| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 24б. Интегралы от произведений присоединенных функции.
Уравнение (5.92) показывает, что при 

Благодаря наличию произведения тригонометрических функций этот интеграл равен нулю и в том случае, если  целое число и
целое число и  независимо от значений
независимо от значений  (см. Двайт, 435, 445 и 465).
(см. Двайт, 435, 445 и 465).
Чтобы определить значение интеграла (5.192) при  необходимо вычислить интеграл от квадрата
необходимо вычислить интеграл от квадрата  по поверхности сферы единичного радиуса.
по поверхности сферы единичного радиуса.
Используя для  выражения (5.182) и (5.115), получим при помощи интегрирования по частям
выражения (5.182) и (5.115), получим при помощи интегрирования по частям

Повторим интегрирование по частям, полагая каждый раз

Произведение  обращается в пуль на границах интервала, поскольку
обращается в пуль на границах интервала, поскольку  содержит множитель
содержит множитель  при
при  при
при  Поэтому после (то
Поэтому после (то  ) - кратного интегрирования по частям получим
) - кратного интегрирования по частям получим

Так как степень  при дифференцировании понижается, второй множитель в подинтегральном выражении оказывается, очевидно, постоянным. Поэтому, сохраняя лишь наивысшую степень и заменив
при дифференцировании понижается, второй множитель в подинтегральном выражении оказывается, очевидно, постоянным. Поэтому, сохраняя лишь наивысшую степень и заменив  на
на  получим, что этот множитель равен
получим, что этот множитель равен

Весь интеграл с учетом формул (5.126) и (5.127) оказывается рапным

При  из формулы (5.192) следует
из формулы (5.192) следует

В случае то  весьма полезным является следующее интегральное соотношение:
весьма полезным является следующее интегральное соотношение:

Для доказательства этой формулы запишем уравнение (5.178), обозначив сначала  а потом
а потом  умножим первое уравнение на у, второе — на у, вычтем и проинтегрируем от — 1 до +1. Для интегрирования в случае
умножим первое уравнение на у, второе — на у, вычтем и проинтегрируем от — 1 до +1. Для интегрирования в случае  перенесем средний член уравнения (5.205)
перенесем средний член уравнения (5.205)
в правую часть, возведем в квадрат, заменим всюду  на
на  умножим на
умножим на  и исключим из результата
и исключим из результата  при помощи уравнения (5.208), возведенного в квадрат и умноженного на
при помощи уравнения (5.208), возведенного в квадрат и умноженного на  При интегрировании от — 1 до +1 все члены, не содержащие
При интегрировании от — 1 до +1 все члены, не содержащие  интегрируются согласно формуле
интегрируются согласно формуле  взаимно уничтожаются; в результате остается
взаимно уничтожаются; в результате остается

Подставляя по формуле (5.190) и интегрируя (см. Двайт, 854.1), находим

При применении вектор-потенциала нам придется пользоваться свойствами ортогональности поверхностных векторных функций  определяемых соотношением
определяемых соотношением

Интегрирование скалярного произведения двух таких функций дает

Заменяя второй член при иомоши уравнения (5.178) и группируя члены, находим

Согласно формулам (5.192) и (5.194), результат равен нулю при  и равен
и равен

при 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКОВ
- ОБОЗНАЧЕНИЯ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОСТАТИКИ
- § 4. Электростатическая индукция.
- § 5. Элементарные электрические заряды.
- § 6. Напряженность электрического поля.
- § 7. Электростатический потенциал.
- § 8а. Электрические диполи и мультиполи.
- § 9. Силовые линии.
- § 10. Эквипотенциальные поверхности.
- § 11а. Теорема Гаусса о потоке электрической индукции.
- § 11б. Силовые линии системы коллинеарных зарядов.
- § 11в. Силовые линии на бесконечности.
- § 12. Максимумы и минимумы потенциала. Теорема Ирншоу.
- § 13. Потенциал двойного электрического слоя.
- § 14. Вектор электрической индукции и силовые трубки.
- § 15. Натяжения в электрическом поле.
- § 16. Теорема Гаусса о потоке электрической индукции для неоднородных сред.
- § 17. Граничные условия и натяжения на поверхности проводников.
- § 18. Граничные условия и натяжения на поверхности диэлектрика.
- § 19. Электрическая индукция и напряженность поля в твердых диэлектриках.
- § 20. Кристаллические диэлектрики.
- Глава II. КОНДЕНСАТОРЫ, ДИЭЛЕКТРИКИ, СИСТЕМЫ ПРОВОДНИКОВ
- § 2. Емкость.
- § 3. Последовательное и параллельное соединение конденсаторов.
- § 4. Сферический конденсатор.
- § 5. Цилиндрический конденсатор.
- § 6. Плоский конденсатор.
- § 7. Защитные кольца.
- § 8. Энергия заряженного конденсатора.
- § 9а. Энергия электрического поля.
- § 9б. Плоский конденсатор с кристаллическим диэлектриком.
- § 10. Натяжения в случае зависимости диэлектрической проницаемости от плотности среды.
- § 11. Электрострикция в жидких диэлектриках.
- § 12. Силы, действующие на проводник в диэлектрике.
- § 13. Теорема взаимности Грина.
- § 14. Суперпозиция полей.
- § 15. Индуцированные заряды на заземленных проводниках.
- § 16. Потенциальные коэффициенты.
- § 17. Собственная и взаимная емкости.
- § 18. Электростатическая экранировка.
- § 19. Потенциальные и емкостные коэффициенты в случае двух отдаленных проводников.
- § 20. Энергия системы зарядов.
- § 21. Силы и моменты сил, действующие на заряженные проводники.
- Глава III. ОБЩИЕ ТЕОРЕМЫ
- § 1. Теорема Остроградского-Гаусса.
- § 2. Теорема Стокса.
- § 3. Уравнения Пуассона и Лапласа.
- § 4. Ортогональные криволинейные координаты.
- § 5. Представление ротора в ортогональных криволинейных координатах.
- § 6. Представление оператора … в различных системах координат.
- § 7. Теорема Грина.
- § 8. Теорема взаимности Грина для диэлектрических сред.
- § 9. Функция Грина.
- § 10. Решение уравнения Пуассона.
- § 11. Теорема единственности при наличии диэлектрических сред.
- § 12. Внесение нового проводника.
- § 13. Эквивалентный слой Грина.
- § 14. Энергия диэлектрического тела в электрическом поле.
- § 15. Изменение электрической энергии системы при увеличении диэлектрической проницаемости.
- § 16. Потенциал аксиально-симметричного поля.
- Глава IV. ДВУХМЕРНОЕ РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА
- § 1. Двухмерные поля и потенциалы.
- § 2. Круговые гармоники.
- § 3. Представление потенциала поля линейного заряда в виде ряда по гармоникам.
- § 4. Проводящий или диэлектрический цилиндр в однородном поле.
- § 5. Диэлектрический цилиндр.
- § 6. Изображение в проводящем цилиндре.
- § 7. Изображение в плоской поверхности проводника или диэлектрика.
- § 8. Задача о диэлектрическом клине.
- § 9. Комплексные величины.
- § 10. Сопряженные функции.
- § 11. Функции потока.
- § 12. Напряженность электрического поля.
- § 13. Функции U и V для поля линейного заряда.
- § 14. Емкость между двумя круглыми цилиндрами.
- § 15. Емкость между цилиндром и плоскостью.
- § 16. Конформные преобразования.
- § 17. Уравнение границы в параметрической форме.
- § 18. Нахождение сопряженных функций.
- § 19. Преобразование Шварца.
- § 20. Многоугольники с одним положительным углом.
- § 21. Многоугольник с углом, равным нулю.
- § 22а. Многоугольники с одним отрицательным углом. Двухмерный диполь. Инверсия.
- § 22б. Изображения при двухмерной инверсии.
- § 23. Многоугольник с двумя углами.
- § 24. Щель, прорезанная в бесконечной плоскости.
- § 25. Римановы поверхности.
- § 26. Задача о круглом цилиндре, расположенном внутри эллиптического.
- § 27а. Условия на границе раздела двух диэлектриков.
- § 27б. Эллиптический диэлектрический цилиндр.
- § 27в. Момент, действующий на диэлектрический цилиндр.
- § 28. Многоугольник с закругленным углом.
- § 29. Плоская решетка из цилиндрических проводов большого диаметра.
- § 30. Случай углов, нецелократных pi/2.
- Глава V. ТРЕХМЕРНОЕ РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА
- § 1. При каких условиях поверхности некоторого семейства могут быть эквипотенциальными?
- § 2. Потенциал поверхностей второго порядка, определяемых уравнением …
- § 3. Заряженный проводящий эллипсоид.
- § 4. Эллиптический и круглый диски.
- § 5. Метод изображений. Проводящие плоскости.
- § 6. Плоская граница двух диэлектриков.
- § 7. Изображение в сферическом проводнике.
- § 8. Пример применения метода изображений для нахождения поля точечного заряда.
- § 9а. Бесконечная система изображений. Задача о двух сферах.
- § 9б. Уравнения в конечных разностях. Задача о двух сферах.
- § 9в. Сфера над плоскостью и две одинаковые сферы.
- § 10. Инверсия в пространстве трех измерений. Геометрические свойства.
- § 11а. Инверсия потенциала и зарядов-изображений.
- § 11б. Пример инверсии изображений.
- § 11в. Инверсия заряженной проводящей поверхности.
- § 11г. Преобразование емкости при инверсии.
- § 12а. Пространствешпле гармоники.
- § 12б. Задача о клипе, ортогонально пересекающемся с поверхностью вращения.
- § 13. Сферические гармоники.
- § 14a. Общие свойства поверхностных гармоник.
- § 14б. Потенциал гармонического распределения заряда.
- § 15. Дифференциальные уравнения поверхностных гармоник.
- § 16а. Зональные гармоники. Уравнение Лежандра.
- § 16в. Полиномы Лежандра. Формула Родрига.
- § 16г. Коэффициенты Лежандра. Обратное расстояние.
- § 16д. Рекуррентные формулы для полиномов Лежандра.
- § 16е. Интеграл от произведения полиномов Лежандра.
- § 16ж. Разложение функций по полиномам Лежандра.
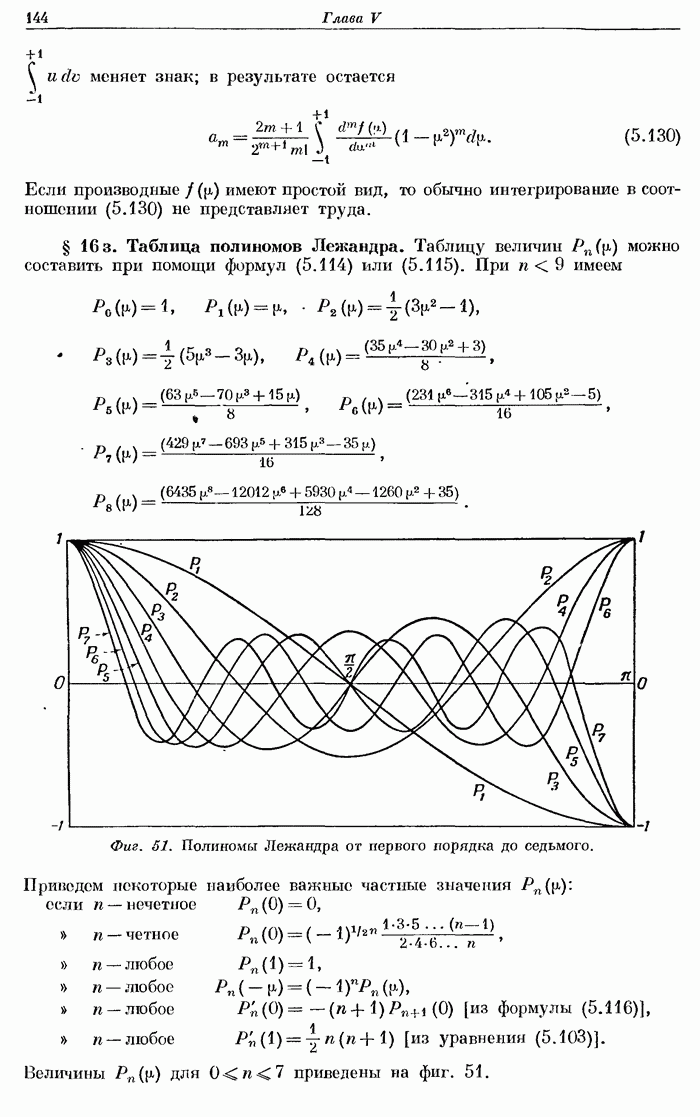
- § 16з. Таблица полиномов Лежандра.
- § 16и. Полиномы Лежандра мнимого аргумента.
- § 17. Потенциал заряженного кольца.
- § 18. Заряженное кольцо в проводящей сфере.
- § 19. Сферическая диэлектрическая оболочка в однородном поле.
- § 20. Сферический конденсатор с малым расстоянием между центрами внутренней и внешней обкладок.
- § 21. Задачи с простой конической границей.
- § 22а. Зональные гармоники второго рода.
- § 22б. Рекуррентные формулы для функций Лежандра второго рода.
- § 22в. Выражение функций Лежандра второго рода через полиномы Лежандра.
- § 22г. Некоторые значения функций Лежандра второго рода.
- § 22д. Функции Лежандра второго рода мнимого аргумента.
- § 22е. Применение функций Лежандра второго рода в теории потенциала.
- § 23. Зональные гармоники нецелого порядка.
- § 24а. Присоединенные функции Лежандра.
- § 24б. Интегралы от произведений присоединенных функции.
- § 24в. Присоединенные функции от мнимого аргумента.
- § 24г. Рекуррентные формулы для присоединенных функций Лежандра.
- § 24д. Некоторые значения присоединенных функций Лежандра.
- § 24е. Равновесные (нейтральные) точки и линии.
- § 25. Биаксиальные гармоники.
- § 26. Конические границы.
- § 27а. Присоединенные функции Лежандра нецелого порядка.
- § 27б. Функция Грина для конуса.
- § 27в. Функция Грина для конической полости.
- § 28а. «Сплюснутые» сфероидальные координаты.
- § 28б. Гармоники сплюснутого сфероида.
- § 28в. Проводящий лист с круглым отверстием.
- § 28г. Момент, действующий на диск в однородном ноле.
- § 28д. Потенциал заряда, распределенного по поверхности сфероида.
- § 28е. Представление потенциала точечного заряда через гармоники сплюснутого сфероида.
- § 29а. Гармоники вытянутого сфероида.
- § 29б. Вытянутый сфероид в однородном поле.
- § 30а. Уравнение Лапласа в цилиндрических координатах.
- § 30б. Уравнение Бесселя и функции Бесселя.
- § 30в. Модифицированное уравнение Бесселя и модифицированные функции Бесселя.
- § 30г. Решение уравнения Бесселя.
- § 30д. Рекуррентные формулы для функций Бесселя
- § 30е. Значения функций Бесееля на бесконечности.
- § 30ж. Интегралы от бесселевых функций.
- § 30з. Разложение в ряд по функциям Бесселя.
- § 30и. Функция Грина для цилиндра. Обратное расстояние.
- § 30к. Функция Грина для цилиндрической полости.
- § 31а. Функции Бесселя нулевого порядка.
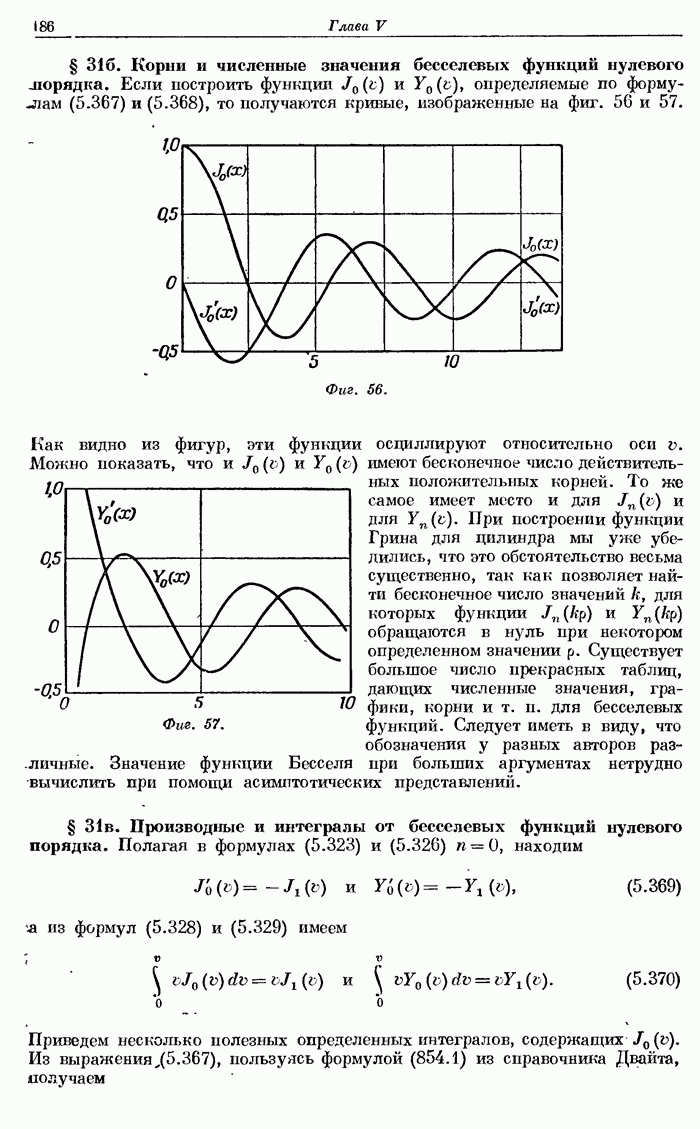
- § 31б. Корни и численные значения бесселевых функций нулевого порядка.
- § 31в. Производные и интегралы от бесселевых функций нулевого порядка.
- § 31г. Поле точечного заряда, расположенного над диэлектрической пластинкой.
- § 31д. Потенциал внутри полого цилиндрического кольца.
- § 32. Функция Бесселя нецелого порядка. Сферические функции Бесселя.
- § 33а. Модифицированные бесселевы функции.
- § 33б. Рекуррентные формулы для модифицированных бесселевых функций.
- § 33в. Значение модифицированных бесселевых функций на бесконечности.
- § 33г. Интеграл от произведения модифицированных бесселевых функций комплексного аргумента.
- § 33д. Функция Грина для кольцевой цилиндрической полости.
- § 34а. Модифицированные бесселевы функции нулевого порядка.
- § 34б. Интегральное представление модифицированных бесселевых функций второго рода.
- § 35. Интегральное представление бесселевых функций пулевого порядка.
- § 36а. Представление обратного расстояния через модифицированные бесселевы функции.
- § 36б. Цилиндрические границы раздела двух диэлектрических сред.
- § 37. Потенциал внутри кольцевой цилиндрической полости.
- § 38. Модифицированные бесселевы функции нецелого порядка.
- § 39. Приближеиные решения. Электростатические линзы.
- § 40. Функции клина.
- Глава VI. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 1. Плотность электрического тока. Уравнение непрерывности.
- § 2. Электродвижущая сила.
- § 3. Закон Ома. Удельное сопротивление.
- § 4. Тепловое действие электрического тока.
- § 5. Линейные проводники. Законы Кирхгофа. Последовательные и параллельные соединения проводников.
- § 6. Расчет электрических цепей. Контурные токи. Мост Уитстона.
- § 7. Цепи из одинаковых звеньев.
- § 8. Линия с непрерывно распределенной утечкой.
- § 9. Общая теория цепей.
- § 10. Сопряженные проводники. Двойной мост Кельвина.
- § 11. Постоянные токи в проводящих средах.
- § 12. Общие теоремы.
- § 13. Двухмерный ток.
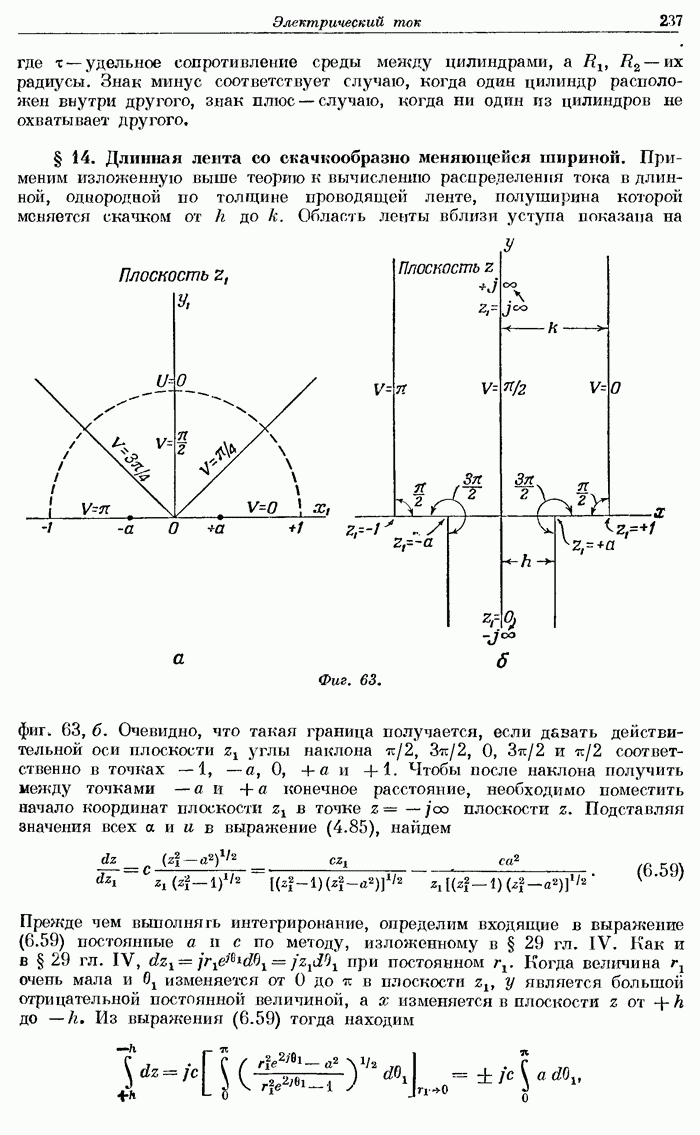
- § 14. Длинная лента со скачкообразно меняющейся шириной.
- § 15. Трехмерное распределение тока.
- § 16. Системы электродов. Две сферы. Удаленные электроды.
- § 17. Задача о проводящем шаре.
- § 18. Задача о сплошном проводящем цилиндре.
- § 19. Сопротивление земли.
- § 20. Токи в тонких изогнутых пленках.
- § 21. Распределение тока в сферической пленке.
- § 22. Поверхность вращения.
- § 23. Предельные значения сопротивления.
- § 24. Токи в анизотропных средах. Слои в земной коре.
- § 25. Ток, обусловленный движением пространственного заряда. Уравнение Чайльда.
- Глава VII. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ТОКОВ
- § 1. Определение единицы силы тока (ампера) через величину магнитного момента.
- § 2. Магнитная индукция и магнитная проницаемость.
- § 3. Магнитный вектор-потенциал. Однородное поле.
- § 4. Теоремы единственности в магнитостатике.
- § 5. Разложение вектор-потенциала но ортогональным функциям.
- § 6. Вектор-потенциал в цилиндрических координатах.
- § 7. Вектор-потенциал в сферических координатах.
- § 8. Выражение для вектор-потенциала через значение магнитной индукции на оси.
- § 9. Уравнение аксиально симметричных трубок магнитной индукции.
- § 10. Вектор-потенциал и поле двухпроводной линии.
- § 11. Вектор-потенциал и поле круглой петли.
- § 12. Поле токов, текущих по сферической пленке.
- § 13. Зональные токи в сферической пленке.
- § 14. Представление поля круглой петли через сферические, гармоники.
- § 15. Закон Био и Савара. Поле прямолинейного провода.
- § 16. Поле соленоида с произвольным шагом намотки.
- § 17. Поле в цилиндрической полости внутри проводящего круглого стержня.
- § 18. Поле токов, текущих вдоль цилиндрической проводящей пленки.
- § 19. Сила, действующая на электрический контур в магнитном ноле.
- § 20. Примеры на вычисление сил взаимодействия между электрическими контурами.
- § 21. Вектор-потенциал и вектор намагниченности.
- § 22. Граничные условия для магнитных полей и для вектор-потенциалов.
- § 23. Пример использования векторов a и A.
- § 24. Метод изображений для токов в случае плоской границы.
- § 25. Магнитная индукция и магнитная проницаемость в кристаллах.
- § 26. Двухмерные магнитные поля.
- § 27. Магнитное экранирование двухпроводной линии.
- § 28. Метод изображений для токов в двухмерных системах.
- § 29. Магнитодвижущая сила и напряженность магнитного поля.
- § 30. Магнитный контур. Тор.
- § 31. Магнитный контур с воздушным зазором.
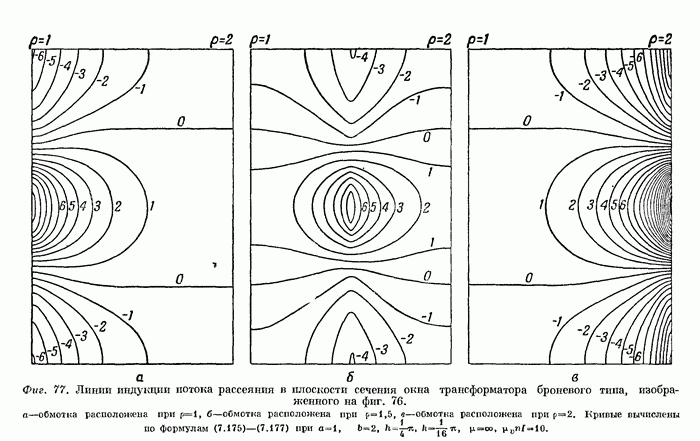
- § 32. Поле в трансформаторе броневого типа.
- § 33. Полюс с расщепленным наконечником. Эффективный воздушный зазор.
- Глава VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 1. Закон индукции Фарадея.
- § 2. Взаимная энергия двух контуров.
- § 3. Энергия магнитного поля.
- § 4. Коэффициент взаимной индукции.
- § 5. Граничные условия для a.
- § 6. Коэффициент взаимной индукции простейших контуров.
- § 7. Коэффициент взаимной индукции двух колец.
- § 8. Переменная взаимная индукция.
- § 9. Самоиндукция.
- § 10. Вычисление самоиндукции. Тонкий провод.
- § 11. Самоиндукция круглой петли.
- § 12. Самоиндукция соленоида.
- § 13. Самоиндукция двухпроводной линии.
- § 14. Энергия n контуров.
- § 15. Натяжения в магнитном поле.
- § 16. Энергия магнетика в статическом магнитном поле.
- Глава IX. ПЕРЕХОДНЫЕ ЯВЛЕНИЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 1. Неустановившиеся электрические процессы.
- § 2. Энергетические соотношевия в электрической цепи.
- § 3. Контур, состоящий из емкости, индуктивности и сопротивления.
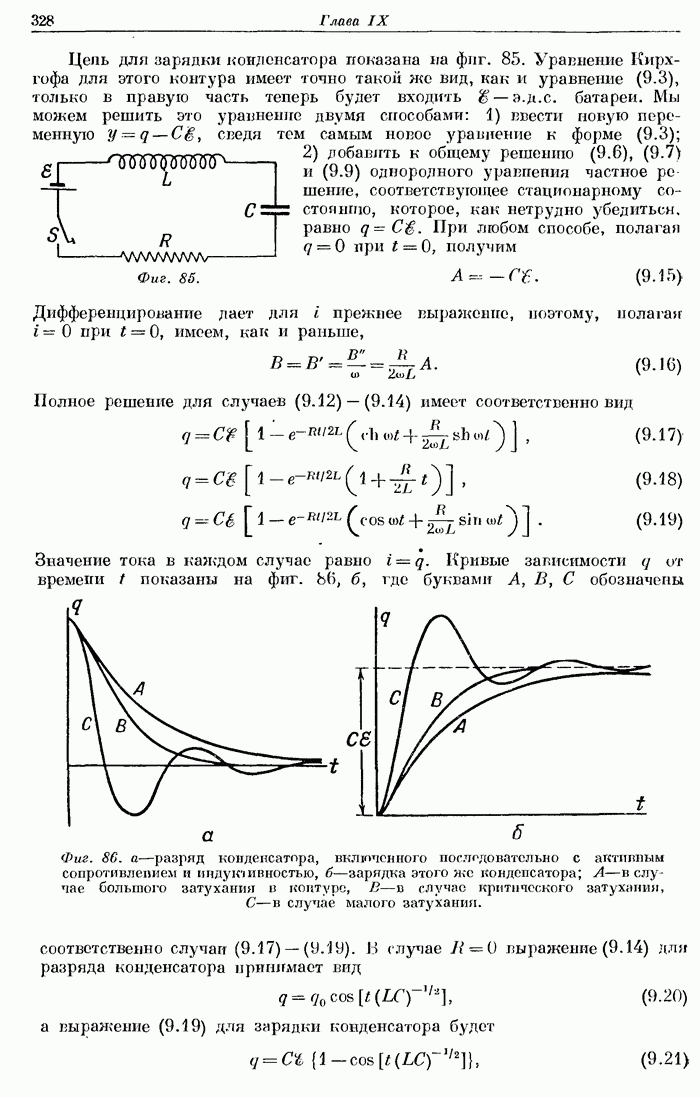
- § 4. Зарядка и разряд конденсатора.
- § 5а. Нарастание и спадание тока в катушке индуктивности.
- § 5б. Индуктивно связанные контуры.
- § 6. Кинетическая энергия и электрокинетический импульс.
- § 7. Общий вид уравнений переходных процессов в цепях.
- § 8. Решение для цепей общего вида.
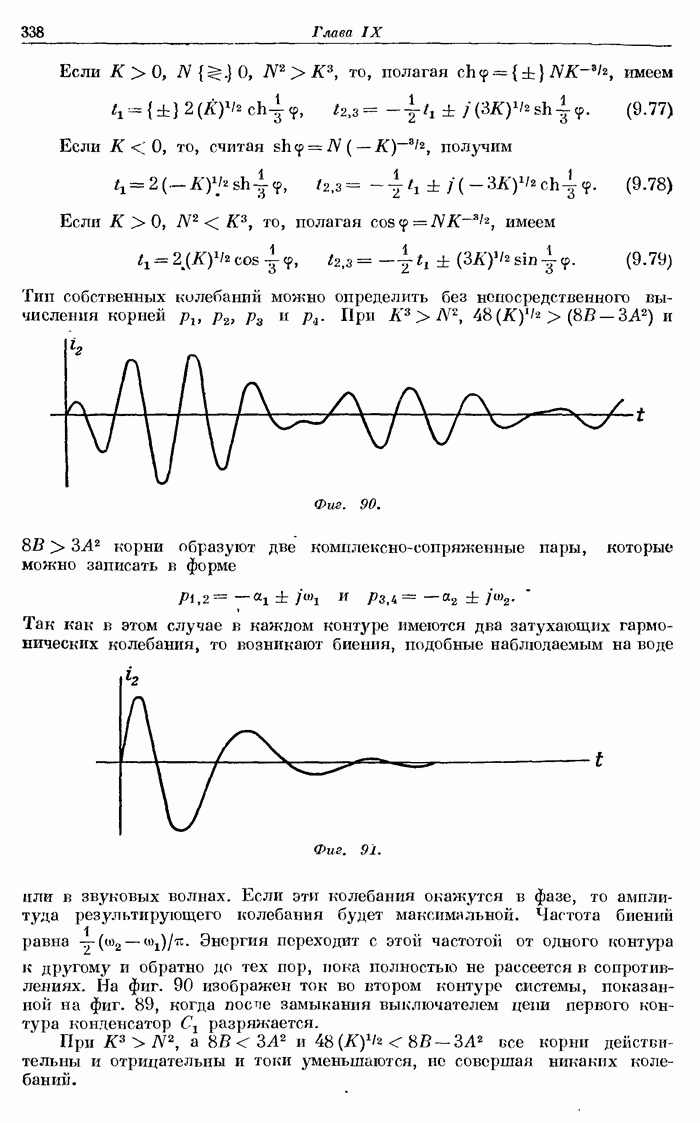
- § 9. Типы собственных колебаний.
- § 10. Цепь, содержащая постоянную э.д.с.
- § 11. Собственные частоты двух индуктивно связанных контуров.
- § 12. Амплитуды колебаний в двух связанных контурах.
- § 13. Колебательный режим.
- § 14. Индуктивно связанные контуры, обладающие малым активным сопротивлением.
- § 15. Настроенные индуктивно связанные контуры, обладающие малым активным сопротивлением.
- § 16. Цепи из одинаковых звеньев.
- § 17. Интегральный эффект переходного процесса.
- § 18. Переходные явления при импульсах конечной продолжительности.
- Глава X. ПЕРЕМЕННЫЕ ТОКИ
- § 1. Гармонические электродвижущие силы. Частное решение.
- § 2. Контур, содержащий сопротивление, емкость и индуктивность.
- § 3. Мощность, эффективные значения, резонанс.
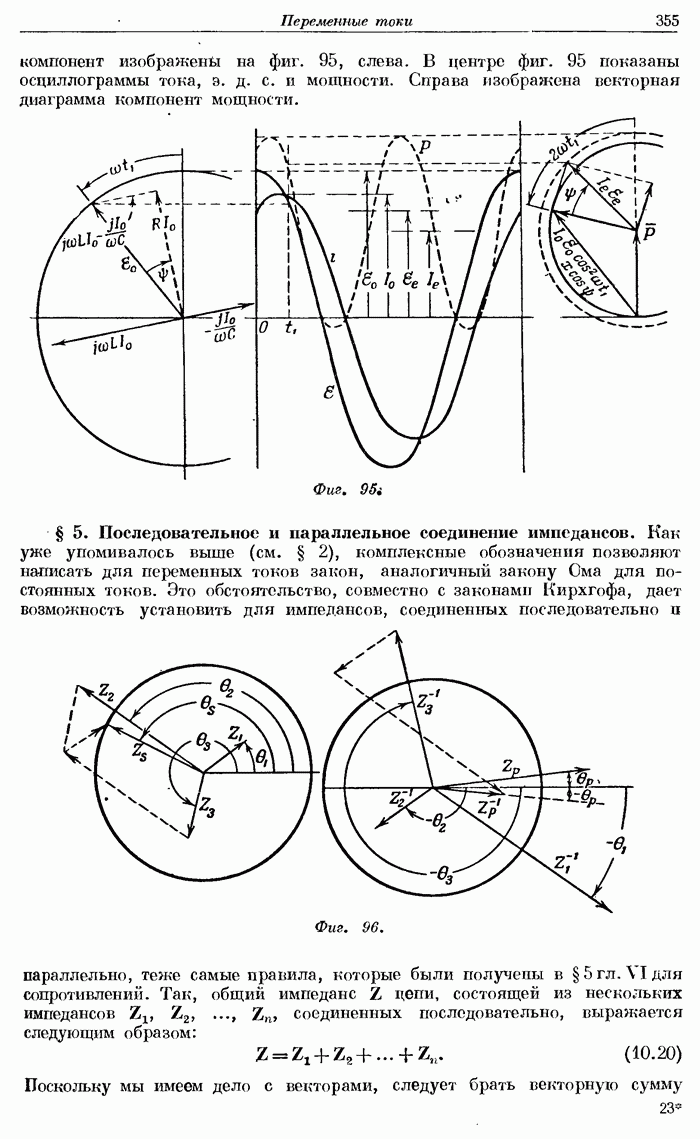
- § 4. Графическое представление. Векторная диаграмма.
- § 5. Последовательное и параллельное соединение импедансов.
- § 6. Передача мощности.
- § 7. Мостик импедансов.
- § 8. Цепь переменного тока в общем случае.
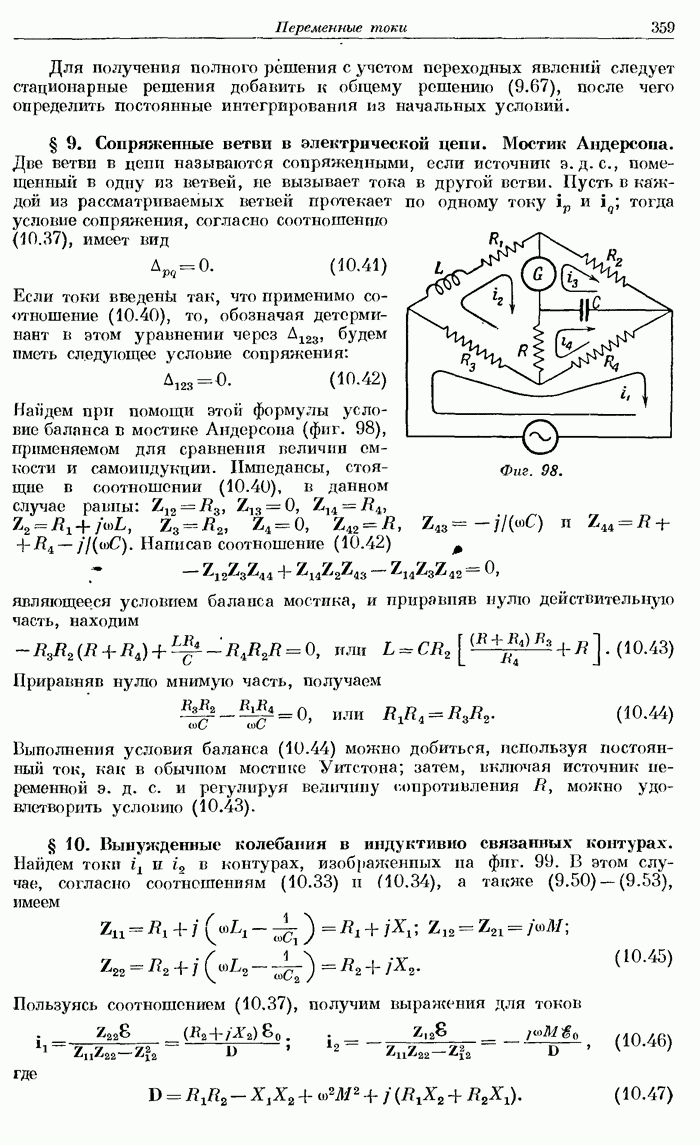
- § 9. Сопряженные ветви в электрической цепи. Мостик Андерсона.
- § 10. Вынужденные колебания в индуктивно связанных контурах.
- § 11. Индуктивно связанные контуры, обладающие малым активным сопротивлением.
- § 12. Настроенные индуктивно связанные контуры, обладающие малым активным сопротивлением.
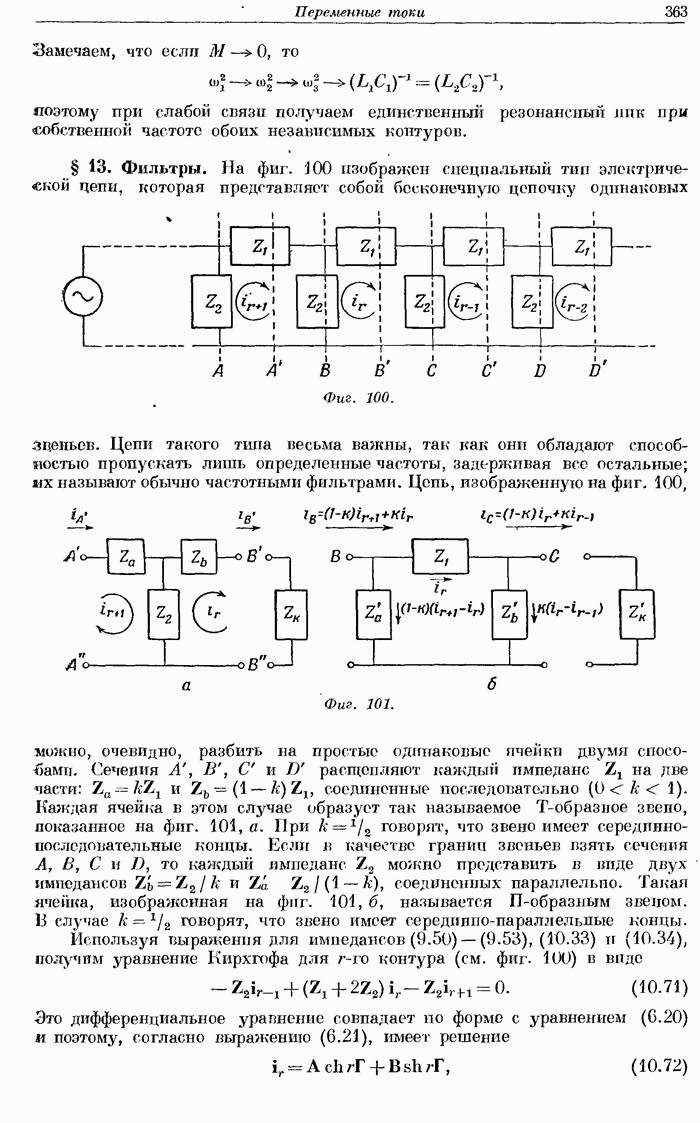
- § 13. Фильтры.
- § 14. Условия на концах в частотных фильтрах.
- § 15. Частотные характеристики фильтров.
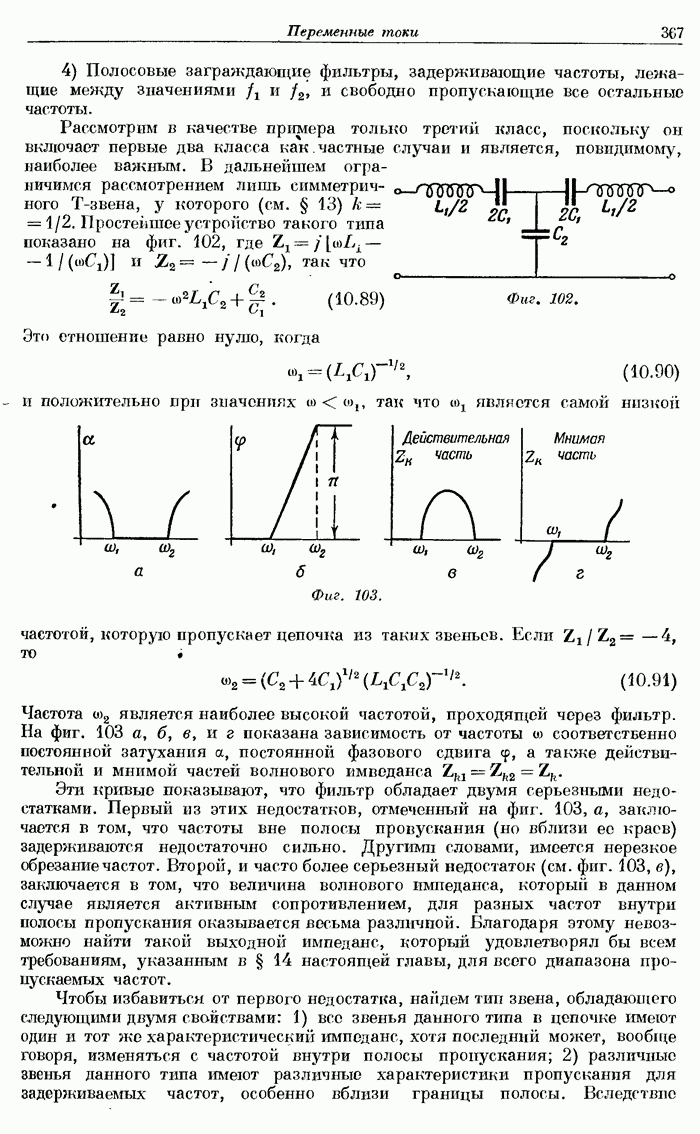
- § 16. Полосовой фильтр.
- § 17. Производные звенья типа M.
- § 18. Выходное устройство фильтра.
- § 19. Линии передачи.
- § 20. Электродвижущие силы несинусоидальной формы. Метод рядов Фурье.
- § 21. Электродвижущие силы несинусоидальной формы. Метод повторяющегося переходного режима.
- § 22. Контур с отрицательным активным сопротивлением.
- Глава XI. ВИХРЕВЫЕ ТОКИ
- § 1. Индуцированные токи в объемных проводниках.
- § 2. Решение уравнения для вектор-потенциала вихревых токов.
- § 3. Скин-эффект в стационарном случае.
- § 4. Скин-эффект в случае полого цилиндрического проводника.
- § 5. Скин-эффект в сплошном цилиндрическом проводнике.
- § 6. Решение в сферических координатах при аксиальной симметрии.
- § 7. Проводящий шар в переменном поле.
- § 8. Мощность, поглощаемая шаром в переменном магнитном поле.
- § 9. Переходные явления в проводящем шаре.
- § 10. Вихревые токи в плоских пластинках.
- § 11. Решение задачи о вихревых токах в плоской бесконечной пластинке методом изображений.
- § 12. Момент, действующий на вращающуюся петлю с током или магнитный диполь.
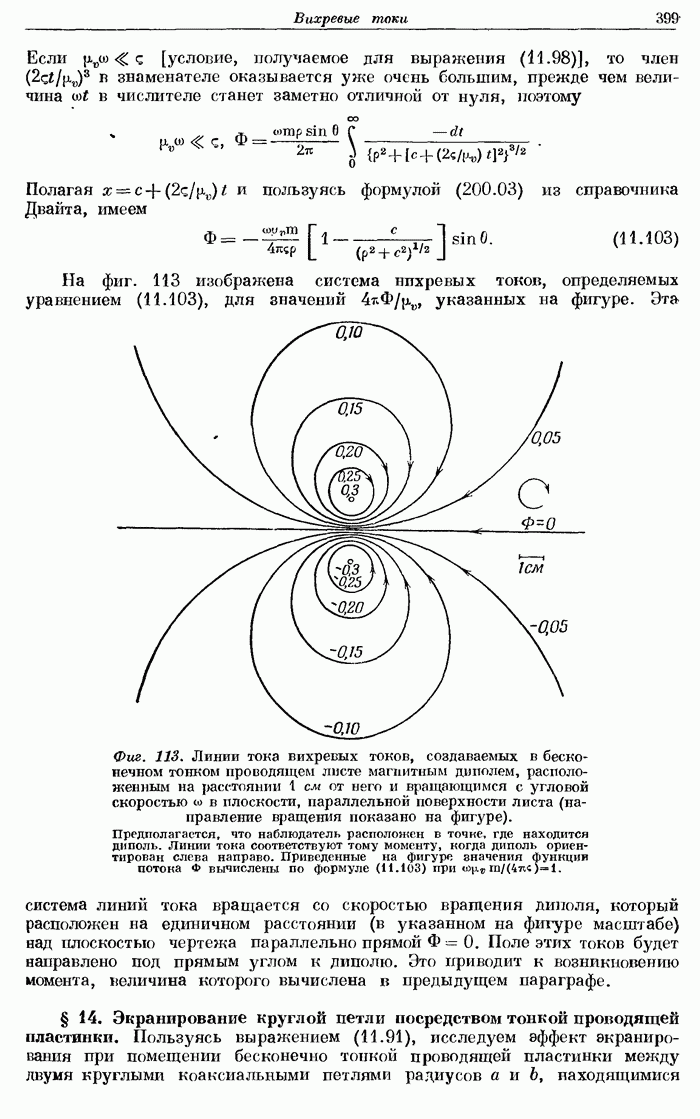
- § 13. Вихревые токи, возбуждаемые вращающимся диполем.
- § 14. Экранирование круглой петли посредством тонкой проводящей пластинки.
- § 15. Зональные вихревые токи в сферической пленке.
- § 16. Вихревые токи в тонкой цилиндрической пленке.
- § 17. Переходные явления при экранировании с помощью толстой цилиндрической оболочки.
- Глава XII. МАГНЕТИЗМ
- § 1. Парамагнетизм и диамагнетизм.
- § 2. Магнитная восприимчивость.
- § 3. Магнитные свойства кристаллов.
- § 4. Кристаллический шар в однородном магнитном поле.
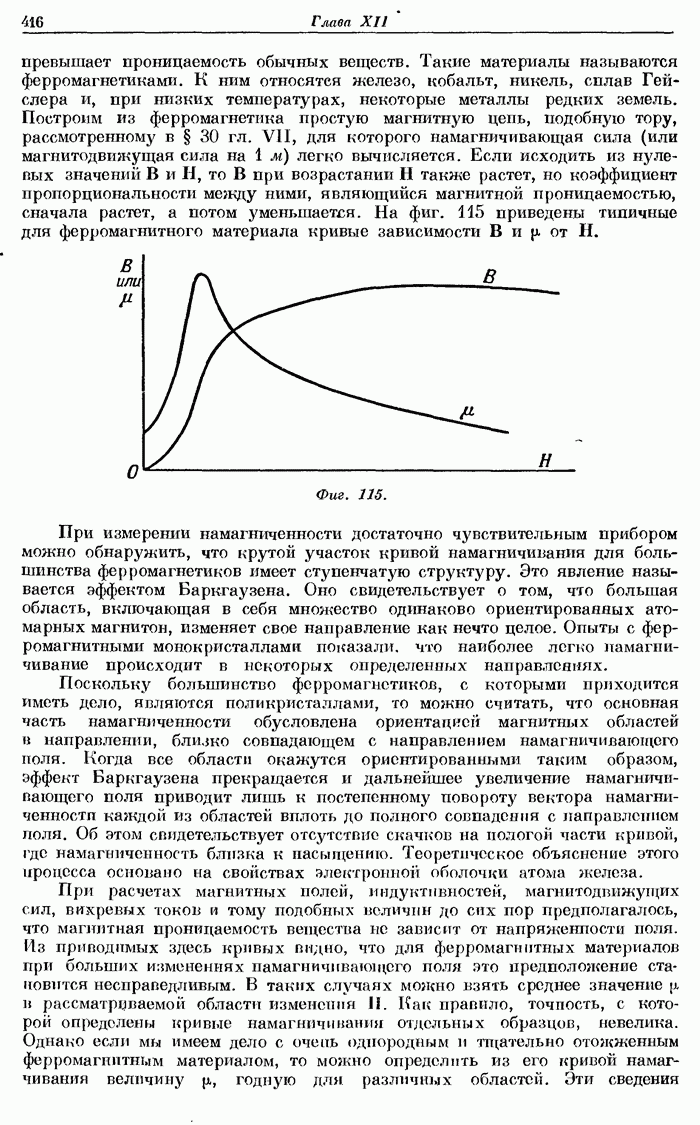
- § 5. Ферромагнетизм.
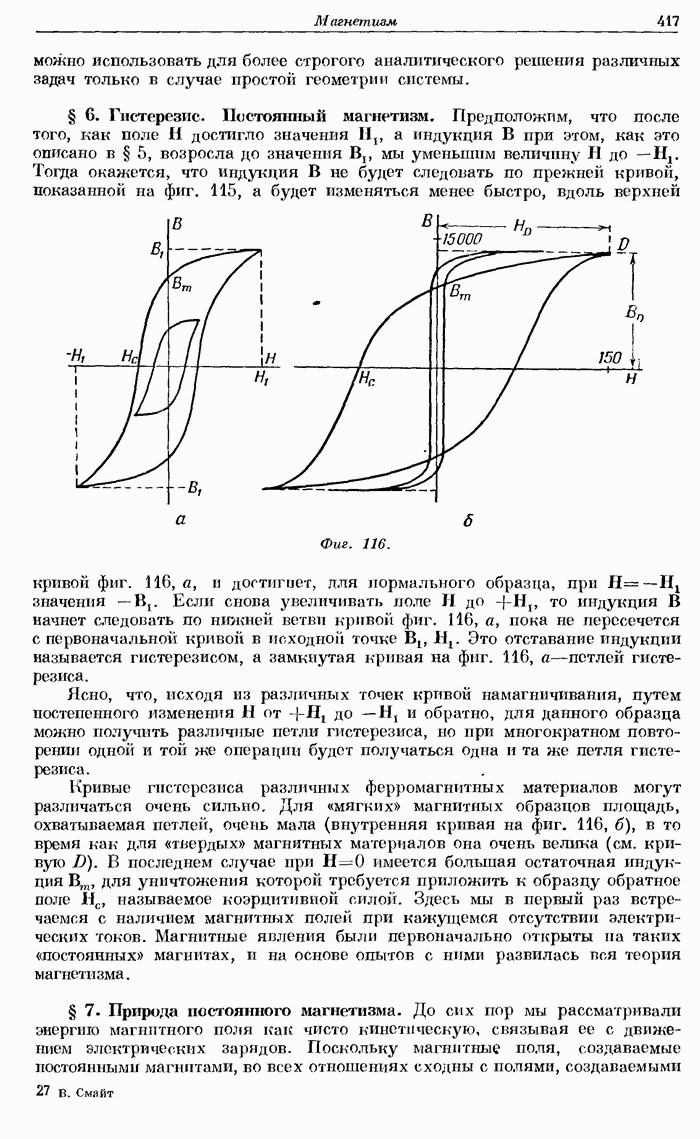
- § 6. Гистерезис. Постоянный магнетизм.
- § 7. Природа постоянного магнетизма.
- § 8. Равномерное намагничивание. Эквивалентный поверхностный ток.
- § 9. Намагниченный шар и цилиндр. Магнитные полюсы.
- § 10. Условия на границе с постоянным магнитом.
- § 11. Сферический постоянный магнит в однородном поле.
- § 12а. Подъемная сила подковообразного магнита.
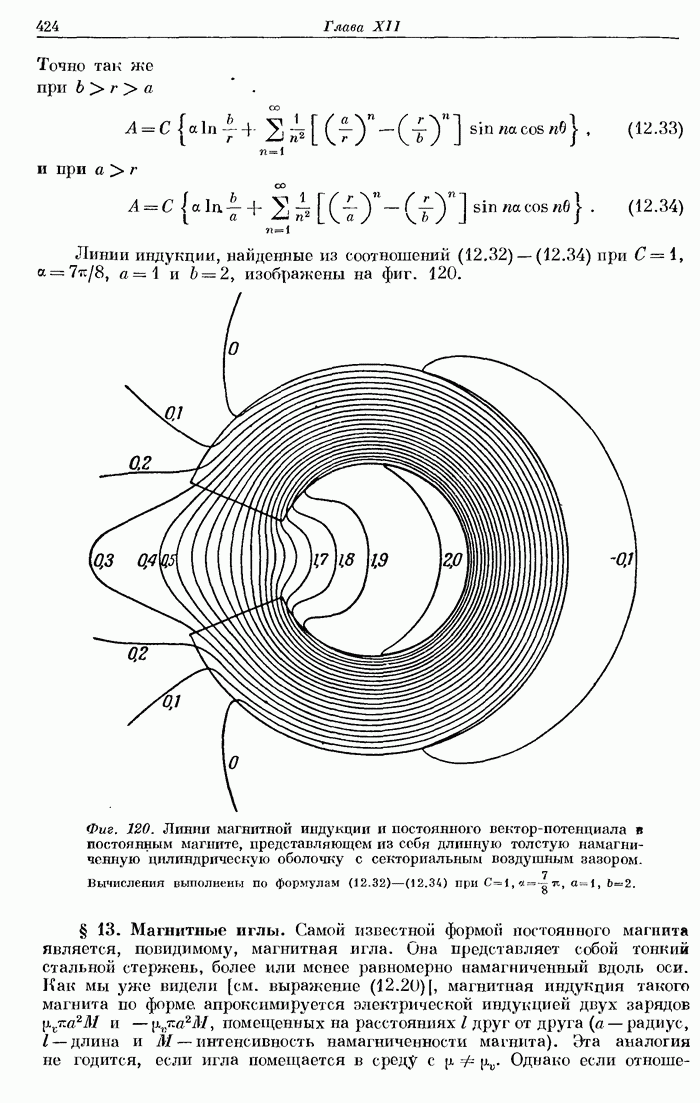
- § 12б. Поле цилиндрического магнита.
- § 13. Магнитные иглы.
- Глава XIII. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 2. Волновое уравнение. Электромагнитные потенциалы. Вектор Герца.
- § 3. Вектор Умова-Пойнтинга.
- § 4. Плоские волны в однородном незаряженном диэлектрике.
- § 5. Скорость распространения волны в анизотропных средах.
- § 6. Поверхность, образованная, лучом, и поляризация в анизотропных средах.
- § 7. Энергия, давление и импульс плоской волны.
- § 8. Отражение и преломление плоских волн.
- § 9. Интенсивности отраженной и преломленной волн.
- § 10. Частота. Длина волны. Эллиптическая поляризация.
- § 11. Полное отражение.
- § 12. Электромагнитные волны в однородных проводниках.
- § 13. Плоские волны в однородных изотропных проводниках.
- § 14. Отражение от проводящей поверхности.
- § 15. Плоские волны вдоль идеально проводящих цилиндрических проводников.
- § 16. Характеристический импеданс среды
- § 17. Отражения от иеоднородностей. Согласующие секции.
- § 18. Комплексный вектор Умова-Пойнтинга.
- § 19. Квазиплоские волны вдоль неидеальных проводников. Двухпроводная линия Лехера.
- § 20. Групповая скорость.
- Глава XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- § 2. Два типа вектор-потенциалов.
- § 3. Сферические электромагнитные волны. Диполь.
- § 4. Запаздывающие потенциалы.
- § 5. Излучение линейной антенны.
- § 6. Поля на больших расстояниях от линейной антенны.
- § 7. Излучение бегущей волны.
- § 8. Коническая линия передачи.
- § 9. Биконическая антенна.
- § 10. Сложные антенны.
- § 11. Влияние земли.
- § 12. Единственность решения.
- § 13. Решения волнового уравнения в сферических координатах.
- § 14. Разложение плоской волны по полиномам Лежандра.
- § 15. Излучение кольцевого тока. Магнитный диполь.
- § 16. Свободные колебания проводящей сферы.
- § 17. Вынужденные колебания диэлектрического или проводящего шара.
- § 18. Решения волнового уравнения в цилиндрических координатах.
- § 19. Разложение плоской волны по цилиндрическим гармоникам
- § 20. Излучение из отверстий в плоском проводящем экране.
- § 21. Диффракция на прямоугольном отверстии в проводящем плоском экране.
- § 22. Ортогональные функции в задаче о диффракции. Излучение открытого конца коаксиальной линии.
- Глава XV. ВОЛНОВОДЫ И ПОЛЫЕ РЕЗОНАТОРЫ
- § 1. Волны в полых цилиндрических трубах.
- § 2. Учет затухания в волноводах.
- § 3. Прямоугольный волновод.
- § 4. Круглый волновод.
- § 5. Коаксиальный волновод.
- § 6. Плоские неоднородности в коаксиальной линии.
- § 7. Возбуждение волноводов.
- § 8. Возбуждение круглого волновода элементом тока.
- § 9. Возбуждение круглого волновода петлей с током.
- § 10. Возбуждение круглого волновода через отверстие.
- § 11. Плоские неоднородности в прямоугольных волноводах.
- § 12. Полые резонаторы. Собственные колебания.
- § 13. Типы независимых собственных колебаний полости.
- § 14. Емкость и индуктивность цилиндрической полости.
- § 15. Затухание собственных колебаний. Активное сопротивление полости.
- § 16. Собственные колебания цилиндрической полости.
- § 17. Свойства прямоугольного резонатора.
- § 18. Свойства резонатора, имеющего форму круглого цилиндра.
- § 19. Многосвязные цилиндрические полые резонаторы.
- § 20. Отрезок коаксиального кабеля как резонатор.
- § 21. Собственные колебания сферической полости.
- § 22. Собственные колебания реальных полых резонаторов.
- § 23. Полые резонаторы сложной формы.
- § 24. Возбуждение полого резонатора петлей с током.
- § 25. Возбуждение круглого цилиндрического резонатора петлей с током.
- § 26. Возбуждение полого резонатора при помощи электрода.
- § 27. Возбуждение полого резонатора через отверстие.
- Глава XVI. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ
- § 1. Постулаты специальной теории относительности.
- § 2. Преобразование Лоренца.
- § 3. Преобразование скорости и ускорения.
- § 4. Зависимость массы от скорости.
- § 5. Преобразование сил.
- § 6. Сила, действующая на заряд, движущийся в магнитном поле.
- § 7. Движение зарядов в однородном магнитном поле.
- § 8. Энергия движущейся заряженной частицы.
- § 9. Критическое магнитное поле в магнетроне.
- § 10. Траектория космической частицы в однородном поле.
- § 11. Магнитное поле движущегося заряда.
- § 12. Запаздывающие поля и потенциалы движущегося заряда.
- § 13. Излучение равномерно ускоренного, прямолинейно движущегося электрона.
- § 14. Преобразование уравнений Максвелла.
- § 15. Определение скорости самолета относительно земли.
- § 16. Движение заряженной частицы в перекрещивающихся электрическом и магнитном полях.
- § 17. Аберрация и эффект Допплера.
- ПРИЛОЖЕНИЕ. СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ ЕДИНИЦ