| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
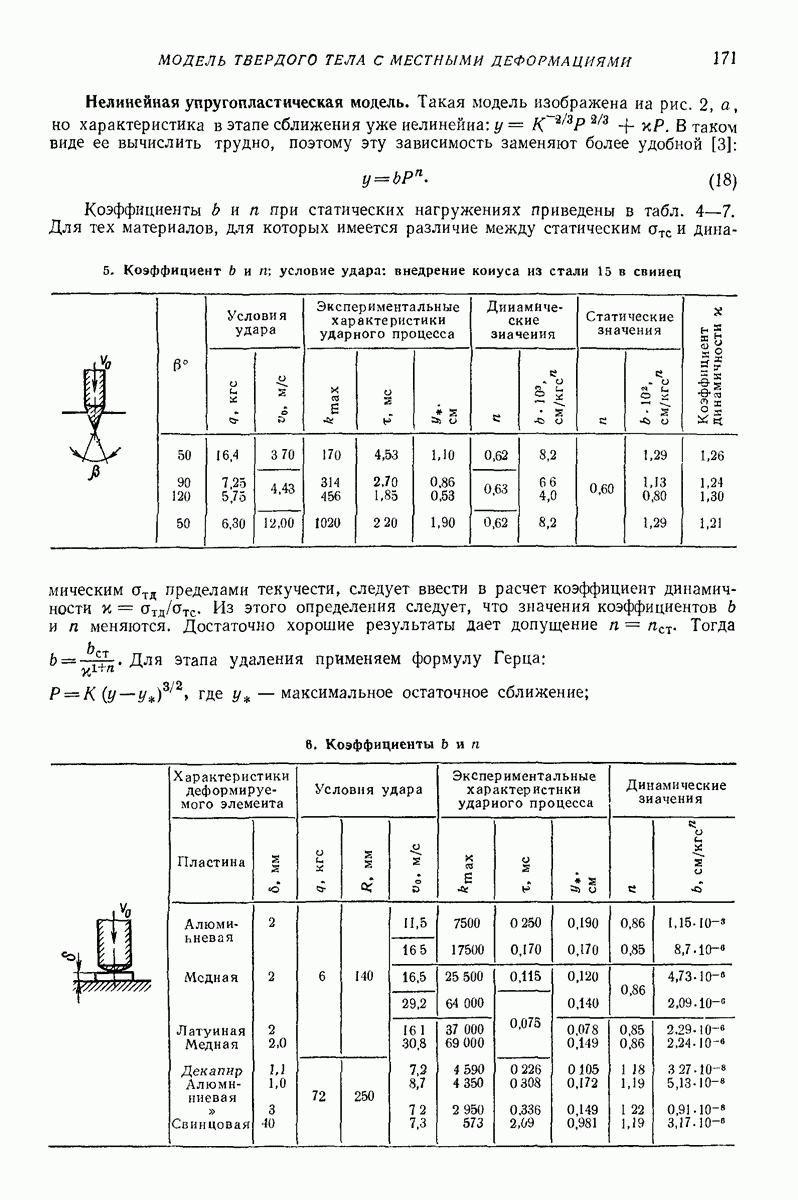
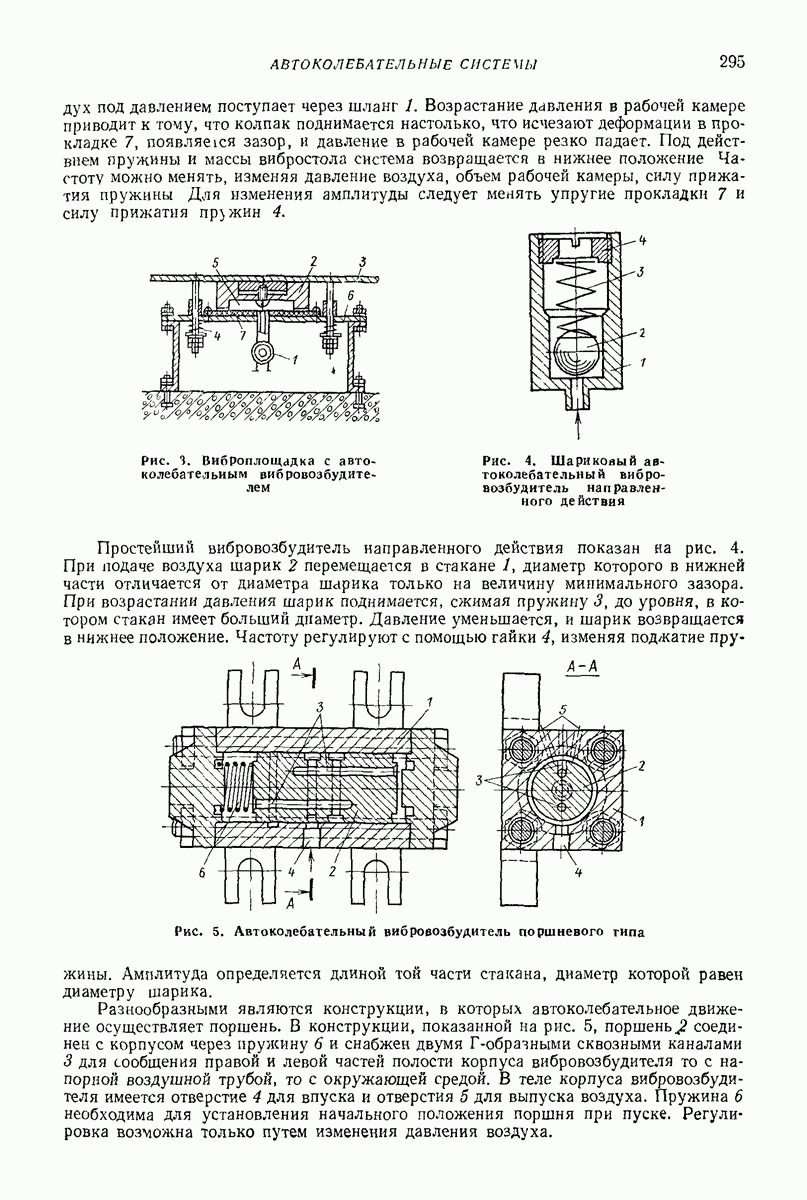
5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
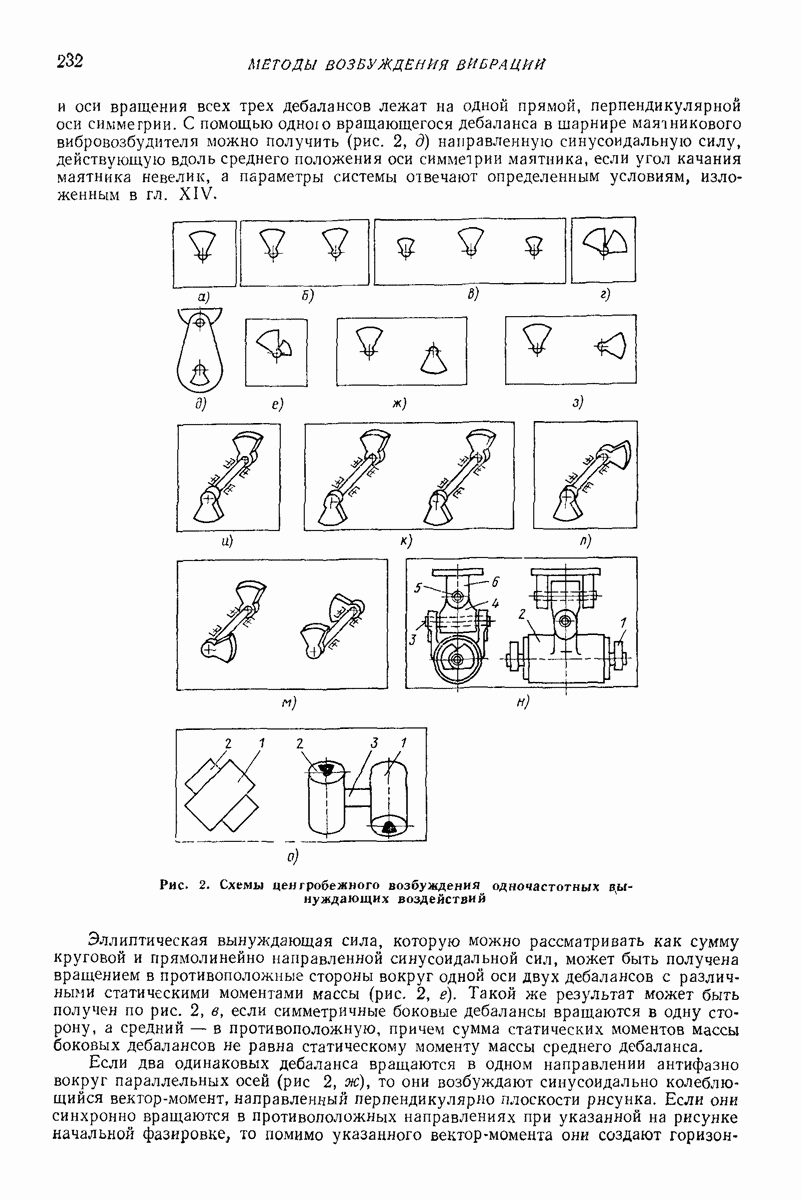
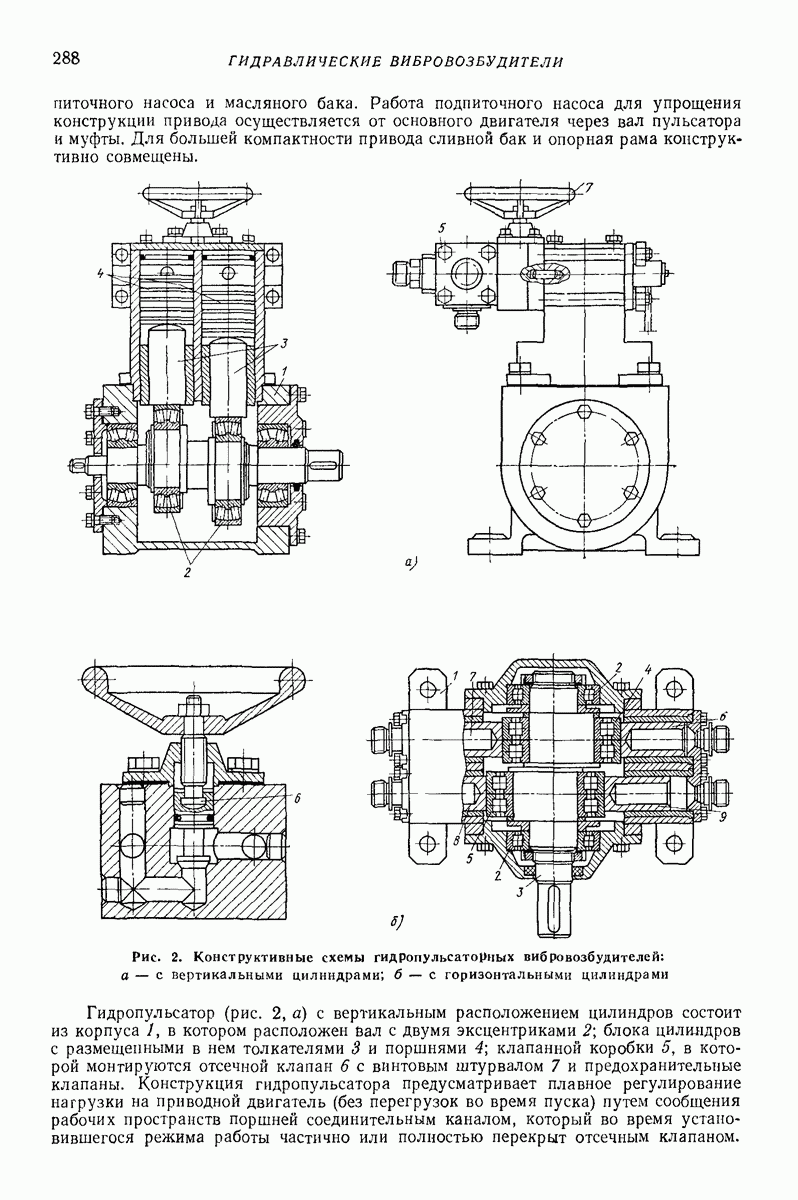
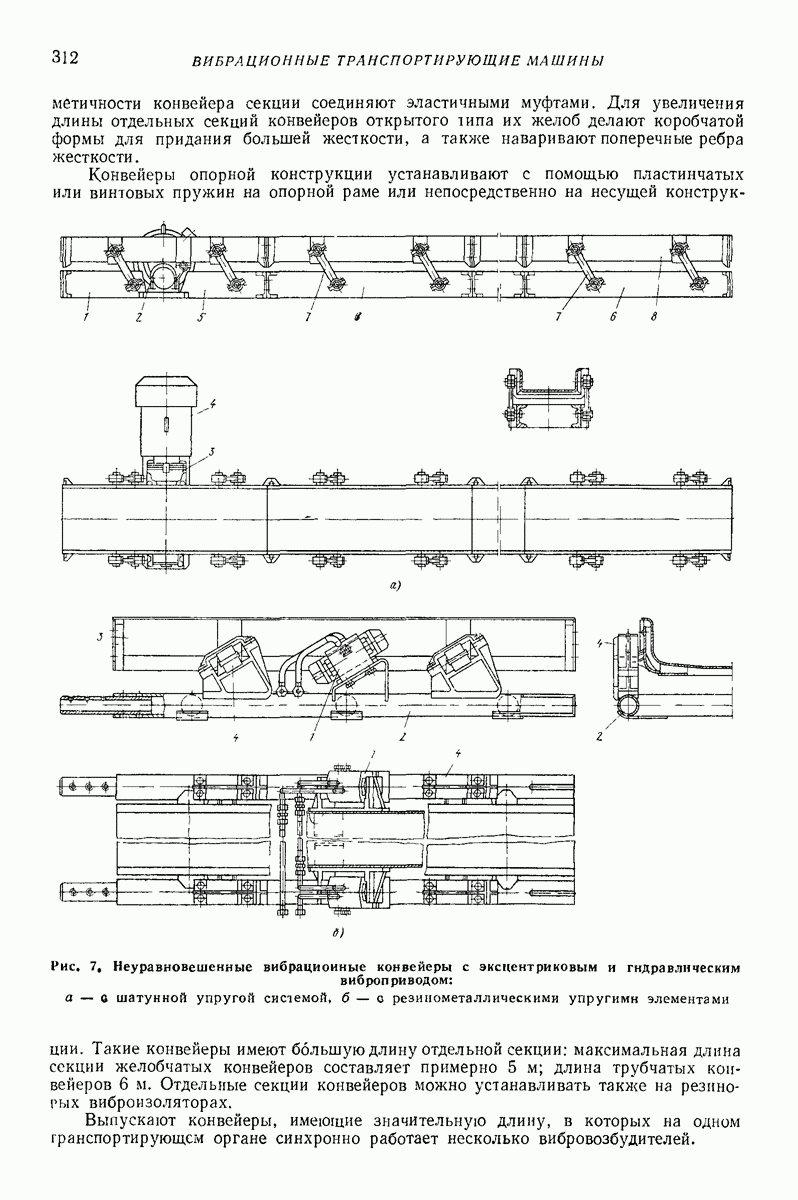
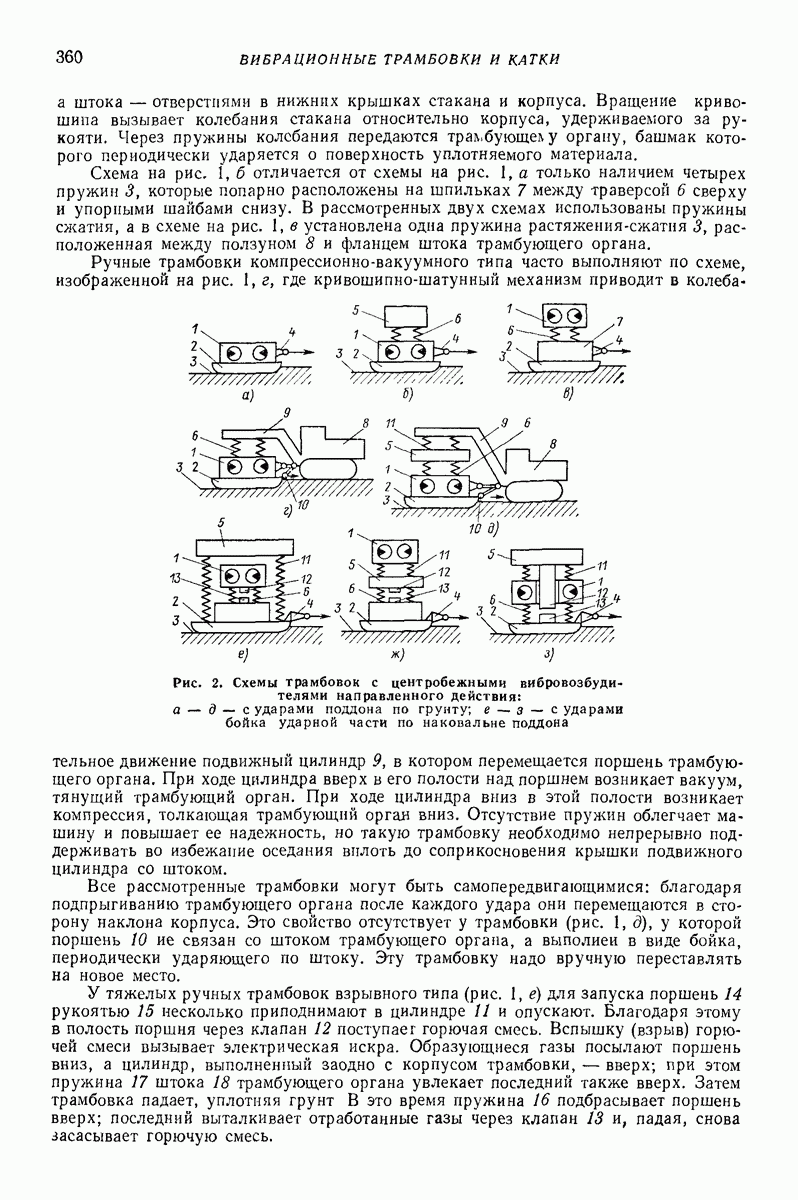
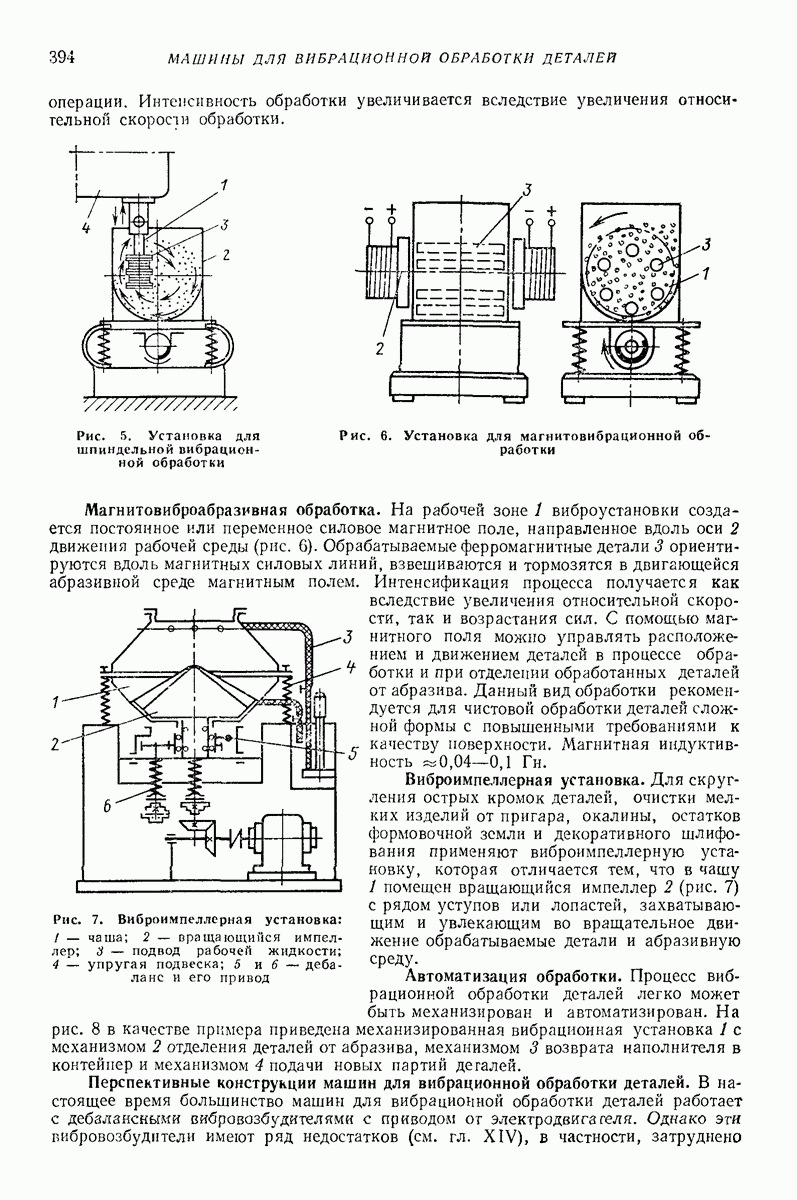
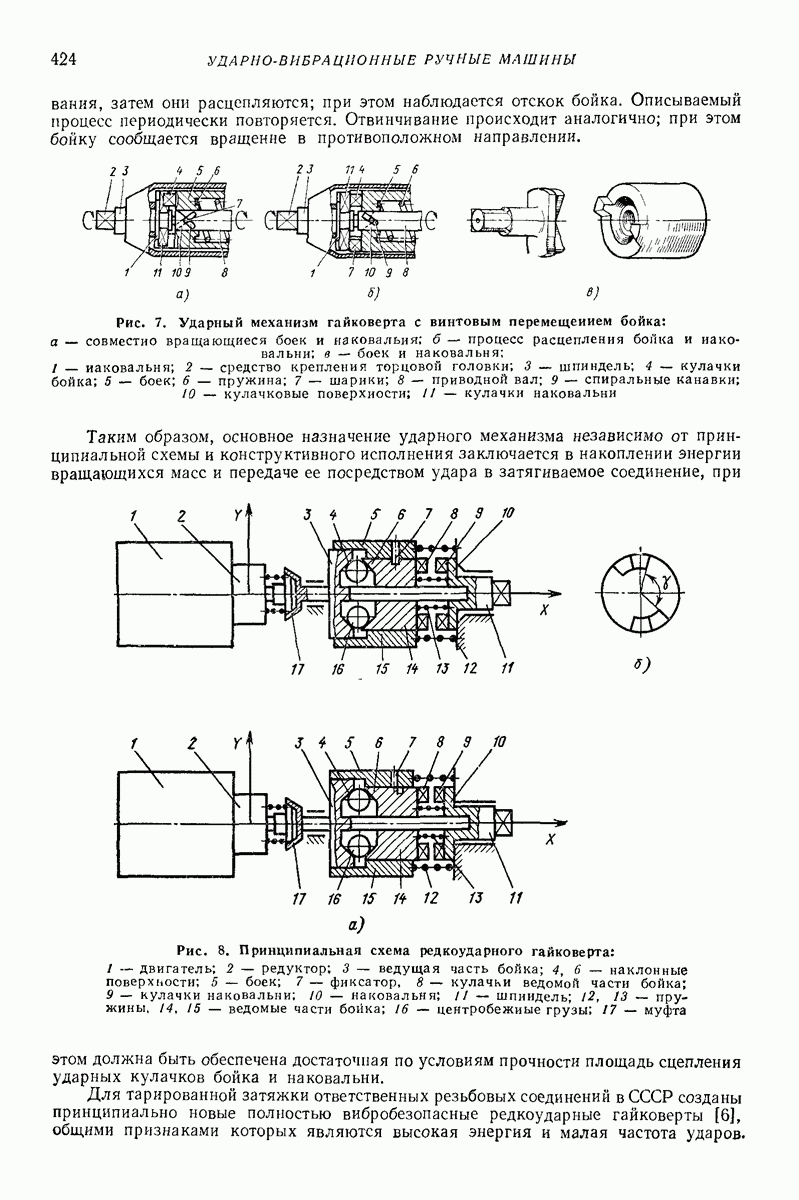
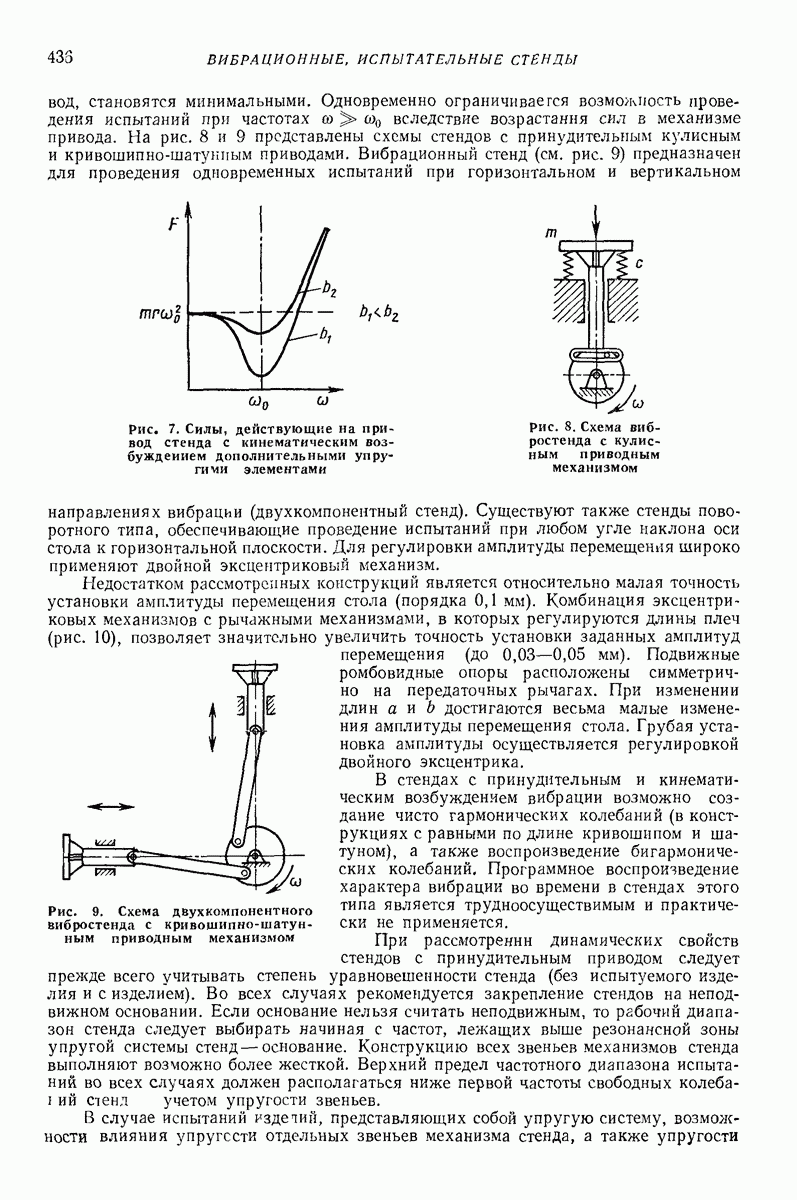
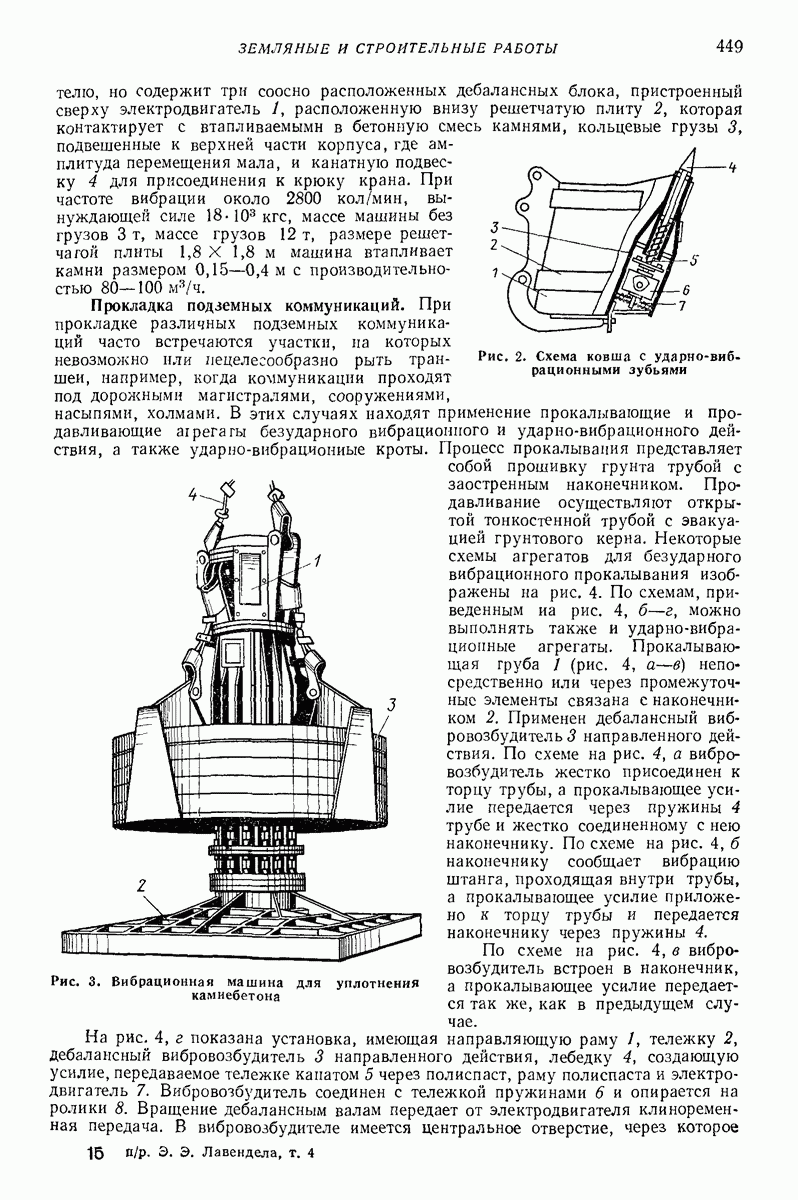
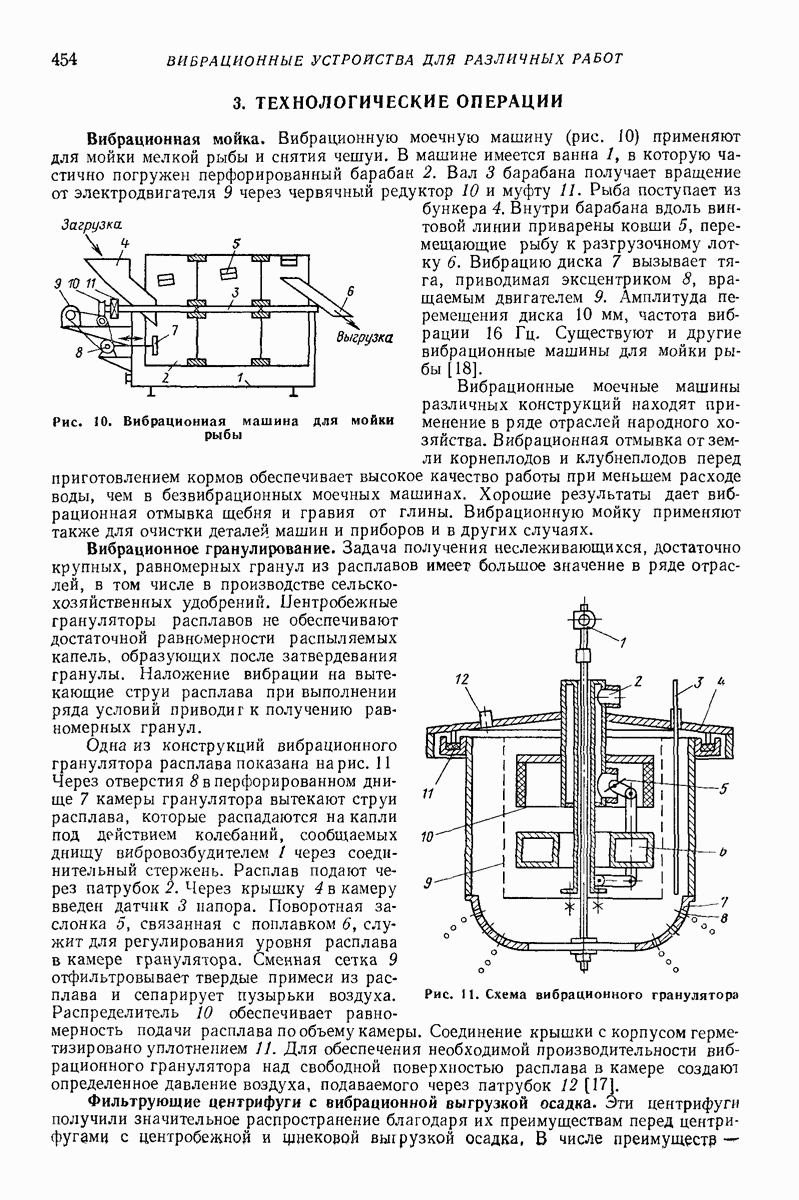
Глубинные (внутренние, погружаемые) вибровозбудители погружают в вибрируемую среду. Они представляют собой центробежные вибровозбудители кругового действия дебалансного или планетарного типа. Двигатель может быть встроенным или вынесенным. На рис. 7 изображена схема дебалансного глубинного вибровозбудителя, вал 2 которого, приводимый во вращение от вынесенного двигателя гибким валом  опирается на подшипники 3, установленные в цилиндрическом корпусе 4. На вал насажен дебаланс 5. Ось вращения дебаланса совпадает с геометрической осью корпуса, погруженного в изотропную среду, со стороны которой при колебаниях прилагаются к корпусу диссипативная и инерционная реакции.
опирается на подшипники 3, установленные в цилиндрическом корпусе 4. На вал насажен дебаланс 5. Ось вращения дебаланса совпадает с геометрической осью корпуса, погруженного в изотропную среду, со стороны которой при колебаниях прилагаются к корпусу диссипативная и инерционная реакции.
Корпус удерживают таким образом, что он не может поворачиваться вокруг своей геометрической оси и перемещаться вдоль нее. Благодаря изотропии окружающей среды, цилиндрической форме корпуса, концентричности дебалансного вала и корпуса и осевой симметрии масс корпуса точки геометрической оси корпуса описывают круговые траектории. Если векторы всех сил, приложенных к корпусу (центробежной силы дебаланса, диссипатнвной и инерционной реакций среды), лежат в одном поперечном сечении корпуса с его центром массы, а линия их действия проходит через этот центр, то при равномерном вращении дебаланса корпус совершает поступательное равномерное круговое движение, при котором все его образующие описывают круговые цилиндрические поверхности одинакового радиуса.

Рис. 7. Глубинный вибровозбуднтель
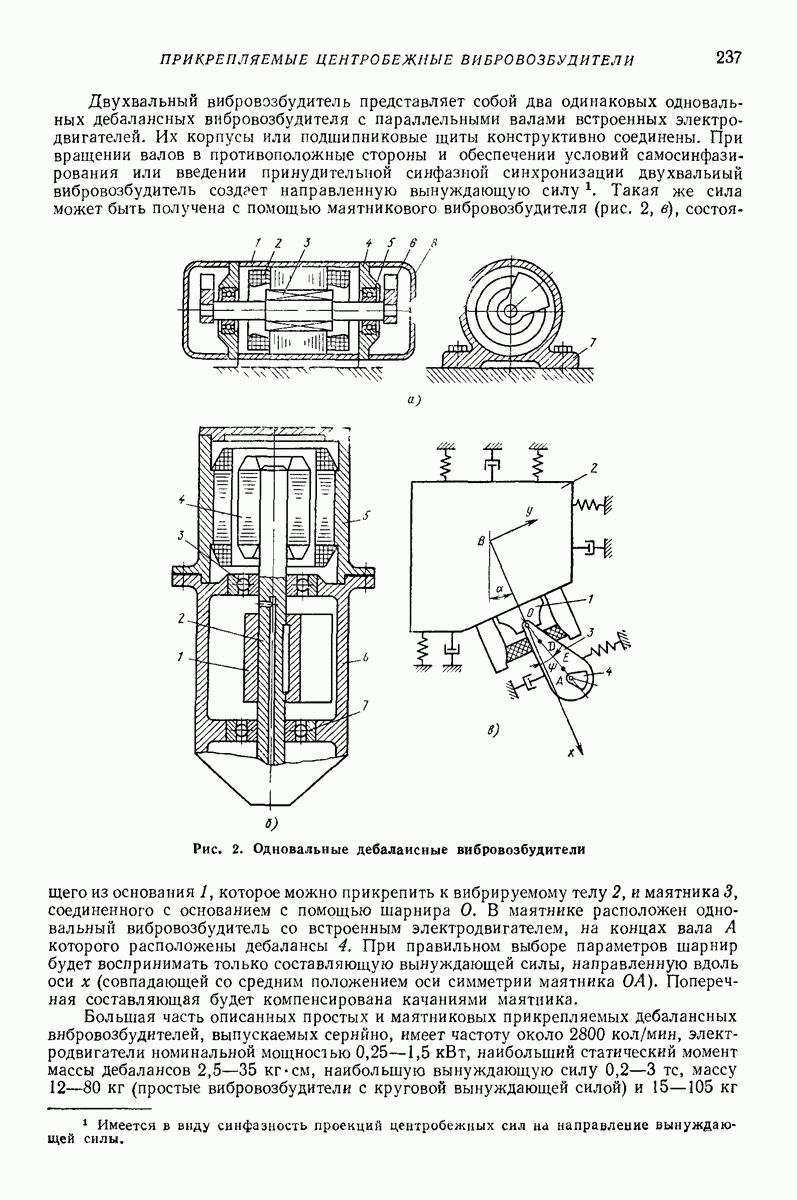
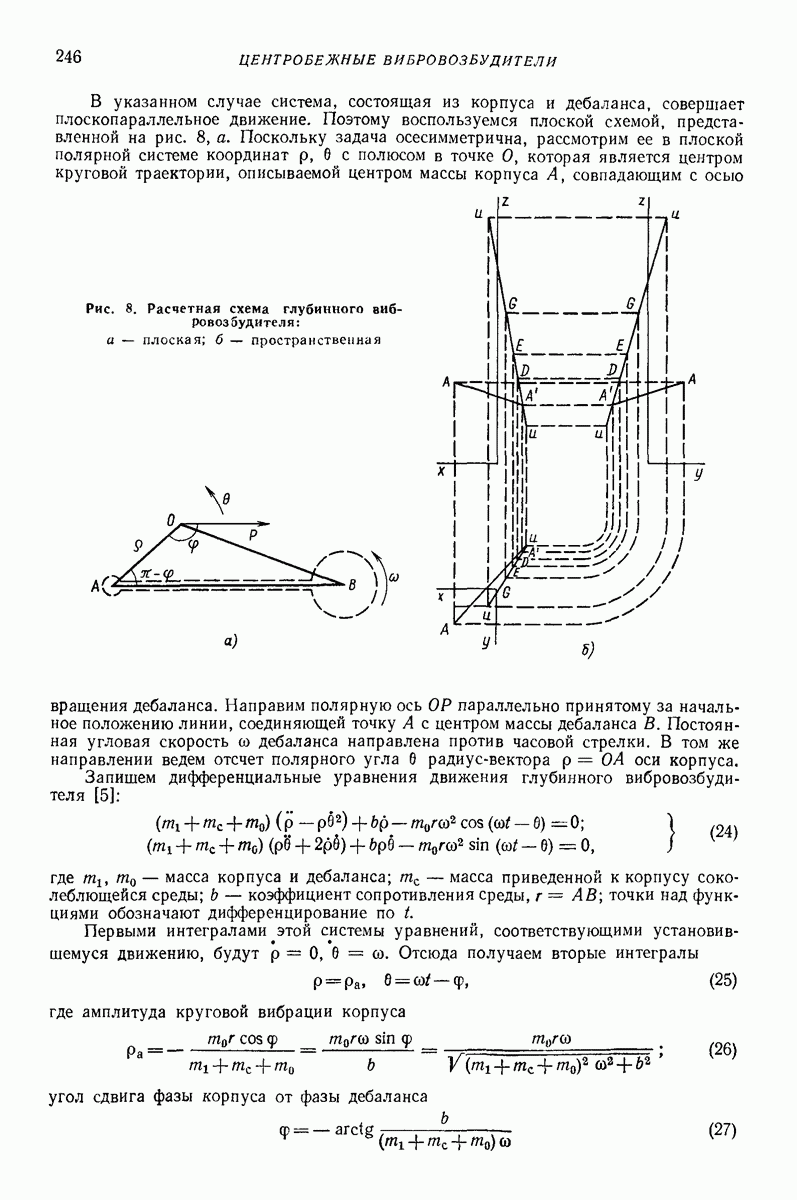
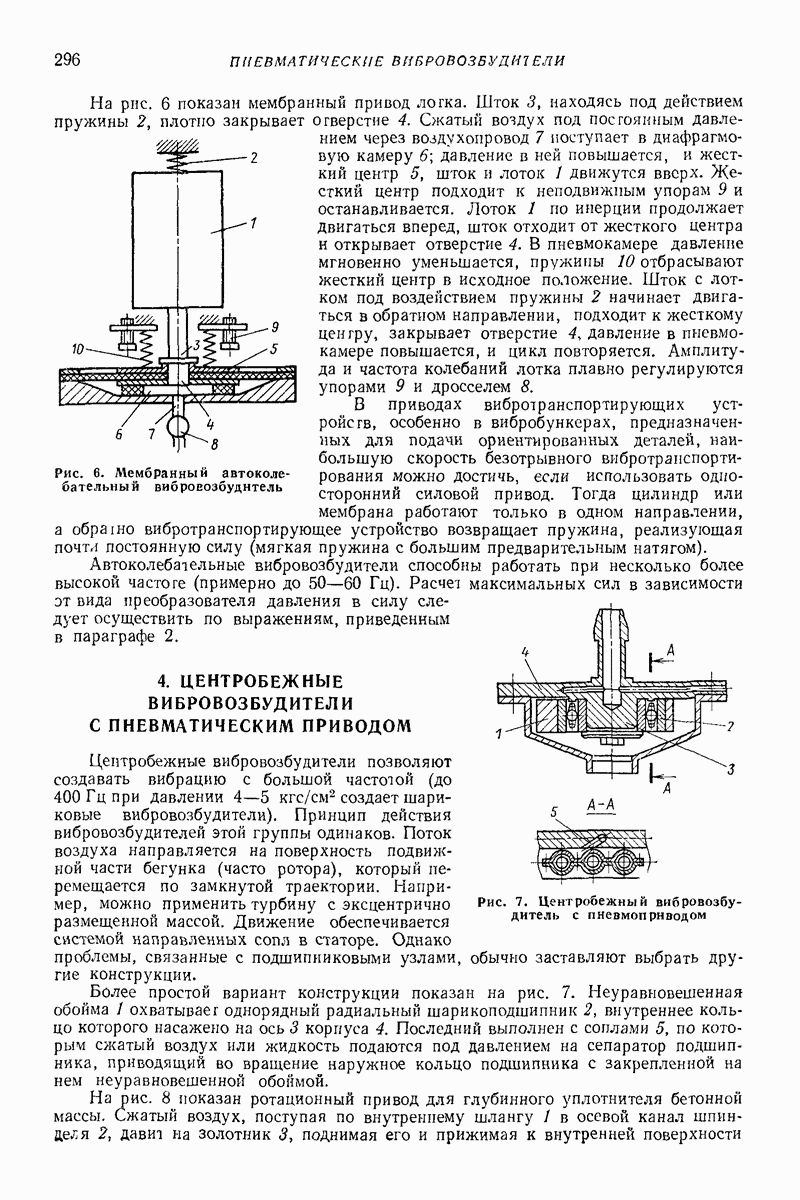
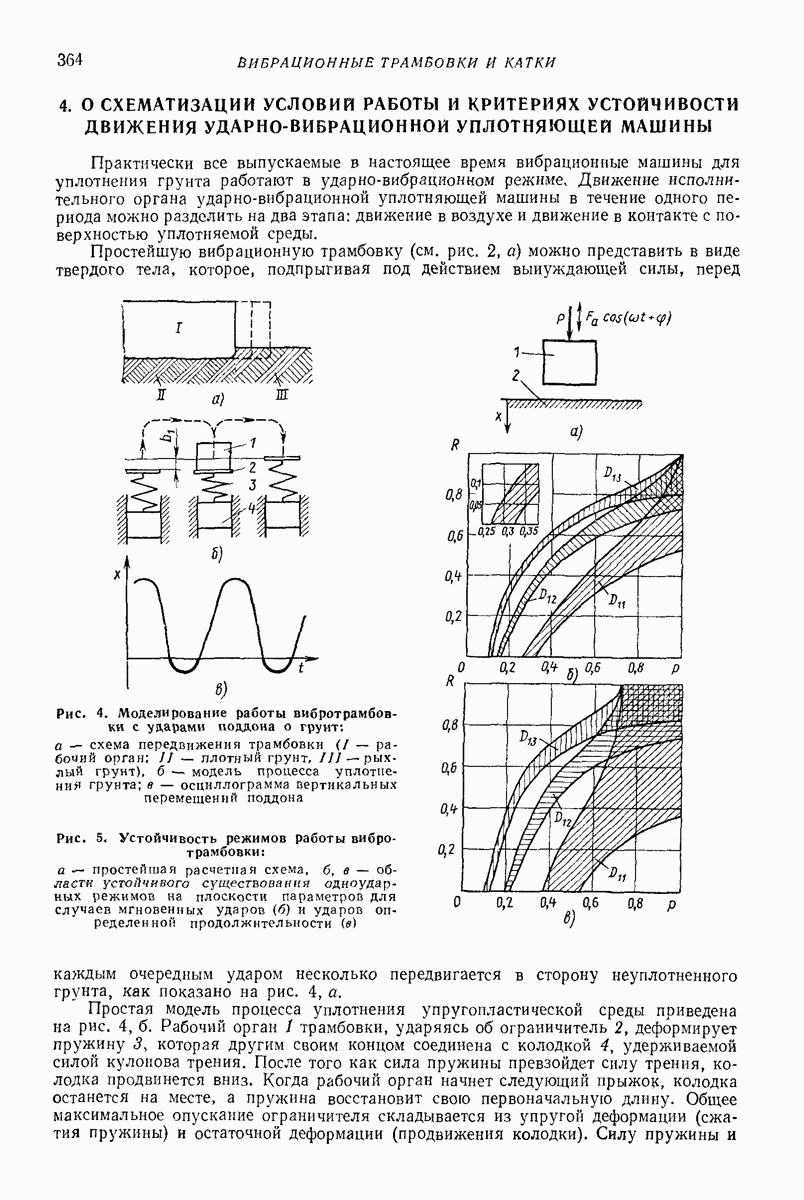
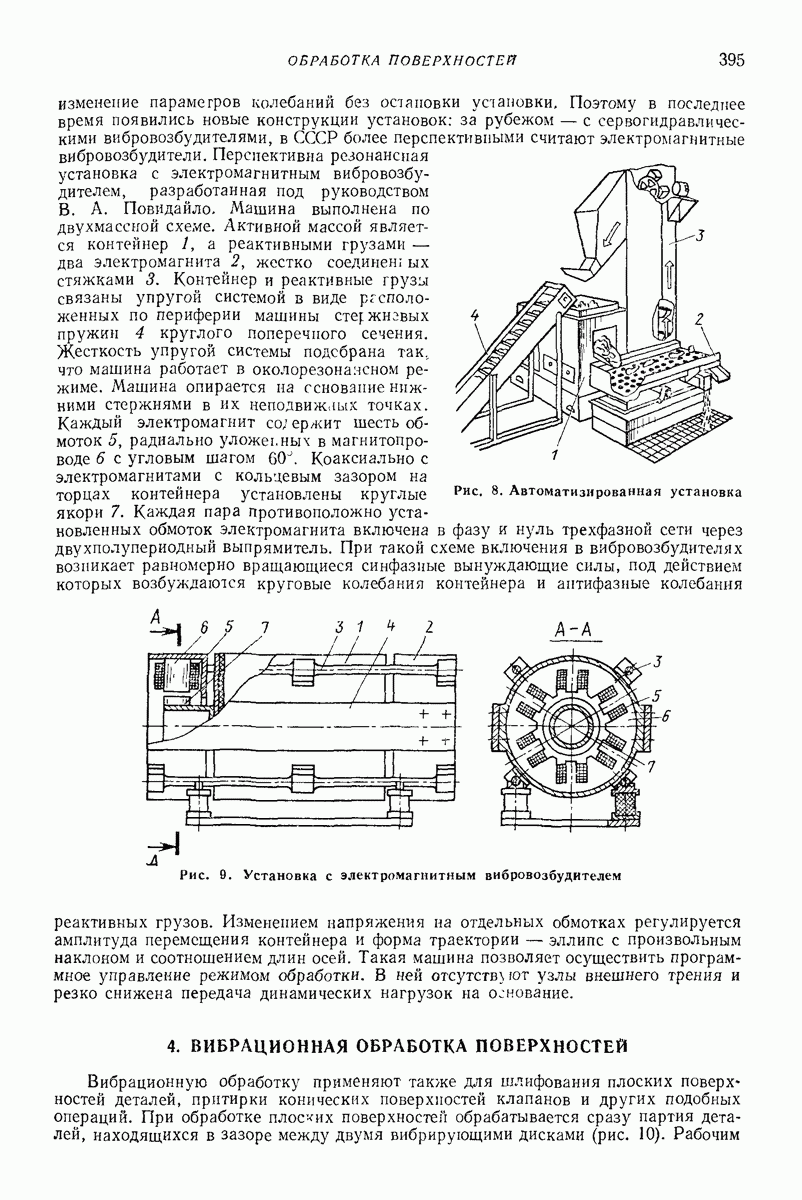
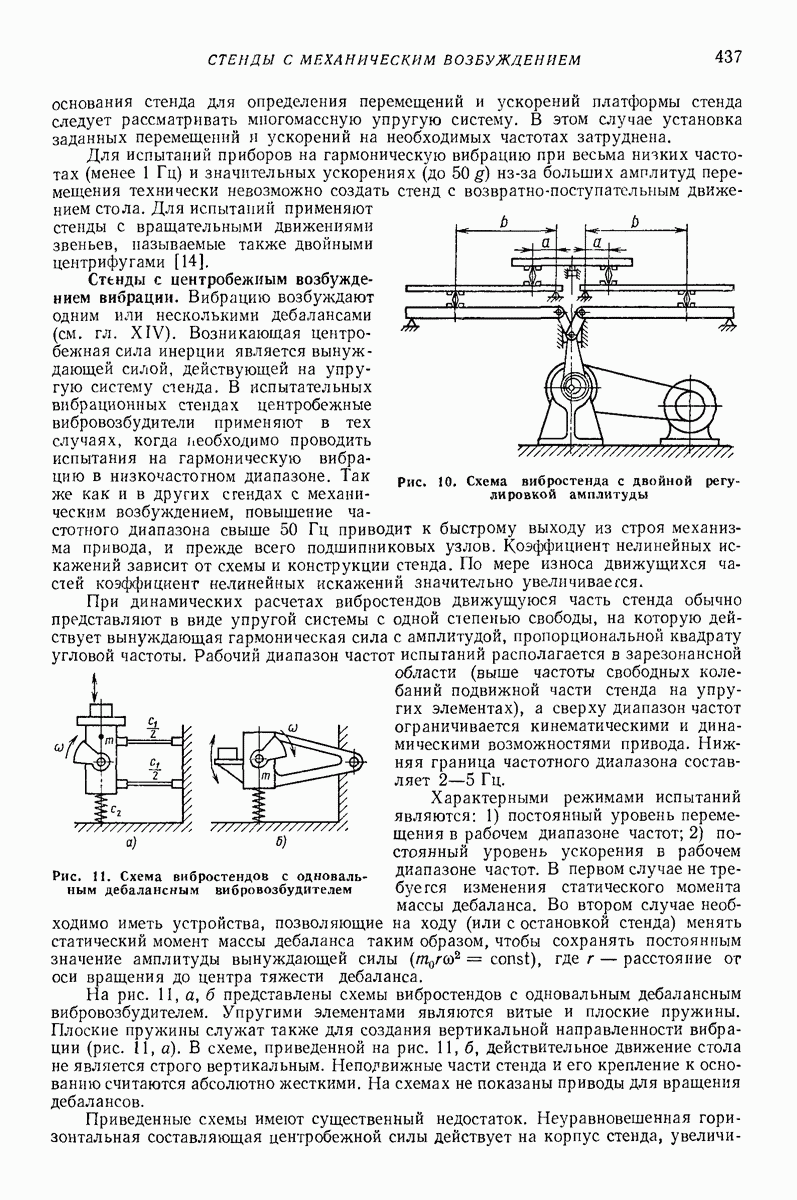
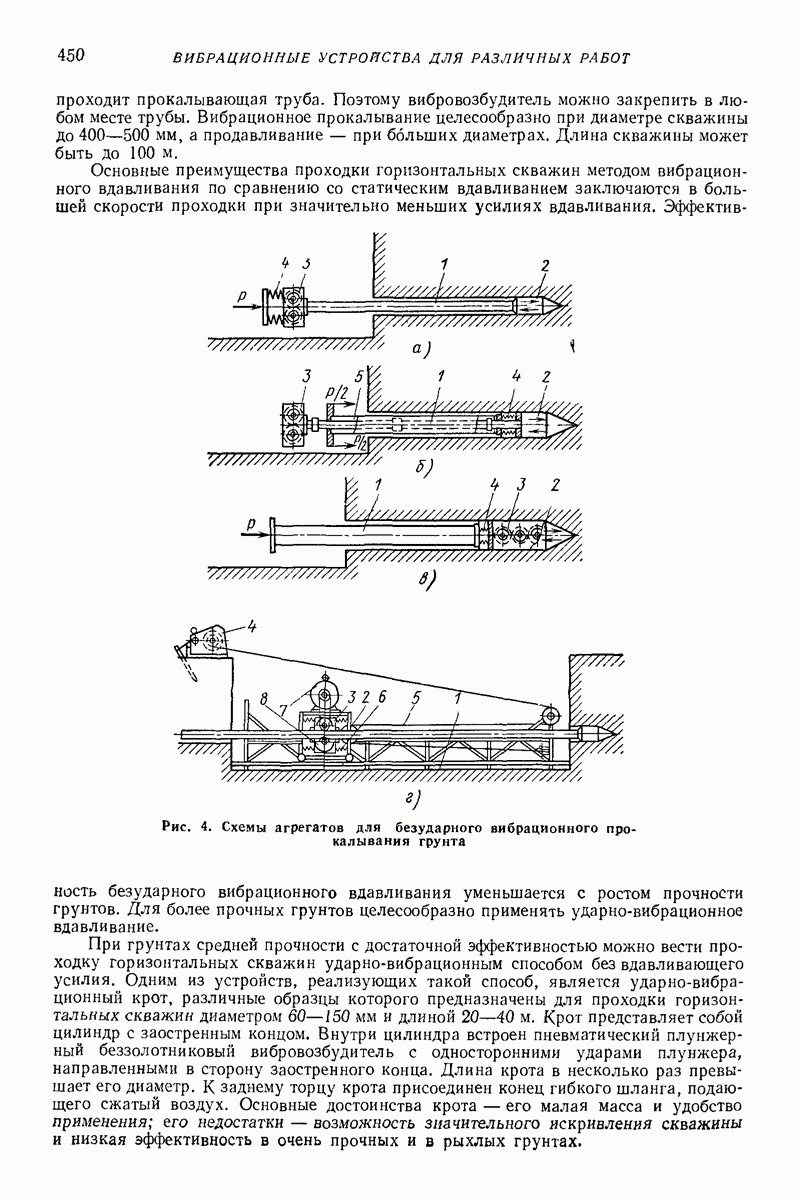
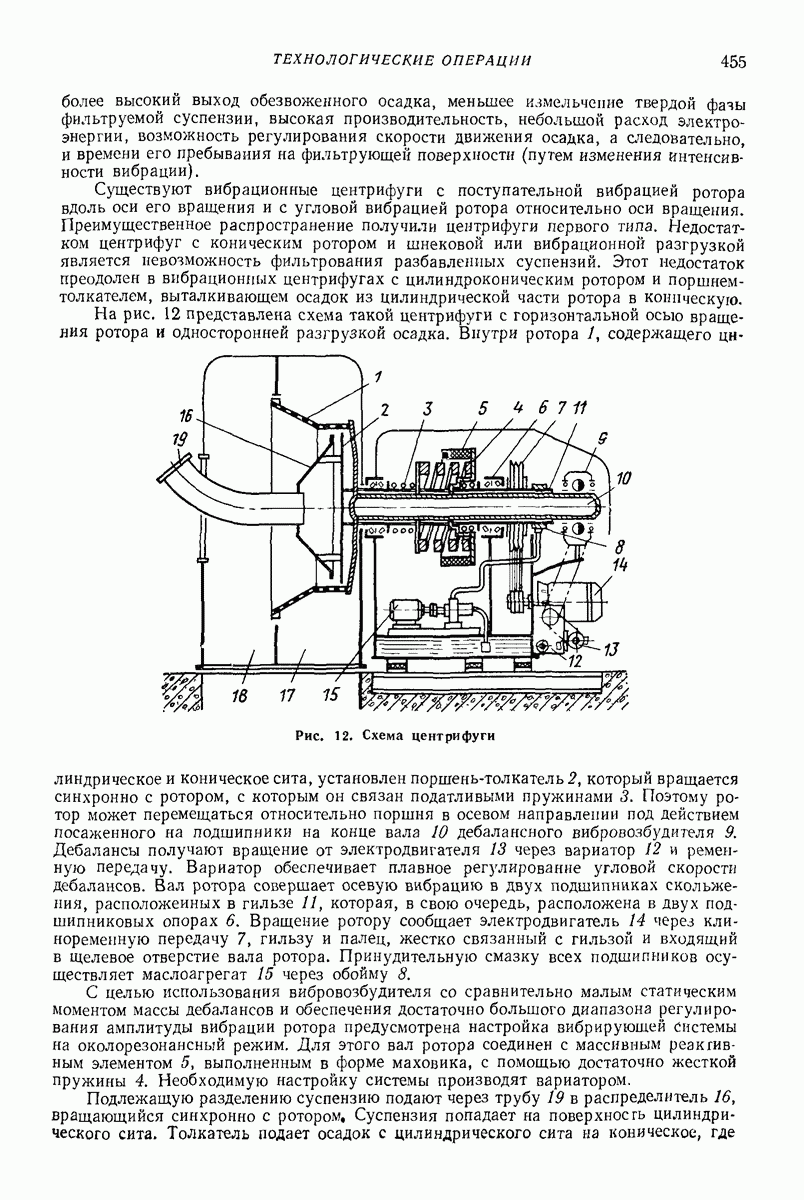
В указанном случае система, состоящая из корпуса и дебаланса, совершает плоскопараллельное движение. Поэтому воспользуемся плоской схемой, представленной на рис. 8, а. Поскольку задача осесимметрична, рассмотрим ее в плоской полярной системе координат  с полюсом в точке О, которая является центром круговой траектории, описываемой центром массы корпуса А, совпадающим с осью вращения дебаланса.
с полюсом в точке О, которая является центром круговой траектории, описываемой центром массы корпуса А, совпадающим с осью вращения дебаланса.

Рис. 8. Расчетная схема глубинного вибровозбудителя: а — плоская;  пространственная
пространственная
Направим полярную ось  параллельно принятому за начальное положению линии, соединяющей точку А с центром массы дебаланса В. Постоянная угловая скорость со дебаланса направлена против часовой стрелки. В том же направлении ведем отсчет полярного угла 6 радиус-вектора
параллельно принятому за начальное положению линии, соединяющей точку А с центром массы дебаланса В. Постоянная угловая скорость со дебаланса направлена против часовой стрелки. В том же направлении ведем отсчет полярного угла 6 радиус-вектора  оси корпуса.
оси корпуса.
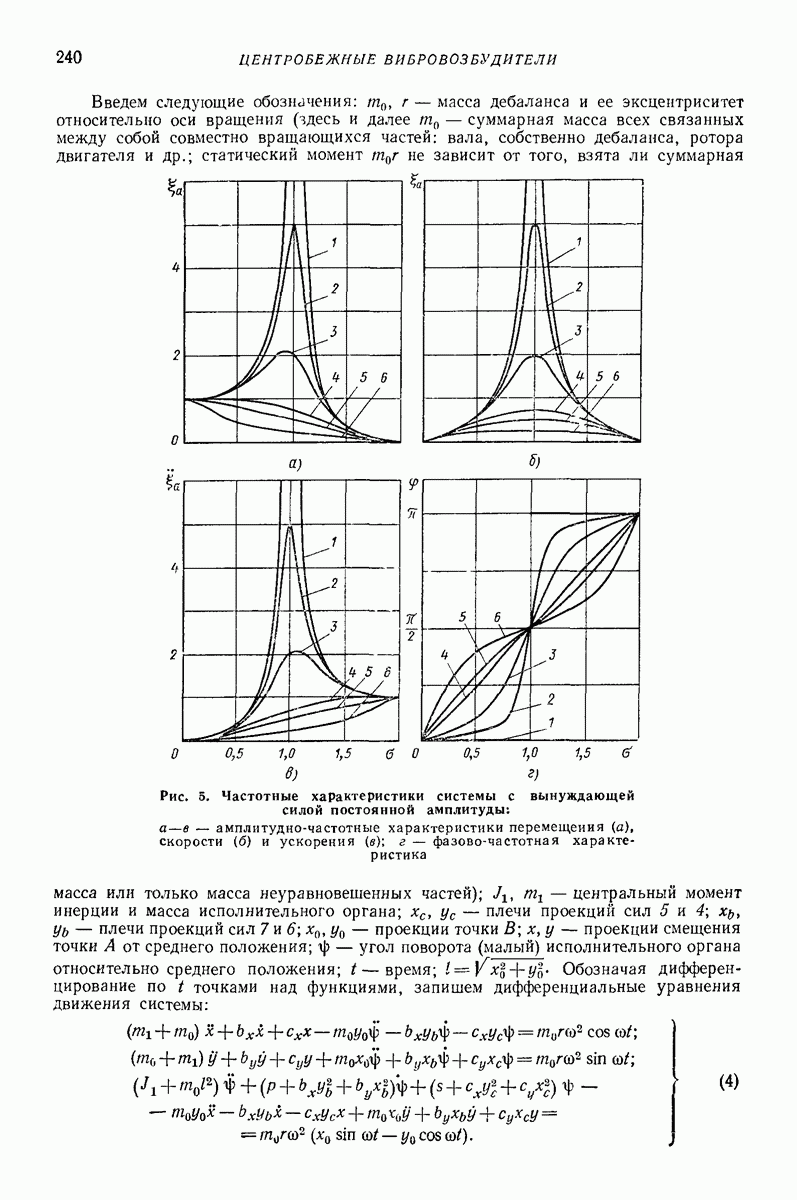
Запишем дифференциальные уравнения движения глубинного вибровозбудителя [5]:

где  масса корпуса и дебаланса;
масса корпуса и дебаланса;  масса приведенной к корпусу соколеблющейся среды;
масса приведенной к корпусу соколеблющейся среды;  коэффициент сопротивления среды,
коэффициент сопротивления среды,  точки над функциями обозначают дифференцирование по
точки над функциями обозначают дифференцирование по 
Первыми интегралами этой системы уравнений, соответствующими установившемуся движению, будут  Отсюда получаем вторые интегралы
Отсюда получаем вторые интегралы

где амплитуда круговой вибрации корпуса

угол сдвига фазы корпуса от фазы дебаланса

находится в пределах  Левый предел соответствует
Левый предел соответствует  правый предел соответствует
правый предел соответствует  .
.
Поскольку при круговой вибрации корпуса вибровозбудителя в изотропной среде модули скорости точек поверхности корпуса и равнодействующей сил диссипативного сопротивления движению корпуса остаются неизменными, текущее значение мощности  необходимой для поддержания колебаний, также остается постоянным. Значение этой мощности
необходимой для поддержания колебаний, также остается постоянным. Значение этой мощности

становится максимальным при  , т. е. при
, т. е. при  и определяется выражением
и определяется выражением

Результаты подсчета мощности по (28) и (29) вдвое превышают соответствующие значения, определяемые (40) и (42) гл. VIII, что вполне естественно, поскольку последние две формулы получены для системы с одной степенью свободы, а в глубинном вибровозбудителе в случае плоскопараллельного движения реализуются две степени свободы.
При вынесенном двигателе к корпусу приложен момент  направленный в сторону вращения дебаланса. При встроенном двигателе к корпусу приложен момент
направленный в сторону вращения дебаланса. При встроенном двигателе к корпусу приложен момент  направленный в сторону, противоположную вращению дебаланса. Здесь
направленный в сторону, противоположную вращению дебаланса. Здесь  механическая мощность на валу электродвигателя;
механическая мощность на валу электродвигателя;  мощность, необходимая для преодоления сопротивления вращению дебалансного вала. Для предотвращения собственного вращения корпуса необходимо извне приложить к нему равный по модулю и противоположно направленный момент. Приведенные значения моментов справедливы, если равнодействующая диссипативных сил среды пересекает ось корпуса вибровозбудителя.
мощность, необходимая для преодоления сопротивления вращению дебалансного вала. Для предотвращения собственного вращения корпуса необходимо извне приложить к нему равный по модулю и противоположно направленный момент. Приведенные значения моментов справедливы, если равнодействующая диссипативных сил среды пересекает ось корпуса вибровозбудителя.
Благодаря осевой симметрии все изложенные результаты сохраняют свою силу при каждом фиксированном значении со и в случаях нелинейной зависимости диссипативной реакции среды от скорости и инерционной реакции среды от ускорения корпуса. Но тогда необходимо знать и подставлять в соответствующие формулы зависимости 
Плоскопараллельное движение корпуса вибровозбудителя нередко признают неприемлемым, поскольку выдвигают требование почти полной неподвижности места прикрепления рукояти к ручному или захватного устройства к подвесному вибровозбудителям. Точку на оси корпуса, амплитуда вибрации которой равна нулю, называют нулевой точкой. С целью получения нулевой точки у верхнего торца корпуса центр массы дебаланса должен быть ниже центра массы всего вибровозбудителя, причем расстояние между указанными центрами масс подлежит определению.
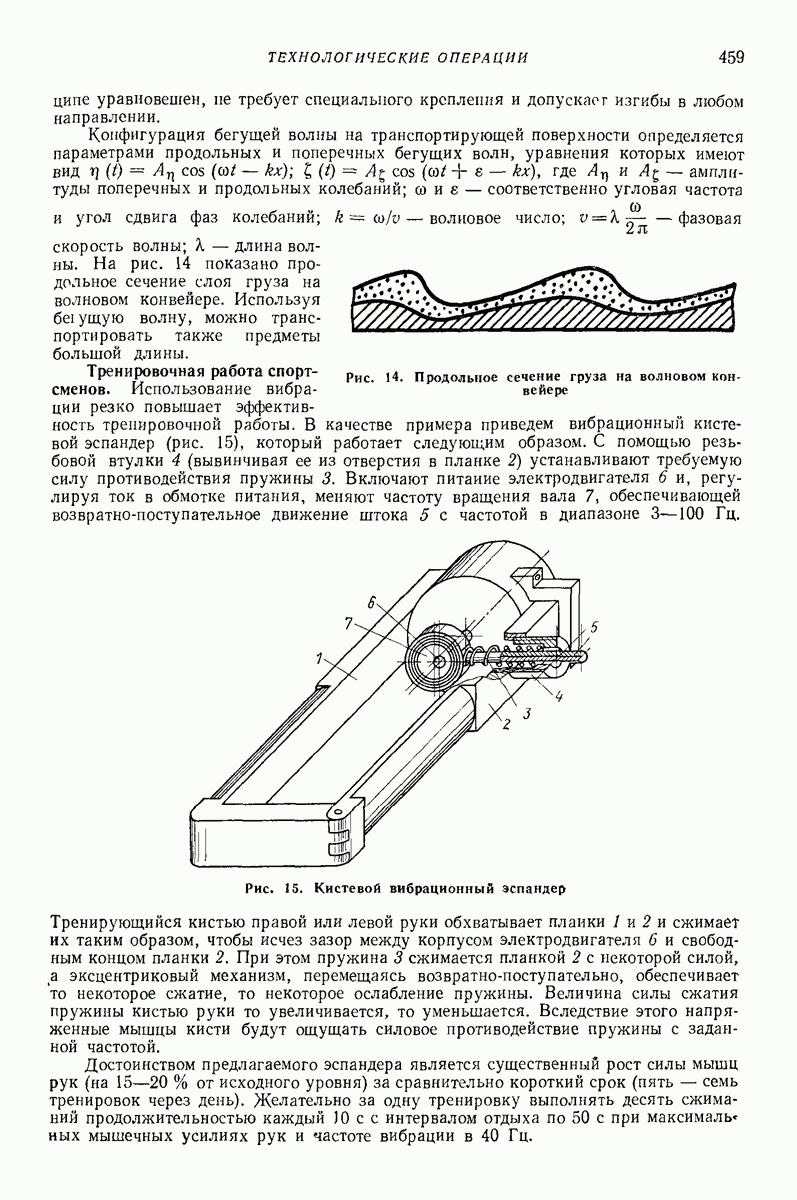
Если движение корпуса вибровозбудителя не плоскопараллельное, то реализуются четыре степени свободы при условии исключения вращения корпуса вокруг своей геометрической оси и перемещения вдоль этой оси. Движение корпуса при такой схематизации будет также осесимметричным. Все точки, расположенные на его геометрической оси, будут описывать окружности вокруг какой-то общей неподвижной оси. Вокруг той же оси будет описывать окружность центр массы дебаланса.
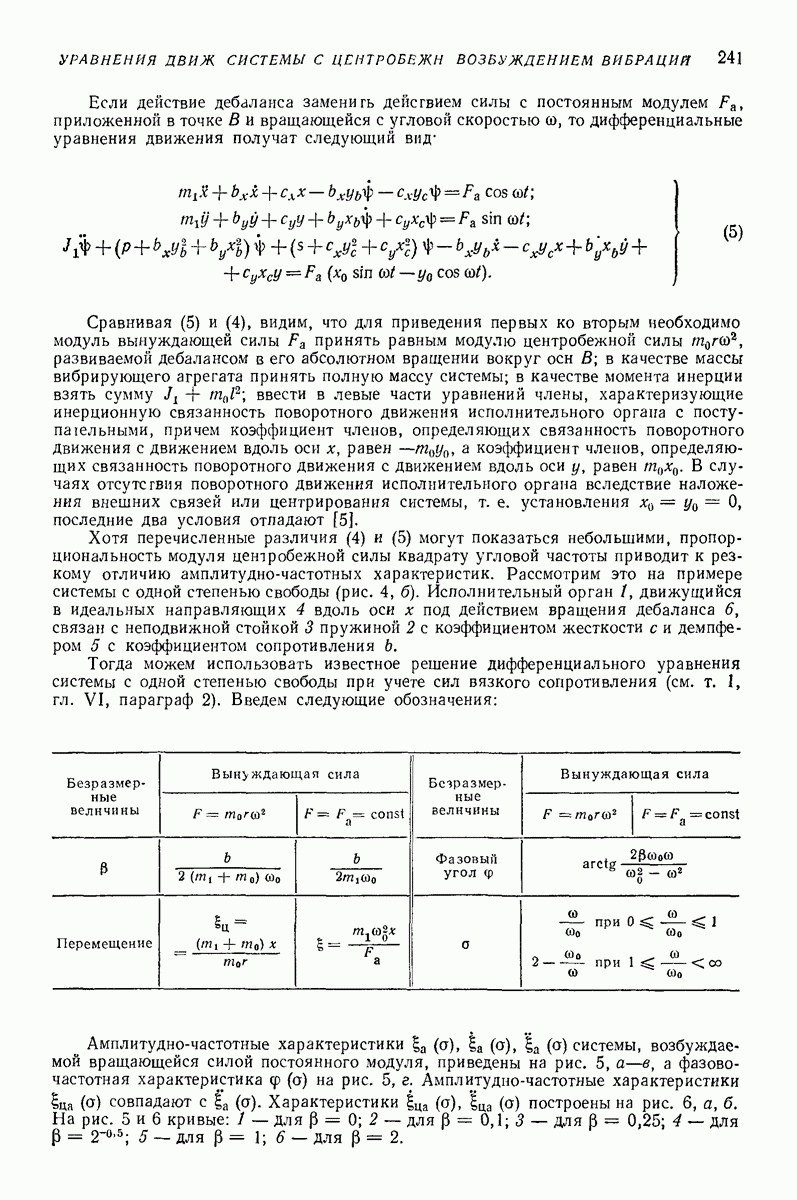
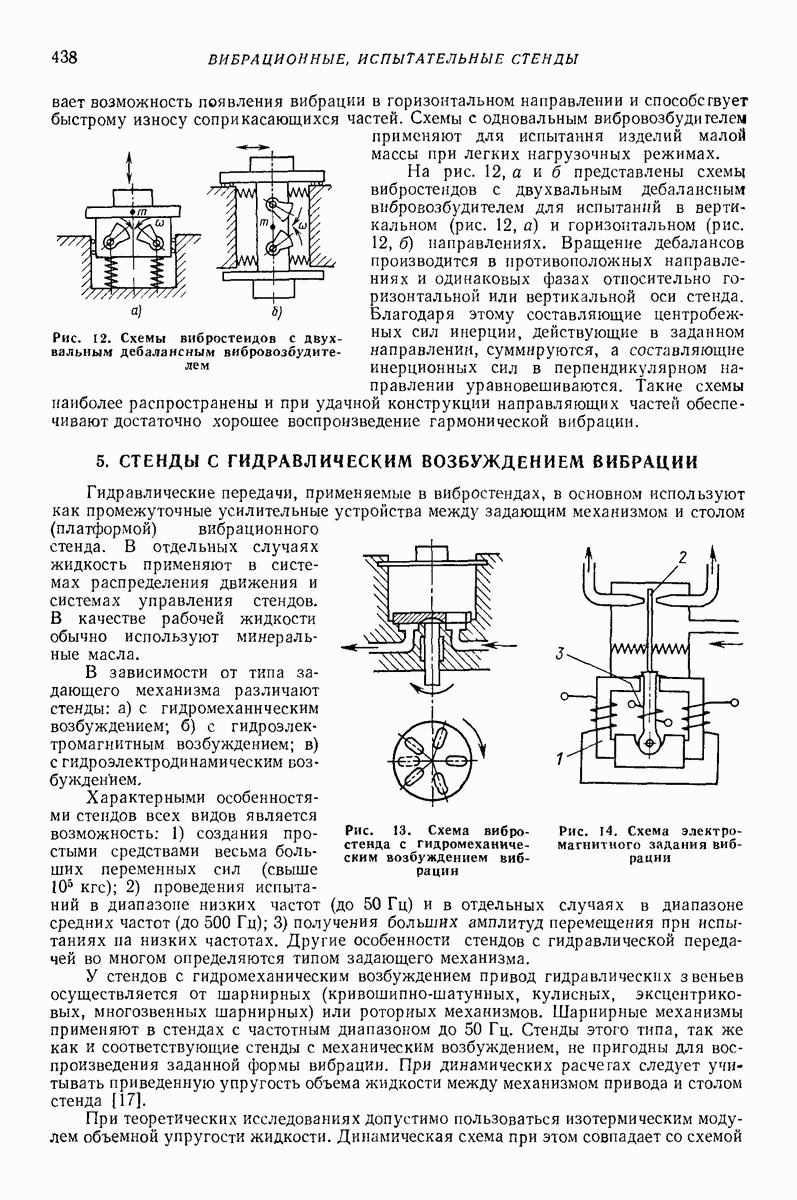
У неподвижной декартовой системы координат совместим ось  с упомянутой неподвижной осью. Оси х и у могут быть расположены произвольно. В левой верхней части рис. 8, б показана проекция на плоскость
с упомянутой неподвижной осью. Оси х и у могут быть расположены произвольно. В левой верхней части рис. 8, б показана проекция на плоскость  геометрической оси
геометрической оси  корпуса, которая является также осью собственного вращения дебаланса. В точке А расположим центр массы дебаланса. Точка А представляет собой проекцию точки А на ось
корпуса, которая является также осью собственного вращения дебаланса. В точке А расположим центр массы дебаланса. Точка А представляет собой проекцию точки А на ось  Полагая малыми угол между осями
Полагая малыми угол между осями  а также отношение эксцентриситета массы дебаланса
а также отношение эксцентриситета массы дебаланса  к длине корпуса, будем считать, что центр масс всего вибровозбуднтеля, включая приведенную к оси
к длине корпуса, будем считать, что центр масс всего вибровозбуднтеля, включая приведенную к оси  соколеблющуюся массу вибрируемой среды, расположен на оси
соколеблющуюся массу вибрируемой среды, расположен на оси  в точке
в точке  Равнодействующая сил диссипативного сопротивления среды приложена в точке
Равнодействующая сил диссипативного сопротивления среды приложена в точке  на оси
на оси  В точке
В точке  расположен центр массы корпуса.
расположен центр массы корпуса.
На рис. 8, б справа показана проекция той же фигуры на плоскость  а внизу — на плоскость
а внизу — на плоскость  Три проекции каждой из перечисленных точек и осей обозначены одинаковыми буквами. В качестве обобщенных координат выберем абсциссу х и ординату у точки
Три проекции каждой из перечисленных точек и осей обозначены одинаковыми буквами. В качестве обобщенных координат выберем абсциссу х и ординату у точки  и углы
и углы  между осью
между осью  и проекцией оси
и проекцией оси  соответственно на плоскости
соответственно на плоскости  Обозначим
Обозначим  момент инерции всего вибровозбудителя относительно центральной оси, перпенднкулярной оси
момент инерции всего вибровозбудителя относительно центральной оси, перпенднкулярной оси 
Линеаризованные дифференциальные уравнения движения корпуса вибровозбудителя можно записать в следующем виде, полагая, что в начальный момент времени отрезок  ориентирован в положительном направлении оси х [5]:
ориентирован в положительном направлении оси х [5]:

Эти уравнения распадаются на две несвязанные подсистемы, из которых первая подсистема образована первым и вторым уравнениями, а вторая подсистема — третьим и четвертым уравнениями. Соответствующие коэффициенты в левых частях первого и третьего уравнений одинаковы, так же как второго и четвертого уравнений. Соответствующие правые части различаются только по фазе синусоидального множителя на угол  , равный углу между осями х и у, что закономерно подчеркивает осевую симметрию движения. Поэтому достаточно рассмотреть первую подсистему.
, равный углу между осями х и у, что закономерно подчеркивает осевую симметрию движения. Поэтому достаточно рассмотреть первую подсистему.
Условием наличия нулевой точки является синфазность  равносильная их пропорциональности, в соответствии с чем
равносильная их пропорциональности, в соответствии с чем  где а — расстояние от точки
где а — расстояние от точки  до нулевой точки. На основании этого первые два уравнения (30) можно записать в следующем виде:
до нулевой точки. На основании этого первые два уравнения (30) можно записать в следующем виде:

Для равенства интегралов первого и второго уравнений (31) необходимо и достаточно, чтобы были соответственно равны коэффициенты при  Равенство коэффициентов при х приводит к соотношению
Равенство коэффициентов при х приводит к соотношению

а равенство коэффициентов при х дает зависимость

Следовательно, условием наличия нулевой точки является приложение равнодействующей сил сопротивления среды в том же поперечном сечении корпуса, в котором расположен центр массы дебаланса. Равенство (33), указывающее положение нулевой точки, можно привести к виду

где  а — расстояние от поперечного сечения корпуса, в котором расположен центр массы дебаланса, до нулевой точки;
а — расстояние от поперечного сечения корпуса, в котором расположен центр массы дебаланса, до нулевой точки;  момент инерции вибровозбудителя относительно нулевой точки.
момент инерции вибровозбудителя относительно нулевой точки.
Интеграл первого уравнения (31), описывающий установившуюся вибрацию, при выполнении условия (32) имеет вид

где

При наличии нулевой точки ось корпуса описывает поверхность кругового конуса. Если условие (32) не выполнено, то нулевая точка отсутствует и ось корпуса описывает иную линейчатую поверхность — однополостный гиперболоид вращения.
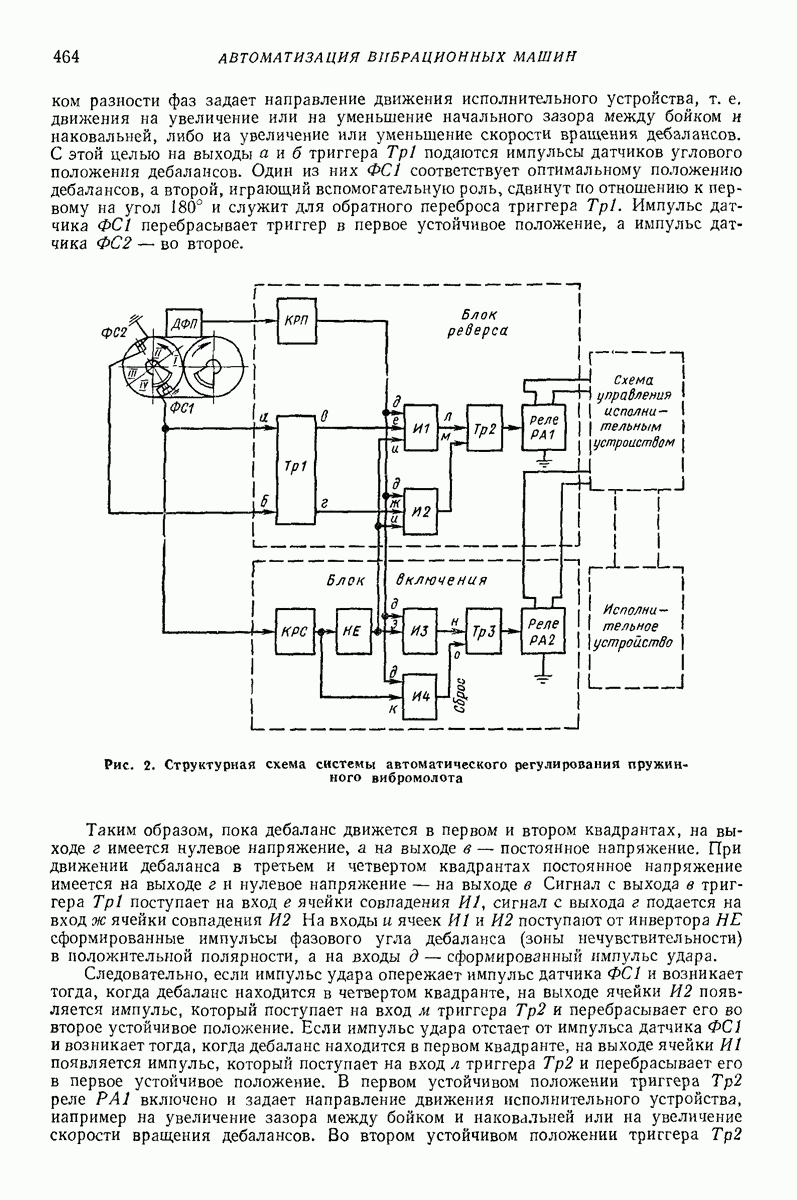
Все изложенные зависимости получены для глубинного дебалансного вибровозбудителя, схематически изображенного на рис. 7. Они в равной мере относятся и к планетарным вибровозбудителям, для которых  обозначает угловую скорость обкатки, за исключением зависимостей, которые определяют момент, приложенный к корпусу со стороны двигателя и подшипников фрикционно-планетарных и зубчато-планетарных вибровозбудигелей, где со обозначает угловую скорость собственного вращения бегунка.
обозначает угловую скорость обкатки, за исключением зависимостей, которые определяют момент, приложенный к корпусу со стороны двигателя и подшипников фрикционно-планетарных и зубчато-планетарных вибровозбудигелей, где со обозначает угловую скорость собственного вращения бегунка.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- Установившиеся режимы движения частицы.
- О методах решения задачи.
- Установившиеся режимы при отсутствии подбрасывания [4-6].
- Установившиеся режимы с подбрасыванием.
- Средние скорость и ускорение частицы в установившихся режимах движения.
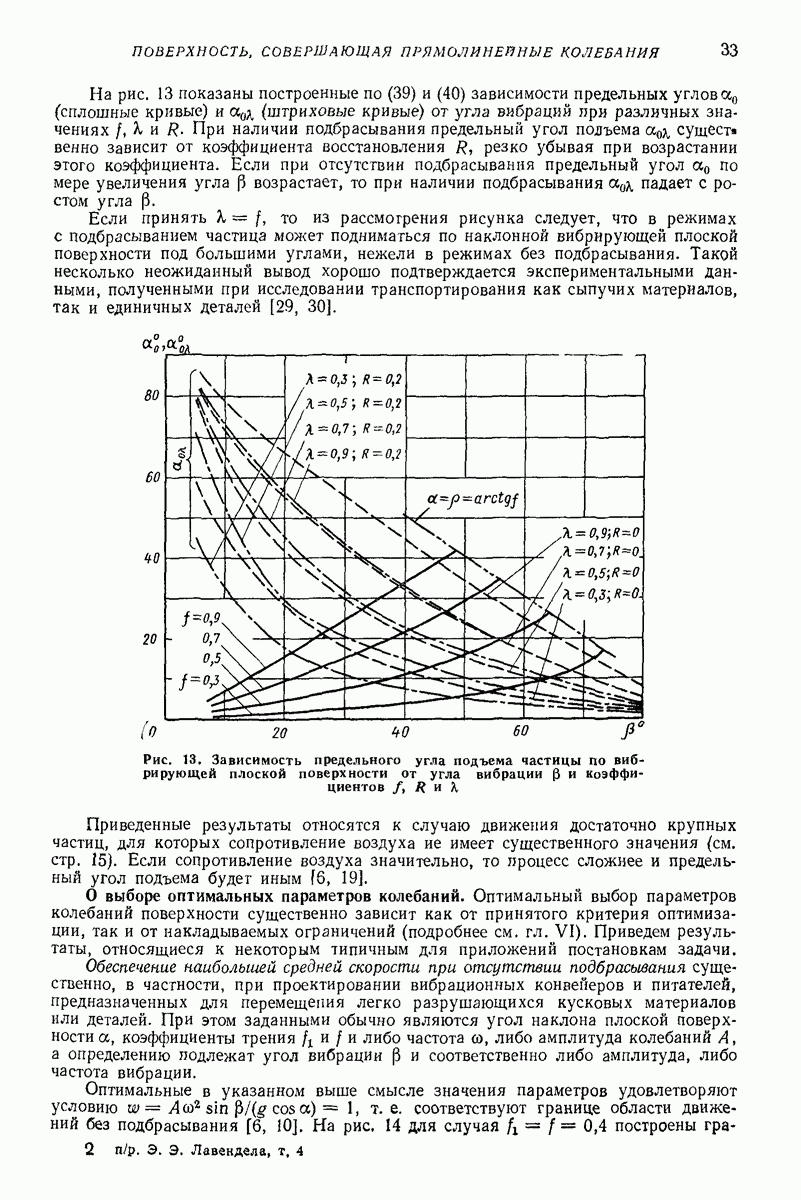
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
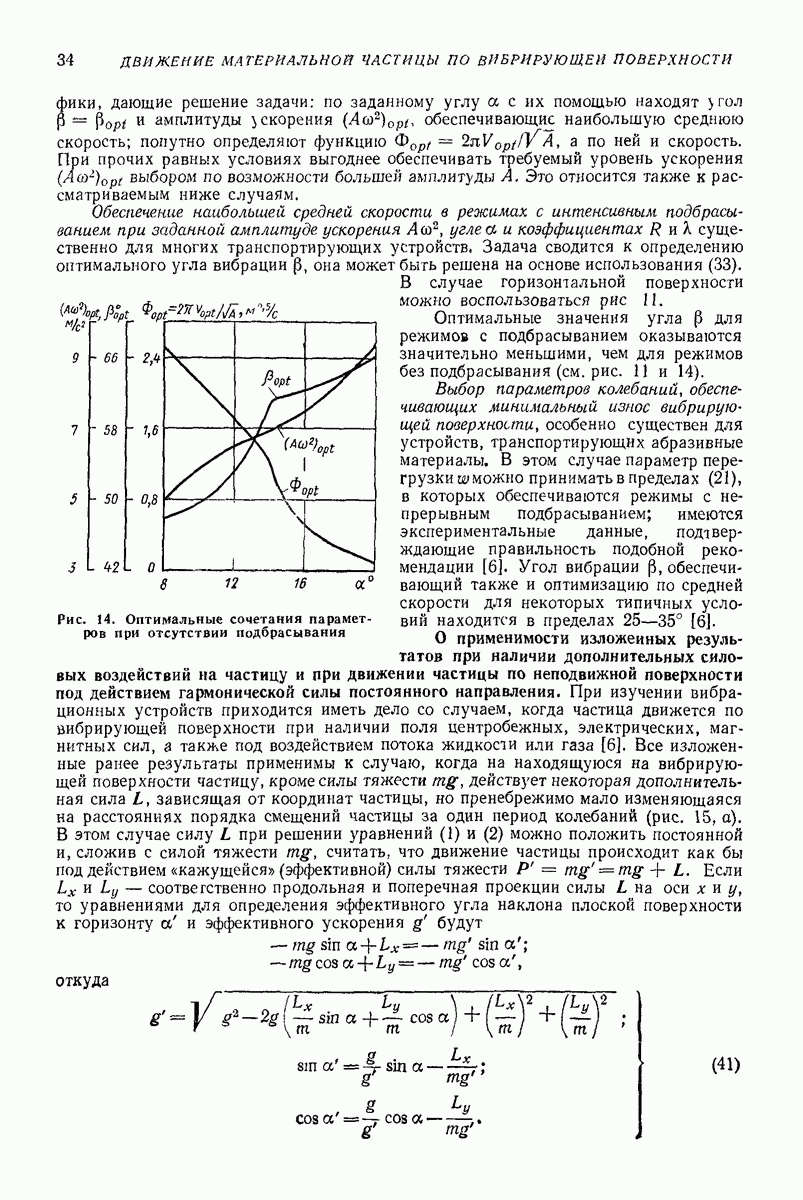
- О выборе оптимальных параметров колебаний.
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
- О влиянии на движение частицы сил вязкого сопротивления.
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
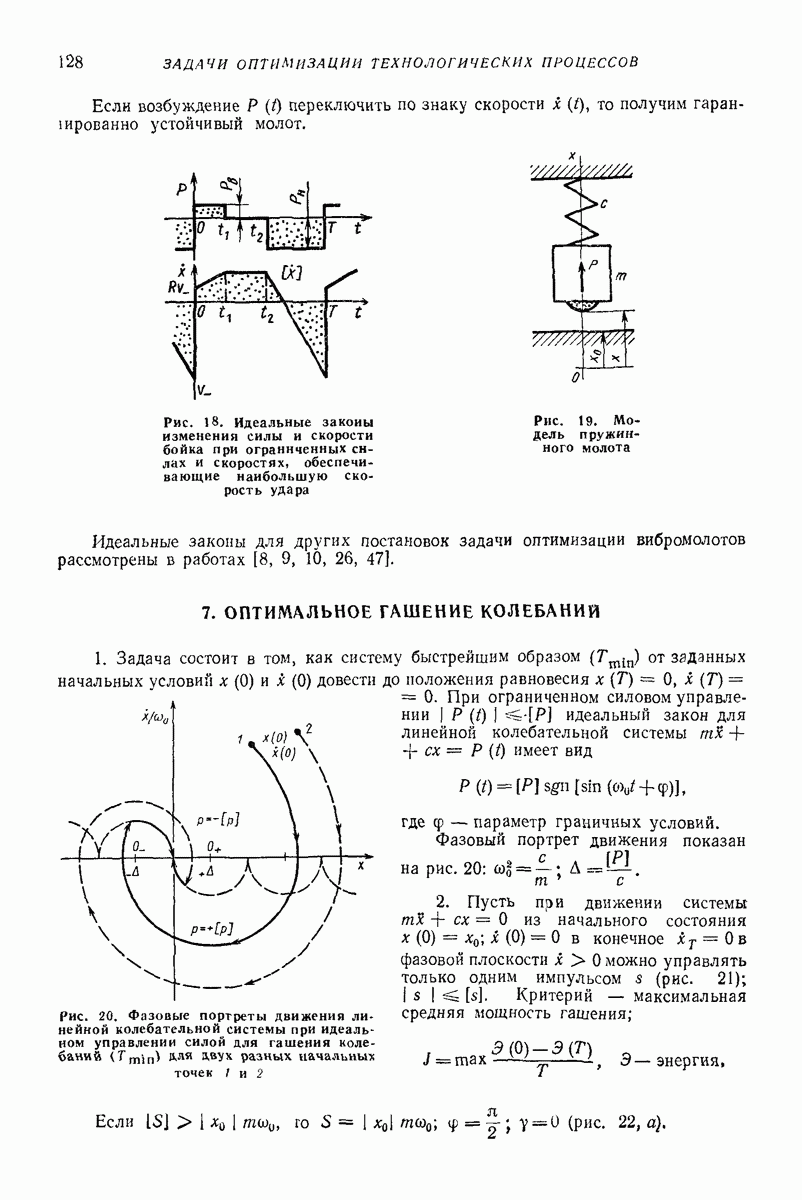
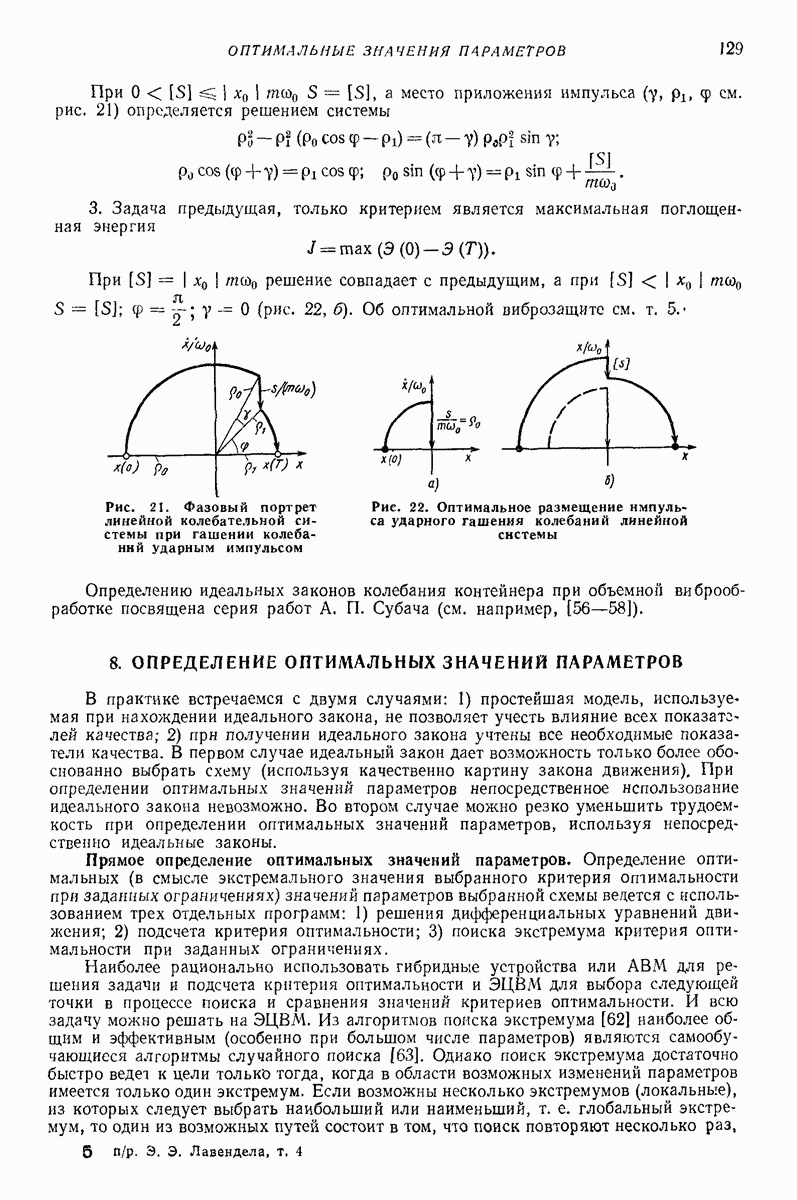
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
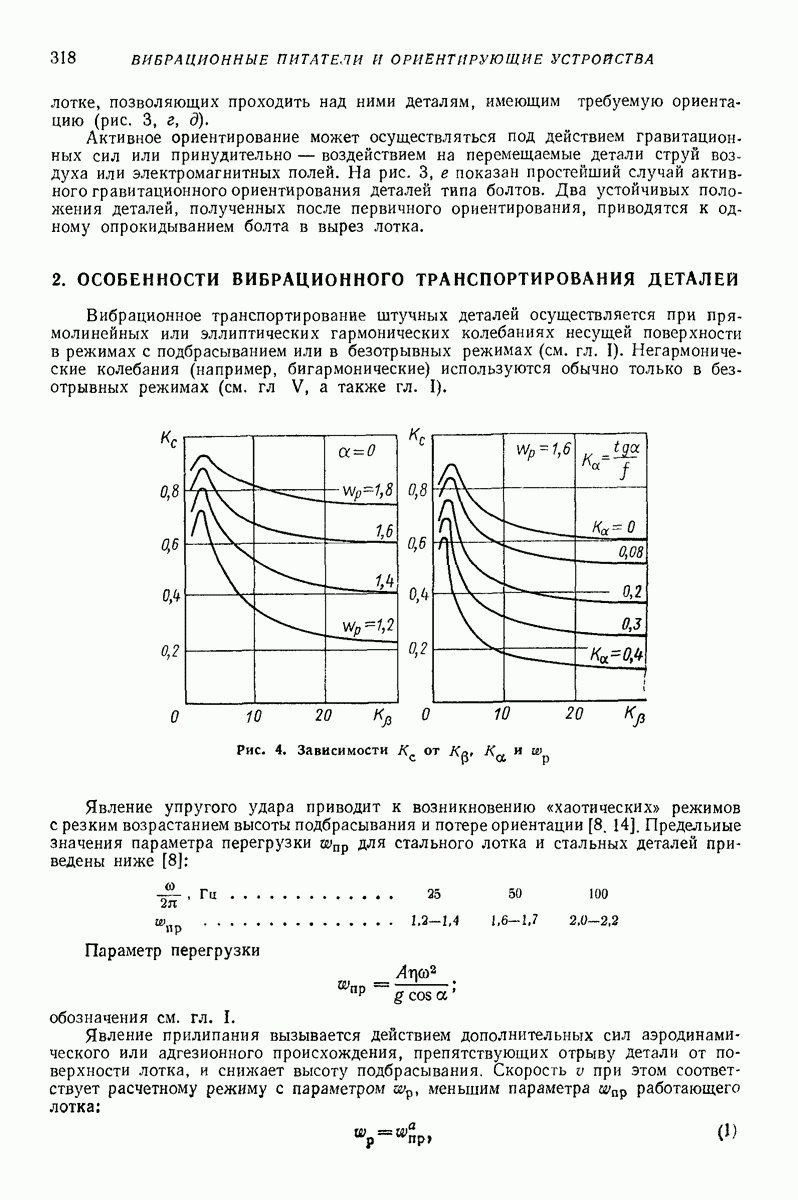
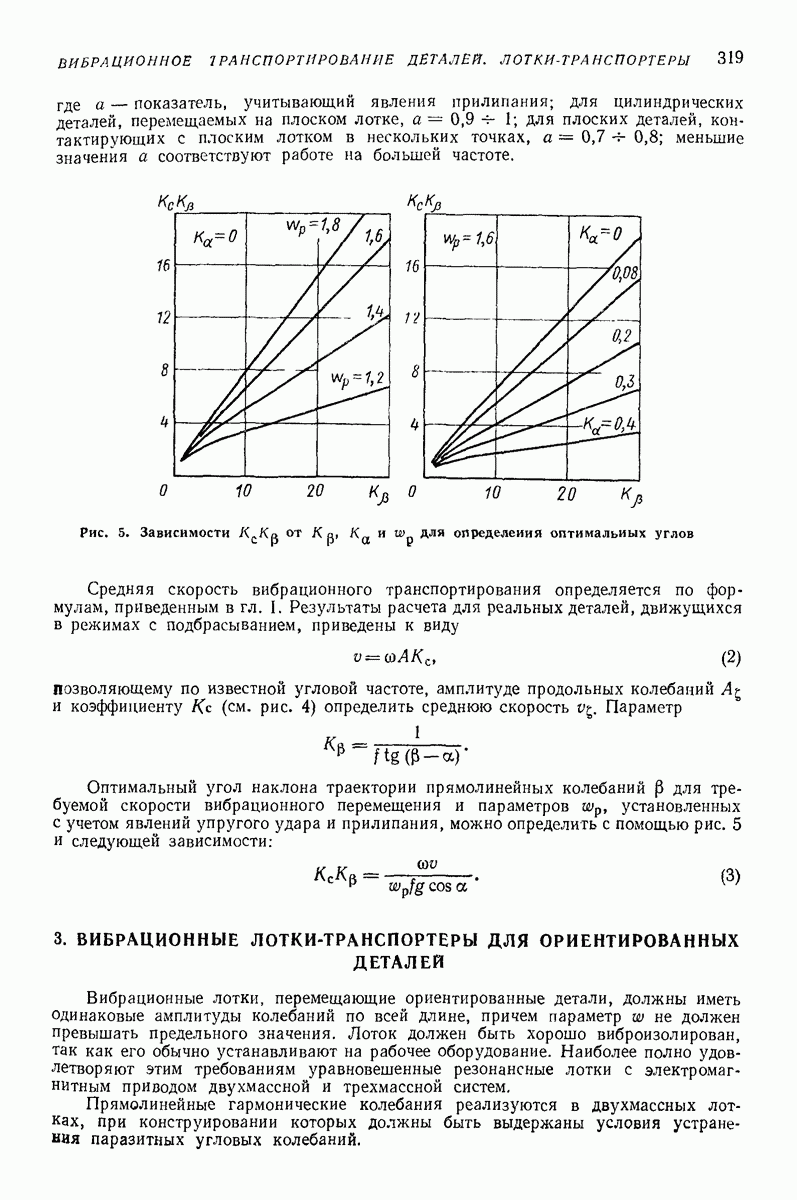
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
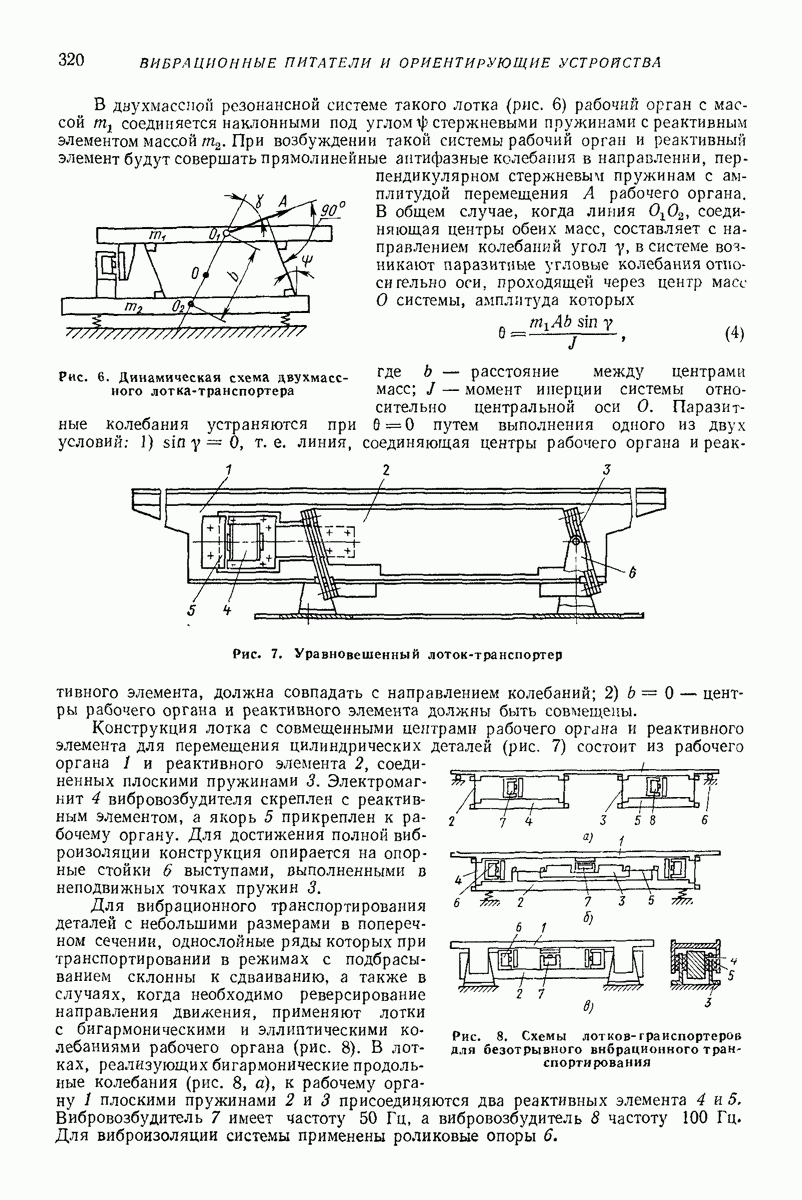
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
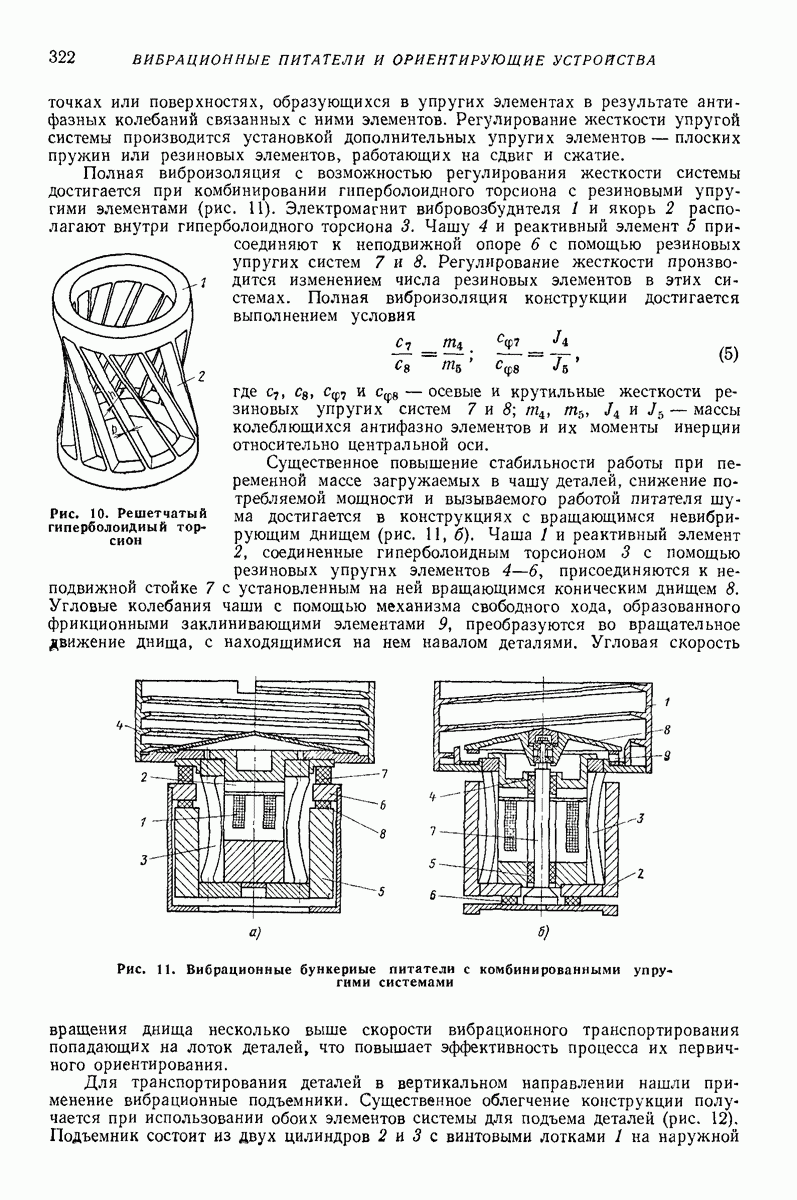
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
- 4. СЕПАРАТОРЫ С ДЕКОЙ
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
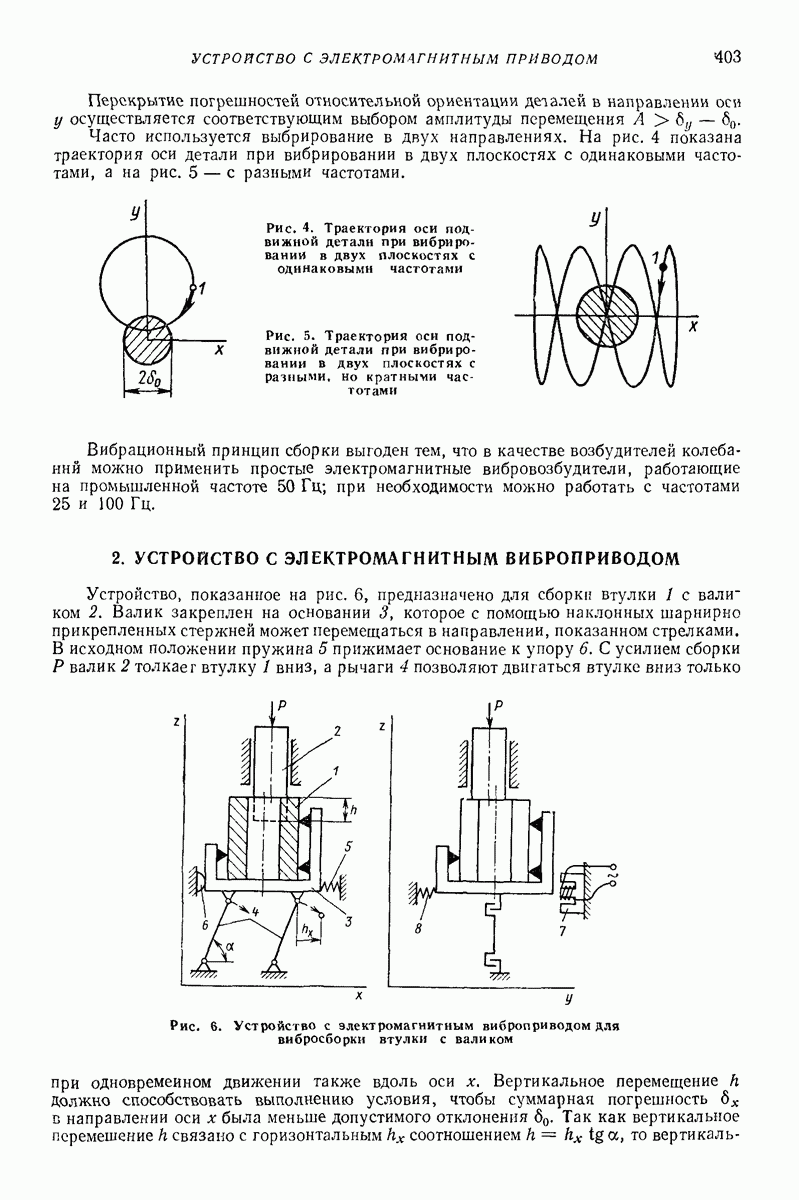
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
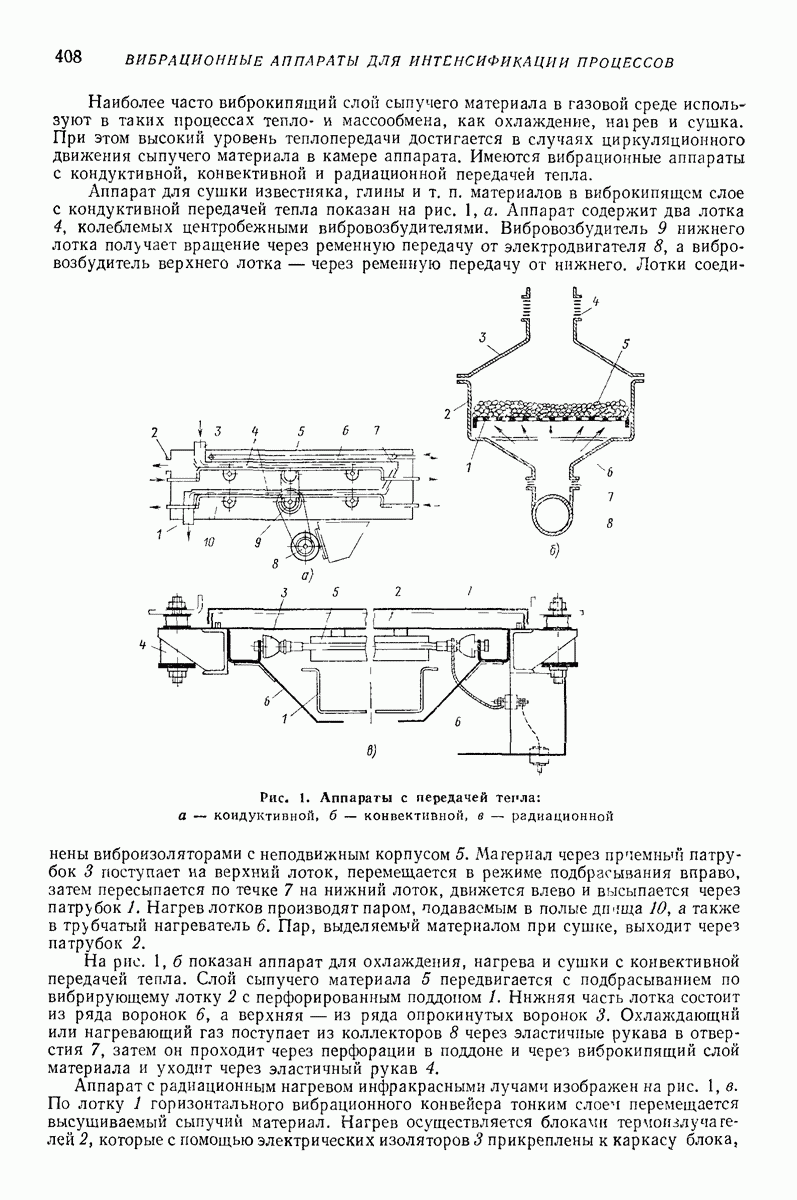
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
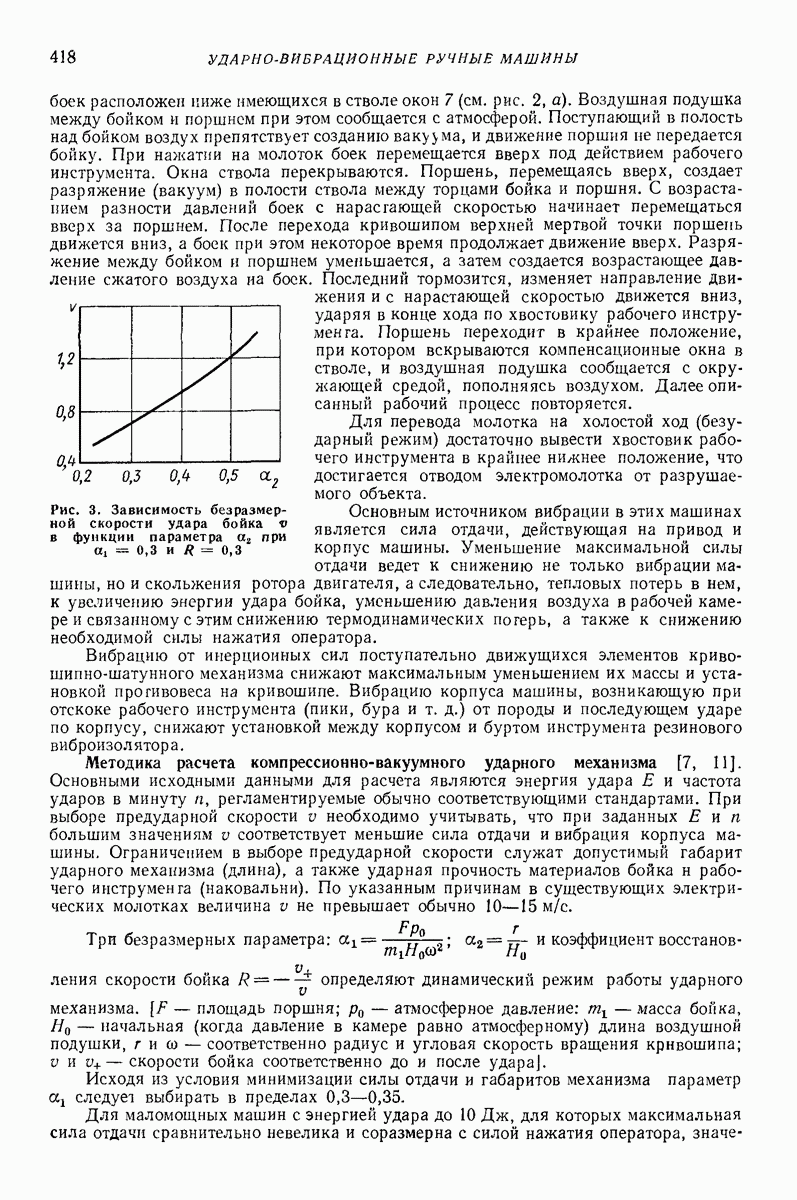
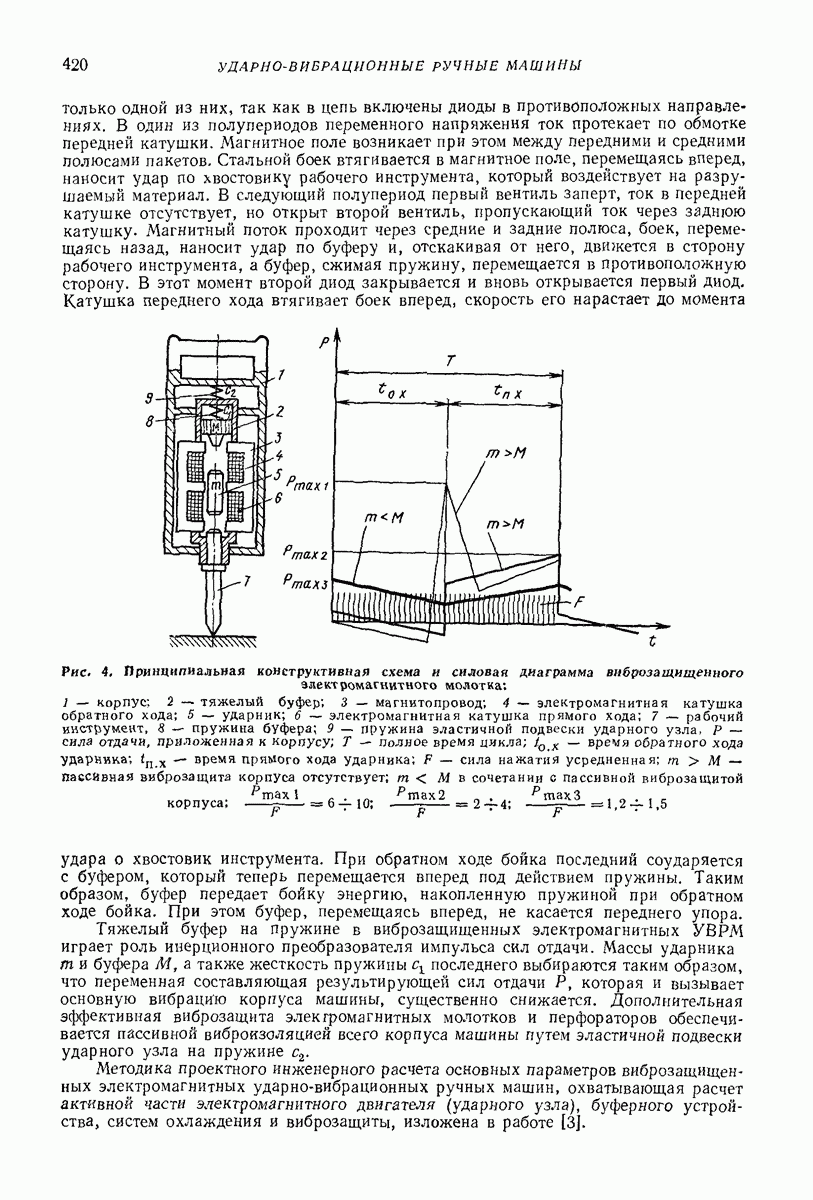
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ