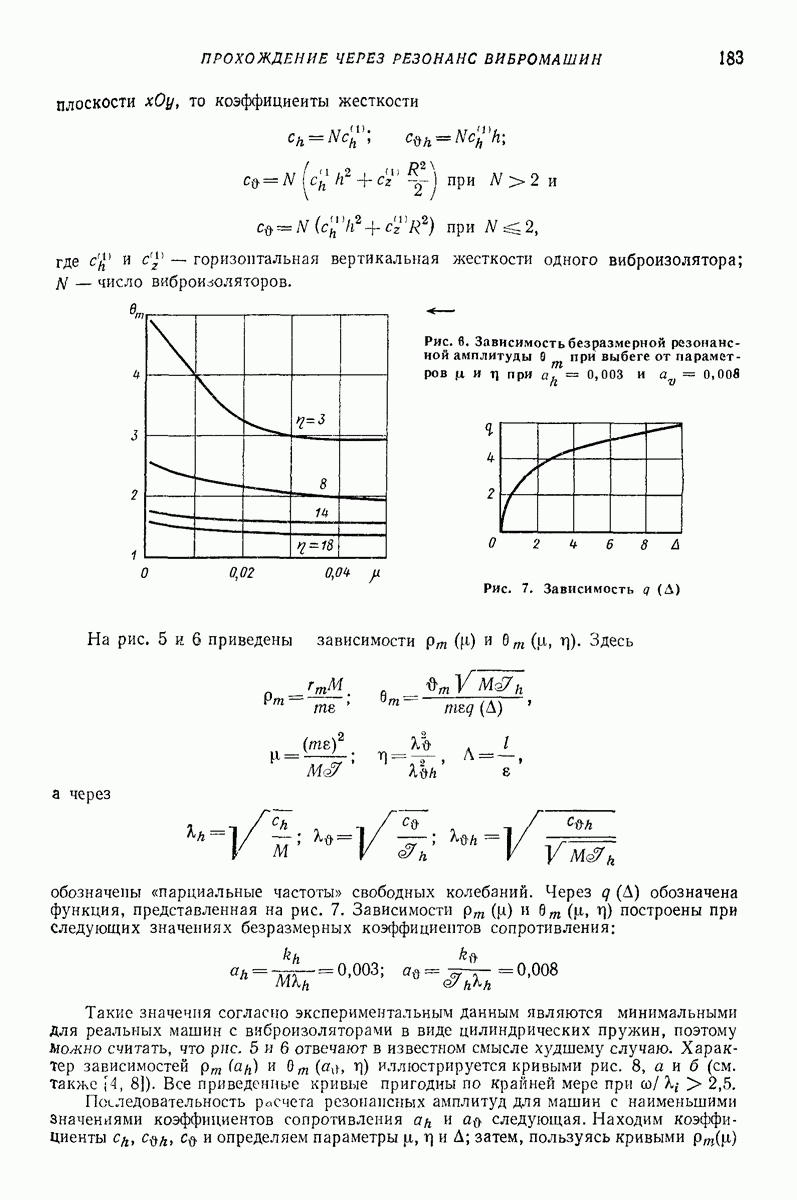
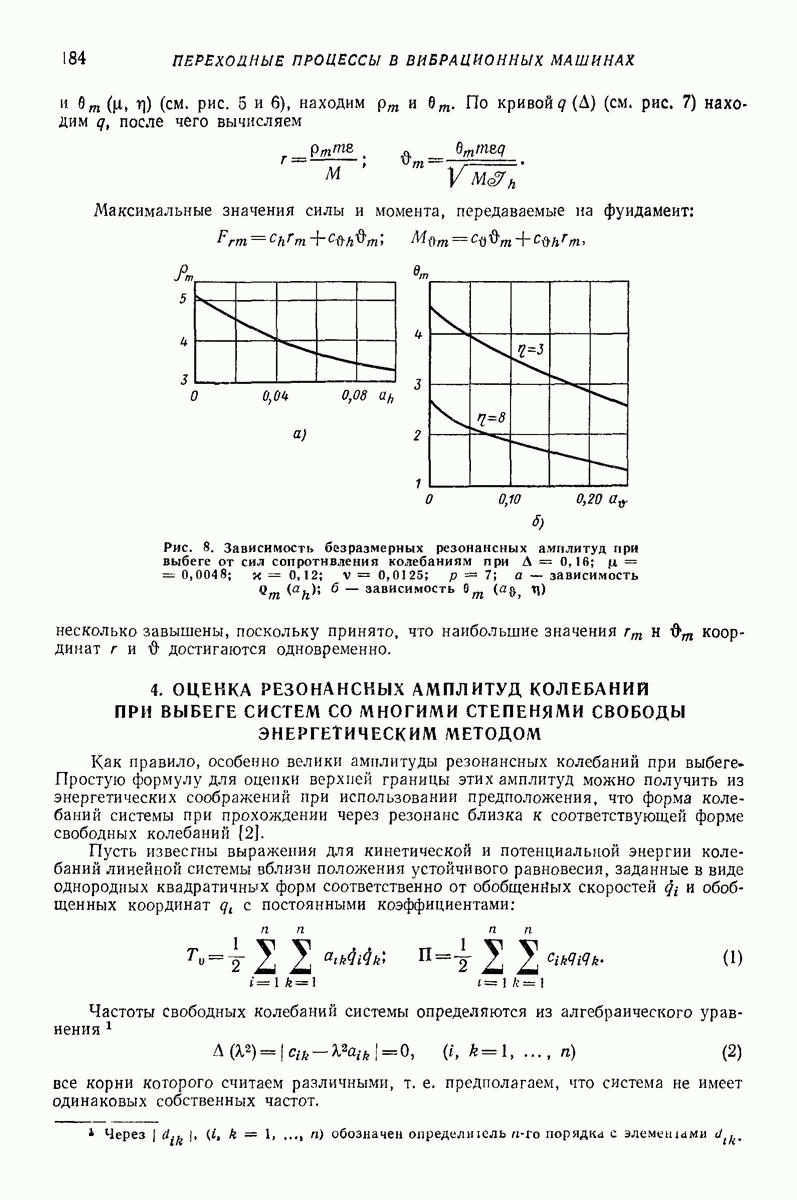
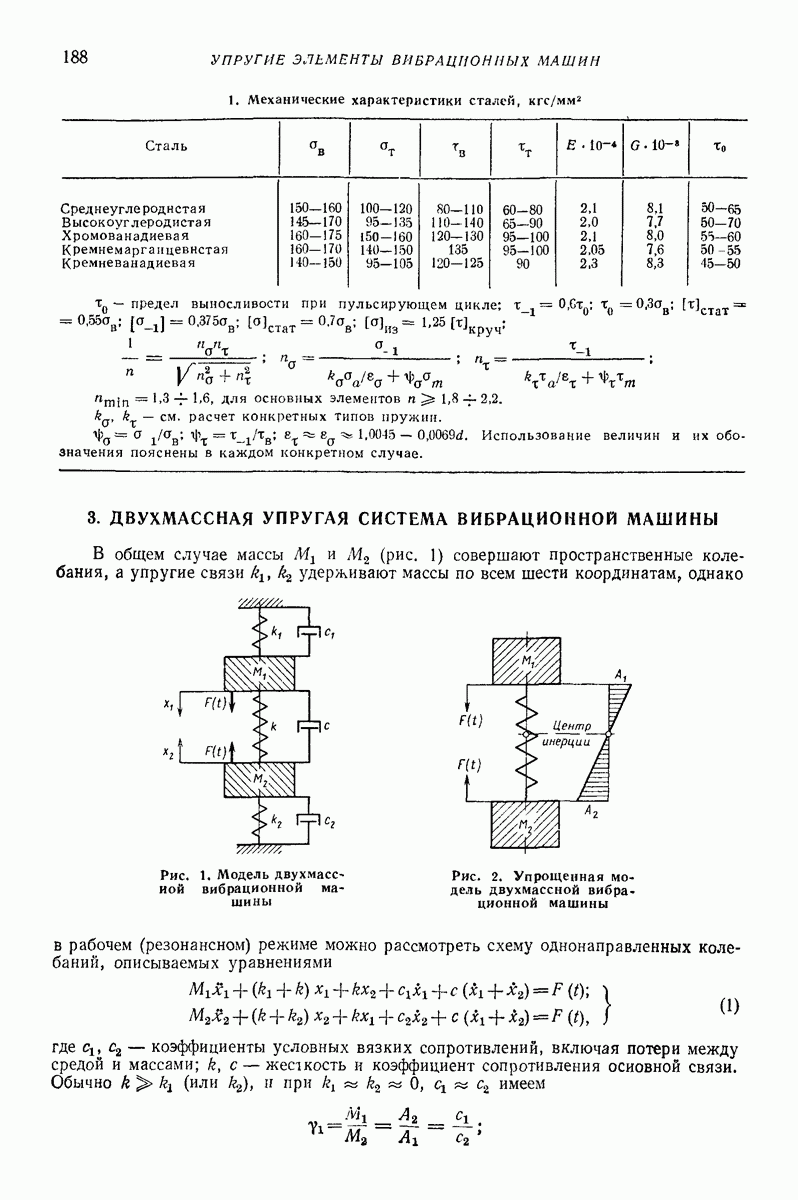
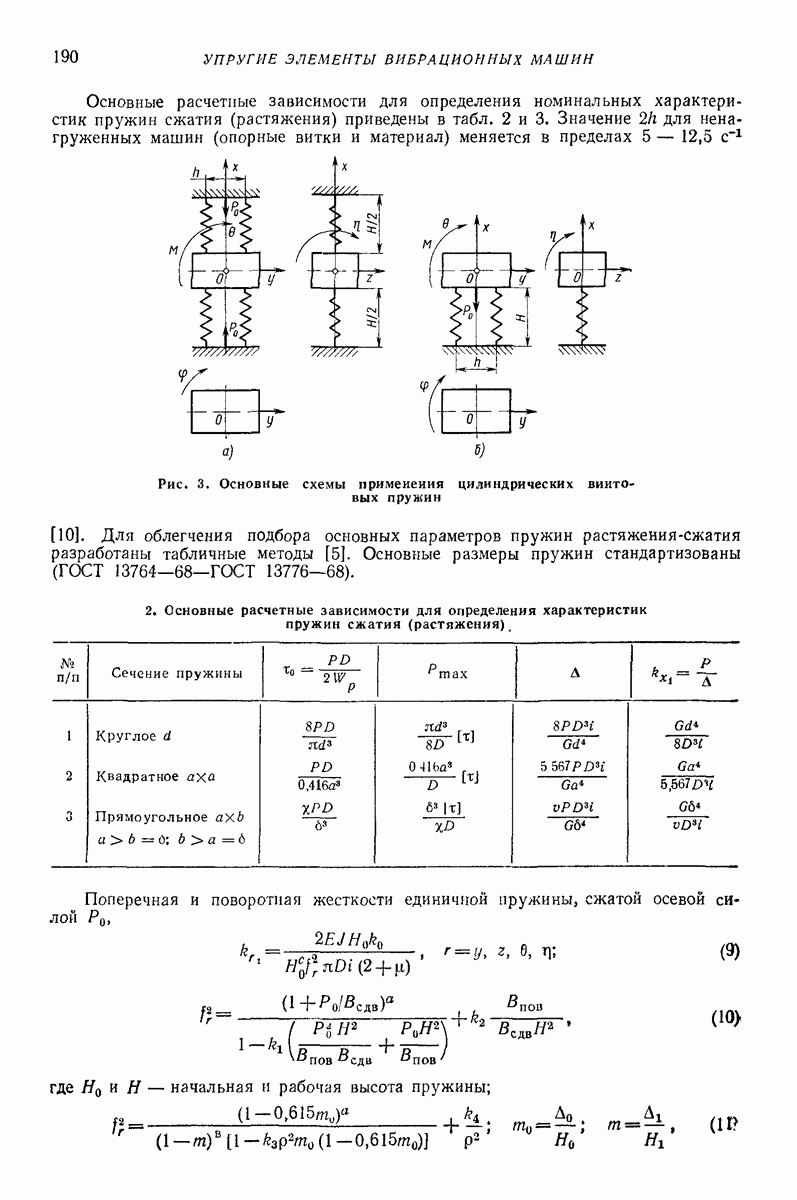
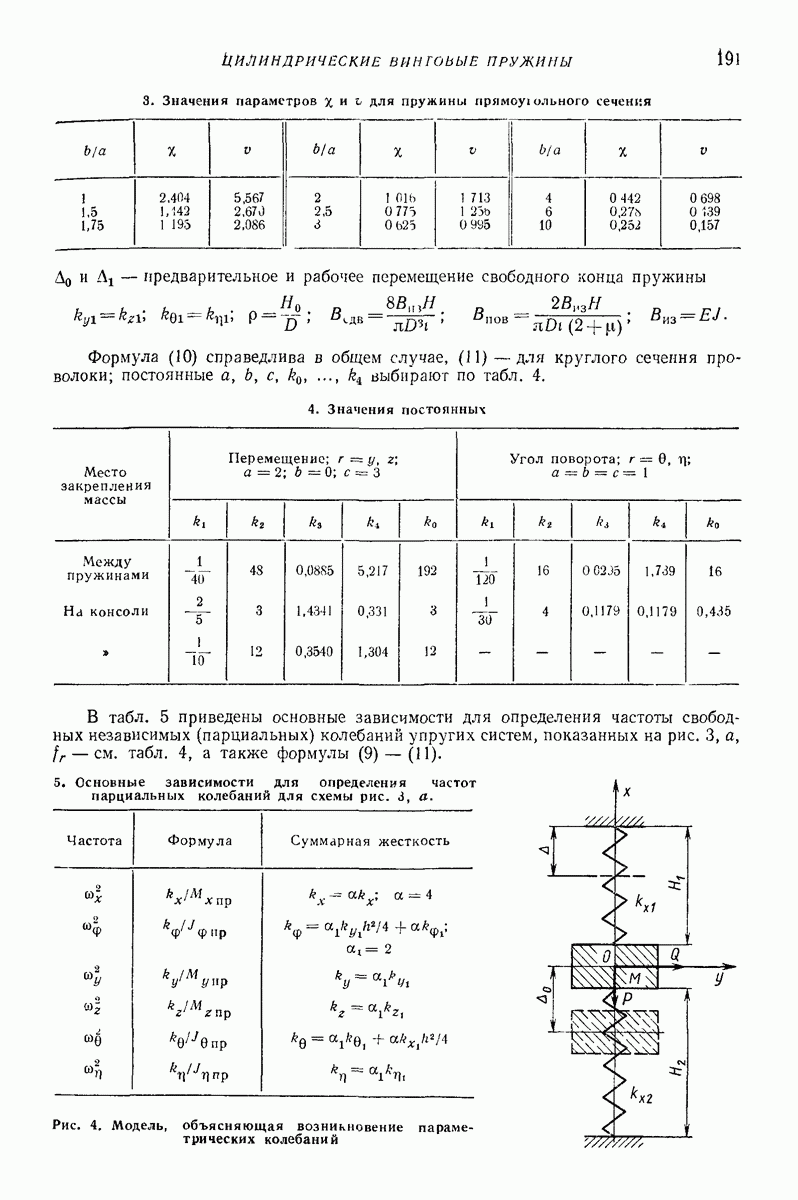
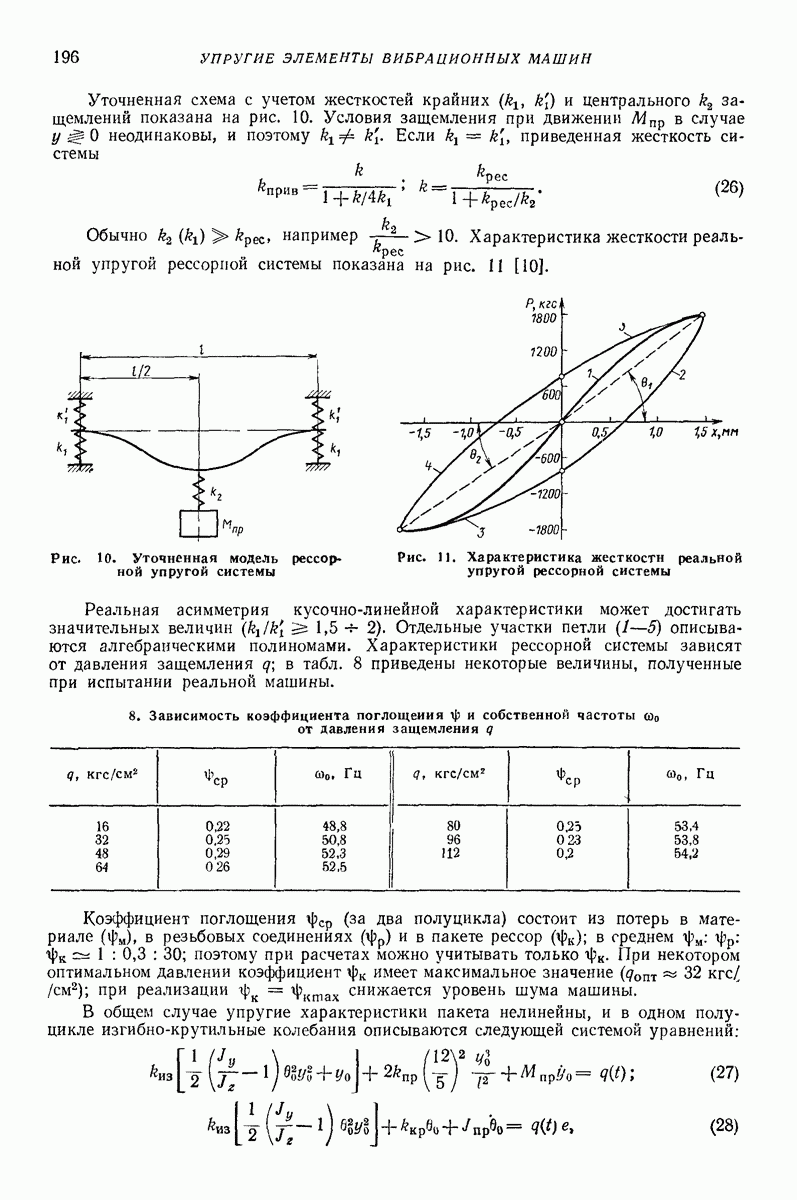
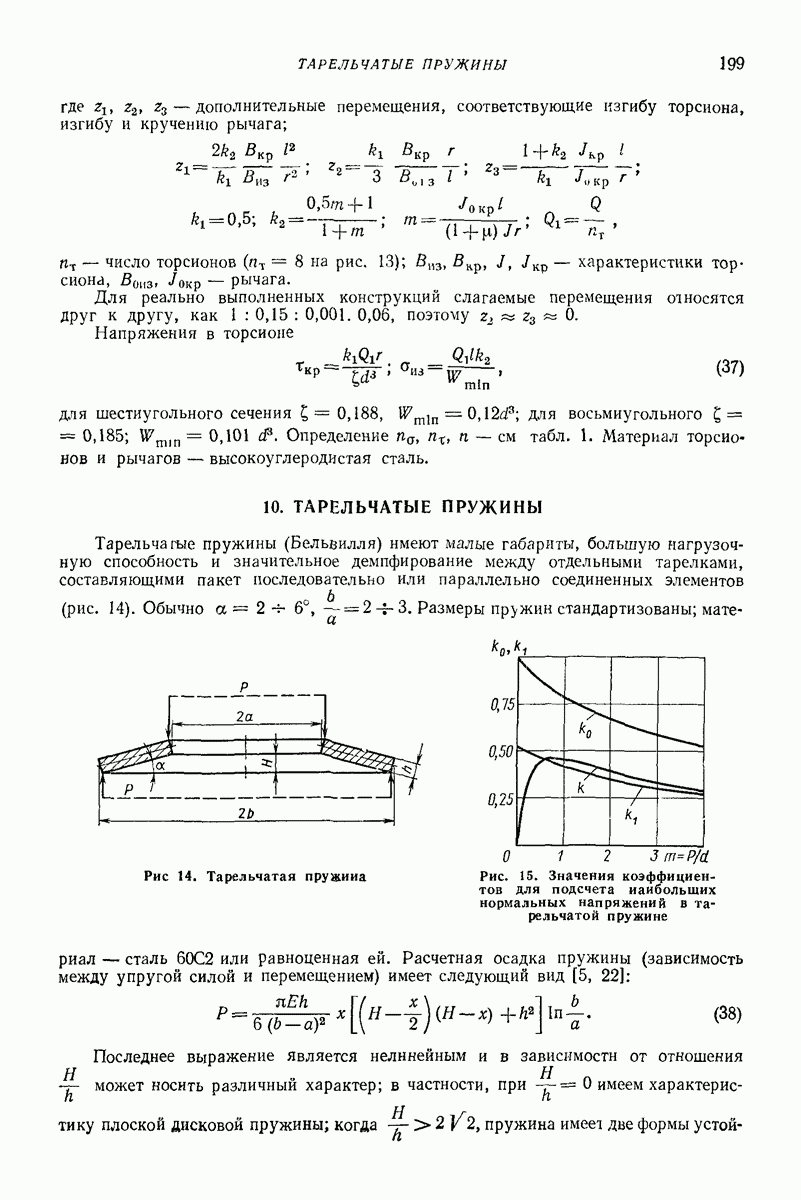
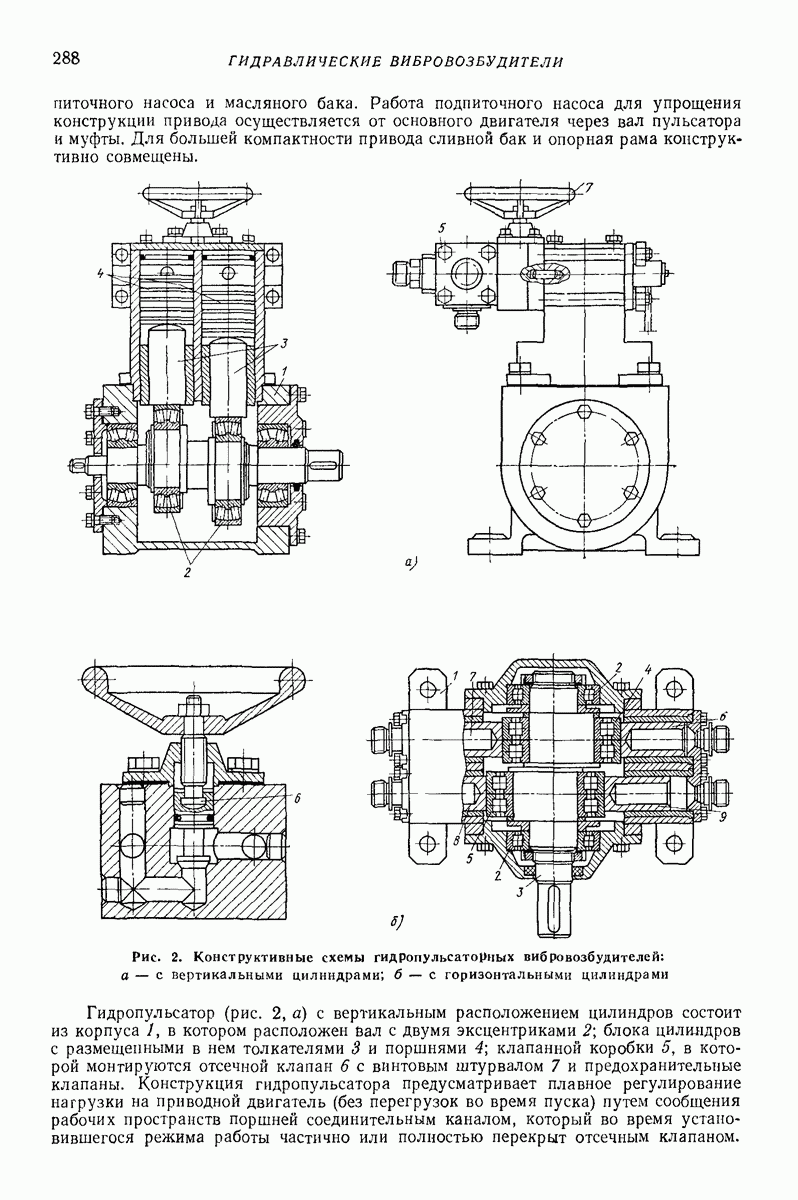
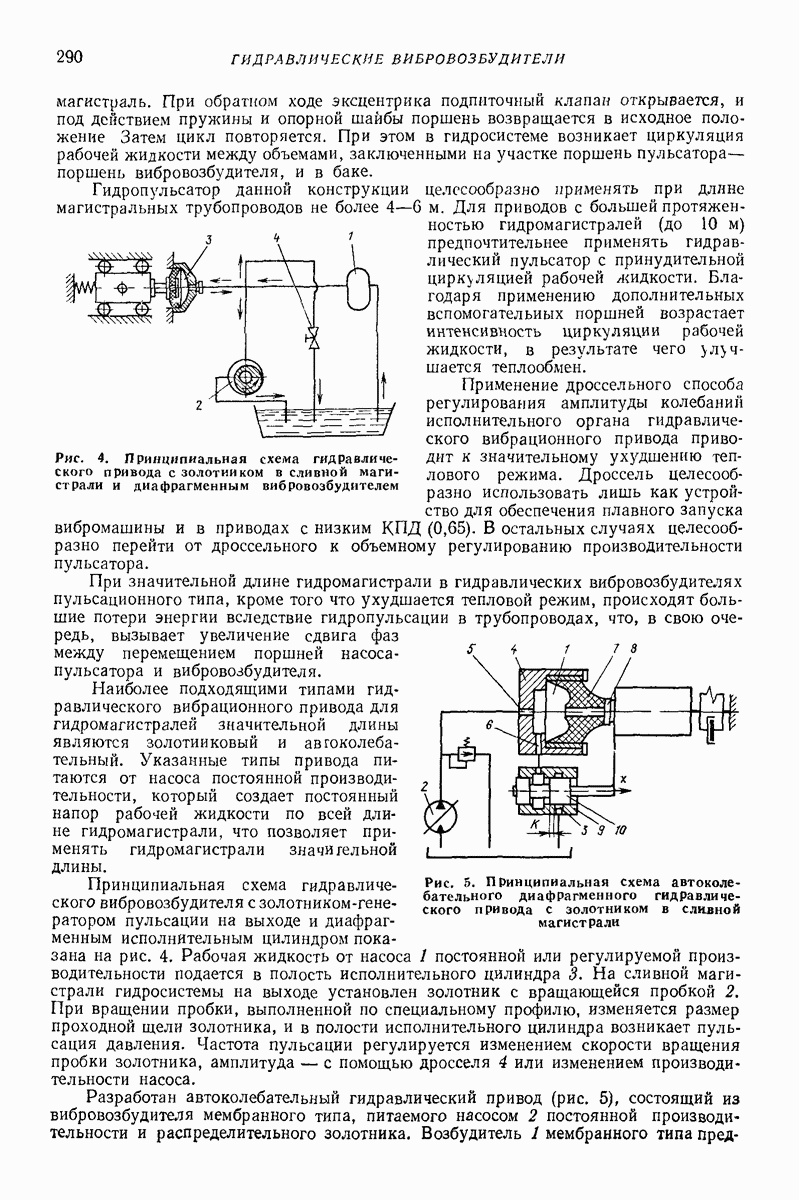
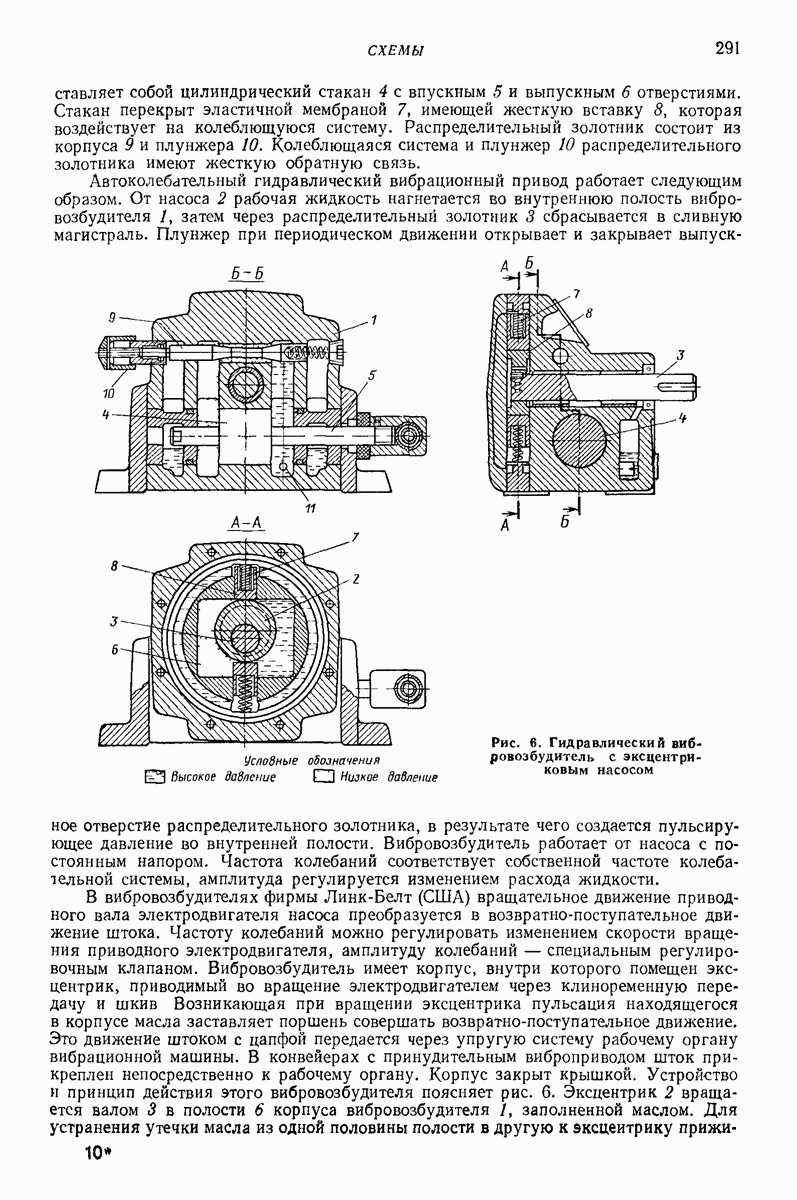
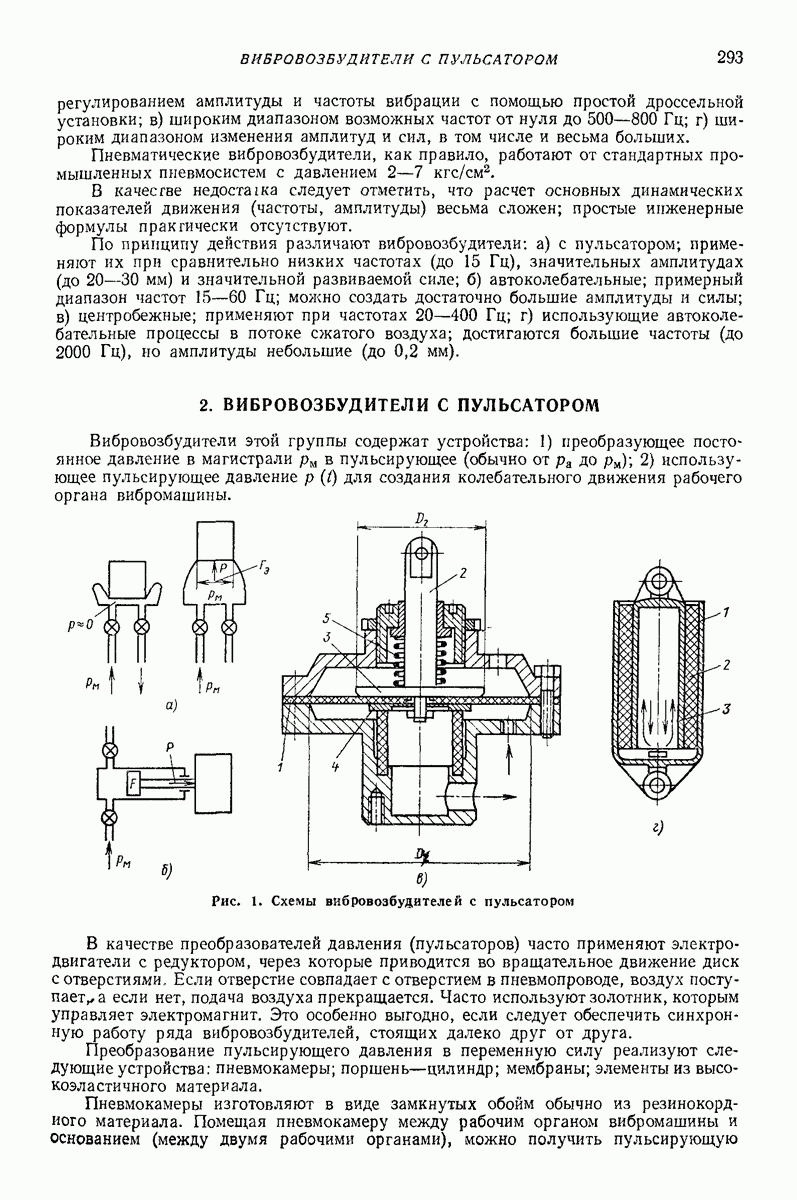
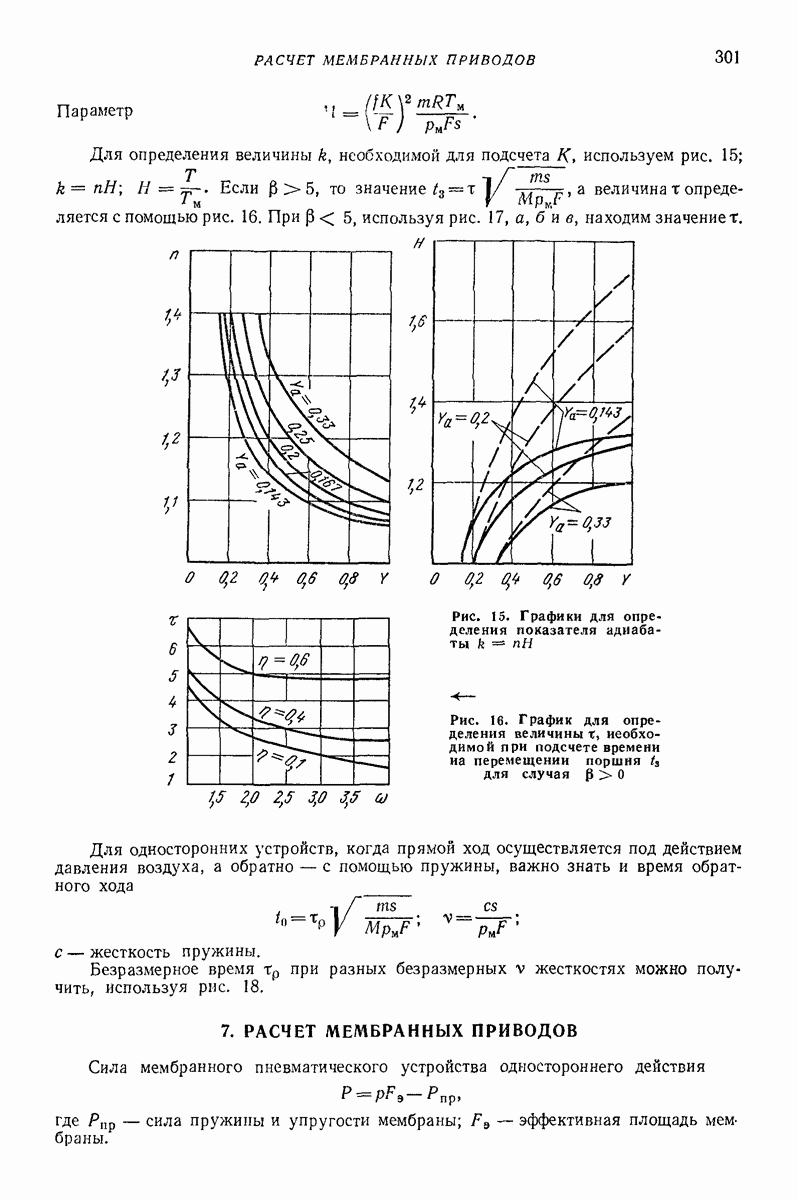
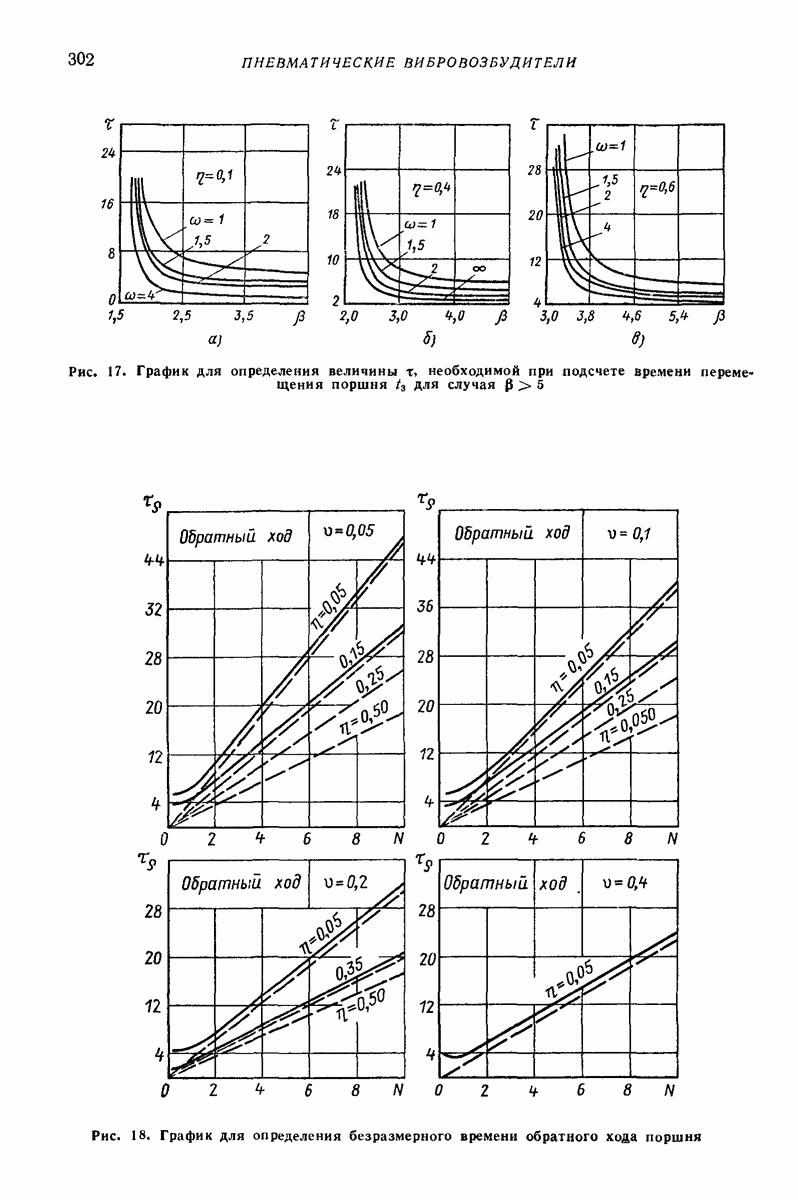
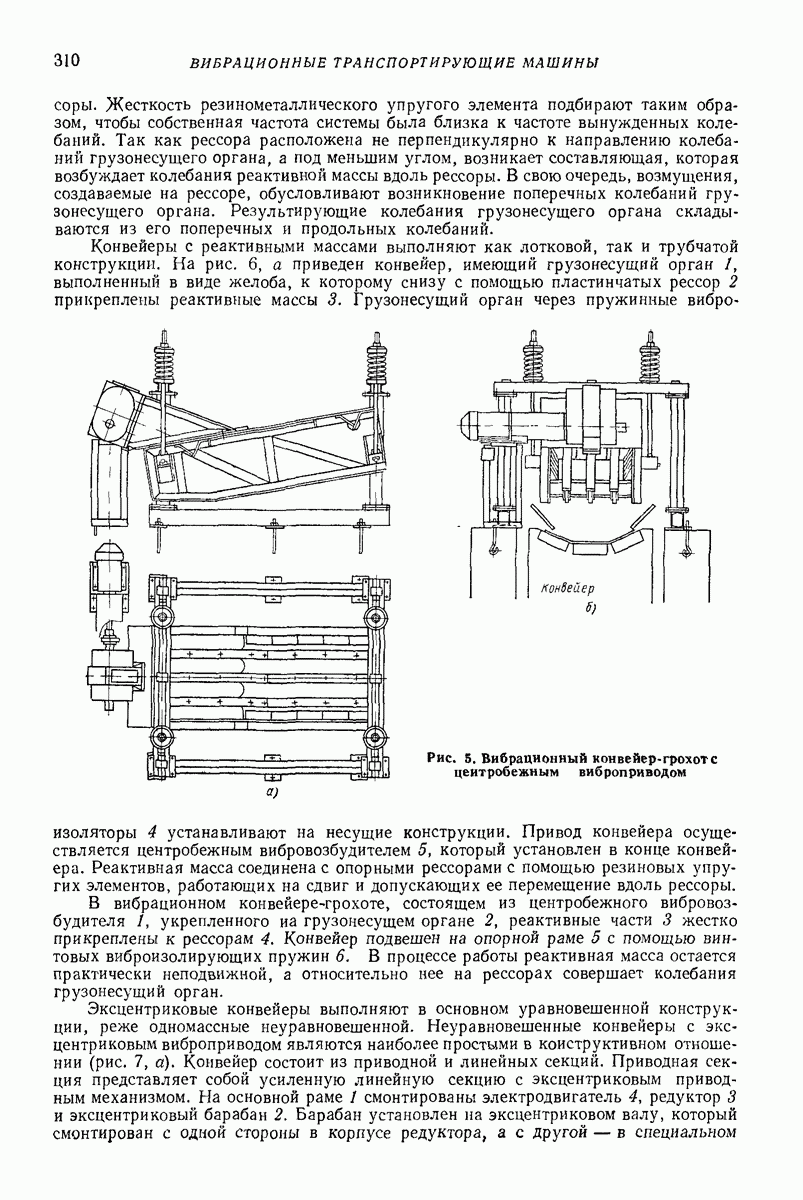
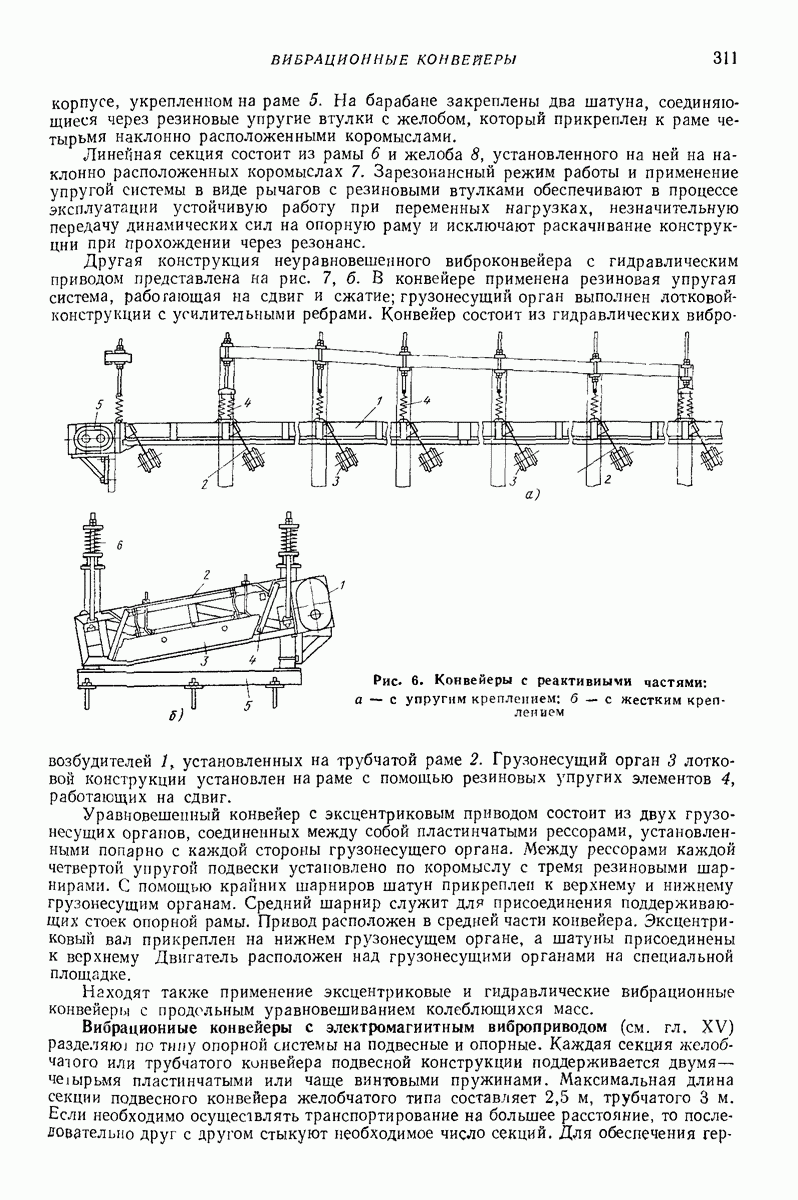
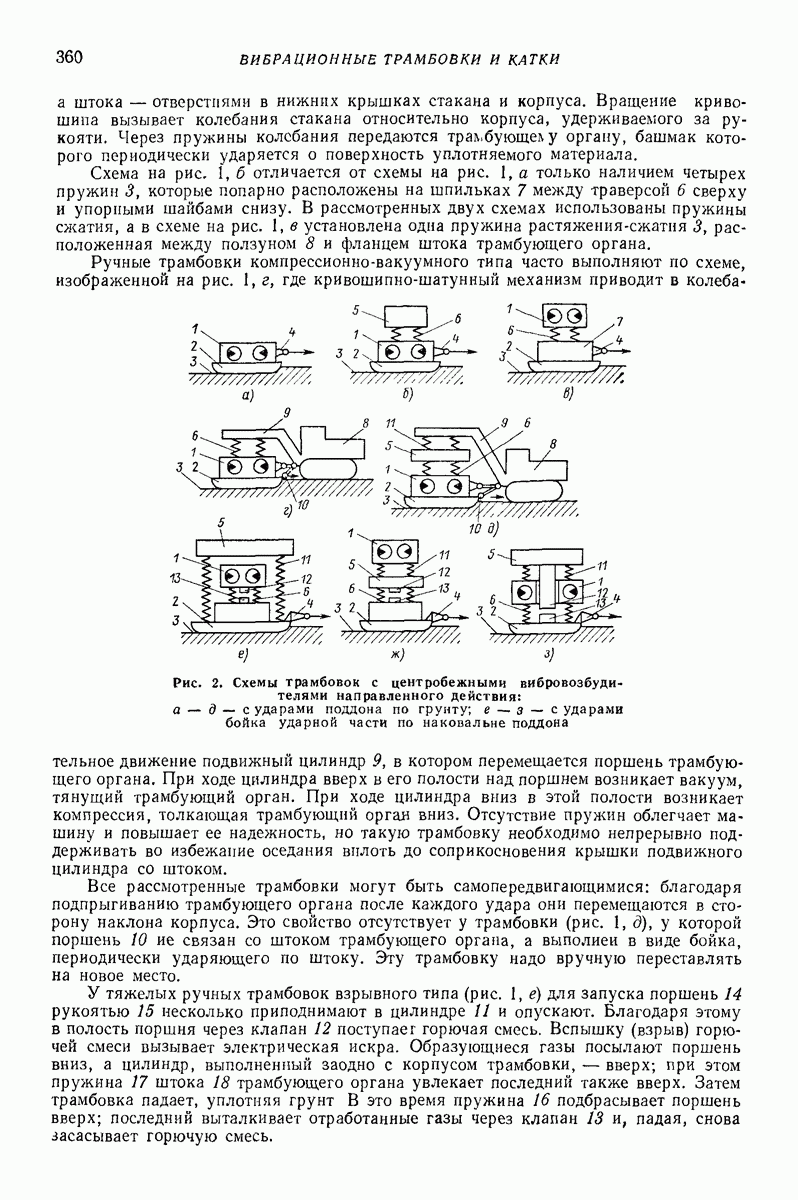
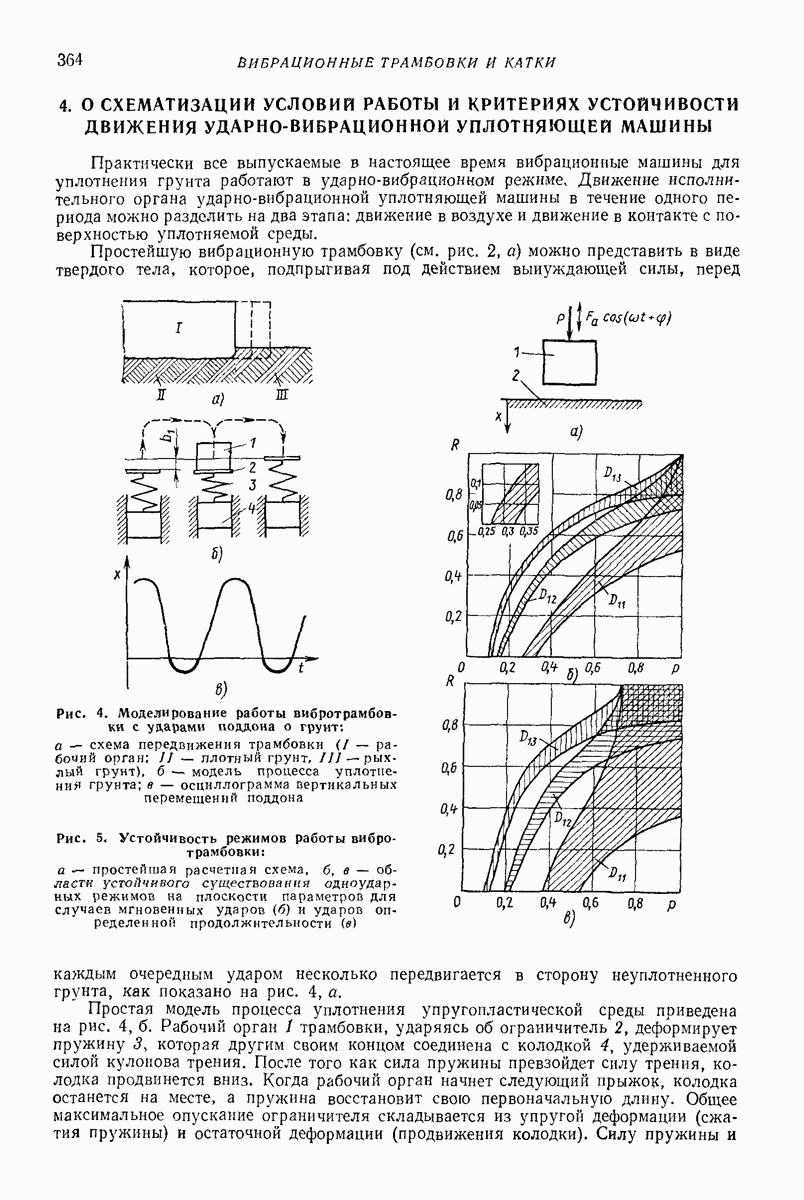
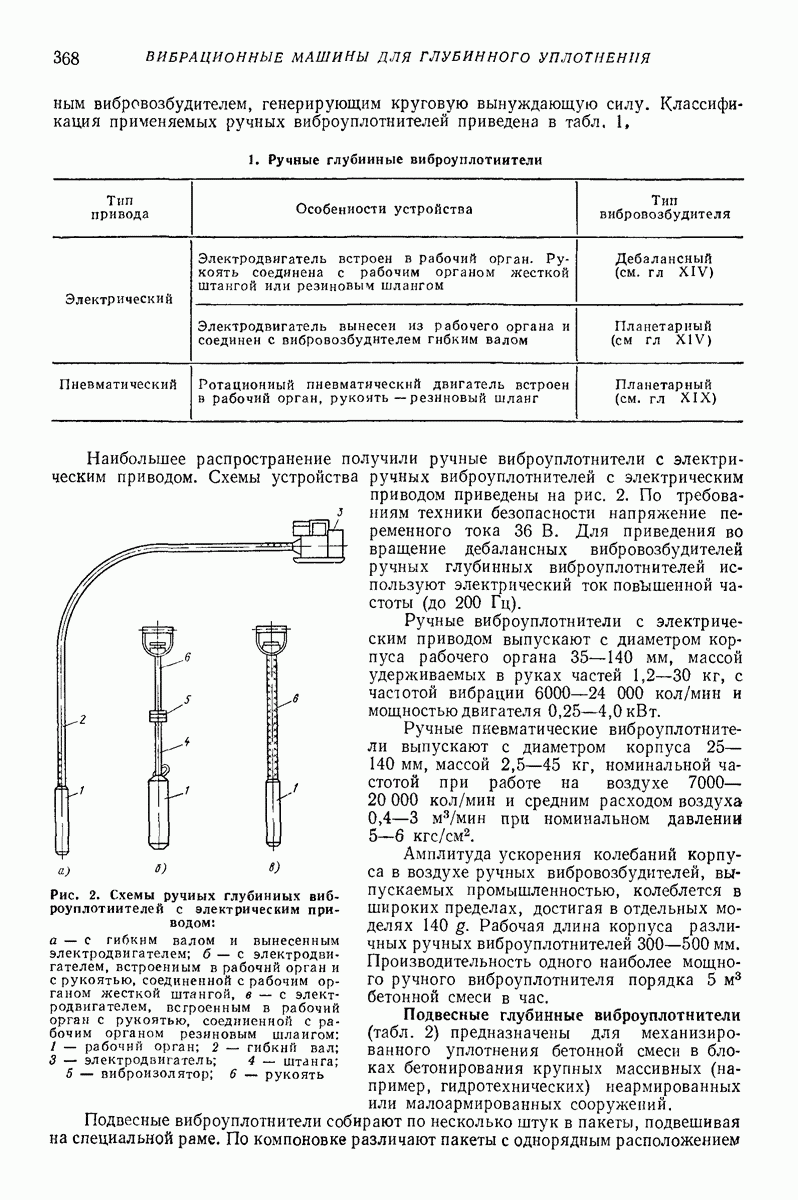
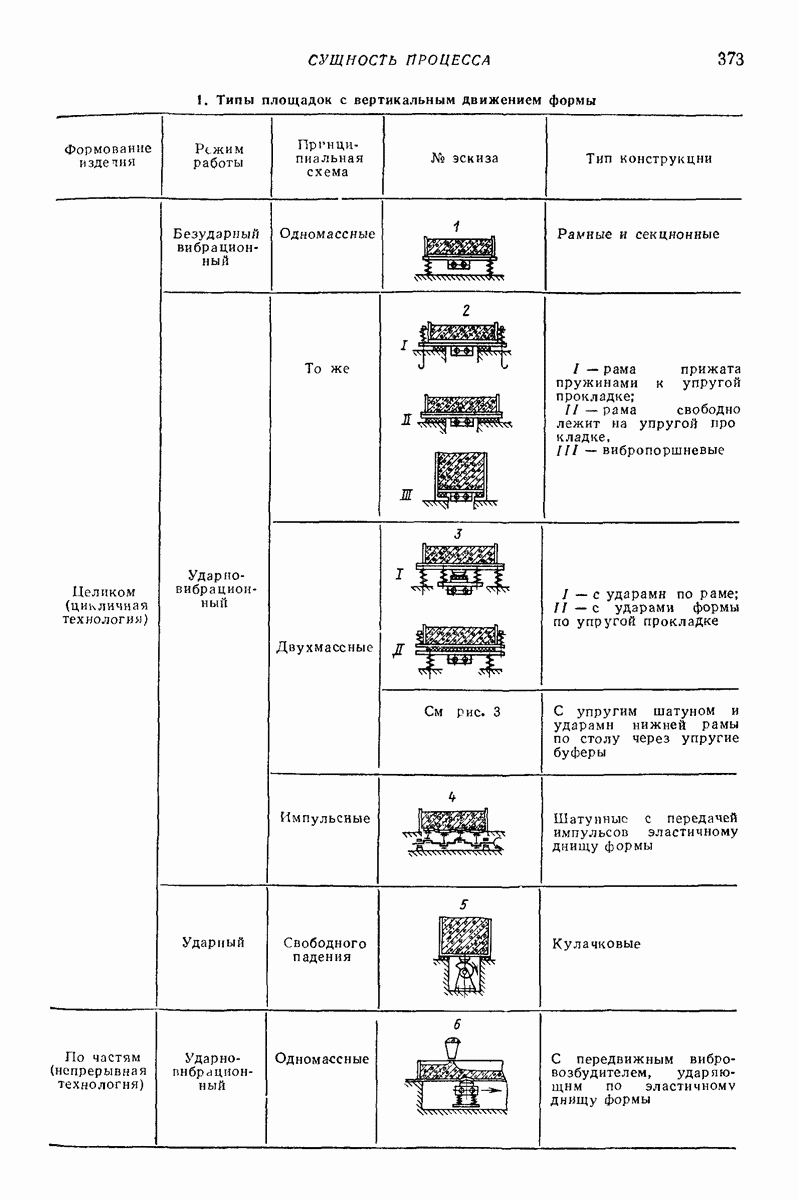
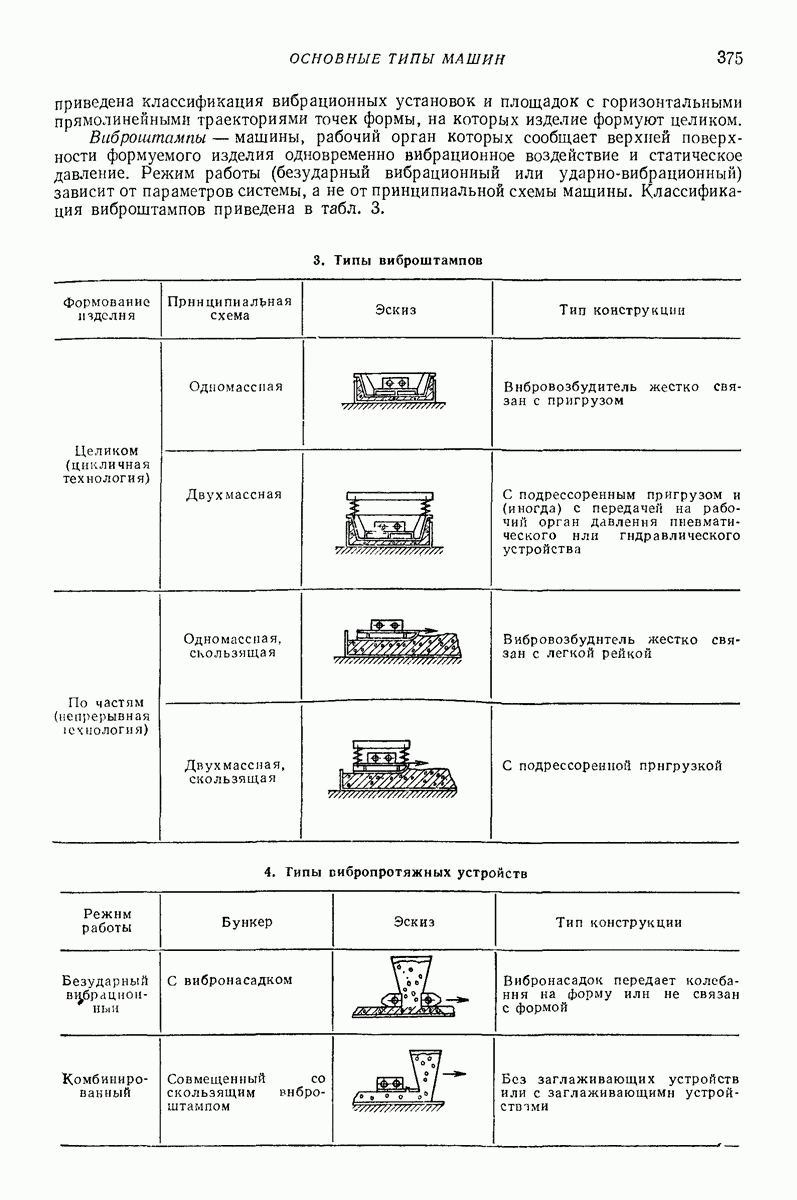
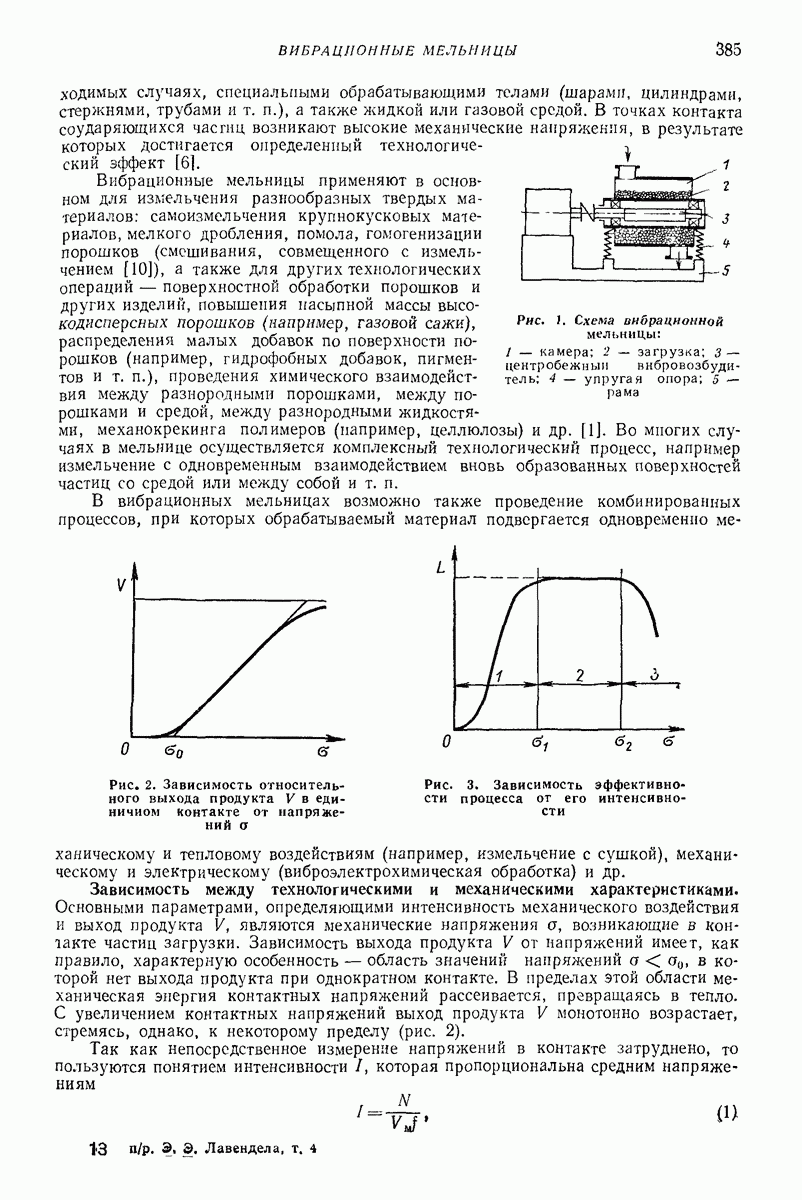
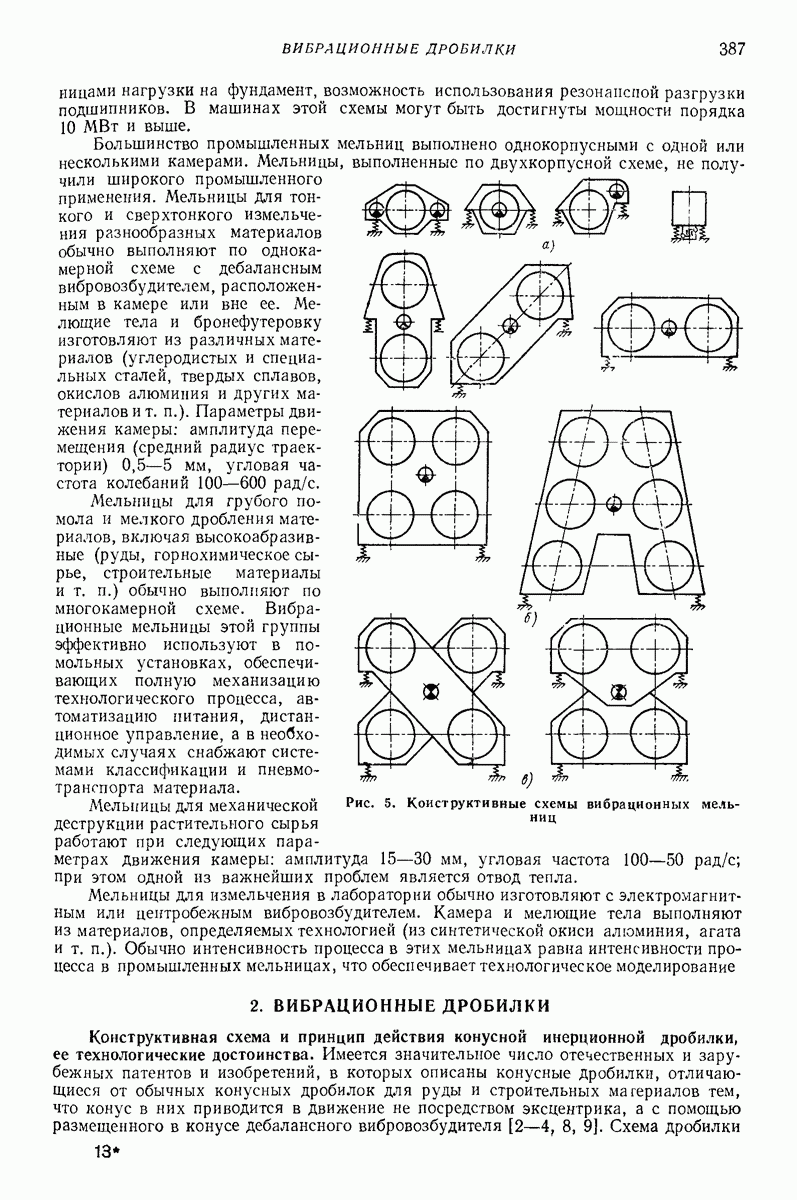
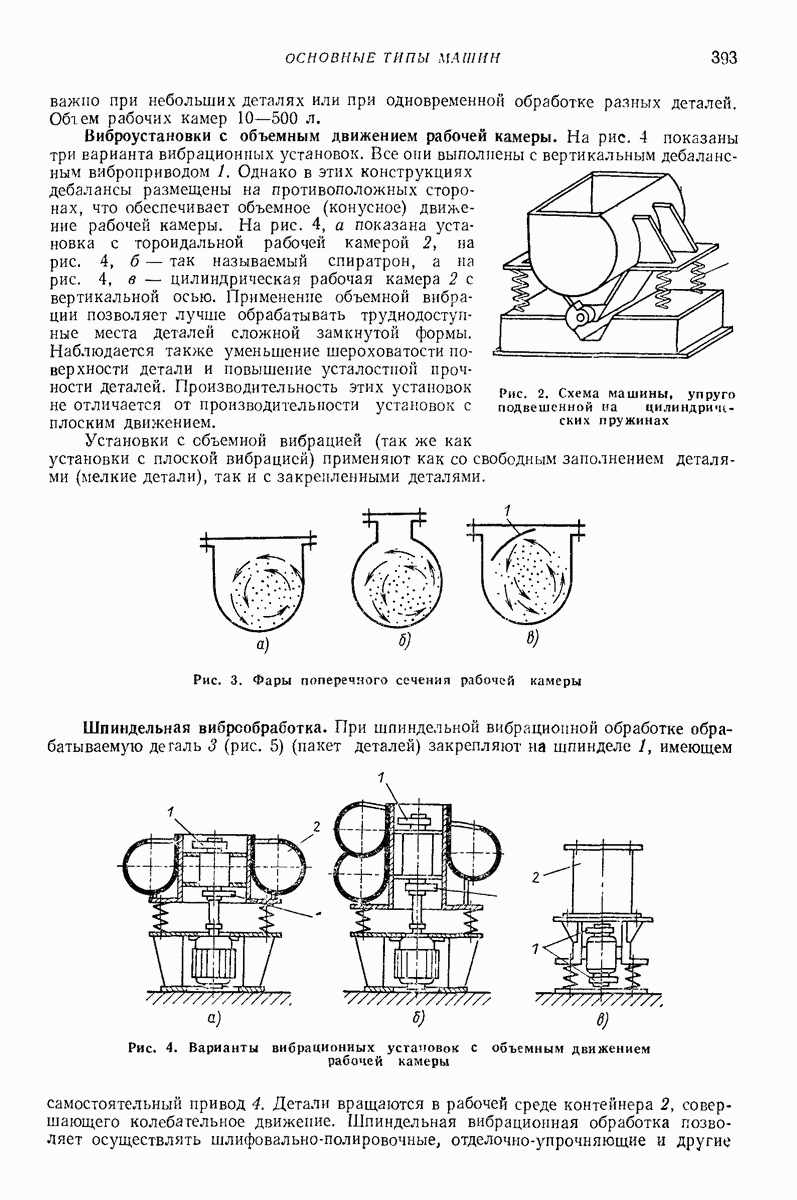
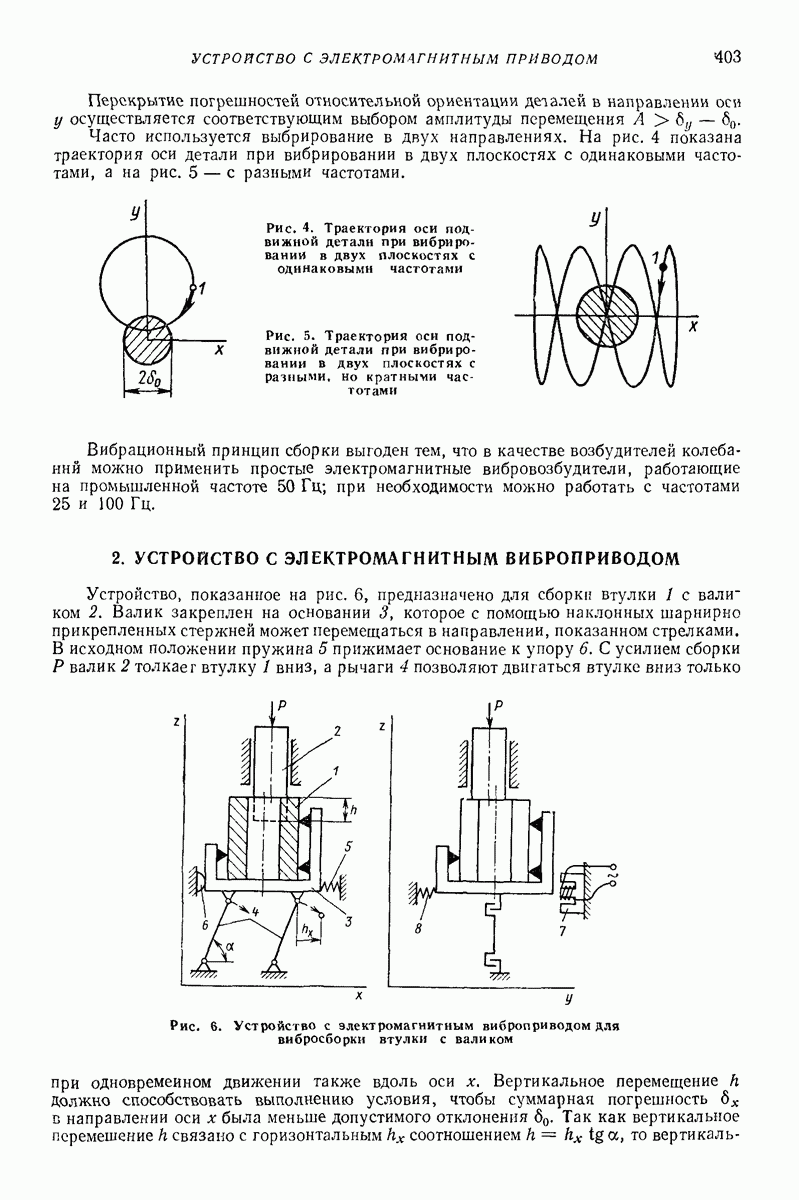
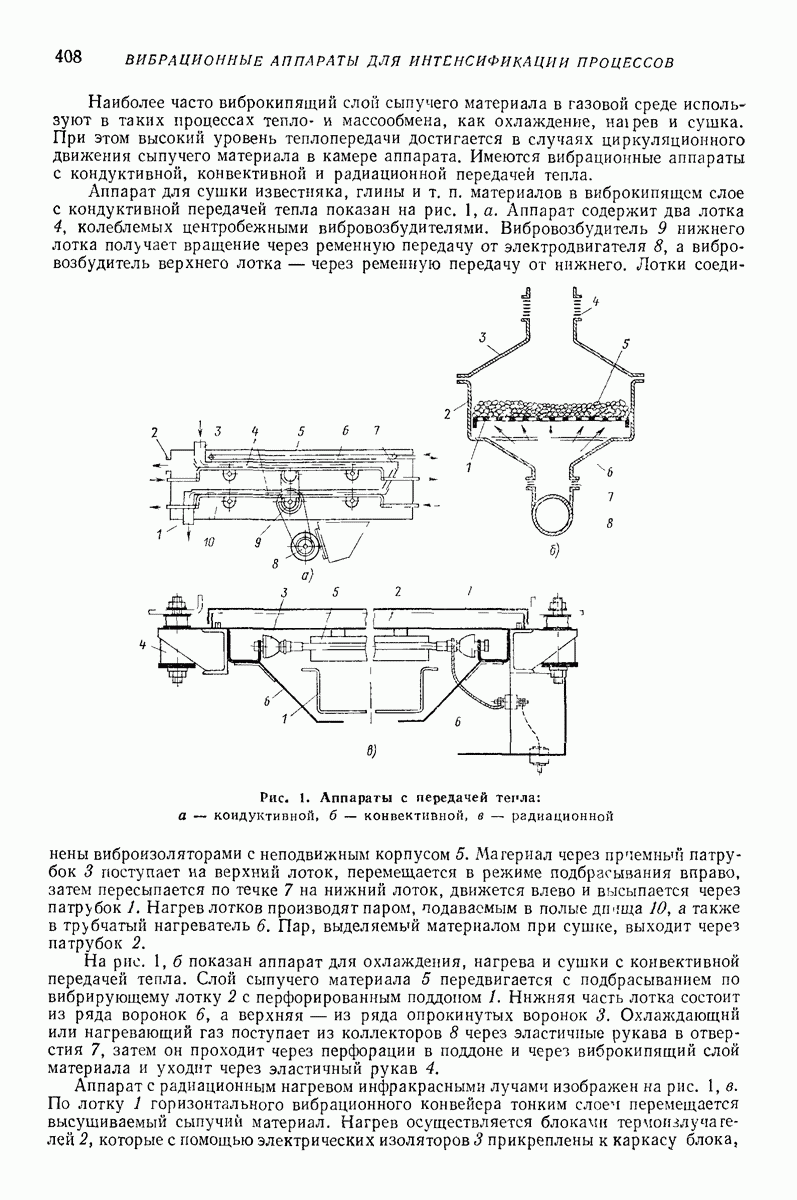
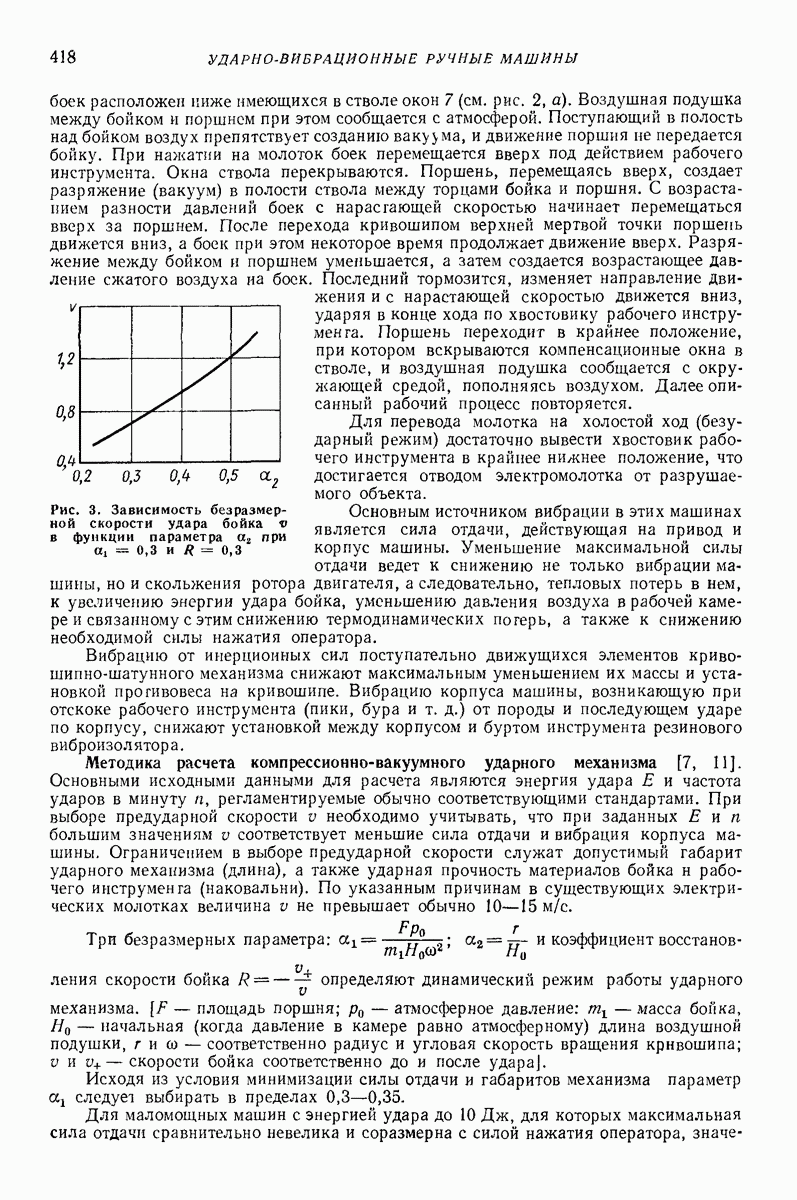
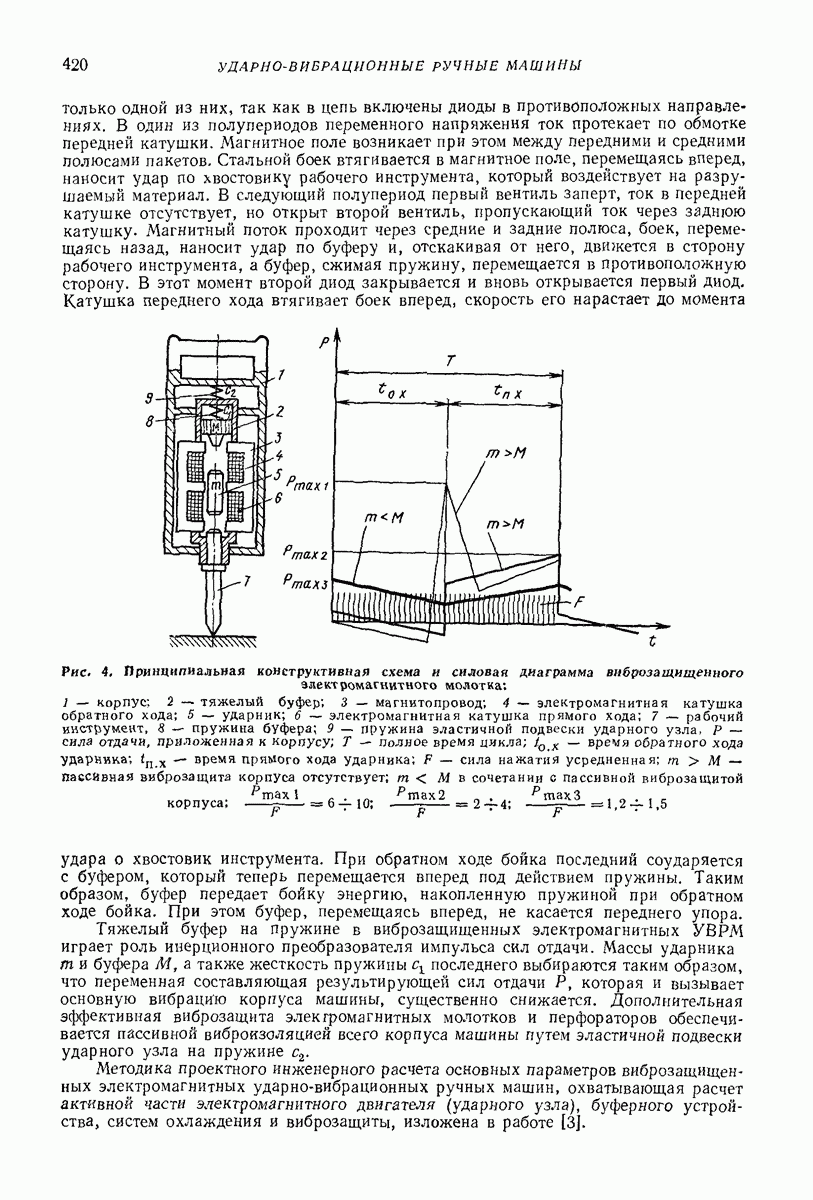
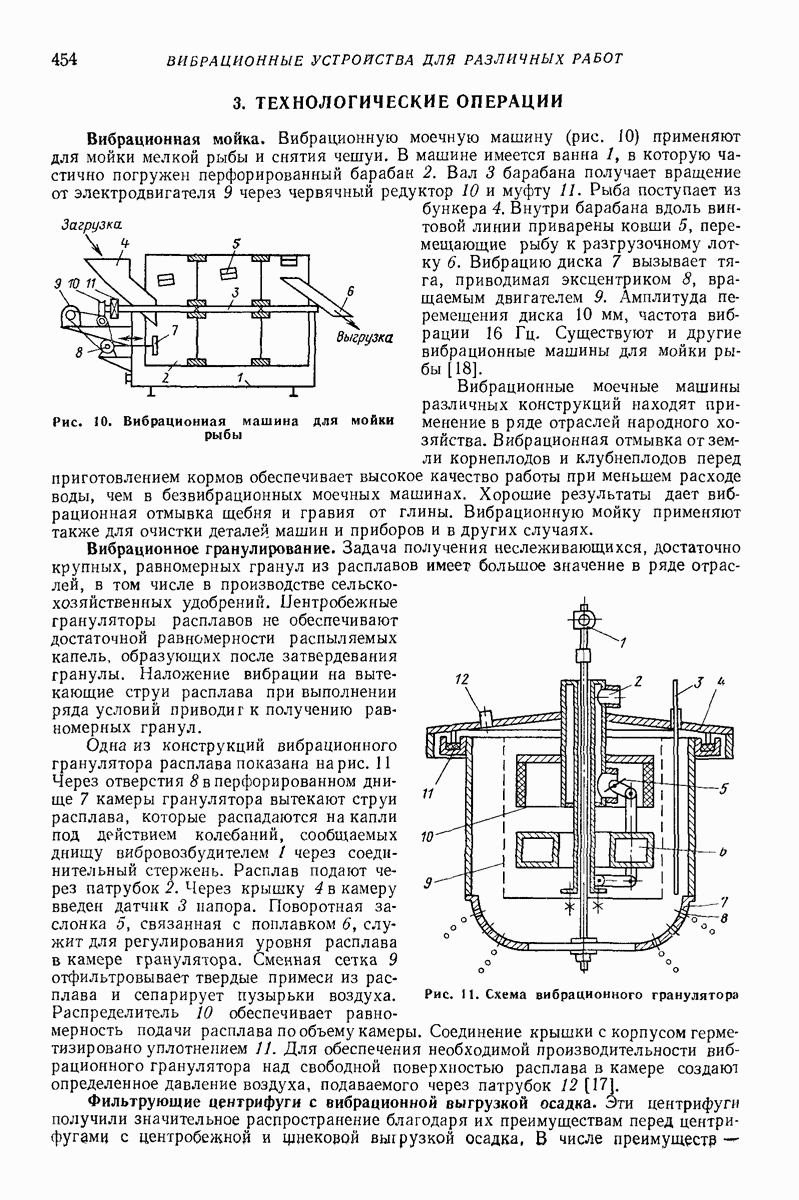
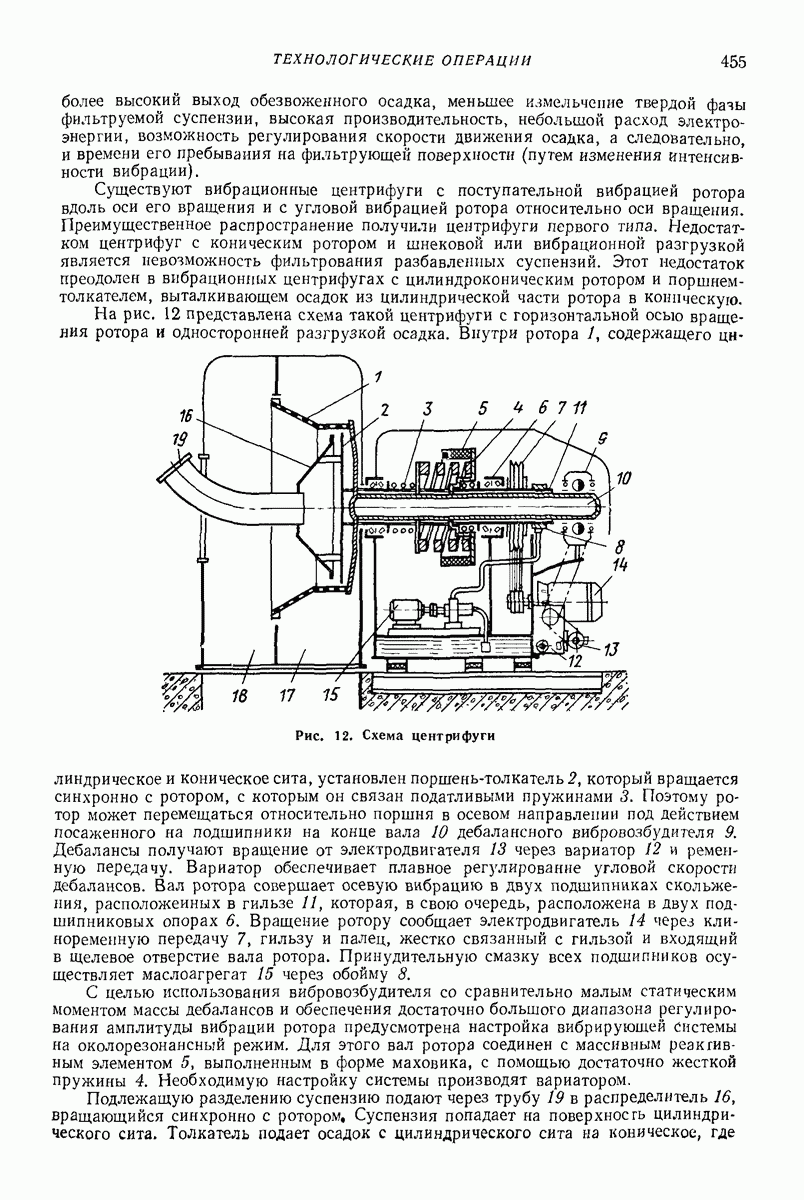
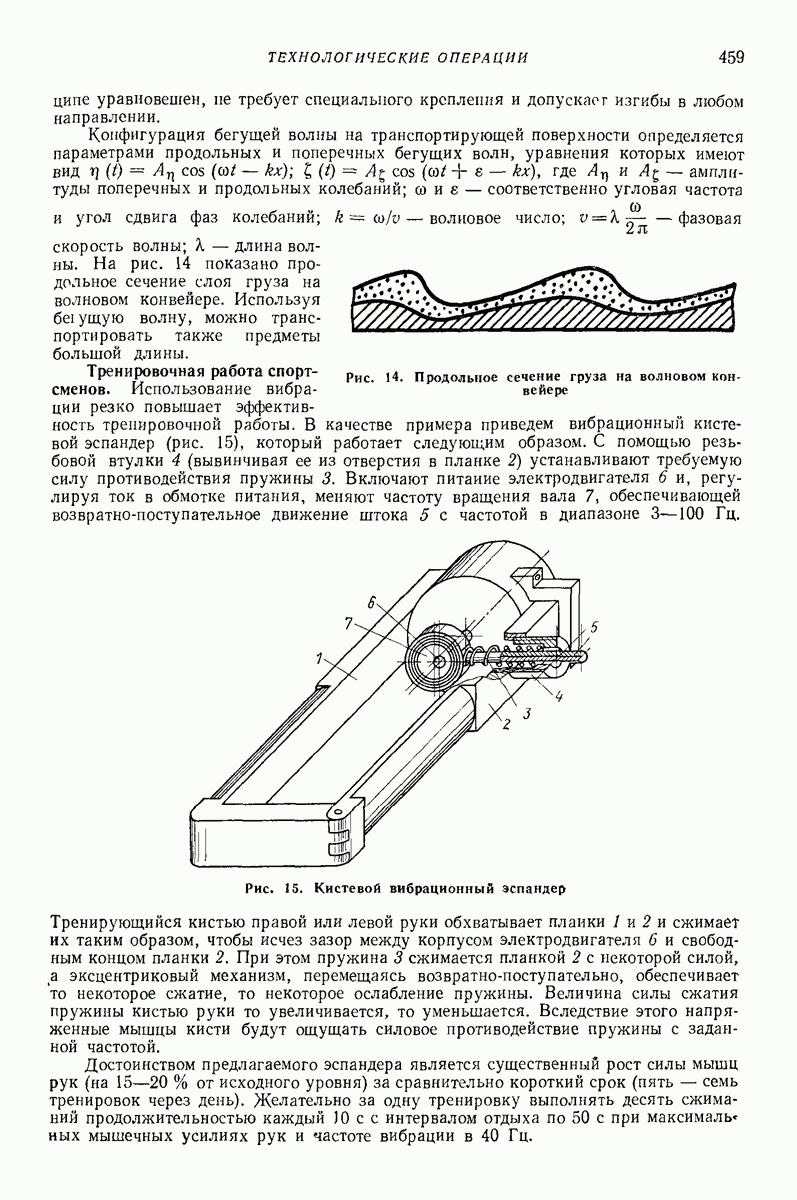
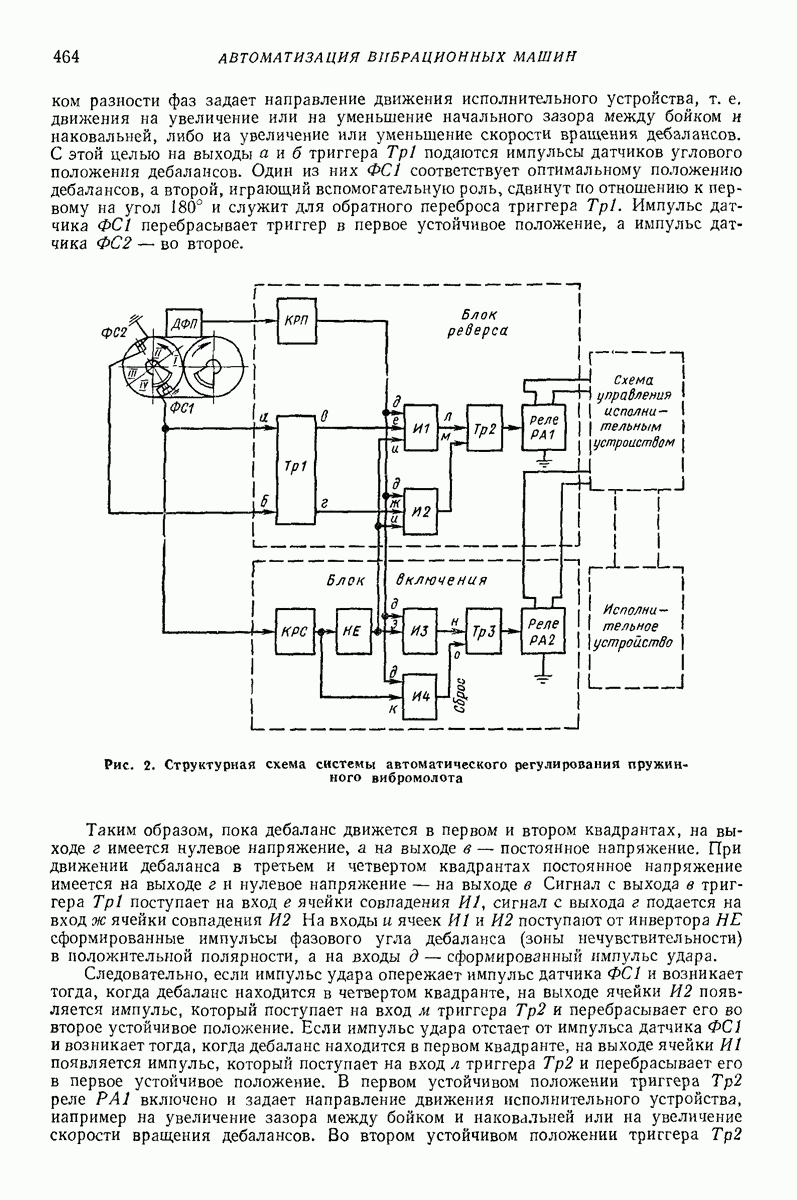
| << Предыдущий параграф | Следующий параграф >> |
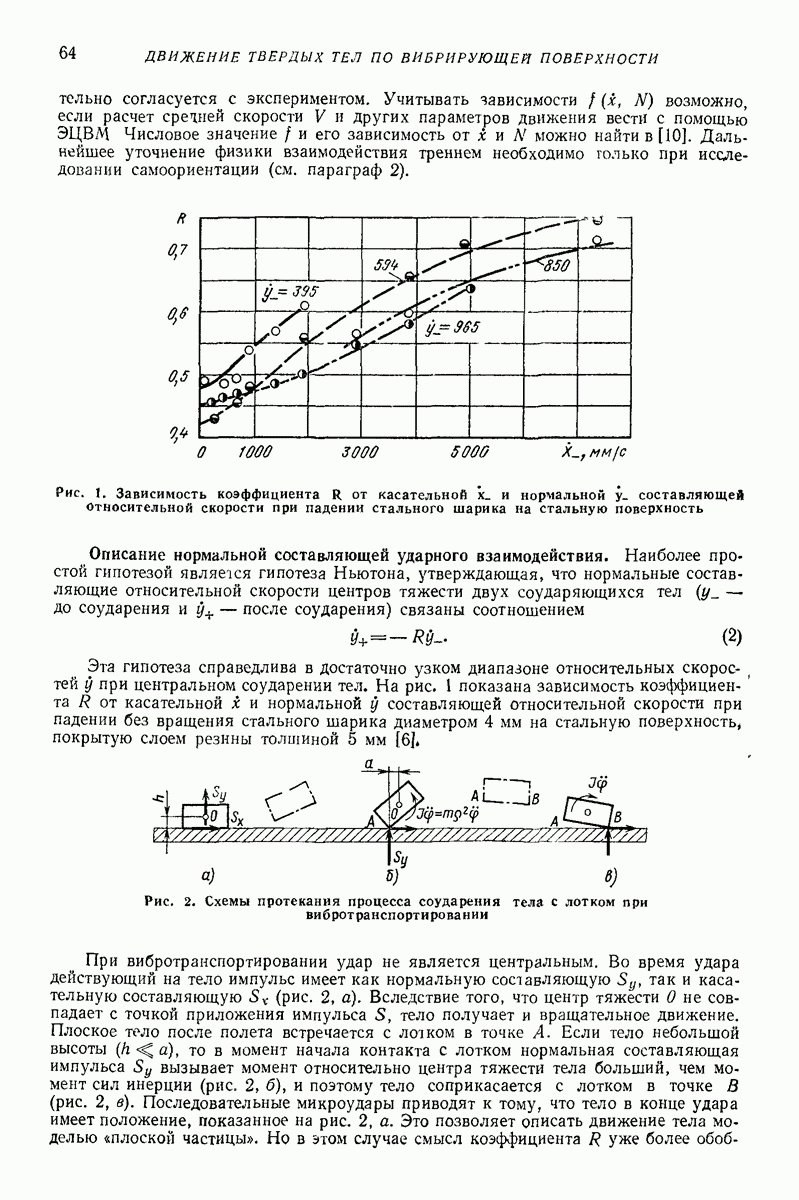
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
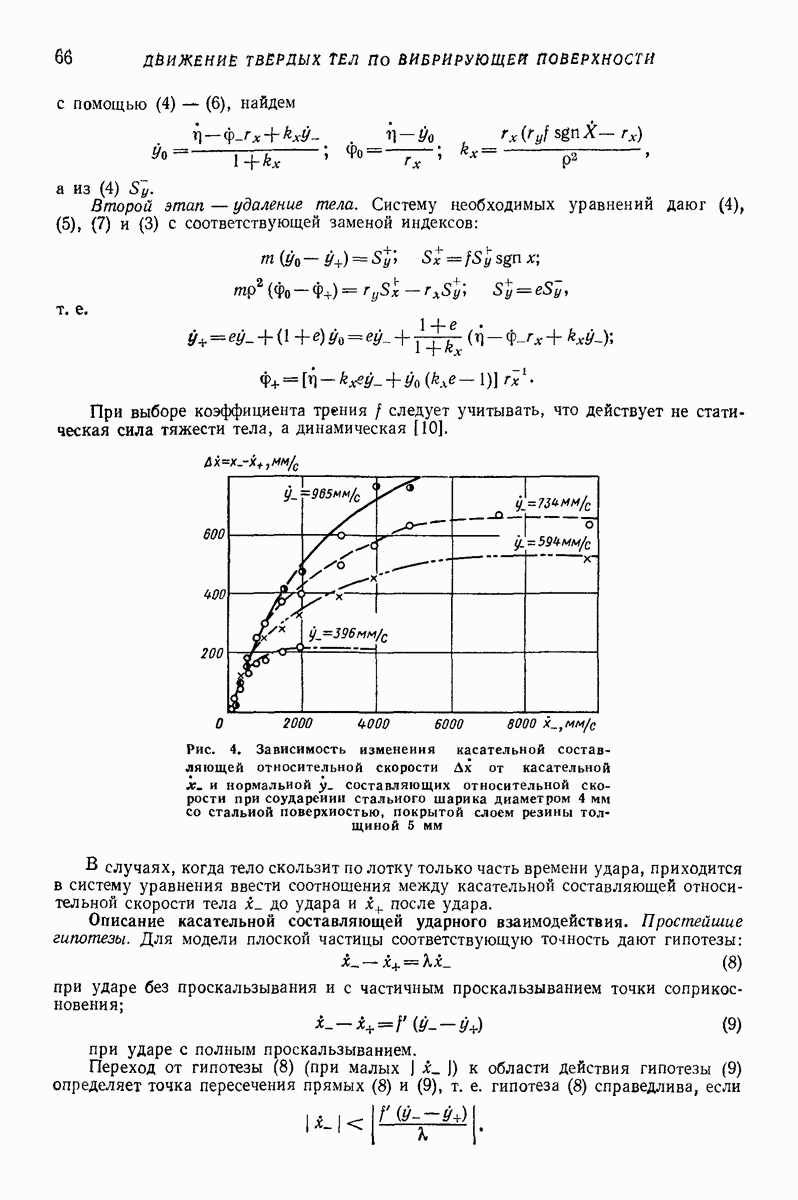
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
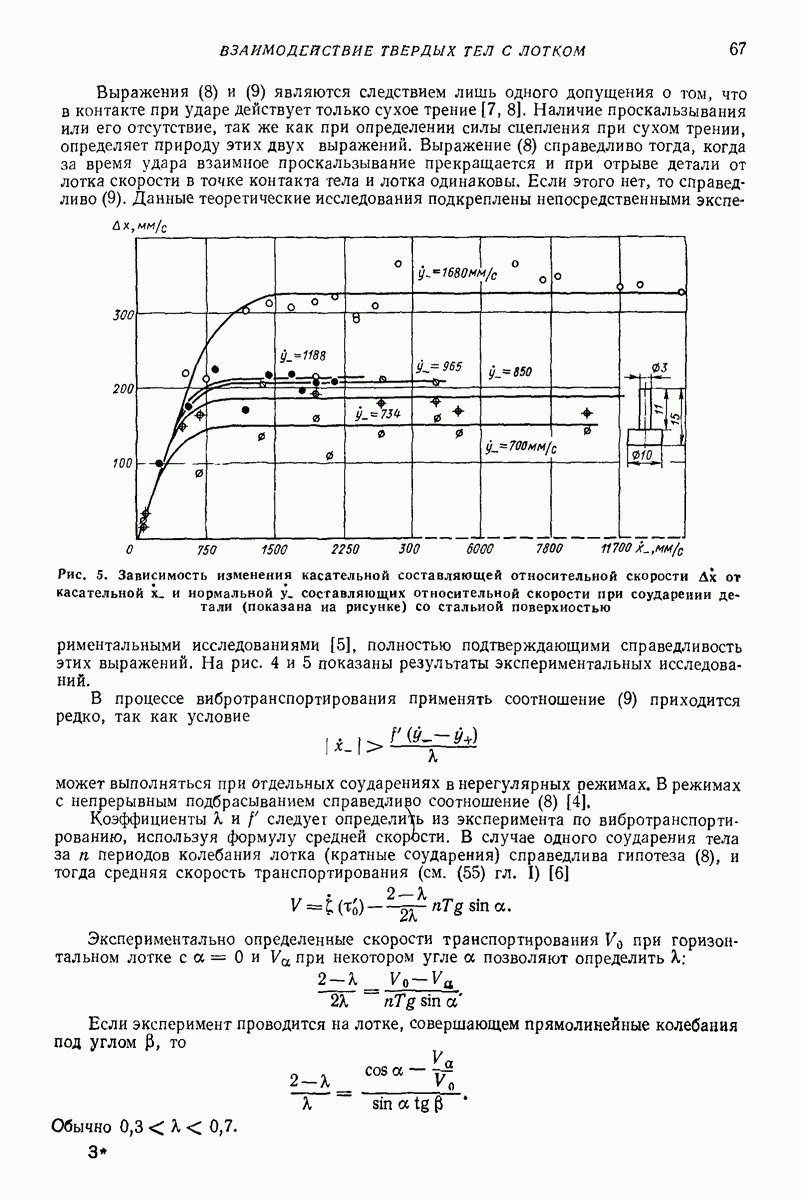
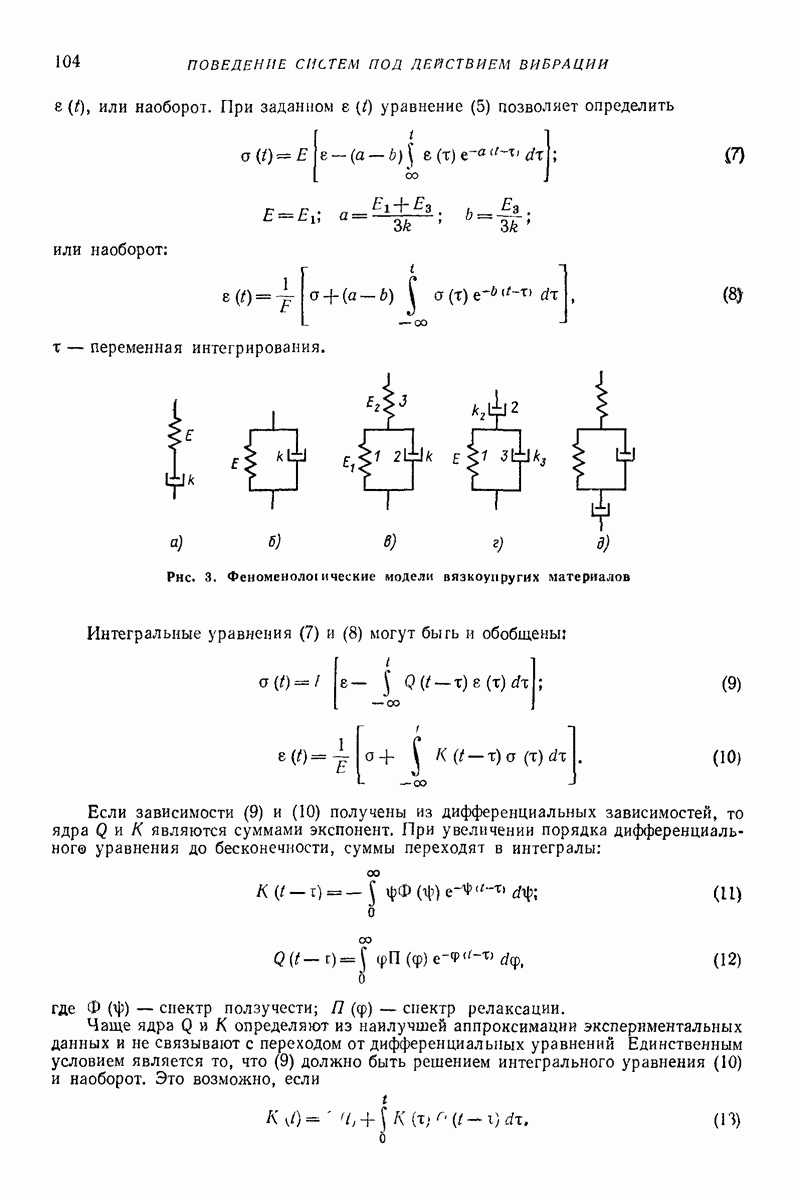
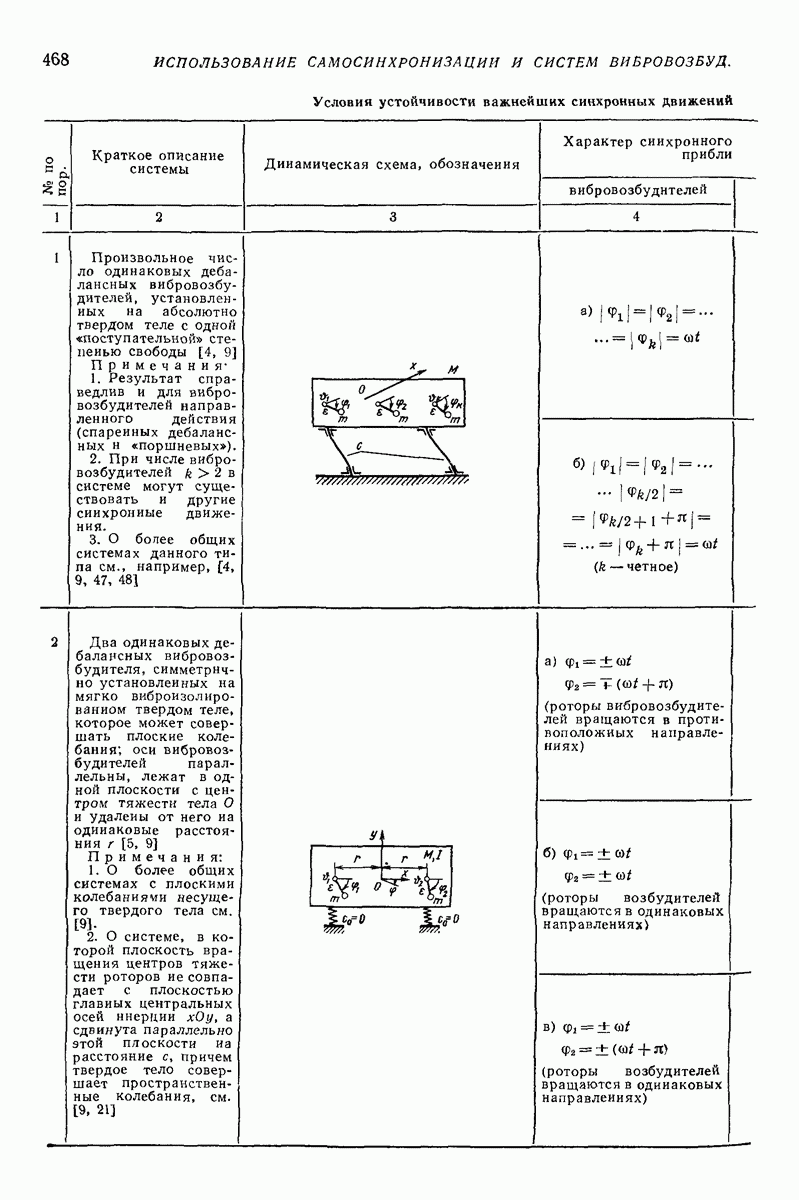
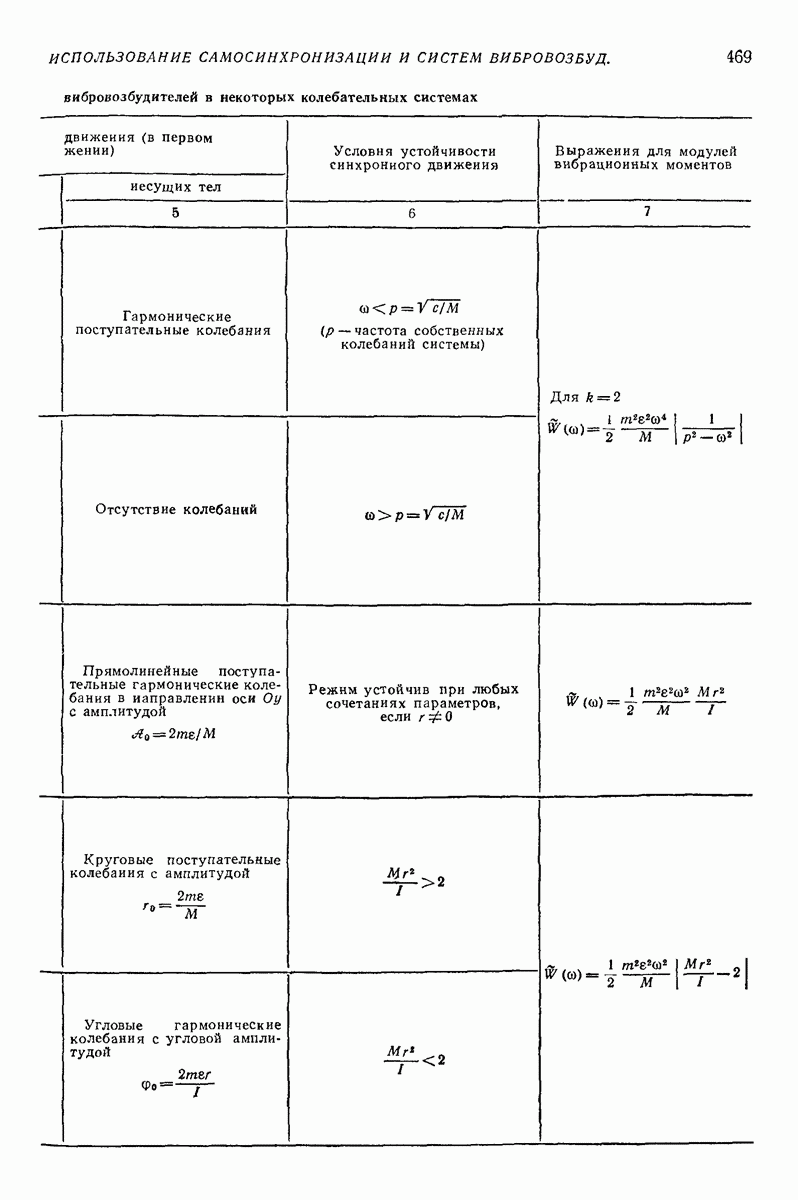
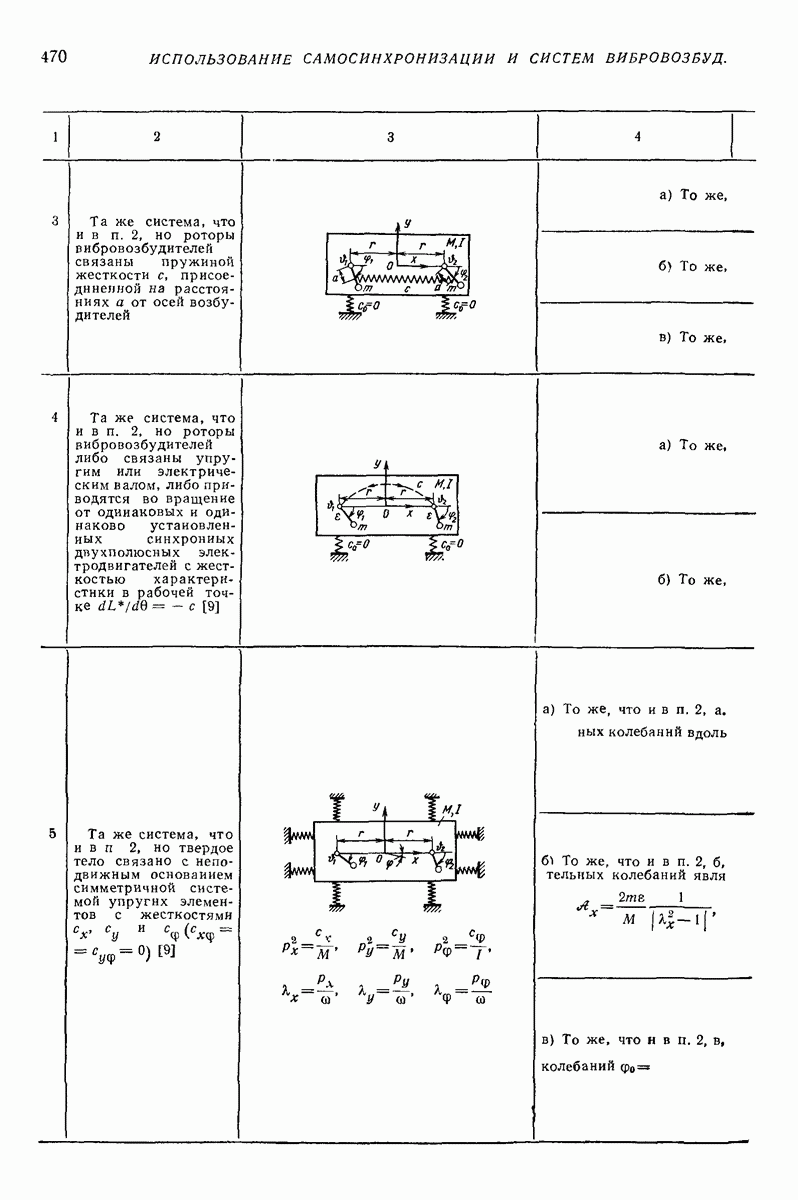
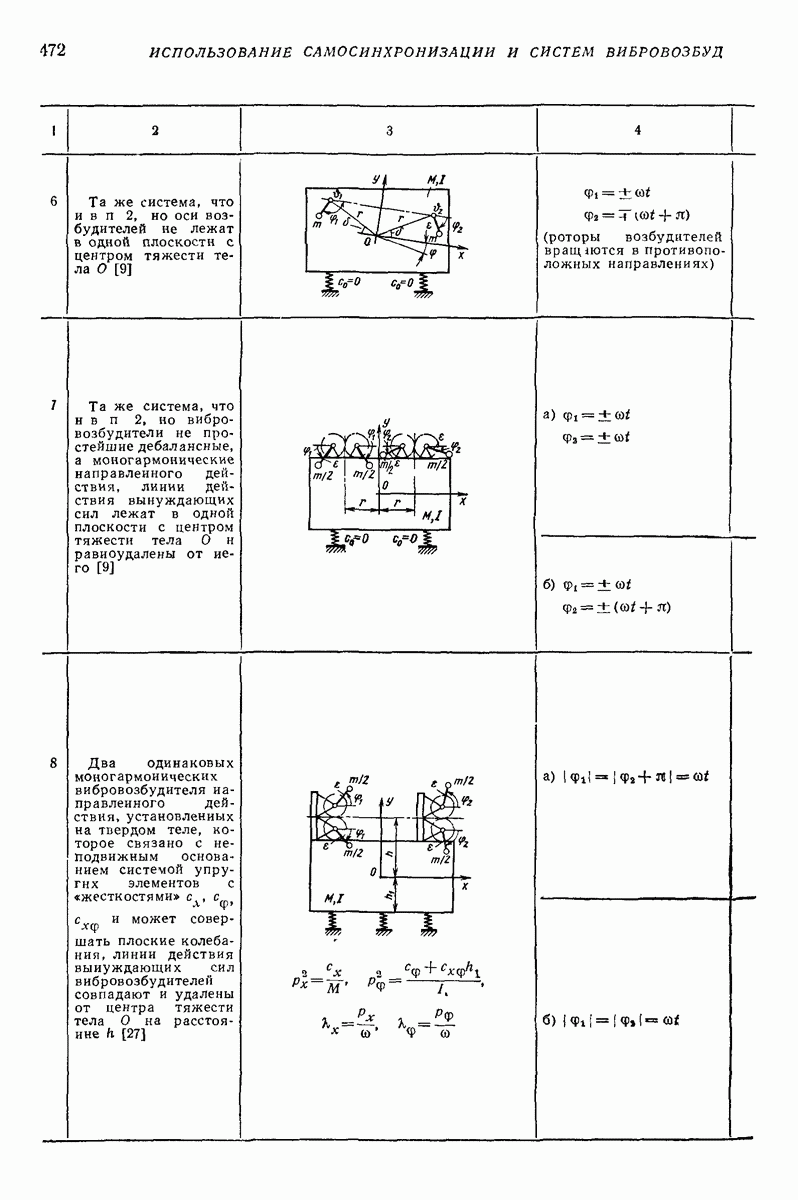
4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
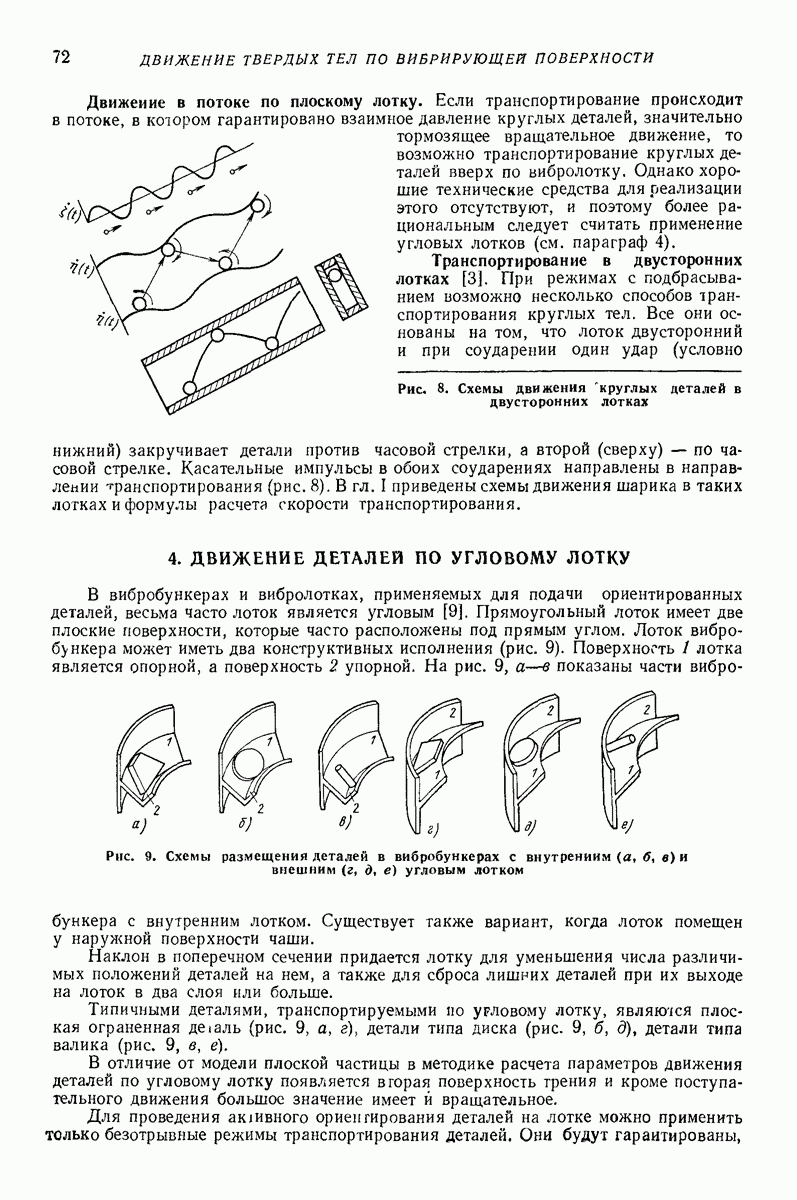
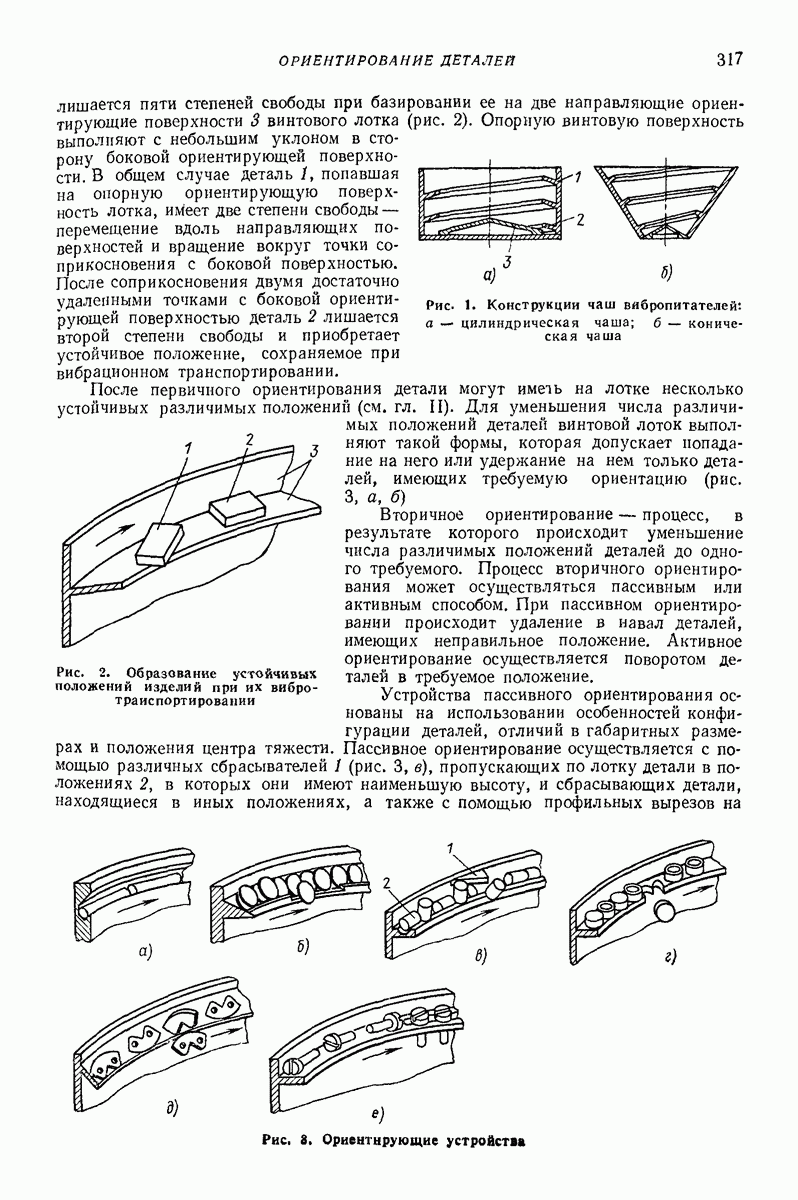
Исследователи, изучающие движение сыпучей среды, из общих законов механики могут предсказать основные качественные черты движения. Поэтому к математическим способам описания неизвестных эмпирических зависимостей, в которых выбор вида аппроксимирующей функции осуществлен формальным образом, обычно не прибегают. Наиболее привычной формой описания движения являются дифференциальные уравнения. Достаточно просто решаются дифференциальные уравнения с постоянными коэффициентами. Поэтому сплошную среду описывают моделью, состоящей из системы твердых тел, связанных взаимно и с поверхностью лотка со стандартными элементами линейной упругости, линейной вязкости, сухого трения с постоянными коэффициентами и простейшими ударными элементами. Такие модели позволяют получить общее решение, поэтапно используя решения линейных систем. Число масс упругих, вязких, ударных элементов сухого грения определяет число постоянных, подлежащих определению из эксперимента. С увеличением числа элементов возрастает точность описания экспериментальных результатов. Такие модели способны описывать с достаточной точностью все необходимые зависимости  вектор а — совокупность всех параметров, влияющих на
вектор а — совокупность всех параметров, влияющих на  пространство параметров, в котором ведется эксперимент. Решение дифференциальных уравнений движения дает теоретические значения
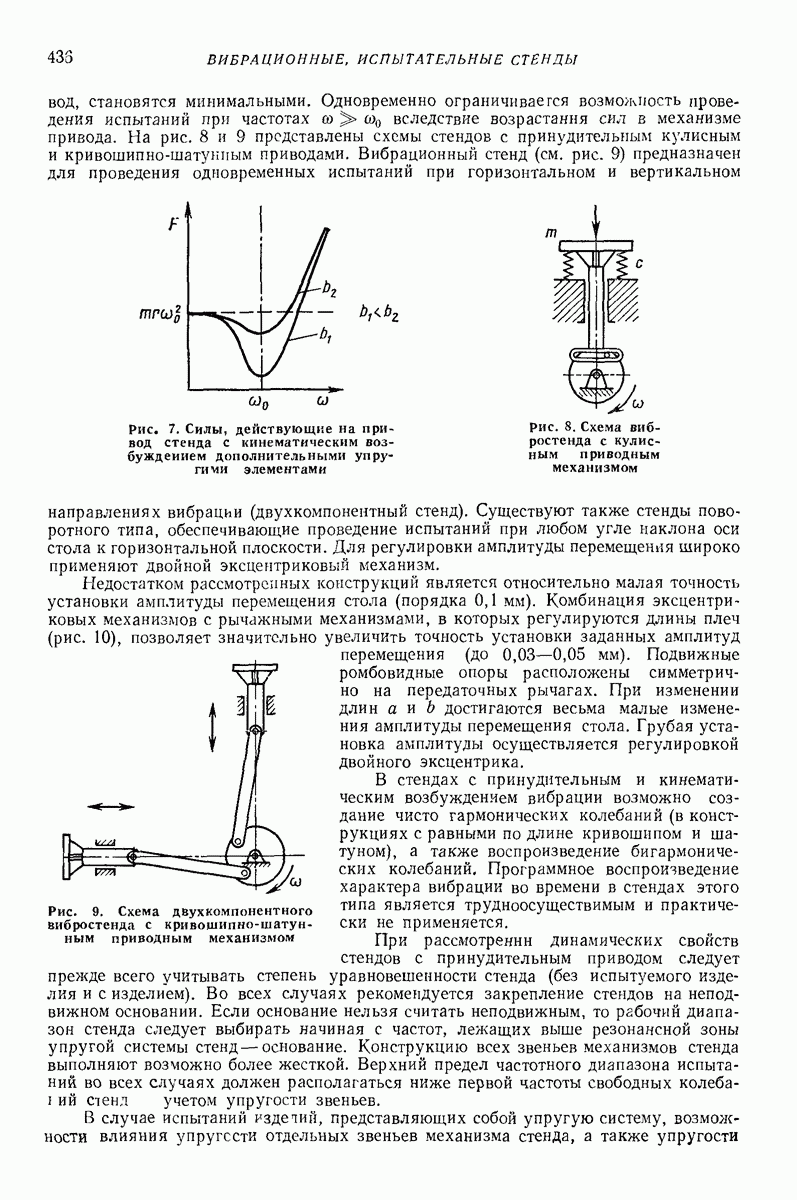
пространство параметров, в котором ведется эксперимент. Решение дифференциальных уравнений движения дает теоретические значения  Но эти значения зависят от численных значений параметров модели
Но эти значения зависят от численных значений параметров модели  Их определяют, минимизируя квадратическую ошибку между экспериментальными значениями
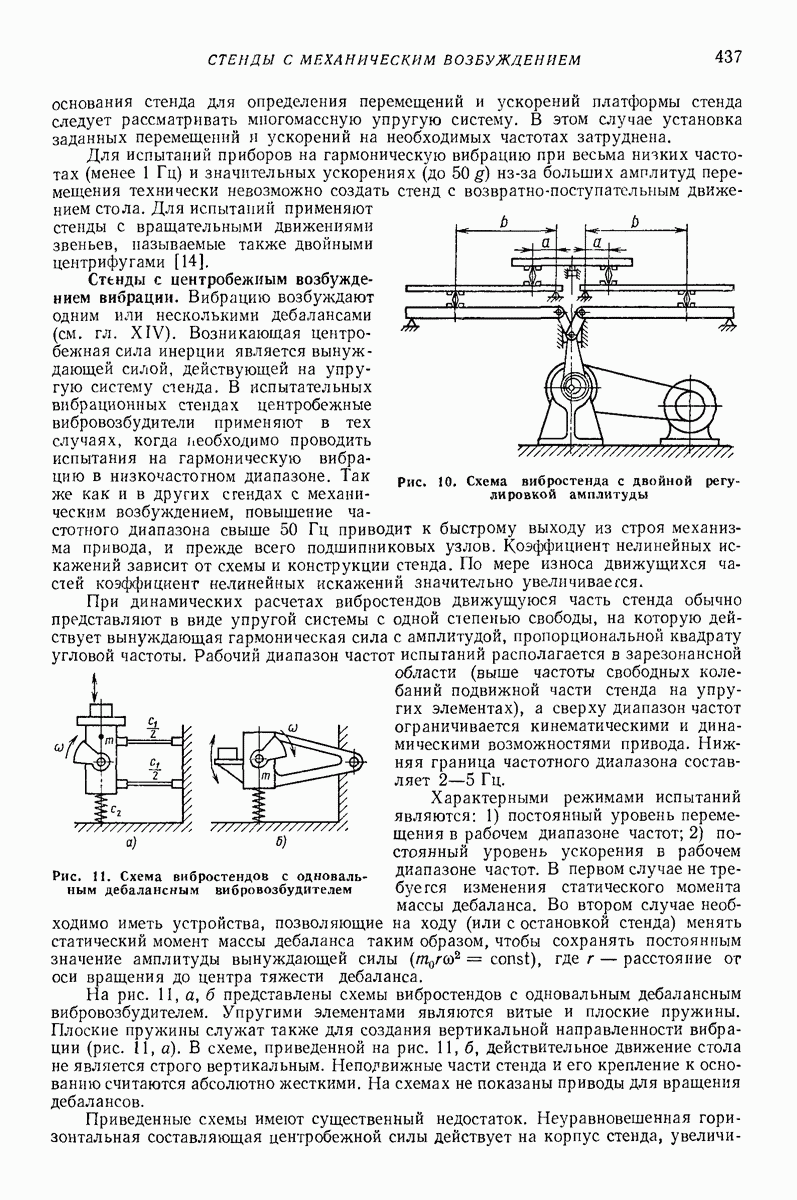
Их определяют, минимизируя квадратическую ошибку между экспериментальными значениями  и теоретическими значениями
и теоретическими значениями  подсчитанными при тех же комбинациях параметров
подсчитанными при тех же комбинациях параметров  при
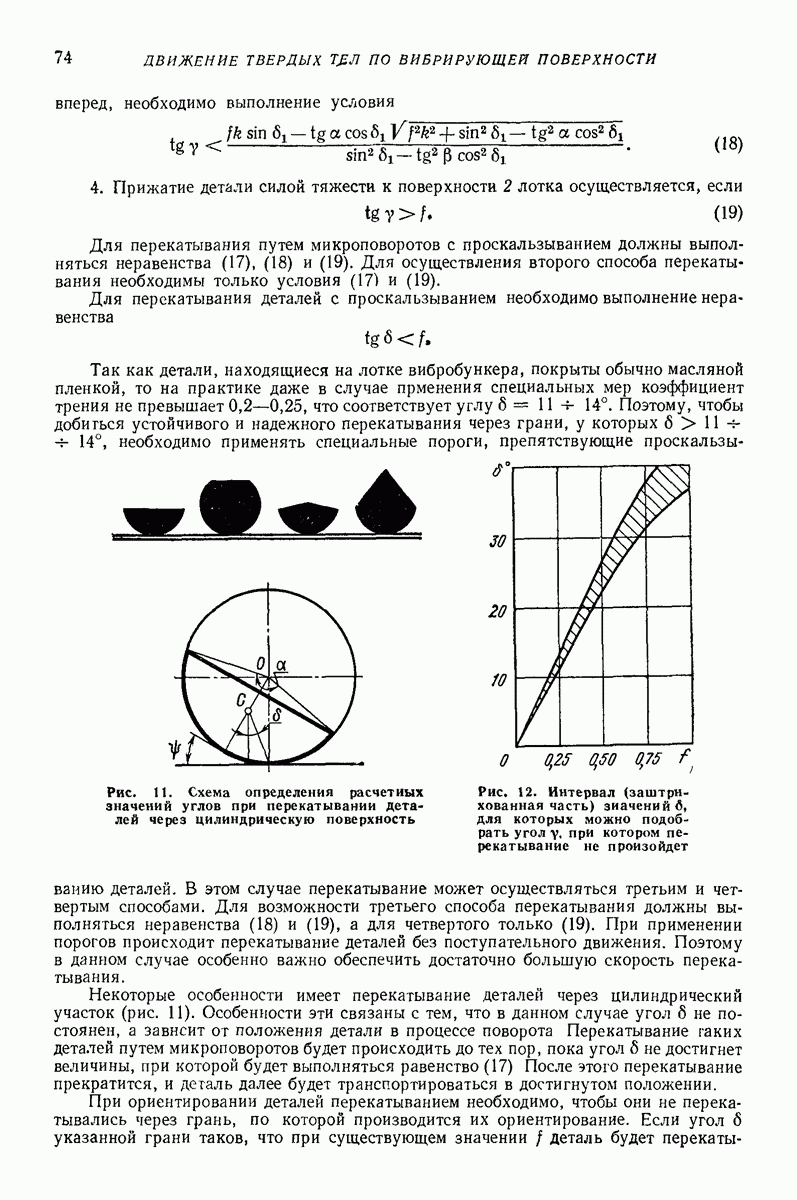
при
которых имеем экспериментальные результаты

Здесь  коэффициент, учитывающий важность совпадения теоретических значений именно в 1-й точке. Если точность аппроксимации должна быть одинаковой (или важность учтена плотностью размещения экспериментальных точек), то
коэффициент, учитывающий важность совпадения теоретических значений именно в 1-й точке. Если точность аппроксимации должна быть одинаковой (или важность учтена плотностью размещения экспериментальных точек), то  знаменателе приведен квадрат среднего значения показателя для нормирования и возможности суммирования ошибок по всем
знаменателе приведен квадрат среднего значения показателя для нормирования и возможности суммирования ошибок по всем  показателям
показателям  Удельный вес
Удельный вес  учитывает важность каждого показателя
учитывает важность каждого показателя  точнее, важность более точной аппроксимации данного
точнее, важность более точной аппроксимации данного  Постоянные модели
Постоянные модели  определяются минимизацией
определяются минимизацией  т. е. формально из системы уравнений
т. е. формально из системы уравнений

Провести аналитический расчет удается только для моделей, не содержащих элементы сухого трения и ударных элементов. Однако именно эти элементы являются определяющими при исследовании вибрационных перемещений. Поэтому наиболее разумным является применение процедуры поиска экстремума в  -мерном пространстве параметров
-мерном пространстве параметров  Применяя эту процедуру, решение системы дифференциальных уравнений модели ведут численно на той же ЭЦВМ для каждой выбранной комбинации значений параметров
Применяя эту процедуру, решение системы дифференциальных уравнений модели ведут численно на той же ЭЦВМ для каждой выбранной комбинации значений параметров  Для относительно хорошо исследованных моделей процедуру поиска можно начинать от хорошего начального приближения значений параметров и программы поиска локального экстремума, что быстро ведет к результату.
Для относительно хорошо исследованных моделей процедуру поиска можно начинать от хорошего начального приближения значений параметров и программы поиска локального экстремума, что быстро ведет к результату.
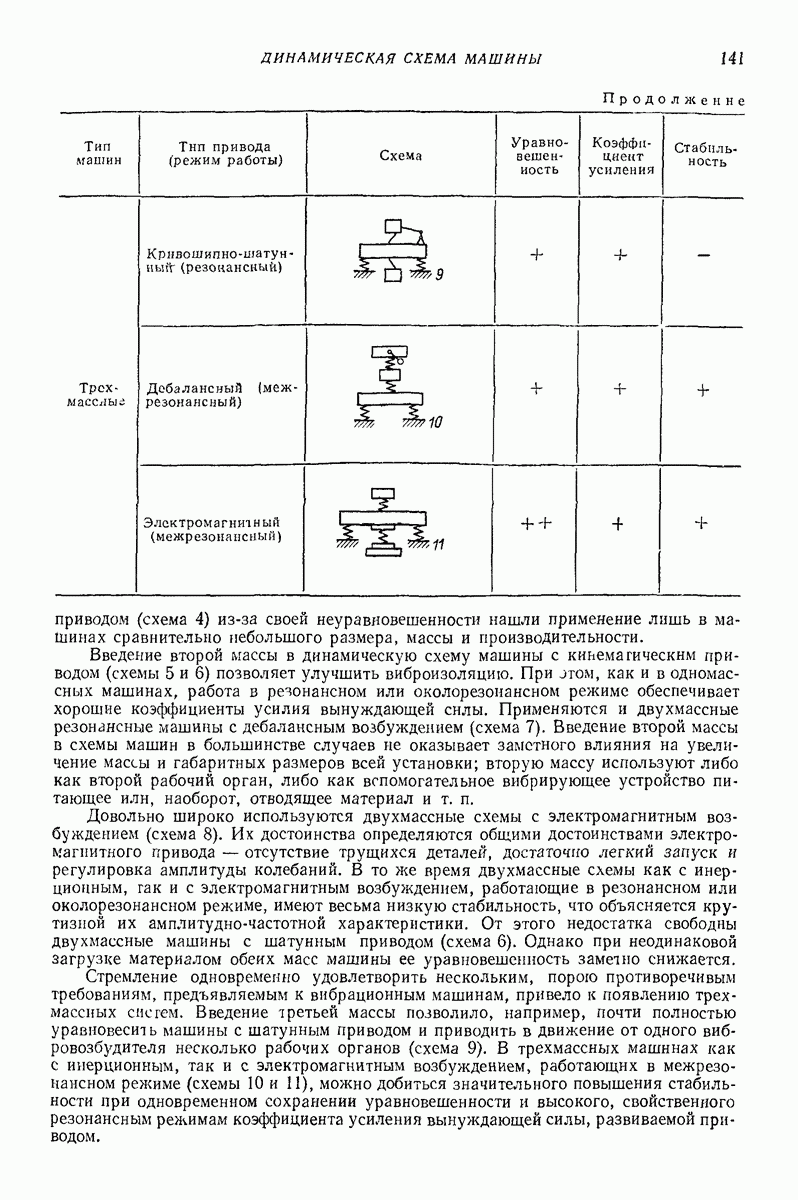
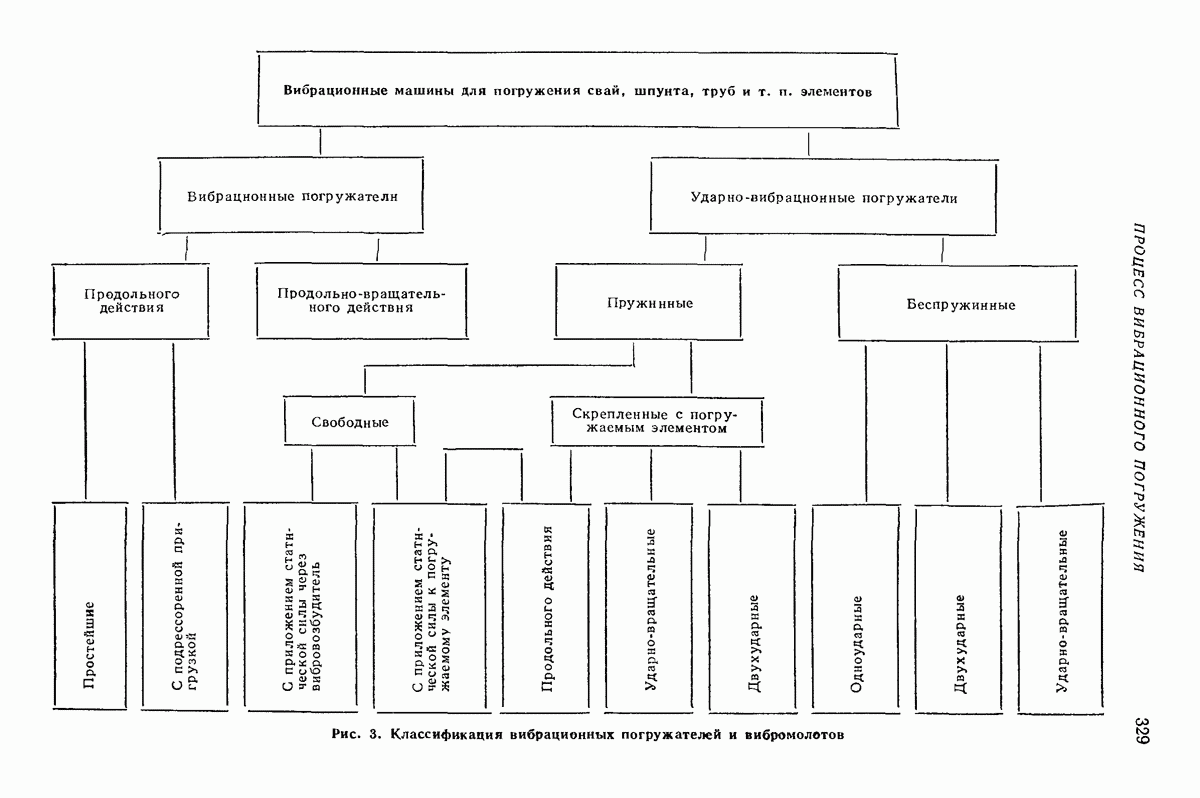
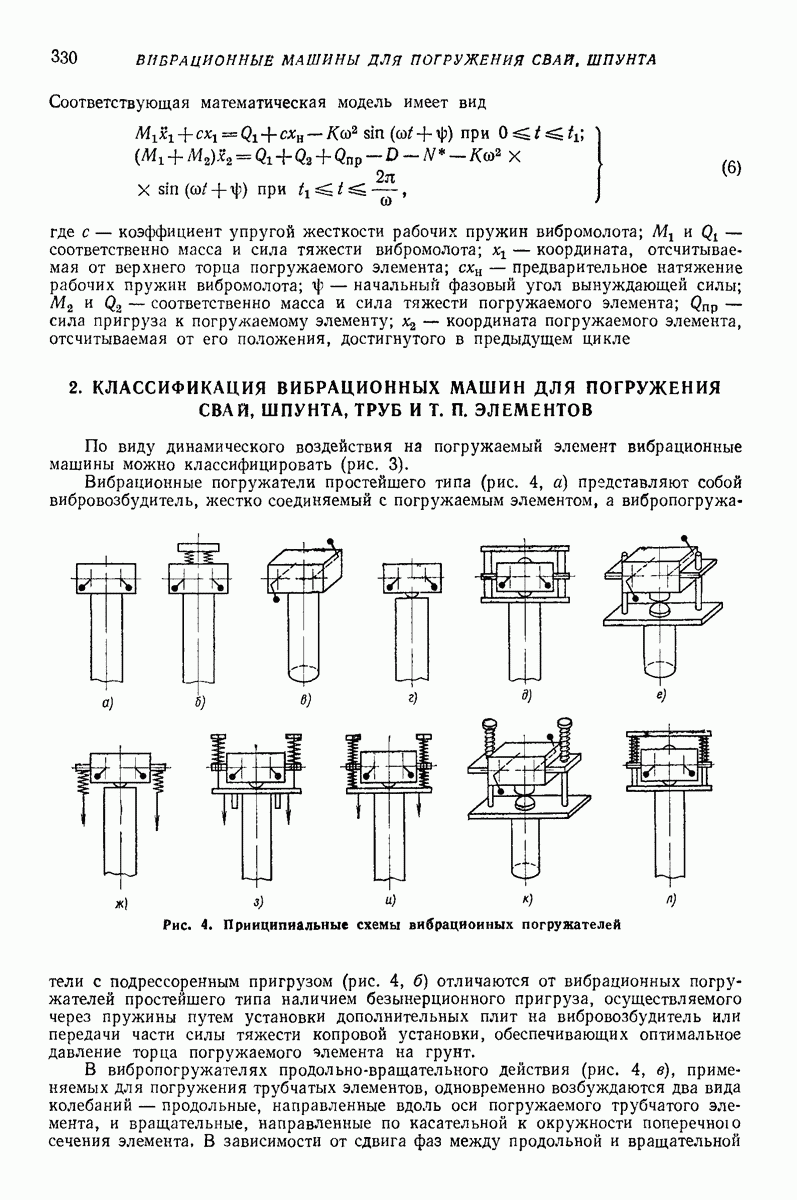
Модели типа систем твердых тел в настоящее время являются наиболее широко используемыми. Эти модели целесообразно применять в случае, когда необходимо прогнозировать поведение сыпучей среды за областью эксперимента или предсказать поведение характеристик, трудно измеряемых в эксперименте. Модельное представление является основой для наиболее правдоподобных прогнозов в новых областях. Это представление имеет и свои недостатки — большая трудоемкость получения практических рекомендаций, так как приходится решать систему дифференциальных уравнений.
Если необходимо установить зависимости между экспериментально определенными величинами в том же диапазоне параметров, то предпочтение надо отдать простой аппроксимации экспериментальных результатов. Непосредственное получение рабочей формулы является менеетрудоемкой операцией, чем определение  Эту аппроксимацию с высокой точностью в широком классе функций по экспериментальным данным в настоящее время можно выполнить на любой ЭЦВМ.
Эту аппроксимацию с высокой точностью в широком классе функций по экспериментальным данным в настоящее время можно выполнить на любой ЭЦВМ.
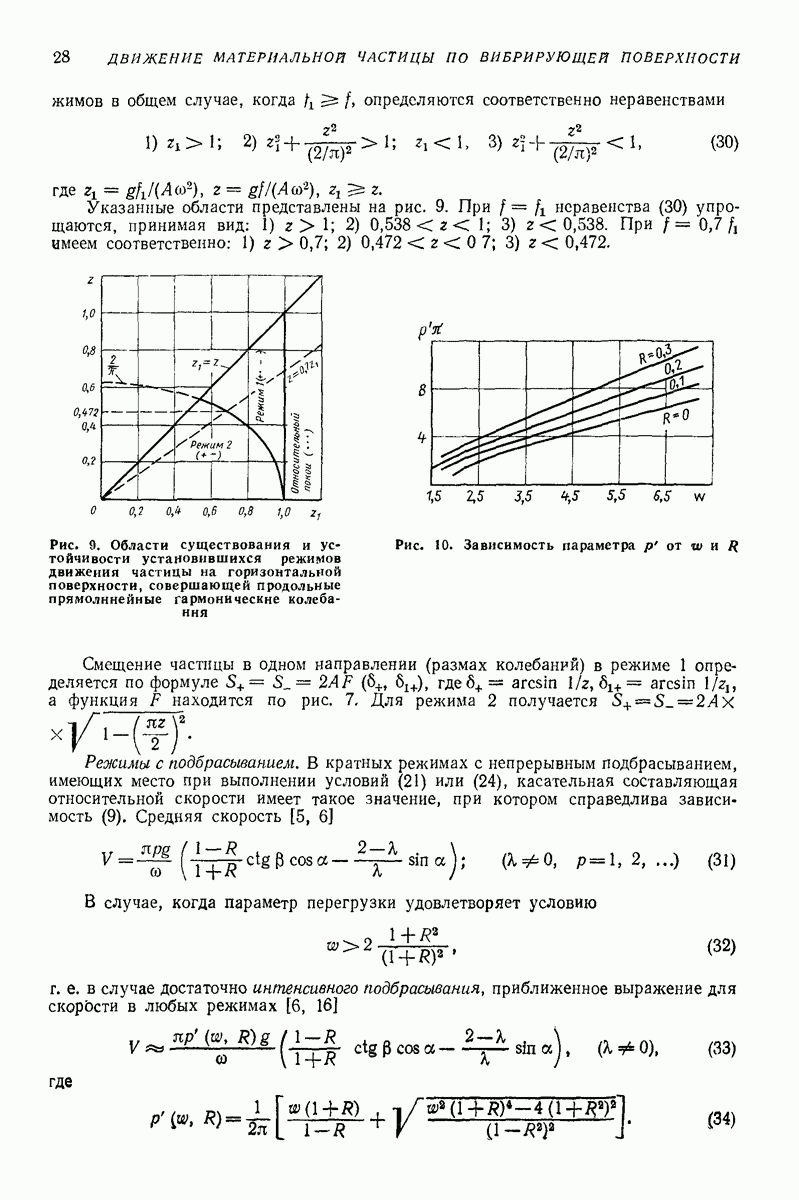
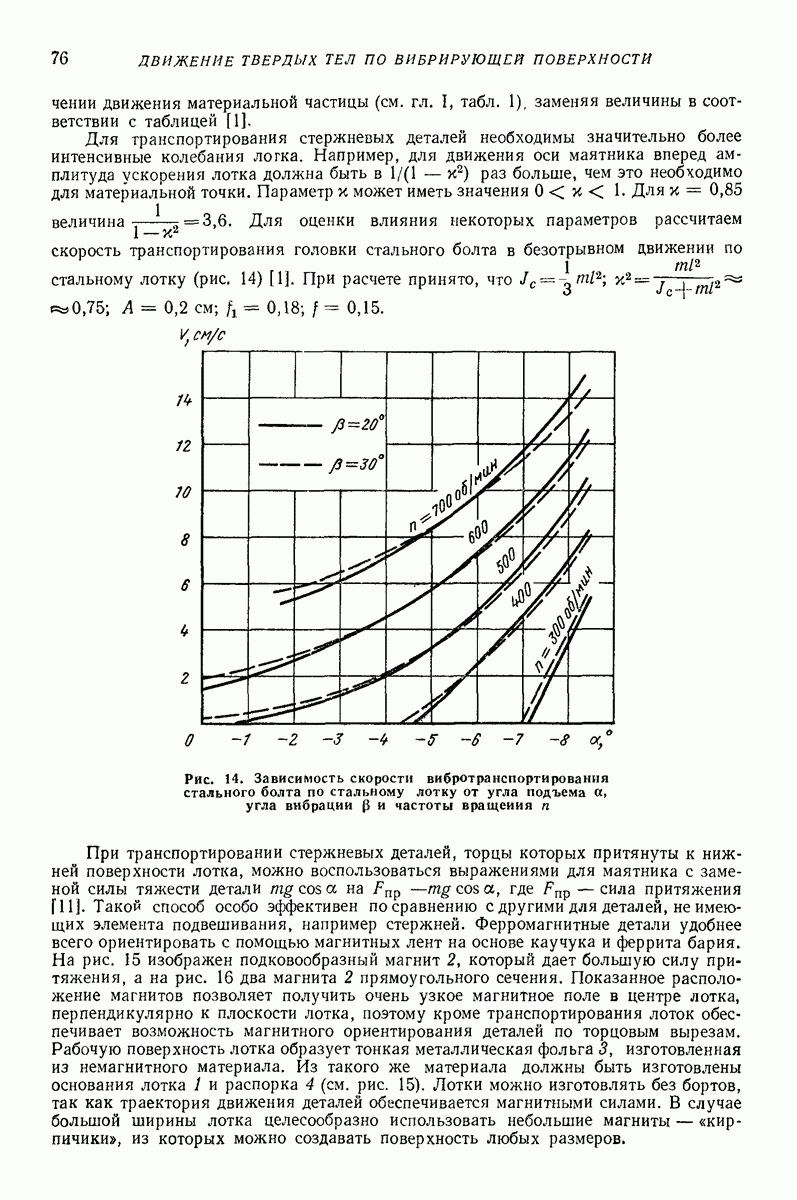
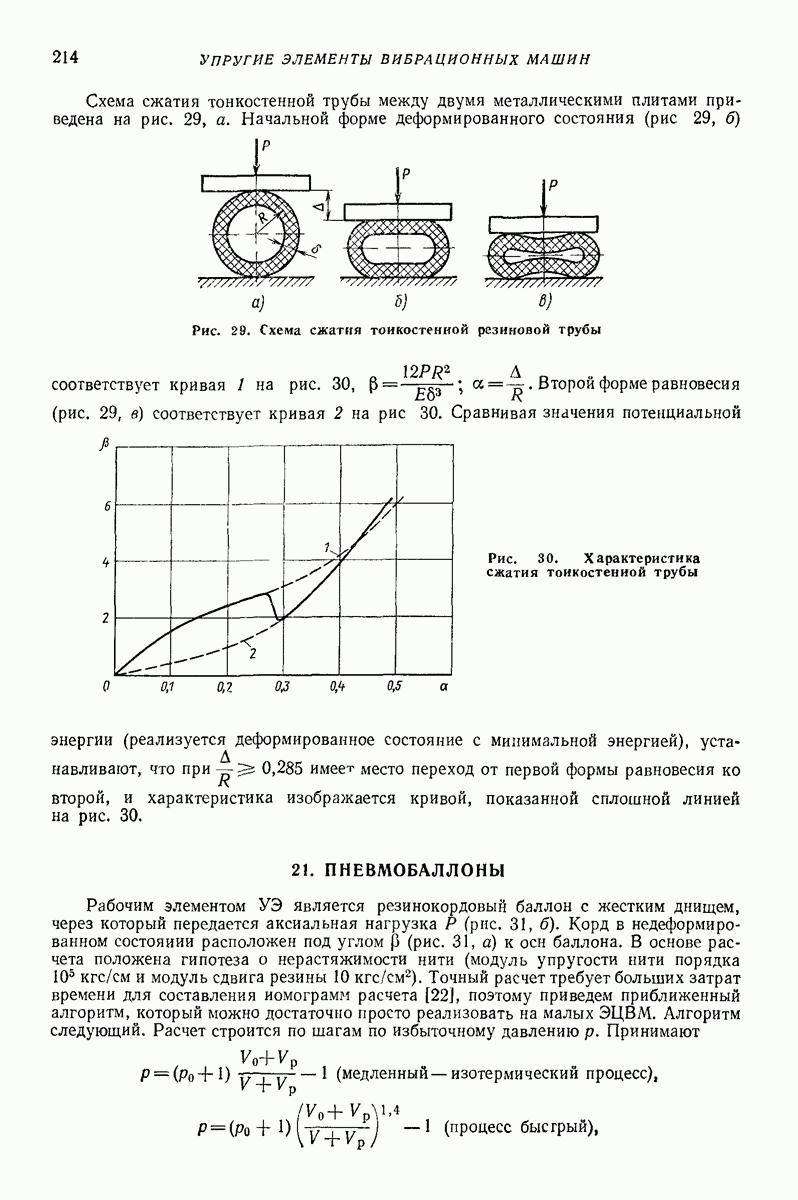
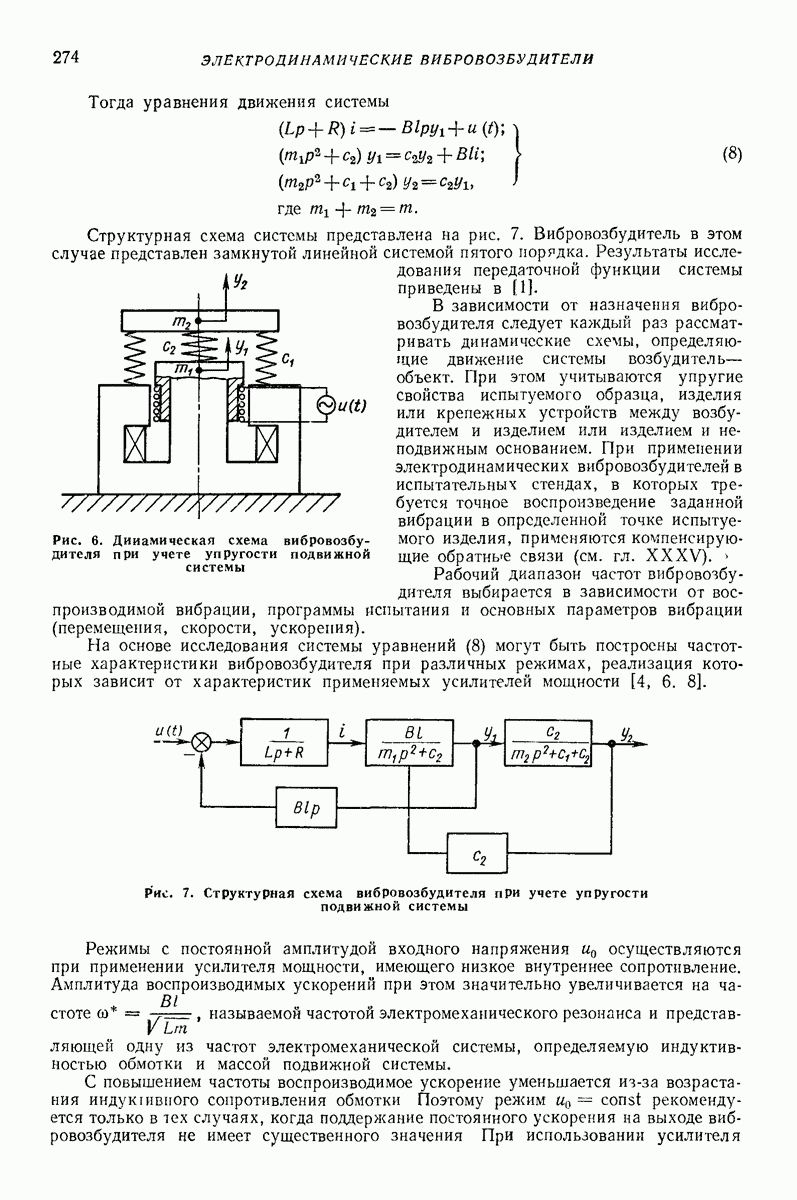
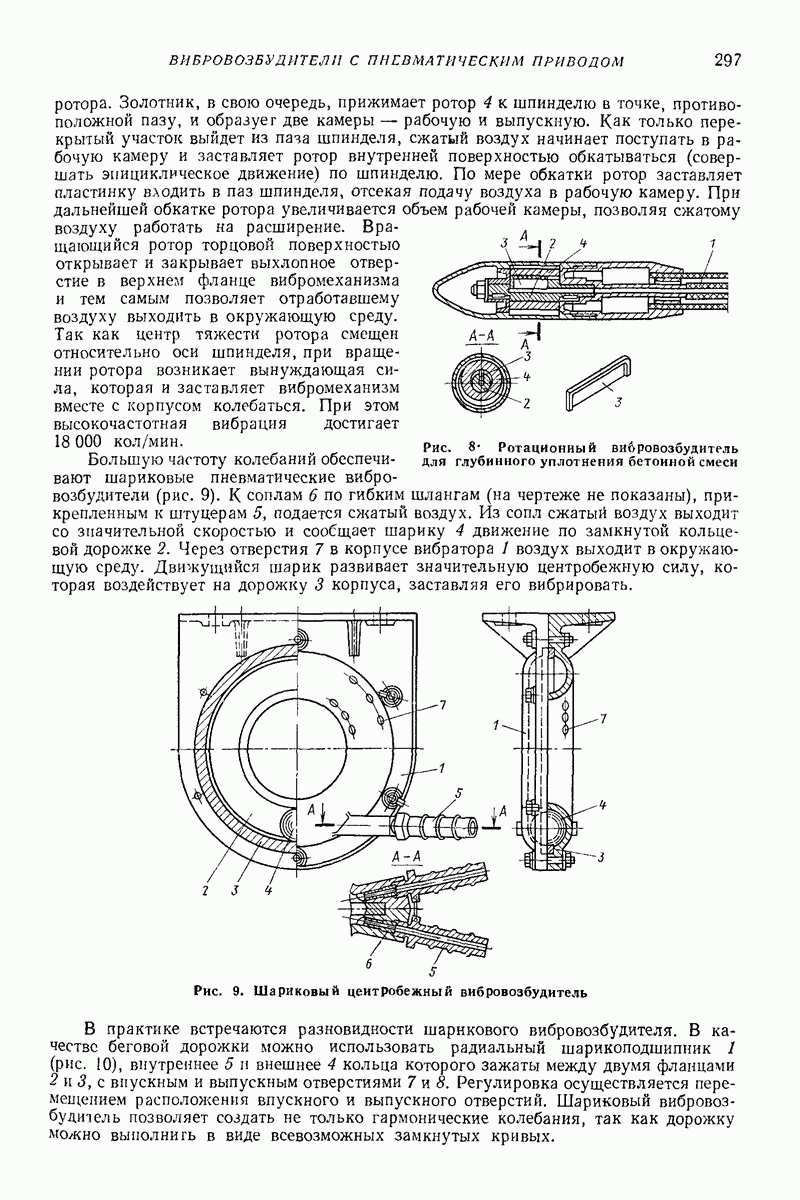
Двухмассная инерционная модель. На рис. 27 представлена двухмассная инерционная модель [16], которая позволяет моделировать упруговязкие и пластические свойства различных сыпучих тел. В качестве примера рассмотрим общий случай вибротранспортирования сыпучего тела по грузонесущему органу вибрационной транспортирующей машины, совершающему прямолинейные колебания.
Модель представляет собой двухмассную колебательную систему с массами  связанными между собой упругими элементами жесткости
связанными между собой упругими элементами жесткости  и демпферами с коэффициентами сопротивления
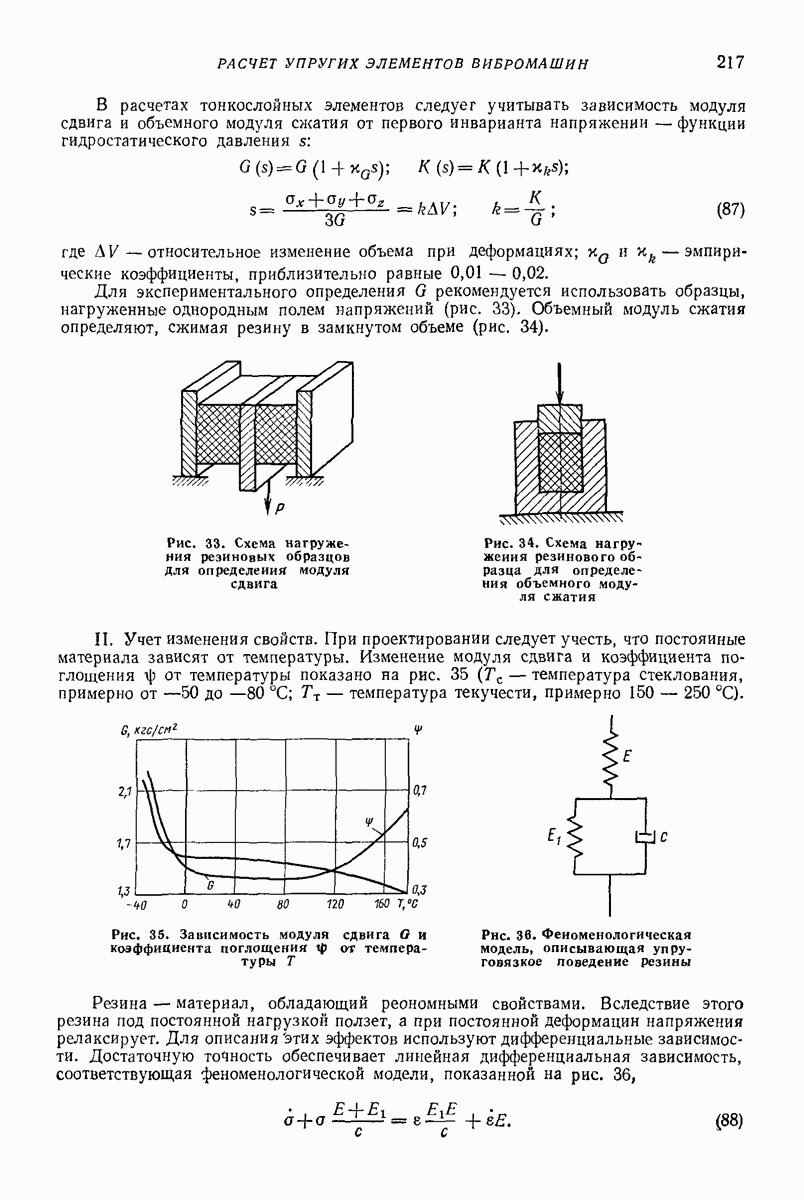
и демпферами с коэффициентами сопротивления  В направлении оси X в режиме совместного движения действуют снлы сухого трения, а в режиме свободного движения силы сопротивления, пропорциональные абсолютной скорости перемещения (демпфер с коэффициентом сопротивления
В направлении оси X в режиме совместного движения действуют снлы сухого трения, а в режиме свободного движения силы сопротивления, пропорциональные абсолютной скорости перемещения (демпфер с коэффициентом сопротивления 
Неибратимые деформации воспроизводятся клиновым элементом и парой сухого трения. В режиме свободного движения массы  та по оси
та по оси  перемещаются, преодолевая вязкостные силы сопротивления, пропорциональные относительной скорости (демпфер с коэффициентом сопротивления
перемещаются, преодолевая вязкостные силы сопротивления, пропорциональные относительной скорости (демпфер с коэффициентом сопротивления  и абсолютной скорости (демпфер с коэффициентом сопротивления
и абсолютной скорости (демпфер с коэффициентом сопротивления 
При движении модели вдоль оси  в случае отсутствия проскальзывания в клиновом элементе уравнение движения следующее:
в случае отсутствия проскальзывания в клиновом элементе уравнение движения следующее:

при наличии проскальзывания в клиновом теле

где  — начальная упругая деформация слоя;
— начальная упругая деформация слоя;  коэффициент, учитывающий уплотнение слоя Сила
коэффициент, учитывающий уплотнение слоя Сила

деформирует сыпучее тело, стремясь вызвать необратимые деформации (сдвинуть клин).

Рис. 27. Двухмассная инерциоиная модель слоя
Деформации модели будут оставаться упругими до того момента, пока деформирующая сила  не превзойдет сопротивление сдвигу клина:
не превзойдет сопротивление сдвигу клина:

Модель находится в контакте с грузонесущим органом до тех пор, пока нормальная реакция не превратится в нуль:

На этапе свободного движения массы  перемещаются совместно:
перемещаются совместно:

Движение массы  в режимах совместного и свободного движения описывается одним уравнением
в режимах совместного и свободного движения описывается одним уравнением

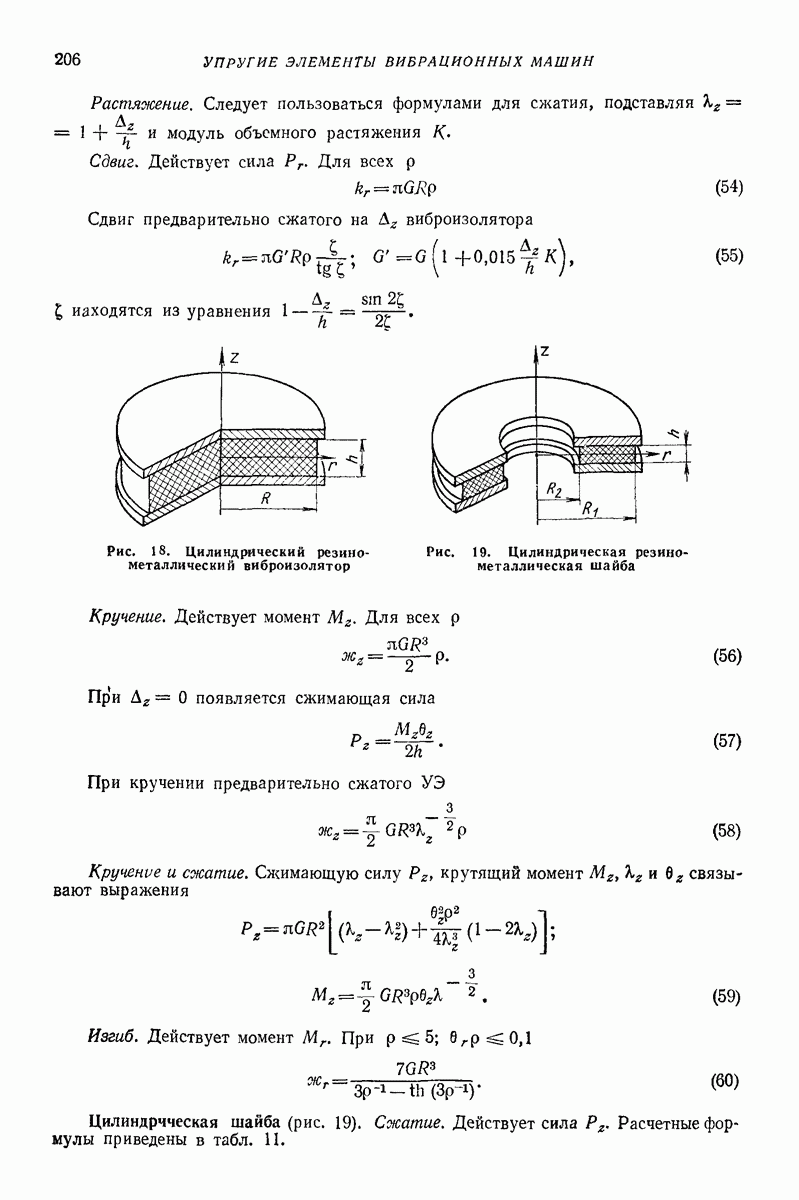
Сила  деформирует сыпучее тело и воздействует на массу
деформирует сыпучее тело и воздействует на массу 
Для массы та на этапе совместного движения характерны следующие режимы: 1) относительное равновесие

модель остается на грузонесущем органе в относительном покое, если сдвигающая массу  сила не превосходит по абсолютной величине предельного значения силы статического трения
сила не превосходит по абсолютной величине предельного значения силы статического трения  (здесь
(здесь  коэффициент трения покоя груза о грузонесущий орган); сила сухого трения меняет свое направление в зависимости от характера движения груза]
коэффициент трения покоя груза о грузонесущий орган); сила сухого трения меняет свое направление в зависимости от характера движения груза]
2) уравнение скольжения сыпучего тела имеет вид

3) на этапе свободного движения уравнение для массы  следующее:
следующее:

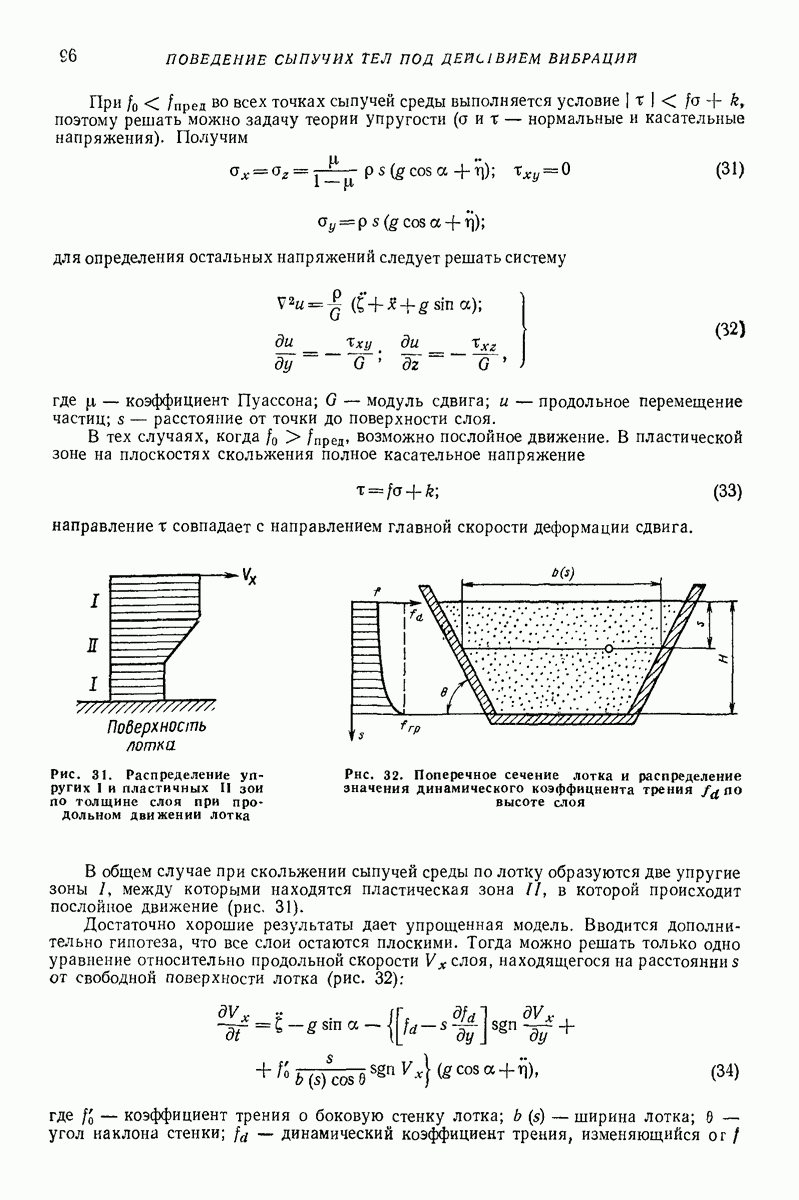
Для нахождения моментов перехода от одного режима движения к другому используют трансцендентные уравнения, которые определяют выбор требуемого уравнения и начальных условий для его решения, так как решение и аналитически, и на электронных моделирующих устройствах производится методом припасовывания.
Момент перехода от участка поперечной упругой деформации модели к пластической  и обратно
и обратно  определяется в результате решения трансцендентного уравнения, полученного приравниванием
определяется в результате решения трансцендентного уравнения, полученного приравниванием 

Переход от скольжения модели к остановке  происходит в момент
происходит в момент  и при условии, что силы статического трения в этот момент больше или равны силе, стремящейся перевести груз в режим проскальзывания:
и при условии, что силы статического трения в этот момент больше или равны силе, стремящейся перевести груз в режим проскальзывания:

Обратный переход от остановки к скольжению (момент  происходит при условии, что силы статического трения не превышают модуля силы, стремящейся перевести модель в режим проскальзывания:
происходит при условии, что силы статического трения не превышают модуля силы, стремящейся перевести модель в режим проскальзывания:

Момент перехода от совместного движения к свободному (момент отрыва груза  определяется в результате решения следующего трансцендентного уравнения:
определяется в результате решения следующего трансцендентного уравнения:

В момент  происходит падение модели груза на грузонесущий орган и начинается фаза соударения. Этот момент определяется трансцендентным уравнением
происходит падение модели груза на грузонесущий орган и начинается фаза соударения. Этот момент определяется трансцендентным уравнением 
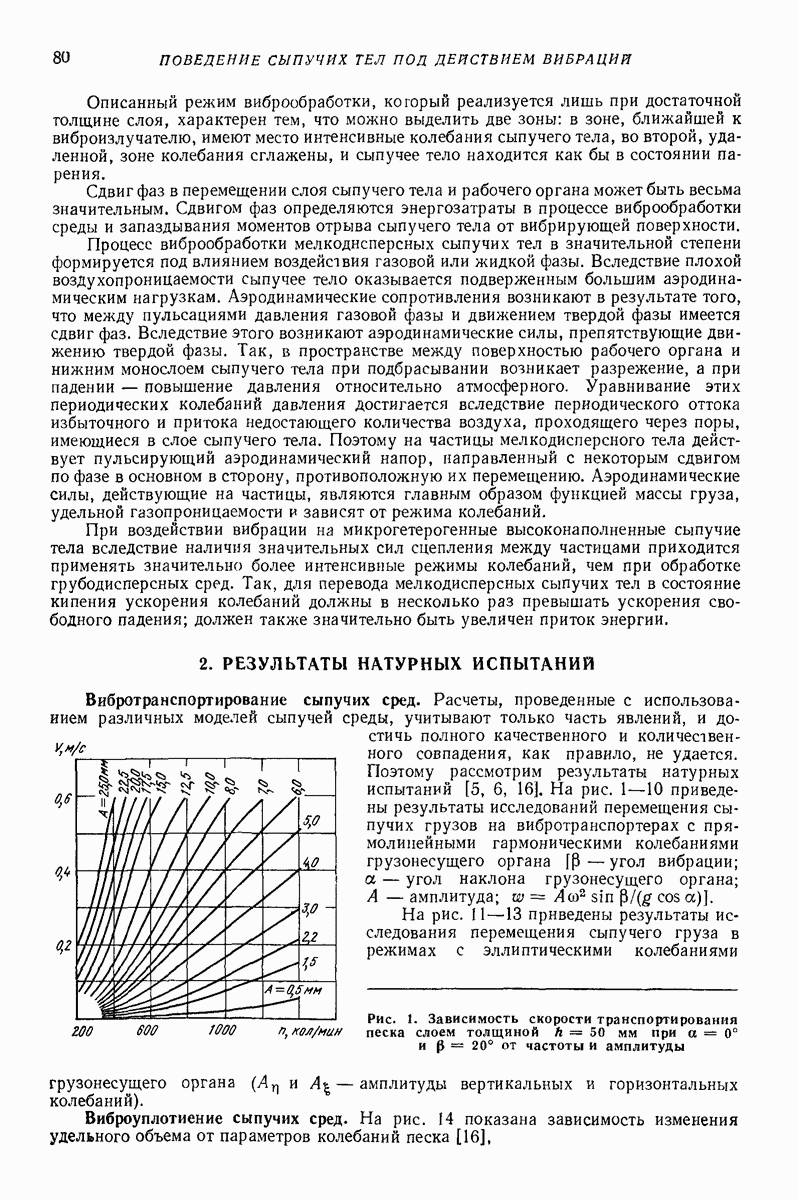
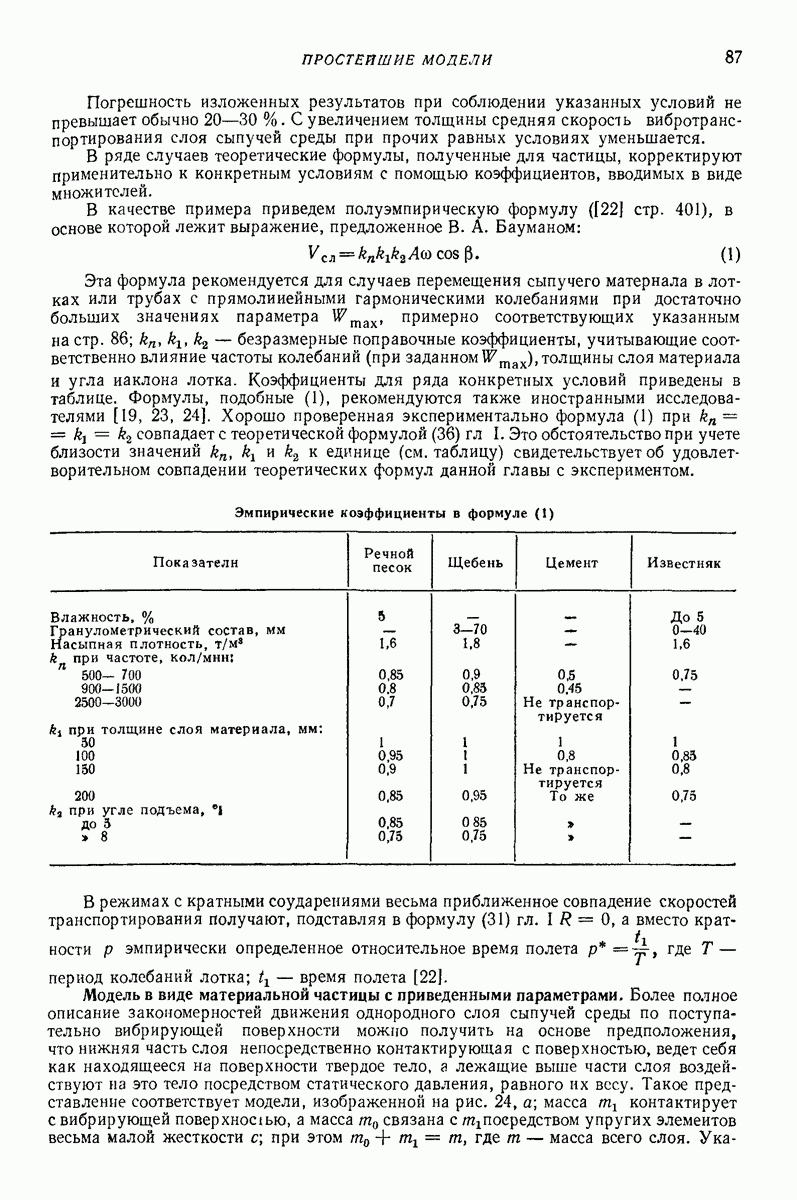
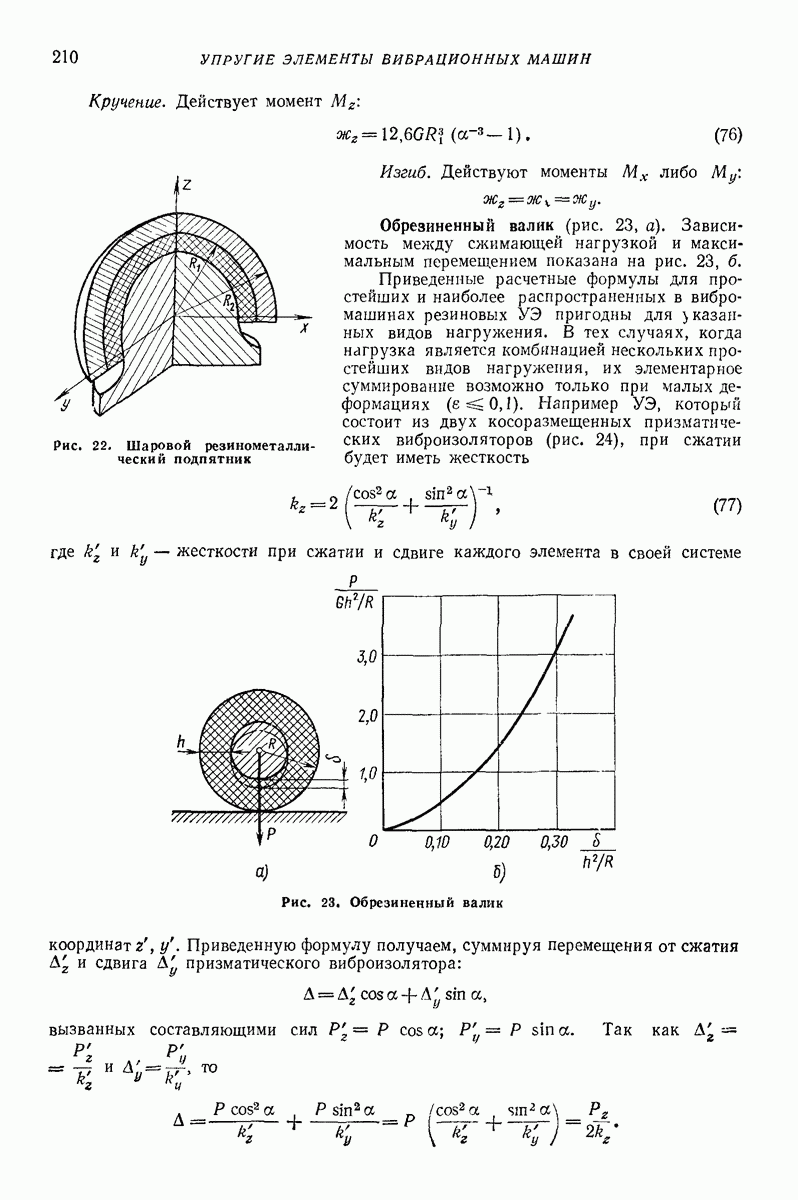
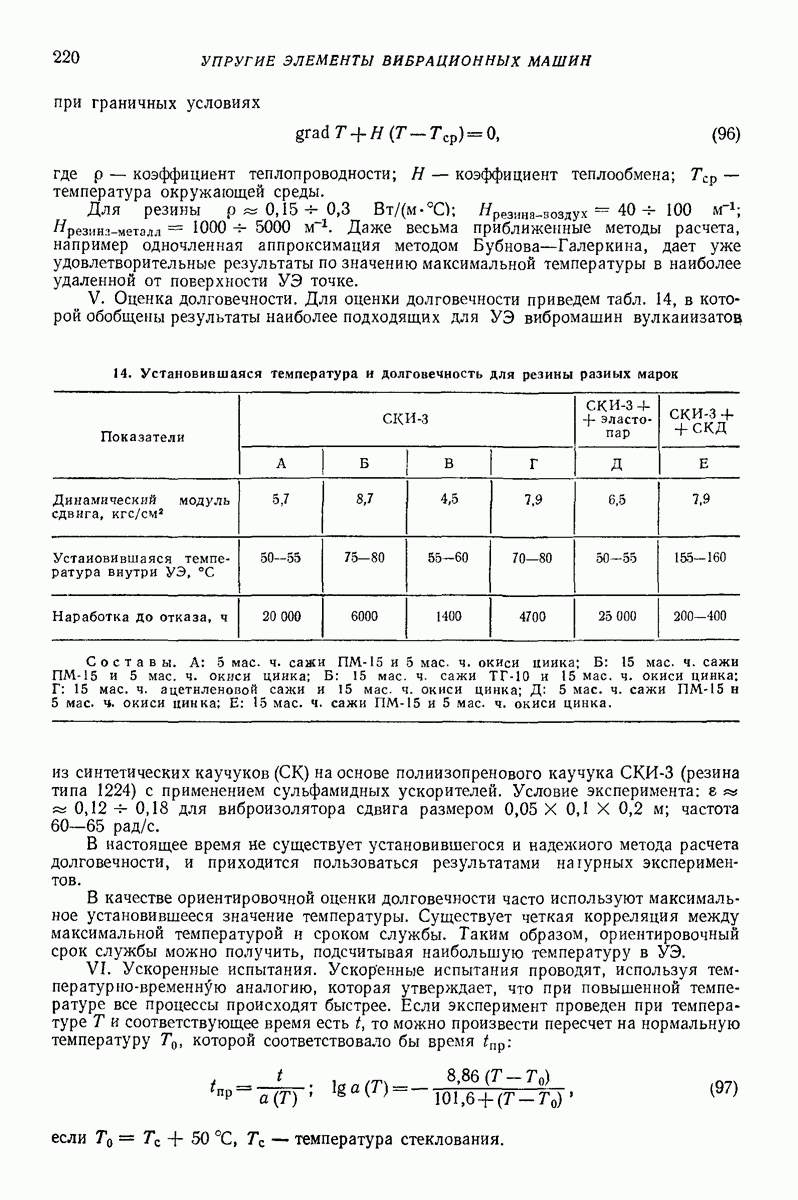
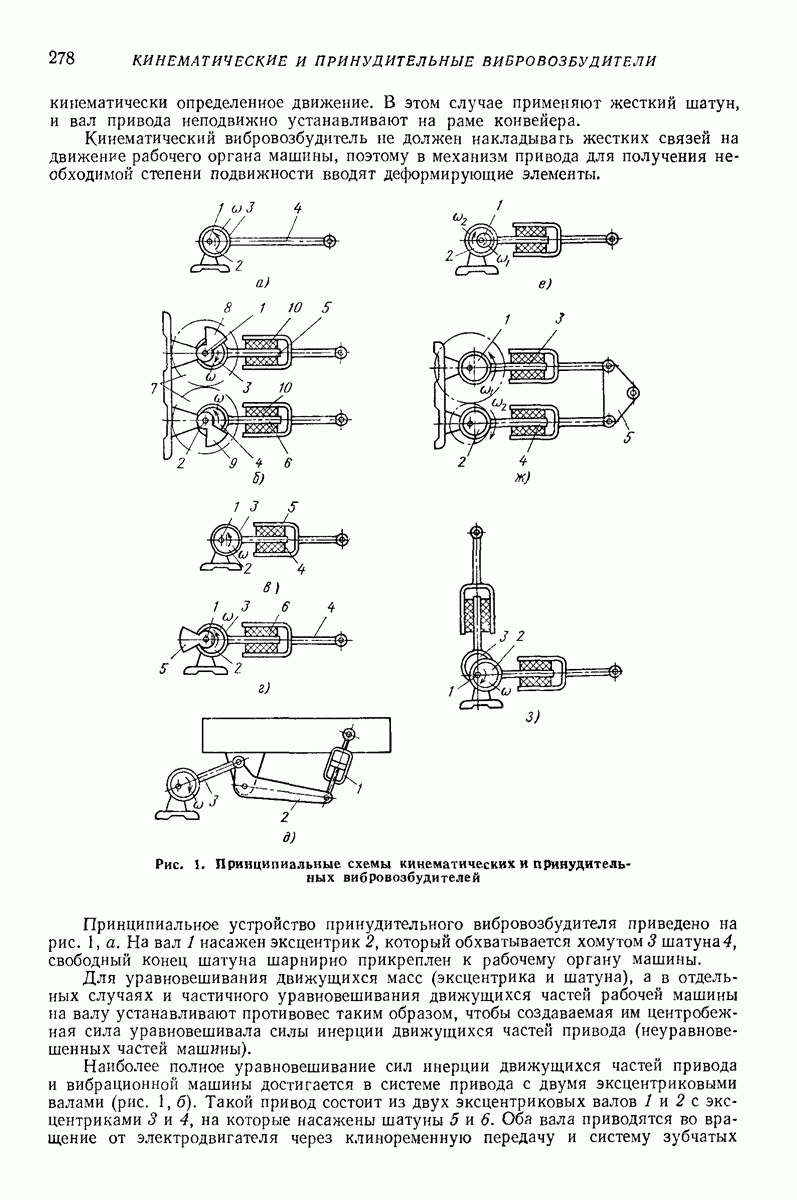
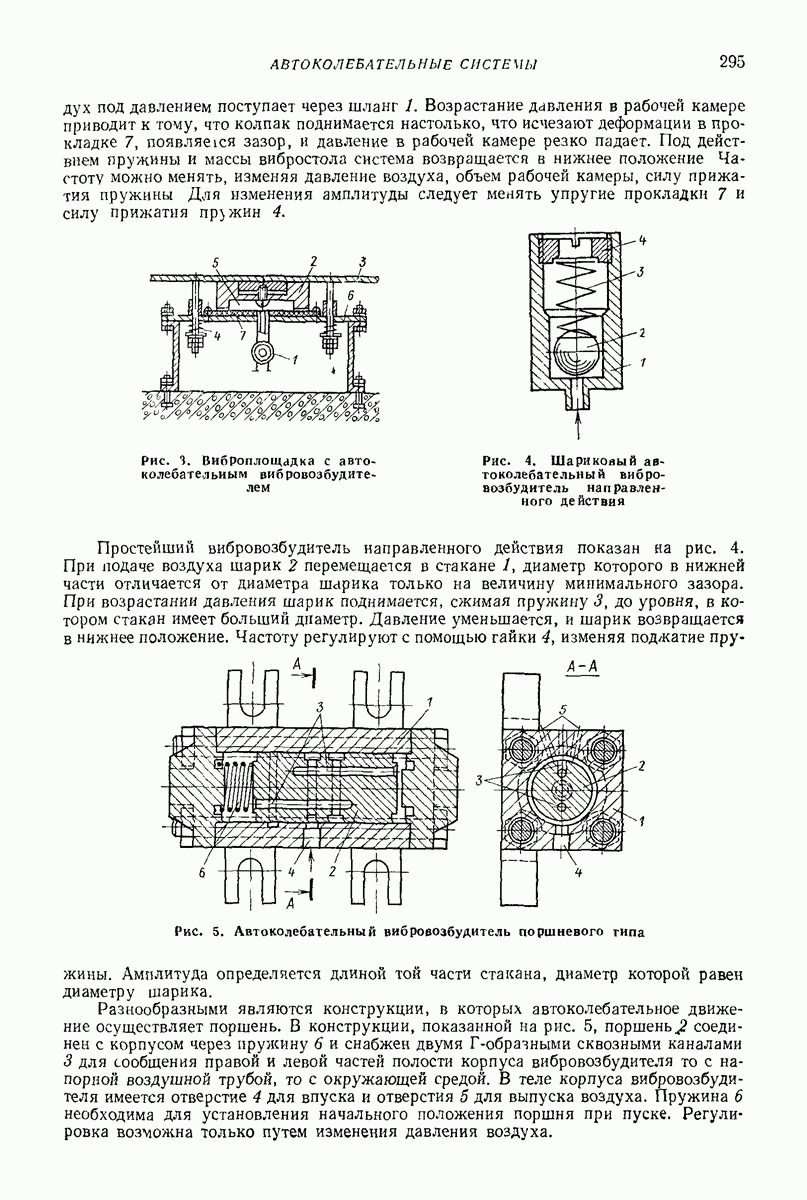
Модели объемной вибрационной обработки. Обработка происходит в прямолинейных, торообразных или спиральных контейнерах с круглым,  -образным, прямоугольным (прямоугольным с закругленными углами) поперечным сечением. Наполненный абразивом и деталями контейнер приводится в вибрационное движение. Успешное снятие слоя материала у детали (очистка поверхностей, удаление острых кромок, шлифование или полирование поверхности) происходит только тогда, когда имеет место достаточно интенсивное движение деталей относительно абразивной массы. Поэтому модели должны быть способны учитывать не только циркуляционную скорость (круговые движения) всей смеси абразива с деталями, но и изменение плотности всей массы. Важным показателем является и сила взаимодействия. На рис. 28 показана модель [9, 16], созданная для описания поведения смеси абразивных частиц и деталей в контейнере с круглым
-образным, прямоугольным (прямоугольным с закругленными углами) поперечным сечением. Наполненный абразивом и деталями контейнер приводится в вибрационное движение. Успешное снятие слоя материала у детали (очистка поверхностей, удаление острых кромок, шлифование или полирование поверхности) происходит только тогда, когда имеет место достаточно интенсивное движение деталей относительно абразивной массы. Поэтому модели должны быть способны учитывать не только циркуляционную скорость (круговые движения) всей смеси абразива с деталями, но и изменение плотности всей массы. Важным показателем является и сила взаимодействия. На рис. 28 показана модель [9, 16], созданная для описания поведения смеси абразивных частиц и деталей в контейнере с круглым  -образным) поперечным сечением Модель представляет собой упругий круг, у которого диаметр изменяется в зависимости от поджатая пружин
-образным) поперечным сечением Модель представляет собой упругий круг, у которого диаметр изменяется в зависимости от поджатая пружин  соединяющих центральные массы абразива
соединяющих центральные массы абразива  и деталей
и деталей  с периферийной суммарной массой
с периферийной суммарной массой  Периферийная масса может двигаться вместе с контейнером, скользить или двигаться в режиме с подбрасыванием. Особенностью модели является допущение, что модель все время является круглой и радиус
Периферийная масса может двигаться вместе с контейнером, скользить или двигаться в режиме с подбрасыванием. Особенностью модели является допущение, что модель все время является круглой и радиус  меняется в зависимости от того, как контейнер воздействует на модель. Массы
меняется в зависимости от того, как контейнер воздействует на модель. Массы  позволяют описать циркуляционную скорость. Взаимные сдвиги
позволяют описать циркуляционную скорость. Взаимные сдвиги
между массами  имитируют силы сухого трения (силы резания) между абразивами и деталями. Энергия соударения между частицами моделируется вязкими элементами
имитируют силы сухого трения (силы резания) между абразивами и деталями. Энергия соударения между частицами моделируется вязкими элементами 

Рис. 28. Модель движения абразива и деталей в установке для виброобъемной обработки
Модель позволяет учитывать и воздействие внешнего силового поля  например магнитные силы. Съем металла считается пропорциональным рассеянной в модели энергии (в вязких элементах
например магнитные силы. Съем металла считается пропорциональным рассеянной в модели энергии (в вязких элементах  и в элементе сухого трения). Энергия, рассеянная при соударении массы
и в элементе сухого трения). Энергия, рассеянная при соударении массы  о контейнер (коэффициент
о контейнер (коэффициент  обычно не считается полезно затраченной для съема металла.
обычно не считается полезно затраченной для съема металла.

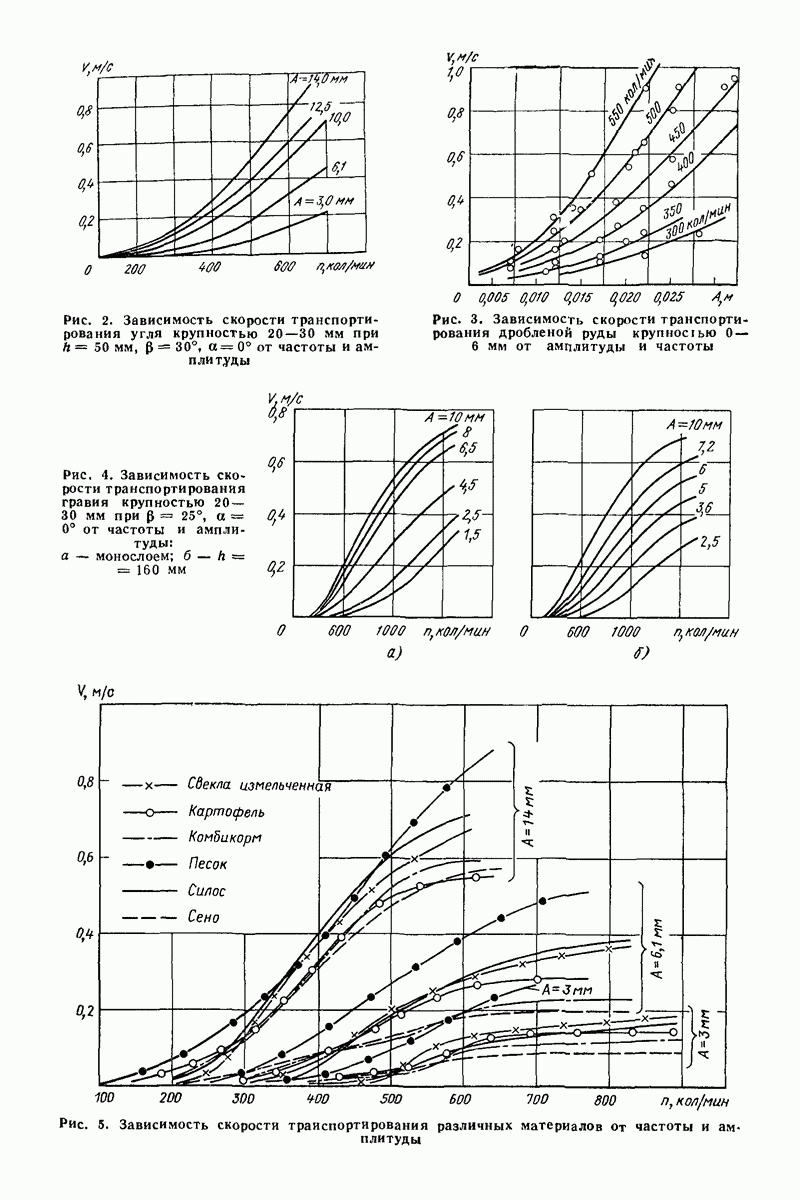
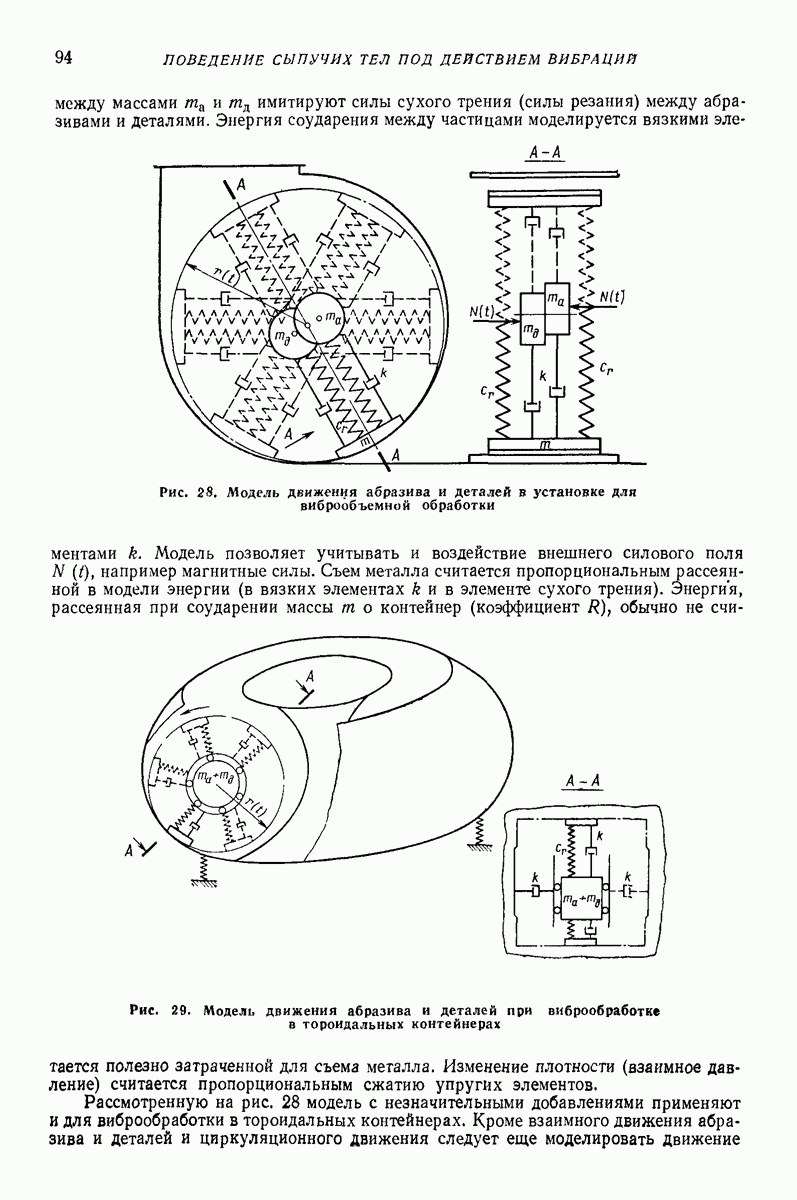
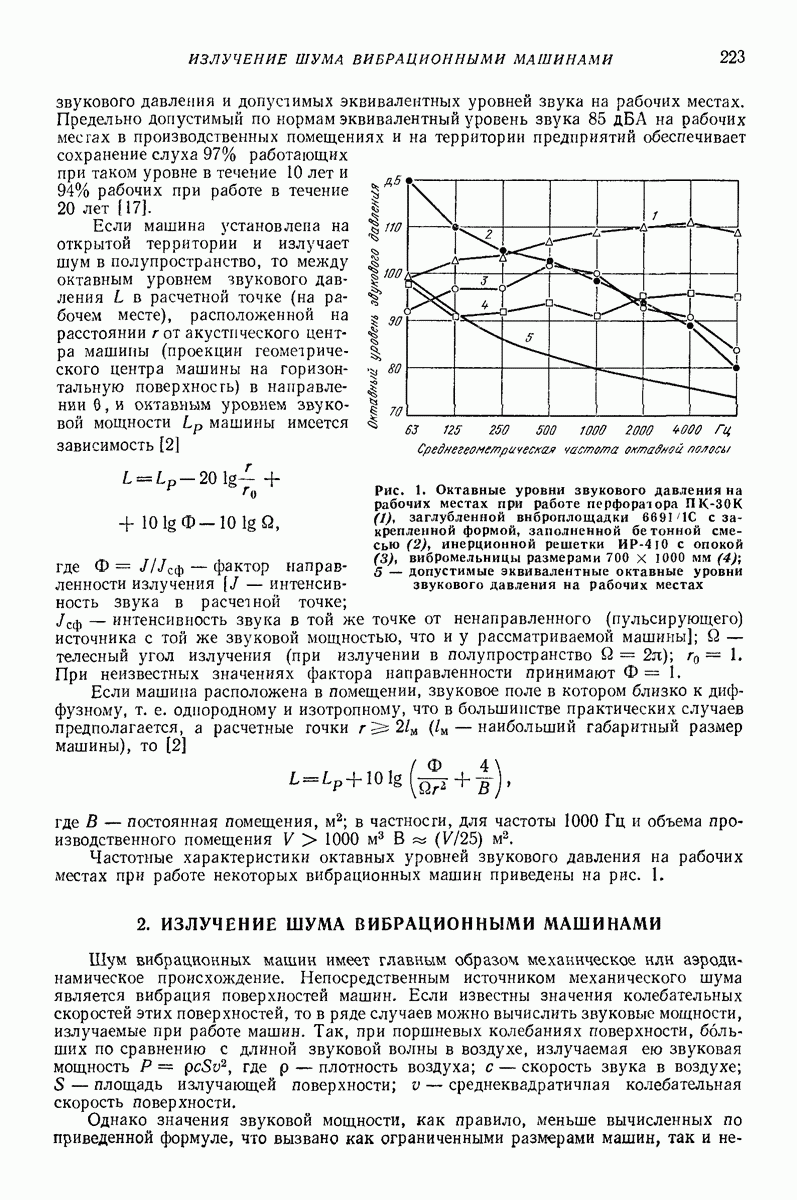
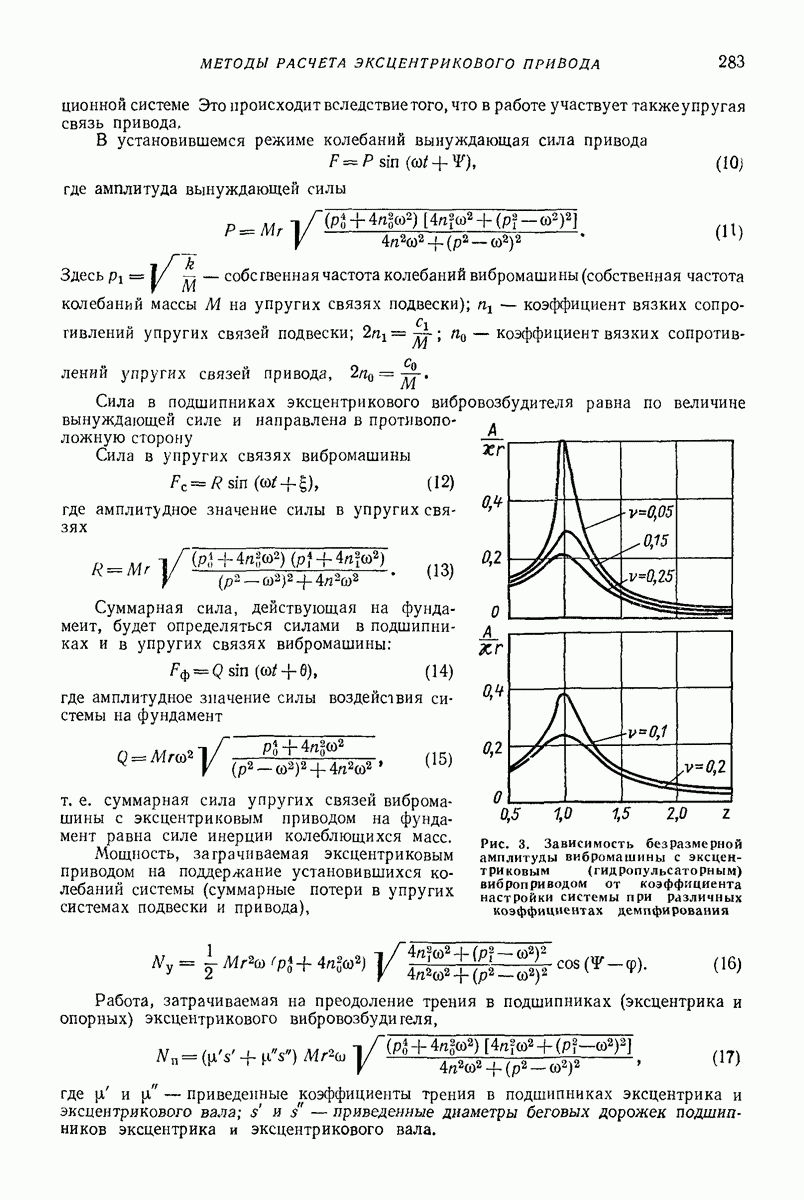
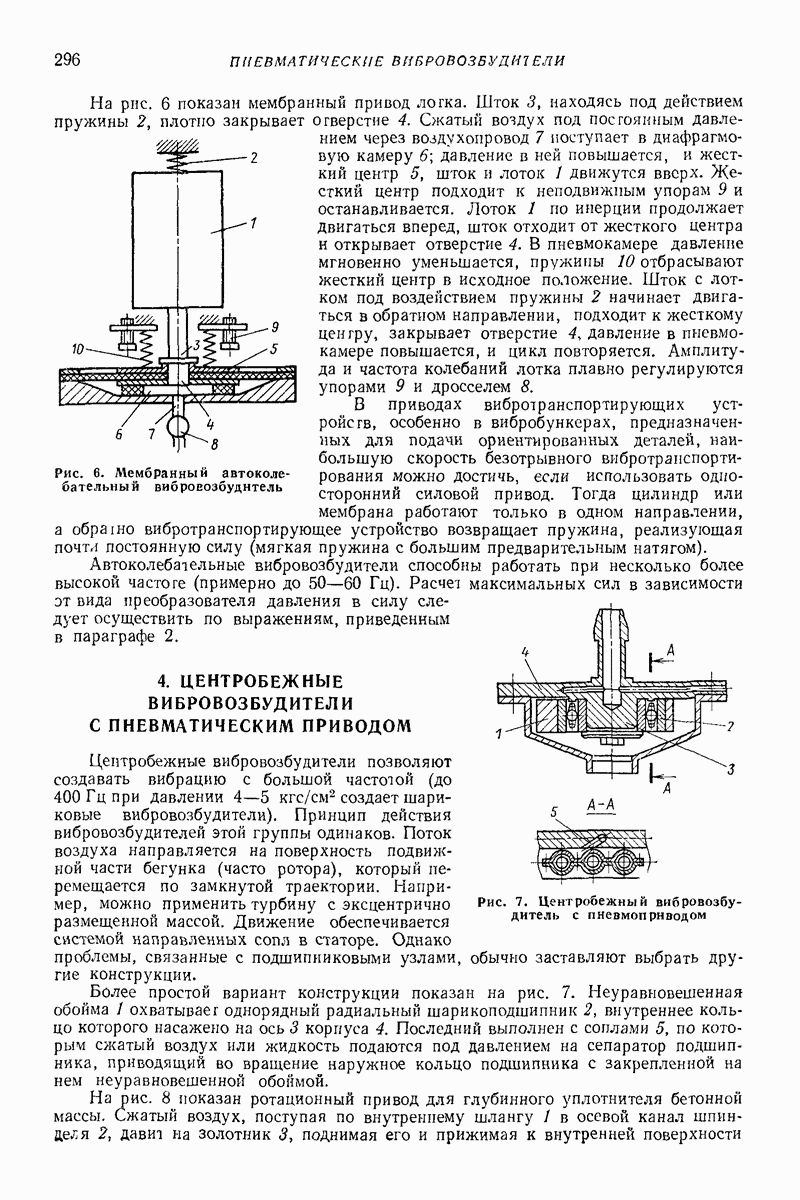
Рис. 29. Модель движения абразива и деталей при виброобработке в тороидальных контейнерах
Изменение плотности (взаимное давление) считается пропорциональным сжатию упругих элементов.
Рассмотренную на рис. 28 модель с незначительными добавлениями применяют и для виброобработки в тороидальных контейнерах. Кроме взаимного движения абразива и деталей и циркуляционного движения следует еще моделировать движение
вдоль тороидальной поверхности. Для учета дополнительных сопротивлений в этом направлении добавляются вязкие элементы (рис. 29). В данной модели энергия взаимодействия абразива и деталей моделируется только вязкими элементами. Для простоты пара трения и разделение массы в центре опущены.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
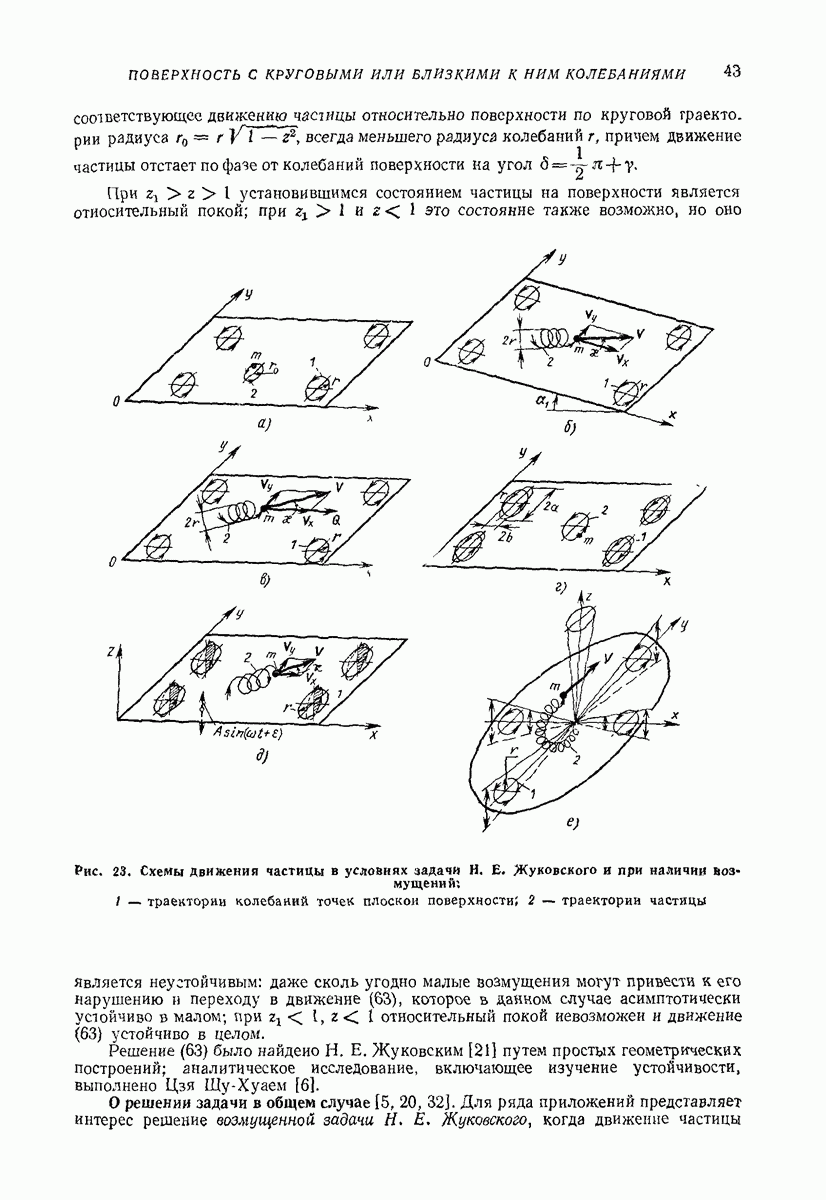
- Установившиеся режимы движения частицы.
- О методах решения задачи.
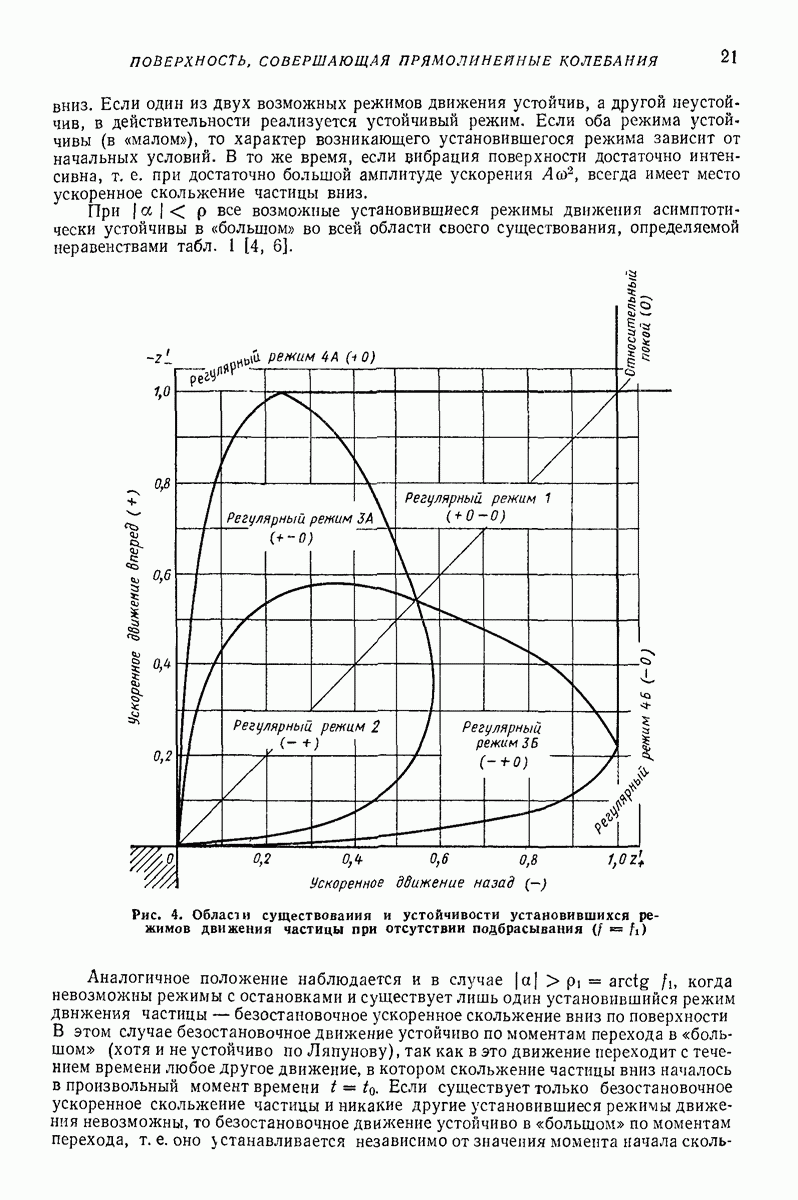
- Установившиеся режимы при отсутствии подбрасывания [4-6].
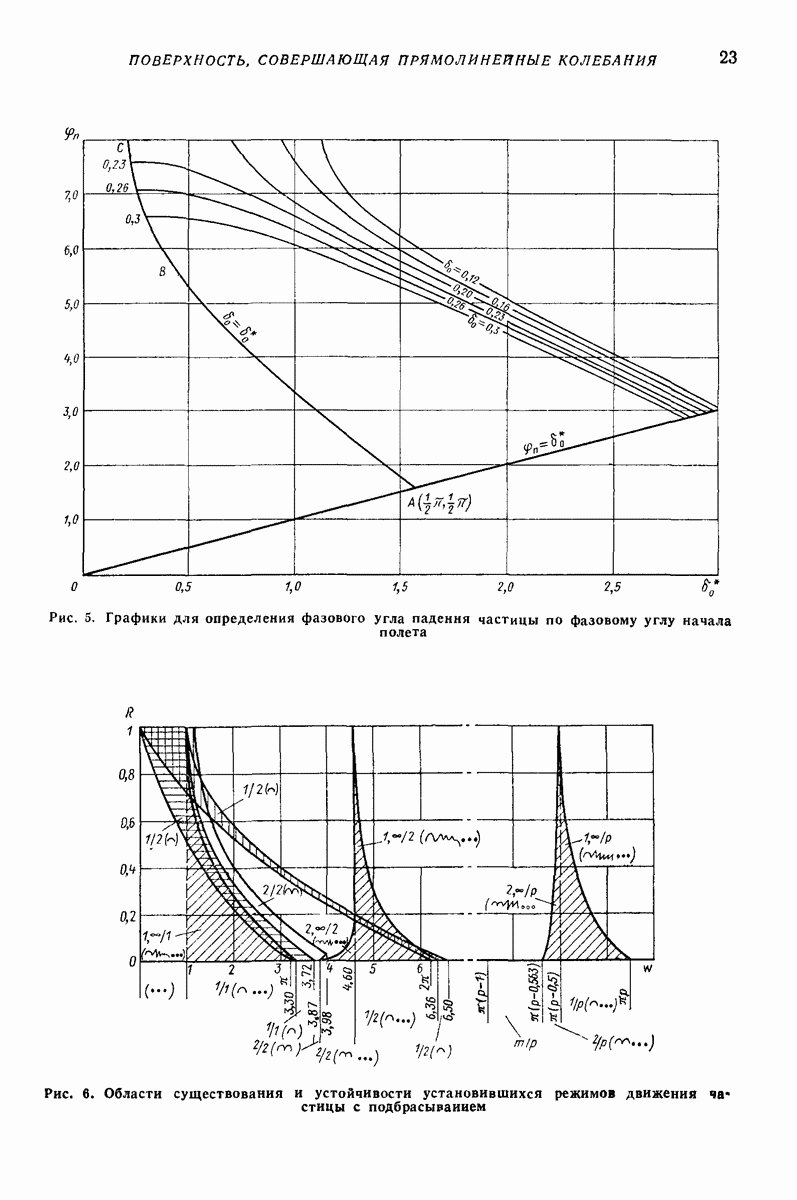
- Установившиеся режимы с подбрасыванием.
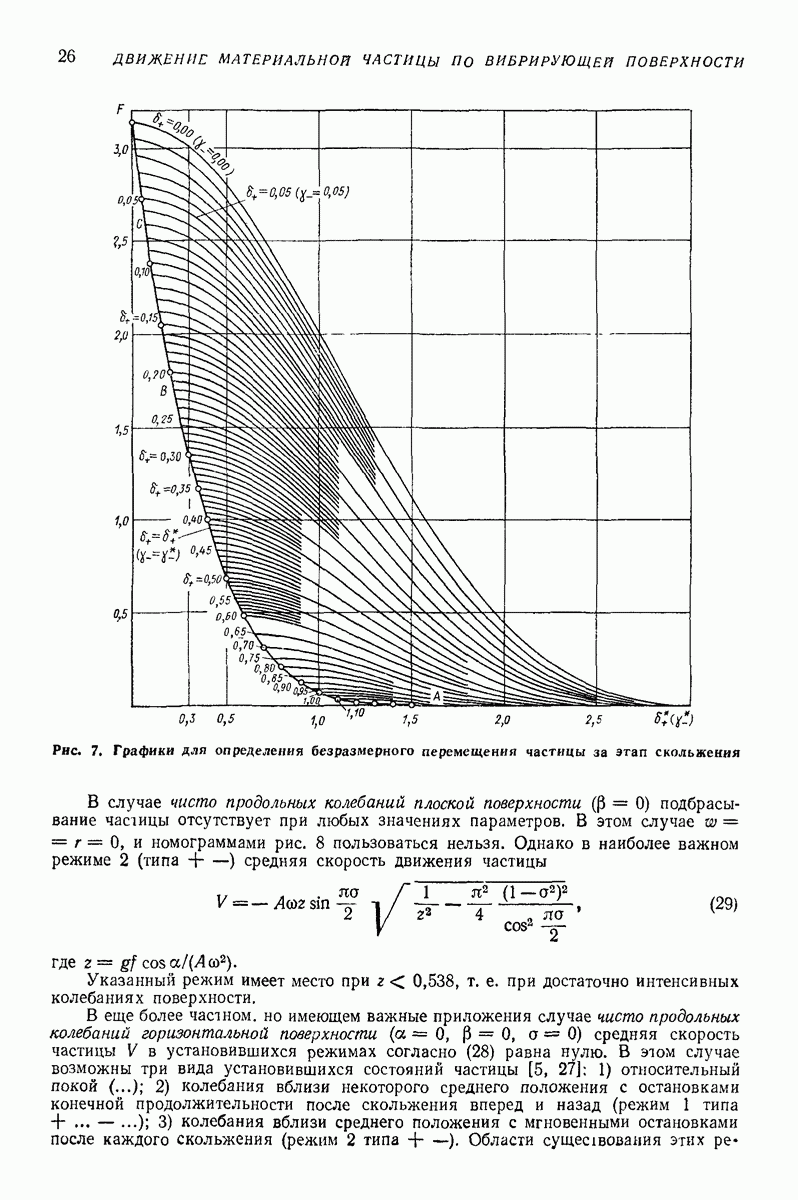
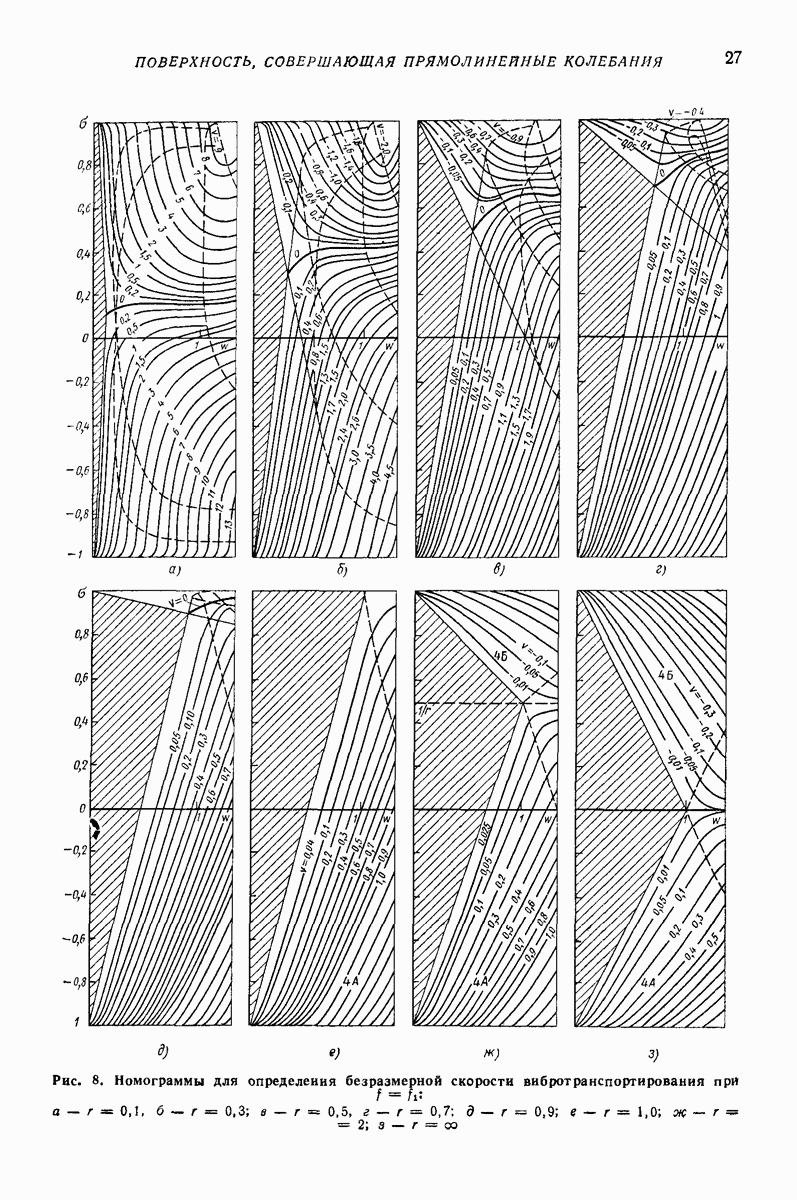
- Средние скорость и ускорение частицы в установившихся режимах движения.
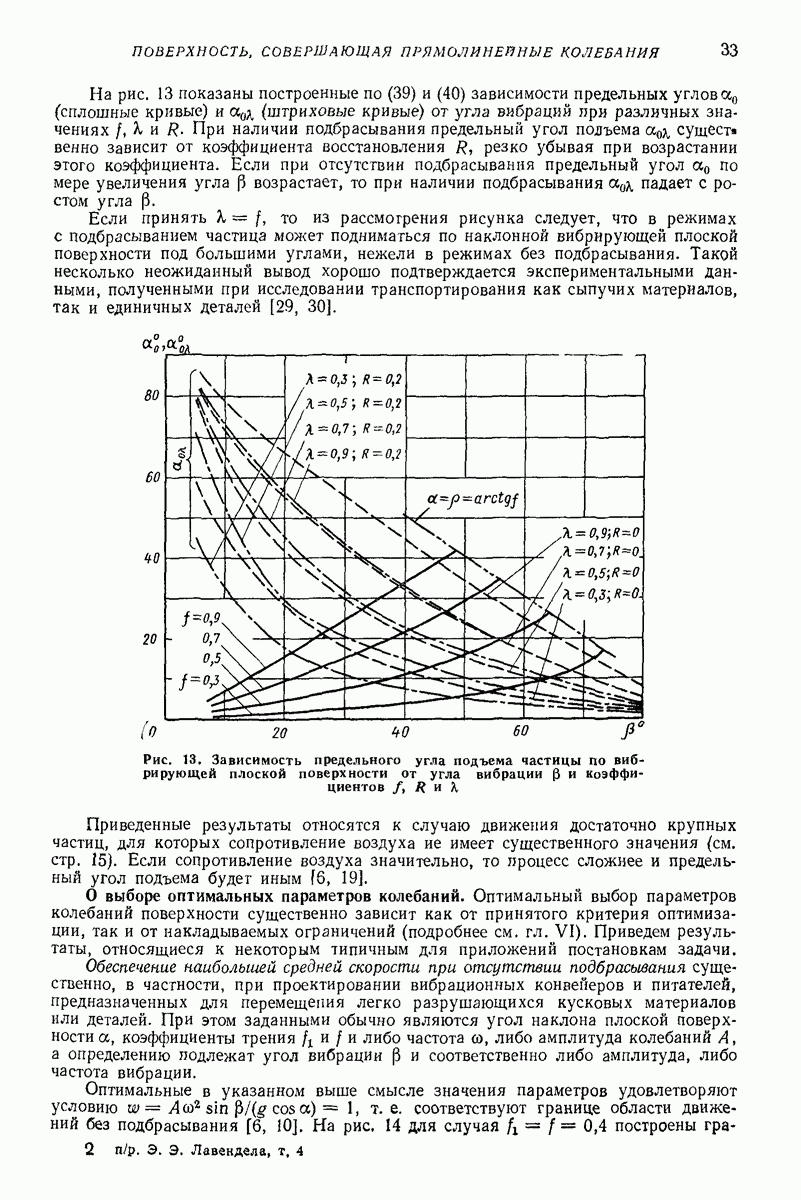
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
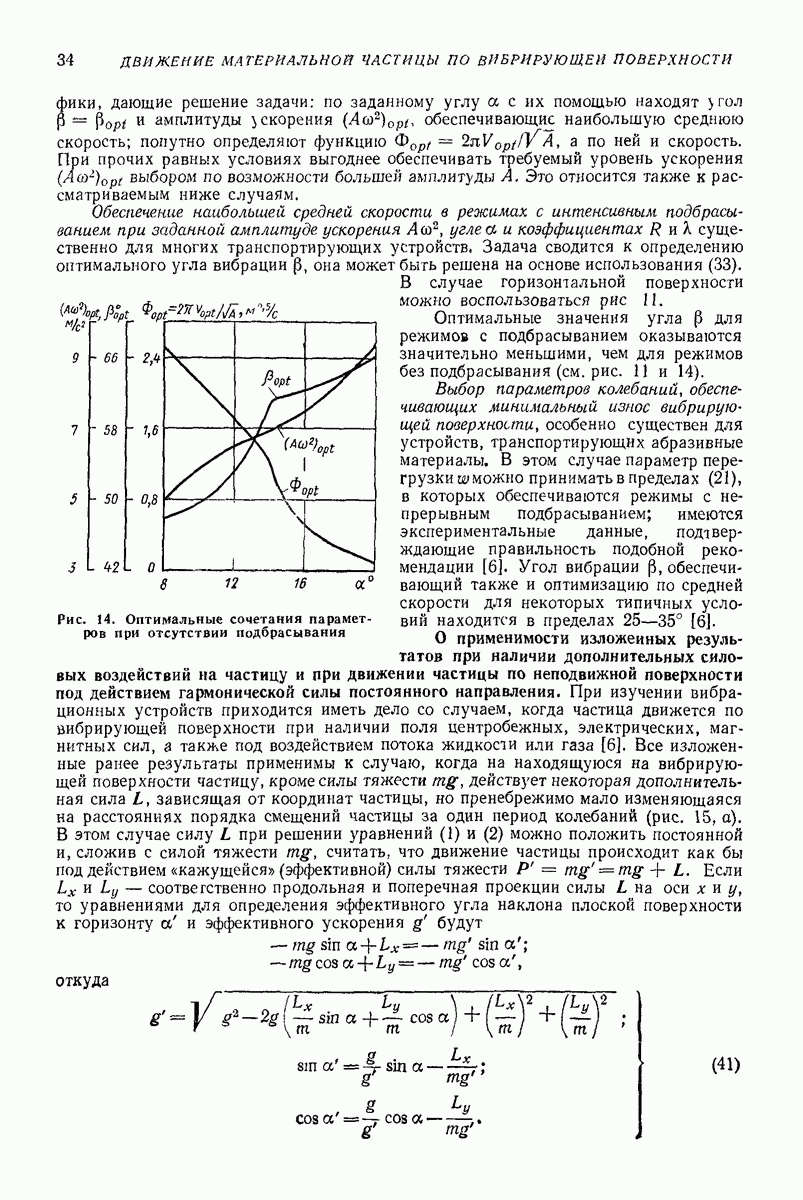
- О выборе оптимальных параметров колебаний.
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
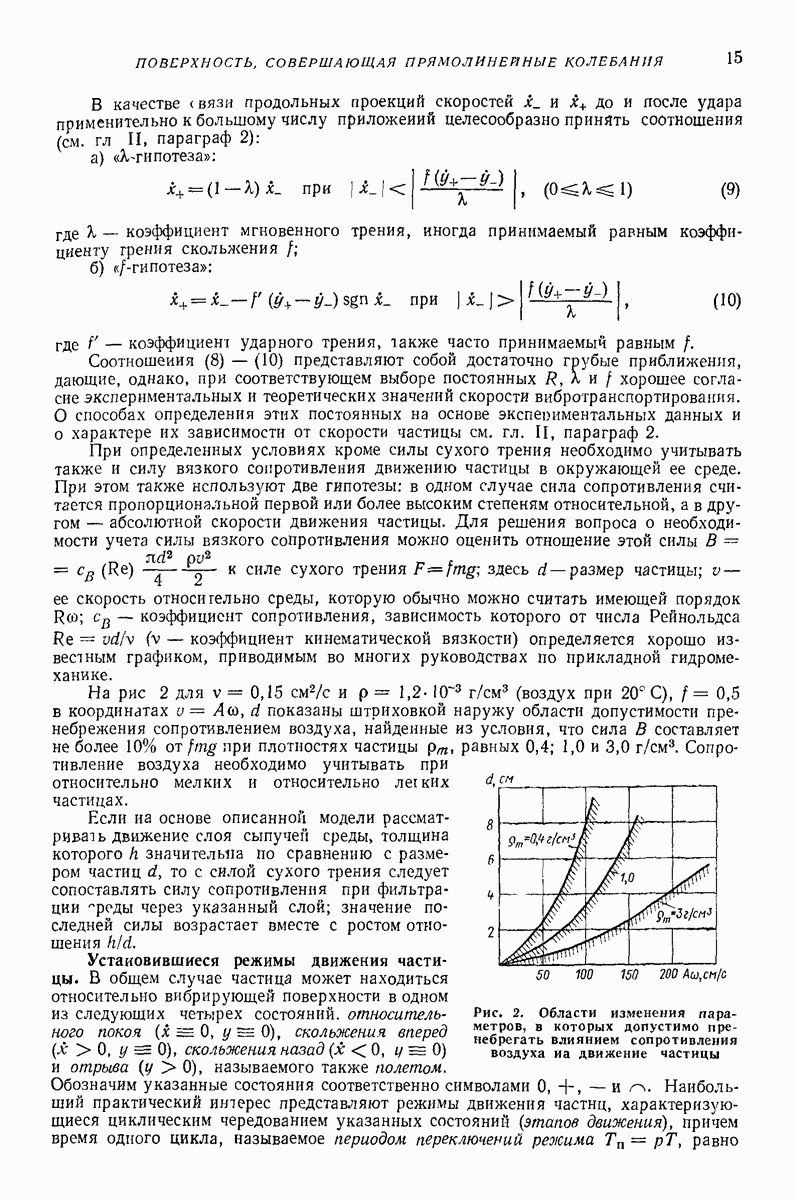
- О влиянии на движение частицы сил вязкого сопротивления.
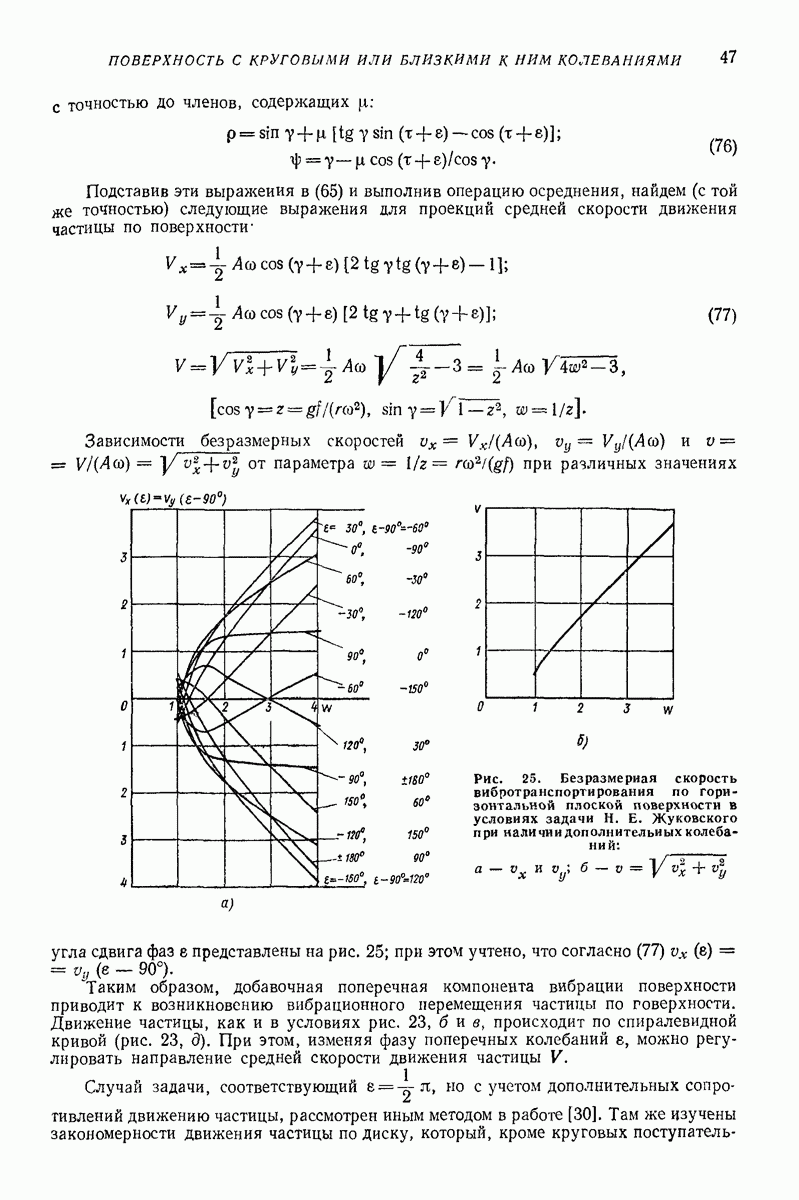
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
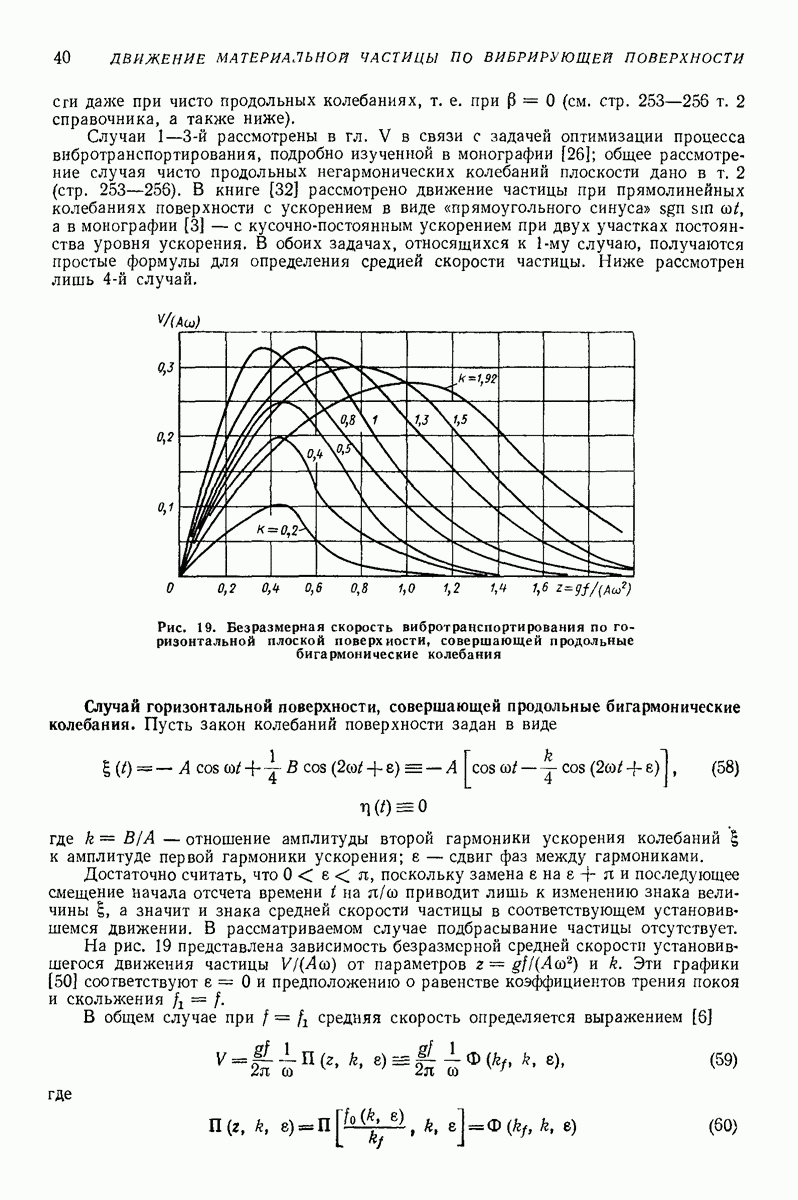
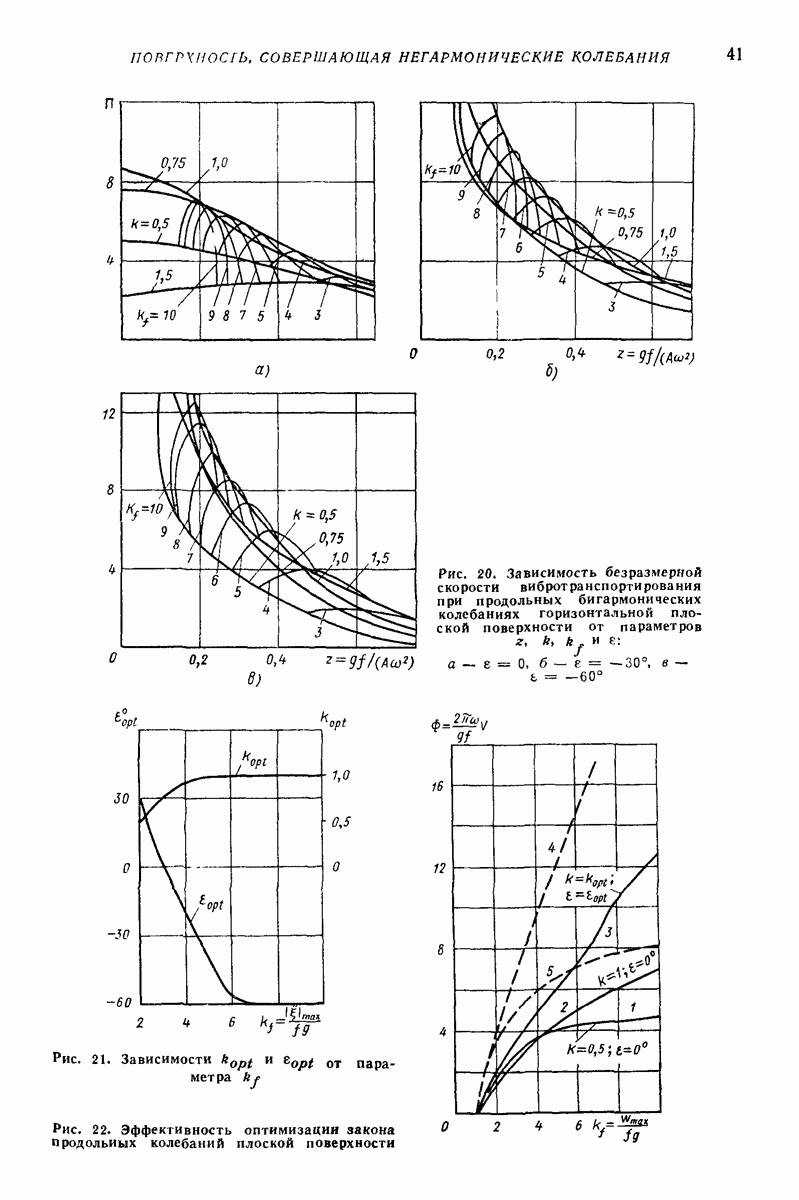
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
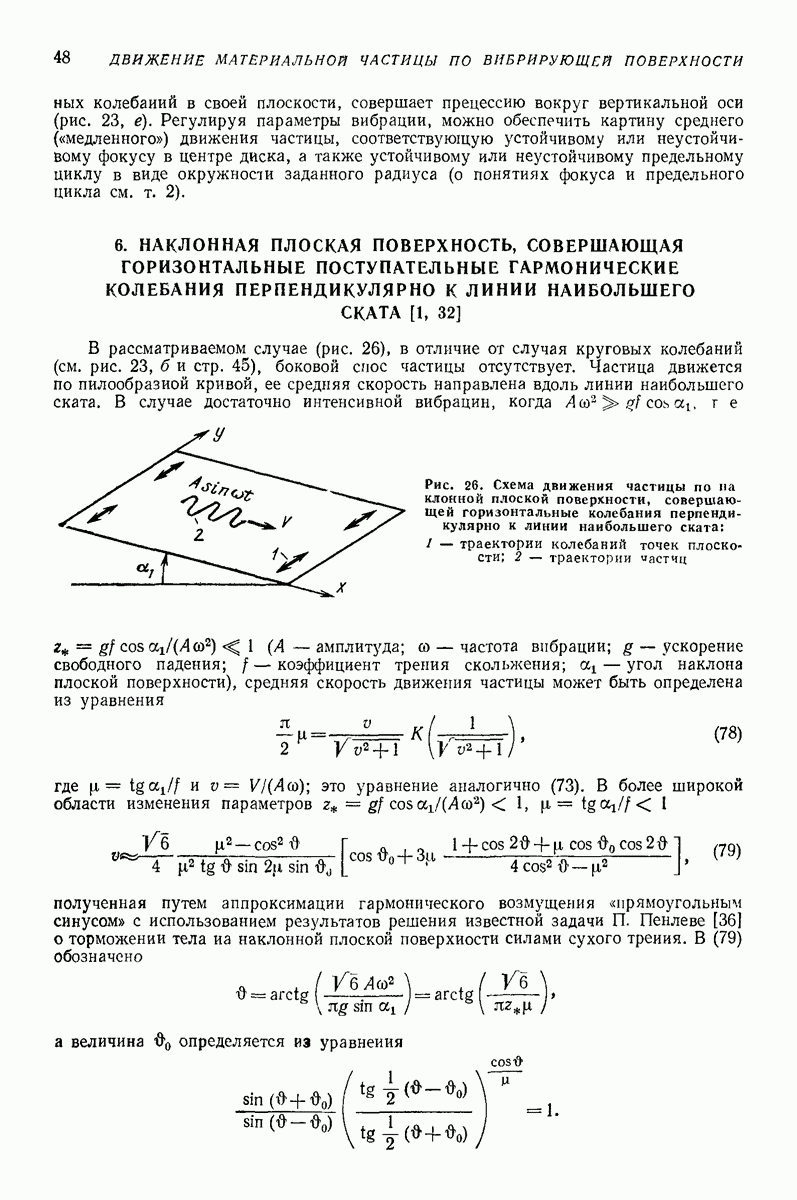
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
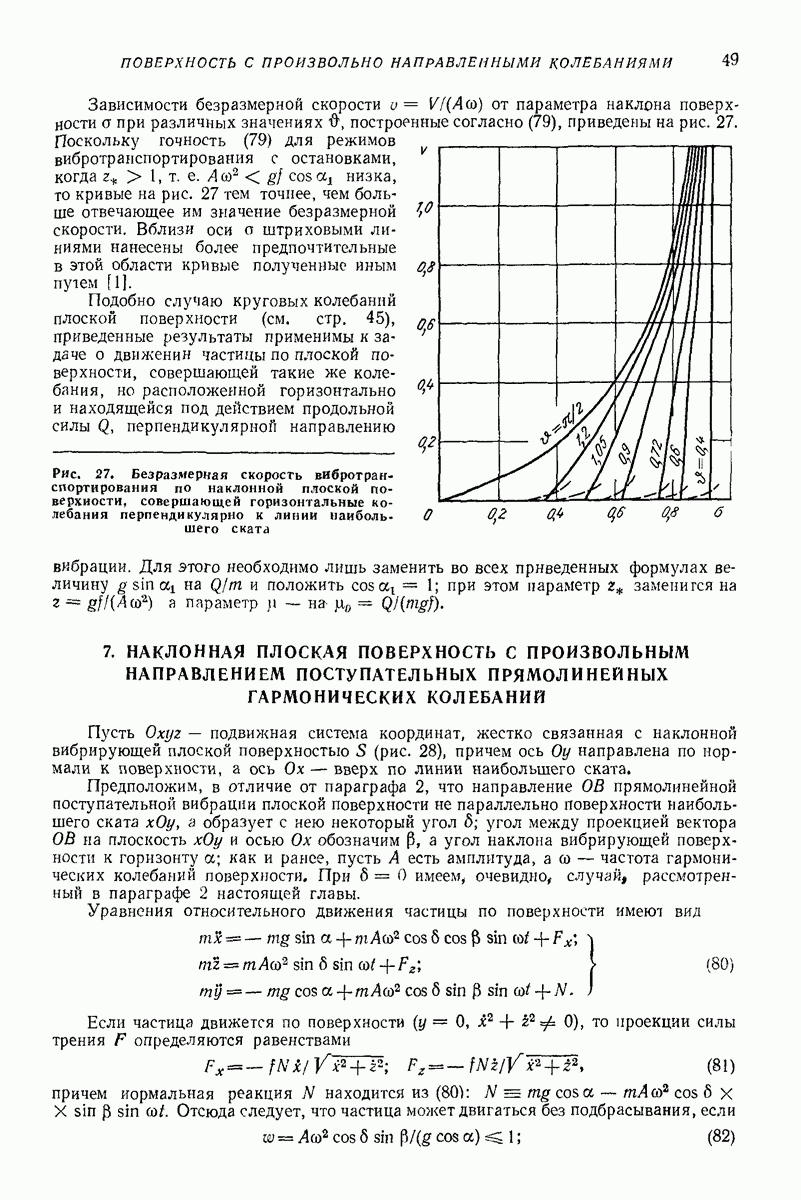
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
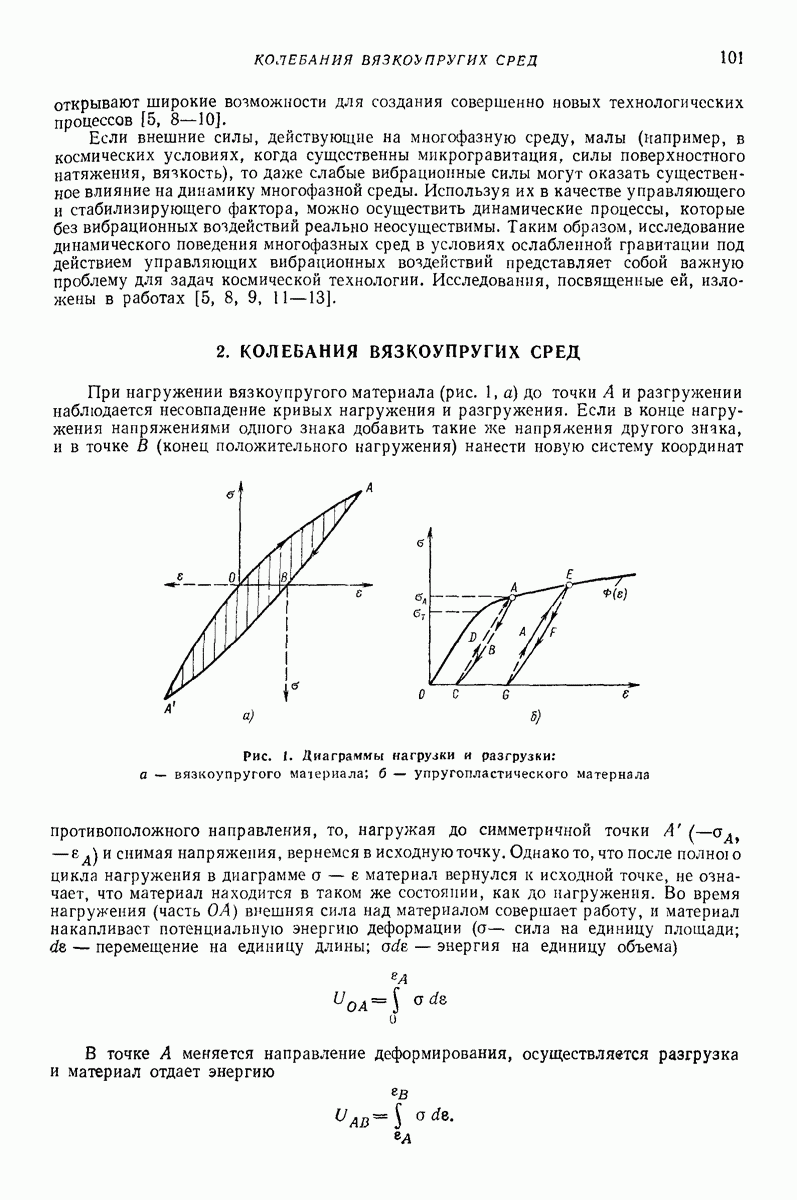
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
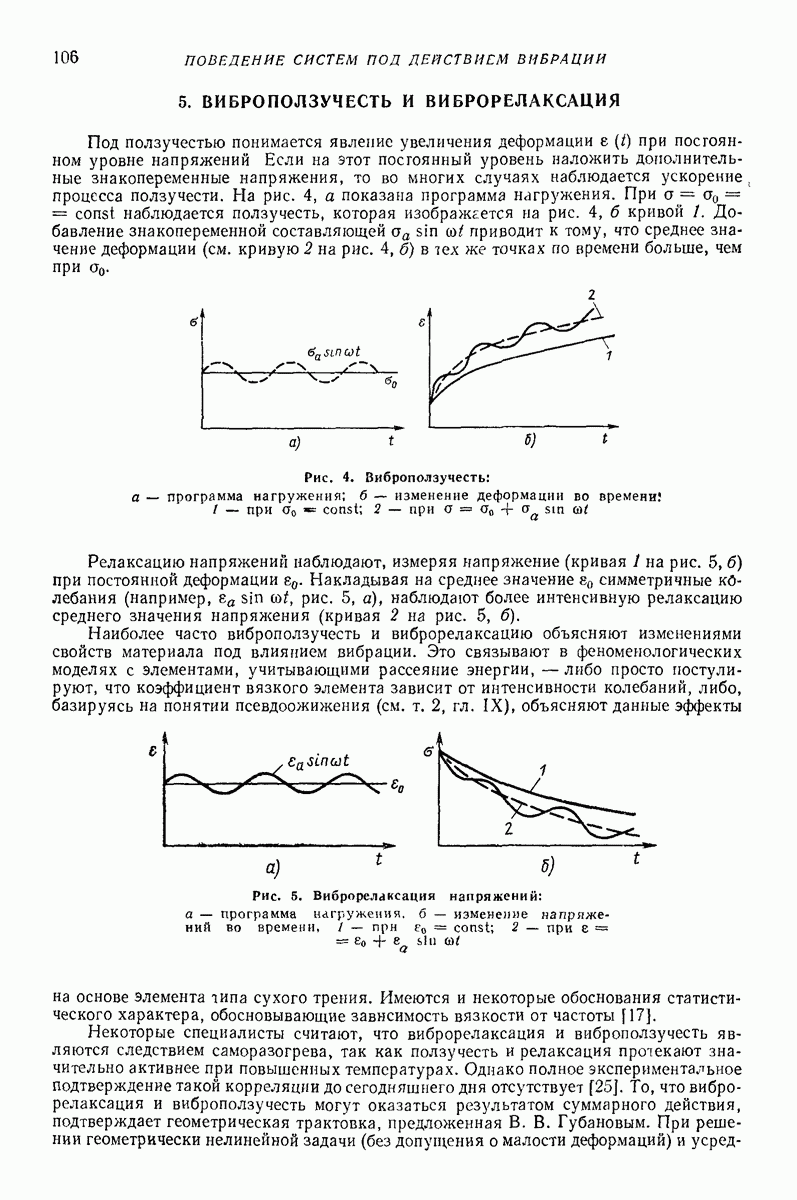
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
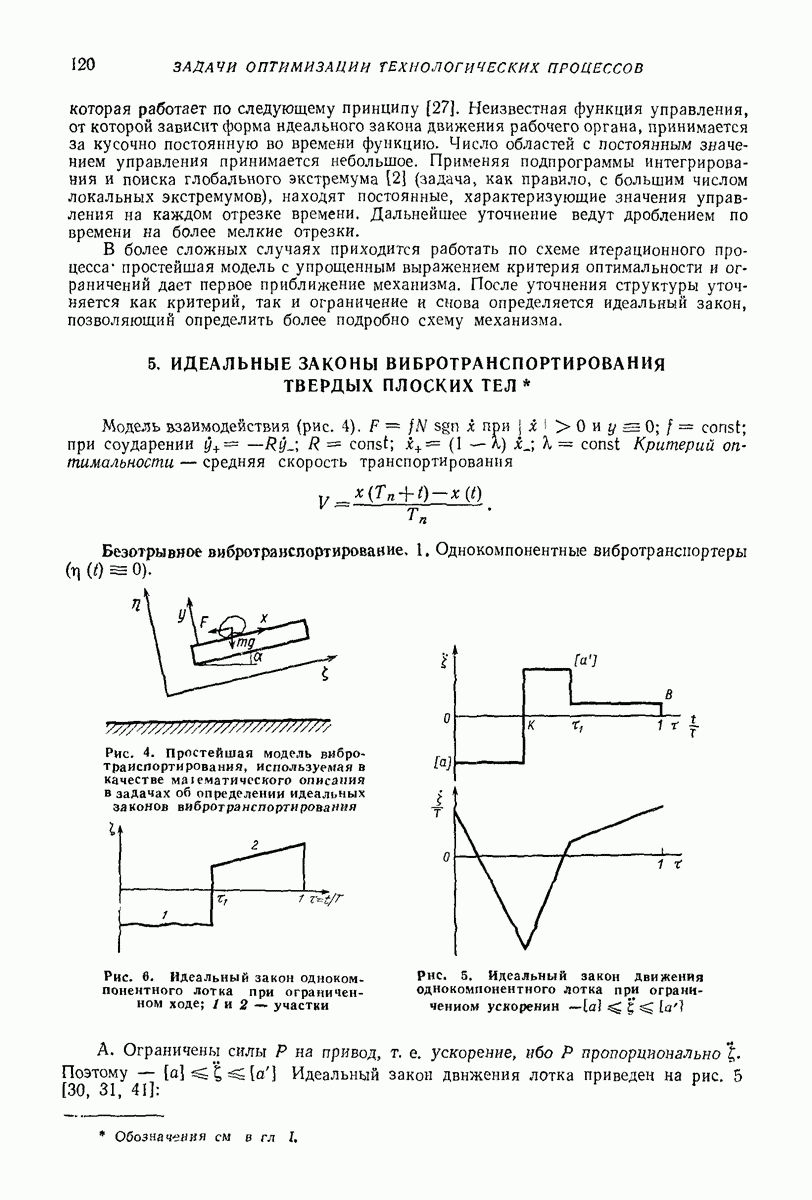
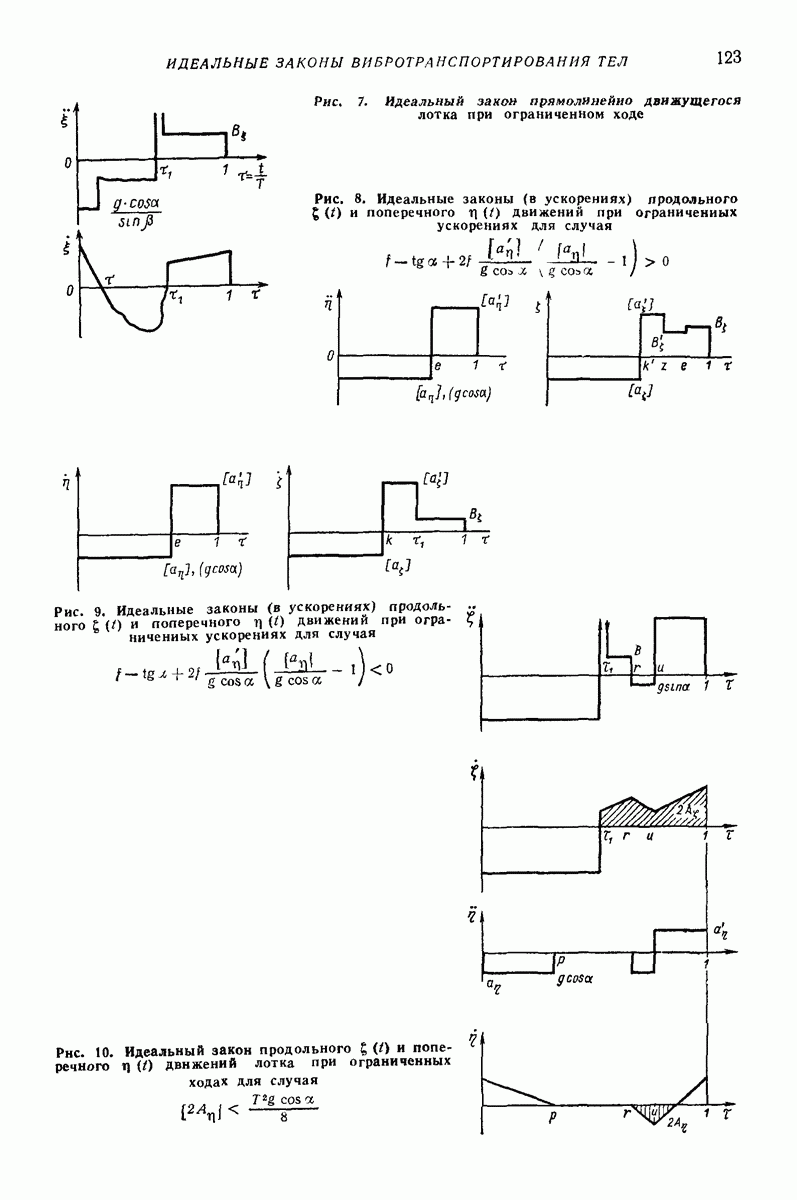
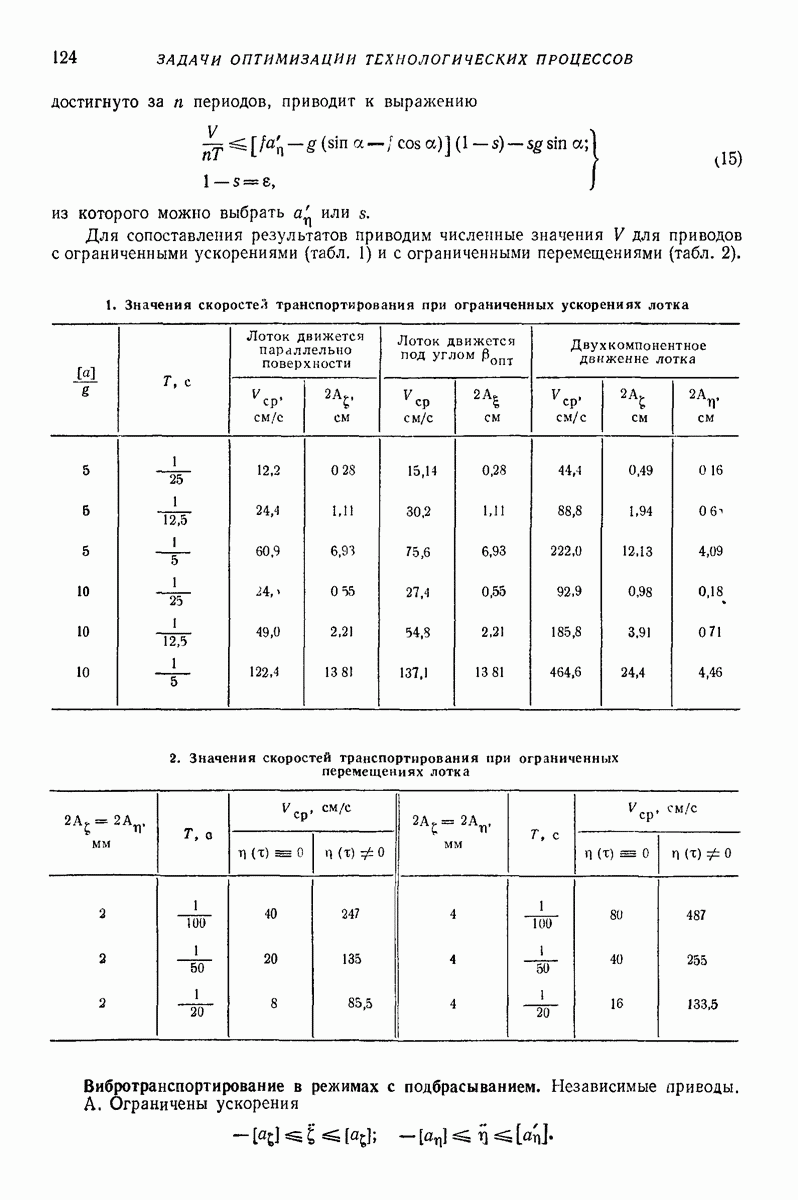
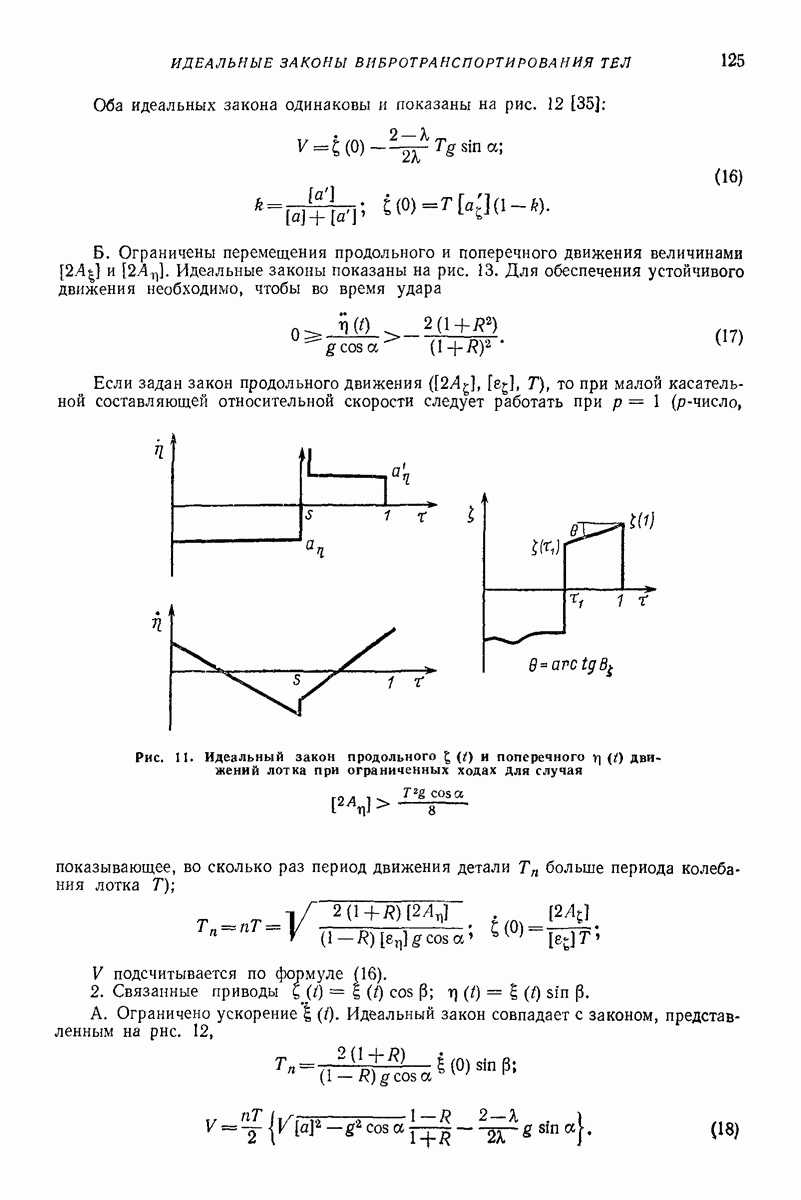
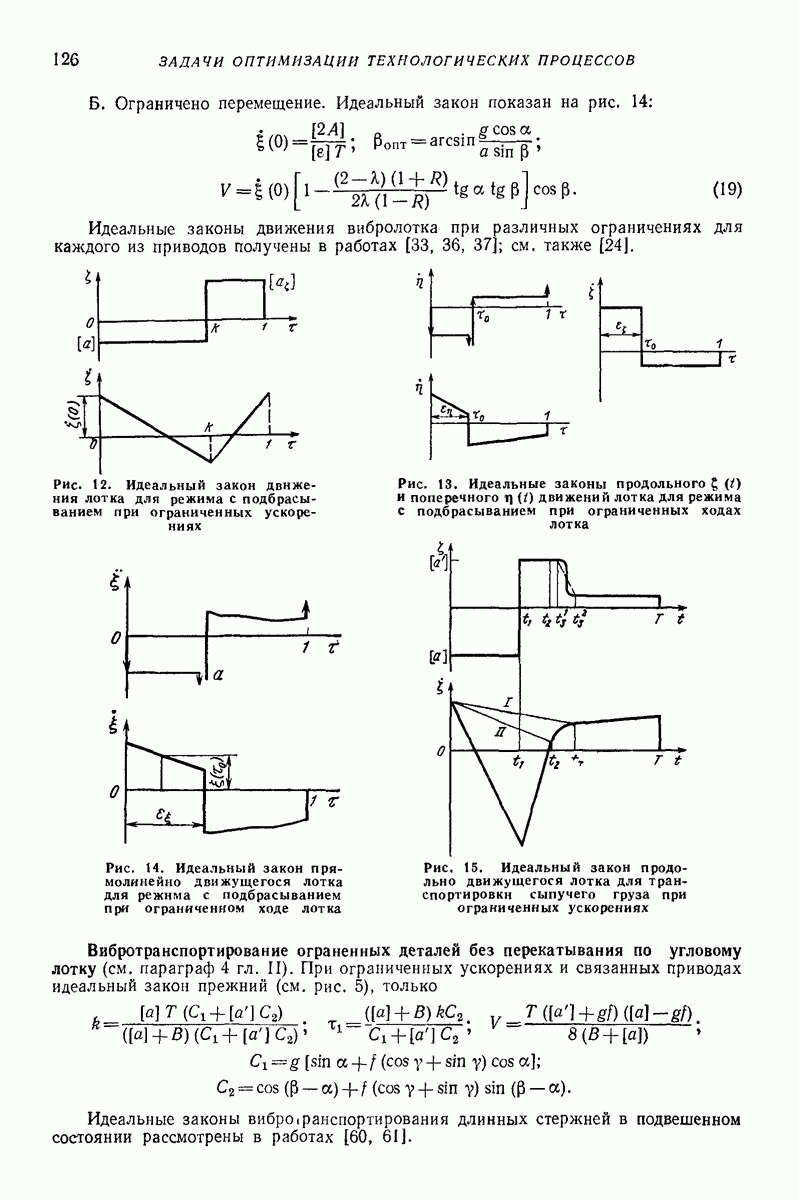
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
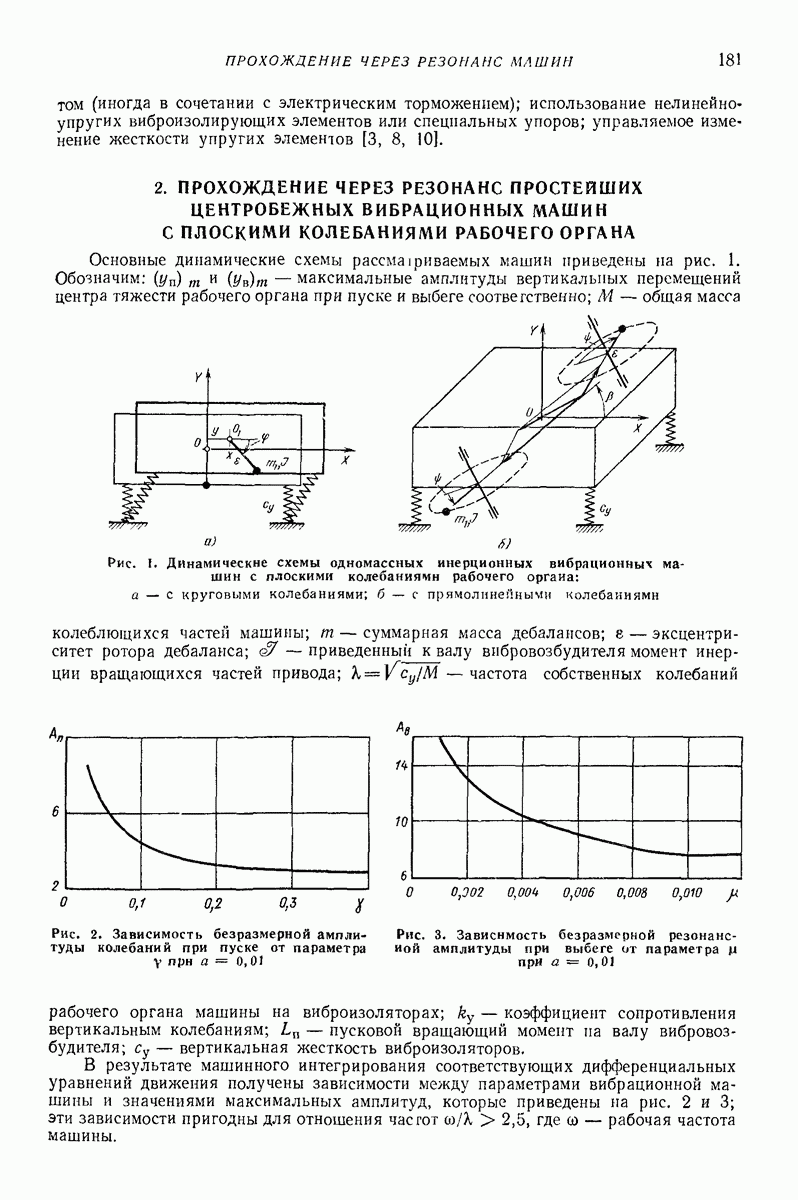
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
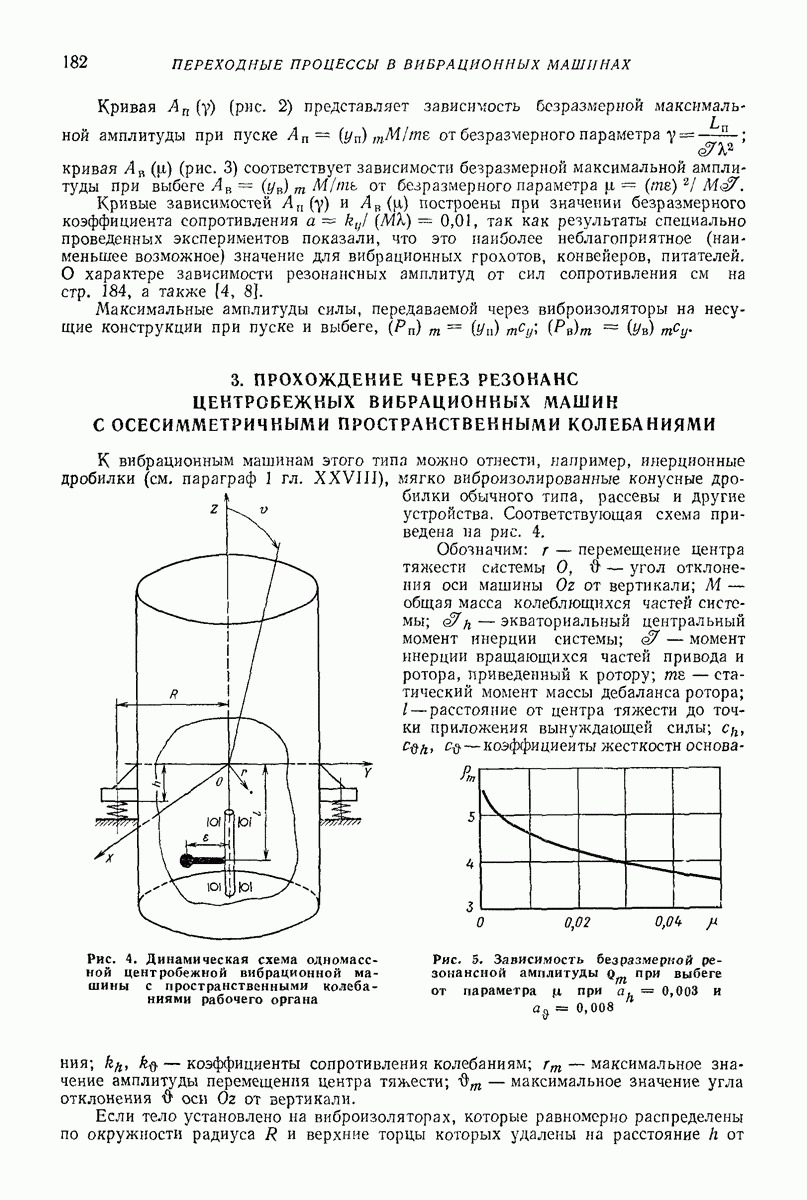
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
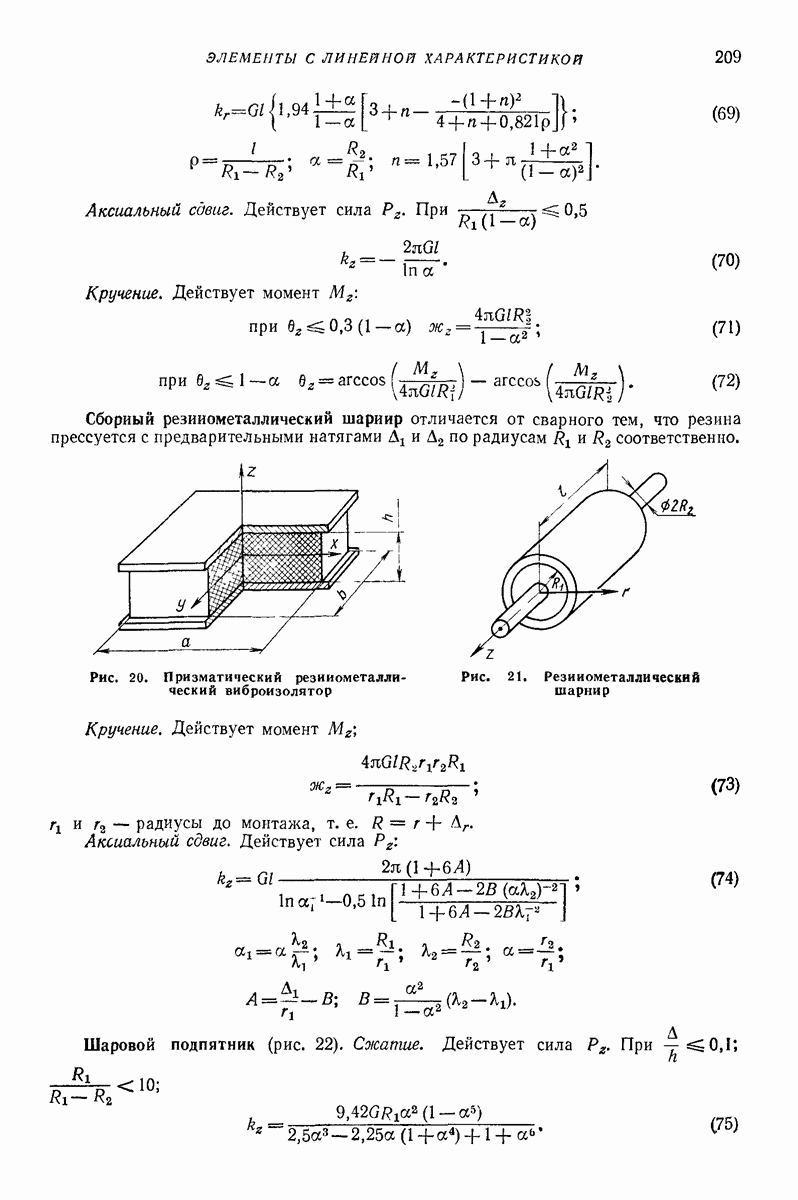
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
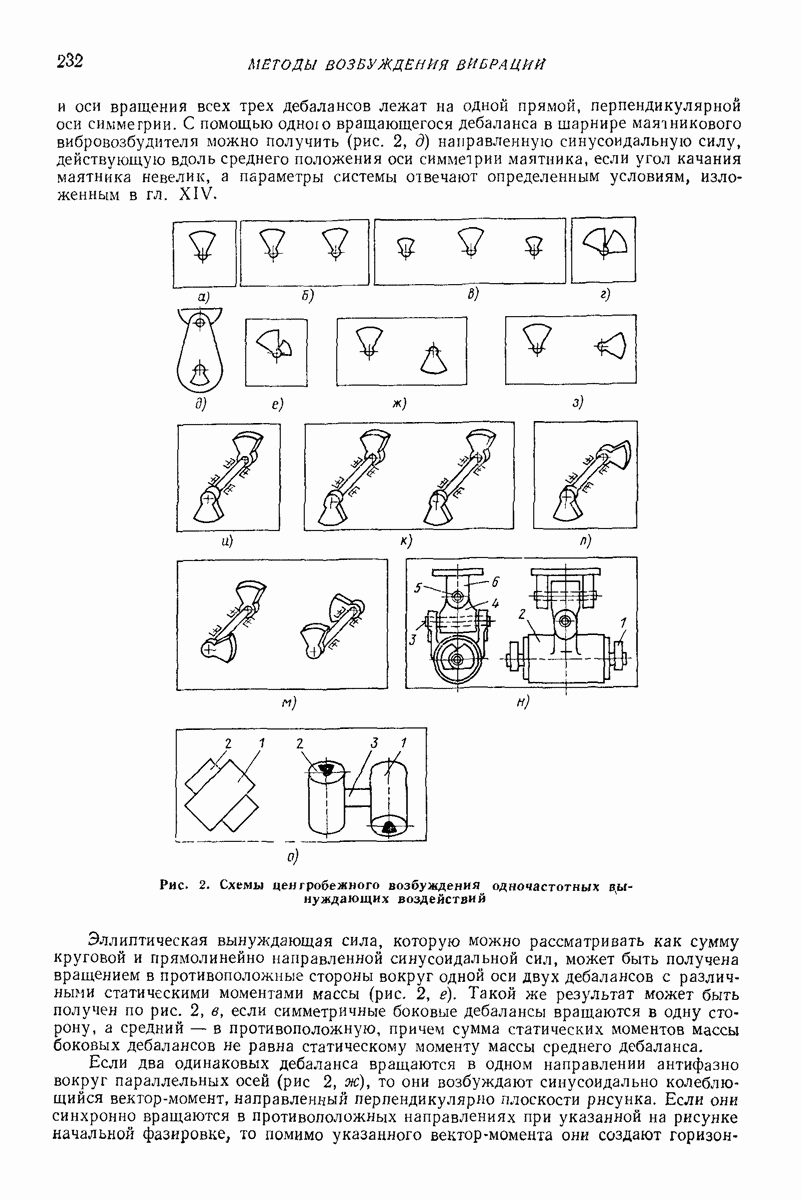
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
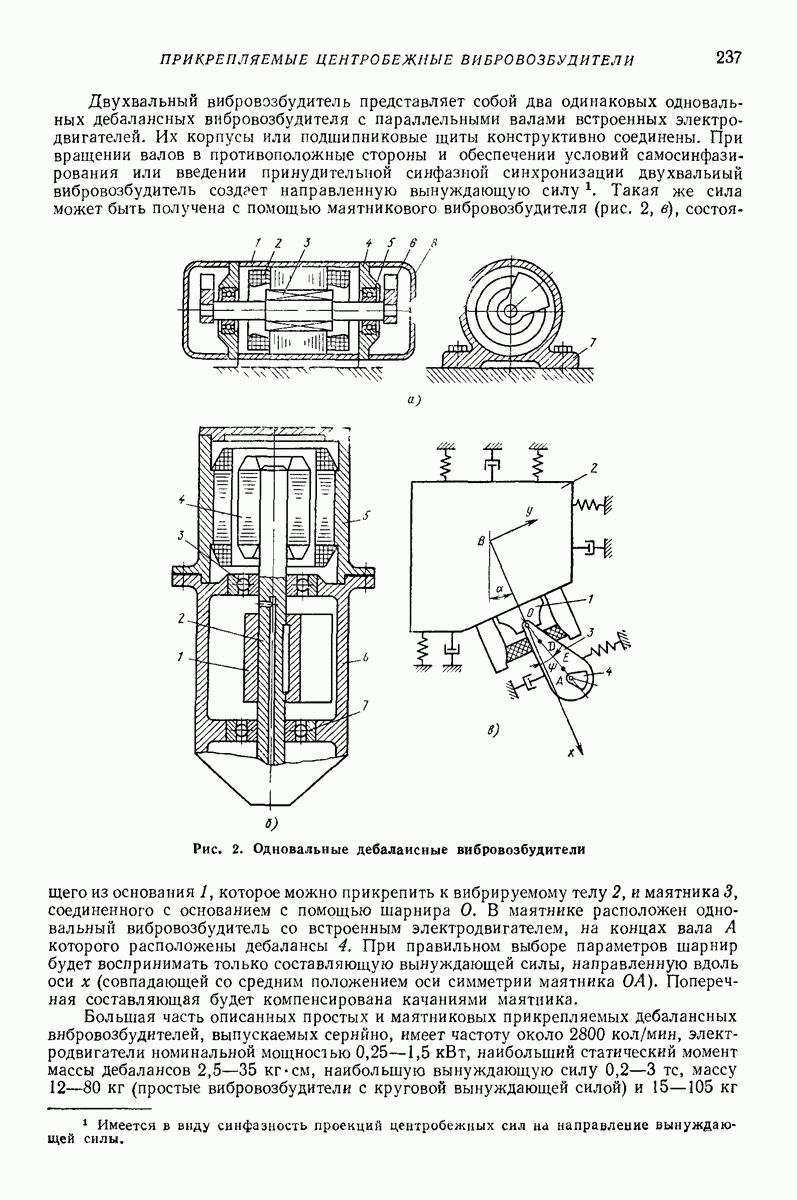
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
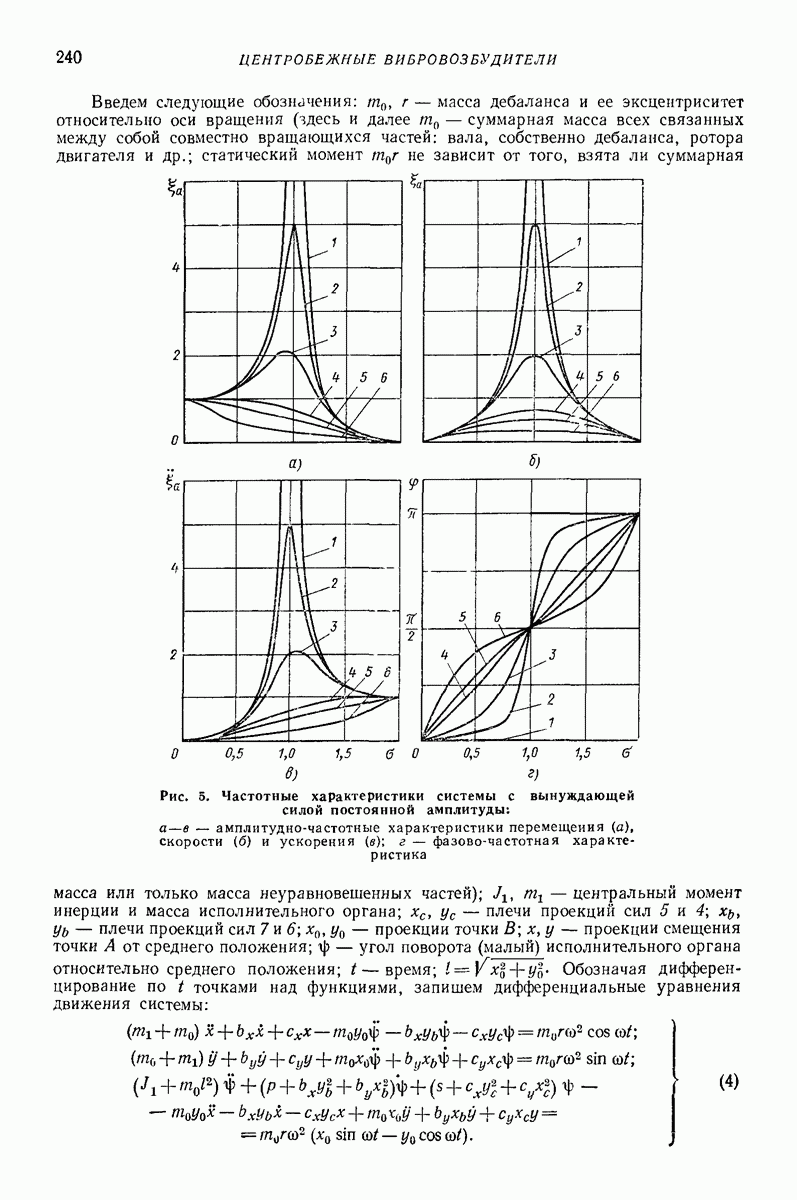
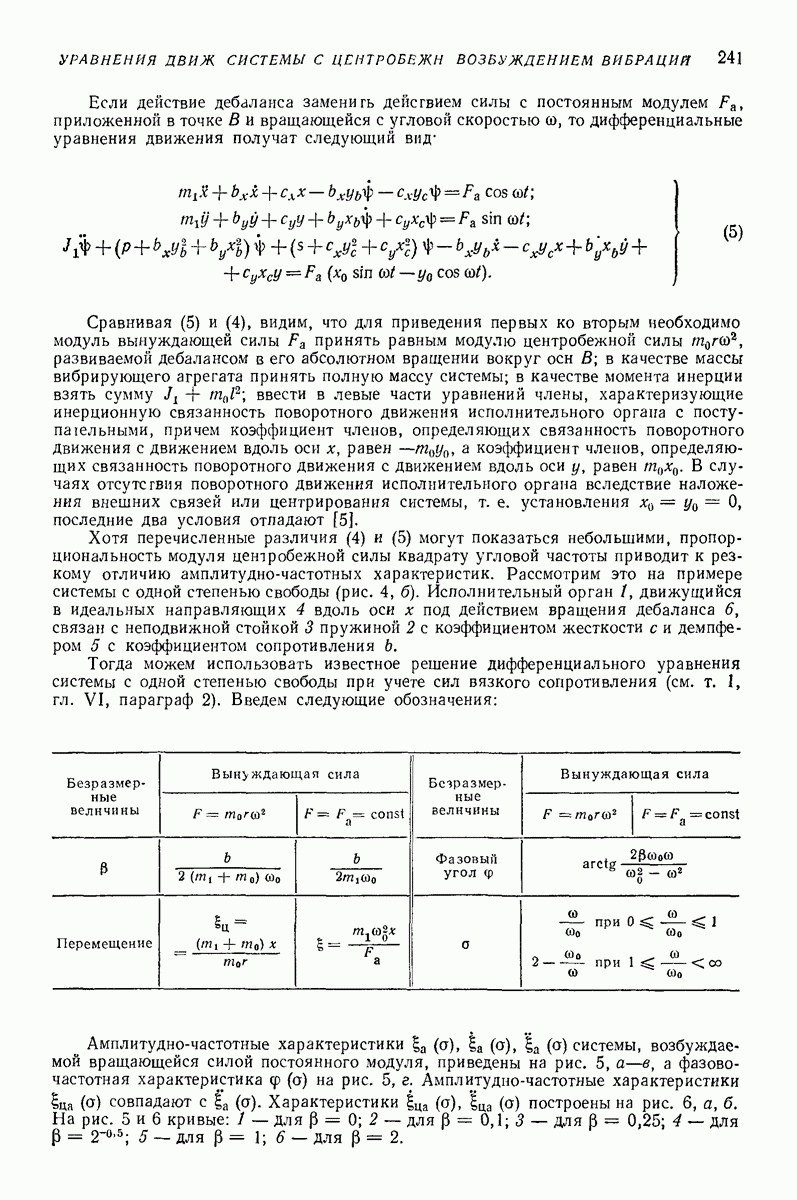
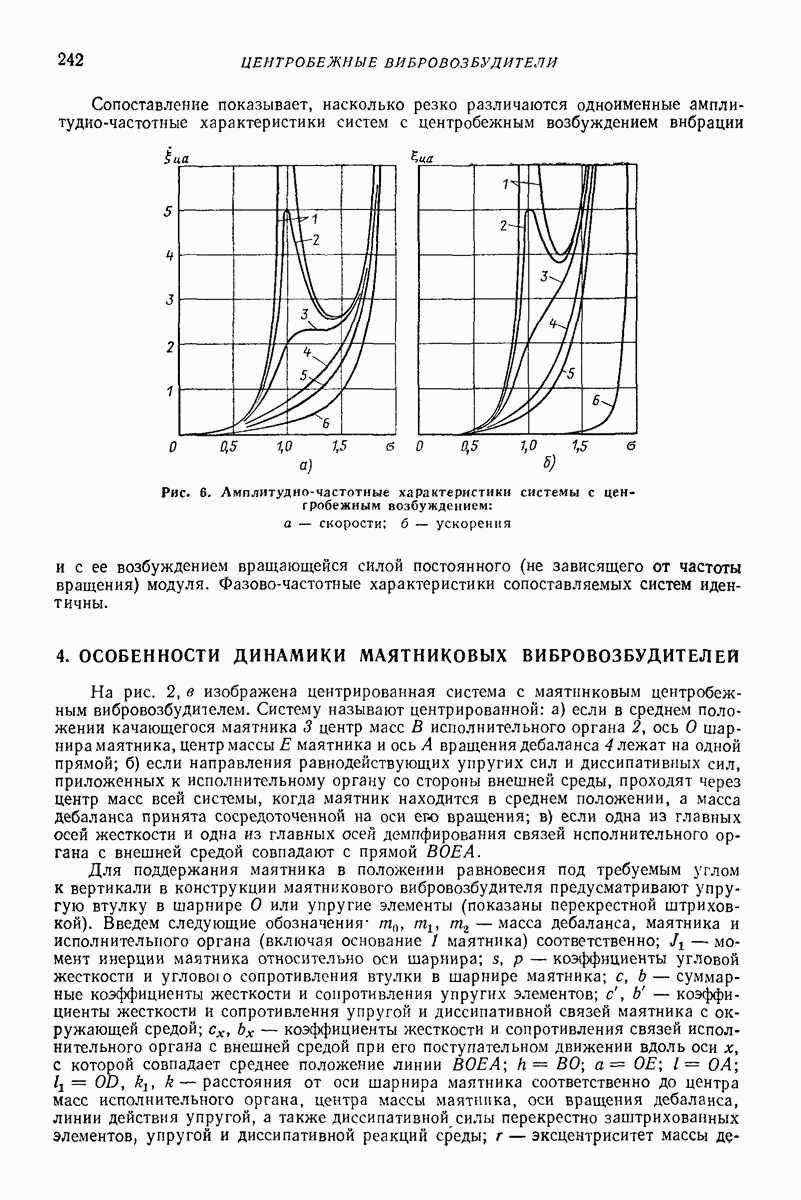
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
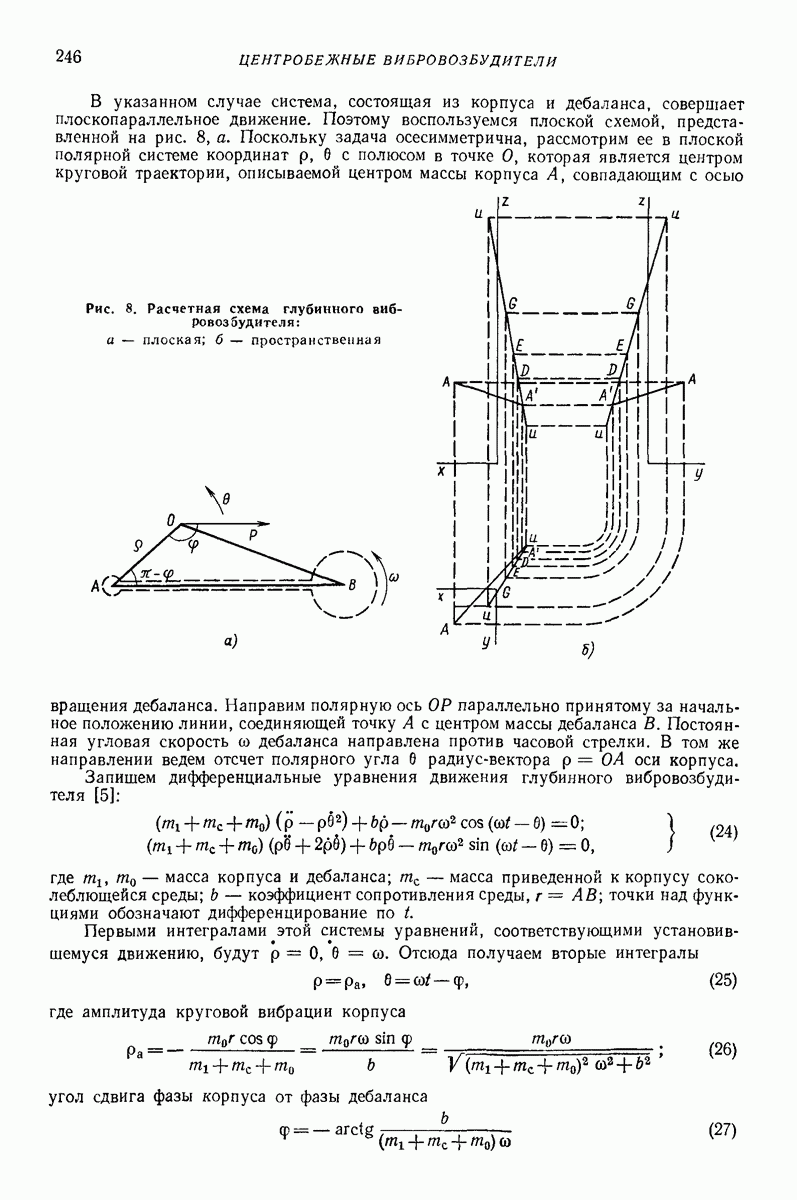
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
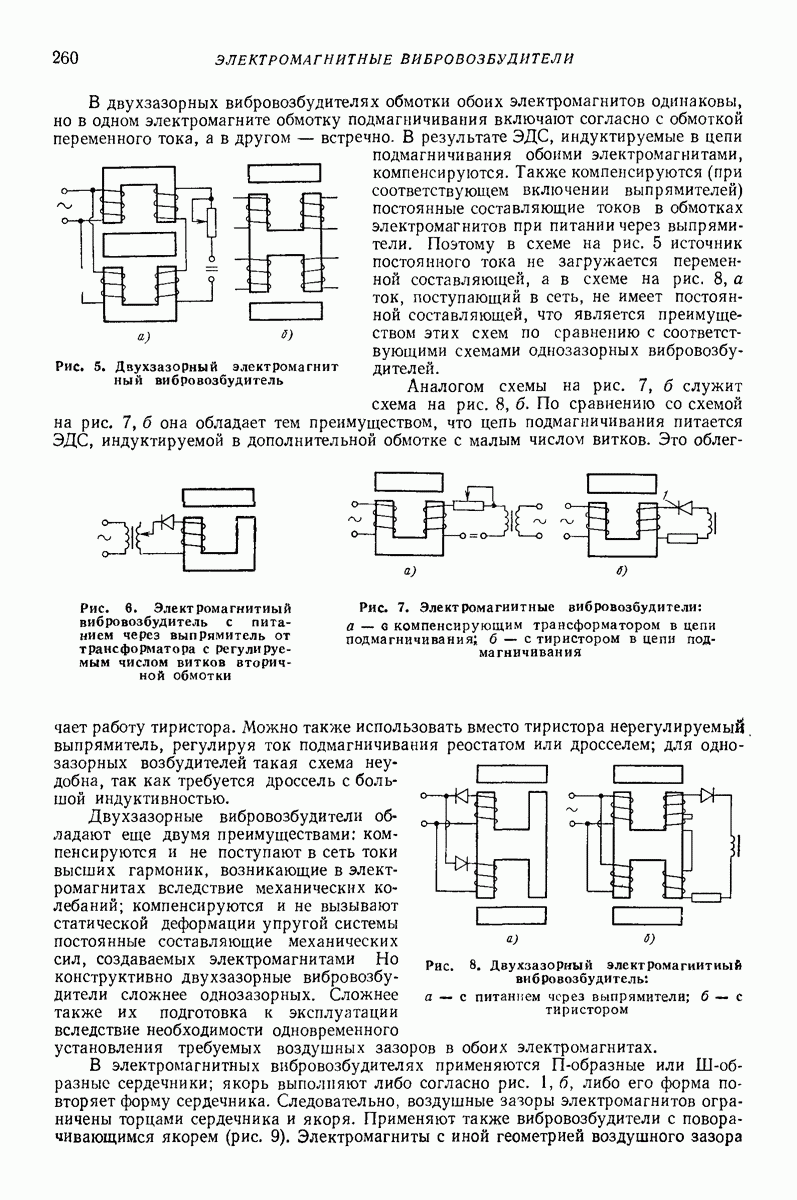
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
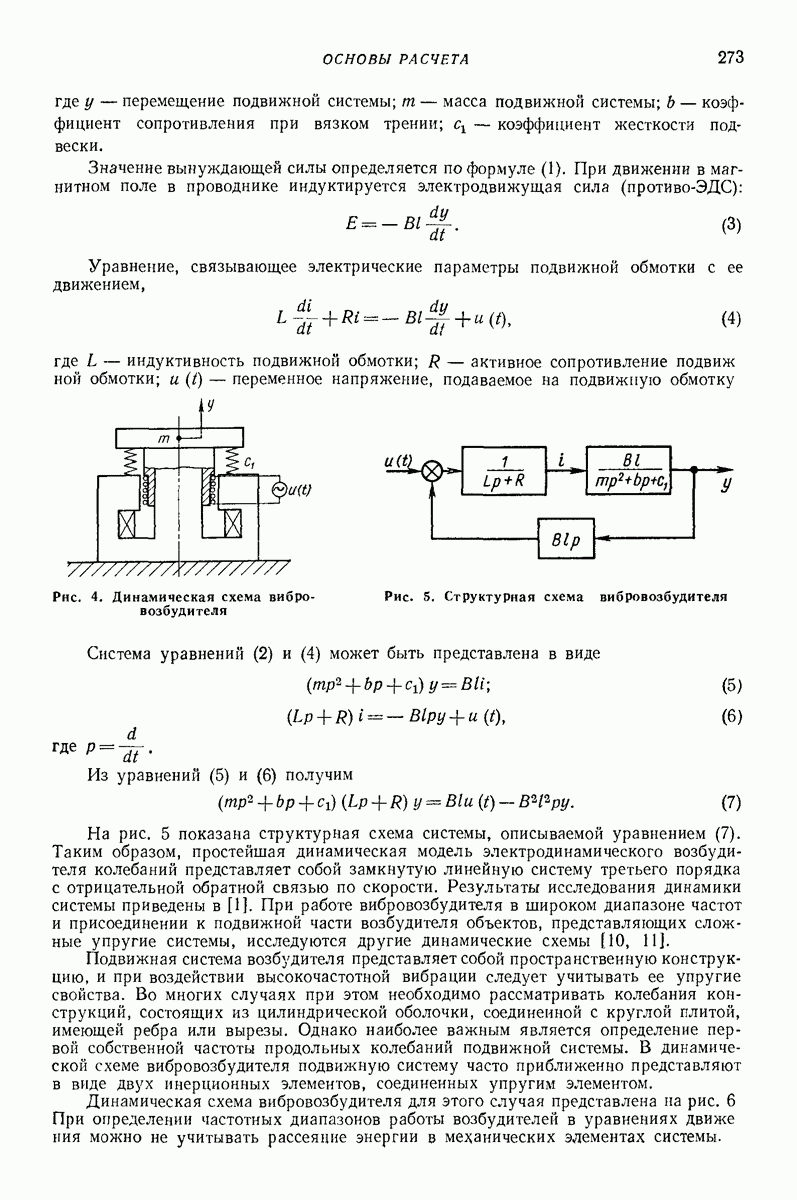
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
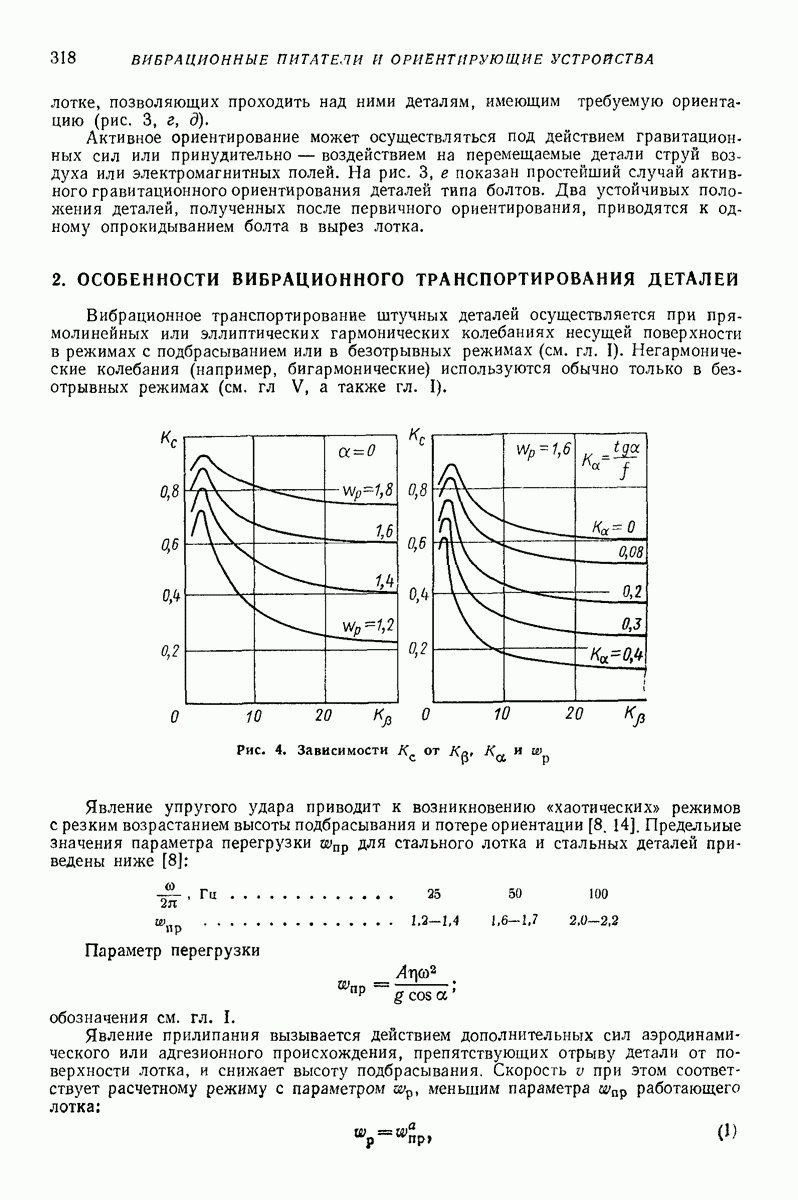
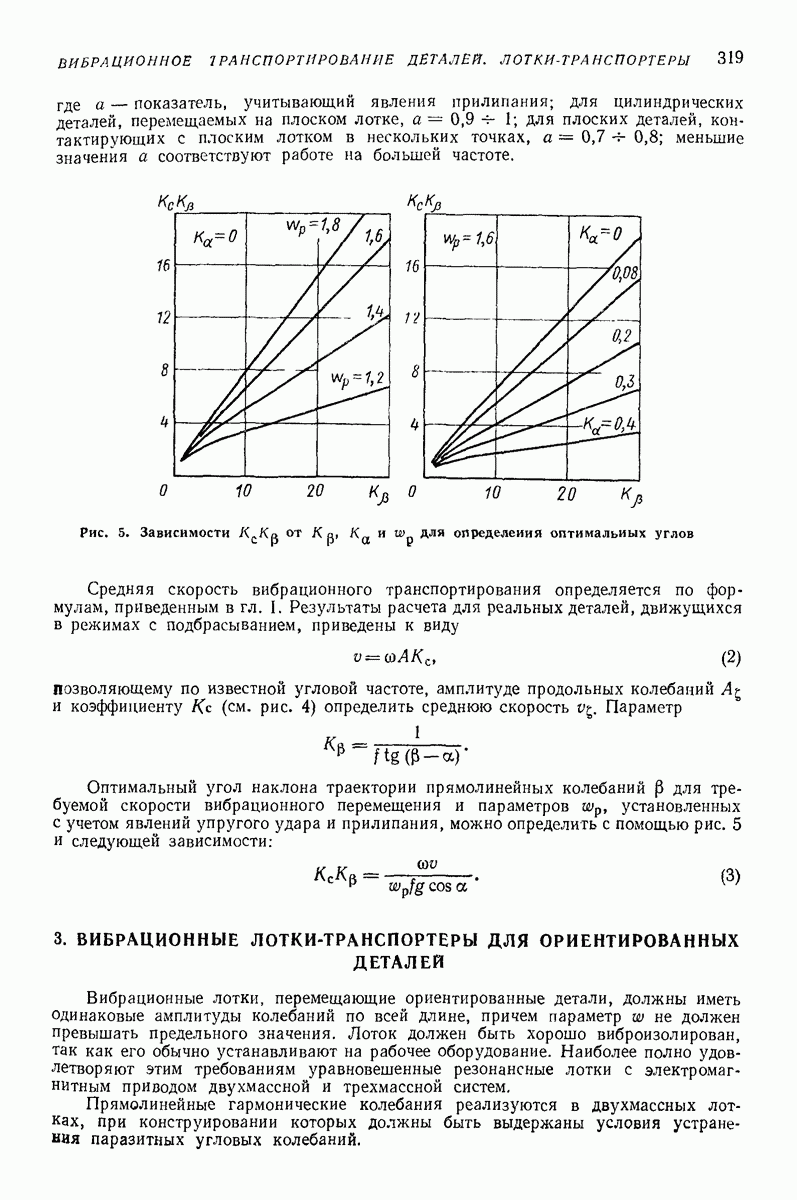
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
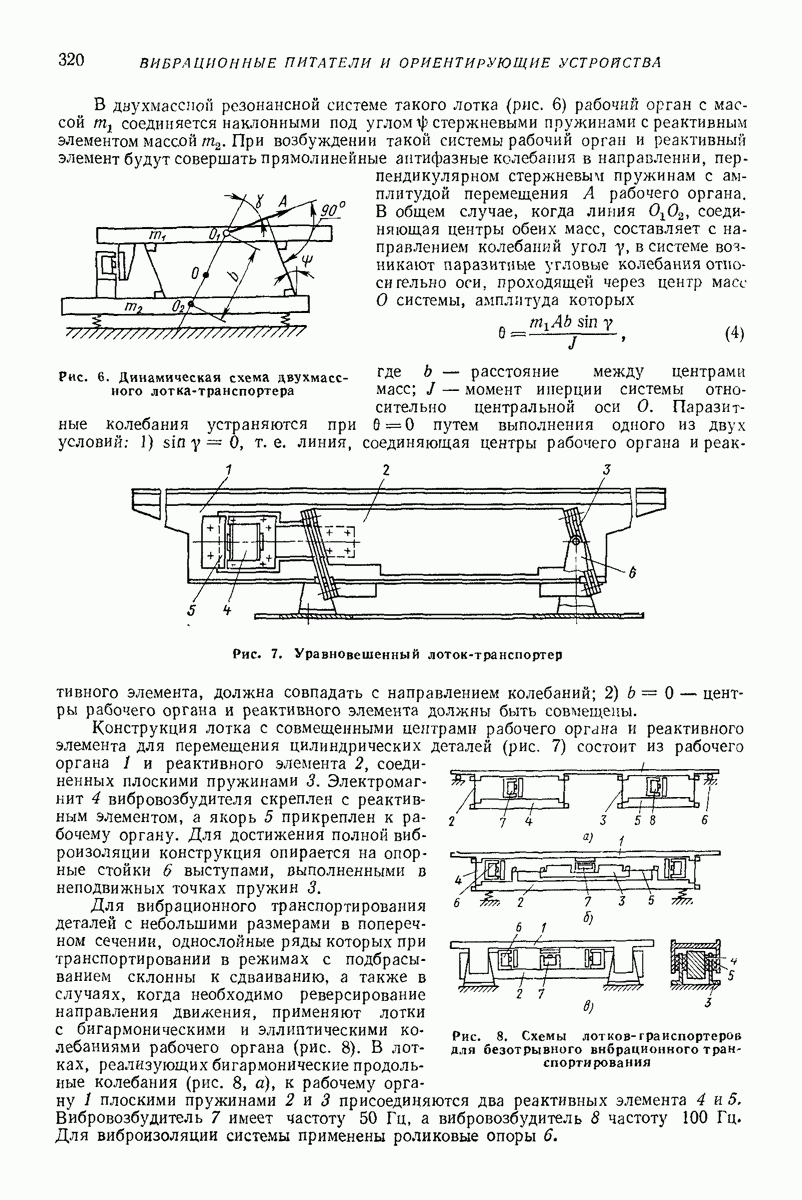
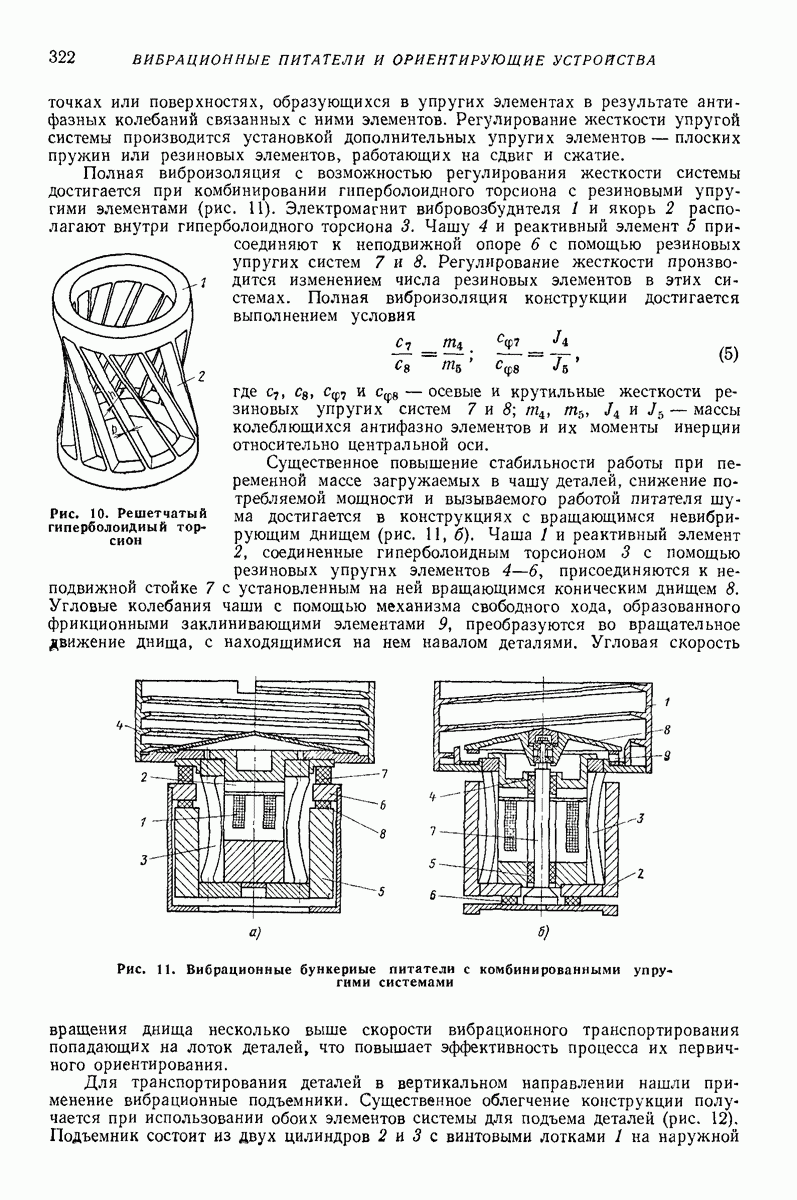
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
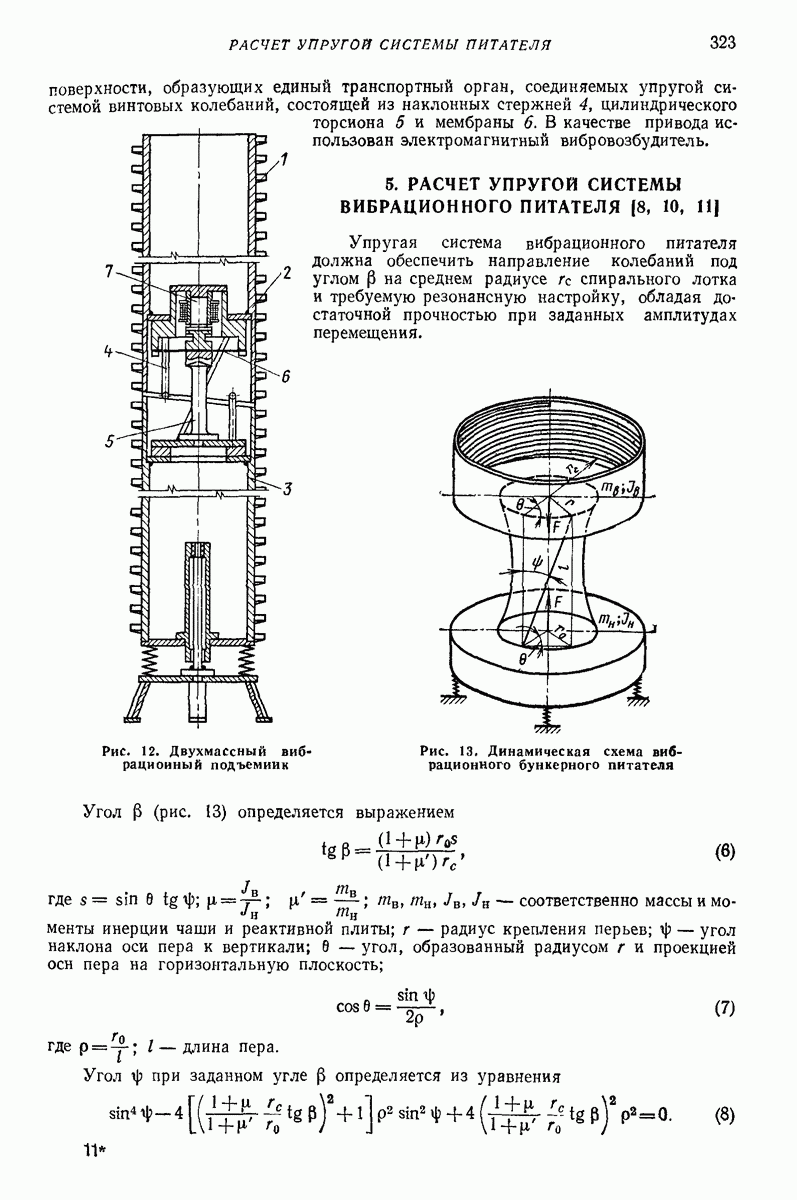
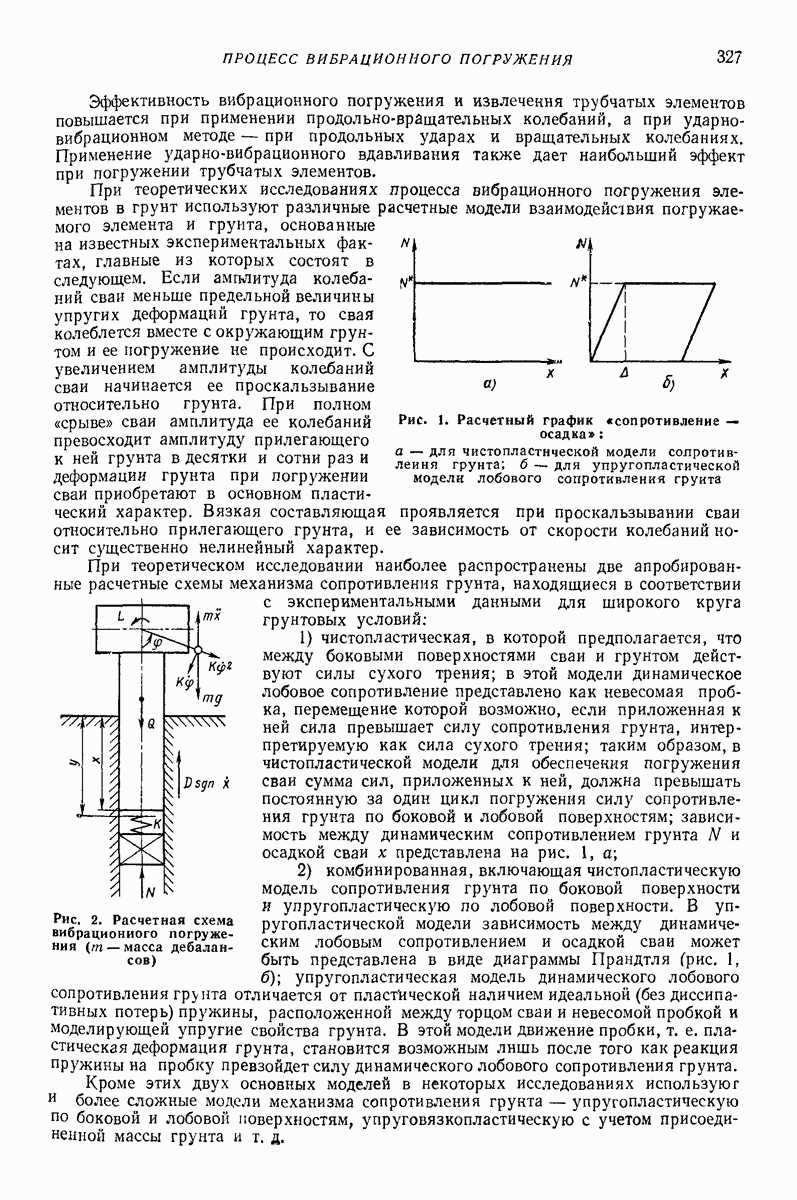
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
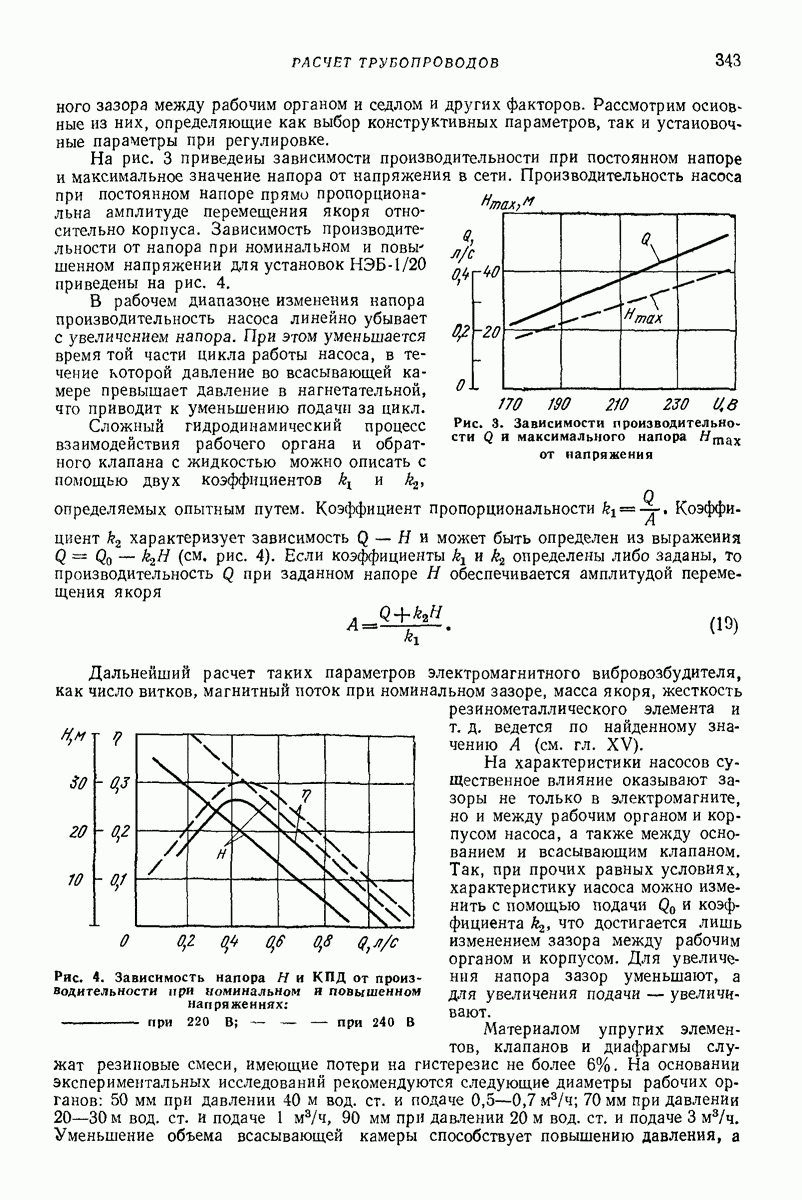
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
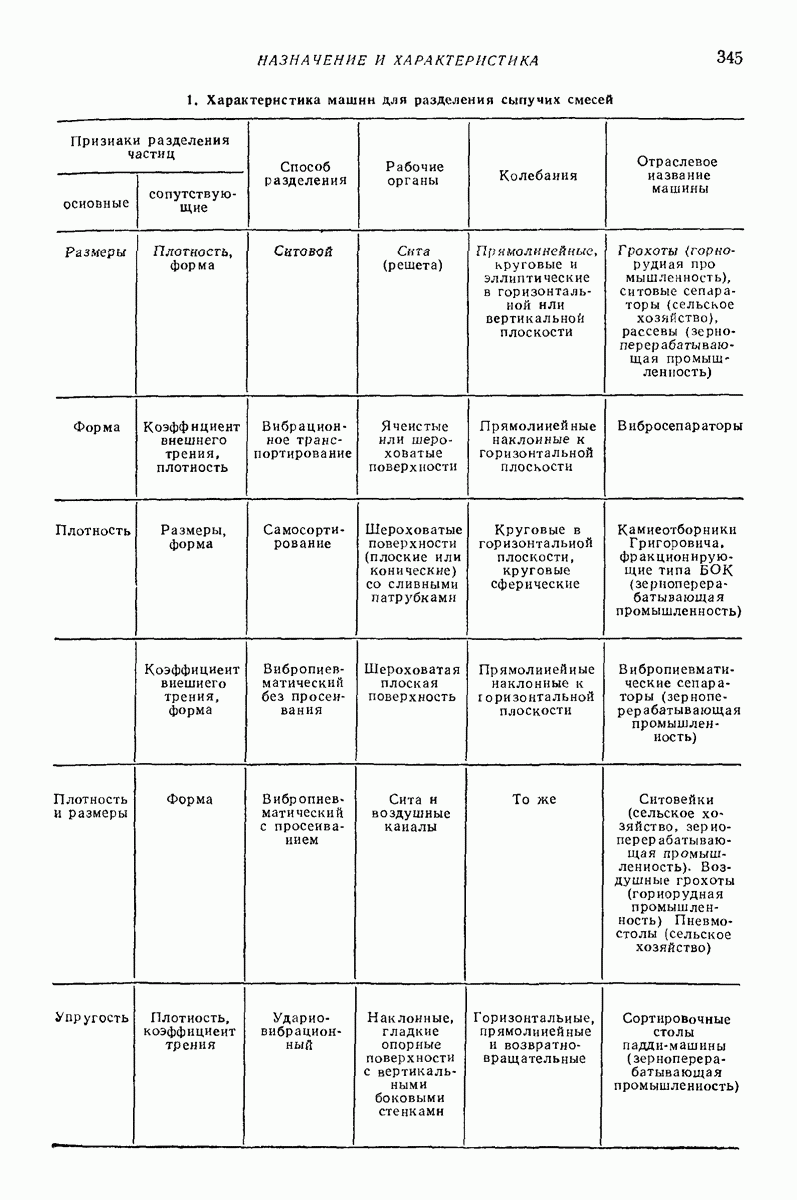
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
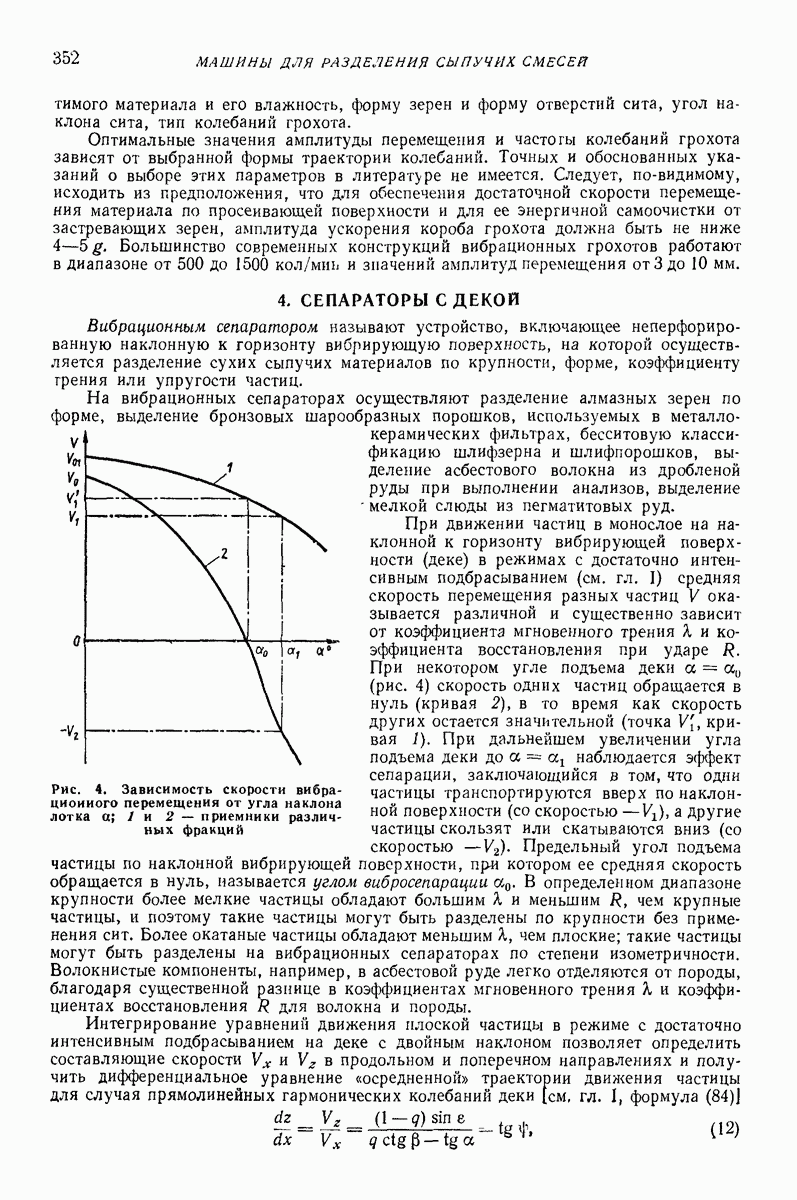
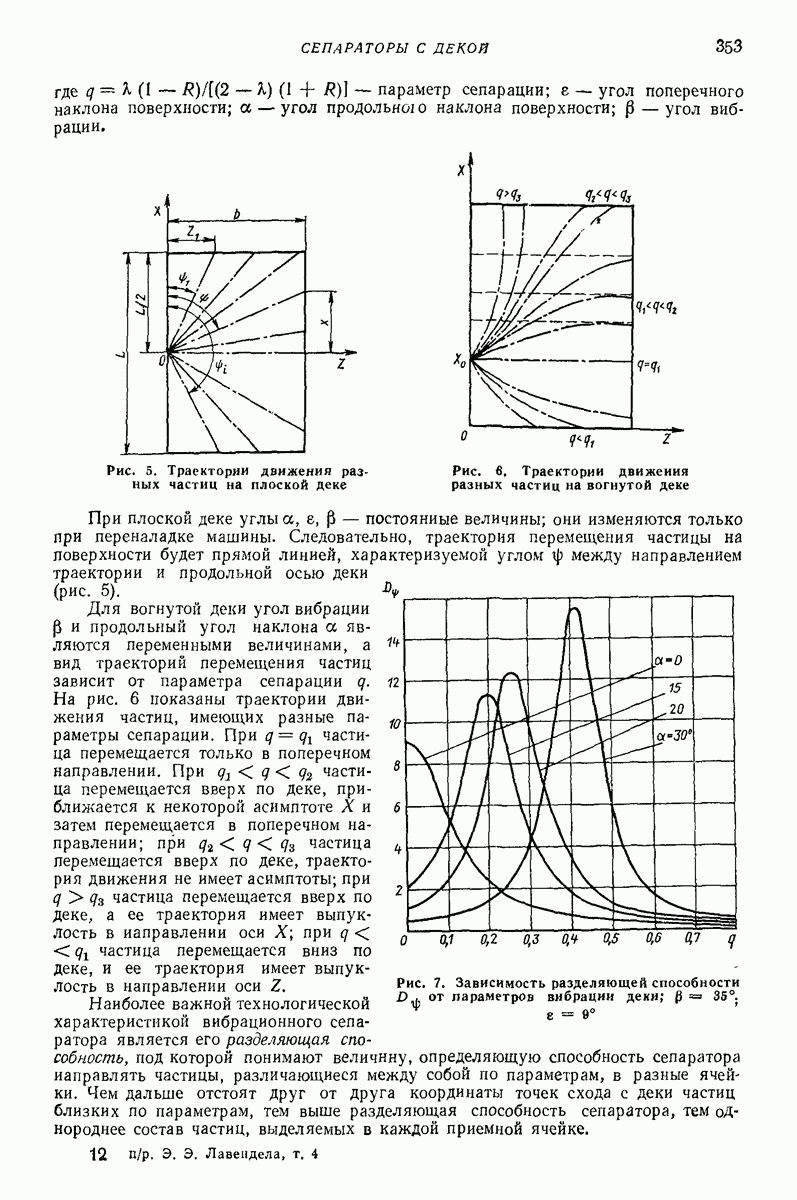
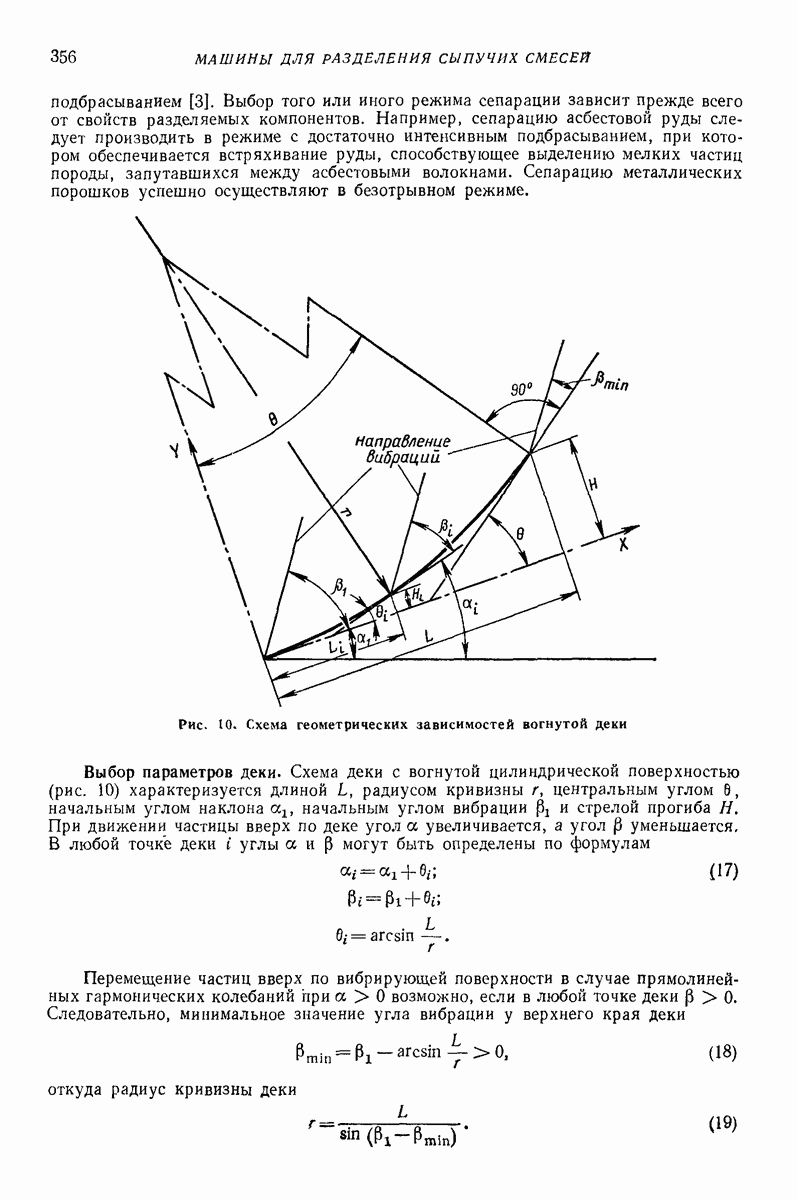
- 4. СЕПАРАТОРЫ С ДЕКОЙ
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
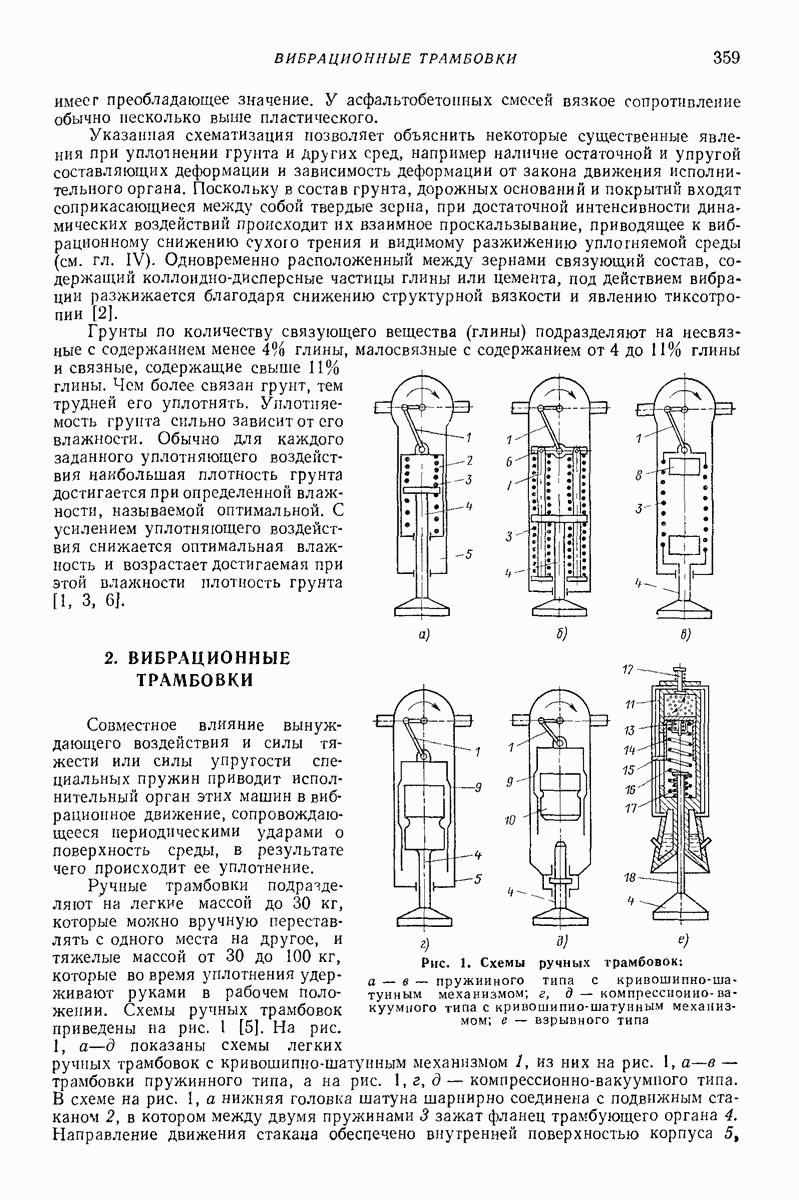
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
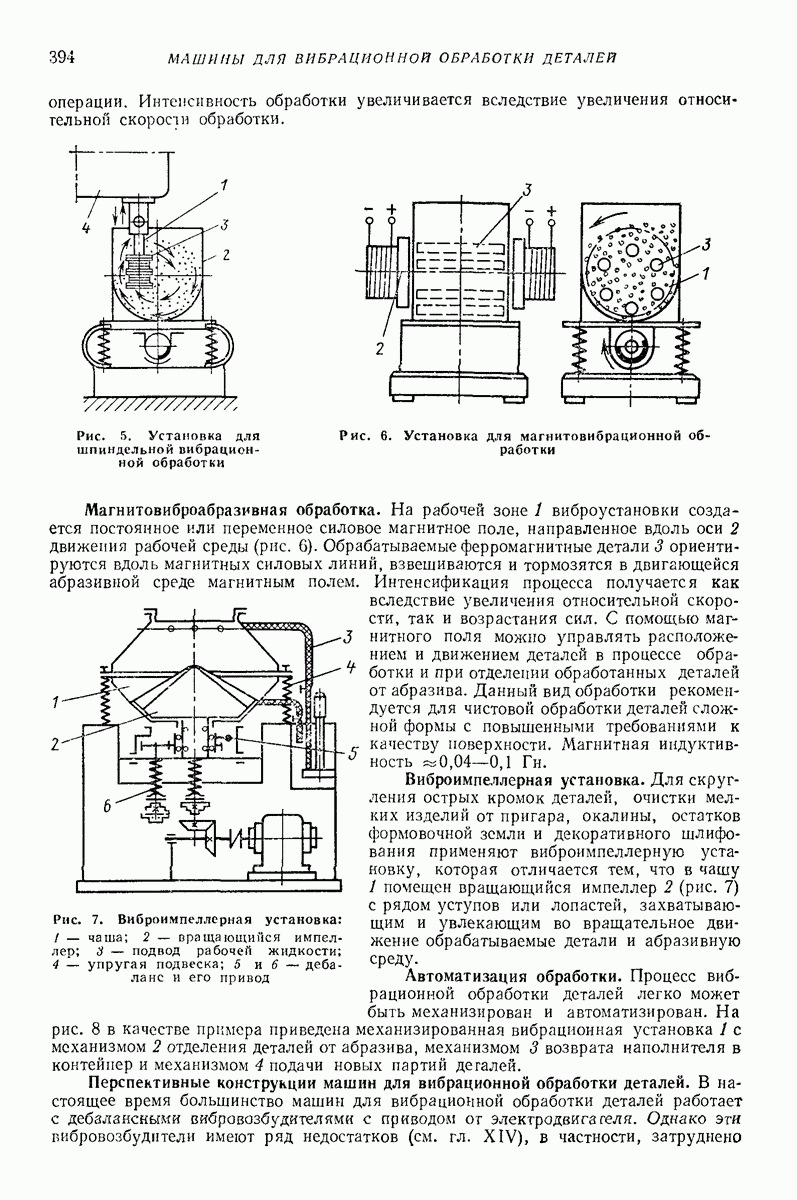
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
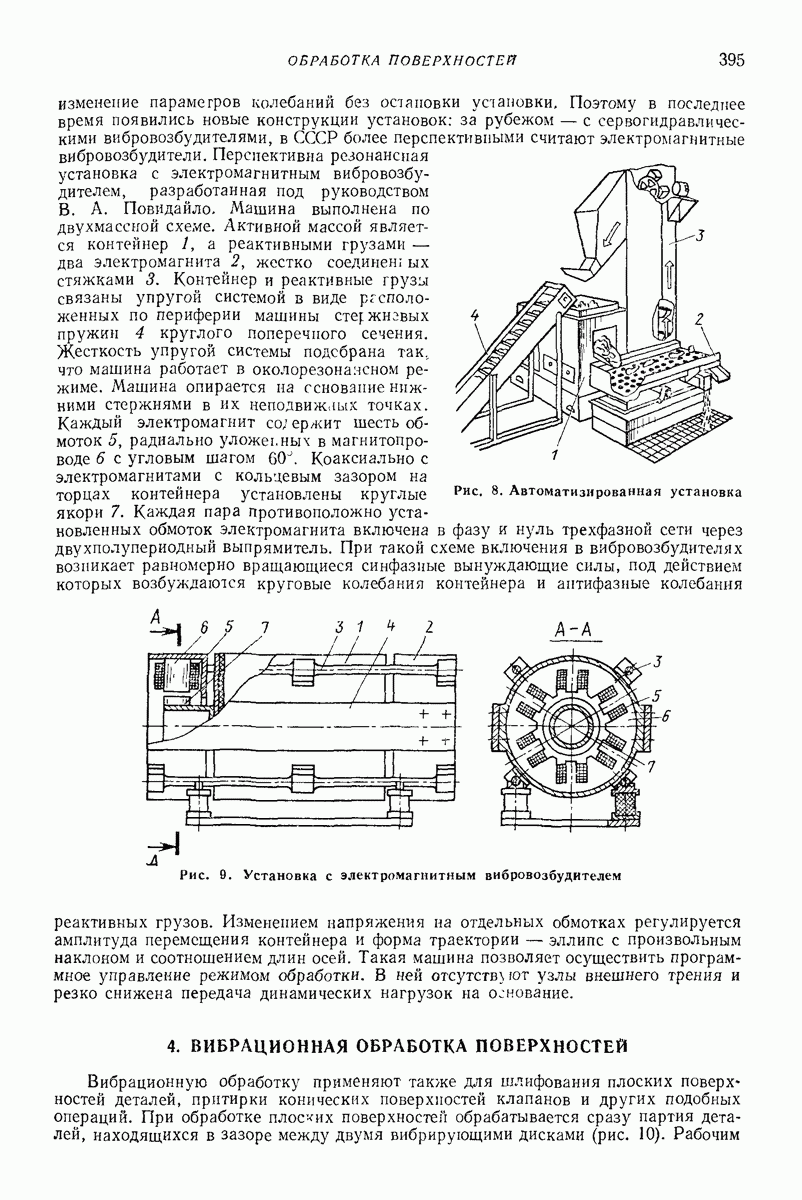
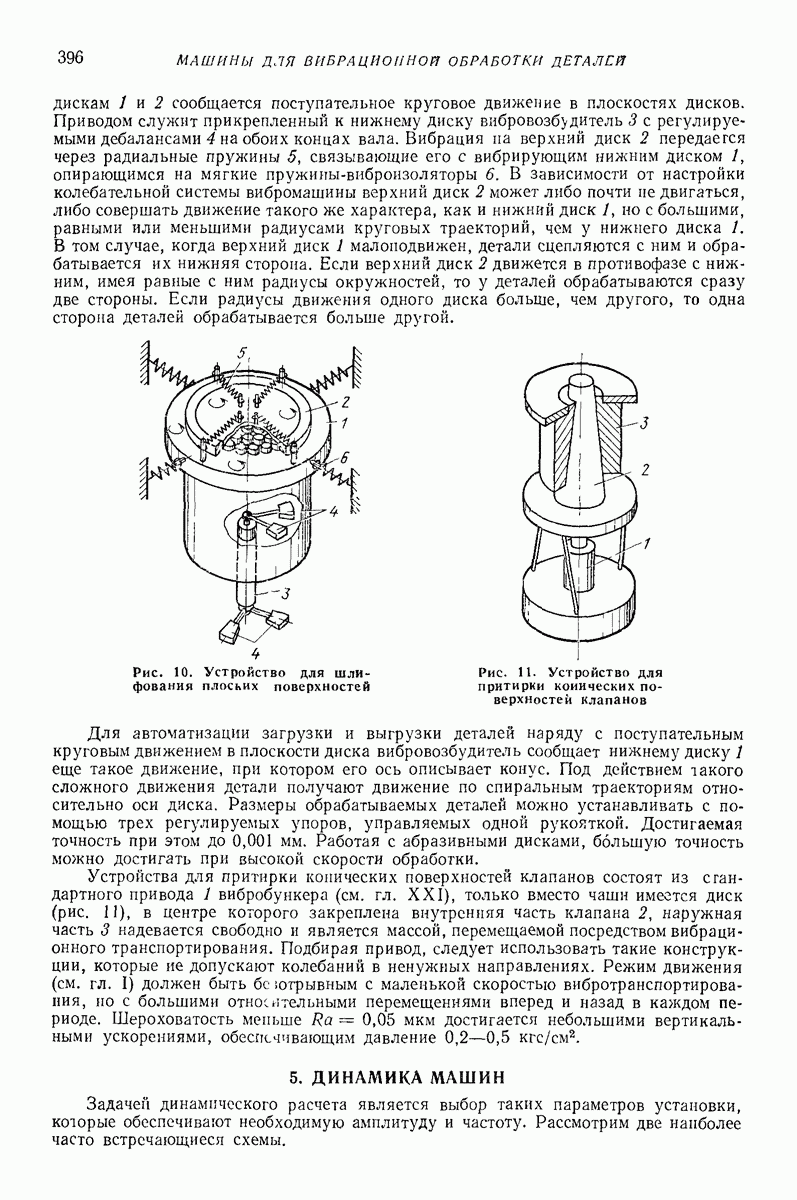
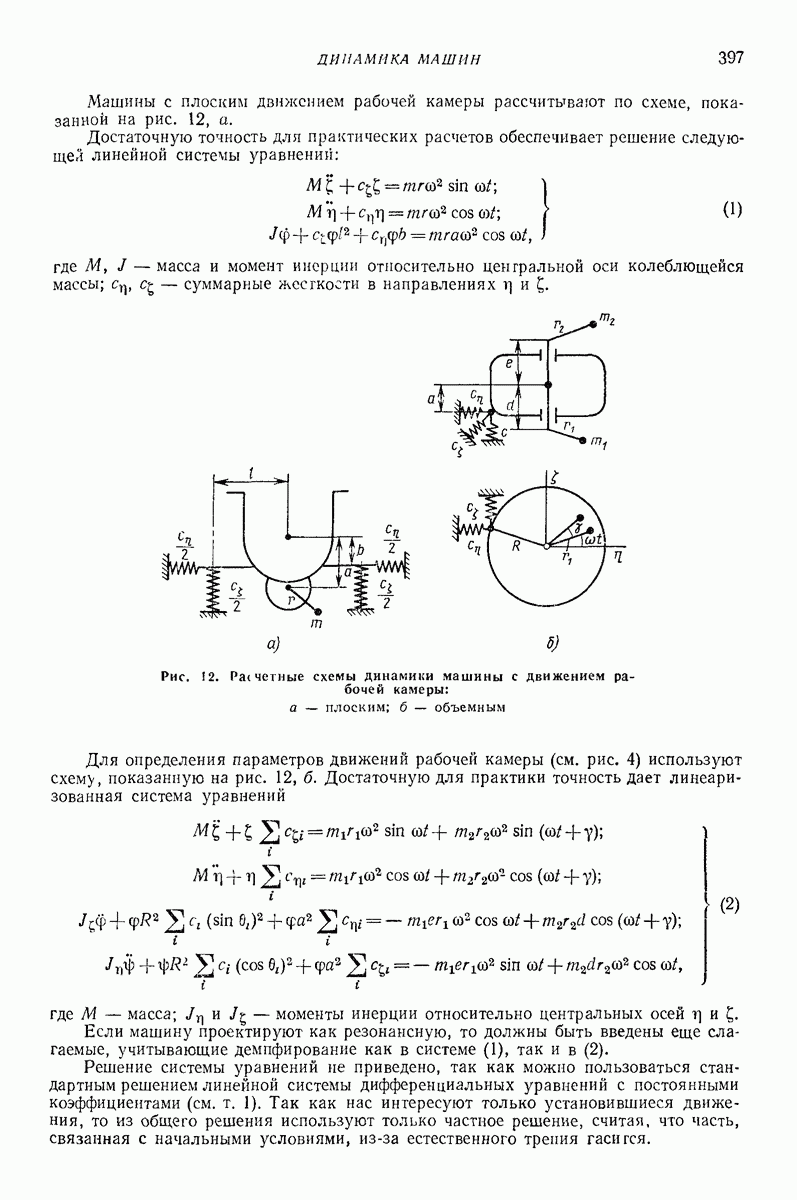
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
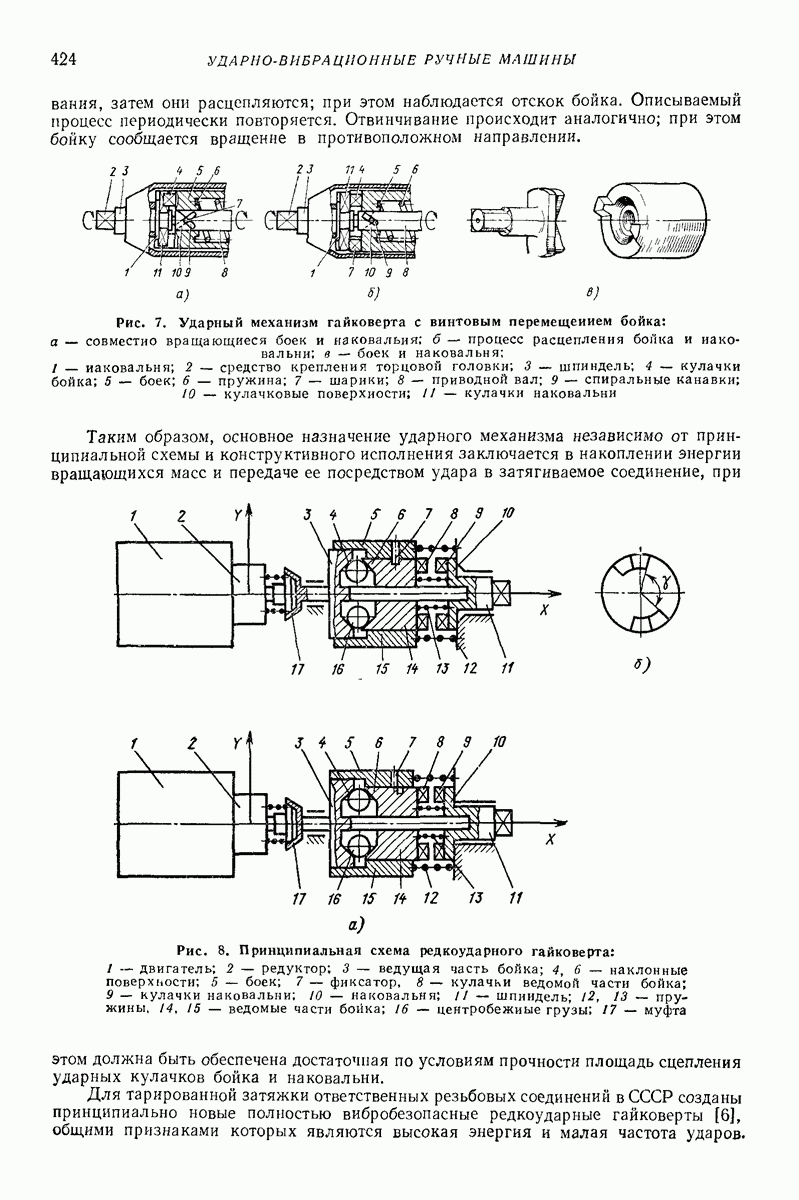
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
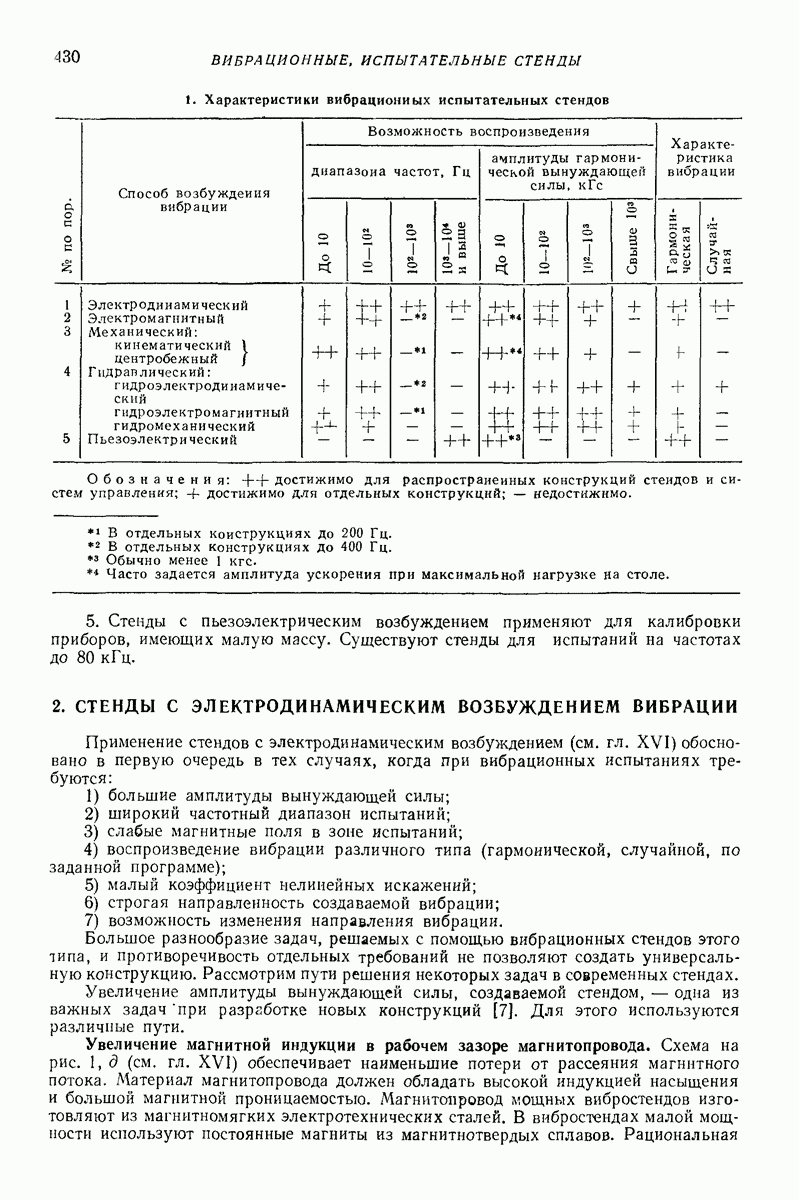
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
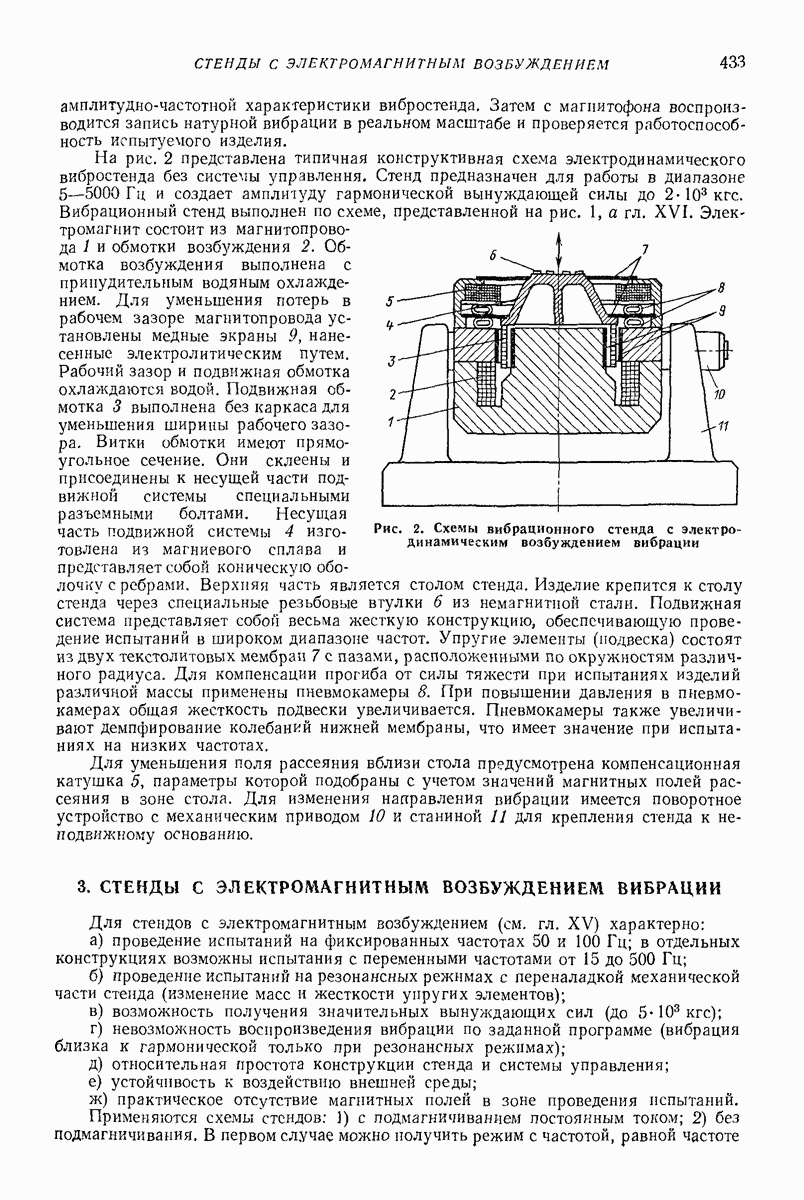
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
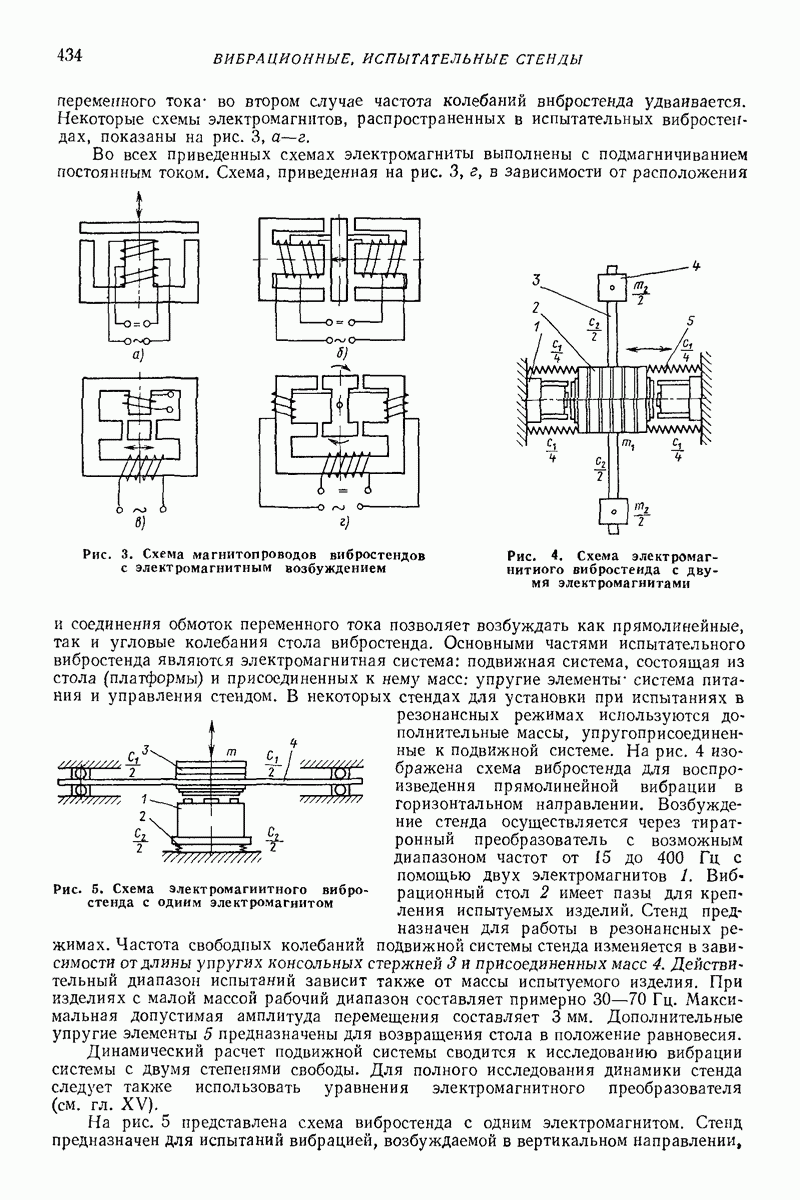
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ