| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Средние скорость и ускорение частицы в установившихся режимах движения.
Определение указанных величин представляет наибольший интерес для приложений. Их вычисление не вызывает существенных затруднений, если найдены моменты перехода от одного этапа к другому в установившемся движении; после этого дело сводится к легко выполняемому интегрированию (1). В результате находится перемещение частицы  за один период переключений
за один период переключений  для регулярных режимов и приращение скорости за тот же период
для регулярных режимов и приращение скорости за тот же период  для режимов ускоренных, а затем средние скорость и ускорение:
для режимов ускоренных, а затем средние скорость и ускорение:

Для практических расчетов удобно пользоваться программой  в Госфонде алгоритмов) В программе автоматически проверяются области применения гипотез взаимодействия частиц с лотком. Время счета на
в Госфонде алгоритмов) В программе автоматически проверяются области применения гипотез взаимодействия частиц с лотком. Время счета на  —15 с.
—15 с.
Режимы без подбрасывания. В наиболее общем случае, когда коэффициенты трения покоя и скольжения  существенно различны, процесс вычисления средней скорости в регулярных режимах сводится к следующему: 1) по (12) и (13) вычисляют
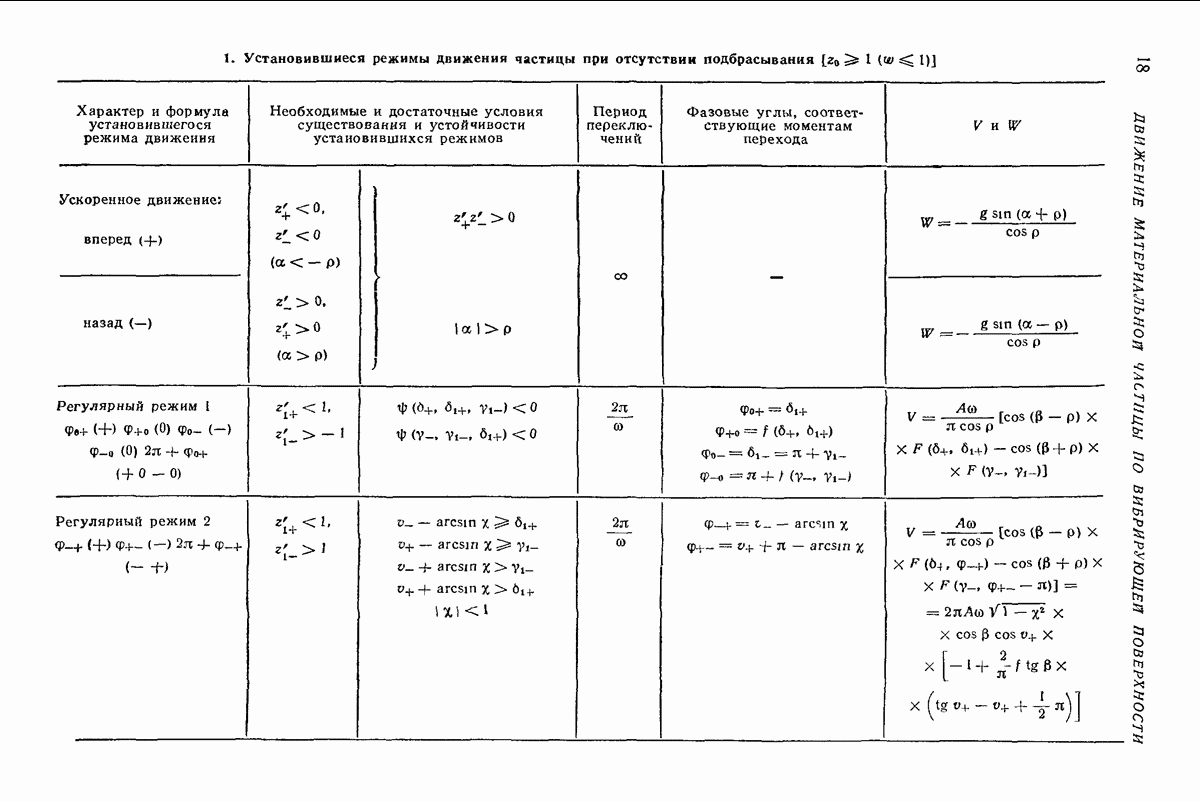
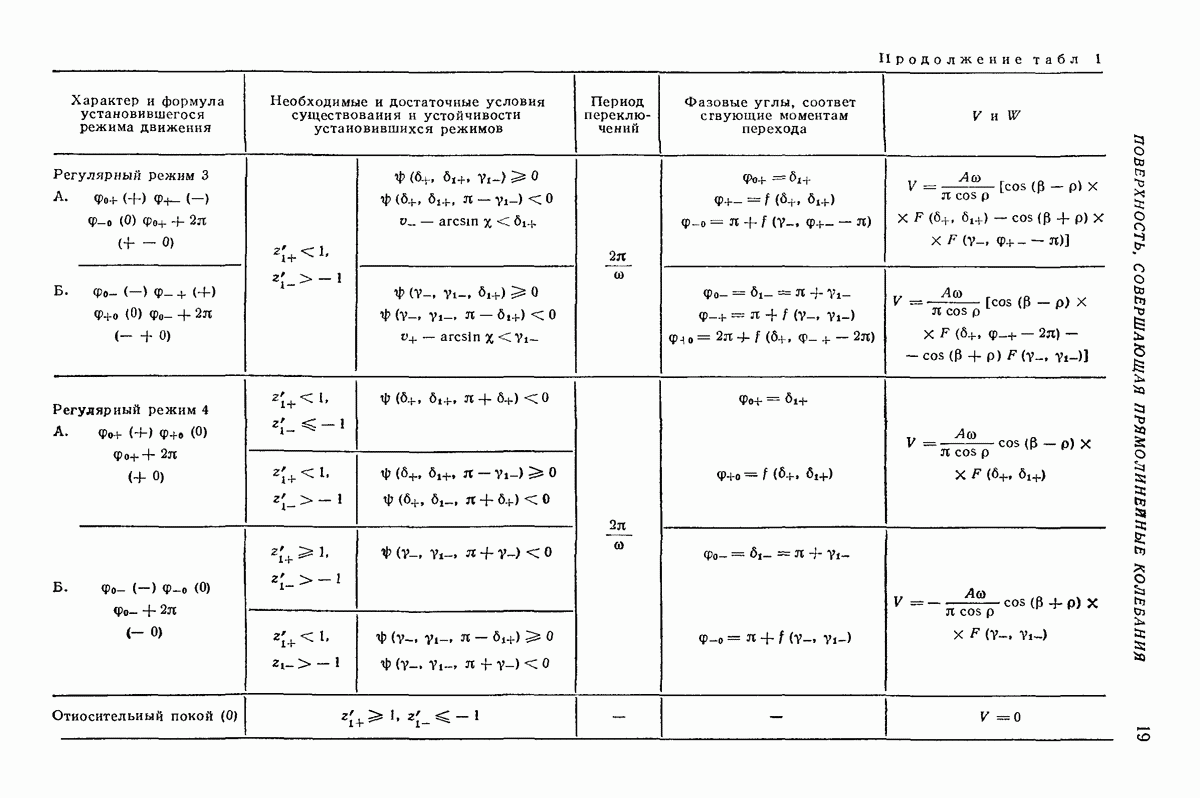
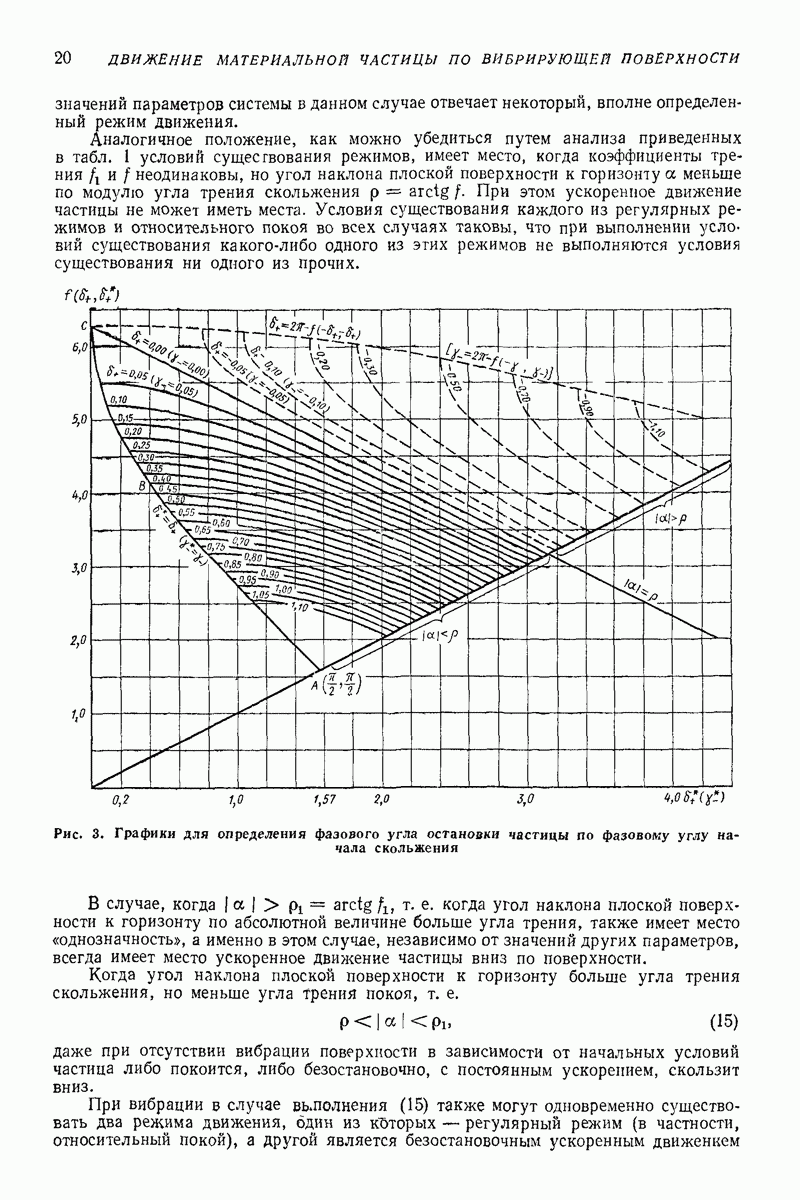
существенно различны, процесс вычисления средней скорости в регулярных режимах сводится к следующему: 1) по (12) и (13) вычисляют  с помощью соотношений, помещенных во второй и трегьей графах табл. 1, при учете (14) и рис. 3 выясняют вид установившегося режима движения частицы; 3) по формулам пятой графы габл. 1 и с помощью рис. 3 находят фазовые углы, соответствующие моментам перехода от одного этапа движения к другому; 4) по формулам последней графы табл 1 и с помощью рис. 7 подсчитывают среднюю скорость V или среднее ускорение
с помощью соотношений, помещенных во второй и трегьей графах табл. 1, при учете (14) и рис. 3 выясняют вид установившегося режима движения частицы; 3) по формулам пятой графы габл. 1 и с помощью рис. 3 находят фазовые углы, соответствующие моментам перехода от одного этапа движения к другому; 4) по формулам последней графы табл 1 и с помощью рис. 7 подсчитывают среднюю скорость V или среднее ускорение 
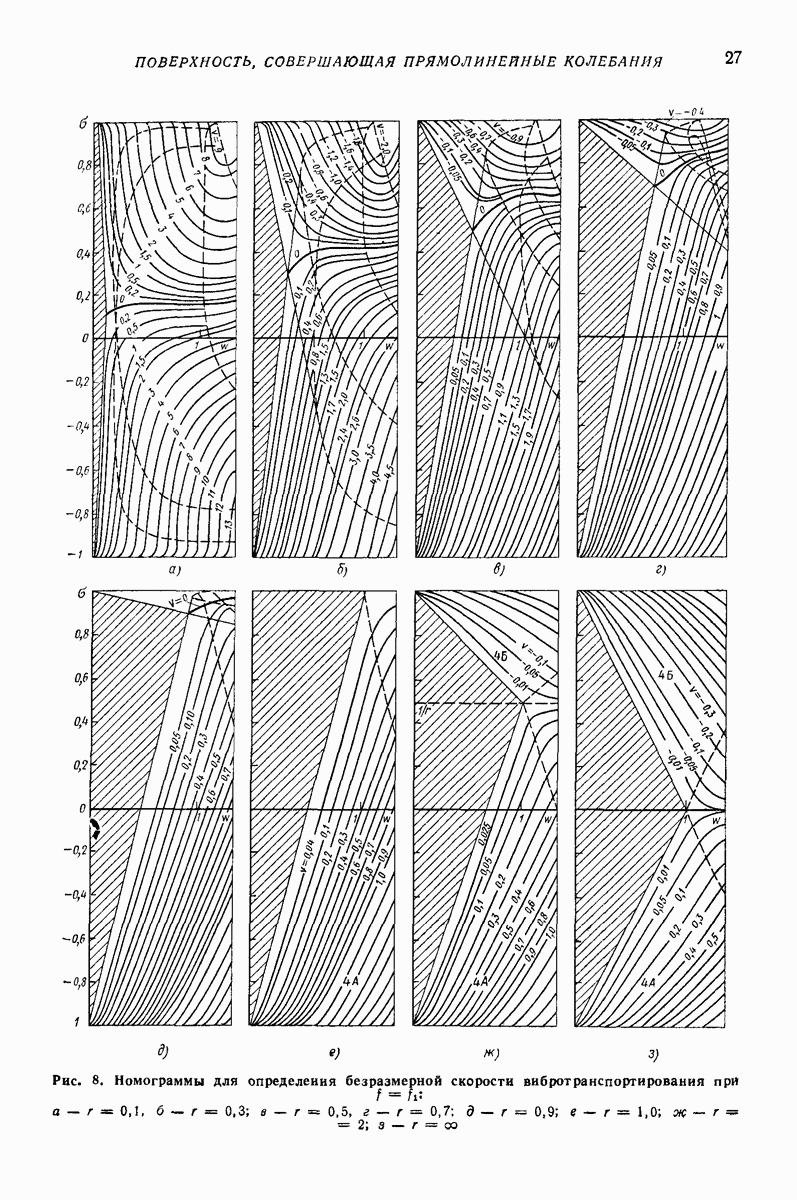
В случае, когда допустимо считать, что  определение средней скорости значительно облегчается. В этом случае можно воспользоваться номограммами [32], приведенными на рис.
определение средней скорости значительно облегчается. В этом случае можно воспользоваться номограммами [32], приведенными на рис.  На этих номограммах сплошные линии соответствуют указанным на них постоянным значениям безразмерной средней скорости движения частицы
На этих номограммах сплошные линии соответствуют указанным на них постоянным значениям безразмерной средней скорости движения частицы

Изолинии безразмерной скорости  нанесены в плоскости безразмерных параметров
нанесены в плоскости безразмерных параметров  где а — параметр наклона плоскости-, каждая из номограмм соответствует определенному значению параметра наклона вибрации
где а — параметр наклона плоскости-, каждая из номограмм соответствует определенному значению параметра наклона вибрации 

Сплошная жирная кривая на номограммах является линией буксования частицы  разделяющей области вибротранспортирования частицы в положительном и отрицательном направлениях Режимам без подбрасывания соответствуют части номограмм, для которых
разделяющей области вибротранспортирования частицы в положительном и отрицательном направлениях Режимам без подбрасывания соответствуют части номограмм, для которых  Примеры определения скорости с использованием приведенных графиков и номограмм см. ниже.
Примеры определения скорости с использованием приведенных графиков и номограмм см. ниже.
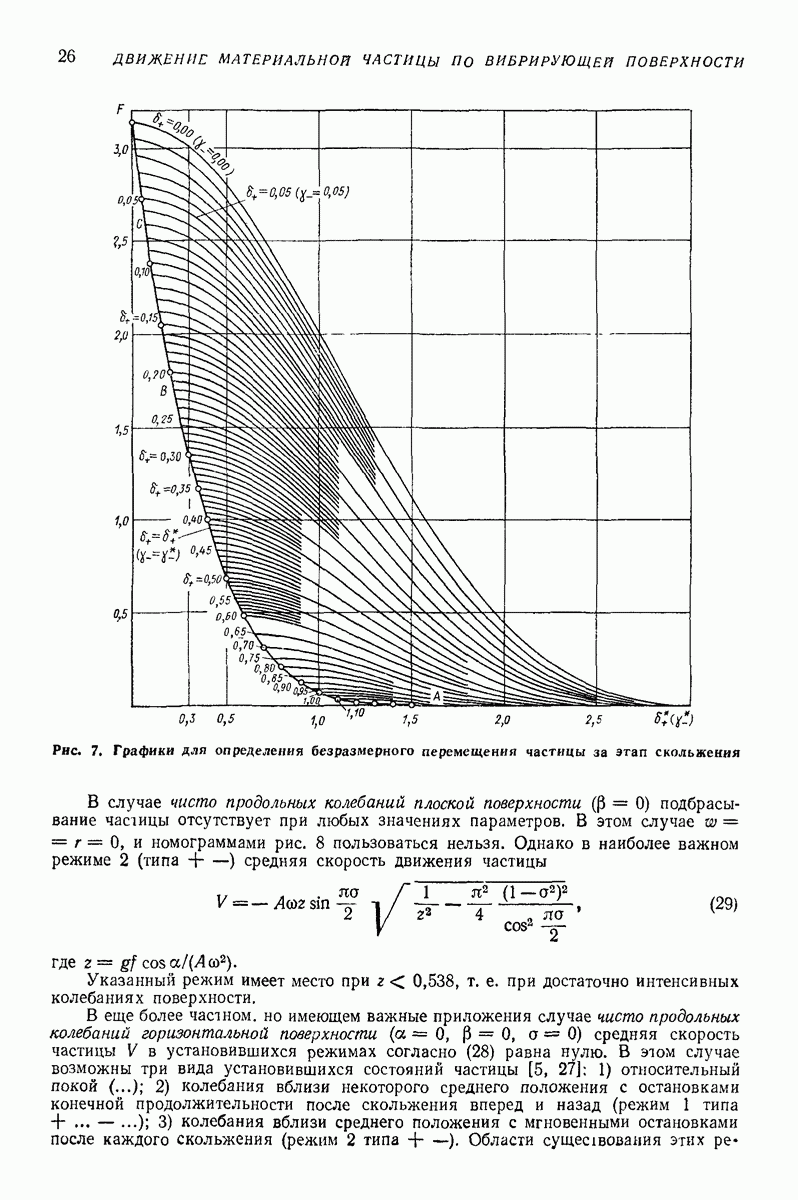
Рис. 7. (см. скан) Графики для определения безразмерного перемещения частицы за этап скольжения
В случае чисто продольных колебаний плоской поверхности  подбрасывание чааицы отсутствует при любых значениях параметров. В этом случае
подбрасывание чааицы отсутствует при любых значениях параметров. В этом случае  и номограммами рис. 8 пользоваться нельзя. Однако в наиболее важном режиме 2 (типа
и номограммами рис. 8 пользоваться нельзя. Однако в наиболее важном режиме 2 (типа  ) средняя скорость движения частицы
) средняя скорость движения частицы

где 
Указанный режим имеет место при  т. е. при достаточно интенсивных колебаниях поверхности.
т. е. при достаточно интенсивных колебаниях поверхности.
В еще более частном, но имеющем важные приложения случае чисто продольных колебаний горизонтальной поверхности  средняя скорость частицы V в установившихся режимах согласно (28) равна нулю. В этом случае возможны три вида установившихся состояний частицы [5, 27]: 1) относительный покой
средняя скорость частицы V в установившихся режимах согласно (28) равна нулю. В этом случае возможны три вида установившихся состояний частицы [5, 27]: 1) относительный покой  колебания вблизи некоторого среднего положения с остановками конечной продолжительности после скольжения вперед и назад (режим 1 типа
колебания вблизи некоторого среднего положения с остановками конечной продолжительности после скольжения вперед и назад (режим 1 типа  ) колебания вблизи среднего положения с мгновенными остановками после каждого скольжения (режим 2 типа
) колебания вблизи среднего положения с мгновенными остановками после каждого скольжения (режим 2 типа  Области сущеавования этих
Области сущеавования этих

(кликните для просмотра скана)
режимов в общем случае, когда  определяются соответственно неравенствами
определяются соответственно неравенствами

где 
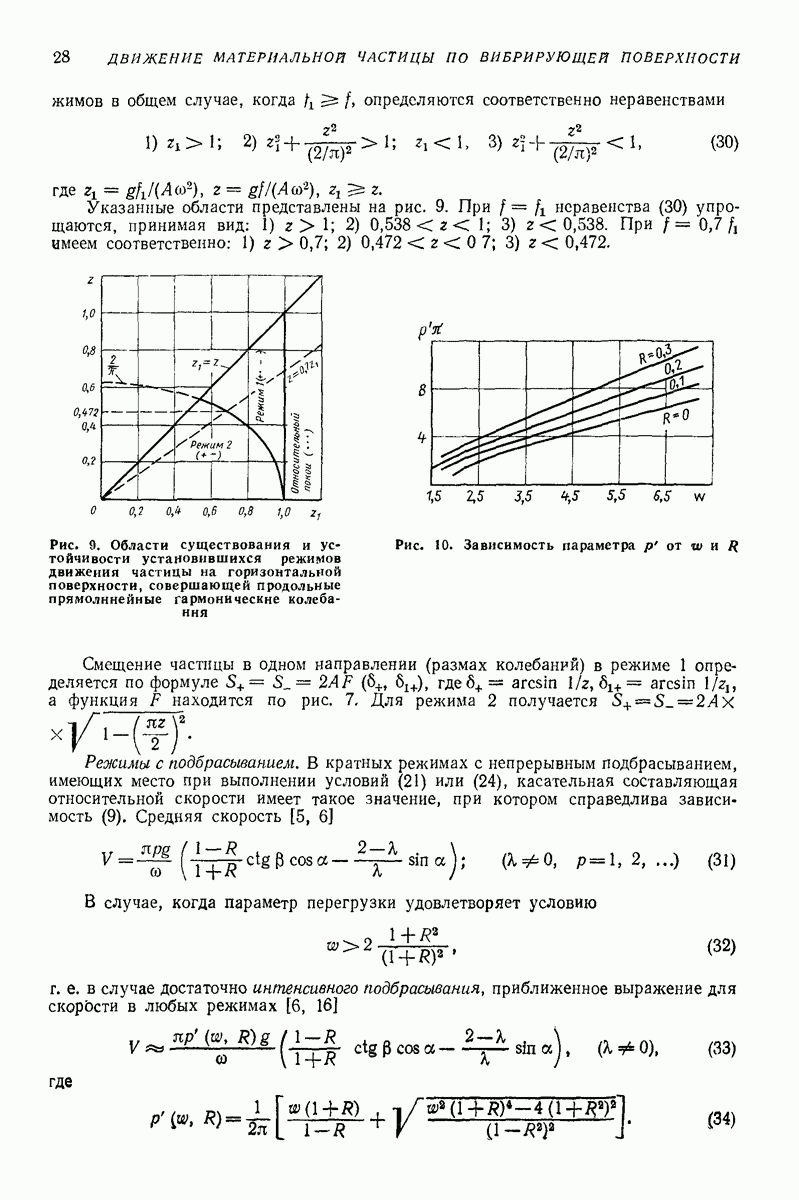
Указанные области представлены на рис. 9. При  неравенства (30) упрощаются, принимая вид: 1)
неравенства (30) упрощаются, принимая вид: 1)  При
При  имеем соответственно: 1)
имеем соответственно: 1)  ; 2)
; 2) 

Рис. 9. Области существования и устойчивости установившихся режимов движения частицы на горизонтальной поверхности, совершающей продольные прямолинейные гармонические колебания

Рис. 10. Зависимость параметра  от
от 
Смещение частицы в одном направлении (размах колебаний) в режиме 1 определяется по формуле  где
где  а функция F находится по рис. 7. Для режима 2 получается
а функция F находится по рис. 7. Для режима 2 получается 
Режимы с подбрасыванием. В кратных режимах с непрерывным подбрасыванием, имеющих место при выполнении условий (21) или (24), касательная составляющая относительной скорости имеет такое значение, при котором справедлива зависимость (9). Средняя скорость [5, 6]

В случае, когда параметр перегрузки удовлетворяет условию

т. е. в случае достаточно интенсивного подбрасывания, приближенное выражение для скорости в любых режимах [6, 16]

где

Формула (33) образована путем интерполяции формулы (31), строго справедливой при  лежащих в интервалах (24), на все промежуточные значения
лежащих в интервалах (24), на все промежуточные значения  причем интерполирующаяся кривая проходит через средние точки интервалов (24).
причем интерполирующаяся кривая проходит через средние точки интервалов (24).
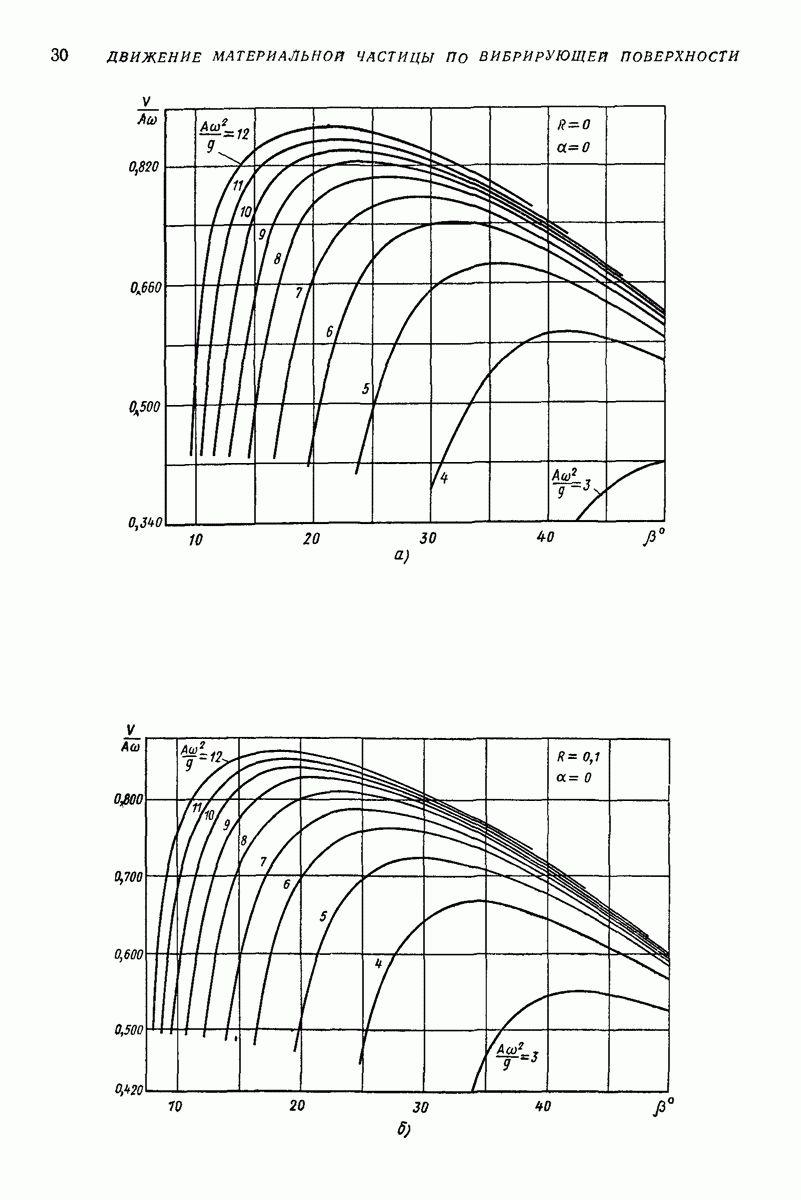
Для облегчения расчетов на рис. 10 представлена функция  соответствующая (34), а на рис. 11, а-а даны зависимости безразмерной величины
соответствующая (34), а на рис. 11, а-а даны зависимости безразмерной величины  от параметра
от параметра  и угла вибраций (5 для случая горизонтальной поверхности
и угла вибраций (5 для случая горизонтальной поверхности  при коэффициенте восстановления
при коэффициенте восстановления  равном 0; 0,1 и 0,2.
равном 0; 0,1 и 0,2.
При интенсивности подбрасывания, отвечающей значениям параметра перегрузки

с погрешностью не выше  можно пренебречь вторым слагаемым в подкоренном выражении (34) по сравнению с первым и принять
можно пренебречь вторым слагаемым в подкоренном выражении (34) по сравнению с первым и принять  Тогда выражение (33) для средней скорости существенно упрощается:
Тогда выражение (33) для средней скорости существенно упрощается:

При  получаем
получаем

т. е. скорость транспортирования оказывается приближенно равной амплитуде продольной проекции скорости колебаний вибрирующей плоской поверхности.
Недостаток приведенных простых приближенных формул состоит в том, что они не отражают зависимость средней скорости от коэффициентов трения и  Однако при наличии интенсивного подбрасывания эта зависимость является довольно слабой, и во многих случаях может не учитываться.
Однако при наличии интенсивного подбрасывания эта зависимость является довольно слабой, и во многих случаях может не учитываться.
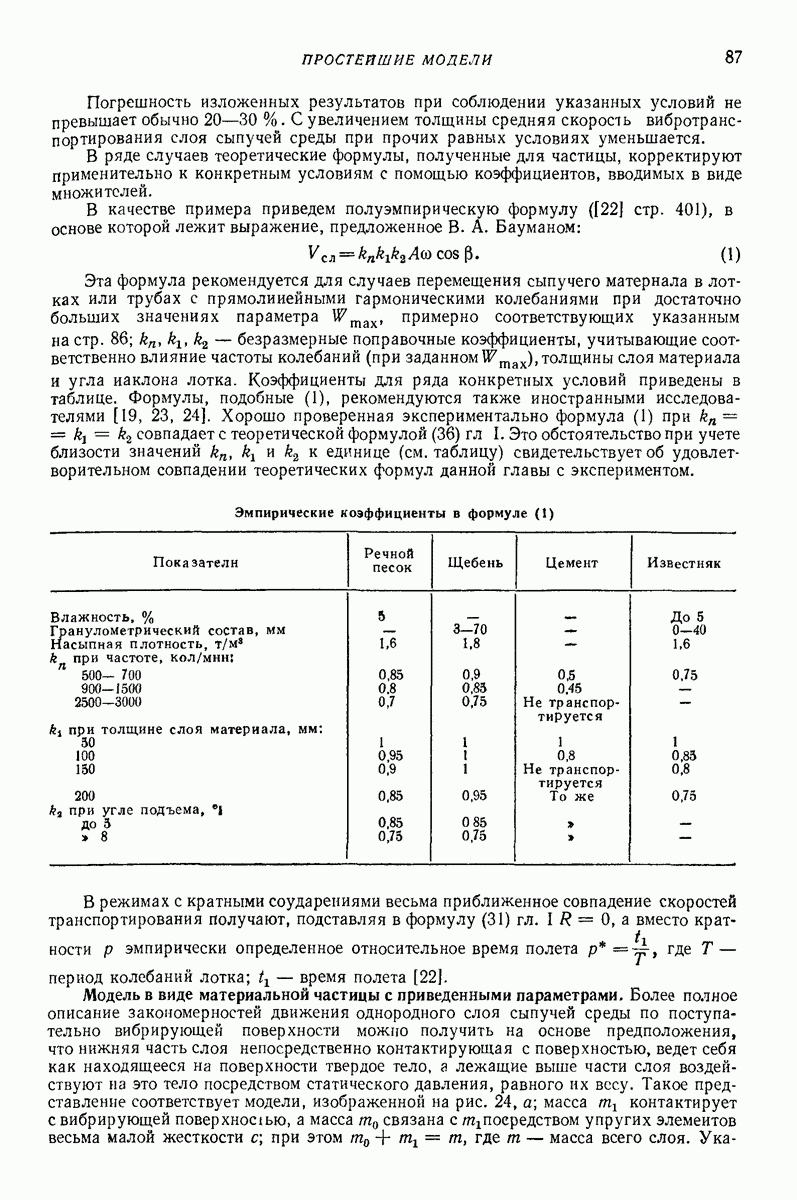
Выражение (36) близко к полуэмпирической формуле В А. Баумана [2] (см. стр. 87), если положить в последней  и опустить близкие к единице эмпирические коэффициенты, а также к другим хорошо проверенным полуэмпирическим формулам, рекомендуемым зарубежными исследователями для случаев транспортирования сыпучих тел [48, 51].
и опустить близкие к единице эмпирические коэффициенты, а также к другим хорошо проверенным полуэмпирическим формулам, рекомендуемым зарубежными исследователями для случаев транспортирования сыпучих тел [48, 51].
В случае режимов со слабоинтенсивным подбрасыванием, когда параметр перегрузки  близок к единице и справедлива
близок к единице и справедлива  -гипотеза (10), для определения скорости вибротранспортирования можно воспользоваться номограммами рис. 8; более полные номограммы, построенные в соответствии с
-гипотеза (10), для определения скорости вибротранспортирования можно воспользоваться номограммами рис. 8; более полные номограммы, построенные в соответствии с  -гипотезой, приведены в [32].
-гипотезой, приведены в [32].
Примеры определения средней скорости. 1. Пусть частота колебаний плоской поверхности  кол/мин, т. е.
кол/мин, т. е.  амплитуда
амплитуда  см; угол наклона к горизонту
см; угол наклона к горизонту  угол вибрации
угол вибрации  коэффициенты трения покоя и скольжения соответственно
коэффициенты трения покоя и скольжения соответственно  В данном случае параметр перегрузки
В данном случае параметр перегрузки  и поэтому частица движется без отрыва от поверхности.
и поэтому частица движется без отрыва от поверхности.
По (12) и (13) находим  Поскольку, согласно (14),
Поскольку, согласно (14),  то в соответствии с неравенствами второй и третьей граф табл. 1 заключаем, что при заданных параметрах реализуется регулярный режим
то в соответствии с неравенствами второй и третьей граф табл. 1 заключаем, что при заданных параметрах реализуется регулярный режим  Поэтому по формуле последней графы табл. 1 с помощью рис. 7 находим
Поэтому по формуле последней графы табл. 1 с помощью рис. 7 находим  .
.
Если принять  то
то  см/с, что близко к ранее найденному
см/с, что близко к ранее найденному  см/с при
см/с при  Вместе с тем, если принять
Вместе с тем, если принять  то тарнм же образом найдем
то тарнм же образом найдем  см/с, т. е. получим значительно меньшую скорость, чем при
см/с, т. е. получим значительно меньшую скорость, чем при 
2. Предположим, что, как и ранее,  но
но  кол/мин
кол/мин  см; коэффициент восстановления при ударе
см; коэффициент восстановления при ударе  При этом
При этом  т. е. осуществляется движение с подбрасыванием. Кроме того,
т. е. осуществляется движение с подбрасыванием. Кроме того,  и поэтому при вычислении V можно пользоваться (33) и (36), а также рис. 11.
и поэтому при вычислении V можно пользоваться (33) и (36), а также рис. 11.

(кликните для просмотра скана)

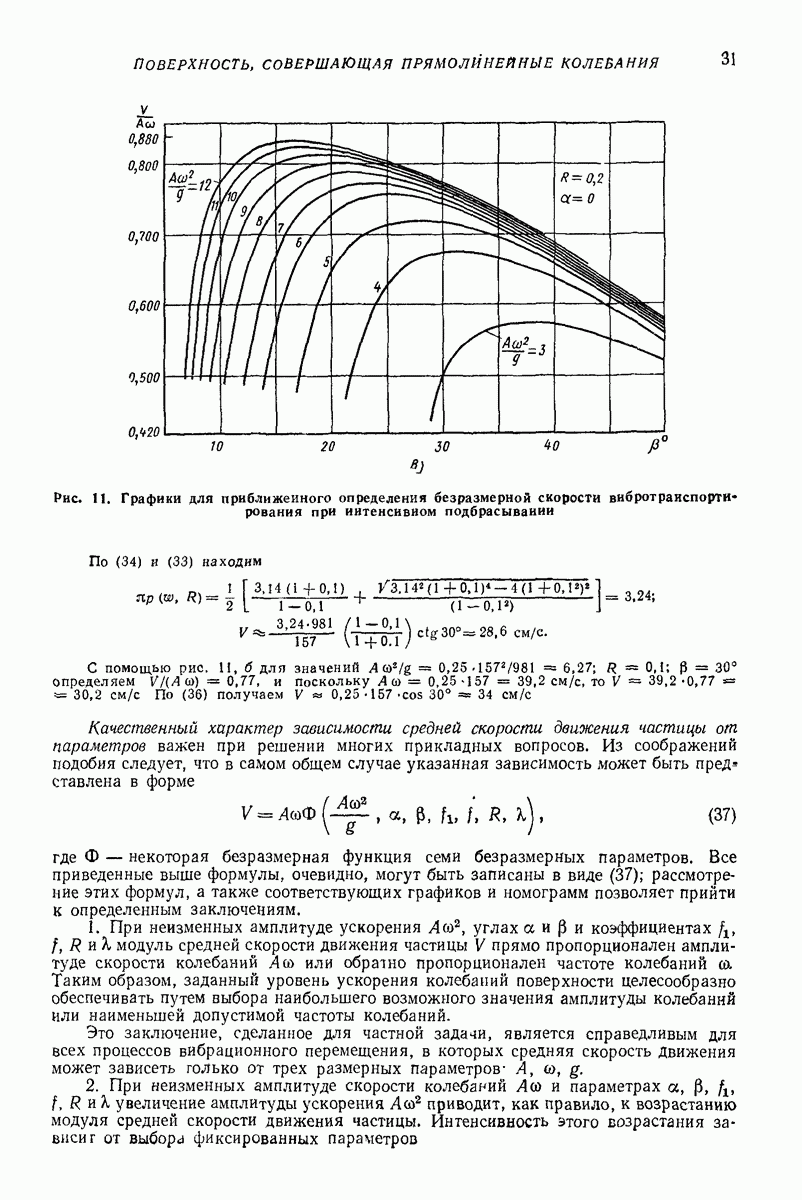
Рис. II. Графики для приближенного определения безразмерной скорости вибротраиспорти рования при интенсивном подбрасывании
По (34) и (33) находим

С помощью рис.  для значений
для значений  определяем
определяем  и поскольку
и поскольку  . По (36) получаем
. По (36) получаем  см/с
см/с
Качественный характер зависимости средней скорости движения частицы от параметров важен при решении многих прикладных вопросов. Из соображений подобия следует, что в самом общем случае указанная зависимость может быть представлена в форме

где  некоторая безразмерная функция семи безразмерных параметров. Все приведенные выше формулы, очевидно, могут быть записаны в виде (37); рассмотрение этих формул, а также соответствующих графиков и номограмм позволяет прийти к определенным заключениям.
некоторая безразмерная функция семи безразмерных параметров. Все приведенные выше формулы, очевидно, могут быть записаны в виде (37); рассмотрение этих формул, а также соответствующих графиков и номограмм позволяет прийти к определенным заключениям.
1. При неизменных амплитуде ускорения  углах а и (5 и коэффициентах
углах а и (5 и коэффициентах  модуль средней скорости движения частицы V прямо пропорционален амплитуде скорости колебаний Лео или обратно пропорционален частоте колебаний
модуль средней скорости движения частицы V прямо пропорционален амплитуде скорости колебаний Лео или обратно пропорционален частоте колебаний  Таким образом, заданный уровень ускорения колебаний поверхности целесообразно обеспечивать путем выбора наибольшего возможного значения амплитуды колебаний или наименьшей допустимой частоты колебаний.
Таким образом, заданный уровень ускорения колебаний поверхности целесообразно обеспечивать путем выбора наибольшего возможного значения амплитуды колебаний или наименьшей допустимой частоты колебаний.
Это заключение, сделанное для частной задали, является справедливым для всех процессов вибрационного перемещения, в которых средняя скорость движения может зависеть только от трех размерных параметров - 
2. При неизменных амплитуде скорости колебаний  и параметрах
и параметрах  увеличение амплитуды ускорения
увеличение амплитуды ускорения  приводит, как правило, к возрастанию модуля средней скорости движения частицы. Интенсивность этого возрастания зависит от выбора фиксированных параметров
приводит, как правило, к возрастанию модуля средней скорости движения частицы. Интенсивность этого возрастания зависит от выбора фиксированных параметров
Отсюда следует (с теми же оговорками), что при постоянной частоте колебаний  и неизменных тех же параметрах модуль средней скорости возрастает с изменением амплитуды колебаний А быстрее, чем по линейному закону При постоянной амплитуде колебаний А и неизменных указанных параметрах модуль средней скорости возрастает с изменением частоты колебаний со быстрее, чем по линейному закону; при этом увеличение частоты
и неизменных тех же параметрах модуль средней скорости возрастает с изменением амплитуды колебаний А быстрее, чем по линейному закону При постоянной амплитуде колебаний А и неизменных указанных параметрах модуль средней скорости возрастает с изменением частоты колебаний со быстрее, чем по линейному закону; при этом увеличение частоты  при неизменной амплитуде А приводит к большему возрастанию скорости, нежели аналогичное увеличение амплитуды А при неизменной частоте
при неизменной амплитуде А приводит к большему возрастанию скорости, нежели аналогичное увеличение амплитуды А при неизменной частоте 
3. При постоянной частоте со и амплитуде А колебаний, а также при неизменных параметрах  зависимость средней скорости от угла вибрации
зависимость средней скорости от угла вибрации  имеет, как правило, один ярко выраженный максимум. Это вытекает из непрерывности функции
имеет, как правило, один ярко выраженный максимум. Это вытекает из непрерывности функции  и того, что V обращается в нуль или становится отрицательной при продольных колебаниях поверхности
и того, что V обращается в нуль или становится отрицательной при продольных колебаниях поверхности  и при поперечных колебаниях
и при поперечных колебаниях 
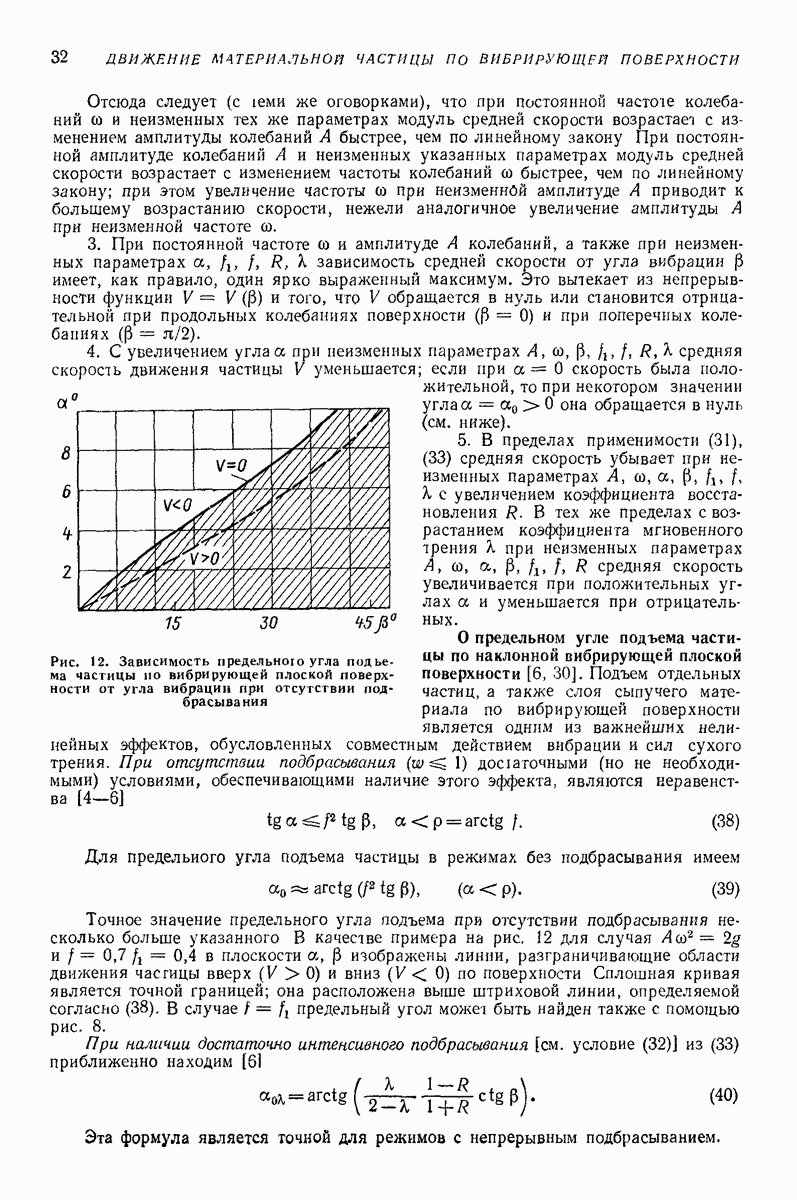
4. С увеличением угла а при неизменных параметрах  средняя скорость движения частицы V уменьшается; если при
средняя скорость движения частицы V уменьшается; если при  скорость была положительной, то при некотором значении угла
скорость была положительной, то при некотором значении угла  она обращается в нуль (см. ниже).
она обращается в нуль (см. ниже).

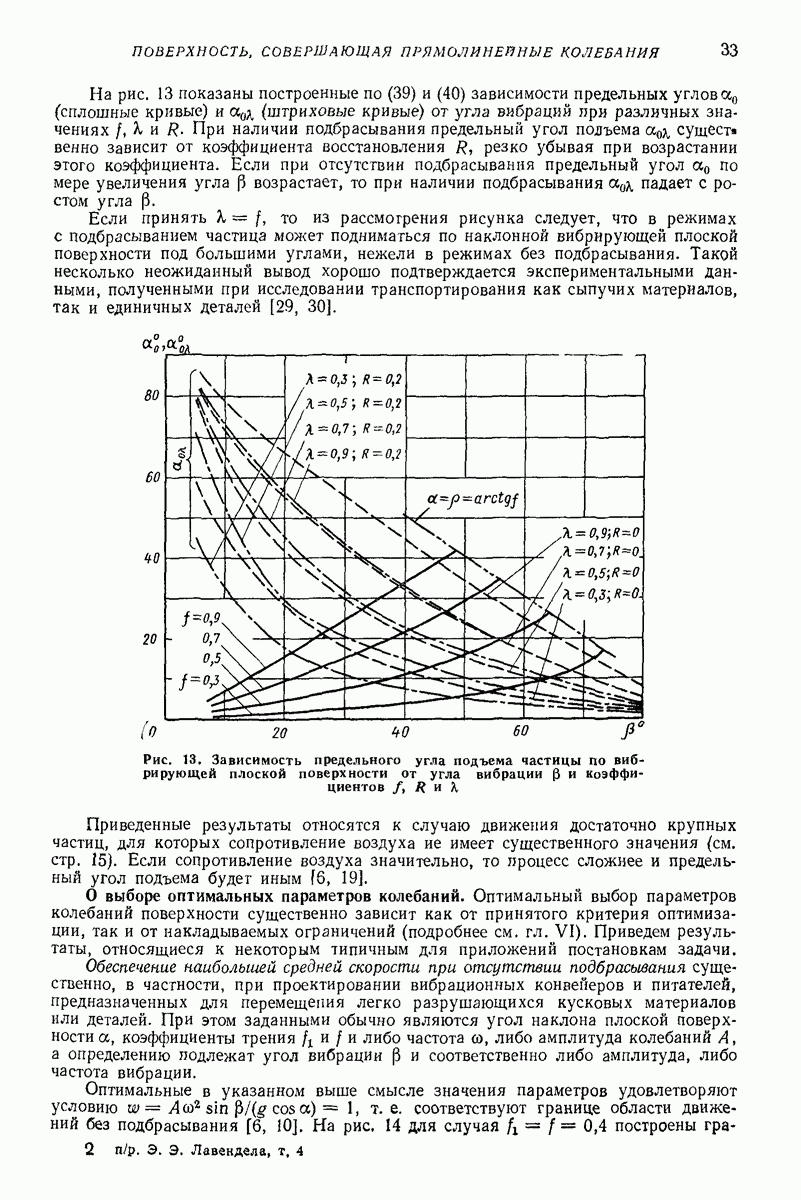
Рис. 12. Зависимость предельного угла подъема частицы но вибрирующей плоской поверхности от угла вибрации при отсутствии подбрасывания
5. В пределах применимости (31), (33) средняя скорость убывает при неизменных параметрах  с увеличением коэффициента восстановления
с увеличением коэффициента восстановления  . В тех же пределах с возрастанием коэффициента мгновенного трения X при неизменных параметрах
. В тех же пределах с возрастанием коэффициента мгновенного трения X при неизменных параметрах  средняя скорость увеличивается при положительных углах а и уменьшается при отрицательных.
средняя скорость увеличивается при положительных углах а и уменьшается при отрицательных.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- Установившиеся режимы движения частицы.
- О методах решения задачи.
- Установившиеся режимы при отсутствии подбрасывания [4-6].
- Установившиеся режимы с подбрасыванием.
- Средние скорость и ускорение частицы в установившихся режимах движения.
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
- О выборе оптимальных параметров колебаний.
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
- О влиянии на движение частицы сил вязкого сопротивления.
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
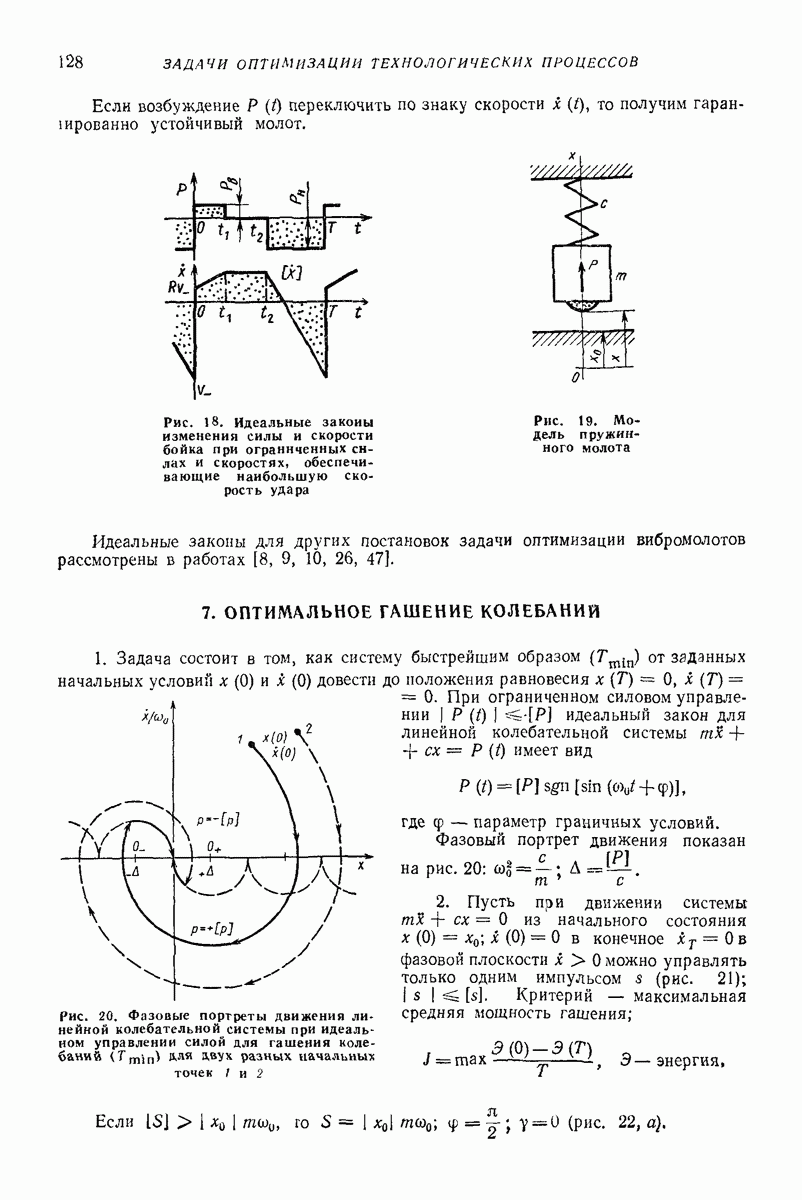
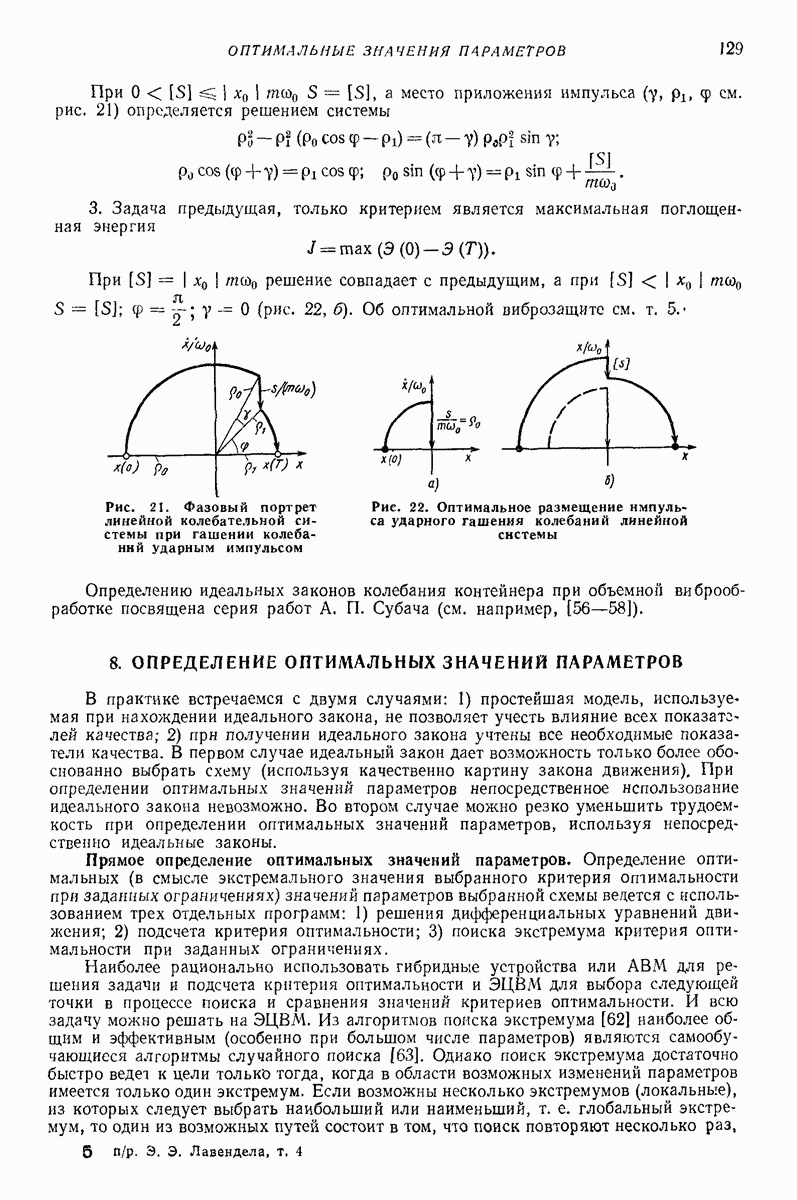
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
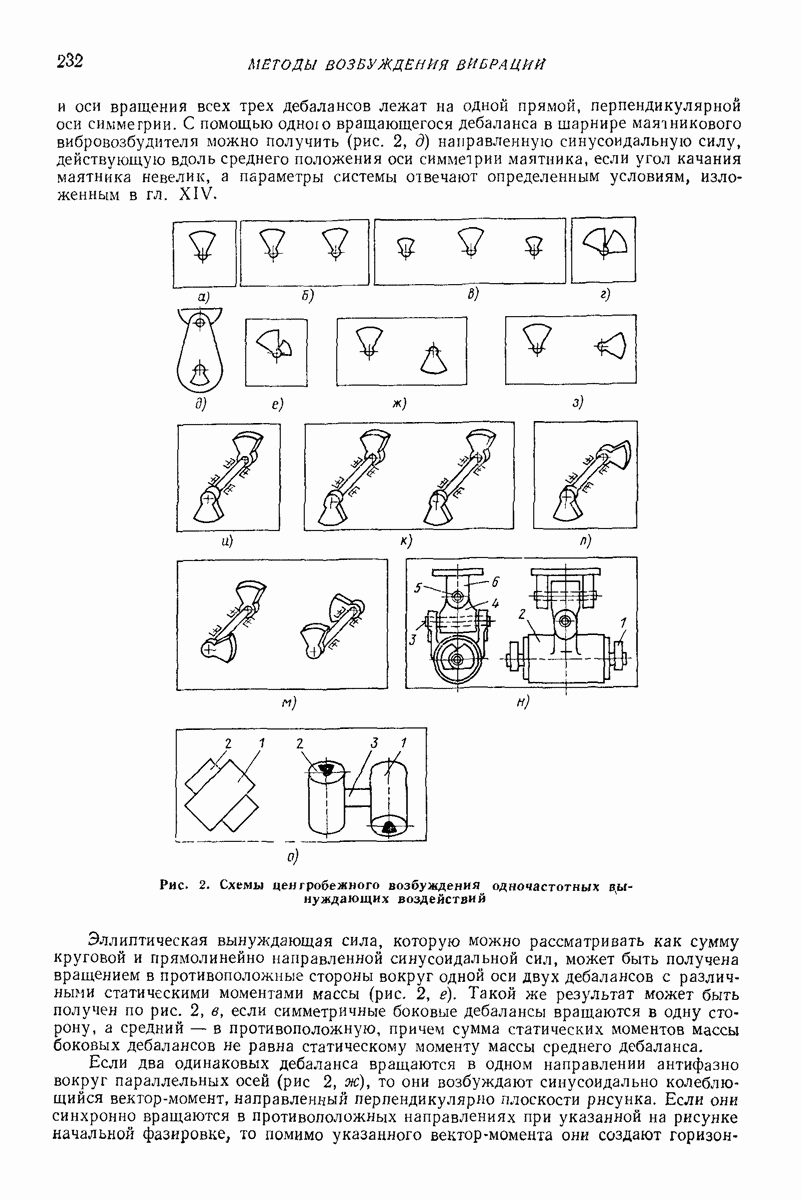
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
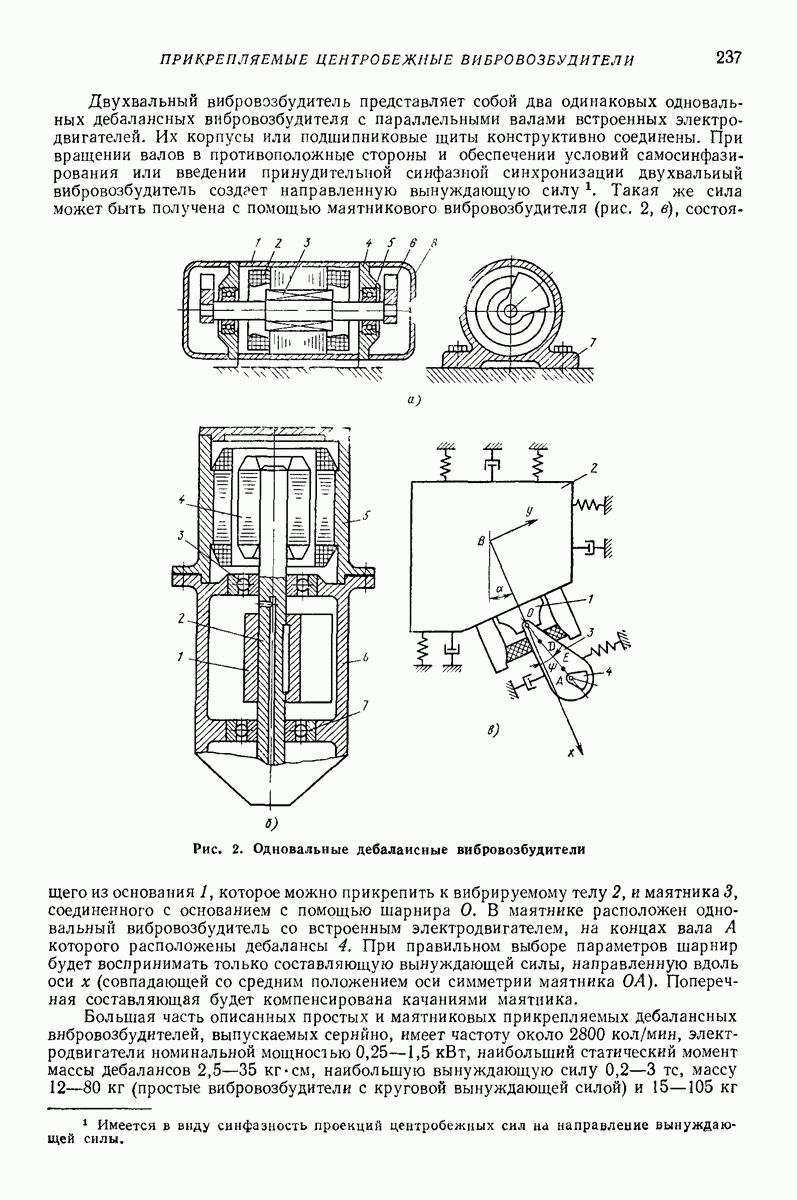
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
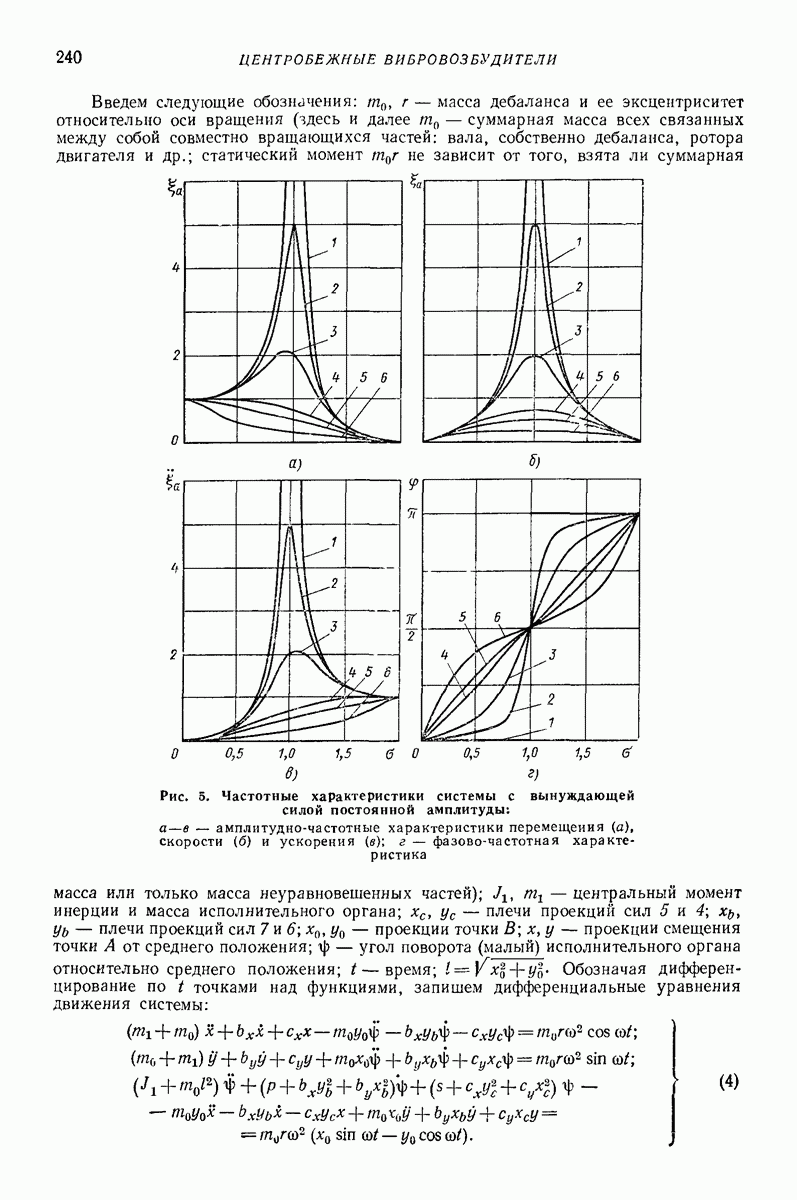
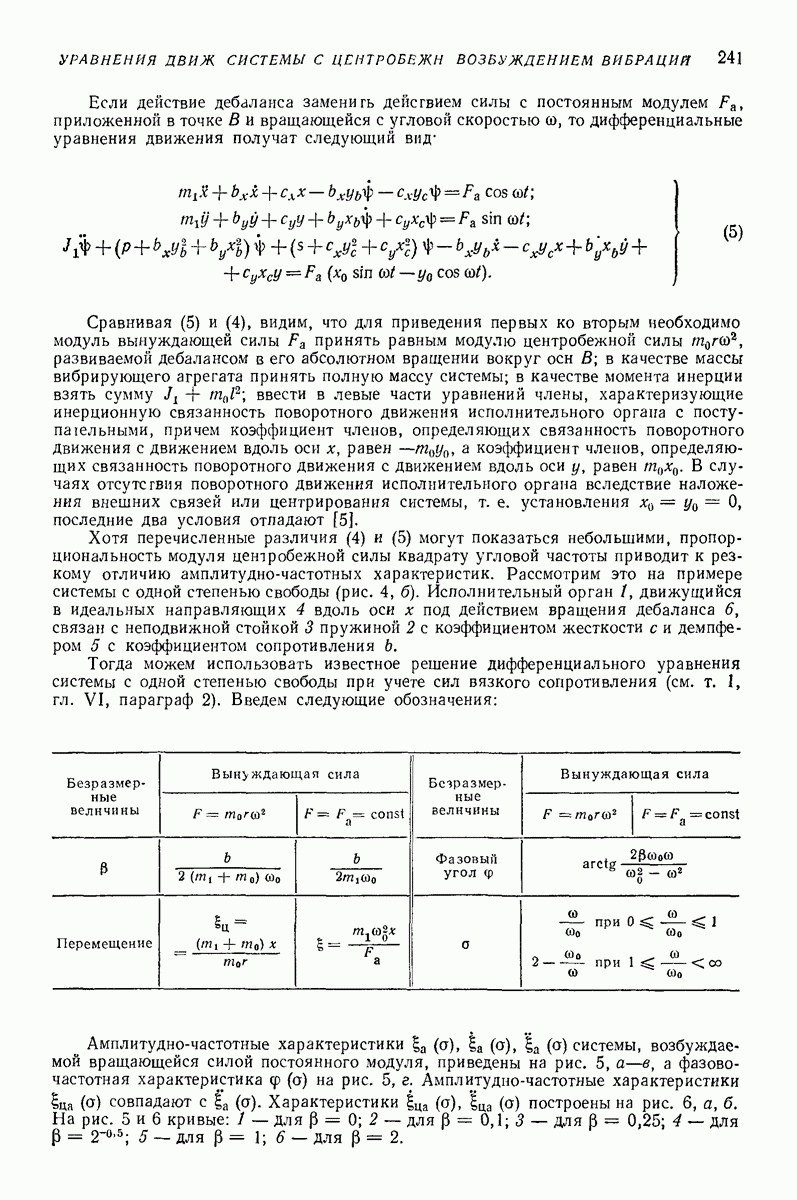
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
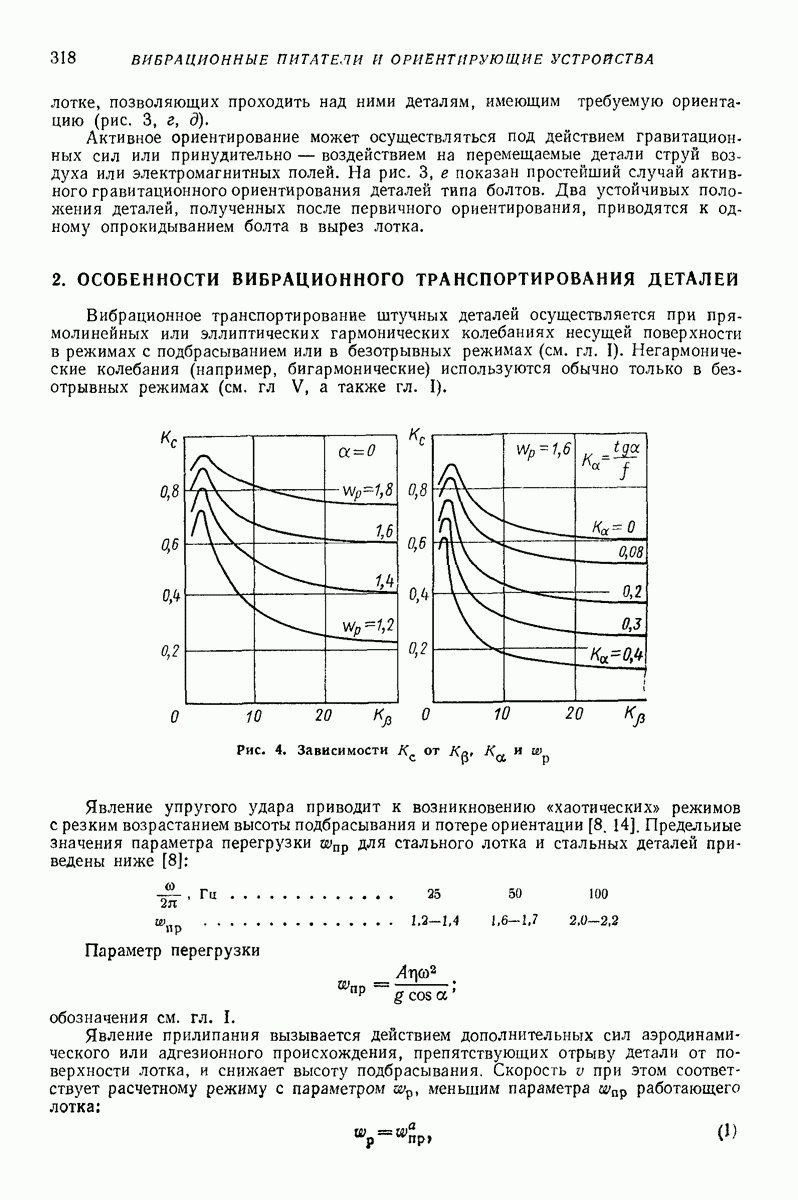
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
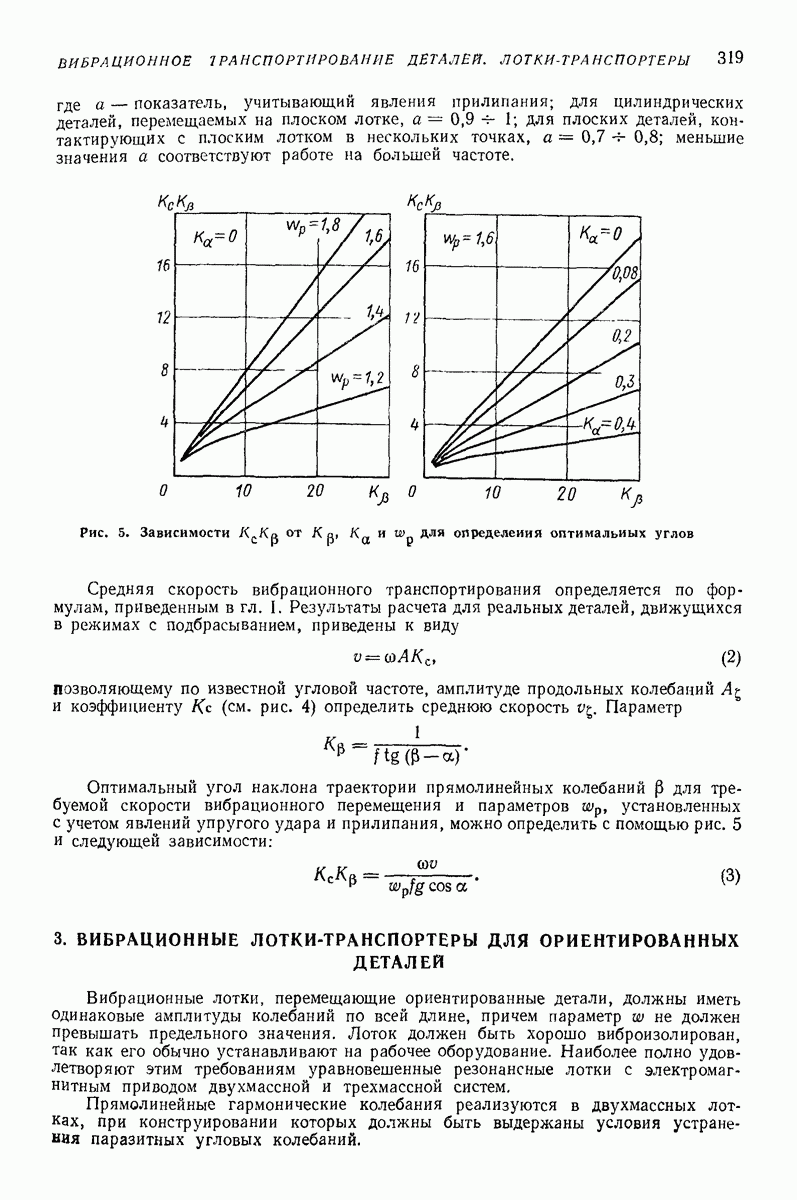
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
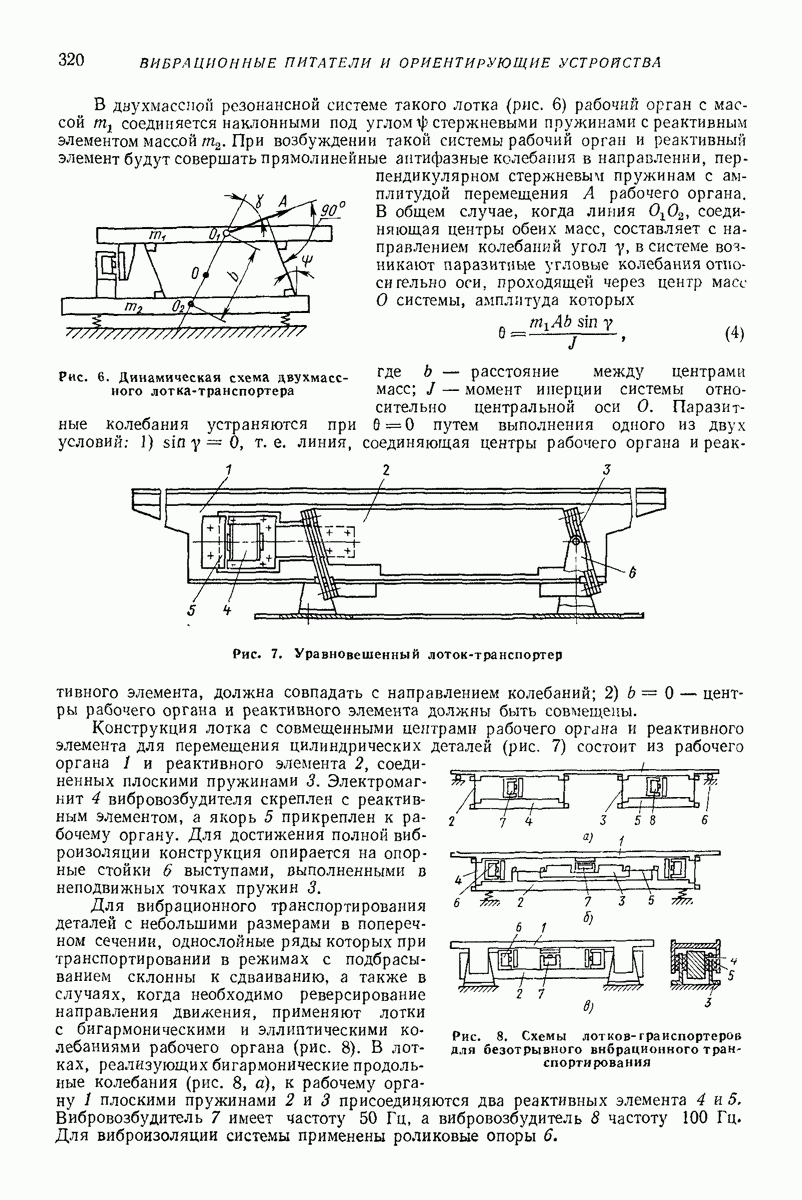
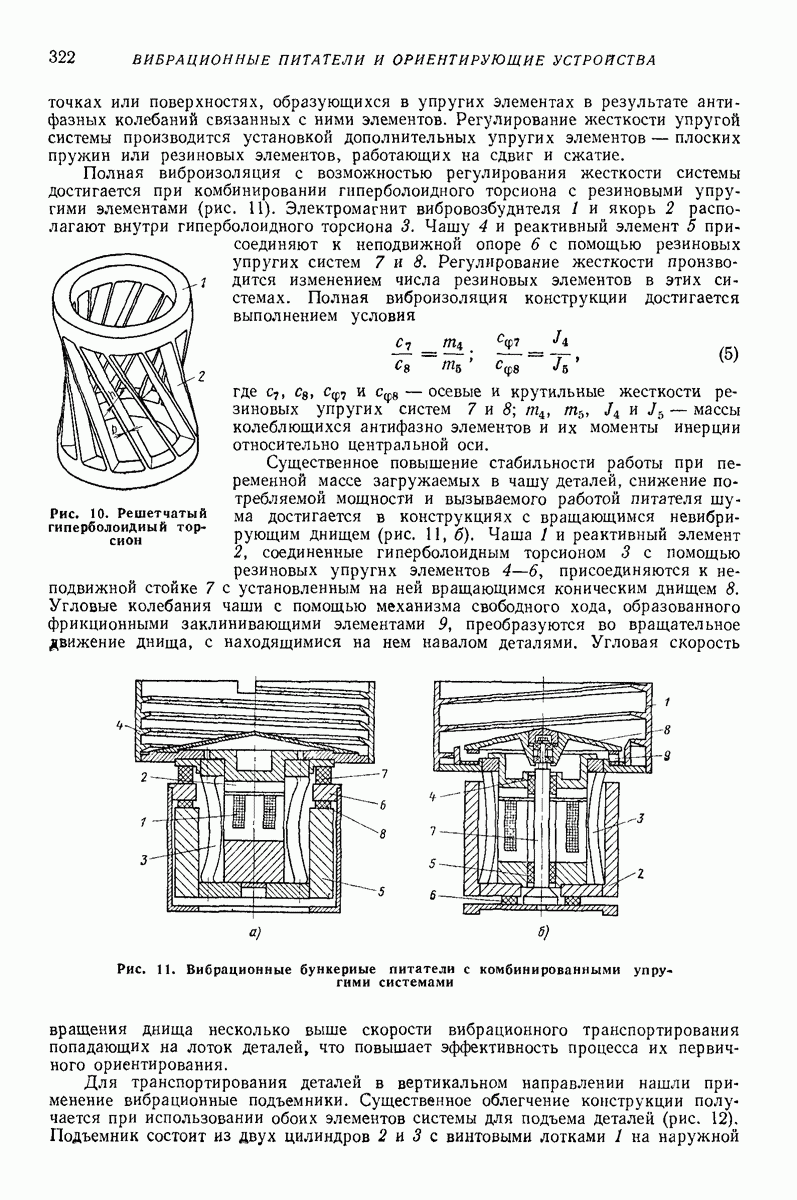
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
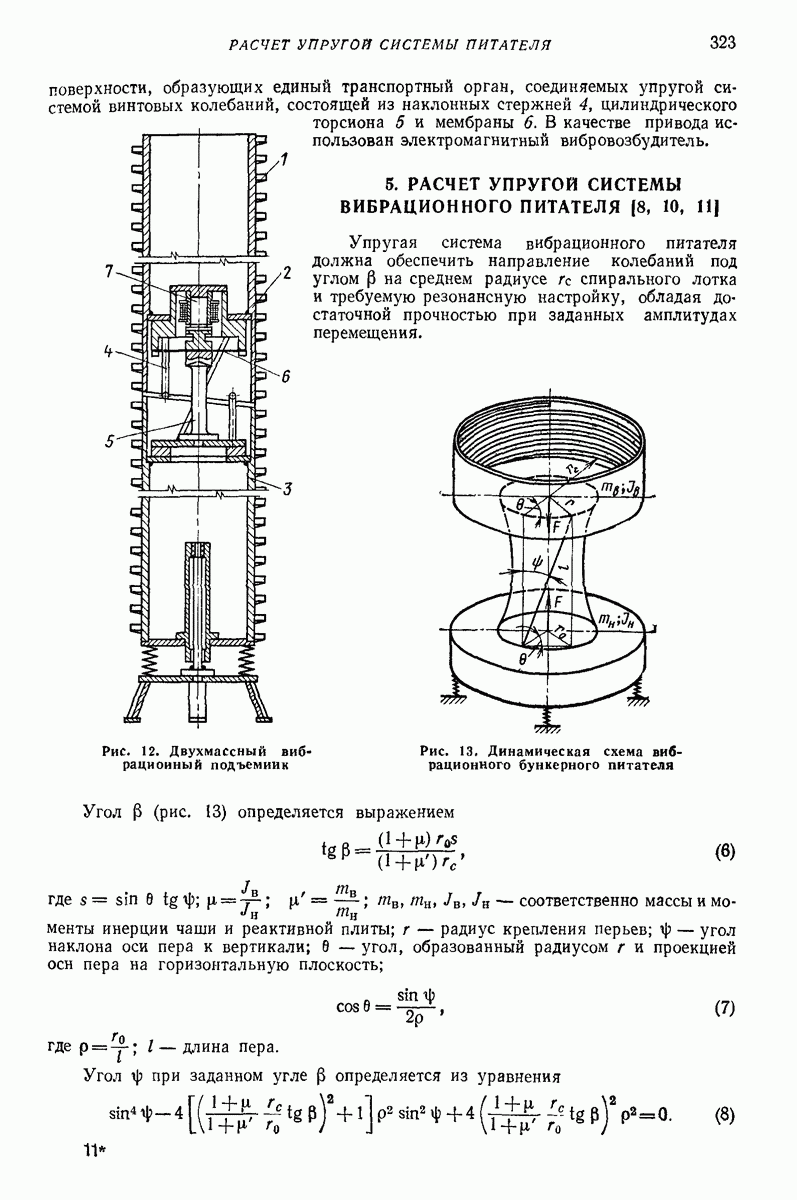
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
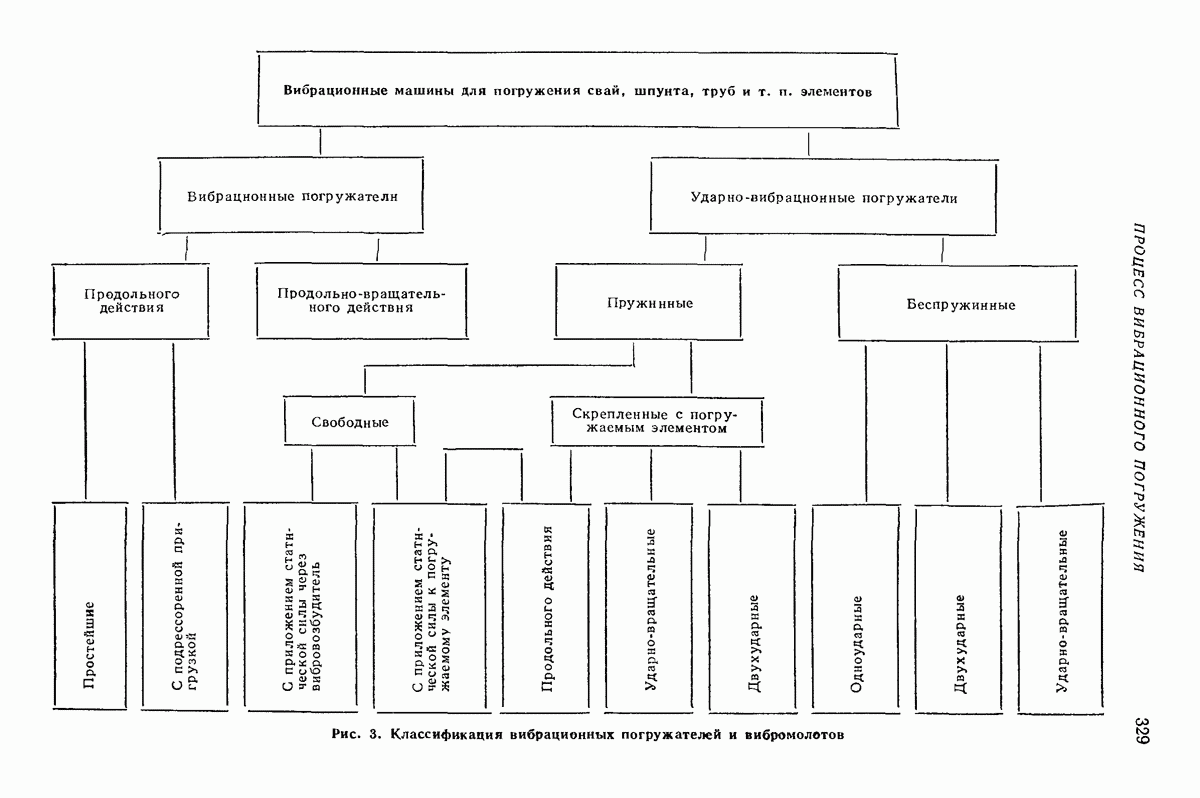
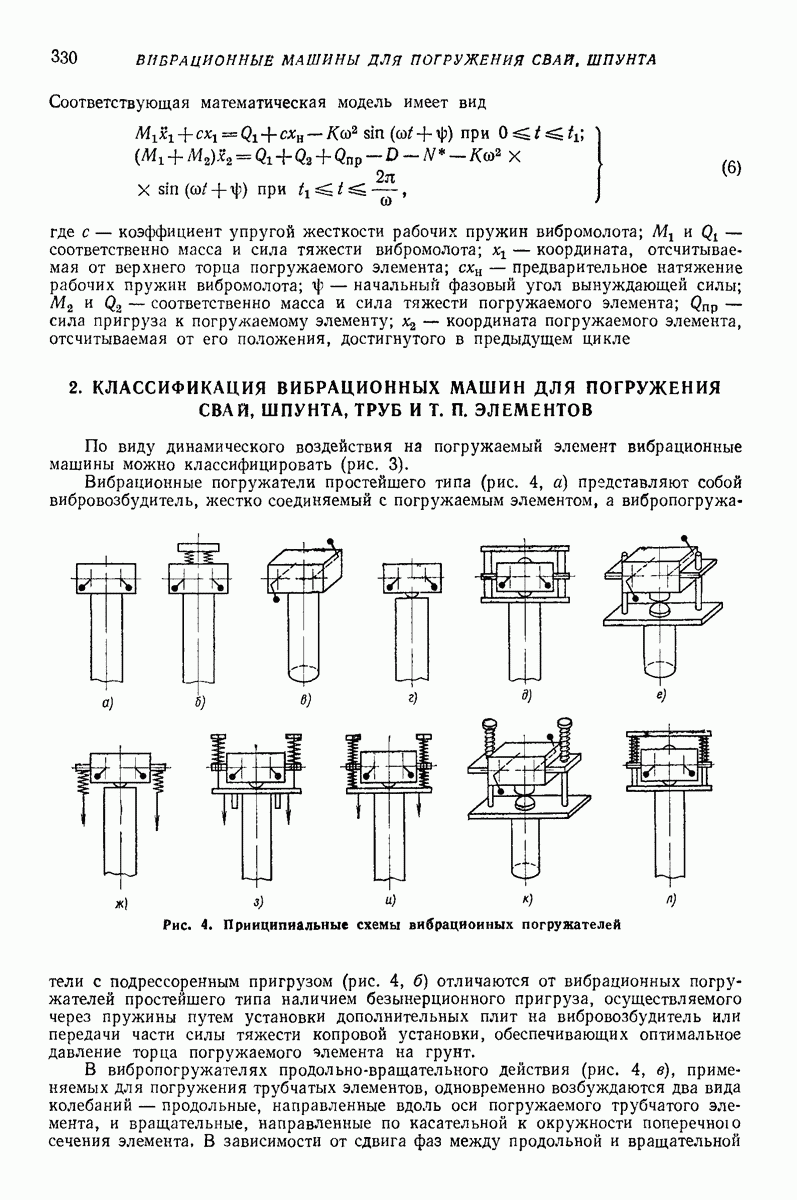
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
- 4. СЕПАРАТОРЫ С ДЕКОЙ
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
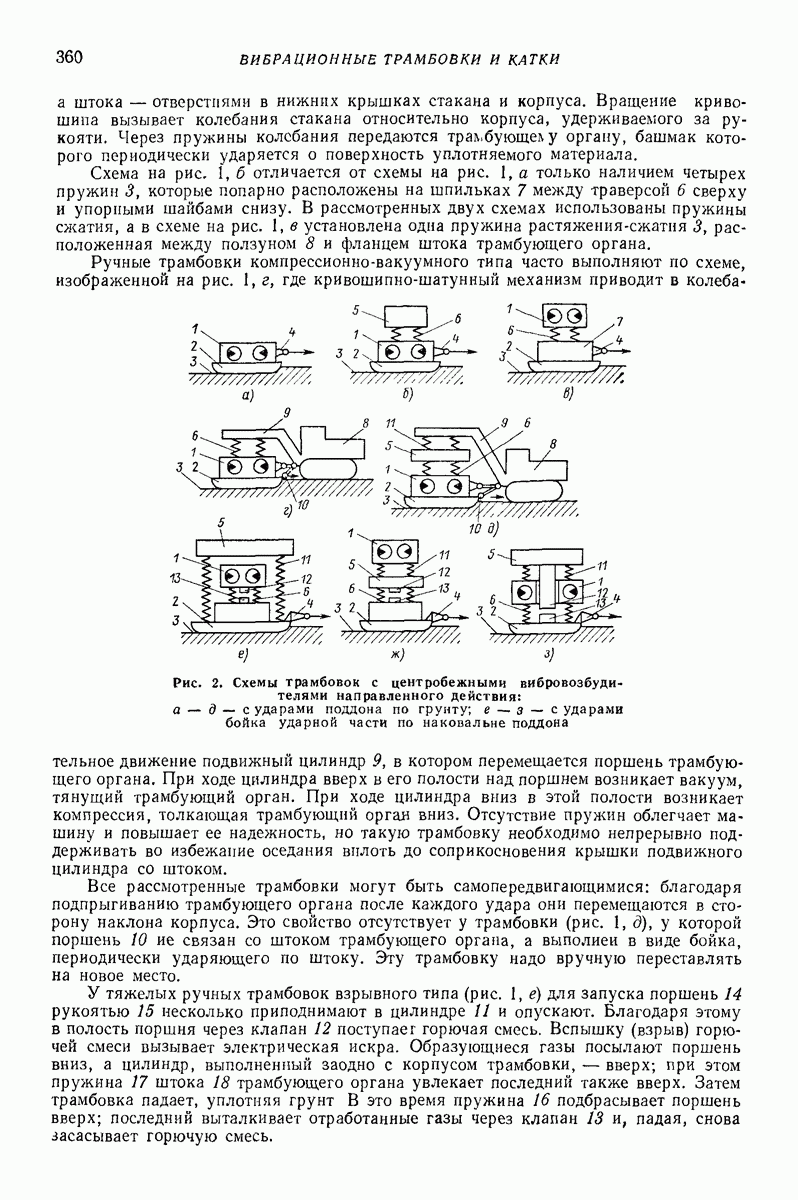
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
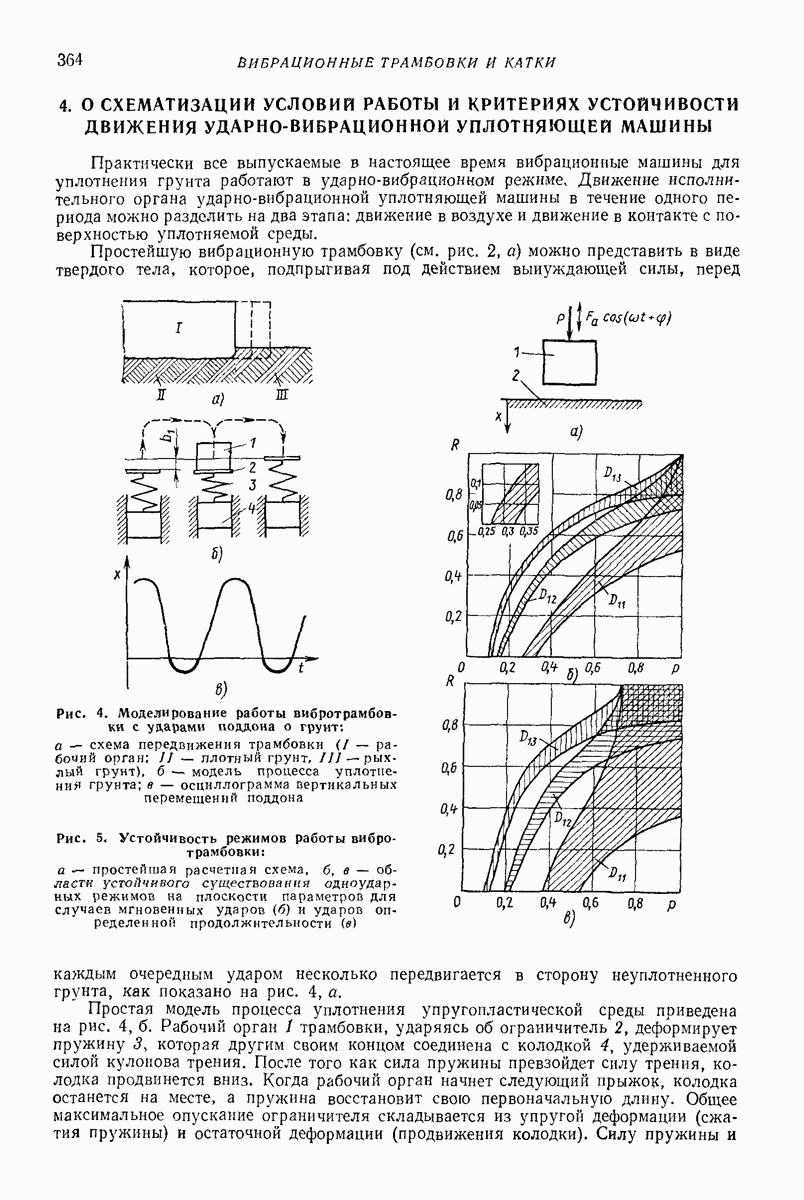
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
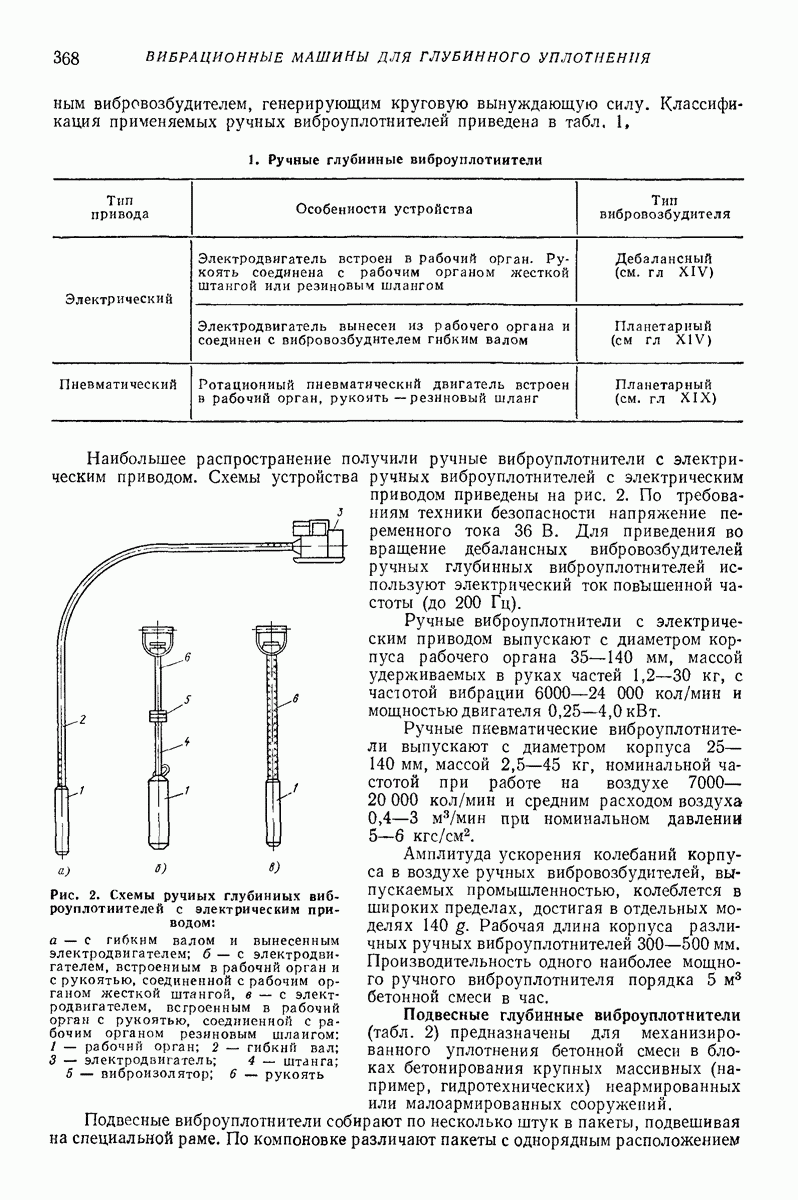
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
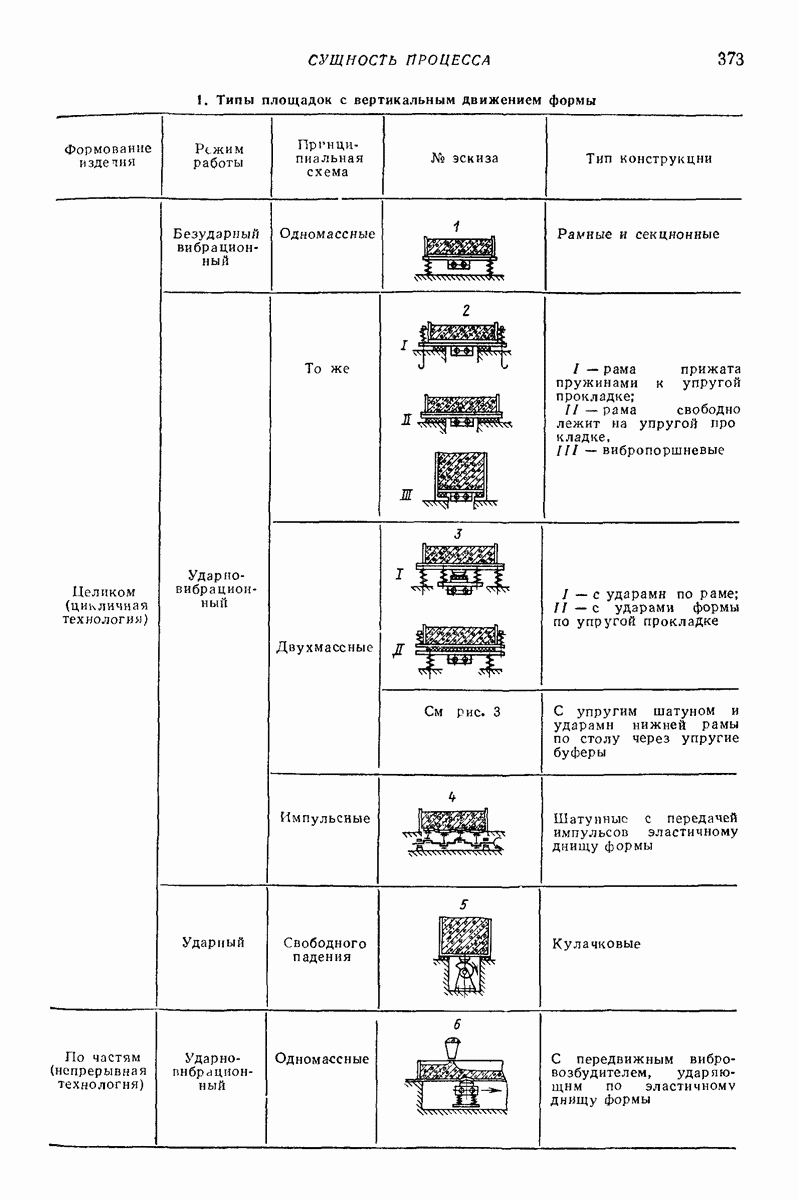
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ