| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
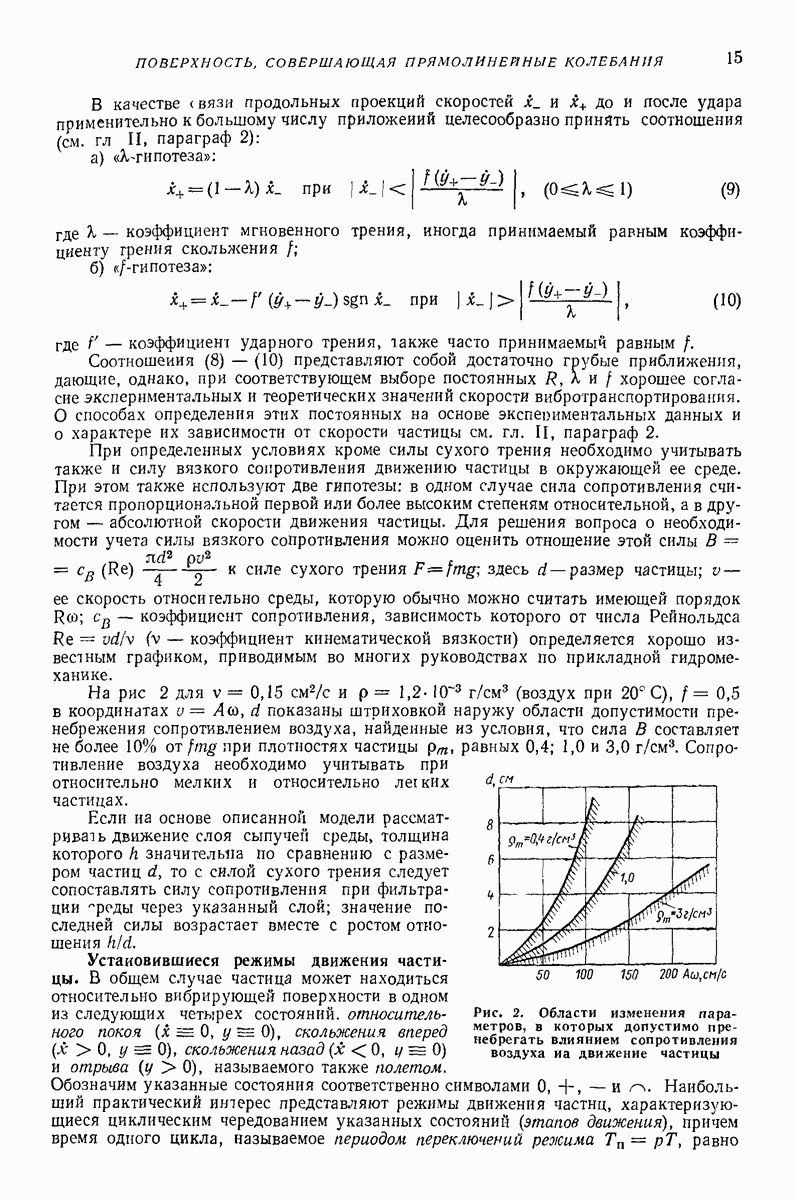
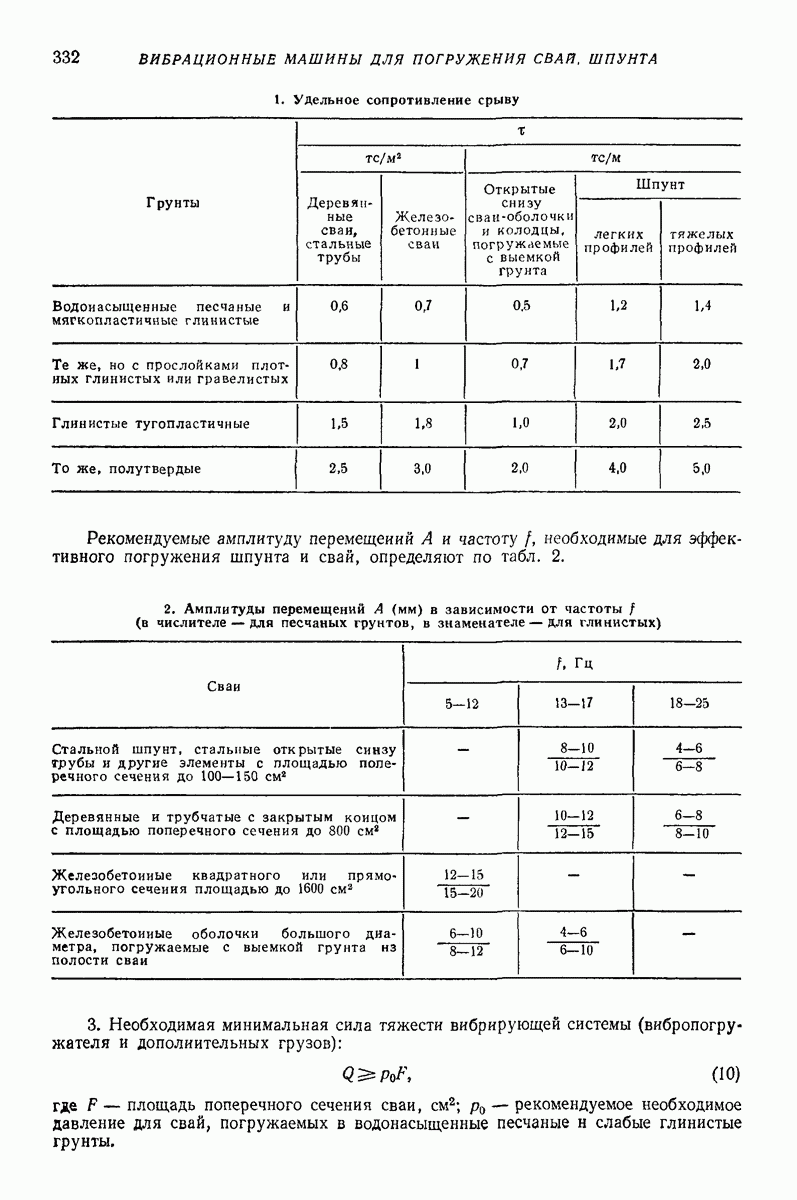
Безотрывное движение. Взаимодействие при безотрывном движении характеризуется коэффициентом трения между телом и поверхностью лотка

где  сила трения;
сила трения;  нормальная реакция.
нормальная реакция.
Приближенная формула не учитывает зависимость  от относительной скорости
от относительной скорости  Однако в задачах о вибротранспортировании диапазон изменений этих величин не очень большой. Если при расчете средней скорости транспортирования V использовать значение
Однако в задачах о вибротранспортировании диапазон изменений этих величин не очень большой. Если при расчете средней скорости транспортирования V использовать значение  соответствующее средним значениям
соответствующее средним значениям  то расчет
то расчет
удовлетворительно согласуется с экспериментом. Учитывать зависимости  возможно, если расчет средней скорости V и других параметров движения вести с помощью ЭЦВМ. Числовое значение
возможно, если расчет средней скорости V и других параметров движения вести с помощью ЭЦВМ. Числовое значение  и его зависимость от
и его зависимость от  можно найти в [10]. Дальнейшее уточнение физики взаимодействия треннем необходимо только при исследовании самоориентации (см. параграф 2).
можно найти в [10]. Дальнейшее уточнение физики взаимодействия треннем необходимо только при исследовании самоориентации (см. параграф 2).

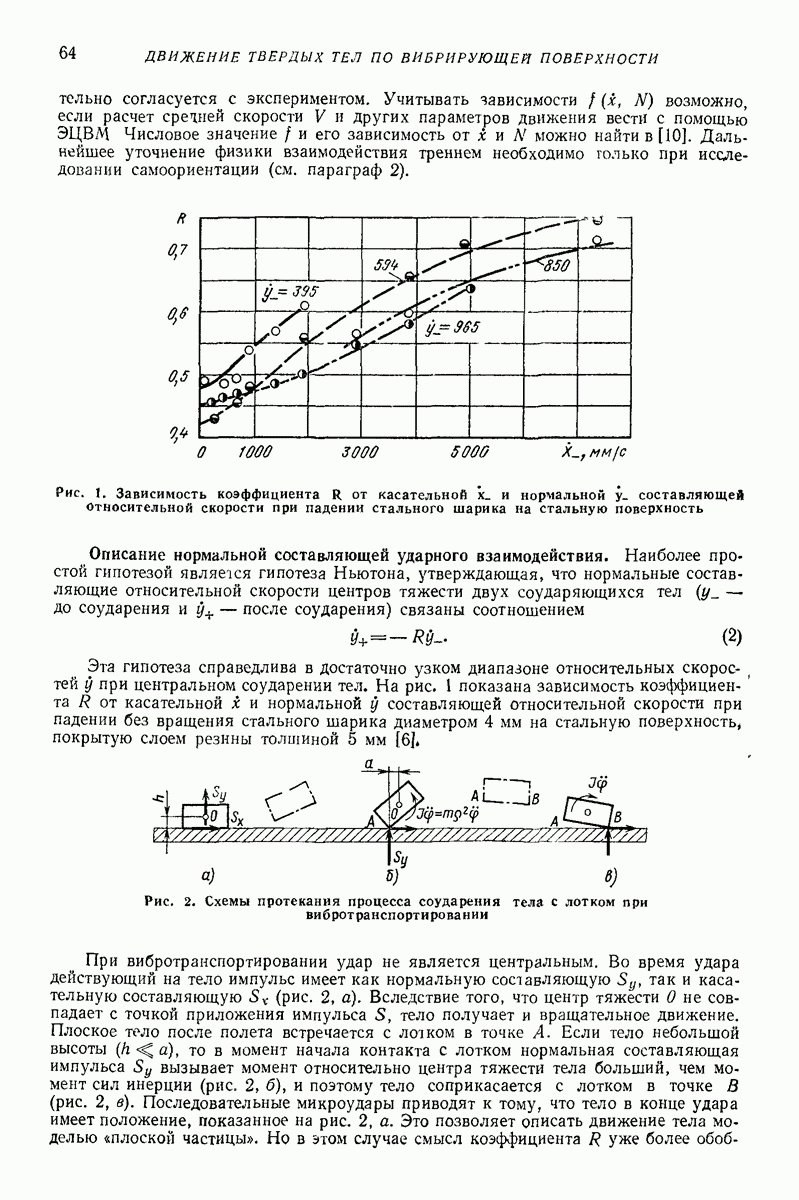
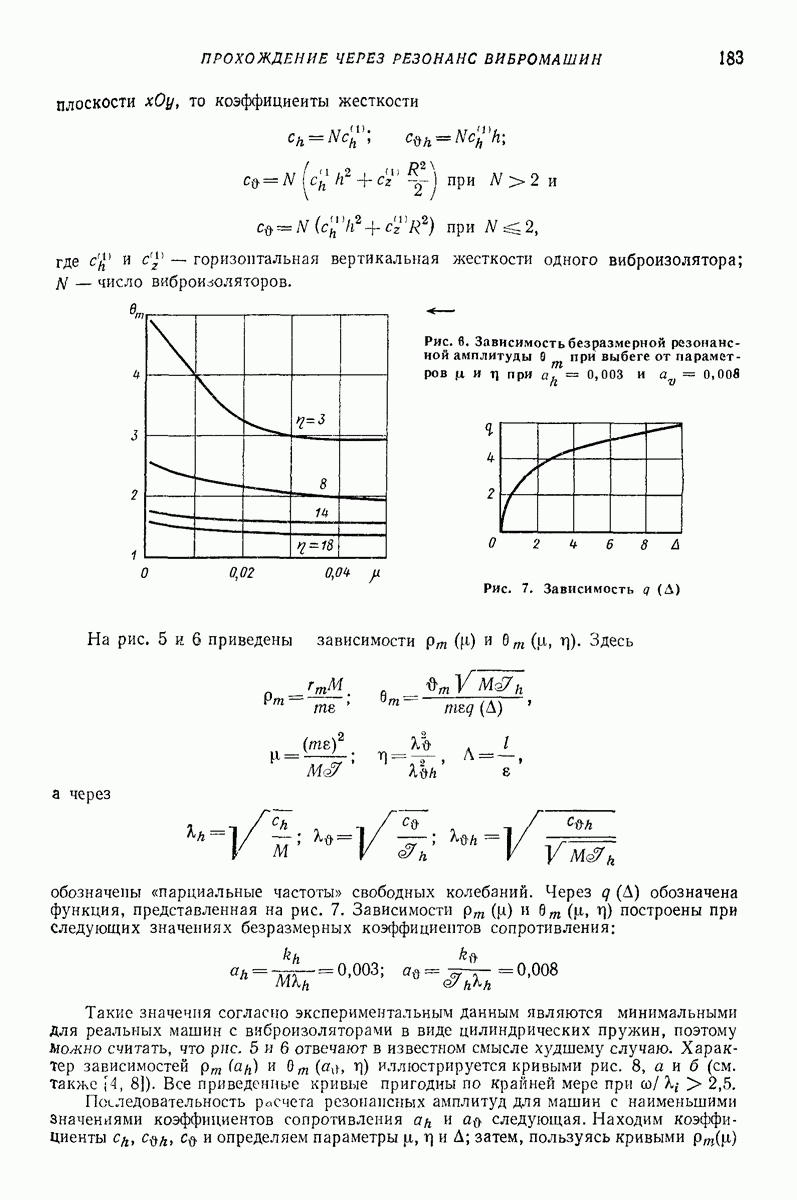
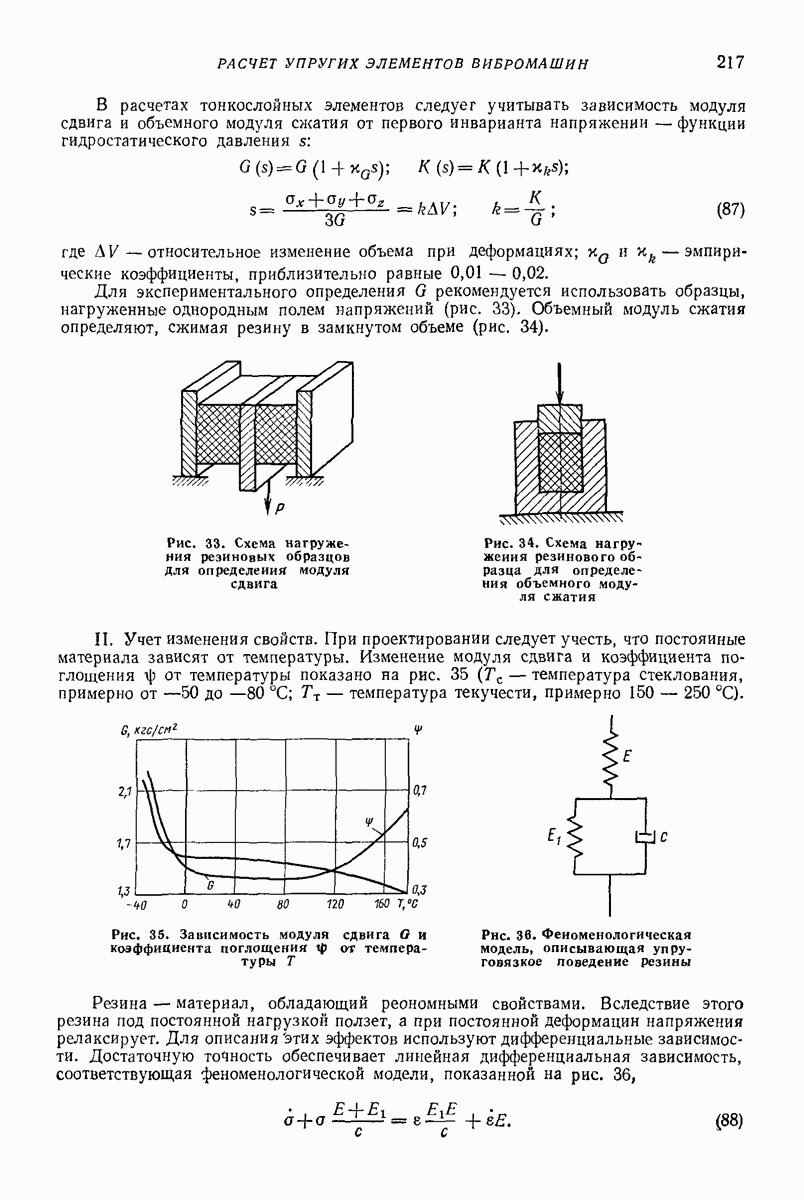
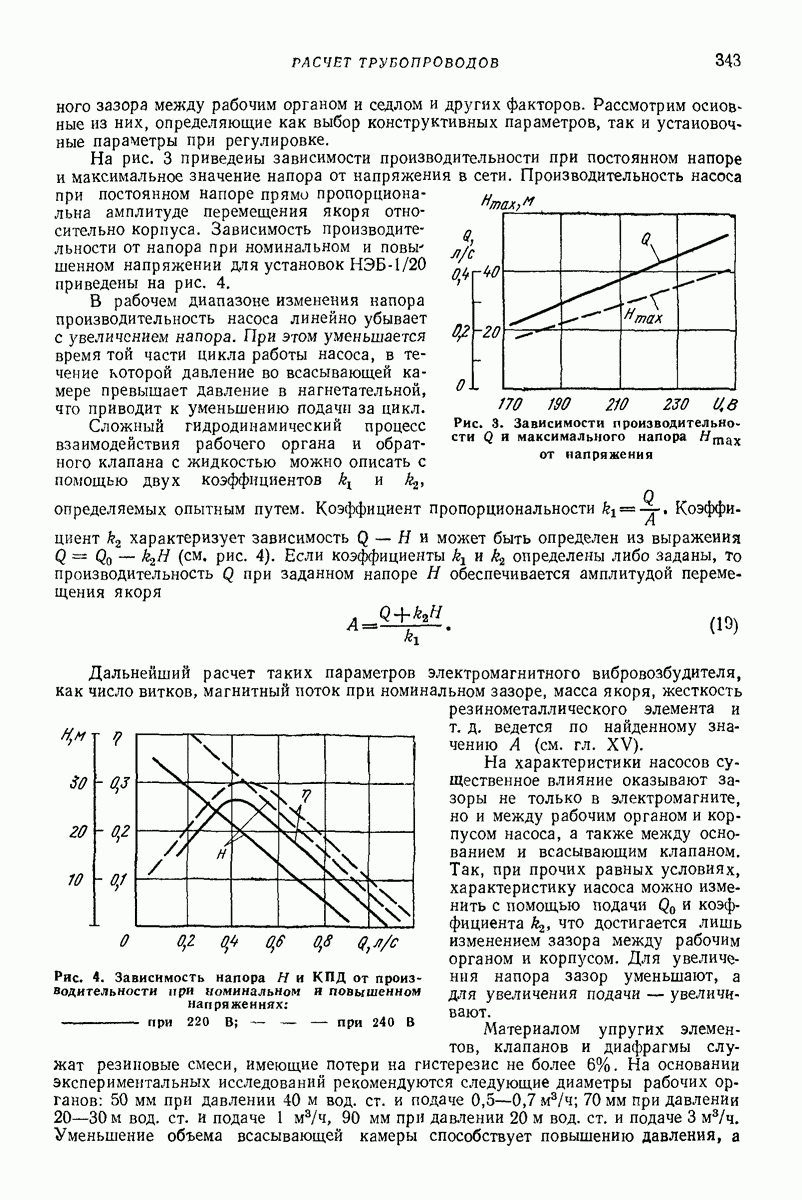
Рис. 1. Зависимость коэффициента  от касательной
от касательной  и нормальной
и нормальной  составляющей относительной скорости при падении стального шарика на стальную поверхность
составляющей относительной скорости при падении стального шарика на стальную поверхность
Описание нормальной составляющей ударного взаимодействия. Наиболее простой гипотезой является гипотеза Ньютона, утверждающая, что нормальные составляющие относительной скорости центров тяжести двух соударяющихся тел  до соударения и
до соударения и  после соударения) связаны соотношением
после соударения) связаны соотношением

Эта гипотеза справедлива в достаточно узком диапазоне относительных скоростей у при центральном соударении тел. На рис. 1 показана зависимость коэффициента  от касательной х и нормальной у составляющей относительной скорости при падении без вращения стального шарика диаметром
от касательной х и нормальной у составляющей относительной скорости при падении без вращения стального шарика диаметром  на стальную поверхность, покрытую слоем резины толшиной
на стальную поверхность, покрытую слоем резины толшиной  [6].
[6].

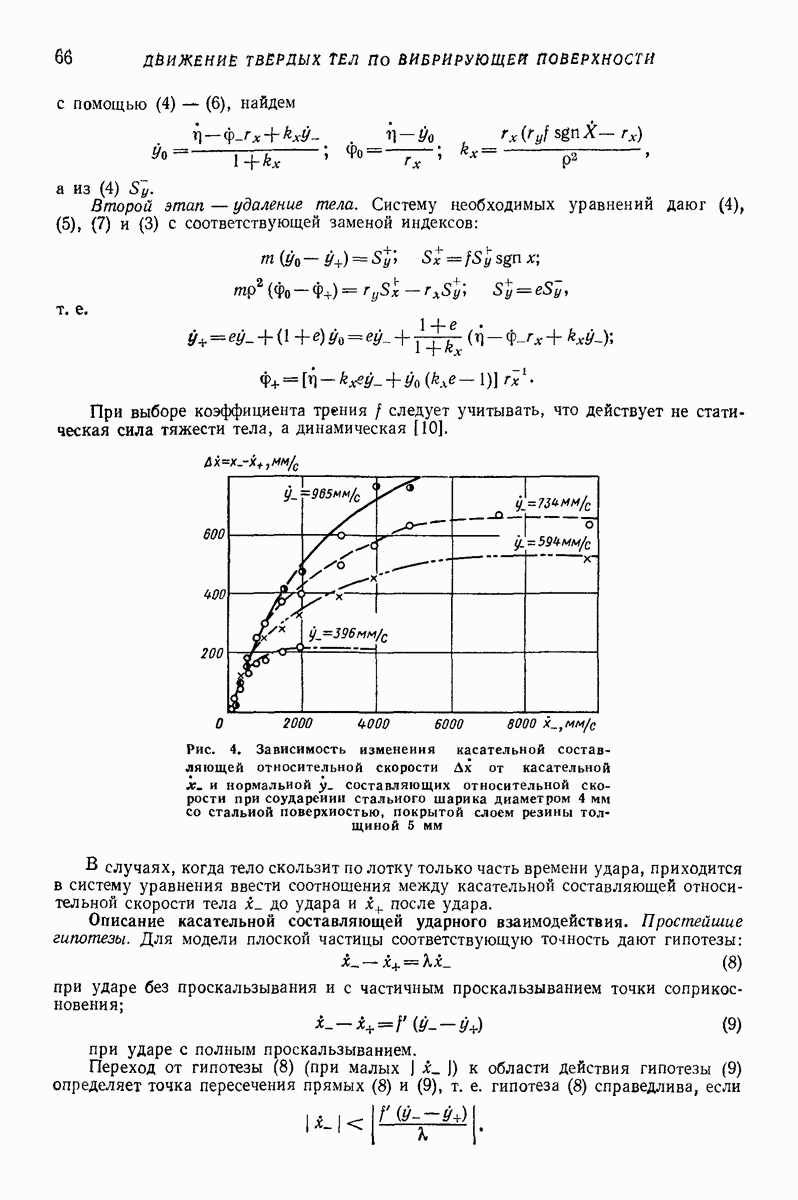
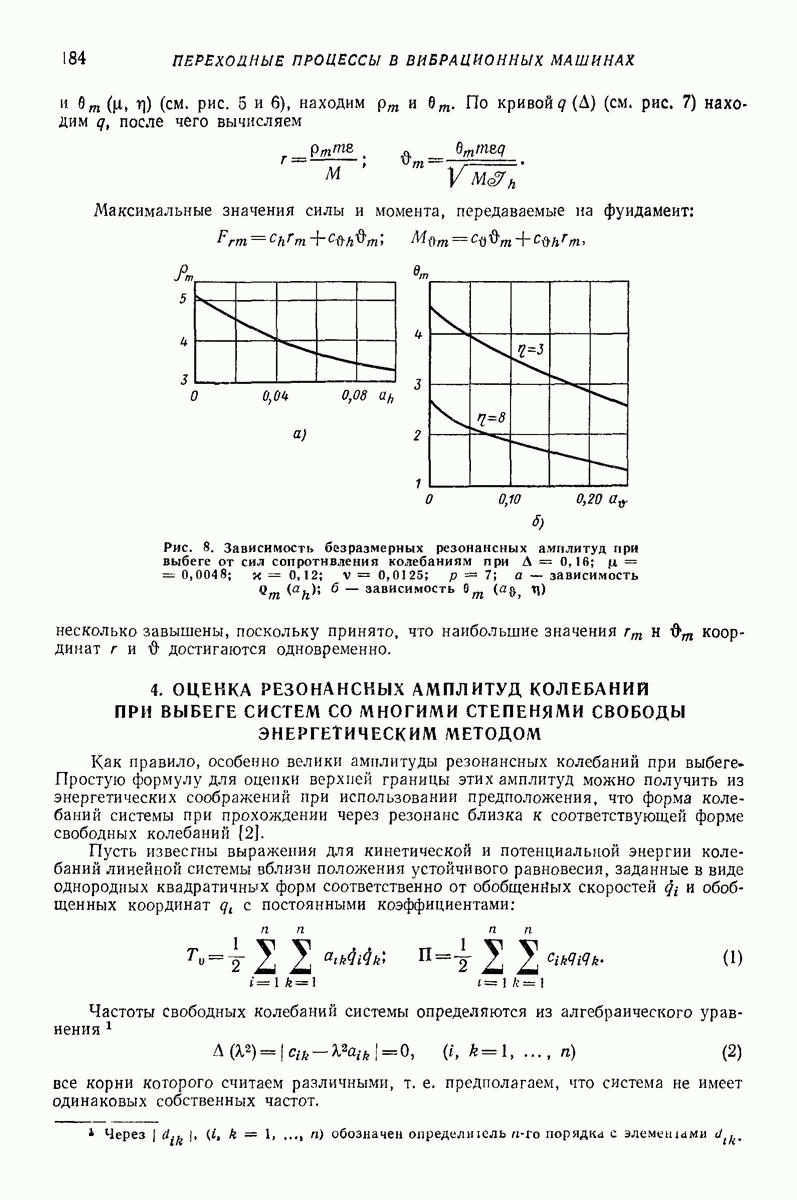
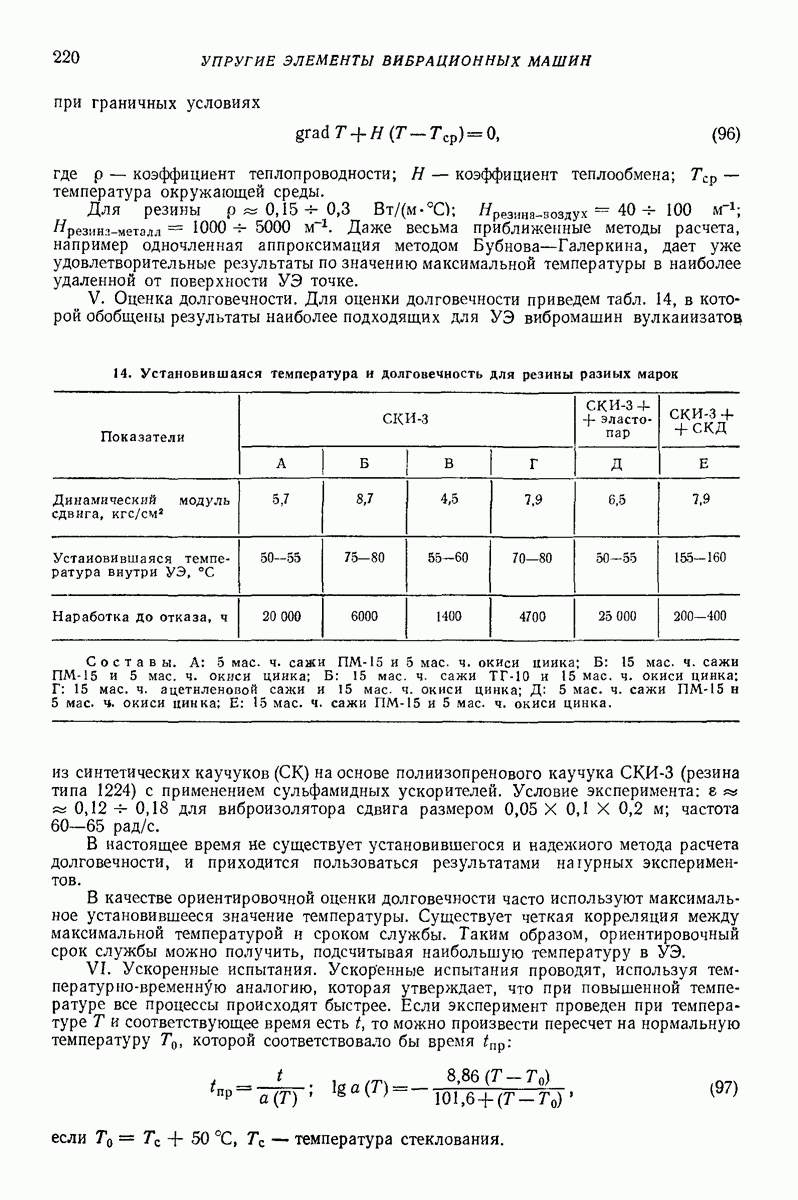
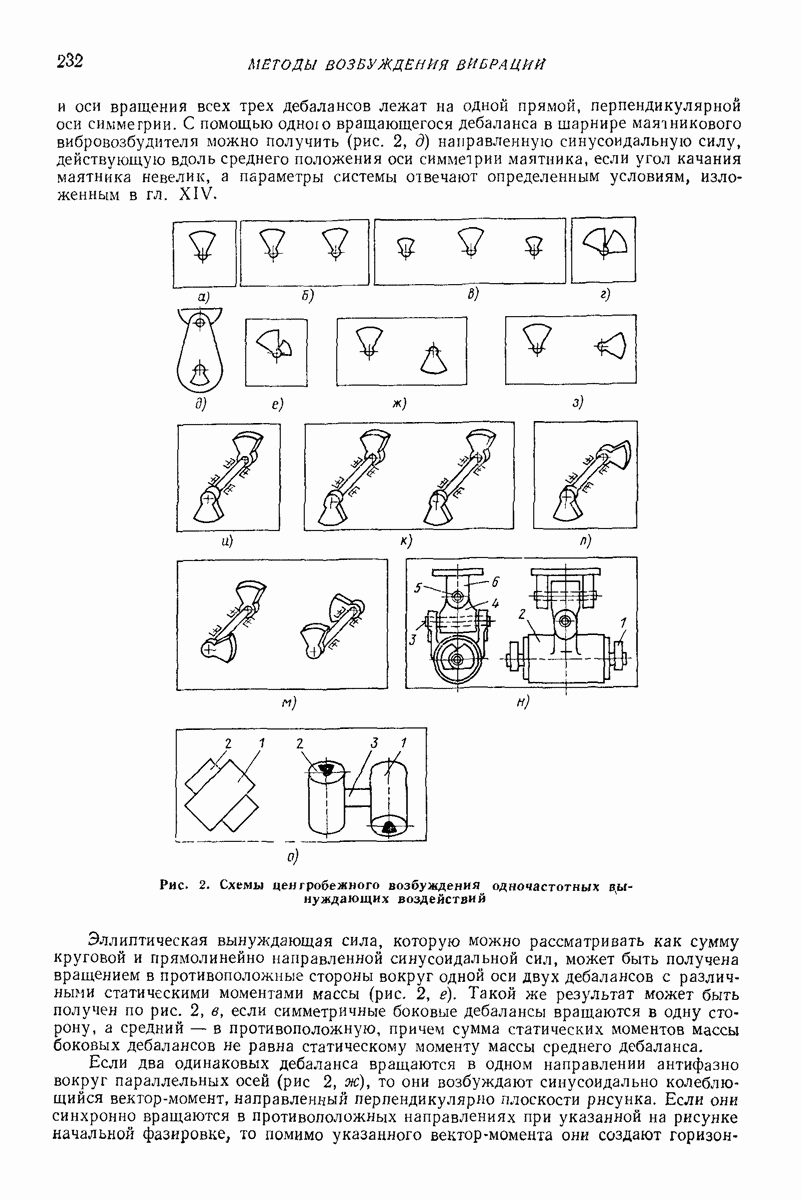
Рис. 2. Схемы протекания процесса соударения тела с лотком при вибротранспортировании
При вибротранспортировании удар не является центральным. Во время удара действующий на тело импульс имеет как нормальную составляющую  так и касательную составляющую
так и касательную составляющую  (рис. 2, а). Вследствие того, что центр тяжести
(рис. 2, а). Вследствие того, что центр тяжести  не совпадает с точкой приложения импульса
не совпадает с точкой приложения импульса  тело получает и вращательное движение. Плоское тело после полета встречается с лотком в точке А. Если тело небольшой высоты
тело получает и вращательное движение. Плоское тело после полета встречается с лотком в точке А. Если тело небольшой высоты  то в момент начала контакта с лотком нормальная составляющая импульса
то в момент начала контакта с лотком нормальная составляющая импульса  вызывает момент относительно центра тяжести тела больший, чем момент сил инерции (рис. 2, б), и поэтому тело соприкасается с лотком в точке В (рис. 2, в). Последовательные микроудары приводят к тому, что тело в конце удара имеет положение, показанное на рис. 2, а. Это позволяет описать движение тела моделью «плоской частицы». Но в этом случае смысл коэффициента
вызывает момент относительно центра тяжести тела больший, чем момент сил инерции (рис. 2, б), и поэтому тело соприкасается с лотком в точке В (рис. 2, в). Последовательные микроудары приводят к тому, что тело в конце удара имеет положение, показанное на рис. 2, а. Это позволяет описать движение тела моделью «плоской частицы». Но в этом случае смысл коэффициента  уже более
уже более
обобщенный, так как нормальные составляющие относительной скорости центра тяжести берутся в начале и в конце серии микроударов. Поэтому  сильно зависит от касательной и нормальной составляющей скорости и конфшурации тела. Значение
сильно зависит от касательной и нормальной составляющей скорости и конфшурации тела. Значение  может быть определено только непосредственно из эксперимента по вибротранспортированию.
может быть определено только непосредственно из эксперимента по вибротранспортированию.
Физически более обоснованной является гипотеза, связывающая кинетические эиергии тел до и после удара [7, 8]. Но так как с этой гипотезой работать сложнее, то используют эквивалентное соотношение импульсов  до соударения и
до соударения и  после соударения
после соударения

где  эмпирический коэффициент.
эмпирический коэффициент.
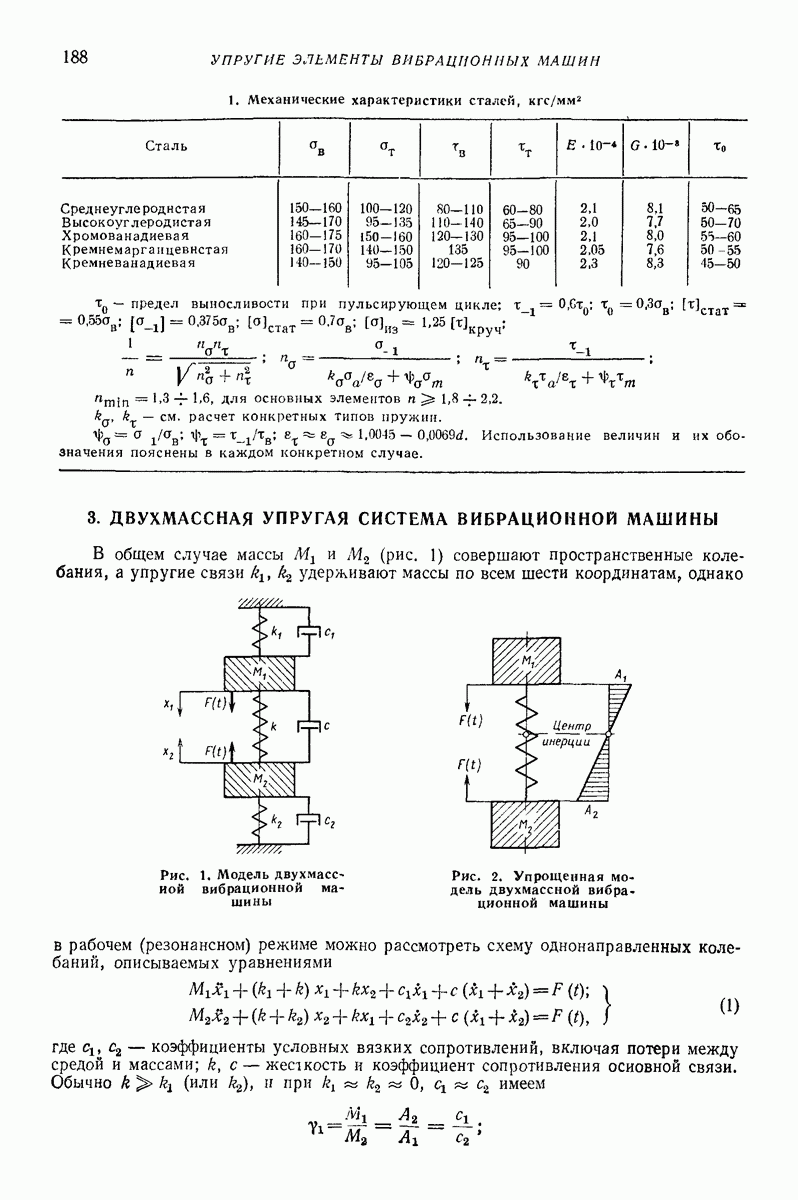
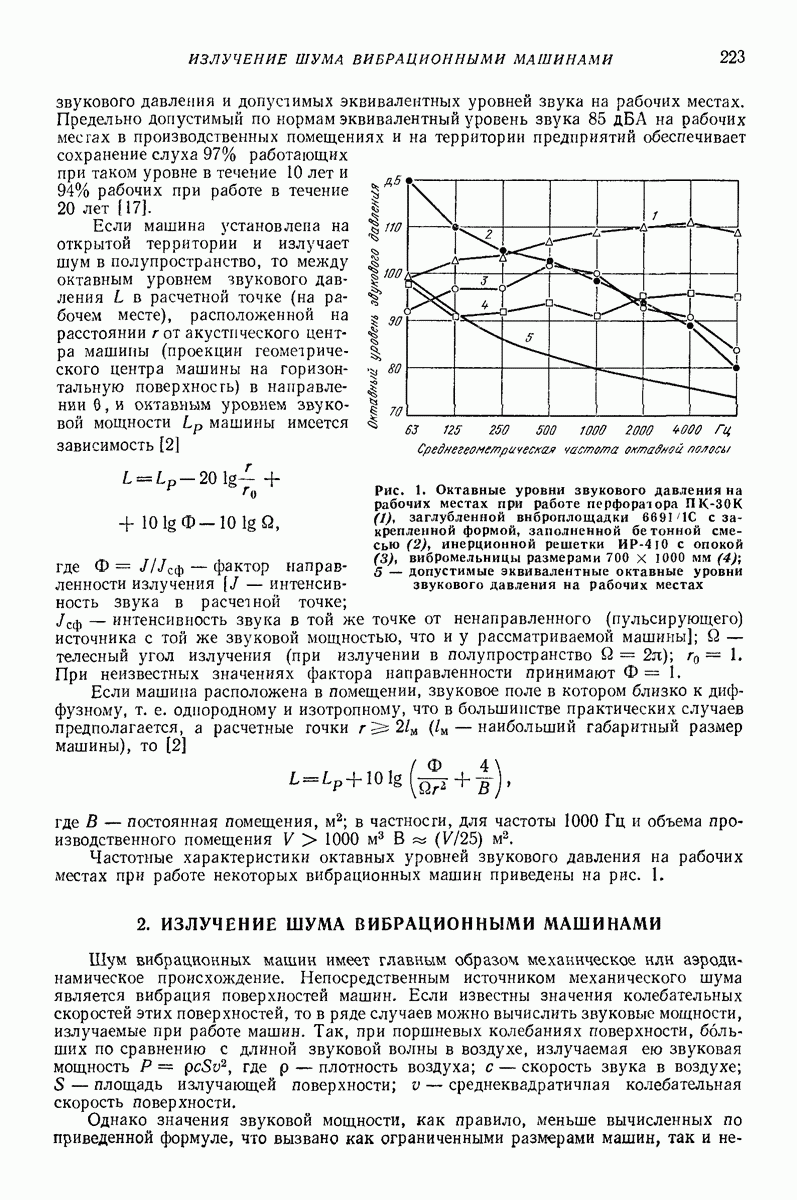
При плоскопараллельном движении (рис. 3) соотношение (3) имеет вид

Определения (3) и (2) совпадают только для центрального удара  или при отсутствии поворота тела [нулю равны угловые скорости в начале удара
или при отсутствии поворота тела [нулю равны угловые скорости в начале удара  (рис. 3, а), в конце удара
(рис. 3, а), в конце удара  (рис. 3, в) и в момент наибольшего сближения
(рис. 3, в) и в момент наибольшего сближения  (рис. 3, б). Тогда скорость центра тяжести
(рис. 3, б). Тогда скорость центра тяжести  совпадает со скоростью точки соприкосновения.
совпадает со скоростью точки соприкосновения.

Рис. 3. Характерные положения тела при соударении с плоской поверхностью: а — в начале удара;  в момент наибольшего сближения; в — в конце удара
в момент наибольшего сближения; в — в конце удара
Определение движения тела в нормальном направлении к поверхности лотка ведется следующим образом [7, 8]. Если относительная скорость достаточно большая и тело все время удара скользит (относительная касательная скорость точки соприкосновения  то весь процесс делитсана два этапа.
то весь процесс делитсана два этапа.
Первый этап — сближение. Уравнения изменения количества движения

и момента количества движения

содержат четыре неизвестные величины — нормальную относительную скорость и угловую скорость  в конце первого этапа и импульсы первого этапа
в конце первого этапа и импульсы первого этапа  Первый этап — сближение заканчивается, когда нормальная составляющая скорости точки соприкосновения (точка В на рис. 3, б)
Первый этап — сближение заканчивается, когда нормальная составляющая скорости точки соприкосновения (точка В на рис. 3, б)  Так как
Так как  где
где  закон движения поверхности лотка в поперечном направлении, то при
закон движения поверхности лотка в поперечном направлении, то при

Присоединив понятие коэффициента трения

с помощью (4) — (6), найдем

Второй этап — удаление тела. Систему необходимых уравнений даюг (4), (5), (7) и (3) с соответствующей заменой индексов:

т. е.

При выборе коэффициента трения  следует учитывать, что действует не статическая сила тяжести тела, а динамическая [10].
следует учитывать, что действует не статическая сила тяжести тела, а динамическая [10].

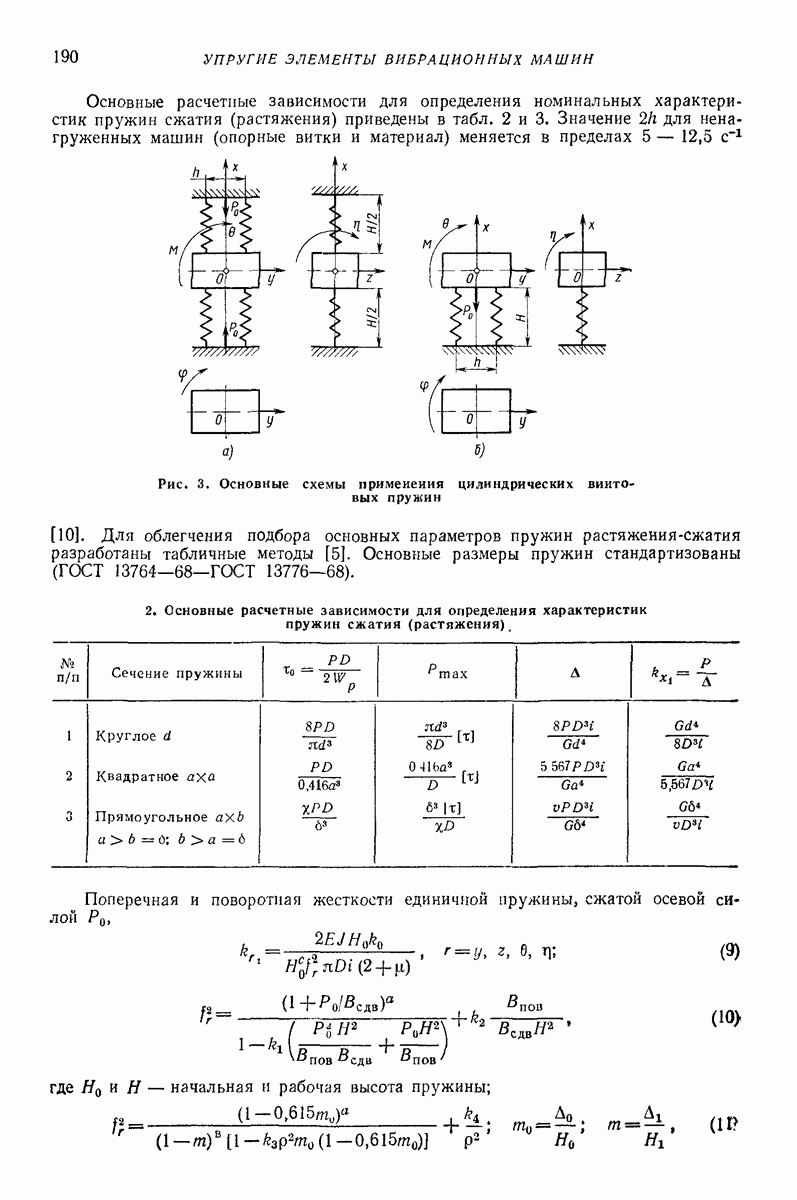
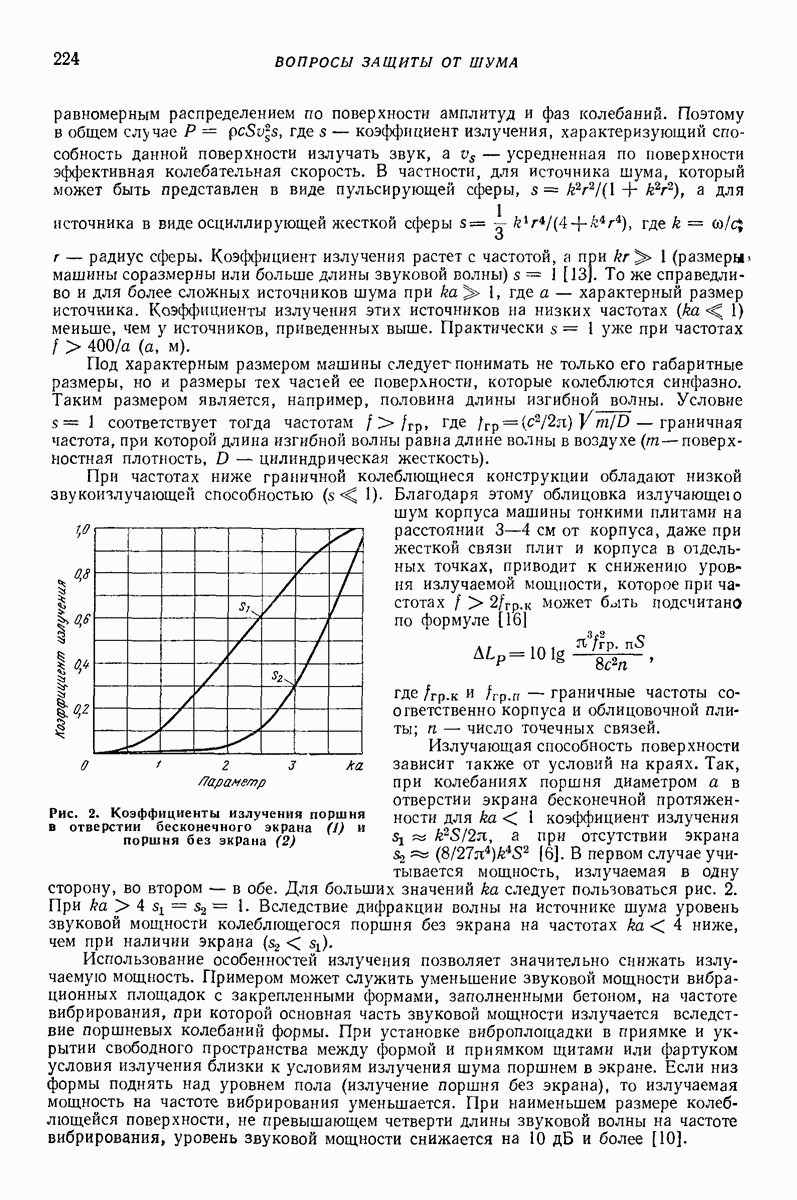
Рис. 4. Зависимость изменения касательной составляющей относительной скорости  от касательной и нормальной составляющих относительной скорости при соударении стального шарика диаметром
от касательной и нормальной составляющих относительной скорости при соударении стального шарика диаметром  со стальной поверхностью, покрытой слоем резины толщиной
со стальной поверхностью, покрытой слоем резины толщиной 
В случаях, когда тело скользит полотку только часть времени удара, приходится в систему уравнения ввести соотношения между касательной составляющей относительной скорости тела  до удара и после удара.
до удара и после удара.
Описание касательной составляющей ударного взаимодействия. Простейшие гипотезы. Для модели плоской частицы соответствующую точность дают гипотезы:

при ударе без проскальзывания и с частичным проскальзыванием точки соприкосновения;

при ударе с полным проскальзыванием.
Переход от гипотезы (8) (при малых  к области действия гипотезы (9) определяет точка пересечения прямых (8) и (9), т. е. гипотеза (8) справедлива, если
к области действия гипотезы (9) определяет точка пересечения прямых (8) и (9), т. е. гипотеза (8) справедлива, если

Выражения (8) и (9) являются следствием лишь одного допущения о том, что в контакте при ударе действует только сухое трение [7, 8]. Наличие проскальзывания или его отсутствие, так же как при определении силы сцепления при сухом трении, определяет природу этих двух выражений. Выражение (8) справедливо тогда, когда за время удара взаимное проскальзывание прекращается и при отрыве детали от лотка скорости в точке контакта тела и лотка одинаковы. Если этого нет, то справедливо (9). Данные теоретические исследования подкреплены непосредственными экспериментальными исследованиями [5], полностью подтверждающими справедливость этих выражений.

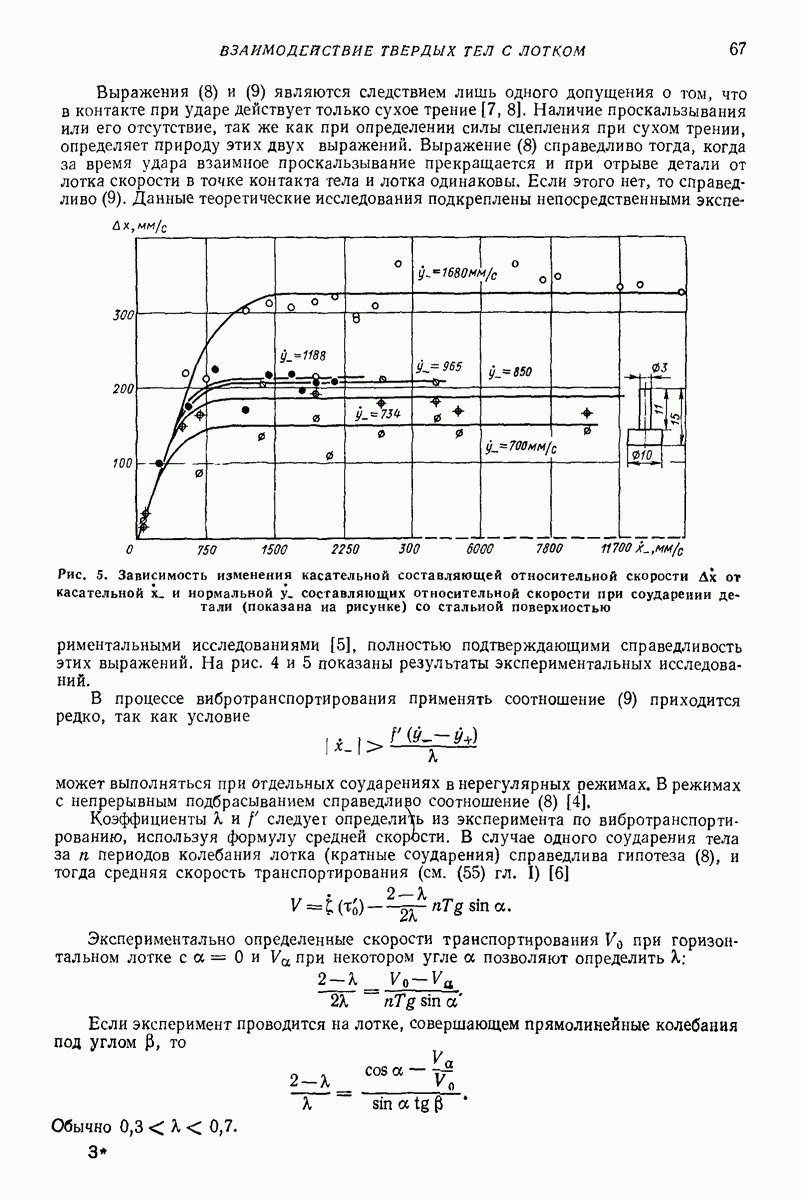
Рис. 5. Зависимость изменения касательной составляющей относительной скорости  от касательной
от касательной  и нормальной у. составляющих относительной скорости при соударении детали (показана на рисунке) со стальной поверхностью
и нормальной у. составляющих относительной скорости при соударении детали (показана на рисунке) со стальной поверхностью
На рис. 4 и 5 показаны результаты экспериментальных исследований.
В процессе вибротранспортирования применять соотношение (9) приходится редко, так как условие

может выполняться при отдельных соударениях в нерегулярных режимах. В режимах с непрерывным подбрасыванием справедливо соотношение (8) [4],
Коэффициенты  следует определить из эксперимента по вибротранспортированию, используя формулу средней скорости. В случае одного соударения тела за
следует определить из эксперимента по вибротранспортированию, используя формулу средней скорости. В случае одного соударения тела за  периодов колебания лотка (кратные соударения) справедлива гипотеза (8), и тогда средняя скорость транспортирования (см. (55) гл. I) [6]
периодов колебания лотка (кратные соударения) справедлива гипотеза (8), и тогда средняя скорость транспортирования (см. (55) гл. I) [6]

Экспериментально определенные скорости транспортирования  при горизонтальном лотке с
при горизонтальном лотке с  при некотором угле а позволяют определить X:
при некотором угле а позволяют определить X:

Если эксперимент проводится на лотке, совершающем прямолинейные колебания под углом  то
то

Обычно 
Естественно, что к можно определить, используя эксперименты и при двух разных а. Тогда только несколько усложняется расчет. Лучшим следует считать вариант, когда разница между обоими углами а достаточно большая, причем эти значения охватывают область, в которой будет использоваться зависимость (8).
Существует формально и вторая возможность для определения k. Предполагая, что  из формулы скорости [(55) гл. I] получим предельный угол подъема
из формулы скорости [(55) гл. I] получим предельный угол подъема  Следовательно, только один эксперимент по определениюапр позволяет определить
Следовательно, только один эксперимент по определениюапр позволяет определить  . Однако таким образом определенное значение к будет весьма далекое от к при значительно меньших а. Это объясняется тем, что, приближаясь к значению
. Однако таким образом определенное значение к будет весьма далекое от к при значительно меньших а. Это объясняется тем, что, приближаясь к значению  из-за стахостического характера удара в части соударений, уже появятся значения х при которых гипотеза (8) должна быть заменена гипотезой (9). Экспериментально определенный к является усредненной величиной. Как видно из экспериментальных исследований (см. рис. 4 и 5), в области, в которой происходит переход от одной гипотезы к другой, наблюдается весьма существенное отклонение от прямой, которой соответствует зависимость (8).
из-за стахостического характера удара в части соударений, уже появятся значения х при которых гипотеза (8) должна быть заменена гипотезой (9). Экспериментально определенный к является усредненной величиной. Как видно из экспериментальных исследований (см. рис. 4 и 5), в области, в которой происходит переход от одной гипотезы к другой, наблюдается весьма существенное отклонение от прямой, которой соответствует зависимость (8).
Гипотеза (8) при экспериментальном подборе коэффициента к позволяет определить среднюю скорость транспортирования и в тех случаях, когда тело имеет и вращательное движение, однако это движение остается неопределенным.
Для определения вращательного движения приходится пользоваться полной системой уравнений, добавляя к ней уравнение изменения количества движения

что позволяет обойтись без гипотез (8) и (9). Имеем несколько типичных случаев.
1. Тело во всем процессе соударения скользит по лотку;  Поперечное движение полностью определяет величины
Поперечное движение полностью определяет величины  Тогда из (7) находим
Тогда из (7) находим  после чего из (10) следует
после чего из (10) следует

Этот случай при вибротранспортировании встречается при значительных относительных скоростях, что может иметь место только в отдельных соударениях в режимах с некратными соударениями.
Более часто приходится встречаться со случаем, когда тело перестает скользить либо на этапе сближения, либо на этапе удаления.
2. Скольжение прекращается на этапе сближения.. Тогда этот этап делится на две фазы. Конец первой фазы определяется условием  Решается система
Решается система

относительно 
Конец второй фазы определяется условием (6). Решается система

На втором этапе решаем систему (12), заменяя индексы  на (0) и (0) на
на (0) и (0) на  вместо уравнения
вместо уравнения  используем соотношение (3):
используем соотношение (3):

3. Скольжение прекращается на этапе удаления тела. Первый этап решается, как при полном проскальзывании. В первой фазе этапа удаления, которая кончается
при  используем систему уравнений (11) с заменой индексов
используем систему уравнений (11) с заменой индексов  на
на  . Рассчитываем величины к,
. Рассчитываем величины к,  Во второй фазе используем систему (12), заменяя индексы
Во второй фазе используем систему (12), заменяя индексы  на
на  вместо последнего соотношения применяем гипотезу (3):
вместо последнего соотношения применяем гипотезу (3):

4. Можно также проанализировать случай, когда во время соударения отсутствует проскальзывание. Так как в практике применения вибрационных машин это встречается крайне редко, то приведем только одно отношение

показывающее, что соотношение импульсов в данном случае зависит от геометрии тела. Другие возможные режимы соударения (скольжение вперед и назад; скольжение вперед — совместное движение — скольжение назад) для вибротранспорта не характерны.
Из рассмотрения систем уравнений вытекают также условия существования каждого вида движения.
Полное проскальзывание будет, если  при любом
при любом  если
если  Скольжение прекратится на этапе сближения, если
Скольжение прекратится на этапе сближения, если  или при любом
или при любом  если
если  где
где 
В этих исследованиях движения достаточно знать динамический коэффициент трения  и величину
и величину  которая может быть определена также из эксперимента при центральном ударе. Проведение расчетов с помощью исследования фаз удара оправданно в задачах об ударном ориентировании деталей. При этом расчет средней скорости транспортирования деталей можно провести только с использованием ЭЦВМ. В случае пространственного движения следует добавить еще два уравнения изменения момента количества движения и одно уравнение изменения количества движения. Принцип решения тот же.
которая может быть определена также из эксперимента при центральном ударе. Проведение расчетов с помощью исследования фаз удара оправданно в задачах об ударном ориентировании деталей. При этом расчет средней скорости транспортирования деталей можно провести только с использованием ЭЦВМ. В случае пространственного движения следует добавить еще два уравнения изменения момента количества движения и одно уравнение изменения количества движения. Принцип решения тот же.
Расчеты движения твердого тела (с использованием постоянных ей  подтверждают справедливость гипотез (8) и (9) в соответствующих условиях, т. е. если коэффициенты
подтверждают справедливость гипотез (8) и (9) в соответствующих условиях, т. е. если коэффициенты  и к определены из непосредственного эксперимента по вибротранспортированию [7].
и к определены из непосредственного эксперимента по вибротранспортированию [7].
Движение деформируемых тел. Во всех рассмотренных моделях время удара бесконечно мало, и его в расчетах принимают равным нулю. Однако с уменьшением жесткости тела время удара занимает все большую часть периода движения тела по лотку, и при расчетах с использованием гипотезы о мгновенности удара появляются слишком большие отклонения по сравнению с экспериментом. Попытка ввести время удара как дополнительную постоянную, как правило, не позволяет ответить на интересующие вопросы.
Простейшим описанием деформируемых тел является одномассная модель с элементами упругости, вязкости и сухого трения, через которые тело соприкасается с лотком. На этапах безотрывного движения приходится решать также уравнение поперечного движения для определения нормальной реакции. В режимах с подбрасыванием условием отрыва является условие исчезновения нормальной реакции  Условием начала взаимного контакта является условие соприкосновения элемента упругости (вязкости, трения) с лотком. Увеличение числа масс в модели транспортируемого тела принципа расчета не изменяет, но расчет резко усложняется. Этими же моделями описывается движение сыпучих сред
Условием начала взаимного контакта является условие соприкосновения элемента упругости (вязкости, трения) с лотком. Увеличение числа масс в модели транспортируемого тела принципа расчета не изменяет, но расчет резко усложняется. Этими же моделями описывается движение сыпучих сред  гл. III).
гл. III).
Если тела очень гибкие,  приходится иметь дело с телом, движение которого не удается описать небольшим числом степеней свободы, то для определения движения следует рекомендовать прямые вариационные методы, Представляется
приходится иметь дело с телом, движение которого не удается описать небольшим числом степеней свободы, то для определения движения следует рекомендовать прямые вариационные методы, Представляется
примерная форма деформированного тела. В этом описании оставляют несколько неизвестных постоянных, которые потом находят с помощью метода Бубнова-Галеркина, метода Ритца или других (см. т. 2, гл. II).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- Установившиеся режимы движения частицы.
- О методах решения задачи.
- Установившиеся режимы при отсутствии подбрасывания [4-6].
- Установившиеся режимы с подбрасыванием.
- Средние скорость и ускорение частицы в установившихся режимах движения.
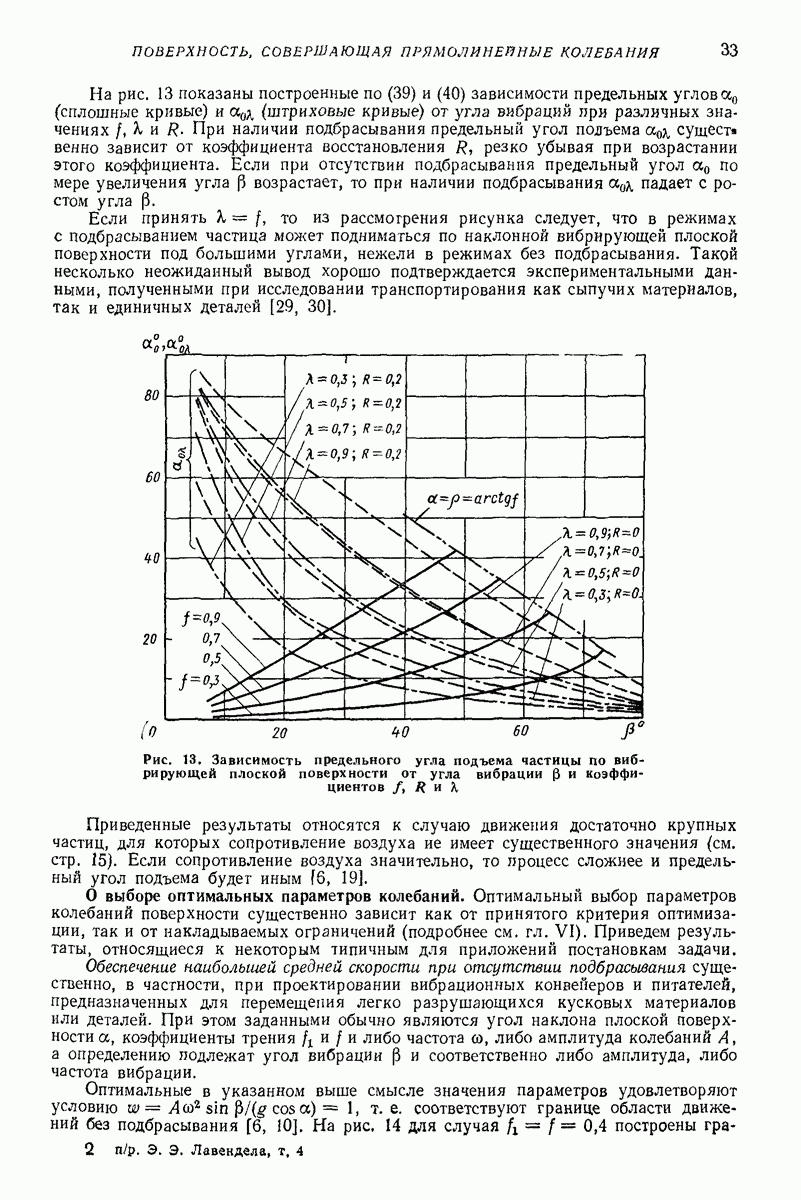
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
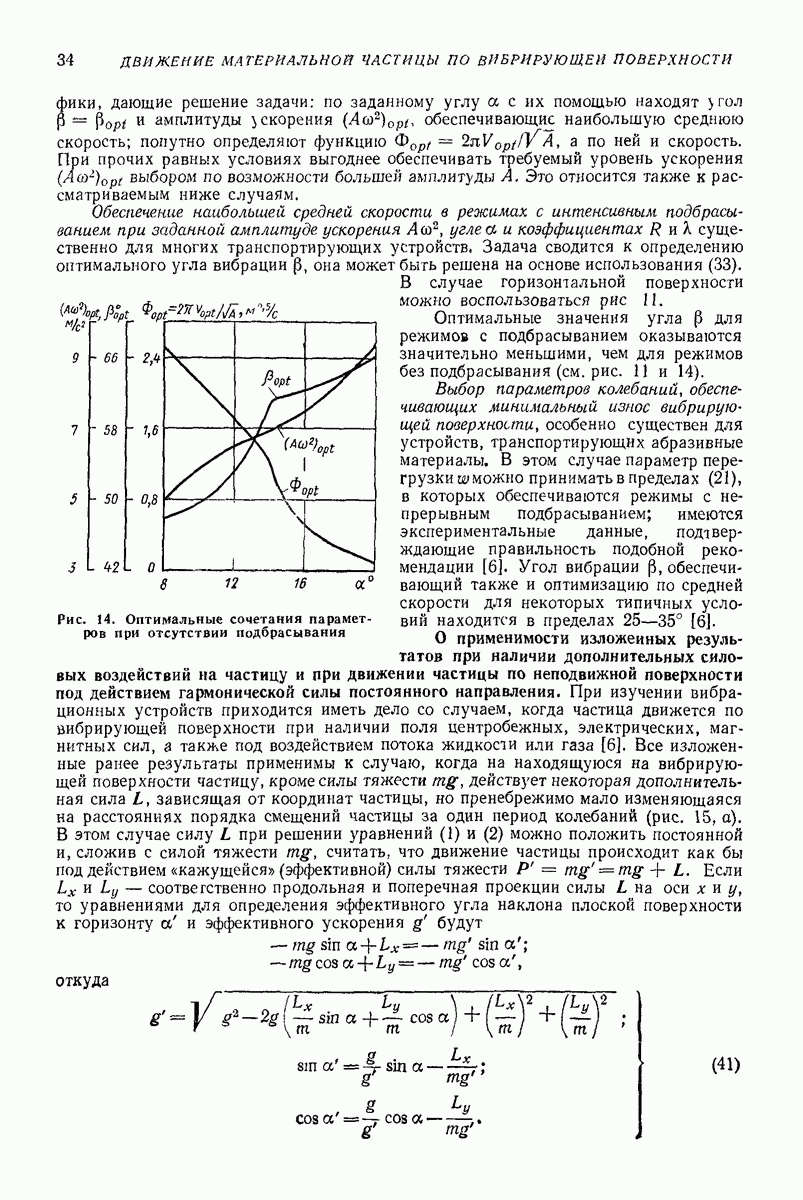
- О выборе оптимальных параметров колебаний.
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
- О влиянии на движение частицы сил вязкого сопротивления.
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
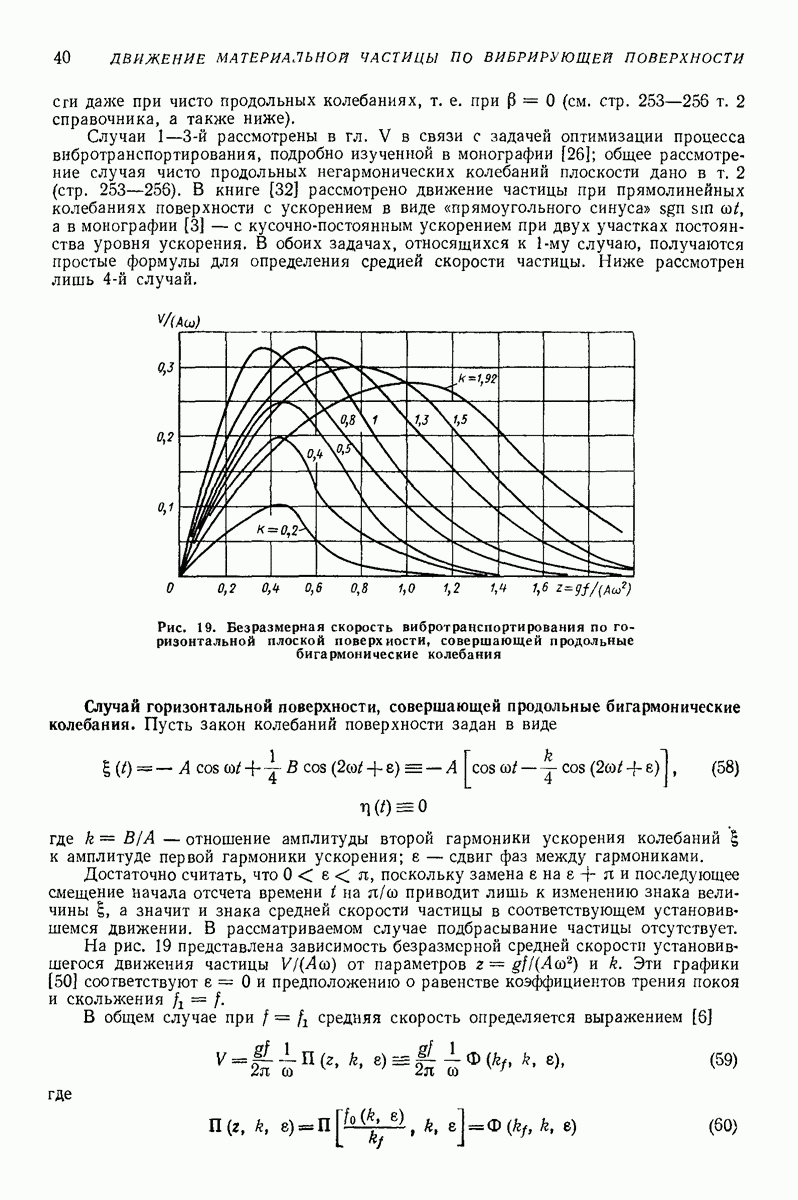
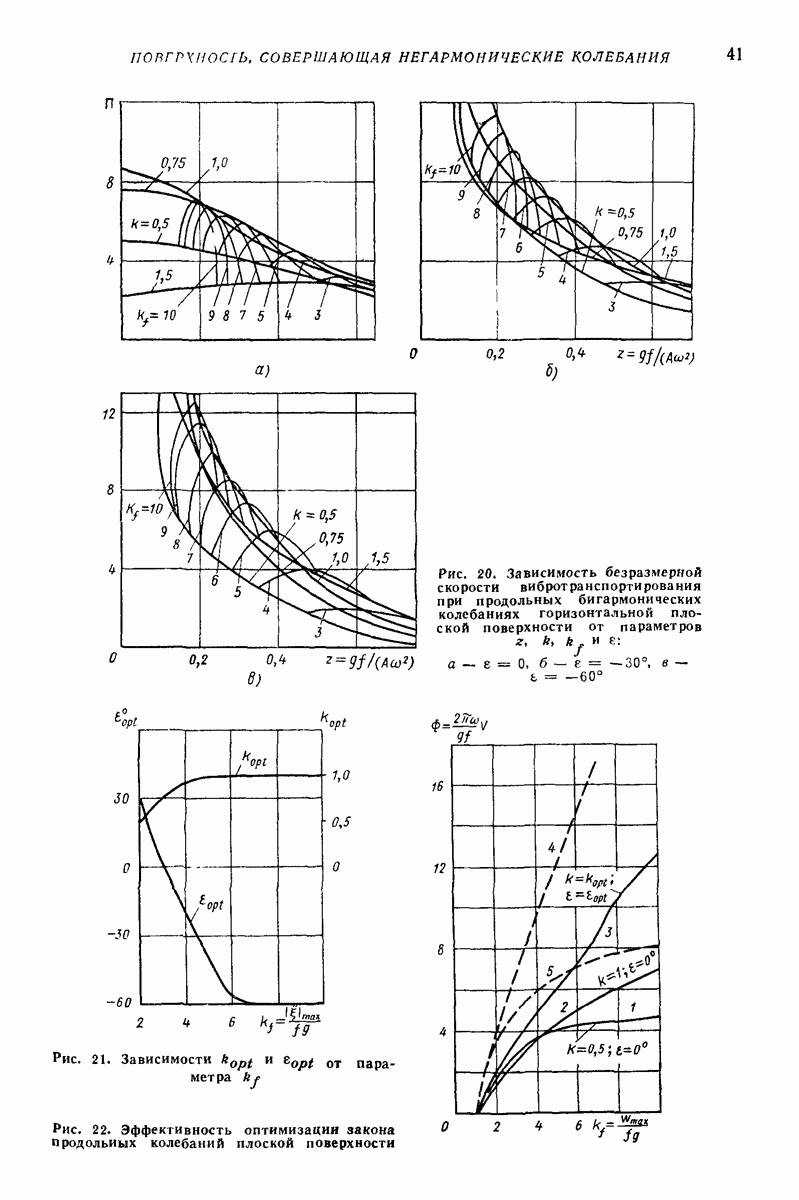
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
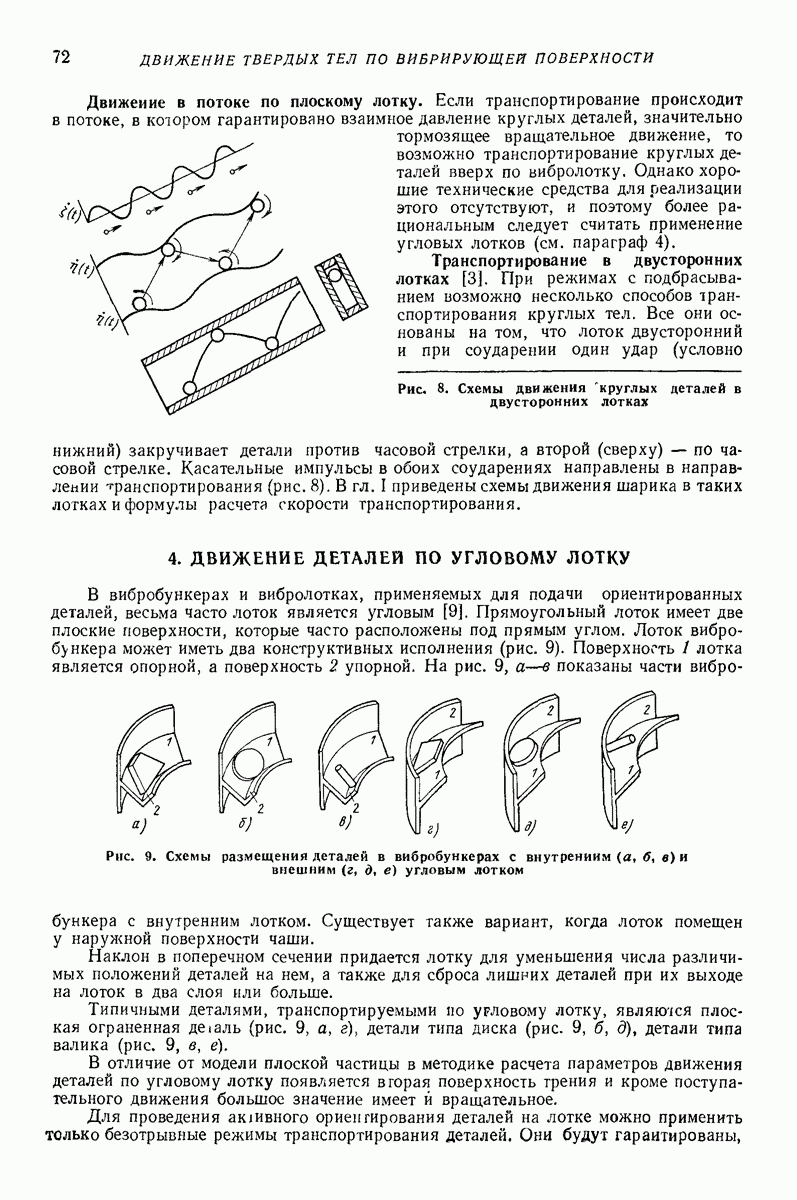
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
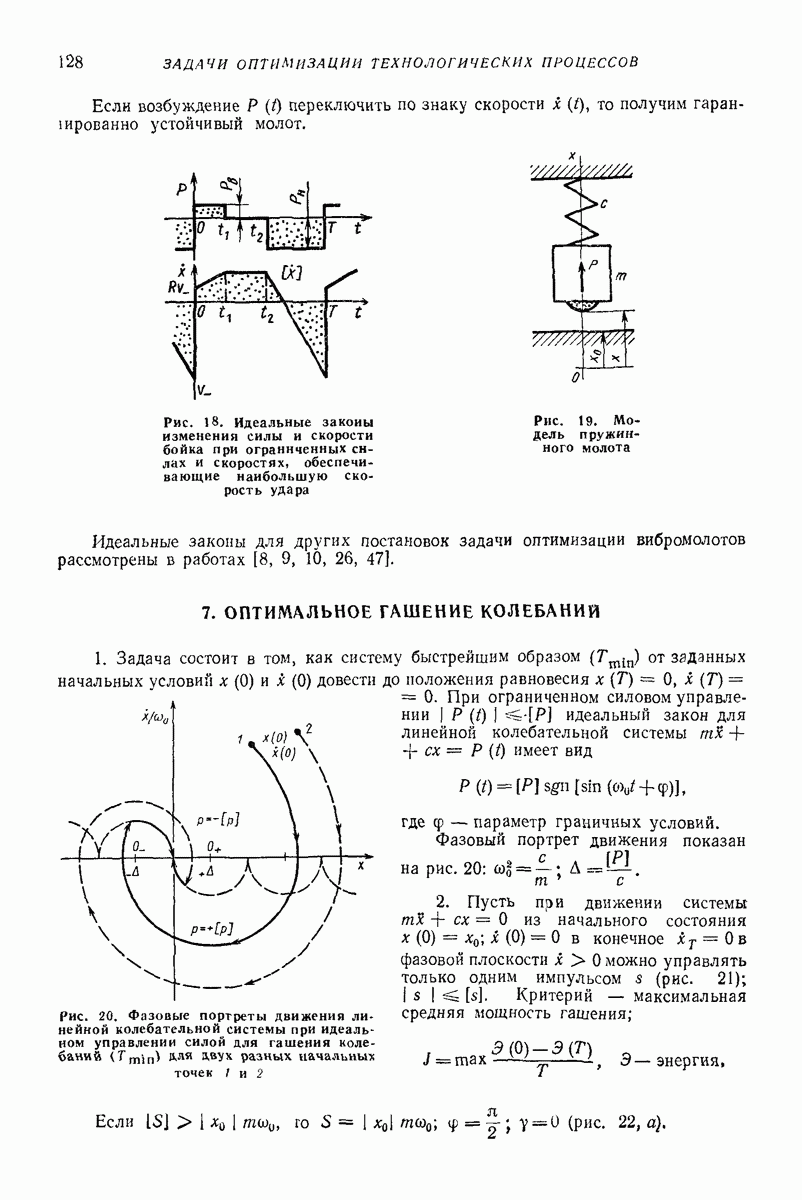
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
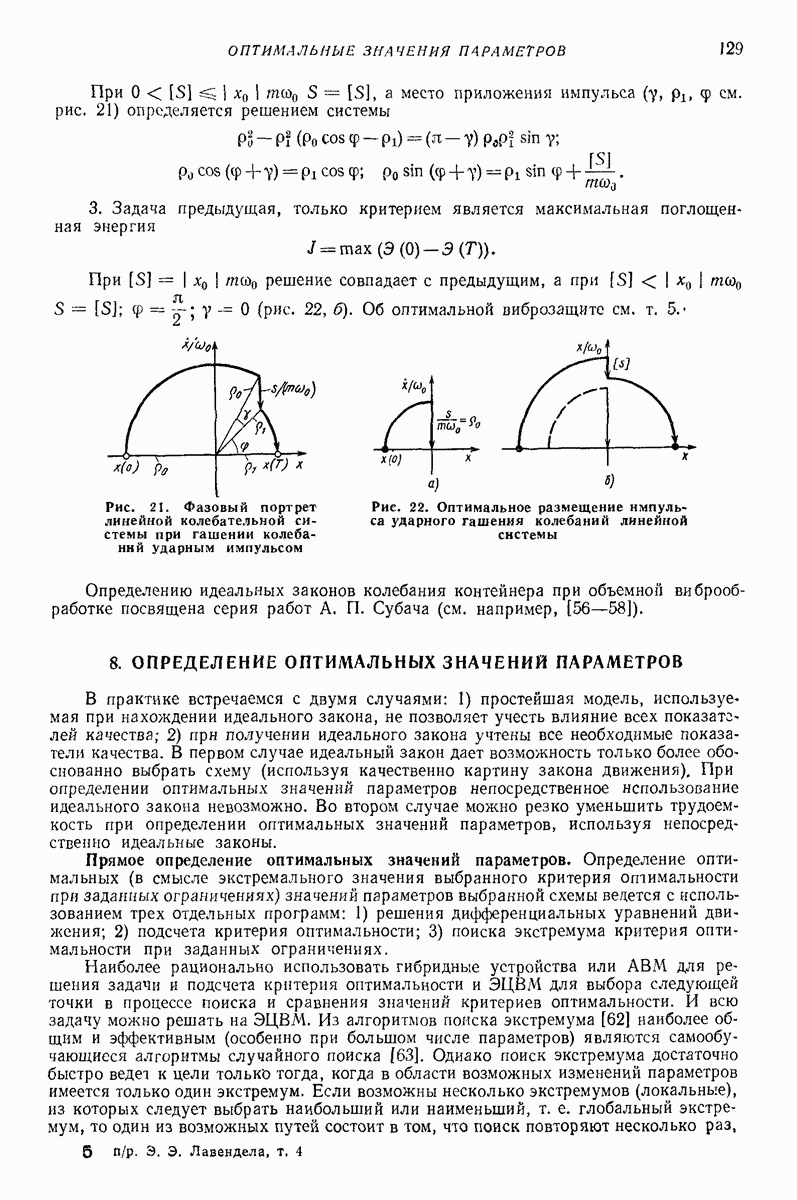
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
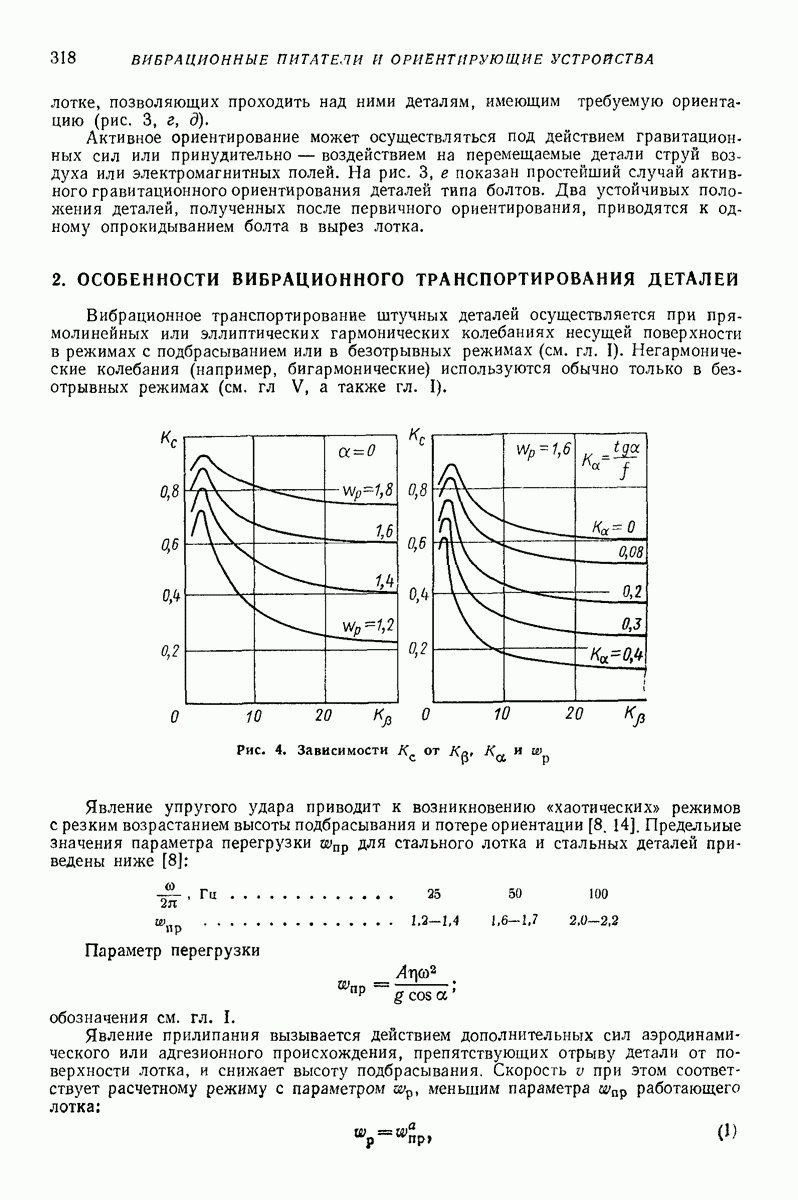
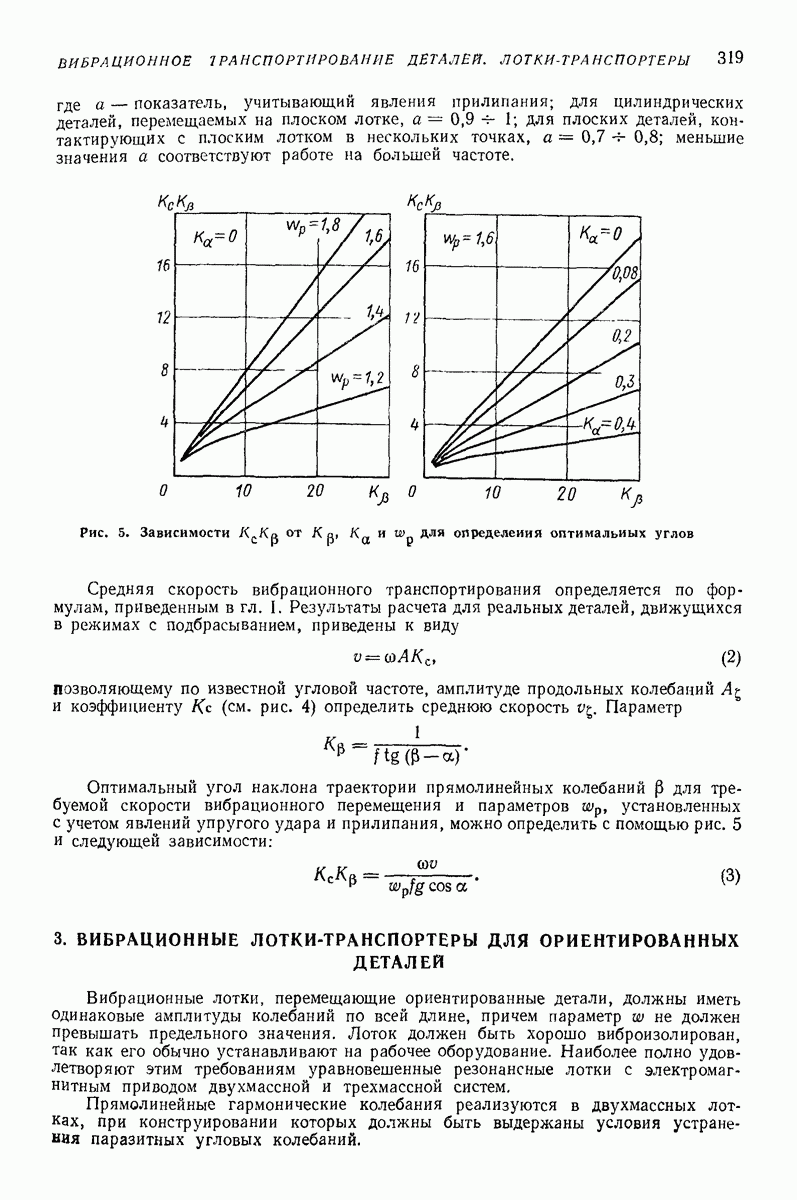
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
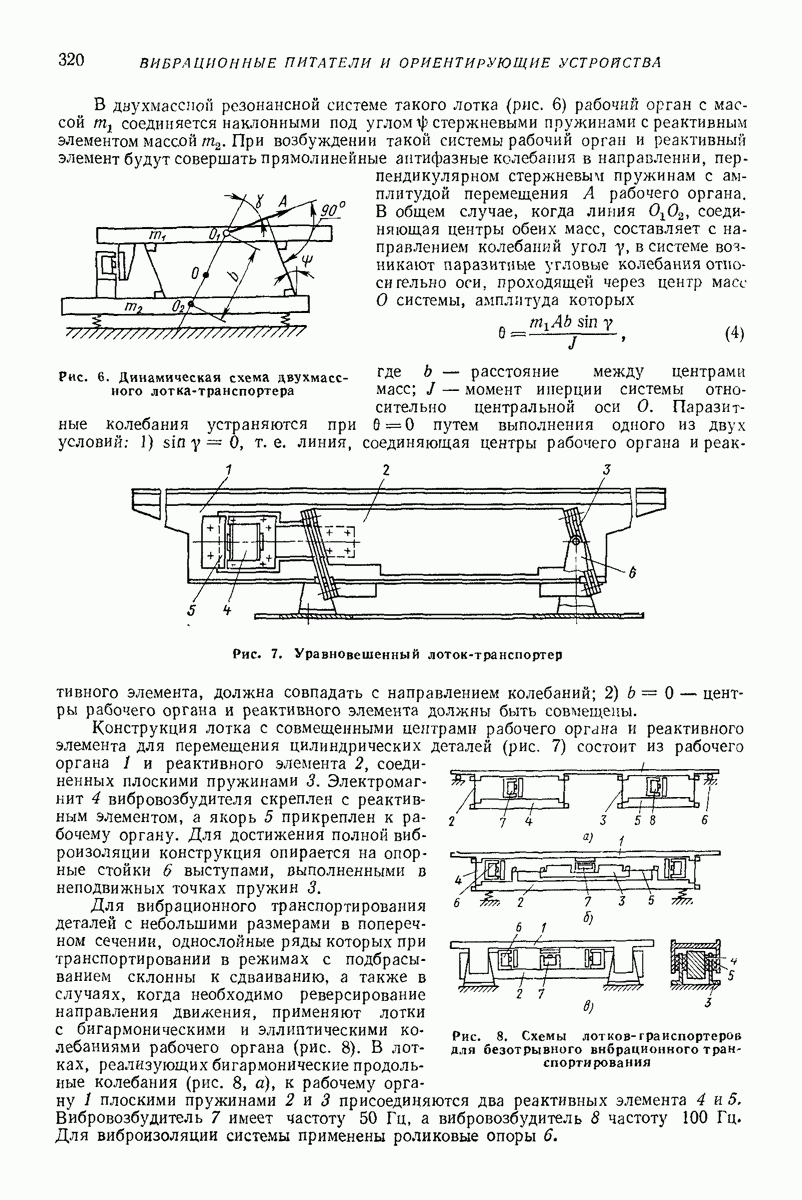
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
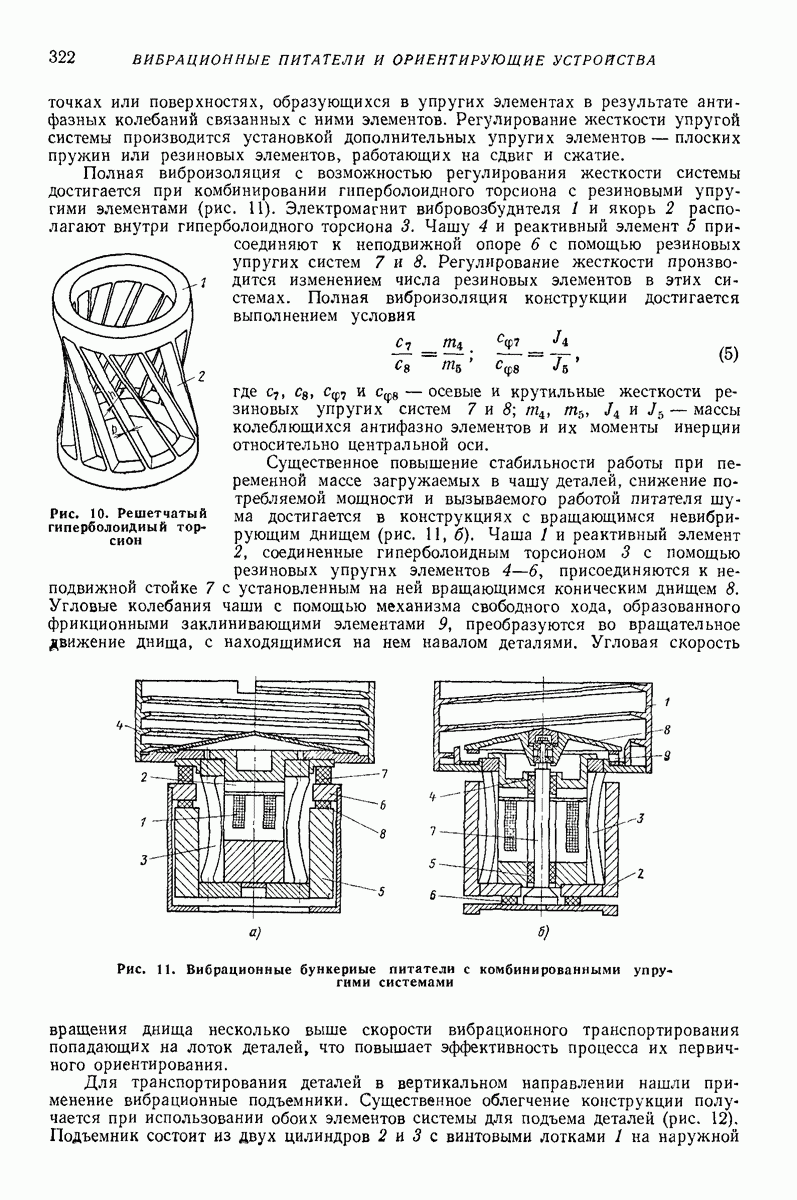
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
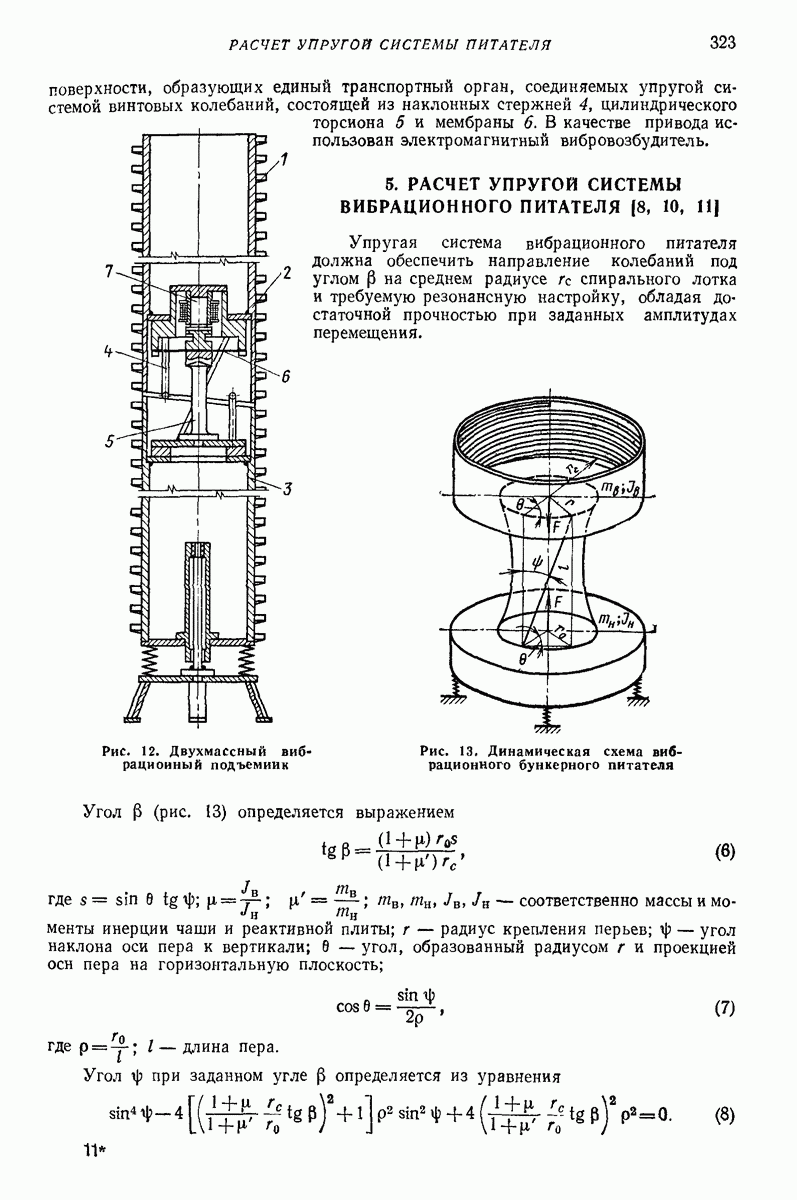
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
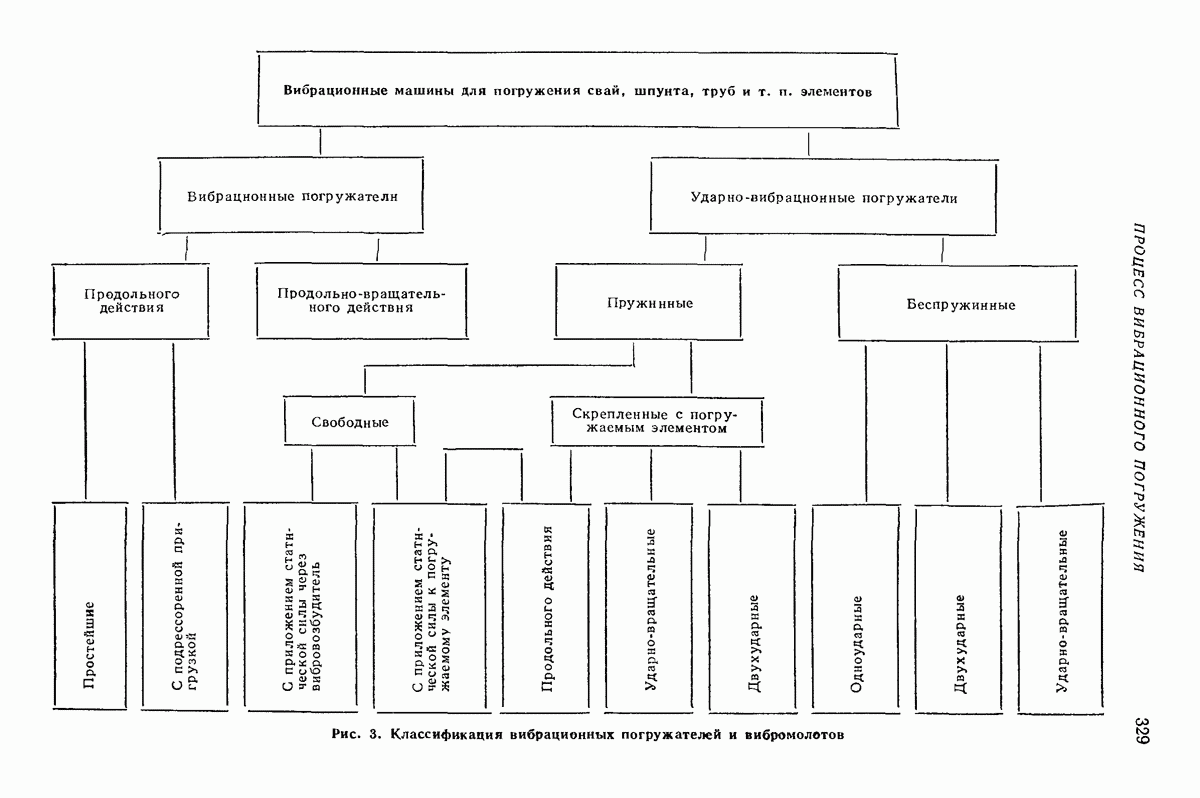
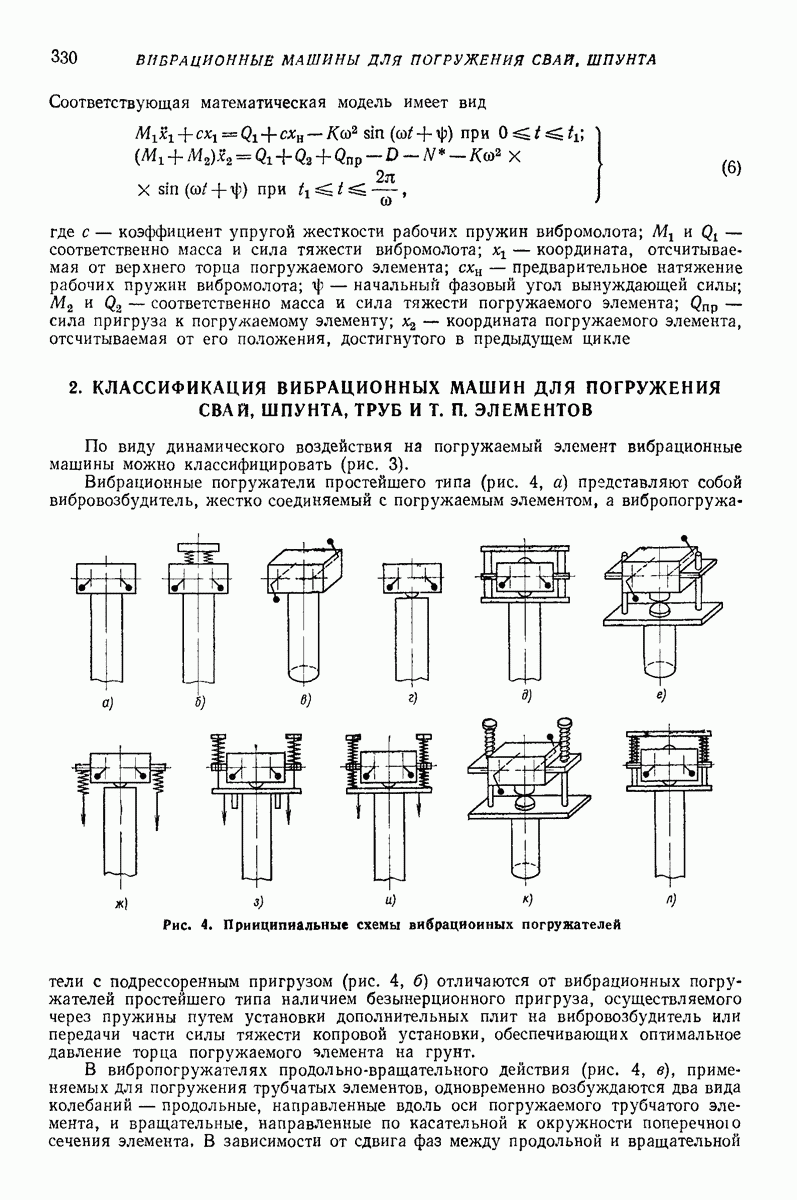
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
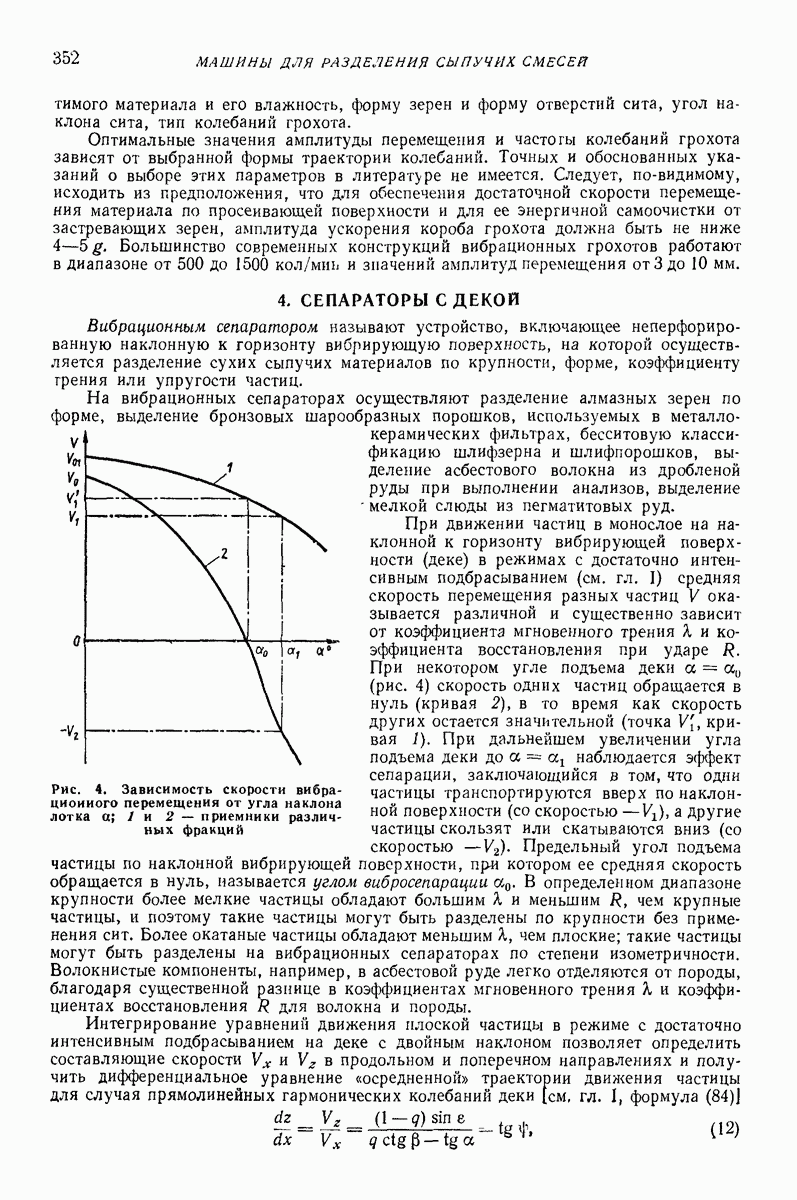
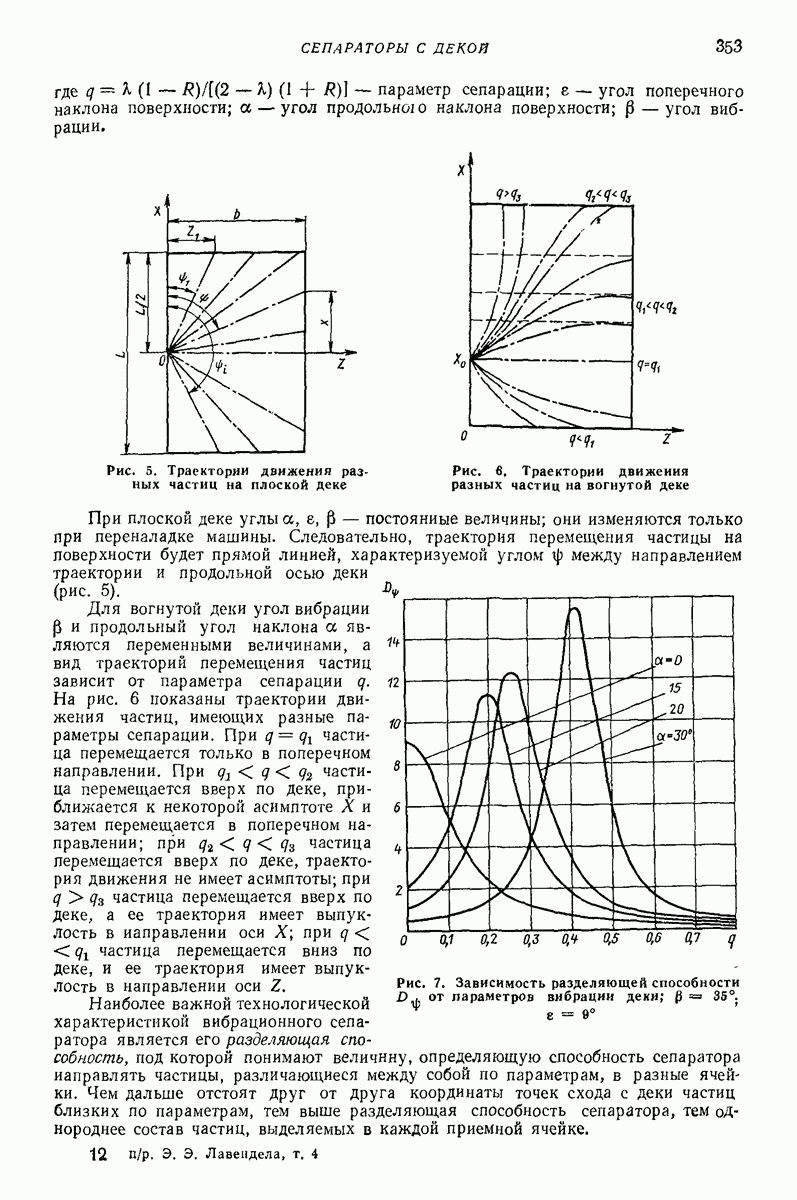
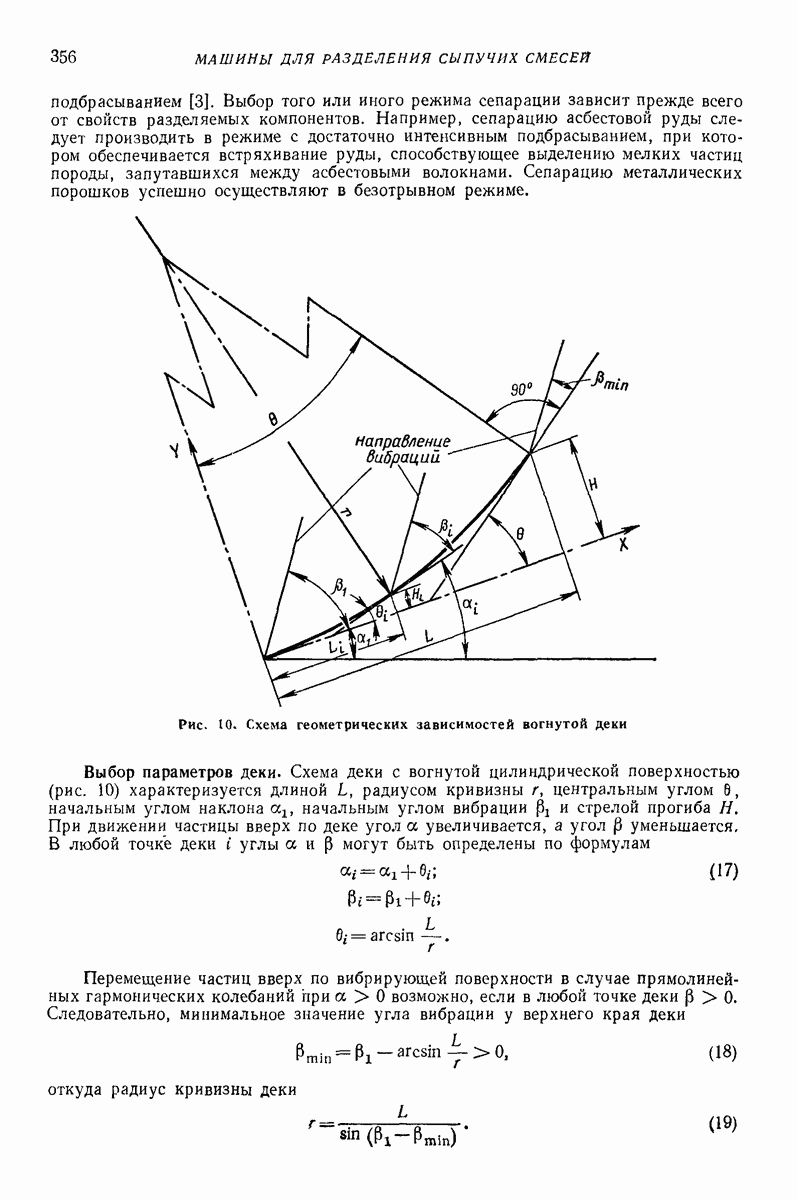
- 4. СЕПАРАТОРЫ С ДЕКОЙ
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
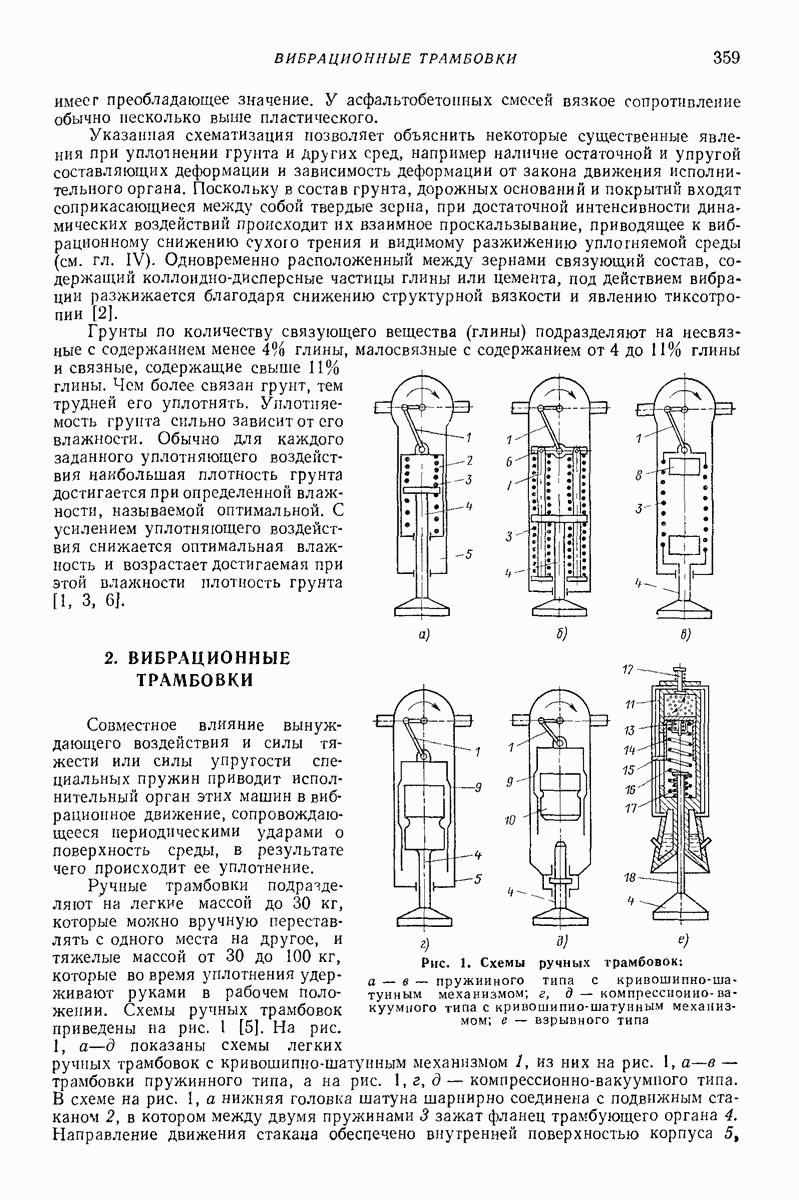
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
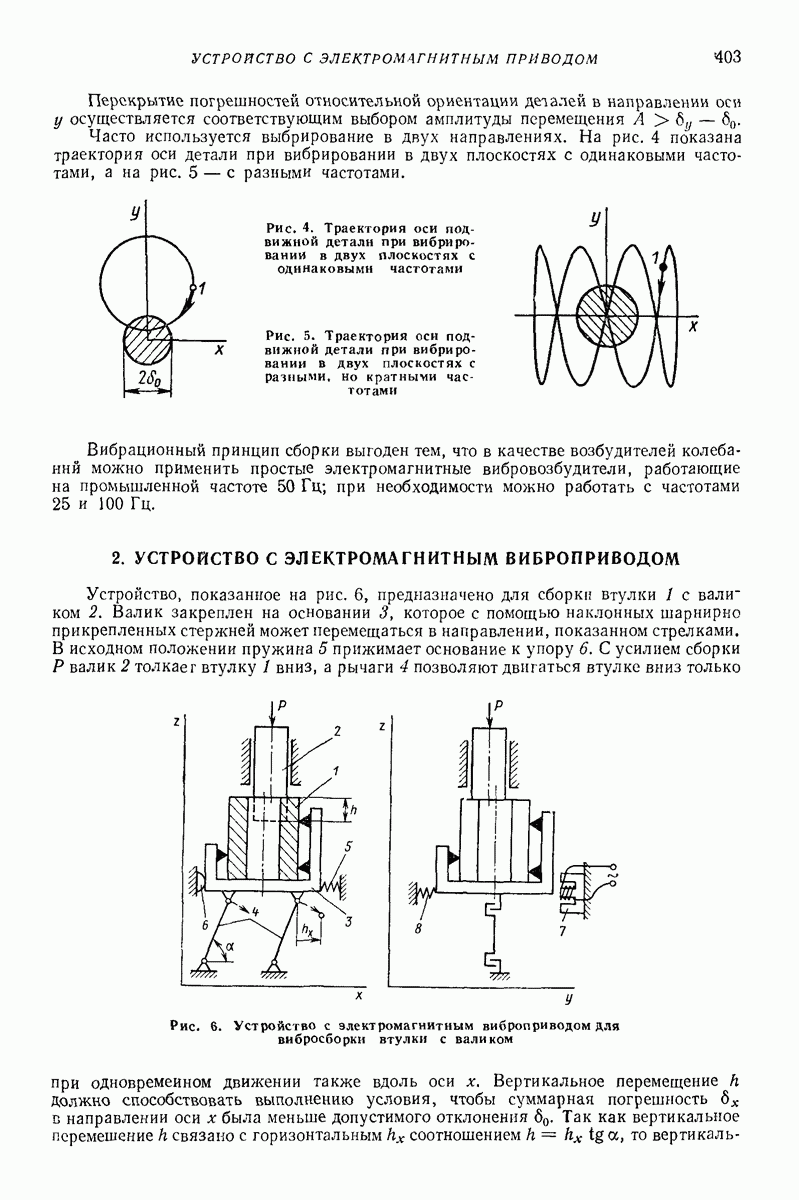
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
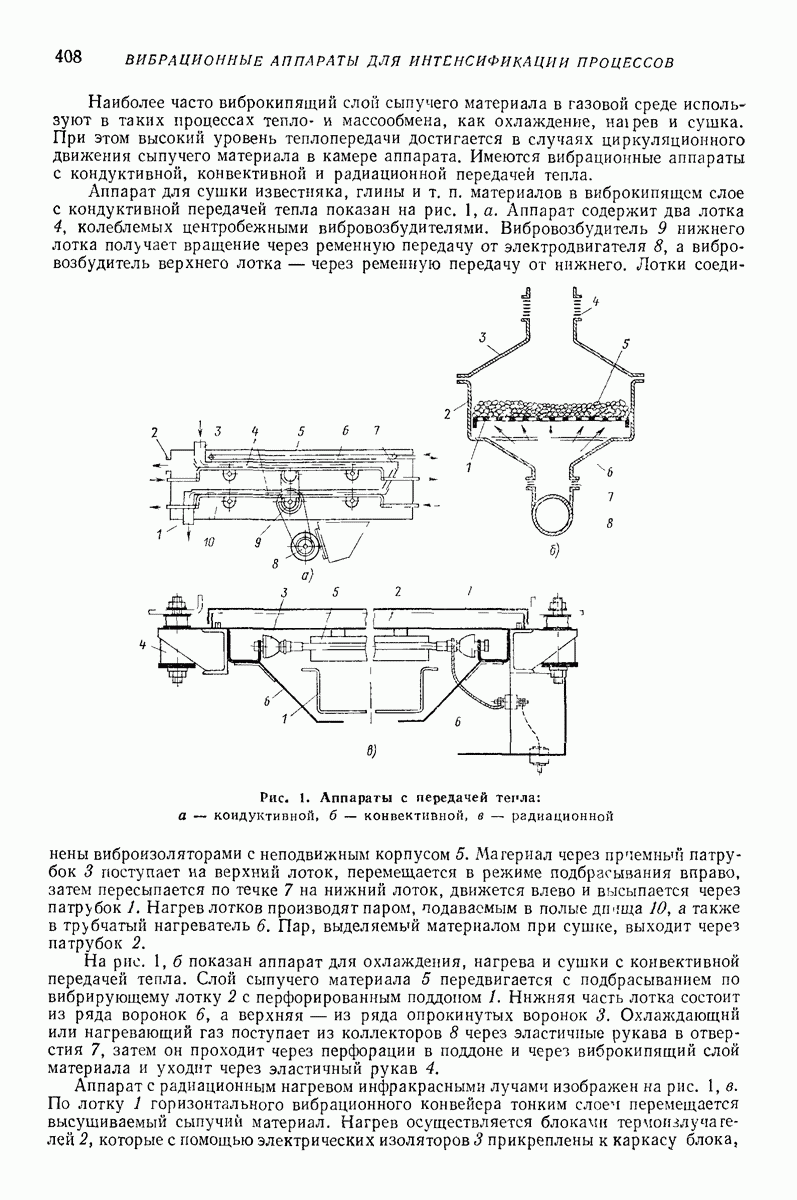
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
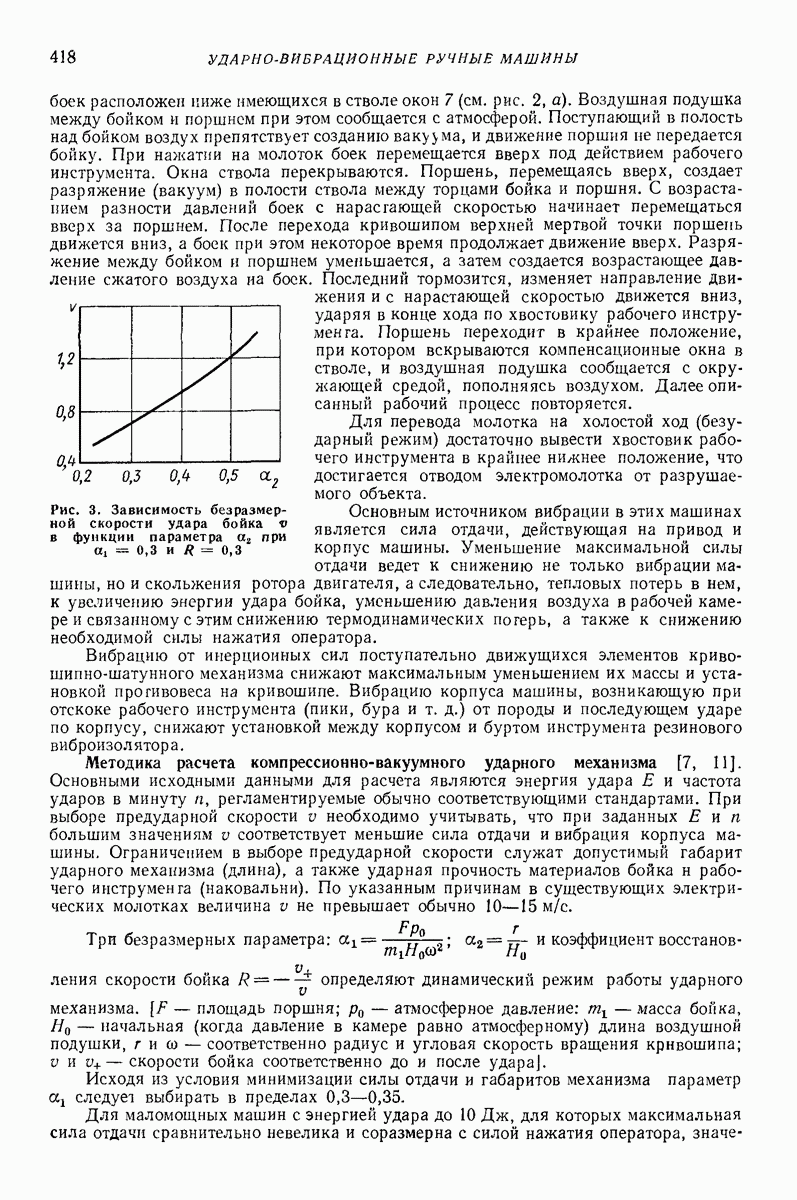
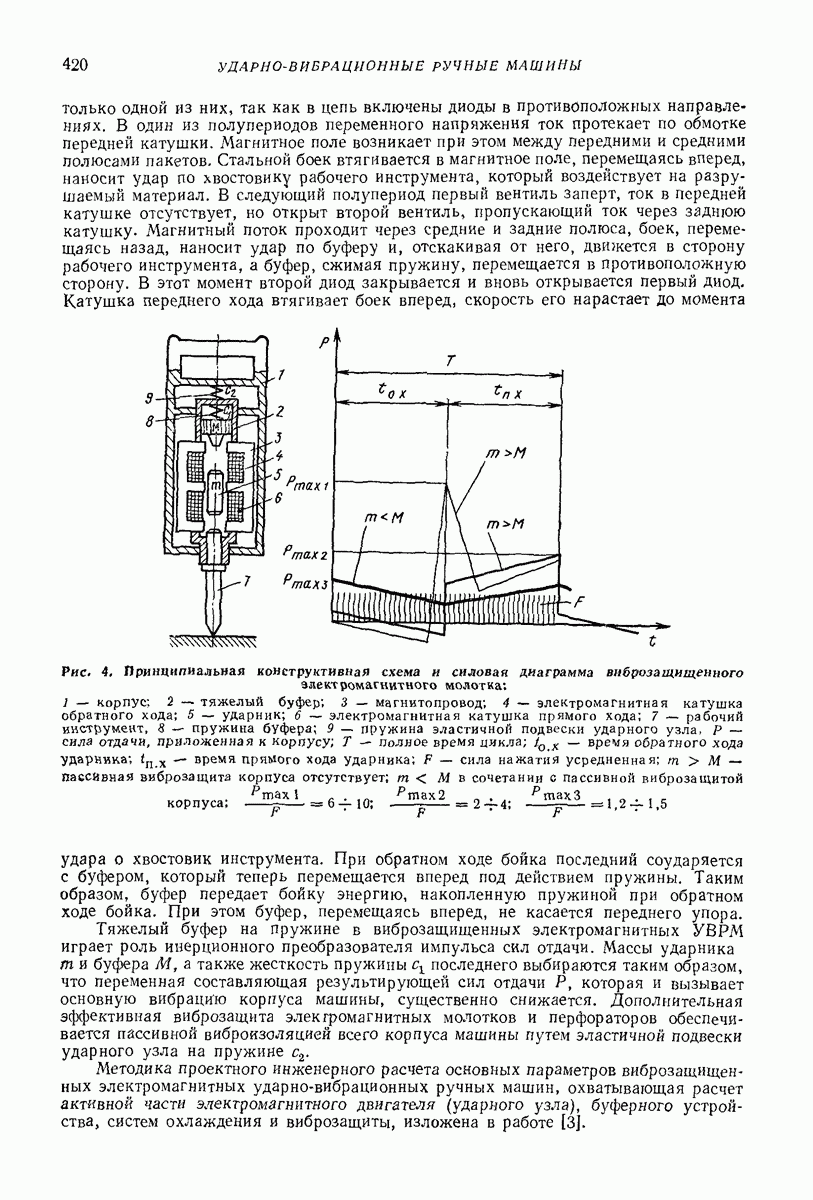
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
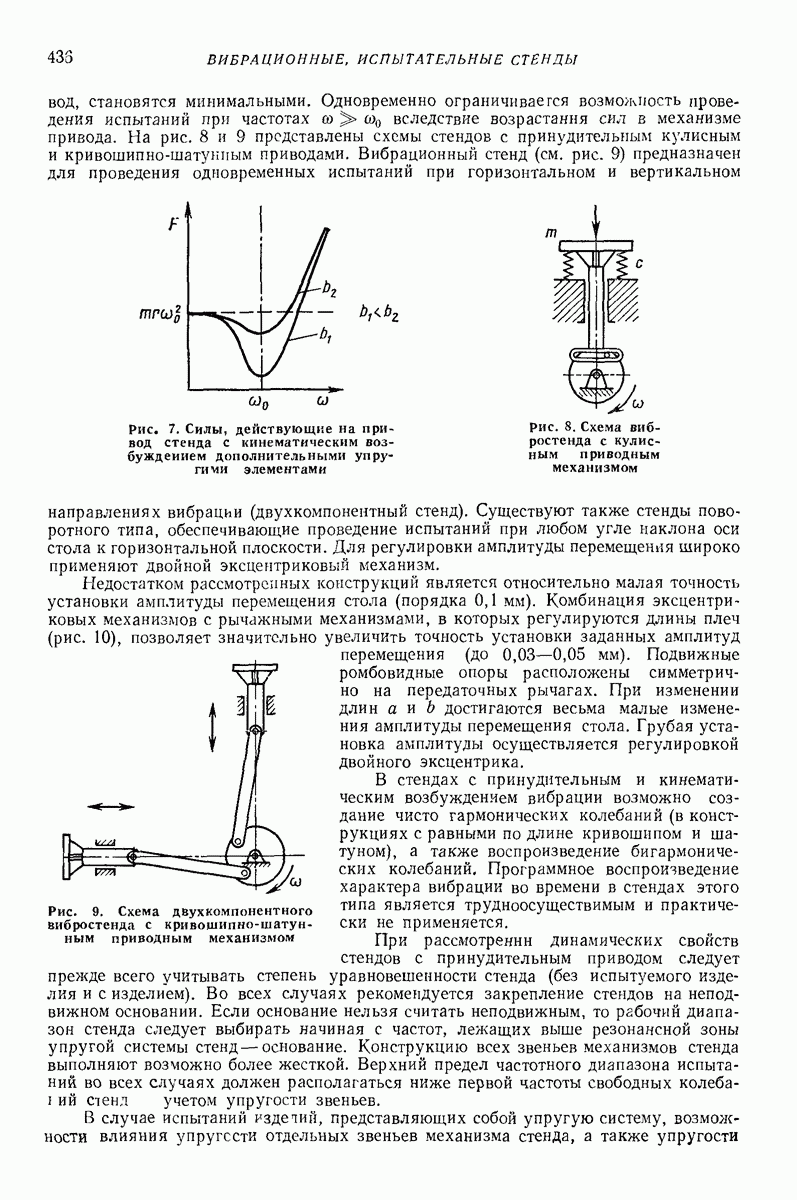
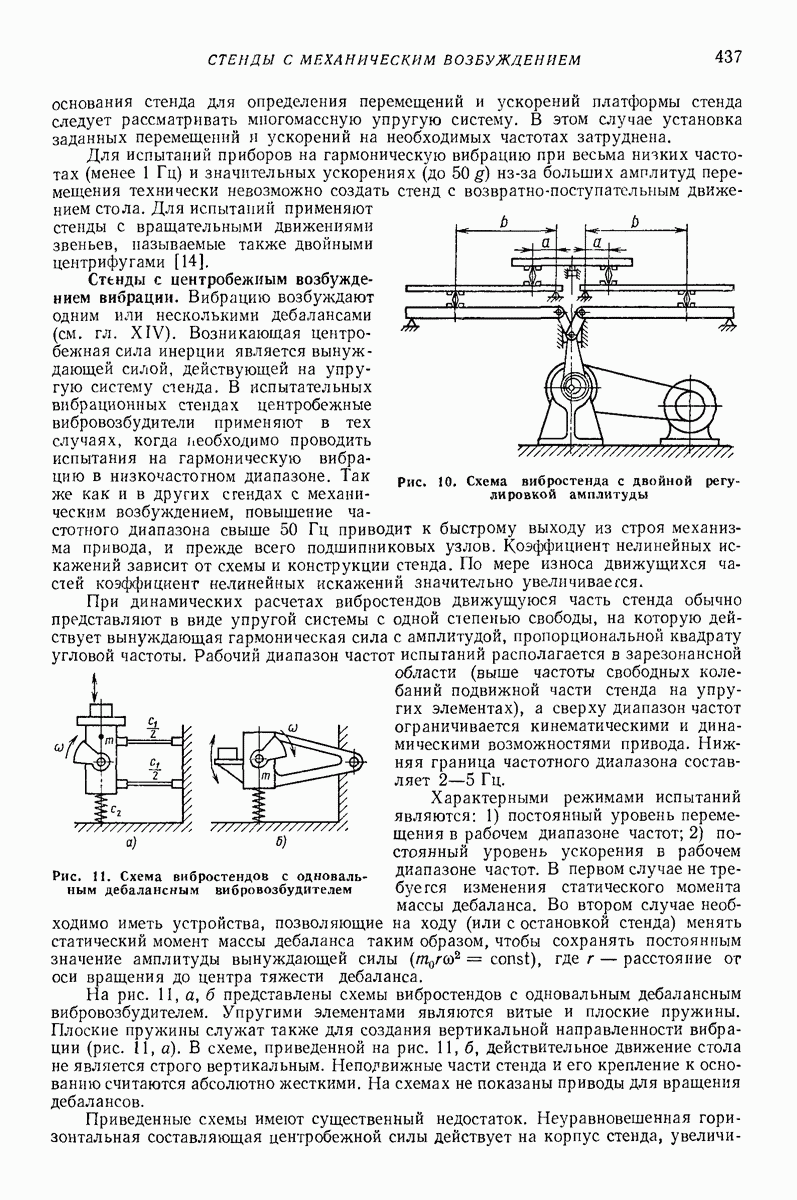
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
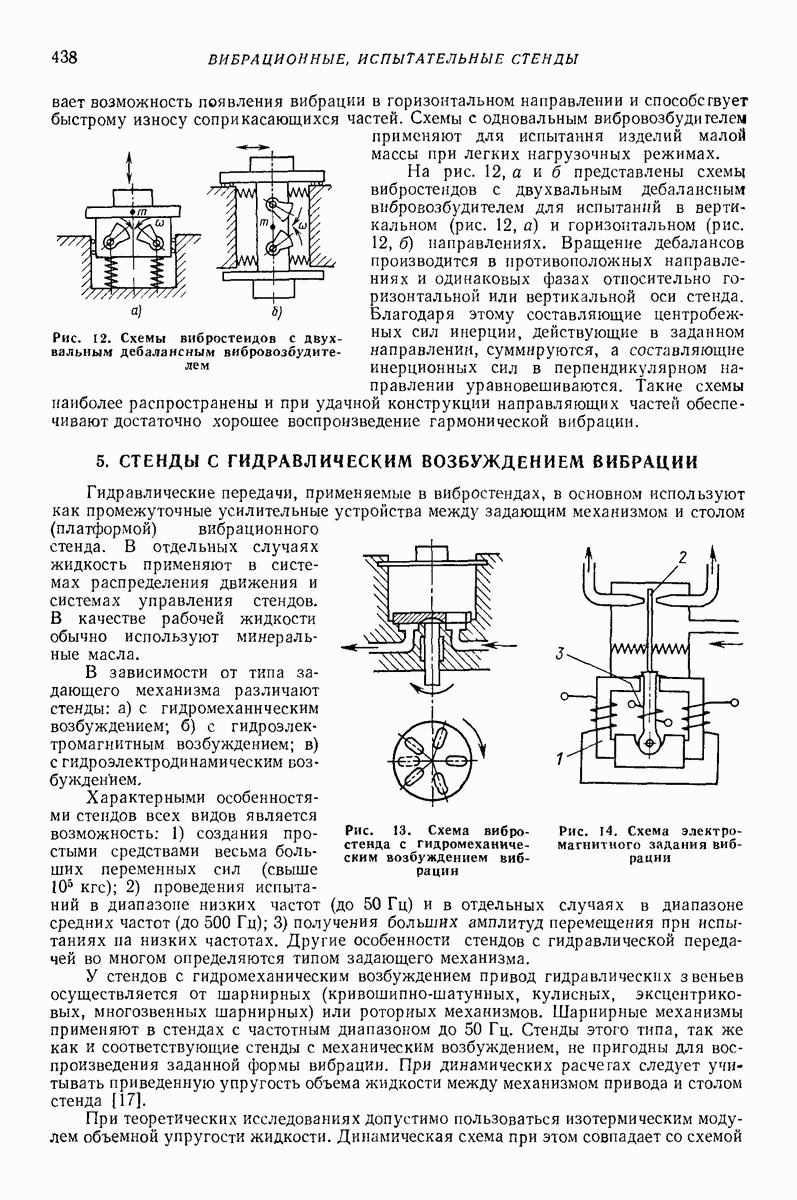
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ