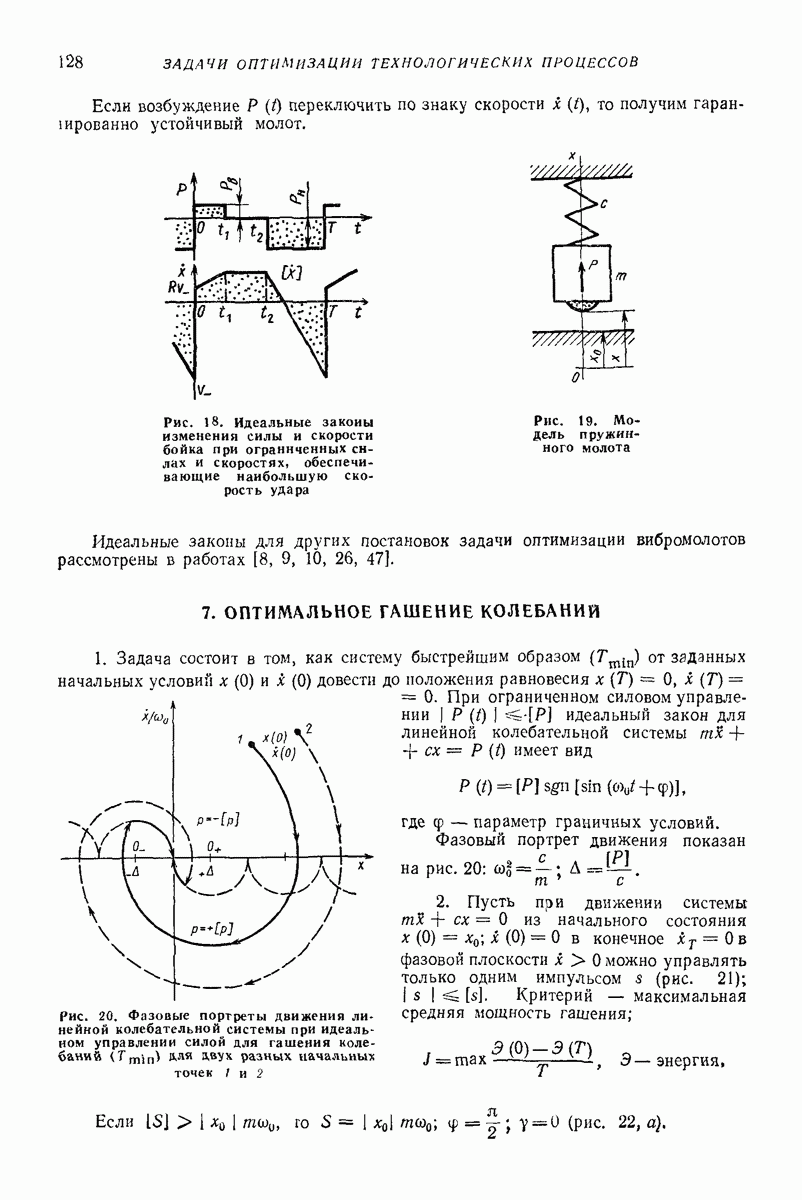
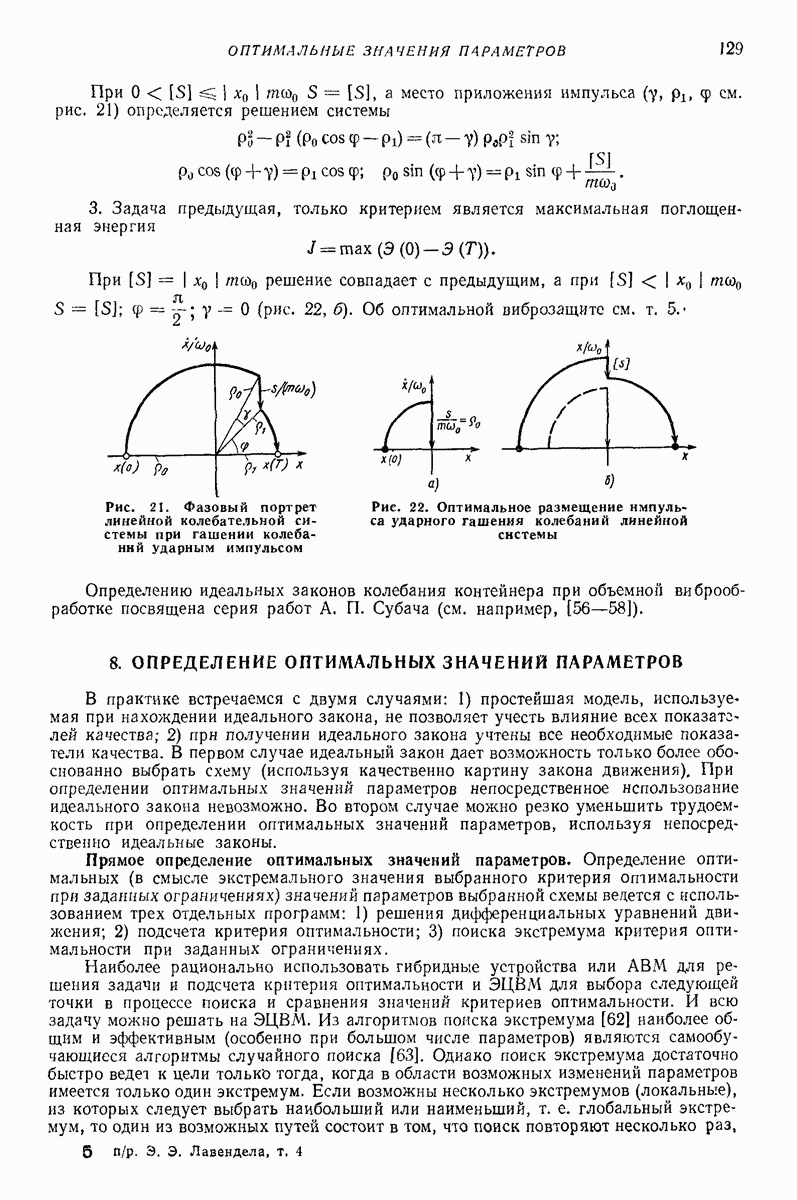
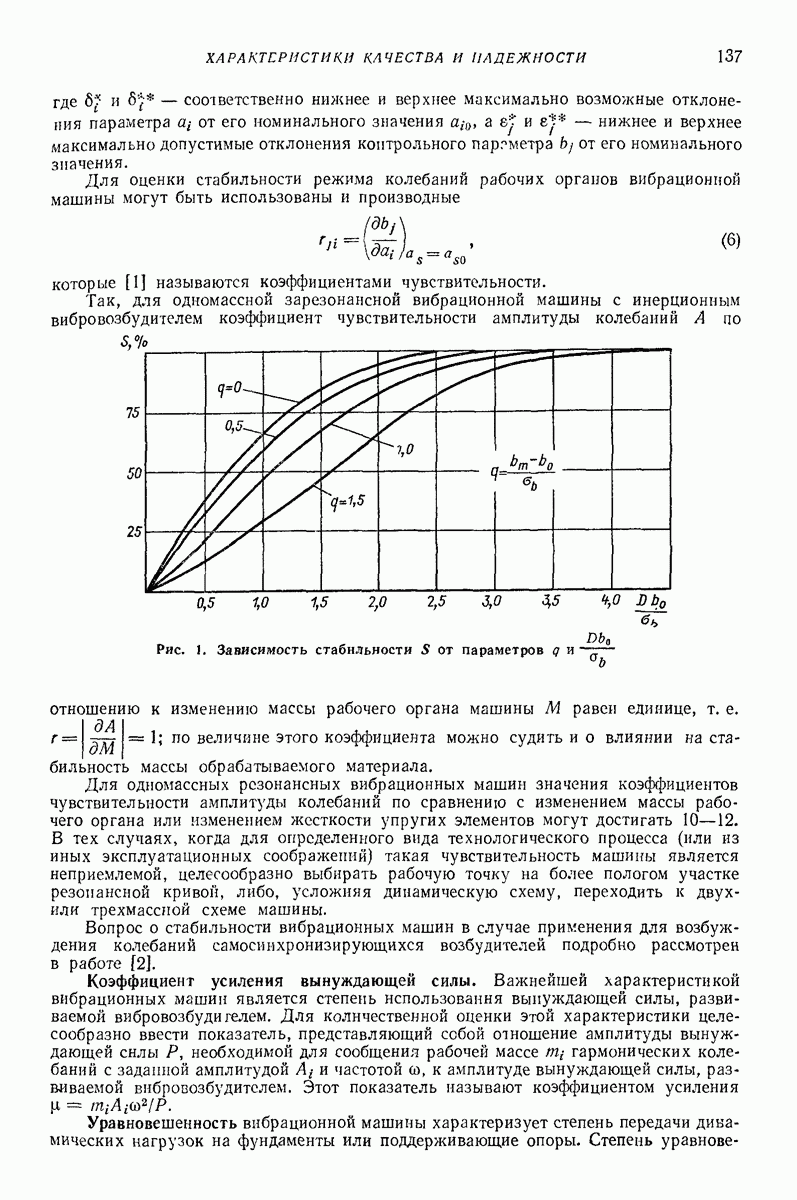
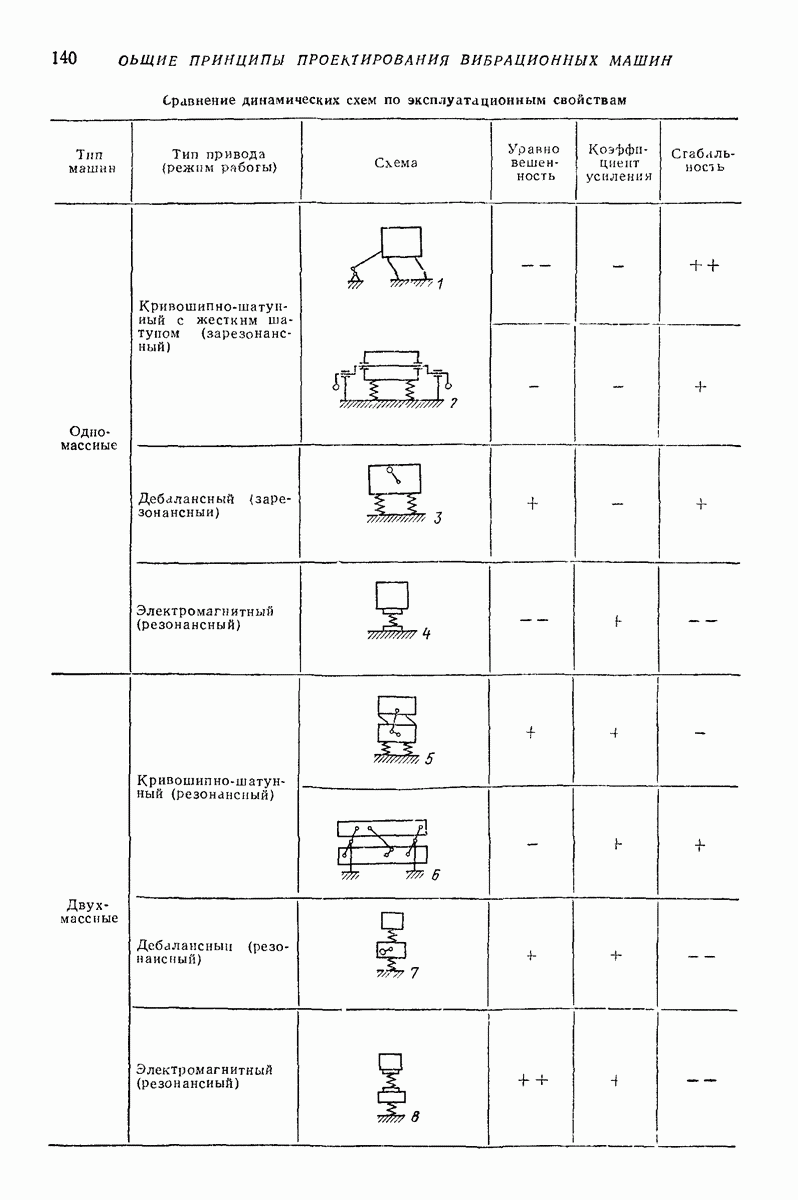
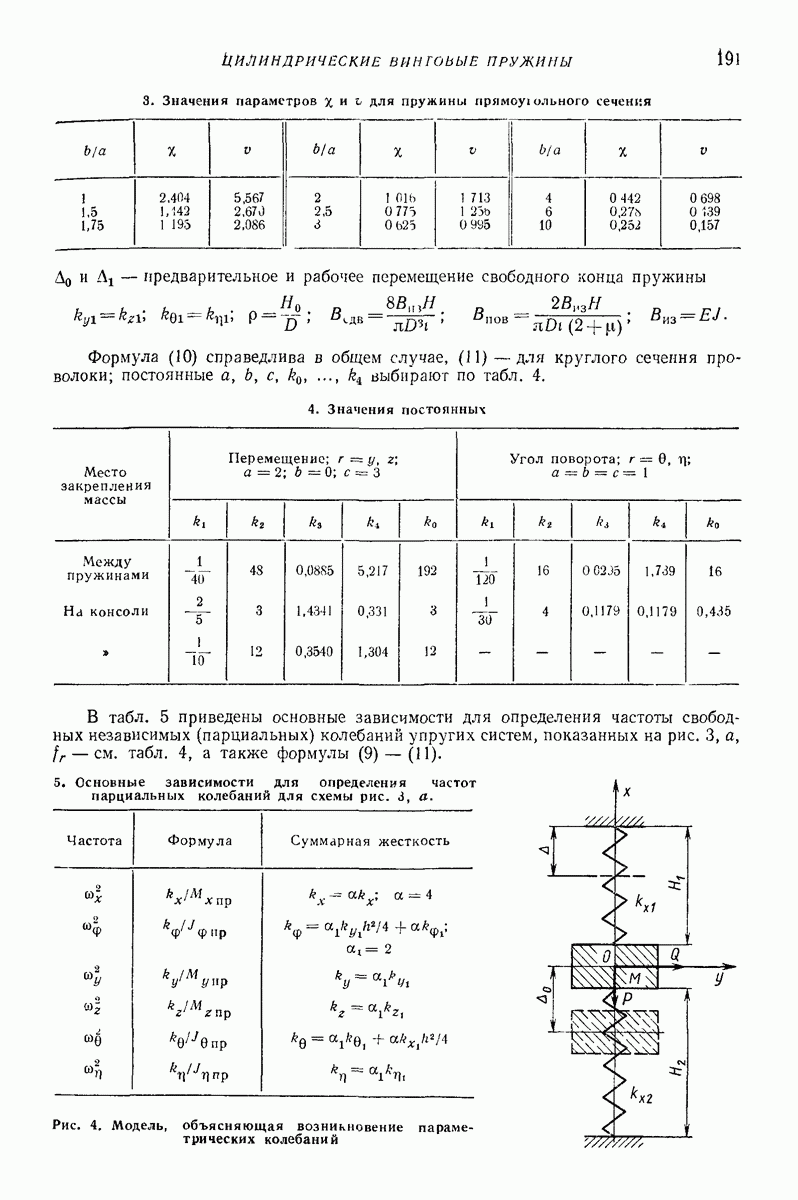
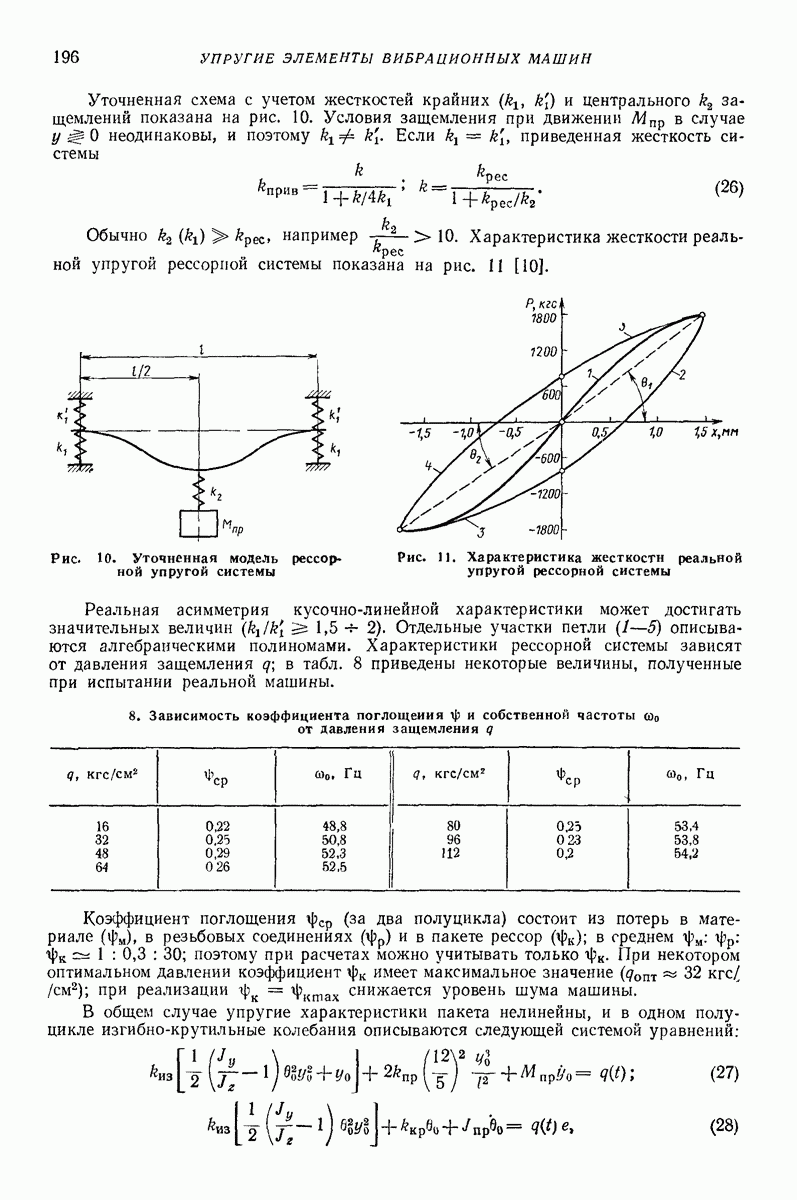
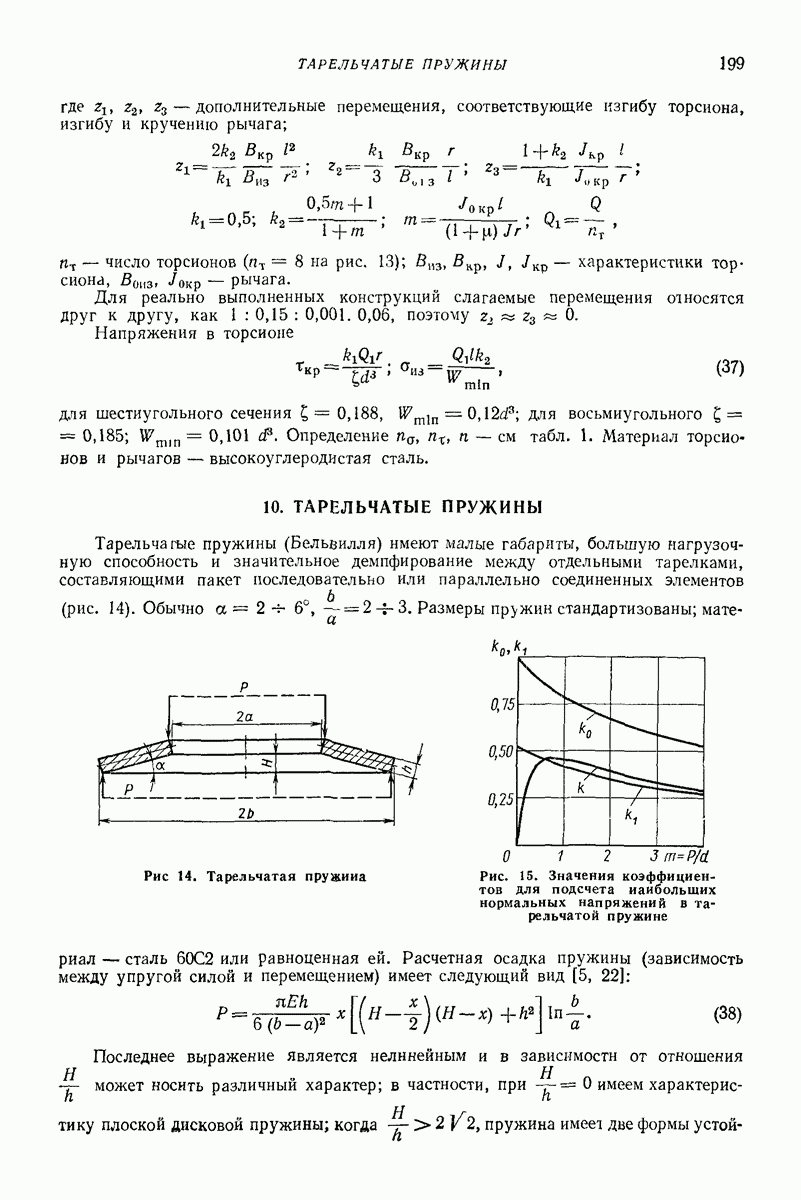
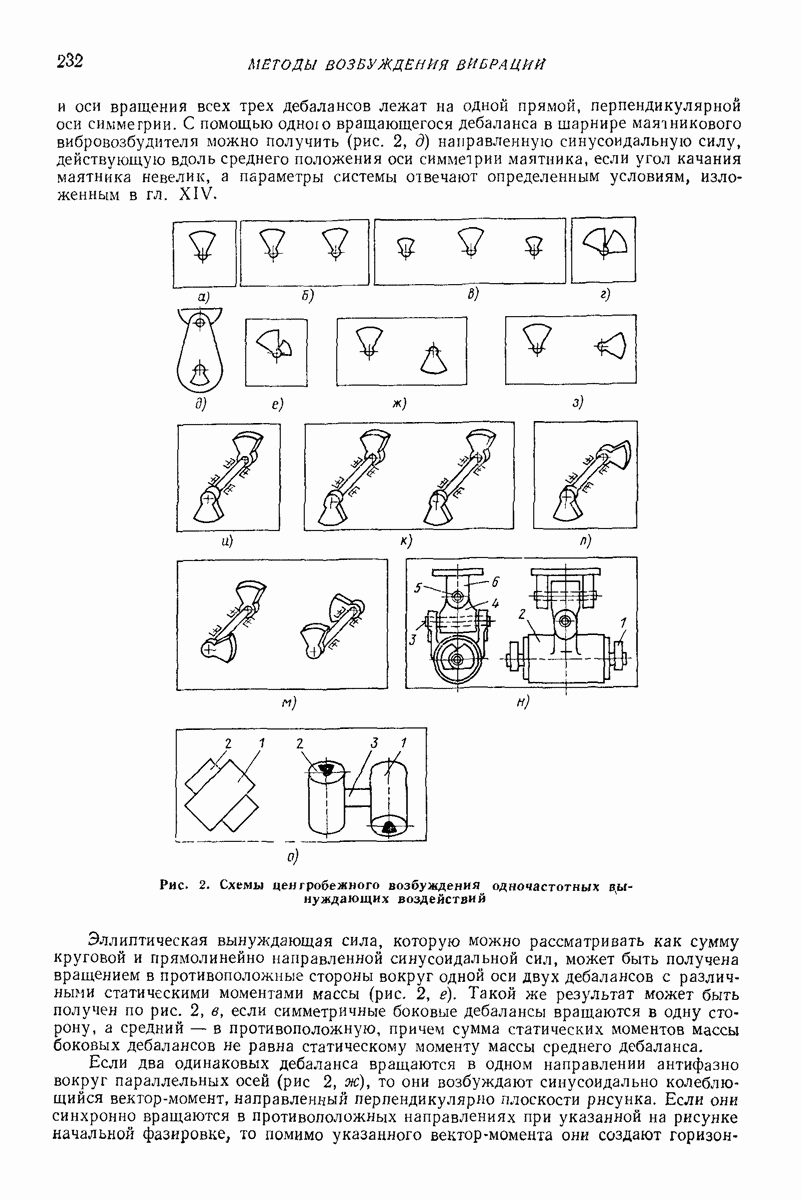
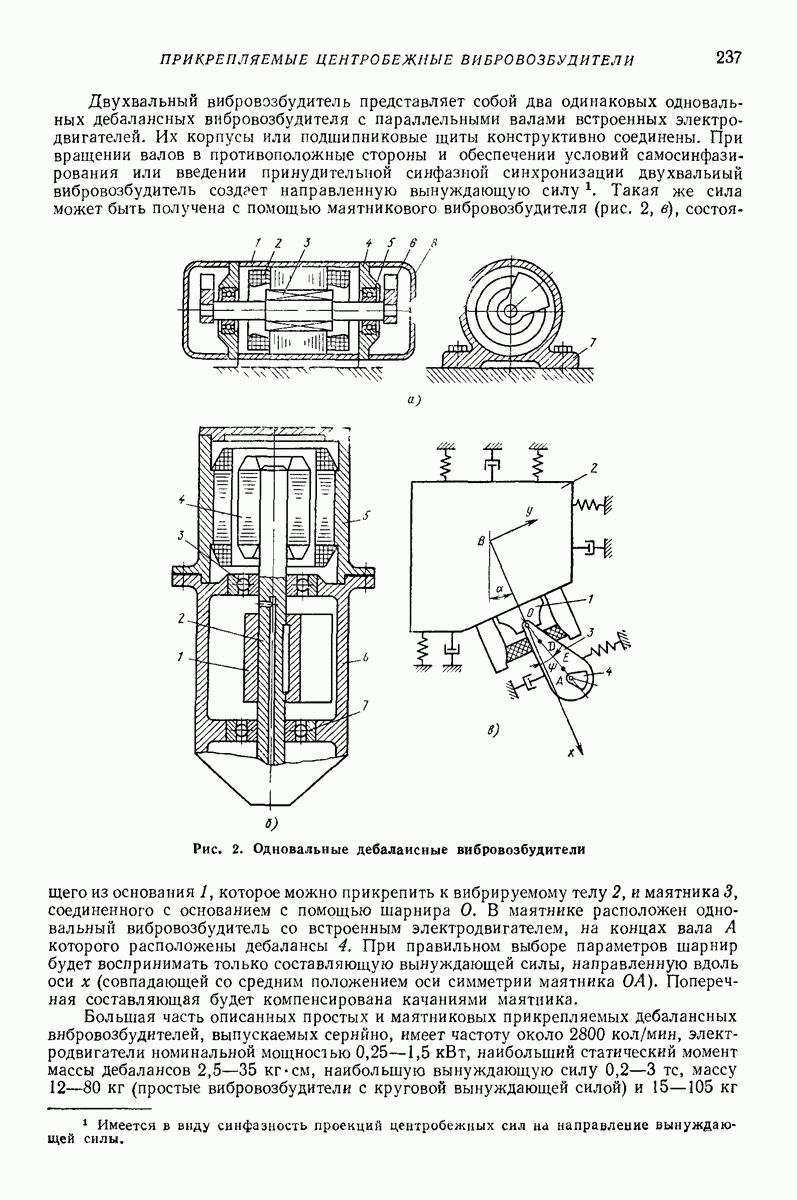
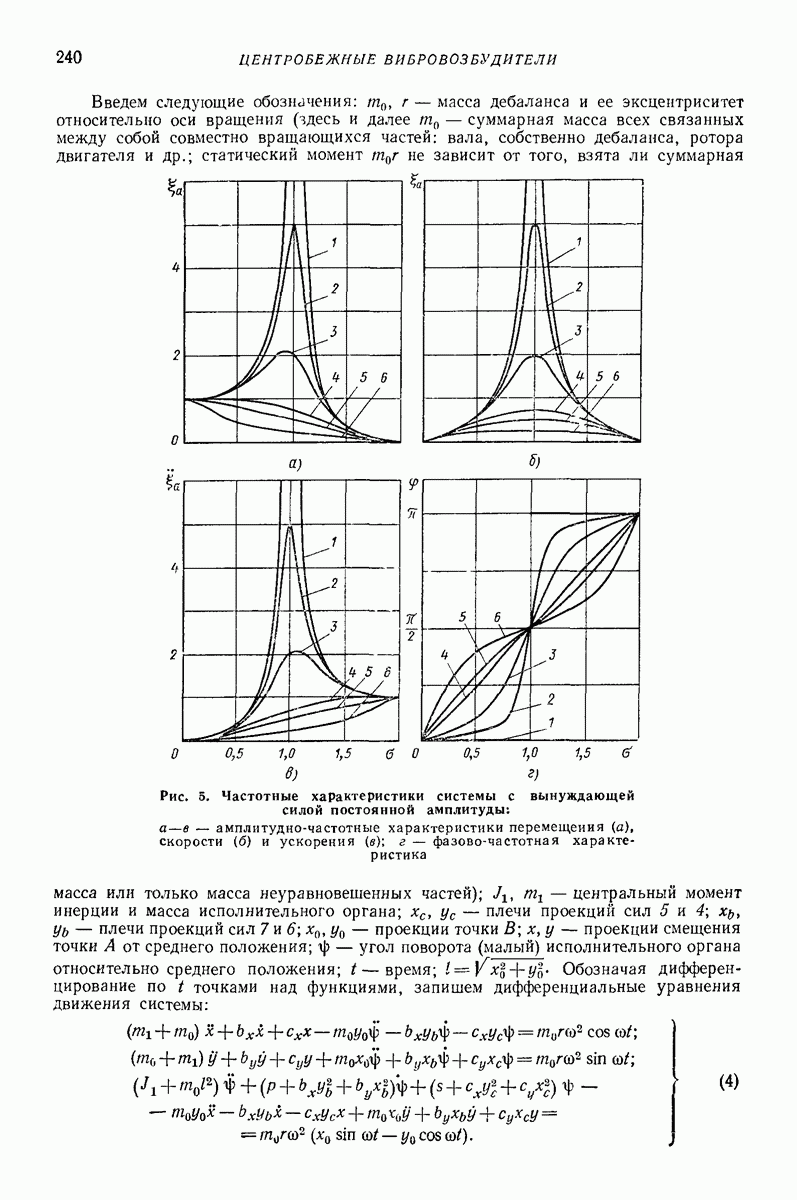
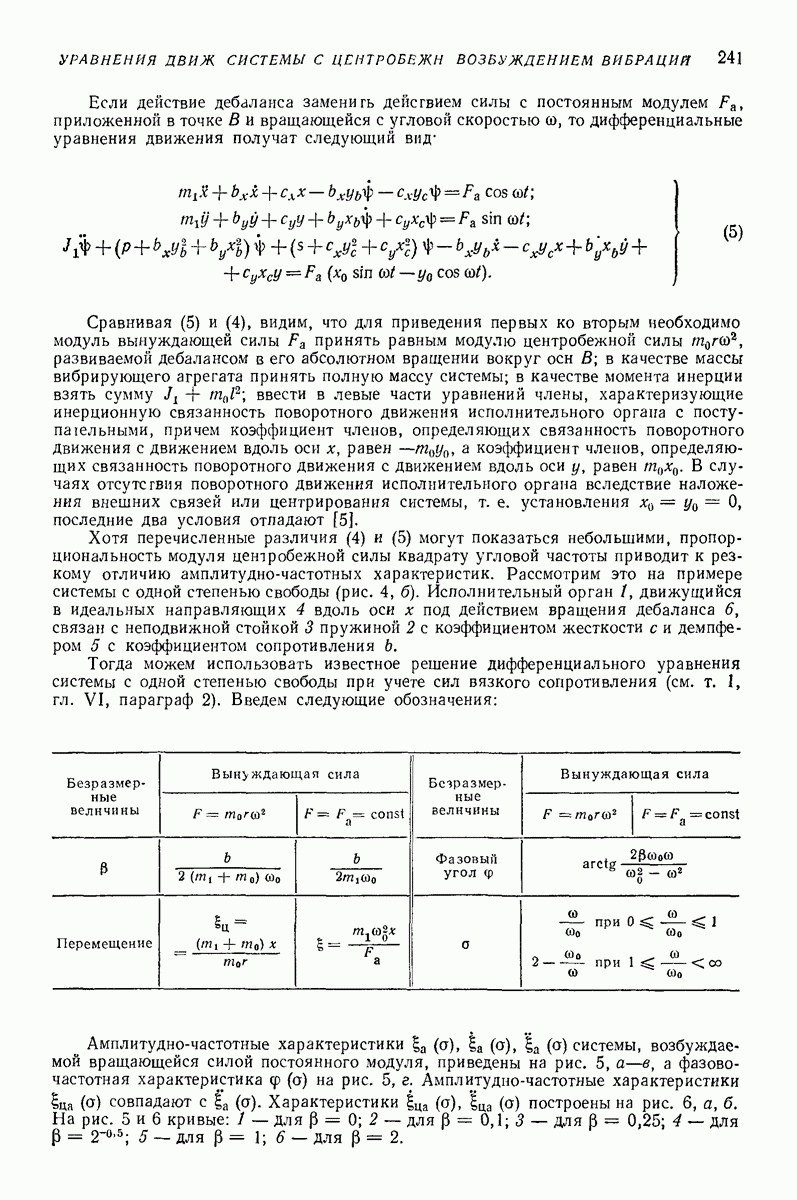
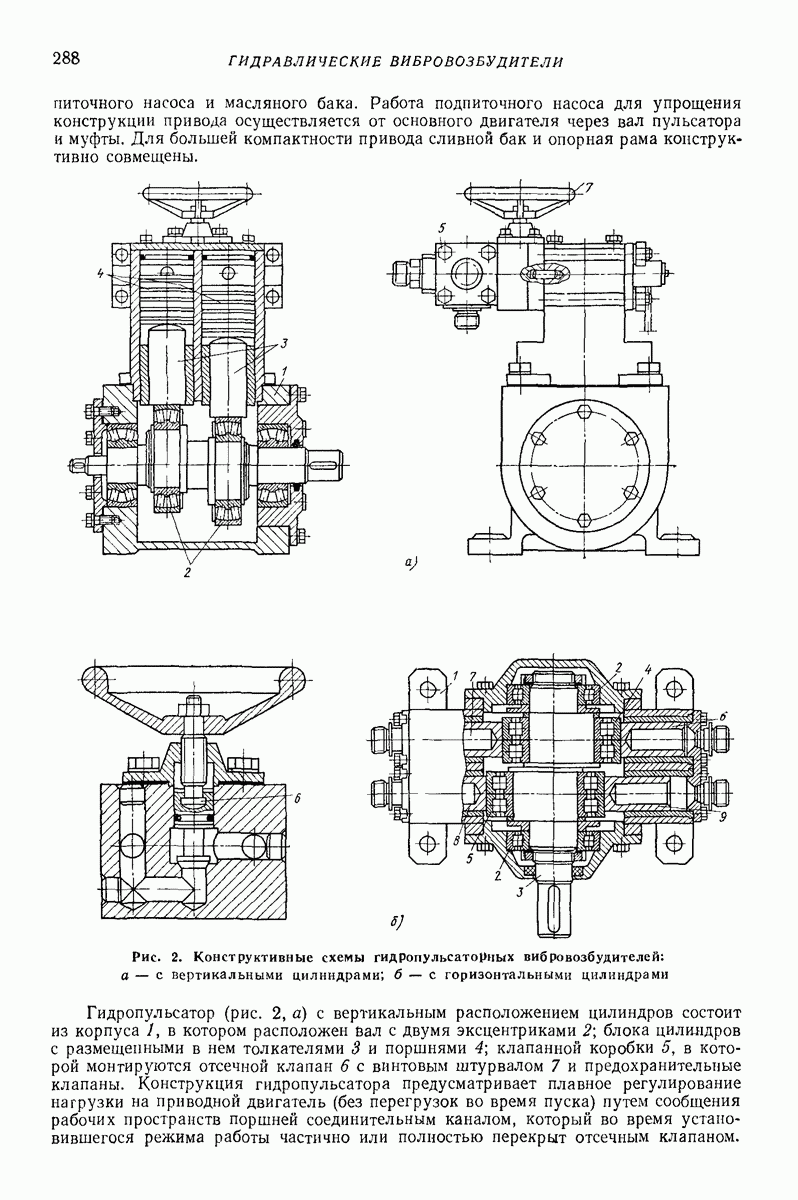
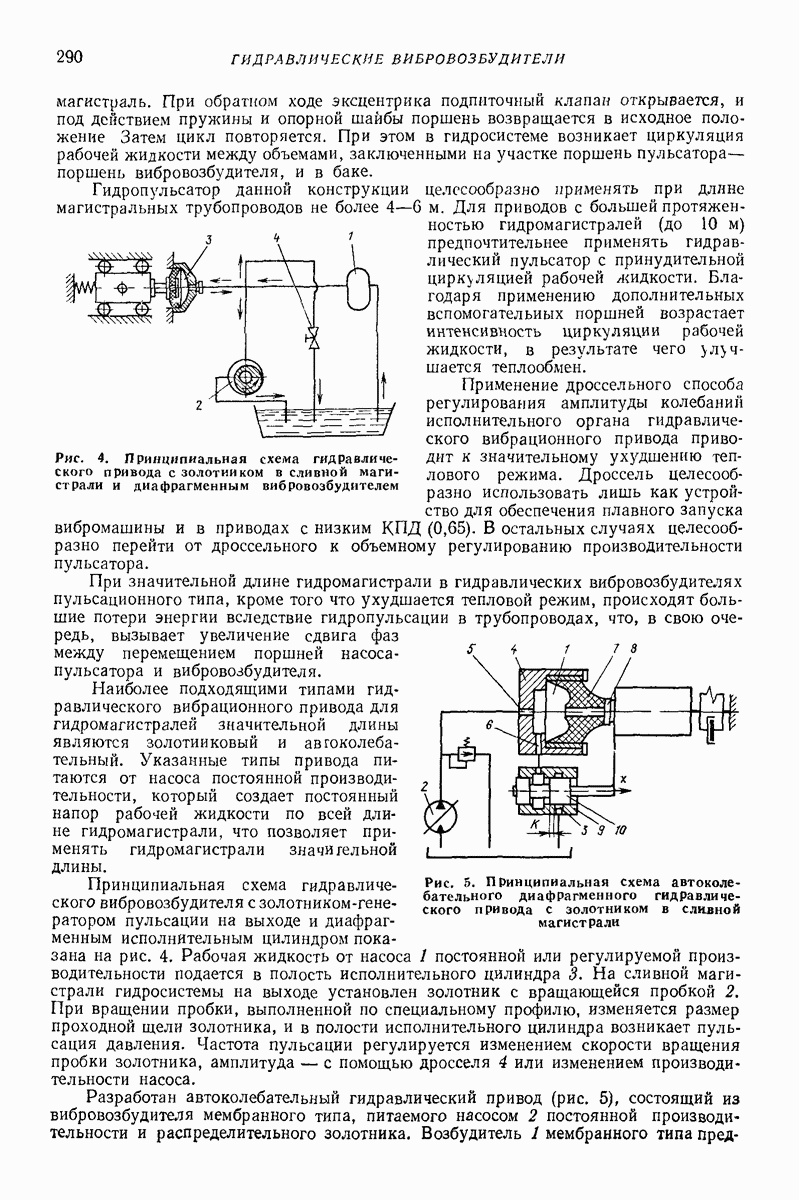
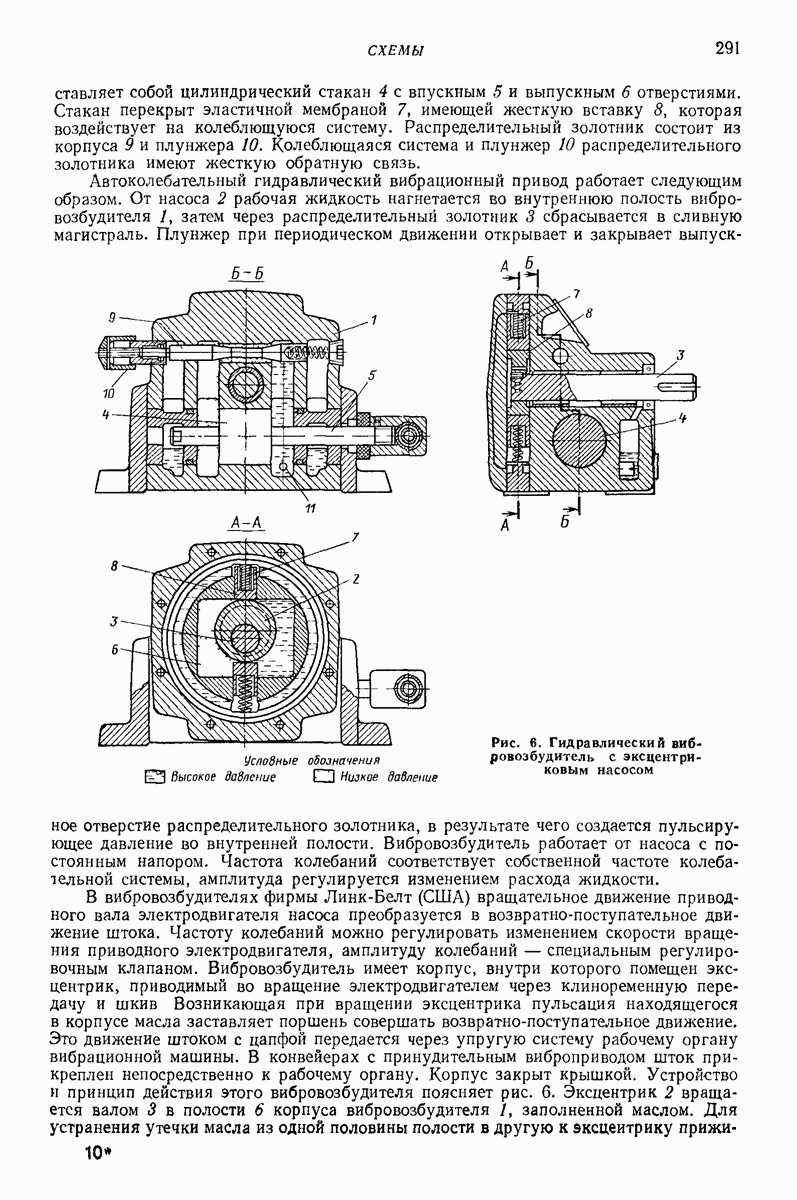
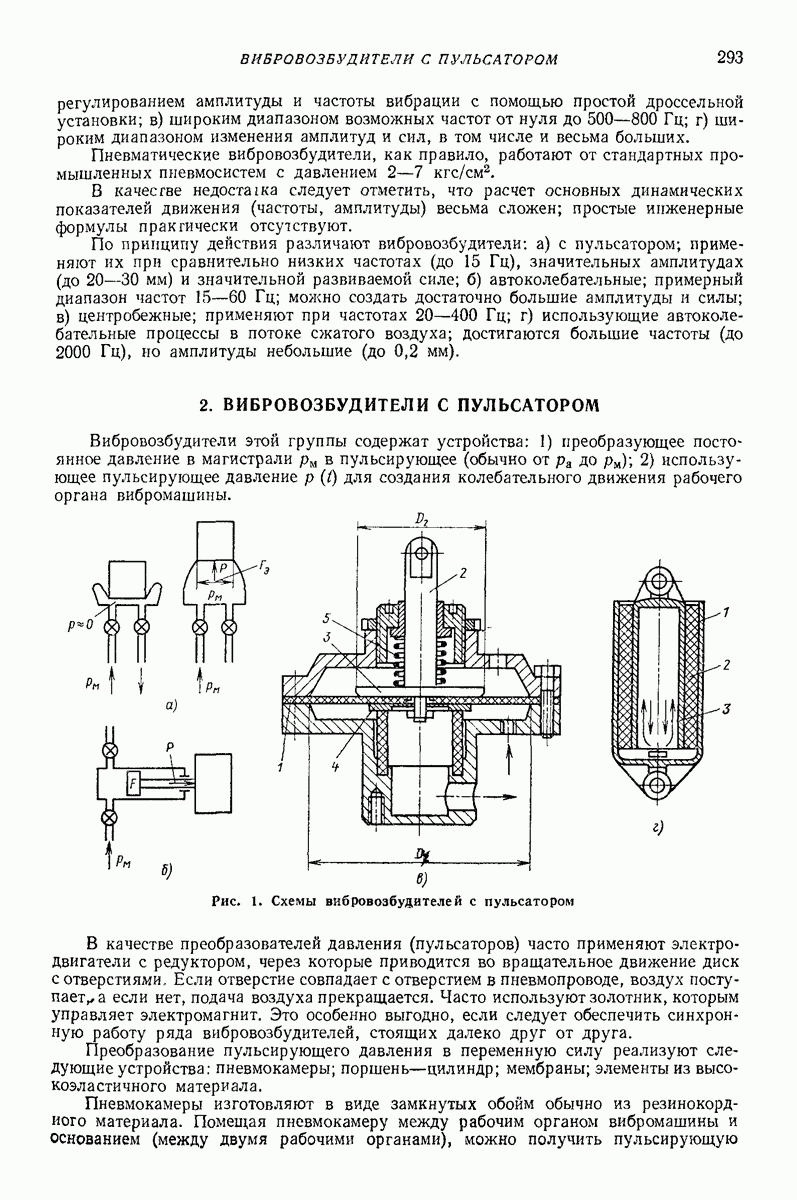
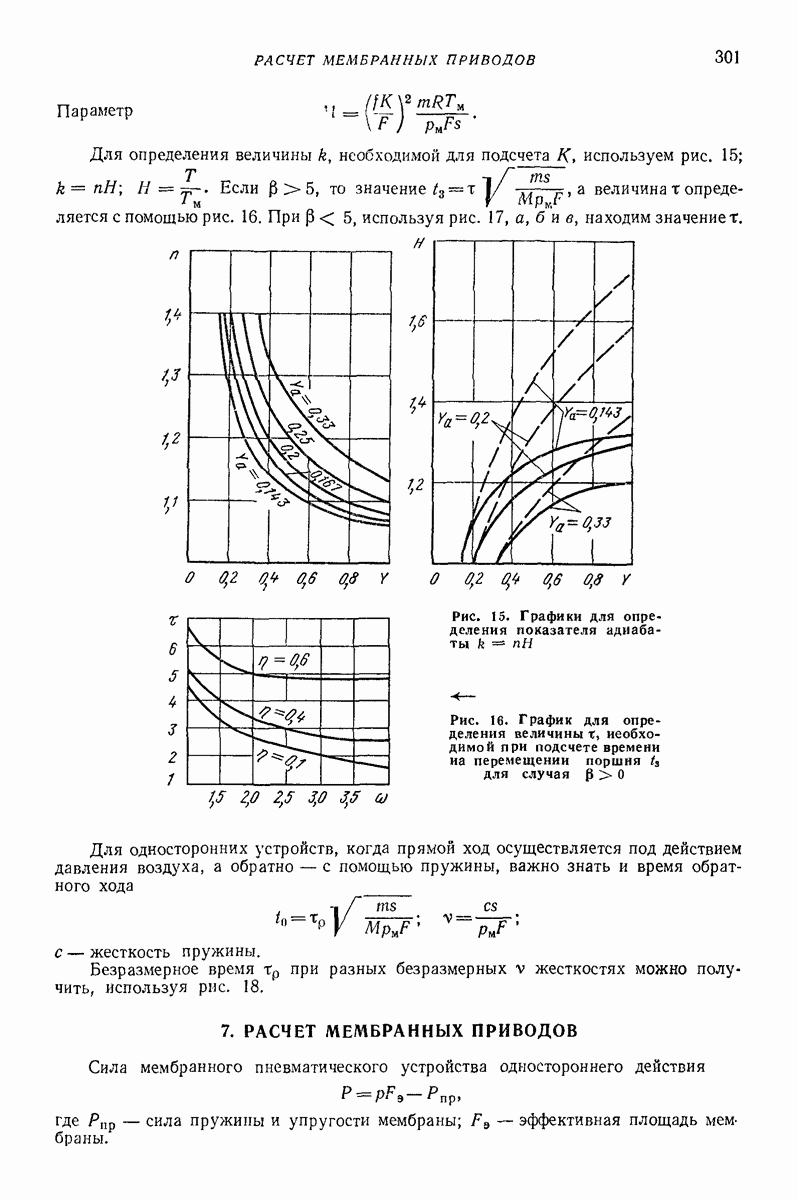
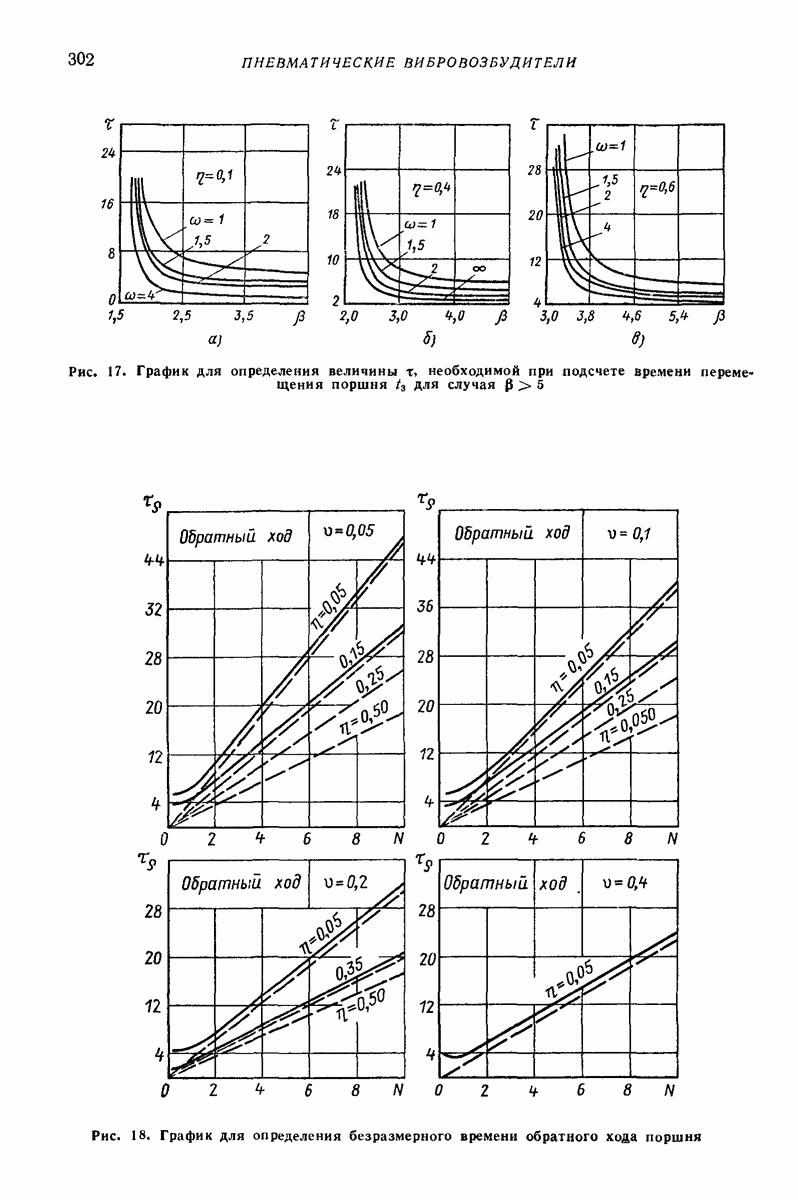
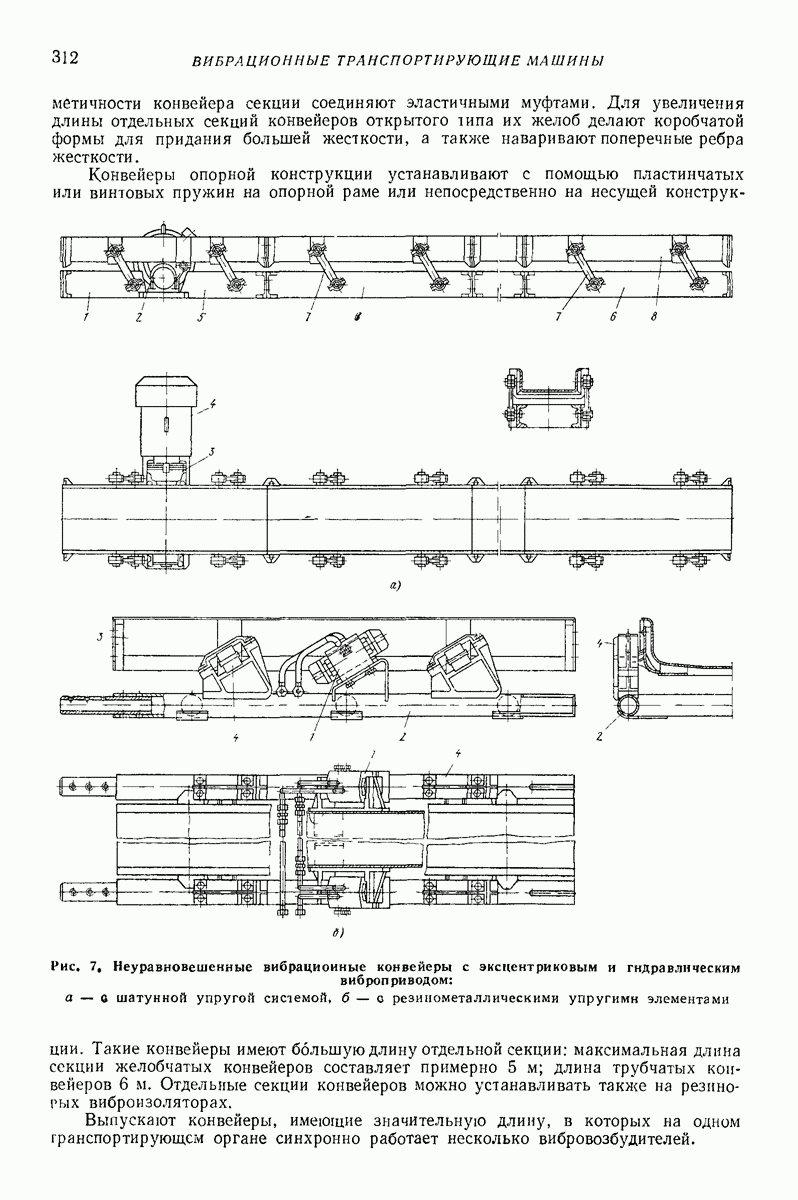
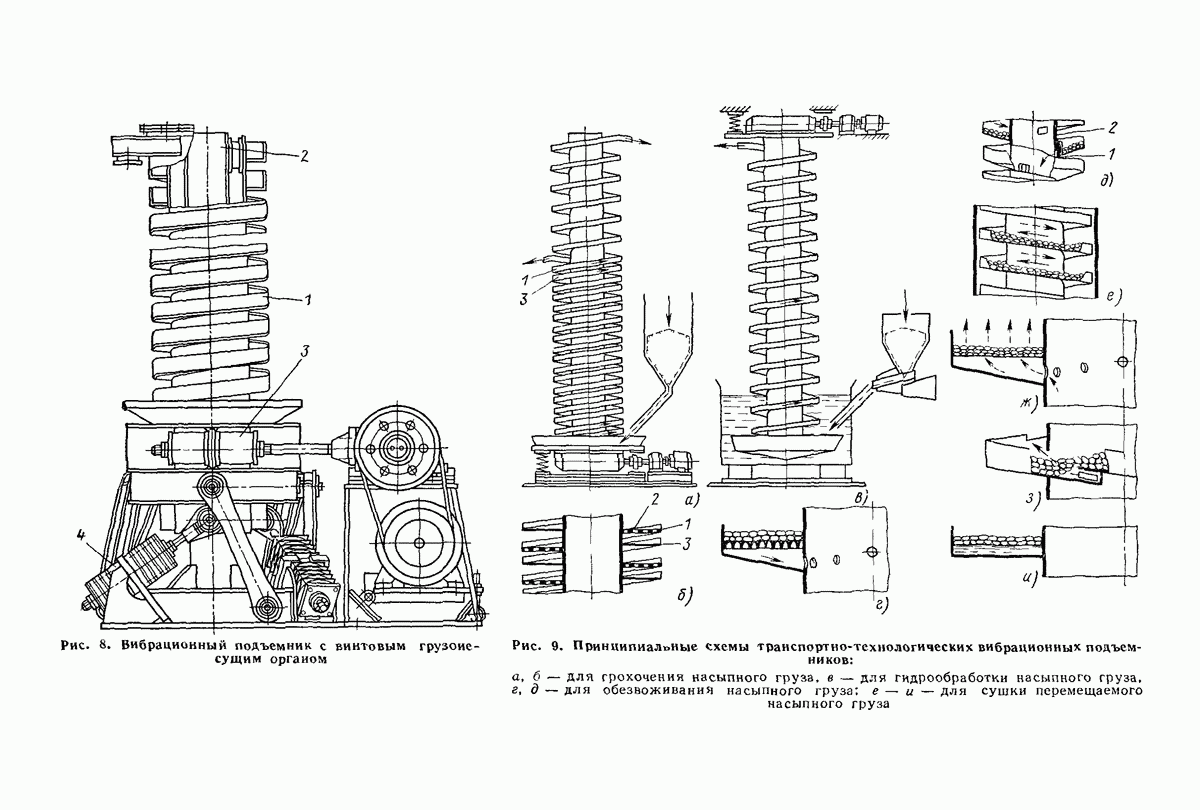
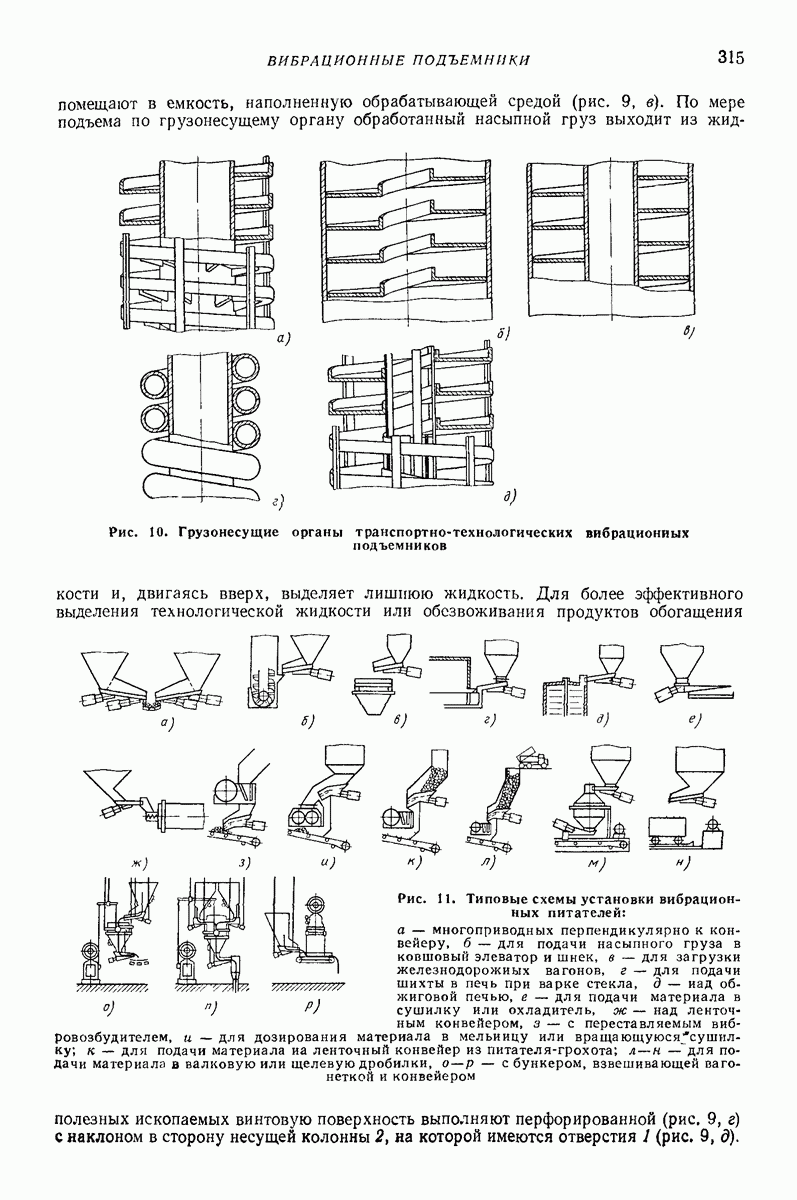
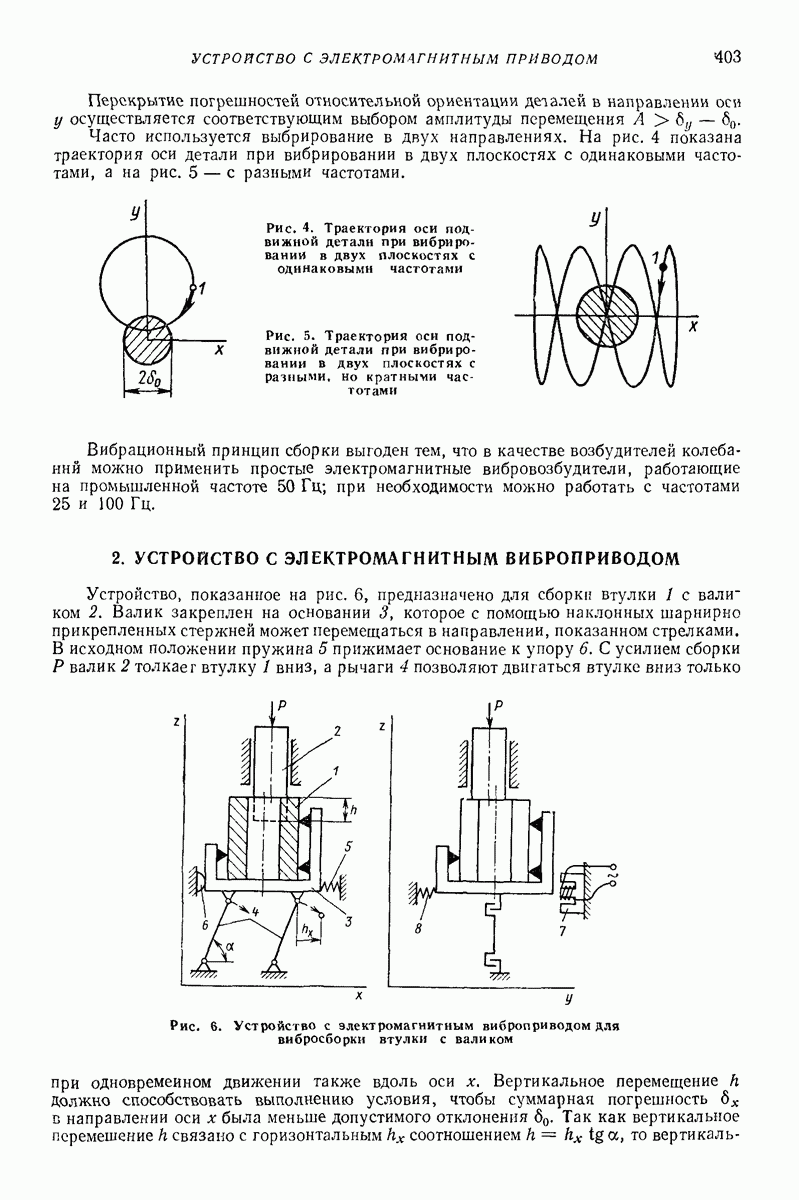
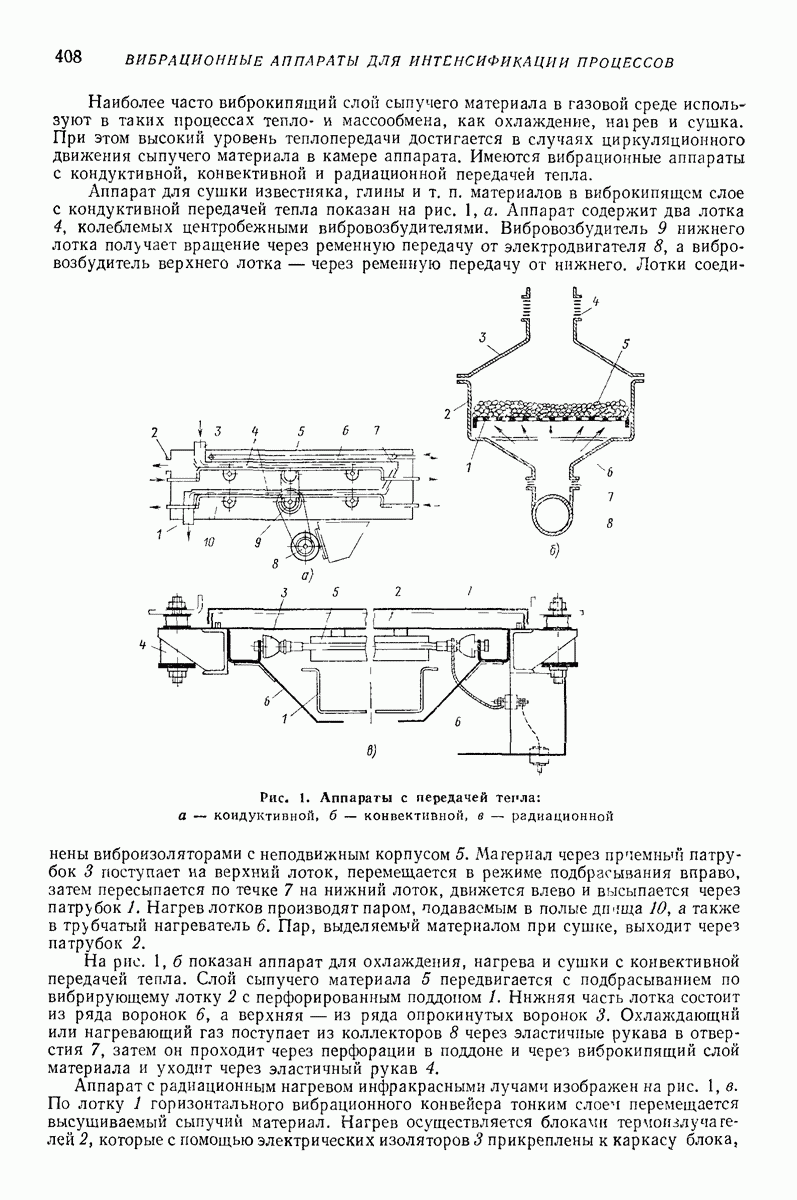
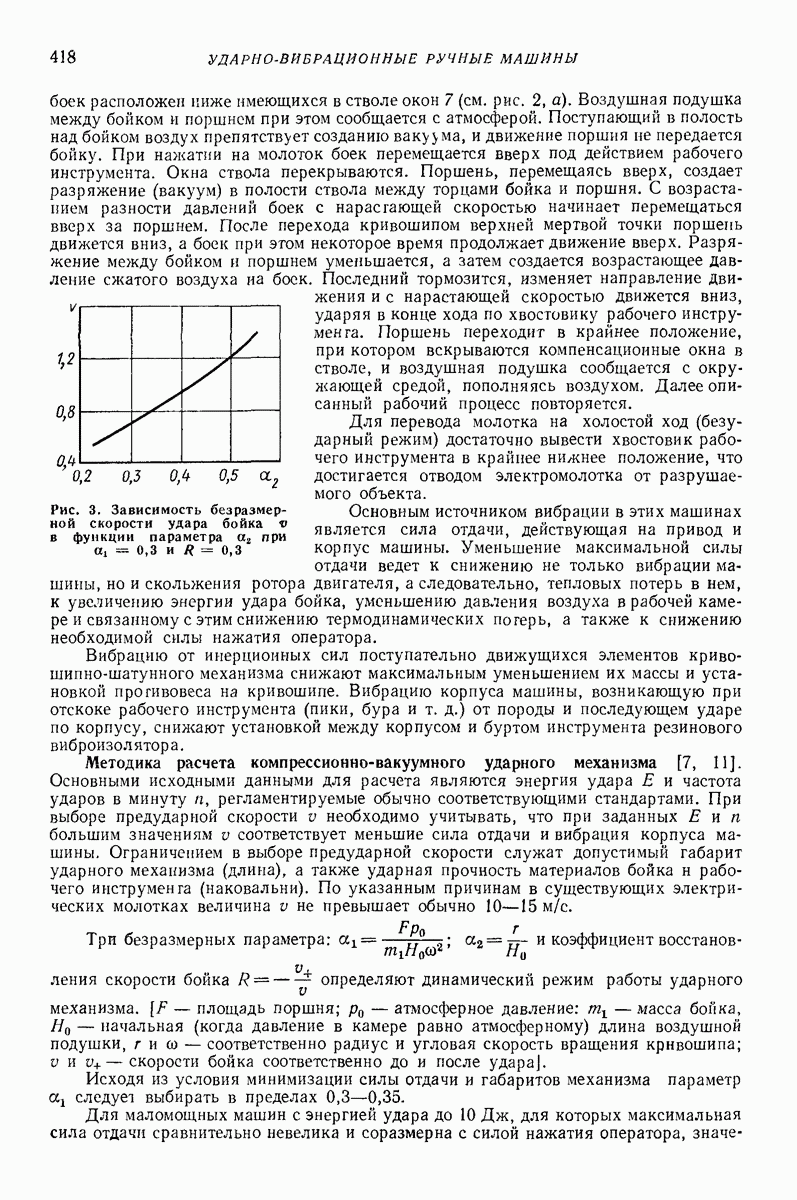
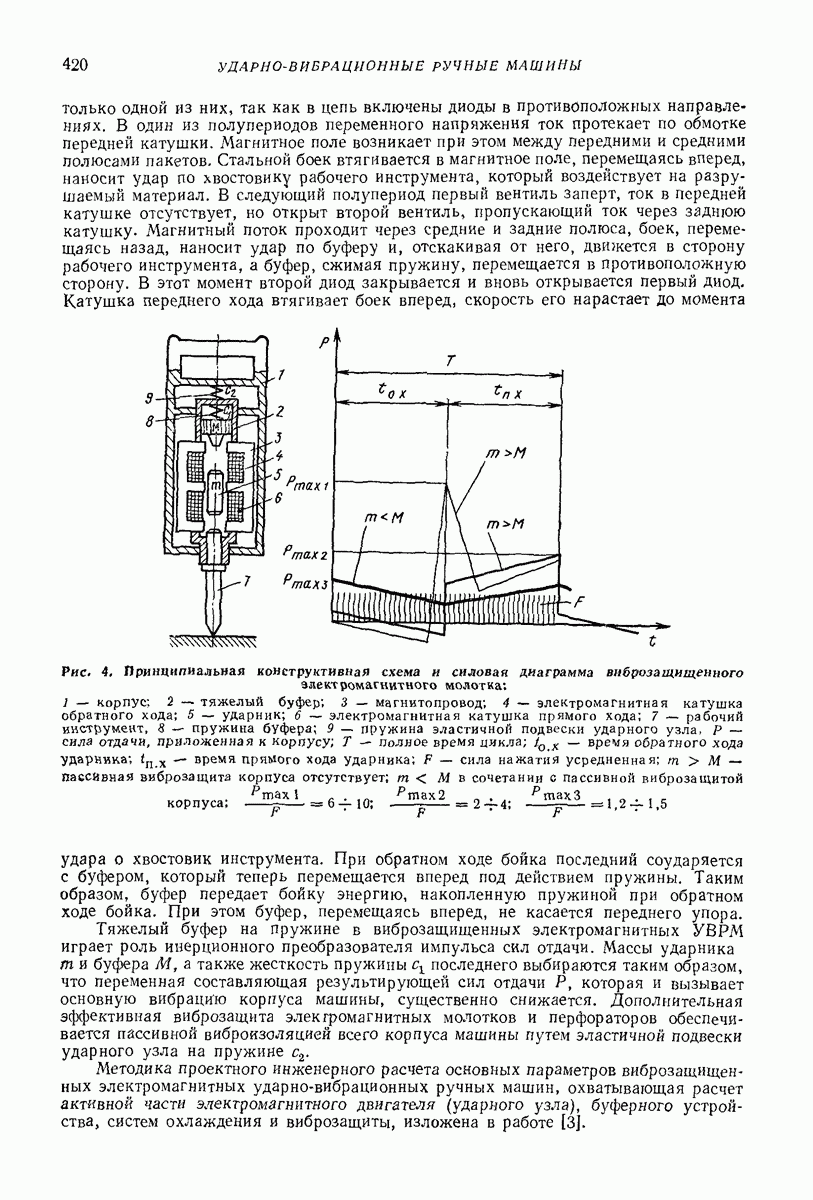
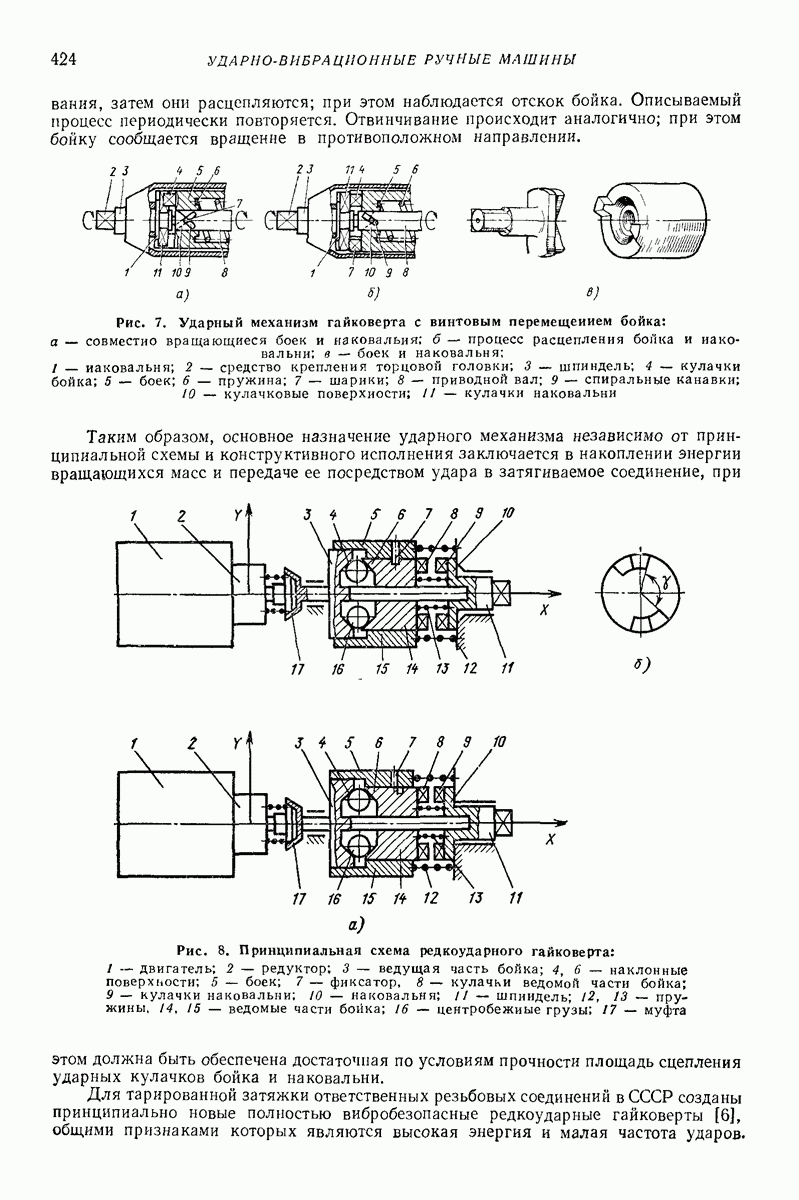
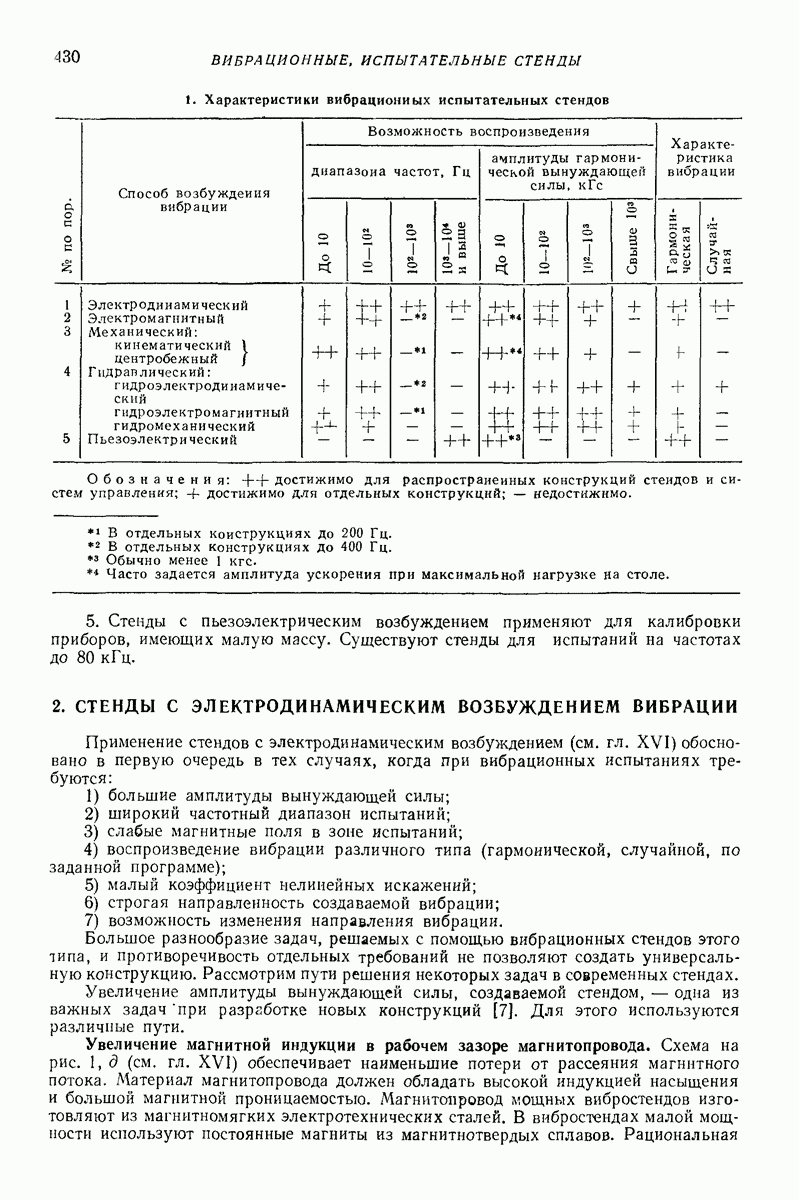
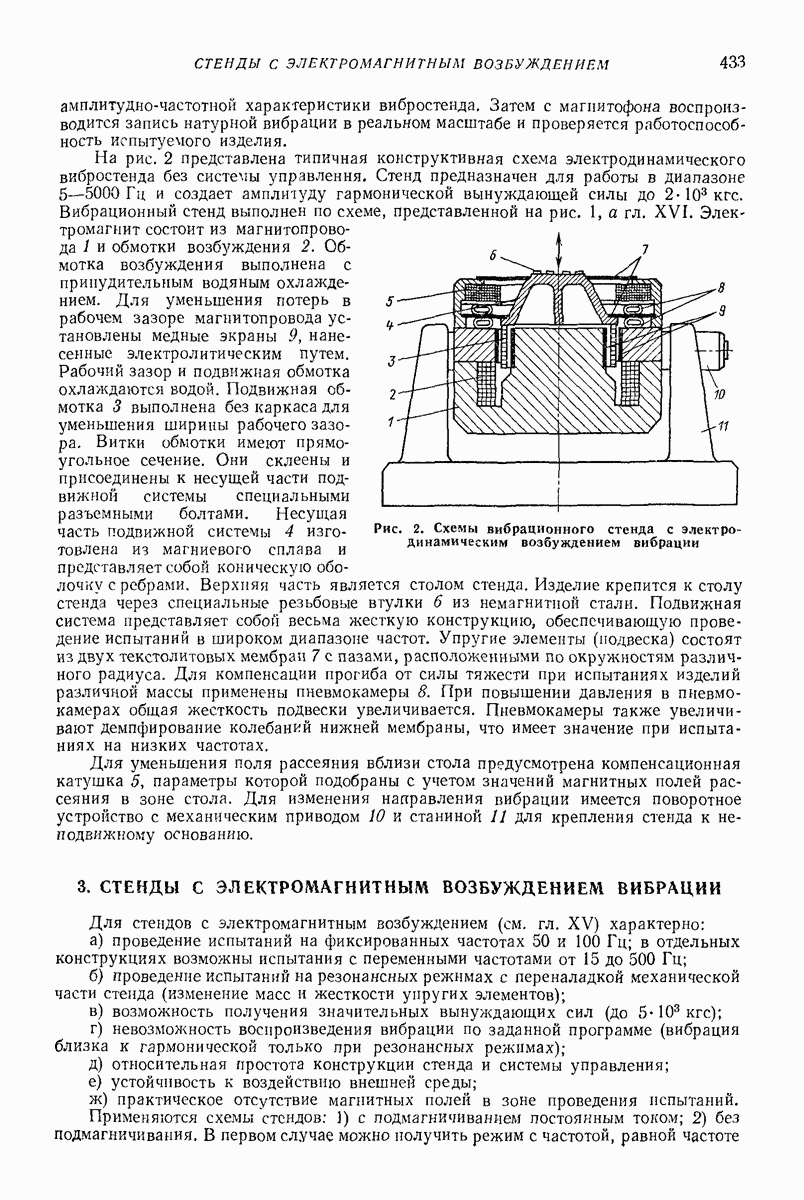
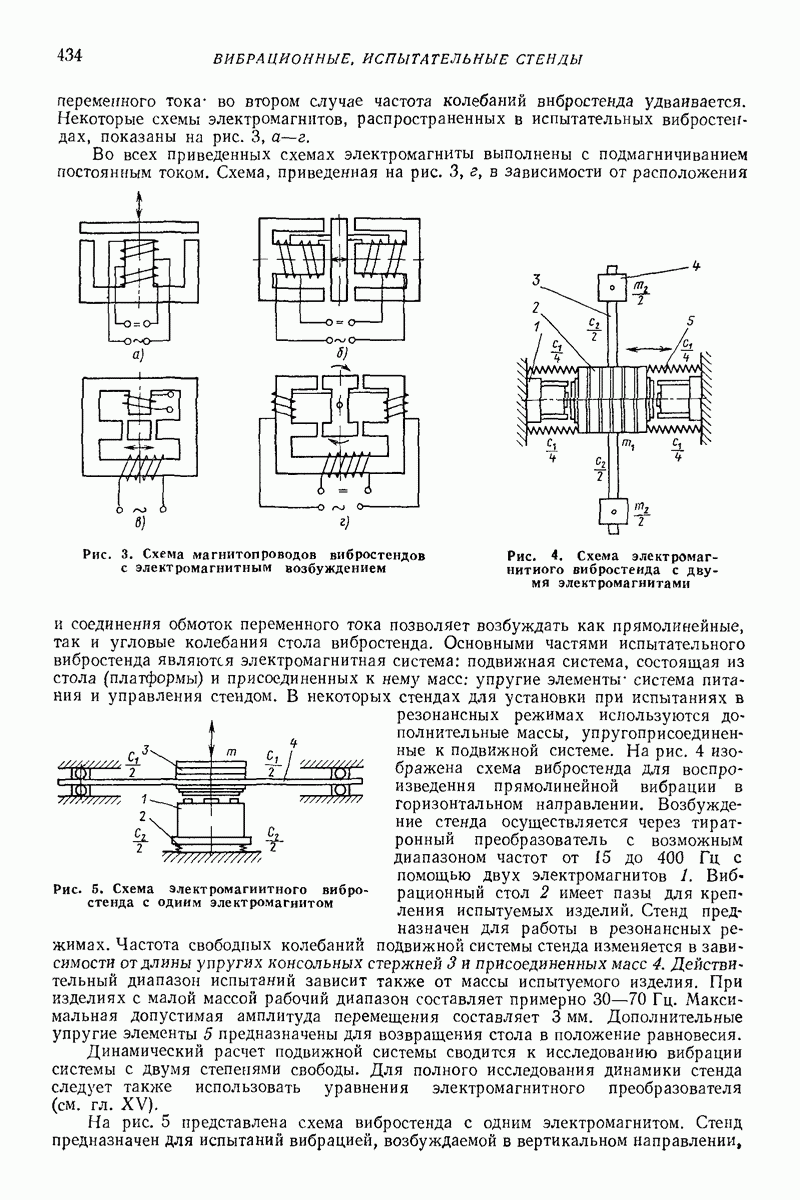
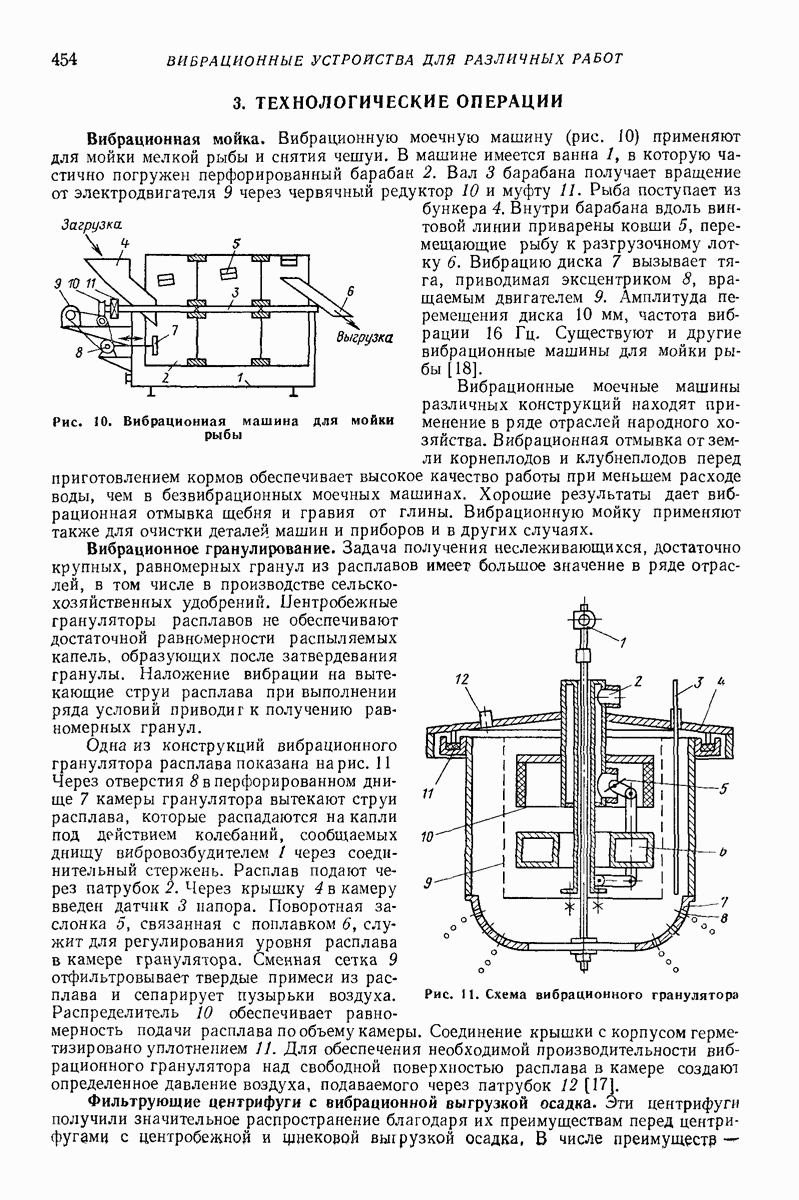
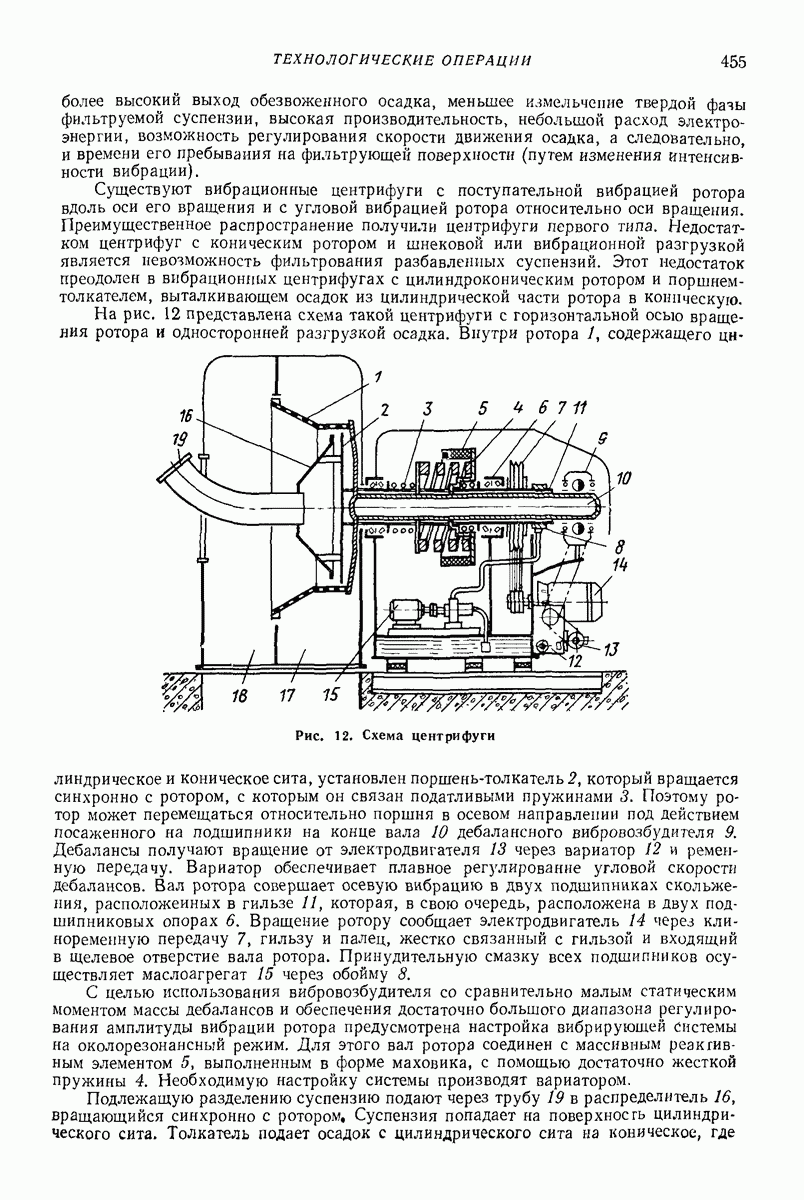
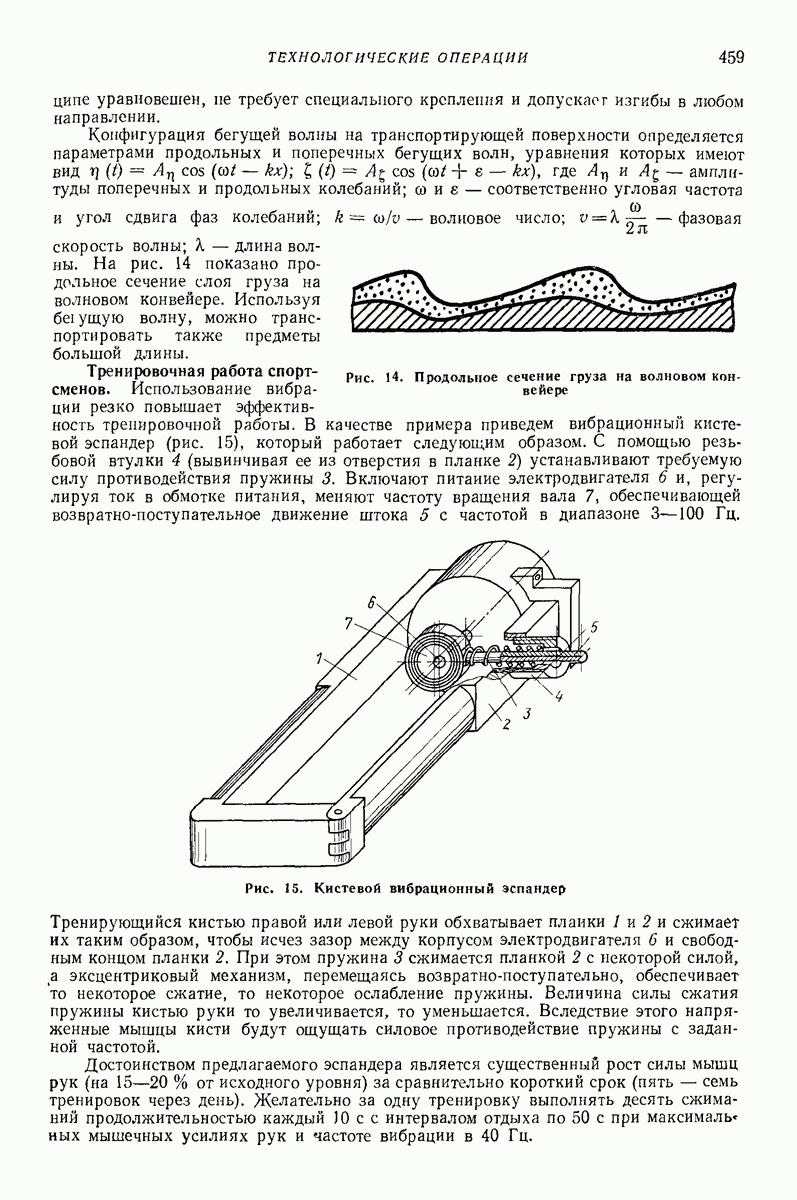
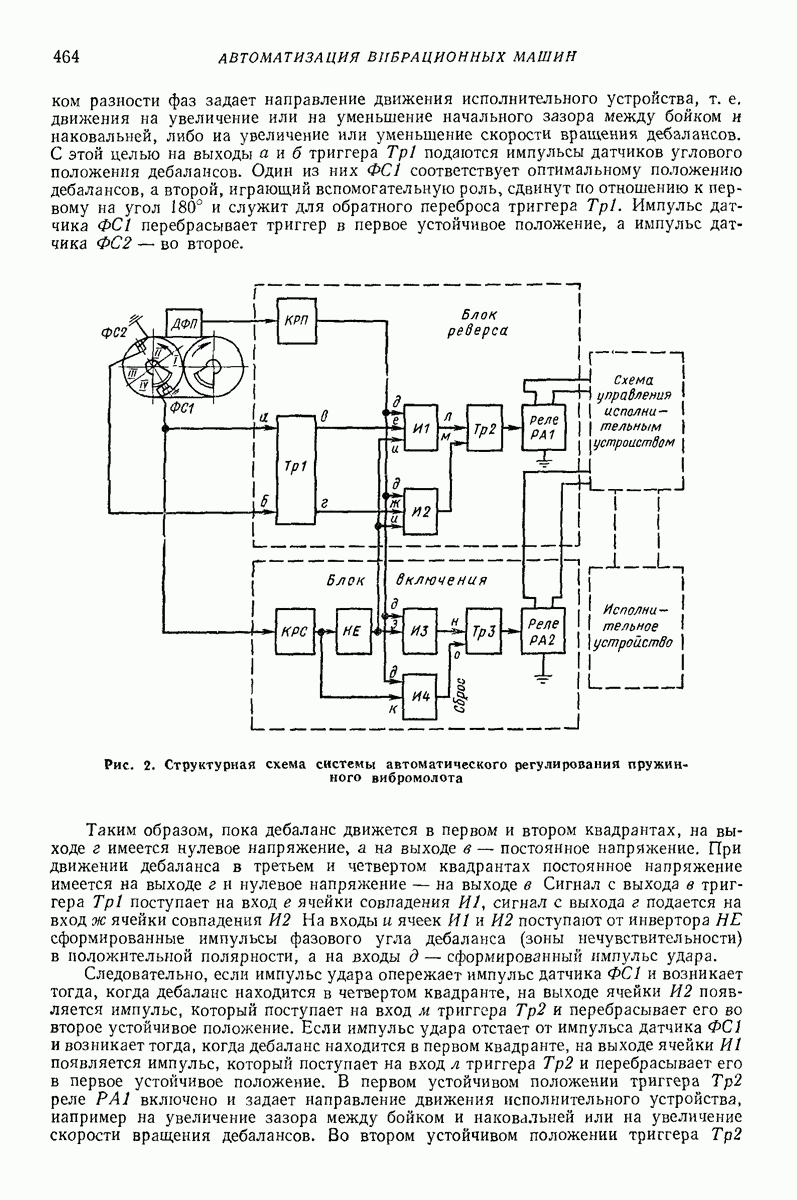
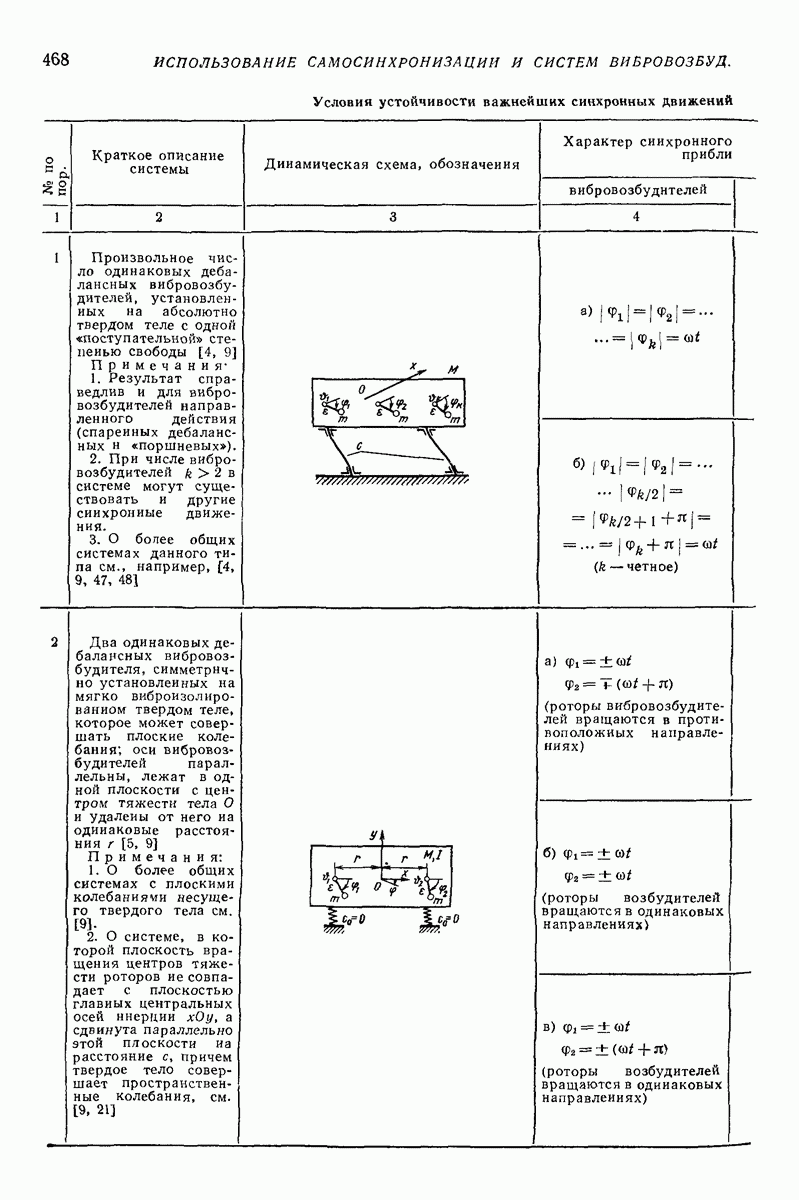
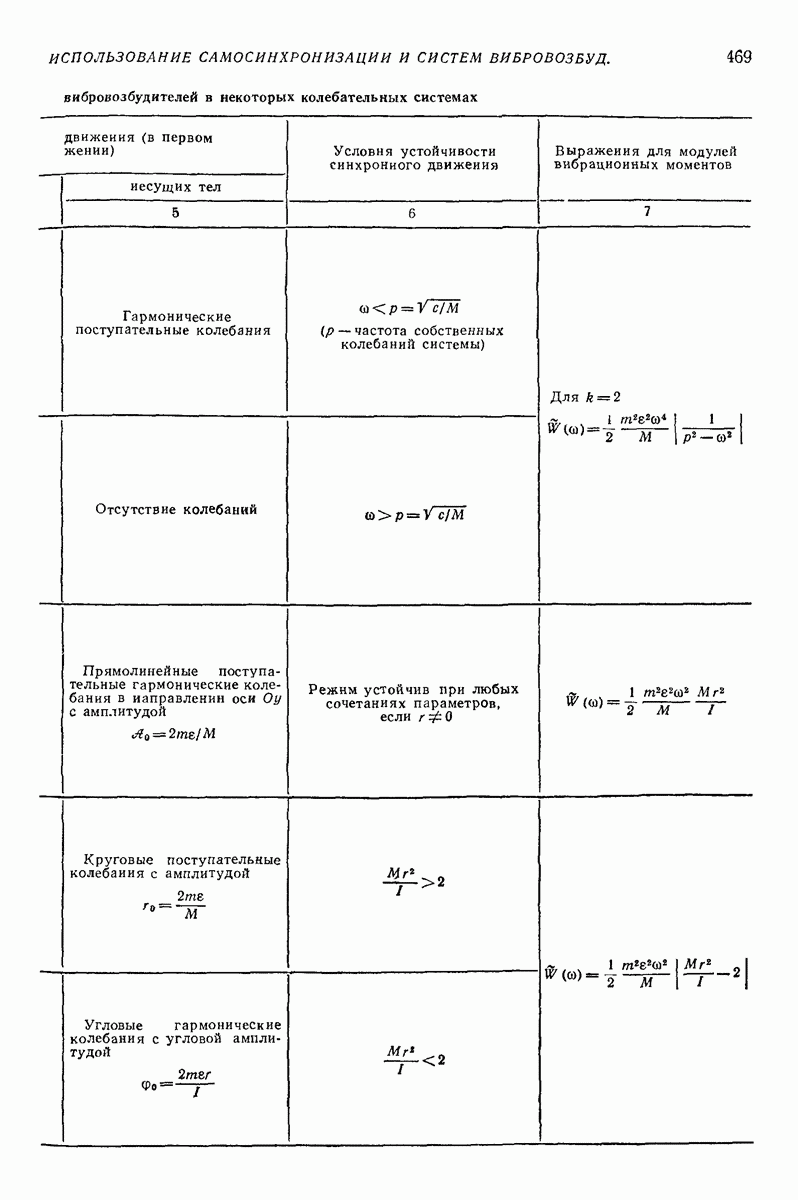
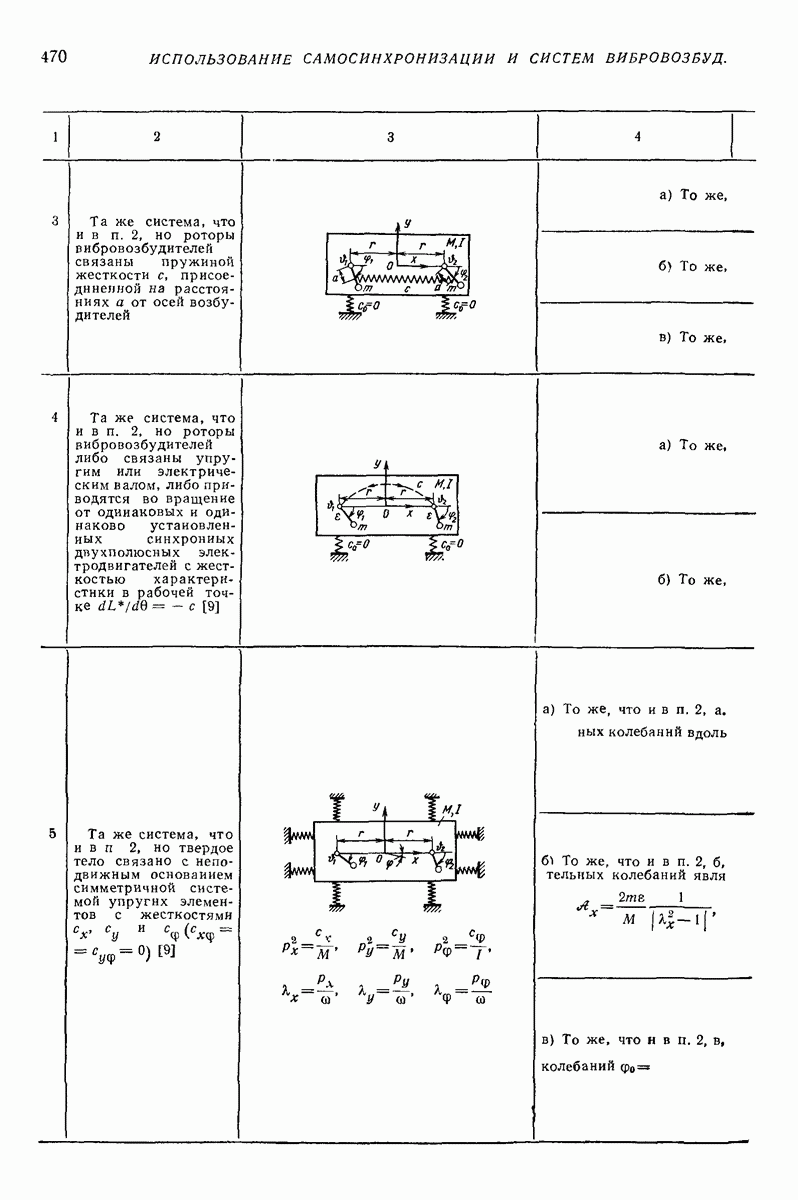
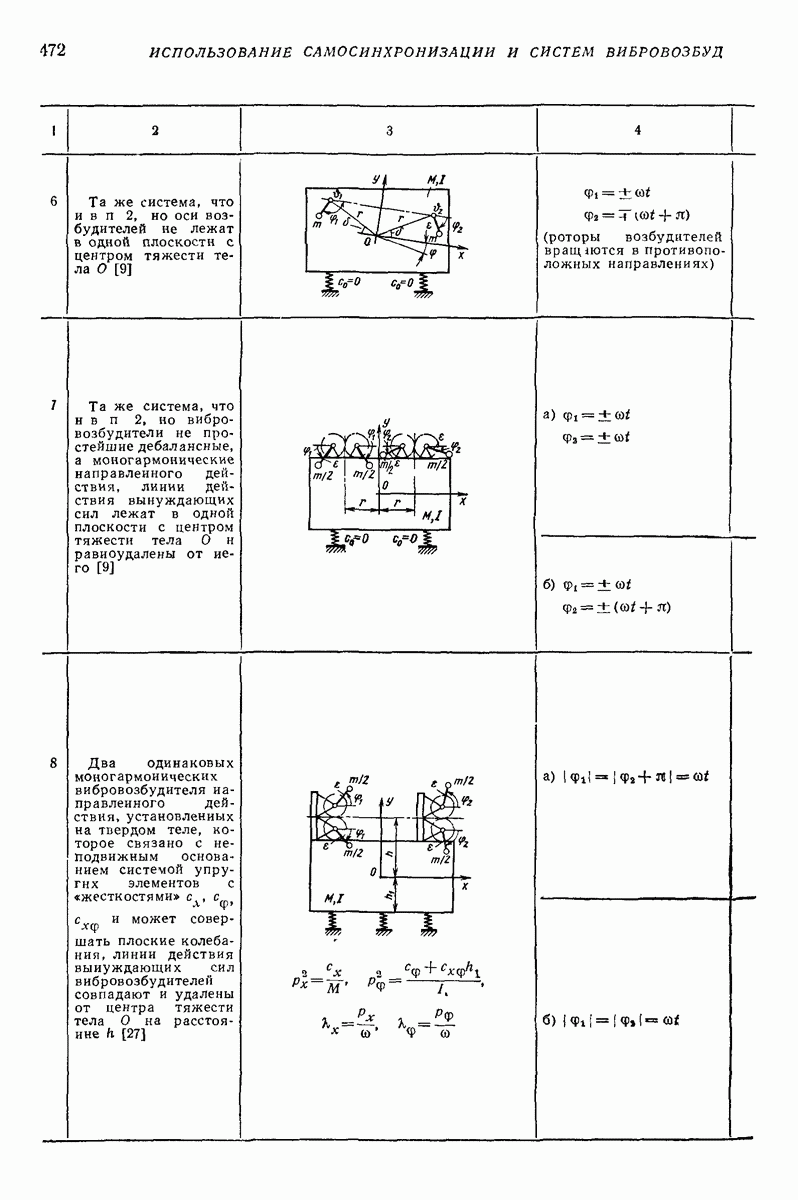
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
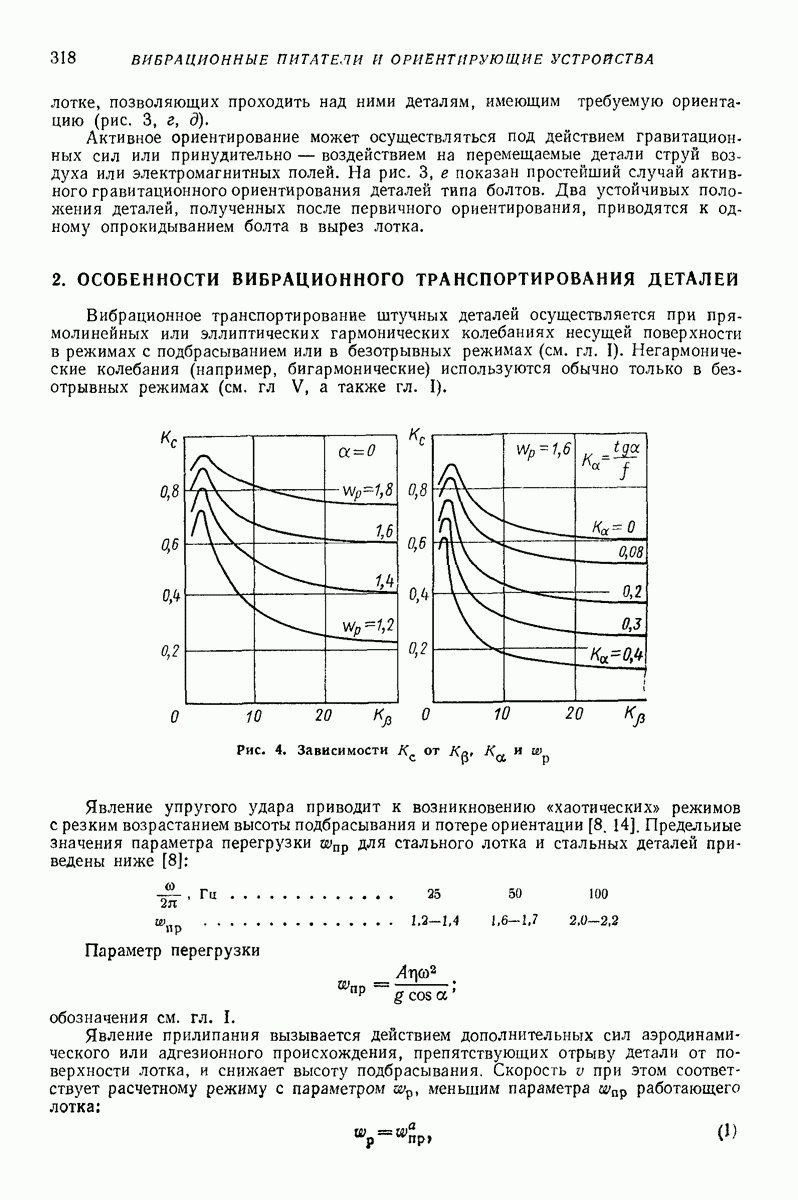
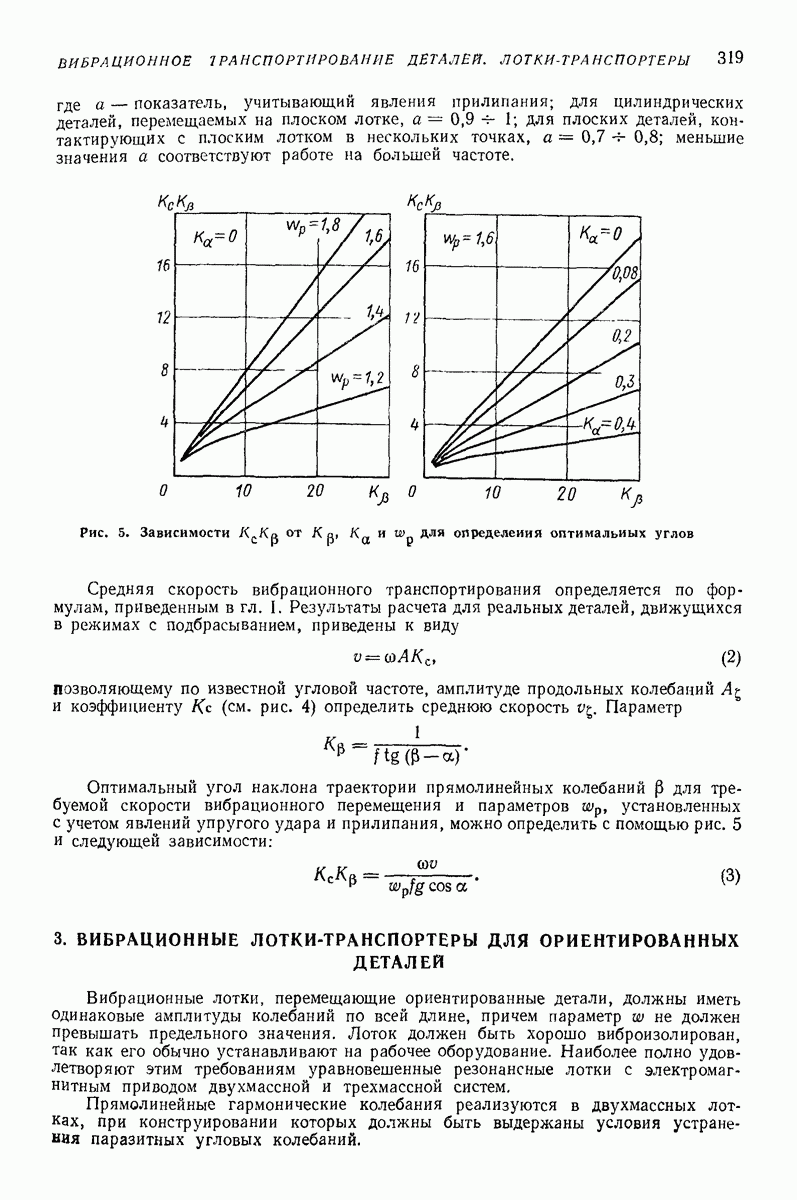
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
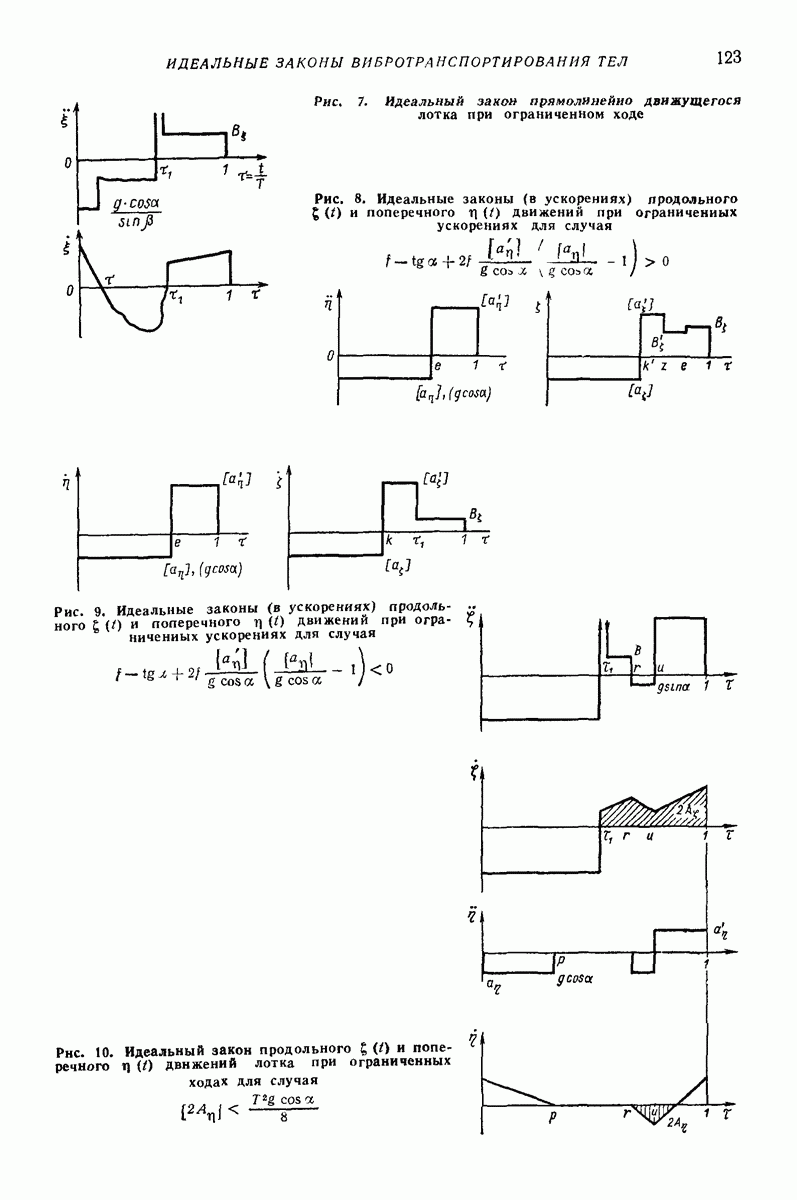
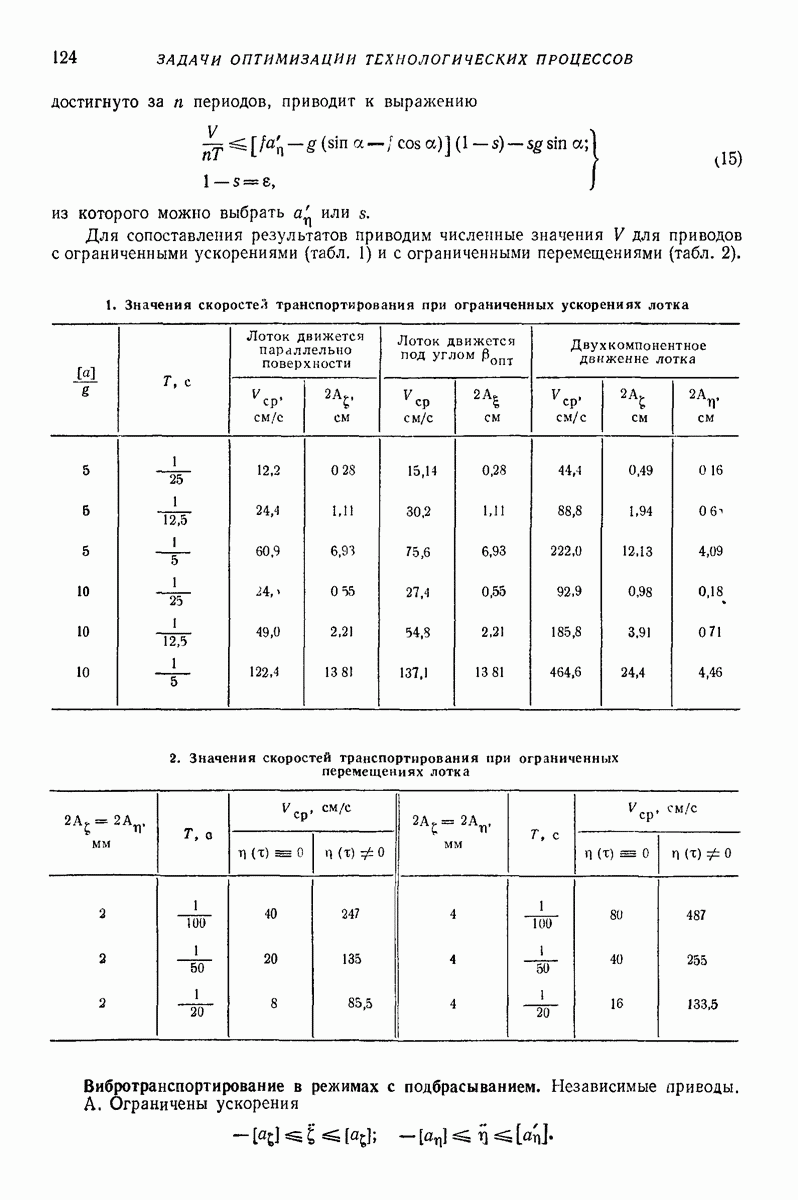
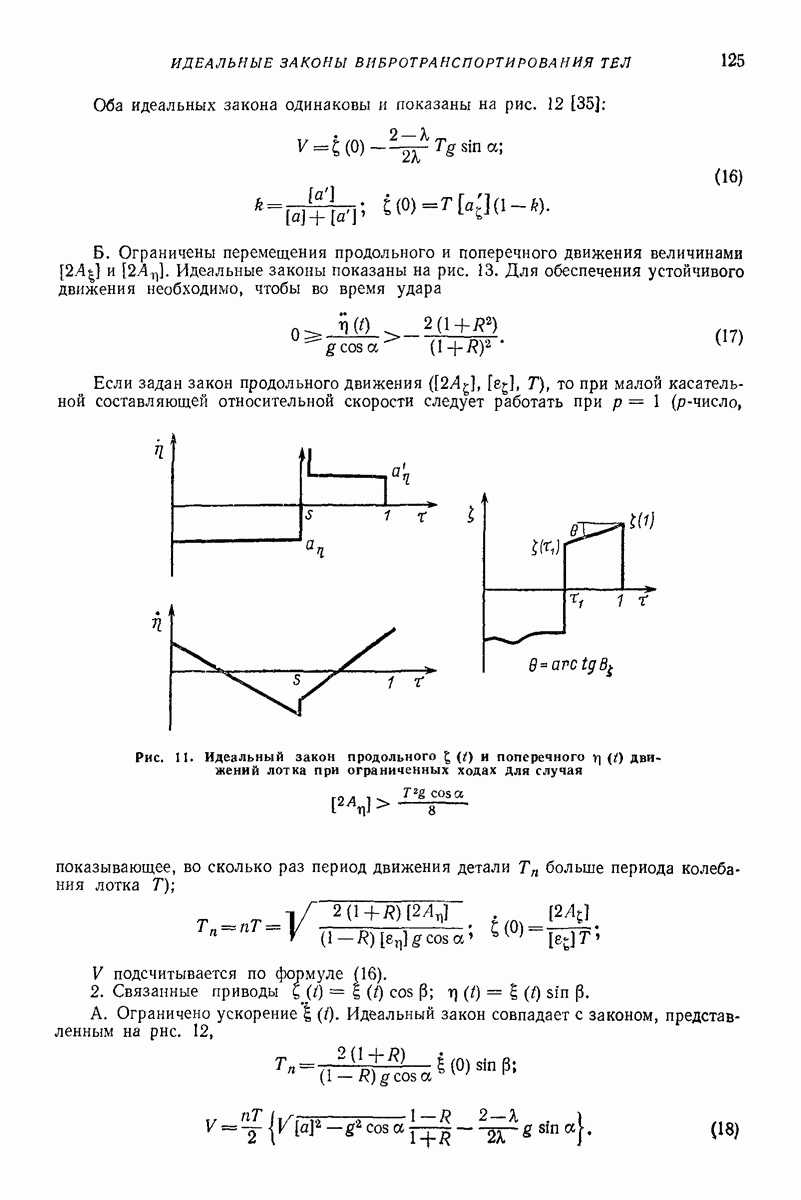
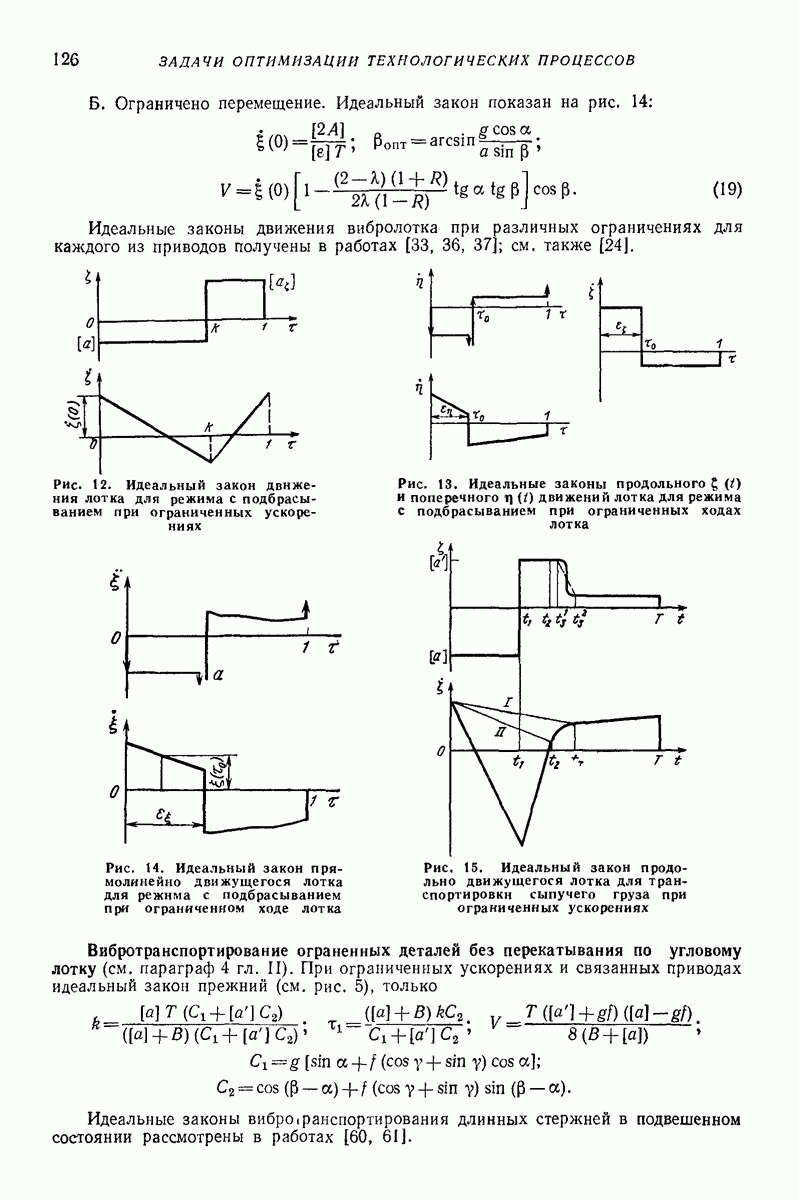
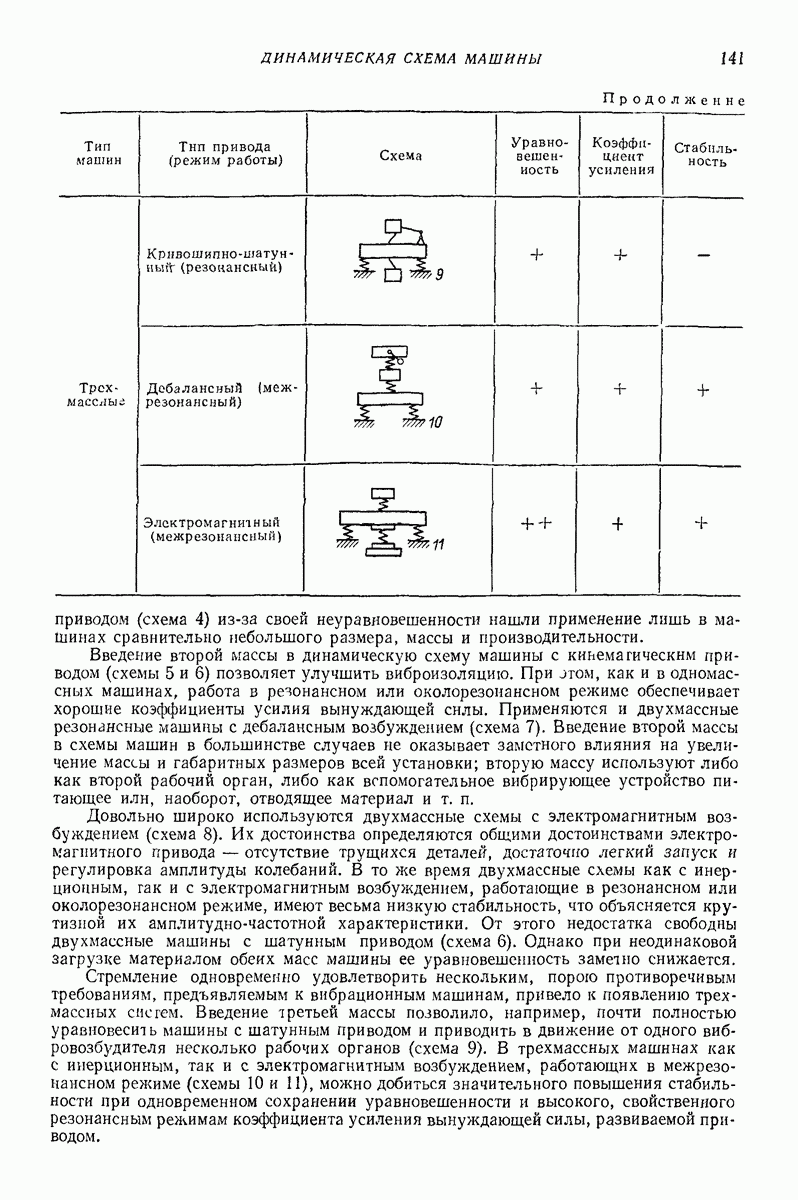
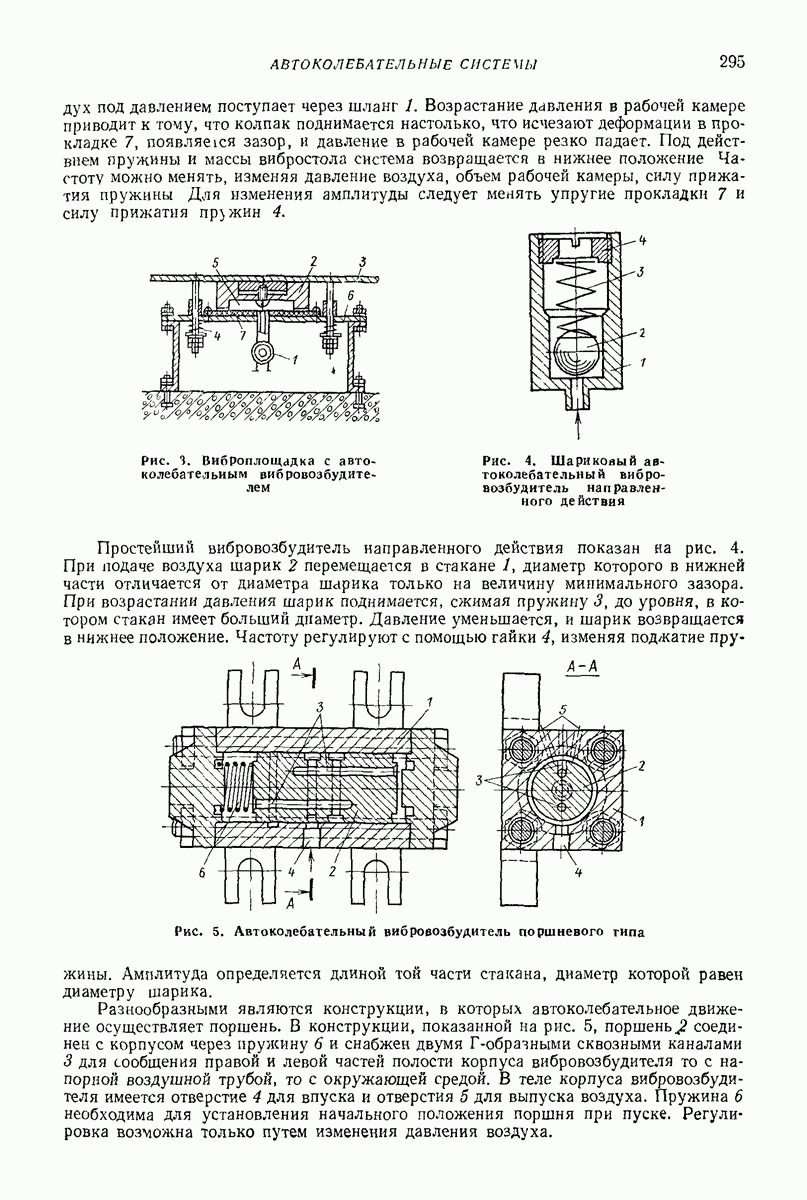
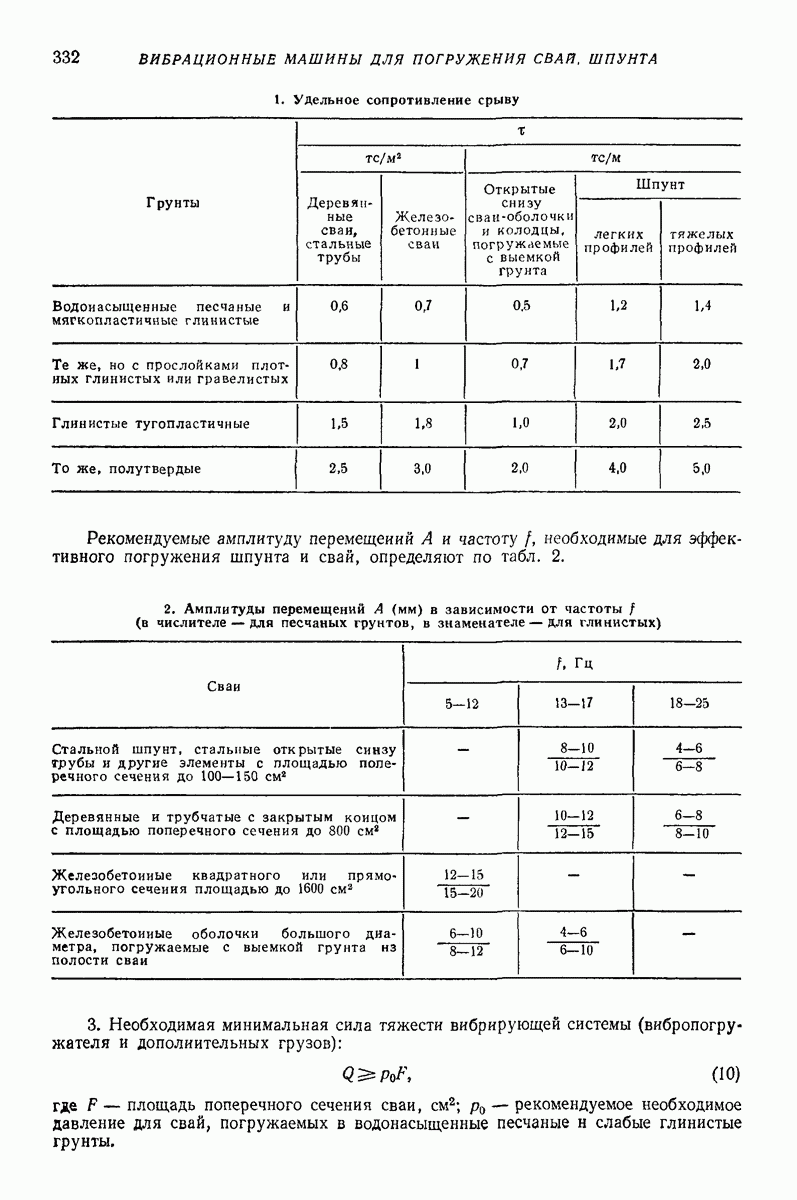
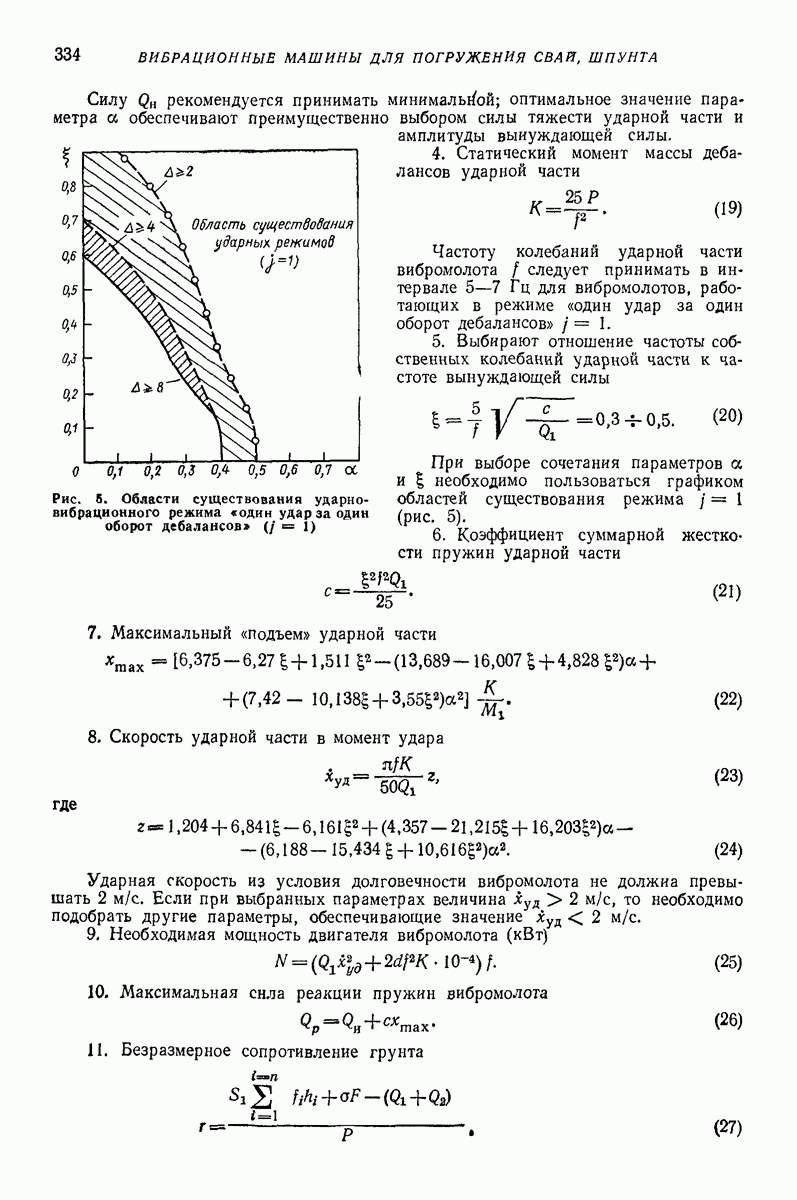
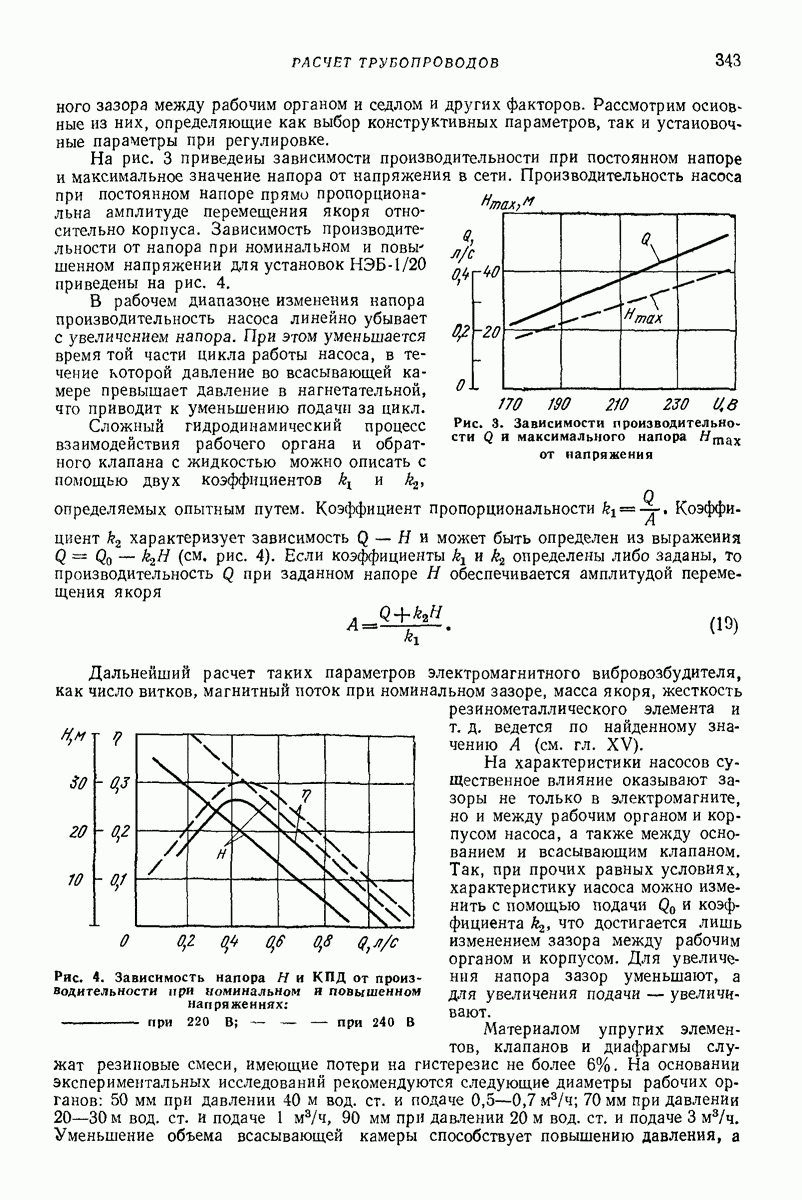
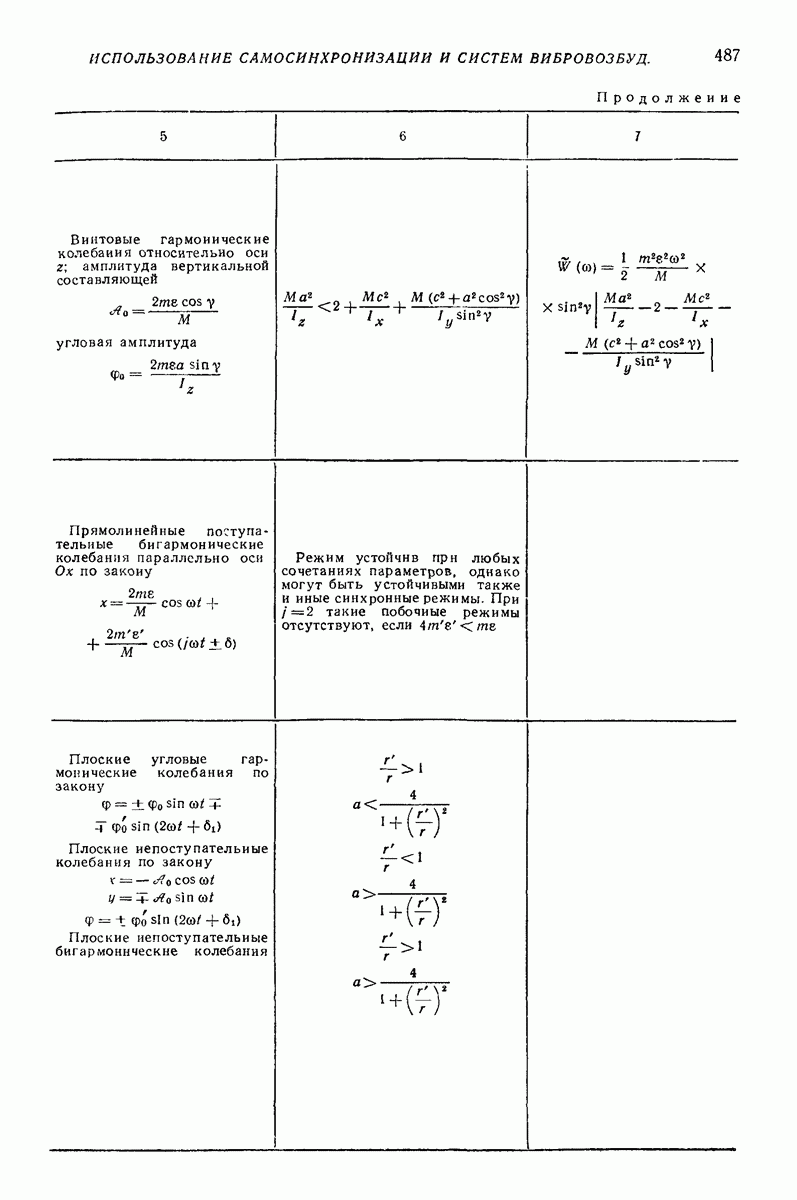
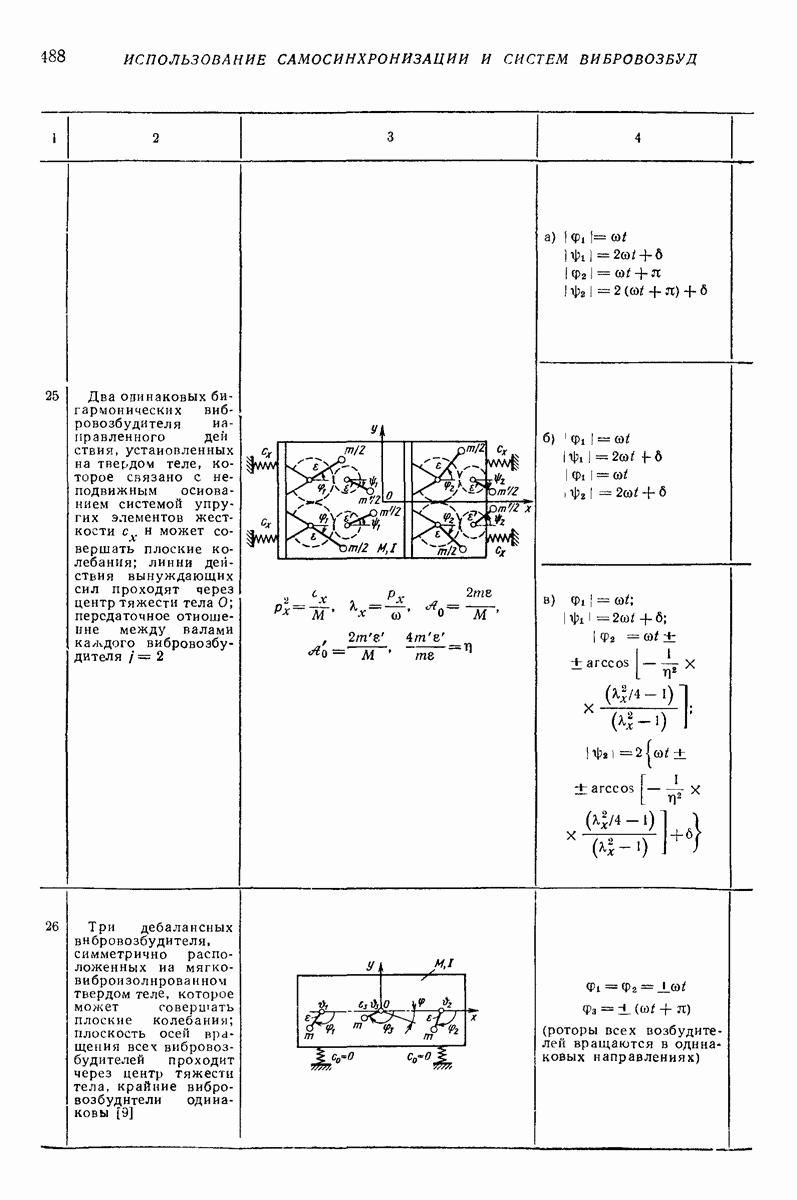
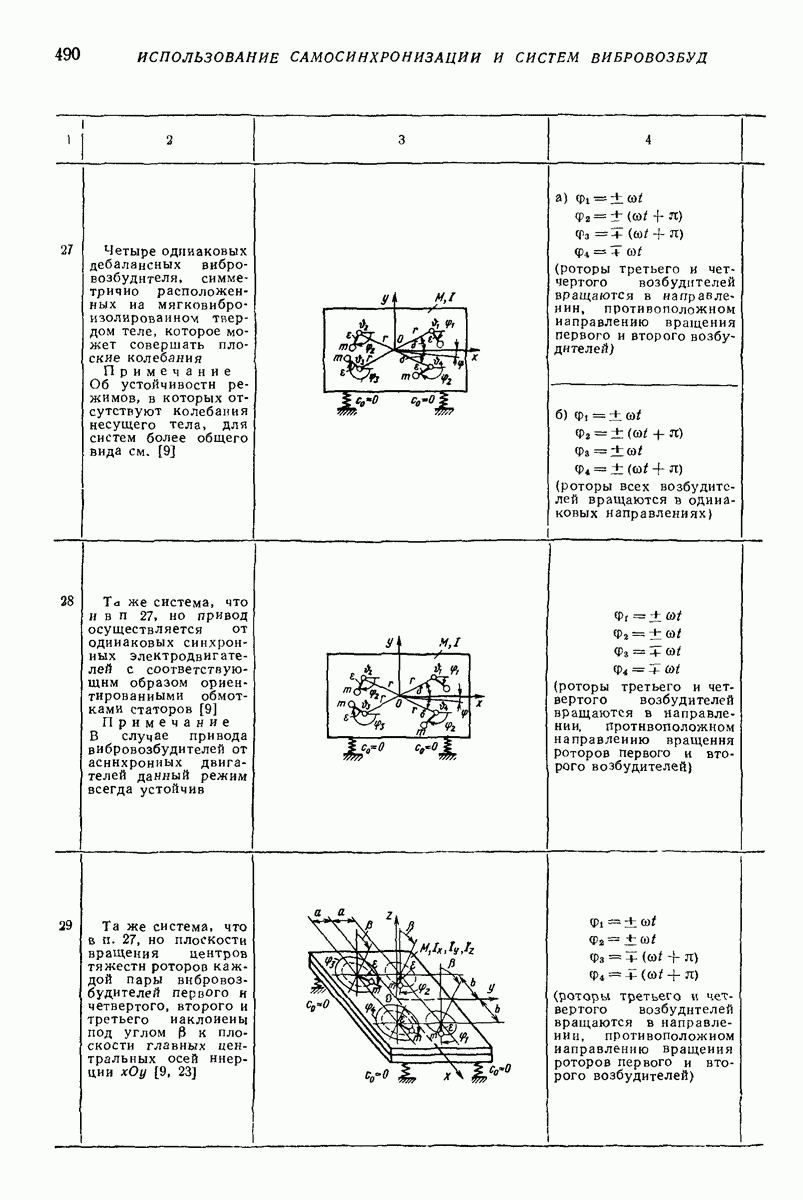
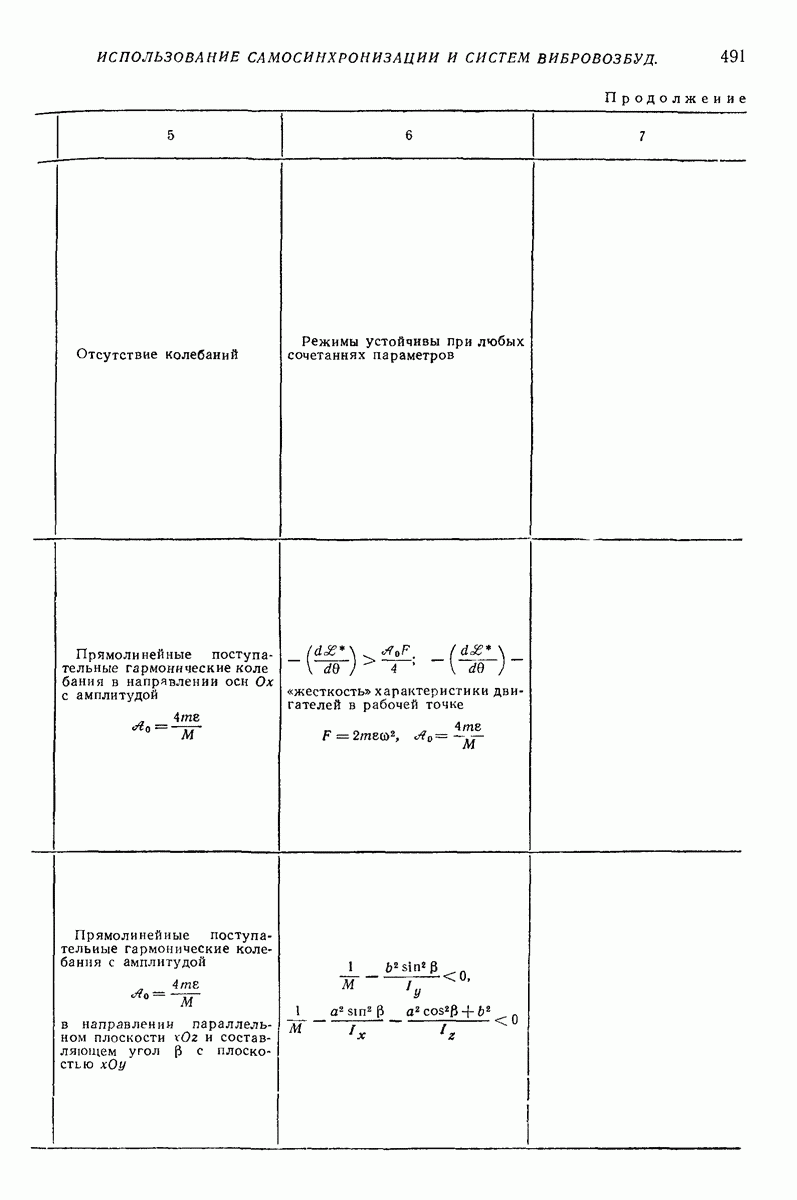
5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
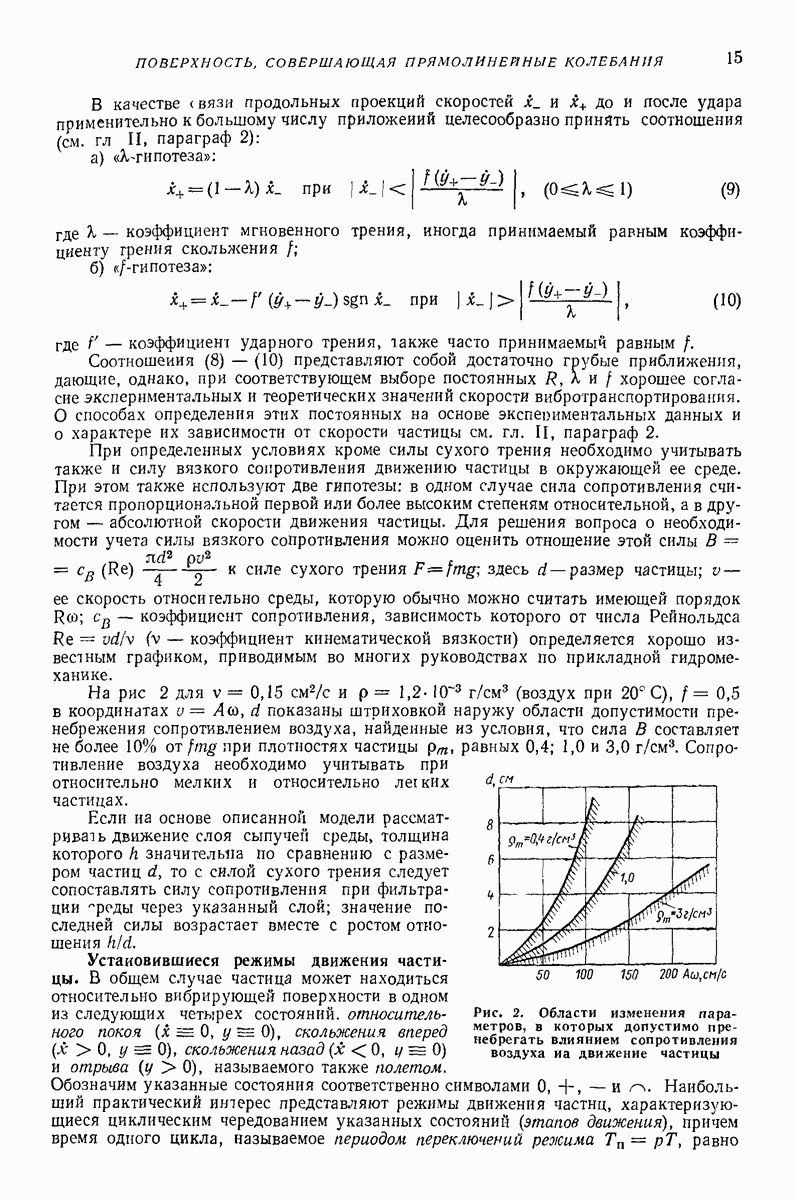
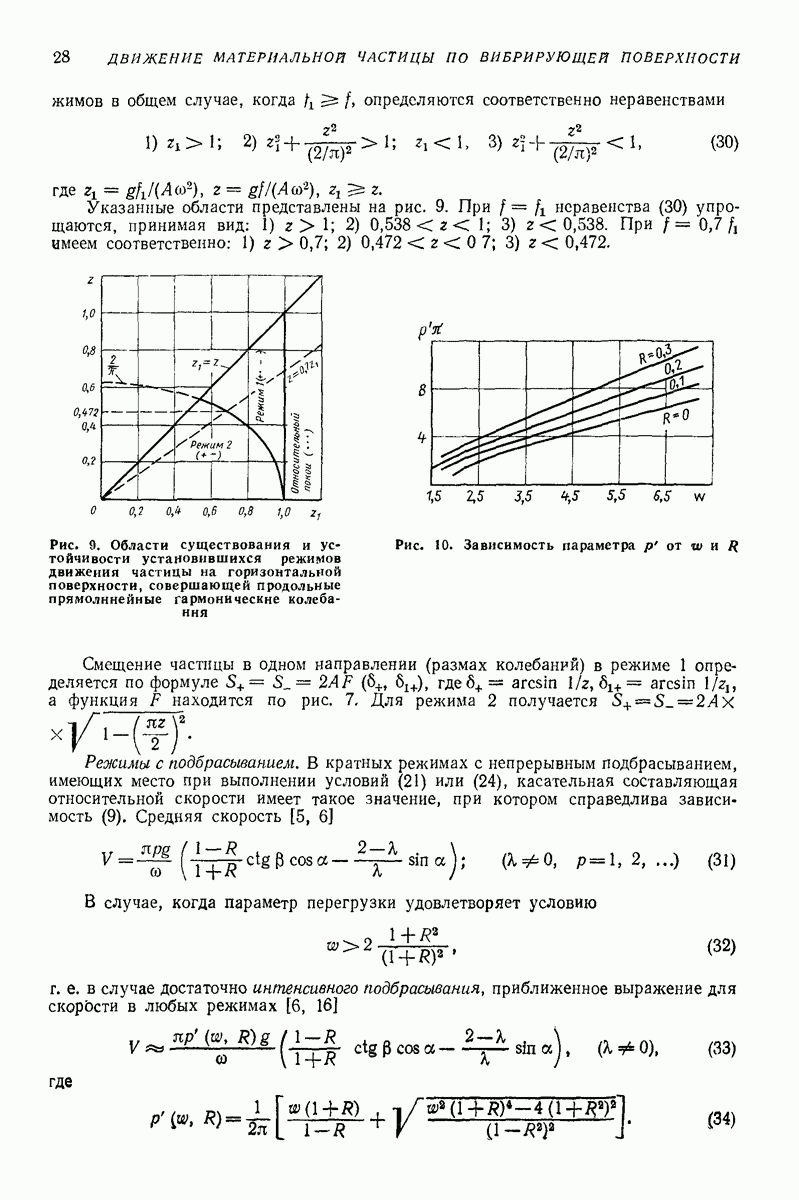
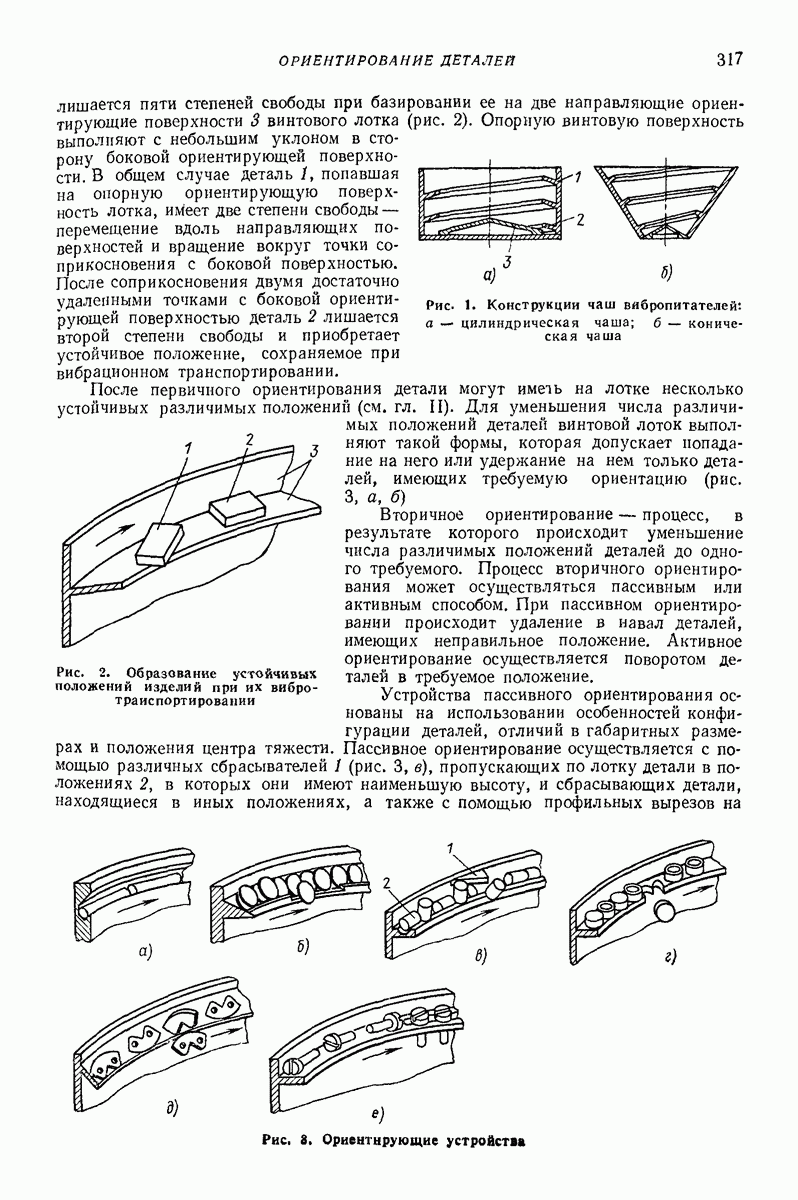
Ниже приведены результаты решения ряда задач о движении частицы по вибрирующей шероховатой плоской поверхности в условиях, близких к условиям классической задачи Н. Е. Жуковского о движении частицы по горизонтальной плоской поверхности, совершающей круговые поступательные колебания. Далее изложен общий подход к рассмотрению класса более сложных задач, характеризующихся наличием разного рода возмущений (наклон поверхности, добавочные силы, дополнительные колебания); этот подход основан на преобразовании системы к «полярным переменным» и использовании метода малого параметра. Затем приведены результаты решения некоторых задач данного класса, интересных в прикладном отношении.
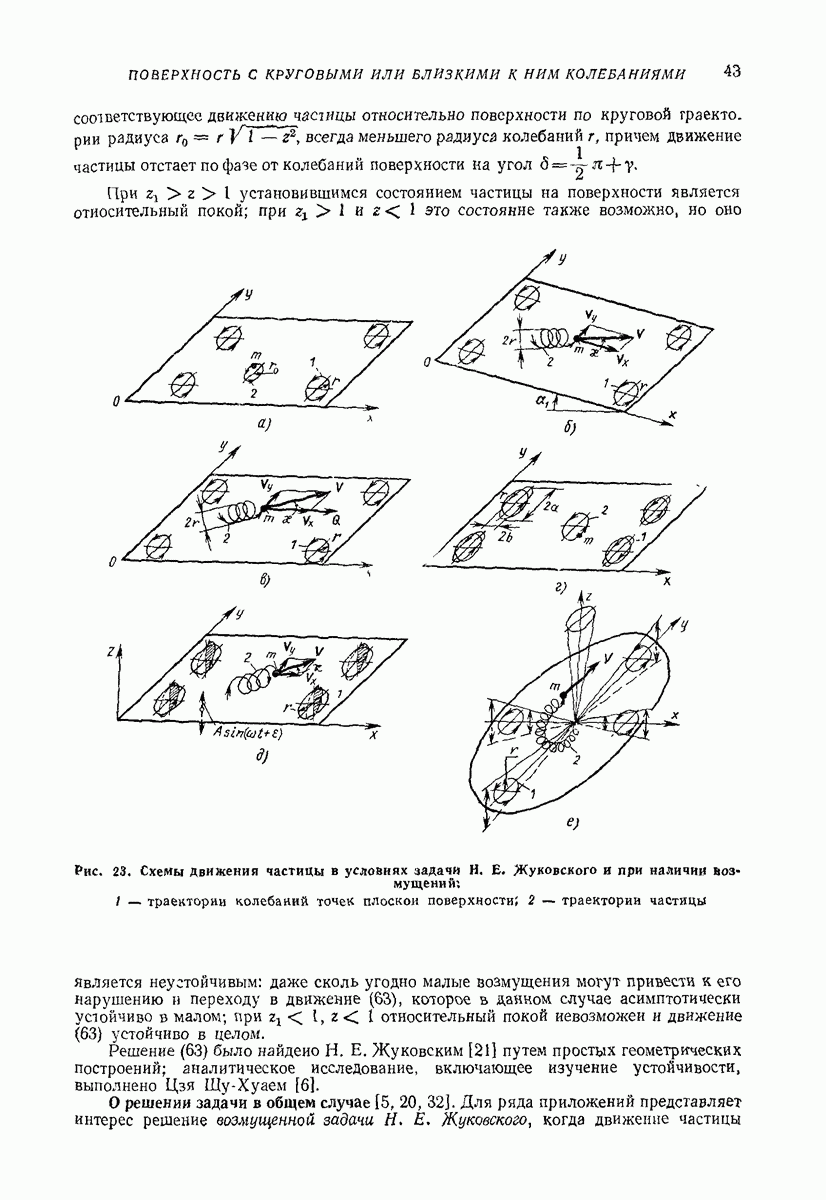
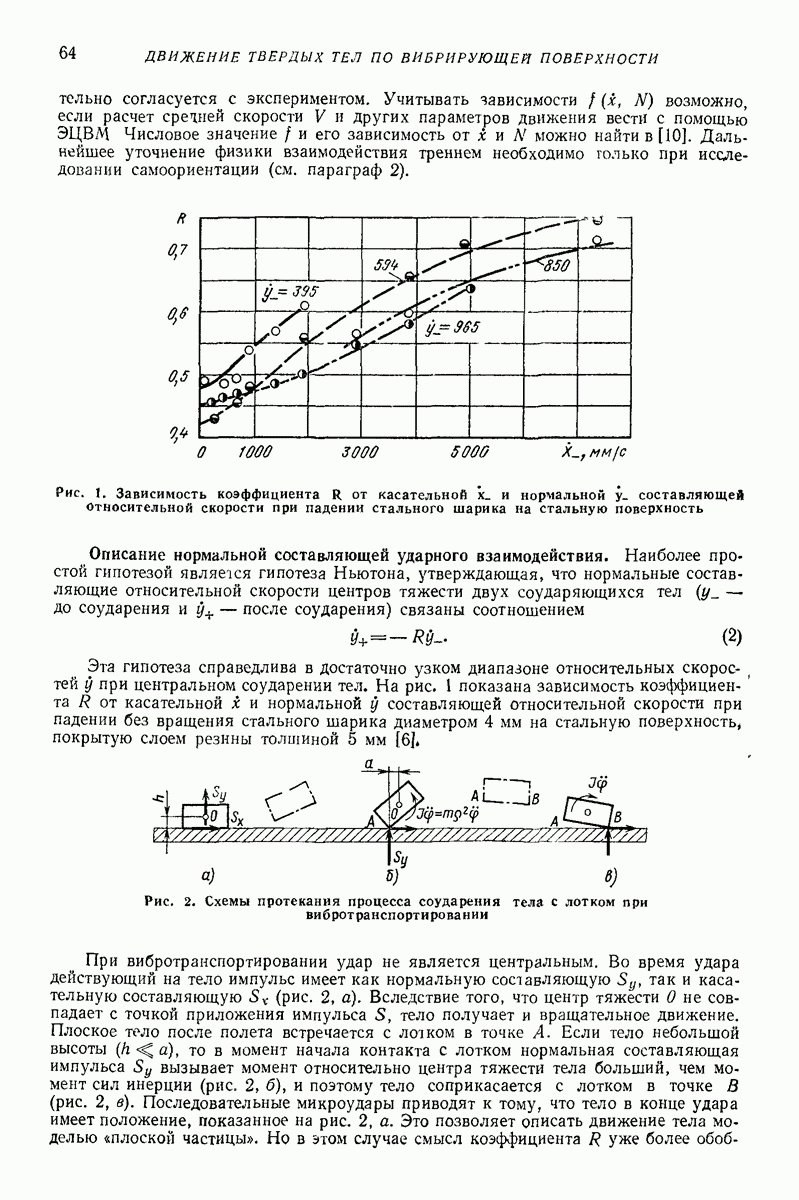
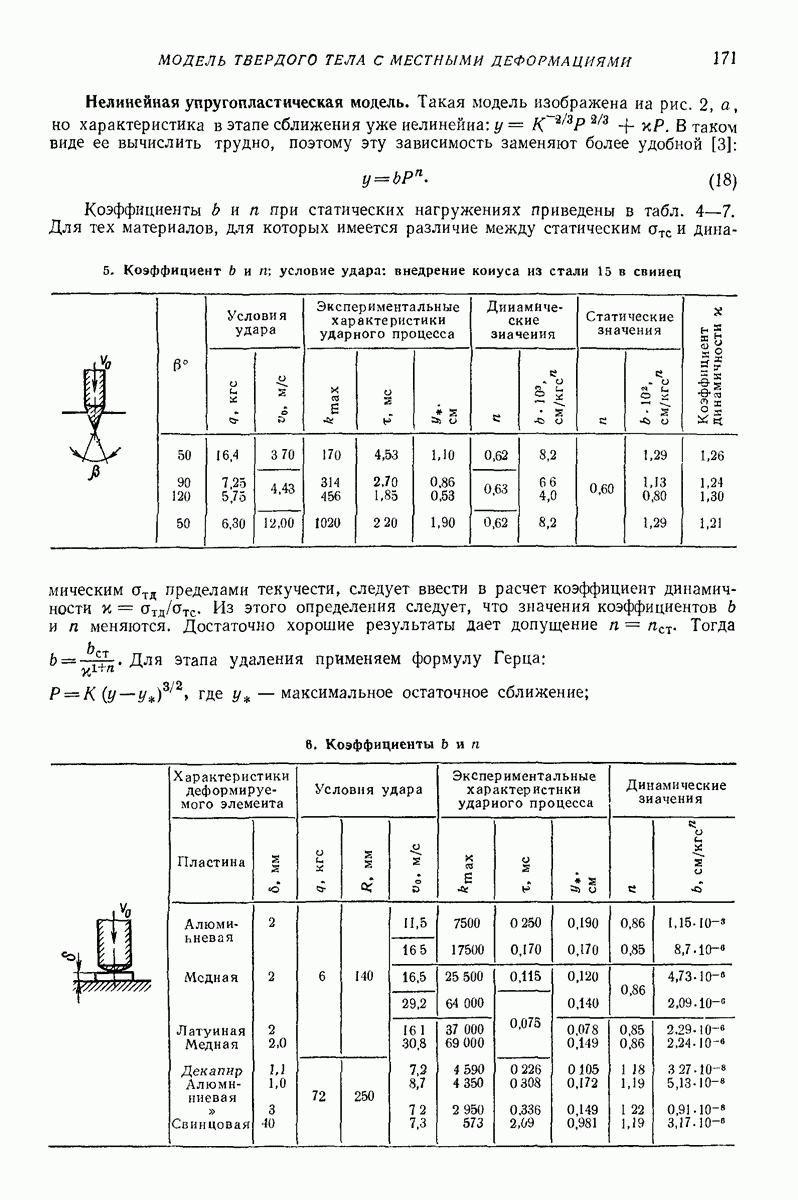
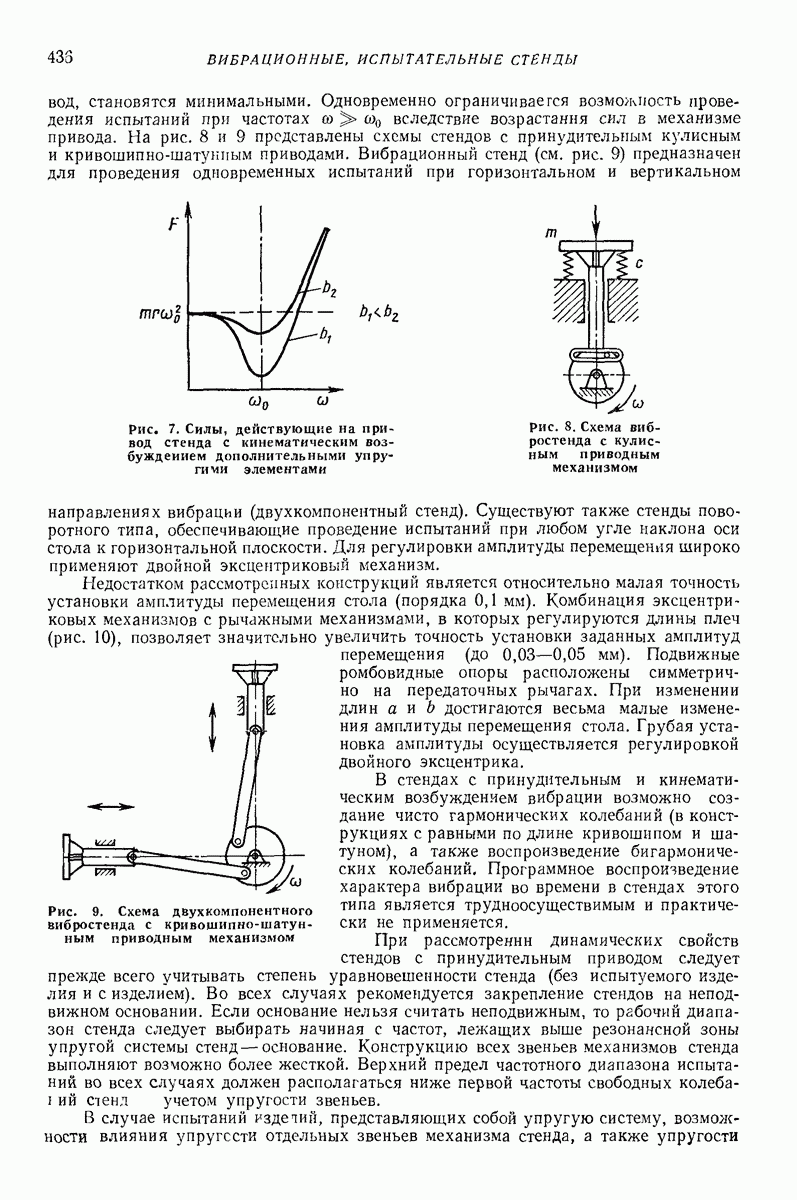
Случай круговых колебаний горизонтальной плоской поверхности (задача Н. Е. Жуковского). Дифференциальные уравнения относительного движения частицы по шероховатой плоской поверхности, совершающей поступательные колебания частоты (о по круговым траекториям некоторого радиуса  имеют вид (рис. 23, а)
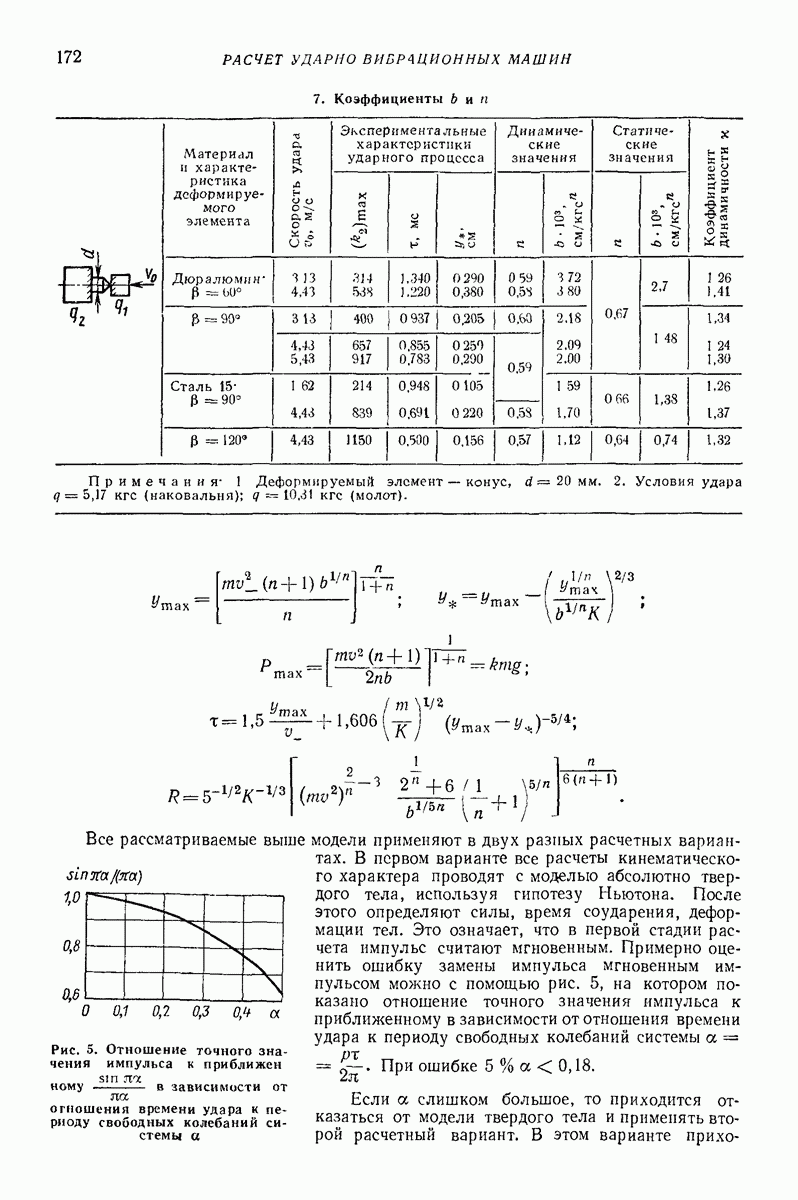
имеют вид (рис. 23, а)

где  коэффициент трения скольжения;
коэффициент трения скольжения;  ускорение свободного падения.
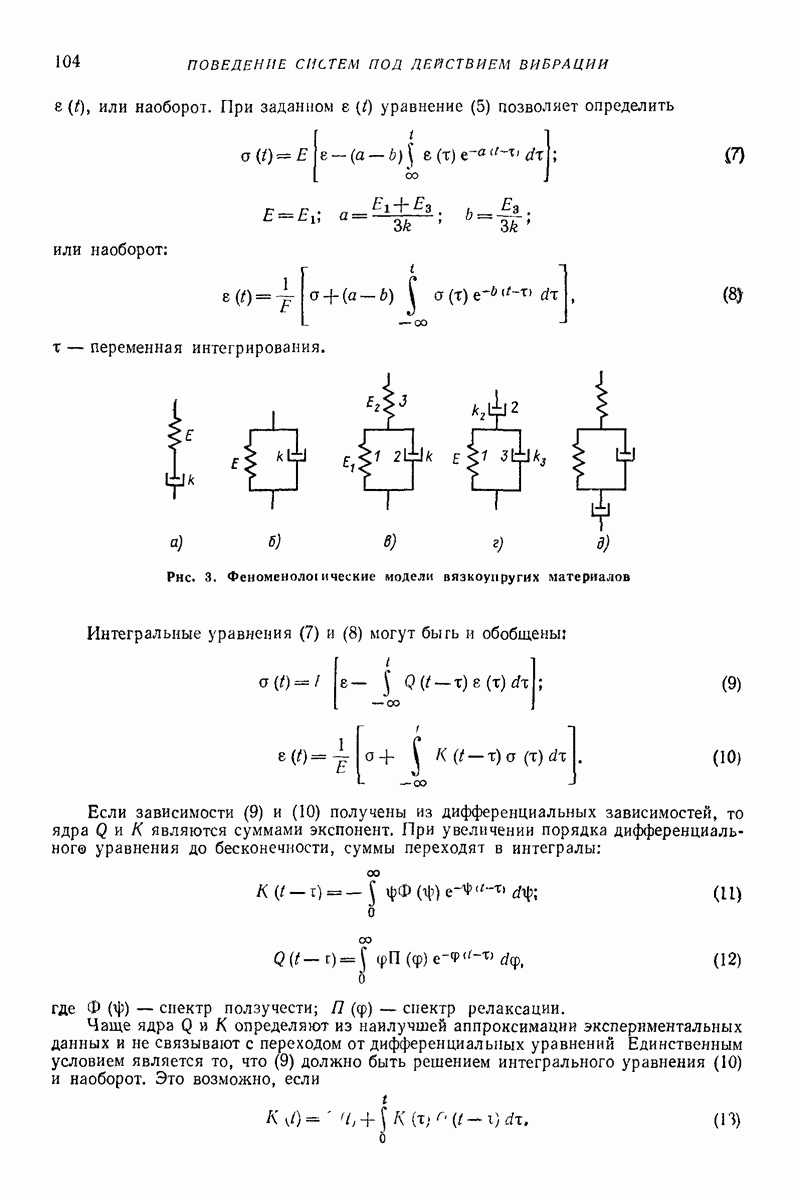
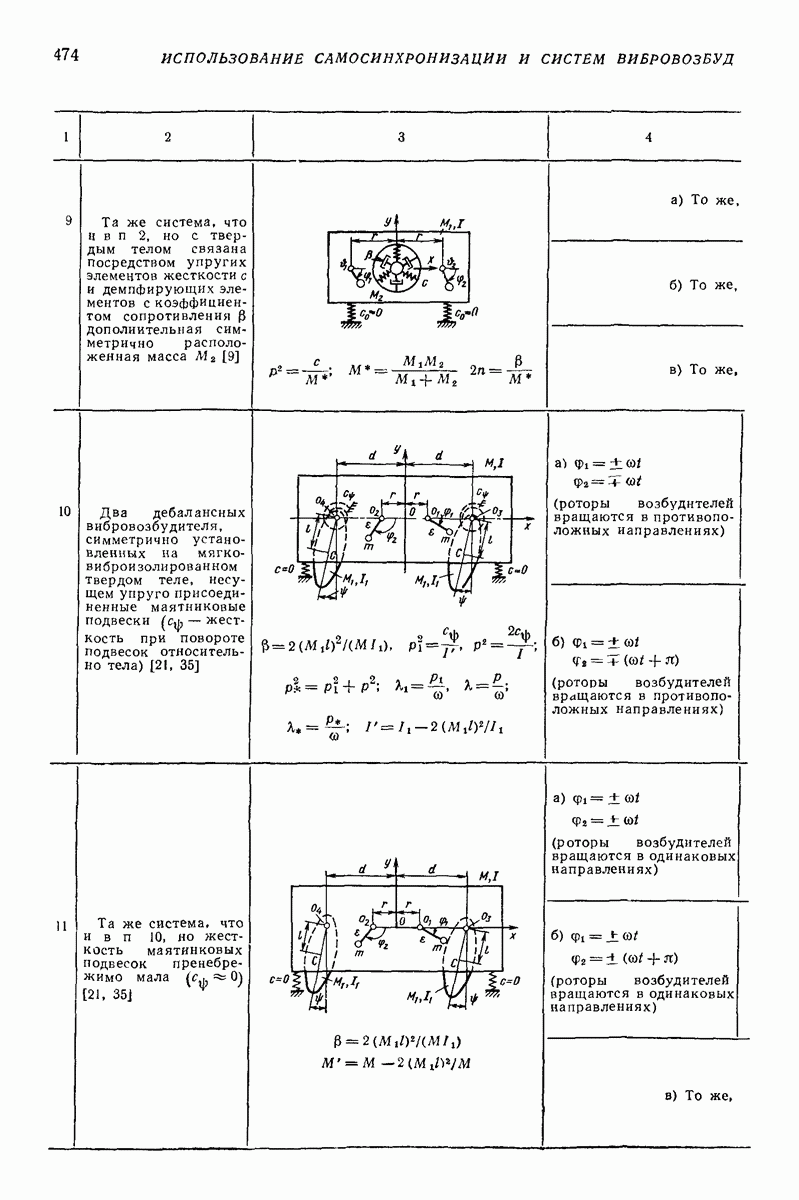
ускорение свободного падения.
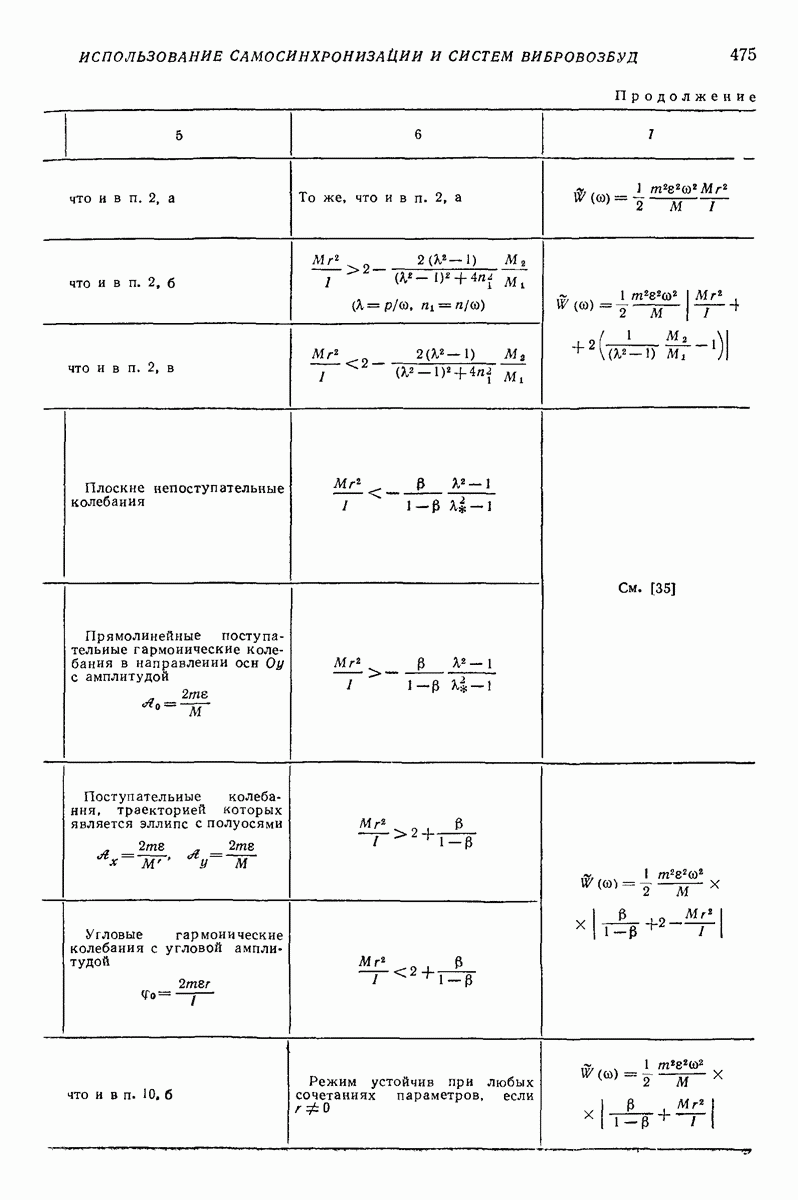
Частица может находиться на поверхности в состоянии относительного покоя  лишь при условии
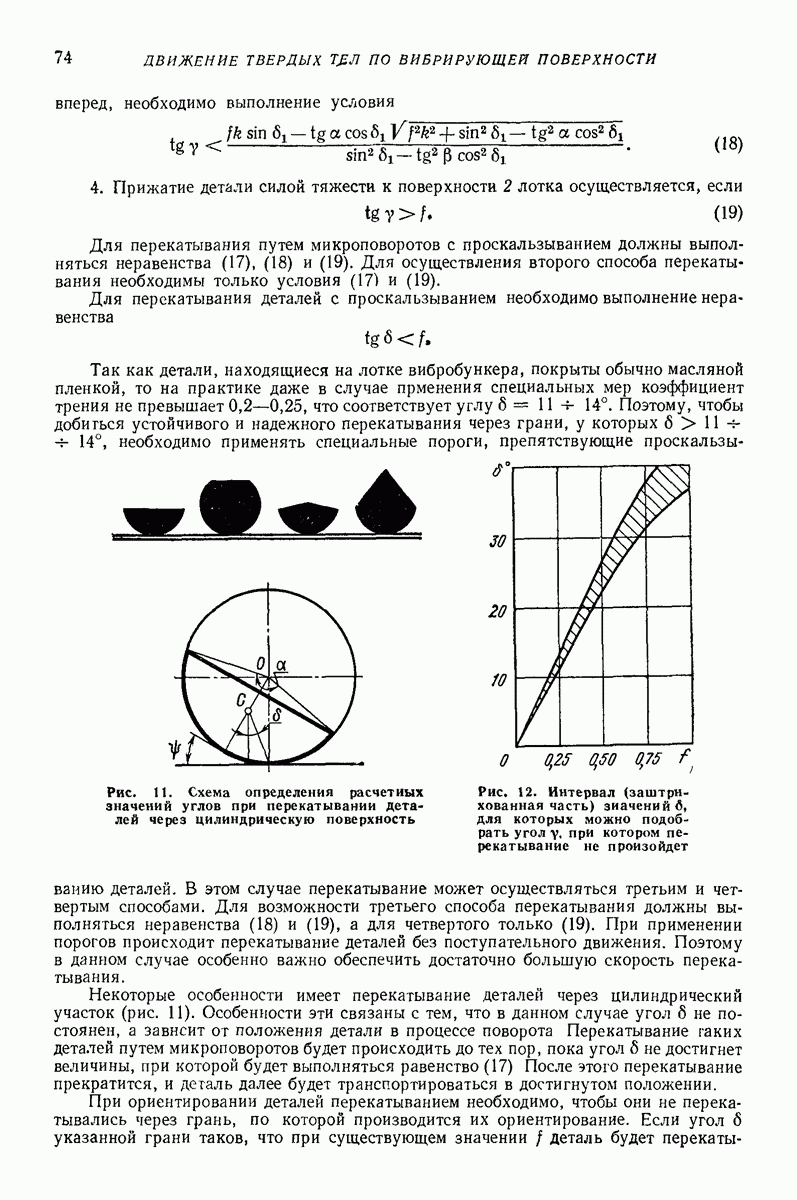
лишь при условии  т. е. что сила инерции в относительном движении
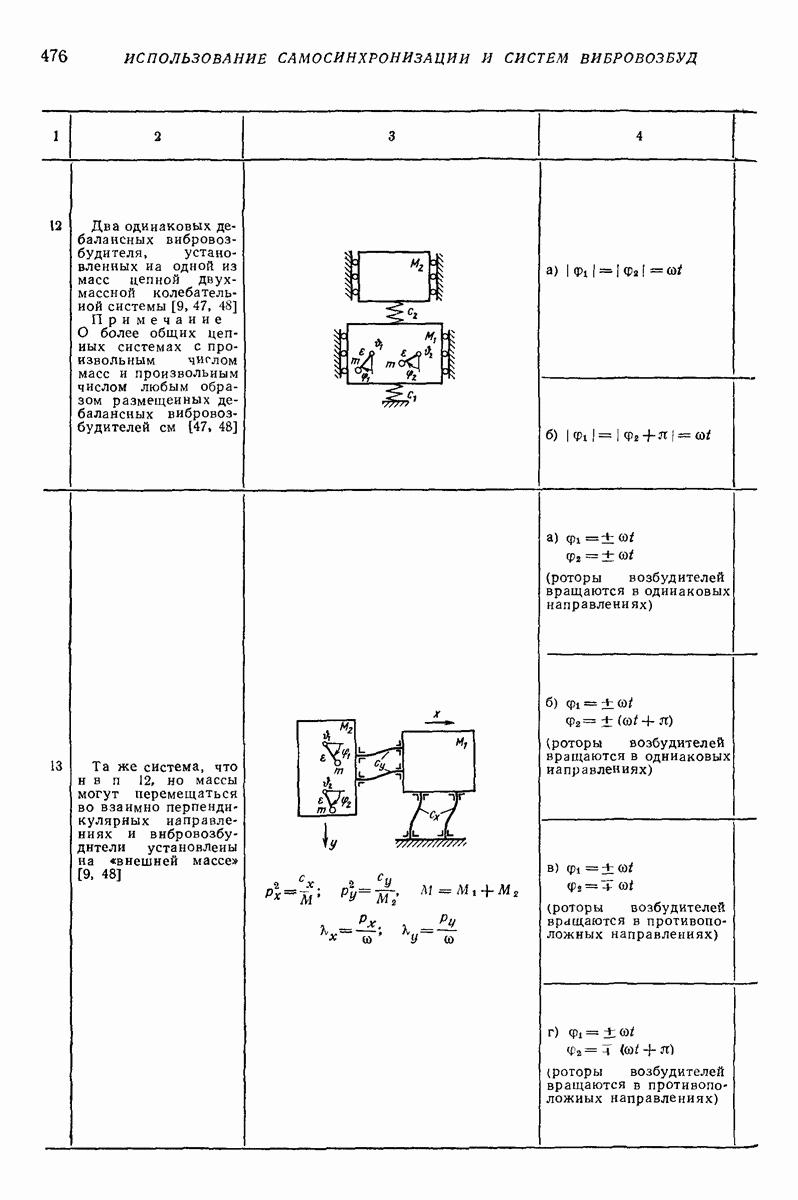
т. е. что сила инерции в относительном движении  не превышает максимального значения силы трения покоя
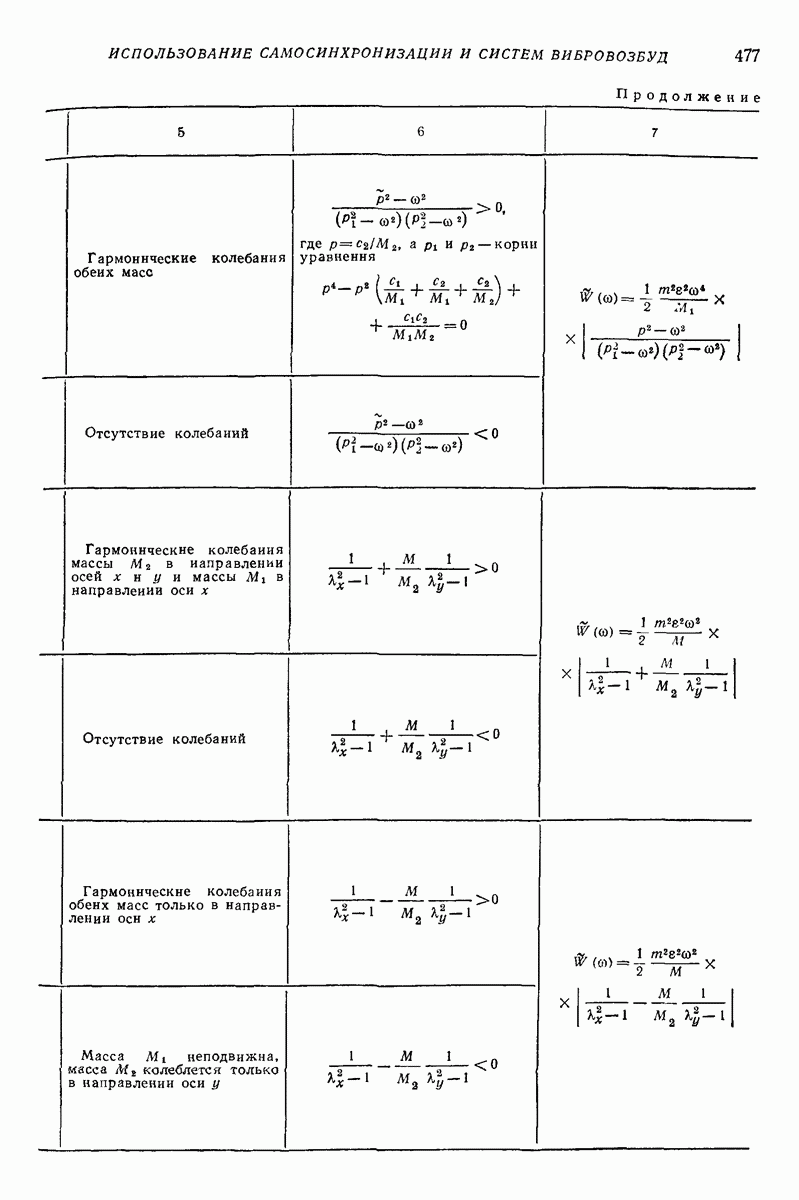
не превышает максимального значения силы трения покоя  — коэффициент трения покоя).
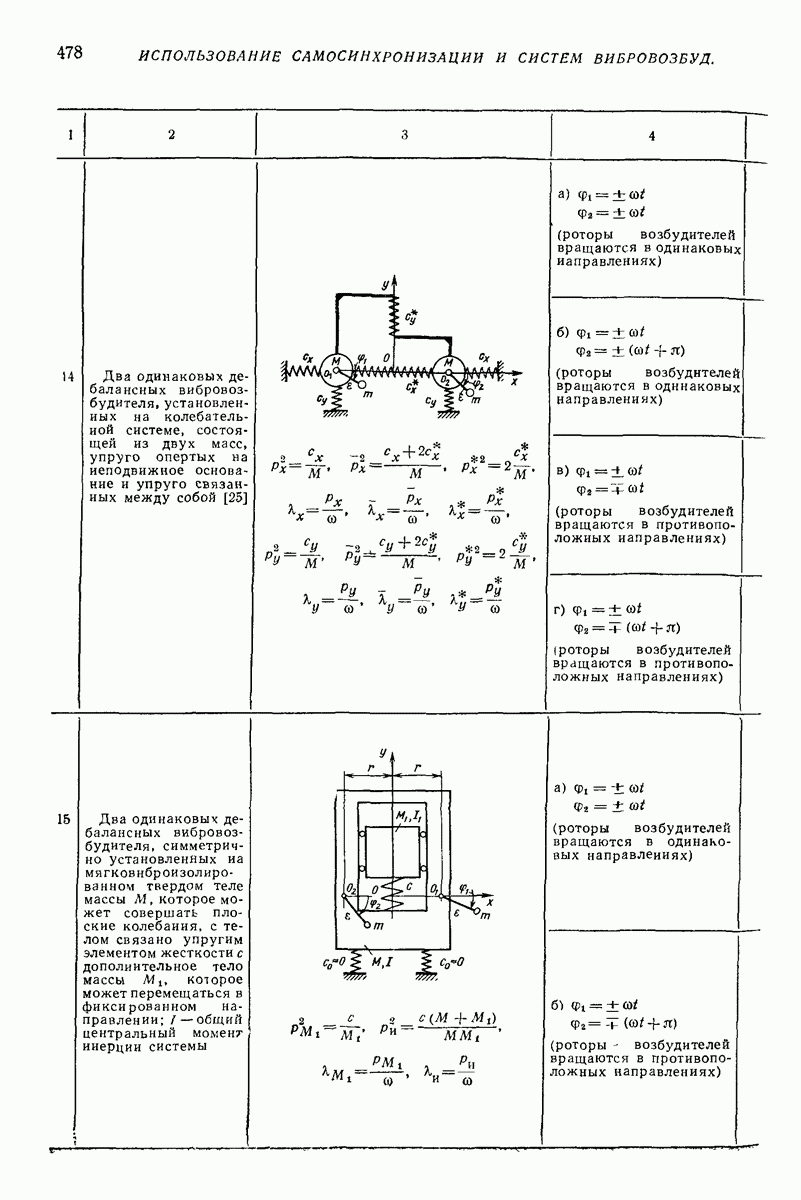
— коэффициент трения покоя).
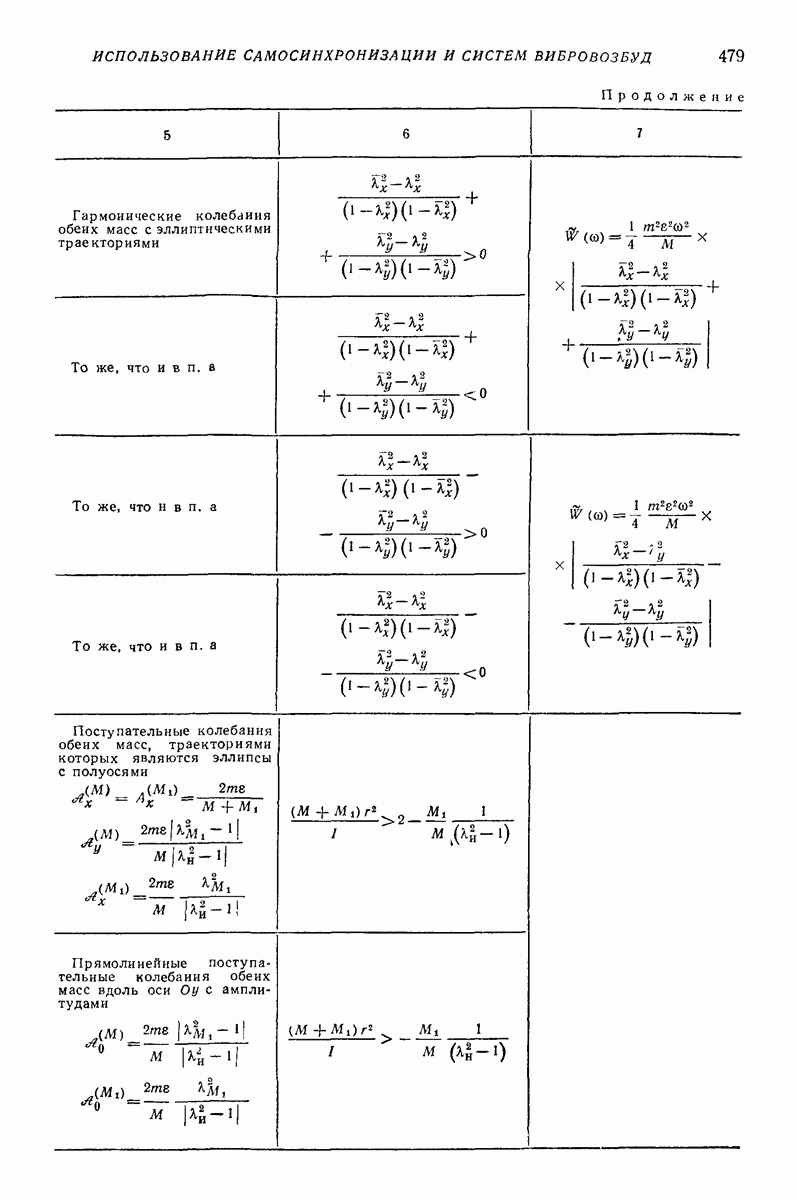
При  уравнения (62) допускают решение
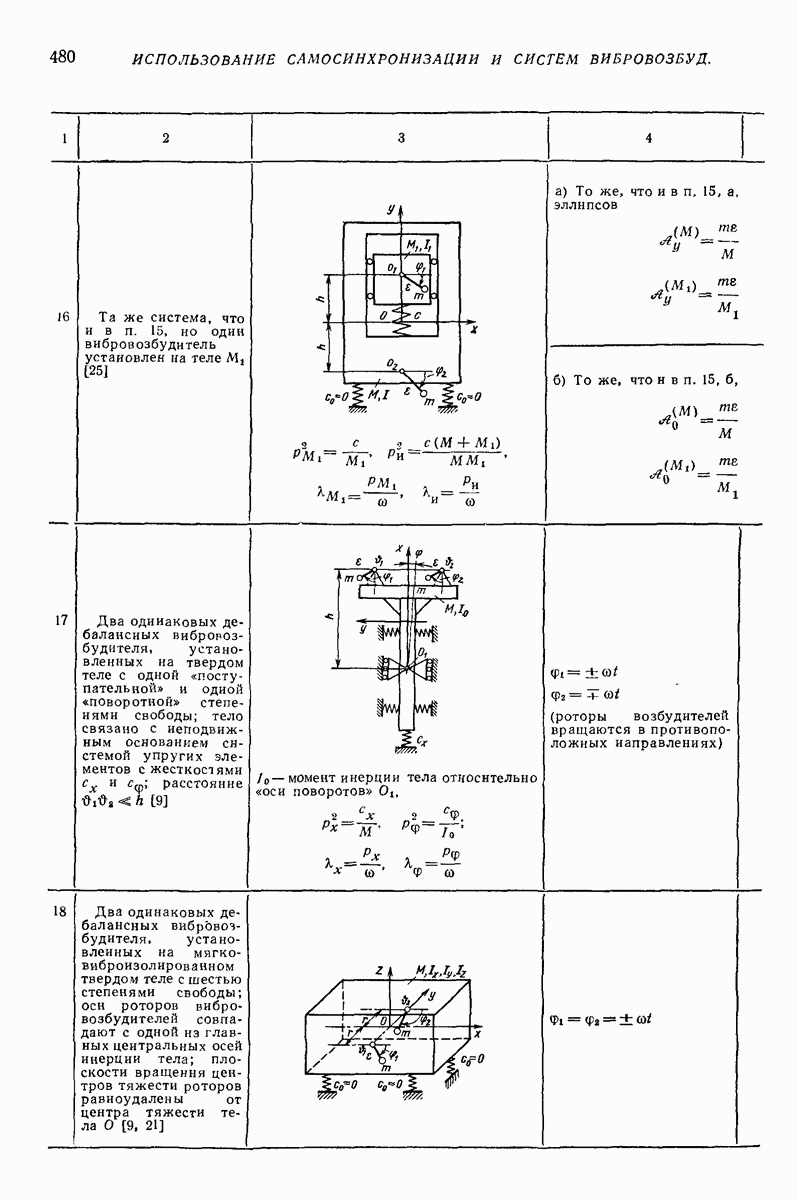
уравнения (62) допускают решение

соответствующее движению частицы относительно поверхности по круговой граектории радиуса  всегда меньшего радиуса колебаний
всегда меньшего радиуса колебаний  причем движение частицы отстает по фазе от колебаний поверхности на угол
причем движение частицы отстает по фазе от колебаний поверхности на угол 
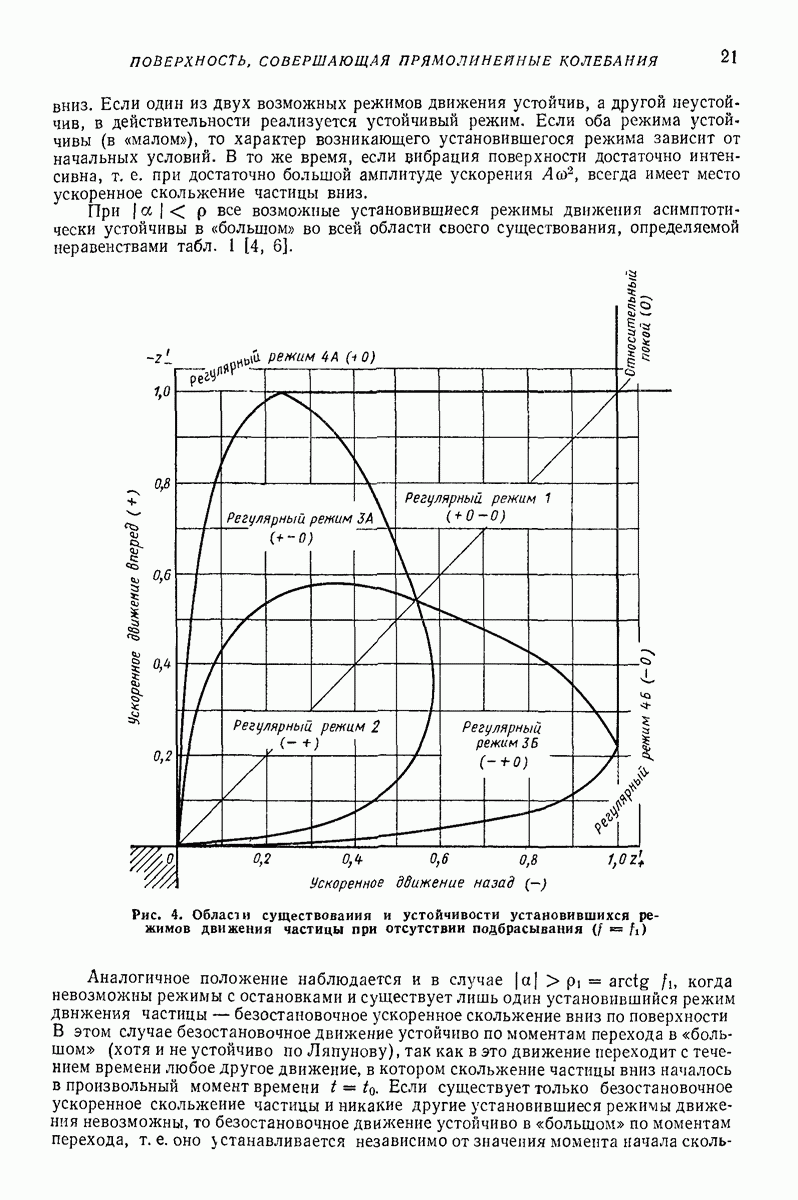
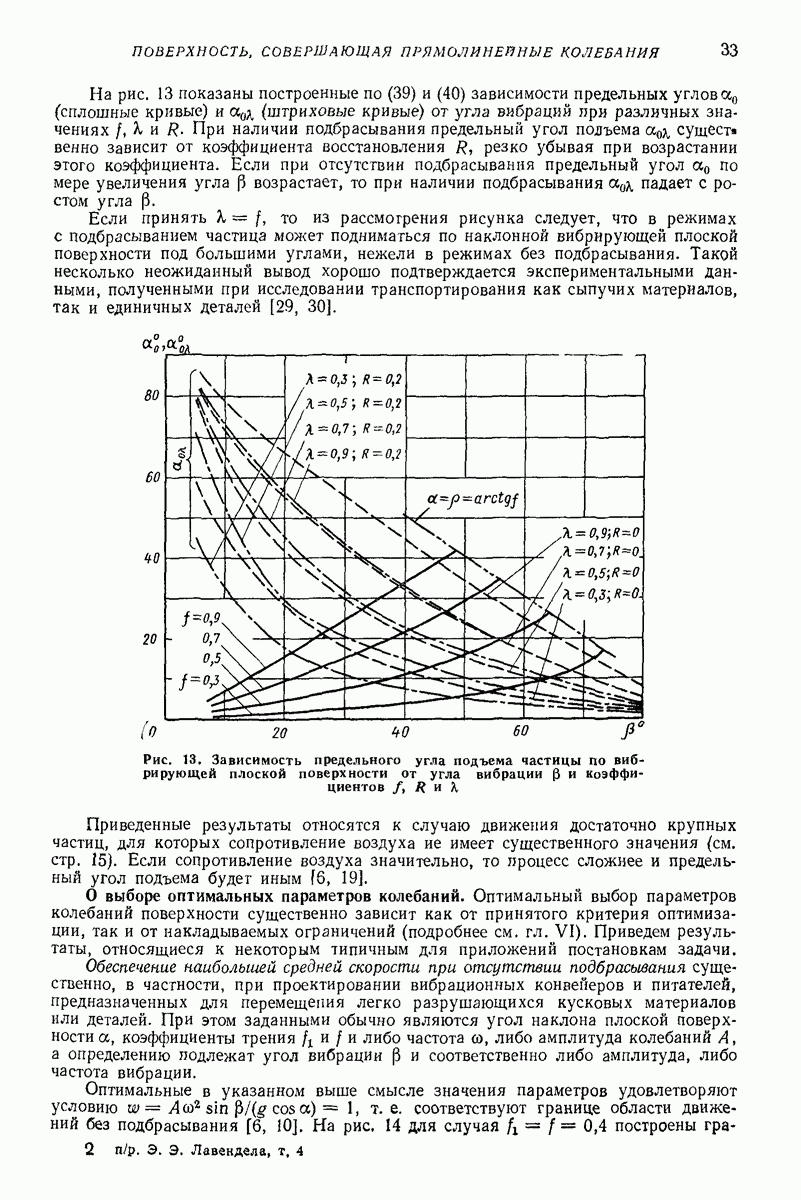
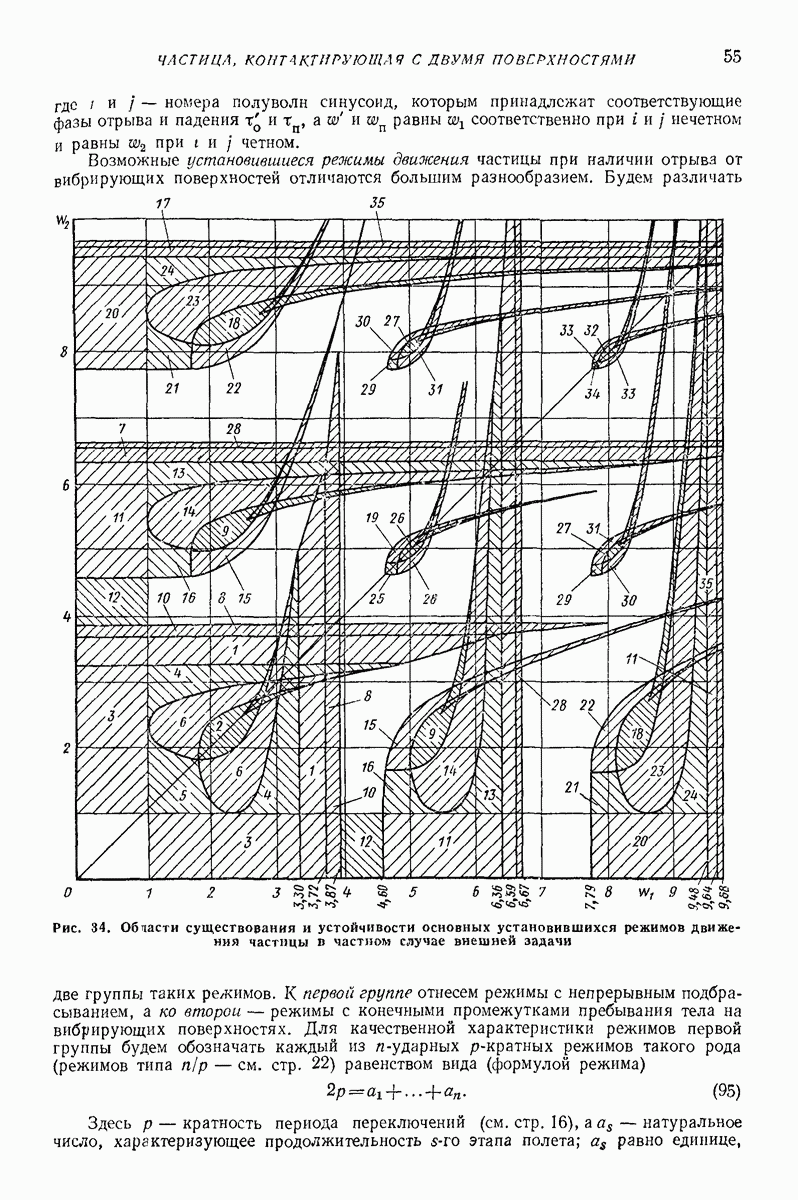
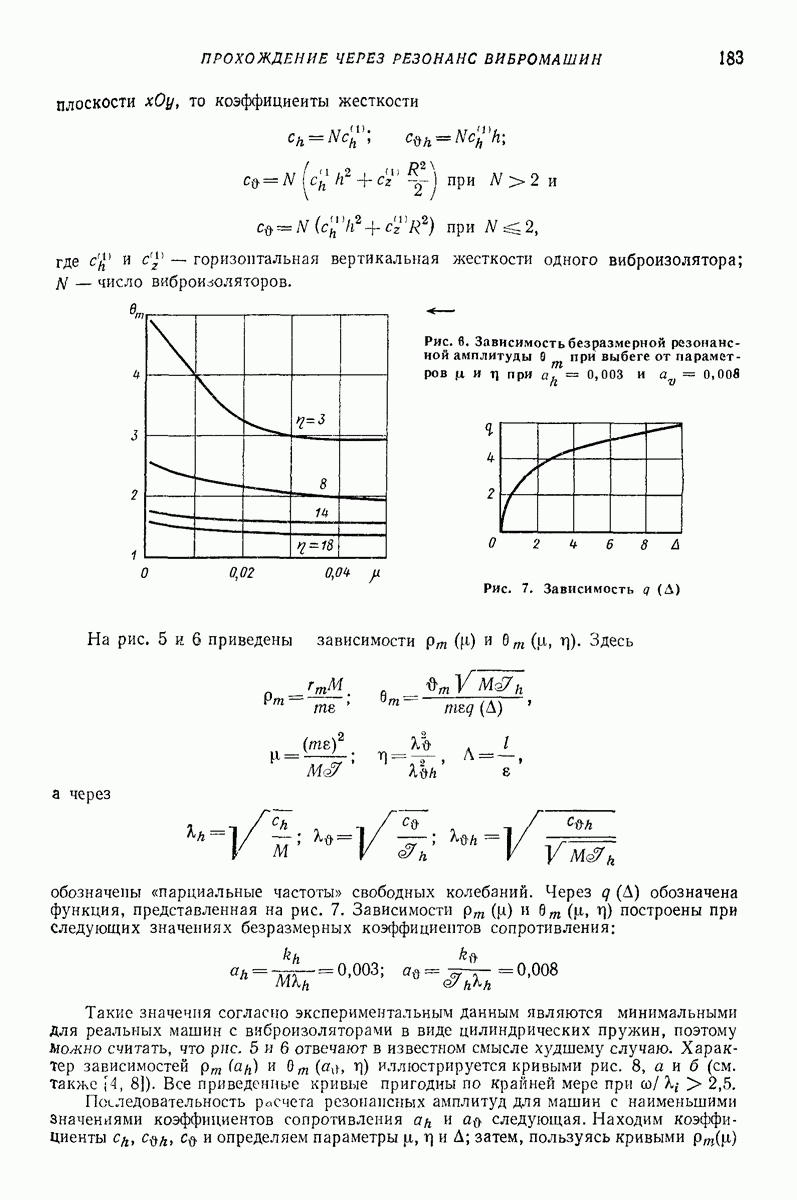
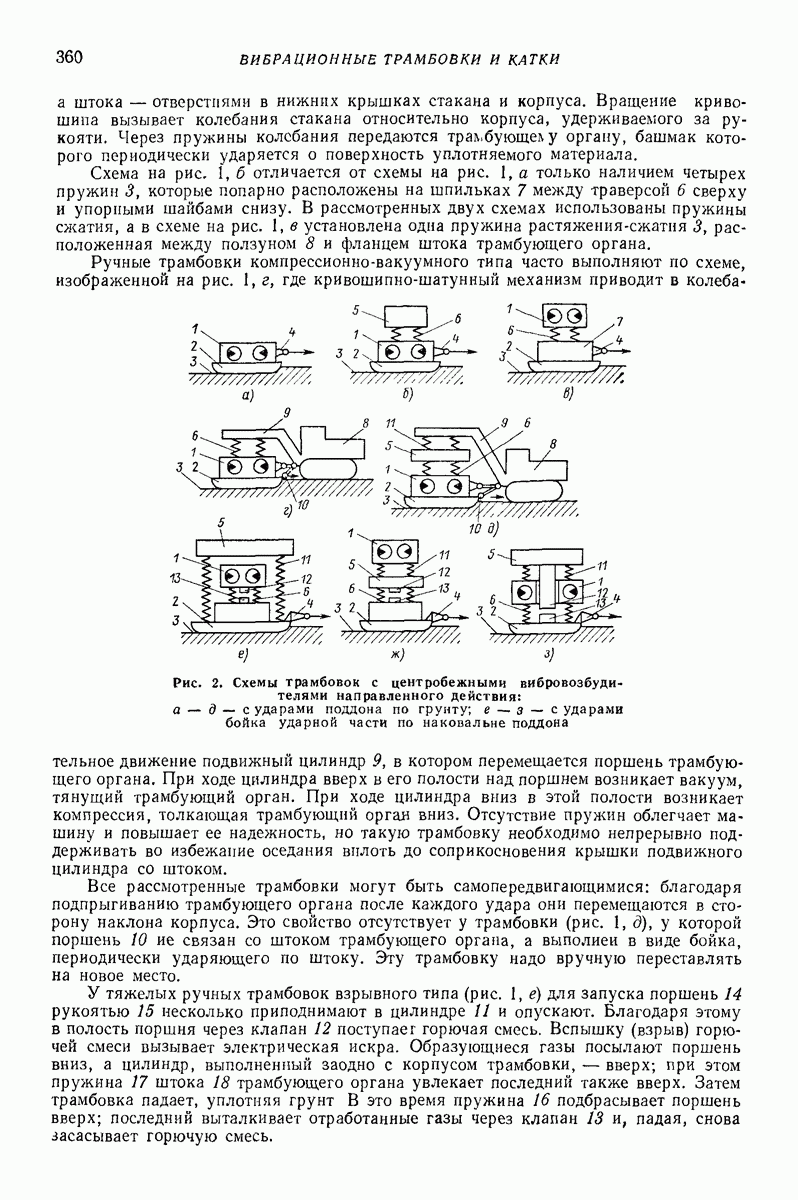
Рис. 23. (см. скан) Схемы движения частицы в условиях задачи Н. Е. Жуковского и при наличии возмущений; 1 — траектории колебаний точек плоской поверхности; 2 — траектории частицы
При  установившимся состоянием частицы на поверхности является относительный покой; при
установившимся состоянием частицы на поверхности является относительный покой; при  это состояние также возможно, но оно является неустойчивым: даже сколь угодно малые возмущения могут привести к его нарушению и переходу в движение (63), которое в данном случае асимптотически устойчиво в малом; при
это состояние также возможно, но оно является неустойчивым: даже сколь угодно малые возмущения могут привести к его нарушению и переходу в движение (63), которое в данном случае асимптотически устойчиво в малом; при  относительный покой невозможен и движение (63) устойчиво в делом.
относительный покой невозможен и движение (63) устойчиво в делом.
Решение (63) было найдено Н. Е. Жуковским [21] путем простых геометрических построений; аналитическое исследование, включающее изучение устойчивости, выполнено Цзя Щу-Хуаем [6].
О решении задачи в общем случае [5, 20, 32]. Для ряда приложений представляет интерес решение возмущенной задачи Н. Е. Жуковского, когда движение частицы
описывается уравнениями

отличающимися от (62) присутствием слагаемых  где
где  малый параметр, а функции
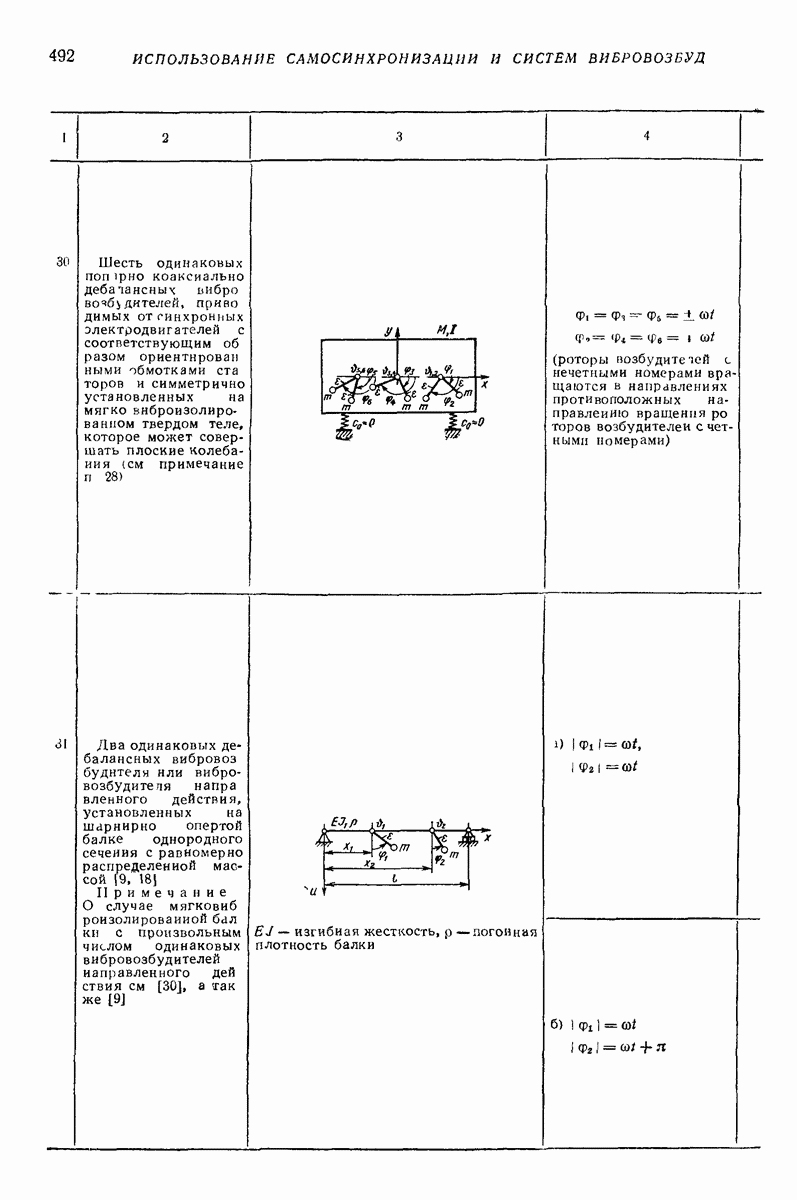
малый параметр, а функции  являются
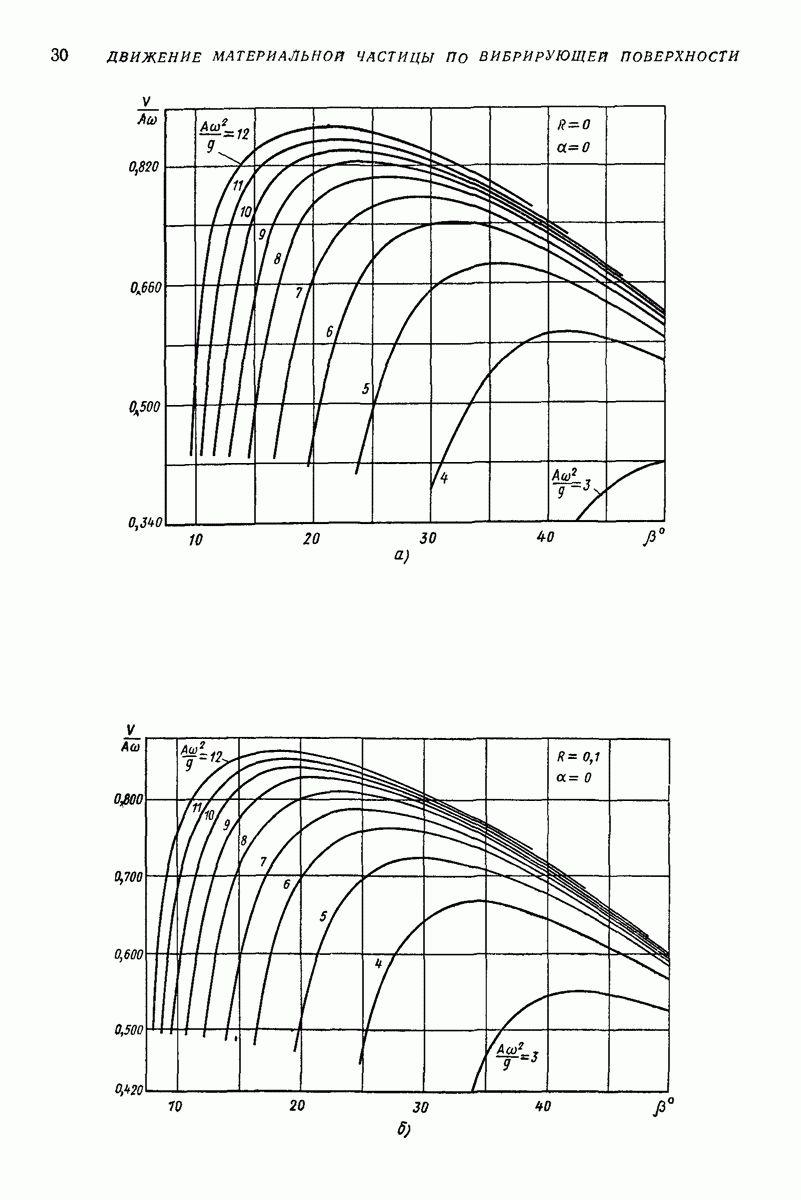
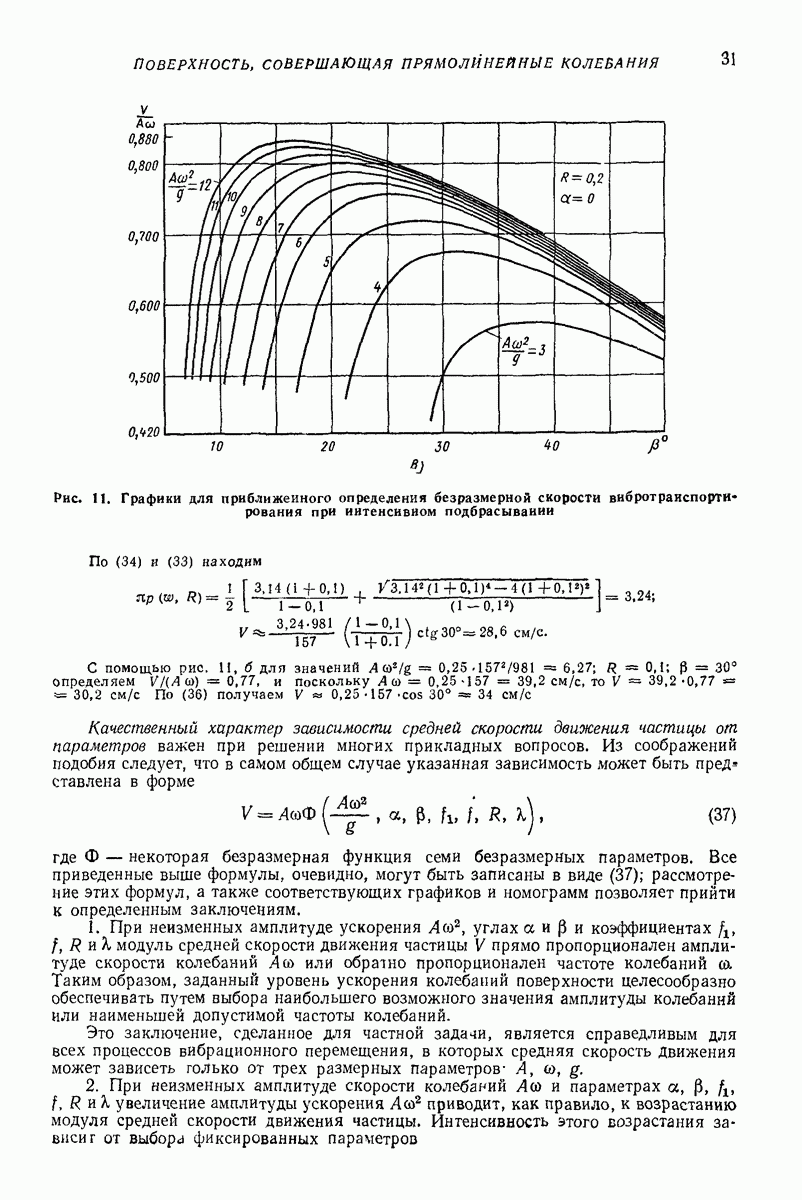
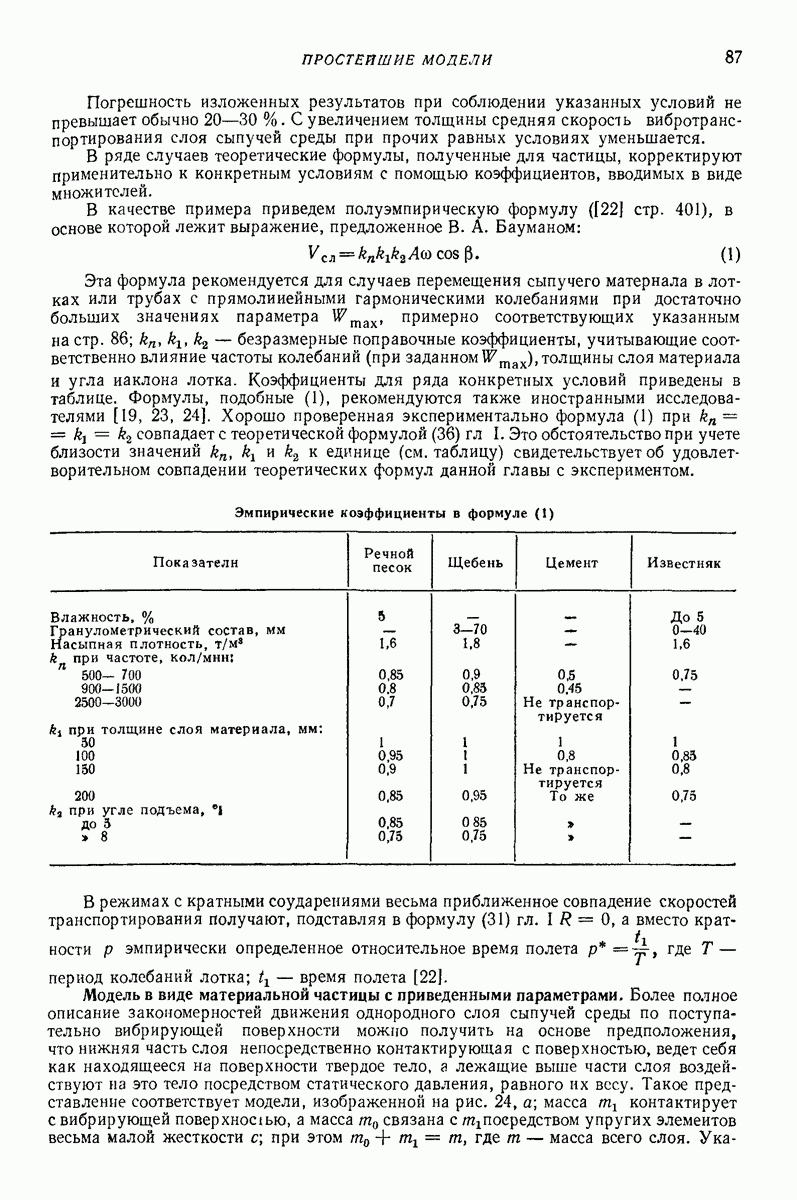
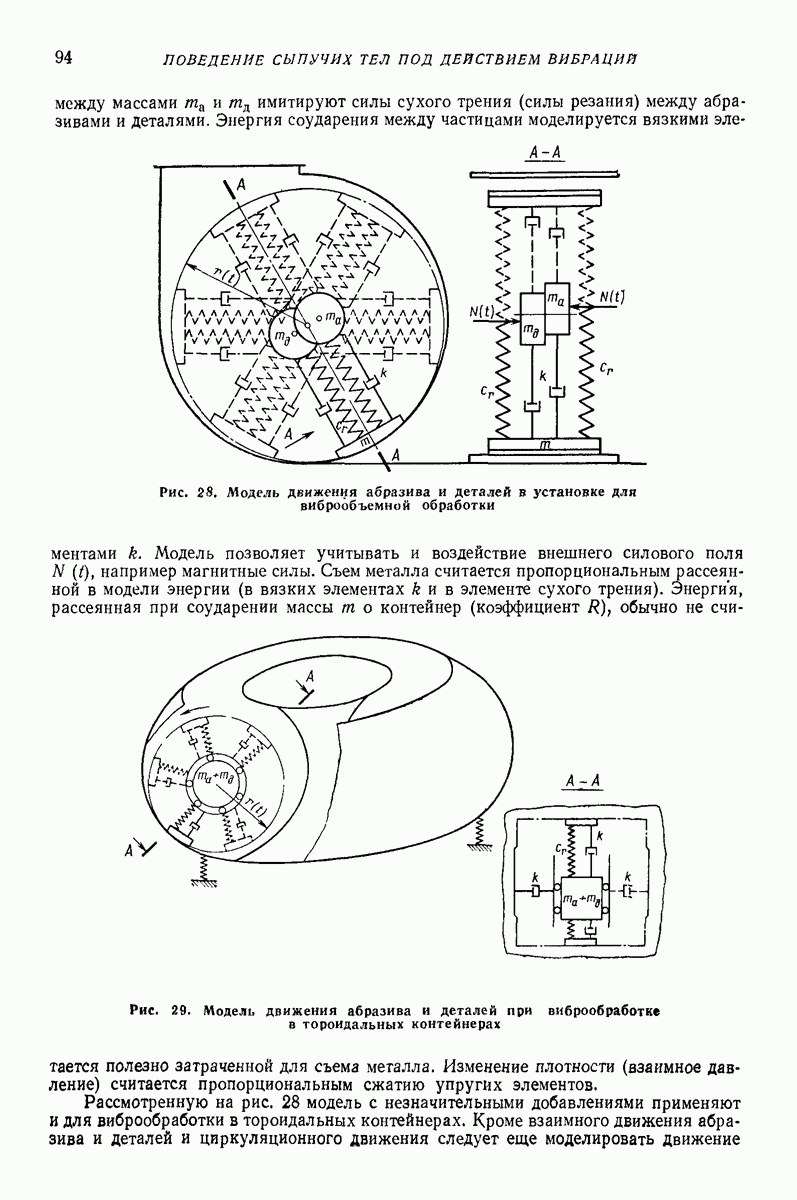
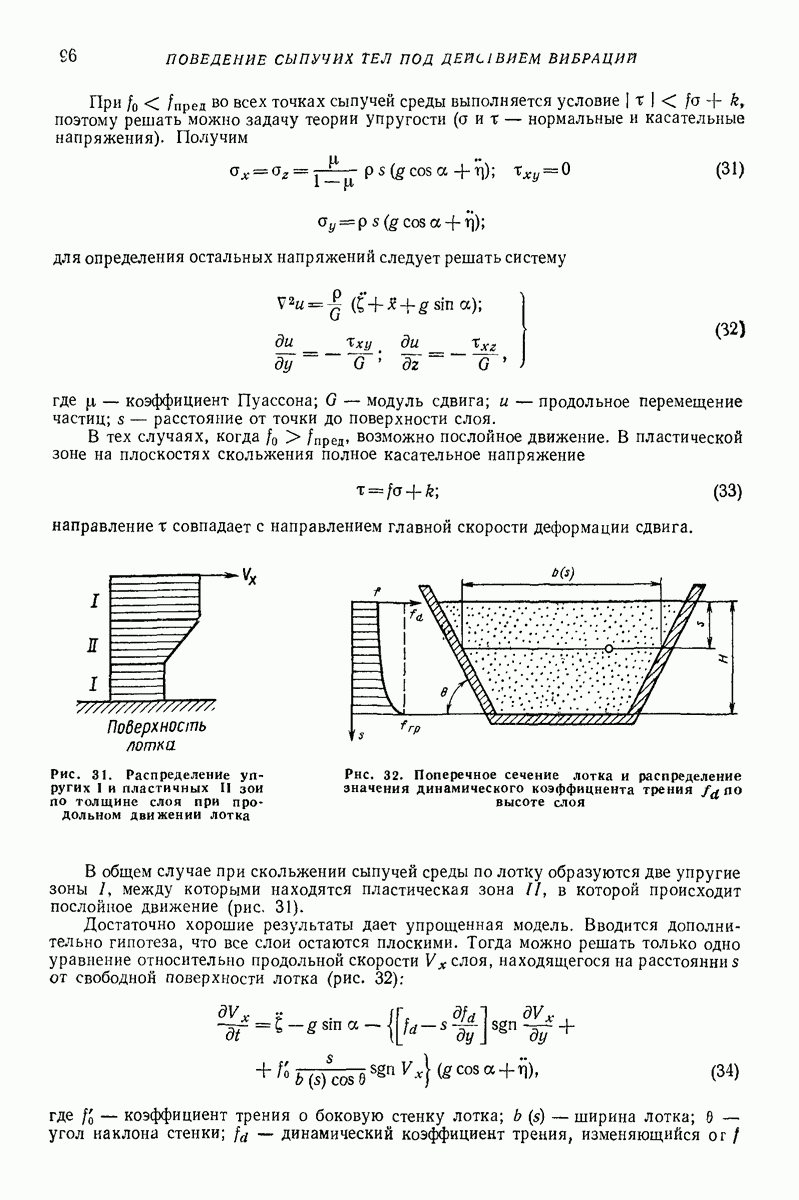
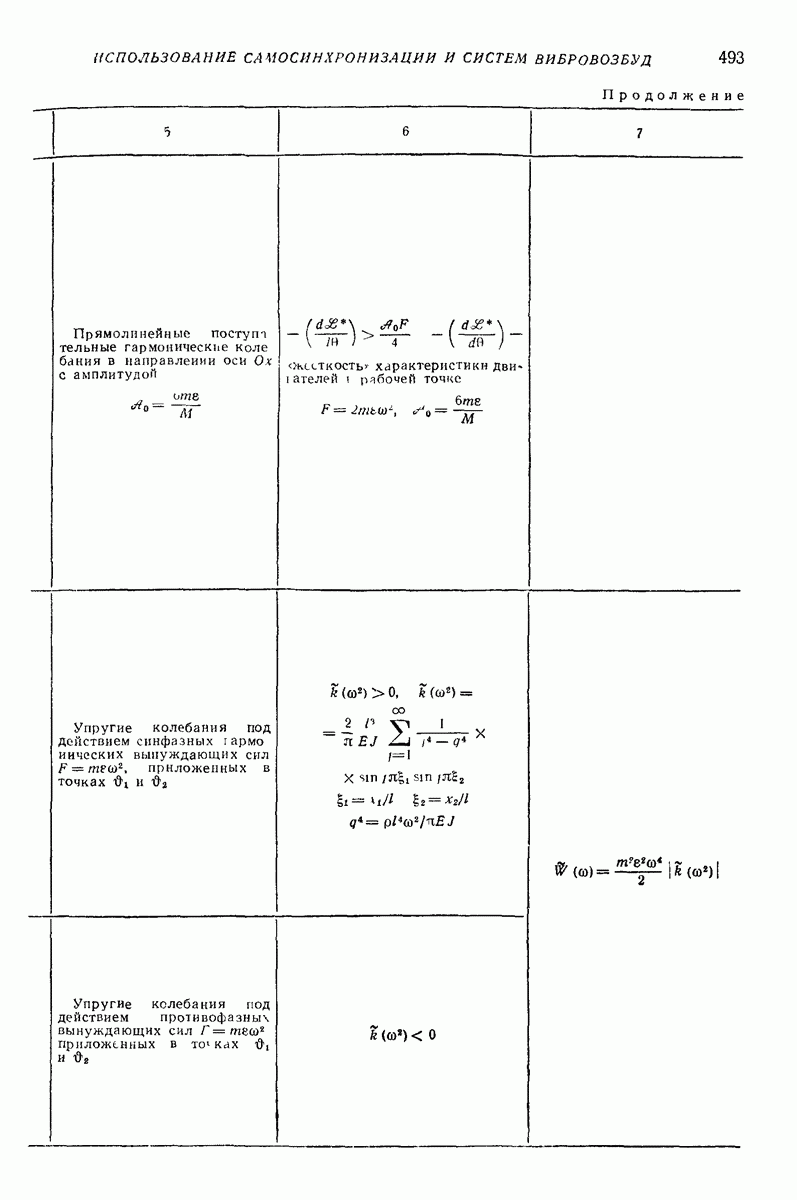
являются  -периодическими по времени
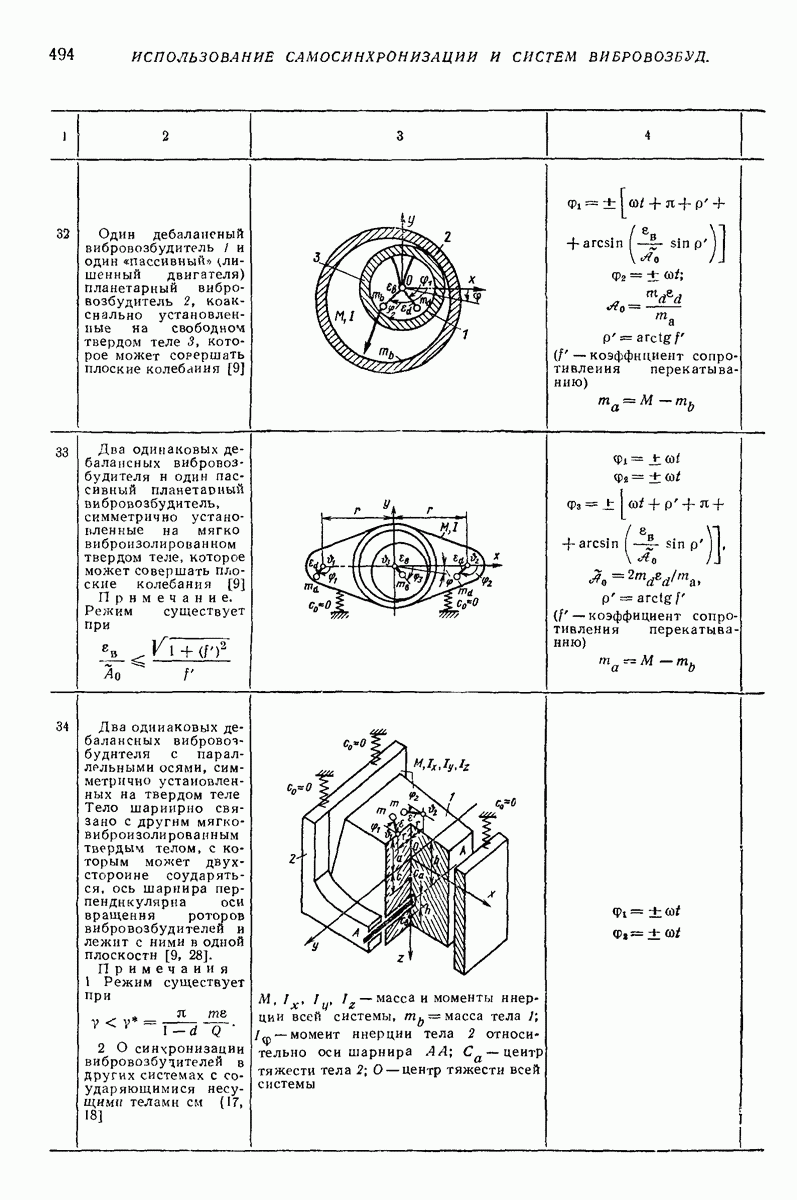
-периодическими по времени 
Для решения (64) часто целесообразно ввести «безразмерное время»  и перейти от неизвестных х и у к «полярным переменным»
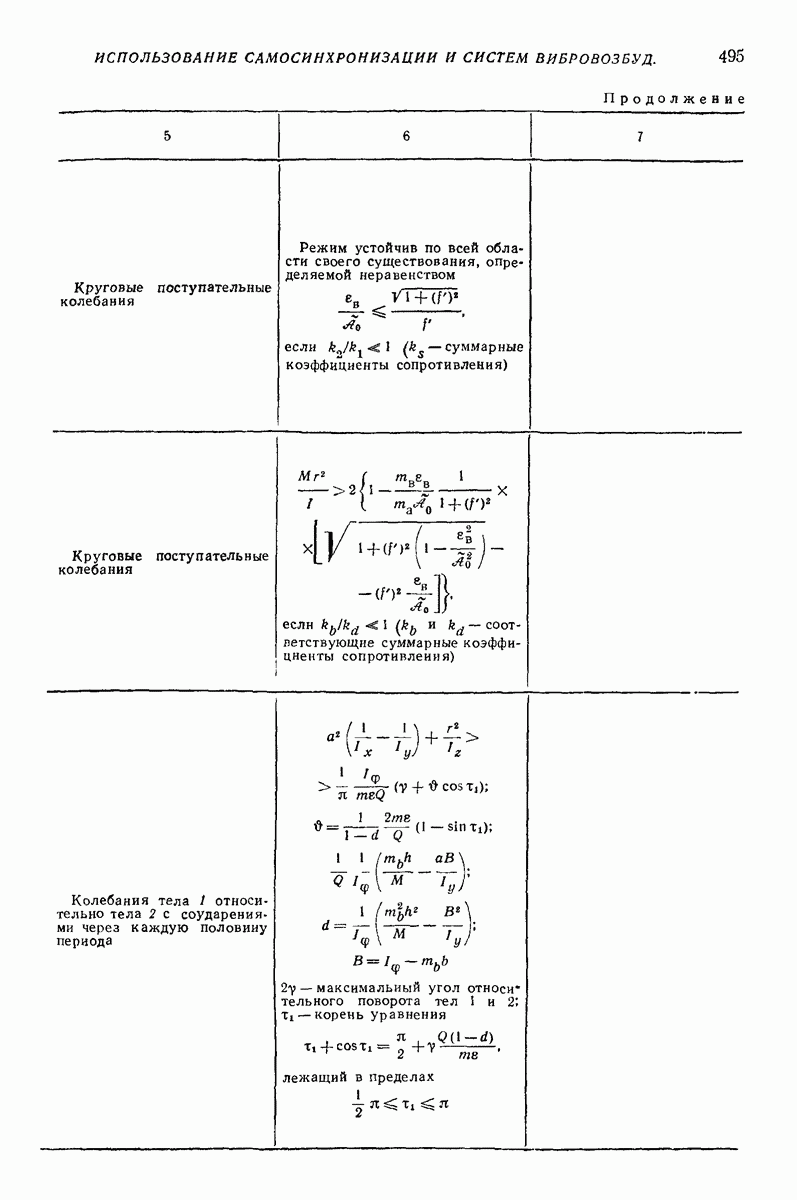
и перейти от неизвестных х и у к «полярным переменным» 

В результате (64) примет вид

где

штрихом обозначено дифференцирование по 
Представляющие основной интерес  -периодические по
-периодические по  решения (66) могут быть эффективно найдены посредством метода малого параметра (см. параграф 3 гл.
решения (66) могут быть эффективно найдены посредством метода малого параметра (см. параграф 3 гл.  в виде рядов
в виде рядов

с  -периодическими коэффициентами.
-периодическими коэффициентами.
Порождающая система  допускает при
допускает при  стационарное решение
стационарное решение  соответствующее решению (63) задачи Н. Е. Жуковского; это решение можно считать
соответствующее решению (63) задачи Н. Е. Жуковского; это решение можно считать  -периодическим по
-периодическим по  Система в вариациях
Система в вариациях

является системой с постоянными коэффициентами; ее характеристическое уравнение  имеет корни с отрицательными вещественными частями, ибо
имеет корни с отрицательными вещественными частями, ибо  Поэтому здесь реализуется простейший случай, когда
Поэтому здесь реализуется простейший случай, когда  -периодические решения у системы (69) отсутствуют. При аналитических по
-периодические решения у системы (69) отсутствуют. При аналитических по  и
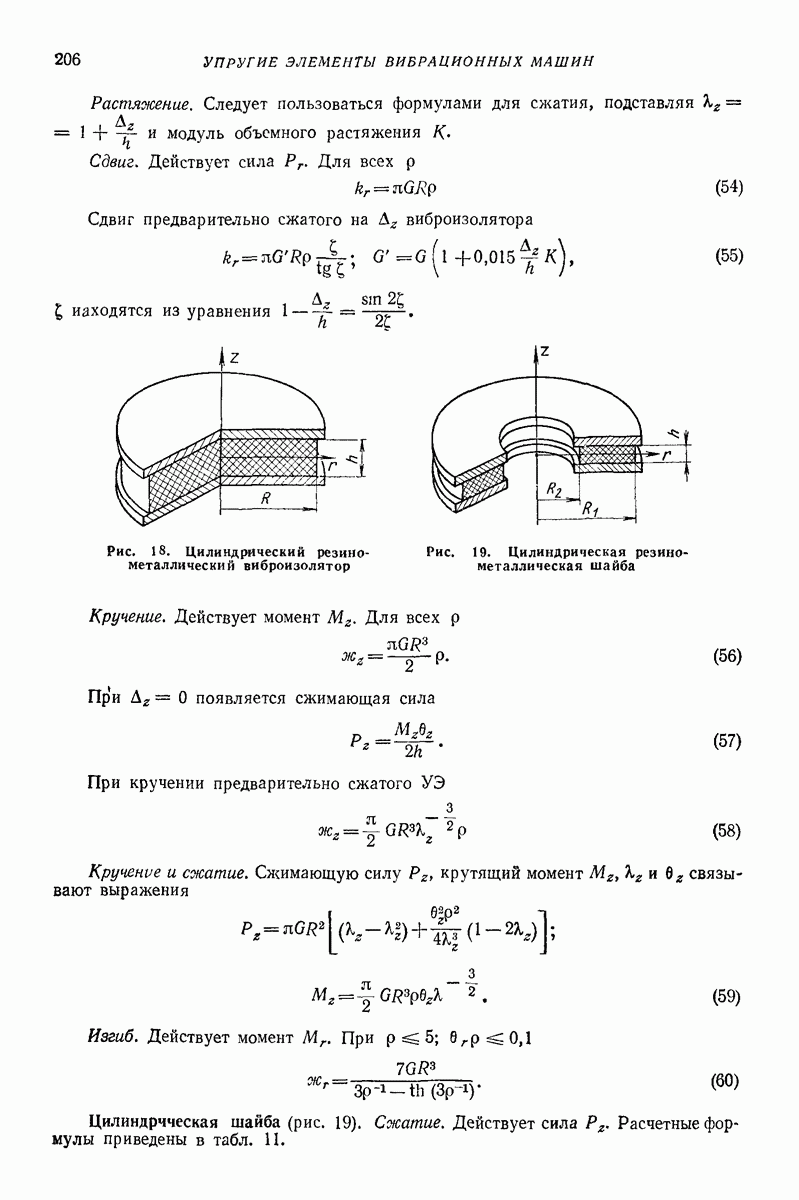
и  функциях
функциях  периодические решения уравнений (66), по крайней мере при достаточно малых
периодические решения уравнений (66), по крайней мере при достаточно малых  будут аналитическими по
будут аналитическими по  и асимптотически устойчивыми. При этом фактическое нахождение коэффициентов рядов (68) не встречает принципиальных трудностей, ибо, несмотря на нелинейность порождающей системы, оно связано с решением линейных неоднородных уравнений с постоянными коэффициентами, однородные части которых совпадают с (69). Так, для нахождения функций
и асимптотически устойчивыми. При этом фактическое нахождение коэффициентов рядов (68) не встречает принципиальных трудностей, ибо, несмотря на нелинейность порождающей системы, оно связано с решением линейных неоднородных уравнений с постоянными коэффициентами, однородные части которых совпадают с (69). Так, для нахождения функций  будем иметь систему уравнений
будем иметь систему уравнений

правые части которых зависят лишь от порождающего решения 
После нахождения величин  с необходимой точностью можно найти с той же точностью проекции скорости частицы
с необходимой точностью можно найти с той же точностью проекции скорости частицы  по (65), а затем средние скорости
по (65), а затем средние скорости 
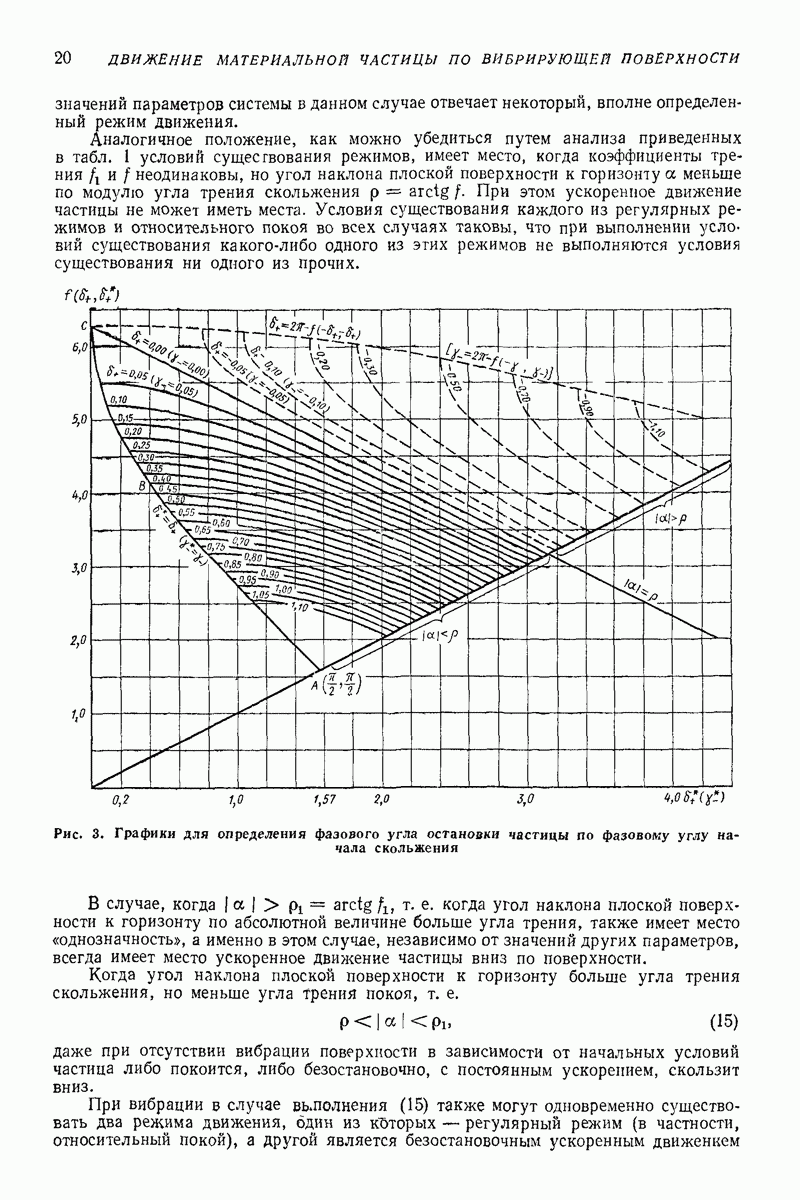
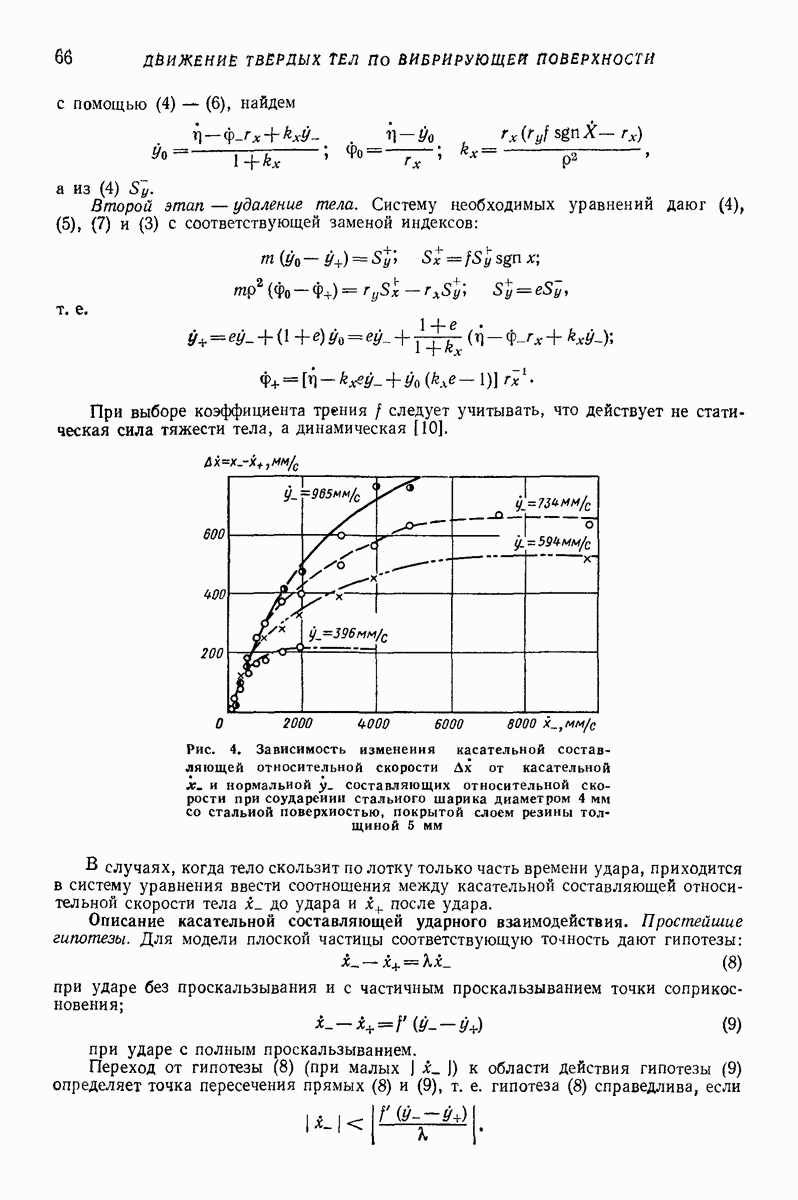
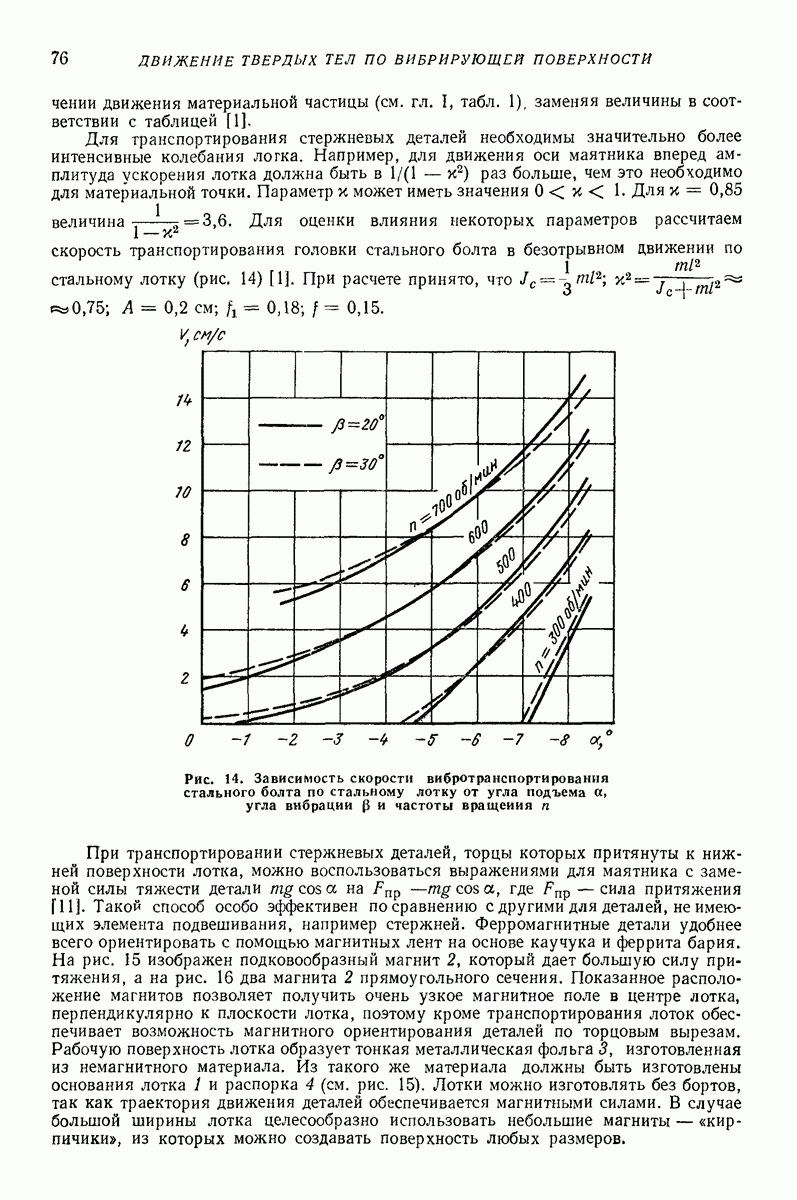
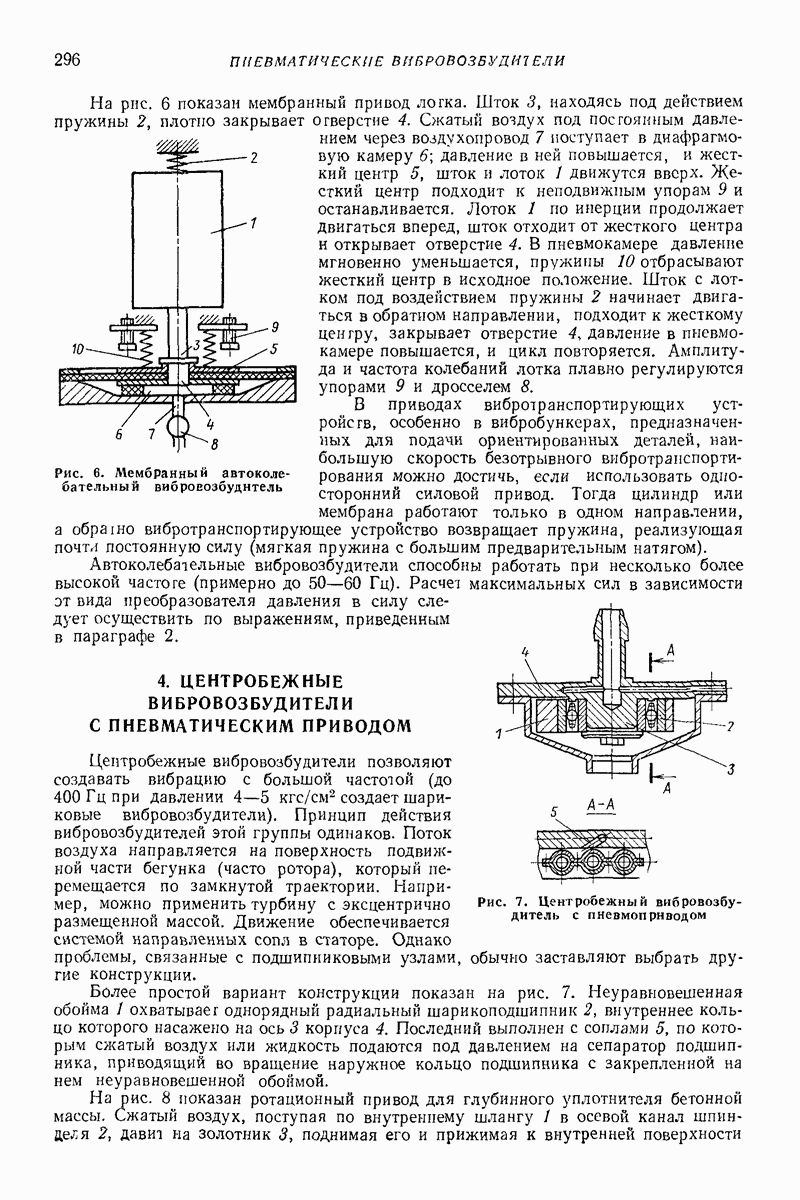
Случай наклонной плоской поверхности и дополнительной постоянной продольной силы. Пусть в отличие от задачи Н. Е. Жуковского вибрирующая плоская поверхность наклонена к горизонту на некоторый относительно малый угол  (отсчитываем этот угол в направлении, противоположном отсчету ранее введенного угла а; рис. 23, б, а также рис. 16). Уравнения движения, соответствующие этому случаю, получатся из (64), если положить в них
(отсчитываем этот угол в направлении, противоположном отсчету ранее введенного угла а; рис. 23, б, а также рис. 16). Уравнения движения, соответствующие этому случаю, получатся из (64), если положить в них  а в левых частях величину
а в левых частях величину  заменить на
заменить на  за малый параметр
за малый параметр  можно принять, например, величину
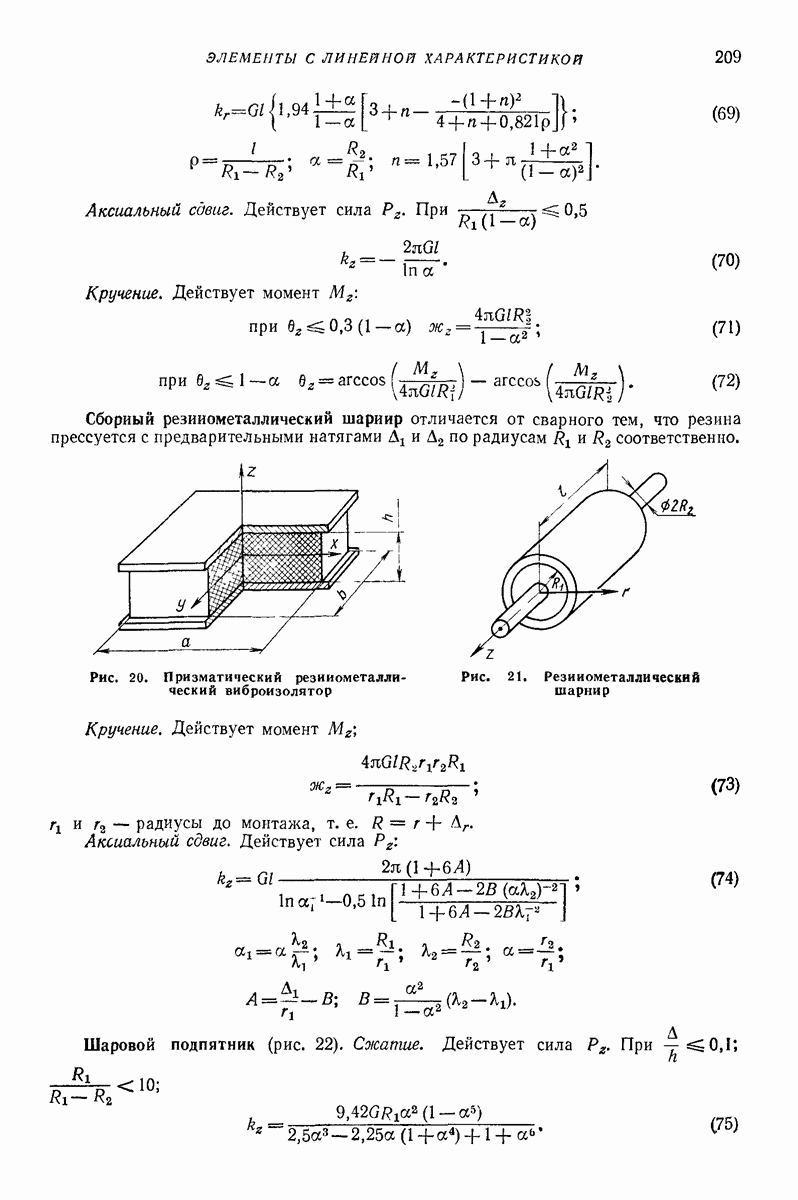
можно принять, например, величину  Решение уравнений изложенным выше способом приводит к выводу, что траекторией относительного движения частицы по поверхности является спиралевидная кривая. Отклонение скорости среднего движения частицы
Решение уравнений изложенным выше способом приводит к выводу, что траекторией относительного движения частицы по поверхности является спиралевидная кривая. Отклонение скорости среднего движения частицы  происходит в ту сторону, в которую направлены абсолютные скорости точек поверхности в моменты ее наинизшего положения (в рассматриваемом случае — в сторону положительного направления оси
происходит в ту сторону, в которую направлены абсолютные скорости точек поверхности в моменты ее наинизшего положения (в рассматриваемом случае — в сторону положительного направления оси  С точностью до величин порядка
С точностью до величин порядка  проекции средней скорости движения частицы по поверхности
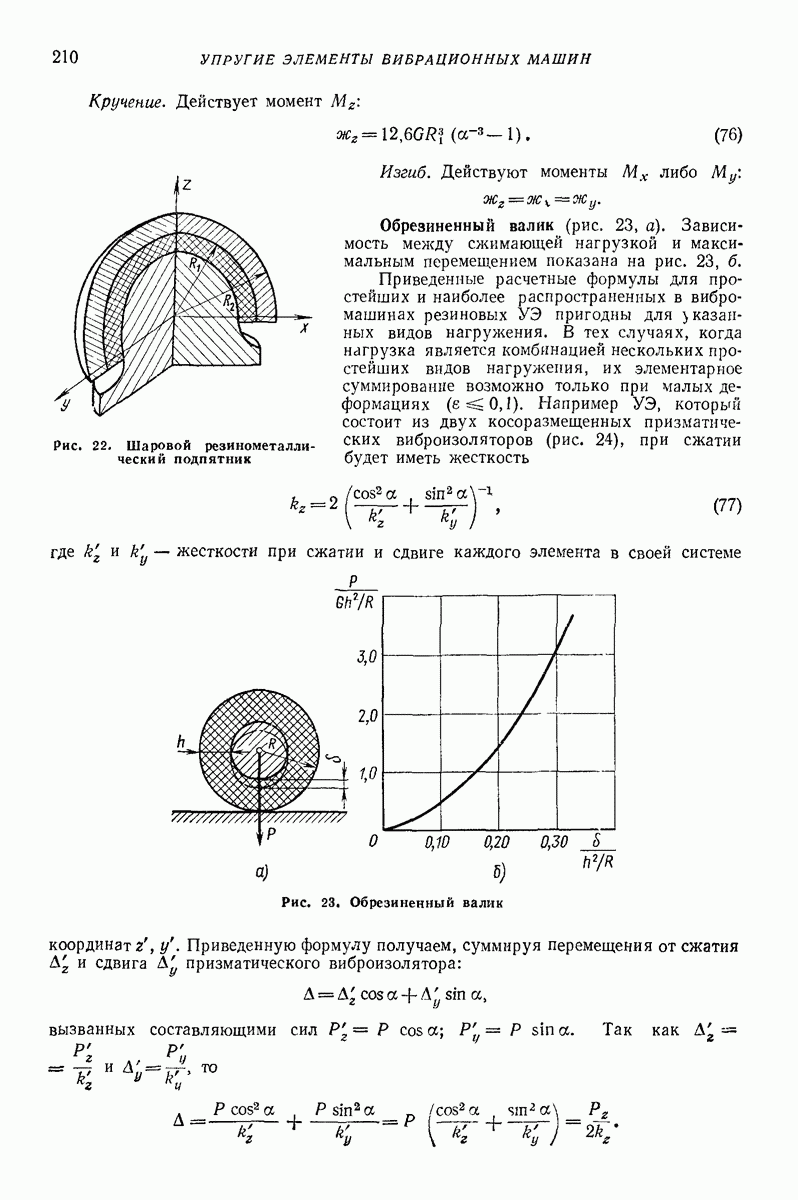
проекции средней скорости движения частицы по поверхности

За период колебаний поверхности  частица описывает «разомкнутую окружность», радиус которой
частица описывает «разомкнутую окружность», радиус которой  т.е. вычисляется аналогично радиусу круговой траектории в задаче Н. Е. Жуковского. С указанной степенью точности скорость бокового сноса частицы не зависит ни от радиуса (амплитуды) траектории колебаний поверхности, ни от коэффициента трения.
т.е. вычисляется аналогично радиусу круговой траектории в задаче Н. Е. Жуковского. С указанной степенью точности скорость бокового сноса частицы не зависит ни от радиуса (амплитуды) траектории колебаний поверхности, ни от коэффициента трения.
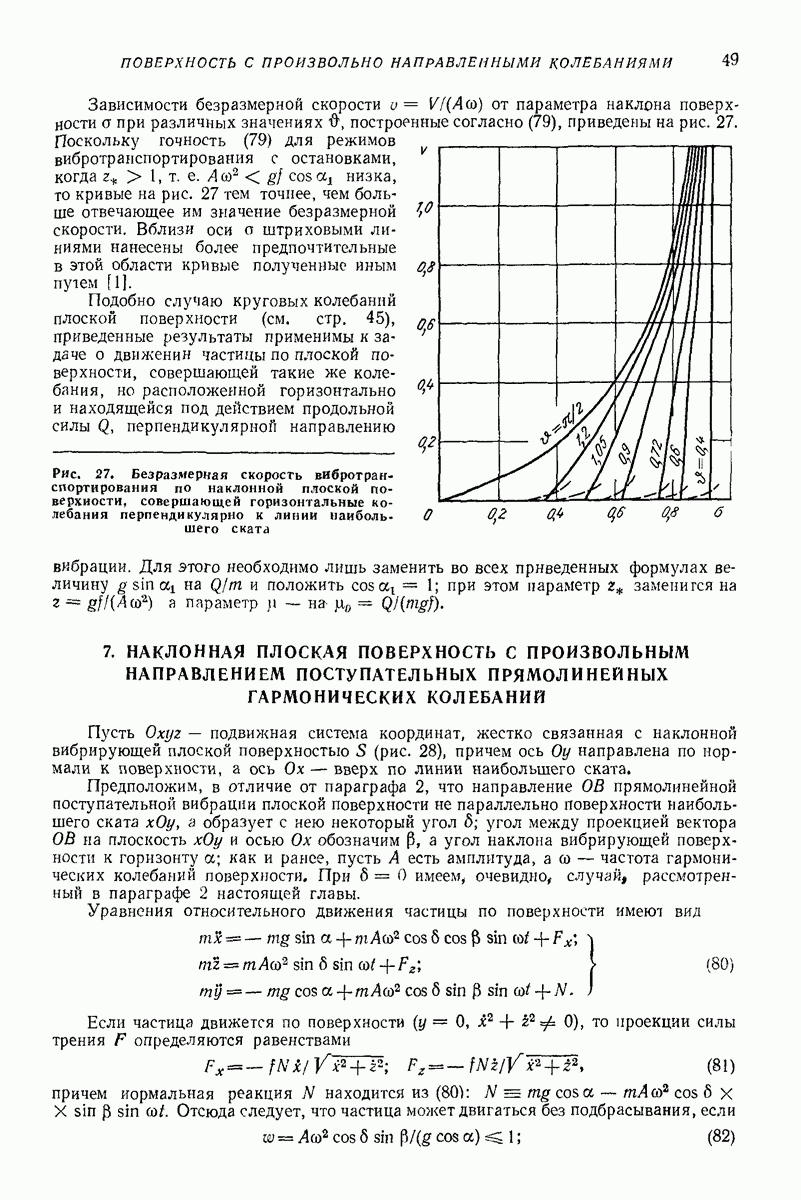
С увеличением интенсивности вибрации, т. е. с уменьшением параметра  величина «угла сноса» (рис. 23, б)
величина «угла сноса» (рис. 23, б)

монотонно убывает до нуля. При  (т. е. при
(т. е. при  скоростью бокового сноса можно пренебречь, положив
скоростью бокового сноса можно пренебречь, положив  при этом скорость V можно приближенно определить из уравнения
при этом скорость V можно приближенно определить из уравнения

где  и
и  — полные эллиптические интегралы соответственно первого и второго рода от модуля
— полные эллиптические интегралы соответственно первого и второго рода от модуля 
Уравнение (73) справедливо и при значительном наклоне поверхности, т. е. когда параметр  имеет порядок единицы.
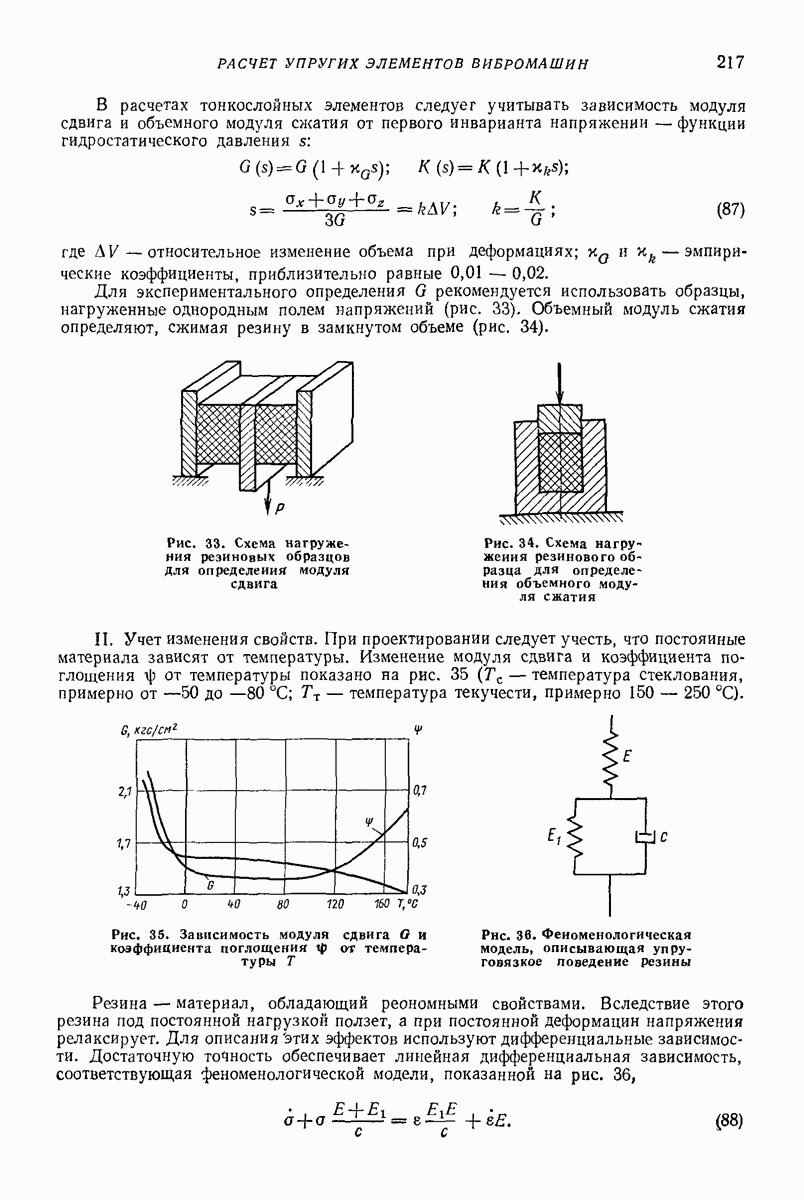
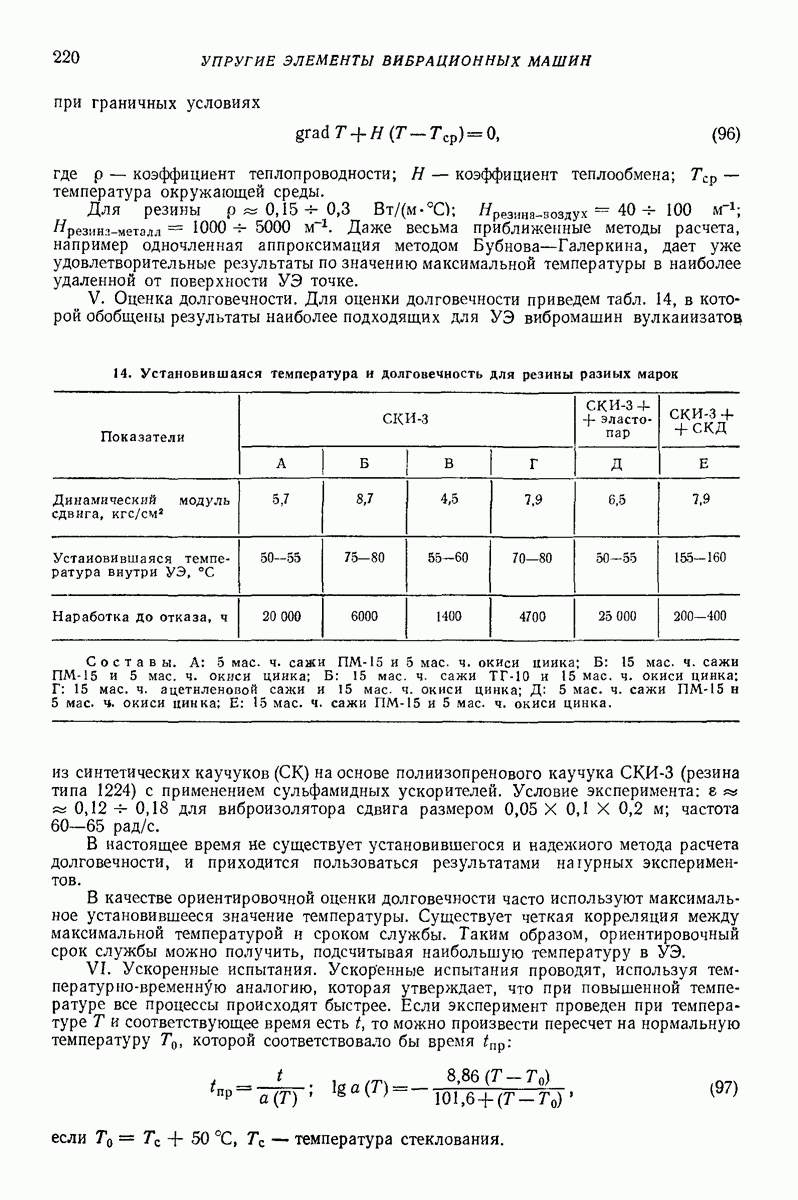
имеет порядок единицы.
При низкой интенсивности вибраций  т.е.
т.е.  приведенные выше формулы утрачивают смысл; в этом случае имеет место движение частицы с шперралами относительного покоя в каждом периоде.
приведенные выше формулы утрачивают смысл; в этом случае имеет место движение частицы с шперралами относительного покоя в каждом периоде.
Изложенные результаты полностью относятся также к случаю, когда вибрирующая поверхность горизонтальна, но на частицу действует дополнительная сила  направленная вдоль оси
направленная вдоль оси  (рис. 23, в) В указанном случае следует лишь заменить во всех приведенных формулах величину
(рис. 23, в) В указанном случае следует лишь заменить во всех приведенных формулах величину  на
на  и положить
и положить  при этом
при этом  заменяется на
заменяется на 
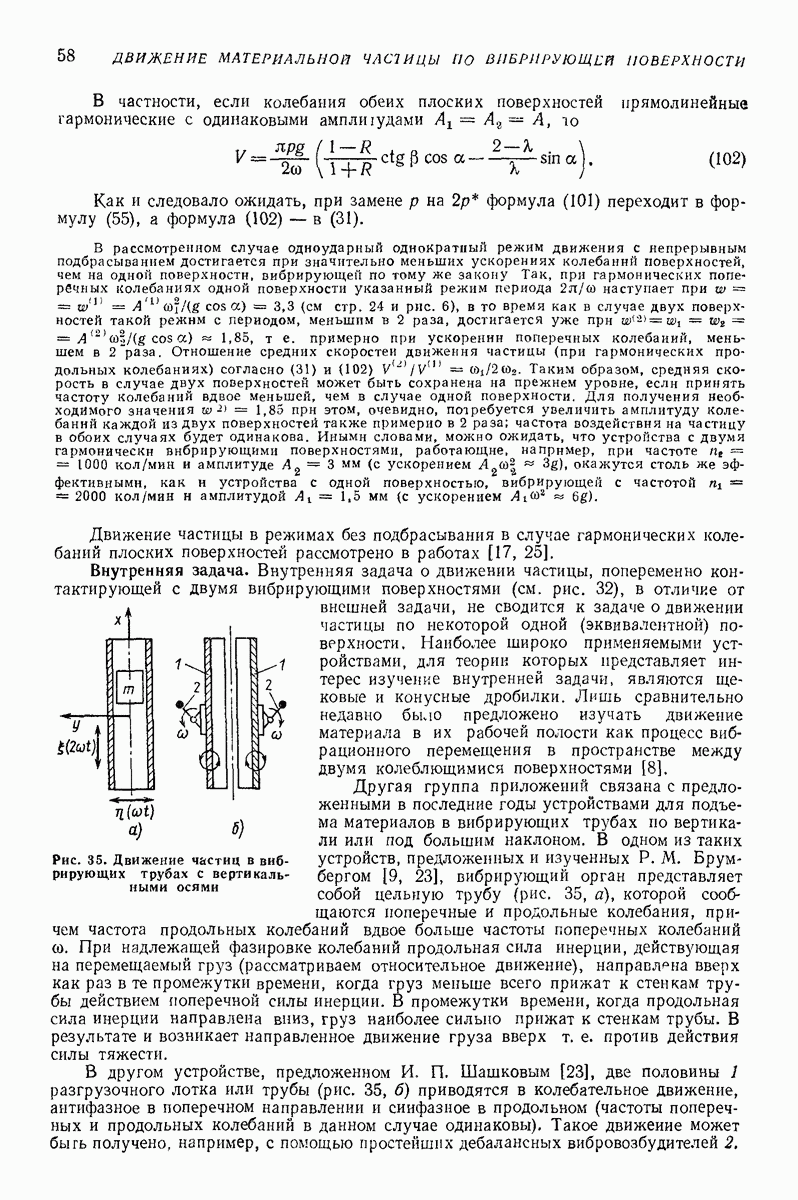
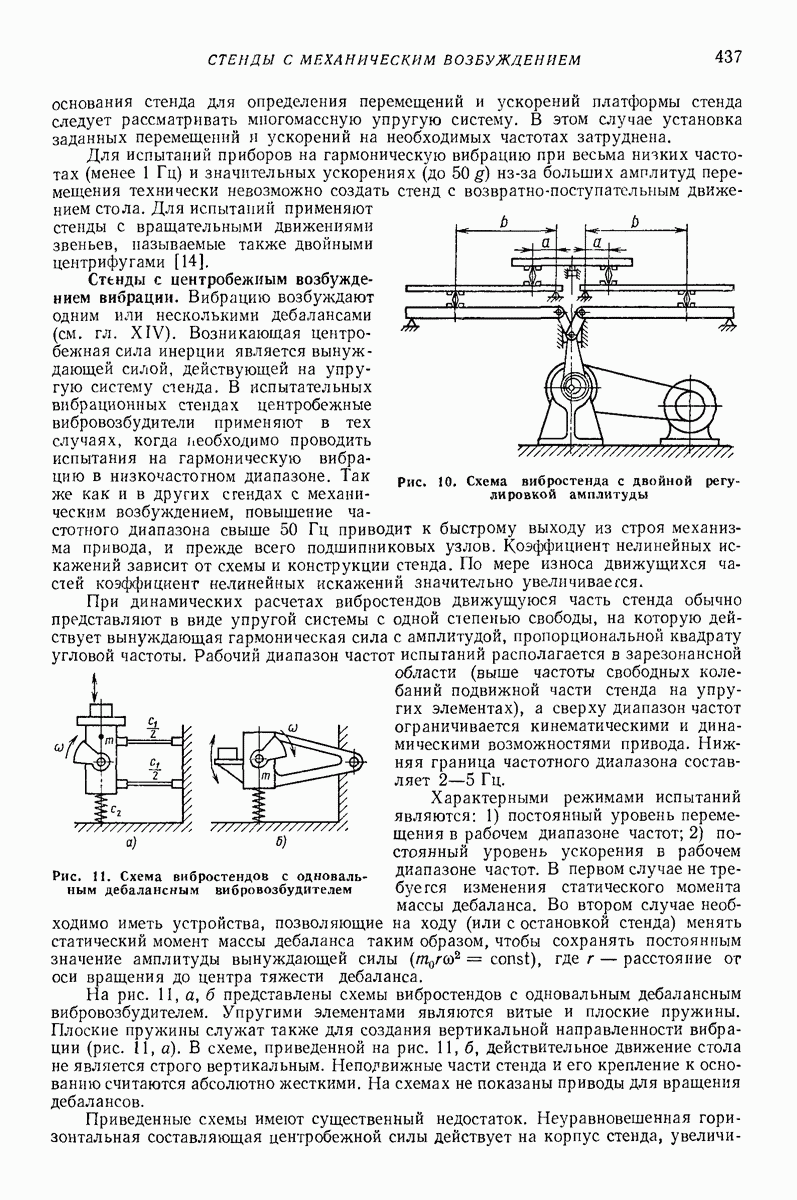
Случай горизонтальной плоской поверхности, совершающей поступательные колебания в горизонтальной плоскости, близкие к круговым. Если горизонтальная поверхность помимо круговых совершает дополнительные малые поступательные колебания в горизонтальной плоскости (рис. 23, г), то в (64) можно положить  где
где  периодические функции
периодические функции  с периодом
с периодом  В частности, если траектории результирующих колебаний — аллипсы с относительно малым эксцентриситетом, то можно принять
В частности, если траектории результирующих колебаний — аллипсы с относительно малым эксцентриситетом, то можно принять  полуоси эллипса, причем большая ось параллельна оси
полуоси эллипса, причем большая ось параллельна оси 

Тогда согласно (67) будем иметь  легко определив периодическое решение (70), найдем величины
легко определив периодическое решение (70), найдем величины  с точностью до членов порядка
с точностью до членов порядка  включительно
включительно

Теперь  соблюдая ту же точность, можно найти скорости х и у, а затем и координаты х и у частицы в устойчивом установившемся движении Траектория частицы в указанном движении имеет вид деформированного эллипса (овала); средняя скорость движения
соблюдая ту же точность, можно найти скорости х и у, а затем и координаты х и у частицы в устойчивом установившемся движении Траектория частицы в указанном движении имеет вид деформированного эллипса (овала); средняя скорость движения  равна нулю.
равна нулю.
2. Значения функций  и
и 
(см. скан)
В случае достаточно интенсивных колебаний, когда  т. е.
т. е.  можно пользоваться приближенным решением
можно пользоваться приближенным решением

где  , причем функции
, причем функции  определяются по табл. 2.
определяются по табл. 2.

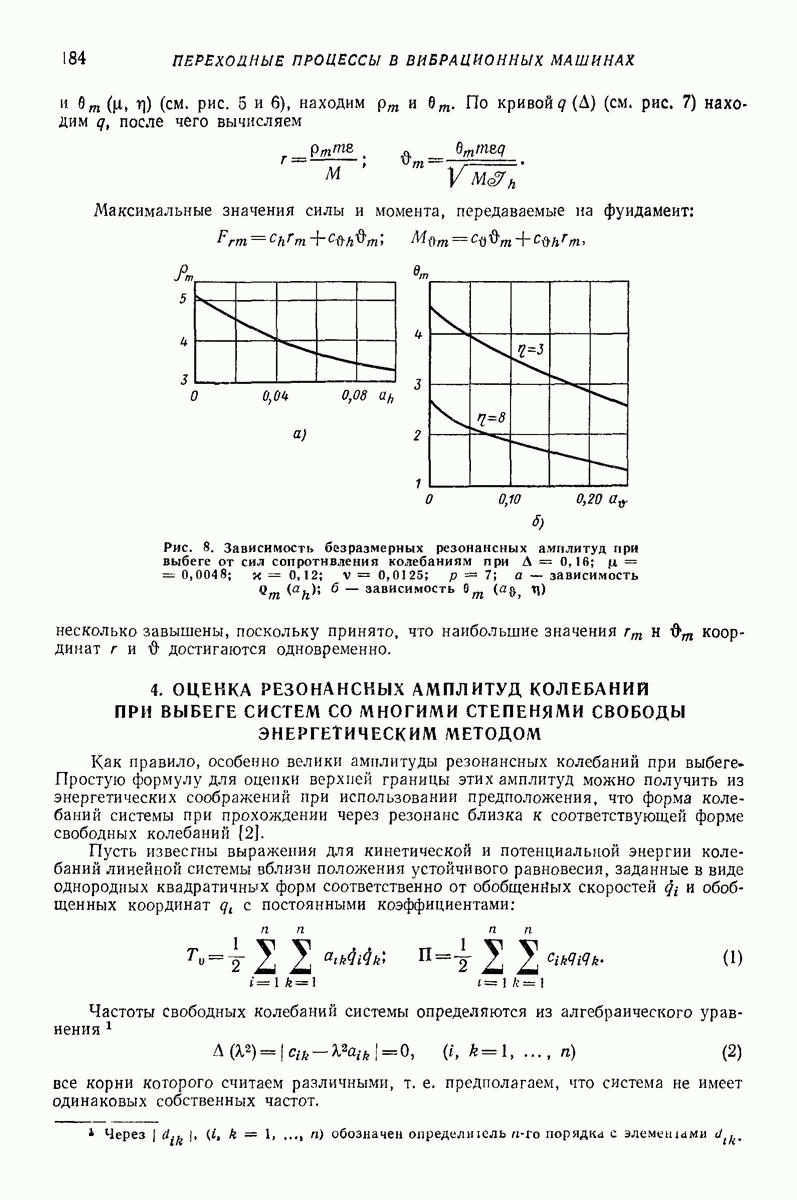
Рис. 24. Годографы скорости частицы при установлении устойчивого движения частицы по плоской поверхности: 
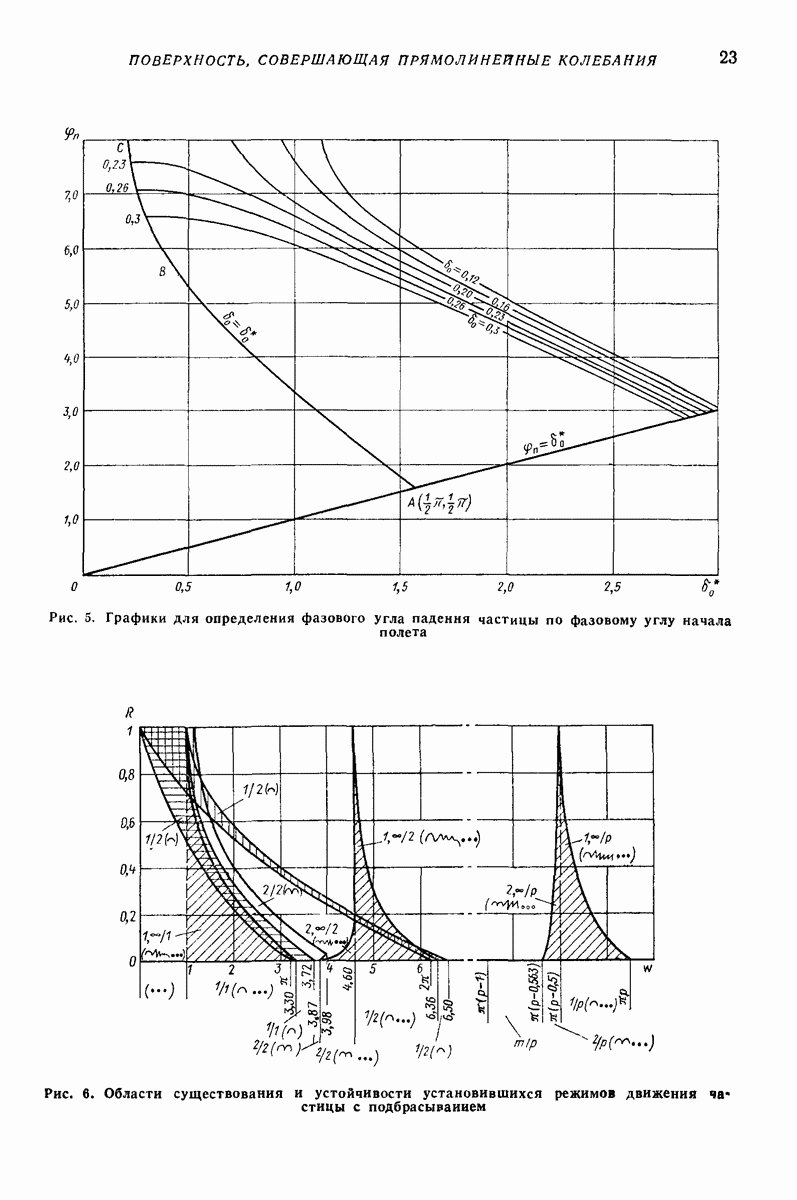
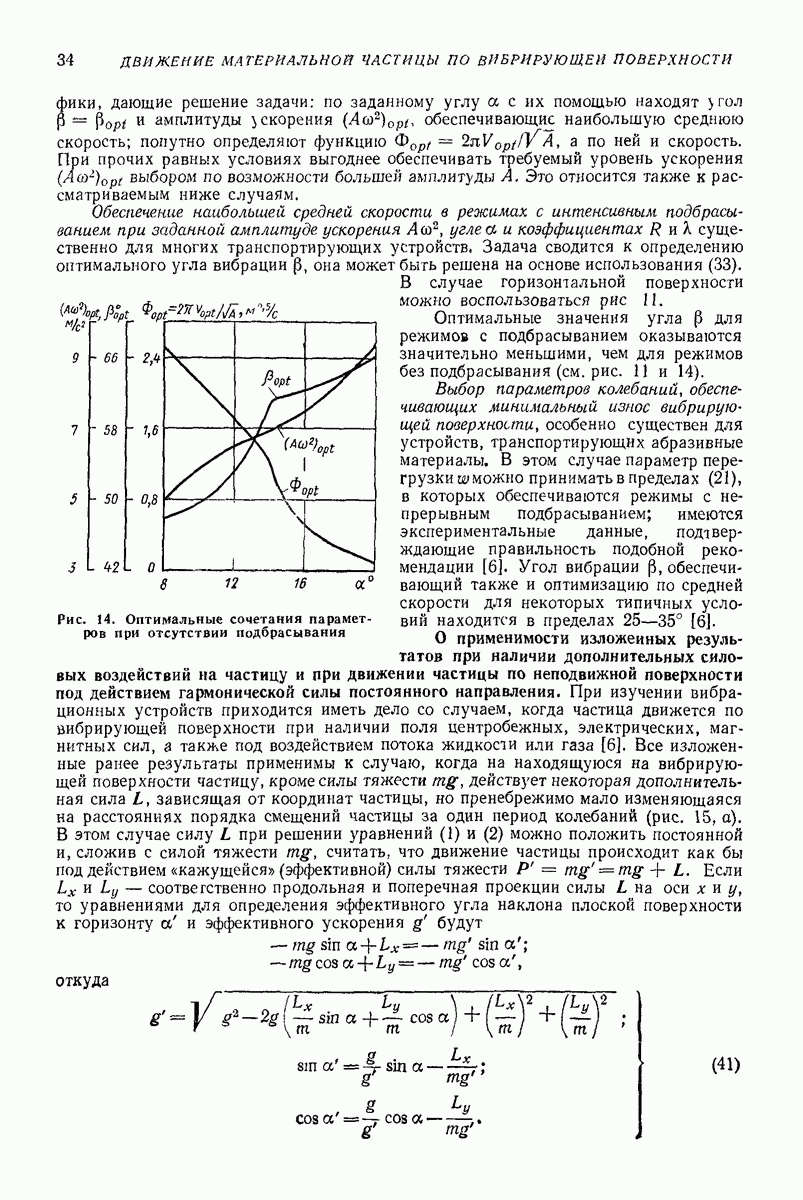
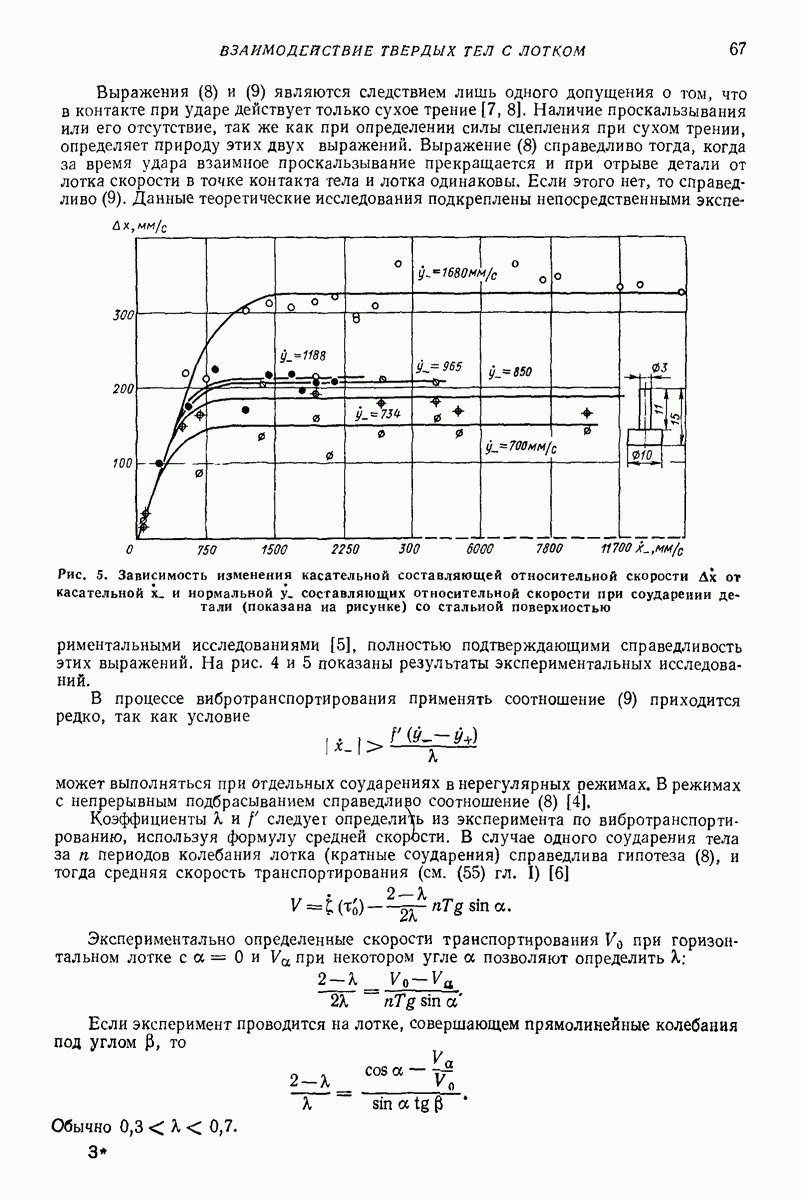
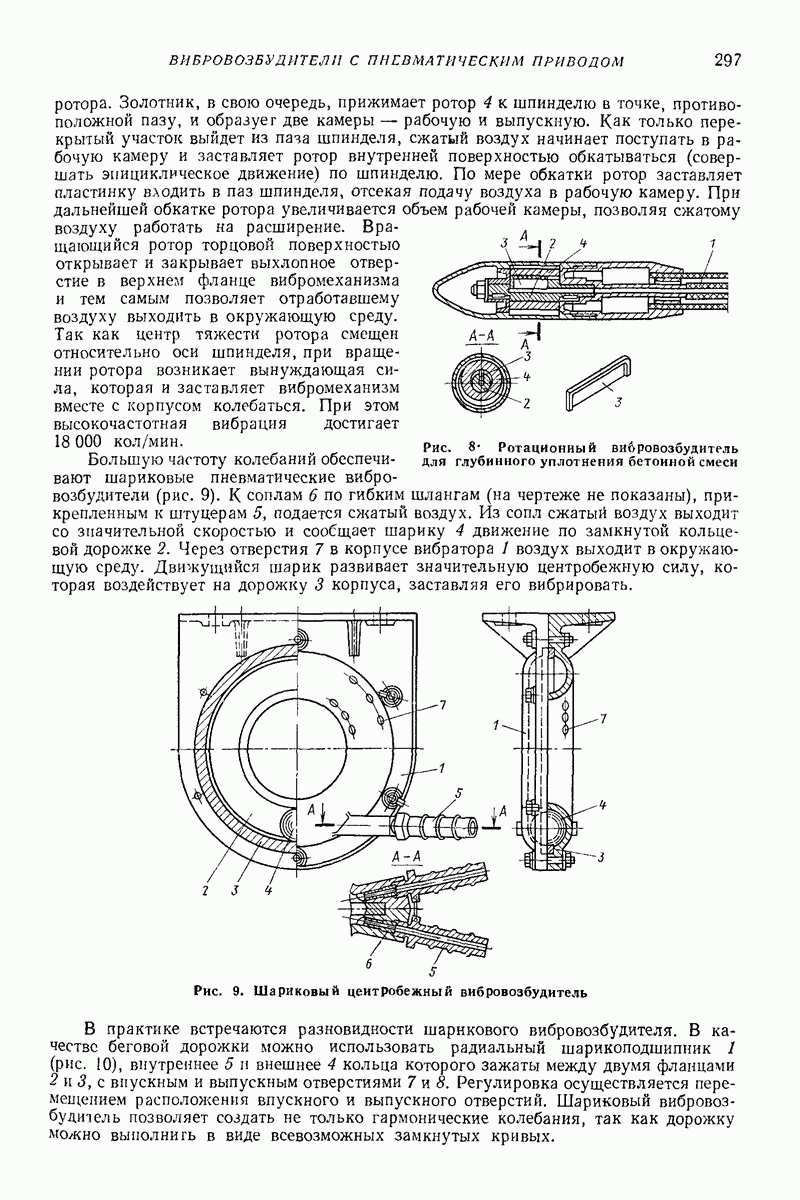
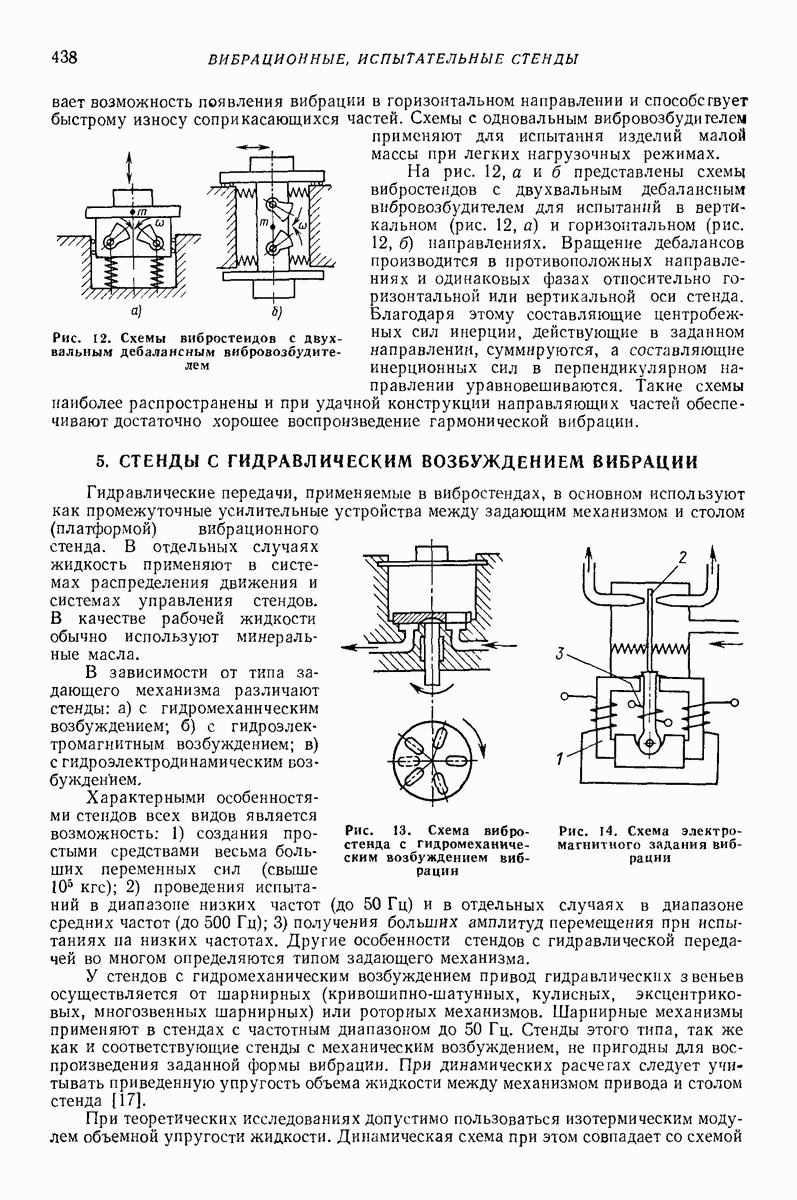
На рис. 24 изображены годографы скорости частицы, полученные в результате решения задачи на электронной моделирующей установке, причем виден процесс установления устойчивого движения, которому соответствуют замкнутые кривые. Отклонение этих кривых от эллипсов увеличивается с уменьшением параметра  Решение (75) получено
Решение (75) получено  Хуаем путем использования метода Бубнова — Галеркина; им же получены кривые на рис. 24 (см [6], где приведен более детальный анализ задачи.)
Хуаем путем использования метода Бубнова — Галеркина; им же получены кривые на рис. 24 (см [6], где приведен более детальный анализ задачи.)
Случай горизонтальной плоской поверхности, совершающей, кроме круговых, дополнительные малые колебания. Когда дополнительные поперечные колебания являются поступательными (рис. 24, б), в (64) следует положить  где
где  периодическая функция
периодическая функция  с периодом
с периодом  характеризующая закон малых поперечных колебаний поверхности. Предполагаем, что
характеризующая закон малых поперечных колебаний поверхности. Предполагаем, что  так что подбрасывание частицы отсутствует. В частности, в случае гармонических поперечных колебаний
так что подбрасывание частицы отсутствует. В частности, в случае гармонических поперечных колебаний  где
где  соответственно амплитуда и фаза колебаний;
соответственно амплитуда и фаза колебаний;  При этом согласно (65) и
При этом согласно (65) и  и после решения (70) находим
и после решения (70) находим
с точностью до членов, содержащих 

Подставив эти выражения в (65) и выполнив операцию осреднения, найдем (с той же точностью) следующие выражения для проекций средней скорости движения частицы по поверхности

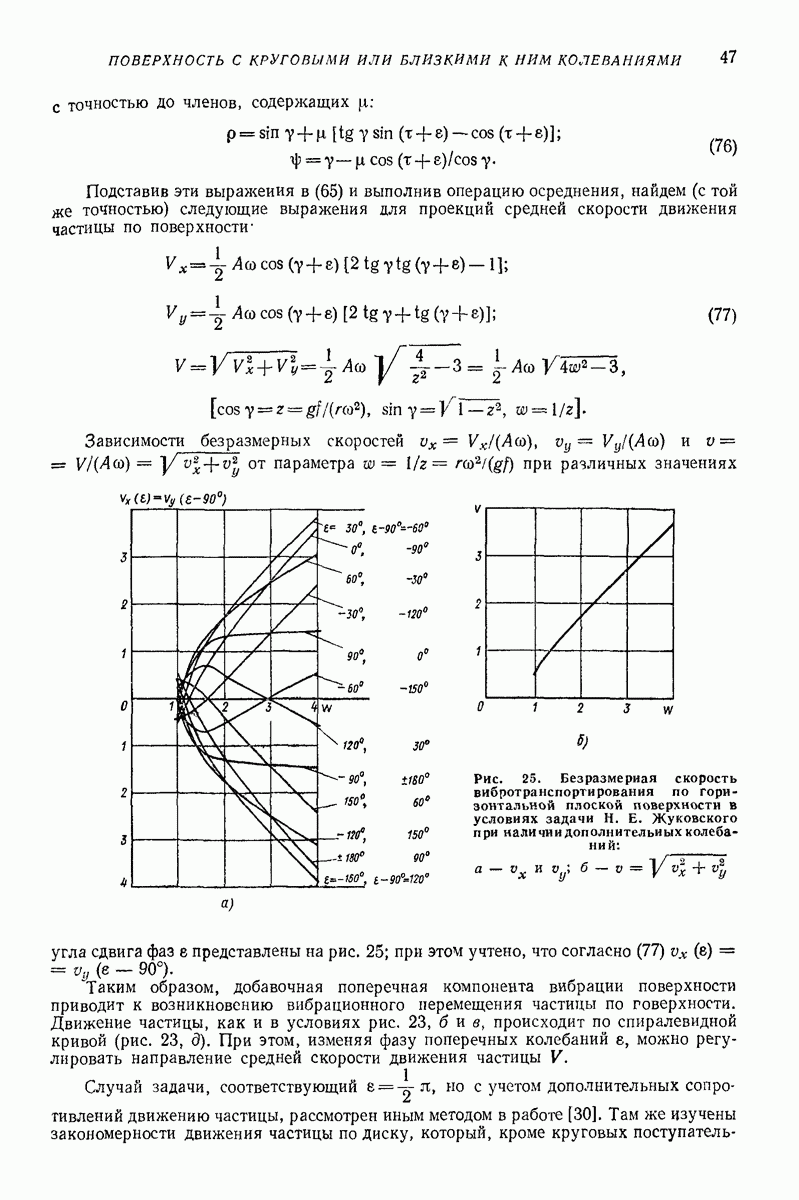
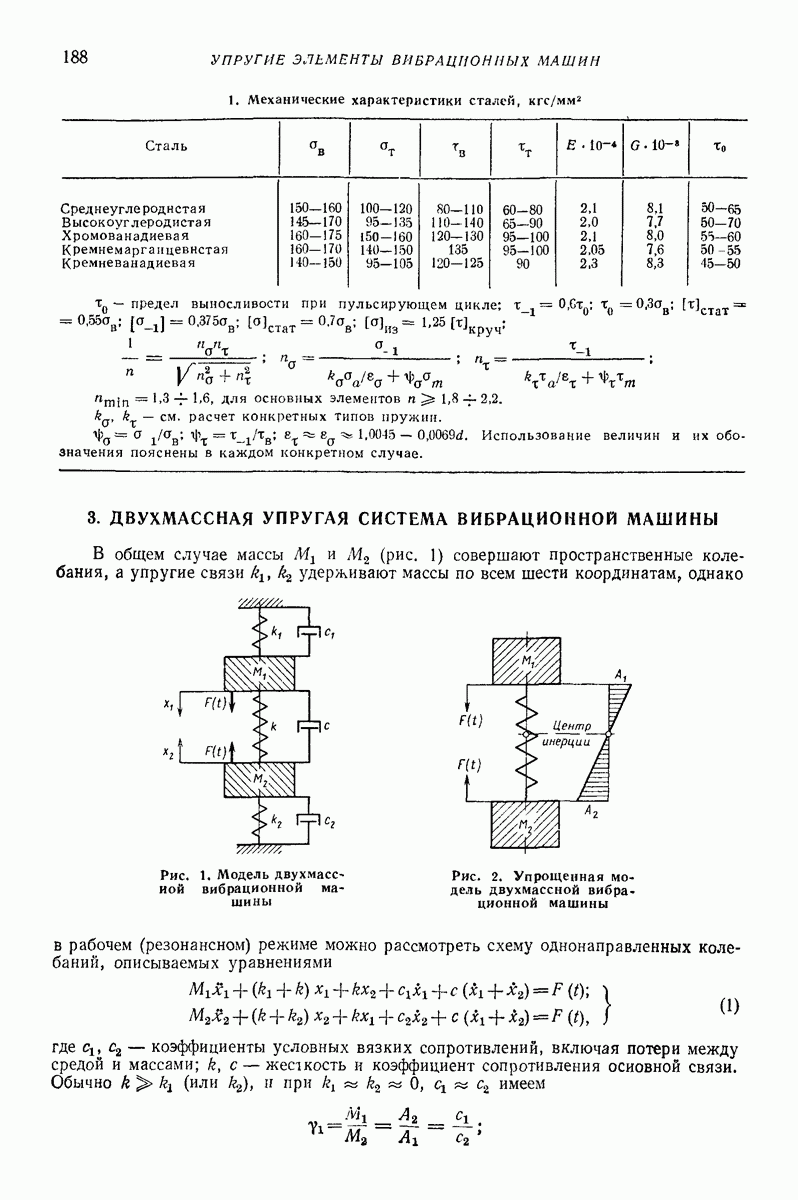
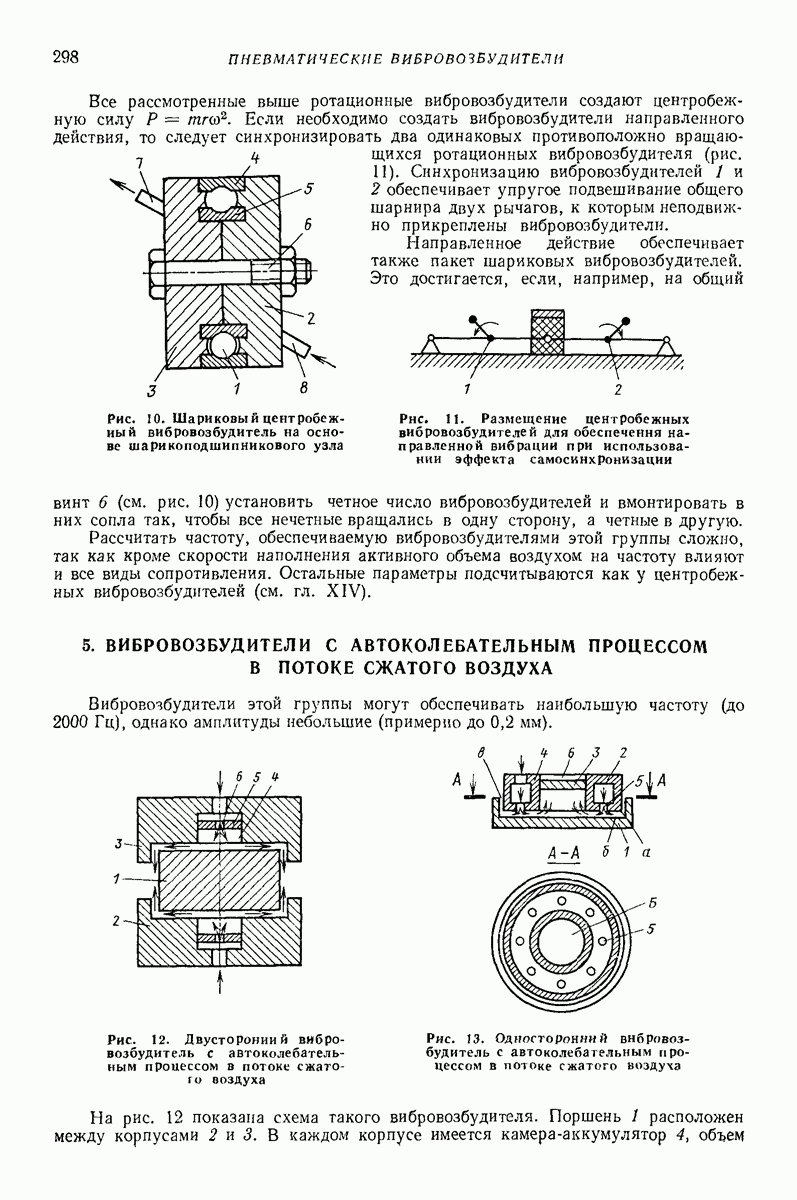
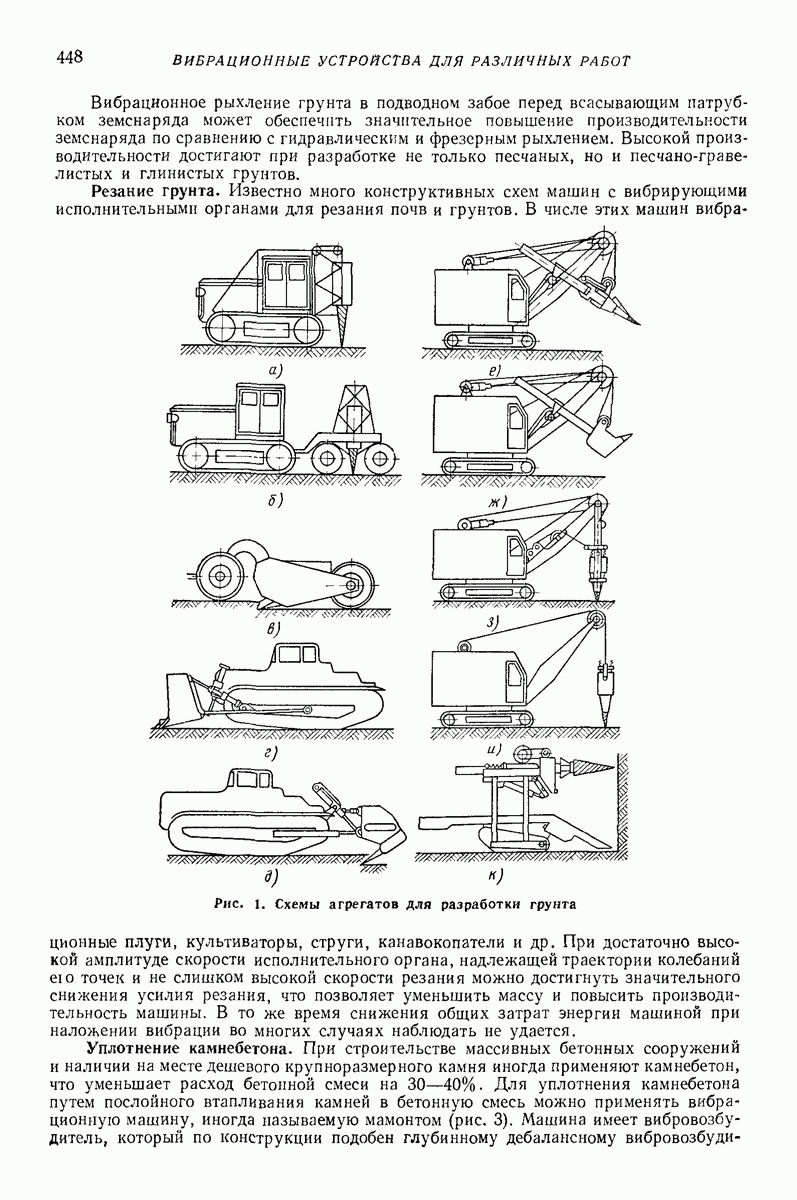
Зависимости безразмерных скоростей  параметра
параметра  при различных значениях угла сдвига фаз
при различных значениях угла сдвига фаз  представлены на рис. 25; при этом учтено, что согласно
представлены на рис. 25; при этом учтено, что согласно 

Рис. 25. Безразмерная скорость вибротранспортирования по горизонтальной плоской поверхности в условиях задачи Н. Е. Жуковского при наличии дополнительных колебаний: 
Таким образом, добавочная поперечная компонента вибрации поверхности приводит к возникновению вибрационного перемещения частицы по говерхности. Движение частицы, как и в условиях рис. 23, б и в, происходит по спиралевидной кривой (рис. 23, 3). При этом, изменяя фазу поперечных колебаний  можно регулировать направление средней скорости движения частицы
можно регулировать направление средней скорости движения частицы 
Случай задачи, соответствующий  с учетом дополнительных сопротивлений движению частицы, рассмотрен иным методом в работе [30]. Там же изучены закономерности движения частицы по диску, который, кроме круговых
с учетом дополнительных сопротивлений движению частицы, рассмотрен иным методом в работе [30]. Там же изучены закономерности движения частицы по диску, который, кроме круговых
поступательных колебаний в своей плоскости, совершает прецессию вокруг вертикальной оси  Регулируя параметры вибрации, можно обеспечить картину среднего («медленного») движения частицы, соответствующую устойчивому или неустойчивому фокусу в центре диска, а также устойчивому или неустойчивому предельному циклу в виде окружности заданного радиуса (о понятиях фокуса и предельного цикла см. т. 2).
Регулируя параметры вибрации, можно обеспечить картину среднего («медленного») движения частицы, соответствующую устойчивому или неустойчивому фокусу в центре диска, а также устойчивому или неустойчивому предельному циклу в виде окружности заданного радиуса (о понятиях фокуса и предельного цикла см. т. 2).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- Установившиеся режимы движения частицы.
- О методах решения задачи.
- Установившиеся режимы при отсутствии подбрасывания [4-6].
- Установившиеся режимы с подбрасыванием.
- Средние скорость и ускорение частицы в установившихся режимах движения.
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
- О выборе оптимальных параметров колебаний.
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
- О влиянии на движение частицы сил вязкого сопротивления.
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
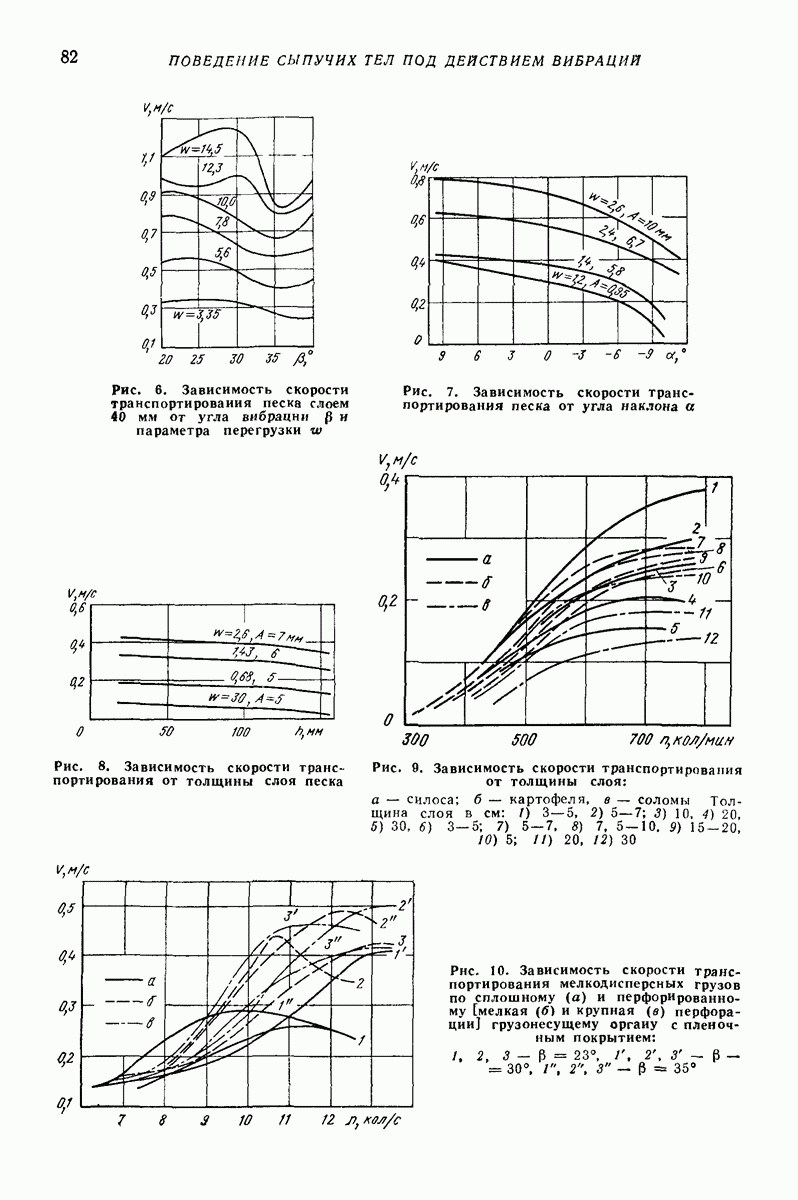
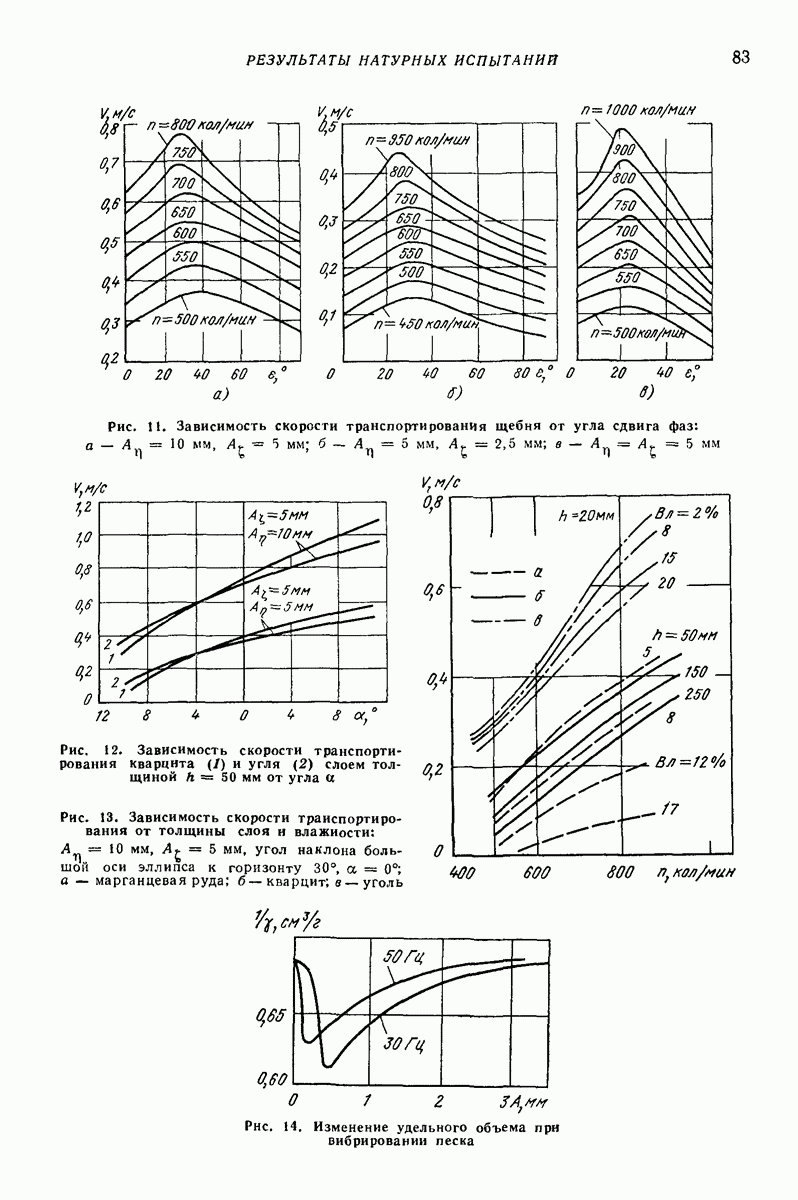
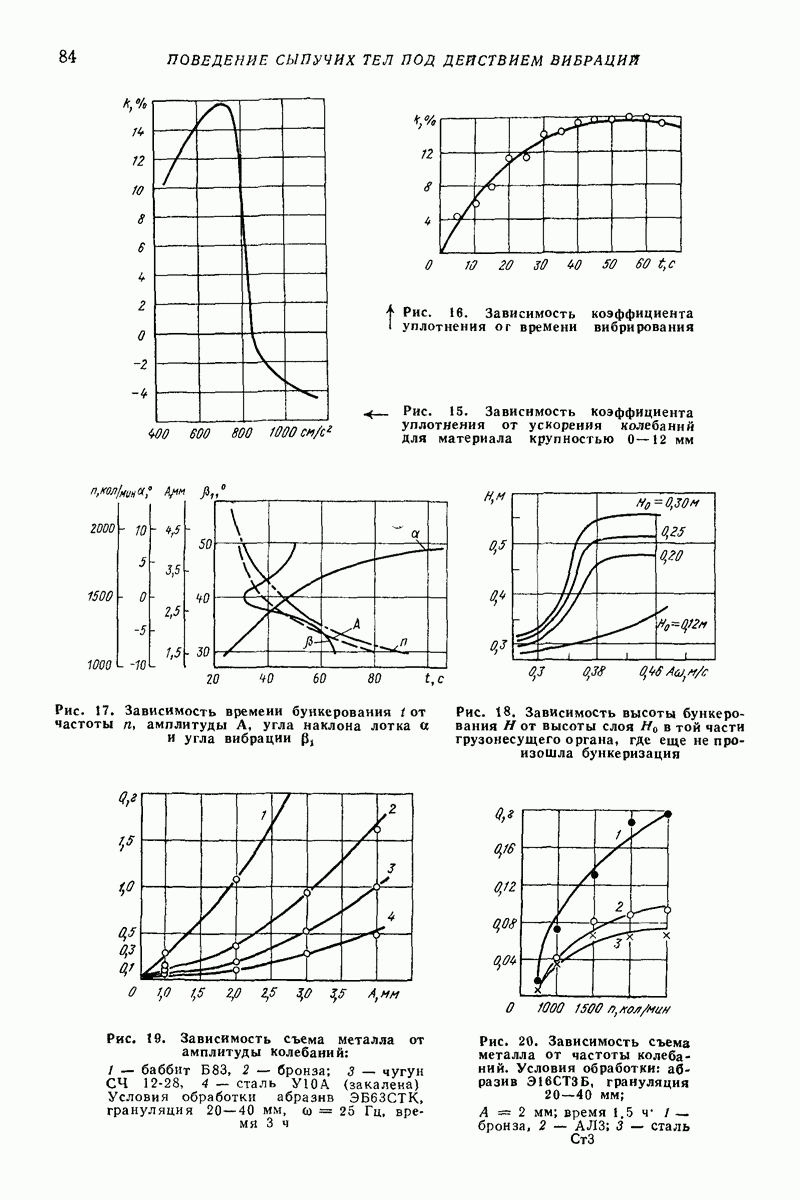
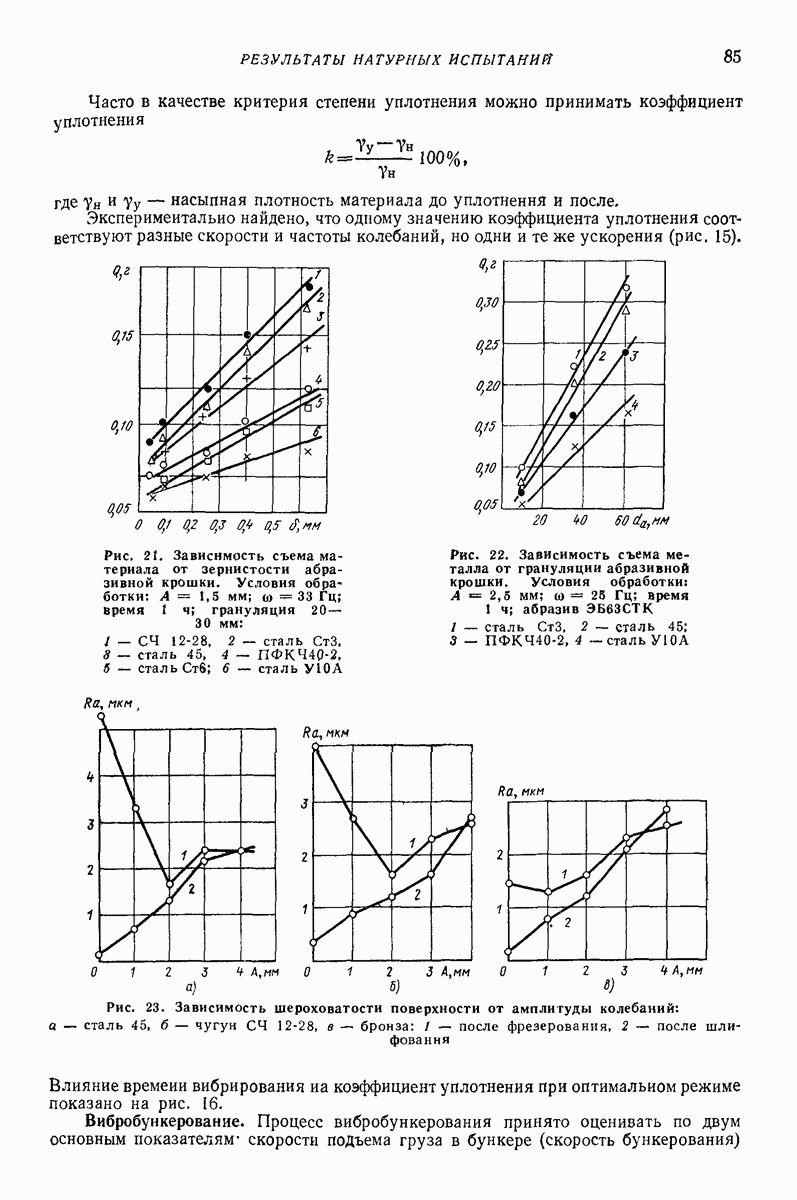
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
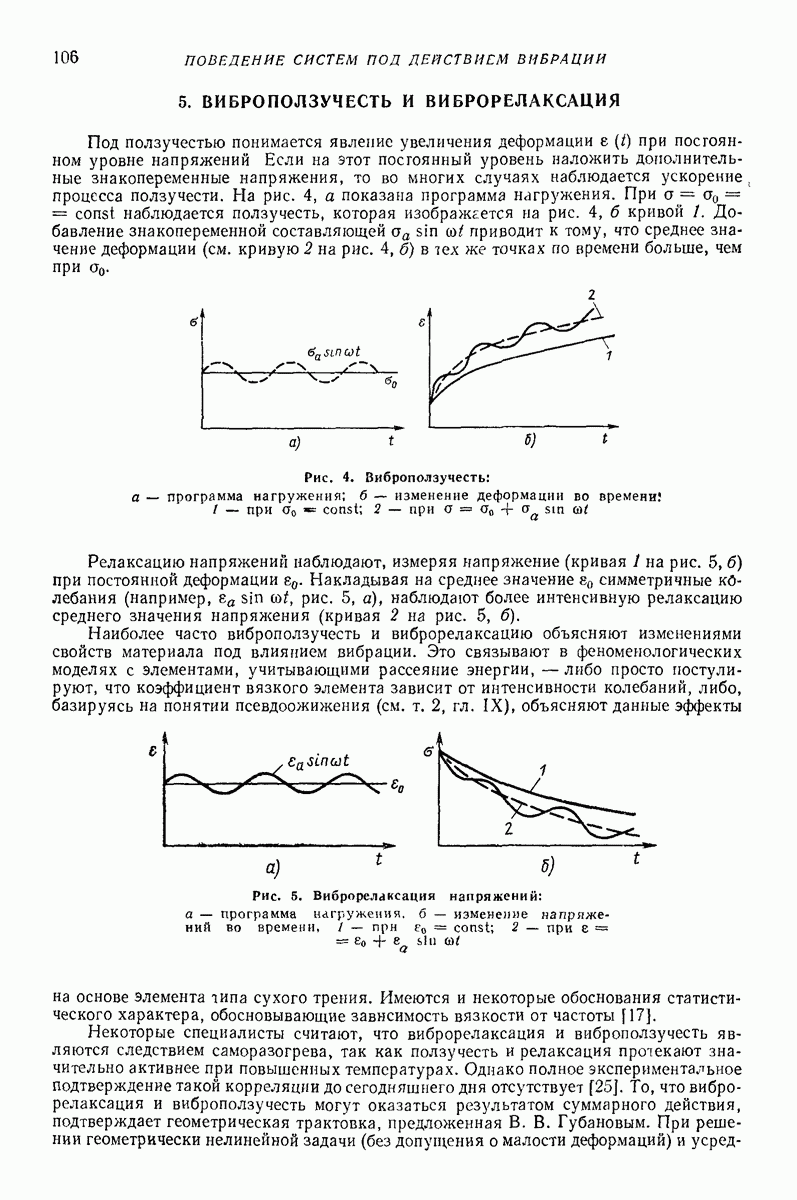
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
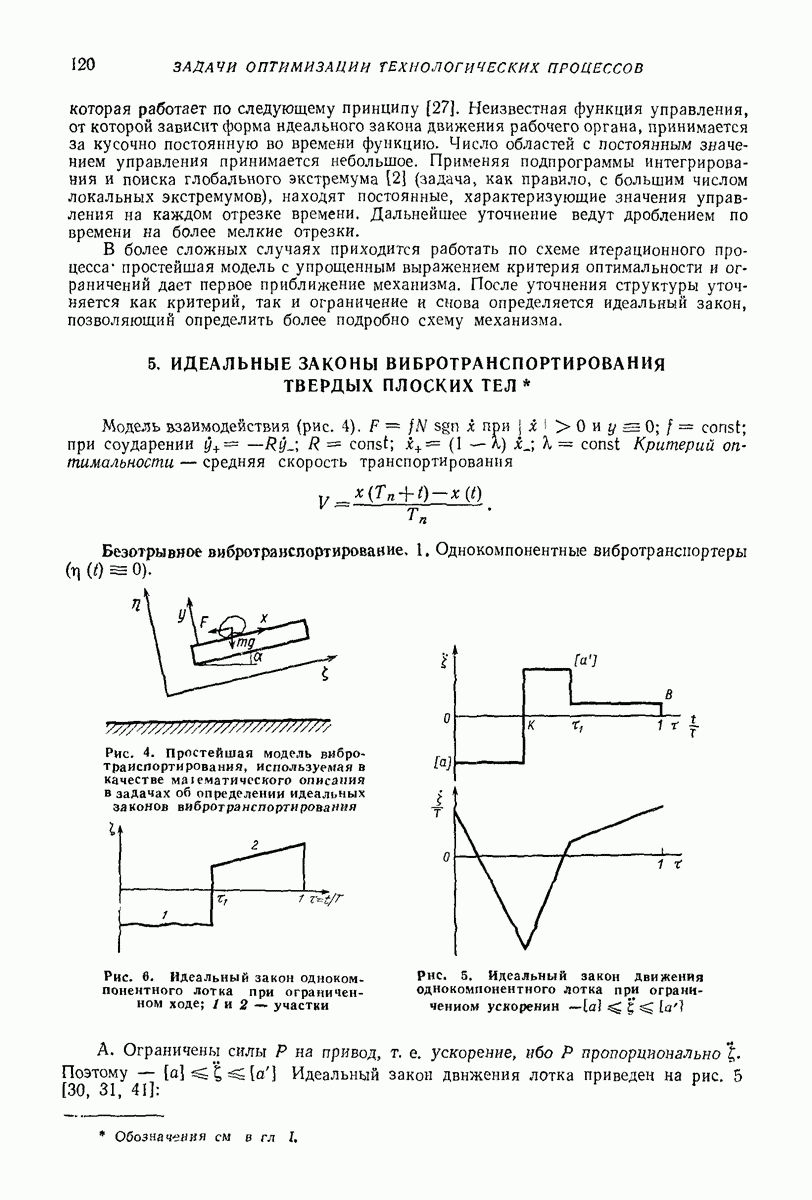
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
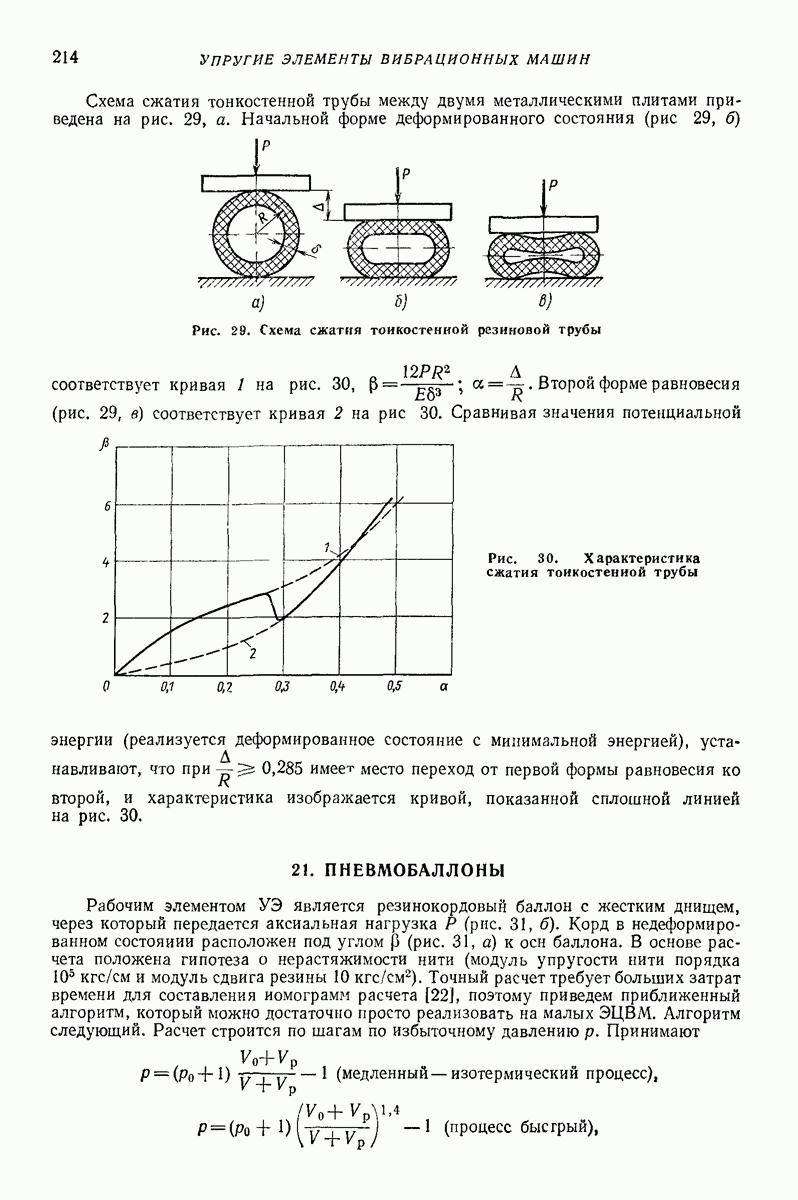
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
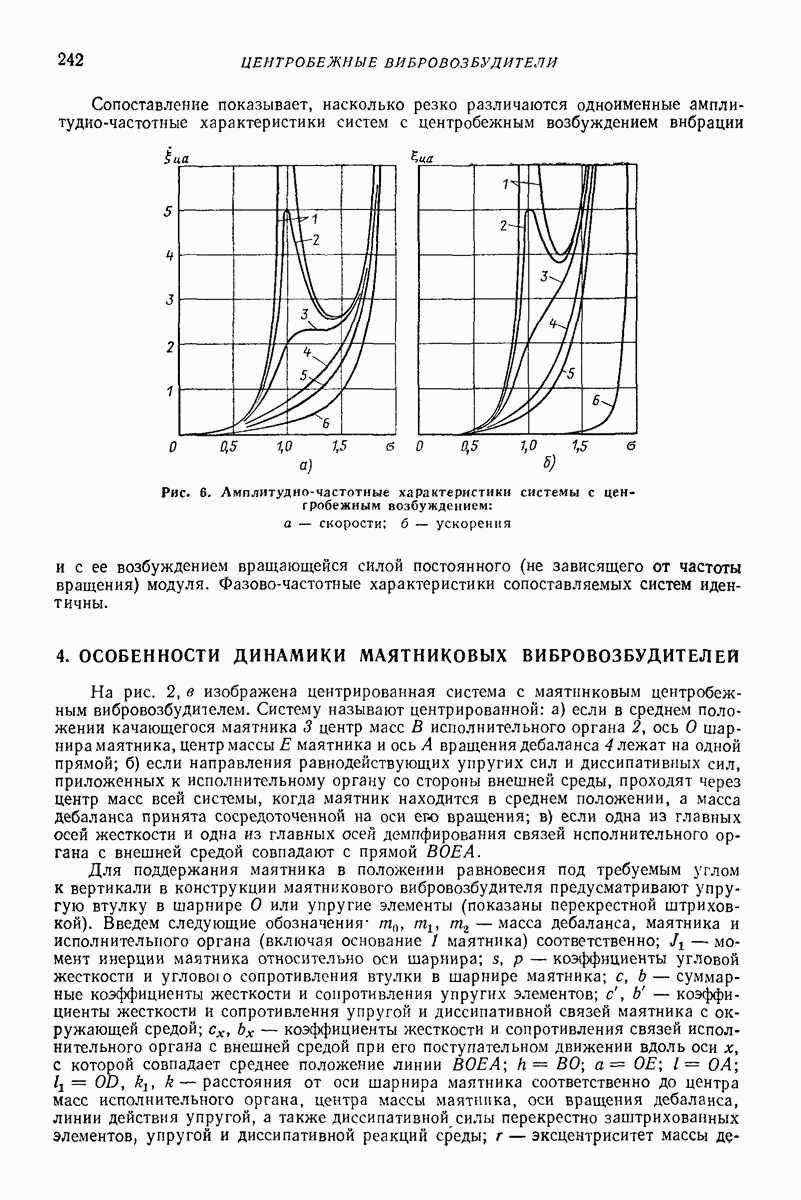
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
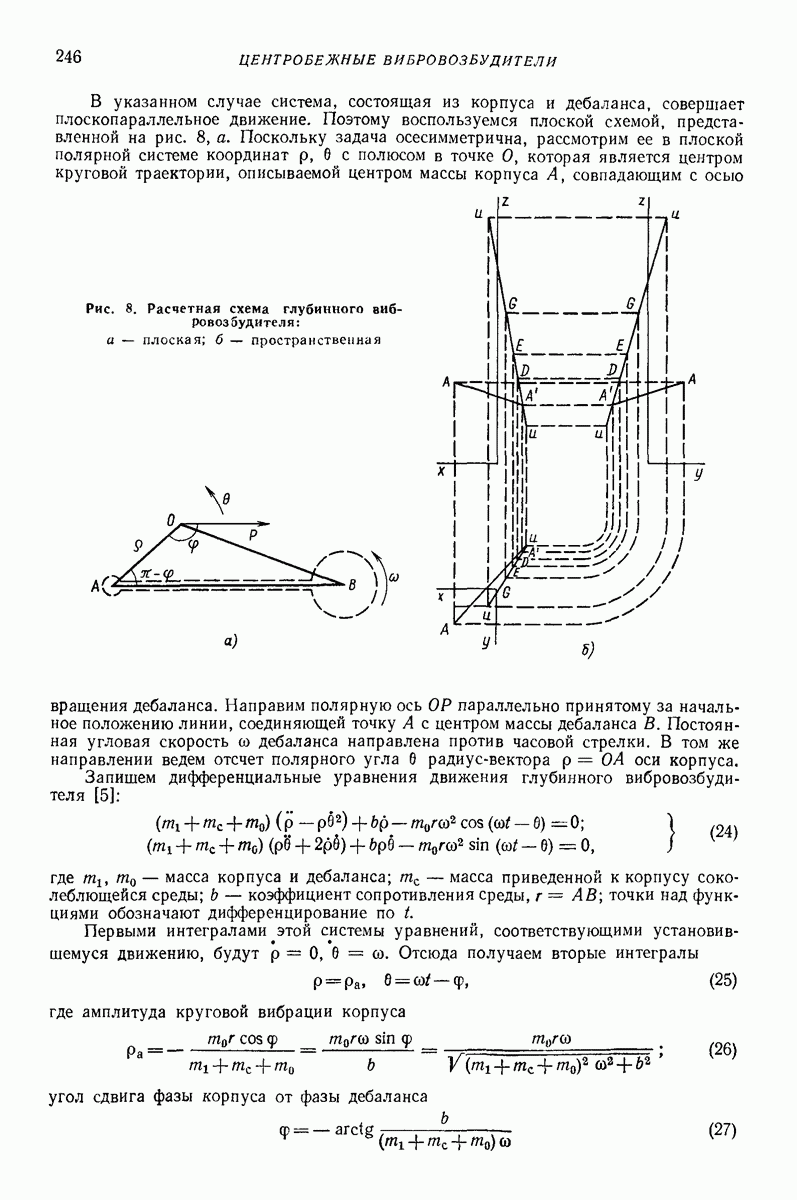
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
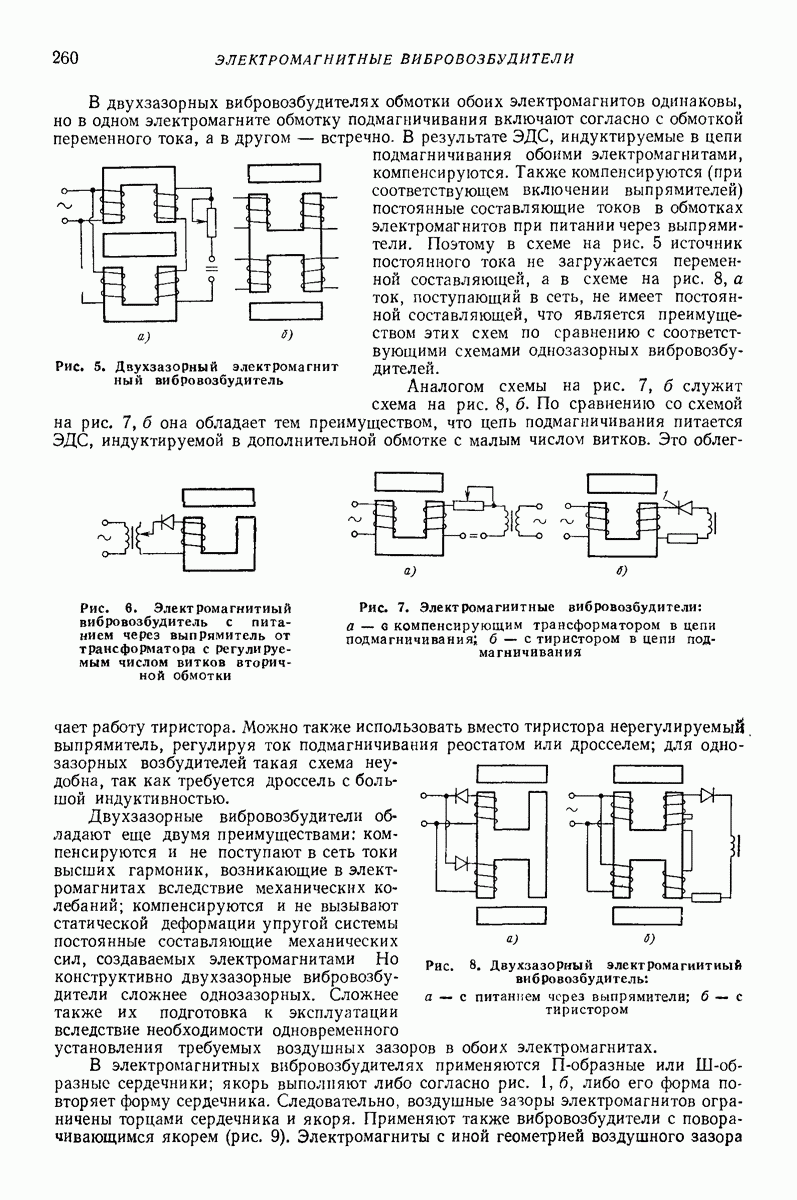
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
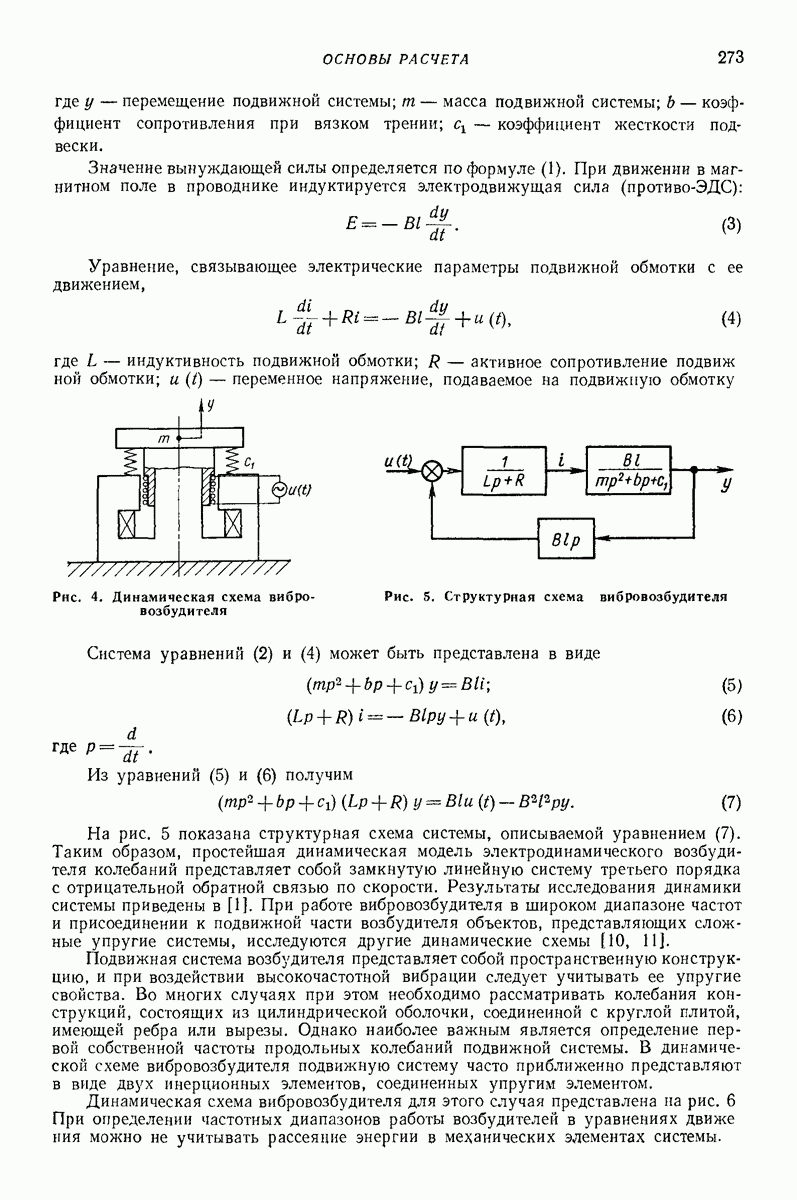
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
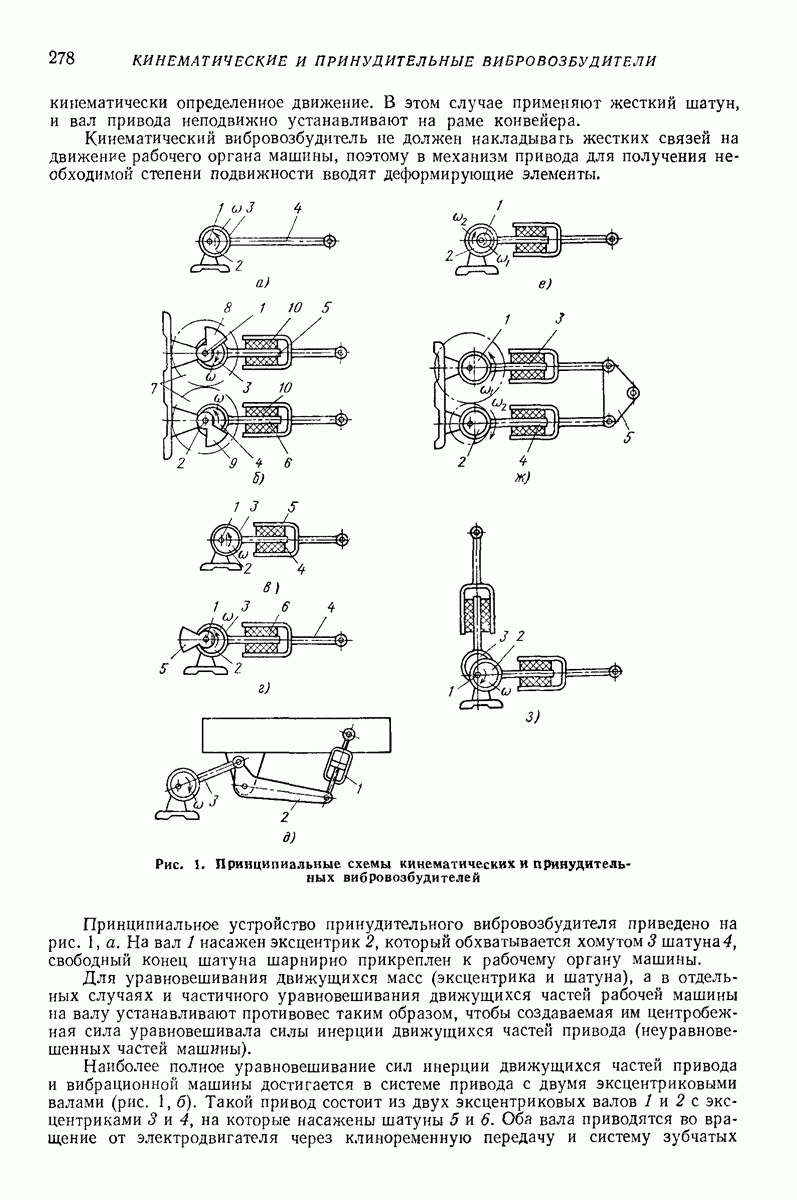
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
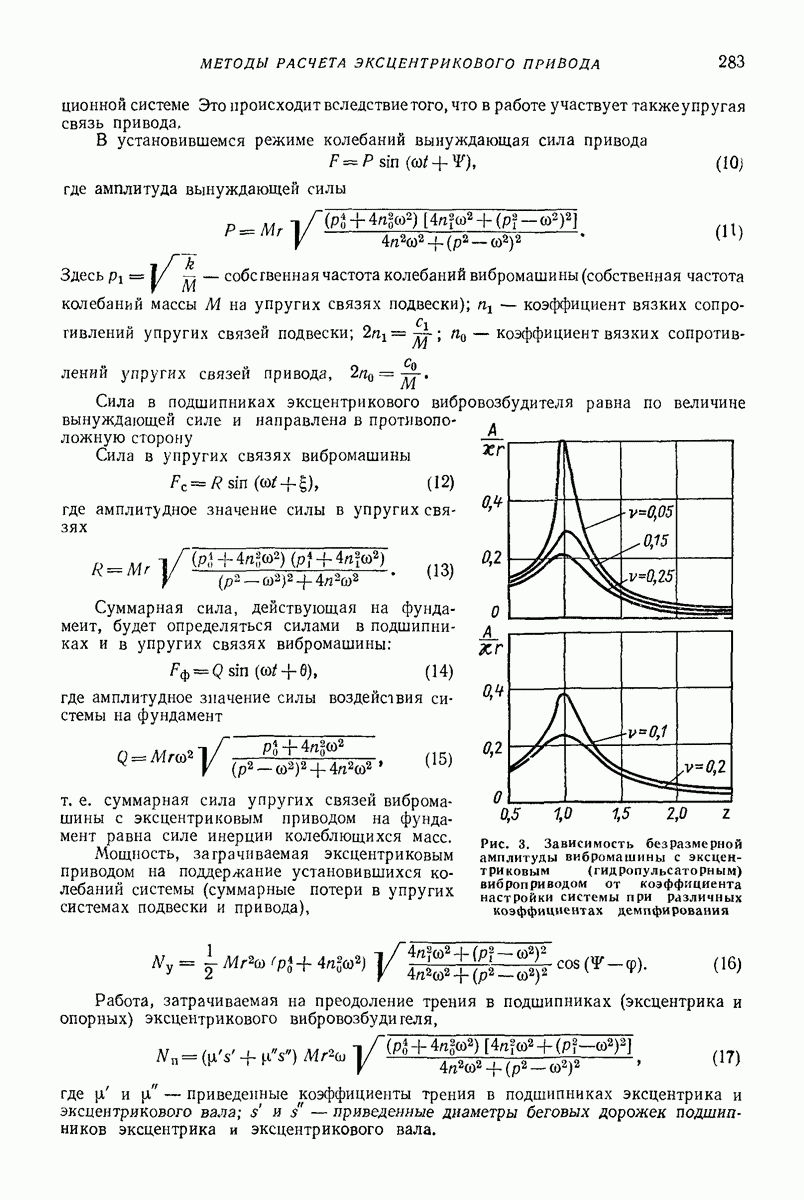
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
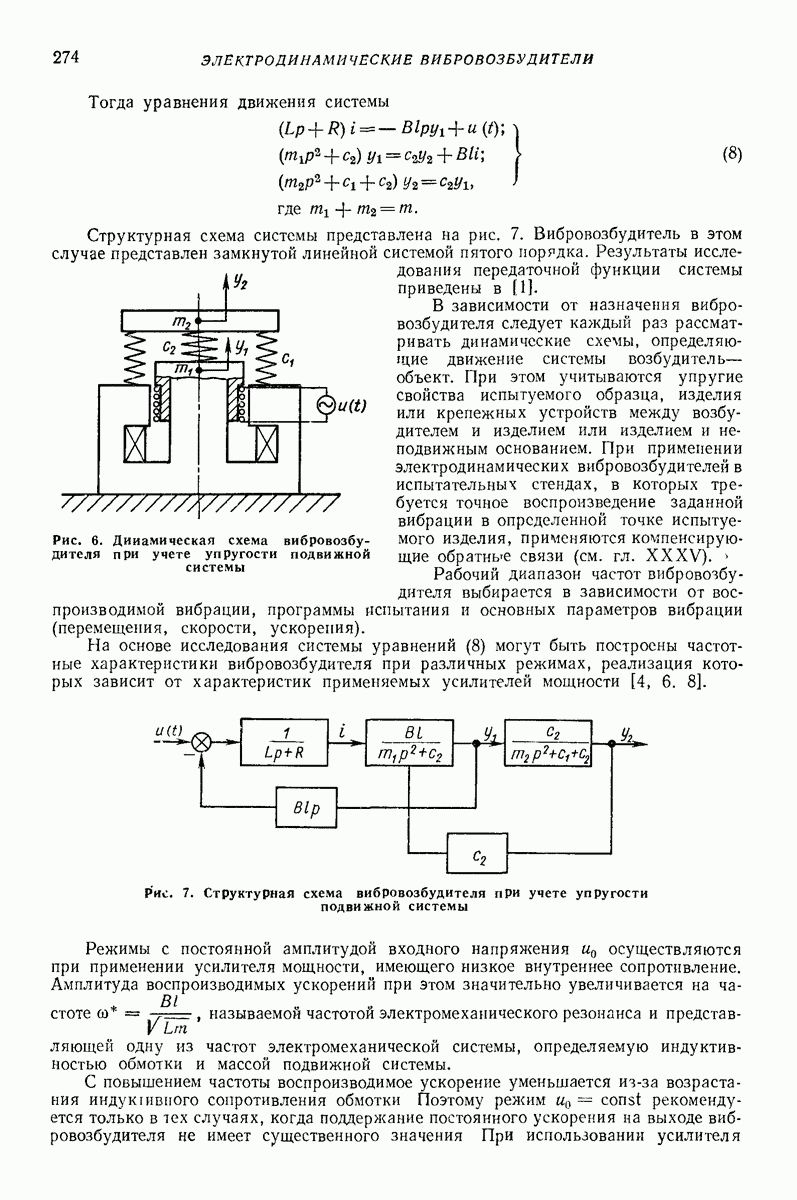
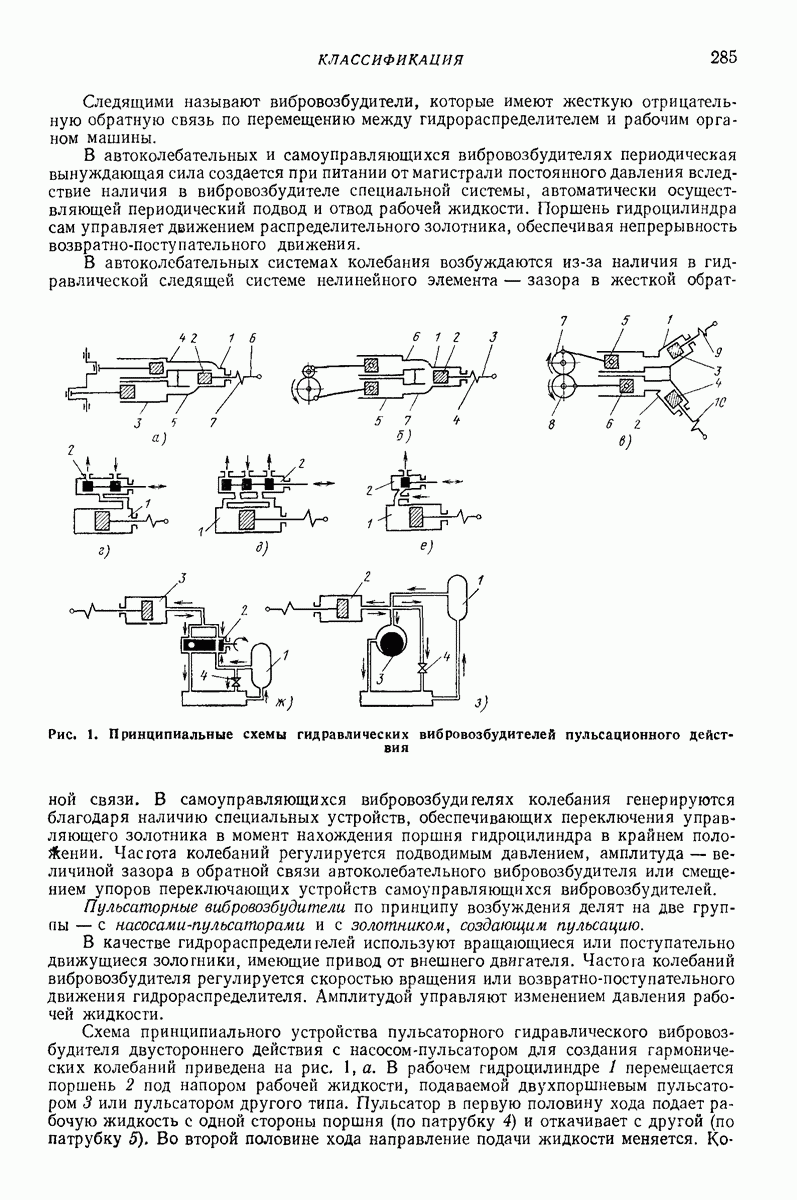
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
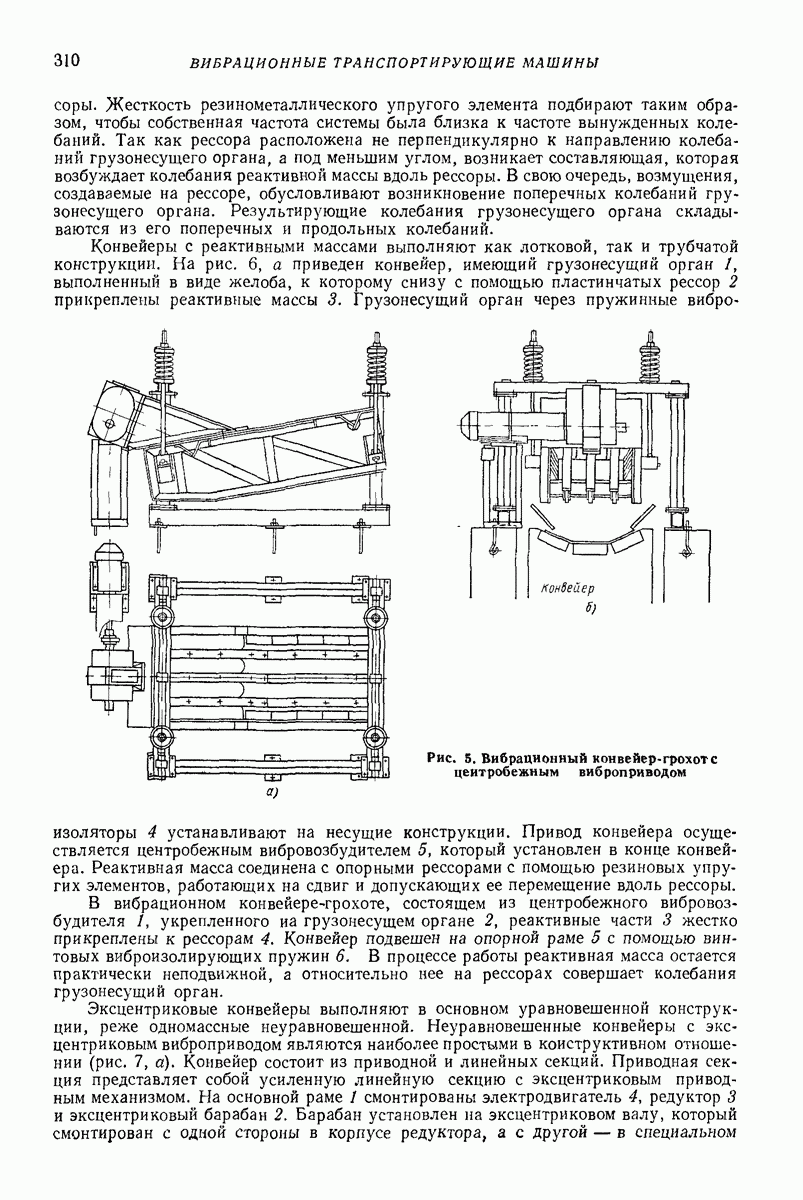
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
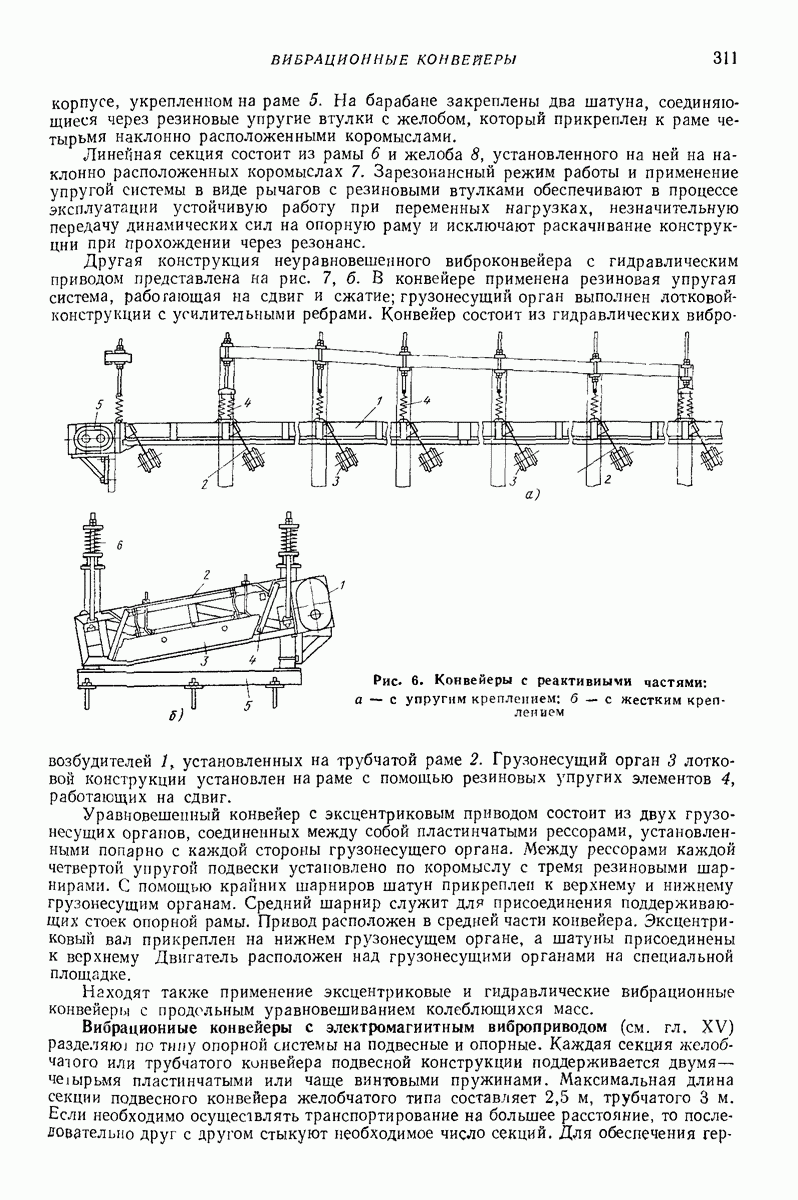
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
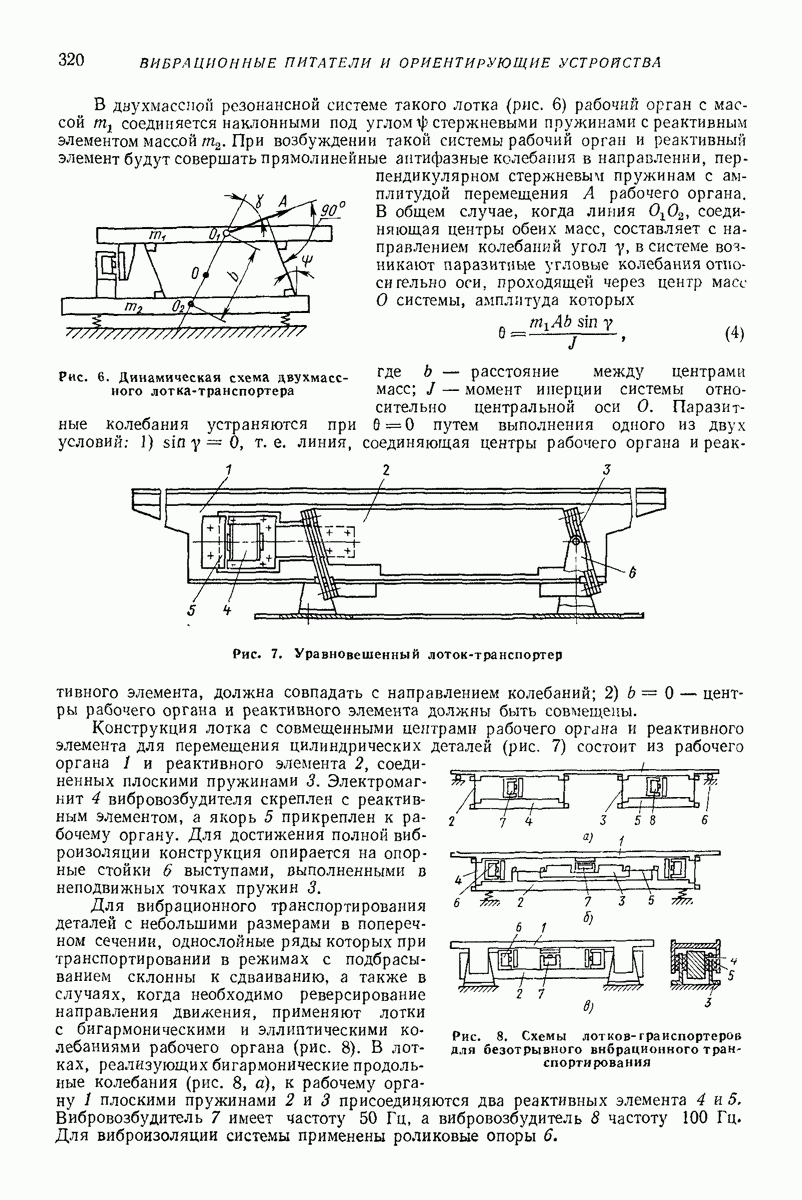
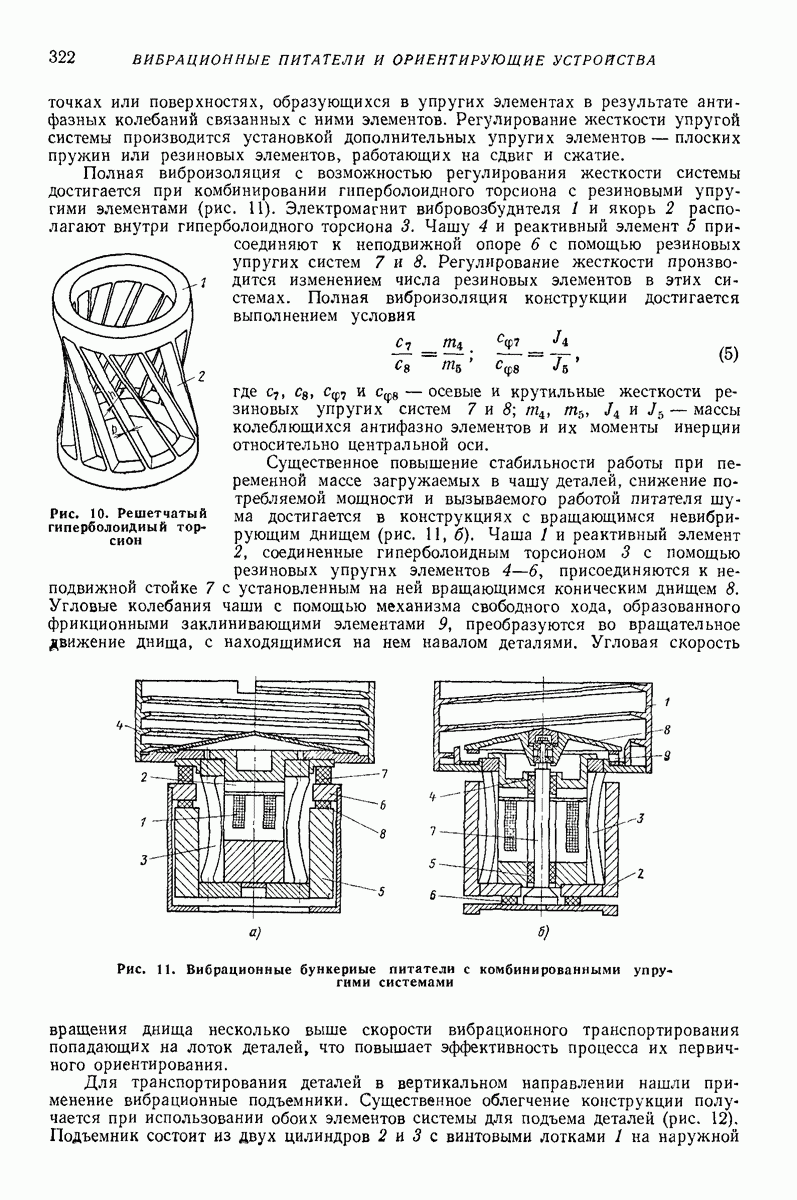
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
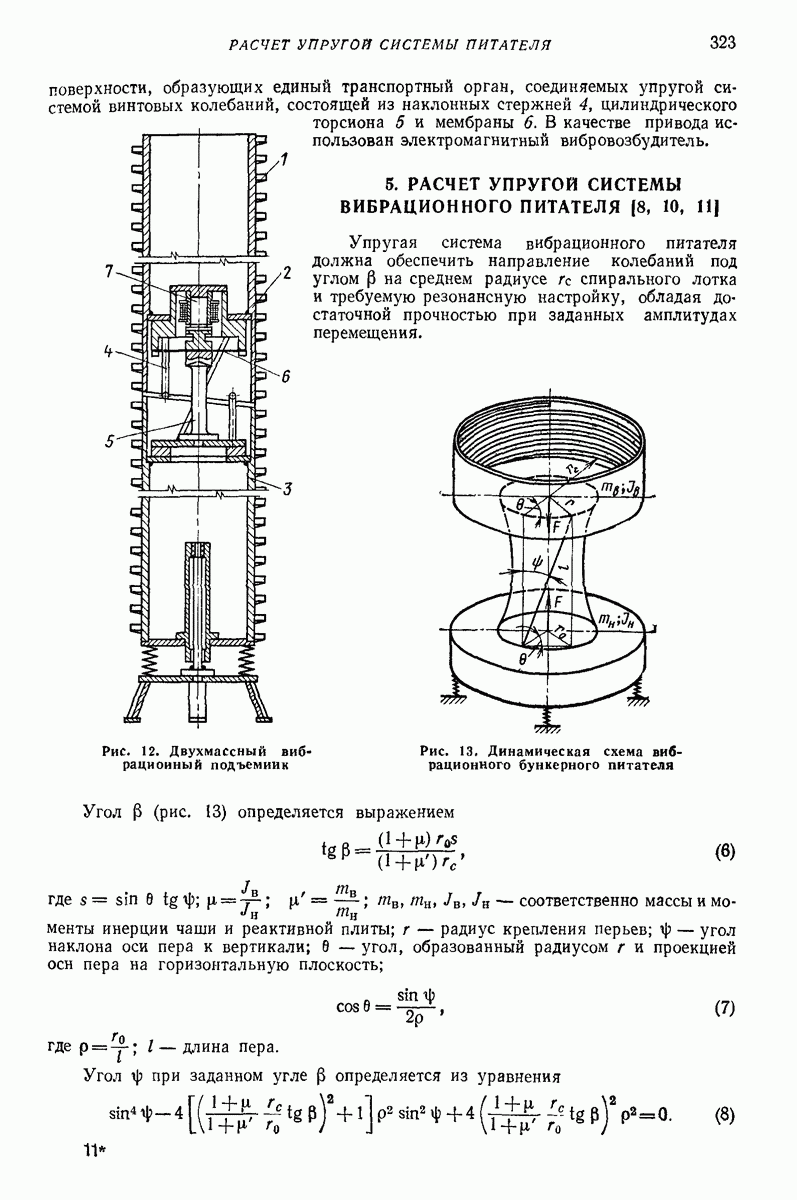
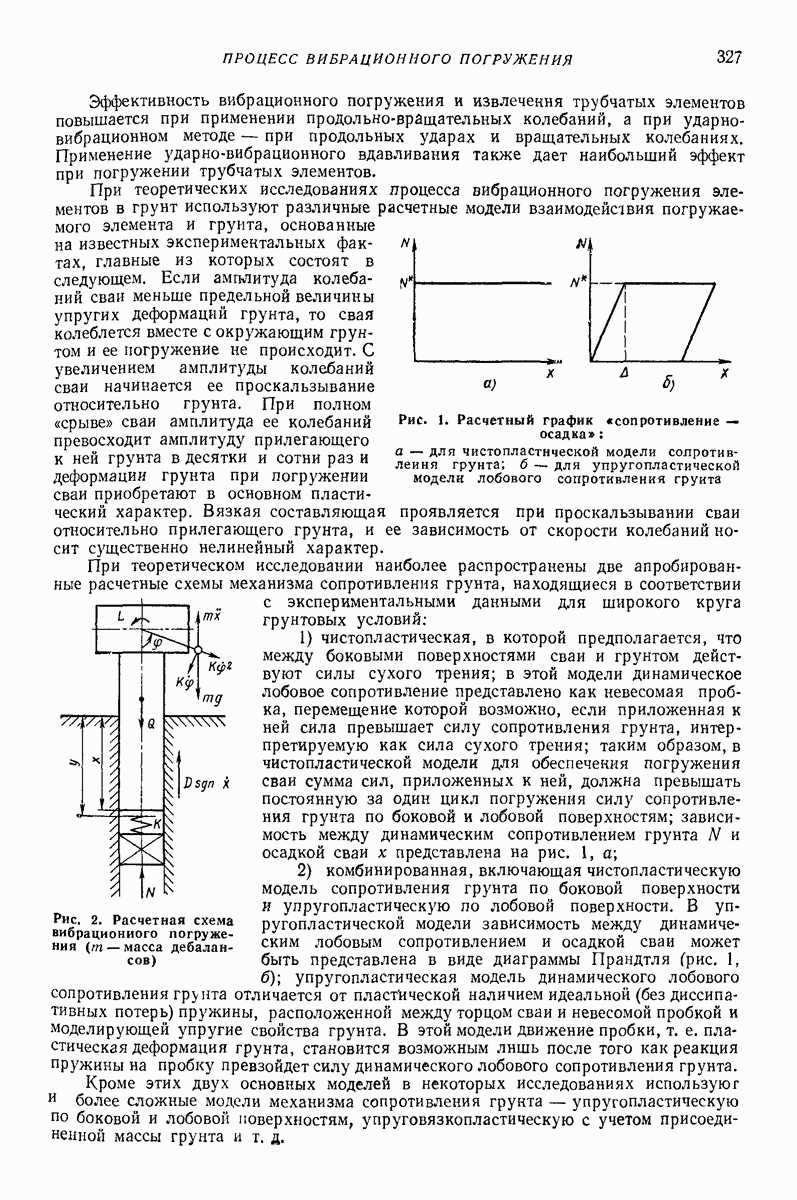
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
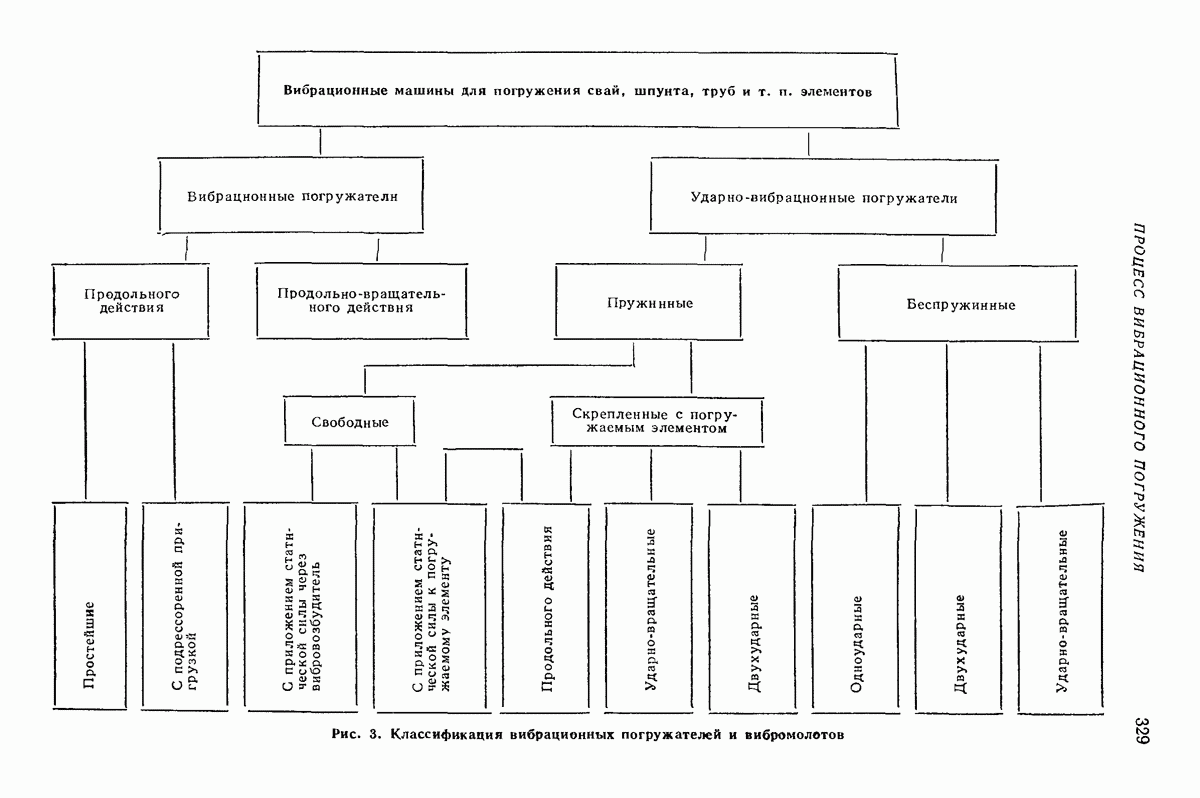
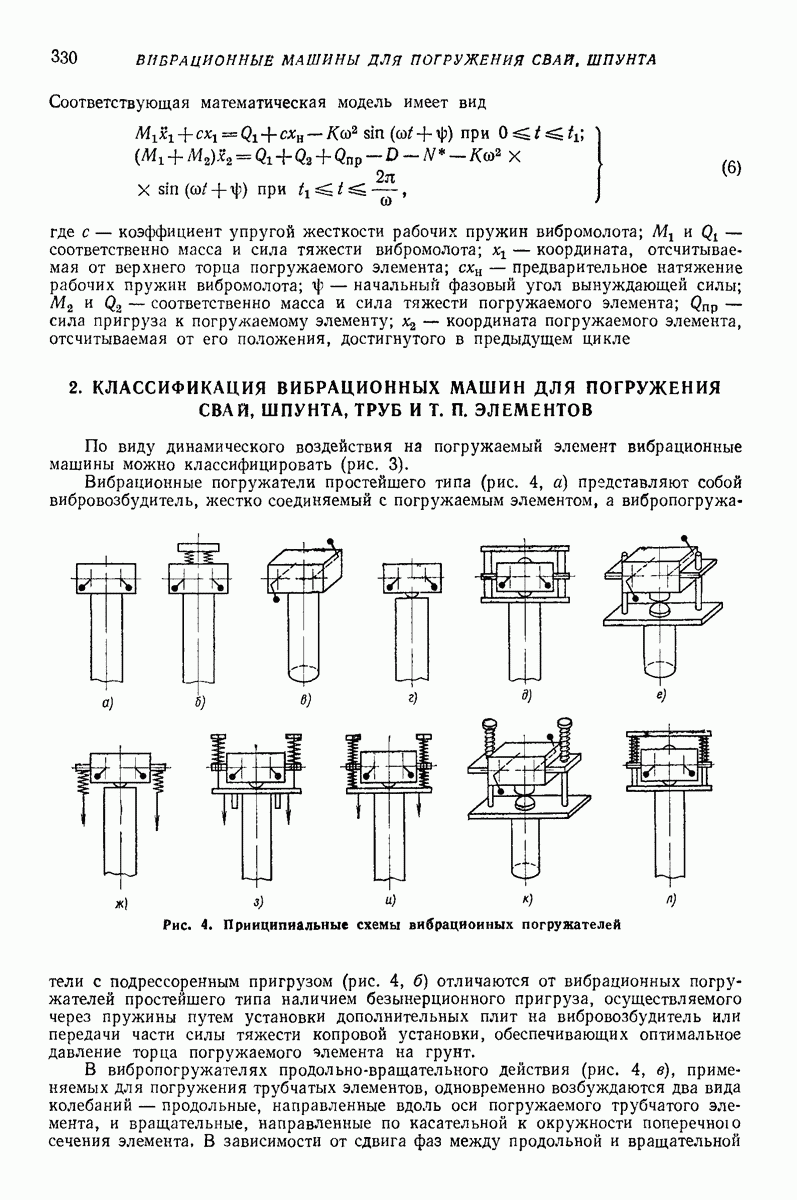
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
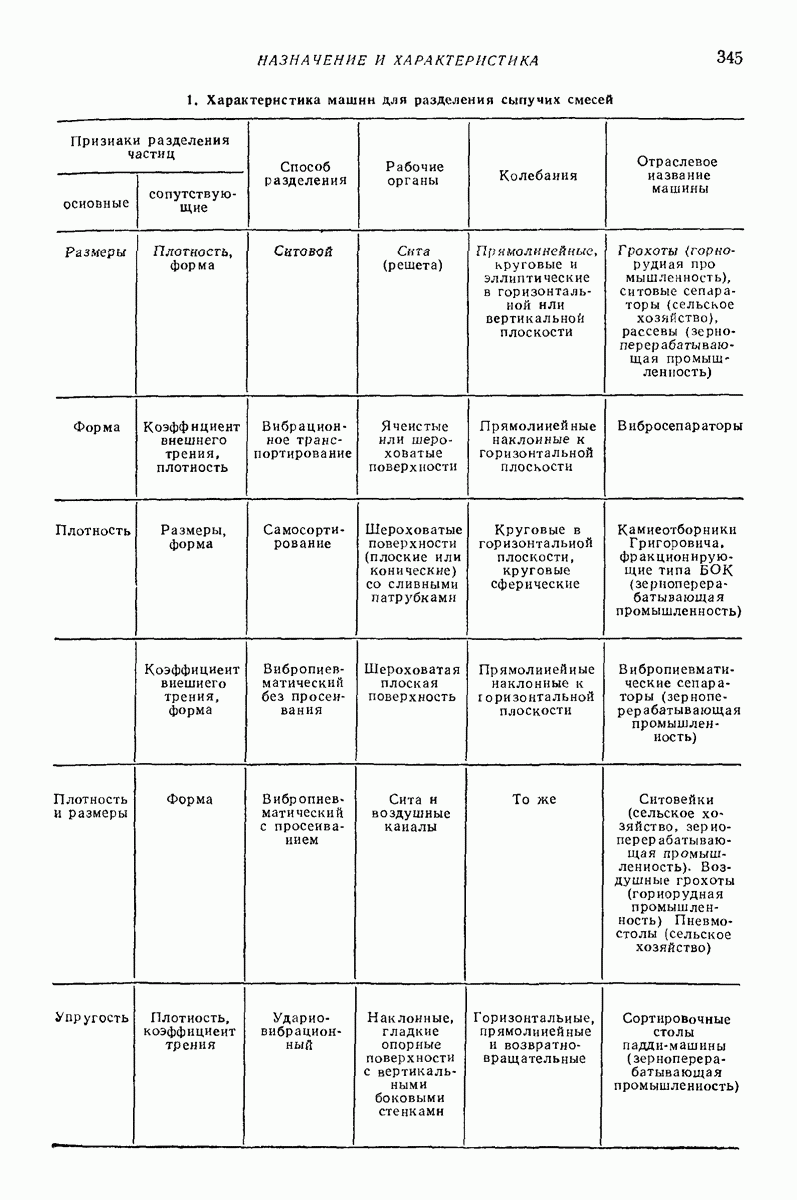
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
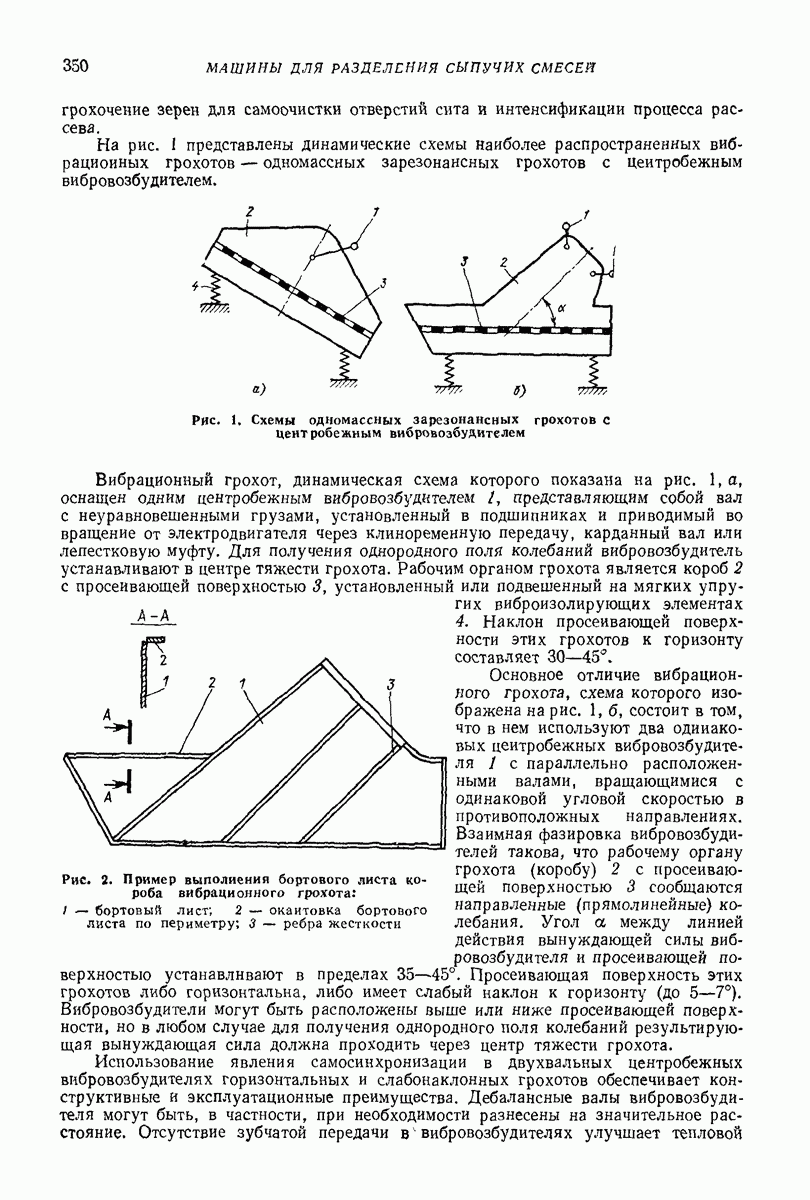
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
- 4. СЕПАРАТОРЫ С ДЕКОЙ
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
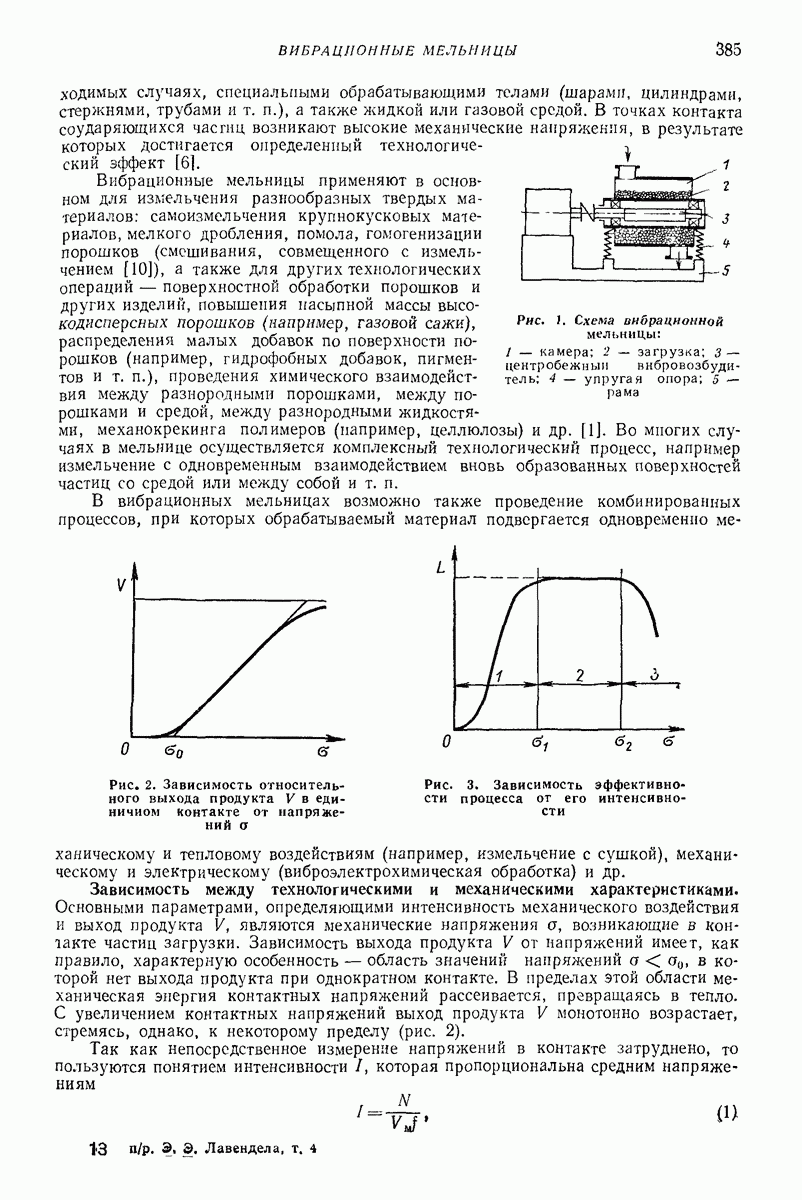
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
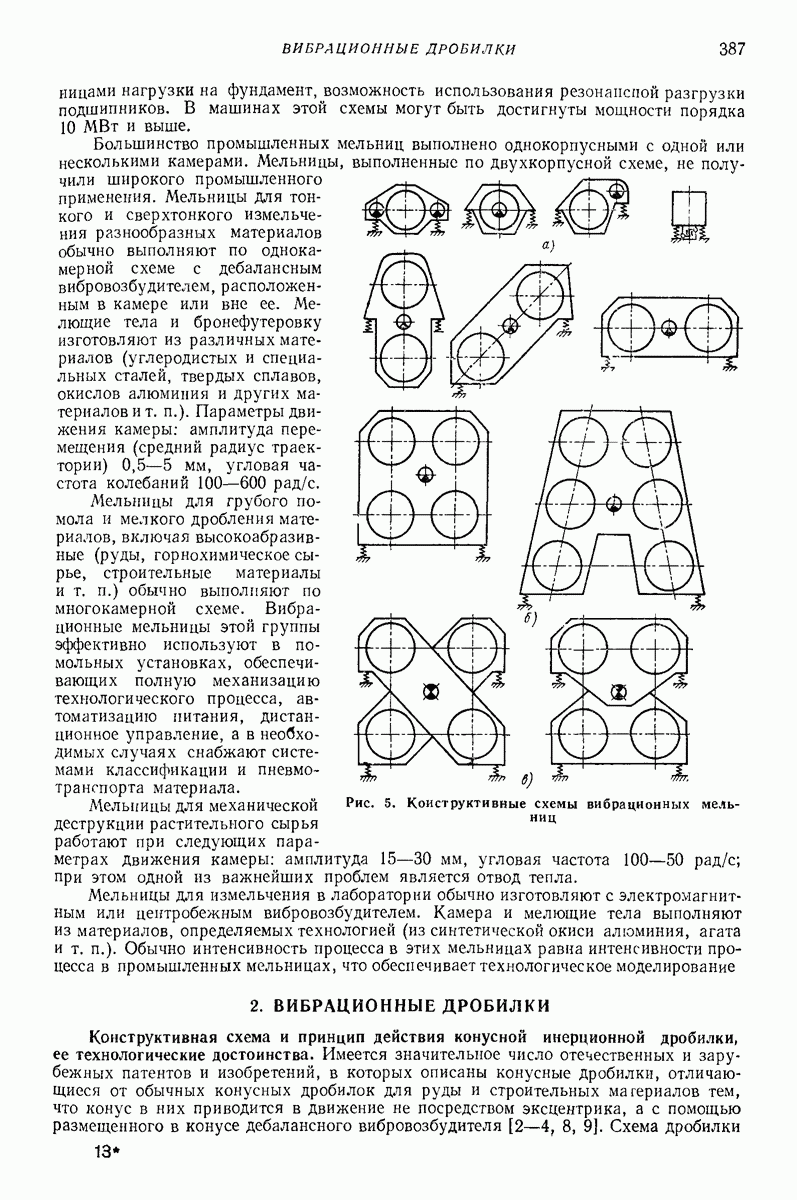
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
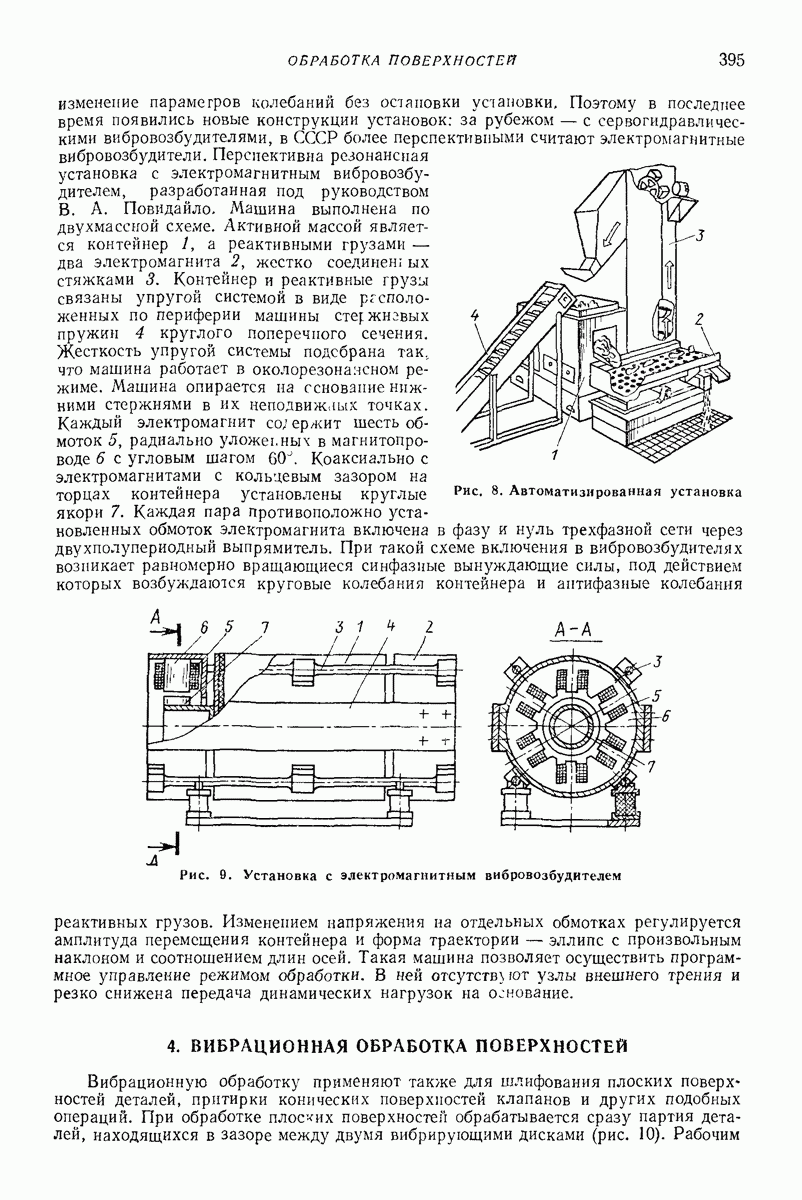
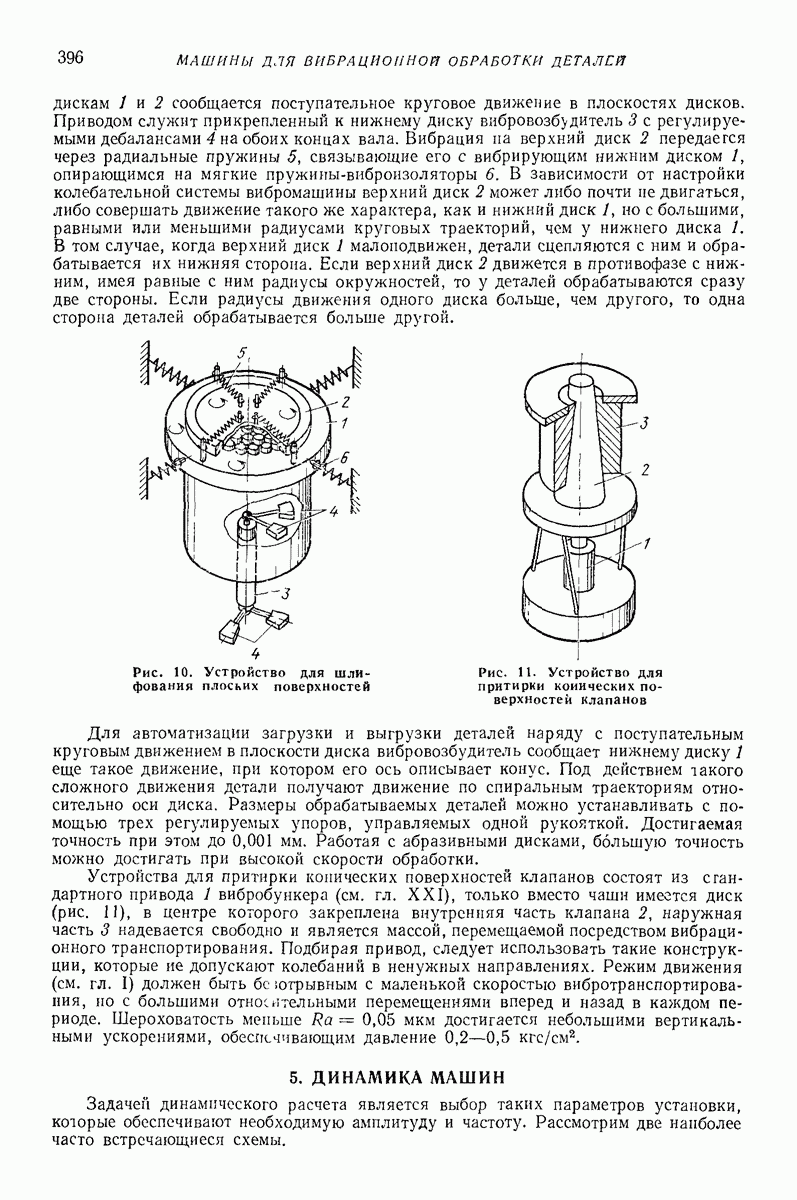
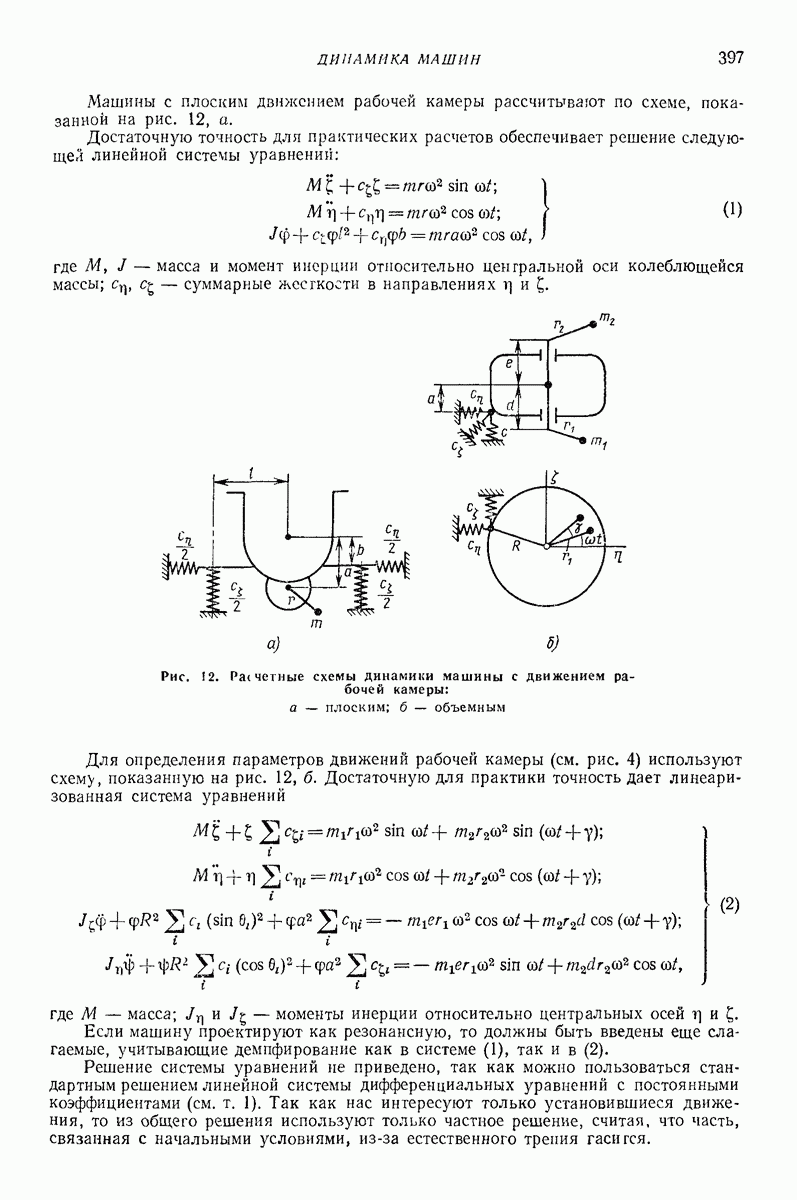
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
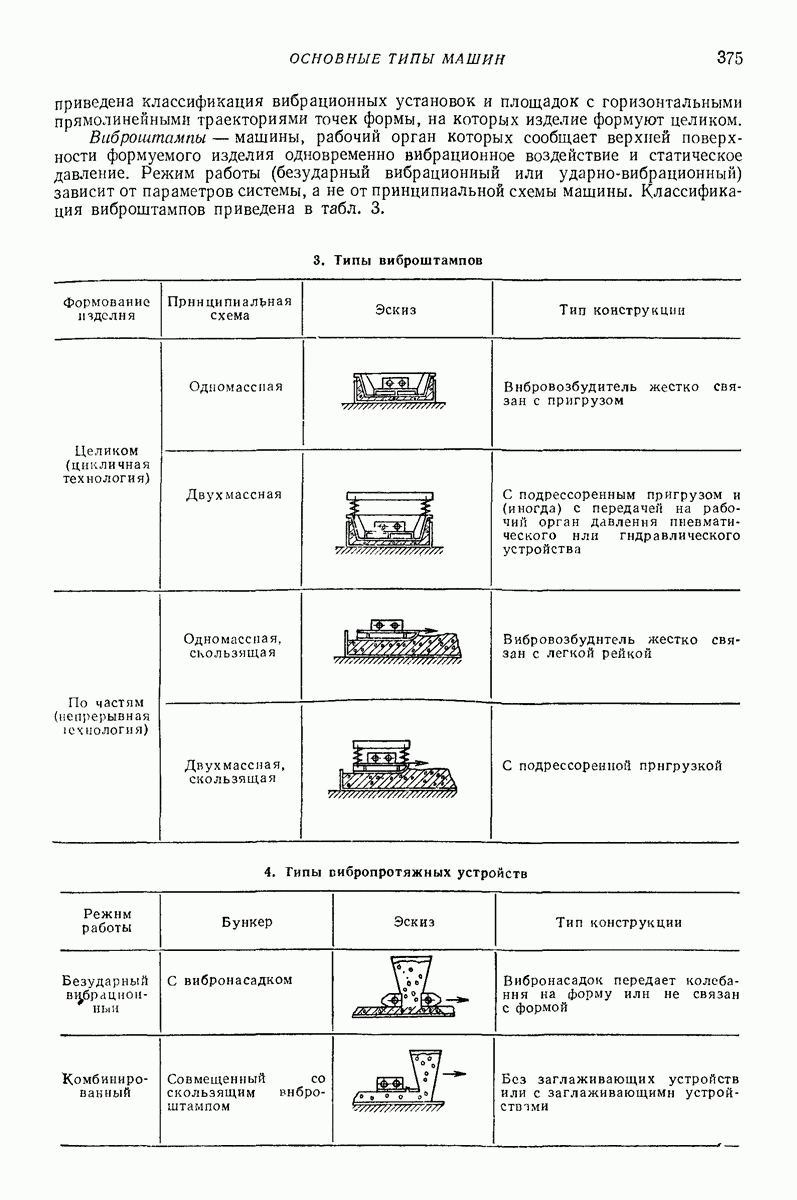
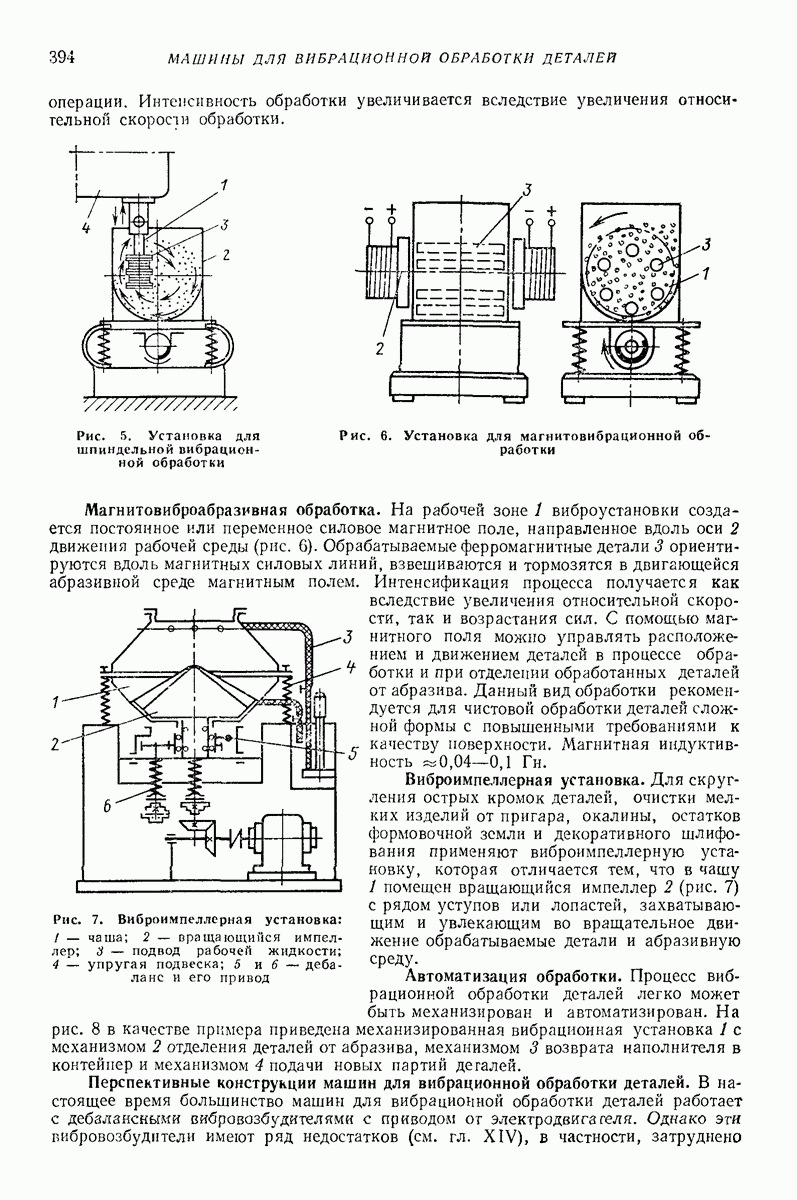
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ