| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
Постановка задачи. Для некоторых приложений представляет интерес исследование движения материальной частицы, попеременно контактирующей с двумя колеблющимися но разным законам поверхностями. При этом возможны два случая.

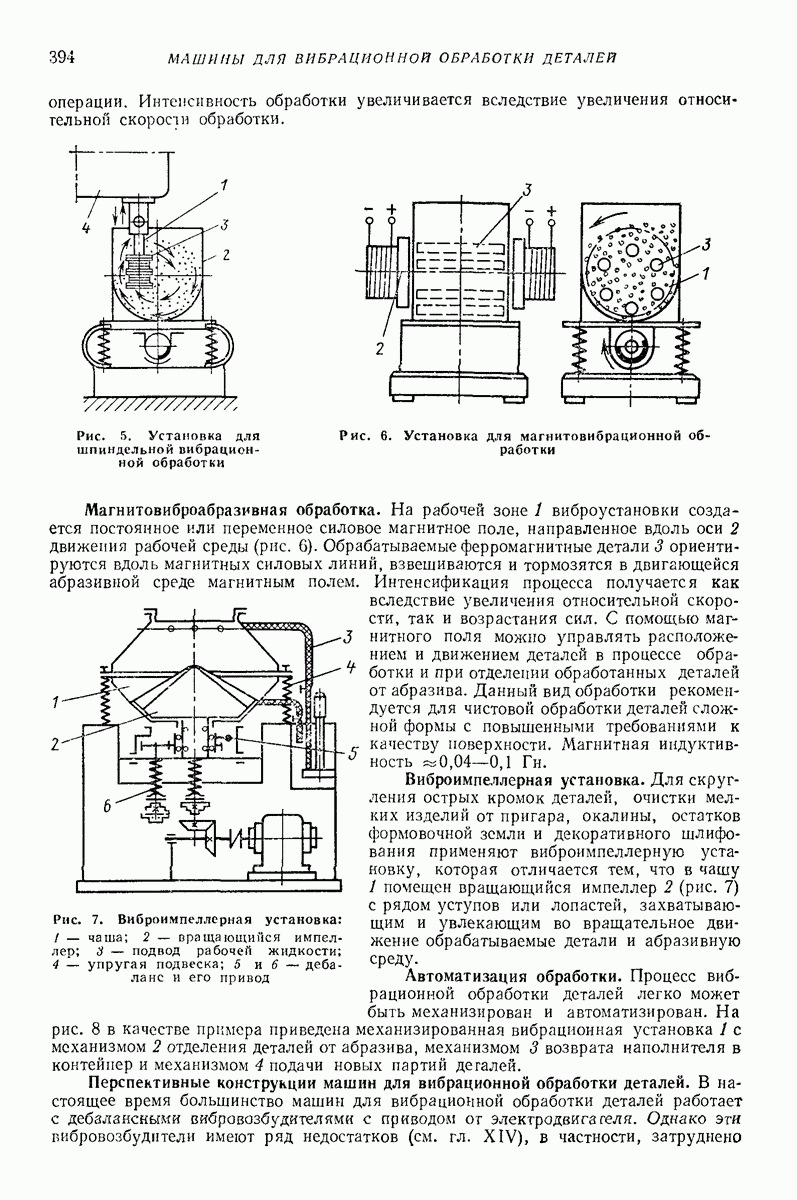
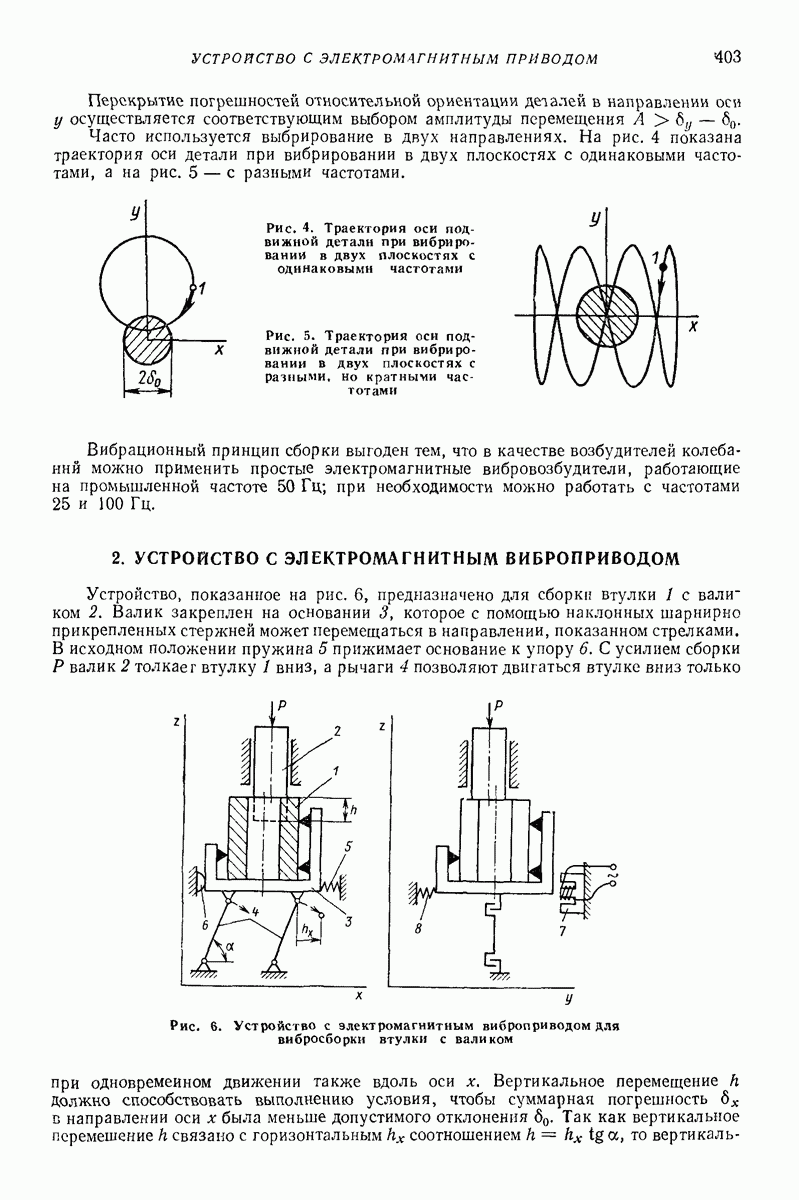
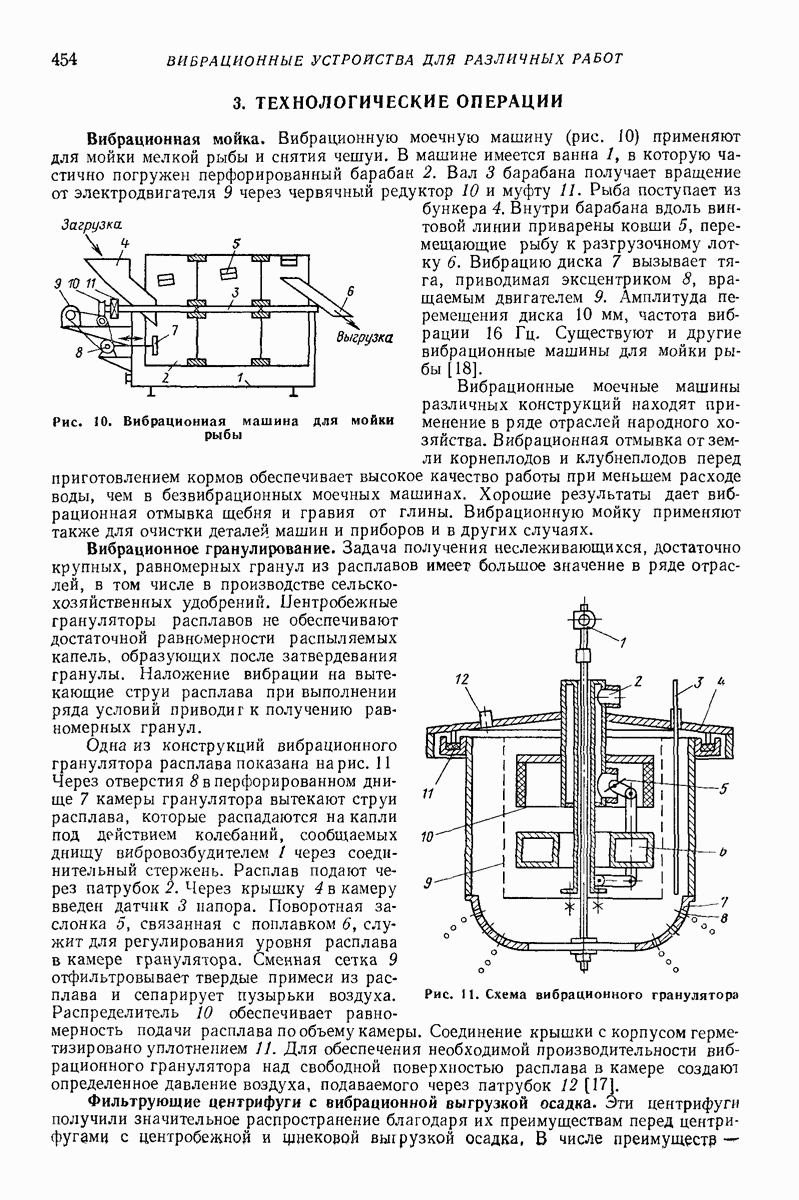
Рис. 30. Частица, попеременно контактирующая с двумя вибрирующими поверхностями (внешняя задача)
В первом случае, который назовем внешней задачей, поверхности как бы пронизывают одна другую в процессе колебаний, так что частица в определенный момент времени может контактировать только с той поверхностью, которая занимает в этот момент верхнее положение. Этот случай представлен на рис. 30, а (1 и 2 — соответственно первая и вторая поверхности и траектории некоторых точек  этих поверхностей). Такой случай реализуется, например, в грохоте, просеивающая поверхность которого образуется двумя группами прямых цилиндрических стержней (рис 30, б) причем стержни группы 1 жестко связаны с одним вибрирующим телом, а стержни группы 2 — с другим; в процессе колебаний стержни каждой группы оказываются попеременно то выше, то ниже стержней другой группы [7, 38]
этих поверхностей). Такой случай реализуется, например, в грохоте, просеивающая поверхность которого образуется двумя группами прямых цилиндрических стержней (рис 30, б) причем стержни группы 1 жестко связаны с одним вибрирующим телом, а стержни группы 2 — с другим; в процессе колебаний стержни каждой группы оказываются попеременно то выше, то ниже стержней другой группы [7, 38]
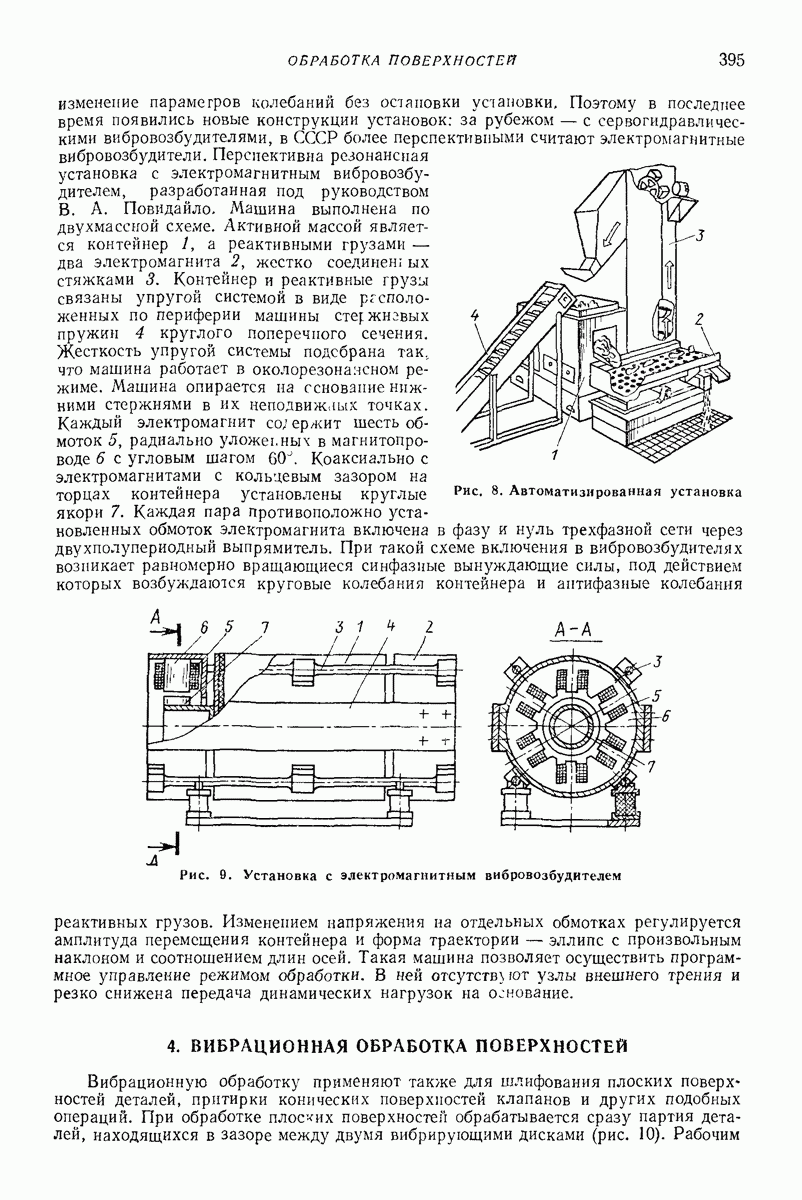
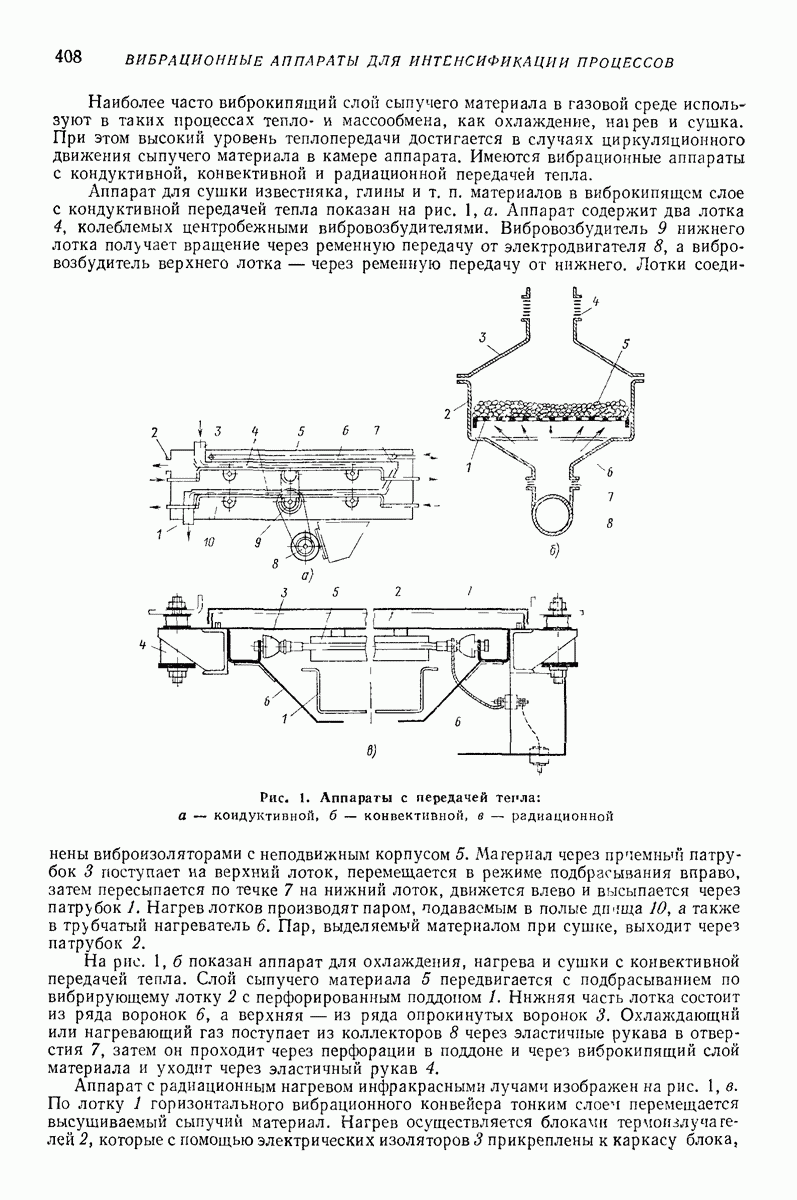
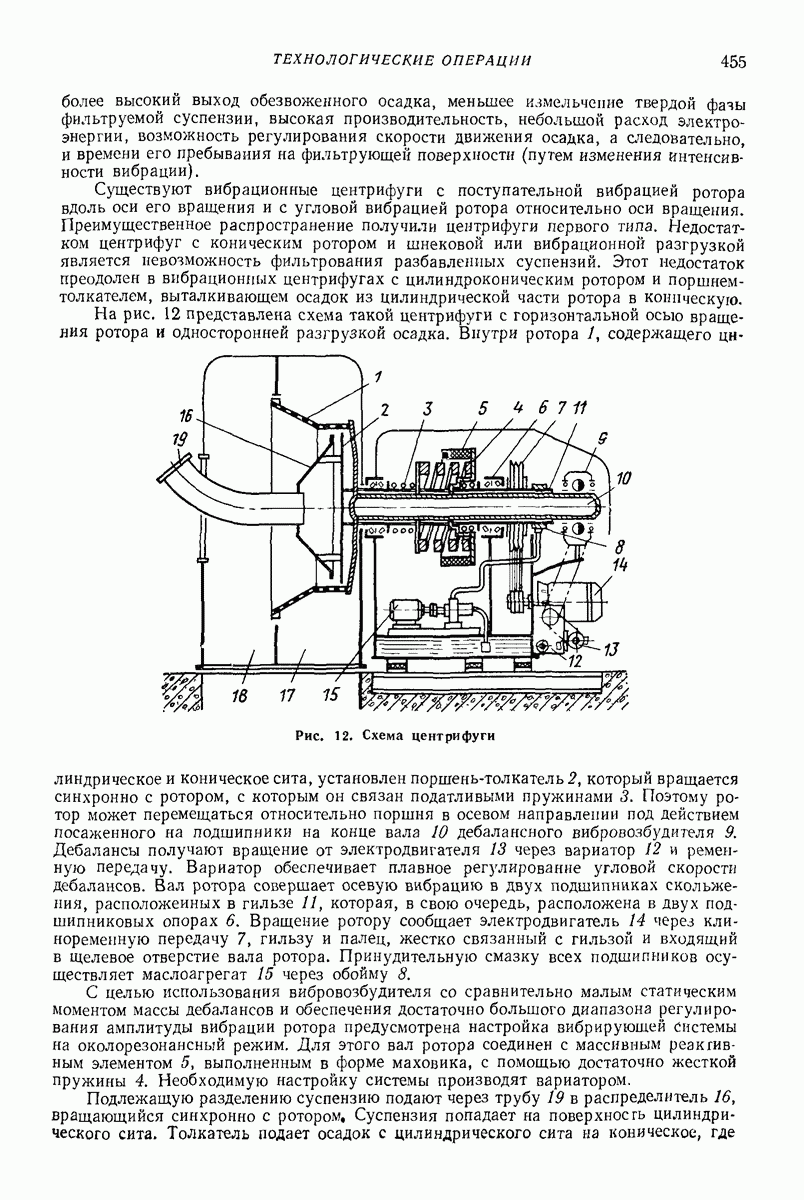
Во втором случае (назовем его внутренней задачей) частица движется в пространстве между двумя вибрирующими поверхностями, соприкасаясь в процессе движения с каждой из них (рис. 31) Изучение такого случая представляет интерес в связи
с теорией щековых и конусных дробилок для разрушения горных пород и строительных материалов [8], теорией некоторых зерноочистительных машин [18], а также устройств, предложенных для подъема грузов в вибрирующих трубах вертикально или под большим наклоном [9, 23].
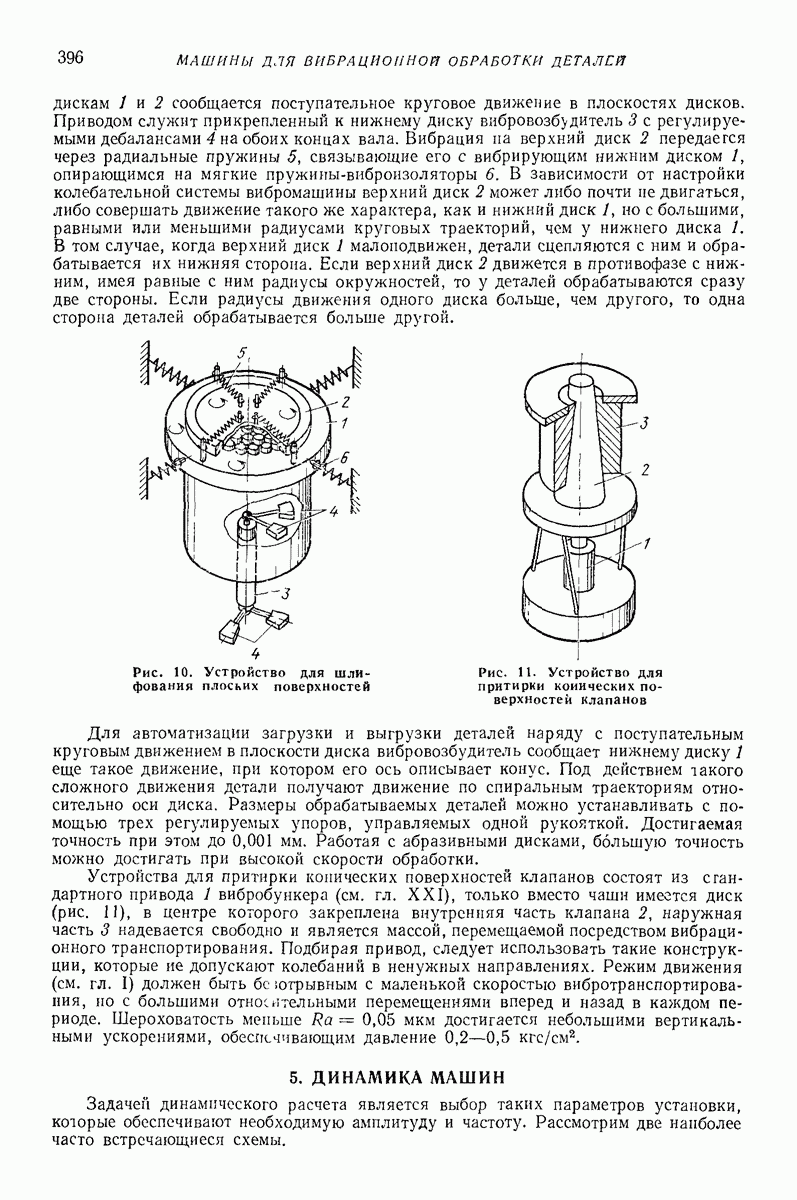
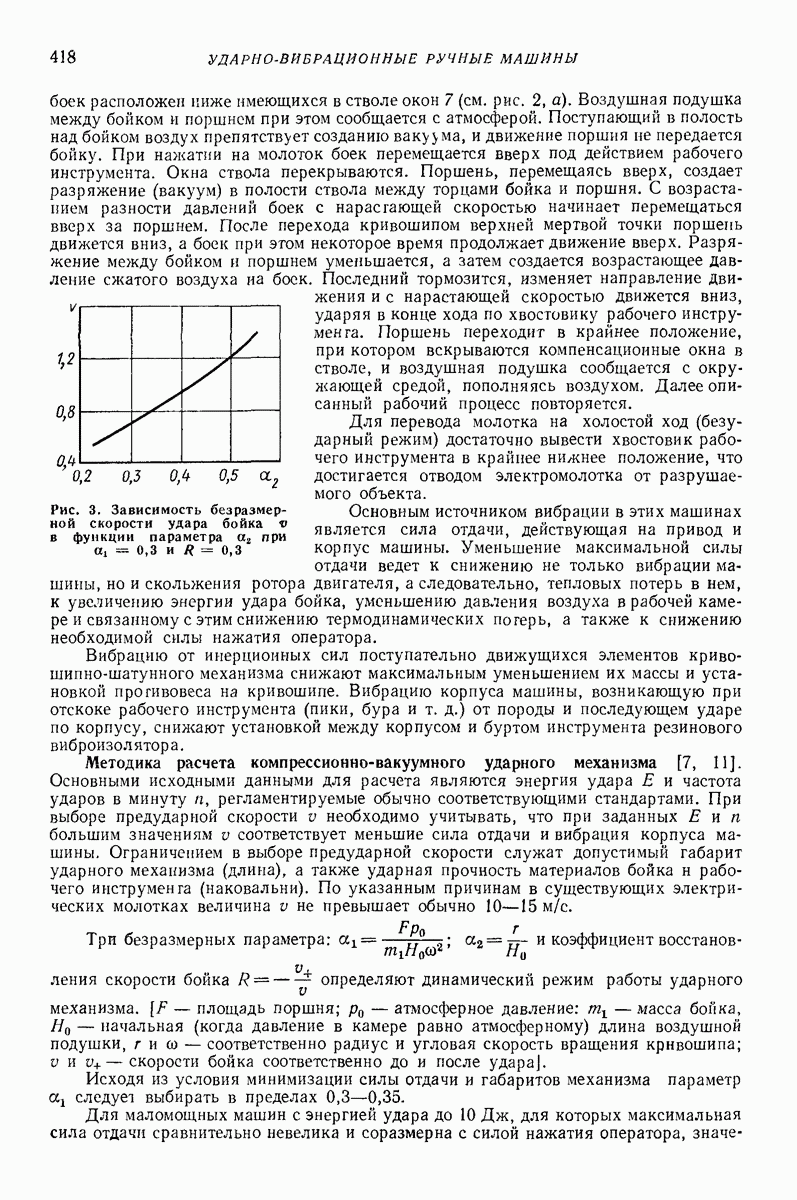
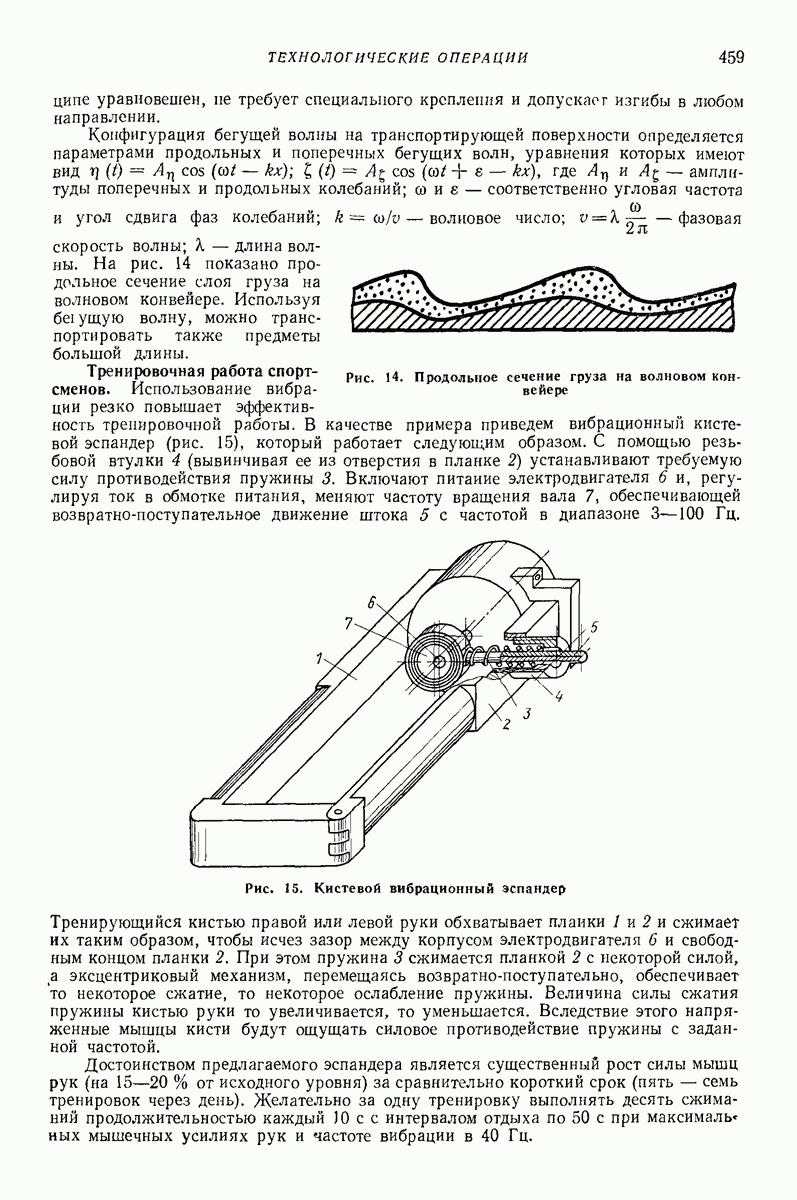
Внешняя задача. Случай гармонических антифазных поперечных колебаний плоских поверхностей [7]. Для многих приложений достаточно рассмотреть случай, когда вибрирующие поверхности представляют собой параллельные наклонные плоские поверхности (рис. 32), совершающие плоские поступательные колебания с одинаковым периодом  траектории которых параллельны плоскости наибольшего ската.
траектории которых параллельны плоскости наибольшего ската.

Рис. 31. Частица, попеременно контактирующая с двумя вибрирующими поверхностями (внутренняя задача)

Рис. 32. Случай параллельных плоских поверхностей в условиях внешней задачи
Пусть  неподвижная система координат, в которой ось
неподвижная система координат, в которой ось  наклонена к горизонту под углом а. Пусть далее
наклонена к горизонту под углом а. Пусть далее  и
и  — системы, связанные с вибрирующими плоскостями 1 и 2 и лежащие в плоскости наибольшего ската. В процессе колебаний абсолютные координаты и
— системы, связанные с вибрирующими плоскостями 1 и 2 и лежащие в плоскости наибольшего ската. В процессе колебаний абсолютные координаты и  точек
точек  и
и  определяются соотношениями
определяются соотношениями

в которых и  и
и  периодические функции времени
периодические функции времени  с некоторым периодом
с некоторым периодом 
Допустим далее, что плоскость 2 в процессе своего движения периодически «пронизывает» плоскость 1, оказываясь попеременно то выше, то ниже ее.
Очевидно, что задача о движении тела по описанной системе двух вибрирующих поверхностей равносильна задаче о движении тела по одной поверхности (назовем ее эквивалентной), колеблющейся по закону

с тем же периодом  т. е. из двух функций с индексами 1 и 2 берется та, для которой
т. е. из двух функций с индексами 1 и 2 берется та, для которой  больше. В моменты времени
больше. В моменты времени  удовлетворяющие равенству
удовлетворяющие равенству  в моменты, отвечающие совпадению вибрирующих поверхностей, проекции скоростей
в моменты, отвечающие совпадению вибрирующих поверхностей, проекции скоростей  претерпевают разрыв первого рода. Таким образом, даже при колебаниях каждой из поверхностей с непрерывными во времени скоростями для скорости колебаний эквивалентной поверхности характерны конечные скачки в некоторые дискретные моменты времени. В результате рассматриваемое устройство позволяет получить преимущества, предоставляемые ударно-вибрационным приводом, и избежать в то же время его недостатка — высоких нагрузок на рабочий орган и
претерпевают разрыв первого рода. Таким образом, даже при колебаниях каждой из поверхностей с непрерывными во времени скоростями для скорости колебаний эквивалентной поверхности характерны конечные скачки в некоторые дискретные моменты времени. В результате рассматриваемое устройство позволяет получить преимущества, предоставляемые ударно-вибрационным приводом, и избежать в то же время его недостатка — высоких нагрузок на рабочий орган и
элементы привода. Этим частично и объясняются технологические достоинства устройств рассматриваемого типа.
Наибольший практический интерес представляет случай движения частицы с отрыгом от вибрирующих поверхностей. Такое движение непременно будет иметь место, если существукп интервалы времени, когда выполняется соотношение

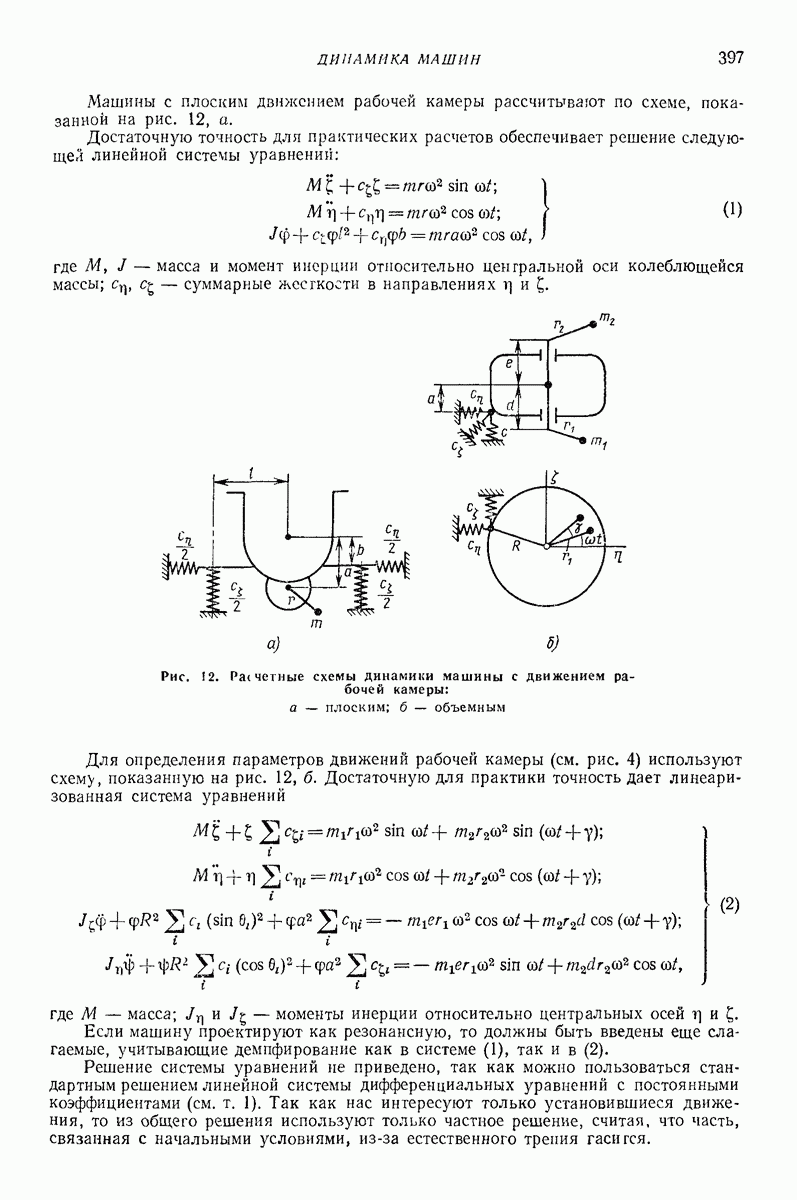
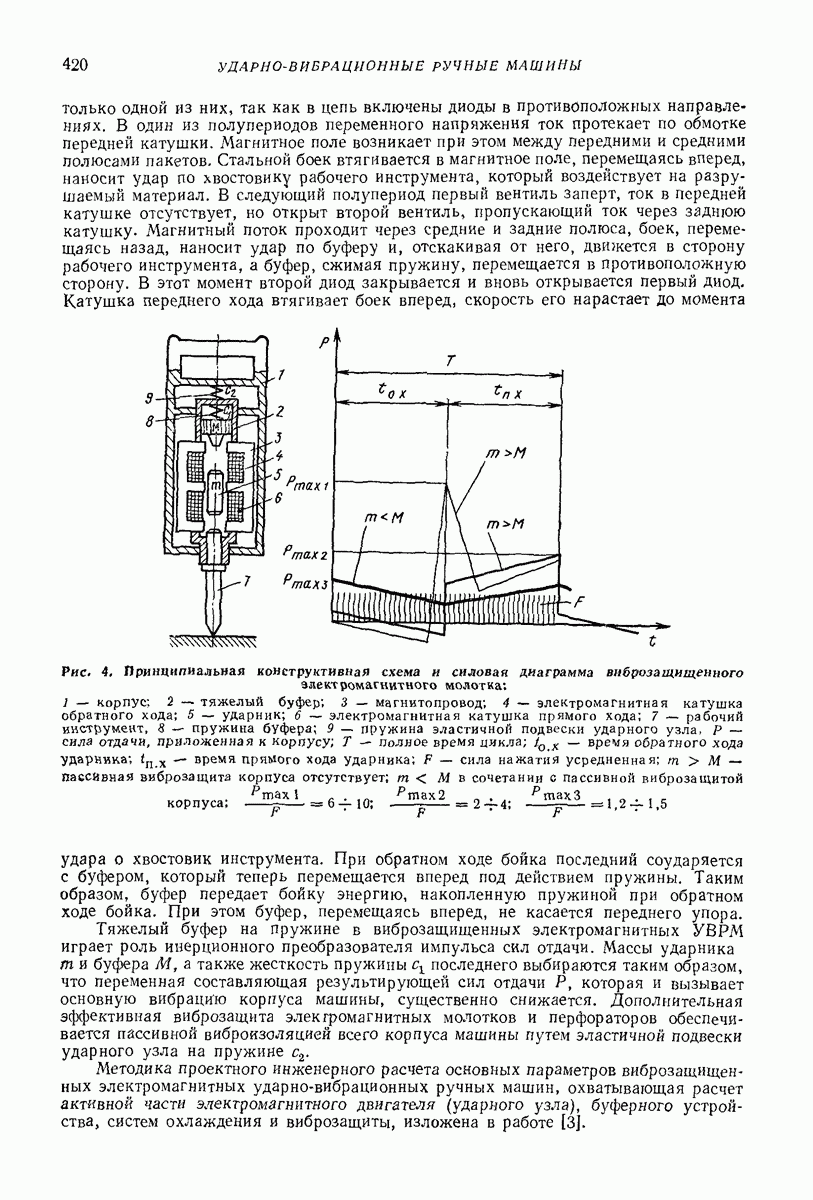
Такие интервалы будем называть интервалами II; моменты времени  для которых неравенство (90) не выполняется, отнесем к интервалам
для которых неравенство (90) не выполняется, отнесем к интервалам 

Рис. 33. Закон поперечных колебании эквивалентной плоской поверхности в частном случае внешней задачи
Существование и устойчивость режимов движения частицы с отрывом полностью определяется законом колебаний эквивалентной плоской поверхности в поперечном направлении  и не зависит от характера продольных колебаний
и не зависит от характера продольных колебаний  а также от продольного движения частицы; изучение продольных колебаний необходимо лишь при определении средней скорости движения частицы.
а также от продольного движения частицы; изучение продольных колебаний необходимо лишь при определении средней скорости движения частицы.
Приведем основные результаты исследования [7], относящиеся к случаю гармонических поперечных колебаний с одинаковой частотой  с различными амплитудами
с различными амплитудами  и противоположными фазами, т. е.
и противоположными фазами, т. е.

При этом плоские поверхности совпадают в моменты  ±1, ±2,
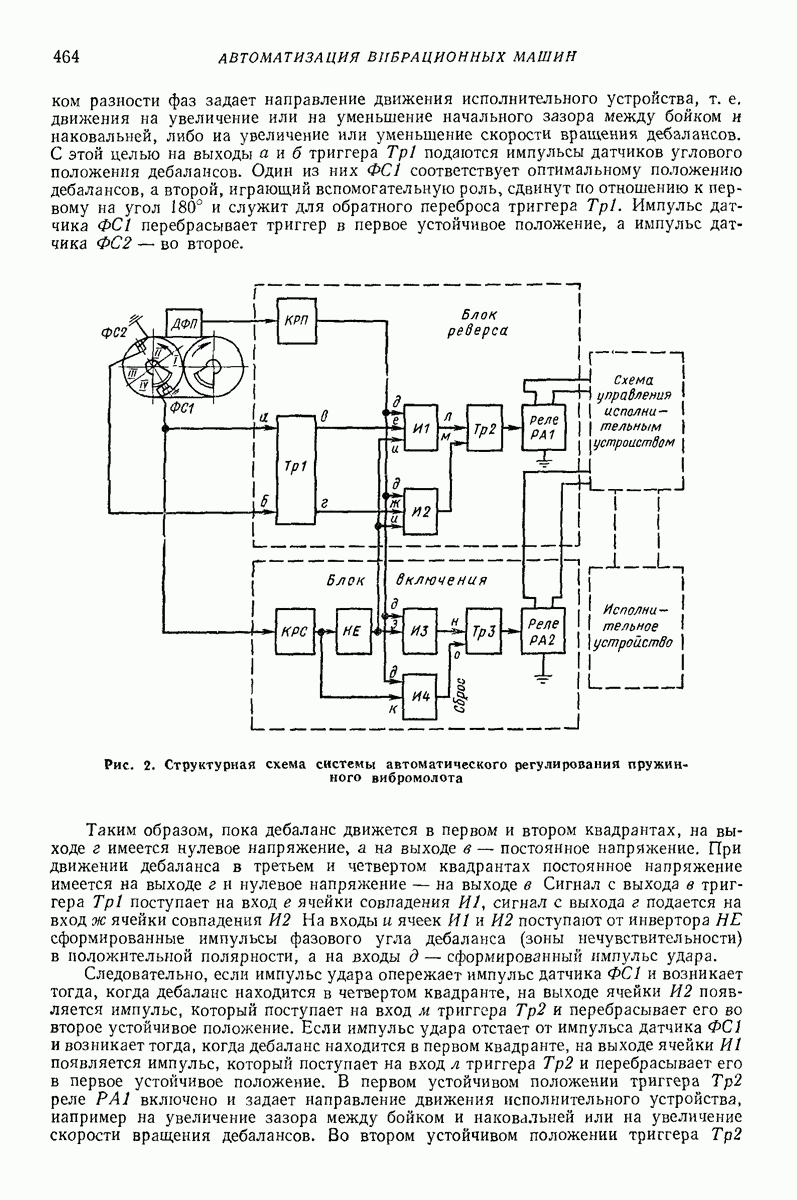
±1, ±2,  а поперечные колебания эквивалентной поверхности определяются соотношениями (рис. 33)
а поперечные колебания эквивалентной поверхности определяются соотношениями (рис. 33)

Соответствующий график представляет собой совокупность полуволн синусоид, причем полуволны с номерами одинаковой четности имеют одинаковые амплитуды.
Условие движения с отрывом (90) в рассматриваемом случае сведется к требованию выполнения, по крайней мере одного из неравенств:

выражающих условия, что амплитудные значения нормальной к плоским поверхностям составляющей ускорения  ) больше нормальной составляющей ускорения силы тяжести
) больше нормальной составляющей ускорения силы тяжести  На рис. 33 эти условия выражаются требованием, чтобы прямая
На рис. 33 эти условия выражаются требованием, чтобы прямая  пересекала полуволны синусоид, причем моментам времени
пересекала полуволны синусоид, причем моментам времени  для которых график функции
для которых график функции  лежит выше прямой
лежит выше прямой  отвечают интервалы II, а прочим моментам времени — интервалы
отвечают интервалы II, а прочим моментам времени — интервалы  Параметры перегрузки
Параметры перегрузки  и
и  можно толковать, согласно (93), как амплитуды поперечных колебаний поверхностей, отнесенные к «критической» амплитуде отвечающей (по крайней мере, при коэффициенте восстановления
можно толковать, согласно (93), как амплитуды поперечных колебаний поверхностей, отнесенные к «критической» амплитуде отвечающей (по крайней мере, при коэффициенте восстановления  переходу от безотрывных к отрывным движениям тела.
переходу от безотрывных к отрывным движениям тела.
Исследование установившихся режимов движения частицы с подбрасыванием при  основывается на следующем трансцендентном уравнении, связывающем фазы отрыва
основывается на следующем трансцендентном уравнении, связывающем фазы отрыва  и падения
и падения  частицы на поверхность
частицы на поверхность  и — соответственно моменты отрыва и падения):
и — соответственно моменты отрыва и падения):

где  номера полуволн синусоид, которым принадлежат соответствующие фазы отрыва и падения
номера полуволн синусоид, которым принадлежат соответствующие фазы отрыва и падения  равны
равны  соответственно при
соответственно при  нечетном и равны
нечетном и равны  при
при  четном.
четном.
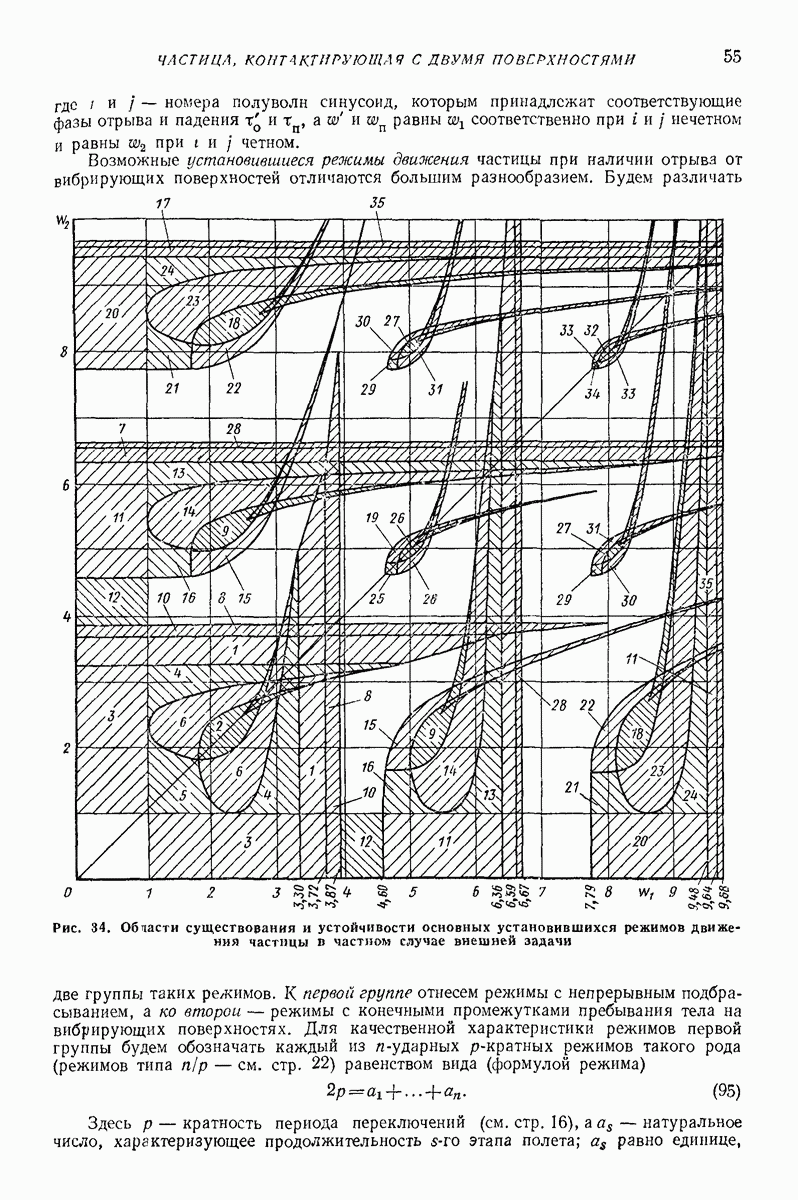
Возможные установившиеся режимы движения частицы при наличии отрыва от вибрирующих поверхностей отличаются большим разнообразием.
Рис. 34. (см. скан) Области существования и устойчивости основных установившихся режимов движения частицы в частном случае внешней задачи
Будем различать две группы таких режимов. К первой группе отнесем режимы с непрерывным подбрасыванием, а ко второй — режимы с конечными промежутками пребывания тела на вибрирующих поверхностях. Для качественной характеристики режимов первой группы будем обозначать каждый из  -ударных
-ударных  -кратных режимов такого рода (режимов типа
-кратных режимов такого рода (режимов типа  см. стр. 22) равенством вида (формулой режима)
см. стр. 22) равенством вида (формулой режима)

Здесь  кратность периода переключений (см. стр. 16),
кратность периода переключений (см. стр. 16),  натуральное число, характеризующее продолжительность
натуральное число, характеризующее продолжительность  этапа полета;
этапа полета;  равно единице,
равно единице,
если момент падения на этом этапе отвечает соседней полуволне синусоиды двум, если падение происходит «через одну полуволну», трем — если «через две полуволны» и т. д.
Число слагаемых  в правой части (95), таким образом, равно числу этапов полета
в правой части (95), таким образом, равно числу этапов полета  в данном режиме, а сумма
в данном режиме, а сумма  числу полуволн синусоид
числу полуволн синусоид  содержащихся в периоде переключений
содержащихся в периоде переключений  Порядок чередования чисел
Порядок чередования чисел  указывает на порядок чередования этапов полета в рассматриваемом режиме. При этом, поскольку любой этап полета может быть принят за начальный, можно не различать режимы, отличающиеся циклической перестановкой чисел а, в правой части (95).
указывает на порядок чередования этапов полета в рассматриваемом режиме. При этом, поскольку любой этап полета может быть принят за начальный, можно не различать режимы, отличающиеся циклической перестановкой чисел а, в правой части (95).
Значительно более разнообразными по структуре могут быть режимы второй группы. Каждому такому режиму при  можно поставить в соответствие равенство вида
можно поставить в соответствие равенство вида

Здесь  по-прежнему кратность периода переключений,
по-прежнему кратность периода переключений,  число, равное двум, единице или нулю в зависимости от числа одновременно выполняющихся неравенств (93), обеспечивающих существование интервалов II. При этом, если
число, равное двум, единице или нулю в зависимости от числа одновременно выполняющихся неравенств (93), обеспечивающих существование интервалов II. При этом, если  то интервалы II существуют в пределах каждой из полуволн синусоид; если
то интервалы II существуют в пределах каждой из полуволн синусоид; если  или наоборот, — только в пределах вдвое меньшего числа полуволн; если
или наоборот, — только в пределах вдвое меньшего числа полуволн; если  то интервалы II не существуют вообще. Таким образом, произведение
то интервалы II не существуют вообще. Таким образом, произведение  равно числу изолированных интервалов II в пределах одного периода переключений. Числа
равно числу изолированных интервалов II в пределах одного периода переключений. Числа  в (96) для этапов пребывания частицы на поверхности равны нулю, а для этапов полета — натуральному числу, равному числу конечных моментов интервалов II, содержащихся внутри данного этапа полета. Общее число таких характерных моментов внутри периода переключений, очевидно, равно
в (96) для этапов пребывания частицы на поверхности равны нулю, а для этапов полета — натуральному числу, равному числу конечных моментов интервалов II, содержащихся внутри данного этапа полета. Общее число таких характерных моментов внутри периода переключений, очевидно, равно  Обозначения режимов второй группы отличаются от обозначений режимов первой группы наличием нулей среди чисел
Обозначения режимов второй группы отличаются от обозначений режимов первой группы наличием нулей среди чисел 
На рис. 34 для случая  и значений
и значений  представлена карта областей существования и устойчивости режимов движения тела не более чем с двумя этапами полета в каждом периоде переключений. В незаштрихованных частях плоскости
представлена карта областей существования и устойчивости режимов движения тела не более чем с двумя этапами полета в каждом периоде переключений. В незаштрихованных частях плоскости  имеют место более сложные режимы. Карга построена на основе решения систем трансцендентных уравнений типа (94) на ЭЦВМ. Номера на карте соответствуют следующим формулам режимов:
имеют место более сложные режимы. Карга построена на основе решения систем трансцендентных уравнений типа (94) на ЭЦВМ. Номера на карте соответствуют следующим формулам режимов:

При этом симметричные режимы, т. е. получающиеся путем замены  на
на  на
на  обозначены одним и тем же номером.
обозначены одним и тем же номером.
В некоторых областях плоскости  одновременно существуют устойчивые установившиеся режимы движения различного вида; имеются также области, где существуют два различных устойчивых режима одного и того же вида. Например, в ромбовидной области вблизи точки
одновременно существуют устойчивые установившиеся режимы движения различного вида; имеются также области, где существуют два различных устойчивых режима одного и того же вида. Например, в ромбовидной области вблизи точки  имеют место два режима вида
имеют место два режима вида  отличающиеся один от другого значениями фазовых углов контакта частицы с плоскостями.
отличающиеся один от другого значениями фазовых углов контакта частицы с плоскостями.
В случае одинаковых амплитуд поперечных колебаний  по существу имеются колебания эквивалентной поверхности с наименьшим периодом
по существу имеются колебания эквивалентной поверхности с наименьшим периодом  вдвое меньшим периода колебаний
вдвое меньшим периода колебаний  каждой из поверхностей. При этом условия существования и устойчивости одноударных
каждой из поверхностей. При этом условия существования и устойчивости одноударных  -кратных режимов с непрерывным подбрасыванием (режимов типа
-кратных режимов с непрерывным подбрасыванием (режимов типа  имеющих период переключений
имеющих период переключений  состоят в выполнении неравенств
состоят в выполнении неравенств

При четных  полет продолжается целое число
полет продолжается целое число  периодов
периодов  и поэтому частица контактирует только с какой-нибудь одной вибрирующей плоской поверхностью; в этом случае условия (97) совпадают с условиями (19), если заменить в
и поэтому частица контактирует только с какой-нибудь одной вибрирующей плоской поверхностью; в этом случае условия (97) совпадают с условиями (19), если заменить в  на
на 
Средняя скорость движения частицы в  -кратных двухударных установившихся режимах (режимах типа
-кратных двухударных установившихся режимах (режимах типа  с формулой
с формулой  при любом законе поперечных и продольных колебаний эквивалентной плоской поверхности имеет вид
при любом законе поперечных и продольных колебаний эквивалентной плоской поверхности имеет вид

Эта формула соответствует гипотезе вязкого ударного трения (см. стр. 15); в ней  фазовые углы контакта частицы с поверхностями, определяемыми из системы двух трансцендентных уравнений, составленных для случая гармонических поперечных колебаний вида (92) из соответствующих уравнений типа (94) при учете условия периодичности поперечного движения частицы. Из (98) вытекают частные случаи.
фазовые углы контакта частицы с поверхностями, определяемыми из системы двух трансцендентных уравнений, составленных для случая гармонических поперечных колебаний вида (92) из соответствующих уравнений типа (94) при учете условия периодичности поперечного движения частицы. Из (98) вытекают частные случаи.
1. Колебания плоских поверхностей — прямолинейные гармонические, направленные под углом (3 к поверхностям; 

Вместо (99) можно использовать формулу

в которой  целые числа в формуле рассматриваемого режима
целые числа в формуле рассматриваемого режима  использование (100) не требует определения
использование (100) не требует определения  т. е. решения трансцендентных уравнений. Из (99) вытекает, что в рассматриваемом случае, при прочих равных условиях, минимальное значение скорости получается при
т. е. решения трансцендентных уравнений. Из (99) вытекает, что в рассматриваемом случае, при прочих равных условиях, минимальное значение скорости получается при  одинаковой продолжительности этапов полета.
одинаковой продолжительности этапов полета.
2. Законы колебаний обеих плоских поверхностей одинаковы, так что наименьший период колебаний фактически равен  а рассматриваемый режим сводится к одноударному
а рассматриваемый режим сводится к одноударному  -кратному режиму:
-кратному режиму:

В частности, если колебания обеих плоских поверхностей прямолинейные гармонические с одинаковыми амплшудами 

Как и следовало ожидать, при замене  на
на  формула (101) переходит в формулу (55), а формула (102) — в (31).
формула (101) переходит в формулу (55), а формула (102) — в (31).
В рассмотренном случае одноударный однократный режим движения с непрерывным подбрасыванием достигается при значительно меньших ускорениях колебаний поверхностей, чем на одной поверхности, вибрирующей по тому же закону Так, при гармонических поперечных колебаниях одной поверхности указанный режим периода  наступает при
наступает при  (см стр. 24 и рис. 6), в то время как в случае двух поверхностей такой режим с периодом, меньшим в 2 раза, достигается уже при —
(см стр. 24 и рис. 6), в то время как в случае двух поверхностей такой режим с периодом, меньшим в 2 раза, достигается уже при —  примерно при ускорении поперечных колебаний, меньшем в 2 раза. Отношение средних скоростей движения частицы (при гармонических продольных колебаниях) согласно (31) и
примерно при ускорении поперечных колебаний, меньшем в 2 раза. Отношение средних скоростей движения частицы (при гармонических продольных колебаниях) согласно (31) и  Таким образом, средняя скорость в случае двух поверхностен может быть сохранена на прежнем уровне, если принять частоту колебаний вдвое меньшей, чем в случае одной поверхности. Для получения необходимого значения
Таким образом, средняя скорость в случае двух поверхностен может быть сохранена на прежнем уровне, если принять частоту колебаний вдвое меньшей, чем в случае одной поверхности. Для получения необходимого значения  при этом, очевидно, потребуется увеличить амплитуду колебаний каждой из двух поверхностей также примерно в 2 раза; частота воздействия на частицу в обоих случаях будет одинакова. Иными словами, можно ожидать, что устройства с двумя гармонически вибрирующими поверхностями, работающие, например, при частоте
при этом, очевидно, потребуется увеличить амплитуду колебаний каждой из двух поверхностей также примерно в 2 раза; частота воздействия на частицу в обоих случаях будет одинакова. Иными словами, можно ожидать, что устройства с двумя гармонически вибрирующими поверхностями, работающие, например, при частоте  кол/мин и амплитуде
кол/мин и амплитуде  (с ускорением
(с ускорением  окажутся столь же эффективными, как и устройства с одной поверхностью, вибрирующей с частотой
окажутся столь же эффективными, как и устройства с одной поверхностью, вибрирующей с частотой  кол/мин и амплитудой
кол/мин и амплитудой  (с ускорением
(с ускорением 
Движение частицы в режимах без подбрасывания в случае гармонических колебаний плоских поверхностей рассмотрено в работах [17, 25].
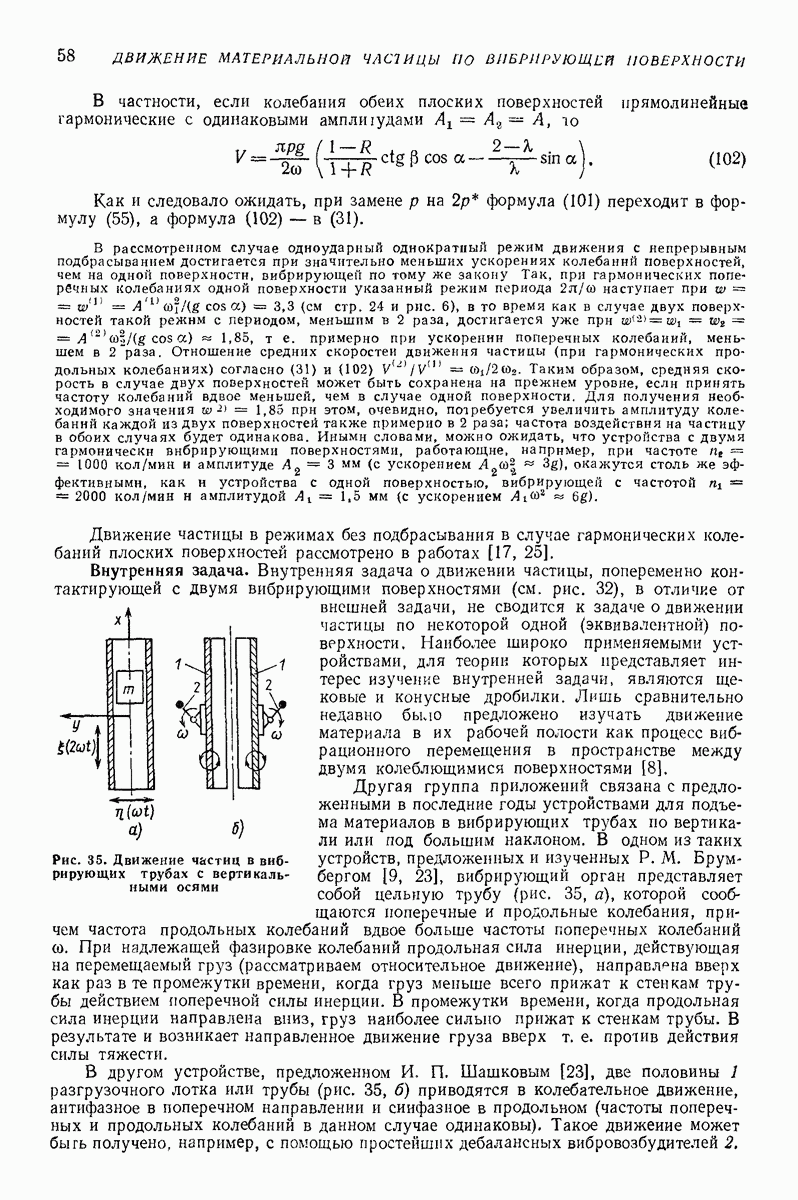
Внутренняя задача. Внутренняя задача о движении частицы, попеременно контактирующей с двумя вибрирующими поверхностями (см. рис. 32), в отличке от внешней задачи, не сводится к задаче о движении частицы по некоторой одной (эквивалентной) поверхности. Наиболее широко применяемыми устройствами, для теории которых представляет интерес изучение внутренней задачи, являются щековые и конусные дробилки. Лишь сравнительно недавно было предложено изучать движение материала в их рабочей полости как процесс вибрационного перемещения в пространстве между двумя колеблющимися поверхностями [8].

Рис. 35. Движение частиц в вибрирующих трубах с вертикальными осями
Другая группа приложений связана с предложенными в последние годы устройствами для подъема материалов в вибрирующих трубах по вертикали или под большим наклоном. В одном из таких устройств, предложенных и изученных  . Брумбергом [9, 23], вибрирующий орган представляет собой цельную трубу (рис. 35, а), которой сообщаются поперечные и продольные колебания, причем частота продольных колебаний вдвое больше частоты поперечных колебаний
. Брумбергом [9, 23], вибрирующий орган представляет собой цельную трубу (рис. 35, а), которой сообщаются поперечные и продольные колебания, причем частота продольных колебаний вдвое больше частоты поперечных колебаний  При надлежащей фазировке колебаний продольная сила инерции, действующая на перемещаемый груз (рассматриваем относительное движение), направлена вверх как раз в те промежутки времени, когда груз меньше всего прижат к стенкам трубы действием поперечной силы инерции. В промежутки времени, когда продольная сила инерции направлена вниз, груз наиболее сильно прижат к стенкам трубы. В результате и возникает направленное движение груза вверх т. е. против действия силы тяжести.
При надлежащей фазировке колебаний продольная сила инерции, действующая на перемещаемый груз (рассматриваем относительное движение), направлена вверх как раз в те промежутки времени, когда груз меньше всего прижат к стенкам трубы действием поперечной силы инерции. В промежутки времени, когда продольная сила инерции направлена вниз, груз наиболее сильно прижат к стенкам трубы. В результате и возникает направленное движение груза вверх т. е. против действия силы тяжести.
В другом устройстве, предложенном  Шашковым [23], две половины 1 разгрузочного лотка или трубы (рис. 35, б) приводятся в колебательное движение, антифазное в поперечном направлении и синфазное в продольном (частоты поперечных и продольных колебаний в данном случае одинаковы). Такое движение может быть получено, например, с помощью простейших дебалансных вибровозбудителей 2.
Шашковым [23], две половины 1 разгрузочного лотка или трубы (рис. 35, б) приводятся в колебательное движение, антифазное в поперечном направлении и синфазное в продольном (частоты поперечных и продольных колебаний в данном случае одинаковы). Такое движение может быть получено, например, с помощью простейших дебалансных вибровозбудителей 2.
Приведем результаты исследования работы первого из описанных устройств. Рассмотрим сначала движение по трубе некоторого тела массы  зазор между которым и стенками трубы отсутствует (см. рис. 35, а). Уравнение относительного движения такого тела имеет вид [9]
зазор между которым и стенками трубы отсутствует (см. рис. 35, а). Уравнение относительного движения такого тела имеет вид [9]

где  коэффициент трения скольжения;
коэффициент трения скольжения;  ускорение свободного падения;
ускорение свободного падения;  периодические функции своих аргументов с периодом
периодические функции своих аргументов с периодом  характеризующие соответственно закон продольных и поперечных колебаний трубы.
характеризующие соответственно закон продольных и поперечных колебаний трубы.
Предполагая, что скорость тела представима в виде  где V — медленная, а
где V — медленная, а  быстрая составляющие, применим для решения (103) метод прямого разделения движений (см. параграф 2 гл.
быстрая составляющие, применим для решения (103) метод прямого разделения движений (см. параграф 2 гл.  При этом, предполагая, что сила трения
При этом, предполагая, что сила трения  мала по сравнению с силами инерции, получим (в соответствии с
мала по сравнению с силами инерции, получим (в соответствии с  гл.
гл.  следующее уравнение медленного движения:
следующее уравнение медленного движения:

в котором

есть приближенное выражение так называемой вибрационной силы, причем скобки  указывают на осреднение заключенного в них выражения по
указывают на осреднение заключенного в них выражения по  за период
за период  . В случае гармонических колебаний трубы
. В случае гармонических колебаний трубы

Подставив (106) в (105) после выполнения усреднения, получим

Здесь  амплитуда скорости продольных колебаний трубы;
амплитуда скорости продольных колебаний трубы;  и
и  безразмерные вибрационная сила и средняя скорость соответственно.
безразмерные вибрационная сила и средняя скорость соответственно.
Из (107) легко получить выражения для любых значений 8, если учесть соотношение  вытекающее из (105) и (106).
вытекающее из (105) и (106).
Зависимости  представлены на рис 36 и 37. Согласно (107) вибрационная снла
представлены на рис 36 и 37. Согласно (107) вибрационная снла  направлена вверх, если она отрицательна, и вниз, если положительна. При
направлена вверх, если она отрицательна, и вниз, если положительна. При  наибольшие по модулю отрицательные значения
наибольшие по модулю отрицательные значения  получаются при
получаются при  что при учете (106) соответствует данному выше качественному объяснению работы устройства; для
что при учете (106) соответствует данному выше качественному объяснению работы устройства; для  и
и  вибрационная сила при
вибрационная сила при  положительна, т. е. направлена вниз, и, значит, транспортирование тела вверх невозможно. Средняя скорость вибротранспортирования V в установившемся движении, согласно (106), может быть найдена из уравнения
положительна, т. е. направлена вниз, и, значит, транспортирование тела вверх невозможно. Средняя скорость вибротранспортирования V в установившемся движении, согласно (106), может быть найдена из уравнения  или с помощью рис. 36. Изменяя параметры
или с помощью рис. 36. Изменяя параметры  можно регулировать скорость подъема тела V в широких пределах, в частности добиться обращения V в нуль, т. е. «зависания» тела в трубе
можно регулировать скорость подъема тела V в широких пределах, в частности добиться обращения V в нуль, т. е. «зависания» тела в трубе
Другим способом — путем точного интегрирования (103) — данная задача рассмотрена Р. М. Брумбергом [9].
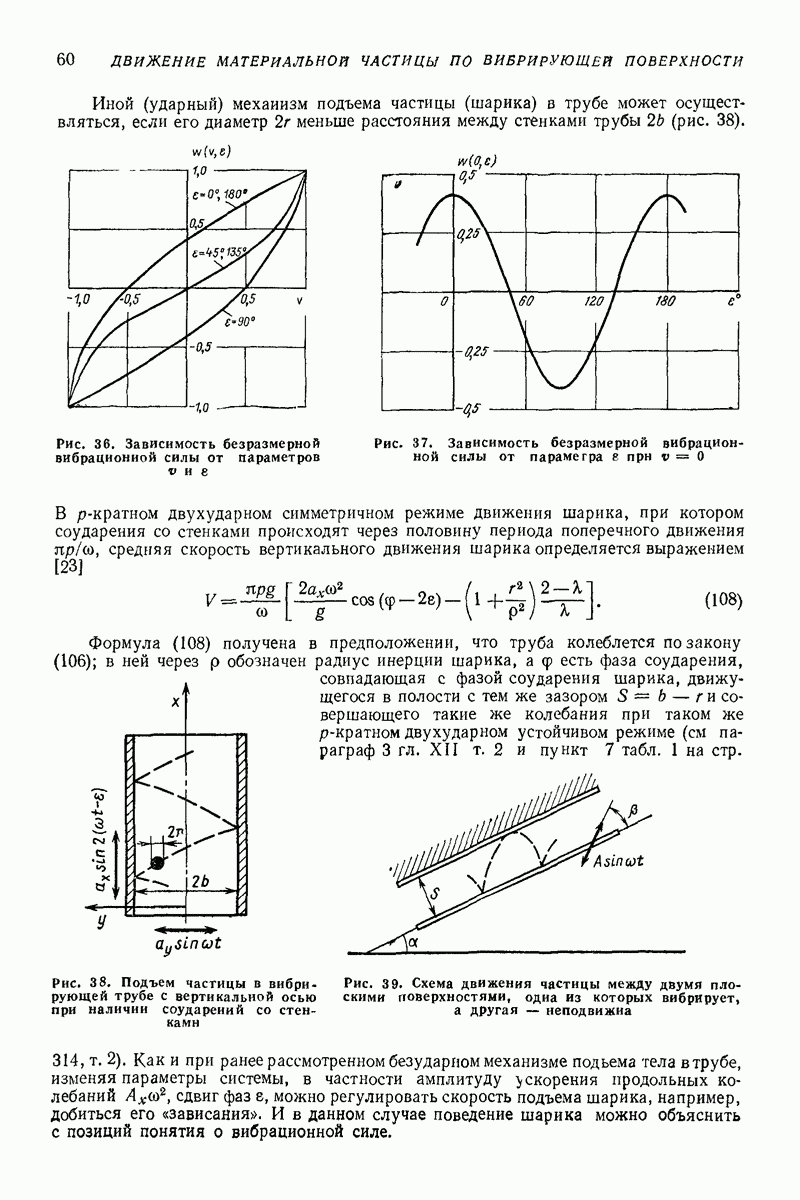
Иной (ударный) механизм подъема частицы (шарика) в трубе может осуществляться, если его диаметр  меньше расстояния между стенками трубы
меньше расстояния между стенками трубы 

Рис. 36. Зависимость безразмерной вибрациониой силы от параметров при 

Рис. 37. Зависимость безразмерной вибрационной силы от параметра в 
В  -кратном двухударном симметричном режиме движения шарика, при котором соударения со стенками происходят через половину периода поперечного движения
-кратном двухударном симметричном режиме движения шарика, при котором соударения со стенками происходят через половину периода поперечного движения  средняя скорость вертикального движения шарика определяется выражением [23]
средняя скорость вертикального движения шарика определяется выражением [23]

Формула (108) получена в предположении, что труба колеблется по закону (106); в ней через  обозначен радиус инерции шарика, а
обозначен радиус инерции шарика, а  есть фаза соударения, совпадающая с фазой соударения шарика, движущегося в полости с тем же зазором
есть фаза соударения, совпадающая с фазой соударения шарика, движущегося в полости с тем же зазором  и совершающего такие же колебания при таком же
и совершающего такие же колебания при таком же  -кратном двухударном устойчивом режиме (см параграф 3 гл.
-кратном двухударном устойчивом режиме (см параграф 3 гл.  и пункт 7 табл. 1 на стр. 314, т. 2).
и пункт 7 табл. 1 на стр. 314, т. 2).

Рис. 3 8. Подъем частицы в вибрирующей трубе с вертикальной осью при наличии соударений со стенками

Рис. 3 9. Схема движения частицы между двумя плоскими поверхностями, одна из которых вибрирует, а другая — неподвижна
Как и при ранее рассмотренном безударном механизме подьема тела втрубе, изменяя параметры системы, в частности амплитуду ускорения продольных колебаний  сдвиг фаз
сдвиг фаз  можно регулировать скорость подъема шарика, например, добиться его «зависания». И в данном случае поведение шарика можно объяснить с позиций понятия о вибрационной силе.
можно регулировать скорость подъема шарика, например, добиться его «зависания». И в данном случае поведение шарика можно объяснить с позиций понятия о вибрационной силе.
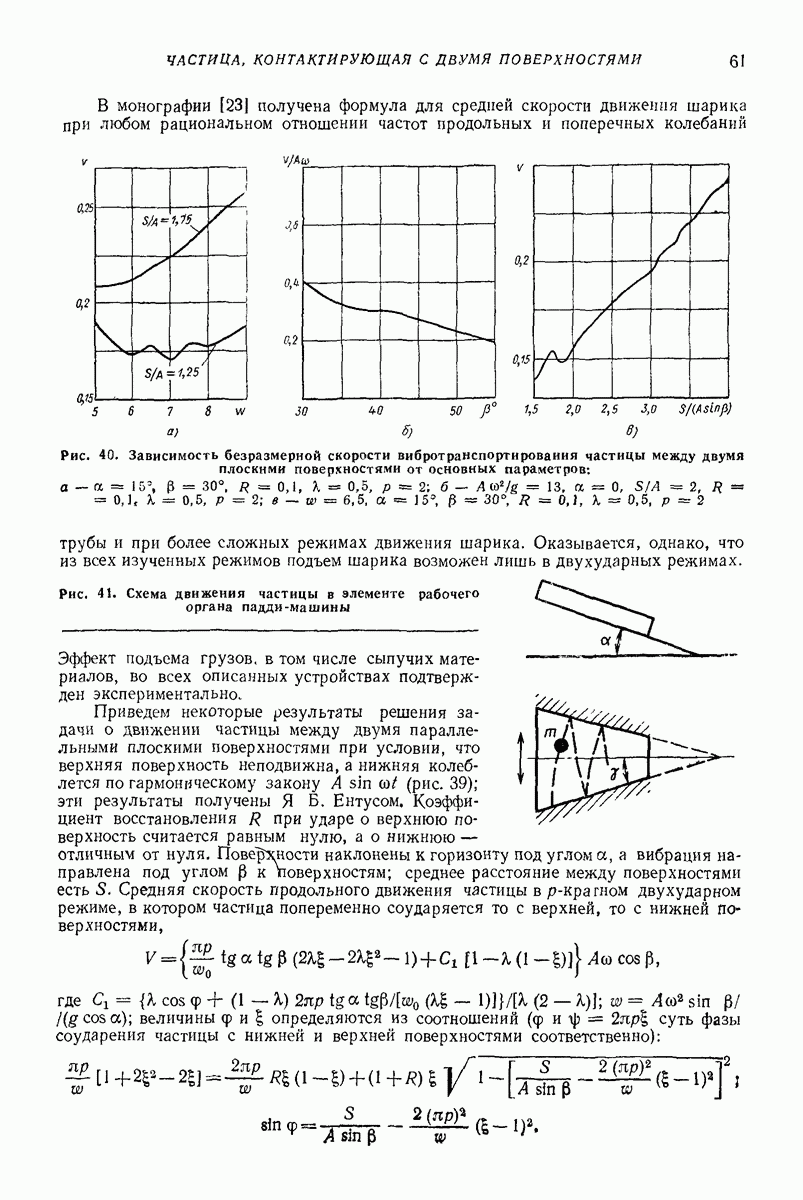
В монографии [23] получена формула для средней скорости движения шарика при любом рациональном отношении частот продольных и поперечных колебаний трубы и при более сложных режимах движения шарика.

Рис. 40. Зависимость безразмерной скорости вибротранспортироваиия частицы между двумя плоскими поверхностями от основных параметров: 
Оказывается, однако, что из всех изученных режимов подъем шарика возможен лишь в двухударных режимах.

Рис. 41. Схема движения частицы в элементе рабочего органа падди-машины
Эффект подъема грузов, в том числе сыпучих материалов, во всех описанных устройствах подтвержден экспериментально.
Приведем некоторые результаты решения задачи о движении частицы между двумя параллельными плоскими поверхностями при условии, что верхняя поверхность неподвижна, а нижняя колеблется по гармоническому закону  (рис. 39); эти результаты получены Я. Б. Ентусом. Коэффициент восстановления
(рис. 39); эти результаты получены Я. Б. Ентусом. Коэффициент восстановления  при ударе о верхнюю поверхность считается равным нулю, а о нижнюю — отличным от нуля. Поверхности наклонены к горизонту под углом
при ударе о верхнюю поверхность считается равным нулю, а о нижнюю — отличным от нуля. Поверхности наклонены к горизонту под углом  , а вибрация направлена под углом
, а вибрация направлена под углом  к поверхностям; среднее расстояние между поверхностями есть
к поверхностям; среднее расстояние между поверхностями есть  Средняя скорость продольного движения частицы в р-кратном двухударном режиме, в котором частица попеременно соударяется то с верхней, то с нижней поверхностями,
Средняя скорость продольного движения частицы в р-кратном двухударном режиме, в котором частица попеременно соударяется то с верхней, то с нижней поверхностями,

где  ; величины
; величины  определяются из соотношений
определяются из соотношений  суть фазы соударения частицы с нижней и верхней поверхностями соответственно):
суть фазы соударения частицы с нижней и верхней поверхностями соответственно):

Указанный режим движения существует при условии  Зависимости безразмерной скорости
Зависимости безразмерной скорости  от параметров системы представлены на рис. 40.
от параметров системы представлены на рис. 40.
К рассматриваемому классу задач относится также изучение движения частицы в падди-машинах, применяемых при очистке зерна [18]. Элемент рабочего органа такой машины представляет собой канал (лоток) с плоским наклонным дном, стенки которого образуют некоторый острый угол у (рис. 41); лотку сообщаются колебания в направлении, перпендикулярном биссектрисе этого угла. Результаты теоретического и экспериментального исследования движения частицы в таком устройстве, при котором она последовательно соударяется с обеими стенками, приводятся в [18].
СПИСОК ЛИТЕРАТУРЫ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- Установившиеся режимы движения частицы.
- О методах решения задачи.
- Установившиеся режимы при отсутствии подбрасывания [4-6].
- Установившиеся режимы с подбрасыванием.
- Средние скорость и ускорение частицы в установившихся режимах движения.
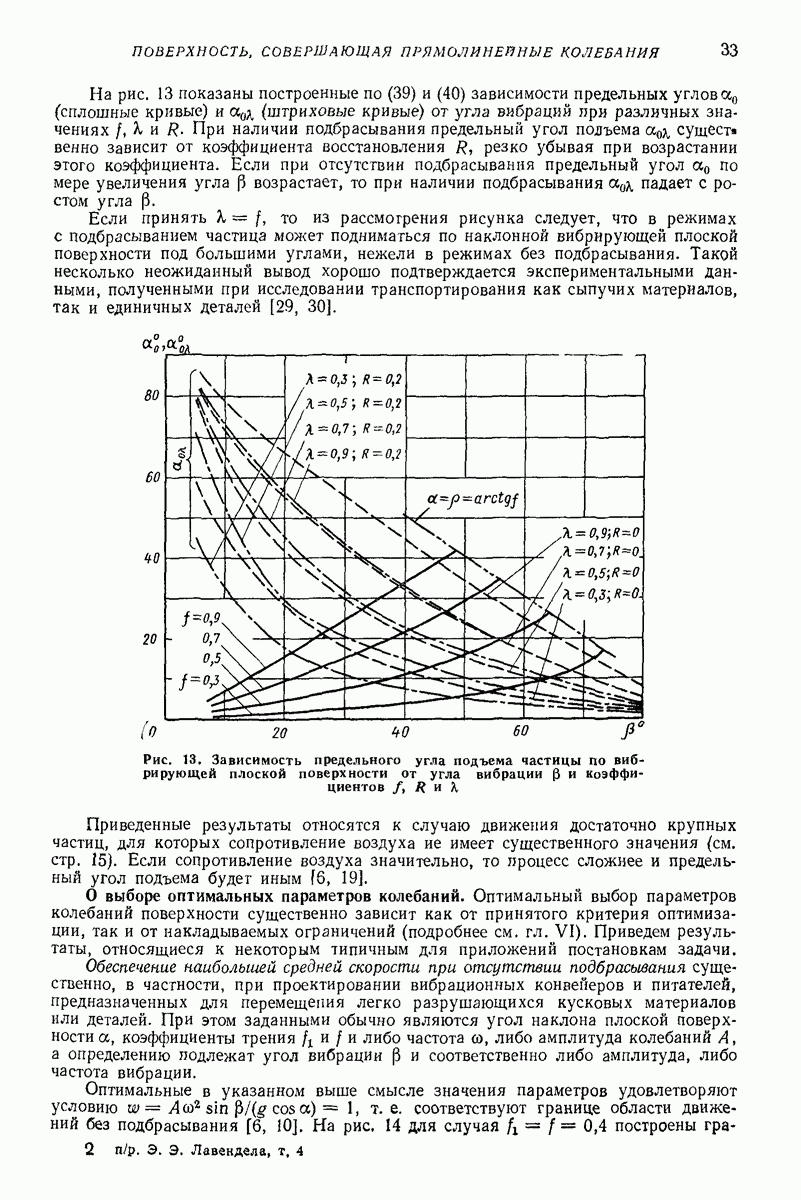
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
- О выборе оптимальных параметров колебаний.
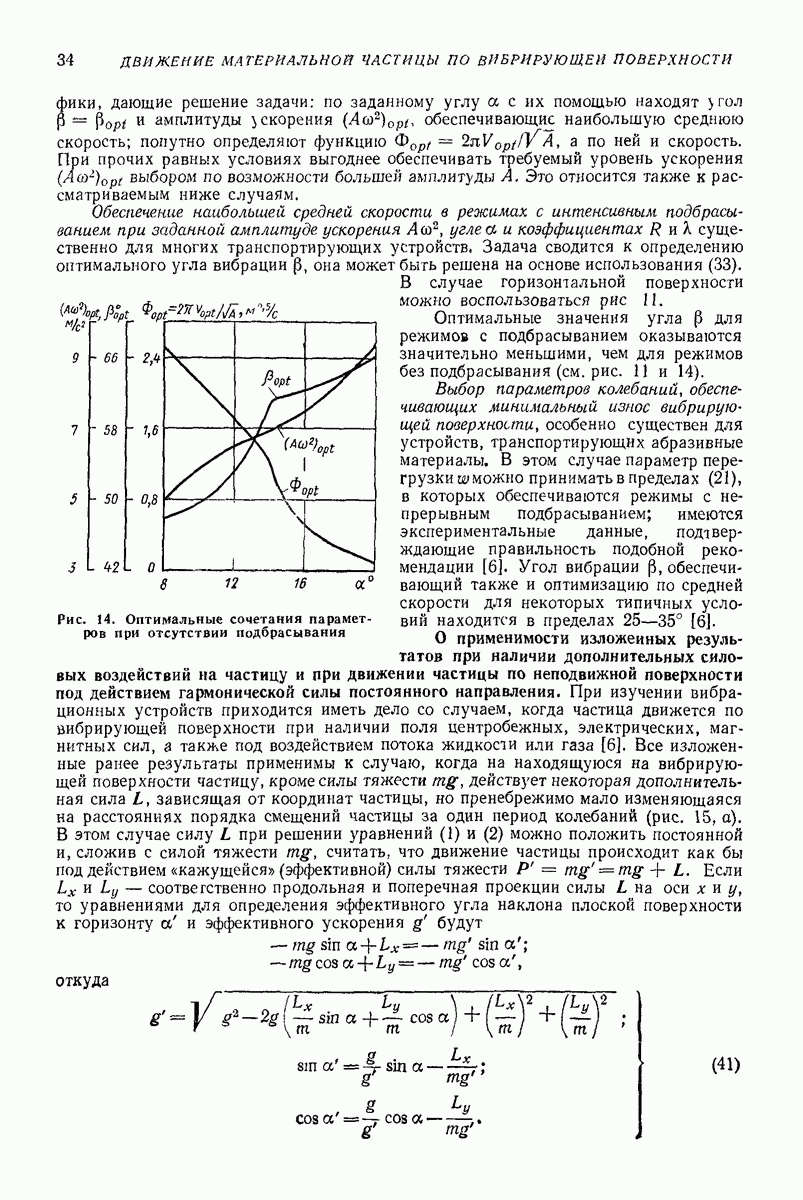
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
- О влиянии на движение частицы сил вязкого сопротивления.
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
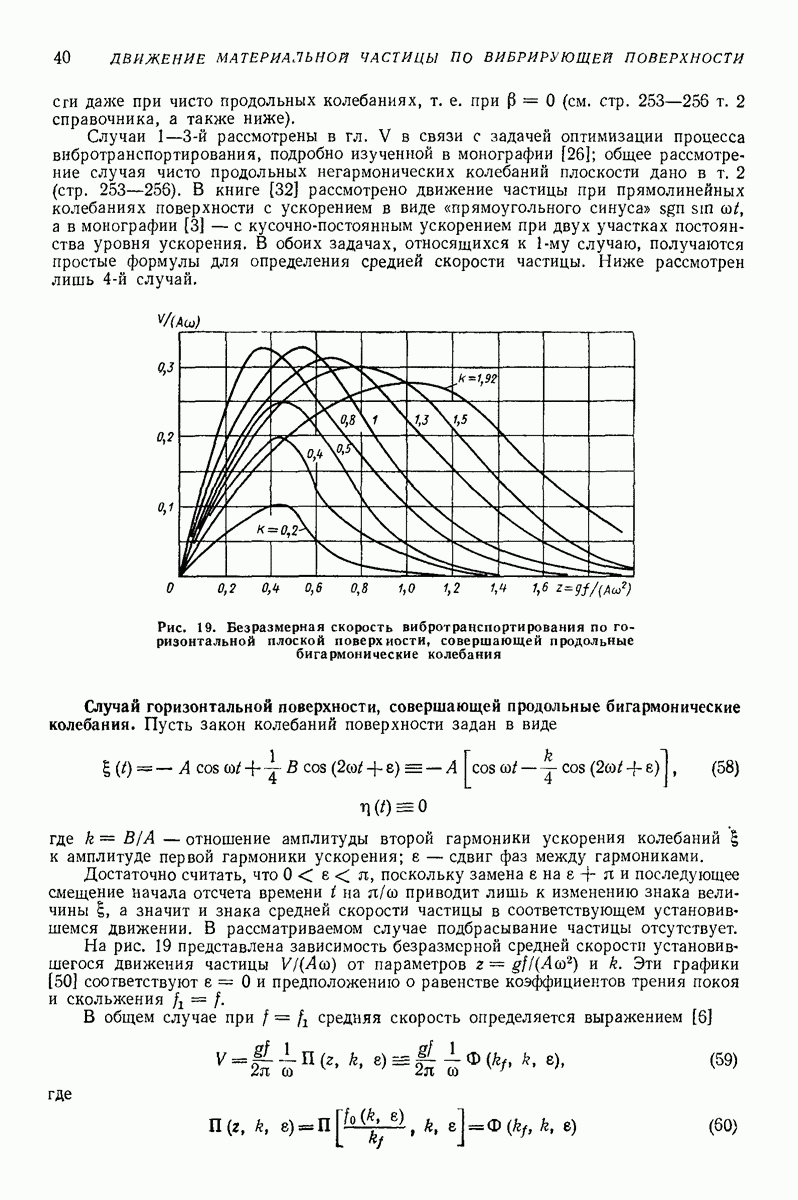
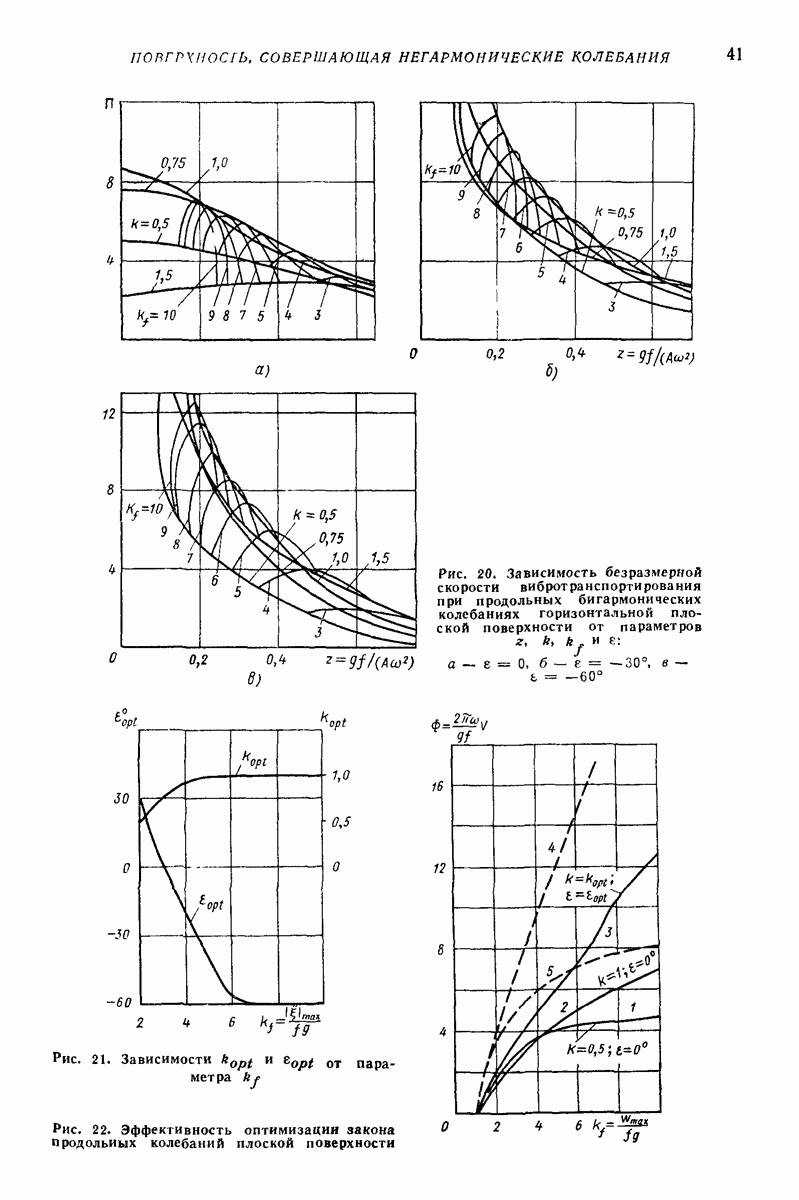
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
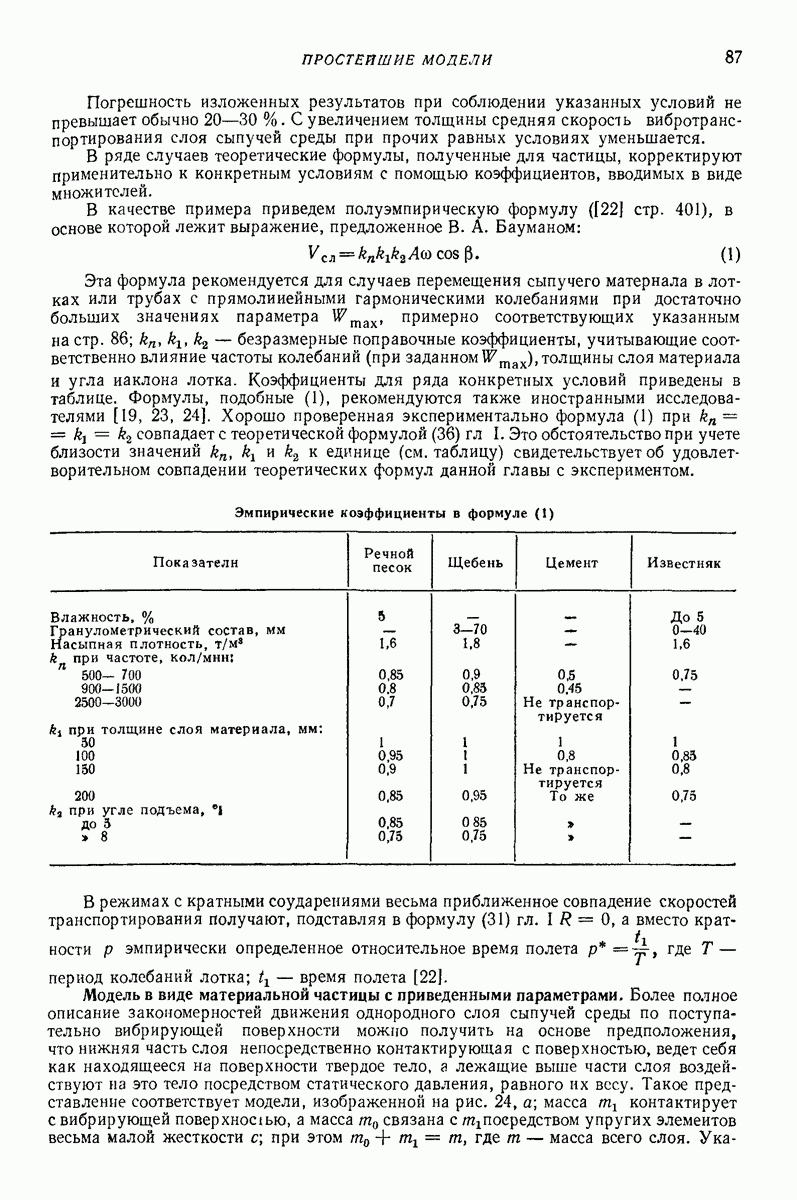
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
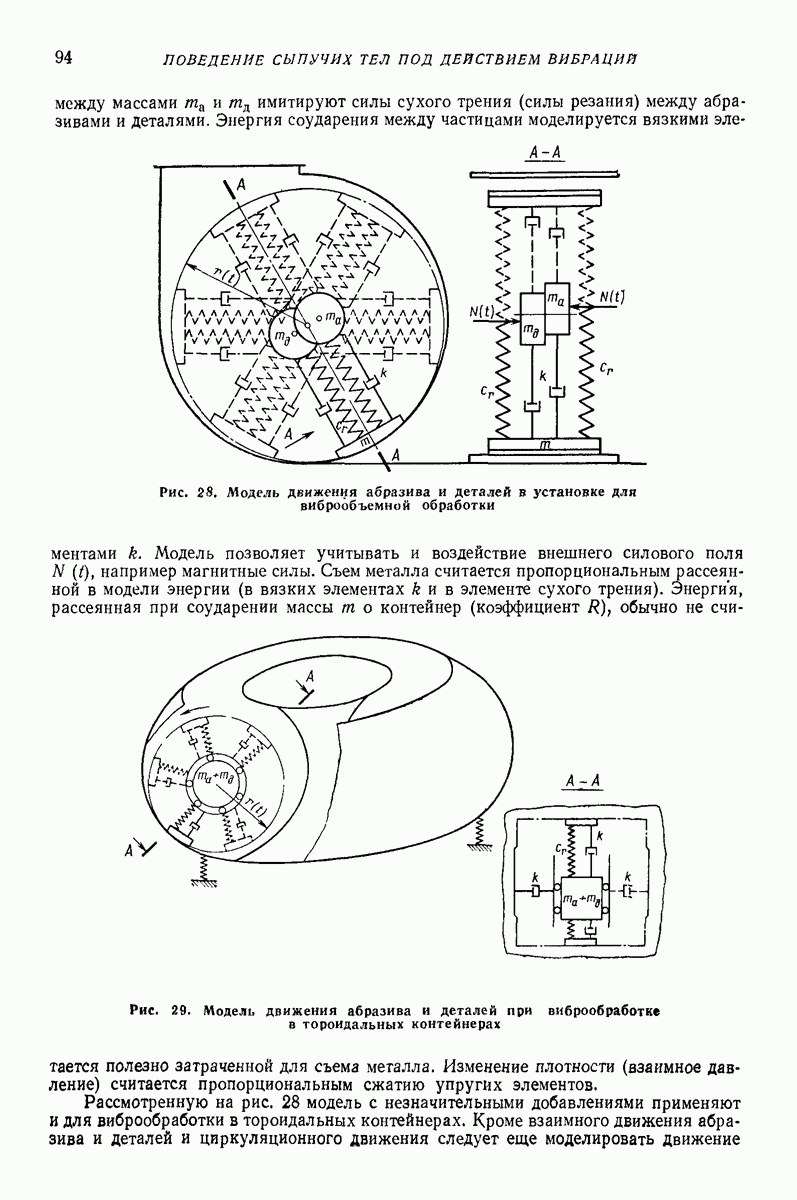
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
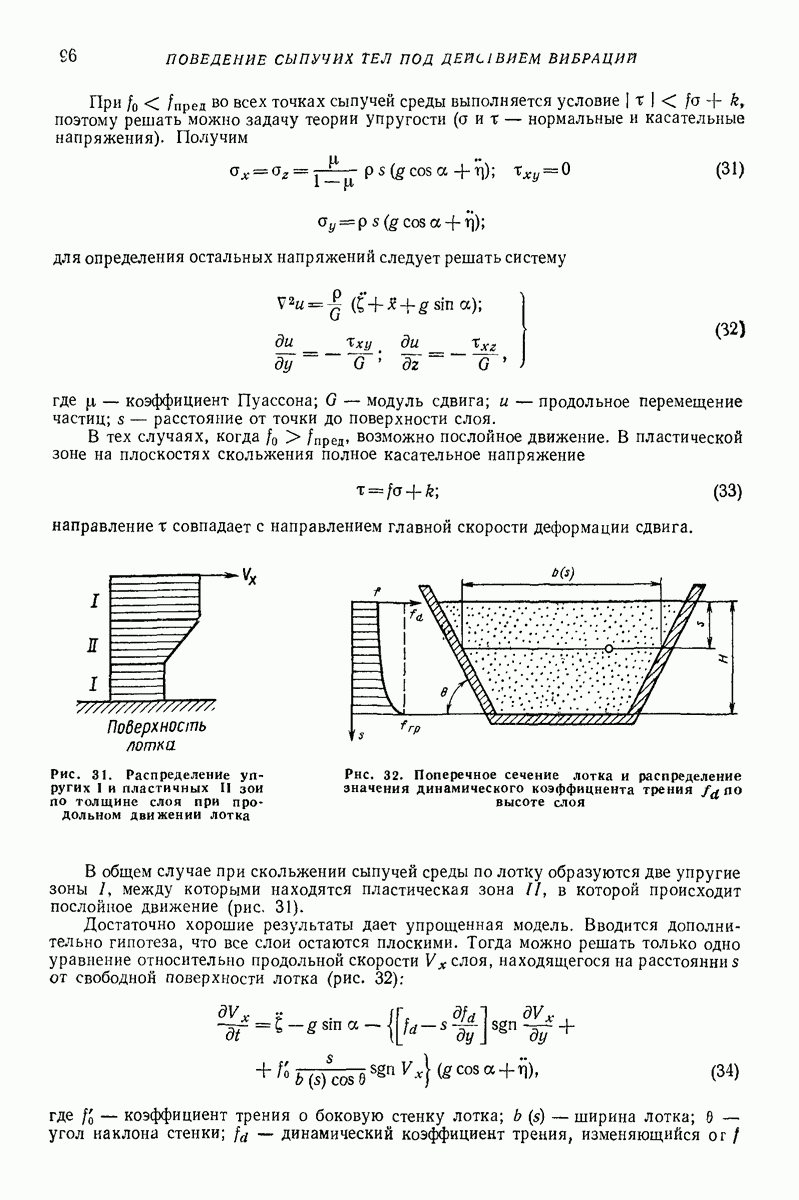
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
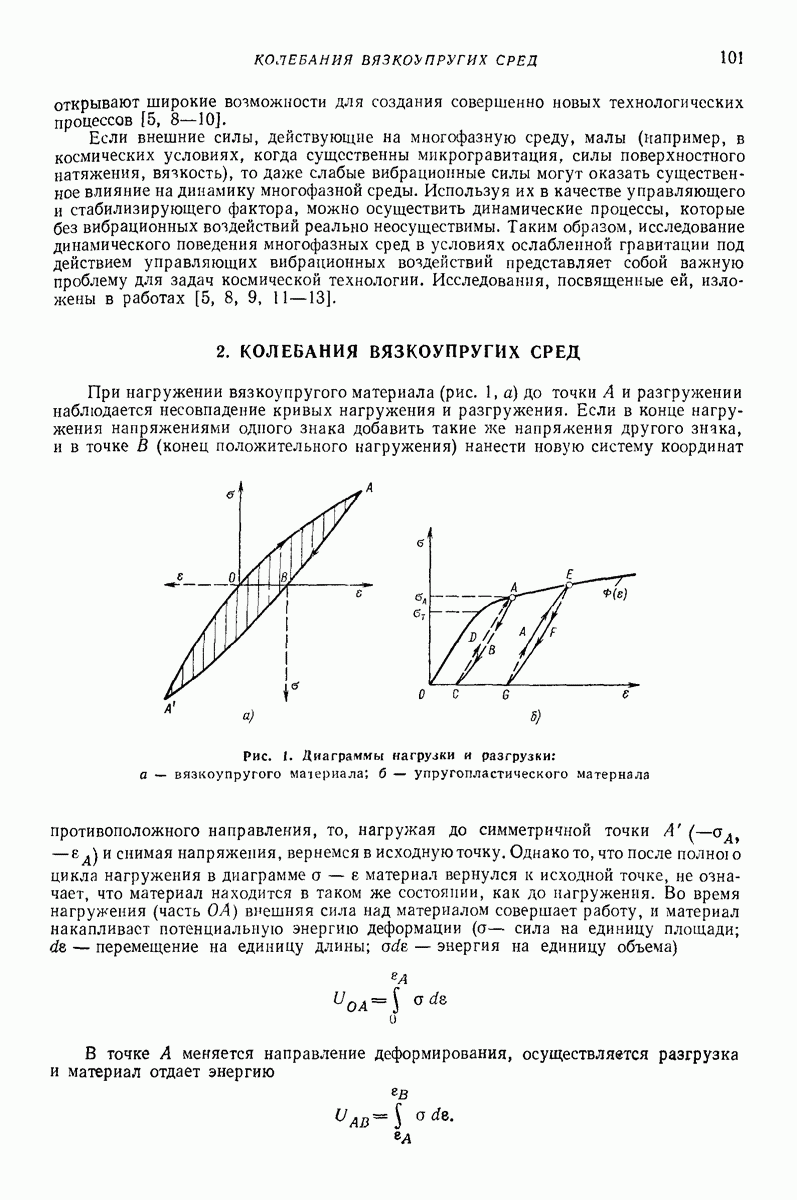
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
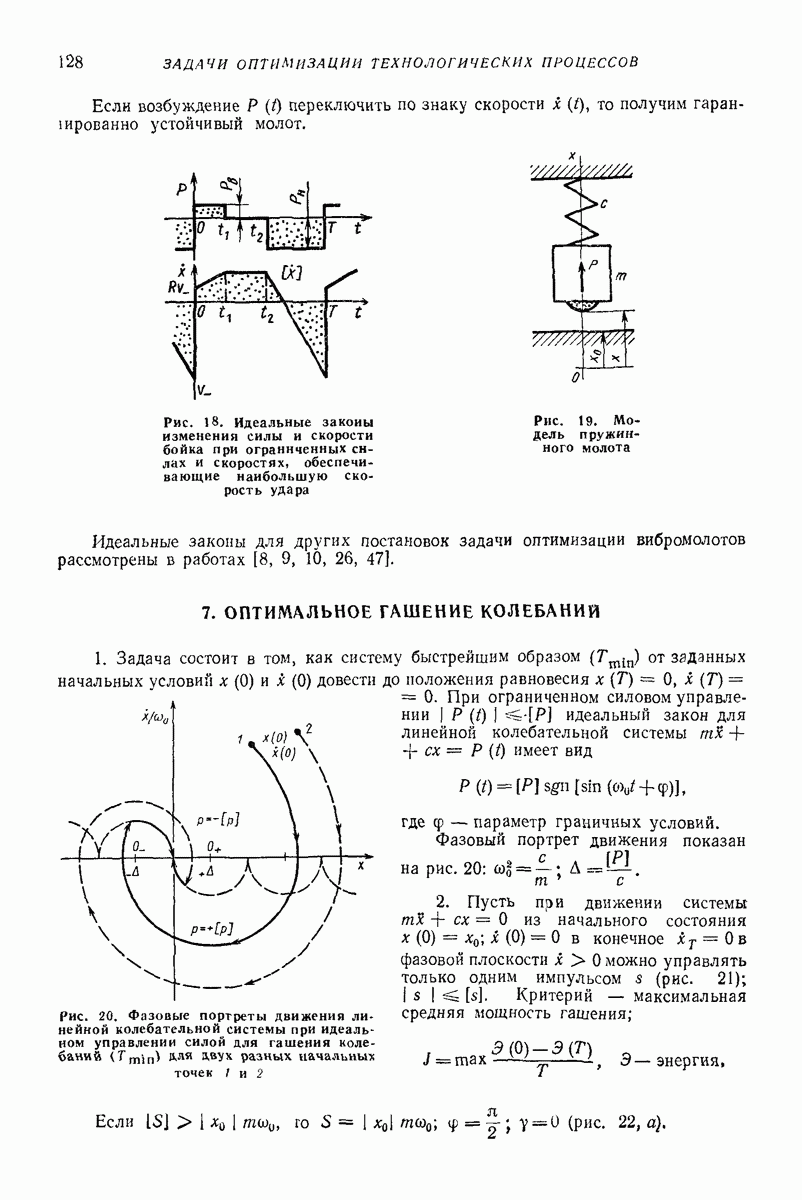
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
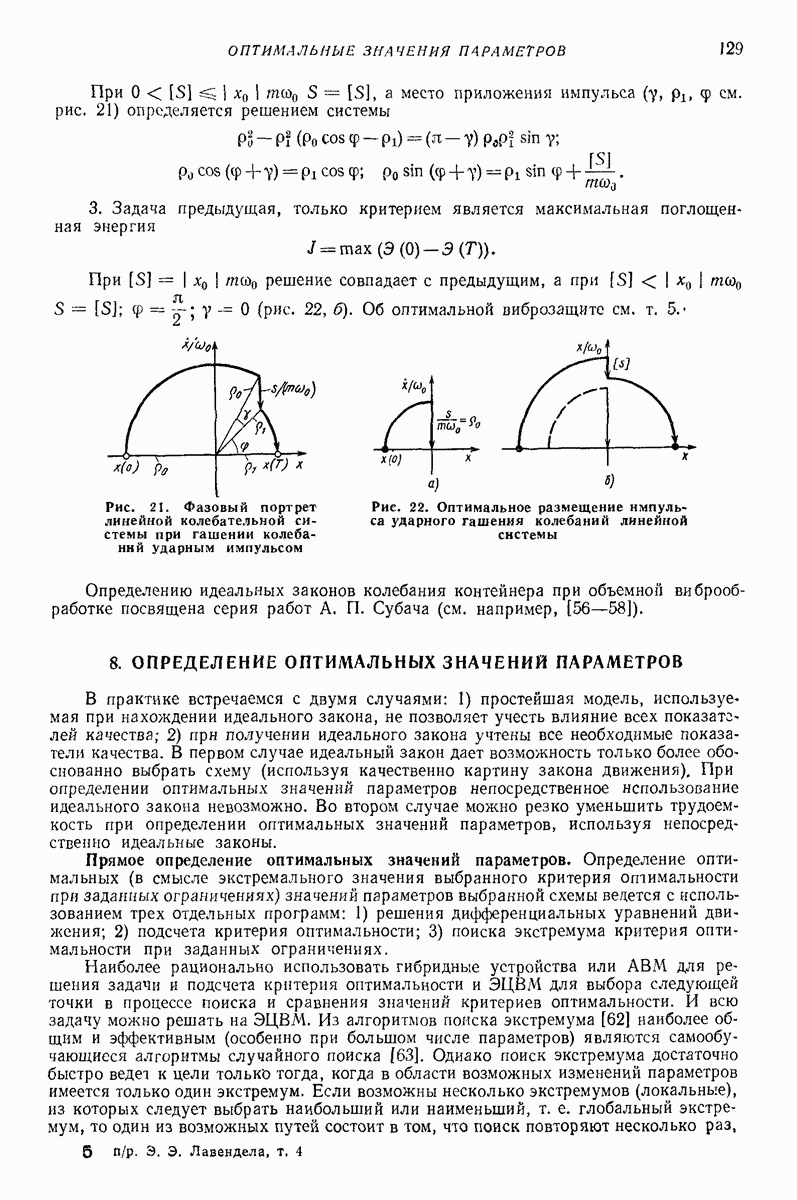
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
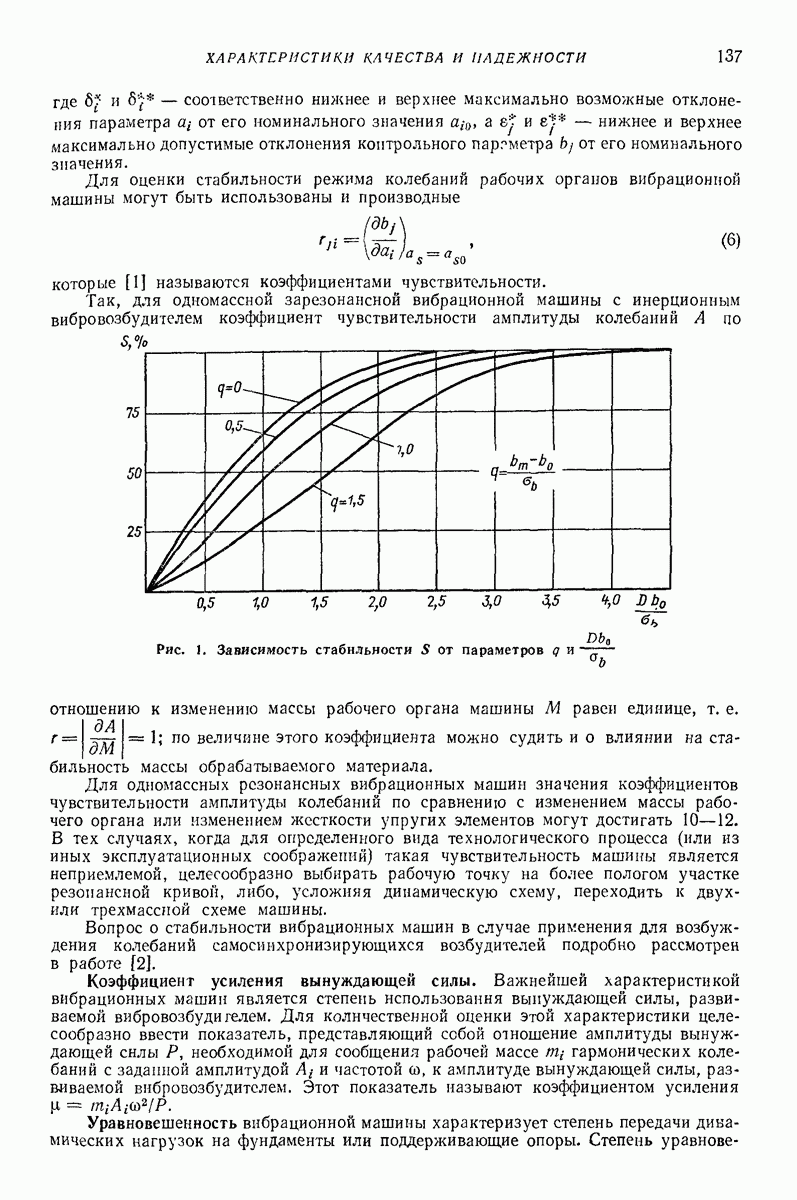
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
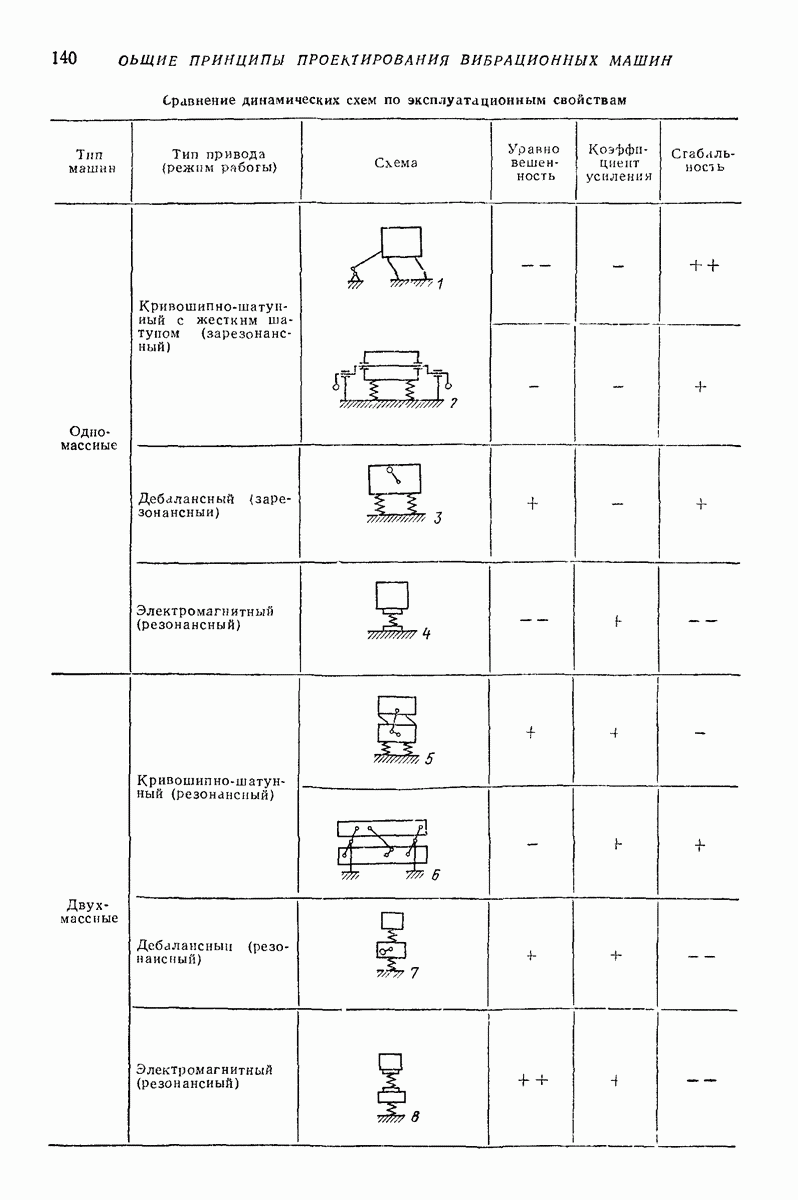
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
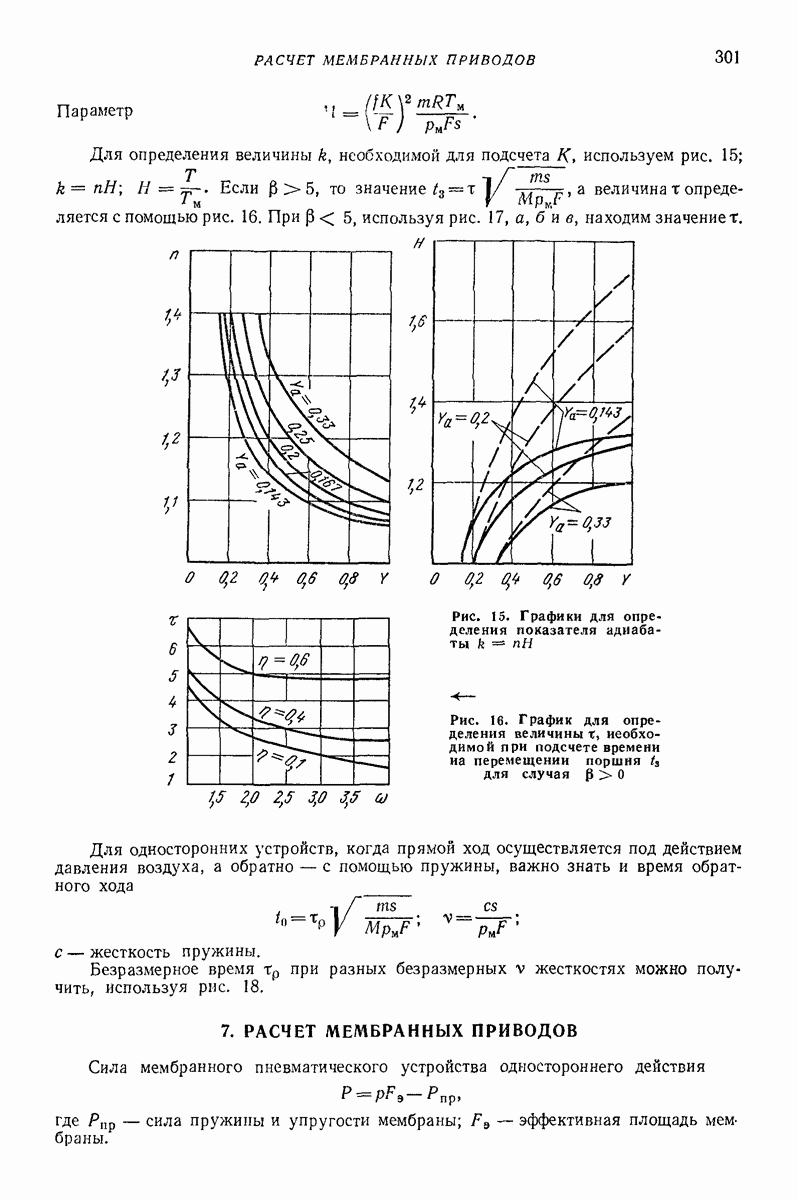
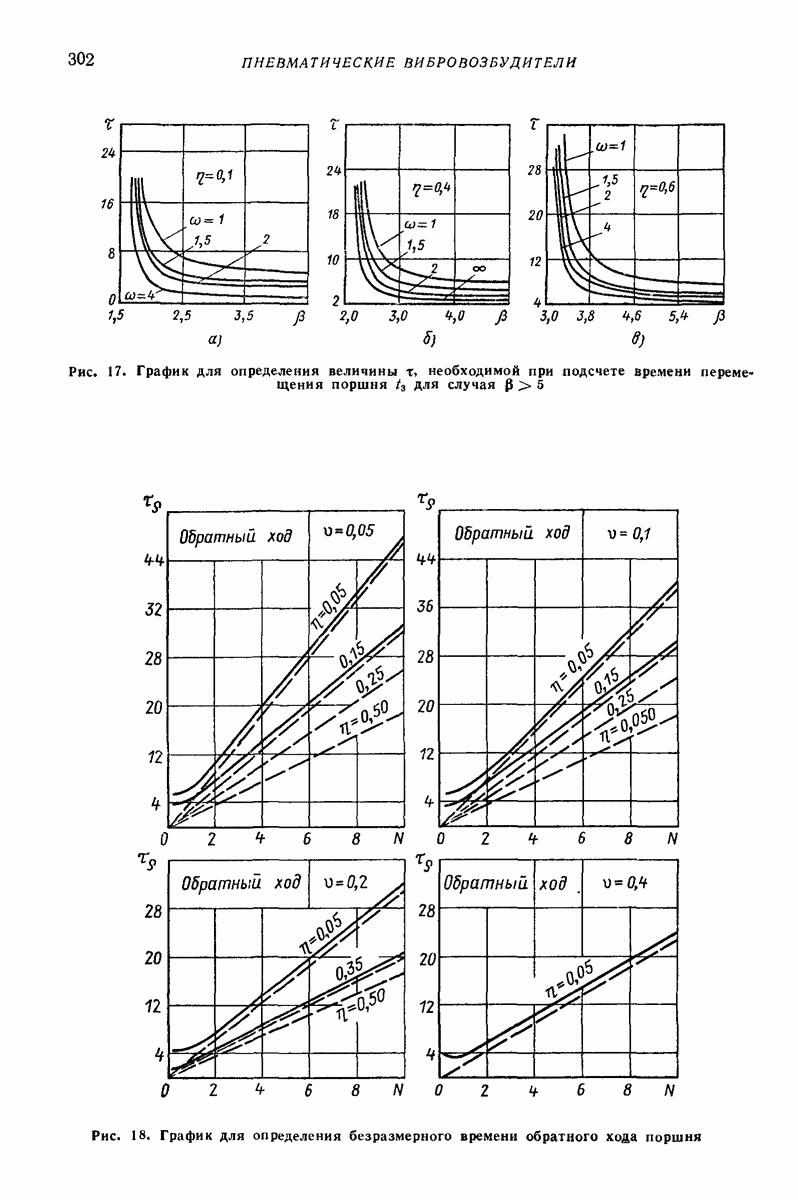
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
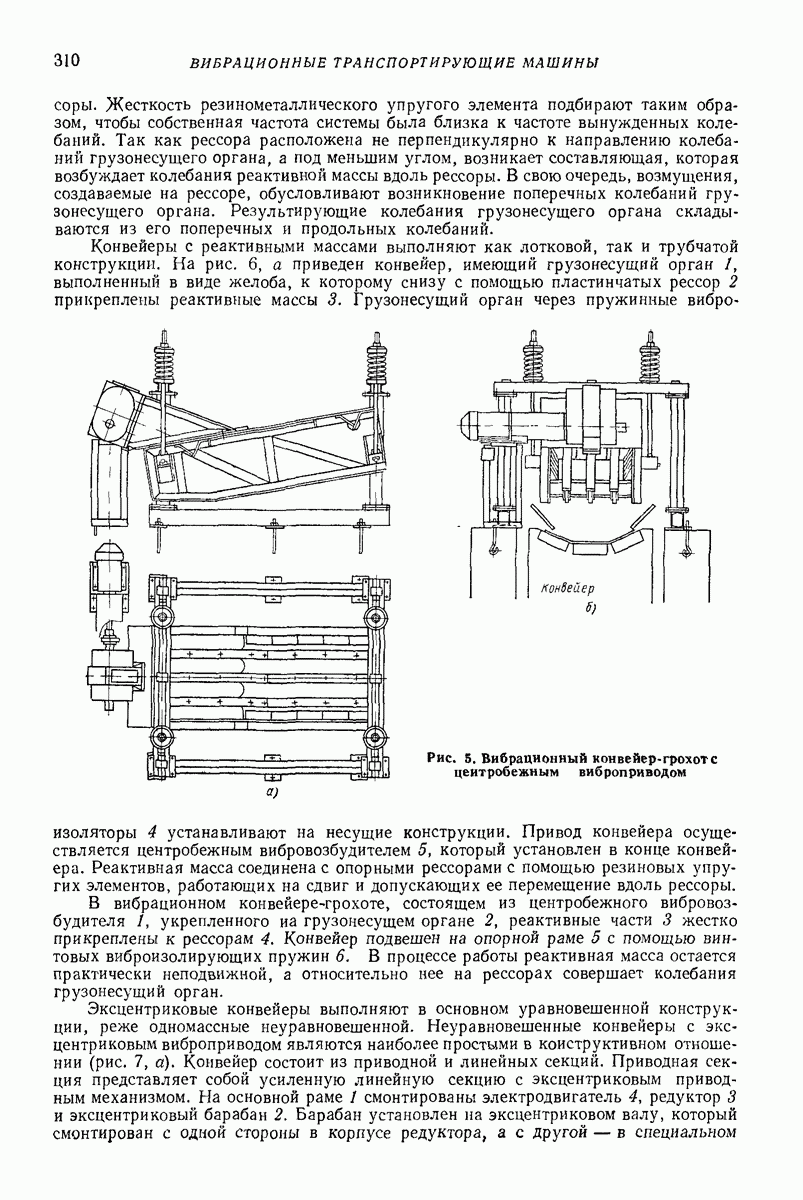
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
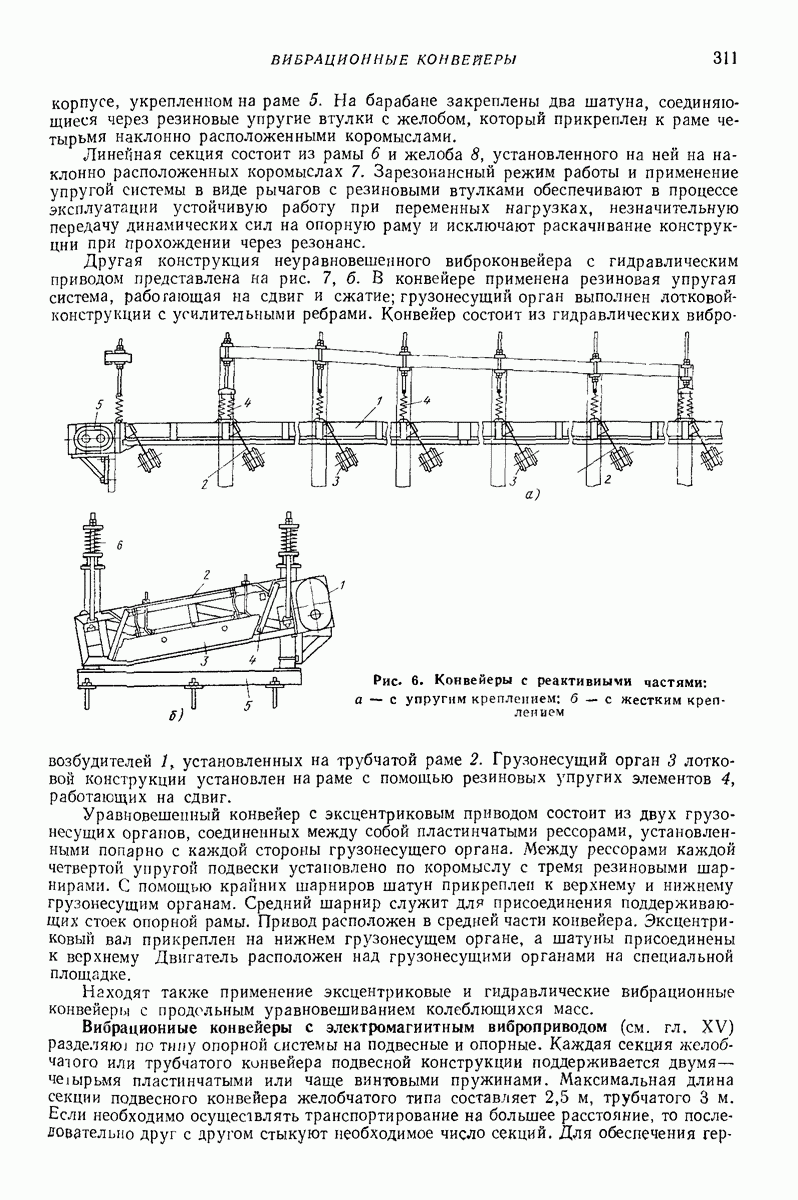
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
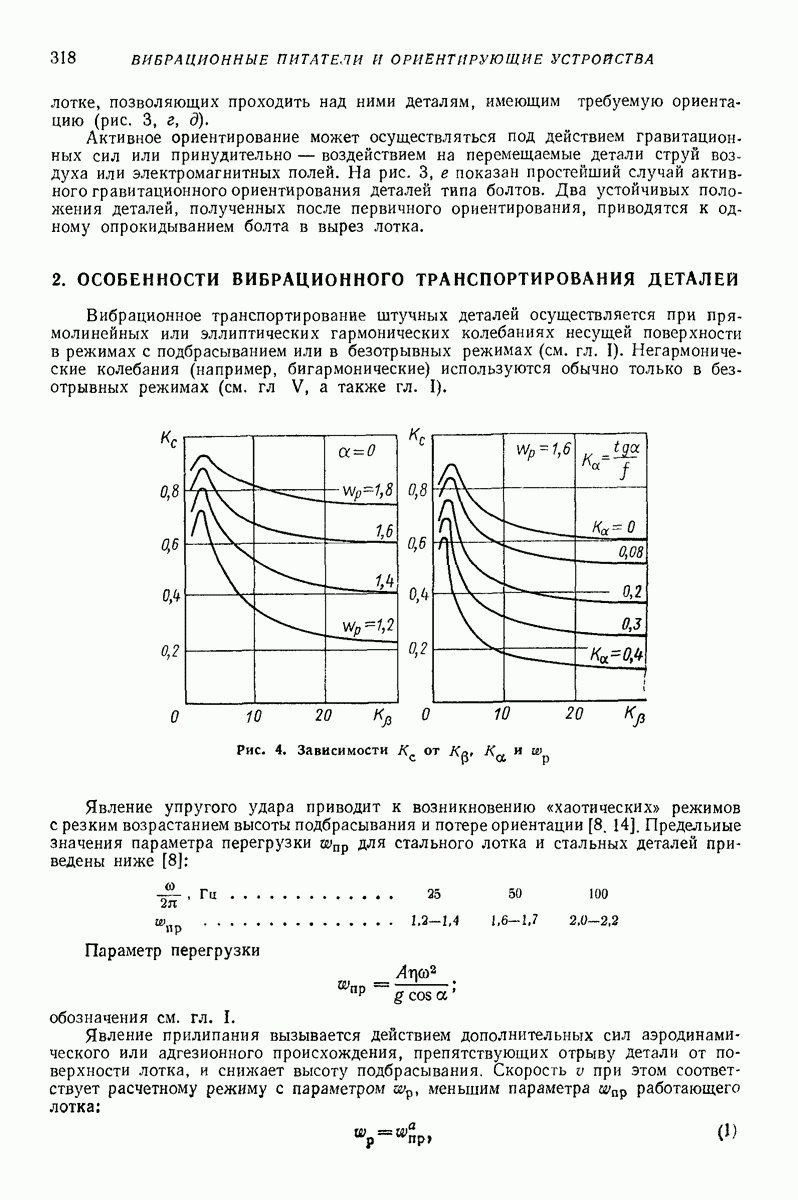
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
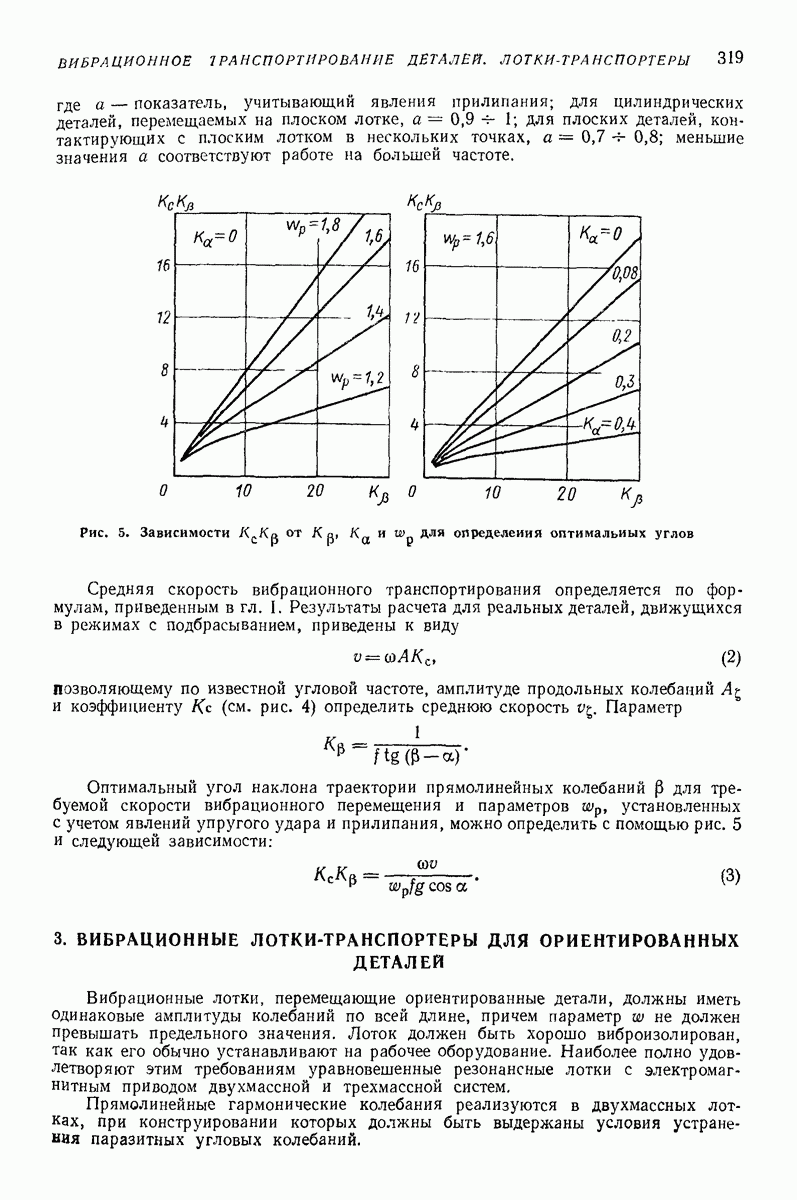
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
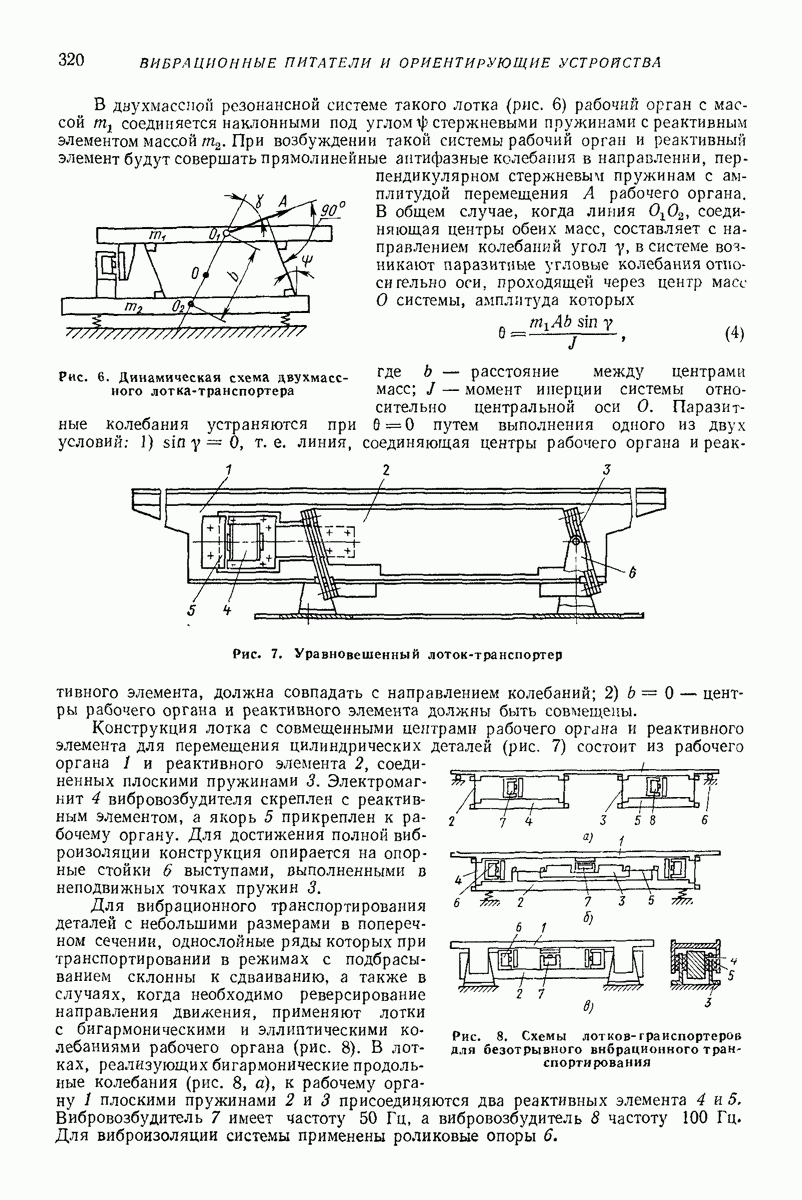
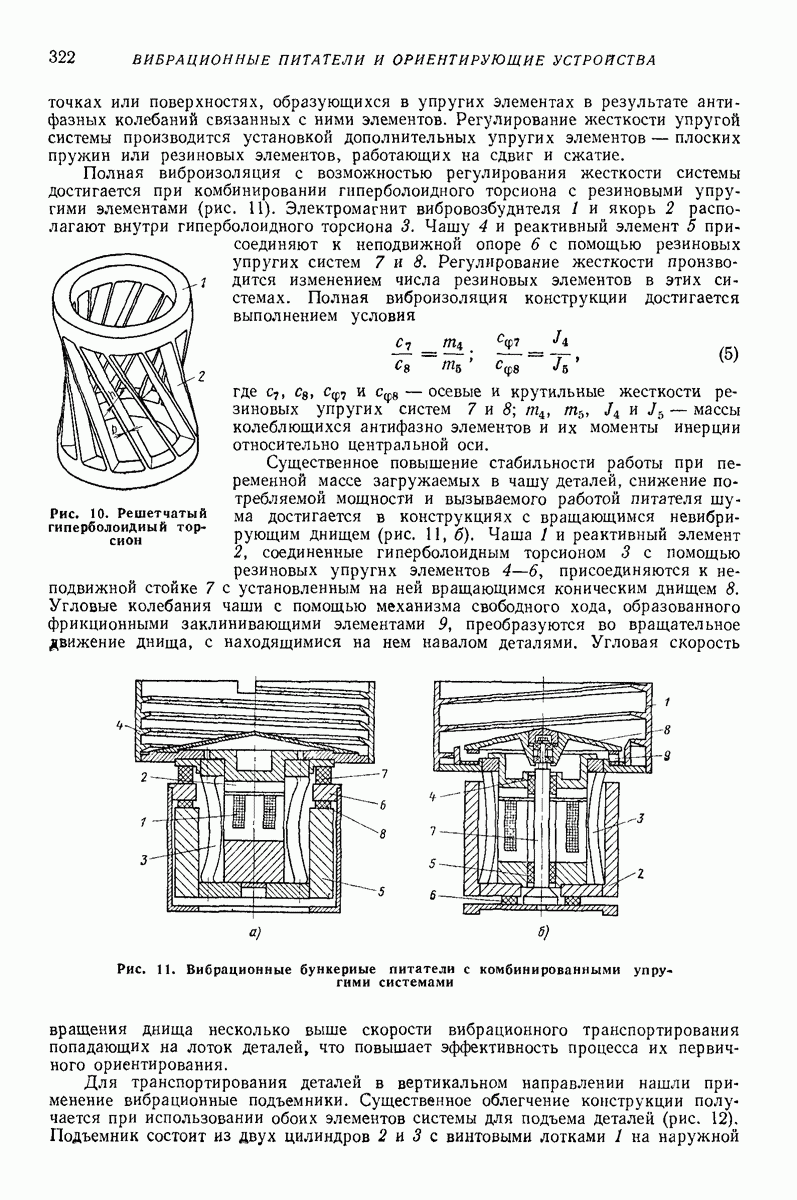
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
- 4. СЕПАРАТОРЫ С ДЕКОЙ
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
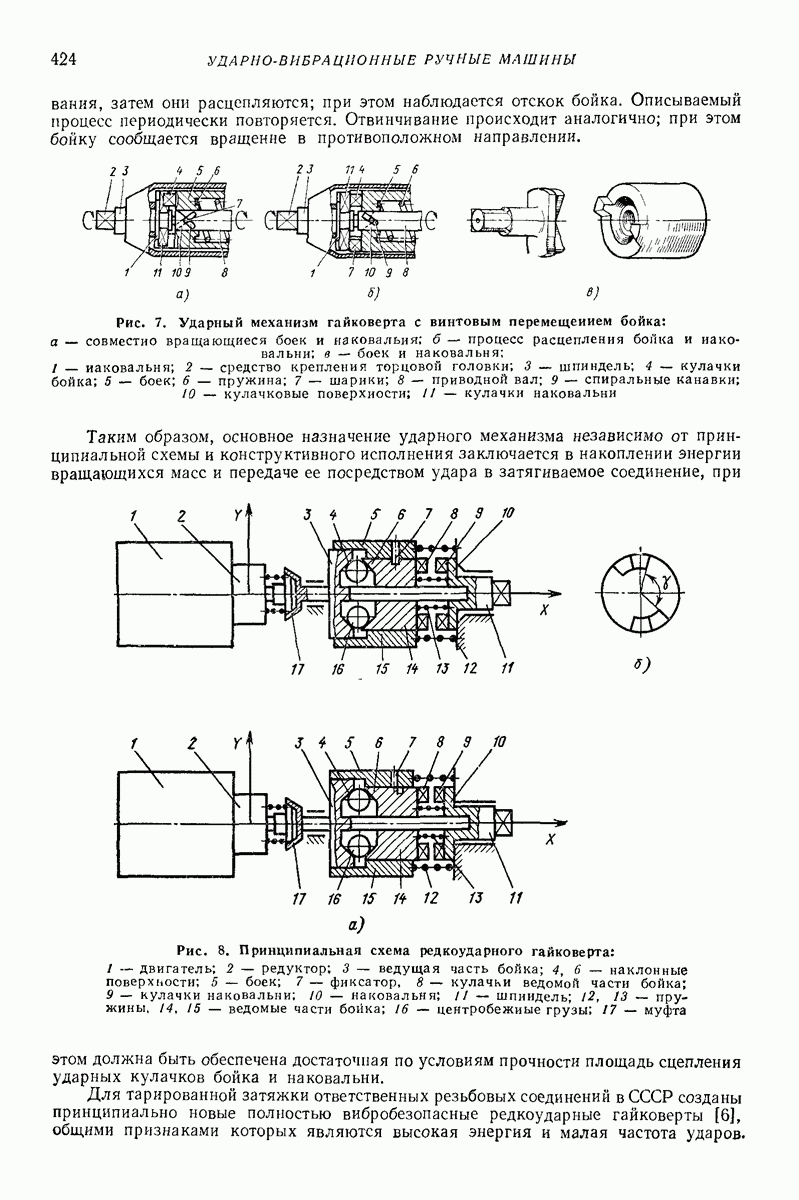
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
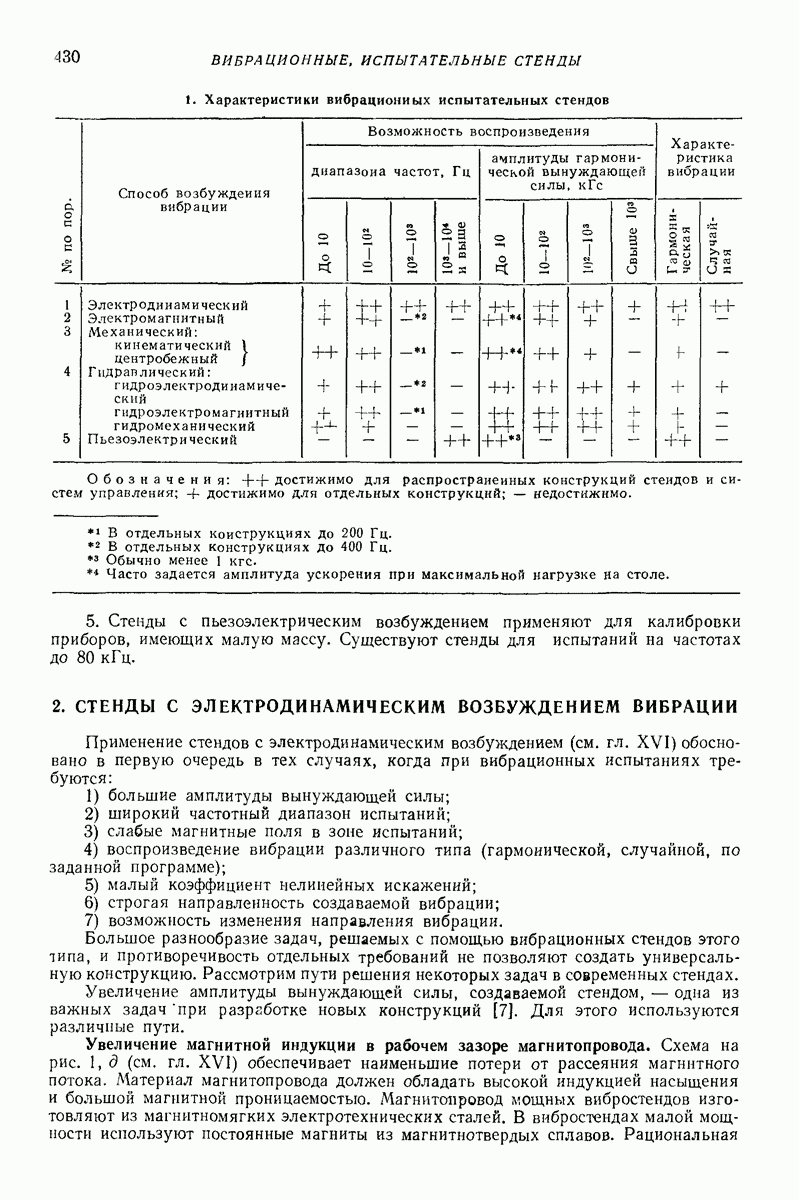
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
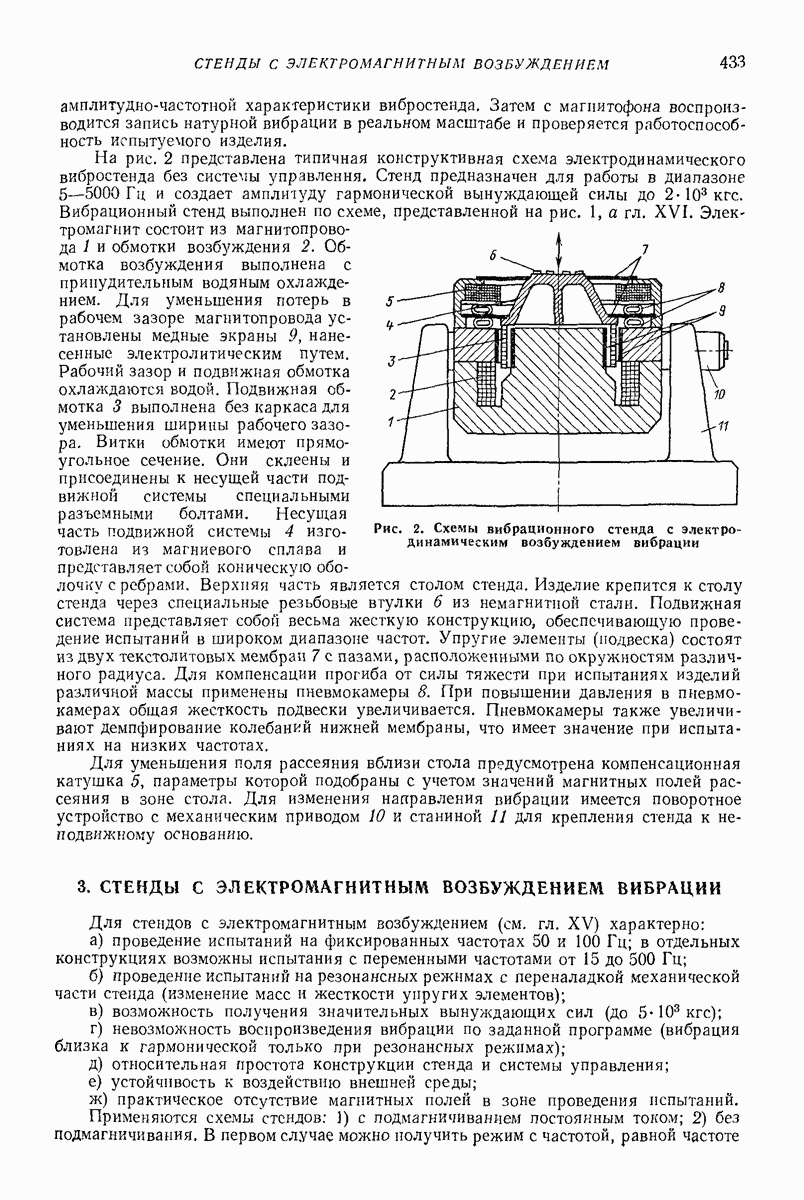
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
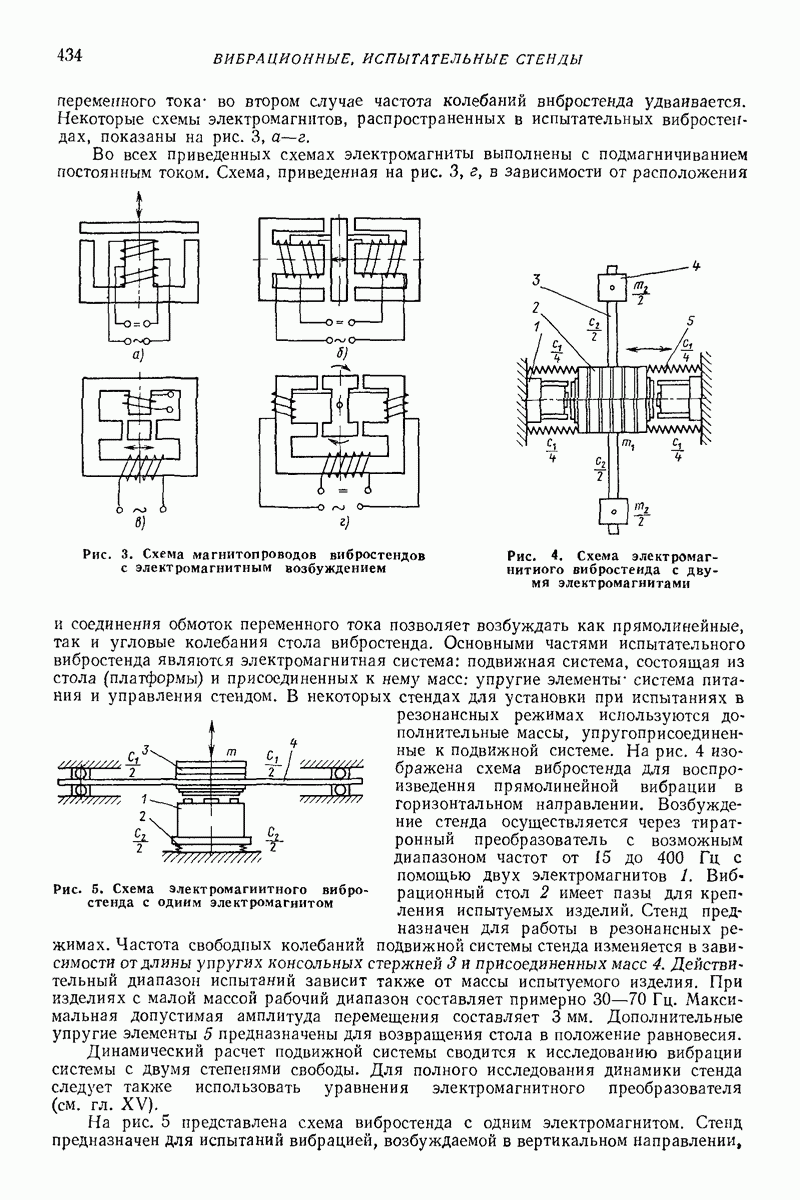
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ