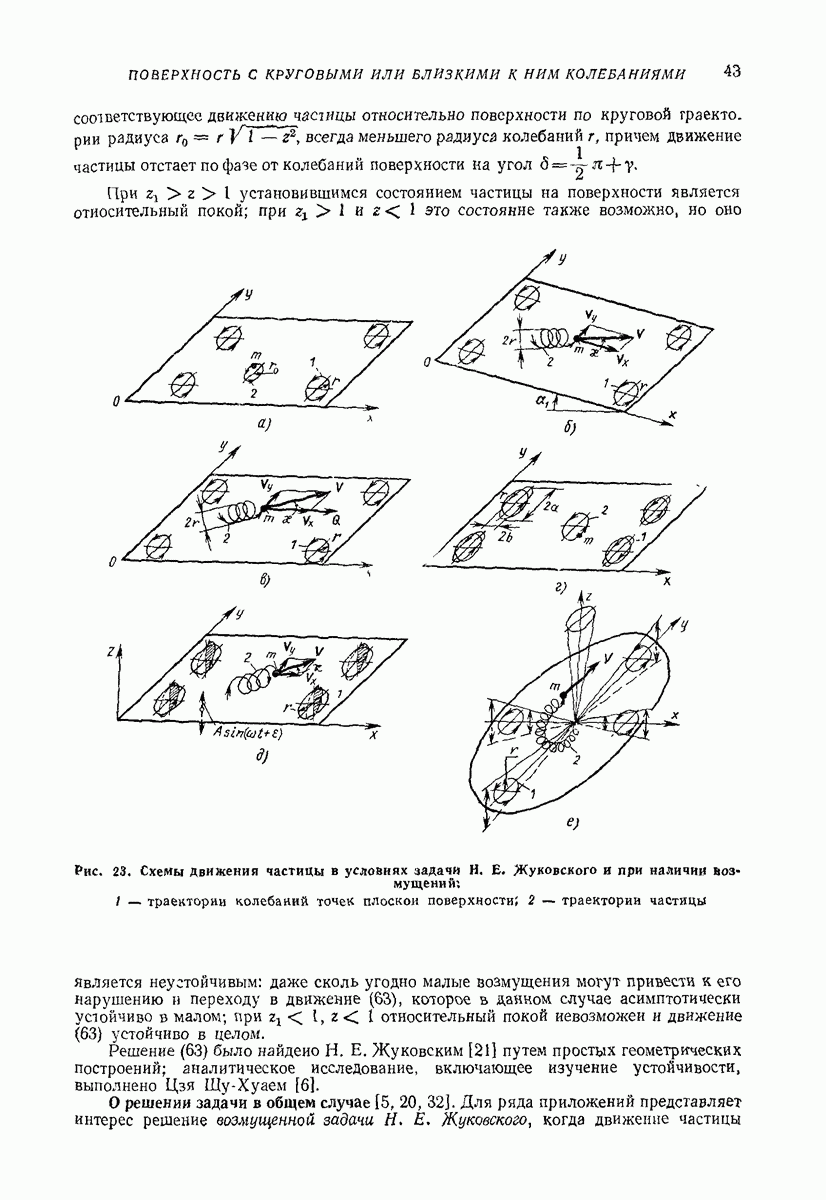
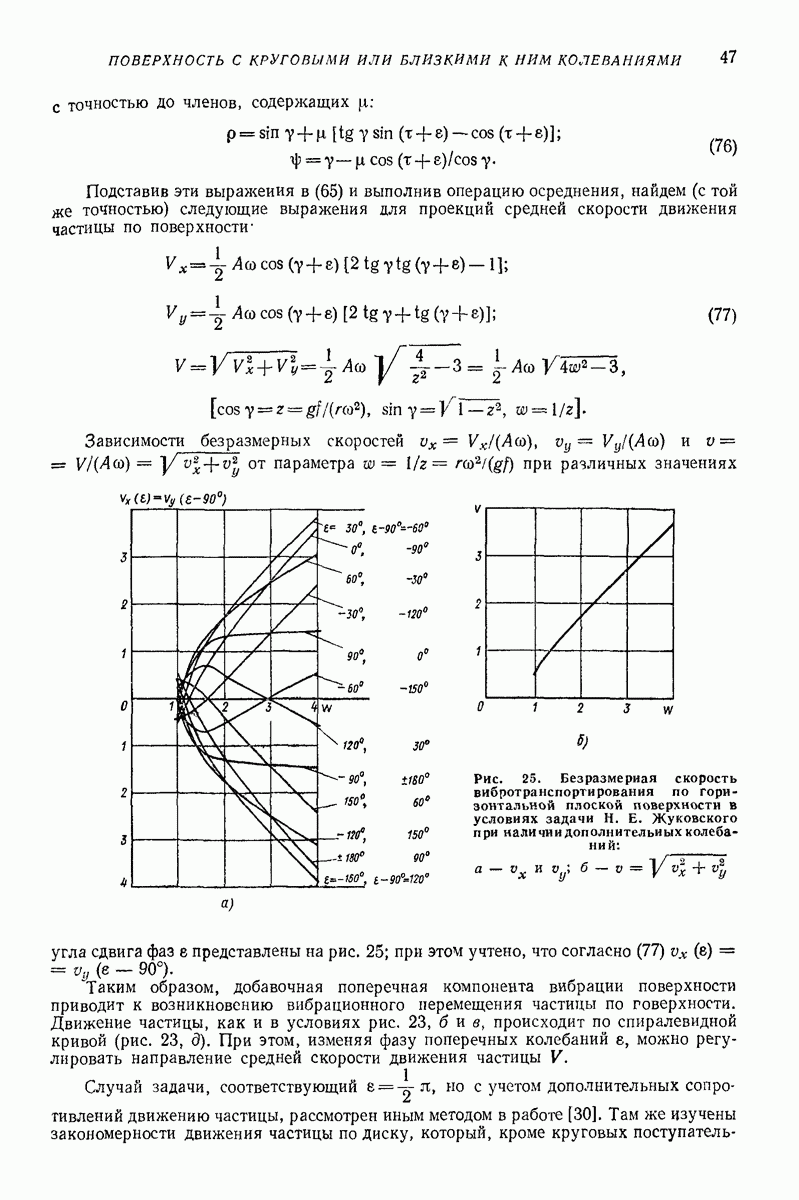
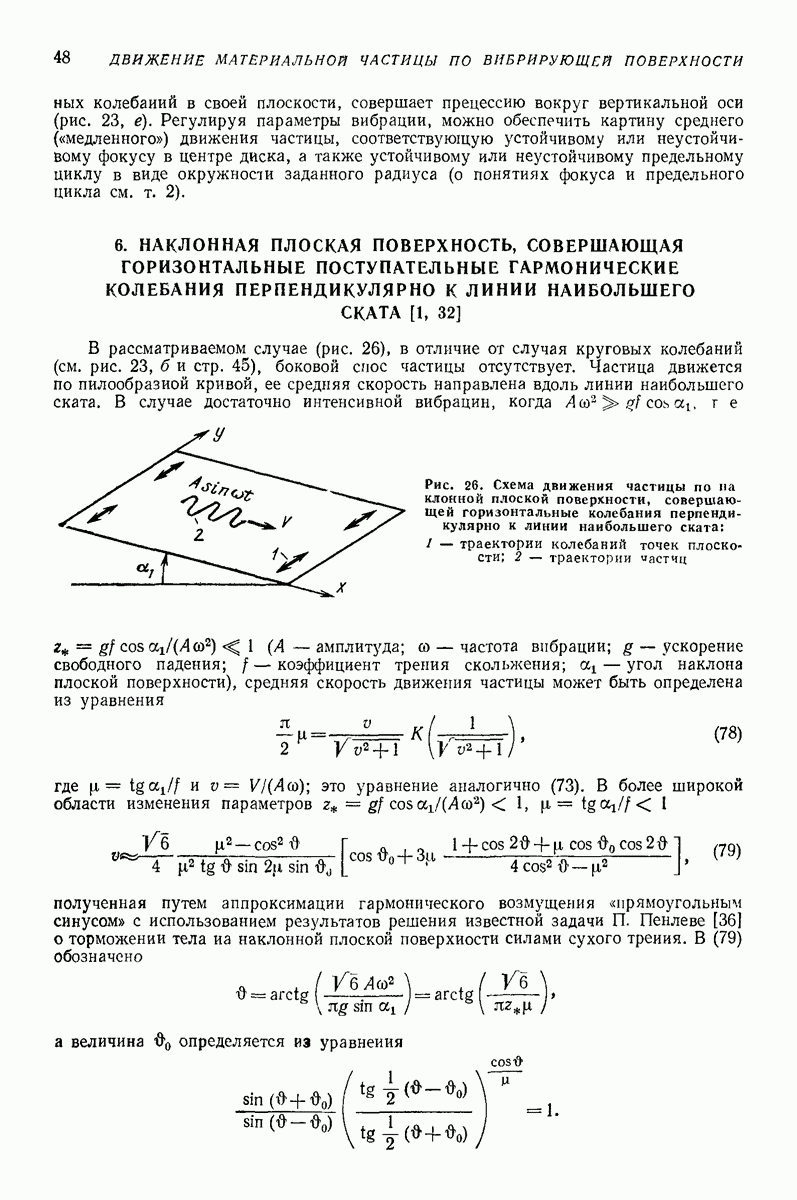
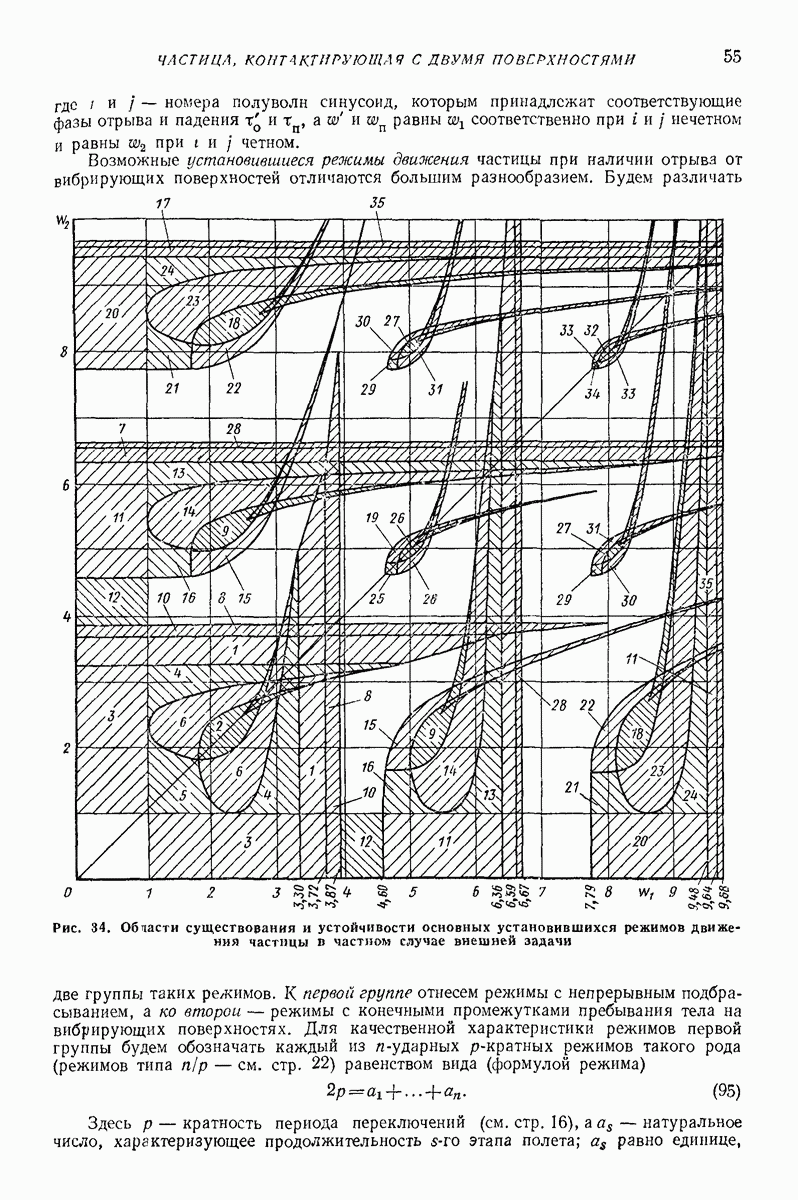
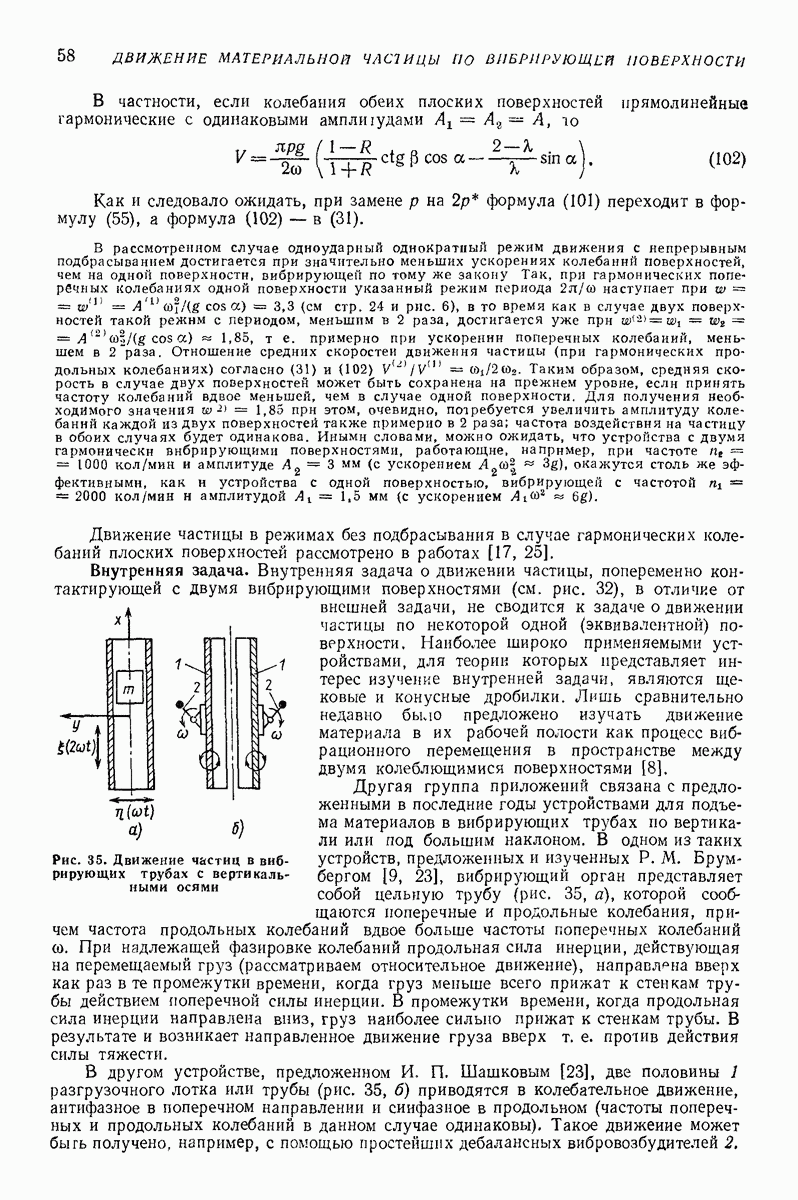
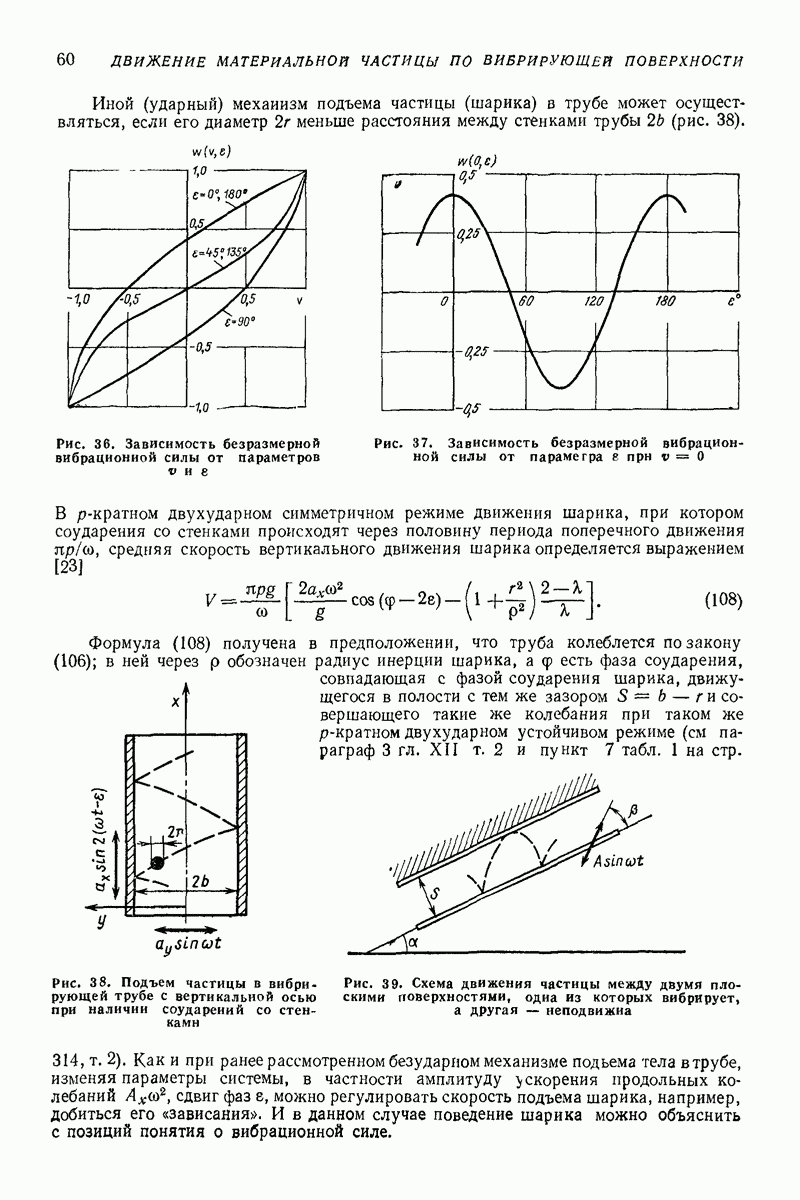
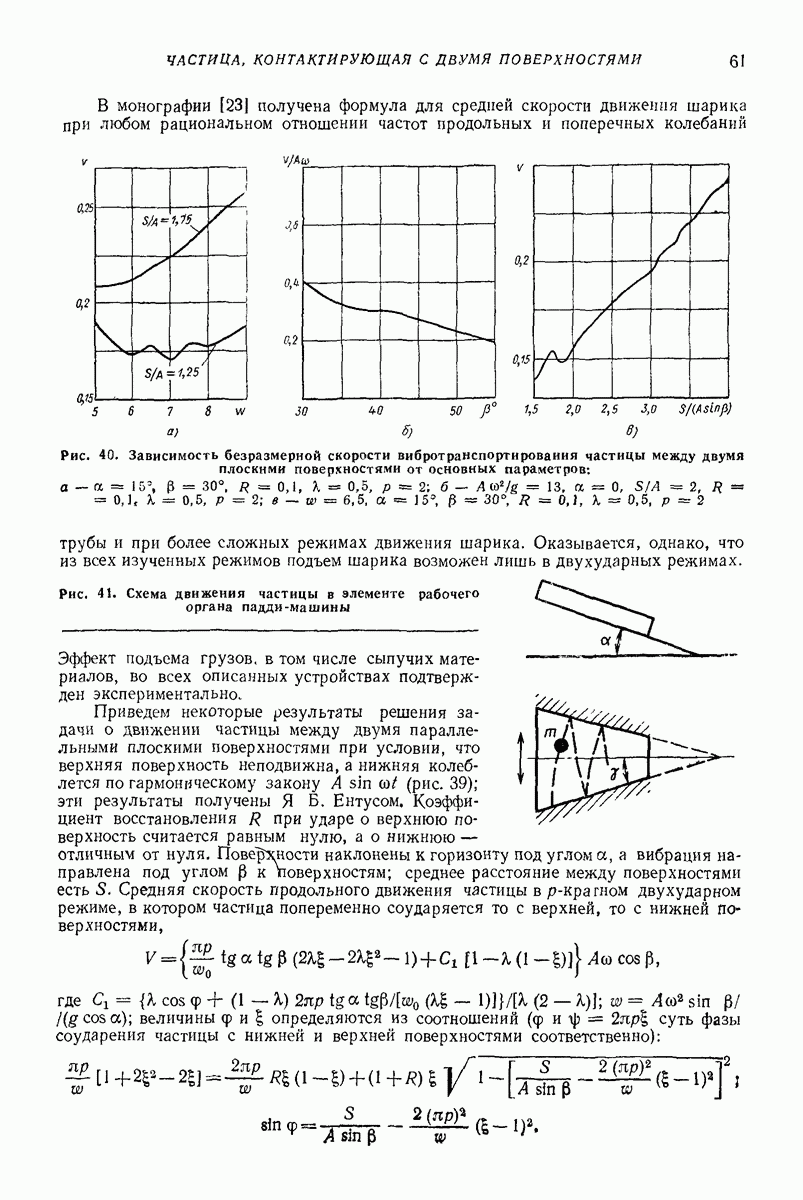
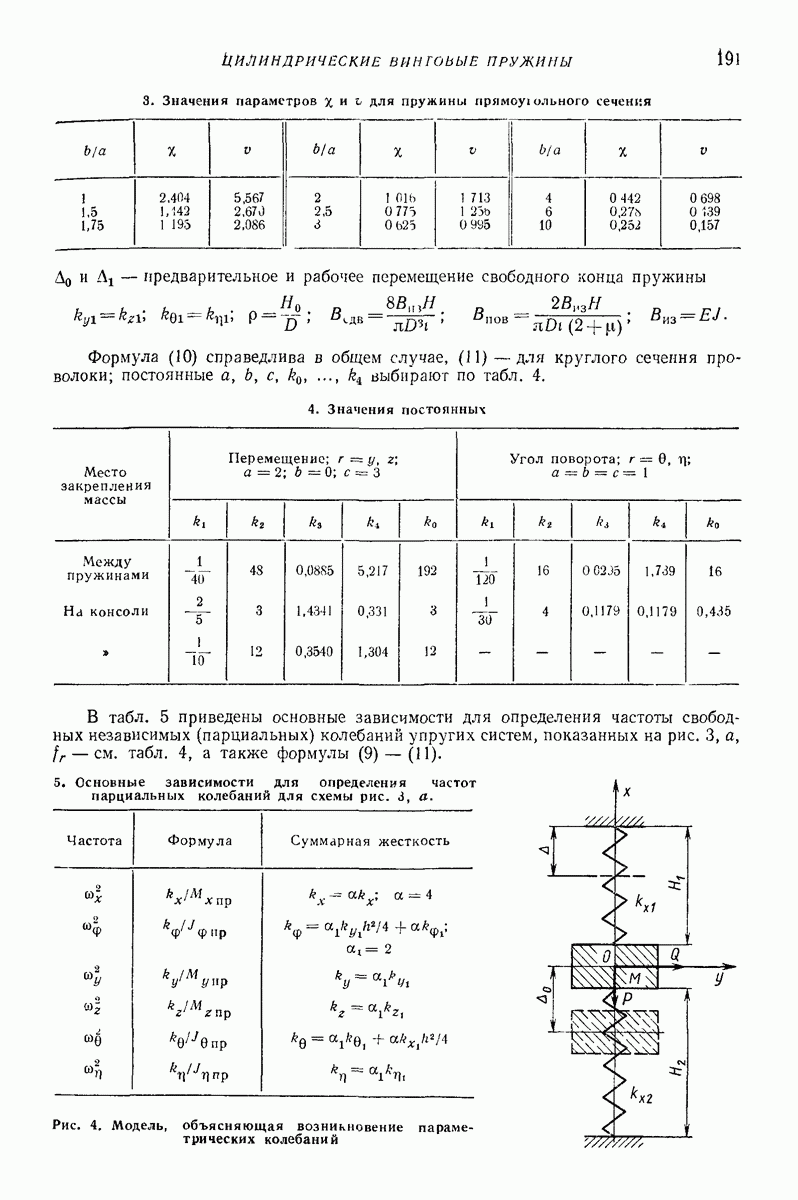
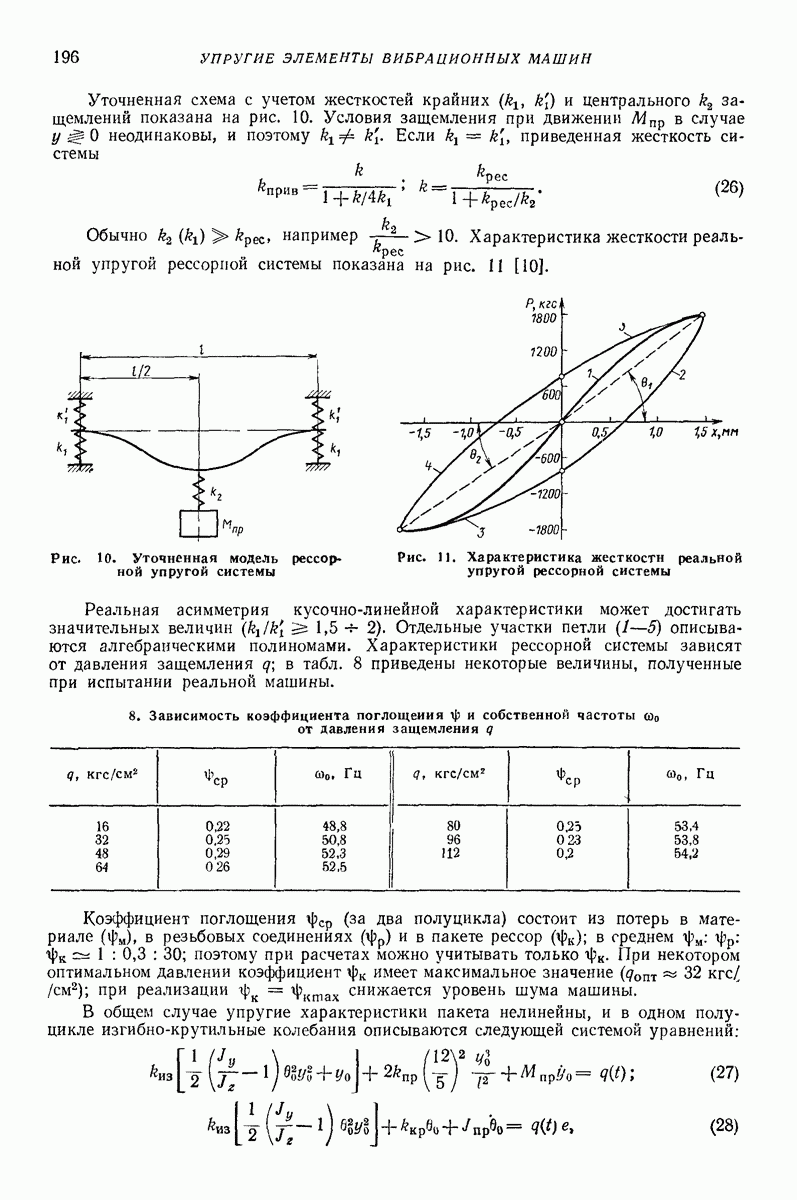
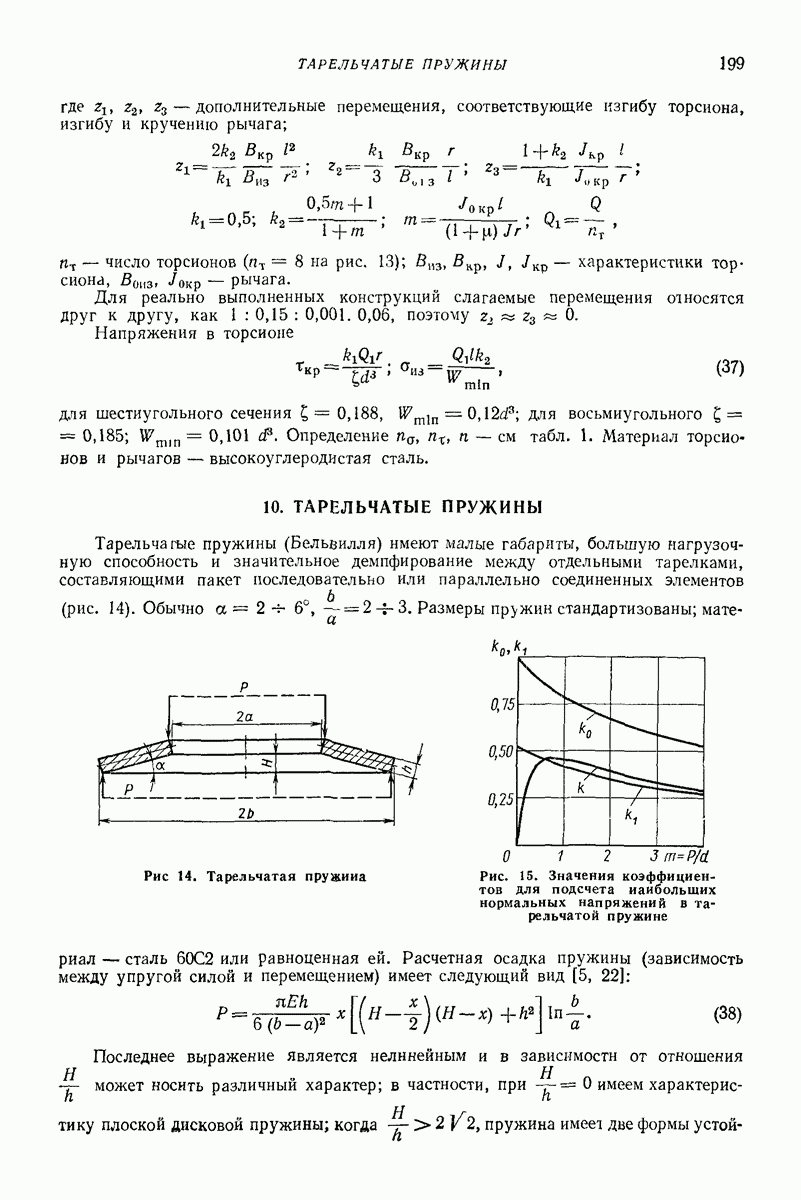
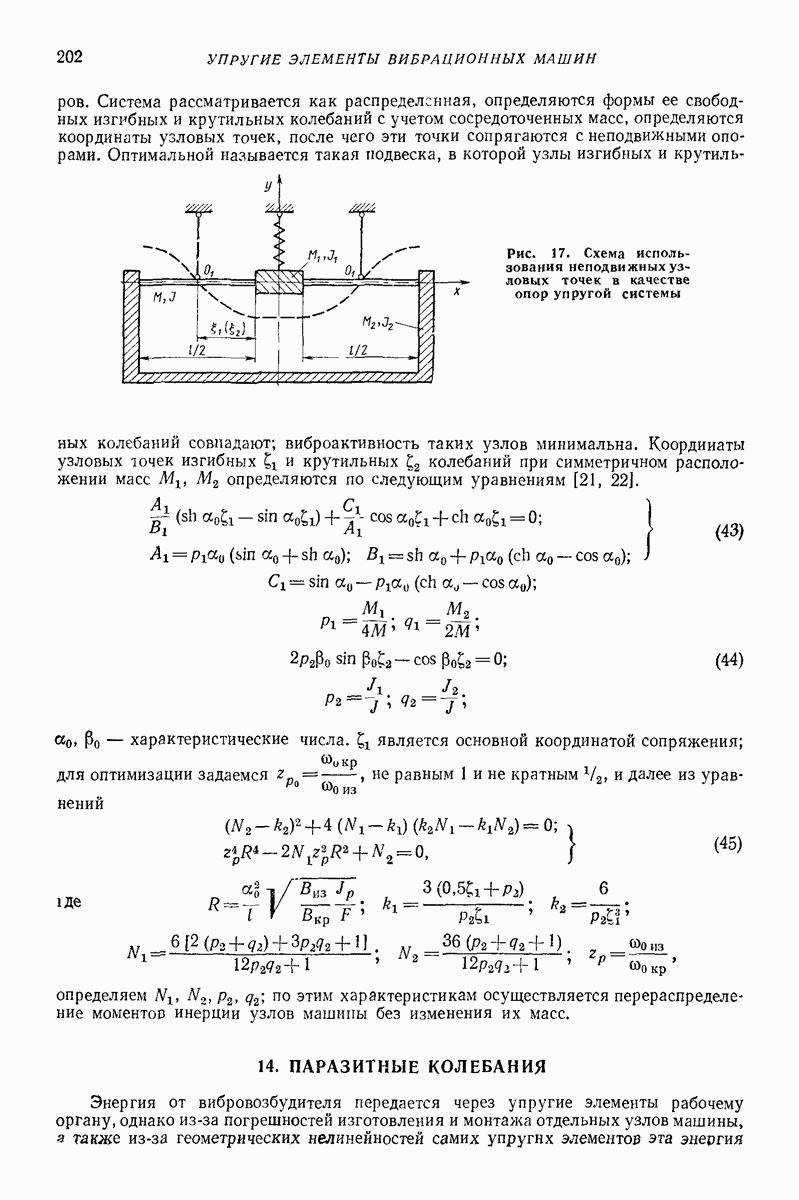
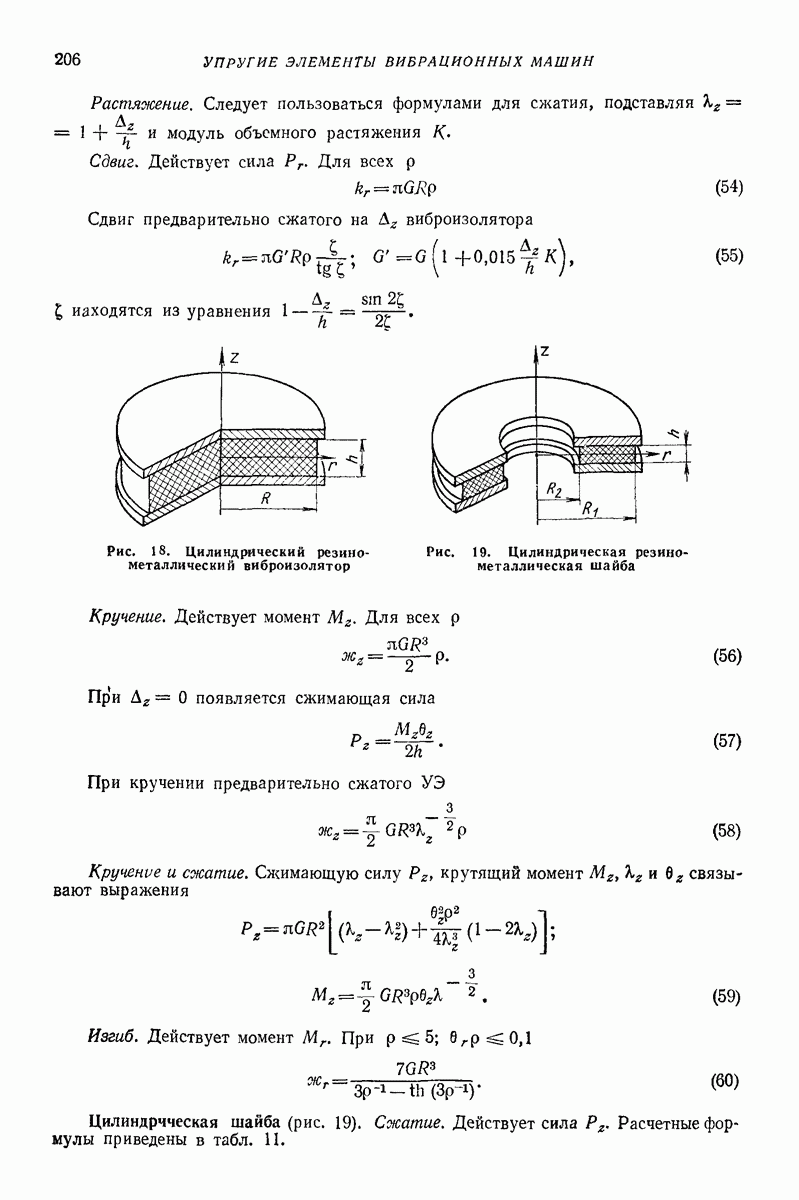
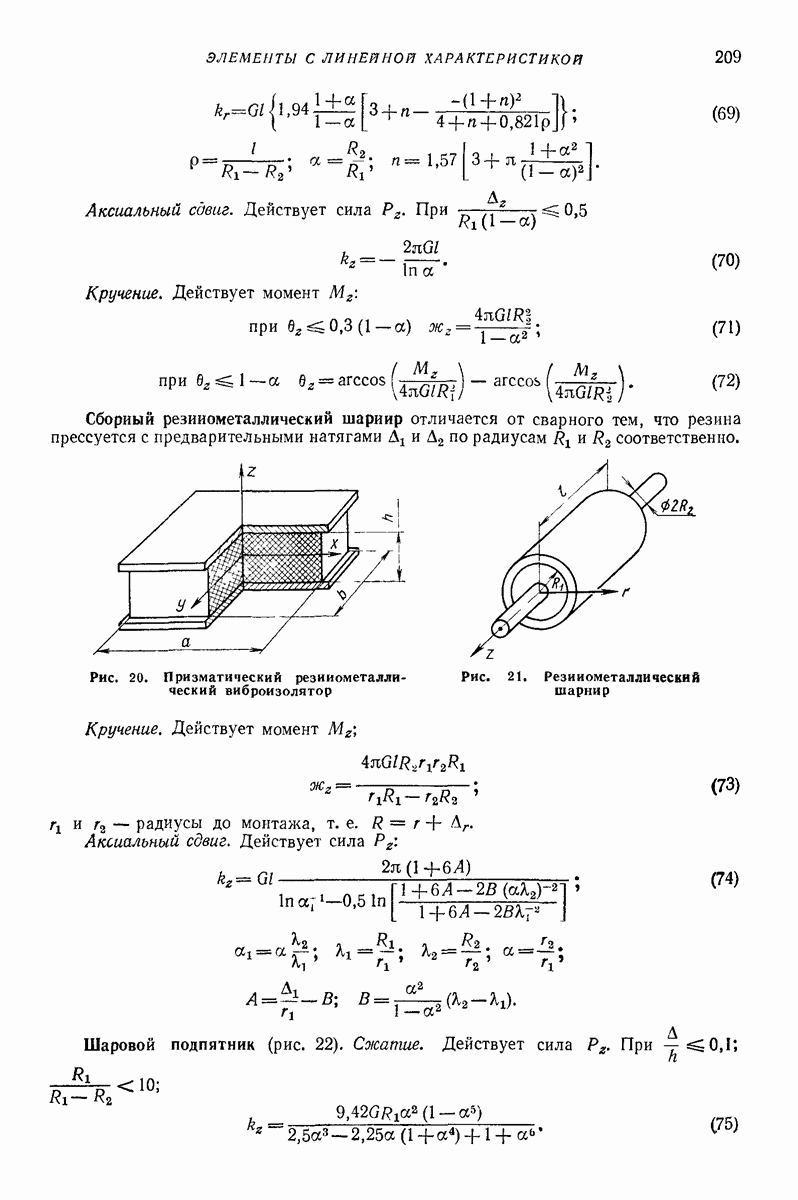
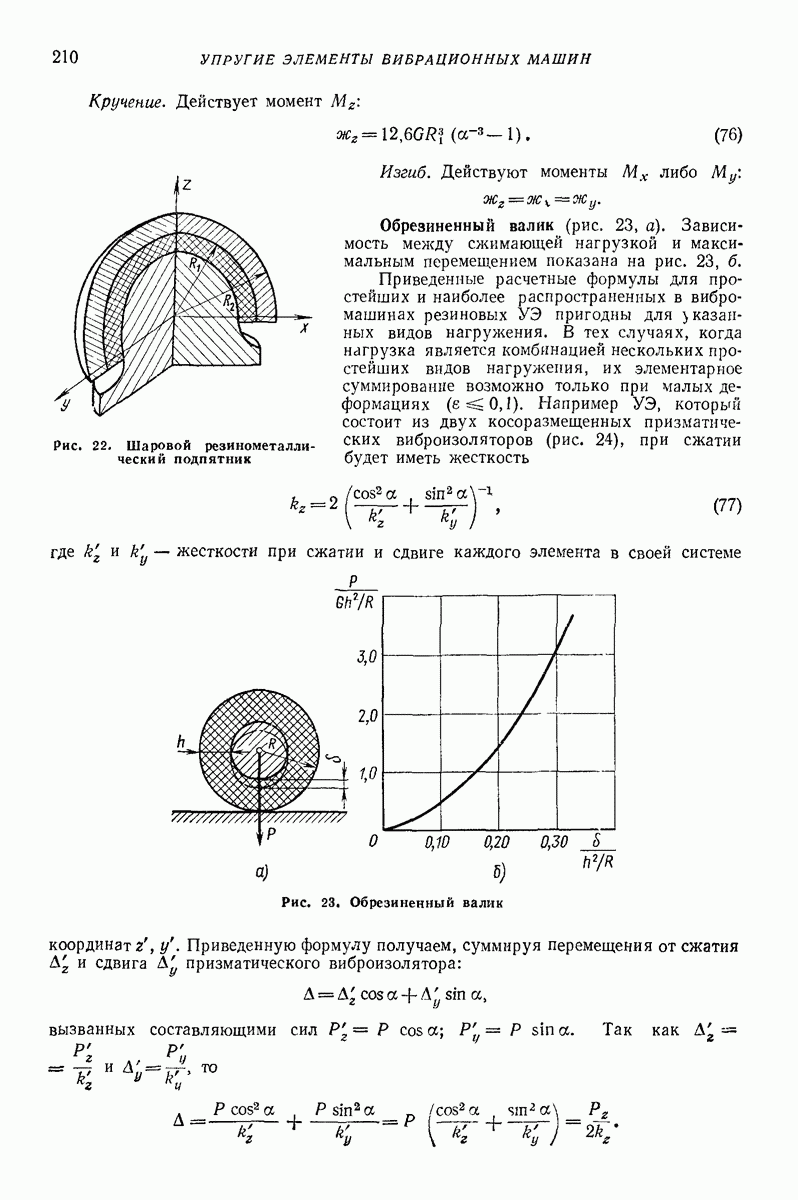
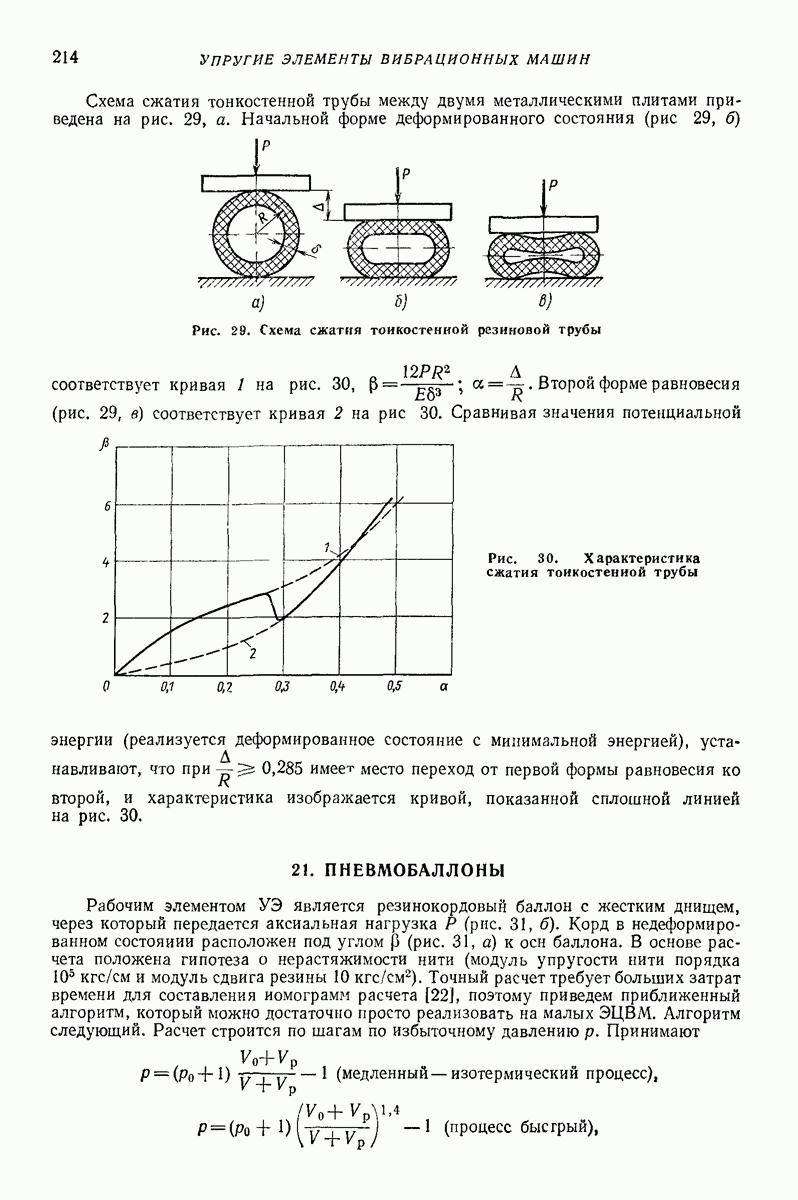
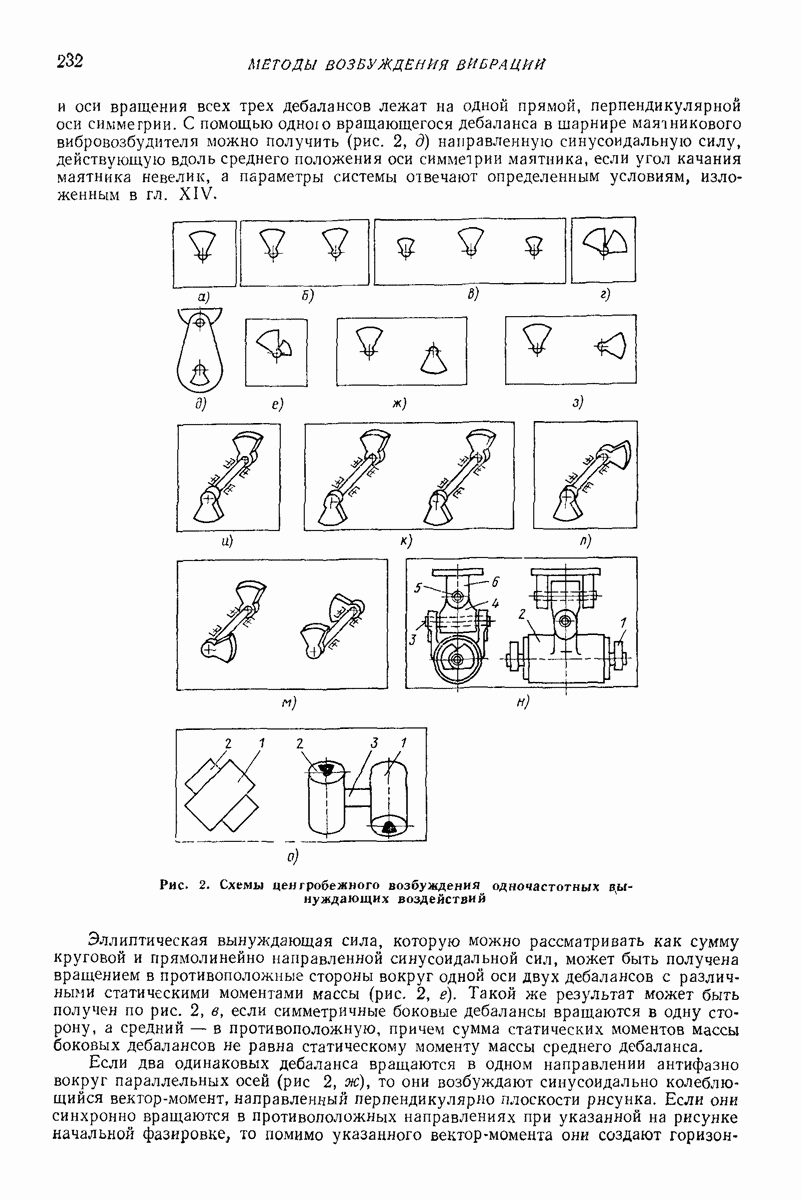
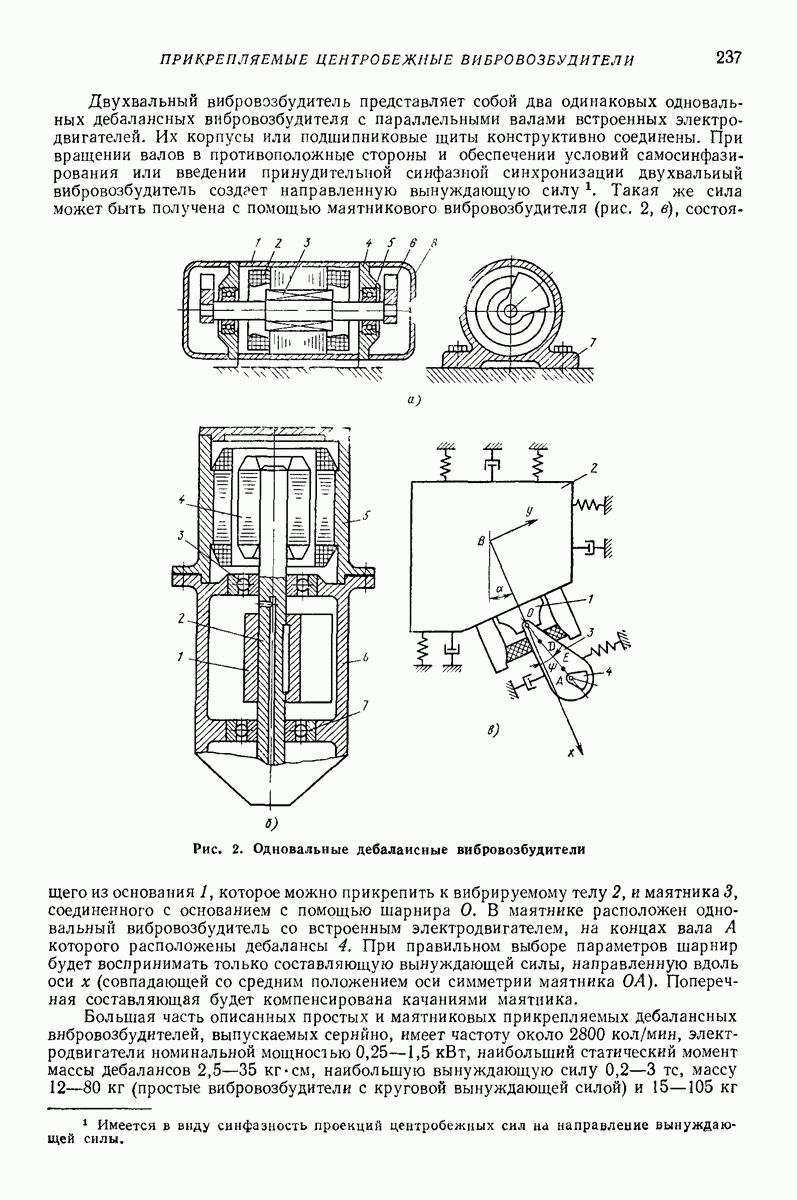
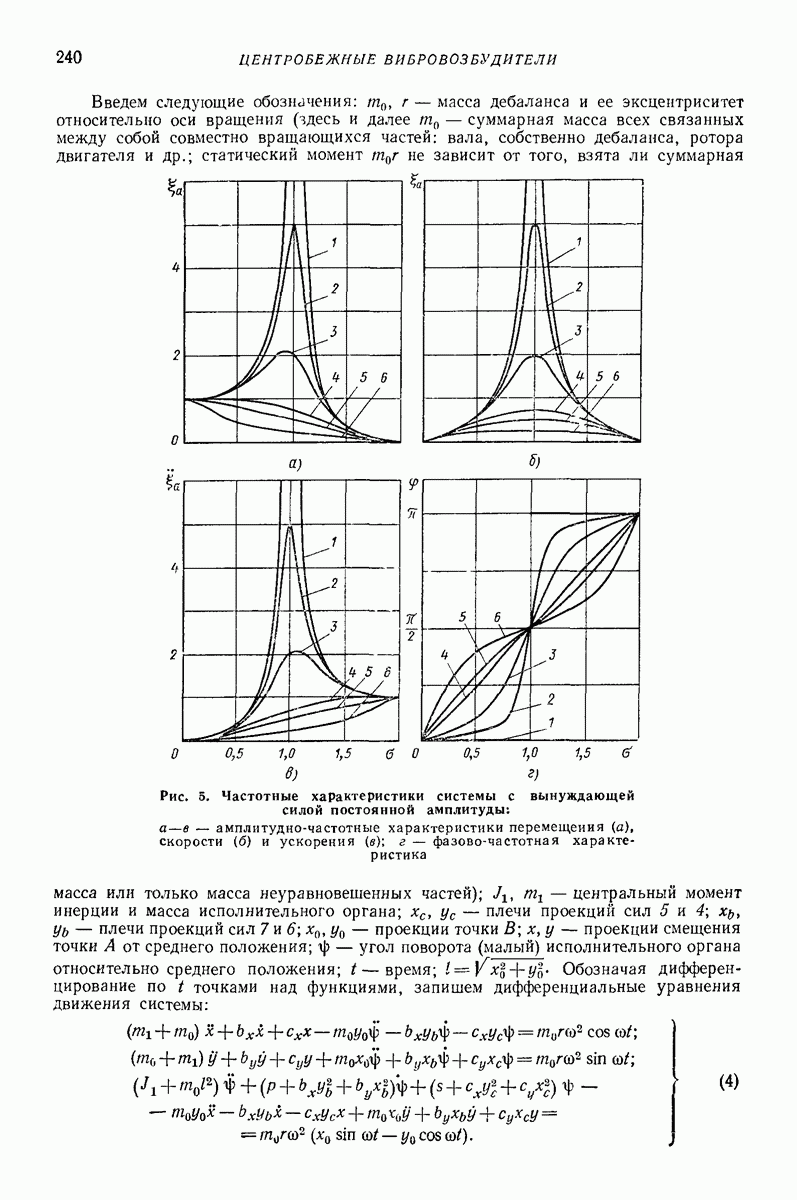
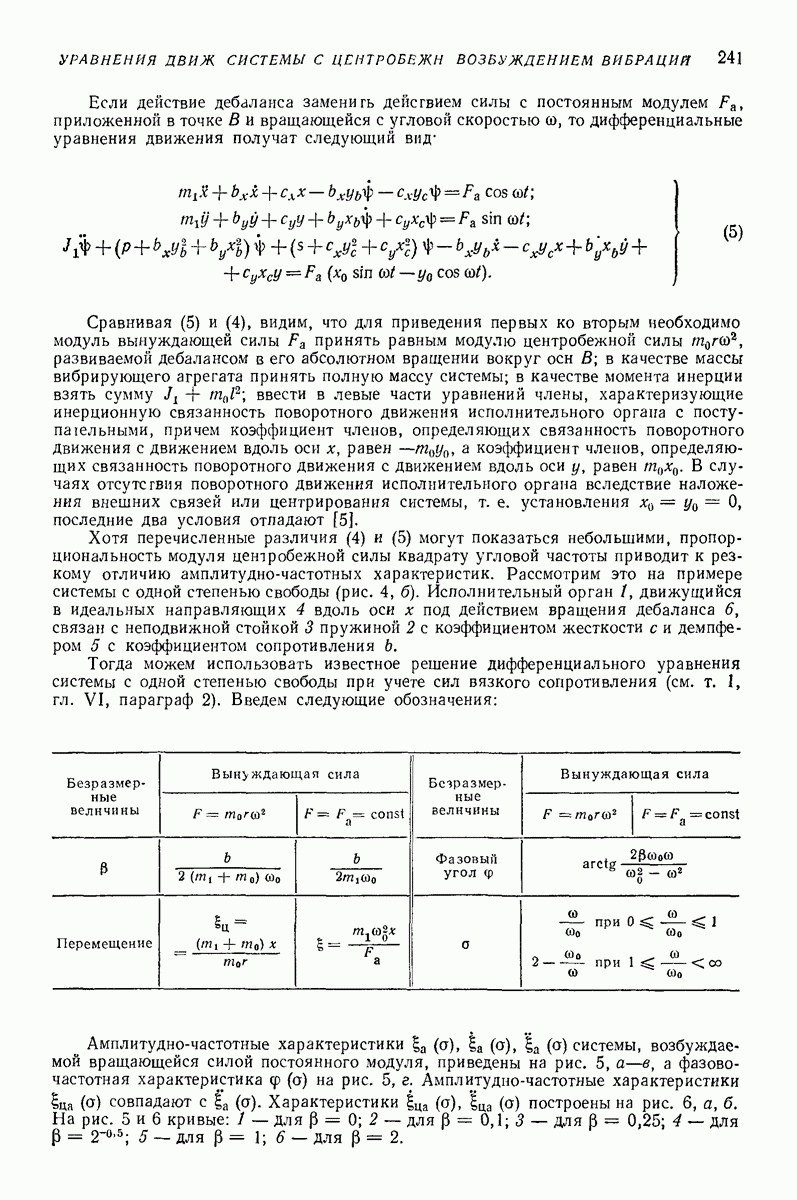
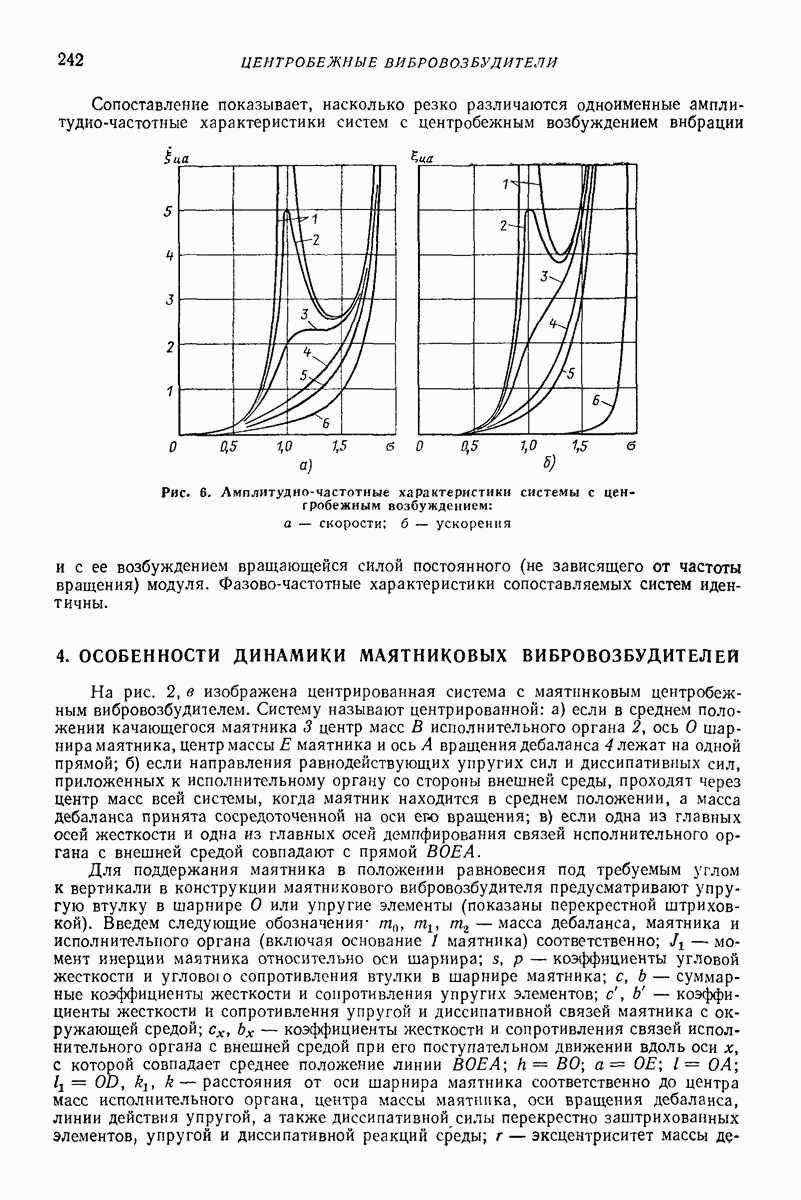
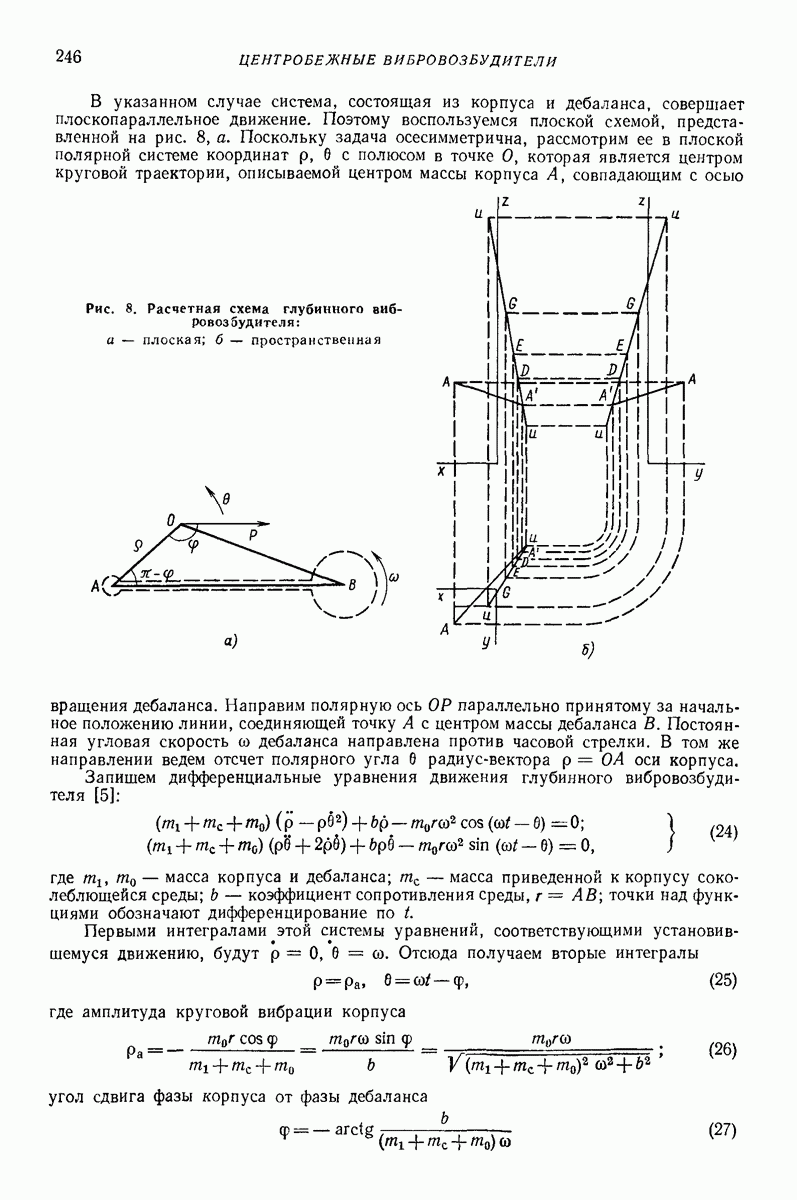
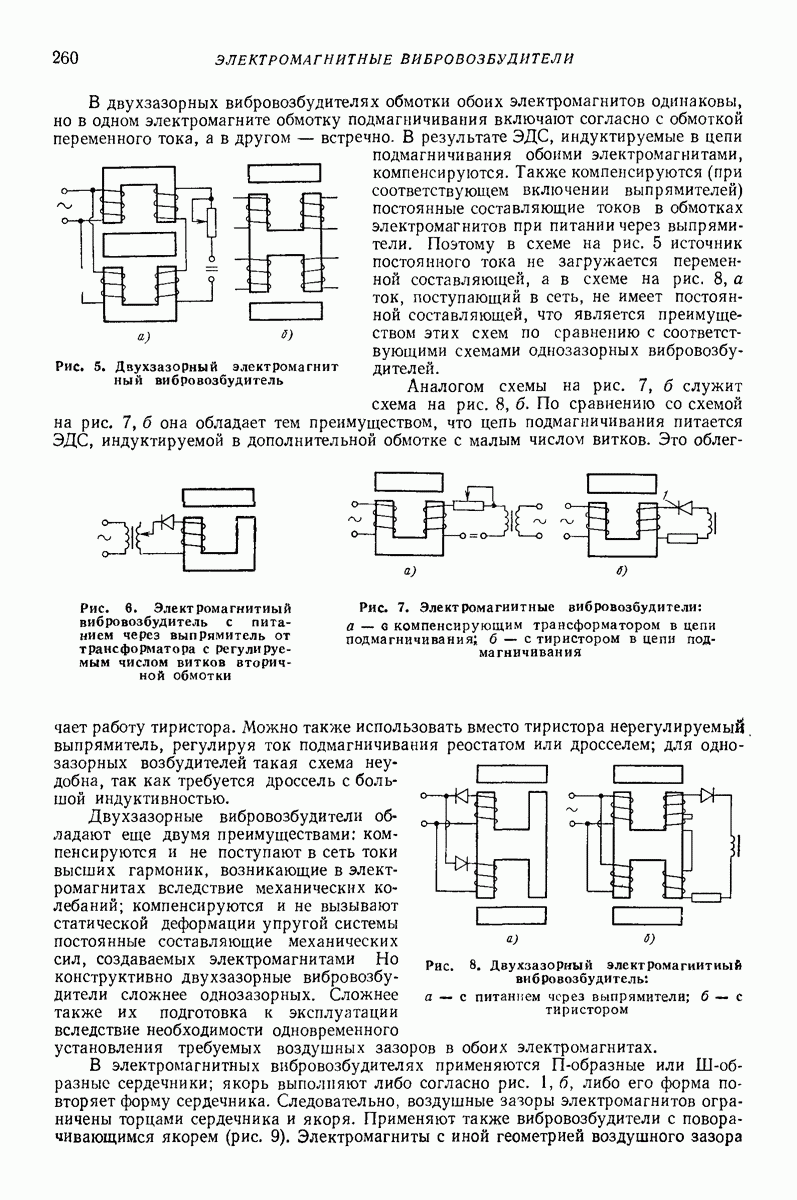
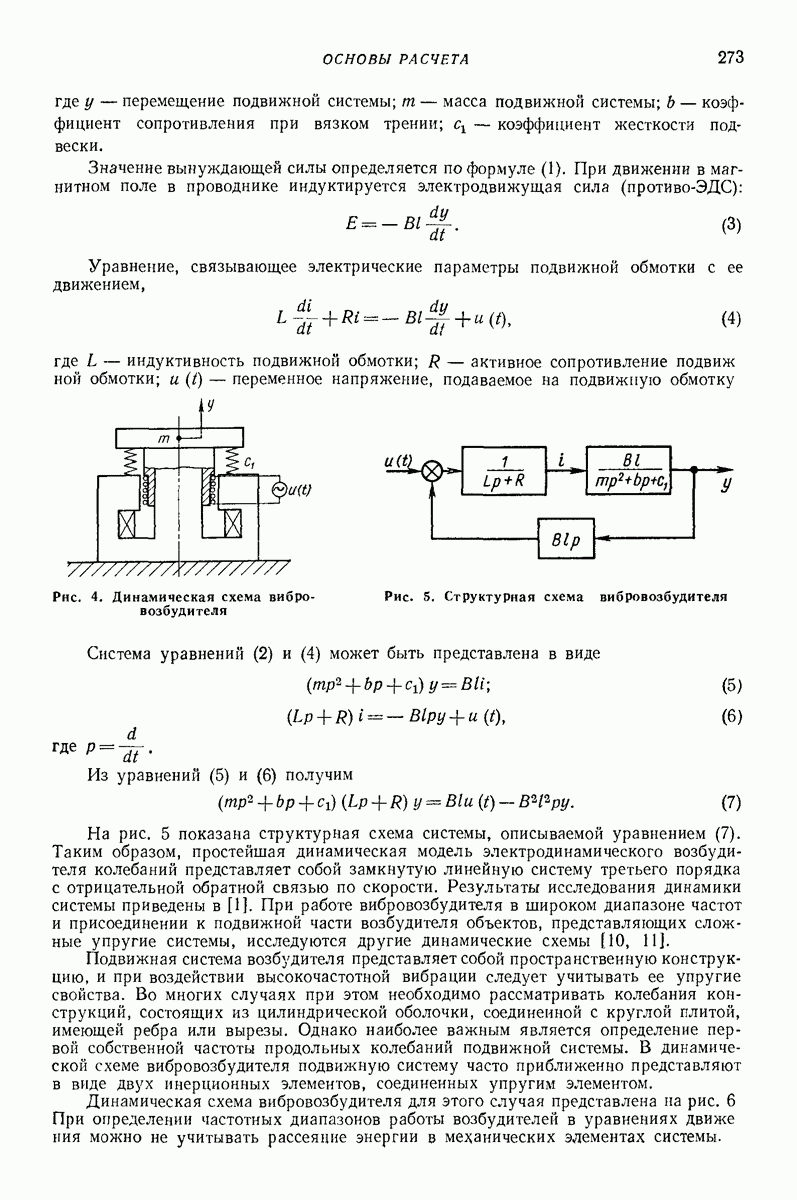
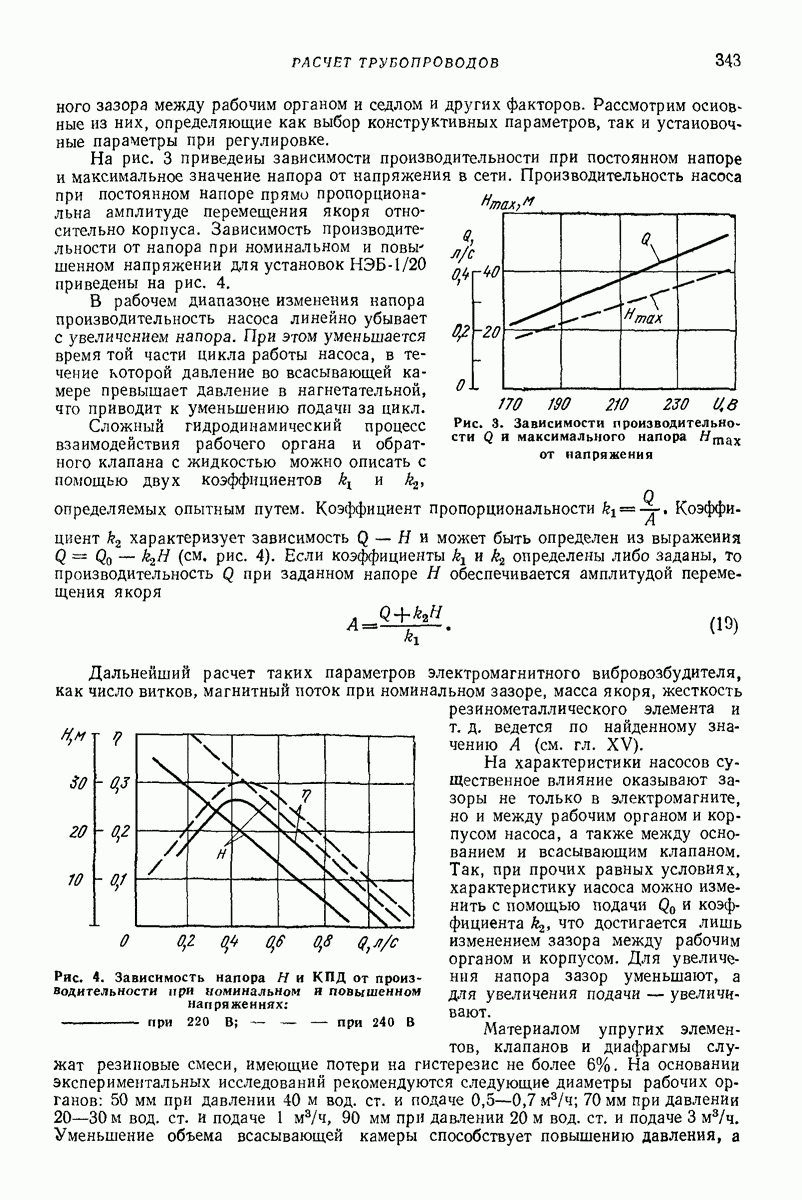
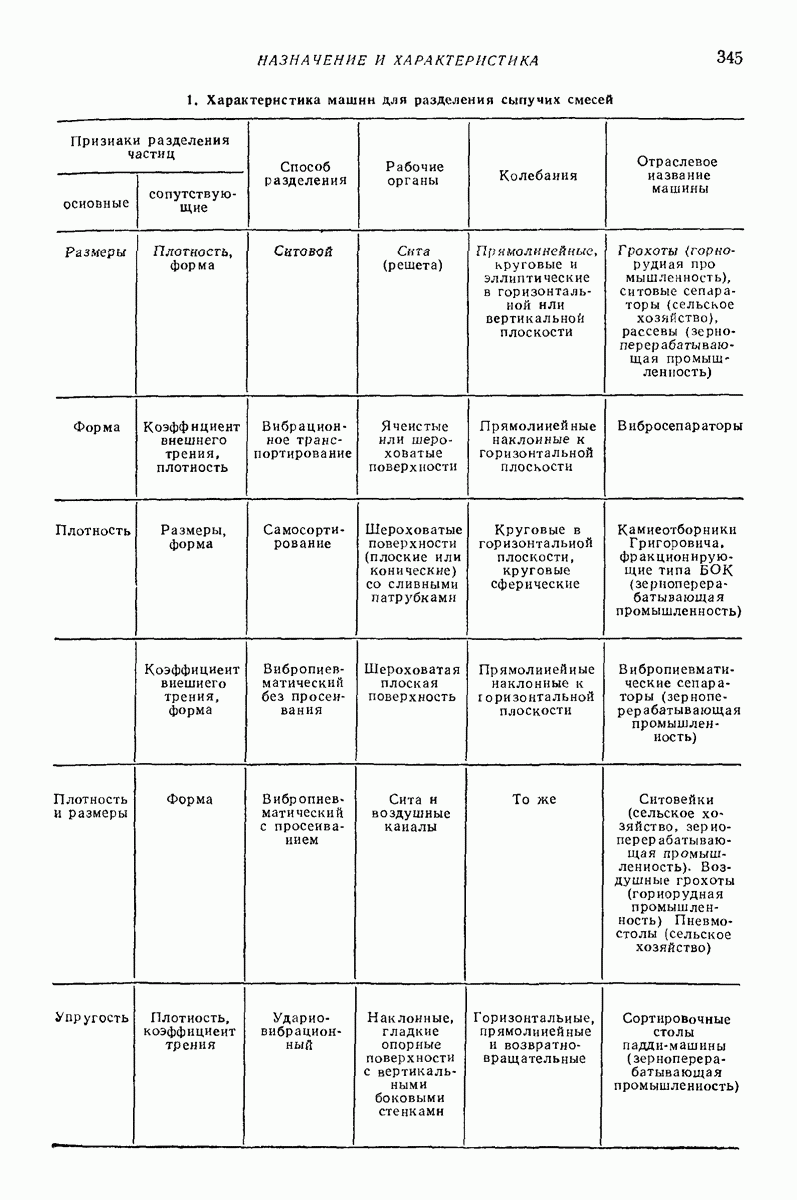
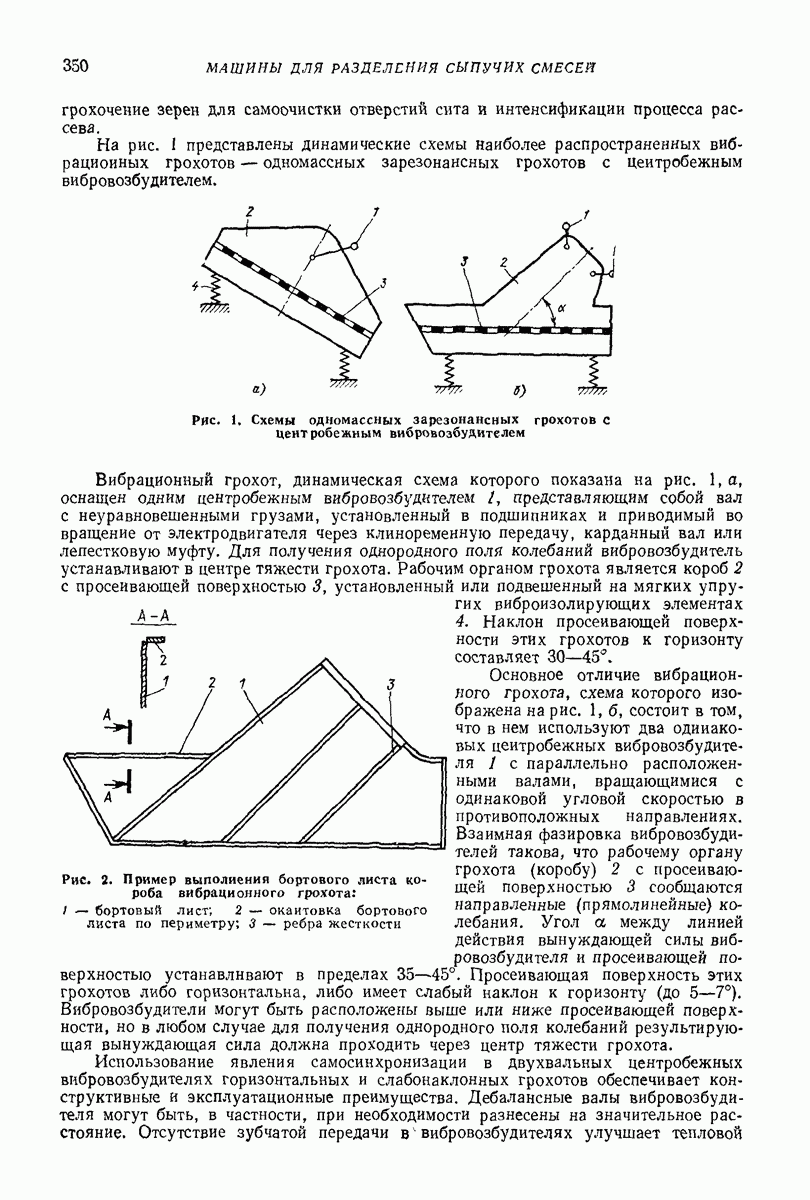
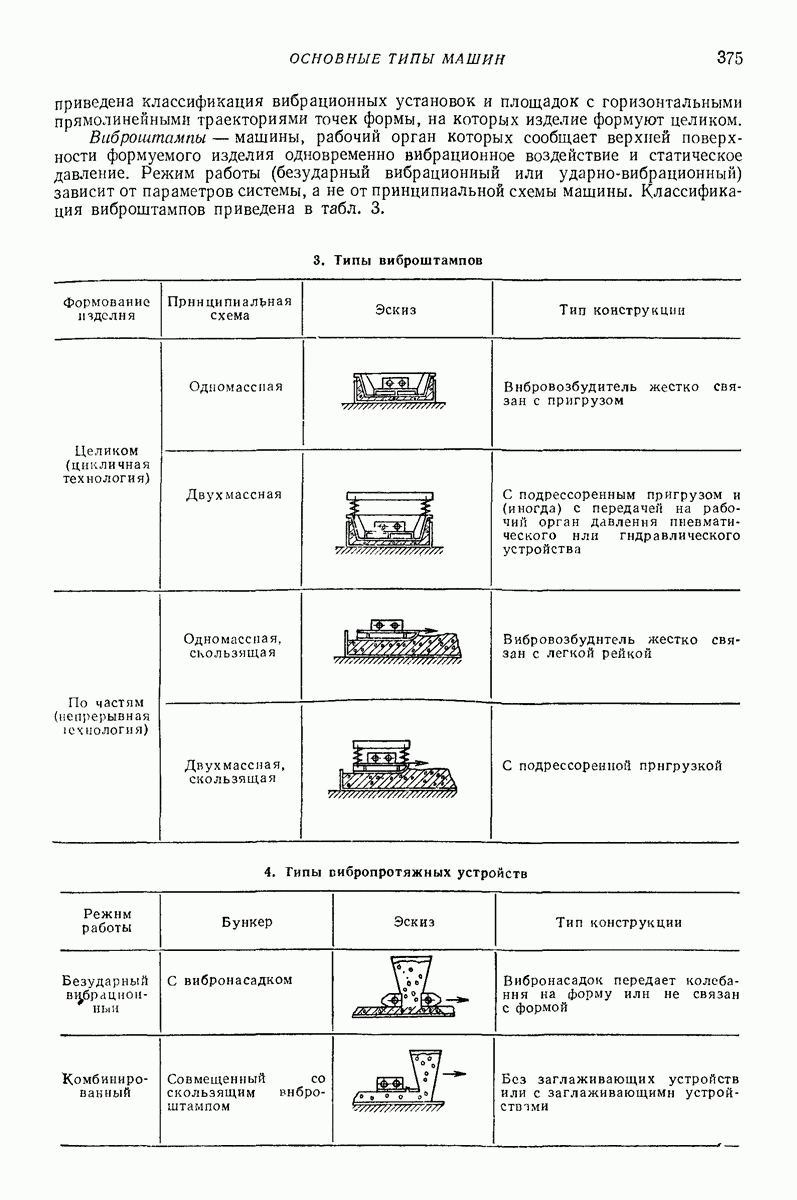
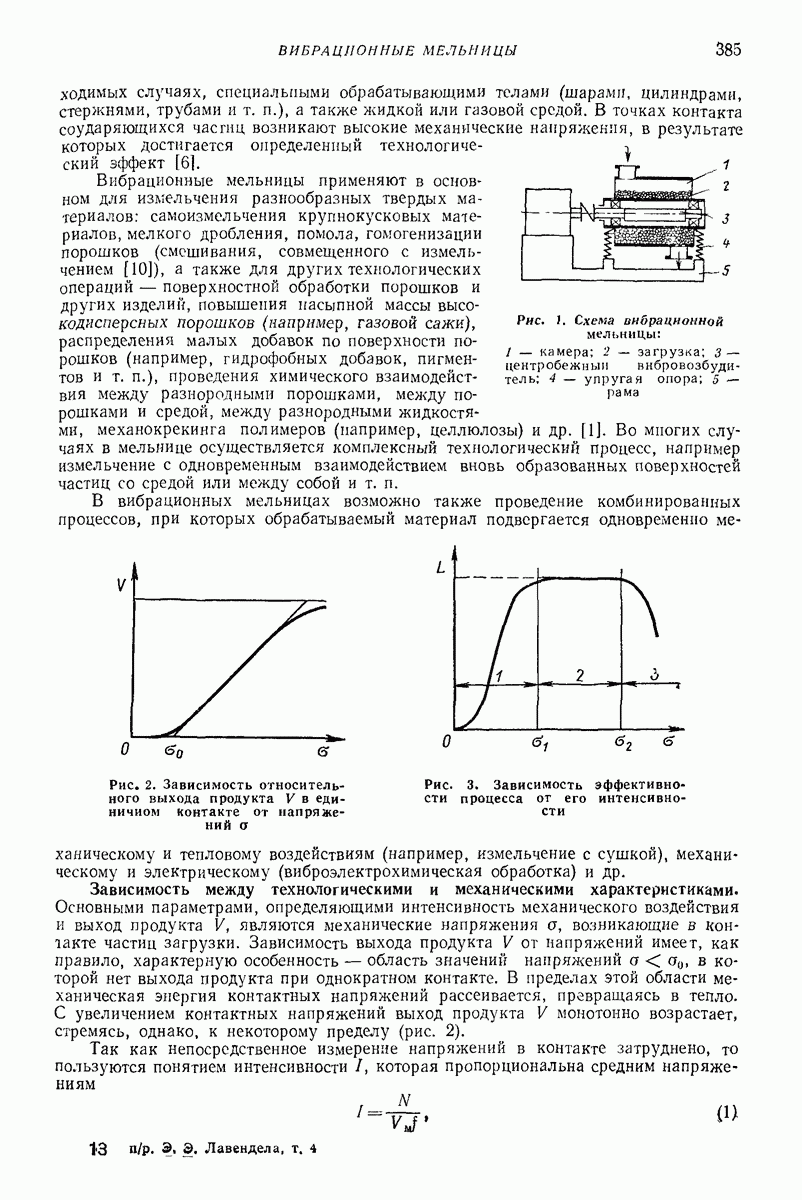
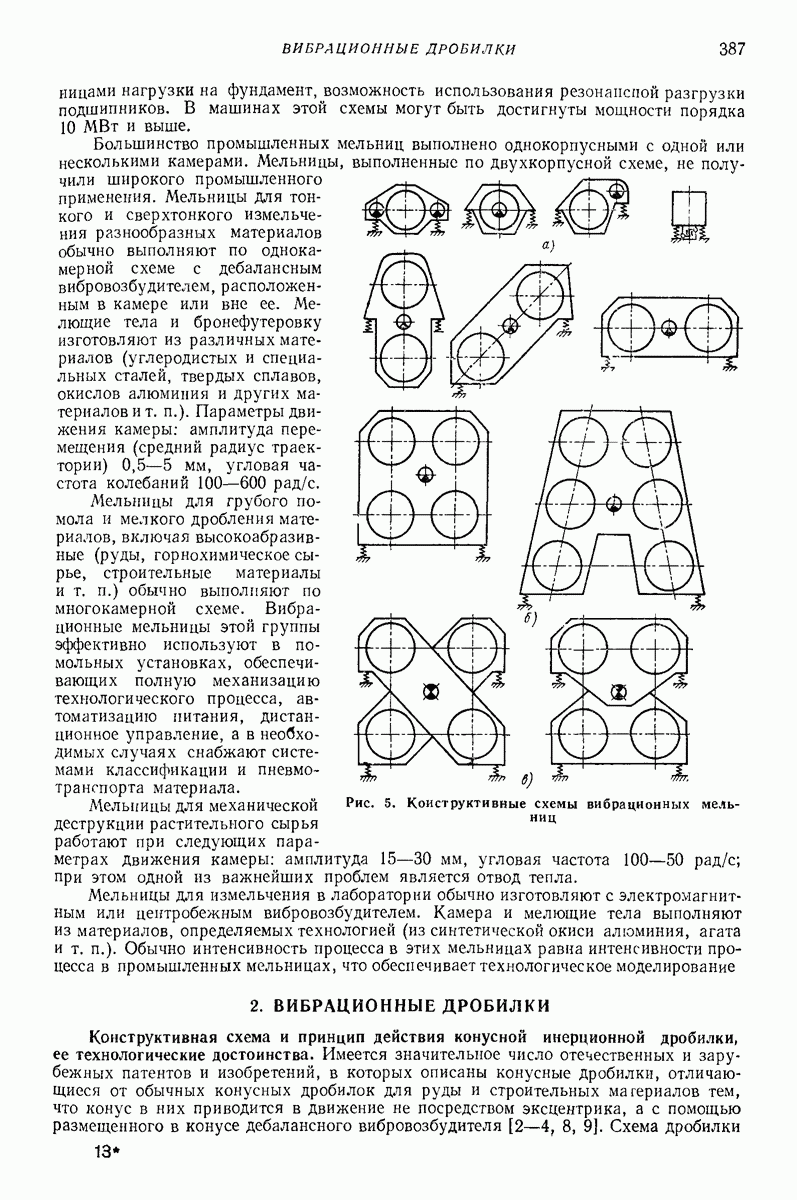
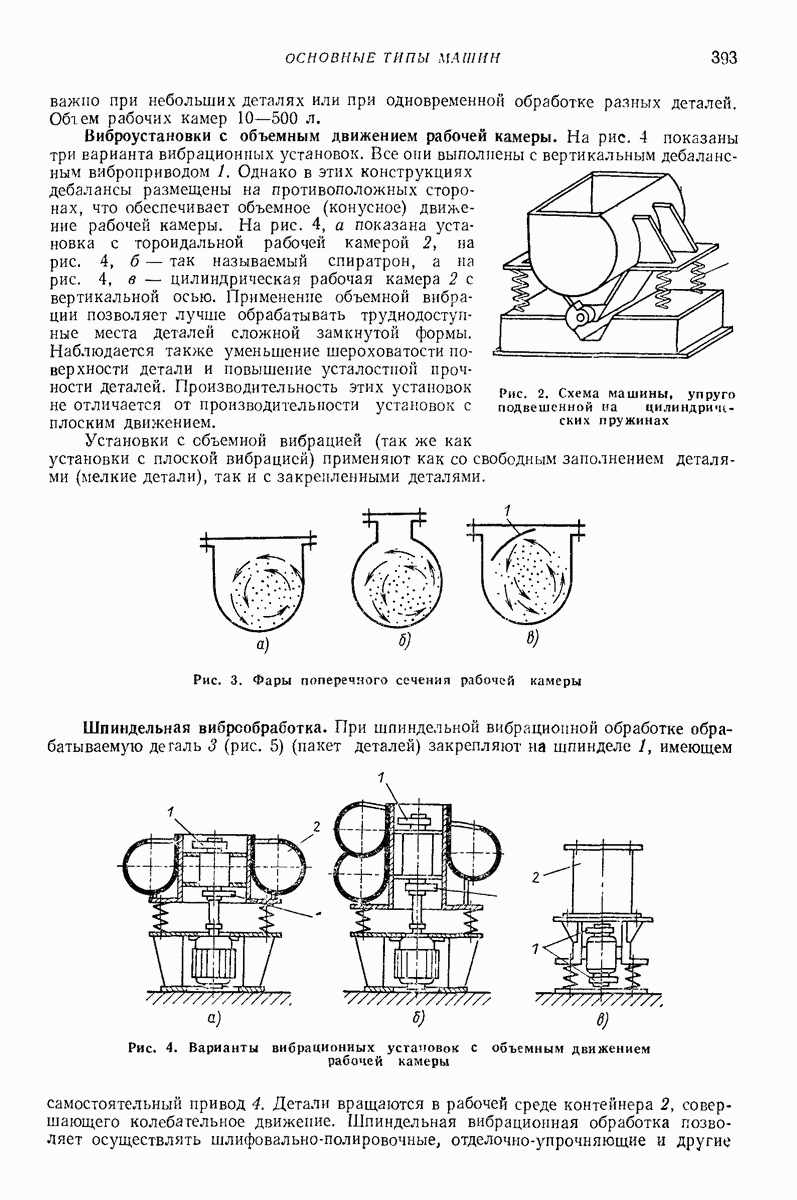
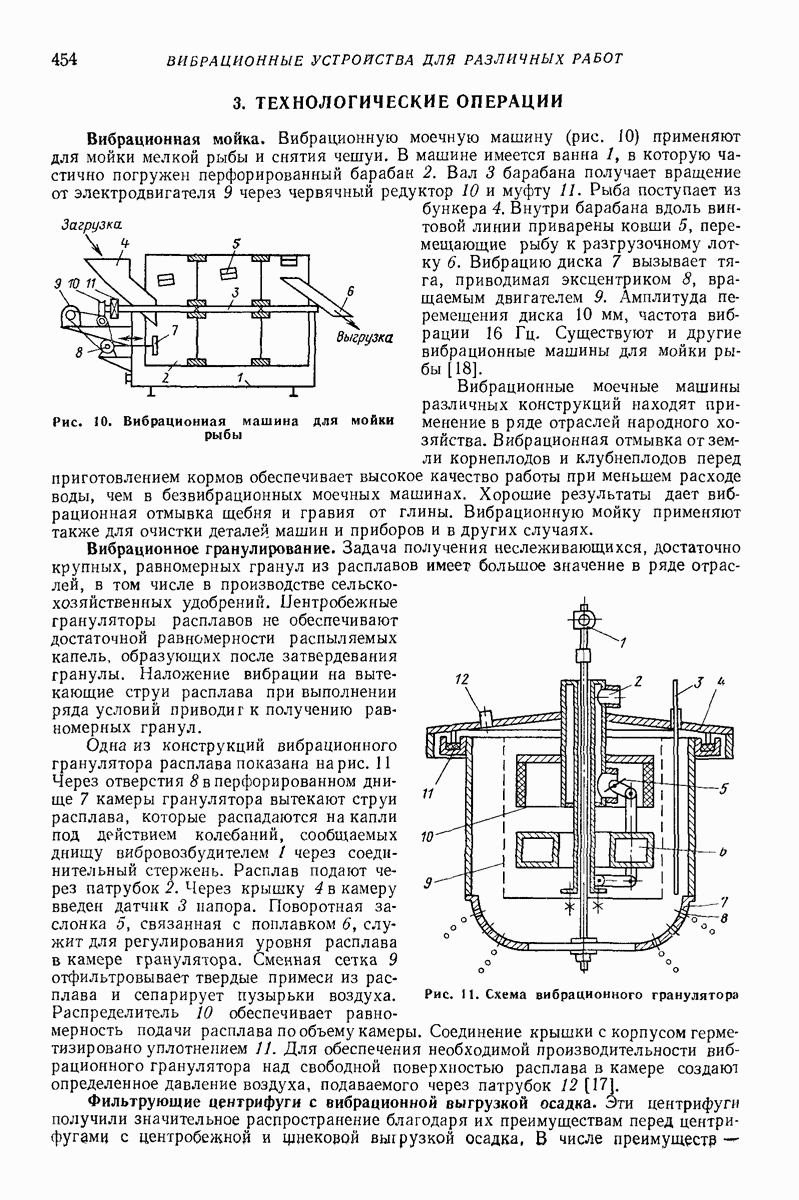
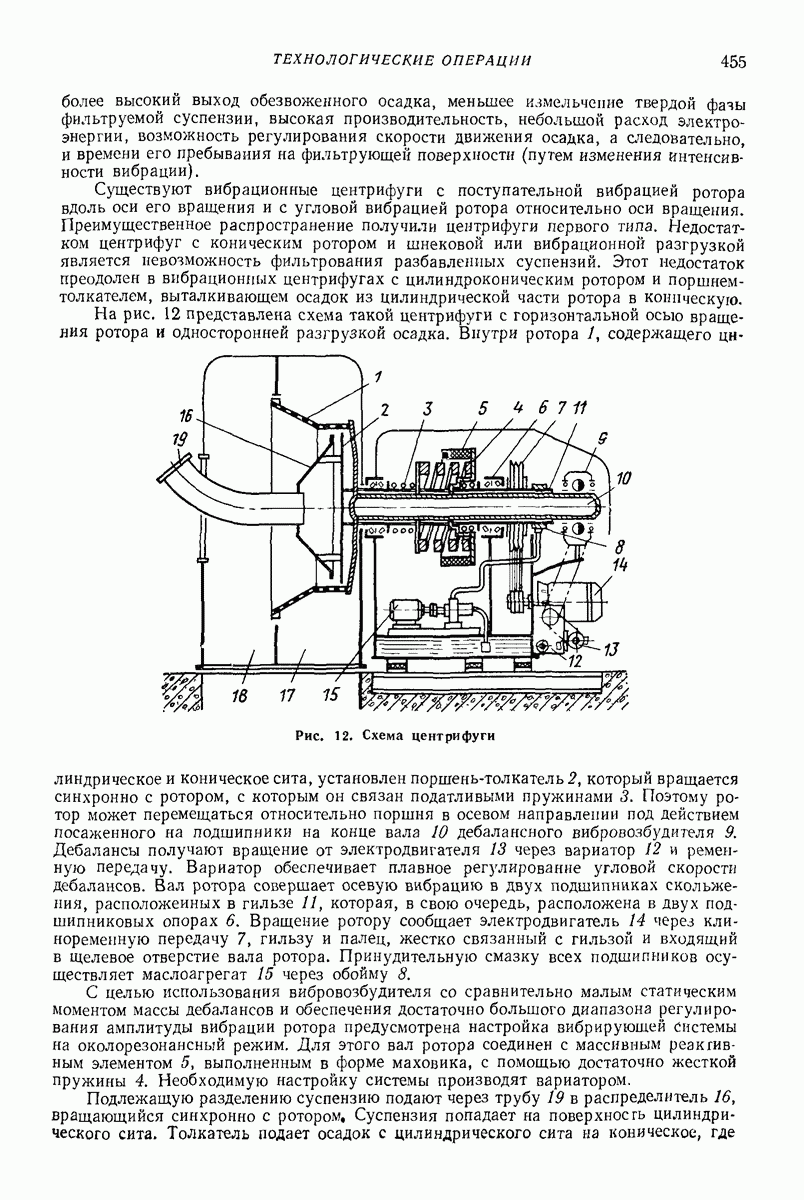
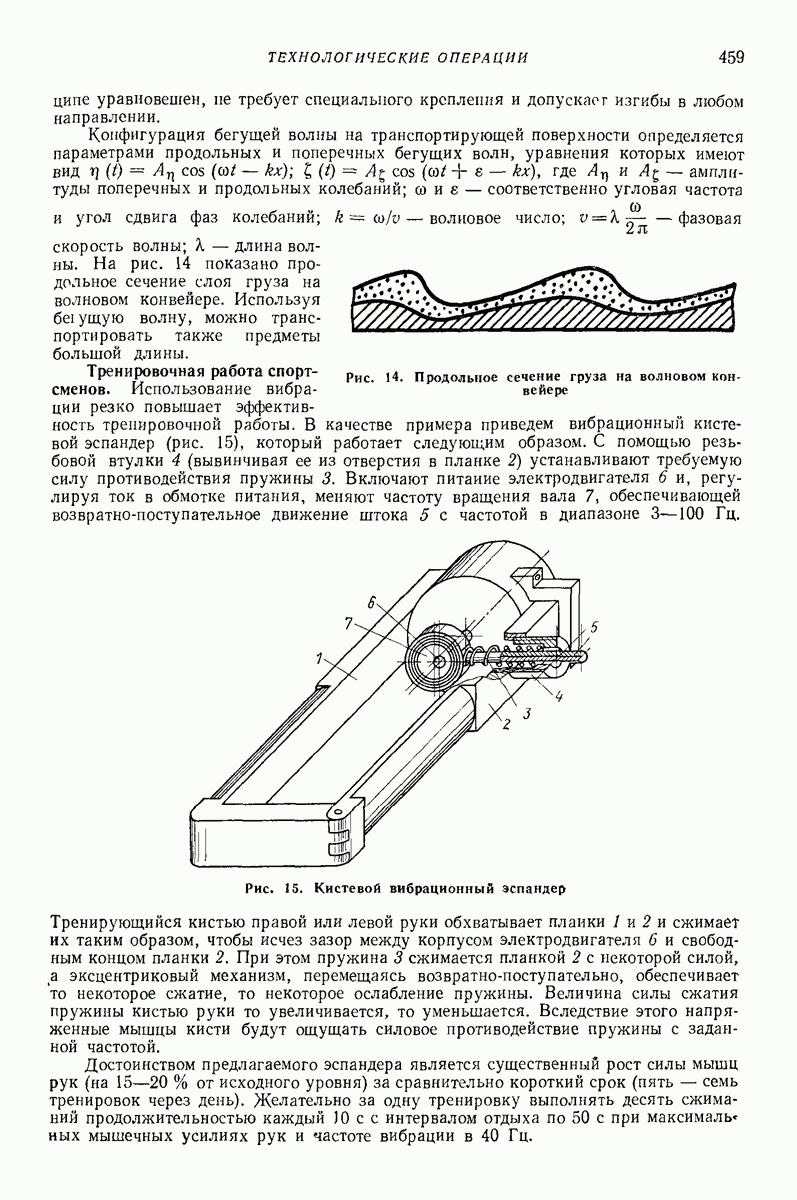
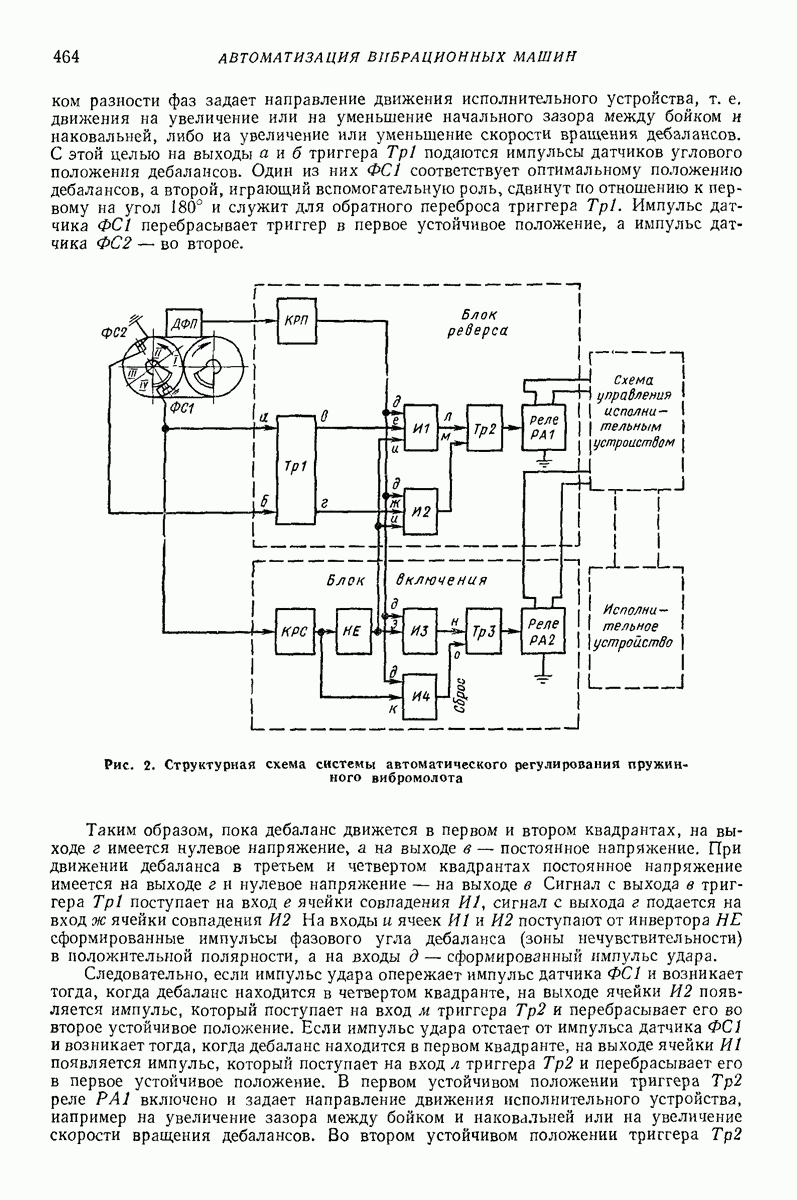
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
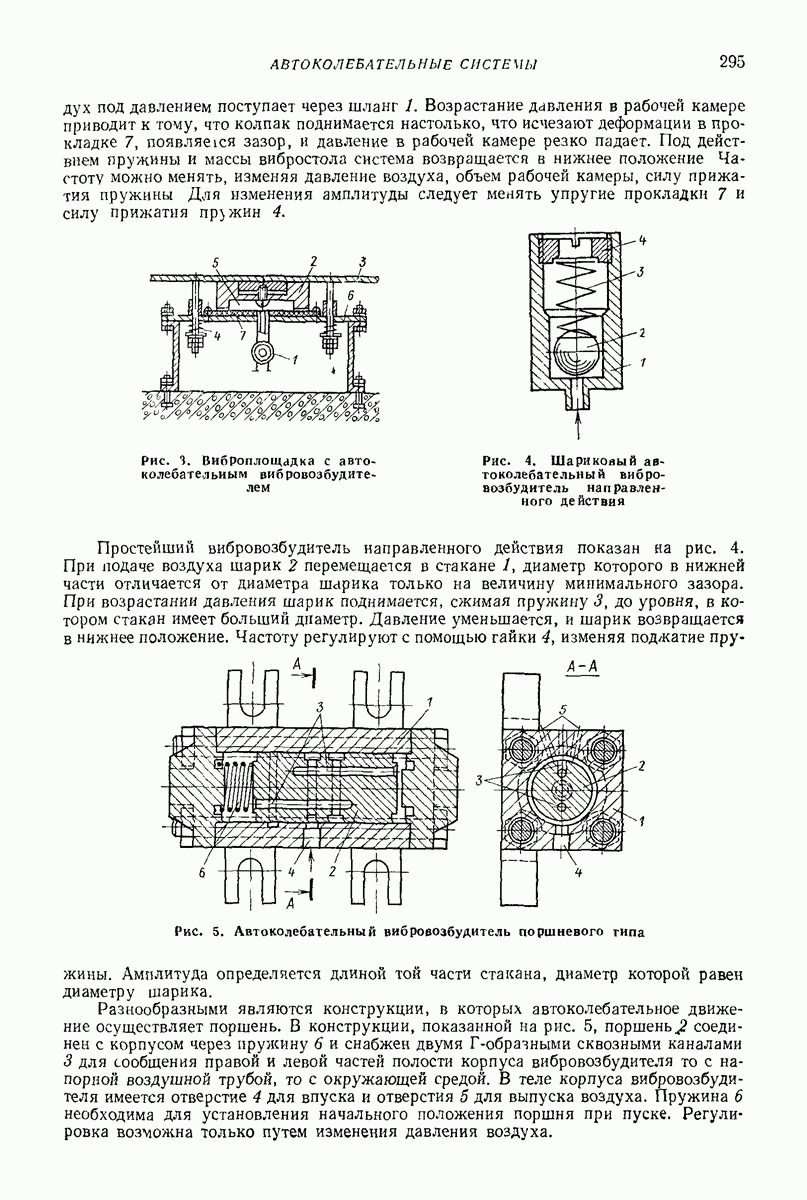
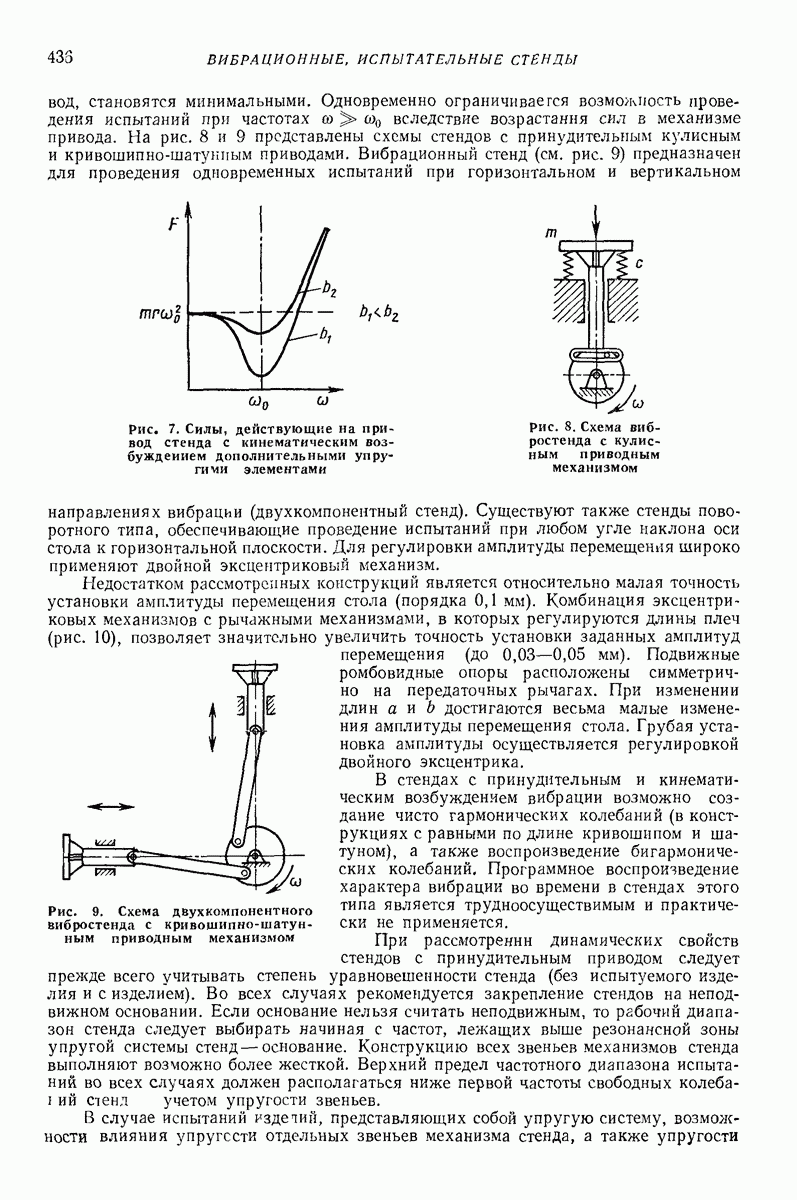
2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
Основные предположения; уравнения движения частицы.
Дифференциальные уравнения относительного движения частицы в осях  жестко связанных с
жестко связанных с
вибрирующей плоскостью, в рассматриваемом случае имеют вид (ось О направлена вдоль  а ось
а ось  поперек плоскости; рис. 1)
поперек плоскости; рис. 1)

Здесь  масса частицы;
масса частицы;  — соответственно амплитуда и частота колебаний плоскости;
— соответственно амплитуда и частота колебаний плоскости;  угол наклона траектории колебаний относительно плоскости (угол вибрации), а — угол наклона плоскости к горизонту;
угол наклона траектории колебаний относительно плоскости (угол вибрации), а — угол наклона плоскости к горизонту;  ускорение свободного падения;
ускорение свободного падения;  нормальная реакция;
нормальная реакция;  сила сопротивления движению частицы, которую вначале будем считать силой сухого (кулонова) трения; условия, когда необходимо учитывать также и силу вязкого трения и некоторые относящиеся к этому случаю результаты, будут приведены ниже.
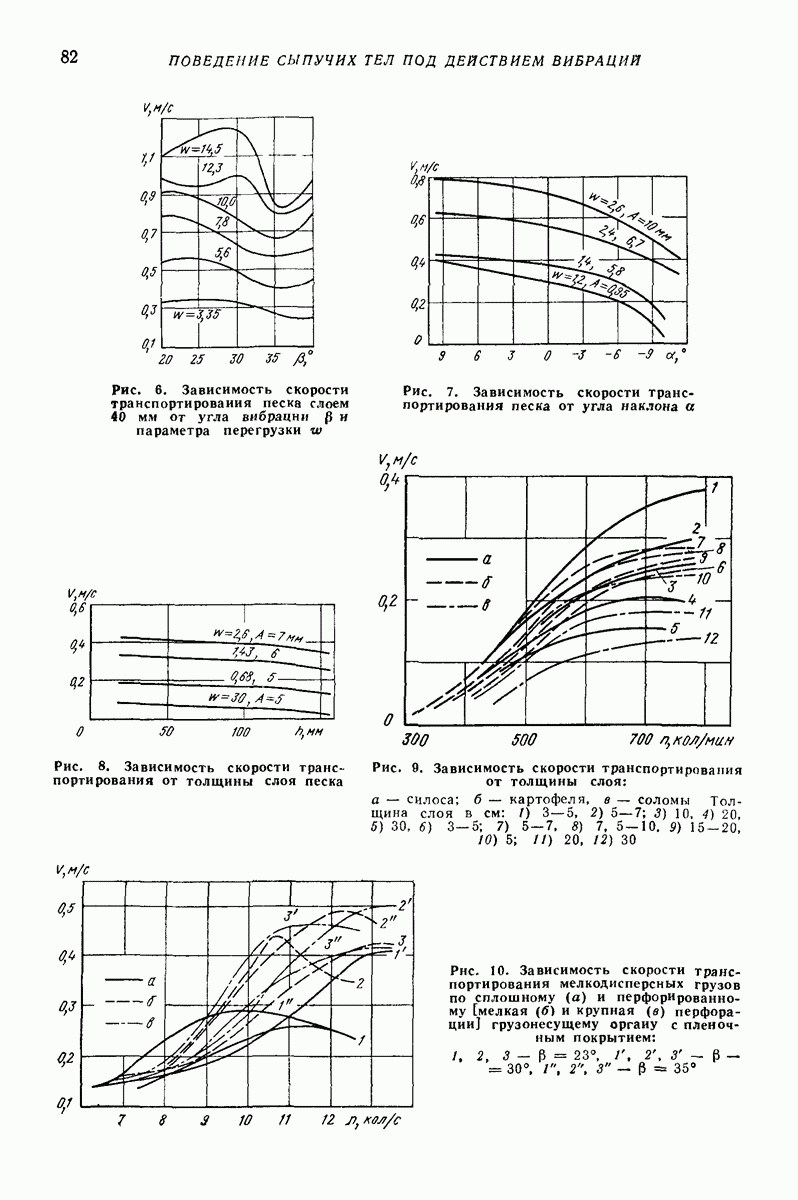
сила сопротивления движению частицы, которую вначале будем считать силой сухого (кулонова) трения; условия, когда необходимо учитывать также и силу вязкого трения и некоторые относящиеся к этому случаю результаты, будут приведены ниже.

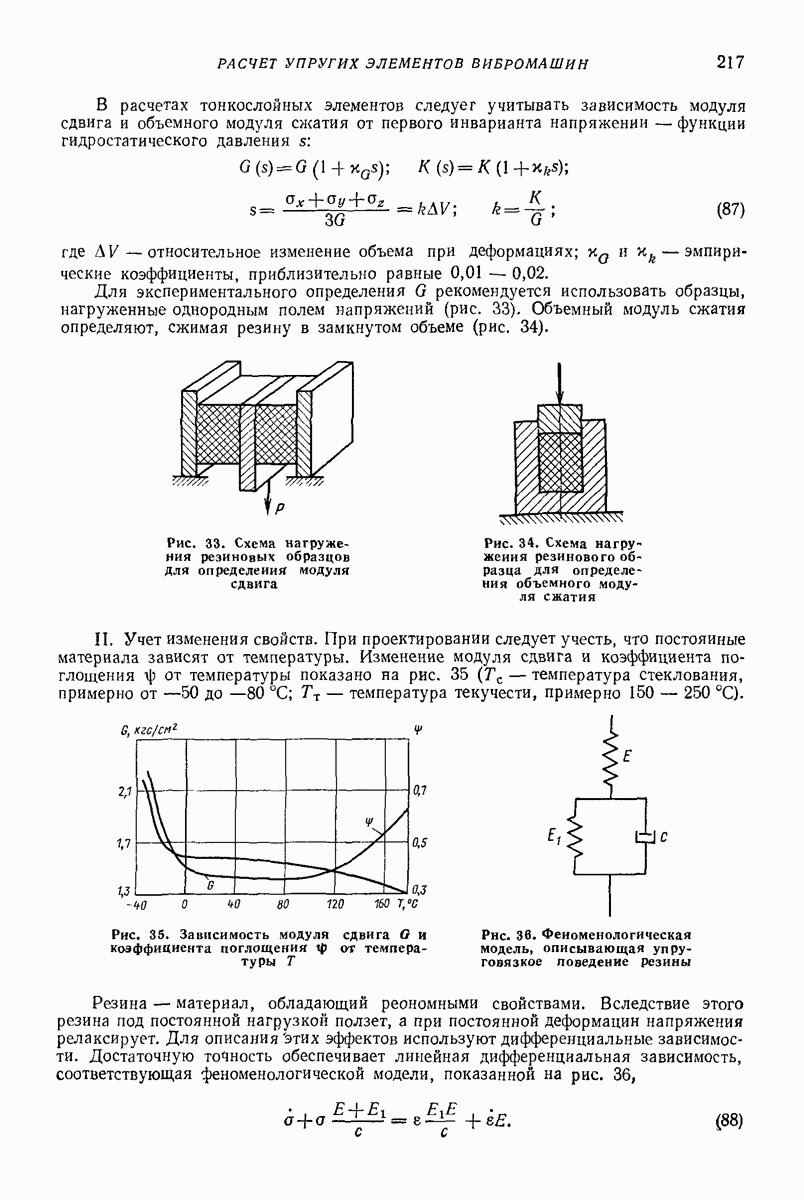
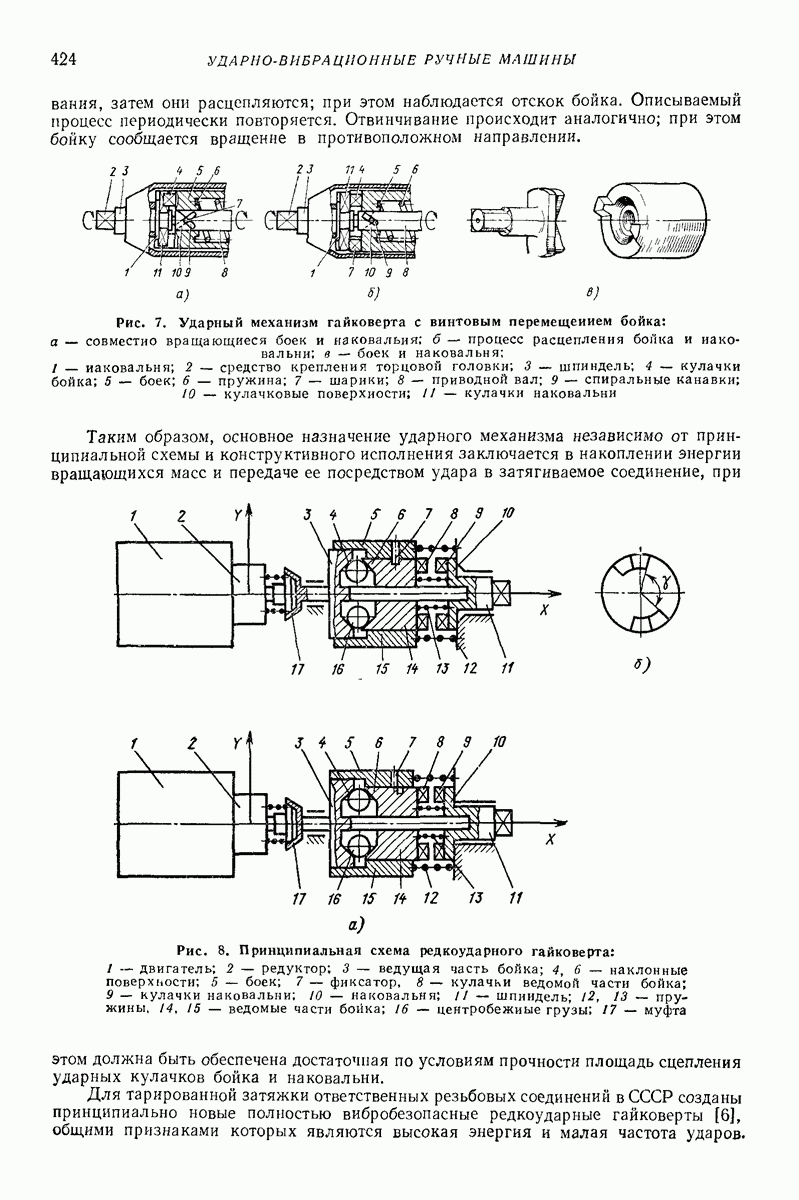
Рис. 1. Материальная частица на плоской поверхности, совершающей прямолинейные гармонические колебания параллельно плоскости наибольшего ската
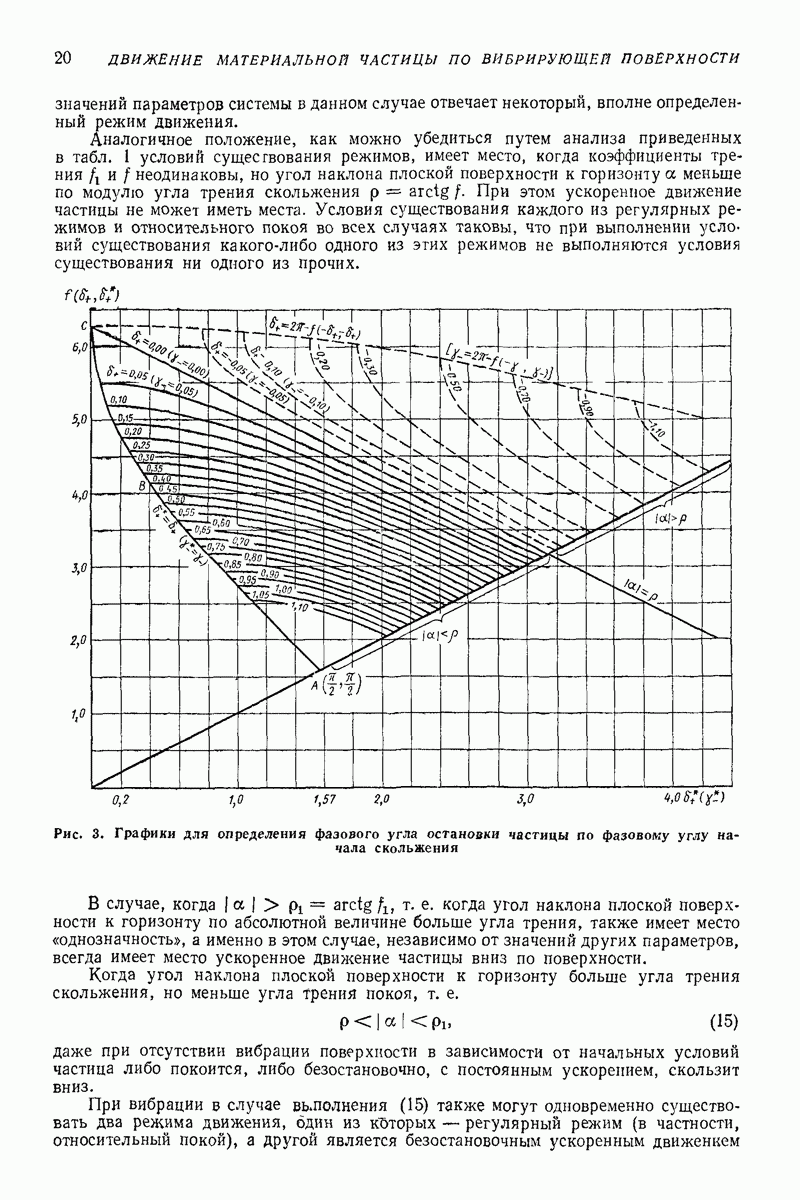
При движении частицы по вибрирующей поверхности 

где  коэффициент трения скольжения, а нормальная реакция определяется из (2):
коэффициент трения скольжения, а нормальная реакция определяется из (2):

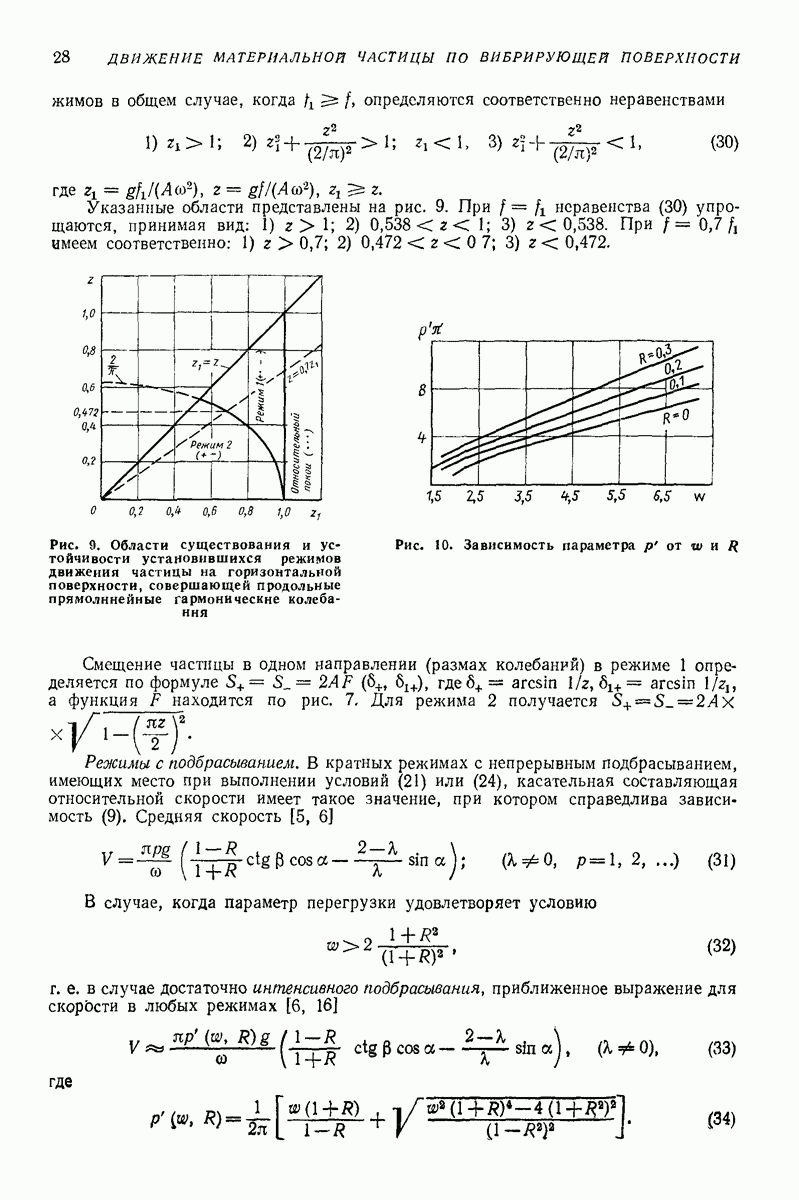
Частица может двигаться без отрыва от поверхности («без подбрасывания»), если  т. е.
т. е.

Параметр  равный отношению амплитуды поперечной составляющей переносной силы инерции
равный отношению амплитуды поперечной составляющей переносной силы инерции  (5 к поперечной составляющей силы тяжести
(5 к поперечной составляющей силы тяжести  назовем параметром перегрузки.
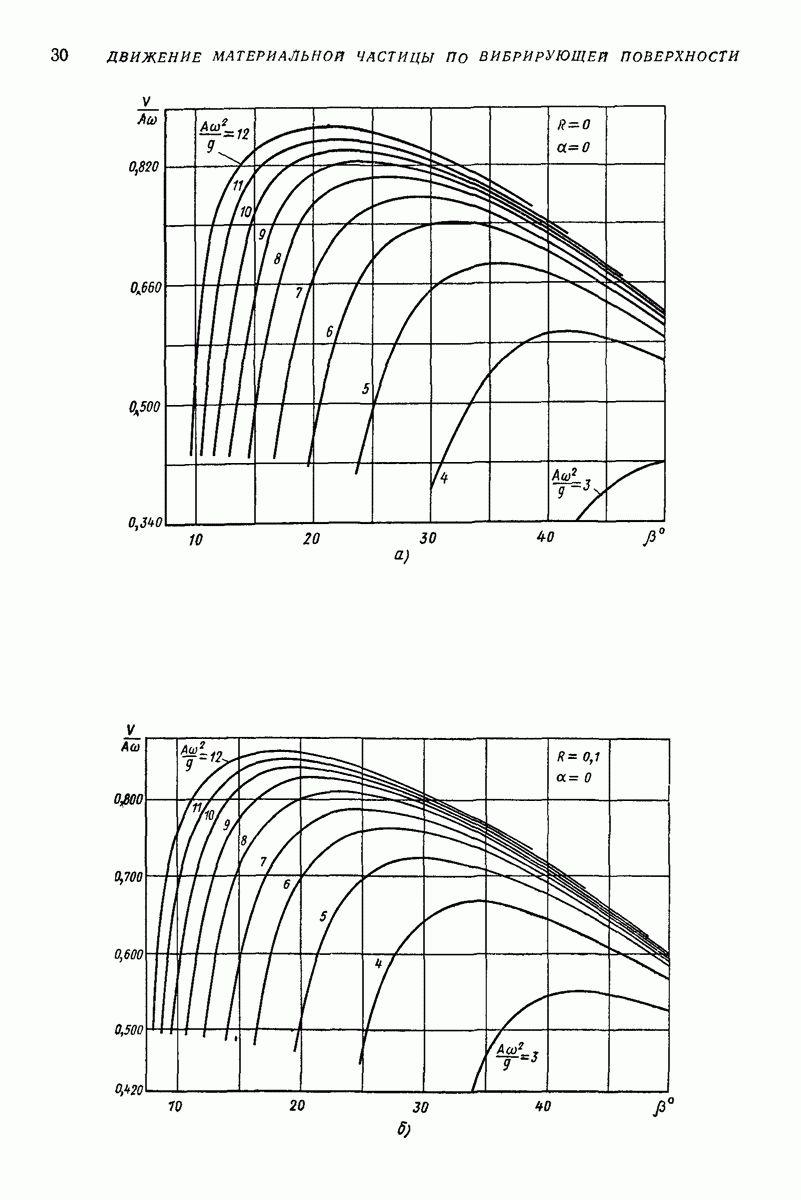
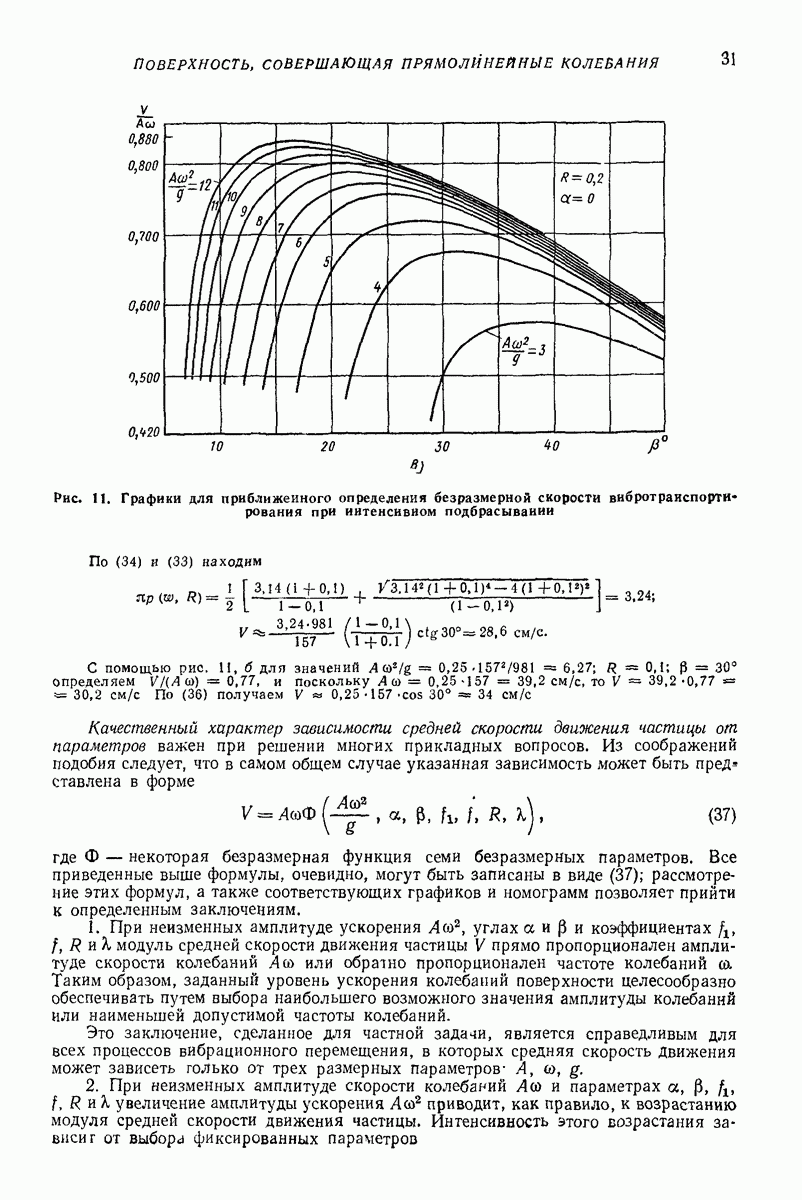
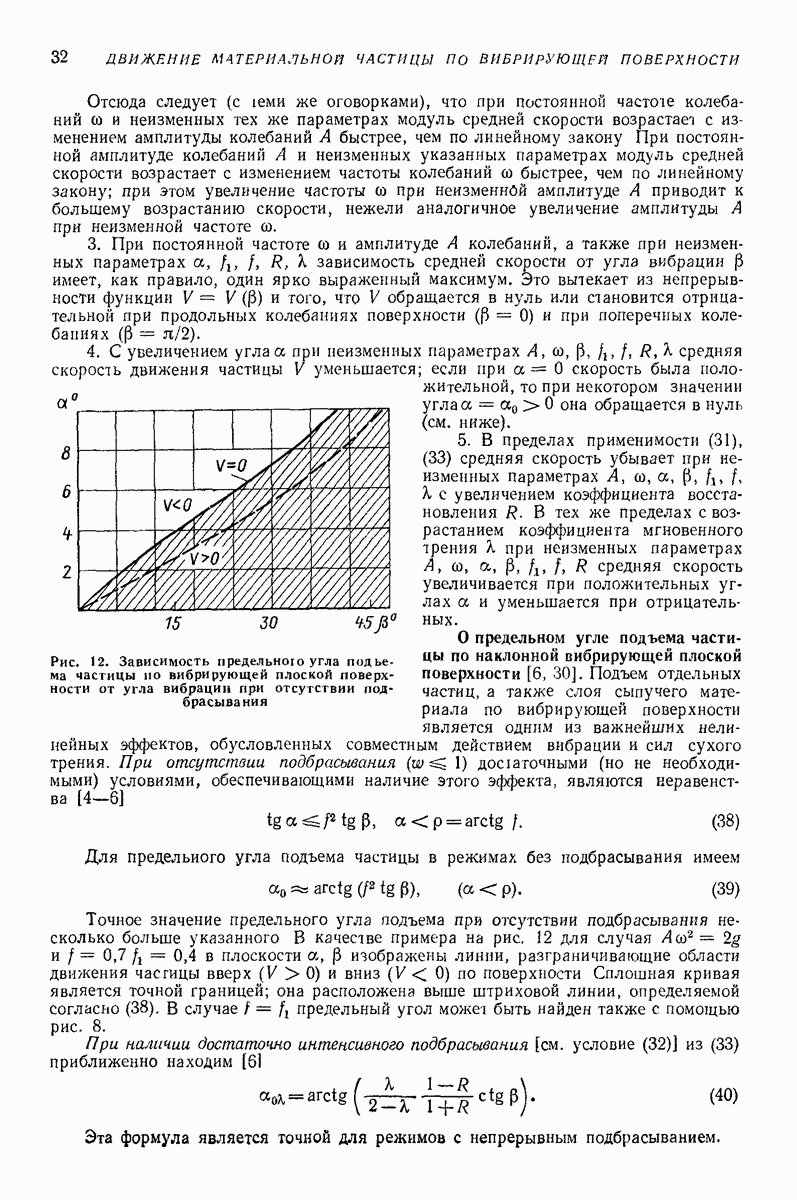
назовем параметром перегрузки.
При относительном покое частицы на поверхности  сила
сила  трения
трения  не определяется (3), а находится из (1):
не определяется (3), а находится из (1): 
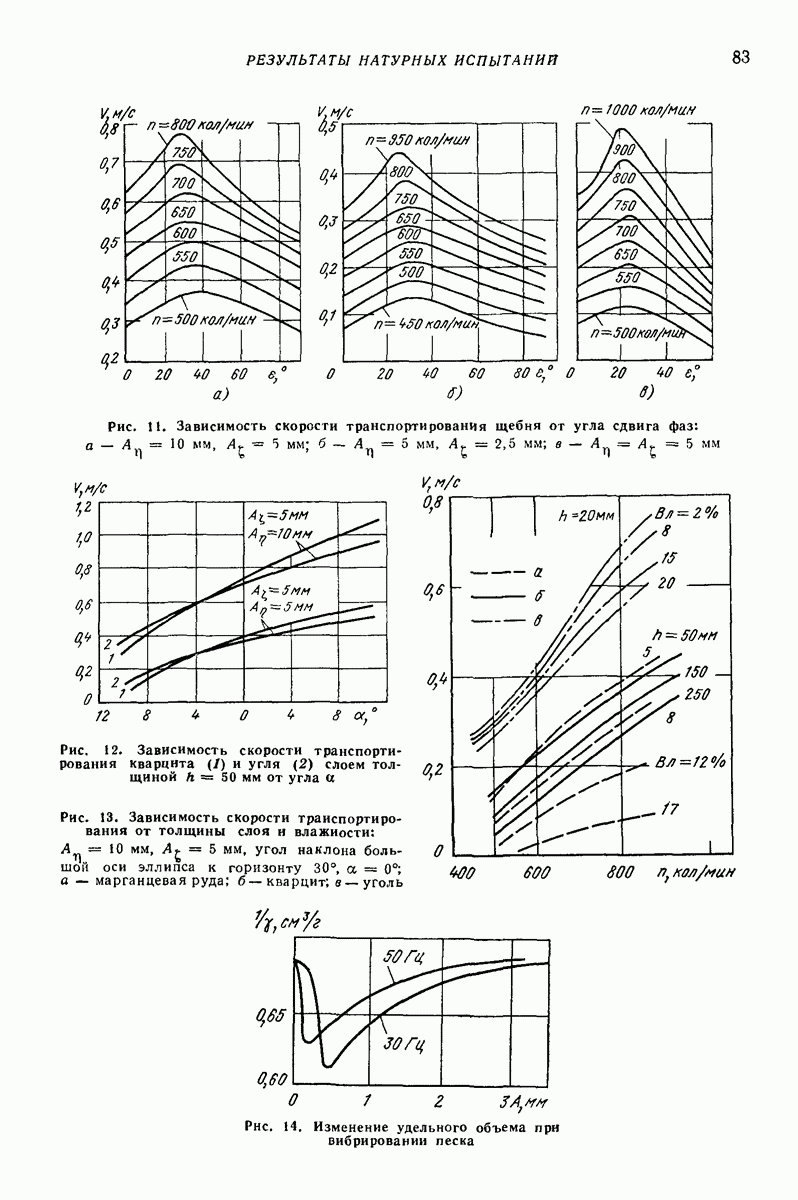
Состояние относительного покоя при этом сохраняется до тех пор, пока выполняется условие

где — коэффициент трения покоя; обычно 
Уравнение скольжения частицы по поверхности  получается из (1) при учете (3) и
получается из (1) при учете (3) и 

где  угол трения скольжения; верхние знаки соответствуют скольжению частицы вперед
угол трения скольжения; верхние знаки соответствуют скольжению частицы вперед  а нижние — назад
а нижние — назад  Уравнения полета частицы
Уравнения полета частицы  получаются из (1) при
получаются из (1) при 
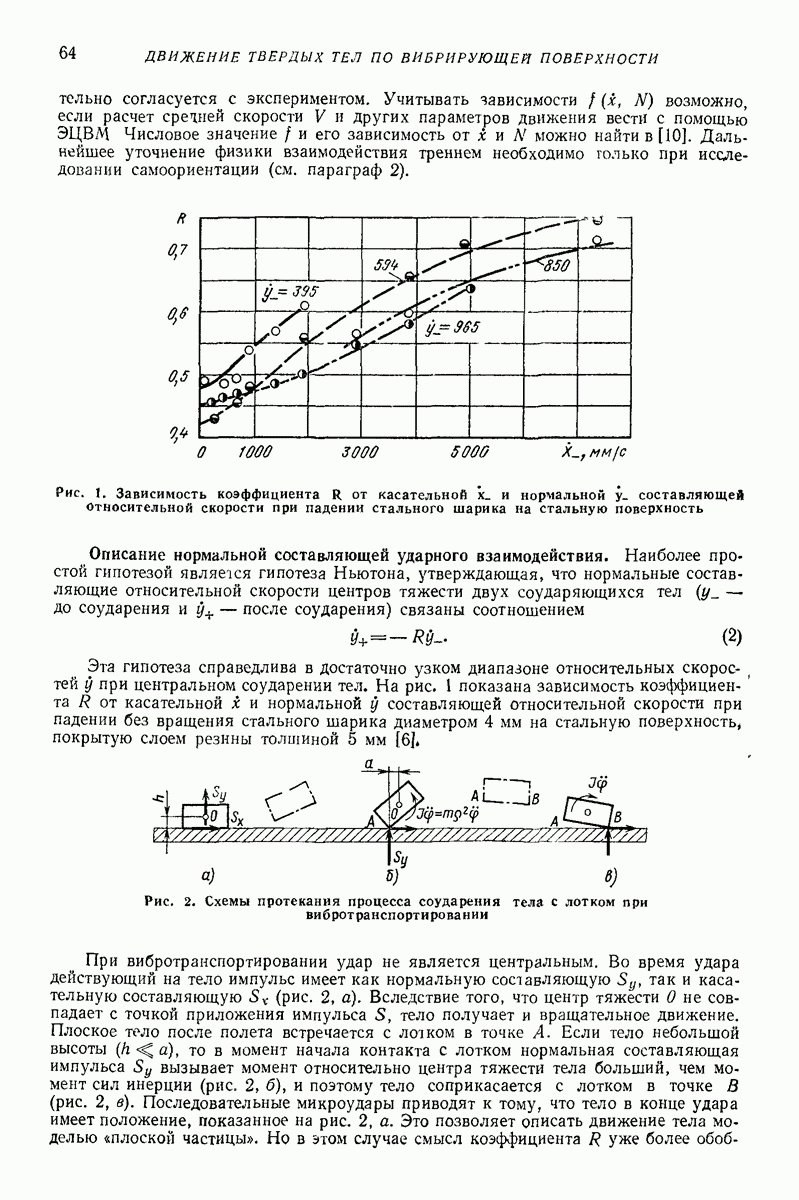
К выписанным соотношениям необходимо добавить равенства, определяющие закон изменения относительной скорости частицы при ее соударении с поверхностью. Обычно соударение считают мгновенным, а изменение нормальной составляющей скорости определяют в соответствии с гипотезой Ньютона:

где  поперечные проекции скорости частицы до и после удара;
поперечные проекции скорости частицы до и после удара;  коэффициент восстановления.
коэффициент восстановления.
В качестве <вязи продольных проекций скоростей  до и после удара применительно к большому числу приложений целесообразно принять соотношения (см. гл II, параграф 2):
до и после удара применительно к большому числу приложений целесообразно принять соотношения (см. гл II, параграф 2):
а)  -гипотеза»:
-гипотеза»:

где  коэффициент мгновенного трения, иногда принимаемый равным коэффициенту грения скольжения
коэффициент мгновенного трения, иногда принимаемый равным коэффициенту грения скольжения 
б)  -гтпотезы
-гтпотезы

где  коэффициент ударного трения, также часто принимаемый равным
коэффициент ударного трения, также часто принимаемый равным 
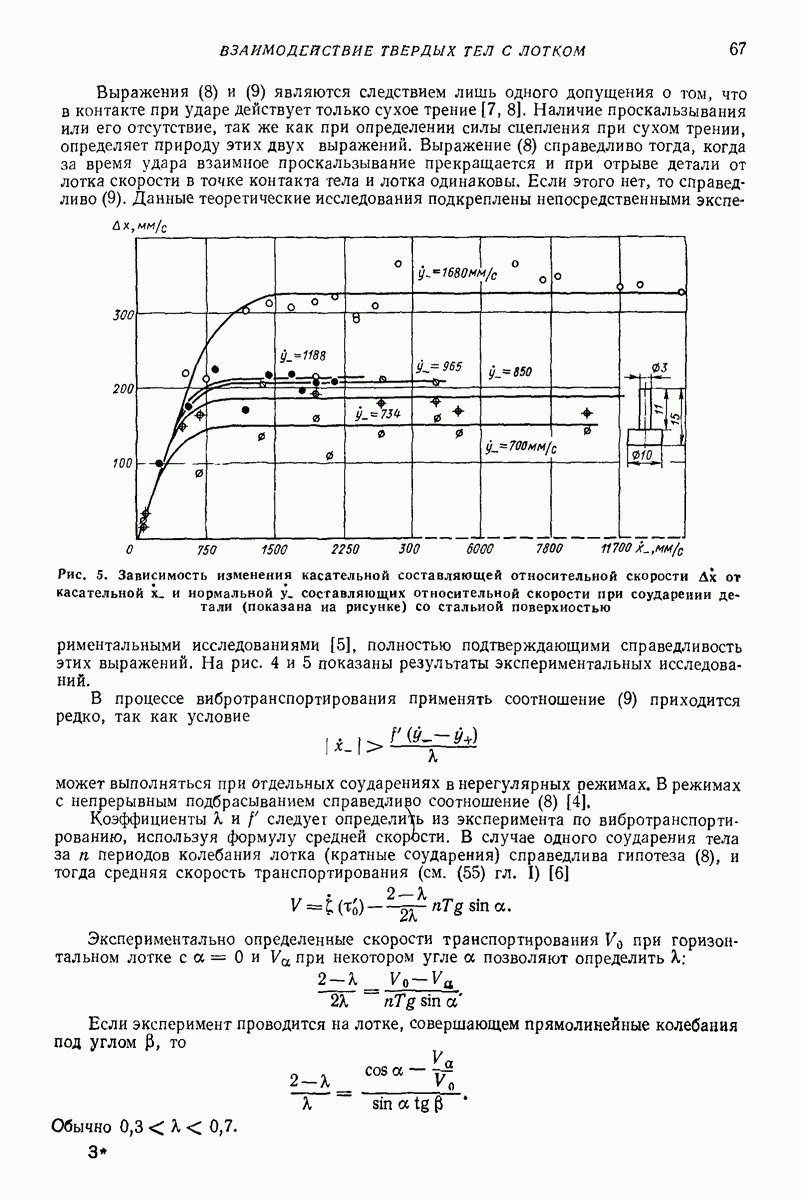
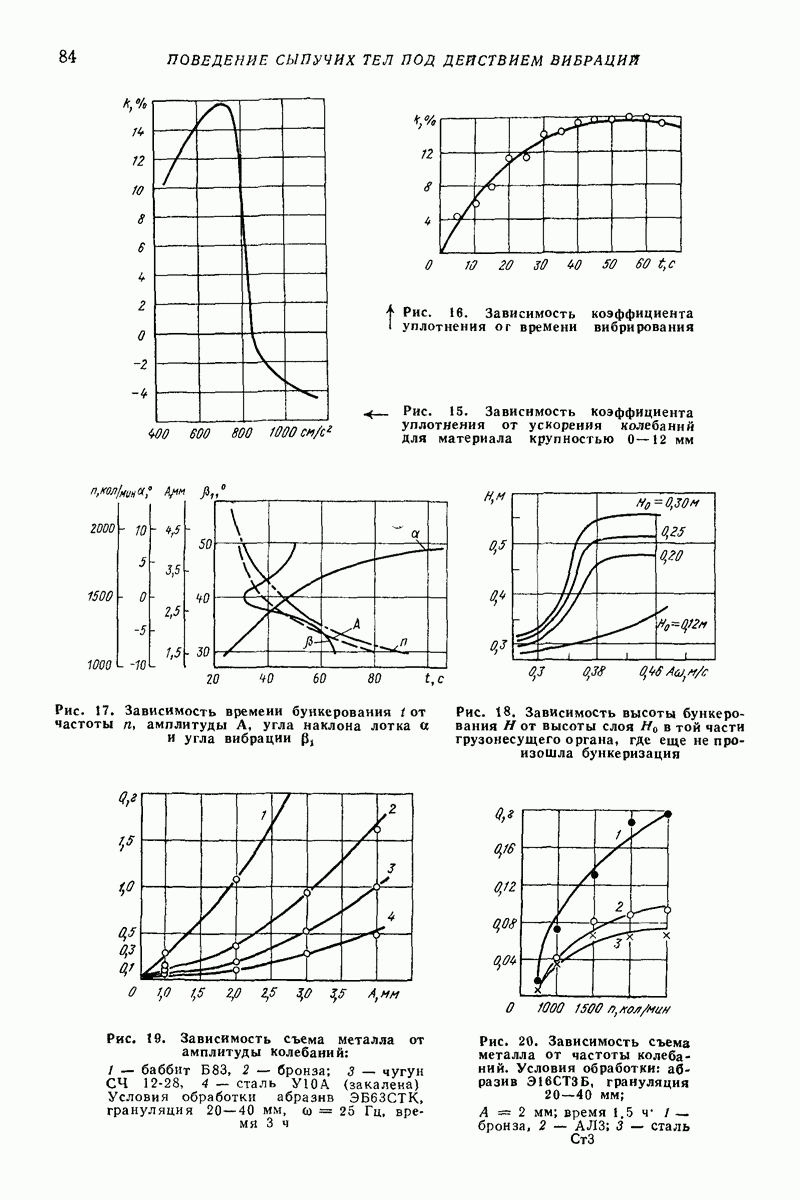
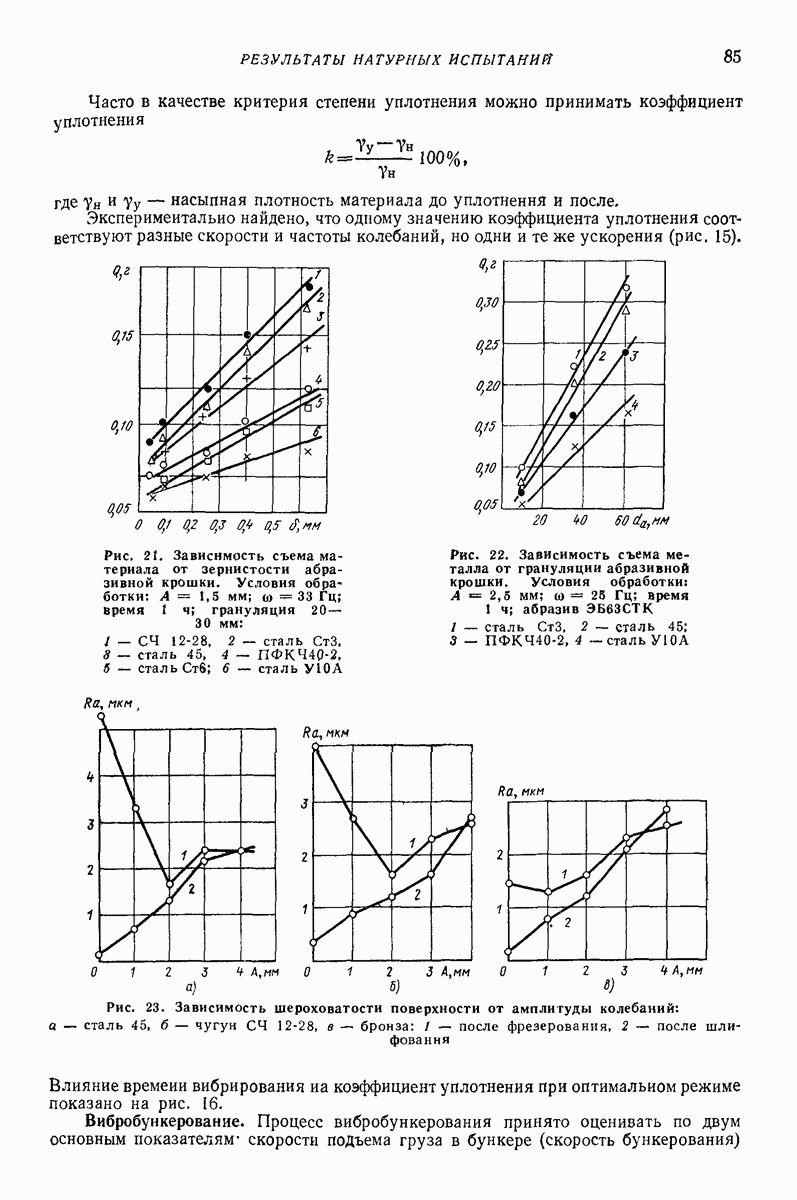
Соотношения (8) — (10) представляют собой достаточно грубые приближения, дающие, однако, при соответствующем выборе постоянных  хорошее согласие экспериментальных и теоретических значений скорости вибротранспортирования. О способах определения этих постоянных на основе экспеоиментальных данных и о характере их зависимости от скорости частицы см. гл. II, параграф 2.
хорошее согласие экспериментальных и теоретических значений скорости вибротранспортирования. О способах определения этих постоянных на основе экспеоиментальных данных и о характере их зависимости от скорости частицы см. гл. II, параграф 2.
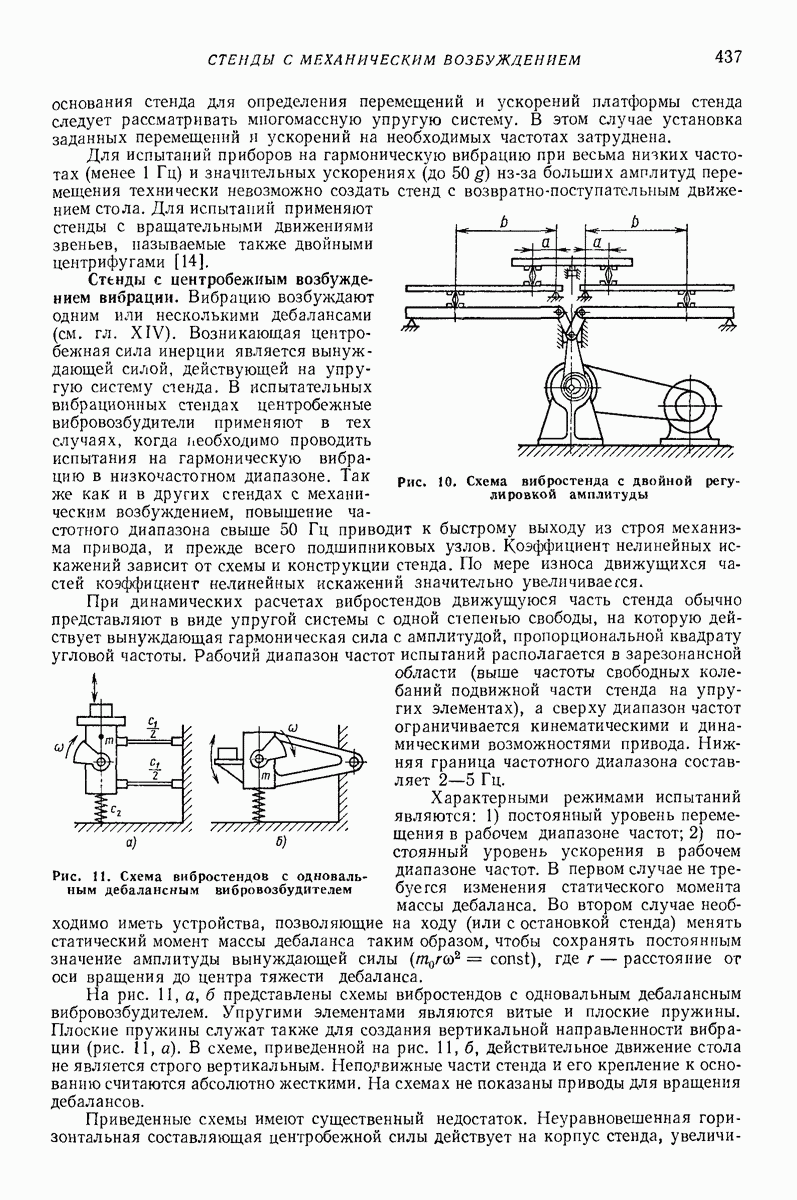
При определенных условиях кроме силы сухого трения необходимо учитывать также и силу вязкого сопротивления движению частицы в окружающей ее среде. При этом также используют две гипотезы: в одном случае сила сопротивления считается пропорциональной первой или более высоким степеням относительной, а в другом — абсолютной скорости движения частицы. Для решения вопроса о необходимости учета силы вязкого сопротивления можно оценить отношение этой силы  к силе сухого трения
к силе сухого трения  здесь
здесь  размер частицы;
размер частицы;  ее скорость относительно среды, которую обычно можно считать имеющей порядок
ее скорость относительно среды, которую обычно можно считать имеющей порядок  коэффициент сопротивления, зависимость которого от числа Рейнольдса
коэффициент сопротивления, зависимость которого от числа Рейнольдса  коэффициент кинематической вязкости) определяется хорошо известным графиком, приводимым во многих руководствах по прикладной гидромеханике.
коэффициент кинематической вязкости) определяется хорошо известным графиком, приводимым во многих руководствах по прикладной гидромеханике.
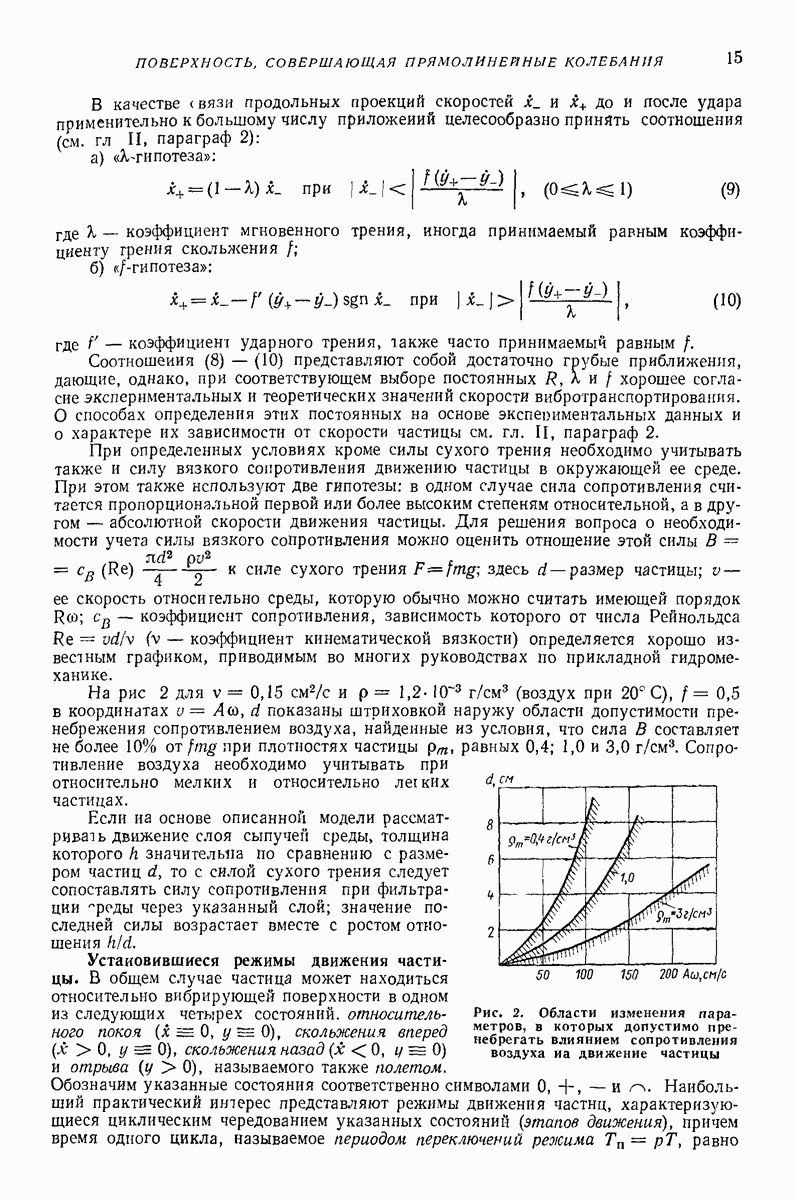
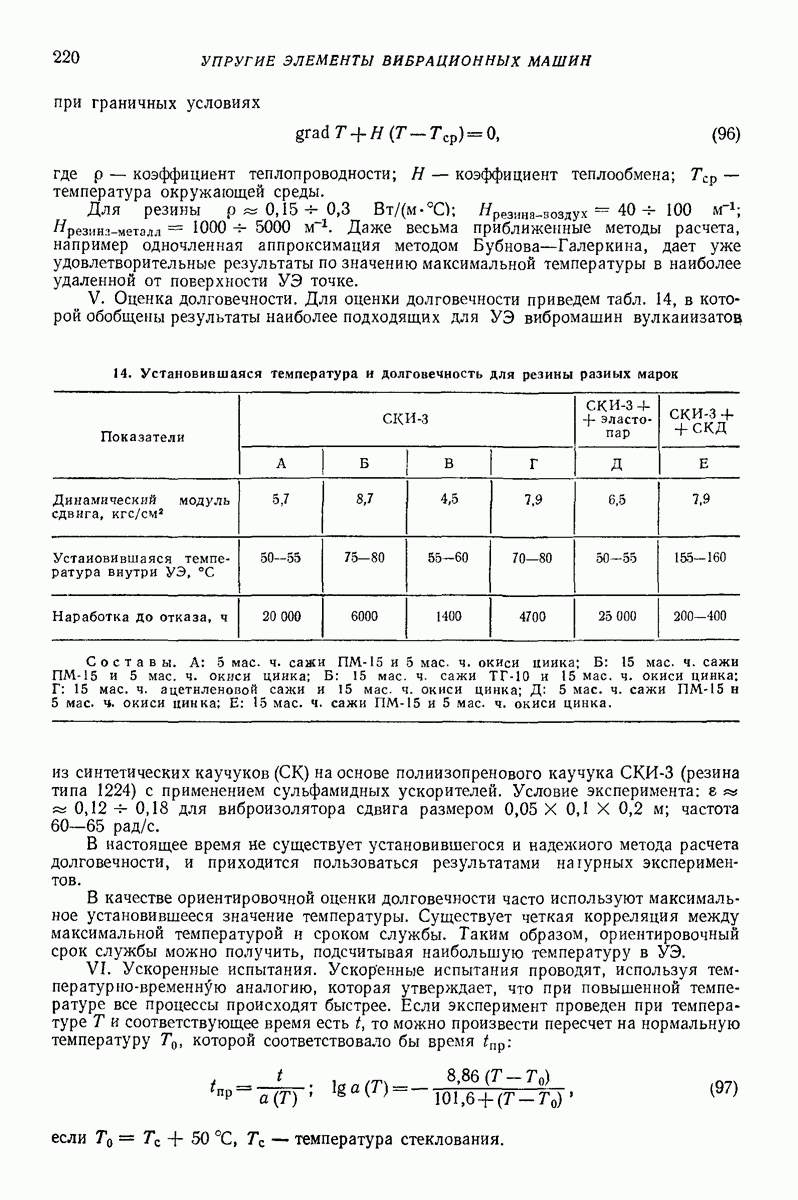
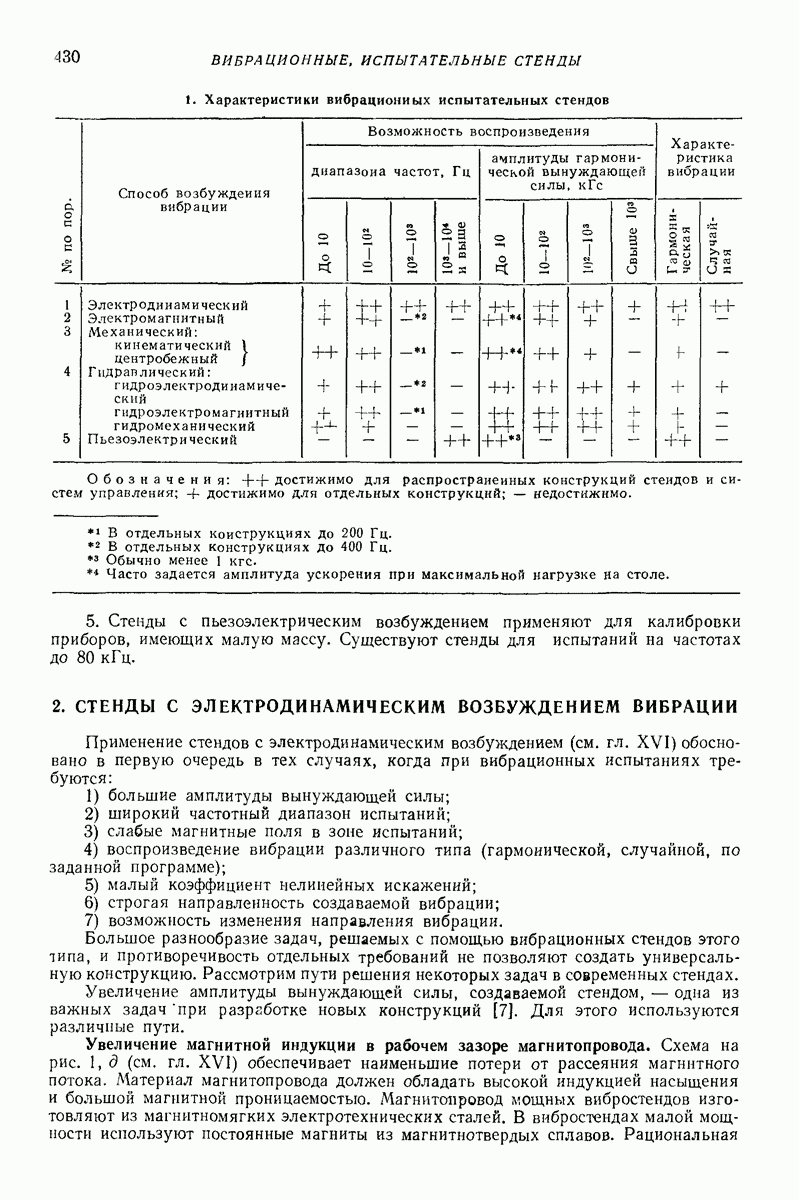
На рис 2 для  (воздух при 20° С),
(воздух при 20° С),  в координатах
в координатах  показаны штриховкой наружу области допустимости пренебрежения сопротивлением воздуха, найденные из условия, что сила В составляет не более 10% от
показаны штриховкой наружу области допустимости пренебрежения сопротивлением воздуха, найденные из условия, что сила В составляет не более 10% от  при плотностях частицы
при плотностях частицы  равных 0,4; 1,0 и
равных 0,4; 1,0 и  Сопротивление воздуха необходимо учитывать при относительно мелких и относительно
Сопротивление воздуха необходимо учитывать при относительно мелких и относительно  частицах.
частицах.

Рис. 2. Области изменения параметров, в которых допустимо пренебрегать влиянием сопротивления воздуха на движение частицы
Если на основе описанной модели рассматривать движение слоя сыпучей среды, толщина которого  значительна по сравнению с размером частиц
значительна по сравнению с размером частиц  то с силой сухого трения следует сопоставлять силу сопротивления при фильтрации среды через указанный слой; значение последней силы возрастает вместе с ростом отношения
то с силой сухого трения следует сопоставлять силу сопротивления при фильтрации среды через указанный слой; значение последней силы возрастает вместе с ростом отношения 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
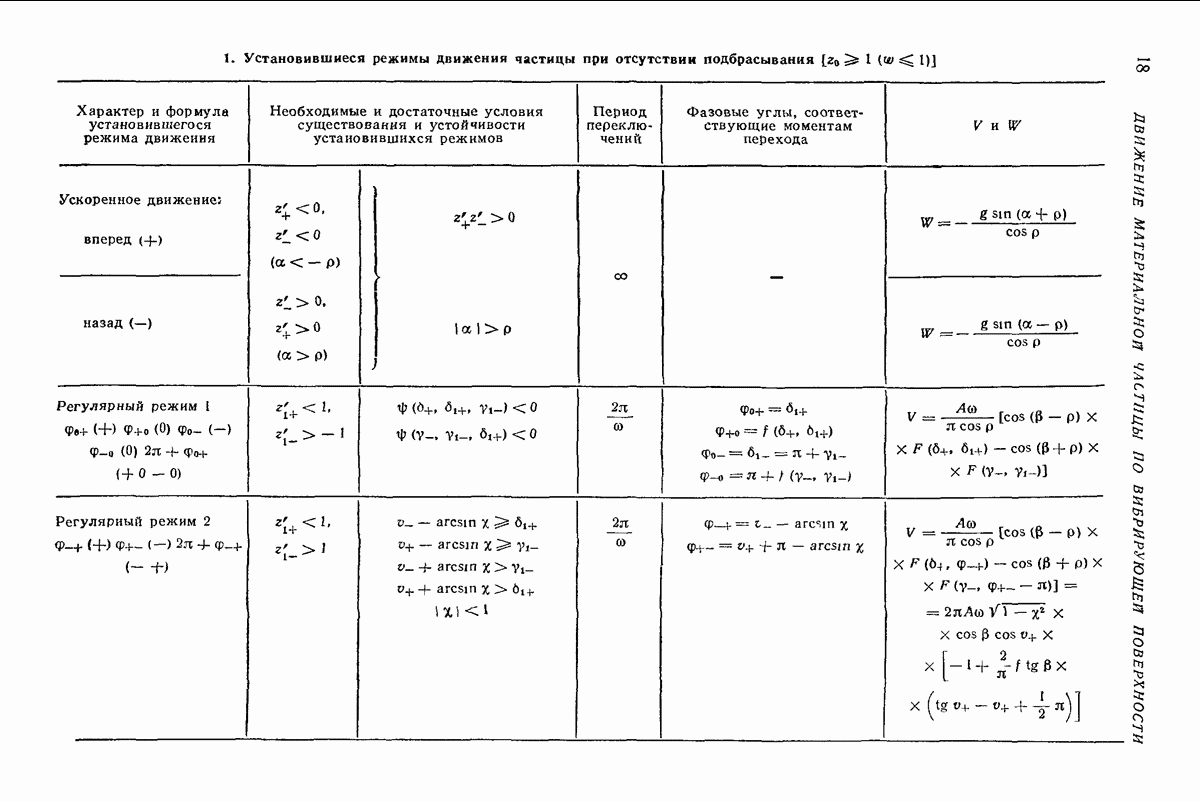
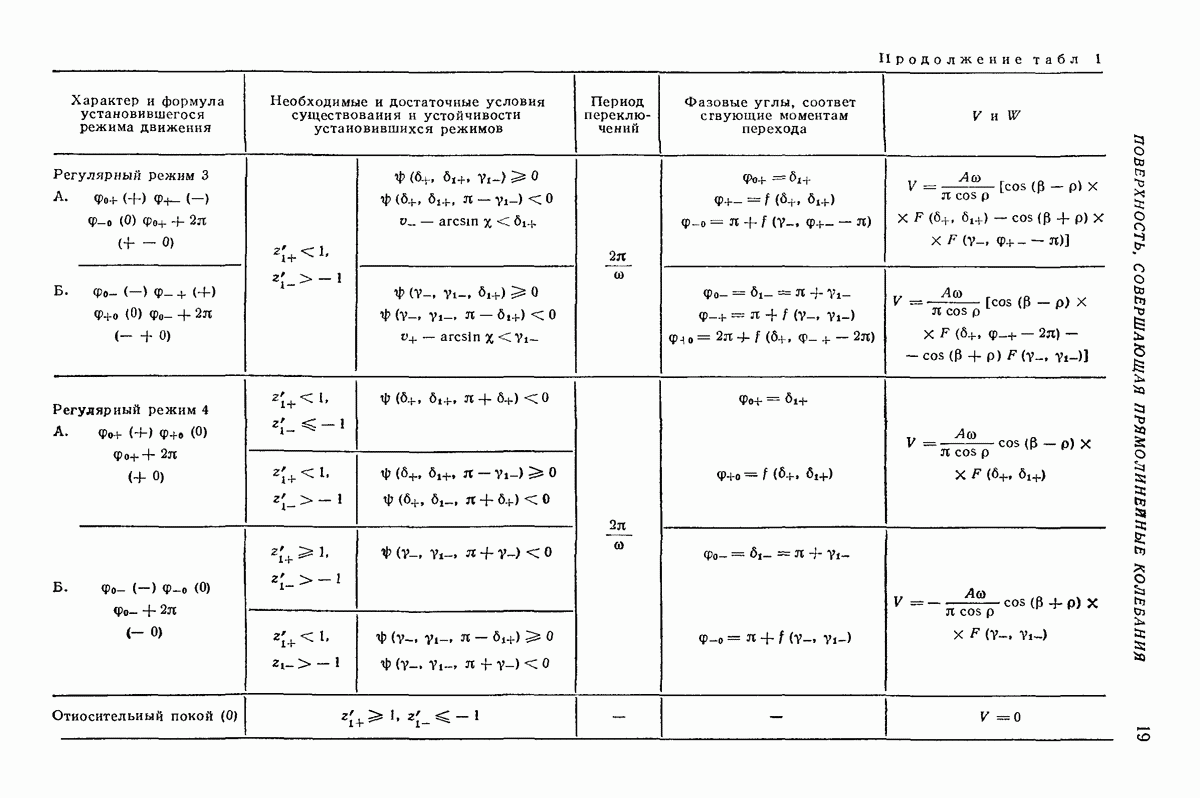
- Установившиеся режимы движения частицы.
- О методах решения задачи.
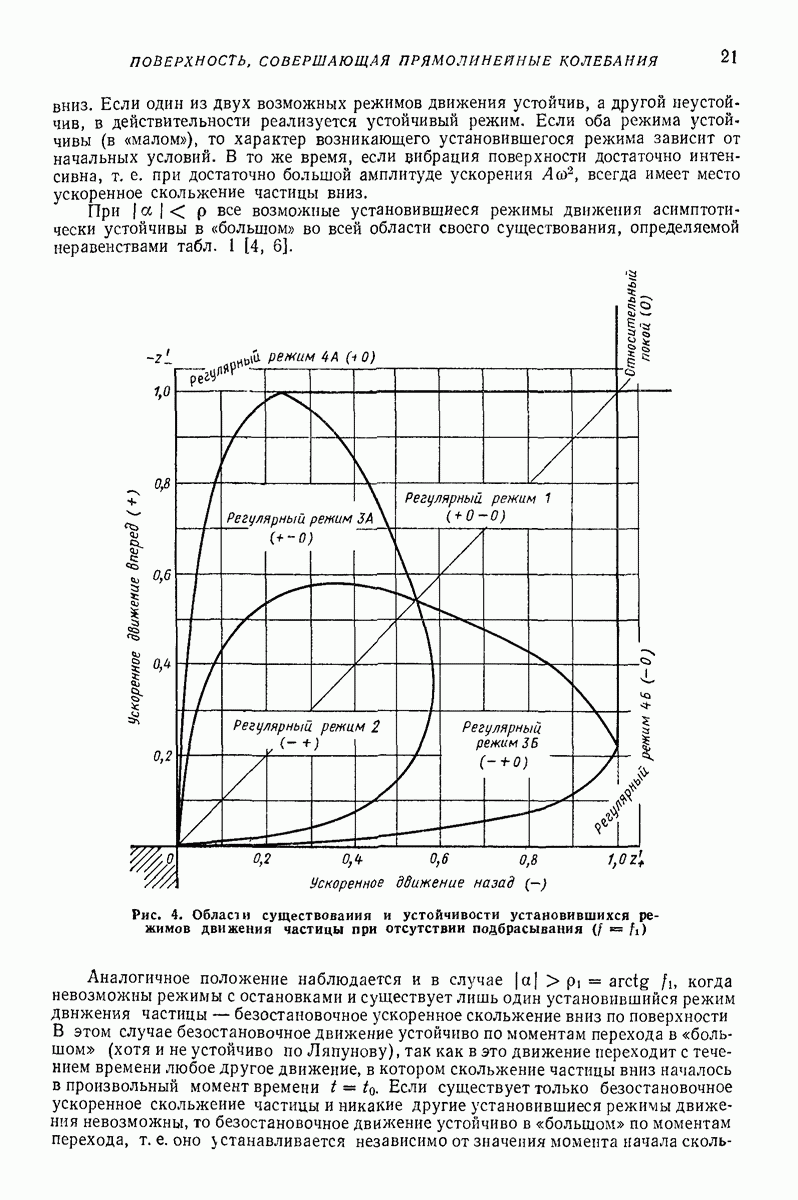
- Установившиеся режимы при отсутствии подбрасывания [4-6].
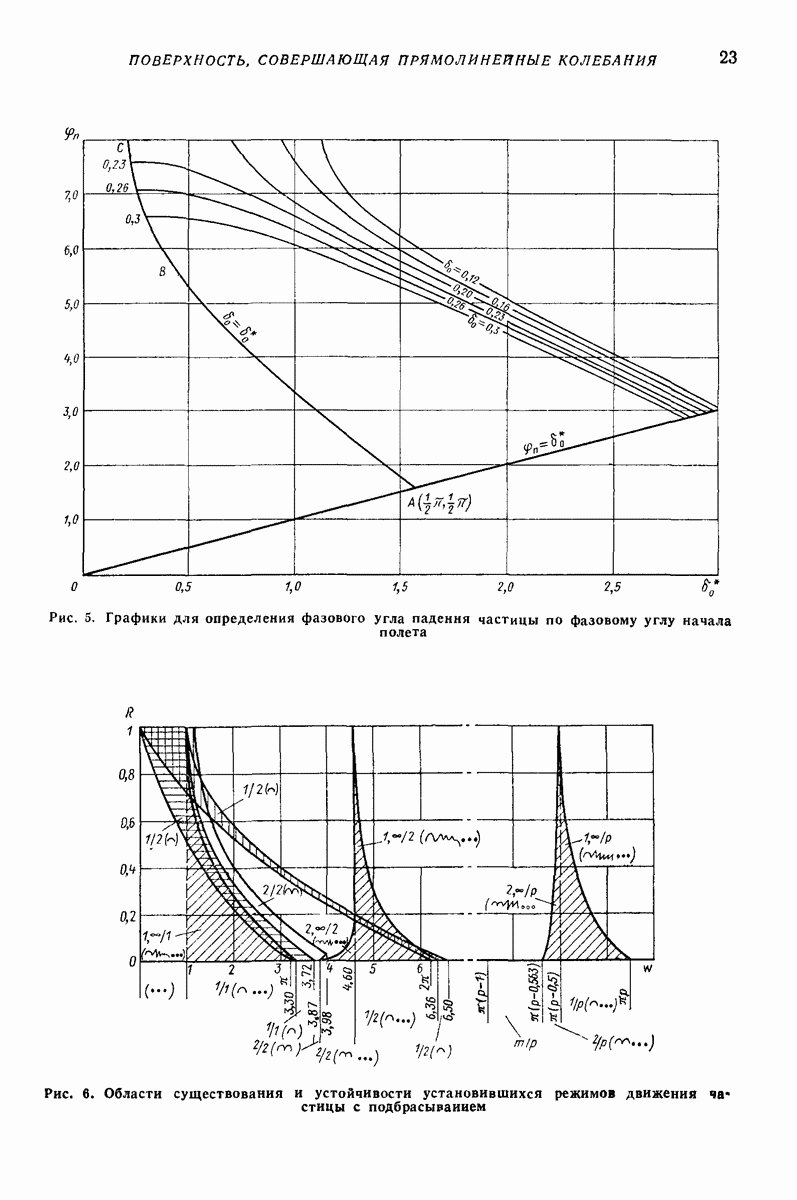
- Установившиеся режимы с подбрасыванием.
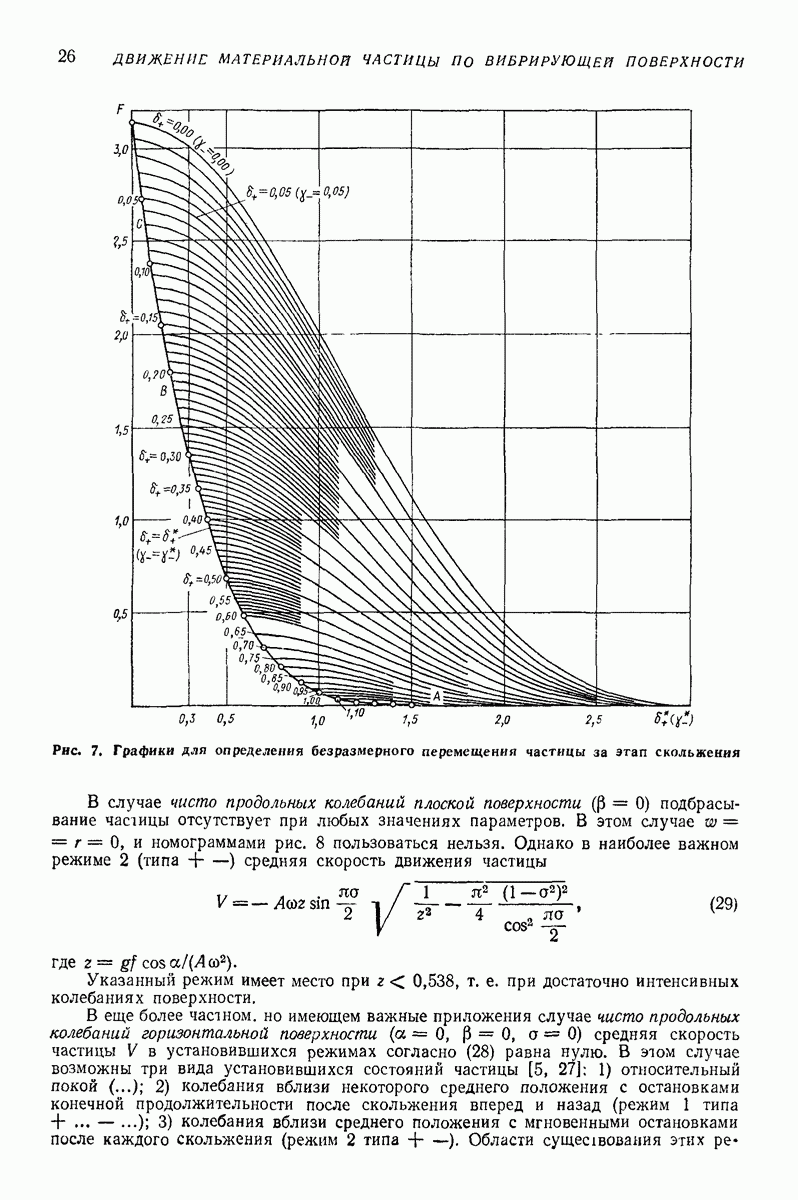
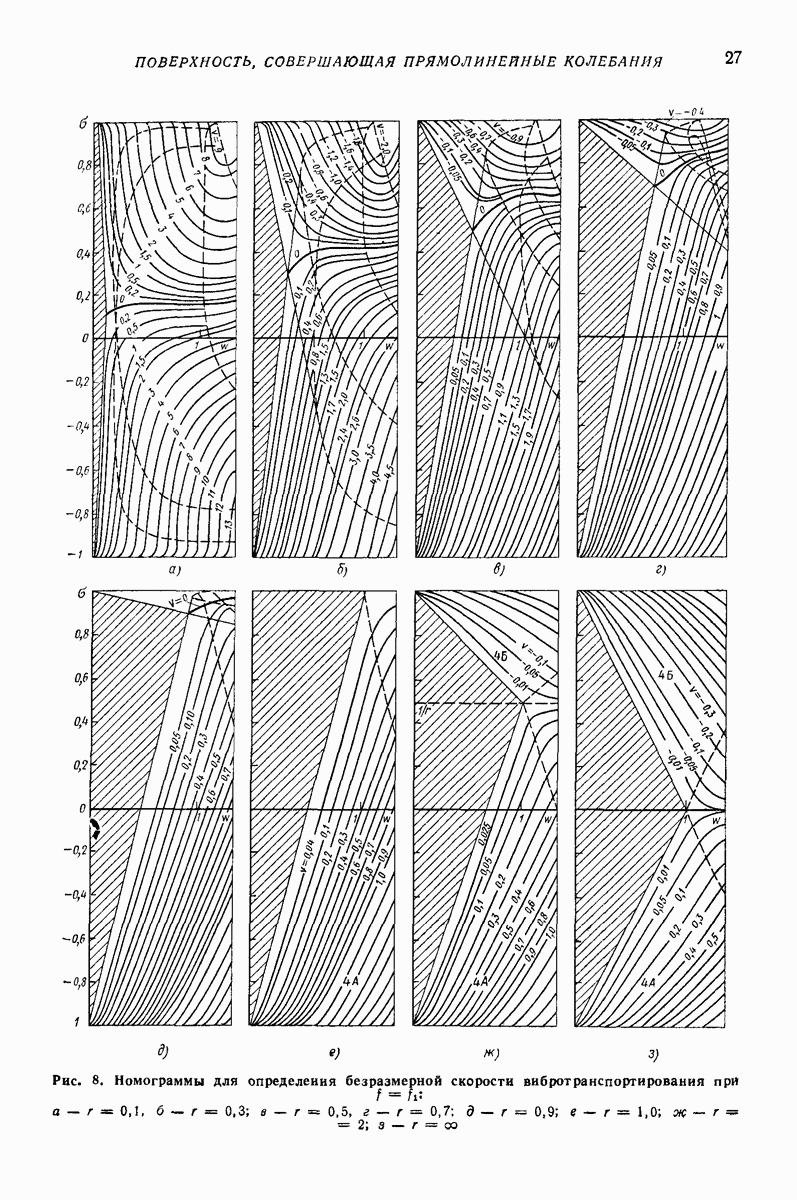
- Средние скорость и ускорение частицы в установившихся режимах движения.
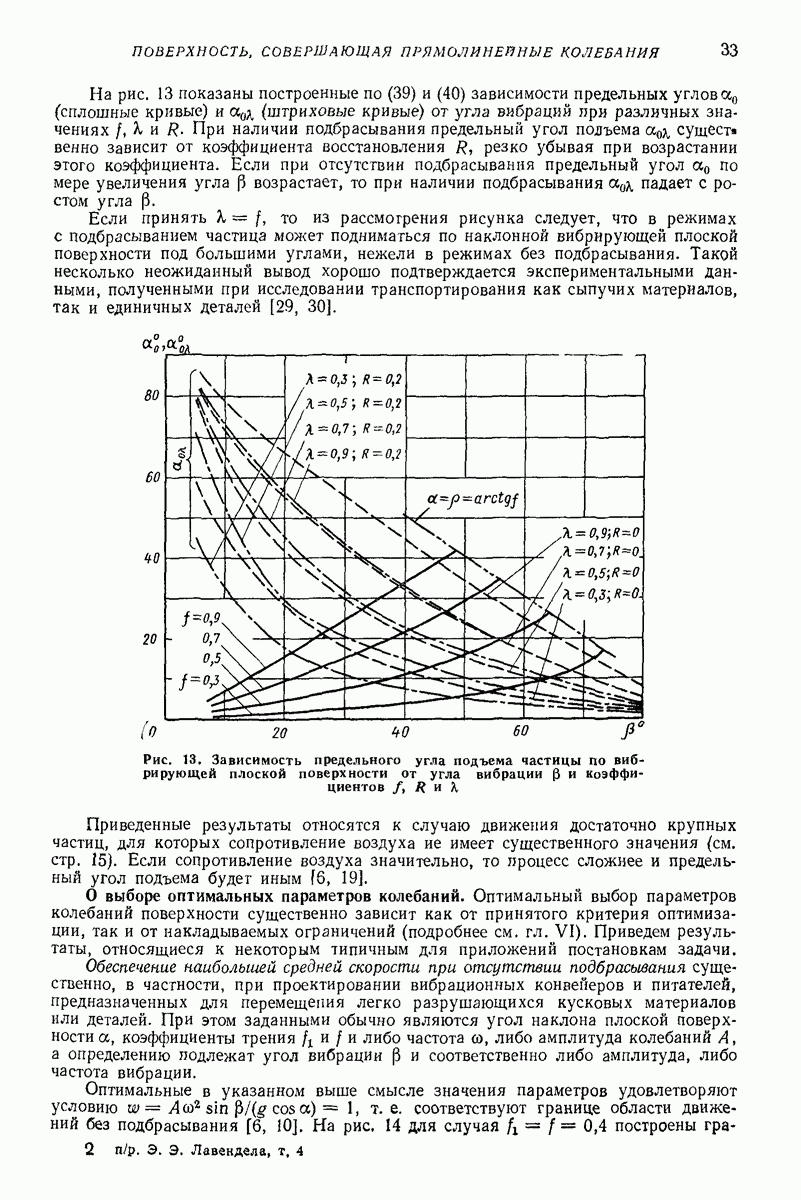
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
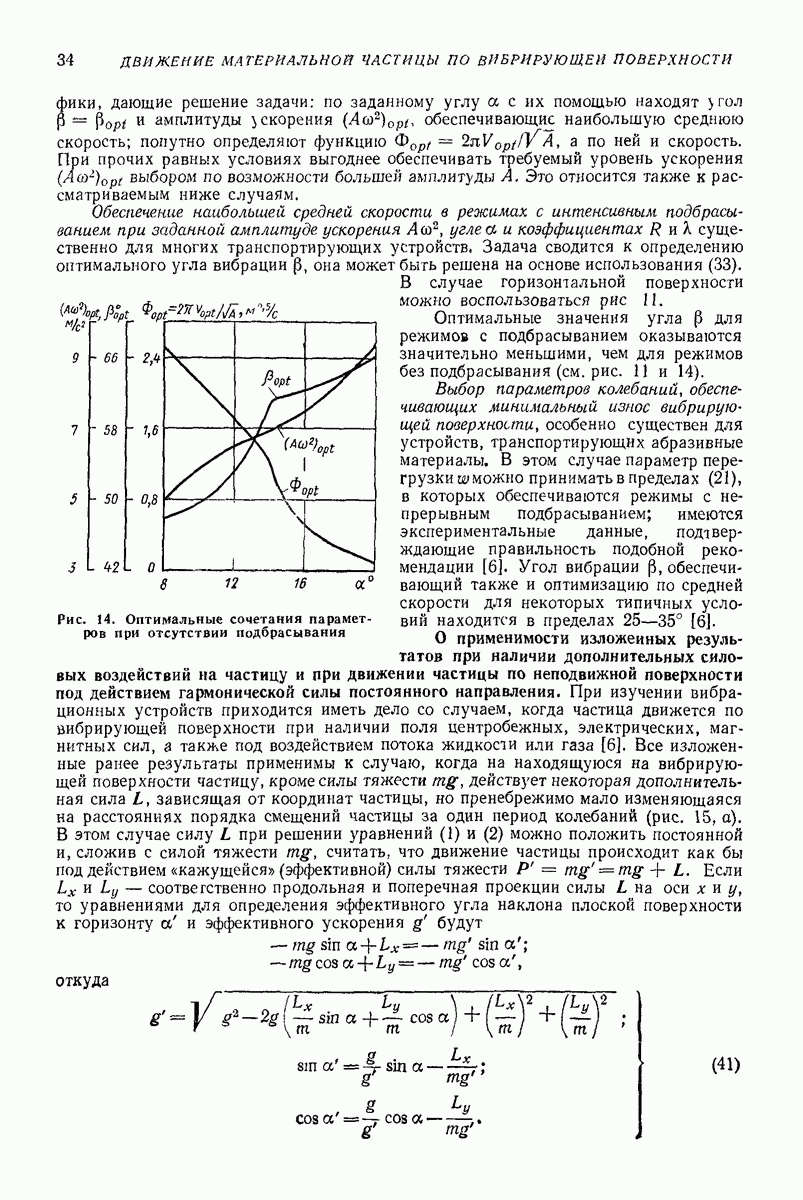
- О выборе оптимальных параметров колебаний.
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
- О влиянии на движение частицы сил вязкого сопротивления.
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
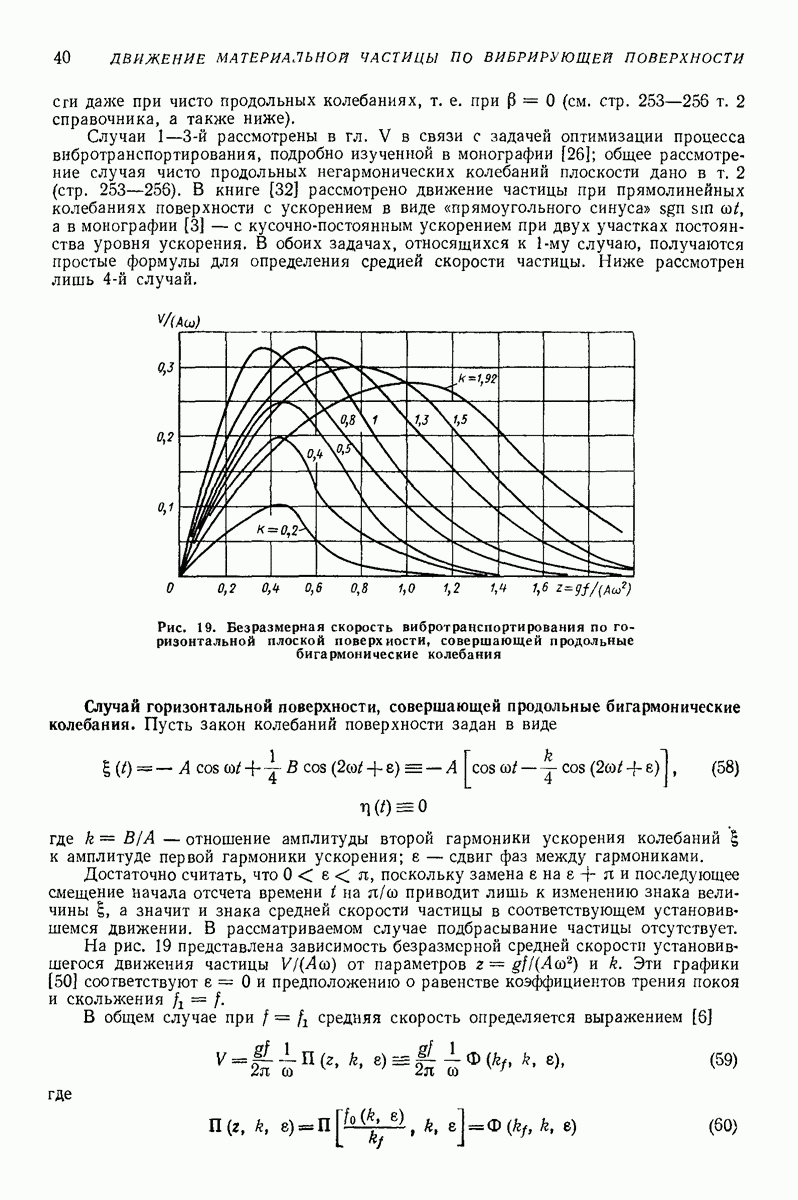
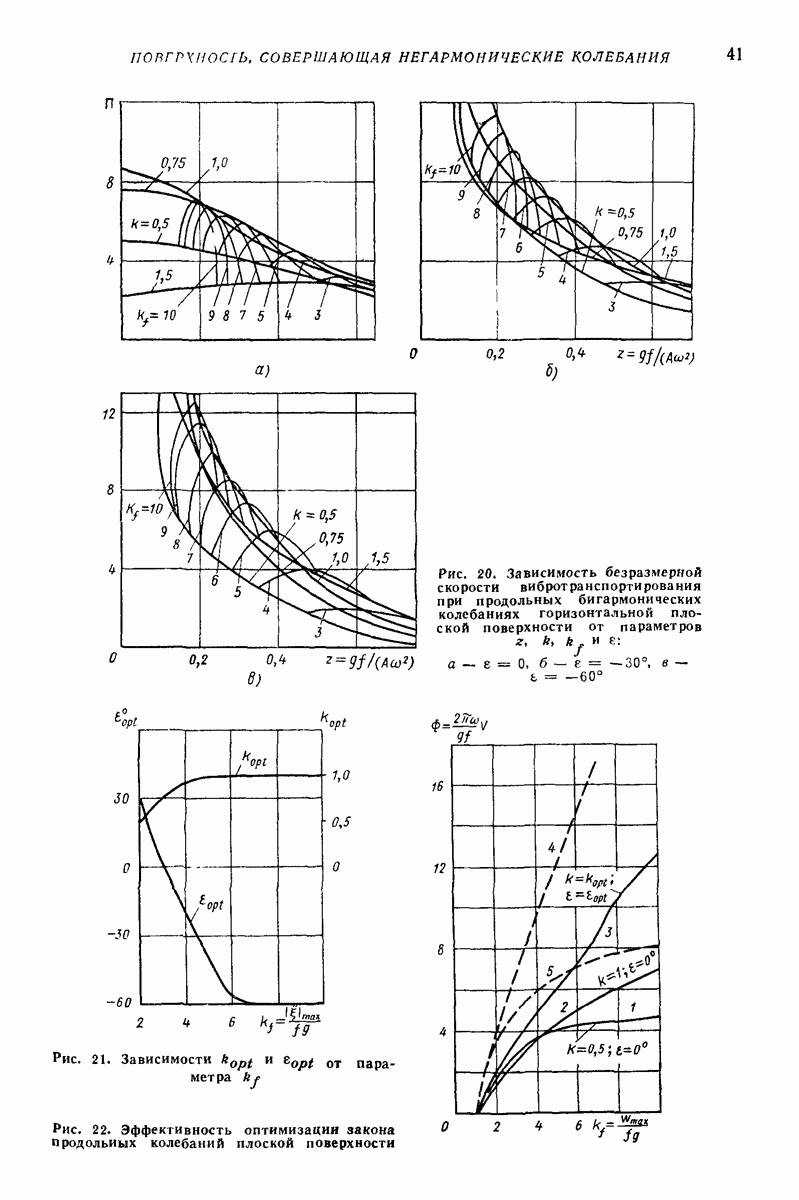
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
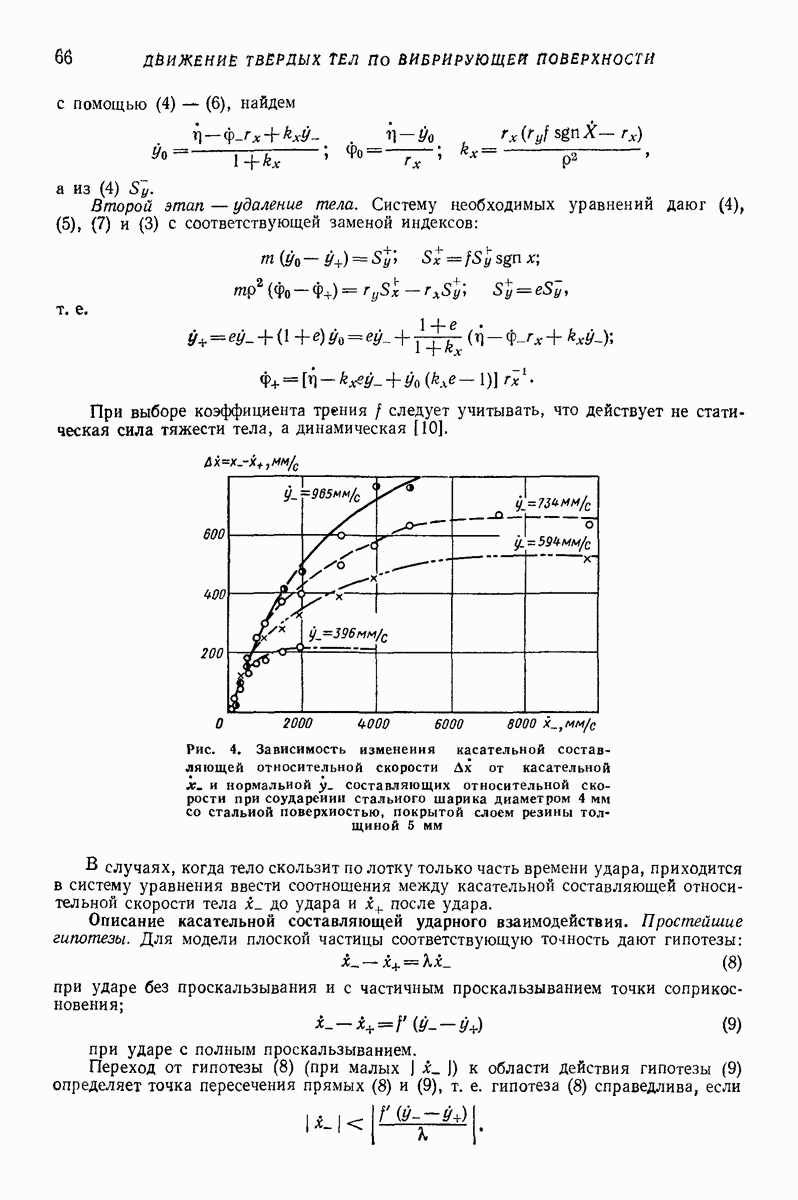
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
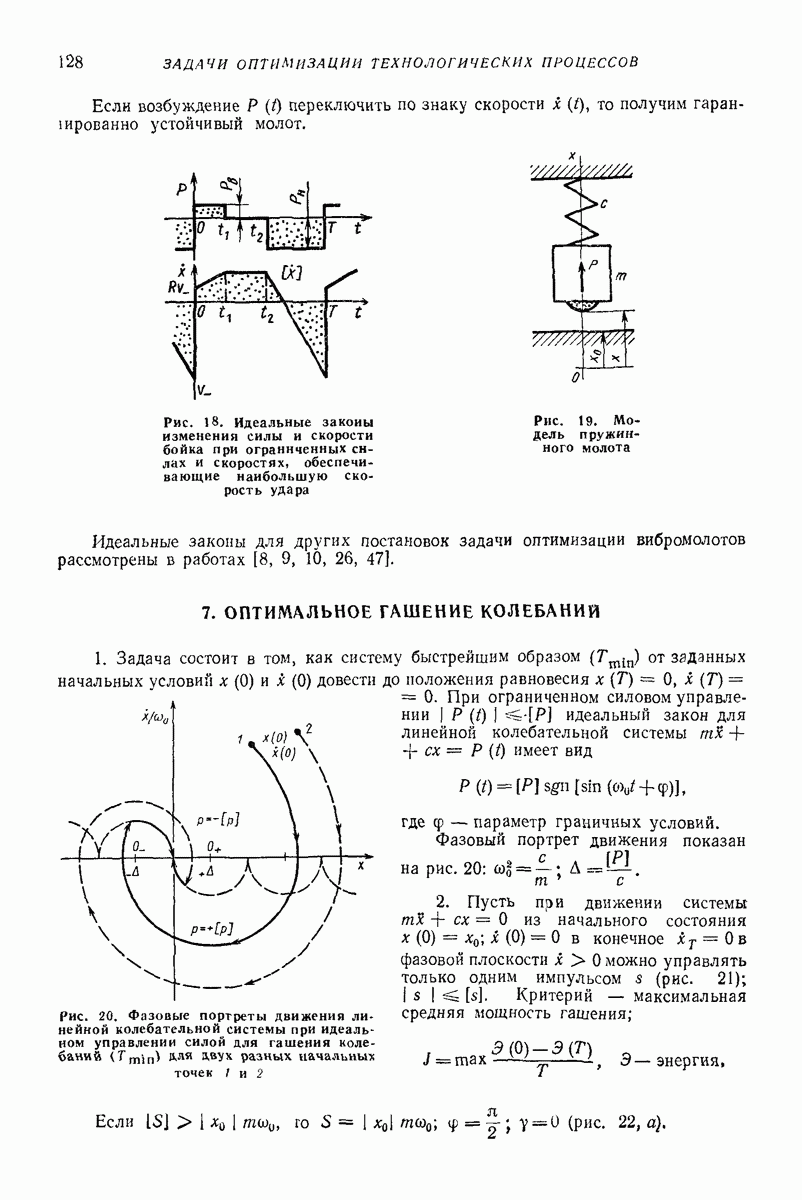
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
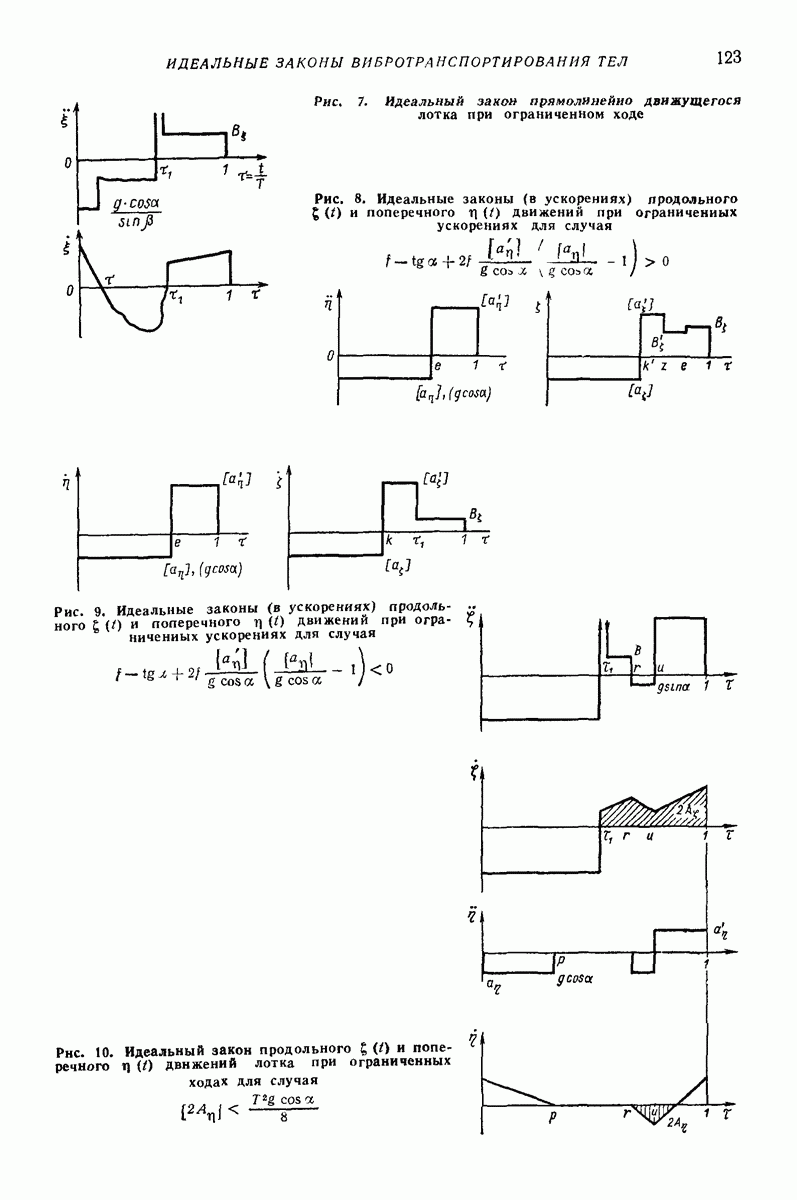
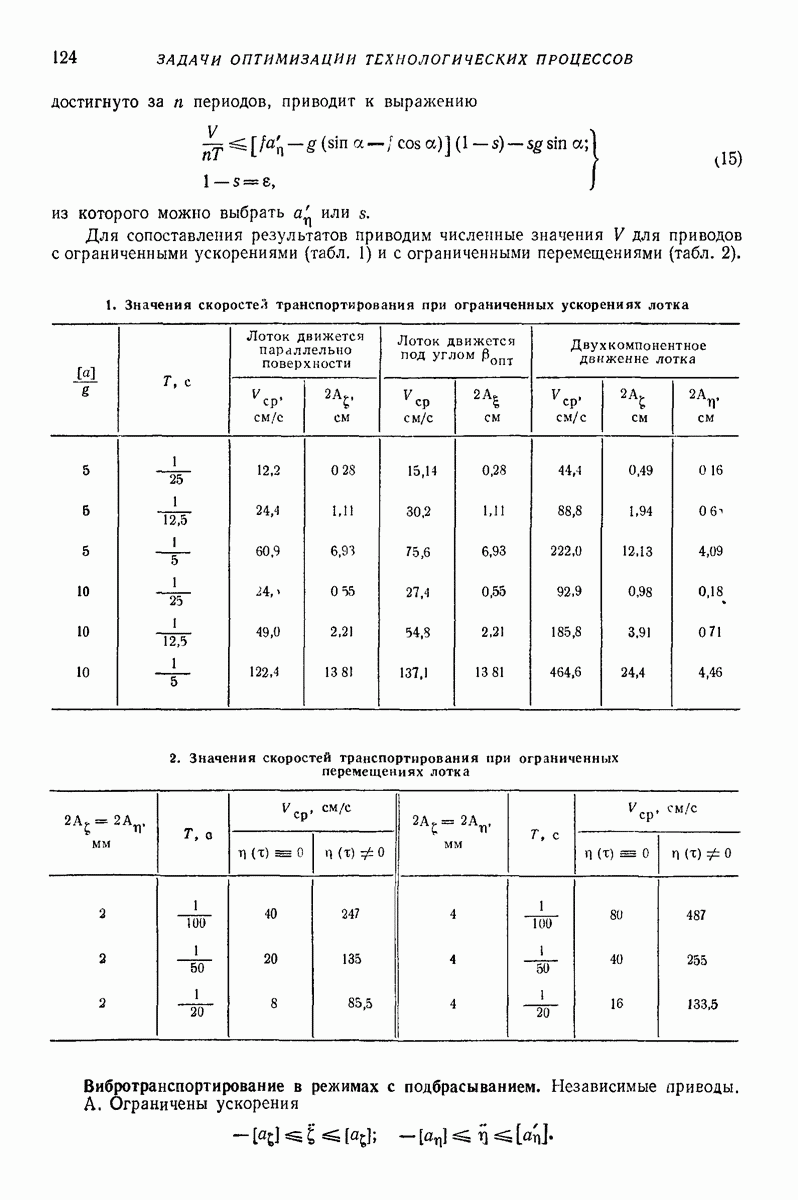
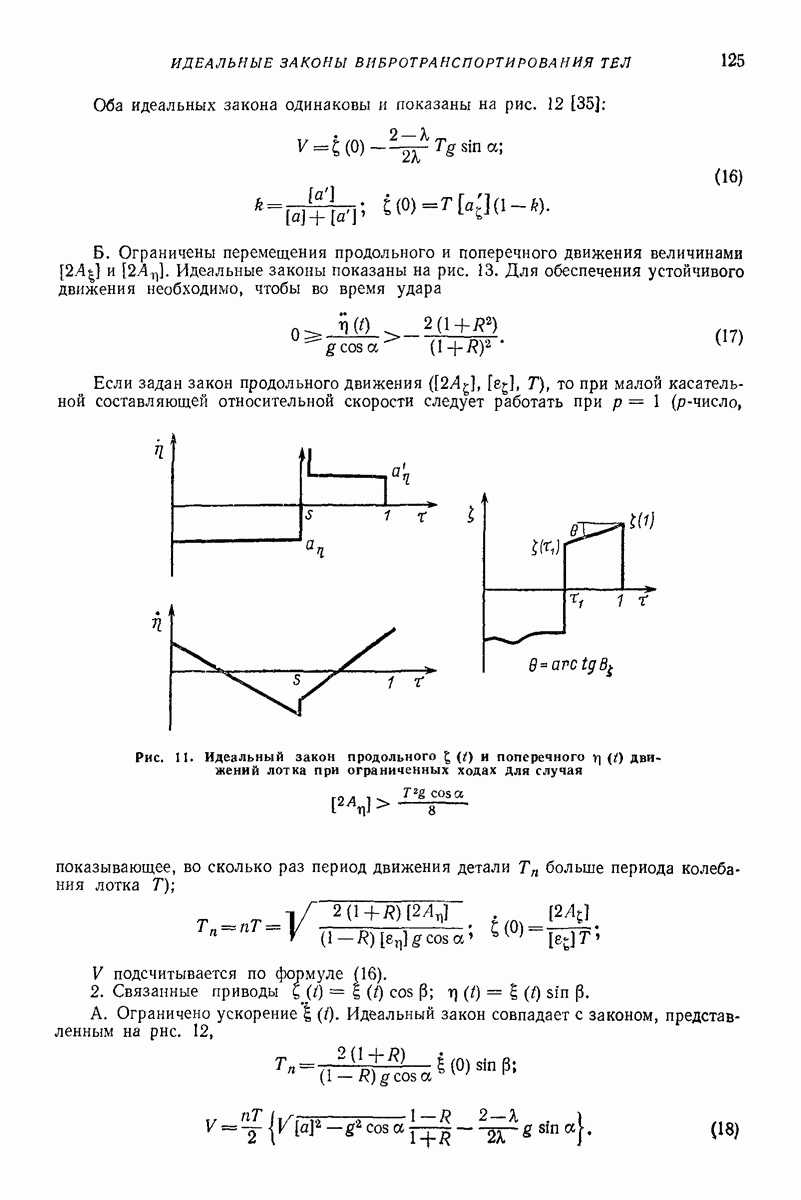
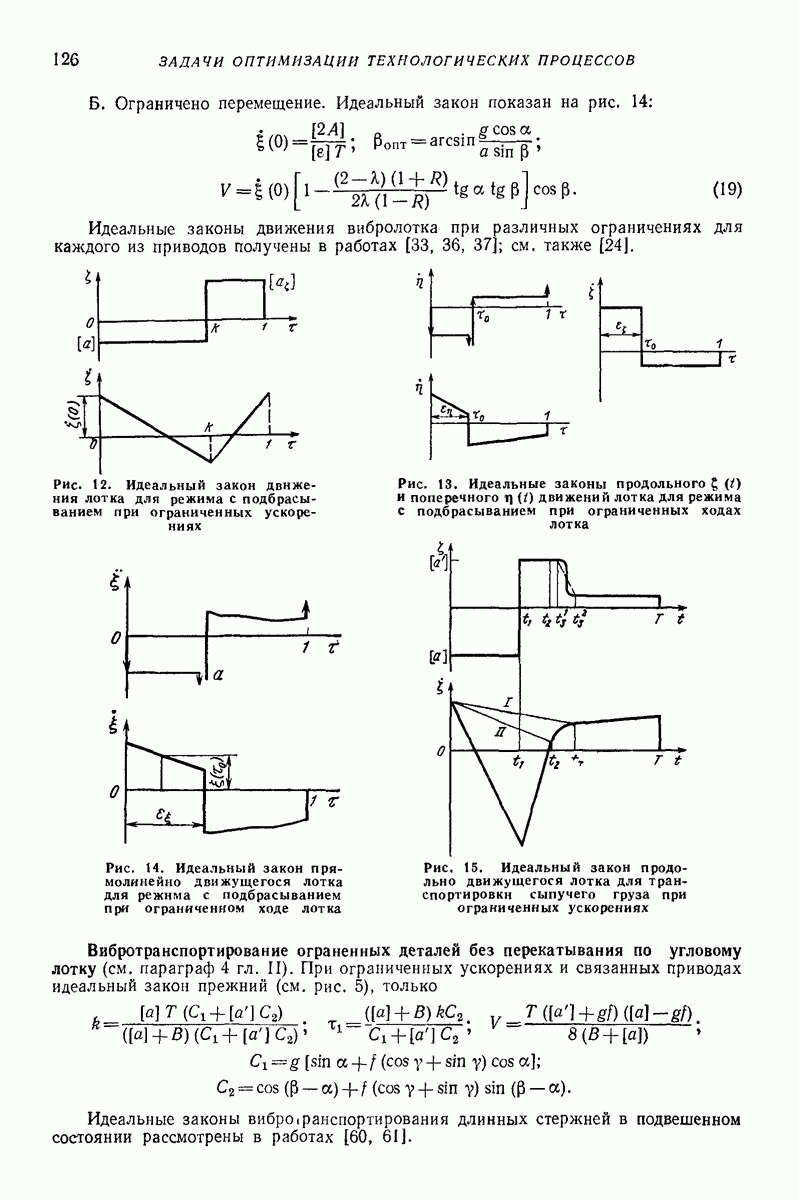
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
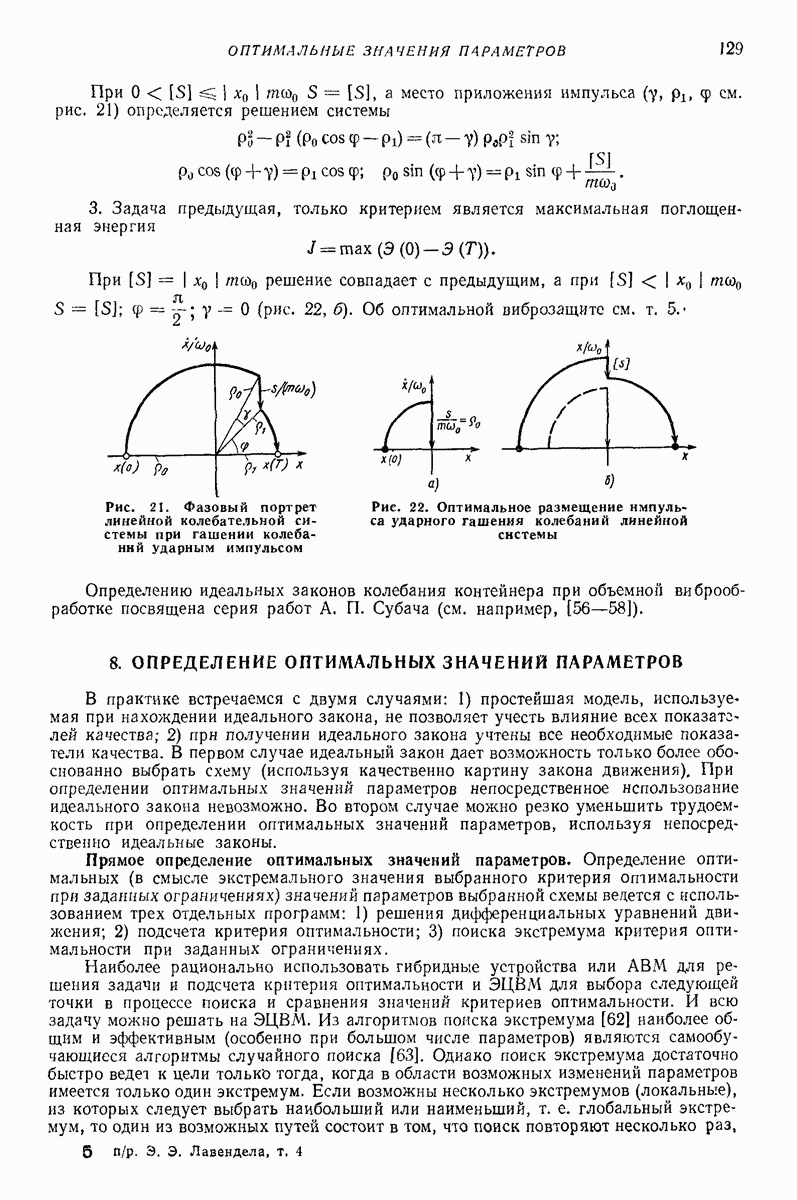
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
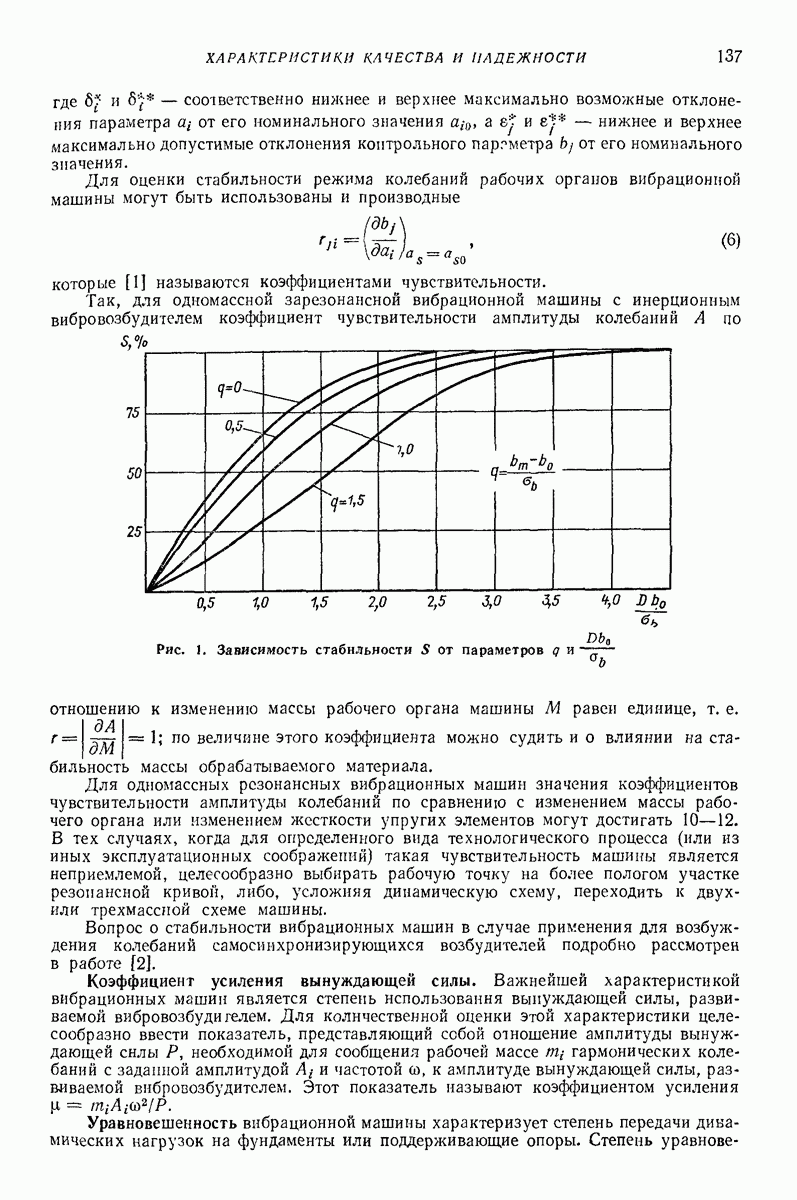
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
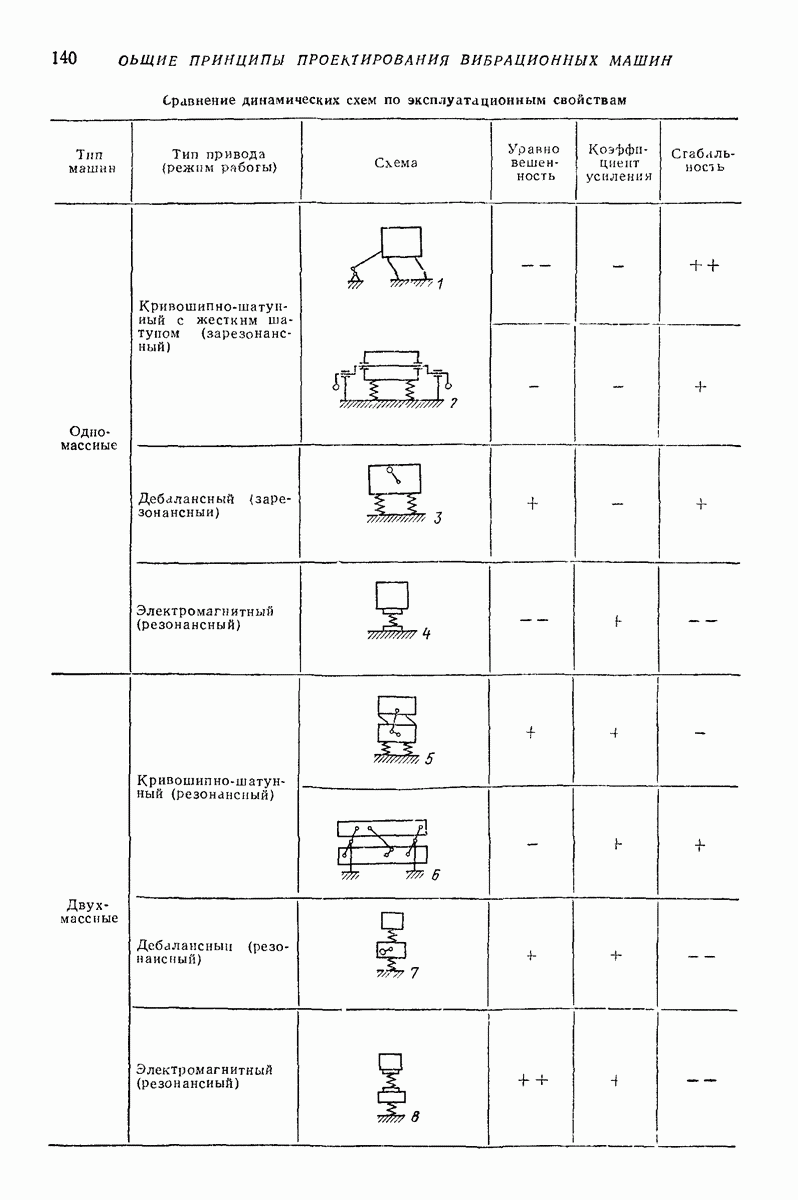
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
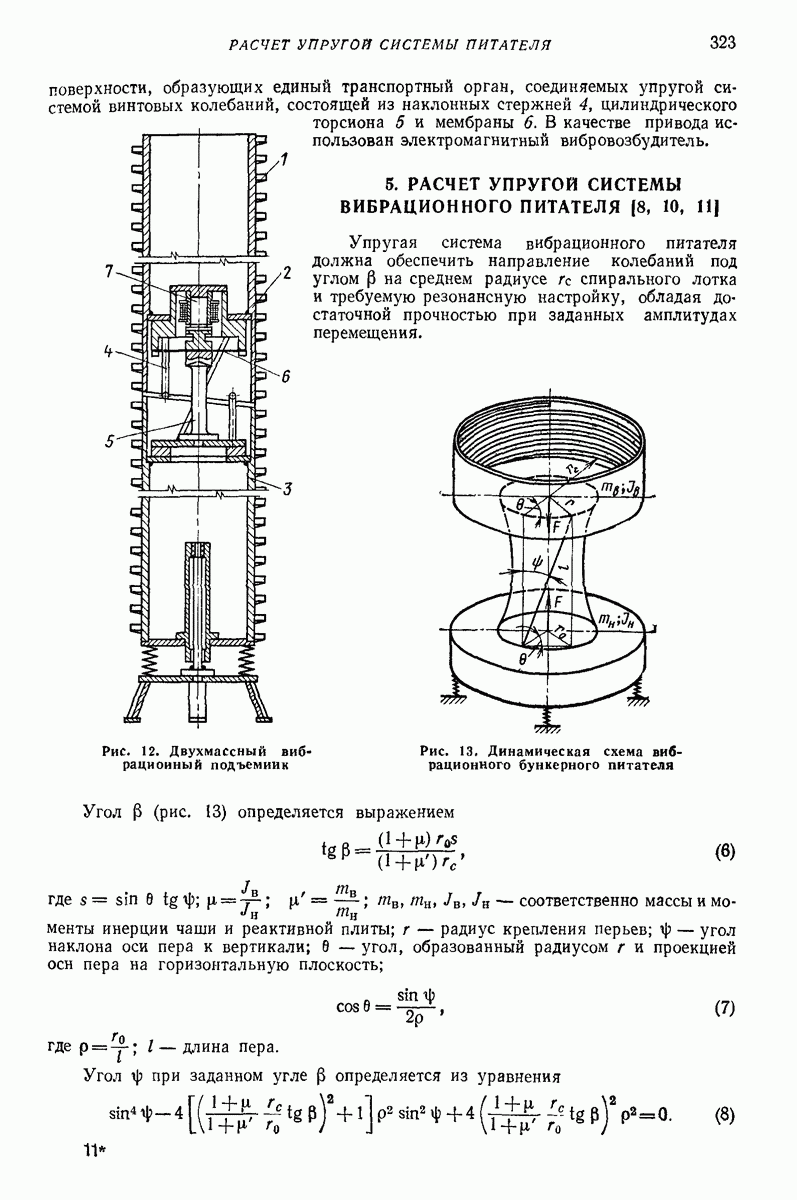
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
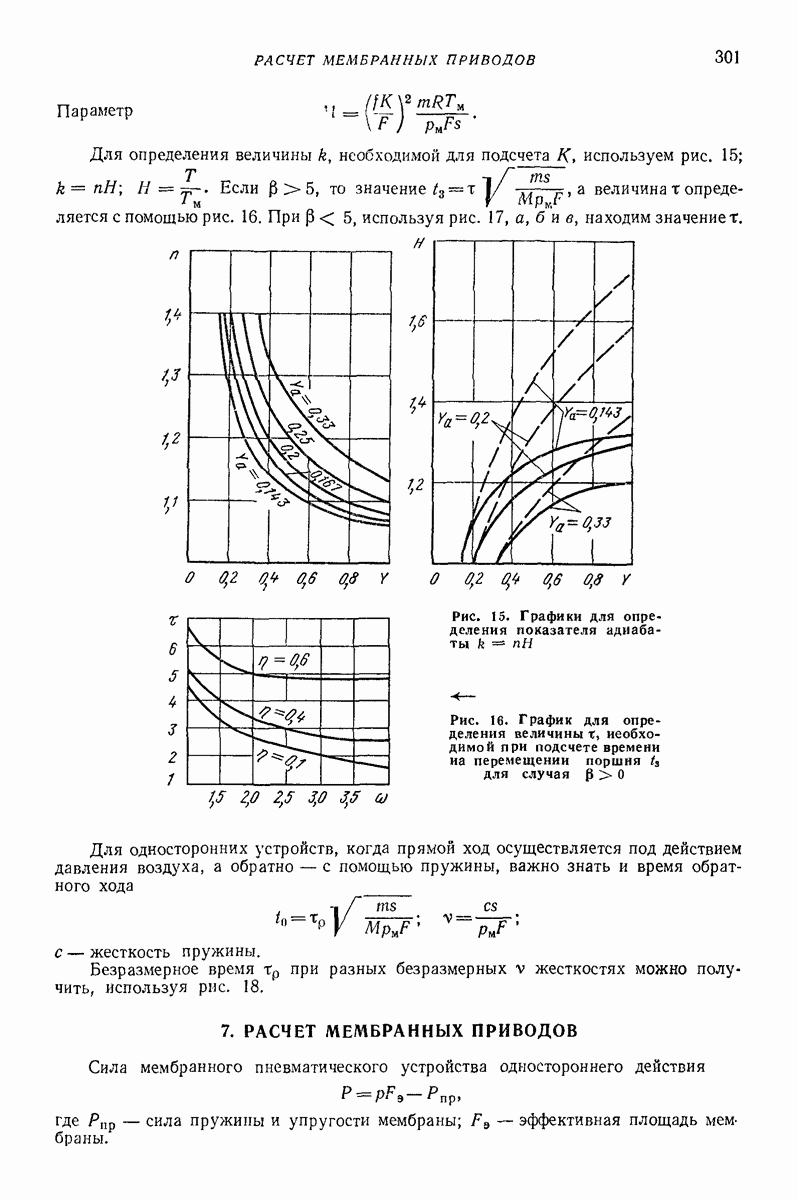
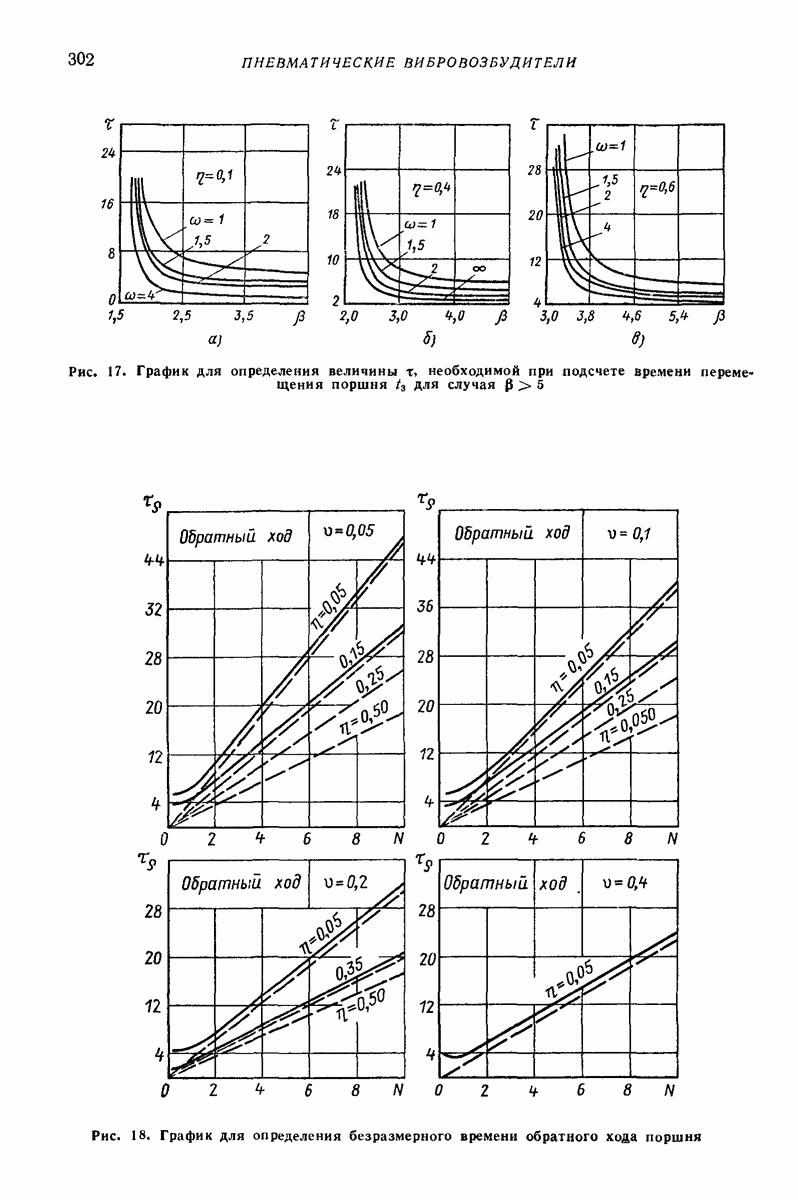
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
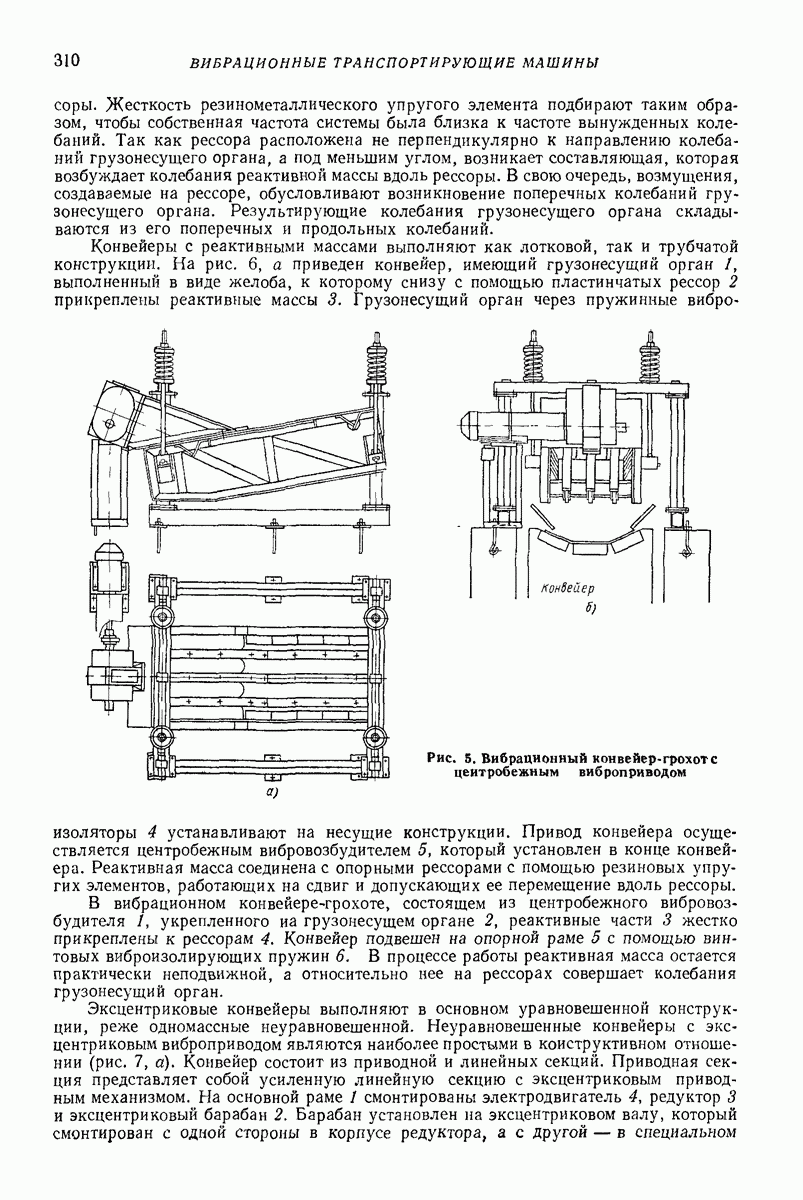
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
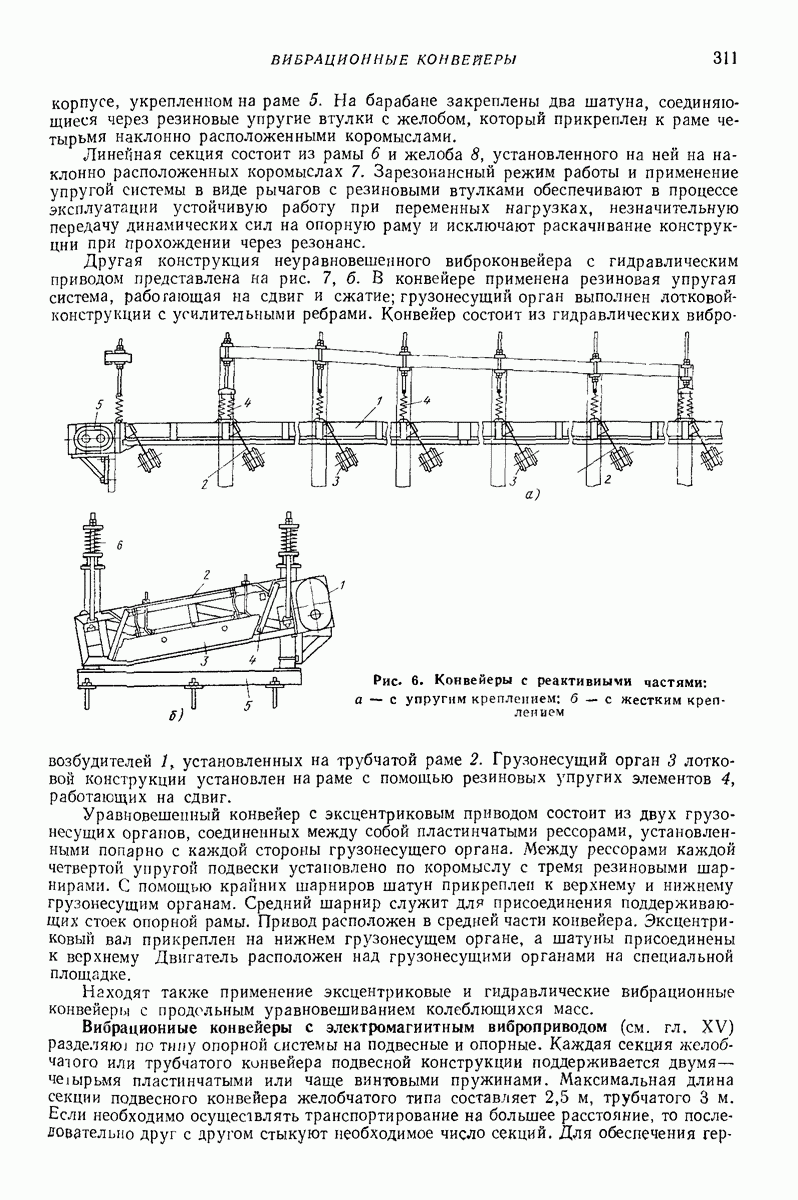
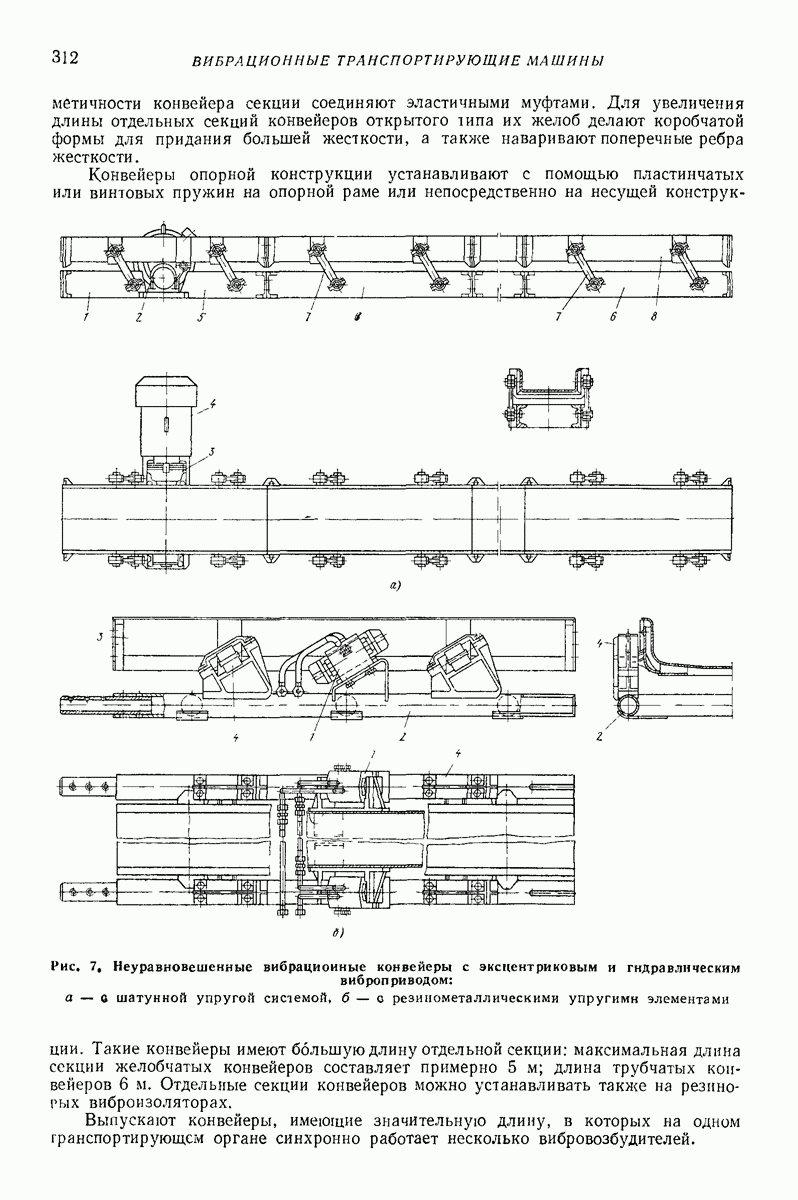
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
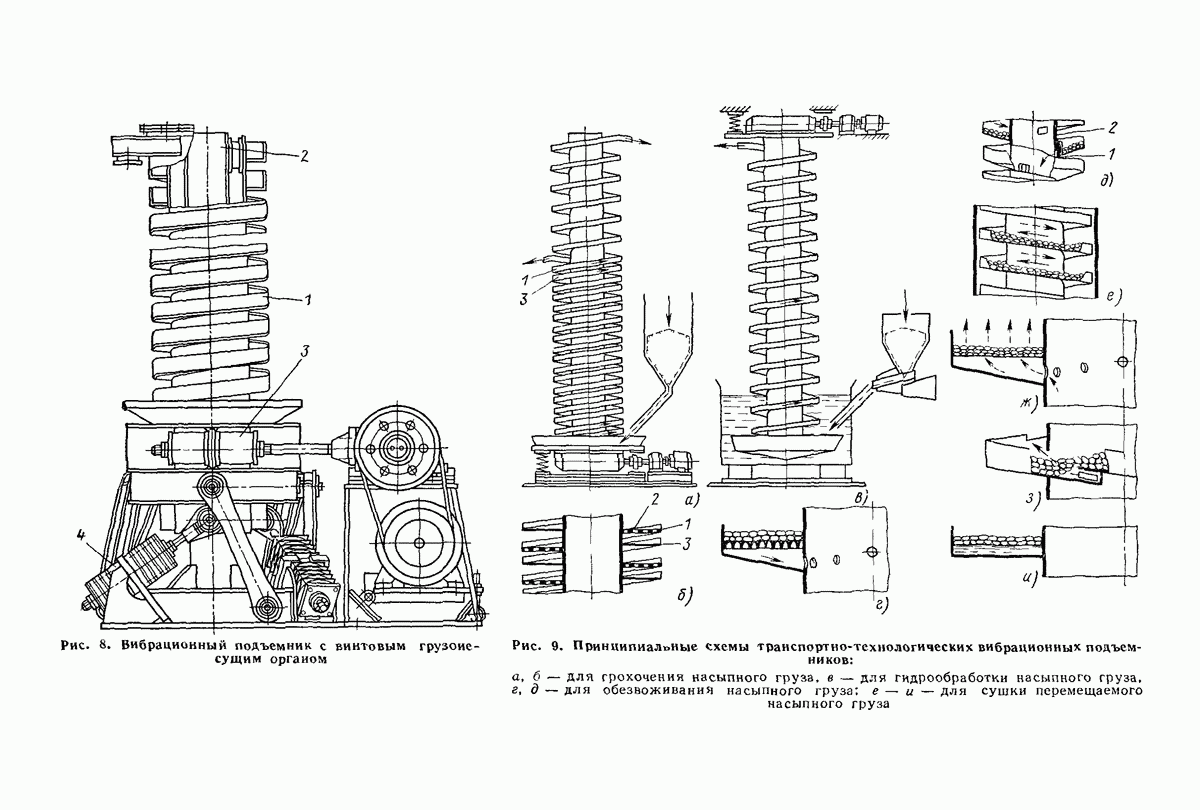
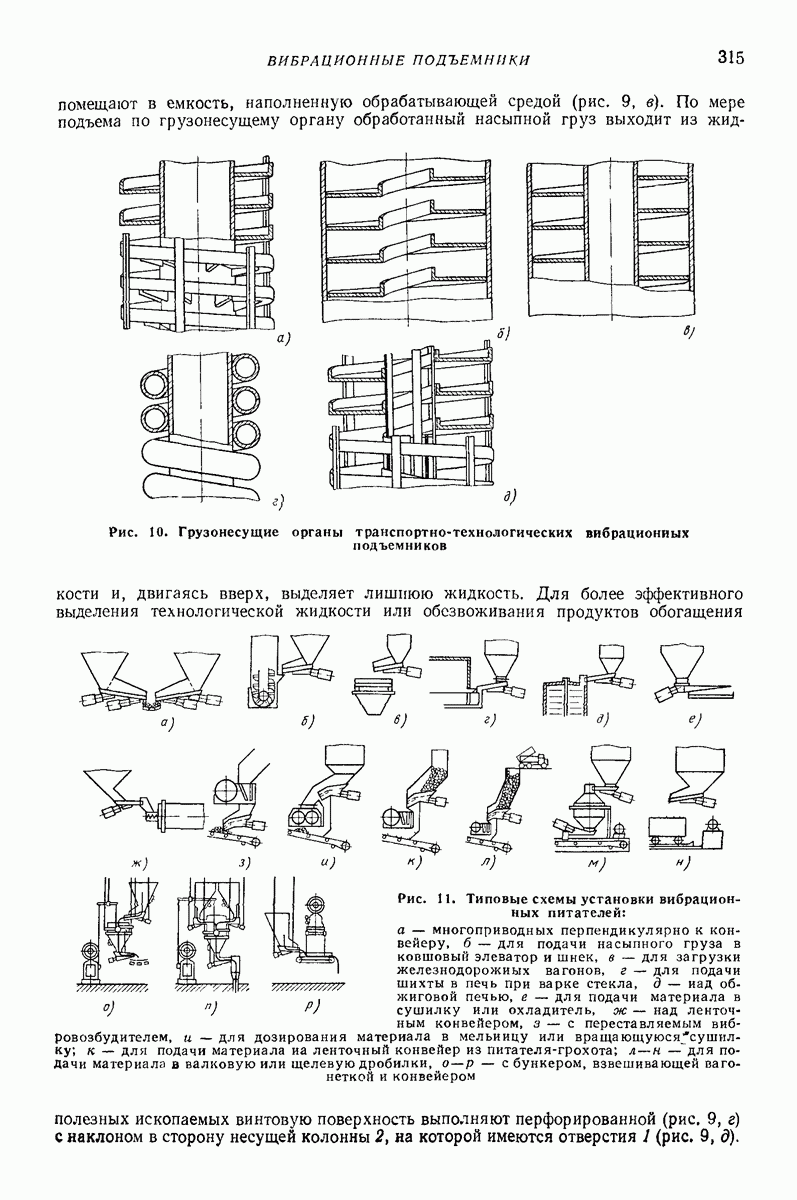
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
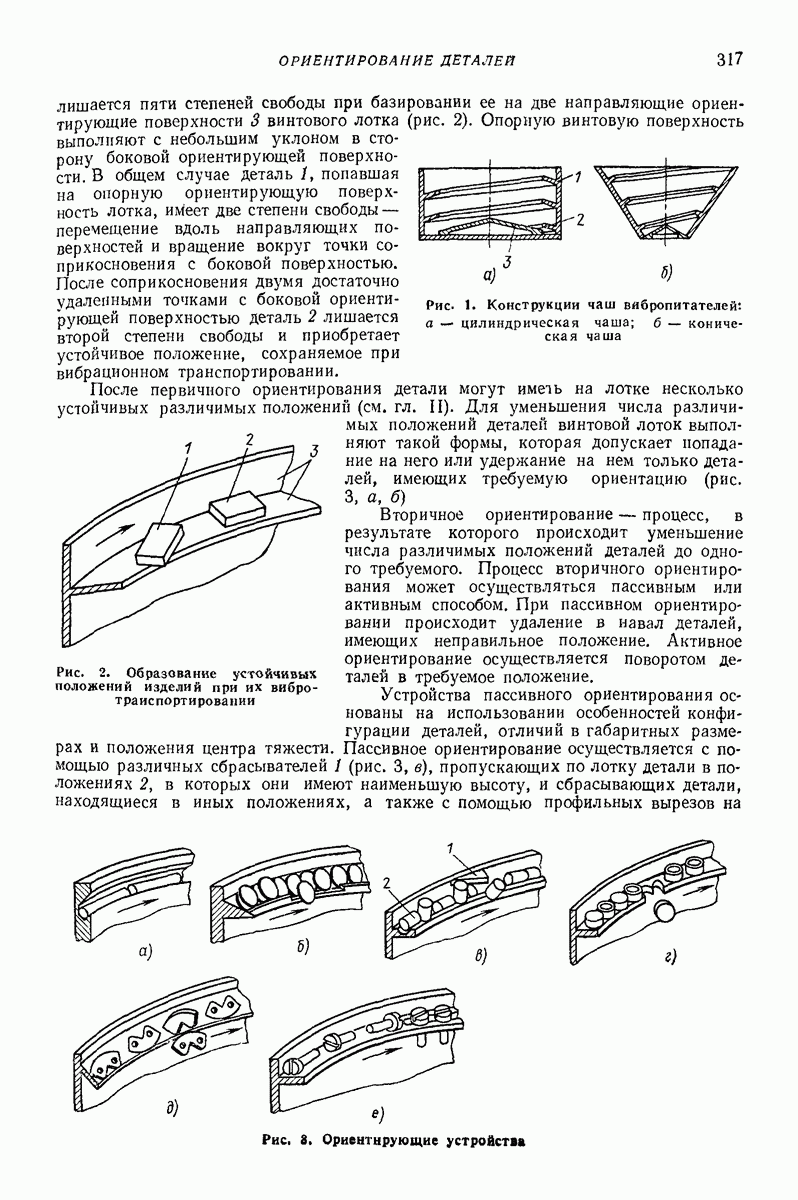
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
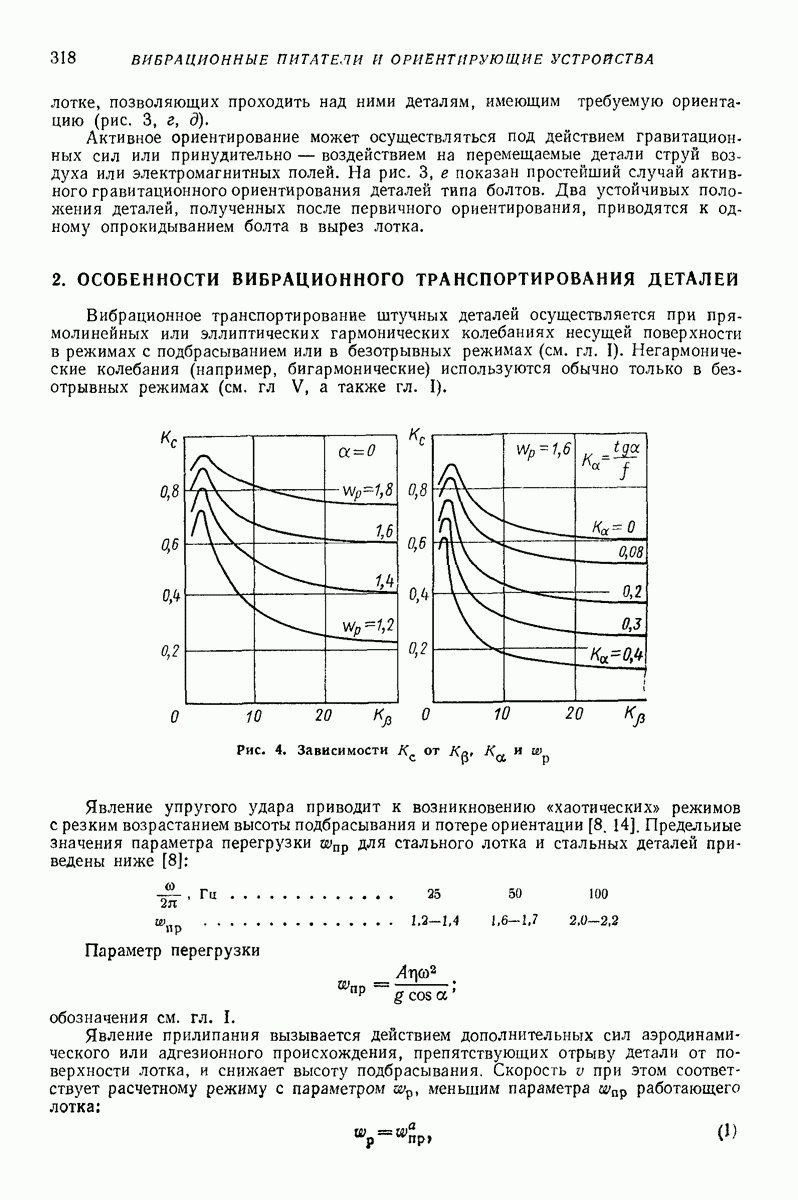
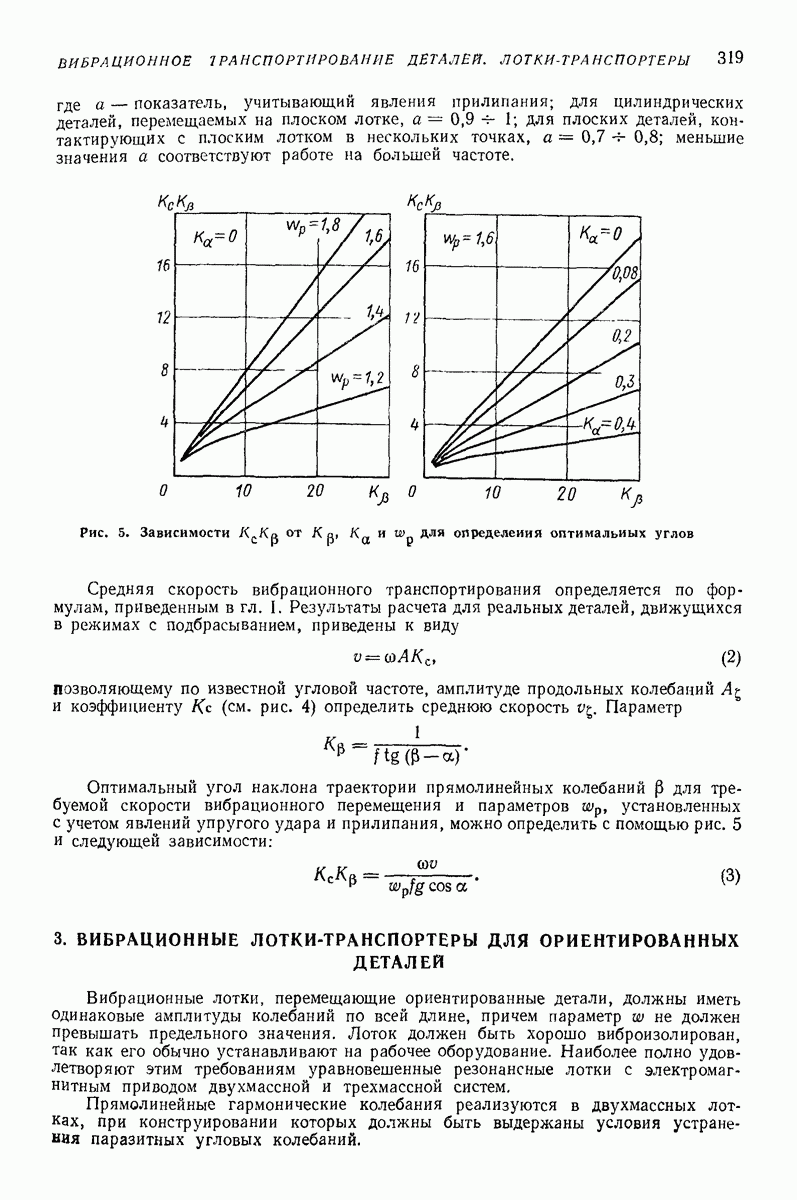
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
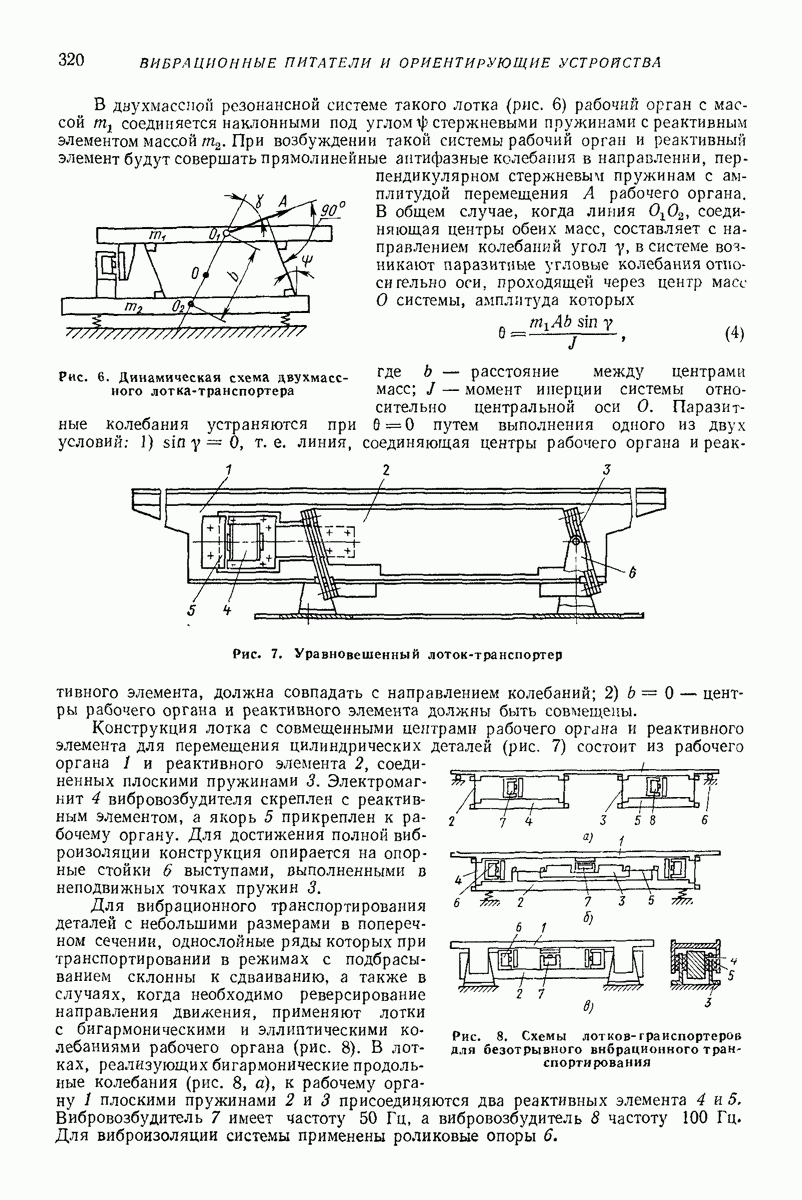
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
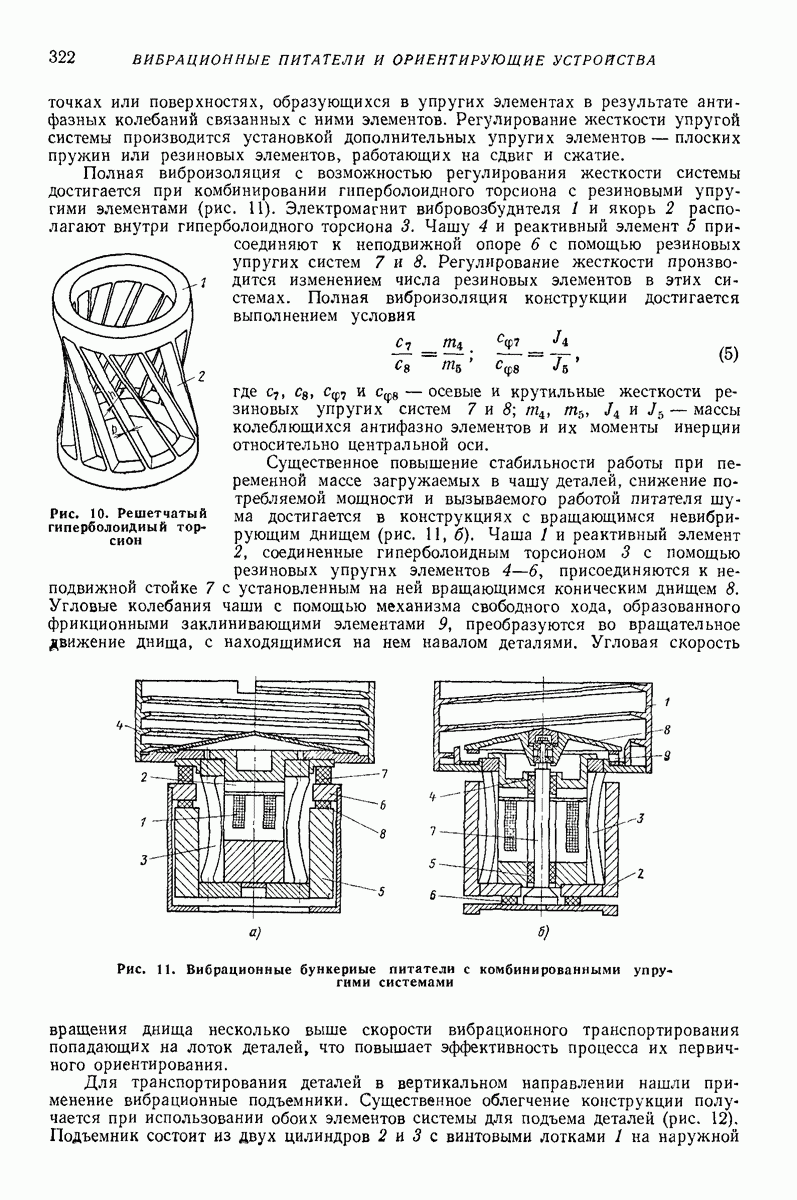
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
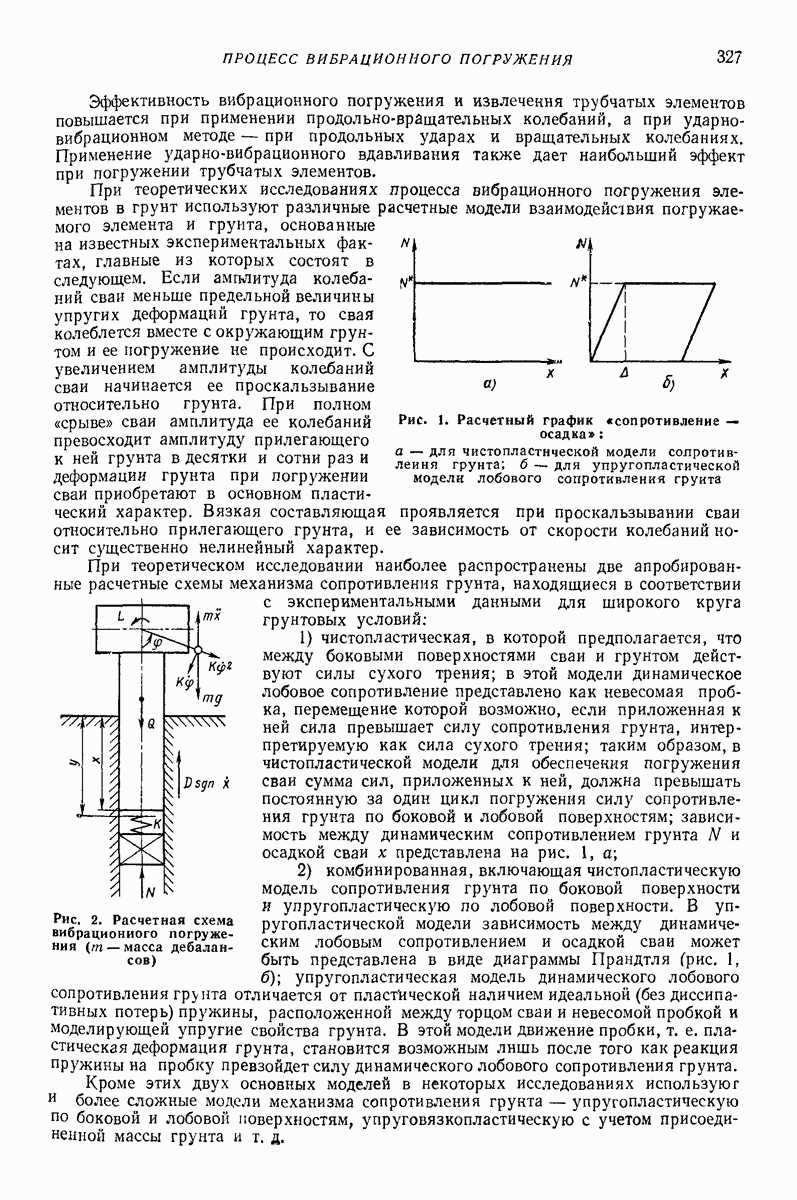
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
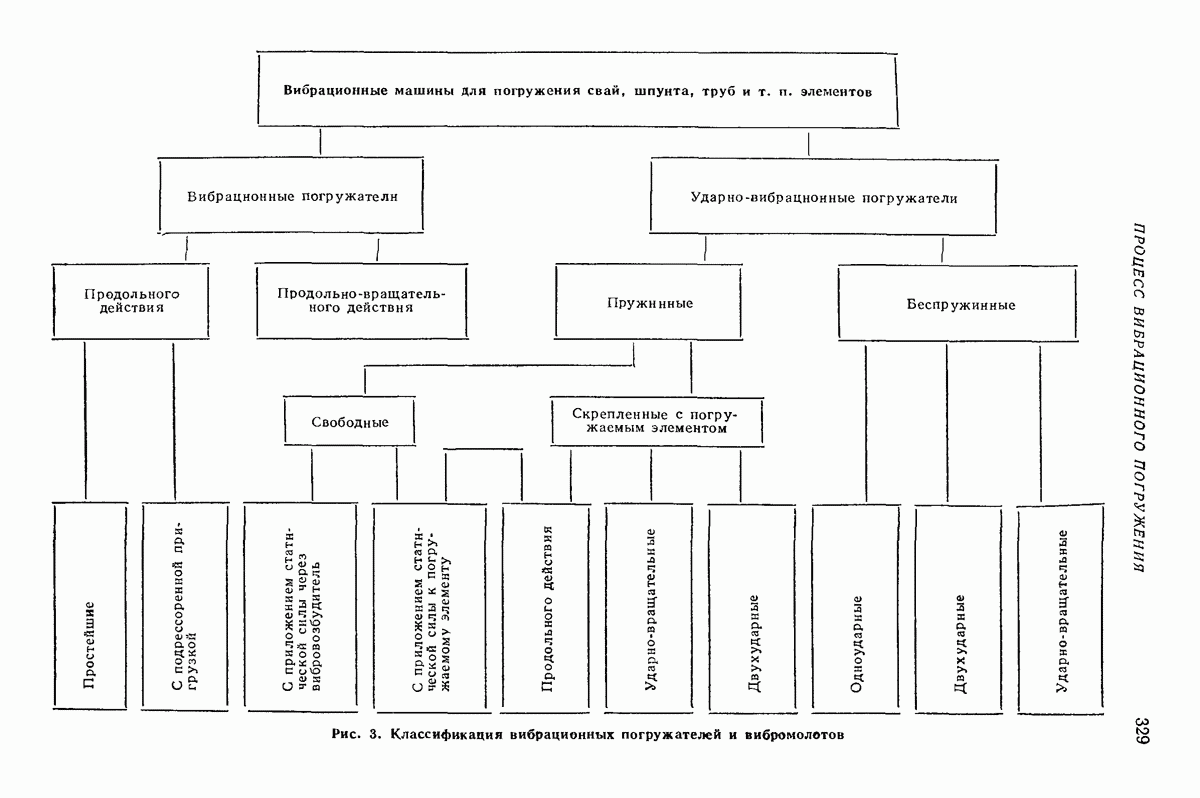
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
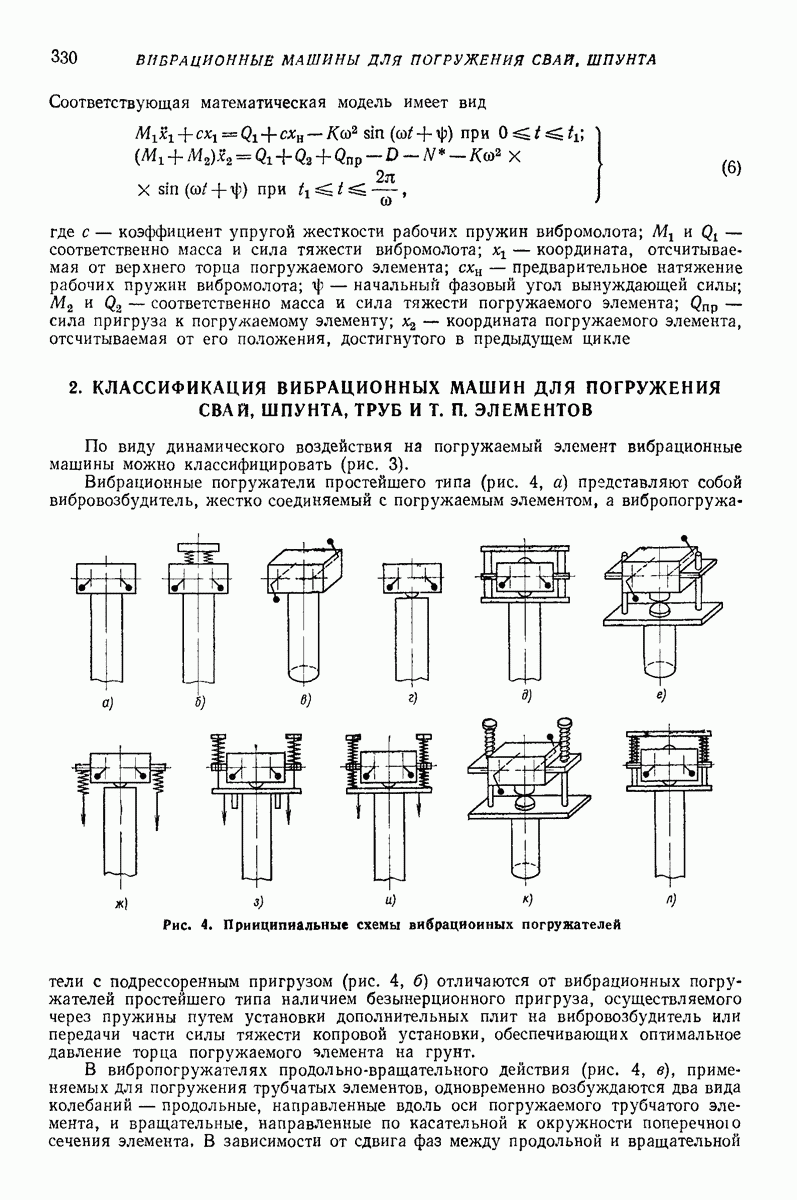
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
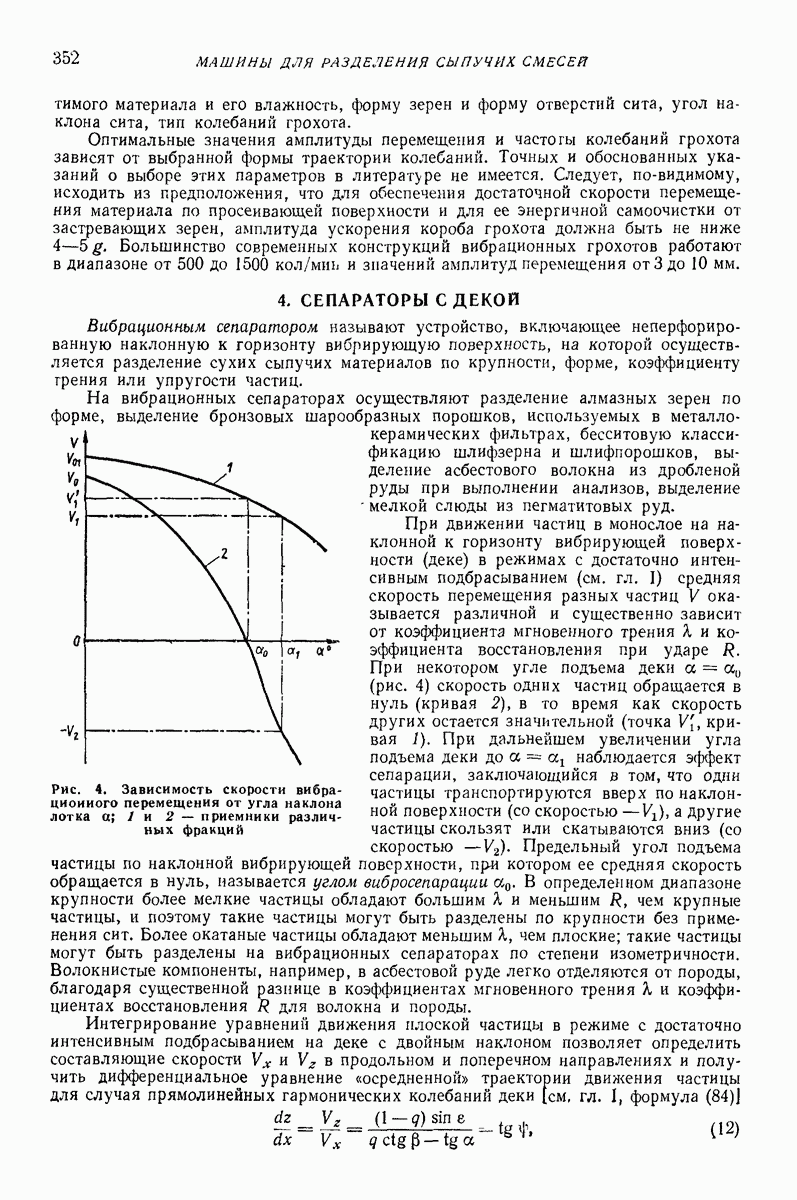
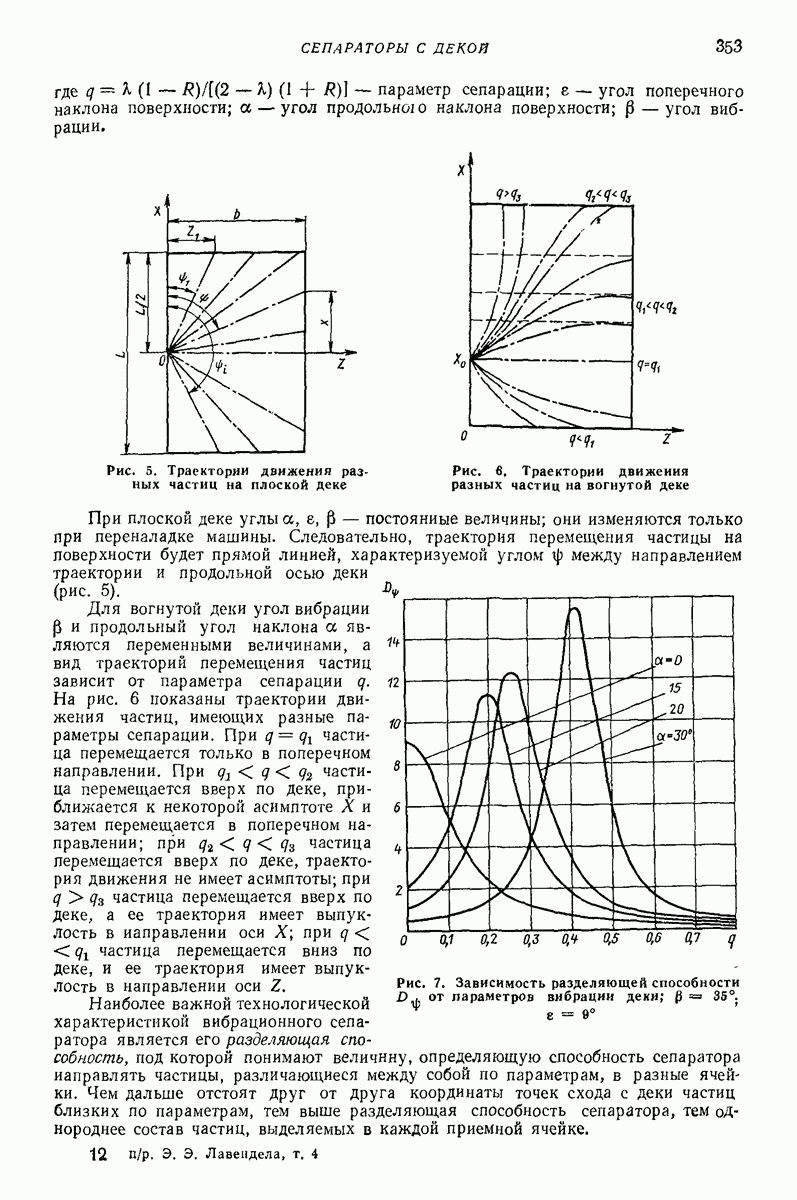
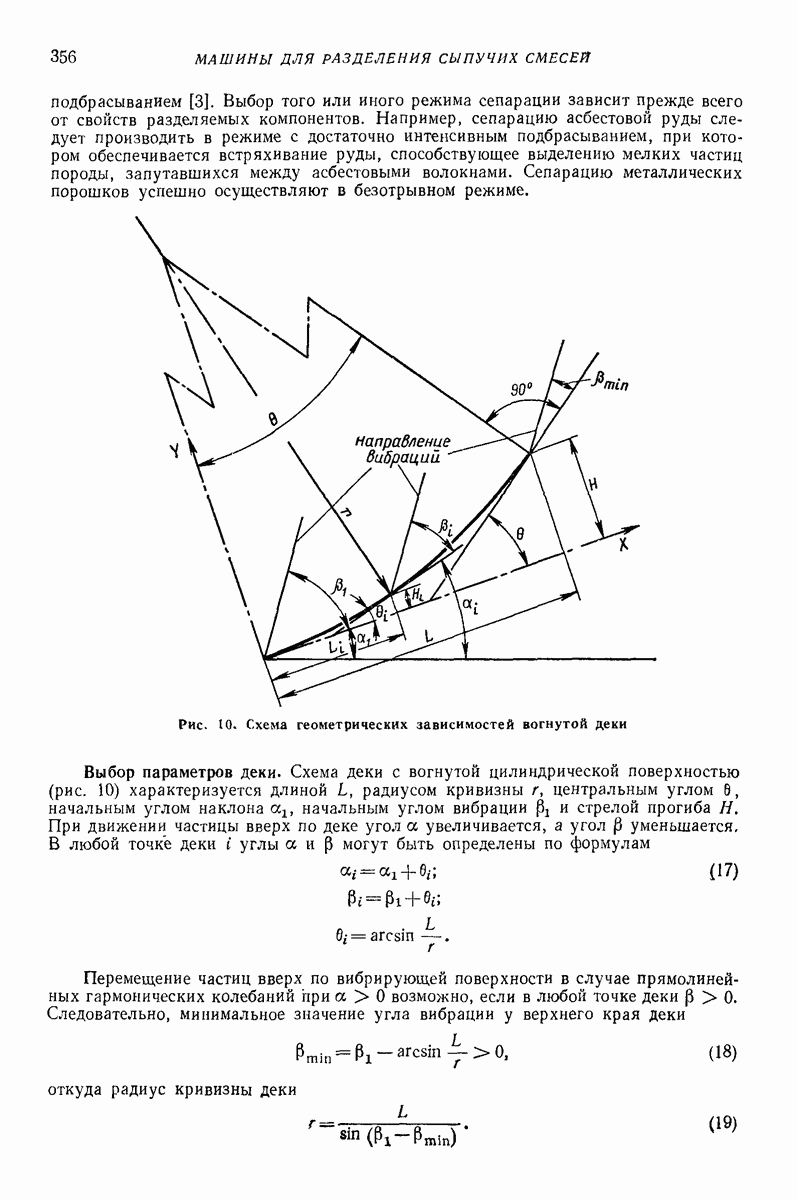
- 4. СЕПАРАТОРЫ С ДЕКОЙ
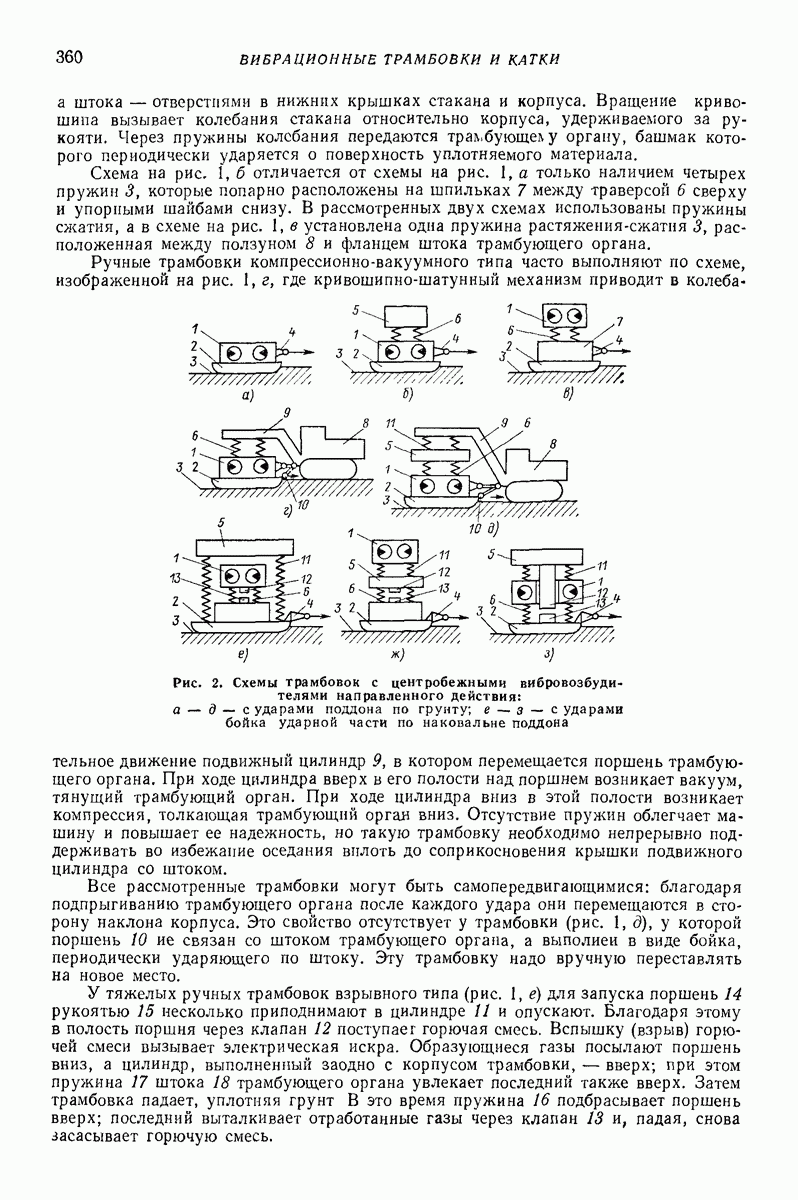
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
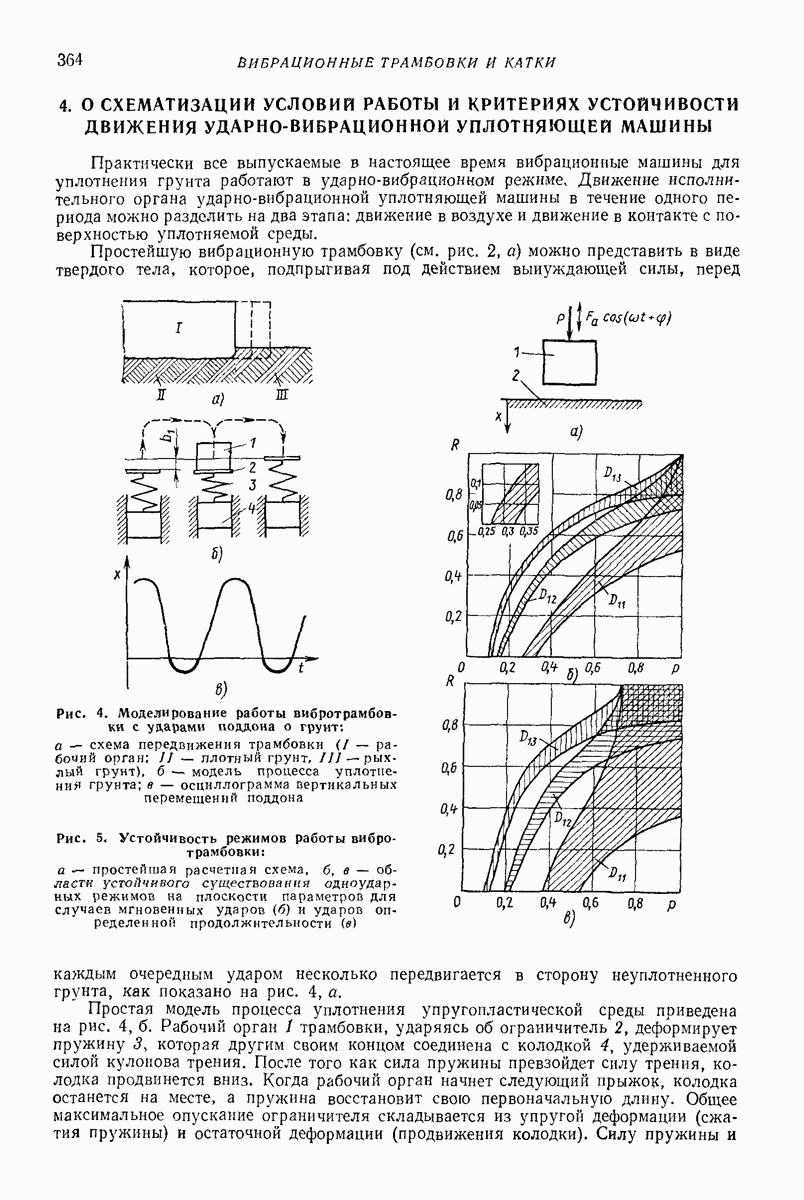
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
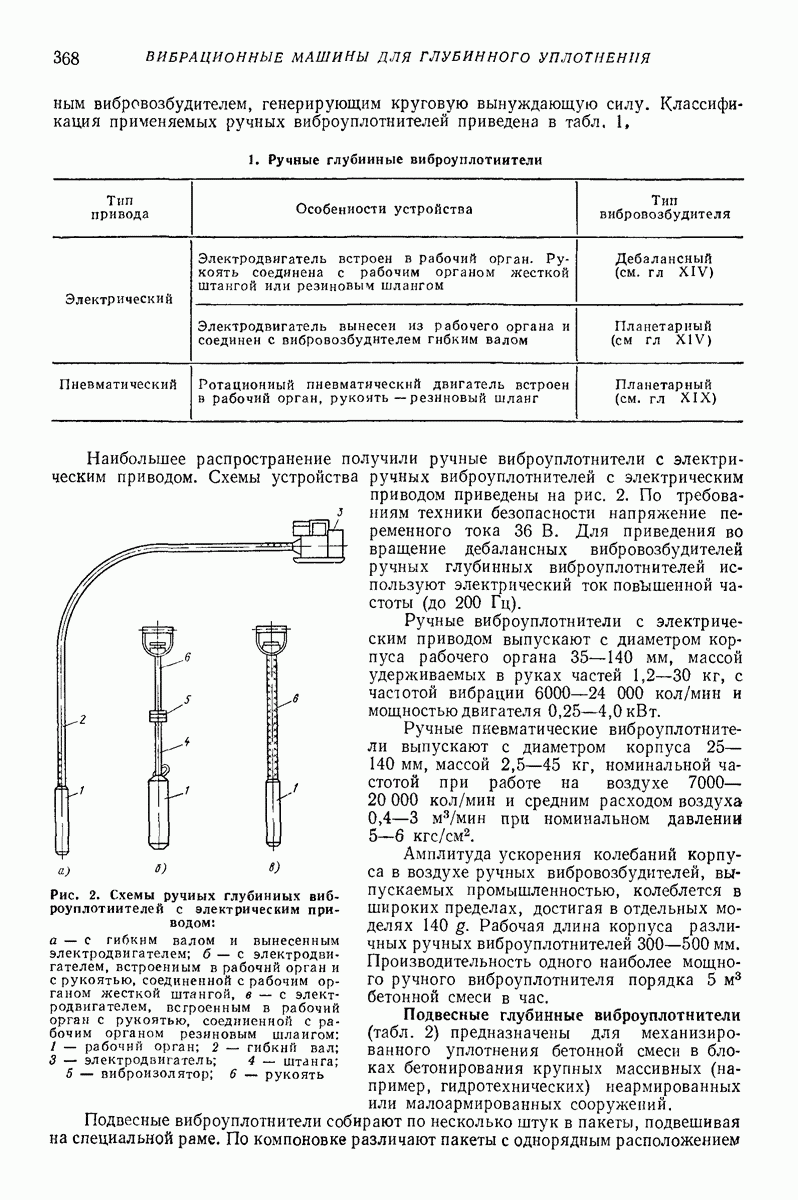
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
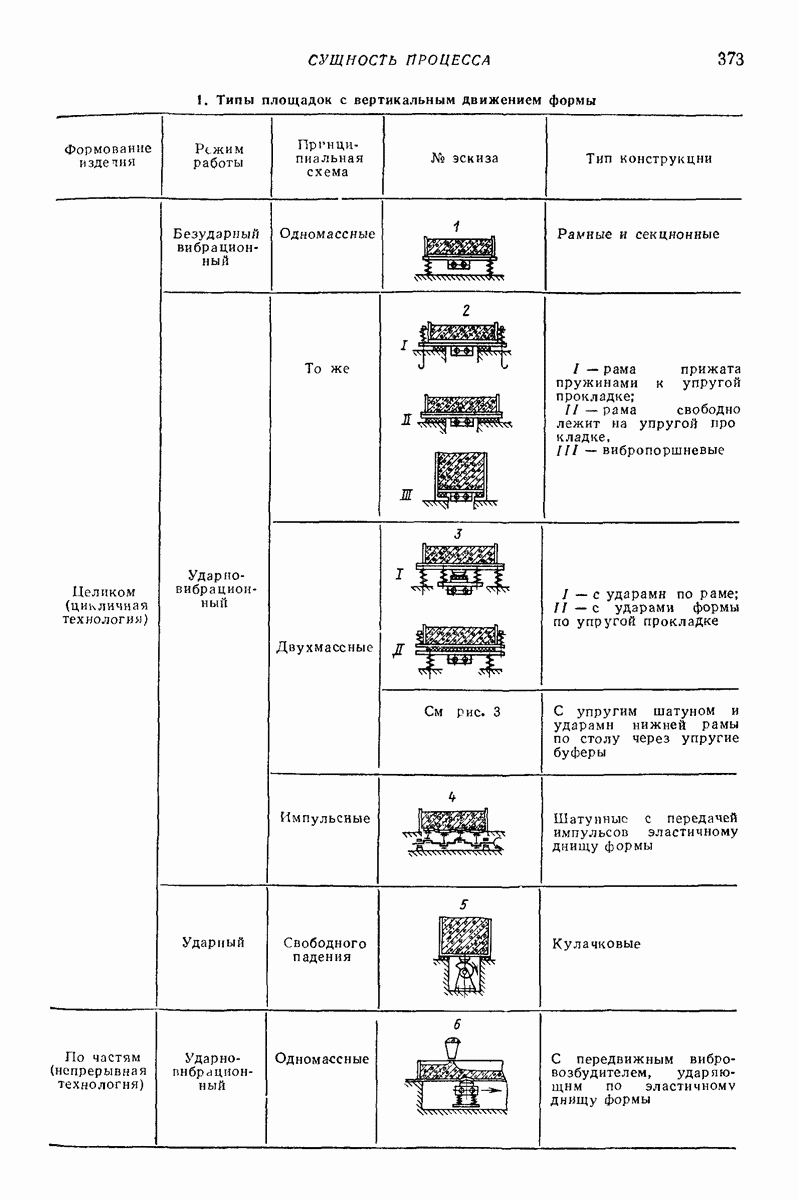
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
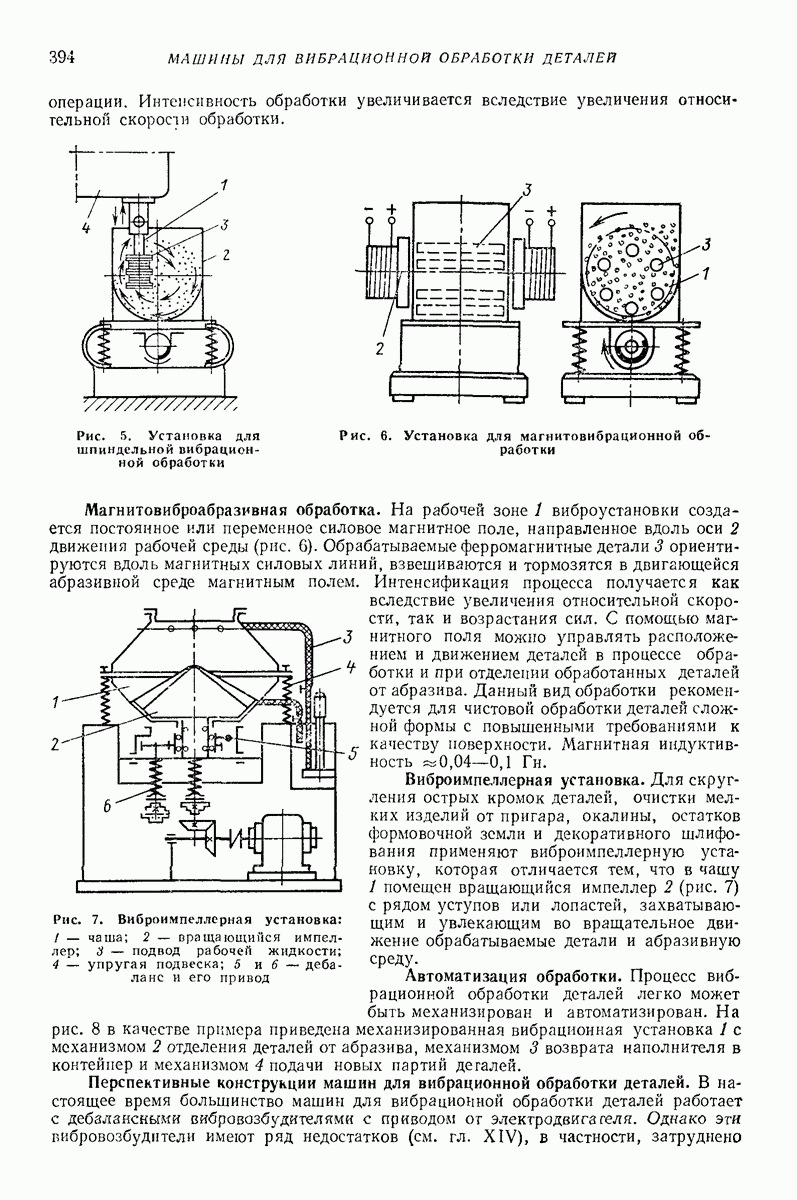
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
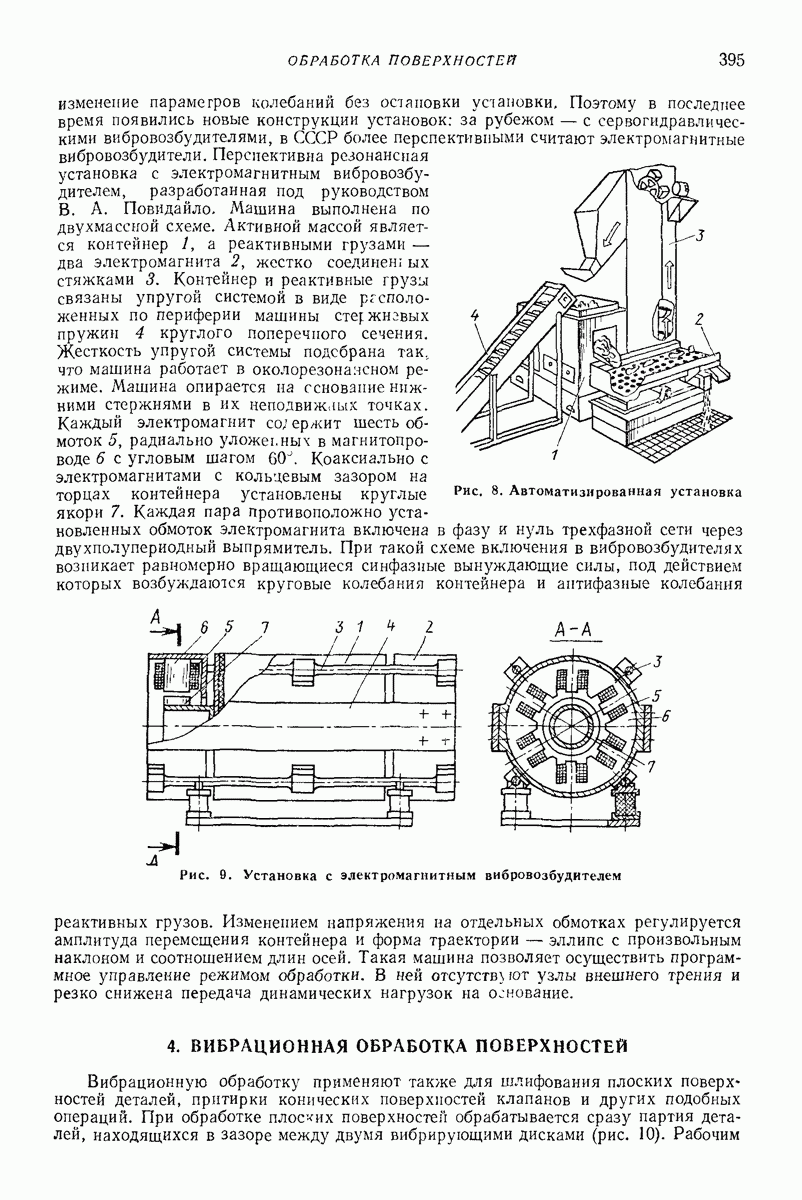
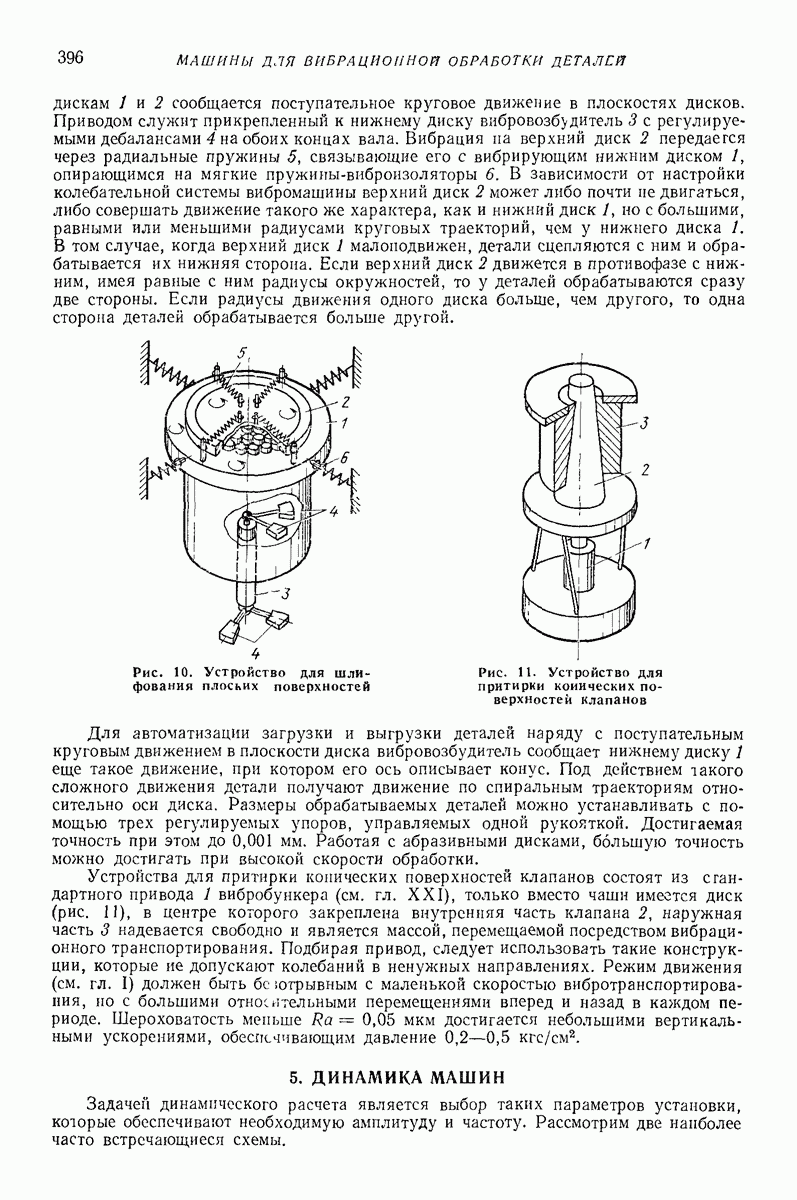
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
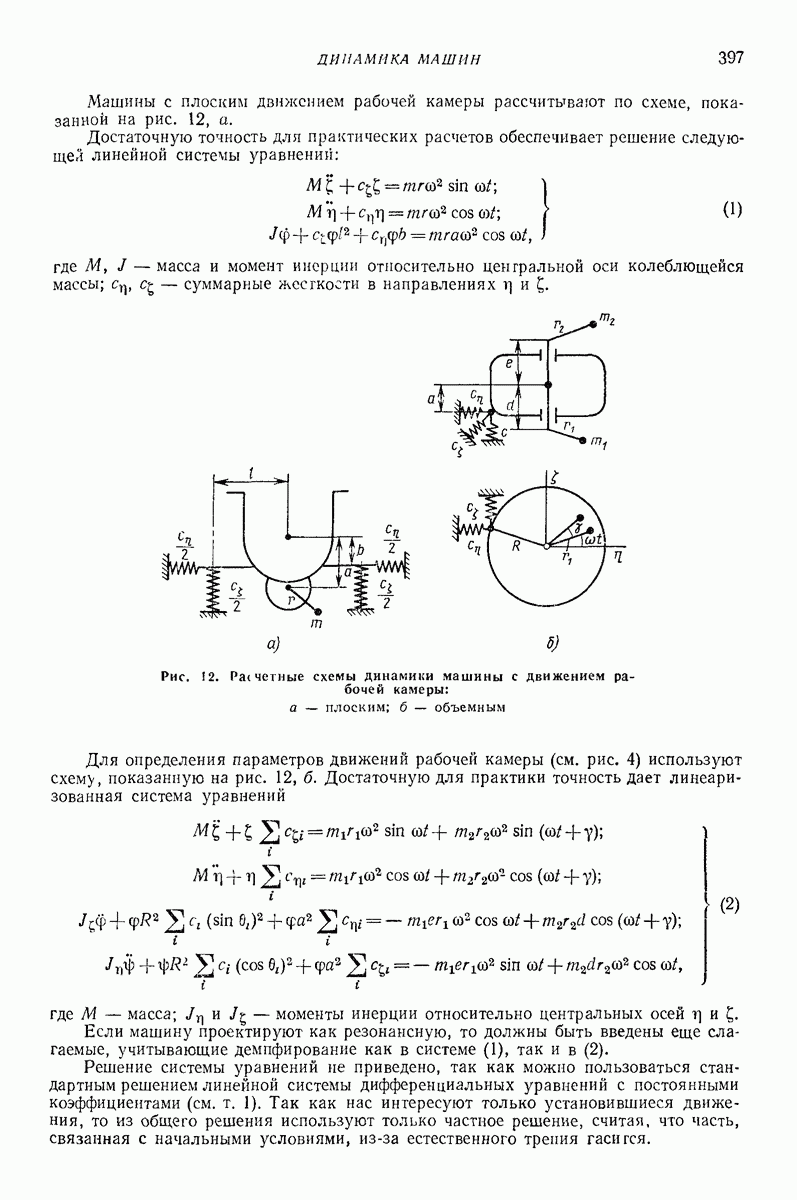
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ