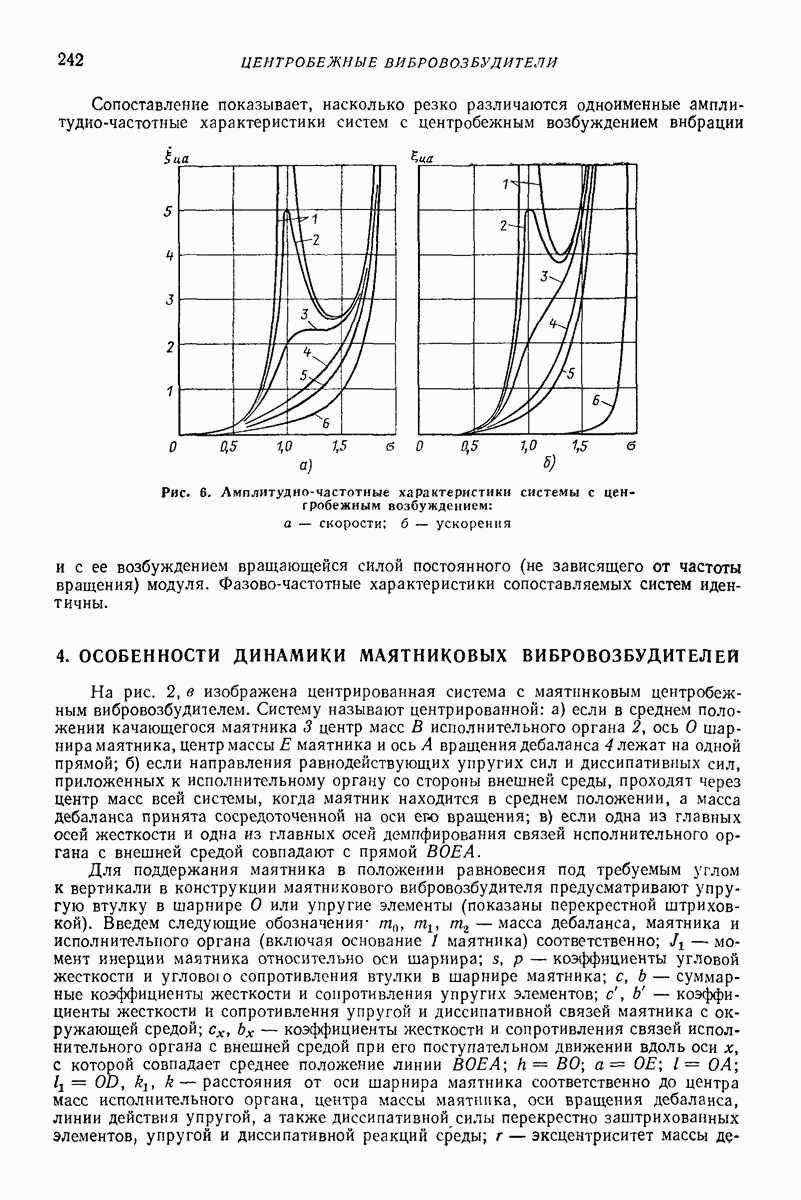
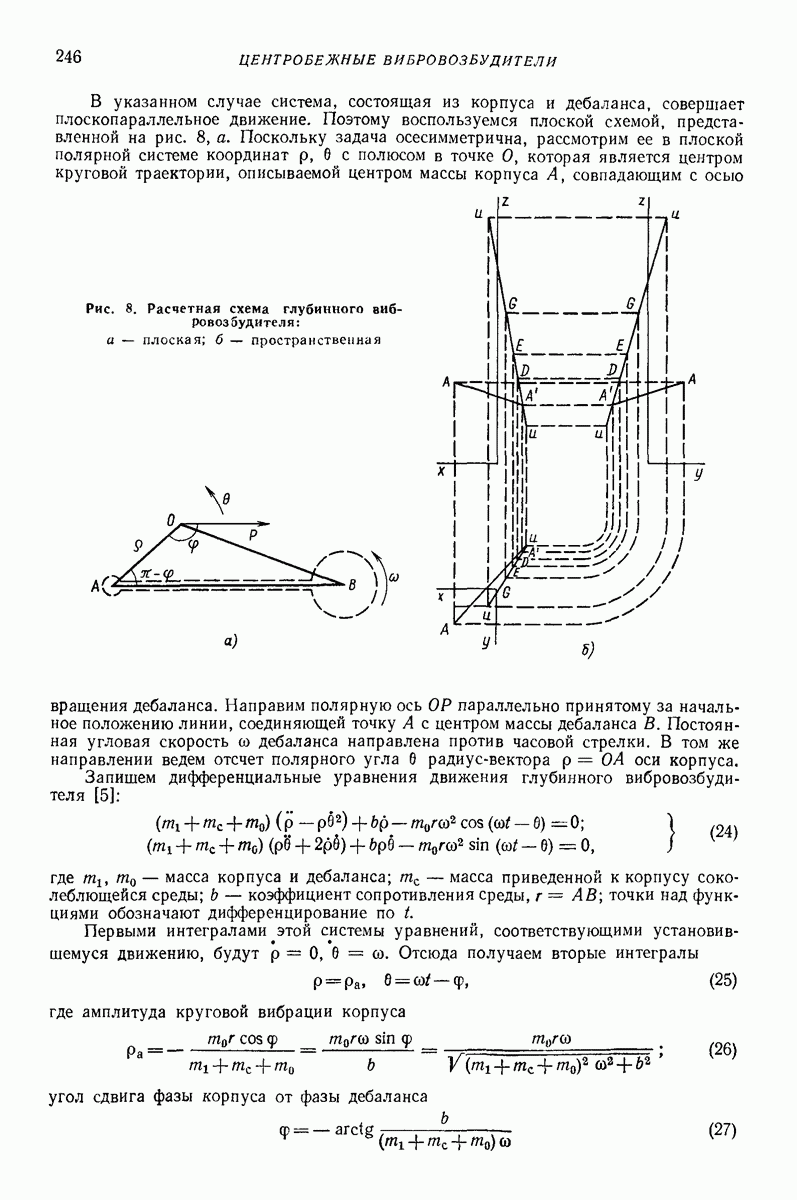
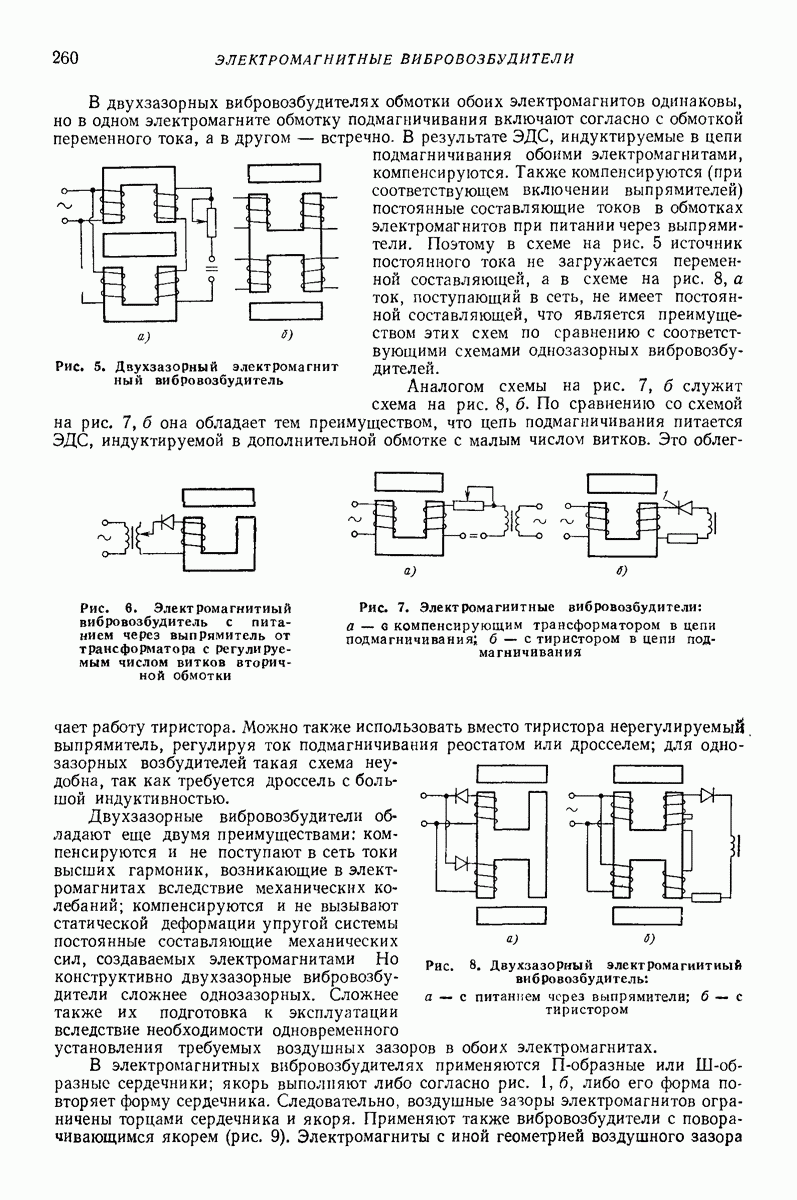
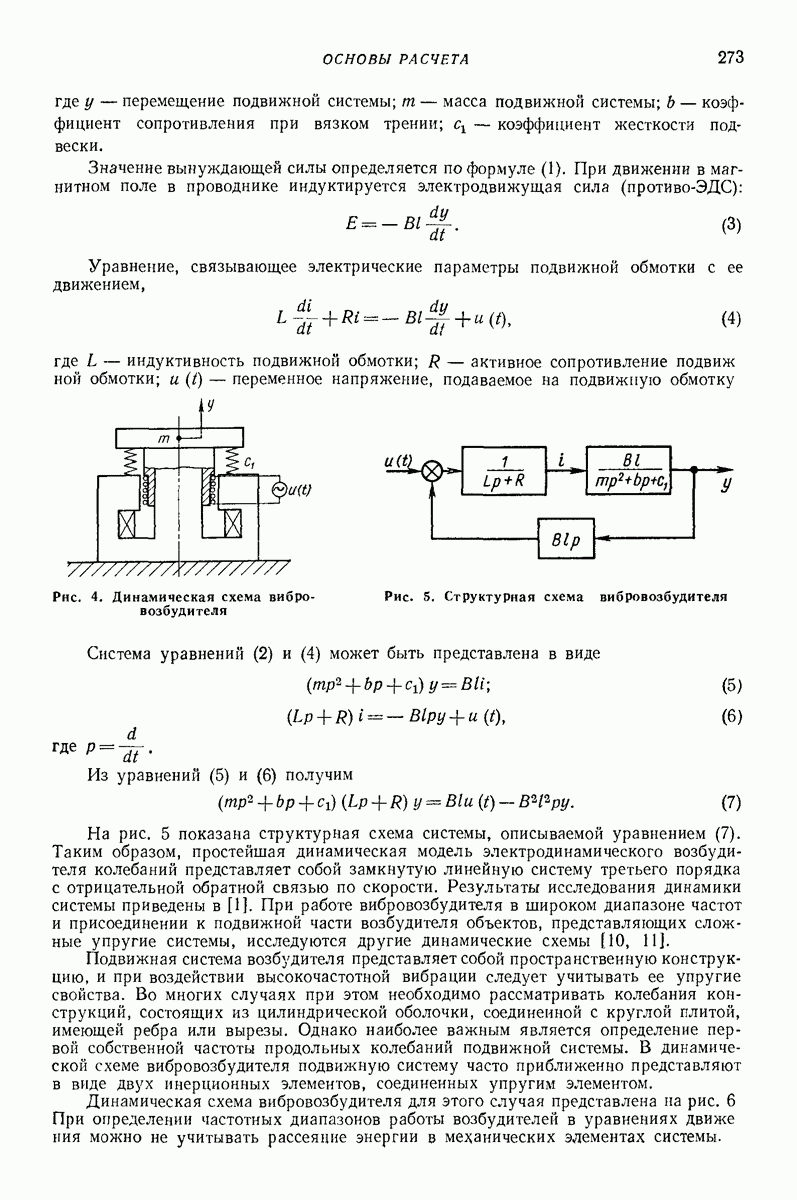
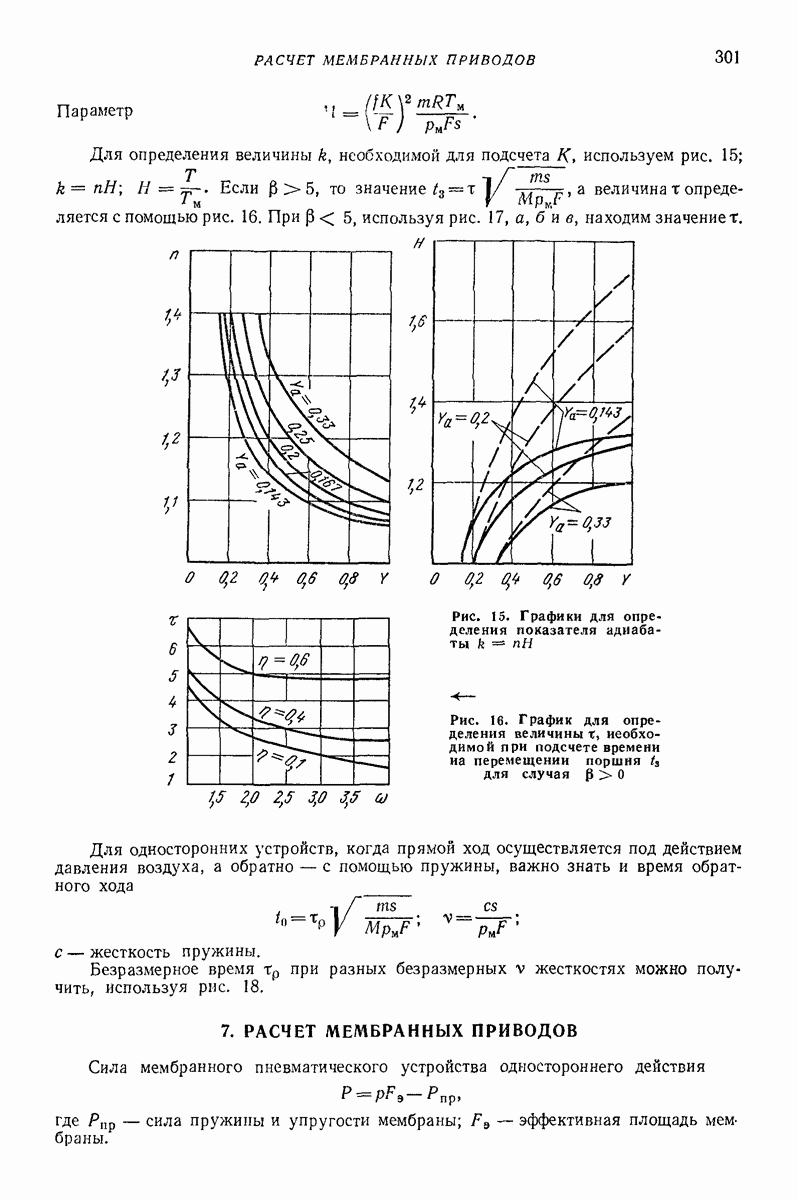
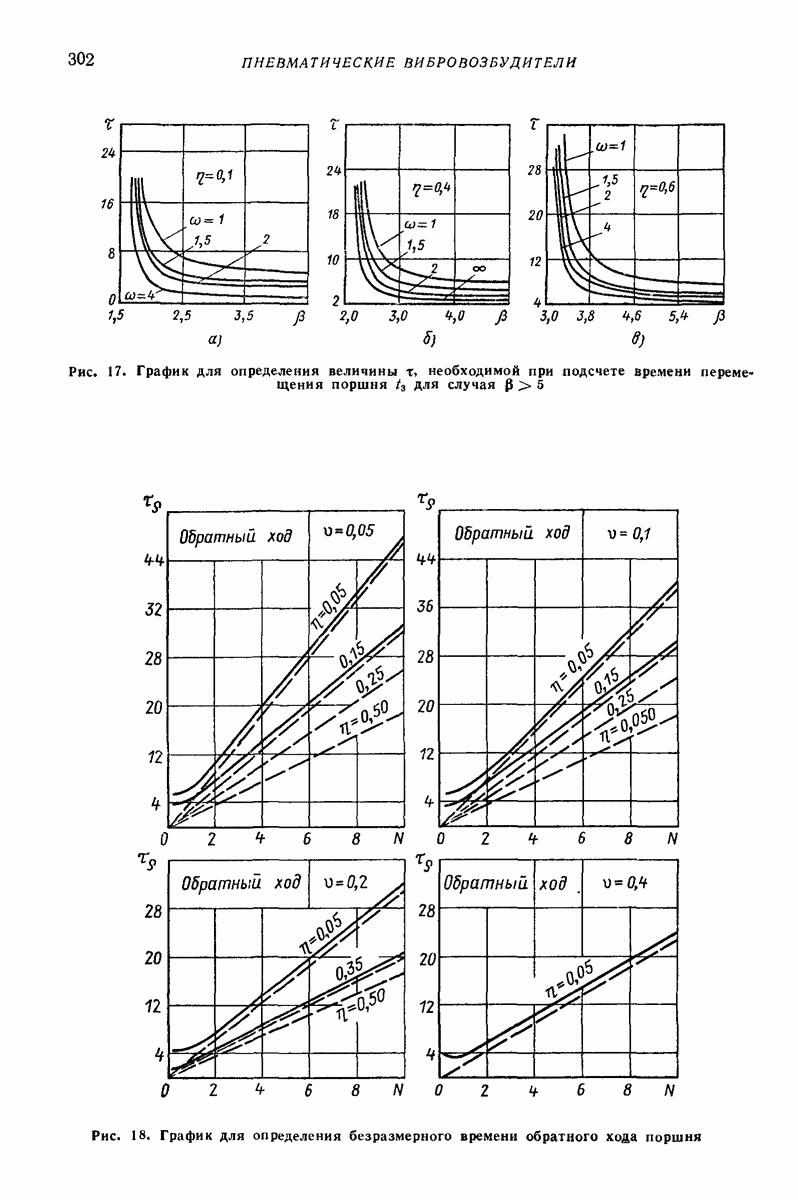
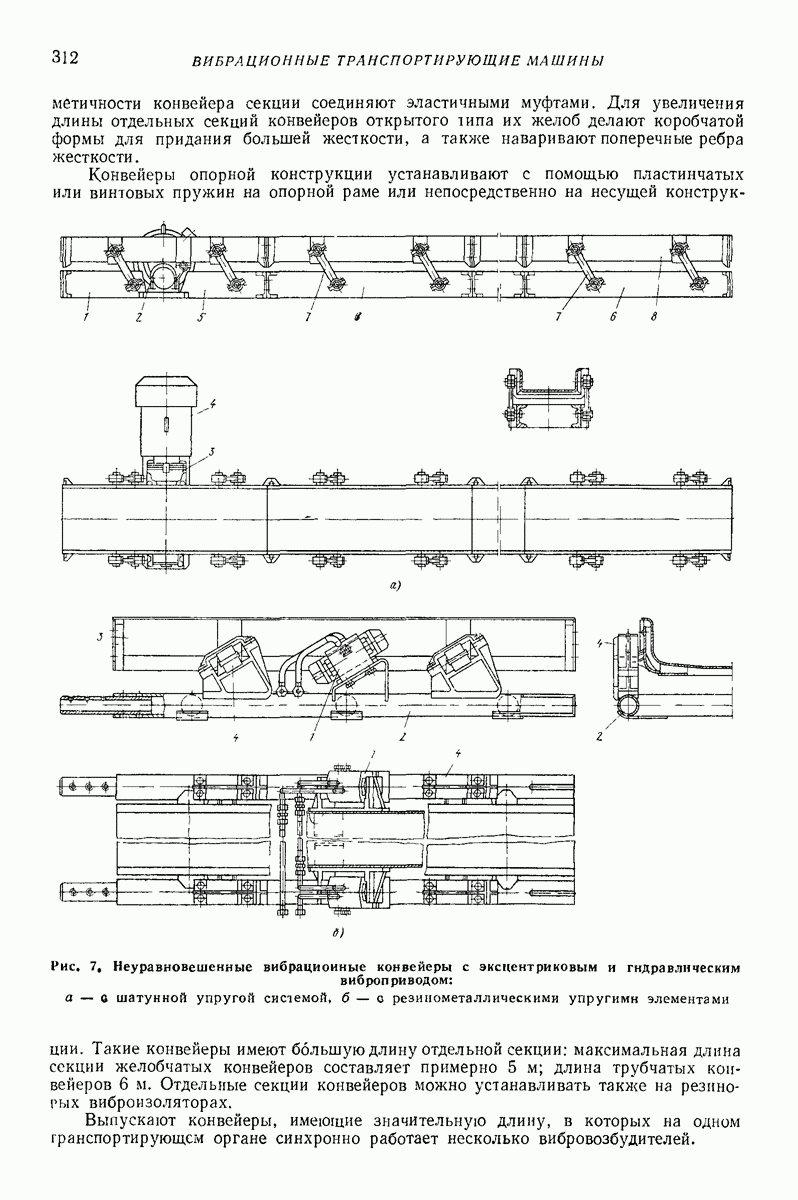
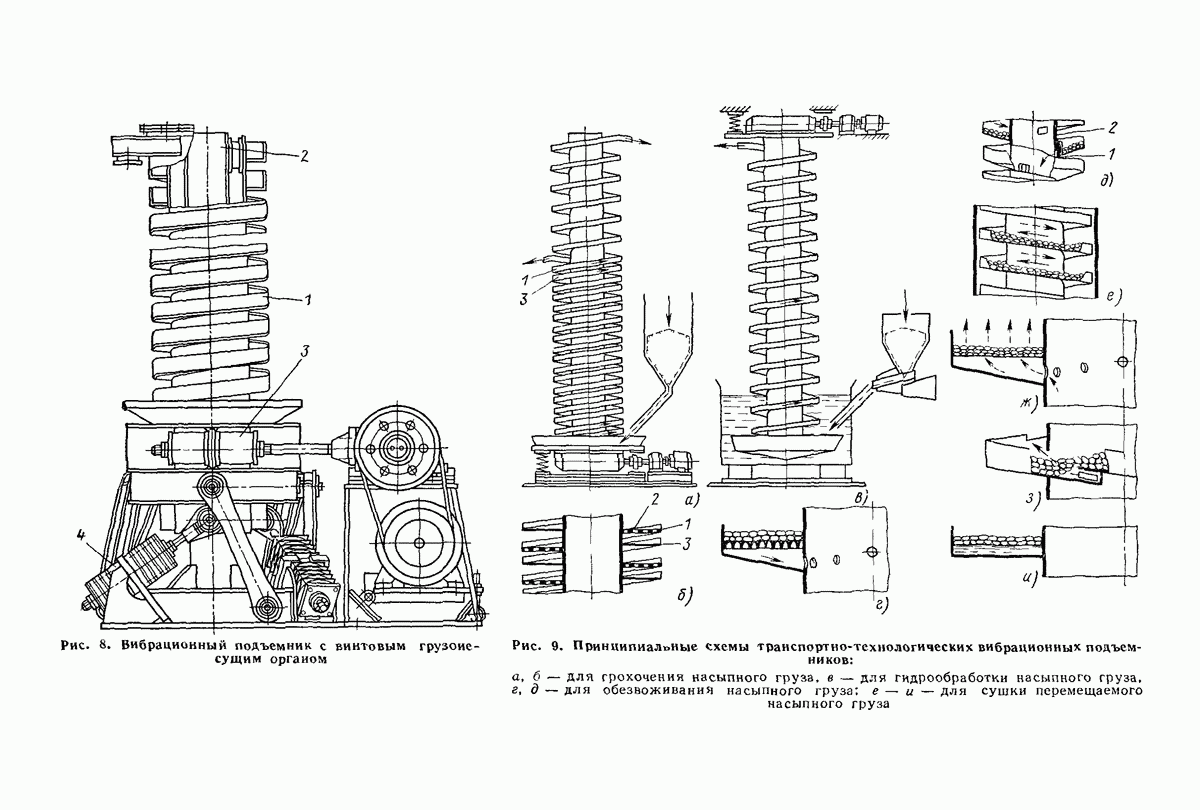
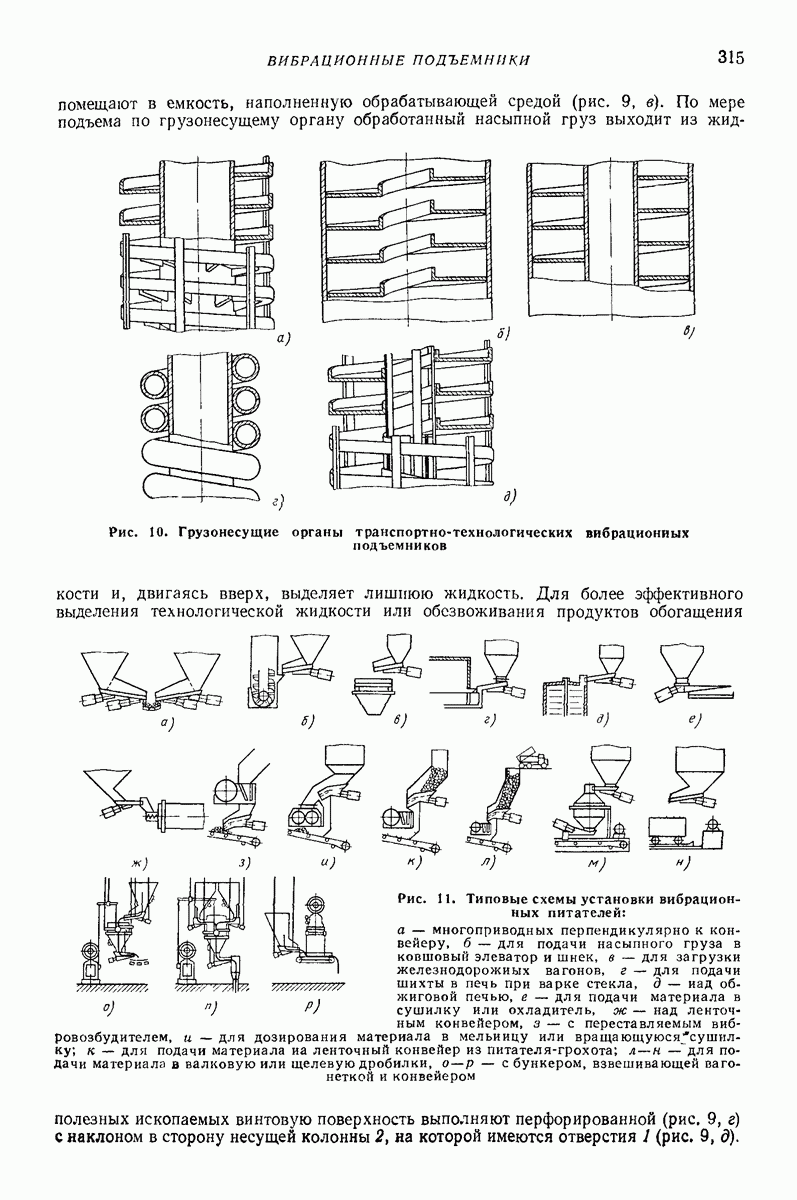
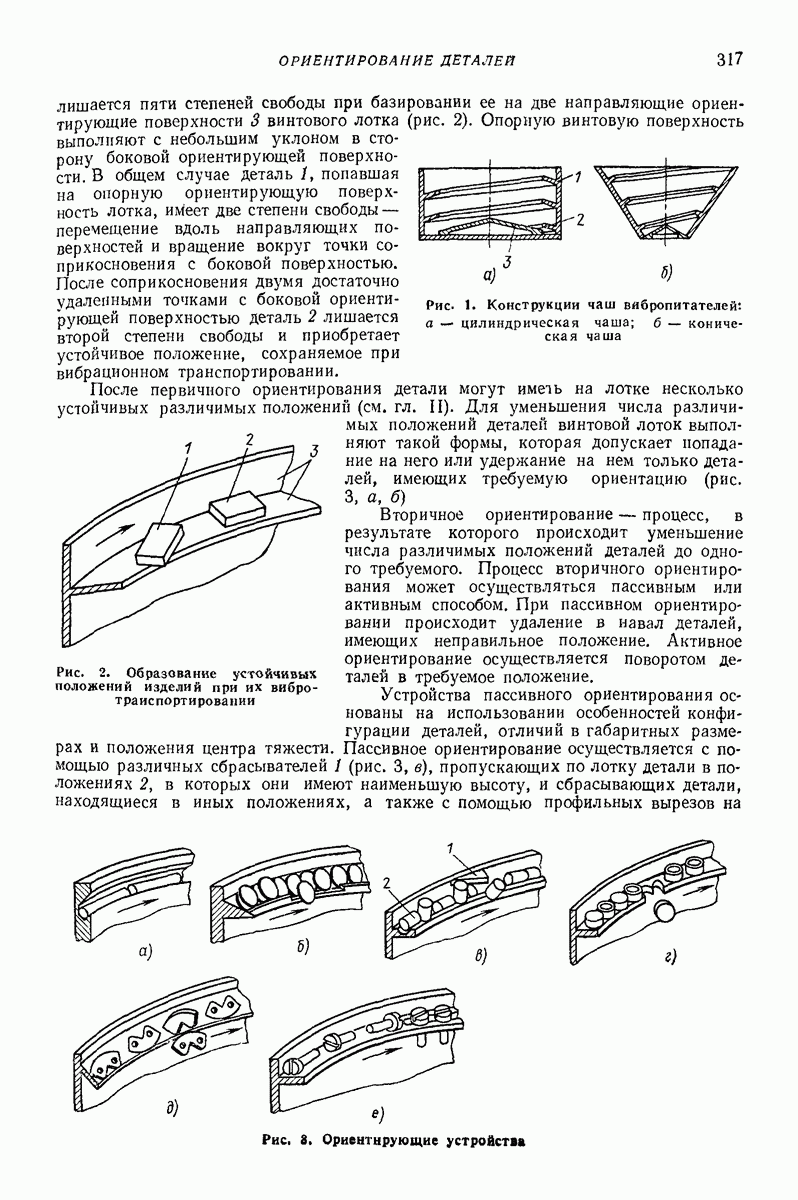
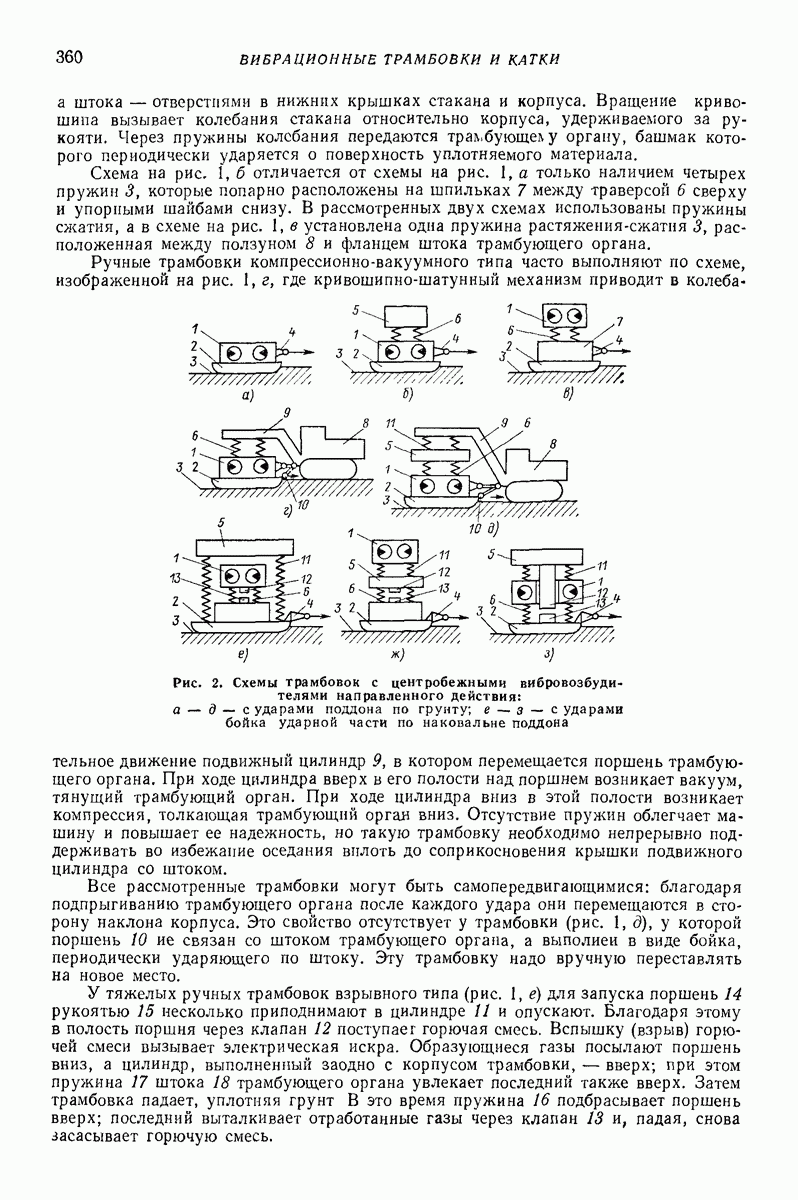
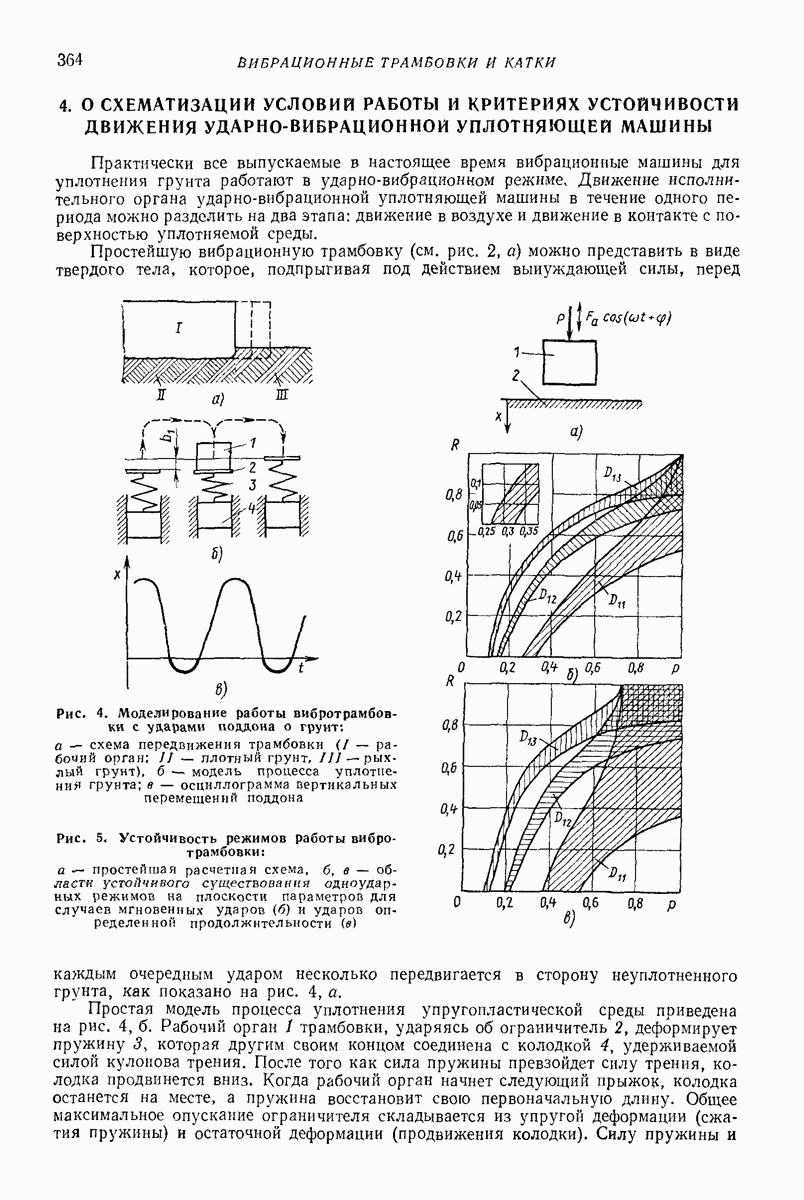
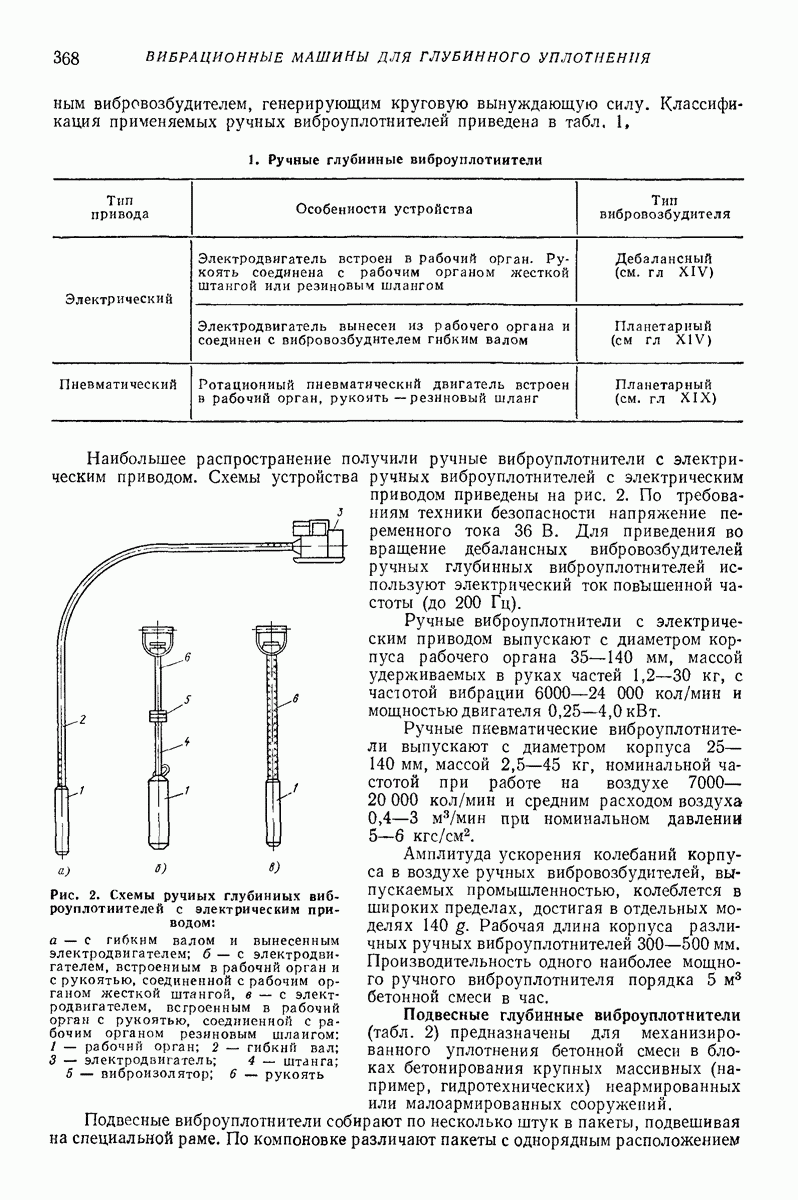
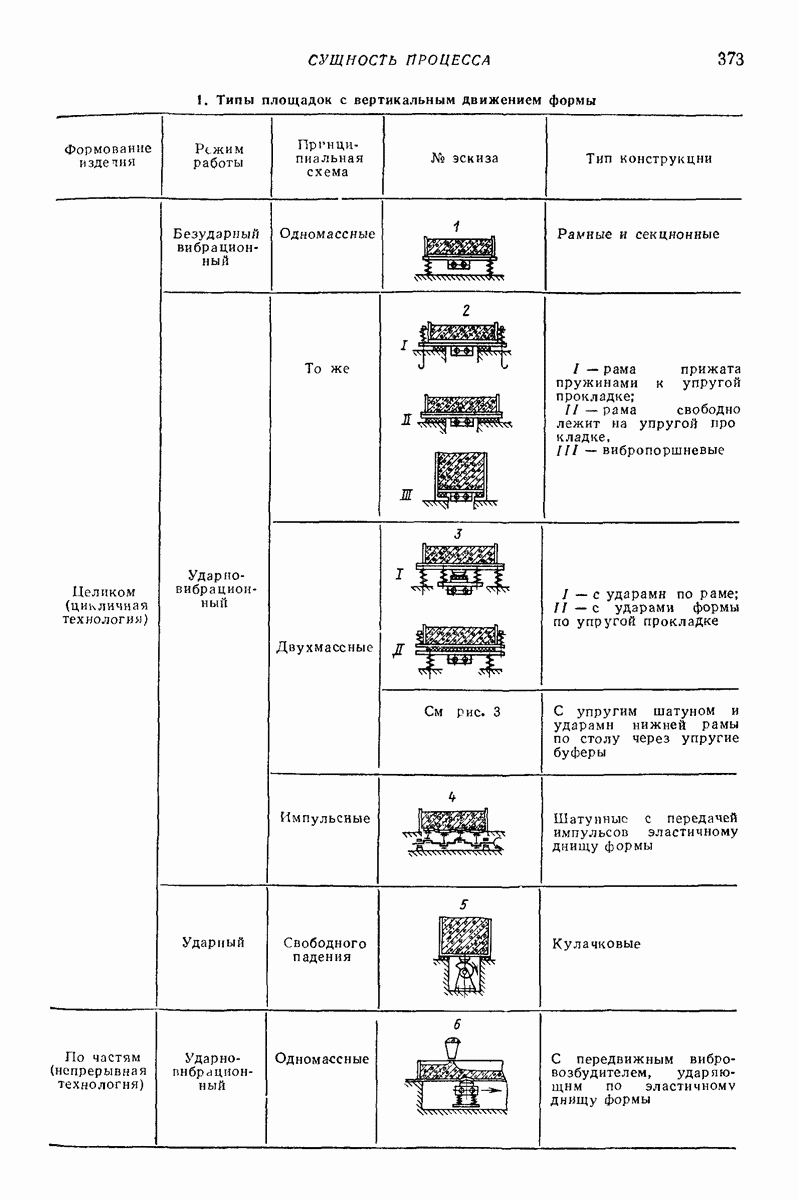
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
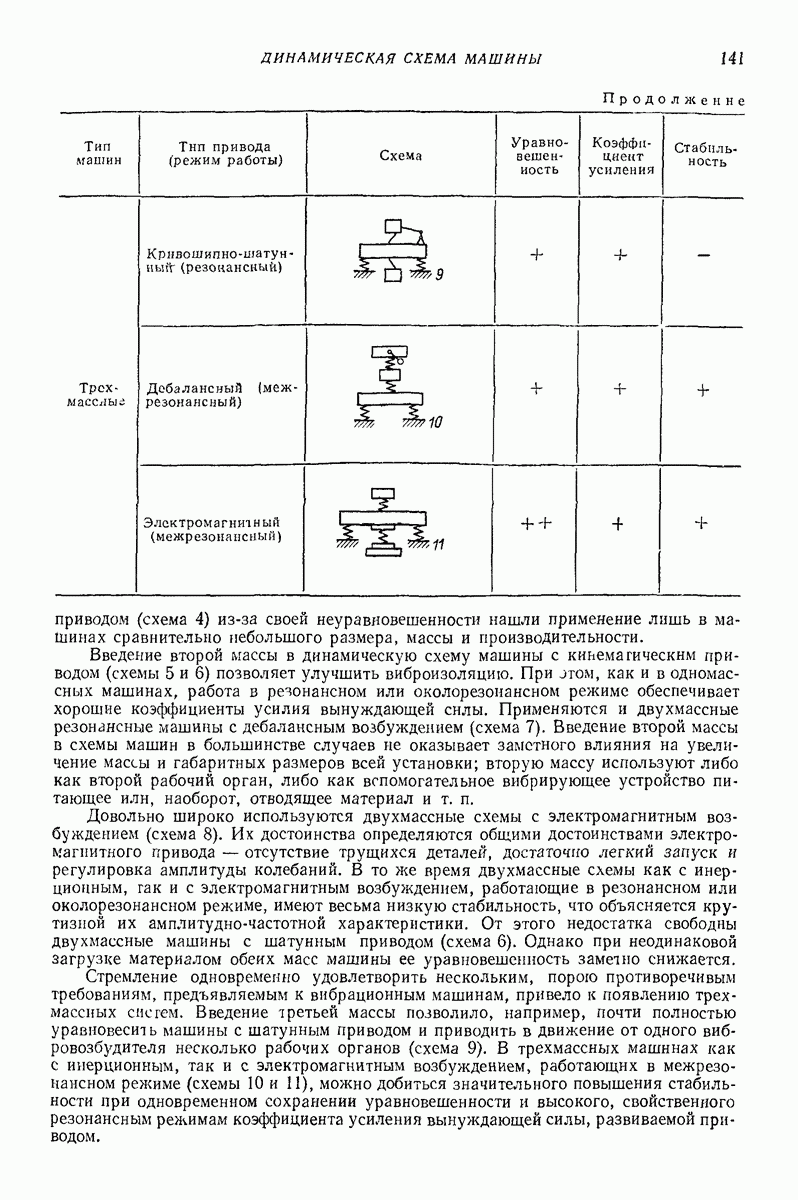
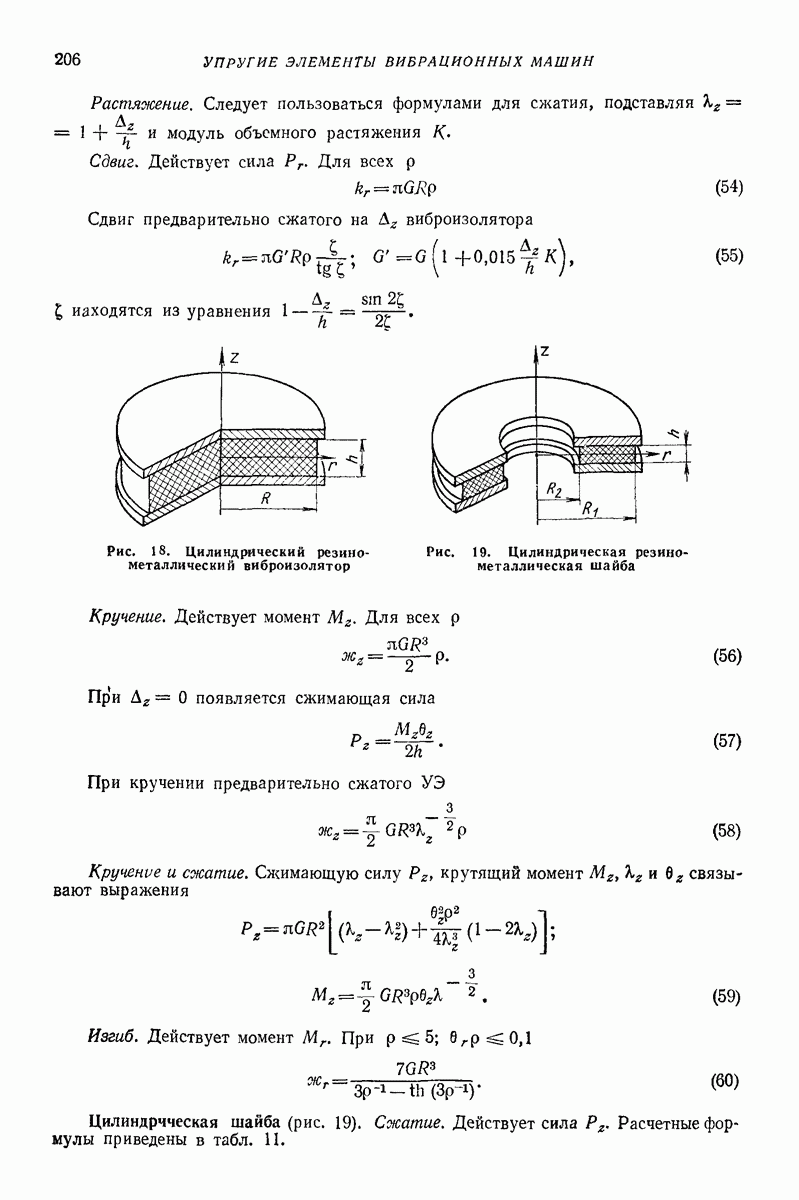
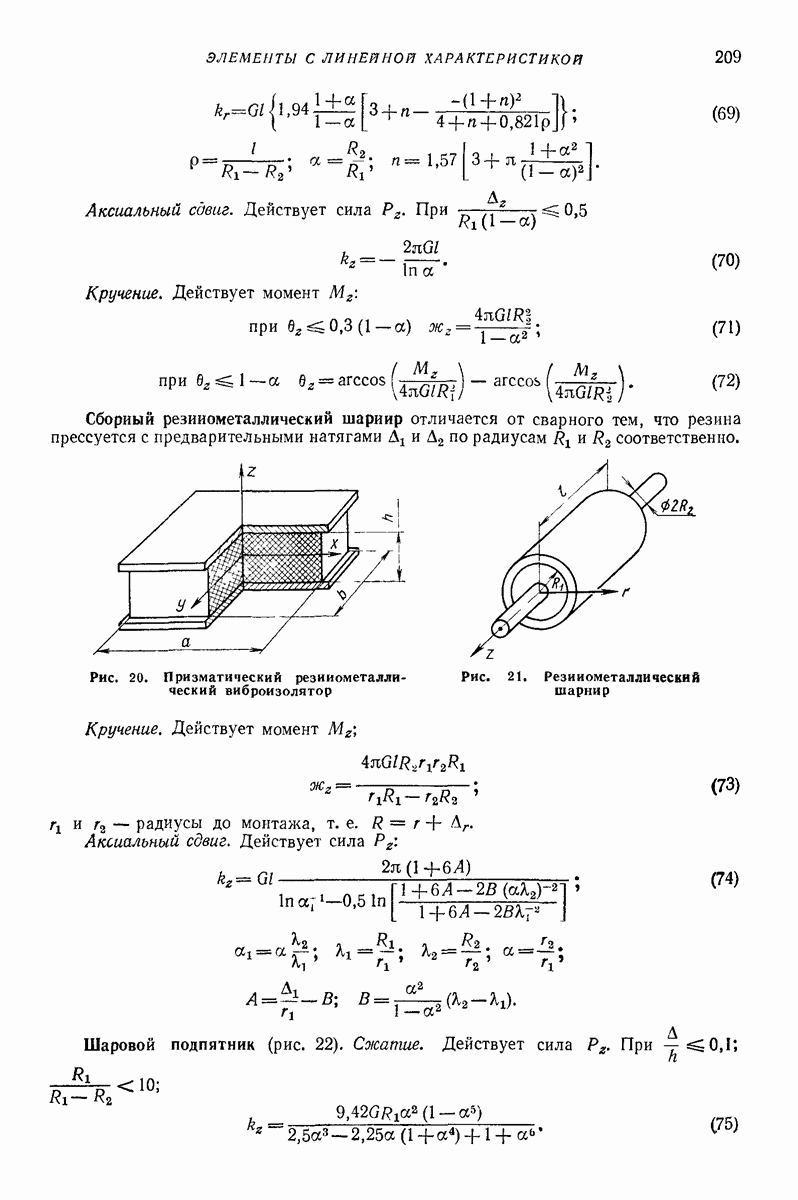
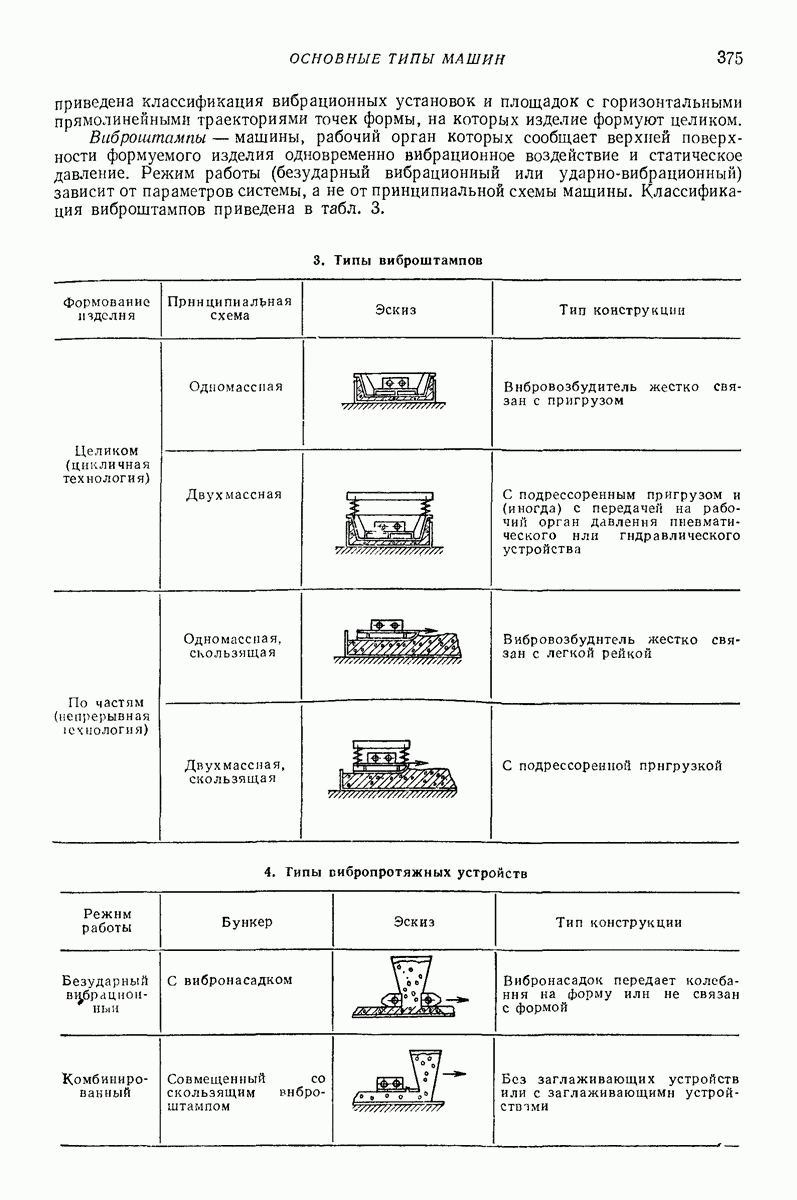
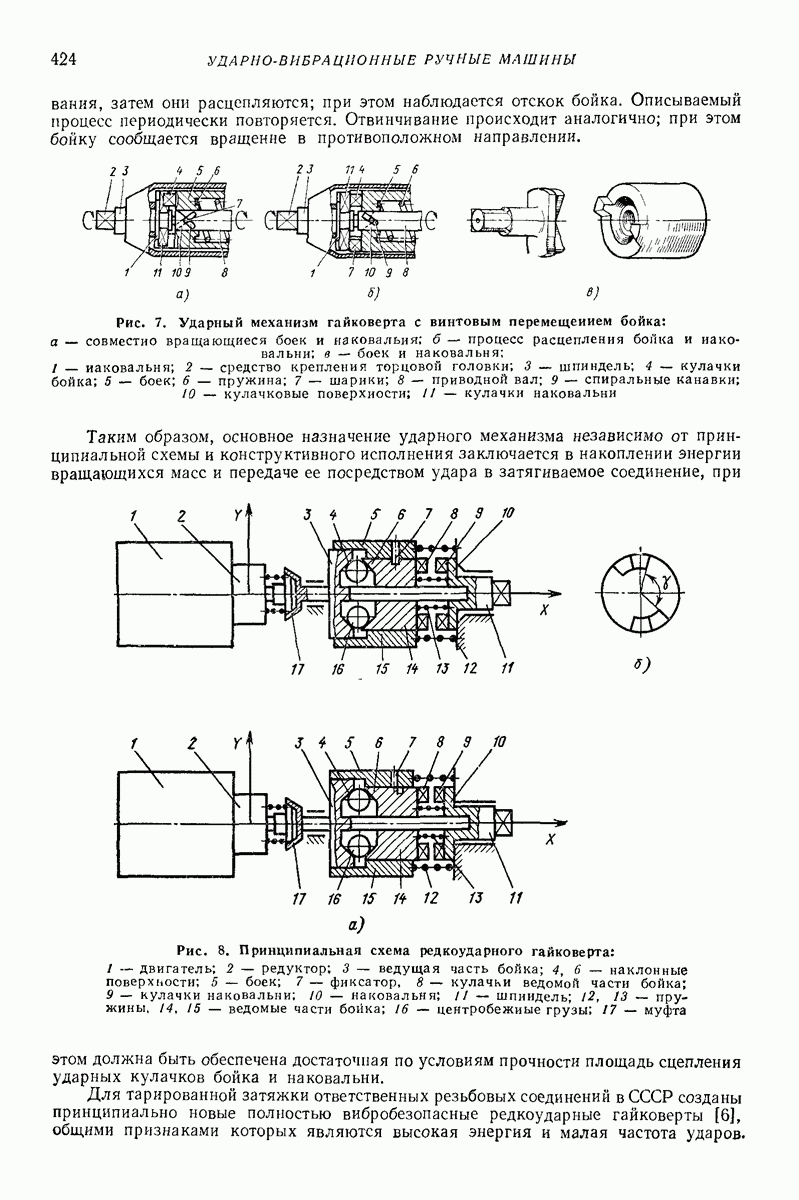
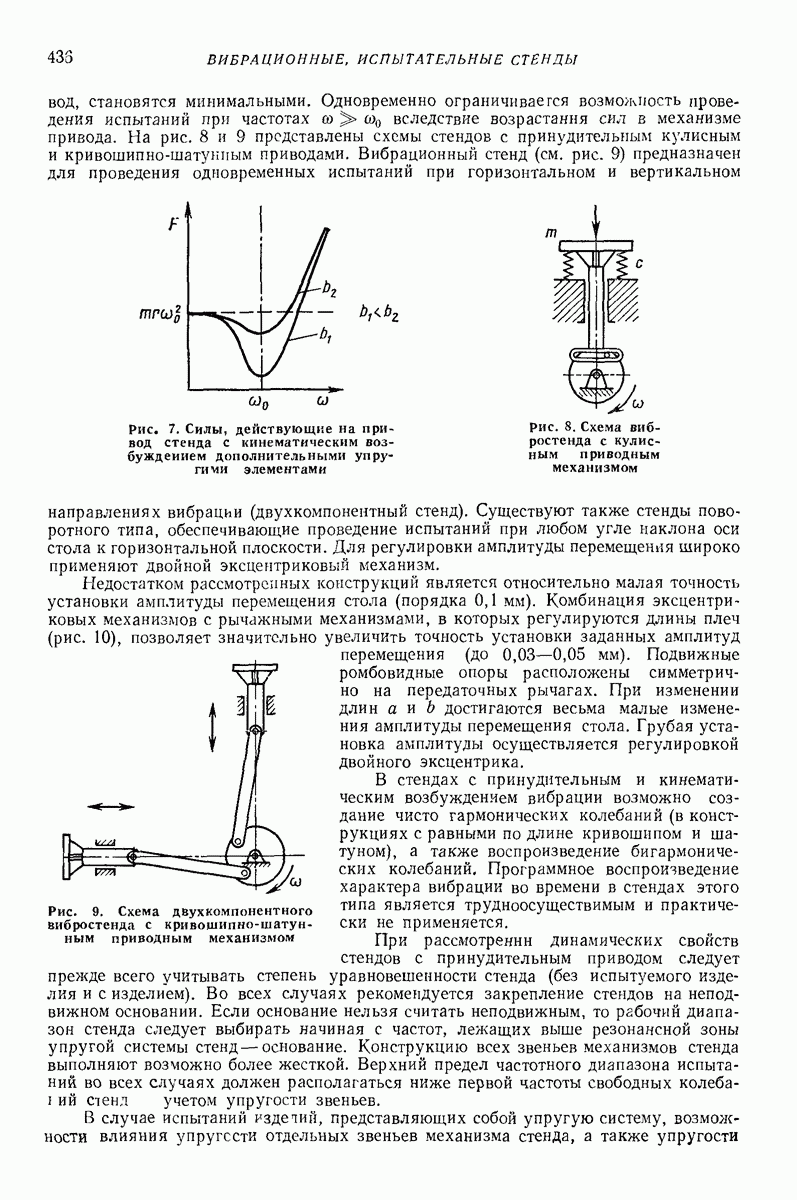
2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
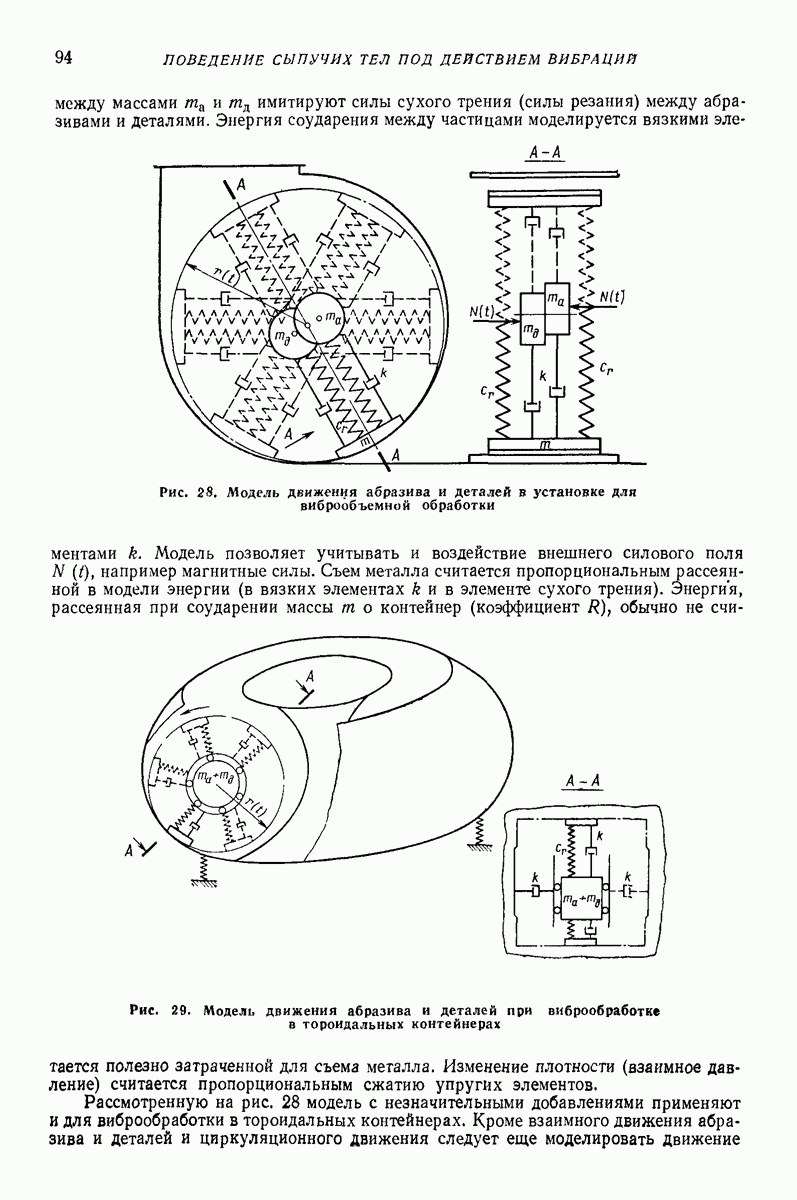
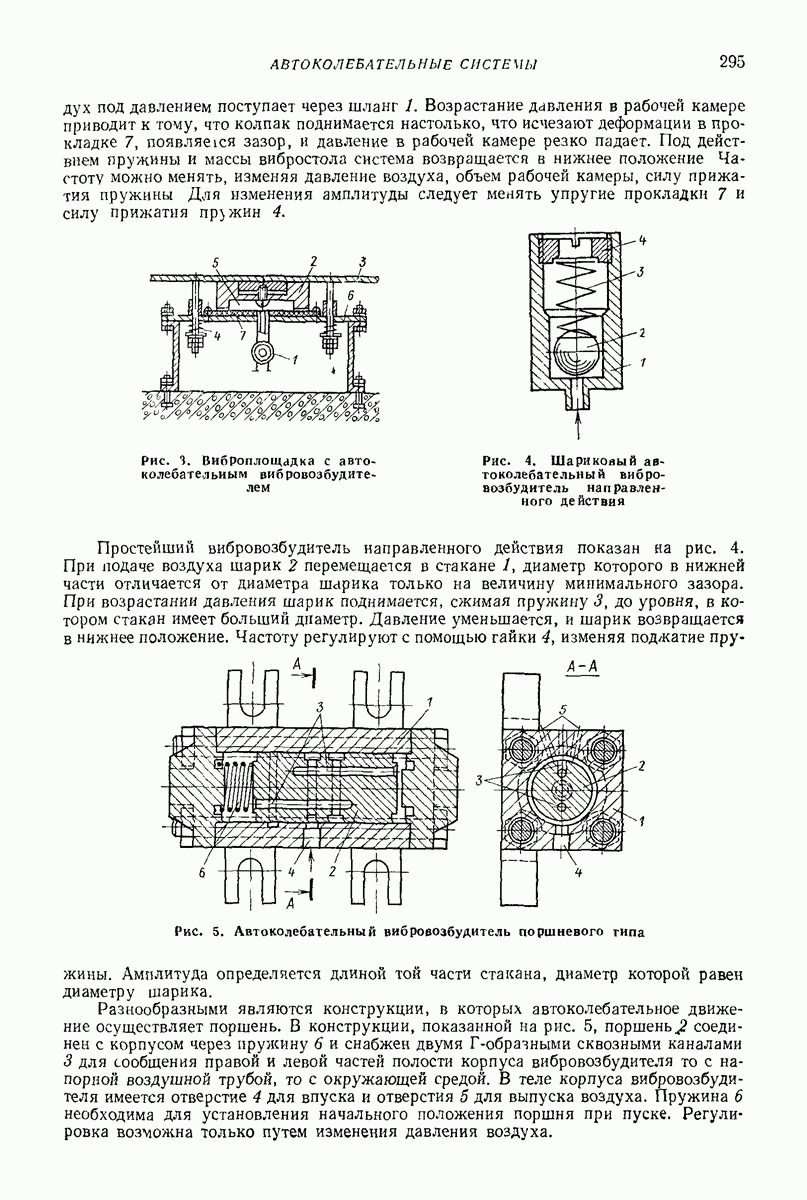
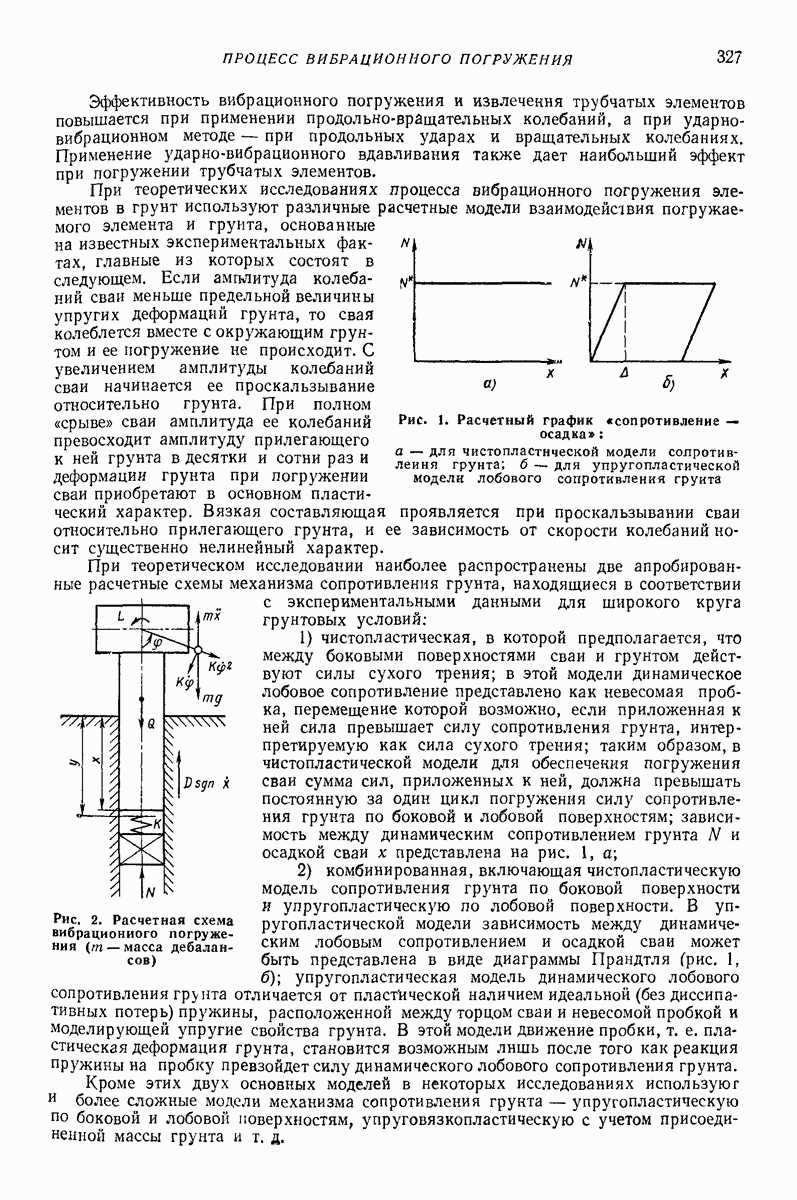
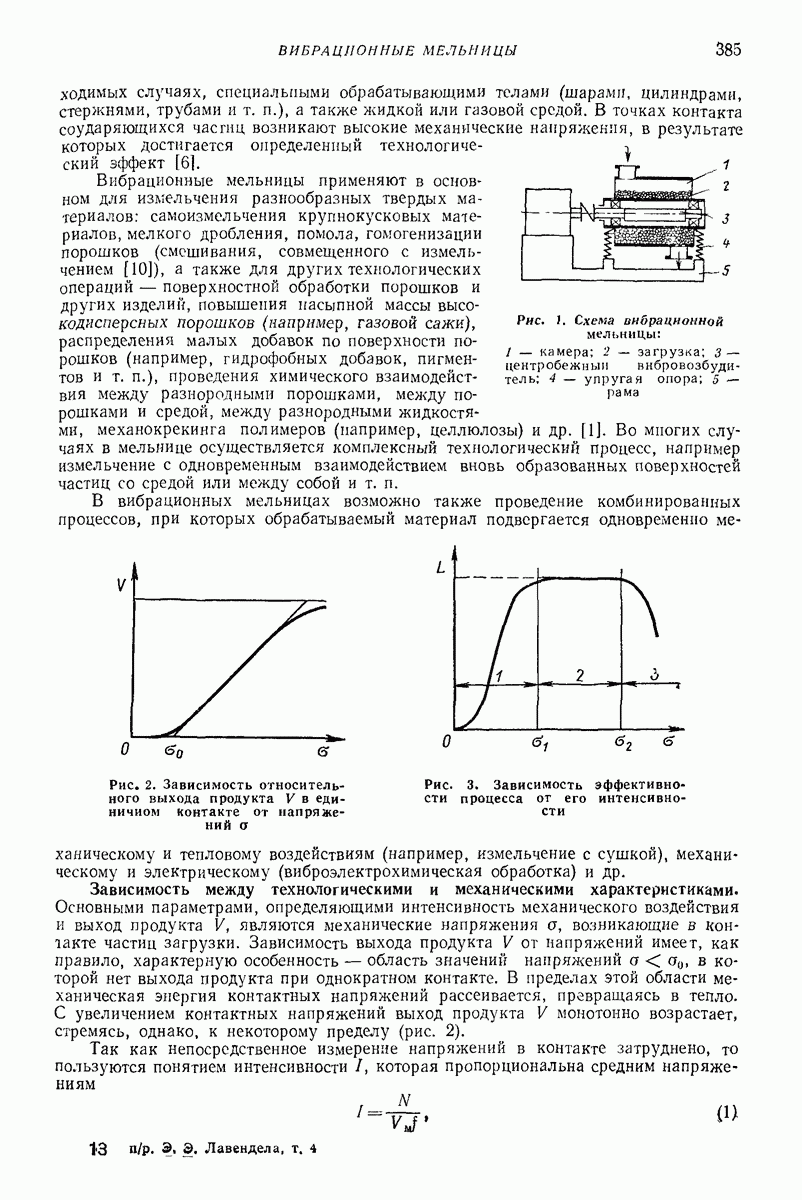
Для определения сил соударения  приходится учитывать податливость при ударе как следствие местных деформаций. При расчете ударно-вибрационных машии приходится встречаться с ударными узлами приводов и ударом в качестве рабочего процесса, т. е. соударением ударного элемента с обрабатываемой средой.
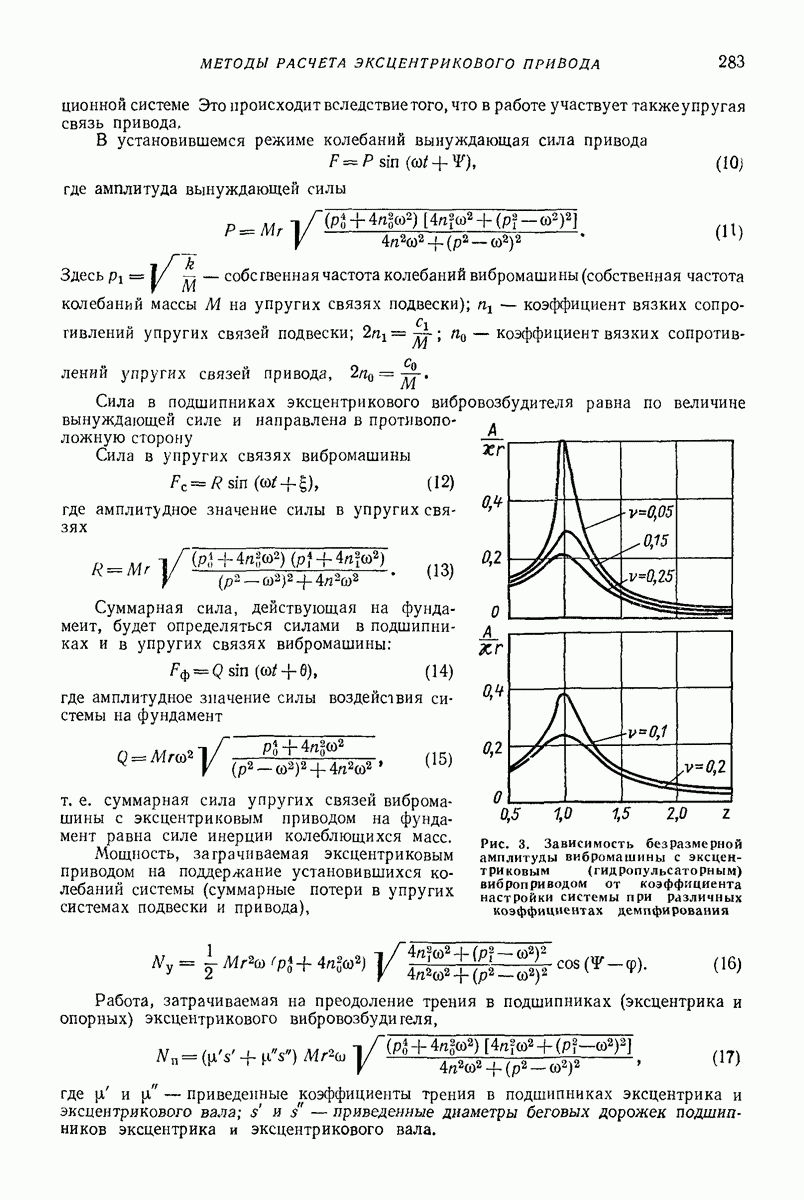
приходится учитывать податливость при ударе как следствие местных деформаций. При расчете ударно-вибрационных машии приходится встречаться с ударными узлами приводов и ударом в качестве рабочего процесса, т. е. соударением ударного элемента с обрабатываемой средой.
В первом случае допускаются только упругие деформации, а пластические нежелательны, так как приводят к быстрому выходу деталей из строя. Во втором случае именно остаточные деформации являются желаемым результатом. Поэтому рассмотрим эти случаи отдельно.
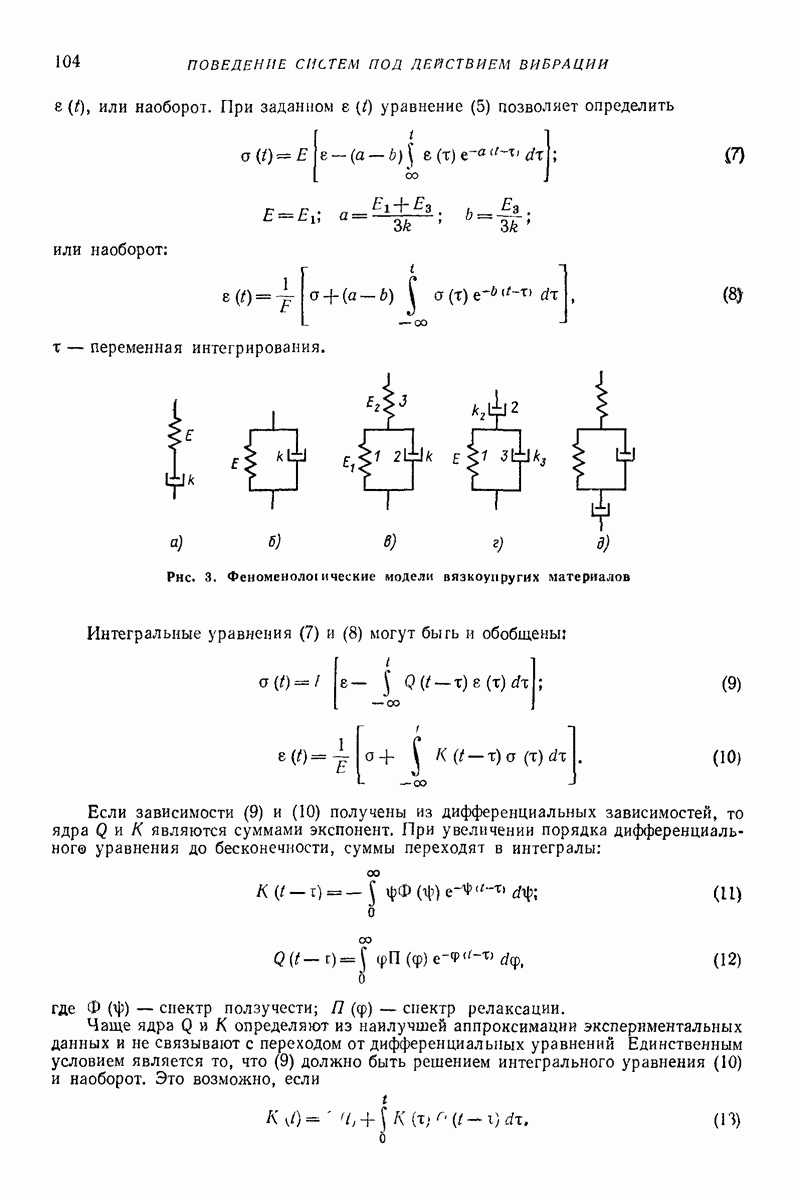
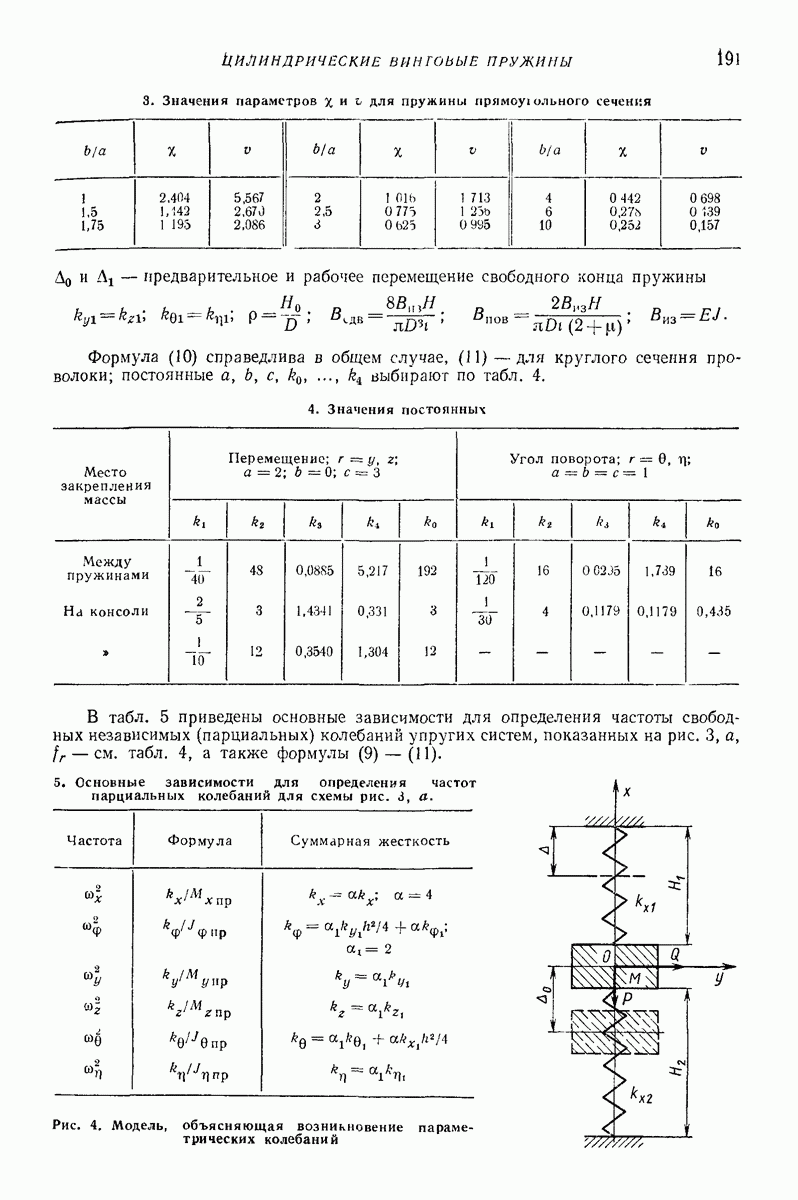
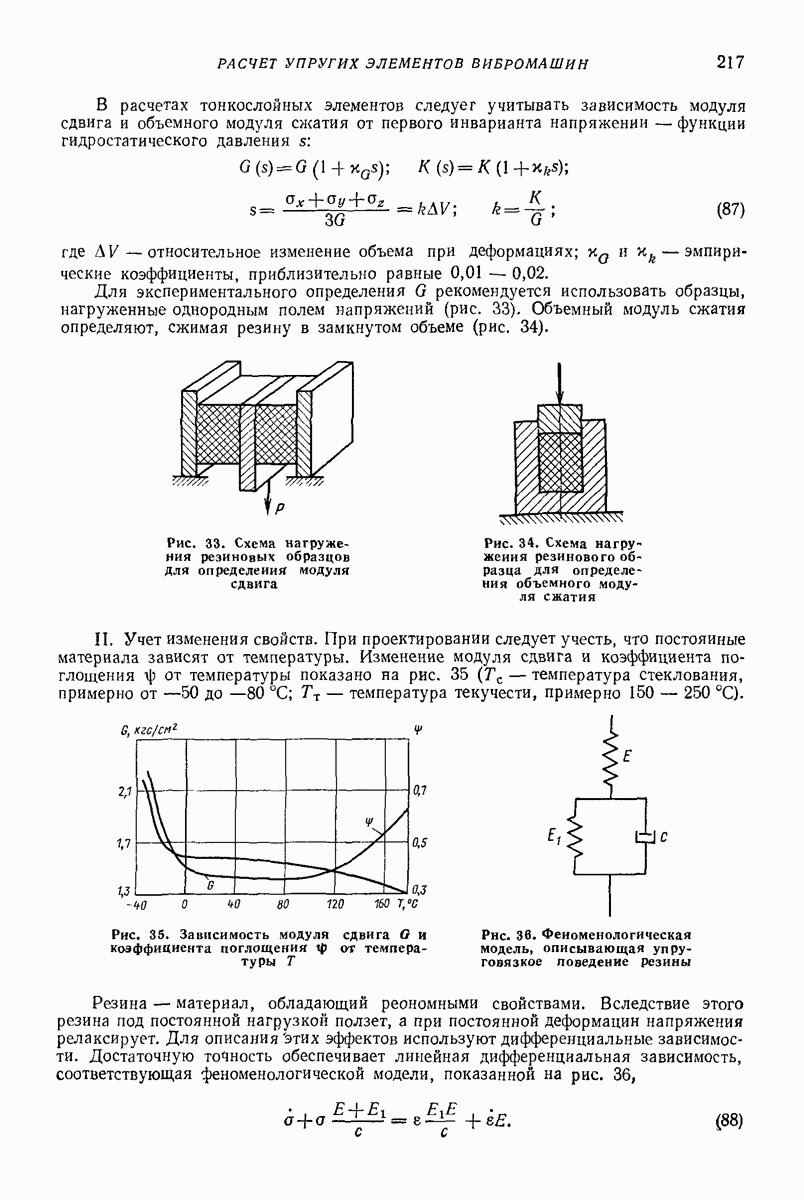
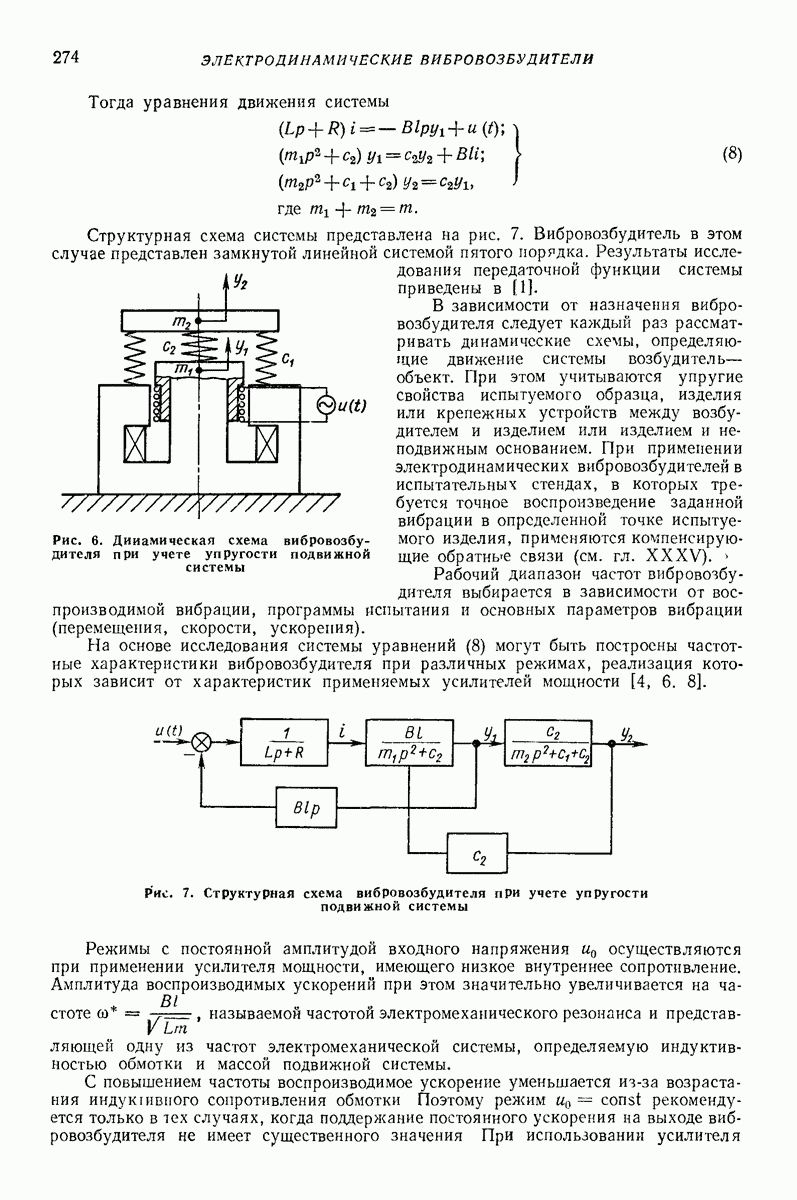
Линейные упругие модели [6, 7]. Как показывают вычисления, часто достаточную точность обеспечивает линеаризованная зависимость упругой силы  Для учета потерь энергии следует ввести вязкие элементы. Простейшие модели такого типа показаны на рис. 1.
Для учета потерь энергии следует ввести вязкие элементы. Простейшие модели такого типа показаны на рис. 1.

Рис. 1. Линейные упругие модели ударного процесса
Модели, представленной на рис. 1, а, соответствует дифференциальное уравнение

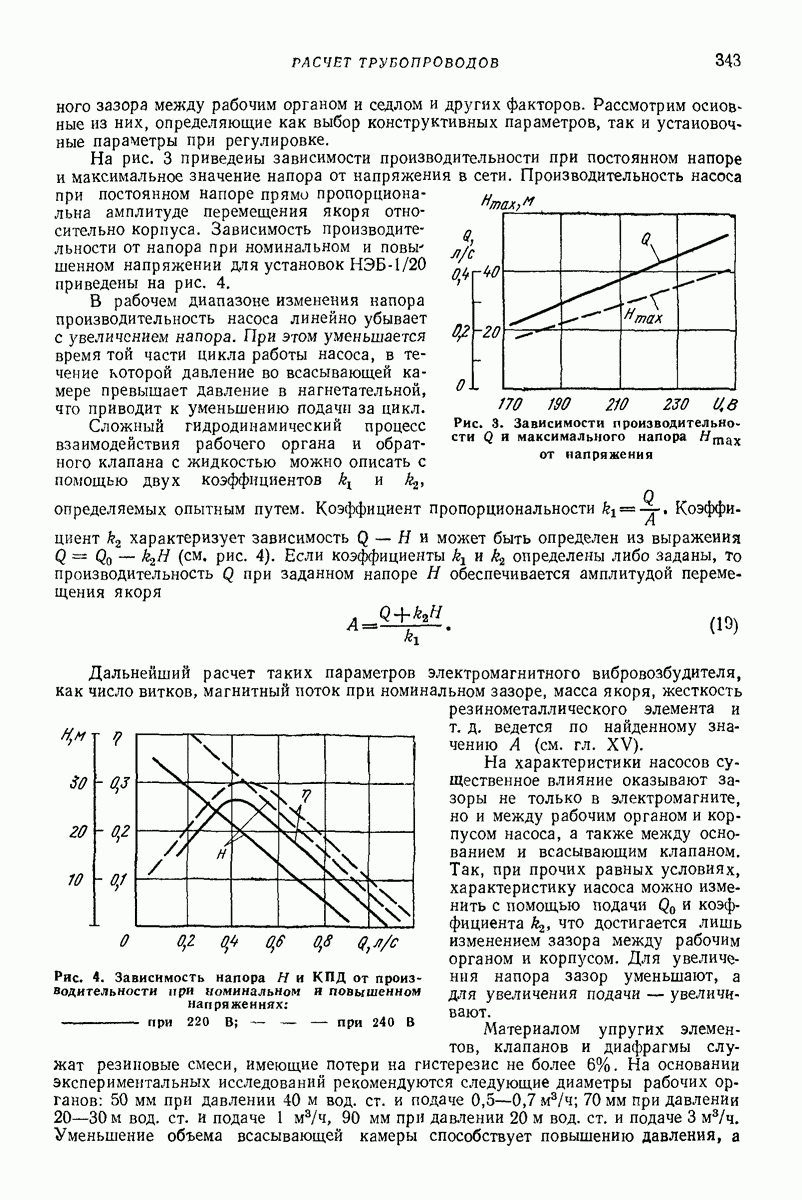
Интегрируем это уравнение после начала ударного контакта при начальных условиях  Значение импульса
Значение импульса  берем из решения (5):
берем из решения (5):

где 
Сила сжатия деформируемого элемента

а ее наибольшее значение

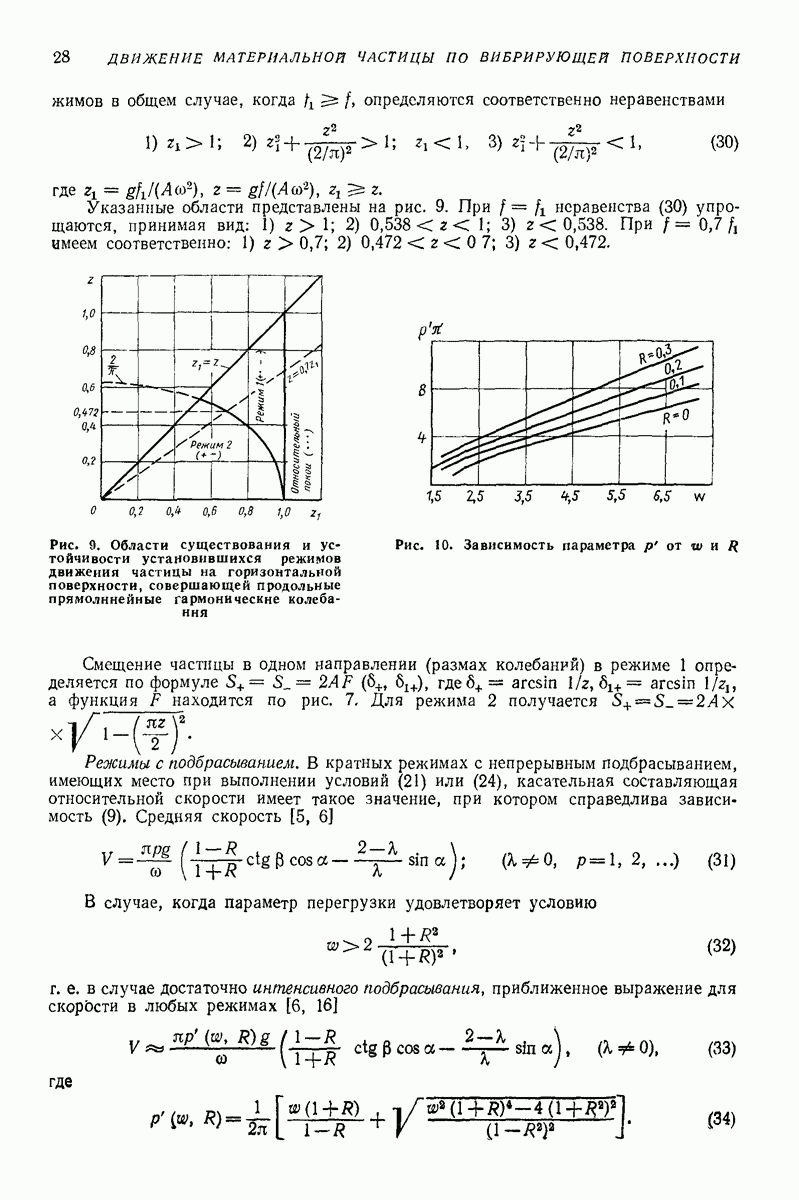
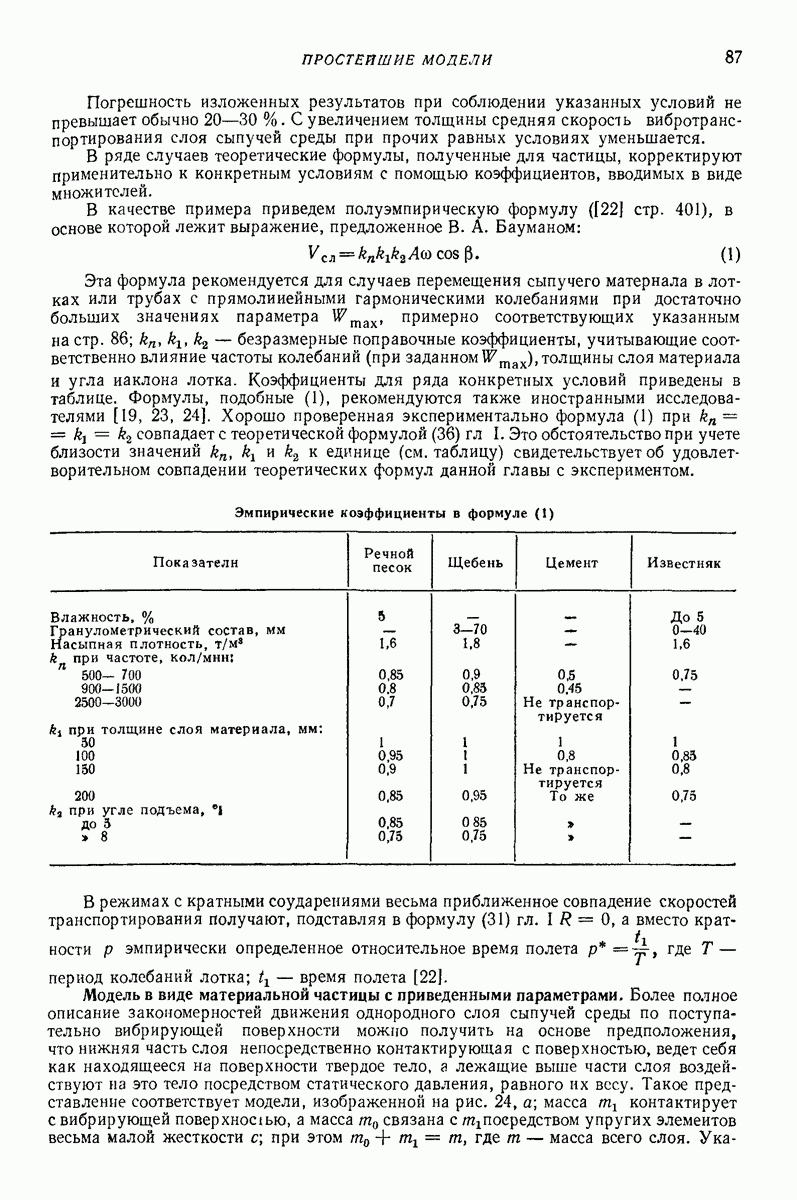
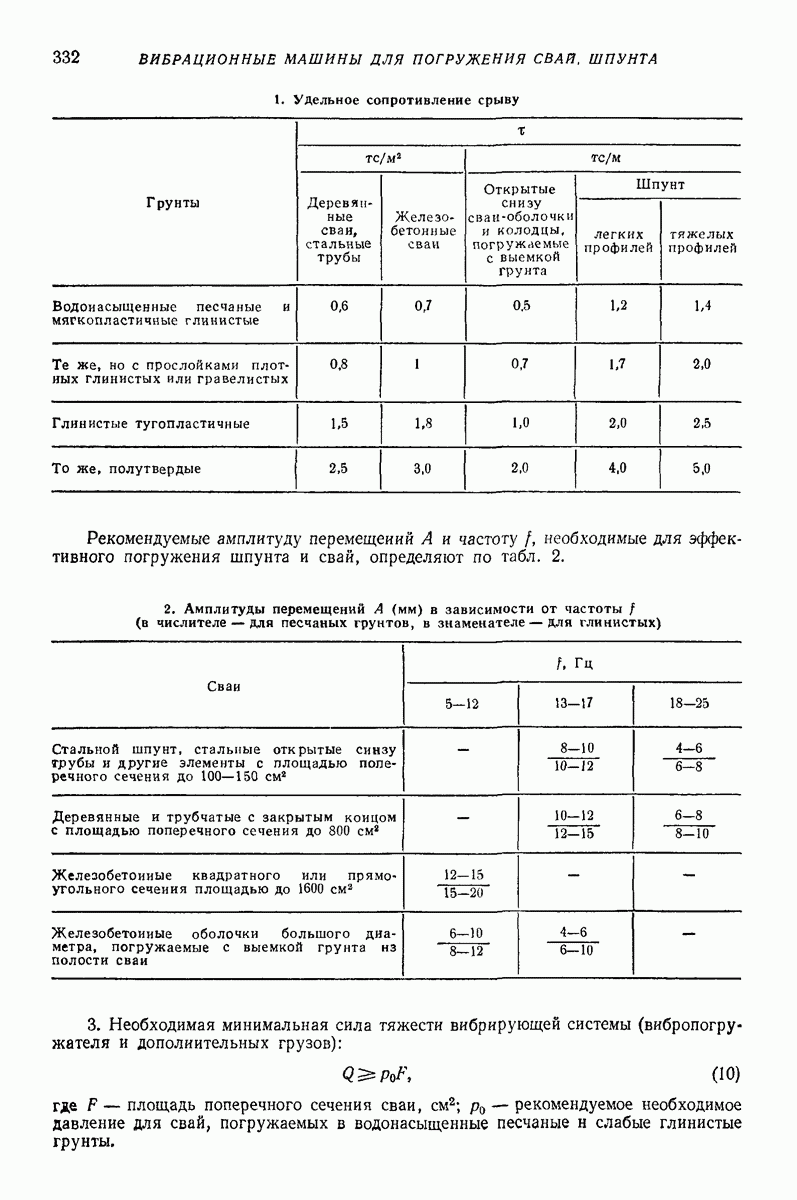
Зависимость коэффициента (3 от безразмерного параметра а приведена в табл. 1.
Для определения продолжительности удара  следует использовать условие отрыва
следует использовать условие отрыва  Результаты такого подсчета приведены в табл. 1. В табл. 1 также помещены данные, позволяющие перейти от значений
Результаты такого подсчета приведены в табл. 1. В табл. 1 также помещены данные, позволяющие перейти от значений  к значению коэффициента а.
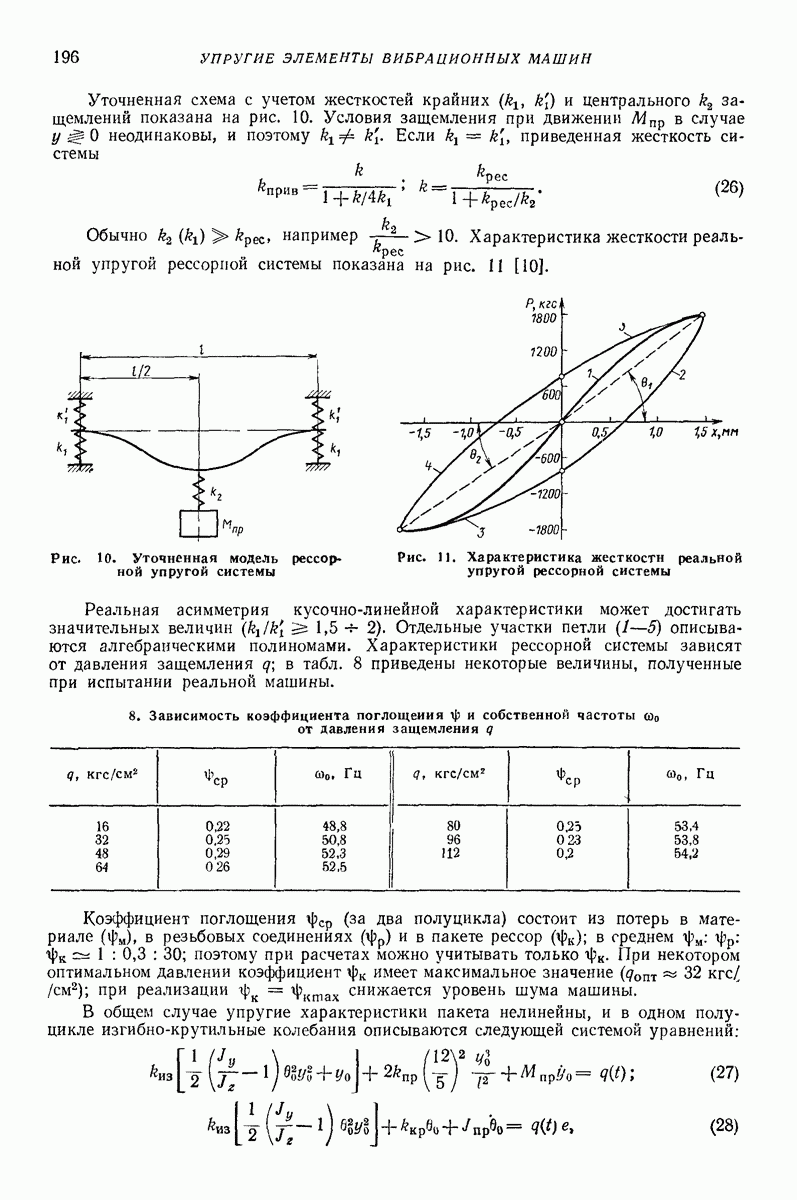
к значению коэффициента а.
1. Параметры модели
(см. скан)
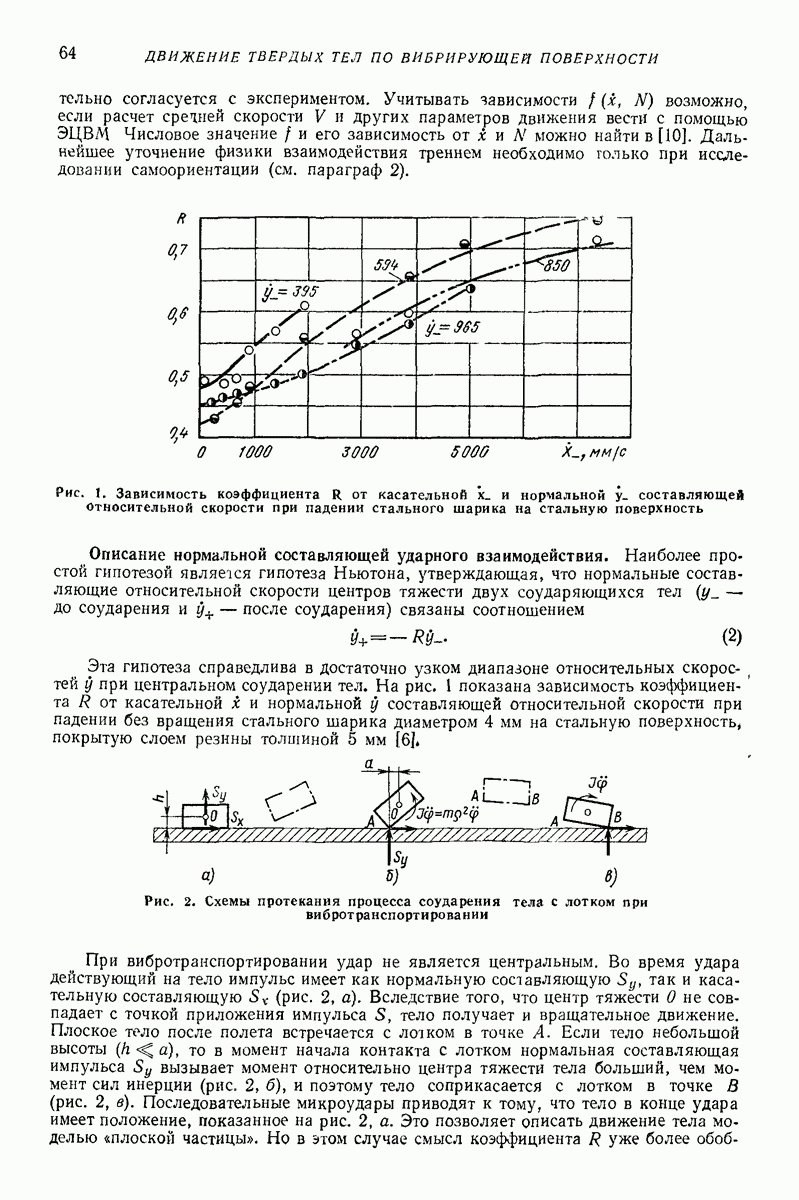
Значение коэффициента  следует определить экспериментально для подобных тел при соответствующей относительной скорости удара, свободном падении и соударении с неподвижной преградой. В этом случае
следует определить экспериментально для подобных тел при соответствующей относительной скорости удара, свободном падении и соударении с неподвижной преградой. В этом случае

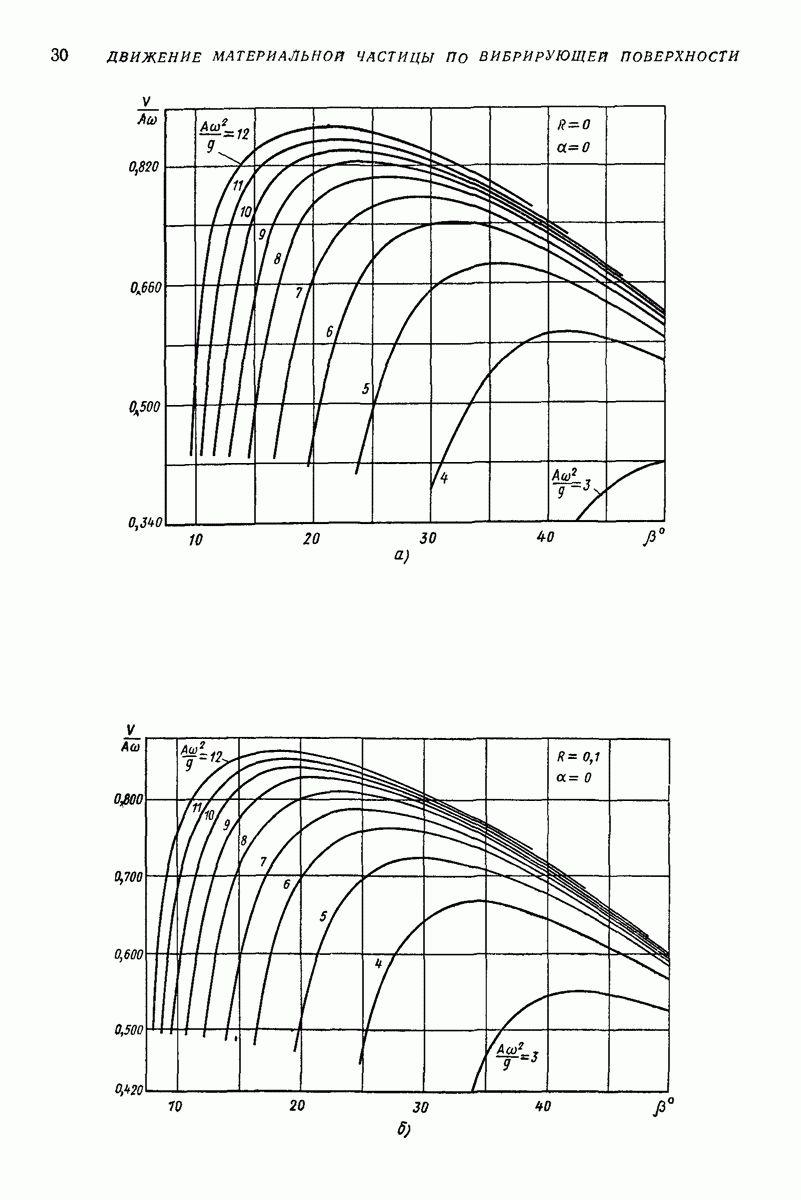
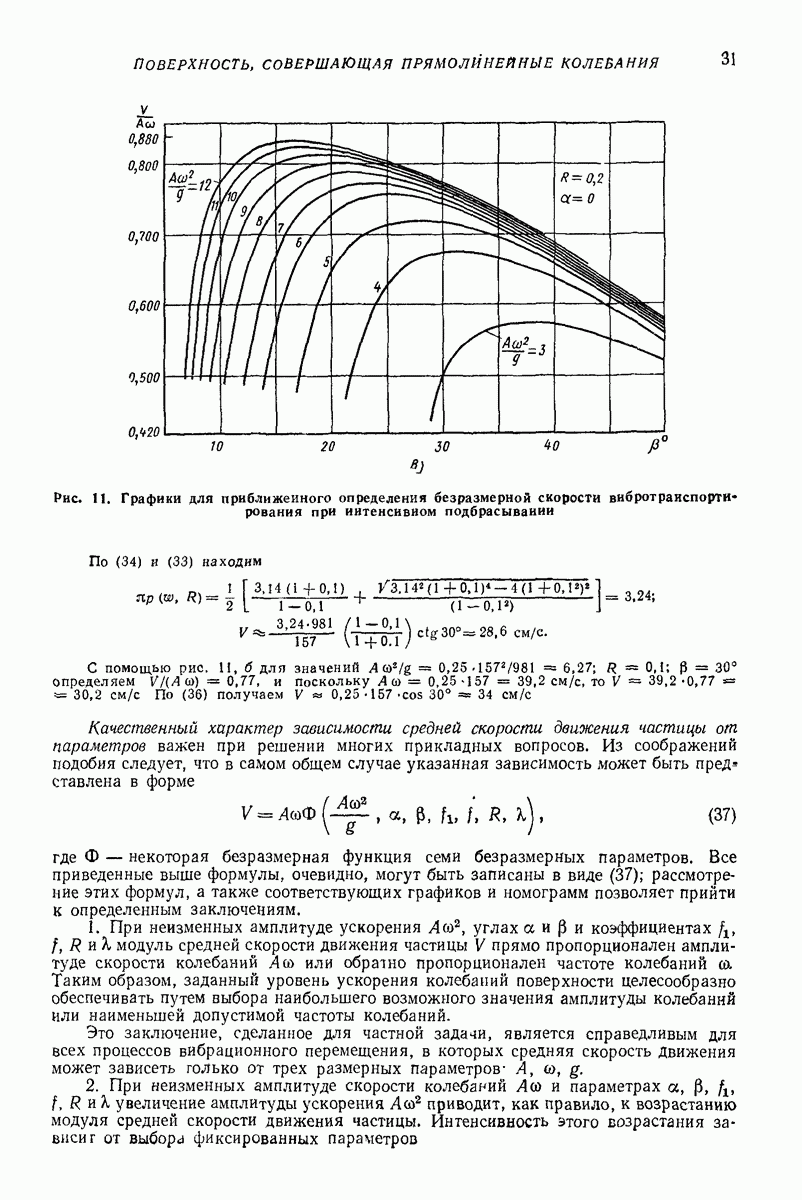
Для наиболее часто используемых материалов  меняется в пределах
меняется в пределах  Теоретическое наибольшее значение
Теоретическое наибольшее значение  примерно 0,92 (кинетическая энергия падения тела переходит в энергию упругих колебаний частиц соударяющихся тел). Жесткость с берут или из линеаризации формулы Герца (15), или из непосредственною эксперимента вдлвливания одного тела в другое.
примерно 0,92 (кинетическая энергия падения тела переходит в энергию упругих колебаний частиц соударяющихся тел). Жесткость с берут или из линеаризации формулы Герца (15), или из непосредственною эксперимента вдлвливания одного тела в другое.
Для модели показанной на рис. 1, б, решение имеет вид

а сила  Соотношения между
Соотношения между  даны в табл 2 Время удара определяется зависимостью
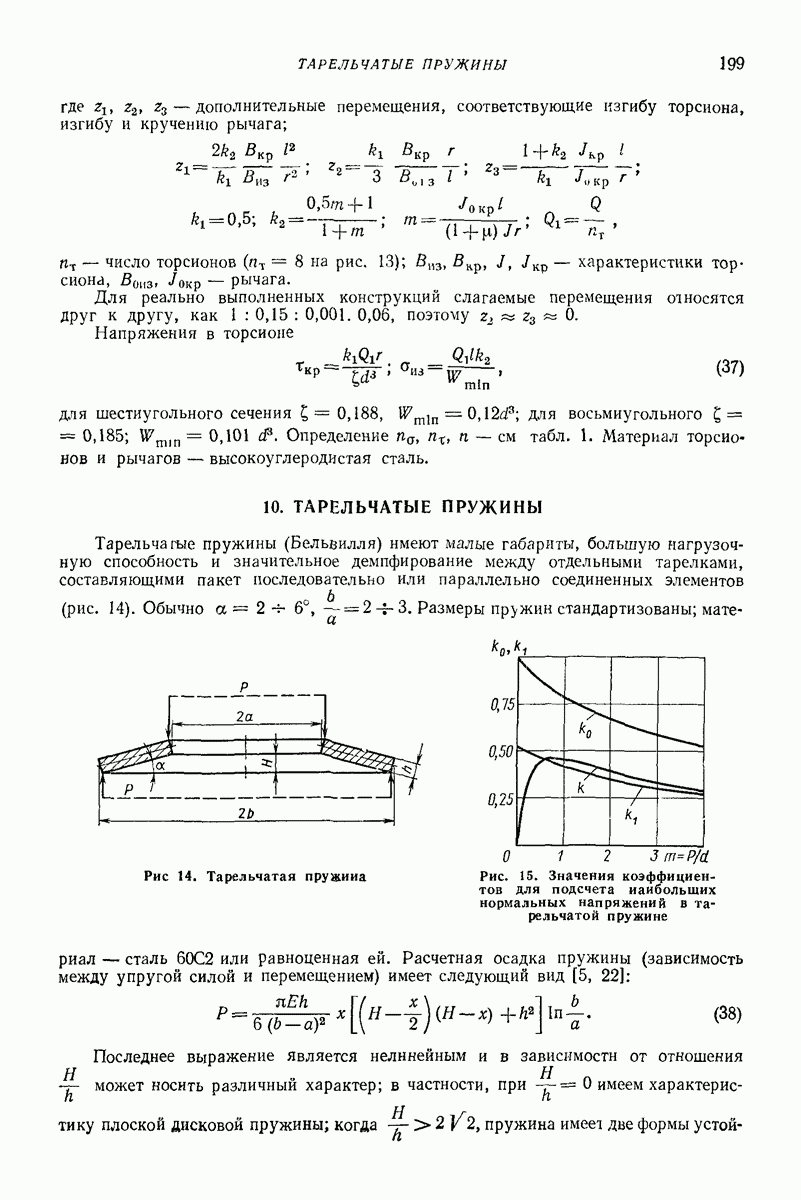
даны в табл 2 Время удара определяется зависимостью

В рассмотренных линейных моделях, содержащих упругие и вязкие элементы, предударная скорость не влияет на продолжительность удара и коэффициент восстановления
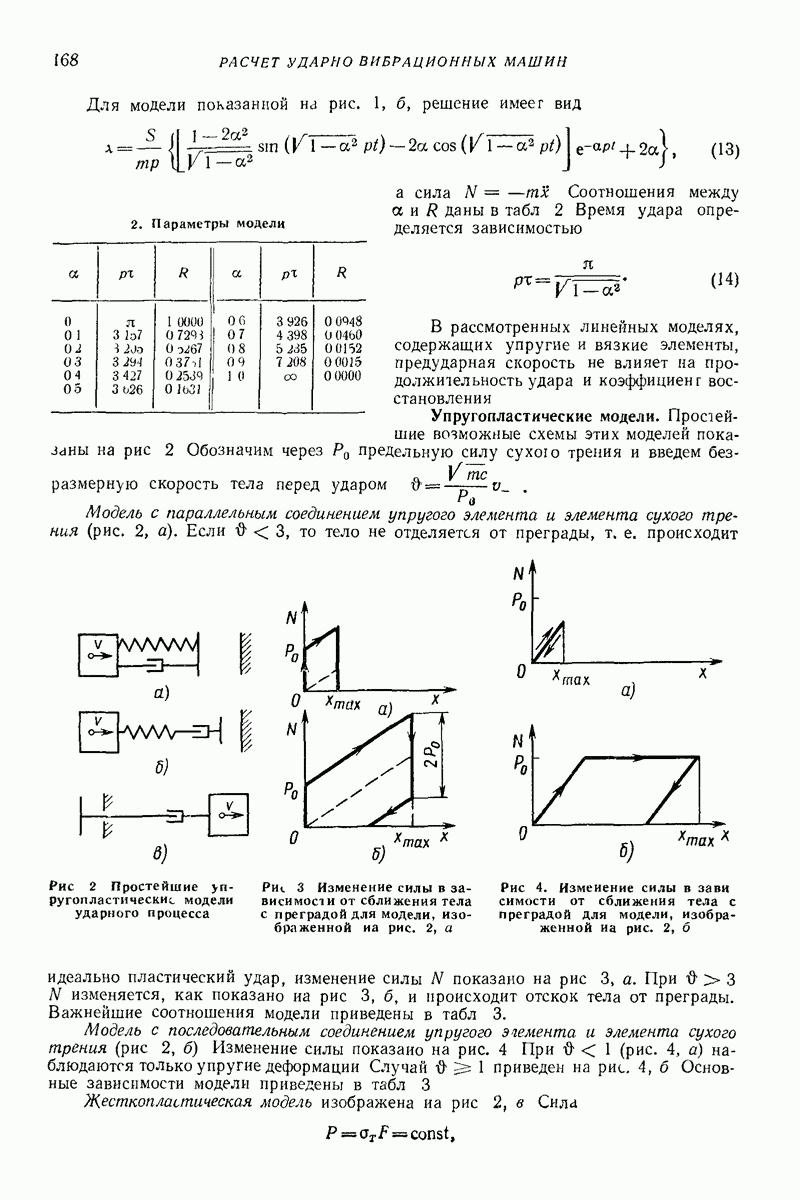
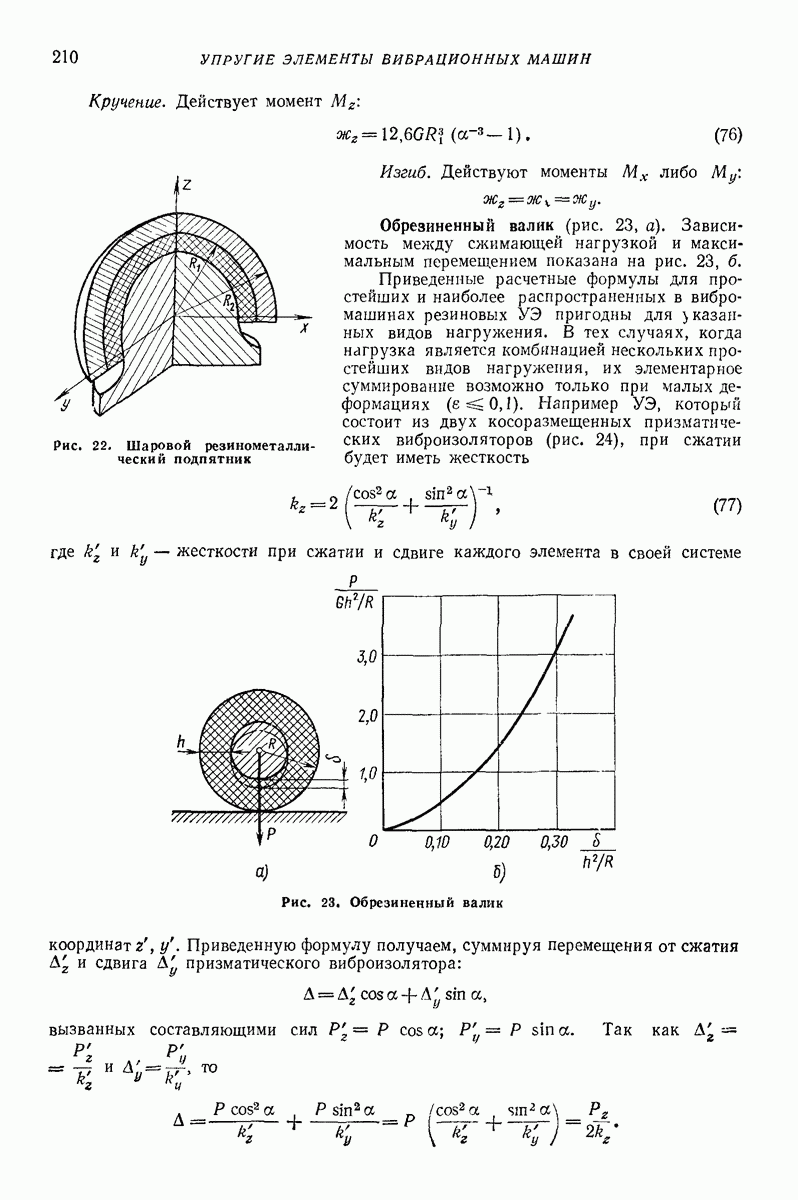
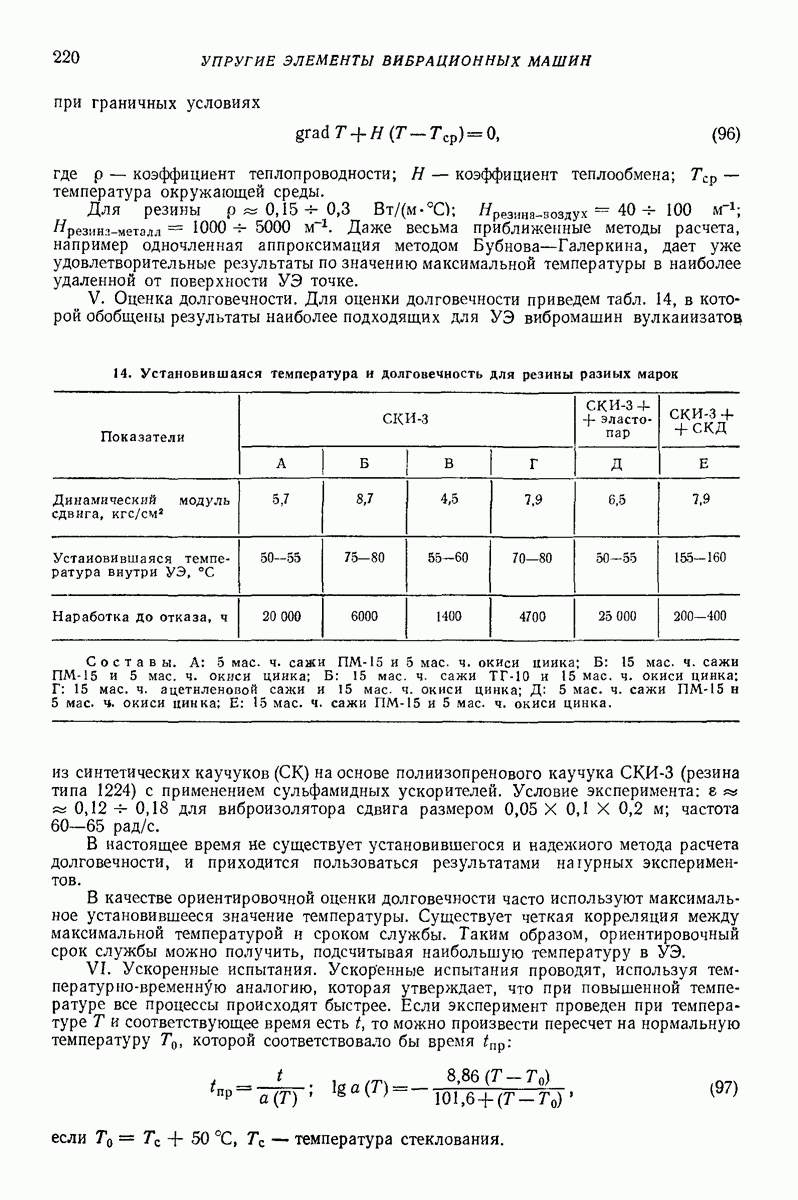
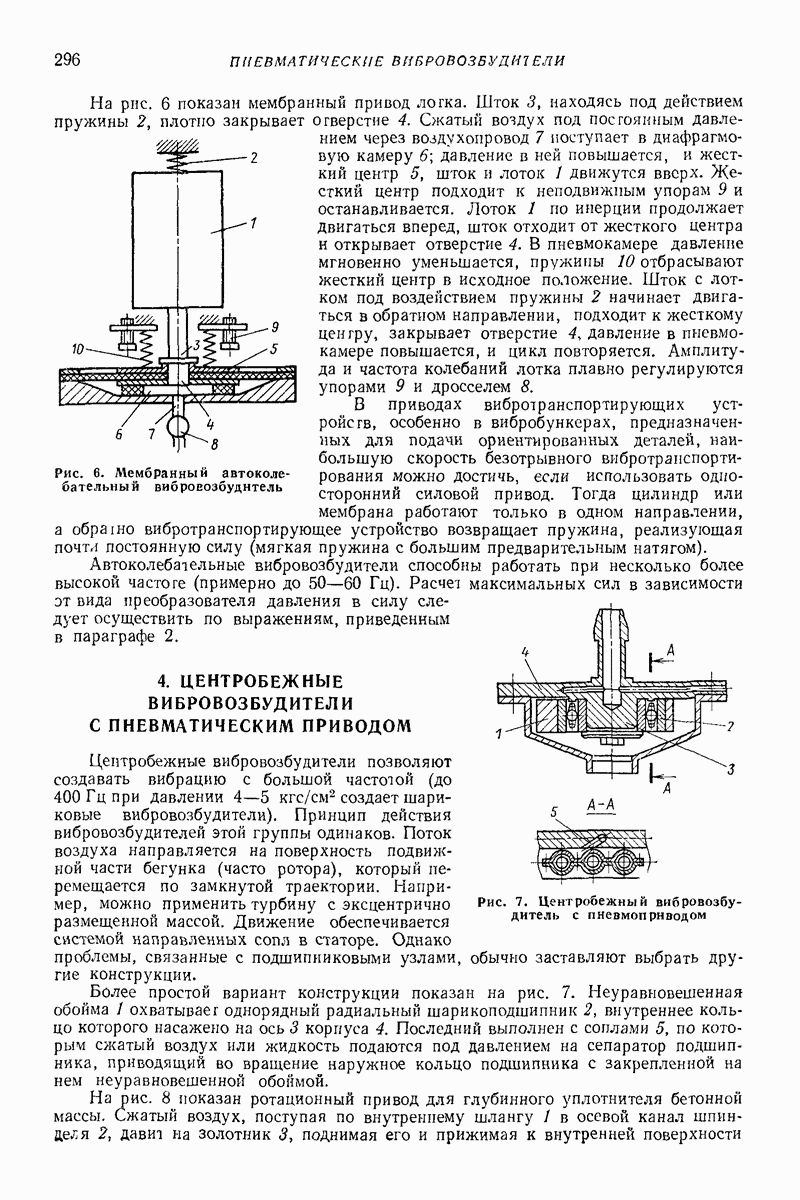
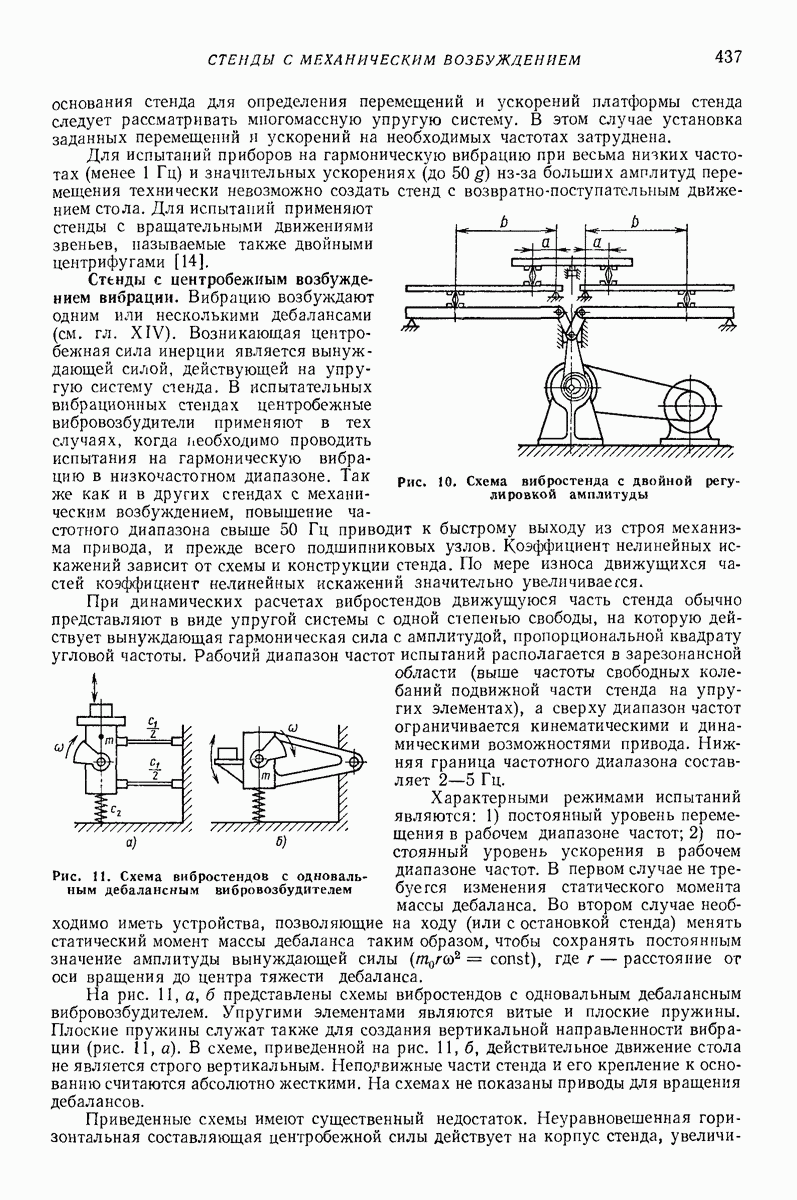
Упругопластические модели. Простейшие возможные схемы этих моделей показаны на рис 2 Обозначим через  предельную силу сухою трения и введем безразмерную скорость тела перед ударом
предельную силу сухою трения и введем безразмерную скорость тела перед ударом 
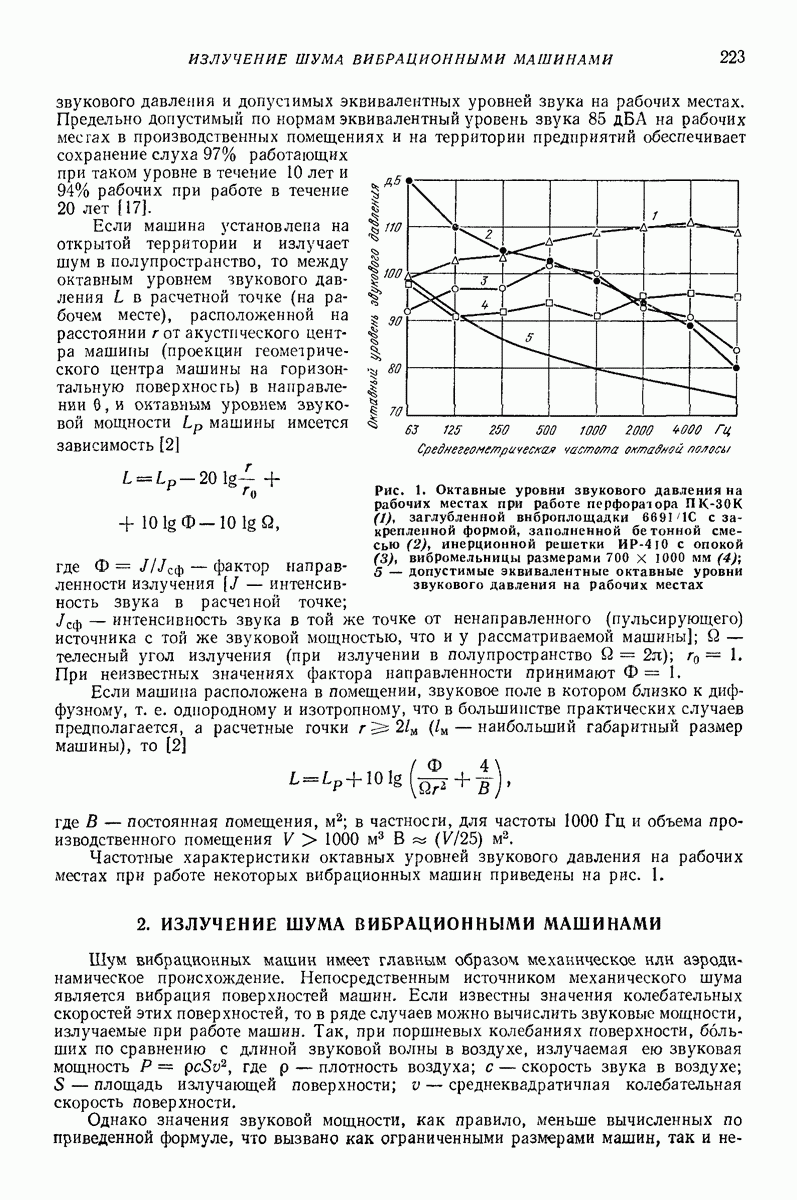
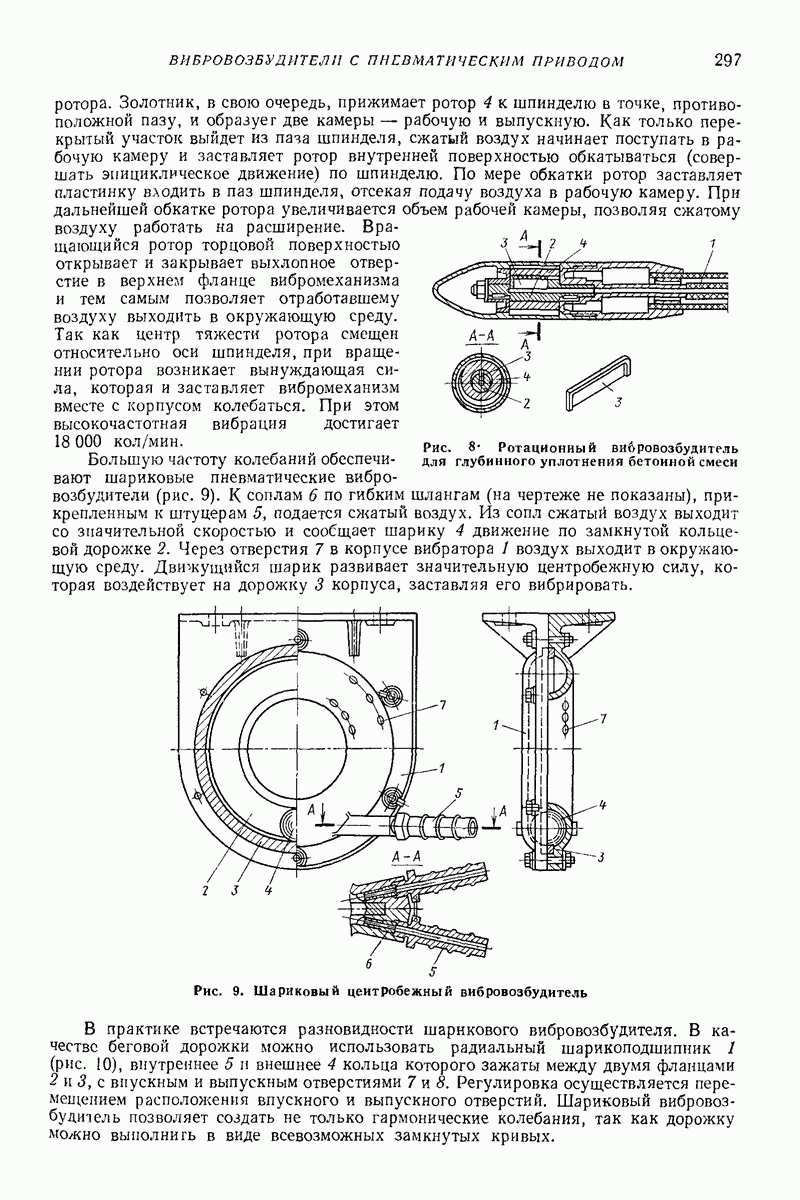
Модель с параллельным соединением упругого элемента и элемента сухого трения (рис. 2, а). Если  то тело не отделяется от преграды, т. е. происходит идеально пластический удар, изменение силы
то тело не отделяется от преграды, т. е. происходит идеально пластический удар, изменение силы  показано на рис 3, а.
показано на рис 3, а.
2. Параметры модели
(см. скан)

Рис. 2 Простейшие упругопластические модели ударного процесса

Рис. 3 Изменение силы в зависимое! и от сближения тела с преградой для модели, изображенной на рис. 2, а

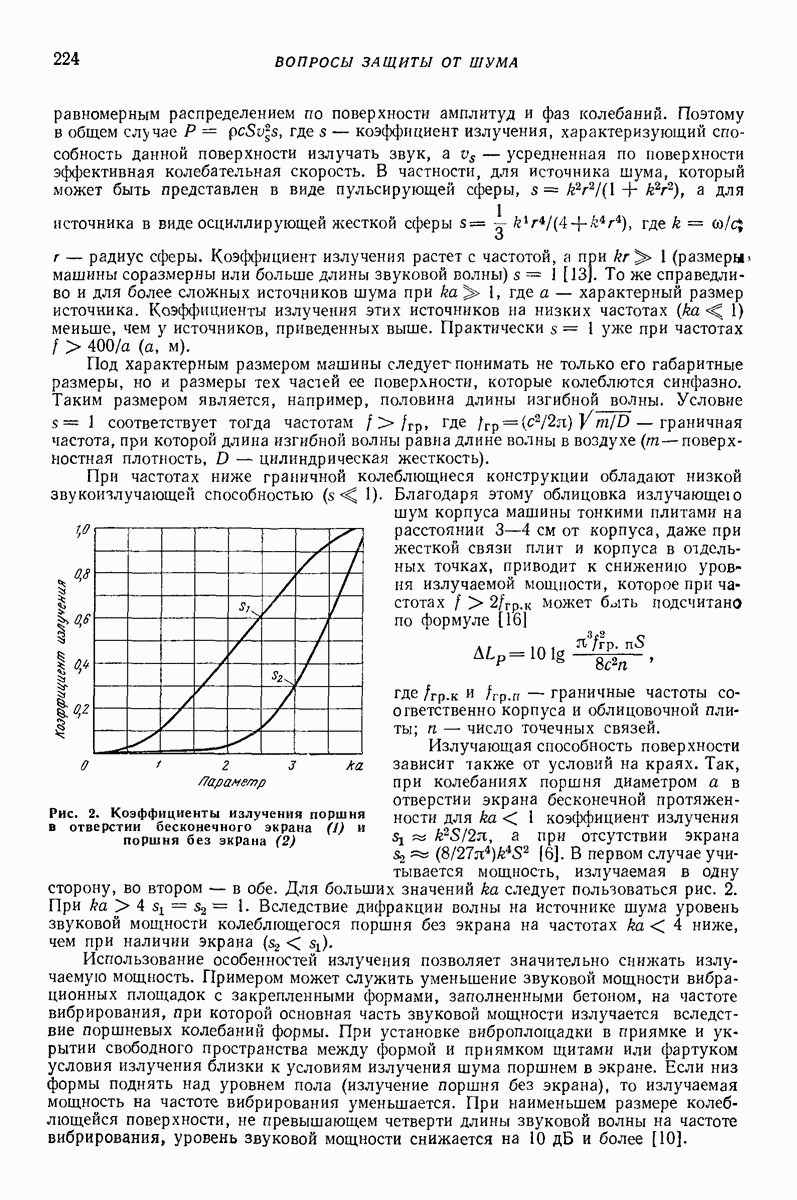
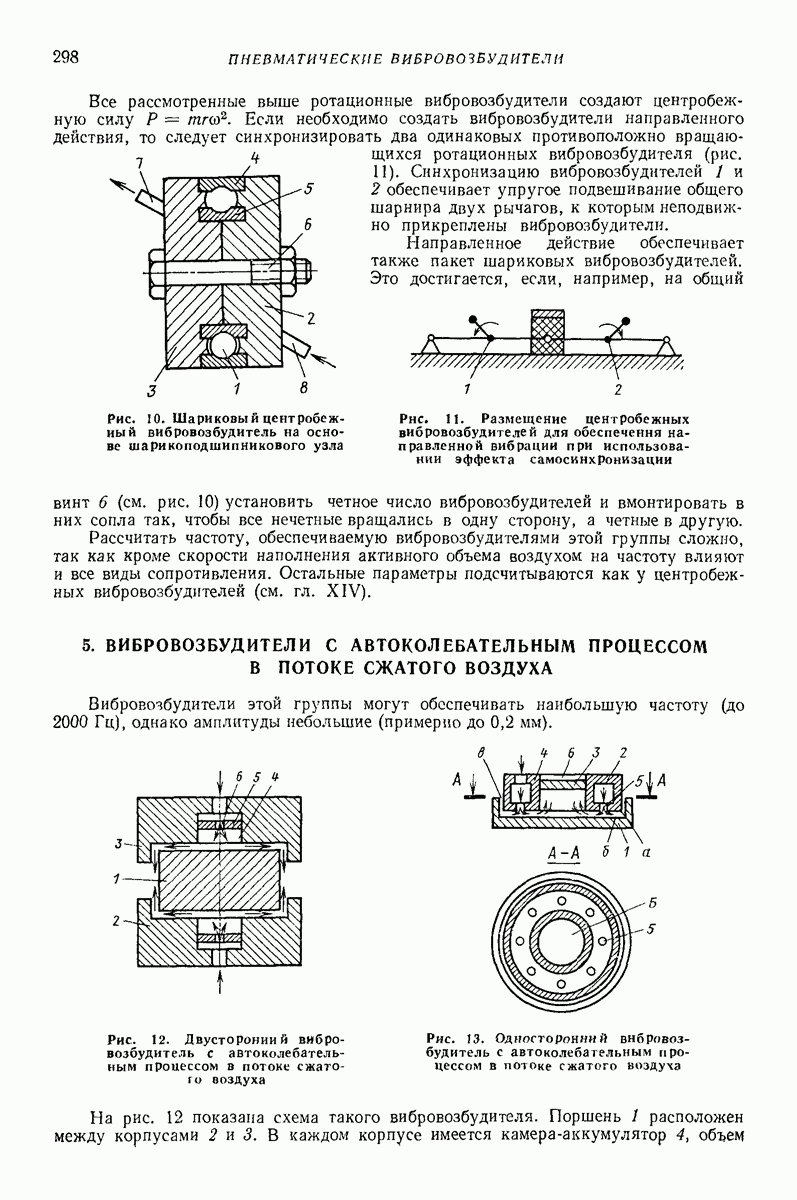
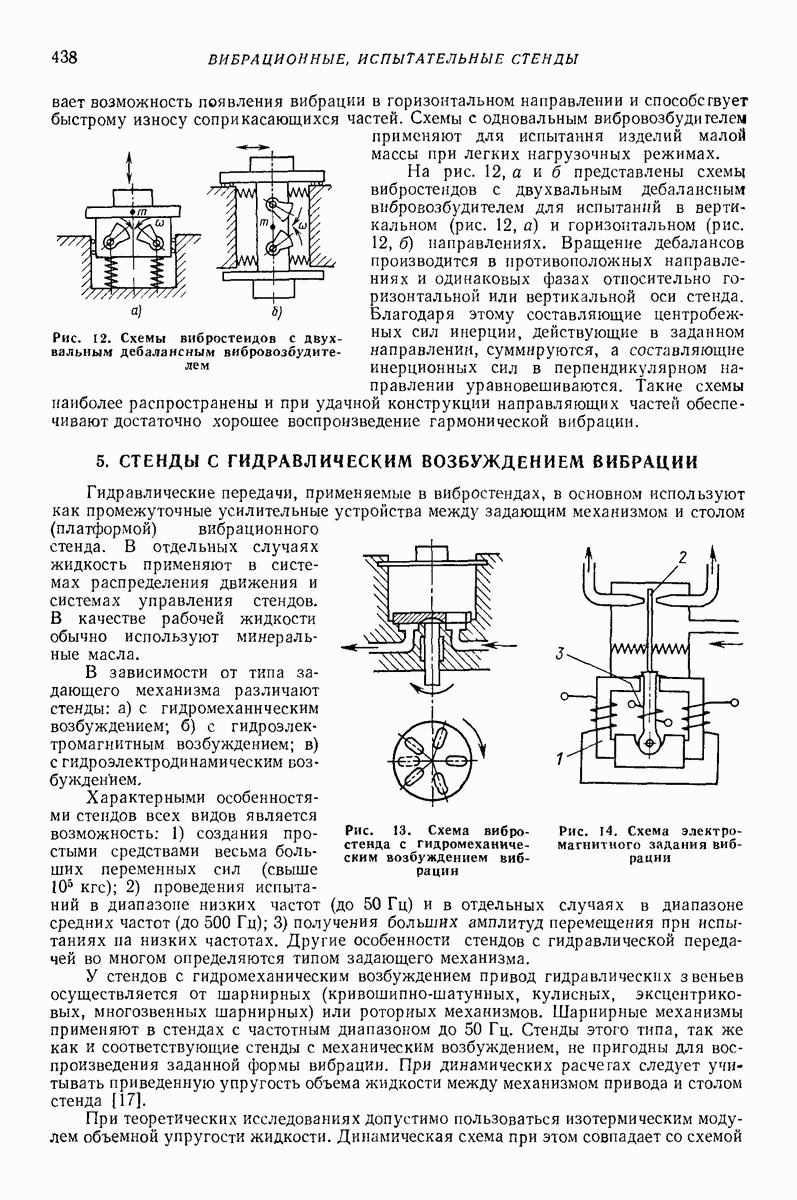
Рис. 4. Изменение силы в зави симости от сближения тела с преградой для модели, изображенной на рис. 2, б
При  изменяется, как показано на рис 3, б, и происходит отскок тела от преграды. Важнейшие соотношения модели приведены в табл 3.
изменяется, как показано на рис 3, б, и происходит отскок тела от преграды. Важнейшие соотношения модели приведены в табл 3.
Модель с последовательным соединением упругого эаемента и элемента сухого трения (рис 2, б) Изменение силы показано на рис. 4 При  (рис. 4, а) наблюдаются только упругие деформации Случай
(рис. 4, а) наблюдаются только упругие деформации Случай  приведен на рис. 4, б Основные зависимости модели приведены в табл 3
приведен на рис. 4, б Основные зависимости модели приведены в табл 3
Жесткопластическая модель изображена на рис 2, в Сила

3. Формулы расчета характерных величин
(см. скан)
где  предел текучести стержня, который является деформируемым элементом;
предел текучести стержня, который является деформируемым элементом;  площадь стержня, обычно предел текучести зависит от скорости деформации
площадь стержня, обычно предел текучести зависит от скорости деформации 

где  статический предел текучести,
статический предел текучести,  эмпирические коэффициенты (для мягкой углеродистой стали
эмпирические коэффициенты (для мягкой углеродистой стали 

где  длина стержня,
длина стержня,  удлинение стержня при ударе.
удлинение стержня при ударе.
Если материал линейно упрочняющийся с модулем упрочнения  то
то

Упругопластические модели описывают зависимости  от скорости Правильную качественную зависимость дает только модель, приведенная на рис. 2, б.
от скорости Правильную качественную зависимость дает только модель, приведенная на рис. 2, б.
Нелинейная вязкоупругая модель. В основу нелинейной упругой зависимости обычно принимают формулу Герца

которая выведена как статическая зависимость между силой  и сближением центров масс
и сближением центров масс  , К — постоянная, зависящая от свойств материала соударяющихся тел и радиусов начальных кривизн
, К — постоянная, зависящая от свойств материала соударяющихся тел и радиусов начальных кривизн  их поверхностей в точке контакта. В случае сферических поверхностей
их поверхностей в точке контакта. В случае сферических поверхностей

где  соответственно модели упругости и коэффициенты Пуассона материалов обоих тел
соответственно модели упругости и коэффициенты Пуассона материалов обоих тел
Рассмотрим соударение двух тел с массами  и введем относительное перемещение тел
и введем относительное перемещение тел 
Тогда дифференциальное уравнение движения имеет вид

В результате решения получаем

Теория Герца достаточно точна, если продолжительность удара  значительно больше наибольшего периода
значительно больше наибольшего периода  свободных колебаний соударяющихся тел. Условие приводит к понятию критической скорости
свободных колебаний соударяющихся тел. Условие приводит к понятию критической скорости

где  плотность материала.
плотность материала.
Формула Герца предполагает также, что материал находится в упругой стадии. Это будет тогда, когда

где  предел упругости; для стали (
предел упругости; для стали ( см/с, т. е. величина малая. Это показывает, что необходимо учитывать пластические деформации.
см/с, т. е. величина малая. Это показывает, что необходимо учитывать пластические деформации.
4. Коэффициенты  деформируемый элемент — конус
деформируемый элемент — конус
(см. скан)
Нелинейная упругопластическая модель. Такая модель изображена на рис. 2, а, но характеристика в этапе сближения уже нелинейна:  В таком виде ее вычислить трудно, поэтому эту зависимость заменяют более удобной [3]:
В таком виде ее вычислить трудно, поэтому эту зависимость заменяют более удобной [3]:

Коэффициенты  при статических нагружениях приведены в табл. 4—7. Для тех материалов, для которых имеется различие между статическим сттс и динамическим
при статических нагружениях приведены в табл. 4—7. Для тех материалов, для которых имеется различие между статическим сттс и динамическим  пределами текучести, следует ввести в расчет коэффициент динамичности
пределами текучести, следует ввести в расчет коэффициент динамичности 
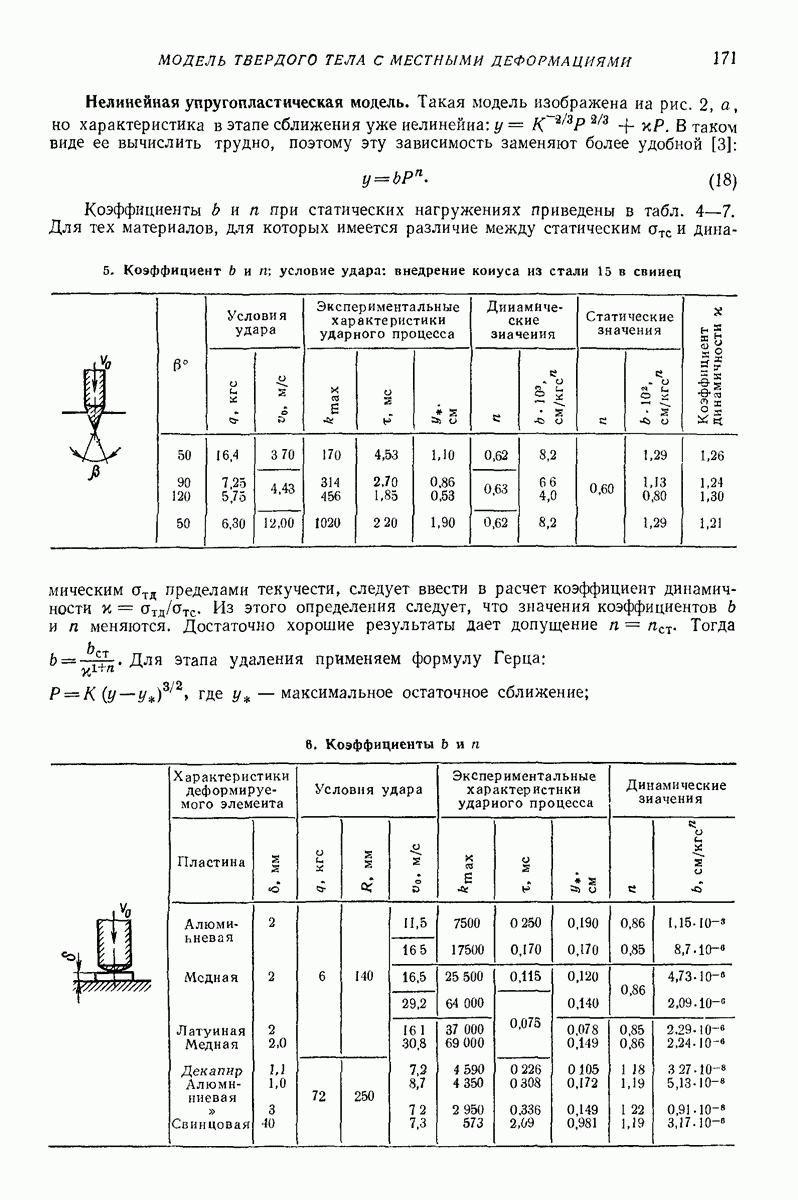
5. Коэффициент  и
и  условие удара: внедрение коиуса из стали 15 в свинец
условие удара: внедрение коиуса из стали 15 в свинец
(см. скан)
Из этого определения следует, что значения коэффициентов  и
и  меняются. Достаточно хорошие результаты дает допущение
меняются. Достаточно хорошие результаты дает допущение  Тогда
Тогда  Для этапа удаления применяем формулу Герца:
Для этапа удаления применяем формулу Герца:  где
где  максимальное остаточное сближение;
максимальное остаточное сближение;
6. Коэффициенты 
(см. скан)
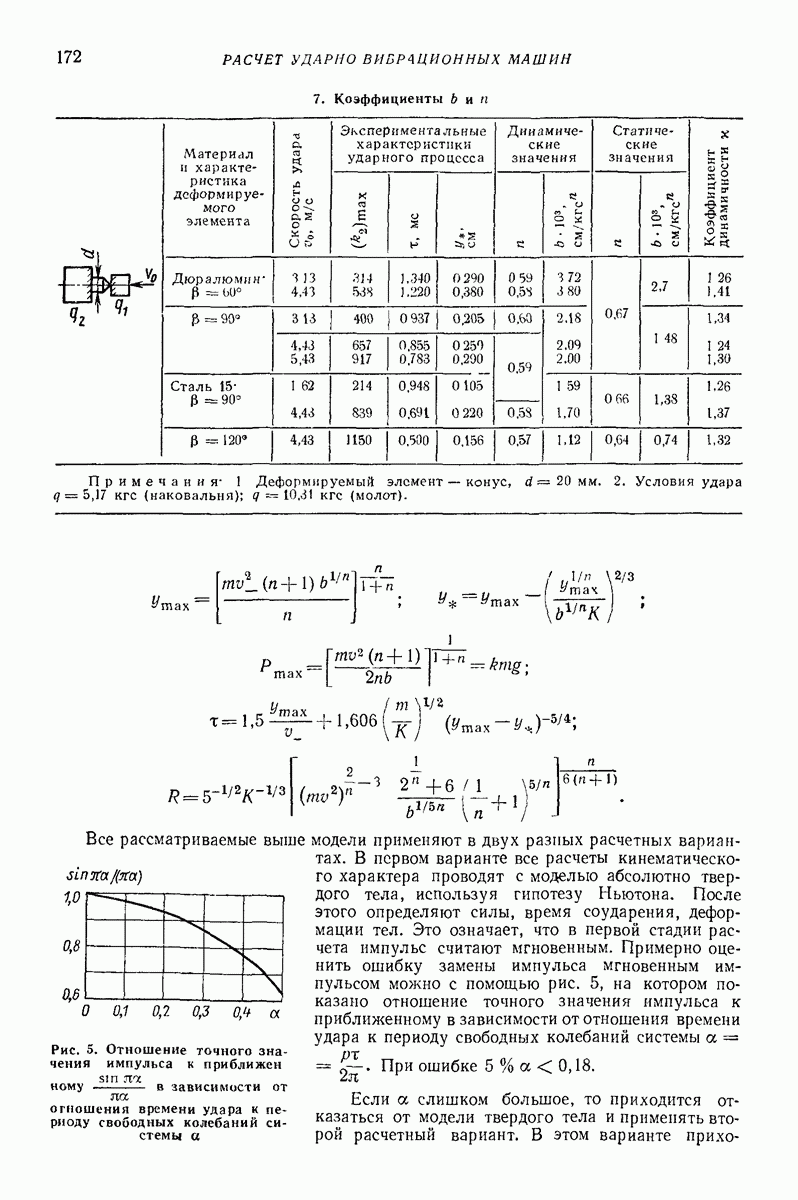
7. Коэффициенты 
(см. скан)

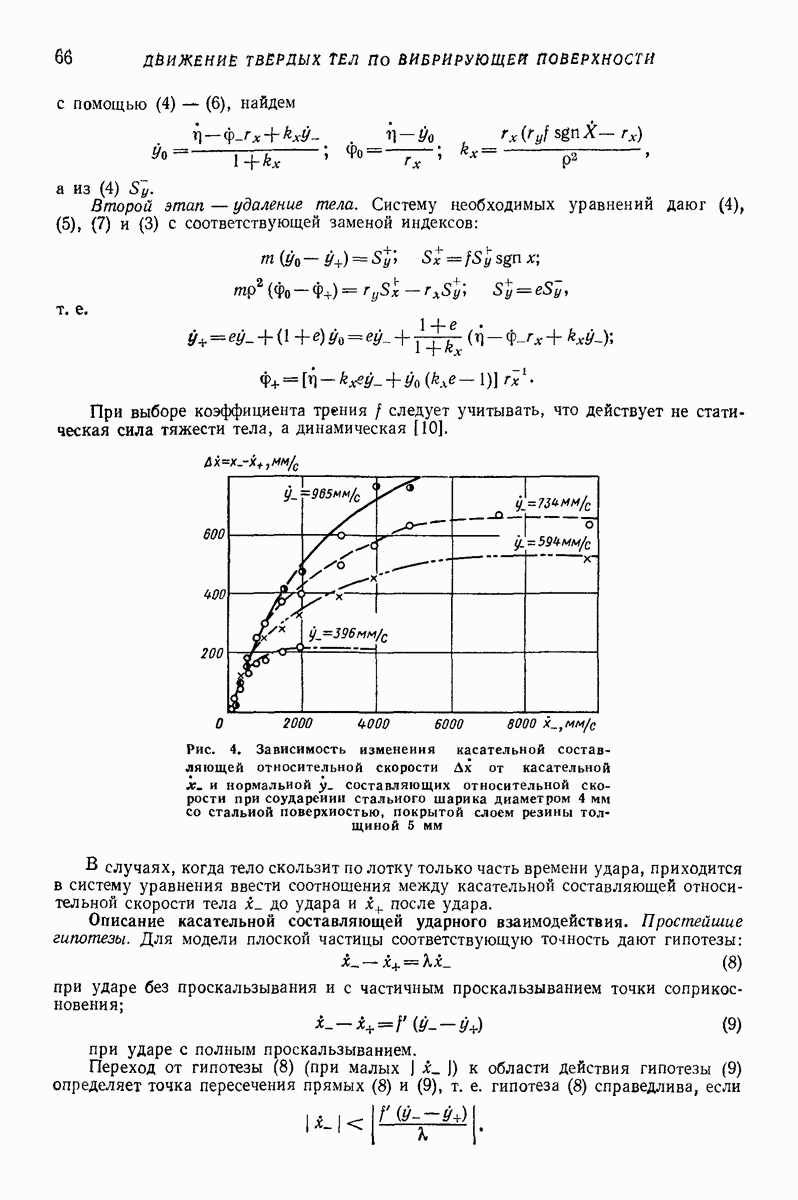
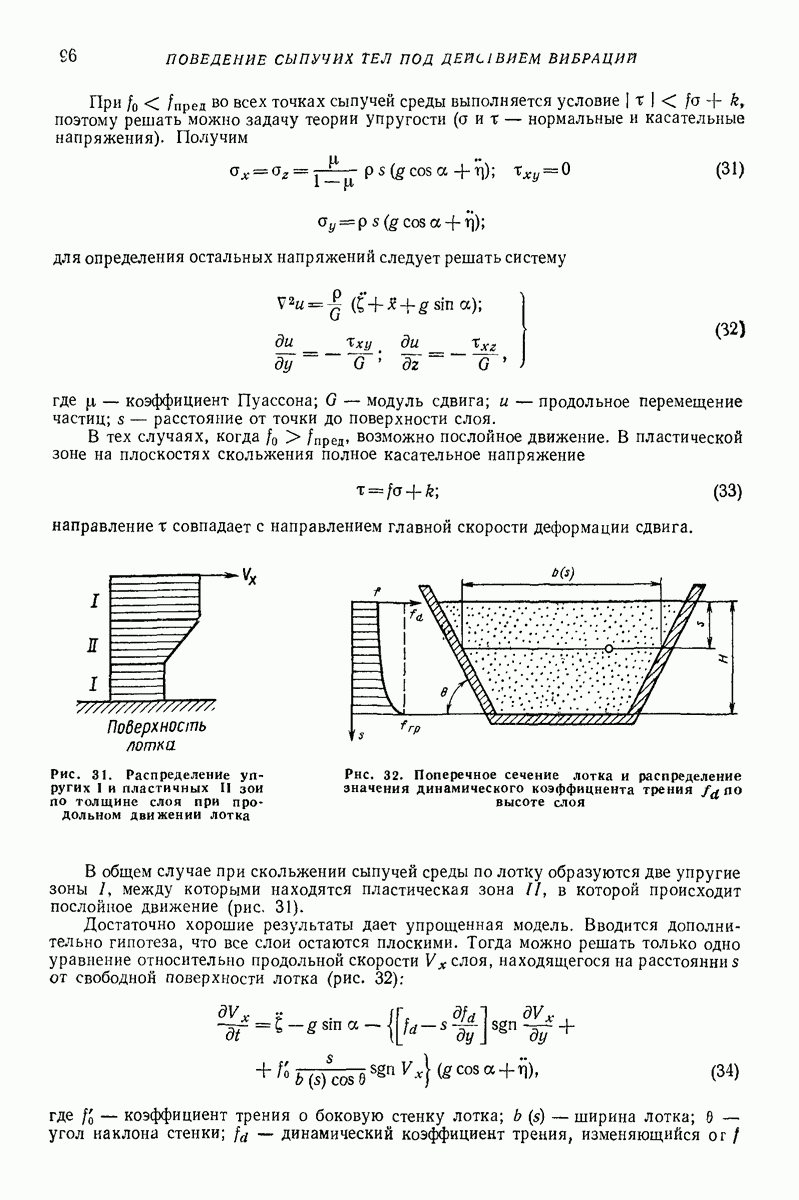
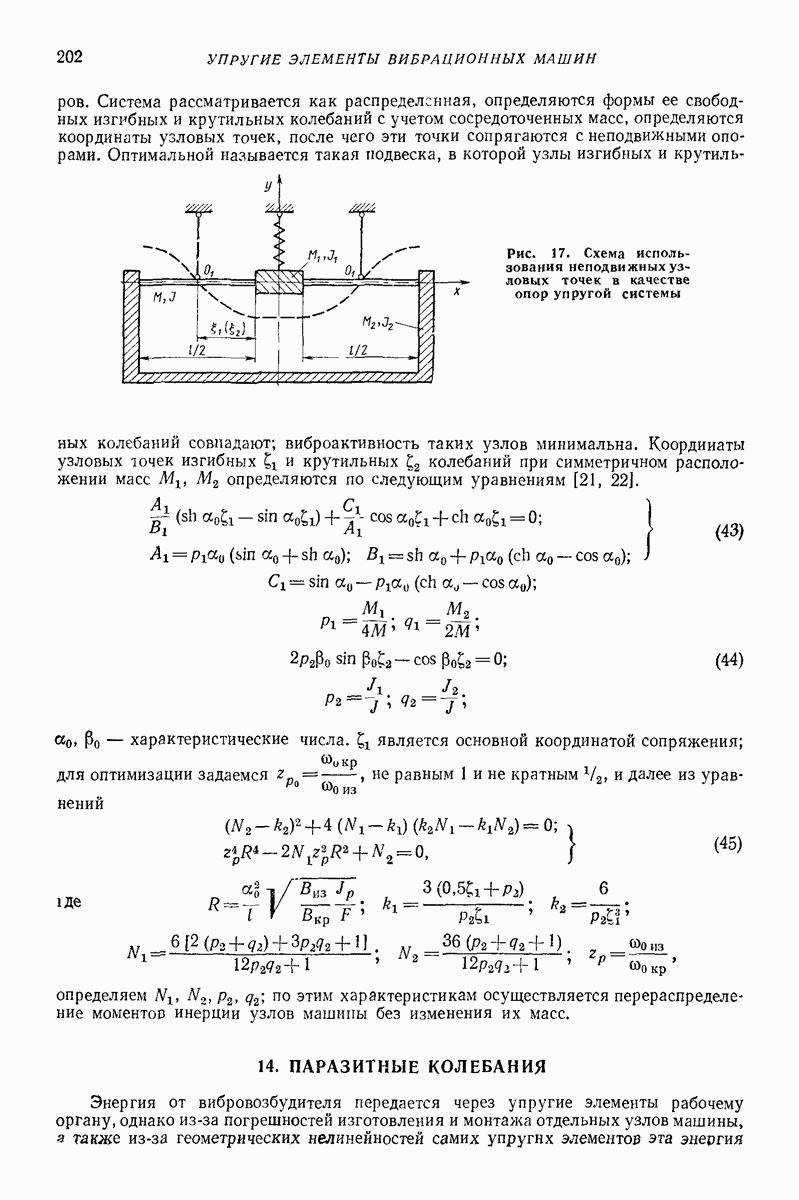
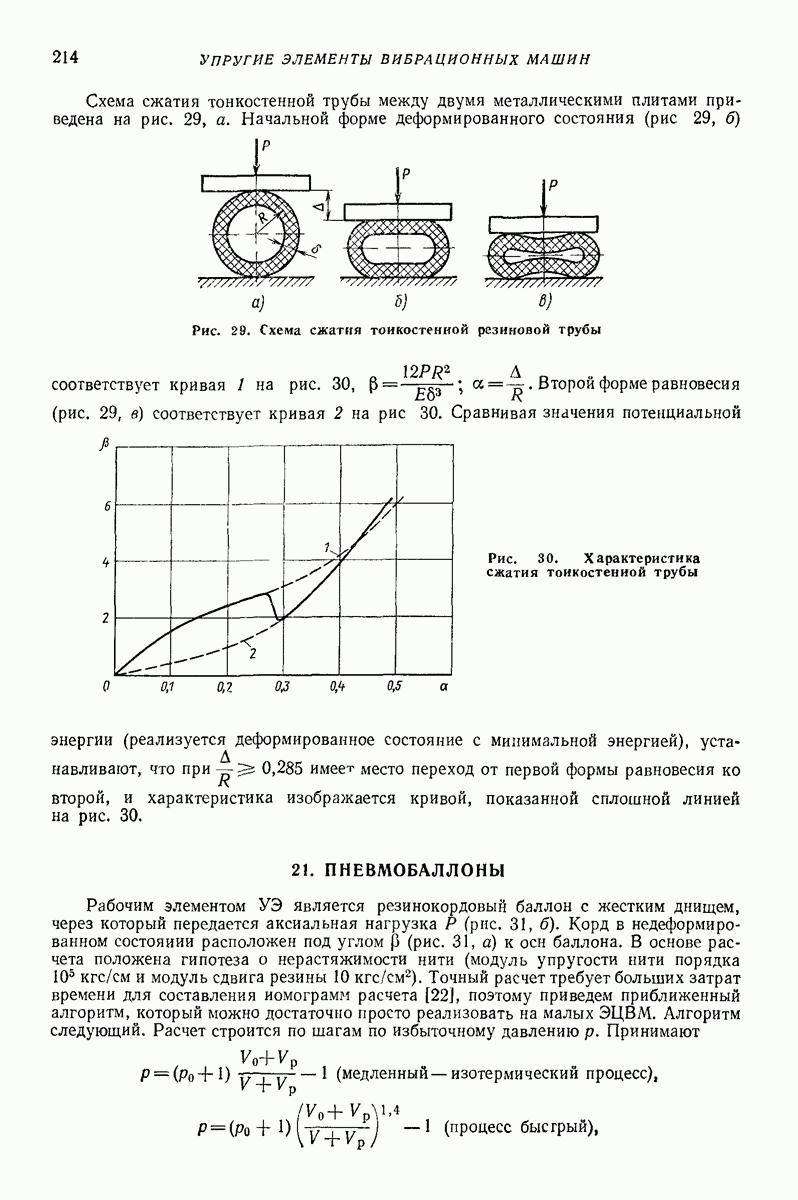
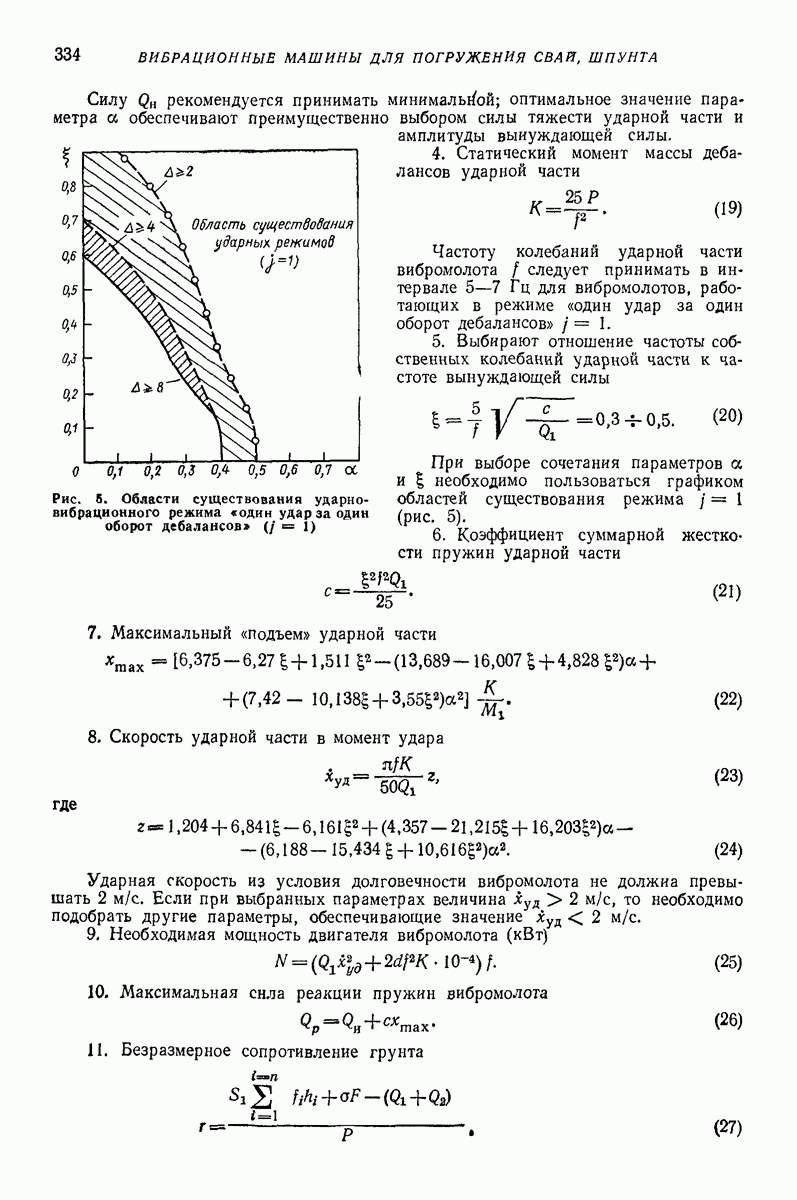
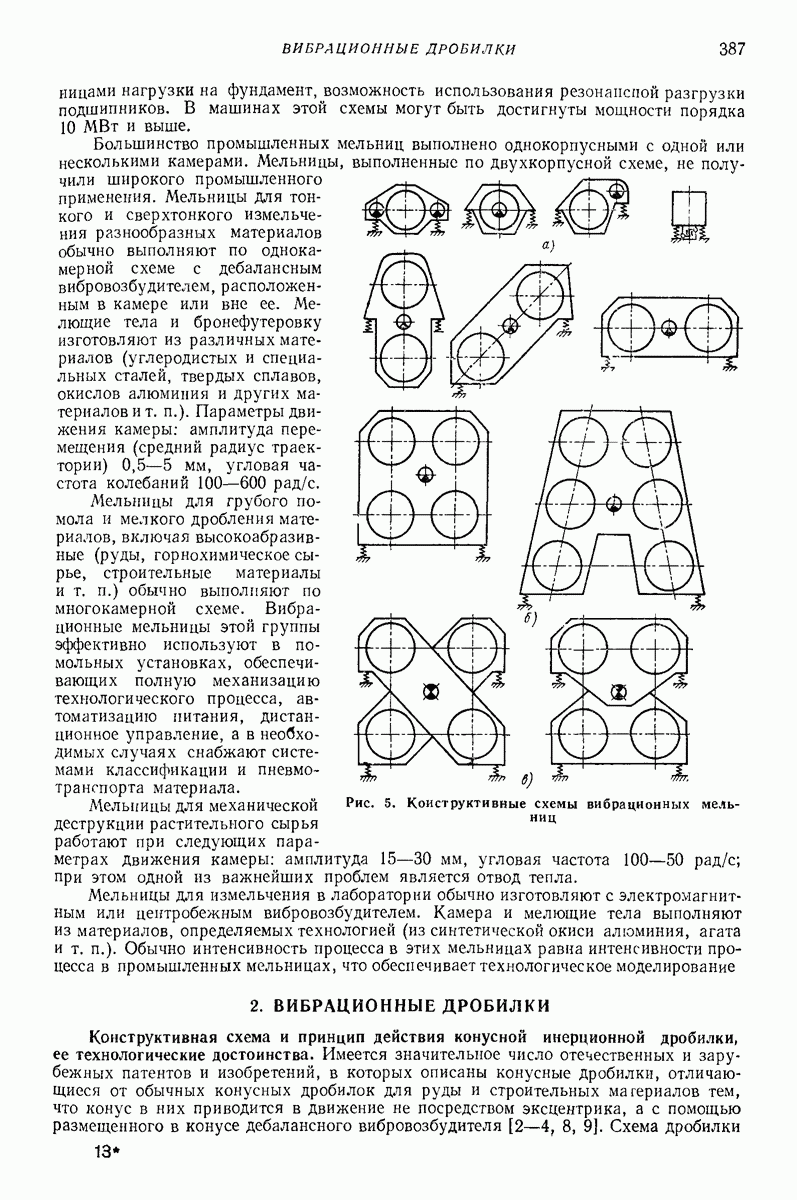
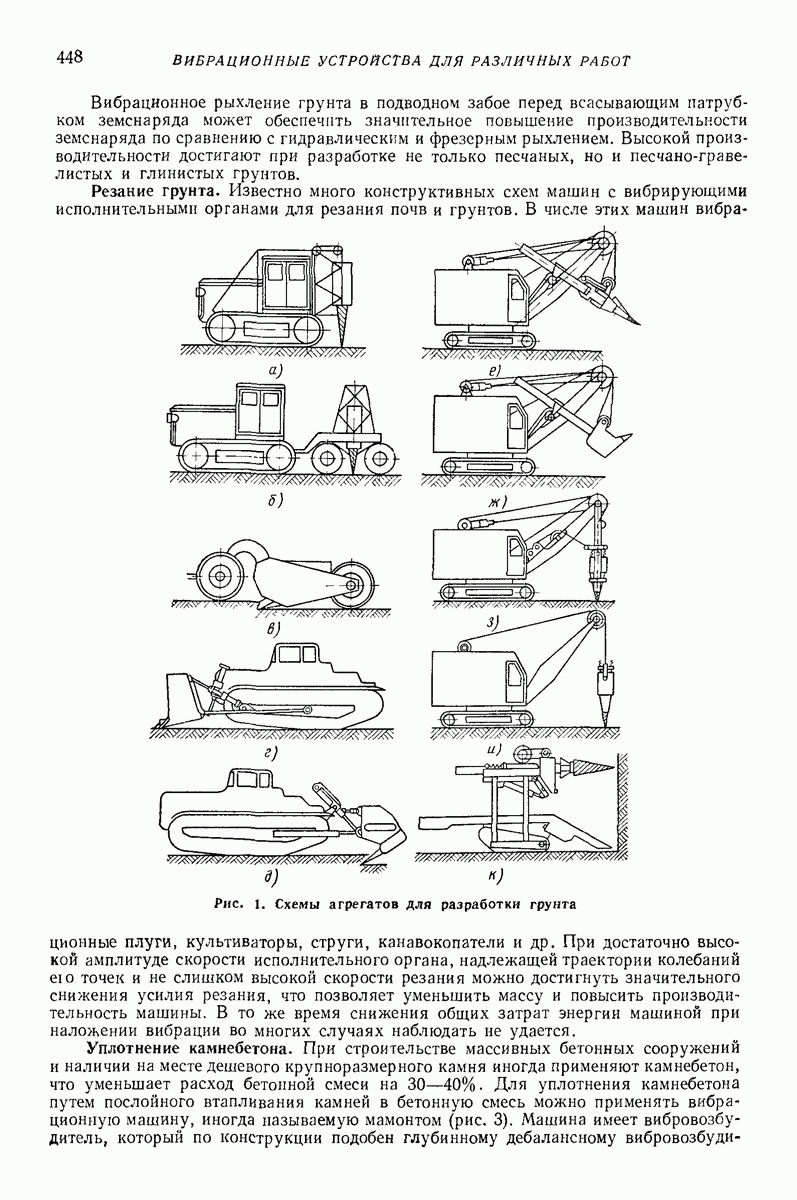
Все рассматриваемые выше модели применяют в двух разных расчетных вариантах. В первом варианте все расчеты кинематического характера проводят с моделью абсолютно твердого тела, используя гипотезу Ньютона. После этого определяют силы, время соударения, деформации тел. Это означает, что в первой стадии расчета импульс считают мгновенным. Примерно оценить ошибку замены импульса мгновенным импульсом можно с помощью рис. 5, на котором показано отношение точного значения импульса к приближенному в зависимости от отношения времени удара к периоду свободных колебаний системы  При ошибке
При ошибке 
Если а слишком большое, то приходится отказаться от модели твердого тела и применять второй расчетный вариант. В этом варианте

Рис. 5. Отношение точного значения импульса к приближенному  в зависимости от отношения времени удара к периоду свободных колебаний системы а
в зависимости от отношения времени удара к периоду свободных колебаний системы а
приходится вместо (5) решать систему дифференциальных уравнений движения одной из моделей твердого тела с присоединенными вязкоупругими или пластическими элементами.
Модельные представления, рассмотренные выше для случая удара по преграде, вполне применимы и в случае соударения двух тел, однако конечные результаты будут зависеть уже от скоростей обоих тел до соударения; для вывода зависимостей (при малых а) следует рассматривать соударение двух моделей (каждая со своими упруговязкопластическими элементами). Ввиду того, что при этом сильно увеличивается число влияющих параметров, представить в замкнутом виде общие решения, как это удается для модели твердого тела (см. т. 2, гл. XII), практически невозможно и приходится получать решение для каждого конкретного случая.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть первая. ВИБРАЦИОННЫЕ ПРОЦЕССЫ
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ ПО ВИБРИРУЮЩЕЙ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ ПРЯМОЛИНЕЙНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- Установившиеся режимы движения частицы.
- О методах решения задачи.
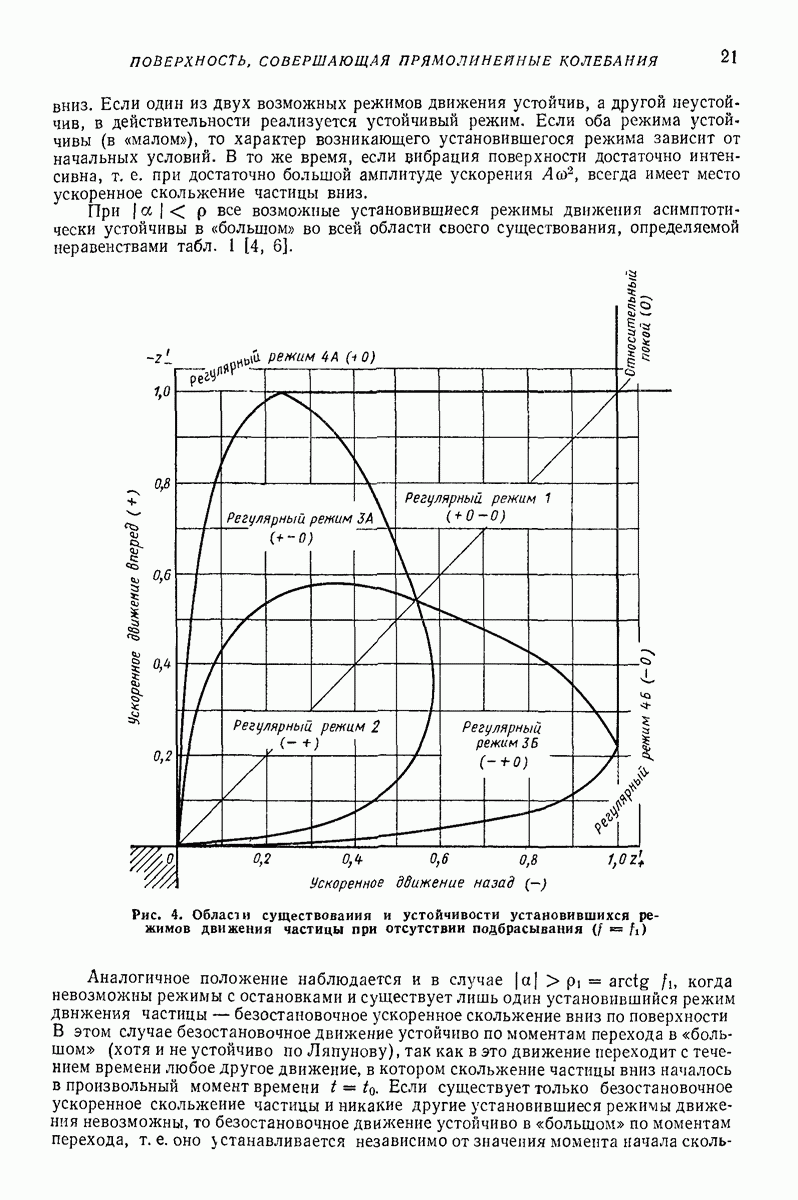
- Установившиеся режимы при отсутствии подбрасывания [4-6].
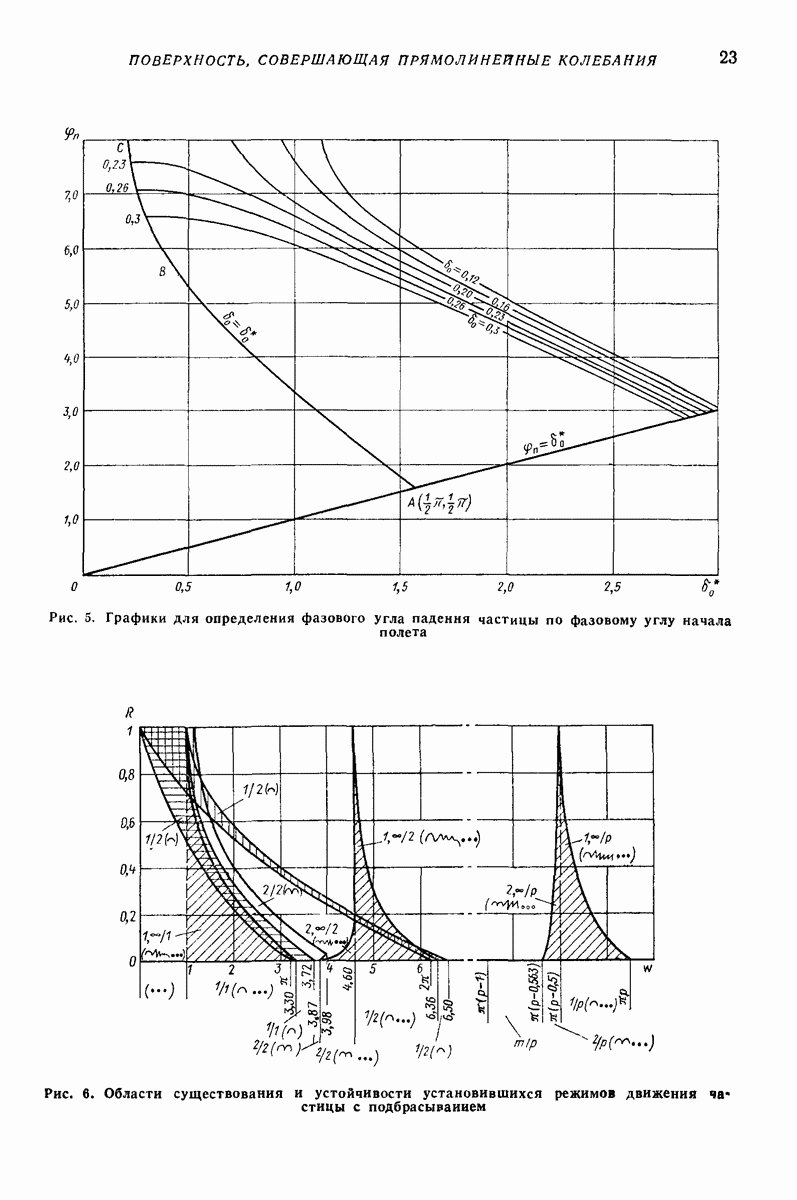
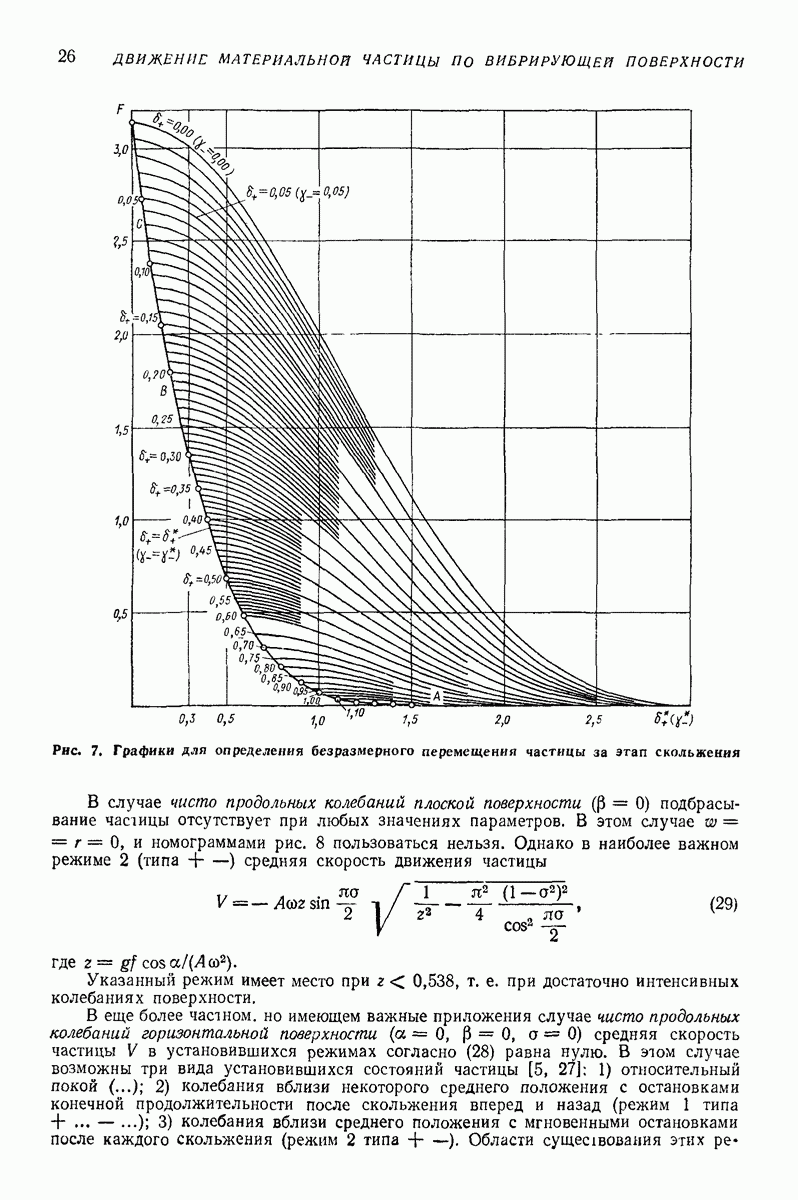
- Установившиеся режимы с подбрасыванием.
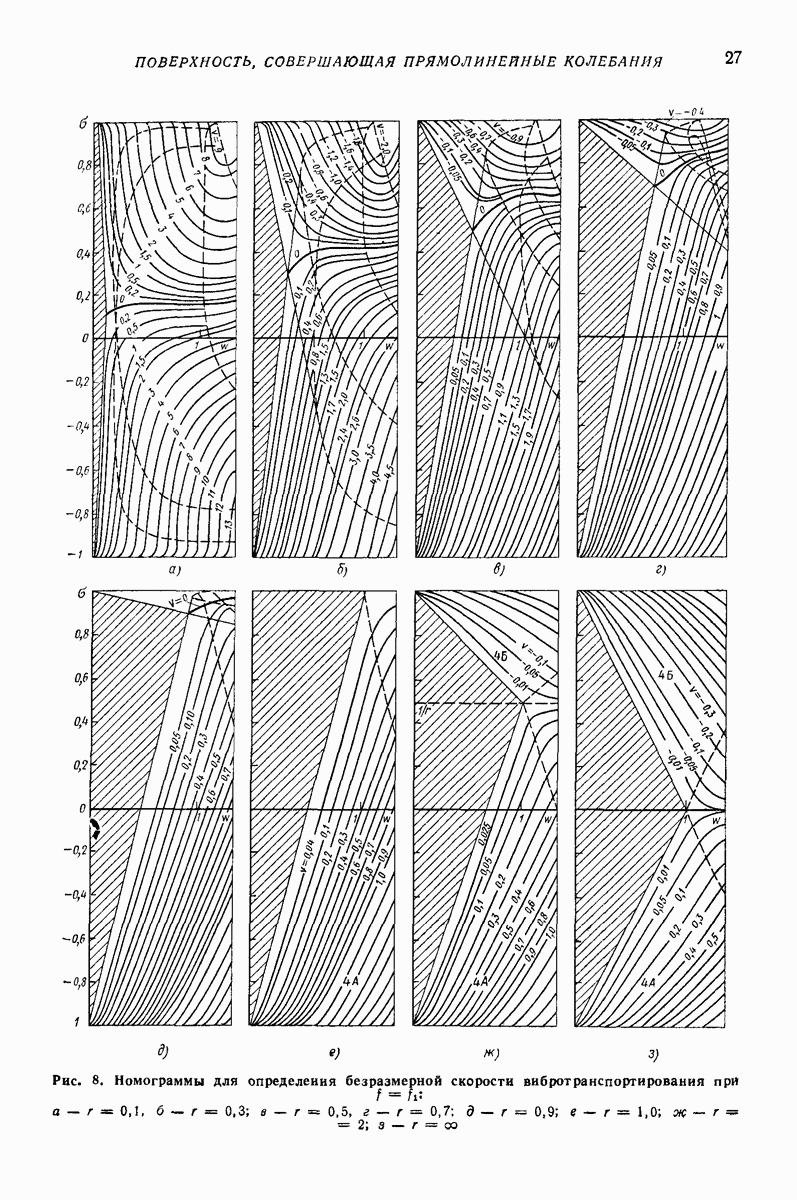
- Средние скорость и ускорение частицы в установившихся режимах движения.
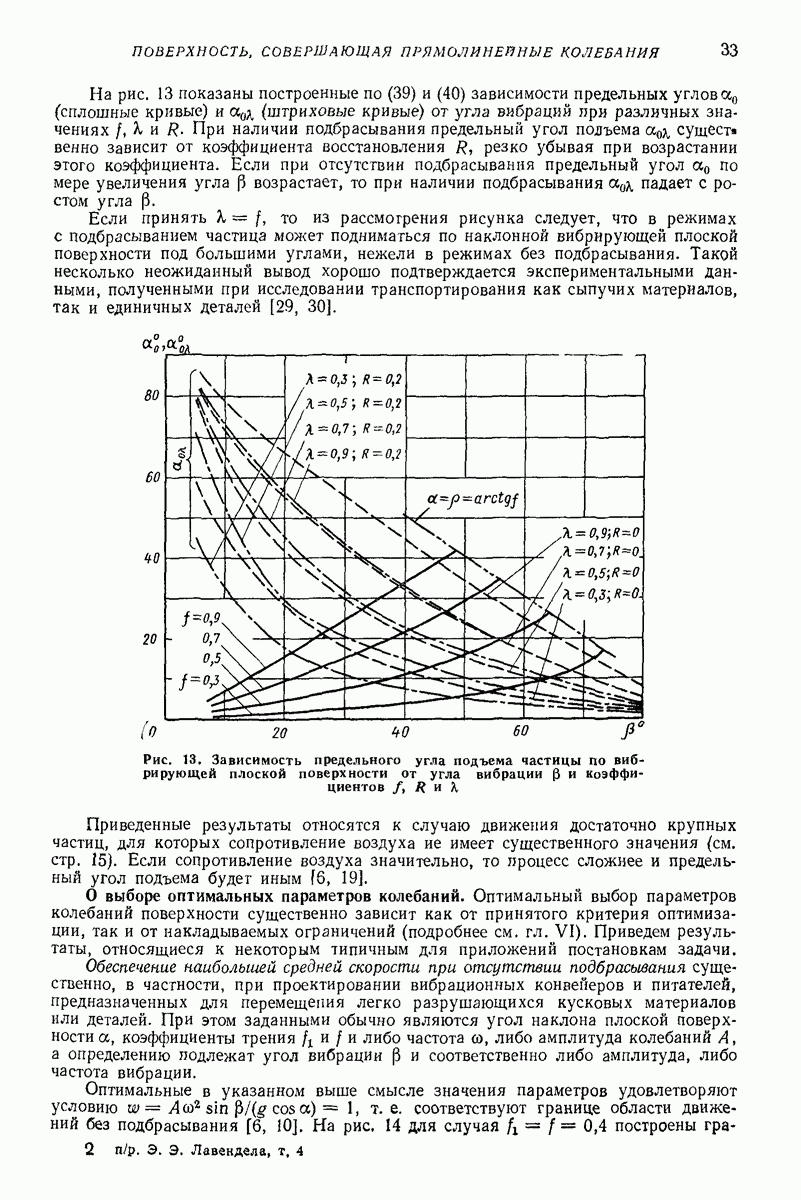
- О предельном угле подъема частицы по наклонной вибрирующей плоской поверхности [6, 30].
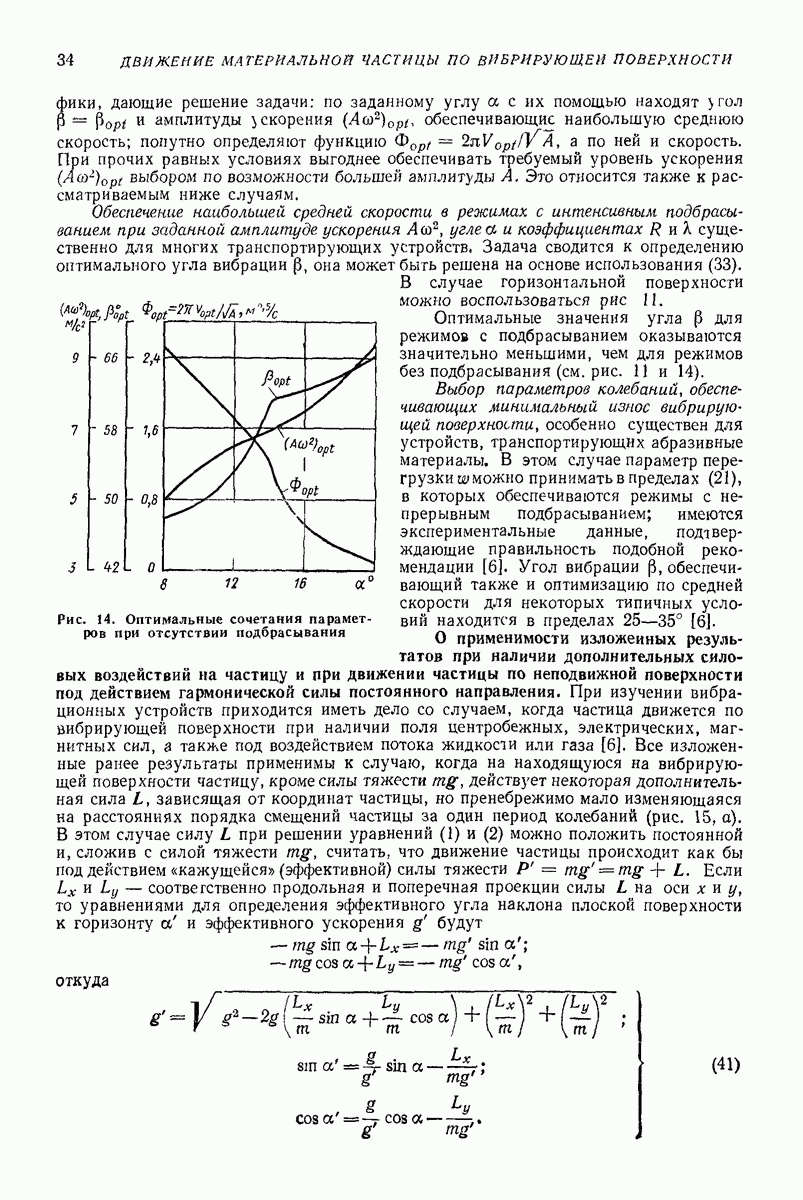
- О выборе оптимальных параметров колебаний.
- О применимости изложенных результатов при наличии дополнительных силовых воздействий на частицу и при движении частицы по неподвижной поверхности под действием гармонической силы постоянного направления.
- Случай анизотропии фрикционных свойств вибрирующей поверхности [32].
- О влиянии на движение частицы сил вязкого сопротивления.
- 3. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ ПАРАЛЛЕЛЬНО ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА [5, 6]
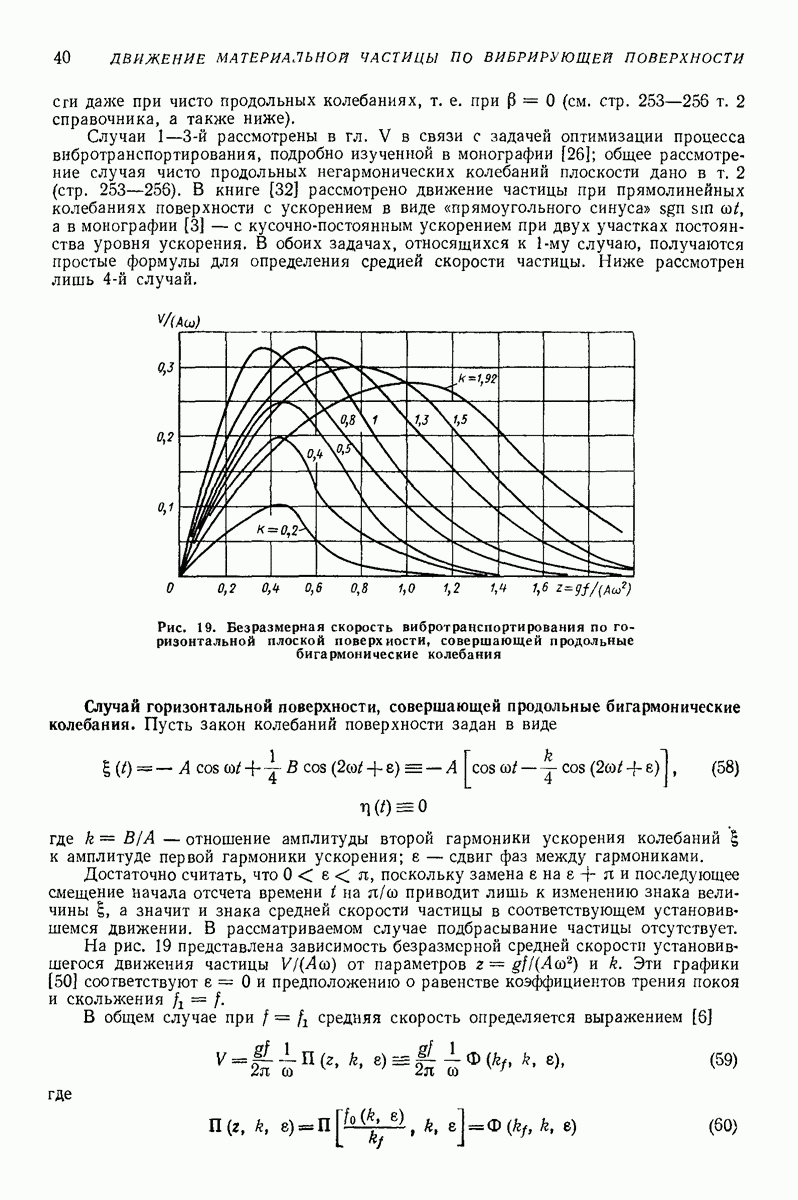
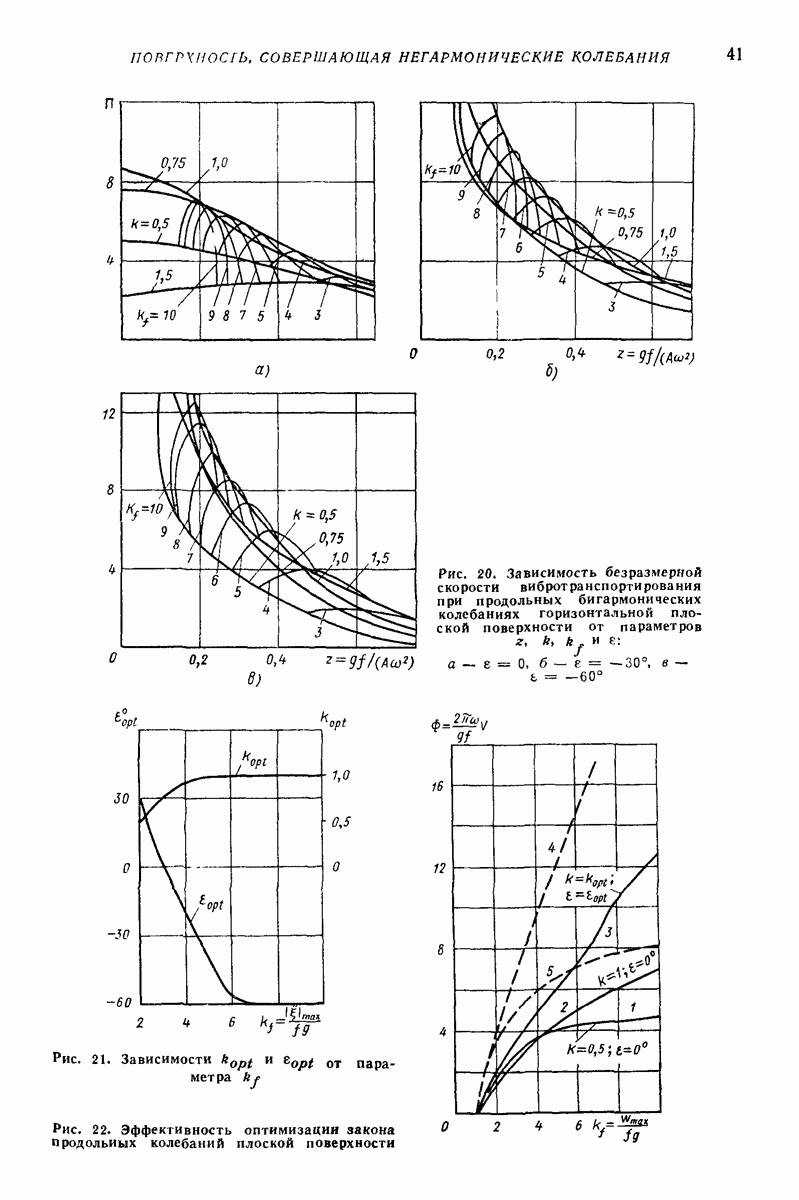
- 4. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
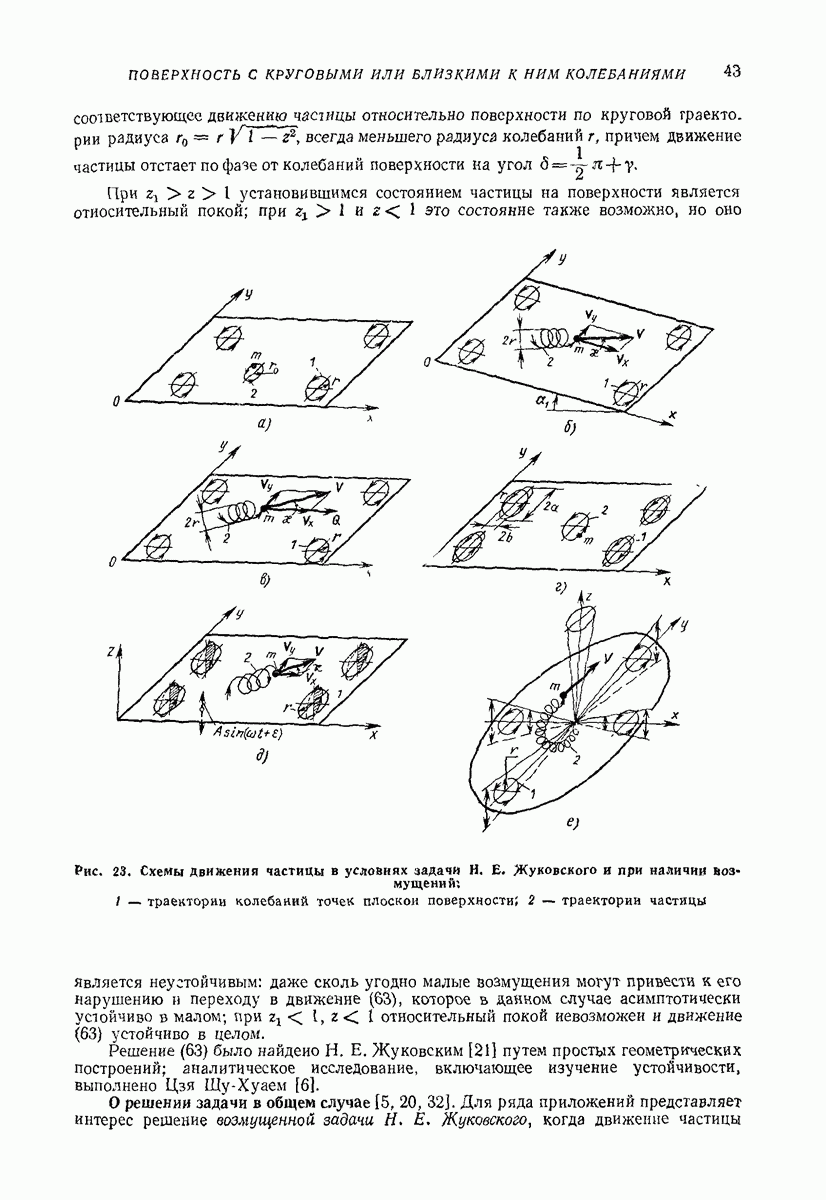
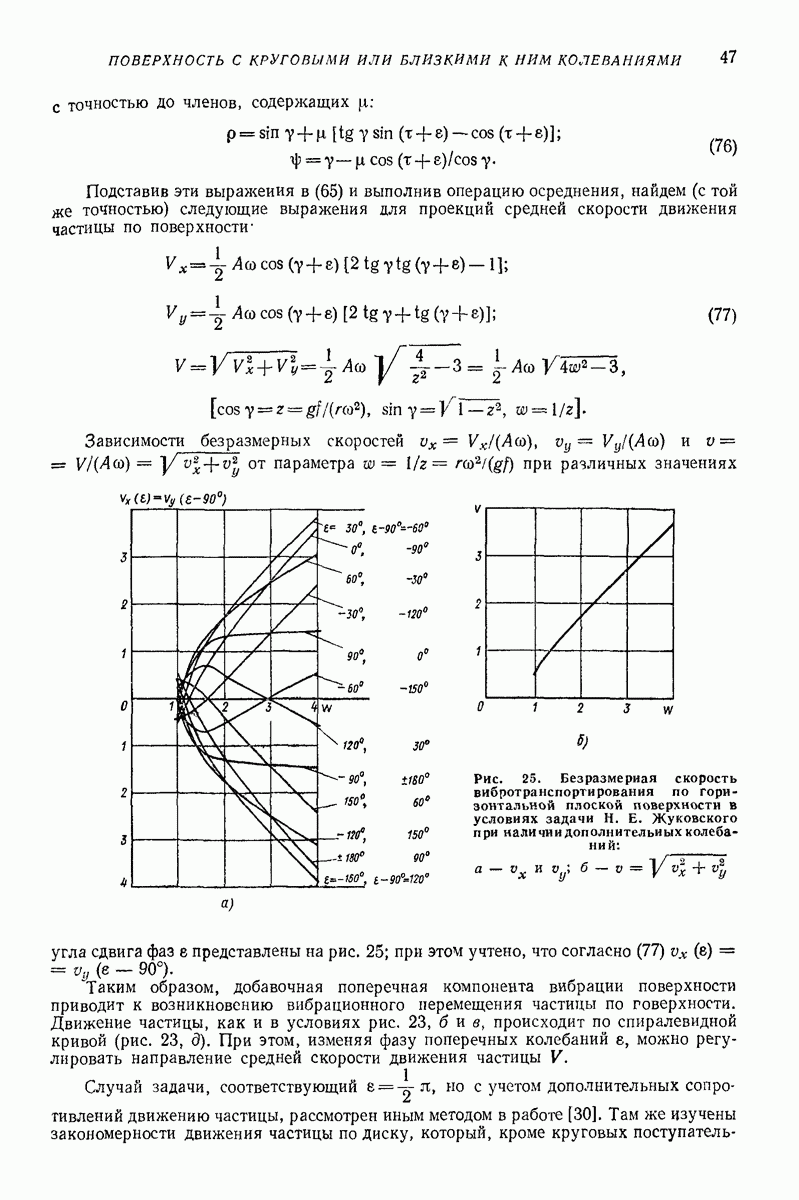
- 5. ГОРИЗОНТАЛЬНАЯ ИЛИ СЛАБОНАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО КРУГОВЫМ ТРАЕКТОРИЯМ, ПАРАЛЛЕЛЬНЫМ ЭТОЙ ЖЕ ПОВЕРХНОСТИ, ИЛИ БЛИЗКИЕ К НИМ
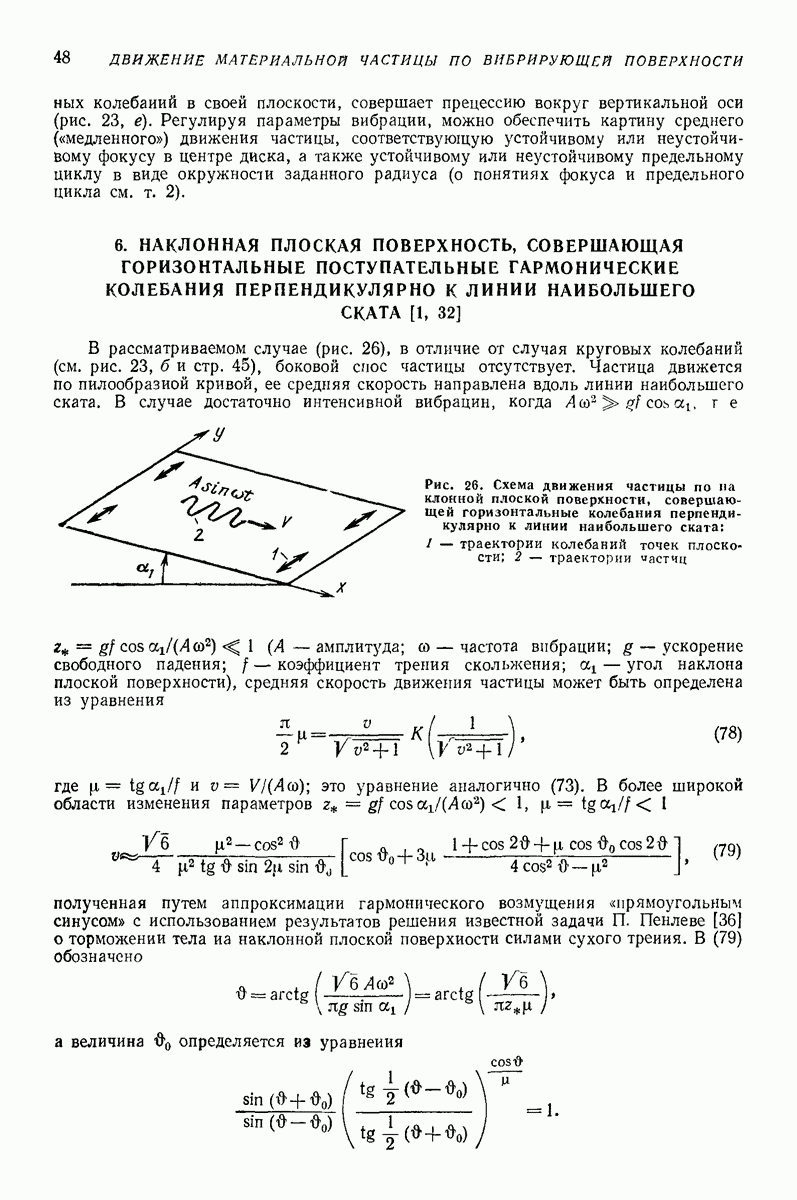
- 6. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ГОРИЗОНТАЛЬНЫЕ ПОСТУПАТЕЛЬНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРПЕНДИКУЛЯРНО К ЛИНИИ НАИБОЛЬШЕГО СКАТА [1, 32]
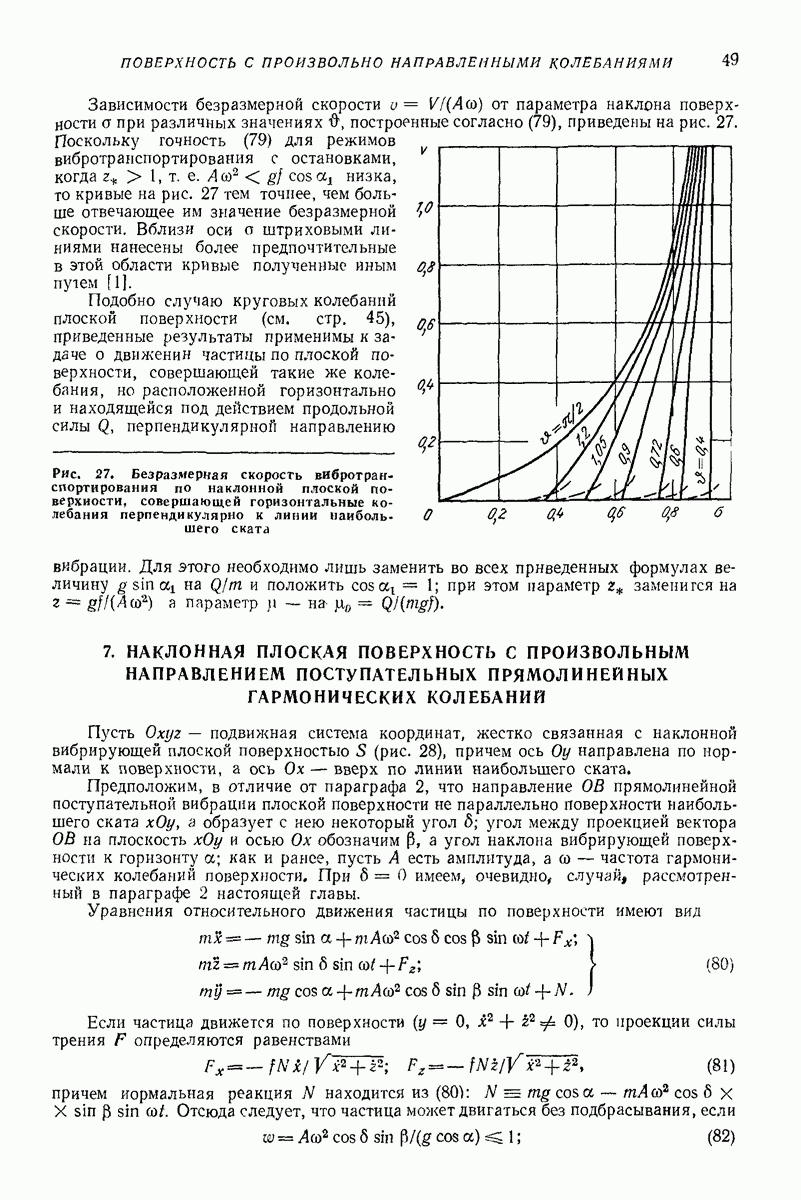
- 7. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ С ПРОИЗВОЛЬНЫМ НАПРАВЛЕНИЕМ ПОСТУПАТЕЛЬНЫХ ПРЯМОЛИНЕЙНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 8. НАКЛОННАЯ ПЛОСКАЯ ПОВЕРХНОСТЬ, СОВЕРШАЮЩАЯ ПОСТУПАТЕЛЬНЫЕ КОЛЕБАНИЯ ПО ЭЛЛИПТИЧЕСКИМ ТРАЕКТОРИЯМ, ПЕРПЕНДИКУЛЯРНЫМ ПЛОСКОСТИ НАИБОЛЬШЕГО СКАТА
- 9. ДВИЖЕНИЕ ЧАСТИЦЫ, ПОПЕРЕМЕННО КОНТАКТИРУЮЩЕЙ С ДВУМЯ ВИБРИРУЮЩИМИ ПОВЕРХНОСТЯМИ
- Глава II. ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ ПО ВИБРИРУЮЩЕЙ ПОВЕРХНОСТИ
- 1. ВЗАИМОДЕЙСТВИЕ ТВЕРДЫХ ТЕЛ С ЛОТКОМ. ГИПОТЕЗЫ И РАСЧЕТ
- 2. САМООРИЕНТАЦИЯ
- 3. ДВИЖЕНИЕ КРУГЛЫХ ТЕЛ
- 4. ДВИЖЕНИЕ ДЕТАЛЕЙ ПО УГЛОВОМУ ЛОТКУ
- 5. ОРИЕНТИРОВАНИЕ СТЕРЖНЕВЫХ ДЕТАЛЕЙ
- Глава III. ПОВЕДЕНИЕ СЫПУЧИХ ТЕЛ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
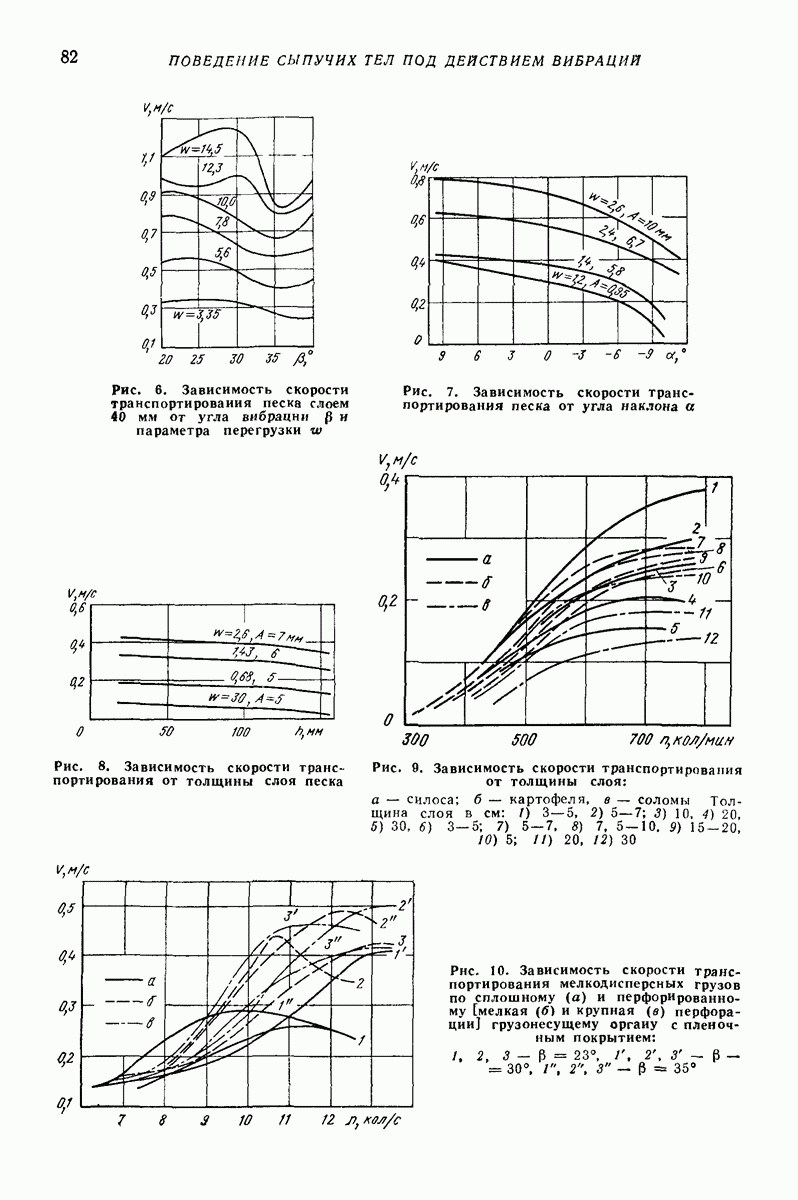
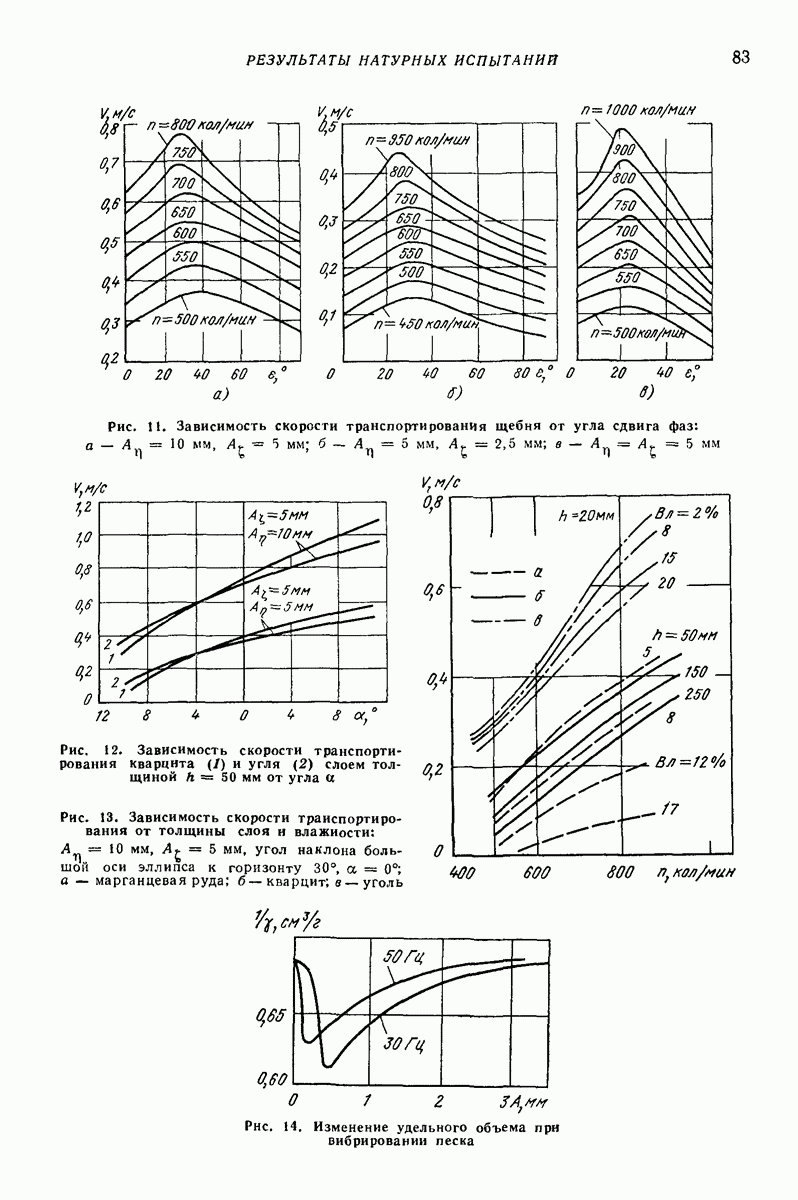
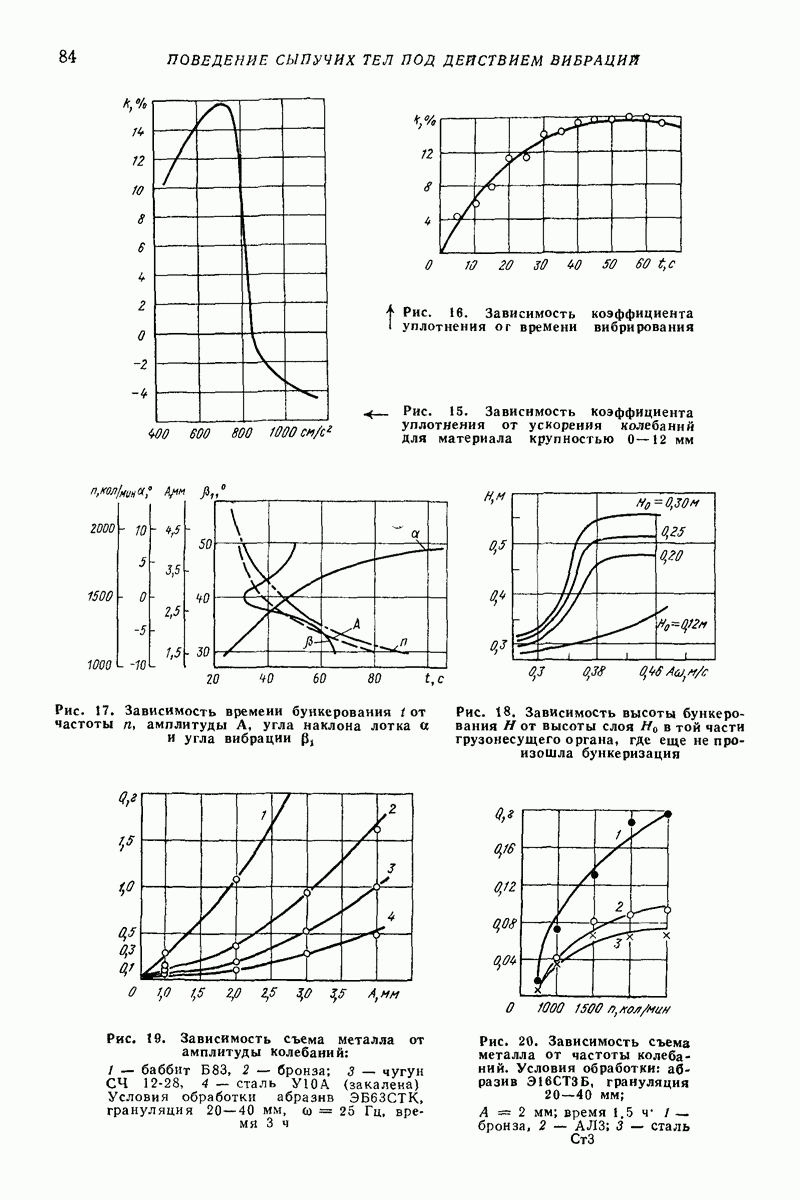
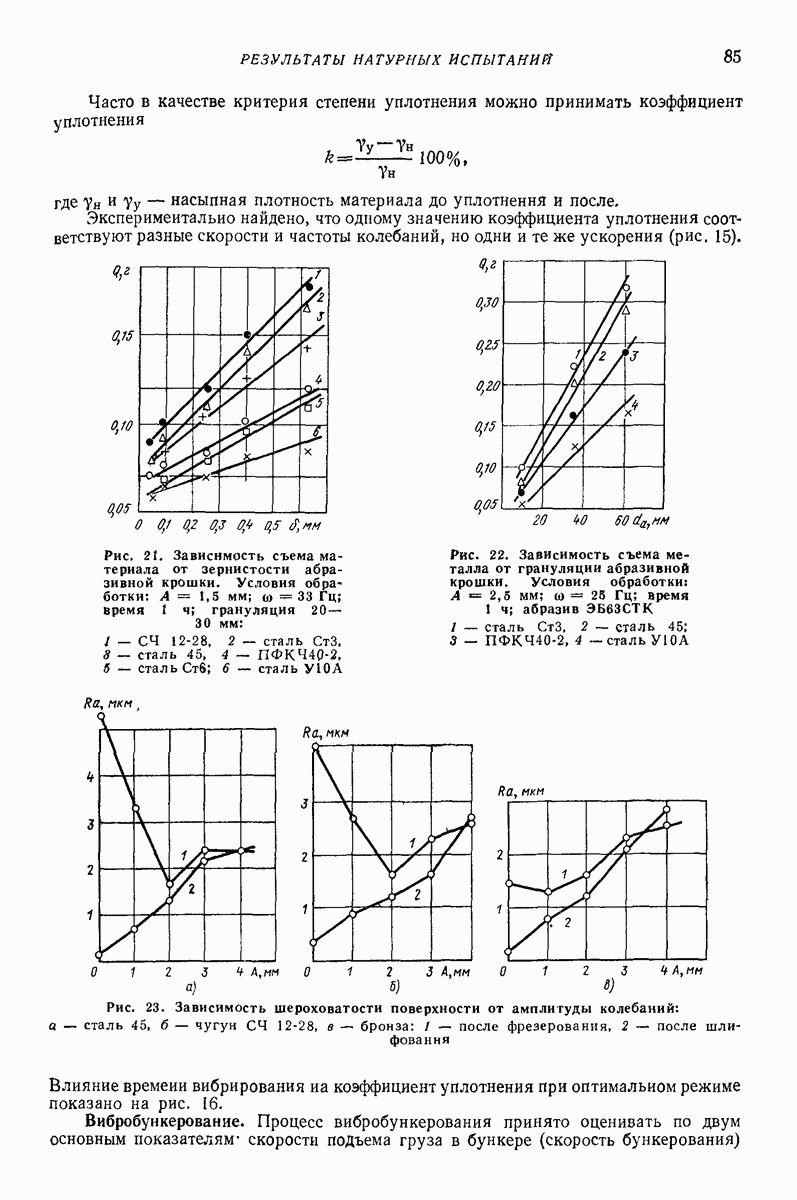
- 2. РЕЗУЛЬТАТЫ НАТУРНЫХ ИСПЫТАНИЙ
- 3. ПРОСТЕЙШИЕ МОДЕЛИ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ СЫПУЧИХ СРЕД
- 4. МОДЕЛИ ТИПА СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- 5. МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- 6. ПОВЕДЕНИЕ СЫПУЧЕЙ СРЕДЫ В СООБЩАЮЩИХСЯ ВИБРИРУЮЩИХ СОСУДАХ
- Глава IV. ПОВЕДЕНИЕ УПРУГОВЯЗКОПЛАСТИЧЕСКИХ И МНОГОФАЗНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ ВИБРАЦИИ
- 2. КОЛЕБАНИЯ ВЯЗКОУПРУГИХ СРЕД
- 3. ДЕЙСТВИЕ ЗНАКОПЕРЕМЕННЫХ НАГРУЗОК НА УПРУГОПЛАСТИЧЕСКИЕ СРЕДЫ
- 4. ПОВЕДЕНИЕ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
- 5. ВИБРОПОЛЗУЧЕСТЬ И ВИБРОРЕЛАКСАЦИЯ
- 6. ДВИЖЕНИЕ ЧАСТИЦЫ ОТНОСИТЕЛЬНО СРЕДЫ
- 7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОФАЗНЫХ СРЕД И МЕТОДЫ ИССЛЕДОВАНИЯ
- 8. ВИБРАЦИОННЫЕ ВОЛНОВЫЕ ЭФФЕКТЫ В МНОГОФАЗНЫХ СРЕДАХ И ИХ ПРИЛОЖЕНИЕ В ТЕХНИКЕ
- Глава V. ЗАДАЧИ ОПТИМИЗАЦИИ ВИБРАЦИОННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- 2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
- 3. КРИТЕРИЙ ОПТИМИЗАЦИИ
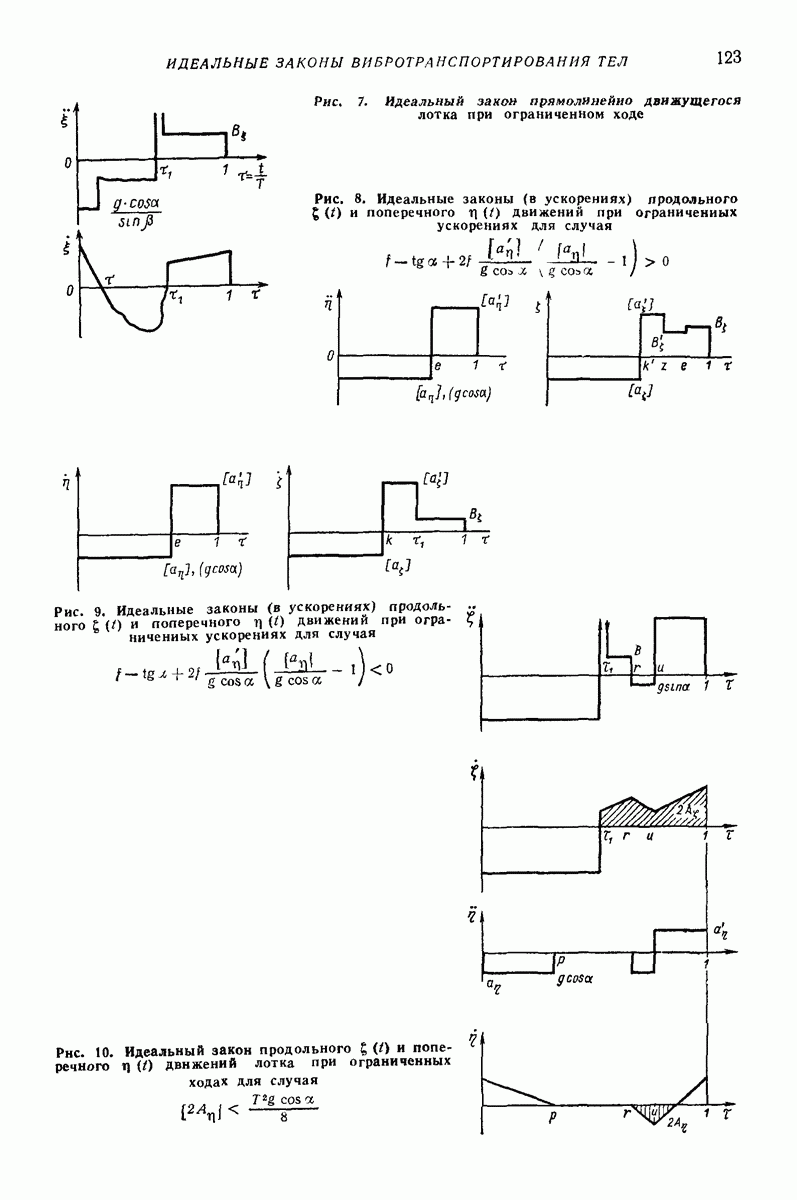
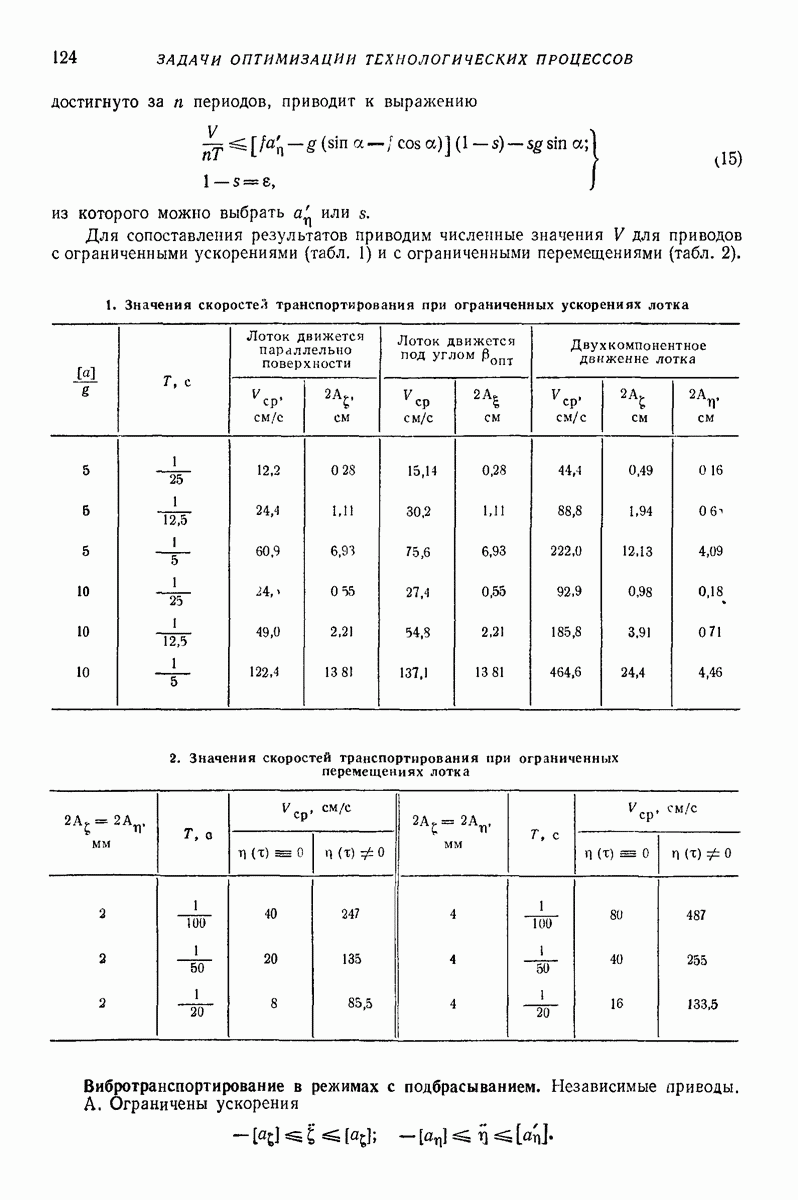
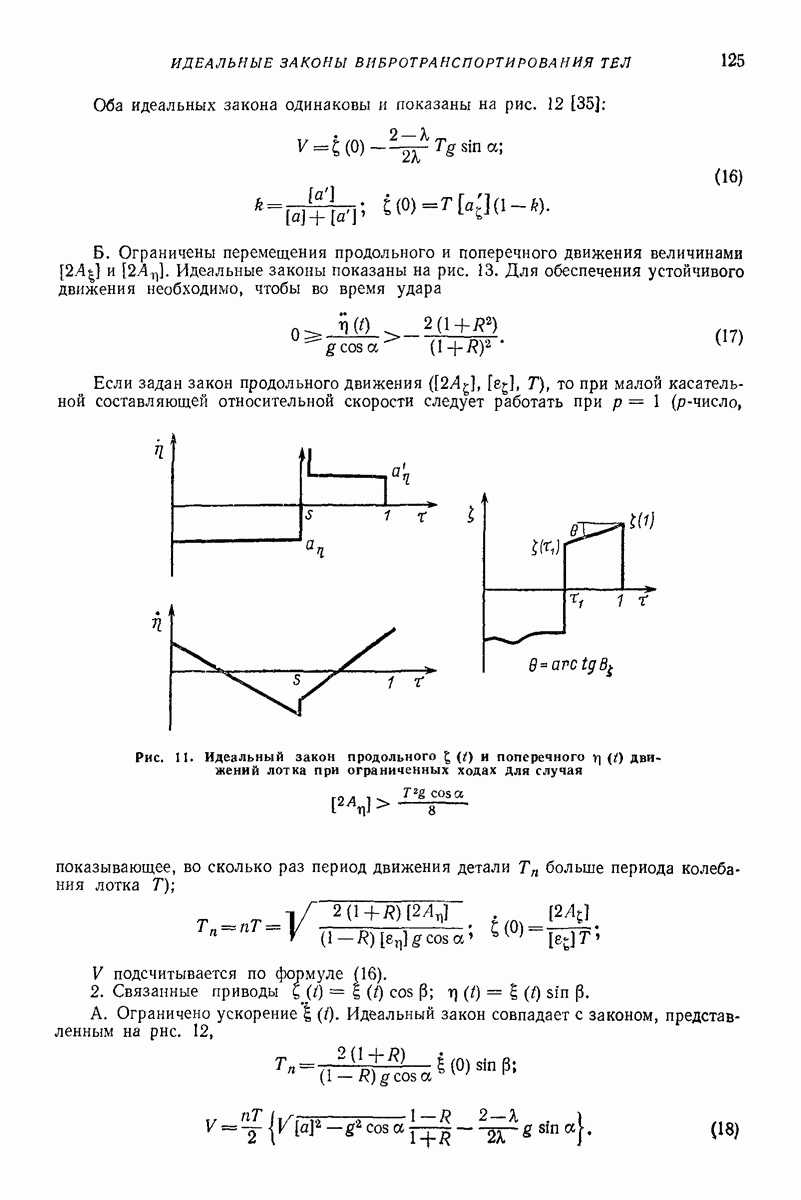
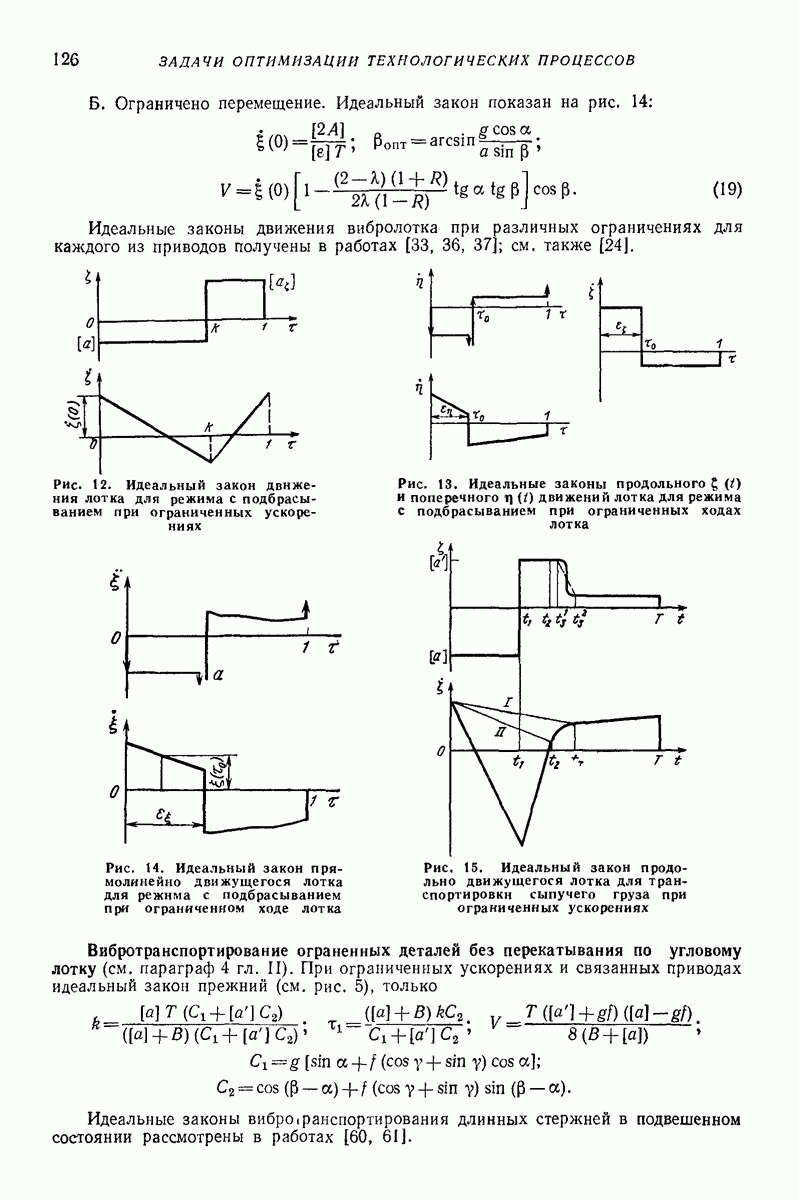
- 4. ПОЛУЧЕНИЕ ИДЕАЛЬНЫХ ЗАКОНОВ ДВИЖЕНИЯ
- 5. ИДЕАЛЬНЫЕ ЗАКОНЫ ВИБРОТРАНСПОРТИРОВАНИЯ ТВЕРДЫХ ПЛОСКИХ ТЕЛ
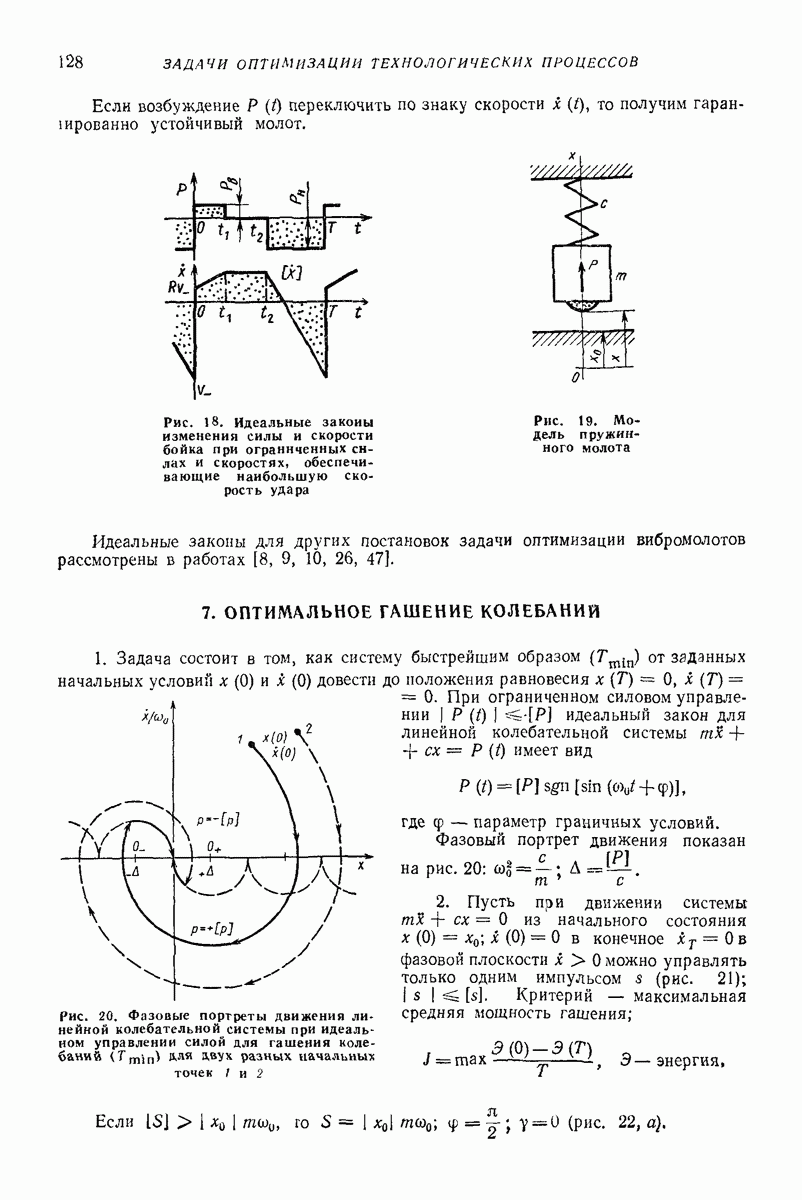
- 6. ИДЕАЛЬНЫЕ ЗАКОНЫ ДЛЯ ВИБРОМОЛОТОВ
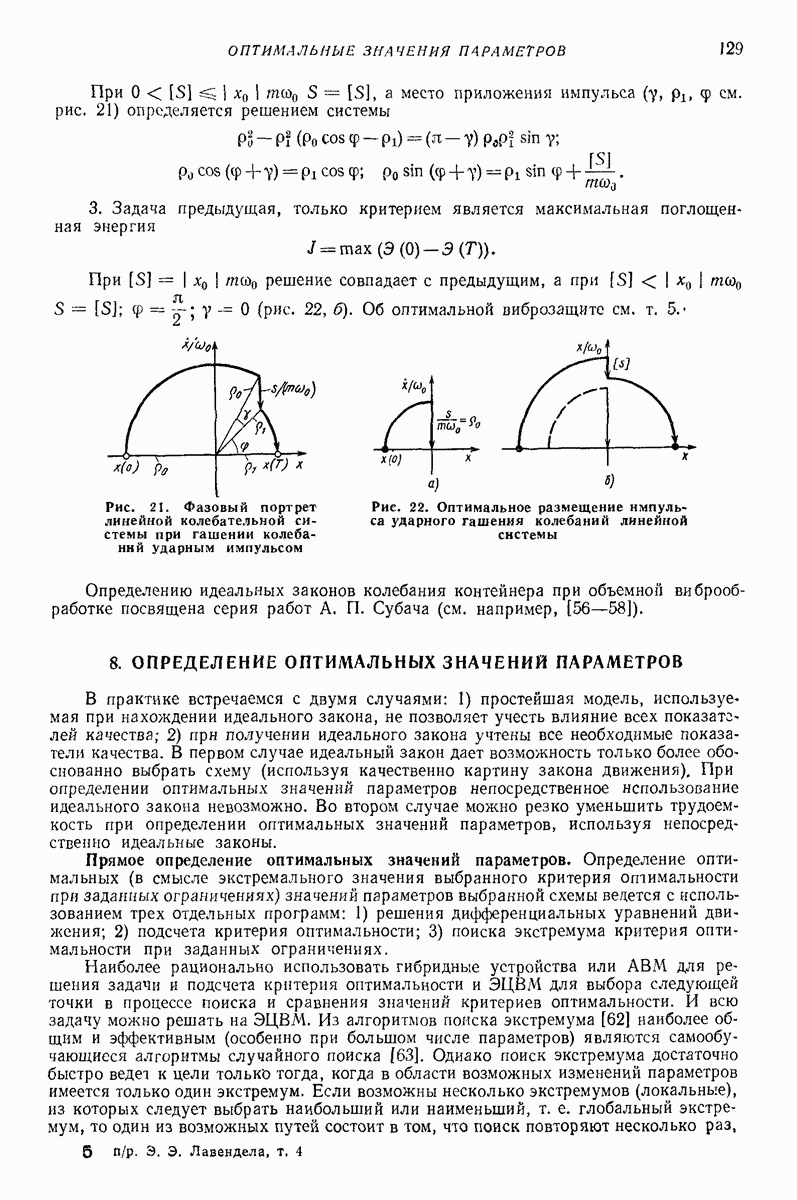
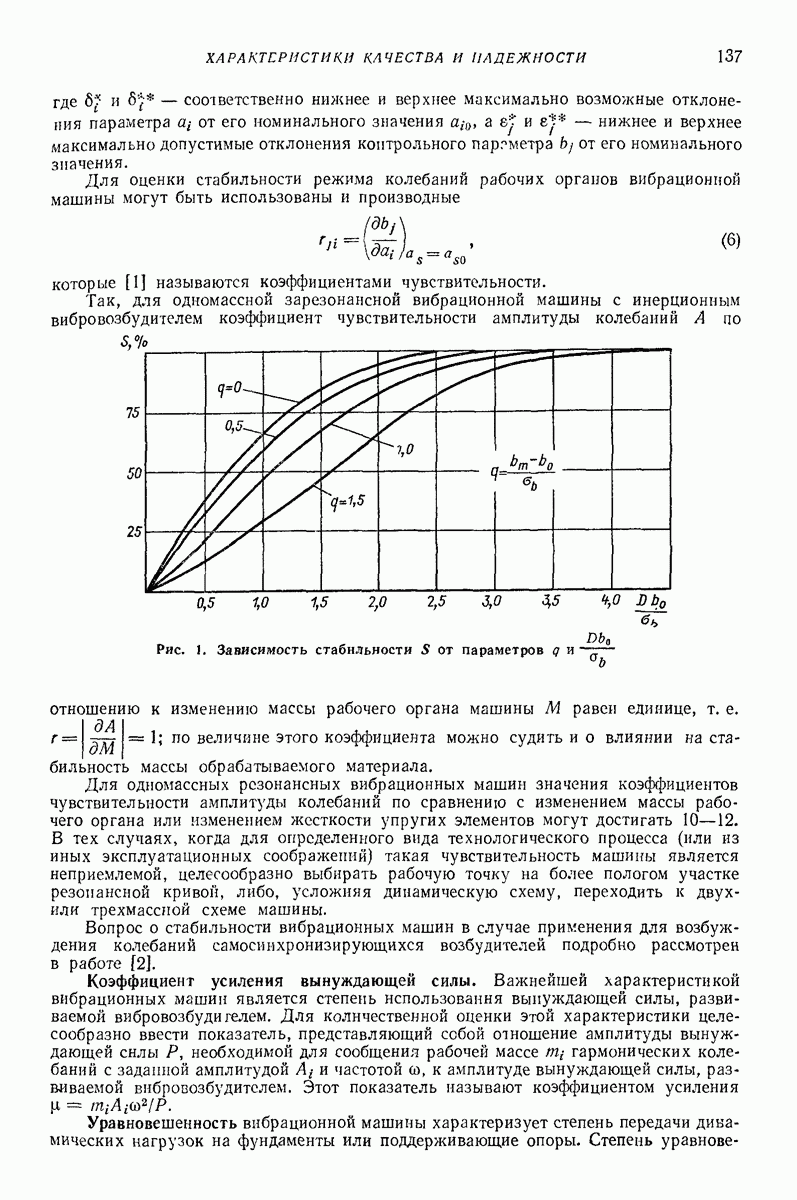
- 7. ОПТИМАЛЬНОЕ ГАШЕНИЕ КОЛЕБАНИЙ
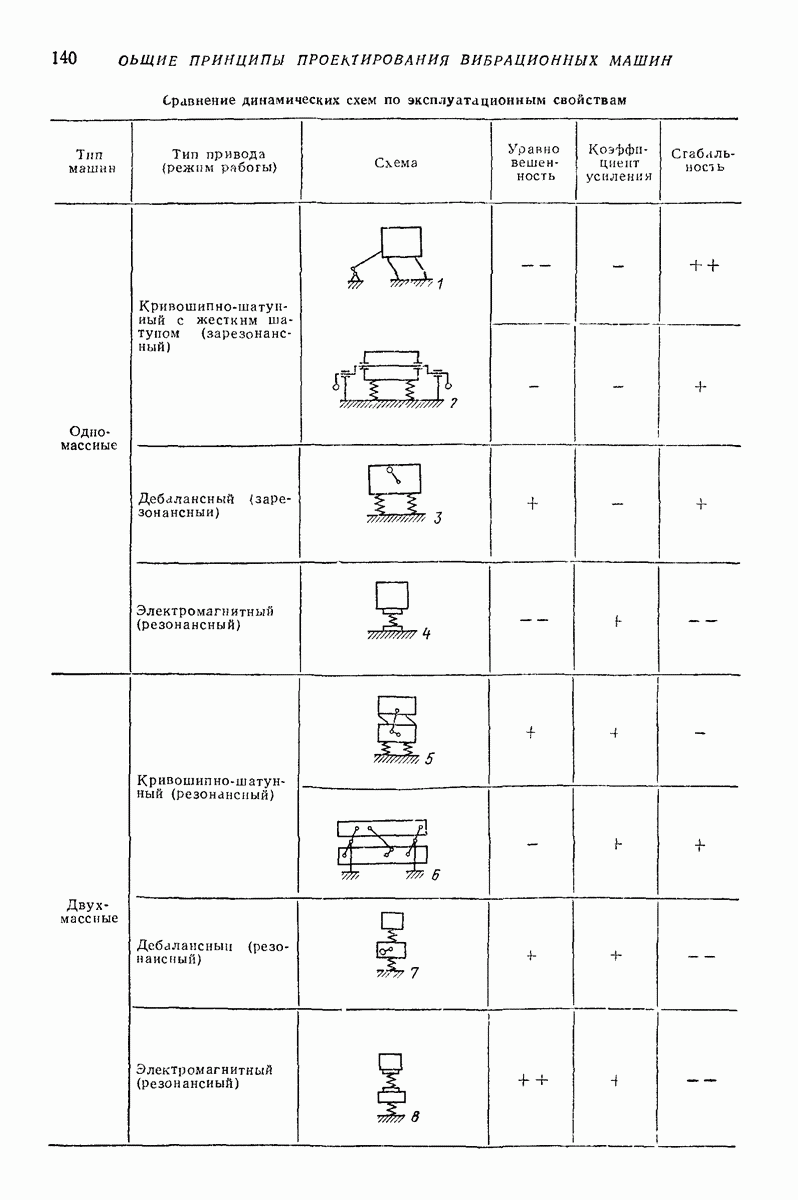
- 8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
- Часть вторая. ПРОЕКТИРОВАНИЕ И РАСЧЕТ ВИБРАЦИОННЫХ МАШИН
- Глава VI. ПРОЕКТИРОВАНИЕ ВИБРАЦИОННЫХ МАШИН
- 2. ВЫБОР ХАРАКТЕРА И ПАРАМЕТРОВ КОЛЕБАНИЙ РАБОЧЕГО ОРГАНА
- 3. ВЫБОР ОБЩЕЙ ДИНАМИЧЕСКОЙ СХЕМЫ ВИБРАЦИОННОЙ МАШИНЫ И СПОСОБА ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
- 4. ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ МАШИН
- Глава VII. СИНТЕЗ ВИБРАЦИОННЫХ ПОЛЕЙ И СОЗДАНИЕ ЗАДАННОГО ПОЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИИ УПРУГОЙ СИСТЕМЫ
- 1. ЗАДАЧА СИНТЕЗА ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ И ЕЕ ОСОБЕННОСТИ [2]
- 2. ПОЛЕ МАЛЫХ КОЛЕБАНИИ ТВЕРДОГО ТЕЛА, ВОЗБУЖДАЕМОЕ СИНХРОННО РАБОТАЮЩИМИ ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 3. ВОЗБУЖДЕНИЕ ВИБРАЦИОННЫХ ПОЛЕЙ УПРУГИХ ТЕЛ
- Глава VIII. РАСЧЕТ БЕЗУДАРНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. ОБЕСПЕЧЕНИЕ ТРЕБУЕМОГО РАЗМАХА ВИБРАЦИИ
- 3. ВЫБОР ВАРИАНТА УСТАНОВКИ ВИБРОВОЗБУДИТЕЛЯ НА ОДНОМ ИЗ ИНЕРЦИОННЫХ ЭЛЕМЕНТОВ МАШИНЫ
- 4. МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОДДЕРЖАНИЯ ВИБРАЦИИ
- 5. ЭКВИВАЛЕНТНЫЕ ЗНАЧЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ
- Глава IX. РАСЧЕТ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 2. МОДЕЛЬ ТВЕРДОГО ТЕЛА С МЕСТНЫМИ ДЕФОРМАЦИЯМИ [6]
- 3. МОДЕЛЬ МНОГОМАССНОЙ СИСТЕМЫ
- 4. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ МАССАМИ И ЗАДАННОЙ ФОРМОЙ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
- 5. МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [6]
- 6. АЛГОРИТМЫ РАСЧЕТА УДАРНО-ВИБРАЦИОННЫХ МАШИН [4]
- Глава X. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ВИБРАЦИОННЫХ МАШИНАХ С ДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
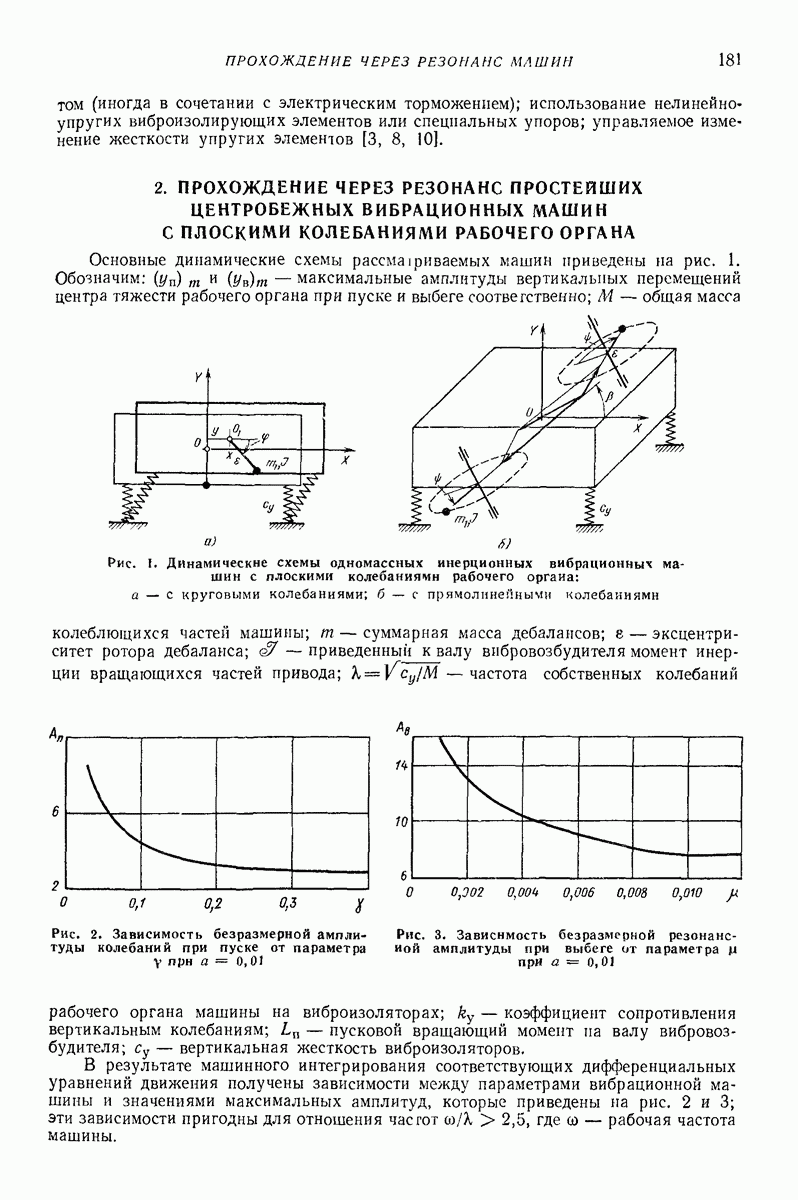
- 2. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ПРОСТЕЙШИХ ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ПЛОСКИМИ КОЛЕБАНИЯМИ РАБОЧЕГО ОРГАНА
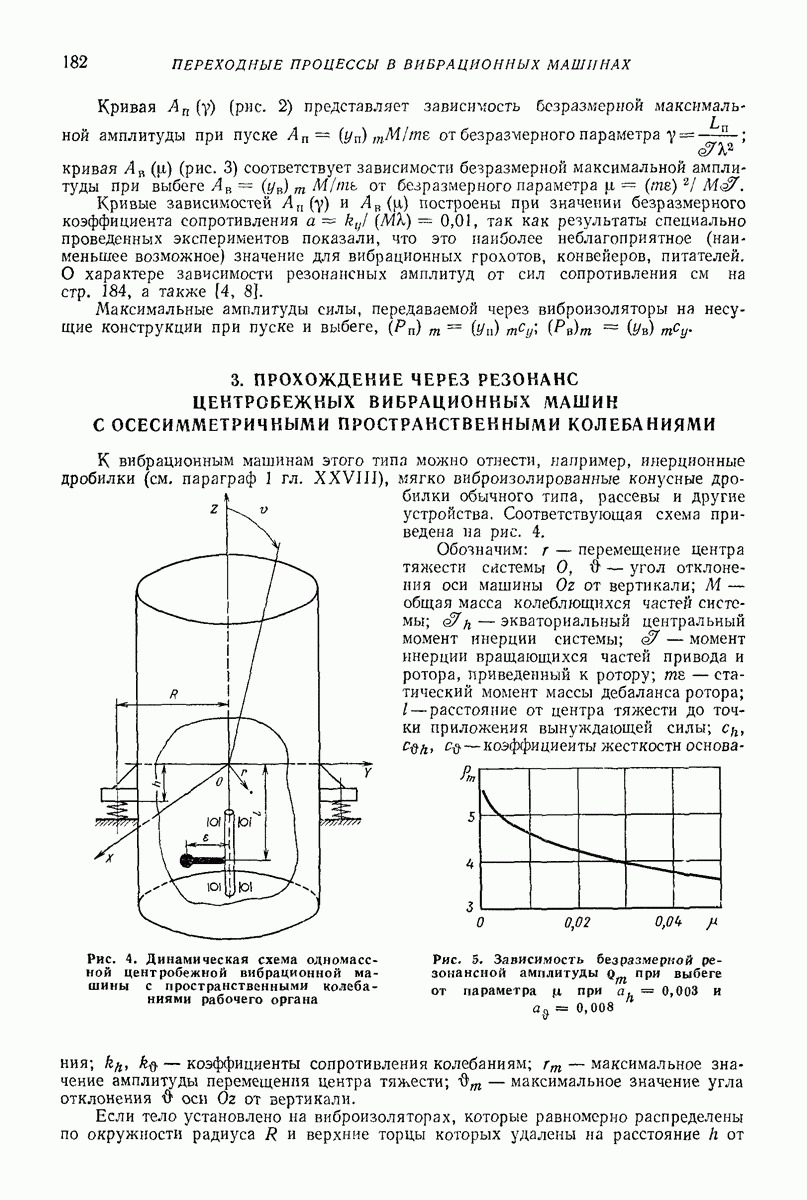
- 3. ПРОХОЖДЕНИЕ ЧЕРЕЗ РЕЗОНАНС ЦЕНТРОБЕЖНЫХ ВИБРАЦИОННЫХ МАШИН С ОСЕСИММЕТРИЧНЫМИ ПРОСТРАНСТВЕННЫМИ КОЛЕБАНИЯМИ
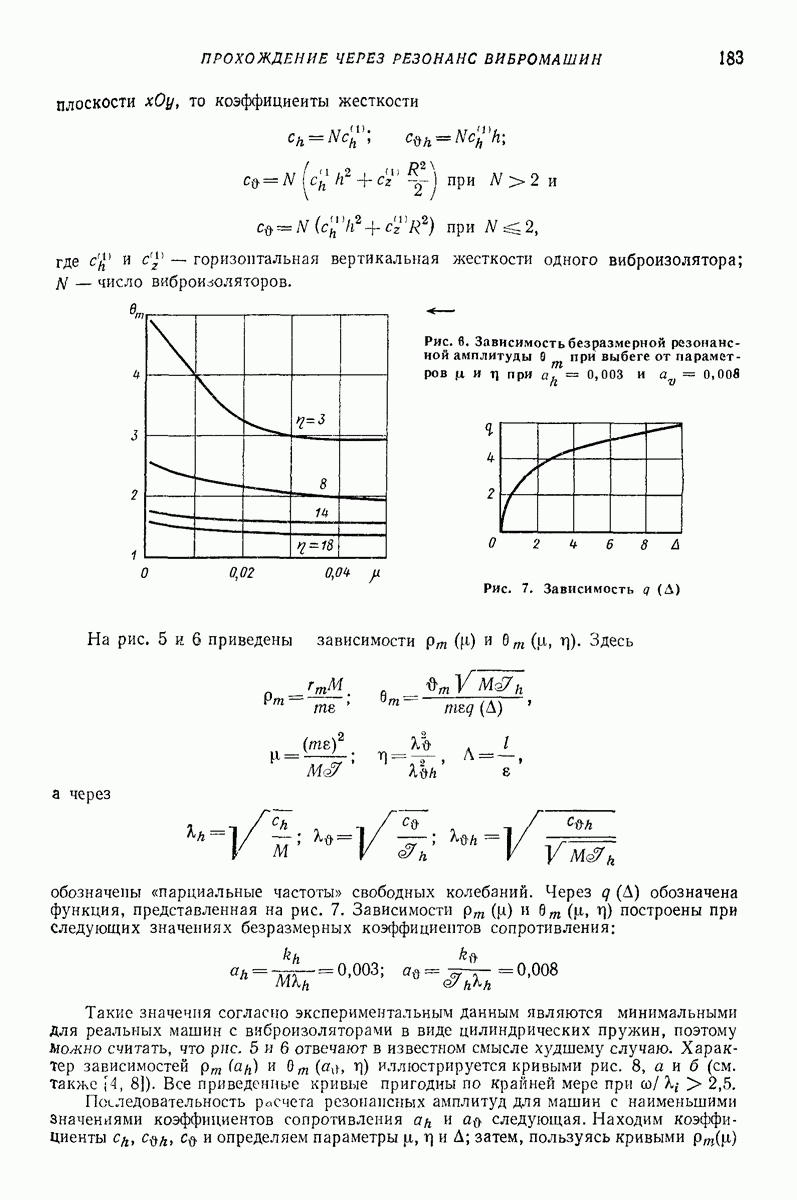
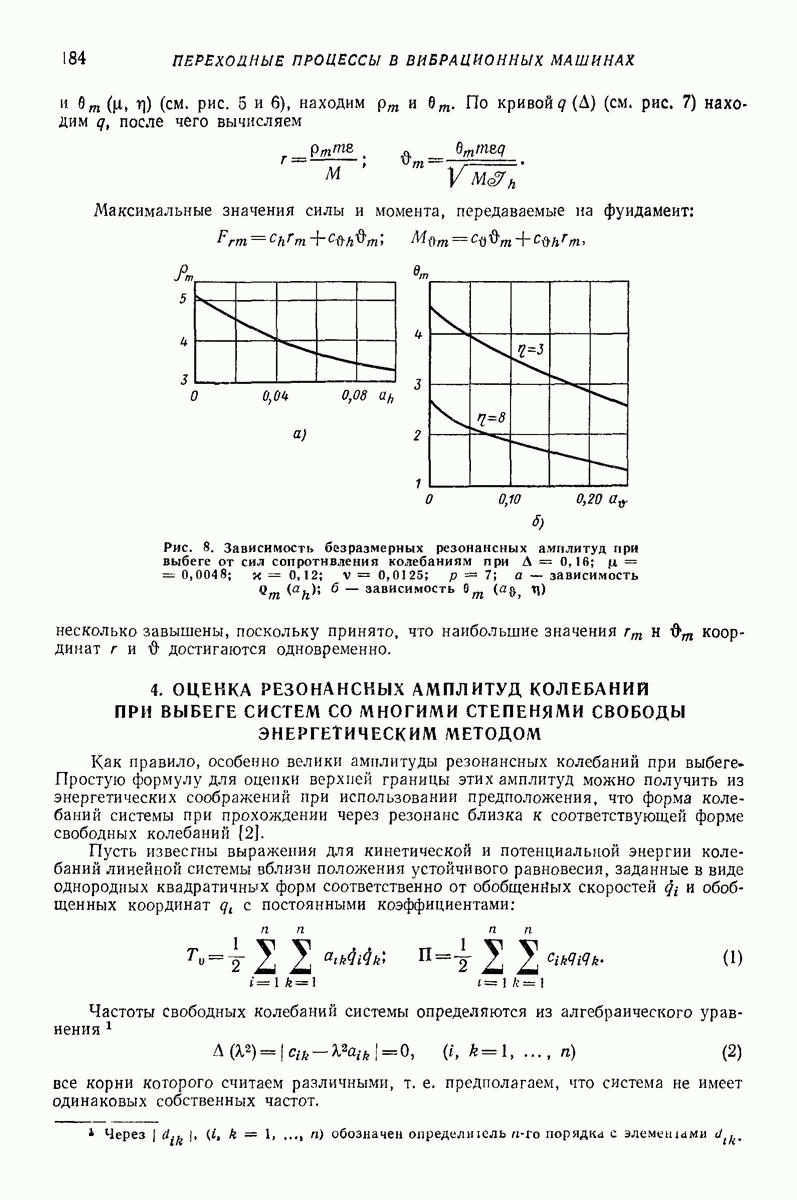
- 4. ОЦЕНКА РЕЗОНАНСНЫХ АМПЛИТУД КОЛЕБАНИЙ ПРИ ВЫБЕГЕ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
- Глава XI. УПРУГИЕ ЭЛЕМЕНТЫ ВИБРАЦИОННЫХ МАШИН
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 2. МАТЕРИАЛЫ МЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ [2, 22]
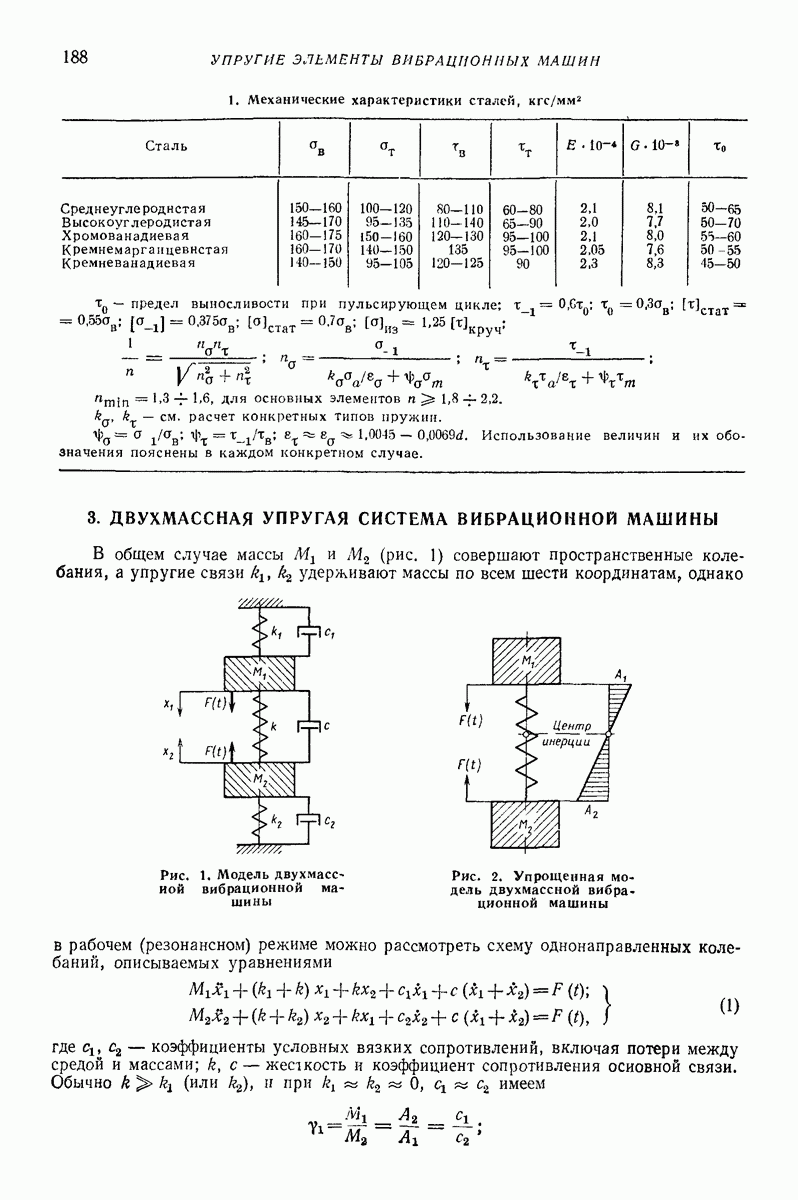
- 3. ДВУХМАССНАЯ УПРУГАЯ СИСТЕМА ВИБРАЦИОННОЙ МАШИНЫ
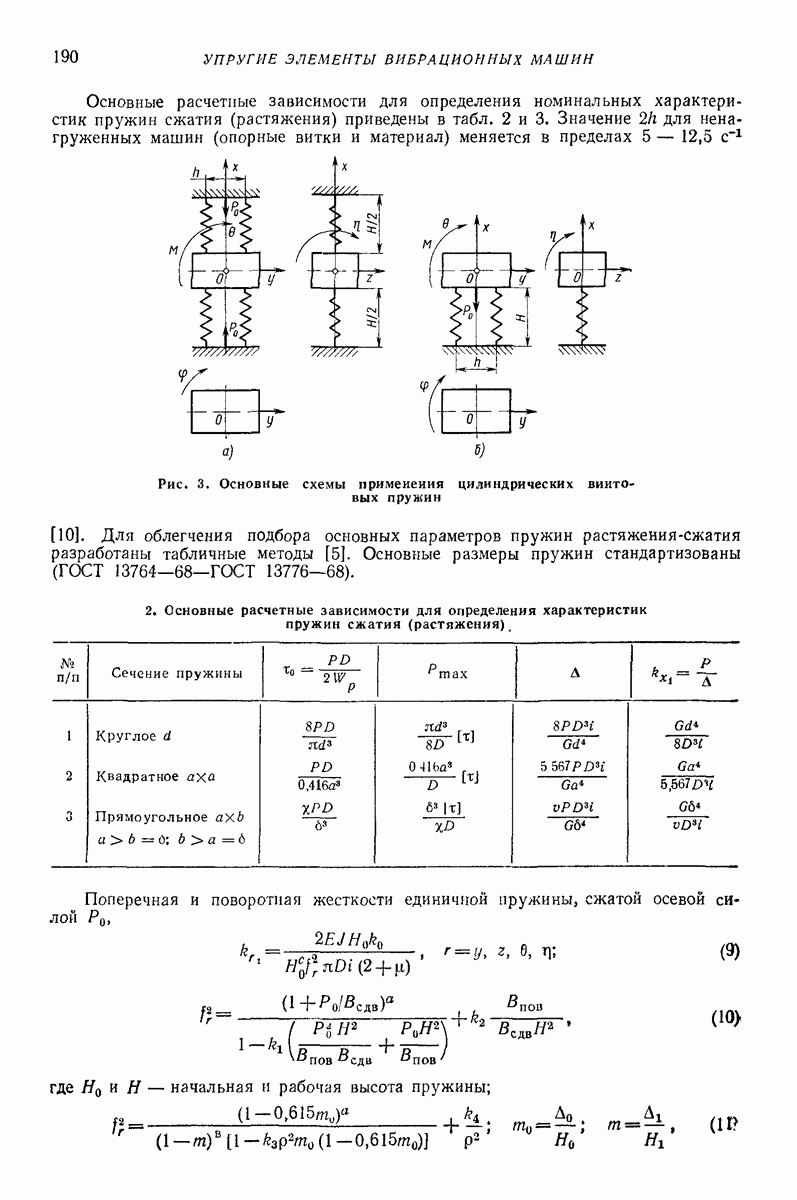
- 4. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ
- 5. ПРОРЕЗНЫЕ ПРУЖИНЫ С ВИНТОВЫМ ПАЗОМ
- 6. КОЛЬЦЕВЫЕ ПРУЖИНЫ
- 7. РЕССОРНАЯ УПРУГАЯ СИСТЕМА
- 8. УПРУГИЕ ЭЛЕМЕНТЫ БУНКЕРНЫХ ВИБРАЦИОННЫХ ПИТАТЕЛЕЙ И ВИБРОПОДЪЕМНИКОВ
- 9. ТОРСИОННЫЕ УПРУГИЕ ЭЛЕМЕНТЫ
- 10. ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ
- 11. ПРИВЕДЕННЫЕ МАССЫ УПРУГИХ ЭЛЕМЕНТОВ
- 12. УПРУГИЕ СИСТЕМЫ С РЕГУЛИРУЕМОЙ ЖЕСТКОСТЬЮ
- 13. ИСПОЛЬЗОВАНИЕ УЗЛОВЫХ ТОЧЕК ОСНОВНЫХ УПРУГИХ ЭЛЕМЕНТОВ В КАЧЕСТВЕ ОПОР ДЛЯ ВИБРОИЗОЛЯТОРОВ
- 14. ПАРАЗИТНЫЕ КОЛЕБАНИЯ
- 15. ГЕНЕРИРОВАНИЕ СУБ- И СУПЕРГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 16. ОБЩАЯ ХАРАКТЕРИСТИКА РЕЗИНОМЕТАЛЛИЧЕСКИХ УПРУГИХ ЭЛЕМЕНТОВ
- 17. УПРУГИЕ ЭЛЕМЕНТЫ С ЛИНЕЙНОЙ (СЛАБОНЕЛИНЕЙНОИ) ХАРАКТЕРИСТИКОЙ [13]
- 18. УПРУГИЕ ЭЛЕМЕНТЫ С ЗАДАННОЙ ЖЕСТКОЙ ХАРАКТЕРИСТИКОЙ
- 19. УПРУГИЕ ЭЛЕМЕНТЫ С РЕЗКО ОТЛИЧАЮЩИМИСЯ ЖЕСТКОСТЯМИ В РАЗНЫХ НАПРАВЛЕНИЯХ
- 20. УПРУГИЕ ЭЛЕМЕНТЫ С МЯГКОЙ ХАРАКТЕРИСТИКОЙ
- 21. ПНЕВМОБАЛЛОНЫ
- 22. РАСЧЕТ УПРУГИХ ЭЛЕМЕНТОВ ВИБРОМАШИН
- Глава XII. ВОПРОСЫ ЗАЩИТЫ ОТ ШУМА ПРИ ПРОЕКТИРОВАНИИ ВИБРАЦИОННЫХ МАШИН
- 2. ИЗЛУЧЕНИЕ ШУМА ВИБРАЦИОННЫМИ МАШИНАМИ
- 3. ЗВУКОВАЯ ВИБРАЦИЯ МАШИН
- Часть третья. ВИБРОВОЗБУДИТЕЛИ
- Глава XIII. МЕТОДЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 2. РАЗЛИЧНЫЕ СПОСОБЫ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 3. ТИПЫ ВИБРОВОЗБУДИТЕЛЕИ
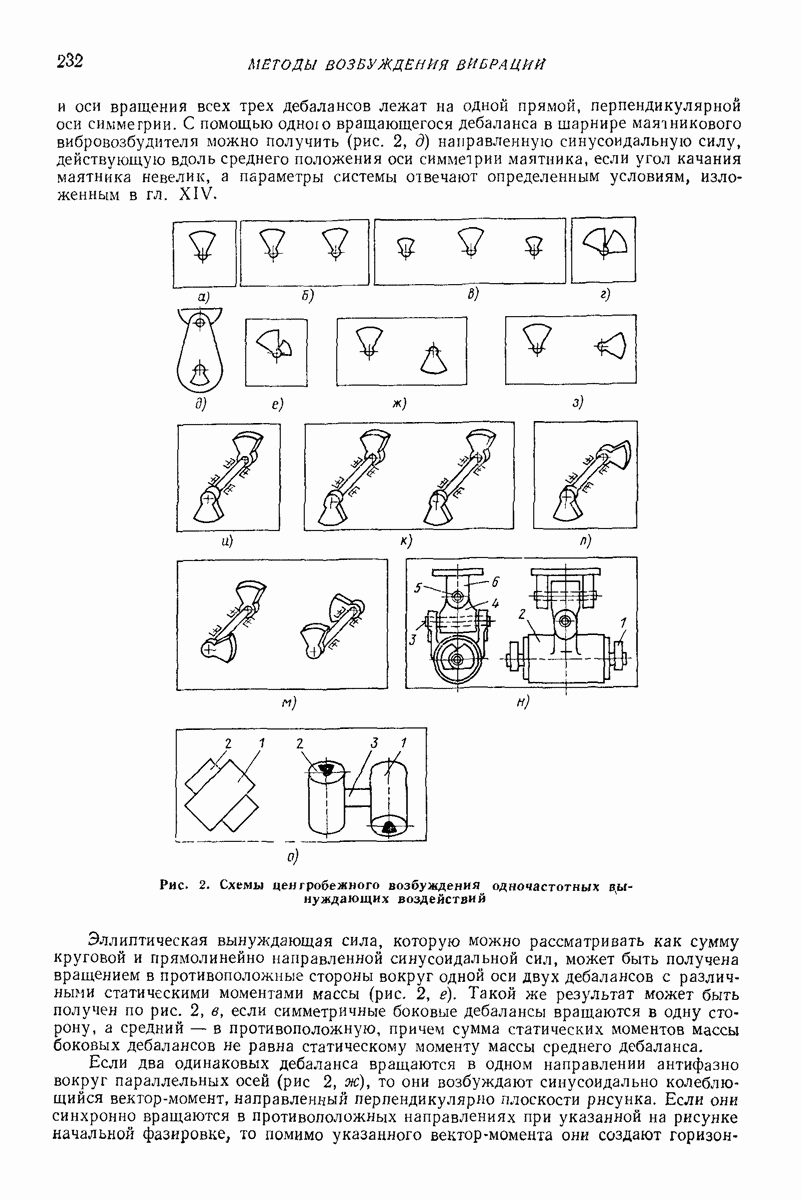
- 4. ЦЕНТРОБЕЖНОЕ ВОЗБУЖДЕНИЕ ОДНОЧАСТОТНЫХ ВЫНУЖДАЮЩИХ СИЛ И МОМЕНТОВ
- Глава XIV. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
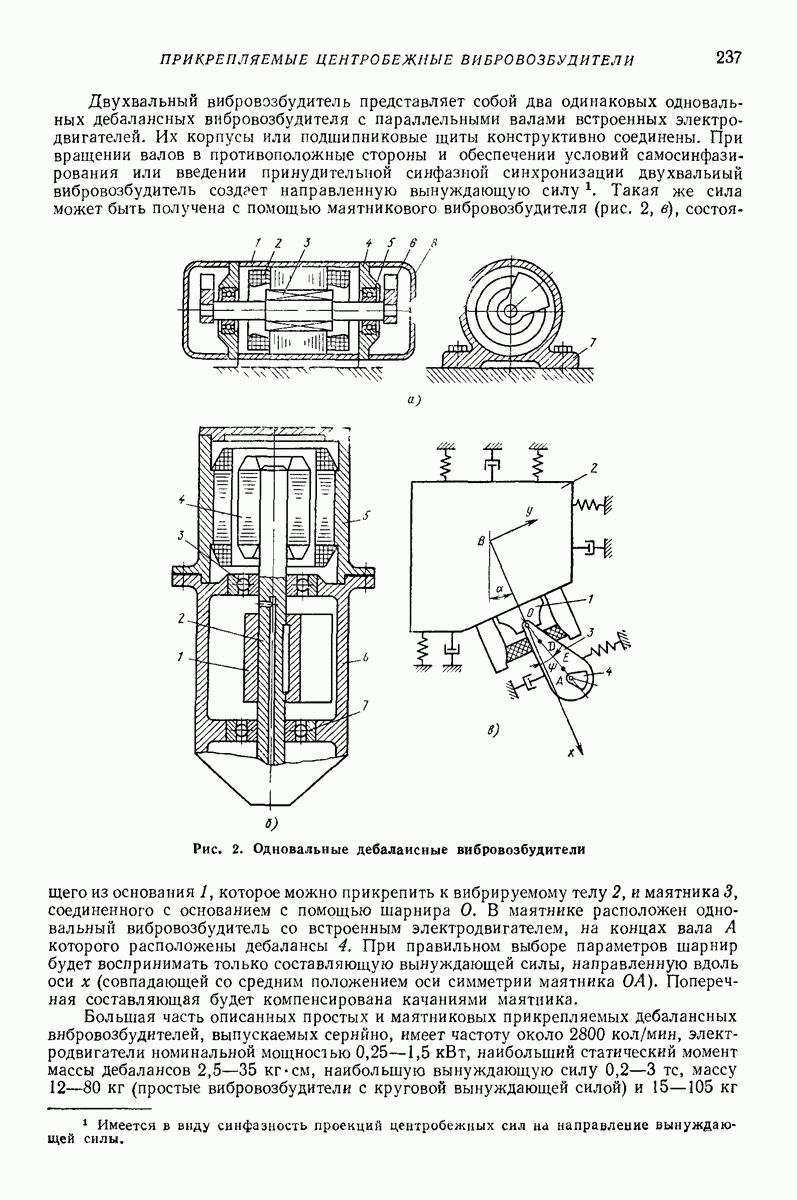
- 2. ПРИКРЕПЛЯЕМЫЕ ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ
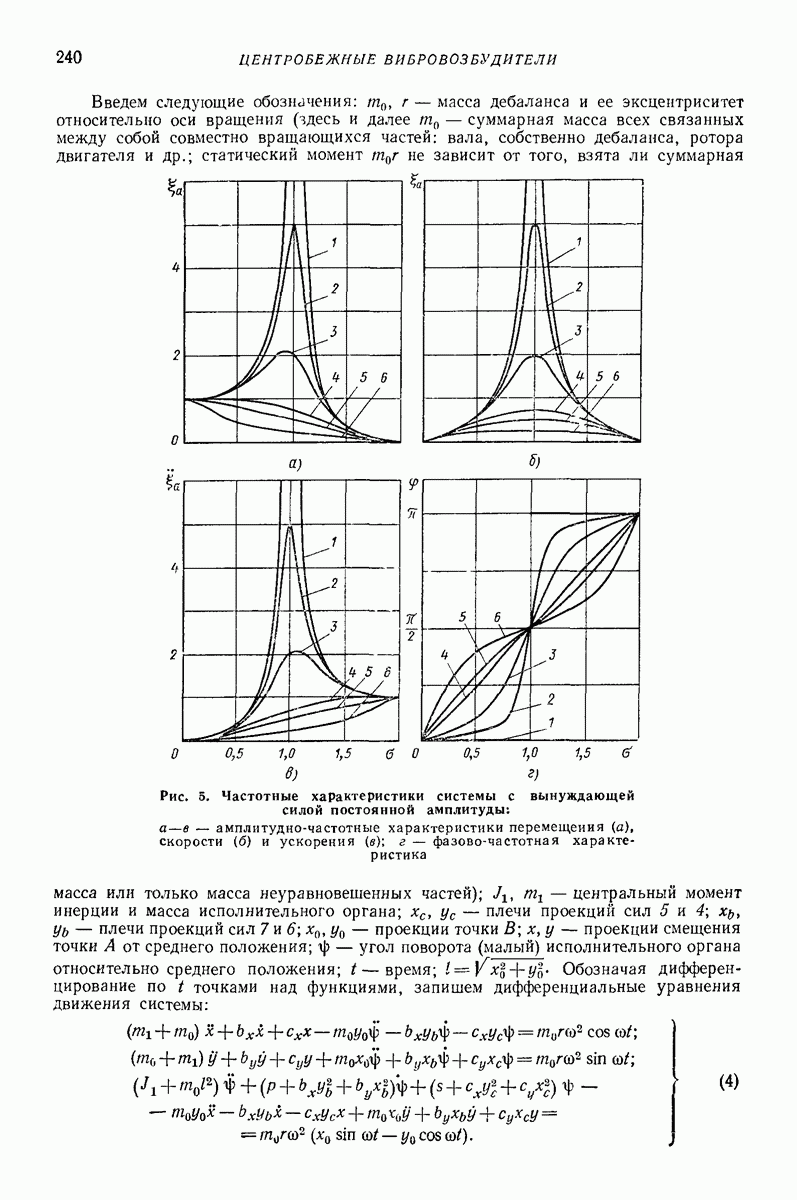
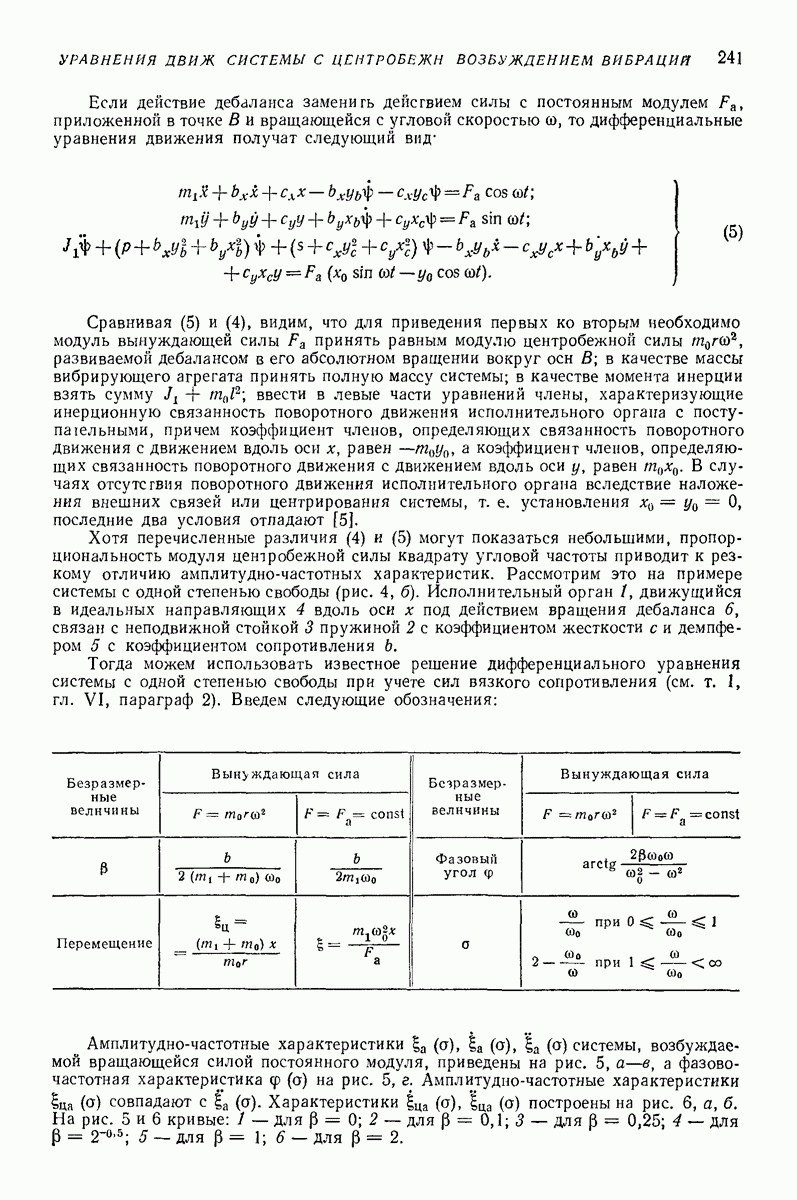
- 3. УРАВНЕНИЯ ДВИЖЕНИЯ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СИСТЕМЫ С ЦЕНТРОБЕЖНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. ОСОБЕННОСТИ ДИНАМИКИ МАЯТНИКОВЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 5. ОСОБЕННОСТИ ДИНАМИКИ ГЛУБИННЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 6. НЕРАВНОМЕРНОСТЬ ВРАЩЕНИЯ ДЕБАЛАНСОВ И НЕСБАЛАНСИРОВАННЫХ БЕГУНКОВ
- 7. СУПЕРГАРМОНИЧЕСКИЙ ВИБРОПРИВОД
- 8. ОПТИМИЗАЦИЯ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ДЕБАЛАНСОВ И РАДИУСА БЕГУНКОВ
- Глава XV. ЭЛЕКТРОМАГНИТНЫЕ ВИБРОВОЗБУДИТЕЛИ
- 1. ОБЩАЯ ХАРАКТЕРИСТИКА ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 2. ЭЛЕКТРИЧЕСКИЕ СХЕМЫ И КЛАССИФИКАЦИЯ
- 3. ОСОБЕННОСТИ ДИНАМИКИ ВИБРАЦИОННЫХ УСТРОЙСТВ С ЭЛЕКТРОМАГНИТНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
- 4. ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ УСТРОЙСТВ И РАСЧЕТ ЭЛЕКТРОМАГНИТОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ ВОЗБУЖДЕНИЯ ВИБРАЦИИ
- 5. НАСТРОЙКА МНОГОПРИВОДНЫХ ВИБРАЦИОННЫХ МАШИН С ПРОТЯЖЕННЫМ РАБОЧИМ ОРГАНОМ
- Глава XVI. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 2. ОСНОВНЫЕ СХЕМЫ
- 3. ОСНОВЫ РАСЧЕТА
- Глава XVII. КИНЕМАТИЧЕСКИЕ И ПРИНУДИТЕЛЬНЫЕ ВИБРОВОЗБУДИТЕЛИ
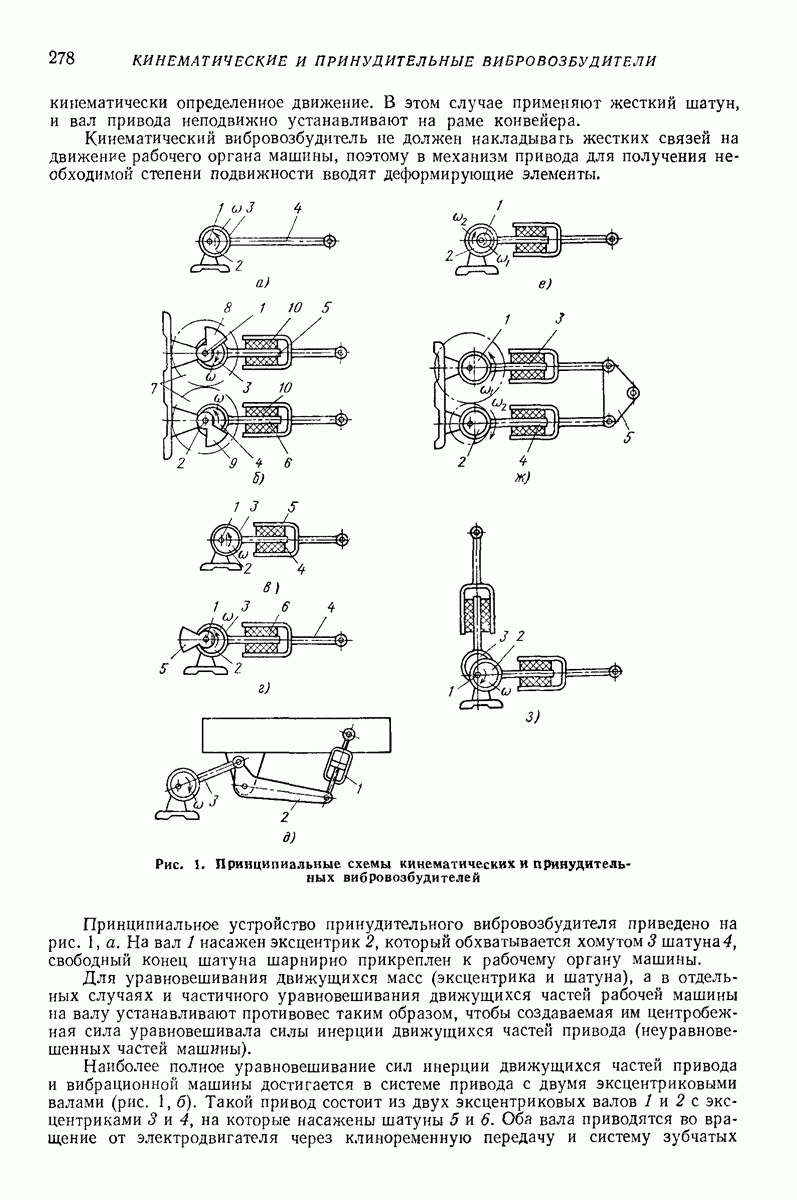
- 1. ПРИНЦИП ДЕЙСТВИЯ КИНЕМАТИЧЕСКИХ И ПРИНУДИТЕЛЬНЫХ ВИБРОВОЗБУДИТЕЛЕЙ
- 2. КЛАССИФИКАЦИЯ
- 3. МЕТОДЫ РАСЧЕТА ЭКСЦЕНТРИКОВОГО ПРИВОДА
- Глава XVIII. ГИДРАВЛИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
- 3. ОСНОВНЫЕ КОНСТРУКТИВНЫЕ СХЕМЫ И РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ
- Глава XIX. ПНЕВМАТИЧЕСКИЕ ВИБРОВОЗБУДИТЕЛИ
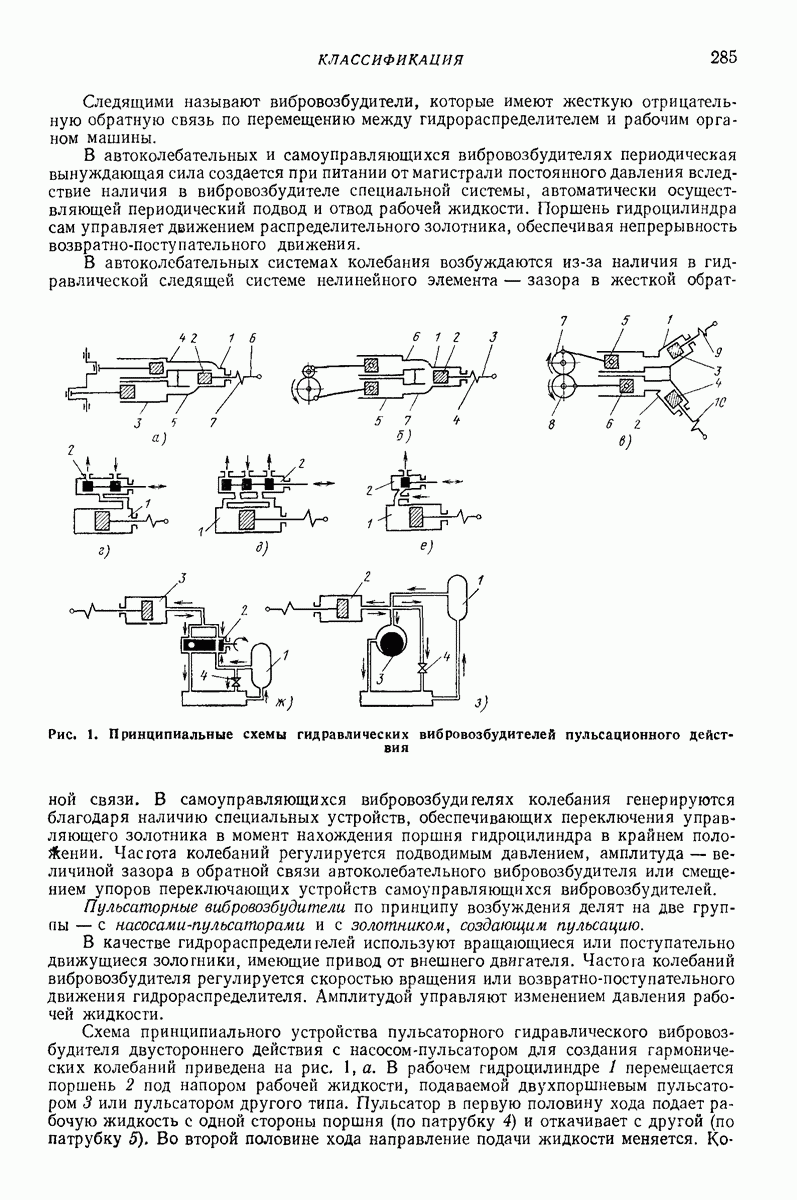
- 2. ВИБРОВОЗБУДИТЕЛИ С ПУЛЬСАТОРОМ
- 3. АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- 4. ЦЕНТРОБЕЖНЫЕ ВИБРОВОЗБУДИТЕЛИ С ПНЕВМАТИЧЕСКИМ ПРИВОДОМ
- 5. ВИБРОВОЗБУДИТЕЛИ С АВТОКОЛЕБАТЕЛЬНЫМ ПРОЦЕССОМ В ПОТОКЕ СЖАТОГО ВОЗДУХА
- 6. РАСЧЕТ ДИНАМИКИ ПОРШНЕВЫХ ПРИВОДОВ
- 7. РАСЧЕТ МЕМБРАННЫХ ПРИВОДОВ
- Часть четвертая. ВИБРАЦИОННЫЕ МАШИНЫ И УСТРОЙСТВА
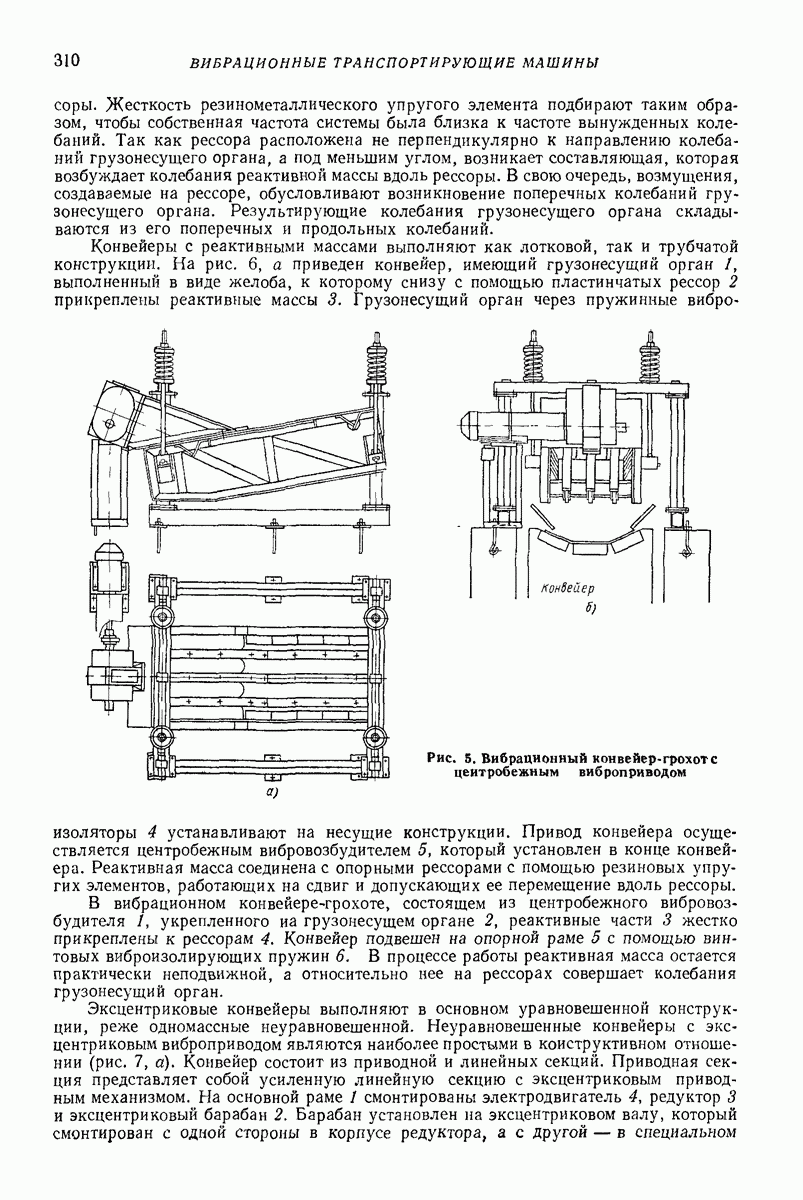
- Глава XX. ВИБРАЦИОННЫЕ ТРАНСПОРТИРУЮЩИЕ МАШИНЫ ДЛЯ НАСЫПНЫХ ГРУЗОВ
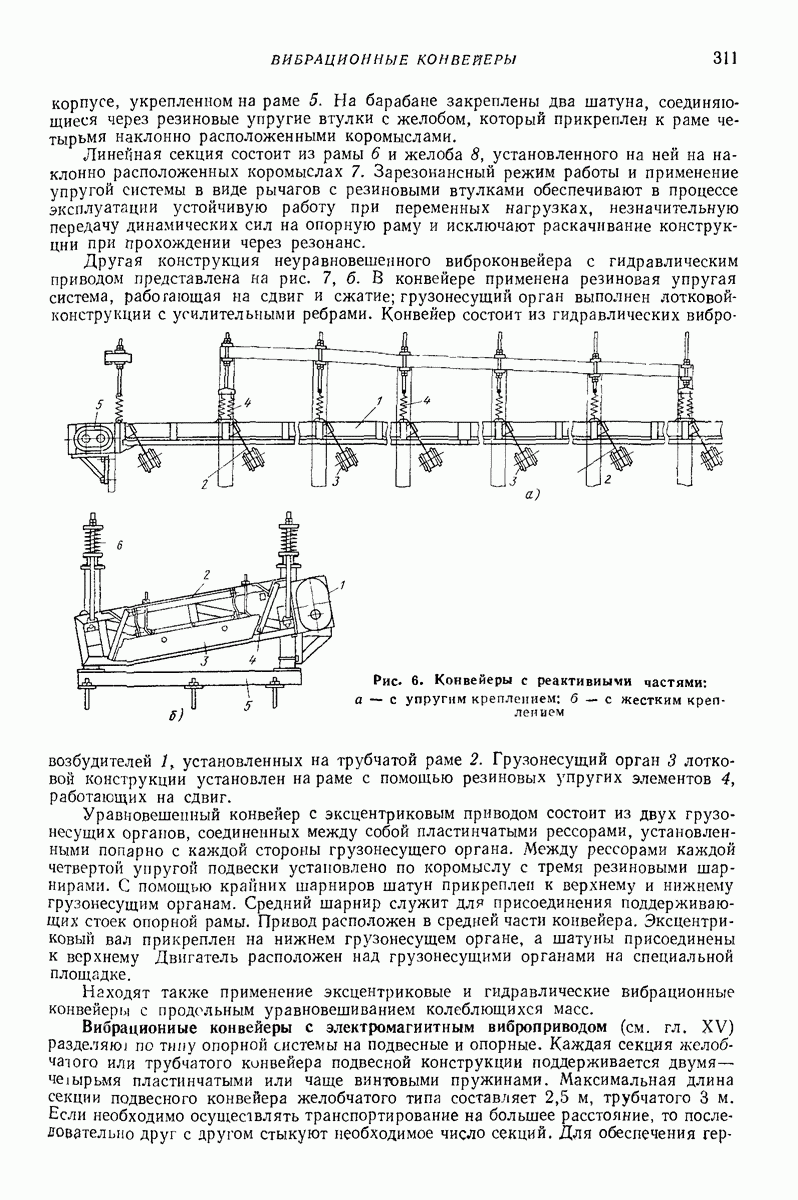
- 3. ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
- 4. ВИБРАЦИОННЫЕ ПОДЪЕМНИКИ
- 5. ВИБРАЦИОННЫЕ ПИТАТЕЛИ
- Глава XXI. ВИБРАЦИОННЫЕ ПИТАТЕЛИ И ОРИЕНТИРУЮЩИЕ УСТРОЙСТВА
- 1. ОРИЕНТИРОВАНИЕ ДЕТАЛЕЙ В ВИБРАЦИОННЫХ ПИТАТЕЛЯХ
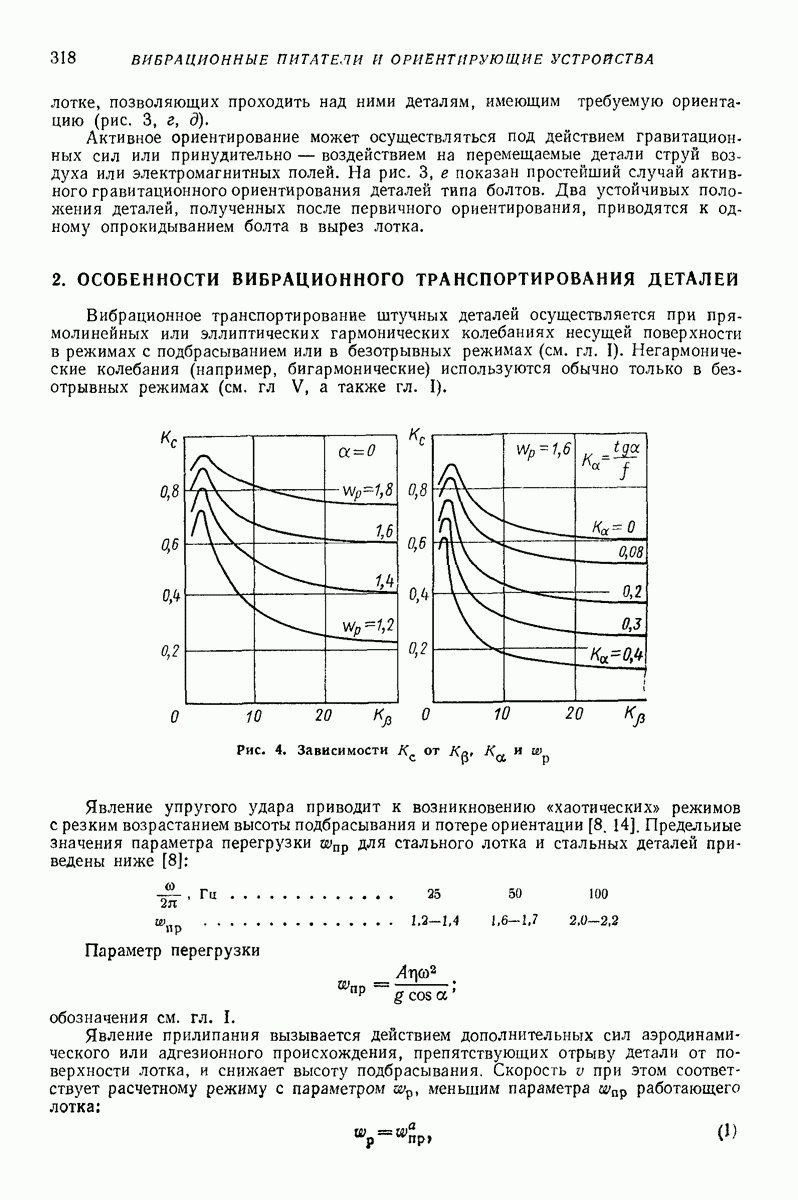
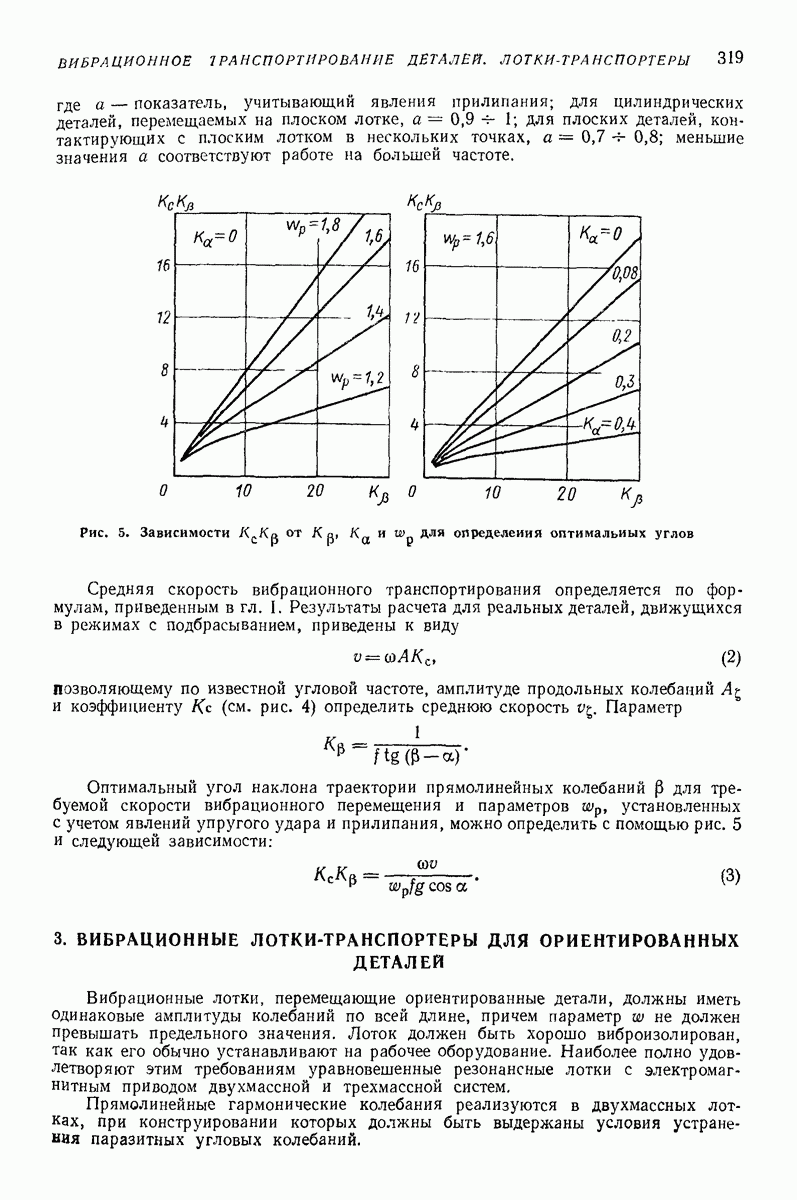
- 2. ОСОБЕННОСТИ ВИБРАЦИОННОГО ТРАНСПОРТИРОВАНИЯ ДЕТАЛЕЙ
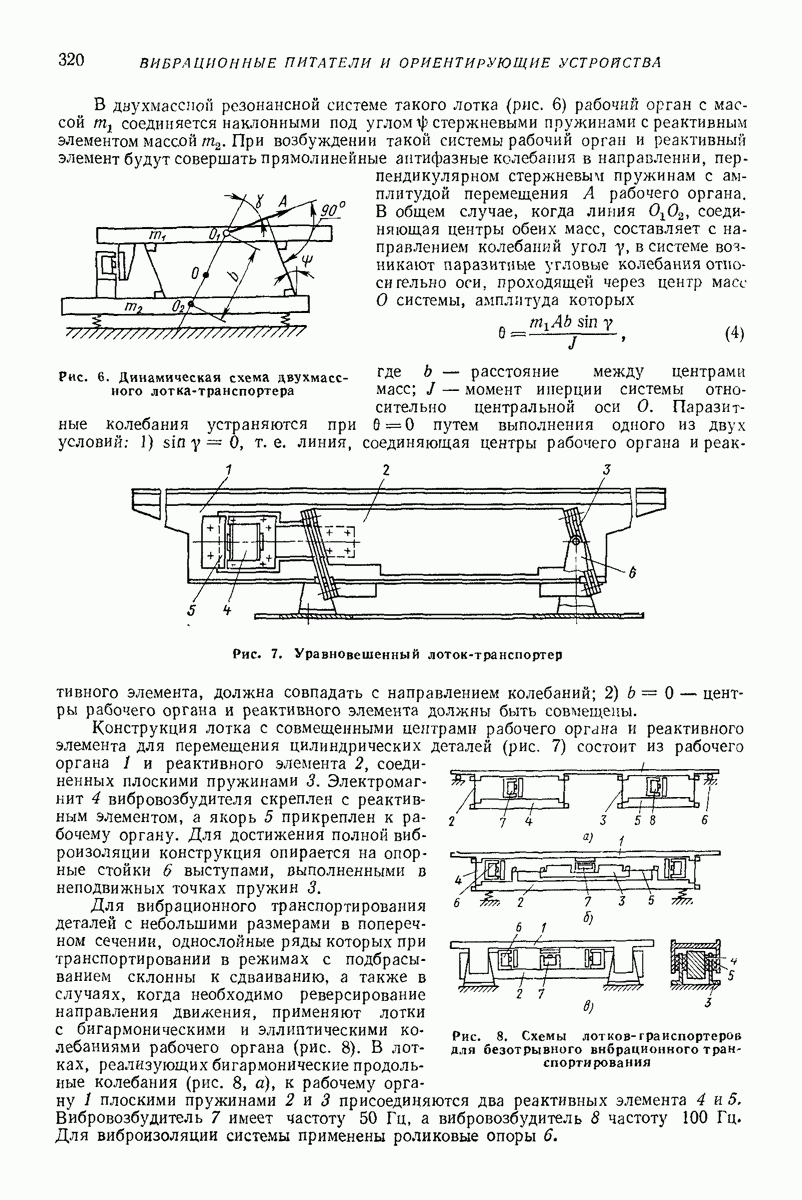
- 3. ВИБРАЦИОННЫЕ ЛОТКИ-ТРАНСПОРТЕРЫ ДЛЯ ОРИЕНТИРОВАННЫХ ДЕТАЛЕЙ
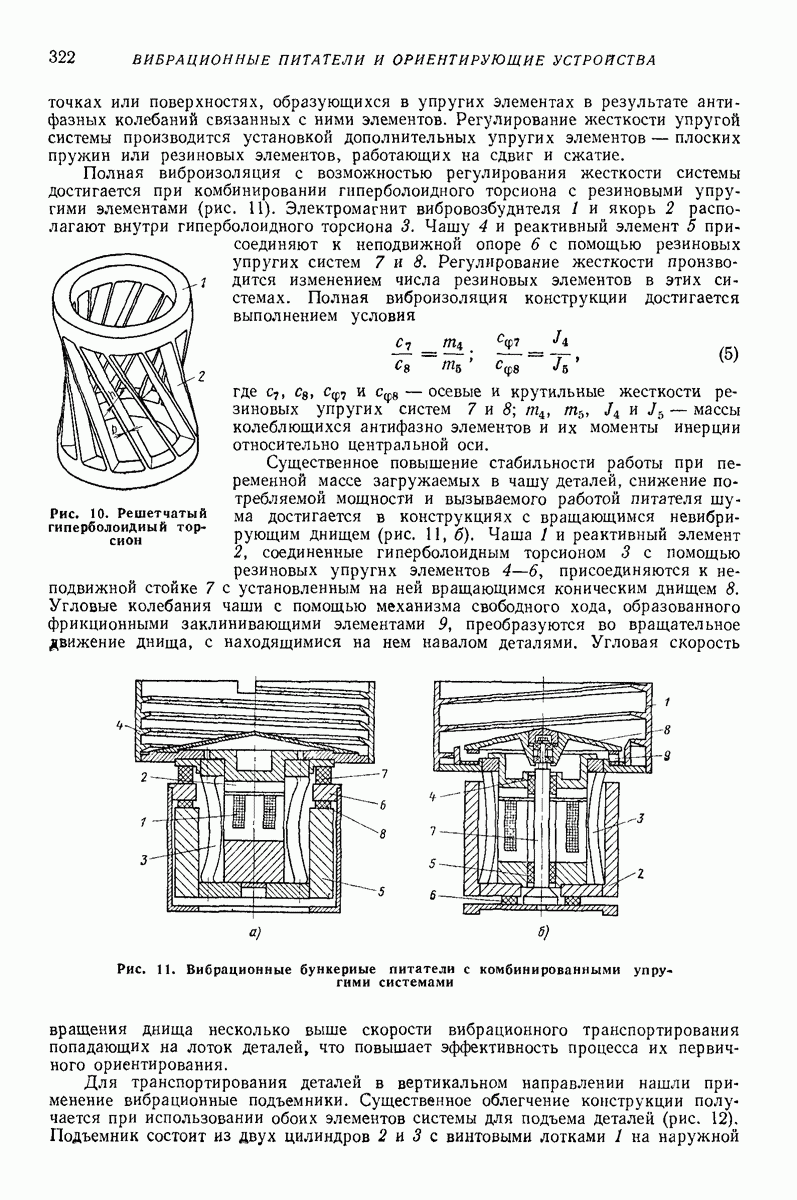
- 4. ВИБРАЦИОННЫЕ БУНКЕРНЫЕ ПИТАТЕЛИ И ПОДЪЕМНИКИ
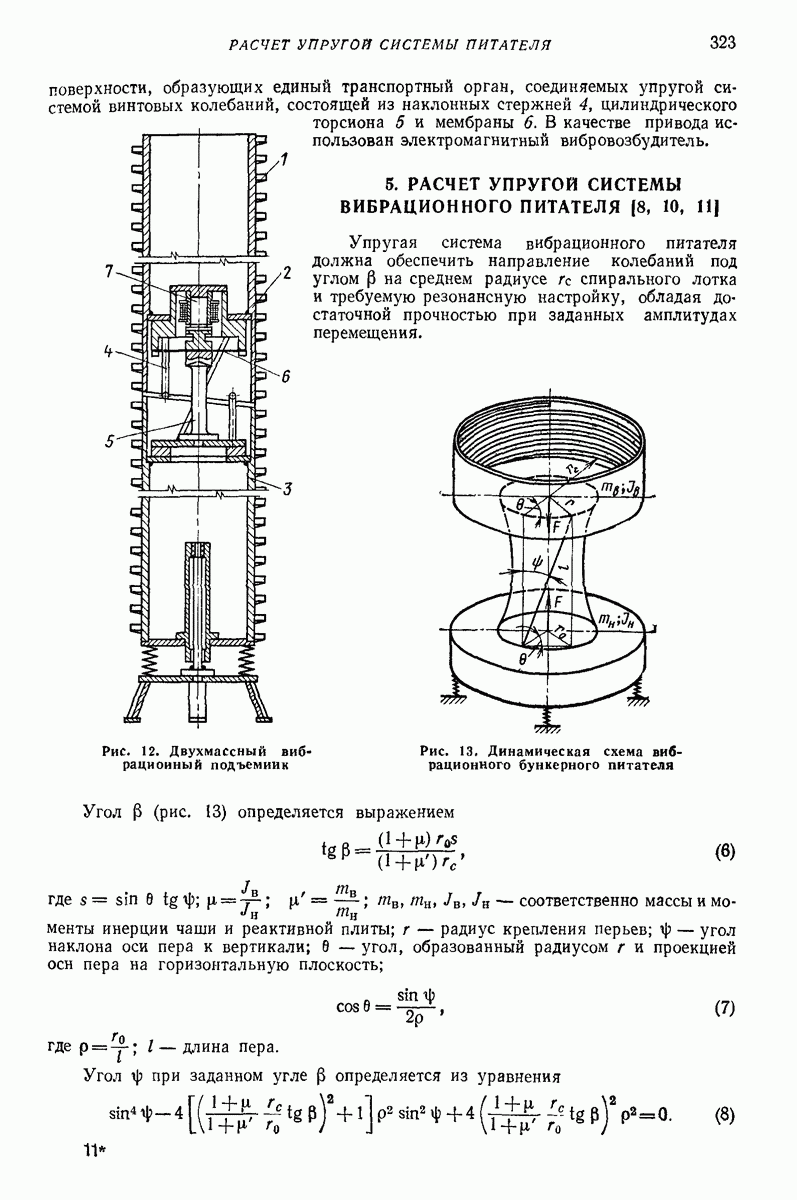
- 5. РАСЧЕТ УПРУГОЙ СИСТЕМЫ ВИБРАЦИОННОГО ПИТАТЕЛЯ (8, 10, 11]
- Глава XXII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА И ДЛЯ ГЕОЛОГИЧЕСКОГО БУРЕНИЯ
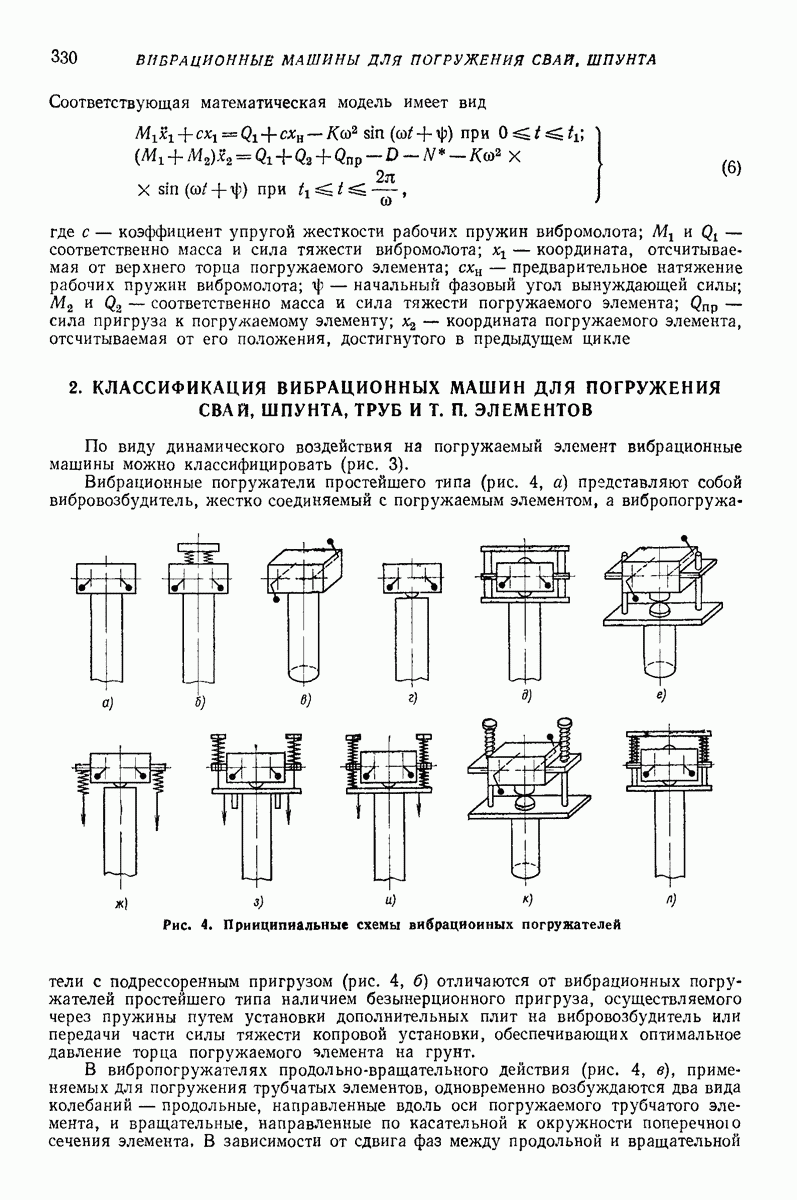
- 2. КЛАССИФИКАЦИЯ ВИБРАЦИОННЫХ МАШИН ДЛЯ ПОГРУЖЕНИЯ СВАЙ, ШПУНТА, ТРУБ И Т. П. ЭЛЕМЕНТОВ
- 3. РАСЧЕТ ПАРАМЕТРОВ ВИБРАЦИОННЫХ И УДАРНО-ВИБРАЦИОННЫХ МАШИН
- Глава XXIII. ВИБРАЦИОННЫЕ НАСОСЫ
- 3. КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ
- 4. РАСЧЕТ ТРУБОПРОВОДОВ
- Глава XXIV. МАШИНЫ ДЛЯ ВИБРАЦИОННОГО РАЗДЕЛЕНИЯ СЫПУЧИХ СМЕСЕЙ
- 2. СИТОВЫЕ (РЕШЕТНЫЕ) СЕПАРАТОРЫ
- 3. ВИБРАЦИОННЫЕ ГРОХОТЫ
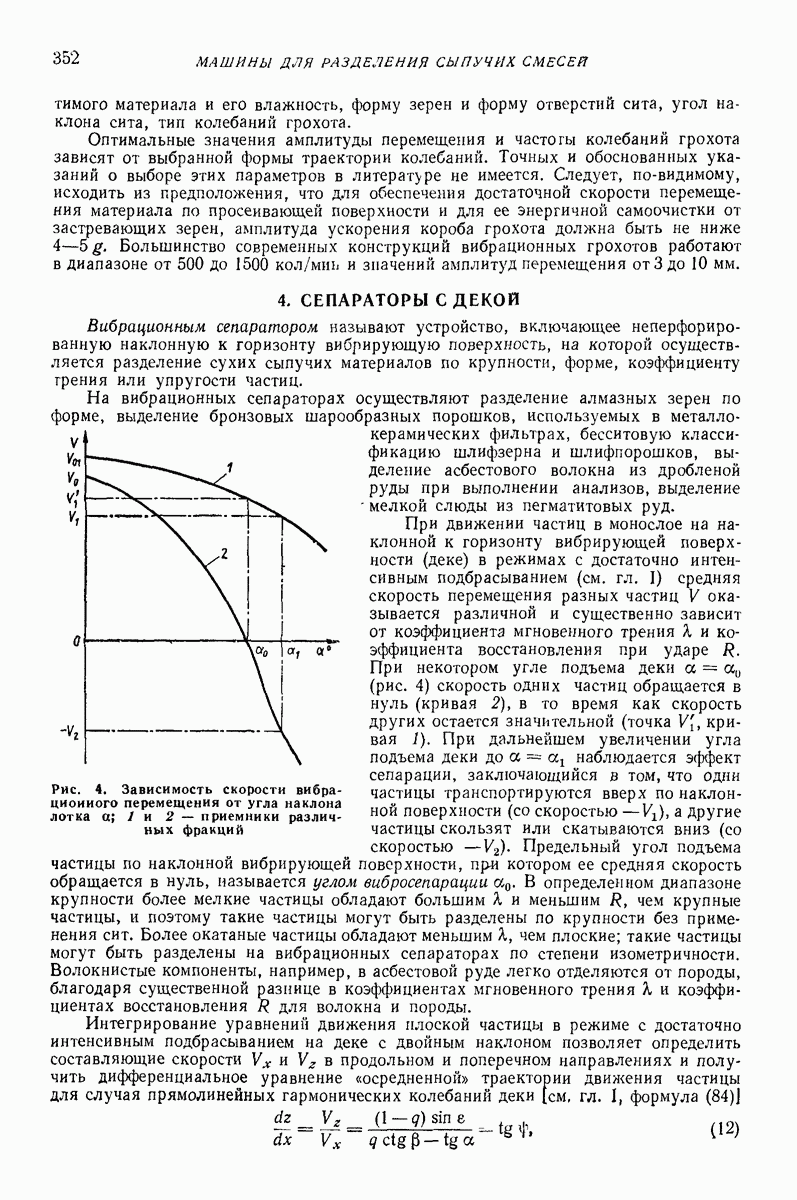
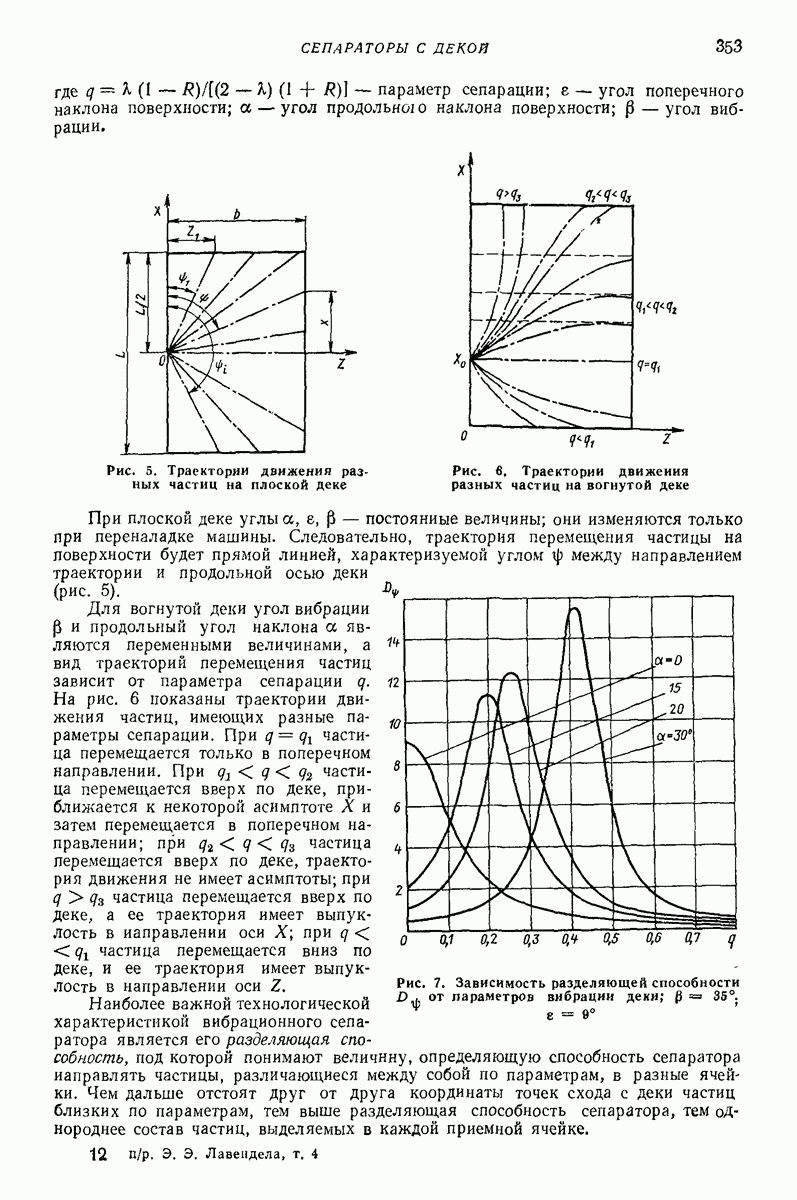
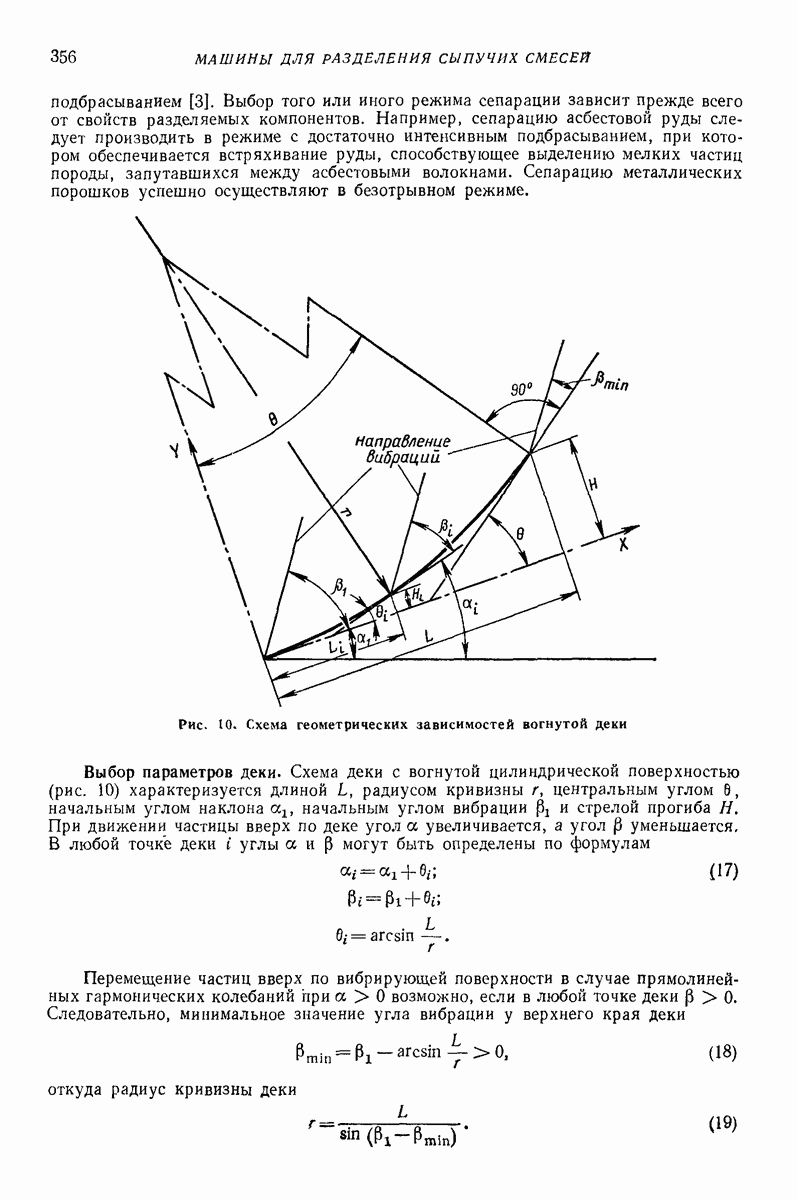
- 4. СЕПАРАТОРЫ С ДЕКОЙ
- Глава XXV. ВИБРАЦИОННЫЕ ТРАМБОВКИ И КАТКИ
- 2. ВИБРАЦИОННЫЕ ТРАМБОВКИ
- 3. ВИБРАЦИОННЫЕ КАТКИ
- 4. О СХЕМАТИЗАЦИИ УСЛОВИИ РАБОТЫ И КРИТЕРИЯХ УСТОЙЧИВОСТИ ДВИЖЕНИЯ УДАРНО-ВИБРАЦИОННОИ УПЛОТНЯЮЩЕЙ МАШИНЫ
- Глава XXVI. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ И ГРУНТА
- 2. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ БЕТОННОЙ СМЕСИ (ГЛУБИННЫЕ ВИБРОУПЛОТНИТЕЛИ)
- 3. ВЫБОР ПАРАМЕТРОВ ГЛУБИННЫХ ВИБРОУПЛОТНИТЕЛЕЙ БЕТОННОЙ СМЕСИ
- 4. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ГЛУБИННОГО УПЛОТНЕНИЯ ГРУНТА
- Глава XXVII. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ФОРМОВАНИЯ ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ
- 2. ОСНОВНЫЕ ТИПЫ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- 3. ВИБРАЦИОННЫЕ ФОРМОВОЧНЫЕ ПЛОЩАДКИ И УСТАНОВКИ
- 4. РАСЧЕТ И ВЫБОР ПАРАМЕТРОВ ВИБРАЦИОННЫХ ФОРМОВОЧНЫХ МАШИН
- Глава XXVIII. ВИБРАЦИОННЫЕ МЕЛЬНИЦЫ И ДРОБИЛКИ
- 2. ВИБРАЦИОННЫЕ ДРОБИЛКИ
- Глава XXIX. МАШИНЫ ДЛЯ ВИБРАЦИОННОЙ ОБРАБОТКИ ДЕТАЛЕЙ
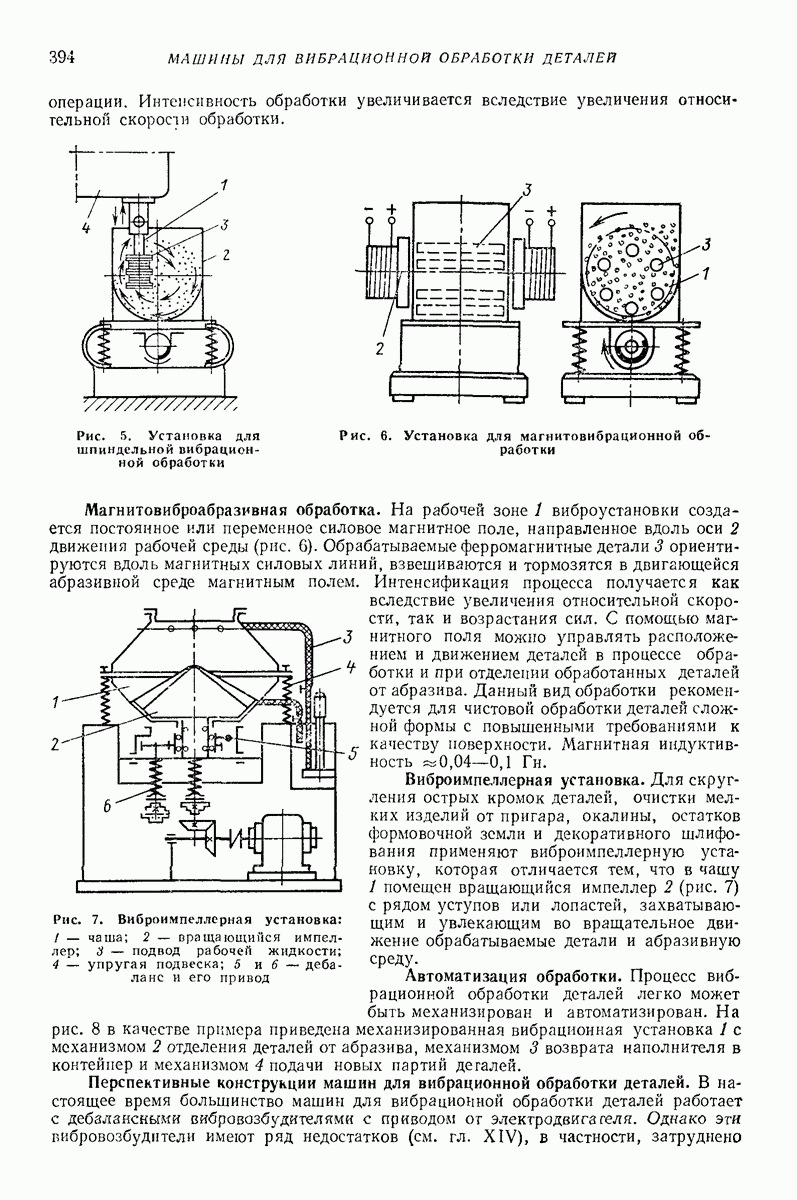
- 1. ТЕХНОЛОГИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ ВИБРАЦИОННОЙ ОБРАБОТКЕ
- 2. КРАТКИЕ СВЕДЕНИЯ О ТЕХНОЛОГИИ
- 3. ОСНОВНЫЕ ТИПЫ МАШИН
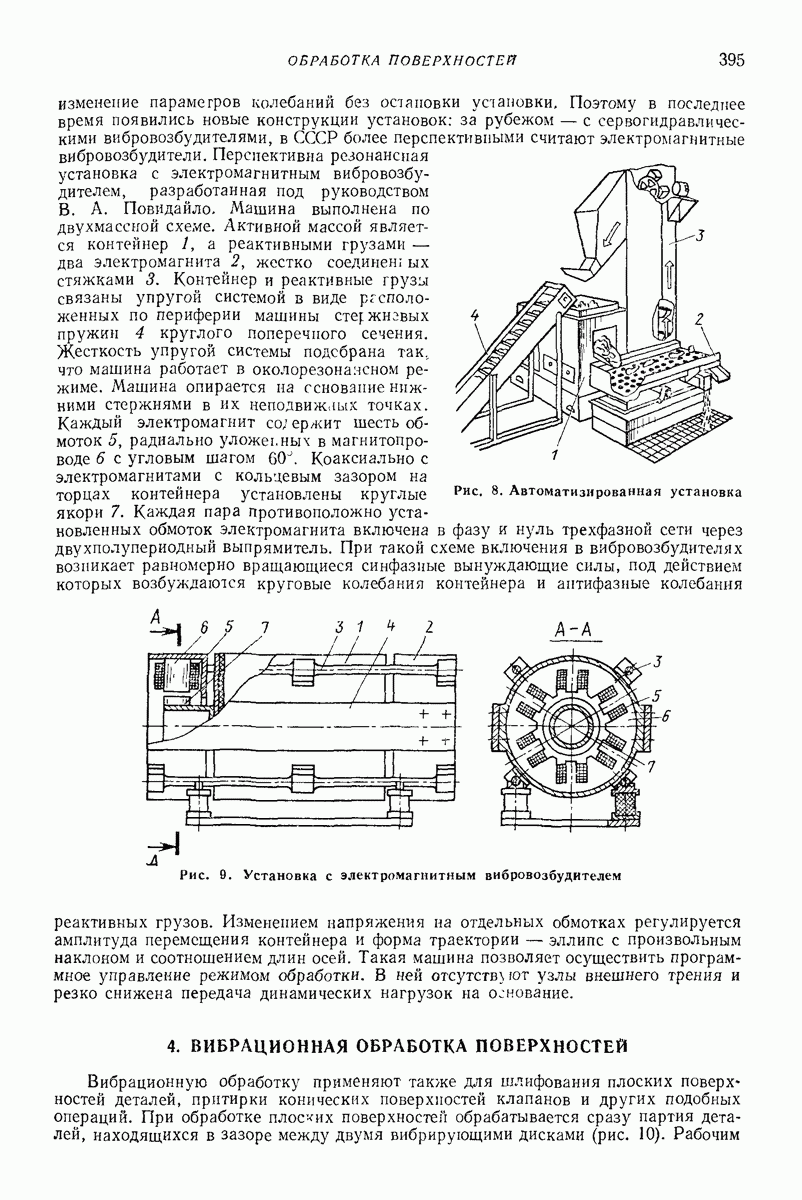
- 4. ВИБРАЦИОННАЯ ОБРАБОТКА ПОВЕРХНОСТЕЙ
- 5. ДИНАМИКА МАШИН
- Глава XXX. ВИБРАЦИОННЫЕ МАШИНЫ ДЛЯ ИЗГОТОВЛЕНИЯ ЛИТЕЙНЫХ ФОРМ И СТЕРЖНЕЙ И ВЫБИВКИ ОПОК
- 2. ВИБРАЦИОННЫЕ ВЫБИВНЫЕ РЕШЕТКИ
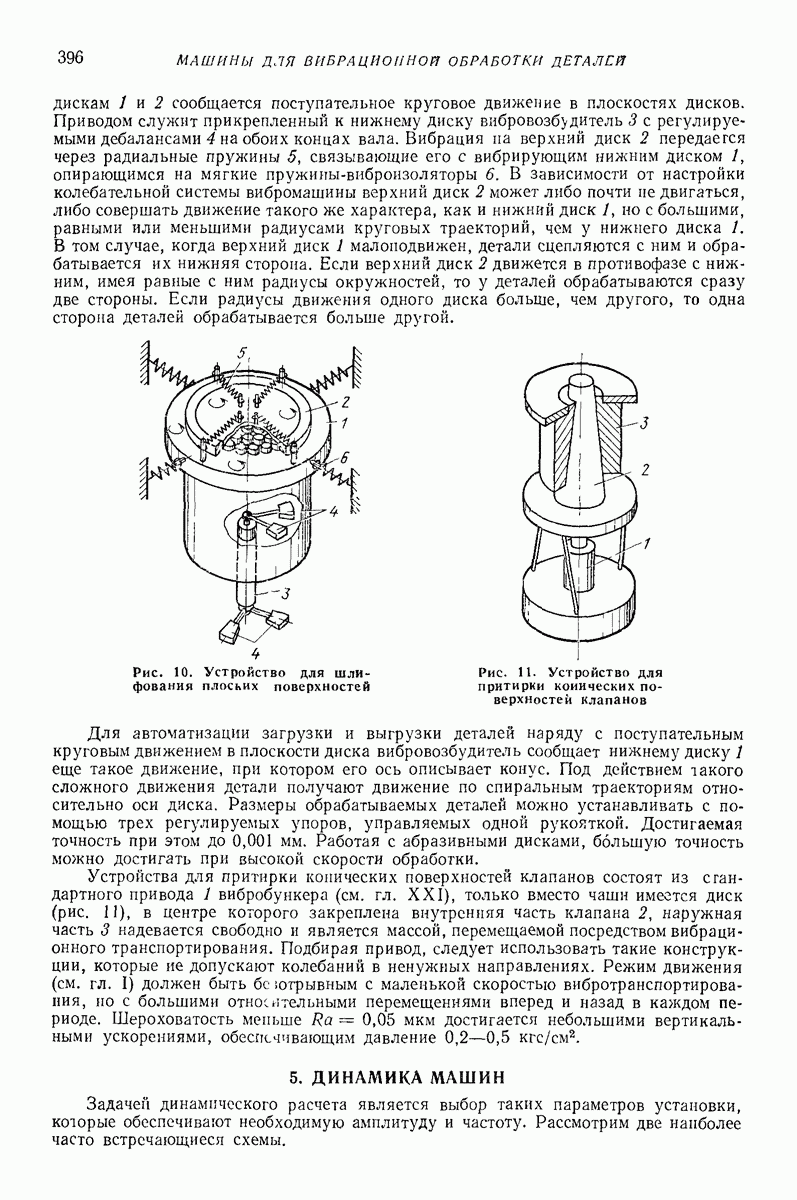
- Глава XXXI. УСТРОЙСТВА ДЛЯ ВИБРАЦИОННОЙ АВТОМАТИЧЕСКОЙ СБОРКИ ДЕТАЛЕЙ
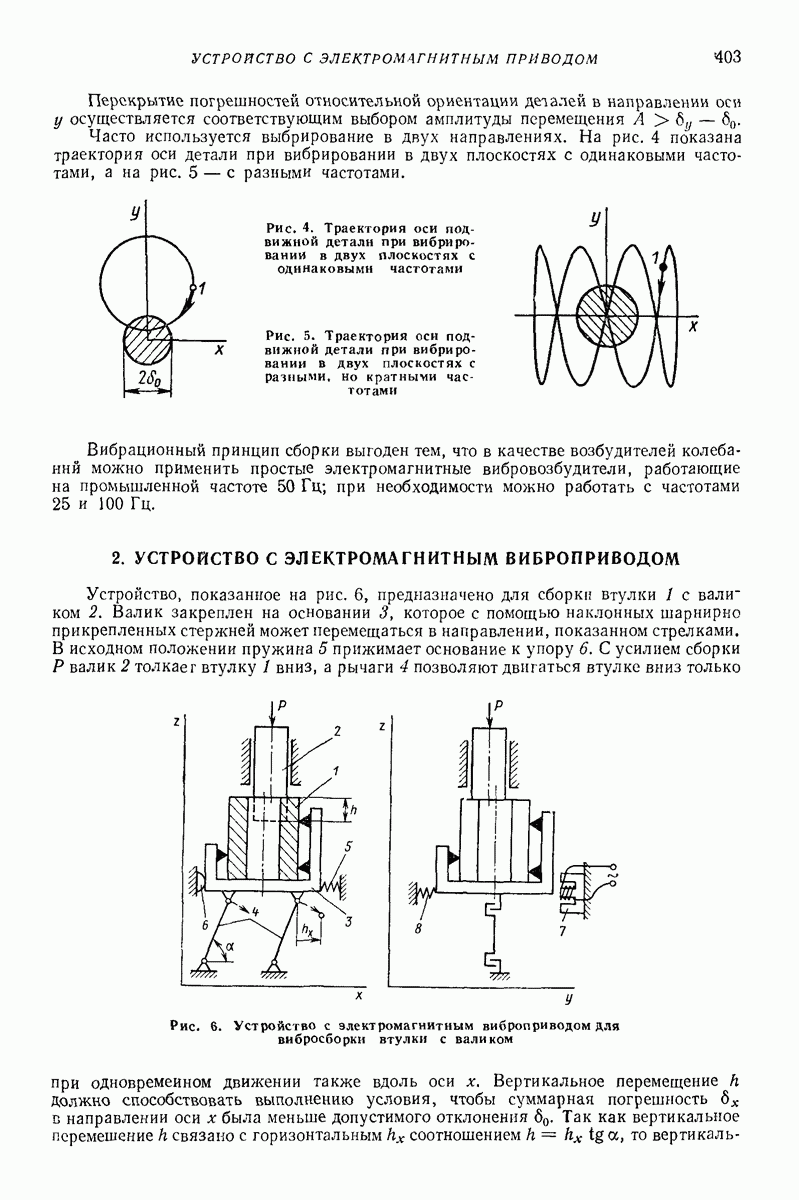
- 2. УСТРОЙСТВО С ЭЛЕКТРОМАГНИТНЫМ ВИБРОПРИВОДОМ
- 3. УСТРОЙСТВО С МЕХАНИЧЕСКИМ ВИБРОПРИВОДОМ
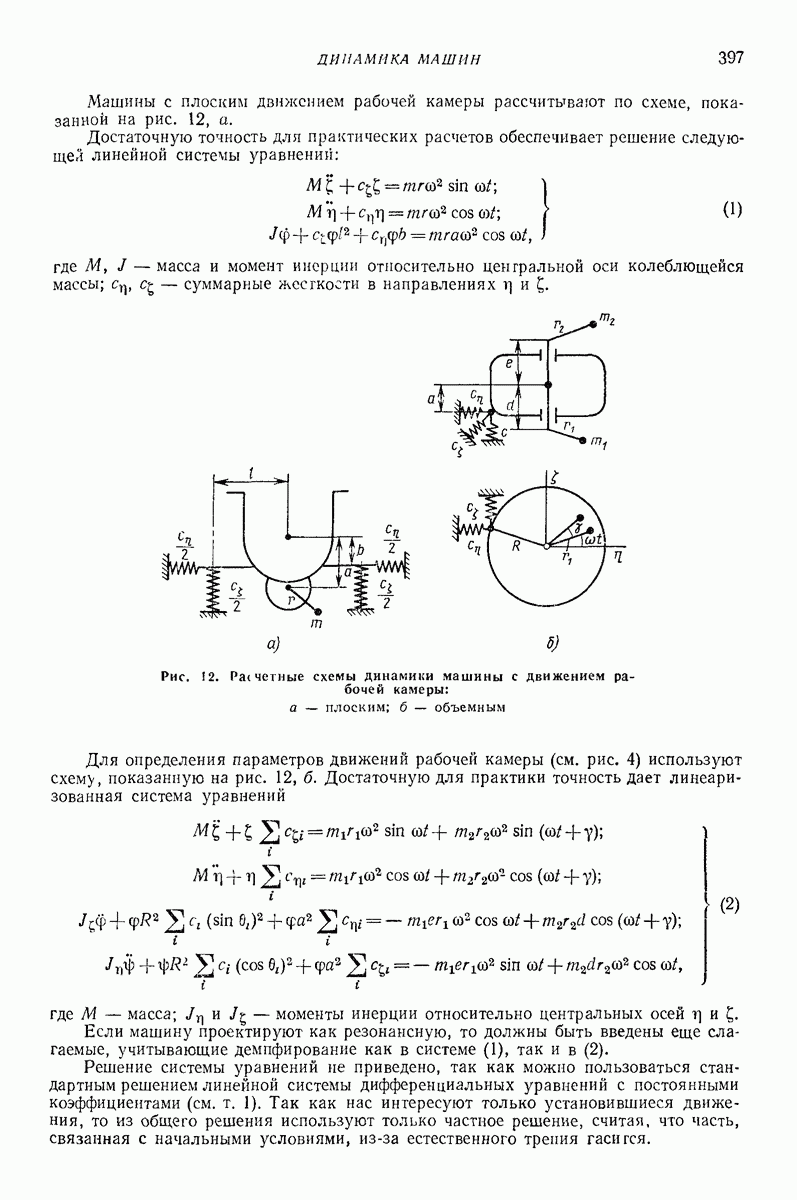
- Глава XXXII. ВИБРАЦИОННЫЕ АППАРАТЫ ДЛЯ ИНТЕНСИФИКАЦИИ ФИЗИЧЕСКИХ ПРОЦЕССОВ И ХИМИЧЕСКИХ РЕАКЦИЙ
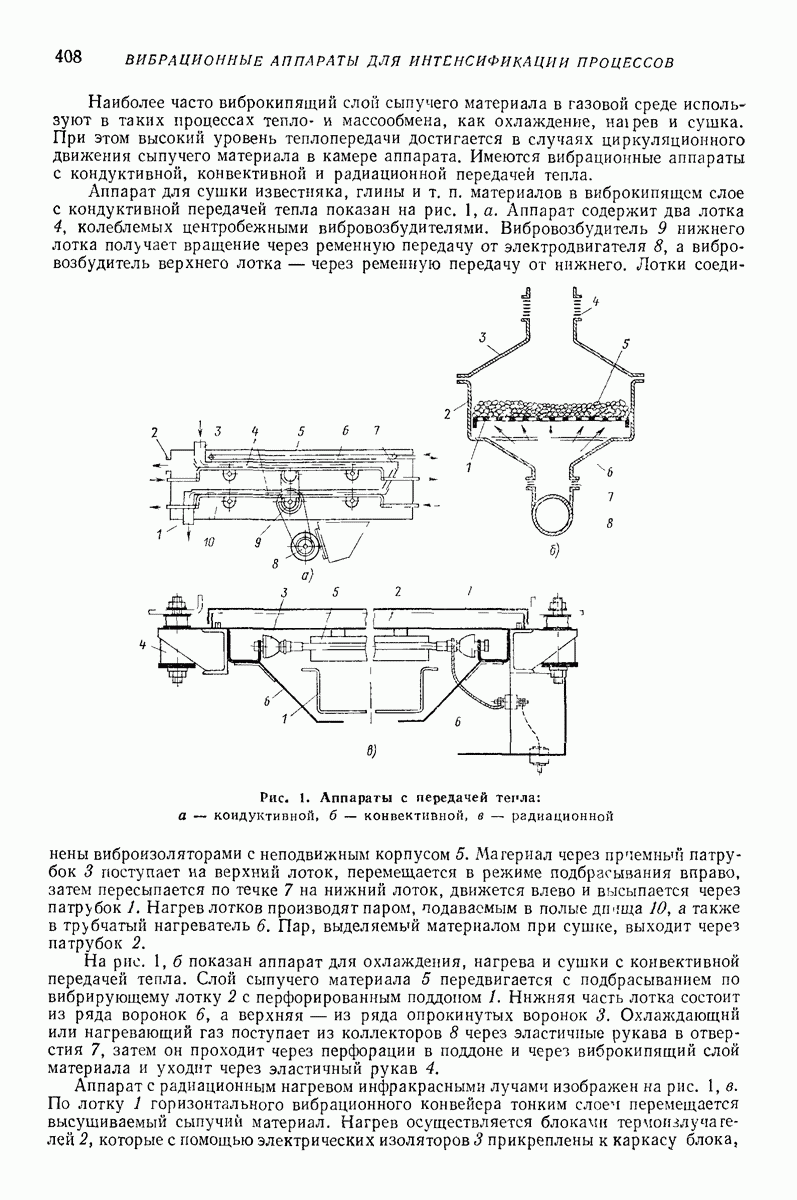
- 2. АППАРАТЫ ДЛЯ СОЗДАНИЯ КИПЯЩЕГО СЛОЯ СЫПУЧЕГО МАТЕРИАЛА
- 3. АППАРАТЫ ДЛЯ ПЕРЕМЕШИВАНИЯ ЖИДКОСТЕЙ И СУСПЕНЗИЙ
- Глава XXXIII. МЕДИЦИНСКИЕ, КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. КОСМЕТИЧЕСКИЕ И БЫТОВЫЕ УСТРОЙСТВА
- Глава XXXIV. УДАРНО-ВИБРАЦИОННЫЕ РУЧНЫЕ МАШИНЫ
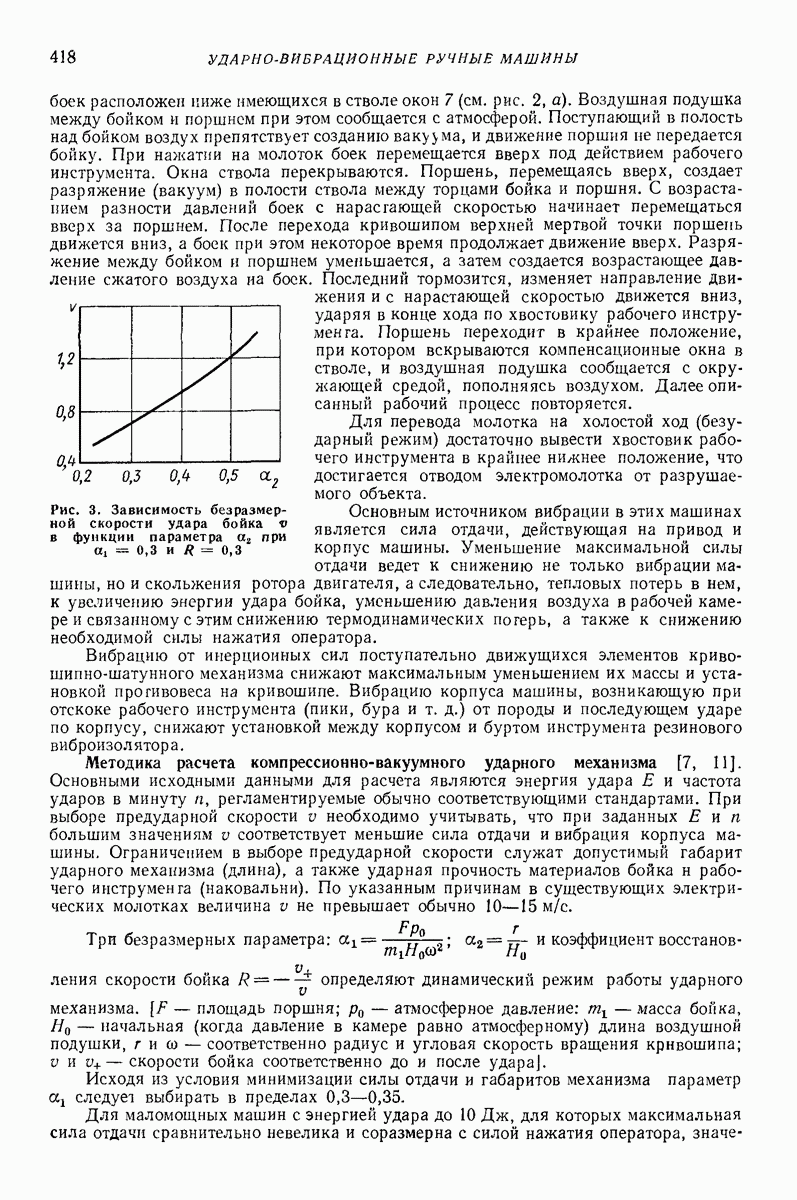
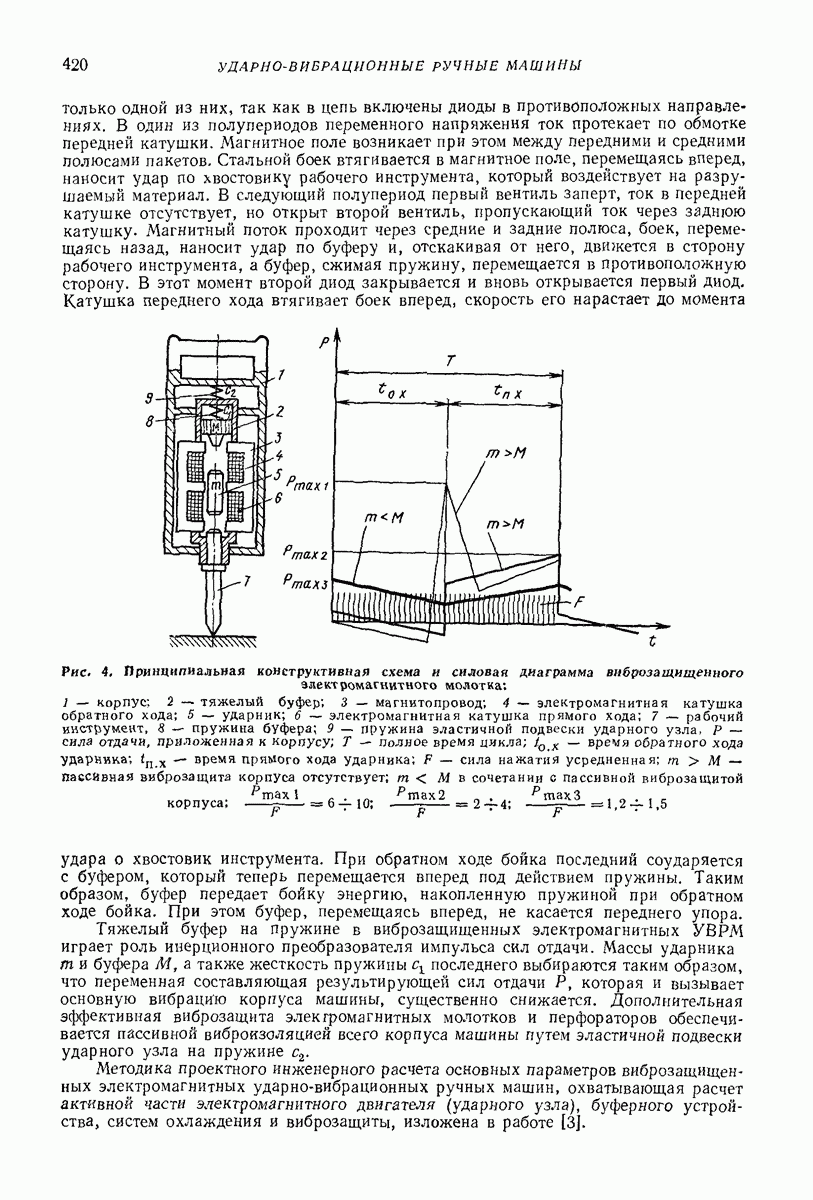
- 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 3. ПНЕВМАТИЧЕСКИЕ МАШИНЫ С ПОСТУПАТЕЛЬНЫМИ УДАРАМИ
- 4. МАШИНЫ С ВРАЩАТЕЛЬНЫМИ УДАРАМИ
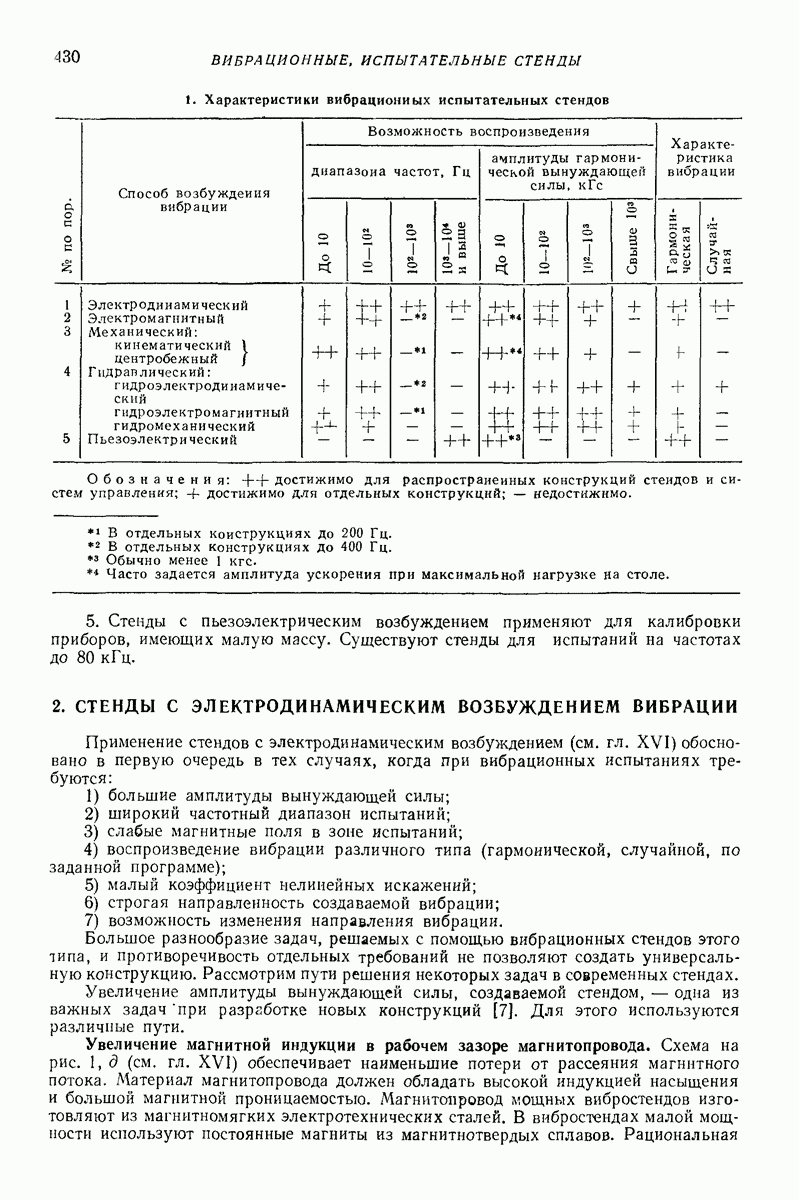
- Глава XXXV. ВИБРАЦИОННЫЕ ИСПЫТАТЕЛЬНЫЕ СТЕНДЫ
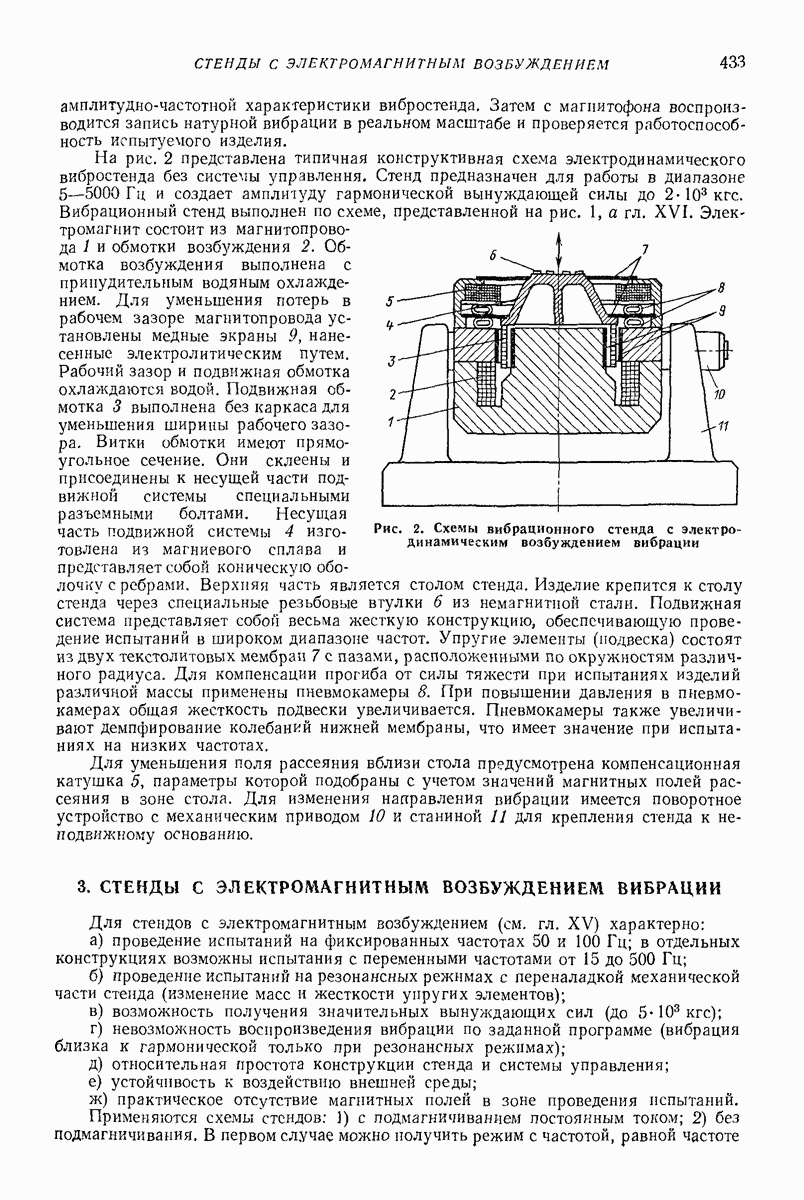
- 2. СТЕНДЫ С ЭЛЕКТРОДИНАМИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
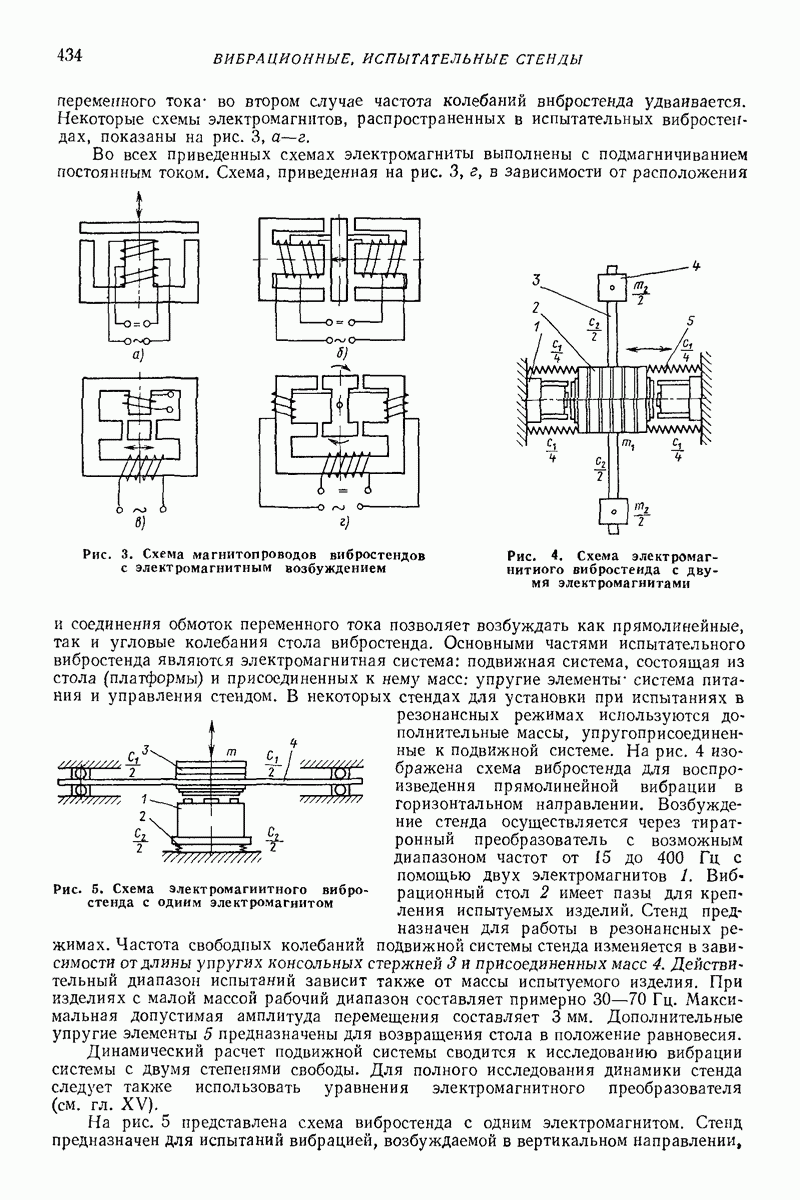
- 3. СТЕНДЫ С ЭЛЕКТРОМАГНИТНЫМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 4. СТЕНДЫ С МЕХАНИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 5. СТЕНДЫ С ГИДРАВЛИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- 6. СТЕНДЫ С ПЬЕЗОЭЛЕКТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ ВИБРАЦИИ
- Глава XXXVI. ВИБРАЦИОННЫЕ ПРИБОРЫ
- 2. ФУНКЦИОНАЛЬНЫЕ ВИБРАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3. ТИПЫ ВИБРАЦИОННЫХ ПРИБОРОВ
- Глава XXXVII. ДРУГИЕ ВИБРАЦИОННЫЕ УСТРОЙСТВА
- 2. РАЗГРУЗОЧНО-ПОГРУЗОЧНЫЕ РАБОТЫ [4-8, 16]
- 3. ТЕХНОЛОГИЧЕСКИЕ ОПЕРАЦИИ
- Глава XXXVIII. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ И РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- 2. АВТОМАТИЗАЦИЯ УДАРНО-ВИБРАЦИОННЫХ МАШИН
- 3. АВТОМАТИЗАЦИЯ РЕЗОНАНСНЫХ ВИБРАЦИОННЫХ МАШИН
- Глава XXXIX. ИСПОЛЬЗОВАНИЕ САМОСИНХРОНИЗАЦИИ И СИСТЕМ ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ ВИБРОВОЗБУДИТЕЛЕЙ ПРИ СИНТЕЗЕ ВИБРАЦИОННЫХ ПОЛЕЙ
- ТЕРМИНЫ