| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
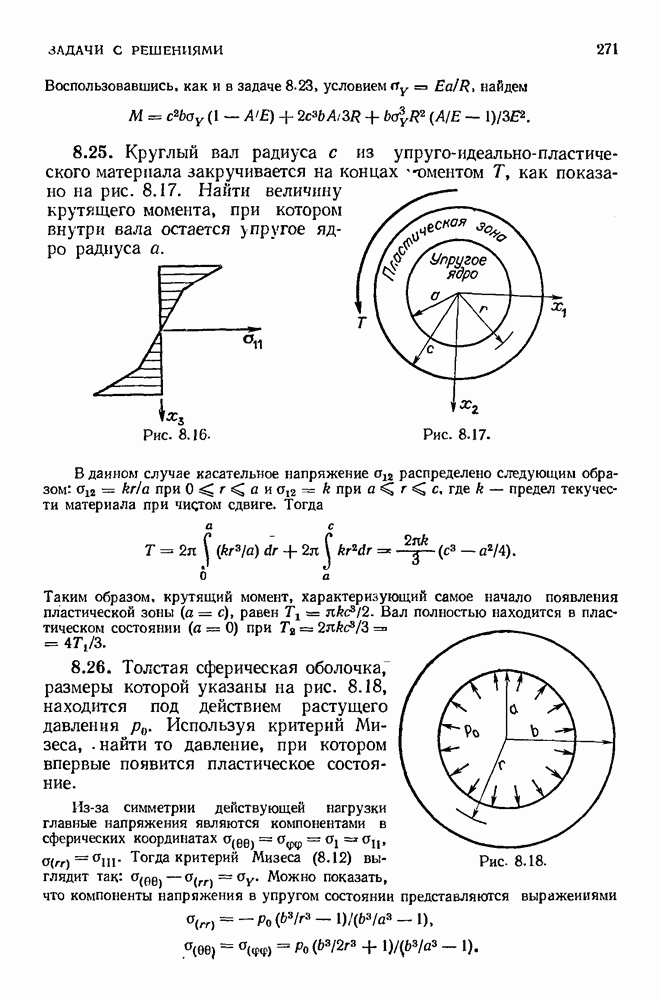
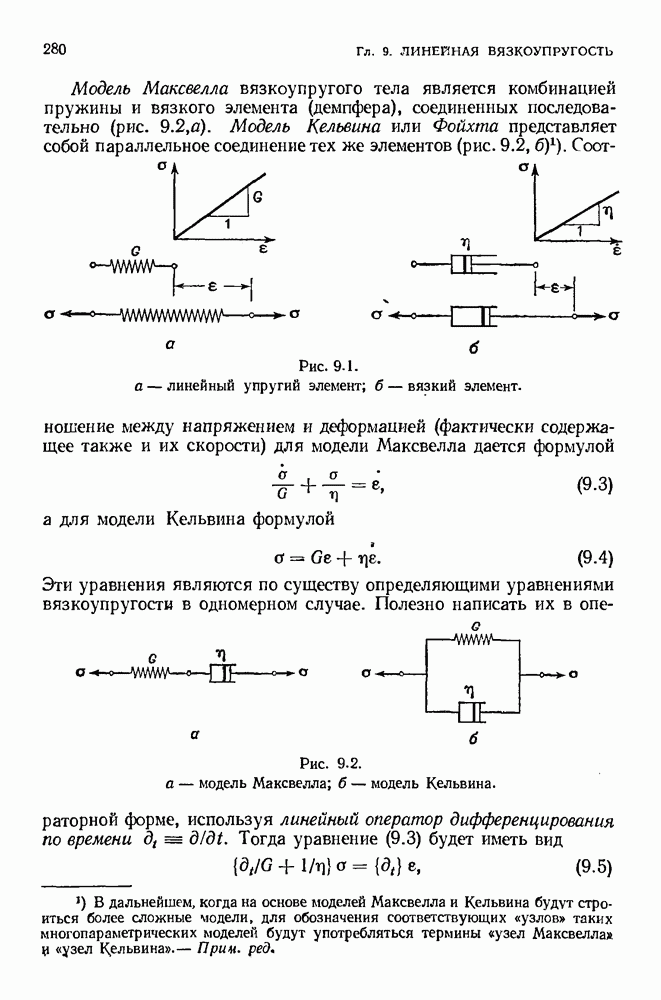
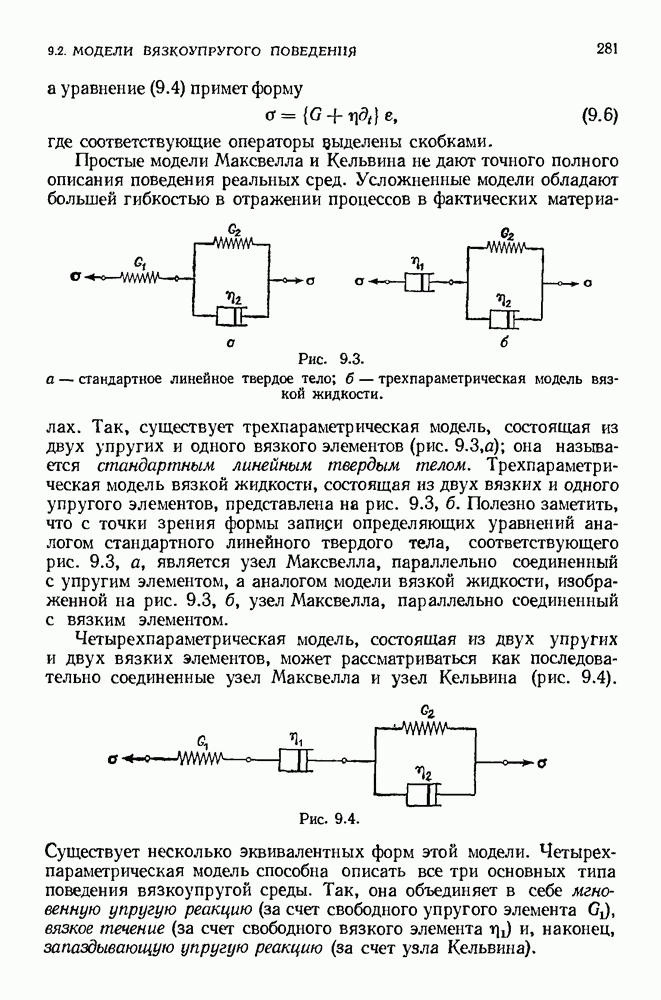
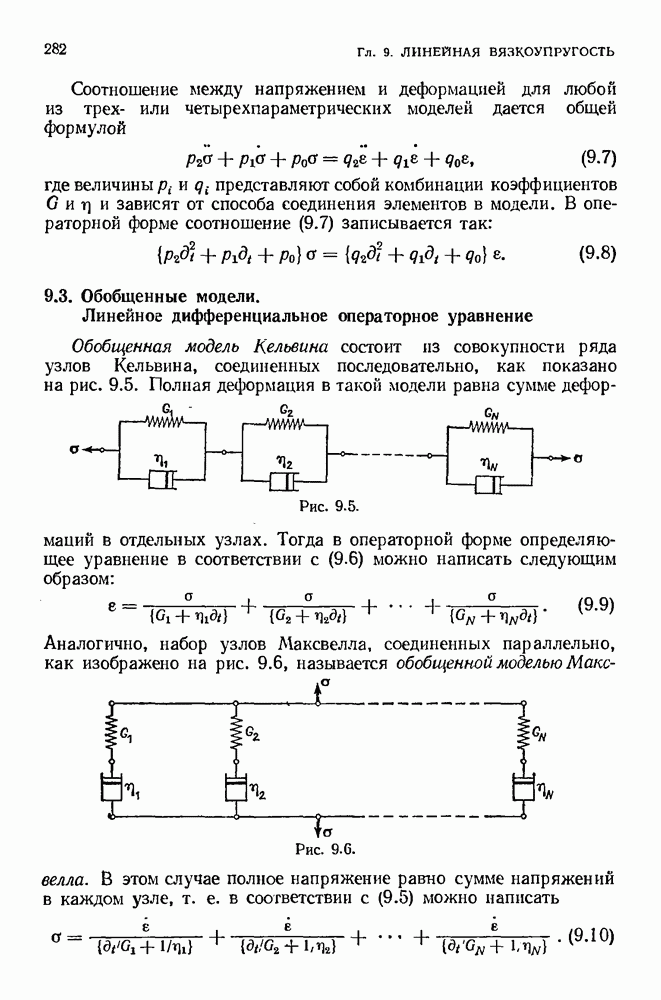
9.7. Трехмерная теория
При создании трехмерной теории линейной вязкоупругости обычно принято рассматривать отдельно вязкоупругое поведение в условиях так называемого чистого сдвига и чистого расширения.
Таким образом, эффекты искажения формы и изменения величины объема изучаются независимо и затем их описания комбинируются, чтобы построить общую теорию. Математически это обеспечивается разложением тензоров напряжений и деформаций на их девиаторную и шаровую части, для каждой из которых затем пишутся определяющие соотношения вязкоупругости. Разложение тензора напряжений дано формулой (2.70)

а разложение тензора малых деформаций — формулой (3.98)

Принимая обозначения, использованные в этих равенствах, запишем в операторной форме трехмерное обобщение определяющих уравнений вязкоупругости (9.13):

и

 и
и  - дифференциальные операторы, определенные в соответствии с (9.14), а числовые множители введены для удобства. Так как практически все материалы упруго реагируют на умеренные гидростатические нагрузки, в качестве операторов
- дифференциальные операторы, определенные в соответствии с (9.14), а числовые множители введены для удобства. Так как практически все материалы упруго реагируют на умеренные гидростатические нагрузки, в качестве операторов  связанных с расширением, обычно берут постоянные и преобразуют соотношения (9.47) к виду
связанных с расширением, обычно берут постоянные и преобразуют соотношения (9.47) к виду

где К — объемный модуль упругости.
Следуя тому же общему правилу разделения эффектов искажения формы и изменения величины объема, напишем трехмерные определяющие соотношения вязкоупругости в форме интегралов ползучести

и интегралов релаксации

Для того чтобы распространить на трехмерный случай описание вязкоупругого процесса при помощи комплексного модуля, требуется ввести комплексный объемный модуль К. Уравнения, раздельно написанные для чистого сдвига и для чистого расширения, таковы:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. Математические основы
- 1.1. Тензоры и механика сплошной среды
- 1.2. Тензоры. Декартовы тензоры. Ранг тензора
- 1.3. Векторы и скаляры
- 1.4. Векторное сложение. Умножение вектора на скаляр
- 1.5. Скалярное и векторное произведения векторов
- 1.6. Диады и диадики
- 1.7. Системы координат. Базисные векторы. Триэдр единичных векторов
- 1.8. Линейные векторные функции. Диадики как линейные векторные операторы
- 1.9. Индексные обозначения. Интервал изменения индексов и соглашение о суммировании
- 1.10. Соглашение о суммировании в символических обозначениях
- 1.11. Преобразование координат. Общее понятие тензора
- 1.12. Метрический тензор. Декартовы тензоры
- 1.13. Законы преобразования декартовых тензоров. Дельта Кронекера. Условия ортогональности
- 1.14. Сложение декартовых тензоров. Умножение на скаляр
- 1.15. Умножение тензоров
- 1.16. Векторное произведение. Тензор Леви-Чивиты. Бивектор
- 1.17. Матрицы Матричные представления декартовых тензоров
- 1.18. Симметрия диадиков, матриц и тензоров
- 1.19. Главные значения и главные направления симметричных тензоров второго ранга
- 1.20. Степени тензоров второго ранга. Соотношение Гамильтона — Кэли
- 1.21. Тензорные поля. Дифференцирование тензоров
- 1.22. Криволинейные интегралы. Теорема Стокса
- 1.23. Теорема Гаусса — Остроградского
- Глава 2. Анализ напряженного состояния
- 2.1. Понятие сплошной среды
- 2.2. Однородность. Изотропия. Массовая плотность
- 2.3. Массовые силы. Поверхностные силы
- 2.4. Принцип напряжения Коши. Вектор напряжения
- 2.5. Напряженное состояние в точке. Тензор напряжений
- 2.6. Связь между тензором напряжений и вектором напряжения
- 2.7. Равновесие сил и моментов. Симметрия тензора напряжений
- 2.8. Законы преобразования напряжений
- 2.9. Поверхности напряжений Коши
- 2.10. Главные напряжения. Инварианты тензора напряжений. Эллипсоид напряжений
- 2.11. Максимальное и минимальное касательное напряжение
- 2.12. Круги Мора для напряжения
- 2.13. Плоское напряженное состояние
- 2.14. Девиатор и шаровой тензор напряжений
- Глава 3. Деформации
- 3.2. Конфигурация сплошной среды. Деформация и течение
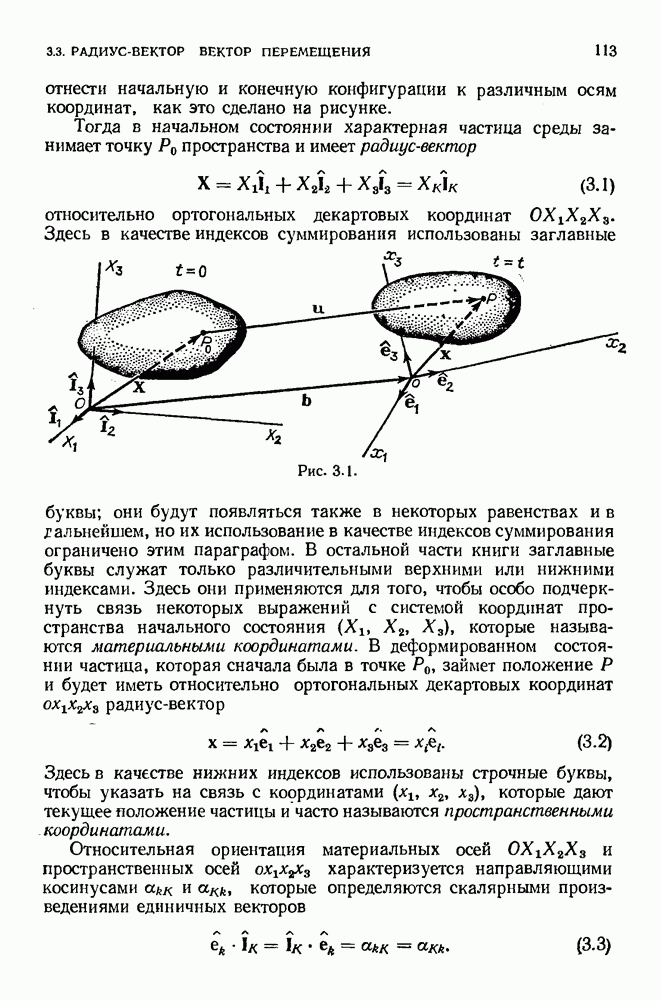
- 3.3. Радиус-вектор. Вектор перемещения
- 3.4. Лагранжево и эйлерово описания движения
- 3.5. Градиенты деформации. Градиенты перемещения
- 3.6. Тензоры деформаций. Тензоры конечных деформаций
- 3.7. Теория малых деформаций. Тензоры бесконечно малых деформаций
- 3.8. Относительное перемещение. Тензор линейного поворота. Вектор поворота
- 3.9. Геометрический смысл тензоров линейных деформаций
- 3.10. Коэффициент длины. Интерпретация конечных деформаций
- 3.11. Тензоры коэффициентов длины. Тензор поворота
- 3.12. Свойства преобразований тензоров деформаций
- 3.13. Главные деформации. Инварианты деформации. Кубическое расширение
- 3.14. Шаровой тензор и девиатор деформаций
- 3.15. Плоская деформация. Круги Мора для деформации
- 3.16. Уравнения совместности для линейных деформаций
- Глава 4. Движение и течение
- 4.1. Движение. Течение. Материальная производная
- 4.2. Скорость. Ускорение. Мгновенное поле скоростей
- 4.3. Траектории. Линии тока. Установившееся движение
- 4.4. Скорость деформации. Завихренность. Приращения деформации
- 4.5. Физическая интерпретация тензоров скоростей деформации и завихренности
- 4.6. Материальные производные по времени от элемента объема, элемента поверхности и линейного элемента
- 4.7. Материальные производные по времени от интеграла по объему, интеграла по поверхности и линейного интеграла
- Глава 5. Основные законы механики сплошной среды
- 5.1. Сохранение массы. Уравнение неразрывности
- 5.2. Теорема об изменении количества движения. Уравнения движения. Уравнения равновесия
- 5.3. Теорема об изменении момента количества движения
- 5.4. Сохранение энергии. Первый закон термодинамики. Уравнение энергии
- 5.5. Уравнения состояния. Энтропия. Второй закон термодинамики
- 5.6. Неравенство Клаузиуса — Дюгема. Диссипативная функция
- 5.7. Определяющие уравнения. Термомеханический и механический континуумы
- Глава 6. Линейная теория упругости
- 6.1. Обобщенный закон Гука. Функция энергии деформации
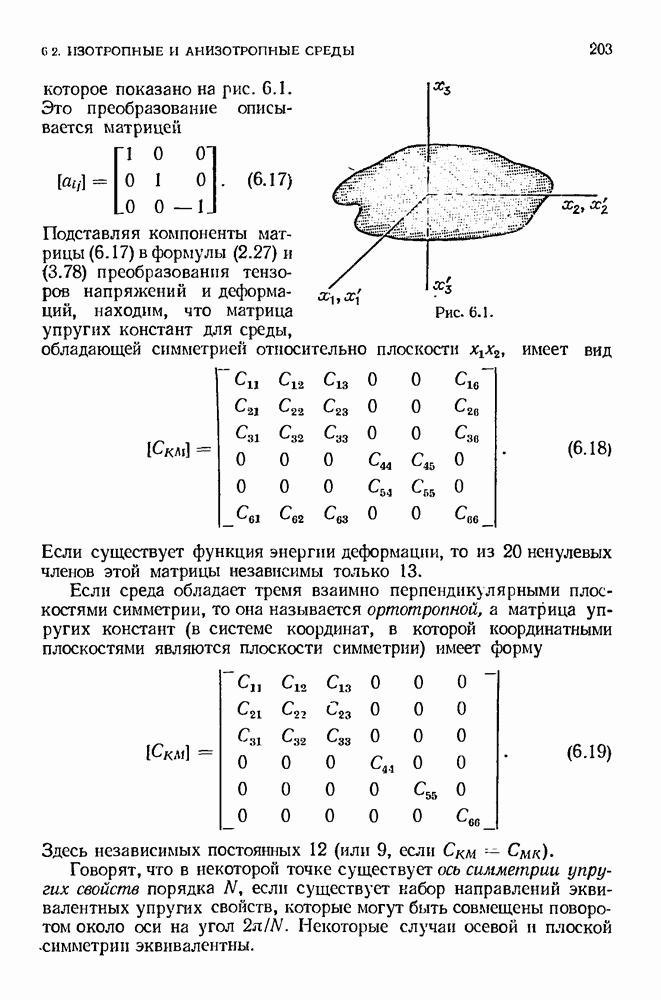
- 6.2. Изотропные и анизотропные среды. Симметрия упругих свойств
- 6.3. Изотропные среды. Упругие постоянные
- 6.4. Постановка статических и динамических задач теории упругости
- 6.5. Теорема о суперпозиции. Единственность решений. Принцип Сен-Венана
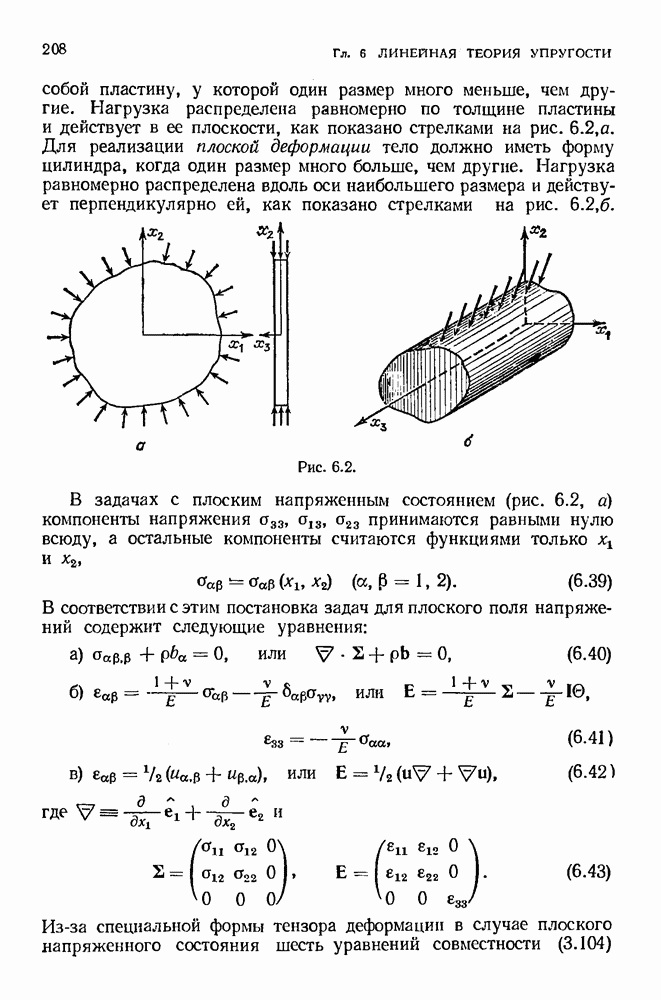
- 6.6. Плоские задачи теории упругости. Плоское напряженное состояние и плоская деформация
- 6.7. Функция напряжений Эри
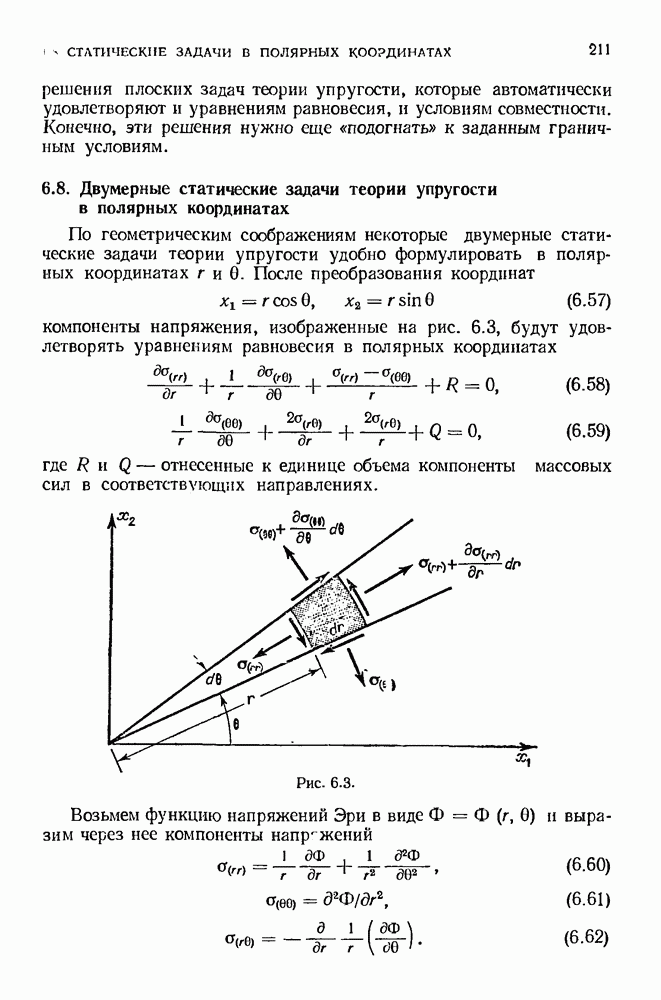
- 6.8. Двумерные статические задачи теории упругости в полярных координатах
- 6.9. Гикерупругость. Гипоупругость
- 6.10. Линейная термоупругость
- Глава 7. Жидкости
- 7.1. Давление жидкости. Тензор вязких напряжений. Баротропное течение
- 7.2. Определяющие уравнения. Стоксовы жидкости. Ньютоновы жидкости
- 7.3. Основные уравнения ньютоновой жидкости. Уравнения Навье — Стокса — Дюгема
- 7.4. Установившееся течение. Гидростатика. Безвихревое течение
- 7.5. Идеальная жидкость. Уравнение Бернулли. Циркуляция
- 7.6. Потенциальное течение. Плоское потенциальное течение
- Глава 8. Теория пластичности
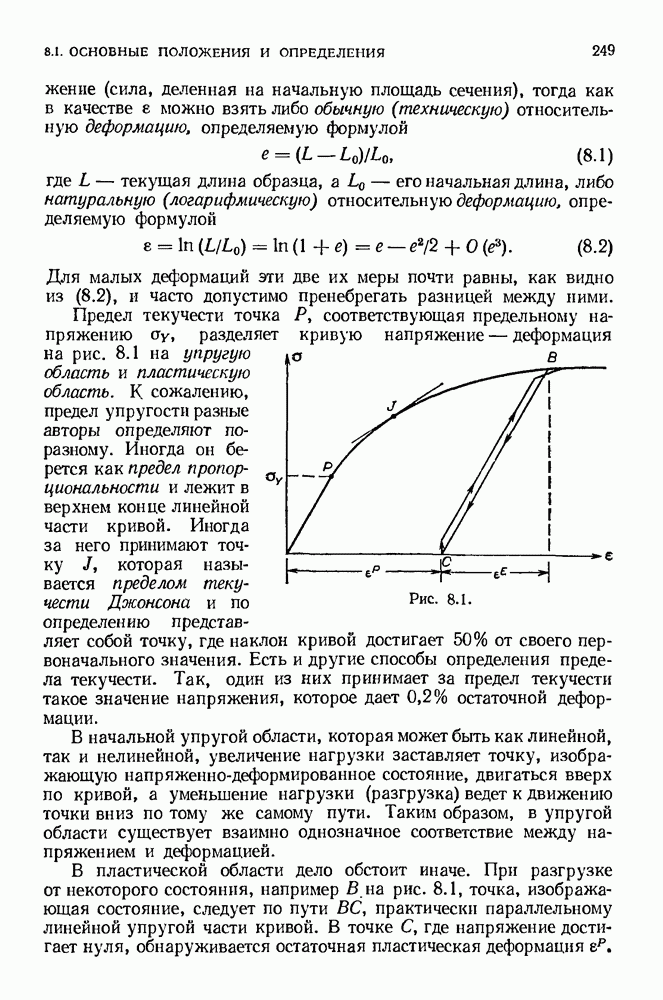
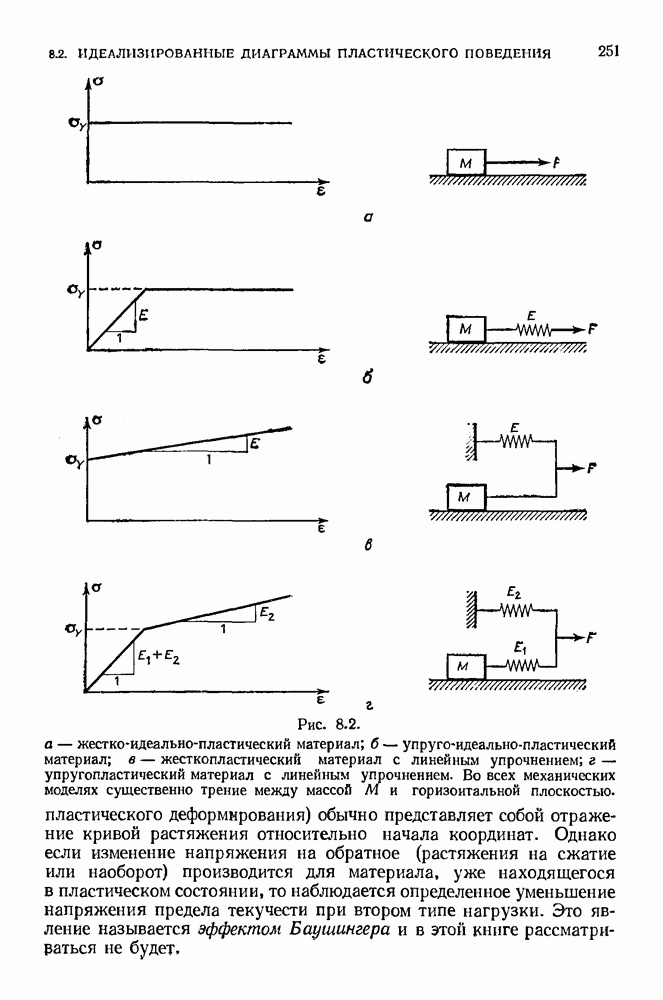
- 8.2. Идеализированные диаграммы пластического поведения
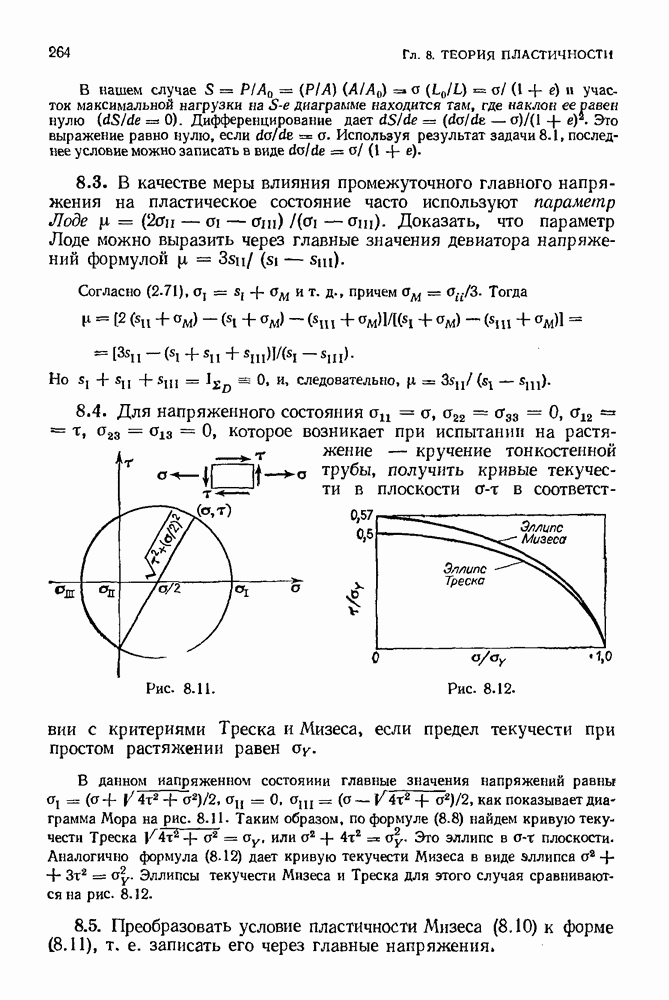
- 8.3. Условия пластичности. Критерии Треска и Мизеса
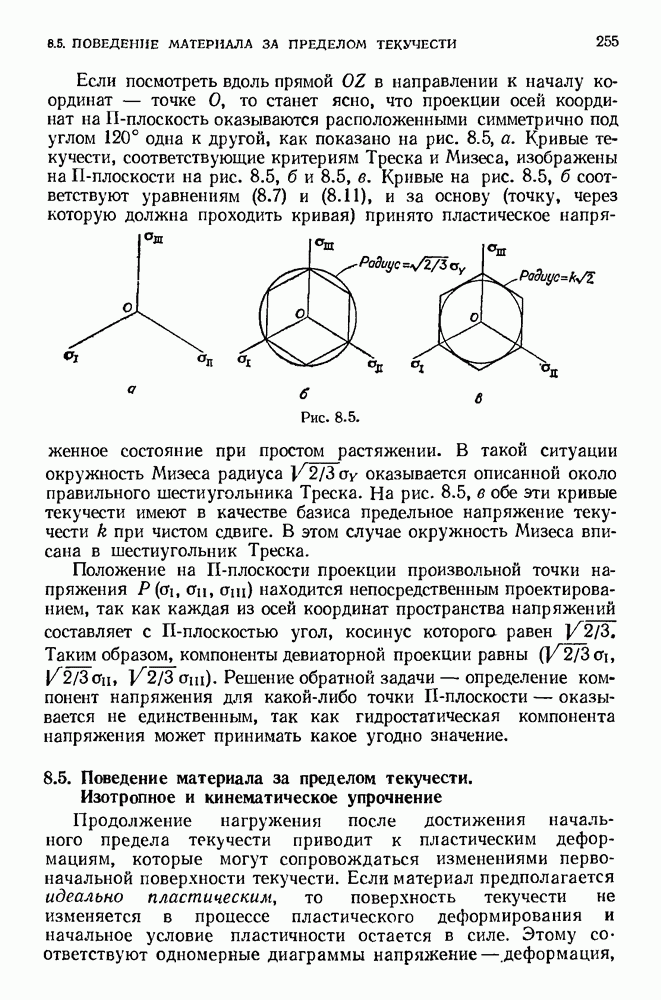
- 8.4. Пространство напряжений. П-плоскость. Поверхность текучести
- 8.5. Поведение материала за пределом текучести. Изотропное и кинематическое упрочнение
- 8.6. Соотношения между напряжениями и деформациями в пластическом состоянии. Теория пластического потенциала
- 8.7. Эквивалентное напряжение. Эквивалентное приращение пластической деформации
- 8.8. Работа на пластических деформациях. Гипотезы упрочнения
- 8.9. Деформационная теория пластичности
- 8.10. Задачи упругопластичности
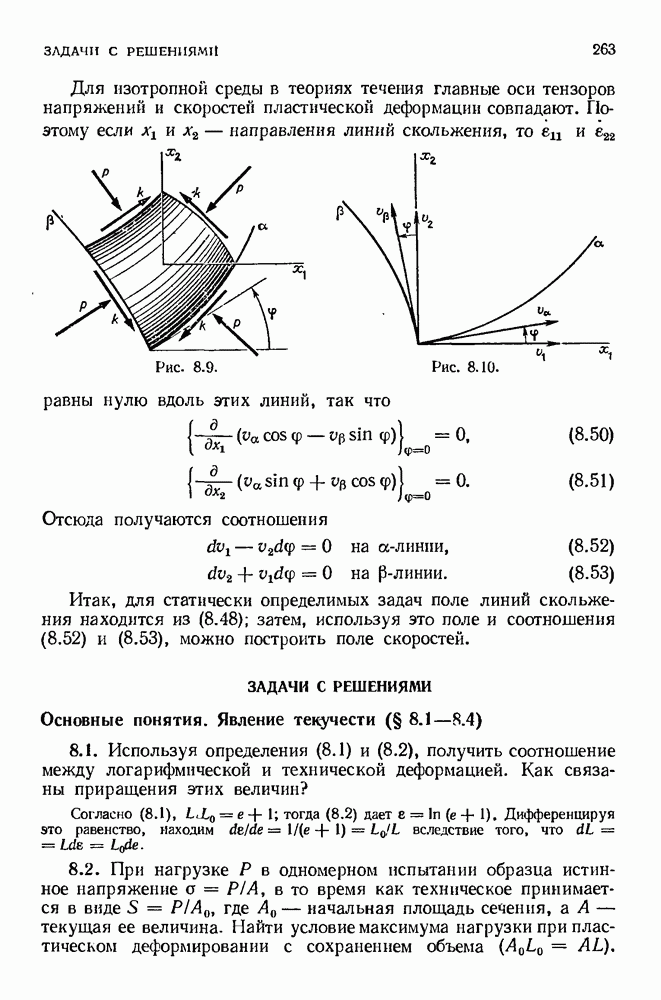
- 8.11. Элементарная теория линий скольжения при плоской пластической деформации
- Глава 9. Линейная вязкоупругость
- 9.1. Вязкоупругое поведение материала
- 9.2. Простейшие механические модели вязкоупругого поведения
- 9.3. Обобщенные модели. Линейное дифференциальное операторное уравнение
- 9.4. Ползучесть и релаксация
- 9.5. Функция ползучести. Функция релаксации. Интегралы наследственности
- 9.6. Комплексные модули и податливости
- 9.7. Трехмерная теория
- 9.8. Анализ вязкоупругого напряженного состояния. Принцип соответствия