| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
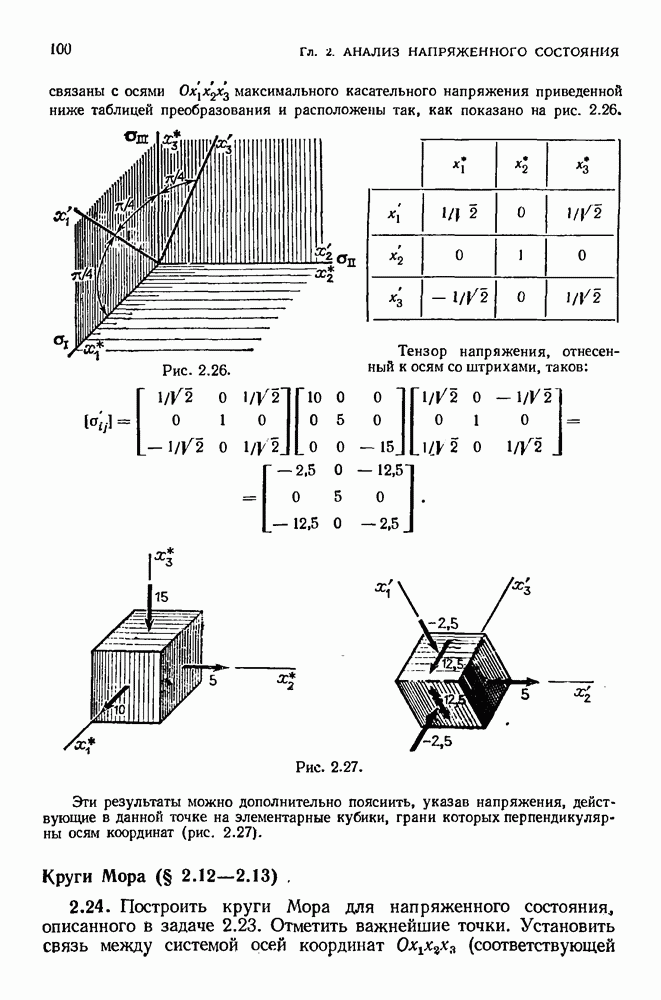
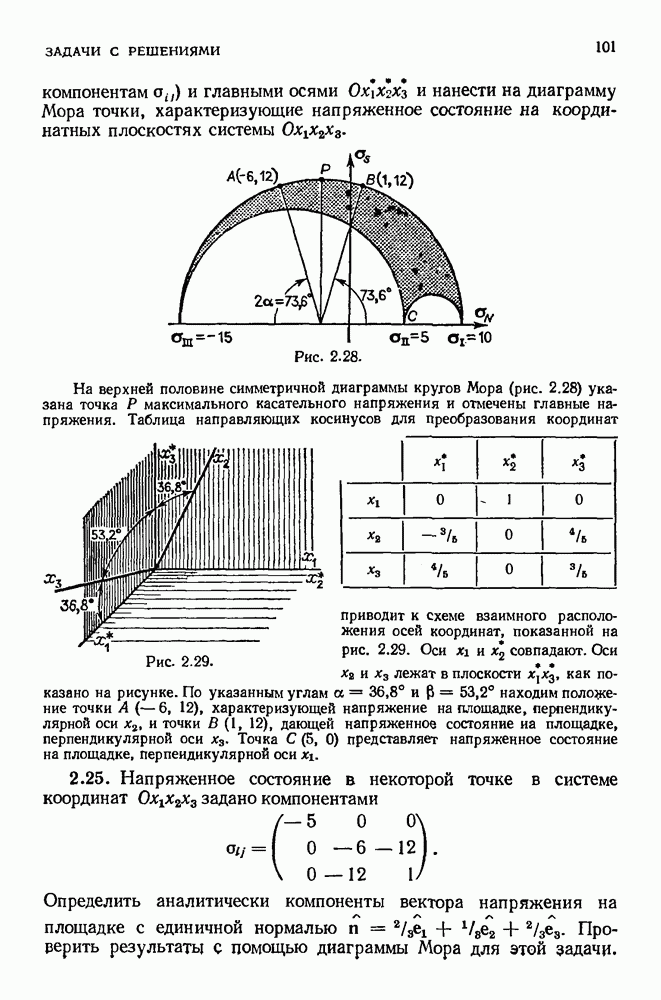
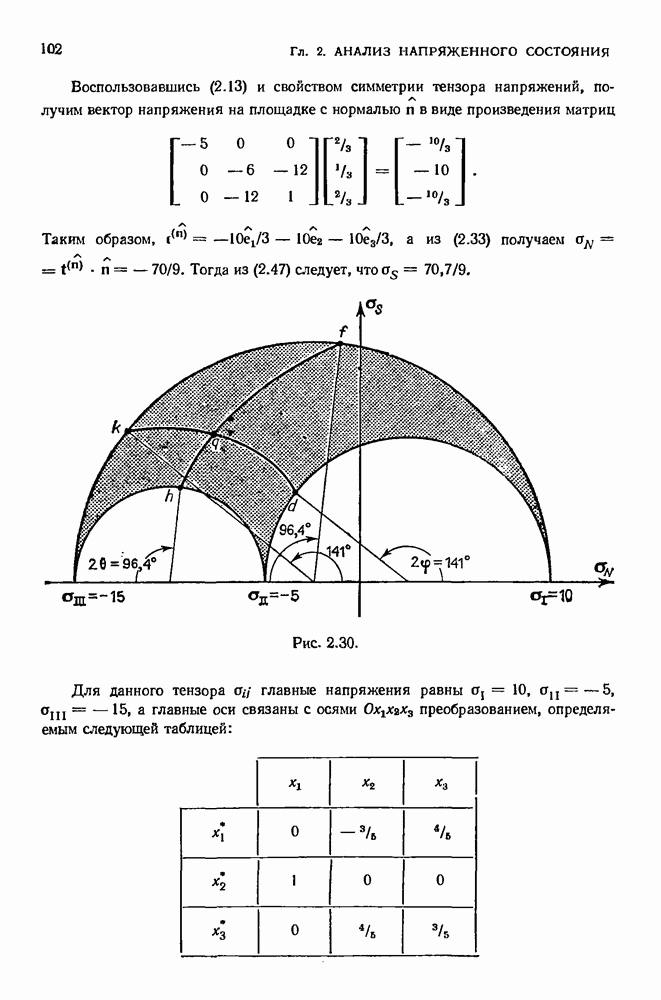
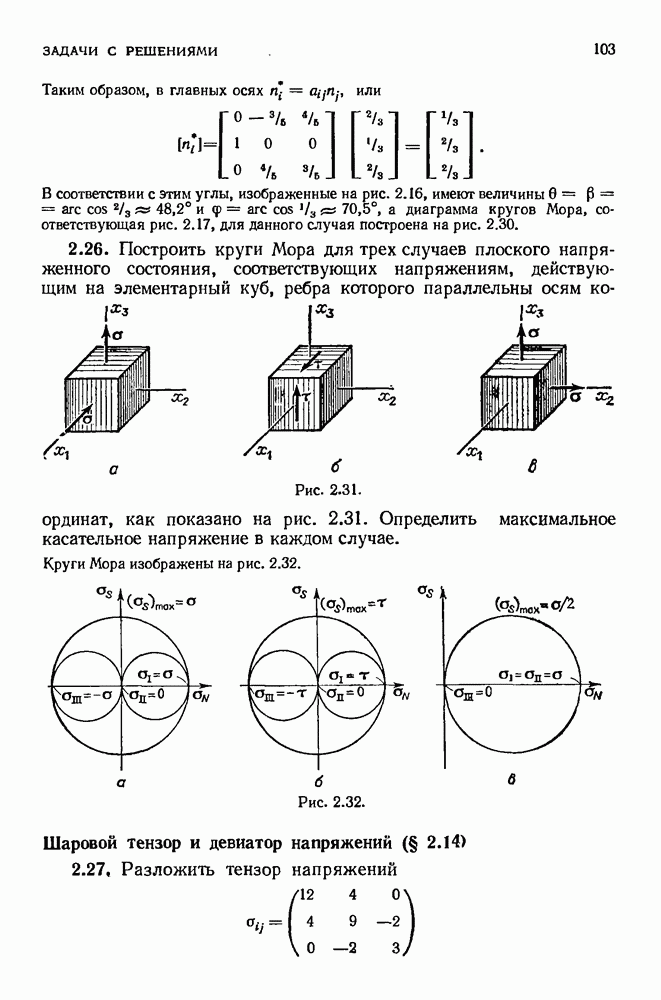
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.21. Тензорные поля. Дифференцирование тензоров
Тензорное поле ставит в соответствие каждой точке пространства и каждому моменту времени  тензор
тензор  где радиус-вектор
где радиус-вектор  меняется в заданной области пространства,
меняется в заданной области пространства,  в заданном интервале времени. Тензорное поле называется непрерывным (или дифференцируемым), если компоненты
в заданном интервале времени. Тензорное поле называется непрерывным (или дифференцируемым), если компоненты  являются непрерывными (или дифференцируемыми) функциями
являются непрерывными (или дифференцируемыми) функциями  Если компоненты тензора зависят только от
Если компоненты тензора зависят только от  то тензорное поле называется стационарным.
то тензорное поле называется стационарным.
В ортогональной декартовой системе координат, где радиус-вектор любой точки имеет вид

поля тензоров различного ранга можно записать в индексных и символических обозначениях, например

б) векторное поле  или
или 
в) поле тензора второго ранга  или
или 
Дифференцирование компонент тензора по координате  обозначается дифференциальным оператором
обозначается дифференциальным оператором  или сокращенно в индексной записи
или сокращенно в индексной записи  что указывает на то, что это тензорный оператор первого ранга. В символических обозначениях для записи этой операции употребляется общеизвестный символ V (набла), который расшифровывается так:
что указывает на то, что это тензорный оператор первого ранга. В символических обозначениях для записи этой операции употребляется общеизвестный символ V (набла), который расшифровывается так:

Частное дифференцирование по переменной  иногда изображают нижним индексом после запятой, как показано в следующих примерах:
иногда изображают нижним индексом после запятой, как показано в следующих примерах:

Эти примеры показывают, что при дифференцировании оператор  приводит к тензору на один порядок выше исходного, если
приводит к тензору на один порядок выше исходного, если  остается свободным индексом (случаи «а» и «в»), и к тензору на один порядок ниже исходного, если
остается свободным индексом (случаи «а» и «в»), и к тензору на один порядок ниже исходного, если  становится индексом суммирования (случай
становится индексом суммирования (случай 
Здесь для справки приведены некоторые важные дифференциальные операторы, часто употребляемые в механике континуума:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. Математические основы
- 1.1. Тензоры и механика сплошной среды
- 1.2. Тензоры. Декартовы тензоры. Ранг тензора
- 1.3. Векторы и скаляры
- 1.4. Векторное сложение. Умножение вектора на скаляр
- 1.5. Скалярное и векторное произведения векторов
- 1.6. Диады и диадики
- 1.7. Системы координат. Базисные векторы. Триэдр единичных векторов
- 1.8. Линейные векторные функции. Диадики как линейные векторные операторы
- 1.9. Индексные обозначения. Интервал изменения индексов и соглашение о суммировании
- 1.10. Соглашение о суммировании в символических обозначениях
- 1.11. Преобразование координат. Общее понятие тензора
- 1.12. Метрический тензор. Декартовы тензоры
- 1.13. Законы преобразования декартовых тензоров. Дельта Кронекера. Условия ортогональности
- 1.14. Сложение декартовых тензоров. Умножение на скаляр
- 1.15. Умножение тензоров
- 1.16. Векторное произведение. Тензор Леви-Чивиты. Бивектор
- 1.17. Матрицы Матричные представления декартовых тензоров
- 1.18. Симметрия диадиков, матриц и тензоров
- 1.19. Главные значения и главные направления симметричных тензоров второго ранга
- 1.20. Степени тензоров второго ранга. Соотношение Гамильтона — Кэли
- 1.21. Тензорные поля. Дифференцирование тензоров
- 1.22. Криволинейные интегралы. Теорема Стокса
- 1.23. Теорема Гаусса — Остроградского
- Глава 2. Анализ напряженного состояния
- 2.1. Понятие сплошной среды
- 2.2. Однородность. Изотропия. Массовая плотность
- 2.3. Массовые силы. Поверхностные силы
- 2.4. Принцип напряжения Коши. Вектор напряжения
- 2.5. Напряженное состояние в точке. Тензор напряжений
- 2.6. Связь между тензором напряжений и вектором напряжения
- 2.7. Равновесие сил и моментов. Симметрия тензора напряжений
- 2.8. Законы преобразования напряжений
- 2.9. Поверхности напряжений Коши
- 2.10. Главные напряжения. Инварианты тензора напряжений. Эллипсоид напряжений
- 2.11. Максимальное и минимальное касательное напряжение
- 2.12. Круги Мора для напряжения
- 2.13. Плоское напряженное состояние
- 2.14. Девиатор и шаровой тензор напряжений
- Глава 3. Деформации
- 3.2. Конфигурация сплошной среды. Деформация и течение
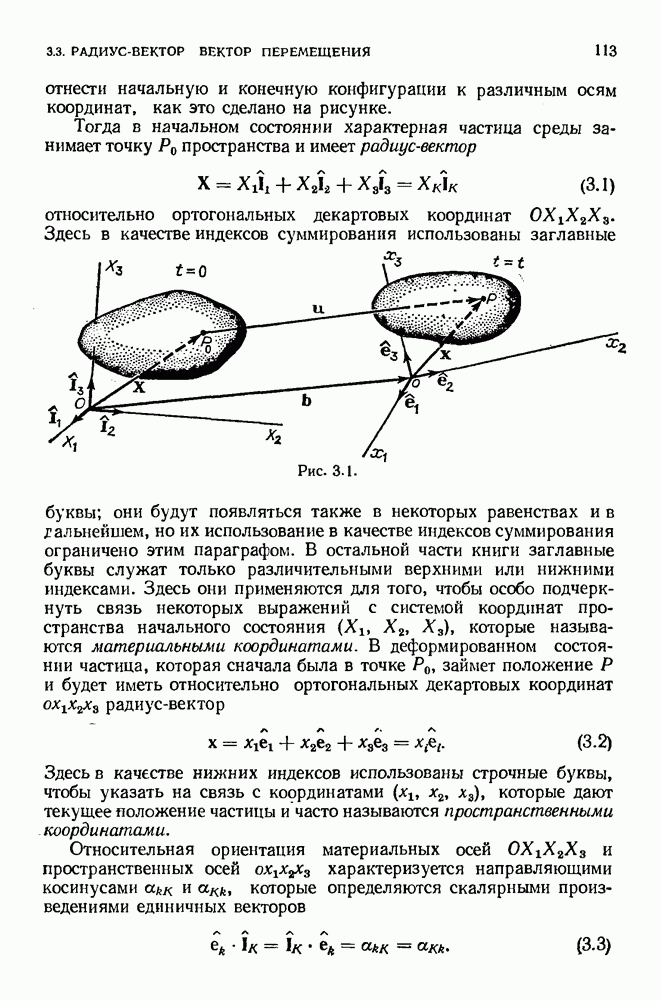
- 3.3. Радиус-вектор. Вектор перемещения
- 3.4. Лагранжево и эйлерово описания движения
- 3.5. Градиенты деформации. Градиенты перемещения
- 3.6. Тензоры деформаций. Тензоры конечных деформаций
- 3.7. Теория малых деформаций. Тензоры бесконечно малых деформаций
- 3.8. Относительное перемещение. Тензор линейного поворота. Вектор поворота
- 3.9. Геометрический смысл тензоров линейных деформаций
- 3.10. Коэффициент длины. Интерпретация конечных деформаций
- 3.11. Тензоры коэффициентов длины. Тензор поворота
- 3.12. Свойства преобразований тензоров деформаций
- 3.13. Главные деформации. Инварианты деформации. Кубическое расширение
- 3.14. Шаровой тензор и девиатор деформаций
- 3.15. Плоская деформация. Круги Мора для деформации
- 3.16. Уравнения совместности для линейных деформаций
- Глава 4. Движение и течение
- 4.1. Движение. Течение. Материальная производная
- 4.2. Скорость. Ускорение. Мгновенное поле скоростей
- 4.3. Траектории. Линии тока. Установившееся движение
- 4.4. Скорость деформации. Завихренность. Приращения деформации
- 4.5. Физическая интерпретация тензоров скоростей деформации и завихренности
- 4.6. Материальные производные по времени от элемента объема, элемента поверхности и линейного элемента
- 4.7. Материальные производные по времени от интеграла по объему, интеграла по поверхности и линейного интеграла
- Глава 5. Основные законы механики сплошной среды
- 5.1. Сохранение массы. Уравнение неразрывности
- 5.2. Теорема об изменении количества движения. Уравнения движения. Уравнения равновесия
- 5.3. Теорема об изменении момента количества движения
- 5.4. Сохранение энергии. Первый закон термодинамики. Уравнение энергии
- 5.5. Уравнения состояния. Энтропия. Второй закон термодинамики
- 5.6. Неравенство Клаузиуса — Дюгема. Диссипативная функция
- 5.7. Определяющие уравнения. Термомеханический и механический континуумы
- Глава 6. Линейная теория упругости
- 6.1. Обобщенный закон Гука. Функция энергии деформации
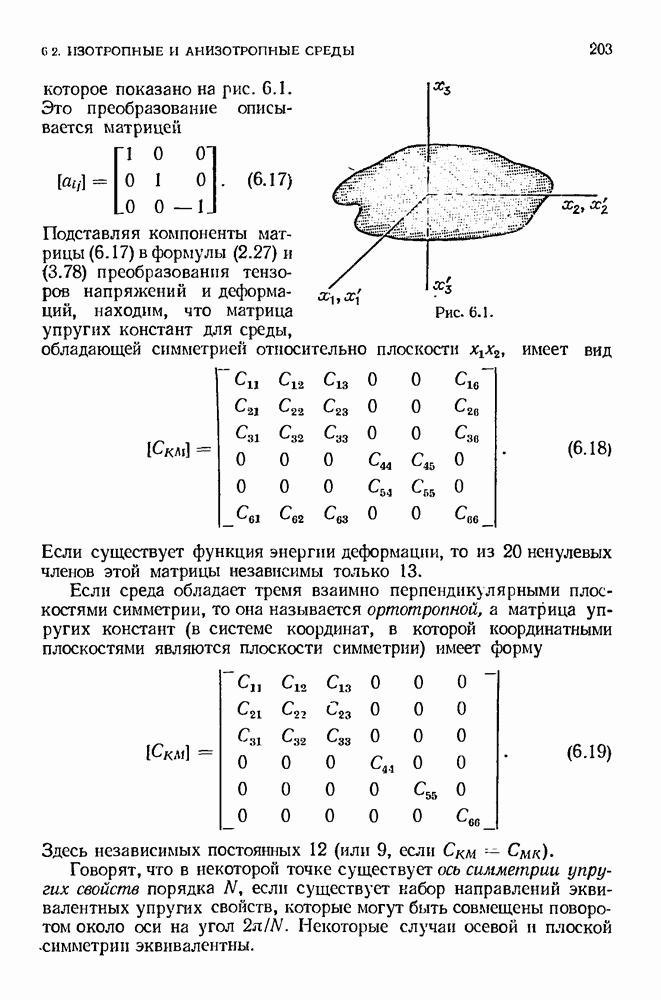
- 6.2. Изотропные и анизотропные среды. Симметрия упругих свойств
- 6.3. Изотропные среды. Упругие постоянные
- 6.4. Постановка статических и динамических задач теории упругости
- 6.5. Теорема о суперпозиции. Единственность решений. Принцип Сен-Венана
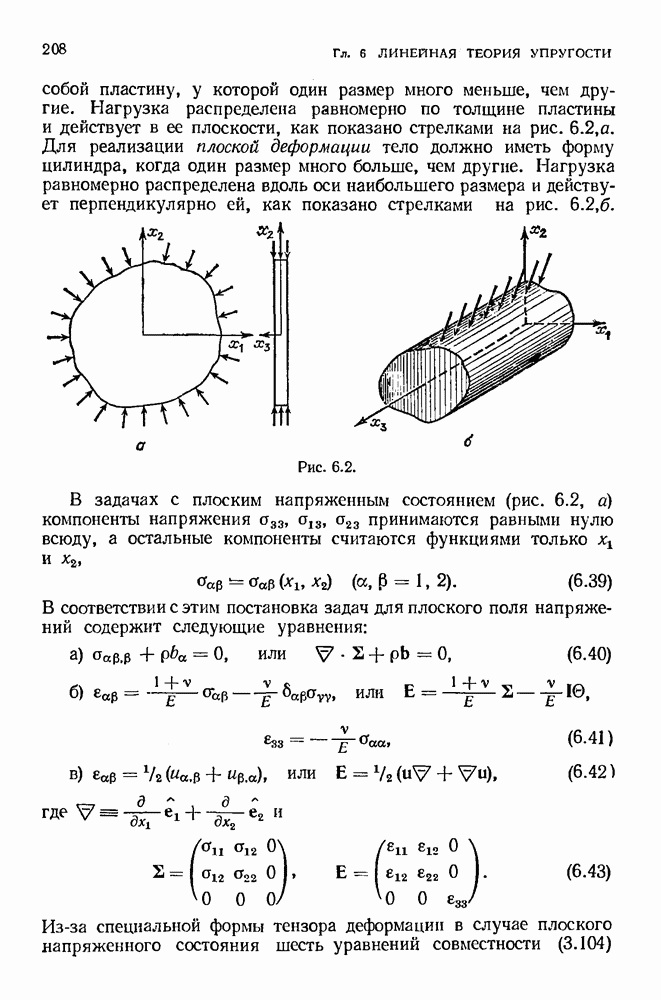
- 6.6. Плоские задачи теории упругости. Плоское напряженное состояние и плоская деформация
- 6.7. Функция напряжений Эри
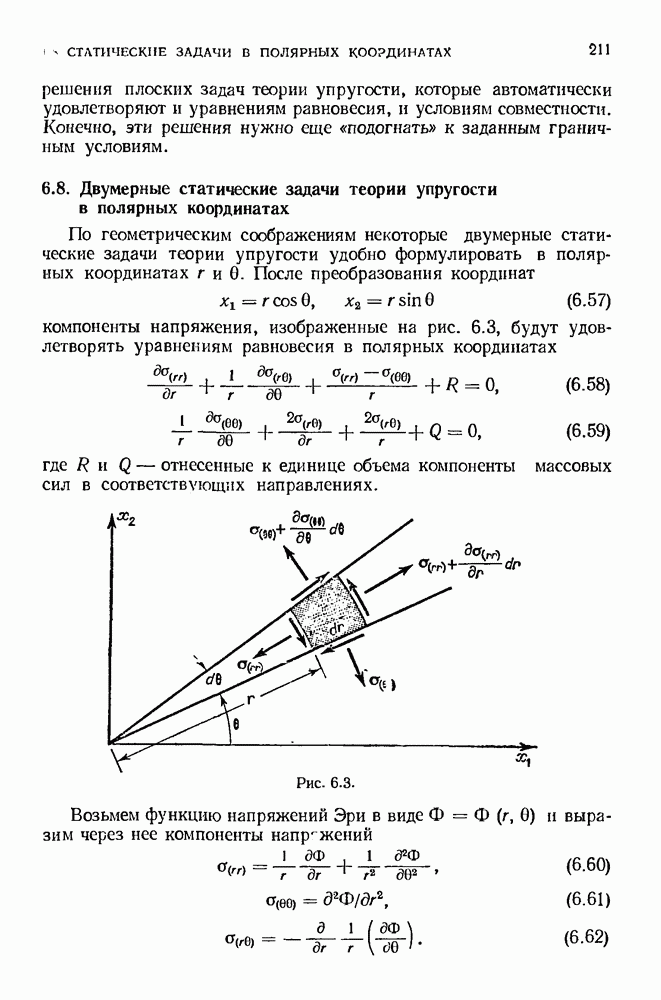
- 6.8. Двумерные статические задачи теории упругости в полярных координатах
- 6.9. Гикерупругость. Гипоупругость
- 6.10. Линейная термоупругость
- Глава 7. Жидкости
- 7.1. Давление жидкости. Тензор вязких напряжений. Баротропное течение
- 7.2. Определяющие уравнения. Стоксовы жидкости. Ньютоновы жидкости
- 7.3. Основные уравнения ньютоновой жидкости. Уравнения Навье — Стокса — Дюгема
- 7.4. Установившееся течение. Гидростатика. Безвихревое течение
- 7.5. Идеальная жидкость. Уравнение Бернулли. Циркуляция
- 7.6. Потенциальное течение. Плоское потенциальное течение
- Глава 8. Теория пластичности
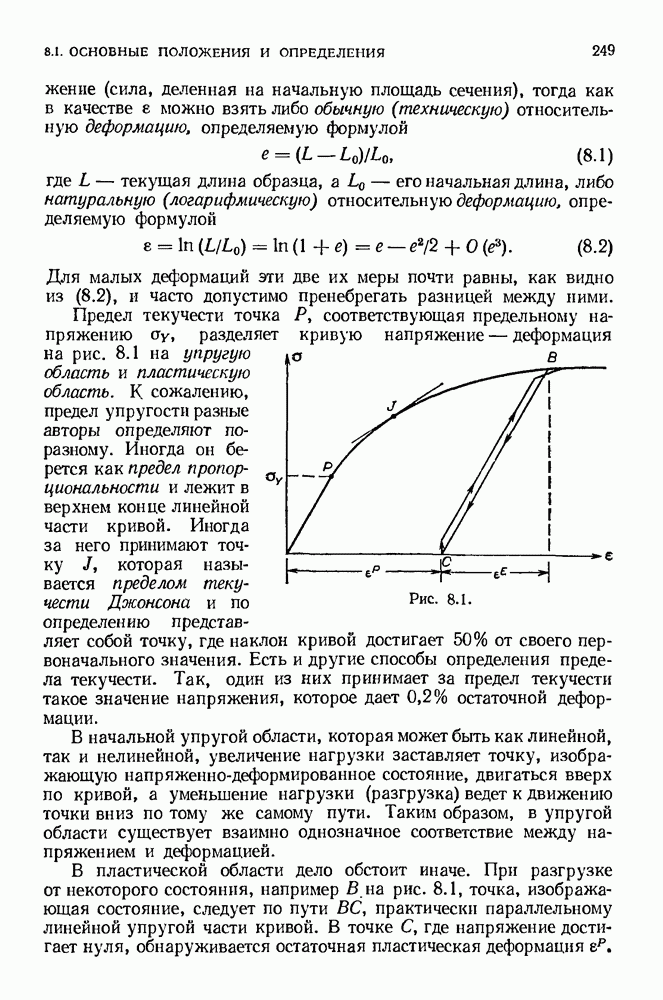
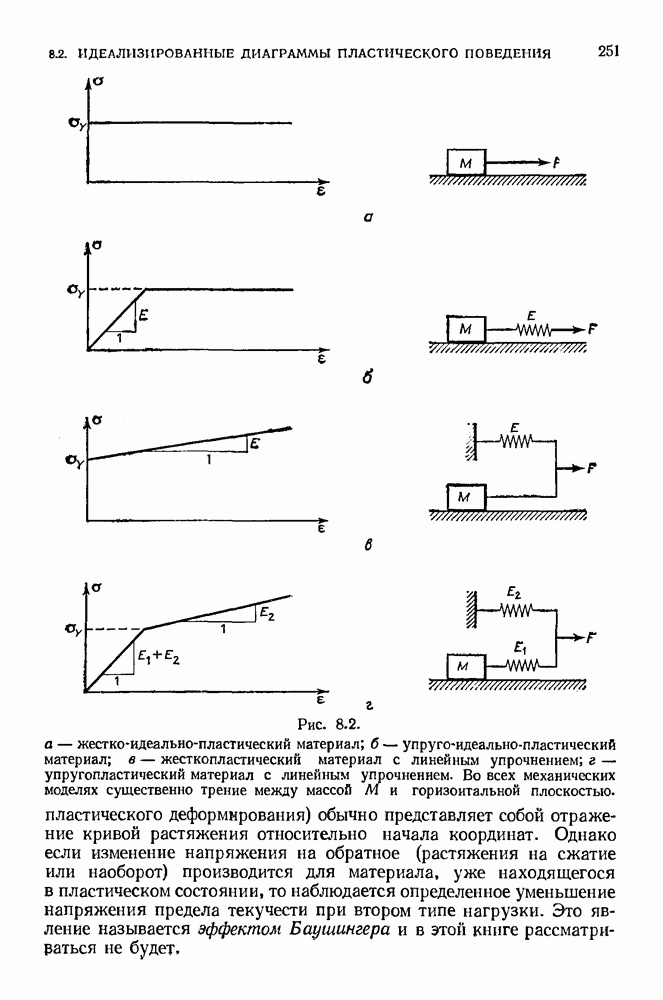
- 8.2. Идеализированные диаграммы пластического поведения
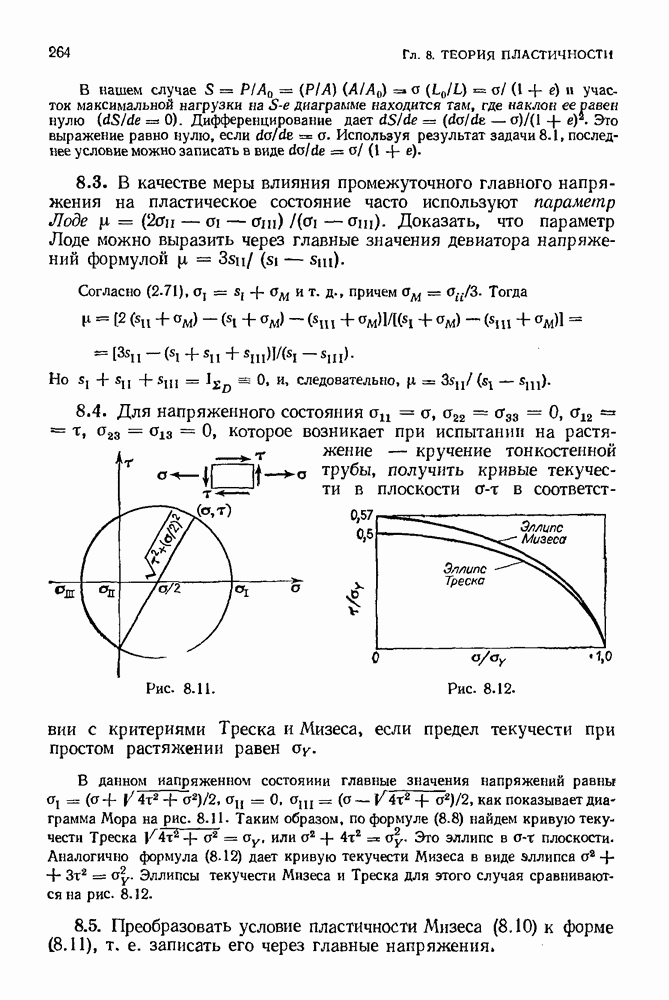
- 8.3. Условия пластичности. Критерии Треска и Мизеса
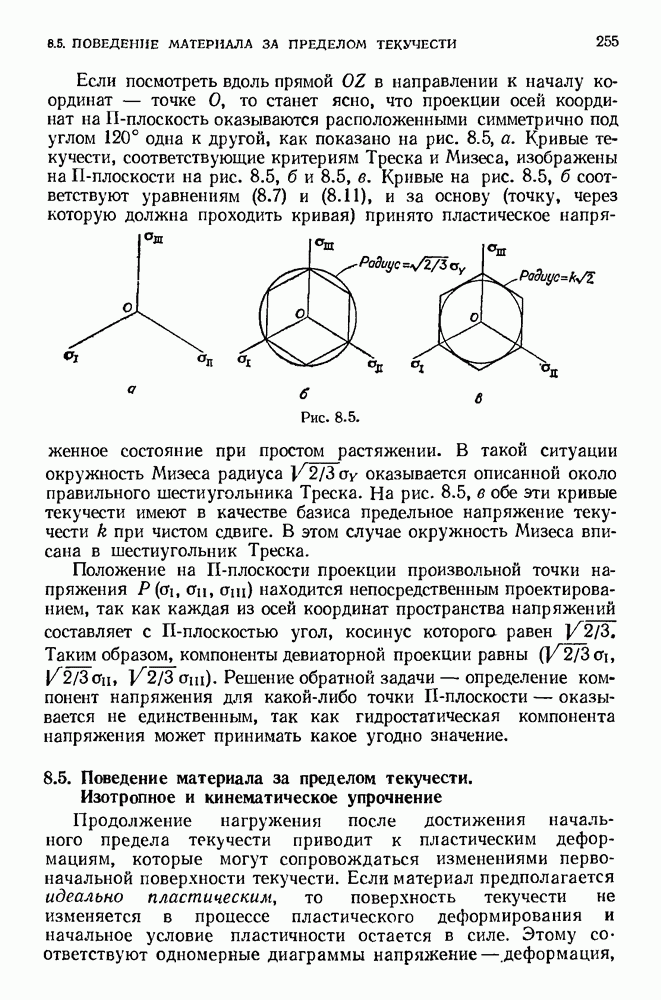
- 8.4. Пространство напряжений. П-плоскость. Поверхность текучести
- 8.5. Поведение материала за пределом текучести. Изотропное и кинематическое упрочнение
- 8.6. Соотношения между напряжениями и деформациями в пластическом состоянии. Теория пластического потенциала
- 8.7. Эквивалентное напряжение. Эквивалентное приращение пластической деформации
- 8.8. Работа на пластических деформациях. Гипотезы упрочнения
- 8.9. Деформационная теория пластичности
- 8.10. Задачи упругопластичности
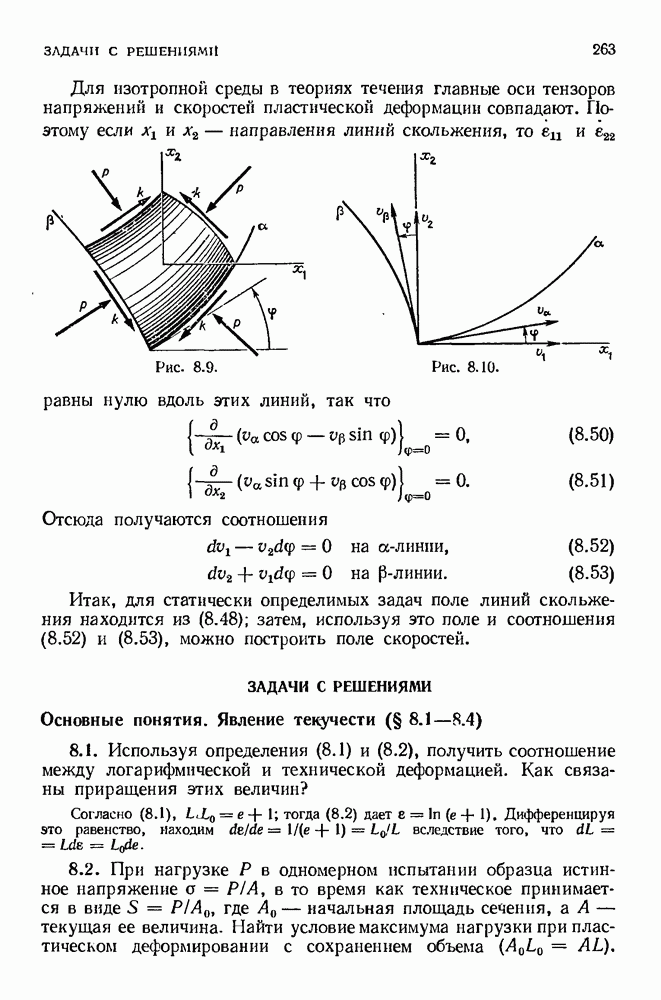
- 8.11. Элементарная теория линий скольжения при плоской пластической деформации
- Глава 9. Линейная вязкоупругость
- 9.1. Вязкоупругое поведение материала
- 9.2. Простейшие механические модели вязкоупругого поведения
- 9.3. Обобщенные модели. Линейное дифференциальное операторное уравнение
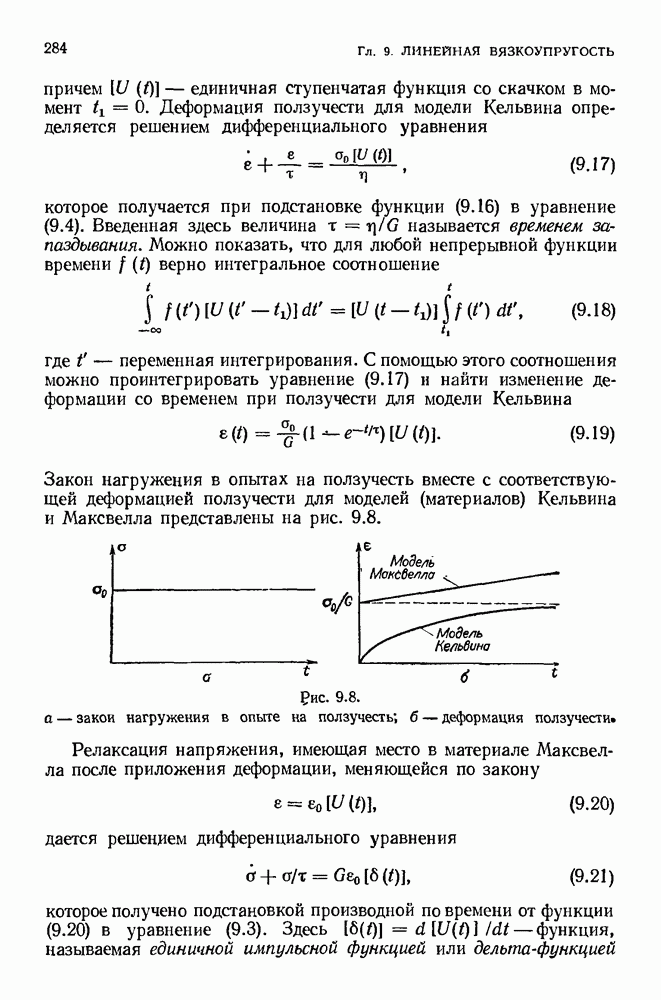
- 9.4. Ползучесть и релаксация
- 9.5. Функция ползучести. Функция релаксации. Интегралы наследственности
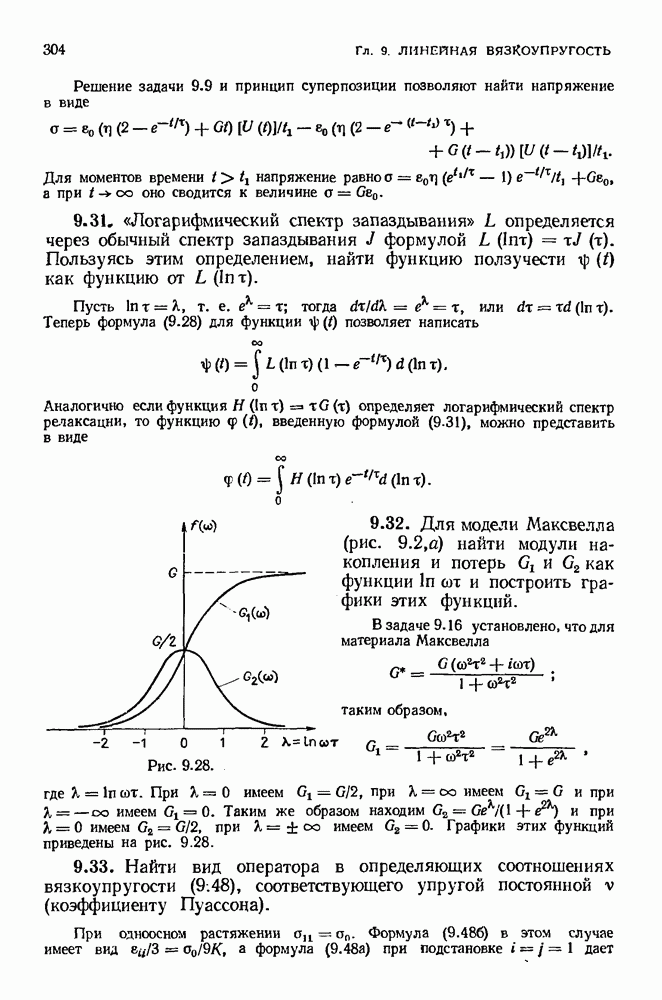
- 9.6. Комплексные модули и податливости
- 9.7. Трехмерная теория
- 9.8. Анализ вязкоупругого напряженного состояния. Принцип соответствия