| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.19. Главные значения и главные направления симметричных тензоров второго ранга
В дальнейшем будут рассматриваться только симметричные тензоры с действительными компонентами. Это несколько проще в математическом отношении, а так как тензоры, важные для механики
сплошной среды, обычно симметричны, то мы не многим жертвуем, принимая такое ограничение.
Для каждого симметричного тензора  заданного в некоторой точке пространства, и для каждого направления в этой точке (характеризуемого единичным вектором
заданного в некоторой точке пространства, и для каждого направления в этой точке (характеризуемого единичным вектором  существует вектор, определяемый внутренним произведением
существует вектор, определяемый внутренним произведением

Здесь  можно рассматривать как линейный векторный оператор, который ставит в соответствие направлению
можно рассматривать как линейный векторный оператор, который ставит в соответствие направлению  вектор
вектор  Если направление таково, что вектор
Если направление таково, что вектор  параллелен
параллелен  то указанное внутреннее произведение выражается скаляром, умноженным на
то указанное внутреннее произведение выражается скаляром, умноженным на  В этом случае
В этом случае

и направление  называется главным направлением или главной осью тензора
называется главным направлением или главной осью тензора  С помощью тождества
С помощью тождества  соотношению (1.129) можно придать форму
соотношению (1.129) можно придать форму

которая представляет систему трех уравнений для четырех неизвестных  и
и  соответствующих каждому главному направлению. В развернутой записи система, которую следует разрешить, имеет вид
соответствующих каждому главному направлению. В развернутой записи система, которую следует разрешить, имеет вид

Заметим прежде всего, что при любом  существует тривиальное решение
существует тривиальное решение  однако нашей целью является получение нетривиального решения. Кроме того, вследствие однородности системы (1.131), не теряя общности, можно ограничиться только решениями, для которых
однако нашей целью является получение нетривиального решения. Кроме того, вследствие однородности системы (1.131), не теряя общности, можно ограничиться только решениями, для которых  Начиная с этого момента мы будем требовать, чтобы это условие выполнялось.
Начиная с этого момента мы будем требовать, чтобы это условие выполнялось.
Для того чтобы система (1.130), или, что то же самое, система (1.131), имела нетривиальное решение, определитель из коэффициентов должен быть равен нулю, т. е.

В развернутом виде это кубическое уравнение относительно  :
:

которое называется характеристическим уравнением тензора  а его скалярные коэффициенты
а его скалярные коэффициенты


называются соответственно первым, вторым и третьим инвариантами тензора  Три корня кубического уравнения (1.133), обозначенные
Три корня кубического уравнения (1.133), обозначенные  называются главными значениями тензора
называются главными значениями тензора  У симметричного тензора с действительными компонентами главные значения действительны; если все они различны, то три главных направления взаимно ортогональны. В главных осях таблица из компонент тензора приводится к диагональной форме:
У симметричного тензора с действительными компонентами главные значения действительны; если все они различны, то три главных направления взаимно ортогональны. В главных осях таблица из компонент тензора приводится к диагональной форме:

Если  то диагональный вид тензора не зависит от выбора осей, соответствующих
то диагональный вид тензора не зависит от выбора осей, соответствующих  и нужно установить только главную ось, соответствующую
и нужно установить только главную ось, соответствующую  Если все главные значения равны, то любое направление является главным. Если главные значения упорядочены, то принято обозначать их через
Если все главные значения равны, то любое направление является главным. Если главные значения упорядочены, то принято обозначать их через  и располагать в порядке убывания:
и располагать в порядке убывания: 
Преобразование от системы  к системе главных осей
к системе главных осей  дается элементами таблицы
дается элементами таблицы

где  направляющие косинусы
направляющие косинусы  главного направления.
главного направления.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. Математические основы
- 1.1. Тензоры и механика сплошной среды
- 1.2. Тензоры. Декартовы тензоры. Ранг тензора
- 1.3. Векторы и скаляры
- 1.4. Векторное сложение. Умножение вектора на скаляр
- 1.5. Скалярное и векторное произведения векторов
- 1.6. Диады и диадики
- 1.7. Системы координат. Базисные векторы. Триэдр единичных векторов
- 1.8. Линейные векторные функции. Диадики как линейные векторные операторы
- 1.9. Индексные обозначения. Интервал изменения индексов и соглашение о суммировании
- 1.10. Соглашение о суммировании в символических обозначениях
- 1.11. Преобразование координат. Общее понятие тензора
- 1.12. Метрический тензор. Декартовы тензоры
- 1.13. Законы преобразования декартовых тензоров. Дельта Кронекера. Условия ортогональности
- 1.14. Сложение декартовых тензоров. Умножение на скаляр
- 1.15. Умножение тензоров
- 1.16. Векторное произведение. Тензор Леви-Чивиты. Бивектор
- 1.17. Матрицы Матричные представления декартовых тензоров
- 1.18. Симметрия диадиков, матриц и тензоров
- 1.19. Главные значения и главные направления симметричных тензоров второго ранга
- 1.20. Степени тензоров второго ранга. Соотношение Гамильтона — Кэли
- 1.21. Тензорные поля. Дифференцирование тензоров
- 1.22. Криволинейные интегралы. Теорема Стокса
- 1.23. Теорема Гаусса — Остроградского
- Глава 2. Анализ напряженного состояния
- 2.1. Понятие сплошной среды
- 2.2. Однородность. Изотропия. Массовая плотность
- 2.3. Массовые силы. Поверхностные силы
- 2.4. Принцип напряжения Коши. Вектор напряжения
- 2.5. Напряженное состояние в точке. Тензор напряжений
- 2.6. Связь между тензором напряжений и вектором напряжения
- 2.7. Равновесие сил и моментов. Симметрия тензора напряжений
- 2.8. Законы преобразования напряжений
- 2.9. Поверхности напряжений Коши
- 2.10. Главные напряжения. Инварианты тензора напряжений. Эллипсоид напряжений
- 2.11. Максимальное и минимальное касательное напряжение
- 2.12. Круги Мора для напряжения
- 2.13. Плоское напряженное состояние
- 2.14. Девиатор и шаровой тензор напряжений
- Глава 3. Деформации
- 3.2. Конфигурация сплошной среды. Деформация и течение
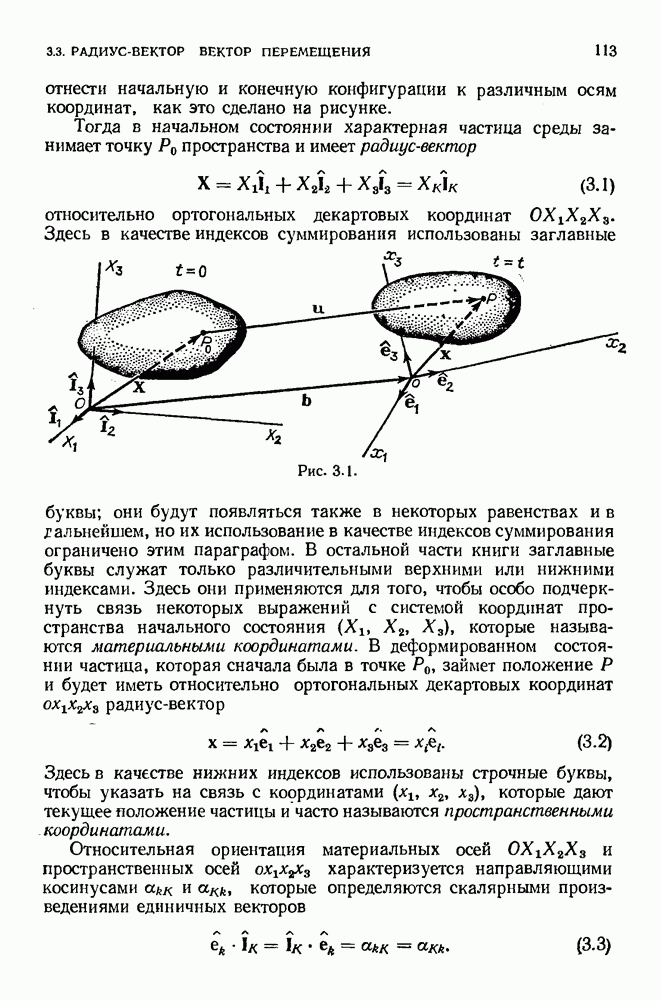
- 3.3. Радиус-вектор. Вектор перемещения
- 3.4. Лагранжево и эйлерово описания движения
- 3.5. Градиенты деформации. Градиенты перемещения
- 3.6. Тензоры деформаций. Тензоры конечных деформаций
- 3.7. Теория малых деформаций. Тензоры бесконечно малых деформаций
- 3.8. Относительное перемещение. Тензор линейного поворота. Вектор поворота
- 3.9. Геометрический смысл тензоров линейных деформаций
- 3.10. Коэффициент длины. Интерпретация конечных деформаций
- 3.11. Тензоры коэффициентов длины. Тензор поворота
- 3.12. Свойства преобразований тензоров деформаций
- 3.13. Главные деформации. Инварианты деформации. Кубическое расширение
- 3.14. Шаровой тензор и девиатор деформаций
- 3.15. Плоская деформация. Круги Мора для деформации
- 3.16. Уравнения совместности для линейных деформаций
- Глава 4. Движение и течение
- 4.1. Движение. Течение. Материальная производная
- 4.2. Скорость. Ускорение. Мгновенное поле скоростей
- 4.3. Траектории. Линии тока. Установившееся движение
- 4.4. Скорость деформации. Завихренность. Приращения деформации
- 4.5. Физическая интерпретация тензоров скоростей деформации и завихренности
- 4.6. Материальные производные по времени от элемента объема, элемента поверхности и линейного элемента
- 4.7. Материальные производные по времени от интеграла по объему, интеграла по поверхности и линейного интеграла
- Глава 5. Основные законы механики сплошной среды
- 5.1. Сохранение массы. Уравнение неразрывности
- 5.2. Теорема об изменении количества движения. Уравнения движения. Уравнения равновесия
- 5.3. Теорема об изменении момента количества движения
- 5.4. Сохранение энергии. Первый закон термодинамики. Уравнение энергии
- 5.5. Уравнения состояния. Энтропия. Второй закон термодинамики
- 5.6. Неравенство Клаузиуса — Дюгема. Диссипативная функция
- 5.7. Определяющие уравнения. Термомеханический и механический континуумы
- Глава 6. Линейная теория упругости
- 6.1. Обобщенный закон Гука. Функция энергии деформации
- 6.2. Изотропные и анизотропные среды. Симметрия упругих свойств
- 6.3. Изотропные среды. Упругие постоянные
- 6.4. Постановка статических и динамических задач теории упругости
- 6.5. Теорема о суперпозиции. Единственность решений. Принцип Сен-Венана
- 6.6. Плоские задачи теории упругости. Плоское напряженное состояние и плоская деформация
- 6.7. Функция напряжений Эри
- 6.8. Двумерные статические задачи теории упругости в полярных координатах
- 6.9. Гикерупругость. Гипоупругость
- 6.10. Линейная термоупругость
- Глава 7. Жидкости
- 7.1. Давление жидкости. Тензор вязких напряжений. Баротропное течение
- 7.2. Определяющие уравнения. Стоксовы жидкости. Ньютоновы жидкости
- 7.3. Основные уравнения ньютоновой жидкости. Уравнения Навье — Стокса — Дюгема
- 7.4. Установившееся течение. Гидростатика. Безвихревое течение
- 7.5. Идеальная жидкость. Уравнение Бернулли. Циркуляция
- 7.6. Потенциальное течение. Плоское потенциальное течение
- Глава 8. Теория пластичности
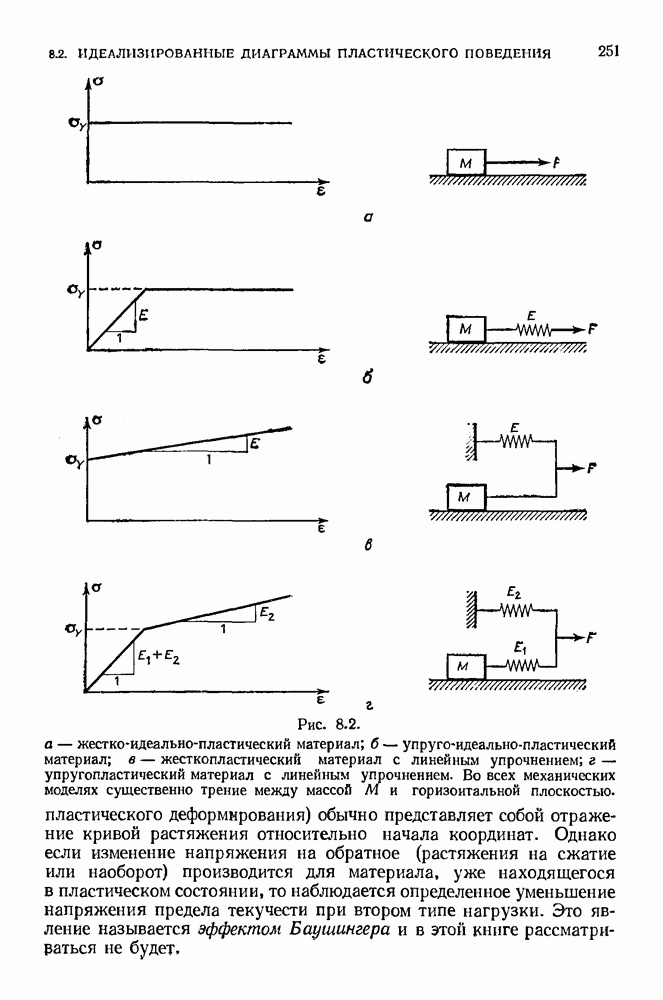
- 8.2. Идеализированные диаграммы пластического поведения
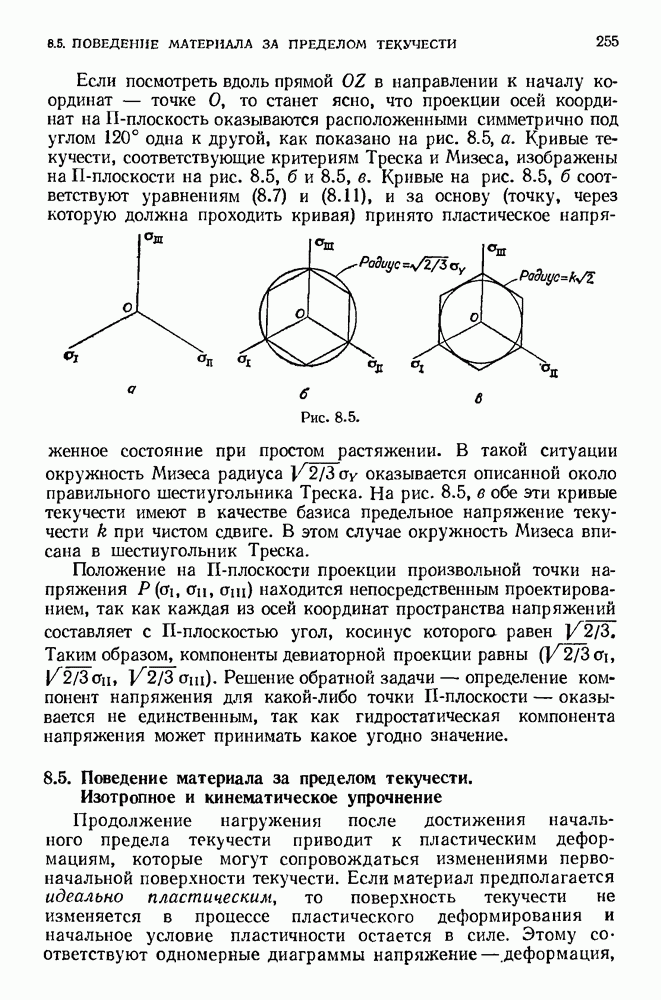
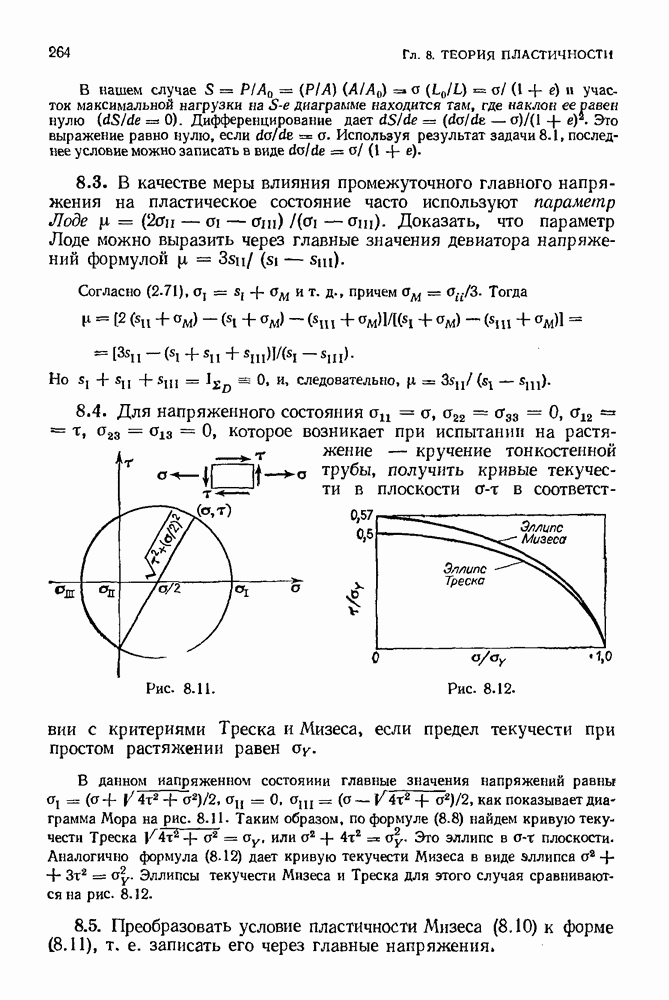
- 8.3. Условия пластичности. Критерии Треска и Мизеса
- 8.4. Пространство напряжений. П-плоскость. Поверхность текучести
- 8.5. Поведение материала за пределом текучести. Изотропное и кинематическое упрочнение
- 8.6. Соотношения между напряжениями и деформациями в пластическом состоянии. Теория пластического потенциала
- 8.7. Эквивалентное напряжение. Эквивалентное приращение пластической деформации
- 8.8. Работа на пластических деформациях. Гипотезы упрочнения
- 8.9. Деформационная теория пластичности
- 8.10. Задачи упругопластичности
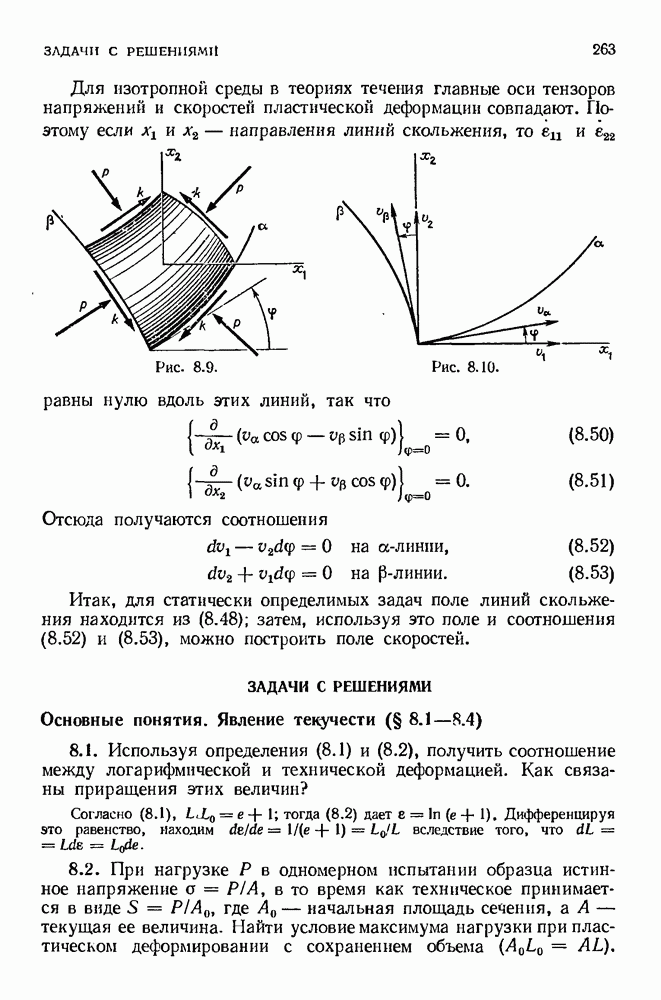
- 8.11. Элементарная теория линий скольжения при плоской пластической деформации
- Глава 9. Линейная вязкоупругость
- 9.1. Вязкоупругое поведение материала
- 9.2. Простейшие механические модели вязкоупругого поведения
- 9.3. Обобщенные модели. Линейное дифференциальное операторное уравнение
- 9.4. Ползучесть и релаксация
- 9.5. Функция ползучести. Функция релаксации. Интегралы наследственности
- 9.6. Комплексные модули и податливости
- 9.7. Трехмерная теория
- 9.8. Анализ вязкоупругого напряженного состояния. Принцип соответствия