| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
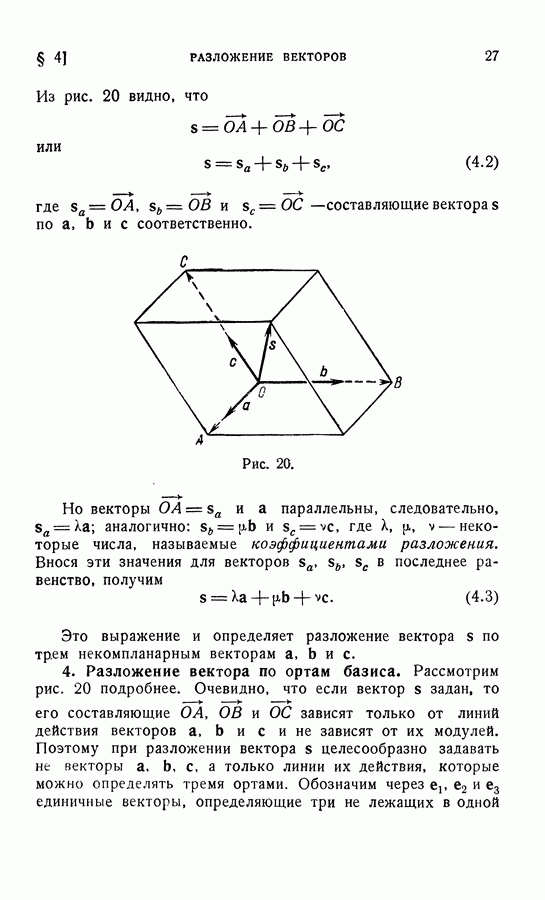
2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
Так как существует бесчисленное множество систем, эквивалентных данной, то большое значение имеет выбор простейшей
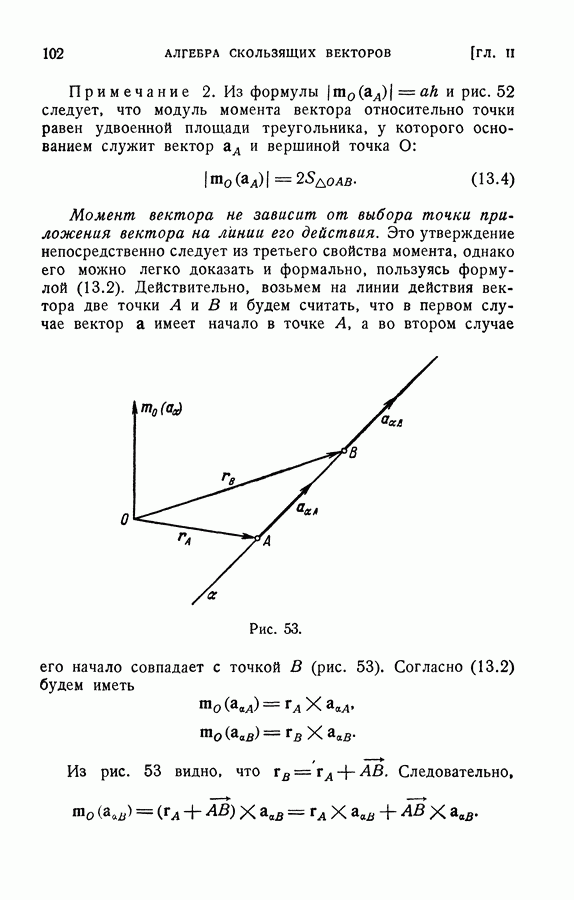
системы. Прежде всего следует остановиться на вопросе, что следует понимать под простейшей системой? Хотя вопрос этот и не имеет точного ответа, однако можно считать, что простейшая система должна содержать наименьшее число векторов. В частности, если данную систему можно привести к нулю, то простейшей системой для данной будем считать нулевую систему, если система приводится к одному вектору, то простейшей системой будвм считать этот вектор. Было показано  что любую систему скользящих векторов можно привести к эквивалентной ей системе двух векторов, однако геометрическое решение, имея большое теоретическое значение, практически неприменимо, так как оно требует много пространственных построений. Поэтому представляет интерес аналитическое решение, свободное от этих недостатков.
что любую систему скользящих векторов можно привести к эквивалентной ей системе двух векторов, однако геометрическое решение, имея большое теоретическое значение, практически неприменимо, так как оно требует много пространственных построений. Поэтому представляет интерес аналитическое решение, свободное от этих недостатков.
Пусть система данных векторов с главным вектором  и главным моментом
и главным моментом  (О — начало координат) эквивалентна двум векторам Р и
(О — начало координат) эквивалентна двум векторам Р и  причем будем считать, что эти векторы приложены в точках
причем будем считать, что эти векторы приложены в точках  соответственно. Уравнения (20.1) примут вид
соответственно. Уравнения (20.1) примут вид

где  и
и  — известные векторы, а векторы
— известные векторы, а векторы  нужно подобрать так, чтобы эта система имела решение. Из первого уравнения выразим Р через
нужно подобрать так, чтобы эта система имела решение. Из первого уравнения выразим Р через 

и внесем это значение во второе уравнение:

Один из векторов,  или
или  можно выбрать произвольно; пусть это будет вектор
можно выбрать произвольно; пусть это будет вектор  Тогда правая часть этого равенства сделается вполне определенным вектором. Вектор
Тогда правая часть этого равенства сделается вполне определенным вектором. Вектор  выберем из условия, что векторы
выберем из условия, что векторы  должны быть взаимно перпендикулярны и, следовательно, их скалярное произведение равняется нулю. Отсюда
должны быть взаимно перпендикулярны и, следовательно, их скалярное произведение равняется нулю. Отсюда

или

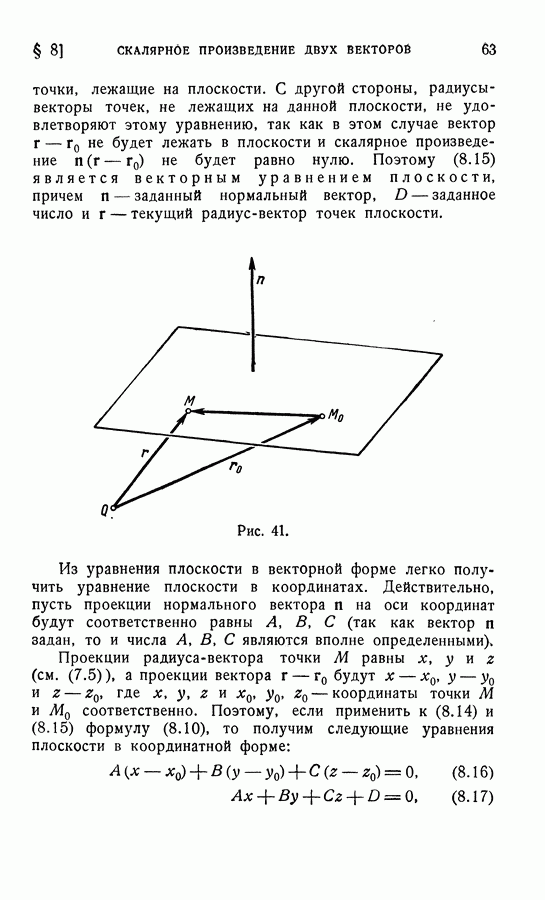
Из этого следует, что точка  должна лежать в плоскости, перпендикулярной к вектору
должна лежать в плоскости, перпендикулярной к вектору  и проходящей через точку
и проходящей через точку  уравнение плоскости (8.15) и (8.14)]. Возьмем на этой плоскости одну точку
уравнение плоскости (8.15) и (8.14)]. Возьмем на этой плоскости одну точку  тем самым будет определен радиус-вектор
тем самым будет определен радиус-вектор  удовлетворяющий условию (20.6). После этого нужно выбрать вектор
удовлетворяющий условию (20.6). После этого нужно выбрать вектор  так, чтобы он обращал в тождество равенство (20.5), и, пользуясь выражением (20.4), найти вектор Р.
так, чтобы он обращал в тождество равенство (20.5), и, пользуясь выражением (20.4), найти вектор Р.
Из приведенного решения видно, что точку приложения одного вектора можно выбрать произвольно, кроме того, имеются большие возможности варьирования при выборе второго вектора (как точки приложения, так и самого вектора).
Все вычисления значительно упрощаются, если совместить начало координат с точкой приложения первого вектора а. В этом случае  и равенства (20.5) и (20.6) примут вид
и равенства (20.5) и (20.6) примут вид

Заметим, что это упрощение не нарушает общности полученного решения, так как оно не ограничивает выбора точки приложения первого вектора, а налагает условие только на выбор начала координат.

Рис. 67.
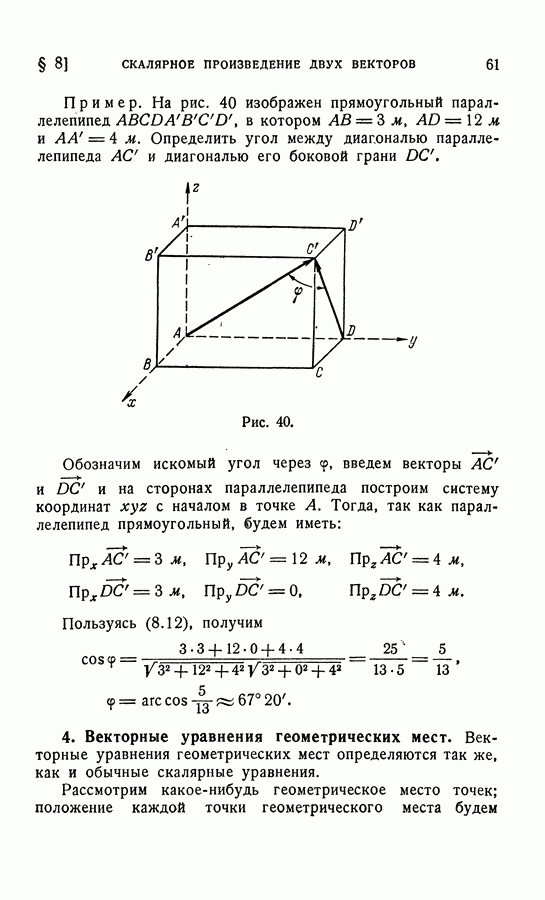
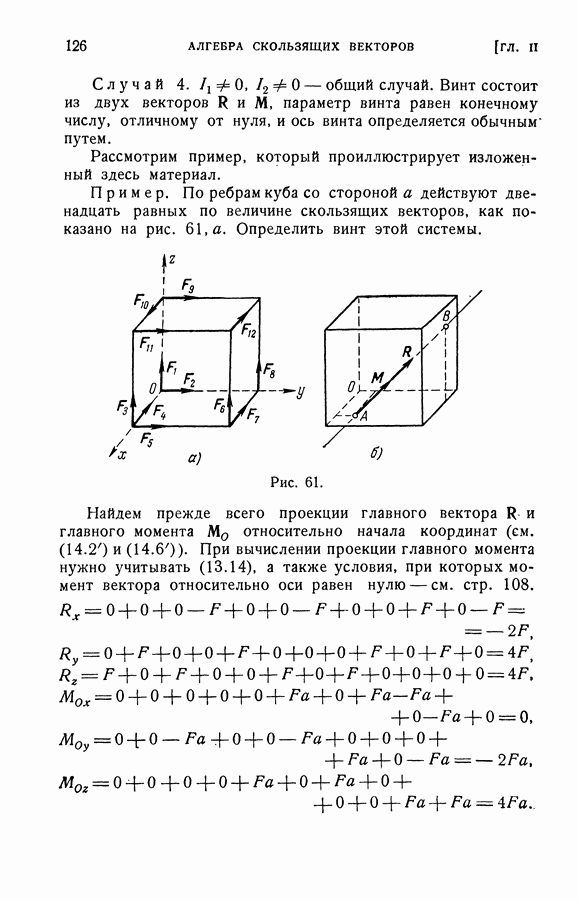
Пример. По ребрам куба, равным а, действуют восемь скользящих, равных по модулю векторов, как показано на рис. 67, а. Требуется заменить эту систему векторов двумя векторами Р и  из которых один проходит через точку О.
из которых один проходит через точку О.
Найдем прежде всего главный вектор и главный момент данной системы (см. (14.2), (14.6), (13.14)):

Так как по условию один вектор проходит через точку О, то  и следует пользоваться формулами (20.7) и (20.8). Запишем уравнение (20.8) в скалярной форме:
и следует пользоваться формулами (20.7) и (20.8). Запишем уравнение (20.8) в скалярной форме:

или для данной задачи:

Положим  тогда
тогда  , следовательно, радиус-вектор
, следовательно, радиус-вектор  определен:
определен:

Векторному уравнению (20.7) относительно  соответствуют три скалярных уравнения, из которых независимых только два (см. (11.11)):
соответствуют три скалярных уравнения, из которых независимых только два (см. (11.11)):

или, учитывая значения 

Первые два уравнения эквивалентны, и из них следует, что  Положим
Положим  тогда из последнего уравнения найдем
тогда из последнего уравнения найдем  Таким образом, вектор
Таким образом, вектор  также определен:
также определен:

Вектор Р найдем из равенства 

Векторы Р и  равны по модулю
равны по модулю  они действуют по диагоналям боковых граней куба, как показано на рис. 67, б. Системы, изображенные на рис.
они действуют по диагоналям боковых граней куба, как показано на рис. 67, б. Системы, изображенные на рис.  эквивалентны. Естественно, что существует бесчисленное множество других решений.
эквивалентны. Естественно, что существует бесчисленное множество других решений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
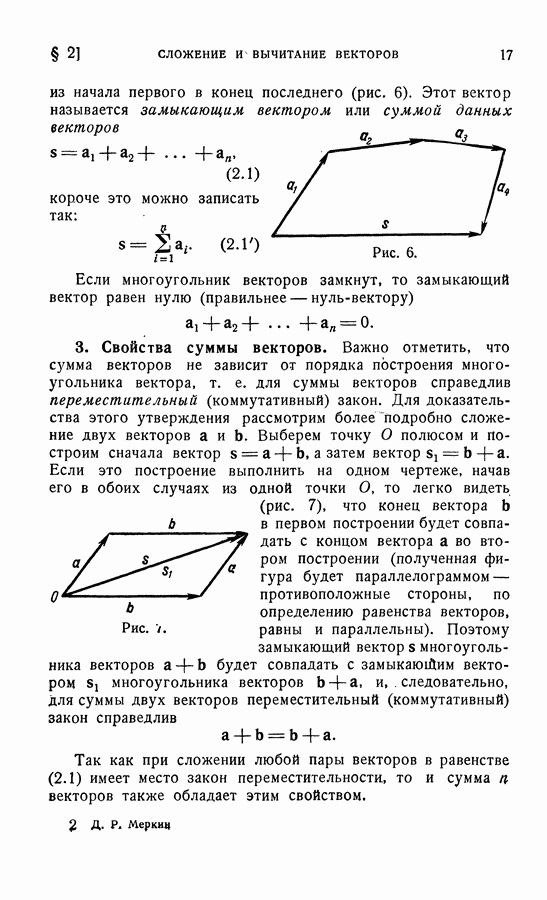
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
- 3. Свойства суммы векторов.
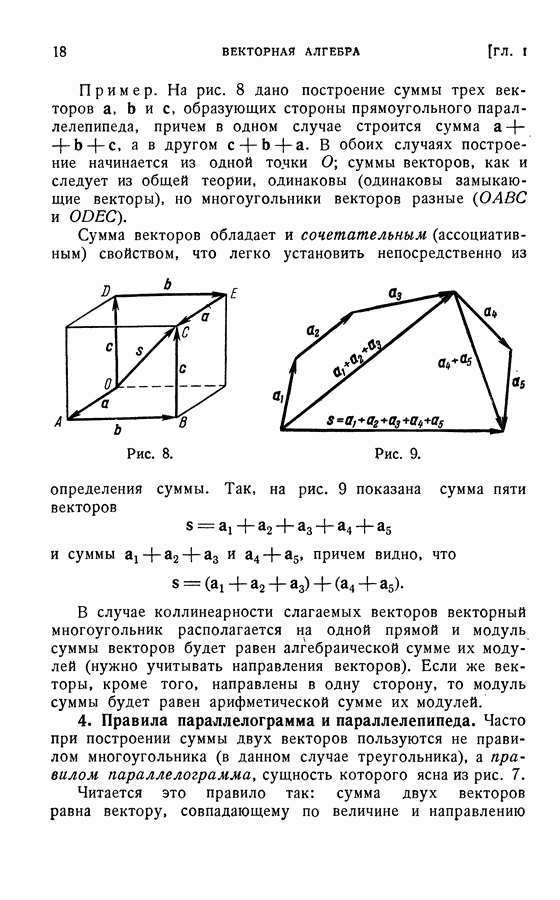
- 4. Правила параллелограмма и параллелепипеда.
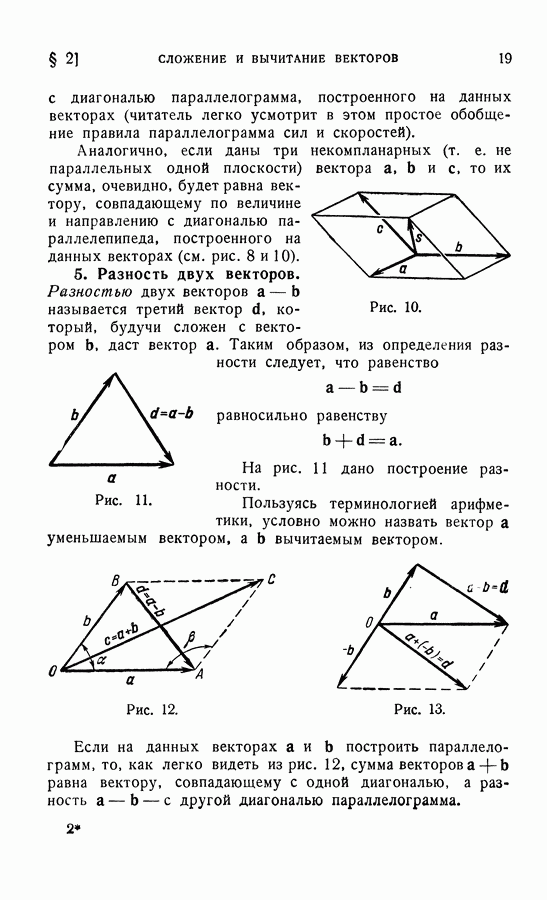
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
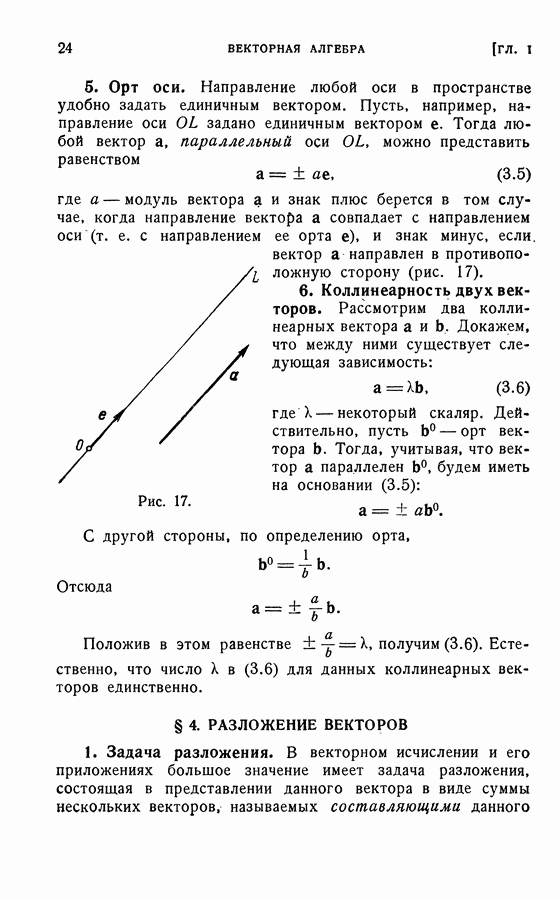
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
- § 6. ПРОЕКЦИИ ВЕКТОРА
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
- 4. Связь между естественным и координатным способами задания вектора.
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
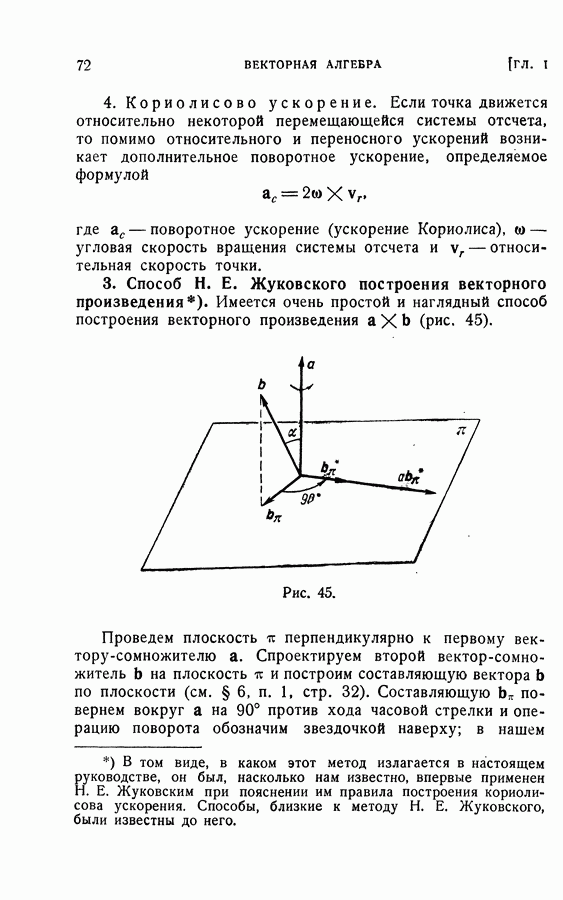
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
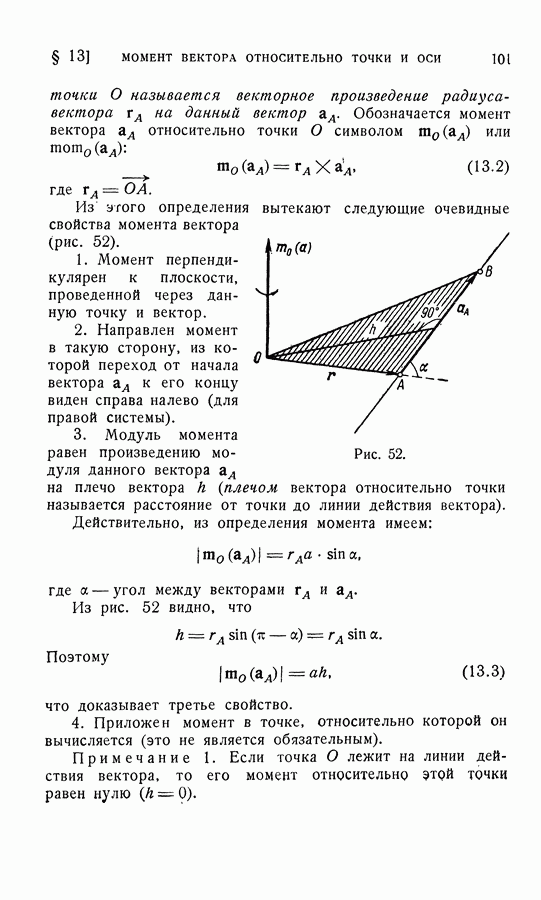
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.