| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
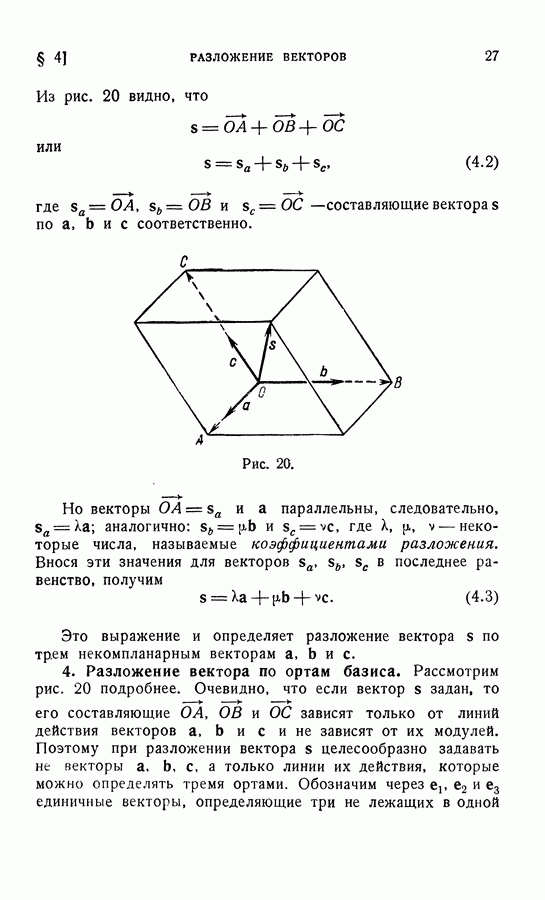
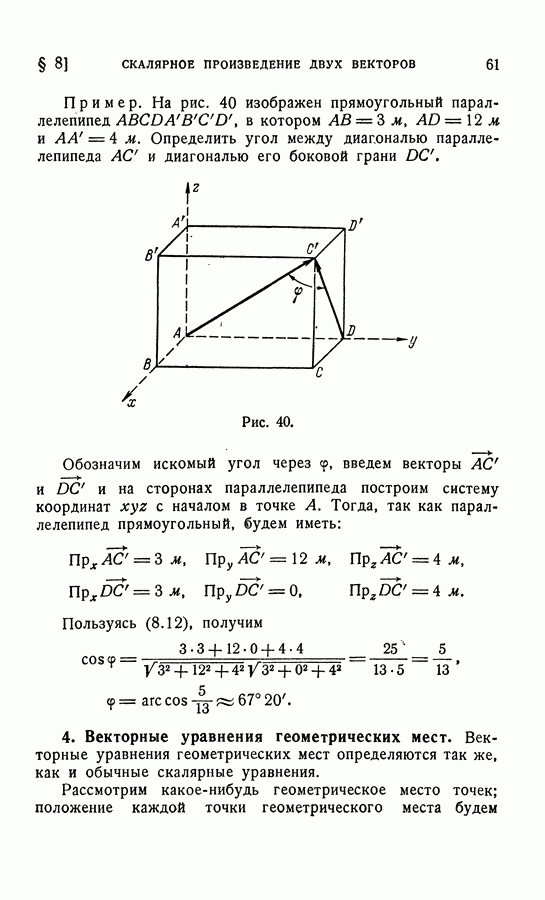
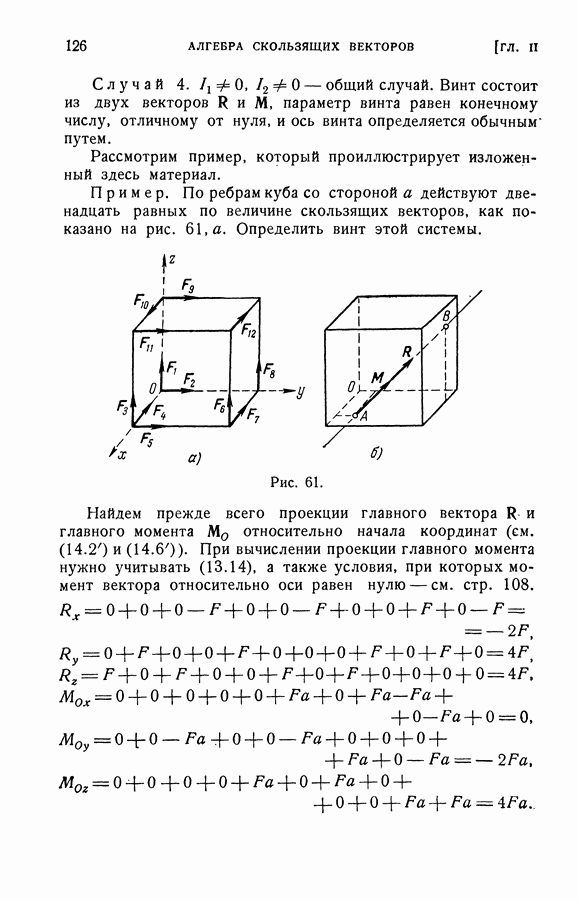
7. Некоторые приложения.
а) Расстояние между двумя точками. Пусть  координаты точки
координаты точки  — координаты точки
— координаты точки  Так как проекции вектора на оси равны разности координат его конца и начала (см. (6.11)), то для вектора
Так как проекции вектора на оси равны разности координат его конца и начала (см. (6.11)), то для вектора  будем иметь
будем иметь

Внося эти выражения в (7.8), получим значение модуля вектора  равное расстоянию
равное расстоянию  между двумя точками
между двумя точками 

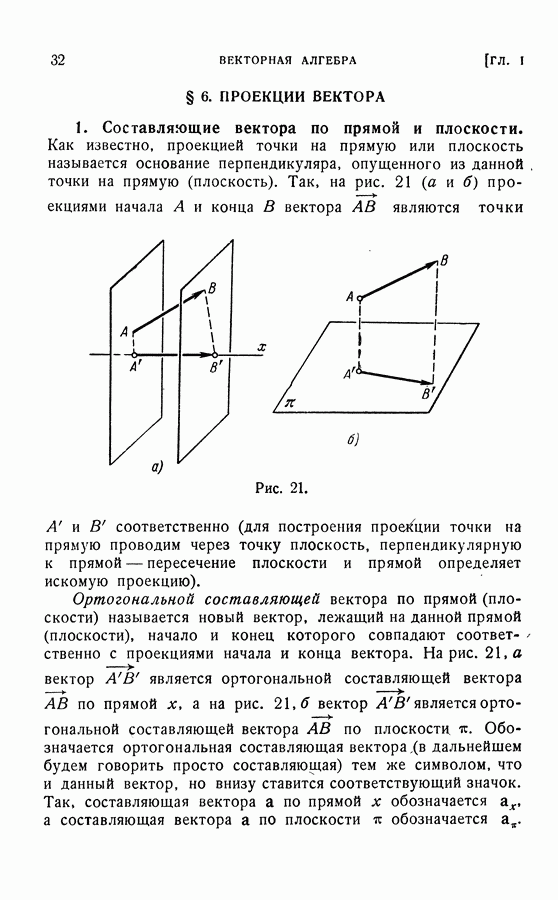
б) Условие коллинеарности двух векторов. Пусть два вектора  коллинеарны. Тогда между ними
коллинеарны. Тогда между ними
существует зависимость вида (см. (3.6))

где X — некоторый скаляр.
Пользуясь свойством (6.7), будем иметь

Отсюда

Так как правые части этих равенств одинаковы, то равны и левые части:

т. е. если векторы коллинеарны, то их проекции пропорциональны (очевидно, справедливо и обратное утверждение).
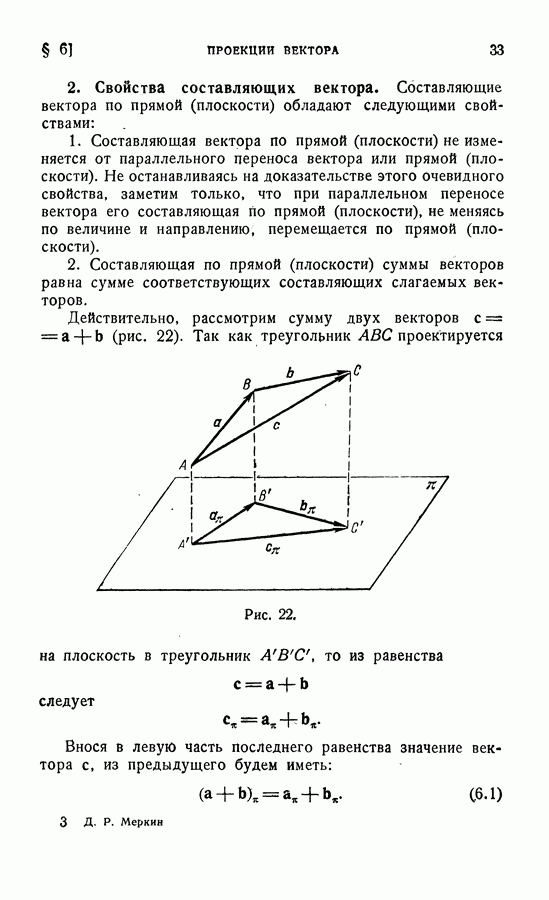
в) Деление отрезка в данном отношении. Задание точки радиусом-вектором позволяет решить следующую важную задачу. Даны две точки  (даны их радиусы-векторы). На прямой
(даны их радиусы-векторы). На прямой  требуется найти точку
требуется найти точку  делящую отрезок
делящую отрезок  в заданном отношении
в заданном отношении  иначе говоря, на отрезке
иначе говоря, на отрезке  требуется найти такую точку (ее радиус-вектор), чтобы выполнялось равенство
требуется найти такую точку (ее радиус-вектор), чтобы выполнялось равенство


Рис. 35.
Составим векторы  (см. рис. 35). Эти векторы коллинеарны, и отношение их модулей равно Следовательно, на основании (3.6) будем иметь:
(см. рис. 35). Эти векторы коллинеарны, и отношение их модулей равно Следовательно, на основании (3.6) будем иметь:

Отсюда найдем радиус-вектор искомой точки:

или

Это векторное равенство равносильно трем скалярным:

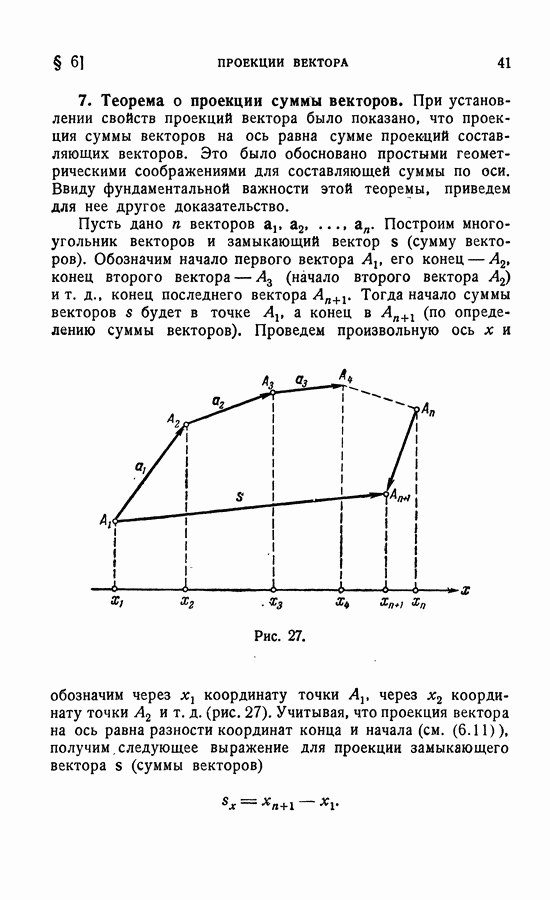
Пример. Определить точку пересечения медиан треугольника, если известны его вершины 
Медиана  делит отрезок
делит отрезок  пополам (рис. 36); следовательно, и для точки
пополам (рис. 36); следовательно, и для точки  справедливо равенство
справедливо равенство


Рис. 36.
Точка пересечения медиан делит отрезок  в отношении
в отношении  поэтому, согласно формуле (7.14),
поэтому, согласно формуле (7.14),

или

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
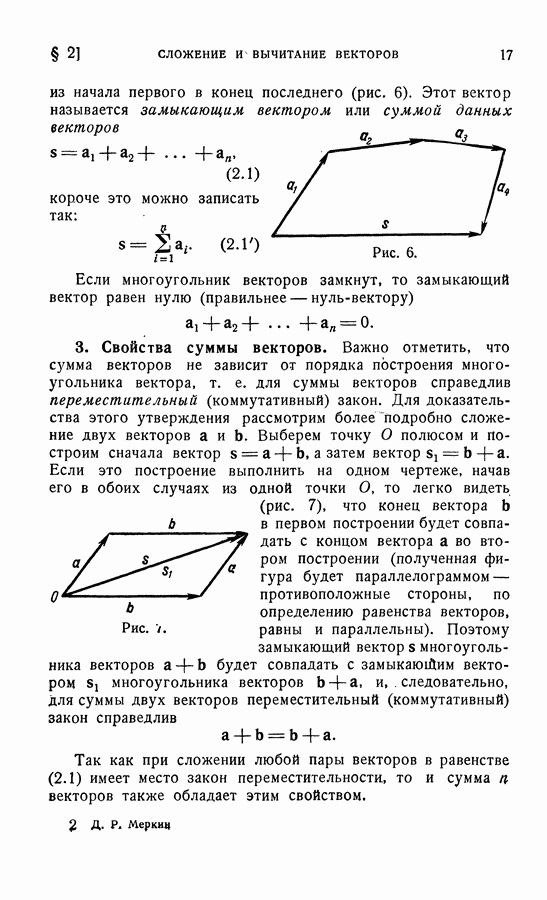
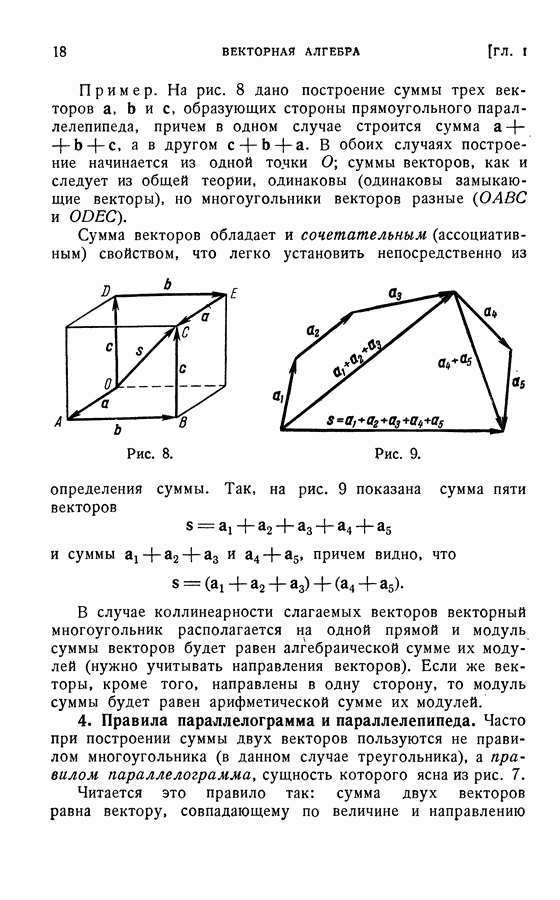
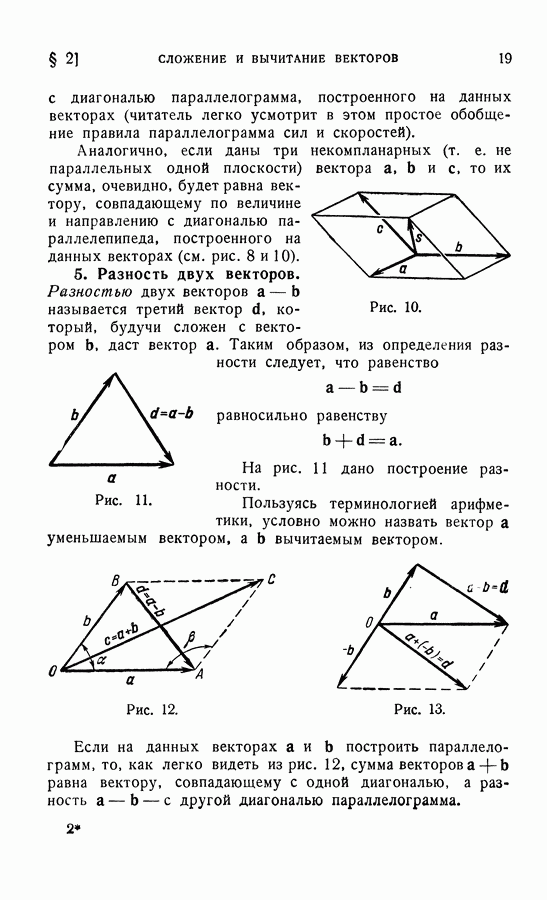
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
- 3. Свойства суммы векторов.
- 4. Правила параллелограмма и параллелепипеда.
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
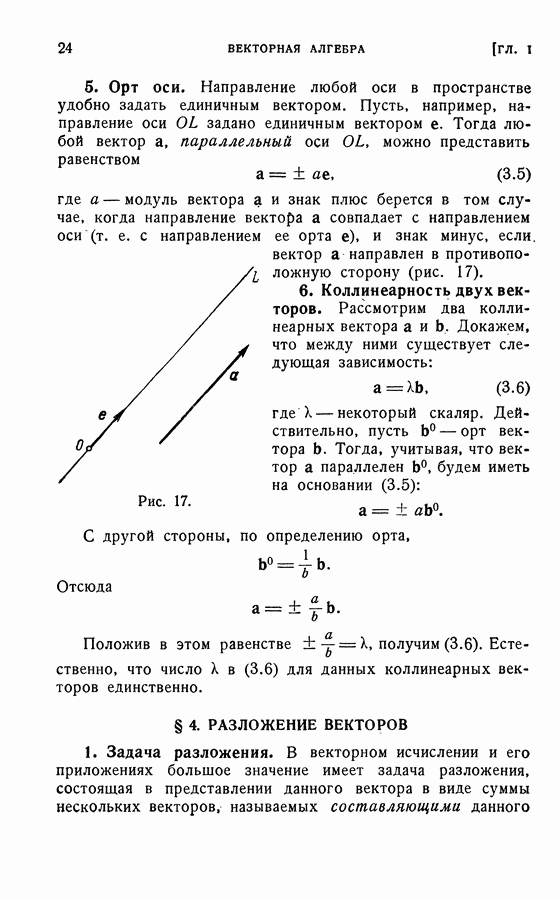
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
- § 6. ПРОЕКЦИИ ВЕКТОРА
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
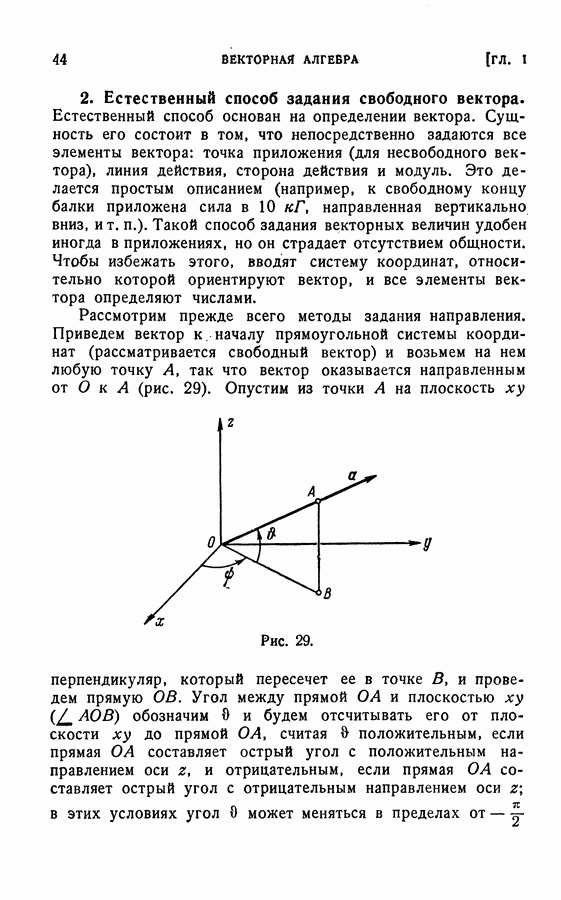
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
- 4. Связь между естественным и координатным способами задания вектора.
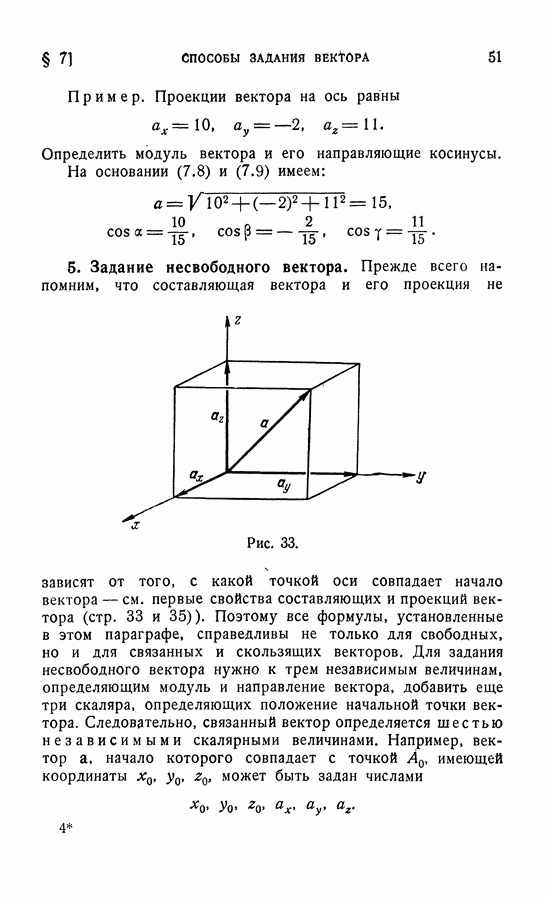
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.