| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Вычисление проекций вектора.
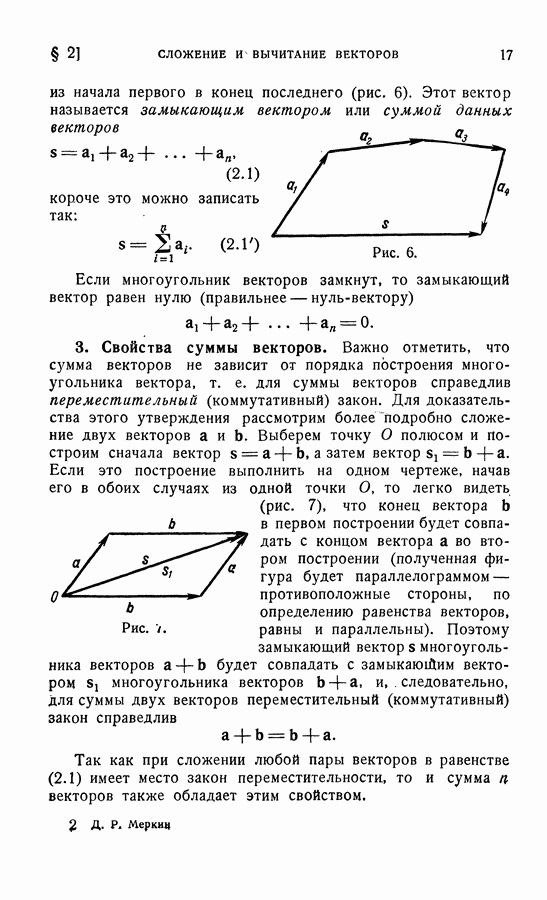
Обозначим через а угол между вектором и осью проекции и перенесем вектор
так, чтобы его начало совпало с какой-нибудь точкой оси. Если направления составляющей вектора  и оси одина ковы, то угол а будет острым и, как видно из рис. 24, а,
и оси одина ковы, то угол а будет острым и, как видно из рис. 24, а,

где а — модуль вектора а. Если же направления вектора  и оси противоположны, то, учитывая знак проекции, будем иметь-(см. рис. 24, б)
и оси противоположны, то, учитывая знак проекции, будем иметь-(см. рис. 24, б)

т. е. предыдущее выражение (нужно помнить, что в данном случае угол а тупой и 

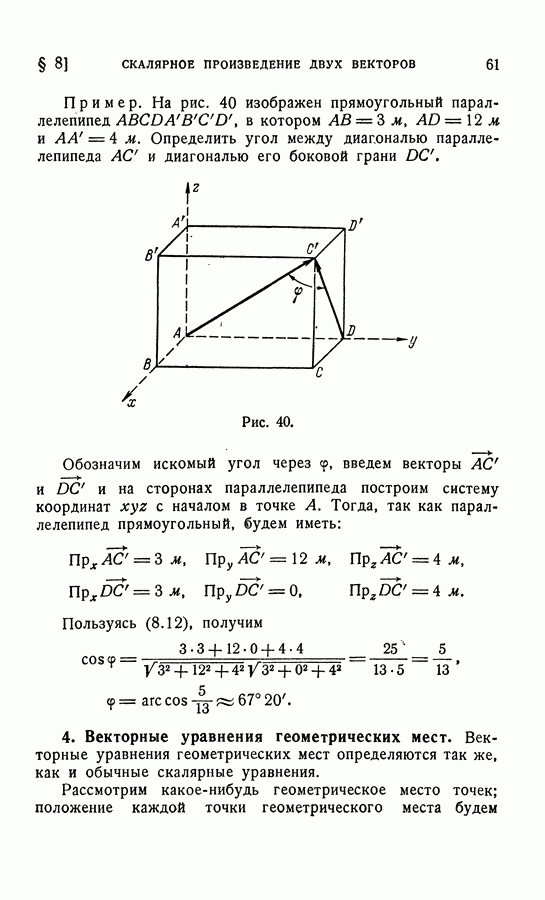
Рис. 24.
Таким образом, проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью:

Кроме этой имеющей исключительно важное значение формулы, для проекции вектора на ось можно дать еще одну очень простую формулу. Установим на оси начало отсчета и выберем масштаб, общий с масштабом векторов. Как известно, координатой точки называется число, выражающее в выбранном масштабе расстояние от начала отсчета оси до проекции данной точки на ось, причем это число берется со знаком плюс, если проекция точки удалена от начала отсчета в сторону направления оси, и со знаком минус в противном случае. Так, например, координатой точки А (рис. 23, б) будет взятое со знаком  число, выражающее длину отрезка
число, выражающее длину отрезка  а координатой точки В будет взятое со знаком — число, определяющее длину отрезка
а координатой точки В будет взятое со знаком — число, определяющее длину отрезка  (мы не останавливаемся на этом
(мы не останавливаемся на этом
подробнее, считая, что читатель знаком с понятием координат точки из курса элементарной математики).
Обозначим через  координату начала, а через
координату начала, а через  координату конца вектора на ось х. Тогда, как видно из рис. 23, а, будем иметь
координату конца вектора на ось х. Тогда, как видно из рис. 23, а, будем иметь

Проекция вектора на ось х будет равна

или, учитывая предыдущие равенства,

Легко видеть, что эта формула имеет общий характер и не зависит от расположения вектора относительно оси и начала отсчета. Действительно, рассмотрим случай, изображённый на рис. 23, б. Из определения координат точек и проекции вектора последовательно получим

(читатель легко проверит справедливость формулы  и и при другом расположении вектора относительно оси и начала отсчета).
и и при другом расположении вектора относительно оси и начала отсчета).
Из (6.11) следует, что проекция вектора на ось равна разности координат конца и начала вектора.
Вычисление проекции вектора на ось встречается весьма часто в самых различных вопросах. Поэтому необходимо выработать твердые навыки вычисления проекций. Можно указать некоторые приемы, облегчающие процесс вычисления проекций.
1. Знак проекции вектора на ось, как правило, можно определить непосредственно из чертежа, а модуль проекции  можно вычислить по формуле
можно вычислить по формуле

где  — острый угол между вектором и осью проекций —
— острый угол между вектором и осью проекций —  если а
если а  если Этом прием, не внося ничего принципиально нового, несколько
если Этом прием, не внося ничего принципиально нового, несколько
облегчает вычисление проекции, так как не требует тригонометрических преобразований.
2. Если требуется определить проекции вектора на две взаимноперпендикулярные оси х и у (предполагается, что вектор лежит в плоскости этих осей) и  — острый угол между вектором и осью х, то
— острый угол между вектором и осью х, то

(знак проекций определяется из чертежа).

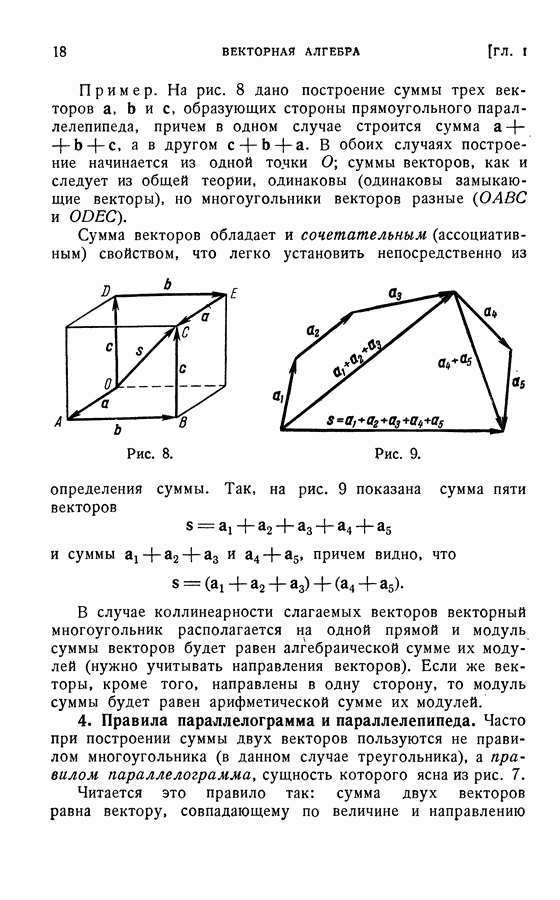
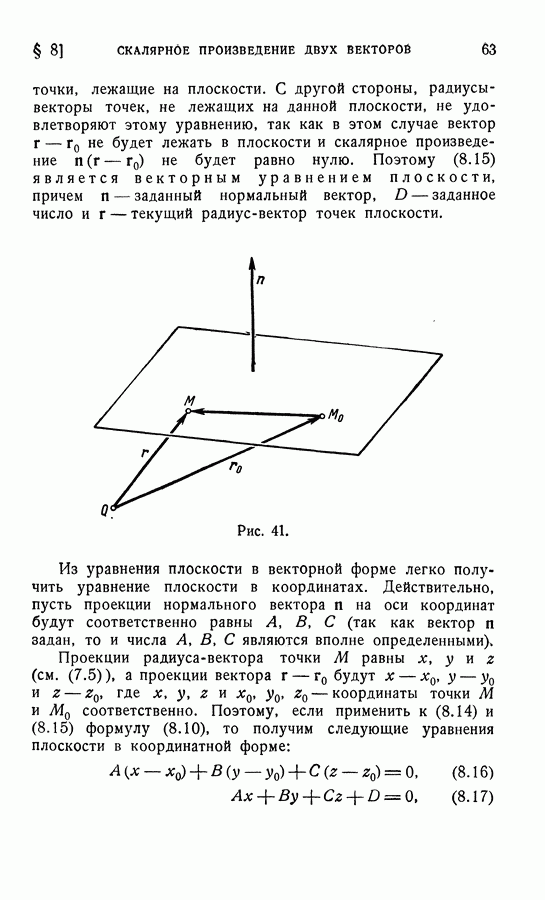
Рис. 25.
Пример. Найти проекции на оси координат х и у силы  изображенной на рис. 25. Из чертежа видно, что обе проекции будут отрицательны. Следовательно,
изображенной на рис. 25. Из чертежа видно, что обе проекции будут отрицательны. Следовательно,

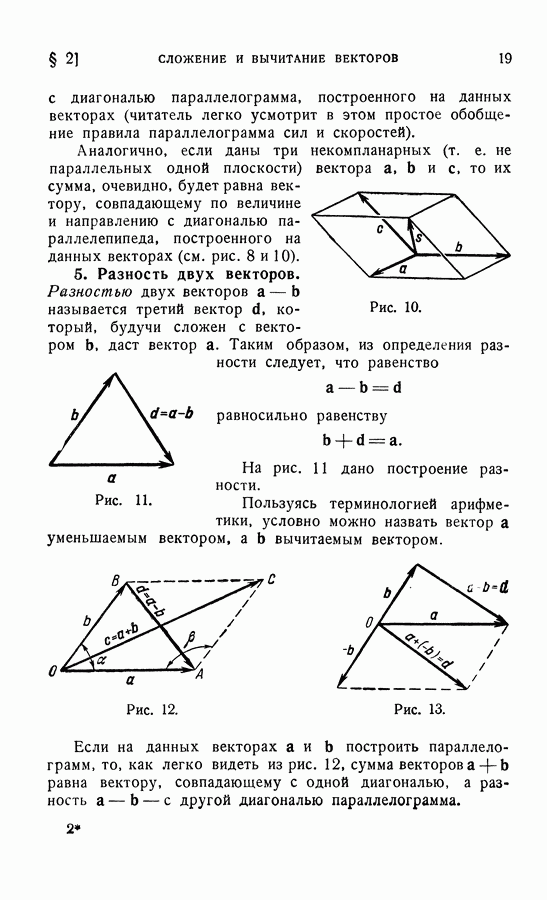
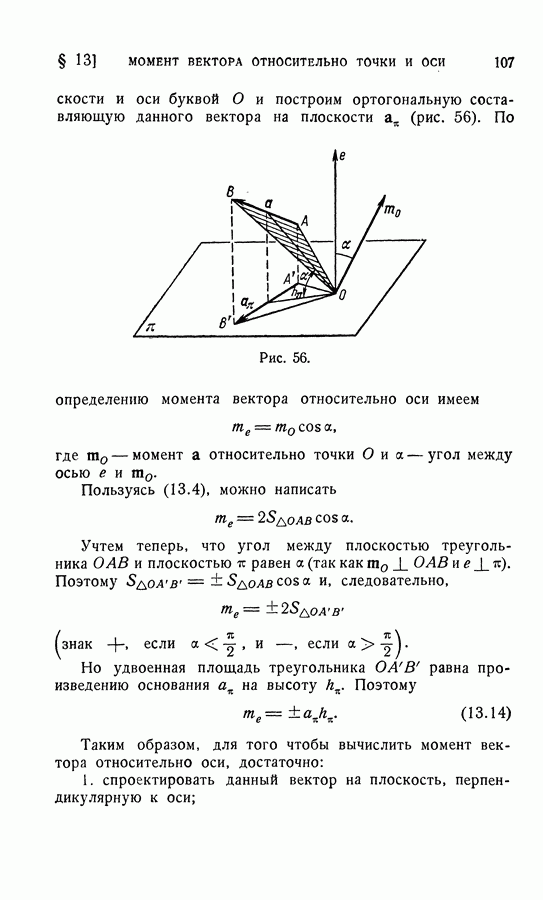
3. Иногда применяется правило двойного проектирования, состоящее в следующем. Пусть дан вектор  и ось
и ось  лежащая в плоскости
лежащая в плоскости  Опустим из конца вектора
Опустим из конца вектора  перпендикуляры на плоскость
перпендикуляры на плоскость  и прямую
и прямую  и соединим затем основания перпендикуляров отрезком прямой линии
и соединим затем основания перпендикуляров отрезком прямой линии  (рис. 26). Обозначим угол между вектором
(рис. 26). Обозначим угол между вектором  и плоскостью
и плоскостью  через
через  угол между
угол между  и
и  через
через  и угол между вектором
и угол между вектором  и осью проекций
и осью проекций  через а. Так как угол
через а. Так как угол  прямой (по построению), то
прямой (по построению), то

Из треугольников  и
и  имеем
имеем

Отсюда

или, сравнивая с выражением для  ,
,

Пользуясь равенством (6.10), получим

Это равенство можно прочитать следующим образом: Для того чтобы получить проекцию вектора на ось, достаточно спроектировать вектор на плоскость, в которой лежит ось проекции, а затем полученную составляющую по плоскости спроектировать на данную ось (правило двойного проектирования).

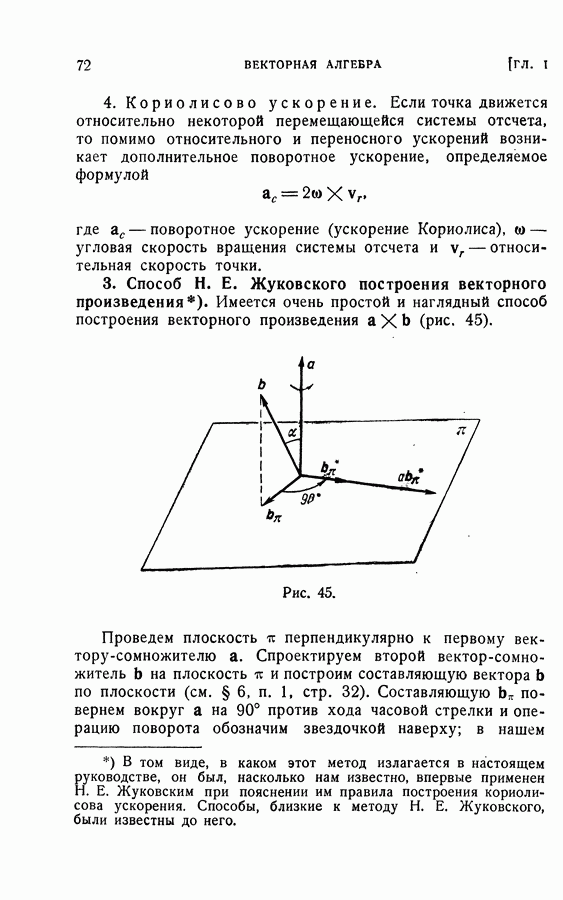
Рис. 26.
Естественно, что при вычислении проекции можно пользоваться просто формулой (6.12), а затем (6.10), но правило двойного проектирования легче запоминается, и оно весьма удобно при решении конкретных задач.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
- 3. Свойства суммы векторов.
- 4. Правила параллелограмма и параллелепипеда.
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
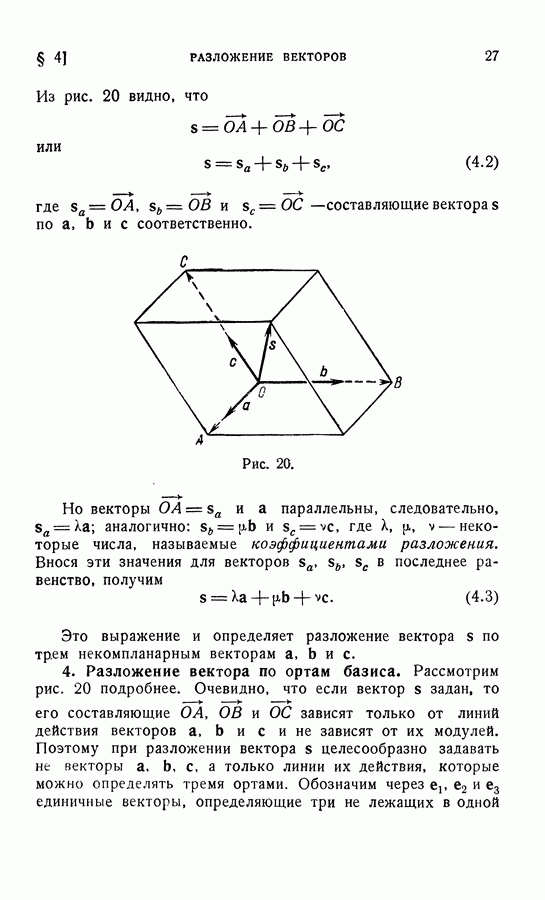
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
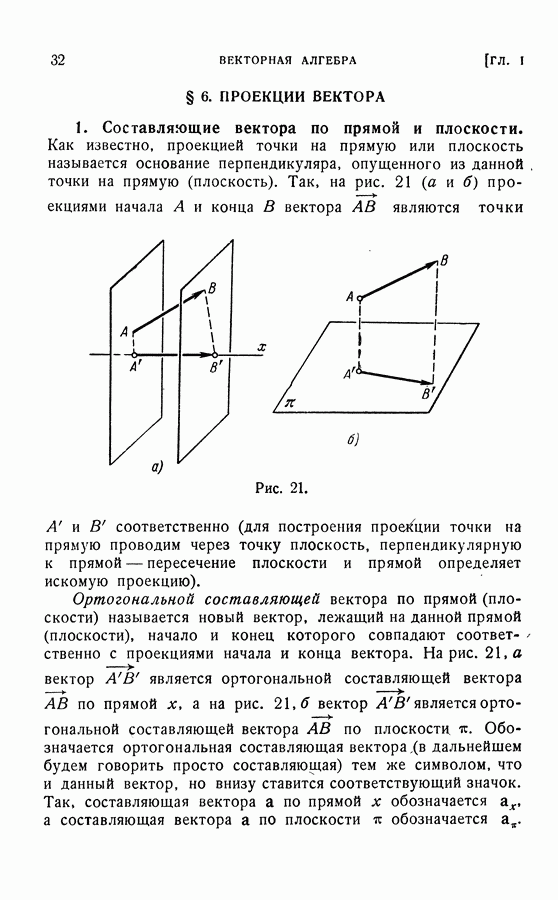
- § 6. ПРОЕКЦИИ ВЕКТОРА
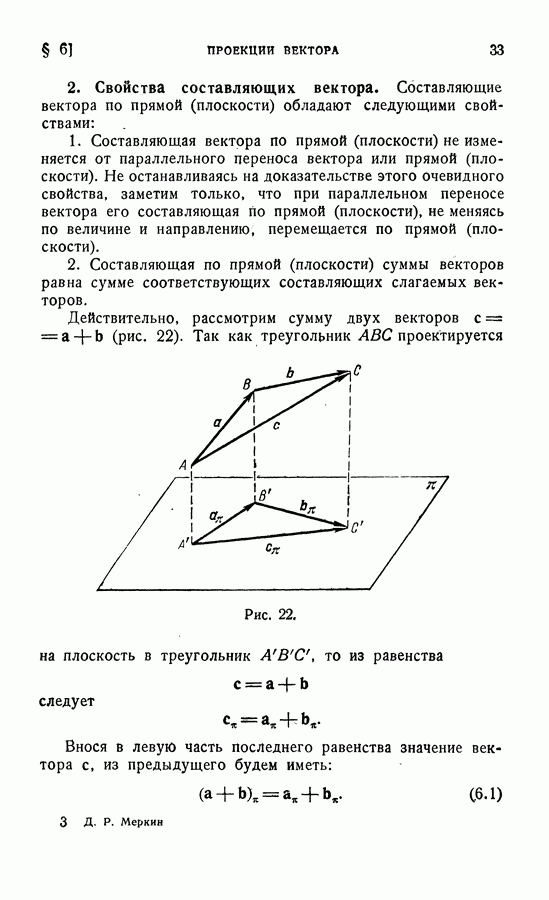
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
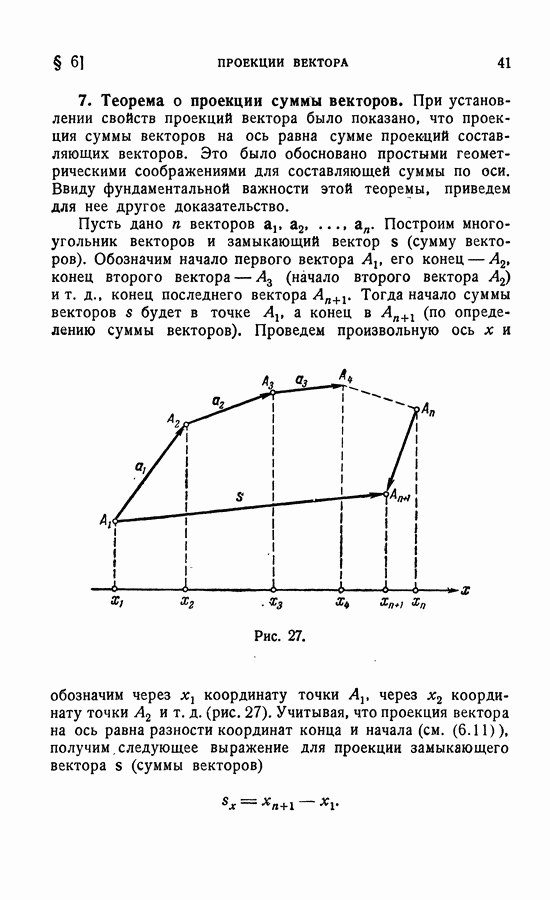
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
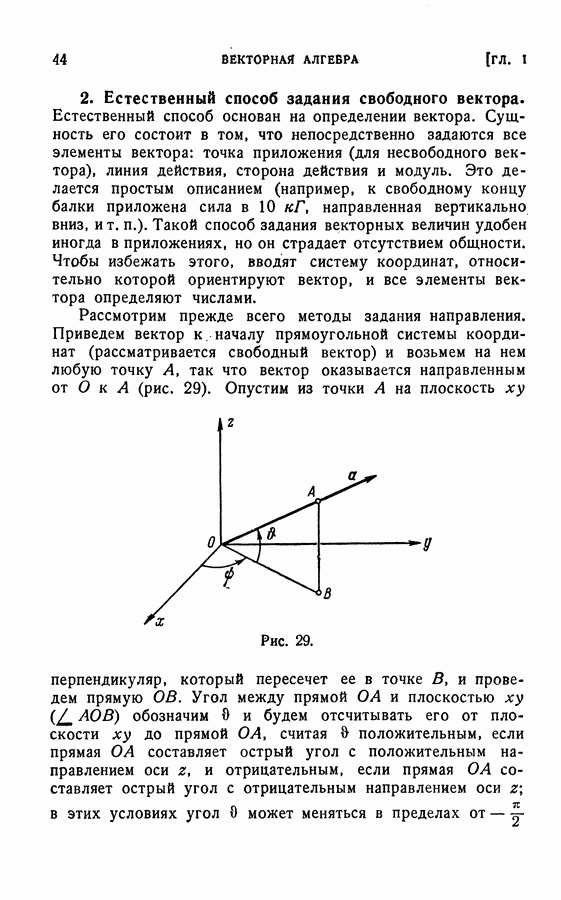
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
- 4. Связь между естественным и координатным способами задания вектора.
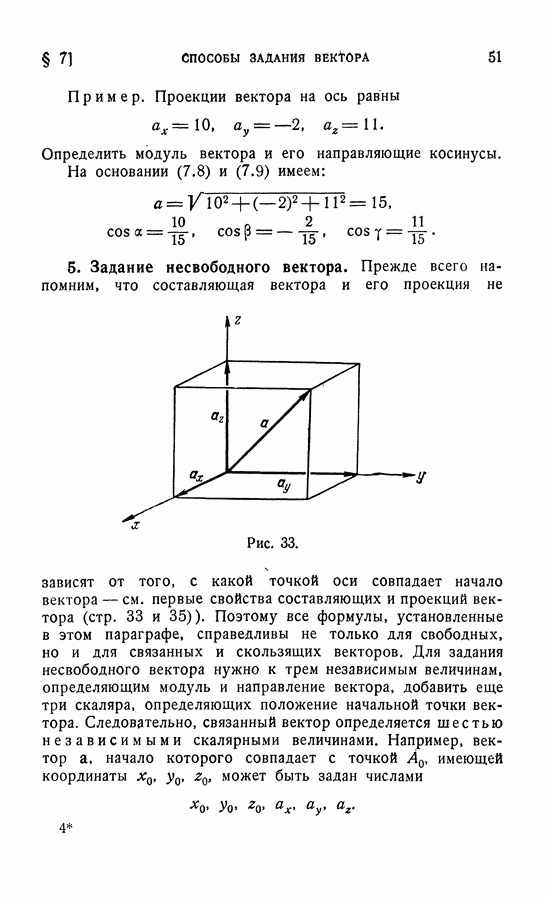
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.