| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
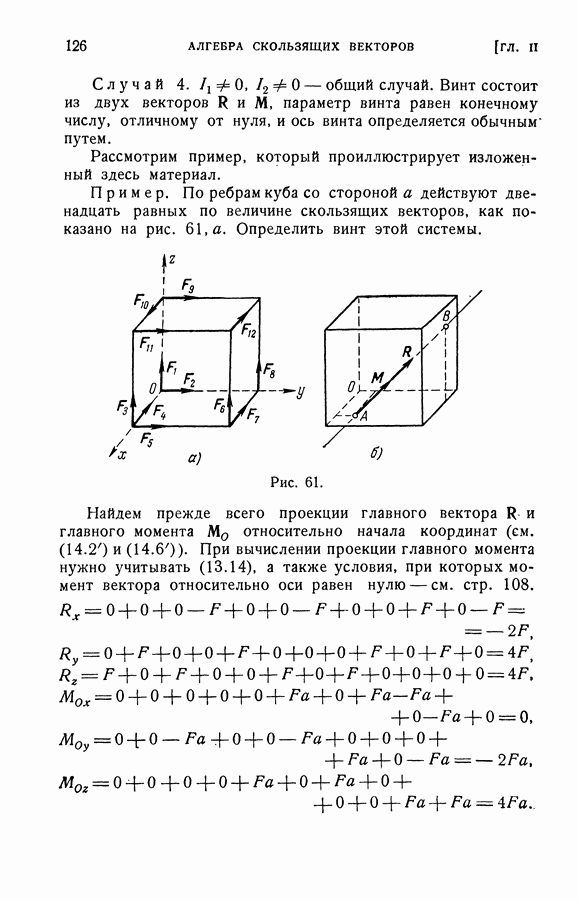
3. Приведение системы скользящих векторов к вектору и паре.
Рассмотрим приведение системы скользящих векторов к другой простейшей системе, а именно к вектору и паре.
Теорема Пуансо. Любую систему скользящих векторов всегда можно привести к одному скользящему вектору и одной паре (среди этих элементов могут быть и нулевые).
Доказательство. Пусть  и
и  главный вектор и главный момент данной системы скользящих векторов
главный вектор и главный момент данной системы скользящих векторов

причем точка О хотя и произвольна, но фиксирована. Рассмотрим систему (см. (19.5))

В этих обозначениях индекс О при  означает, что линия действия вектора
означает, что линия действия вектора  проходит через точку О, а тот же индекс в
проходит через точку О, а тот же индекс в  означает, что этот вектор-момент равен главному моменту данной системы относительно точки О.
означает, что этот вектор-момент равен главному моменту данной системы относительно точки О.
Главный вектор системы (20.10) согласно (19.6) равен  а главный момент этой системы относительно того же полюса О равен
а главный момент этой системы относительно того же полюса О равен  так как
так как  (вектор
(вектор  по условию проходит через точку О). Таким образом, системы (20.9) и (20.10) имеют равные главные векторы и главные моменты; в силу основной теоремы они эквивалентны.
по условию проходит через точку О). Таким образом, системы (20.9) и (20.10) имеют равные главные векторы и главные моменты; в силу основной теоремы они эквивалентны.
Доказательство теоремы Пуансо теперь следует из того что момент  представляет некоторую пару, плоскость которой перпендикулярна к
представляет некоторую пару, плоскость которой перпендикулярна к 
Приведение системы скользящих векторов к вектору и паре является наиболее простой математической операцией. Действительно, достаточно вычислить главный вектор и главный момент системы. Тогда система, составленная из главного вектора, проходящего через полюс О, и пары, момент которой равен главному моменту, будет эквивалентна данной системе (естественно, что можно говорить о системе, состоящей из скользящего вектора  и свободного вектора момента
и свободного вектора момента  ).
).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
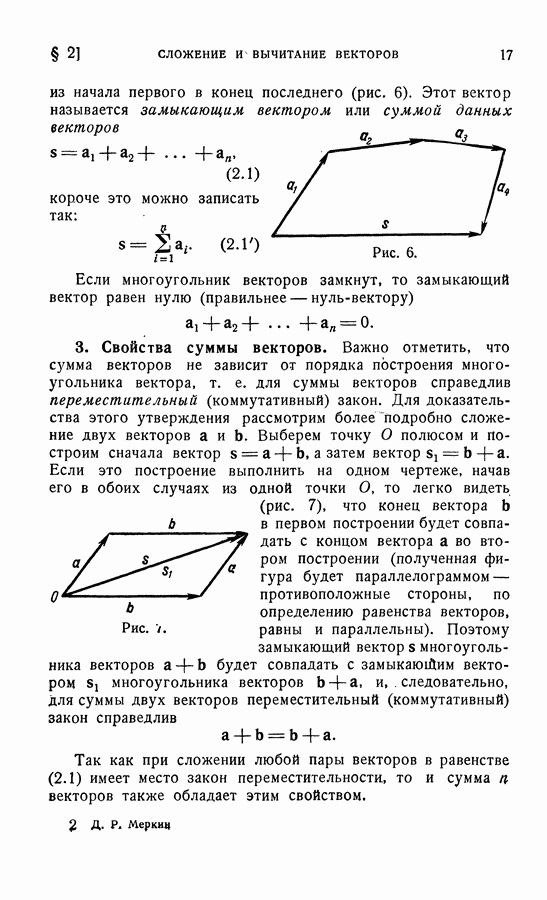
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
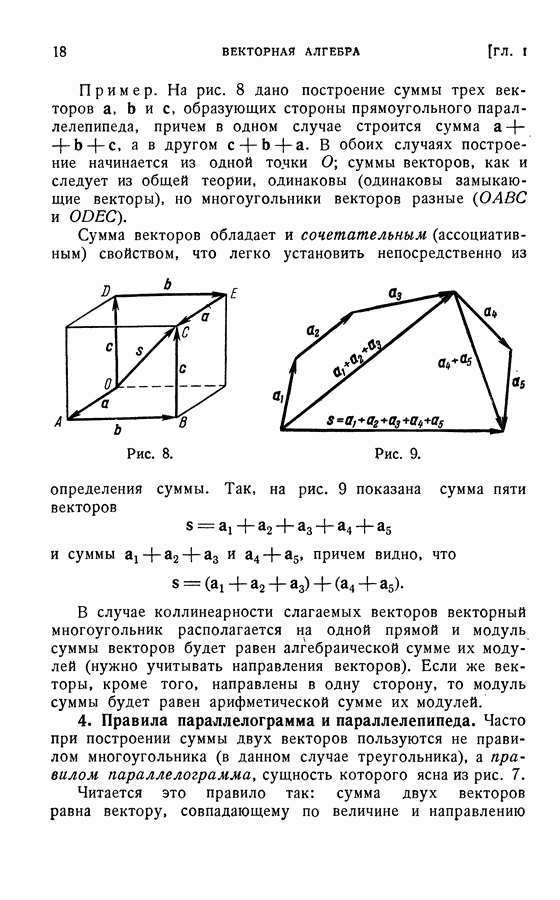
- 3. Свойства суммы векторов.
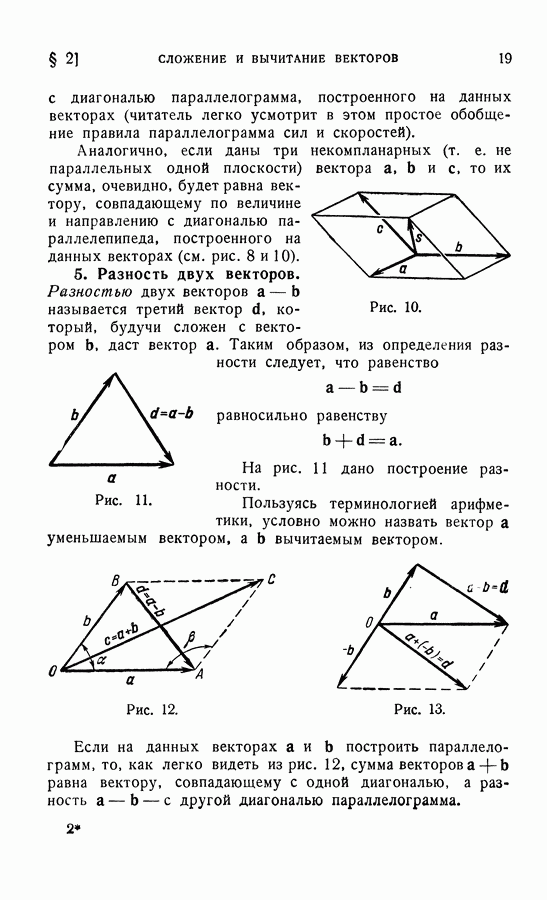
- 4. Правила параллелограмма и параллелепипеда.
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
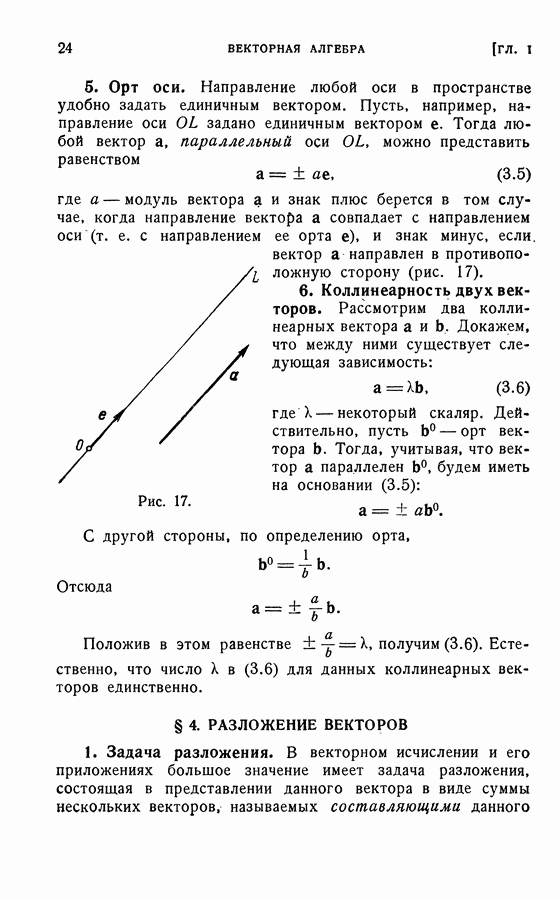
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
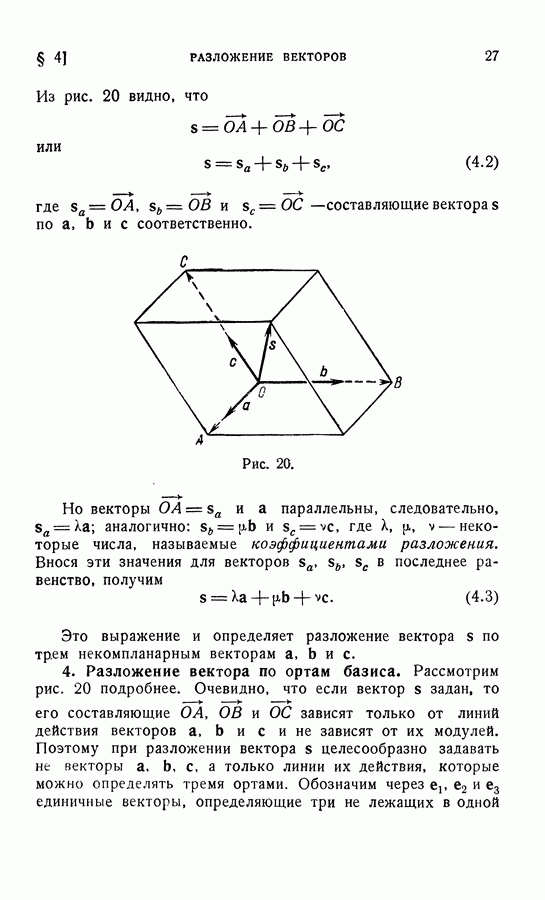
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
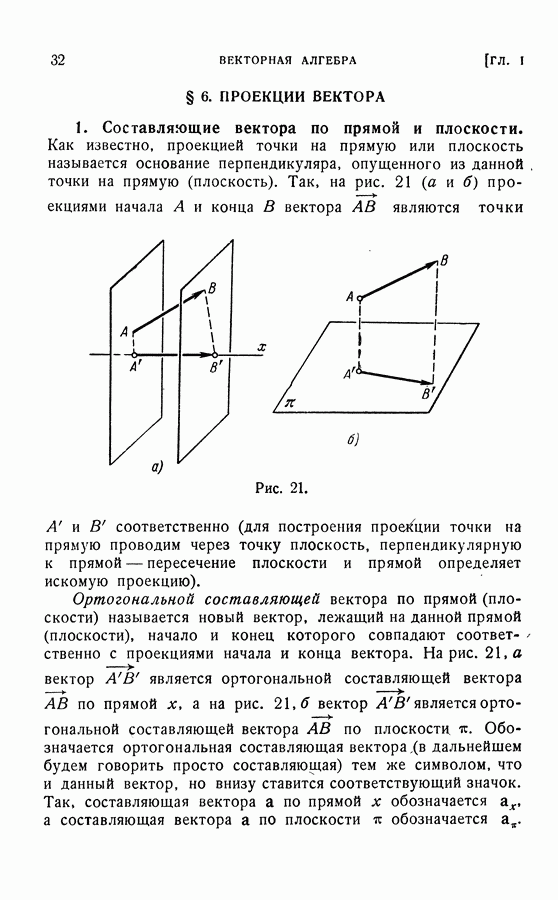
- § 6. ПРОЕКЦИИ ВЕКТОРА
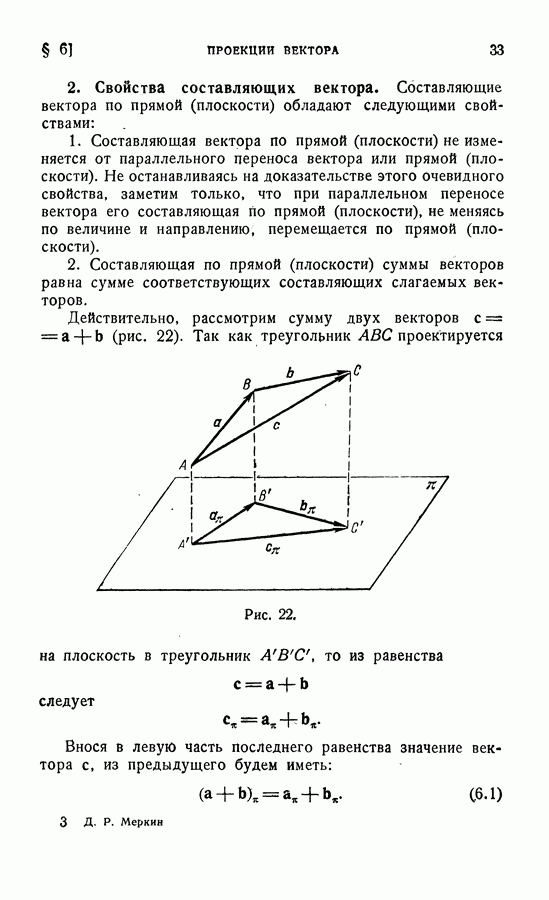
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
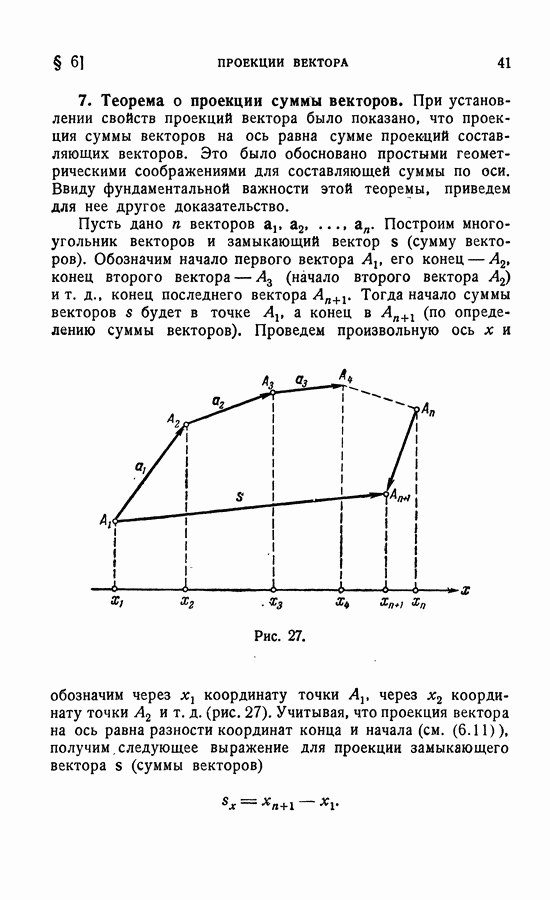
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
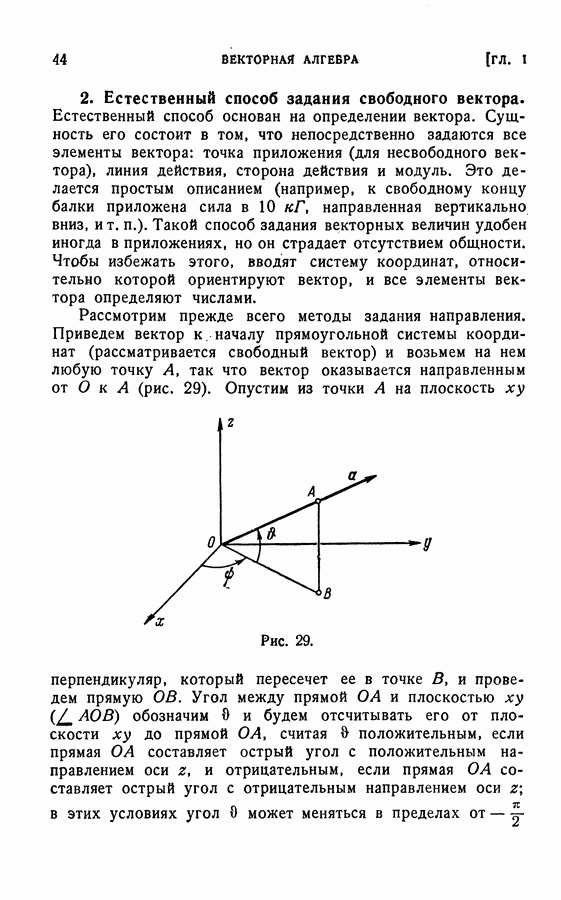
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
- 4. Связь между естественным и координатным способами задания вектора.
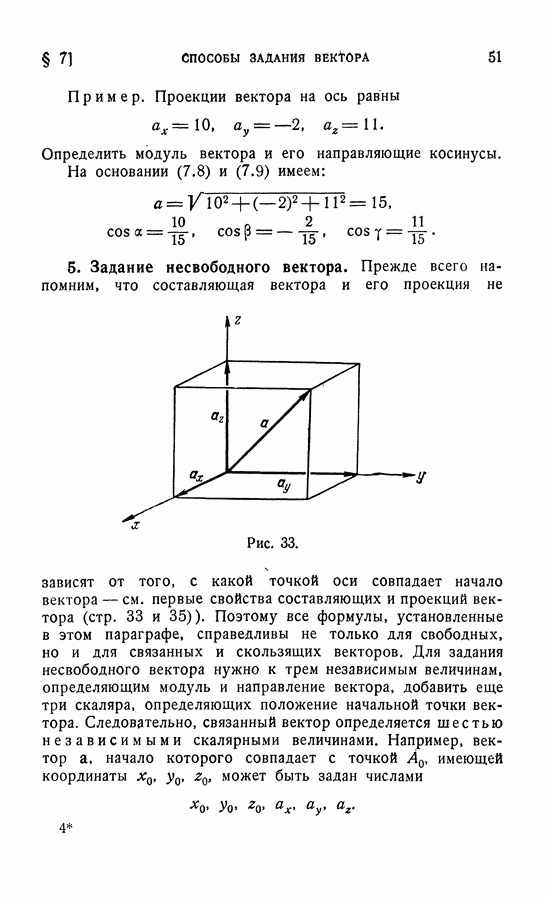
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.