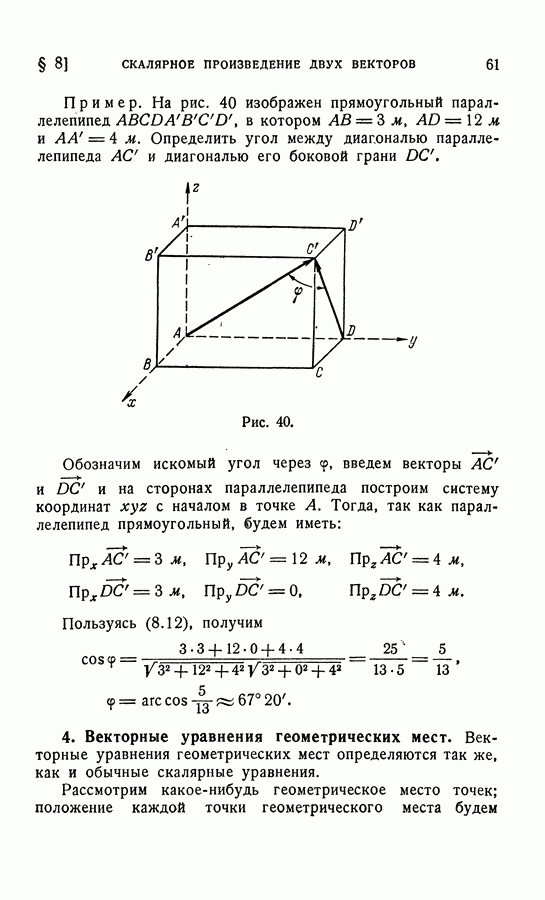
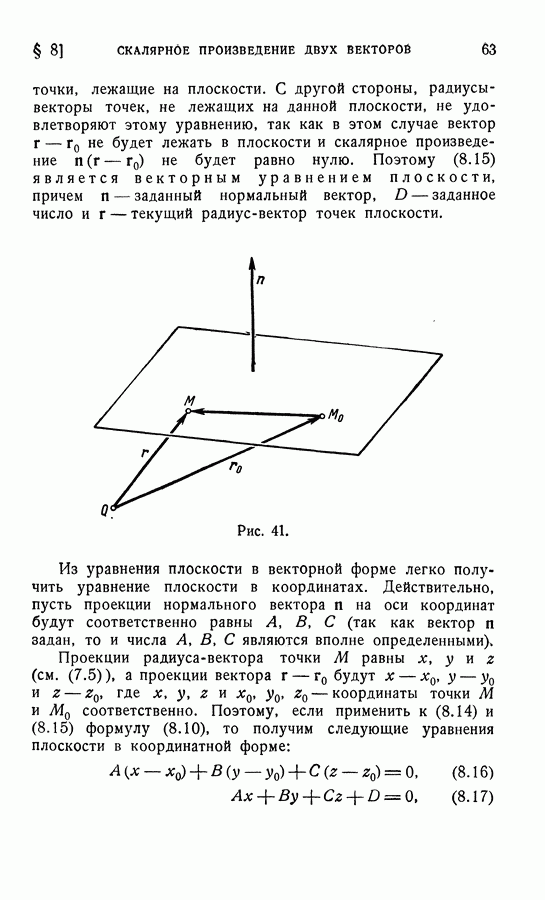
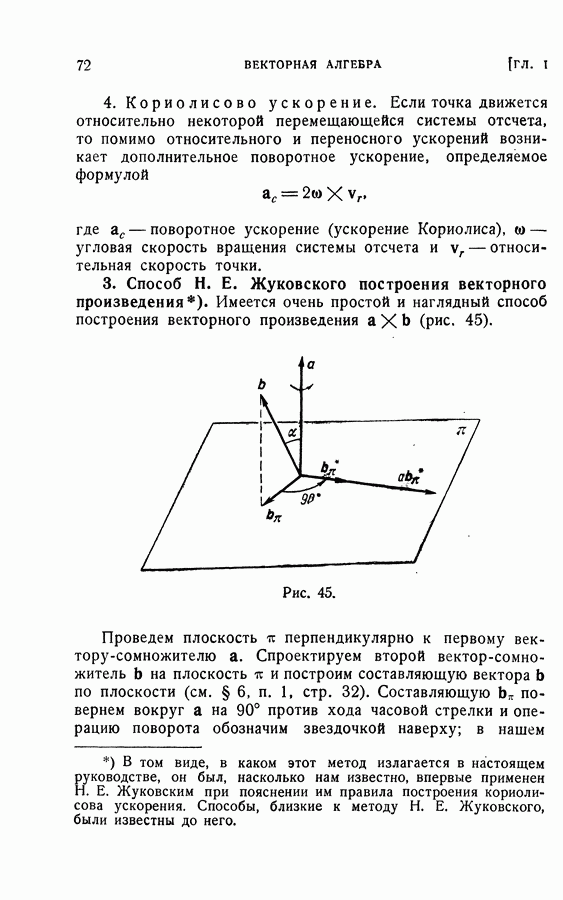
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
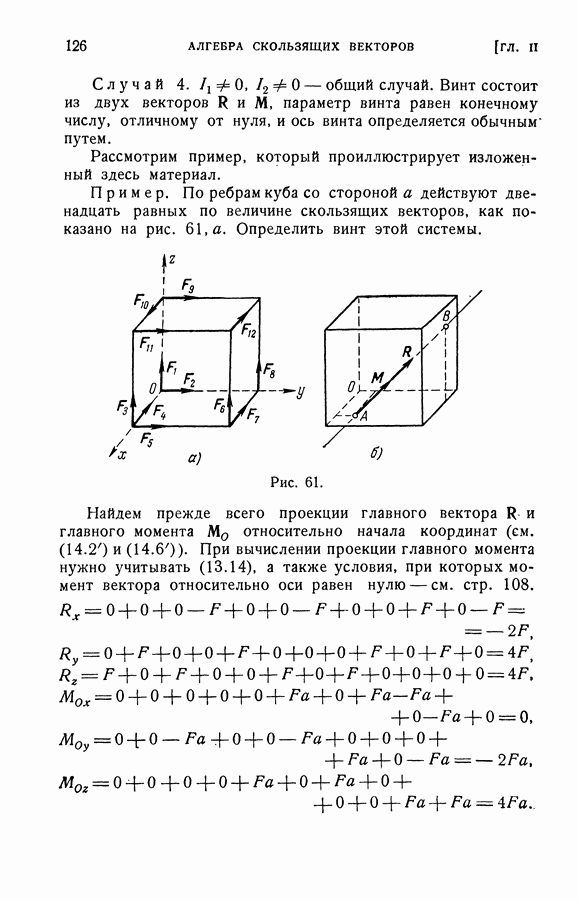
7. Инварианты системы векторов.
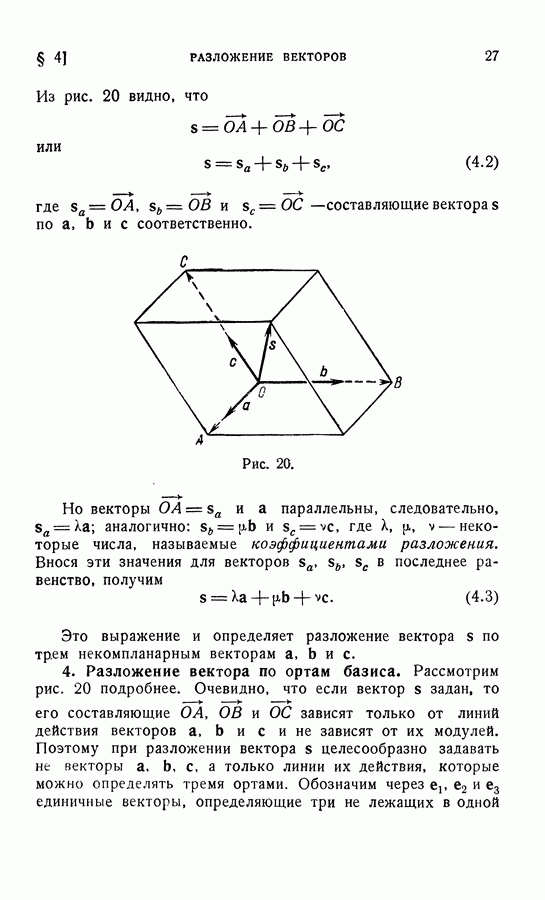
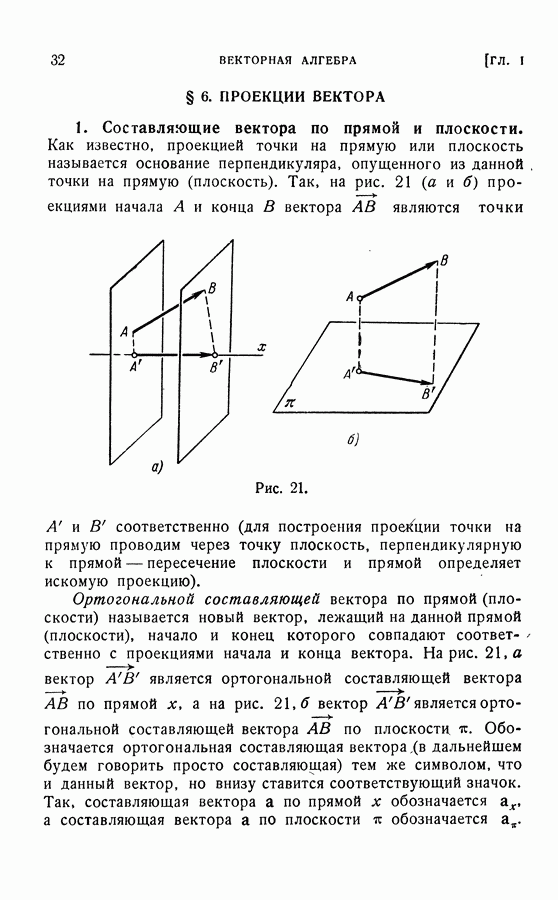
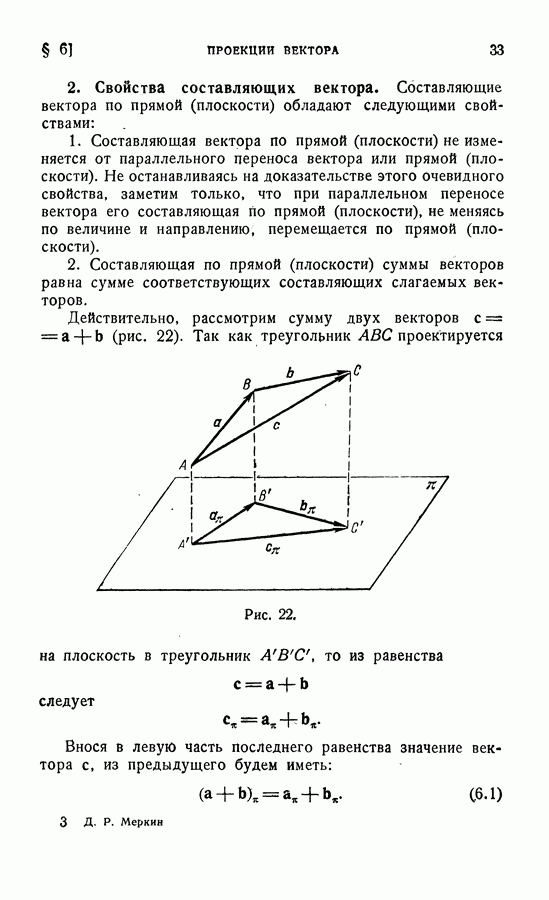
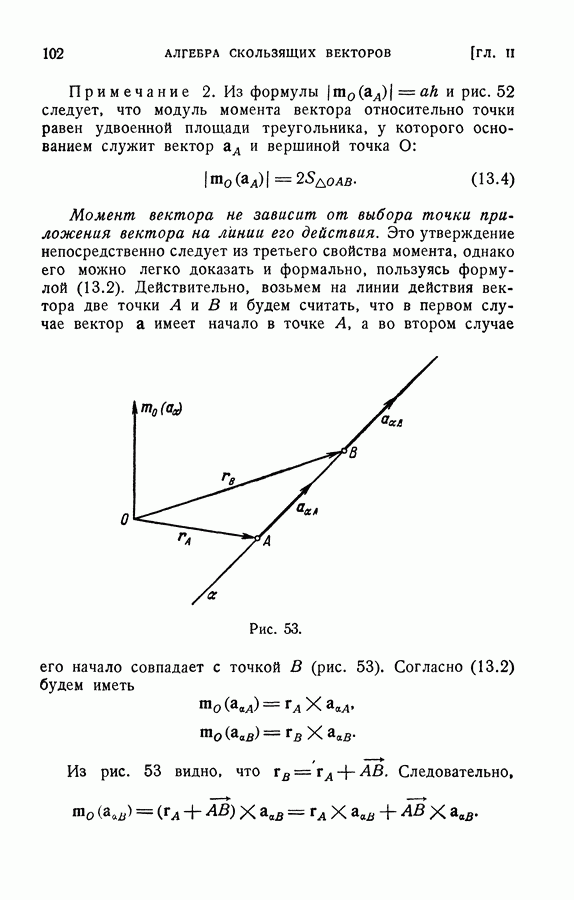
Рассмотрим систему векторов  и вычислим главный вектор системы
и вычислим главный вектор системы  Очевидно, что величина и направление главного вектора не зависят от того, в какой точке пространства мы выберем его начало (по определению главного вектора). Поэтому главный вектор называют первым инвариантом системы векторов.
Очевидно, что величина и направление главного вектора не зависят от того, в какой точке пространства мы выберем его начало (по определению главного вектора). Поэтому главный вектор называют первым инвариантом системы векторов.
В более узком смысле этого слова под первым инвариантом системы векторов будем понимать независимость модуля главного вектора от выбора полюса

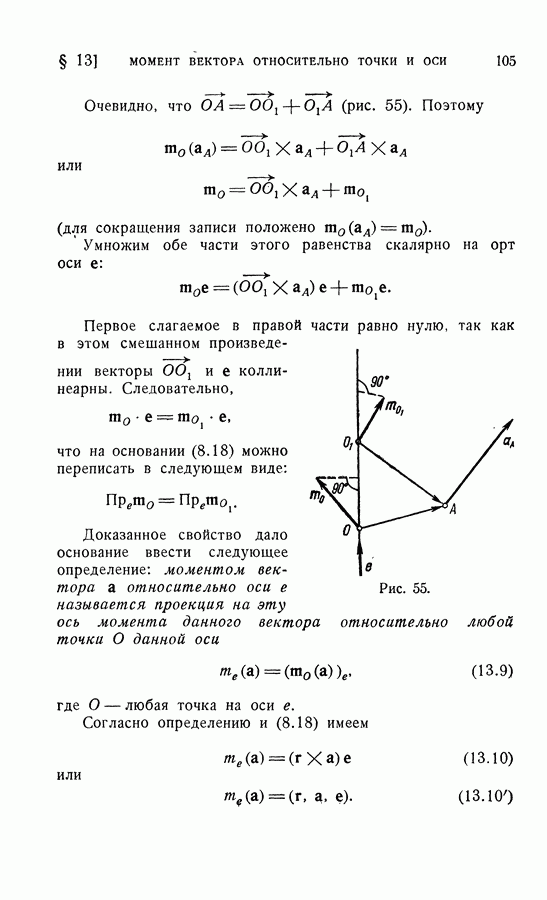
Возьмем теперь две произвольные точки О и  и вычислим относительно этих точек главные моменты
и вычислим относительно этих точек главные моменты  Очевидно, что
Очевидно, что  моменты будут, вообще геворя, различны (см. (14.10) и следствия). Составим скалярное произведение
моменты будут, вообще геворя, различны (см. (14.10) и следствия). Составим скалярное произведение  и воспользуемся выражением (14.11)
и воспользуемся выражением (14.11)

или

Учтем теперь, что скалярное произведение векторов  и
и  равно нулю (так как эти векторы взаимно перпендикулярны). Поэтому
равно нулю (так как эти векторы взаимно перпендикулярны). Поэтому

т. е. скалярное произведение главного момента системы векторов на главный вектор той же системы не зависит от выбора полюса. На этом основании вторым инвариантом системы векторов называют скалярное произведение главного вектора на главный момент

или в проекциях

где  - проекции главного момента, вычисленного относительно произвольной точки пространства, например относительно начала координат, и
- проекции главного момента, вычисленного относительно произвольной точки пространства, например относительно начала координат, и  — проекции главного вектора.
— проекции главного вектора.
Непосредственно из определений следует, что инварианты системы векторов  являются одновременно инвариантами и относительно преобразований осей (см. (12.1) и (12.2)), однако смешивать эти понятия нельзя.
являются одновременно инвариантами и относительно преобразований осей (см. (12.1) и (12.2)), однако смешивать эти понятия нельзя.
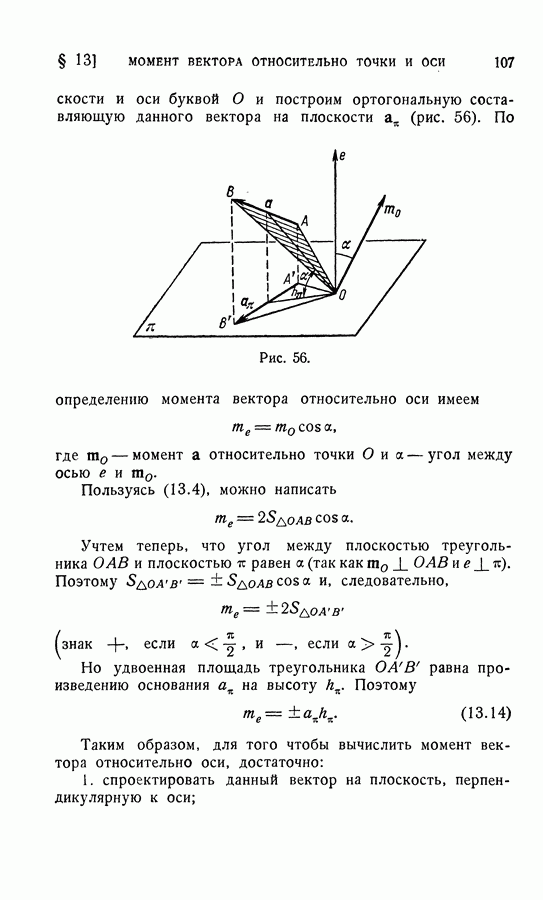
При главном векторе  отличном от нуля, второму инварианту можно дать очень простую геометрическую интерпретацию. На основании определения скалярного произведения второй инвариант можно записать в следующей форме:
отличном от нуля, второму инварианту можно дать очень простую геометрическую интерпретацию. На основании определения скалярного произведения второй инвариант можно записать в следующей форме:

где — угол между векторами  и
и  Так как главный вектор
Так как главный вектор  не связан с выбором точки О, то выражение
не связан с выбором точки О, то выражение

не зависит от выбора полюса. С другой стороны, произведение  равно проекции главного момента на направление главного вектора. Поэтому при
равно проекции главного момента на направление главного вектора. Поэтому при  проекция главного момента на направление главного вектора не зависит от выбора полюса О, относительно которого
проекция главного момента на направление главного вектора не зависит от выбора полюса О, относительно которого
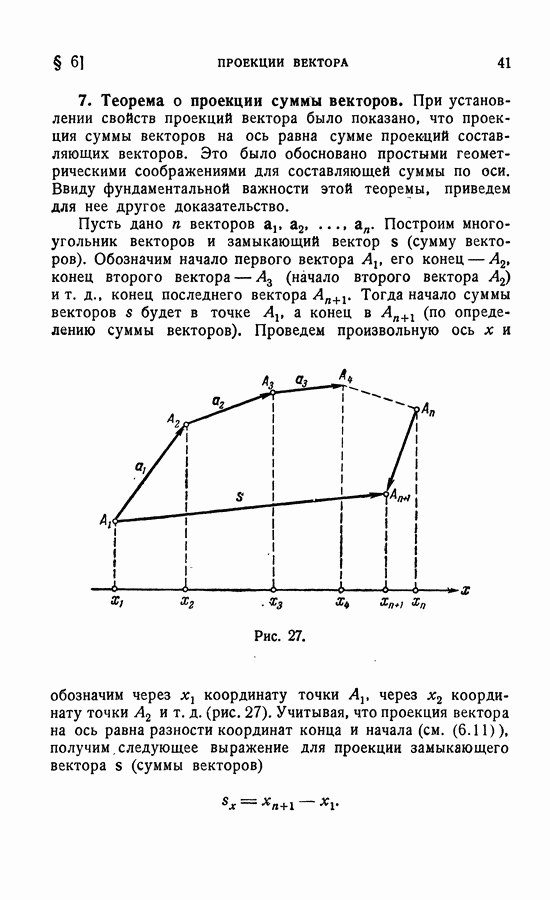
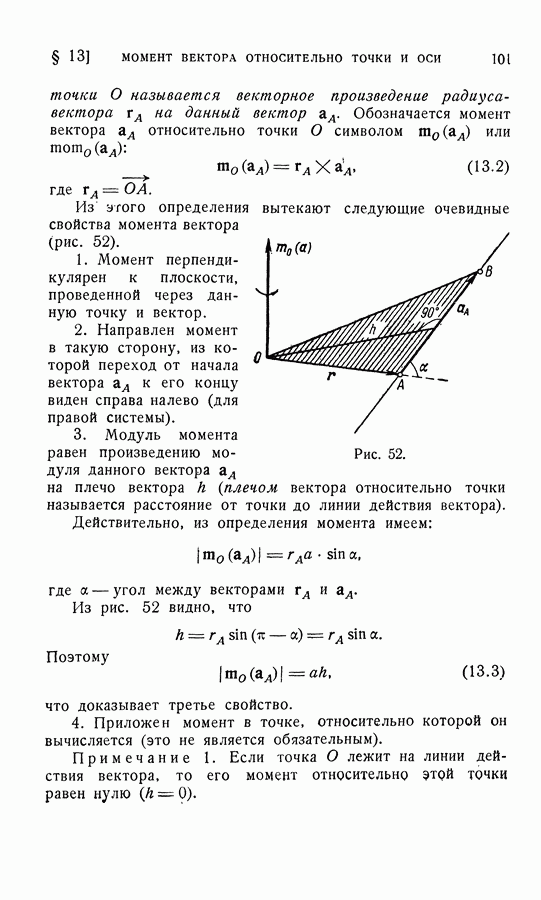
вычисляется главный момент  (рис. 59), но сам главный момент
(рис. 59), но сам главный момент  зависит от выбора полюса.
зависит от выбора полюса.

Рис. 59.
Величина этой проекции определяется формулой

или

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
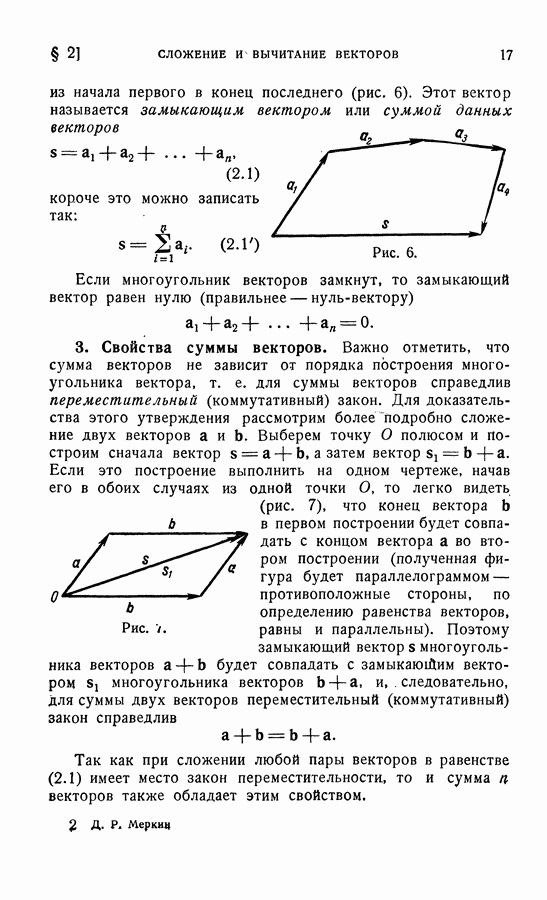
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
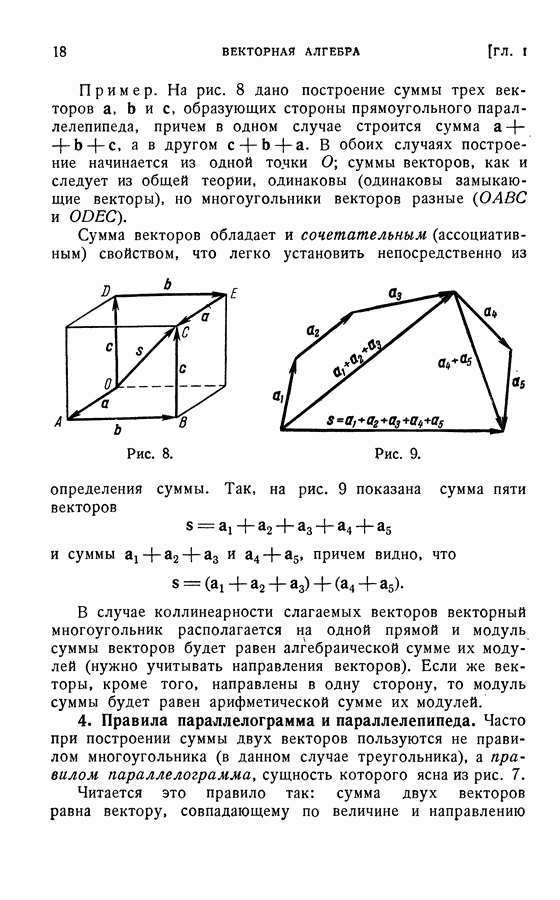
- 3. Свойства суммы векторов.
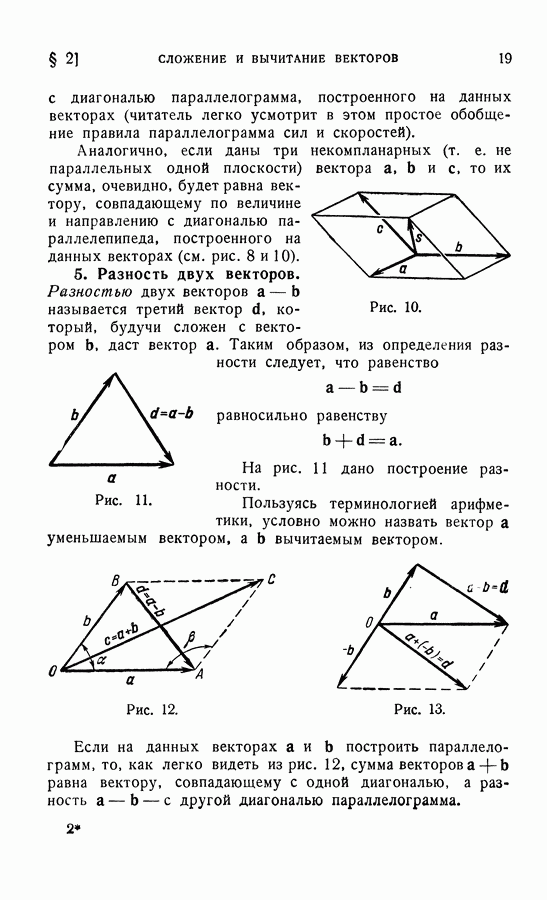
- 4. Правила параллелограмма и параллелепипеда.
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
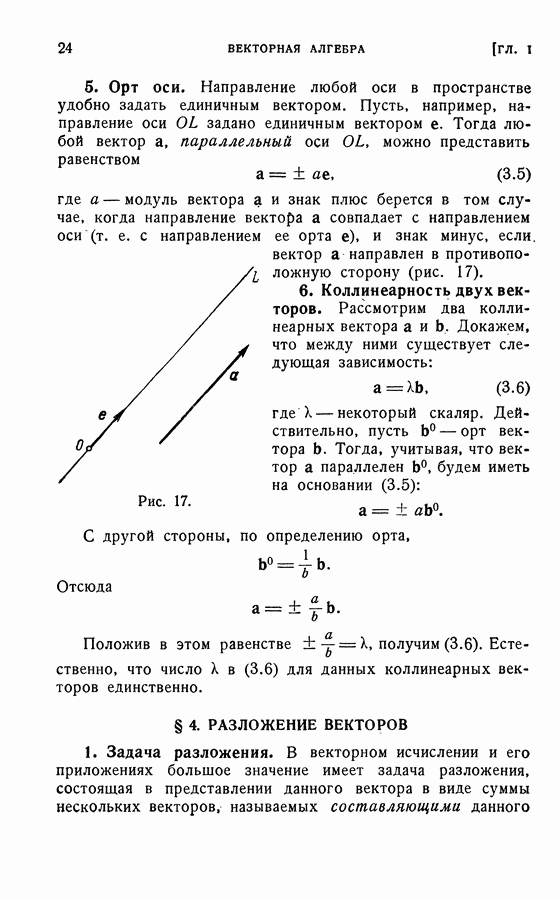
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
- § 6. ПРОЕКЦИИ ВЕКТОРА
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
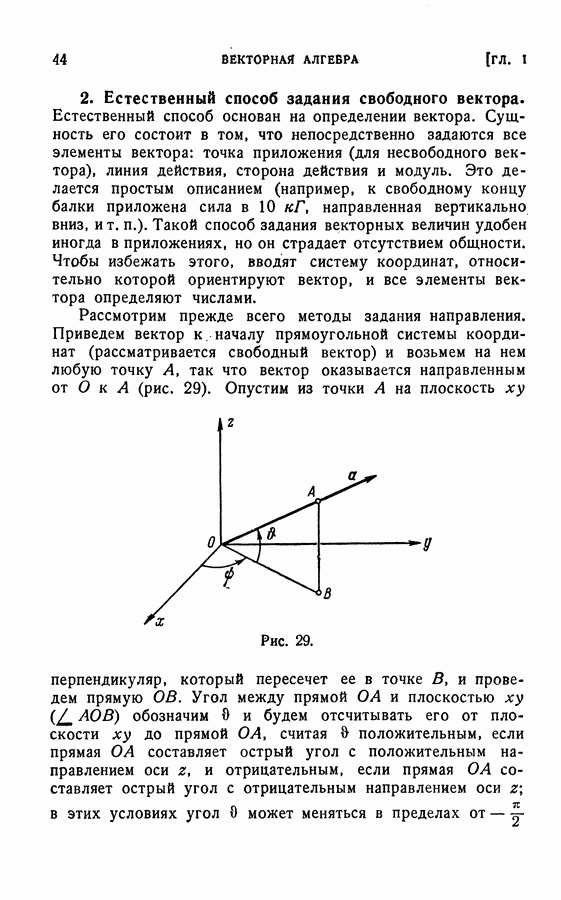
- 2. Естественный способ задания свободного вектора.
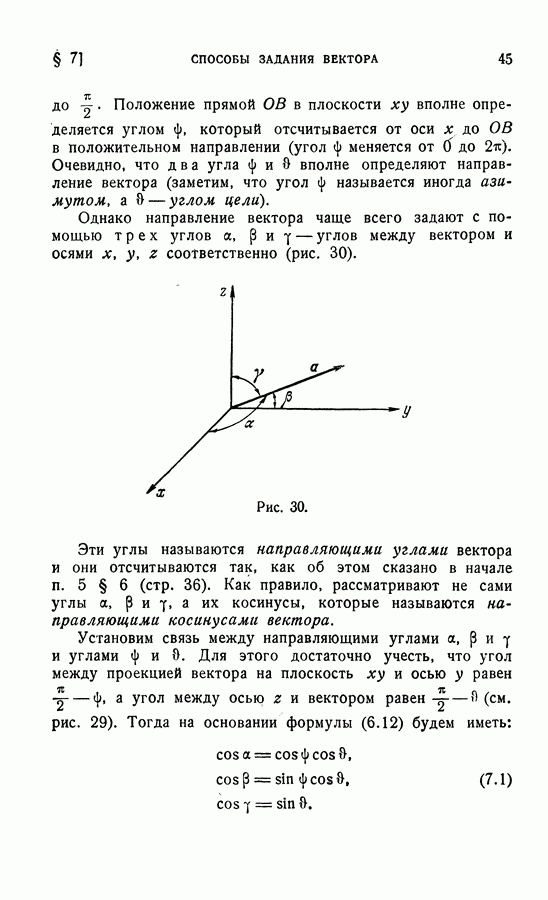
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
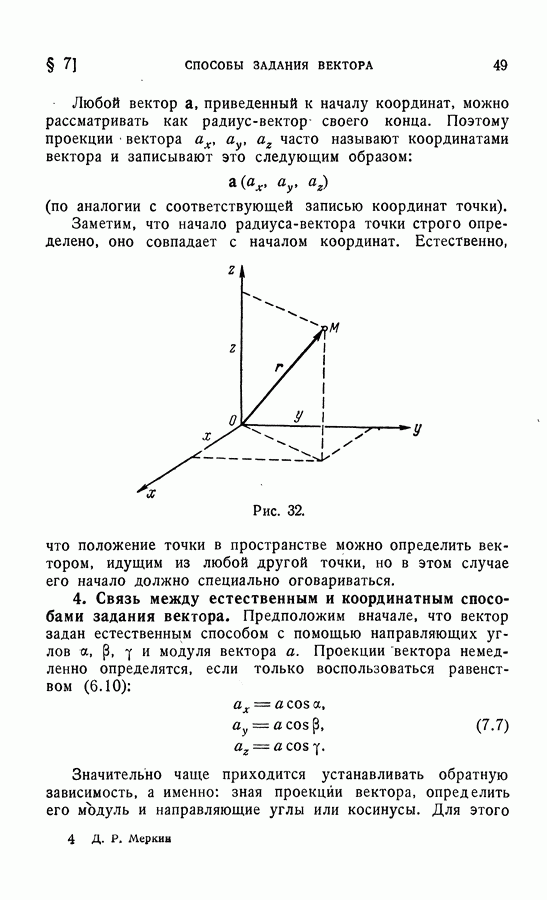
- 4. Связь между естественным и координатным способами задания вектора.
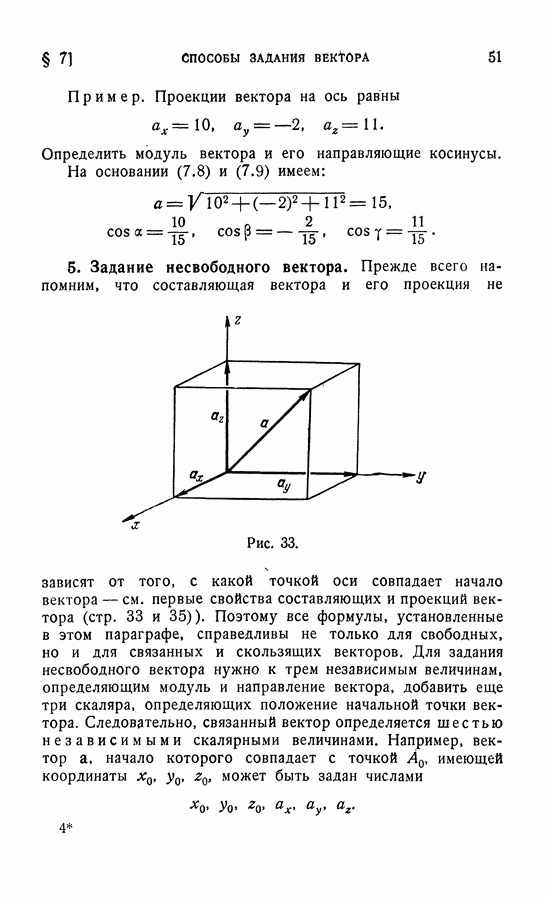
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.