| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
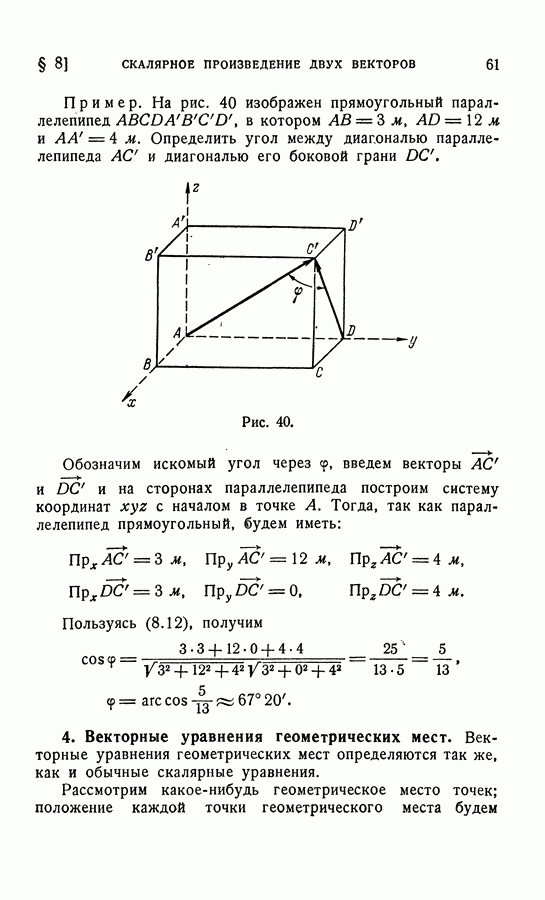
1. Смешанное произведение трех векторов.
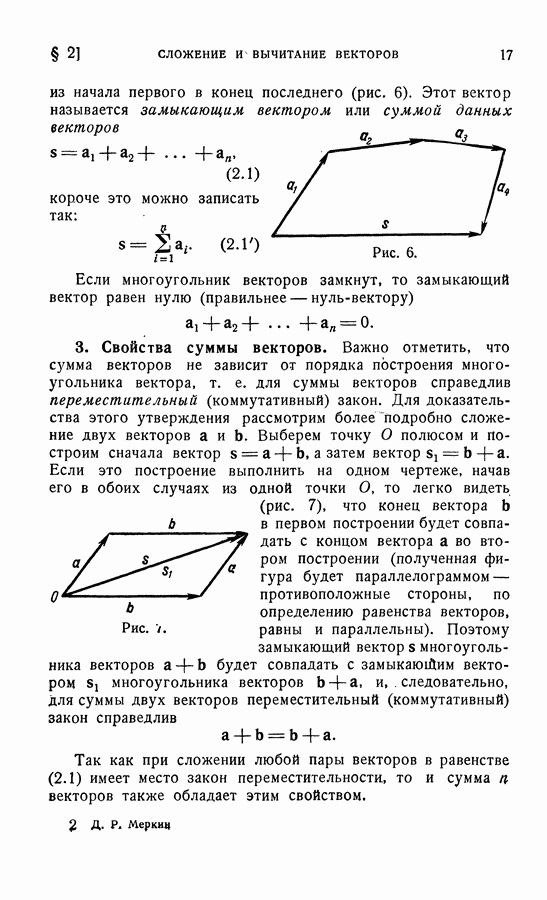
Рассмотрим три вектора  с и составим произведение
с и составим произведение

В этом произведении вектор а сначала умножается векторно на  а затем полученный вектор
а затем полученный вектор  умножается скалярно на с. Такое произведение называется смешанным. Очевидно, что в результате должен получиться скаляр (последнее действие — скалярное произведение двух векторов
умножается скалярно на с. Такое произведение называется смешанным. Очевидно, что в результате должен получиться скаляр (последнее действие — скалярное произведение двух векторов  и с). Вычислим это число, пользуясь тем, что скалярное произведение двух векторов равно сумме произведений их одноименных проекций — см. (8.10):
и с). Вычислим это число, пользуясь тем, что скалярное произведение двух векторов равно сумме произведений их одноименных проекций — см. (8.10):

Внесем в это выражение значения проекций вектора  из (9.15):
из (9.15):

Правая часть этого равенства равна определителю третьего порядка:

что нетрудно проверить, разложив определитель, например, по элементам третьей строки.
Легко установить следующие основные свойства смешанного произведения.
а) Смешанное произведение не изменяется от перестановки действий, т. е.

Действительно, рассмотрим произведение

(эту перестановку множителей можно делать, так как скалярное произведение обладает свойством переместительности). Воспользуемся теперь (10.1), изменив соответственно данному случаю обозначения:

Переставим в этом определителе последнюю строку на место второй, а вторую на место третьей, затем вторую строку поставим на место первой, а первую на место второй. При каждой перестановке строк определитель меняет знак на обратный, поэтому при сделанных двух перестановках определитель не изменится, но в результате последний определитель будет совпадать с определителем (10.1), что доказывает равенство (10.2).
Это свойство дает основание обозначать смешанное произведение следующим сокращенным образом:

не уточняя без особой необходимости, где стоят знаки векторного и скалярного произведений. В соответствии с этим обозначением формула (10.1) примет вид

б) Смешанное произведение не изменяется от циклической (круговой) перестановки сомножителей:

Действительно, пользуясь свойством а) и переместительным свойством скалярного произведения, последовательно получим

в) От перестановки местами двух сомножителей, смешанное произведение, не изменяя своей абсолютной величины, меняет знак на противоположный:

Этсг свойство доказывается следующей цепочкой равенств:

г) Если два вектора коллинеарны, то смешанное произведение равно нулю. Действительно, пусть а и с коллинеарны. Имеем

так как векторное произведение двух коллинеарных векторов равно нулю. В частности, если в смешанном произведении имеется два равных вектора, то оно равно нулю:

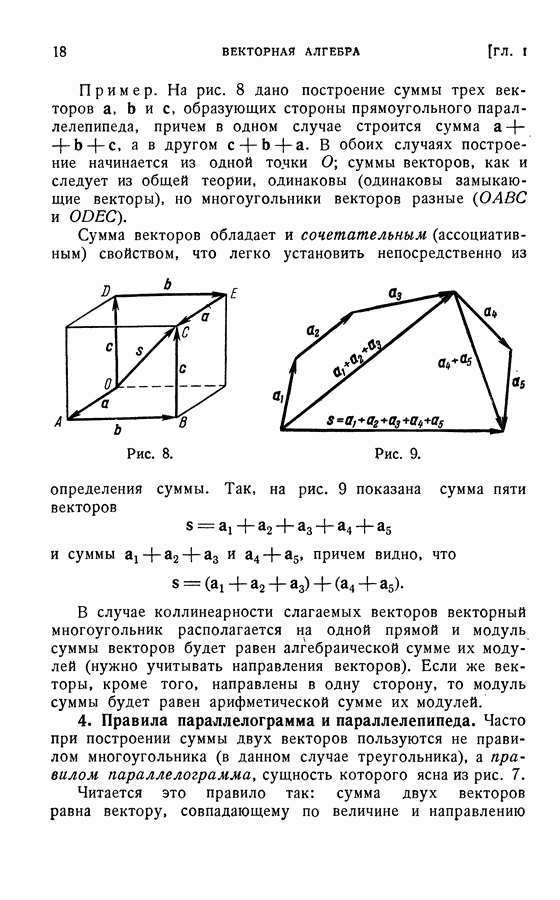
Смешанное произведение трех векторов имеет простой геометрический смысл — с точностью до знака оно равно объему параллелепипеда, построенного на данных векторах.

Рис. 48.
Для доказательства построим на данных векторах параллелепипед (предполагается, что векторы не компланарны) и вектор  (рис. 48). Обозначим:
(рис. 48). Обозначим:  — площадь основания параллелепипеда (основания, построенного на векторах
— площадь основания параллелепипеда (основания, построенного на векторах  — его высота и а — угол между векторами
— его высота и а — угол между векторами 
Согласно определению скалярного произведения, имеем

Из рис. 48 видно, что с  Следовательно,
Следовательно,

что равно объему параллелепипеда.
На рис. 48 тройка векторов  с является правой, в результате чего угол
с является правой, в результате чего угол  оказался острым и
оказался острым и  Если тройка векторов
Если тройка векторов  с будет левой, то угол а будет
с будет левой, то угол а будет
тупым и  . В этом случае произведение
. В этом случае произведение  хотя и будет отрицательно, но по абсолютной величине оно равно высоте параллелепипеда
хотя и будет отрицательно, но по абсолютной величине оно равно высоте параллелепипеда  Итак, можно сделать следующий вывод: смешанное произведение с точностью до знака равно объему параллелепипеда, построенного на векторах-сомножителях, причем это произведение будет положительно, если тройка данных векторов является правой, и отрицательно, если тройка векторов левая (при принятой правой системе):
Итак, можно сделать следующий вывод: смешанное произведение с точностью до знака равно объему параллелепипеда, построенного на векторах-сомножителях, причем это произведение будет положительно, если тройка данных векторов является правой, и отрицательно, если тройка векторов левая (при принятой правой системе):

Рассмотрим условия, при которых смешанное произведение трех векторов равно нулю. Очевидно, что это возможно в следующих случаях:
1) среди множителей имеется хотя бы один нулевой вектор;
2) если два (или все три) вектора коллинеарны — см. свойство г);
3) векторы а, b и с компланарны. Действительно, в этом случае  с и, следовательно,
с и, следовательно, 
Третий случай по существу охватывает первые два случая, так как если среди трех векторов имеется хотя бы два коллинеарных или хотя бы один нулевой, то все три вектора компланарны (см. § 1, п. 7, стр. 15). Итак, для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю:

или, сравнивая с (10.3),

Таково необходимое и достаточное условие компланарности трех векторов, выраженное через проекции. Условие (10.8) или, что то же самое, (10.9) является очень удобным и часто применяется в приложениях.
Пример. Даны три точки, не лежащие на одной прямой:

Написать уравнение плоскости, проходящей через эти три точки.
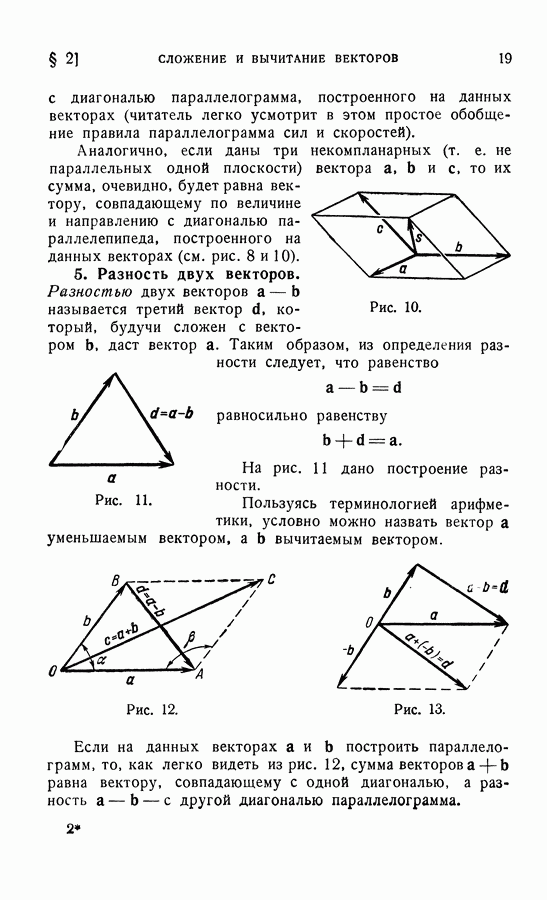
Возьмем в плоскости произвольную точку  и построим векторы
и построим векторы  и
и  (рис. 49).
(рис. 49).

Рис. 49.
Все три вектора лежат в одной плоскости, следовательно, они компланарны и их смешанное произведение равно нулю:

или

где  — радиусы-векторы точек
— радиусы-векторы точек  соответственно. Этому равенству удовлетворяют радиусы-векторы
соответственно. Этому равенству удовлетворяют радиусы-векторы  любых точек, лежащих на плоскости, и не удовлетворяют радиусы-векторы точек, не лежащих на плоскости (так как в последнем случае векторы
любых точек, лежащих на плоскости, и не удовлетворяют радиусы-векторы точек, не лежащих на плоскости (так как в последнем случае векторы  не будут компланарны). Следовательно, (10.10) есть уравнение плоскости в векторной форме. Для того чтобы написать уравнение плоскости в координатной форме, достаточно воспользоваться формулой (10.9):
не будут компланарны). Следовательно, (10.10) есть уравнение плоскости в векторной форме. Для того чтобы написать уравнение плоскости в координатной форме, достаточно воспользоваться формулой (10.9):

Заметим, что если точки  лежат на одной прямой, то векторы
лежат на одной прямой, то векторы  будут коллинеарны и на основании свойства г) смешанного произведения равенство
будут коллинеарны и на основании свойства г) смешанного произведения равенство
(10.10), а следовательно, и (10.10) будет выполняться тождественно при любых  т. е. при любых х, у и z. Геометрически это означает, что при этих условиях существует бесчисленное множество плоскостей, проходящих через данные три точки (через прямую в пространстве можно провести бесчисленное множество плоскостей).
т. е. при любых х, у и z. Геометрически это означает, что при этих условиях существует бесчисленное множество плоскостей, проходящих через данные три точки (через прямую в пространстве можно провести бесчисленное множество плоскостей).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
- 3. Свойства суммы векторов.
- 4. Правила параллелограмма и параллелепипеда.
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
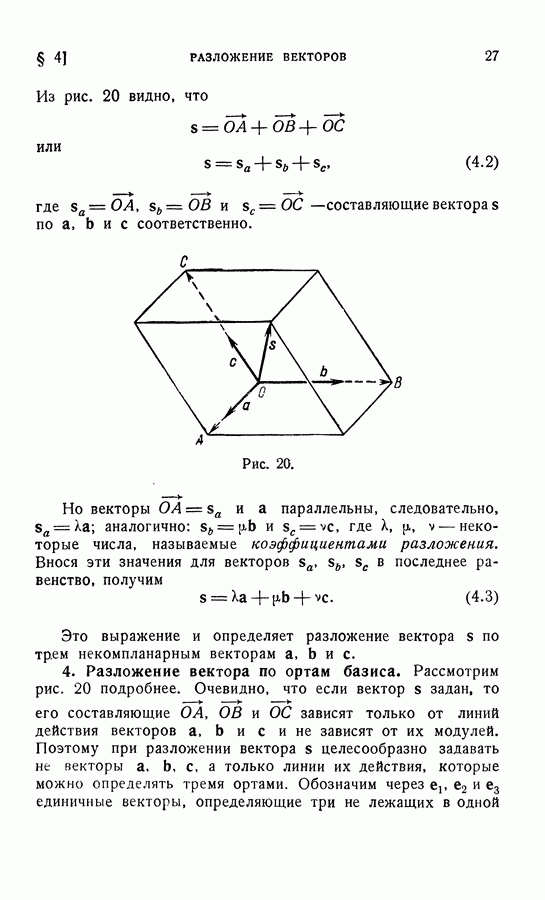
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
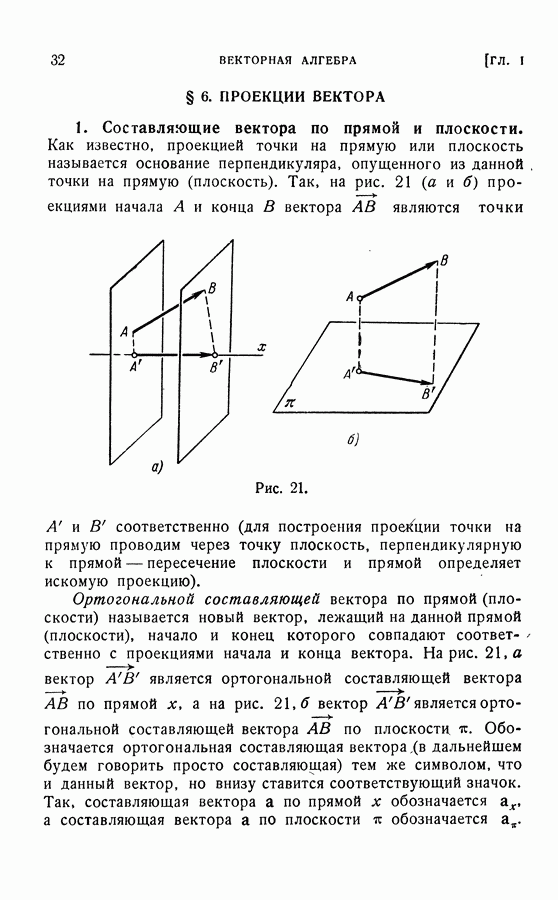
- § 6. ПРОЕКЦИИ ВЕКТОРА
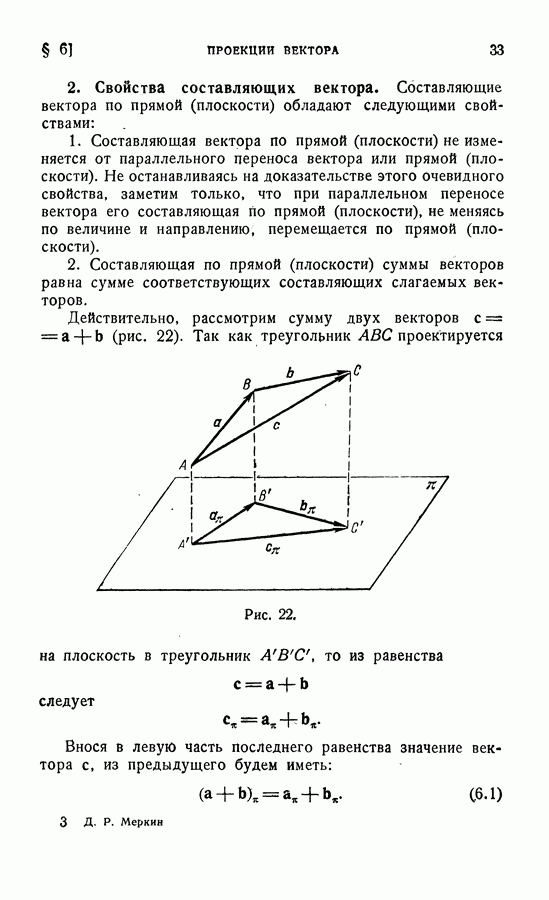
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
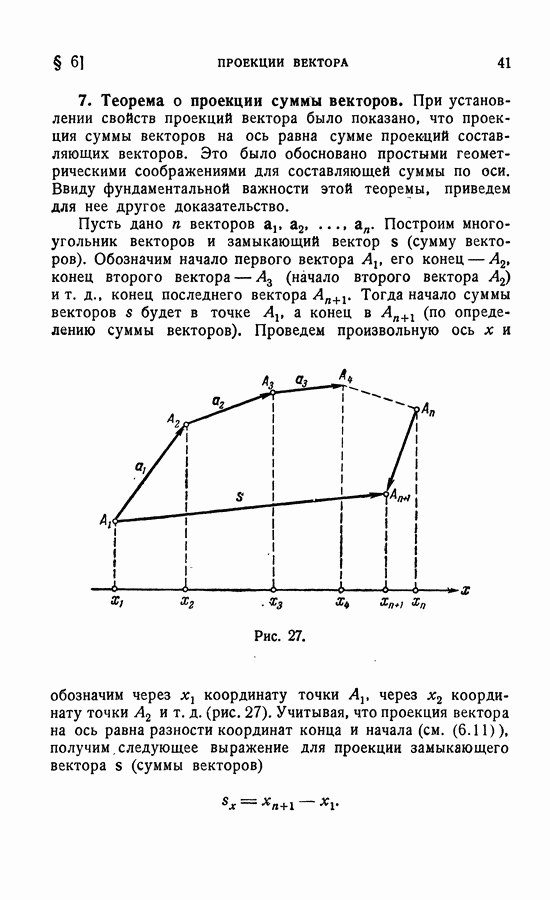
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
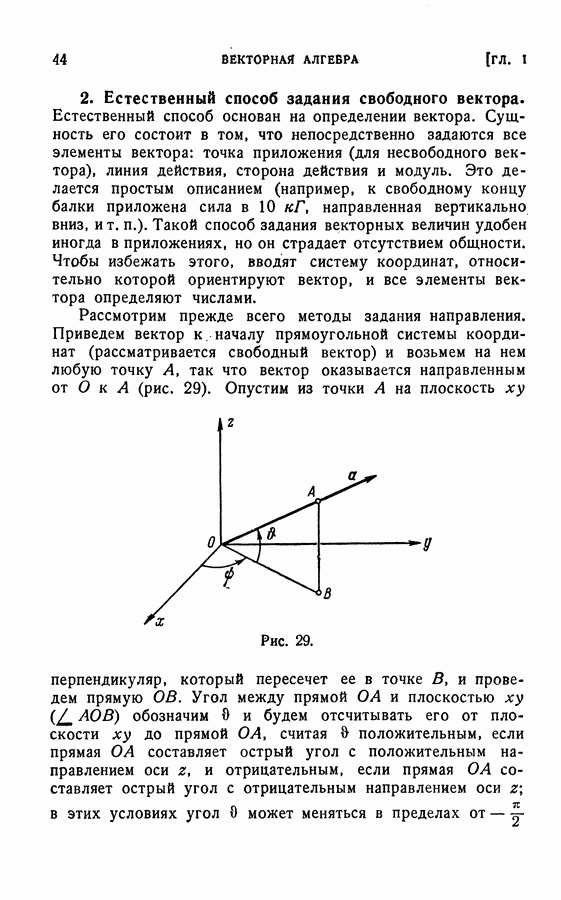
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
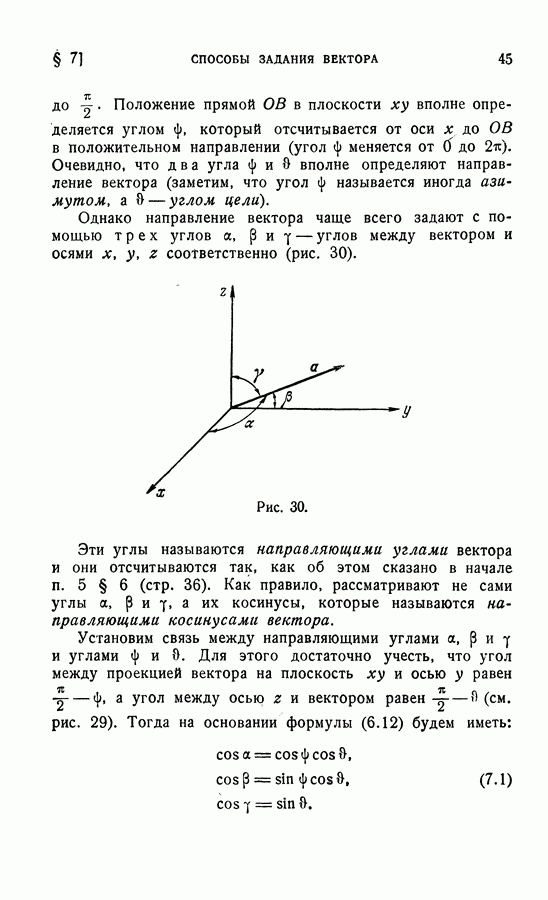
- 4. Связь между естественным и координатным способами задания вектора.
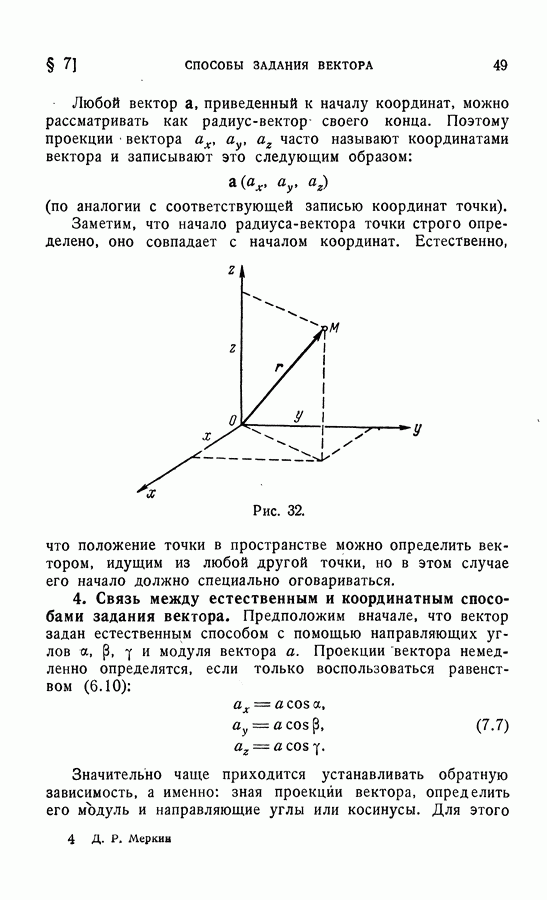
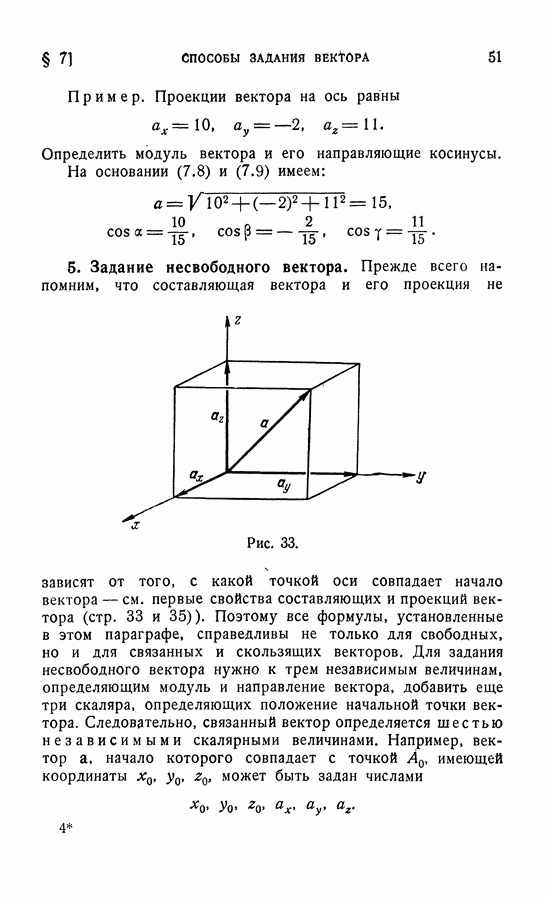
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
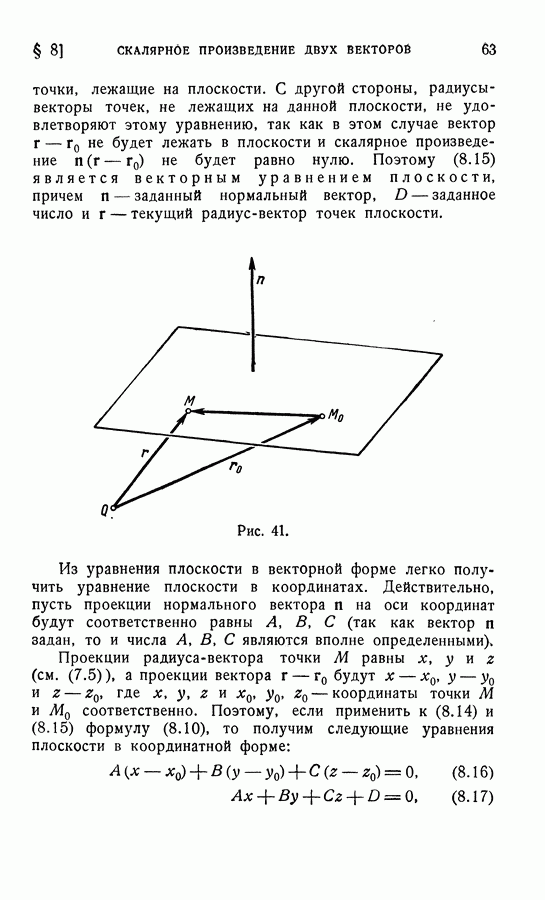
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
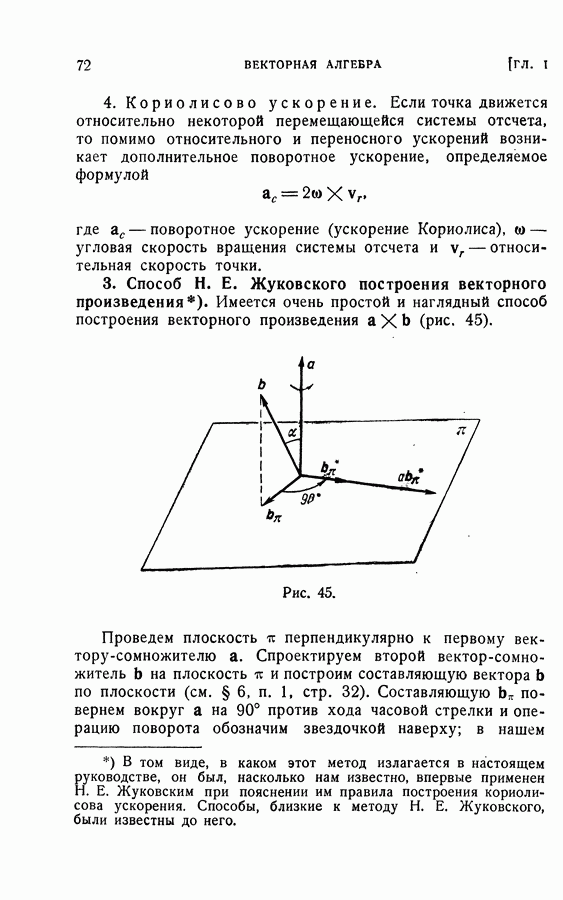
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
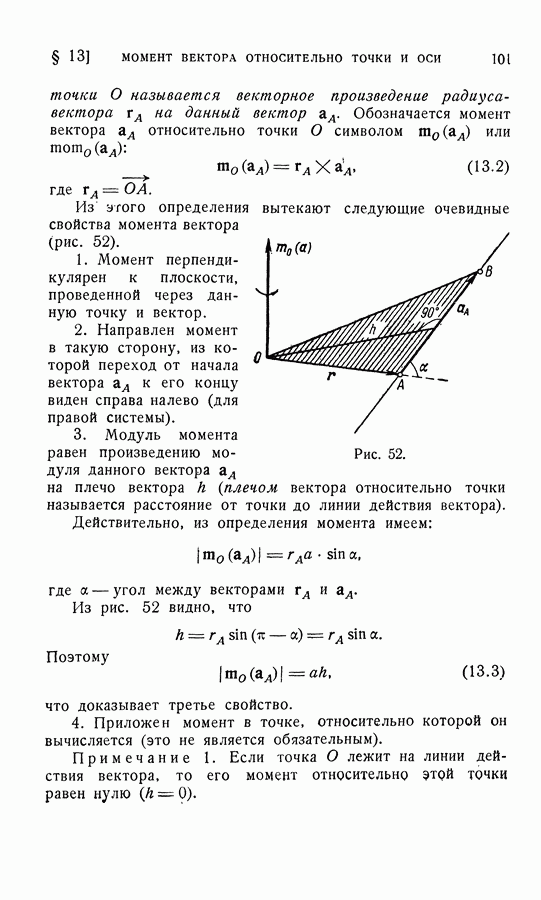
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.