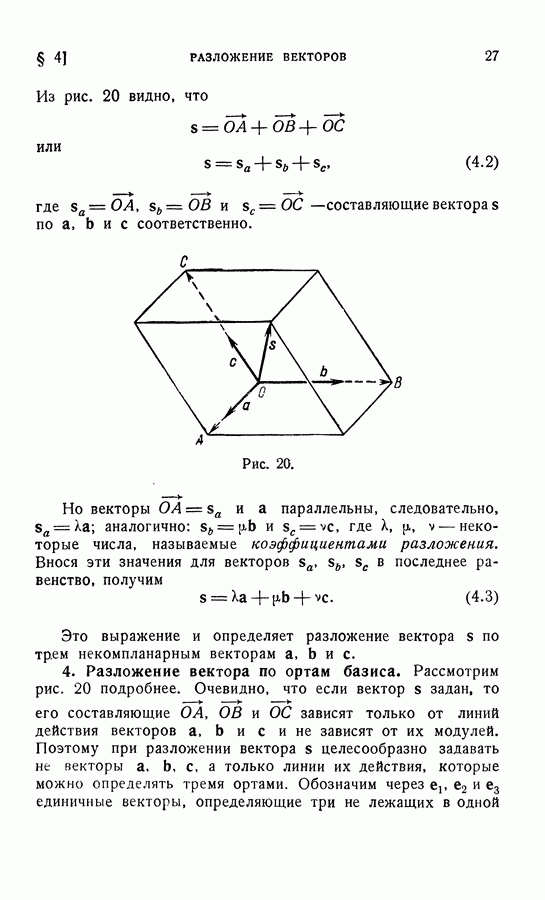
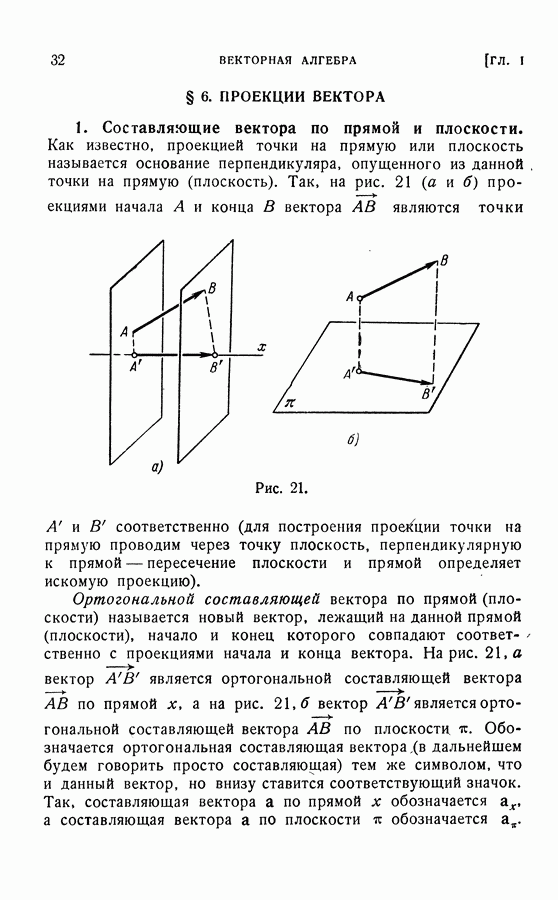
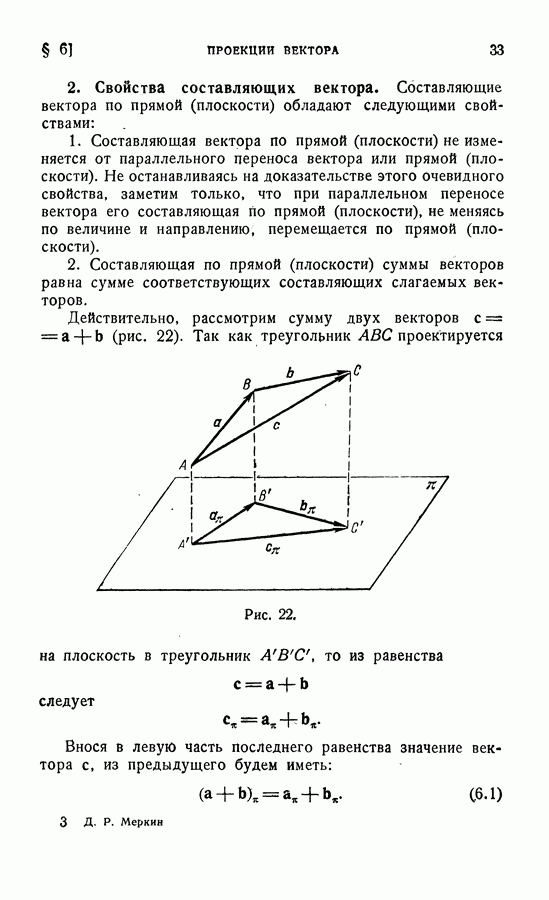
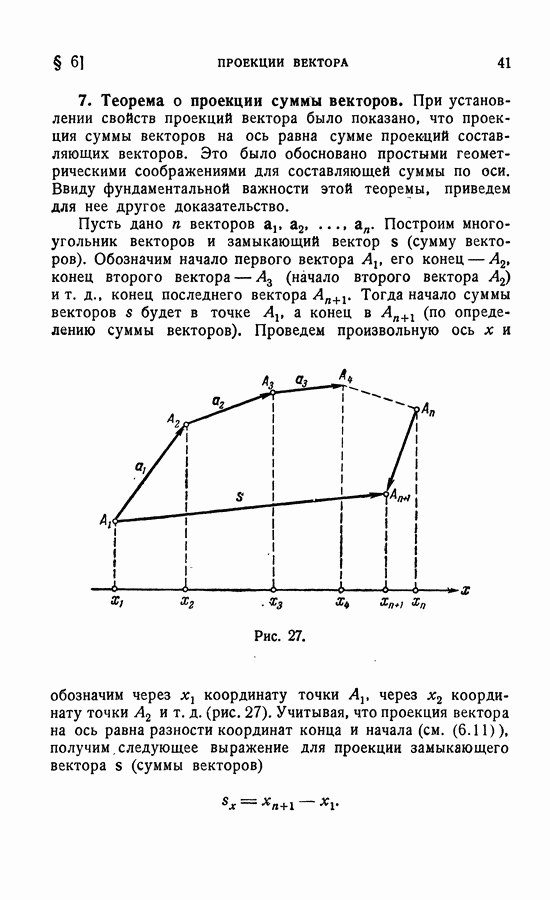
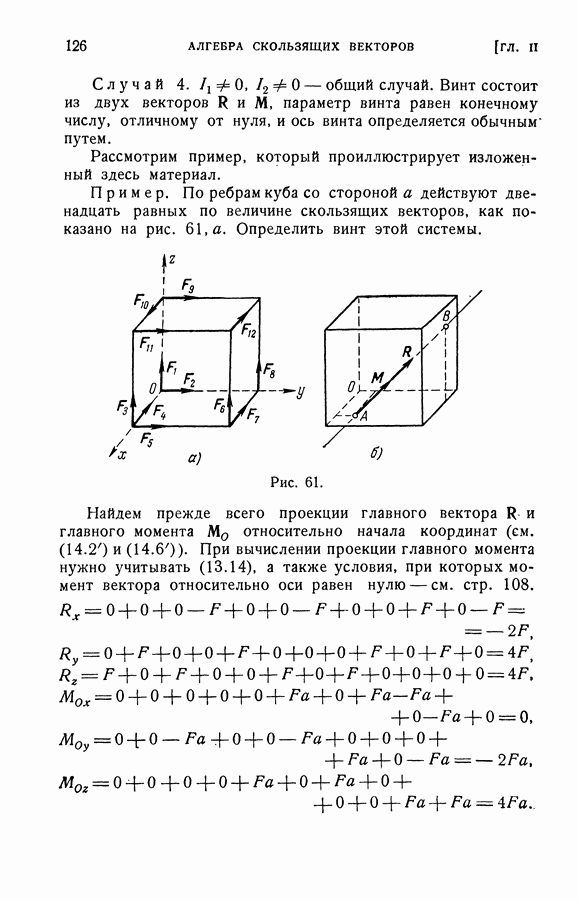
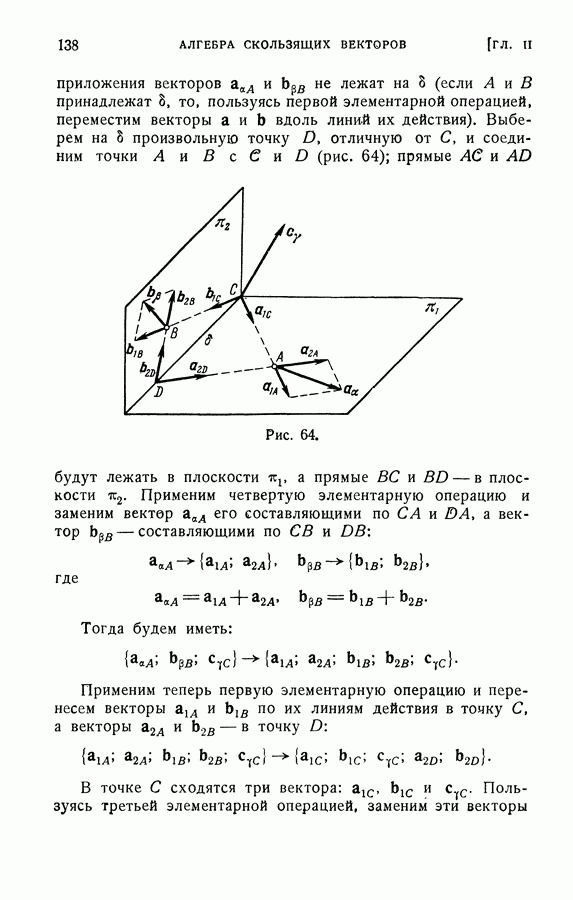
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
10. Понятие о винте.
В этом пункте мы кратко остановимся на понятии винта (дополнительно о нем см.
п. 3 § 19). Прежде всего напомним, что вектор и момент вектора, главный вектор и главный момент системы  и
и  это векторы разной природы, разной размерности. Рассмотрим скользящий вектор
это векторы разной природы, разной размерности. Рассмотрим скользящий вектор  лежащий на некоторой прямой а, и некоторый вектор М, коллинеарный ему и имеющий размерность момента вектора
лежащий на некоторой прямой а, и некоторый вектор М, коллинеарный ему и имеющий размерность момента вектора  Совокупность двух таких векторов называется винтом. В зависимости от природы вектора
Совокупность двух таких векторов называется винтом. В зависимости от природы вектора  можно говорить о динамическом винте, кинематическом винте, электродинамическом винте и т. п. Вектор
можно говорить о динамическом винте, кинематическом винте, электродинамическом винте и т. п. Вектор  называется амплитудой винта, прямая а — основанием или осью винта, вектор М — моментом. Так как векторы
называется амплитудой винта, прямая а — основанием или осью винта, вектор М — моментом. Так как векторы  и М коллинеарны, то между ними должна существовать линейная зависимость
и М коллинеарны, то между ними должна существовать линейная зависимость

причем число  имеющее всегда размерность длины, называется параметром винта (параметр винта
имеющее всегда размерность длины, называется параметром винта (параметр винта  будет положительным числом, если векторы R и М направлены в одну сторону, и отрицательным, если эти векторы направлены в разные стороны).
будет положительным числом, если векторы R и М направлены в одну сторону, и отрицательным, если эти векторы направлены в разные стороны).
Остановимся прежде всего на вопросе о числе независимых параметров, определяющих винт, и на способе задания винта. Амплитуда винта по определению является скользящим вектором. Как было показано (см. п. 5 § 13), скользящий вектор, включая линию его действия, определяется пятью независимыми скалярными величинами. Следовательно, для задания амплитуды винта  и его оси требуется пять независимых скалярных параметров. Момент винта М можно определить, пользуясь равенством (14.22), которое в дополнение к известному вектору
и его оси требуется пять независимых скалярных параметров. Момент винта М можно определить, пользуясь равенством (14.22), которое в дополнение к известному вектору  требует знания еще одного числа — параметра винта
требует знания еще одного числа — параметра винта  Таким образом, винт вполне определяется шестью независимыми скалярами. Какие величины удобнее всего выбрать для задания винта? Существует несколько способов задания винта. Остановимся на некоторых из них.
Таким образом, винт вполне определяется шестью независимыми скалярами. Какие величины удобнее всего выбрать для задания винта? Существует несколько способов задания винта. Остановимся на некоторых из них.
1. Винт может быть определен модулем амплитуды  параметром винта
параметром винта  и теми четырьмя величинами, которые определяют положение оси винта (прямая в пространстве определяется четырьмя независимыми параметрами). Недостаток этого способа состоит в том, что направление амплитуды на оси винта остается неопределенным.
и теми четырьмя величинами, которые определяют положение оси винта (прямая в пространстве определяется четырьмя независимыми параметрами). Недостаток этого способа состоит в том, что направление амплитуды на оси винта остается неопределенным.
2. Амплитуда винта  как скользящий вектор может быть определена шестью числами:
как скользящий вектор может быть определена шестью числами:  где первые три числа равны проекциям амплитуды, а вторые три числа равны моментам амплитуды относительно тех же осей координат (см. п. 5 § 13). Между этими числами имеется одна зависимость (условие перпендикулярности):
где первые три числа равны проекциям амплитуды, а вторые три числа равны моментам амплитуды относительно тех же осей координат (см. п. 5 § 13). Между этими числами имеется одна зависимость (условие перпендикулярности):

так что независимых величин здесь только пять.
Шестым числом, определяющим винт, будет параметр винта  Если винт обозначить символом
Если винт обозначить символом  то можно записать:
то можно записать:

или сокращенно:

где  — момент амплитуды
— момент амплитуды  относительно начала координат в предположении, что амплитуда находится на оси винта (векторы
относительно начала координат в предположении, что амплитуда находится на оси винта (векторы  и подчинены условию ортогональности). Необходимо иметь в виду, что при этом способе задания винта вектор определяет не момент винта, а момент амплитуды относительно начала координат. Момент винта М вычисляется по формуле (14.22), и его проекции равны:
и подчинены условию ортогональности). Необходимо иметь в виду, что при этом способе задания винта вектор определяет не момент винта, а момент амплитуды относительно начала координат. Момент винта М вычисляется по формуле (14.22), и его проекции равны:

3. Очень часто винт задают следующими величинами:  где
где  — координаты любой точки оси винта (одну из них можно выбрать произвольно):
— координаты любой точки оси винта (одну из них можно выбрать произвольно):

или сокращенно:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
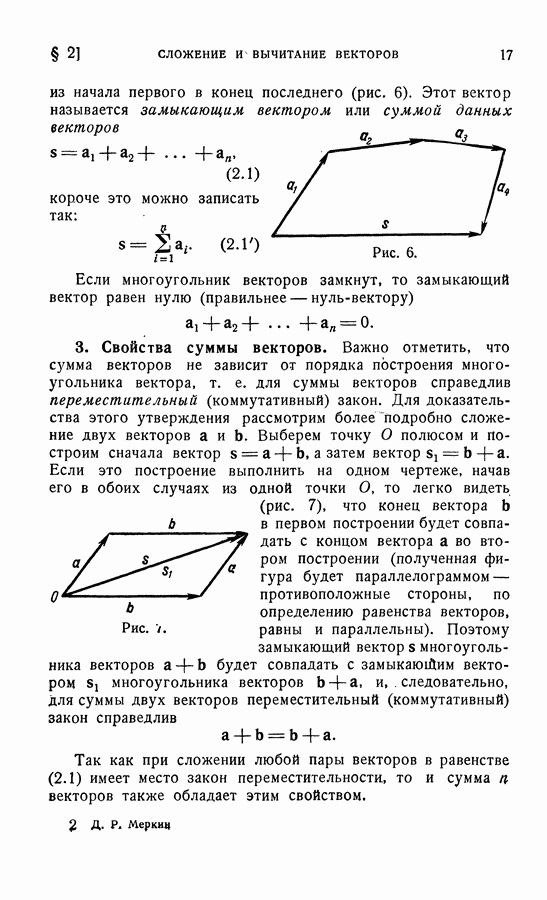
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
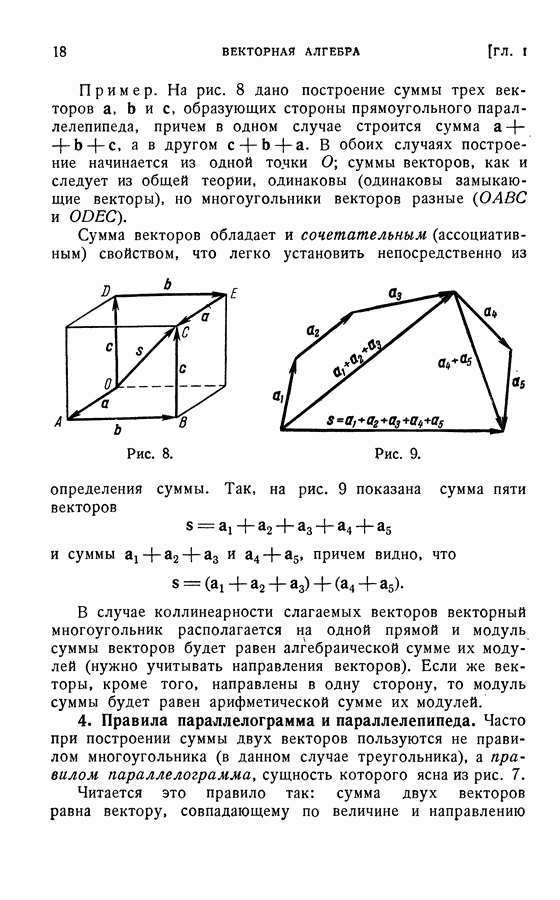
- 3. Свойства суммы векторов.
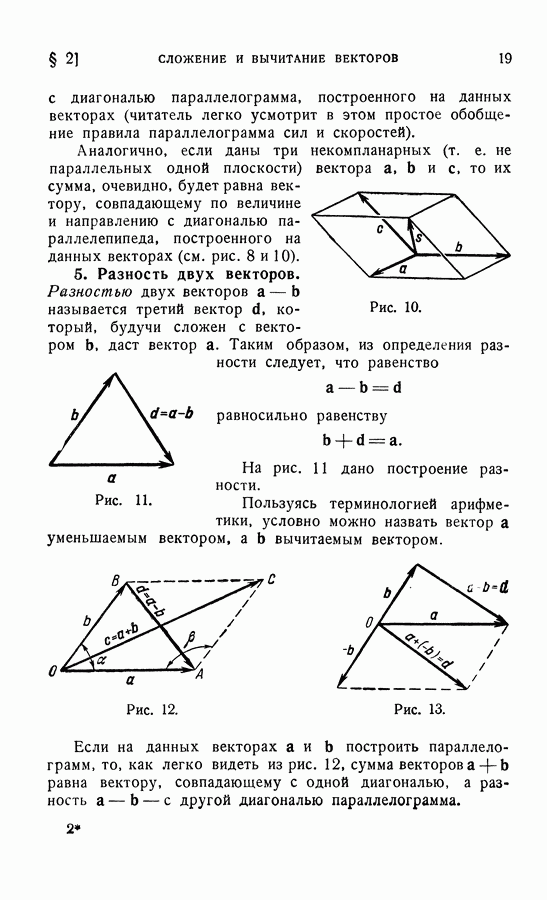
- 4. Правила параллелограмма и параллелепипеда.
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
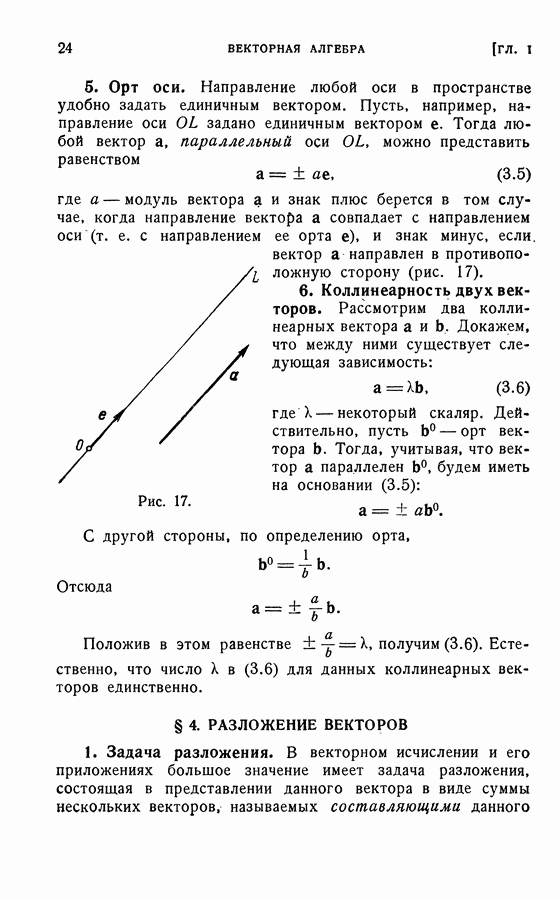
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
- § 6. ПРОЕКЦИИ ВЕКТОРА
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
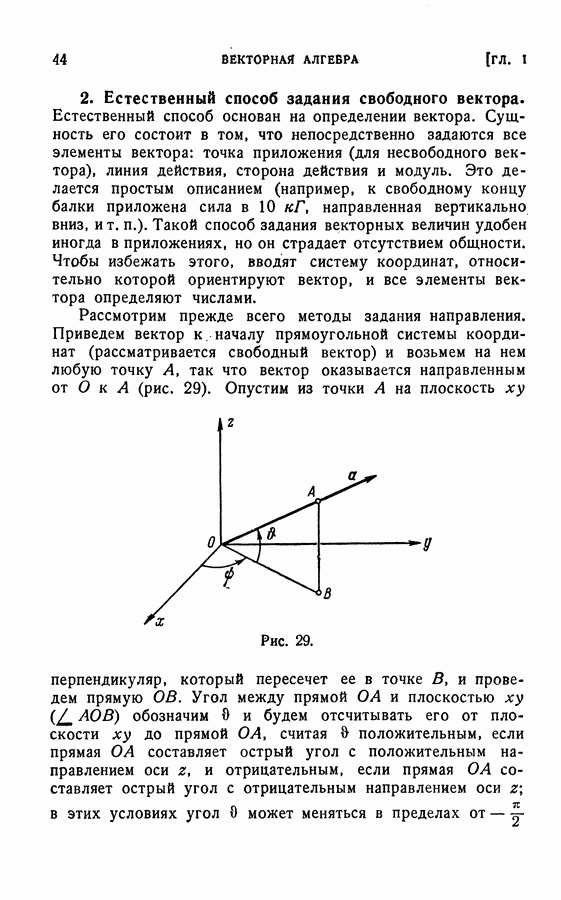
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
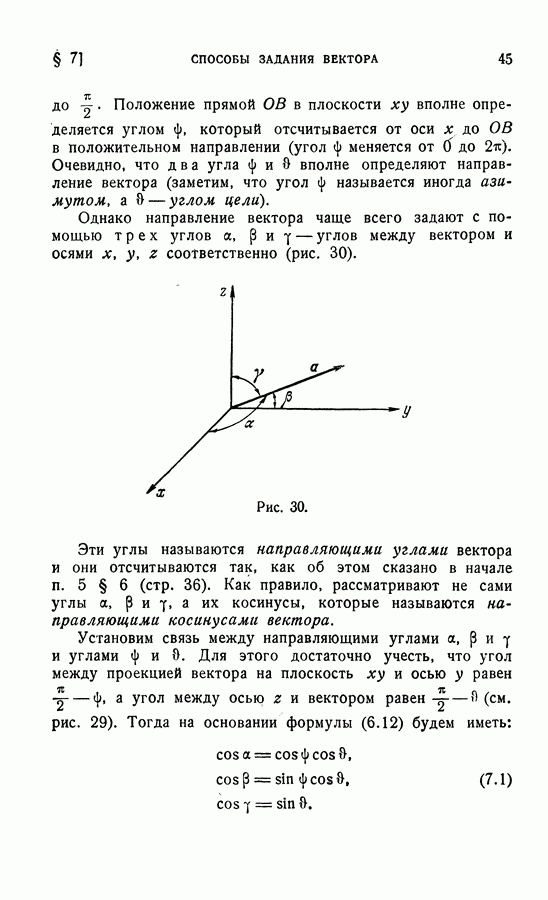
- 4. Связь между естественным и координатным способами задания вектора.
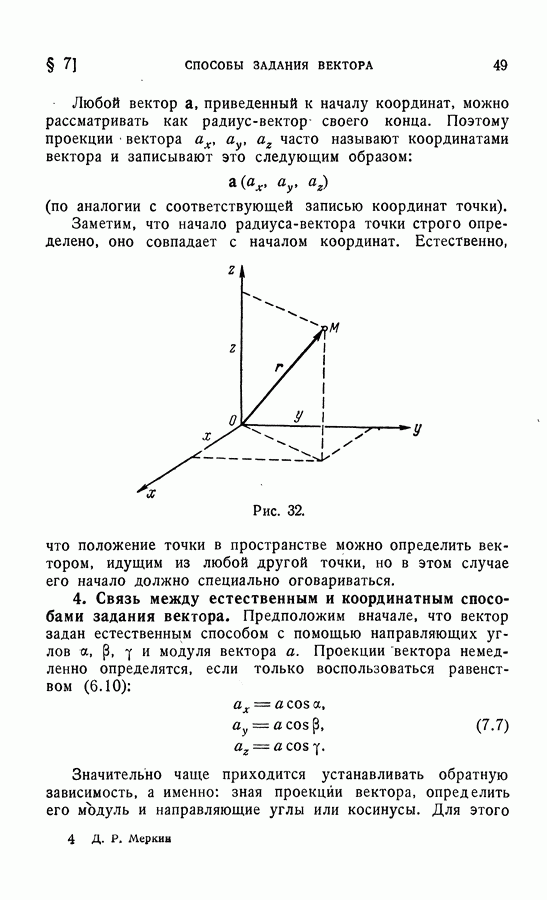
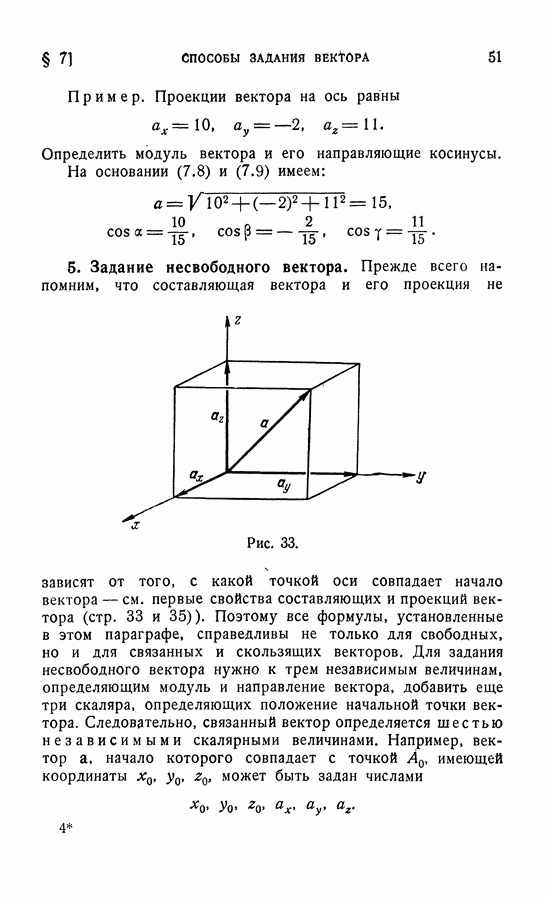
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.