| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Основные определения и аксиомы.
Две системы векторов будем считать эквивалентными, если они вызывают одинаковое состояние некоторого объекта или одинаково характеризуют данное явление. В данном определении эквивалентности имеются некоторые термины («одинаковое состояние», «одинаково характеризуют»), которые не являются математически точными. Поэтому введем некоторые дополнительные определения и аксиомы, которые позволят подойти к понятию эквивалентности математически.
Эквивалентность будем обозначать знаком  запись
запись

означает, что система векторов  эквивалентна системе
эквивалентна системе  , наоборот, система векторов
, наоборот, система векторов  эквивалентна системе
эквивалентна системе 
Из определения свободных и скользящих векторов следует, что если векторы свободны, то

где А и В — любые точки пространства. Если же векторы скользящие, то

где А и В — любые точки на а (см. (13.1)).
Если система векторов  эквивалентна одному вектору
эквивалентна одному вектору 

то говорят, что данная система векторов имеет равнодействующий вектор или приводится к равнодействующему вектору. Заметим сразу же, что далеко не всегда систему векторов можно привести к одному равнодействующему вектору.
Если система векторов  эквивалентна нулевой системе, то будем говорить, что данная система векторов эквивалентна нулю или уравновешена:
эквивалентна нулевой системе, то будем говорить, что данная система векторов эквивалентна нулю или уравновешена:

Вопрос о признаках, определяющих нулевую систему, сейчас не ставится, однако из данных определений вытекает, что один вектор а будет эквивалентен нулю в том и только том случае, если он равен нулю. Иначе говоря, из  следует, что
следует, что  и наоборот.
и наоборот.
Первая аксиома. Если к данной системе векторов присоединить или от данной системы отбросить систему, эквивалентную нулю, то в результате получится новая система, эквивалентная данной. То есть, если

то будет справедливо следующее соотношение:

Таким образом, первая аксиома устанавливает, что из (15.4) следует (15.5) и, наоборот, из (15.5) следует (15.4).
Все сделанные до сих пор определения и первая аксиома относятся к любой совокупности векторов, содержащей векторы разной природы. Понятно, что такие общие определения требуют более детального подхода в конкретных случаях. Прежде всего условимся, что дальнейшие определения и аксиомы будут относиться к векторам одной размерности (случаи разной размерности векторов будут специально оговариваться), Таким образом, если нет специальной оговорки, то векторы, входящие в систему, можно подвергать формальным математическим операциям сложения и вычитания.
Вторая аксиома. Два вектора, имеющие общее начало, эквивалентны одному вектору, приложенному к той же точке и равному их сумме:

где

Эта аксиома является по существу перефразировкой хорошо известных правил сложения двух сил, приложенных к одной точке, сложения скоростей и т. п.
Следствие 1. Система векторов, приложенных к одной точке, эквивалентна одному равнодействующему вектору, имеющему то же начало и равному сумме данных векторов.
Действительно, применим последовательно вторую аксиому сначала к первой паре векторов, затем присоединим третий вектор и т. д. Таким образом,

где

Следствие 2. Для того чтобы система векторов, приложенных к одной точке, была эквивалентна нулю, необходимо и достаточно, чтобы их сумма равнялась нулю.
Для доказательства достаточно заменить данную систему векторов  одним вектором Кл и учесть, что один вектор эквивалентен нулю тогда и только тогда, когда он равен нулю. Следовательно, условие
одним вектором Кл и учесть, что один вектор эквивалентен нулю тогда и только тогда, когда он равен нулю. Следовательно, условие

является необходимым и достаточным, чтобы система векторов, имеющих общее начало, была уравновешена.
Следствие 3. Система, составленная из суммы двух взаимно противоположных систем (см. (14.1)), эквивалентна нулю:

(так как любые два вектора  взаимно уравновешены).
взаимно уравновешены).
Следствие 4. Если справедливо

то будет выполняться и следующее соотношение:

и наоборот.
Действительно, присоединим к системе  систему (15.10), эквивалентную нулю (первая аксиома):
систему (15.10), эквивалентную нулю (первая аксиома):

Учитывая (15.9) и применяя снова первую аксиому, получим (15.11).
Первые две аксиомы и очевидные следствия имеют общий характер. Они справедливы как для системы свободных векторов, так и для систем скользящих и несвободных векторов. Следующая аксиома относится только к скользящим векторам.
Третья аксиома (аксиома системы скользящих векторов). Совокупность двух скользящих векторов эквивалентна нулю тогда и только тогда, когда они равны по величине, действуют по одной прямой и направлены в. противоположные стороны.
На рис. 62 показаны две пары скользящих векторов, каждая из которых эквивалентна нулю.

Рис. 62.
Заметим сразу же, что если бы векторы, изображенные на рис. 62, были несвободными, то они не были бы эквивалентны нулю.
Следствие. Сумма двух взаимно противоположных систем скользящих векторов эквивалентна нулю:

Полезно сравнить это соотношение с (15.9). В последнем взаимно уравновешенные векторы  приложены к одной точке, и поэтому (15.9) справедливо не только для скользящих, но и для несвободных, связанных векторов. В (15.12) уравновешенные векторы
приложены к одной точке, и поэтому (15.9) справедливо не только для скользящих, но и для несвободных, связанных векторов. В (15.12) уравновешенные векторы  лежат на
лежат на
одной прямой и, как правило, приложены к разным точкам. Поэтому (15.12) справедливо только для скользящих векторов и не справедливо для несвободных, связанных векторов.
Примечание 1. Пользуясь определением скользящих векторов и формулами (15.8) и (15.9), легко показать, что если два скользящих вектора лежат на одной прямой, равны по величине и обратны по направлению, то они эквивалентны нулю (сумма этих векторов равна нулю, а так как они скользящие и действуют по одной прямой, то их можно привести к одному началу). Однако обратное утверждение не может быть доказано, и поэтому введена третья аксиома. -
Примечание 2. Третья аксиома может служить признаком скользящих векторов в том смысле, что. если для системы векторов справедлива третья аксиома, то векторы, входящие в систему, скользящие. Действительно, пусть для данной системы векторов справедлива третья аксиома и  - любой вектор этой системы. Возьмем на а произвольную точку В и добавим к данному вектору два уравновешенных вектора
- любой вектор этой системы. Возьмем на а произвольную точку В и добавим к данному вектору два уравновешенных вектора  (это можно сделать на основании первой аксиомы и (15.9)). В результате получим (рис. 63)
(это можно сделать на основании первой аксиомы и (15.9)). В результате получим (рис. 63)


Рис. 63.
Учтем теперь, что по условию третья аксиома применима и, следовательно, два вектора  эквивалентны нулю. Тогда, снова применяя первую аксиому и отбрасывая эти векторы, будем иметь
эквивалентны нулю. Тогда, снова применяя первую аксиому и отбрасывая эти векторы, будем иметь

или

и так как В — произвольная точка на а, то вектор  — скользящий.
— скользящий.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
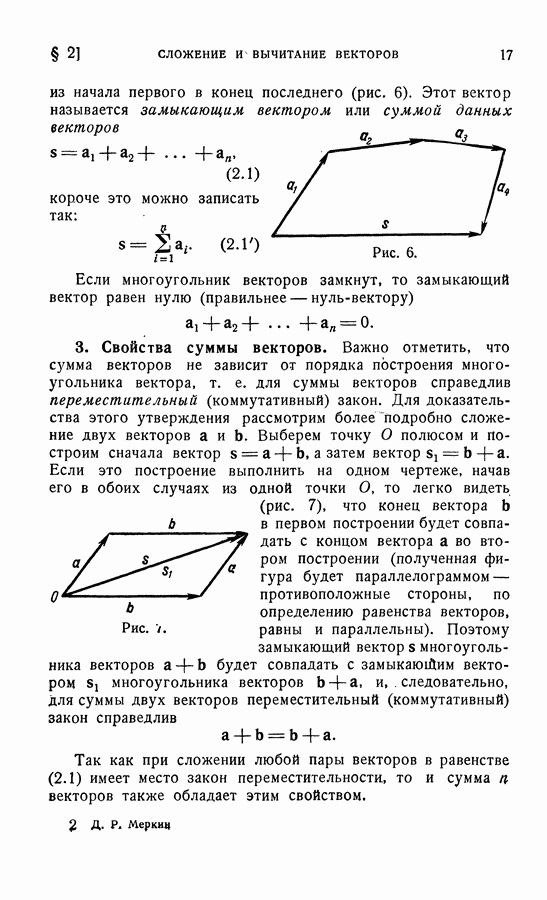
- 2. Сумма векторов.
- 3. Свойства суммы векторов.
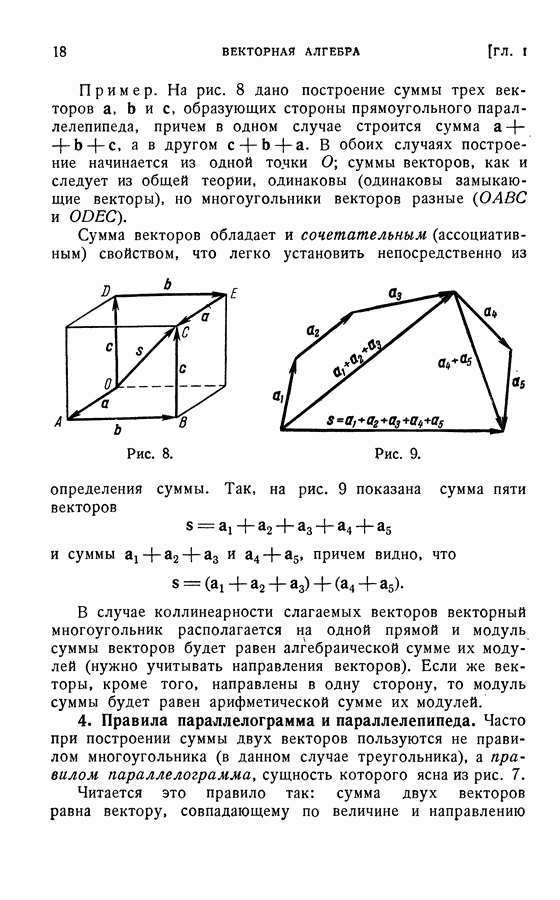
- 4. Правила параллелограмма и параллелепипеда.
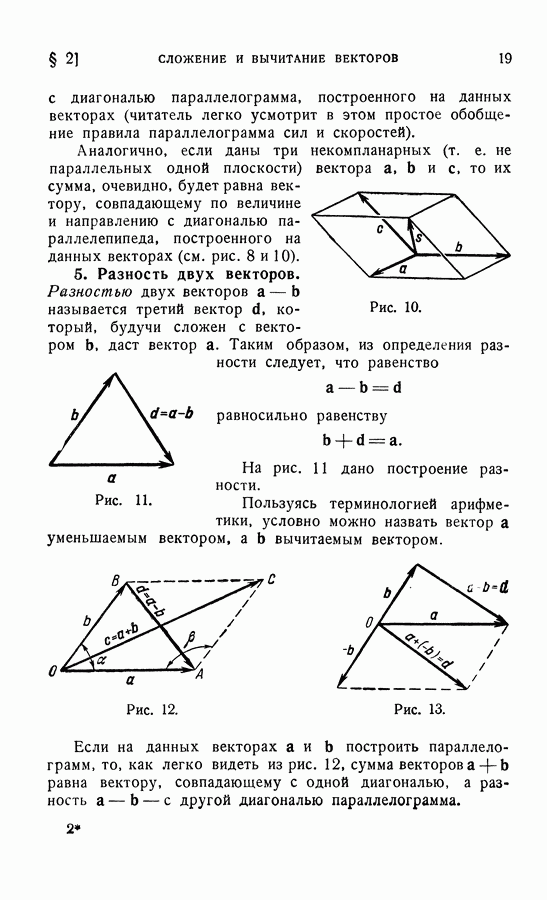
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
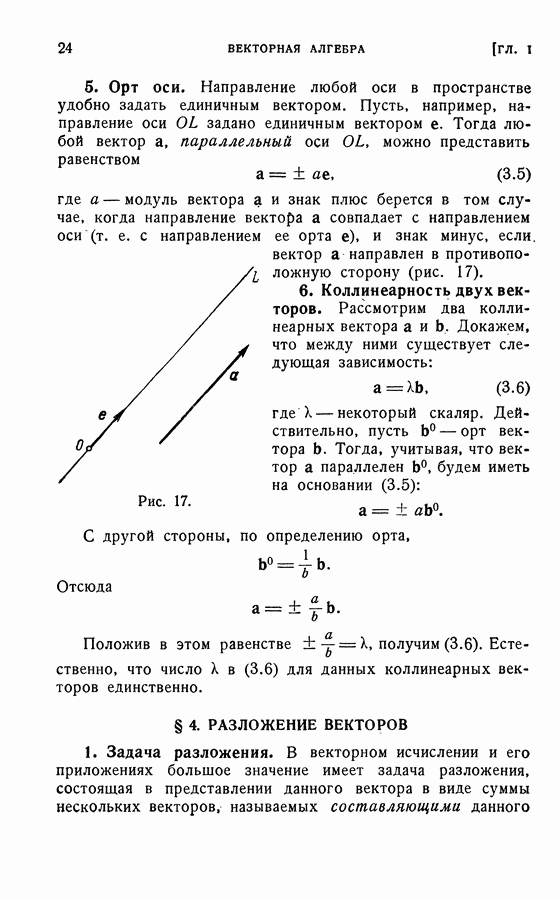
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
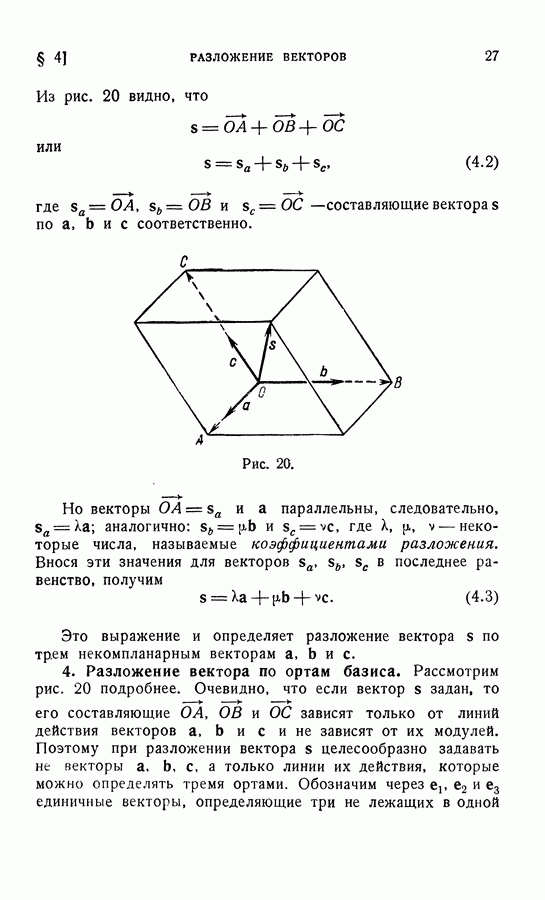
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
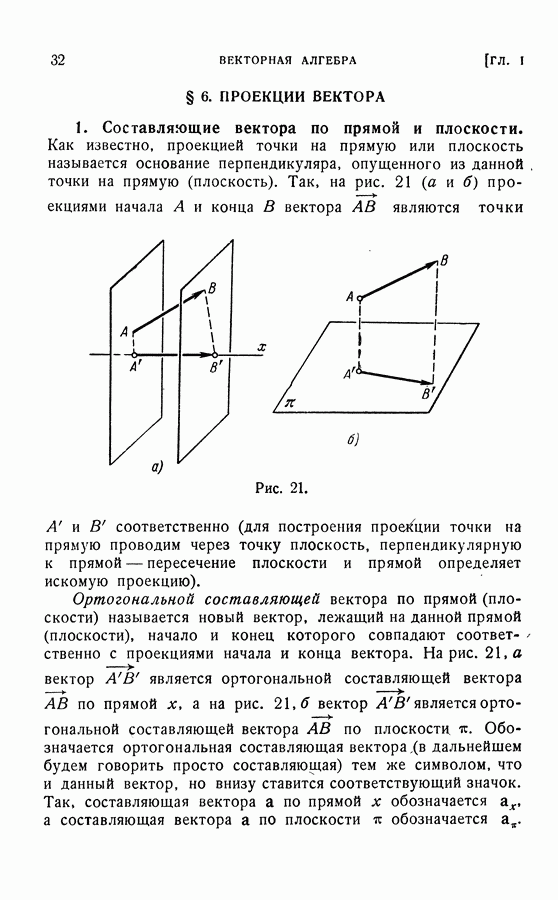
- § 6. ПРОЕКЦИИ ВЕКТОРА
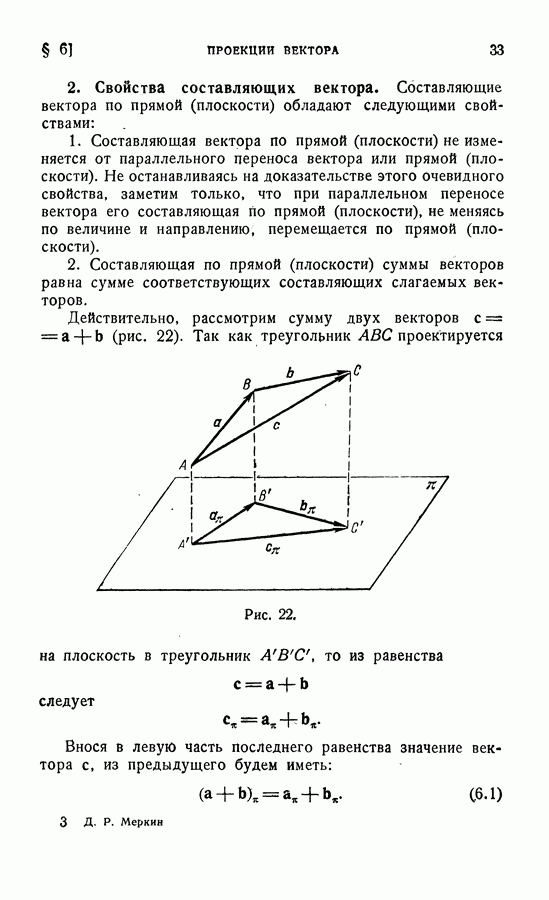
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
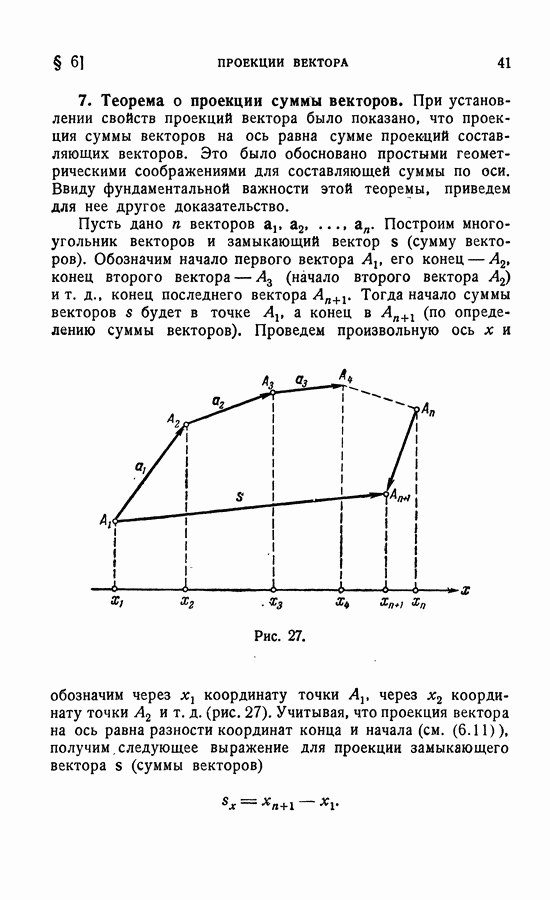
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
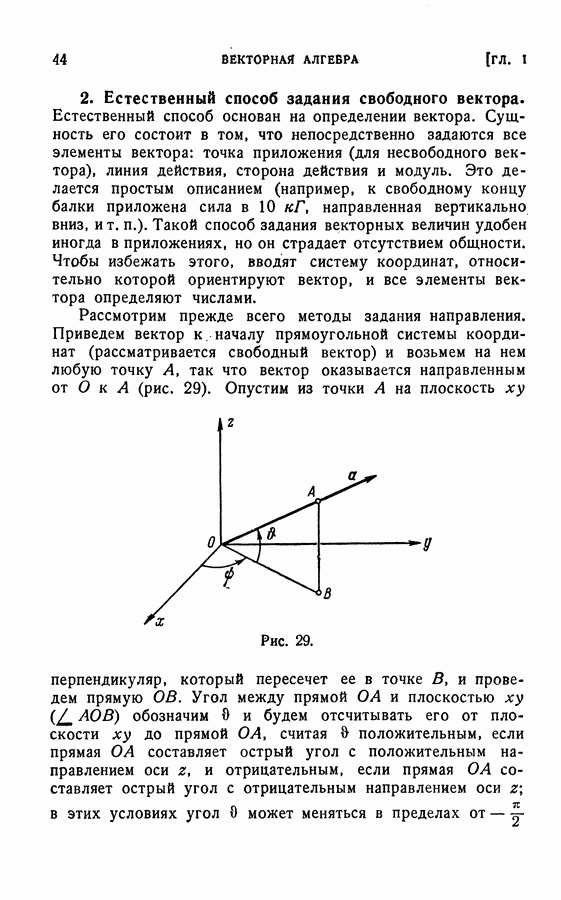
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
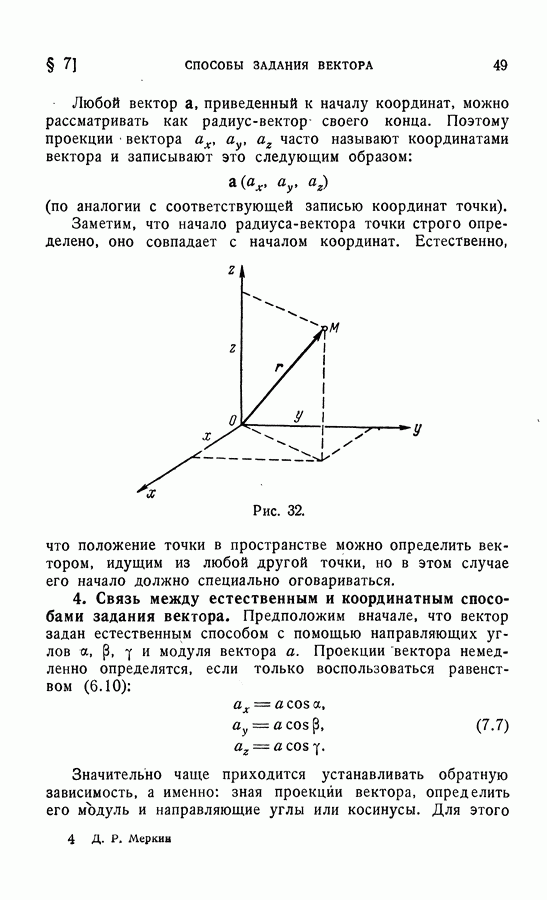
- 4. Связь между естественным и координатным способами задания вектора.
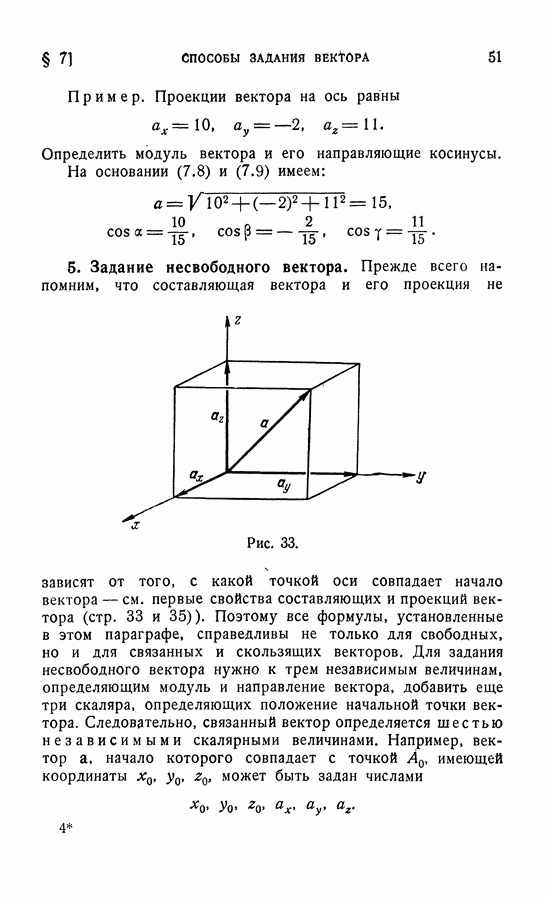
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.