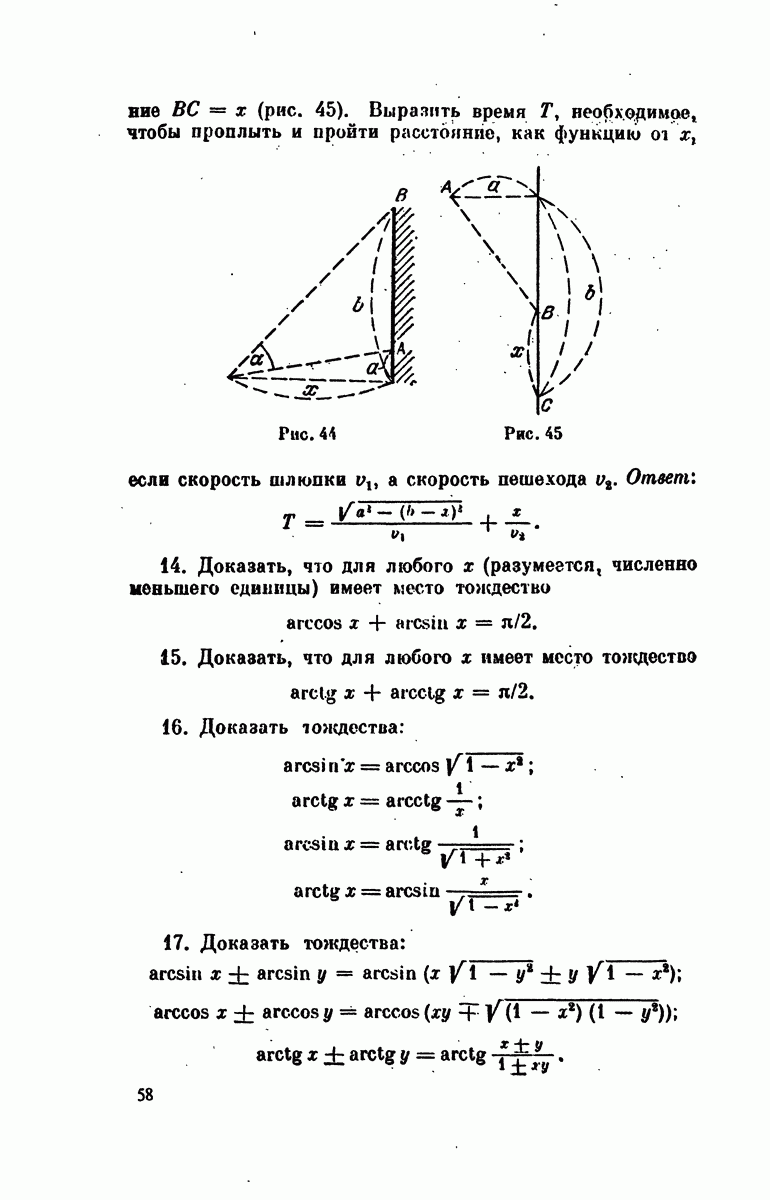
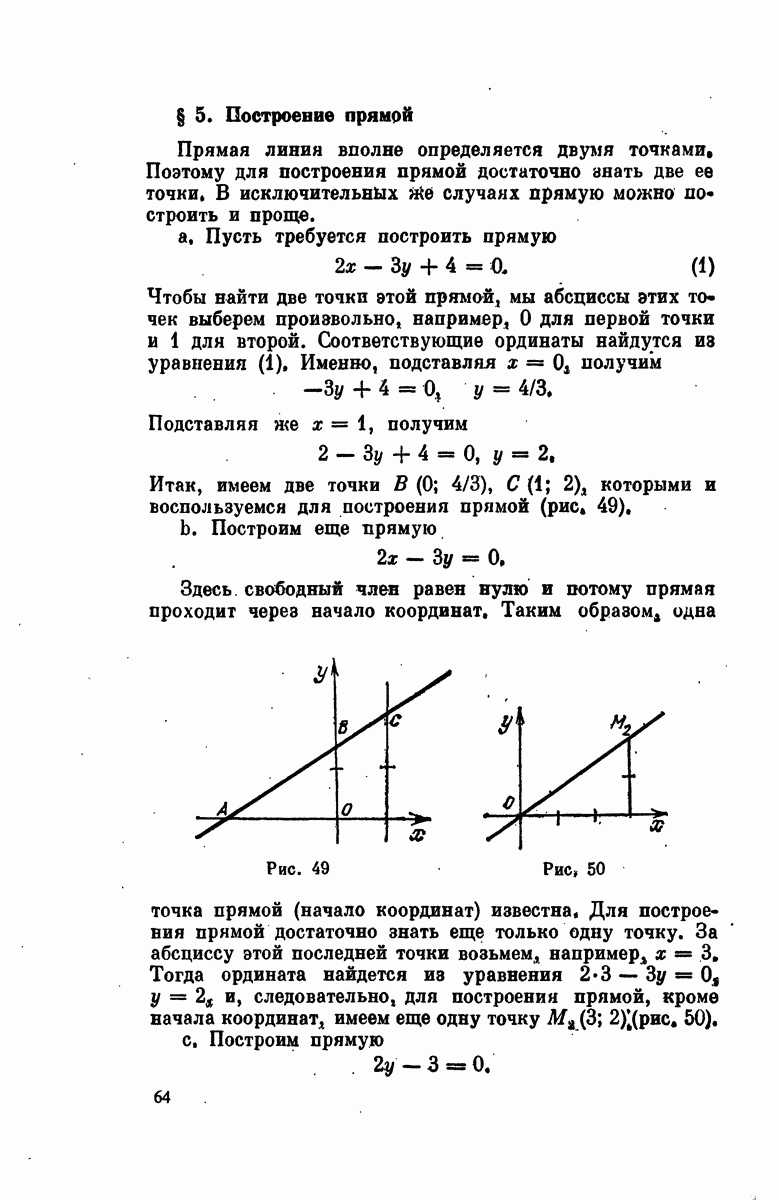
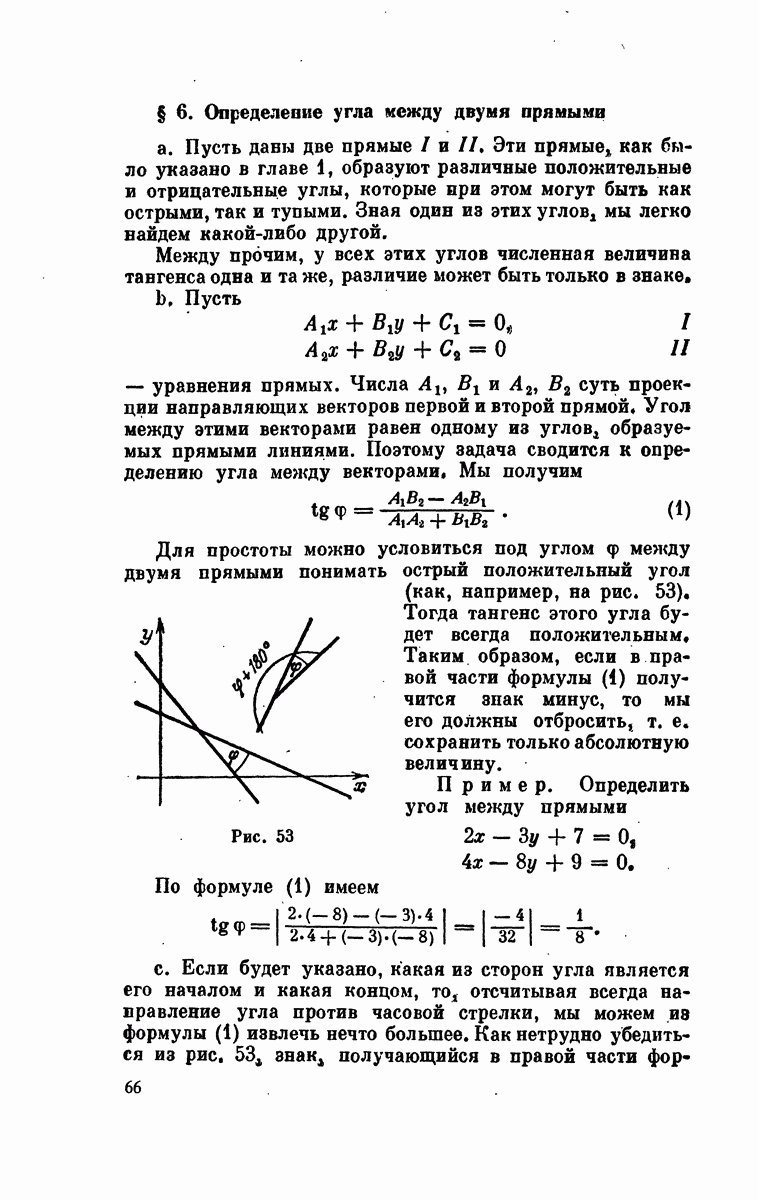
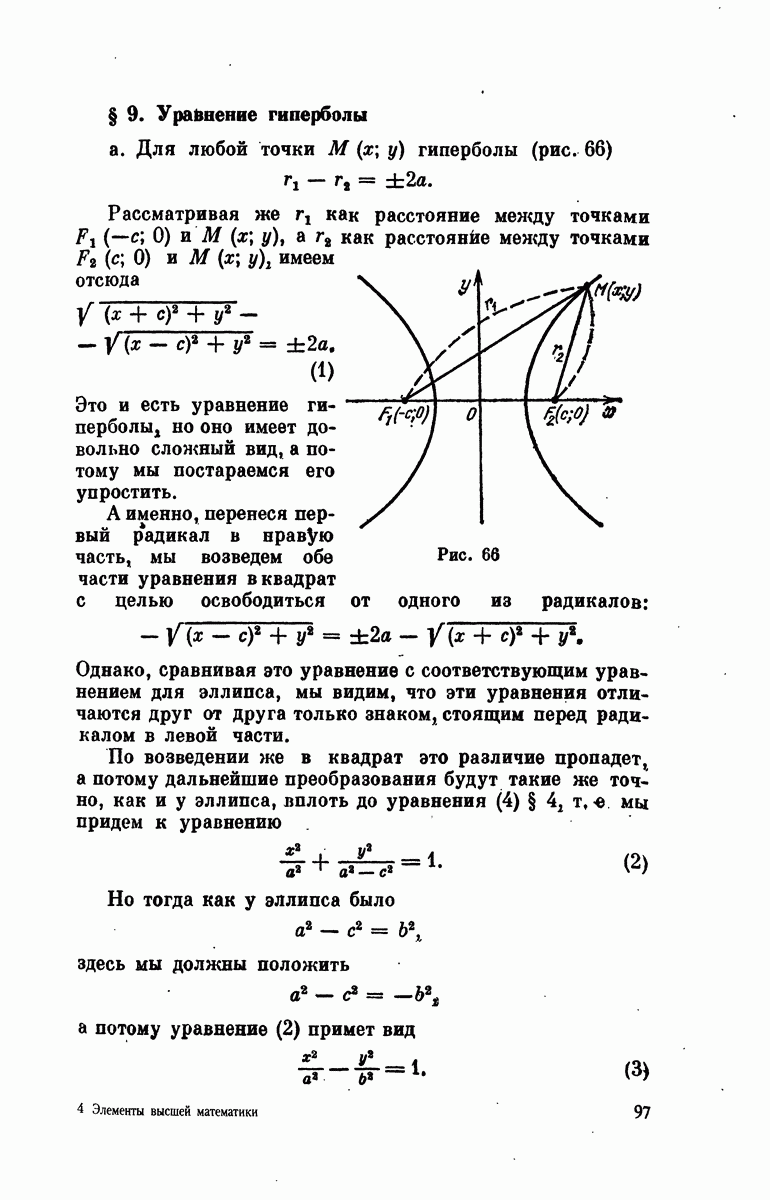
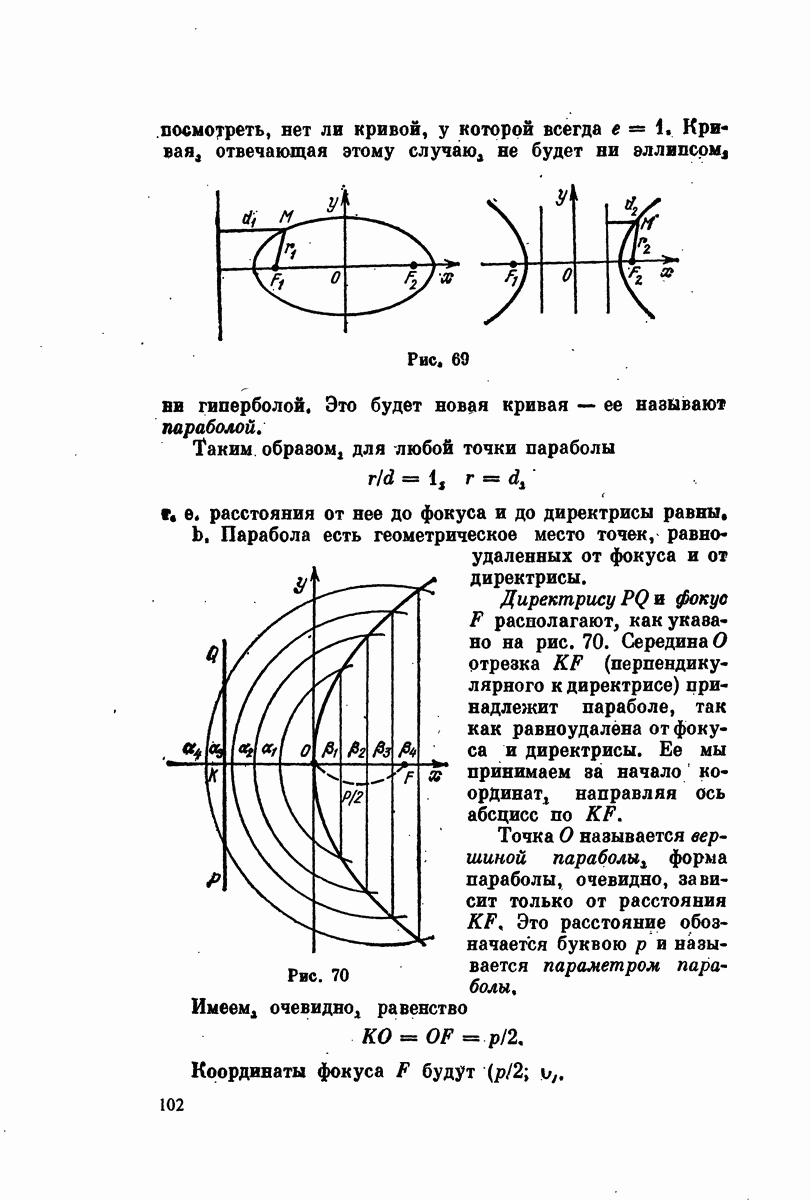
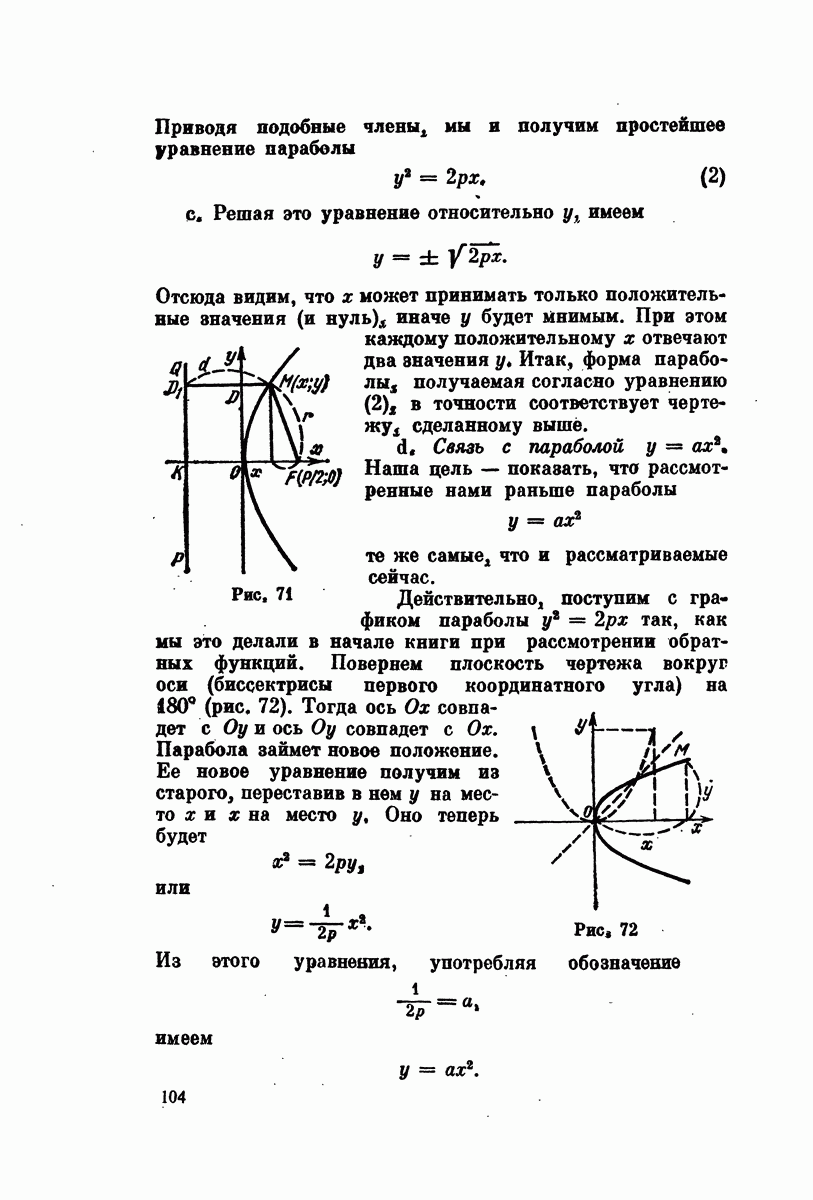
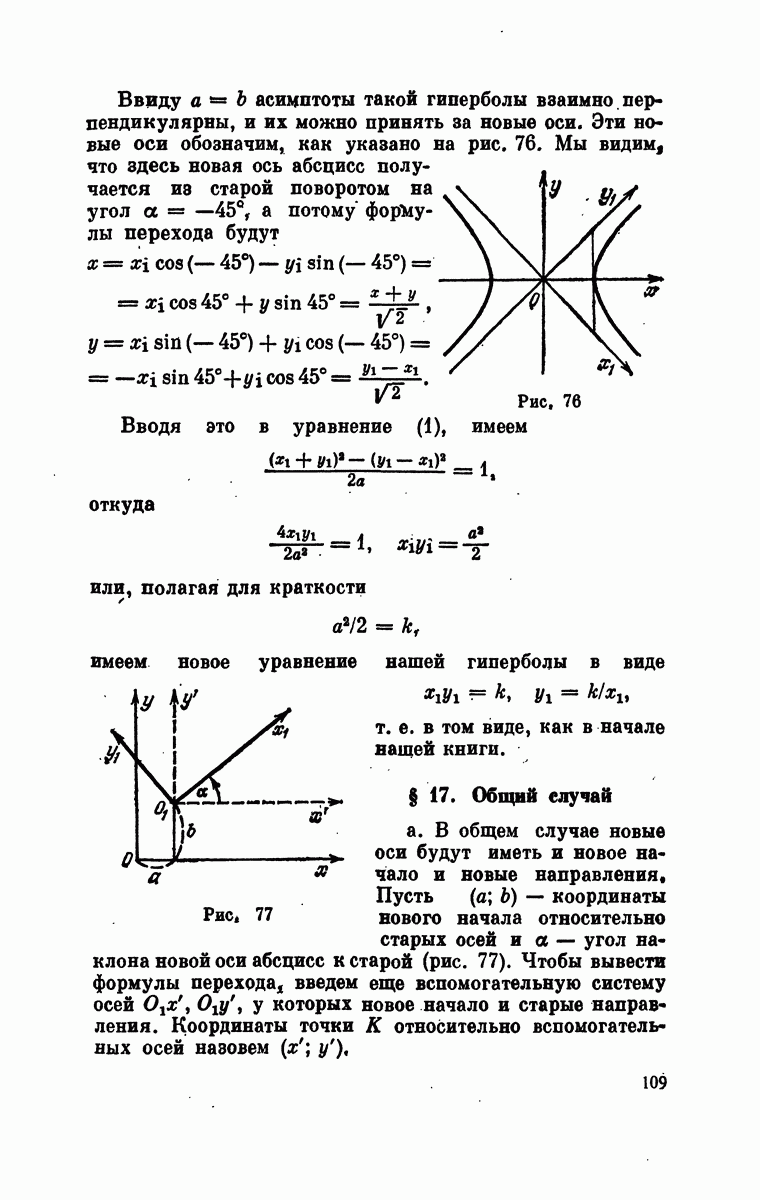
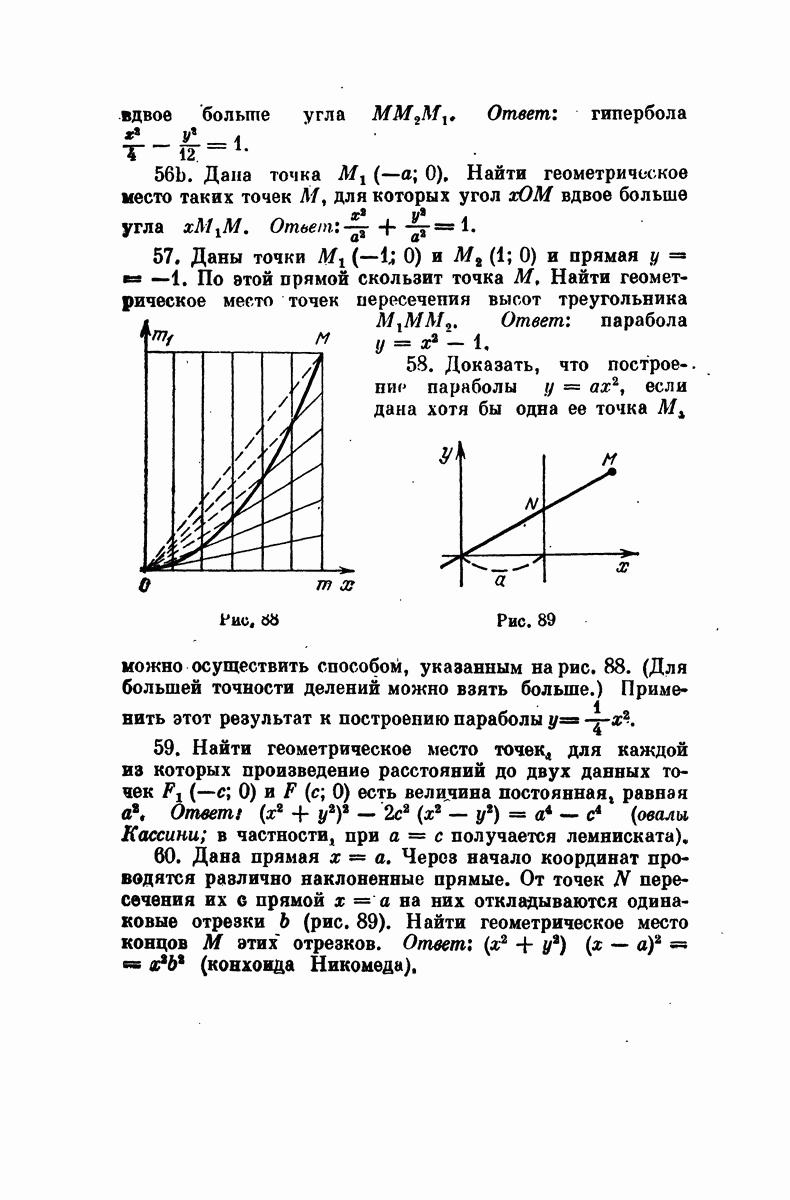
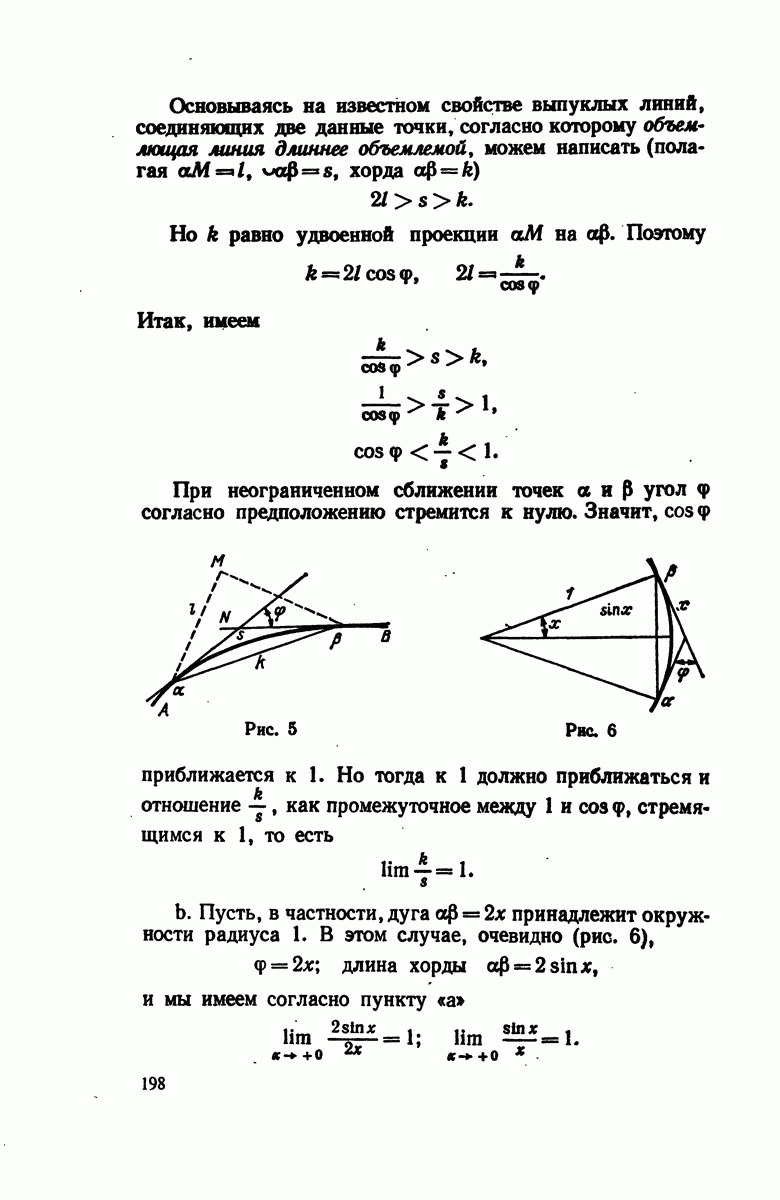
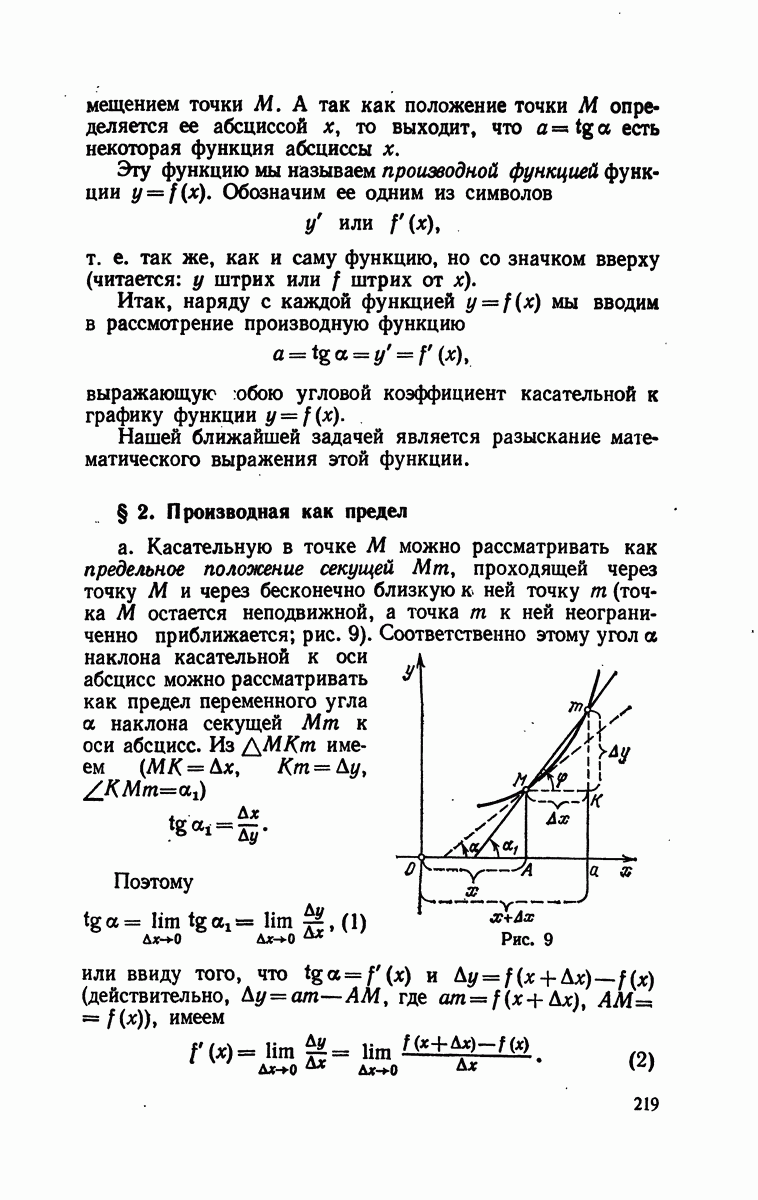
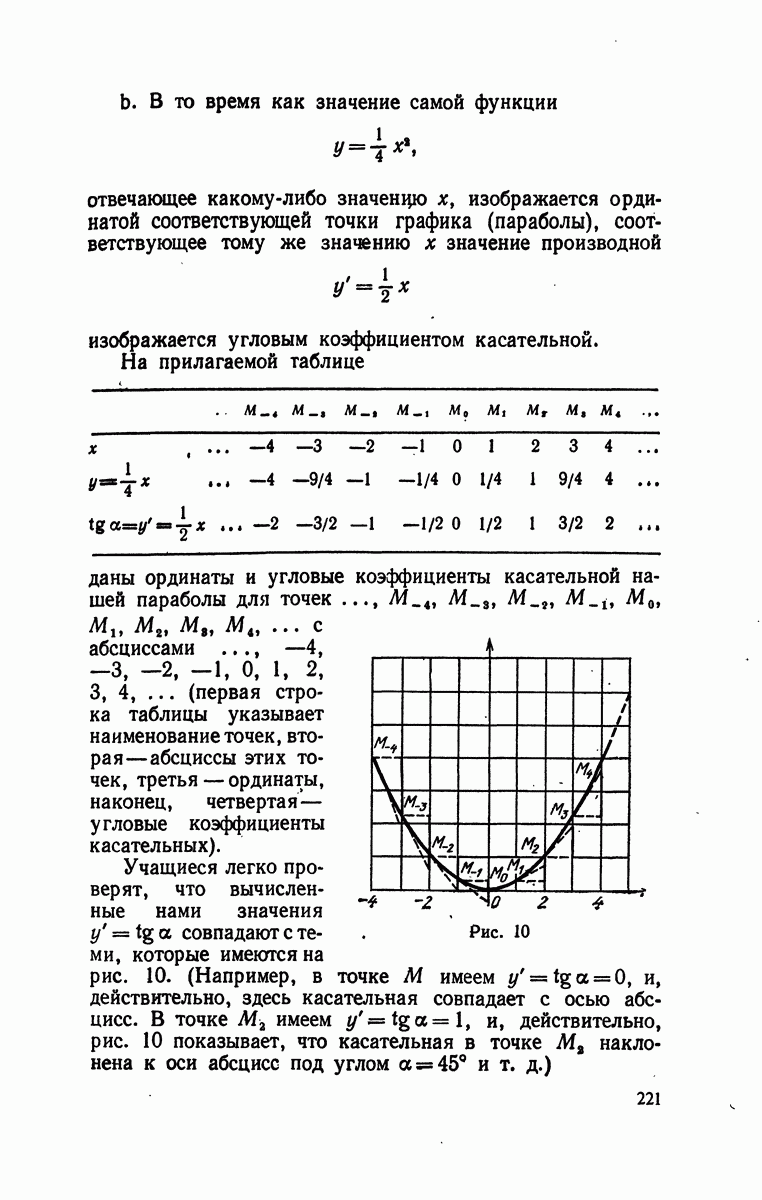
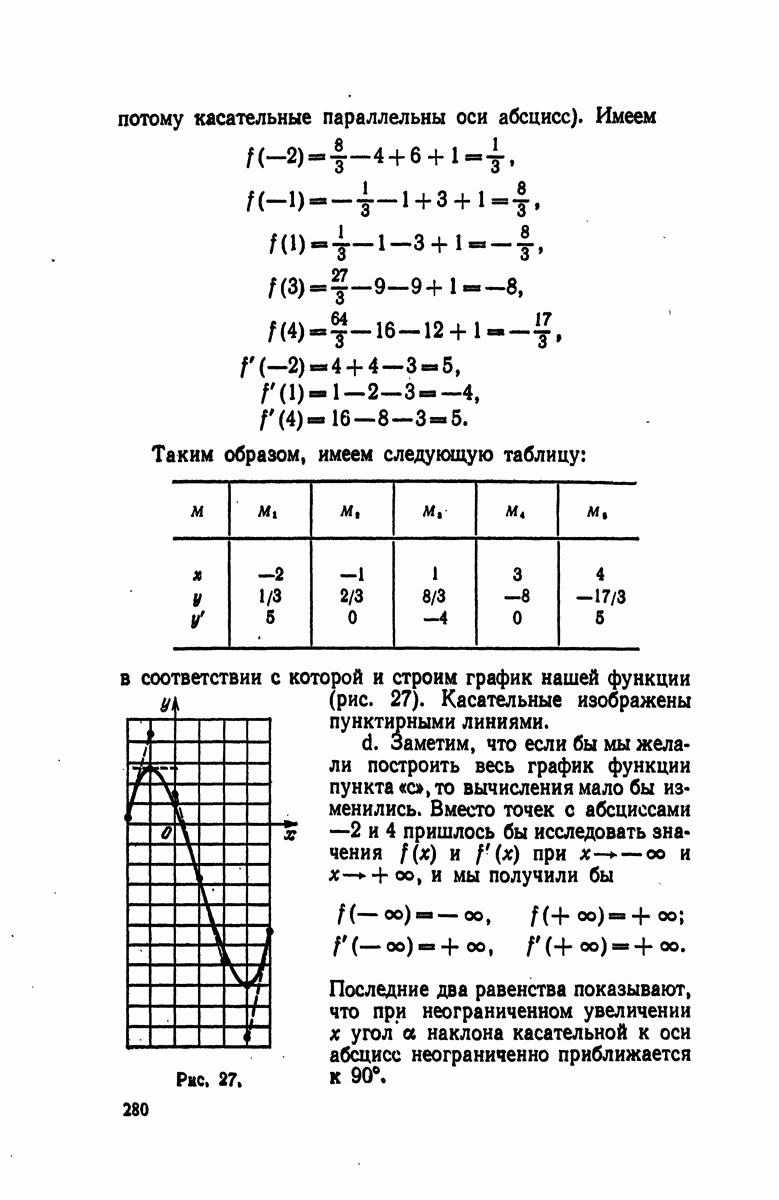
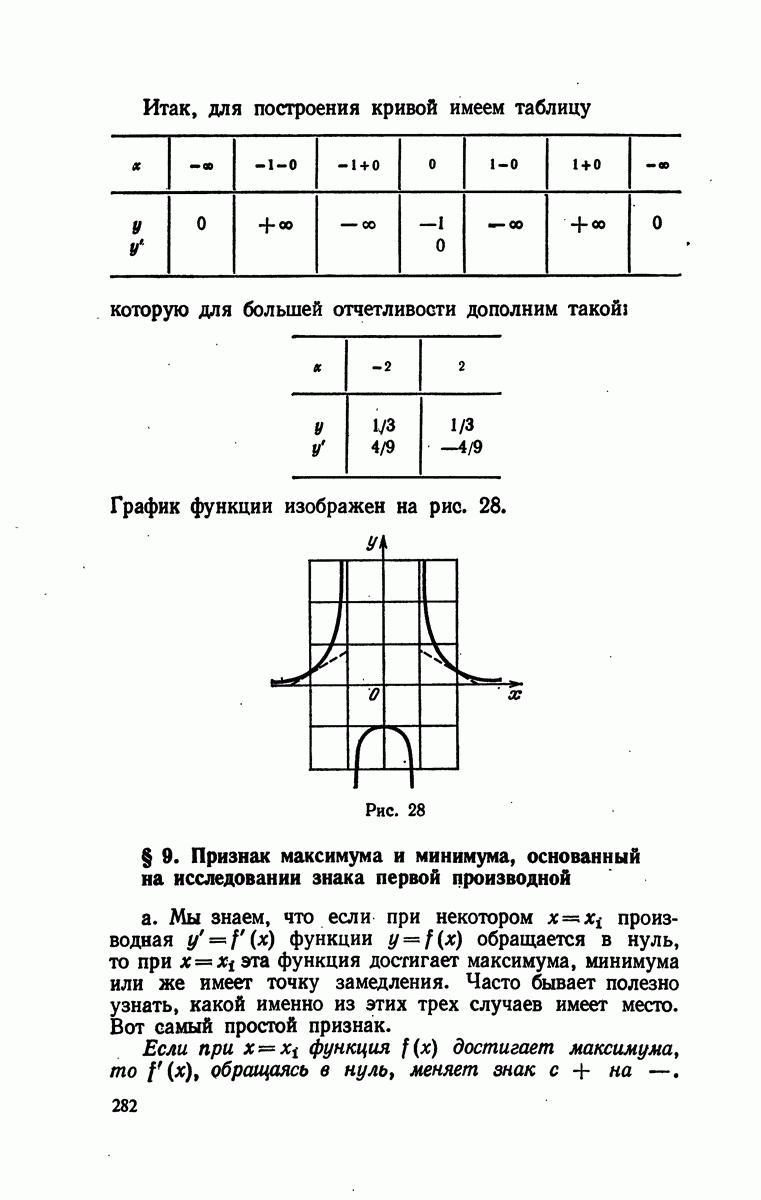
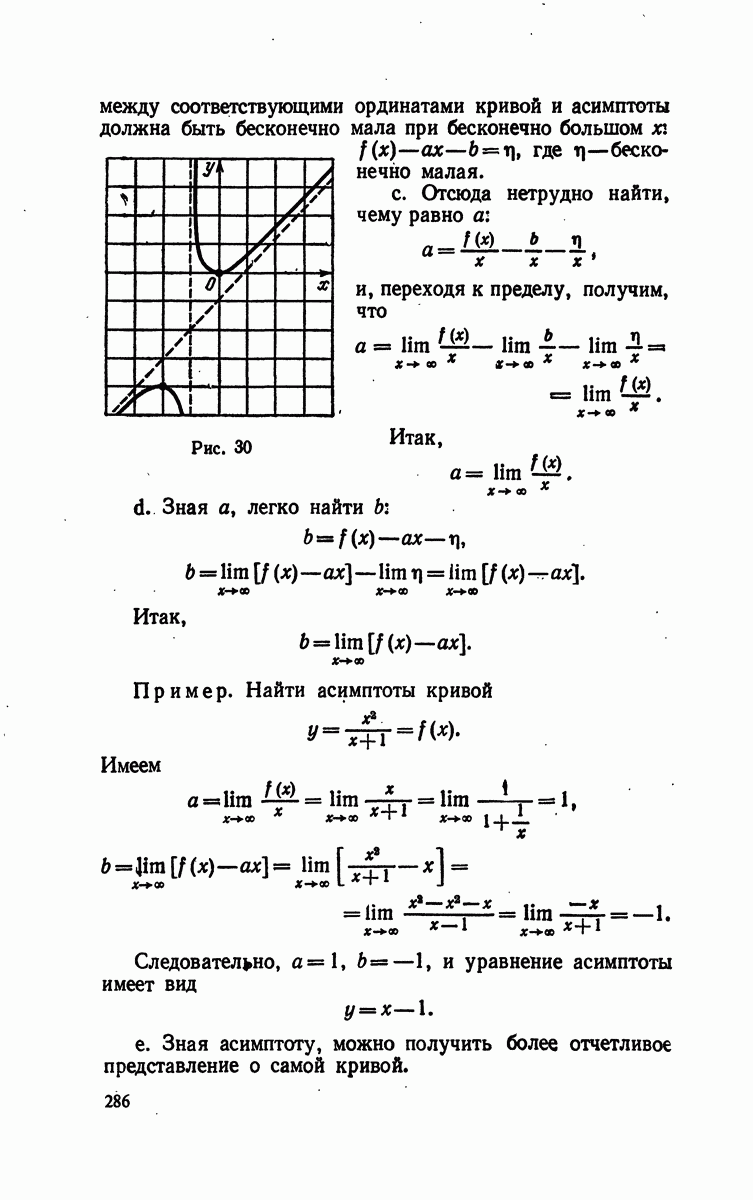
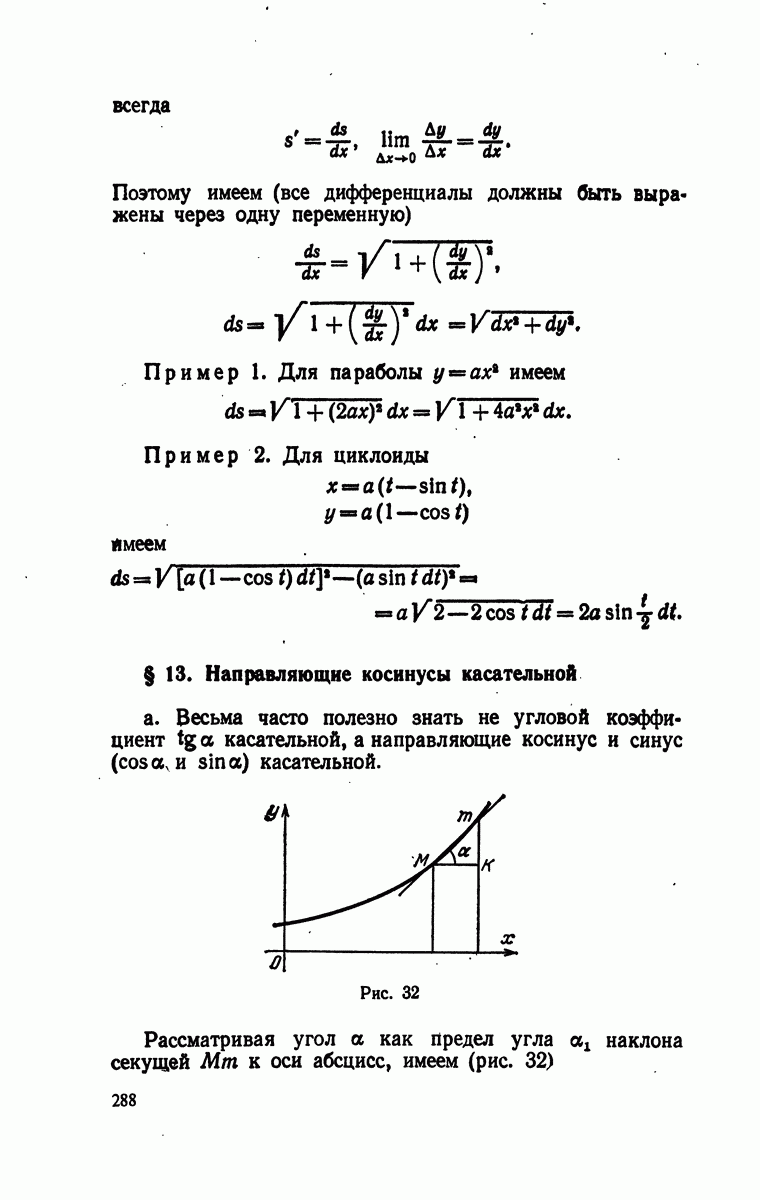
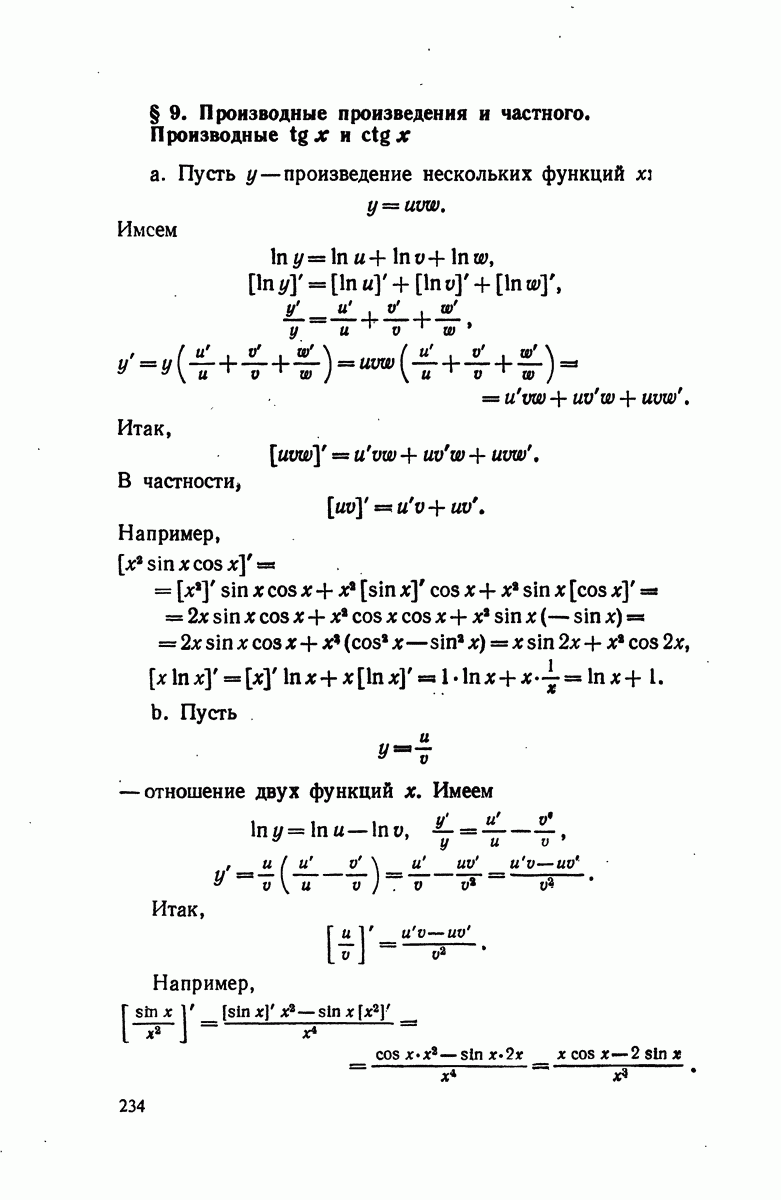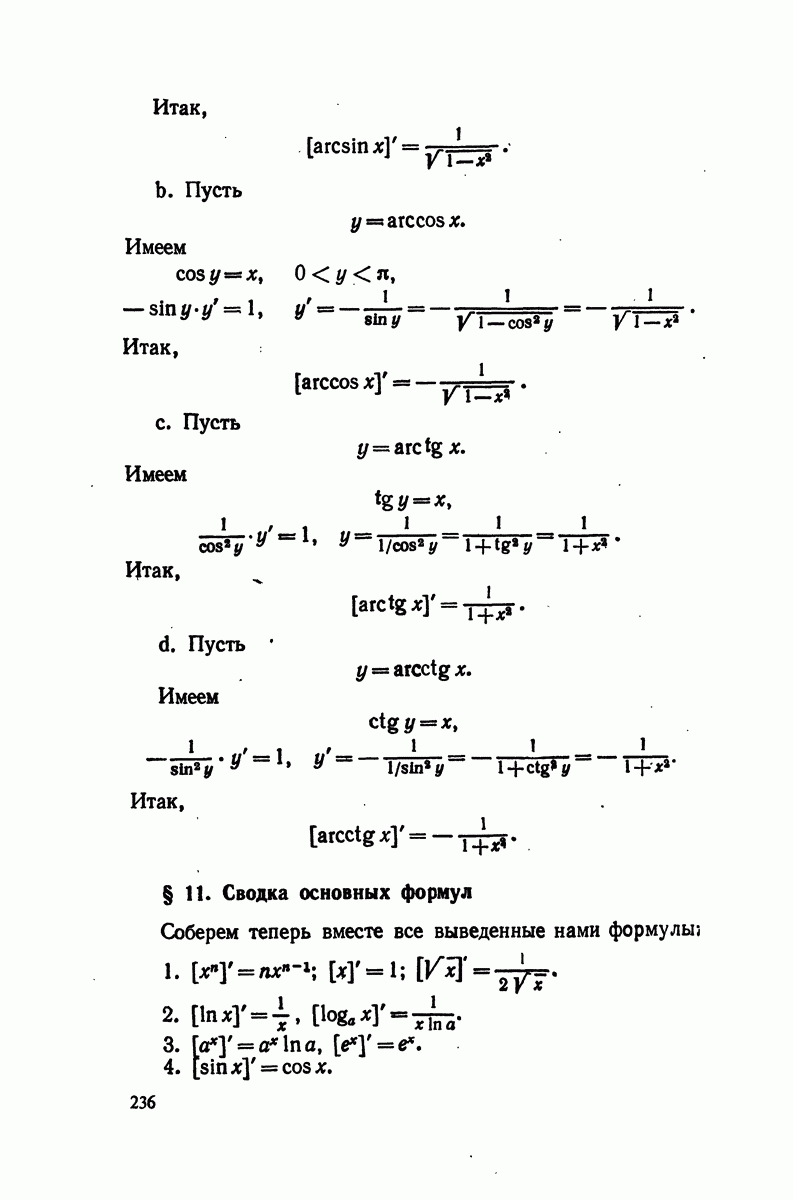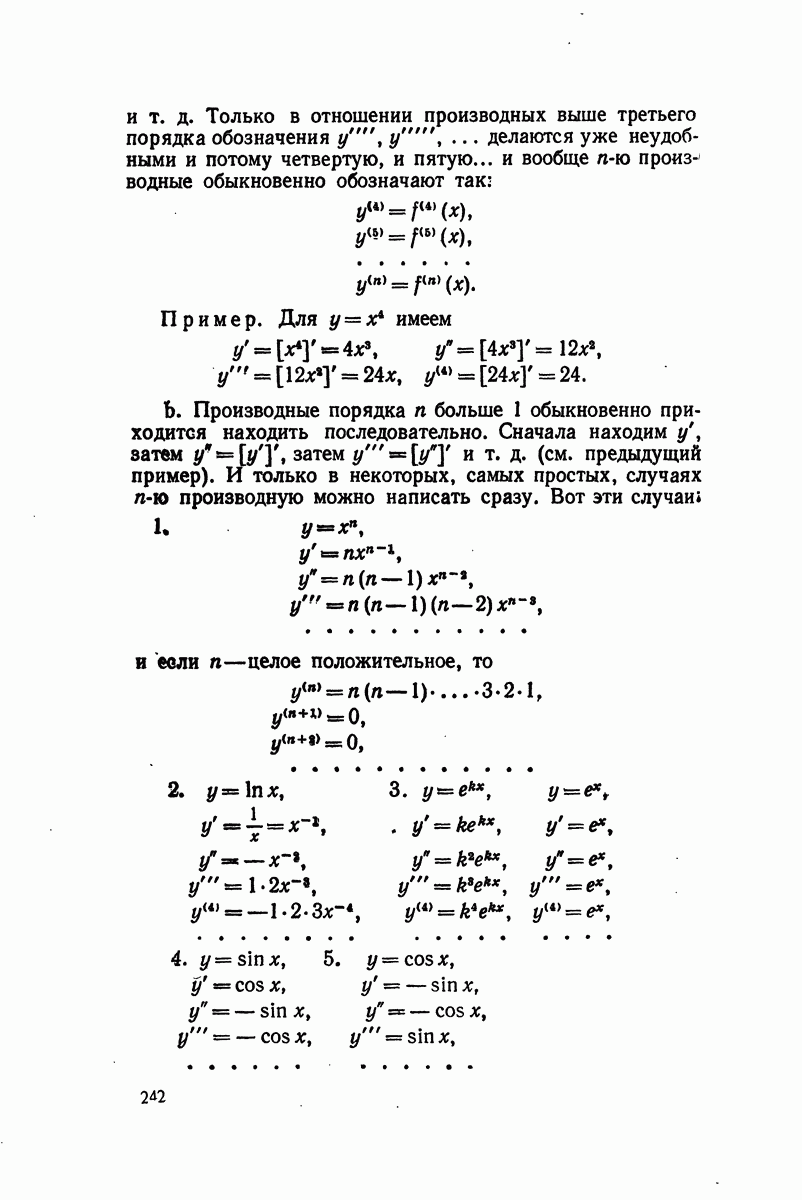| Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ПРЕДИСЛОВИЕ
В России исторически сложилось так, что представление об образовании включает в себя органичное единство школы как системы приобретения знаний, фундаментальной науки как показателя уровня подготовки специалистов и гуманитарной культуры как основы духовного единства народов, населяющих нашу страну.
Формулируя задачи образования, академик А. Н. Крылов говорил: «Школа не может дать вполне законченного знания; главная задача школы — дать общее развитие, дать необходимые навыки, одним словом... главная задача школы — научить учиться, и для того, кто в школе научится учиться, практическая деятельность всю его жизнь будет наилучшей школой».
Отметим, что особенность отечественной школы состоит в сочетании четкости рассуждений с глубиной содержания и простотой, доступностью, конкретностью изложения материала, которые всегда предпочитаются формальным конструкциям. Практическое воплощение данных идей подразумевает наличие высококвалифицированных и творчески мыслящих преподавателей.
Математическое образование и математическая культура составляют стержень научного знания, и значение математики как основы фундаментальных исследований постоянно возрастает.
Для решения этих задач требуются учебники, отражающие в определенной полноте современное состояние исследований и мировоззренческие принципы данной области науки.
Предлагаемые к публикации избранные учебники по математике реализуют указанный выше подход. Они написаны, в основном, профессорами Московского государственного университета им. М. В. Ломоносова.
Книга И. М. Виноградова «Элементы высшей математики (Аналитическая геометрия. Дифференциальное исчисление.
Основы теории чисел)» написана на основе лекций по высшей математике, которые автор читал в Ленинградском политехническом институте, а также его широко известного учебника по теории чисел. Математика воспринимается автором этой книги как мощное орудие для решения проблем естествознания. Поэтому он стремится возможно быстрее дать в руки студентов это орудие, на большом количестве простых, но принципиально важных примеров научить пользоваться ими. При этом он не делает различия, будет ли впоследствии оно применяться в инженерной работе или в абстрактных математических исследованиях. Часть, посвященная теории чисел, является классическим учебником, который стал настольной книгой специалистов в этой области.
Предполагается также издать учебники Г. И. Архипова, В. А. Садовничего, В. Н. Чубарикова «Лекции по математическому анализу», И. И. Привалова «Введение в теорию функций комплексного переменного», В. А. Садовничего «Теория операторов», С. Б. Гашкова, В. Н. Чубарикова «Арифметика. Алгоритмы. Сложность вычислений» и др.
Надеюсь, что данные книги положат начало новой серии базовых учебников по высшей математике для вузов с повышенным уровнем математической подготовки.
Кроме практической ценности эта серия призвана подвести некоторые итоги работы российских ученых и педагогов — математиков по созданию базовых учебников по математике на рубеже второго и третьего тысячелетий. Серия не ограничивается конечным числом изданий. В дальнейшем предполагается продолжить отбор и издание учебников как ныне здравствующих, так и ушедших из жизни авторов, которые отвечают изложенной выше концепции, не потеряли своей новизны и актуальности и пользуются заслуженной популярностью и авторитетом у студентов и педагогов.
Академик Российской Академии наук В. А. Садовничий
| Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- § 1. Ось
- § 2. Вектор
- § 3. Направленные углы
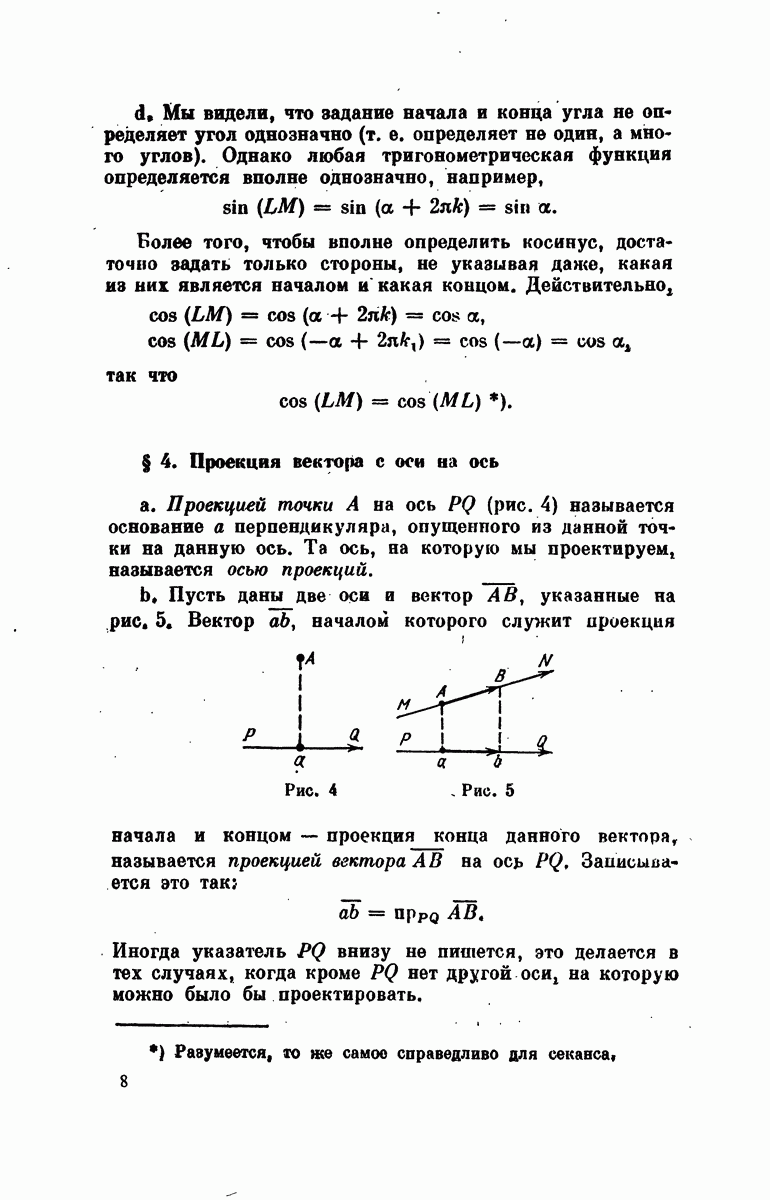
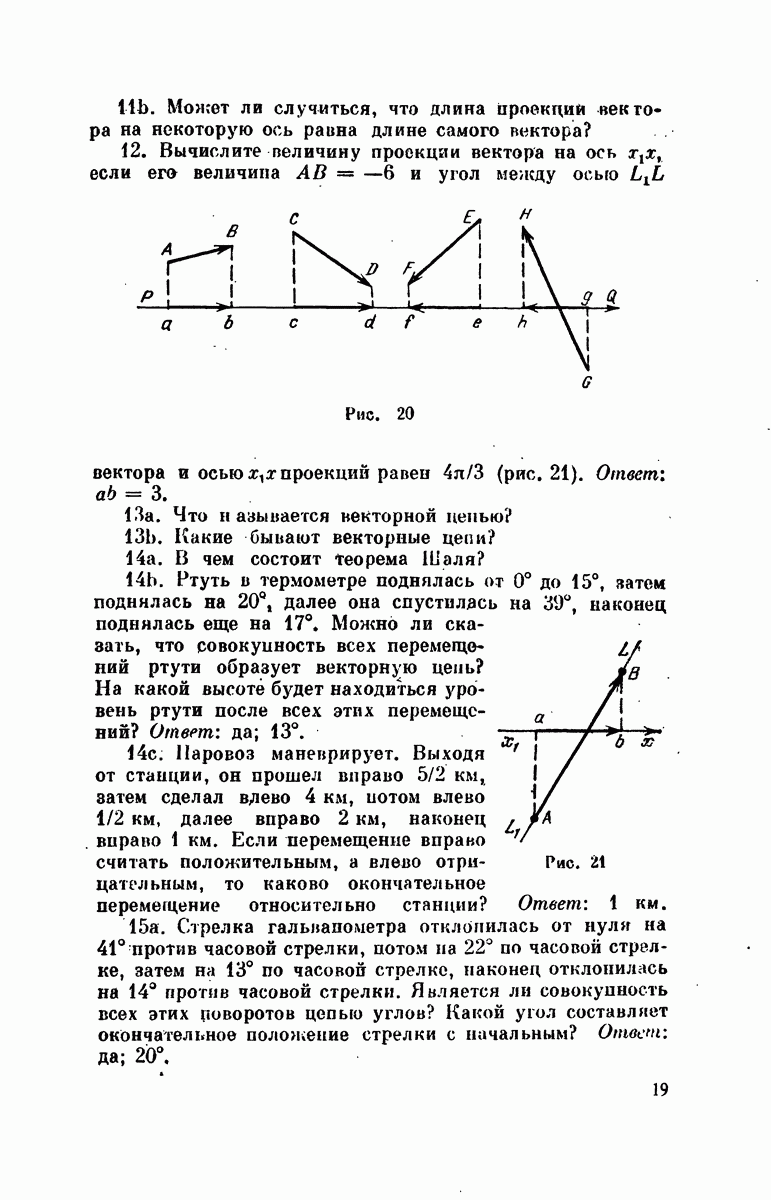
- § 4. Проекция вектора с оси на ось
- § 5. Векторные цепи
- § 6. Цепи углов
- § 7. Проекции вектора на две взаимно перпендикулярные оси
- § 8. Угол между двумя лекторами. Условия параллельности и перпендикулярности
- S 9. Упражнения и контрольные вопросы
- Глава 2. КООРДИНАТЫ
- § 1. Метод координат
- § 2. Основные задачи, решаемые методом координат
- § 3. Упражнения
- Глава 3. ФУНКЦИИ
- § 1. Переменные в постоянные
- § 2. Понятие о функциональной зависимости
- § 3. Классификация математических функций
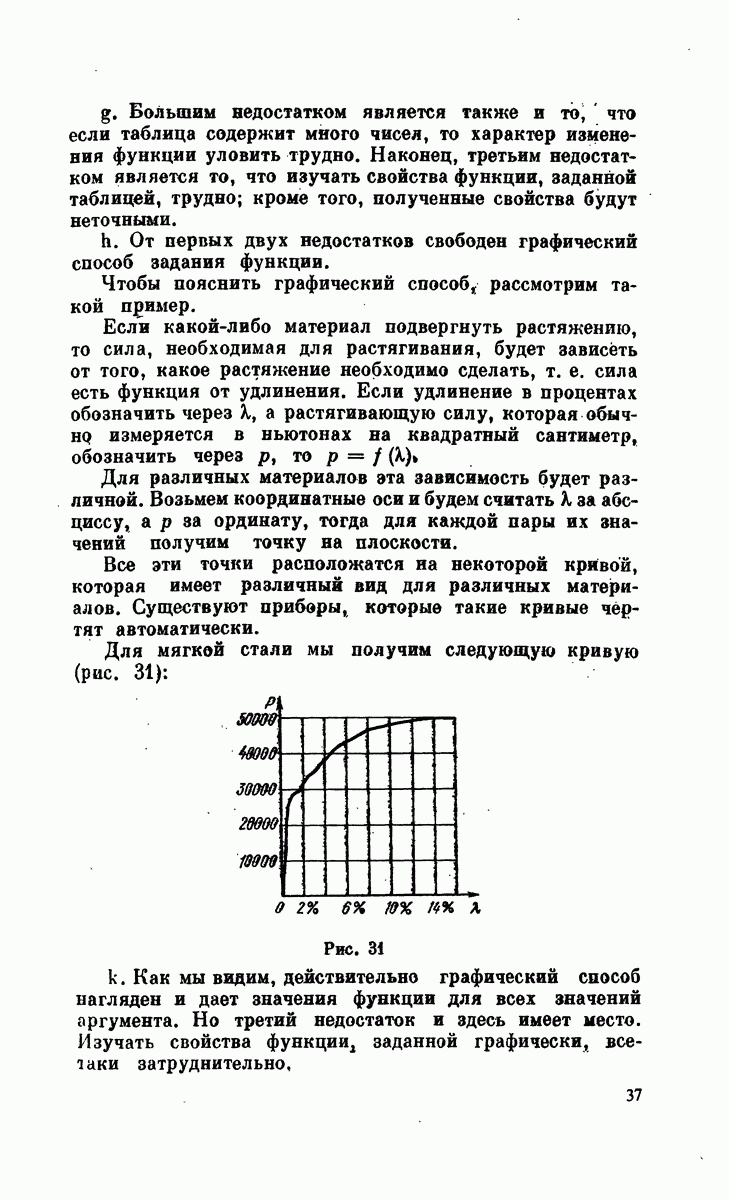
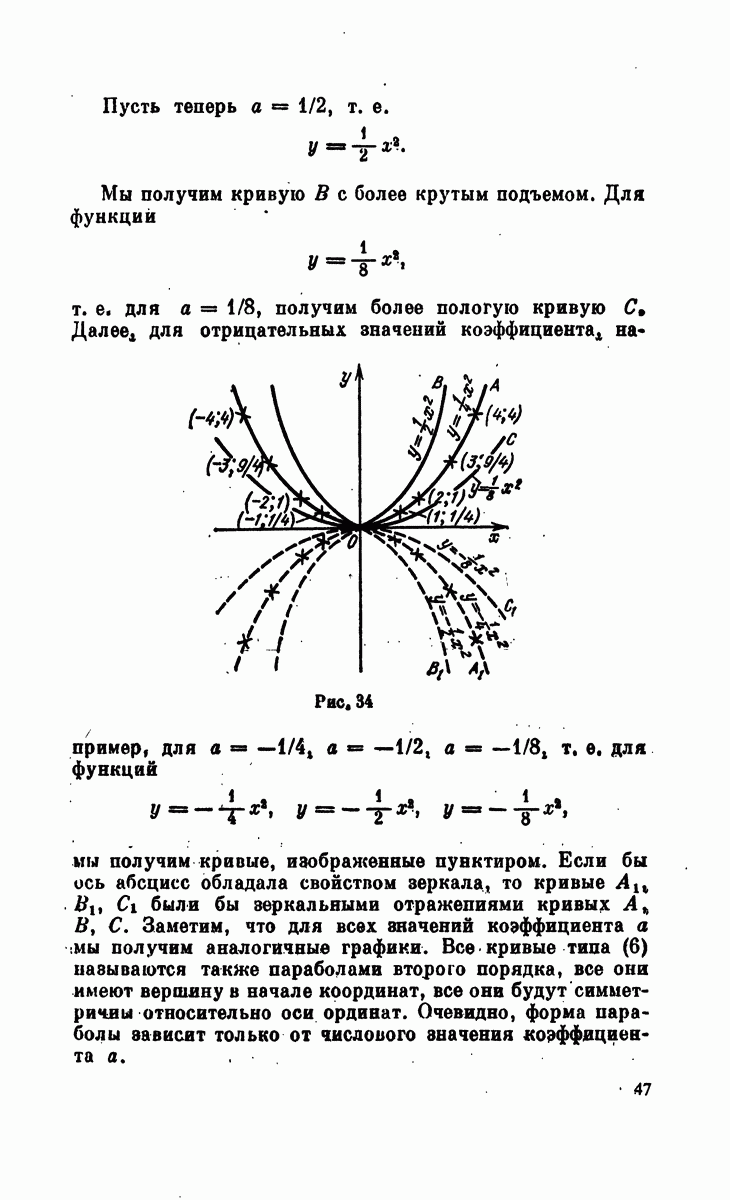
- § 4. Обзор и графическое изображение простейших функции одного аргумента
- § 5. Обратные функции
- § 6. Понятие об уравнении линии
- § 7. Упражнения
- Глава 4. ПРЯМАЯ
- § 1. Уравнение прямой, проходящей через данную точку
- § 2. Общее уравнение прямой
- § 3. Частные случаи
- § 4. Переход к уравнению с угловым коэффициентом
- § 5. Построение прямой
- § 6. Определение угла между двумя прямыми
- § 7. Условие совпадения прямых
- § 8 Пересечение прямых
- § 9. Расстояние от точки до прямой
- § 10. Другой подход к выводу уравнения прямой
- § 11. Прямая, проходящая через две точки
- § 12. Уравнение прямой в отрезках на осях
- § 13. Задачи на прямую линию
- Глава 5. ПРОСТЕЙШИЕ КРИВЫЕ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- § 1. Окружность
- § 2. Эллипс. Построение посредством нитн. Зависимость между полуосями и полуфокусным расстоянием
- § 3. Построение эллипса по точкам
- § 4. Уравнение эллипса
- § 5. Связь эллипса с окружностью
- § 6. Директрисы эллипса
- § 7. Гипербола. Построение посредством нити
- § 8. Построение гиперболы по точкам
- § 9. Уравнение гиперболы
- § 10. Асимптоты. Геометрическое значение b
- § 11. Директрисы гиперболы
- § 12. Парабола. Построение по точкам
- § 13. Уравнение параболы
- § 14. Преобразование координат
- § 15. Пример на упрощение уравнения кривой путем параллельного переноса осей
- § 16. Поворот осей
- § 17. Общий случай
- § 18. Полярные координаты
- § 19. Спираль Архимеда
- § 20. Логарифмическая спираль
- § 21. Примеры на составление полярных уравнений кривых
- § 22. Выражение прямоугольных координат через полярные
- § 23. Уравнение лемнискаты
- § 24. Параметрическое задание линий
- § 25. Построение графика
- § 26. Циклоида
- § 27. Упражнения
- Глава 6. ВЕКТОРЫ, ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
- § 1. Оси, векторы, углы
- § 2. Проекции
- § 3. Проекции на три взаимно перпендикулярные оси. Длина вектора через проекции
- § 4. Простейшие зависимости, содержащие величину вектора, проекции и направляющие косинусы
- § 5. Проекция вектора на оси. Косинус угла между двумя векторами. Скалярное произведение векторов
- § 6. Координаты
- § 7. Выражение проекций вектора через координаты конца и начала
- § 8. Выражение длины вектора через координаты концов. Расстояние между двумя точками
- § 9. Деление отрезка в данном отношении
- § 10. График уравнения с двумя переменными
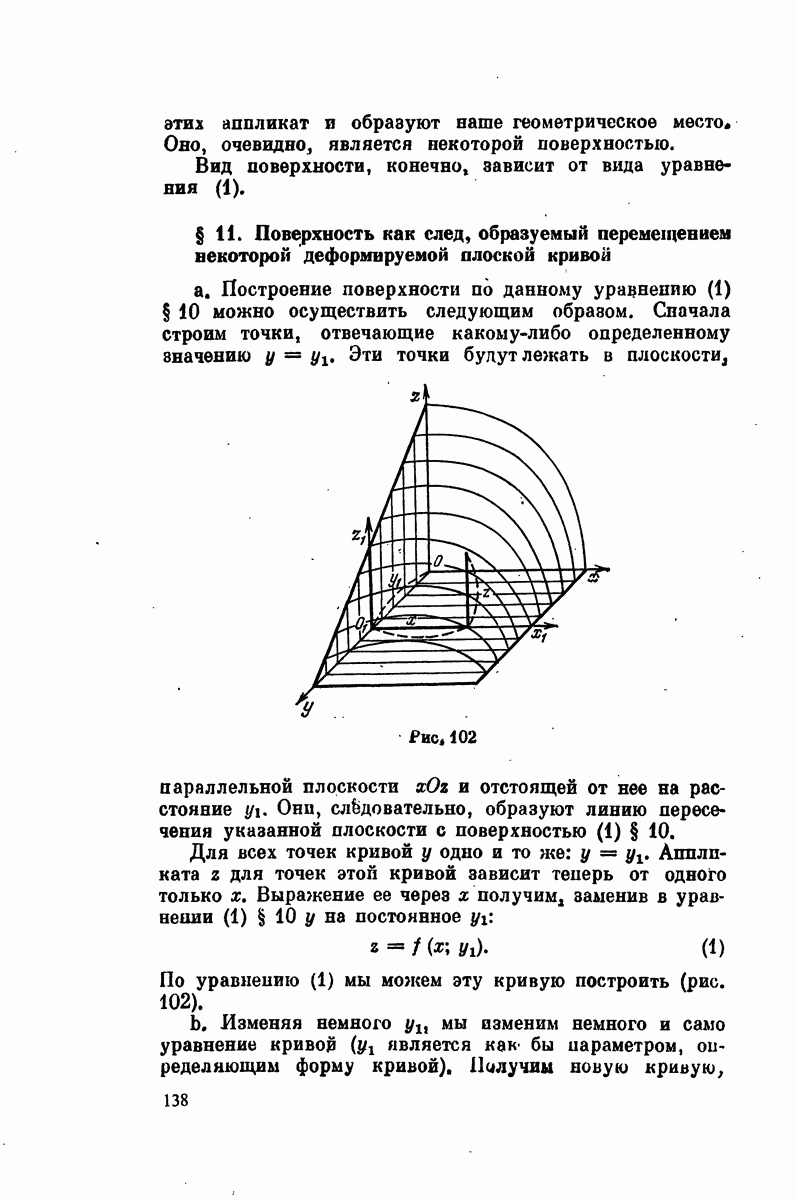
- § 11. Поверхность как след, образуемый перемещением некоторой деформируемой плоской кривой
- § 12. Цилиндрические поверхности
- § 13. Обратная задача. Уравнение шаровой поверхности
- § 14. Уравнение плоскости, проходящей через данную точку
- § 15. Общее уравнение плоскости
- § 16. Частные случаи
- § 17. Выяснение расположения плоскости относительно осей
- § 18. Угол между плоскостями. Условие параллельности. Условие перпендикулярности
- § 19. Условие совпадения плоскостей
- § 20. Расстояние от точке до плоскости
- § 21. Прямая как пересечение двух плоскостей
- § 22. Прямая, проходящая через данную точку
- § 23. Прямая, проходящая через две точки
- § 24. Переход от системы уравнений прямой в общем виде к системе в виде пропорций
- § 25. Угол между прямыми. Условие параллельности. Условие перпендикулярности
- § 26. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности
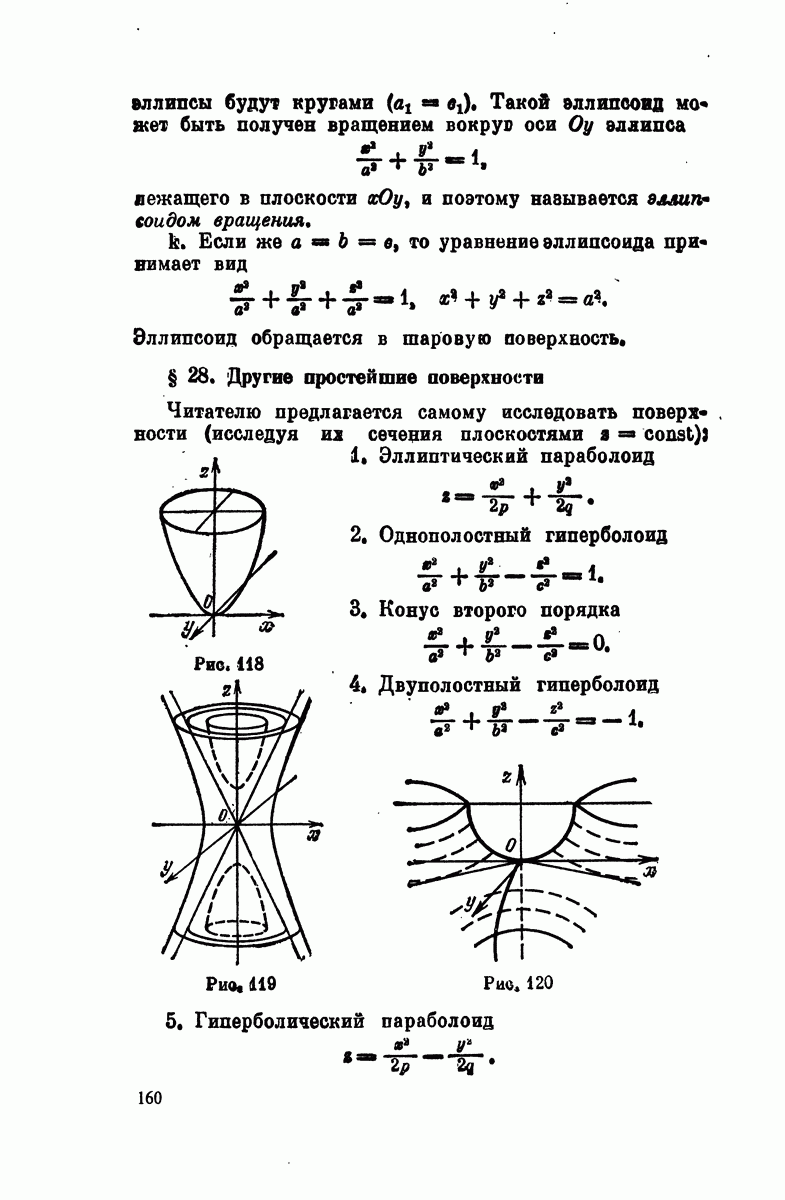
- § 27. Простейшие поверхности. Эллипсоид
- § 28. Другие простейшие поверхности
- § 29. Кривая в пространстве как пересечение двух поверхностей
- § 30. Параметрические уравнения
- § 31. Винтовая линия
- § 32. Параметрические уравнения в механике
- § 33. Переход от параметрического представления к общему и обратно
- § 34. Преобразование координат
- § 35. Упражнения
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. Бесконечно малые
- § 2. Понятие предела переменной величины
- § 3. Понятие бесконечно большой
- § 4. Свойства бесконечно малых
- § 5. Основные свойства пределов
- § 6. Предел непрерывной функции
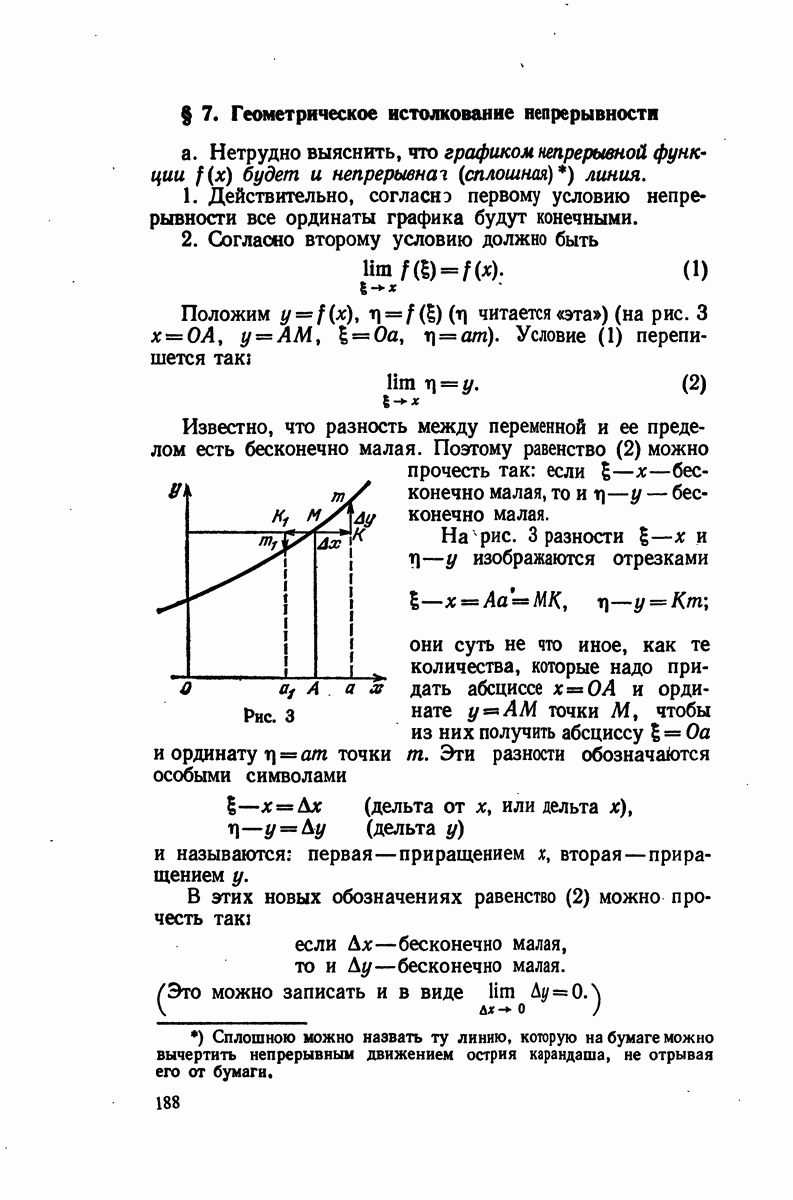
- § 7. Геометрическое истолкование непрерывности
- § 8. Свойство непрерывной функции
- § 9. Предел функции, зависящей от нескольких переменных
- § 10. Особые случаи разыскания предела
- § 11. Замечательный тригонометрический предел
- § 12. Признак существования предела
- § 13. Сходимость бесконечных рядов
- § 14. Простейшие признаки сходимости
- § 15. Основание натуральных логарифмов
- § 16. Порядок бесконечно малых
- § 17. Упражнения
- Глава 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная как угловой коэффициент касательной
- § 2. Производная как предел
- § 3. Пояснение общей теории на примере. Уравнения касательной и нормали
- § 4. Механическое значение производной
- § 5. Производные трех простейших функций
- § 6. Производная постоянного и суммы. Вынесение постоянного множителя за знак производной
- § 7. Производная сложной функции
- § 8. Разыскание производных путем логарифмирования. Производные функции х^n при любом n к функции а^x.
- § 9. Производные произведения и частного. Производные tg x и ctg x.
- § 10. Производные обратных тригонометрических функций
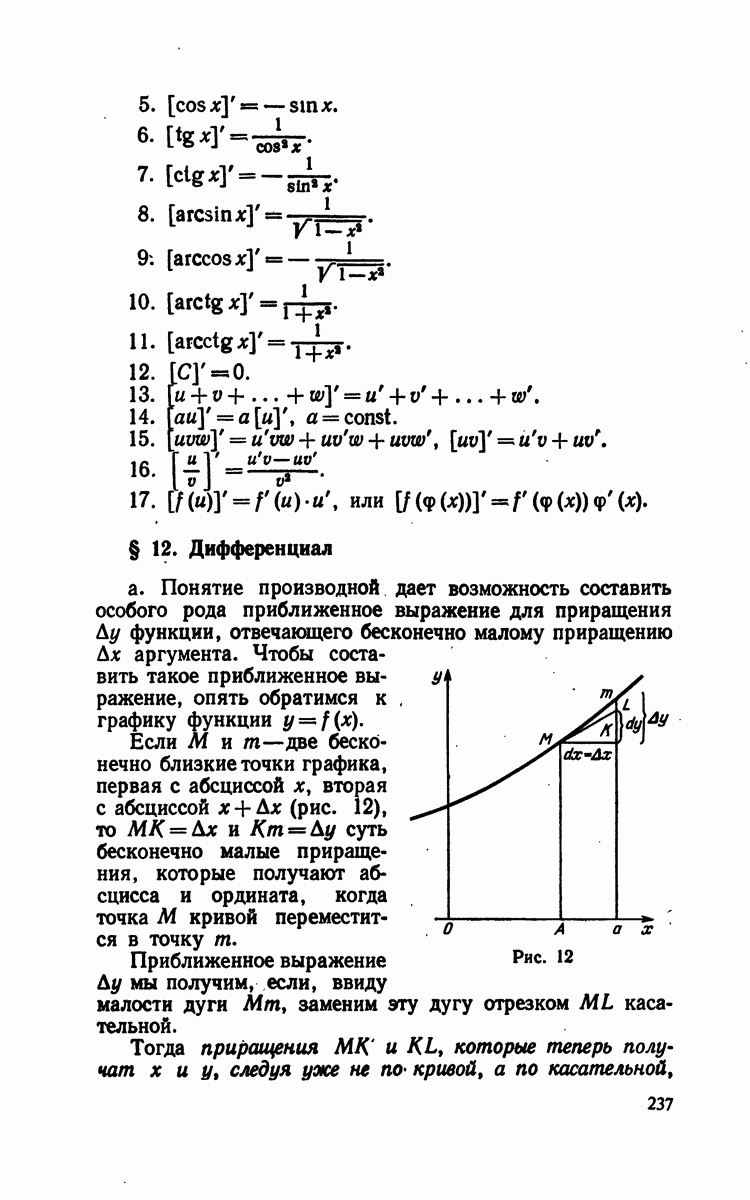
- § 11. Сводка основных формул
- § 12. Дифференциал
- § 13. Основные формулы для дифференциалов
- § 14. Высшие производные
- § 15. Высшие дифференциалы
- § 16. Дифференцирование неявных функций
- § 17. Дифференцирование функций, заданных параметрическим способом
- § 18. Преобразование дифференциалов к новой переменной
- § 19. Упражнения
- Глава 3. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- § 1. Непрерывность первой производной
- § 2. Возрастание и убывание функций. Максимум и минимум
- § 3. Приложение к построению графиков
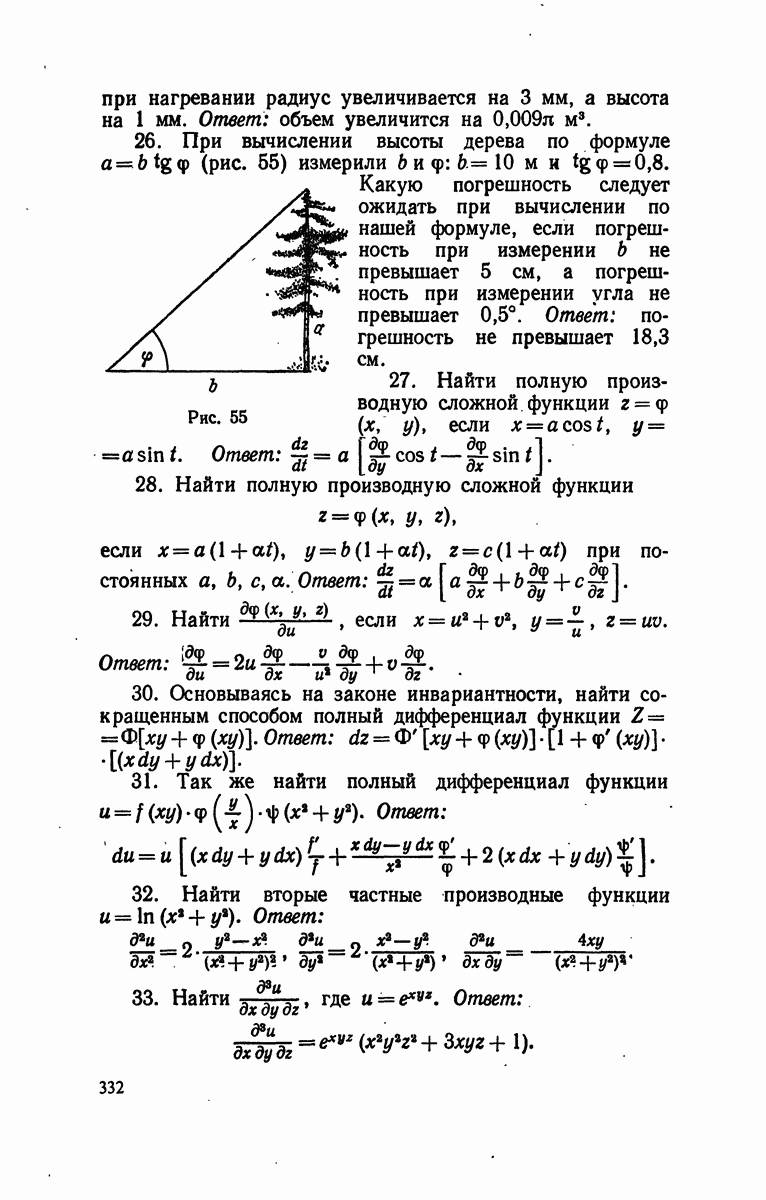
- § 4. Наибольшее и наименьшее значения функции
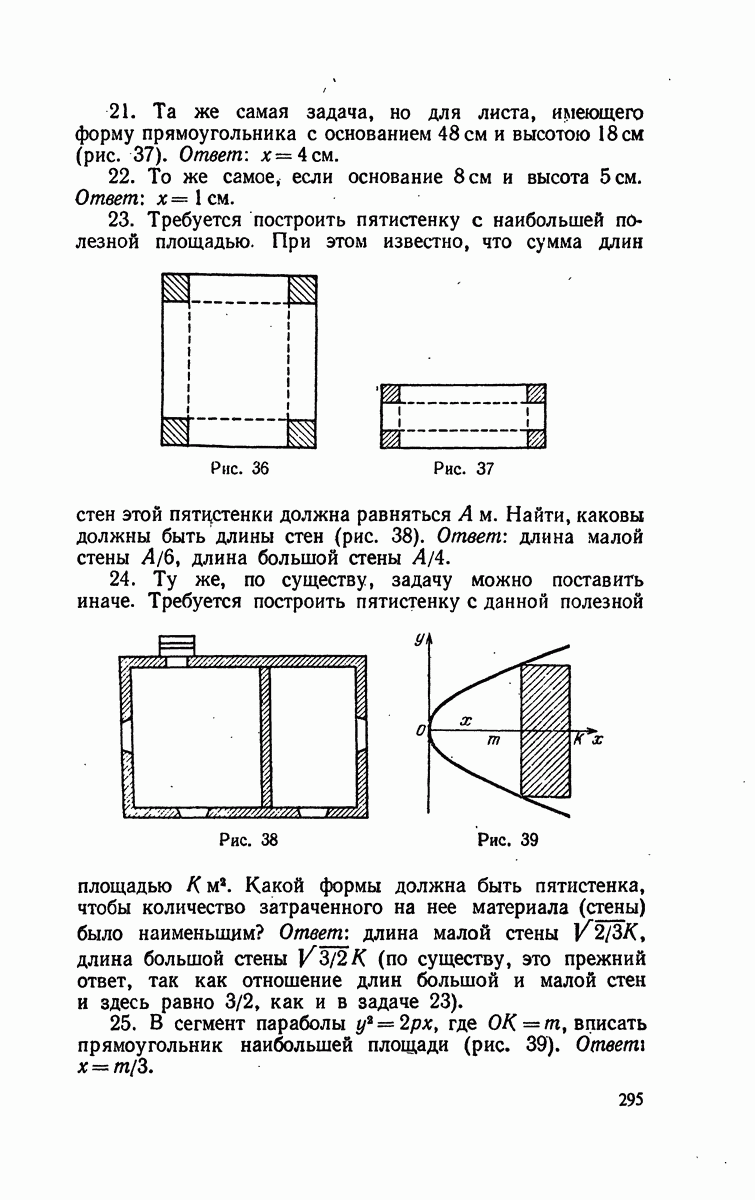
- § 5. Прикладные задачи на наибольшее и наименьшее значения
- § 6. Направление выпуклости, точки перегиба
- § 7. Приложение к построению графиков
- § 8. Построение графиков разрывных функций
- § 9. Признак максимума и минимума, основанный на исследовании знака первой производной
- § 10. Признак максимума и минимума, основанный на исследовании знака второй и высших производных
- § 11. Асимптоты
- § 12. Дифференциал дуги
- § 13. Направляющие косинусы касательной
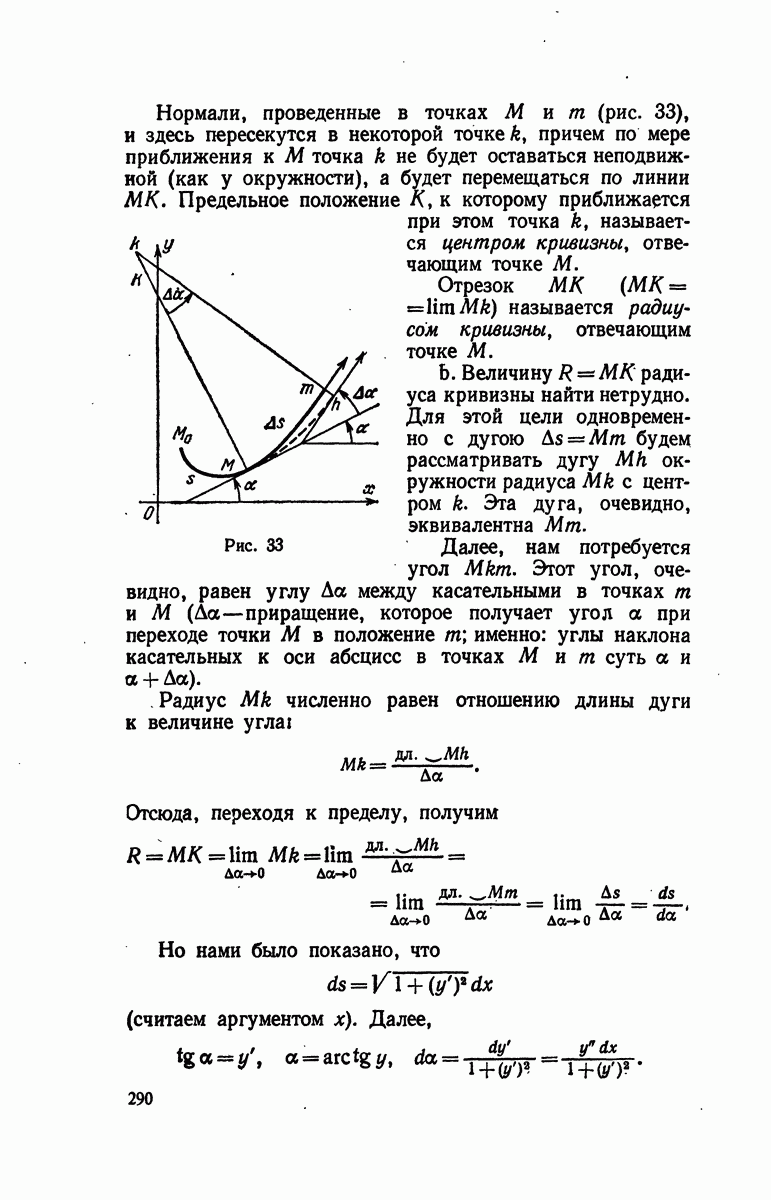
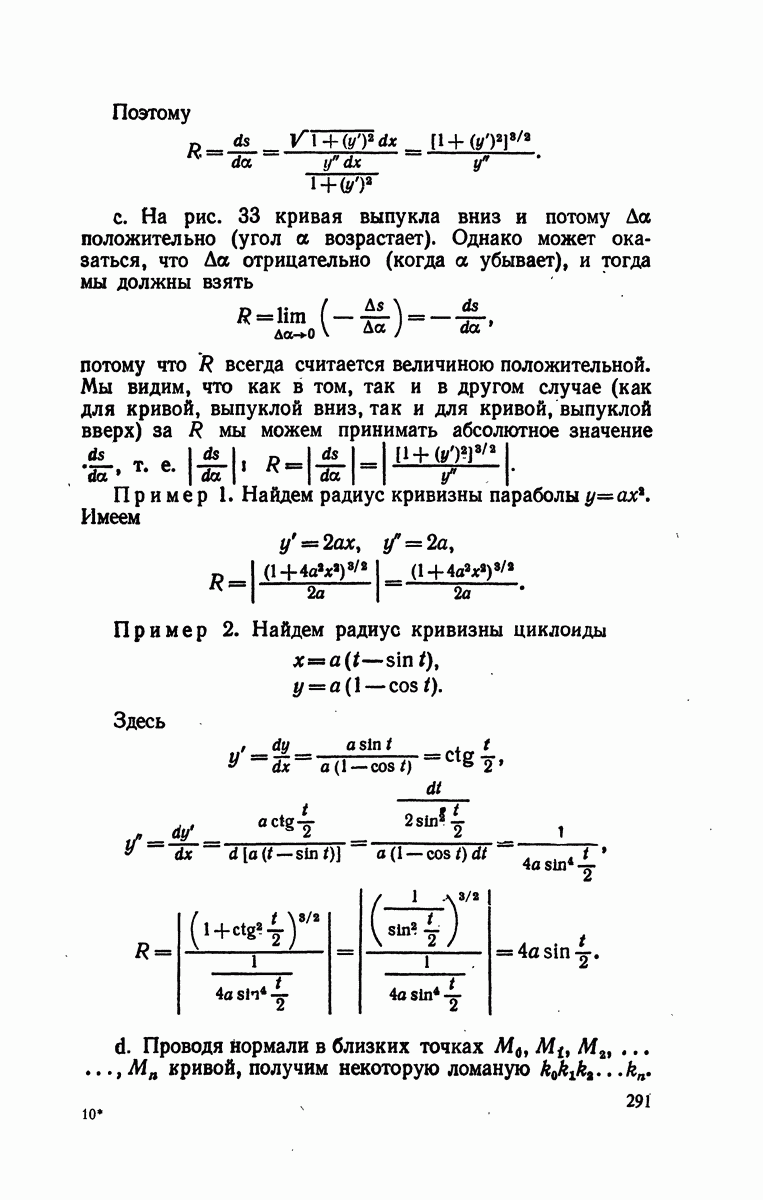
- § 14. Радиус кривизны, центр кривизны
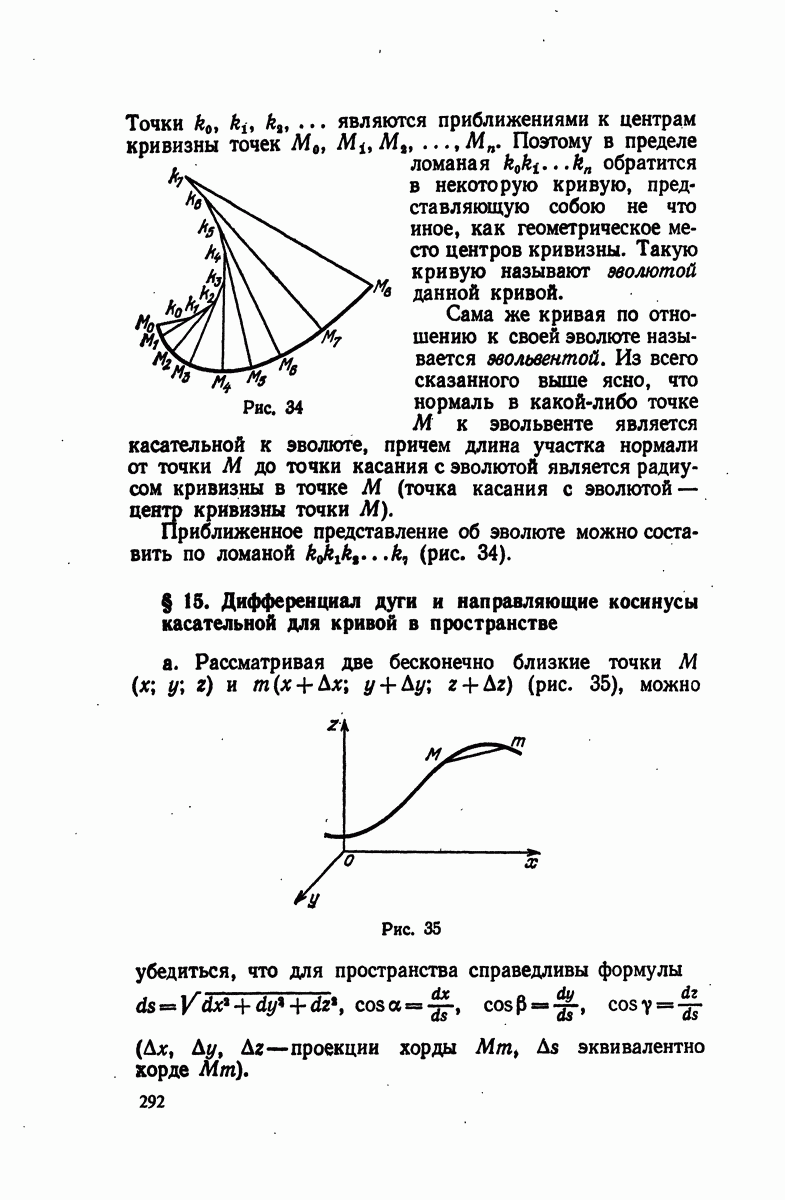
- § 15. Дифференциал дуги и направляющие косинусы касательной для кривой в пространстве
- § 16. Упражнения
- Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
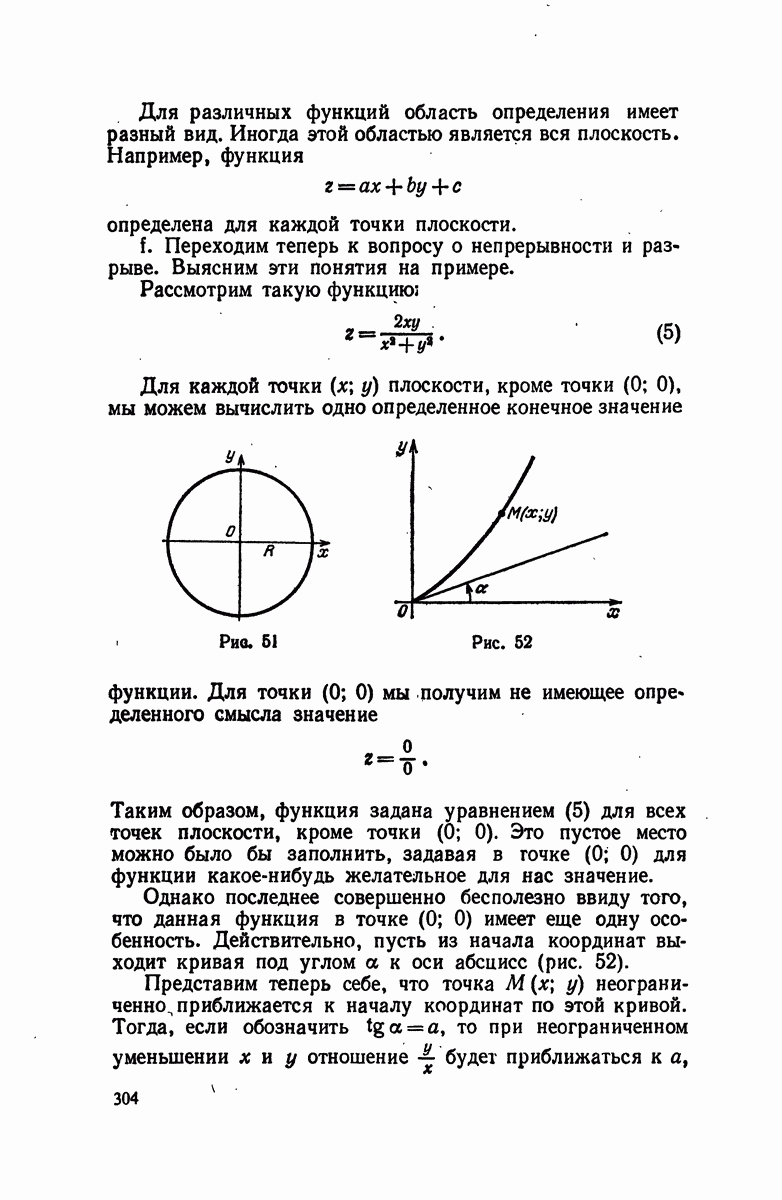
- § 1. Функции многих переменных. Область определения. Непрерывность
- § 2. Частные производные и полный дифференциал
- § 3. Частные производные и полный дифференциал сложной функции многих переменных
- § 4. Дифференцирование неявных функций
- § 5. Частные производные и полные дифференциалы высшего порядка
- § 6. Упражнения
- ЧАСТЬ ТРЕТЬЯ. ОСНОВЫ ТЕОРИИ ЧИСЕЛ
- Глава 1. ТЕОРИЯ ДЕЛИМОСТИ
- § 2. Общий наибольший делитель
- § 3. Общее наименьшее кратное
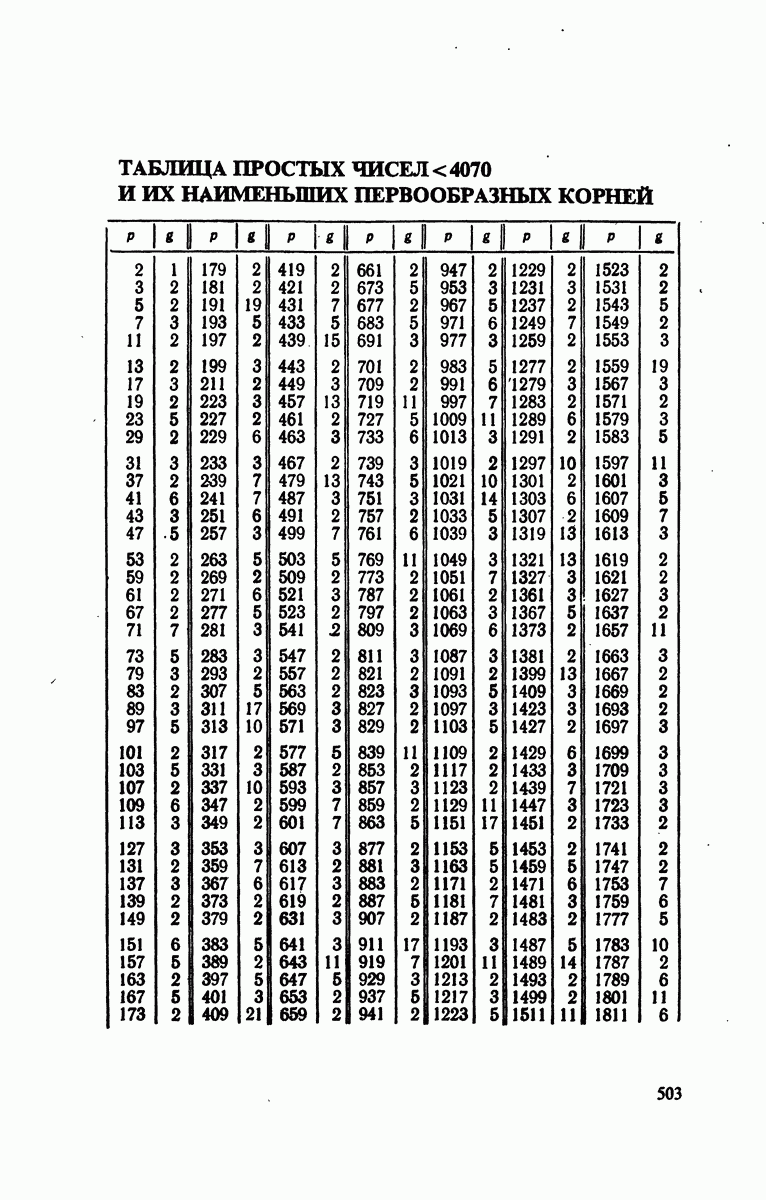
- § 4. Простые числа
- § 5. Единственность разложения на простые сомножители
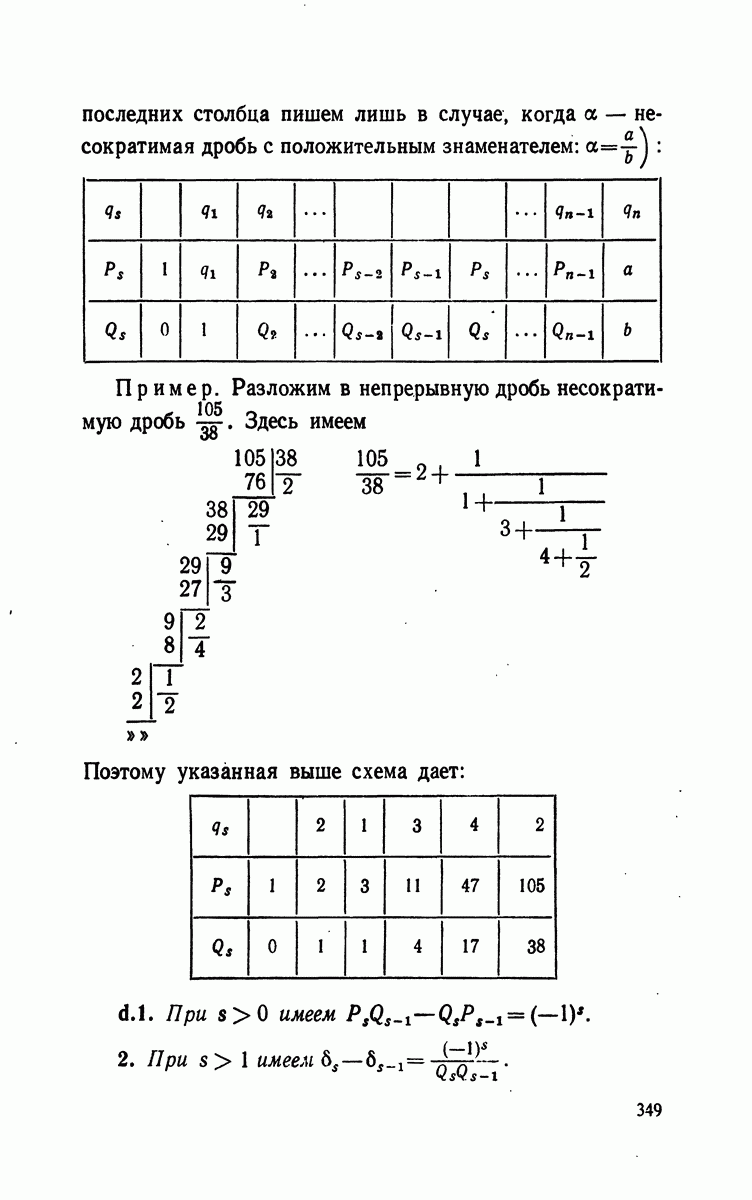
- § 6. Непрерывные дроби и их связь с алгоритмом Евклида
- Вопросы к главе 1
- Глава 2. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
- § 1. Функции [x] и {x}
- § 2. Мультипликативные функции
- § 3. Число делителей и сумма делителей
- § 4. Функция Мёбиуса
- § 5. Функция Эйлера
- Вопросы к главе II
- Глава 3. СРАВНЕНИЯ
- § 2. Свойства сравнений, подобные свойствам равенств
- § 3. Дальнейшие свойства сравнений
- § 4. Полная система вычетов
- § 5. Приведенная система вычетов
- § 6. Теоремы Эйлера и Ферма
- Вопросы к главе 3
- Глава 4. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
- § 2. Сравнения первой степени
- § 3. Система сравнений первой степени
- § 4. Сравнения любой степени по простому модулю
- § 5. Сравнения любой степени по составному модулю
- Вопросы к главе 4
- Глава 5. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
- § 2. Символ Лежандра
- § 3. Символ Якоби
- § 4. Случай составного модуля
- Вопросы к главе 5
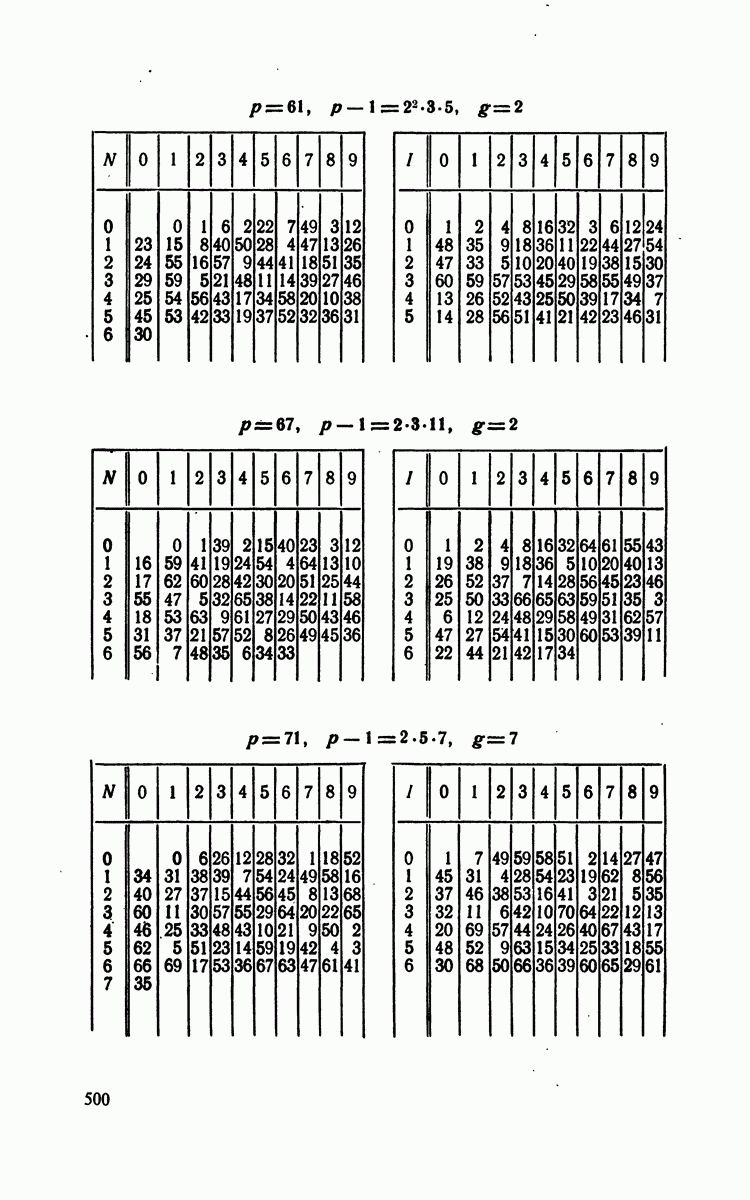
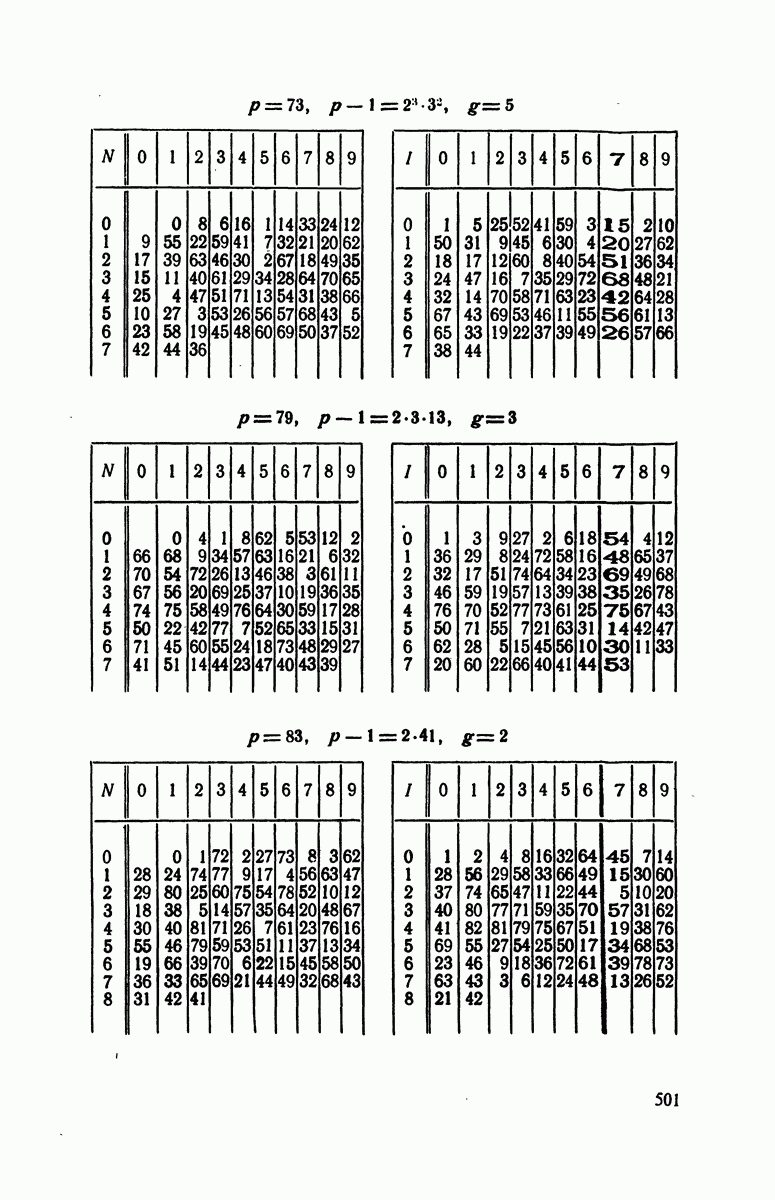
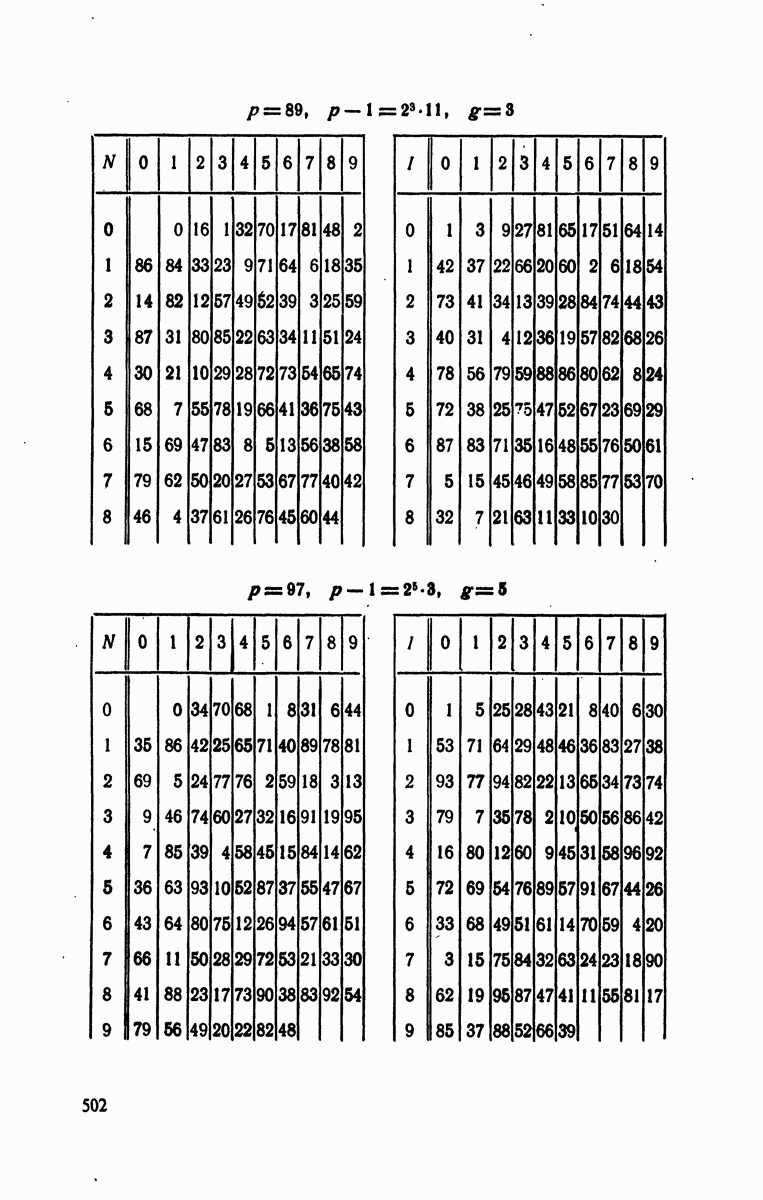
- Глава 6. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- § 2. Первообразные корни по модулям
- § 3. Разыскание первообразных корней по модулям
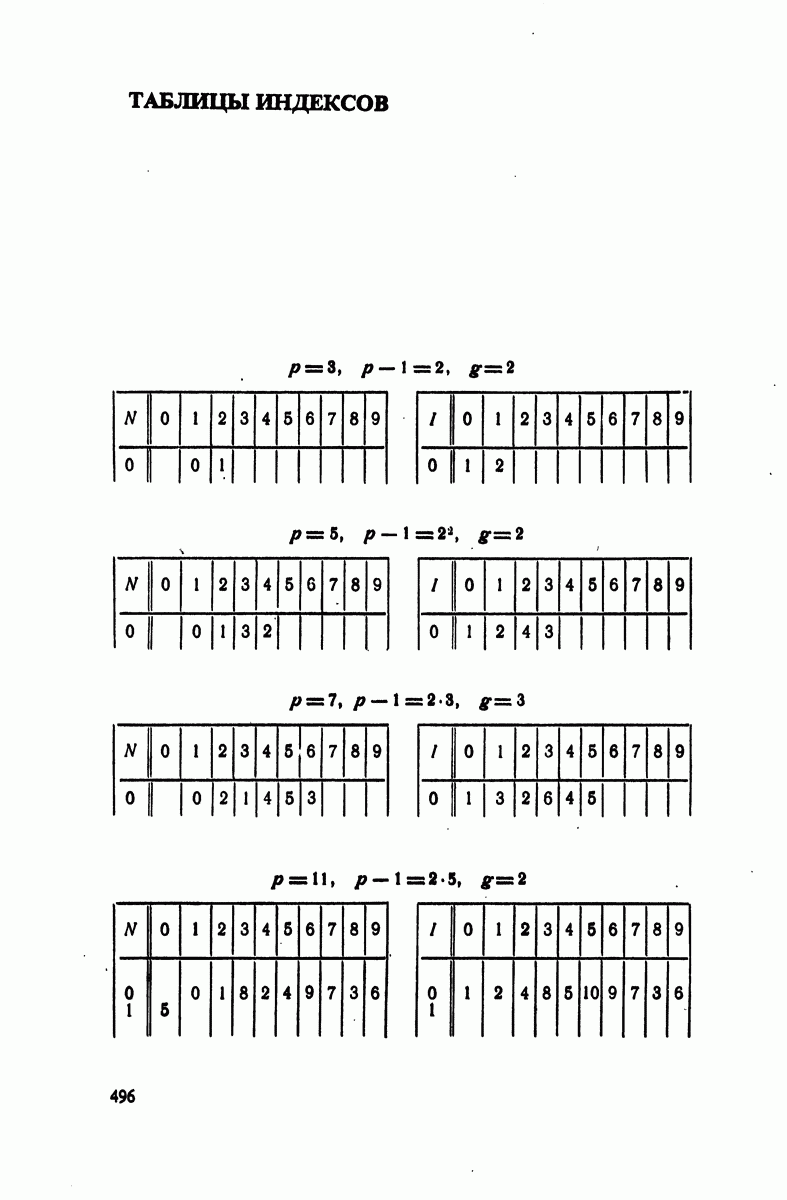
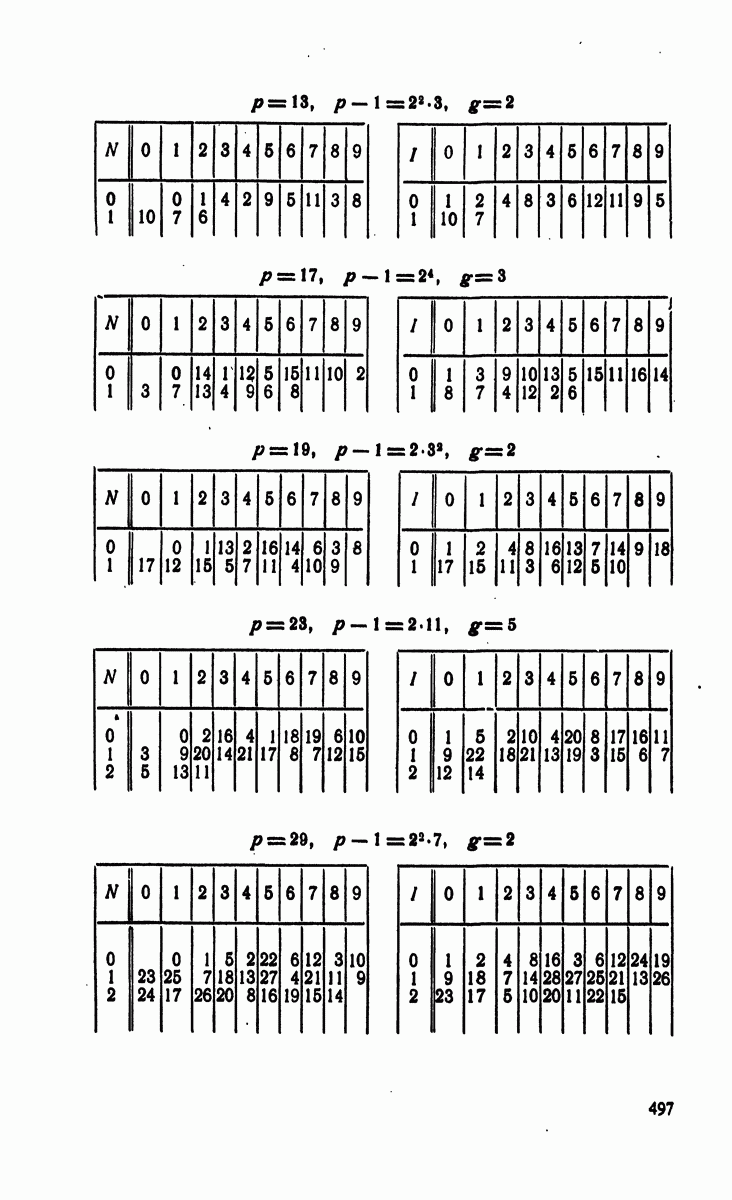
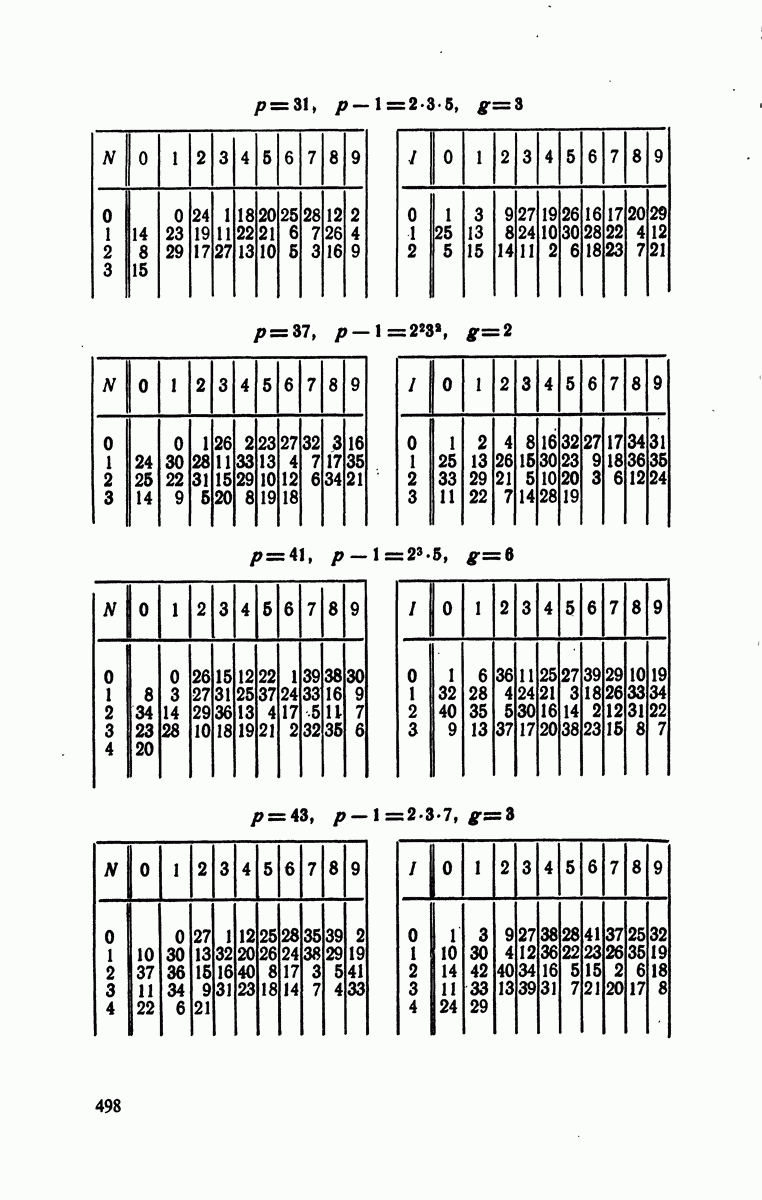
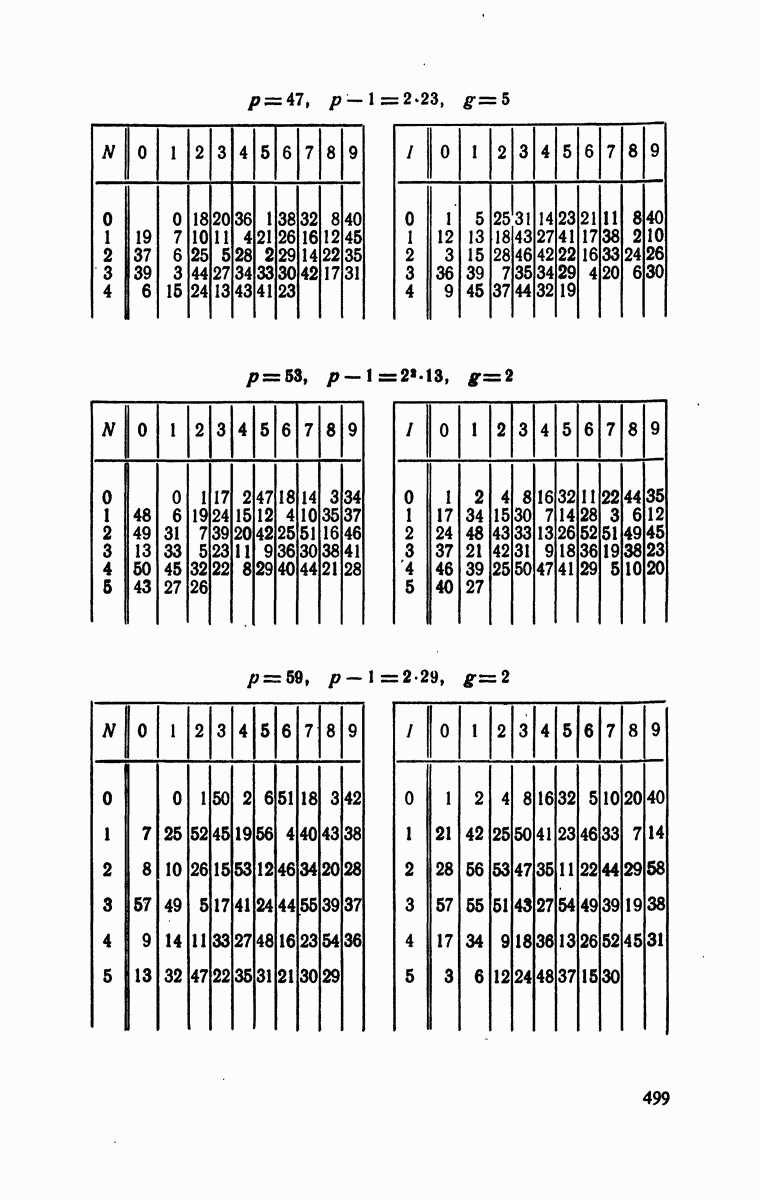
- § 4. Индексы по модулям
- § 5. Следствия предыдущей теории
- § 6. Индексы по модулю 2^a
- § 7. Индексы по любому составному модулю
- Вопросы к главе 6
- Глава 7. ХАРАКТЕРЫ
- § 2. Важнейшие свойства характеров
- Вопросы к главе 7
- РЕШЕНИЯ ВОПРОСОВ
- Решения к главе 2
- Решения к главе 3
- Решения к главе 4
- Решения к главе 5
- Решения к главе 6
- ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ