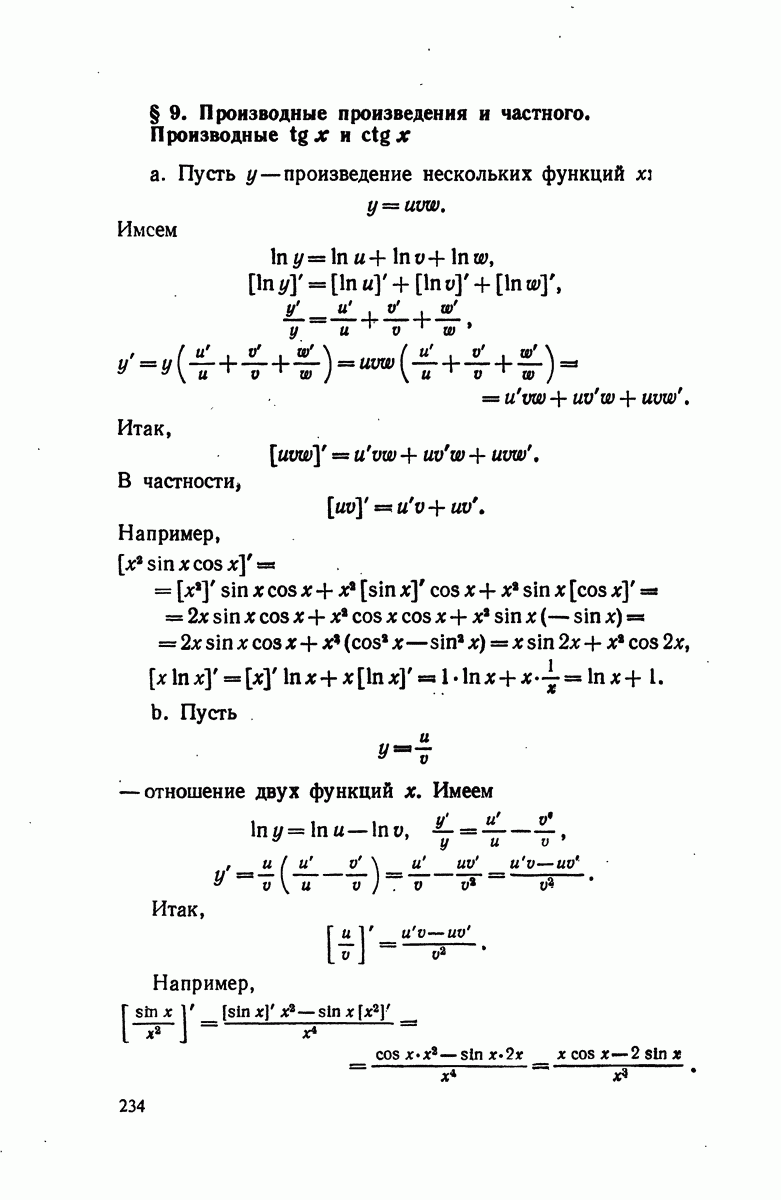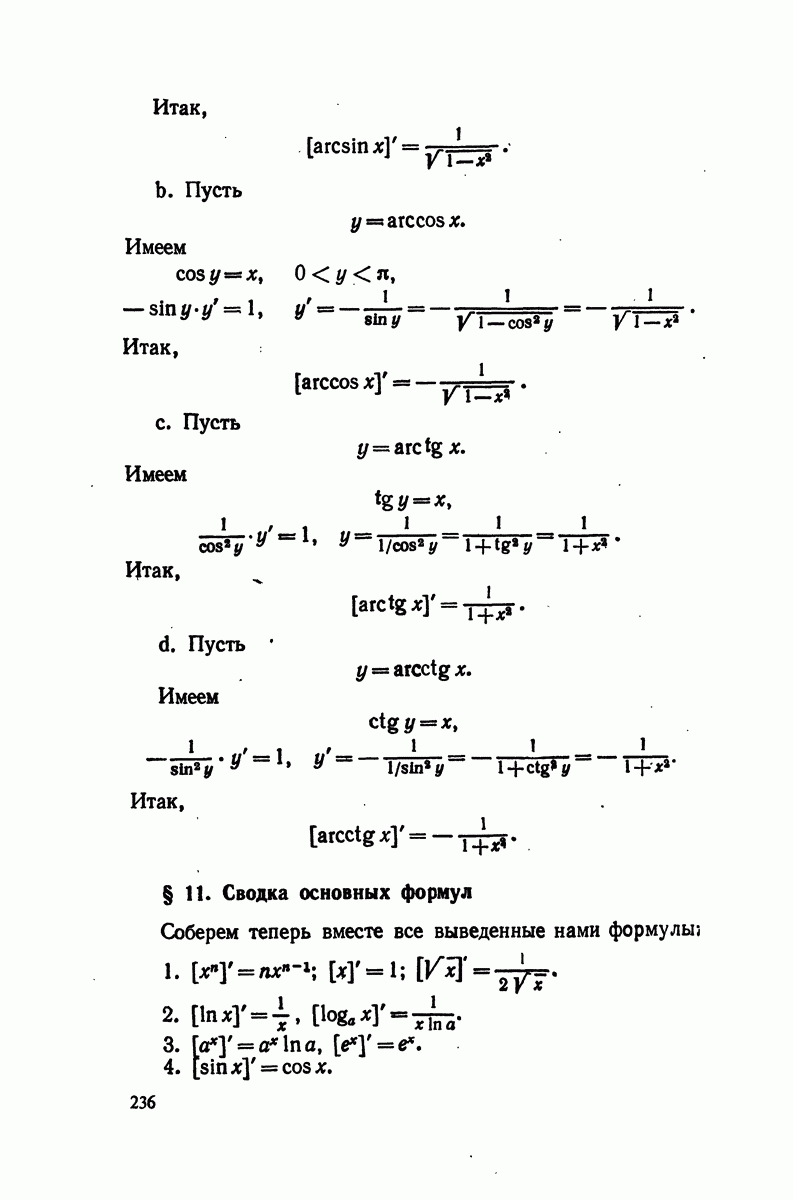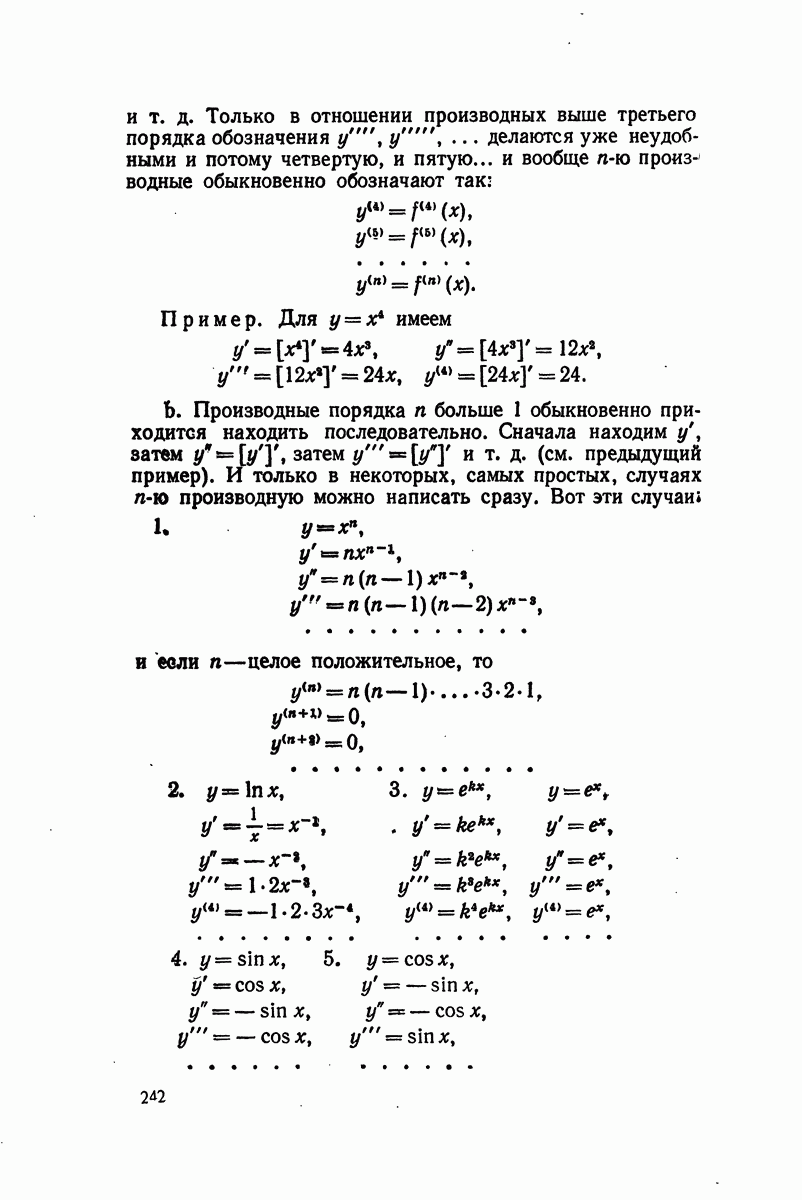| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Понятие бесконечно большой
а. Вместе с понятием бесконечно малой нам потребуется и понятие бесконечно большой величины. В то время как для бесконечно малой нельзя поставить никаких границ ее приближению к нулю, для бесконечно большой величины, наоборот, нельзя поставить никаких границ ее увеличению (по абсолютной величине). Называя какую-либо величину  бесконечно большой, мы должны быть уверены в том, что какое бы большое положительное число N мы ни задали, в изменении переменной
бесконечно большой, мы должны быть уверены в том, что какое бы большое положительное число N мы ни задали, в изменении переменной  обязательно наступит момент, начиная с которого абсолютная величина
обязательно наступит момент, начиная с которого абсолютная величина  этой переменной будет оставаться больше
этой переменной будет оставаться больше 
Отмечая это характерное свойство бесконечно большой, мы дадим ей такое определение.
Бесконечно большой мы называем такую переменную  , относительно которой мы уверены в следующем:
, относительно которой мы уверены в следующем:
Какое бы большое положительное число N мы ни задали, в изменении  наступит момент, начиная с которого абсолютная величина
наступит момент, начиная с которого абсолютная величина  переменной
переменной  будет оставаться больше
будет оставаться больше 
b. И здесь мы считаем необходимым особенно подчеркнуть то, что свойство бесконечно большой начиная с некоторого момента численно оставаться больше N должно обнаруживаться при любом N, как бы велико N ни было задано.
Например, после того как  по абсолютной величине уже остается больше N, при дальнейшем изменении
по абсолютной величине уже остается больше N, при дальнейшем изменении  наступит момент, начиная с которого
наступит момент, начиная с которого  и при дальнейшем изменении
и при дальнейшем изменении  — моменты, начиная с которых
— моменты, начиная с которых

Иначе, если  — бесконечно большая, то при ее изменении последовательно наступят моменты, начиная с которых
— бесконечно большая, то при ее изменении последовательно наступят моменты, начиная с которых

с. Относительно бесконечно большой величины часто говорят также, что она стремится к бесконечности. В связи с этим запись того, что  — бесконечно большая, можно производить одним из двух следующих способов:
— бесконечно большая, можно производить одним из двух следующих способов:

или

(Знак  есть символ бесконечности.)
есть символ бесконечности.)
d. В частности, если начиная с некоторого момента все значения бесконечно большой я положительны, пишут

e. Если же начиная с некоторого момента все значения бесконечно большой  отрицательны, то пишут
отрицательны, то пишут

f. Примерами бесконечно больших могут служить переменные  , принимающие такие последовательные значения:
, принимающие такие последовательные значения:

Относительно двух первых можно написать, в частности,

тогда как относительно  , можно лишь написать
, можно лишь написать

Легко показать, что дробь

с бесконечно малым знаменателем а (не обращающимся в нуль) будет бесконечно большой.
Действительно, задав произвольно большое положительное N и положив  видим, что начиная с момента, когда
видим, что начиная с момента, когда  будет оставаться меньше
будет оставаться меньше  , будем иметь
, будем иметь

Таким образом, какое бы большое положительное число N мы ни задали, в изменении величины  наступит момент, начиная с которого
наступит момент, начиная с которого

Значит,  — бесконечно большая.
— бесконечно большая.
h. Наоборот, дробь

с бесконечно большим знаменателем  будет бесконечно малой.
будет бесконечно малой.
Задав произвольно малое положительное число  и положив
и положив  видим, что начиная с момента, когда
видим, что начиная с момента, когда  будет оставаться больше N, будем иметь
будет оставаться больше N, будем иметь

Таким образом, какое бы малое положительное число в мы ни задали, наступит момент, начиная с которого

Значит, а — бесконечно малая.
i. Переменная  абсолютная величина
абсолютная величина  которой остается не больше некоторой постоянной А, т. е. переменная
которой остается не больше некоторой постоянной А, т. е. переменная  которая всегда удовлетворяет условию
которая всегда удовлетворяет условию

называется ограниченной.
Например, ограниченной будет величина

потому что всегда

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- § 1. Ось
- § 2. Вектор
- § 3. Направленные углы
- § 4. Проекция вектора с оси на ось
- § 5. Векторные цепи
- § 6. Цепи углов
- § 7. Проекции вектора на две взаимно перпендикулярные оси
- § 8. Угол между двумя лекторами. Условия параллельности и перпендикулярности
- S 9. Упражнения и контрольные вопросы
- Глава 2. КООРДИНАТЫ
- § 1. Метод координат
- § 2. Основные задачи, решаемые методом координат
- § 3. Упражнения
- Глава 3. ФУНКЦИИ
- § 1. Переменные в постоянные
- § 2. Понятие о функциональной зависимости
- § 3. Классификация математических функций
- § 4. Обзор и графическое изображение простейших функции одного аргумента
- § 5. Обратные функции
- § 6. Понятие об уравнении линии
- § 7. Упражнения
- Глава 4. ПРЯМАЯ
- § 1. Уравнение прямой, проходящей через данную точку
- § 2. Общее уравнение прямой
- § 3. Частные случаи
- § 4. Переход к уравнению с угловым коэффициентом
- § 5. Построение прямой
- § 6. Определение угла между двумя прямыми
- § 7. Условие совпадения прямых
- § 8 Пересечение прямых
- § 9. Расстояние от точки до прямой
- § 10. Другой подход к выводу уравнения прямой
- § 11. Прямая, проходящая через две точки
- § 12. Уравнение прямой в отрезках на осях
- § 13. Задачи на прямую линию
- Глава 5. ПРОСТЕЙШИЕ КРИВЫЕ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- § 1. Окружность
- § 2. Эллипс. Построение посредством нитн. Зависимость между полуосями и полуфокусным расстоянием
- § 3. Построение эллипса по точкам
- § 4. Уравнение эллипса
- § 5. Связь эллипса с окружностью
- § 6. Директрисы эллипса
- § 7. Гипербола. Построение посредством нити
- § 8. Построение гиперболы по точкам
- § 9. Уравнение гиперболы
- § 10. Асимптоты. Геометрическое значение b
- § 11. Директрисы гиперболы
- § 12. Парабола. Построение по точкам
- § 13. Уравнение параболы
- § 14. Преобразование координат
- § 15. Пример на упрощение уравнения кривой путем параллельного переноса осей
- § 16. Поворот осей
- § 17. Общий случай
- § 18. Полярные координаты
- § 19. Спираль Архимеда
- § 20. Логарифмическая спираль
- § 21. Примеры на составление полярных уравнений кривых
- § 22. Выражение прямоугольных координат через полярные
- § 23. Уравнение лемнискаты
- § 24. Параметрическое задание линий
- § 25. Построение графика
- § 26. Циклоида
- § 27. Упражнения
- Глава 6. ВЕКТОРЫ, ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
- § 1. Оси, векторы, углы
- § 2. Проекции
- § 3. Проекции на три взаимно перпендикулярные оси. Длина вектора через проекции
- § 4. Простейшие зависимости, содержащие величину вектора, проекции и направляющие косинусы
- § 5. Проекция вектора на оси. Косинус угла между двумя векторами. Скалярное произведение векторов
- § 6. Координаты
- § 7. Выражение проекций вектора через координаты конца и начала
- § 8. Выражение длины вектора через координаты концов. Расстояние между двумя точками
- § 9. Деление отрезка в данном отношении
- § 10. График уравнения с двумя переменными
- § 11. Поверхность как след, образуемый перемещением некоторой деформируемой плоской кривой
- § 12. Цилиндрические поверхности
- § 13. Обратная задача. Уравнение шаровой поверхности
- § 14. Уравнение плоскости, проходящей через данную точку
- § 15. Общее уравнение плоскости
- § 16. Частные случаи
- § 17. Выяснение расположения плоскости относительно осей
- § 18. Угол между плоскостями. Условие параллельности. Условие перпендикулярности
- § 19. Условие совпадения плоскостей
- § 20. Расстояние от точке до плоскости
- § 21. Прямая как пересечение двух плоскостей
- § 22. Прямая, проходящая через данную точку
- § 23. Прямая, проходящая через две точки
- § 24. Переход от системы уравнений прямой в общем виде к системе в виде пропорций
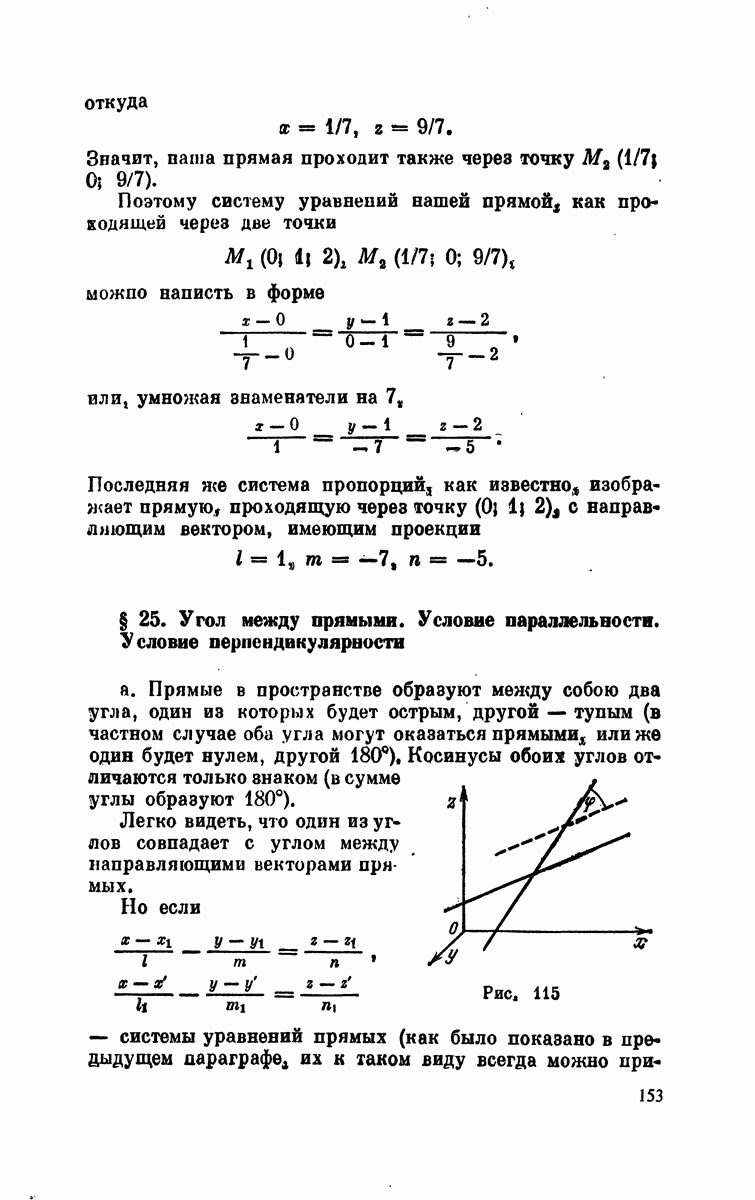
- § 25. Угол между прямыми. Условие параллельности. Условие перпендикулярности
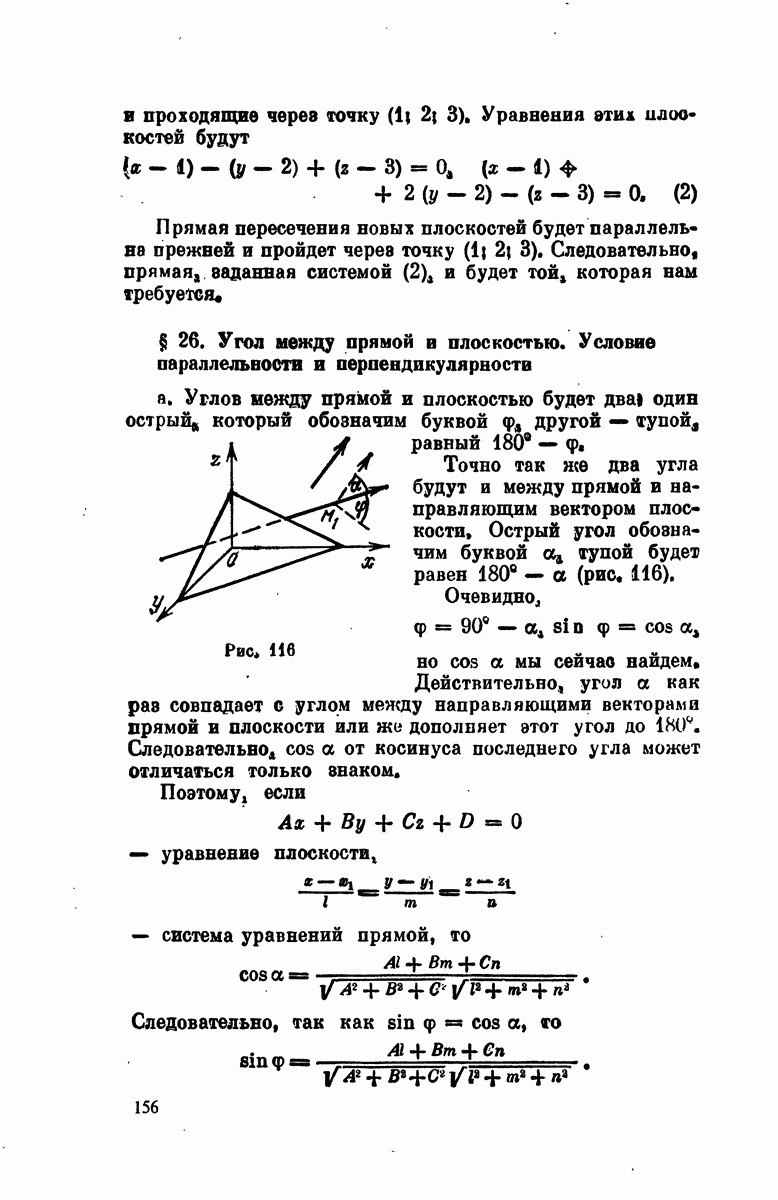
- § 26. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности
- § 27. Простейшие поверхности. Эллипсоид
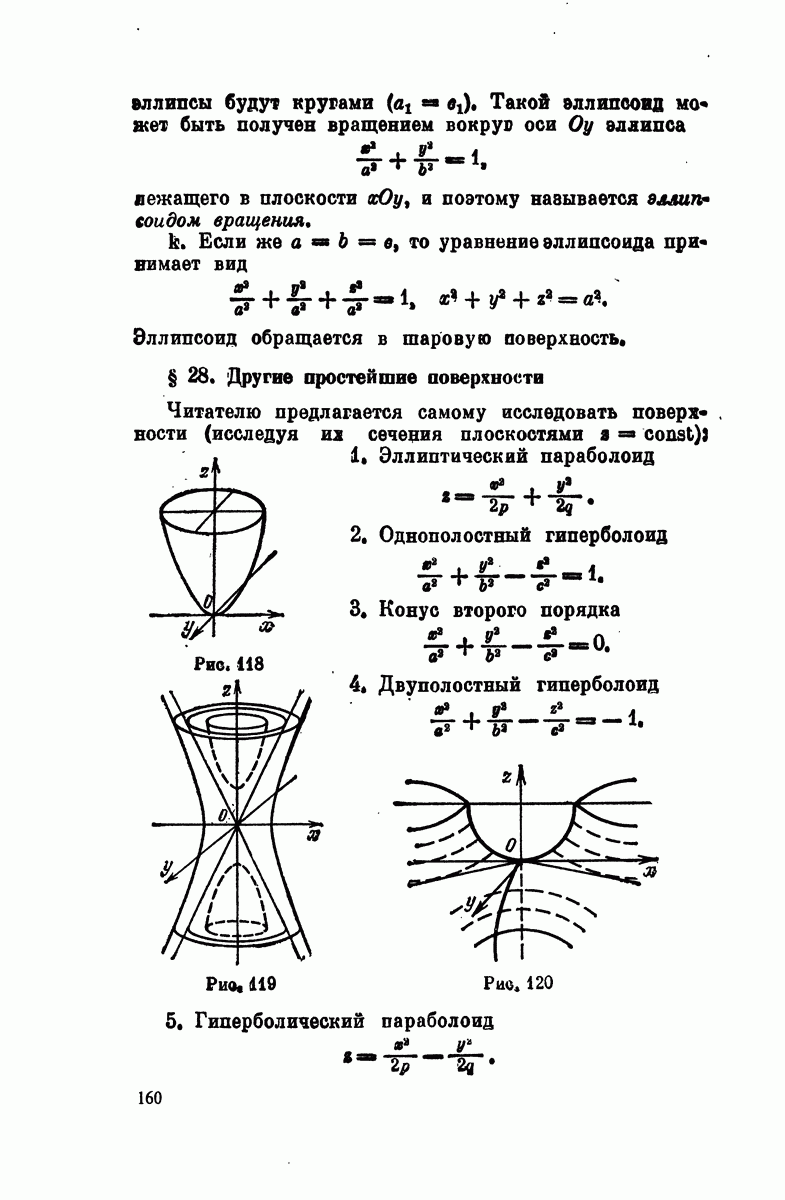
- § 28. Другие простейшие поверхности
- § 29. Кривая в пространстве как пересечение двух поверхностей
- § 30. Параметрические уравнения
- § 31. Винтовая линия
- § 32. Параметрические уравнения в механике
- § 33. Переход от параметрического представления к общему и обратно
- § 34. Преобразование координат
- § 35. Упражнения
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. Бесконечно малые
- § 2. Понятие предела переменной величины
- § 3. Понятие бесконечно большой
- § 4. Свойства бесконечно малых
- § 5. Основные свойства пределов
- § 6. Предел непрерывной функции
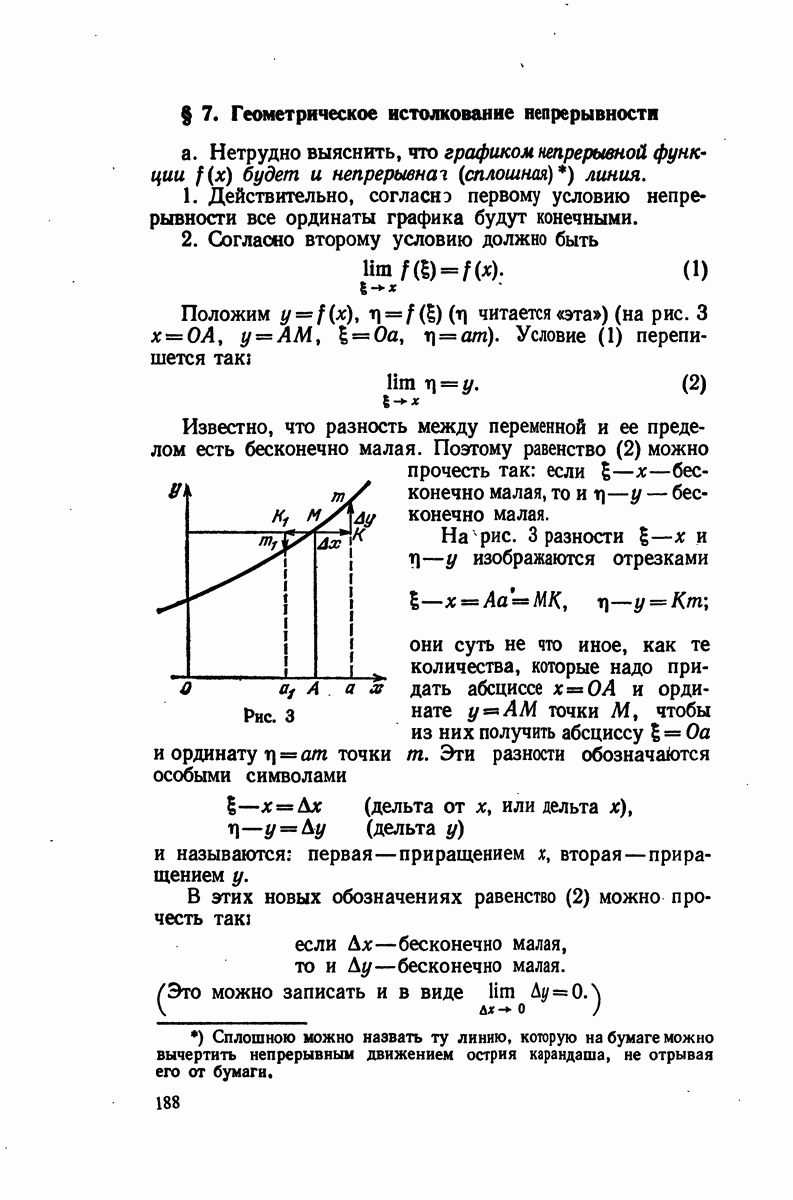
- § 7. Геометрическое истолкование непрерывности
- § 8. Свойство непрерывной функции
- § 9. Предел функции, зависящей от нескольких переменных
- § 10. Особые случаи разыскания предела
- § 11. Замечательный тригонометрический предел
- § 12. Признак существования предела
- § 13. Сходимость бесконечных рядов
- § 14. Простейшие признаки сходимости
- § 15. Основание натуральных логарифмов
- § 16. Порядок бесконечно малых
- § 17. Упражнения
- Глава 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная как угловой коэффициент касательной
- § 2. Производная как предел
- § 3. Пояснение общей теории на примере. Уравнения касательной и нормали
- § 4. Механическое значение производной
- § 5. Производные трех простейших функций
- § 6. Производная постоянного и суммы. Вынесение постоянного множителя за знак производной
- § 7. Производная сложной функции
- § 8. Разыскание производных путем логарифмирования. Производные функции х^n при любом n к функции а^x.
- § 9. Производные произведения и частного. Производные tg x и ctg x.
- § 10. Производные обратных тригонометрических функций
- § 11. Сводка основных формул
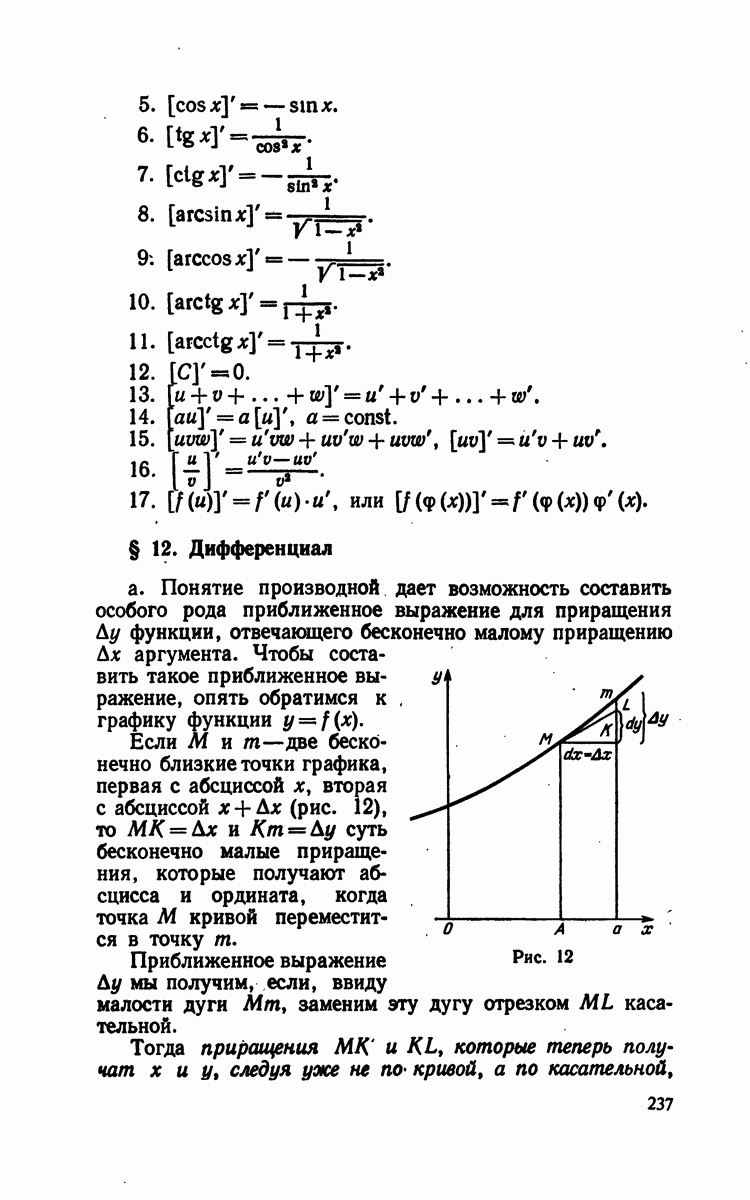
- § 12. Дифференциал
- § 13. Основные формулы для дифференциалов
- § 14. Высшие производные
- § 15. Высшие дифференциалы
- § 16. Дифференцирование неявных функций
- § 17. Дифференцирование функций, заданных параметрическим способом
- § 18. Преобразование дифференциалов к новой переменной
- § 19. Упражнения
- Глава 3. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- § 1. Непрерывность первой производной
- § 2. Возрастание и убывание функций. Максимум и минимум
- § 3. Приложение к построению графиков
- § 4. Наибольшее и наименьшее значения функции
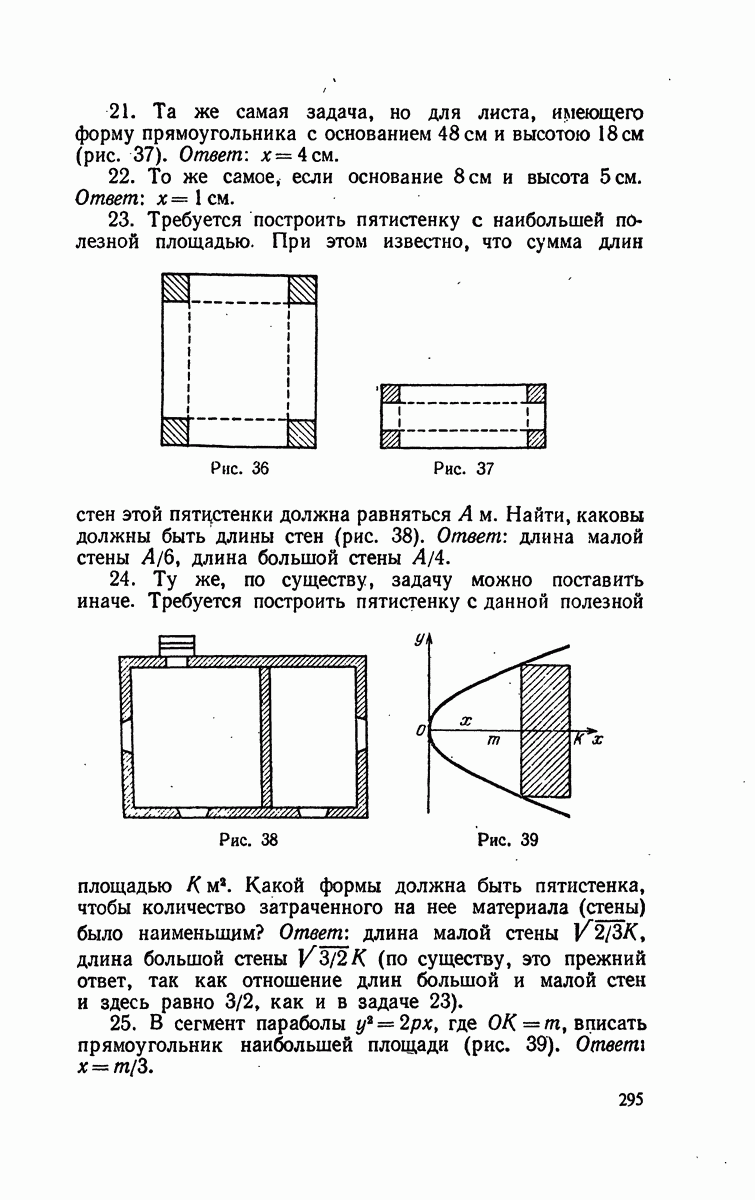
- § 5. Прикладные задачи на наибольшее и наименьшее значения
- § 6. Направление выпуклости, точки перегиба
- § 7. Приложение к построению графиков
- § 8. Построение графиков разрывных функций
- § 9. Признак максимума и минимума, основанный на исследовании знака первой производной
- § 10. Признак максимума и минимума, основанный на исследовании знака второй и высших производных
- § 11. Асимптоты
- § 12. Дифференциал дуги
- § 13. Направляющие косинусы касательной
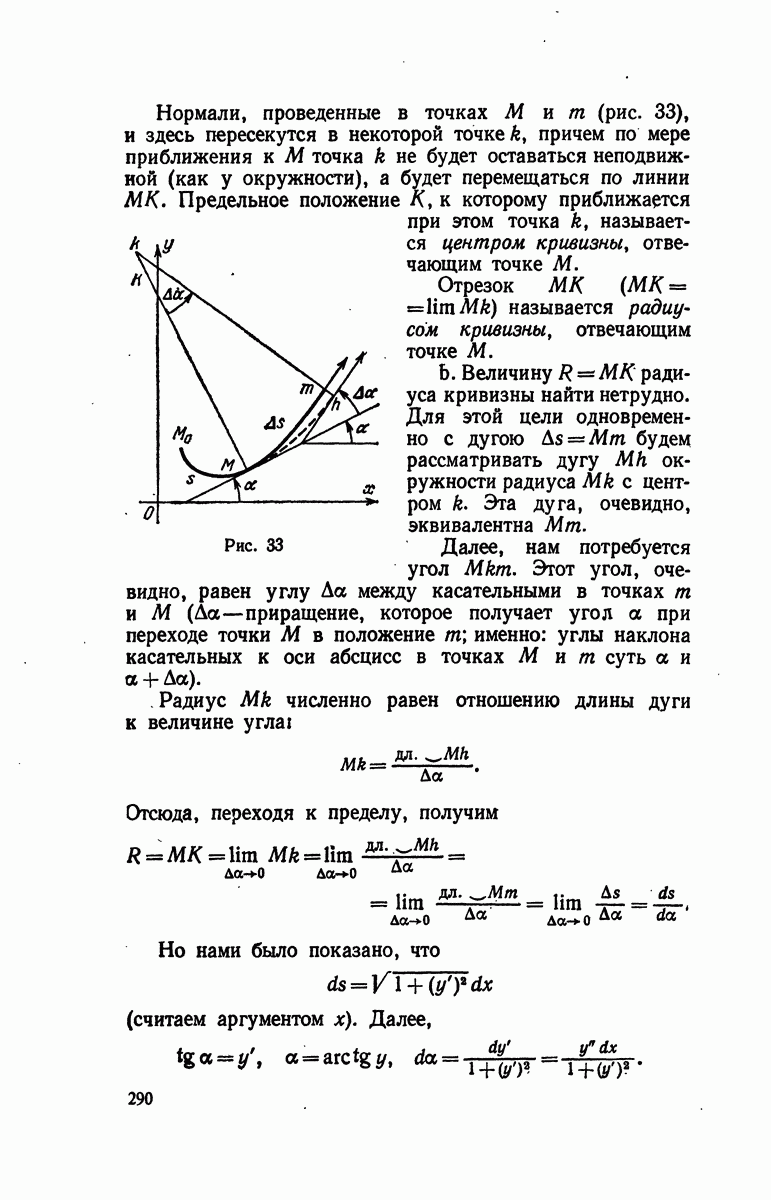
- § 14. Радиус кривизны, центр кривизны
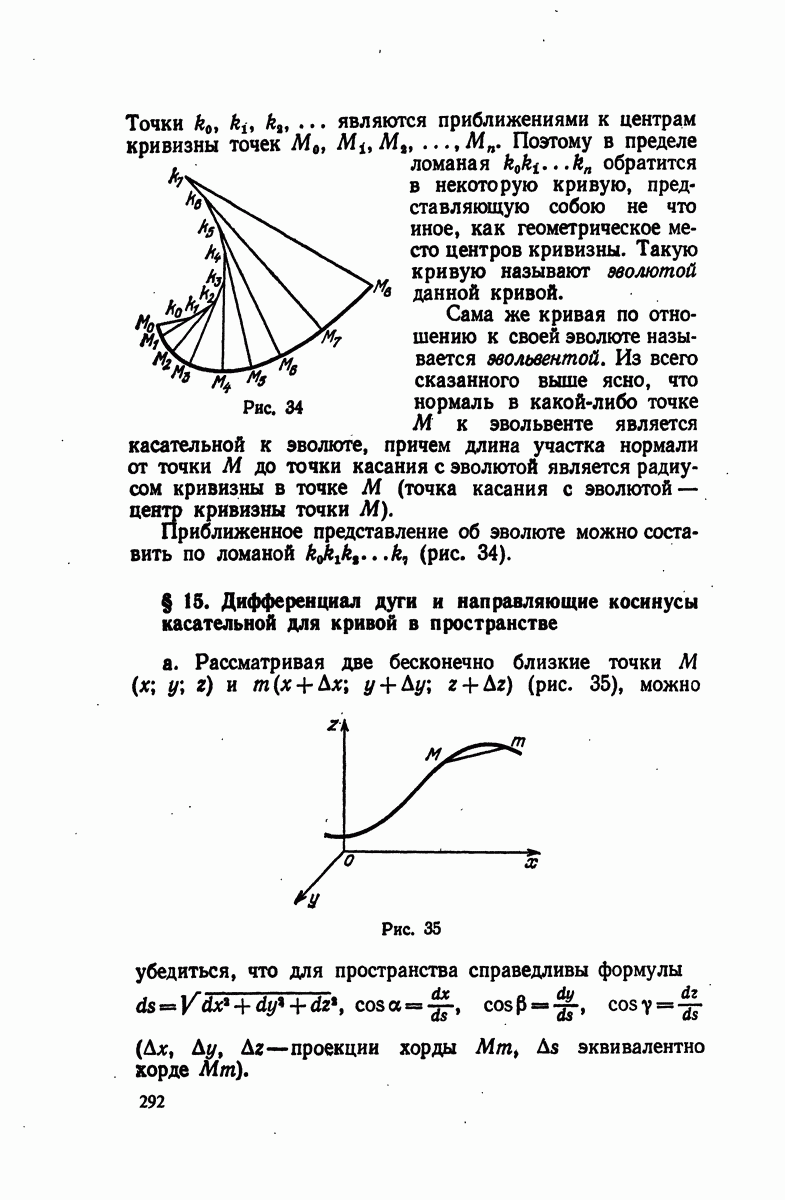
- § 15. Дифференциал дуги и направляющие косинусы касательной для кривой в пространстве
- § 16. Упражнения
- Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 1. Функции многих переменных. Область определения. Непрерывность
- § 2. Частные производные и полный дифференциал
- § 3. Частные производные и полный дифференциал сложной функции многих переменных
- § 4. Дифференцирование неявных функций
- § 5. Частные производные и полные дифференциалы высшего порядка
- § 6. Упражнения
- ЧАСТЬ ТРЕТЬЯ. ОСНОВЫ ТЕОРИИ ЧИСЕЛ
- Глава 1. ТЕОРИЯ ДЕЛИМОСТИ
- § 2. Общий наибольший делитель
- § 3. Общее наименьшее кратное
- § 4. Простые числа
- § 5. Единственность разложения на простые сомножители
- § 6. Непрерывные дроби и их связь с алгоритмом Евклида
- Вопросы к главе 1
- Глава 2. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
- § 1. Функции [x] и {x}
- § 2. Мультипликативные функции
- § 3. Число делителей и сумма делителей
- § 4. Функция Мёбиуса
- § 5. Функция Эйлера
- Вопросы к главе II
- Глава 3. СРАВНЕНИЯ
- § 2. Свойства сравнений, подобные свойствам равенств
- § 3. Дальнейшие свойства сравнений
- § 4. Полная система вычетов
- § 5. Приведенная система вычетов
- § 6. Теоремы Эйлера и Ферма
- Вопросы к главе 3
- Глава 4. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
- § 2. Сравнения первой степени
- § 3. Система сравнений первой степени
- § 4. Сравнения любой степени по простому модулю
- § 5. Сравнения любой степени по составному модулю
- Вопросы к главе 4
- Глава 5. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
- § 2. Символ Лежандра
- § 3. Символ Якоби
- § 4. Случай составного модуля
- Вопросы к главе 5
- Глава 6. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- § 2. Первообразные корни по модулям
- § 3. Разыскание первообразных корней по модулям
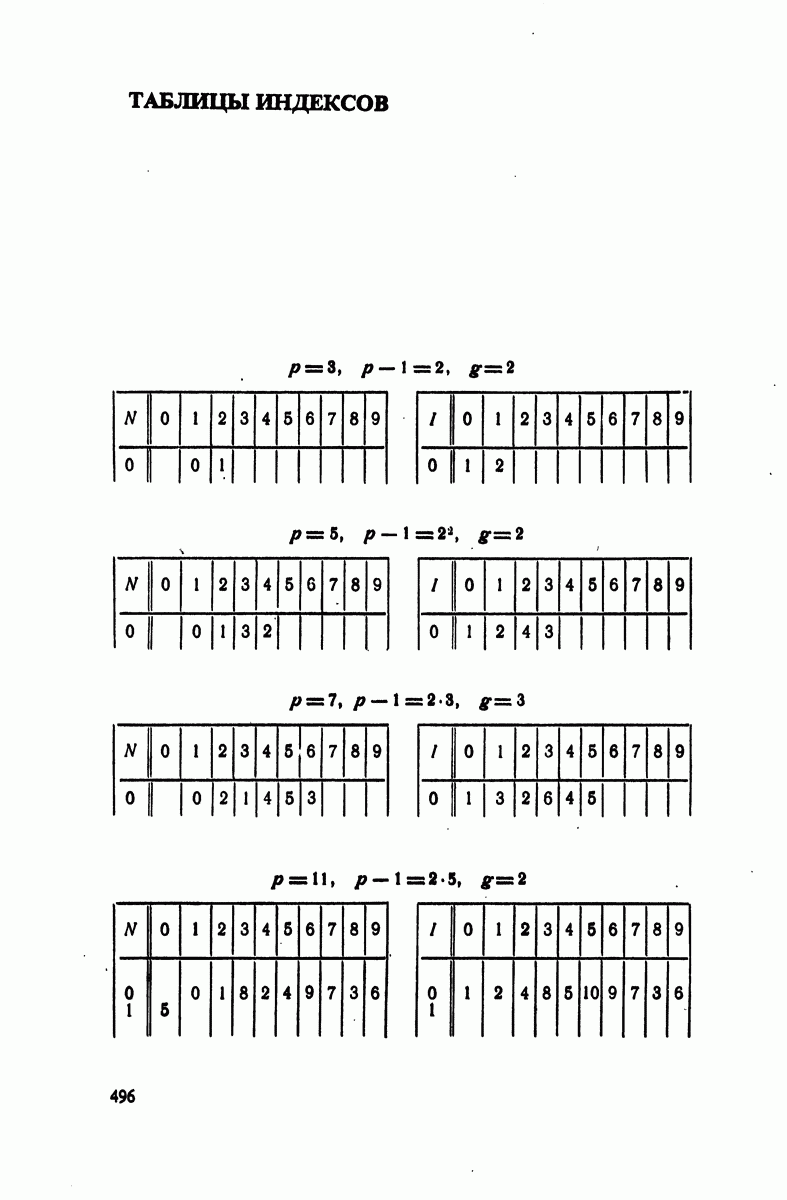
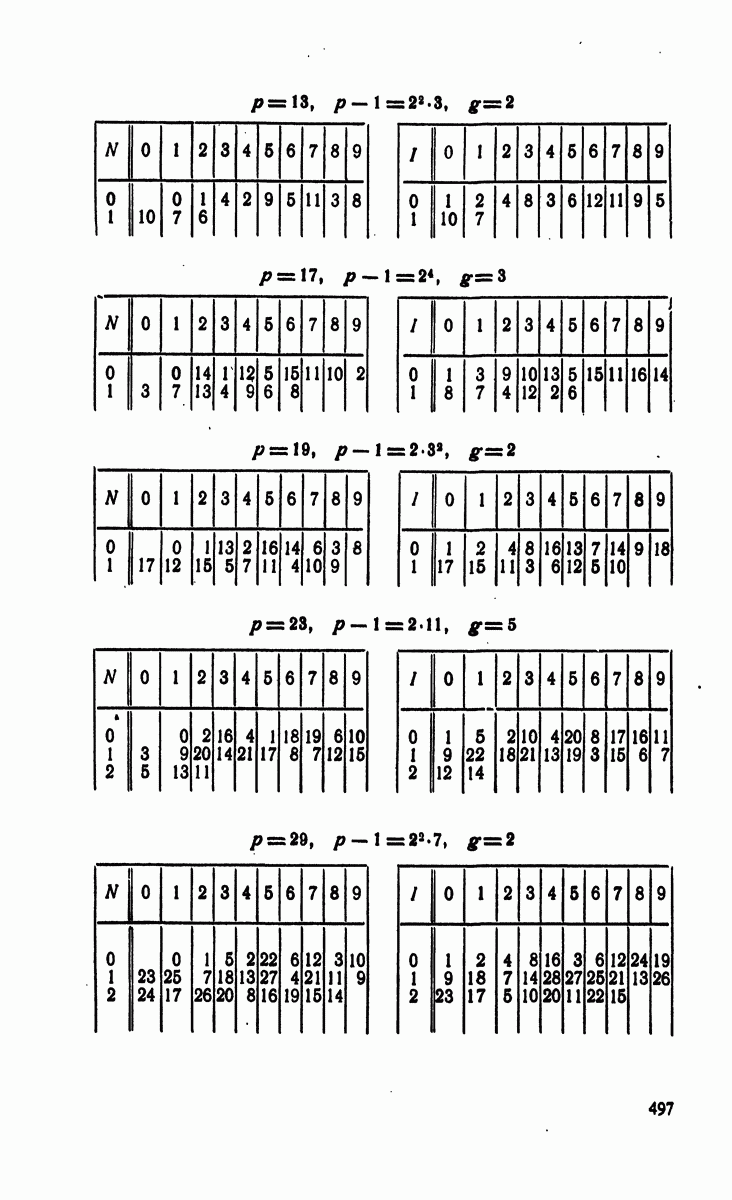
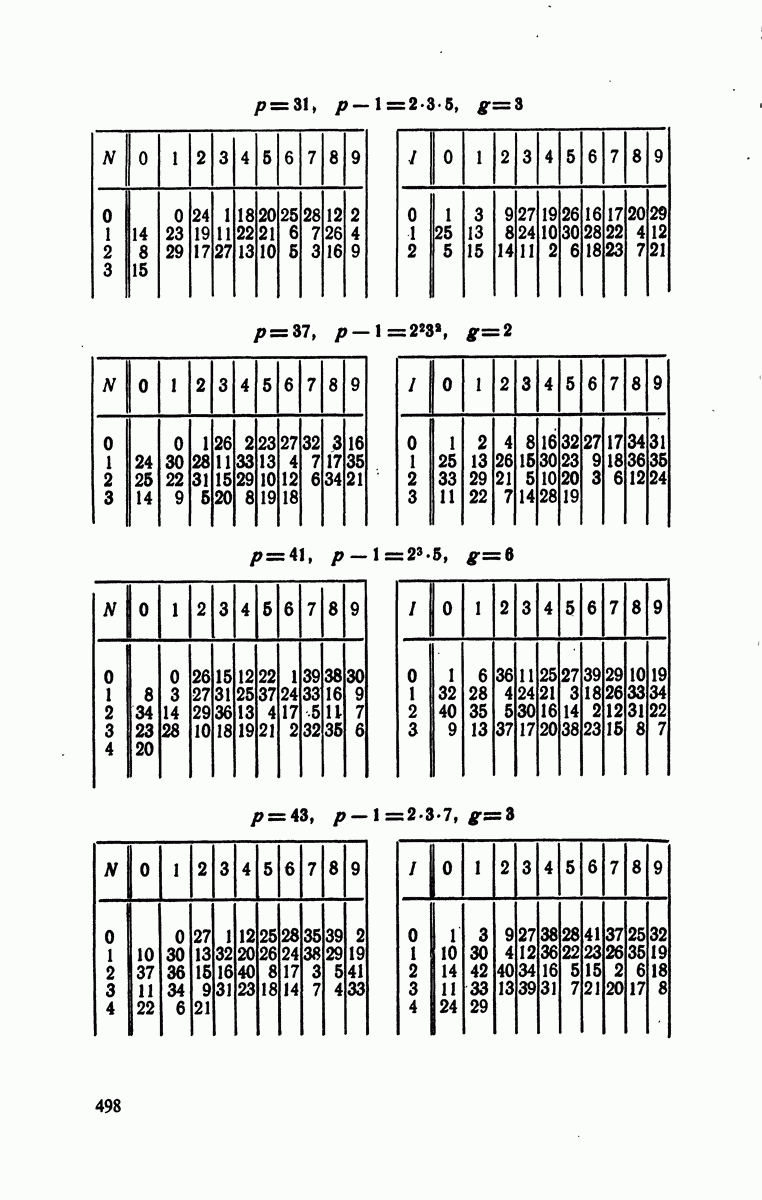
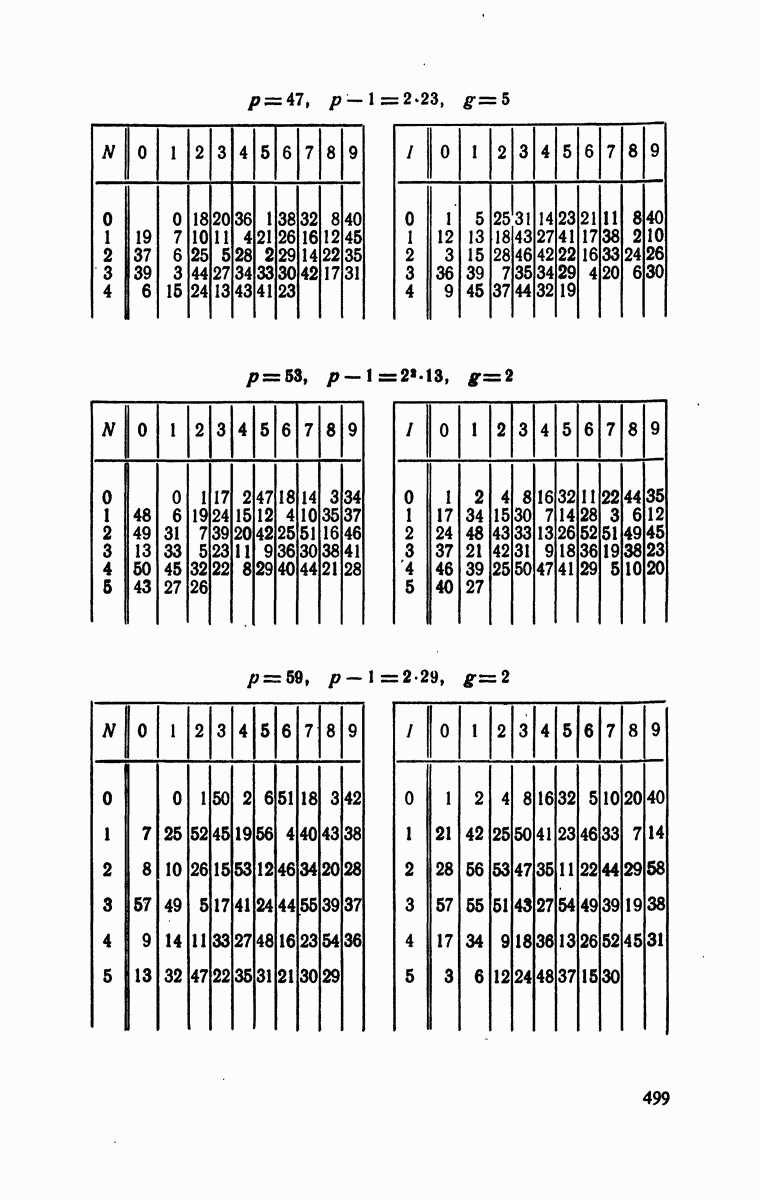
- § 4. Индексы по модулям
- § 5. Следствия предыдущей теории
- § 6. Индексы по модулю 2^a
- § 7. Индексы по любому составному модулю
- Вопросы к главе 6
- Глава 7. ХАРАКТЕРЫ
- § 2. Важнейшие свойства характеров
- Вопросы к главе 7
- РЕШЕНИЯ ВОПРОСОВ
- Решения к главе 2
- Решения к главе 3
- Решения к главе 4
- Решения к главе 5
- Решения к главе 6
- ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ