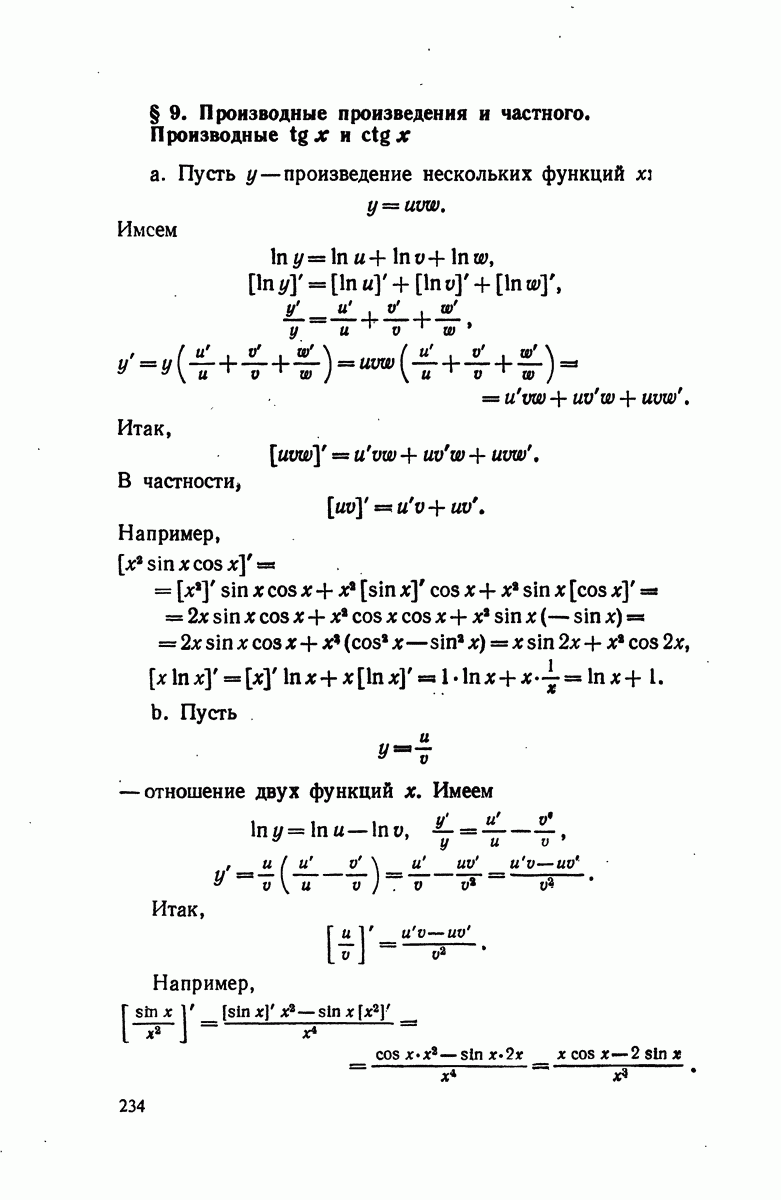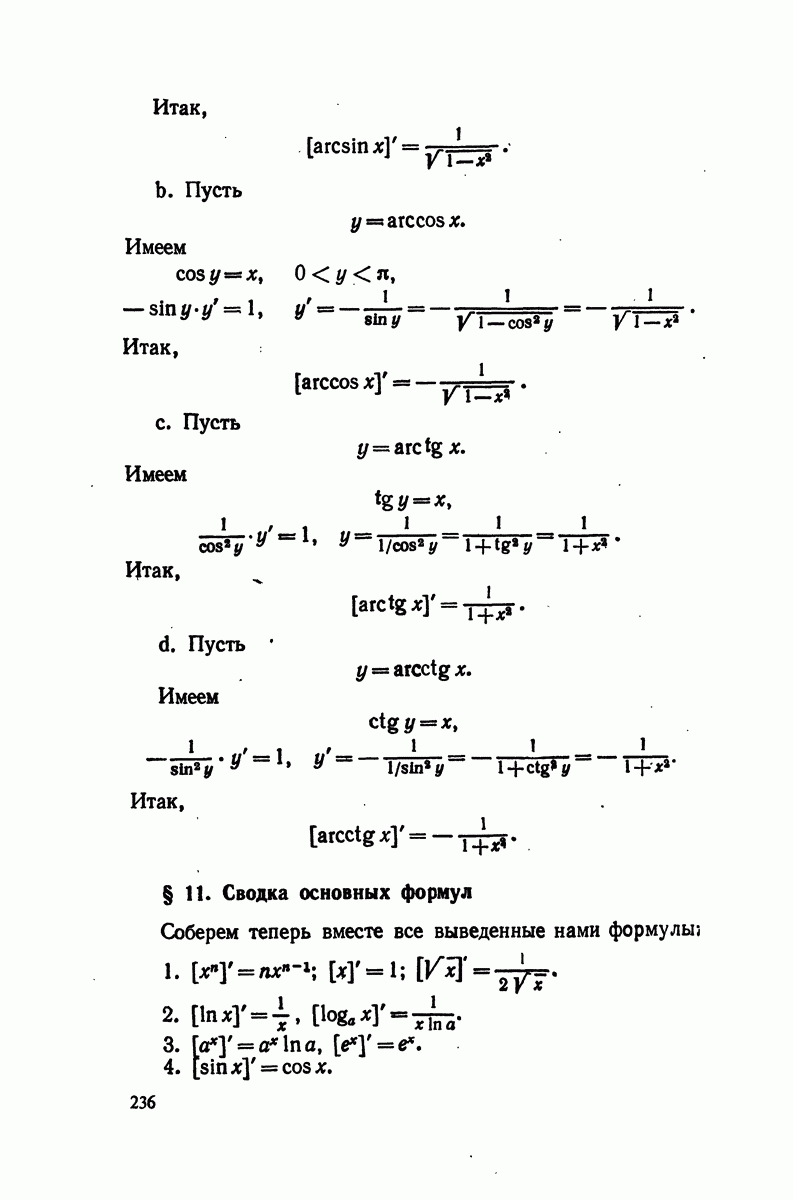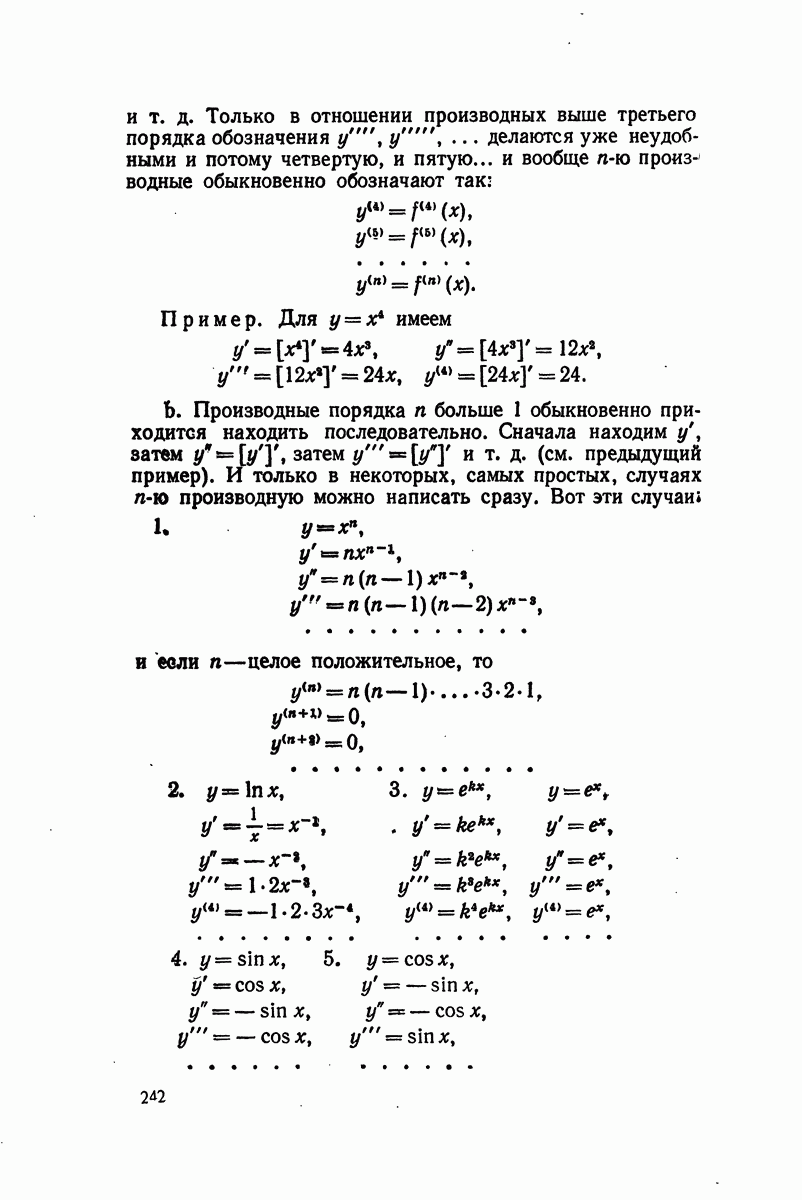| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Обзор и графическое изображение простейших функции одного аргумента
а. Мы начнем с рассмотрения наиболее простых функций.
Пусть мы имеем функцию первого порядка

Сначала разберем еще более простой случай

т. е. тот частный случай, когда 
Составим таблицу, давая  произвольные, например, целые значения, и вычисляя соответствующие значения у.
произвольные, например, целые значения, и вычисляя соответствующие значения у.

Примем теперь пары значений х и у за координаты точек и будем наносить на бумагу эти точки. Предположим сначала, что число А; положительно и что оно изображается отрезком  , а единица длины — отрезком
, а единица длины — отрезком  ; тогда, соединяя все точки, получим прямую АВ, изображенную на рис. 33.
; тогда, соединяя все точки, получим прямую АВ, изображенную на рис. 33.
В таблице даны семь пар значений  , эти пары нам дали семь точек.
, эти пары нам дали семь точек.
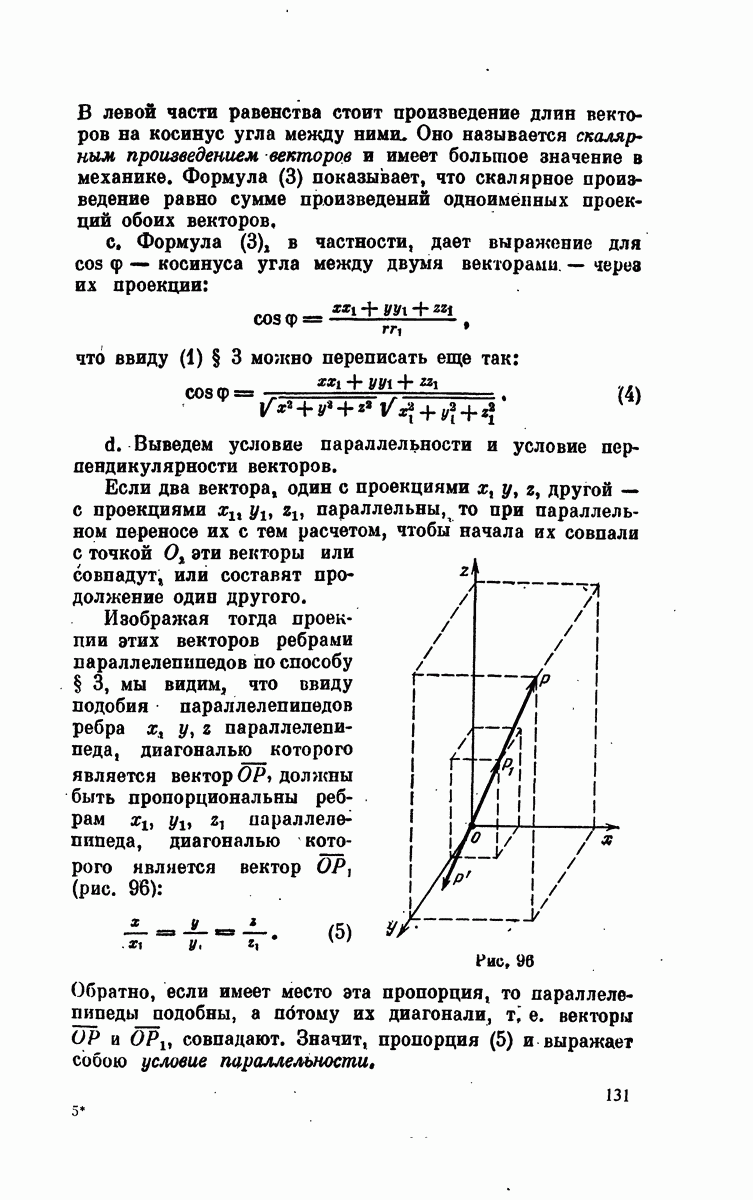
Но, очевидно, и любая пара значений х и у, полученная из уравнения (2), дает точку, лежащую на той же прямой. Обратно, любая точка (х; у) этой прямой имеет координаты, удовлетворяющие уравнению (2). Это следует непосредственно из подобия треугольников  Действительно,
Действительно,

т. е.

откуда

Из равенства (4) мы усматриваем, что

где а есть угол наклона прямой к положительному на правлению оси абсцисс.
Если k — число отрицательное, то для положительных значений х мы получим отрицательные значения у и обратно,

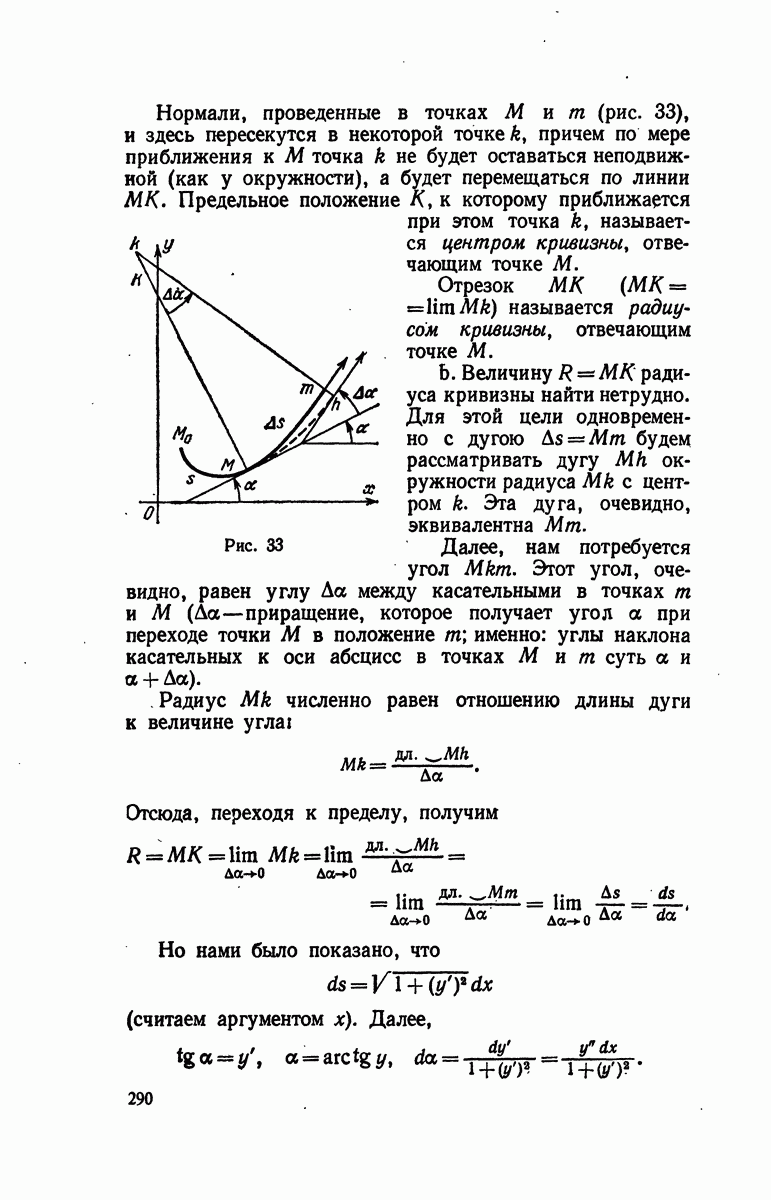
Рис. 33
Теперь мы получим прямую  , которая проходит также через начало координат но из второго угла в четвертый, а следовательно, наклонена к оси абсцисс под тупым углом
, которая проходит также через начало координат но из второго угла в четвертый, а следовательно, наклонена к оси абсцисс под тупым углом 
Нетрудно видеть, что

откуда

Таким образом, и здесь

Итак, графиком функции (2) всегда будет прямая линия, проходящая через начало координат и составляющая с положительным направлением оси абсцисс угол, тангенс которого равен коэффициенту при х. Этот коэффициент определяет собой наклон прямой к оси абсцисс. Если он положителен, то прямая проходит из первого координатного угла в третий, если же он отрицателен, то прямая проходит из второго угла в четвертый.
Поэтому число к называется угловым коэффициентом прямой.
b. Возьмем теперь прямую АВ

и подпимем ее вверх на расстояние b так, чтобы она заняла положение EF (см. рис. 33). Тогда все ординаты прямой АВ увеличатся на одно и то же положительное число  и мы получим уравнение
и мы получим уравнение

Если число b будет отрицательно, то мы получим прямую СМ, сдвинутую вниз. Следовательно, уравнение (1) выражает прямую, не проходящую через начало координат, но отсекающую на оси ординат отрезок, равный  и имеющую угловой коэффициент к. При различных b и к мы можем получить все прямые плоскости (кроме прямыху параллельных оси
и имеющую угловой коэффициент к. При различных b и к мы можем получить все прямые плоскости (кроме прямыху параллельных оси  ).
).
Итак, графиком функции первого порядка всегда является прямая, поэтому уравнение (1) называется уравнением прямой с угловым коэффициентом.
c. В частности, если  то получим прямую PQ (см. рис. 33), параллельную оси абсцисс, отстоящую от нее на расстояние, равное
то получим прямую PQ (см. рис. 33), параллельную оси абсцисс, отстоящую от нее на расстояние, равное  Уравнение ее примет вид
Уравнение ее примет вид

т. е. функция первого порядка выродилась в постоянное число.
В дальнейшем постоянное число мы будем рассматривать как такую переменную величину, у которой все числовые значения равны. Поэтому можно сказать, что график постоянного числа есть прямая, параллельная оси абсцисс, отстоящая от нее на расстояние, равное этому постоянному числу, взятому по абсолютной величине.
d. Функции первого порядка очень часто встречаются в науке. Нередко зависимость, выраженную функцией первого порядка, называют линейным законом. Приведем конкретный пример: мы знаем, что если тело движется равномерно ускоренно, то, обозначая через  начальную скорость, через g ускорение, через t время и через v скорость, мы будем иметь формулу:
начальную скорость, через g ускорение, через t время и через v скорость, мы будем иметь формулу:

Таким образом, изменение скорости в равномерно ускоренном движении подчиняется линейному закону.
e. Частным случаем линейного закона будет зависимость

Мы замечаем, что если х увеличить в несколько раз, то численная величина у также увеличится во столько же раз; если х уменьшится в некоторое число раз, то численная величина у уменьшится во столько же раз.
Такая функциональная зависимость называется прямой пропорциональностью. Общим математическим выражением прямой пропорциональности является уравнение (2), причем число к носит название коэффициента пропорциональности.
Если начальная скорость  , то зависимость скорости или времени в равномерно ускоренном движении выразится так:
, то зависимость скорости или времени в равномерно ускоренном движении выразится так:

Коэффициентом пропорциональности здесь является постоянное ускорение 
f. Теперь займемся графическим изображением функций второго порядка.
Мы рассмотрим лишь частный случай

Пусть для определенности, сначала  , т. е.
, т. е.

Составляем таблицу

Построим по этой таблице точки. По нанесенным точкам схематически обрисовывается контур кривой  изображенной на рис. 34.
изображенной на рис. 34.
Полученная кривая называется параболой второго порядка, точка О называется ее вершиной. Мы здесь пользовались так называемым способом построения кривой по точкам. Это наиболее употребительный и простой способ вычерчивания графиков функций. Заметим, что чем подробнее мы составим таблицу, т. е. чем меньше промежутки будем брать для последовательных значений аргумента, тем точнее мы построим кривую.
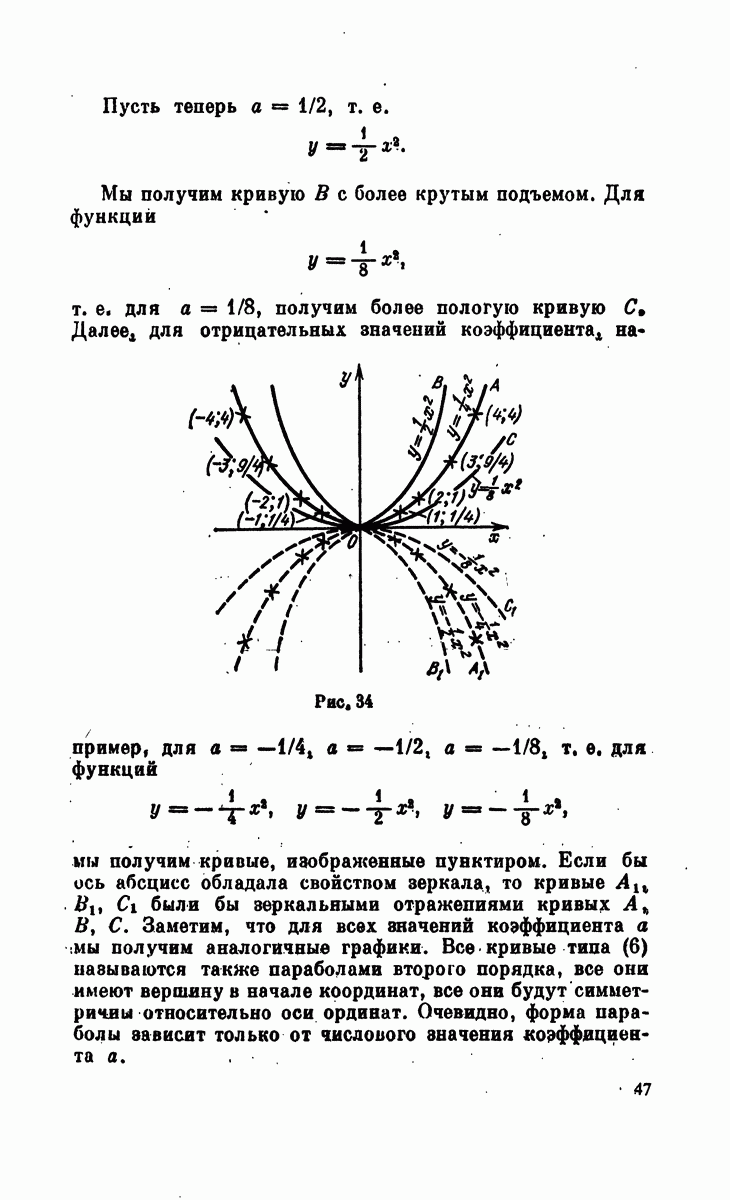
Пусть теперь  , т. е.
, т. е.

Мы получим кривую В с более крутым подъемом. Для функций

т. е. для а  получим более пологую кривую С.
получим более пологую кривую С.

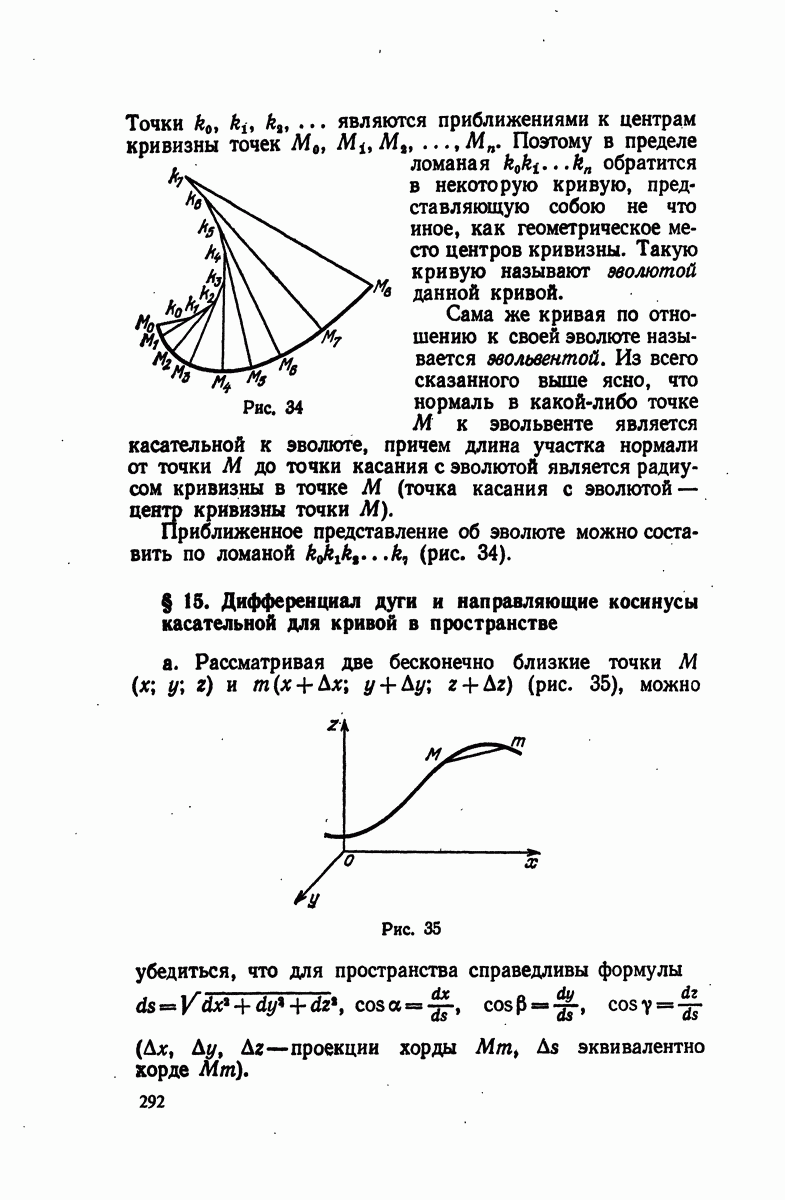
Рис. 34
Далее для отрицательных значений коэффициента например, для  , т. е. для функций
, т. е. для функций

мы получим кривые, изображенные пунктиром. Если бы ось абсцисс обладала свойством зеркала, то кривые  были бы зеркальными отражениями кривых
были бы зеркальными отражениями кривых  . Заметим, что для всех значений коэффициента а мы получим аналогичные графики. Все кривые типа (6) называются также парабодами второго порядка, все она имеют вершину в начале координат, все они будут симметричны относительно оси ординат. Очевидно, форма параболы зависит только от числового значения коэффициента а.
. Заметим, что для всех значений коэффициента а мы получим аналогичные графики. Все кривые типа (6) называются также парабодами второго порядка, все она имеют вершину в начале координат, все они будут симметричны относительно оси ординат. Очевидно, форма параболы зависит только от числового значения коэффициента а.
Если мы пожелаем вычерчивать графики функции второго порядка общего типа

то получим также параболы, но вершины их не будут находиться в начале координат; это будет строго доказано позднее.
д. Функции второго порядка в науке встречаются часто. Когда мы говорим о табличном задании функций то приводим пример зависимости напряжений в ободе махового колеса от скорости его вращения. Эта зависимость может быть очень точно выражена формулой

где  — плотность материала колеса.
— плотность материала колеса.
Еще пример: при равномерно ускоренномдвижепии путь зависит от времени, и эта зависимость выражается формулой

где g — ускорение силы тяжести,  — начальная скорость,
— начальная скорость,  — начальный путь, S — путь, пройденный за время
— начальный путь, S — путь, пройденный за время 
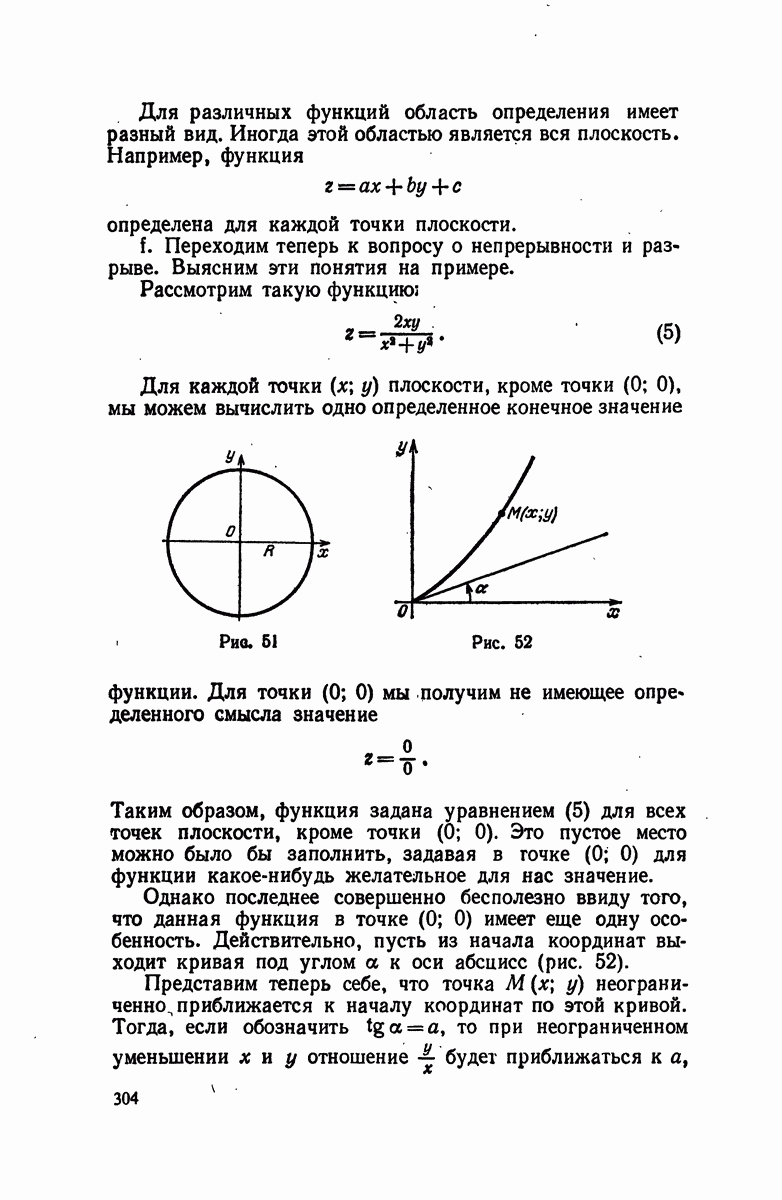
h. Теперь займемся дробными функциями. Для простоты мы рассмотрим только один частный; но очень важный случай

При построении графиков дробных функций мы нередко встречаемся с одной характерной особенностью, которая отлично видна даже на этом простом примере, а именно, при составлении таблицы для данной функции мы аргументу можем задавать любые значения, за исключением  так как на нуль делить нельзя. Таким образом, при
так как на нуль делить нельзя. Таким образом, при  наша функция не существует. Последнее обстоятельство вынуждает нас осмотреть окрестности нуля. Для этого мы будем задавать аргументу численно уменьшающиеся положительные и отрицательные значения осторожно подходя к нулю справа и слева, например, так как это показано в нижеследующей таблице, где для определенности мы взяли
наша функция не существует. Последнее обстоятельство вынуждает нас осмотреть окрестности нуля. Для этого мы будем задавать аргументу численно уменьшающиеся положительные и отрицательные значения осторожно подходя к нулю справа и слева, например, так как это показано в нижеследующей таблице, где для определенности мы взяли 

Построим теперь график нашей функции (рис. 35).

Рис. 35
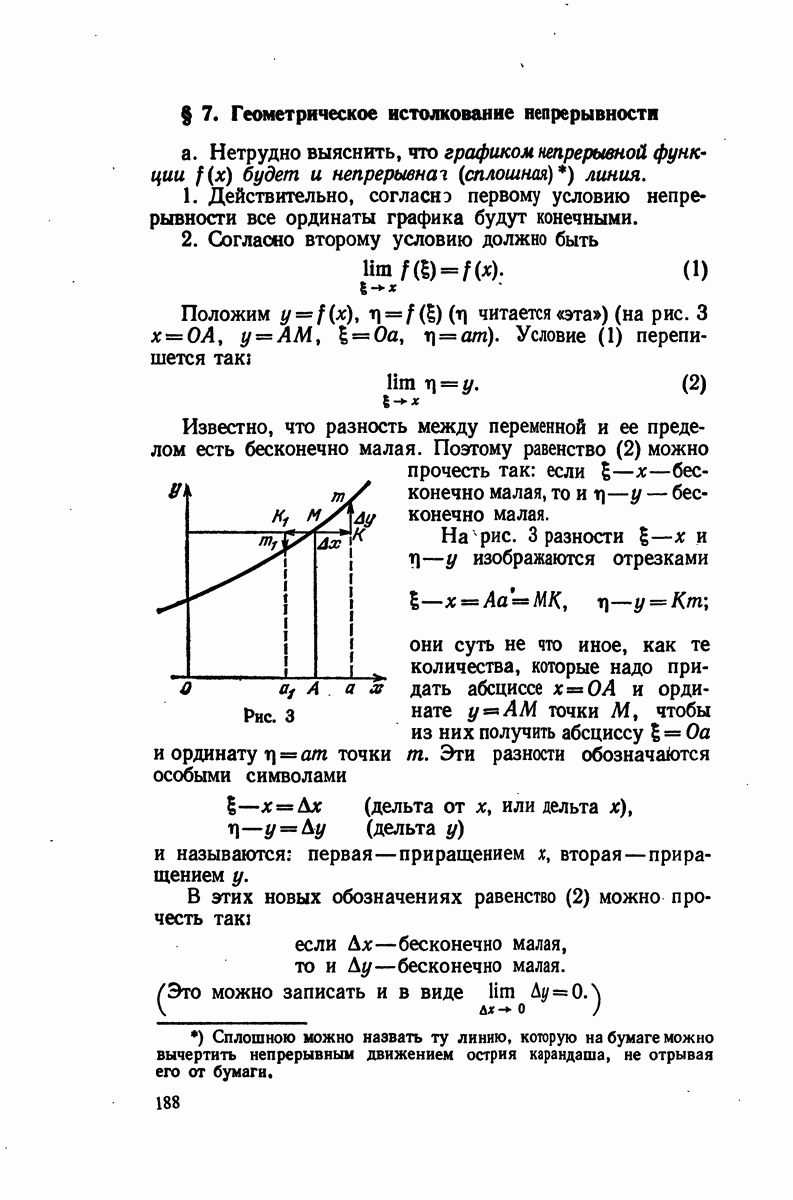
Мы изобразили график функции сплошной линией. При рассмотрении его нетрудно заметить, что кривая состоит из двух ветвей, совершенно отделенных друг от друга координатными осями, так что одна ветвь расположена в первом координатном углу, а другая — в третьем.
Если мы проследим ход кривой, безгранично удаляясь  от начала координат в обе стороны по горизонтальному и но вертикальному направлениям, то убедимся, что каждая ветвь неограниченно приближается к координатным осям, но никогда их не достигает. Заметим, что, вообще, если мы встречаемся с какой-либо кривой, которая неограниченно стремится к некоторой прямой, то такая прямая называется асимптотой кривой. Таким образом, изображенная на чертеже кривая имеет две асимптоты, одной является ось абсцисс, другой ось ординат.
от начала координат в обе стороны по горизонтальному и но вертикальному направлениям, то убедимся, что каждая ветвь неограниченно приближается к координатным осям, но никогда их не достигает. Заметим, что, вообще, если мы встречаемся с какой-либо кривой, которая неограниченно стремится к некоторой прямой, то такая прямая называется асимптотой кривой. Таким образом, изображенная на чертеже кривая имеет две асимптоты, одной является ось абсцисс, другой ось ординат.
Если мы возьмем  , то получим кривую, изображенную на чертеже пунктиром; она является зеркальным отражением первой кривой относительно оси абсцисс, а также и относительно оси ординат.
, то получим кривую, изображенную на чертеже пунктиром; она является зеркальным отражением первой кривой относительно оси абсцисс, а также и относительно оси ординат.
Для других значений к мы получим аналогичные кривые. Все кривые типа (1) называются равнобочными гиперболами, все они имеют своими асимптотами координатные оси, все они состоят из двух отдельных ветвей причем при положительных к ветви будут расположены в первом и третьем координатных углах, а при отрицательных к ветви будут расположены во втором и четвертом координатных углах.
k. Уравнение (1) показывает, что если величину аргумента  увеличить в несколько раз, то численная величина функции у уменьшается во столько же раз, и обратно: при уменьшении аргумента в несколько раз численное значение функции во столько же раз увеличивается.
увеличить в несколько раз, то численная величина функции у уменьшается во столько же раз, и обратно: при уменьшении аргумента в несколько раз численное значение функции во столько же раз увеличивается.
Такая зависимость называется обратной пропорциональностью, и уравнение (8) выражает математически в общем виде закон обратной пропорциональности.
Приведем конкретный пример на закон обратной пропорциональности.
Из фивики известно, что при постоянных массе газа и температуре произведение величины объема газа на величину его давления есть величина постоянная.
Если обозначить объем через а давление через  то можем написать
то можем написать  или же
или же  где с — постоянная величина.
где с — постоянная величина.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- § 1. Ось
- § 2. Вектор
- § 3. Направленные углы
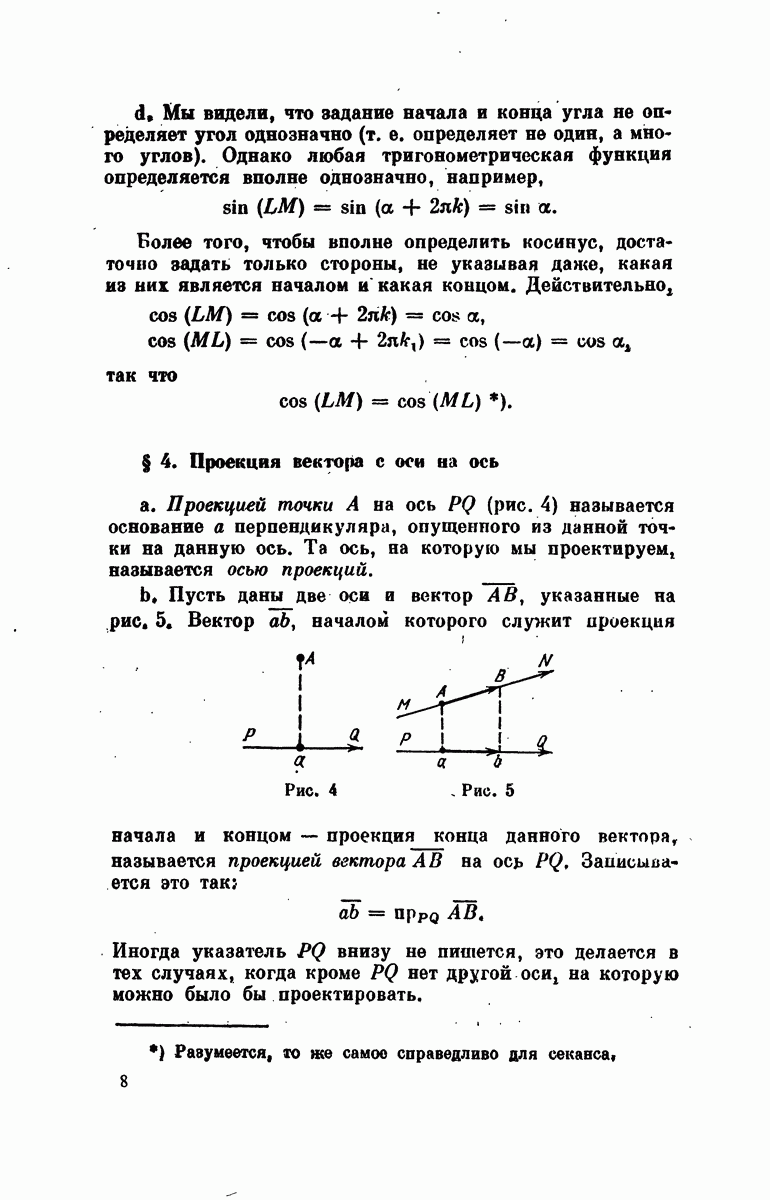
- § 4. Проекция вектора с оси на ось
- § 5. Векторные цепи
- § 6. Цепи углов
- § 7. Проекции вектора на две взаимно перпендикулярные оси
- § 8. Угол между двумя лекторами. Условия параллельности и перпендикулярности
- S 9. Упражнения и контрольные вопросы
- Глава 2. КООРДИНАТЫ
- § 1. Метод координат
- § 2. Основные задачи, решаемые методом координат
- § 3. Упражнения
- Глава 3. ФУНКЦИИ
- § 1. Переменные в постоянные
- § 2. Понятие о функциональной зависимости
- § 3. Классификация математических функций
- § 4. Обзор и графическое изображение простейших функции одного аргумента
- § 5. Обратные функции
- § 6. Понятие об уравнении линии
- § 7. Упражнения
- Глава 4. ПРЯМАЯ
- § 1. Уравнение прямой, проходящей через данную точку
- § 2. Общее уравнение прямой
- § 3. Частные случаи
- § 4. Переход к уравнению с угловым коэффициентом
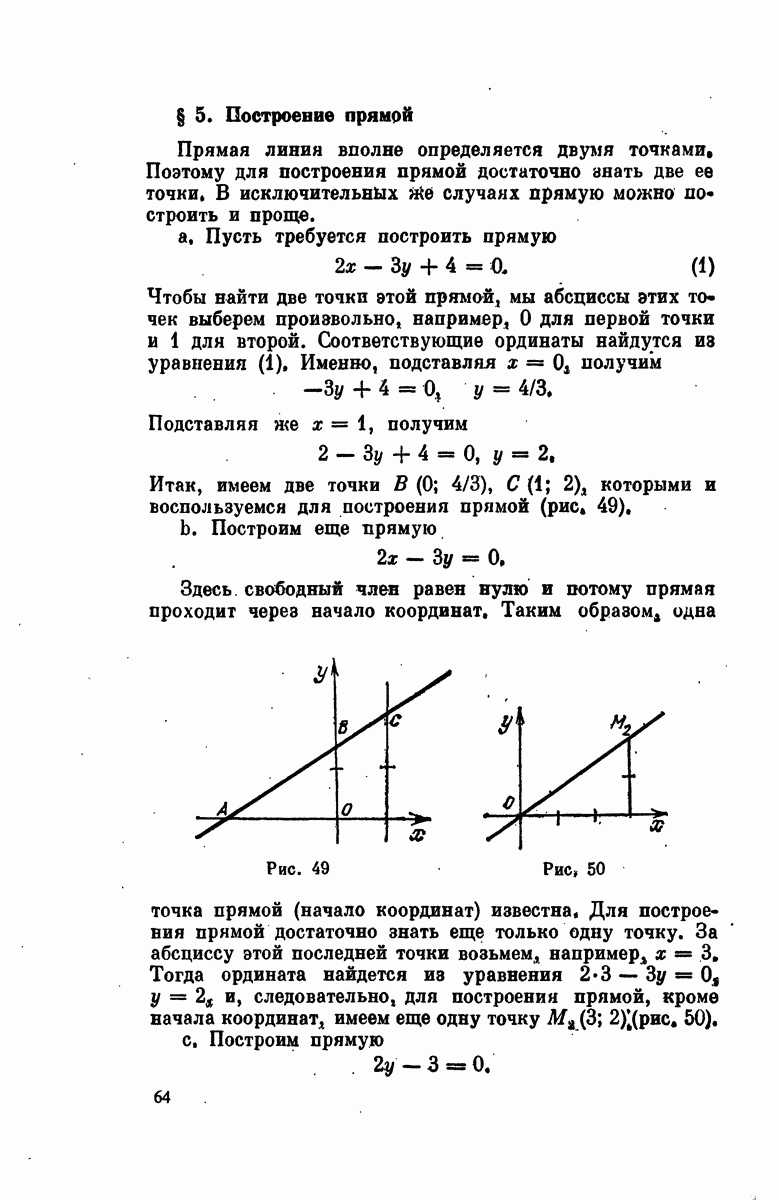
- § 5. Построение прямой
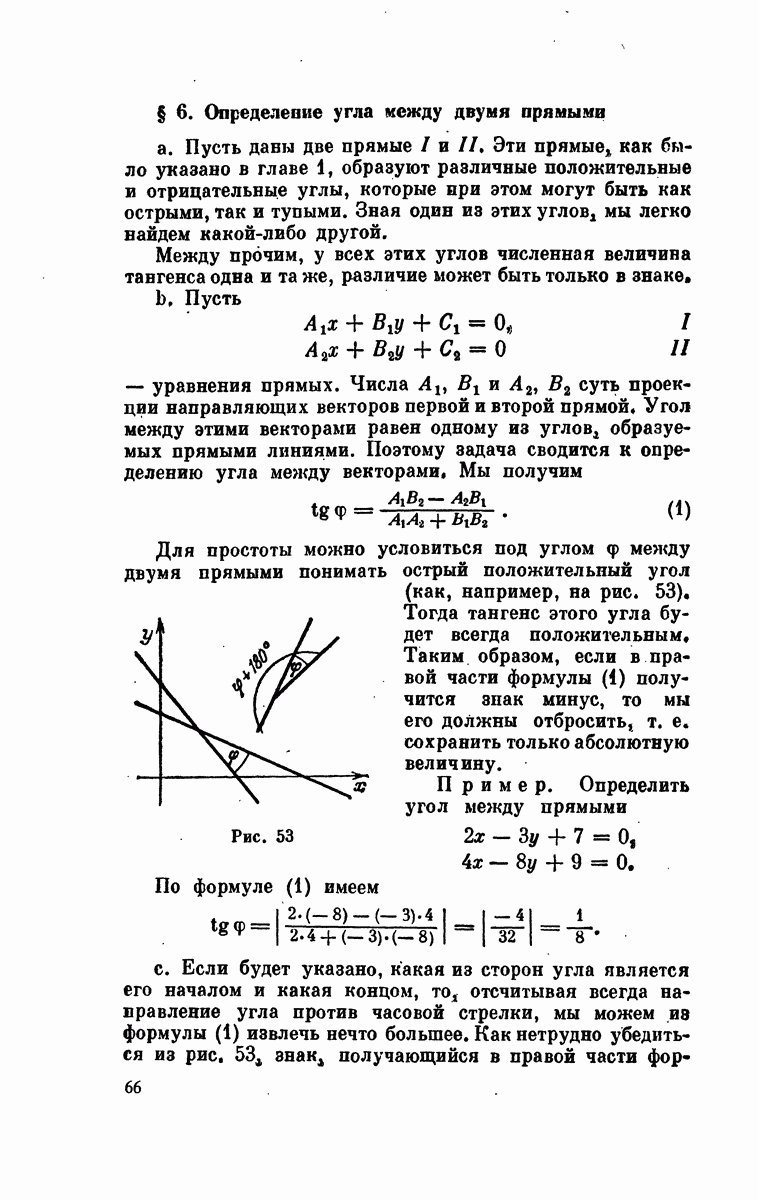
- § 6. Определение угла между двумя прямыми
- § 7. Условие совпадения прямых
- § 8 Пересечение прямых
- § 9. Расстояние от точки до прямой
- § 10. Другой подход к выводу уравнения прямой
- § 11. Прямая, проходящая через две точки
- § 12. Уравнение прямой в отрезках на осях
- § 13. Задачи на прямую линию
- Глава 5. ПРОСТЕЙШИЕ КРИВЫЕ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- § 1. Окружность
- § 2. Эллипс. Построение посредством нитн. Зависимость между полуосями и полуфокусным расстоянием
- § 3. Построение эллипса по точкам
- § 4. Уравнение эллипса
- § 5. Связь эллипса с окружностью
- § 6. Директрисы эллипса
- § 7. Гипербола. Построение посредством нити
- § 8. Построение гиперболы по точкам
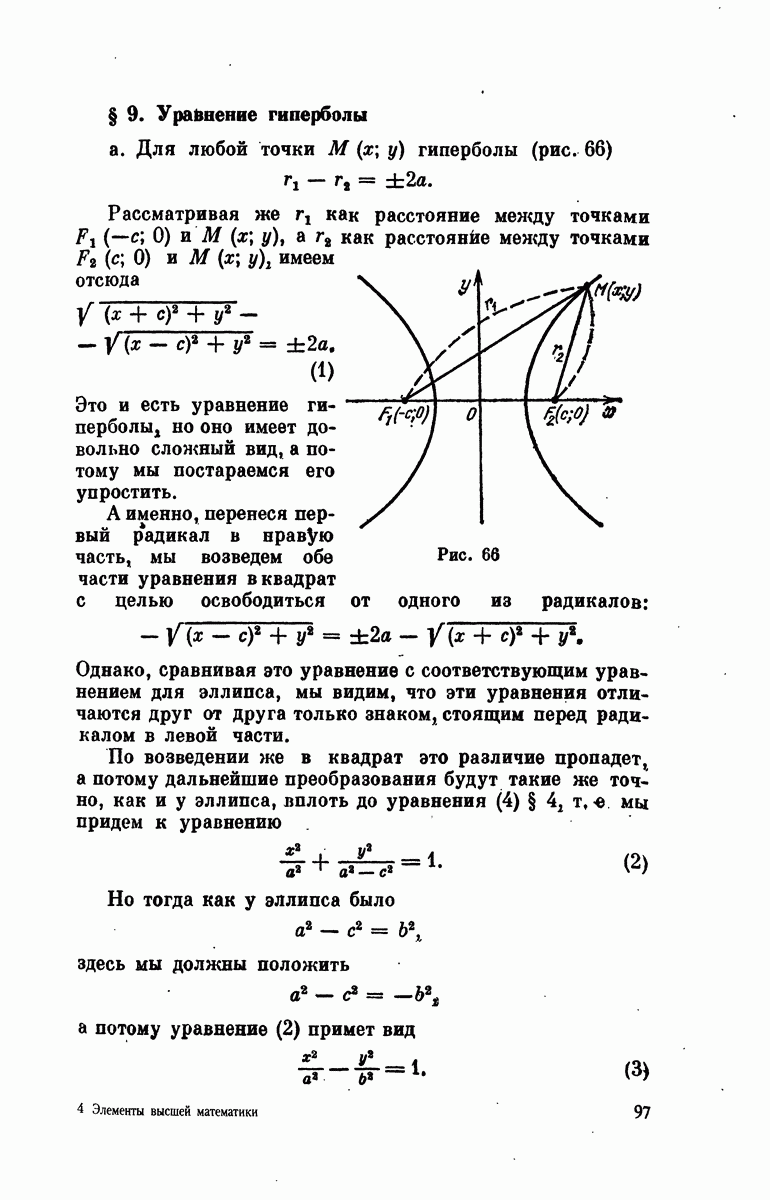
- § 9. Уравнение гиперболы
- § 10. Асимптоты. Геометрическое значение b
- § 11. Директрисы гиперболы
- § 12. Парабола. Построение по точкам
- § 13. Уравнение параболы
- § 14. Преобразование координат
- § 15. Пример на упрощение уравнения кривой путем параллельного переноса осей
- § 16. Поворот осей
- § 17. Общий случай
- § 18. Полярные координаты
- § 19. Спираль Архимеда
- § 20. Логарифмическая спираль
- § 21. Примеры на составление полярных уравнений кривых
- § 22. Выражение прямоугольных координат через полярные
- § 23. Уравнение лемнискаты
- § 24. Параметрическое задание линий
- § 25. Построение графика
- § 26. Циклоида
- § 27. Упражнения
- Глава 6. ВЕКТОРЫ, ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
- § 1. Оси, векторы, углы
- § 2. Проекции
- § 3. Проекции на три взаимно перпендикулярные оси. Длина вектора через проекции
- § 4. Простейшие зависимости, содержащие величину вектора, проекции и направляющие косинусы
- § 5. Проекция вектора на оси. Косинус угла между двумя векторами. Скалярное произведение векторов
- § 6. Координаты
- § 7. Выражение проекций вектора через координаты конца и начала
- § 8. Выражение длины вектора через координаты концов. Расстояние между двумя точками
- § 9. Деление отрезка в данном отношении
- § 10. График уравнения с двумя переменными
- § 11. Поверхность как след, образуемый перемещением некоторой деформируемой плоской кривой
- § 12. Цилиндрические поверхности
- § 13. Обратная задача. Уравнение шаровой поверхности
- § 14. Уравнение плоскости, проходящей через данную точку
- § 15. Общее уравнение плоскости
- § 16. Частные случаи
- § 17. Выяснение расположения плоскости относительно осей
- § 18. Угол между плоскостями. Условие параллельности. Условие перпендикулярности
- § 19. Условие совпадения плоскостей
- § 20. Расстояние от точке до плоскости
- § 21. Прямая как пересечение двух плоскостей
- § 22. Прямая, проходящая через данную точку
- § 23. Прямая, проходящая через две точки
- § 24. Переход от системы уравнений прямой в общем виде к системе в виде пропорций
- § 25. Угол между прямыми. Условие параллельности. Условие перпендикулярности
- § 26. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности
- § 27. Простейшие поверхности. Эллипсоид
- § 28. Другие простейшие поверхности
- § 29. Кривая в пространстве как пересечение двух поверхностей
- § 30. Параметрические уравнения
- § 31. Винтовая линия
- § 32. Параметрические уравнения в механике
- § 33. Переход от параметрического представления к общему и обратно
- § 34. Преобразование координат
- § 35. Упражнения
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. Бесконечно малые
- § 2. Понятие предела переменной величины
- § 3. Понятие бесконечно большой
- § 4. Свойства бесконечно малых
- § 5. Основные свойства пределов
- § 6. Предел непрерывной функции
- § 7. Геометрическое истолкование непрерывности
- § 8. Свойство непрерывной функции
- § 9. Предел функции, зависящей от нескольких переменных
- § 10. Особые случаи разыскания предела
- § 11. Замечательный тригонометрический предел
- § 12. Признак существования предела
- § 13. Сходимость бесконечных рядов
- § 14. Простейшие признаки сходимости
- § 15. Основание натуральных логарифмов
- § 16. Порядок бесконечно малых
- § 17. Упражнения
- Глава 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная как угловой коэффициент касательной
- § 2. Производная как предел
- § 3. Пояснение общей теории на примере. Уравнения касательной и нормали
- § 4. Механическое значение производной
- § 5. Производные трех простейших функций
- § 6. Производная постоянного и суммы. Вынесение постоянного множителя за знак производной
- § 7. Производная сложной функции
- § 8. Разыскание производных путем логарифмирования. Производные функции х^n при любом n к функции а^x.
- § 9. Производные произведения и частного. Производные tg x и ctg x.
- § 10. Производные обратных тригонометрических функций
- § 11. Сводка основных формул
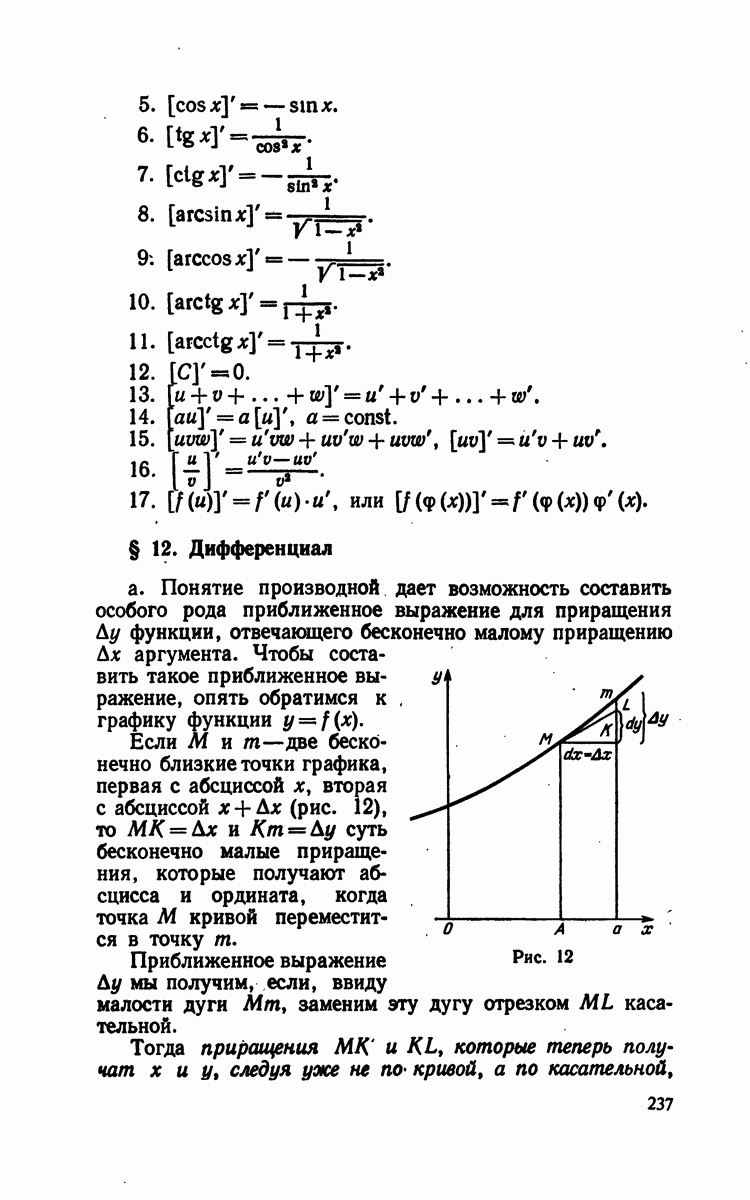
- § 12. Дифференциал
- § 13. Основные формулы для дифференциалов
- § 14. Высшие производные
- § 15. Высшие дифференциалы
- § 16. Дифференцирование неявных функций
- § 17. Дифференцирование функций, заданных параметрическим способом
- § 18. Преобразование дифференциалов к новой переменной
- § 19. Упражнения
- Глава 3. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- § 1. Непрерывность первой производной
- § 2. Возрастание и убывание функций. Максимум и минимум
- § 3. Приложение к построению графиков
- § 4. Наибольшее и наименьшее значения функции
- § 5. Прикладные задачи на наибольшее и наименьшее значения
- § 6. Направление выпуклости, точки перегиба
- § 7. Приложение к построению графиков
- § 8. Построение графиков разрывных функций
- § 9. Признак максимума и минимума, основанный на исследовании знака первой производной
- § 10. Признак максимума и минимума, основанный на исследовании знака второй и высших производных
- § 11. Асимптоты
- § 12. Дифференциал дуги
- § 13. Направляющие косинусы касательной
- § 14. Радиус кривизны, центр кривизны
- § 15. Дифференциал дуги и направляющие косинусы касательной для кривой в пространстве
- § 16. Упражнения
- Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 1. Функции многих переменных. Область определения. Непрерывность
- § 2. Частные производные и полный дифференциал
- § 3. Частные производные и полный дифференциал сложной функции многих переменных
- § 4. Дифференцирование неявных функций
- § 5. Частные производные и полные дифференциалы высшего порядка
- § 6. Упражнения
- ЧАСТЬ ТРЕТЬЯ. ОСНОВЫ ТЕОРИИ ЧИСЕЛ
- Глава 1. ТЕОРИЯ ДЕЛИМОСТИ
- § 2. Общий наибольший делитель
- § 3. Общее наименьшее кратное
- § 4. Простые числа
- § 5. Единственность разложения на простые сомножители
- § 6. Непрерывные дроби и их связь с алгоритмом Евклида
- Вопросы к главе 1
- Глава 2. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
- § 1. Функции [x] и {x}
- § 2. Мультипликативные функции
- § 3. Число делителей и сумма делителей
- § 4. Функция Мёбиуса
- § 5. Функция Эйлера
- Вопросы к главе II
- Глава 3. СРАВНЕНИЯ
- § 2. Свойства сравнений, подобные свойствам равенств
- § 3. Дальнейшие свойства сравнений
- § 4. Полная система вычетов
- § 5. Приведенная система вычетов
- § 6. Теоремы Эйлера и Ферма
- Вопросы к главе 3
- Глава 4. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
- § 2. Сравнения первой степени
- § 3. Система сравнений первой степени
- § 4. Сравнения любой степени по простому модулю
- § 5. Сравнения любой степени по составному модулю
- Вопросы к главе 4
- Глава 5. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
- § 2. Символ Лежандра
- § 3. Символ Якоби
- § 4. Случай составного модуля
- Вопросы к главе 5
- Глава 6. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- § 2. Первообразные корни по модулям
- § 3. Разыскание первообразных корней по модулям
- § 4. Индексы по модулям
- § 5. Следствия предыдущей теории
- § 6. Индексы по модулю 2^a
- § 7. Индексы по любому составному модулю
- Вопросы к главе 6
- Глава 7. ХАРАКТЕРЫ
- § 2. Важнейшие свойства характеров
- Вопросы к главе 7
- РЕШЕНИЯ ВОПРОСОВ
- Решения к главе 2
- Решения к главе 3
- Решения к главе 4
- Решения к главе 5
- Решения к главе 6
- ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ