| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 13. Задачи на прямую линию
1а. Написать уравнение прямой, проходящей через точку  , если известно, что перпендикулярный к прямой направляющий вектор имеет проекции
, если известно, что перпендикулярный к прямой направляющий вектор имеет проекции  Ответ:
Ответ: 
Написать уравнение прямой» если известно, что она проходит через начало координат, а ее направляющий вектор имеет проекции  Ответ:
Ответ: 
2а. Написать уравнение прямой, проходящей через точку М (0; 5), если известно, что проекция направляющего вектора на ось абсцисс в три раза больше его проекции на ось ординат. Ответ: 
Написать уравнение прямой, проходящей через точку М (1; 1), если ее направляющий вектор является биссектрисой второго координатного угла. Ответ: 
3а. Каковы проекции направляющего вектора для прямой

и какова длина этого вектора? Ответ: длина вектора равна 17.
3b. Что произойдет с направляющим вектором прямой

если обе части уравнения умножить на какое-либо положительное число N? Ответ: направляющий вектор изменит свою длину в N раз, но направление его не изменится.
4а. Проверить, лежит ли точка (5; 7) на прямой  Отвёт; лежит
Отвёт; лежит
4b. На прямой  найти точку, у которой абсцисса
найти точку, у которой абсцисса 
5а. Найти на прямой  такую точку, у которой абсцисса равна ординате. Ответ:
такую точку, у которой абсцисса равна ординате. Ответ: 
5b. На прямой  найти такую точку, у которой абсцисса в десять раз больше ординаты. Ответ:
найти такую точку, у которой абсцисса в десять раз больше ординаты. Ответ:  .
.
6а. На прямой  найти точку, у которой абсцисса на 4 больше ординаты. Ответ:
найти точку, у которой абсцисса на 4 больше ординаты. Ответ: 
6b. На прямой  найти точку, у которой ордината
найти точку, у которой ордината  Ответ:
Ответ: 
7а. На прямой  найти точку, равноудаленную от
найти точку, равноудаленную от  в (2; 1). Ответ: (3; 3).
в (2; 1). Ответ: (3; 3).
7b. На прямой  найти точку, равноотстоящую от точек (1; 1) и (4; 2). Ответ: (2; 3),
найти точку, равноотстоящую от точек (1; 1) и (4; 2). Ответ: (2; 3),
8а. Построить прямые:

8b. Построить прямые:

9а. Какая прямая имеет уравнение 
Какая прямая имеет уравневие  ?
?
10а. Построить прямые:

10b. Построить прямые:

11а. Вычислить тангенс острого угла между прямыми  Ответ:
Ответ:  . Вычислить тангенс острого угла между прямыми
. Вычислить тангенс острого угла между прямыми  . Ответ:
. Ответ: 
12а. Найти острый угол между прямыми  Ответ:
Ответ:  45°,
45°,
12b. Найти острый угол между прямыми  . Ответ:
. Ответ:  .
.
13а. Привести к виду с угловым коэффициентом уравнения прямых:

13b. Найти острый угол между прямыми  . Ответ:
. Ответ:  .
.
14а. Вычислить тангенс острого угла между прямыми  Ответ:
Ответ: 
14b. Вычислить тангенс острого угла между прямыми и 

14с. Вычислить тангенс угла между прямыми  Ответ:
Ответ: 
15а. Будут ли параллельны прямые 
Будут ли параллельны прямые 
16а. Будут ли перпендикулярны прямые

16b. Будут ли перпендикулярны прямые

17а. Даны прямые:

Какие из них параллельны и какие перпендикулярны?
17b. Почему следует считать, что прямые

параллельны?
17с. Почему следует считать, что прямые

перпендикулярны?
18а. Через точку (5; 2) провести прямую параллельно прямой  Ответ:
Ответ: 
18b. Написать уравнение прямой, проходящей через точку  параллельно прямой
параллельно прямой  . Ответ:
. Ответ: 
19а. Через точку  провести прямую перпендикулярно прямой
провести прямую перпендикулярно прямой  . Ответ:
. Ответ:  . Через точку
. Через точку  провести прямую перпендикулярно прямой
провести прямую перпендикулярно прямой  . Ответ:
. Ответ:  .
.
20а. Через точку  провести прямую параллельно прямой
провести прямую параллельно прямой  . Ответ:
. Ответ:  .
.
20b. Через точку (3; —1) провести прямую перпендикулярно прямой  . Ответ:
. Ответ:  .
.
21а. Через точку  провести прямую под углом 45° к прямой
провести прямую под углом 45° к прямой  . Ответ:
. Ответ: 
Через точку  провести прямую под углом 45° к прямой
провести прямую под углом 45° к прямой  . Ответ:
. Ответ: 
22а. Через точку (1; 2) провести прямую, наклоненную к прямой  под углом, тангенс которого равен 5. Ответ:
под углом, тангенс которого равен 5. Ответ:  .
.
22b. Через точку (3; —4) провести прямую, наклоненную к прямой  под углом, тангенс которого равен 2. Ответ:
под углом, тангенс которого равен 2. Ответ: 
23а. Совпадают ли прямые  ? Ответ: совпадают,
? Ответ: совпадают,
23b. Совпадают ли прямые  ? Ответ: не совпадают.
? Ответ: не совпадают.
24а. Найти точку пересечения прямых  . Ответ:
. Ответ:  .
.
24b. Найти точку пересечения прямых  . Ответ:
. Ответ: 
25а. Пересекаются ли прямые  Если нет, то почему?
Если нет, то почему?
25b. Можно ли сказать, что совпадающие прямые пересекаются? Если да, то сколько точек пересечения имеют совпадающие прямые?
26а. Найти координаты вершин треугольника, если стороны заданы уравнениями  . Ответ: (1; 2), (2; 1), (3; 3).
. Ответ: (1; 2), (2; 1), (3; 3).
26b. Найти вершины треугольника, если его стороны заданы уравнениями  Ответ:
Ответ:  .
.
27а. Через точку пересечения прямых  провести прямую параллельно примой
провести прямую параллельно примой  Ответ:
Ответ: 
Через точку пересечения прямых  провести прямую перпендикулярно прямой
провести прямую перпендикулярно прямой 
28а. Написать уравнение высоты треугольника, образованного прямыми  если известно, что высота опущена из точки пересечения первых двух прямых на третью. Ответ:
если известно, что высота опущена из точки пересечения первых двух прямых на третью. Ответ: 
28b. Через точку пересечения прямых  провести прямую параллельно прямой
провести прямую параллельно прямой  Ответ:
Ответ: 
29. Через точку пересечения прямых  провести прямую перпендикулярно прямой
провести прямую перпендикулярно прямой  в 0. Ответ:
в 0. Ответ: 
30а, Найти расстояние от точки (1; 1) до прямой  Ответ:
Ответ: 
Доказать, что расстояния от точки  до прямых
до прямых  одинаковы (равны 2).
одинаковы (равны 2).
31а. Доказать, что расстояние между двумя параллельными прямыми  выражается формулой
выражается формулой 
Найти расстояние между параллельными прямыми  Ответ:
Ответ: 
Найти расстояние между параллельными прямыми  Ответъ
Ответъ 
32а. Написать уравнение прямой, параллельной прямым  и проходящей посередине между ними. Ответ:
и проходящей посередине между ними. Ответ: 
Написать уравнение прямой, параллельной прямым  и делящей расстояние между ними в отношении
и делящей расстояние между ними в отношении  в направлении от первой прямой ко второй. Ответ:
в направлении от первой прямой ко второй. Ответ: 
32с. Провести прямую параллельво прямым

расположенную между ними так, чтобы расстояние ее до первой прямой было в два раза больше расстояния до второй прямой. Ответ:  .
.
33. Проследить за тем, какой знак имеет выражение

для различных точек плоскости:
a) Для точек, лежащих выше прямой  Ответ:
Ответ:  при
при  — при
— при  .
.
b) Для точек, лежащих ниже этой прямой. Ответ: — при.  при
при  .
.
c) Для точек, Лежащих справа от этой прямой Ответ:  при
при  — при
— при  .
.
d) Для точек, лежащих слева от этой прямой. Ответ: — при  при
при 
е) Для точек, лежащих по ту же сторону от прямой, что и начало координат. Ответ:  при
при  — при
— при 
f) Для точек, лежащих по другую сюрону от начала координат относительно этой прямой. Ответ: — при  при
при  .
.
34а. Узнать, лежит  точка (1; 2) выше или ниже прямой
точка (1; 2) выше или ниже прямой  Ответ: выше.
Ответ: выше.
34b. То же для точки  относительно прямой
относительно прямой  Ответ: выше.
Ответ: выше.
34с. Лежнт ли точка (3; 7) справа или слева от прямой  Ответ: слева.
Ответ: слева.
35а. Лежат ли точка  и начало координат по одну сторону или по разные стороны относительно прямой
и начало координат по одну сторону или по разные стороны относительно прямой  Ответ: по одну сторону.
Ответ: по одну сторону.
35b. Лежат ли точки (1; 2) и  одну или
одну или  разные стороны от прямой
разные стороны от прямой  Ответ: по разные стороны.
Ответ: по разные стороны.
36. Доказать, что точка (2; 2) находится внутри треугольника, заданного уравнениями сторон 
37а. Доказать, что если даны прямые  то уравнения обеих биссектрис двух смежных углов, образованных этими прямыми, будут
то уравнения обеих биссектрис двух смежных углов, образованных этими прямыми, будут

37b. Написать уравнение биссектрисы того угла между прямыми  в котором лежит точка
в котором лежит точка  Ответ:
Ответ: 
38. Черев точку (1; 1) провести прямую, равноудаленную от точек (6; 1) и (2) 5) и проходящую между ними, Ответ: 
39а. Вывести формулу для вычисления расстояния от точки до прямой, исходя из тех соображений, что удвоенная площадь треугольника вершинами которого служат точки  пересечения прямой с осями и данная точка
пересечения прямой с осями и данная точка  выражается произведением искомого расстояния на длину
выражается произведением искомого расстояния на длину 
39b. Доказать, что расстояние  от начала координат
от начала координат  прямой -
прямой -  выражается формулой
выражается формулой

40. Написать уравнение прямой, проходящей через точку (1; —1) и отстоящей от точки (4; 0) на расстояние 1. Ответ: две прямые 
41. Через точку (1; 0) провести прямую, проходящую над точкой (10; 3) на расстоянии 3 единиц от последней» Ответ: 
42. Написать уравнение прямой параллельной прямой

и отстоящей от нее на расстояние 2 единиц. Ответ: две прямые 
43а. Найти отражение точки (1; 8) относительно прямой  как в зеркале. Ответ: (7, 0). Указание. Отражением точки М относительно прямой РХР называется точка
как в зеркале. Ответ: (7, 0). Указание. Отражением точки М относительно прямой РХР называется точка  лежащая на продолжении перпендикуляра, опущенного на прямую из точки
лежащая на продолжении перпендикуляра, опущенного на прямую из точки  причем прямая делит расстояние между М и
причем прямая делит расстояние между М и  пополам.
пополам.
43b. Найти отражение точки (3; 3) относительно прямой  Ответ:
Ответ: 
44а. Написать уравнения сторон треугольника с вершинами  . Ответ:
. Ответ: 
Написать уравнения сторон треугольника, заданного вершинами  Ответ:
Ответ: 
45а. Провести прямую через точку (1; 2) и через точку пересечения прямых  . Ответ:
. Ответ: 
Провести прямую через точку  точку пересечения прямых
точку пересечения прямых  Ответ
Ответ 
Через точку пересечения прямых  провести прямую так, чтобы ее начальная ордината (отрезок на оси ординат) равнялась
провести прямую так, чтобы ее начальная ордината (отрезок на оси ординат) равнялась  . Ответ:
. Ответ: 
46. Даны вершины треугольника  Написать уравпение высоты, опущенной из точки
Написать уравпение высоты, опущенной из точки  Ответ:
Ответ: 
47. Найти площадь треугольника по координатам его вершин  вычисляя длину стороны и опущенного на нее перпендикуляра.
вычисляя длину стороны и опущенного на нее перпендикуляра. 

48а. Привести к виду в отрезках на осях уравнение  и построить эту прямую. Ответ;
и построить эту прямую. Ответ; 
48b. Привести к виду в отрезках на осях, а затем построить прямые:

49. Отрезки, отсекаемые прямой на осях, суть  Написать уравнение прямой в форме с углбвым коэффициентом. Ответ:
Написать уравнение прямой в форме с углбвым коэффициентом. Ответ: 
50. Написать уравнение прямой в форме в отрезках на осях, если дано, что она наклонена к оси абсцисс под углом 45° и отсекает на оси ординат отрезок длиной 1.
Ответ: 
51а. Черев точку (2; 1) провести прямую так, чтобы она отсекала от первого координатного угла площадь, равную 4. Ответ: 
Написать уравнение прямой, параллельной прямой  и отсекающей от первого координатного угла площадь, равную 5. Ответ:
и отсекающей от первого координатного угла площадь, равную 5. Ответ: 
52. Даны уравнения сторон треугольника 
a) Найти вершины. Ответ:  .
.
b) Найти центр масс. Ответ: (2; 4/3).
c) Найти уравнения медиан. Ответ: 
Найти уравнения высот. Ответ:  .
.
e) Найти прямые, проходящие через вершины параллельно сторонам. Ответ:  .
.
f) Вычислить периметр. Ответ: периметр равен  .
.
g) Вычислить длины высот. Ответ: 
Вычислить площадь этого треугольника. Ответ:  .
.
k) Найти центр и радиус описанного круга. Ответ центр 
1) Вычислить тангенсы углов этого треугольника» Ответ: 
53. Световой луч, падая из точки  и отражаясь от прямой
и отражаясь от прямой  проходит затем через точку
проходит затем через точку  Написать уравнение луча падающего и луча отраженного. Ответ:
Написать уравнение луча падающего и луча отраженного. Ответ: 
54. Доказать, что в равностороннем треугольнике сумма расстояний от любой внутренней точки до сторон постоянна, а именно равна стороне, умноженной на 
55. Даны две точки  . На оси абсцисс найти точку М так, чтобы угол
. На оси абсцисс найти точку М так, чтобы угол  был прямой. (Решить: а) не пользуясь уравнением прямой, b) пользуясь им.) Ответ: (4; 0).
был прямой. (Решить: а) не пользуясь уравнением прямой, b) пользуясь им.) Ответ: (4; 0).
56а. Основание равнобедренного треугольника имеет уравнение  Одна из боковых сторон имеет уравнение
Одна из боковых сторон имеет уравнение  Найта уравнение другой боковой стороны, если известно, что она проходит через точку (8; 9). Ответ:
Найта уравнение другой боковой стороны, если известно, что она проходит через точку (8; 9). Ответ: 
56b. Даны уравнения боковых сторон равнобедренного треугольника  точка (1; 2) на его основании. Написать уравнение основания. Ответ:
точка (1; 2) на его основании. Написать уравнение основания. Ответ: 
57. Написать уравнение прямой, равноудаленной отточек  Ответ:
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- § 1. Ось
- § 2. Вектор
- § 3. Направленные углы
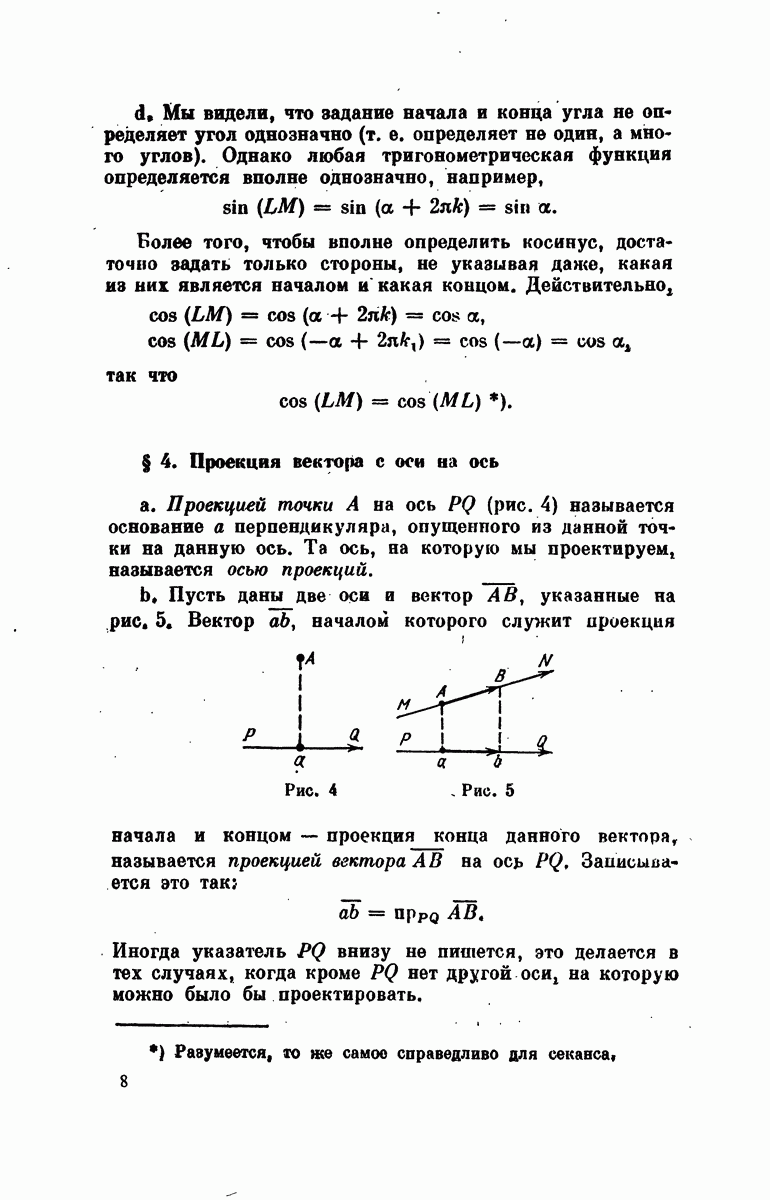
- § 4. Проекция вектора с оси на ось
- § 5. Векторные цепи
- § 6. Цепи углов
- § 7. Проекции вектора на две взаимно перпендикулярные оси
- § 8. Угол между двумя лекторами. Условия параллельности и перпендикулярности
- S 9. Упражнения и контрольные вопросы
- Глава 2. КООРДИНАТЫ
- § 1. Метод координат
- § 2. Основные задачи, решаемые методом координат
- § 3. Упражнения
- Глава 3. ФУНКЦИИ
- § 1. Переменные в постоянные
- § 2. Понятие о функциональной зависимости
- § 3. Классификация математических функций
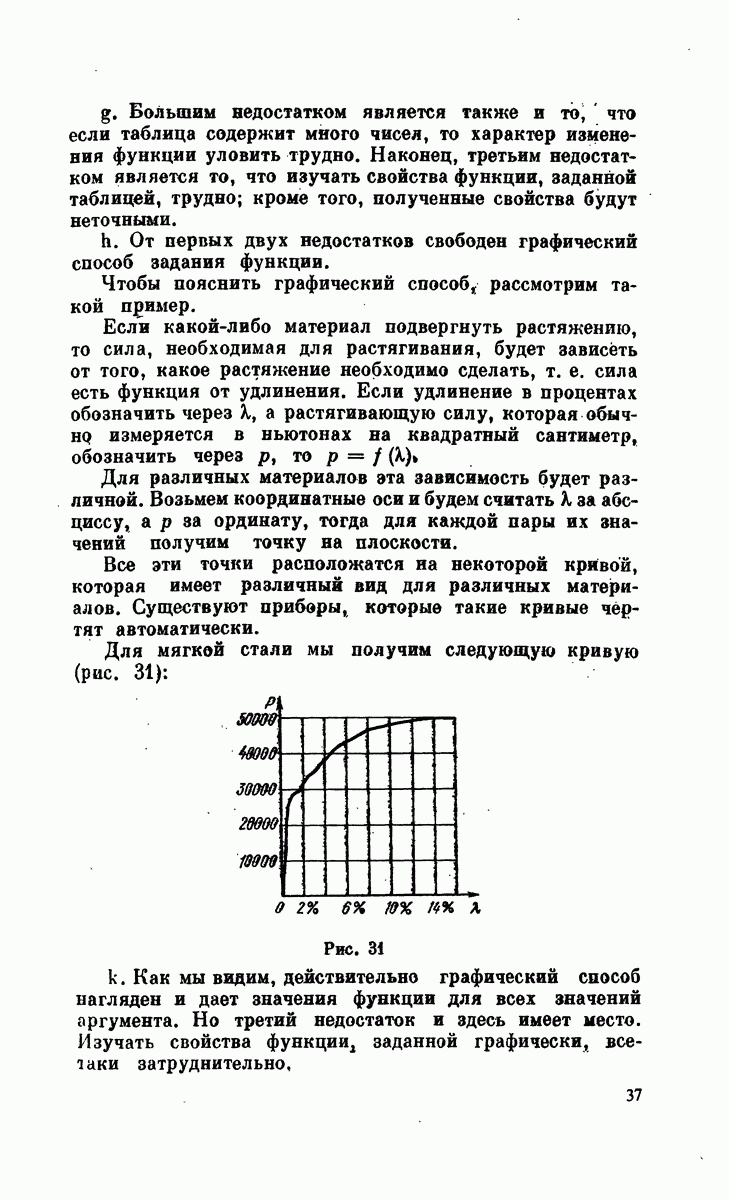
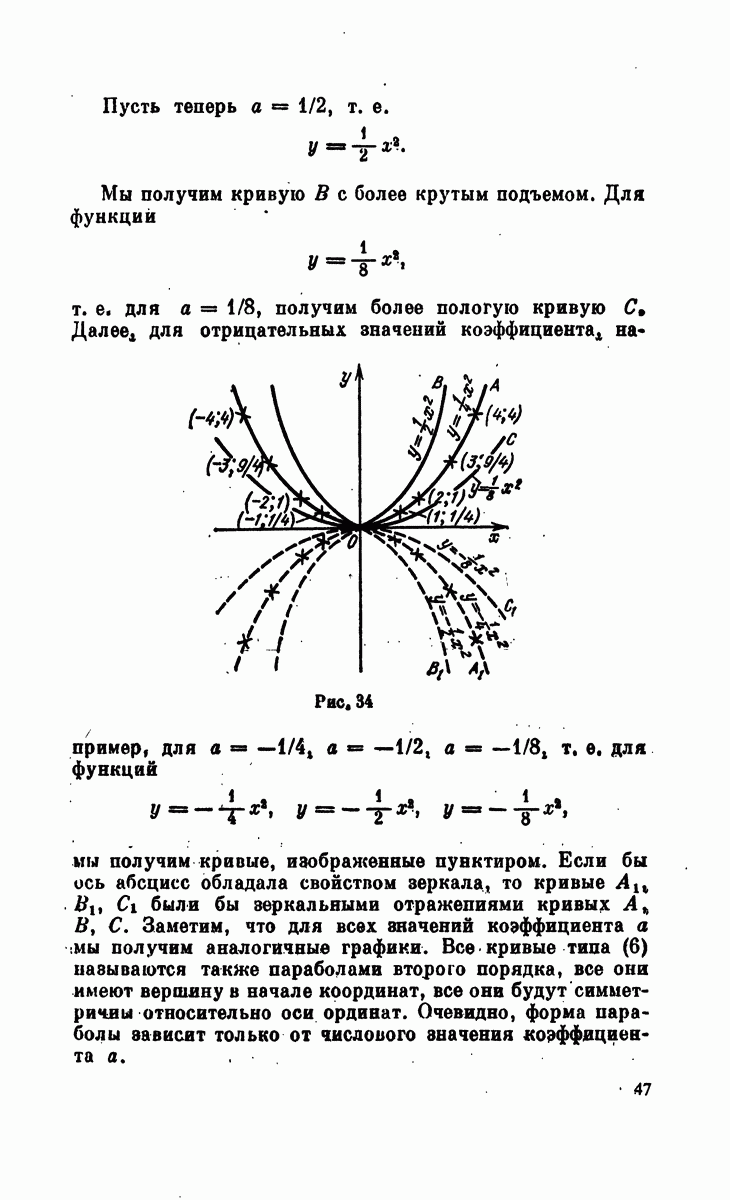
- § 4. Обзор и графическое изображение простейших функции одного аргумента
- § 5. Обратные функции
- § 6. Понятие об уравнении линии
- § 7. Упражнения
- Глава 4. ПРЯМАЯ
- § 1. Уравнение прямой, проходящей через данную точку
- § 2. Общее уравнение прямой
- § 3. Частные случаи
- § 4. Переход к уравнению с угловым коэффициентом
- § 5. Построение прямой
- § 6. Определение угла между двумя прямыми
- § 7. Условие совпадения прямых
- § 8 Пересечение прямых
- § 9. Расстояние от точки до прямой
- § 10. Другой подход к выводу уравнения прямой
- § 11. Прямая, проходящая через две точки
- § 12. Уравнение прямой в отрезках на осях
- § 13. Задачи на прямую линию
- Глава 5. ПРОСТЕЙШИЕ КРИВЫЕ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- § 1. Окружность
- § 2. Эллипс. Построение посредством нитн. Зависимость между полуосями и полуфокусным расстоянием
- § 3. Построение эллипса по точкам
- § 4. Уравнение эллипса
- § 5. Связь эллипса с окружностью
- § 6. Директрисы эллипса
- § 7. Гипербола. Построение посредством нити
- § 8. Построение гиперболы по точкам
- § 9. Уравнение гиперболы
- § 10. Асимптоты. Геометрическое значение b
- § 11. Директрисы гиперболы
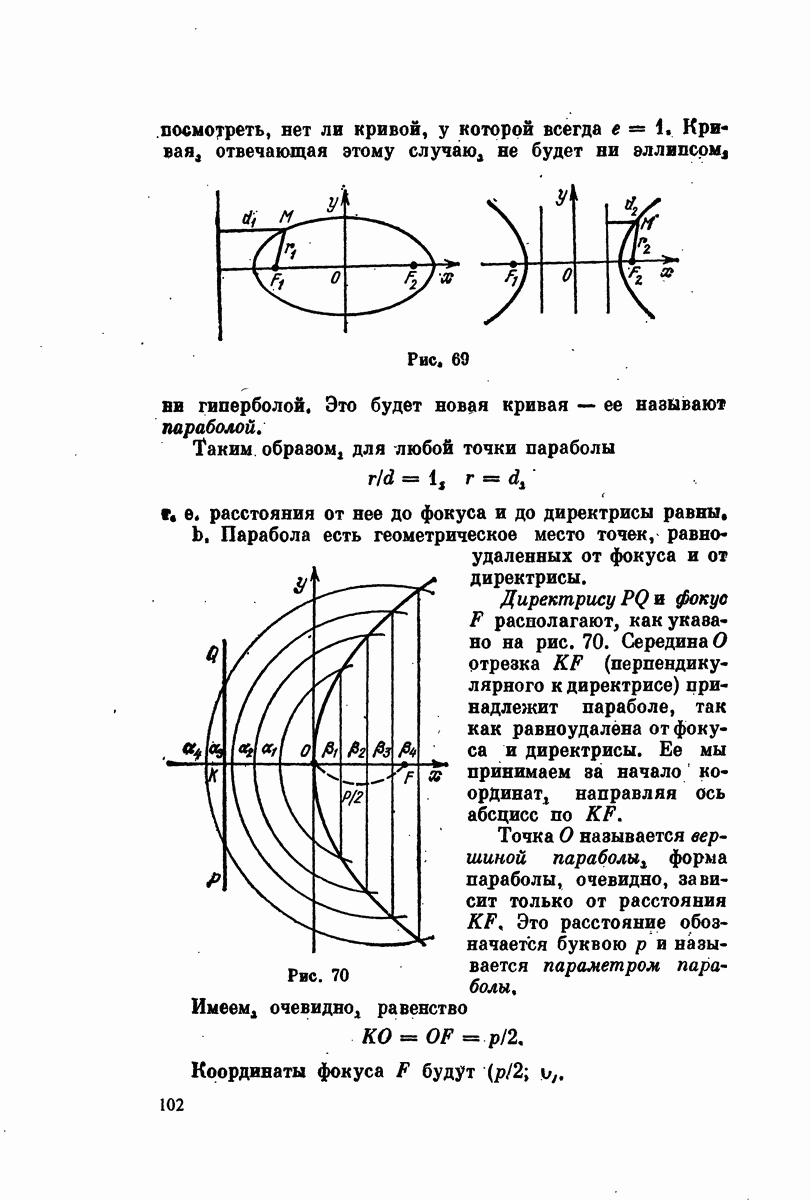
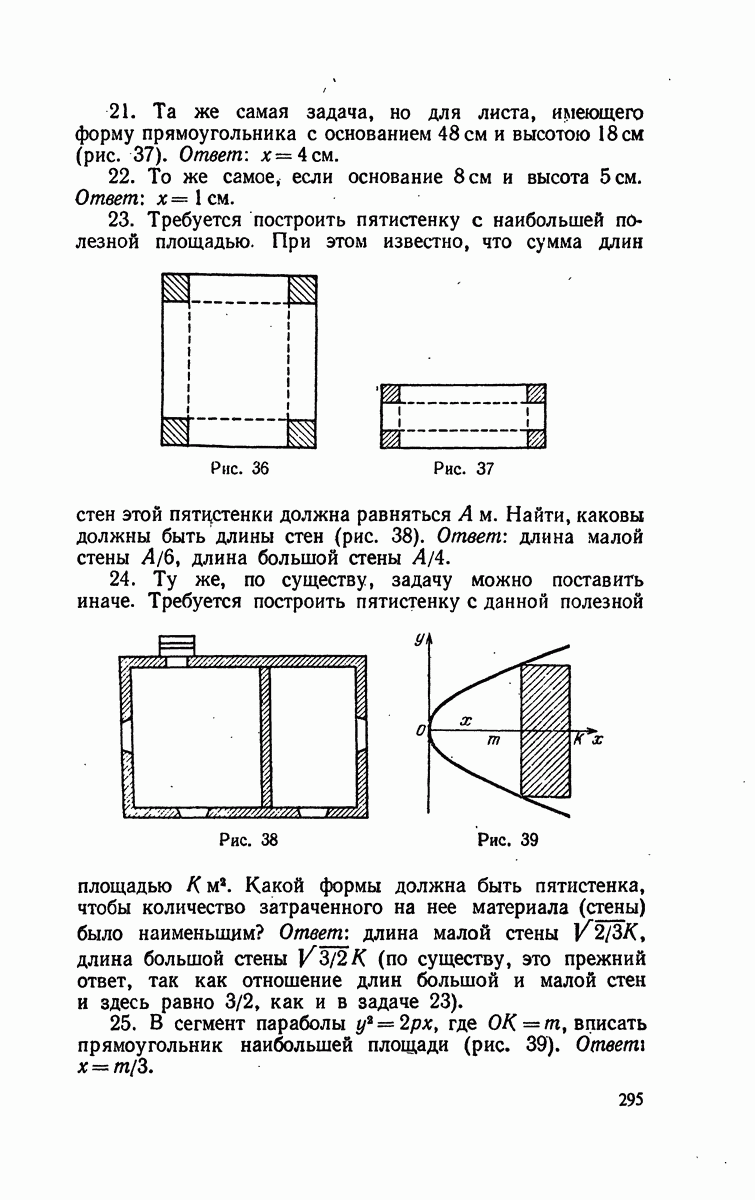
- § 12. Парабола. Построение по точкам
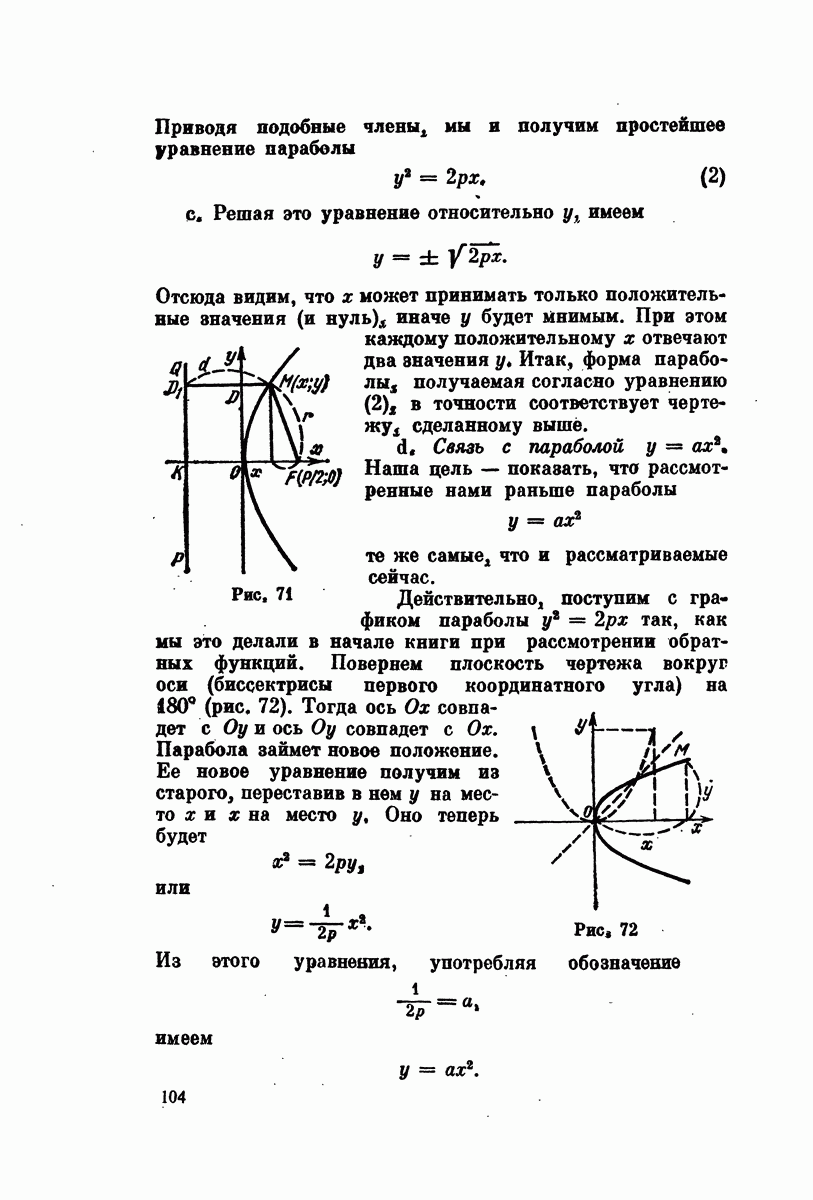
- § 13. Уравнение параболы
- § 14. Преобразование координат
- § 15. Пример на упрощение уравнения кривой путем параллельного переноса осей
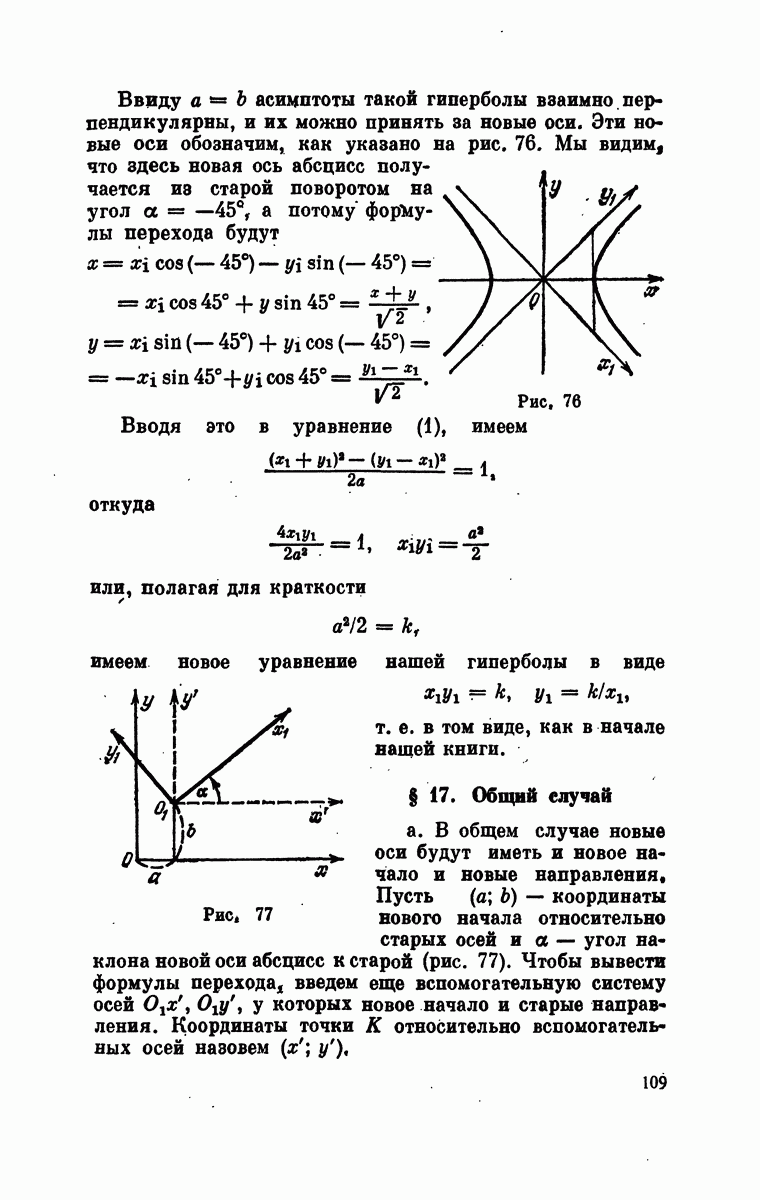
- § 16. Поворот осей
- § 17. Общий случай
- § 18. Полярные координаты
- § 19. Спираль Архимеда
- § 20. Логарифмическая спираль
- § 21. Примеры на составление полярных уравнений кривых
- § 22. Выражение прямоугольных координат через полярные
- § 23. Уравнение лемнискаты
- § 24. Параметрическое задание линий
- § 25. Построение графика
- § 26. Циклоида
- § 27. Упражнения
- Глава 6. ВЕКТОРЫ, ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
- § 1. Оси, векторы, углы
- § 2. Проекции
- § 3. Проекции на три взаимно перпендикулярные оси. Длина вектора через проекции
- § 4. Простейшие зависимости, содержащие величину вектора, проекции и направляющие косинусы
- § 5. Проекция вектора на оси. Косинус угла между двумя векторами. Скалярное произведение векторов
- § 6. Координаты
- § 7. Выражение проекций вектора через координаты конца и начала
- § 8. Выражение длины вектора через координаты концов. Расстояние между двумя точками
- § 9. Деление отрезка в данном отношении
- § 10. График уравнения с двумя переменными
- § 11. Поверхность как след, образуемый перемещением некоторой деформируемой плоской кривой
- § 12. Цилиндрические поверхности
- § 13. Обратная задача. Уравнение шаровой поверхности
- § 14. Уравнение плоскости, проходящей через данную точку
- § 15. Общее уравнение плоскости
- § 16. Частные случаи
- § 17. Выяснение расположения плоскости относительно осей
- § 18. Угол между плоскостями. Условие параллельности. Условие перпендикулярности
- § 19. Условие совпадения плоскостей
- § 20. Расстояние от точке до плоскости
- § 21. Прямая как пересечение двух плоскостей
- § 22. Прямая, проходящая через данную точку
- § 23. Прямая, проходящая через две точки
- § 24. Переход от системы уравнений прямой в общем виде к системе в виде пропорций
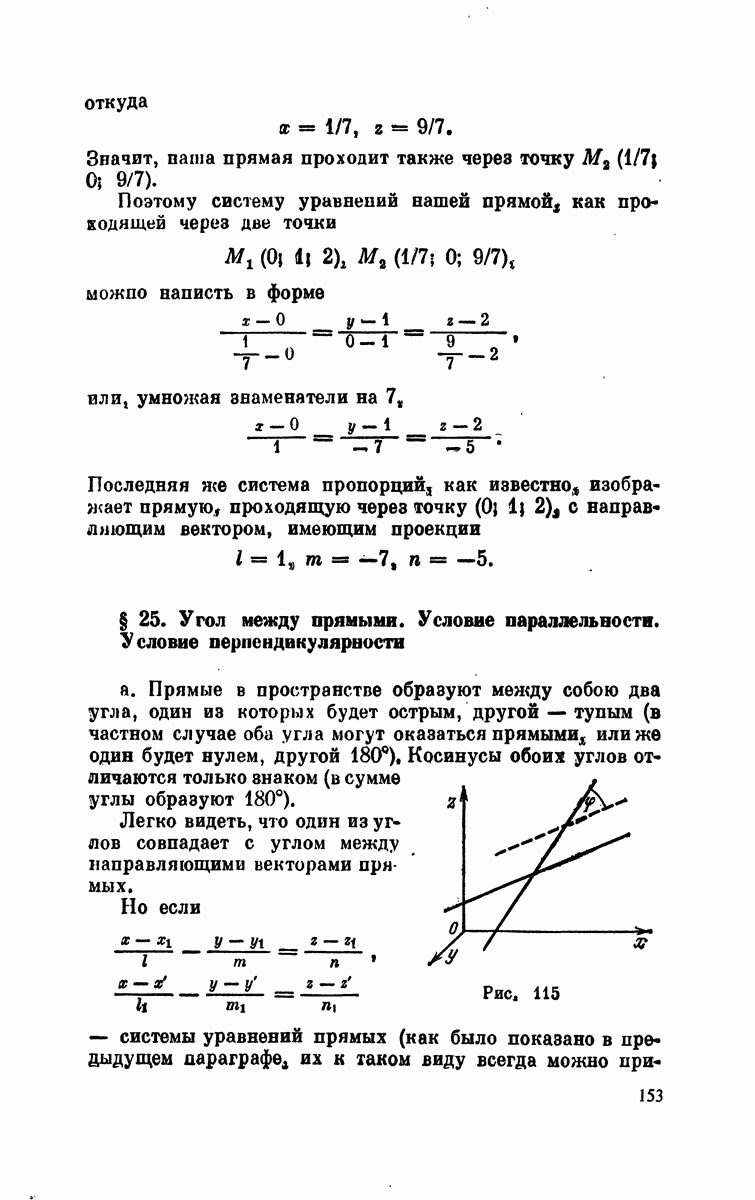
- § 25. Угол между прямыми. Условие параллельности. Условие перпендикулярности
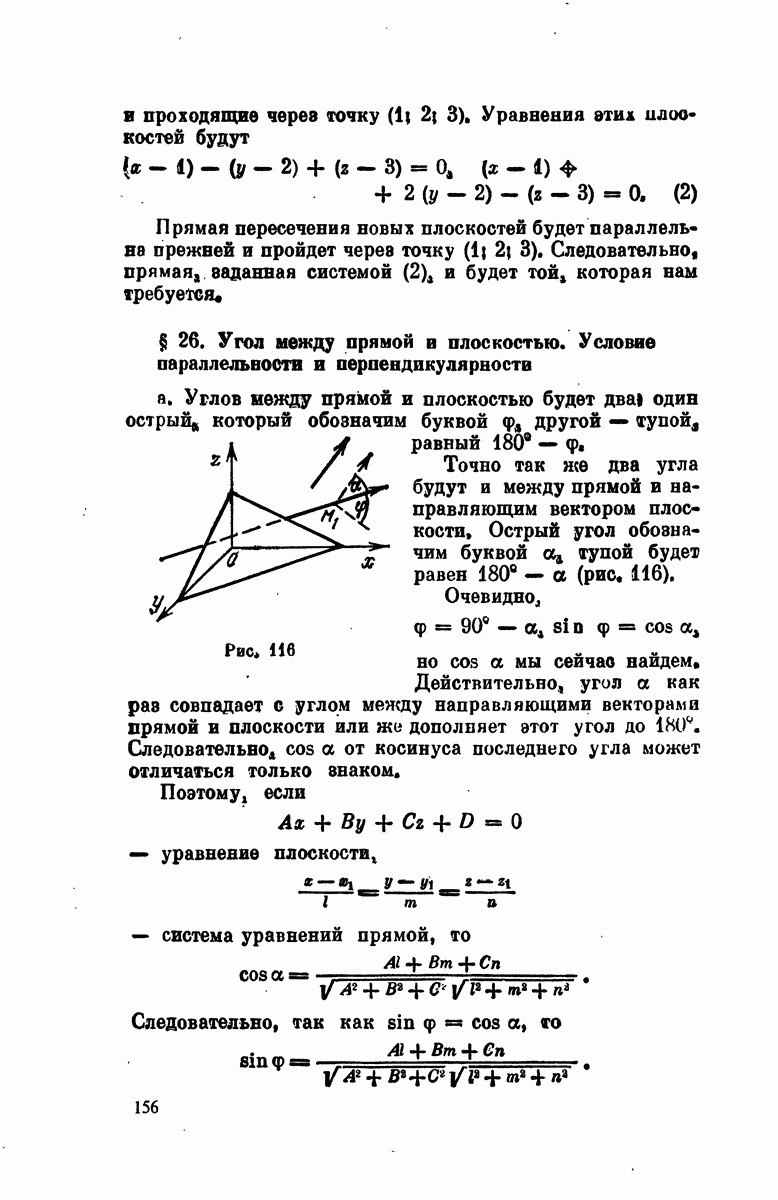
- § 26. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности
- § 27. Простейшие поверхности. Эллипсоид
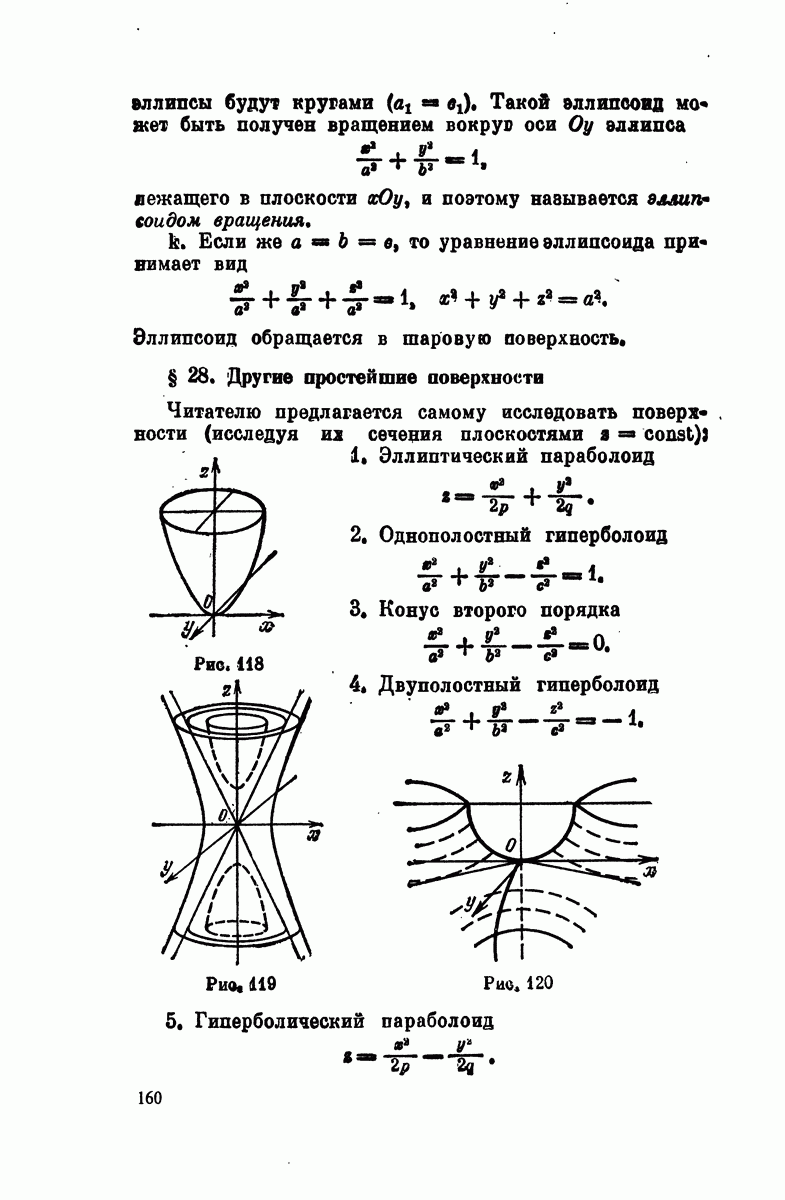
- § 28. Другие простейшие поверхности
- § 29. Кривая в пространстве как пересечение двух поверхностей
- § 30. Параметрические уравнения
- § 31. Винтовая линия
- § 32. Параметрические уравнения в механике
- § 33. Переход от параметрического представления к общему и обратно
- § 34. Преобразование координат
- § 35. Упражнения
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. Бесконечно малые
- § 2. Понятие предела переменной величины
- § 3. Понятие бесконечно большой
- § 4. Свойства бесконечно малых
- § 5. Основные свойства пределов
- § 6. Предел непрерывной функции
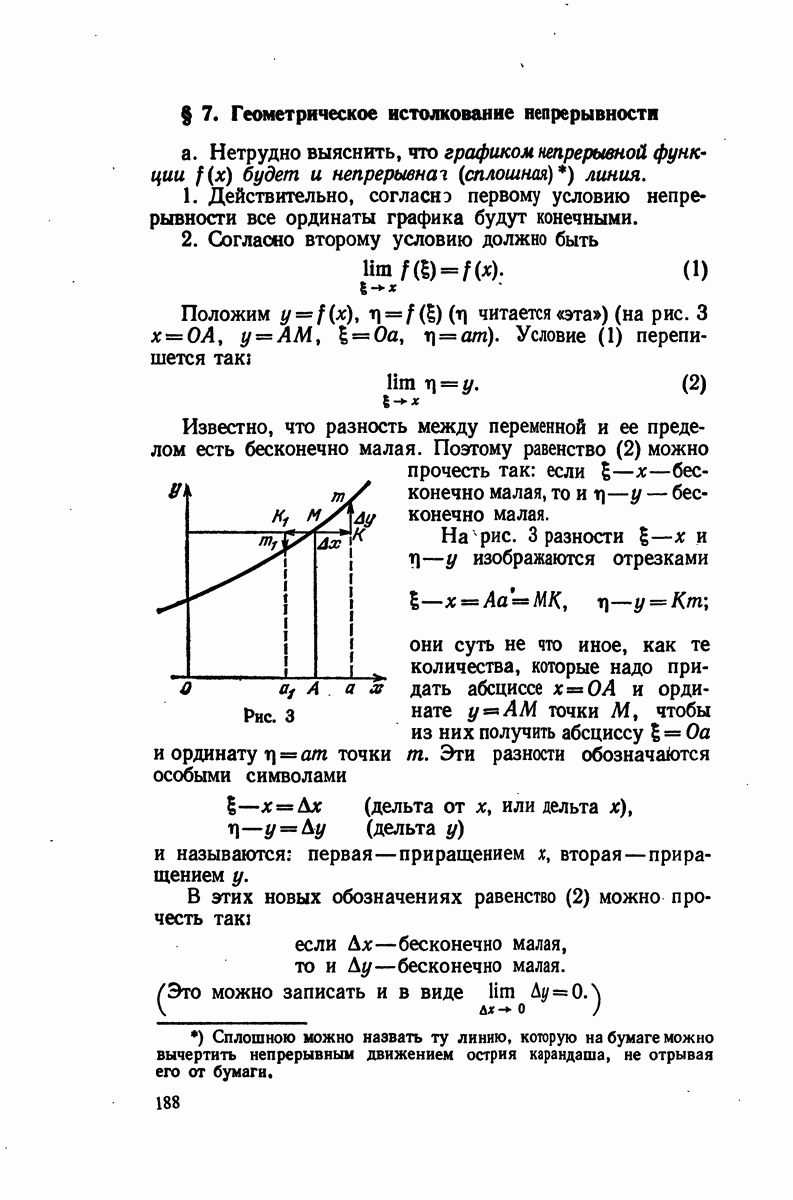
- § 7. Геометрическое истолкование непрерывности
- § 8. Свойство непрерывной функции
- § 9. Предел функции, зависящей от нескольких переменных
- § 10. Особые случаи разыскания предела
- § 11. Замечательный тригонометрический предел
- § 12. Признак существования предела
- § 13. Сходимость бесконечных рядов
- § 14. Простейшие признаки сходимости
- § 15. Основание натуральных логарифмов
- § 16. Порядок бесконечно малых
- § 17. Упражнения
- Глава 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная как угловой коэффициент касательной
- § 2. Производная как предел
- § 3. Пояснение общей теории на примере. Уравнения касательной и нормали
- § 4. Механическое значение производной
- § 5. Производные трех простейших функций
- § 6. Производная постоянного и суммы. Вынесение постоянного множителя за знак производной
- § 7. Производная сложной функции
- § 8. Разыскание производных путем логарифмирования. Производные функции х^n при любом n к функции а^x.
- § 9. Производные произведения и частного. Производные tg x и ctg x.
- § 10. Производные обратных тригонометрических функций
- § 11. Сводка основных формул
- § 12. Дифференциал
- § 13. Основные формулы для дифференциалов
- § 14. Высшие производные
- § 15. Высшие дифференциалы
- § 16. Дифференцирование неявных функций
- § 17. Дифференцирование функций, заданных параметрическим способом
- § 18. Преобразование дифференциалов к новой переменной
- § 19. Упражнения
- Глава 3. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- § 1. Непрерывность первой производной
- § 2. Возрастание и убывание функций. Максимум и минимум
- § 3. Приложение к построению графиков
- § 4. Наибольшее и наименьшее значения функции
- § 5. Прикладные задачи на наибольшее и наименьшее значения
- § 6. Направление выпуклости, точки перегиба
- § 7. Приложение к построению графиков
- § 8. Построение графиков разрывных функций
- § 9. Признак максимума и минимума, основанный на исследовании знака первой производной
- § 10. Признак максимума и минимума, основанный на исследовании знака второй и высших производных
- § 11. Асимптоты
- § 12. Дифференциал дуги
- § 13. Направляющие косинусы касательной
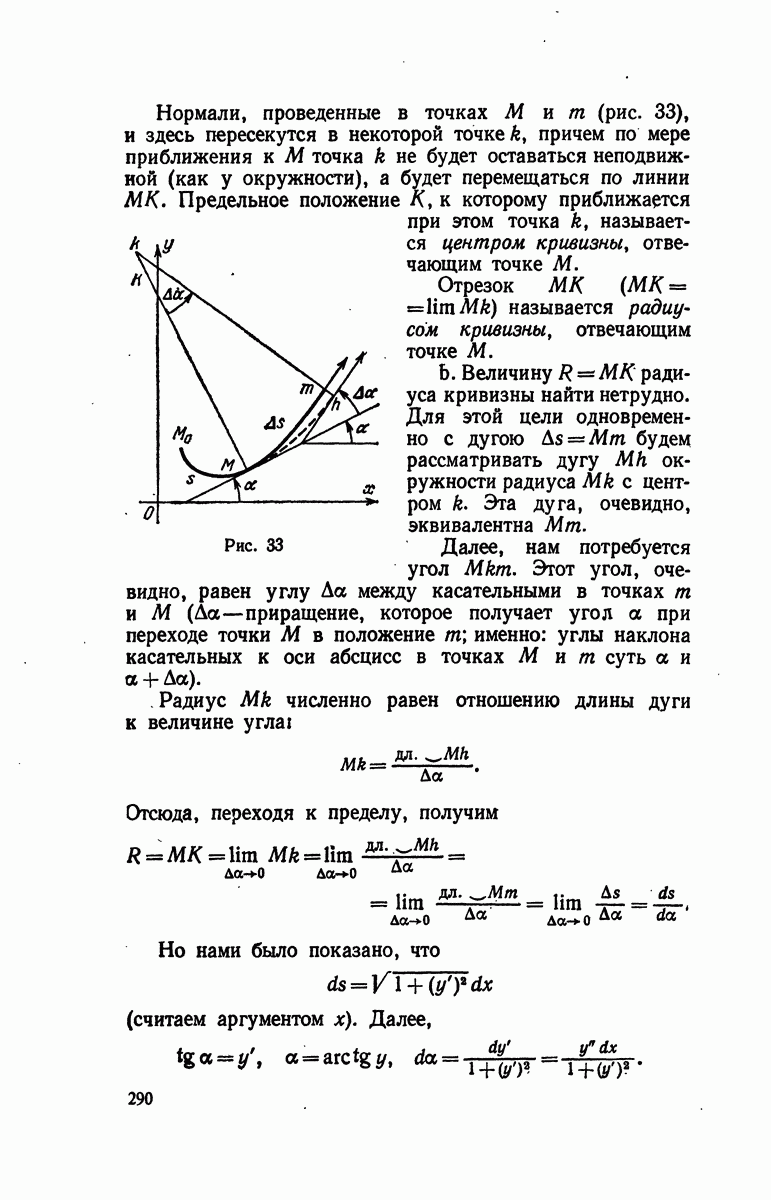
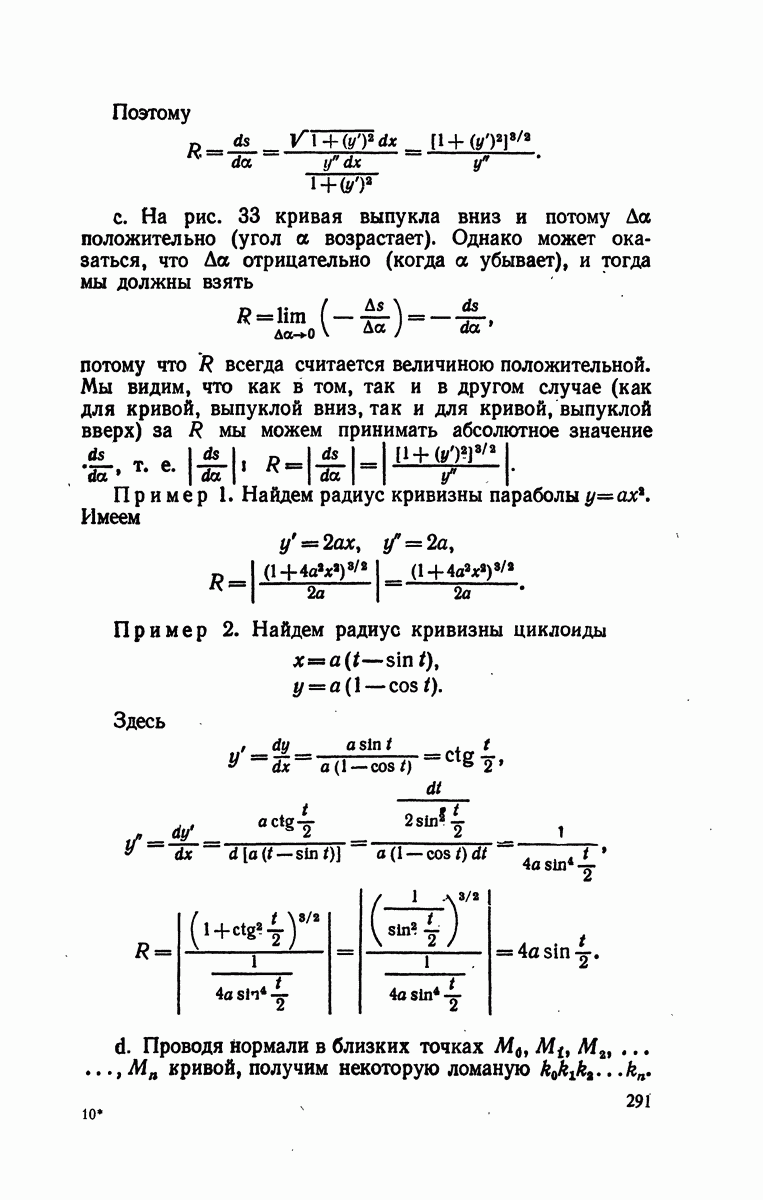
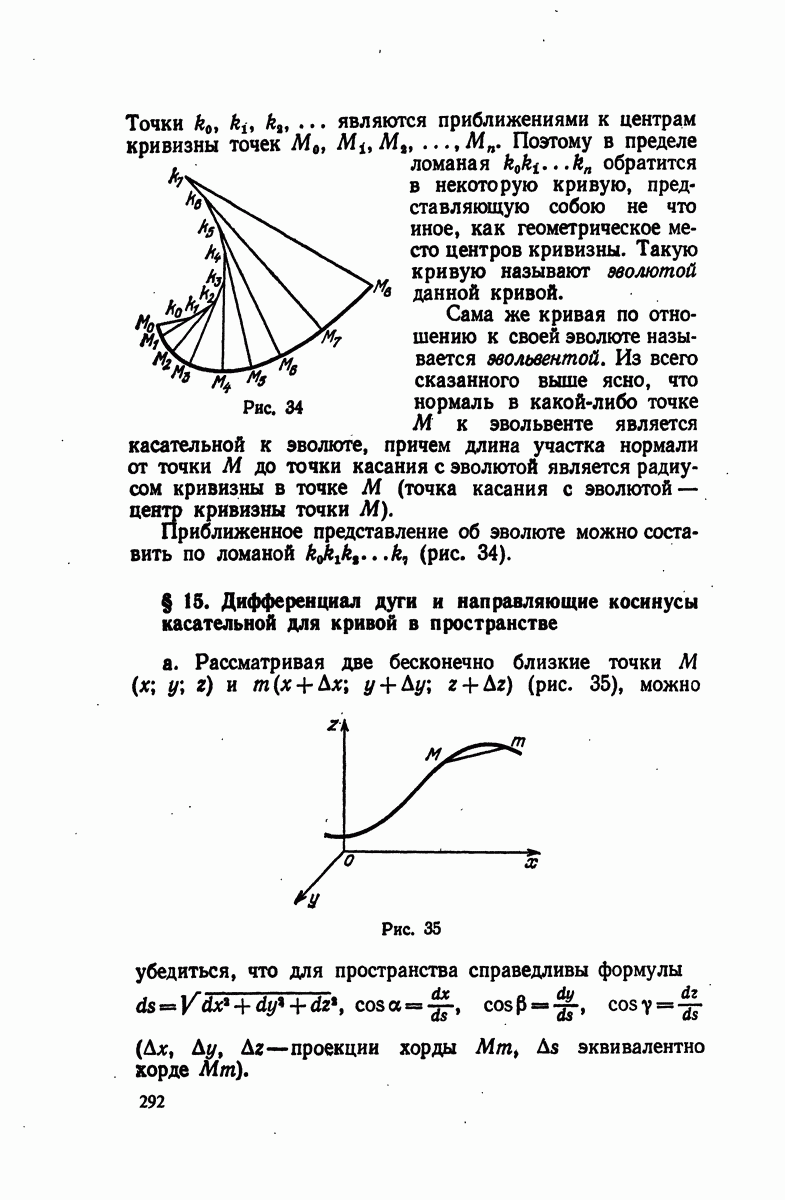
- § 14. Радиус кривизны, центр кривизны
- § 15. Дифференциал дуги и направляющие косинусы касательной для кривой в пространстве
- § 16. Упражнения
- Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 1. Функции многих переменных. Область определения. Непрерывность
- § 2. Частные производные и полный дифференциал
- § 3. Частные производные и полный дифференциал сложной функции многих переменных
- § 4. Дифференцирование неявных функций
- § 5. Частные производные и полные дифференциалы высшего порядка
- § 6. Упражнения
- ЧАСТЬ ТРЕТЬЯ. ОСНОВЫ ТЕОРИИ ЧИСЕЛ
- Глава 1. ТЕОРИЯ ДЕЛИМОСТИ
- § 2. Общий наибольший делитель
- § 3. Общее наименьшее кратное
- § 4. Простые числа
- § 5. Единственность разложения на простые сомножители
- § 6. Непрерывные дроби и их связь с алгоритмом Евклида
- Вопросы к главе 1
- Глава 2. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
- § 1. Функции [x] и {x}
- § 2. Мультипликативные функции
- § 3. Число делителей и сумма делителей
- § 4. Функция Мёбиуса
- § 5. Функция Эйлера
- Вопросы к главе II
- Глава 3. СРАВНЕНИЯ
- § 2. Свойства сравнений, подобные свойствам равенств
- § 3. Дальнейшие свойства сравнений
- § 4. Полная система вычетов
- § 5. Приведенная система вычетов
- § 6. Теоремы Эйлера и Ферма
- Вопросы к главе 3
- Глава 4. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
- § 2. Сравнения первой степени
- § 3. Система сравнений первой степени
- § 4. Сравнения любой степени по простому модулю
- § 5. Сравнения любой степени по составному модулю
- Вопросы к главе 4
- Глава 5. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
- § 2. Символ Лежандра
- § 3. Символ Якоби
- § 4. Случай составного модуля
- Вопросы к главе 5
- Глава 6. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
- § 2. Первообразные корни по модулям
- § 3. Разыскание первообразных корней по модулям
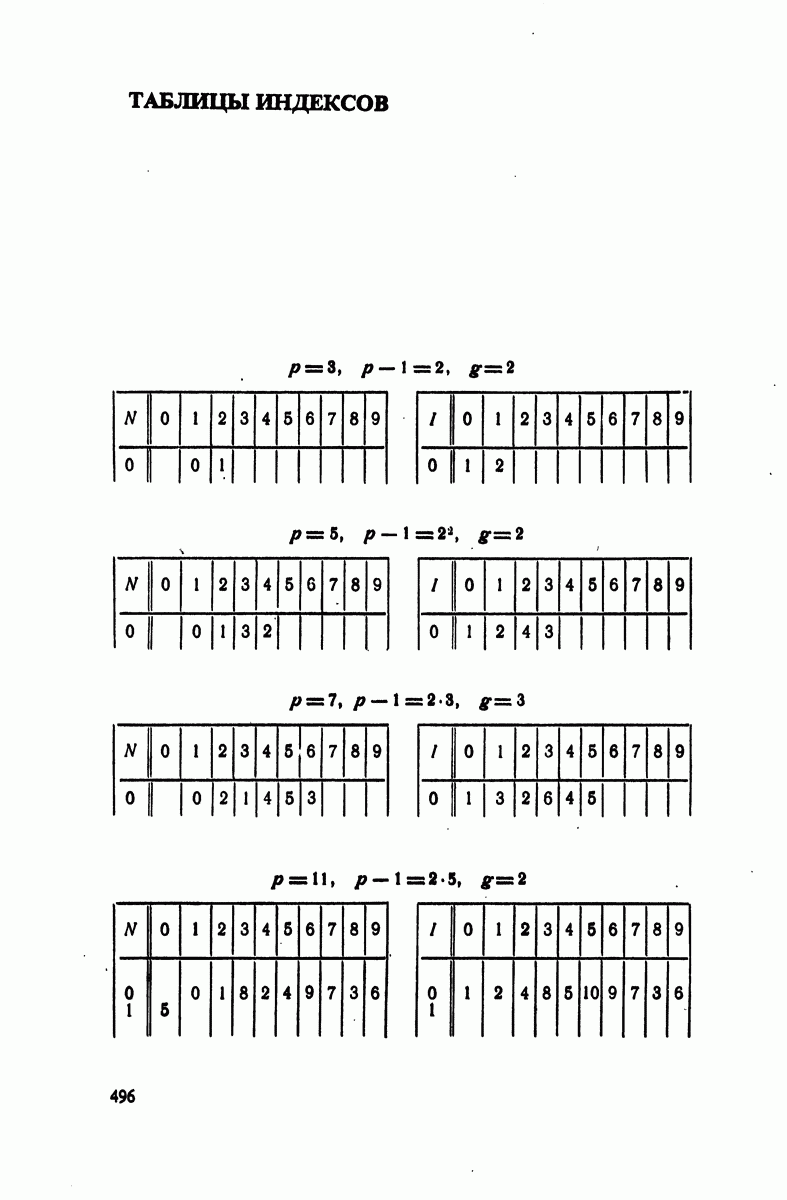
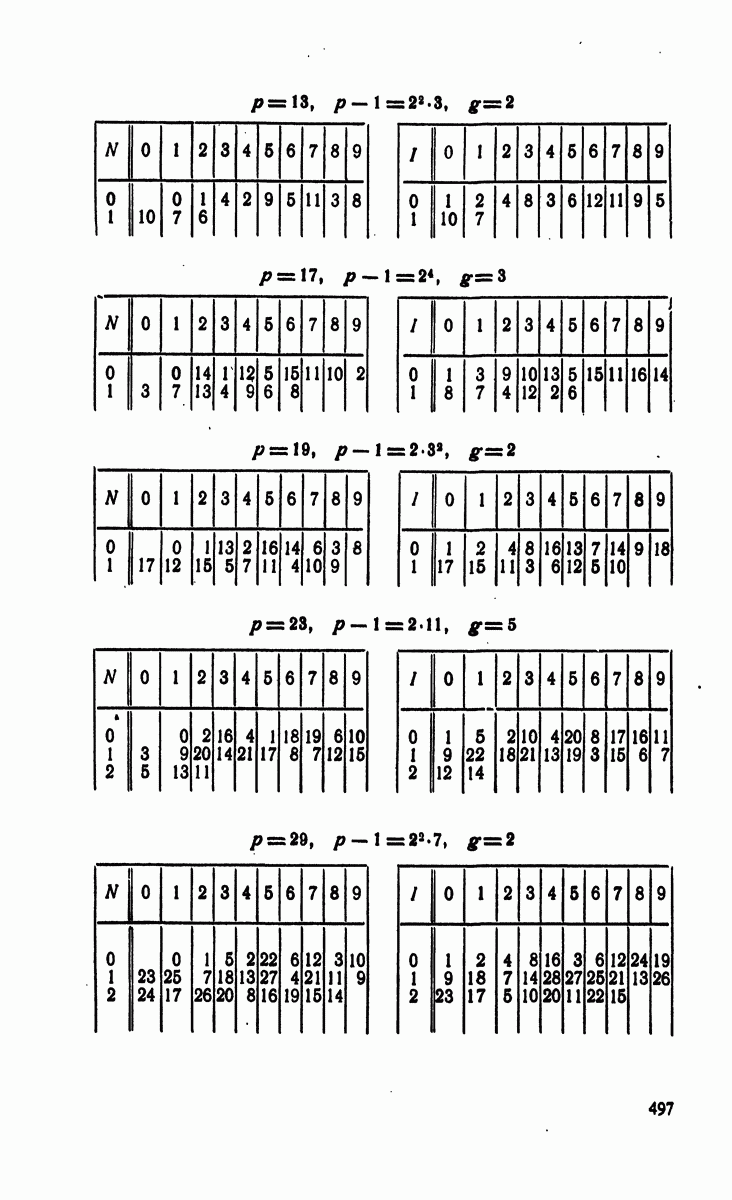
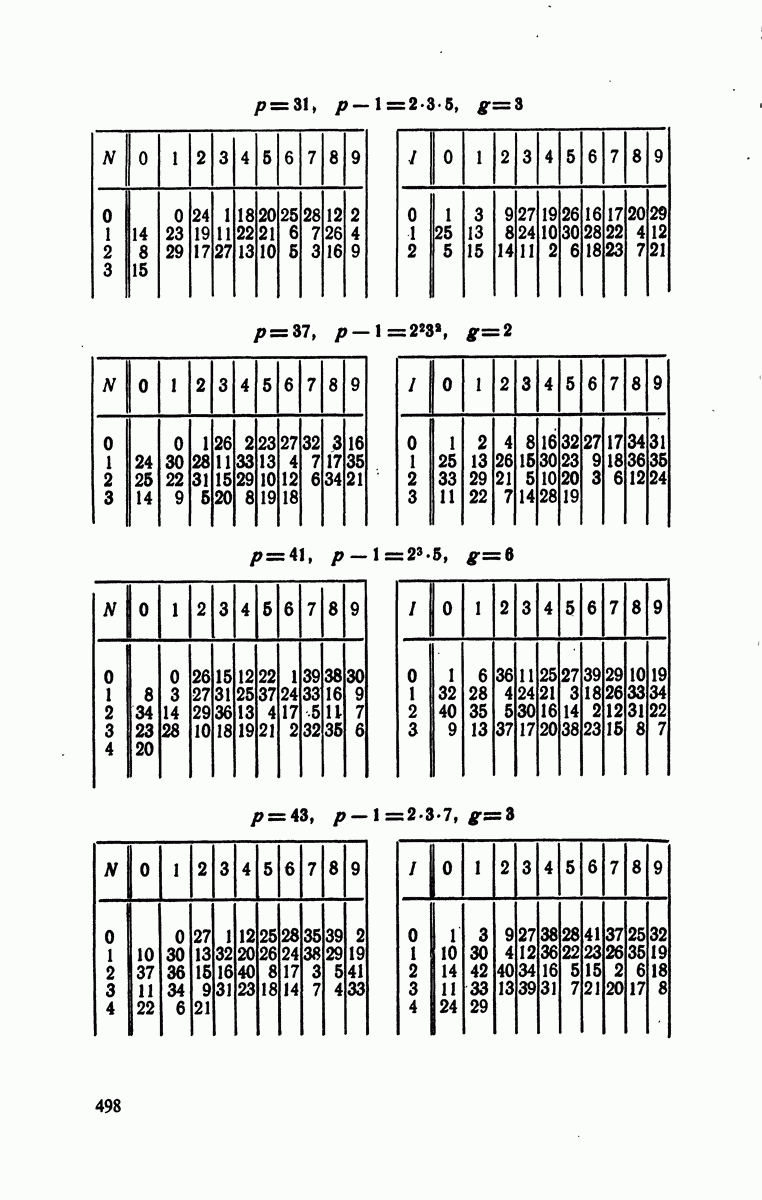
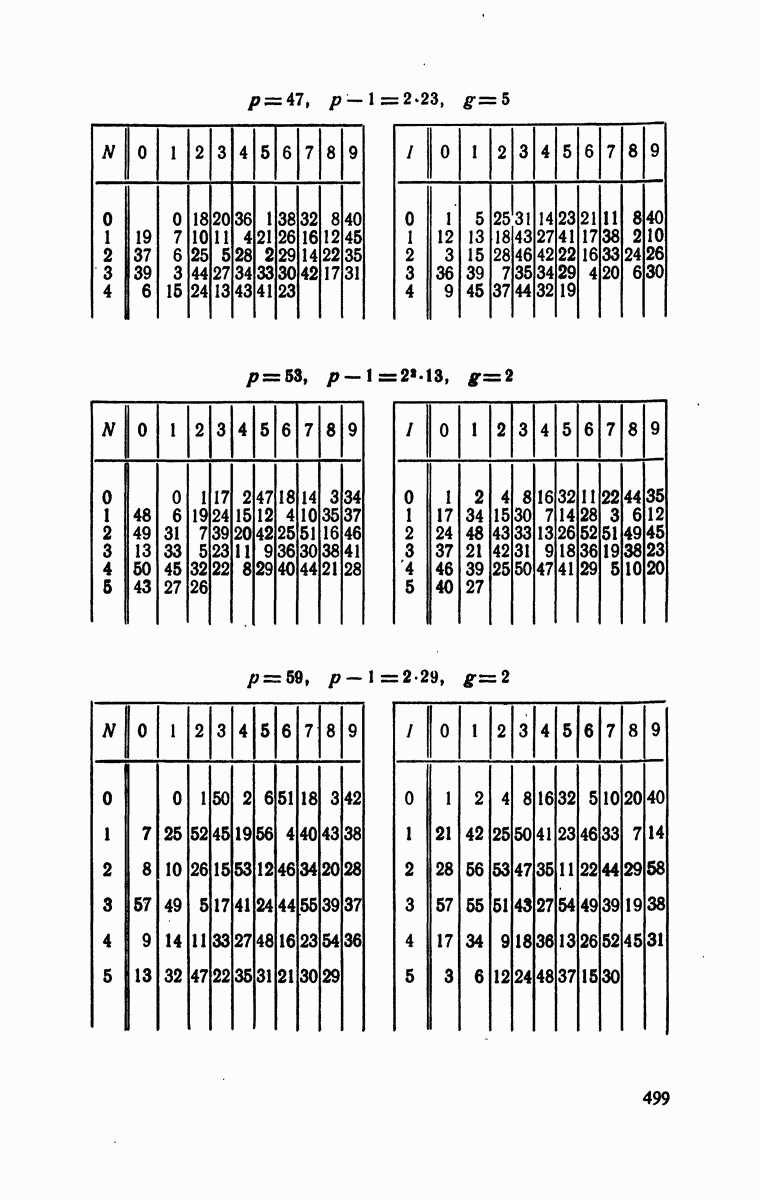
- § 4. Индексы по модулям
- § 5. Следствия предыдущей теории
- § 6. Индексы по модулю 2^a
- § 7. Индексы по любому составному модулю
- Вопросы к главе 6
- Глава 7. ХАРАКТЕРЫ
- § 2. Важнейшие свойства характеров
- Вопросы к главе 7
- РЕШЕНИЯ ВОПРОСОВ
- Решения к главе 2
- Решения к главе 3
- Решения к главе 4
- Решения к главе 5
- Решения к главе 6
- ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ