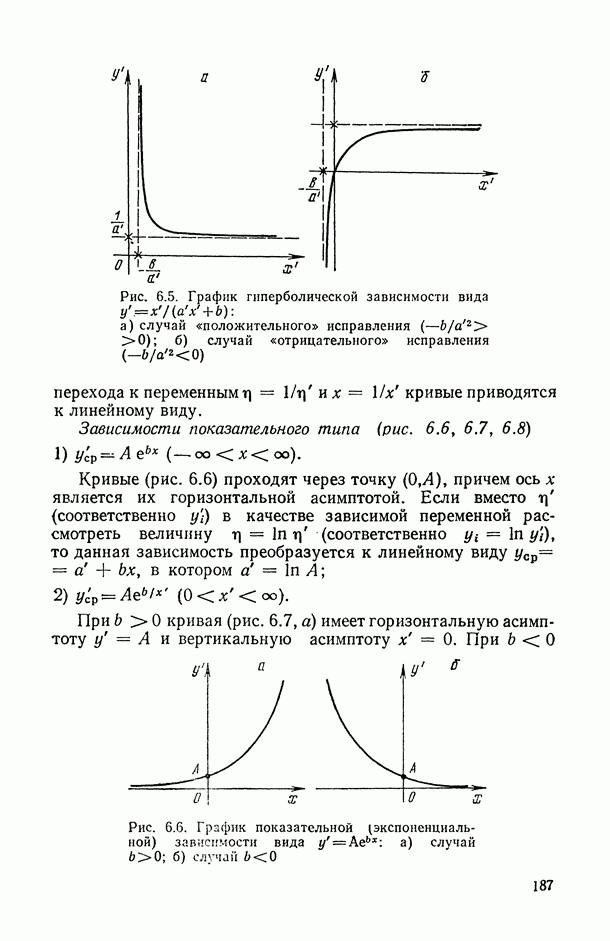
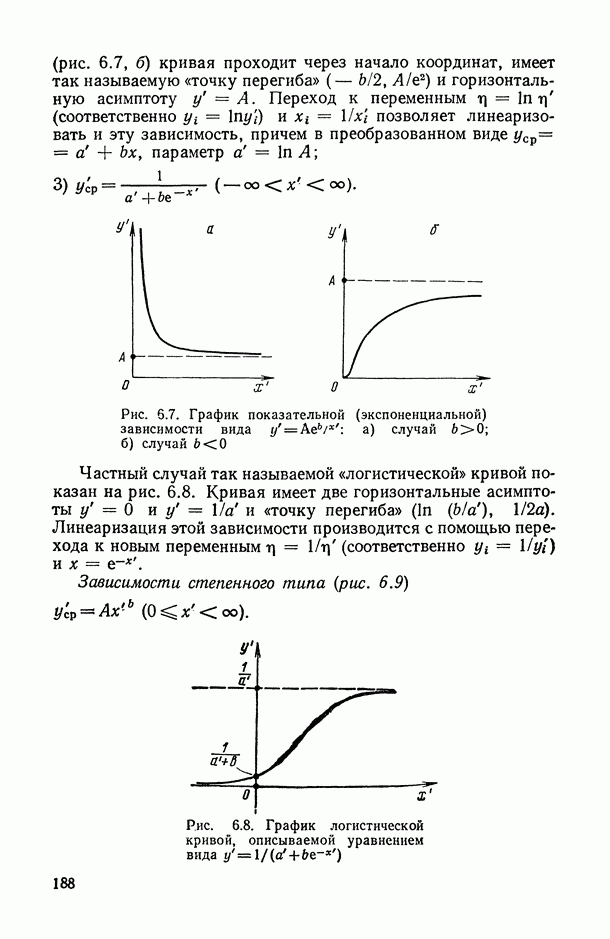
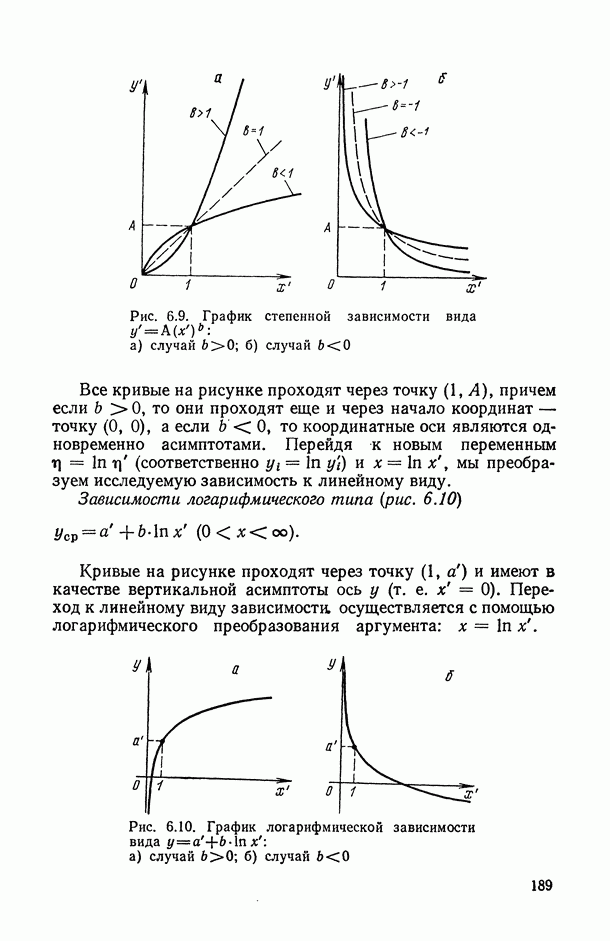
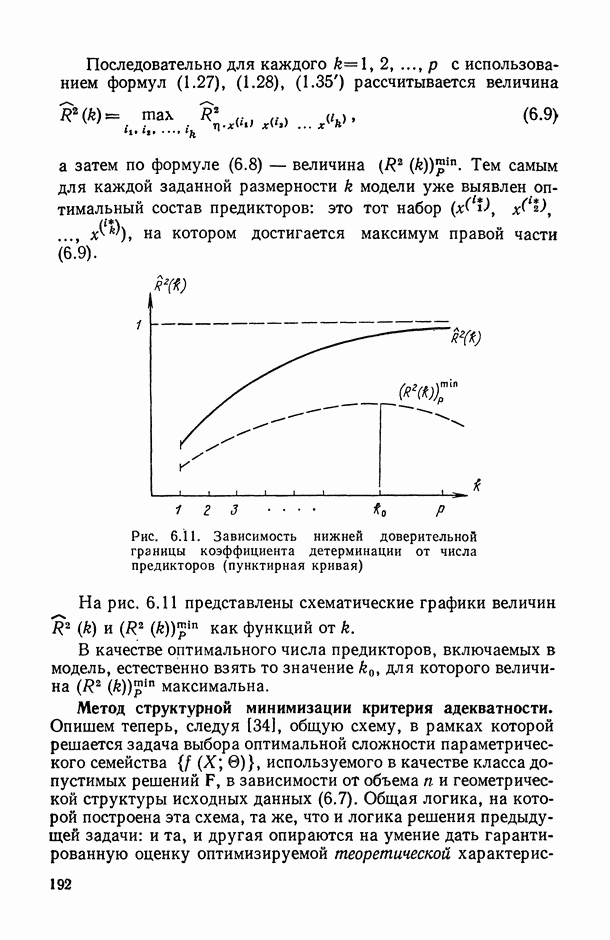
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
Имеется ли вообще какая-либо связь между исследуемыми переменными, какова структура этих связей и как измерить их тесноту? — эти вопросы исследователь ставит перед собой уже на ранней стадии статистического исследования зависимостей (см. описание этапа 3 в § В.6).
В частности, исследователь должен уметь: а) выбрать (с учетом специфики и природы анализируемых переменных) подходящий измеритель статистической связи (индекс или коэффициент корреляции, корреляционное отношение, какую-либо информационную характеристику связи, ранговый коэффициент корреляции и т. п.); б) оценить (с помощью точечной и интервальной оценок) его числовое значение по имеющимся выборочным данным; в) проверить гипотезу о том, что полученное числовое значение анализируемого измерителя связи действительно свидетельствует о наличии статистической связи (или, как говорят, проверить исследуемую корреляционную характеристику на статистически значимое ее отличие от нуля); г) проанализировать структуру связей между компонентами исследуемого многомерного признака, снабдив проведенный анализ специальным плоским геометрическим представлением исследуемой структуры, в котором компоненты (переменные) изображаются точками, а связи между ними — соединяющими их отрезками (см. рис. 4.1 и 4.2). Описанию методов и моделей, цривлекаемых для решения всех тих вопросов, и посвящен данный раздел.
Глава 1. АНАЛИЗ ТЕСНОТЫ СВЯЗИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ
1.1. Анализ парных связей
1.1.1. Понятие индекса корреляции.
Прежде чем приступать к исследованию конкретного вида связей между рассматриваемыми переменными, т. е. к оценке неизвестных параметров В в соотношениях типа

следует выяснить, существует ли вообще эта связь, и, в случае положительного ответа, попытаться установить степень тесноты этой связи.
Во введении (§ В.5) описаны различные типы зависимостей, которые могут наблюдаться между исследуемыми переменными. Умение правильно классифицировать каждую конкретную многомерную систему наблюдений играет решающую роль при выборе соответствующих математико-статистических методов поиска изучаемой зависимости и при ее неформальной, физически содержательной интерпретации.
Однако в данном пункте в целях унификации подхода к решению исследуемой в этой главе задачи мы временно прибегнем к некоторому формальному обобщению рассмотренных ранее схем В, С и D. В частности, будет предложен подход, при котором во всех вышеупомянутых схемах зависимостей исследуемая независимая переменная интерпретируется как случайная переменная (параметр) от которой зависит закон условного распределения зависимой переменной  .
.
Итак, при каждом фиксированном значении  распределение зависимой переменной
распределение зависимой переменной  задается плотностью
задается плотностью  зависящей от X. Соответственно будут зависеть от X и математическое ожидание
зависящей от X. Соответственно будут зависеть от X и математическое ожидание  , и дисперсия
, и дисперсия  . Природа же исследуемой многомерной схемы, т. е. тип искомой зависимости, будет определяться спецификой частного закона распределения наблюдаемой независимой переменной
. Природа же исследуемой многомерной схемы, т. е. тип искомой зависимости, будет определяться спецификой частного закона распределения наблюдаемой независимой переменной
Очевидно, в схеме В (наблюдения производятся в фиксированных точках  без случайных ошибок в регистрации независимой переменной) случайную величину
без случайных ошибок в регистрации независимой переменной) случайную величину  следует рассматривать как дискретную с областью мыслимых значений
следует рассматривать как дискретную с областью мыслимых значений  (не исключается возможность повторения одинаковых значений
(не исключается возможность повторения одинаковых значений  в этом ряду) и с частным законом распределения
в этом ряду) и с частным законом распределения  , задаваемым вероятностями
, задаваемым вероятностями 
В схеме  плотность
плотность  частного распределения определяется, помимо набора наблюдаемых абсцисс
частного распределения определяется, помимо набора наблюдаемых абсцисс  законами распределения ошибок измерения
законами распределения ошибок измерения  .
.
Если  — число различных уровней
— число различных уровней  структурной компоненты X, при которых снимались экспериментальные данные
структурной компоненты X, при которых снимались экспериментальные данные  — плотность распределения ошибки
— плотность распределения ошибки  то
то

где  — число наблюдений, произведенных «на уровне»
— число наблюдений, произведенных «на уровне» 
В схемах С и  объясняющие наблюдаемые переменные соответственно
объясняющие наблюдаемые переменные соответственно  по своей природе случайны, следовательно, им также соответствует некоторая плотность частного распределения
по своей природе случайны, следовательно, им также соответствует некоторая плотность частного распределения  .
.
Если рассмотреть случай единственного результирующего показателя  и мысленно спроектировать все точки исследуемой многомерной системы на ось его возможных значений О у, то получим выборку из одномерного закона с плотностью
и мысленно спроектировать все точки исследуемой многомерной системы на ось его возможных значений О у, то получим выборку из одномерного закона с плотностью  характеризующего вероятностную природу безусловной случайной величины
характеризующего вероятностную природу безусловной случайной величины  При такой интерпретации очевидно, что плотность частного (безусловного) распределения
При такой интерпретации очевидно, что плотность частного (безусловного) распределения  получается как смесь соответствующих условных плотностей
получается как смесь соответствующих условных плотностей  , а именно:
, а именно:  (в схеме
(в схеме  в дальнейшем при усреднении по
в дальнейшем при усреднении по  мы не будем специально оговаривать случай схемы В, подразумевая переход от интегрирования по X к суммированию по
мы не будем специально оговаривать случай схемы В, подразумевая переход от интегрирования по X к суммированию по  Соответственно в нашем дальнейшем изложении будут участвовать характеристики
Соответственно в нашем дальнейшем изложении будут участвовать характеристики

Рассмотрим, например, частный случай схемы С, когда вектор исследуемых показателей

—  -мерная нормальная случайная величина [14, с. 173], и пусть
-мерная нормальная случайная величина [14, с. 173], и пусть  — соответственно векторы средних значений объясняющих переменных
— соответственно векторы средних значений объясняющих переменных  и результирующих показателей
и результирующих показателей  — ковариационные матрицы [14, с. 138] соответственно векторов
— ковариационные матрицы [14, с. 138] соответственно векторов 
Тогда можно показать (см., например, [20, с. 45]), что условное распределение вектора результирующих показателей  при условии, что значения объясняющих переменных зафиксированы на уровне
при условии, что значения объясняющих переменных зафиксированы на уровне  (т. е. при условии
(т. е. при условии  также нормально с условным средним значением
также нормально с условным средним значением

и ковариационной матрицей

Из (1.3) и (1.4), в частности, следует:
а) функция  регрессии
регрессии  по
по  при совместном нормальном законе распределения исследуемых показателей линейна по X;
при совместном нормальном законе распределения исследуемых показателей линейна по X;
б) ковариационная матрица условного распределения вектора результирующих показателей  не зависит от X;
не зависит от X;
в) если рассматривается парная регрессионная зависимость, т. е. зависимость единственного результирующего показателя  от единственной объясняющей переменной
от единственной объясняющей переменной  в схеме С, причем распределение случайной величины
в схеме С, причем распределение случайной величины  подчиняется двумерному нормальному закону, то условное распределение случайной величины
подчиняется двумерному нормальному закону, то условное распределение случайной величины  тоже нормально с условным средним значением (функцией регрессии)
тоже нормально с условным средним значением (функцией регрессии)

и с дисперсией

(здесь и  — средние значения соответственно объясняющей переменной
— средние значения соответственно объясняющей переменной  и результирующего показателя
и результирующего показателя  и — их дисперсии, а
и — их дисперсии, а  — коэффициент корреляции между ними, см., например, [14, гл. 5]).
— коэффициент корреляции между ними, см., например, [14, гл. 5]).
Будем рассматривать в дальнейшем (если специально не оговорено противное) случай единственного результирующего показателя, т. е. случай 
Итак, величина  характеризует полную вариацию (дисперсию) исследуемого результирующего показателя
характеризует полную вариацию (дисперсию) исследуемого результирующего показателя  в то время как
в то время как  определяет дисперсию функции регрессии
определяет дисперсию функции регрессии  — усредненную (по различным значениям
— усредненную (по различным значениям  ) величину условной дисперсии
) величину условной дисперсии  , т. е. среднюю величину дисперсии неконтролируемой остаточной случайной компоненты
, т. е. среднюю величину дисперсии неконтролируемой остаточной случайной компоненты  (см. соотношения (В. 14), (В.16), (В.21)).
(см. соотношения (В. 14), (В.16), (В.21)).
Воспользовавшись соотношением (2в.3.6) из [117, с. 94], получим следующее полезное соотношение, связывающее три вышеупомянутые меры случайного разброса:

Это означает, что полная вариация исследуемой зависимой переменной складывается из контролируемой нами вариации функции регрессии и из не поддающейся нашему контролю вариации остаточной случайной компоненты. Очевидно, связь между  в соотношениях (В. 14), (В. 16), (В.21) и т. п. будет тем теснее, тем определеннее, чем менее «размазанными» окажутся участвующие в них остаточные неконтролируемые случайные компоненты
в соотношениях (В. 14), (В. 16), (В.21) и т. п. будет тем теснее, тем определеннее, чем менее «размазанными» окажутся участвующие в них остаточные неконтролируемые случайные компоненты  и
и 
Можно, в частности, задаться вопросом: какая доля степени изменчивости интересующего нас зависимого признака (т. е. какая доля дисперсии с) обусловливается изменчивостью описывающей его функции независимой переменной  (т. е. ее дисперсией
(т. е. ее дисперсией  ) Так мы приходим к понятию наиболее общей характеристики степени тесноты связи между
) Так мы приходим к понятию наиболее общей характеристики степени тесноты связи между  — индекса корреляции
— индекса корреляции  , где
, где

Из (1.5) и (1.6) непосредственно следует, что 
При этом минимальное значение индекса корреляции  соответствует полному отсутствию варьирования
соответствует полному отсутствию варьирования  с изменением
с изменением  а это означает полное отсутствие какого-либо влияния
а это означает полное отсутствие какого-либо влияния  , т. е., как говорят, отсутствие корреляционной связи между результирующим показателем
, т. е., как говорят, отсутствие корреляционной связи между результирующим показателем  и объясняющими переменными
и объясняющими переменными
В то же время максимальное значение индекса корреляции  соответствует полному отсутствию варьирования остаточной случайной компоненты
соответствует полному отсутствию варьирования остаточной случайной компоненты  . А поскольку среднее значение остаточной случайной компоненты равно нулю, то она практически исчезает из разложений (В. 14), (В. 16), (В.21). Это означает наличие чисто функциональной связи между
. А поскольку среднее значение остаточной случайной компоненты равно нулю, то она практически исчезает из разложений (В. 14), (В. 16), (В.21). Это означает наличие чисто функциональной связи между  и, следовательно, возможность детерминированного восстановления значений
и, следовательно, возможность детерминированного восстановления значений  по соответствующим значениям объясняющих переменных
по соответствующим значениям объясняющих переменных
Таким образом, введенный с помощью (1.6) индекс корреляции  между результирующим показателем
между результирующим показателем  и объясняющими переменными
и объясняющими переменными  формально определен для любой двумерной системы наблюдений. Квадрат его величины
формально определен для любой двумерной системы наблюдений. Квадрат его величины  показывает, какая доля дисперсии исследуемого результирующего показателя
показывает, какая доля дисперсии исследуемого результирующего показателя  определяется (детерминируется) изменчивостью (дисперсией) соответствующей функции регрессии
определяется (детерминируется) изменчивостью (дисперсией) соответствующей функции регрессии  от аргумента
от аргумента  , поэтому часто называется коэффициентом детерминации. Соответственно оставшаяся доля дисперсии
, поэтому часто называется коэффициентом детерминации. Соответственно оставшаяся доля дисперсии  объясняется воздействием неконтролируемой случайной остаточной компоненты («помехи»), а следовательно, определяет ту верхнюю границу точности, с которой мы сможем восстанавливать (предсказывать) значения
объясняется воздействием неконтролируемой случайной остаточной компоненты («помехи»), а следовательно, определяет ту верхнюю границу точности, с которой мы сможем восстанавливать (предсказывать) значения  по заданным значениям объясняющих переменных
по заданным значениям объясняющих переменных  .
.
Наилучшие методы построения статистической оценки  для неизвестного теоретического значения индекса корреляции
для неизвестного теоретического значения индекса корреляции  так же как и различные варианты его интерпретации, зависят от ряда исходных предпосылок каждой конкретной двумерной схемы (общий вид функции
так же как и различные варианты его интерпретации, зависят от ряда исходных предпосылок каждой конкретной двумерной схемы (общий вид функции  , вид распределения многомерной случайной величины
, вид распределения многомерной случайной величины  и т. п.). Описание их поэтому дается ниже отдельно для каждого из некоторых специальных частных случаев.
и т. п.). Описание их поэтому дается ниже отдельно для каждого из некоторых специальных частных случаев.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
- В.3. Математический инструментарий
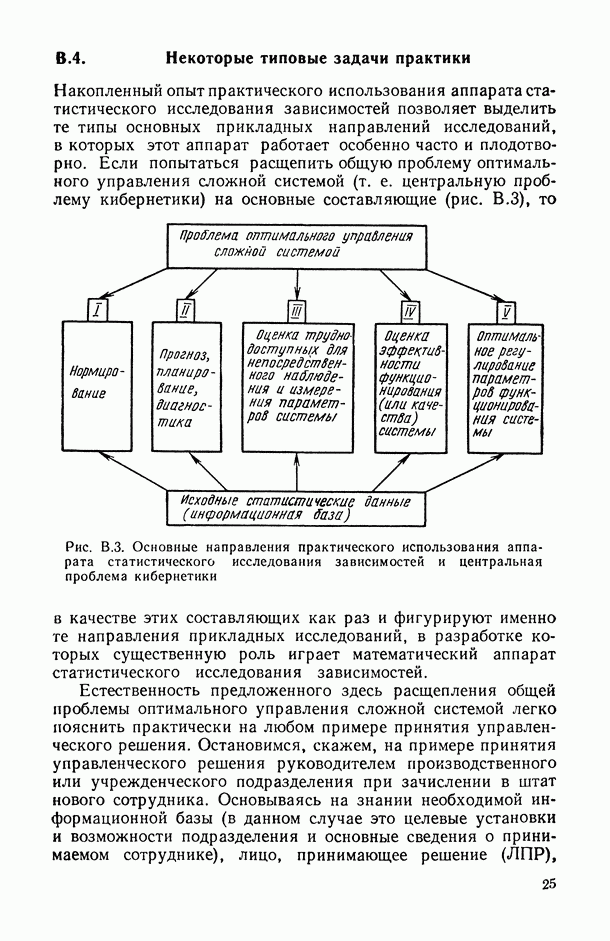
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
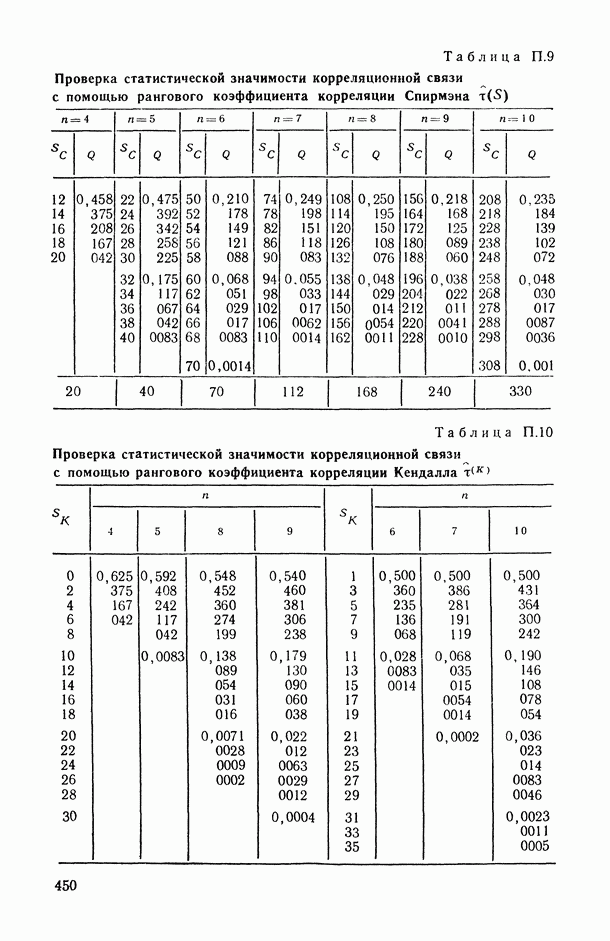
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
- 2.3. Анализ множественных ранговых связей
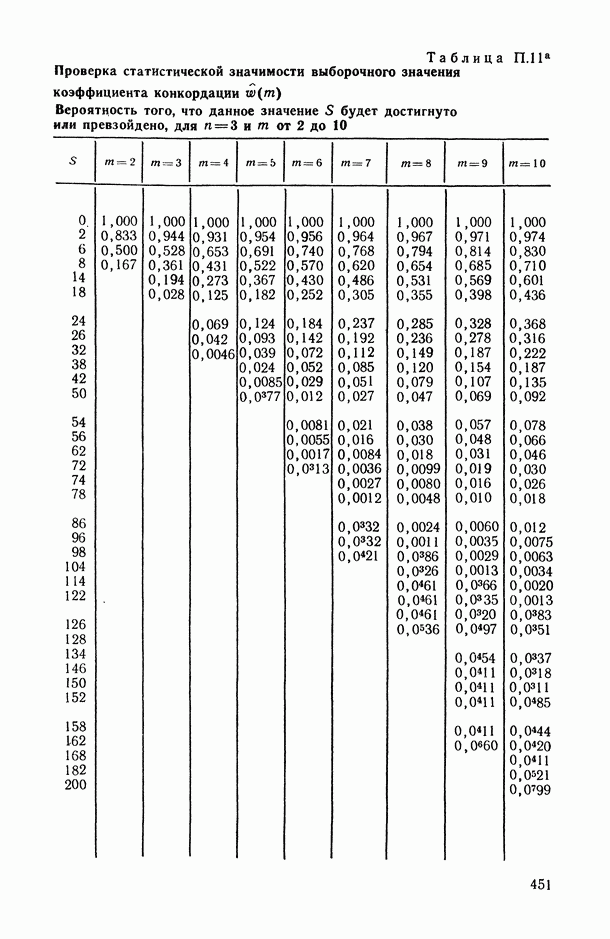
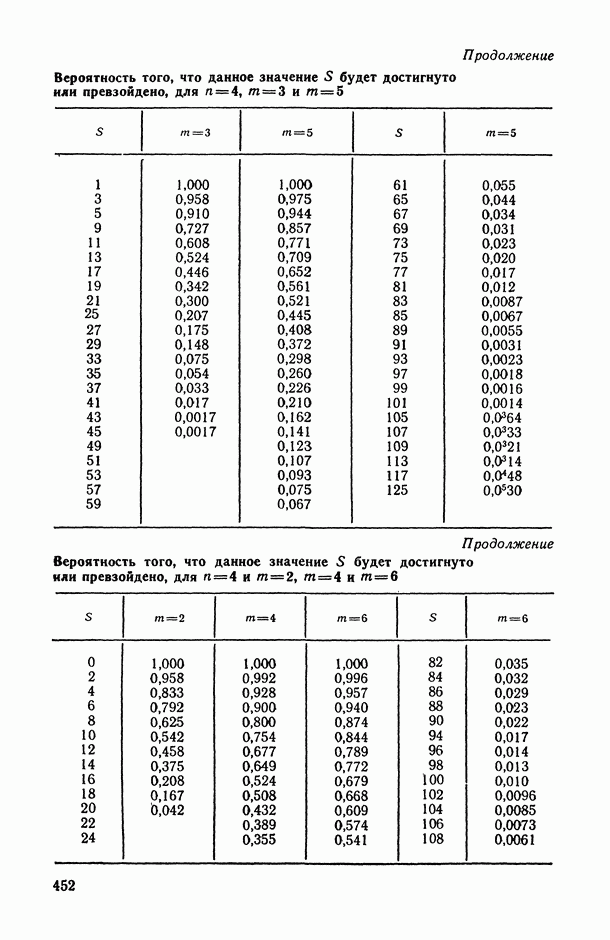
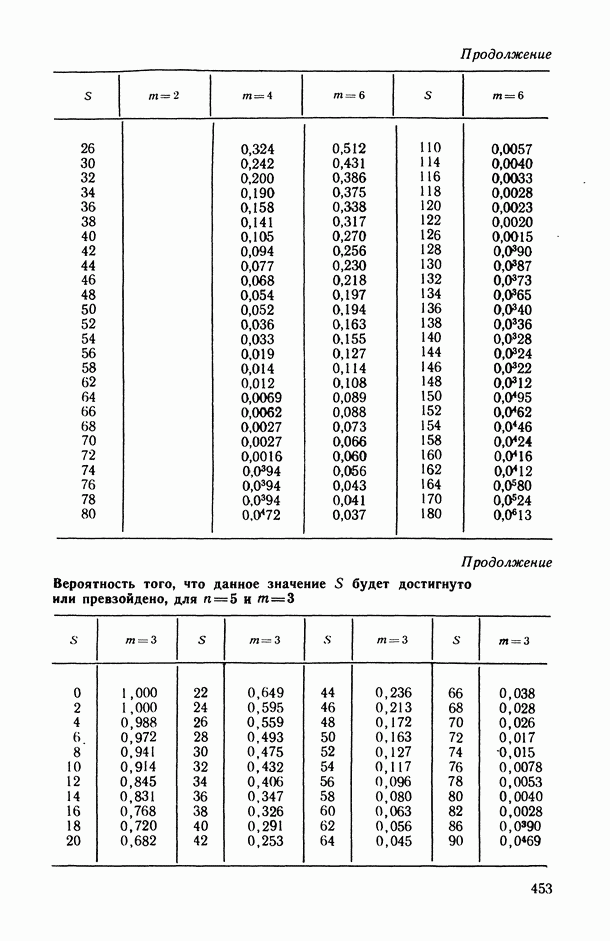
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
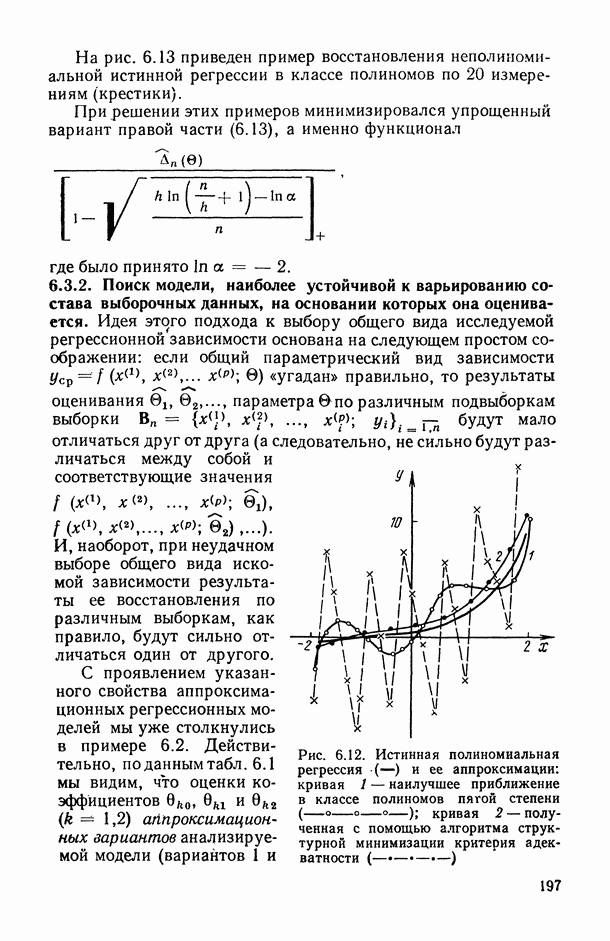
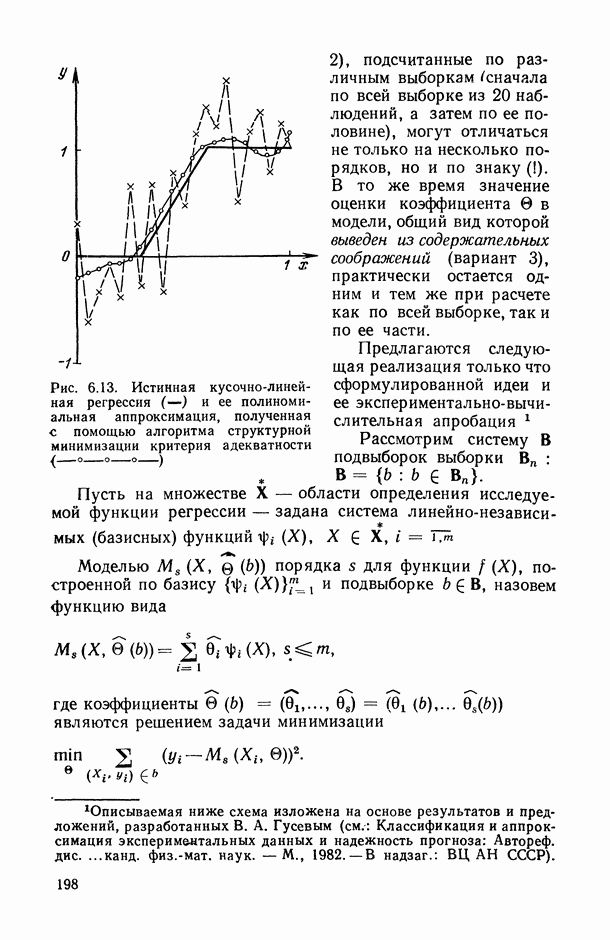
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
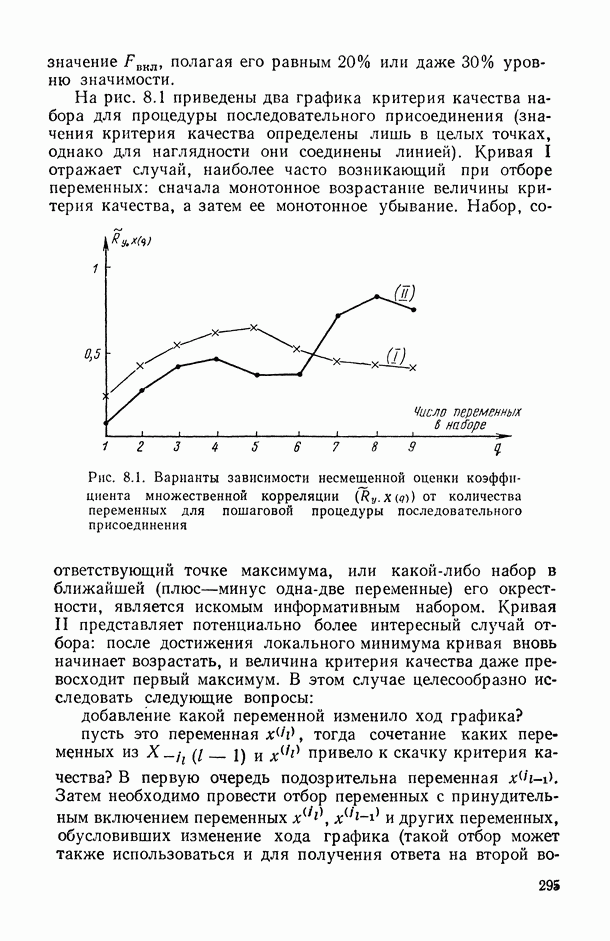
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
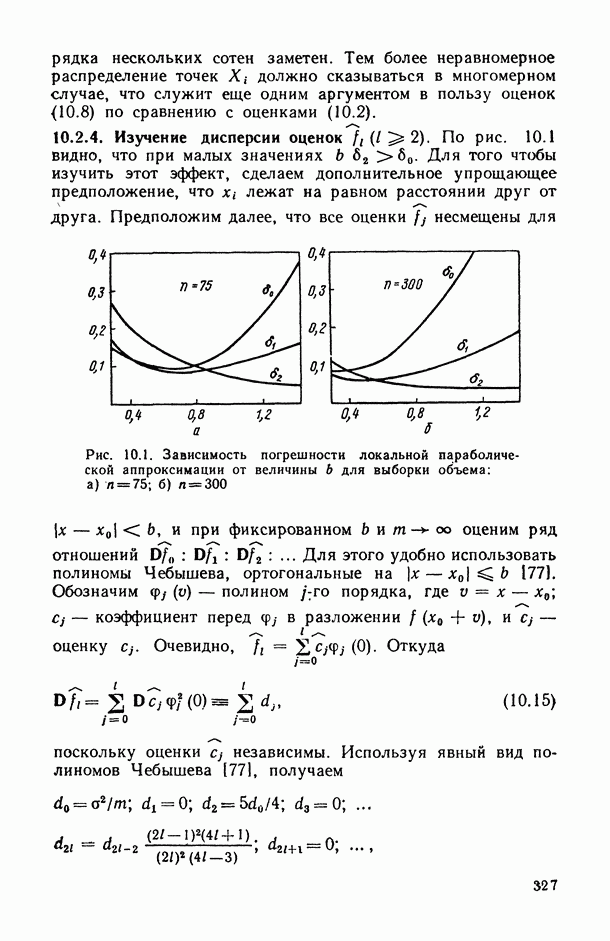
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
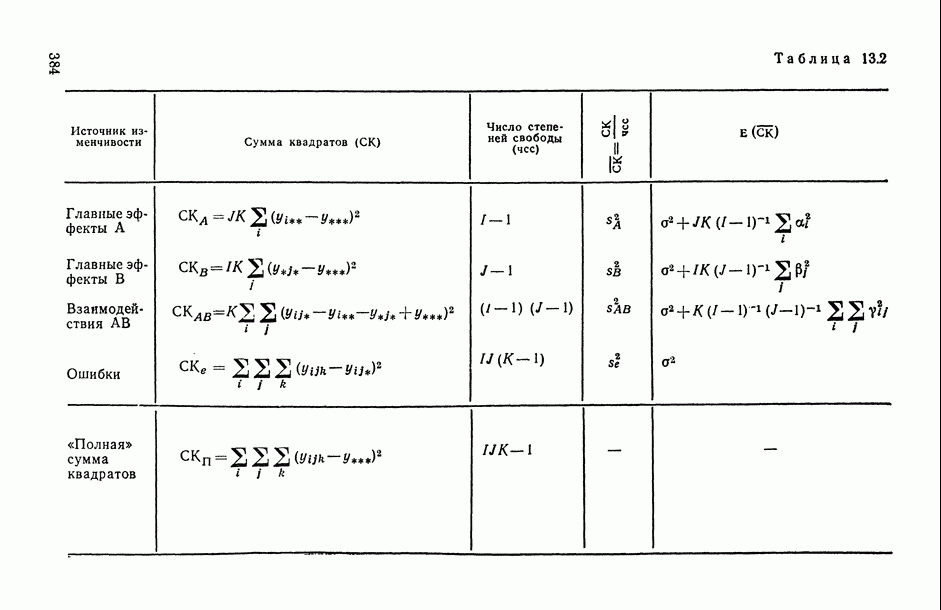
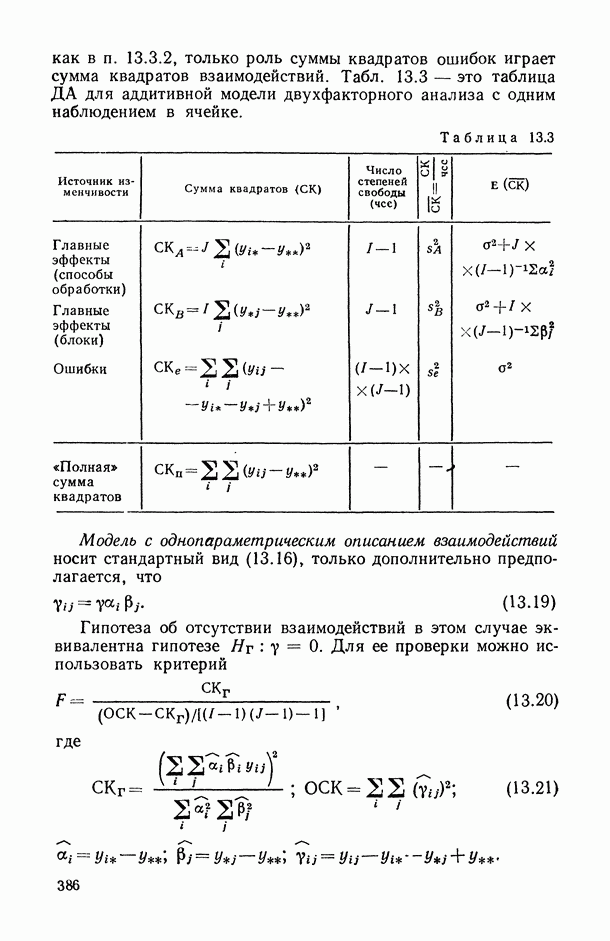
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
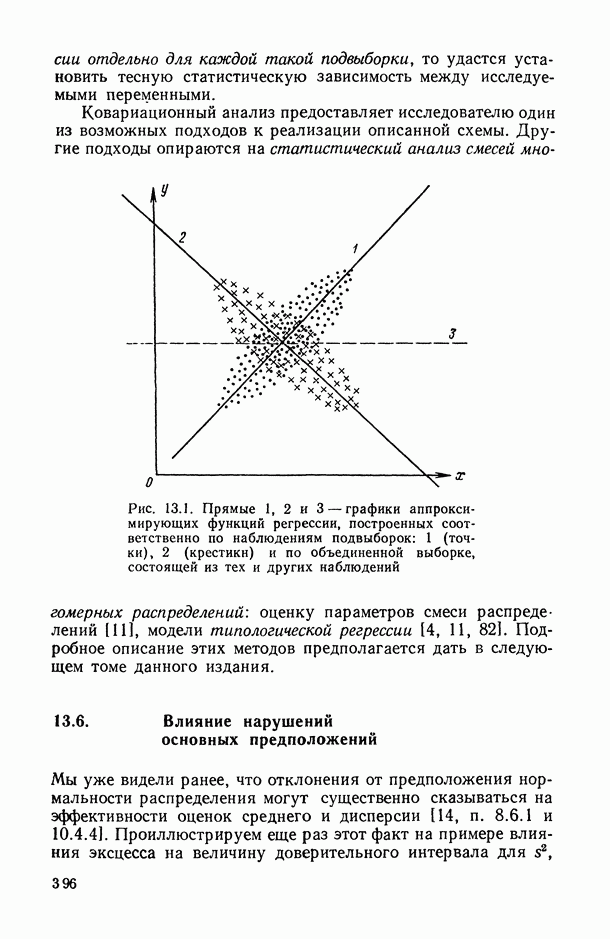
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
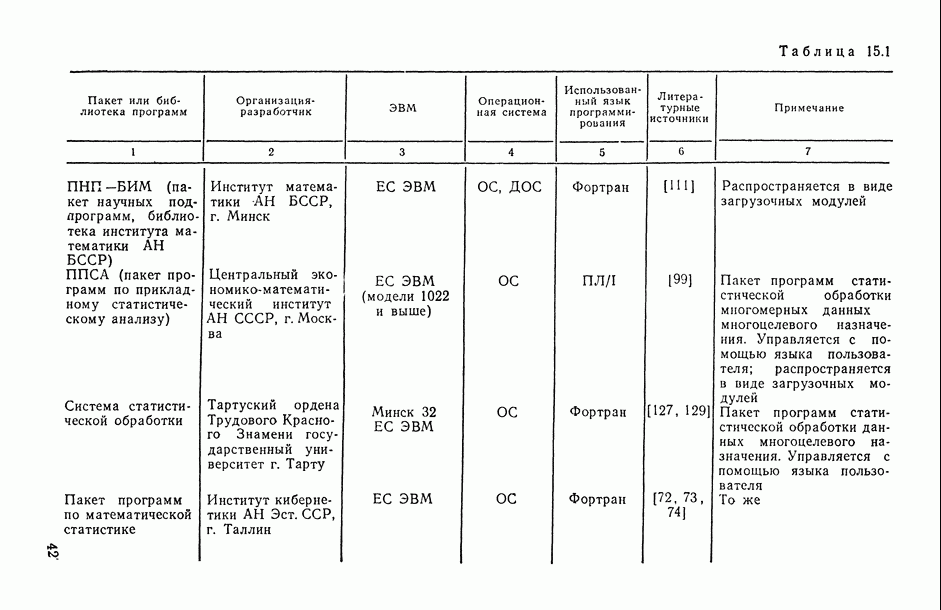
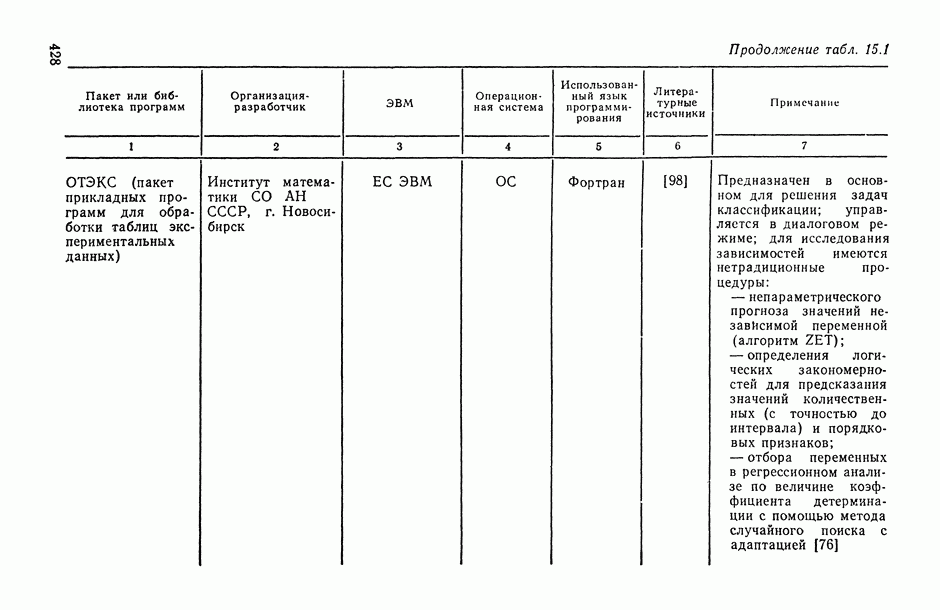
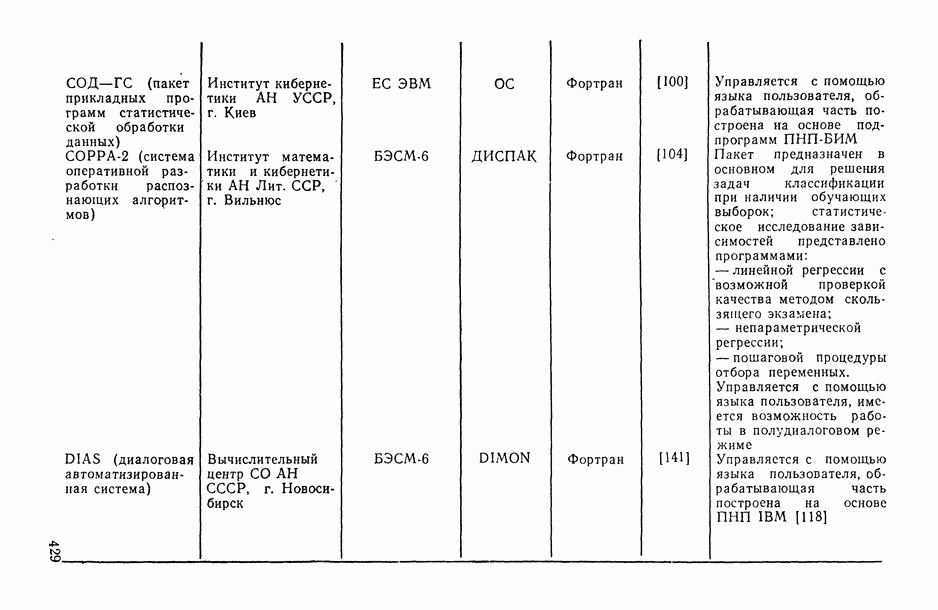
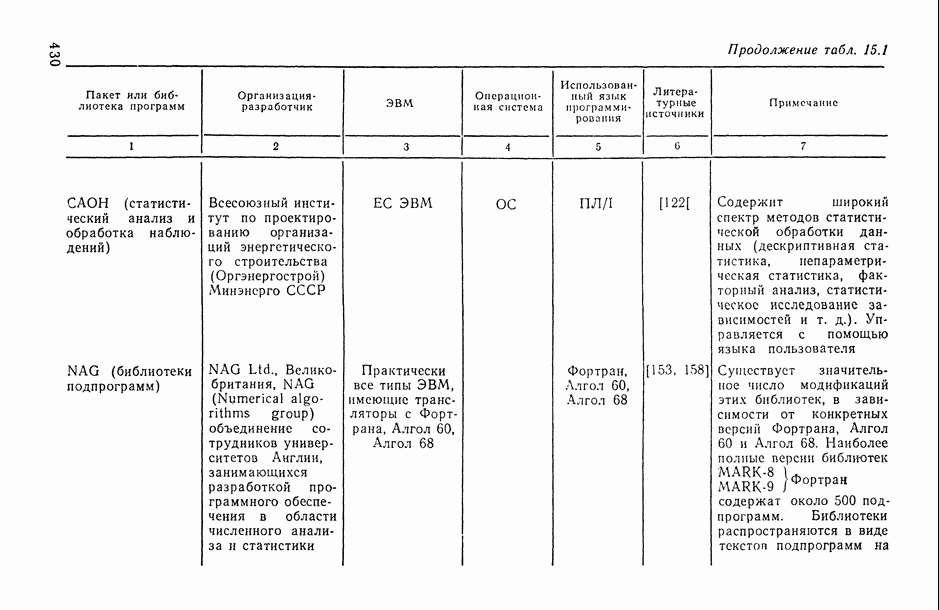
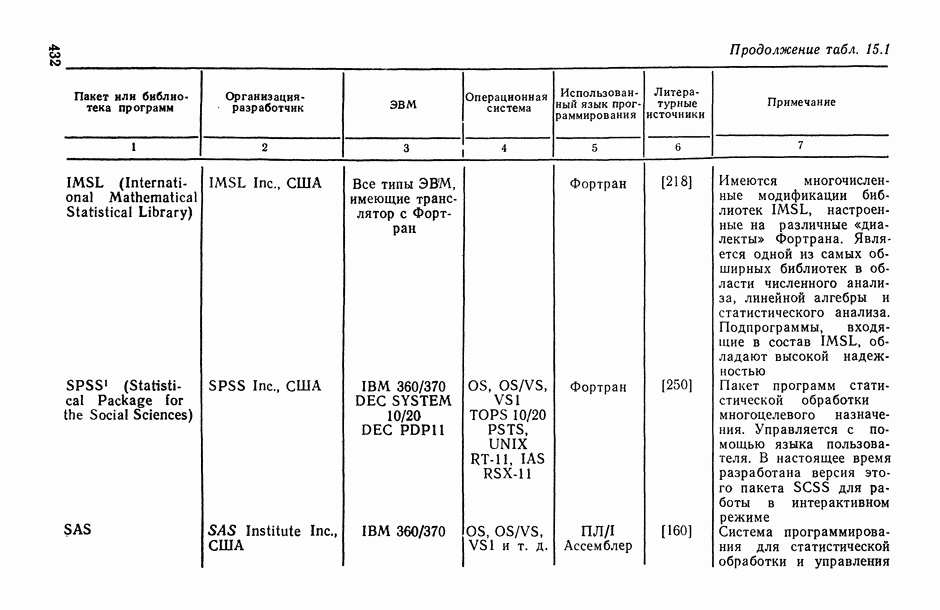
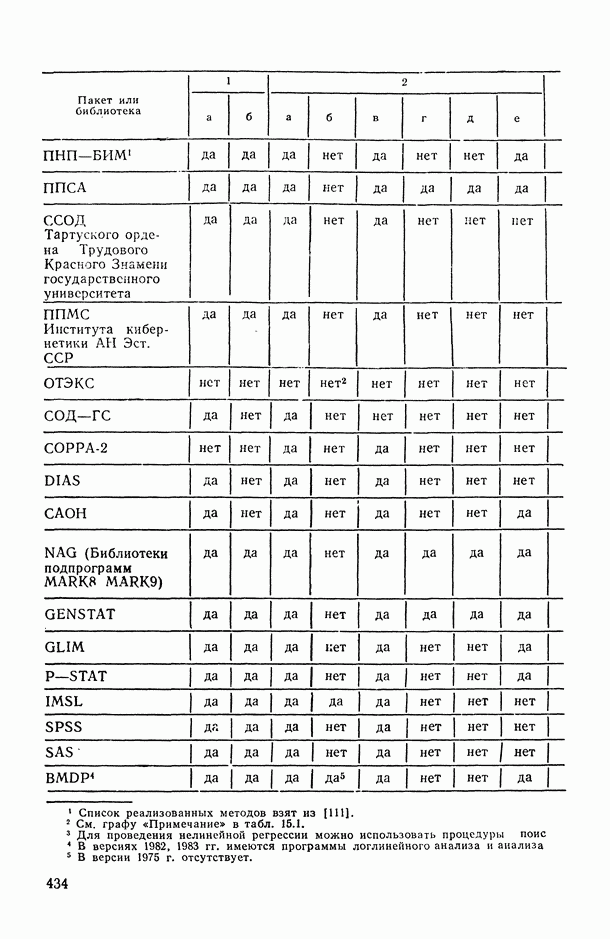
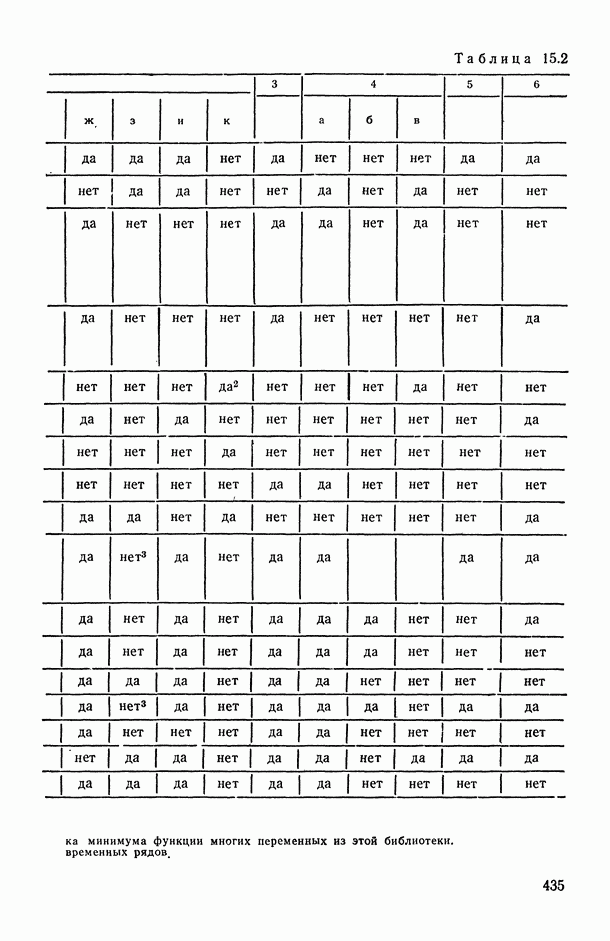
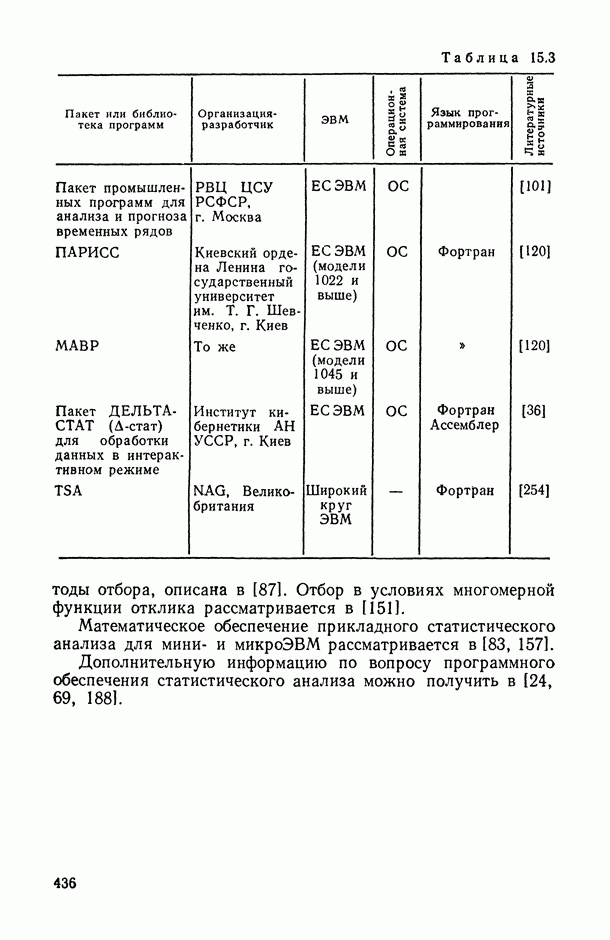
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
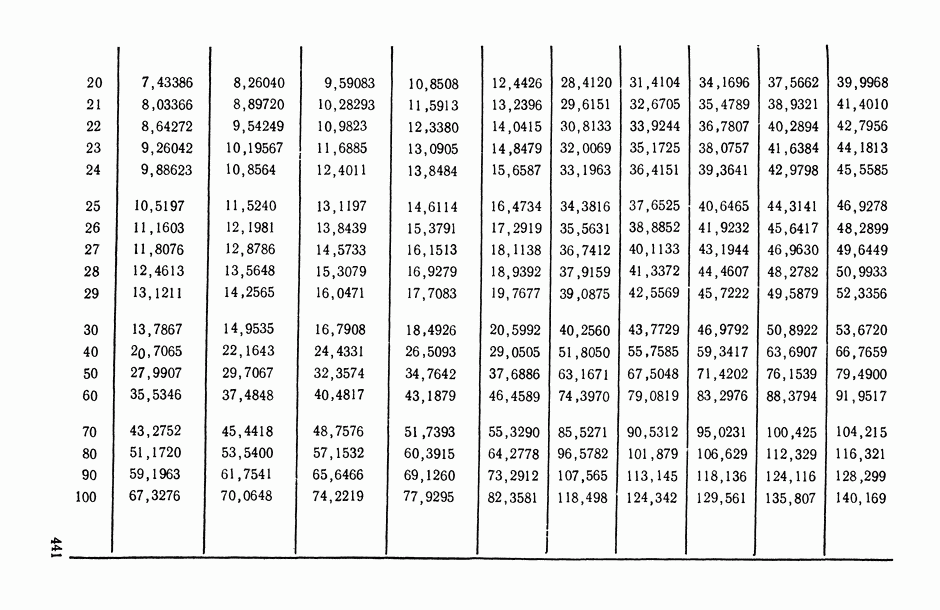
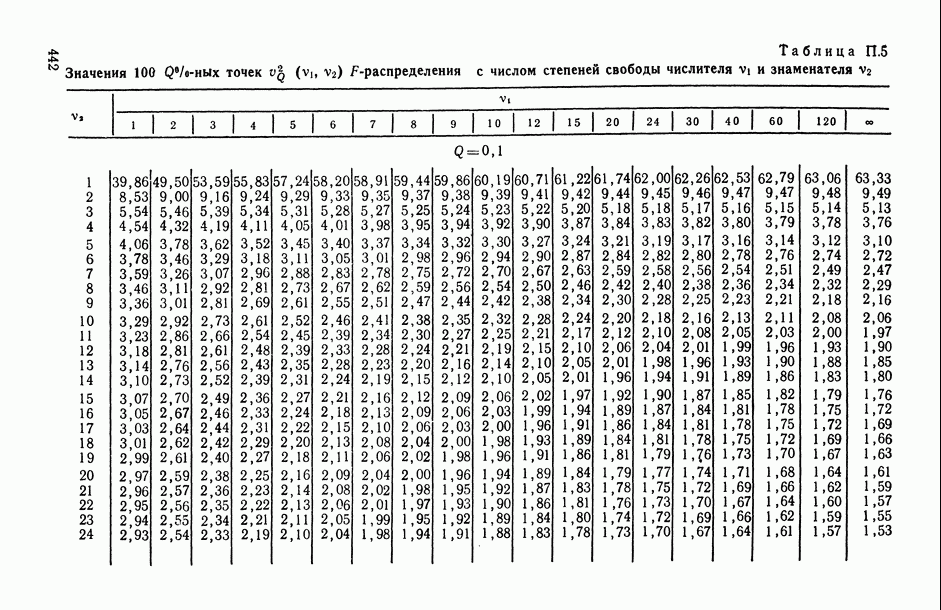
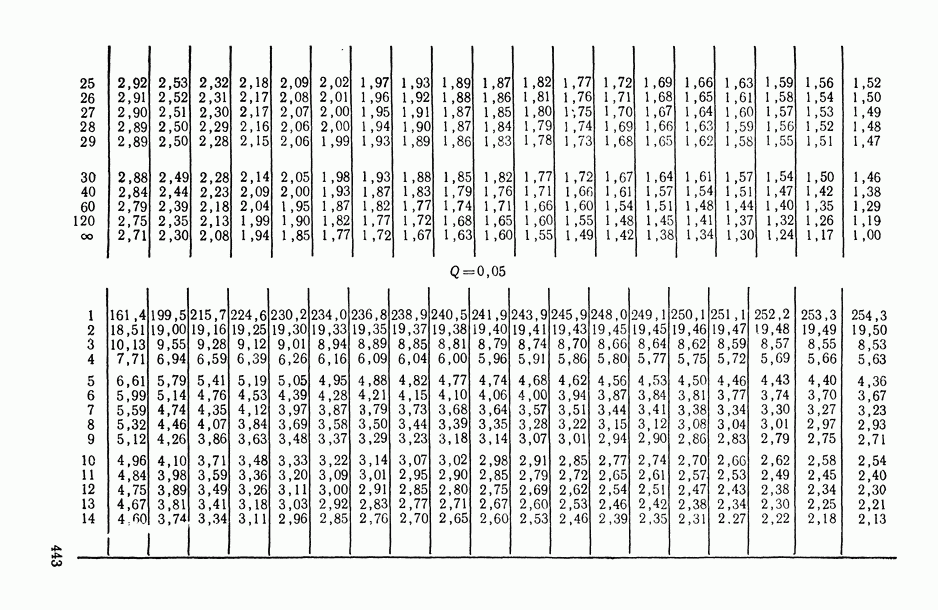
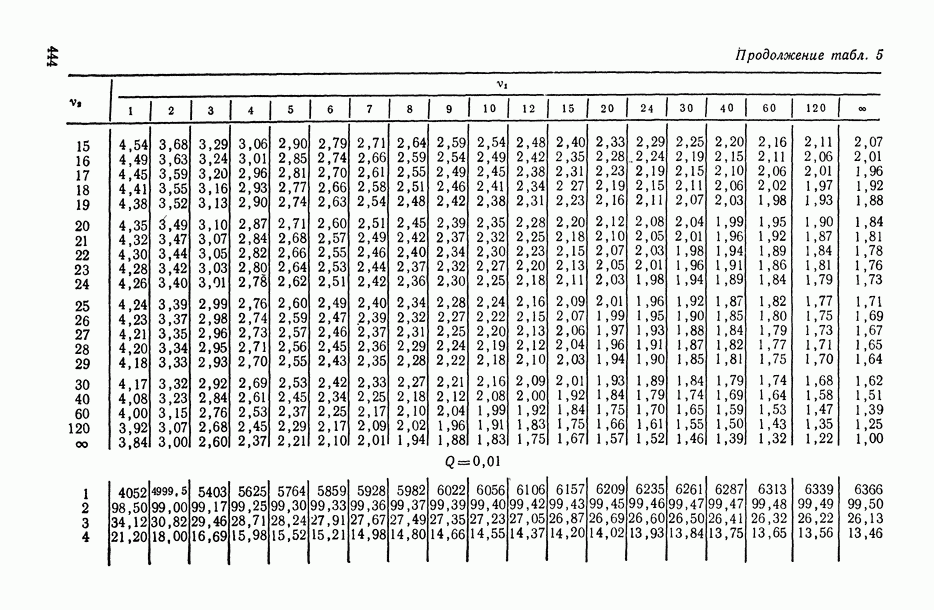
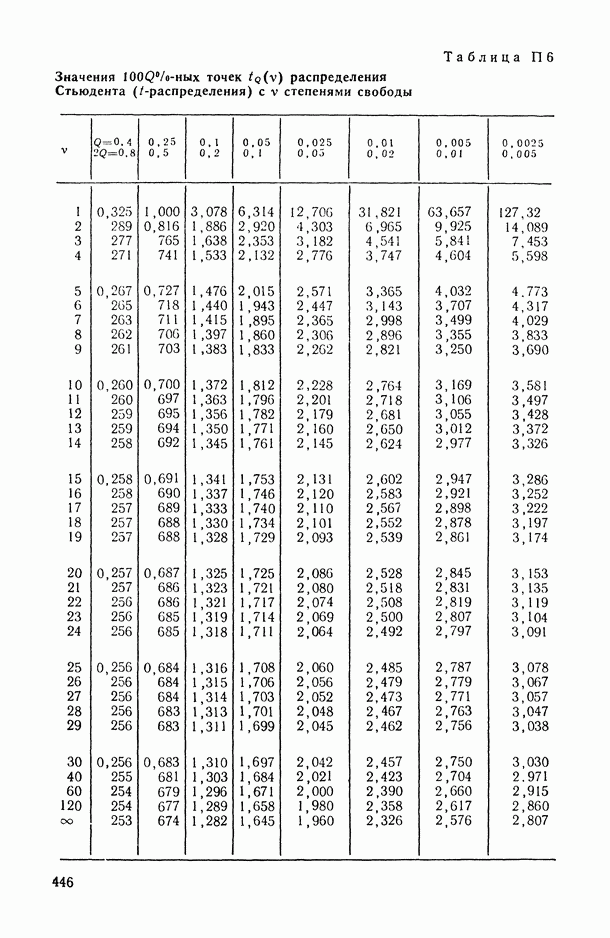
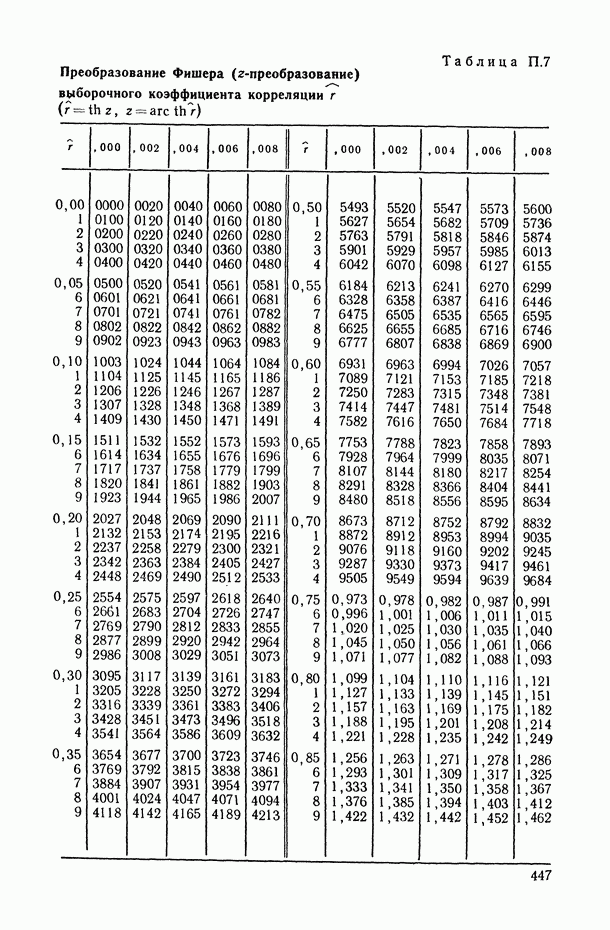
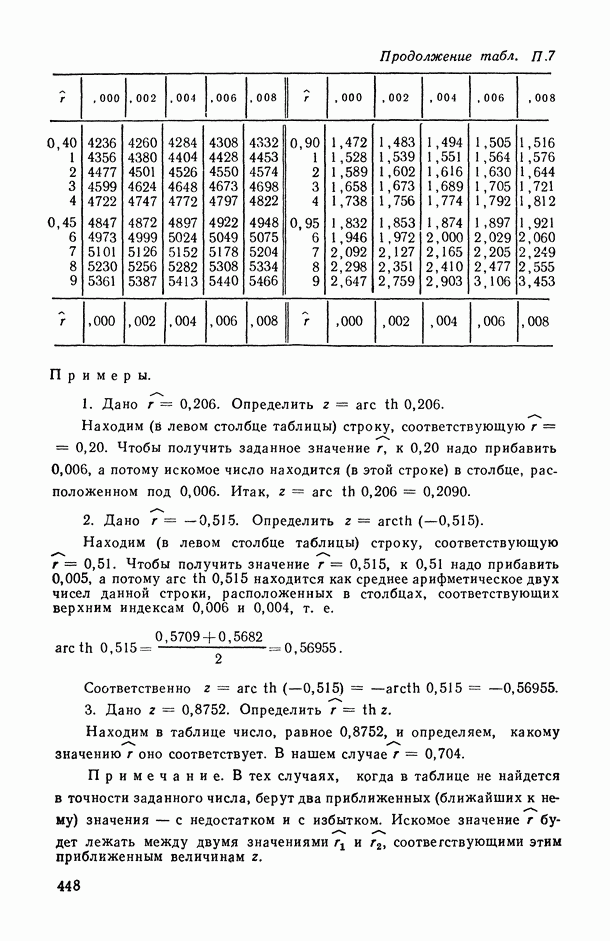
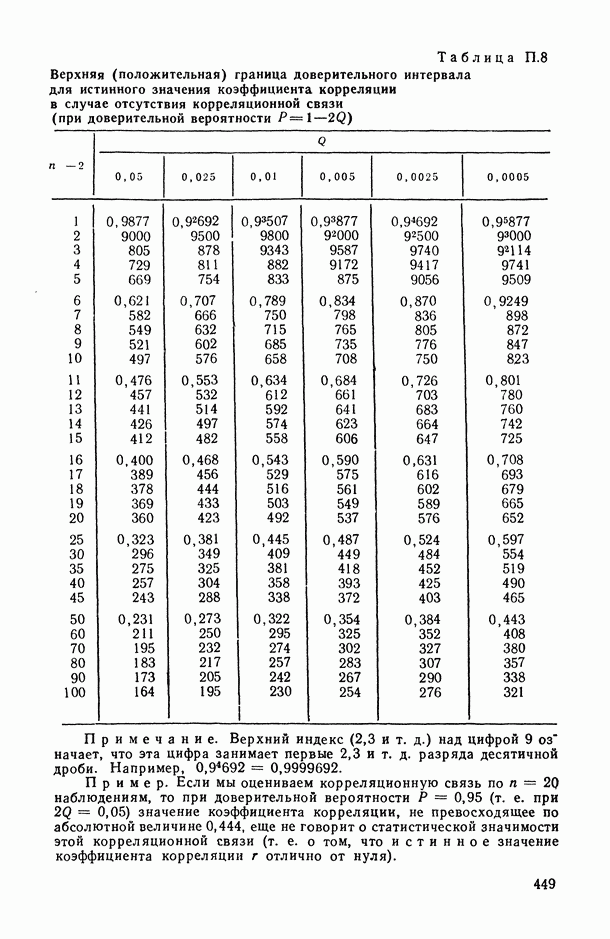
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
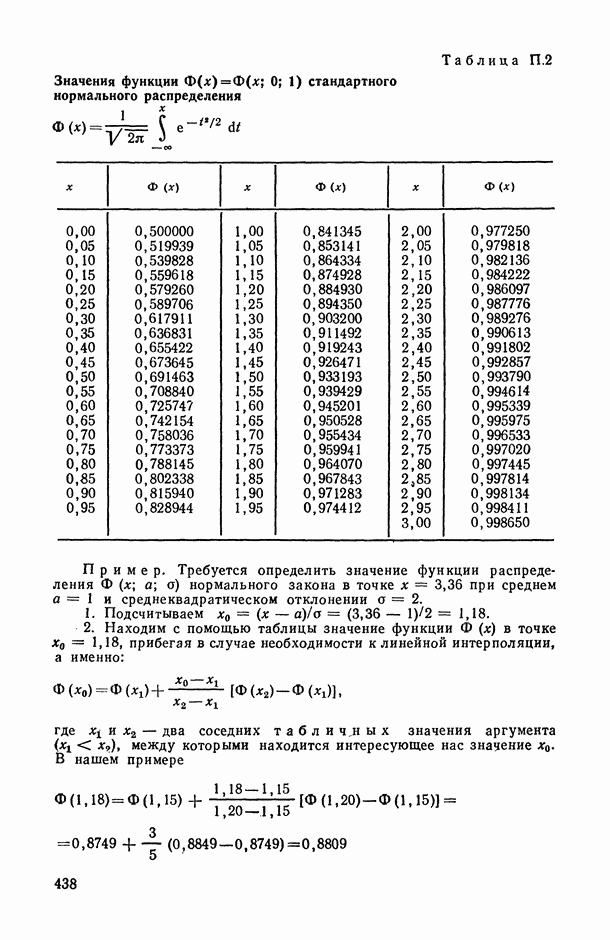
- Таблица П.2. Значения функции стандартного нормального распределения
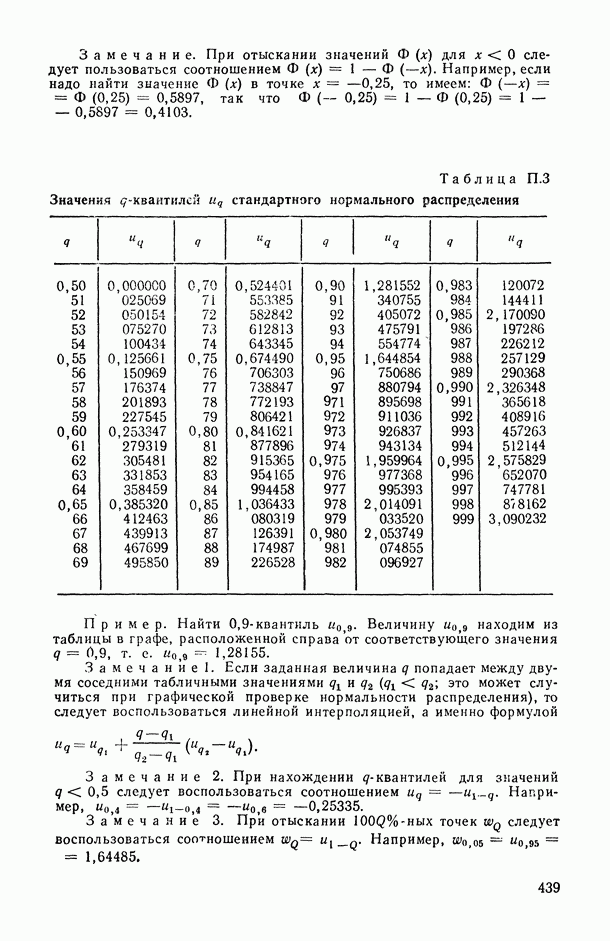
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
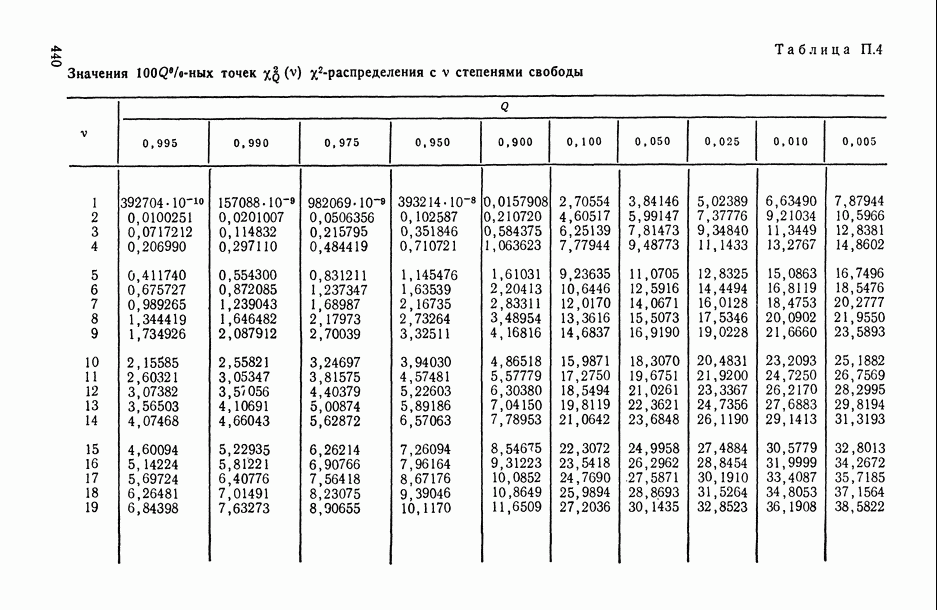
- СПИСОК ЛИТЕРАТУРЫ