| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
На практике далеко не всегда исходя из профессиональных соображений удается найти аналитический вид регрессионной зависимости. Использование же для ее описания одного из стандартных классов функций может привести к заметной систематической ошибке. Для уменьшения этой опасности прибегают к методам локального (при заданном значении регрессора) оценивания регрессии (§ 10.1-10.2) или же разбивают область возможных значений регрессора на несколько частей и для каждой из них строят свое аналитическое описание регрессионной зависимости (§ 10.3).
Построение простейших непараметрических оценок рассматривается в п. 10.1.1. Их слабое место: недостаточно эффективное использование гладкости регрессии и особенностей геометрического расположения выборочных значений регрессора. Возможны два пути борьбы с этим недостатком: 1) усложнение весовой функции в (10.2) и 2) локальное использование обычной параметрической регрессии для оценки коэффициентов при первых членах разложения регрессионной кривой (поверхности) в ряд Тейлора в окрестности изучаемой точки.
В этой главе принят второй путь как более наглядный и традиционный для статистики.
10.1. Непараметрическое оценивание регрессии
10.1.1. Роль и место непараметрических методов.
Непараметрический подход к оцениванию позволяет ослабить два основных требования классической постановки регрессионной задачи. Первое предположение о том, что  как функция X представима в виде
как функция X представима в виде  , где
, где  — известная функция своих аргументов, а В — вектор неизвестных параметров, оцениваемый по выборочным данным, — заменяется на более слабое предположение, что
— известная функция своих аргументов, а В — вектор неизвестных параметров, оцениваемый по выборочным данным, — заменяется на более слабое предположение, что  — непрерывная и гладкая функциях. Второе — требование постоянства
— непрерывная и гладкая функциях. Второе — требование постоянства  дисперсии случайной погрешности — заменяется на предположение непрерывности
дисперсии случайной погрешности — заменяется на предположение непрерывности  .
.
В простейшей непараметрической оценке выбирается некоторая непустая окрестность точки  и, предполагая, что в этой окрестности
и, предполагая, что в этой окрестности  приблизительно постоянна, полагаем
приблизительно постоянна, полагаем

где суммирование в числителе и знаменателе проводится по всем выборочным точкам  . Формуле (10.1) можно придать несколько другой вид, удобный для дальнейших обобщений. Введем весовую функцию
. Формуле (10.1) можно придать несколько другой вид, удобный для дальнейших обобщений. Введем весовую функцию  если
если  и равную нулю в противном случае. Тогда (10.1) перепишется в виде
и равную нулю в противном случае. Тогда (10.1) перепишется в виде

Классическая непараметрическая оценга регрессии получается из (10.2) путем предположения, что

где  — известная функция неотрицательного аргумента, стремящаяся к нулю при и
— известная функция неотрицательного аргумента, стремящаяся к нулю при и  ; b — параметр масштаба, задающий размер окрестности. Обычно полагают
; b — параметр масштаба, задающий размер окрестности. Обычно полагают

Поскольку в непараметрических оценках  используется не вся выборка, а только ее часть — совокупность пар
используется не вся выборка, а только ее часть — совокупность пар  входящими в окрестность
входящими в окрестность  где приближенно верны классические предположения, то в случае, когда 1) классические предположения верны для всей области изменения X и 2) параметрическое представление регрессионной зависимости известно исследователю, непараметрические оценки всегда менее эффективны по сравнению с классическими. Однако они имеют меньшее смещение, когда эти предположения нарушаются. В реальных задачах, выбирая метод оценивания регрессии, следует стремиться сбалансировать обе погрешности: случайную, как правило, уменьшающуюся при расширении объема используемой выборки, и систематическую, растущую при этом.
где приближенно верны классические предположения, то в случае, когда 1) классические предположения верны для всей области изменения X и 2) параметрическое представление регрессионной зависимости известно исследователю, непараметрические оценки всегда менее эффективны по сравнению с классическими. Однако они имеют меньшее смещение, когда эти предположения нарушаются. В реальных задачах, выбирая метод оценивания регрессии, следует стремиться сбалансировать обе погрешности: случайную, как правило, уменьшающуюся при расширении объема используемой выборки, и систематическую, растущую при этом.
10.1.2. Примеры.
Прежде чем переходить к последовательному изложению непараметрических оценок, приведем два примера их использования, заимствованных из опубликованных работ.
Пример 10.1 [49]. Для анализа производительности труда изучалась зависимость у — выработки  на одного рабочего в строительно-монтажном тресте от — объема (млн. руб.) строительно-монтажных работ (СМР);
на одного рабочего в строительно-монтажном тресте от — объема (млн. руб.) строительно-монтажных работ (СМР);  — рентабельности в процентах к сметной стоимости СМР;
— рентабельности в процентах к сметной стоимости СМР;  — объема продукции подсобных предприятий в процентах к сметной стоимости СМР;
— объема продукции подсобных предприятий в процентах к сметной стоимости СМР;  — ритмичности СМР в течение года по кварталам
— ритмичности СМР в течение года по кварталам  — фактической стоимости потребленных материалов в процентах к общей стоимости СМР;
— фактической стоимости потребленных материалов в процентах к общей стоимости СМР;  — фондоемкости;
— фондоемкости;  — текучести кадров к среднемесячному числу рабочих. За единицу наблюдения был взят строительно-монтажный трест. Выборка объема
— текучести кадров к среднемесячному числу рабочих. За единицу наблюдения был взят строительно-монтажный трест. Выборка объема 
После проведения классического регрессионного анализа с отсевом незначимых факторов была получена модель 
Эта модель легко интерпретировалась с точки зрения экономического содержания. Действительно,  являются ведущими аргументами, увеличение которых положительно сказывается на выработке, а
являются ведущими аргументами, увеличение которых положительно сказывается на выработке, а  — это производство продукции внутри треста, которое в силу малой мощности предприятий не может быть рентабельным, но без него невозможно строительство. Погрешность аппроксимации в терминах
— это производство продукции внутри треста, которое в силу малой мощности предприятий не может быть рентабельным, но без него невозможно строительство. Погрешность аппроксимации в терминах  — среднего абсолютного относительного отклонения и
— среднего абсолютного относительного отклонения и  — стандартного отклонения составила для (10.4)
— стандартного отклонения составила для (10.4)

Оценка той же регрессионной зависимости с помощью непараметрической процедуры (10.2) дала заметно лучшее приближение: енецар  . Правда, интерпретация непараметрической модели сложнее. Работа не оканчивается получением оценок значений регрессии в заданных точках, а требуется еще установить, как в среднем меняется регрессионная зависимость при изменении аргументов. Часто атому не уделяется должного внимания. Пример 10.2 [22, 88]. Рассматривалась модельная одномерная задача, где
. Правда, интерпретация непараметрической модели сложнее. Работа не оканчивается получением оценок значений регрессии в заданных точках, а требуется еще установить, как в среднем меняется регрессионная зависимость при изменении аргументов. Часто атому не уделяется должного внимания. Пример 10.2 [22, 88]. Рассматривалась модельная одномерная задача, где  — случайная величина, равномерно распределенная на отрезке
— случайная величина, равномерно распределенная на отрезке  . В качестве меры погрешности
. В качестве меры погрешности  метода аппроксимации бралось
метода аппроксимации бралось 
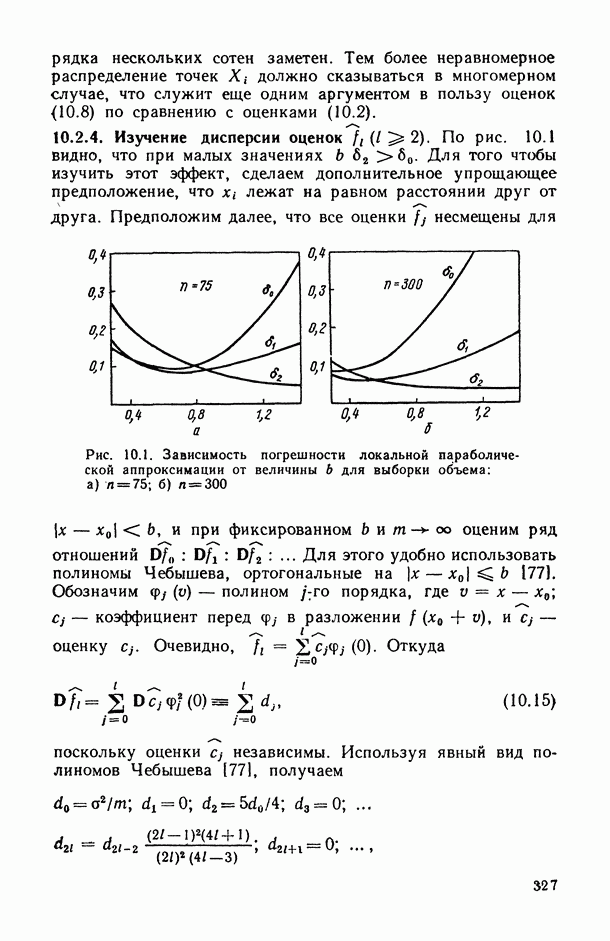
На рис. 10.1 показаны значения  , соответствующие непараметрическому оцениванию с помощью метода локальной параболической (порядка i) аппроксимации (§ 10.2) с весовой функцией
, соответствующие непараметрическому оцениванию с помощью метода локальной параболической (порядка i) аппроксимации (§ 10.2) с весовой функцией  Параметрическое оценивание с неадекватно предположенной моделью
Параметрическое оценивание с неадекватно предположенной моделью  в обоих случаях
в обоих случаях  дало значительно большую погрешность
дало значительно большую погрешность 
По рисунку видно, что при использовании неадекватной параметрической модели погрешность наибольшая. Локальная параболическая аппроксимация с использованием полинома второй степени лучше, чем традиционно применяемая аппроксимация полиномом нулевой степени. Первая не только дает наименьшую погрешность, но и значительно устойчивее к выбору величины b.
10.1.3. Выбор параметра масштаба b.
Это наиболее ответственный момент при использовании непараметрических оценок типа (10.2). Здесь возможны два подхода: 1) выбор единого значения b для всей области изменения X (так обычно поступают на практике) и 2) локальный выбор b в зависимости от того, насколько близко к искомой точке  расположены точки
расположены точки  выборки.
выборки.
В первом случае целесообразно построить как функцию b кривую

задающую асимптотически (при  ) несмещенную оценку величины среднеквадратической погрешности непараметрической аппроксимации.
) несмещенную оценку величины среднеквадратической погрешности непараметрической аппроксимации.
Подходящее значение  находится из условия, что
находится из условия, что  для всех
для всех 
Локальный выбор b целесообразен, когда  расположены в области интересующих нас значений очень неравномерно. В этом случае можно, например, потребовать, чтобы b
расположены в области интересующих нас значений очень неравномерно. В этом случае можно, например, потребовать, чтобы b  — величина b в точке
— величина b в точке  — выбиралось из условия
— выбиралось из условия

где  — некоторое наперед заданное число. Для нахождения оптимального значения
— некоторое наперед заданное число. Для нахождения оптимального значения  можно воспользоваться описанной выше процедурой, но с заменой в (10.5) в левой части
можно воспользоваться описанной выше процедурой, но с заменой в (10.5) в левой части  на
на  , а в правой под знаком второй суммы b — на
, а в правой под знаком второй суммы b — на  , где
, где  определяется (10.6). Так же как b, гаопт находится из условия минимизации
определяется (10.6). Так же как b, гаопт находится из условия минимизации  .
.
10.1.4. Более эффективное использование гладкости.
Если регрессионная поверхность достаточно гладкая и в окрестности  может приближенно считаться линейной, т. е.
может приближенно считаться линейной, т. е.

где  — неизвестный вектор, зависящий только от
— неизвестный вектор, зависящий только от  то для оценки
то для оценки  вместо (10.2) можно воспользоваться оценкой
вместо (10.2) можно воспользоваться оценкой

где 

для  . Для обоснования (10.8) заметим, что предложенная точечная оценка есть обычная мнк-оценка постоянного члена в случае линейной поверхности регрессии, когда в (10.7) отброшены члены, обозначенные
. Для обоснования (10.8) заметим, что предложенная точечная оценка есть обычная мнк-оценка постоянного члена в случае линейной поверхности регрессии, когда в (10.7) отброшены члены, обозначенные  . В примере 10.2 мы видели, что эта оценка (соответственно
. В примере 10.2 мы видели, что эта оценка (соответственно  ) может быть значительно лучше оценки (10.2) (соответственно
) может быть значительно лучше оценки (10.2) (соответственно  ). Она специально рассчитана на случай, когда
). Она специально рассчитана на случай, когда  не заполняют равномерно пространство возможных значений X.
не заполняют равномерно пространство возможных значений X.
Использование оценки (10.8) вместо (10.2) открывает возможность содержательной интерпретации регрессионной зависимости, на необходимость чего было обращено внимание в примере 10.1.
Для этого достаточно наряду с оценкой  построить
построить  — оценку вектора
— оценку вектора  в (10.7)
в (10.7)

Сравнение 0 (X) для разных значений X дает возможность оценить, как, насколько меняется влияние изучаемых факторов на регрессию в разных областях пространства возможных значений X.
При использовании формул (10.8), (10.9) выбор величины b можно производить так же, как указано в предыдущем пункте.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
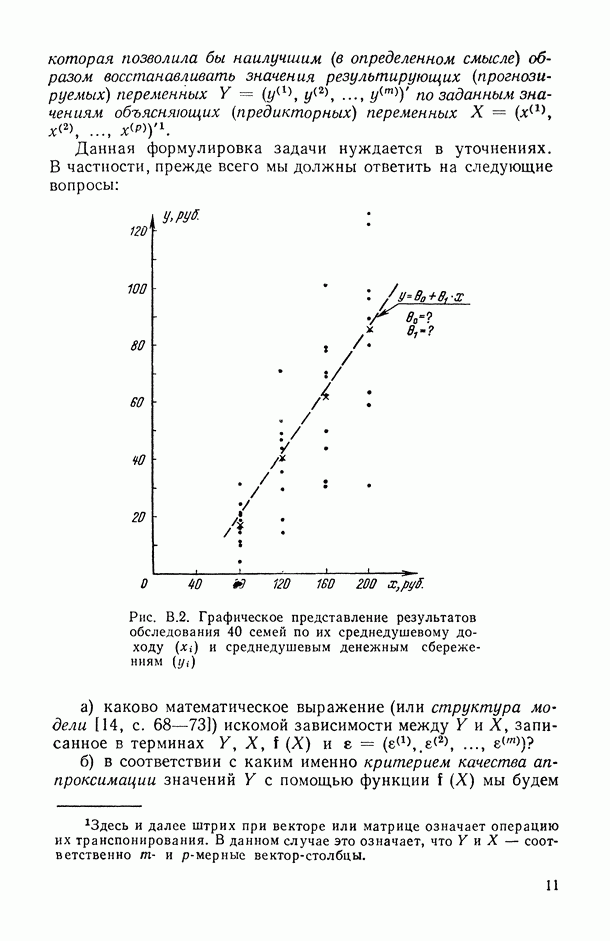
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
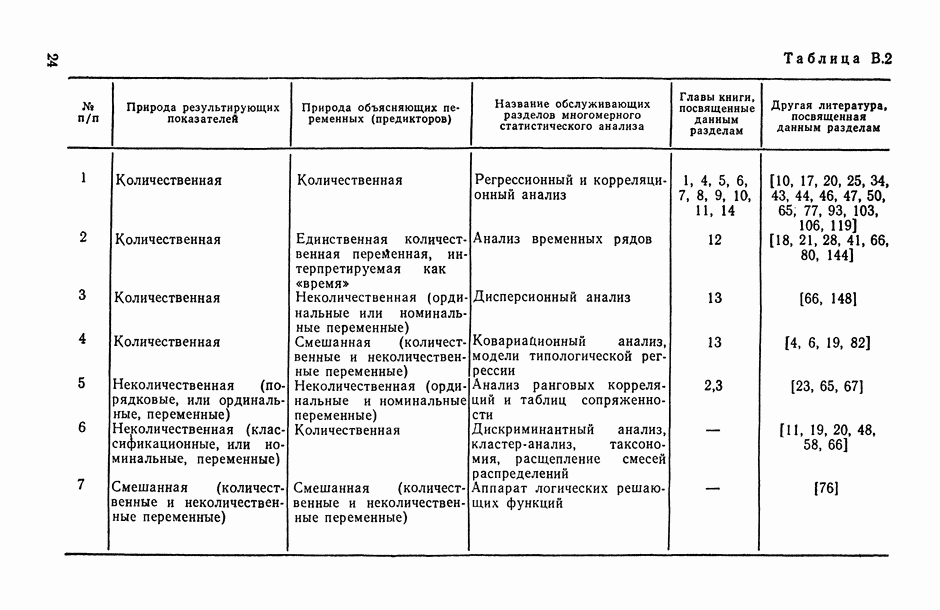
- В.3. Математический инструментарий
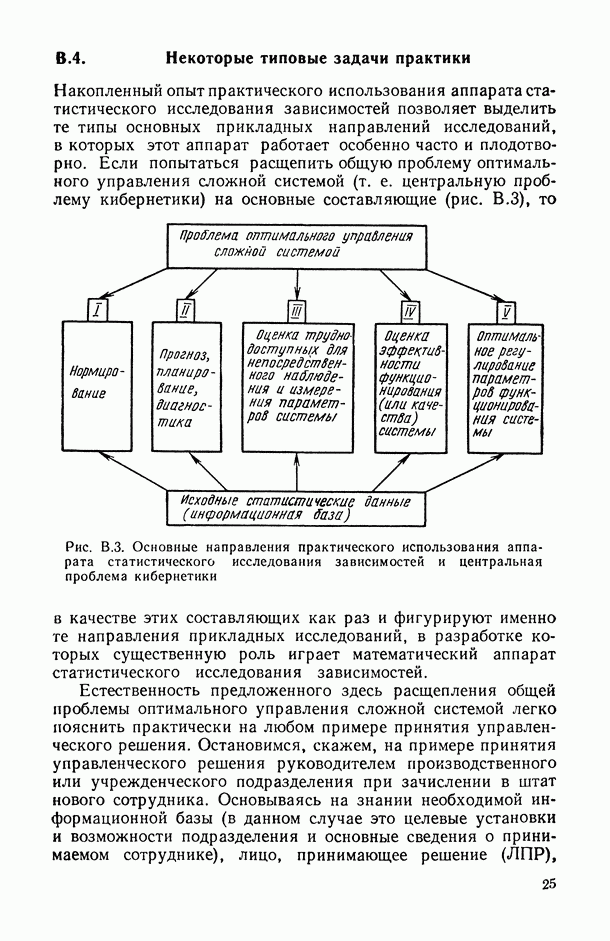
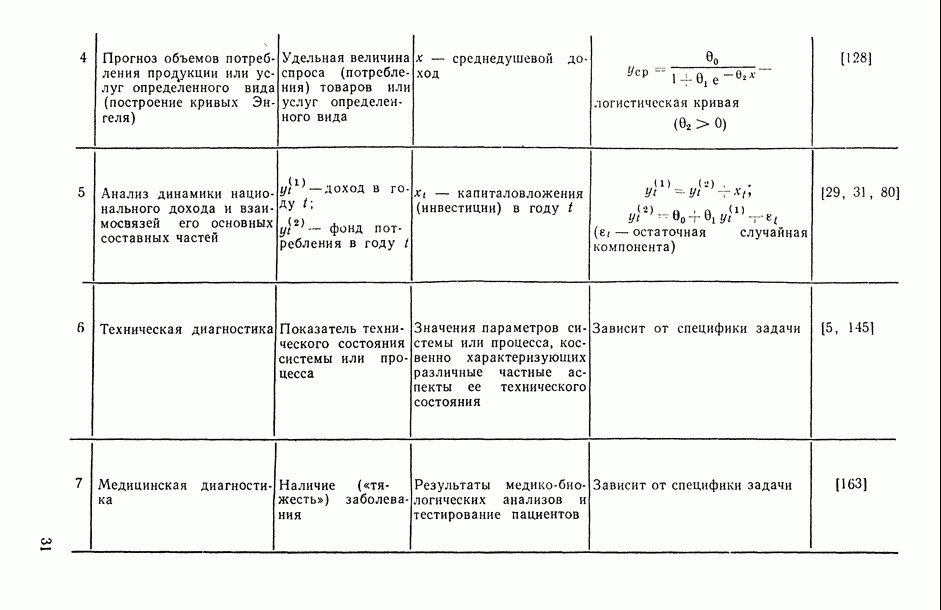
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
- 2.3. Анализ множественных ранговых связей
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
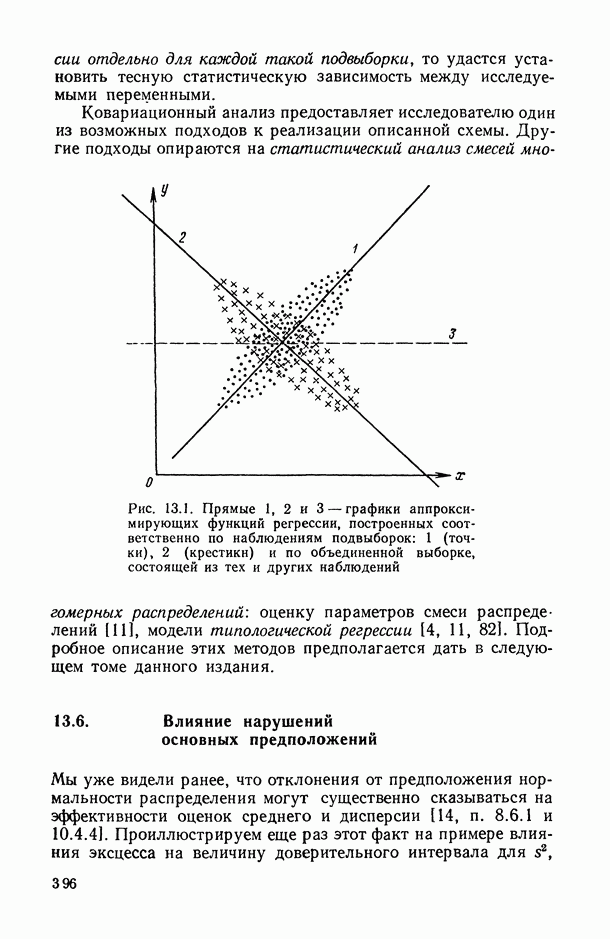
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
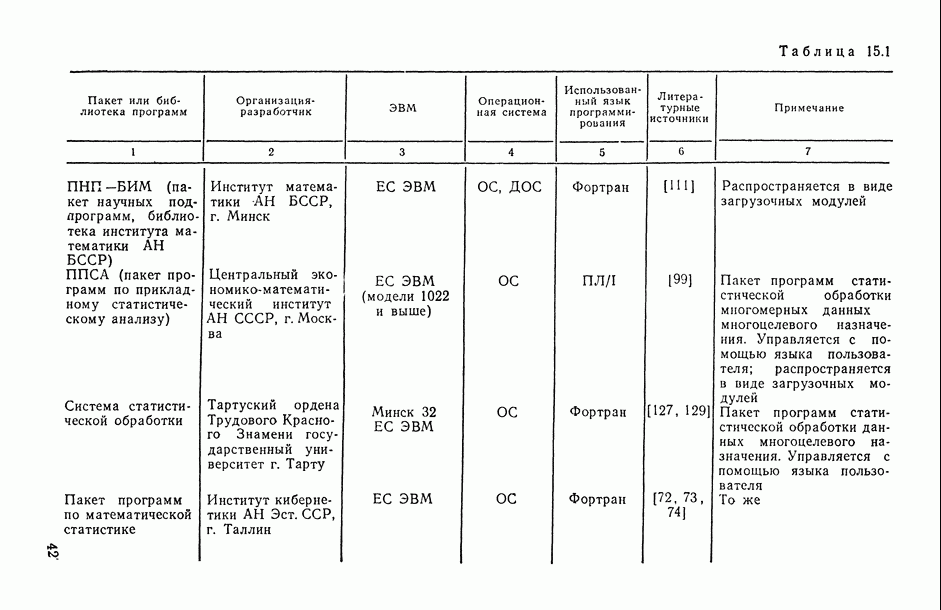
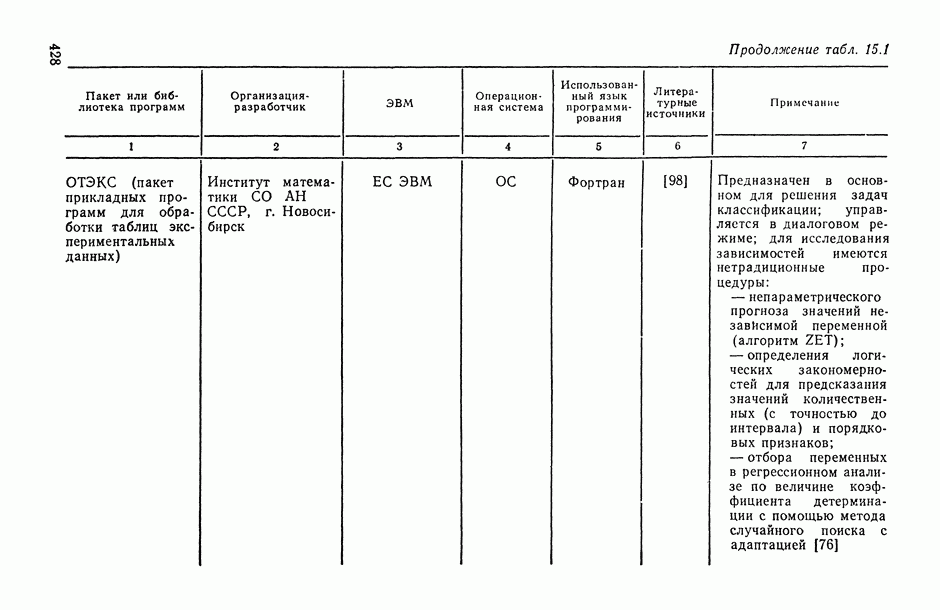
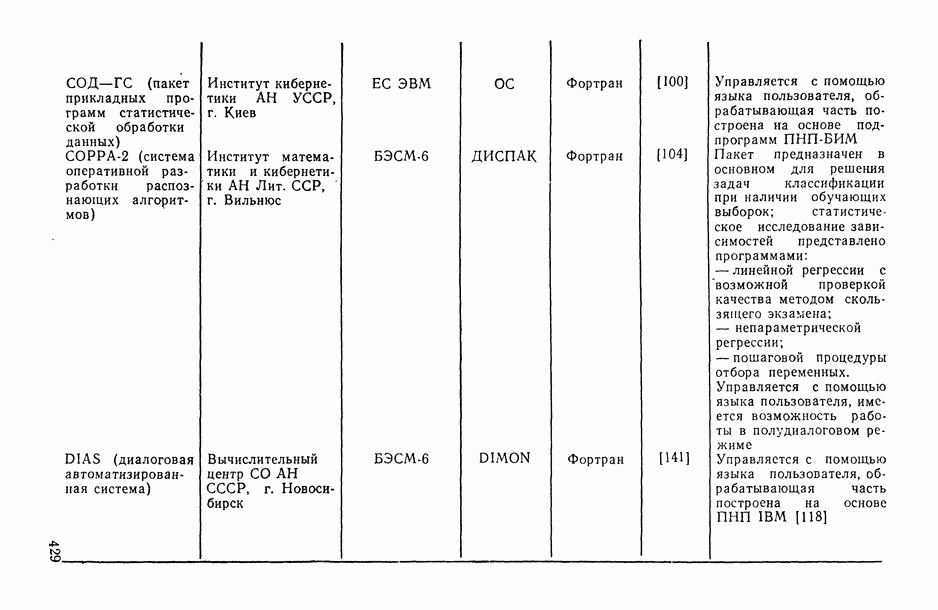
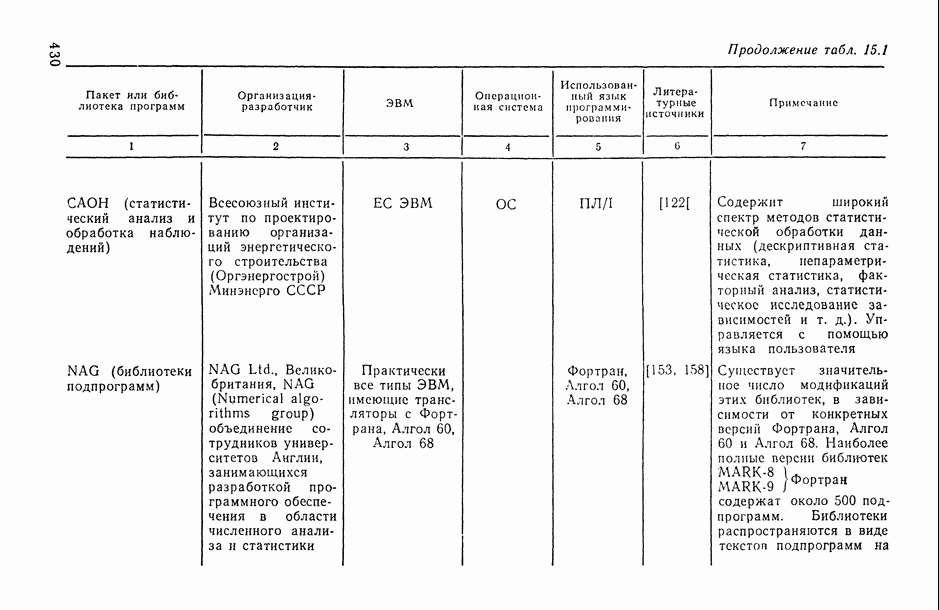
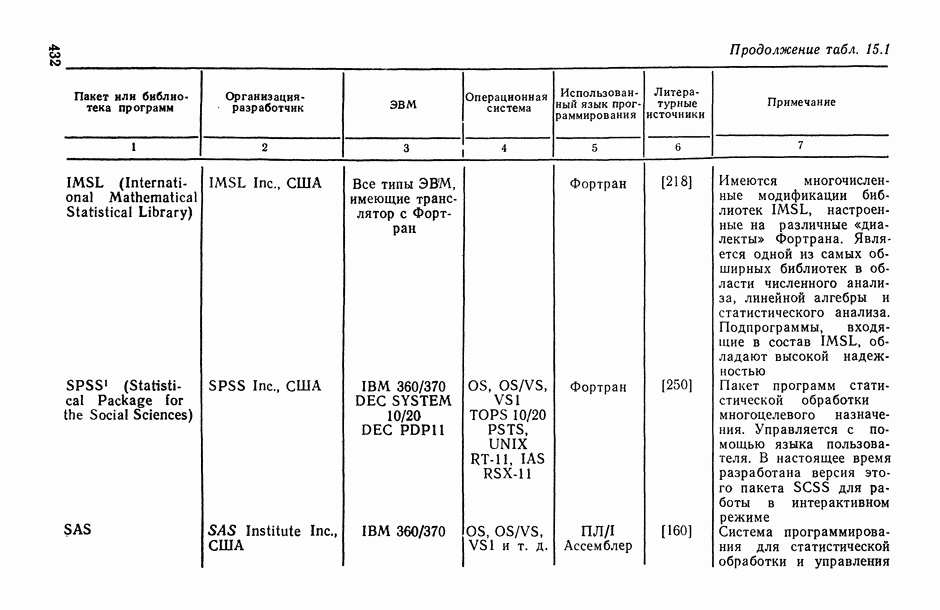
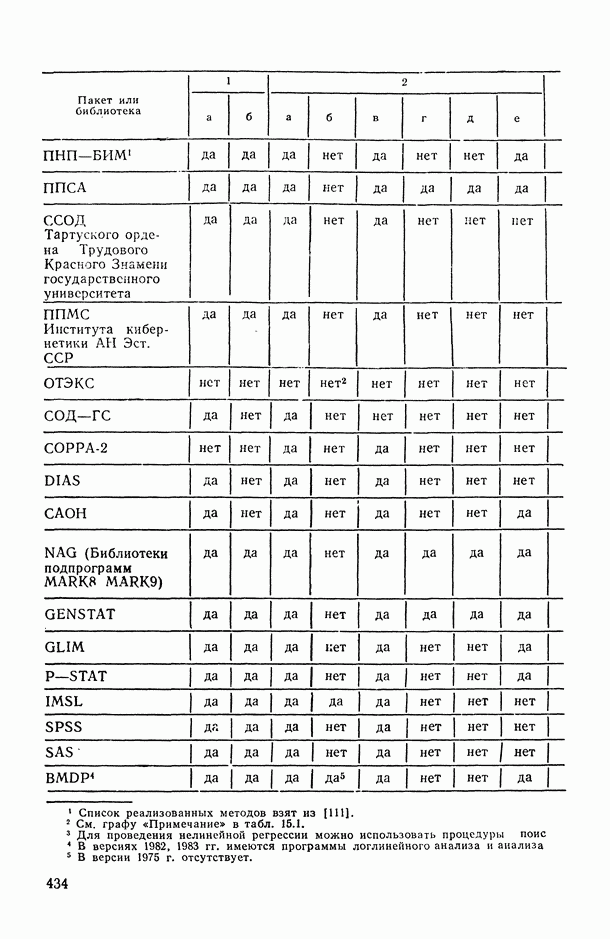
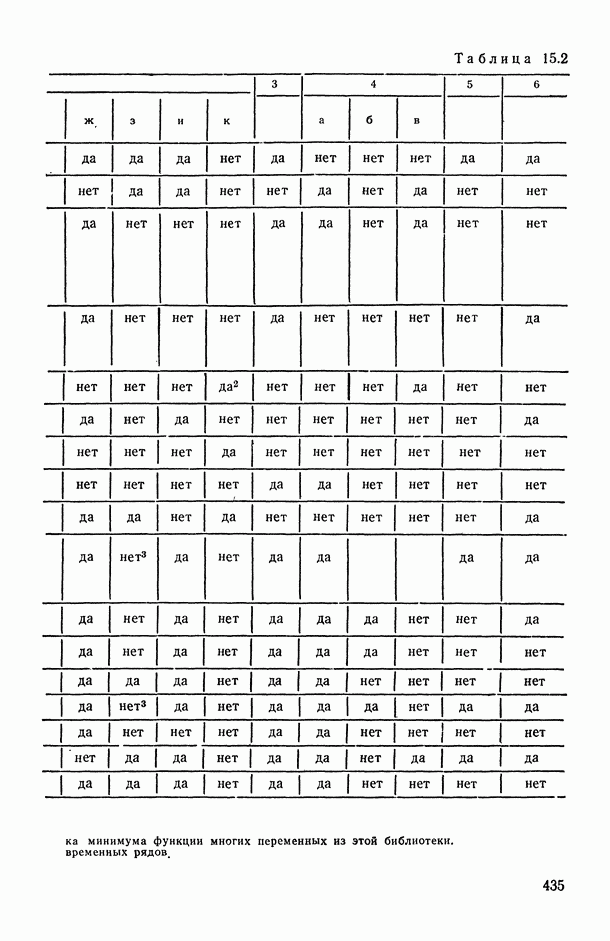
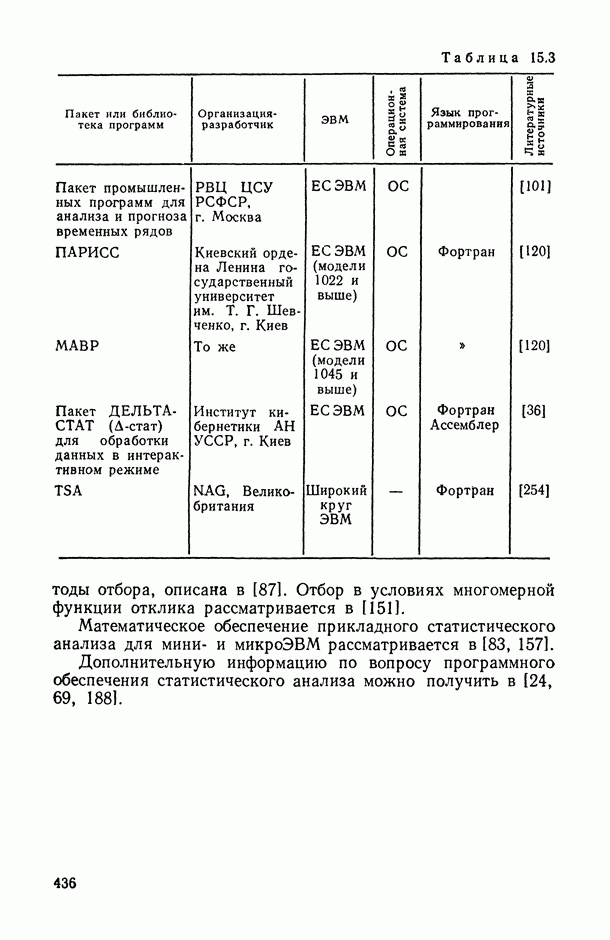
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
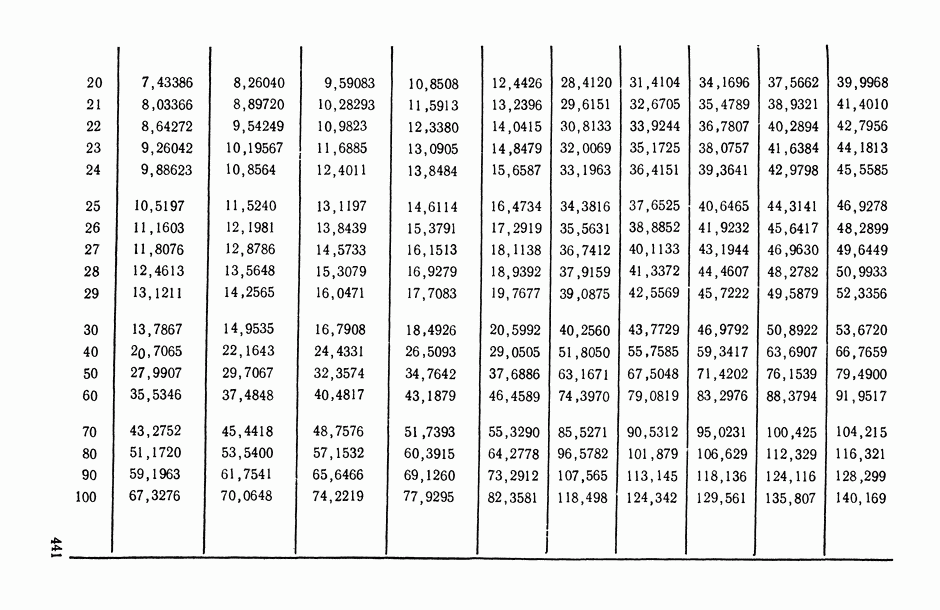
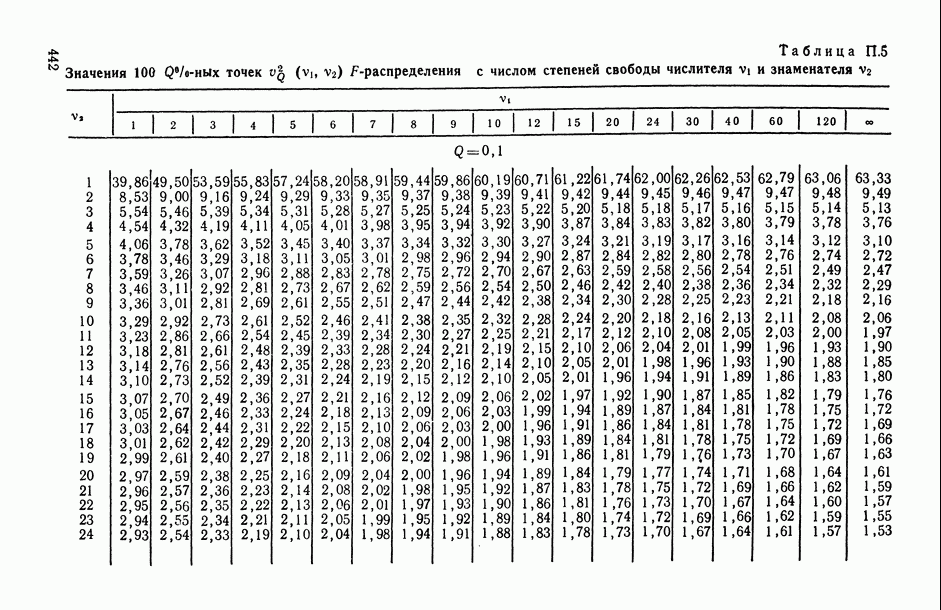
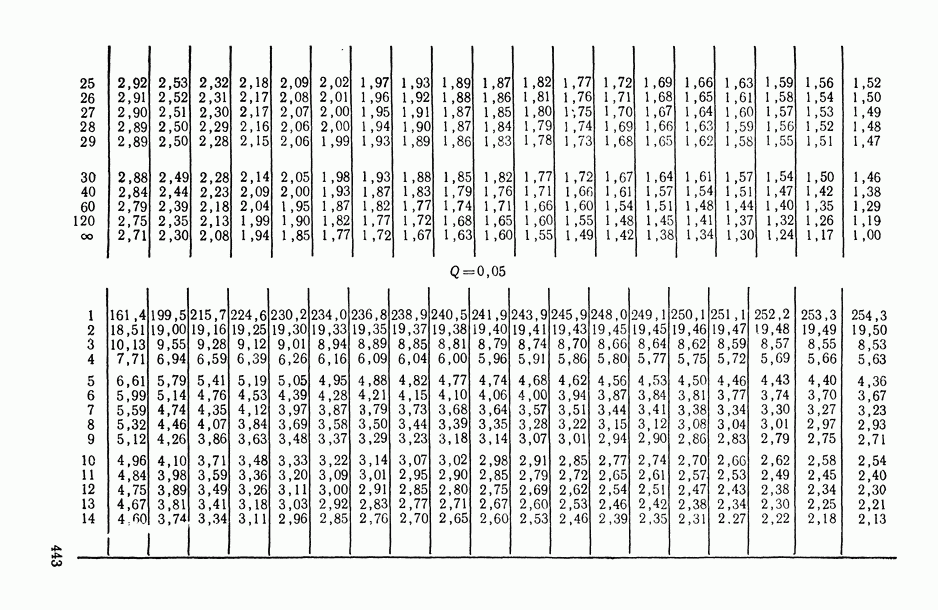
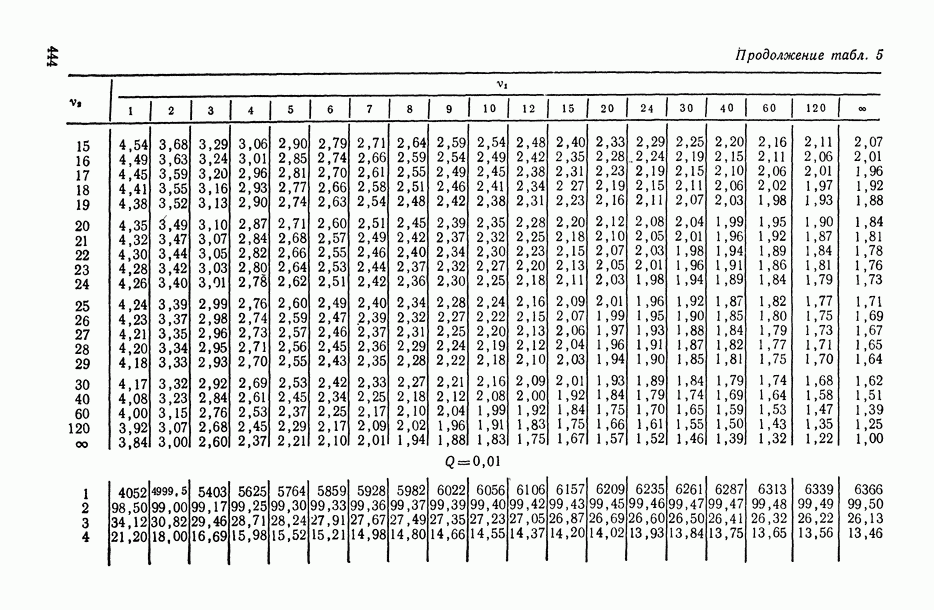
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
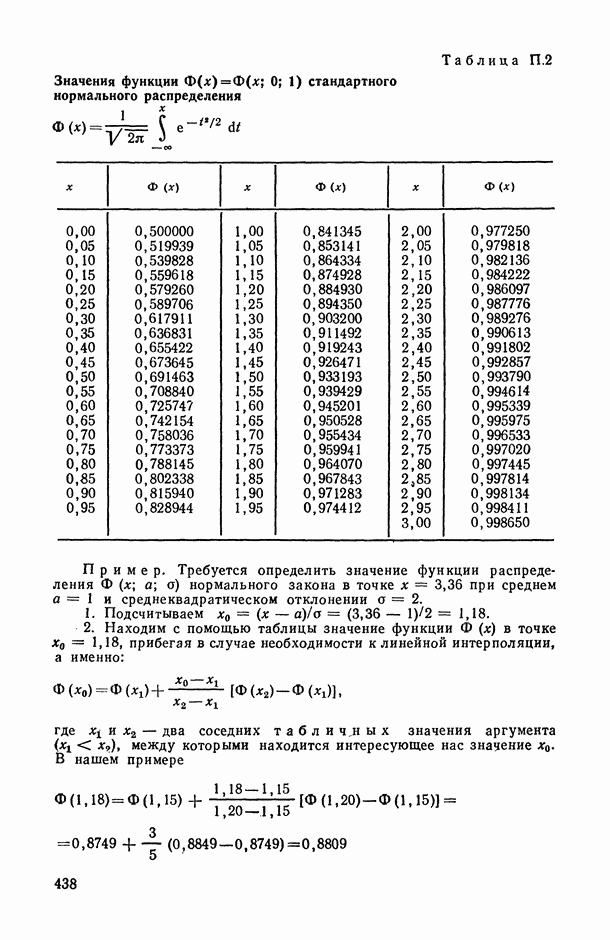
- Таблица П.2. Значения функции стандартного нормального распределения
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ