| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
При отклонениях исследуемой зависимости от линейного вида, как уже отмечалось, коэффициент корреляции  теряет свой смысл как характеристика степени тесноты связи. В этих случаях исследователь должен воспользоваться имеющимися у него двумерными выборочными данными
теряет свой смысл как характеристика степени тесноты связи. В этих случаях исследователь должен воспользоваться имеющимися у него двумерными выборочными данными  с целью построения оценок для определенной выше, в некотором смысле универсальной теоретической характеристики степени тесноты связи — индекса корреляции (см. формулу (1.6)). Способ построения таких оценок выбирается в зависимости от природы имеющихся у нас выборочных данных и от характера некоторых дополнительных допущений.
с целью построения оценок для определенной выше, в некотором смысле универсальной теоретической характеристики степени тесноты связи — индекса корреляции (см. формулу (1.6)). Способ построения таких оценок выбирается в зависимости от природы имеющихся у нас выборочных данных и от характера некоторых дополнительных допущений.
Корреляционное отношение. Наиболее привлекательной в этом смысле является ситуация, в которой характер выборочных данных (их количество, «плотность» расположения на плоскости) допускает их группировку по оси объясняющей переменной и возможность подсчета так называемых «частных» средних ординат  внутри каждого
внутри каждого  интервала группирования.
интервала группирования.
Пусть такое группирование данных произведено. При этом, как обычно, k — число интервалов группирования по оси абсцисс; (i = 1, 2, ..., k) — число выборочных точек, попавших  интервал группирования;
интервал группирования;  — среднее значение ординат точек, попавших в i-й интервал группирования. Тогда, как легко понять, выборочным аналогом (оценкой) введенной ранее дисперсии of будет величина
— среднее значение ординат точек, попавших в i-й интервал группирования. Тогда, как легко понять, выборочным аналогом (оценкой) введенной ранее дисперсии of будет величина

где общее среднее  .
.
Соответственно получаем оценку для в виде

где выборочная дисперсия  индивидуальных результатов наблюдения
индивидуальных результатов наблюдения  около общего среднего у вычисляется по формуле
около общего среднего у вычисляется по формуле

Величину  принято называть корреляционным отношением зависимой переменной
принято называть корреляционным отношением зависимой переменной  по независимой переменной Его вычисление не обременено никакими дополнительными допущениями относительно общего вида регрессионной зависимости (1.1). Однако, в отличие от коэффициента корреляции, корреляционное отношение несимметрично по отношению к исследуемым переменным, т. е., вообще говоря,
по независимой переменной Его вычисление не обременено никакими дополнительными допущениями относительно общего вида регрессионной зависимости (1.1). Однако, в отличие от коэффициента корреляции, корреляционное отношение несимметрично по отношению к исследуемым переменным, т. е., вообще говоря,  . Кроме того, корреляционное отношение, по определению, является величиной неотрицательной, так как под ним подразумевается результат извлечения арифметического значения корня квадратного из
. Кроме того, корреляционное отношение, по определению, является величиной неотрицательной, так как под ним подразумевается результат извлечения арифметического значения корня квадратного из  .
.
В остальном свойства корреляционного отношения во многом похожи на свойства коэффициента корреляции.
Из (1.5) и (1.6), в частности, немедленно следует, что подобно коэффициенту корреляции корреляционное отношение не может быть больше единицы. Из  следует наличие однозначной функциональной связи между
следует наличие однозначной функциональной связи между  , и, наоборот, однозначная функциональная связь между
, и, наоборот, однозначная функциональная связь между  свидетельствует о том, что
свидетельствует о том, что  . Далее, отсутствие корреляционной связи между
. Далее, отсутствие корреляционной связи между  означает, что условные средние
означает, что условные средние  сохраняют постоянное значение, равное общему среднему у, а потому
сохраняют постоянное значение, равное общему среднему у, а потому  Наоборот, если
Наоборот, если  и следовательно, частные средние
и следовательно, частные средние  не зависят от
не зависят от  т. е. соответствующая линия регрессии параллельна горизонтальной оси.
т. е. соответствующая линия регрессии параллельна горизонтальной оси.
Отметим, что между  нет какой-либо простой зависимости. Некоррелированность
нет какой-либо простой зависимости. Некоррелированность  с
с  (т. е. равенство нулю величины
(т. е. равенство нулю величины  ) не влечет за собой непосредственно некоррелированности
) не влечет за собой непосредственно некоррелированности  с
с  . Возможны ситуации, в которых один из этих показателей принимает нулевое значение, в то время как другой равен единице. Допустим, например, что
. Возможны ситуации, в которых один из этих показателей принимает нулевое значение, в то время как другой равен единице. Допустим, например, что  принимает значения:
принимает значения:  с вероятностями 1/3 каждое. В этом случае
с вероятностями 1/3 каждое. В этом случае  (в силу симметрии параболы относительно оси
(в силу симметрии параболы относительно оси  и симметричности распределения
и симметричности распределения  ).
).
Можно показать, что корреляционное отношение  не может быть меньше абсолютной величины коэффициента корреляции
не может быть меньше абсолютной величины коэффициента корреляции  , характеризующего зависимость между теми же переменными. В случае линейной зависимости эти две характеристики связи совпадают. Это позволяет использовать величину разности
, характеризующего зависимость между теми же переменными. В случае линейной зависимости эти две характеристики связи совпадают. Это позволяет использовать величину разности  в качестве меры отклонения регрессионной зависимости от линейного вида (см. п. 6.3.3).
в качестве меры отклонения регрессионной зависимости от линейного вида (см. п. 6.3.3).
И наконец, все замечания относительно смысловой интерпретации коэффициента корреляции  (в частности, о логическом соотношении понятий «корреляционная зависимость, связь между переменными, их причинная взаимообусловленность») остаются в силе и для корреляционного отношения.
(в частности, о логическом соотношении понятий «корреляционная зависимость, связь между переменными, их причинная взаимообусловленность») остаются в силе и для корреляционного отношения.
Проверка гипотезы об отсутствии корреляционной связи Какую величину корреляционного отношения можно признать статистически значимо отличающейся от нуля, т. е.достаточной для статистически обоснованного вывода о наличии корреляционной связи между исследуемыми переменными? Ведь так же, как и в случае прямолинейного типа зависимости, принципиально возможны ситуации, когда отклонение от нуля полученной величины корреляционного отношения  является статистически незначимым, т. е. обусловленным лишь неизбежными случайными колебаниями выборки.
является статистически незначимым, т. е. обусловленным лишь неизбежными случайными колебаниями выборки.
Для построения соответствующего критерия воспользуемся фактом приближенной  —
—  -распределенности случайной величины
-распределенности случайной величины

справедливым в предположении, что  (или, что то
(или, что то  и что условные распределения зависимой переменной
и что условные распределения зависимой переменной  при любом фиксированном
при любом фиксированном  описываются нормальным законом с постоянной дисперсией
описываются нормальным законом с постоянной дисперсией  (см., например, [65, с. 401]).
(см., например, [65, с. 401]).
Поэтому, если окажется, что

то гипотеза об отсутствии корреляционной связи между  отвергается с уровнем значимости а (здесь, как и ранее,
отвергается с уровнем значимости а (здесь, как и ранее,  -
-  -ная точка
-ная точка  -распределения с числом степеней свободы числителя
-распределения с числом степеней свободы числителя  и знаменателя
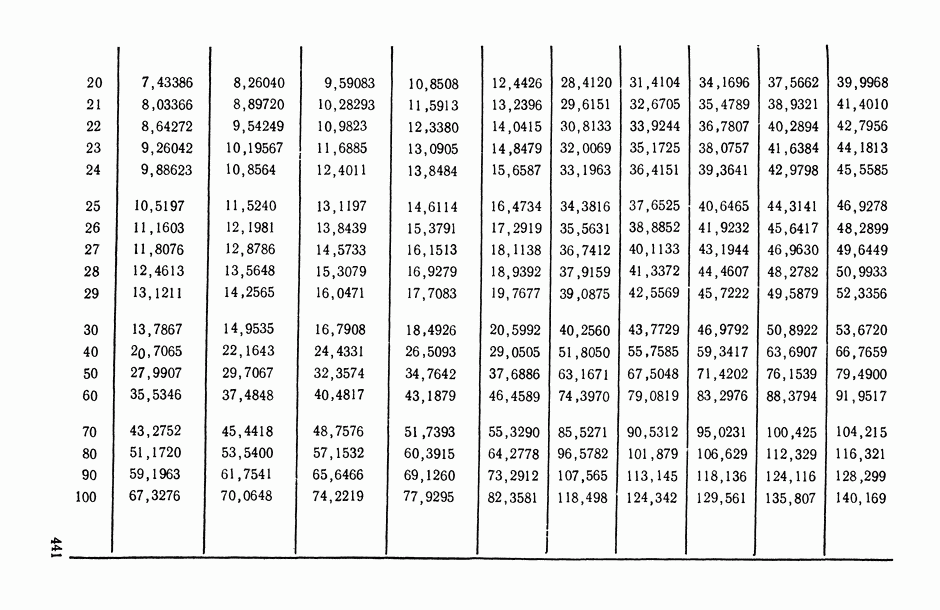
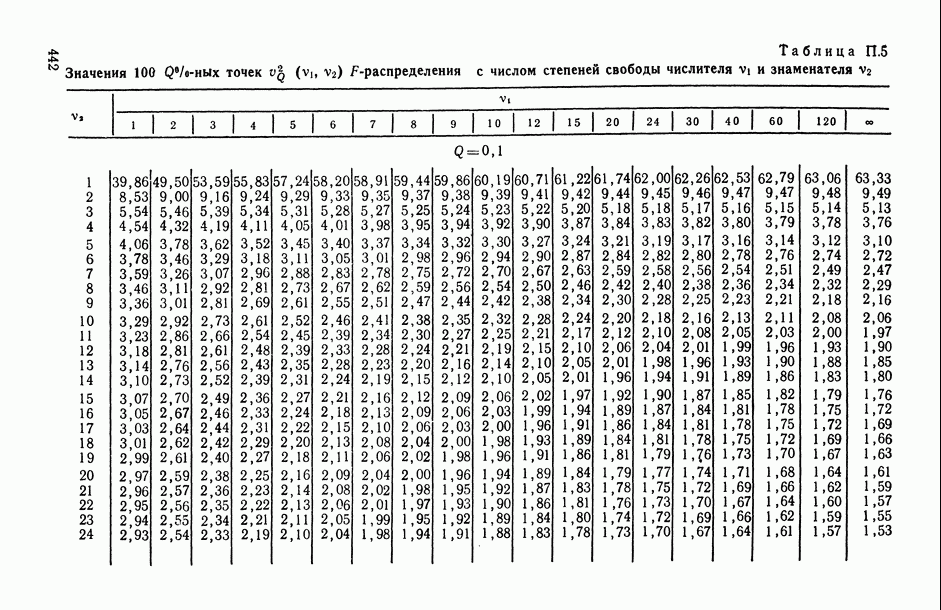
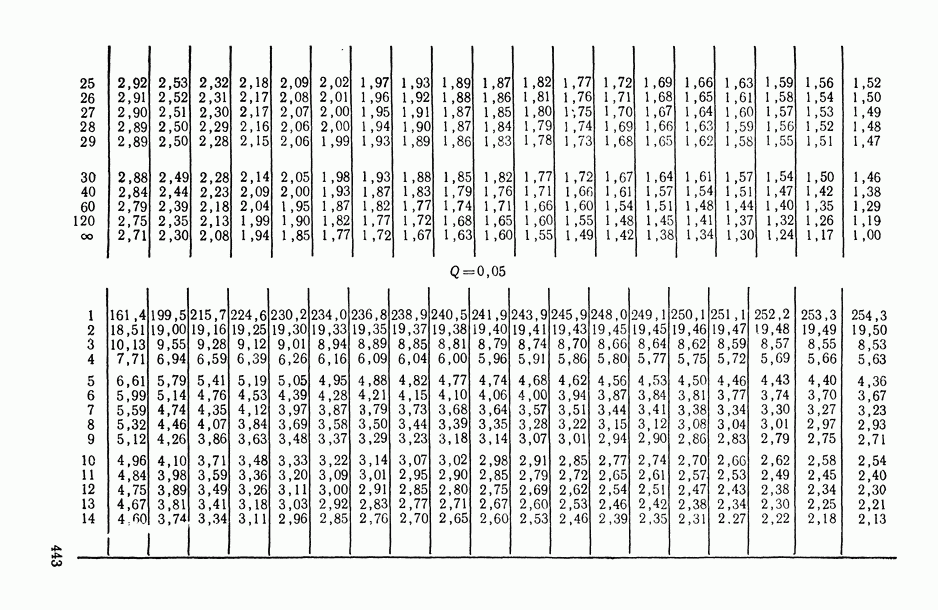
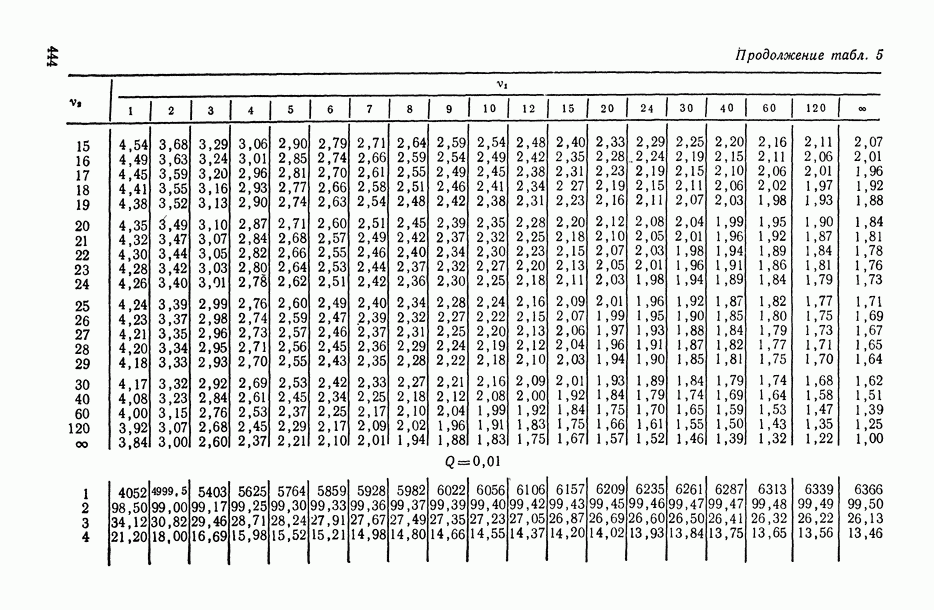
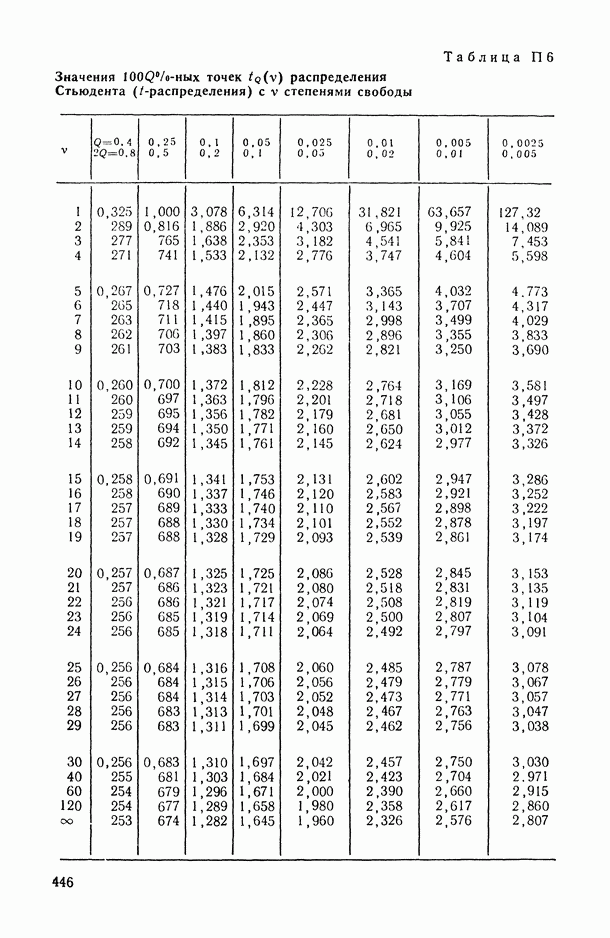
и знаменателя  находится из табл. П.5). При выполнении обратного неравенства значение корреляционного отношения
находится из табл. П.5). При выполнении обратного неравенства значение корреляционного отношения  признается статистически незначимым, т. е. делается вывод об отсутствии корреляционной связи между
признается статистически незначимым, т. е. делается вывод об отсутствии корреляционной связи между  и
и
Доверительные интервалы для истинного значения корреляционного отношения  можно построить, опираясь на тот факт, что статистика
можно построить, опираясь на тот факт, что статистика

приближенно подчиняется так называемому «нецентральному  -распределению», который оказывается справедливым в предположении
-распределению», который оказывается справедливым в предположении  -нормальности случайных величин
-нормальности случайных величин  и при любом отличном от нуля истинном значении корреляционного отношения
и при любом отличном от нуля истинном значении корреляционного отношения 
Действительно, как известно (см., например, [14, гл. 61), случайная величина

подчиняется нецентральному  -распределению с числами степеней свободы числителя и знаменателя соответственно
-распределению с числами степеней свободы числителя и знаменателя соответственно  параметром нецентральности а, если
параметром нецентральности а, если  суть взаимно независимые нормальные случайные величины, обладающие одинаковыми дисперсиями, причем
суть взаимно независимые нормальные случайные величины, обладающие одинаковыми дисперсиями, причем  а
а

Намечая доказательство сформулированного выше утверждения о статистике  определенной формулой (1.17), заметим, что в нашем случае в роли случайных величин
определенной формулой (1.17), заметим, что в нашем случае в роли случайных величин  грубо говоря, выступают значения
грубо говоря, выступают значения  а в роли случайных величин
а в роли случайных величин  — значения
— значения  Отметим также следующие соотношения, в справедливости (в некоторых случаях приближенной) которых нетрудно убедиться:
Отметим также следующие соотношения, в справедливости (в некоторых случаях приближенной) которых нетрудно убедиться:

(здесь  ) — неизвестная нам функция регрессии
) — неизвестная нам функция регрессии  по
по  — средняя точка
— средняя точка  интервала группирования по оси асбцисс, а
интервала группирования по оси асбцисс, а  — среднее значение функции регрессии):
— среднее значение функции регрессии):

И наконец, параметр нецентральности в соответствии с (1.18) и с учетом (1.6) в нашем случае имеет вид

Далее воспользуемся тем (см., например, [30, с. 99]), что распределение статистики  при
при  достаточно хорошо аппроксимируется обычным (центральным)
достаточно хорошо аппроксимируется обычным (центральным)  -распределением с числом степеней свободы числителя, приблизительно равным
-распределением с числом степеней свободы числителя, приблизительно равным  числом степеней свободы знаменателя, равным
числом степеней свободы знаменателя, равным  Поэтому в нашем случае распределение статистики
Поэтому в нашем случае распределение статистики

приближенно описывается  -распределением с числом степеней свободы числителя
-распределением с числом степеней свободы числителя

и числом степеней свободы знаменателя 
Таким образом, получаем следующее правило построения приближенных доверительных интервалов для истинного значения корреляционного отношения 
1) пользуясь формулой (1.16), вычисляем точечную оценку  для истинного значения корреляционного отношения
для истинного значения корреляционного отношения 
2) по формуле (1.19) подсчитываем вспомогательное число степеней свободы v числителя для аппроксимирующего центрального  -распределения;
-распределения;
3) задавшись уровнем доверия  , с помощью табл. П.5 находим 100
, с помощью табл. П.5 находим 100  -ную точку
-ную точку  и
и  -ную точку
-ную точку  -распределения с числом степеней свободы числителя
-распределения с числом степеней свободы числителя  и знаменателя
и знаменателя 
4) утверждаем, что приблизительно с вероятностью  истинное значение корреляционного отношение
истинное значение корреляционного отношение  удовлетворяет неравенствам
удовлетворяет неравенствам

Проиллюстрируем работоспособность описанного метода на следующем примере. Пусть в результате обработки 132 экспериментальных точек  получено выборочное значение корреляционного отношения
получено выборочное значение корреляционного отношения  . При этом мы воспользовались разбиением диапазона изменения независимой переменной на
. При этом мы воспользовались разбиением диапазона изменения независимой переменной на  равных интервалов группирования. Соответственно получаем в качестве вспомогательного числа степеней свободы числителя величину
равных интервалов группирования. Соответственно получаем в качестве вспомогательного числа степеней свободы числителя величину  (частное округляем до целого числа). Задавшись доверительной вероятностью
(частное округляем до целого числа). Задавшись доверительной вероятностью  , из табл. П.5 находим (полагая
, из табл. П.5 находим (полагая  ):
):

И наконец, в соответствии с формулой (1.20) находим левый ( ) и правый (
) и правый ( ) концы доверительного интервала для истинного значения
) концы доверительного интервала для истинного значения 

Таким образом, при точечной оценке  истинное значение заключено в пределах от
истинное значение заключено в пределах от  до
до  с вероятностью, приблизительно равной 0,9, т. е.
с вероятностью, приблизительно равной 0,9, т. е.  .
.
В этом примере хорошо видна существенная несимметричность концов интервальной оценки относительно точечной оценки (правый конец интервальной оценки отстоит от точечной оценки на 0,33, в то время как левый конец — всего лишь на 
Для значений точечных оценок  , близких к нулю или к единице, левый или правый конец интервальной оценки может терять содержательный смысл, выходя за пределы отрезка [0, 1]. В этом случае в качестве левого или правого конца интервальной оценки следует брать соответствующее граничное значение — нуль или единицу (причина подобных нежелательных ситуаций — в аппроксимационном подходе к решению данной задачи). Однако описанный прием все-таки следует признать гораздо более точным, чем применяемый иногда метод построения интервальных оценок для
, близких к нулю или к единице, левый или правый конец интервальной оценки может терять содержательный смысл, выходя за пределы отрезка [0, 1]. В этом случае в качестве левого или правого конца интервальной оценки следует брать соответствующее граничное значение — нуль или единицу (причина подобных нежелательных ситуаций — в аппроксимационном подходе к решению данной задачи). Однако описанный прием все-таки следует признать гораздо более точным, чем применяемый иногда метод построения интервальных оценок для  необоснованно использующий приблизительную
необоснованно использующий приблизительную  -нормальность статистики
-нормальность статистики 
Оценка индекса корреляции по несгруппированным данным. Если характер имеющихся у нас выборочных данных  таков, что не допускает их сколько-нибудь удовлетворительной группировки по оси объясняющей переменной (недостаточно велико
таков, что не допускает их сколько-нибудь удовлетворительной группировки по оси объясняющей переменной (недостаточно велико  , точки
, точки  ) слишком «разрежены» на плоскости), то построению оценок для
) слишком «разрежены» на плоскости), то построению оценок для  мы вынуждены предпослать принятие той или иной гипотезы об общем виде регрессионной функции (1.1). О статистических методах проверки подобного рода гипотез см. ниже, гл. 6. Пусть, например, в результате анализа, описанного в гл. 6, нами принята гипотеза о том, что интересующая нас регрессионная зависимость
мы вынуждены предпослать принятие той или иной гипотезы об общем виде регрессионной функции (1.1). О статистических методах проверки подобного рода гипотез см. ниже, гл. 6. Пусть, например, в результате анализа, описанного в гл. 6, нами принята гипотеза о том, что интересующая нас регрессионная зависимость  имеет вид алгебраического полинома второго порядка, т. е.
имеет вид алгебраического полинома второго порядка, т. е.  Тогда для оценки введенной ранее характеристики степени тесноты связи между исследуемыми переменными
Тогда для оценки введенной ранее характеристики степени тесноты связи между исследуемыми переменными  — коэффициента детерминации
— коэффициента детерминации  (или индекса корреляции
(или индекса корреляции  ) исследователю приходится вначале вычислить оценки
) исследователю приходится вначале вычислить оценки  для неизвестных параметров — коэффициентов
для неизвестных параметров — коэффициентов  , входящих в уравнение регрессии (см. гл. 7). И лишь после этого, ориентируясь на правую часть формулы (1.6), мы получим в качестве оценки для величину:
, входящих в уравнение регрессии (см. гл. 7). И лишь после этого, ориентируясь на правую часть формулы (1.6), мы получим в качестве оценки для величину:

так как нетрудно показать [65], что величина

является в данном случае выборочным аналогом (оценкой) теоретической дисперсии  участвующей в (1.6).
участвующей в (1.6).
Пусть в общем случае нами принята гипотеза об общем виде интересующей нас зависимости  , где
, где  — некоторая известная функция аргумента
— некоторая известная функция аргумента  зависящая от
зависящая от  неизвестного параметра
неизвестного параметра  .
.
Тогда, пользуясь рекомендациями гл. 7, строим оценки  неизвестных параметров, входящих в описание функции регрессии, после чего вычисляем оценку
неизвестных параметров, входящих в описание функции регрессии, после чего вычисляем оценку  коэффициента детерминации
коэффициента детерминации  по формуле
по формуле

Замечание. Можно показать, что, как и следовало ожидать, в частном случае  оценка, определяемая соотношением (1.21), совпадает с квадратом выборочного коэффициента корреляции
оценка, определяемая соотношением (1.21), совпадает с квадратом выборочного коэффициента корреляции 
Следует отметить, что вычисление и использование выборочных характеристик степени тесноты связи типа (1.21) затруднено по меньшей мере тремя обстоятельствами: 1) необходимостью предварительного выбора общего вида регрессионной зависимости; 2) необходимостью предварительного вычисления оценок для входящих в уравнение регрессии неизвестных параметров; 3) отсутствием строгих рекомендаций по их проверке на статистическую значимость и по построению соответствующих интервальных оценок.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
- В.3. Математический инструментарий
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
- 2.3. Анализ множественных ранговых связей
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
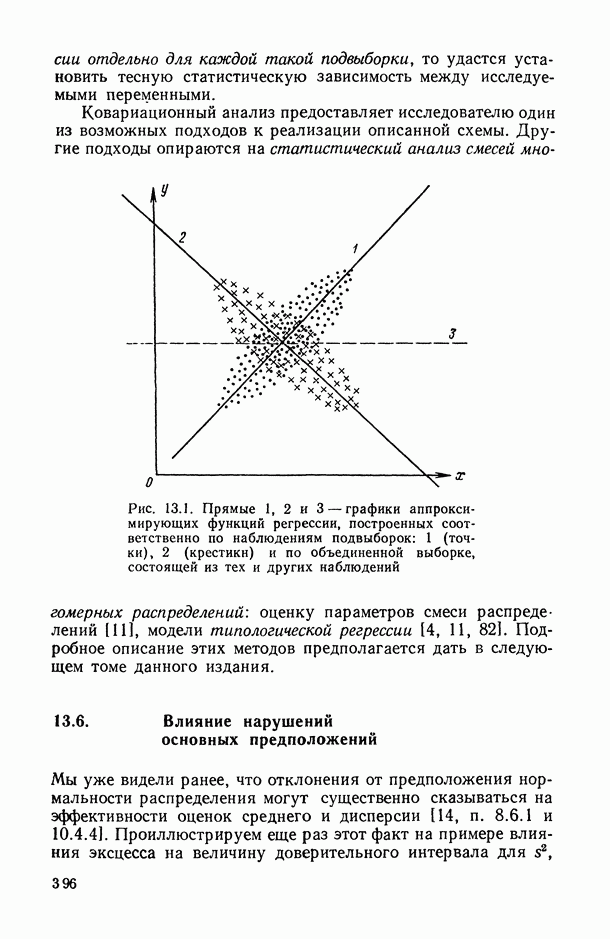
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
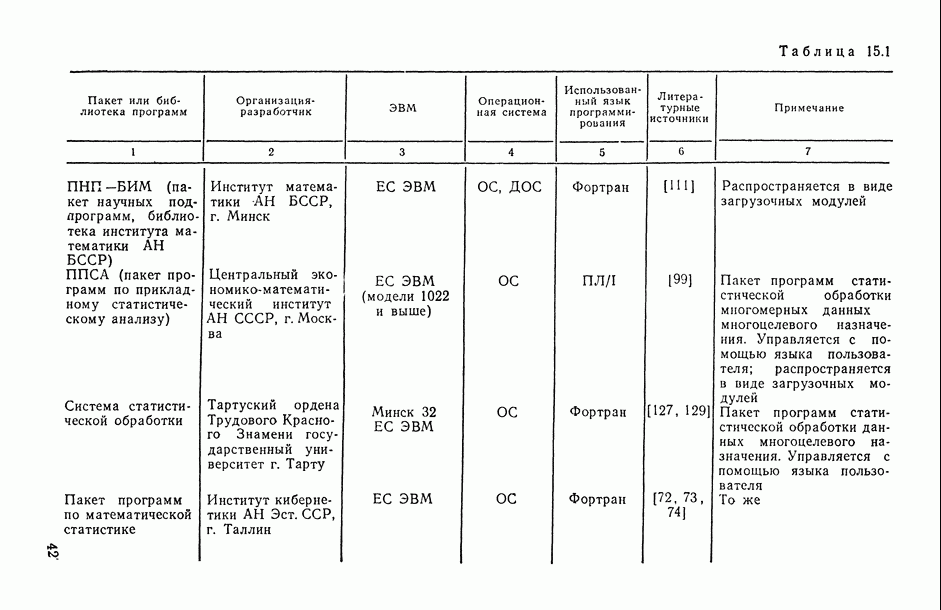
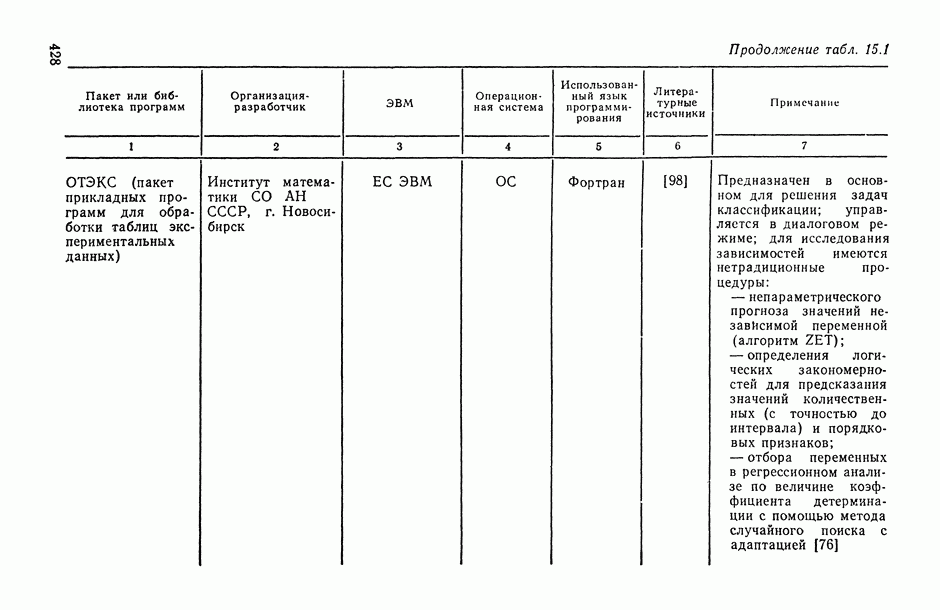
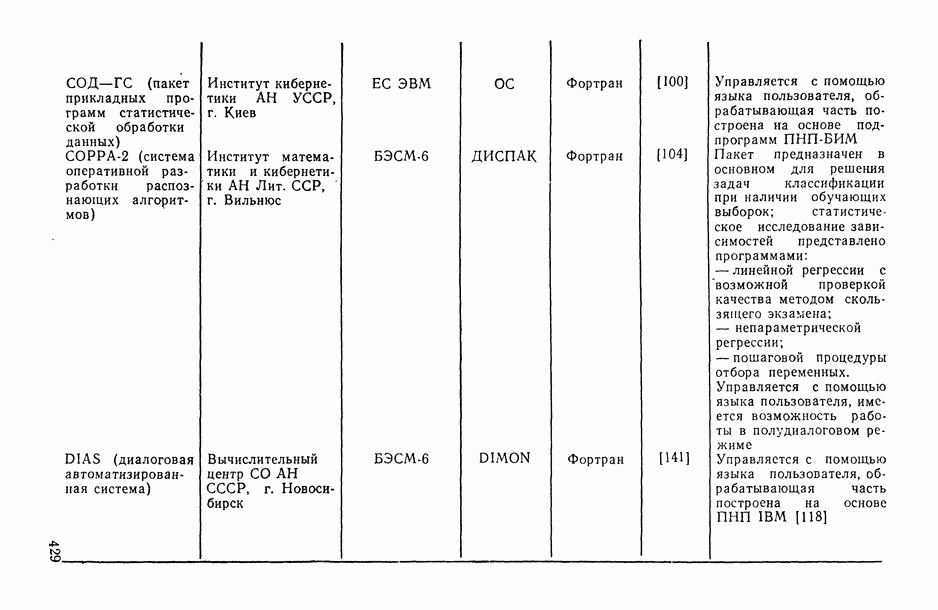
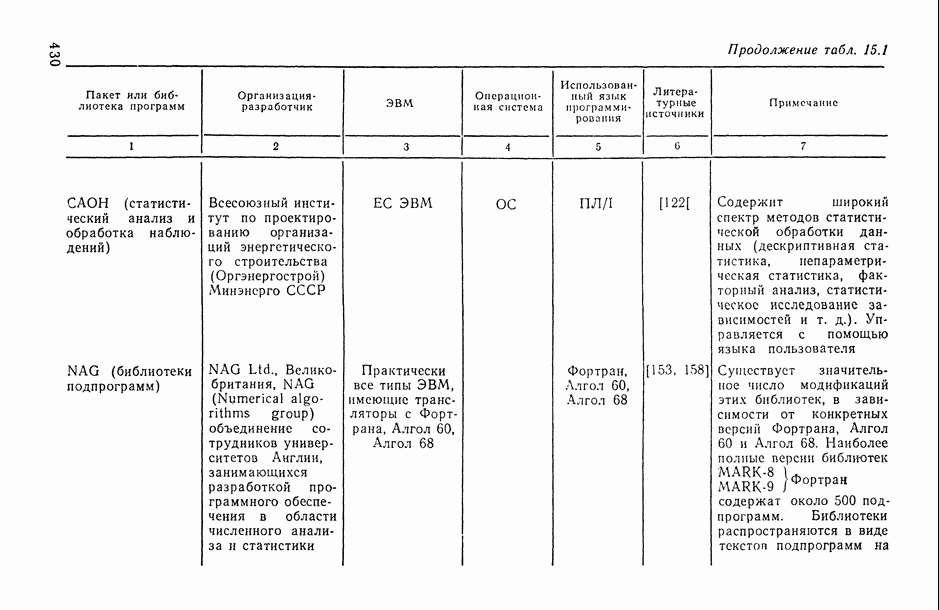
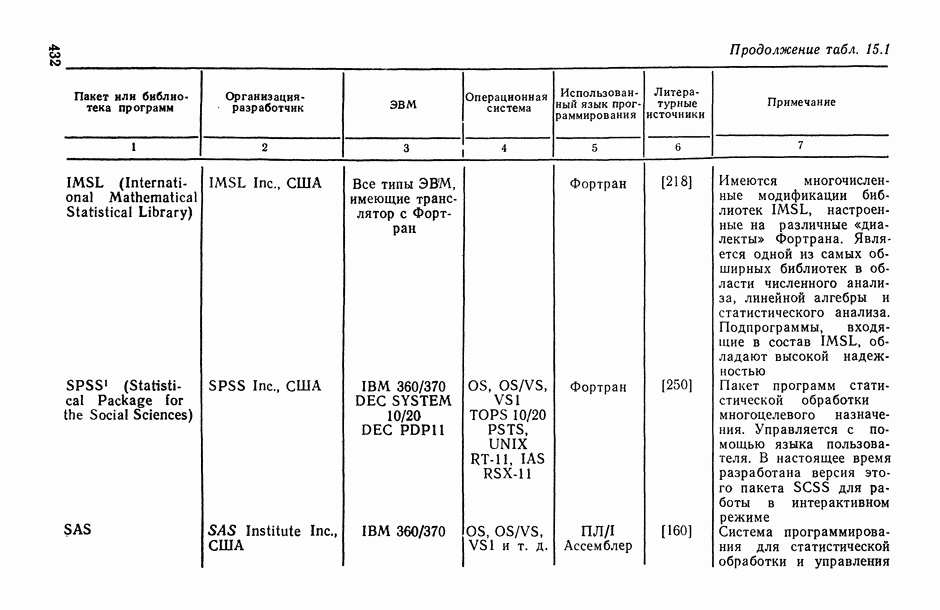
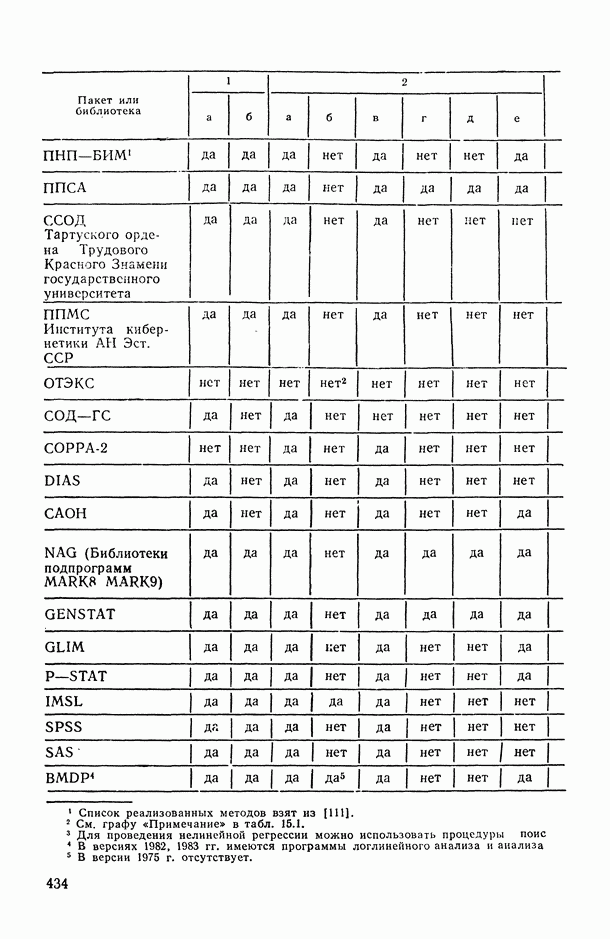
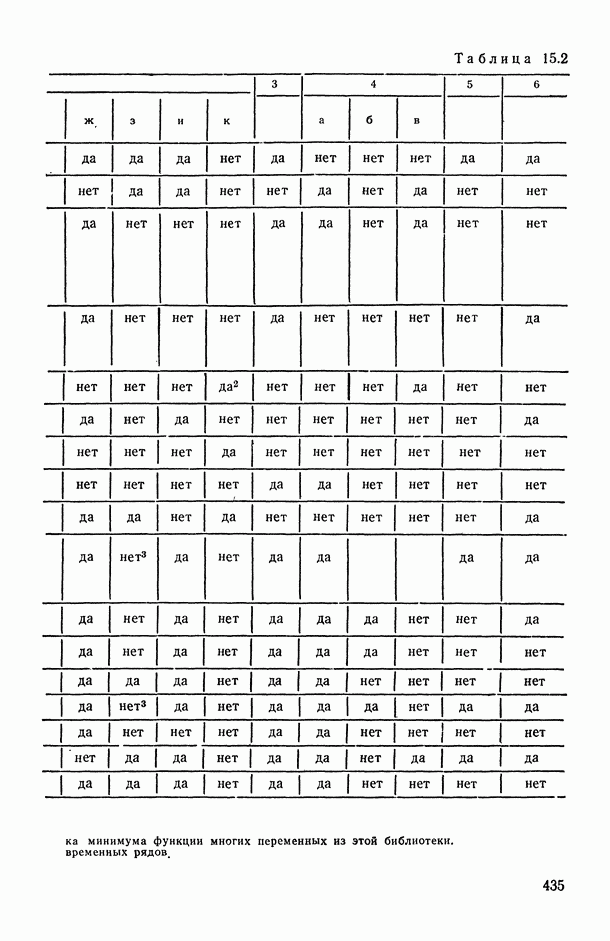
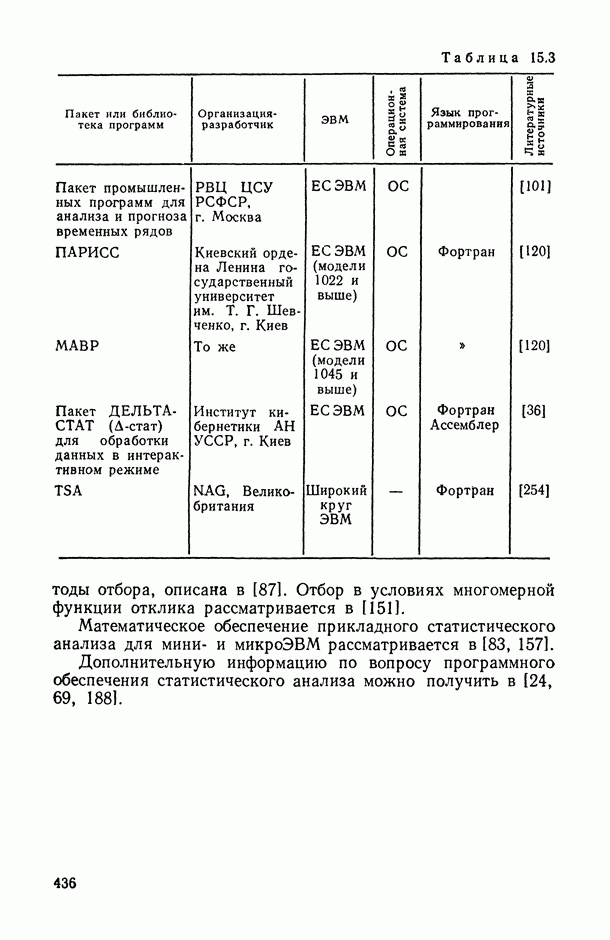
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
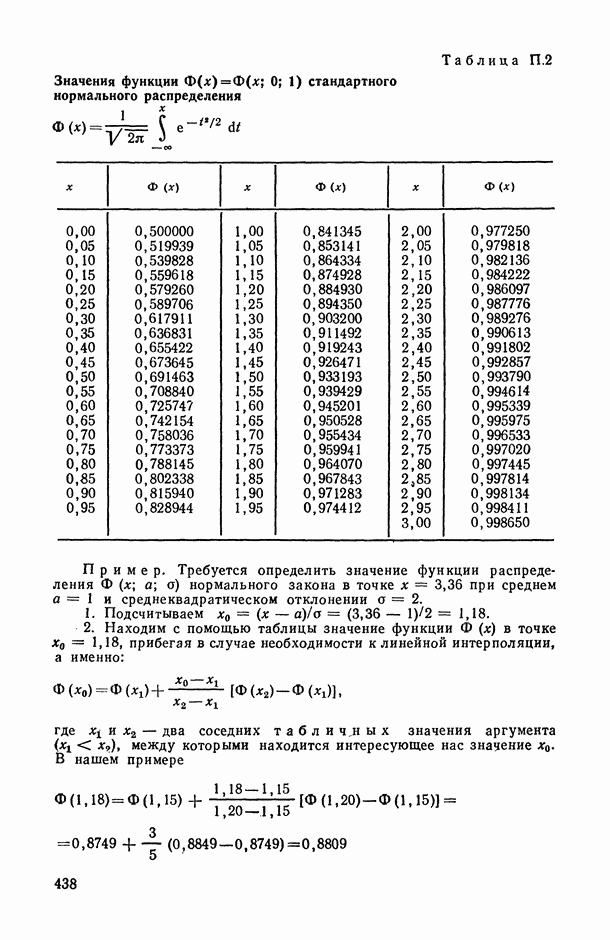
- Таблица П.2. Значения функции стандартного нормального распределения
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ