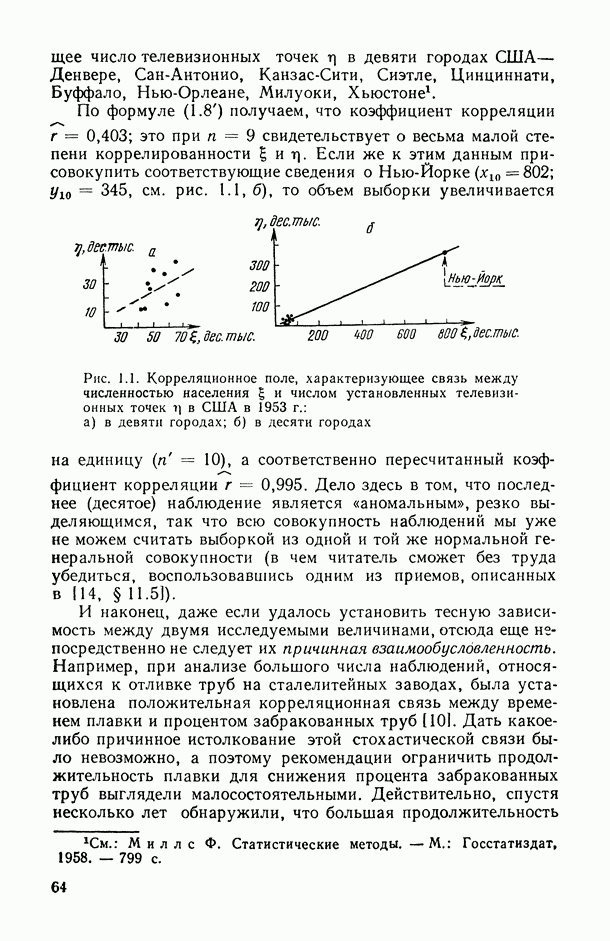
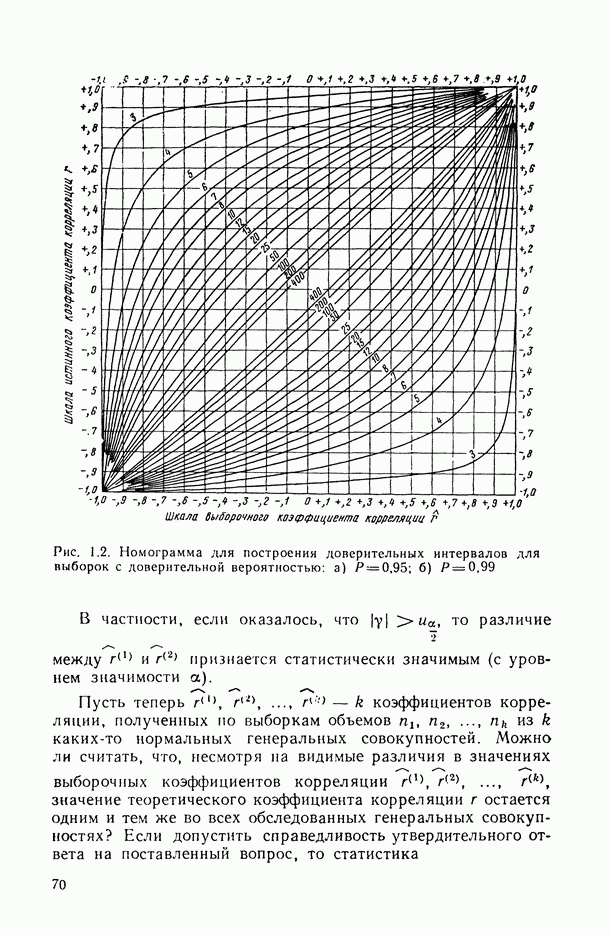
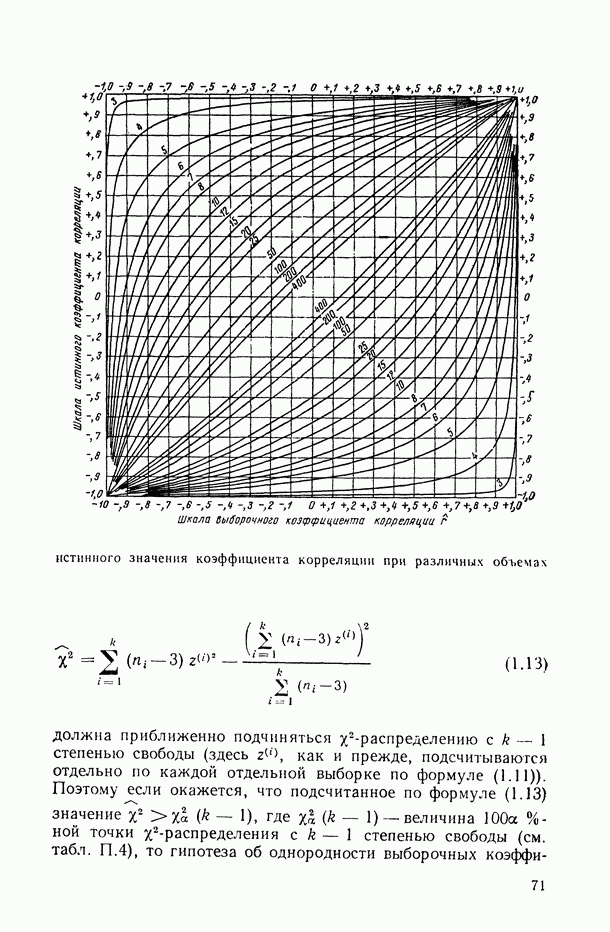
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
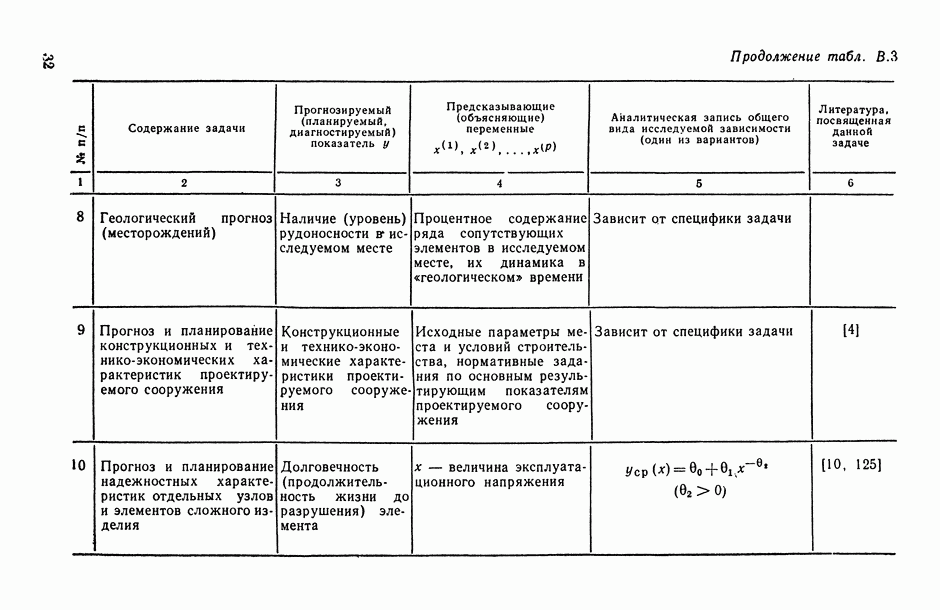
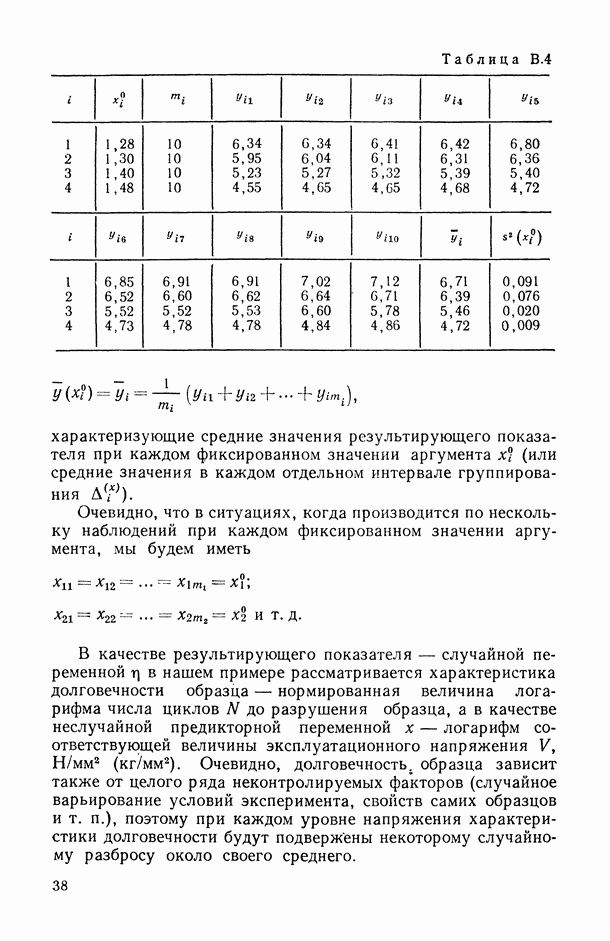
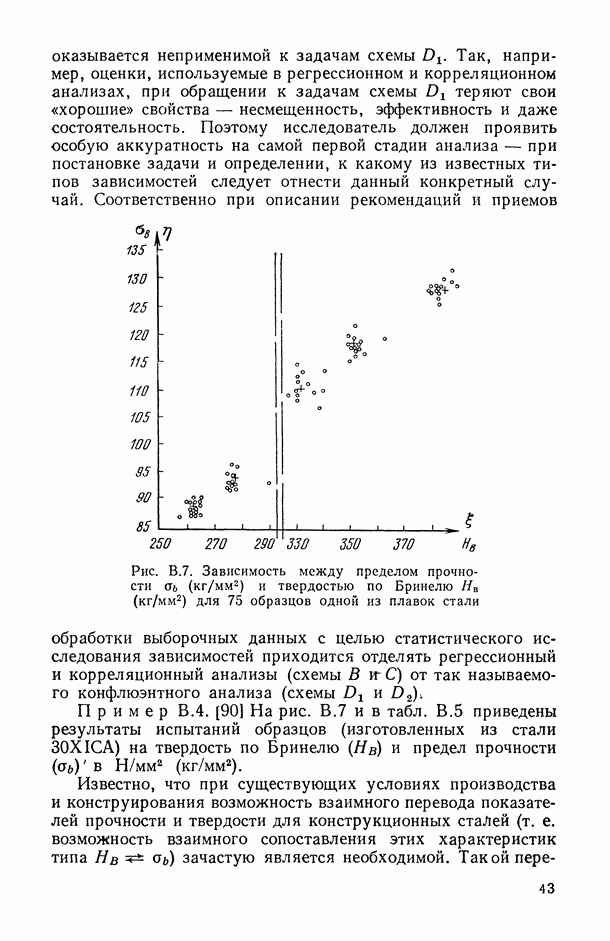
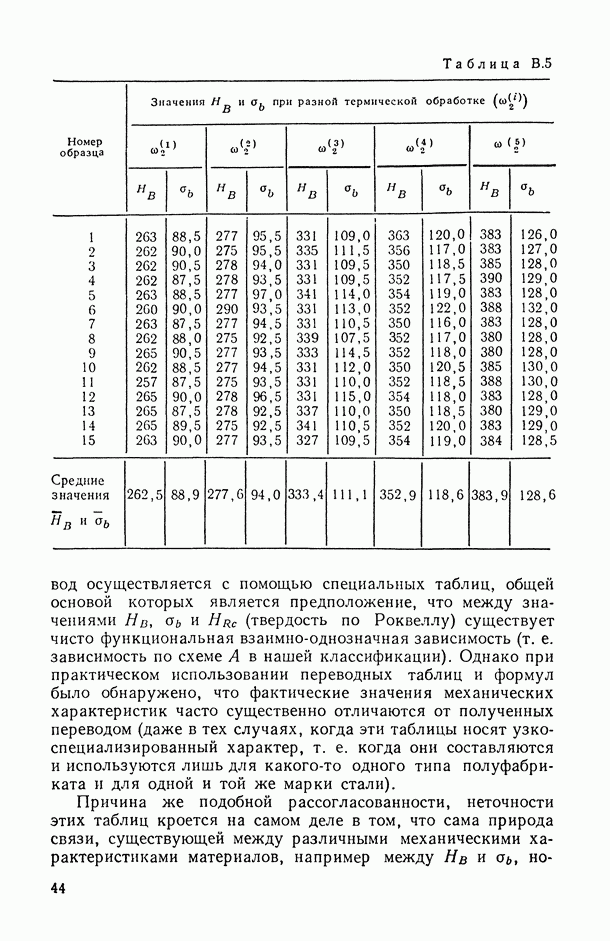
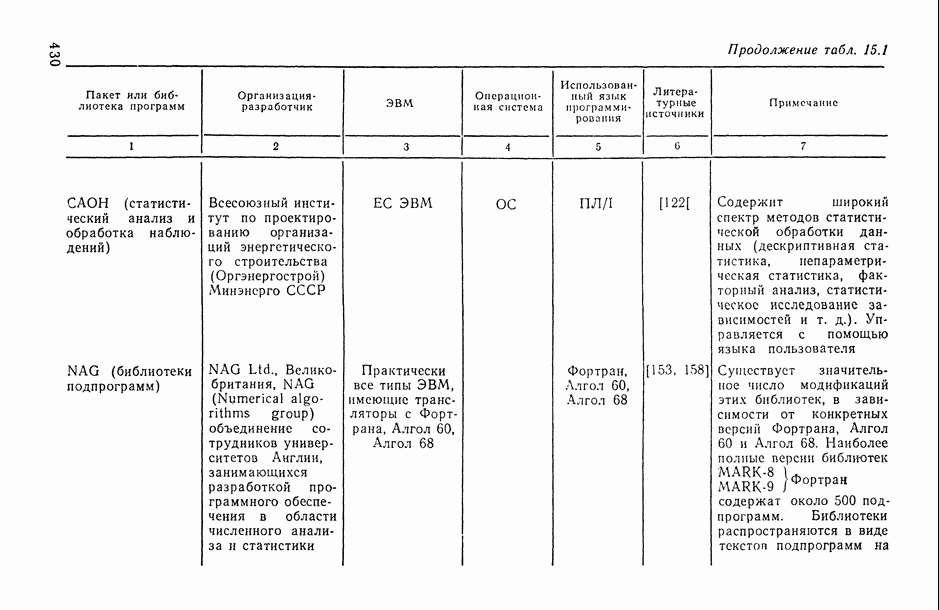
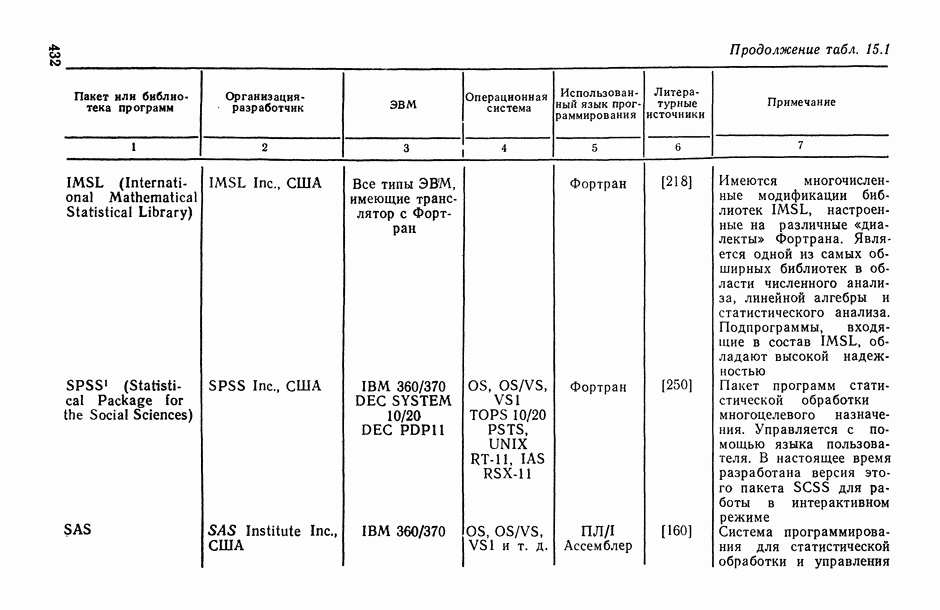
11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
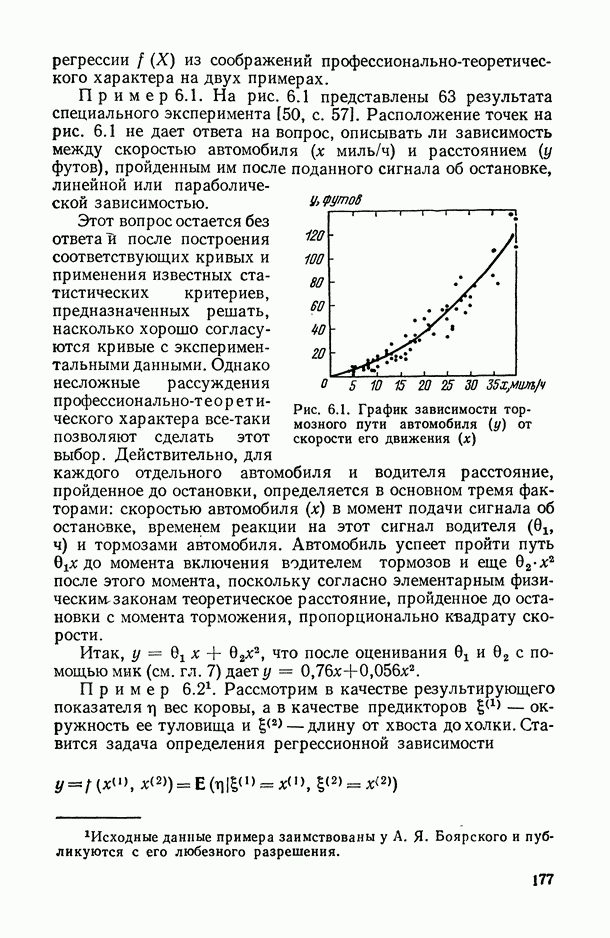
Воспользуемся полученными в предыдущем пункте рекомендациями для анализа точности моделей линейной и полиномиальной регрессии. Нас будет интересовать, в частности, конкретизация формул (11.18) и (11.19) в этих случаях.
Парная линейная регрессия. Рассматривается модель вида (11.1), в которой размерность предиктора  , а система базисных функций задается соотношениями:
, а система базисных функций задается соотношениями:  так что в конечном счете анализируется зависимость вида
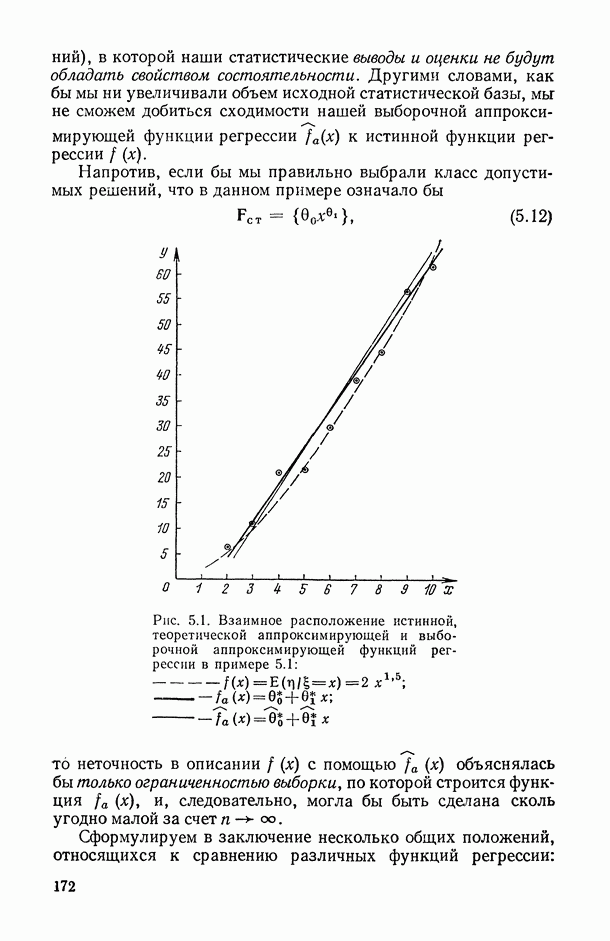
так что в конечном счете анализируется зависимость вида  или
или

Тогда

где  — арифметические средние значения наблюденных величин предиктора
— арифметические средние значения наблюденных величин предиктора  и результирующего показателя у соответственно.
и результирующего показателя у соответственно.
Далее

так что (в соответствии с (11.18) и (11.19)) с вероятностью Р будем иметь выполнение неравенств (при заданном фиксированном значении предиктора  ):
):

где  как и прежде,
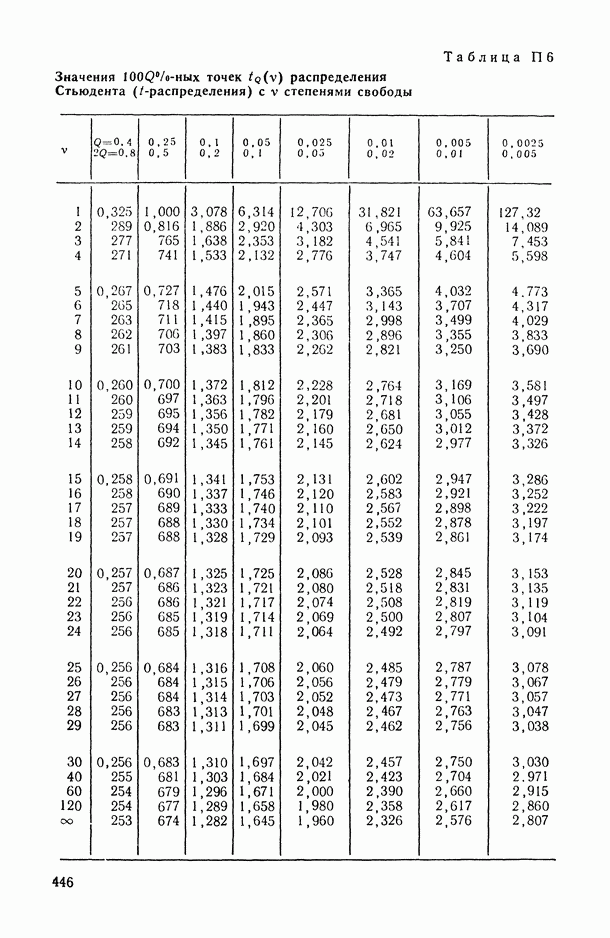
как и прежде,  -ная точка распределения Стьюдента с v степенями свободы;
-ная точка распределения Стьюдента с v степенями свободы;  — оценка остаточной дисперсии (см. (11.12)), т. е.
— оценка остаточной дисперсии (см. (11.12)), т. е.

а  — оценки наименьших квадратов неизвестных коэффициентов
— оценки наименьших квадратов неизвестных коэффициентов  (см. (11.9)), т. е.
(см. (11.9)), т. е.

Из (11.18") и (11.19), в частности, видно, что: а) величина погрешности и в том и в другом случае зависит от того, при каком именно значении предиктора  производится оценка, причем эта погрешность (и соответственно ширина доверительного интервала) увеличивается по мере удаления заданного значения
производится оценка, причем эта погрешность (и соответственно ширина доверительного интервала) увеличивается по мере удаления заданного значения  от среднего арифметического
от среднего арифметического  и наблюденных значений предикторной переменной; б) погрешность оценивания неизвестной функции регрессии
и наблюденных значений предикторной переменной; б) погрешность оценивания неизвестной функции регрессии  пропорциональна величине
пропорциональна величине  и, следовательно, неограниченно убывает с ростом объема выборки
и, следовательно, неограниченно убывает с ростом объема выборки  по которой производится оценивание; в) погрешность оценивания индивидуального
по которой производится оценивание; в) погрешность оценивания индивидуального  не среднего) значения результирующего показателя
не среднего) значения результирующего показателя  с помощью вычисленной по методу наименьших квадратов функции регрессии
с помощью вычисленной по методу наименьших квадратов функции регрессии  при неограниченном увеличении объема выборки (т. е. при
при неограниченном увеличении объема выборки (т. е. при  ) в отличие от предыдущей погрешности не убывает до нуля, но стремится, как это и должно быть (в соответствии с допущением (11.2)), к величине
) в отличие от предыдущей погрешности не убывает до нуля, но стремится, как это и должно быть (в соответствии с допущением (11.2)), к величине  -ной точки
-ной точки  -нормального распределения, т. е. к величине
-нормального распределения, т. е. к величине  а (поскольку, как известно [71],
а (поскольку, как известно [71],  -распределение сходится к стандартному нормальному при
-распределение сходится к стандартному нормальному при  а следовательно, при
а следовательно, при  , где
, где  -квантиль стандартного нормального распределения; а
-квантиль стандартного нормального распределения; а  в силу состоятельности
в силу состоятельности  .
.
Множественная линейная регрессия. Обобщим модель (11.4) на случай  предикторных переменных
предикторных переменных  Запишем исследуемую модель
Запишем исследуемую модель  в терминах центрированных наблюденных переменных, т. е.
в терминах центрированных наблюденных переменных, т. е.

Тогда получаем следующую интерпретацию общих обозначений п. 11.1.1 и 11.1.2:

выборочные ковариации переменных и [14, п. 5.6.7]. Соответственно

где —  элемент матрицы, обратной к выборочной ковариационной матрице предиктора X.
элемент матрицы, обратной к выборочной ковариационной матрице предиктора X.
Таким образом,

Поэтому в соответствии с (11.18) и (11.19) с вероятностью Р можно гарантировать выполнение следующих неравенств при заданном фиксированном векторном значении  предикторных переменных:
предикторных переменных:

Предварительный переход к центрированным переменным обусловил то, что правые части (11.18") и (11.19") не учитывают погрешности в оценке неизвестного теоретического среднего  . Модификация левых и правых частей (11.18") и (11.19"), соответствующая возвращению к исходной (нецент-рированной) записи модели, заключается в следующем: в левые части неравенств надо прибавить (внутри прямых скобок) величину
. Модификация левых и правых частей (11.18") и (11.19"), соответствующая возвращению к исходной (нецент-рированной) записи модели, заключается в следующем: в левые части неравенств надо прибавить (внутри прямых скобок) величину  , а в правые части (под знак радикала) — соответственно единицу и
, а в правые части (под знак радикала) — соответственно единицу и  изменив в обоих случаях число степеней свободы у процентной точки
изменив в обоих случаях число степеней свободы у процентной точки  -распределения на
-распределения на  Нетрудно увидеть, что записанные в таком модифицированном виде неравенства (11.18") и (11.19") дают в качестве своего частного случая при
Нетрудно увидеть, что записанные в таком модифицированном виде неравенства (11.18") и (11.19") дают в качестве своего частного случая при  неравенства (11.18") и (11.19).
неравенства (11.18") и (11.19).
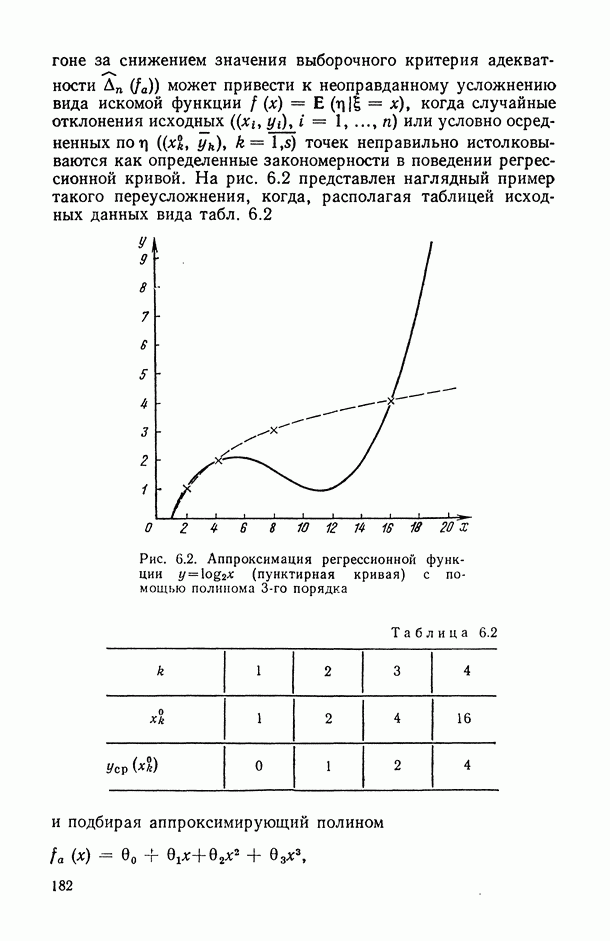
Полиномиальная регрессия. Рассмотрим случай скалярного (т. е. одномерного,  предиктора
предиктора  и пусть искомая функция регрессии
и пусть искомая функция регрессии  принадлежит классу алгебраических полиномов степени
принадлежит классу алгебраических полиномов степени  , т. е.
, т. е.

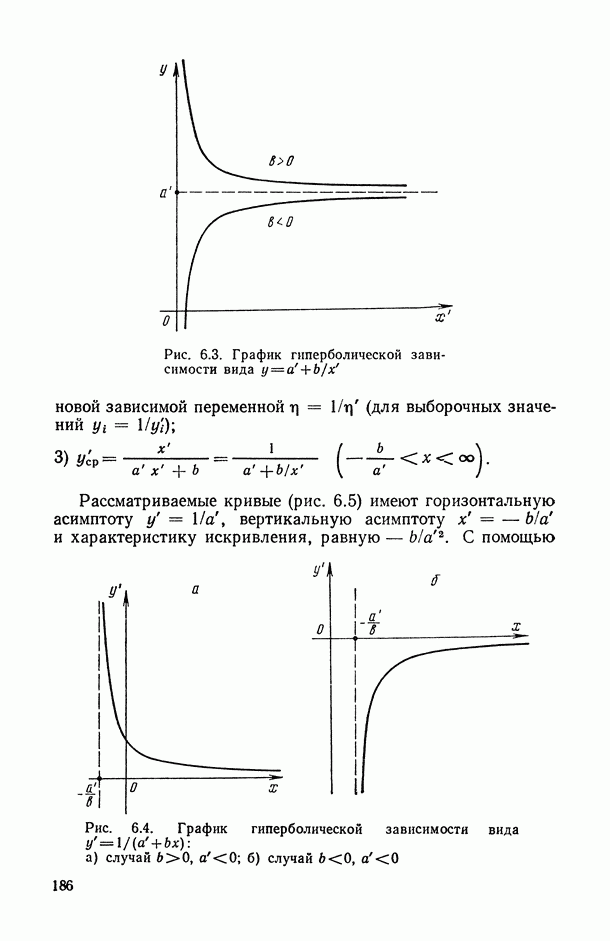
Ограничимся для определенности случаем  (переход к общему случаю
(переход к общему случаю  осуществляется очевидным образом без каких-либо затруднений) и представим функцию регрессии в системе базисных функций
осуществляется очевидным образом без каких-либо затруднений) и представим функцию регрессии в системе базисных функций  являющихся ортогональными (на совокупности наблюденных значений предиктора
являющихся ортогональными (на совокупности наблюденных значений предиктора  полиномами Чебышева (см. гл. 7, а также [10, с. 131; 77, с. 275]), т. е.
полиномами Чебышева (см. гл. 7, а также [10, с. 131; 77, с. 275]), т. е.

где

Взаимная ортогональность полиномов  (на системе наблюдений
(на системе наблюдений  ) означает, что
) означает, что

что обеспечивает диагональность матрицы  . В частности, имеем
. В частности, имеем

Полученные в соответствии с (11.9) мнк-оценки  оказываются статистачески взаимно независимыми и имеют дисперсии
оказываются статистачески взаимно независимыми и имеют дисперсии 
Учитывая, что в данном случае

можно (в соответствии с (11.18) и (11.19)) гарантировать с вероятностью Р выполнение неравенств (при заданном значении  ):
):

где

 —
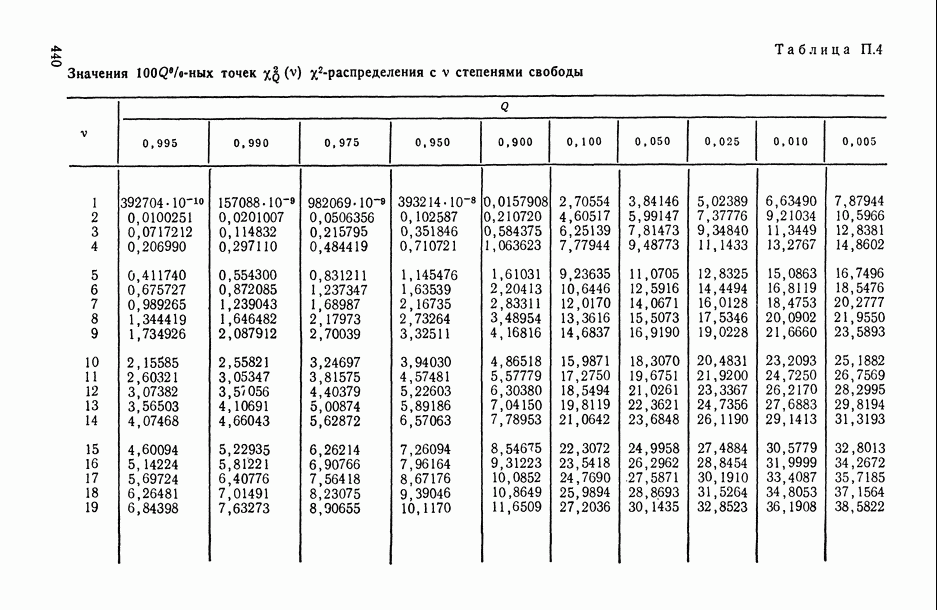
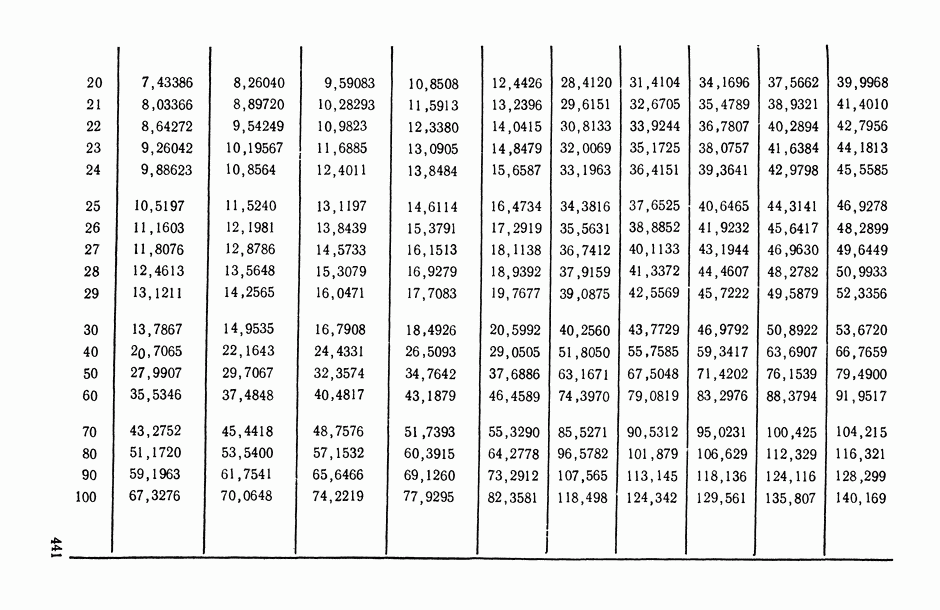
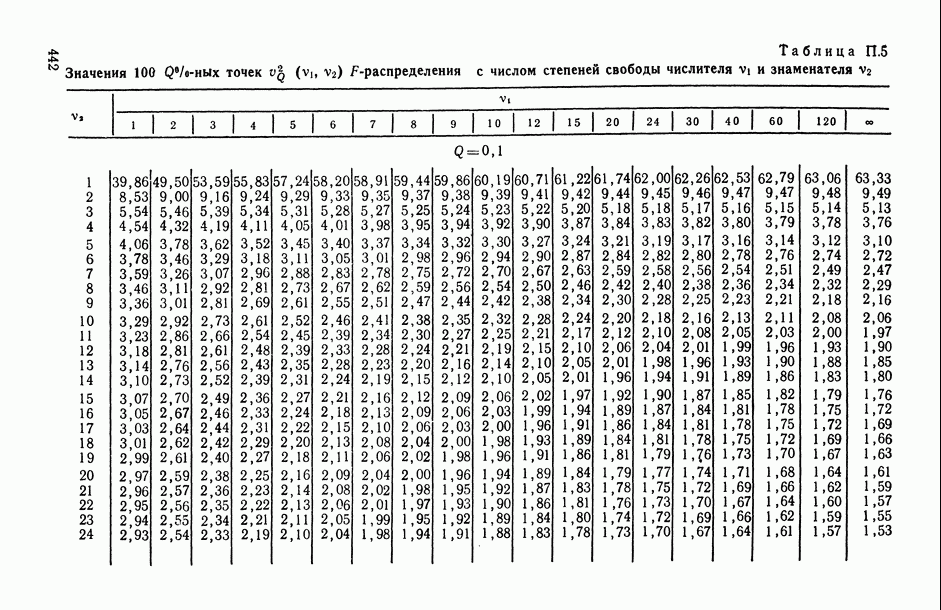
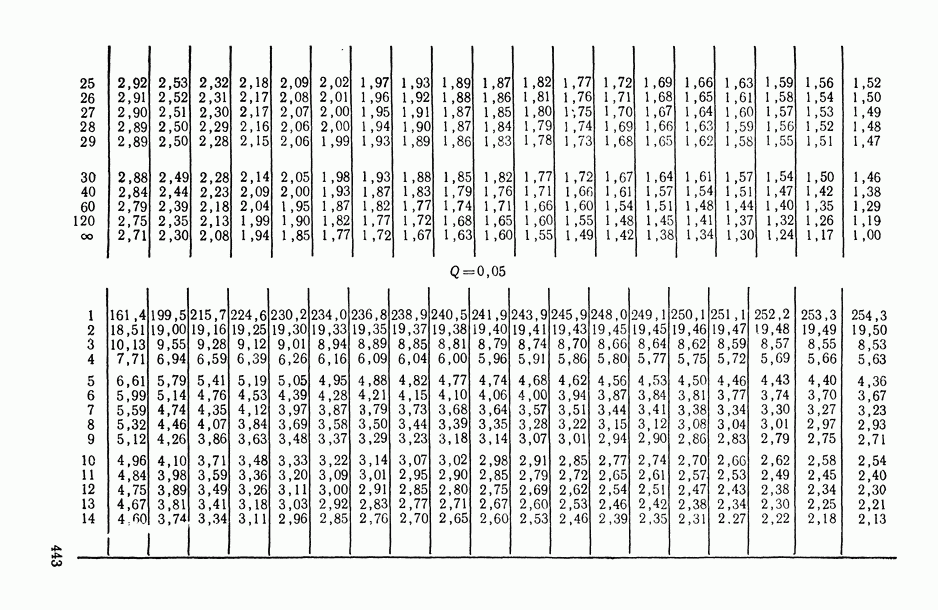
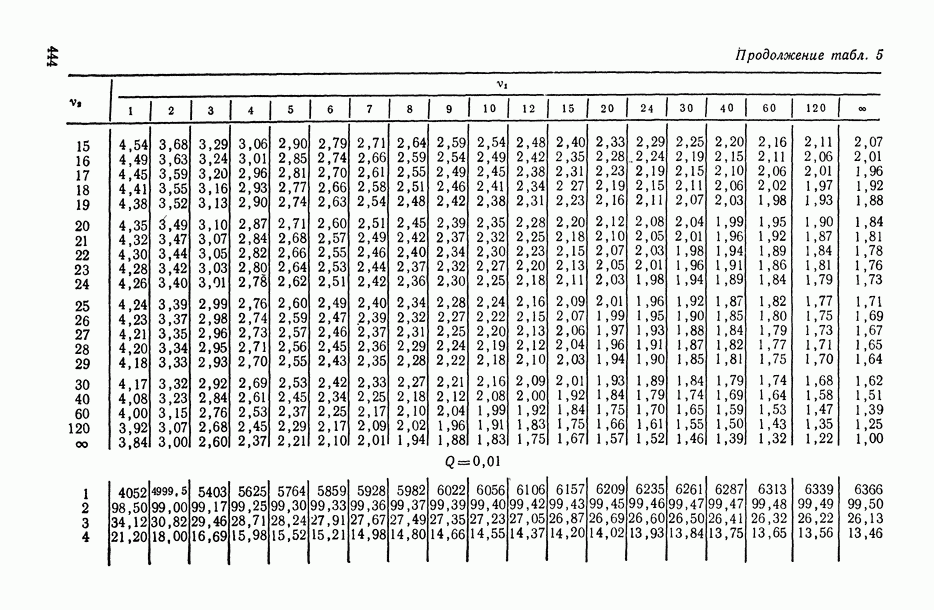
—  -ная точка распределения Стьюдента с v степенями свободы (определяется из табл. П.6).
-ная точка распределения Стьюдента с v степенями свободы (определяется из табл. П.6).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
- В.3. Математический инструментарий
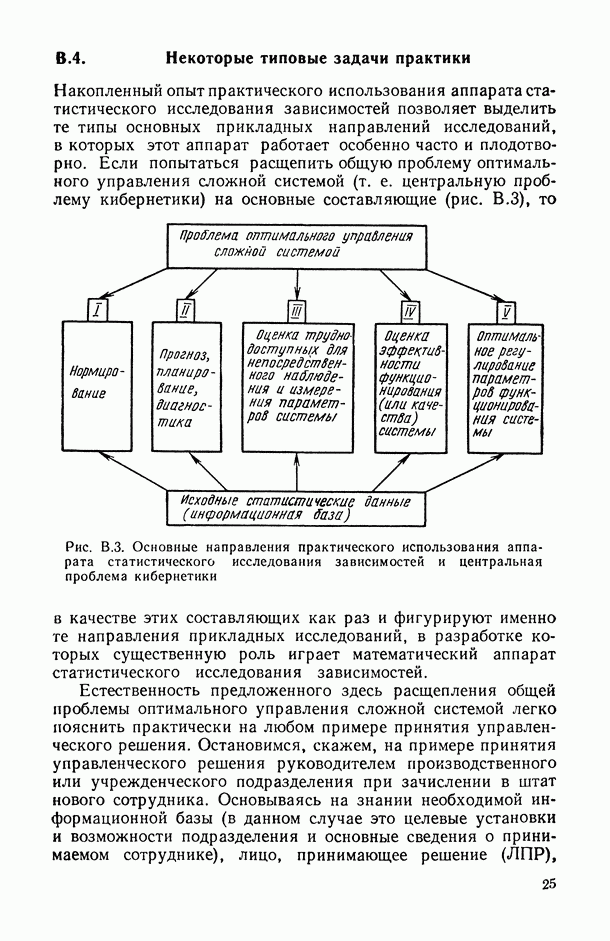
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
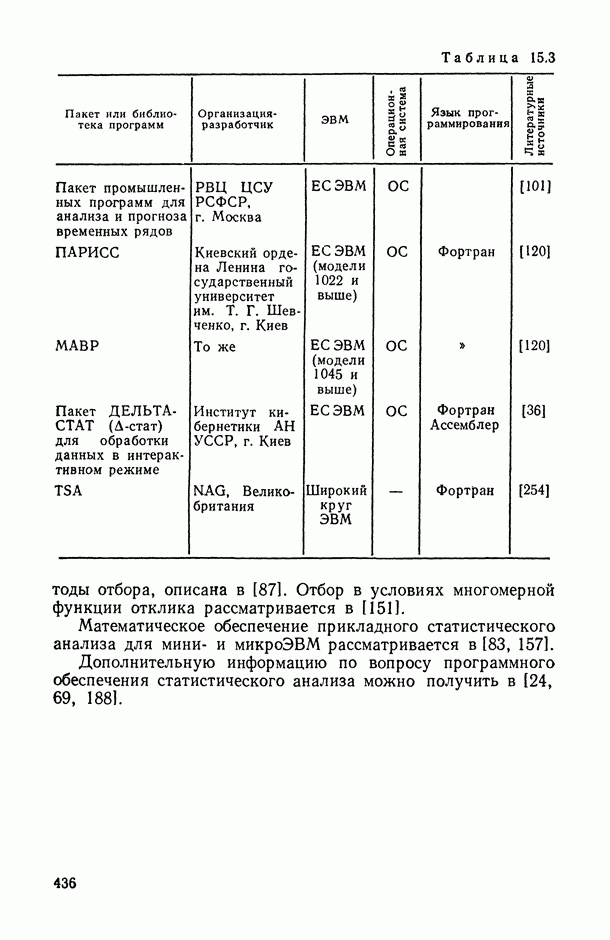
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
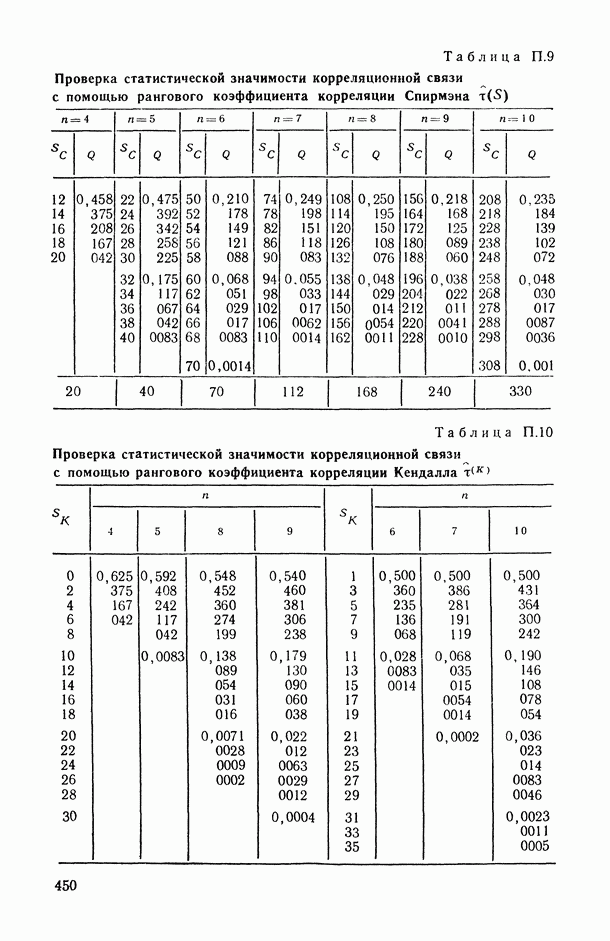
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
- 2.3. Анализ множественных ранговых связей
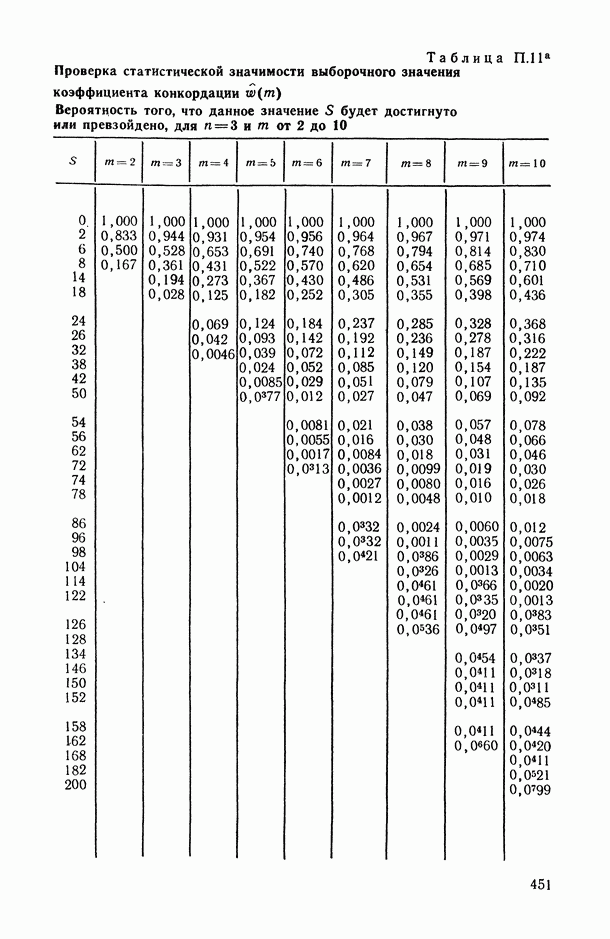
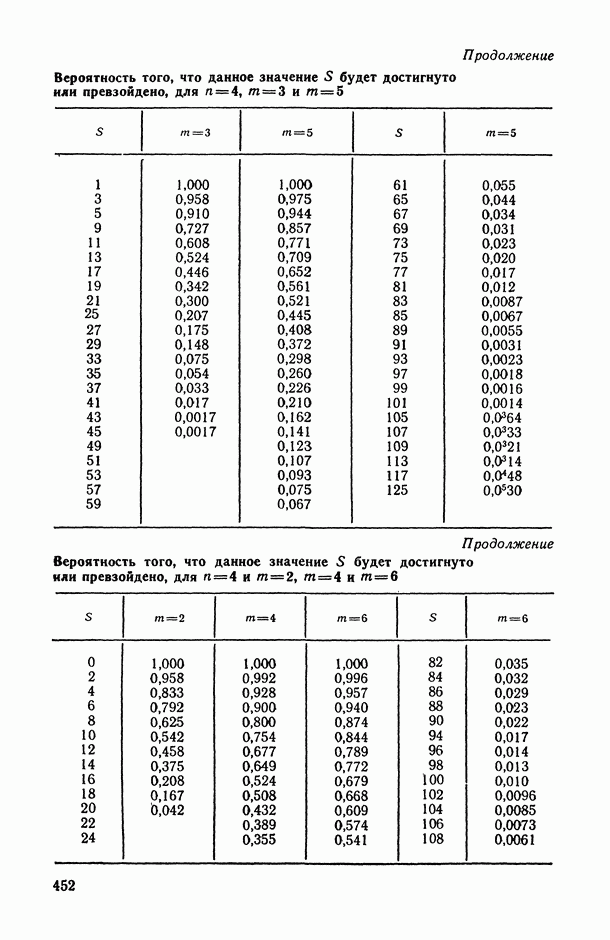
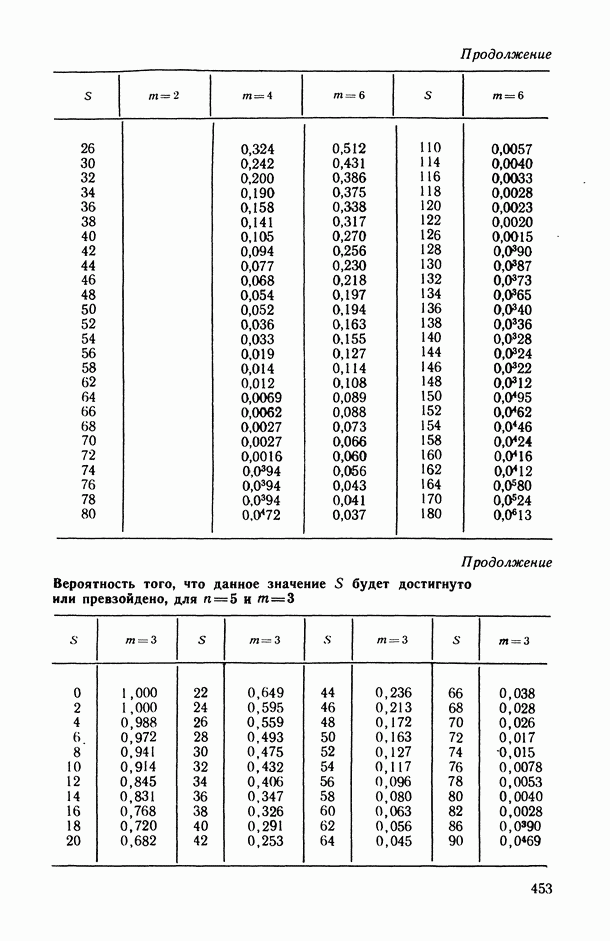
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
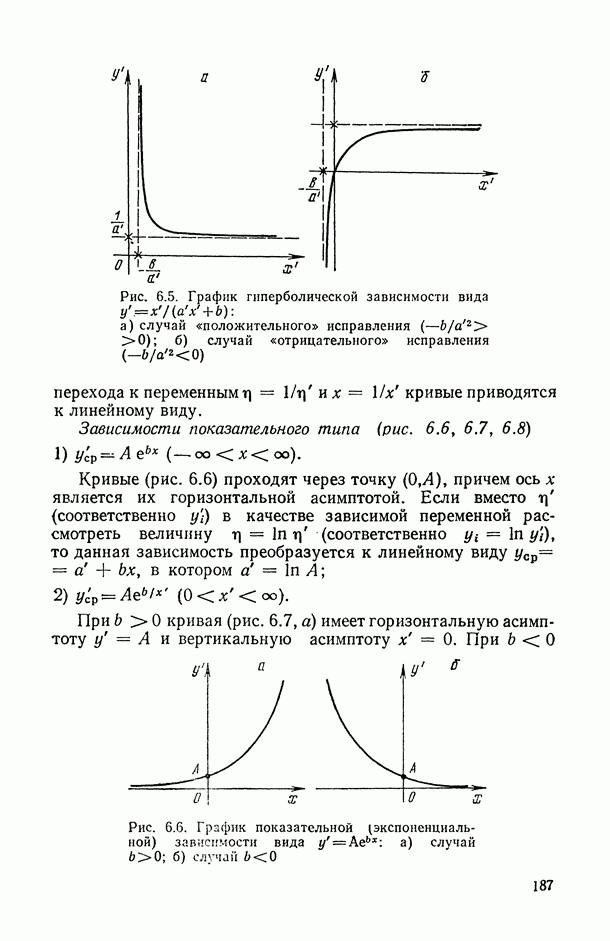
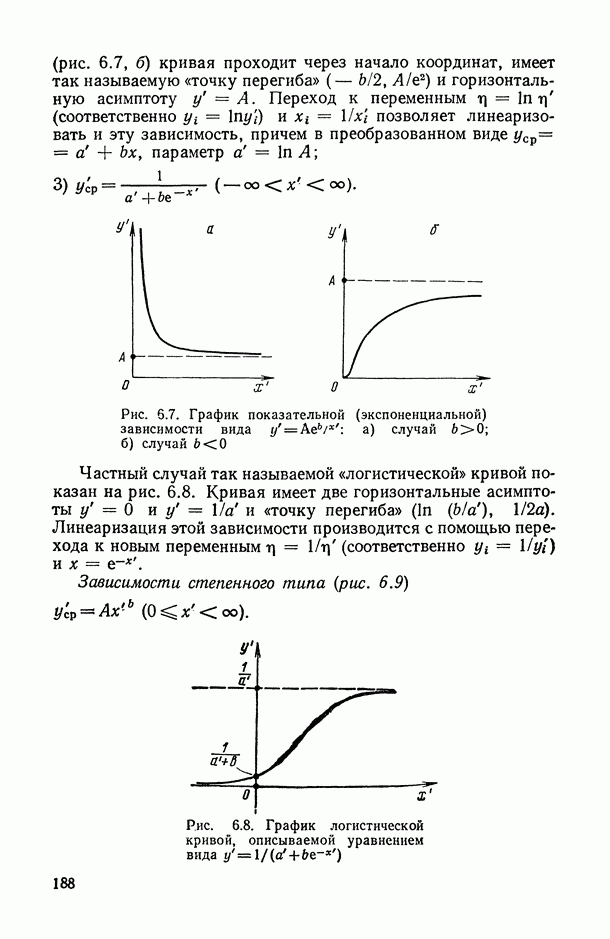
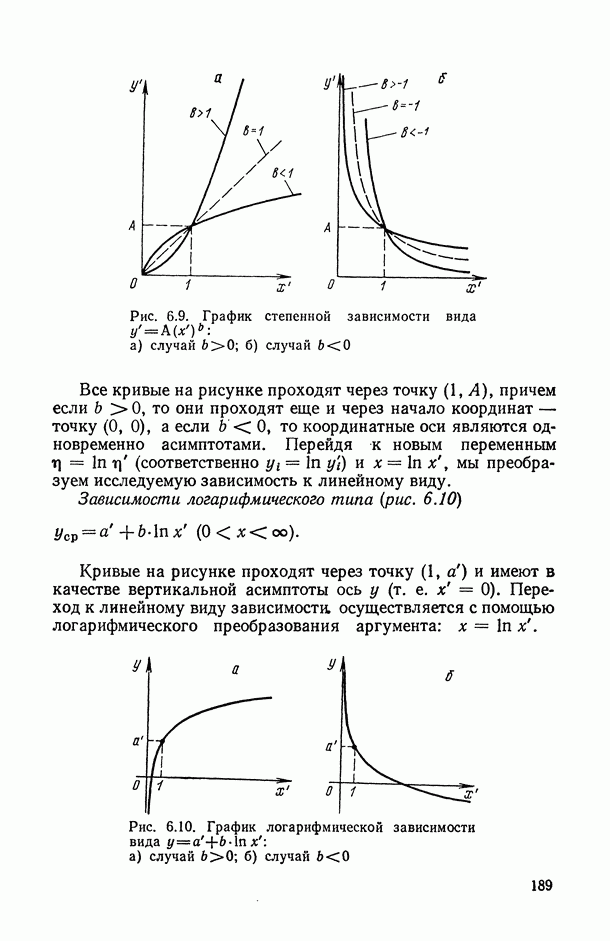
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
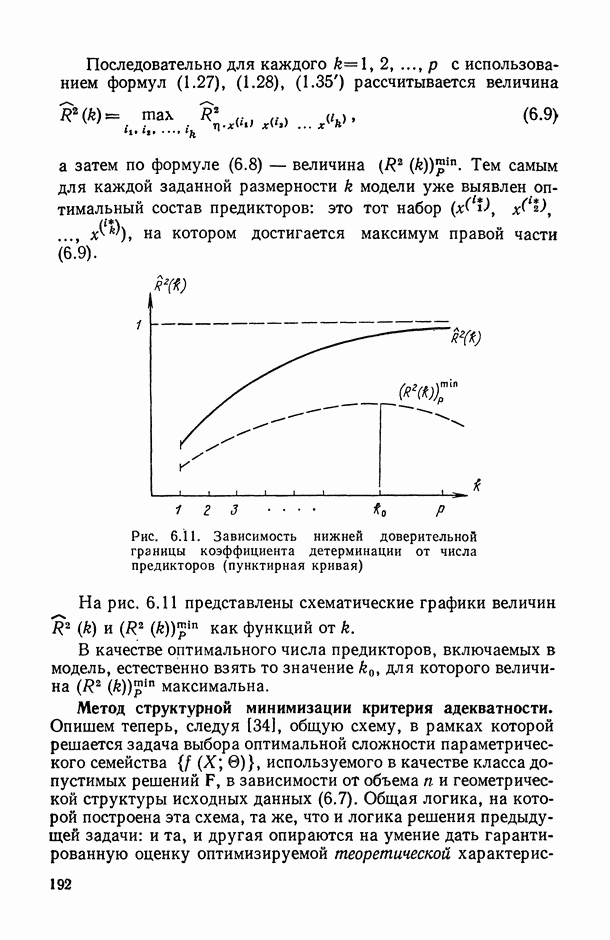
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
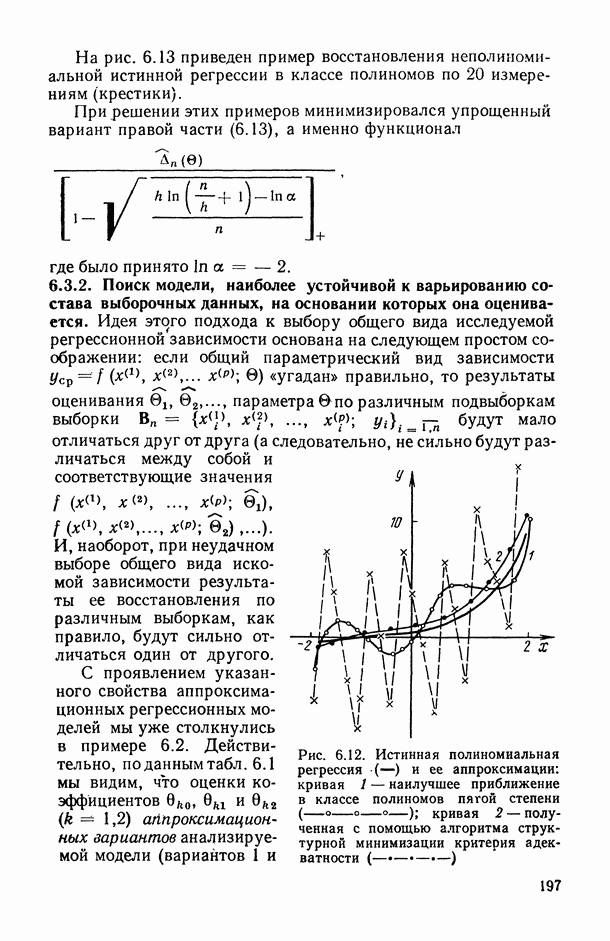
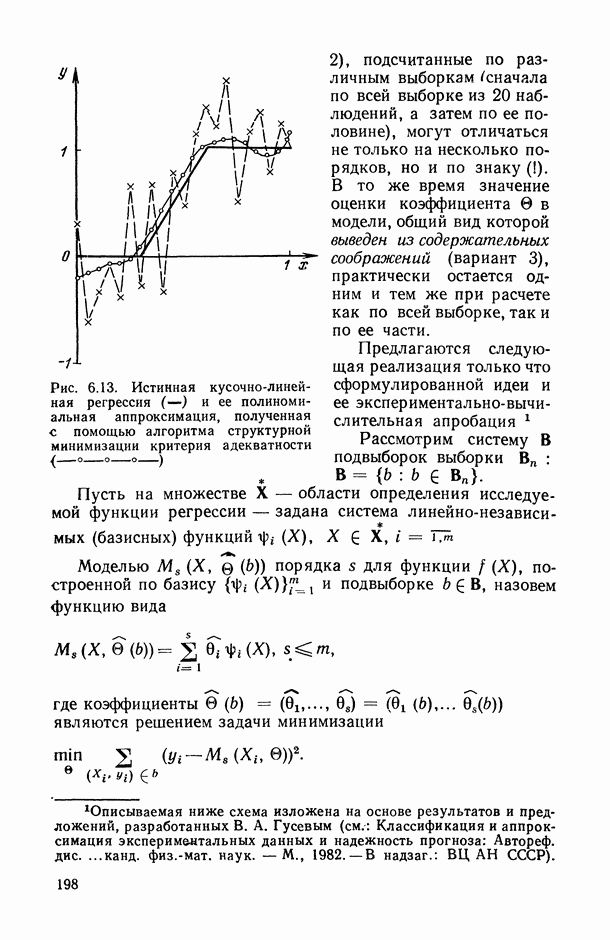
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
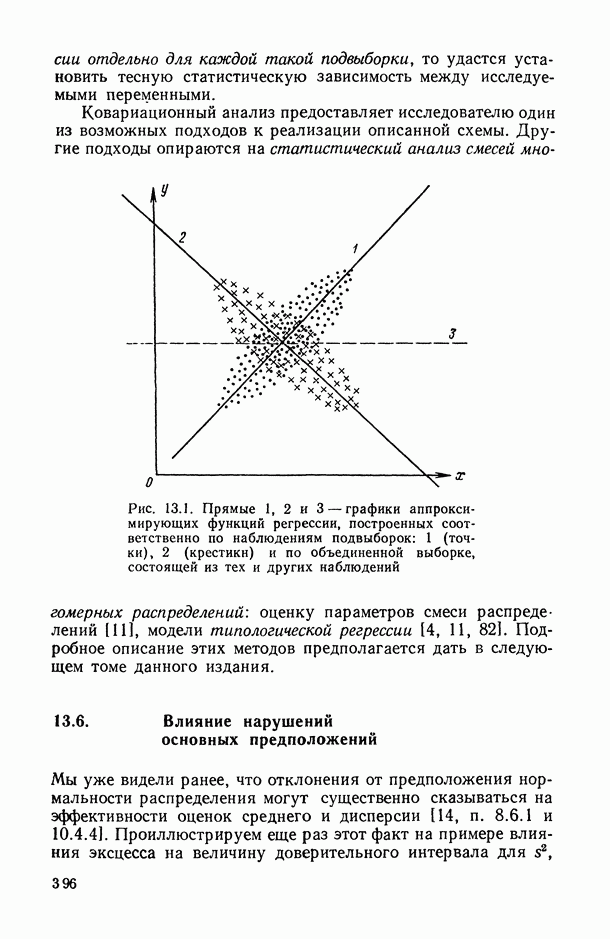
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
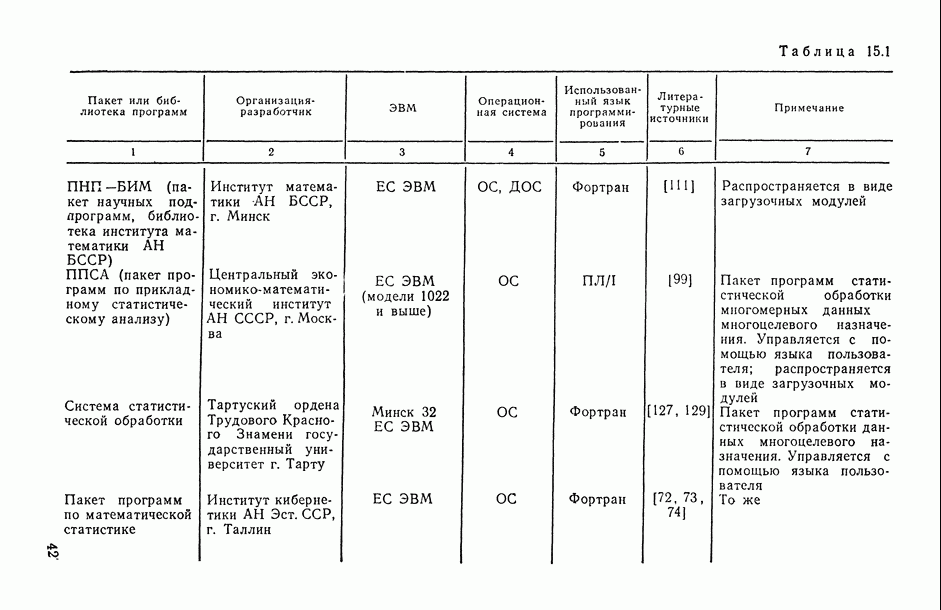
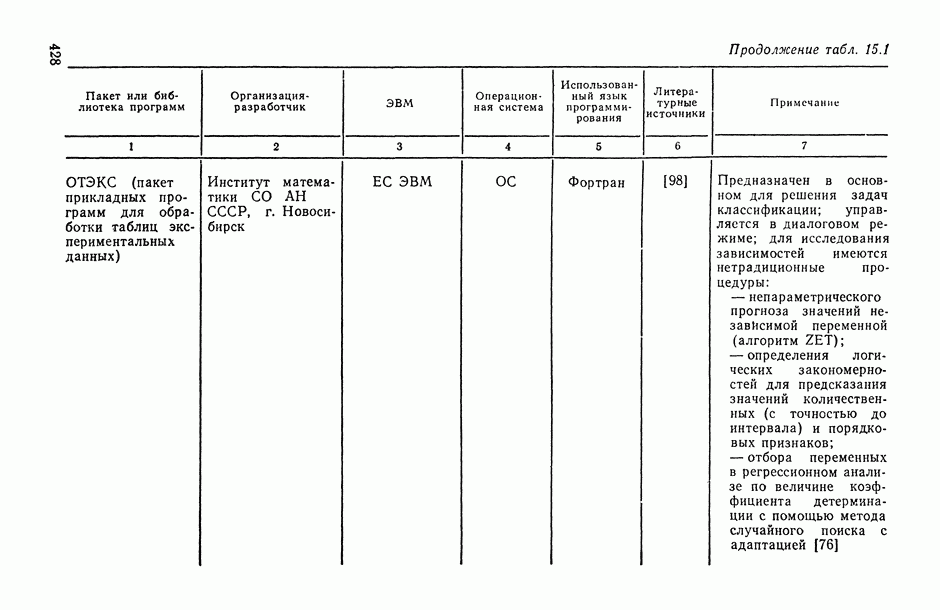
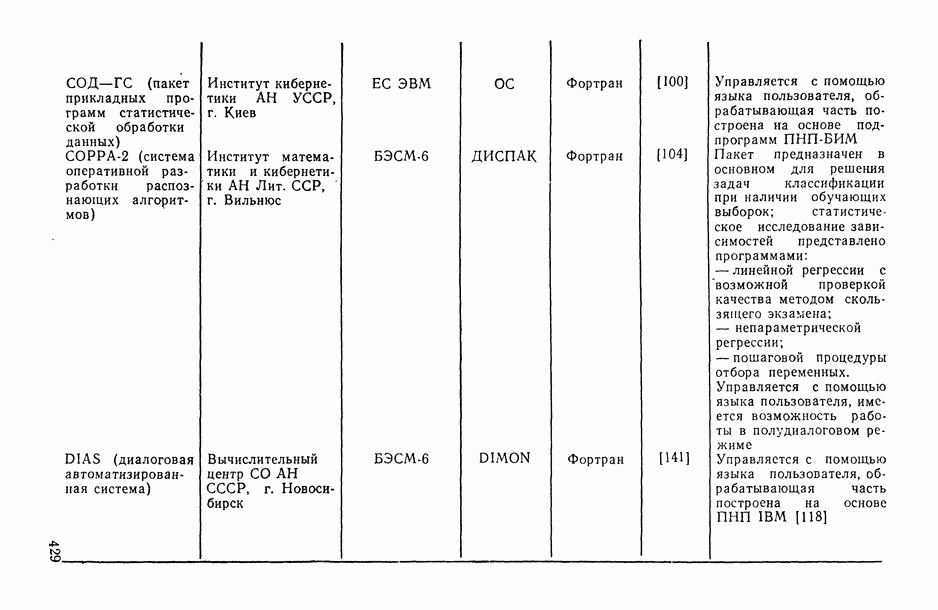
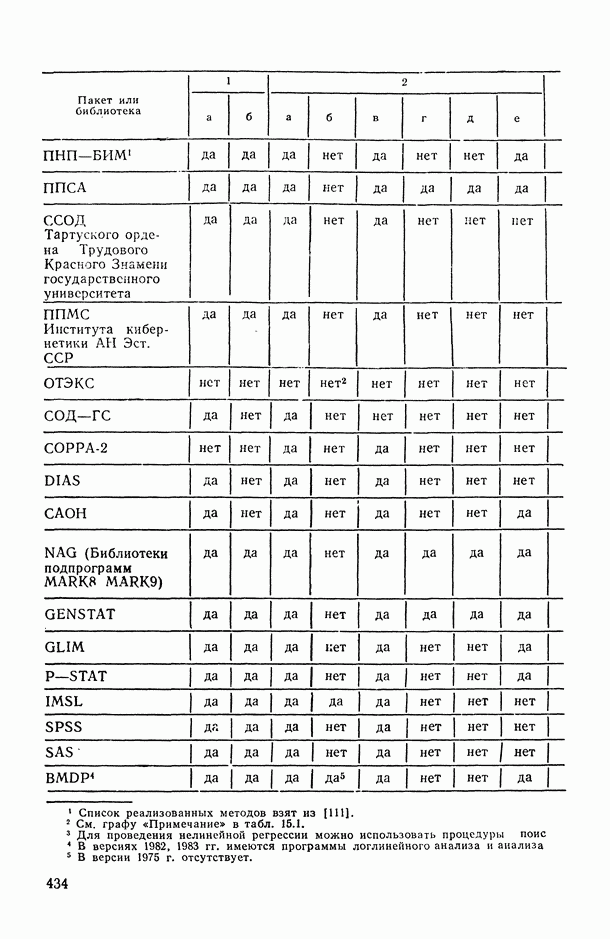
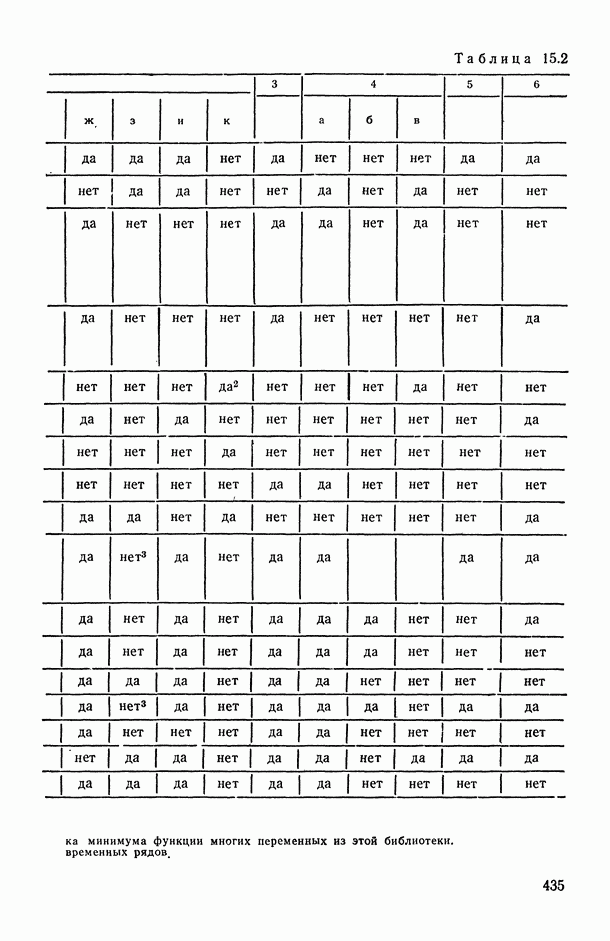
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
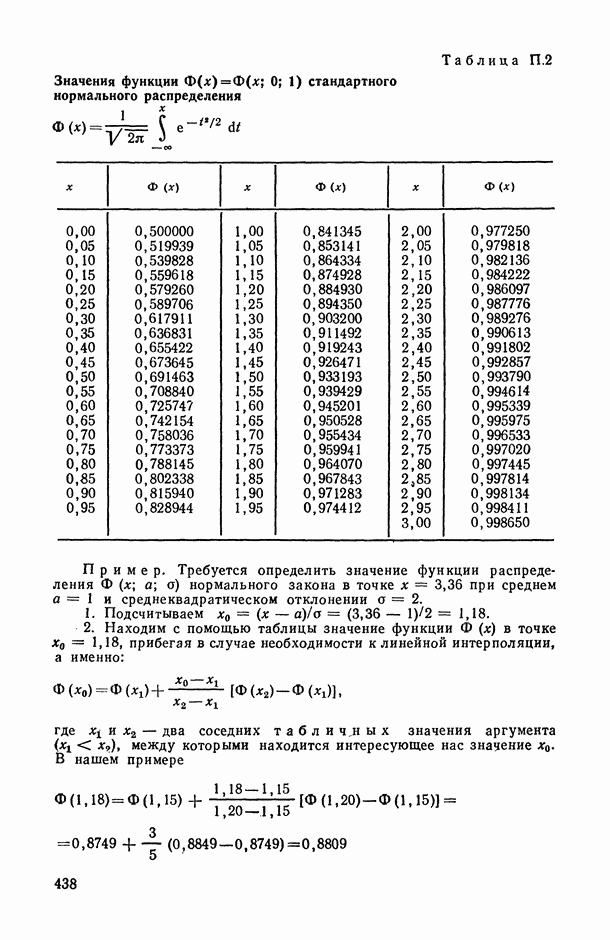
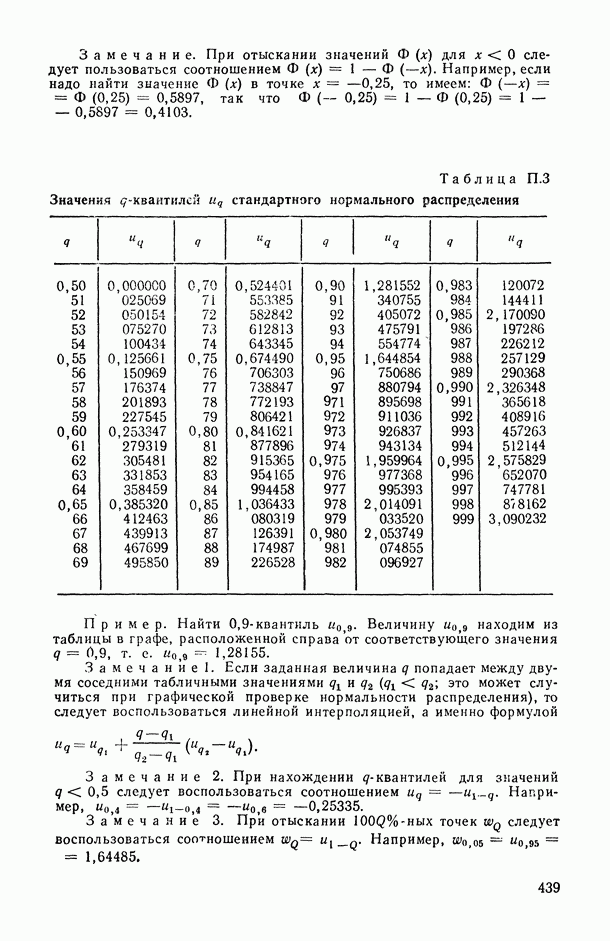
- Таблица П.2. Значения функции стандартного нормального распределения
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ