| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.3. Полный двухфакторный дисперсионный анализ
13.3.1. Взаимодействия.
Рассмотрим полный двухфакторный эксперимент с факторами А и В, имеющими соответственно  градаций (уровней). Обозначим
градаций (уровней). Обозначим  - среднее значение результата эксперимента при сочетании i-гo уровня фактора А с
- среднее значение результата эксперимента при сочетании i-гo уровня фактора А с  уровнем фактора В (среднее значение в
уровнем фактора В (среднее значение в  -ячейке прямоугольной таблицы, в которой строкам соответствуют градации фактора А, а столбцам — градации фактора В). Пусть
-ячейке прямоугольной таблицы, в которой строкам соответствуют градации фактора А, а столбцам — градации фактора В). Пусть  системы
системы  весов, выбранные в соответствии с градациями факторов А и В. Например, если фактор А — тип почвы, а В — сорт, результат эксперимента — урожай, то и может быть пропорционально площадям с
весов, выбранные в соответствии с градациями факторов А и В. Например, если фактор А — тип почвы, а В — сорт, результат эксперимента — урожай, то и может быть пропорционально площадям с  типом почвы,
типом почвы,  — площадям, занятым
— площадям, занятым  сортом. Средним значением
сортом. Средним значением  уровня (фактора) А называют
уровня (фактора) А называют 
В рассмотренном выше примере  — ожидаемая средняя урожайность на
— ожидаемая средняя урожайность на  типе почвы при условии, что выбор сорта при посеве не зависит от типа почвы и пропорционален
типе почвы при условии, что выбор сорта при посеве не зависит от типа почвы и пропорционален  Эти условия выполняются, в частности, когда либо тип почвы оказывает приблизительно одинаковое влияние на урожайность всех сортов, либо низка общая культура земледелия, и землепользователю просто неизвестны или он лишен возможности использовать оптимальные сочетания сорта и типа почвы. Аналогично определяется среднее
Эти условия выполняются, в частности, когда либо тип почвы оказывает приблизительно одинаковое влияние на урожайность всех сортов, либо низка общая культура земледелия, и землепользователю просто неизвестны или он лишен возможности использовать оптимальные сочетания сорта и типа почвы. Аналогично определяется среднее  уровня (фактора)
уровня (фактора)  . В примере
. В примере  — это ожидаемая средняя урожайность
— это ожидаемая средняя урожайность  сорта при случайном распределении его по полям, пропорциональном
сорта при случайном распределении его по полям, пропорциональном 
Генеральным средним называют

Главный эффект  уровня А определяется как
уровня А определяется как  Очевидно,
Очевидно,  удовлетворяют условию
удовлетворяют условию
 (13.12)
(13.12)
Аналогично главный эффект  уровня В определяется как
уровня В определяется как  удовлетворяют условию
удовлетворяют условию
 (13.13)
(13.13)
Взаимодействием i-го уровня А с  уровнем В называют
уровнем В называют

Взаимодействия удовлетворяют условиям:
 (13.14)
(13.14)
Итак, математическая модель для средних имеет вид

где  удовлетворяют уравнениям
удовлетворяют уравнениям 
Очень важным для практического использования ДА является следующее утверждение [148, § 4.1]:
Если при некоторой системе весов  все взаимодействия равны нулю, то они равны нулю при любой другой системе весов. В этом случае модель называют аддитивной. В аддитивной модели каждое сравнение средних
все взаимодействия равны нулю, то они равны нулю при любой другой системе весов. В этом случае модель называют аддитивной. В аддитивной модели каждое сравнение средних  или
или  и главных эффектов
и главных эффектов  или
или  имеет значение, не зависящее от системы весов
имеет значение, не зависящее от системы весов 
Содержательная интерпретация результатов ДА проста и наглядна, когда мы решаем  основании статистических или других соображений), что взаимодействия отсутствуют. В этом случае заключением о главных эффектах можно завершить весь анализ. Однако если гипотеза об отсутствии взаимодействий была принята на основании только того, что она не была отвергнута некоторым
основании статистических или других соображений), что взаимодействия отсутствуют. В этом случае заключением о главных эффектах можно завершить весь анализ. Однако если гипотеза об отсутствии взаимодействий была принята на основании только того, что она не была отвергнута некоторым  -критерием, то следует посмотреть мощность этого критерия и оценить, насколько статистически невыявленные взаимодействия могут повлиять на интерпретацию результатов.
-критерием, то следует посмотреть мощность этого критерия и оценить, насколько статистически невыявленные взаимодействия могут повлиять на интерпретацию результатов.
Часто величины взаимодействий могут быть уменьшены с помощью подходящего преобразования наблюдаемых случайных величин [14, п. 10.3.4]. Пример использования преобразования с целью сделать модель аддитивной можно найти в [170].
Среди статистиков нет единого мнения о целесообразности изучения главных эффектов в условиях статистически значимых взаимодействий. Нам кажется, что этот вопрос носит, скорее, содержательный, чем формально-математический характер. Если введенные средние имеют смысл, то изучение их свойств целесообразно. Наконец, взаимодействия могут быть значимы статистически, но относительно малы по сравнению с главными эффектами.
Всюду в дальнейшем, если не оговорено противное, будет выбираться система весов:  Такие веса иногда называют равными.
Такие веса иногда называют равными.
13.3.2. Двухфакторный анализ с равным числом К наблюдений в ячейках (К > 1).
Обозначим  наблюдение в
наблюдение в  -ячейке, тогда математическая модель имеет вид
-ячейке, тогда математическая модель имеет вид
 (13.16)
(13.16)
где  независимы и имеют нормальное распределение со средним, равным нулю, и дисперсией
независимы и имеют нормальное распределение со средним, равным нулю, и дисперсией  а константы
а константы  удовлетворяют соотношениям (13.12)-(13.14) с равными весами. Обычно проверяются следующие гипотезы:
удовлетворяют соотношениям (13.12)-(13.14) с равными весами. Обычно проверяются следующие гипотезы:

Оценки для параметров строятся аналогично тому, как это делается в § 13.2.1:

Возьмем тождество

возведем в квадрат его правую и левую части и просуммируем по всем значениям индексов  . Так как все смешанные произведения при суммировании равны нулю, получаем
. Так как все смешанные произведения при суммировании равны нулю, получаем

Поскольку сумма рангов слагаемых правой части (13.17) совпадает с рангом квадратичной формы левой части, согласно теореме Кохрана получаем, что суммы квадратов правой части независимы и соответственно распределены как  с числом степеней свободы, совпадающим с рангом соответствующей формы. Таким образом, критерии для проверки гипотез
с числом степеней свободы, совпадающим с рангом соответствующей формы. Таким образом, критерии для проверки гипотез  могут быть построены как соответствующие
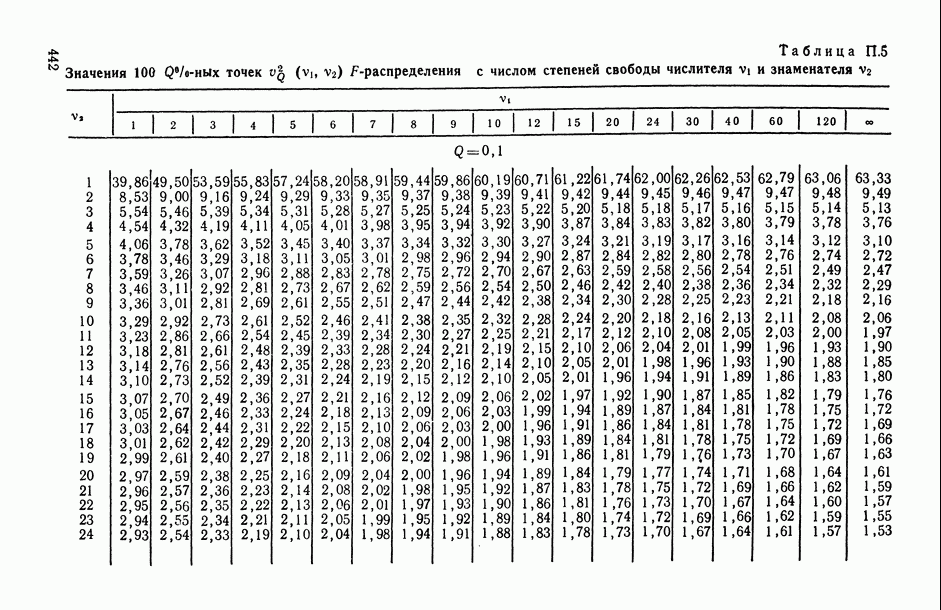
могут быть построены как соответствующие  -отношения
-отношения  определены в таблице ДА для двухфакторного анализа с
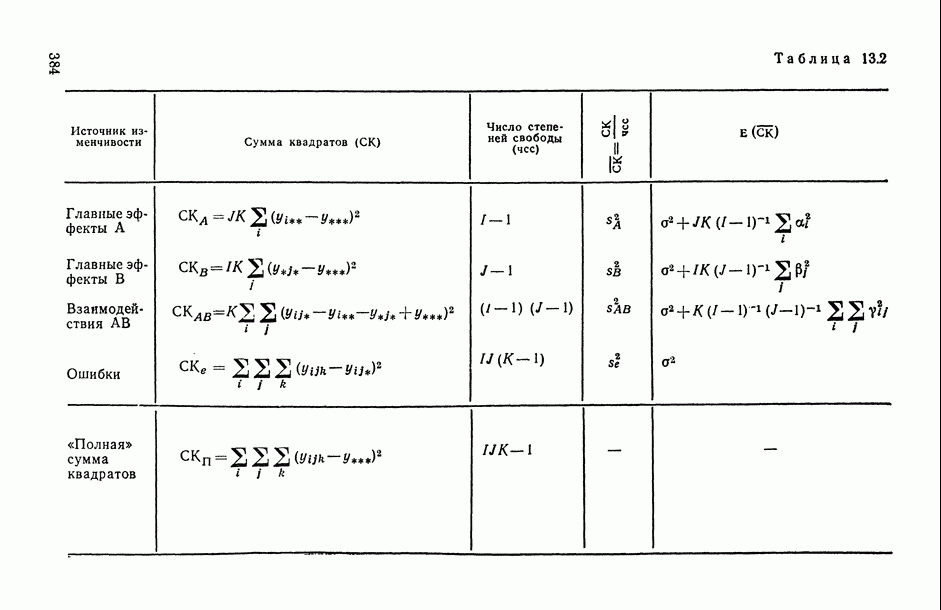
определены в таблице ДА для двухфакторного анализа с  наблюдениями в ячейке (табл. 13.2).
наблюдениями в ячейке (табл. 13.2).
Таблица 13.2
(см. скан)
Доверительные интервалы для сравнений  могут быть построены с помощью
могут быть построены с помощью  -метода аналогично тому, как это сделано в случае однофакторного анализа. Г-метод может быть также применен к разностям главных эффектов. Однако к взаимодействиям он уже не применим.
-метода аналогично тому, как это сделано в случае однофакторного анализа. Г-метод может быть также применен к разностям главных эффектов. Однако к взаимодействиям он уже не применим.
13.3.3. Случай неравных.
В общем случае не существует простого разложения, подобного (13.17). Поэтому остаются две возможности: либо воспользоваться точным, но громоздким методом анализа, изложенным, например, в монографии [148], либо применить приближенный метод. Последний заключается в следующем. Приближенно считают, что

где  независимы и нормально распределены с нулевым средним и дисперсией
независимы и нормально распределены с нулевым средним и дисперсией  удовлетворяют соотношениям
удовлетворяют соотношениям  Оценка
Оценка  в этом случае строится с помощью
в этом случае строится с помощью  Далее анализ проводится так же, как в п. 13.3.2 с
Далее анализ проводится так же, как в п. 13.3.2 с  .
.
В частном случае, когда для всех  где
где  при выборе
при выборе  разложение типа (13.17) имеет место, и ДА проводится с очевидными изменениями в табл. 13.2.
разложение типа (13.17) имеет место, и ДА проводится с очевидными изменениями в табл. 13.2.
13.3.4. Случай.
Как правило, подобные данные возникают при использовании планов с рандомизированными блоками, когда можно априори ожидать, что или взаимодействие между изучаемым фактором А (способом обработки) и фактором В (блоком) мало в среднем, или что существует малопараметрическая параметризация взаимодействий. Ниже указываются основные модели.
Аддитивная модель без взаимодействий
 (13.18)
(13.18)
где  а независимы, нормально распределены
а независимы, нормально распределены  . При рандомизированных блоках
. При рандомизированных блоках  отражает суммарное влияние двух источников случайных отклонений: отклонения, связанного со случайностью расположения фактора А в блоке, и отклонения, равного случайной погрешности воспроизведения эксперимента при заданном расположении А в блоке.
отражает суммарное влияние двух источников случайных отклонений: отклонения, связанного со случайностью расположения фактора А в блоке, и отклонения, равного случайной погрешности воспроизведения эксперимента при заданном расположении А в блоке.
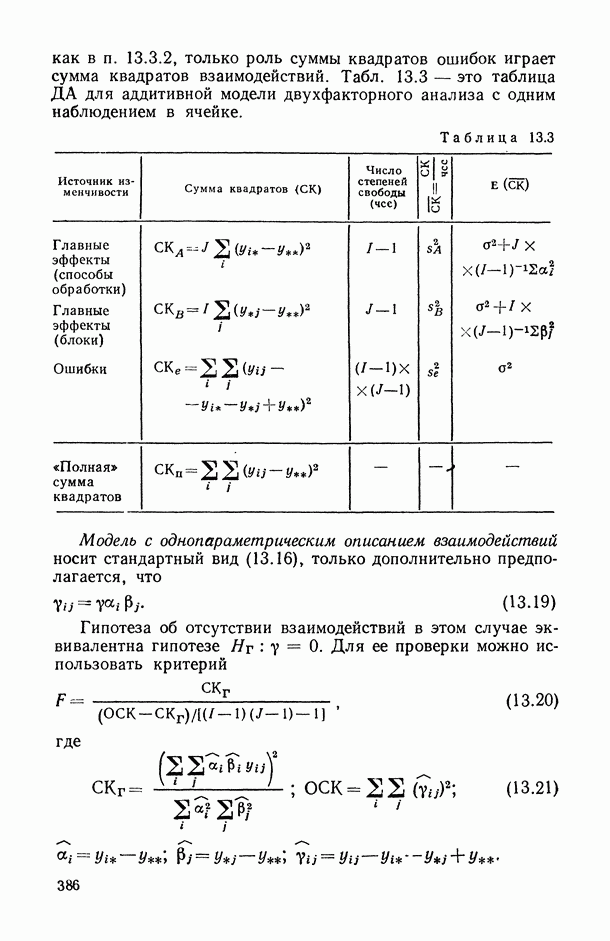
Поскольку в аддитивной модели предполагается, что взаимодействия отсутствуют, проверка гипотез  проводится так же, как в п. 13.3.2, только роль суммы квадратов ошибок играет сумма квадратов взаимодействий. Табл. 13.3 — это таблица ДА для аддитивной модели двухфакторного анализа с одним наблюдением в ячейке.
проводится так же, как в п. 13.3.2, только роль суммы квадратов ошибок играет сумма квадратов взаимодействий. Табл. 13.3 — это таблица ДА для аддитивной модели двухфакторного анализа с одним наблюдением в ячейке.
Таблица 13.3

Модель с однопараметрическим описанием взаимодействий носит стандартный вид (13.16), только дополнительно предполагается, что
 (13.19)
(13.19)
Гипотеза об отсутствии взаимодействий в этом случае эквивалентна гипотезе  . Для ее проверки можно использовать критерий
. Для ее проверки можно использовать критерий
 (13.20)
(13.20)
где

Критерий F в (13.20) при  имеет
имеет  -распределение с
-распределение с  степенями свободы. Гипотезы
степенями свободы. Гипотезы  проверяются так же, как в п. 13.3.2, только сумма квадратов ошибок определяется как
проверяются так же, как в п. 13.3.2, только сумма квадратов ошибок определяется как  и имеет на одну степень свободы меньше, чем в табл. 13.3.
и имеет на одну степень свободы меньше, чем в табл. 13.3.
Более реалистической является модель с  параметрическим описанием взаимодействий [217]. Она похожа на предыдущую, только в ней предполагается, что взаимодействия пропорциональны произведению не главных факторов, а некоторых констант, оцениваемых по выборке,
параметрическим описанием взаимодействий [217]. Она похожа на предыдущую, только в ней предполагается, что взаимодействия пропорциональны произведению не главных факторов, а некоторых констант, оцениваемых по выборке,

Пусть  - матрица с
- матрица с  определенными, как в (13.21), тогда
определенными, как в (13.21), тогда  и определяются, как выше, а
и определяются, как выше, а  где
где  наибольшее собственное число матрицы
наибольшее собственное число матрицы  ;
;  -нормализованный собственный вектор
-нормализованный собственный вектор  , соответствующий собственному числу
, соответствующий собственному числу  аналогичный вектор
аналогичный вектор  . Для проверки гипотезы
. Для проверки гипотезы  используется отношение типа (13.20) с естественной заменой
используется отношение типа (13.20) с естественной заменой  на
на  . Однако распределение отношения сложнее и не сводится к
. Однако распределение отношения сложнее и не сводится к  -распределению.
-распределению.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
- В.3. Математический инструментарий
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
- 2.3. Анализ множественных ранговых связей
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
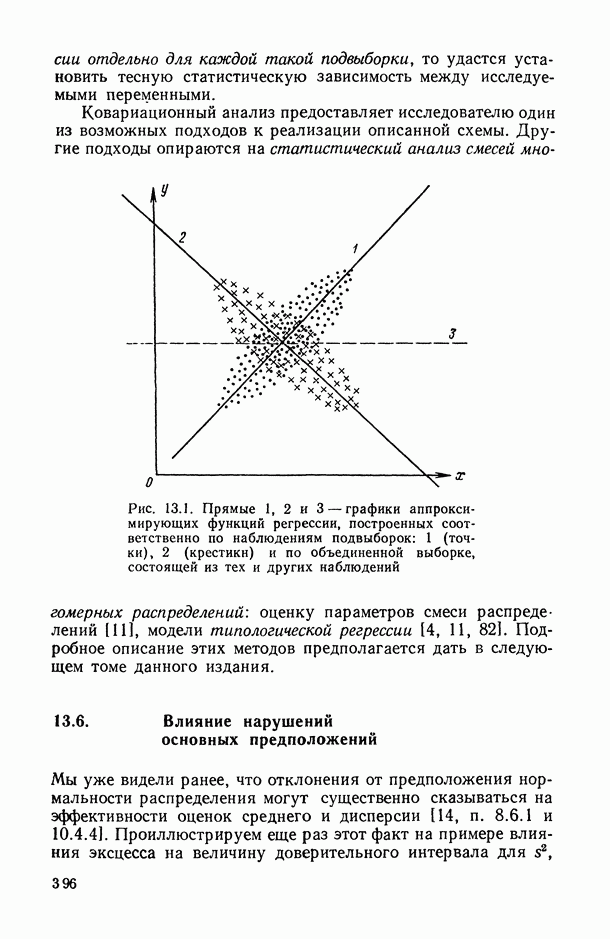
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
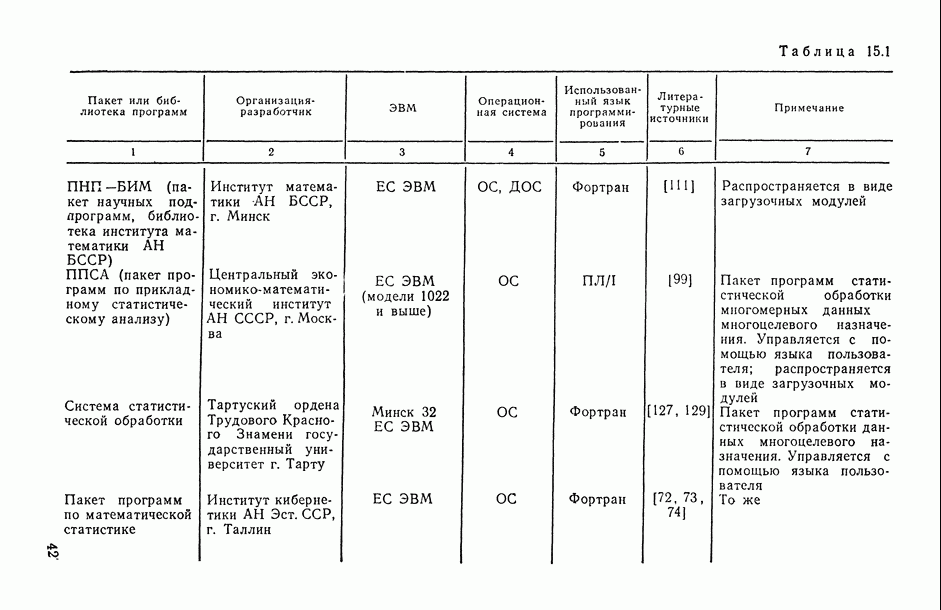
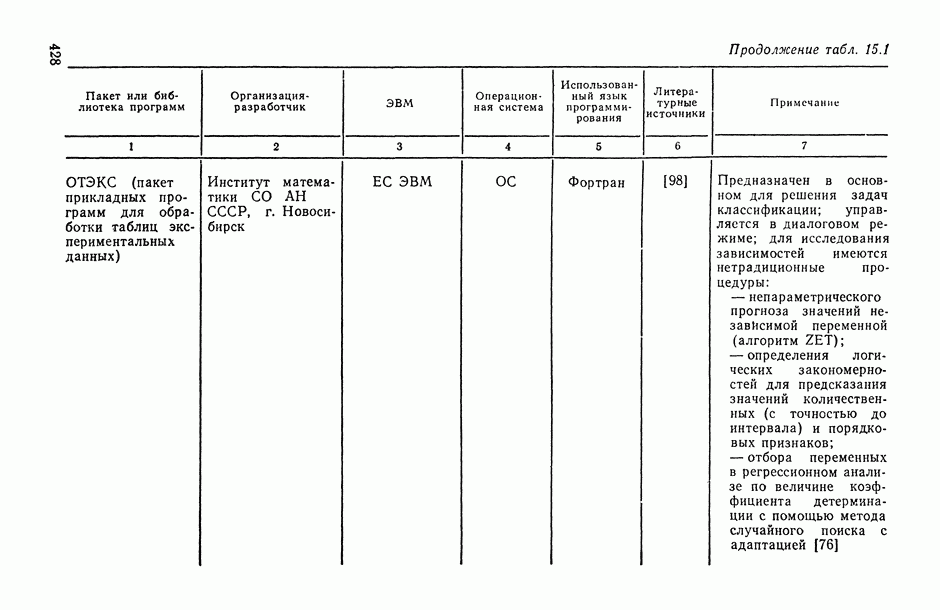
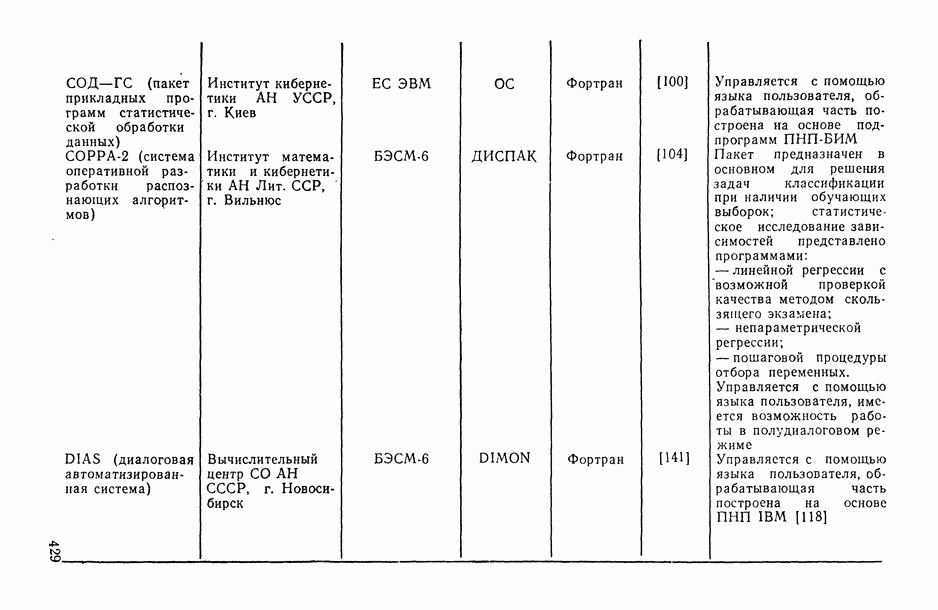
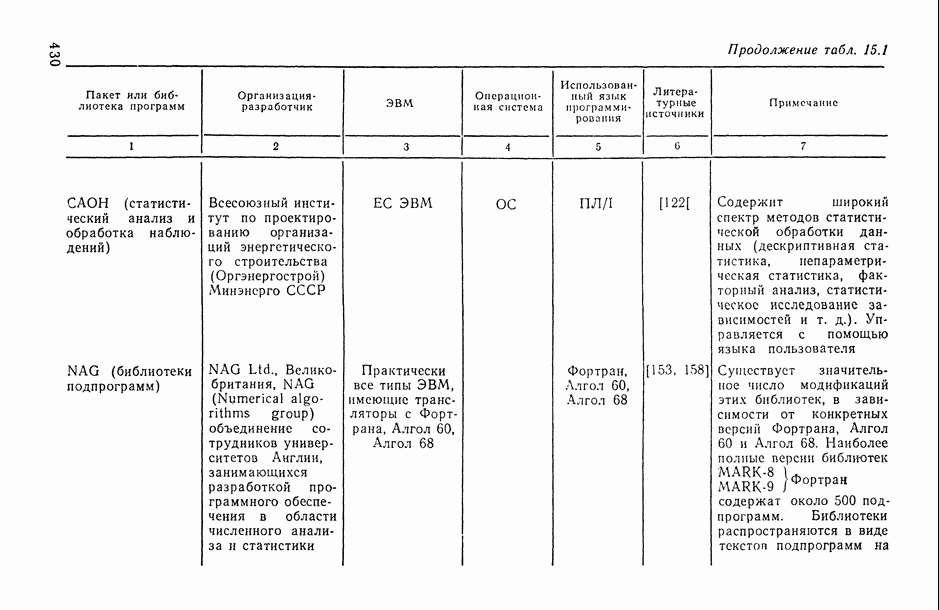
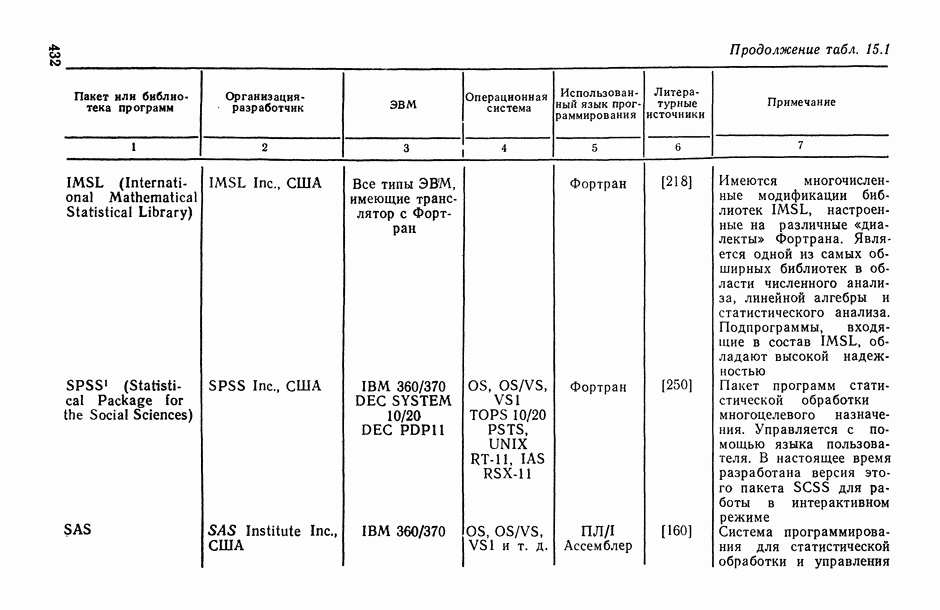
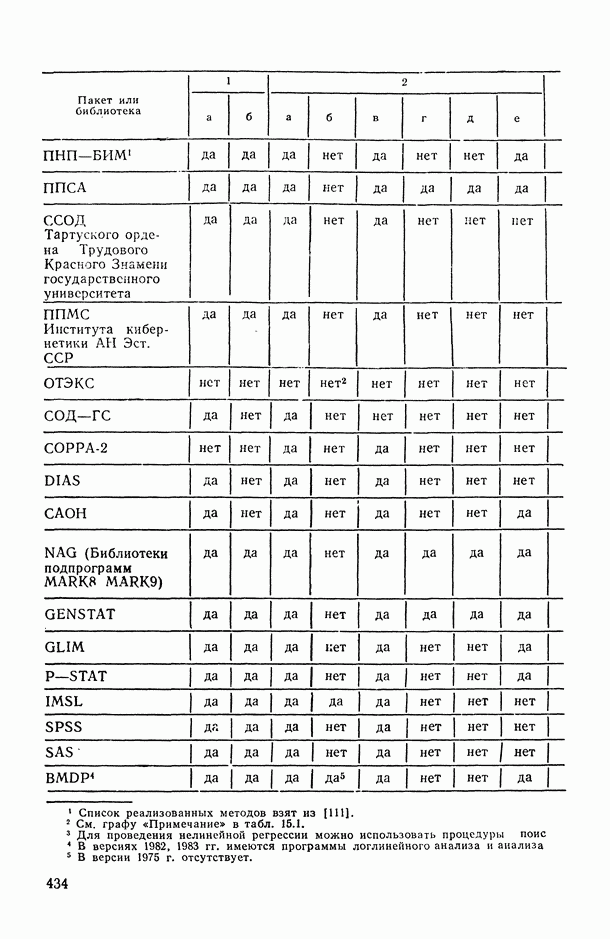
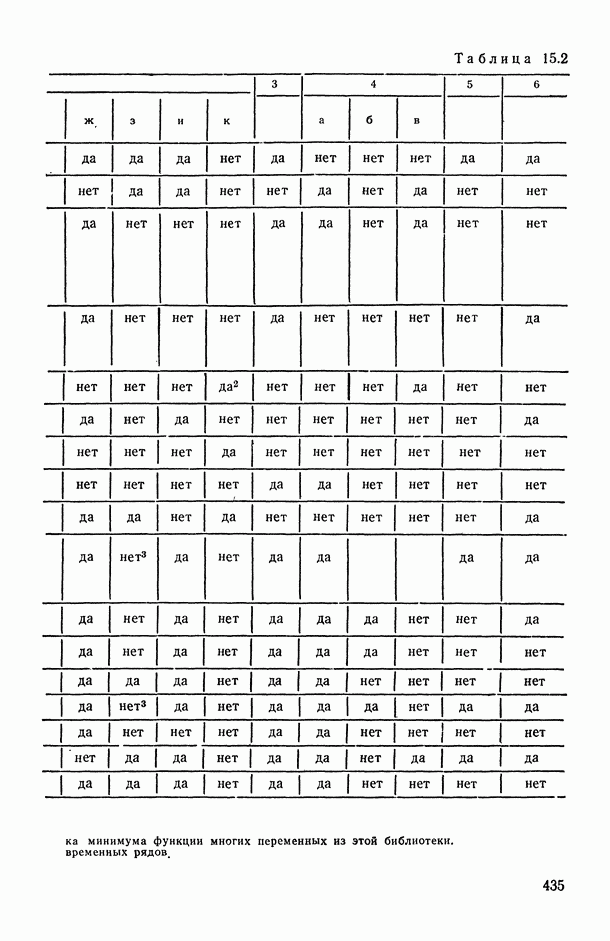
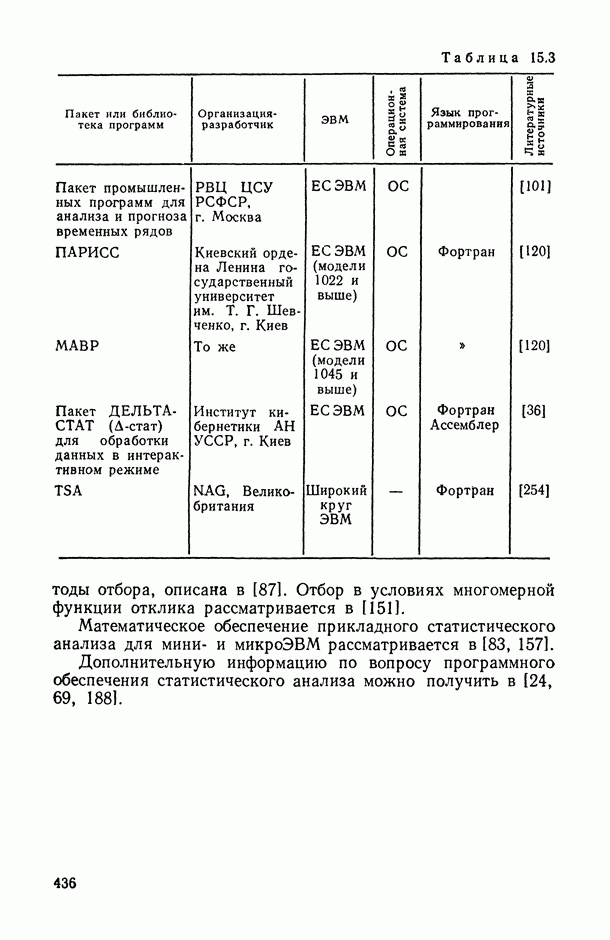
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
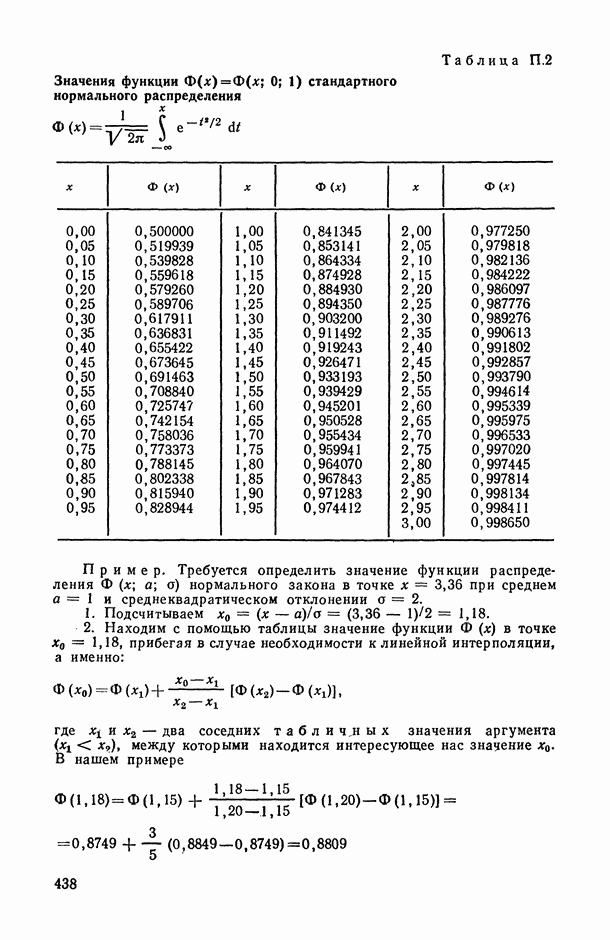
- Таблица П.2. Значения функции стандартного нормального распределения
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ