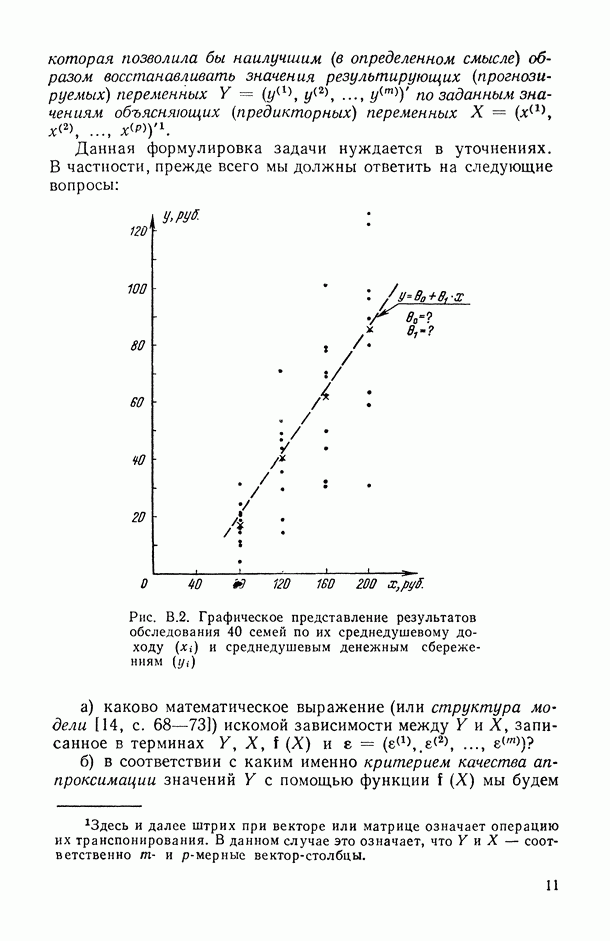
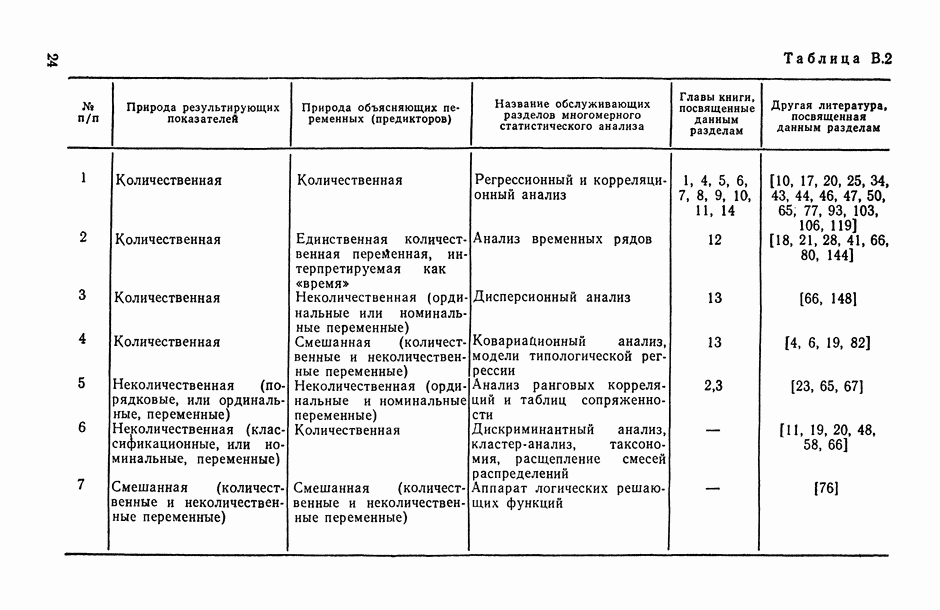
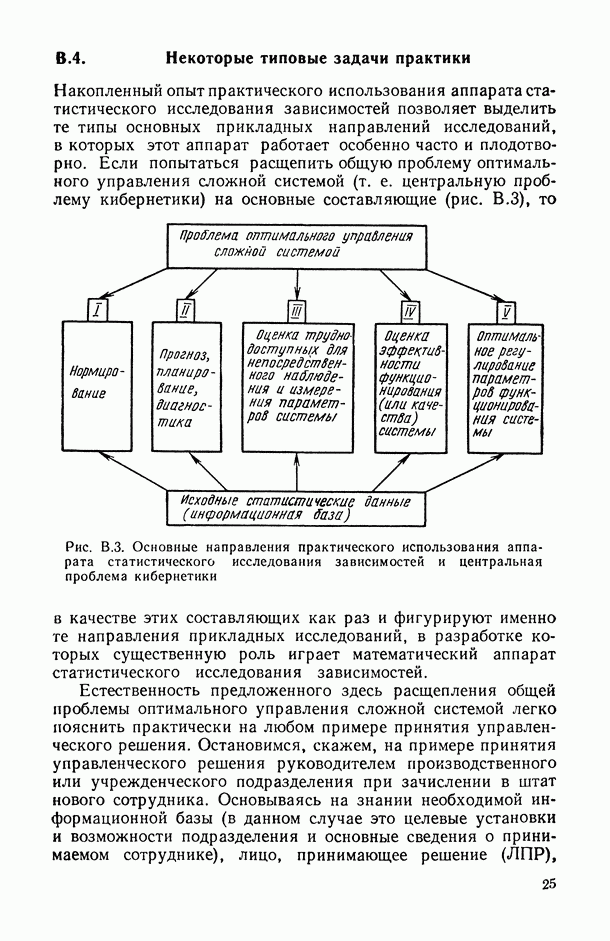
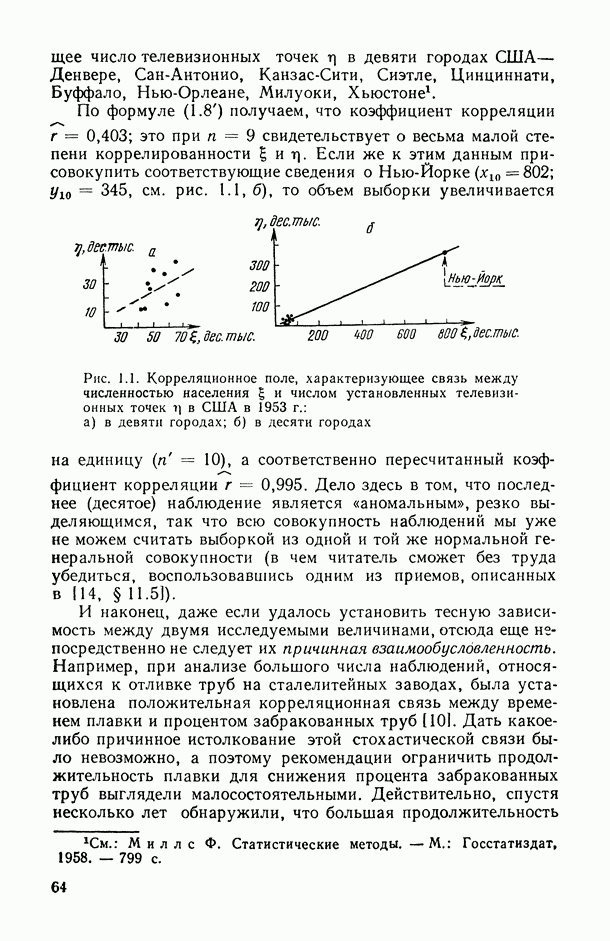
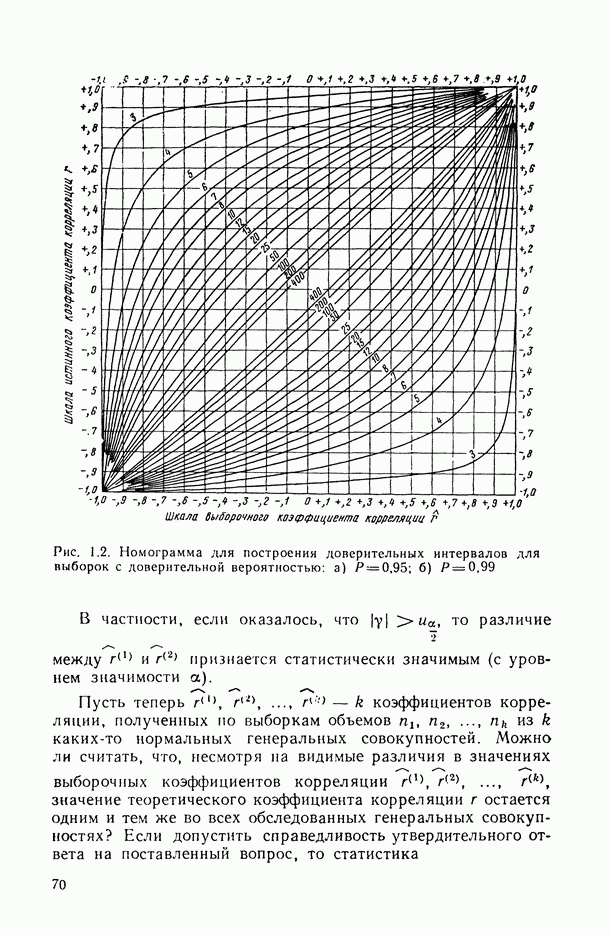
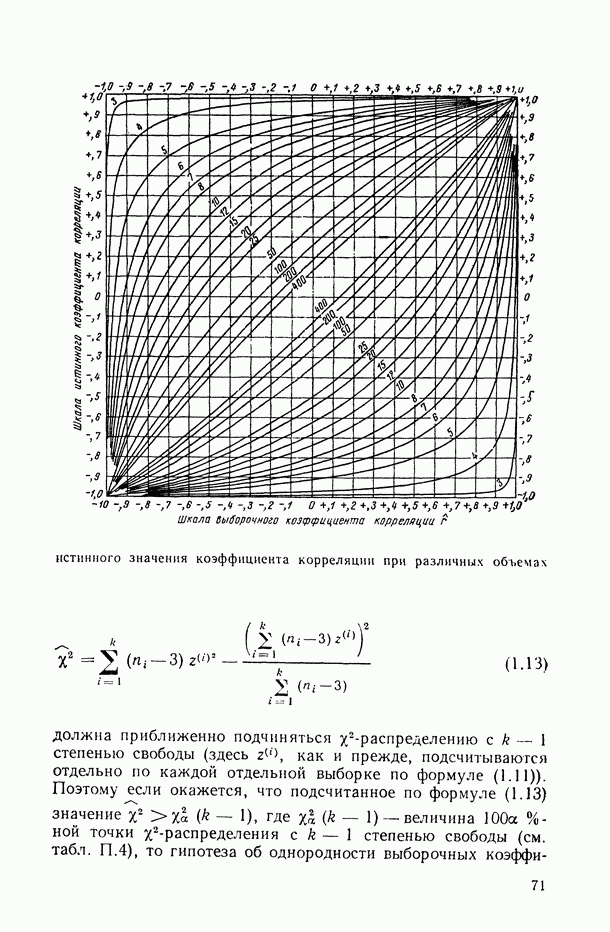
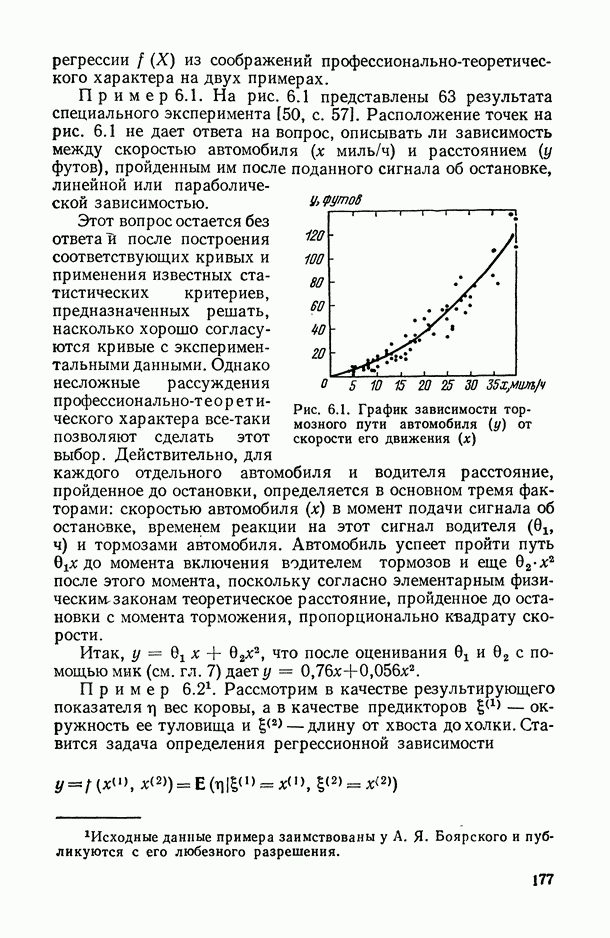
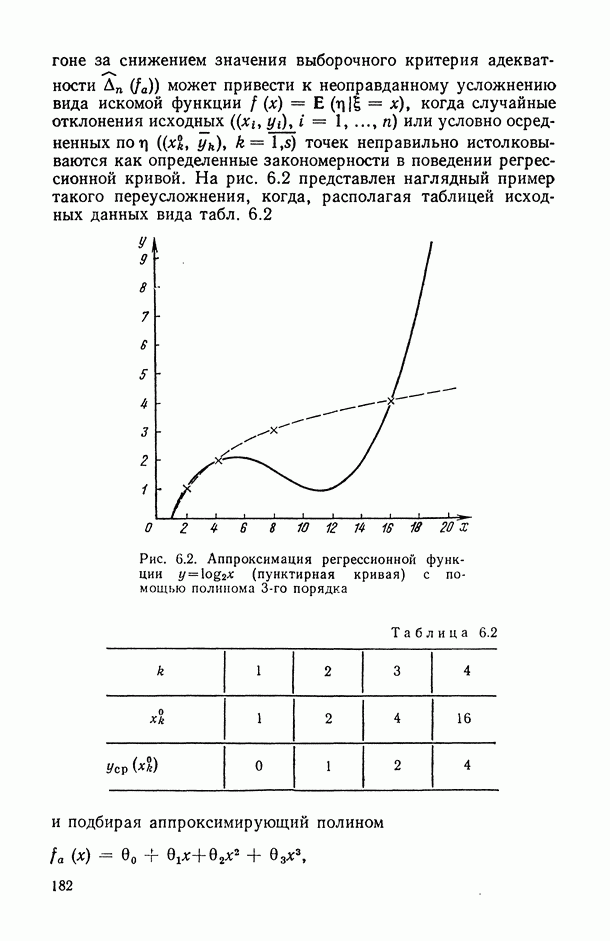
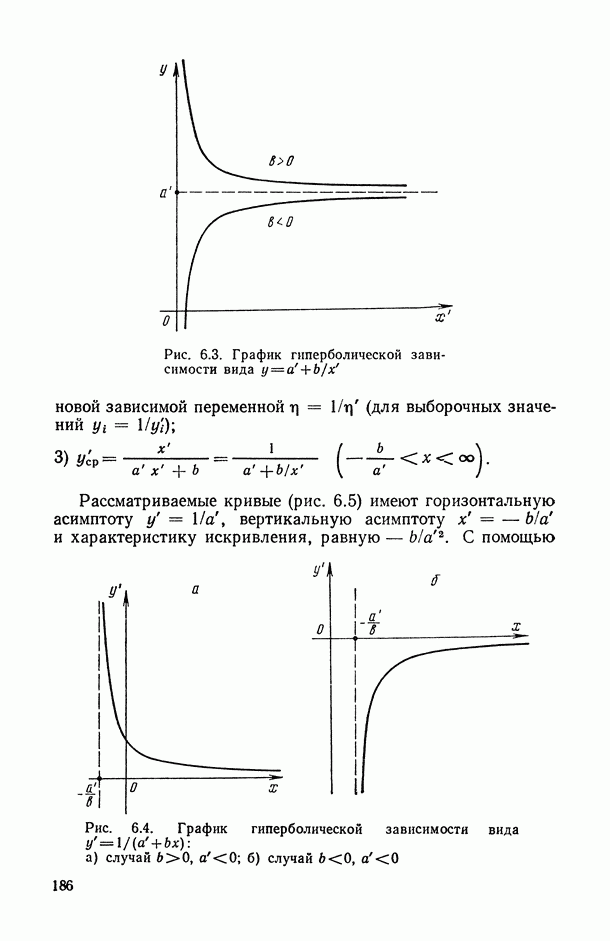
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
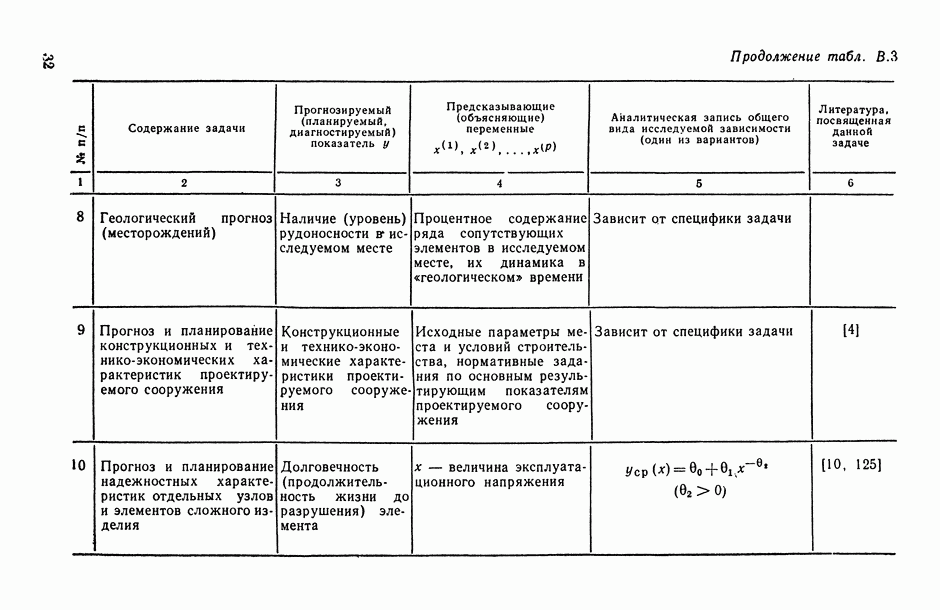
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
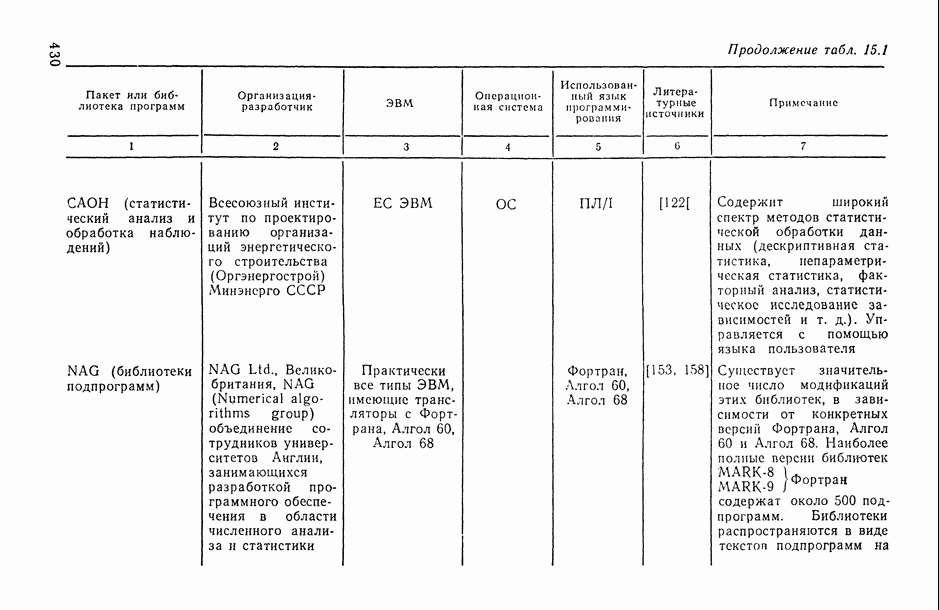
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
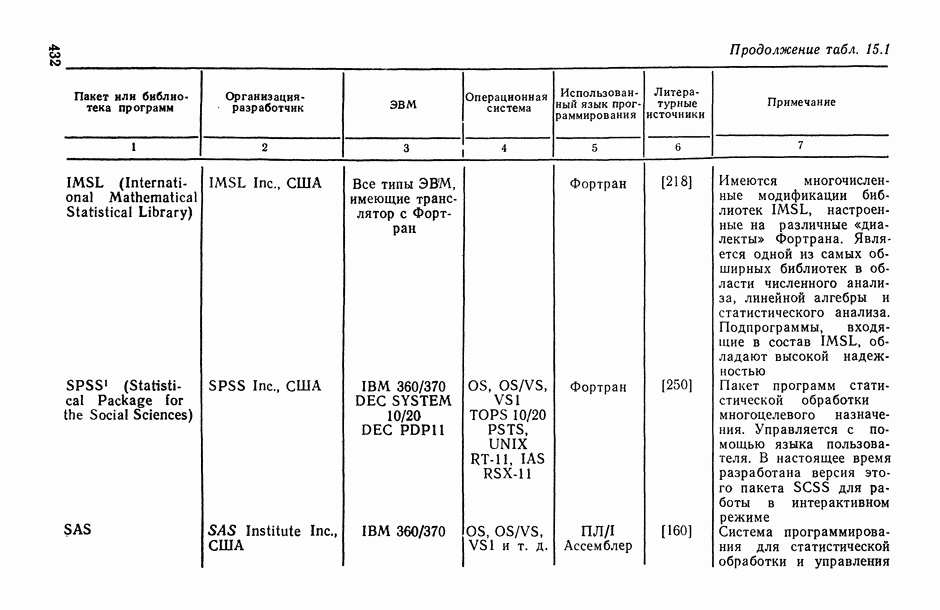
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
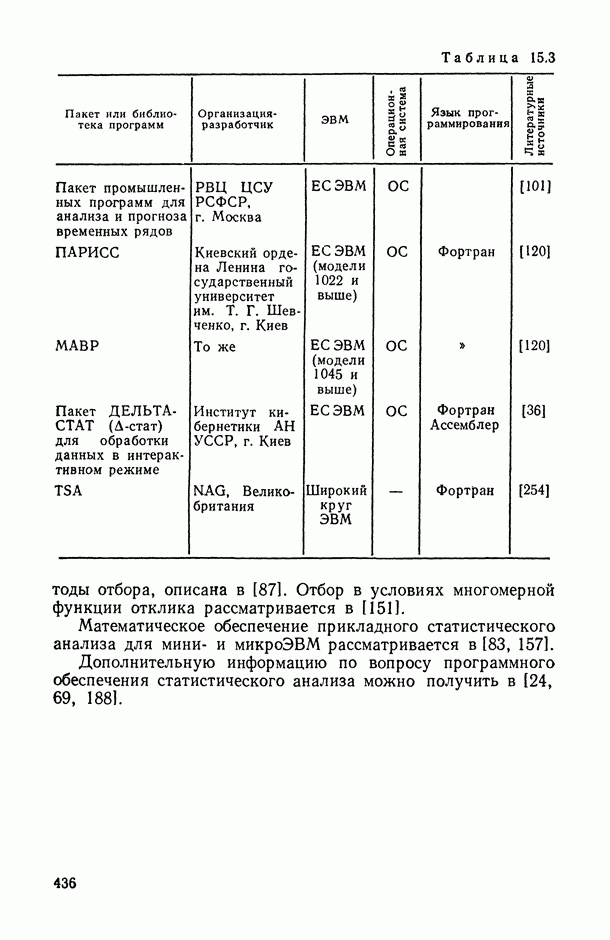
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
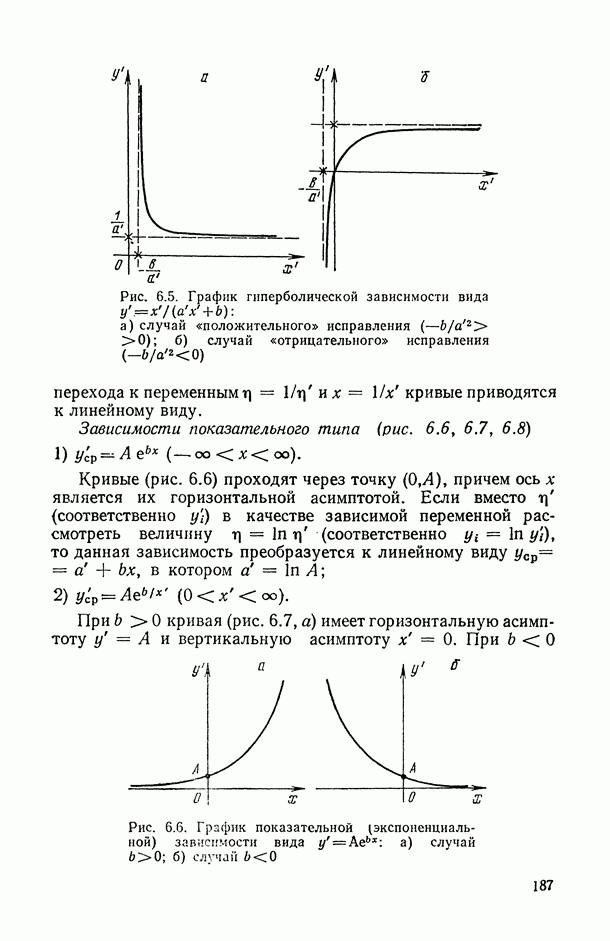
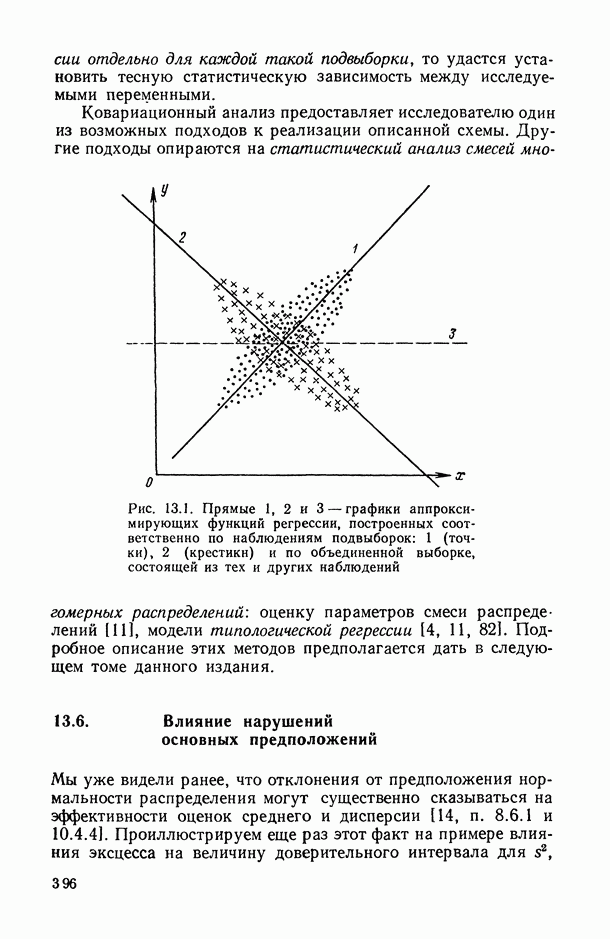
5.3. Взаимоотношения различных регрессий
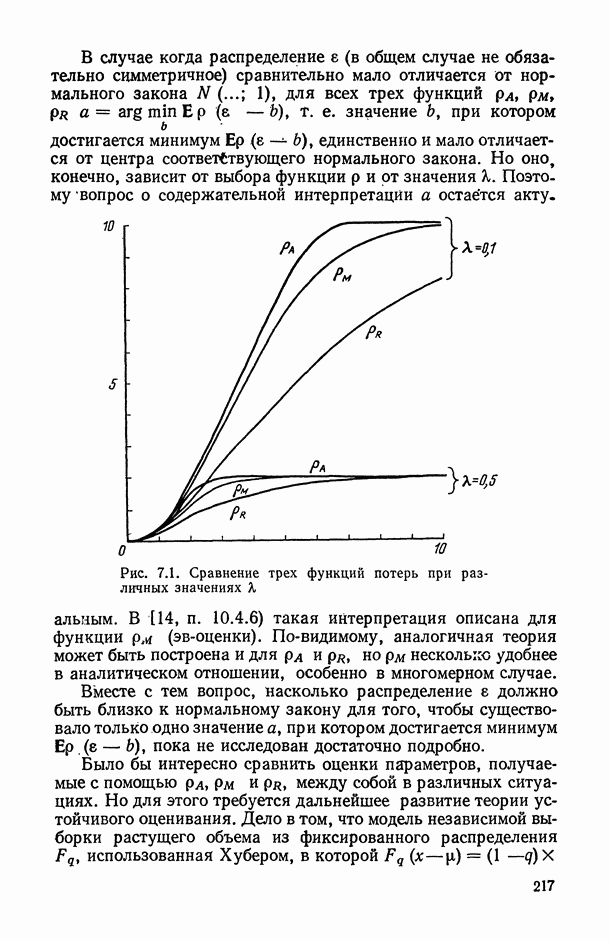
Взаимоотношения истинной и  -регрессий существенно зависят от вероятностной природы регрессионных остатков
-регрессий существенно зависят от вероятностной природы регрессионных остатков  в моделях типа (5.1) и от способа выбора класса допустимых решений F. Попробуем вначале понять эти взаимоотношения на примере.
в моделях типа (5.1) и от способа выбора класса допустимых решений F. Попробуем вначале понять эти взаимоотношения на примере.
Пример 5.1. Результирующий показатель  связан с объясняющей переменной
связан с объясняющей переменной  соотношением
соотношением

где регрессионный остаток  — случайная величина, подчиняющаяся нормальному закону распределения со средним значением
— случайная величина, подчиняющаяся нормальному закону распределения со средним значением  и с дисперсией
и с дисперсией  а диапазон возможных значений
а диапазон возможных значений  определяется, отрез ком [2; 10]. Очевидно, истинная функция регрессии в данном случае имеет вид
определяется, отрез ком [2; 10]. Очевидно, истинная функция регрессии в данном случае имеет вид

Предположим, нам не известен точный вид соотношения (5.8) и соответственно не известно уравнение функции регрессии (5.9).
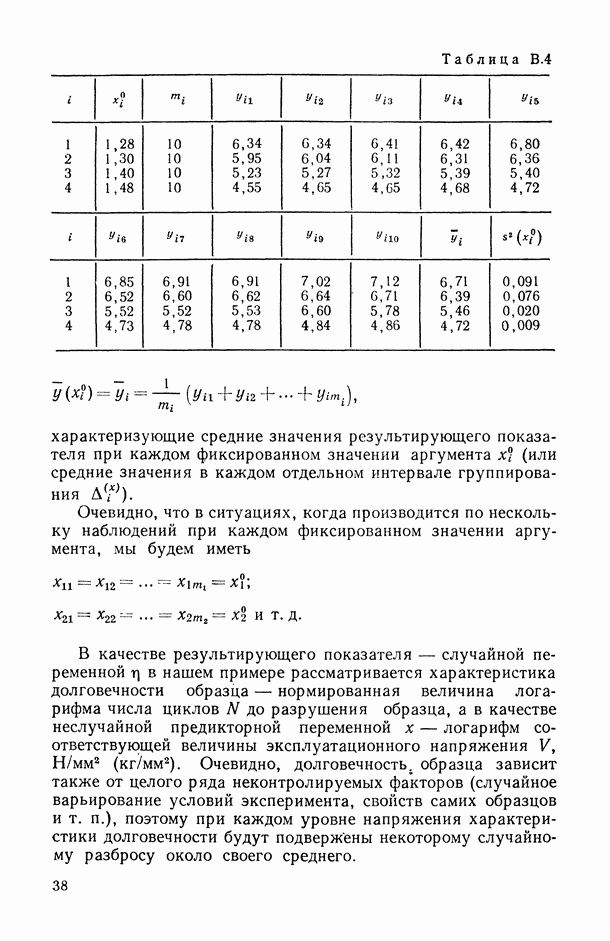
Однако мы располагаем следующей системой двумерных наблюдений  , генерируемых моделью (5.8), т. е. связанных соотношением
, генерируемых моделью (5.8), т. е. связанных соотношением  (табл. 5.1)
(табл. 5.1)
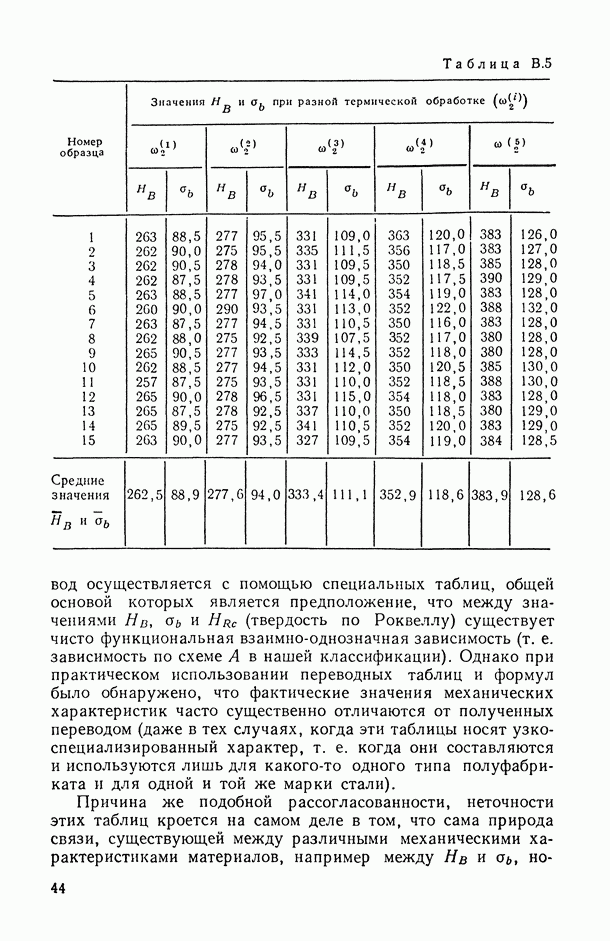
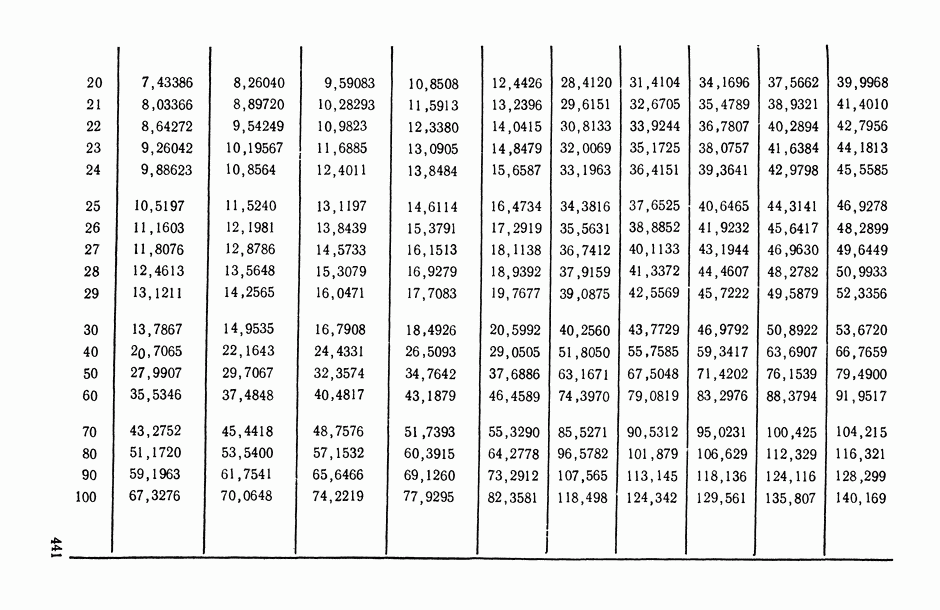
Таблица 5.1

Расположение точек — наблюдений на рис. 5.1 дает нам основание ограничить класс допустимых решений только линейными зависимостями, т. е. определить в качестве класса допустимых решений параметрическое семейство

Имея априорную информацию о типе распределения регрессионных остатков, остановим свой выбор на квадратичной функции потерь. Решая оптимизационную задачу вида

получаем оценки  для неизвестных параметров
для неизвестных параметров  участвующих в записи аппроксимирующей функции
участвующих в записи аппроксимирующей функции  График соответствующей выборочной аппроксимирующей функции регрессии
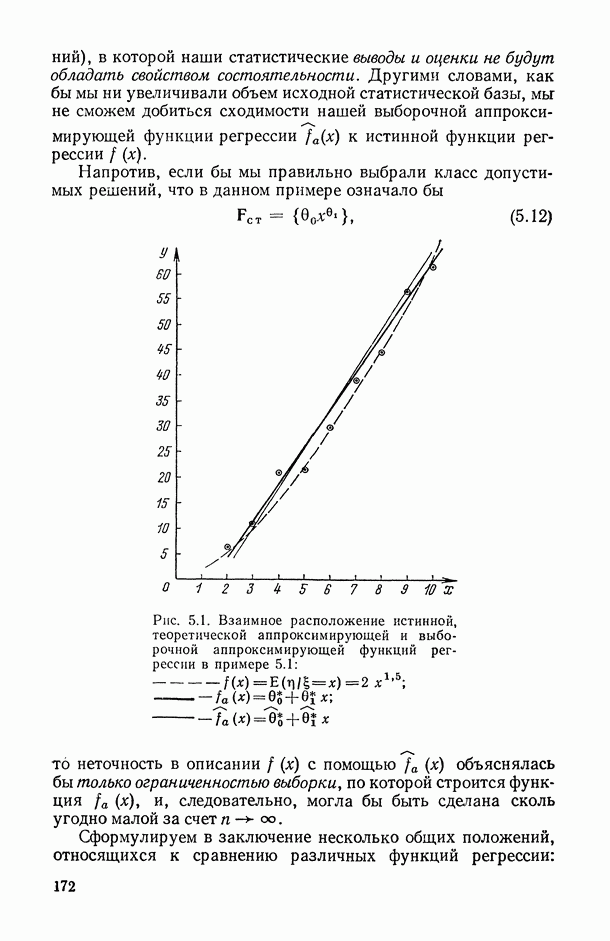
График соответствующей выборочной аппроксимирующей функции регрессии  изображен на рис. 5.1. Для сравнения на том же рисунке изображены графики истинной функции регрессии
изображен на рис. 5.1. Для сравнения на том же рисунке изображены графики истинной функции регрессии  и теоретической аппроксимирующей функции регрессии
и теоретической аппроксимирующей функции регрессии  Последняя характеризует результат, к которому мы бы неограниченно приближались (в смысле сходимости по вероятности), решая оптимизационную задачу (5.11) для неограниченно расширяющейся по объему выборки
Последняя характеризует результат, к которому мы бы неограниченно приближались (в смысле сходимости по вероятности), решая оптимизационную задачу (5.11) для неограниченно расширяющейся по объему выборки  . Поскольку мы «не угадали» класс допустимых решений (истинная функция регрессии не принадлежит к выбранному нами классу (5.10)), то в данном случае мы находимся в ситуации (к сожалению, достаточно типичной для практики статистических исследований), в которой наши статистические выводы и оценки не будут обладать свойством состоятельности.
. Поскольку мы «не угадали» класс допустимых решений (истинная функция регрессии не принадлежит к выбранному нами классу (5.10)), то в данном случае мы находимся в ситуации (к сожалению, достаточно типичной для практики статистических исследований), в которой наши статистические выводы и оценки не будут обладать свойством состоятельности.
Другими словами, как бы мы ни увеличивали объем исходной статистической базы, мы не сможем добиться сходимости нашей выборочной аппроксимирующей функции регрессии  к истинной функции регрессии
к истинной функции регрессии  .
.
Напротив, если бы мы правильно выбрали класс допустимых решений, что в данном примере означало бы

то неточность в описании  с помощью
с помощью  объяснялась бы только ограниченностью выборки, по которой строится функция
объяснялась бы только ограниченностью выборки, по которой строится функция  , и, следовательно, могла бы быть сделана сколь угодно малой за счет
, и, следовательно, могла бы быть сделана сколь угодно малой за счет 

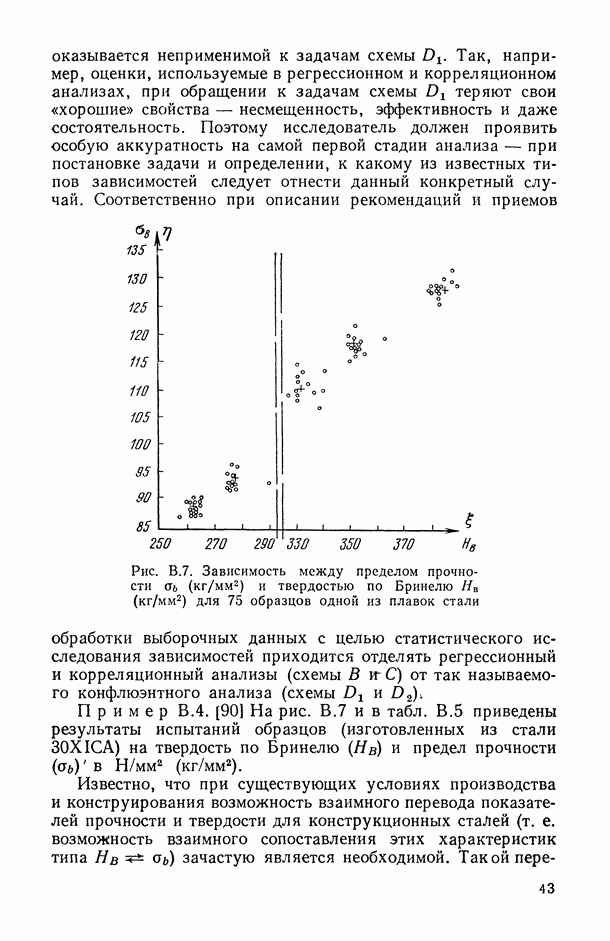
Рис. 5.1. Взаимное расположение истинной, теоретической аппроксимирующей и выборочной аппроксимирующей функций регрессии в примере 5.1: 
Сформулируем в заключение несколько общих положений, относящихся к сравнению различных функций регрессии:
а) истинная регрессия  является одновременно среднеквадратической, т. е. дает решение оптимизационной задачи вида (5.6) при квадратичной функции потерь
является одновременно среднеквадратической, т. е. дает решение оптимизационной задачи вида (5.6) при квадратичной функции потерь  и при отсутствии ограничений на класс допустимых решений F (доказательство приведено в п. 1.3.1);
и при отсутствии ограничений на класс допустимых решений F (доказательство приведено в п. 1.3.1);
б) для широкого класса критериев адекватности  выборочная аппроксимирующая функция регрессии
выборочная аппроксимирующая функция регрессии  сходится (по вероятности) к теоретической аппроксимирующей функции регрессии
сходится (по вероятности) к теоретической аппроксимирующей функции регрессии  при
при 
в) в случае удачного выбора класса допустимых решений, т. е. при  , теоретическая аппроксимирующая функция регрессии
, теоретическая аппроксимирующая функция регрессии  (при надлежащем выборе критериев адекватности
(при надлежащем выборе критериев адекватности  ) совпадает с истинной и соответственно выборочная аппроксимирующая функция регрессии
) совпадает с истинной и соответственно выборочная аппроксимирующая функция регрессии  будет сходиться (по вероятности) к истинной;
будет сходиться (по вероятности) к истинной;
г) в случае неудачного выбора класса допустимых решений, т. е. при  ошибку в описании истинной функции регрессии
ошибку в описании истинной функции регрессии  с помощью выборочной аппроксимирующей функции регрессии
с помощью выборочной аппроксимирующей функции регрессии  удобно представить в виде суммы двух компонент: ошибки выборки и ошибки аппроксимации. При этом ошибка выборки (разность
удобно представить в виде суммы двух компонент: ошибки выборки и ошибки аппроксимации. При этом ошибка выборки (разность  )
)  при
при  стремится (по вероятности) к нулю, в то время как ошибка аппроксимации (разность
стремится (по вероятности) к нулю, в то время как ошибка аппроксимации (разность  )
)  не стремится к нулю ни при каком выборе критерия адекватности
не стремится к нулю ни при каком выборе критерия адекватности  .
.
Обсуждение мотивов выбора вида функции потерь  (и соответственно критерия адекватности
(и соответственно критерия адекватности  ) приводится в гл. 7.
) приводится в гл. 7.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
- В.3. Математический инструментарий
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
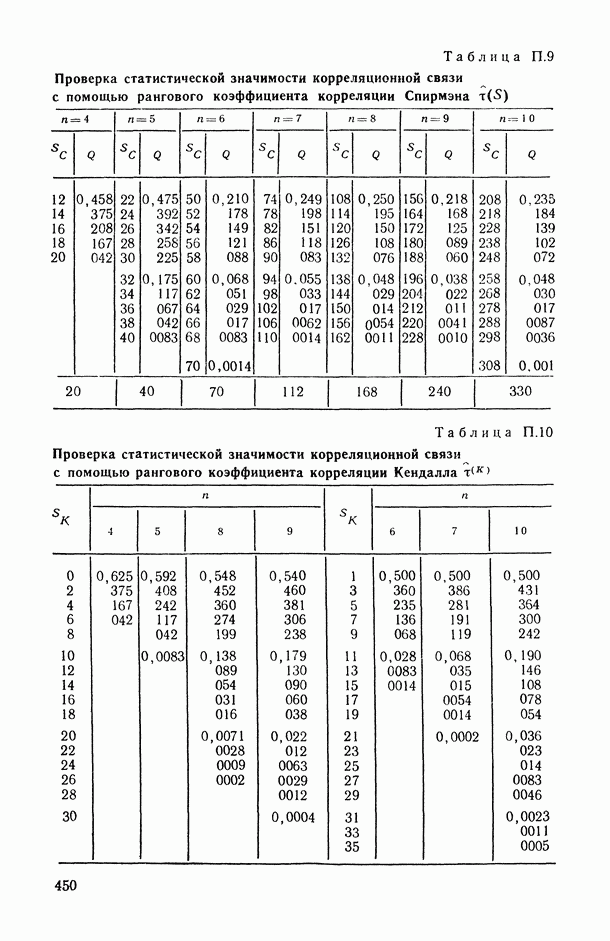
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
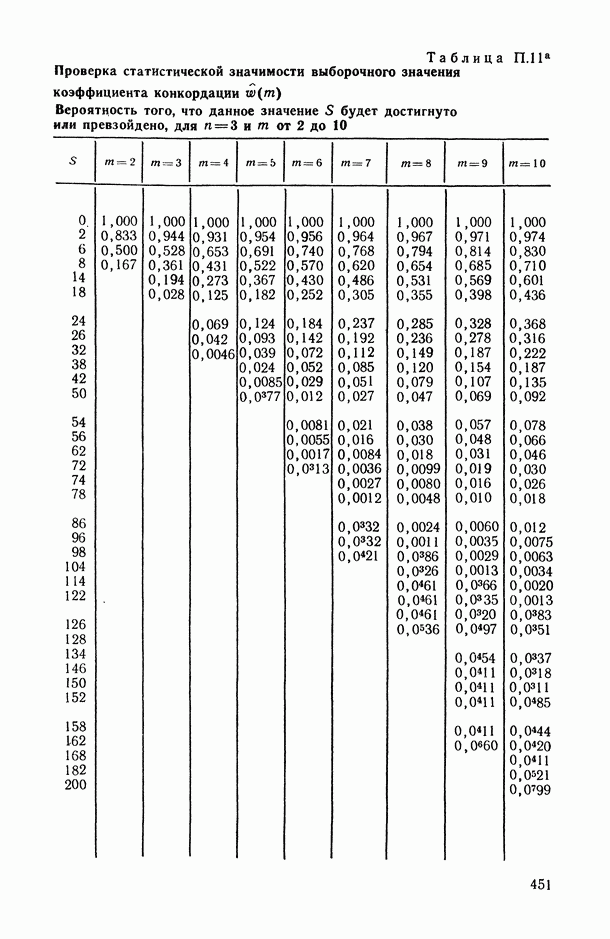
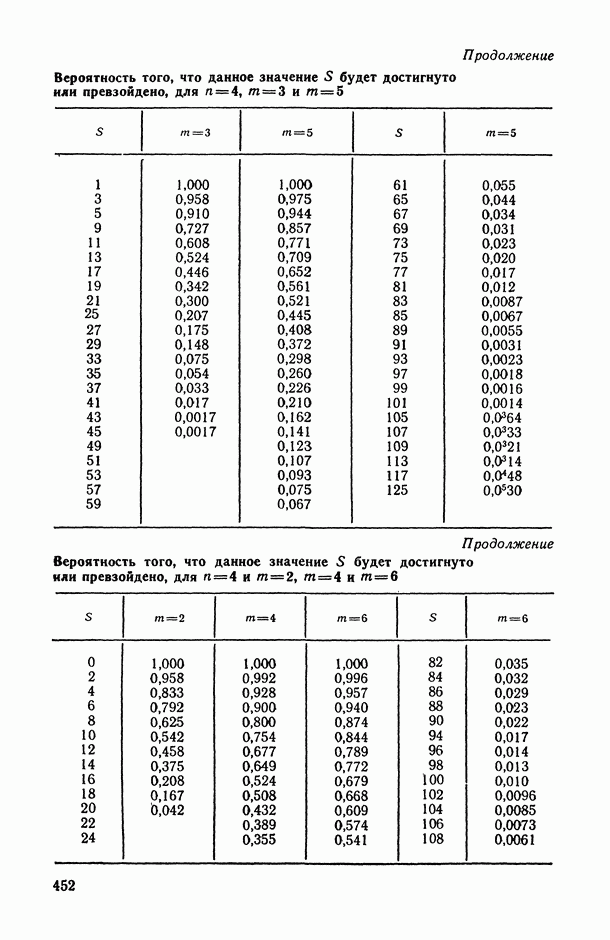
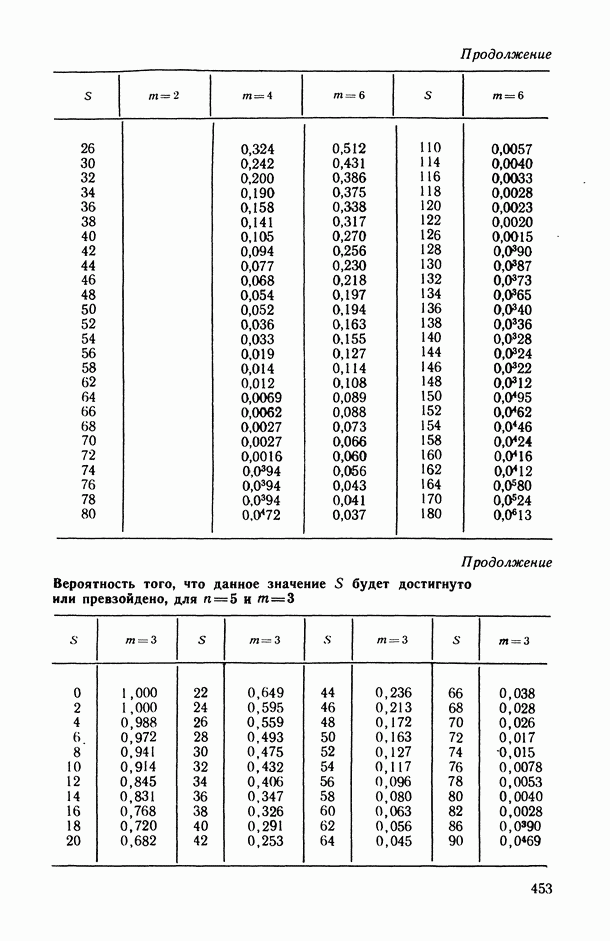
- 2.3. Анализ множественных ранговых связей
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
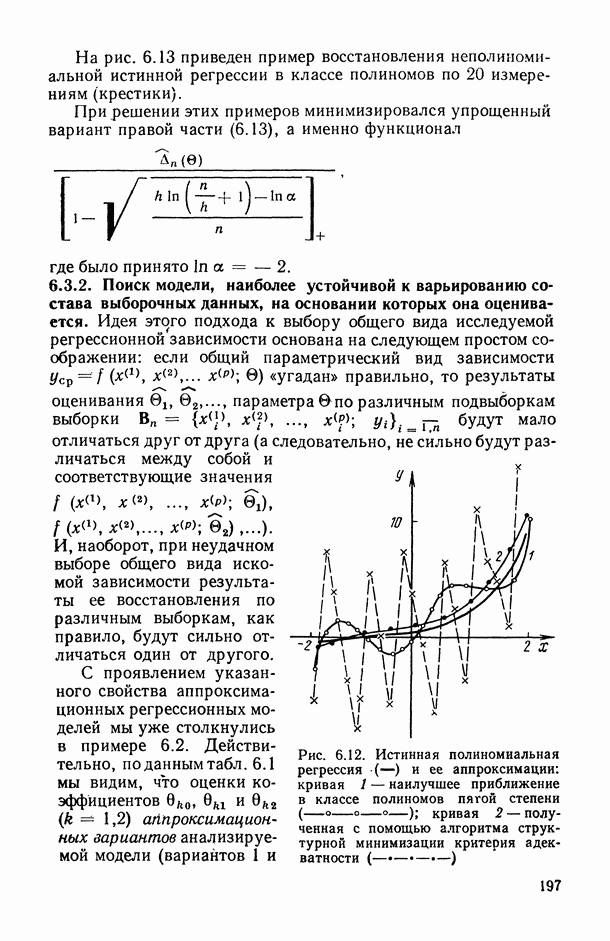
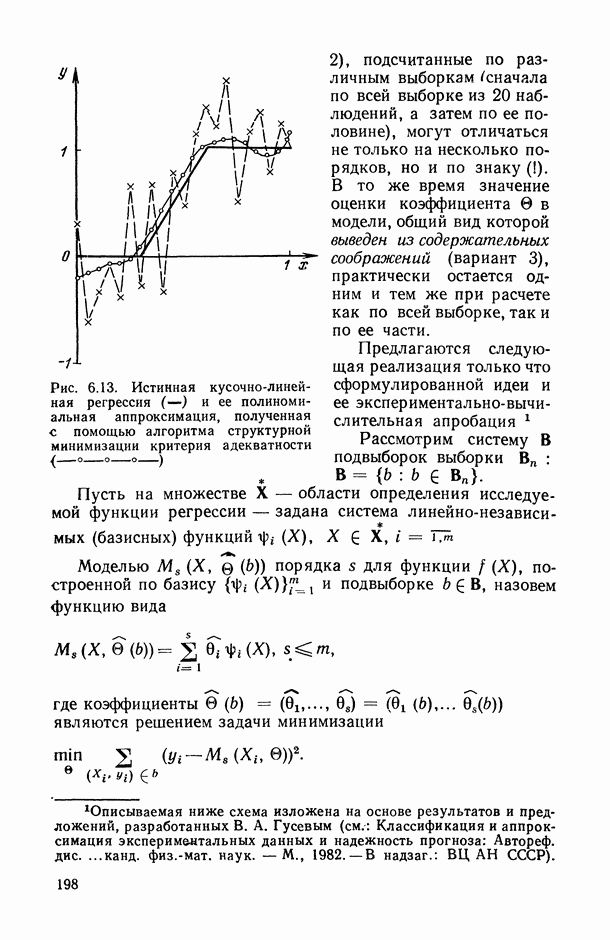
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
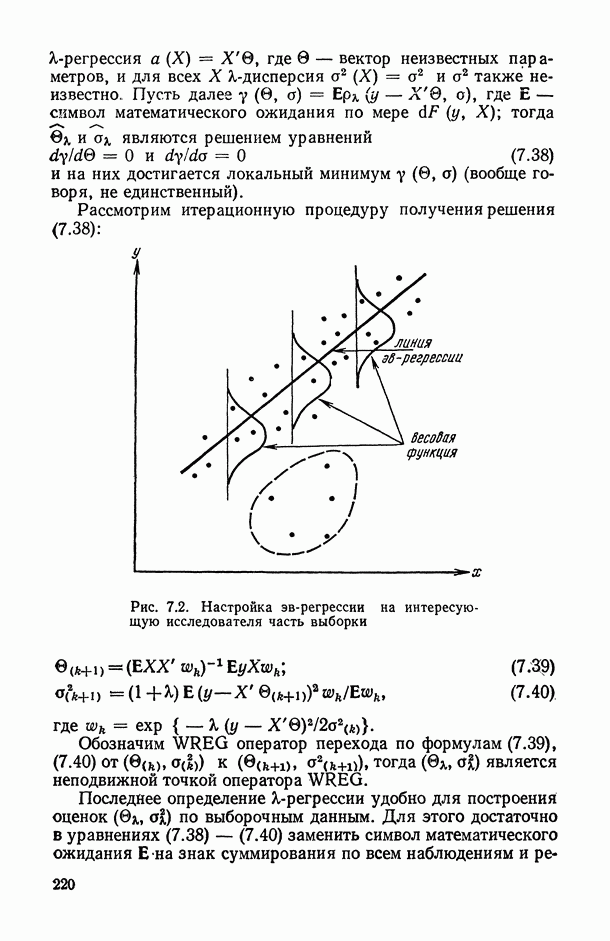
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
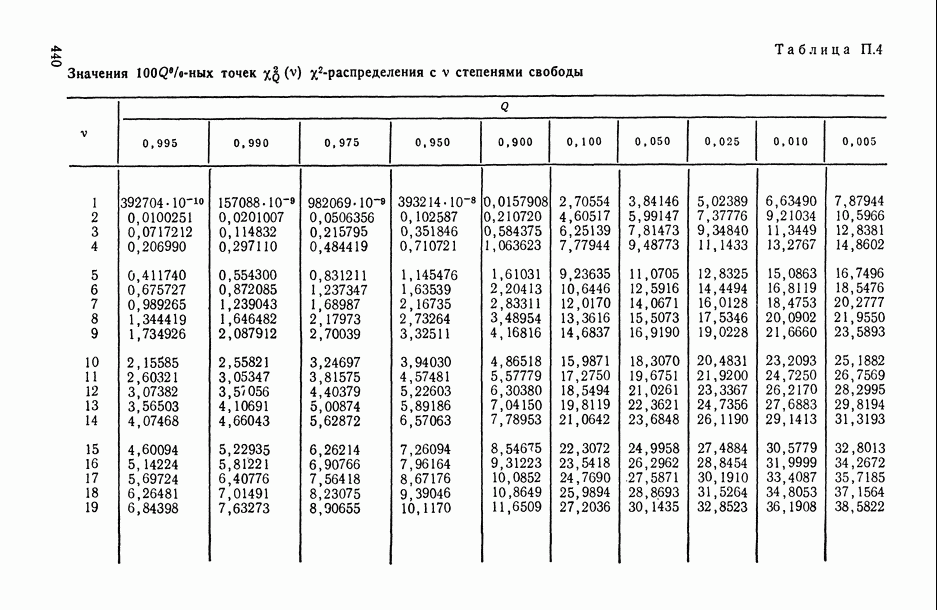
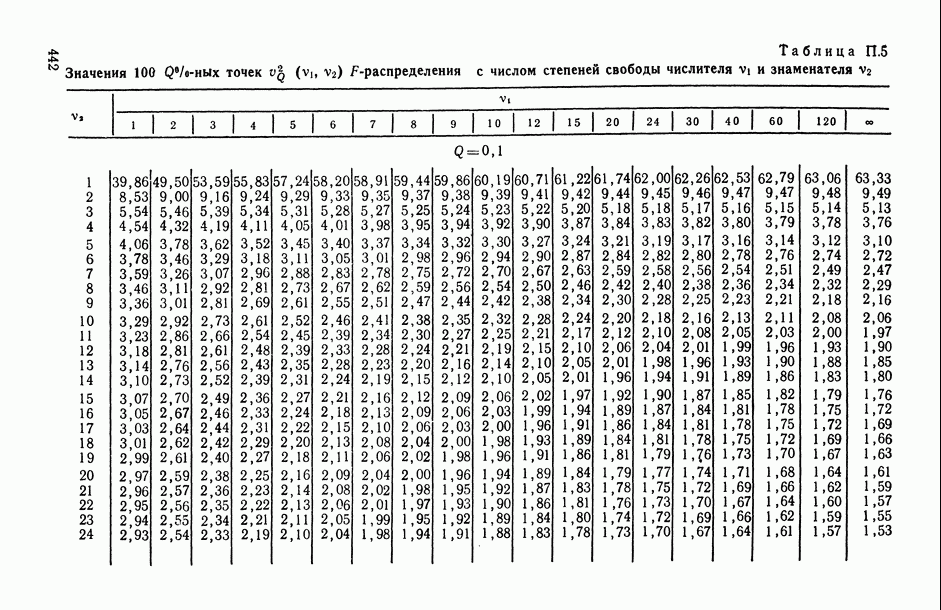
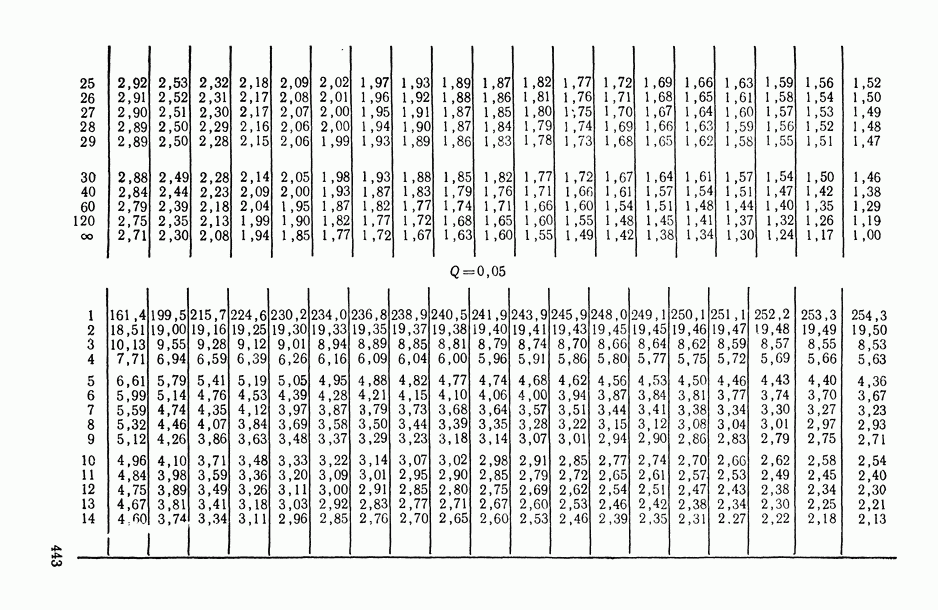
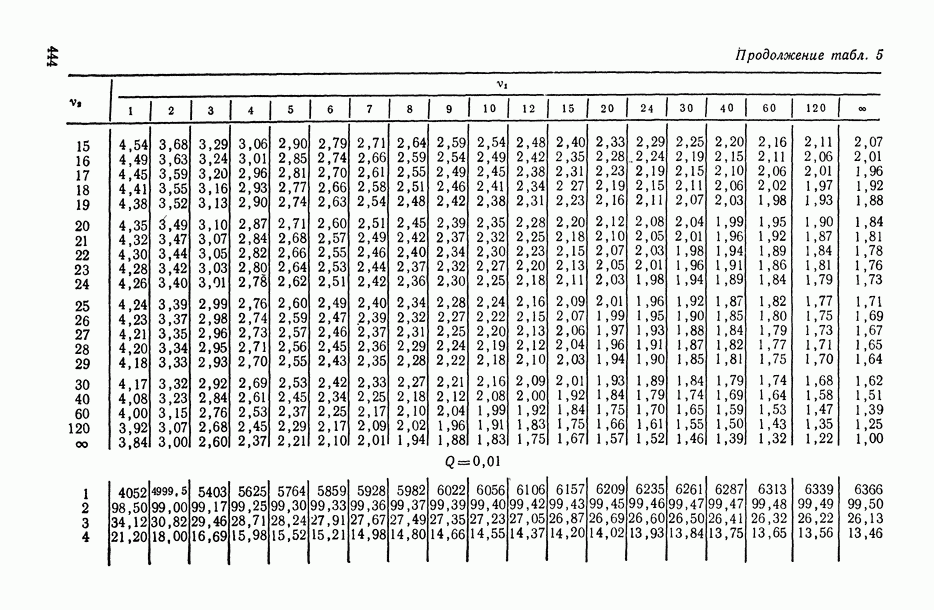
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
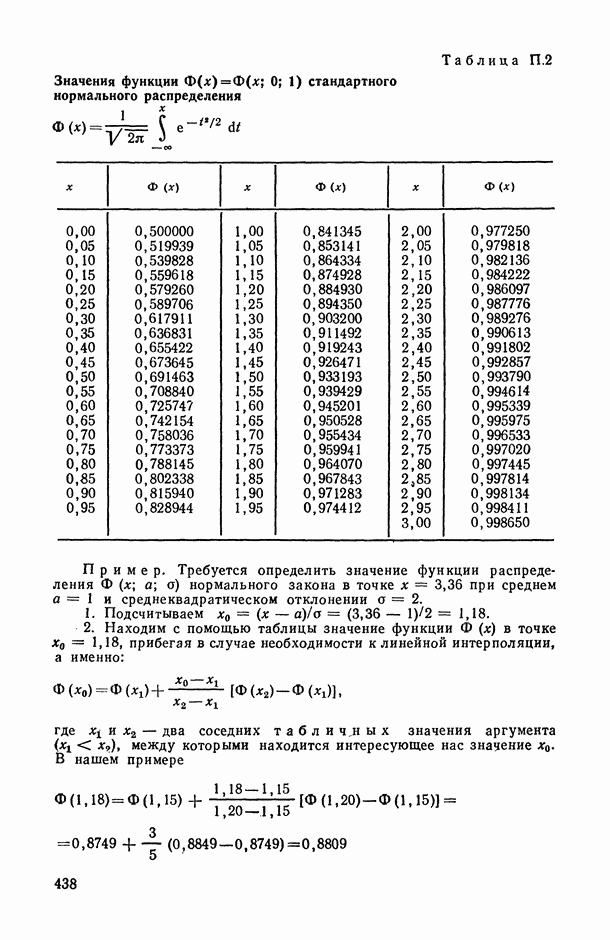
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
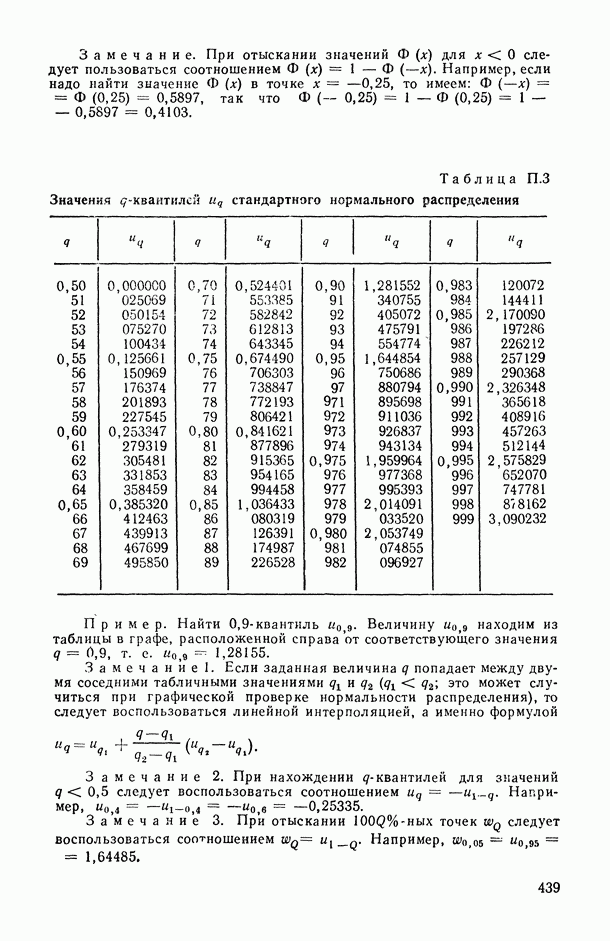
- Таблица П.2. Значения функции стандартного нормального распределения
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ