| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.5. Методы, не использующие вычисления производных
9.5.1. Основные подходы к устранению необходимости вычисления производных.
Как уже отмечалось, существенным недостатком методов, изложенных в предыдущих параграфах, является необходимость подсчета производных  а в методе Ньютона — и вторых производных
а в методе Ньютона — и вторых производных  на каждой итерации. При сложных функциях
на каждой итерации. При сложных функциях  это, во-первых, оказывается утомительным с программистской точки зрения, а во-вторых, приводит к громоздким вычислениям на каждой итерации.
это, во-первых, оказывается утомительным с программистской точки зрения, а во-вторых, приводит к громоздким вычислениям на каждой итерации.
Возможно несколько способов избавления от необходимости подсчета производных:
использование методов прямого поиска (нулевого порядка), таких, как симплекс-метод, метод случайного поиска и т. п. [185], аппроксимация производных конечно-разностными аналогами, специальные методы аппроксимации матриц  позволяющие реализовать итерационные процедуры, близкие по эффективности к процедурам Ньютона и Ньютона—Гаусса, но с меньшим объемом вычислений.
позволяющие реализовать итерационные процедуры, близкие по эффективности к процедурам Ньютона и Ньютона—Гаусса, но с меньшим объемом вычислений.
Прямые методы минимизации оказались малоэффективными для задач регрессионного типа даже по сравнению с градиентными методами [251. К тому же после отыскания с их помощью экстремальных значений В требуется проведение объемистых вычислений по нахождению статистических характеристик, описывающих качество оценок.
Конечно-разностная аппроксимация хотя и избавляет потребителя от утомительной работы по составлению дополнительных программ для вычисления производных, но не решает проблемы сокращения объема вычислений. Чаще всего она приводит к его заметному увеличению.
Наиболее перспективными и удобными оказались методы третьей группы. Они завоевали весьма прочное место во многих статистических пакетах (см., например, [169]).
9.5.2. Разностные аналоги метода Ньютона — Гаусса.
Основная идея, на которую опираются методы третьей группы, за ключается в использовании на (s + 1)-й итерации информации, полученной на предыдущих s итерациях, для построения разумных аппроксимаций элементов матрицы  и компонент градиента
и компонент градиента 
При решении регрессионных задач хорошо зарекомендовали себя методы, являющиеся, по существу, аппроксимациями метода Ньютона—Гаусса. По-видимому, работа [236] является в этом направлении пионерской. Упрощенный и непосредственно приспособленный к задачам регрессии алгоритм предложен в [242], см. также [1691. Достаточно подробный анализ алгоритмов подобного типа и их дальнейшее развитие содержатся в [37, 38]. Данную совокупность методов целесообразно назвать методами Ньютона—Гаусса без подсчета производных. Как и обычный метод Ньютона—Гаусса (см. п. 9.4.2), эти методы опираются на линейную аппроксимацию функций  в окрестности точки
в окрестности точки 

В отличие от метода Ньютона—Гаусса коэффициенты  не совпадают с производными
не совпадают с производными  а подсчитываются по значениям функции
а подсчитываются по значениям функции  полученным по прошлым итерациям. В принципе величины
полученным по прошлым итерациям. В принципе величины  могут быть подсчитаны самыми различными способами, но в программах по регрессионному анализу оказывается очень удобным отыскивать их с помощью все того же мнк. Определим
могут быть подсчитаны самыми различными способами, но в программах по регрессионному анализу оказывается очень удобным отыскивать их с помощью все того же мнк. Определим  как решение задачи мнк:
как решение задачи мнк:

где  веса, описывающие вклад того или иного значения
веса, описывающие вклад того или иного значения  При этом s значений получены непосредственно из итерационной процедуры, а выбор остальных q значений параметров
При этом s значений получены непосредственно из итерационной процедуры, а выбор остальных q значений параметров  будет объяснен позднее. В частности, в алгоритме, предложенном в [242],
будет объяснен позднее. В частности, в алгоритме, предложенном в [242],  , а остальные веса полагаются нулевыми.
, а остальные веса полагаются нулевыми.
Хорошие результаты дает выбор весов вида  где
где  — убывающая функция, например
— убывающая функция, например 
Можно показать, что

где

Подставляя теперь в (9.2) приближенное значение функции  (ср. с § 9.4), получим, что функция
(ср. с § 9.4), получим, что функция  достигает своего минимума при
достигает своего минимума при  , где
, где

После несложных преобразований приходим к очень удобной в вычислительном плане формуле

где 
Итерационная процедура Ньютона—Гаусса, опирающаяся на (9.18), принимает вид

Выбор  осуществляется по одному из правил, принимаемых для процедуры Ньютона—Гаусса с переменным шагом.
осуществляется по одному из правил, принимаемых для процедуры Ньютона—Гаусса с переменным шагом.
Остановимся на некоторых особенностях процедуры (9.19). Ее основное достоинство состоит в том, что на каждом шаге до. статочно всего одного вычисления функции  (естественно при всех
(естественно при всех  . Данное свойство оказывается чрезвычайно полезным при сложных функциях
. Данное свойство оказывается чрезвычайно полезным при сложных функциях  , например, в тех случаях, когда эта функция удовлетворяет некоторому дифференциальному уравнению, допускающему лишь численное решение, для получения которого требуются специальные объемистые вычисления.
, например, в тех случаях, когда эта функция удовлетворяет некоторому дифференциальному уравнению, допускающему лишь численное решение, для получения которого требуются специальные объемистые вычисления.
Процедура (9.19) содержит операцию обращения матрицы, от которой можно было бы избавиться, заменив ее обращением с помощью рекуррентных формул.
Однако, как правило, трудоемкость этой операции несущественна по сравнению с трудоемкостью подсчета значений функций  .
.
В [242] утверждается, что вместо непосредственного обращения матрицы  целесообразно использовать пошаговые процедуры, применяемые при отборе существенных факторов (см. гл. 8). Подобный прием особенно удобен при функциях
целесообразно использовать пошаговые процедуры, применяемые при отборе существенных факторов (см. гл. 8). Подобный прием особенно удобен при функциях  «овражного» типа (матрица
«овражного» типа (матрица  плохо обусловлена).
плохо обусловлена).
Для определения  требуется подсчет функций
требуется подсчет функций  по крайней мере в
по крайней мере в  точке
точке  На последующих итерациях достаточно проведения подсчета функций
На последующих итерациях достаточно проведения подсчета функций  лишь в одной точке
лишь в одной точке  Однако при плохо обусловленных матрицах
Однако при плохо обусловленных матрицах  рекомендуется использовать в (9.17) дополнительные значения функций, подсчитанные в точках
рекомендуется использовать в (9.17) дополнительные значения функций, подсчитанные в точках  . Таким образом, упоминавшееся ранее q равно
. Таким образом, упоминавшееся ранее q равно  Дополнительные точки рекомендуется располагать на направлениях, ортогональных к направлению, определяемому (9.17).
Дополнительные точки рекомендуется располагать на направлениях, ортогональных к направлению, определяемому (9.17).
При линейной параметризации метод Ньютона—Гаусса без подсчета производных дает точное решение задачи мнк на первой итерации, если 
На наш взгляд, выигрыш в объеме вычислений при переходе от итерационной процедуры (9.18) к более сложным процедурам весьма сомнителен ввиду резкого увеличения сложности расчетов на каждой итерации.
9.5.3. Некоторые замечания о выборе длины шага.
Один из главных недостатков изложенного метода состоит в следующем. Как показано ранее, существенным свойством квазиградиентных методов является возможность отыскания такого (может быть, достаточно малого) шага  , в выбранном направлении, который приводит к уменьшению значения минимизируемой функции. Это имеет место всякий раз, когда направление минимизации составляет острый угол с антиградиентом. Выбор же направления в формуле (9.19) не гарантирует нам этого. Поэтому даже при малых
, в выбранном направлении, который приводит к уменьшению значения минимизируемой функции. Это имеет место всякий раз, когда направление минимизации составляет острый угол с антиградиентом. Выбор же направления в формуле (9.19) не гарантирует нам этого. Поэтому даже при малых  мы будем не в состоянии уменьшить значение
мы будем не в состоянии уменьшить значение  . В [242] предлагается попеременно для
. В [242] предлагается попеременно для  пробовать как положительные, так и отрицательные значения. Например, если задаться коэффициентом редукции
пробовать как положительные, так и отрицательные значения. Например, если задаться коэффициентом редукции  , то можно положить
, то можно положить  , где
, где  тогда соответствует первому
тогда соответствует первому  , для которого
, для которого  . Однако и эта процедура иногда может не привести к уменьшению функции, (например, в случае, когда направление минимизации ортогонально градиенту).
. Однако и эта процедура иногда может не привести к уменьшению функции, (например, в случае, когда направление минимизации ортогонально градиенту).
Тогда следующую точку можно искать методом случайного поиска, в окрестности данной 
9.5.4. Разностные аналоги метода Ньютона.
В предыдущем пункте отправной точкой при конструировании итерационных процедур служила доступность. информации лишь о функциях  . Иногда в регрессионных задачах оказывается сравнительно просто подсчитать производные
. Иногда в регрессионных задачах оказывается сравнительно просто подсчитать производные  Подчеркнем, что речь идет о непосредственном подсчете величины
Подчеркнем, что речь идет о непосредственном подсчете величины  а не их разностных аналогов, которые требуют, по крайней мере
а не их разностных аналогов, которые требуют, по крайней мере  вычисления функций
вычисления функций  Обращение к разностным формулам для вычисления делает применение изложенной ниже группы методов бессмысленным. Каждый шаг, ими определяемый, будет по трудоемкости близок к нескольким шагам из итерационных процедур, рассмотренных в п. 9.4.1 и 9.5.2.
Обращение к разностным формулам для вычисления делает применение изложенной ниже группы методов бессмысленным. Каждый шаг, ими определяемый, будет по трудоемкости близок к нескольким шагам из итерационных процедур, рассмотренных в п. 9.4.1 и 9.5.2.
По-видимому, наиболее известным из рассматриваемой группы методов является метод Дэвидона—Флетчера—Пауэлла. Идея, лежащая в основе данных методов, состоит в отыскании на каждом шаге направлений спуска, близких к направлению метода Ньютона, но без использования матрицы вторых производных.
Матрица  аппроксимирующая матрицу
аппроксимирующая матрицу  . из метода Ньютона, может быть, например, выбрана как решение системы
. из метода Ньютона, может быть, например, выбрана как решение системы

где Н — симметричная матрица.
Решение системы (9.20) при  неоднозначно, поэтому возможны различные способы конструирования матрицы Н Различные методы рассматриваемой группы отличаются способами конструирования этой матрицы и правилами выбора направлений
неоднозначно, поэтому возможны различные способы конструирования матрицы Н Различные методы рассматриваемой группы отличаются способами конструирования этой матрицы и правилами выбора направлений  , если они не определены однозначно. Матрица
, если они не определены однозначно. Матрица  должна удовлетворять одновременно уравнениям (9.20) при всех
должна удовлетворять одновременно уравнениям (9.20) при всех 
Приведем способы конструирования матриц  для некоторых наиболее распространенных методов (см. [108, 115, 240, 211]):
для некоторых наиболее распространенных методов (см. [108, 115, 240, 211]):
а) метод сопряженных градиентов:

где  матрицу
матрицу  часто выбирают единичной или диагональной с элементами
часто выбирают единичной или диагональной с элементами 
б) метод Дэвидона—Флетчера—Пауэлла:

в) измененный вариант метода Дэвидона—Флетчера—Пауэлла:

При квадратичной функции  (в нашем случае — линейной параметризации) после
(в нашем случае — линейной параметризации) после  шагов матрица Н, подсчитываемая любым из методов а)-в), в точности совпадает с матрицей
шагов матрица Н, подсчитываемая любым из методов а)-в), в точности совпадает с матрицей  определенной в п. 9.3. Иными словами, при
определенной в п. 9.3. Иными словами, при  в этом случае точное решение исходной экстремальной задачи будет заведомо получено за
в этом случае точное решение исходной экстремальной задачи будет заведомо получено за  шагов. Если
шагов. Если  выбирается из условия наискорейшего спуска в направлении
выбирается из условия наискорейшего спуска в направлении  , то при выполнении не слишком ограничительных условий последовательность
, то при выполнении не слишком ограничительных условий последовательность  сходится при
сходится при  к
к  со сверхлинейной скоростью независимо от выбора
со сверхлинейной скоростью независимо от выбора 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
- В.3. Математический инструментарий
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
- 2.3. Анализ множественных ранговых связей
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
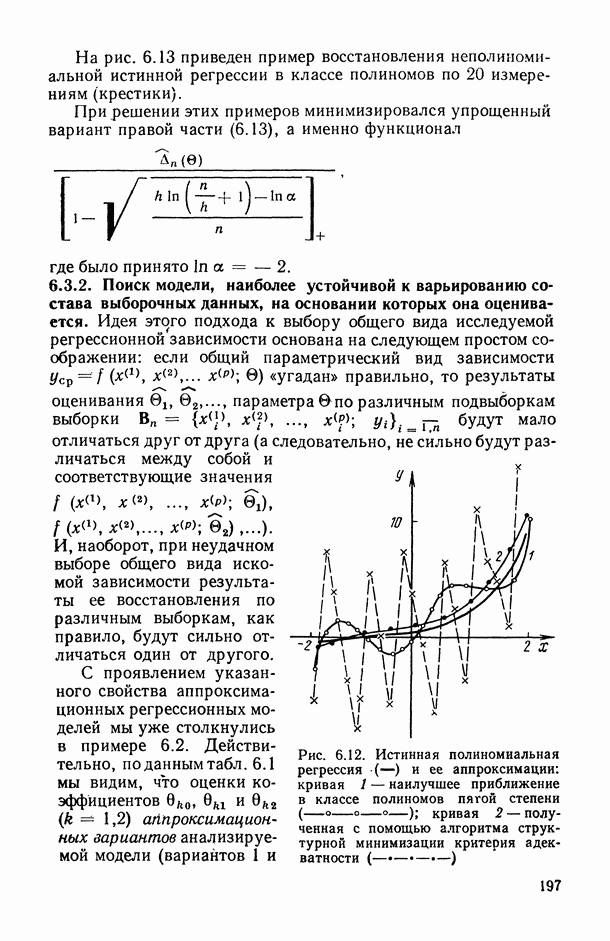
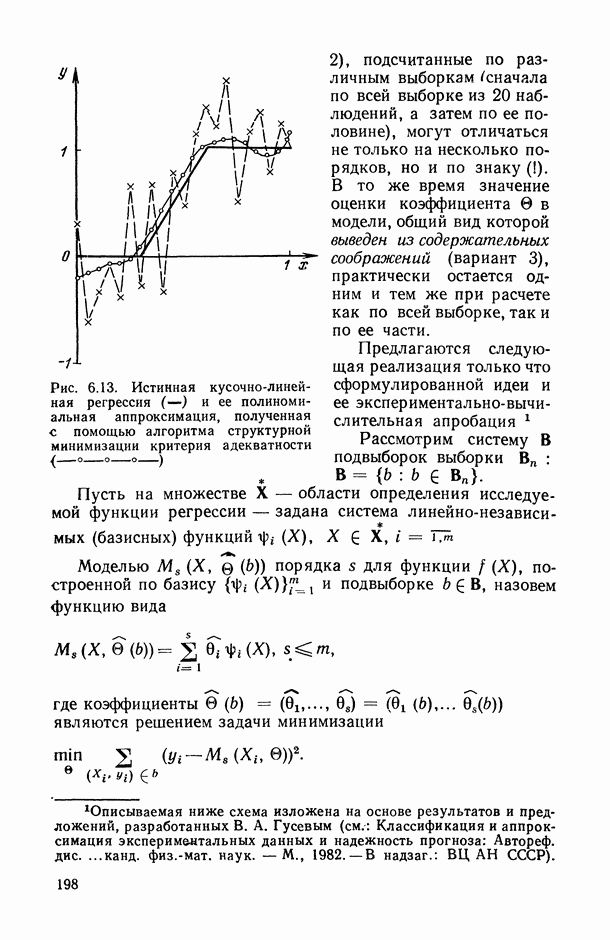
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
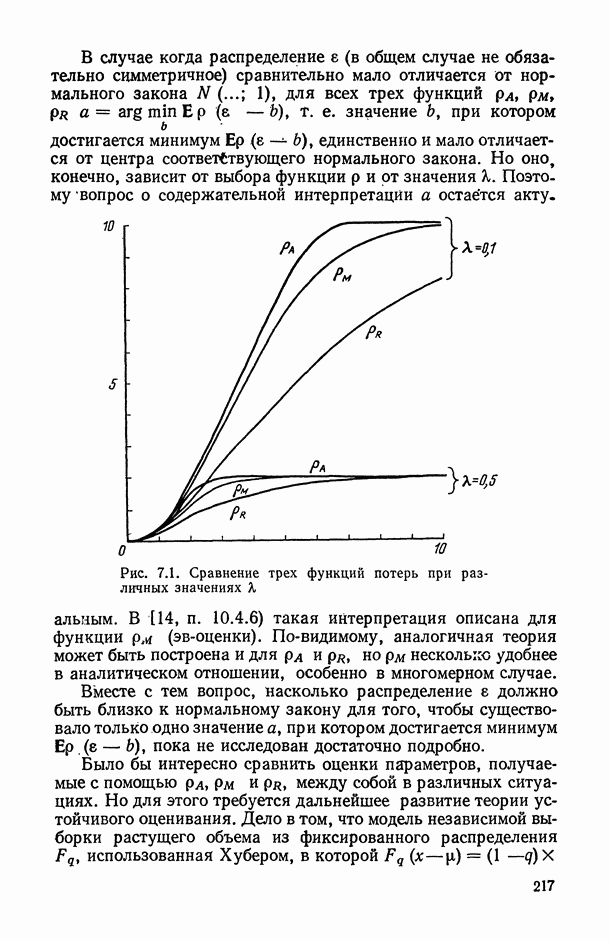
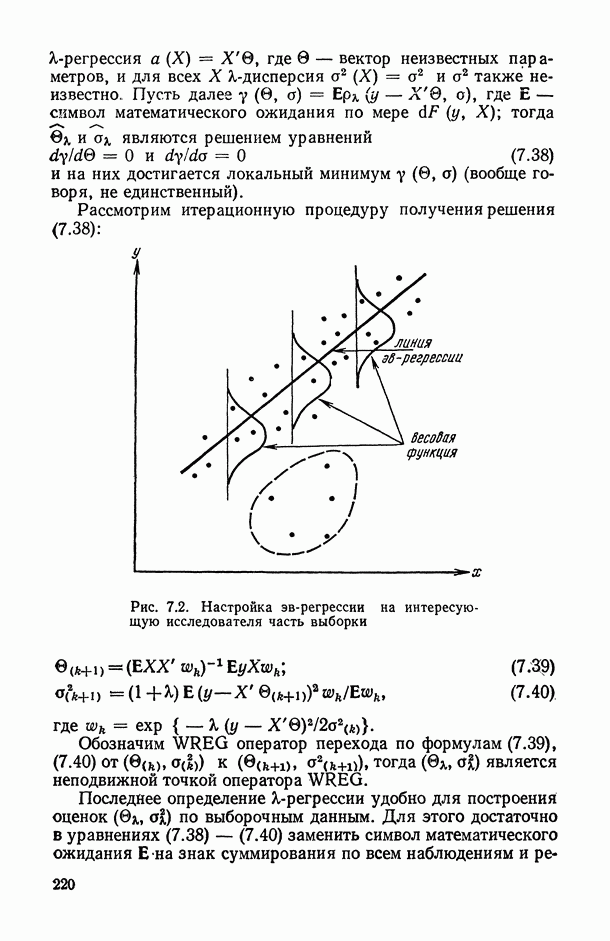
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
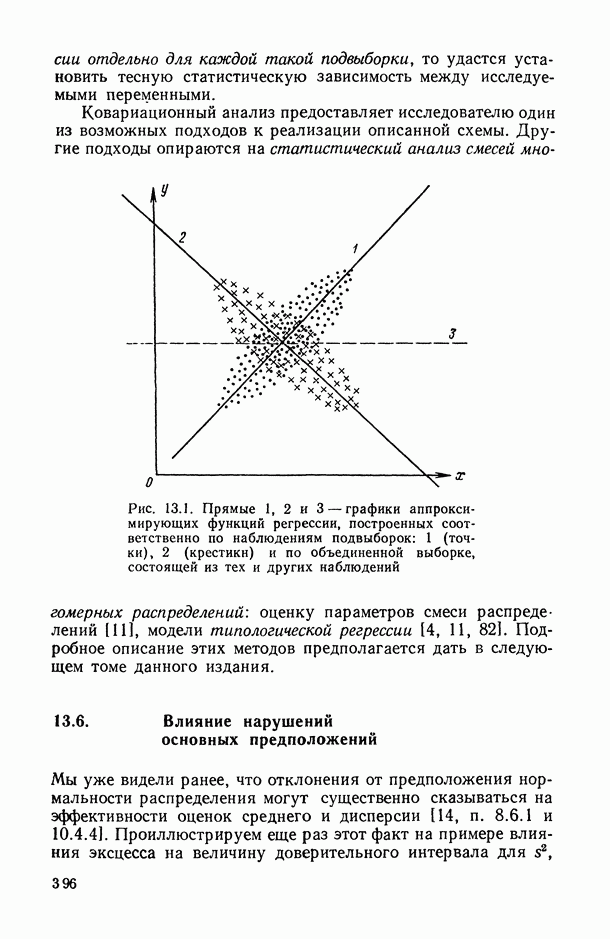
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
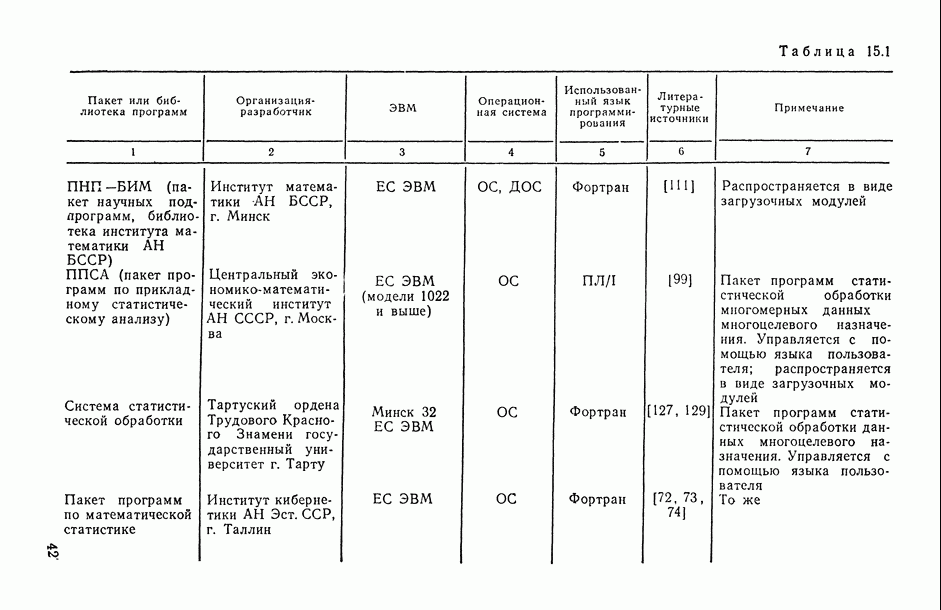
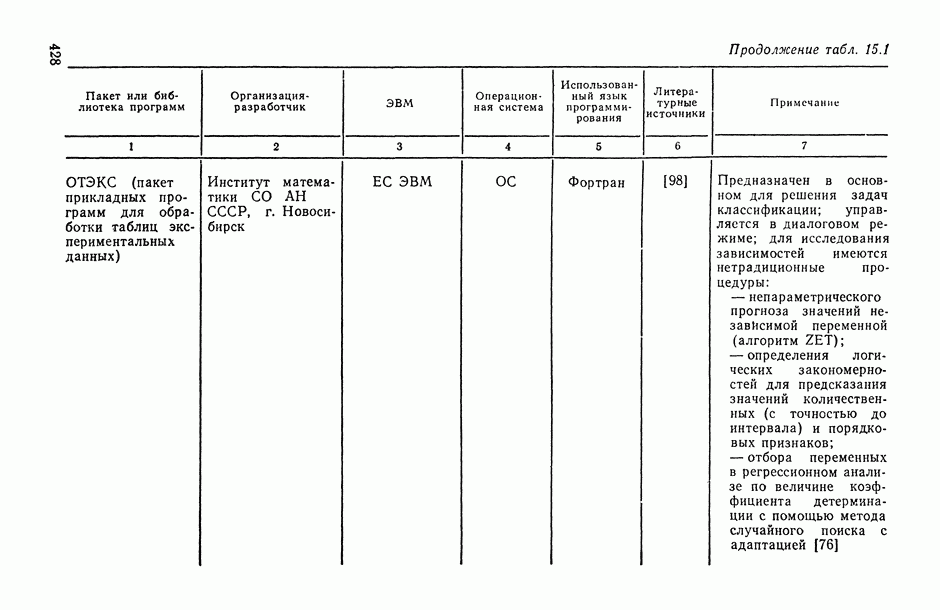
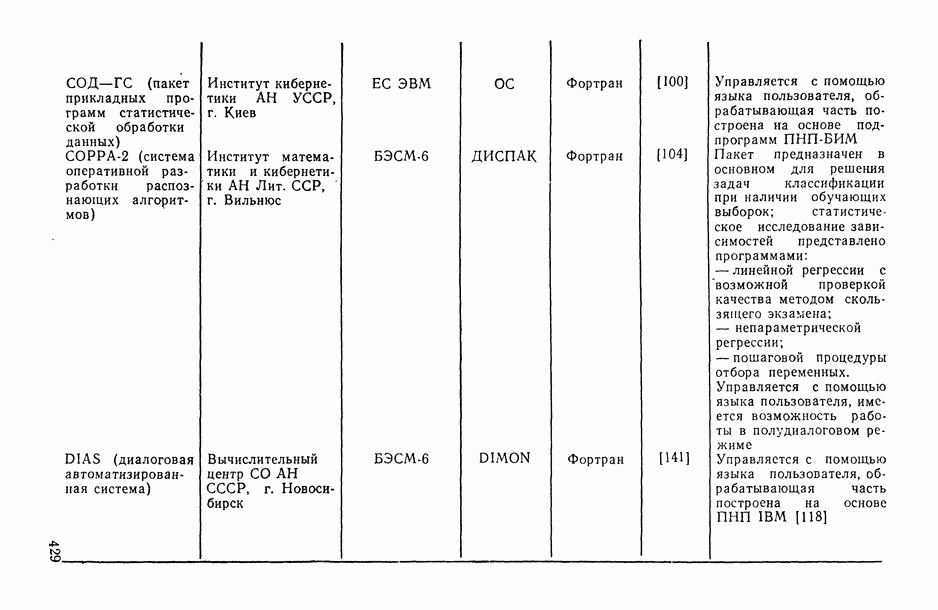
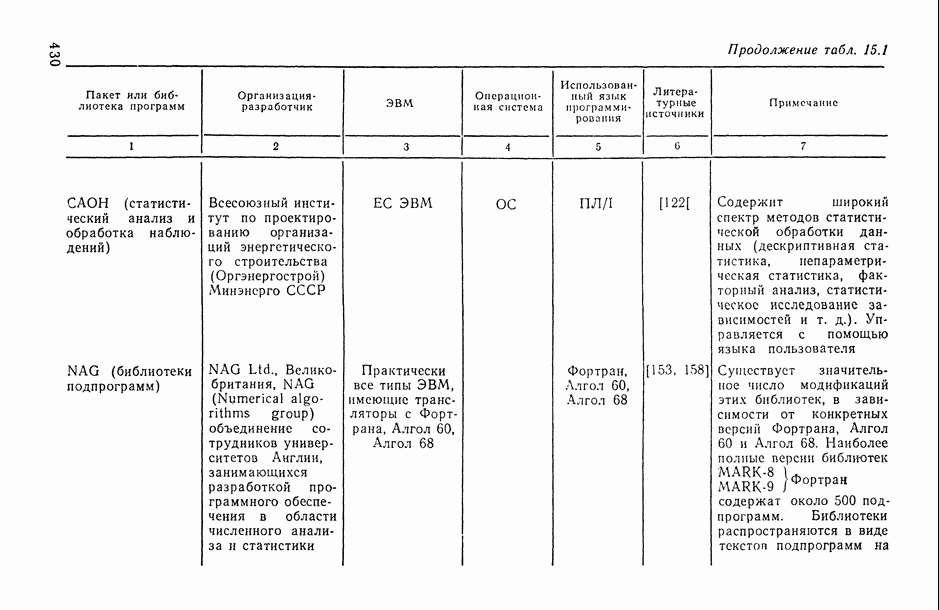
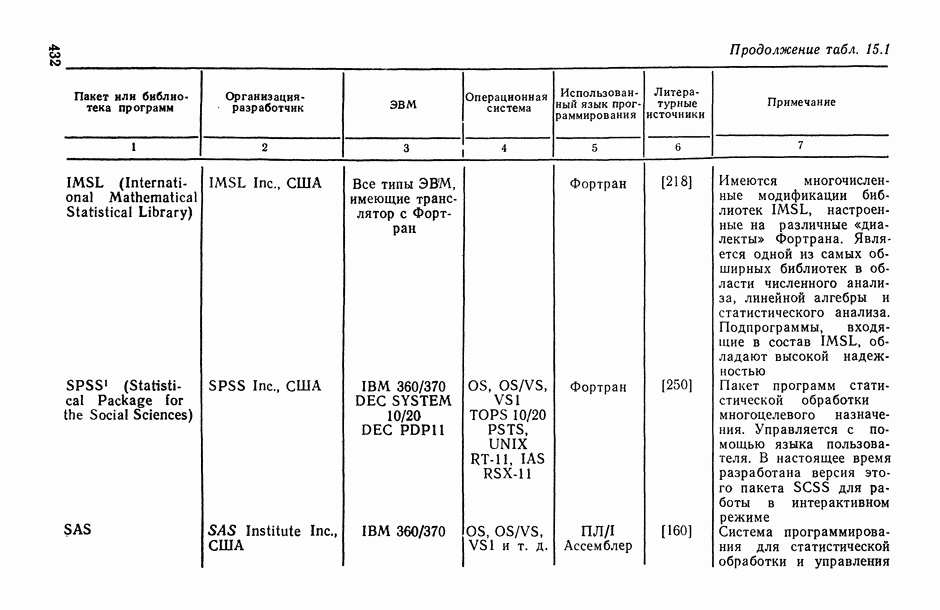
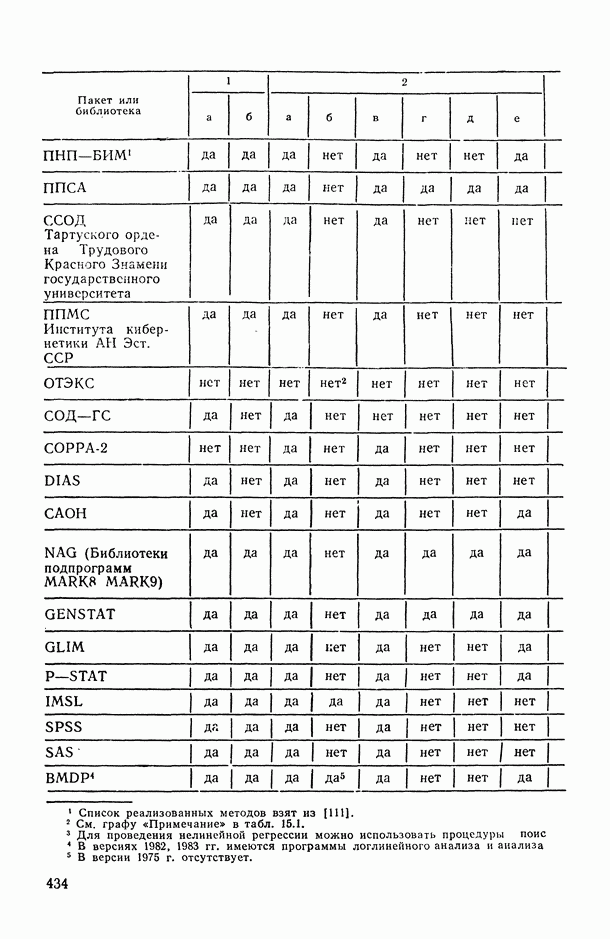
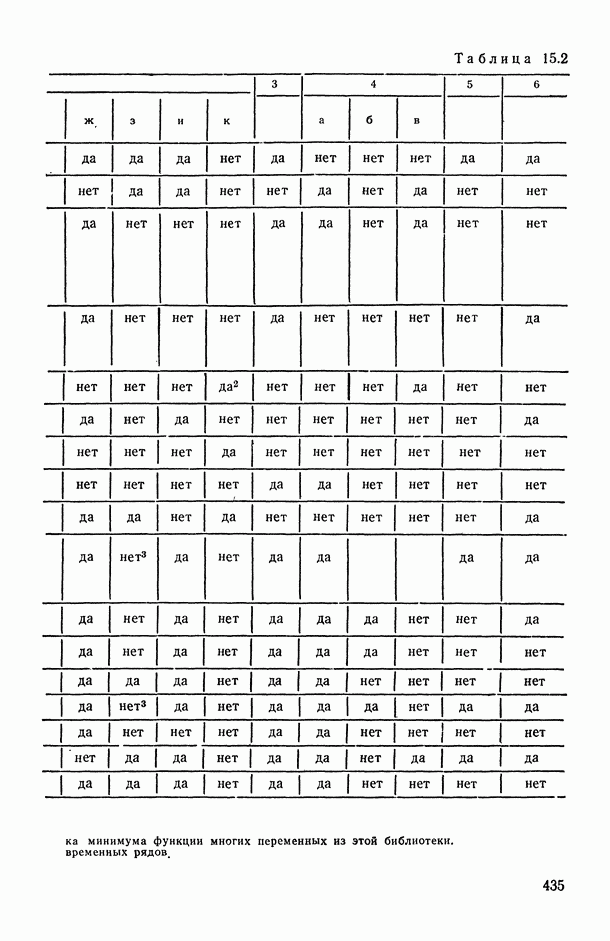
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
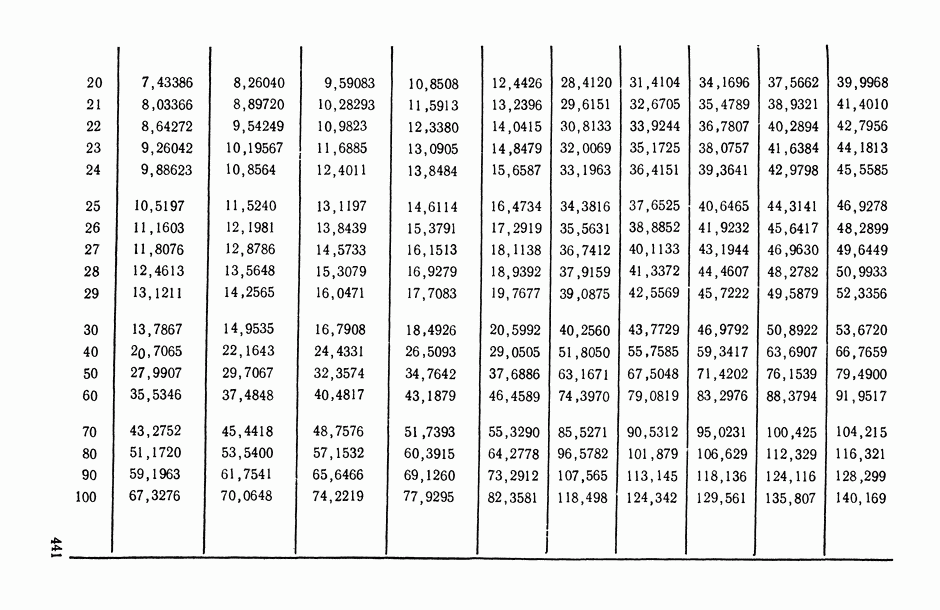
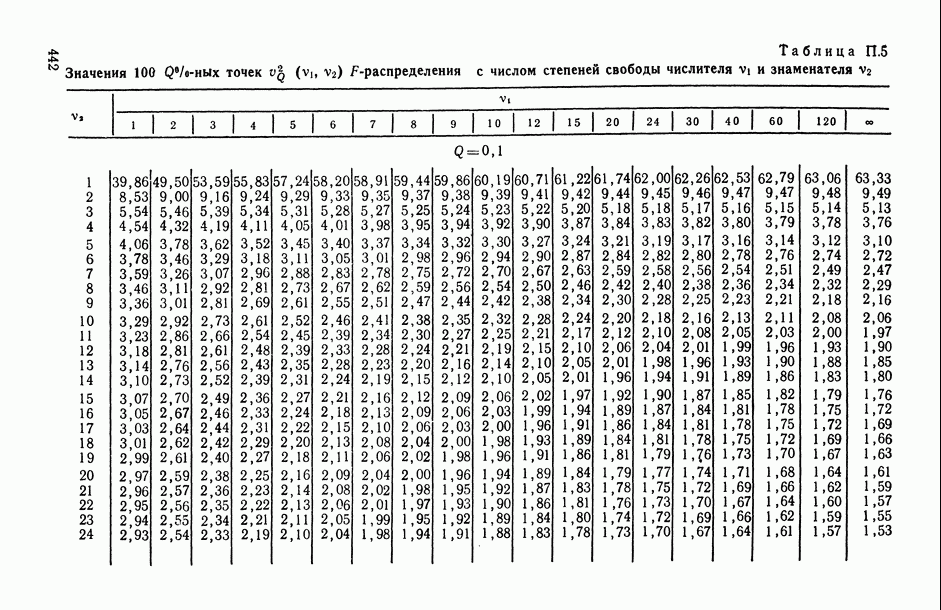
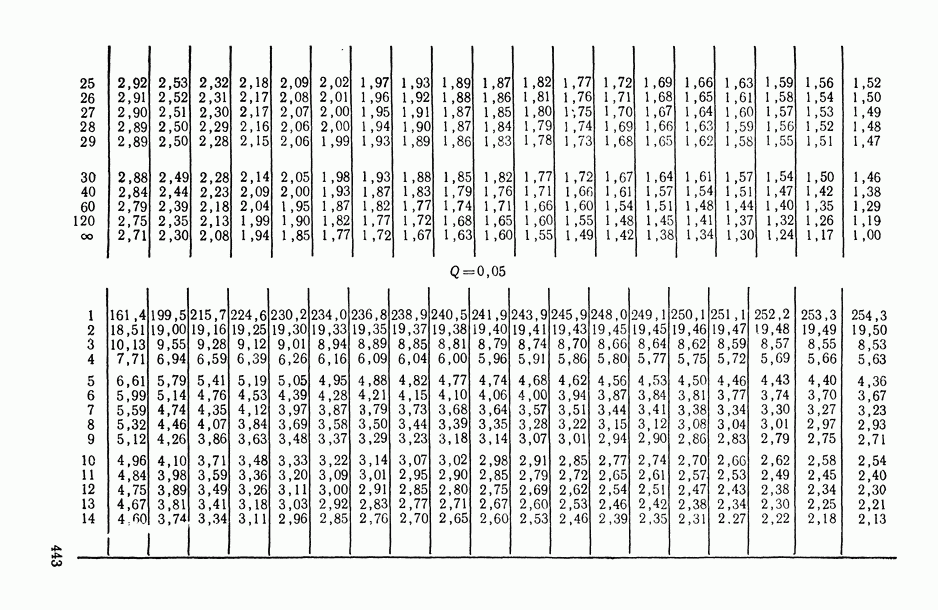
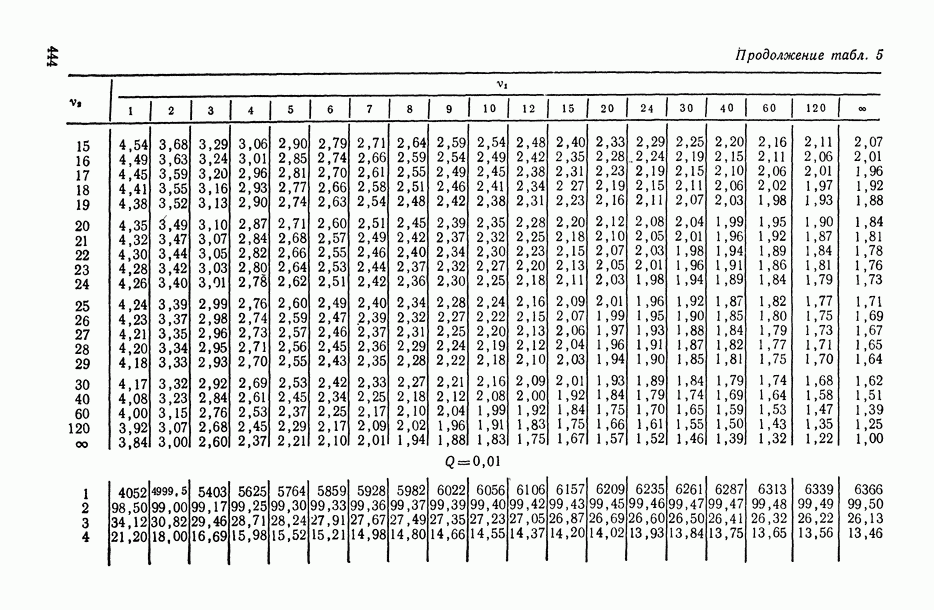
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
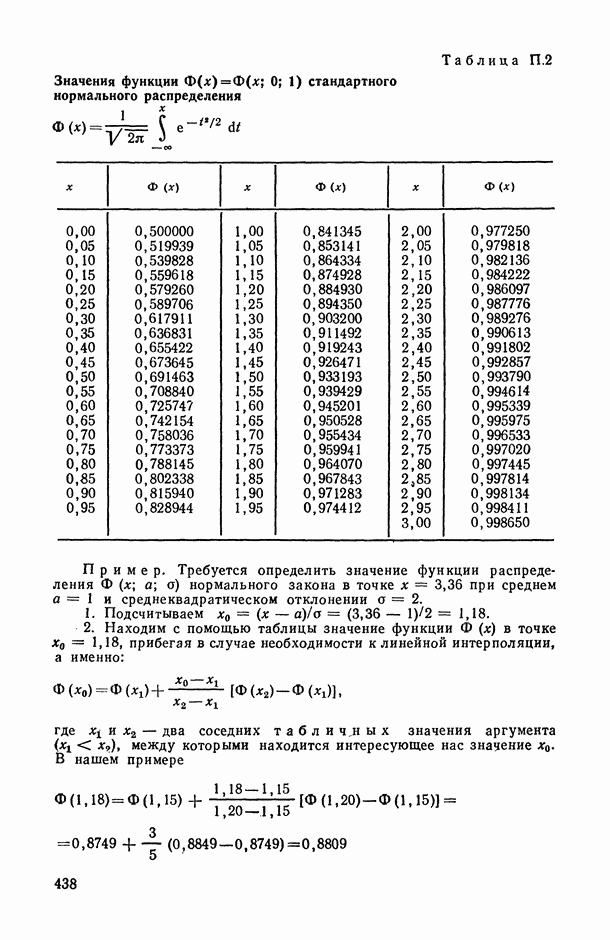
- Таблица П.2. Значения функции стандартного нормального распределения
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ