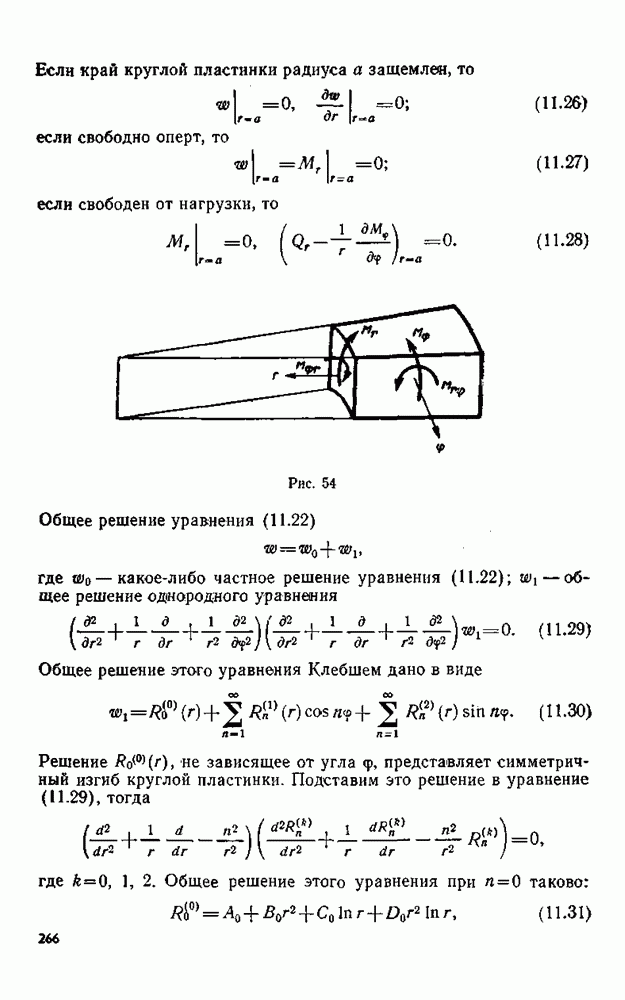
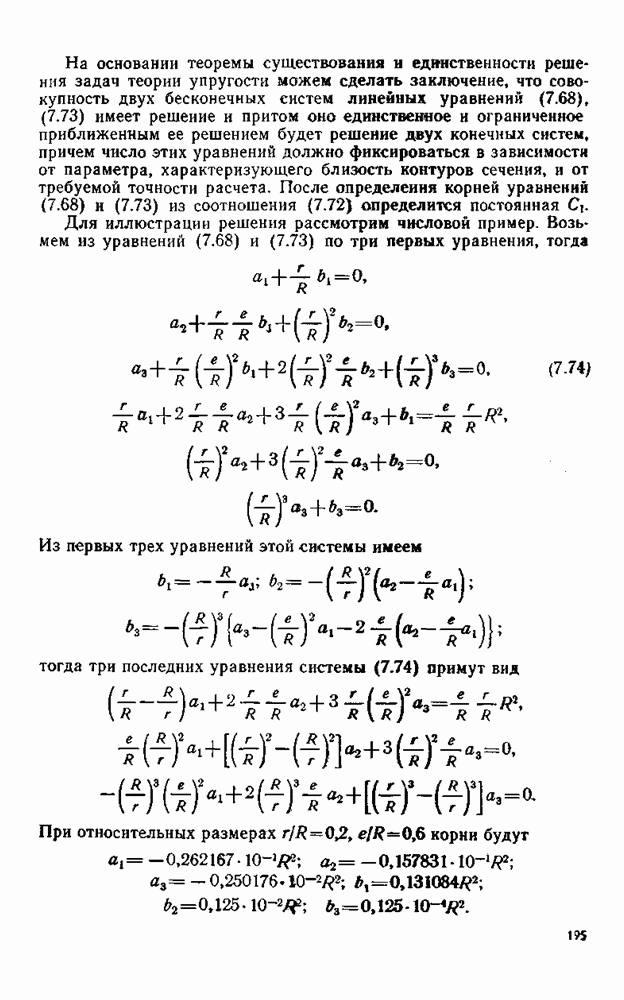| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 9. Тензор напряжений
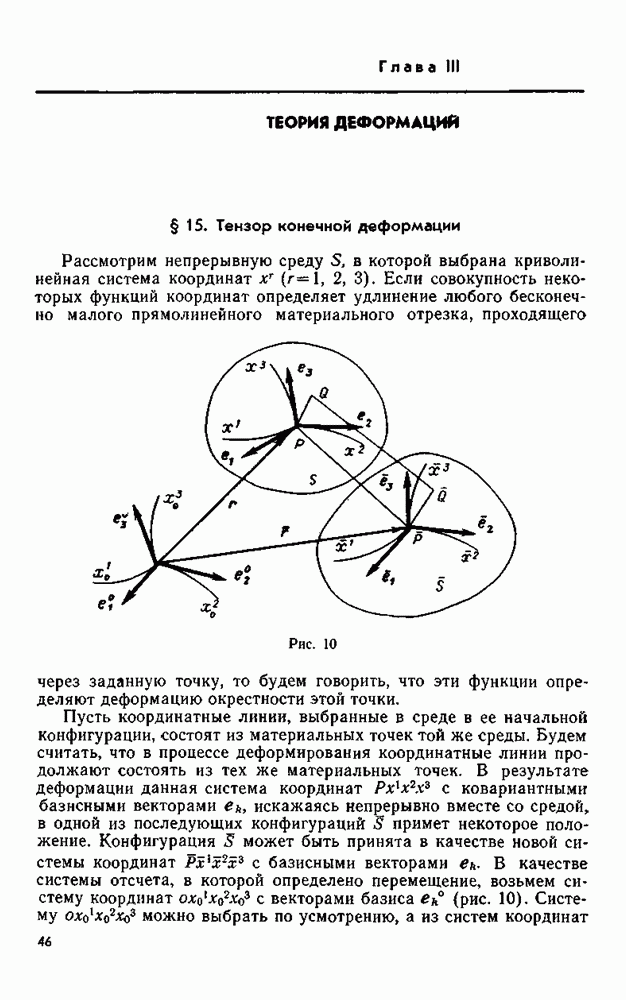
Выберем в теле некоторую точку  и проведем через нее координатные линии произвольной криволинейной системы координат
и проведем через нее координатные линии произвольной криволинейной системы координат 
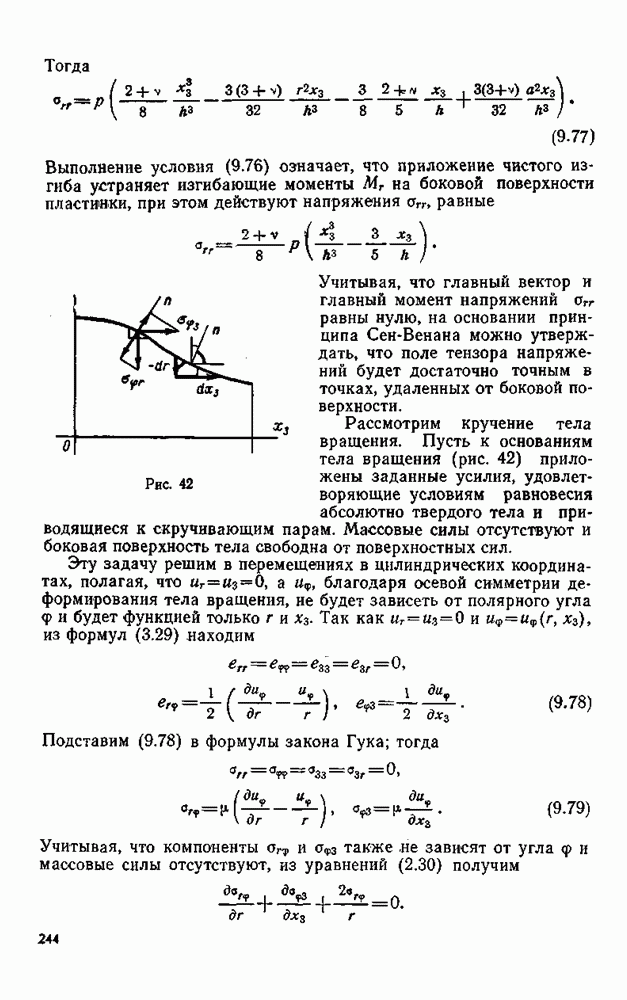
Рассмотрим в точке  тетраэдр, мысленно выделенный из недеформированного тела тремя координатными поверхностями, определяемыми ковариантными базисными векторами и поверхностью, внешней нормалью к которой служит некоторое направление
тетраэдр, мысленно выделенный из недеформированного тела тремя координатными поверхностями, определяемыми ковариантными базисными векторами и поверхностью, внешней нормалью к которой служит некоторое направление  — единичный вектор), проходящее через ту же точку
— единичный вектор), проходящее через ту же точку  (рис. 6).
(рис. 6).
Рассмотрим движение тетраэдра. Обозначим через  соответственно площади поверхностей
соответственно площади поверхностей  и
и  .
.

Рис. 5

Рис. 6
На указанных поверхностях, нормалями которых служат соответственно векторы взаимного базиса  и единичная нормаль
и единичная нормаль  , действуют
, действуют  где
где  векторы напряжения в координатных площадках с нормалями
векторы напряжения в координатных площадках с нормалями  Кроме того, массовая сила выделенного элемента равна
Кроме того, массовая сила выделенного элемента равна  (здесь
(здесь  ускорение;
ускорение;  плотность материала недеформированной среды).
плотность материала недеформированной среды).
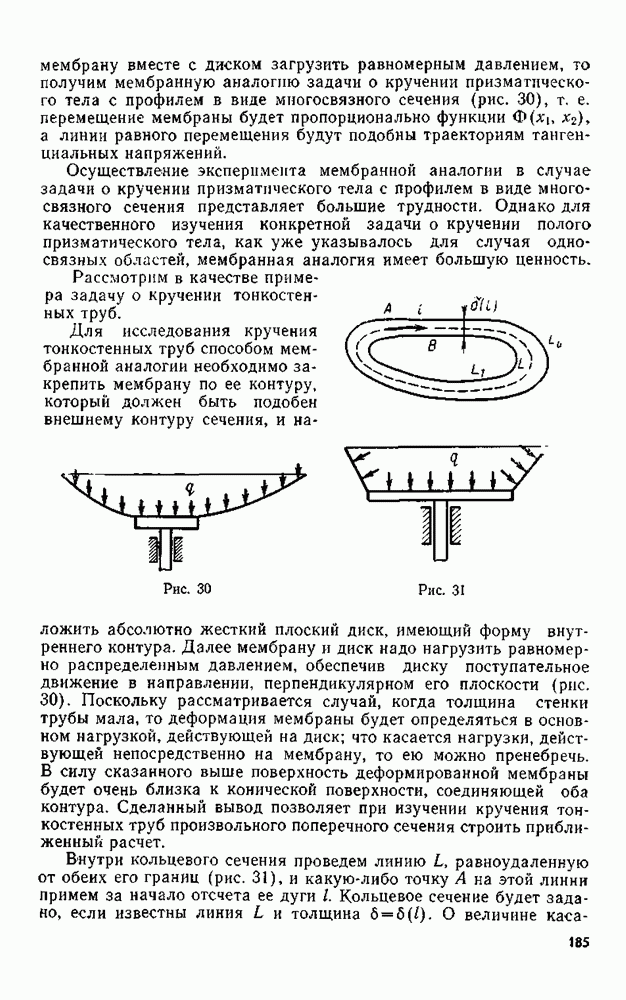
На основании принципа отвердевания и начала Даламбера уравнение движения тетраэдра будет иметь вид

Здесь во втором слагаемом суммирование ведется по индексу  от 1 до 3. Поскольку для тетраэдра сумма векторов площадей равна нулю, то
от 1 до 3. Поскольку для тетраэдра сумма векторов площадей равна нулю, то

Учитывая, что  ковариантные компоненты единичного вектора), вместо (2.10) будем иметь
ковариантные компоненты единичного вектора), вместо (2.10) будем иметь

откуда

Подставим это в (2.9), тогда

Пусть при постоянном направлении  расстояние от точки
расстояние от точки  до поверхности
до поверхности  стремится к нулю. Принимая во внимание, что
стремится к нулю. Принимая во внимание, что  из последнего уравнения найдем
из последнего уравнения найдем

Вектор напряжения  может быть представлен тремя составляющими по отношению к векторам ковариантного базиса
может быть представлен тремя составляющими по отношению к векторам ковариантного базиса  т. е.
т. е.

Подставляя (2.12) в (2.11), получим

Учитывая, что  где
где  контравариантные компоненты вектора напряжения, найдем
контравариантные компоненты вектора напряжения, найдем

В (2.13) двойное суммирование ведется по индексам  а в (2.14) — одинарное суммирование по индексу
а в (2.14) — одинарное суммирование по индексу 
Формула (2.14) определяет контравариантные компоненты вектора напряжения на площадке, заданной нормалью  поэтому на основании теоремы о признаке тензора заключаем, что величины
поэтому на основании теоремы о признаке тензора заключаем, что величины  составляют контравариантные компоненты тензора второго ранга. Тензор называется контравариантным тензором напряжений.
составляют контравариантные компоненты тензора второго ранга. Тензор называется контравариантным тензором напряжений.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
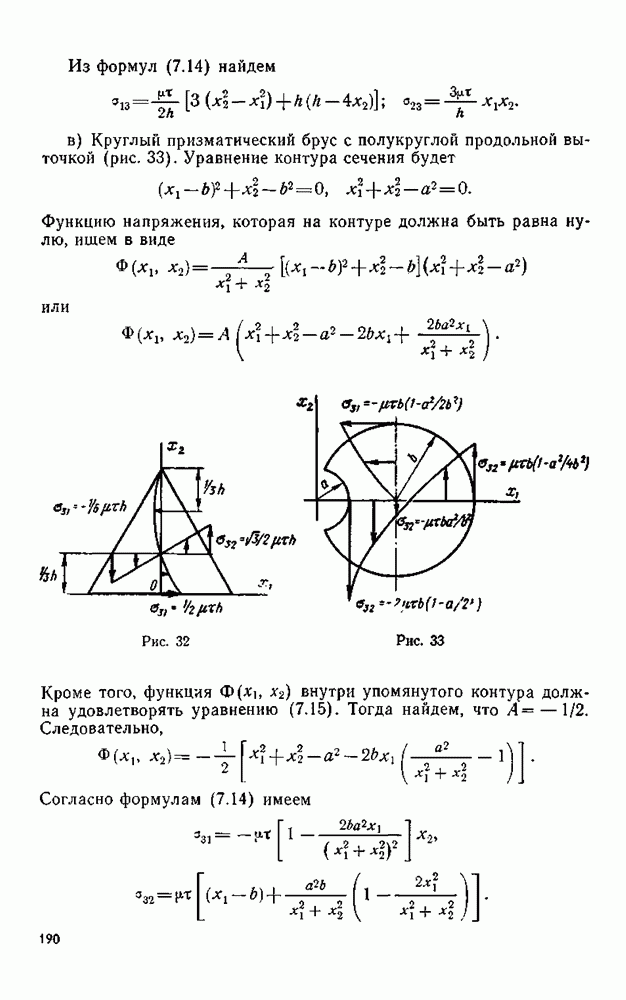
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
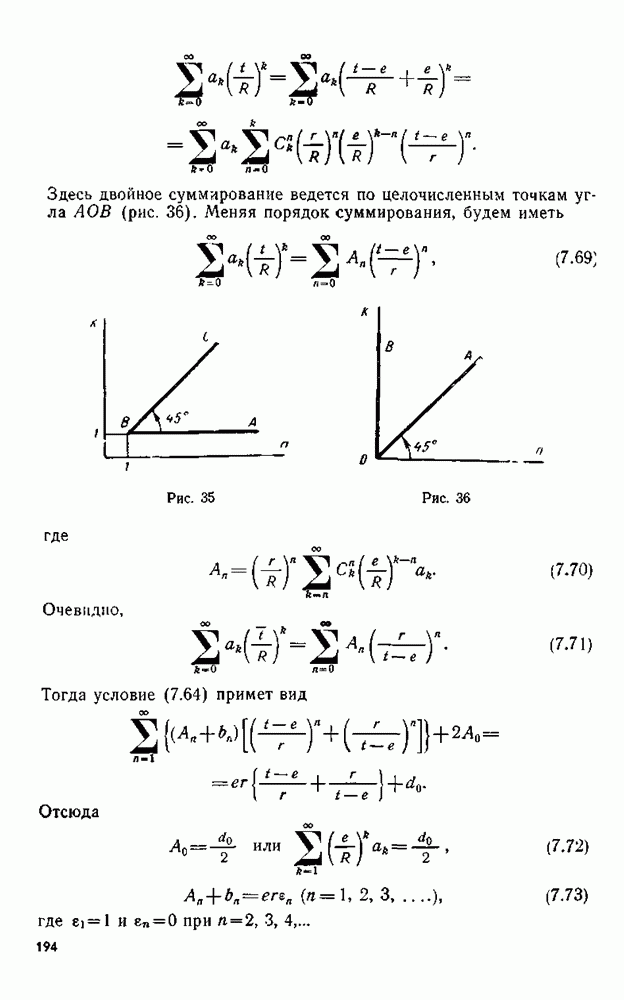
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки