Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН

§ 81. Две типа волн

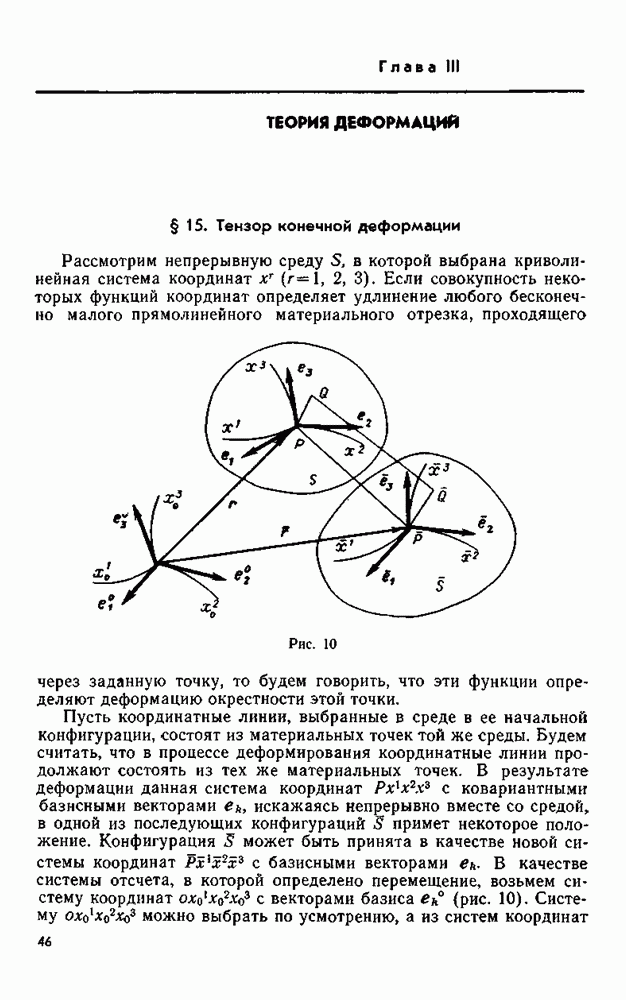
Пуассоном впервые доказано существование в однородной изотропной среде двух типов волн; один из типов волн носит название волн сжатия — разрежения, другой — волн сдвига. Им было показано, что они характеризуются различными скоростями распространения фронта, а также тем, что в волнах сжатия — разрежения отсутствует вращение частиц, а сдвиговые волны не сопровождаются изменением объема.

Перейдем к доказательству существования двух типов волн. Будем рассматривать безграничную среду. Представим массовые силы действующие на эту среду, и поле перемещений и в виде

Здесь — скалярные функции координат и времени векторные функции координат и времени

Из (10.2) следует

Подставляя в уравнения движения упругой среды (5.5) выражения (10.1), (10.2), учитывая (10.3) и изменяя порядок дифференциальных операторов, получим

Здесь обозначено

Легко видеть, что (10.4) будет удовлетворено, если положить

Таким образом, доказано, что векторное поле и, определяемое (10.2), является решением уравнения (5.5), если функции

удовлетворяют (10.6) и функция называется продольным потенциалом, поперечным потенциалом.

Возникает вопрос, есть ли у этих уравнений решения, которые нельзя представить в указанном нами виде. Можно показать, что таких решений нет. Отметим некоторые важные следствия.

а. Пусть а начальные условия таковы, что при Тогда для определения получается однородное уравнение (10.7) с нулевыми начальными условиями. Это означает, что всегда; из уравнения (10.2) следует тогда, что

Это показывает, что в волне, описываемой функцией не происходит вращение частиц среды, т. е. каждая из них движется поступательно. Поэтому такие волны называются продольными. Следует подчеркнуть еще раз, что если и в некоторый момент волновое поле имеет продольный характер, то оно остается продольным всегда, т. е. продолыные волны в изотропной однородной и безграничной среде при своем распространении не генерируют поперечных.

Уравнение (10.6), описывающее продольные волны, является неоднородным волновым уравнением. Известно, что если функция и начальные условия в конечной части пространства отличны от нуля, то поверхность, отделяющая возмущенную область от невозмущенной (фронт волны), распространяется в направлении своей нормали в сторону невозмущенной области со скоростью

Пусть теперь а начальные условия таковы, что при Тогда . В таком поле объемное расширение равно нулю. Действительно,

Волны, обладающие таким свойством, называются поперечными или волнами сдвига. Поперечные волны, распространяясь в безграничной среде, не генерируют продольных волн. Скорость распространения фронта поперечных волн равна

В однородной среде с границей продольные и поперечные волны распространяются независимо лишь до того момента, пока фронт не пересечет границу. Тогда образуются так называемые отраженные волны обоих типов, так как обычно системе граничных условий нельзя удовлетворить, введя отраженную волну какого-либо одного типа.

Рассмотрим несколько примеров.

1. Плоская продольная волна. Пусть массовые силы отсутствуют, поперечный потенциал тождественно равен нулю, а продольный потенциал зависит только от Тогда уравнение (10,6) превращается в уравнение колебаний струны

и имеет решение вида

где произвольные, дважды дифференцируемые функции.

Первое слагаемое в (10.8) представляет волну постоянной формы, распространяющуюся со скоростью в положительном направлении оси а второе — волну постоянной формы, распространяющуюся в противоположном направлении.

Перемещение, соответствующее решению (10.8), на основе (10.2) будет

Выражение (10.9) показывает, что на каждой плоскости, перпендикулярной к оси при фиксированном при переходе от точки к точке волновое поле не меняется и параллельно оси Если направление распространения плоской волны не совпадает с осью то поле перемещений будет описываться более сложными формулами, хотя физическая картина останется той же. Выведем соответствующие формулы.

Пусть направление распространения плоских продольных волн составляет с координатными осями углы, косинусы которых есть Обозначим через расстояние, отсчитываемое вдоль прямой, параллельной направлению Для простоты рассмотрим волну, распространяющуюся в одном направлении. Подставляя вместо его выражение , получим

Из (10.2) для компонентов вектора перемещения получим

2. Сферическая продольная волна. Рассмотрим случай, когда продольный потенциал в сферической системе координат зависит лишь от радиуса и времени Поперечный потенциал вновь тождественно равен нулю. Массовые силы не действуют.

В этом случае в сферических координатах уравнение (10.6) принимает вид

или

Решение этого уравнения будет

отсюда

Первое слагаемое (10.10) представляет волну, расходящуюся от центра, а второе — волну, сходящуюся к центру.

Рассмотрим волну, расходящуюся от центра. Поскольку продольный потенциал зависит лишь от то в сферических координатах отличной от нуля проекцией вектора будет

Выражение (10.11) указывает, что перемещение направлено строго по радиусу и не меняется при переходе от точки к точке, если они лежат на одной и той же сфере (при фиксированном времени).

Важно подчеркнуть, что при стремящемся к нулю, стремится к бесконечности, это же происходит с деформациями и напряжениями. Вообще говоря, уравнения Ляме не годятся для описания среды, испытывающей большие деформации. Но формально эти уравнения такие решения допускают и они пригодны и удобны для описания реальных процессов, когда ограничено снизу. Пусть, например, упругая волна вызвана равномерным давлением, приложенным к поверхности сферической полости радиуса Тогда формула (10.11) описывает решение в области и особенность при оказывается вне области, в которой ищется решение. В этом примере функция фигурирующая в формуле легко определяется по заданному на полости давлению

Итак, решение (10.11) имеет особенность при Такая особенность называется центром расширения. Отметим, что в отличие от плоской волны, которая при распространении не меняет своей формы, сферическая волна свою форму меняет. В самом деле, коэффициенты — и — в формуле (10.11) показывают, что амплитуды волны с изменением меняются.

3. Плоская поперечная волна. Пусть снова массовые силы отсутствуют; продольный потенциал а поперечный потенциал имеет лишь один отличный от нуля компонент который зависит только от Тогда из (10.7) получаем

Отсюда

Для простоты будем рассматривать только волну, распространяющуюся в положительном направлении оси Для проекций вектора перемещения получим формулы

Здесь направление оси направление распространеиия волны. Однако, в отличие от плоской продольной волны, скорость ее распространения равна а направление перемещения ее совпадает с направлением распространения волны, а перпендикулярно ему (в данном случае перемещение направлено вдоль оси

Нетрудно убедиться, что объемное расширение в такой волне, как и в общем случае поперечной волны, равно нулю

Согласно формулам (3.27) для компонентов тензора вращения частиц получим

т. е. частицы вращаются вдоль оси, параллельной оси