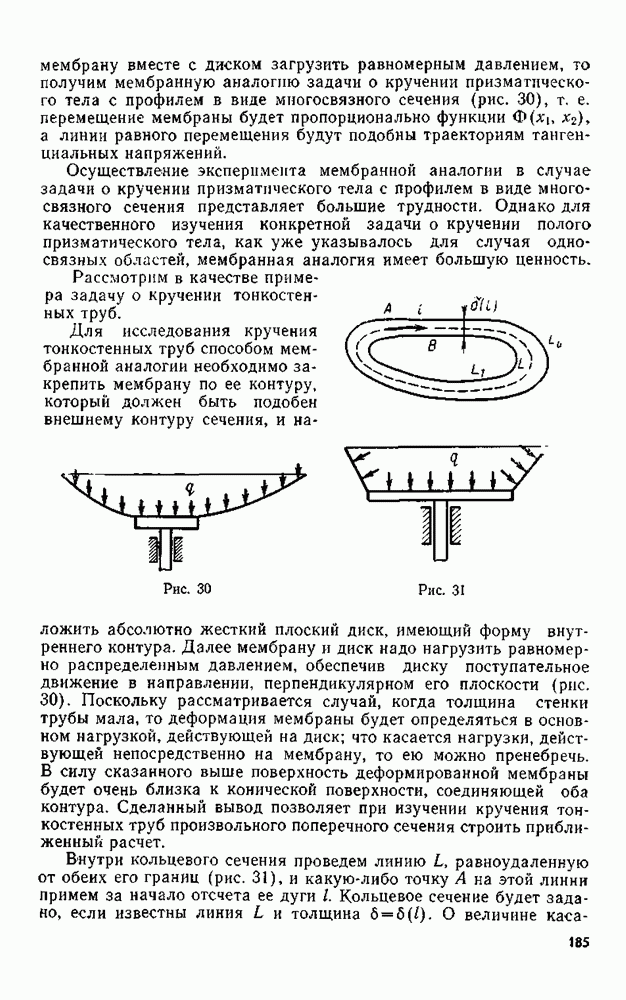
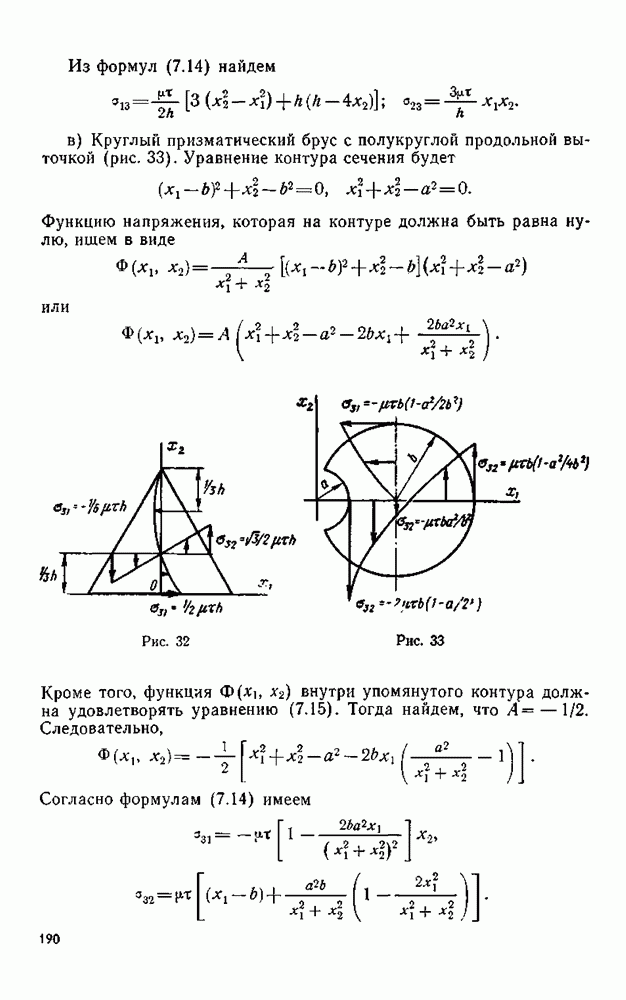
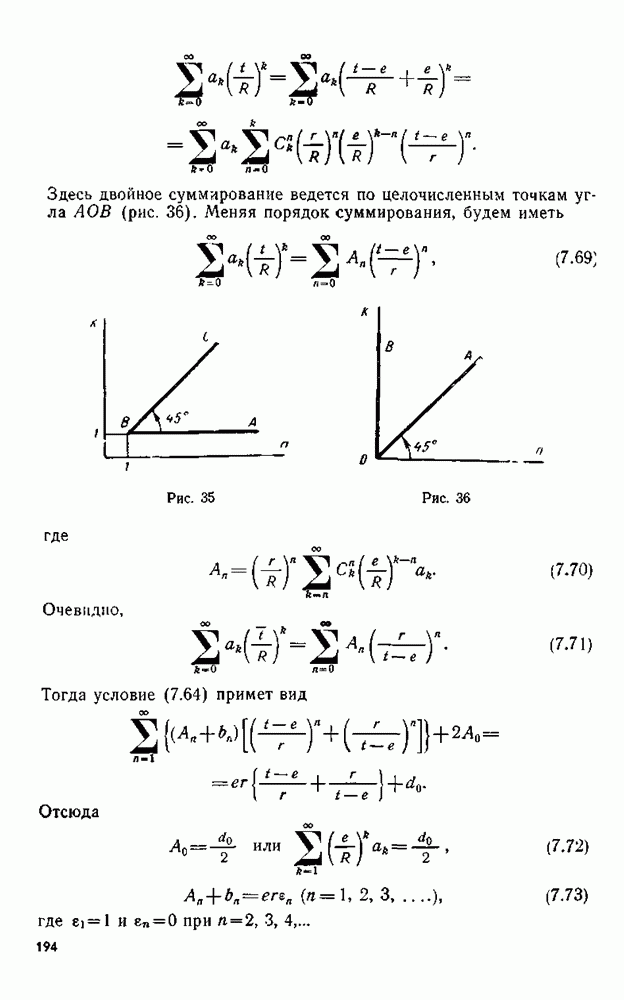
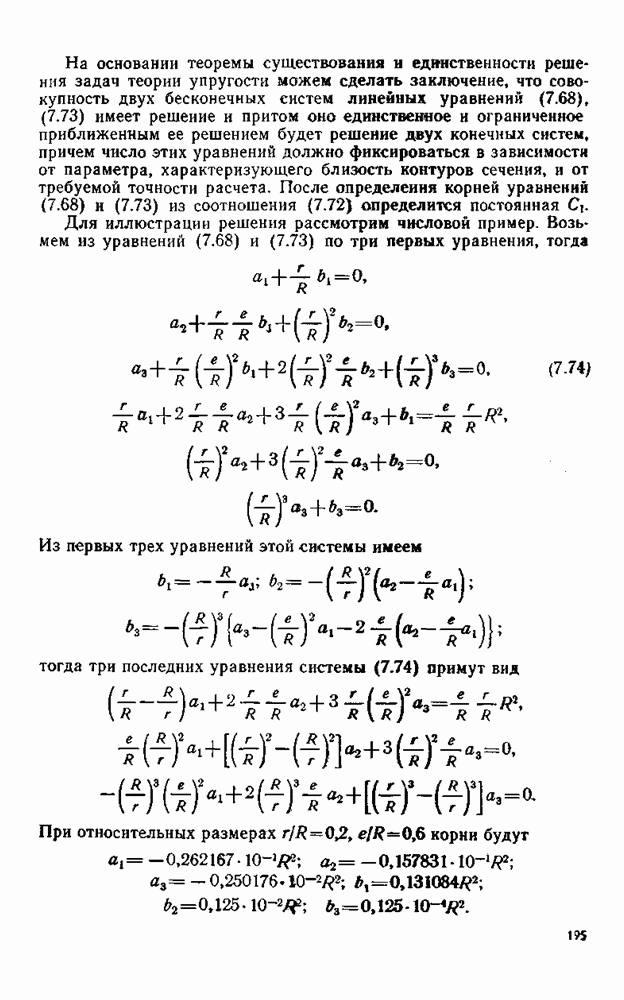| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
§ 59. Кручение призматического тела произвольного односвязного поперечного сечения
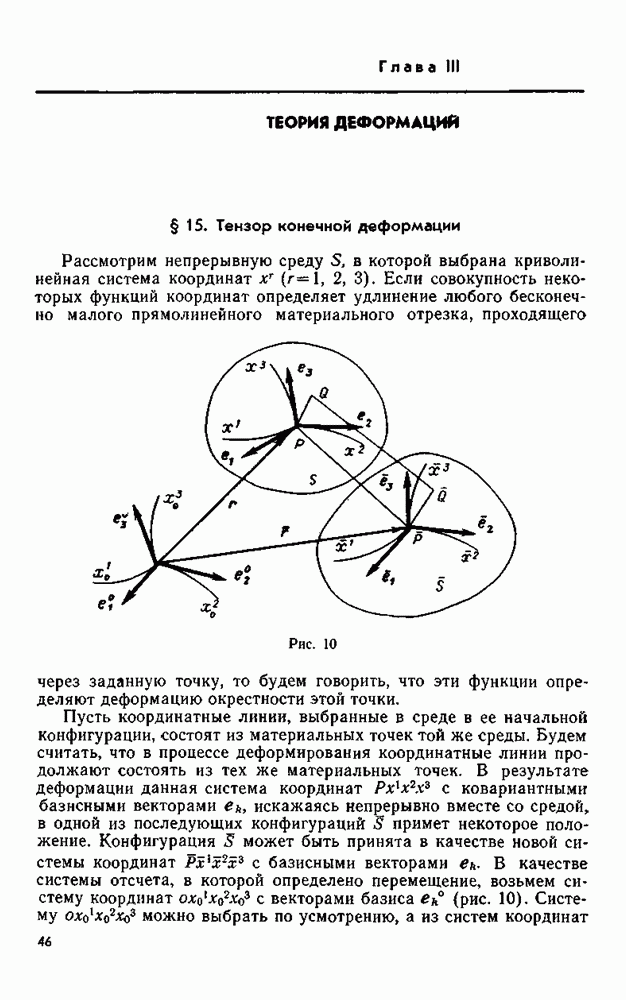
Пусть к основаниям однородного изотропного призматического тела приложены силы, приводящиеся к скручивающим парам. Кроме того, массовые силы отсутствуют, и боковая поверхность тел свободна от внешних сил.
Направим ось  параллельно образующим боковой поверхности, а оси
параллельно образующим боковой поверхности, а оси  возьмем на одном из оснований бруса (рис. 28).
возьмем на одном из оснований бруса (рис. 28).
Задача об упругом равновесии призматического тела при указанных условиях сводится к нахождению величин  удовлетворяющих в области, запятой телом, дифференциальным уравнениям равновесия (2.25) при отсутствии массовых сил и формулам закона Гука (4.35), а также граничным условиям на боковой поверхности и основаниях призматического тела.
удовлетворяющих в области, запятой телом, дифференциальным уравнениям равновесия (2.25) при отсутствии массовых сил и формулам закона Гука (4.35), а также граничным условиям на боковой поверхности и основаниях призматического тела.

Рис. 28
Поставленная в таком виде задача представляет большие математические трудности. Поэтому на основании принципа Сен-Венана, при достаточно большой длине призматического тела по сравнению с размерами его оснований, мы можем смягчить граничные условия на основаниях таким образом, чтобы главный вектор и главный момент сил, приложенных к основаниям, имели заданные значения; при этом действительное распределение сил на основаниях практически не оказывает влияния на части тела, находящиеся вдали от них. Такое интегральное удовлетворение условий на основаниях создает довольно широкий произвол в выборе решения.
Сен-Венан, исходя из вышеуказанных предположений, своим полуобратный методом решил указанную проблему в перемещениях. Решение в перемещениях поставленной проблемы Сен-Венан ищет в виде

где  постоянная величина, называемая степенью закручивания, а
постоянная величина, называемая степенью закручивания, а  некоторая функция, подлежащая определению.
некоторая функция, подлежащая определению.
Перемещения (7.1) показывают, что поперечные сечения не остаются плоскими, а искривляются, причем все сечения одинаково.
Из формул закона Гука (4.35) с учетом формул (3.26) для компонентов тензора напряжений  соответствующих перемещениям (7.1), получим
соответствующих перемещениям (7.1), получим

и

Подставляя (7.2) и (7.3) в дифференциальные уравнения равновесия (2.25), когда массовые силы отсутствуют, мы увидим, что первые два из них удовлетворяются тождественно, а третье уравнение

Последнее соотношение показывает, что функция  называемая функцией кручения Сен-Венана, должна быть гармонической функцией переменных
называемая функцией кручения Сен-Венана, должна быть гармонической функцией переменных  в области
в области  занятой поперечным сечением тела. Из третьей формулы (7.1) вытекает, что перемещение «з также должно быть гармонической функцией.
занятой поперечным сечением тела. Из третьей формулы (7.1) вытекает, что перемещение «з также должно быть гармонической функцией.
Учитывая, что внешняя нормаль  к контуру любого поперечного сечения перпендикулярна к оси
к контуру любого поперечного сечения перпендикулярна к оси  имеем
имеем  Тогда первые два условия (2.22), ввиду отсутствия внешних сил на боковой поверхности и по условию (7.3), будут удовлетворены тождественно; третье условие (2.22) на
Тогда первые два условия (2.22), ввиду отсутствия внешних сил на боковой поверхности и по условию (7.3), будут удовлетворены тождественно; третье условие (2.22) на  с учетом (7,2) примет вид
с учетом (7,2) примет вид

где через  обозначена граница области
обозначена граница области 
Учитывая, что

вместо (7.5) на  получим
получим

где — производная  по нормали
по нормали 
Задача определения функции  есть, таким образом, задача Неймана для уравнения Лапласа. Легко показать, что в нашем случае условие существования решения задачи Неймана выполняется. Действительно,
есть, таким образом, задача Неймана для уравнения Лапласа. Легко показать, что в нашем случае условие существования решения задачи Неймана выполняется. Действительно,


При соблюдении этого условия решение задачи Неймана определяется с точностью до произвольного постоянного слагаемого. Это слагаемое не существенно, ибо замена функции  на
на  с не меняет напряженного состояния, что следует из формул (7.2), а вызывает, как показывает третья формула (7.1), лишь жесткое поступательное перемещение тела вдоль оси
с не меняет напряженного состояния, что следует из формул (7.2), а вызывает, как показывает третья формула (7.1), лишь жесткое поступательное перемещение тела вдоль оси 
Для гармонической функции  справедливо тождество
справедливо тождество

на основании которого, с учетом граничного условия (7.6), обнаруживаем, что главный вектор касательных напряжений, приложенных в поперечном сечении, равен нулю. Действительно,

На основании формулы Гаусса — Остроградского из последнего равенства получим

В последней формуле, учитывая граничное условие (7.6), мы будем иметь V]  аналогично доказывается, что
аналогично доказывается, что  Поэтому касательные напряжения, приложенные в поперечном сечении, сводятся к паре сил, момент которой равен (рис. 28)
Поэтому касательные напряжения, приложенные в поперечном сечении, сводятся к паре сил, момент которой равен (рис. 28)

Внося в эту формулу значения  из формул (7.2), окончательно получим
из формул (7.2), окончательно получим

В этой формуле

Из условия равновесия на основаниях имеем  откуда
откуда

где  называется крутящим моментом;
называется крутящим моментом;  жесткостью при кручении.
жесткостью при кручении.
Принимая во внимание формулу (7.6), из формулы Гаусса — Остроградского найдем

С другой стороны, на основании первой формулы Грина

Следовательно,

Умножим обе части последнего соотношения на  и сложим с (7.9), получим
и сложим с (7.9), получим

Отсюда следует, что всегда 
Введем гармоническую функцию  сопряженную с функцией
сопряженную с функцией  тогда по условиям Коши — Римана будем иметь
тогда по условиям Коши — Римана будем иметь

Граничное условие, которому удовлетворяет функция  получится из (7.6), если внести туда условия (7.10) и учесть (6.27). В результате получаем
получится из (7.6), если внести туда условия (7.10) и учесть (6.27). В результате получаем

Интегрируя обе части этого равенства по контуру поперечного сечения, будем иметь

Для компонентов тензора напряжений на основании (7.2) с учетом условий (7.10) мы получим формулы

Из этих формул хорошо видно, что решение задачи не изменится, если в функции  прибавить постоянную величину.
прибавить постоянную величину.
Следовательно, определение функции сведено к задаче Дирихле для уравнения Лапласа.
Часто вместо функции  вводят другую
вводят другую  называемую функцией напряжений при кручении или функцией напряжений Прандтля. Эта функция определяется формулой
называемую функцией напряжений при кручении или функцией напряжений Прандтля. Эта функция определяется формулой

В этом случае из (7.12) будем иметь

Из (7,13), учитывая, что

получим

Для функции  граничное условие на основании (7.11) примет вид
граничное условие на основании (7.11) примет вид

Таким образом, задача определения  есть задача Дирихле для уравнения Пуассона (7.15) при граничном условии (7.16). Из формулы (7.8) с учетом (7.14) для определения крутящего момента будем иметь
есть задача Дирихле для уравнения Пуассона (7.15) при граничном условии (7.16). Из формулы (7.8) с учетом (7.14) для определения крутящего момента будем иметь

Эта формула показывает, что величина момента  не меняется, если к функции
не меняется, если к функции  прибавить любую постоянную. Записав (7,17) в виде
прибавить любую постоянную. Записав (7,17) в виде

и применив к первому интегралу формулу Гаусса — Остроградского, получим

Принимая в (7.16) постоянную С равной нулю, что допустимо, так как изменение  на постоянную величину не меняет решения задачи, что видно из (7.14) и (7.17), вместо формулы (7.18) будем иметь
на постоянную величину не меняет решения задачи, что видно из (7.14) и (7.17), вместо формулы (7.18) будем иметь

Эта важная формула принадлежит Прандтлю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки