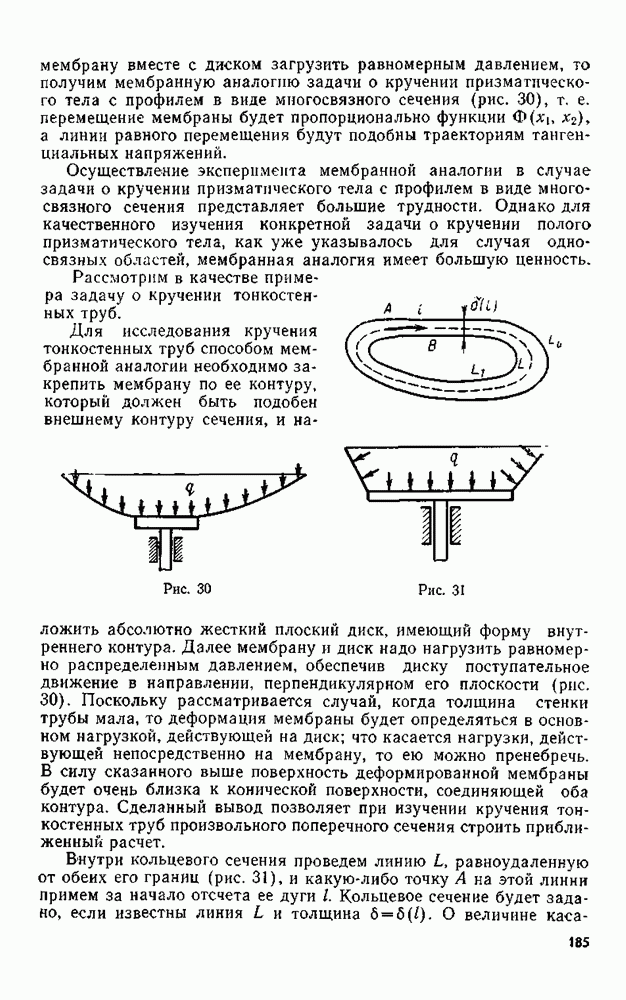
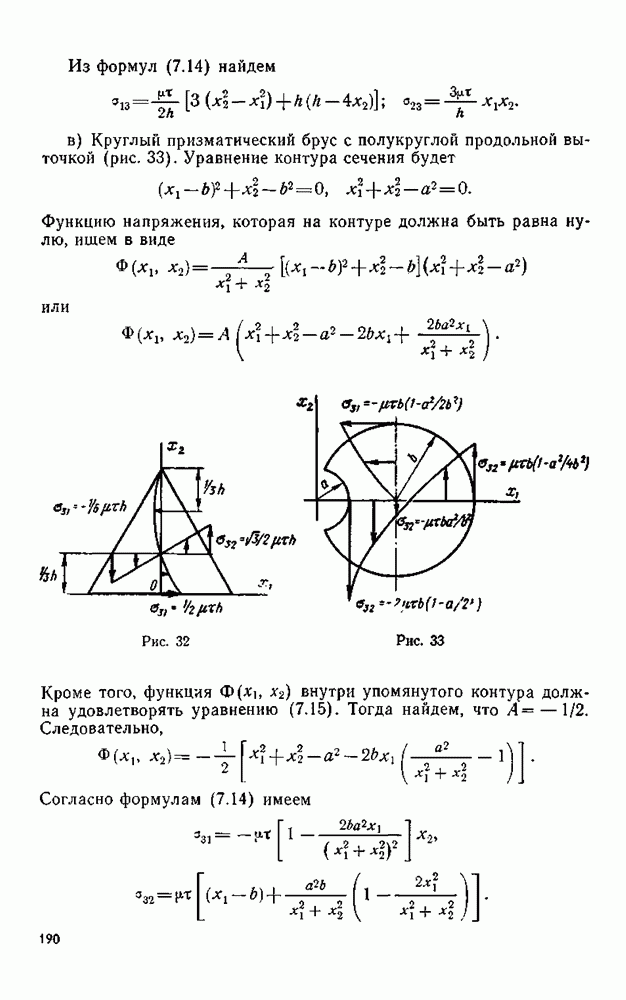
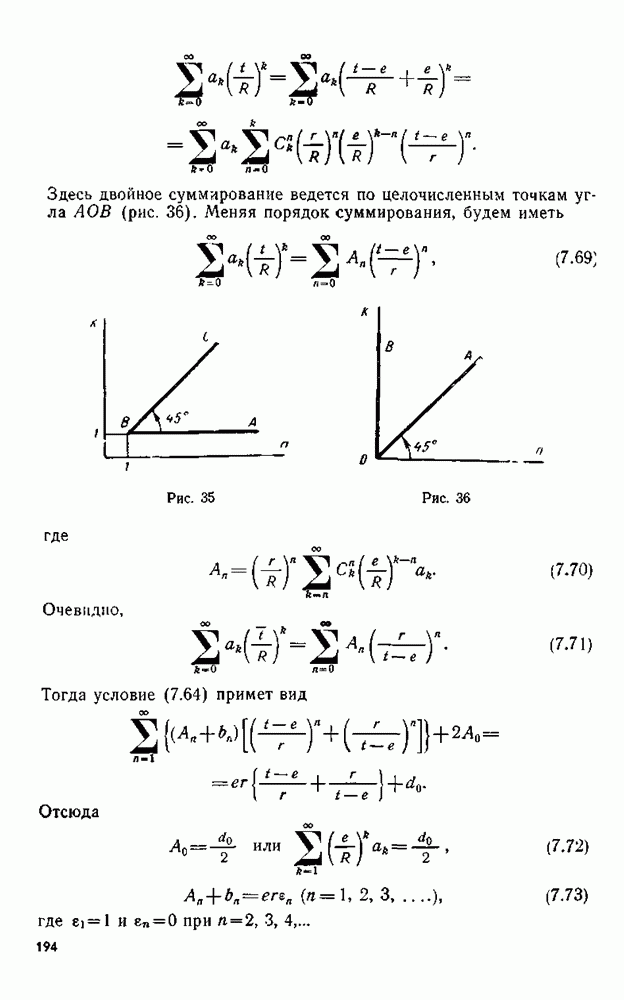
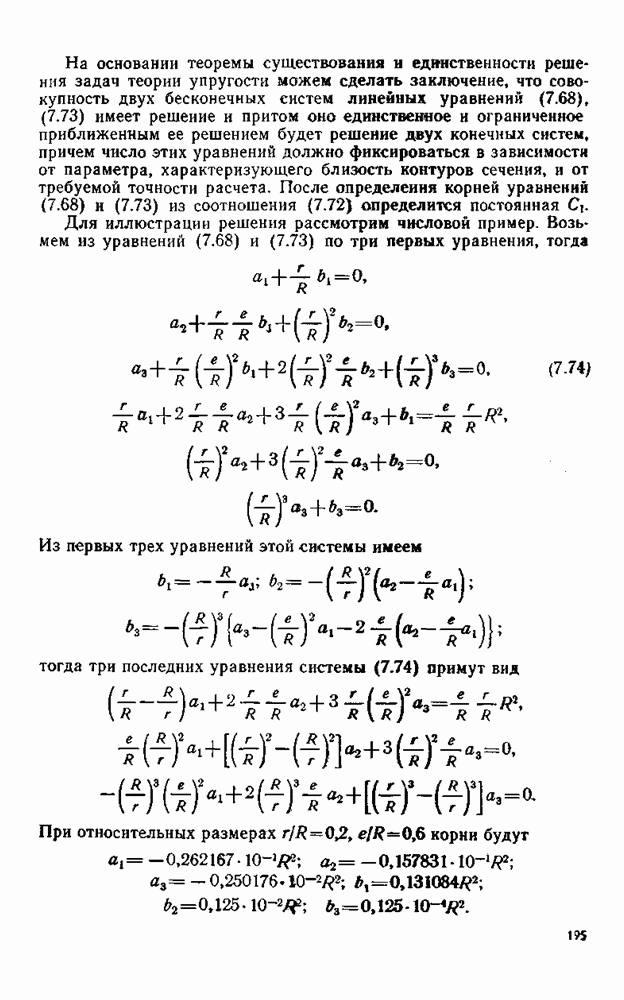| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
Для решения трехмерных статических задач теории упругости мы не располагаем таким эффективным аналитическим аппаратом, как в плоской теории упругости. Здесь мы рассмотрим такие частные решения уравнения равновесия в случае отсутствия массовых сил, для которых вблизи определенных точек перемещение неограниченно возрастает. Эти точки должны лежать вне тела или содержаться в особых полостях внутри него. Следует отметить, что наиболее простой тип изолированной особой точки представляет собою точка приложения сосредоточенной силы.
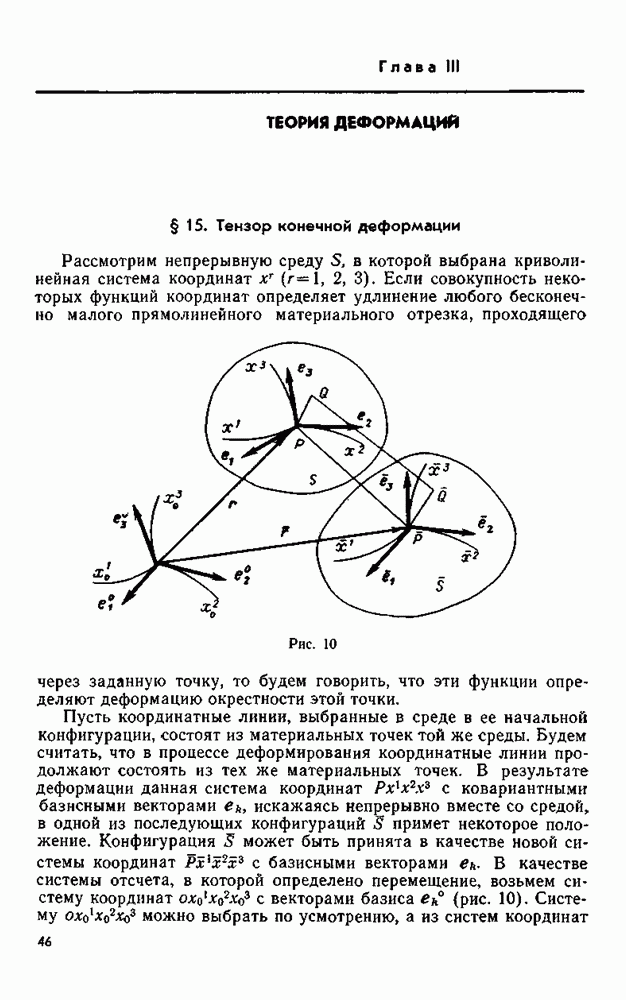
§ 75. Решения Кельвина и Буссинеска — Папковича
Если на тело действуют массовые оилы, то векторное уравнение равновесия имеет вид (5.7). Будем предполагать, что область, занятая телом, простирается безгранично по всем направлениям, а массовая сила  от нуля в области
от нуля в области  совпадающей либо со всей областью
совпадающей либо со всей областью  либо с частью ее.
либо с частью ее.
Приводим общую форму частного решения, данную Кельвином. Выразим вектор перемещения при помощи скалярного потенциала  и векторного потенциала
и векторного потенциала  формулой
формулой

Здесь V — оператор Гамильтона.
Предположим также, что массовые силы могут быть представлены в виде

Используя в уравнении равновесия (5.7) векторное тождество

придем к уравнению

Из (9.1) вычислим

Подставляя эти соотношения и (9.2) в уравнение равновесия (9.3), найдем

Это уравнение будет удовлетворено, если положить

Таким образом, частное решение уравнения (9.3) можно получить на основе частных решений уравнений Пуассона (9.4), имеющих, как известно из теории потенциала, вид

где  -расстояние от точки
-расстояние от точки  области
области  для которой вычисляются функции
для которой вычисляются функции  и
и  ; интегралы распространяются по области
; интегралы распространяются по области  вне которой массовые силы равны нулю (рис. 39); функции
вне которой массовые силы равны нулю (рис. 39); функции  определяются по формулам
определяются по формулам

которые вытекают из условия, что массовую силу  можно представить в виде (9.2). Действительно, при
можно представить в виде (9.2). Действительно, при  из (9.2) найдем
из (9.2) найдем

или при 


Рис. 39
Частные решения этих уравнений могут быть представлены в виде

Применим формулу Гаусса — Остроградского к первому равенству (9.9); тогда

где  поверхность области
поверхность области 
Полагая, что массовая сила непрерывна в области  вплоть до ее границы (тогда на этой границе
вплоть до ее границы (тогда на этой границе  а так же
а так же  вместо (9.10) получим (9.7). Таким же образом, из трех оставшихся уравнений (9.9) найдем
вместо (9.10) получим (9.7). Таким же образом, из трех оставшихся уравнений (9.9) найдем

Эти три скалярные равенства эквивалентны одному векторному равенству (9.8).
Для получения решения Буссинеска — Папковича общее решение уравнения равновесия (9.3) представим в виде

где  радиус-вектор точки тела;
радиус-вектор точки тела;  неизвестные постоянные;
неизвестные постоянные;  - неизвестные функции координат.
- неизвестные функции координат.
Действуя на обе части равенства (9.11) оператором  и учитывая векторные тождества
и учитывая векторные тождества 
найдем

Так как

из (9.11) будем иметь

Учитывая (9.12), (9.13) и  в уравнении (9.3), будем иметь
в уравнении (9.3), будем иметь

Это уравнение будет удовлетворено, если положить

Из второго уравнения (9.14) найдем

Приняв  из третьего уравнения будем иметь
из третьего уравнения будем иметь

Подставив (9.15) в первое уравнение (9.14), получим

Таким образом, решение уравнения равновесия (9.3) может быть найдено в форме (9.11), если векторная функция  и скалярная функция
и скалярная функция  удовлетворяют соответственно уравнениям Пуассона (9.15) и (9.16). Решение Буссинеска — Папковича включает четыре скалярные функции - скалярную функцию
удовлетворяют соответственно уравнениям Пуассона (9.15) и (9.16). Решение Буссинеска — Папковича включает четыре скалярные функции - скалярную функцию  и три проекции вектора
и три проекции вектора  Представление, в котором
Представление, в котором  является не гармонической, а бигармонической функцией, было дано Буссинеском и независимо от него Б. Г. Галеркиным.
является не гармонической, а бигармонической функцией, было дано Буссинеском и независимо от него Б. Г. Галеркиным.
Некоторые задачи можно решить, не используя такого количества функции. Если, например, в решении (9.11) принять  то получим простое решение вида
то получим простое решение вида

На основании первого уравнения (9.14) функция  является
является
гармонической; кроме того из третьего уравнения (9.14) следует, что решение (9.17) годно для случая, когда отсутствуют массовые силы.
Из (9.17) найдем, что

Таким образом, для простого решения вида (9.17) объемная деформация тождественно равна нулю.
На основании формул (4.35) для решения вида (9.17) формулы тензора напряжений примут вид

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки