| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Метрический тензор
Рассмотрим две бесконечно близкие точки  пространства. Эти точки определяют бесконечно малый вектор
пространства. Эти точки определяют бесконечно малый вектор  не зависящий от выбора системы координат. Длину вектора
не зависящий от выбора системы координат. Длину вектора  обозначим через
обозначим через  Если
Если  по условию определяет единичный вектор, направленный по прямой
по условию определяет единичный вектор, направленный по прямой  то
то

Проведем из точки  координатные линии, которые не лежат в одной плоскости и, вообще говоря, не ортогональны. Обозначим через с
координатные линии, которые не лежат в одной плоскости и, вообще говоря, не ортогональны. Обозначим через с  систему векторов, направленных по касательным к координатным линиям с длиной, не равной единице; тогда
систему векторов, направленных по касательным к координатным линиям с длиной, не равной единице; тогда

где  бесконечно малые векторы, определяющие параллелепипед, диагональю которого является вектор
бесконечно малые векторы, определяющие параллелепипед, диагональю которого является вектор  т. е.
т. е.

Отсюда, согласно правилам скалярного умножения векторов, найдем

где

Система векторов  называется ковариантным базисом координатной системы.
называется ковариантным базисом координатной системы.
В квадратичной форме дифференциалов  коэффициенты
коэффициенты  как явствует из (1.28), образуют симметричную матрицу
как явствует из (1.28), образуют симметричную матрицу  Таким образом, на основании теоремы о признаке тензора
Таким образом, на основании теоремы о признаке тензора  являются компонентами ковариантного тензора, называемого ковариантным метрическим тензором.
являются компонентами ковариантного тензора, называемого ковариантным метрическим тензором.
При использовании криволинейных координат целесообразно ввести, наряду с основным базисом  взаимный контравариантный базис
взаимный контравариантный базис  т. е. тройку векторов
т. е. тройку векторов  связанных с основными векторами
связанных с основными векторами  формулами;
формулами;

где  символы Кронекера.
символы Кронекера.
Для этого достаточно принять

Из (1.29) тзкже следует, что

Итак,  перпендикулярен плоскости
перпендикулярен плоскости 
Если система координат ортогональна, то, очевидно, [см. (1.30) и (1.31)] базисные векторы  совпадут по направлениям, но их величины, вообще говоря, различны.
совпадут по направлениям, но их величины, вообще говоря, различны.
Представим вектор  как линейную комбинацию векторов
как линейную комбинацию векторов 

Учитывая соотношения (1.28) и (1.29), получим  следовательно,
следовательно,  Отсюда по правилу Крамера найдем
Отсюда по правилу Крамера найдем

Здесь  алгебраическое дополнение элемента
алгебраическое дополнение элемента  в детерминанте
в детерминанте 
Из (1.32) на основании (1.29) будем иметь

Величины  являются симметричными. Подставляя (1.32) в (1.29), будем иметь
являются симметричными. Подставляя (1.32) в (1.29), будем иметь 
Отсюда заключаем, что величины  являются компонентами контравариантного
являются компонентами контравариантного  Тензор
Тензор  называется контравариантным
называется контравариантным
метрическим тензором. Компоненты этого тензора  могут быть вычислены при помощи (1.33).
могут быть вычислены при помощи (1.33).
Умножим теперь контравариаитный вектор  на метрический тензор
на метрический тензор  и свернем; тогда мы получим ковариантный вектор
и свернем; тогда мы получим ковариантный вектор  который мы обозначим через
который мы обозначим через  Следовательно,
Следовательно,

Таким же образом

Векторы  связанные формулами (1.34) и (1.35), называются ассоциированными векторами. Как видно из формул (1.34) и (1.35), мы легко можем вычислить компоненты одного из векторов
связанные формулами (1.34) и (1.35), называются ассоциированными векторами. Как видно из формул (1.34) и (1.35), мы легко можем вычислить компоненты одного из векторов  по компонентам другого. Поэтому
по компонентам другого. Поэтому  удобно рассматривать как различные соответственно ковариантные и контравариантные компоненты одного и того же векора А.
удобно рассматривать как различные соответственно ковариантные и контравариантные компоненты одного и того же векора А.
Тензор  называется смешанным метрическим тензором. Легко доказать, что
называется смешанным метрическим тензором. Легко доказать, что  совпадает с тензором Кронекера. Действительно, на основании формул (1.34), (1.35) и (1.36) имеем
совпадает с тензором Кронекера. Действительно, на основании формул (1.34), (1.35) и (1.36) имеем

откуда

Для того чтобы эти соотношения выполнялись при всех значениях  компоненты смешанного метрического тензора
компоненты смешанного метрического тензора  следует выбрать следующим образом:
следует выбрать следующим образом:

Рассмотрим теперь ковариантный тензор  Если нужно поднять первый индекс
Если нужно поднять первый индекс  тогда тензор
тогда тензор  следует умножить на
следует умножить на  и затем свернуть относительно первого индекса, т. е.
и затем свернуть относительно первого индекса, т. е.

Для того чтобы можно было узнать, какой индекс был поднят, на его место ставят точку. Например, в равенстве

поднят второй индекс k. Оба индекса можно поднять по формуле

Эти операции, очевидно, можно полностью перенести на тензоры любого ранга. Все тензоры, полученные один из другого указанным способом, называются ассоциированными; компоненты их
также могут быть рассмотрены как компоненты одного и того же тензора.
В прямолинейной прямоугольной системе координат квадрат расстояния между точками А с координатами  с координатами
с координатами  будет
будет

Так как

Теперь формуле (1.38) можно придать вид

Введя обозначение

последней формуле придадим вид

На основании теоремы о признаке тензора заключаем, что  ковариантный тензор.
ковариантный тензор.
Определим значения контравариантных и ковариантных компонентов вектора а, заданного в точке  пространства. Проведем через эту точку три координатные поверхности
пространства. Проведем через эту точку три координатные поверхности

Пересечение этих координатных поверхностей определит три координатные линии.
Вычислим углы, образуемые направлениями  с осями прямоугольной декартовой системы координат
с осями прямоугольной декартовой системы координат  Вдоль
Вдоль  возьмем элементарный вектор
возьмем элементарный вектор  длина его определится по формуле
длина его определится по формуле

Здесь суммирование ведется по индексу  от 1 до 3. Учитывая, что вдоль координатной линии
от 1 до 3. Учитывая, что вдоль координатной линии  координаты
координаты  зависят только от координаты
зависят только от координаты  последней формуле придадим вид
последней формуле придадим вид

или, в силу формул (1.39),

Тогда выражение для косинуса угла между направлением и осью  примет вид
примет вид

Как известно, формула для косинуса угла между направлением  (или между вектором
(или между вектором  и осью имеет вид
и осью имеет вид

Учитывая, что в прямоугольной декартовой системе координат компоненты тензора  равны
равны  в силу (1.10) будем иметь
в силу (1.10) будем иметь

отсюда

На основании этой формулы из (1.43) найдем

Обозначим контравариантные и ковариантные компоненты векторов через  и
и  а его компоненты в прямоугольной декартовой системе координат — через
а его компоненты в прямоугольной декартовой системе координат — через  Далее
Далее  обозначают проекции вектора а соответственно на
обозначают проекции вектора а соответственно на  Учитывая, что
Учитывая, что  орты прямоугольной декартовой системы координат), согласно основной формуле для проекции вектора на заданное направление получим
орты прямоугольной декартовой системы координат), согласно основной формуле для проекции вектора на заданное направление получим

другой стороны, на основании формул (1.5) и (1.7) имеем

Подставляя эти выражения соответственно в (1.45) и (1.46), окончательно получим


Отметим еще раз, что в (1.47) и (1.48) по индексу к никакого суммирования производить не следует. Если криволинейиая система координат ортогональна, то направления не к совпадут, тогда  обозначим их через
обозначим их через 
Если криволинейная система координат ортогональна, то, как известно,

где Ни — коэффициенты Лямэ.
В этом случае из (1.47) и (1.48) получим

Величины  называются физическими проекциями вектора а. Обозначим теперь тензор второго ранга в прямолинейных прямоугольных координатах
называются физическими проекциями вектора а. Обозначим теперь тензор второго ранга в прямолинейных прямоугольных координатах  через
через  физические проекции этого тензора в криволинейных ортогональных координатах
физические проекции этого тензора в криволинейных ортогональных координатах  через
через  а его контравариаитные компоненты через
а его контравариаитные компоненты через  тогда по формулам преобразования компонентов тензора (1.10) будем иметь
тогда по формулам преобразования компонентов тензора (1.10) будем иметь

Учитывая здесь (1.44) и то, что  можем написать
можем написать 

На основании (1.13)

тогда

Учитывая, что  будем иметь
будем иметь

Определим угол  между двумя произвольными векторами
между двумя произвольными векторами  заданными в одной точке. Векторы
заданными в одной точке. Векторы  можно определить линейной комбинацией вида
можно определить линейной комбинацией вида

Скалярное произведение векторов  равно
равно

или

С другой стороны,

где

Подставляя (1.51) и (1.53) в (1.52), найдем

Из последнего получим условие ортогональности двух векторов 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
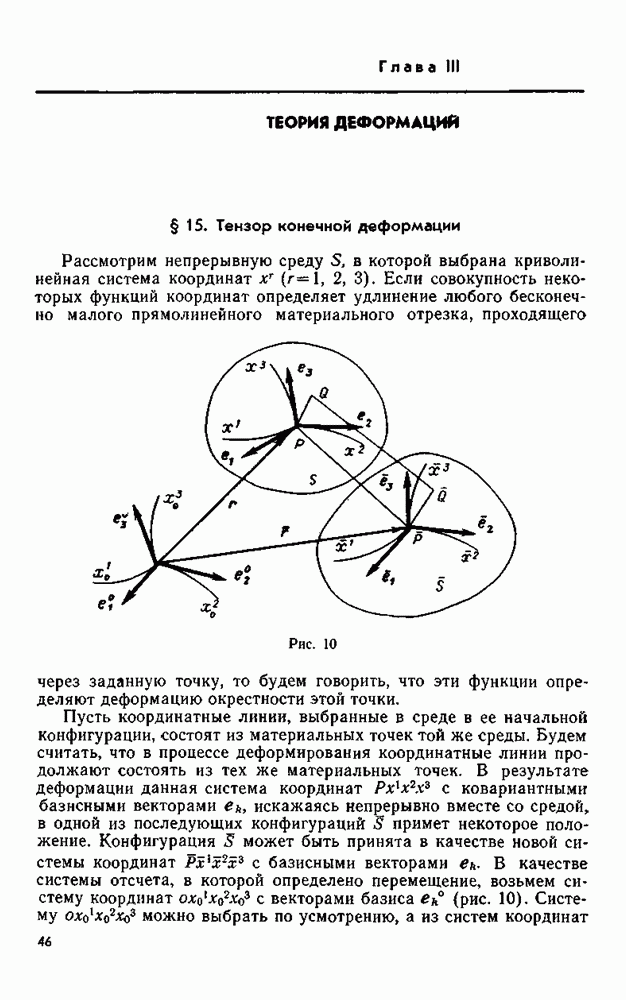
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки