| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 42. Функция напряжений Эри
Решение задач плоской теории упругости значительно упрощается, если массовыми силами пренебречь либо в силу их малости, либо, имея в виду, что всегда задачу при наличии массовых сил можно свести к задаче без массовых сил, если найти какое-либо частное решение соответствующих неоднородных дифференциальных уравнений равновесия, В дальнейшем будем предполагать, что массовые силы отсутствуют.
В плоской задаче теории упругости большую роль играет введенная впервые Эри вспомогательная функция. Следует отметить, что благодаря введению этой функции был создан плодотворный метод решения задач плоской теории упругости.
В случае отсутствия массовых сил уравнения (6.5) примут вид

Первое уравнение (6.21) показывает, что выражение  является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции  следовательно,
следовательно,

Таким же образом из второго уравнения имеем

где  некоторая функция. Сравнение этих формул для одной и той же величины дает соотношение
некоторая функция. Сравнение этих формул для одной и той же величины дает соотношение

которое показывает, что выражение  представляет со бой полный дифференциал некоторой функции
представляет со бой полный дифференциал некоторой функции  так что
так что

откуда

Подставляя значения  в формулы (6.22) и (6,23), получим
в формулы (6.22) и (6,23), получим

Эти формулы были впервые получены Эри. Функция  называется функцией напряжения Эри.
называется функцией напряжения Эри.

Рис. 17
Очевидно, если допустить, что имеют место соотношения (6.24), уравнения (6.21) будут удовлетворены тождественно. Кроме того, как известно, для того, чтобы величины  соответствовали действительному напряженному состоянию, они должны удовлетворять условию совместности
соответствовали действительному напряженному состоянию, они должны удовлетворять условию совместности  т. е.
т. е.

С другой стороны, из соотношений (6.24) имеем

Учитывая последнее равенство, из (6.25) окончательно получим

где

В дальнейшем мы будем считать, что функция напряжений в области имеет непрерывные производные вплоть до четвертого порядка.
Таким образом, для того чтобы функция напряжений определяла некоторое действительное напряженное состояние, необходимо и достаточно, чтобы она была бигармонической.
Выведем теперь контурные условия, которым должна удовлетворять функция Эри. Допуская, что на границе данной области заданы внешние силы  преобразуем контурные условия (6.12).
преобразуем контурные условия (6.12).
Мы будем в дальнейшем предполагать, что контуры простые, т. е. не самопересекающиеся, и достаточно гладкие.
Выразим  через производные координат
через производные координат  по дуге I, отсчитываемой в положительном направлении вдоль рассматриваемого контура. Из рис. 17 имеем
по дуге I, отсчитываемой в положительном направлении вдоль рассматриваемого контура. Из рис. 17 имеем

Внося (6.24) и (6.27) в контурные условия (6.12), получим на 

или

Для произвольной точки  контура
контура  введем обозначения
введем обозначения

Тогда, интегрируя равенства (6.28), получим

Итак, приращения функций  при переходе из точки
при переходе из точки  в точку
в точку  (эти точки лежат на одном и том же контуре) равны соответственно проекциям на ось
(эти точки лежат на одном и том же контуре) равны соответственно проекциям на ось  и на ось
и на ось  результирующего вектора внешних сил, приложенных к контуру между этими двумя точками. Имея формулы (6.30), нетрудно найти производные
результирующего вектора внешних сил, приложенных к контуру между этими двумя точками. Имея формулы (6.30), нетрудно найти производные

Внося значения  из (6.30) в (6.31) и интегрируя полученный результат по I, будем иметь
из (6.30) в (6.31) и интегрируя полученный результат по I, будем иметь

Формула (6.33) показывает, что по заданным на любой контуре значениям внешних сил можно вычислить значение  в любой точке того же контура с точностью до линейного слагаемого вида
в любой точке того же контура с точностью до линейного слагаемого вида

Следует отметить, что это слагаемое для компонентов тензора напряжений, вычисляемых формулами (6.24), выпадает.
Если заданная область односвязна, то на контуре  можно
можно  принять равными нулю. Если область многосвязна, то, положив постоянные
принять равными нулю. Если область многосвязна, то, положив постоянные  равными нулю на каком-либо одном из контуров, мы не можем распоряжаться остальными по произволу.
равными нулю на каком-либо одном из контуров, мы не можем распоряжаться остальными по произволу.
Подставляя значения  из (6.30) в (6.32), определим значение нормальной производной
из (6.30) в (6.32), определим значение нормальной производной

по заданным внешним силам, приложенным на контурах.
Таким образом, решение плоской задачи теории упругости сводится к определению бигармонической функции по известным на контурах значениям этой функции и ее нормальной производной.
При полном обходе любого замкнутого контура в силу формул (6.30), (6.33) будем иметь

где  соответственно проекции на ось
соответственно проекции на ось  и на ось
и на ось  главного вектора внешних сил, приложенных к рассматриваемому контуру. Интегрируя (6.36) по частям, получим
главного вектора внешних сил, приложенных к рассматриваемому контуру. Интегрируя (6.36) по частям, получим

где  и — координаты произвольной точки
и — координаты произвольной точки  рассматриваемого контура
рассматриваемого контура  с которой начинается полный обход. Третий член (6.37) определяет значение главного момента всех внешних сил, приложенных к рассматриваемому контуру, относительно произвольно выбранного начала координат.
с которой начинается полный обход. Третий член (6.37) определяет значение главного момента всех внешних сил, приложенных к рассматриваемому контуру, относительно произвольно выбранного начала координат.
Формулы (6.35) и (6,37) позволяют установить условия однозначности функции  и ее производных
и ее производных  Функция
Функция 
и ее производные  будут однозначными в том случае, если главный вектор и главный момент внешних сил, приложенных к каждому контуру области, в отдельности равны нулю; если главный вектор равен нулю, то функция будет, вообще говоря, неоднозначной, а ее производные
будут однозначными в том случае, если главный вектор и главный момент внешних сил, приложенных к каждому контуру области, в отдельности равны нулю; если главный вектор равен нулю, то функция будет, вообще говоря, неоднозначной, а ее производные  будут однозначными функциями; если же главный вектор не равен нулю, то неоднозначными будут как сама функция
будут однозначными функциями; если же главный вектор не равен нулю, то неоднозначными будут как сама функция  так и ее производные.
так и ее производные.

Рис. 18
Ряд интересных решений уравнения (6.26) можно получить, задавшись функцией Эри в виде полиномов различных степеней. В качестве простейшего примера выберем функцию Эри в виде полинома второй степени, который, очевидно, удовлетворяет уравнению (6.26)

В случае отсутствия массовых сил по формулам Эри (6.24) для компонентов тензора напряжений получим

Таким образом, все три компонента постоянны по всей области. Для прямоугольной полосы со сторонами, параллельными осям координат (рис. 18), силы, приложенные к контуру, где  , в силу формулы (6.12) будут
, в силу формулы (6.12) будут

Уравнению (6.26) также удовлетворяет полином третьей степени

На основании формулы (6.24) компоненты напряжений будут

Предполагая  мы получим
мы получим

Эта система компонентов тензора напряжений соответствует чистому изгибу прямоугольной полосы внешними силами, приложенными  обоих ее концах
обоих ее концах  Эти внешние силы на основании формул
Эти внешние силы на основании формул  должны быть равны
должны быть равны  на конце
на конце  на конце
на конце  Главный вектор и главный момент этих сил, очевидно,
Главный вектор и главный момент этих сил, очевидно,
будут

здесь  — толщина полосы;
— толщина полосы;  — высота полосы.
— высота полосы.
Согласно принципу Сен-Венана найденное решение применимо вдали от концов полосы также для случая, когда вместо внешних сил, приложенных на обоих концах полосы и распределенных во закону (6.39), действуют статически эквивалентные пары сил с моментом  причем вблизи места приложения пар напряженное состояние будет отличаться от (6.39). Если не равен пул» только коэффициент
причем вблизи места приложения пар напряженное состояние будет отличаться от (6.39). Если не равен пул» только коэффициент  то отличным от нуля компонентом тензора напряжений будет нормальное напряжение
то отличным от нуля компонентом тензора напряжений будет нормальное напряжение  Если же только один из коэффициентов
Если же только один из коэффициентов  не равен нулю, например
не равен нулю, например  то в дополнение к нормальному напряжению
то в дополнение к нормальному напряжению  появляется касательное напряжение
появляется касательное напряжение  Когда используются полиномы более высокой степени, чем третья, то бигармоническое уравнение удовлетворяется при некоторых соотношениях между их коэффициентами
Когда используются полиномы более высокой степени, чем третья, то бигармоническое уравнение удовлетворяется при некоторых соотношениях между их коэффициентами
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
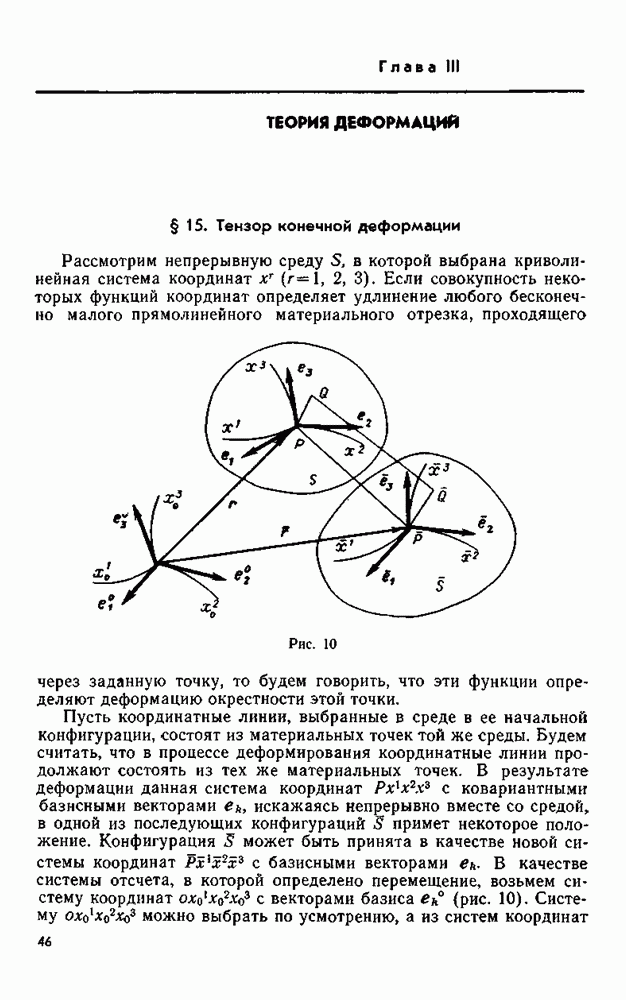
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки