| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 38. Простейшие задачи теории упругости
К простейшим задачам теории упругости мы будем относить те из них, в которых в любой точке тела компоненты напряжений, а следовательно, и деформаций постоянны или линейно зависят от координат. Очевидно, в простейших задачах соотношения Бельтрами — Митчелла или уравнения сплошности деформаций удовлетворяются тождественно. Эти задачи решаются полуобратным методом.
1. Всестороннее равномерное давление.
Пусть тело подвержено всестороннему равномерному внешнему давлению  единичный вектор по нормали к поверхности тела). Массовыми силами пренебрегаем. Зададимся тензором напряжений в виде
единичный вектор по нормали к поверхности тела). Массовыми силами пренебрегаем. Зададимся тензором напряжений в виде

который удовлетворяет дифференциальным уравнениям равновесия (2.25), а также соотношениям Бельтрами — Митчелла.
Определим внешние силы, вызывающие в рассматриваемом теле тензор напряжений в виде (5.47); на основании формул (2.22) имеем

или

т. е. вектор напряжения, приложенный на поверхности тела, должен представлять собой давление  что имеет место по заданию. Таким образом, во всех точках тела любые три взаимно перпендикулярные сечения суть главные площадки. На основании обобщенного закона Гука (4.50) компоненты тензора деформаций будут равны
что имеет место по заданию. Таким образом, во всех точках тела любые три взаимно перпендикулярные сечения суть главные площадки. На основании обобщенного закона Гука (4.50) компоненты тензора деформаций будут равны

Допустим, что данное тело закреплено в некоторой точке, которую примем за начало координатных осей, и в этой точке закреплено элементарное волокно, расположенное на оси  кроме того, стеснен поворот элементарного волокна, расположенного на оси
кроме того, стеснен поворот элементарного волокна, расположенного на оси  в плоскости
в плоскости  Аналитическая запись этих условий закрепления соответственно для всех
Аналитическая запись этих условий закрепления соответственно для всех  такова
такова

Подставляя решение (5.48) в формулы (3.44) и учитывая условия закрепления (5.49), после несложных вычислений определим проекции вектора упругого перемещения.

Следовательно, перемещения точек тела радиальные, причем они растут пропорционально расстоянию от начала координат и симметричны относительно него.
2. Осевое растяжение призматического бруса.
Пусть призматическое тело с прямолинейной осью и перпендикулярными к ней основаниями произвольной формы подвержено осевому растяжению. Массовыми силами пренебрегаем. Тензор напряжений, выбранный в виде

удовлетворяет дифференциальным уравнениям равновесия  также соотношениям Бельтрами — Митчелла. Определим внешние силы, вызывающие в данном призматическом теле тензор напряжений вида (5.51). В силу формул (2.22) имеем: на боковой поверхности бруса
также соотношениям Бельтрами — Митчелла. Определим внешние силы, вызывающие в данном призматическом теле тензор напряжений вида (5.51). В силу формул (2.22) имеем: на боковой поверхности бруса 

на основаниях бруса 

Равенства (5.52) показывают, что боковая поверхность тела должна быть свободна от внешних сил, что вполне справедливо, так как на тело действуют только осевые силы. Равенства (5.53) показывают, что на основаниях бруса должны быть приложены равномерно распределенные растягивающие усилия интенсивностью  Фактически передача растягивающей силы на рассматриваемый брус может сильно отличаться от равномерно распределенных растягивающих сил. Однако, согласно принципу Сен-Венана, на достаточо удаленной от оснований бруса части его решение
Фактически передача растягивающей силы на рассматриваемый брус может сильно отличаться от равномерно распределенных растягивающих сил. Однако, согласно принципу Сен-Венана, на достаточо удаленной от оснований бруса части его решение  можно принять за точное.
можно принять за точное.
На основании обобщенного закона Гука (4.50) компоненты тензора деформаций будут равны

В центре тяжести верхнего сечения бруса, в котором расположено начало координат, как и В первой задаче, примем граничные условия

Подставляя решение (5.44) в формулы (3.44), с учетом (5.55) получим

Первые две формулы (5.56) показывают, что во всех поперечных
сечениях перемещения  одинаковы и пропорциональны расстоянию данной точки поперечного сечения до оси бруса. Третья формула (5.56) показывает, что плоские сечения после деформации остаются плоскими. В курсе сопротивления материалов последний результат принимается за исходное предположение, носящее название «гипотеза плоских сечений».
одинаковы и пропорциональны расстоянию данной точки поперечного сечения до оси бруса. Третья формула (5.56) показывает, что плоские сечения после деформации остаются плоскими. В курсе сопротивления материалов последний результат принимается за исходное предположение, носящее название «гипотеза плоских сечений».
3. Растяжение призматического бруса под действием собственного веса.
а) Пусть призматический брус длиной I, закрепленный своим верхним концом, подвержен деформации растяжения под действием собственного веса. Обозначим через  плотность материала. Оси системы координат выберем так, чтобы начало ее поместилось в центре тяжести верхнего основания, перпендикулярного к оси бруса, и одна из осей системы, направленная вертикально вниз, например,
плотность материала. Оси системы координат выберем так, чтобы начало ее поместилось в центре тяжести верхнего основания, перпендикулярного к оси бруса, и одна из осей системы, направленная вертикально вниз, например,  совпала с осью бруса. Тогда проекции массовой силы будут
совпала с осью бруса. Тогда проекции массовой силы будут

Пользуясь полуобратным методом Сен-Венана, выберем компоненты тензора напряжений в виде

Здесь  пока неизвестные постоянные. Этими компонентами тензора напряжений соотношения Бельтрами — Митчелла удовлетворяются тождественно; тождественно удовлетворяются также первые два уравнения равновесия, а из третьего уравнения получаем
пока неизвестные постоянные. Этими компонентами тензора напряжений соотношения Бельтрами — Митчелла удовлетворяются тождественно; тождественно удовлетворяются также первые два уравнения равновесия, а из третьего уравнения получаем

В силу этого будем иметь

Учитывая формулы (5.57) и имея в виду, что  где
где  внешняя нормаль к поверхности бруса, для проекции силы, действующей на боковой поверхности бруса, на основании (2.22) будем иметь
внешняя нормаль к поверхности бруса, для проекции силы, действующей на боковой поверхности бруса, на основании (2.22) будем иметь

Как видно из последних равенств, боковая поверхность бруса должна быть свободна от сил, что имеет место в действительности, так как брус находится под действием лишь собственного веса. На нижнем основании бруса при  имеем
имеем

где  внешняя нормаль нижнего основания. Согласно формулам (2.22)
внешняя нормаль нижнего основания. Согласно формулам (2.22)

В силу условий задачи нижнее основание свободно от сил, поэтому

откуда

Окончательно имеем

Поступая аналогичным образом, на верхнем основании бруса при  будем иметь
будем иметь

Это соответствует такому закреплению верхнего основания, при котором в нем возникают только нормальные, равномерно распределенные по всему основанию напряжения. Такое закрепление практически осуществить не представляется возможным, но в силу принципа Сен-Венана решение (5.57) может быть принято за точное и при любом другом способе закрепления.
На основании обобщенного закона Гука компоненты тензора деформаций будут

При граничных условиях (5,55) второй задачи с учетом (5.59) из формул (3.44) будем иметь

Точки, лежащие на оси бруса, как показывает третья формула (5.60), перемещаются лишь вдоль этой оси.
Так как в поперечных сечениях бруса отсутствуют касательные напряжения, а следовательно, и сдвиги, то эти сечения после деформации бруса останутся нормальными ко всем волокнам и, как показывает третья формула (5.60), сечения обращаются в параболоиды вращения, обращенные выпуклостью вниз.
б) Призматический брус длиной I, закрепленный своим верхним концом, находится под действием своего веса и силы  приложенной к свободному концу в направлении оси бруса. Поместим начало координат в центре тяжести верхнего сечения и одну из осей
приложенной к свободному концу в направлении оси бруса. Поместим начало координат в центре тяжести верхнего сечения и одну из осей  направим вдоль оси бруса вниз. Исходя из принципа Сен-Венана, заменим силу
направим вдоль оси бруса вниз. Исходя из принципа Сен-Венана, заменим силу  статически ей эквивалентной, равномерно распределенной по нижнему основанию бруса нагрузкой интенсивностью
статически ей эквивалентной, равномерно распределенной по нижнему основанию бруса нагрузкой интенсивностью  площадь нижнего основания, перпендикулярного к
площадь нижнего основания, перпендикулярного к
оси бруса); тогда, в силу линейности задачи, решение будет представлено в виде суммы решений второй и третьей задач.
4. Кручение круглого призматического бруса.
Пусть на крайних поперечных сечениях круглого призматического бруса с осью  действуют пары сил, моменты которых по величине равны, но знаки различны; в этом случае брус подвержен деформации кручения (рис. 14); боковая поверхность бруса свободна от поверхностных сил и объемные силы отсутствуют
действуют пары сил, моменты которых по величине равны, но знаки различны; в этом случае брус подвержен деформации кручения (рис. 14); боковая поверхность бруса свободна от поверхностных сил и объемные силы отсутствуют 
Элементарное решение задачи в теории сопротивления материалов основывается на предположении, что поперечные сечения бруса, оставаясь плоскими, с сохранением между собой расстояний поворачиваются относительно друг друга и их радиусы не искривляются.

Рис. 14
Если принять во внимание это предположение, то проекции вектора перемещения некоторой точки в каком-либо поперечном сечении бруса будет

где  постоянный угол закручивания, рассчитанный на единицу длины бруса.
постоянный угол закручивания, рассчитанный на единицу длины бруса.
Проверим, совместимы ли эти перемещения со всеми основными уравнениями теории упругости. Подставив (5.61) в формулы  для компонентов тензора деформаций будем иметь
для компонентов тензора деформаций будем иметь

Объемная деформация

Как видно из формул (5.62), уравнения совместности Сен-Венана удовлетворяются тождественно.
Учитывая, что массовые силы равны нулю и имеет место соотношение (5.63), убеждаемся, что (5.61) удовлетворяют уравнениям упругого равновесия Ляме 
На основании обобщенного закона Гука компоненты напряжений будут

Таким образом, в любом поперечном сечении бруса действуют только два компонента касательных напряжений. Подставляя (5.64) в формулы (2.22), на боковой поверхности, где  будем иметь
будем иметь  Следовательно, боковая поверхность бруса должна быть свободна от напряжений, что действительно имеет место. Далее, подставляя (5.64) в формулы (2.22) для крайних поперечных сечений
Следовательно, боковая поверхность бруса должна быть свободна от напряжений, что действительно имеет место. Далее, подставляя (5.64) в формулы (2.22) для крайних поперечных сечений  получим поверхностные силы, соответствующие решению (5.61), в виде
получим поверхностные силы, соответствующие решению (5.61), в виде

Таким образом, решение (5.61) приводит к выводу, что в крайних поперечных сечениях бруса должны действовать только касательные силы, распределенные по закону (5.64). Главный вектор и главный момент этих сил относительно центра круга будут

В силу того, что оси  проходят через центр тяжести круга, статические моменты его площади будут
проходят через центр тяжести круга, статические моменты его площади будут

Окончательно имеем

где  полярный момент инерции площади круга,
полярный момент инерции площади круга,

здесь  радиус окружности.
радиус окружности.
Осуществление передачи внешних сил на концах бруса по закону (5.64) практически невозможно, но на основании принципа Сен-Венана решение (5.64) можно считать точным при любом законе передачи внешних сил, если соблюдены условия статической эквивалентности, т. е. постоянную  выбираем так (это возможно), чтобы момент
выбираем так (это возможно), чтобы момент  приложенной пары сил на одном из крайних сечений был равен равнодействующему моменту
приложенной пары сил на одном из крайних сечений был равен равнодействующему моменту  , т.е.
, т.е.

откуда получаем

что дает закон Гука при кручении круглого призматического бруса.
5. Чистый изгиб призматического бруса.
Примем ось бруса за  а главные центральные оси инерции поперечного сечения за оси
а главные центральные оси инерции поперечного сечения за оси  при этом ось
при этом ось  направим в сторону растянутых волокон (рис. 15).
направим в сторону растянутых волокон (рис. 15).

Рис. 15
Предположим, что боковая поверхность бруса свободна от внешних сил и массовые силы отсутствуют. Кроме того, пусть в крайних сечениях рассматриваемого бруса приложены две пары сил, плоскости действия которых совпадают с одной из главных его плоскостей, моменты их равны по величине и знаки противоположны. В этом случае брус подвергается чистому изгибу и, как известно из теории сопротивления материалов, решение этой задачи основано на предположении, что каждое поперечное сечение, оставаясь плоским, поворачивается вокруг центральной оси этого сечения, перпендикулярной плоскости действия пар (нейтральная ось —  на определенный угол. Положим, что компоненты тензора напряжений
на определенный угол. Положим, что компоненты тензора напряжений

где а — некоторая постоянная;  расстояние точки поперечного сечения, в которой вычисляется нормальное напряжение
расстояние точки поперечного сечения, в которой вычисляется нормальное напряжение  до нейтральной оси этого сечения.
до нейтральной оси этого сечения.
Проверим, совместимы ли компоненты напряжений с основными уравнениями теории упругости. Ввиду того, что рассматриваемая задача также является простейшей задачей теории упругости, компоненты тензора напряжений (5.65) тождественно удовлетворяют соотношениям Бельтрами — Митчелла. Компоненты тензора напряжений (5.65) также удовлетворяют уравнениям упругого равновесия.
На боковой поверхности бруса, где  на основании формул (2.22) с учетом (5.65) будем иметь
на основании формул (2.22) с учетом (5.65) будем иметь

Таким образом, боковая поверхность должна быть свободна от внешних сил, что имеет место в действительности.
В крайних сечениях, где  также на основании формул (2.22) с учетом (5.65) имеем
также на основании формул (2.22) с учетом (5.65) имеем

Формулы (5.66) показывают, что в крайних сечениях бруса должны быть приложены только нормальные напряжения, распределенные по закону (5,66). Главный вектор и главный момент этих сил будут

Учитывая, что оси  направлены вдоль главных центральных осей инерции поперечного сечения, статический момент относительно оси
направлены вдоль главных центральных осей инерции поперечного сечения, статический момент относительно оси  и центробежный момент инерции площади сечения относительно осей
и центробежный момент инерции площади сечения относительно осей  равны нулю, окончательно имеем
равны нулю, окончательно имеем

где  момент инерции площади сечения относительно нейтральной оси
момент инерции площади сечения относительно нейтральной оси 
На практике осуществить передачу внешних сил по закону (5.66) не представляется возможным; поэтому, исходя из принципа Сен-Венана, вместо этих сил можно взять нагрузку в виде изгибающих моментов так, чтобы было выполнено условие эквивалентности

откуда

и, таким образом,

На основании обобщенного закона Гука для компонентов тензора деформаций будем иметь

Поместим начало координат в центре тяжести левого крайнего сечения, в котором закрепим брус так, чтобы удовлетворялись условия

Тогда из (3.44) с учетом условий закрепления и формул (5.67) после некоторых преобразований для определения перемещений получим формулы

Ось бруса до деформации  как показывают формулы (5.68), оставаясь в плоскости
как показывают формулы (5.68), оставаясь в плоскости  называемой плоскостью изгиба, после деформации обращается в параболу
называемой плоскостью изгиба, после деформации обращается в параболу

Кривизна упругой линии с точностью до малых величин высшего порядка равна

Подставляя выражение  получаем формулу
получаем формулу

определяющую кривизну оси бруса, пропорциональную величина изгибающего момента. Так как кривизна постоянна, то упругая лнвия — парабола с точностью до малых величин высшего порядка может быть заменена окружностью.
Как следует из формулы для перемещения  любое поперечное сечение
любое поперечное сечение  после деформации переходит в плоское сечение.
после деформации переходит в плоское сечение.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
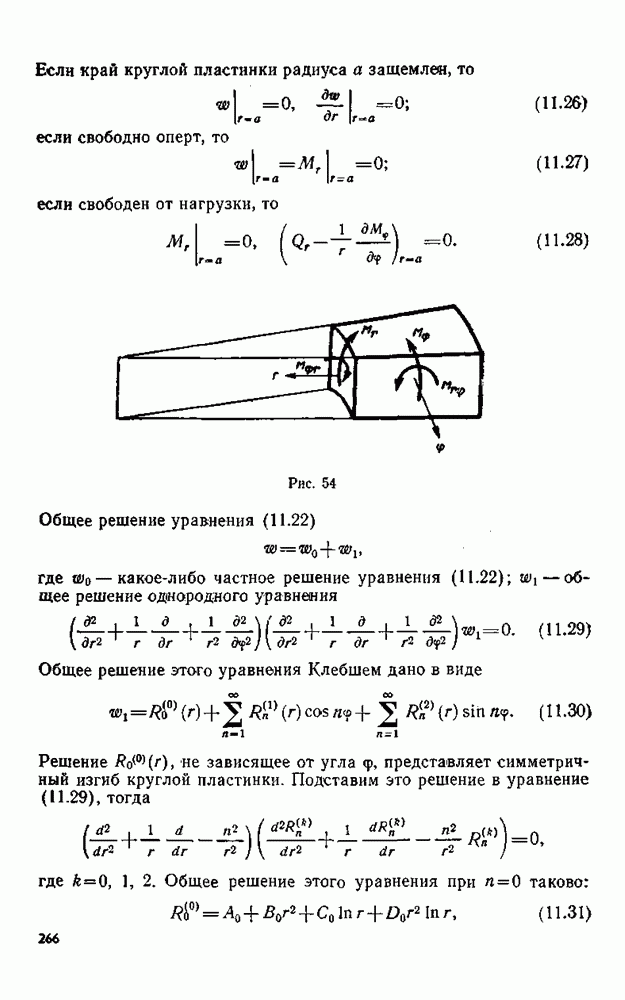
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки