Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ

§ 15. Тензор конечной деформации

Рассмотрим непрерывную среду в которой выбрана криволинейная система координат ). Если совокупность некоторых функций координат определяет удлинение любого бесконечно малого прямолинейного материального отрезка, проходящего через заданную точку, то будем говорить, что эти функции определяют деформацию окрестности этой точки.

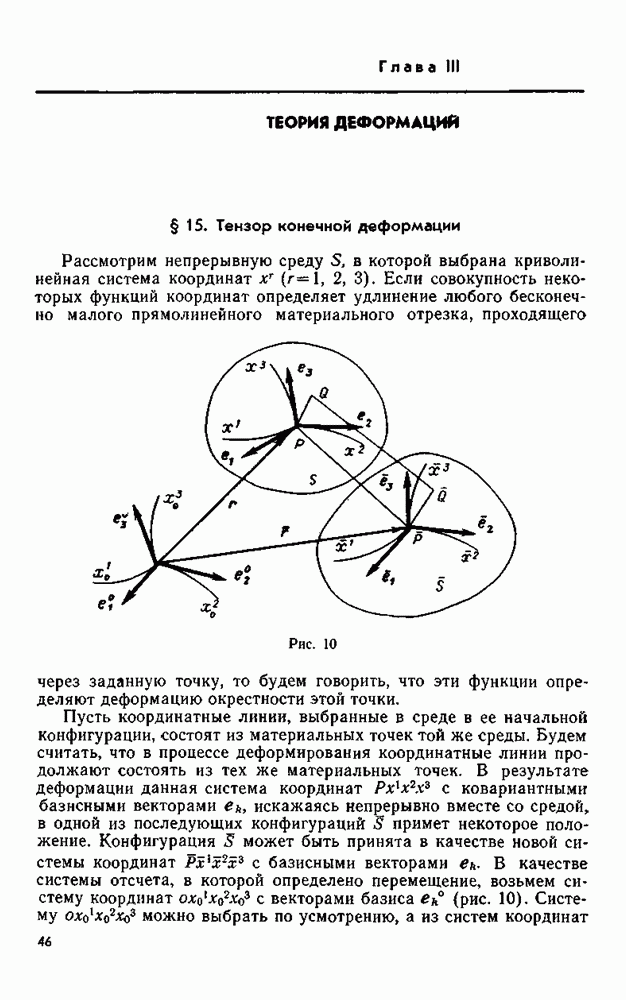
Рис. 10

Пусть координатные линии, выбранные в среде в ее начальной конфигурации, состоят из материальных точек той же среды. Будем считать, что в процессе деформирования координатные линии продолжают состоять из тех же материальных точек. В результате деформации данная система координат с ковариантными базисными векторами искажаясь непрерывно вместе со средой, в одной из последующих конфигураций примет некоторое положение. Конфигурация может быть принята в качестве новой системы координат с базисными векторами . В качестве системы отсчета, в которой определено перемещение, возьмем систему координат с векторами базиса (рис. 10). Систему можно выбрать по усмотрению, а из систем координат

произвольно можно выбрать только одну: если выбрана система то система определится деформацией наоборот.

Согласно формуле (1.27) для квадратов линейных элементов конфигураций соответственно имеем

Здесь ковариантные метрические тензоры соответственно в компоненты бесконечно малого вектора определяющего положение точки относительно точки компоненты вектора (см. рис. 10), который в силу непрерывности является бесконечно малым.

Деформированное состояние тела определяется разностью

На основании (1.6) этой разности придадим вид

где

в свою очередь,

Из (3.2) видно, что являются компонентами симметричного коварнантного тензора второго ранга, который называется тензором деформации. Когда все для всех точек, то и тело не деформируется. Относительное удлинение линейного элемента адоль координатной линии по определению, равно

Согласно формулам (1.40)

Учитывая (3.6) в (3,5), получим

Отсюда, используя (3.3), найдем

Здесь по индексу суммирование не производится; корень взят со знаком плюс, так как при относительное удлинение равно нулю.

Косинус угла между двумя линейными элементами которые до деформации были направлены вдоль координатных линий согласно формулам (1.54), (1.6) и (3.6) определится по формуле

В силу (3.4) этой формуле придадим вид

Определив из и подставив в последнюю формулу, найдем

Формулы (3.7) и (3.8) показывают, что шесть компонентов тензора деформаций, определяемые формулами (3.3), позволяют полностью вычислить удлинения вдоль координатных линий, исходящих из некоторой точки тела, и угол между двумя линейными элементами после деформации, которые до деформации были направлены вдоль координатных линий Так как угол между координатными линиями до деформации известен, то определится и изменение этого угла.

Теперь через компоненты вектора перемещения и определим компоненты тензора деформации Из рис. 10 видно, что

Пусть с являются соответственно базисными векторами, тогда на основании (1.26)

Из векторного уравнения (3.9) следует

Подставляя (3.10) в последние соотношения, будем иметь

Так как для конфигурации соответственно

то на основании правил скалярного умножения и формул найдем

Подставив (3.12) в (3.3), получим

Относительно системы координат вектор и представим в виде

здесь суммирование производится по индексу а. Тогда, учитывая (1.57), (1.79), (1.65) и (1.80), найдем

где есть ковариантные производные соответственно контравариантного и ковариантного векторов, равные

Следует отметить, что здесь символы Кристоффеля должны быть вычислены по метрическим тензорам для конфигурации 5. Подставляя (3.15) в (3.13) окончательно будем иметь

По формулам (3.17) при помощи ковариантных производных ковариантных и контравариантных компонентов вектора перемещения и в системе направлений базисных векторов вычисляются компоненты тензора деформации.