| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 58. Решение бигармонического уравнения для невесомой полуплоскости
Для решения плоской задачи теории упругости в случае отсутствия массовых сил, как было установлено в § 42, приходится интегрировать двумерное бигармоническое уравнение (6.26). Решение этого уравнения приведем для полуплоскости, ограниченной прямой. Пусть эта полуплоскость в прямоугольной системе координат занимает область 
Умножим (6.26) на  и проинтегрируем по переменной от
и проинтегрируем по переменной от  до
до  тогда
тогда

На основании формулы (6.220) равенству (6.237) придадим вид

или

где

Корни характеристического уравнения дифференциального уравнения (6.238) равны

Тогда общее решение (6.238) будет иметь вид

Для получения ограниченного решения необходимо положить  при этом
при этом

Коэффициенты  определяются граничными условиями задачи. По формуле обращения Фурье (6.217) и (6.239) найдем
определяются граничными условиями задачи. По формуле обращения Фурье (6.217) и (6.239) найдем

Таким образом, функцию напряжений можно получить квадратурой.
Умножим формулы Эри (6.24) на  и проинтегрируем по аргументу
и проинтегрируем по аргументу  от
от  до
до  учитывая формулы (6.216), (6.220) и (6.239), найдем
учитывая формулы (6.216), (6.220) и (6.239), найдем

Из (6.242), (6.243) и (6.244) по формуле обращения Фурье получим

Этим методом решим две задачи.
1. Полуплоскость, к границе которой приложена распределенная сила. Примем ось  за границу полуплоскости и направим ось
за границу полуплоскости и направим ось  внутрь этой полуплоскости. Допустим, что на границе
внутрь этой полуплоскости. Допустим, что на границе  заданы
заданы  и на полуплоскость не действуют массовые силы. Будем считать, что при
и на полуплоскость не действуют массовые силы. Будем считать, что при  компоненты тензора напряжений стремятся к нулю. В решении (6.240) интегральные постоянные
компоненты тензора напряжений стремятся к нулю. В решении (6.240) интегральные постоянные  определятся из граничных условий
определятся из граничных условий

Умножим эти условия на  и проинтегрируем по переменной
и проинтегрируем по переменной  тогда при
тогда при  будем иметь
будем иметь

Подставляя (6.240) в (6.242) и (6.244), из граничных условий (6.246) найдем

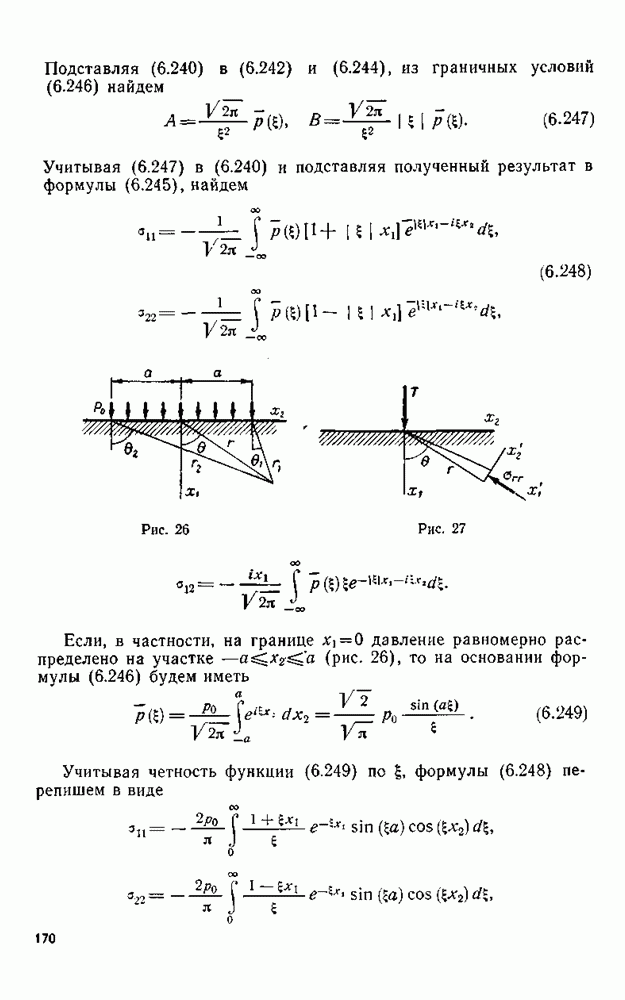
Учитывая (6.247) в (6.240) и подставляя полученный результат в формулы (6.245), найдем


Рис. 26

Рис. 27

Если, в частности, на границе  давление равномерно распределено на участке —
давление равномерно распределено на участке —  (рис. 26), то на основании формулы (6.246) будем иметь
(рис. 26), то на основании формулы (6.246) будем иметь

Учитывая четность функции (6.249) по  формулы (6.248) перепишем в виде
формулы (6.248) перепишем в виде


Вычисляя теперь эти интегралы, найдем компоненты тензора напряжений

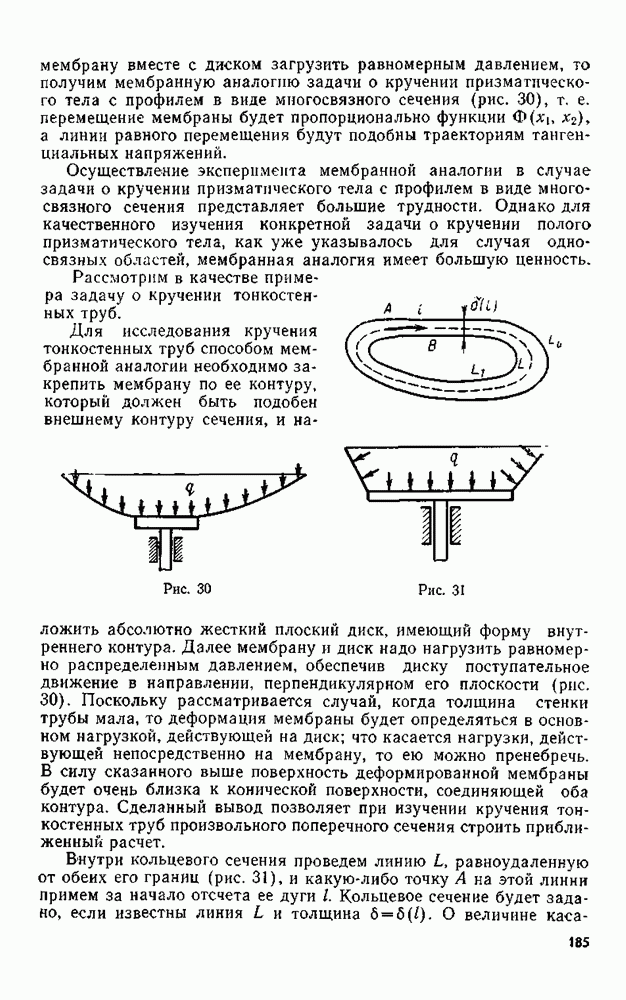
где, согласно рис. 26,

2. Полуплоскость, к границе которой приложена сосредоточенная сила. Рассмотрим распределение напряжений в полуплоскости (рис. 27), к границе которой в начале координат приложена в направлении оси  сосредоточенная сила
сосредоточенная сила  а массовые силы отсутствуют. Решение этой задачи может быть получено из решения (6.248), если в формуле (6.249) предположить, что
а массовые силы отсутствуют. Решение этой задачи может быть получено из решения (6.248), если в формуле (6.249) предположить, что  и
и  Тогда
Тогда

Учитывая (6.251) в формулах (6.248), после вычислений интегралов найдем

где

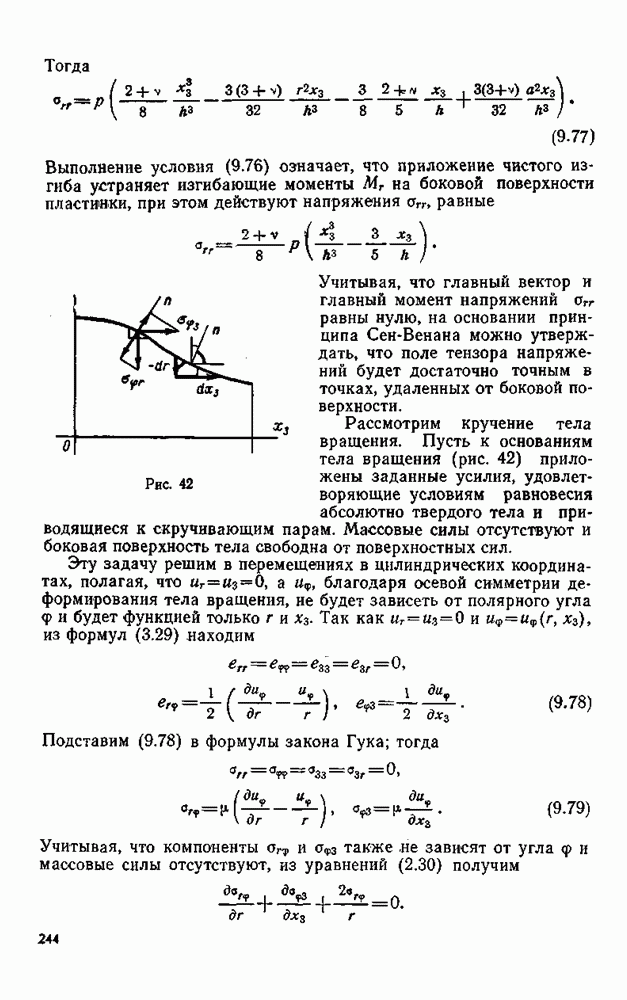
При  компоненты тензора напряжений беспредельно возрастают. Вычислим нормальное и тангенциальное напряжения в площадке, перпендикулярной к радиусу-вектору. Возьмем за повернутые оси координат оси, совпадающие с направлениями нормали и касательной к данной площадке (рис. 27). На основании формул (1.13)
компоненты тензора напряжений беспредельно возрастают. Вычислим нормальное и тангенциальное напряжения в площадке, перпендикулярной к радиусу-вектору. Возьмем за повернутые оси координат оси, совпадающие с направлениями нормали и касательной к данной площадке (рис. 27). На основании формул (1.13)

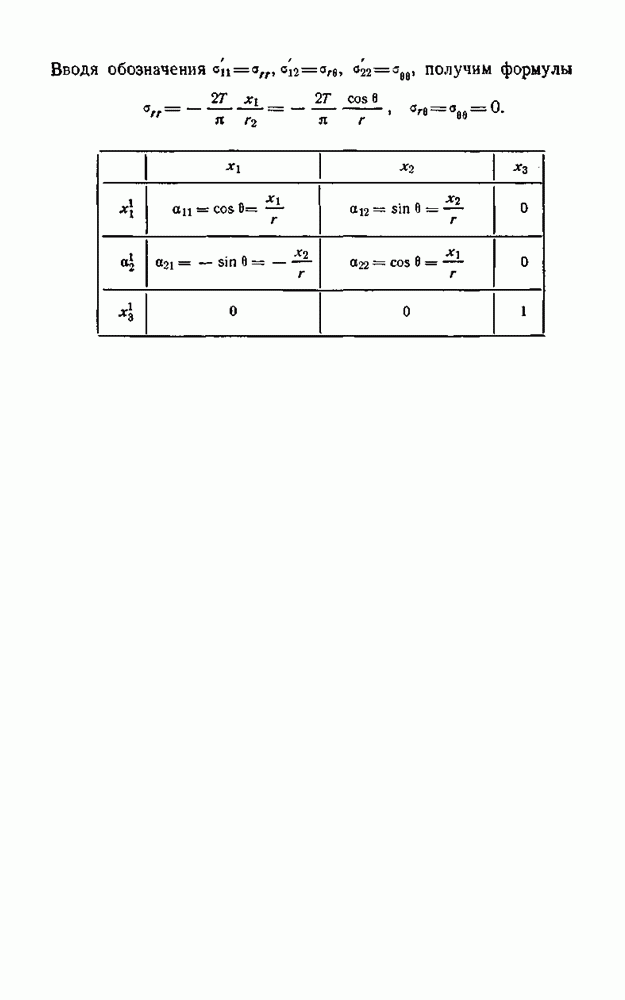
и таблицы находим

Вводя обозначения  получим формулы
получим формулы

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
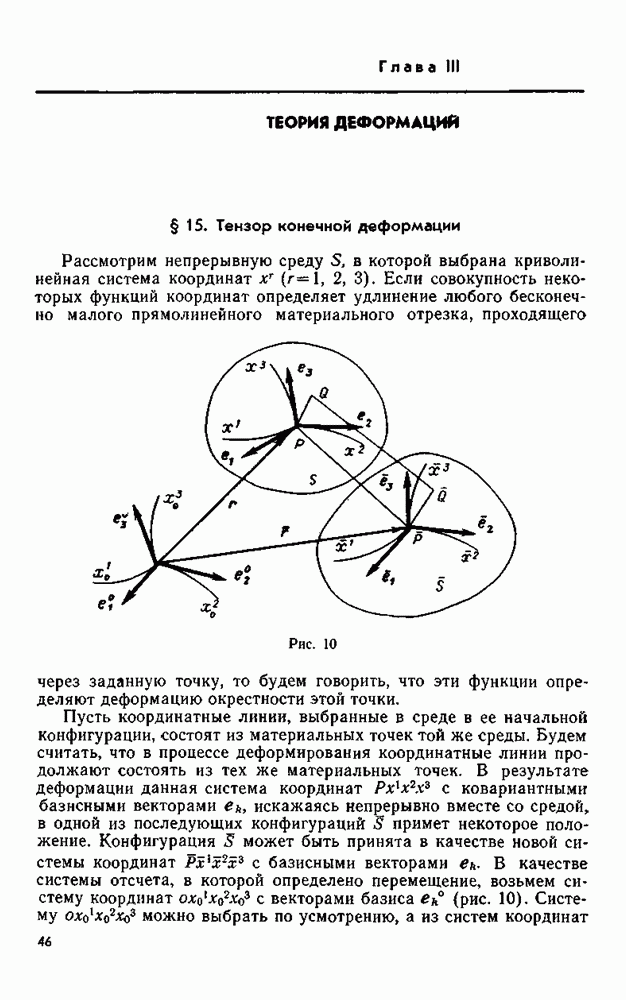
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки