| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 79. Симметричная деформация тела вращения
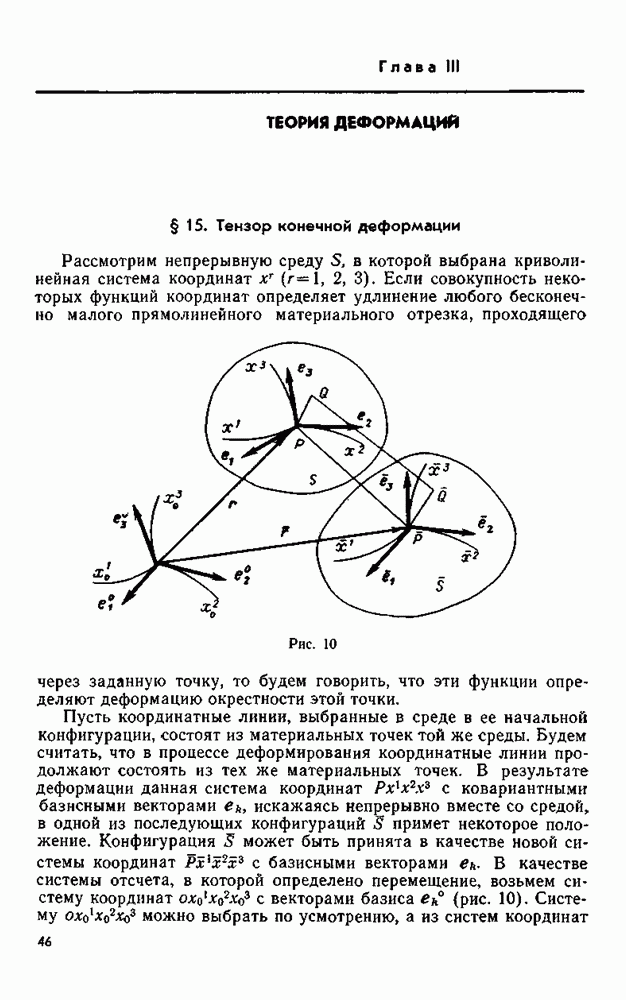
Пусть тело, представляющее собой тело вращения около оси  деформируется под действием поверхностных сил (массовые силы отсутствуют) симметрично относительно этой оси вращения. Тогда перемещение в направлении, перпендикулярном плоскости, проходящей через ось
деформируется под действием поверхностных сил (массовые силы отсутствуют) симметрично относительно этой оси вращения. Тогда перемещение в направлении, перпендикулярном плоскости, проходящей через ось  будет равно нулю, а две другие проекции
будет равно нулю, а две другие проекции  не будут зависеть от полярного угла
не будут зависеть от полярного угла  Для решения этой задачи удобно пользоваться цилиндрическими координатами
Для решения этой задачи удобно пользоваться цилиндрическими координатами  Компоненты симметрического тензора деформаций в цилиндрической системе координат, согласно формулам (3.29), будут иметь вид
Компоненты симметрического тензора деформаций в цилиндрической системе координат, согласно формулам (3.29), будут иметь вид

Подставим (9.50) в формулы закона Гука и выразим коэффициенты Ляме  через
через  ; тогда будем иметь
; тогда будем иметь

Если положить

то формулы (9.51) примут вид

где  -функция напряжений.
-функция напряжений.
Функции (9.53) тождественно удовлетворяют первым двум дифференциальным уравнениям равновесия (2.30), а третье уравнение принимает вид

При этом условии функции (9.53) тождественно удовлетворяют уравнениям совмеспности (5.37), Таким образом, задача симметричной деформации тела вращения сводится к нахождению решения бигармонического уравнения, удовлетворяющего соответствующим граничным условиям.
Приведем решение задачи о симметричной деформации сплошного круглого цилиндра, возникшей под действием сил, приложенных на его боковой поверхности и симметрично распределенных
относительно его оси. Для решения этой задачи определим из уравнения (9.54) функцию напряжений  Очевидно, решение уравнения
Очевидно, решение уравнения

будет также решением уравнения (9.54). Это решение можно взять в виде

Тогда из уравнения (9.55) для функции  получим обыкновенное дифференциальное уравнение
получим обыкновенное дифференциальное уравнение

Учитывая, что одно из фундаментальных решений уравнения (9.57) обращается в бесконечность при  будем интересоваться ограниченным решением, которое имеет вид
будем интересоваться ограниченным решением, которое имеет вид

Ряд в скобках выражения (9.58) называется бесселевой функцией нулевого порядка с мнимым аргументом  и обозначается символом
и обозначается символом  тогда вместо (9.56) будем иметь
тогда вместо (9.56) будем иметь

Производная от бесселевой функции по мнимому аргументу  с отрицательным знаком называется бесселевой функцией первого порядка и обозначается символом
с отрицательным знаком называется бесселевой функцией первого порядка и обозначается символом  Непосредственной проверкой легко установить, что имеет место соотношение
Непосредственной проверкой легко установить, что имеет место соотношение

если

Учитывая, что функция  является решением уравнения (9.57), придем к заключению, что функция
является решением уравнения (9.57), придем к заключению, что функция  является решением уравнения
является решением уравнения

Следовательно, решение уравнения (9.54) можно представить в виде

Таким образом, на основании (9.59) и (9.60), функцию напряжений можно представить в виде

Подставив эту функцию напряжений  в формулы (9.52), найдем компоненты тензора напряжений; например, для
в формулы (9.52), найдем компоненты тензора напряжений; например, для  будем иметь
будем иметь

где  вполне определенные функции, выраженные через
вполне определенные функции, выраженные через  и
и  которые здесь не приводятся.
которые здесь не приводятся.
На основании (9.62) граничные условия на боковой поверхности цилиндра будут

Соответствующим подбором постоянных  можно изучить различные случаи симметричной относительно оси цилиндра нагрузки, действующей на его боковой поверхности. Напрнмер, для случая, когда на боковую поверхность цилиндра действуют нормальные давления
можно изучить различные случаи симметричной относительно оси цилиндра нагрузки, действующей на его боковой поверхности. Напрнмер, для случая, когда на боковую поверхность цилиндра действуют нормальные давления  касательные силы
касательные силы  и когда
и когда  длина цилиндра), из формул
длина цилиндра), из формул  найдем
найдем

Отсюда получим значения постоянных с] и  Если решение уравнения (9.54) взять в виде
Если решение уравнения (9.54) взять в виде

то соответствующим подбором постоянных  получим решение задачи, когда на боковую поверхность цилиндра действуют нормальные давления
получим решение задачи, когда на боковую поверхность цилиндра действуют нормальные давления  и касательные силы
и касательные силы  .
.
Таким образом, комбинируя решения (9.61) и (9.65) и пользуясь принципом сложения действия сил, мы можем получить любое симметричное относительно оси цилиндра распределение нормальных и касательных сил на его боковой поверхности. При этом на торцах цилиндра могут возникнуть некоторые силы, распределенные симметрично относительно оси цилиндра. Налагая на эти силы осевую растягивающую или сжимающую силу, всегда можем добиться того, чтобы равнодействующая всех сил обращалась в нуль. Согласно принципу Сен-Венана влиянием этих сил на напряженное состояние на некотором расстоянии от торцов можно пренебречь.
Теперь рассмотрим задачу об изгибе круглой пластинки постоянной толщины.
Известно, что в сферической системе координат в случае осевой симметрии битарионическое уравнение таково

Рассмотрим сначала уравнение Лапласа

и найдем его частные решения в виде

где  целое положительное число.
целое положительное число.
Подставим (9.67) в (9.68), тогда

Замена независимой переменной  приводит уравнение (9.69) к уравнению Лежандра
приводит уравнение (9.69) к уравнению Лежандра

решение которого ищем в виде многочлена

Подставив это выражение в уравнение (9.70), Найдем

Отсюда

Следовательно,

Подставим это решение в (9.68). Учитывая, что

при  получим следующие решения уравнения (9.67):
получим следующие решения уравнения (9.67):


Здесь  неизвестные постоянные коэффициенты. Эти решения являются, очевидно, также решениями уравнения (9.66).
неизвестные постоянные коэффициенты. Эти решения являются, очевидно, также решениями уравнения (9.66).
Если  является решением уравнения (9.67), то легко установить, что
является решением уравнения (9.67), то легко установить, что  является решением уравнения (9.66). Действительно,
является решением уравнения (9.66). Действительно,

Подставим последнее соотношение в уравнение (9.66), тогда, учитывая, что  является решением уравнения (9.67), будем иметь
является решением уравнения (9.67), будем иметь

 последовательно, умножением решений (9.71) на
последовательно, умножением решений (9.71) на  получим решения уравнения (9.66), которые уже не будут решениями уравнения (9.67)
получим решения уравнения (9.66), которые уже не будут решениями уравнения (9.67)

С помощью предыдущих решений рассмотрим различные случаи симметрично нагруженной круглой пластинки (рис. 41).
а) На основании (9.71) и (9.72) функцию напряжений  представим в виде полинома третьей степени
представим в виде полинома третьей степени

Подставим эту функцию в формулы (9.53), тогда



Рис. 41
Таким образом, для функции напряжений (9.73) компоненты тензора напряжений являются постоянными по всей пластинке. Постоянные  определятся, если на торцах и боковой поверхности пластинки соответственно заданы равномерно распределенные
определятся, если на торцах и боковой поверхности пластинки соответственно заданы равномерно распределенные 
б) Теперь при помощи (9.71) и (9.72) функцию напряжений представим в виде

На основании формул (9.53) получим

Если положить  тогда
тогда

Постоянная 64 определится, если на боковой поверхности пластинки задано постоянное значение изгибающего момента  Тогда
Тогда

Данное условие является интегральным, но согласно принципу Сен-Венана найденное напряженное состояние будет достаточно точным в точках, удаленных от боковой поверхности пластинки.
Из последнего соотношения найдем

Тогда

Это решение представляет чистый изгиб пластинки моментами, равномерно распределенными по ее боковой поверхности.
в) Исходя из (9.71) и (9.72), возьмем функцию напряжений

Для этой функции напряжения таковы

К напряжениям  прибавим равномерное в направлении оси
прибавим равномерное в направлении оси  растяжение
растяжение  тогда получим компоненты тензора напряжений, которые содержат четыре постоянных
тогда получим компоненты тензора напряжений, которые содержат четыре постоянных  и
и 
Пусть имеем граничные условия

 интенсивность равномерной нагрузки.
интенсивность равномерной нагрузки.
Подставив в эти граничные условия выражения тензора напряжений, определим постоянные  и
и  Следовательно,
Следовательно,

Напряжения  на боковой поверхности пластинки дают изгибающие моменты
на боковой поверхности пластинки дают изгибающие моменты  равномерно распределенные по контуру.
равномерно распределенные по контуру.
Чтобы получить решение для свободно опертой пластинки, к компонентам тензора напряжений (9.75) прибавим напряжении чистого изгиба, и постоянную  определим так, чтобы на боковой поверхности
определим так, чтобы на боковой поверхности 

Тогда

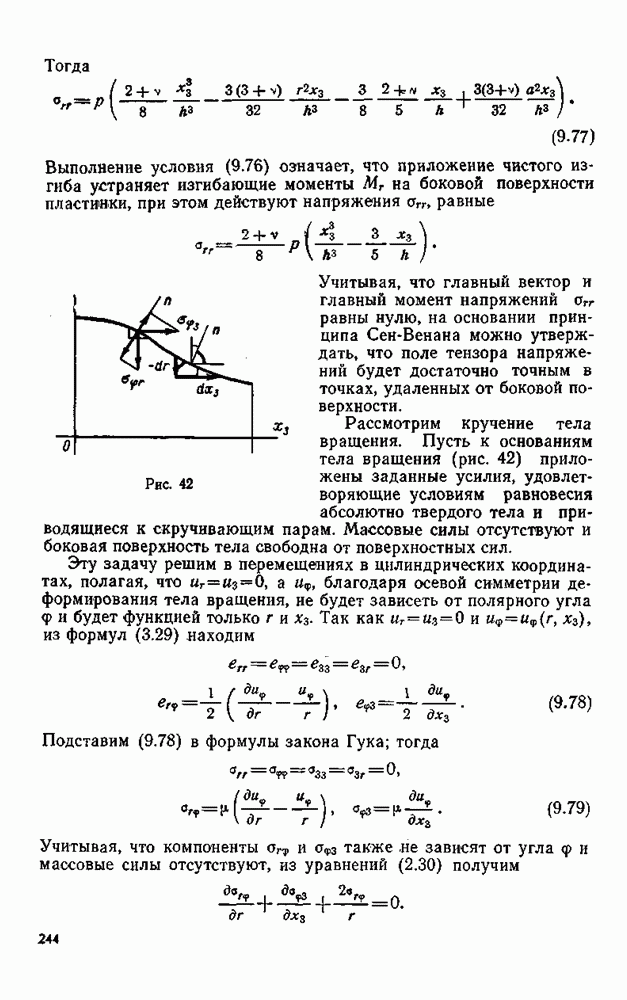
Выполнение условия (9.76) означает, что приложение чистого изгиба устраняет изгибающие моменты  на боковой поверхности пластинки, при этом действуют напряжения
на боковой поверхности пластинки, при этом действуют напряжения  равные
равные

Учитывая, что главный вектор и главный момент напряжений  равны нулю, на основании принципа Сен-Венана можно утверждать, что поле тензора напряжений будет достаточно точным в точках, удаленных от боковой поверхности.
равны нулю, на основании принципа Сен-Венана можно утверждать, что поле тензора напряжений будет достаточно точным в точках, удаленных от боковой поверхности.

Рис. 42
Рассмотрим кручение тела вращения. Пусть к основаниям тела вращения (рис. 42) приложены заданные усилия, удовлетворяющие условиям равновесия абсолютно твердого тела и приводящиеся к скручивающим парам. Массовые силы отсутствуют и боковая поверхность тела свободна от поверхностных сил.
Эту задачу решим в перемещениях в цилиндрических координатах, полагая, что  благодаря осевой симметрии деформирования тела вращения, не будет зависеть от полярного угла
благодаря осевой симметрии деформирования тела вращения, не будет зависеть от полярного угла  и будет функцией только
и будет функцией только  Так как
Так как  из формул (3.29) находим
из формул (3.29) находим

Подставим (9.78) в формулы закона Гука; тогда

Учитывая, что компоненты  также не зависят от угла
также не зависят от угла  и массовые силы отсутствуют, из уравнений (2,30) получим
и массовые силы отсутствуют, из уравнений (2,30) получим

Последнему уравнению придадим вид

Решение уравнения (9.80) будет

Здесь функция  называемая функцией напряжений, определится из уравнений совместности.
называемая функцией напряжений, определится из уравнений совместности.
Условия совместности деформаций (3.40) с учетом (9.79) для данной задачи примут вид

С учетом (9.81) второе уравнение примет вид

Последнее удовлетворяется, если

Непосредственной проверкой легко убедиться, что при условии (9.82) первое уравнение удовлетворяется тождественно. Таким образом, условие совместности деформаций для данной задачи имеет вид (9.82),
Граничное условие для функции  определится из следующего рассуждения. В силу того, что боковая поверхность бруса свободна от поверхностных сил, сумма проекций касательных напряжений
определится из следующего рассуждения. В силу того, что боковая поверхность бруса свободна от поверхностных сил, сумма проекций касательных напряжений  действующих в точках границы осевого сечения на нормаль к границе (рис, 42), должна обращаться в нуль, т. е.
действующих в точках границы осевого сечения на нормаль к границе (рис, 42), должна обращаться в нуль, т. е.

Согласно рис. 42 имеем

где  элемент дуги границы.
элемент дуги границы.
Подставляя (9.81) и (9.84) в граничное условие (9.83), найдем

откуда  или
или 
Величина крутящего момента связана с функцией  соотношением
соотношением

Если тело вращения имеет форму конуса (рис. 43), то на поверхности его имеет место соотношение


Рис. 43
Очевидно, любая функция аргумента, представляющего собой левую часть (9.86), будет величиной постоянной на поверхности конуса. Попытаемся функцию напряжений искать в виде

где  неизвестные постоянные.
неизвестные постоянные.
На основании вышесказанного эта функция на поверхности конуса удовлетворяет условию  Функция (9.87) удовлетворяет уравнению (9.82), если принять
Функция (9.87) удовлетворяет уравнению (9.82), если принять

Таким образом,

Постоянную А определяем из (9.85)

Согласно формулам (9.81) касательные напряжения будут

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
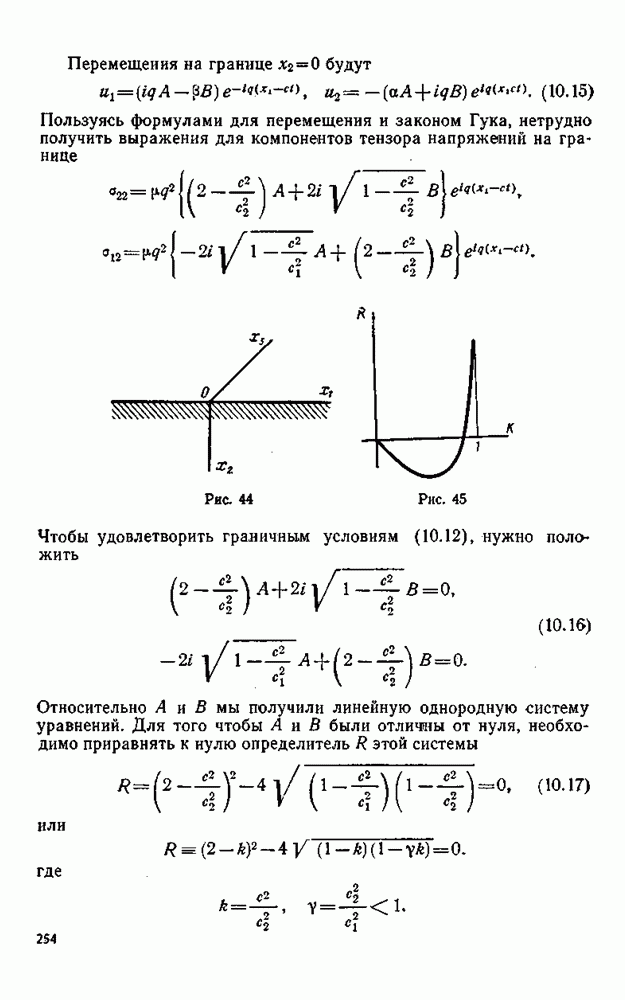
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
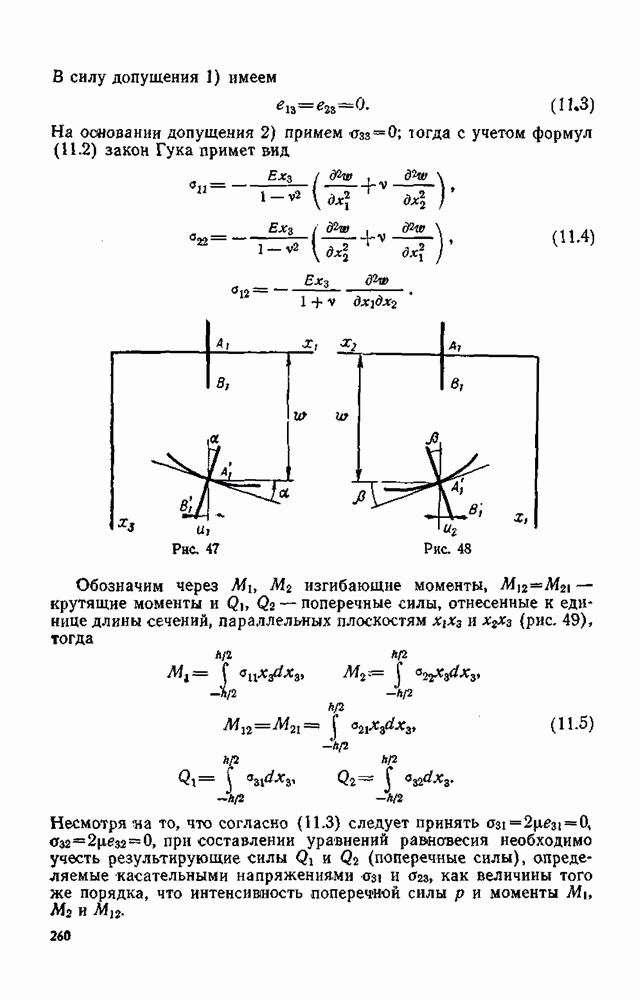
- § 84. Дифференциальное уравнение изгиба тонких пластинок
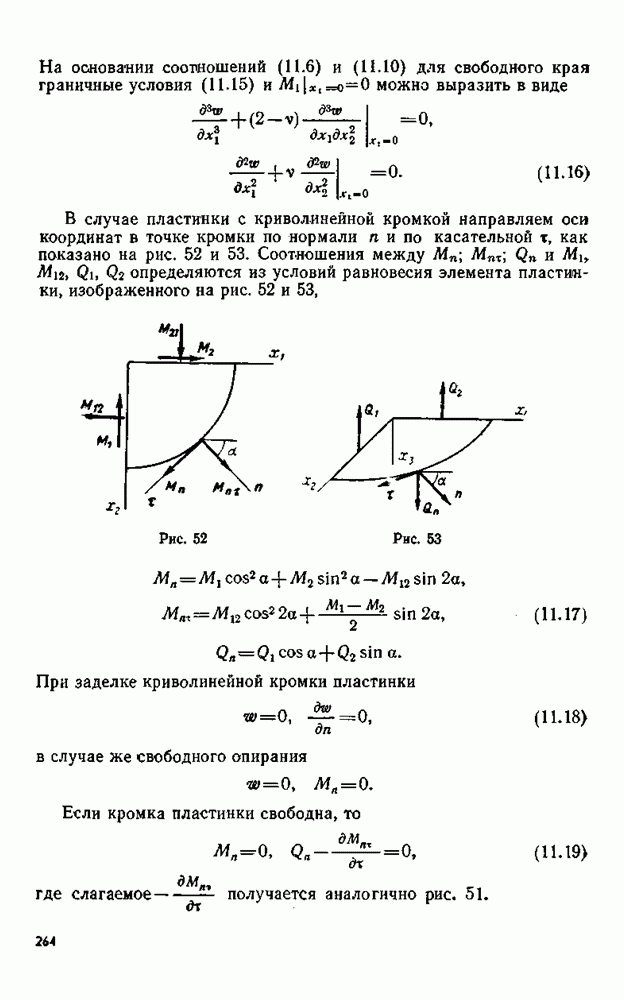
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки