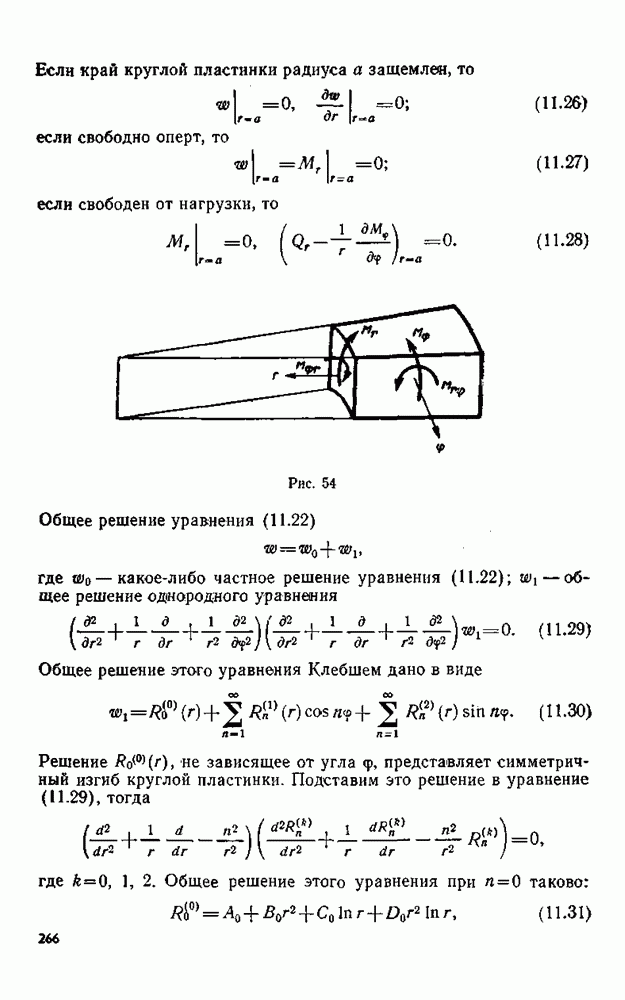
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
Под основными граничными задачами плоской теории упругости, аналогично тому, как для трехмерного тела (§ 34), мы будем понимать следующие задачи:
Первая основная задача. Определение упругого равновесия, когда заданы внешние силы, приложенные к границе  области 5.
области 5.
Вторая основная задача. Определение упругого равновесия, когда заданы перемещения точек границы 
Основная смешанная задача. Определение упругого равновесия, когда на одной части границы заданы приложенные к ней силы, а на другой — перемещения точек.
Если область 5 бесконечна, то в случае первой основной задачи должны быть заданы напряжения на бесконечности, т. е.  и
и  в случае же второй основной задачи и основной смешанной задачи — величины
в случае же второй основной задачи и основной смешанной задачи — величины  Допуская, что решение указанных задач существует, его единственность для конечной области можно доказать аналогично доказательству, приведенному в случае соответствующих пространственных задач; на доказательстве теоремы единственности для бесконечной области мы не останавливаемся; при надобности читатель сможет ознакомиться с ним в монографии Н. И. Мусхелишвили «Некоторые основные задачи математической теории упругости».
Допуская, что решение указанных задач существует, его единственность для конечной области можно доказать аналогично доказательству, приведенному в случае соответствующих пространственных задач; на доказательстве теоремы единственности для бесконечной области мы не останавливаемся; при надобности читатель сможет ознакомиться с ним в монографии Н. И. Мусхелишвили «Некоторые основные задачи математической теории упругости».
Из формул (6.67), (6.77), (6.78) видно, что решение плоской задачи теории упругости сводится к отысканию пары функций комплексного переменного  аналитических в данной области 5, при этом на ее границе
аналитических в данной области 5, при этом на ее границе  эти функции
эти функции  должны удовлетворять определенным условиям, отвечающим какой-либо из сформулированных задач.
должны удовлетворять определенным условиям, отвечающим какой-либо из сформулированных задач.
Будем считать, что граница  области
области  не пересекает себя, замкнута и в каждой точке имеет касательную. Кроме того, примем, что компоненты вектора перемещения и тензора напряжений непрерывны вплоть до границы
не пересекает себя, замкнута и в каждой точке имеет касательную. Кроме того, примем, что компоненты вектора перемещения и тензора напряжений непрерывны вплоть до границы 
1. Для первой основной задачи функции  в случае конечной односвязной области
в случае конечной односвязной области  ограниченной контуром
ограниченной контуром  должны на основании (6.74) удовлетворять краевому условию
должны на основании (6.74) удовлетворять краевому условию

Здесь  аффикс точки
аффикс точки  и
и  ее декартовы координаты, причем
ее декартовы координаты, причем

где  заданные значения проекций внешних сил, действующих на
заданные значения проекций внешних сил, действующих на 
Выражение слева в (6.109) дает граничное значение функции  когда
когда  оставаясь внутри области
оставаясь внутри области  стремится к точке
стремится к точке  контура
контура  Это граничное условие существует в силу принятого предположения о непрерывности компонентов тензора напряжений вплоть до контура
Это граничное условие существует в силу принятого предположения о непрерывности компонентов тензора напряжений вплоть до контура  (Следует отметить, что в формуле (6.74) дуга, обозначенная через А В, целиком лежит в области 5. Однако в силу предположения о непрерывности компонентов тензора напряжений вплоть до контура, мы вполне законно применили эту формулу для случая, когда дуга
(Следует отметить, что в формуле (6.74) дуга, обозначенная через А В, целиком лежит в области 5. Однако в силу предположения о непрерывности компонентов тензора напряжений вплоть до контура, мы вполне законно применили эту формулу для случая, когда дуга  принадлежит контуру
принадлежит контуру 
2. Для второй основной задачи функции  в случае той же конечной односвязной области 5, должны на основании
в случае той же конечной односвязной области 5, должны на основании
(6.67) удовлетворять на контуре  соотношению
соотношению

где  — заданные значения перемещения точки
— заданные значения перемещения точки 
Здесь, так же как и выше, левая часть равенства (6.111) представляет собой граничное значение выражения

Это граничное значение существует, так как

а по условию, принятому нами выше,  непрерывны вплоть до контура
непрерывны вплоть до контура 
3. Для первой основной задачи в случае бесконечной области  ограниченной замкнутым контуром
ограниченной замкнутым контуром  регулярные в ней функции
регулярные в ней функции  на основании условия (6.109) с учетом формул (6.104) и (6.105), должны удовлетворять краевому соотношению
на основании условия (6.109) с учетом формул (6.104) и (6.105), должны удовлетворять краевому соотношению

При этом введено обозначение

Когда точка  описывает контур
описывает контур  в положительном направлении, выражения
в положительном направлении, выражения  получают соответственно приращения
получают соответственно приращения  так что приращение выражения
так что приращение выражения  как легко убедиться, будет равно нулю. Поэтому функция
как легко убедиться, будет равно нулю. Поэтому функция  является однозначной и непрерывной на
является однозначной и непрерывной на 
4. Для второй основной задачи в случае бесконечной же области  ограниченной контуром
ограниченной контуром  для функций
для функций  на основании формулы (6.111) с учетом формул (6.104) и (6.105) будем иметь краевое условие
на основании формулы (6.111) с учетом формул (6.104) и (6.105) будем иметь краевое условие

где

Как видно из (6.115), правая часть равенства (6.114) представляет собой однозначную и непрерывную на  функцию, поскольку таковыми являются все содержащиеся в ней члены.
функцию, поскольку таковыми являются все содержащиеся в ней члены.
5. В основной смешанной задаче будем иметь условия вида  тех частях границы, где заданы проекции вектора напряжения, и условия вида (6.111) на остальных ее частях, где заданы проекции вектора перемещения.
тех частях границы, где заданы проекции вектора напряжения, и условия вида (6.111) на остальных ее частях, где заданы проекции вектора перемещения.
Выше мы убедились, что условие непрерывности компонентов тензора напряжений вплоть до границы  области 5 приводит к непрерывности вплоть до границы выражения
области 5 приводит к непрерывности вплоть до границы выражения

а условие непрерывности проекции вектора перемещения — к непрерывности вплоть до границы выражения

Очевидно, что выражение  может быть непрерывным вплоть до границы без обязательного соблюдения условия непрерывности (вплоть до границы
может быть непрерывным вплоть до границы без обязательного соблюдения условия непрерывности (вплоть до границы  компонентов тензора напряжений. Поэтому последнее условие может быть заменено более слабым условием непрерывности вплоть до границы указанного выражения.
компонентов тензора напряжений. Поэтому последнее условие может быть заменено более слабым условием непрерывности вплоть до границы указанного выражения.  дальнейшем будем считать, что для двух первых основных задач функции
дальнейшем будем считать, что для двух первых основных задач функции  непрерывно продолжимы на все точки границы
непрерывно продолжимы на все точки границы  области
области  это накладывает сильное условие на нскомые функции, но и значительно упрощает рассуждения при применении методов эффективного решения основных задач.
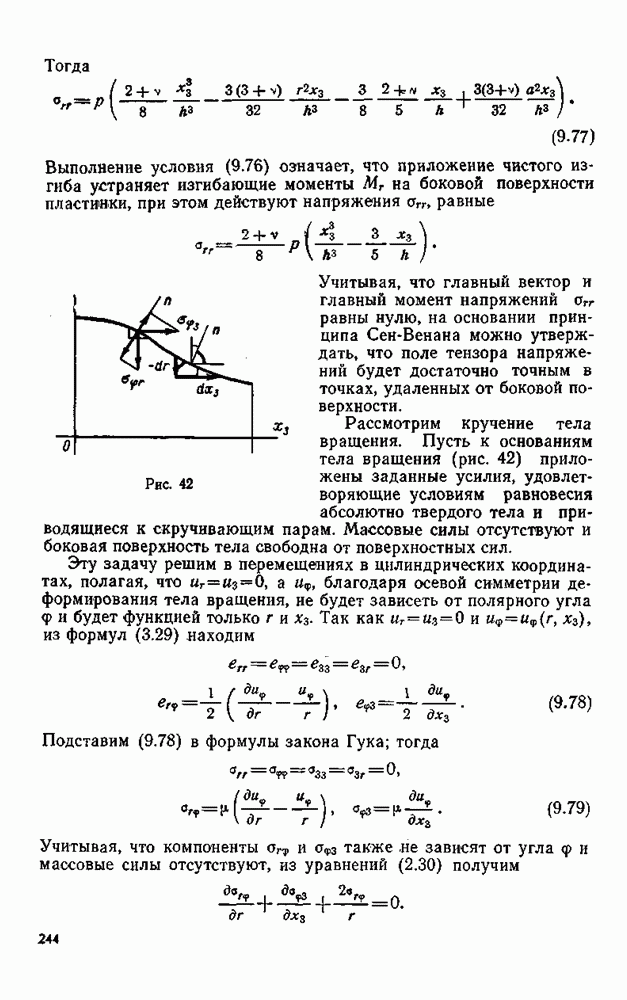
это накладывает сильное условие на нскомые функции, но и значительно упрощает рассуждения при применении методов эффективного решения основных задач.
Условие непрерывности  в случае первой основной задачи исключает разрывные внешние нагрузки, например сосредоточенные силы; для смешанной задачи функции
в случае первой основной задачи исключает разрывные внешние нагрузки, например сосредоточенные силы; для смешанной задачи функции  в отдельности не будут непрерывными в точках стыка.
в отдельности не будут непрерывными в точках стыка.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
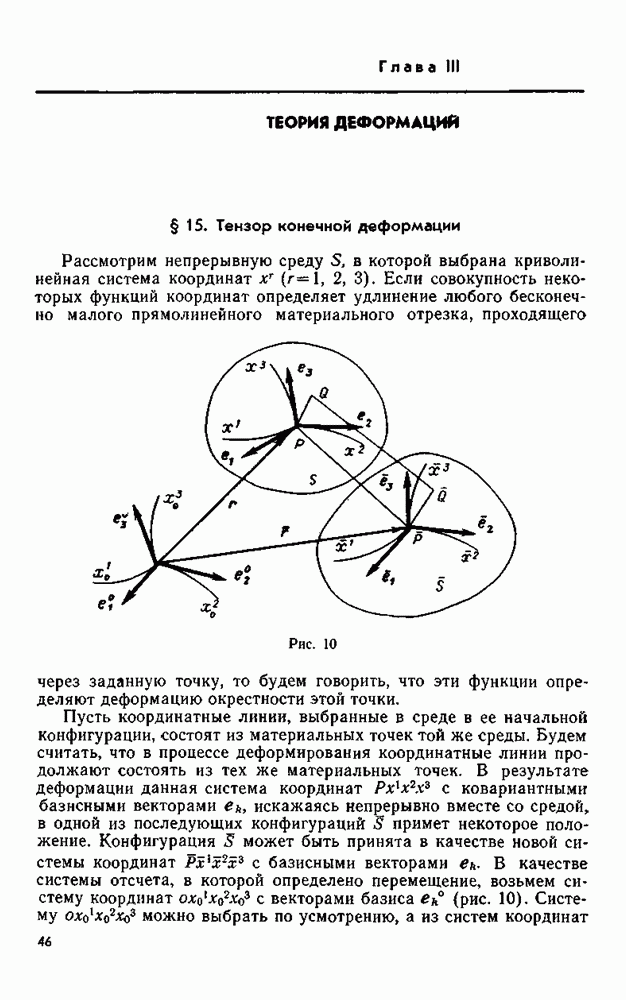
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки