| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 55. Решение граничных задач для полуплоскости
Приводим некоторые обозначения. Пусть  является некоторой функцией комплексного переменного
является некоторой функцией комплексного переменного  определенной в некоторой области плоскости
определенной в некоторой области плоскости  Тогда через
Тогда через  будем обозначать функцию, принимающую сопряженные с
будем обозначать функцию, принимающую сопряженные с  значения в точках I, сопряженных с
значения в точках I, сопряженных с 

или

где

Легко заметить, что если  голоморфна в некоторой области
голоморфна в некоторой области  то
то  голоморфна в области
голоморфна в области  представляющей собой область, симметричную области
представляющей собой область, симметричную области  относительно действительной оси. В самом деле, положим, что
относительно действительной оси. В самом деле, положим, что  голоморфна в
голоморфна в  тогда в области
тогда в области  имеет место
имеет место

Учитывая в условиях  соотношения (6.183), в области
соотношения (6.183), в области  будем иметь
будем иметь

Последние соотношения показывают, что функции  удовлетворяют условиям
удовлетворяют условиям  в области
в области 
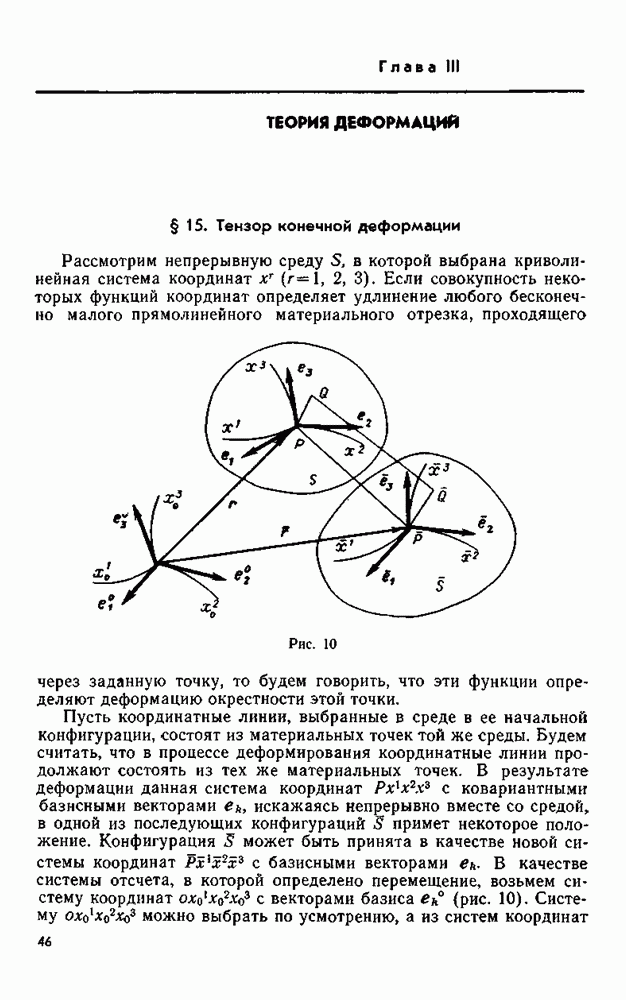
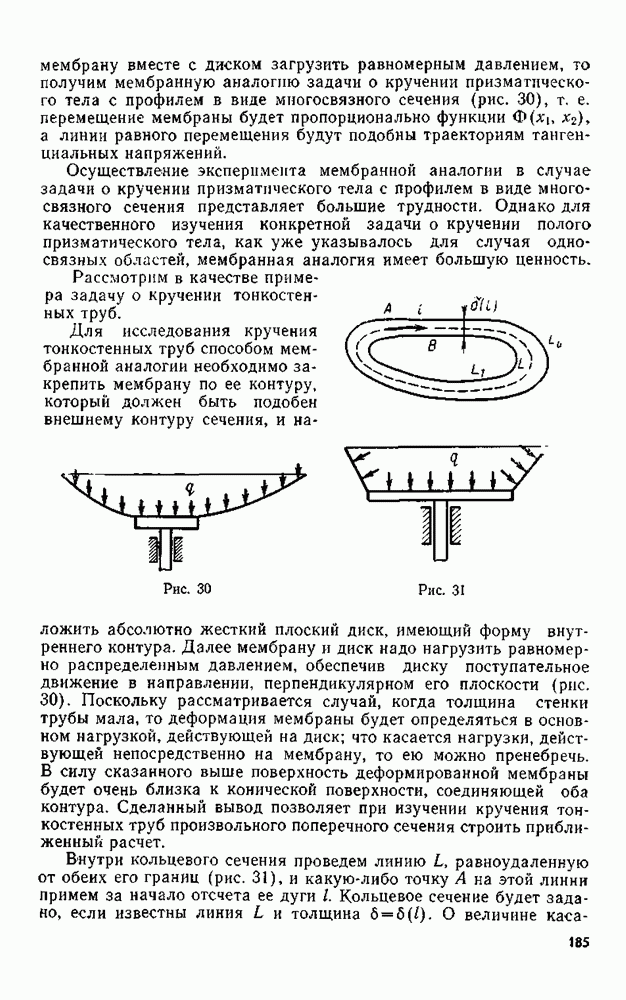
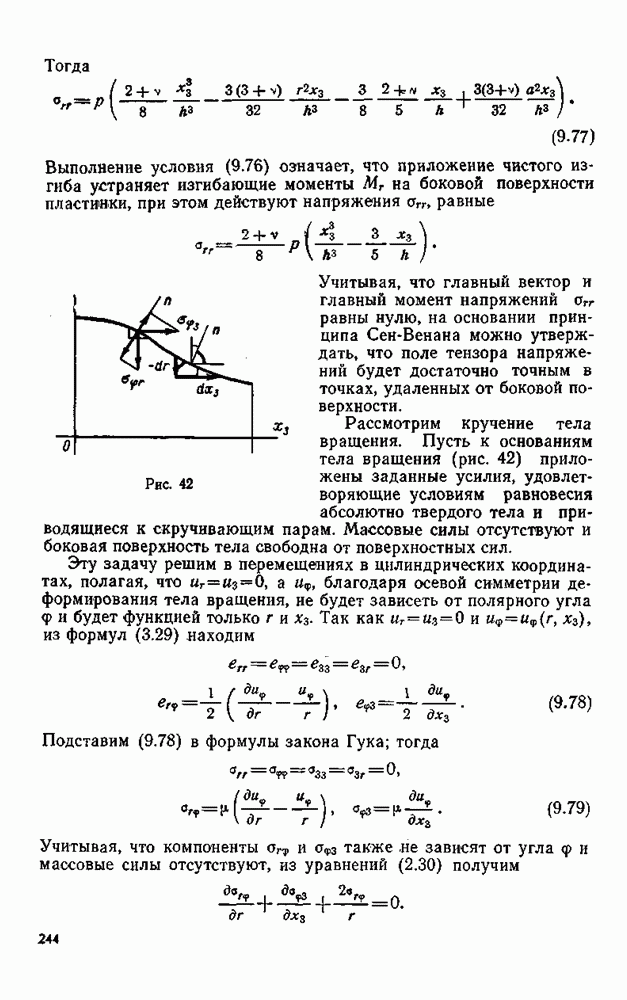
Пусть тело занимает нижнюю полуплоскость, ограниченную прямой, которую примем за ось абсцисс. Обозначим нижнюю полуплоскость  остающуюся справа, если двигаться по оси
остающуюся справа, если двигаться по оси  в положительном направлении, через
в положительном направлении, через  а верхнюю полуплоскость — через
а верхнюю полуплоскость — через 
Пусть функция  определена в
определена в  тогда функция
тогда функция  будет определена в область
будет определена в область  и пусть существует граничное значение
и пусть существует граничное значение  где аффикс некоторой точки оси
где аффикс некоторой точки оси  тогда из формулы (6.182 непосредственно следует, что существует и граничное значение
тогда из формулы (6.182 непосредственно следует, что существует и граничное значение  причем
причем

или

Пусть в области  определены комплексные потенциалы
определены комплексные потенциалы  и имеются ненагруженные отрезки границы
и имеются ненагруженные отрезки границы 
Приведем формулы (6.77), (6.78) и (6.83) к удобному для применения виду; с этой целью построим аналитическое продолжение функции  через ненагруженные отрезки границы. Из формул (6.77) и (6.78) в области имеем
через ненагруженные отрезки границы. Из формул (6.77) и (6.78) в области имеем

где

Возьмем функцию

определяемую этим равенством в области 
На основании вышесказанного ясно, что функция  определяемая равенством (6.186), будет голоморфной в области
определяемая равенством (6.186), будет голоморфной в области 
Напишем в  вместо
вместо  считая, что
считая, что  находится в и перейдем к сопряженным значениям, тогда
находится в и перейдем к сопряженным значениям, тогда

отсюда

формула (6.187) определяет функцию  в области через функцию
в области через функцию  продолженную и на верхнюю полуплоскость.
продолженную и на верхнюю полуплоскость.
На границе  выражение (6.186) (при
выражение (6.186) (при  со стороны
со стороны
области  примет вид
примет вид

Выражение (6.185) на границе  имеет вид
имеет вид

поэтому на тех участках границы, где  найдем
найдем

Сравнивая (6.188) и (6.190) и учитывая (6.184) [в силу определения  получим
получим

Следовательно, функция  определенная с помощью (6.186) в верхней полуплоскости, является аналитическим продолжением через ненагруженные участки границы голоморфной в нижней полуплоскости функции
определенная с помощью (6.186) в верхней полуплоскости, является аналитическим продолжением через ненагруженные участки границы голоморфной в нижней полуплоскости функции  иными словами, функция
иными словами, функция  определяемая формулой (6.186), представляет кусочно-голоморфную функцию по всей плоскости, разрезанной вдоль нагруженных участков границы
определяемая формулой (6.186), представляет кусочно-голоморфную функцию по всей плоскости, разрезанной вдоль нагруженных участков границы 
Из равенства, сопряженного с выражением (6.189), на ненагруженных участках следует продолжимость через них функции  Представим соотношение (6.185) в иной форме. Для этого подставим (6.187) в (6.78) и (6.185), получим удобные для применения формулы
Представим соотношение (6.185) в иной форме. Для этого подставим (6.187) в (6.78) и (6.185), получим удобные для применения формулы

Преобразуем теперь формулу (6.83). С этой целью продолжим голоморфную в области  функцию
функцию  в область
в область  так, чтобы в этой области
так, чтобы в этой области

где  дается правой частью (6.186). (Как выяснено, она при наличии ненагруженных участков аналитически продолжает сквозь них искомую функцию
дается правой частью (6.186). (Как выяснено, она при наличии ненагруженных участков аналитически продолжает сквозь них искомую функцию  регулярную в нижней полуплоскости.) Учитывая формулу (6.186), последнему соотношению придадим вид
регулярную в нижней полуплоскости.) Учитывая формулу (6.186), последнему соотношению придадим вид

при этом в области  будем иметь
будем иметь

Из этого уравнения вытекает, что в области  справедливо соотношение
справедливо соотношение

При помощи его формула (6.83) примет вид

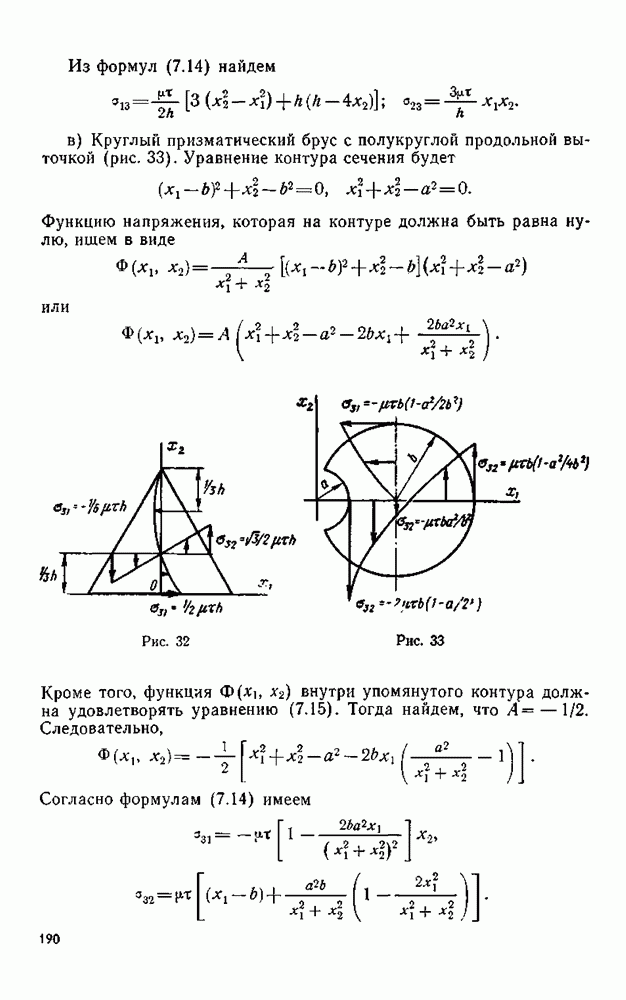
В дальнейшем будем предполагать, что кроме, быть может, конечного числа точек  функция
функция  на контуре
на контуре  непрерывна слева и справа и, кроме того,
непрерывна слева и справа и, кроме того,

для любой точки контура, тогда как вблизи точек справедливо неравенство

Эти условия обеспечивают непрерывную продолжимость тензора напряжений и вектора перемещения на все точки границы, кроме, быть может, точек 
Будем считать, что при больших  функции
функции  могут быть представлены следующим образом:
могут быть представлены следующим образом:

где  — постоянны; символ О обозначает величину такую, что
— постоянны; символ О обозначает величину такую, что  от
от  и стремится к нулю при
и стремится к нулю при  к этим условиям присоединим еще условия, что при больших
к этим условиям присоединим еще условия, что при больших  имеют место выражения:
имеют место выражения:

где

При этих соотношениях компоненты тензора напряжений на бесконечности равны нулю.
Пусть  представляет собой главный вектор сил, приложенных к отрезку
представляет собой главный вектор сил, приложенных к отрезку  границы
границы  со стороны области
со стороны области  Подставляя (6.198) в формулу (6.74), при удалении конца А влево, а конца В вправо независимо друг от друга, найдем
Подставляя (6.198) в формулу (6.74), при удалении конца А влево, а конца В вправо независимо друг от друга, найдем

Здесь  расстояния точек
расстояния точек  от начала координат и
от начала координат и  величина, стремящаяся к нулю при
величина, стремящаяся к нулю при  Для того чтобы главный вектор
Для того чтобы главный вектор  оставался конечным, когда
оставался конечным, когда 
независимо друг от друга, следует принять

тогда

С другой стороны, должно иметь место соотношение

где  — главный вектор внешних сил, приложенных ко всей границе (он будет всегда конечен, если силы приложены на конечном участке границы); следовательно,
— главный вектор внешних сил, приложенных ко всей границе (он будет всегда конечен, если силы приложены на конечном участке границы); следовательно,

Из двух линейных уравнений (6.199) и (6.200) имеем

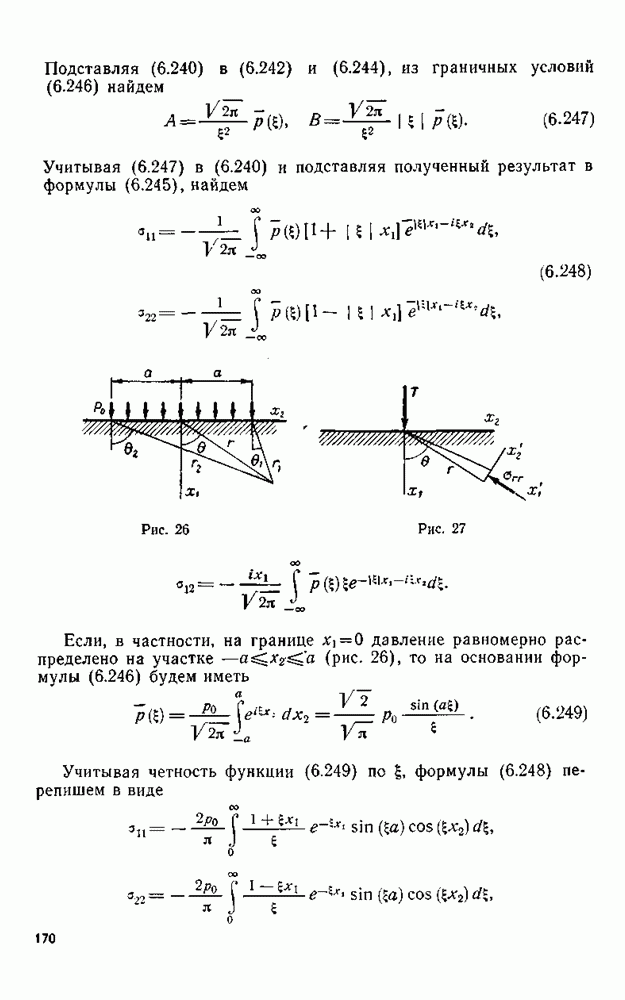
1. Решение первой основной задачи. В этой задаче на контуре  внешние силы задаются следующим образом:
внешние силы задаются следующим образом:

где  — соответственно давление и касательная сила, удовлетворяющие условию Гельдера на контуре
— соответственно давление и касательная сила, удовлетворяющие условию Гельдера на контуре  включая окрестность бесконечно удаленной точки. Кроме того,
включая окрестность бесконечно удаленной точки. Кроме того,  Согласно (6.193) и (6.195) граничное условие примет вид
Согласно (6.193) и (6.195) граничное условие примет вид

Из (6.202) видно, что решение первой основной задачи сведено к определению кусочно-голоморфной функции по заданному скачку. Решение этой задачи, исчезающее на бесконечности, согласно (6.149) будет

Зная функцию  можно по формулам (6.192), (6.193) и (6.194) определить компоненты тензора напряжений
можно по формулам (6.192), (6.193) и (6.194) определить компоненты тензора напряжений  и вектора перемещения
и вектора перемещения 
2. Решение второй основной задачи. Здесь значения компонентов вектора перемещения на контуре  задаются в виде
задаются в виде

где  — заданные функции, имеющие производные, удовлетворяющие условию Гельдера, включая и бесконечно удаленную точку, и
— заданные функции, имеющие производные, удовлетворяющие условию Гельдера, включая и бесконечно удаленную точку, и 
Продифференцируем (6.194) по  при этом граничное условие (6.204) примет вид
при этом граничное условие (6.204) примет вид

Введем кусочно-голоморфную функцию, обозначаемую через  так, чтобы
так, чтобы

Тогда граничное условие (6.205) примет вид

Из этого уравнения видно, что вторая основная задача также сведена к определению кусочно-голоморфной функции по заданному скачку; ее решение имеет вид

Таким образом, из (6.206) окончательно имеем

3. Решение основной смешанной задачи. Пусть на совокупности конечного числа  отрезков
отрезков  границы
границы  заданы проекции вектора перемещения
заданы проекции вектора перемещения  а на ее остальной части — проекции внешней силы
а на ее остальной части — проекции внешней силы  Совокупность отрезков
Совокупность отрезков  обозначим через V, остальную часть границы — через
обозначим через V, остальную часть границы — через  Поскольку нам уже известно решение первой основной задачи, то влияние заданных на
Поскольку нам уже известно решение первой основной задачи, то влияние заданных на  сил удобнее учесть отдельно; в соответствии с этим мы всегда может предполагать, что на
сил удобнее учесть отдельно; в соответствии с этим мы всегда может предполагать, что на  составляющие
составляющие 
Таким образом, краевые условия для рассматриваемой несколько видоизмененной смешанной задачи принимают вид

где  — заданная на
— заданная на  функция. Упомянутая задача связана с расчетом штампов.
функция. Упомянутая задача связана с расчетом штампов.
Если в условии (6.208) величина  является постоянной на
является постоянной на  тогда, не нарушая общности, ее можно положить равной нулю, ибо в этом случае значение с влияет только на жесткое поступательное перемещение всей системы. Здесь предпологается, что дополнительно задан главный вектор
тогда, не нарушая общности, ее можно положить равной нулю, ибо в этом случае значение с влияет только на жесткое поступательное перемещение всей системы. Здесь предпологается, что дополнительно задан главный вектор  сил, приложенных к
сил, приложенных к 
Основная смешанная задача в такой постановке соответствует случаю  жестко соединенных штампов.
жестко соединенных штампов.
В случае, когда  какие-то постоянные), можно на
какие-то постоянные), можно на  не нарушая общности, произвольно зафиксировать только одну из них, остальные же постоянные
не нарушая общности, произвольно зафиксировать только одну из них, остальные же постоянные  подлежат определению. В этом случае, в отличие от предыдущего, предполагается, что заданы главные векторы
подлежат определению. В этом случае, в отличие от предыдущего, предполагается, что заданы главные векторы  сил, приложенных к каждому отрезку
сил, приложенных к каждому отрезку  в отдельности. Такая формулировка задачи соответствует действию
в отдельности. Такая формулировка задачи соответствует действию  штампов, независимо совершающих вертикальные перемещения. Когда
штампов, независимо совершающих вертикальные перемещения. Когда  названные задачи совпадают. На основании (6.208) для обеих задач граничное условие (6.205) на
названные задачи совпадают. На основании (6.208) для обеих задач граничное условие (6.205) на  примет вид
примет вид

В силу (6.193), с учетом (6.195), граничное условие (6.209) на  эквивалентно соотношению
эквивалентно соотношению  так что функция
так что функция  является голоморфной во всей плоскости, разрезанной вдоль
является голоморфной во всей плоскости, разрезанной вдоль  Следовательно, решение основной смешанной задачи сведено к неоднородной задаче Римана.
Следовательно, решение основной смешанной задачи сведено к неоднородной задаче Римана.
Положим, что  на V удовлетворяет условию Гельдера. Тогда решение задачи (6.210), не исчезающее на бесконечности, может быть представлено в виде
на V удовлетворяет условию Гельдера. Тогда решение задачи (6.210), не исчезающее на бесконечности, может быть представлено в виде

где  -частное решение однородной задачи, соответствующей (6.210), голоморфное во всей плоскости, разрезанной вдоль
-частное решение однородной задачи, соответствующей (6.210), голоморфное во всей плоскости, разрезанной вдоль  оно равно
оно равно

причем постоянная

Кроме того  — некоторый полином.
— некоторый полином.
В силу того, что голоморфная функция  должна исчезать на бесконечности, полином
должна исчезать на бесконечности, полином  не должен иметь степень выше
не должен иметь степень выше  поэтому
поэтому

Коэффициенты Со,  полинома
полинома  определяются из дополнительных условий задачи. В случае, когда
определяются из дополнительных условий задачи. В случае, когда  на отрезке
на отрезке  в качестве таких условий принимается равенство главного вектора
в качестве таких условий принимается равенство главного вектора  сил, приложенных к каждому отрезку
сил, приложенных к каждому отрезку  заданным величинам.
заданным величинам.
Согласно (6.202) имеем

где  аффикс точки
аффикс точки  . В этом соотношении, учитывая (6.210), будем иметь на
. В этом соотношении, учитывая (6.210), будем иметь на 

Применяя к правой части (6.211) формулу Сохоцкого — Племеля, найдем

Внеся отсюда значение  в условие (6.212), получим
в условие (6.212), получим

Подставляя в очевидное соотношение

значение подынтегральной функции из предшествующего равенства, придем к системе  линейных уравнений для постоянных
линейных уравнений для постоянных  ее однозначная разрешимость следует из единственности решения исходной смешанной задачи.
ее однозначная разрешимость следует из единственности решения исходной смешанной задачи.
Для решения задачи, когда  на
на  вычислим значения
вычислим значения  на ненагруженной части
на ненагруженной части  границы
границы  Учитывая, что в этом случае функция
Учитывая, что в этом случае функция  продолжима
продолжима  ненагруженные отрезки границы V, согласно формулам
ненагруженные отрезки границы V, согласно формулам  получим
получим

Здесь  — аффикс точки
— аффикс точки 
С другой стороны, на ненагруженных участках  имеем очевидное соотношение
имеем очевидное соотношение

Учитывая в этом соотношении формулу (6.215), придем к системе  линейных уравнений для
линейных уравнений для 
Дополнительное уравнение получим, используя заданную величину главного вектора  сил, приложенных к
сил, приложенных к  На основании первых формул (6.197) и (6.201) имеем
На основании первых формул (6.197) и (6.201) имеем

с другой стороны, исходя из формулы (6.211), находим  Следовательно,
Следовательно,

Таким образом, остается лишь определить  из упомянутой системы
из упомянутой системы  уравнений, однозначная разрешимость которой вытекает из единственности решения исходной задачи.
уравнений, однозначная разрешимость которой вытекает из единственности решения исходной задачи.
В случае, когда  что соответствует прямолинейному основанию штампа, параллельному границе
что соответствует прямолинейному основанию штампа, параллельному границе  формулы (6.211), (6.213), (6.214) и (6.215), в силу обращения в них интегрального члена в нуль, значительно упрощаются.
формулы (6.211), (6.213), (6.214) и (6.215), в силу обращения в них интегрального члена в нуль, значительно упрощаются.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
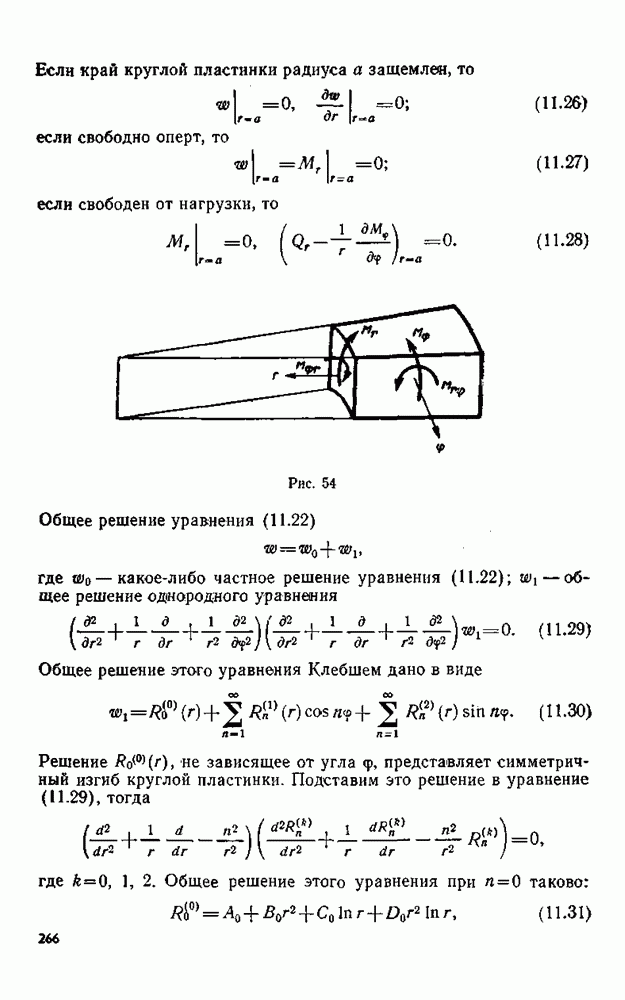
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки