§ 63. Аналогии при кручении

а. Мембранная аналогия. Мембраной называется тонкая пленка, не оказывающая сопротивления изгибу, а сопротивляющаяся только растяжению.

Пусть однородная мембрана постоянной толщины натянута одинаково по всем направлениям силой на плоский контур того же очертания, что и контур поперечного сечения скручиваемого призматического тела, и нагружена нормальной к ней равномерно распределенной нагрузкой на единицу площади. Пусть оси координат лежат в плоскости мембраны, которая провисает под действием нагрузки на величину

Рис. 29

Выведем дифференциальное уравнение равновесия; для этого вырежем элемент, имеющий форму прямоугольника со сторонами (рис. 29). Приравняем к нулю сумму проекций на ось всех сил, действующих на него;

Отсюда получим уравнение для прогиба равномерно нагруженной мембраны

Так как на контуре мембраны прогиб равен нулю, следовательно, контурное условие будет

Таким образом, контурное условие (7.34) тождественно совпадает с контурным условием для функции Если положить тогда дифференциальное уравнение (7.15) совпадет с (7.33). Внесем в уравнение (7.33), тогда

С другой стороны, имеем

Из последних двух уравнений Тогда

Следовательно, задача кручения призматического тела может быть решена путем измерения прогибов равномерно нагруженной мембраны.

Если рассечь мембрану плоскостями то полученные линии равного перемещения в задаче кручения будут совпадать с траекториями касательных напряжений Уклон мембраны в направлении внешней нормали к линии равного перемещения в некоторой ее точке определяет касательное напряжение в соответствующей точке сечения, т. е. Действительно,

откуда

Согласно этой формуле наибольший угол наклона мембраны определяет наибольшее касательное напряжение.

Жесткость призматического тела при кручении определяется объемом у, ограниченным поверхностью деформированной мембраны, и плоскостью ее до деформации, т. е. Действительно, так как

а также учитывая, что

найдем откуда

Ценность мембранной аналогии заключается не только в том, что она позволяет экспериментально исследовать проблему кручения, но и в том, что при помощи этой аналогии можно без какого-либо эксперимента в каждой конкретной задаче о кручении призматического тела составить качественное представление о виде траекторий касательных напряжений и о наибольшем тангенциальном напряжении.

Мембранная аналогия легко обобщается и на случай полых призматических тел. В этом случае, как явствует из соотношения которое выведено из сравнения уравнений (7.15) и (7.33), должны быть соблюдены следующие условия:

1) внешний контур мембраны должен быть подобным внешнему контуру сечеиия призматического тела и закреплен неподвижно;

2) все внутренние контуры сечения призматического тела должны быть имитированы абсолютно жесткими плоскими невесомыми дисками, параллельными друг другу, и должны получить поступательные перемещения константы, входящие в граничные условия на внутренних контурах сечения призматического тела);

3) эти диски должны быть загружены тем же равномерно распределенным нормальным давлением что и сама мембрана. Последнее обстоятельство вытекает из теоремы о циркуляции касательных напряжений в задаче о кручении, в справедливости чего сейчас убедимся.

Подставим в (7.32), тогда

Здесь — уклон мембраны в направлении внешней нормали к внутреннему контуру площадь, ограниченная внутренним контуром

Умножив обе части (7.37) на величину равномерного натяжения мембраны будем иметь

Очевидно, левая часть этого равенства есть сумма проекций сил натяжения мембраны в сечении ее по данному контуру на направление, перпендикулярное плоскости контура

Таким образом, (7.38) дает условие равновесия каждого диска под действием равномерно распределенного давления и натяжения мембраны в сечении ее по контуру этих дисков. Если такого рода

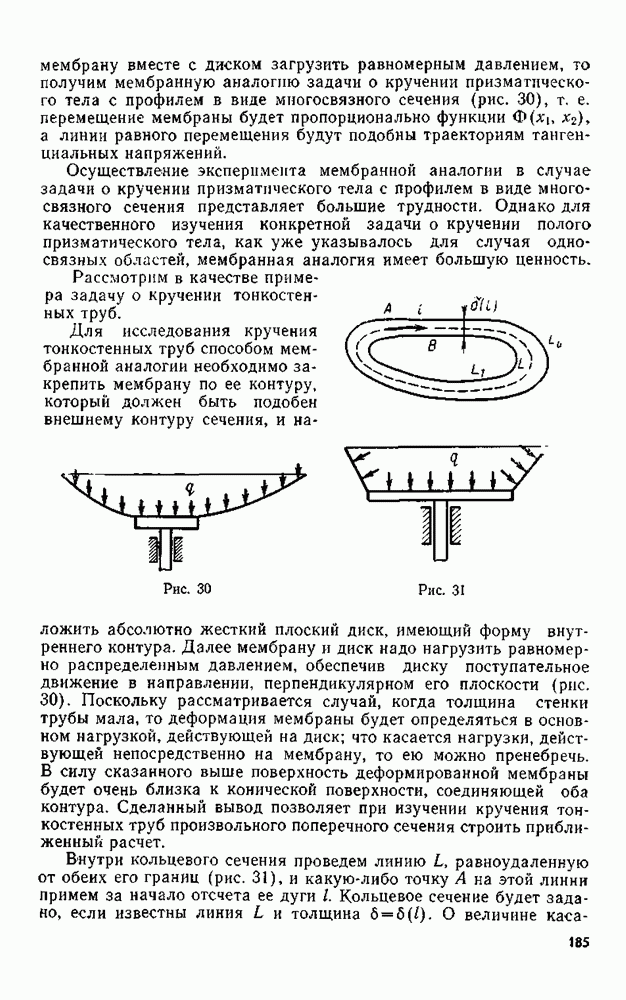
мембрану вместе с диском загрузить равномерным давлением, то получим мембранную аналогию задачи о кручении призматического тела с профилем в виде многосвязного сечения перемещение мембраны будет пропорционально функции а линии равного перемещения будут подобны траекториям тангенциальных напряжений.

Осуществление эксперимента мембранной аналогии в случае задачи о кручении призматического тела с профилем в виде многосвязного сечения представляет большие трудности. Однако для качественного изучения конкретной задачи о кручении полого призматического тела, как уже указывалось для случая односвязных областей, мембранная аналогия имеет большую ценность.

Рассмотрим в качестве примера задачу о кручении тонкостенных труб.

Рис. 30

Рис. 31

Для исследования кручения тонкостенных труб способом мембранной аналогии необходимо закрепить мембрану по ее контуру, который должен быть подобен внешнему контуру сечения, и наложить абсолютно жесткий плоский диск, имеющий форму внутреннего контура. Далее мембрану и диск надо нагрузить равномерно распределенным давлением, обеспечив диску поступательное движение в направлении, перпендикулярном его плоскости (рис. 30). Поскольку рассматривается случай, когда толщина стенки трубы мала, то деформация мембраны будет определяться в основном нагрузкой, действующей на диск; что касается нагрузки, действующей непосредственно на мембрану, то ею можно пренебречь. В силу сказанного выше поверхность деформированной мембраны будет очень близка к конической поверхности, соединяющей оба контура. Сделанный вывод позволяет при изучении кручения тонкостенных труб произвольного поперечного сечения строить приближенный расчет.

Внутри кольцевого сечения проведем линию равноудаленную от обеих его границ (рис. 31), и какую-либо точку А на этой линии примем за начало отсчета ее дуги I Кольцевое сечение будет задано, если известны линия и толщина . О величине

касательного напряжения в данной точке можно приблизительно судить по среднему уклону мембраны в этой точке, поэтому приблизительное значение тангенциального напряжения в точке В определится формулой

Полагая, что на внешнем контуре будем иметь

Как видно из этой формулы,

Из формулы (7.26) имеем

где площадь, ограниченная внутренним контуром; — постоянное значение функции на внутреннем контуре.

Учитывая, что среднее значение функции на линии приближенно равно последней формуле придадим вид

В правой части (7.41) выражение внутри скобок представляет собой площадь, ограниченную средним контуром поэтому формулу (7.41) перепишем в виде

где

С другой стороны, на основании (7,32) имеем

Исключим из формул (7.42) и (7.43), тогда

где

Формула (7.44) дана Бредтом.

Из сравнения формул (7.39) и (7.42) найдем

Эта формула также принадлежит Бредту.

б. Гидродинамическая аналогия Буссинеска. Рассмотрим ламинарное движение вязкой жидкости по призматической трубе с поперечным сечением, совпадающим с поперечным сечением призматического тела, кручение которого исследуется. Обозначим ось трубы через Скорость текущей по трубе жидкости должна удовлетворять уравнению Пуассона

где - падение гидродинамического давления по оси трубы, принимаемое постоянным.

На стенках трубы имеем условие Рейнольдса

Таким образом, контурное условие (7,46) тождественно совпадает с контурным условием для функции

Если положить тогда дифференциальное уравнение (7.15) совпадает с (7.45). Внесем в уравнение (7.45) и полученное уравнение сравним с уравнением (7.15); тогда

и