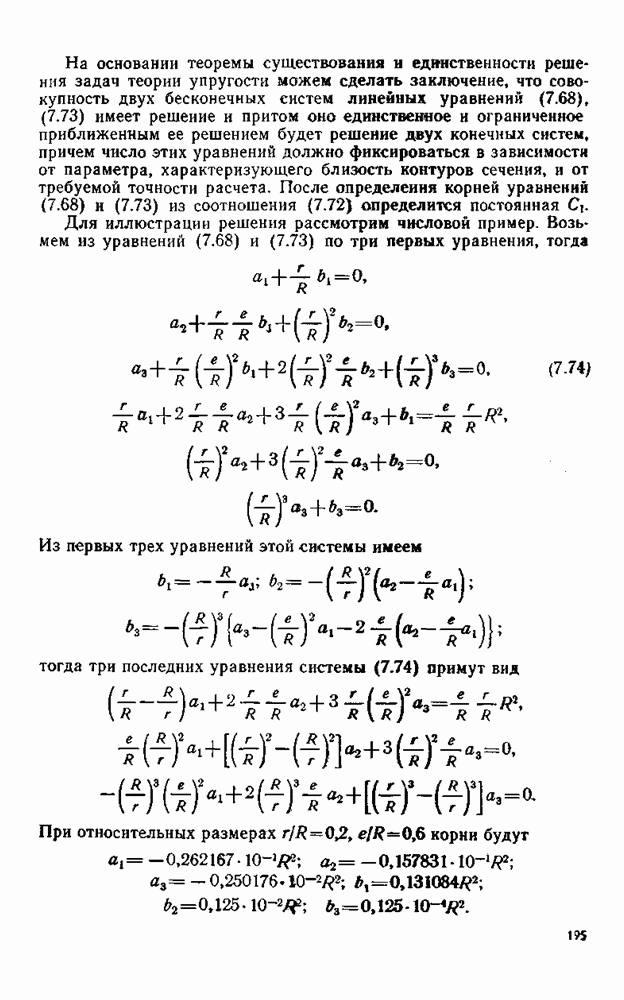| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
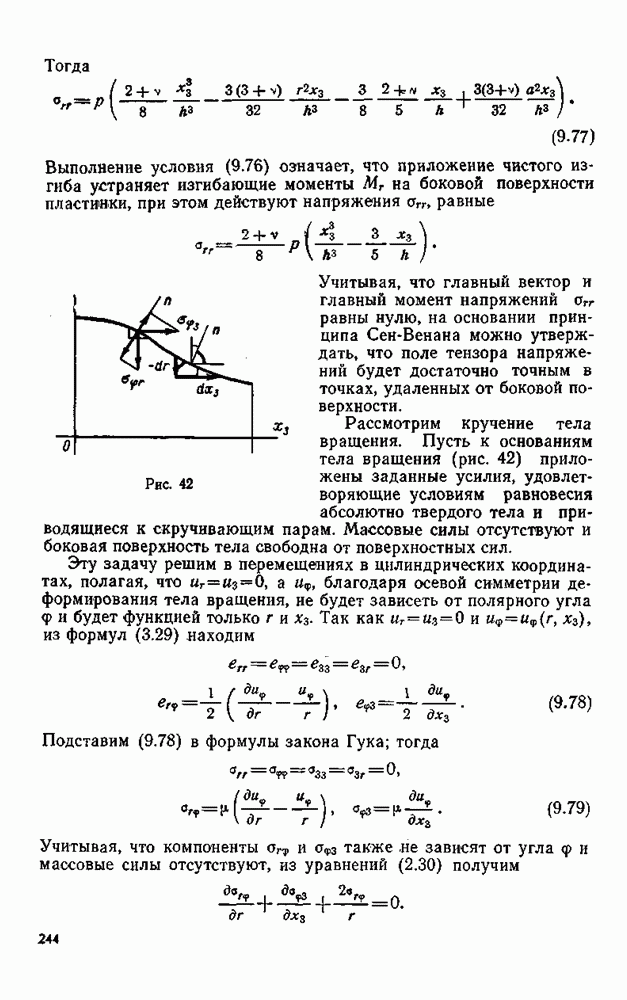
§ 10. Уравнения движения и равновесия в компонентах тензора напряжений
Известно, что для составления уравнений движения абсолютно твердого тела необходимо и достаточно приравнять нулю главный вектор и главный момент действующих на него внешних сил и сил инерции.
Для того, чтобы составить уравнения движения деформируемого тела, необходимо и достаточно приравнять нулю главный вектор, главный момент сил и сил инерции, приложенных к каждой части тела, которую можно мысленно из него выделить.
Равенство нулю главного вектора, главного момента указанных сил налагает определенные условия (к нахождению которых мы переходим) на изменение компонентов тензора напряжений при переходе от одной точки тела к другой. В дальнейшем будем
предполагать, что компоненты тензора напряжений непрерывны и имеют непрерывные частные производные во всех точках тела. Мысленно вырежем внутри тела некоторый произвольный объем  ограниченный достаточно гладкой поверхностью
ограниченный достаточно гладкой поверхностью  Главный вектор и главный момент объемных сил
Главный вектор и главный момент объемных сил  действующих на элемент объема
действующих на элемент объема  выделенного из объема
выделенного из объема  сил инерции
сил инерции  приложенных к этому элементу в случае динамической нагрузки, и поверхностных сил
приложенных к этому элементу в случае динамической нагрузки, и поверхностных сил  действующих на элемент
действующих на элемент  должны равняться нулю, т. е.
должны равняться нулю, т. е.

Так как компонент силы  в направлении единичного вектора
в направлении единичного вектора  равен
равен  и компонент силы
и компонент силы  в том же направлении равен
в том же направлении равен  вместо (2.15) можно написать
вместо (2.15) можно написать

Учитывая (2.14) и формулу Гаусса — Остроградского (1.94), поверхностному интегралу в (2.17) придадим вид

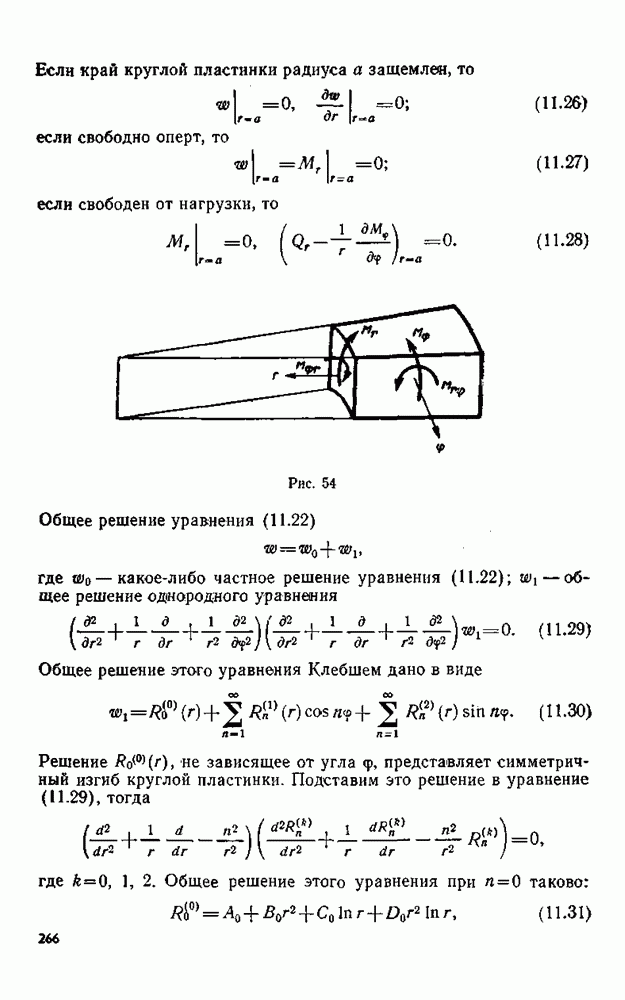
Подставив это в (2.17), получим

Отсюда в силу непрерывности подынтегральной функции, произвольности вектора  и объема
и объема  следует, что подынтегральная функция должна обращаться в нуль в каждой точке тела
следует, что подынтегральная функция должна обращаться в нуль в каждой точке тела

Если тело находится в равновесии, то ускорение элемента  будет равно нулю, и уравнение примет вид
будет равно нулю, и уравнение примет вид

Здесь  ковариантная производная тензора напряжений суммирование производится по индексу
ковариантная производная тензора напряжений суммирование производится по индексу  от 1 до 3.
от 1 до 3.
Уравнения (2.19) и (2.20), связывающие изменение компонентов тензора напряжений с массовыми силами в любой точке внутри
тела, соответственно называются уравнениями движения и уравнениями равновесия дефомнруемого тела в контра вариантной форме. Эти уравнения, в которые входят девять компонентов тензора напряжений, являются неоднородными уравнениями первого порядка в частных производных. В случае отсутствия массовых сил эти уравнения будут однородными.
Так как компонент момента  в направлении единичного вектора
в направлении единичного вектора  равен
равен  компонент момента
компонент момента  в том же направлении равен
в том же направлении равен  и радиус-вектор точки
и радиус-вектор точки  можно представить в видто с учетом формулы
можно представить в видто с учетом формулы  вместо (2.16) напишем
вместо (2.16) напишем

Принимая во внимание формулу (2.13) и формулу Гаусса — Остроградского (1.94), поверхностному интегралу в уравнении (2.20) придадим вид

Так как  уравнение (2.20) запишем в виде
уравнение (2.20) запишем в виде

Так как  поэтому
поэтому

На основании формулы  , произвольности объема
, произвольности объема  и непрерывности подынтегральной функции имеем
и непрерывности подынтегральной функции имеем

Заметив, что  последнему соотношению придадим вид
последнему соотношению придадим вид

Развернув это выражение, будем иметь

Так как направление  произвольно, заключаем, что
произвольно, заключаем, что

Таким образом, доказана симметричность тензора напряжений. Следовательно, тензор напряжений, характеризующий напряженное состояние в данной точке, определяется шестью независимыми компонентами.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
- ВВЕДЕНИЕ
- Глава I. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- § 1. Определения скаляра, вектора и тензора
- § 2. Сложение, умножение и свертывание тензоров. Признак тензора
- § 3. Метрический тензор
- § 4. Дифференцирование базисных векторов. Символы Кристоффеля
- § 5. Параллельное векторное поле
- § 6. Тензор Римана — Кристоффеля. Производная вектора. Формула Гаусса — Остроградского, e-тензор
- Глава II. ТЕОРИЯ НАПРЯЖЕНИЙ
- § 8. Метод сечений. Вектор напряжения
- § 9. Тензор напряжений
- § 10. Уравнения движения и равновесия в компонентах тензора напряжений
- § 11. Условия на поверхности
- § 12. Уравнения движения и равновесия в декартовой системе координат
- § 13. Уравнения движения и равновесия в цилиндрических и сферических координатах
- § 14. Определение главных нормальных напряжений
- Глава III. ТЕОРИЯ ДЕФОРМАЦИЙ
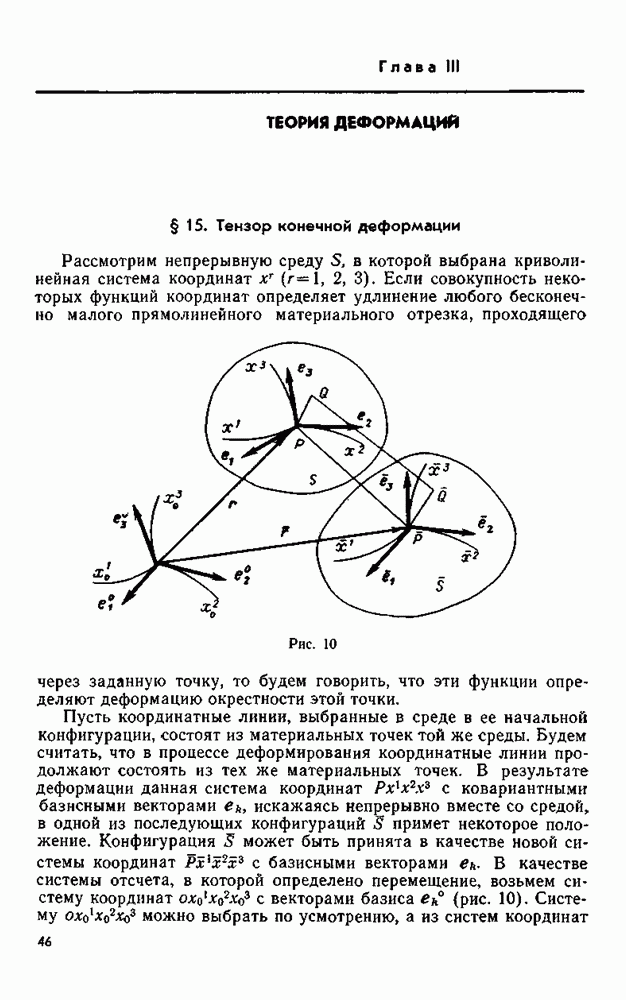
- § 15. Тензор конечной деформации
- § 16. Тензор малой деформации
- § 17. Уравнения совместности деформаций
- § 18. Тензор деформаций в декартовой системе координат
- § 19. Компоненты тензоров малой деформации и вращения в цилиндрических и сферических координатах
- § 20. Главные относительные удлинения
- § 21. Уравнения совместности деформаций в некоторых системах координат (условия Сен-Венана)
- § 22. Определение перемещений по компонентам тензора малой деформации
- Глава IV. СВЯЗЬ МЕЖДУ НАПРЯЖЕННЫМ И ДЕФОРМИРОВАННЫМ СОСТОЯНИЯМИ
- § 23. Обобщенный закон Гука
- § 24. Работа внешних сил
- § 25. Потенциал тензора напряжений
- § 26. Потенциал в случае линейно-упругого тела
- § 27. Различные случаи упругой симметрии тела
- § 28. Температурные напряжения
- § 29. Интеграл энергии для уравнений движения упругого тела
- § 30. Тождество Бетти
- § 31. Теорема Клапейрона
- ГЛАВА V. ПОЛНАЯ СИСТЕМА ОСНОВНЫХ УРАВНЕНИЙ ТЕОРИИ УПРУГОСТИ
- § 32. Уравнения упругого равновесия и движения в перемещениях
- § 33. Уравнения в компонентах напряжений
- § 34. Основные граничные задачи статики упругого тела. Единственность решения
- § 35. Основные задачи динамики упругого тела
- § 36. Принцип Сен-Венана (принцип смягчения граничных условий)
- § 37. Прямые и обратные решения задач теории упругости. Полуобратный метод Сен-Венана
- § 38. Простейшие задачи теории упругости
- ГЛАВА VI. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- § 39. Плоская деформация
- § 40. Плоское напряженное состояние
- § 41. Обобщенное плоское напряженное состояние
- § 42. Функция напряжений Эри
- § 43. Функция Эри в полярных координатах. Задача Ляме
- § 44. Комплексное представление бигармонической функции, компонентов вектора перемещения и тензора напряжений
- § 45. Степень определенности введенных функций и ограничения, накладываемые на них
- § 46. Основные граничные задачи и приведение их к задачам теории функций комплексного переменного
- § 47. Теорема Мориса Леви
- § 48. Метод конформных отображений
- § 49. Интеграл типа Коши
- § 50. Теореме Гарнака
- § 51. Краевая задача Римана
- § 52. Приведение основных краевых задач к функциональным уравнениям
- § 53. Равновесие кругового полого цилиндра
- § 54. Бесконечная пластинка с эллиптическим отверстием
- § 55. Решение граничных задач для полуплоскости
- § 56. Некоторые сведения об интегральном преобразовании Фурье
- § 57. Бесконечная плоскость, деформируемая под действием массовых сил
- § 58. Решение бигармонического уравнения для невесомой полуплоскости
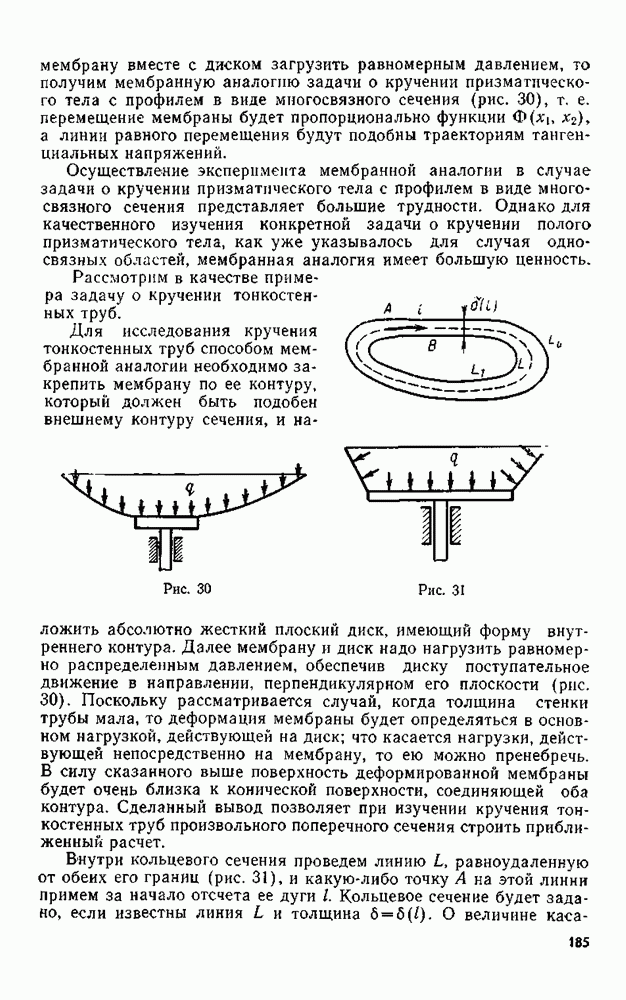
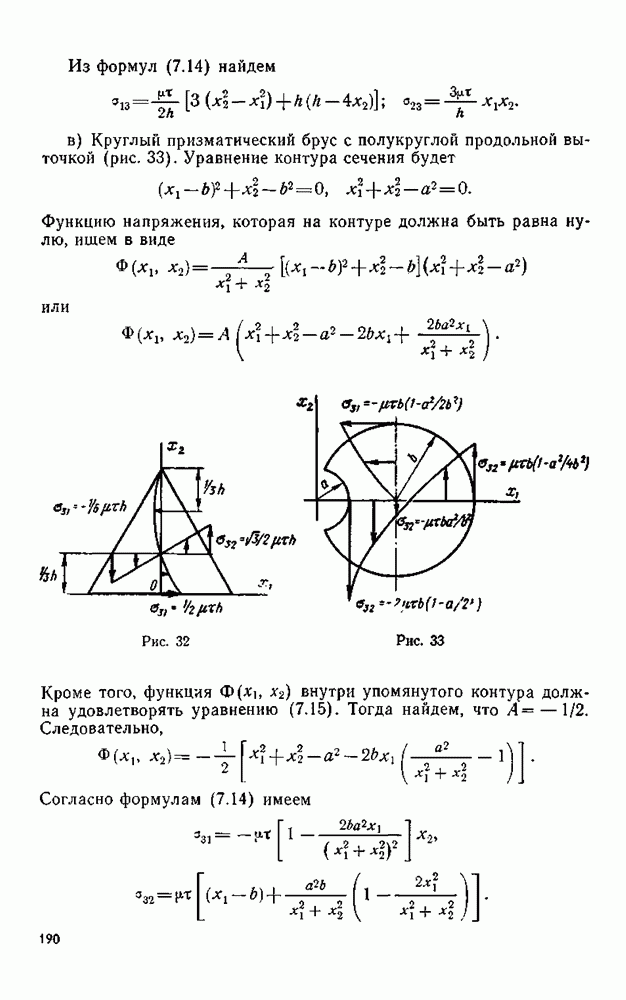
- Глава VII. КРУЧЕНИЕ И ИЗГИБ ПРИЗМАТИЧЕСКИХ ТЕЛ
- § 59. Кручение призматического тела произвольного односвязного поперечного сечения
- § 60. Некоторые свойства касательных напряжений
- § 61. Кручение полых призматических тел
- § 62. Теорема о циркуляции касательного напряжения
- § 63. Аналогии при кручении
- § 64. Комплексная функция кручения
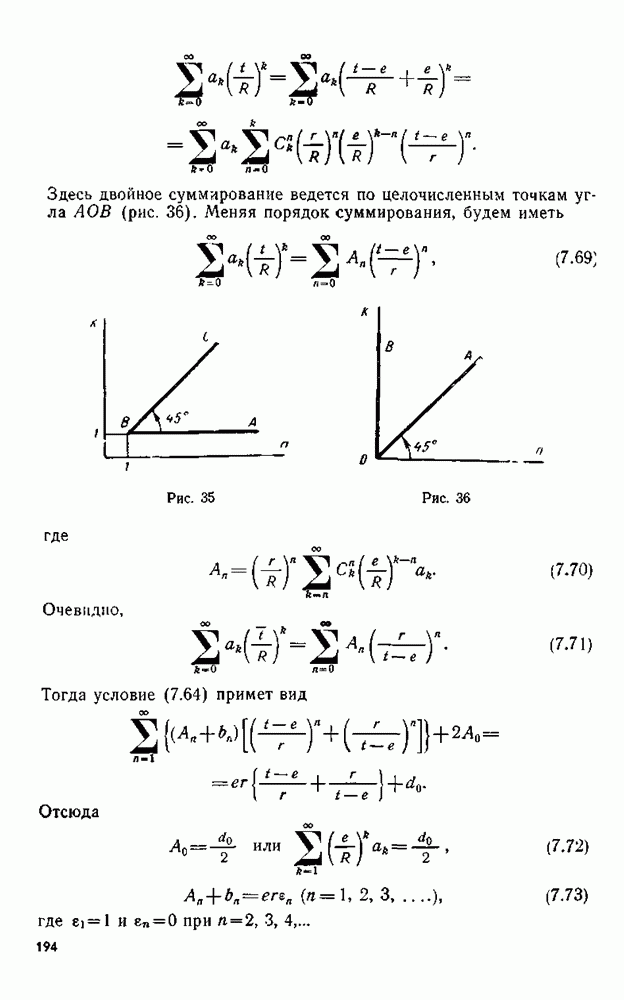
- § 65. Решение частных задач кручения
- § 66. Изгиб призматического тела, закрепленного одним концом
- § 67. Центр изгиба
- § 68. Изгиб призматического тела с эллиптическим поперечным сечением
- Глава VIII. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УПРУГОСТИ. ВАРИАЦИОННЫЕ МЕТОДЫ
- § 69. Теорема взаимности Бетти
- § 70. Принцип минимума потенциальной энергии
- § 71. Принцип минимума дополнительной работы — принцип Кастильяно
- § 72. Метод Рэлея-Ритца
- § 73. Вариационный принцип Рейсснера
- § 74. Уравнения равновесия и граничные условия для геометрически нелинейного тела
- Глава IX. ТРЕХМЕРНЫЕ СТАТИЧЕСКИЕ ЗАДАЧИ
- § 75. Решения Кельвина и Буссинеска — Папковича
- § 76. Элементарные решения Буссинеска первого и второго рода
- § 77. Давление на поверхность полубесконечного тела
- § 78. Задача Герца о давлении двух соприкасающихся тел
- § 79. Симметричная деформация тела вращения
- § 80. Температурные напряжения
- Глава X. ТЕОРИЯ РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН
- § 82. Поверхностные волны Рэлея
- § 83. Волны Лява
- Глава XI. ТЕОРИЯ ТОНКИХ ПЛАСТИНОК
- § 84. Дифференциальное уравнение изгиба тонких пластинок
- § 85. Граничные условия
- § 86. Уравнение изгиба пластинки в полярных координатах
- § 87. Симметричный изгиб круглой пластинки