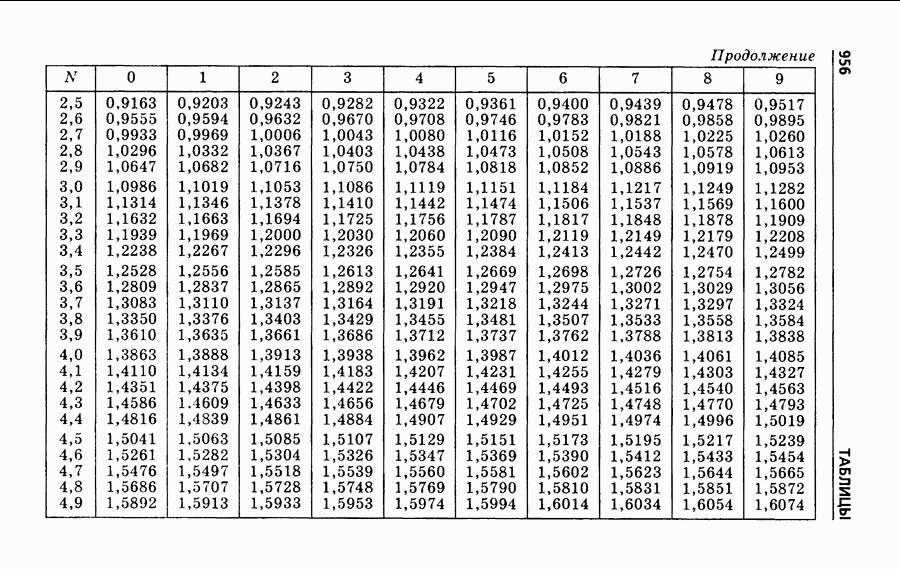
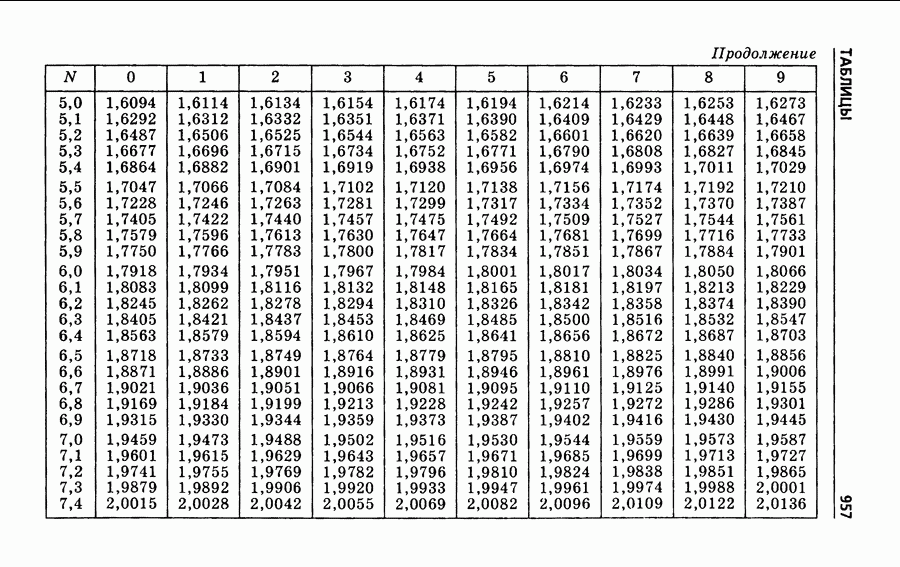
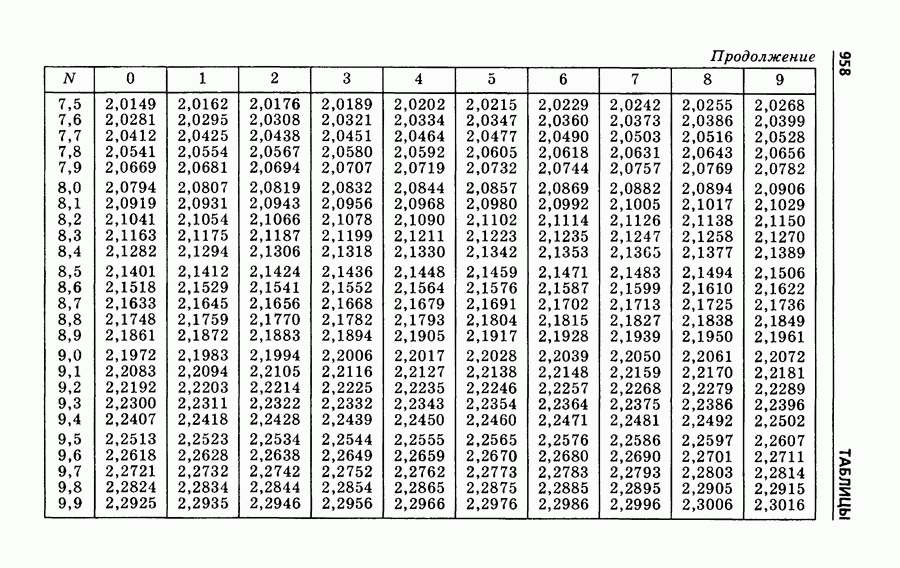
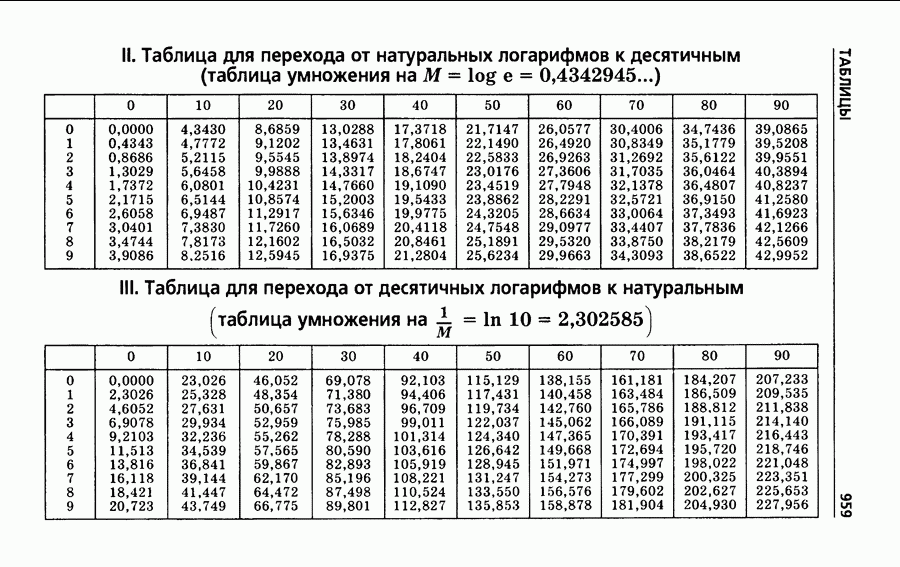
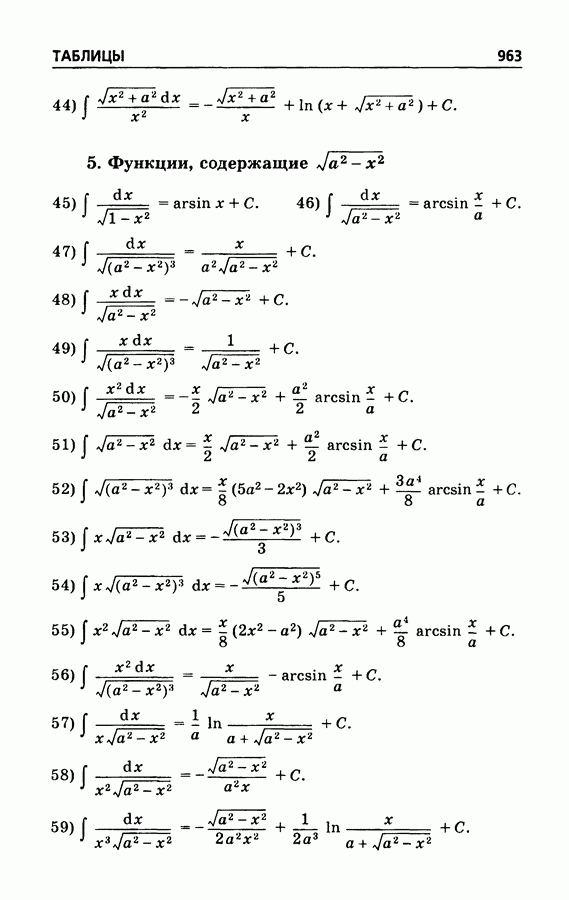| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
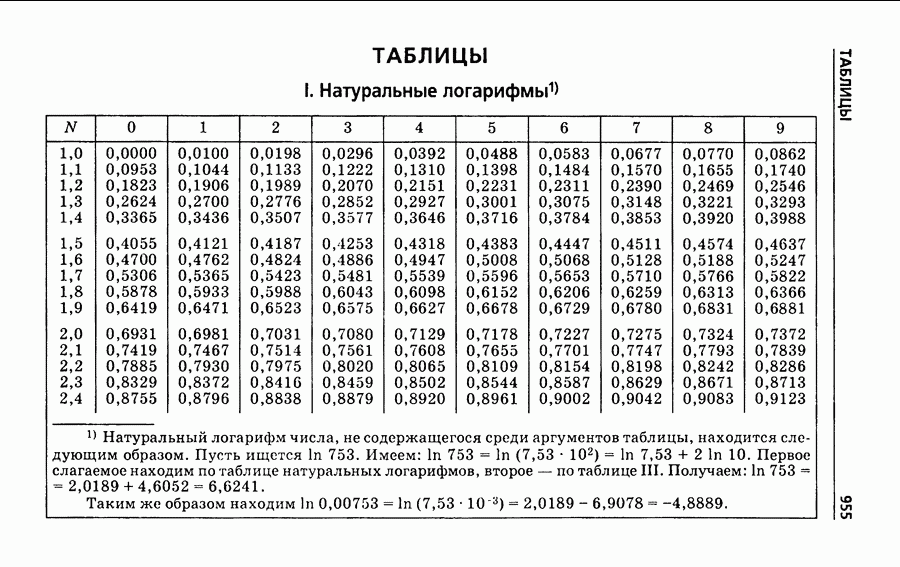
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 398. Дифференцирование и интегрирование степенного ряда
Теорема 1. Если степенной ряд имеет радиус сходимости  и сумму
и сумму

то ряд, полученный его почленным дифференцированием, имеет тот же радиус сходимости  и его сумма есть производная функции
и его сумма есть производная функции

Следовательно, сумма степенного ряда есть дифференцируемая функция; притом она имеет производные любого порядка (так как к ряду (2) снова можно применить теорему 1 и т. д.).
Замечание 1. Если ряд (1) расходится на каком-либо конце промежутка  то на этом конце ряд (2) тоже расходится. Сходимость же ряда (1) на конце промежутка
то на этом конце ряд (2) тоже расходится. Сходимость же ряда (1) на конце промежутка  может сохраниться в ряде (2), но может и нарушиться.
может сохраниться в ряде (2), но может и нарушиться.
Замечание 2. Сходимость ряда (2) несколько хуже, чем ряда (1) (так как  по абсолютному значению больше, чем
по абсолютному значению больше, чем  ).
).
Пример 1. Последовательно дифференцируя

у которого  получаем ряды с тем же радиусом сходимости. Их суммы есть последовательные производные от
получаем ряды с тем же радиусом сходимости. Их суммы есть последовательные производные от  :
:

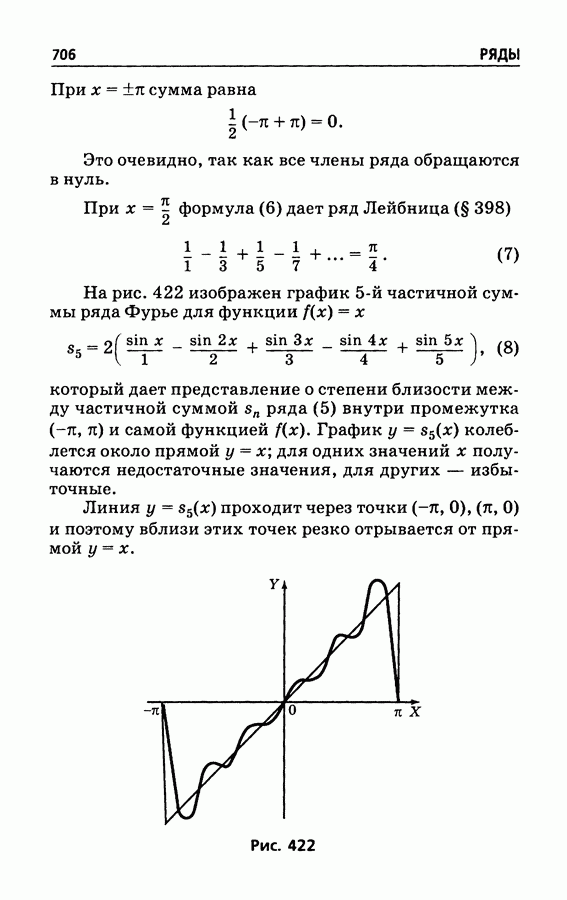
Ряд (3) расходится на обоих концах промежутка сходимости, ряды (4)-(6) - тоже.
Пример 2. Ряд (3) получается дифференцированием ряда

Ряд (7) расходится при  и сходится при
и сходится при  но после дифференцирования сходимость на конце
но после дифференцирования сходимость на конце  нарушается.
нарушается.
Теорема 2. Ряд, полученный почленным интегрированием ряда (1) в пределах от нуля до  имеет тот же радиус сходимости и его сумма равна
имеет тот же радиус сходимости и его сумма равна 

Замечание 3. Если ряд (1) сходится на одном из концов промежутка  то на этом конце ряд (8) тоже сходится, и формула (8) остается в силе. Расходимость же ряда (1) на конце промежутка
то на этом конце ряд (8) тоже сходится, и формула (8) остается в силе. Расходимость же ряда (1) на конце промежутка  может сохраниться в ряде (8), но может и нарушиться. Сходимость ряда (8) несколько лучше, чем ряда (1).
может сохраниться в ряде (8), но может и нарушиться. Сходимость ряда (8) несколько лучше, чем ряда (1).
Пример 3. Радиус сходимости геометрической прогрессии

равен единице. Интегрируя почленно, получаем (при  ):
):

Радиус сходимости ряда (10) тоже равен единице. На конце  ряд (9) расходится, а ряд (10) сходится (по признаку Лейбница), и мы имеем:
ряд (9) расходится, а ряд (10) сходится (по признаку Лейбница), и мы имеем:

На конце  ряд (10), как и (9), расходится (по интегральному признаку).
ряд (10), как и (9), расходится (по интегральному признаку).
Пример 4. Интегрируя почленно ряд

(§ 272, пример 2), для которого  получаем:
получаем:

где  любое число. Отсюда находим разложение функции
любое число. Отсюда находим разложение функции 

Здесь тоже 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- § 1. Понятие о предмете аналитической геометрии
- § 2. Координаты
- § 3. Прямоугольная система координат
- § 4. Прямоугольные координаты
- § 5. Координатные углы
- § 6. Косоугольная система координат
- § 7. Уравнение линии
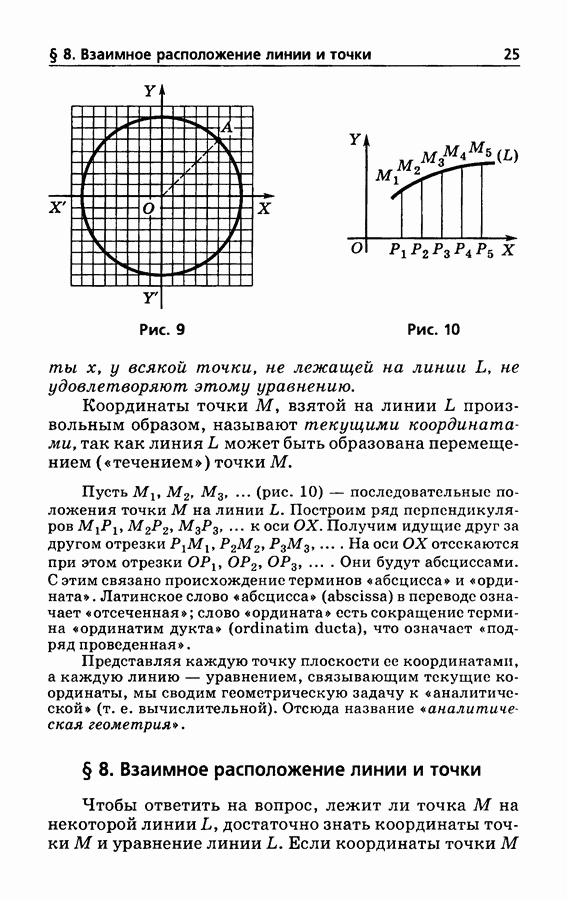
- § 8. Взаимное расположение линии и точки
- § 9. Взаимное расположение двух линий
- § 10. Расстояние между двумя точками
- § 11. Деление отрезка в данном отношении
- § 11а. Деление отрезка пополам
- § 12. Определитель второго порядка
- § 13. Площадь треугольника
- § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом)
- § 15. Прямая, параллельная оси
- § 16. Общее уравнение прямой
- § 17. Построение прямой по ее уравнению
- § 18. Условие параллельности прямых
- § 19. Пересечение прямых
- § 20. Условие перпендикулярности двух прямых
- § 21. Угол между двумя прямыми
- § 22. Условие, при котором три точки лежат на одной прямой
- § 23. Уравнение прямой, проходящей через две точки
- § 24. Пучок прямых
- § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой
- § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- § 27. Взаимное расположение прямой и пары точек
- § 28. Расстояние от точки до прямой
- § 29. Полярные параметры прямой
- § 30. Нормальное уравнение прямой
- § 31. Приведение уравнения прямой к нормальному виду
- § 32. Отрезки на осях
- § 33. Уравнение прямой в отрезках
- § 34. Преобразование координат (постановка вопроса)
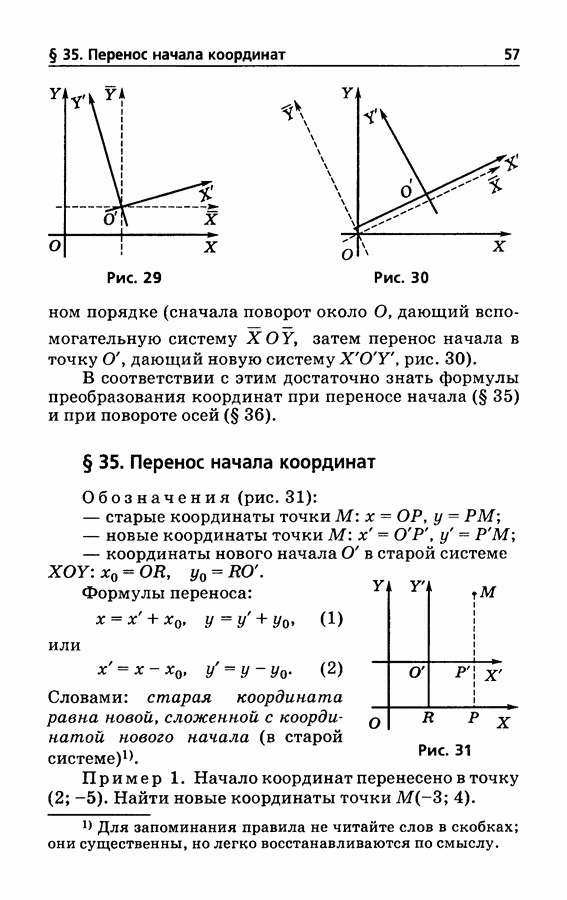
- § 35. Перенос начала координат
- § 36. Поворот осей
- § 37. Алгебраические линии и их порядок
- § 38. Окружность
- § 39. Нахождение центра и радиуса окружности
- § 40. Эллипс как сжатая окружность
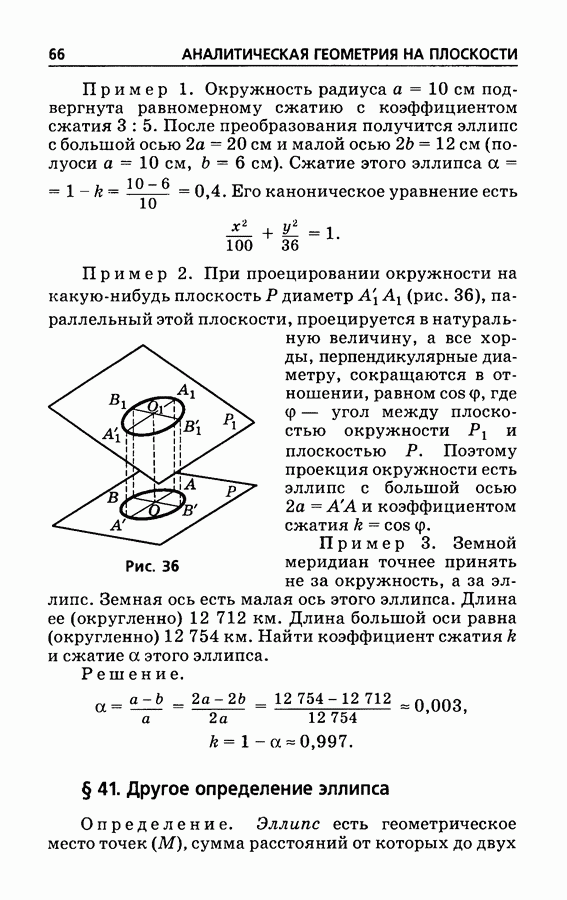
- § 41. Другое определение эллипса
- § 42. Построение эллипса по его осям
- § 43. Гипербола
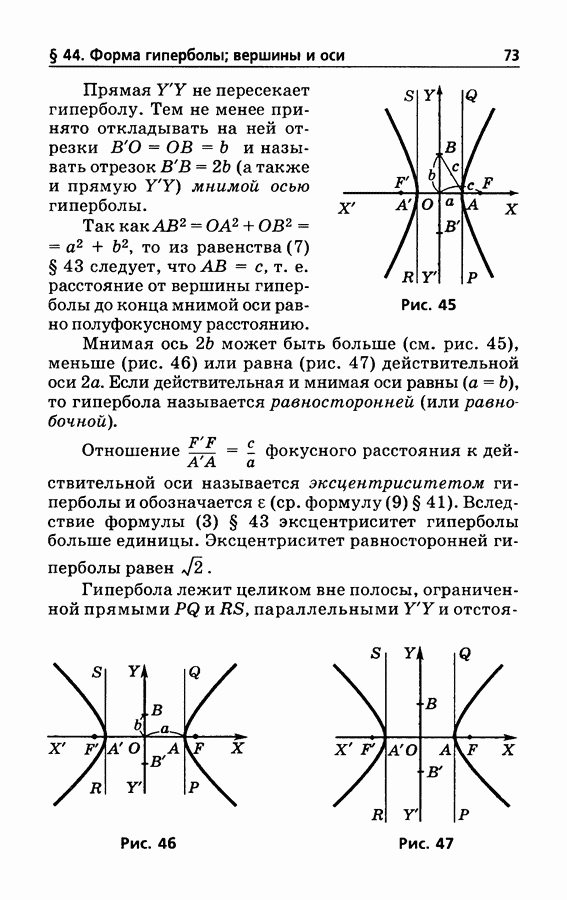
- § 44. Форма гиперболы; вершины и оси
- § 45. Построение гиперболы по ее осям
- § 46. Асимптоты гиперболы
- § 47. Сопряженные гиперболы
- § 48. Парабола
- § 49. Построение параболы по данному параметру p
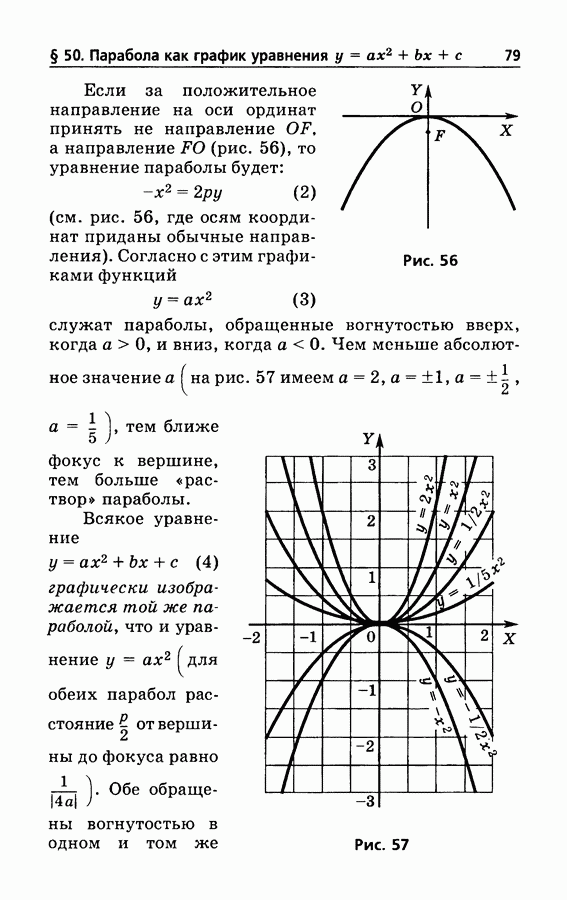
- § 50. Парабола как график уравнения y=ax^2+bx+c
- § 51. Директрисы эллипса и гиперболы
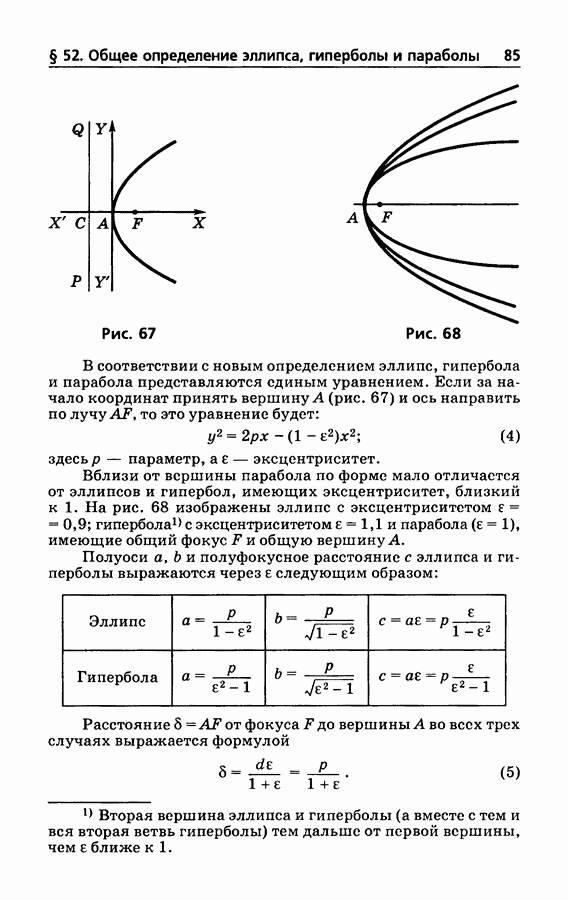
- § 52. Общее определение эллипса, гиперболы и параболы
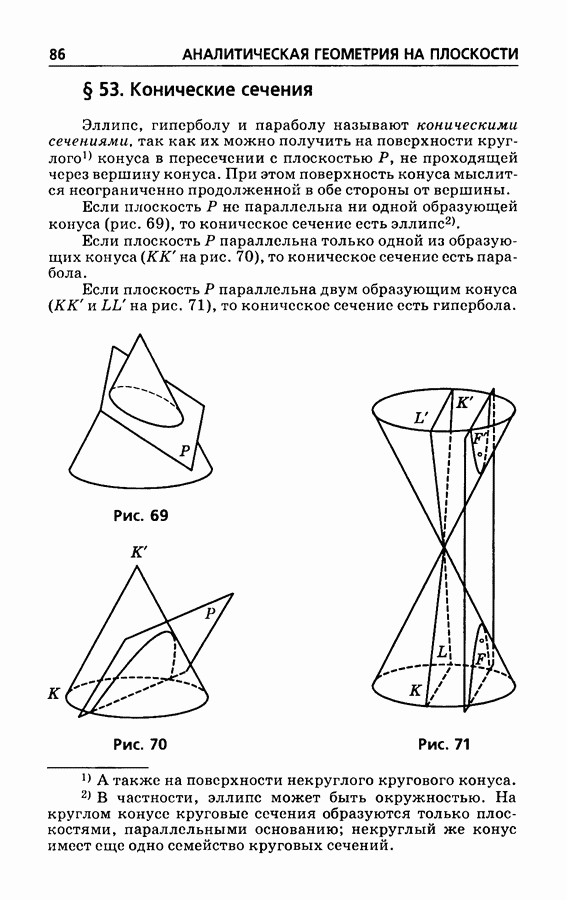
- § 53. Конические сечения
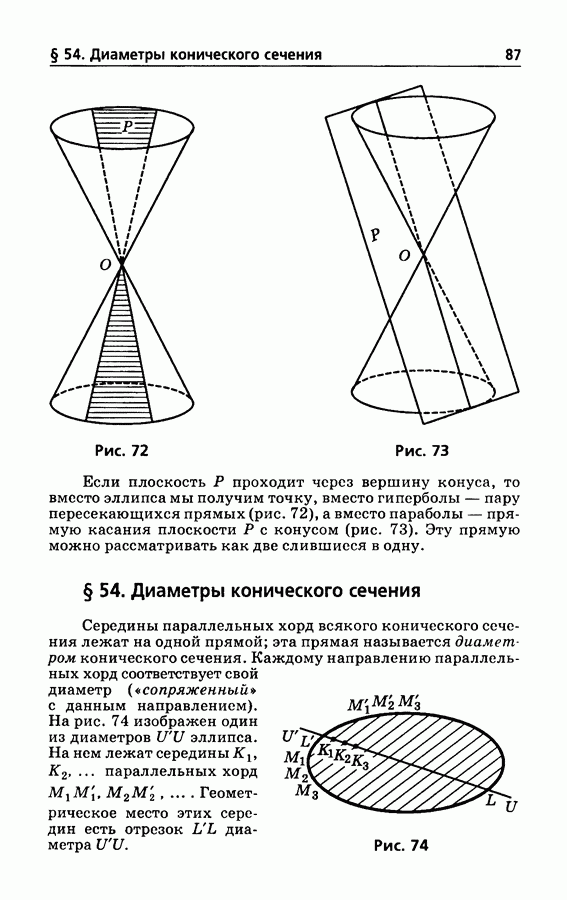
- § 54. Диаметры конического сечения
- § 55. Диаметры эллипса
- § 56. Диаметры гиперболы
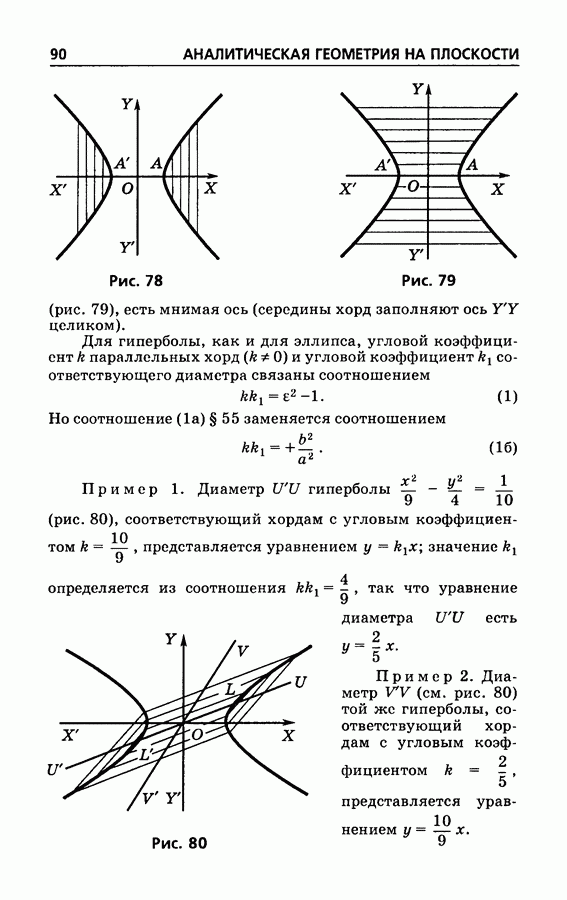
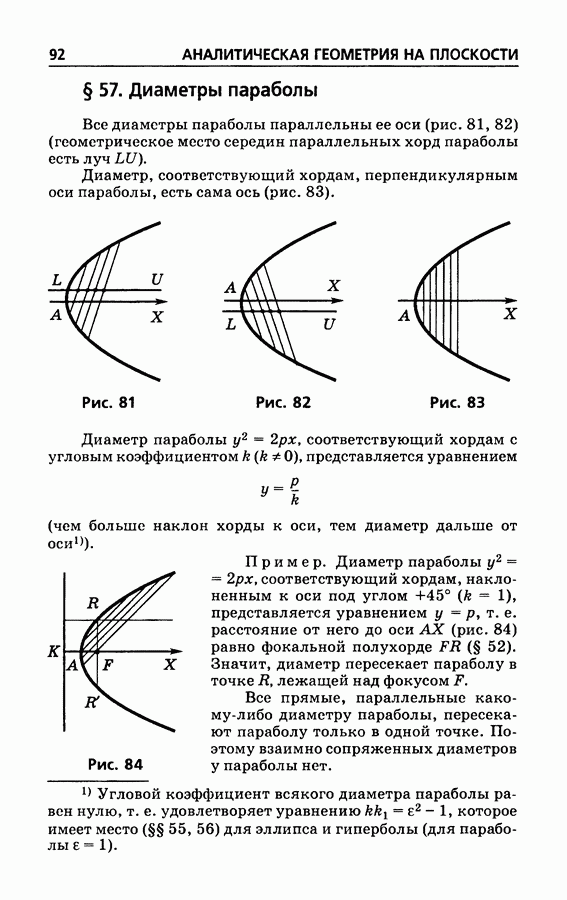
- § 57. Диаметры параболы
- § 58. Линии второго порядка
- § 59. Запись общего уравнения второй степени
- § 60. Упрощение уравнения второй степени; общие замечания
- § 61. Предварительное преобразование уравнения второй степени
- § 62. Завершающее преобразование уравнения второй степени
- § 63. О приемах, облегчающих упрощение уравнения второй степени
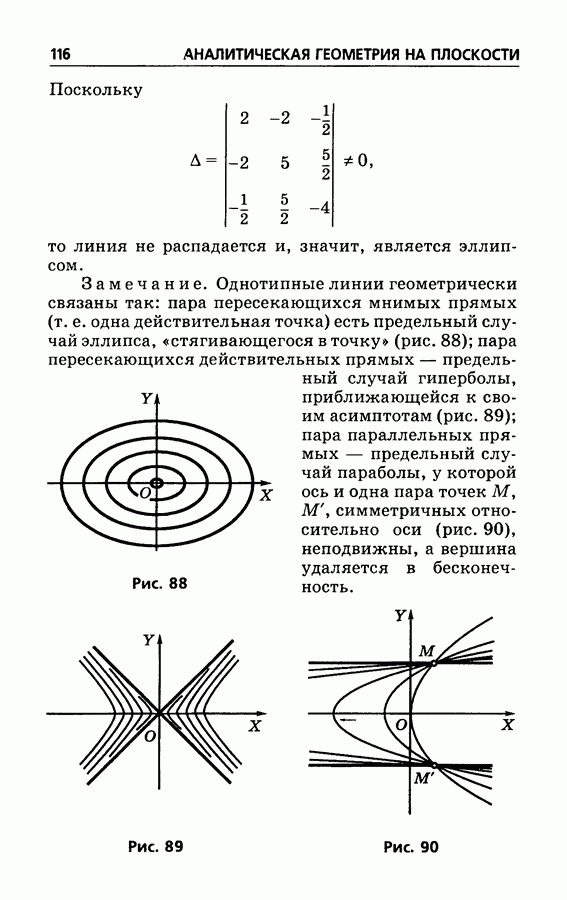
- § 64. Признак распадения линий второго порядка
- § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка
- § 66. Инварианты уравнения второй степени
- § 67. Три типа линий второго порядка
- § 68. Центральные и нецентральные линии второго порядка
- § 69. Нахождение центра центральной линии второго порядка
- § 70. Упрощение уравнения центральной линии второго порядка
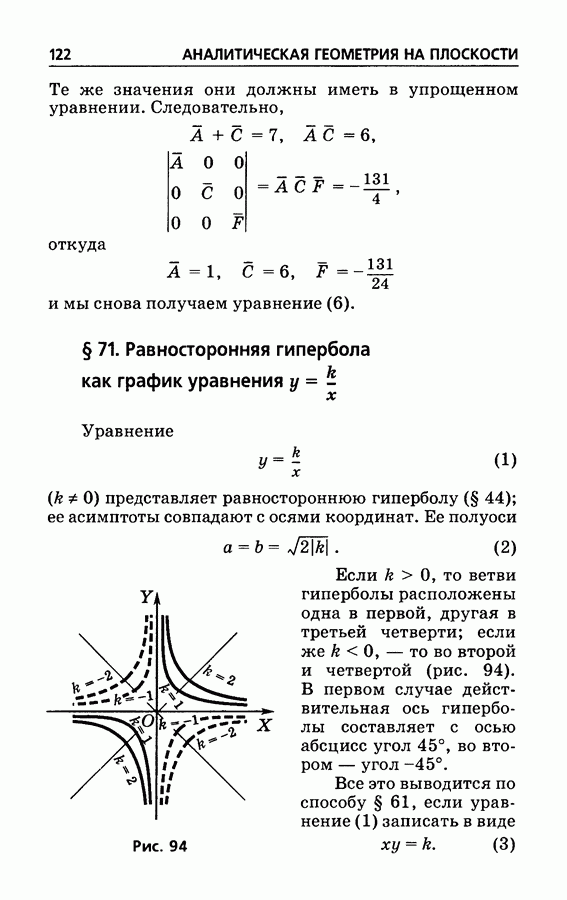
- § 71. Равносторонняя гипербола как график уравнения y=k/x
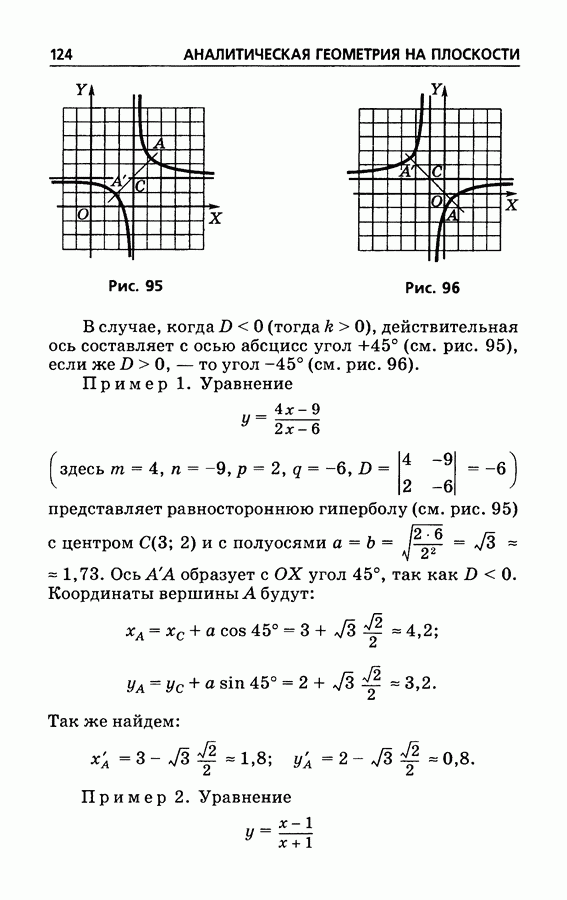
- § 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q)
- § 73. Полярные координаты
- § 74. Связь между полярными и прямоугольными координатами
- § 75. Архимедова спираль
- § 76. Полярное уравнение прямой
- § 77. Полярное уравнение конического сечения
- АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- § 78. Понятие о векторах и скалярах
- § 79. Вектор в геометрии
- § 80. Векторная алгебра
- § 81. Коллинеарные векторы
- § 82. Нуль-вектор
- § 83. Равенство векторов
- § 84. Приведение векторов к общему началу
- § 85. Противоположные векторы
- § 86. Сложение векторов
- § 87. Сумма нескольких векторов
- § 88. Вычитание векторов
- § 89. Умножение и деление вектора на число
- § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор)
- § 91. Проекция точки на ось
- § 92. Проекция вектора на ось
- § 93. Основные теоремы о проекциях вектора
- § 94. Прямоугольная система координат в пространстве
- § 95. Координаты точки
- § 96. Координаты вектора
- § 97. Выражения вектора через компоненты и через координаты
- § 98. Действия над векторами, заданными своими координатами
- § 99. Выражение вектора через радиусы-векторы его начала и конца
- § 100. Длина вектора. Расстояние между двумя точками
- § 101. Угол между осью координат и вектором
- § 102. Признак коллинеарности (параллельности) векторов
- § 103. Деление отрезка в данном отношении
- § 104. Скалярное произведение двух векторов
- § 104а. Физический смысл скалярного произведения
- § 105. Свойства скалярного произведения
- § 106. Скалярные произведения основных векторов
- § 107. Выражение скалярного произведения через координаты сомножителей
- § 108. Условие перпендикулярности векторов
- § 109. Угол между векторами
- § 110. Правая и левая системы трех векторов
- § 111. Векторное произведение двух векторов
- § 112. Свойства векторного произведения
- § 113. Векторные произведения основных векторов
- § 114. Выражение векторного произведения через координаты сомножителей
- § 115. Компланарные векторы
- § 116. Смешанное произведение
- § 117. Свойства смешанного произведения
- § 118. Определитель третьего порядка
- § 119. Выражение смешанного произведения через координаты сомножителей
- § 120. Признак компланарности в координатной форме
- § 121. Объем параллелепипеда
- § 122. Двойное векторное произведение
- § 123. Уравнение плоскости
- § 124. Особые случаи положения плоскости относительно системы координат
- § 125. Условие параллельности плоскостей
- § 126. Условие перпендикулярности плоскостей
- § 127. Угол между двумя плоскостями
- § 128. Плоскость, проходящая через данную точку параллельно данной плоскости
- § 129. Плоскость, проходящая через три точки
- § 130. Отрезки на осях
- § 131. Уравнение плоскости в отрезках
- § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости
- § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям
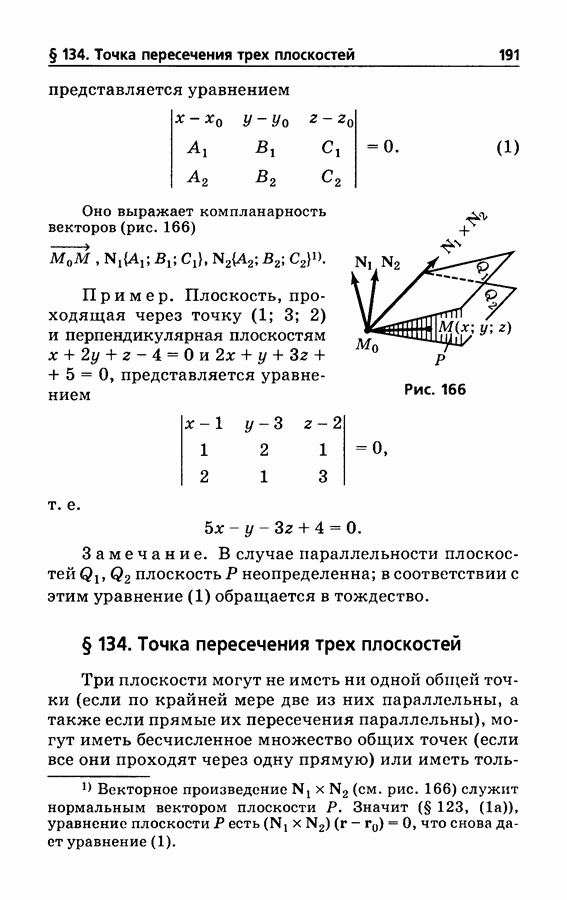
- § 134. Точка пересечения трех плоскостей
- § 135. Взаимное расположение плоскости и пары точек
- § 136. Расстояние от точки до плоскости
- § 137. Полярные параметры плоскости
- § 138. Нормальное уравнение плоскости
- § 139. Приведение уравнения плоскости к нормальному виду
- § 140. Уравнения прямой в пространстве
- § 141. Условие, при котором два уравнения первой степени представляют прямую
- § 142. Пересечение прямой с плоскостью
- § 143. Направляющий вектор
- § 144. Углы между прямой и осями координат
- § 145. Угол между двумя прямыми
- § 146. Угол между прямой и плоскостью
- § 147. Условия параллельности и перпендикулярности прямой и плоскости
- § 148. Пучок плоскостей
- § 149. Проекции прямой на координатные плоскости
- § 150. Симметричные уравнения прямой
- § 151. Приведение уравнений прямой к симметричному виду
- § 152. Параметрические уравнения прямой
- § 153. Пересечение плоскости с прямой, заданной параметрически
- § 154. Уравнения прямой, проходящей через две данные точки
- § 155. Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой
- § 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости
- § 157. Уравнение плоскости, проходящей через данную точку и данную прямую
- § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым
- § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой
- § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости
- § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую
- § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую
- § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости
- § 164. Уравнения общего перпендикуляра к двум данным прямым
- § 165. Кратчайшее расстояние между двумя прямыми
- § 165а. Правые и левые пары прямых
- § 166. Преобразование координат
- § 167. Уравнение поверхности
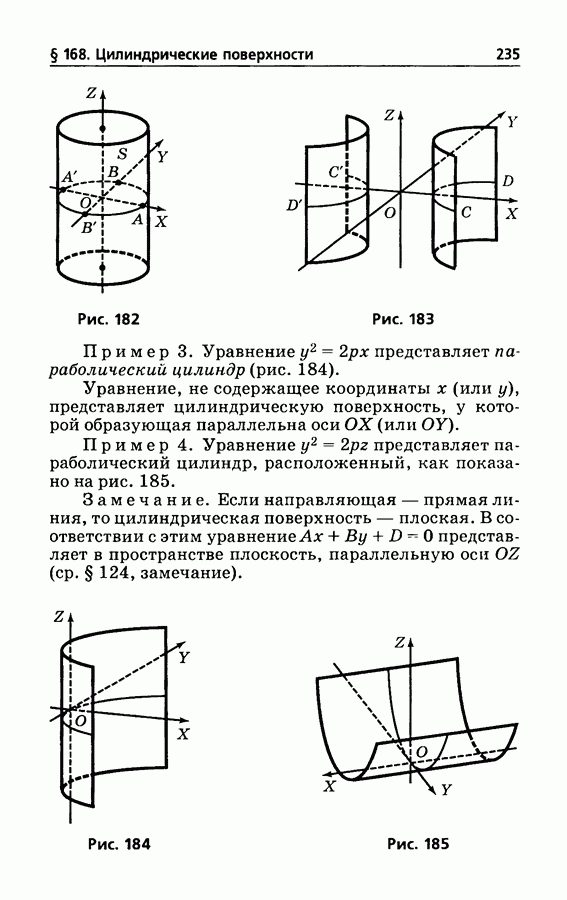
- § 168. Цилиндрические поверхности, у которых образующие параллельны одной из осей координат
- § 169. Уравнения линии
- § 170. Проекция линии на координатную плоскость
- § 171. Алгебраические поверхности и их порядок
- § 172. Сфера
- § 173. Эллипсоид
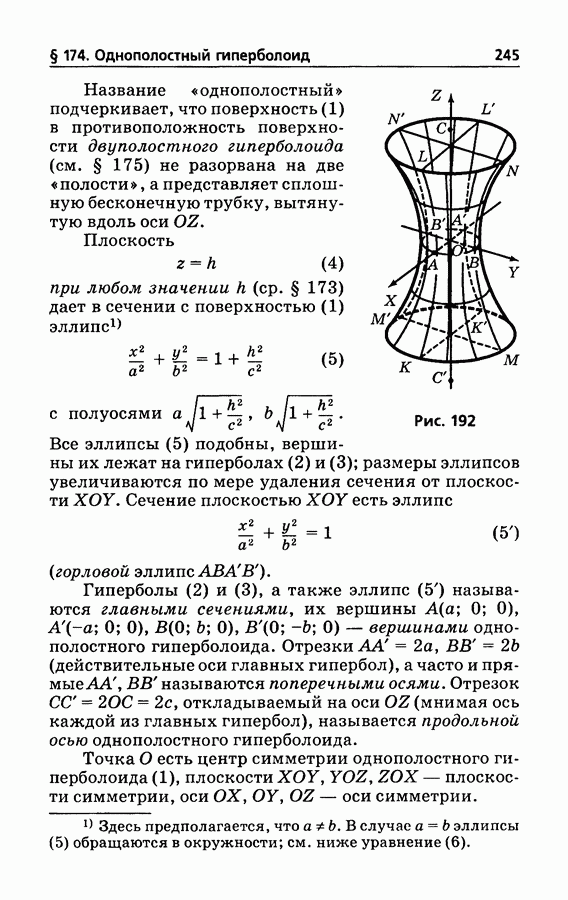
- § 174. Однополостный гиперболоид
- § 175. Двуполостный гиперболоид
- § 176. Конус второго порядка
- § 177. Эллиптический параболоид
- § 178. Гиперболический параболоид
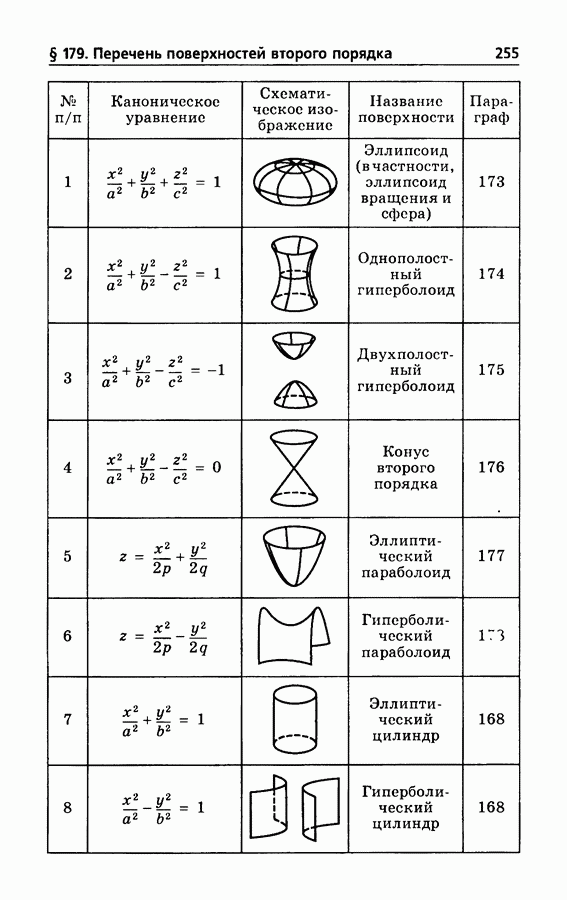
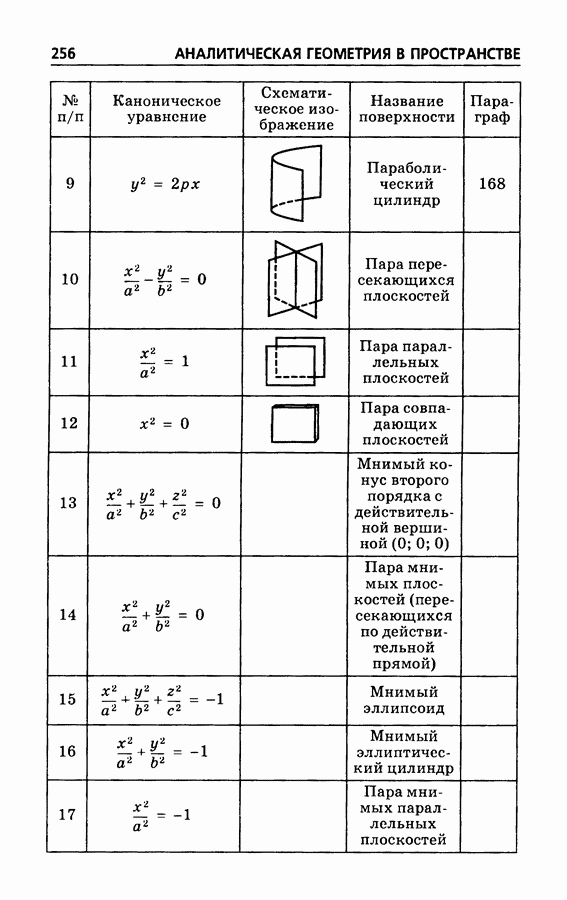
- § 179. Перечень поверхностей второго порядка
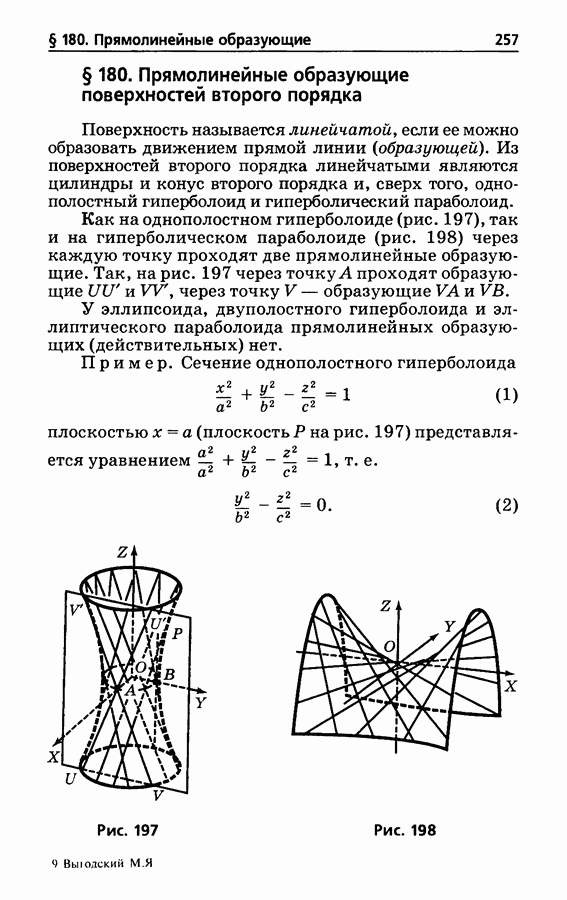
- § 180. Прямолинейные образующие поверхностей второго порядка
- § 181. Поверхности вращения
- § 182. Определители второго и третьего порядков
- § 183. Определители высших порядков
- § 184. Свойства определителей
- § 185. Практический прием вычисления определителей
- § 186. Применение определителей к исследованию и решению системы уравнений
- § 187. Два уравнения с двумя неизвестными
- § 188. Два уравнения с двумя неизвестными
- § 189. Однородная система двух уравнений с тремя неизвестными
- § 190. Два уравнения с двумя неизвестными
- § 190а. Система n уравнений с n неизвестными
- ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- § 192. Рациональные числа
- § 193. Действительные (вещественные) числа
- § 194. Числовая ось
- § 195. Переменные и постоянные величины
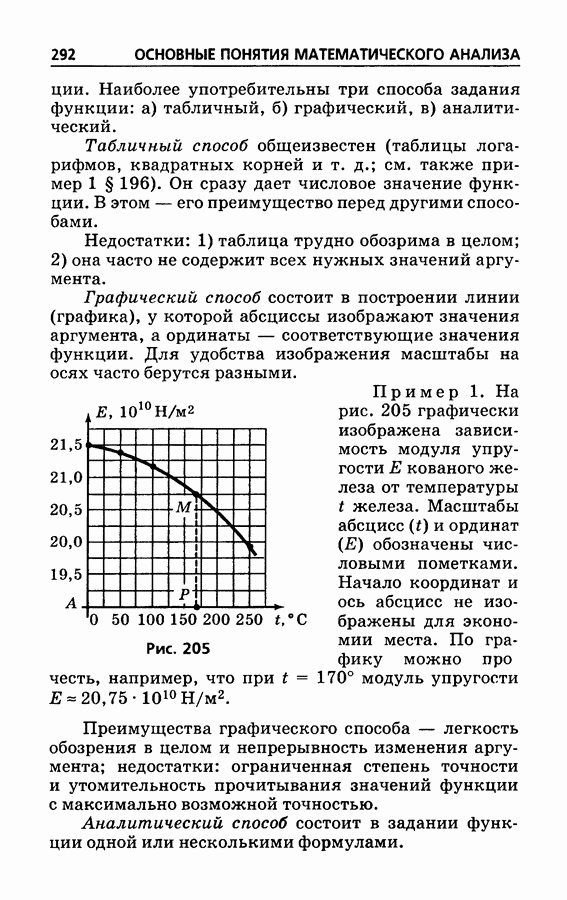
- § 196. Функция
- § 197. Способы задания функции
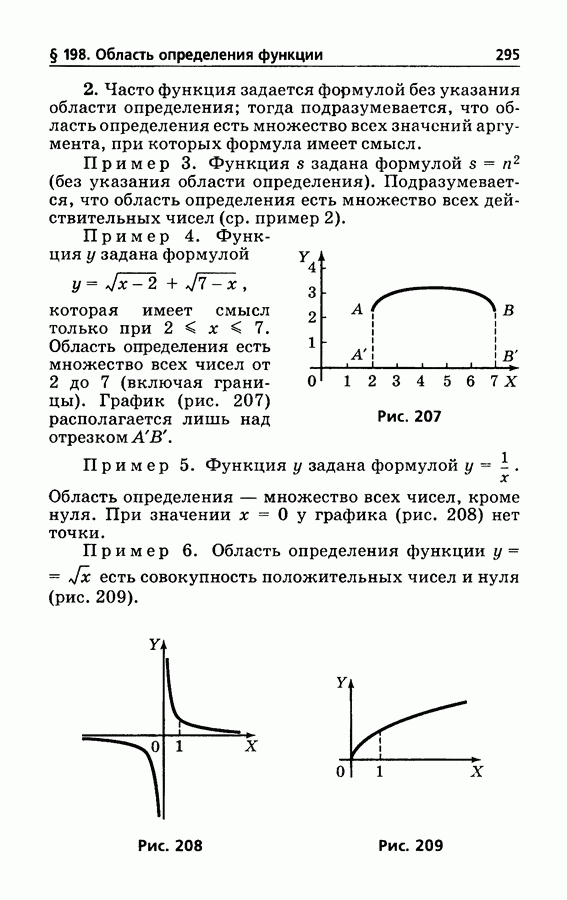
- § 198. Область определения функции
- § 199. Промежуток
- § 200. Классификация функций
- § 201. Основные элементарные функции
- § 202. Обозначение функции
- § 203. Предел последовательности
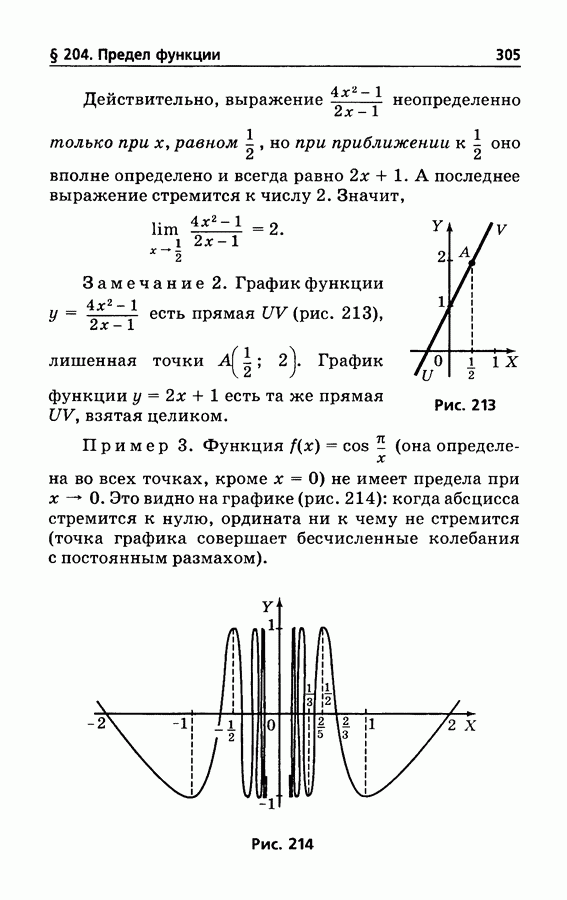
- § 204. Предел функции
- § 205. Определение предела функции
- § 206. Предел постоянной величины
- § 207. Бесконечно малая величина
- § 208. Бесконечно большая величина
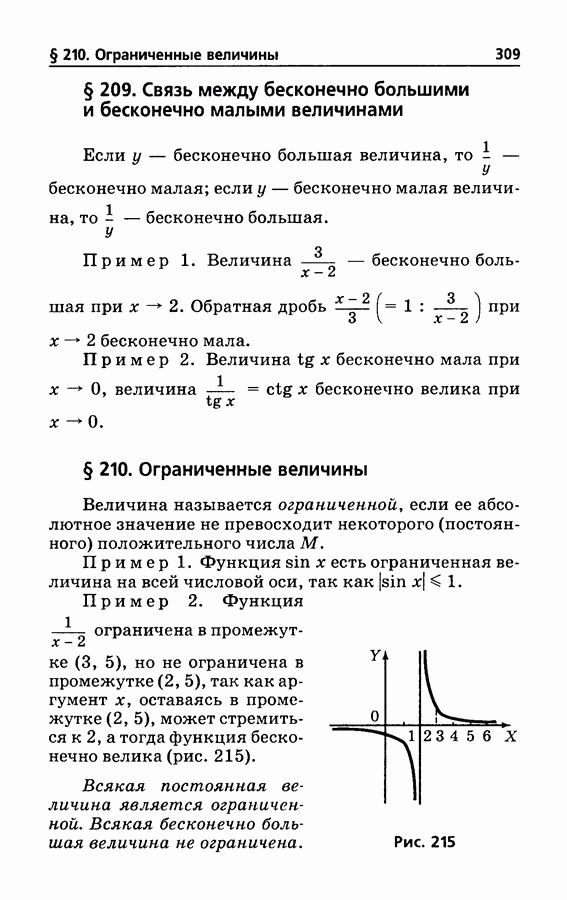
- § 209. Связь между бесконечно большими и бесконечно малыми величинами
- § 210. Ограниченные величины
- § 211. Расширение понятия предепа
- § 212. Основные свойства бесконечно малых величин
- § 213. Основные теоремы о пределах
- § 214. Число е
- § 215. Предел sinx/x при x стремящемся к 0
- § 216. Эквивалентные бесконечно малые величины
- § 217. Сравнение бесконечно малых величин
- § 217а. Приращение переменной величины
- § 218. Непрерывность функции в точке
- § 219. Свойства функций, непрерывных в точке
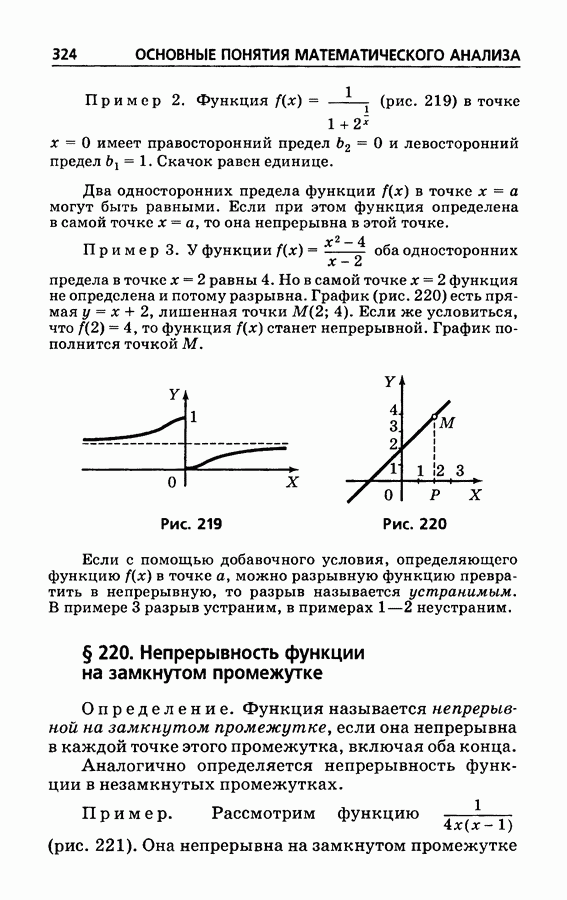
- § 219а. Односторонний предел; скачок функции
- § 220. Непрерывность функции на замкнутом промежутке
- § 221. Свойства функций, непрерывных на замкнутом промежутке
- ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 223. Скорость
- § 224. Определение производной функции
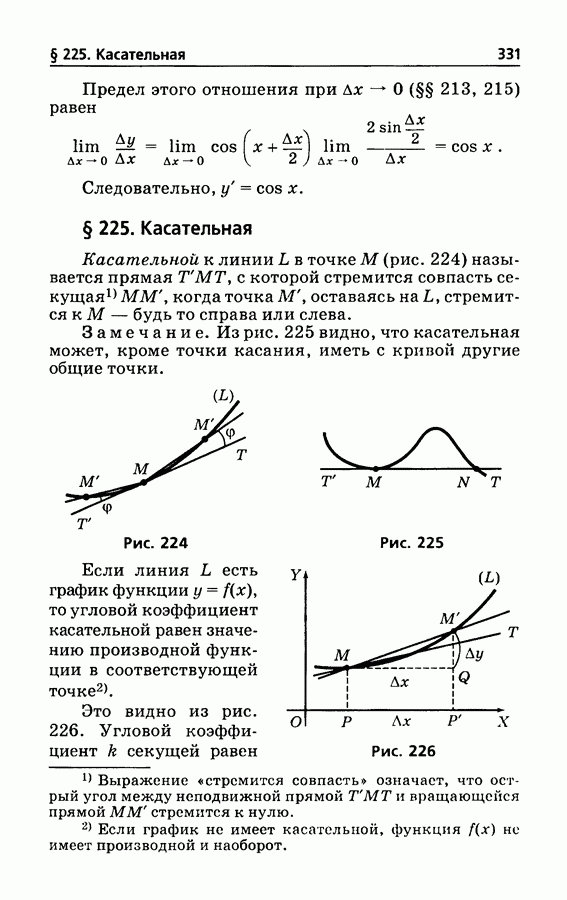
- § 225. Касательная
- § 226. Производные некоторых простейших функций
- § 227. Свойства производной
- § 228. Дифференциал
- § 229. Механический смысл дифференциала
- § 230. Геометрический смысл дифференциала
- § 231. Дифференцируемые функции
- § 232. Дифференциалы некоторых простейших функций
- § 233. Свойства дифференциала
- § 234. Инвариантность выражения f'(x)dx
- § 235. Выражение производной через дифференциалы
- § 236. Функция от функции (сложная функция)
- § 237. Дифференциал сложной функции
- § 238. Производная сложной функции
- § 239. Дифференцирование произведения
- § 240. Дифференцирование частного (дроби)
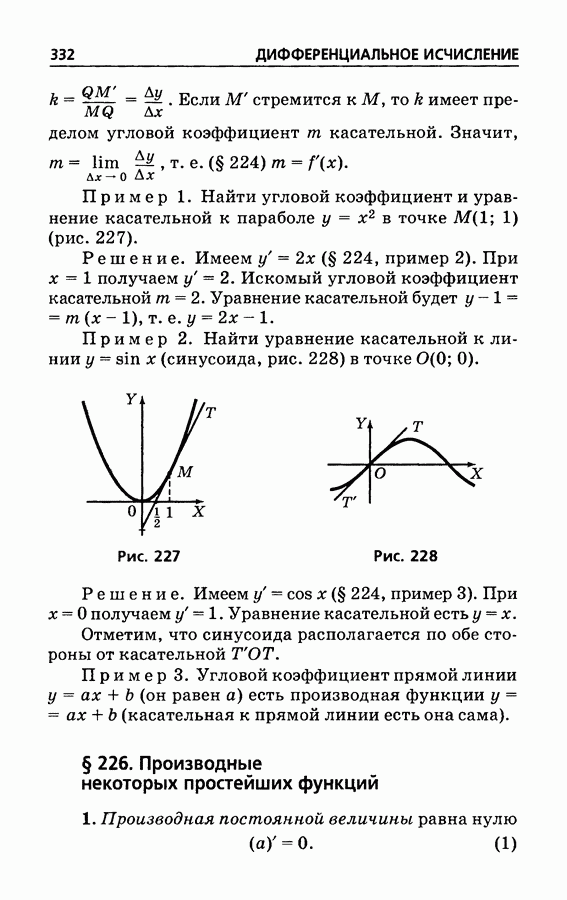
- § 241. Обратная функция
- § 242. Натуральные логарифмы
- § 243. Дифференцирование логарифмической функции
- § 244. Логарифмическое дифференцирование
- § 245. Дифференцирование показательной функции
- § 246. Дифференцирование тригонометрических функций
- § 247. Дифференцирование обратных тригонометрических функций
- § 247а. Некоторые поучительные примеры
- § 248. Дифференциал в приближенных вычислениях
- § 249. Применение дифференциала к оценке погрешности формул
- § 250. Дифференцирование неявных функций
- § 251. Параметрическое задание линии
- § 252. Параметрическое задание функции
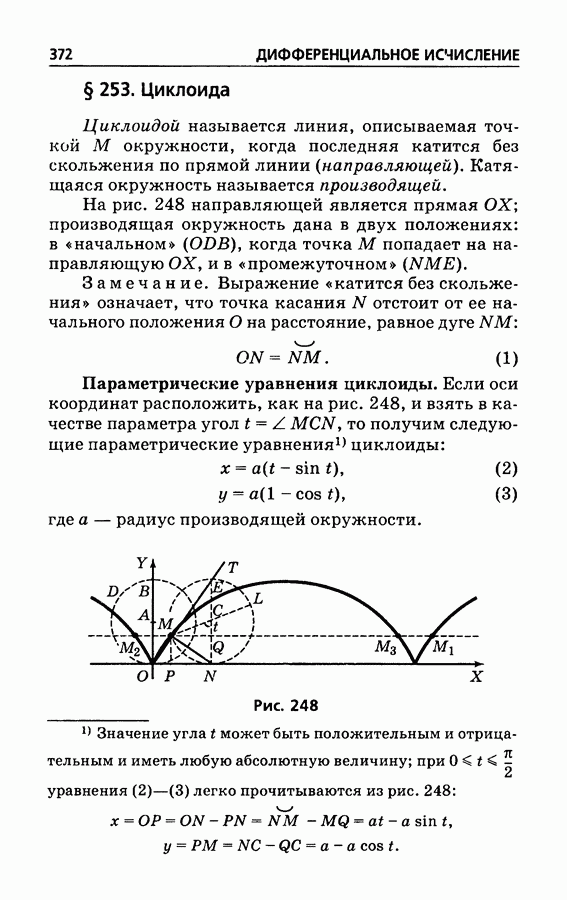
- § 253. Циклоида
- § 254. Уравнение касательной к плоской линии
- § 254а. Касательные к кривым второго порядка
- § 255. Уравнение нормали
- § 256. Производные высших порядков
- § 257. Механический смысл второй производной
- § 258. Дифференциалы высших порядков
- § 259. Выражение высших производных через дифференциалы
- § 260. Высшие производные функций, заданных параметрически
- § 261. Высшие производные неявных функций
- § 262. Правило Лейбница
- § 263. Теорема Ролля
- § 264. Теорема Лагранжа о среднем значении
- § 265. Формула конечных приращений
- § 266. Обобщенная теорема о среднем значении (Коши)
- § 267. Раскрытие неопределенности вида 0/0
- § 268. Раскрытие неопределенности вида бесконесность на бесконечность
- § 269. Неопределенные выражения других видов
- § 270. Исторические сведения о формуле Тейлора
- § 271. Формула Тейлора
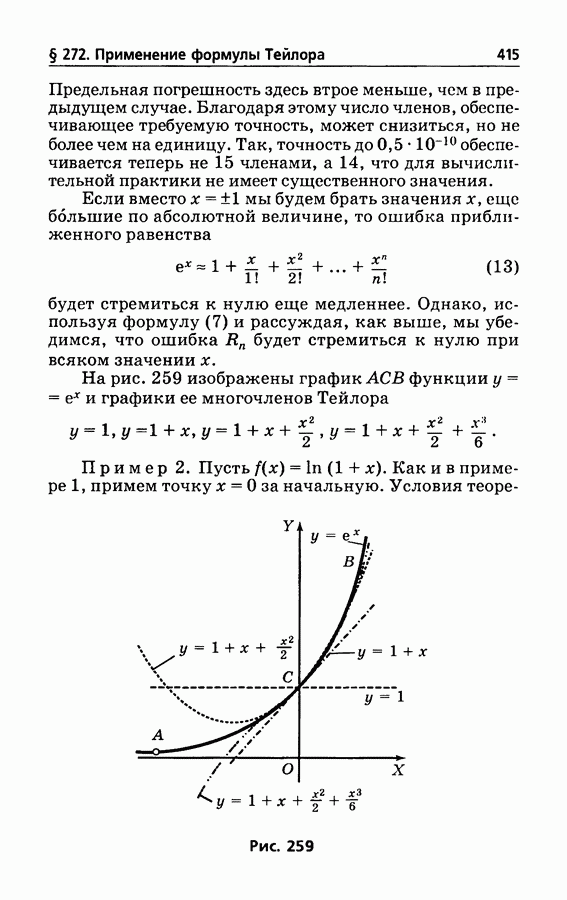
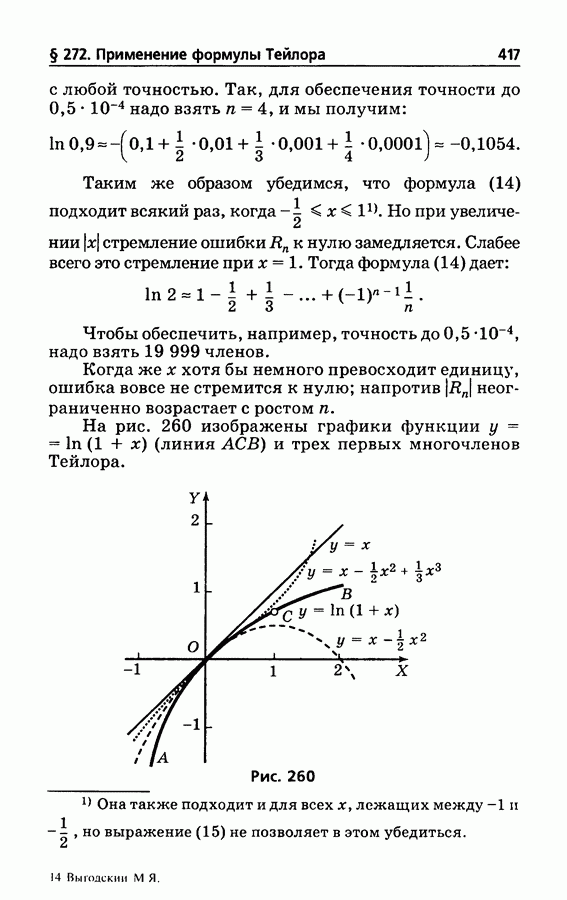
- § 272. Применение формулы Тейлора к вычислению значений функции
- § 273. Возрастание и убывание функции
- § 274. Признаки возрастания и убывания функции в точке
- § 274а. Признаки возрастания и убывания функции в промежутке
- § 275. Максимум и минимум
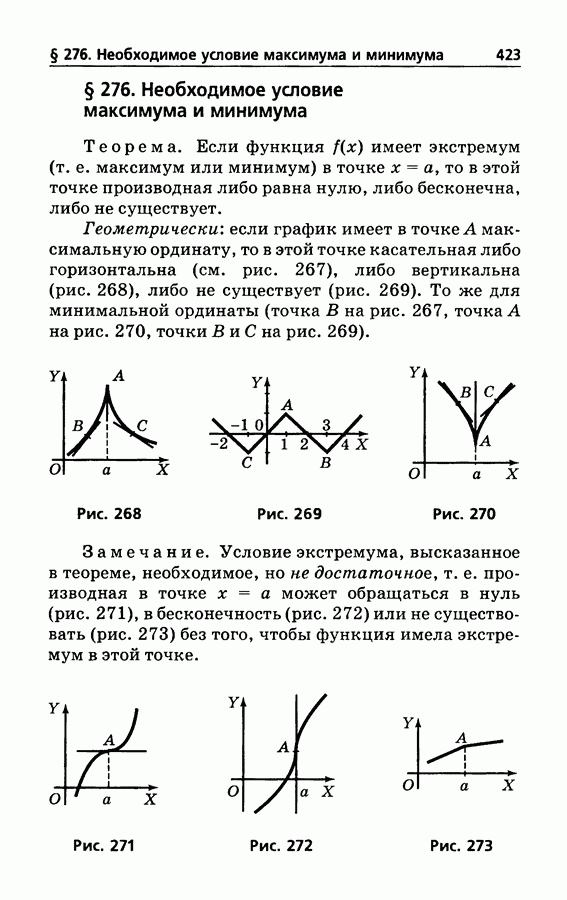
- § 276. Необходимое условие максимума и минимума
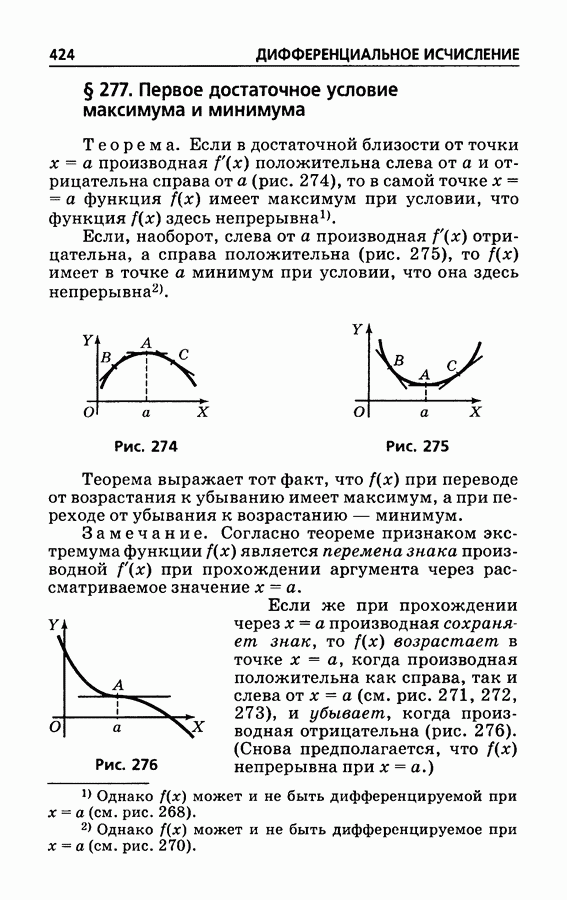
- § 277. Первое достаточное условие максимума и минимума
- § 278. Правило нахождения максимумов и минимумов
- § 279. Второе достаточное условие максимума и минимума
- § 280. Нахождение наибольшего и наименьшего значений функции
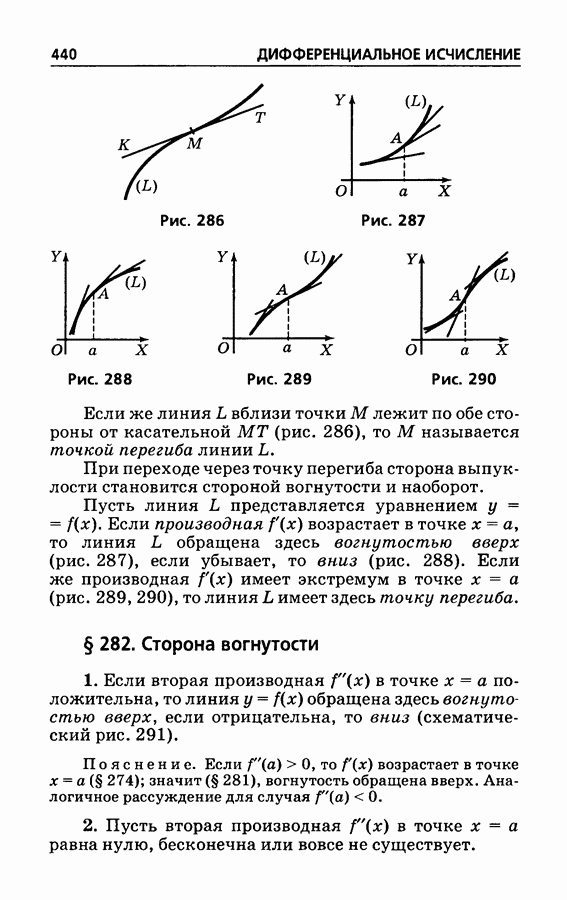
- § 281. Выпуклость плоских кривых; точка перегиба
- § 282. Сторона вогнутости
- § 283. Правило для нахождения точек перегиба
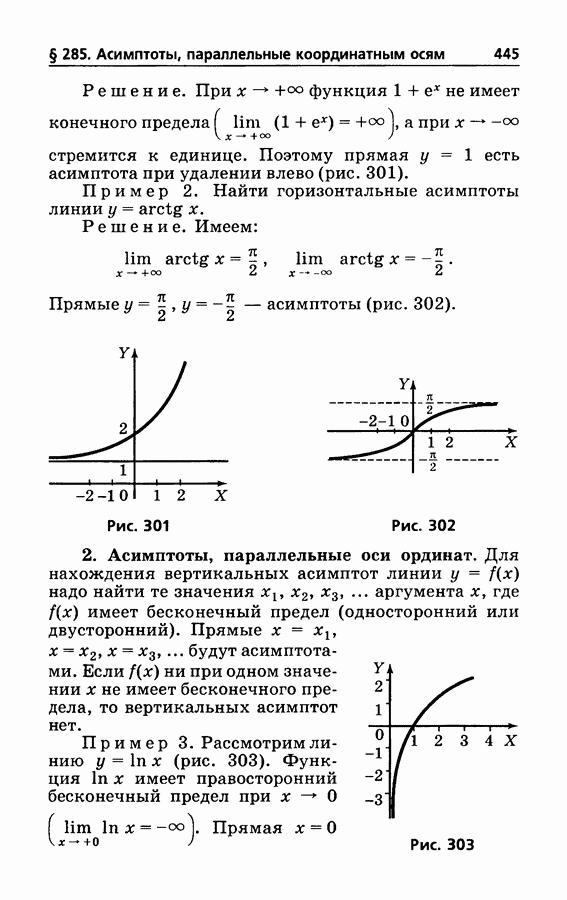
- § 284. Асимптоты
- § 285. Нахождение асимптот, параллельных координатным осям
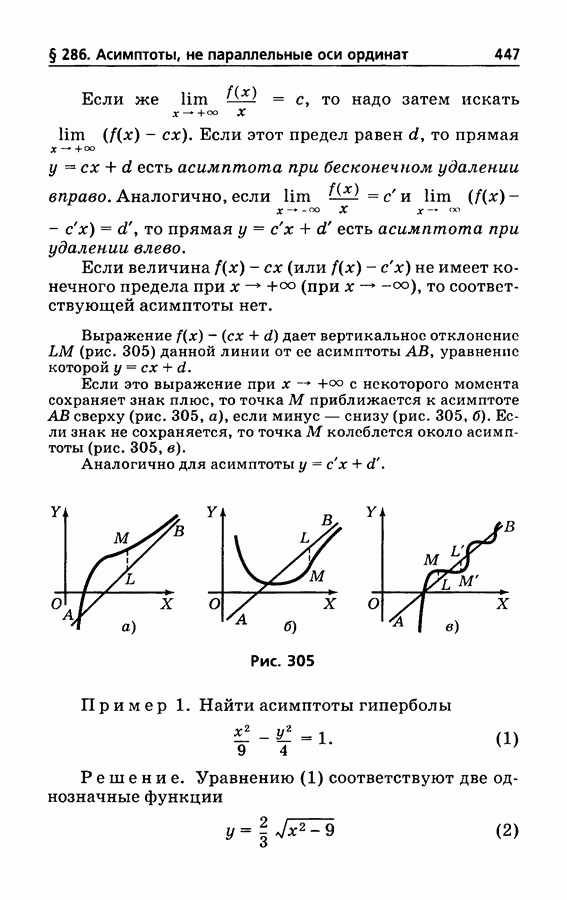
- § 286. Нахождение асимптот, не параллельных оси ординат
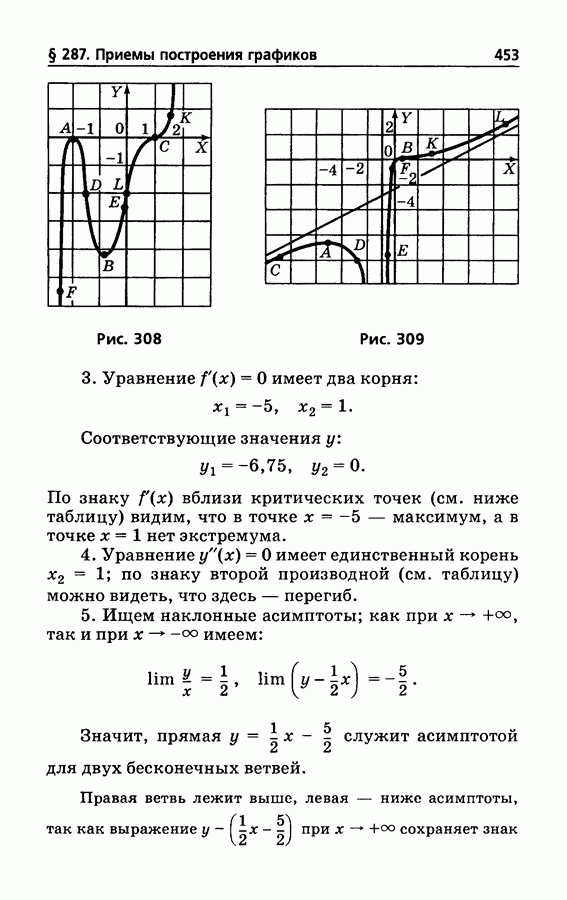
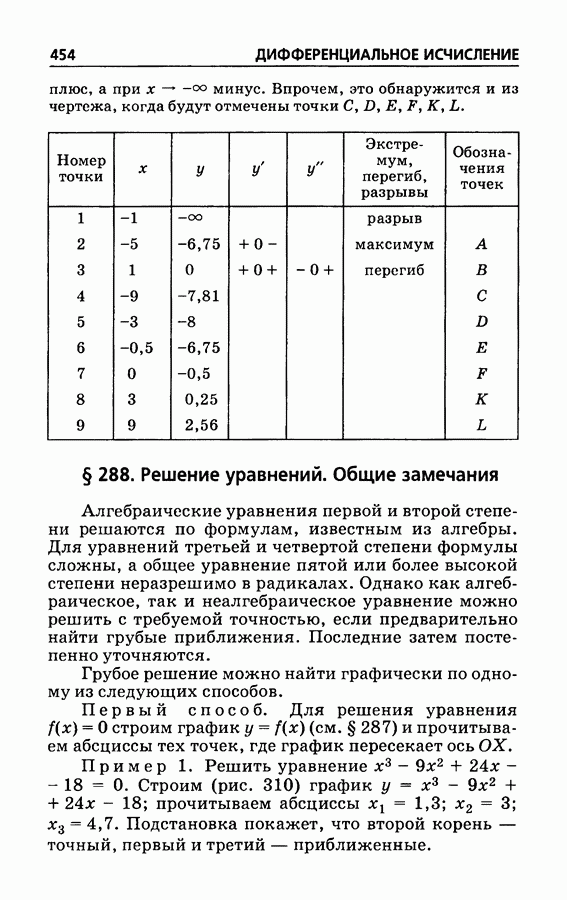
- § 287. Приемы построения графиков
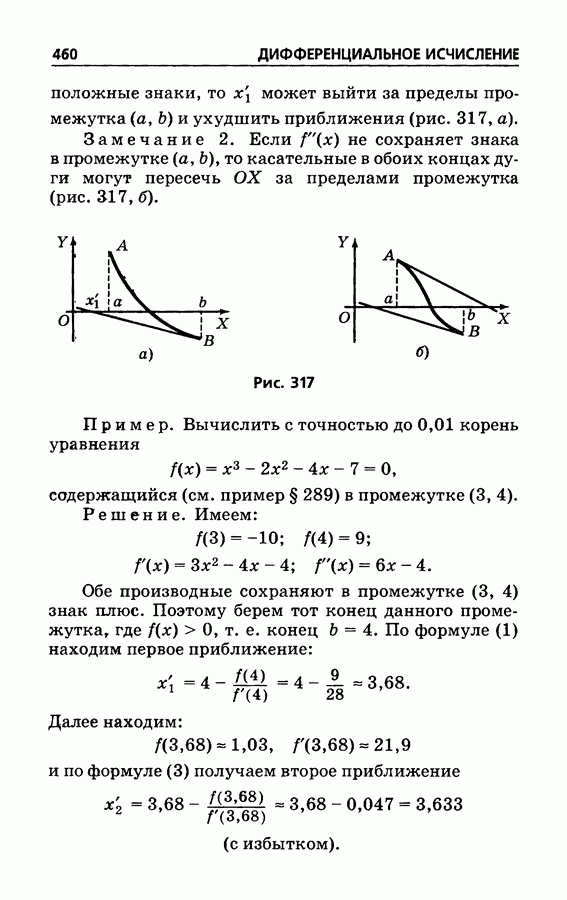
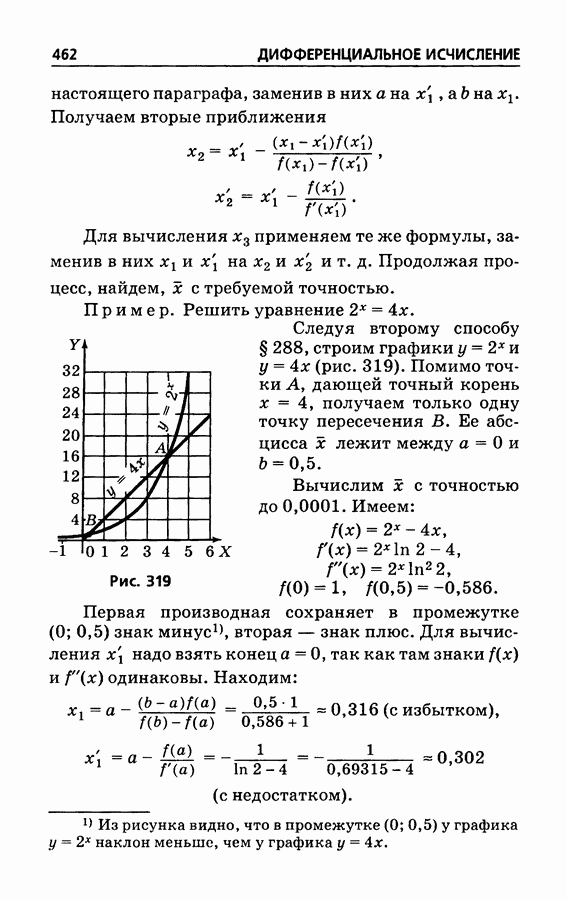
- § 288. Решение уравнений. Общие замечания
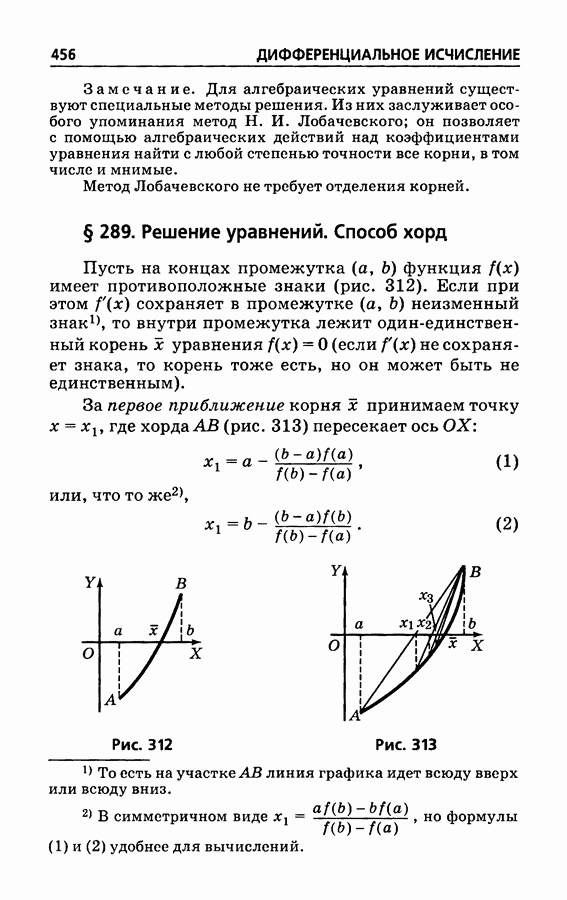
- § 289. Решение уравнений. Способ хорд
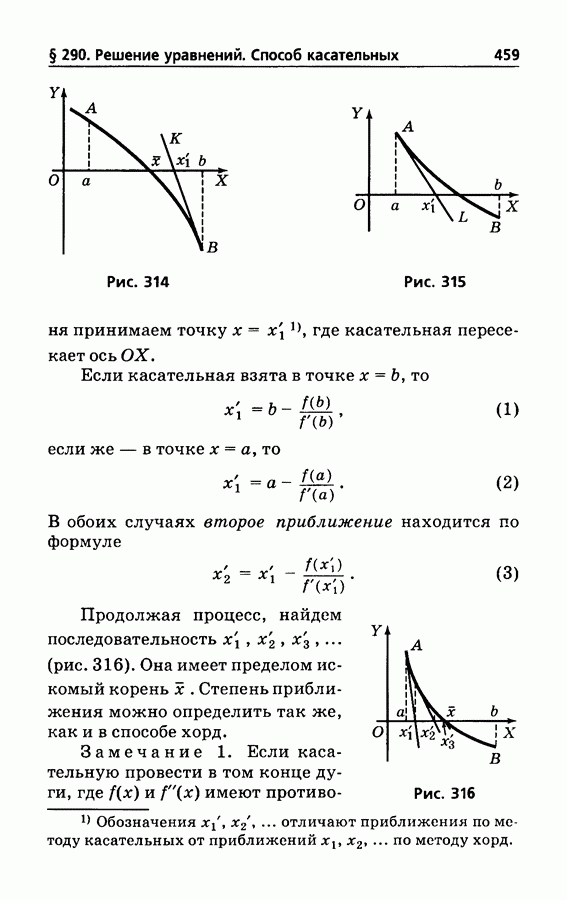
- § 290. Решение уравнений. Способ касательных
- § 291. Комбинированный метод хорд и касательных
- ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 293. Первообразная функция
- § 294. Неопределенный интеграл
- § 295. Геометрический смысл интегрирования
- § 296. Вычисление постоянной интегрирования по начальным данным
- § 297. Свойства неопределенного интеграла
- § 298. Таблица интегралов
- § 299. Непосредственное интегрирование
- § 300. Способ подстановки (интегрирование через вспомогательную переменную)
- § 301. Интегрирование по частям
- § 302. Интегрирование некоторых тригонометрических выражений
- § 303. Тригонометрические подстановки
- § 304. Рациональные функции
- § 304а. Исключение целой части
- § 305. О приемах интегрирования рациональных дробей
- § 306. Интегрирование простейших рациональных дробей
- § 307. Интегрирование рациональных функций (общий метод)
- § 308. О разложении многочлена на множители
- § 309. Об интегрируемости в элементарных функциях
- § 310. Некоторые интегралы, зависящие от радикалов
- § 311. Интеграл от биномиального дифференциала
- § 312. Интегралы вида …
- § 313. Интегралы вида S R(sinx, cosx)dx
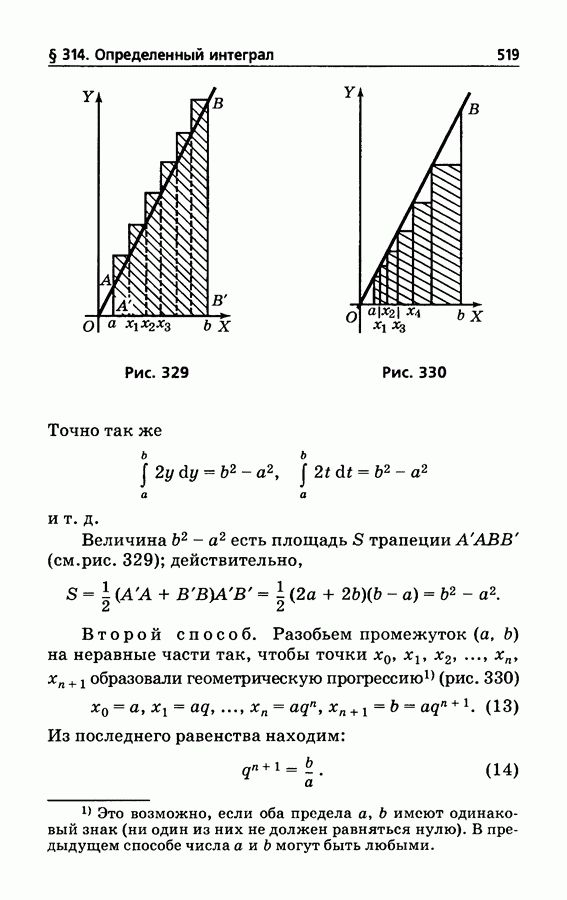
- § 314. Определенный интеграл
- § 315. Свойства определенного интеграла
- § 316. Геометрический смысл определенного интеграла
- § 317. Механический смысл определенного интеграла
- § 318. Оценка определенного интеграла
- § 318а. Неравенство Буняковского
- § 319. Теорема о среднем интегрального исчисления
- § 320. Определенный интеграл как функция верхнего предела
- § 321. Дифференциал интеграла
- § 322. Интеграл дифференциала. Формула Ньютона — Лейбница
- § 323. Вычисление определенного интеграла с помощью неопределенного
- § 324. Определенное интегрирование по частям
- § 325. Способ подстановки в определенном интеграле
- § 326. О несобственных интегралах
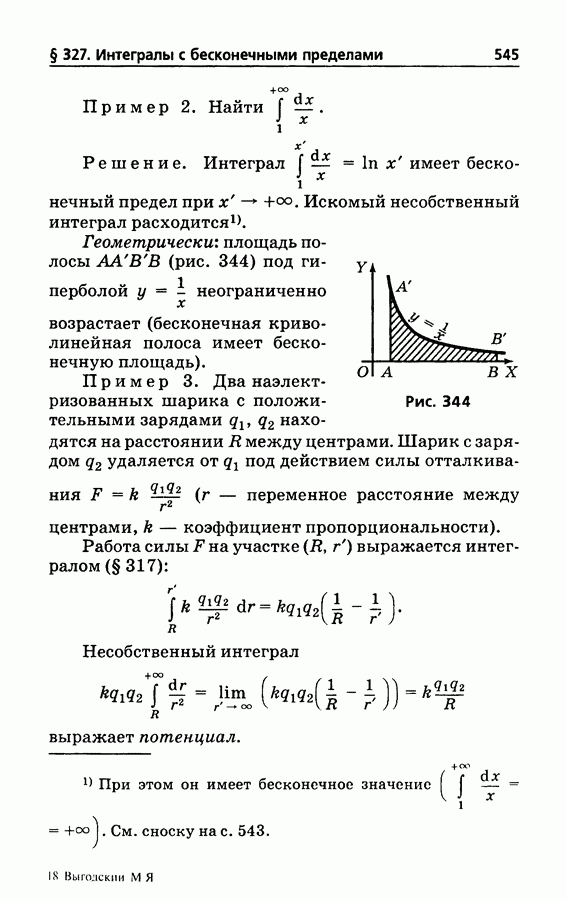
- § 327. Интегралы с бесконечными пределами
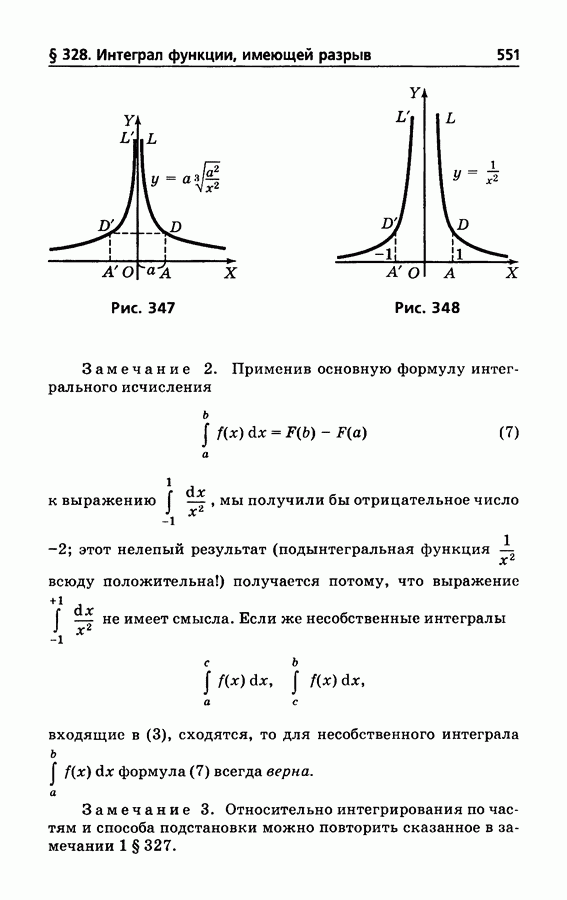
- § 328. Интеграл функции, имеющей разрыв
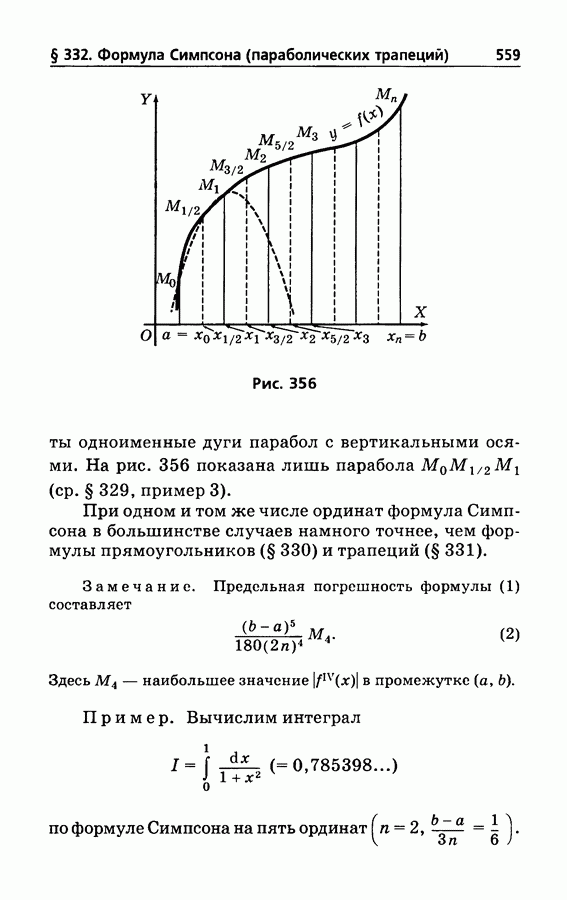
- § 329. О приближенном вычислении интеграла
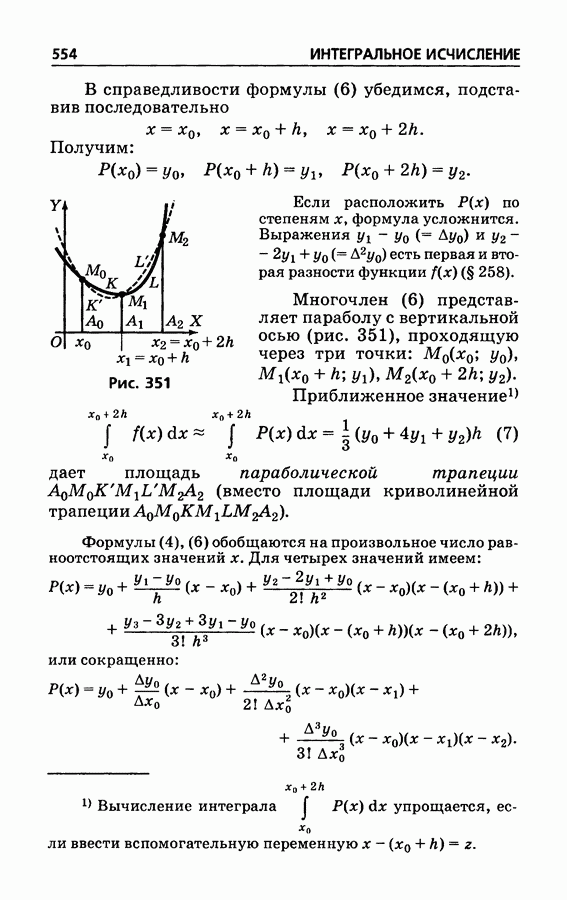
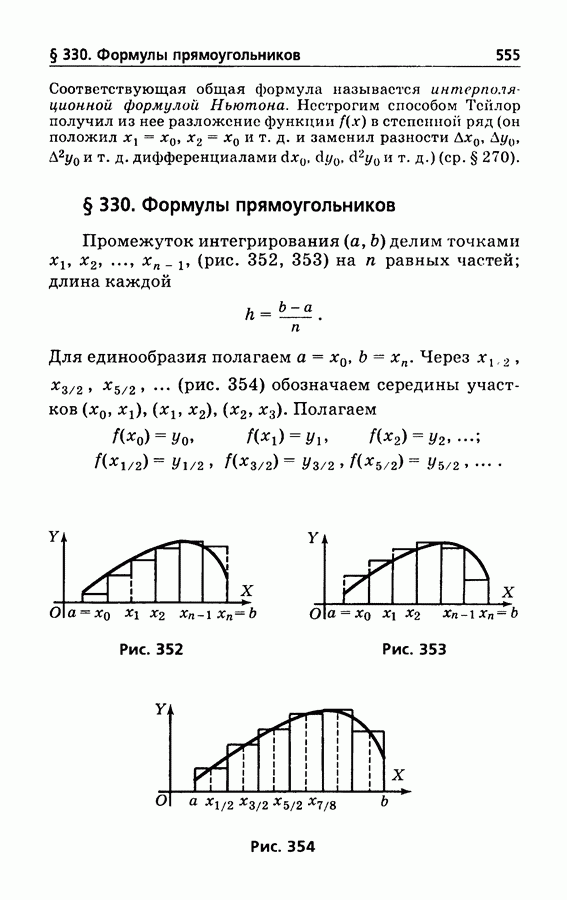
- § 330. Формулы прямоугольников
- § 331. Формула трапеций
- § 332. Формула Симпсона (параболических трапеций)
- § 333. Площади фигур, отнесенных к прямоугольным координатам
- § 334. Схема применения определенного интеграла
- § 335. Площади фигур, отнесенных к полярным координатам
- § 336. Объем тела по поперечным сечениям
- § 337. Объем тела вращения
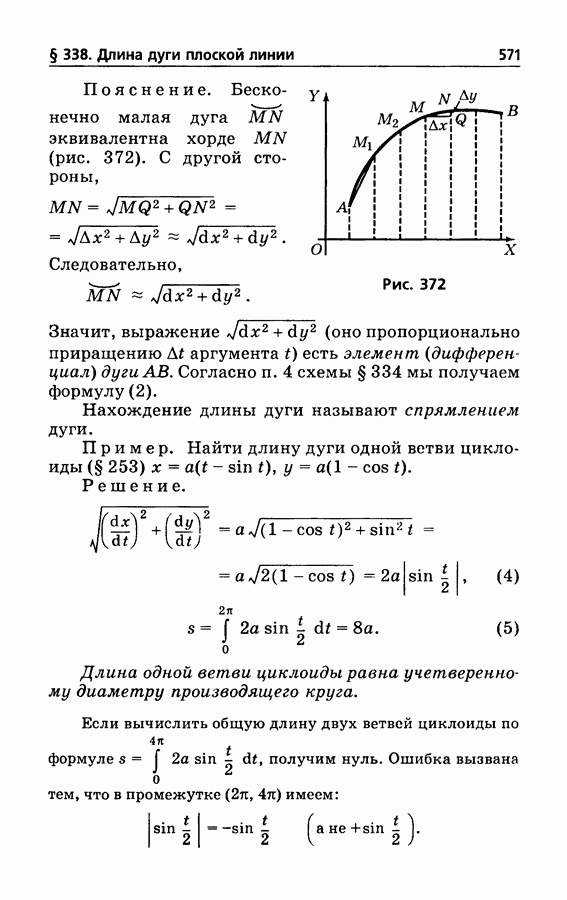
- § 338. Длина дуги плоской линии
- § 339. Дифференциал дуги
- § 340. Длина дуги и ее дифференциал в полярных координатах
- § 341. Площадь поверхности вращения
- ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ
- § 342. Кривизна
- § 343. Центр, радиус и круг кривизны плоской линии
- § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии
- § 345. Эволюта плоской линии
- § 346. Свойства эволюты плоской линии
- § 347. Развертка (эвольвента) плоской линии
- § 348. Параметрическое задание пространственной линии
- § 349. Винтовая линия
- § 350. Длина дуги пространственной линии
- § 351. Касательная к пространственной линии
- § 352. Нормальная плоскость
- § 353. Вектор-функция скалярного аргумента
- § 354. Предел вектор-функции
- § 355. Производная вектор-функции
- § 356. Дифференциал вектор-функции
- § 357. Свойства производной и дифференциала вектор-функции
- § 358. Соприкасающаяся плоскость
- § 359. Главная нормаль. Сопутствующий трехгранник
- § 360. Взаимное расположение линии и плоскости
- § 361. Основные векторы сопутствующего трехгранника
- § 362. Центр, ось и радиус кривизны пространственной линии
- § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии
- § 364. О знаке кривизны
- § 365. Кручение
- РЯДЫ
- § 367. Определение ряда
- § 368. Сходящиеся и расходящиеся ряды
- § 369. Необходимое условие сходимости ряда
- § 370. Остаток ряда
- § 371. Простейшие действия над рядами
- § 372. Положительные ряды
- § 373. Сравнение положительных рядов
- § 374. Признак Даламбера для положительного ряда
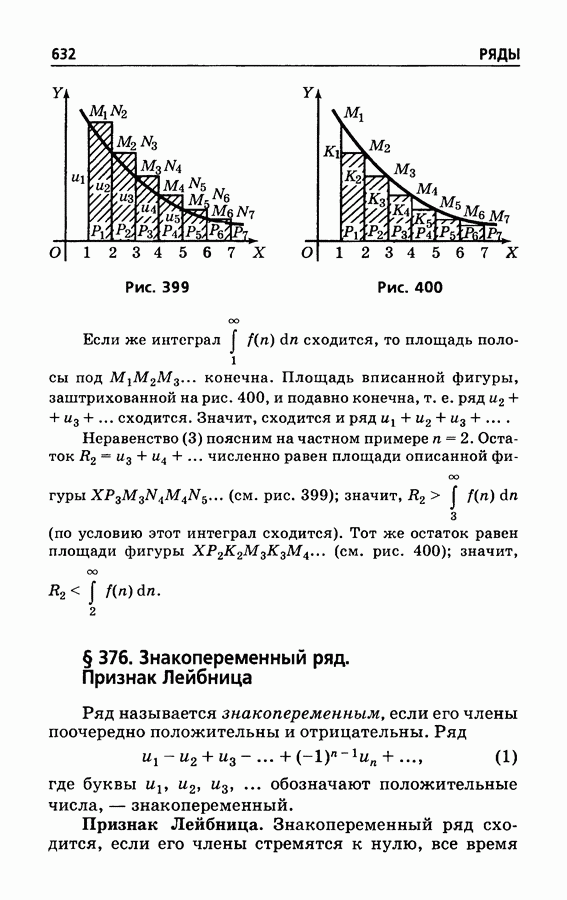
- § 375. Интегральный признак сходимости
- § 376. Знакопеременный ряд. Признак Лейбница
- § 377. Абсолютная и условная сходимость
- § 378. Признак Даламбера для произвольного ряда
- § 379. Перестановка членов ряда
- § 380. Группировка членов ряда
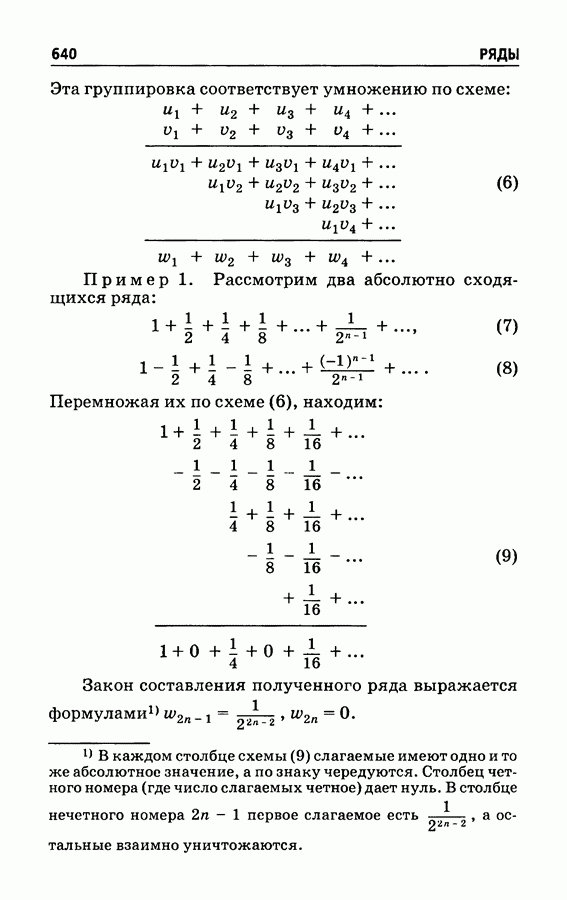
- § 381. Умножение рядов
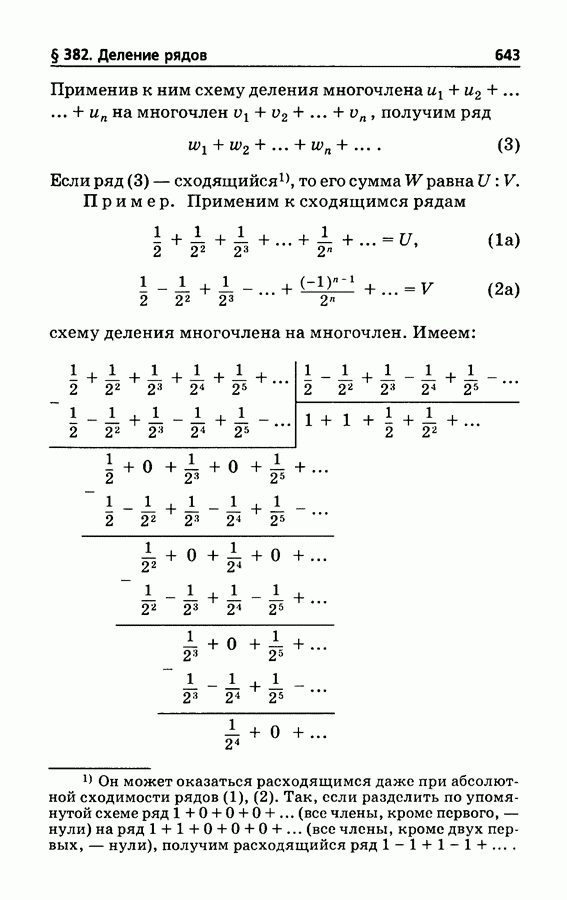
- § 382. Деление рядов
- § 383. Функциональный ряд
- § 384. Область сходимости функционального ряда
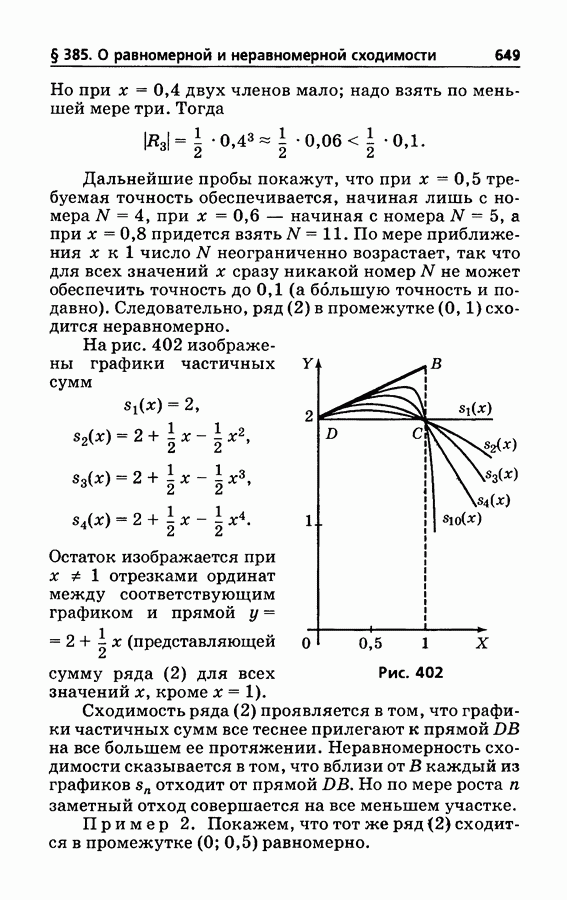
- § 385. О равномерной и неравномерной сходимости
- § 386. Определение равномерной и неравномерной сходимости
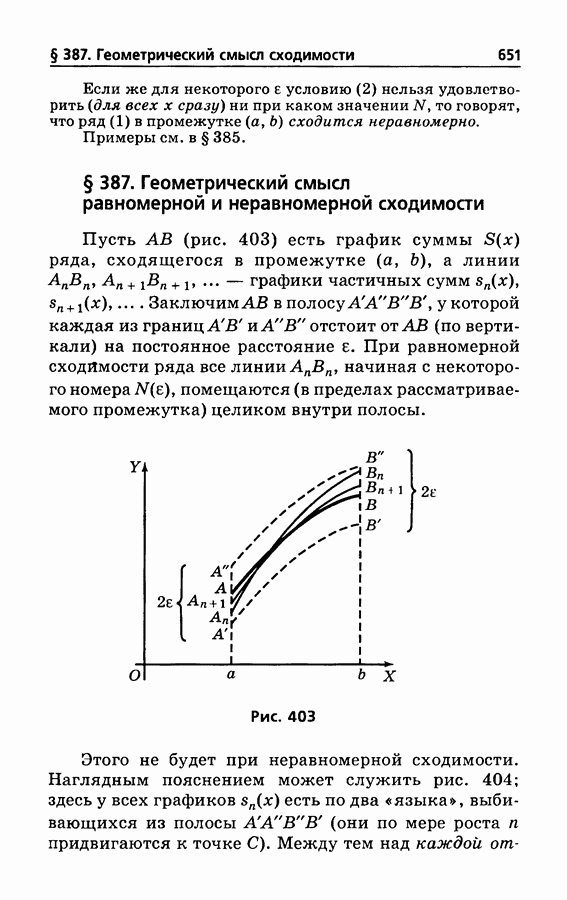
- § 387. Геометрический смысл равномерной и неравномерной сходимости
- § 388. Признак равномерной сходимости; правильные ряды
- § 389. Непрерывность суммы ряда
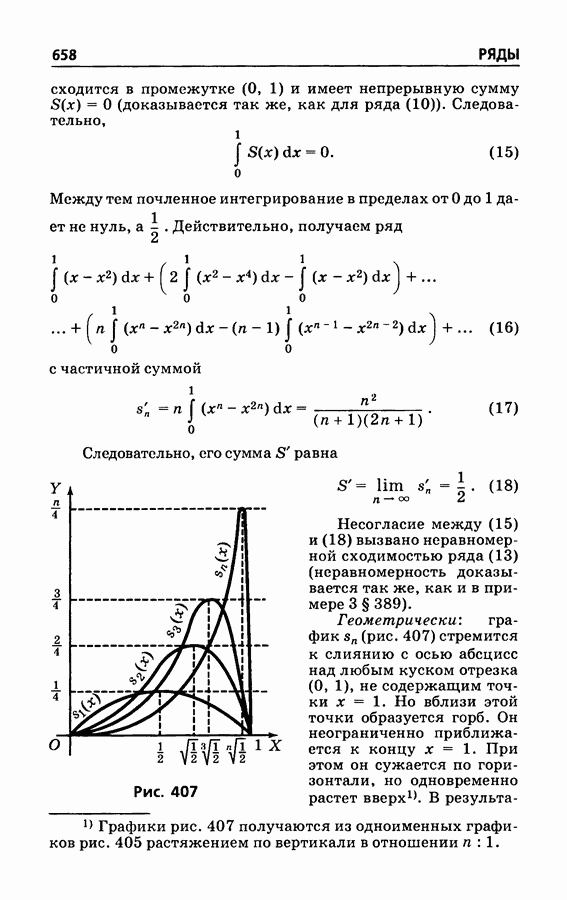
- § 390. Интегрирование рядов
- § 391. Дифференцирование рядов
- § 392. Степенной ряд
- § 393. Промежуток и радиус сходимости степенного ряда
- § 394. Нахождение радиуса сходимости
- § 395. Область сходимости ряда, расположенного по степеням х — х0
- § 396. Теорема Абеля
- § 397. Действия со степенными рядами
- § 398. Дифференцирование и интегрирование степенного ряда
- § 399. Ряд Тейлора
- § 400. Разложение функции в степенной ряд
- § 401. Разложение элементарных функций в степенные ряды
- § 402. Применение рядов к вычислению интегралов
- § 403. Гиперболические функции
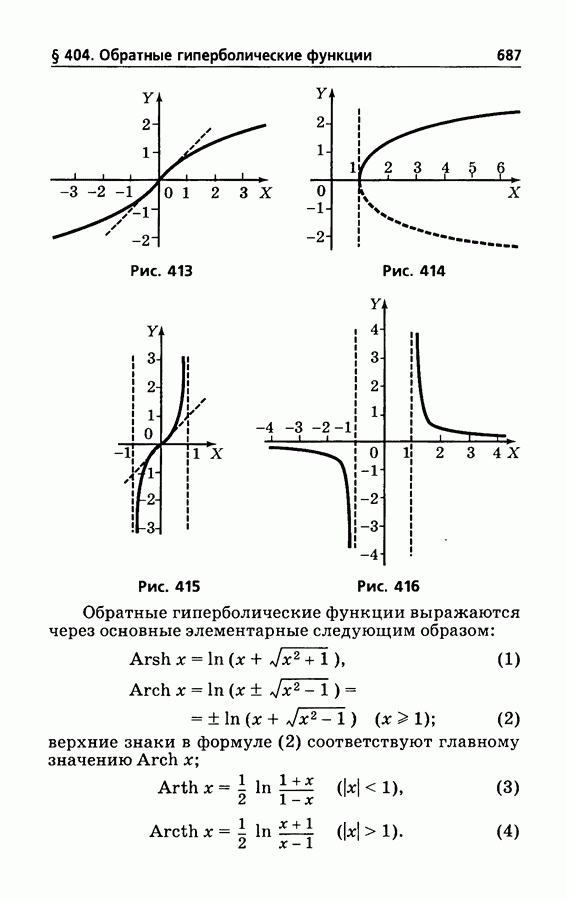
- § 404. Обратные гиперболические функции
- § 405. Происхождение наименований гиперболических функций
- § 406. О комплексных числах
- § 407. Комплексная функция действительного аргумента
- § 408. Производная комплексной функции
- § 409. Возведение положительного числа в комплексную степень
- § 410. Формула Эйлера
- § 411. Тригонометрический ряд
- § 412. Исторические сведения о тригонометрических рядах
- § 413. Ортогональность системы функций cos nx, sin nx
- § 414. Формулы Эйлера-Фурье
- § 415. Ряд Фурье
- § 416. Ряд Фурье для непрерывной функции
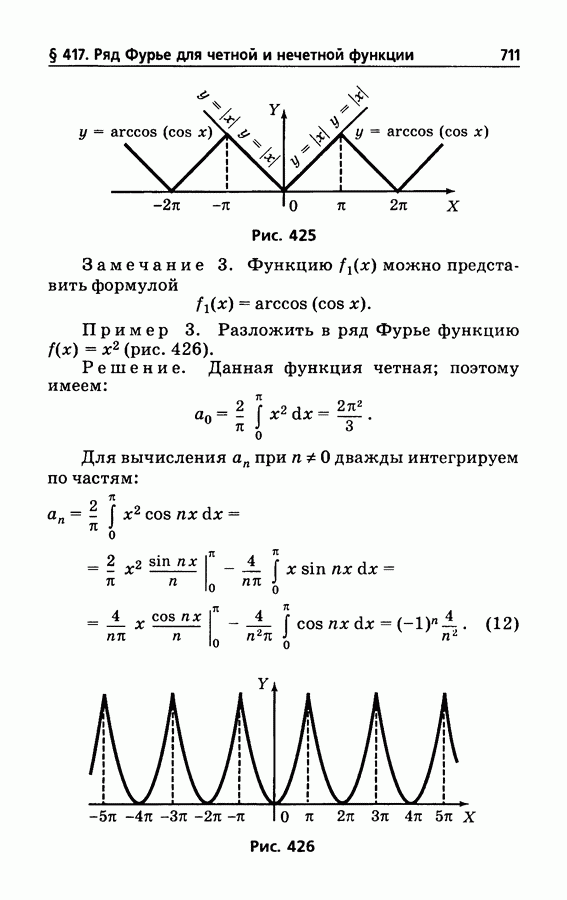
- § 417. Ряд Фурье для четной и нечетной функции
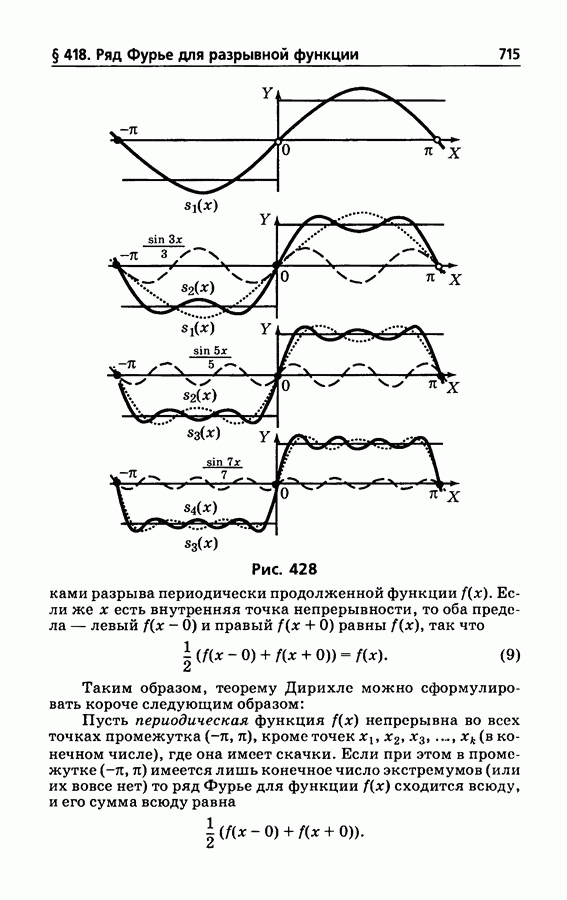
- § 418. Ряд Фурье для разрывной функции
- ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ
- § 420. Функция трех и большего числа аргументов
- § 421. Способы задания функций нескольких аргументов
- § 422. Предел функции нескольких аргументов
- § 424. Непрерывность функции нескольких аргументов
- § 425. Частные производные
- § 426. Геометрический смысл частных производных для случая двух аргументов
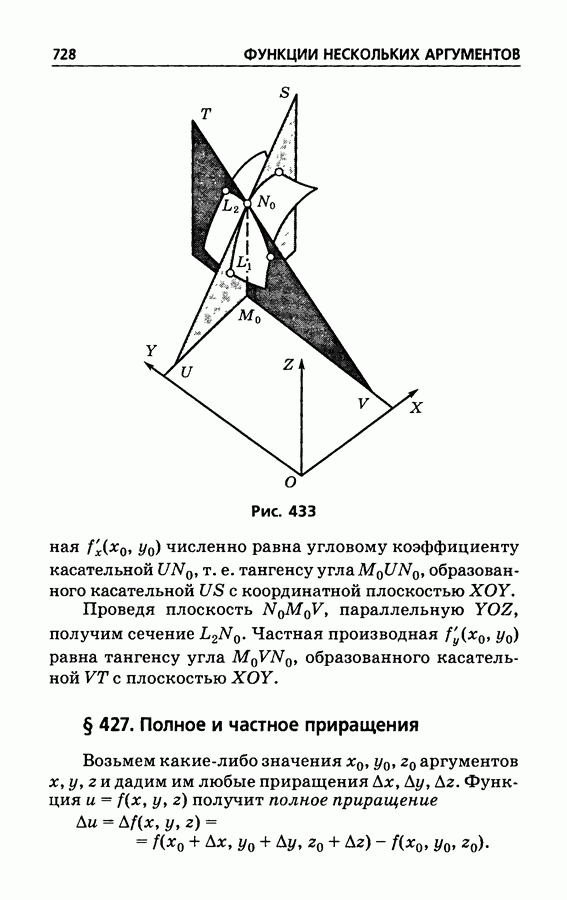
- § 427. Полное и частное приращения
- § 428. Частный дифференциал
- § 429. О выражении частной производной через дифференциал
- § 430. Полный дифференциал
- § 431. Геометрический смысл полного дифференциала (случай двух аргументов)
- § 432. Инвариантность выражения … полного дифференциала
- § 433. Техника дифференцирования
- § 434. Дифференцируемые функции
- § 435. Касательная плоскость и нормаль к поверхности
- § 436. Уравнение касательной плоскости
- § 437. Уравнения нормали
- § 438. Дифференцирование сложной функции
- § 439. Замена прямоугольных координат полярными
- § 440. Формулы для производных сложной функции
- § 441. Полная производная
- § 442. Дифференцирование неявной функции нескольких переменных
- § 443. Частные производные высших порядков
- § 444. Полные дифференциалы высших порядков
- § 445. Техника повторного дифференцирования
- § 446. Условное обозначение дифференциалов
- § 447. Формула Тейлора для функции нескольких аргументов
- § 448. Экстремум (максимум и минимум) функции нескольких аргументов
- § 449. Правило нахождения экстремума
- § 450. Достаточные условия экстремума (случай двух аргументов)
- § 451. Двойной интеграл
- § 452. Геометрический смысл двойного интеграла
- § 453. Свойства двойного интеграла
- § 454. Оценка двойного интеграла
- § 455. Вычисление двойного интеграла (простейший случай)
- § 456. Вычисление двойного интеграла (общий случай)
- § 457. Функция точки
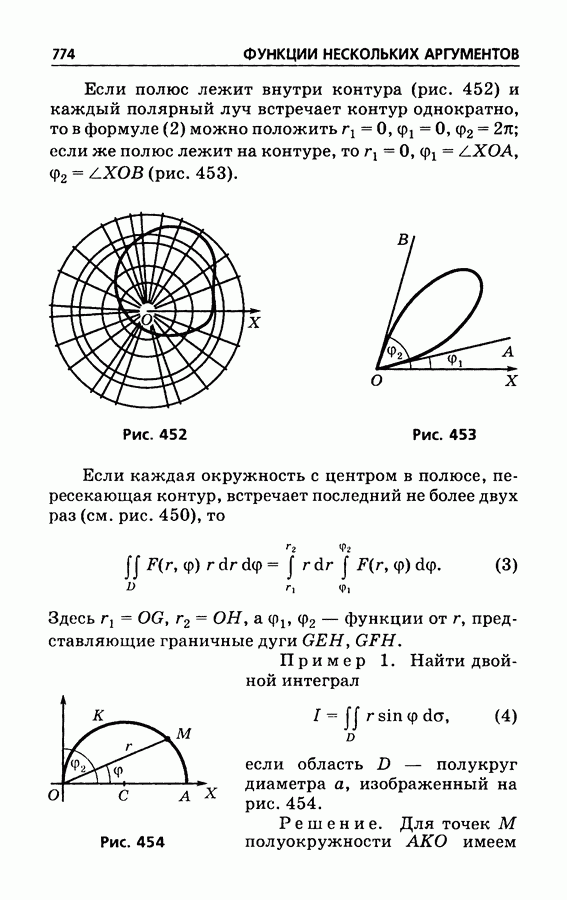
- § 458. Выражение двойного интеграла через полярные координаты
- § 459. Площадь куска поверхности
- § 460. Тройной интеграл
- § 461. Вычисление тройного интеграла (простейший случай)
- § 462. Вычисление тройного интеграла (общий случай)
- § 463. Цилиндрические координаты
- § 464. Выражение тройного интеграла через цилиндрические координаты
- § 465. Сферические координаты
- § 466. Выражение тройного интеграла через сферические координаты
- § 467. Схема применения двойного и тройного интегралов
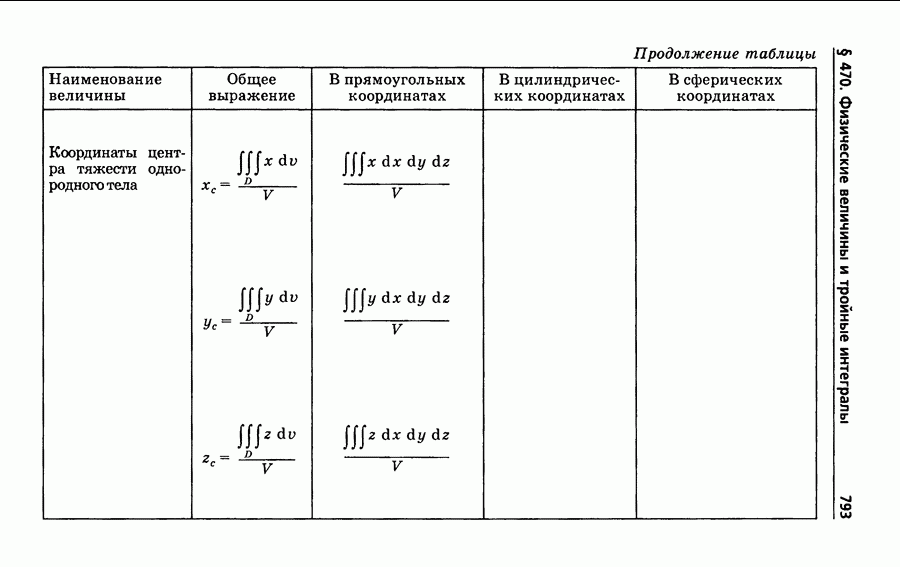
- § 468. Момент инерции
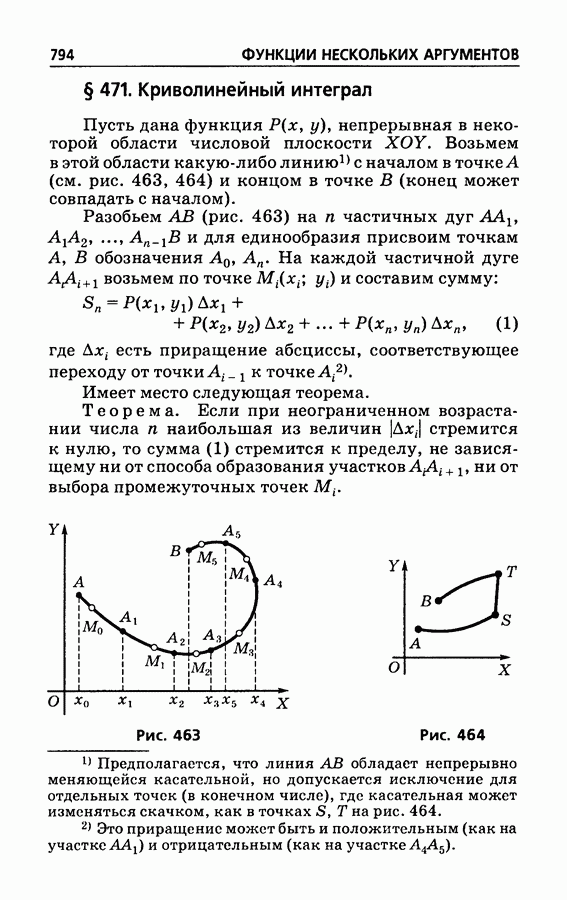
- § 471. Криволинейный интеграл
- § 472. Механический смысл криволинейного интеграла
- § 473. Вычисление криволинейного интеграла
- § 474. Формула Грина
- § 475. Условие, при котором криволинейный интеграл не зависит от пути
- § 476. Другая форма условия предыдущего параграфа
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 478. Уравнение первого порядка
- § 479. Геометрический смысл уравнения первого порядка
- § 480. Изоклины
- § 481. Частное и общее решения уравнения первого порядка
- § 482. Уравнения с разделенными переменными
- § 483. Разделение переменных. Особое решение
- § 484. Уравнение в полных дифференциалах
- § 484а. Интегрирующий множитель
- § 485. Однородное уравнение
- § 486. Линейное уравнение первого порядка
- § 487. Уравнение Клеро
- § 488. Огибающая
- § 489. Об интегрируемости дифференциальных уравнений
- § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера
- § 491. Интегрирование дифференциальных уравнений с помощью рядов
- § 492. О составлении дифференциальных уравнений
- § 493. Уравнение второго порядка
- § 494. Уравнение n-го порядка
- § 495. Случаи понижения порядка
- § 496. Линейное уравнение второго порядка
- § 497. Линейное уравнение второго порядка с постоянными коэффициентами
- § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части
- § 498а. Связь между случаями 1 и 3 § 498
- § 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью
- § 500. Линейные уравнения любого порядка
- § 501. Метод вариации постоянных
- § 502. Системы дифференциальных уравнений. Линейные системы
- НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
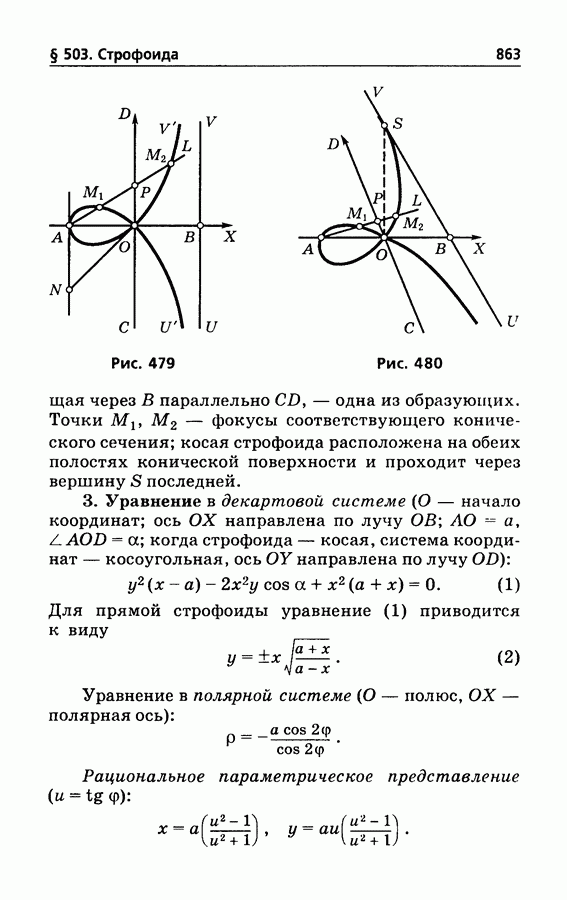
- § 503. Строфоида
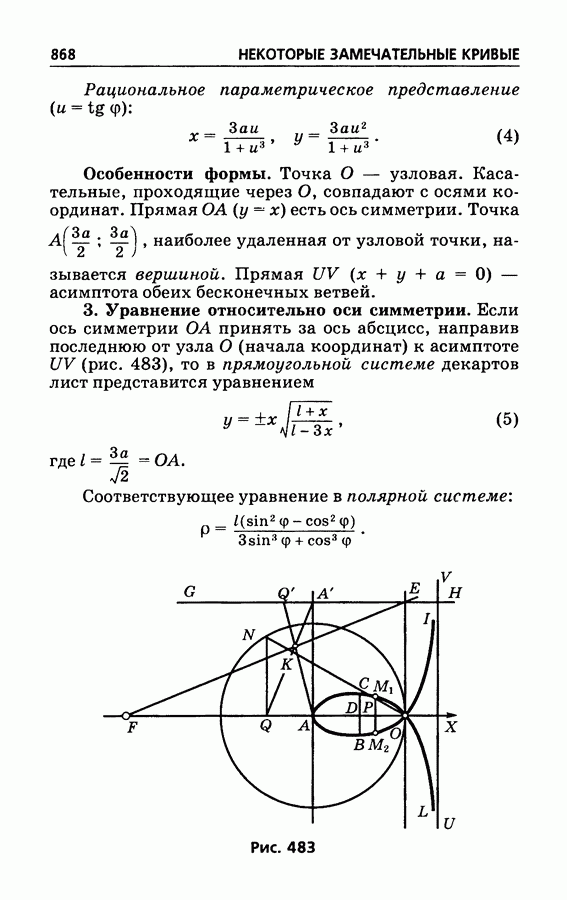
- § 504. Циссоида Диокла
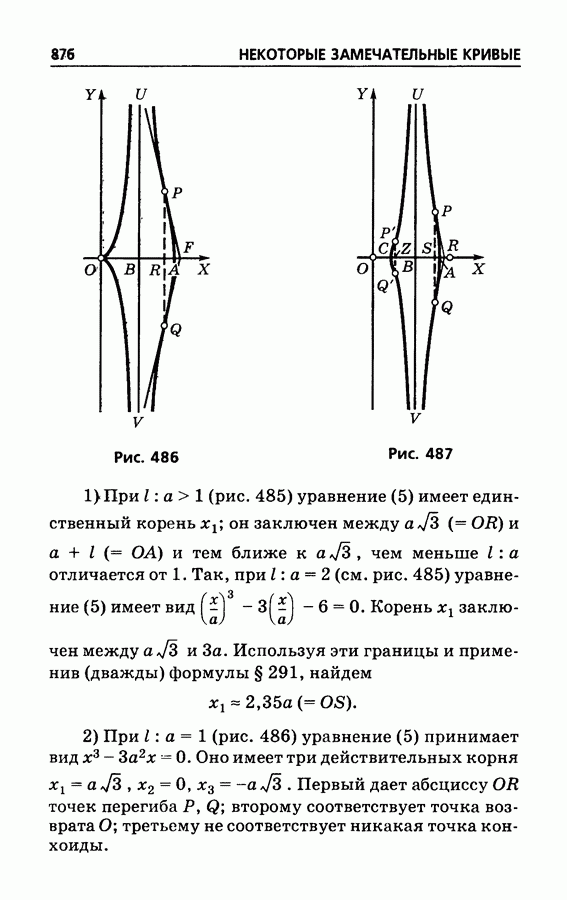
- § 505. Декартов лист
- § 506. Верзьера Аньези
- § 507. Конхоида Никомеда
- § 508. Улитка Паскаля; кардиоида
- § 509. Линия Кассини
- § 510. Лемниската Бернулли
- § 511. Архимедова спираль
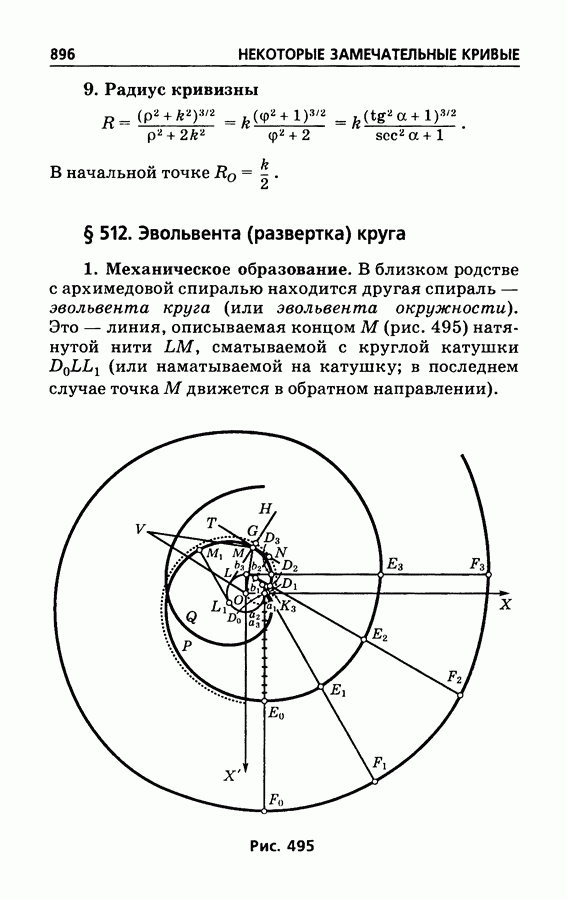
- § 512. Эвольвента (развертка) круга
- § 513. Логарифмическая спираль
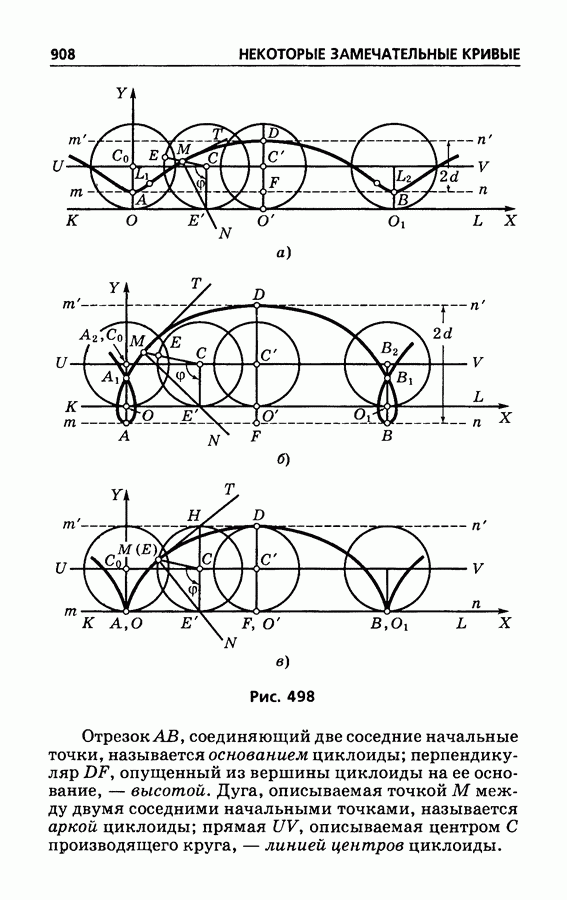
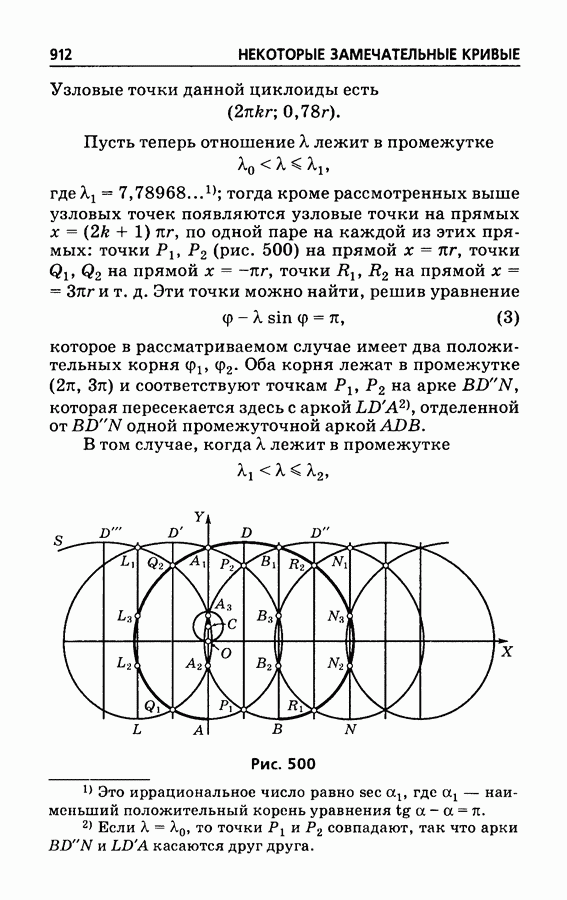
- § 514. Циклоиды
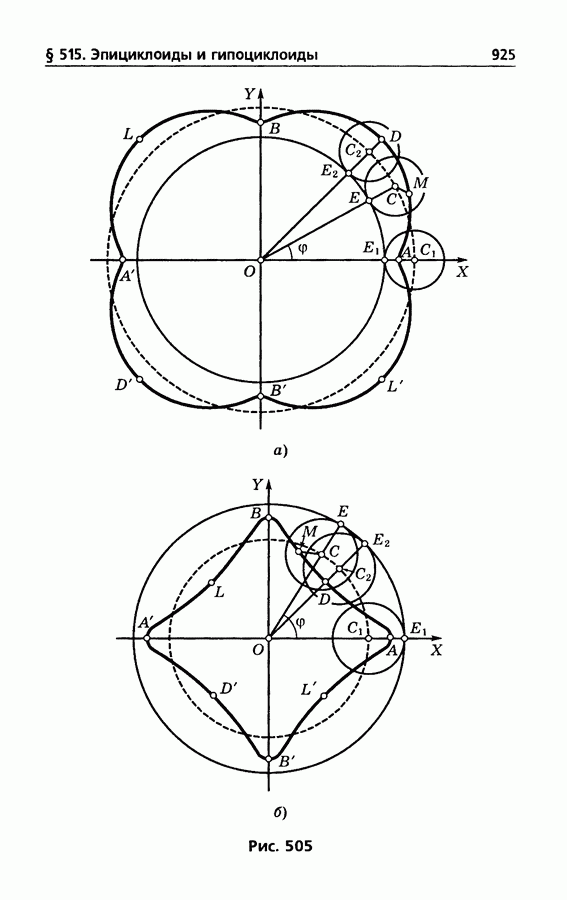
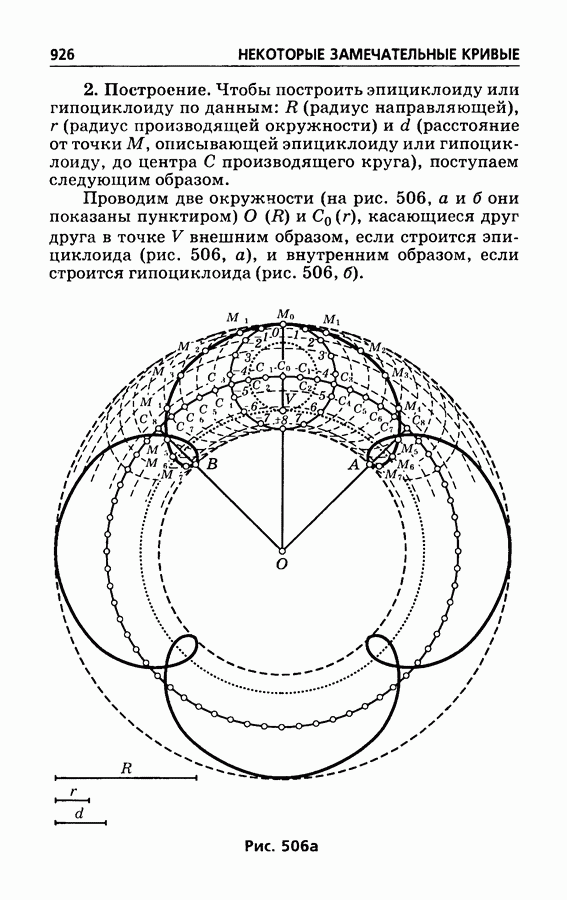
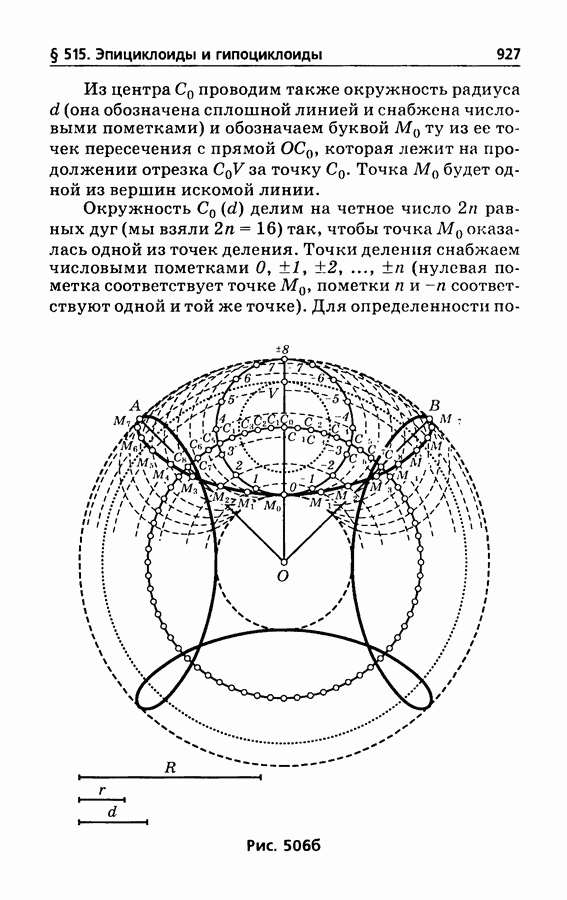
- § 515. Эпициклоиды и гипоциклоиды
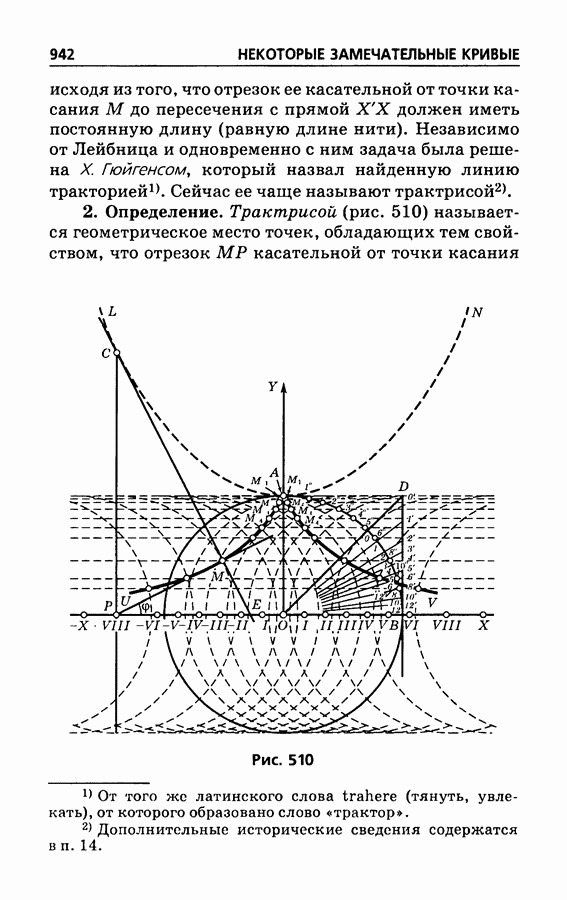
- § 516. Трактриса
- § 517. Цепная линия