| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
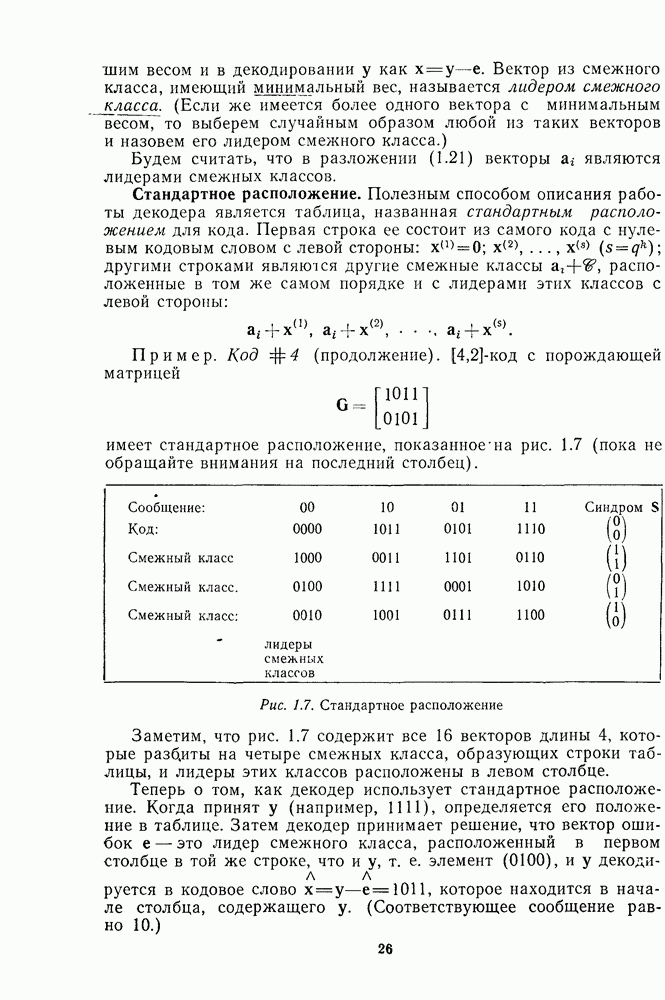
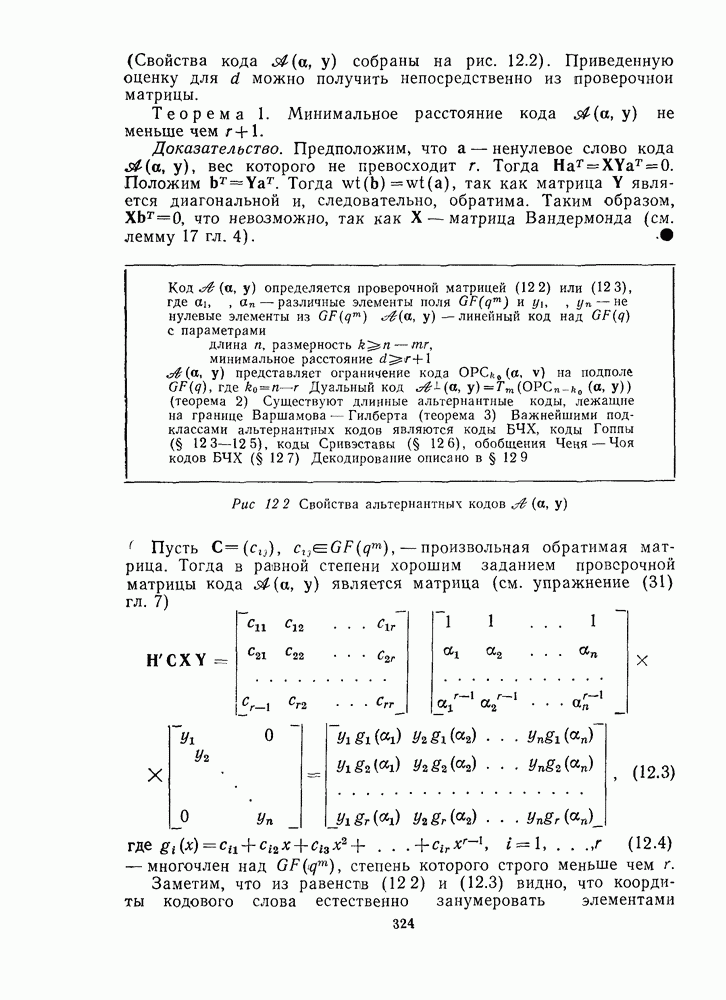
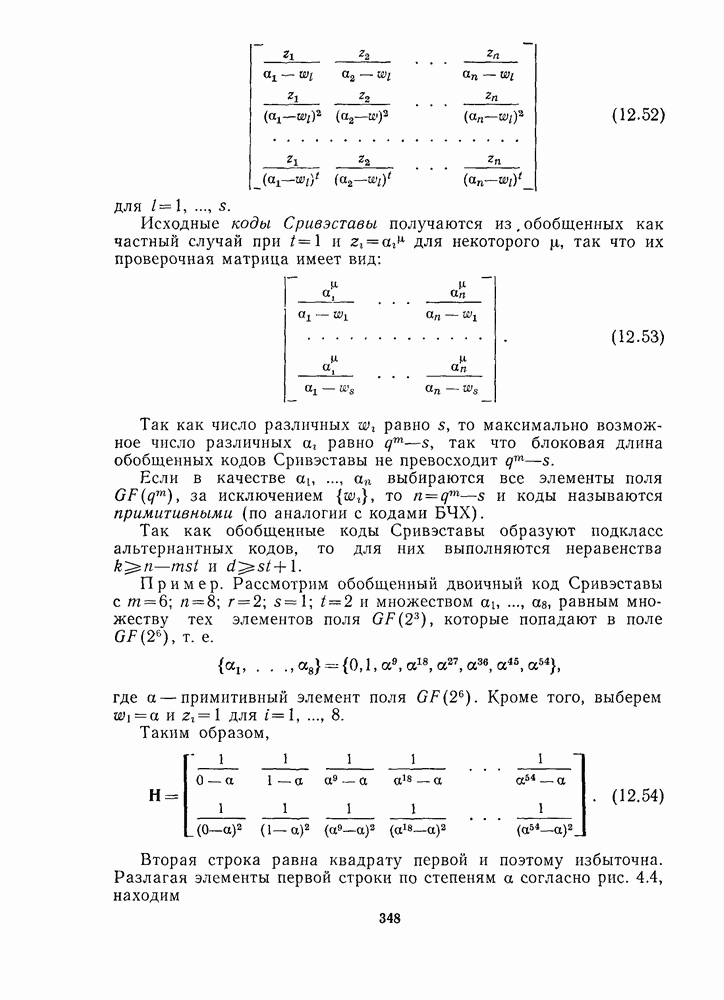
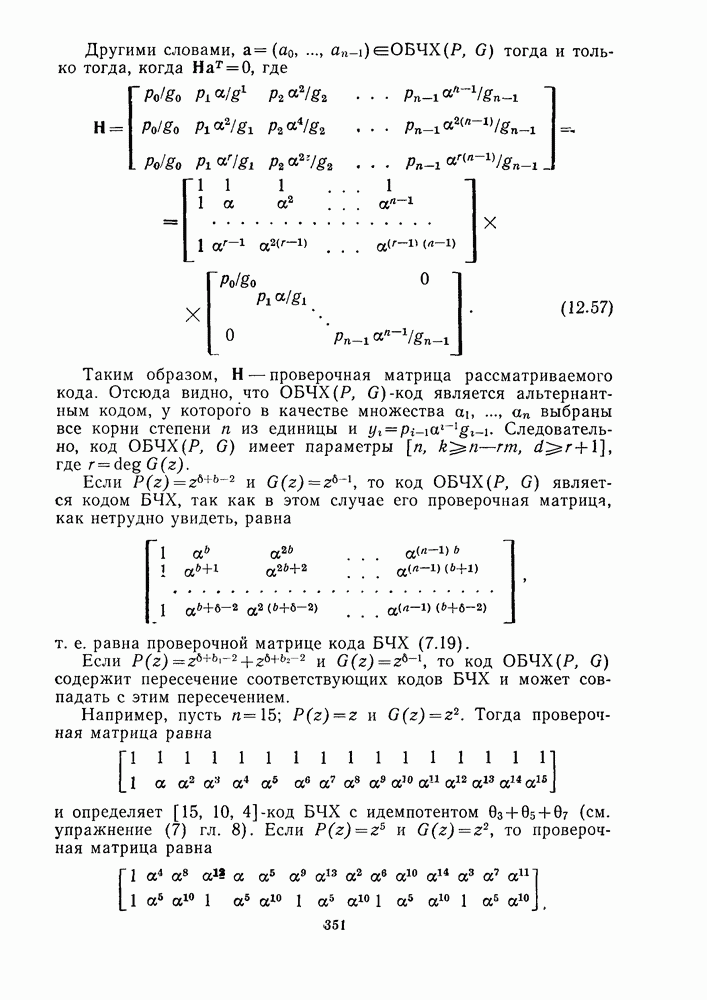
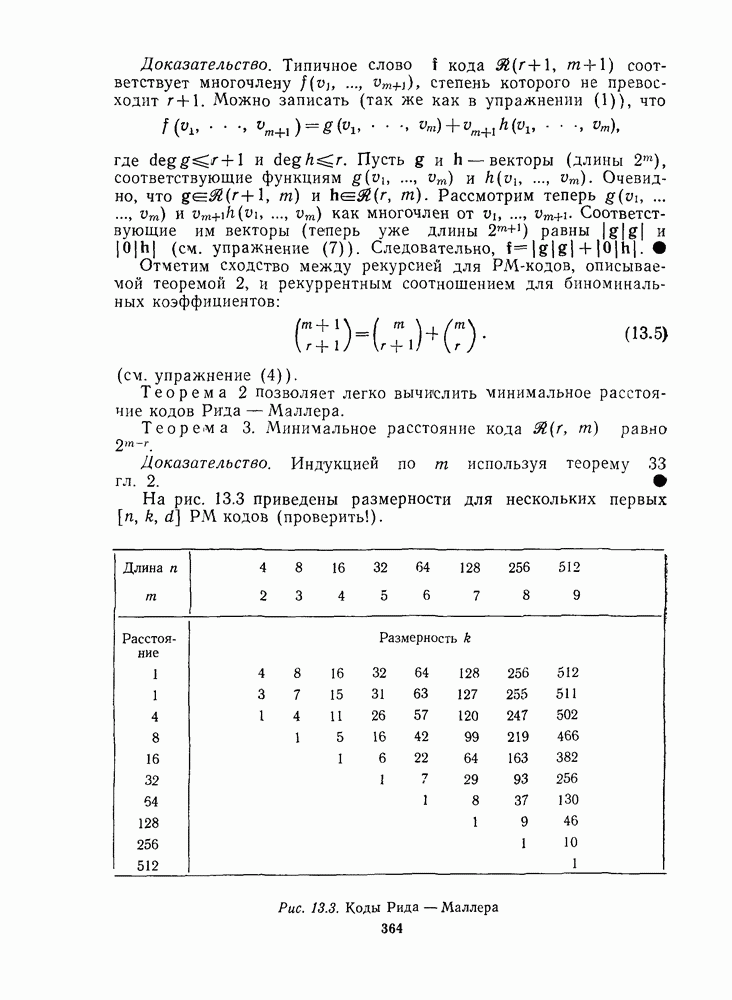
2.2. ГРАНИЦА ПЛОТКИНА
Теорема 1. (Граница Плоткина.) Для любого  -кода при
-кода при  справедливо неравенство
справедливо неравенство

Доказательство. Вычислим сумму

двумя способами. Во-первых, так как при  расстояние
расстояние  то сумма не меньше чем
то сумма не меньше чем  . С другой стороны, пусть А обозначает
. С другой стороны, пусть А обозначает  -матрицу, строками которой являются все кодовые слова. Предположим, что
-матрицу, строками которой являются все кодовые слова. Предположим, что  столбец А содержит
столбец А содержит  нулей и
нулей и  единиц. Тогда вклад этого столбца в нашу сумму равен
единиц. Тогда вклад этого столбца в нашу сумму равен  и поэтому эта сумма равна
и поэтому эта сумма равна

Если число  четное, то максимум этого выражения достигается при
четное, то максимум этого выражения достигается при  для всех
для всех  и поэтому сумма не превышает
и поэтому сумма не превышает  Таким образом, мы имеем:
Таким образом, мы имеем:

или

Но число  четное, и поэтому
четное, и поэтому

С другой стороны, если число  нечетное, то сумма не превышает
нечетное, то сумма не превышает  и вместо (2.2) получим
и вместо (2.2) получим

Отсюда следует, что

(4). Предполагая, что  -матрица Адамара существует, показать, что
-матрица Адамара существует, показать, что

[Указание. Использовать коды  из гл. 2 на с. 57].
из гл. 2 на с. 57].
(5). Показать, что

(6). Показать, что

причем равенство достигается тогда и только тогда, когда существует система Штейнера  до,
до,  (ср. § 2.5).
(ср. § 2.5).
Таким образом, из известных фактов о системах Штейнера (см. Чин [277], Колленс [300], Дембовский [370], Деннистон [372], Дуайен и Роза [386], Ханани [595—600], Ди Паола и др. [1020], Вигт [1423, 1424]) вытекают соответствующие результаты о величине  . Так, например, системы Штейнера
. Так, например, системы Штейнера  существуют для всех
существуют для всех  равных степени простого числа [370, гл. 6], и поэтому
равных степени простого числа [370, гл. 6], и поэтому

Аналогично унитарные поляры проективных геометрий [370, с. 104] дают равенство

Упражнение (6) показывает также, что определение величины  является в общем случае очень трудной проблемой. Так, например, из (17.10) следует, что
является в общем случае очень трудной проблемой. Так, например, из (17.10) следует, что  причем равенство достигается тогда и только тогда, когда существует проективная плоскость порядка 10.
причем равенство достигается тогда и только тогда, когда существует проективная плоскость порядка 10.
Следующие результаты приводятся без доказательств.
Теорема 6. (Шонхейм [1158]; см. также Форт и Хедлунд [446], Шонхейм [1161], Спенсер [1259] и Свифт (1294].)

Если существуют матрицы Адамара всех возможных порядков (что, однако, до сих пор еще не доказано), то на самом деле в уравнениях (2.3) — (2.6) выполняются равенства. Таким образом, граница Плоткина является точной в том смысле, что существуют коды, достигающие этой границы. В этом и заключается теорема Левенштейна, которая доказывается в следующем параграфе.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРОВ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Часть I: Глава 1. Линейные коды
- 1.1. ЛИНЕЙНЫЕ КОДЫ
- 1.2. СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.3. НА ПРИЕМНОМ КОНЦЕ
- 1.4. НЕМНОГО ПОДРОБНЕЕ О ДЕКОДИРОВАНИИ ЛИНЕЙНОГО КОДА
- 1.5. ВЕРОЯТНОСТЬ ОШИБКИ
- 1.6. ТЕОРЕМА ШЕННОНА О СУЩЕСТВОВАНИИ ХОРОШИХ КОДОВ
- 1.7. КОДЫ ХЭММИНГА
- 1.8. ДУАЛЬНЫЙ КОД
- 1.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (II)
- 1.10. НЕКОТОРЫЕ ОБЩИЕ СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.11. КРАТКОЕ СОДЕРЖАНИЕ ГЛ. 1
- Глава 2. Нелинейные коды, матрицы Адамара, t-схемы и код Голея
- 2.1. НЕЛИНЕЙНЫЕ КОДЫ
- 2.2. ГРАНИЦА ПЛОТКИНА
- 2.3. МАТРИЦЫ АДАМАРА И КОДЫ АДАМАРА
- 2.4. КОНФЕРЕНС-МАТРИЦЫ
- 2.5. t-СХЕМЫ
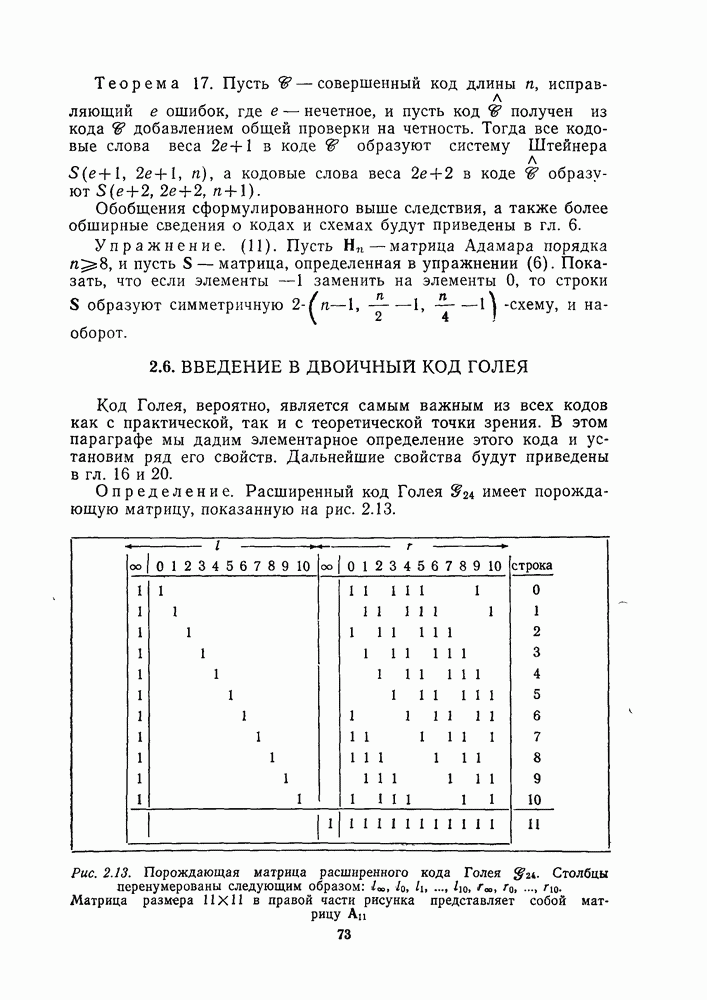
- 2.6. ВВЕДЕНИЕ В ДВОИЧНЫЙ КОД ГОЛЕЯ
- 2.7. СИСТЕМА ШТЕЙНЕРА S(5,6,12) И НЕЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОДНУ ОШИБКУ
- 2.8. ВВЕДЕНИЕ В КОД НОРДСТРОМА—РОБИНСОНА
- 2.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (III)
- Глава 3. Введение в коды БЧХ и конечные поля
- 3.1. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (I)
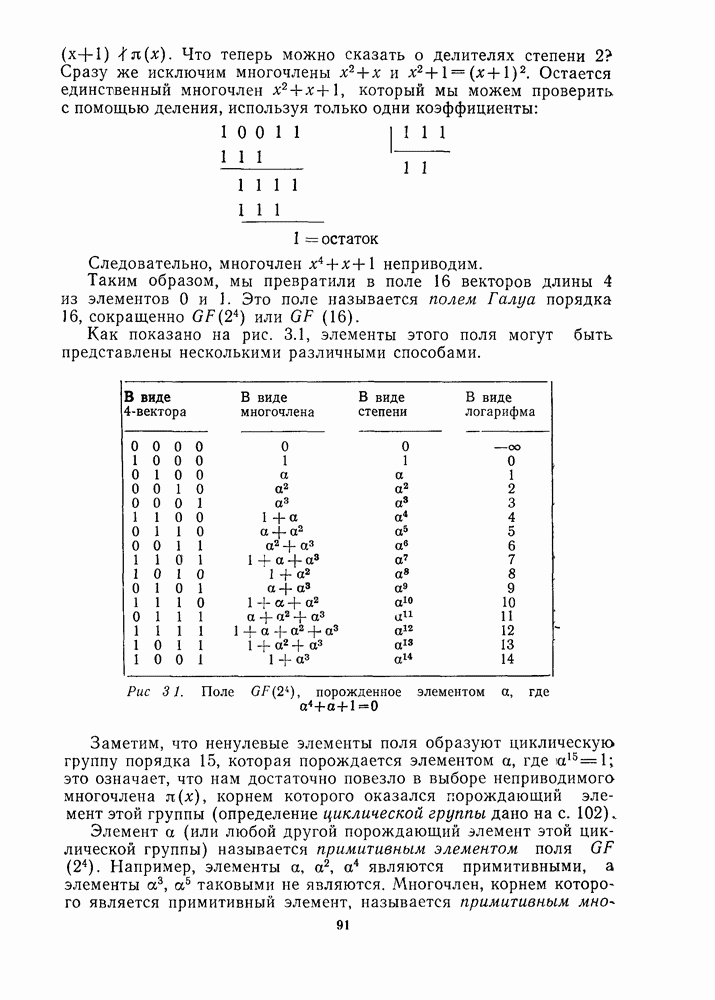
- 3.2. ПОСТРОЕНИЕ ПОЛЯ GF(16)
- 3.3. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (II)
- 3.4. ВЫЧИСЛЕНИЯ В КОНЕЧНОМ ПОЛЕ
- Глава 4. Конечные поля
- 4.2. КОНЕЧНЫЕ ПОЛЯ ОСНОВЫ ТЕОРИИ
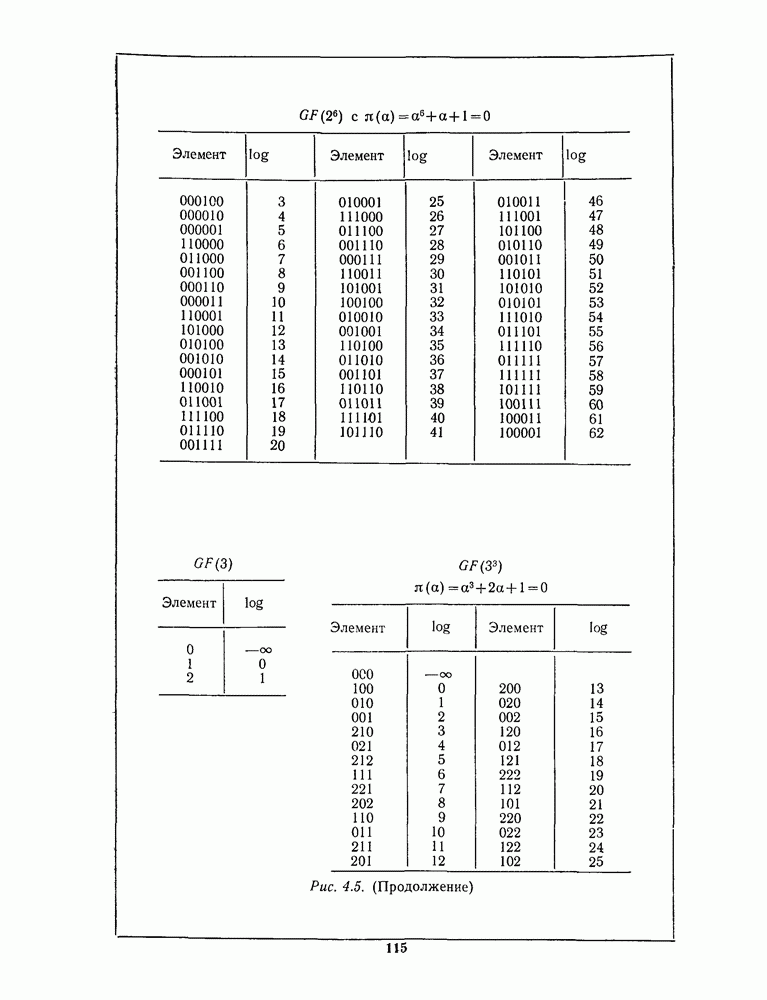
- 4.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ
- 4.4. КАК НАХОДИТЬ НЕПРИВОДИМЫЕ МНОГОЧЛЕНЫ
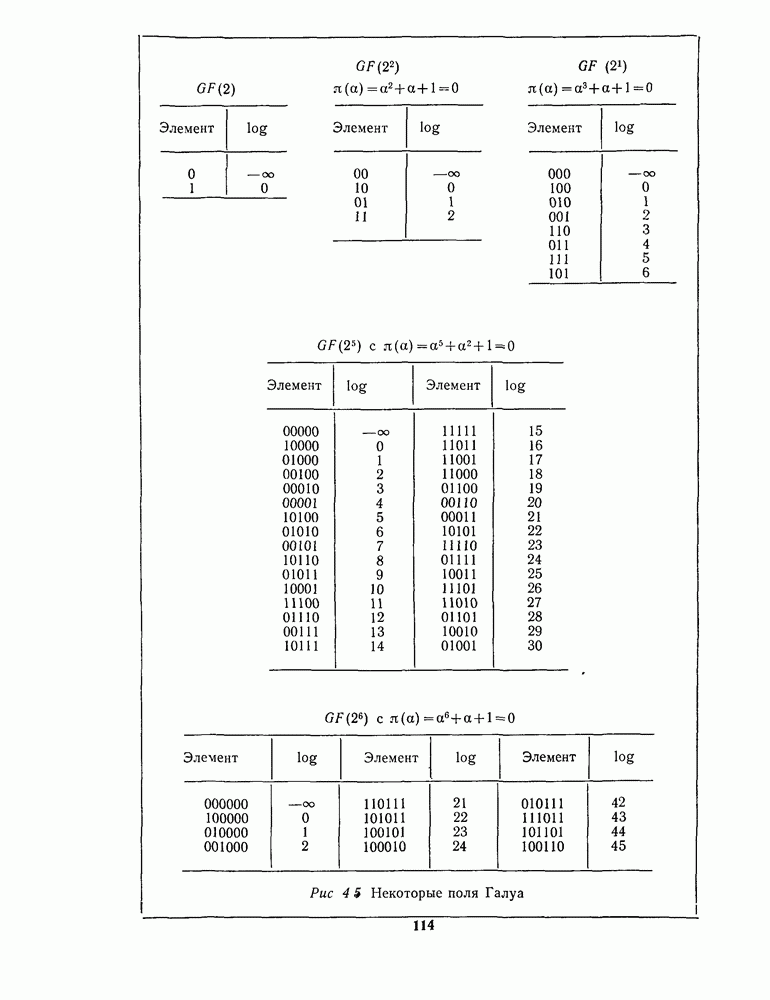
- 4.5. ТАБЛИЦЫ МАЛЫХ ПОЛЕЙ
- 4.6. ГРУППА АВТОМОРФИЗМОВ ПОЛЯ GF(p^m)
- 4.7. ЧИСЛО НЕПРИВОДИМЫХ МНОГОЧЛЕНОВ
- 4.8. БАЗИСЫ GF(p^m) НАД GF(p)
- 4.9. ЛИНЕАРИЗОВАННЫЕ МНОГОЧЛЕНЫ И НОРМАЛЬНЫЕ БАЗИСЫ
- Глава 5. Дуальные коды и их весовые спектры
- 5.2. ВЕСОВОЙ СПЕКТР КОДА, ДУАЛЬНОГО К ДВОИЧНОМУ ЛИНЕЙНОМУ КОДУ
- 5.3. ГРУППОВАЯ АЛГЕБРА
- 5.4. ХАРАКТЕРЫ
- 5.5. ТЕОРЕМА МАК-ВИЛЬЯМС ДЛЯ НЕЛИНЕЙНЫХ КОДОВ
- 5.6. ОБОБЩЕННЫЕ ТЕОРЕМЫ МАК-ВИЛЬЯМС ДЛЯ ЛИНЕЙНЫХ КОДОВ
- 5.7. СВОЙСТВА МНОГОЧЛЕНОВ КРАВЧУКА
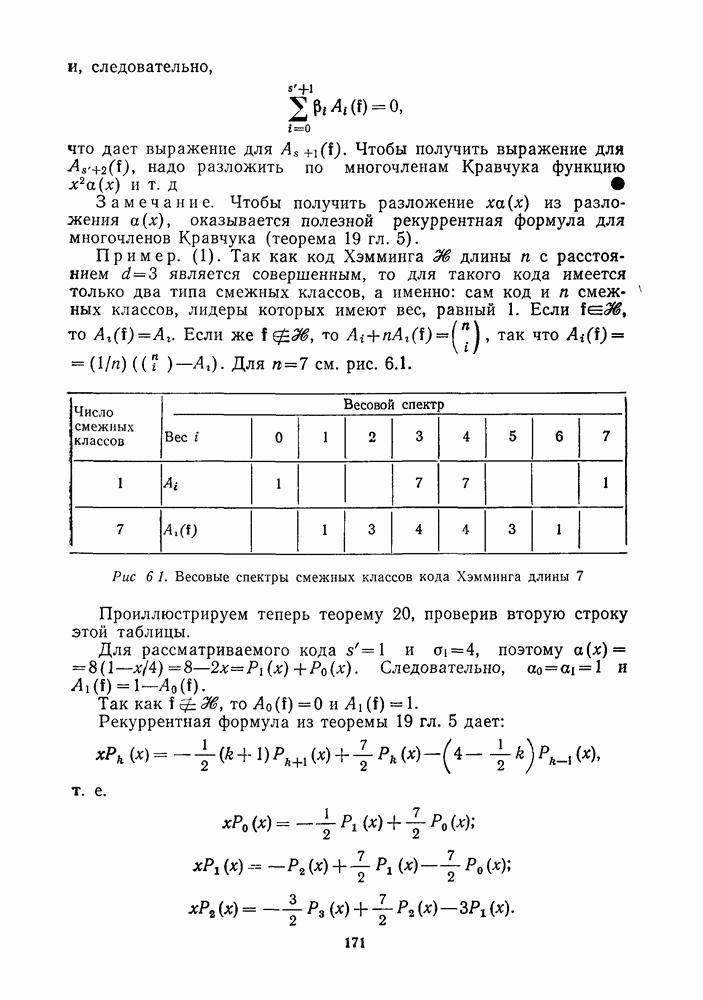
- Глава 6. Коды, схемы и совершенные коды
- 6.2. ЧЕТЫРЕ ФУНДАМЕНТАЛЬНЫХ ПАРАМЕТРА КОДА
- 6.3. ЯВНАЯ ФОРМУЛА ДЛЯ СПЕКТРА ВЕСОВ И РАССТОЯНИЙ
- 6.4. ПОСТРОЕНИЕ СХЕМ ИЗ КОДОВ ПРИ …
- 6.5. ДУАЛЬНЫЙ КОД ТАКЖЕ ПОРОЖДАЕТ СХЕМЫ
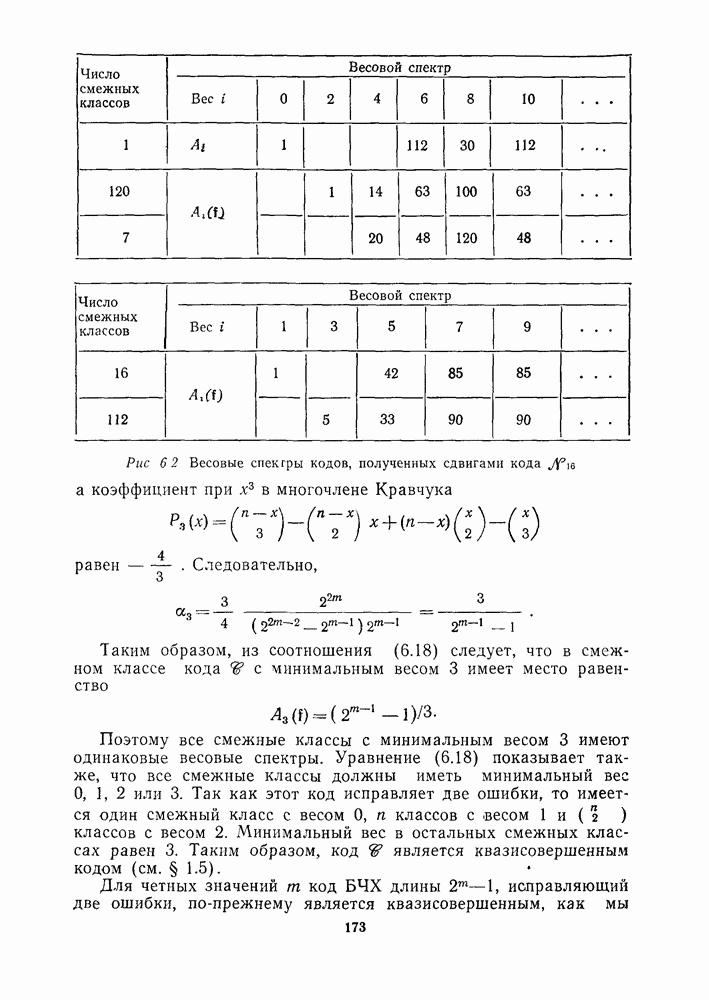
- 6.6. ВЕСОВОЙ СПЕКТР КОДА, ПОЛУЧЕННОГО В РЕЗУЛЬТАТЕ СДВИГА
- 6.7. ПОСТРОЕНИЕ СХЕМ ИЗ НЕЛИНЕЙНЫХ КОДОВ ПРИ …
- 6.8. СОВЕРШЕННЫЕ КОДЫ
- 6.9. КОДЫ НАД GF(q)
- 6.10. НЕ СУЩЕСТВУЕТ НЕИЗВЕСТНЫХ СОВЕРШЕННЫХ КОДОВ
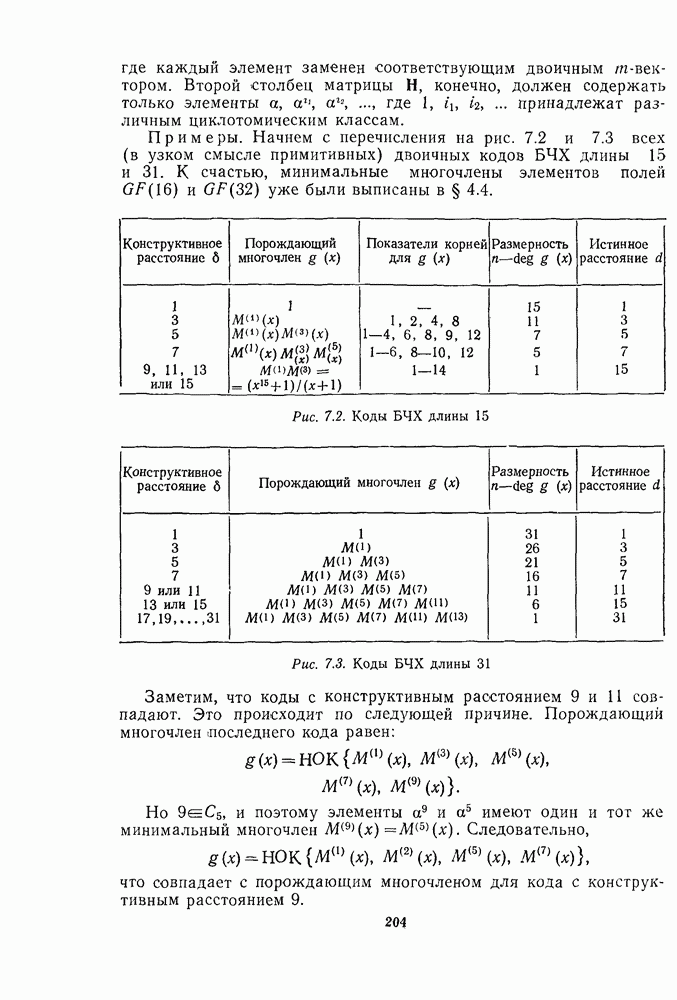
- Глава 7. Циклические коды
- 7.2. ОПРЕДЕЛЕНИЕ ЦИКЛИЧЕСКОГО КОДА
- 7.3. ПОРОЖДАЮЩИЙ МНОГОЧЛЕН
- 7.4. ПРОВЕРОЧНЫЙ МНОГОЧЛЕН
- 7.5. ДЕЛИТЕЛИ МНОГОЧЛЕНА x^n-1
- 7.6. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ t ОШИБОК
- 7.7. ИСПОЛЬЗОВАНИЕ МАТРИЦЫ НАД GF(q^m) ДЛЯ ЗАДАНИЯ КОДА НАД GF(q)
- 7.8. КОДИРОВАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- Глава 8. Циклические коды (продолжение): идемпотенты и многочлены Мэттсона-Соломона
- 8.2. ИДЕМПОТЕНТЫ
- 8.3. МИНИМАЛЬНЫЕ ИДЕАЛЫ, НЕПРИВОДИМЫЕ КОДЫ И ПРИМИТИВНЫЕ ИДЕМПОТЕНТЫ
- 8.4. ВЕСОВОЙ СПЕКТР МИНИМАЛЬНЫХ КОДОВ
- 8.5. ГРУППЫ АВТОМОРФИЗМОВ КОДА
- 8.6. МНОГОЧЛЕН МЭТТСОНА—СОЛОМОНА
- 8.7. НЕКОТОРЫЕ ВЕСОВЫЕ СПЕКТРЫ
- Глава 9. Коды БЧХ
- 9.2. ИСТИННОЕ МИНИМАЛЬНОЕ РАССТОЯНИЕ КОДА БЧХ
- 9.3. ЧИСЛО ИНФОРМАЦИОННЫХ СИМВОЛОВ КОДОВ БЧХ
- 9.4. ТАБЛИЦА КОДОВ БЧХ
- 9.5. ДЛИННЫЕ КОДЫ БЧХ
- 9.6. ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 9.7. КВАДРАТНЫЕ УРАВНЕНИЯ НАД GF(2^m)
- 9.8. КВАЗИСОВЕРШЕННОСТЬ КОДОВ БЧХ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
- 9.9. ГРАНИЦА КАРЛИЦА—УШИЯМЫ
- 9.10. АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ НЕКОТОРЫХ ВЕСОВЫХ СПЕКТРОВ
- 9.11. КОДЫ НЕ-БЧХ, ИСПРАВЛЯЮЩИЕ ТРИ ОШИБКИ
- Глава 10. Коды Рида-Соломона и коды Юстесена
- 10.2. КОДЫ РИДА-СОЛОМОНА
- 10.3. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
- 10.4. ИДЕМПОТЕНТЫ КОДОВ РИДА-СОЛОМОНА
- 10.5. ОТОБРАЖЕНИЕ КОДОВ НАД GF(2^m) В ДВОИЧНЫЕ КОДЫ
- 10.6. ИСПРАВЛЕНИЕ ПАКЕТОВ ОШИБОК
- 10.7. КОДИРОВАНИЕ КОДОВ РИДА—СОЛОМОНА
- 10.9. ИЗБЫТОЧНЫЕ ВЫЧЕТНЫЕ КОДЫ
- 10.10. ДЕКОДИРОВАНИЕ КОДОВ РИДА-СОЛОМОНА
- 10.11. КОДЫ ЮСТЕСЕНА И КАСКАДНЫЕ КОДЫ
- Глава 11. Коды МДР
- 11.2. ПОРОЖДАЮЩАЯ И ПРОВЕРОЧНАЯ МАТРИЦЫ
- 11.3. ВЕСОВОЙ СПЕКТР КОДА МДР
- 11.4. МАТРИЦЫ, У КОТОРЫХ ВСЕ КВАДРАТНЫЕ ПОДМАТРИЦЫ НЕВЫРОЖДЕНЫ
- 11.5. КОДЫ МДР, ПОЛУЧЕННЫЕ ИЗ КОДОВ РИДА-СОЛОМОНА
- 11.6. n-МНОЖЕСТВА
- 11.7. ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ
- 11.8. ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
- Глава 12. Альтернантные коды, коды Гоппы и другие обобщения кодов БЧХ
- 12.2. АЛЬТЕРНАНТНЫЕ КОДЫ
- 12.3. КОДЫ ГОППЫ
- 12.4. ДАЛЬНЕЙШИЕ СВОЙСТВА КОДОВ ГОППЫ
- 12.5. ЦИКЛИЧНОСТЬ УДЛИНЕННЫХ КОДОВ ГОППЫ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
- 12.6. ОБОБЩЕННЫЕ КОДЫ СРИВЭСТАВЫ
- 12.7. ОБОБЩЕНИЕ ЧЕНЯ—ЧОЯ КОДОВ БЧХ
- 12.8. АЛГОРИТМ ЕВКЛИДА
- 12.9. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- Часть II: Глава 13. Коды Рида-Маллера
- 13.2. БУЛЕВЫ ФУНКЦИИ
- 13.3. КОДЫ РИДА-МАЛЛЕРА
- 13.4. РИДА-МАЛЕРА КОДЫ И ГЕОМЕТРИИ
- 13.5. ВЕКТОРЫ МИНИМАЛЬНОГО ВЕСА ПОРОЖДАЮТ КОД
- 13.6. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (I)
- 13.7. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (II)
- 13.8. ДРУГИЕ ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.9. ГРУППЫ АВТОМОРФИЗМОВ РИДА-МАЛЕРА КОДОВ
- 13.10. МНОГОЧЛЕНЫ МЭТТСОНА—СОЛОМОНА ДЛЯ РИДА-МАЛЕРА КОДОВ
- 13.11. ДЕЙСТВИЕ ПОЛНОЙ АФФИННОЙ ГРУППЫ НА МНОГОЧЛЕНАХ МЭТТСОНА—СОЛОМОНА
- Глава 14. Коды Рида-Маллера первого порядка
- 14.2. ПСЕВДОШУМОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 14.3. СМЕЖНЫЕ КЛАССЫ ПО КОДУ РИДА—МАЛЛЕРА ПЕРВОГО ПОРЯДКА
- 14.4. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ КОДА R(1, m)
- 14.5. МАКСИМАЛЬНО-НЕЛИНЕЙНЫЕ ФУНКЦИИ
- Глава 15. Коды Рида-Маллера первого порядка Кердока и Препараты
- 15.2. ВЕСОВОЙ СПЕКТР КОДА РИДА—МАЛЛЕРА ВТОРОГО ПОРЯДКА
- 15.3. СПЕКТР ВЕСОВ ПРОИЗВОЛЬНЫХ КОДОВ РИДА—МАЛЛЕРА
- 15.4. ПОДКОДЫ РАЗМЕРНОСТИ 2m В КОДАХ R(2, m)* И R(2, m)
- 15.5. КОД КЕРДОКА И ЕГО ОБОБЩЕНИЯ
- 15.6. КОД ПРЕПАРАТЫ
- 15.7. ОБОБЩЕНИЕ ГЕТАЛСА КОДОВ ПРЕПАРАТЫ
- Глава 16. Квадратично-вычетные коды
- 16.2. ОПРЕДЕЛЕНИЕ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.3. ИДЕМПОТЕНТЫ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.4. РАСШИРЕННЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.5. ГРУППА АВТОМОРФИЗМОВ КВ-КОДОВ
- 16.6. ДВОИЧНЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.7. ДВАЖДЫ ЦИРКУЛЯНТНЫЕ И КВАЗИЦИКЛИЧЕСКИЕ КОДЫ
- 16.8. КВАДРАТИЧНО-ВЫЧЕТНЫЕ И СИММЕТРИЧНЫЕ КОДЫ НАД GF{3)
- 16.9. ДЕКОДИРОВАНИЕ ЦИКЛИЧЕСКИХ И НЕКОТОРЫХ ДРУГИХ КОДОВ
- Глава 17. Границы для объема кода
- 17.2. ГРАНИЦЫ ДЛЯ A(n, d, w)
- 17.3. ГРАНИЦЫ ДЛЯ A(n, d)
- 17.4. ГРАНИЦЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 17.5. ГРАНИЦА ГРАЙСМЕРА
- 17.6. ПОСТРОЕНИЕ ЛИНЕЙНЫХ КОДОВ; АНТИКОДЫ
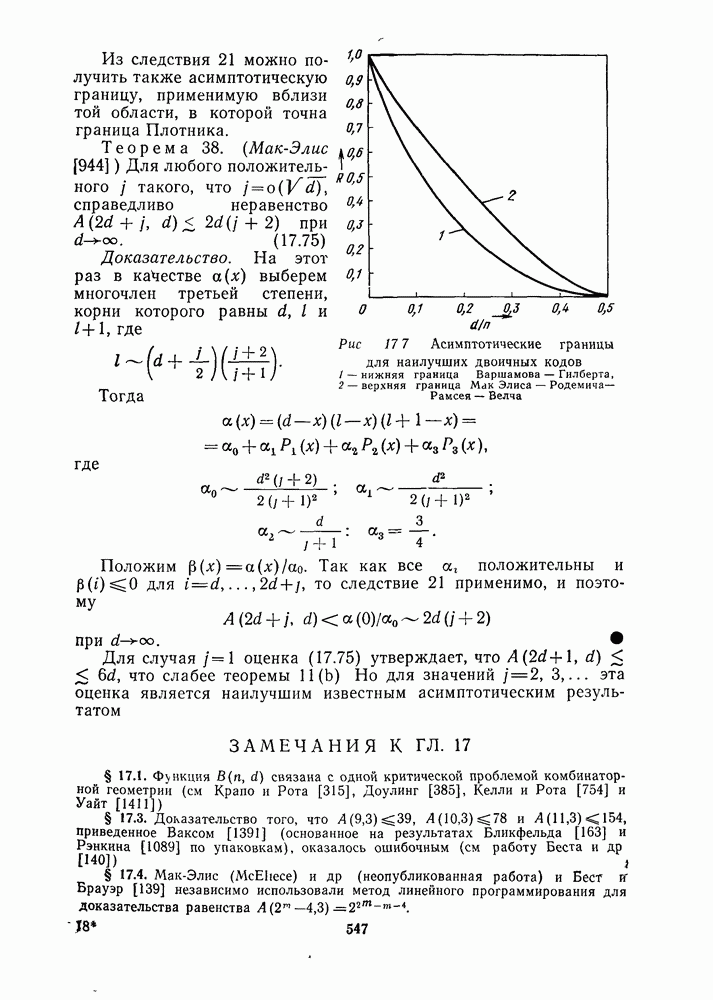
- 17.7. АСИМПТОТИЧЕСКИЕ ГРАНИЦЫ
- Глава 18. Методы комбинирования кодов
- I. ПРОИЗВЕДЕНИЕ КОДОВ И ИХ ОБОБЩЕНИЕ
- 18.2. ПРЯМОЕ ПРОИЗВЕДЕНИЕ КОДОВ
- 18.3. НЕ ВСЕ ЦИКЛИЧЕСКИЕ КОДЫ ЯВЛЯЮТСЯ ПРЯМЫМИ ПРОИЗВЕДЕНИЯМИ ЦИКЛИЧЕСКИХ КОДОВ
- 18.4. ДРУГОЙ СПОСОБ ПРЕДСТАВЛЕНИЯ НЕПРИВОДИМЫХ ЦИКЛИЧЕСКИХ кодов В ВИДЕ ПРОИЗВЕДЕНИЯ КОДОВ
- 18.5. КАСКАДНЫЕ КОДЫ: (*)-КОНСТРУКЦИЯ
- 18.6. ОБЩИЙ ПОДХОД К РАЗЛОЖЕНИЮ ЦИКЛИЧЕСКИХ КОДОВ
- II. ДРУГИЕ МЕТОДЫ КОМБИНИРОВАНИЯ КОДОВ
- 18.7. МЕТОДЫ ПОСТРОЕНИЯ, КОТОРЫЕ УВЕЛИЧИВАЮТ ДЛИНУ
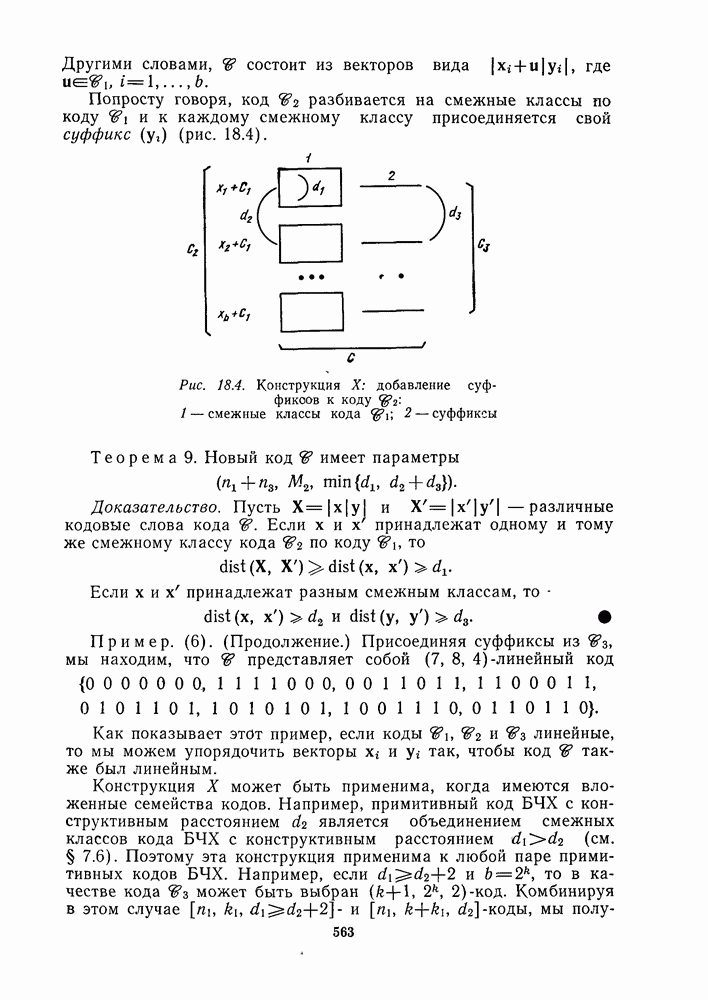
- 18.7.1. КОНСТРУКЦИЯ X: ДОБАВЛЕНИЕ СУФФИКСОВ К КОДОВЫМ СЛОВАМ
- 18.7.2. КОНСТРУКЦИЯ Х4: КОМБИНИРОВАНИЕ ЧЕТЫРЕХ КОДОВ
- 18.7.3. КОДЫ, ИСПРАВЛЯЮЩИЕ ОДИНОЧНЫЕ И ДВОЙНЫЕ ОШИБКИ
- 18.7.4. КОНСТРУКЦИЯ …
- 18.7.5. КОНСТРУКЦИЯ ПИРЕТА
- 18.8. КОНСТРУКЦИИ, СВЯЗАННЫЕ С КАСКАДНЫМИ КОДАМИ
- 18.8.2. ОБОБЩЕННЫЕ КАСКАДНЫЕ КОДЫ ЗИНОВЬЕВА
- 18.9. МЕТОДЫ УКОРОЧЕНИЯ КОДОВ
- 18.9.2. КОНСТРУКЦИИ ХЕЛГЕРТА И СТИНАФФА
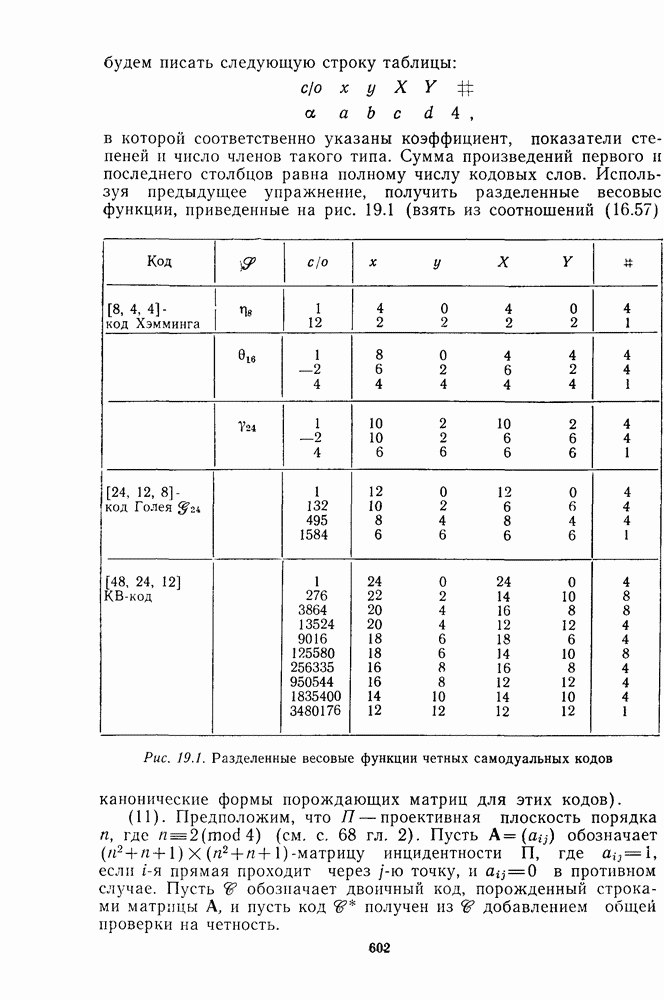
- Глава 19. Самодуальные коды и теория инвариантов
- 19.2. ВВЕДЕНИЕ В ТЕОРИЮ ИНВАРИАНТОВ
- 19.3. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ИНВАРИАНТОВ
- 19.4. ОБОБЩЕНИЯ ТЕОРЕМЫ ГЛИСОНА
- 19.5. НЕСУЩЕСТВОВАНИЕ НЕКОТОРЫХ ОЧЕНЬ ХОРОШИХ КОДОВ
- 19.6. ХОРОШИЕ САМОДУАЛЬНЫЕ КОДЫ СУЩЕСТВУЮТ
- Глава 20. Коды Голея
- 20.2. ГРУППА МАТЬЕ M24
- 20.3. ГРУППА М24 5-ТРАНЗИТИВНА
- 20.4. ПОРЯДОК ГРУППЫ М24 РАВЕН 24•23•22•21•20•48
- 20.5. СИСТЕМА ШТЕЙНЕРА S(5, 8, 24) ЕДИНСТВЕННА
- 20.6. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
- 20.7. ГРУППЫ АВТОМОРФИЗМОВ ТРОИЧНЫХ КОДОВ ГОЛЕЯ
- 20.8. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
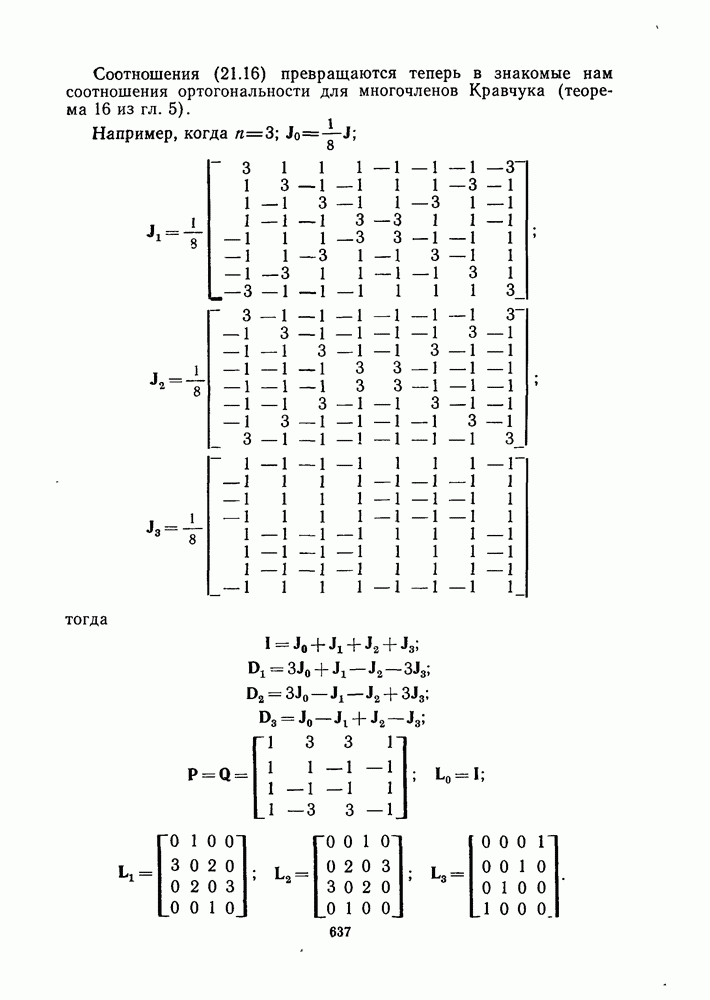
- Глава 21. Схемы отношений
- 21.2. СХЕМЫ ОТНОШЕНИЙ
- 21.3. СХЕМА ОТНОШЕНИЙ ХЭММИНГА
- 21.4. МЕТРИЧЕСКИЕ СХЕМЫ
- 21.5. СИМПЛЕКТИЧЕСКИЕ ФОРМЫ
- 21.6. СХЕМА ДЖОНСОНА
- 21.7. ПОДМНОЖЕСТВА СХЕМ ОТНОШЕНИЙ
- 21.8. ПОДМНОЖЕСТВА СИМПЛЕКТИЧЕСКИХ ФОРМ
- 21.9. t-СХЕМЫ И ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
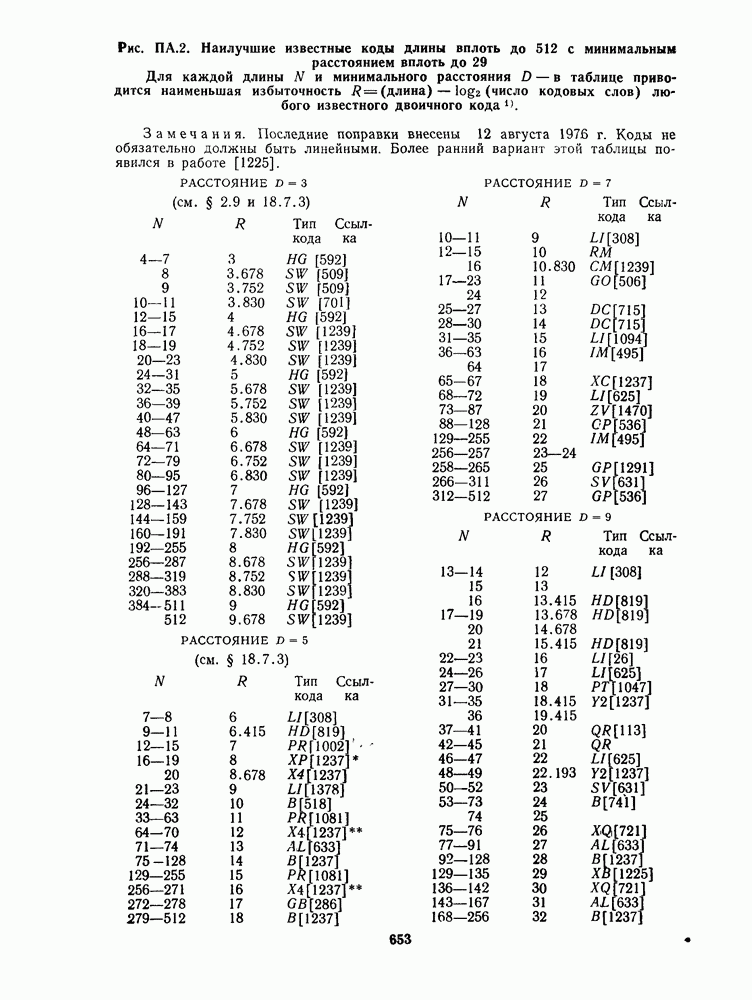
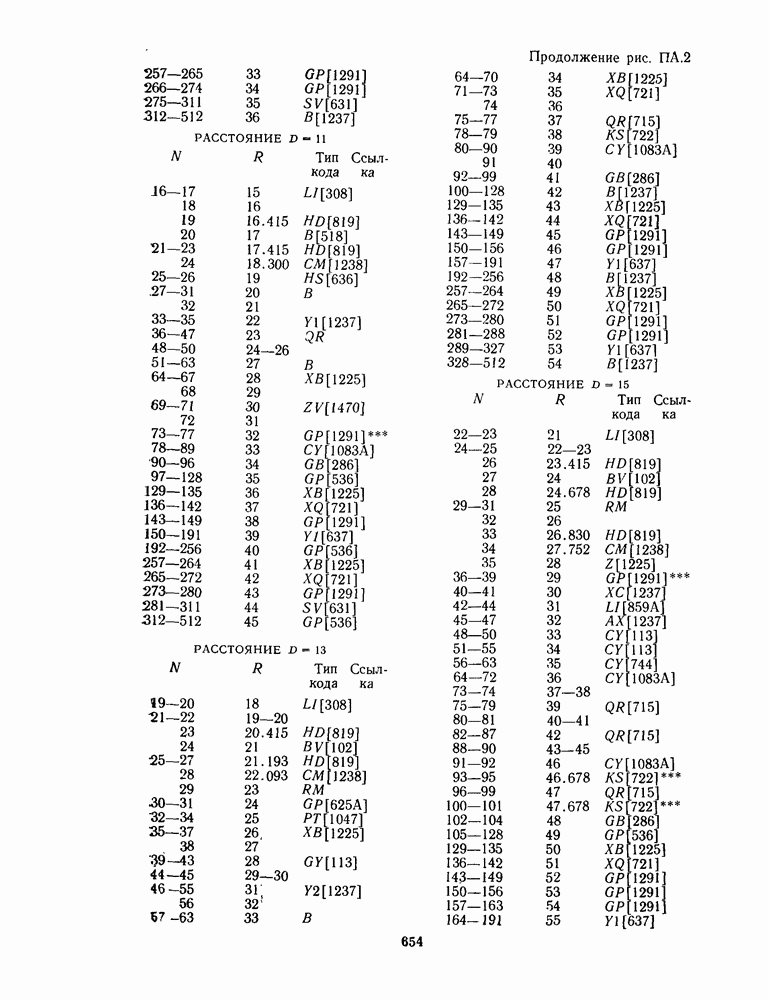
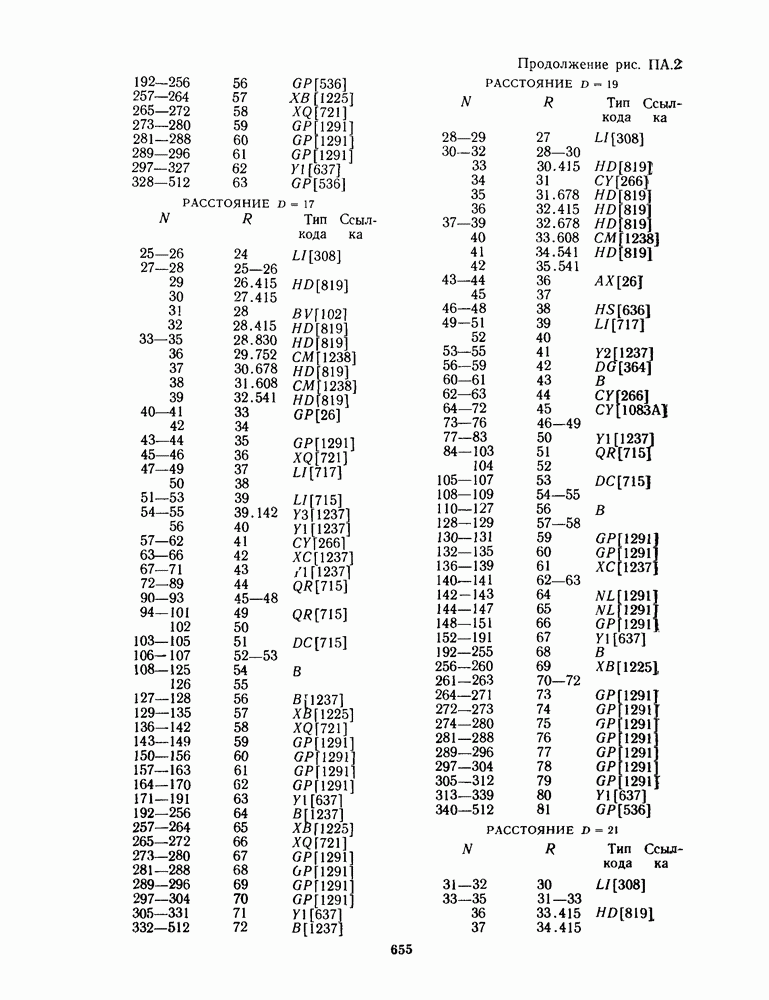
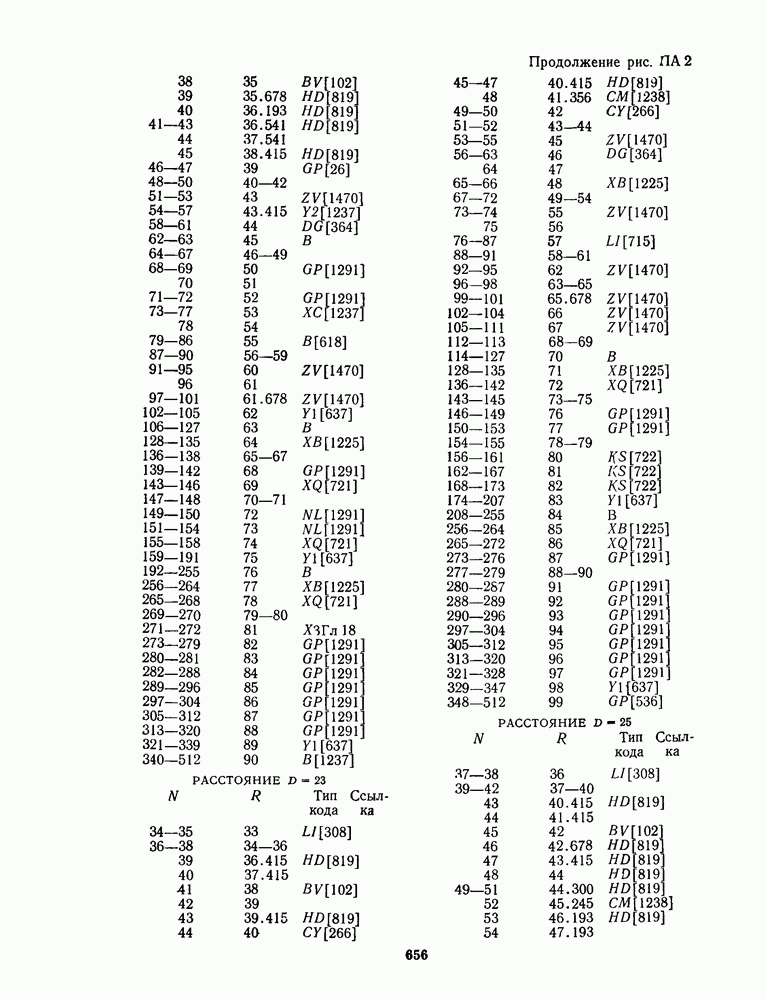
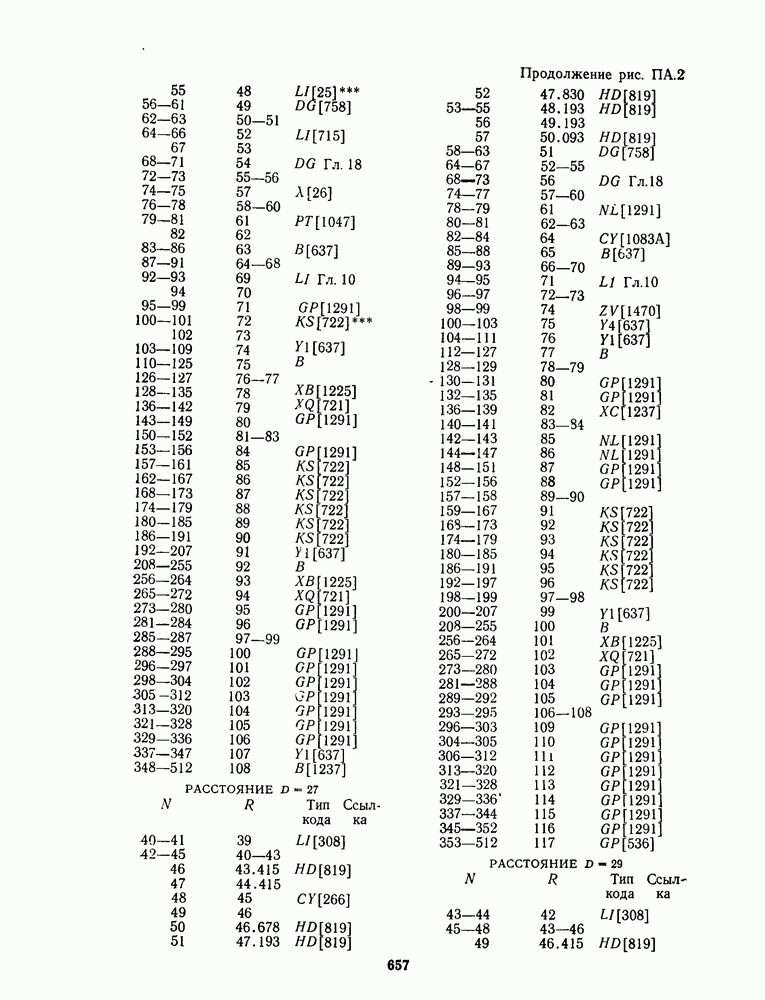
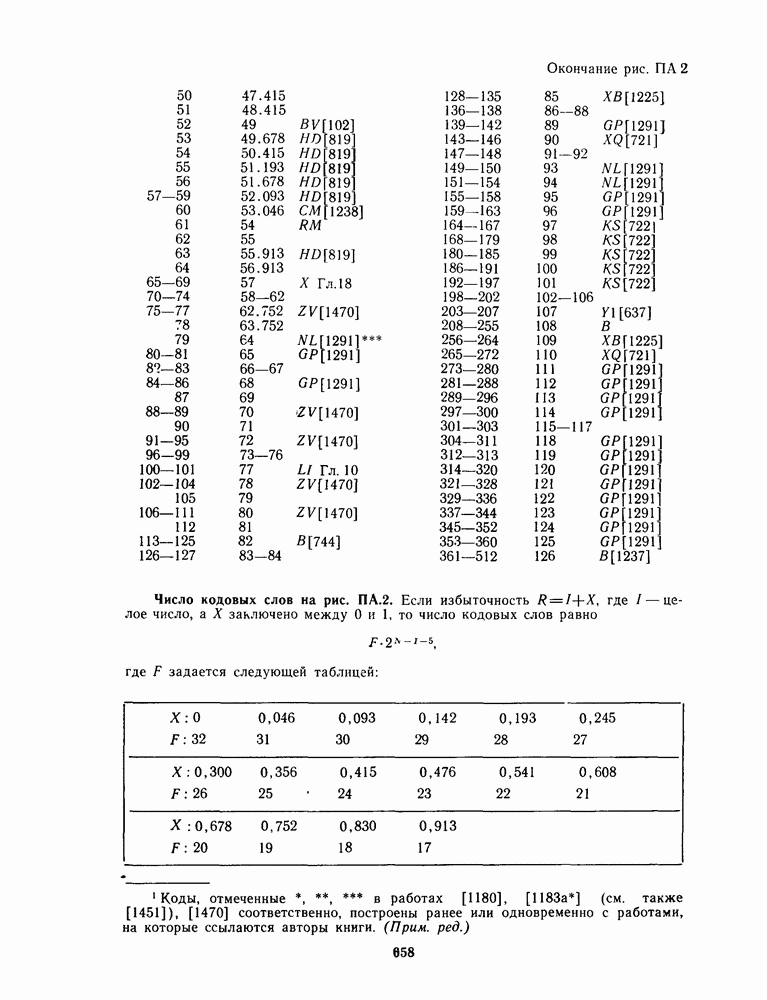
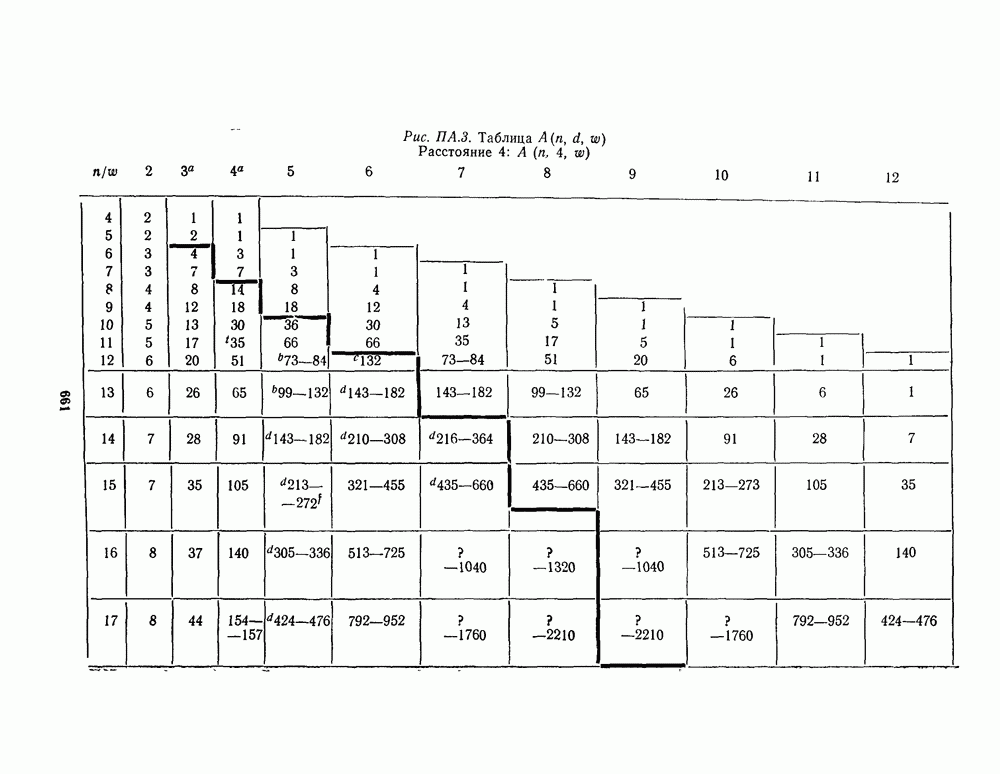
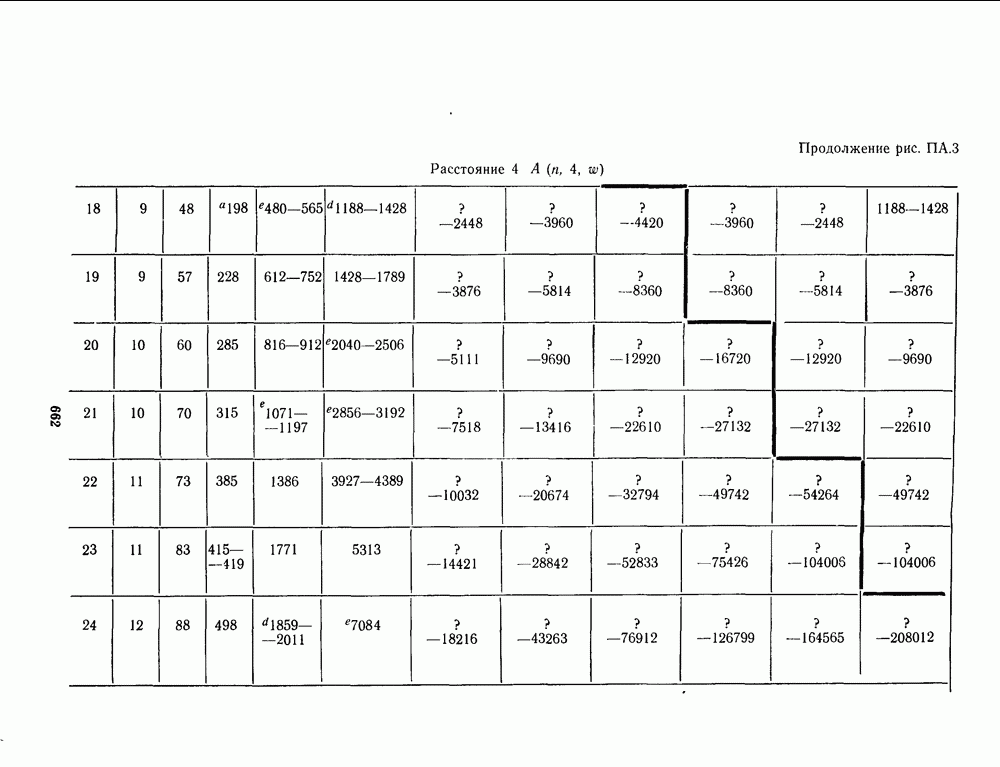
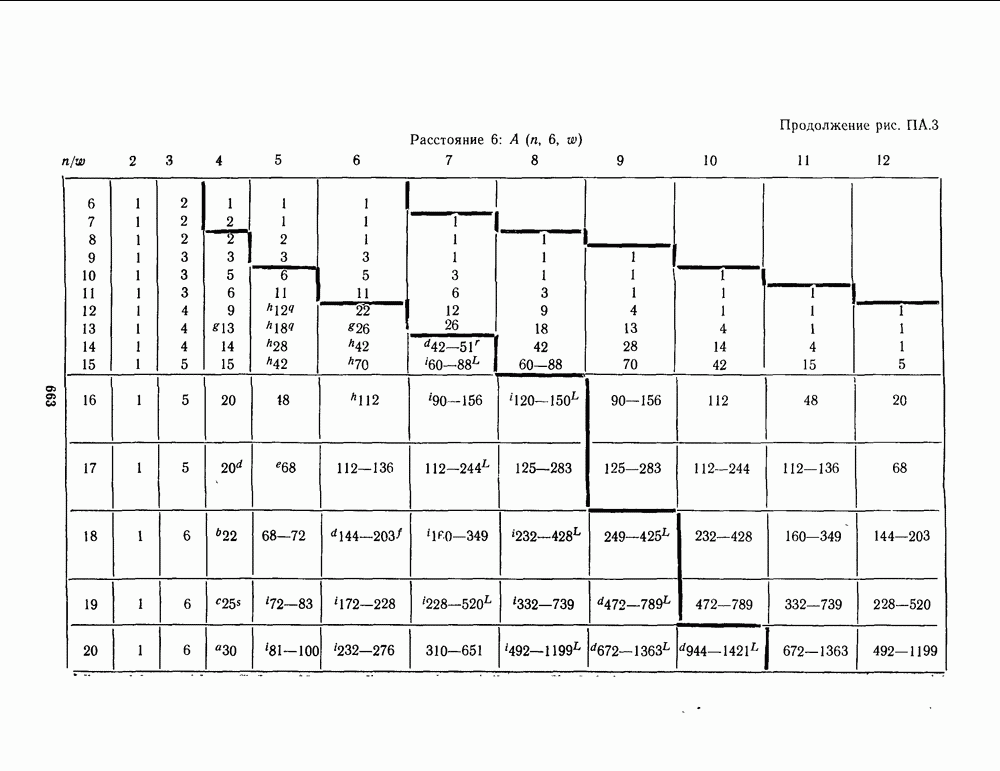
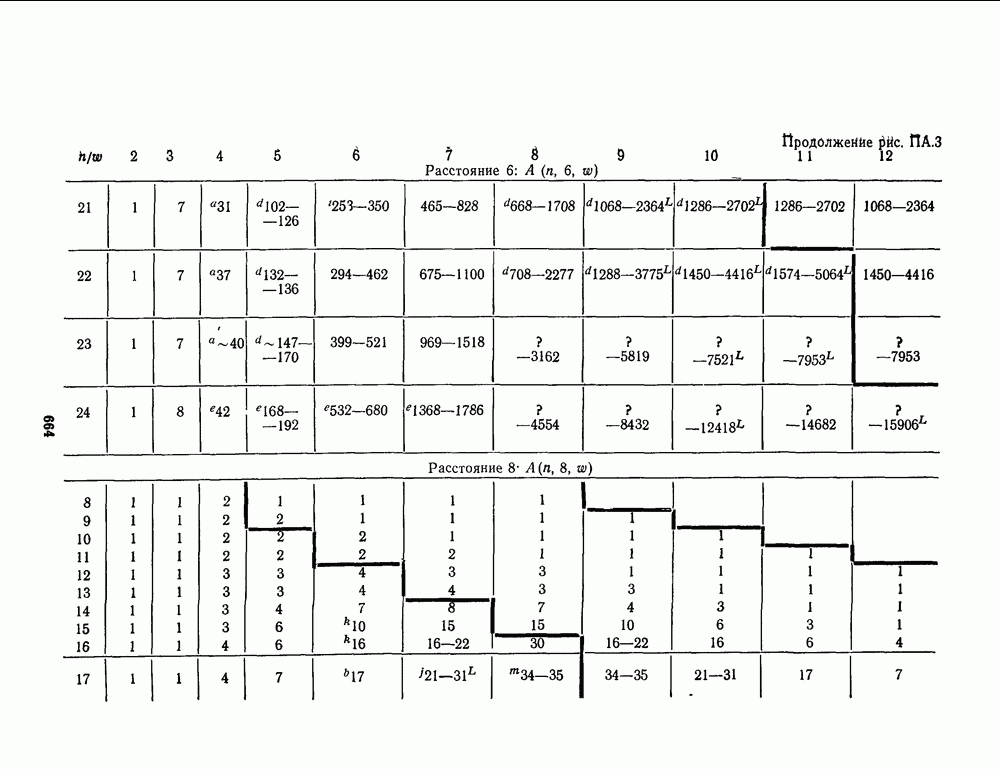
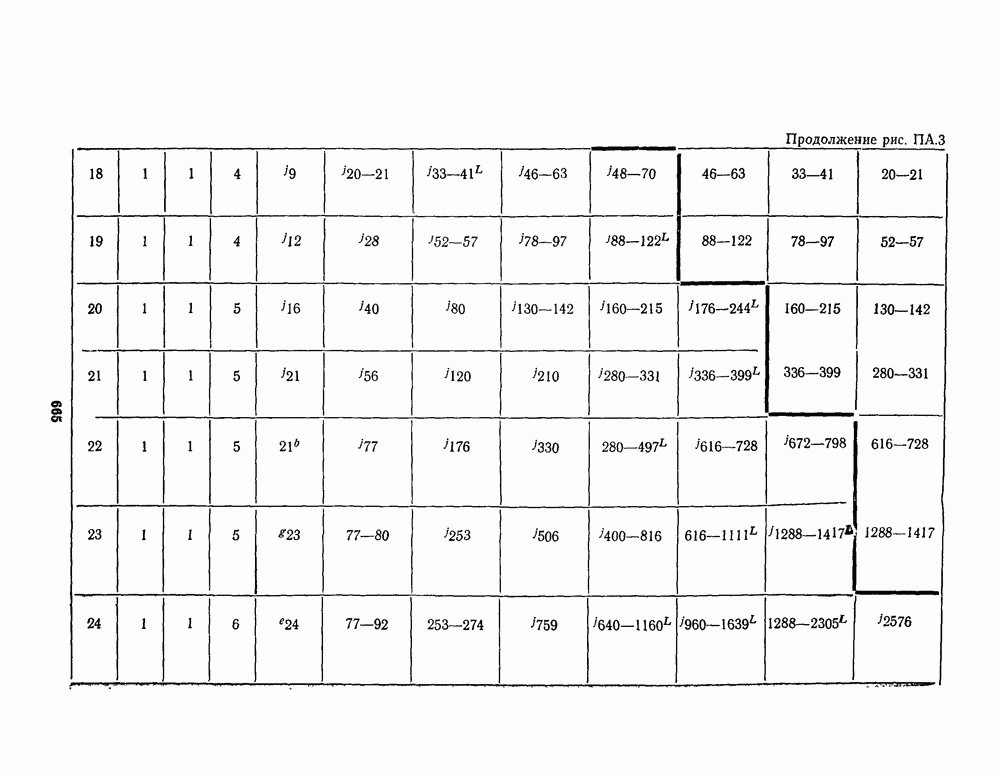
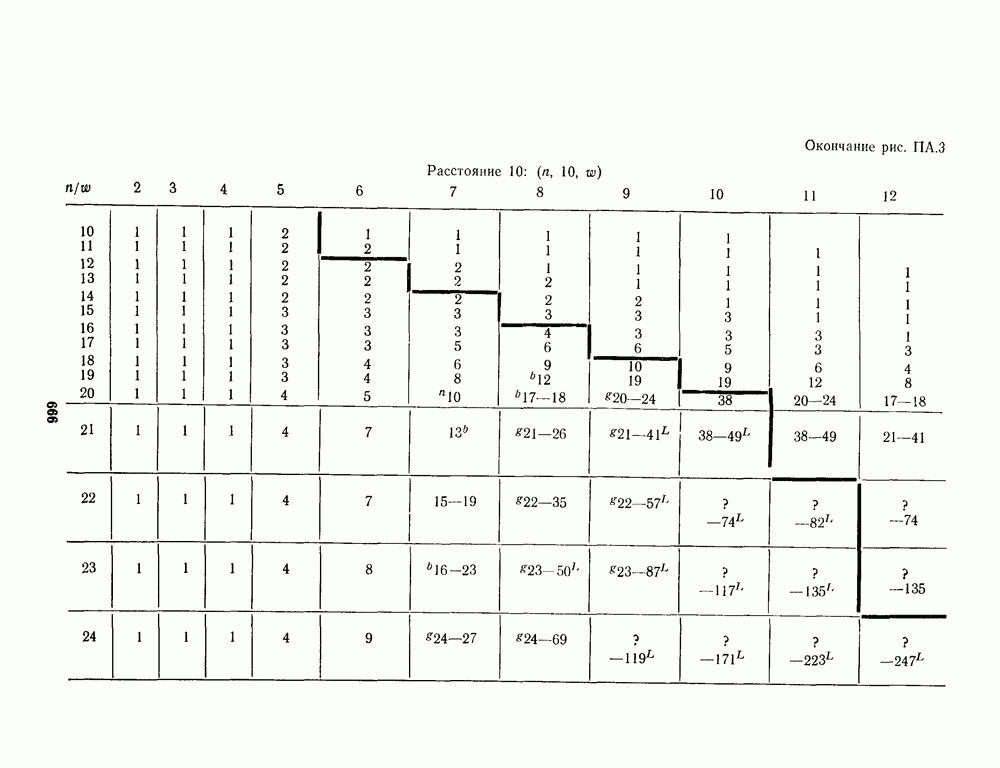
- ПРИЛОЖЕНИЕ А. ТАБЛИЦЫ НАИЛУЧШИХ ИЗВЕСТНЫХ КОДОВ
- ПРИЛОЖЕНИЕ В. КОНЕЧНЫЕ ГЕОМЕТРИИ