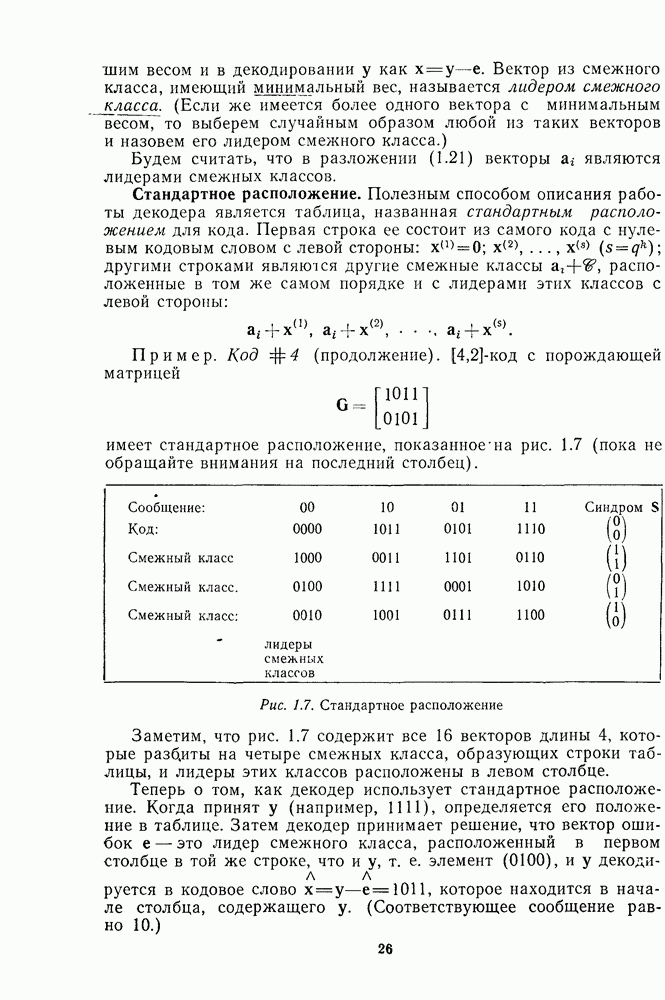
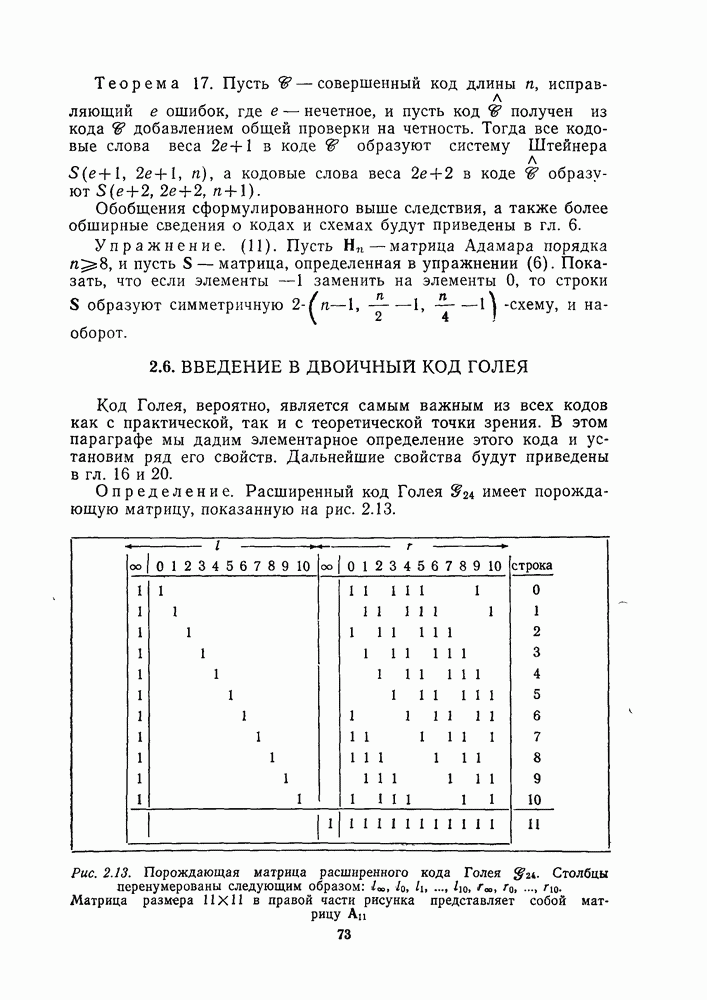
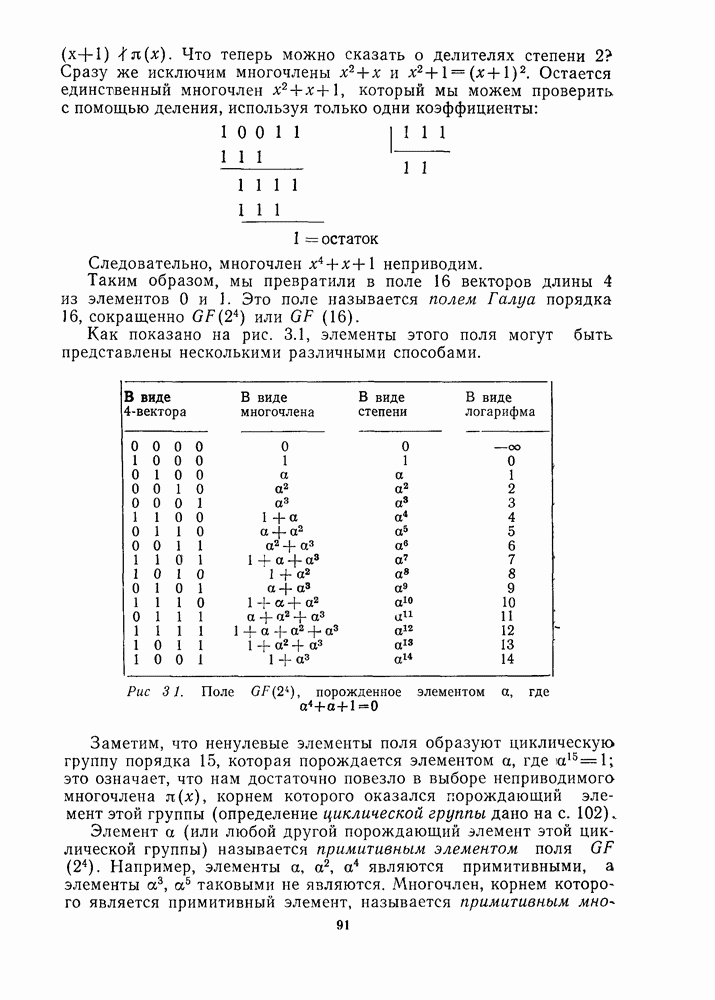
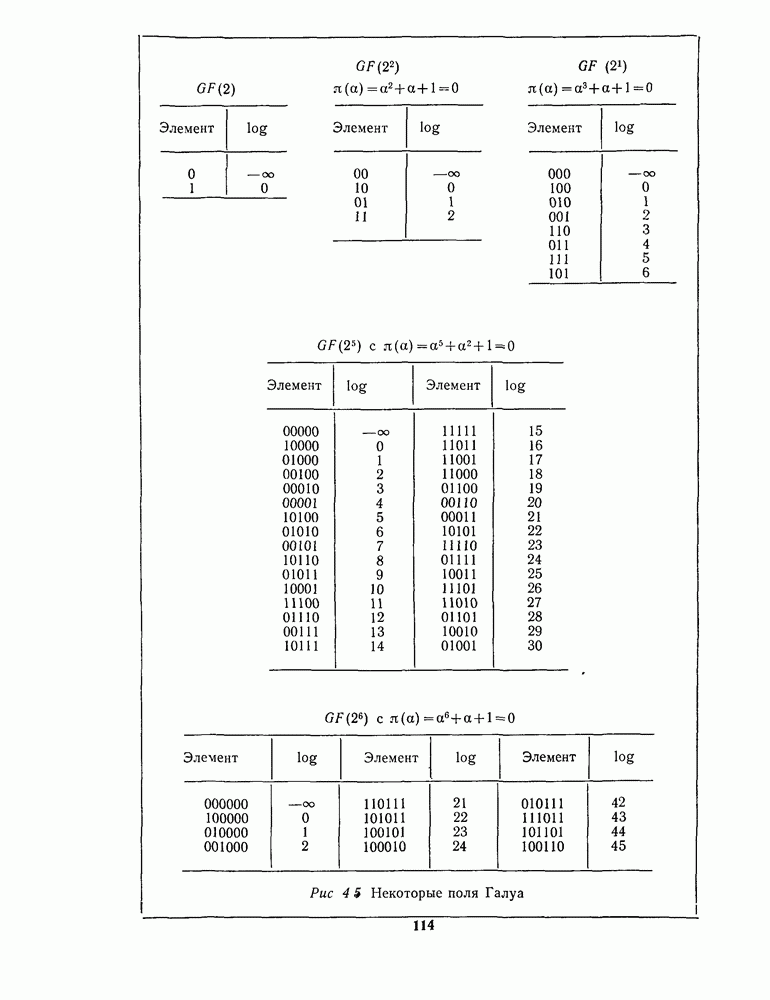
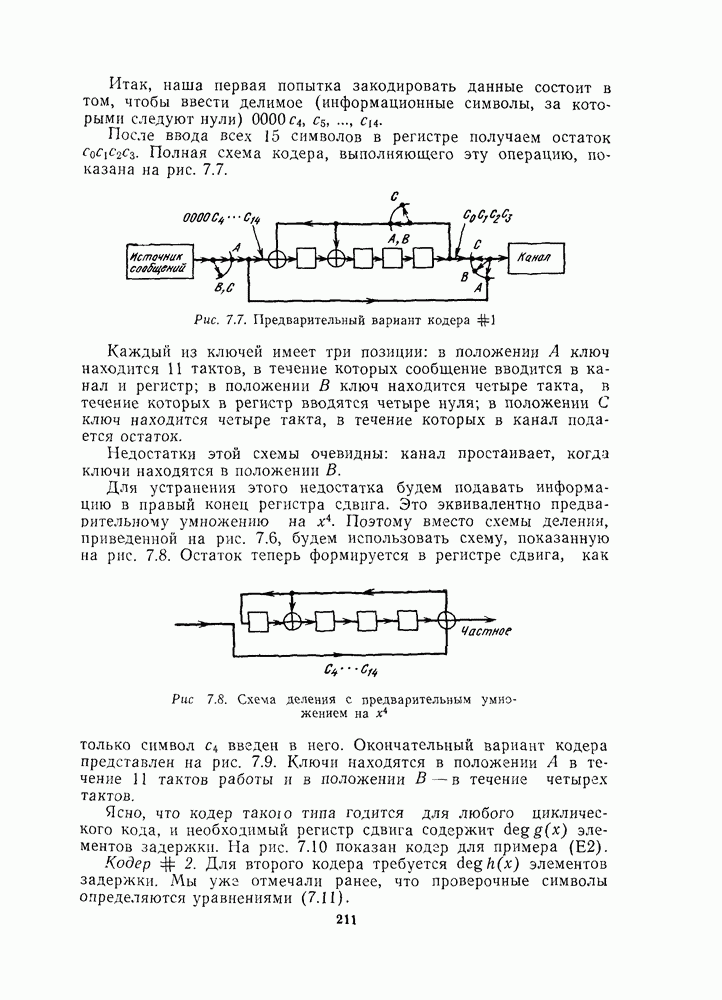
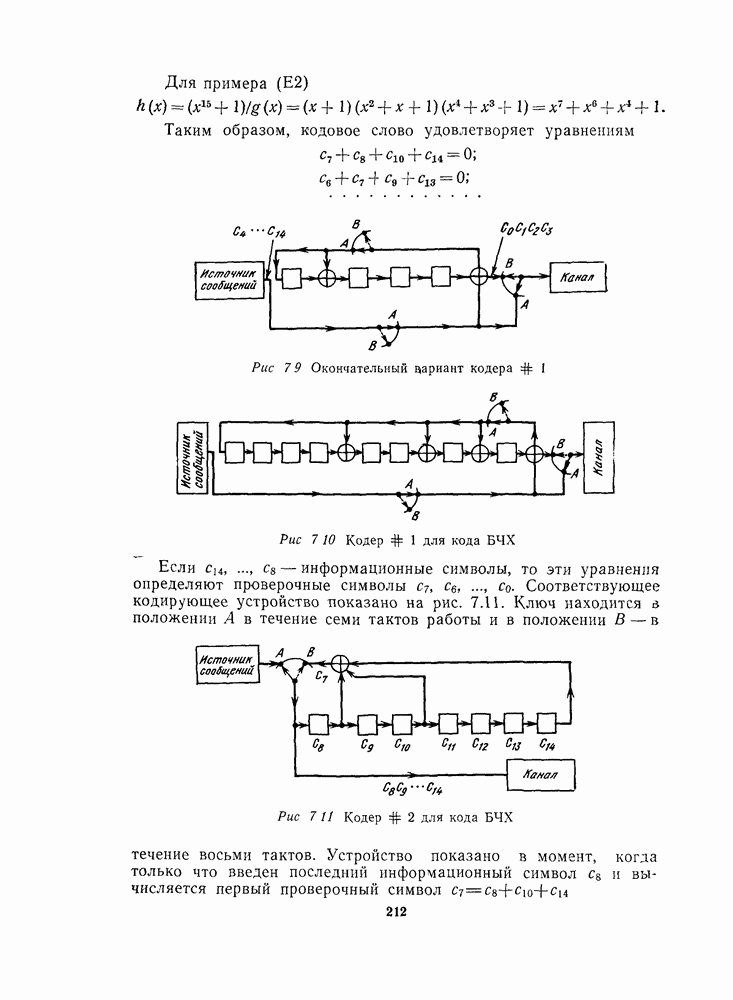
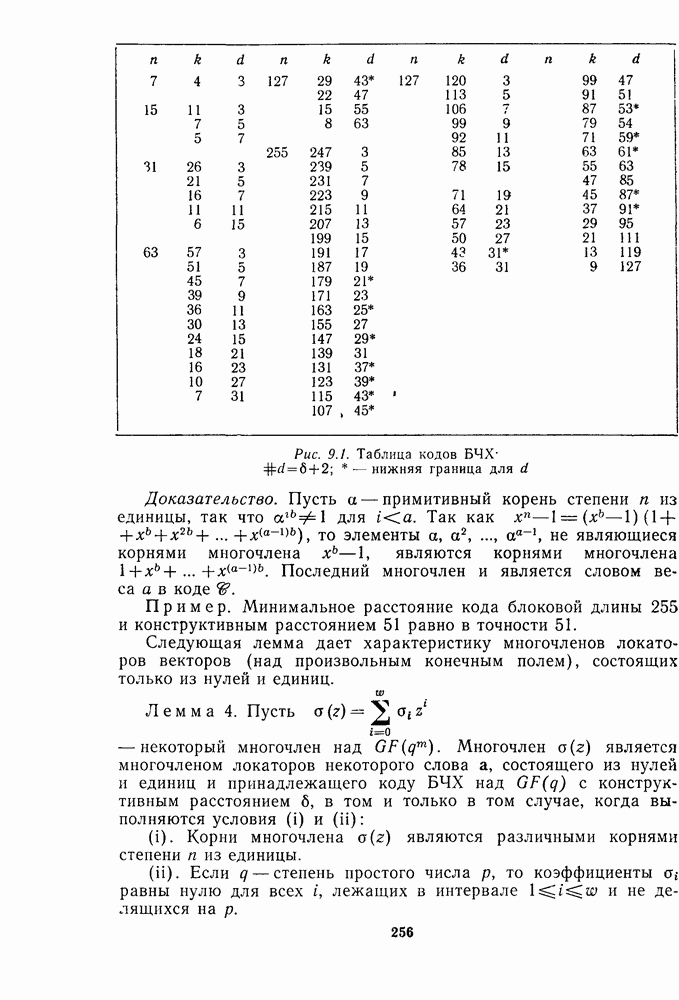
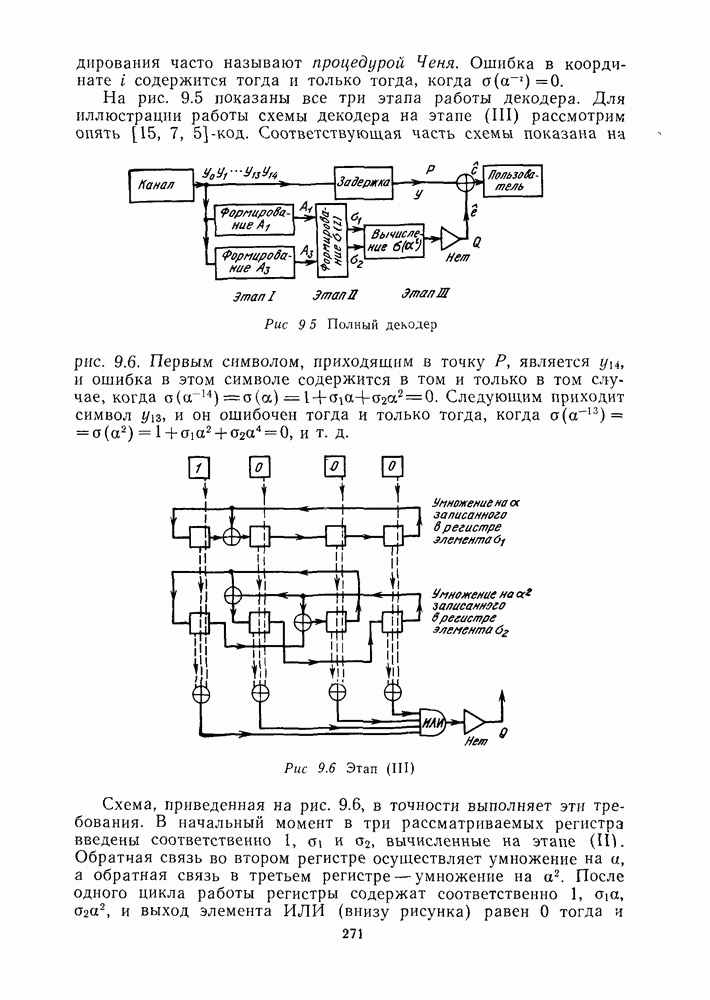
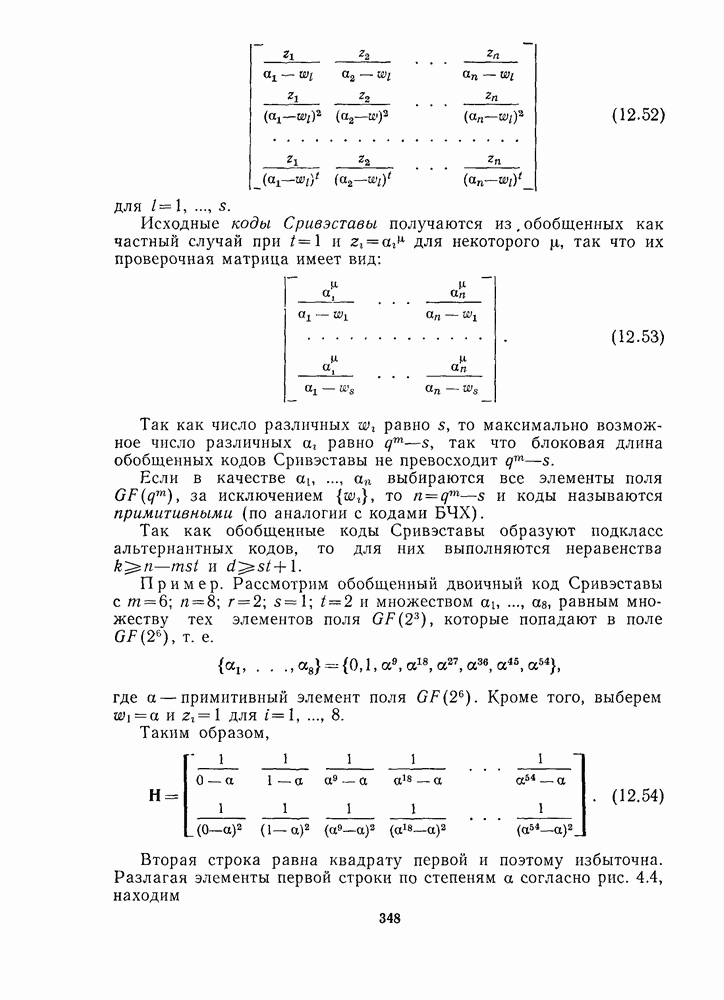
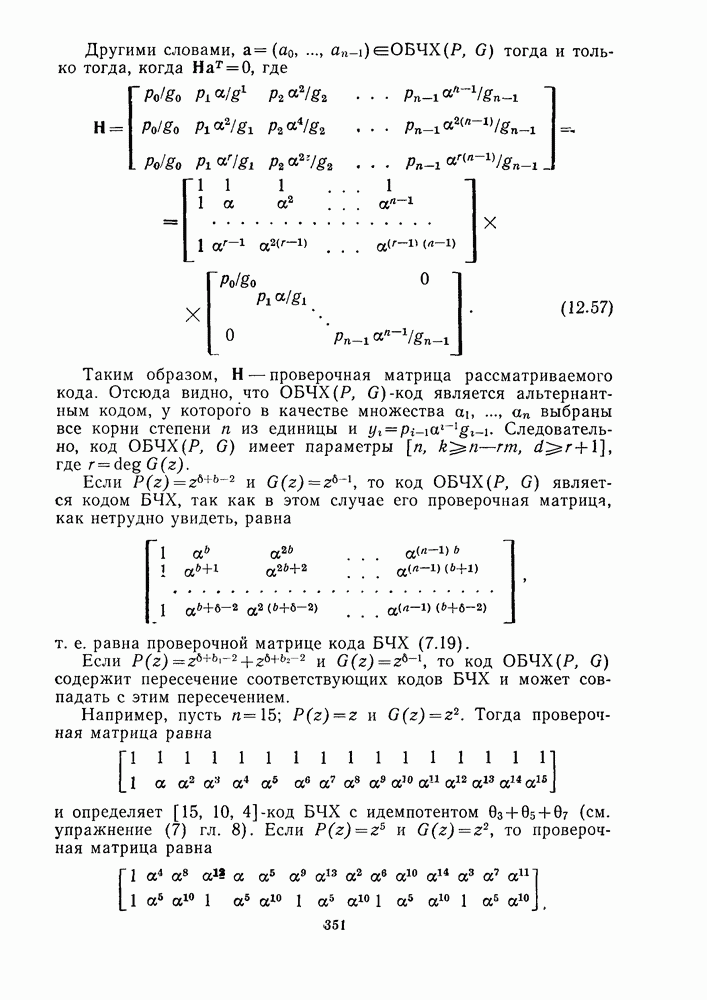
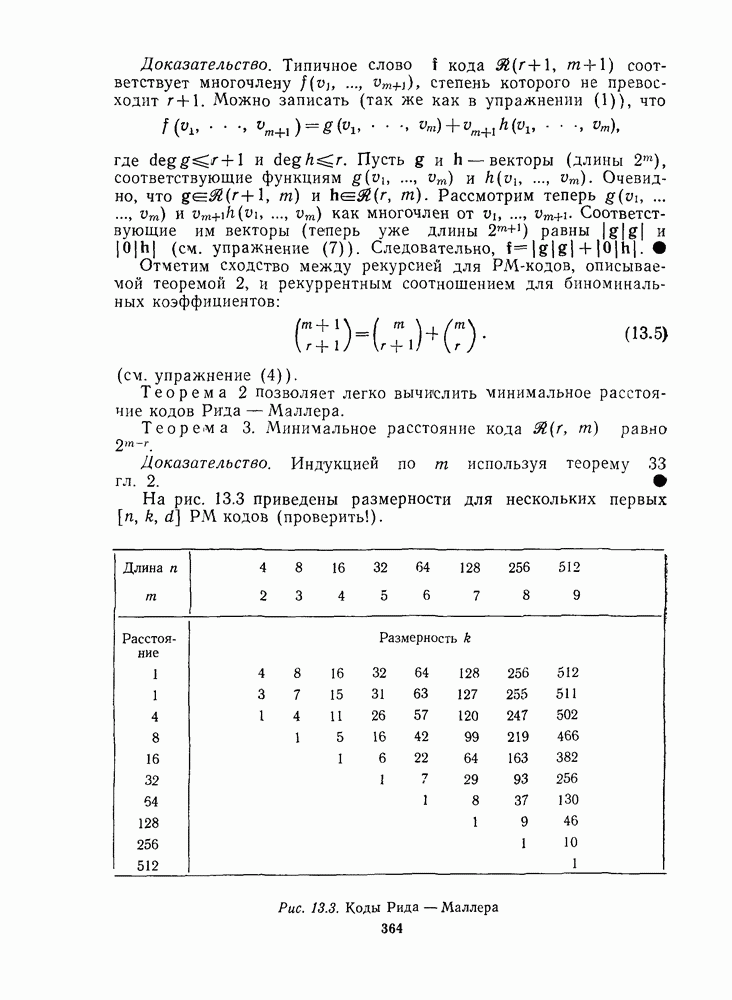
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
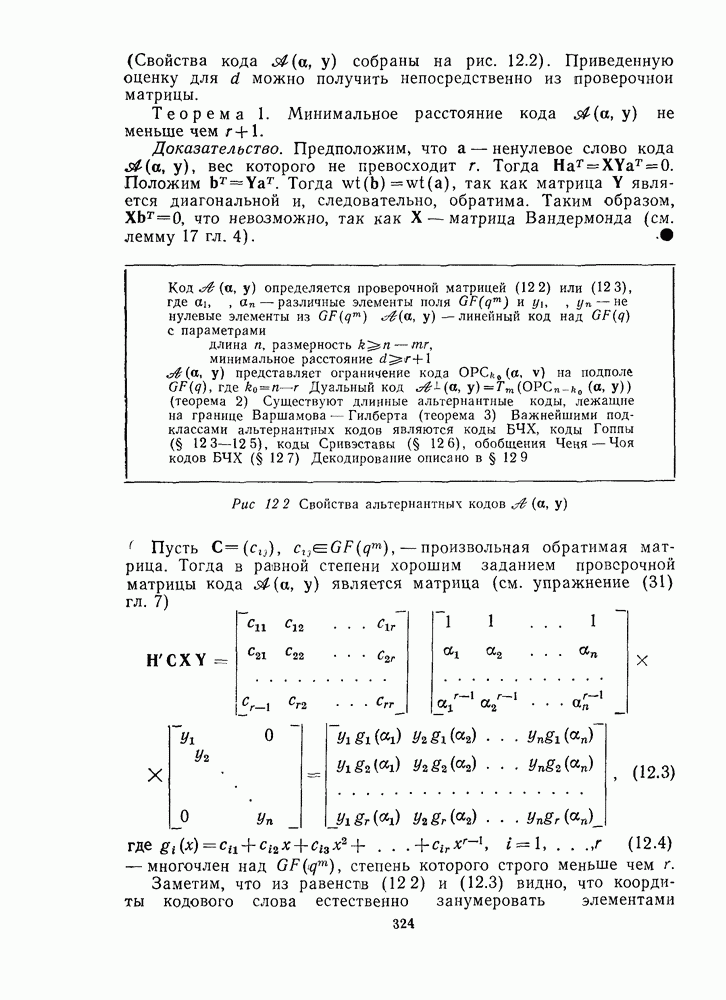
4.2. КОНЕЧНЫЕ ПОЛЯ ОСНОВЫ ТЕОРИИ
Характеристика поля. Пусть  произвольное конечное поле порядка
произвольное конечное поле порядка  содержит единичный элемент 1, и так как
содержит единичный элемент 1, и так как  конечно, то не могут быть различными все элементы
конечно, то не могут быть различными все элементы  Стедовательно, существует наименьшее число
Стедовательно, существует наименьшее число  такое, что
такое, что  Это
Это  должно быть простым числом (так как если
должно быть простым числом (так как если  то либо
то либо  либо
либо  и называется характеристикой поля Характеристика поля GF(24), построенного в гл 3, равна 2 Если характеристика поля
и называется характеристикой поля Характеристика поля GF(24), построенного в гл 3, равна 2 Если характеристика поля  равна
равна  то
то  для произвольного элемента
для произвольного элемента 
Таким образом,  содержит
содержит  элементов
элементов  Сумма и произведение этих
Сумма и произведение этих
элементов имеют такой же вид, так что эти  элементов образуют подполе
элементов образуют подполе  поля
поля  Если
Если  то в
то в  нет других элементов и
нет других элементов и 
Другие элементы в F. Предположим, что  и выберем в
и выберем в  максимальное множество линейно независимых над
максимальное множество линейно независимых над  элементов, скажем,
элементов, скажем,  Тогда
Тогда  содержит все элементы вида
содержит все элементы вида  и не содержит никаких других. Следовательно,
и не содержит никаких других. Следовательно,  является векторным пространством размерности
является векторным пространством размерности  над
над  и содержит
и содержит  элементов для некоторого простого
элементов для некоторого простого  и некоторого целого
и некоторого целого  (иначе, порядок
(иначе, порядок  равен
равен  Пусть
Пусть  обозначает множество всех
обозначает множество всех  ненулевых элементов поля
ненулевых элементов поля 
Важнейшим специфическим свойством конечных полей, отличающим их от бесконечных полей, является следующее.
Теорема  образует циклическую мультипликативную группу порядка
образует циклическую мультипликативную группу порядка  (Конечная мультипликативная циклическая группа определяется как множество элементов
(Конечная мультипликативная циклическая группа определяется как множество элементов  при условии
при условии  Элемент а называется образующей группы.)
Элемент а называется образующей группы.)
Доказательство То что  является мультипликативной группой, следует из определения поля. Пусть
является мультипликативной группой, следует из определения поля. Пусть  Так как мощность
Так как мощность  равна
равна  то
то  может принимать не более
может принимать не более  различных значений. Следовательно, найдутся целые числа
различных значений. Следовательно, найдутся целые числа  такие, что
такие, что  или
или  Наименьшее такое
Наименьшее такое  называется порядком элемента а.
называется порядком элемента а.
Выберем теперь а так, чтобы его порядок  был максимально возможным Покажем, что порядок I любого элемента
был максимально возможным Покажем, что порядок I любого элемента  делит число
делит число  Пусть я— простое число такое, что
Пусть я— простое число такое, что  взаимно просты с
взаимно просты с  Тогда элемент
Тогда элемент  имеет порядок
имеет порядок  а элемент имеет порядок
а элемент имеет порядок  а порядок элемента
а порядок элемента  равен
равен  (см. упражнение (7)). Следовательно,
(см. упражнение (7)). Следовательно,  так как в противном случае
так как в противном случае  не является максимальным. Таким образом, если некоторая степень простого числа является делителем
не является максимальным. Таким образом, если некоторая степень простого числа является делителем  то она является также делителем
то она является также делителем  следовательно, I делит
следовательно, I делит  Отсюда следует, что каждый элемент
Отсюда следует, что каждый элемент  из
из  удовлетворяет уравнению
удовлетворяет уравнению  Это означает, что многочлен
Это означает, что многочлен  делится
делится  . А так как
. А так как  содержит
содержит  элементов, то
элементов, то  Но
Но  следовательно,
следовательно,  Поэтому Прея
Поэтому Прея  и ненулевые элементы поля
и ненулевые элементы поля  образуют циклическую группу
образуют циклическую группу 
Следствие 3. (Теорема Ферма.) Каждый элемент  поля
поля  порядка
порядка  удовлетворяет тождеству
удовлетворяет тождеству  или, эквивалентно, является корнем уравнения
или, эквивалентно, является корнем уравнения 
Таким образом,

В поле  порядка
порядка  элемент а называется примитивным, если его порядок равен
элемент а называется примитивным, если его порядок равен  (см § 3.2) Отсюда следует, что любой ненулевой элемент поля
(см § 3.2) Отсюда следует, что любой ненулевой элемент поля  явчяется степенью элемента а Вторым следствием из теоремы 2 является
явчяется степенью элемента а Вторым следствием из теоремы 2 является
Теорема 4 Любое конечное поле  содержит примитивным элемент
содержит примитивным элемент
Доказательство В качестве примитивного элемента выберем образующий элемент а циклической группы 
Очень полезной оказывается следующая лемма Лемма 5 В любом поле характеристики  Доказательство Согласно упражнению (18) гл. 1
Доказательство Согласно упражнению (18) гл. 1

где 
При 

так как числитель содержит множитель  а знаменатель — нет В частности, в поле характеристики 2 имеем
а знаменатель — нет В частности, в поле характеристики 2 имеем

В заключение этого параграфа рассмотрим одно применение следствия 3 Воспользовавшись им в поле  получим следующий важный результат
получим следующий важный результат

для любого целого  не делящегося на
не делящегося на  Это стандартная формулировка теоремы Ферма, из которой, например, следует, что
Это стандартная формулировка теоремы Ферма, из которой, например, следует, что

или, иначе, 
Упражнения. (5) Производная многочлена над конечным полем. Если

то определим производную равенством

Показать, что:

(iii). Если  делит
делит  то
то  делит
делит  .
.
(iv). Если ни в каком расширении поля многочлен  не имеет кратных корней, то
не имеет кратных корней, то  взаимно просты.
взаимно просты.
(v). Если  то
то  состоит только из четных степеней и является полным квадратом,
состоит только из четных степеней и является полным квадратом, 
(6). Предположим, что  конечное расширение поля
конечное расширение поля  содержащее все корни многочлена
содержащее все корни многочлена  .
.
(i). Показать, что все корни многочлена  различны. [Указание. Показать, что этот многочлен взаимно прост со своей производной.]
различны. [Указание. Показать, что этот многочлен взаимно прост со своей производной.]
(ii). Доказать непосредственно, что эти корни образуют поле.
(7). Пусть  коммутативная группа, содержащая элементы
коммутативная группа, содержащая элементы  соответственно порядков
соответственно порядков 
Показать, что если  то
то 
Показать, что если  взаимно просты, то порядок элемента
взаимно просты, то порядок элемента  равен
равен 
Показать, что если  то порядок элемента
то порядок элемента  равен
равен 
(8).  - функция Эйлера (или тотиент-функция), определяется для любого целого положительного числа
- функция Эйлера (или тотиент-функция), определяется для любого целого положительного числа  как число чисел, не превосходящих
как число чисел, не превосходящих  и взаимно простых с
и взаимно простых с  .
.
(i). Показать, что

где  пробегает все простые делители числа
пробегает все простые делители числа  .
.
(ii). Показать, что

где суммирование ведется по всем делителям  числа
числа  включая
включая  и
и  .
.
(iii). Доказать теорему Ферма — Эйлера: если  взаимно просты, то
взаимно просты, то 
(9). Пусть  обозначает число примитивных элементов поля
обозначает число примитивных элементов поля  Показать, что
Показать, что  где
где  функция Эйлера, определенная в задаче 8. Отсюда вывести, что
функция Эйлера, определенная в задаче 8. Отсюда вывести, что 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРОВ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Часть I: Глава 1. Линейные коды
- 1.1. ЛИНЕЙНЫЕ КОДЫ
- 1.2. СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.3. НА ПРИЕМНОМ КОНЦЕ
- 1.4. НЕМНОГО ПОДРОБНЕЕ О ДЕКОДИРОВАНИИ ЛИНЕЙНОГО КОДА
- 1.5. ВЕРОЯТНОСТЬ ОШИБКИ
- 1.6. ТЕОРЕМА ШЕННОНА О СУЩЕСТВОВАНИИ ХОРОШИХ КОДОВ
- 1.7. КОДЫ ХЭММИНГА
- 1.8. ДУАЛЬНЫЙ КОД
- 1.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (II)
- 1.10. НЕКОТОРЫЕ ОБЩИЕ СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.11. КРАТКОЕ СОДЕРЖАНИЕ ГЛ. 1
- Глава 2. Нелинейные коды, матрицы Адамара, t-схемы и код Голея
- 2.1. НЕЛИНЕЙНЫЕ КОДЫ
- 2.2. ГРАНИЦА ПЛОТКИНА
- 2.3. МАТРИЦЫ АДАМАРА И КОДЫ АДАМАРА
- 2.4. КОНФЕРЕНС-МАТРИЦЫ
- 2.5. t-СХЕМЫ
- 2.6. ВВЕДЕНИЕ В ДВОИЧНЫЙ КОД ГОЛЕЯ
- 2.7. СИСТЕМА ШТЕЙНЕРА S(5,6,12) И НЕЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОДНУ ОШИБКУ
- 2.8. ВВЕДЕНИЕ В КОД НОРДСТРОМА—РОБИНСОНА
- 2.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (III)
- Глава 3. Введение в коды БЧХ и конечные поля
- 3.1. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (I)
- 3.2. ПОСТРОЕНИЕ ПОЛЯ GF(16)
- 3.3. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (II)
- 3.4. ВЫЧИСЛЕНИЯ В КОНЕЧНОМ ПОЛЕ
- Глава 4. Конечные поля
- 4.2. КОНЕЧНЫЕ ПОЛЯ ОСНОВЫ ТЕОРИИ
- 4.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ
- 4.4. КАК НАХОДИТЬ НЕПРИВОДИМЫЕ МНОГОЧЛЕНЫ
- 4.5. ТАБЛИЦЫ МАЛЫХ ПОЛЕЙ
- 4.6. ГРУППА АВТОМОРФИЗМОВ ПОЛЯ GF(p^m)
- 4.7. ЧИСЛО НЕПРИВОДИМЫХ МНОГОЧЛЕНОВ
- 4.8. БАЗИСЫ GF(p^m) НАД GF(p)
- 4.9. ЛИНЕАРИЗОВАННЫЕ МНОГОЧЛЕНЫ И НОРМАЛЬНЫЕ БАЗИСЫ
- Глава 5. Дуальные коды и их весовые спектры
- 5.2. ВЕСОВОЙ СПЕКТР КОДА, ДУАЛЬНОГО К ДВОИЧНОМУ ЛИНЕЙНОМУ КОДУ
- 5.3. ГРУППОВАЯ АЛГЕБРА
- 5.4. ХАРАКТЕРЫ
- 5.5. ТЕОРЕМА МАК-ВИЛЬЯМС ДЛЯ НЕЛИНЕЙНЫХ КОДОВ
- 5.6. ОБОБЩЕННЫЕ ТЕОРЕМЫ МАК-ВИЛЬЯМС ДЛЯ ЛИНЕЙНЫХ КОДОВ
- 5.7. СВОЙСТВА МНОГОЧЛЕНОВ КРАВЧУКА
- Глава 6. Коды, схемы и совершенные коды
- 6.2. ЧЕТЫРЕ ФУНДАМЕНТАЛЬНЫХ ПАРАМЕТРА КОДА
- 6.3. ЯВНАЯ ФОРМУЛА ДЛЯ СПЕКТРА ВЕСОВ И РАССТОЯНИЙ
- 6.4. ПОСТРОЕНИЕ СХЕМ ИЗ КОДОВ ПРИ …
- 6.5. ДУАЛЬНЫЙ КОД ТАКЖЕ ПОРОЖДАЕТ СХЕМЫ
- 6.6. ВЕСОВОЙ СПЕКТР КОДА, ПОЛУЧЕННОГО В РЕЗУЛЬТАТЕ СДВИГА
- 6.7. ПОСТРОЕНИЕ СХЕМ ИЗ НЕЛИНЕЙНЫХ КОДОВ ПРИ …
- 6.8. СОВЕРШЕННЫЕ КОДЫ
- 6.9. КОДЫ НАД GF(q)
- 6.10. НЕ СУЩЕСТВУЕТ НЕИЗВЕСТНЫХ СОВЕРШЕННЫХ КОДОВ
- Глава 7. Циклические коды
- 7.2. ОПРЕДЕЛЕНИЕ ЦИКЛИЧЕСКОГО КОДА
- 7.3. ПОРОЖДАЮЩИЙ МНОГОЧЛЕН
- 7.4. ПРОВЕРОЧНЫЙ МНОГОЧЛЕН
- 7.5. ДЕЛИТЕЛИ МНОГОЧЛЕНА x^n-1
- 7.6. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ t ОШИБОК
- 7.7. ИСПОЛЬЗОВАНИЕ МАТРИЦЫ НАД GF(q^m) ДЛЯ ЗАДАНИЯ КОДА НАД GF(q)
- 7.8. КОДИРОВАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- Глава 8. Циклические коды (продолжение): идемпотенты и многочлены Мэттсона-Соломона
- 8.2. ИДЕМПОТЕНТЫ
- 8.3. МИНИМАЛЬНЫЕ ИДЕАЛЫ, НЕПРИВОДИМЫЕ КОДЫ И ПРИМИТИВНЫЕ ИДЕМПОТЕНТЫ
- 8.4. ВЕСОВОЙ СПЕКТР МИНИМАЛЬНЫХ КОДОВ
- 8.5. ГРУППЫ АВТОМОРФИЗМОВ КОДА
- 8.6. МНОГОЧЛЕН МЭТТСОНА—СОЛОМОНА
- 8.7. НЕКОТОРЫЕ ВЕСОВЫЕ СПЕКТРЫ
- Глава 9. Коды БЧХ
- 9.2. ИСТИННОЕ МИНИМАЛЬНОЕ РАССТОЯНИЕ КОДА БЧХ
- 9.3. ЧИСЛО ИНФОРМАЦИОННЫХ СИМВОЛОВ КОДОВ БЧХ
- 9.4. ТАБЛИЦА КОДОВ БЧХ
- 9.5. ДЛИННЫЕ КОДЫ БЧХ
- 9.6. ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 9.7. КВАДРАТНЫЕ УРАВНЕНИЯ НАД GF(2^m)
- 9.8. КВАЗИСОВЕРШЕННОСТЬ КОДОВ БЧХ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
- 9.9. ГРАНИЦА КАРЛИЦА—УШИЯМЫ
- 9.10. АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ НЕКОТОРЫХ ВЕСОВЫХ СПЕКТРОВ
- 9.11. КОДЫ НЕ-БЧХ, ИСПРАВЛЯЮЩИЕ ТРИ ОШИБКИ
- Глава 10. Коды Рида-Соломона и коды Юстесена
- 10.2. КОДЫ РИДА-СОЛОМОНА
- 10.3. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
- 10.4. ИДЕМПОТЕНТЫ КОДОВ РИДА-СОЛОМОНА
- 10.5. ОТОБРАЖЕНИЕ КОДОВ НАД GF(2^m) В ДВОИЧНЫЕ КОДЫ
- 10.6. ИСПРАВЛЕНИЕ ПАКЕТОВ ОШИБОК
- 10.7. КОДИРОВАНИЕ КОДОВ РИДА—СОЛОМОНА
- 10.9. ИЗБЫТОЧНЫЕ ВЫЧЕТНЫЕ КОДЫ
- 10.10. ДЕКОДИРОВАНИЕ КОДОВ РИДА-СОЛОМОНА
- 10.11. КОДЫ ЮСТЕСЕНА И КАСКАДНЫЕ КОДЫ
- Глава 11. Коды МДР
- 11.2. ПОРОЖДАЮЩАЯ И ПРОВЕРОЧНАЯ МАТРИЦЫ
- 11.3. ВЕСОВОЙ СПЕКТР КОДА МДР
- 11.4. МАТРИЦЫ, У КОТОРЫХ ВСЕ КВАДРАТНЫЕ ПОДМАТРИЦЫ НЕВЫРОЖДЕНЫ
- 11.5. КОДЫ МДР, ПОЛУЧЕННЫЕ ИЗ КОДОВ РИДА-СОЛОМОНА
- 11.6. n-МНОЖЕСТВА
- 11.7. ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ
- 11.8. ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
- Глава 12. Альтернантные коды, коды Гоппы и другие обобщения кодов БЧХ
- 12.2. АЛЬТЕРНАНТНЫЕ КОДЫ
- 12.3. КОДЫ ГОППЫ
- 12.4. ДАЛЬНЕЙШИЕ СВОЙСТВА КОДОВ ГОППЫ
- 12.5. ЦИКЛИЧНОСТЬ УДЛИНЕННЫХ КОДОВ ГОППЫ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
- 12.6. ОБОБЩЕННЫЕ КОДЫ СРИВЭСТАВЫ
- 12.7. ОБОБЩЕНИЕ ЧЕНЯ—ЧОЯ КОДОВ БЧХ
- 12.8. АЛГОРИТМ ЕВКЛИДА
- 12.9. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- Часть II: Глава 13. Коды Рида-Маллера
- 13.2. БУЛЕВЫ ФУНКЦИИ
- 13.3. КОДЫ РИДА-МАЛЛЕРА
- 13.4. РИДА-МАЛЕРА КОДЫ И ГЕОМЕТРИИ
- 13.5. ВЕКТОРЫ МИНИМАЛЬНОГО ВЕСА ПОРОЖДАЮТ КОД
- 13.6. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (I)
- 13.7. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (II)
- 13.8. ДРУГИЕ ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.9. ГРУППЫ АВТОМОРФИЗМОВ РИДА-МАЛЕРА КОДОВ
- 13.10. МНОГОЧЛЕНЫ МЭТТСОНА—СОЛОМОНА ДЛЯ РИДА-МАЛЕРА КОДОВ
- 13.11. ДЕЙСТВИЕ ПОЛНОЙ АФФИННОЙ ГРУППЫ НА МНОГОЧЛЕНАХ МЭТТСОНА—СОЛОМОНА
- Глава 14. Коды Рида-Маллера первого порядка
- 14.2. ПСЕВДОШУМОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 14.3. СМЕЖНЫЕ КЛАССЫ ПО КОДУ РИДА—МАЛЛЕРА ПЕРВОГО ПОРЯДКА
- 14.4. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ КОДА R(1, m)
- 14.5. МАКСИМАЛЬНО-НЕЛИНЕЙНЫЕ ФУНКЦИИ
- Глава 15. Коды Рида-Маллера первого порядка Кердока и Препараты
- 15.2. ВЕСОВОЙ СПЕКТР КОДА РИДА—МАЛЛЕРА ВТОРОГО ПОРЯДКА
- 15.3. СПЕКТР ВЕСОВ ПРОИЗВОЛЬНЫХ КОДОВ РИДА—МАЛЛЕРА
- 15.4. ПОДКОДЫ РАЗМЕРНОСТИ 2m В КОДАХ R(2, m)* И R(2, m)
- 15.5. КОД КЕРДОКА И ЕГО ОБОБЩЕНИЯ
- 15.6. КОД ПРЕПАРАТЫ
- 15.7. ОБОБЩЕНИЕ ГЕТАЛСА КОДОВ ПРЕПАРАТЫ
- Глава 16. Квадратично-вычетные коды
- 16.2. ОПРЕДЕЛЕНИЕ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.3. ИДЕМПОТЕНТЫ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.4. РАСШИРЕННЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.5. ГРУППА АВТОМОРФИЗМОВ КВ-КОДОВ
- 16.6. ДВОИЧНЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.7. ДВАЖДЫ ЦИРКУЛЯНТНЫЕ И КВАЗИЦИКЛИЧЕСКИЕ КОДЫ
- 16.8. КВАДРАТИЧНО-ВЫЧЕТНЫЕ И СИММЕТРИЧНЫЕ КОДЫ НАД GF{3)
- 16.9. ДЕКОДИРОВАНИЕ ЦИКЛИЧЕСКИХ И НЕКОТОРЫХ ДРУГИХ КОДОВ
- Глава 17. Границы для объема кода
- 17.2. ГРАНИЦЫ ДЛЯ A(n, d, w)
- 17.3. ГРАНИЦЫ ДЛЯ A(n, d)
- 17.4. ГРАНИЦЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 17.5. ГРАНИЦА ГРАЙСМЕРА
- 17.6. ПОСТРОЕНИЕ ЛИНЕЙНЫХ КОДОВ; АНТИКОДЫ
- 17.7. АСИМПТОТИЧЕСКИЕ ГРАНИЦЫ
- Глава 18. Методы комбинирования кодов
- I. ПРОИЗВЕДЕНИЕ КОДОВ И ИХ ОБОБЩЕНИЕ
- 18.2. ПРЯМОЕ ПРОИЗВЕДЕНИЕ КОДОВ
- 18.3. НЕ ВСЕ ЦИКЛИЧЕСКИЕ КОДЫ ЯВЛЯЮТСЯ ПРЯМЫМИ ПРОИЗВЕДЕНИЯМИ ЦИКЛИЧЕСКИХ КОДОВ
- 18.4. ДРУГОЙ СПОСОБ ПРЕДСТАВЛЕНИЯ НЕПРИВОДИМЫХ ЦИКЛИЧЕСКИХ кодов В ВИДЕ ПРОИЗВЕДЕНИЯ КОДОВ
- 18.5. КАСКАДНЫЕ КОДЫ: (*)-КОНСТРУКЦИЯ
- 18.6. ОБЩИЙ ПОДХОД К РАЗЛОЖЕНИЮ ЦИКЛИЧЕСКИХ КОДОВ
- II. ДРУГИЕ МЕТОДЫ КОМБИНИРОВАНИЯ КОДОВ
- 18.7. МЕТОДЫ ПОСТРОЕНИЯ, КОТОРЫЕ УВЕЛИЧИВАЮТ ДЛИНУ
- 18.7.1. КОНСТРУКЦИЯ X: ДОБАВЛЕНИЕ СУФФИКСОВ К КОДОВЫМ СЛОВАМ
- 18.7.2. КОНСТРУКЦИЯ Х4: КОМБИНИРОВАНИЕ ЧЕТЫРЕХ КОДОВ
- 18.7.3. КОДЫ, ИСПРАВЛЯЮЩИЕ ОДИНОЧНЫЕ И ДВОЙНЫЕ ОШИБКИ
- 18.7.4. КОНСТРУКЦИЯ …
- 18.7.5. КОНСТРУКЦИЯ ПИРЕТА
- 18.8. КОНСТРУКЦИИ, СВЯЗАННЫЕ С КАСКАДНЫМИ КОДАМИ
- 18.8.2. ОБОБЩЕННЫЕ КАСКАДНЫЕ КОДЫ ЗИНОВЬЕВА
- 18.9. МЕТОДЫ УКОРОЧЕНИЯ КОДОВ
- 18.9.2. КОНСТРУКЦИИ ХЕЛГЕРТА И СТИНАФФА
- Глава 19. Самодуальные коды и теория инвариантов
- 19.2. ВВЕДЕНИЕ В ТЕОРИЮ ИНВАРИАНТОВ
- 19.3. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ИНВАРИАНТОВ
- 19.4. ОБОБЩЕНИЯ ТЕОРЕМЫ ГЛИСОНА
- 19.5. НЕСУЩЕСТВОВАНИЕ НЕКОТОРЫХ ОЧЕНЬ ХОРОШИХ КОДОВ
- 19.6. ХОРОШИЕ САМОДУАЛЬНЫЕ КОДЫ СУЩЕСТВУЮТ
- Глава 20. Коды Голея
- 20.2. ГРУППА МАТЬЕ M24
- 20.3. ГРУППА М24 5-ТРАНЗИТИВНА
- 20.4. ПОРЯДОК ГРУППЫ М24 РАВЕН 24•23•22•21•20•48
- 20.5. СИСТЕМА ШТЕЙНЕРА S(5, 8, 24) ЕДИНСТВЕННА
- 20.6. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
- 20.7. ГРУППЫ АВТОМОРФИЗМОВ ТРОИЧНЫХ КОДОВ ГОЛЕЯ
- 20.8. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
- Глава 21. Схемы отношений
- 21.2. СХЕМЫ ОТНОШЕНИЙ
- 21.3. СХЕМА ОТНОШЕНИЙ ХЭММИНГА
- 21.4. МЕТРИЧЕСКИЕ СХЕМЫ
- 21.5. СИМПЛЕКТИЧЕСКИЕ ФОРМЫ
- 21.6. СХЕМА ДЖОНСОНА
- 21.7. ПОДМНОЖЕСТВА СХЕМ ОТНОШЕНИЙ
- 21.8. ПОДМНОЖЕСТВА СИМПЛЕКТИЧЕСКИХ ФОРМ
- 21.9. t-СХЕМЫ И ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
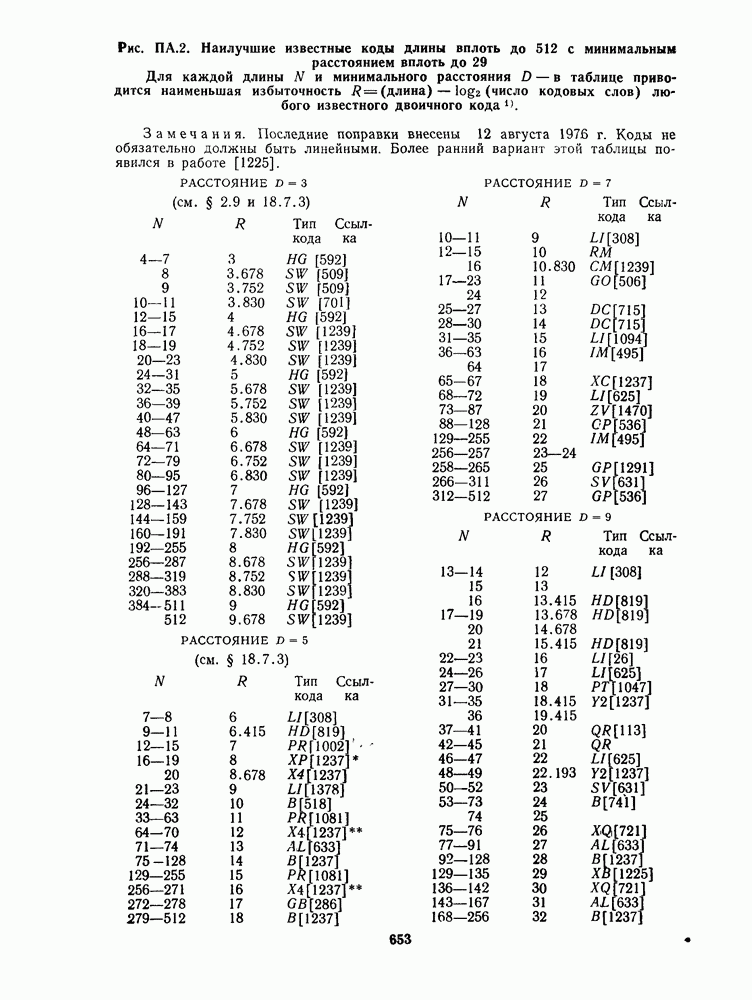
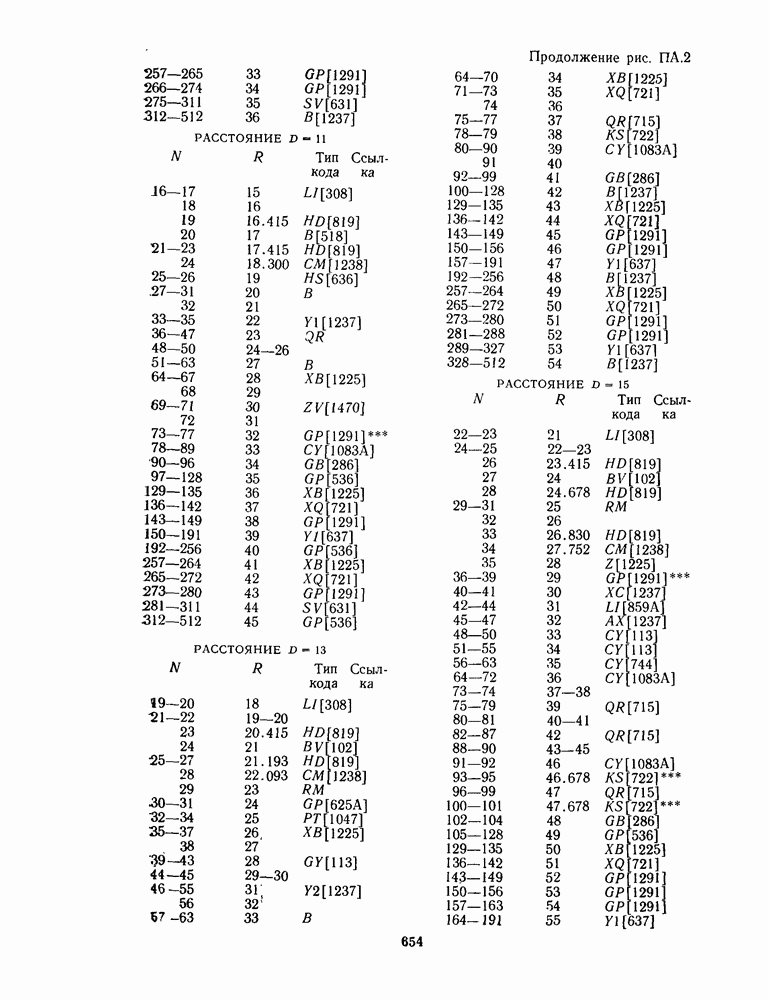
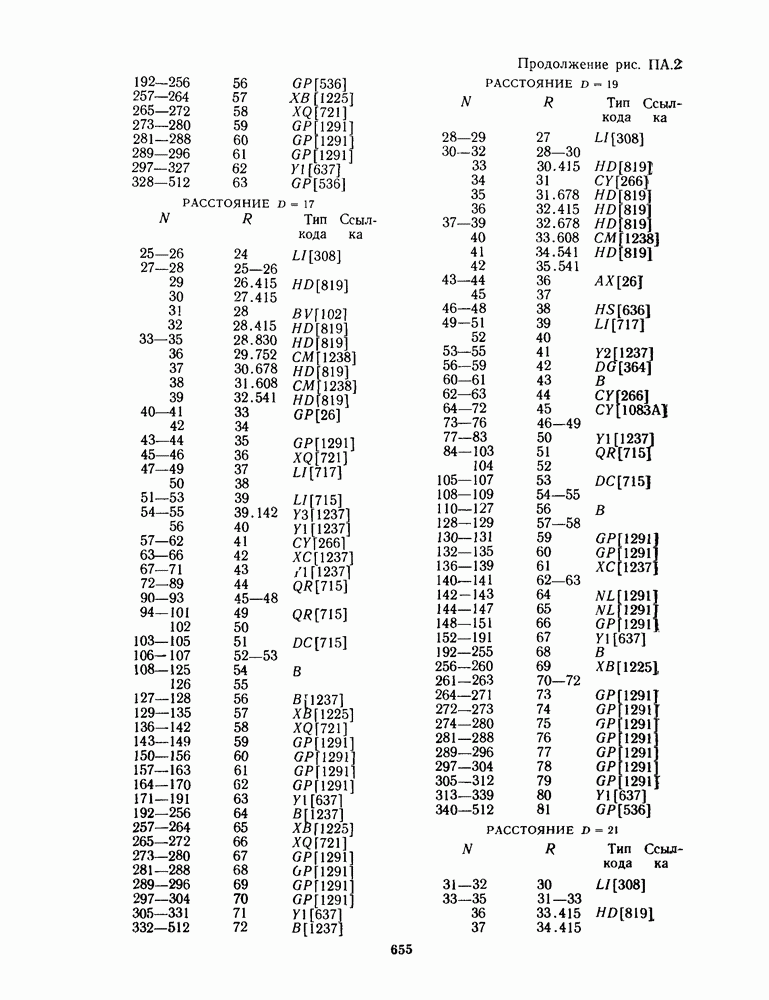
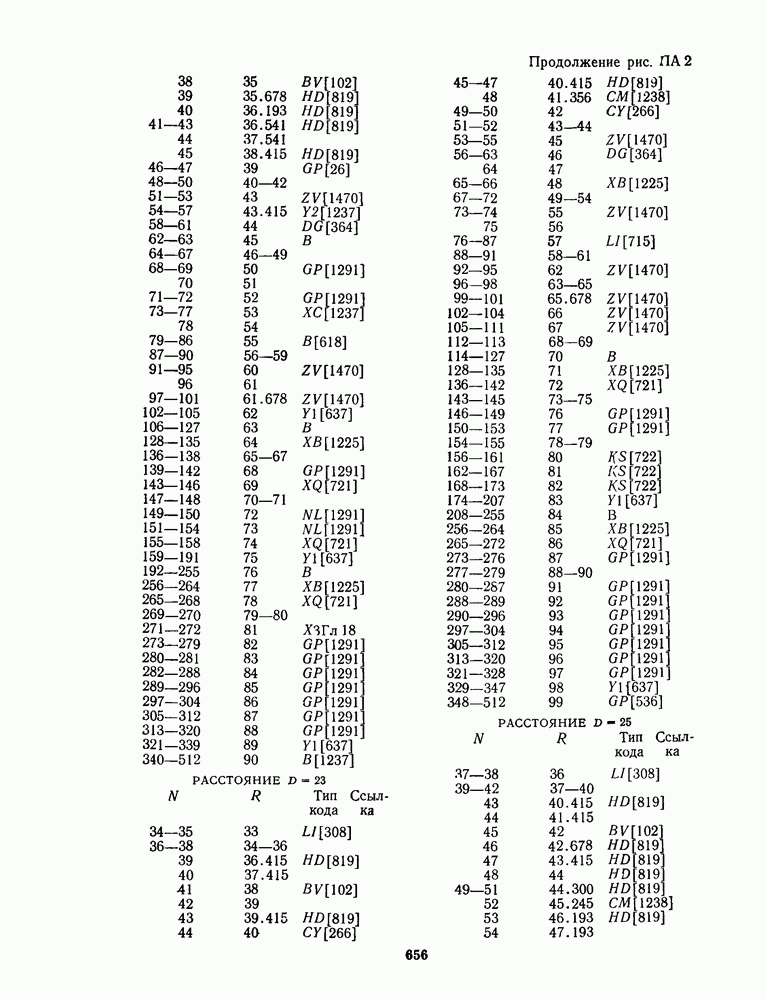
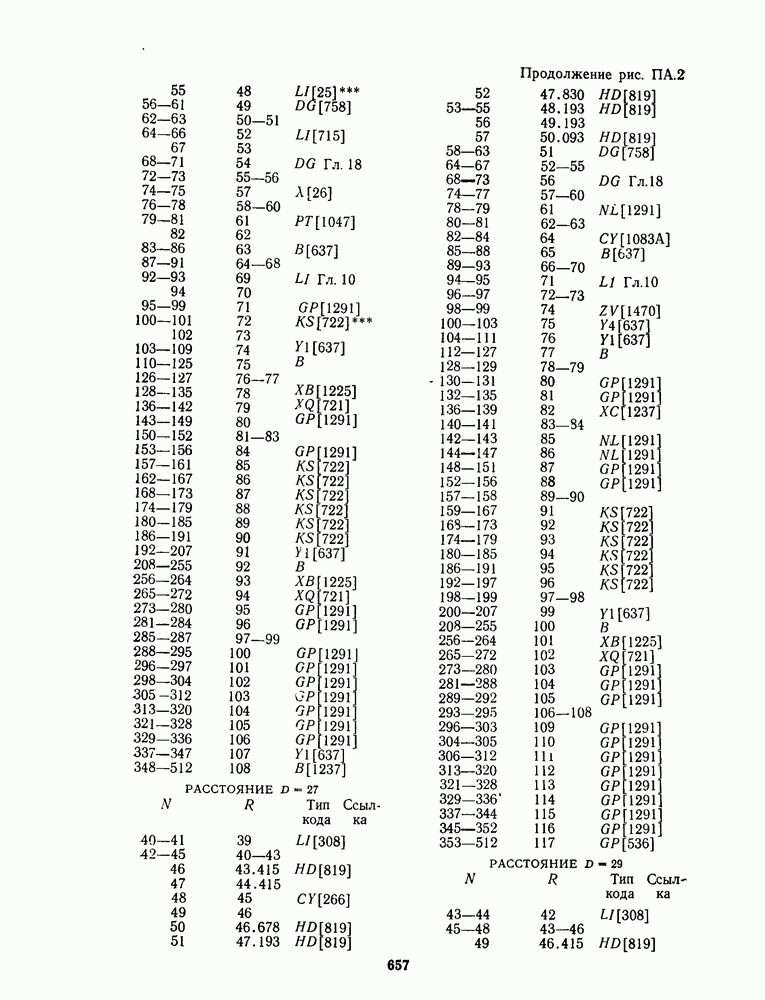
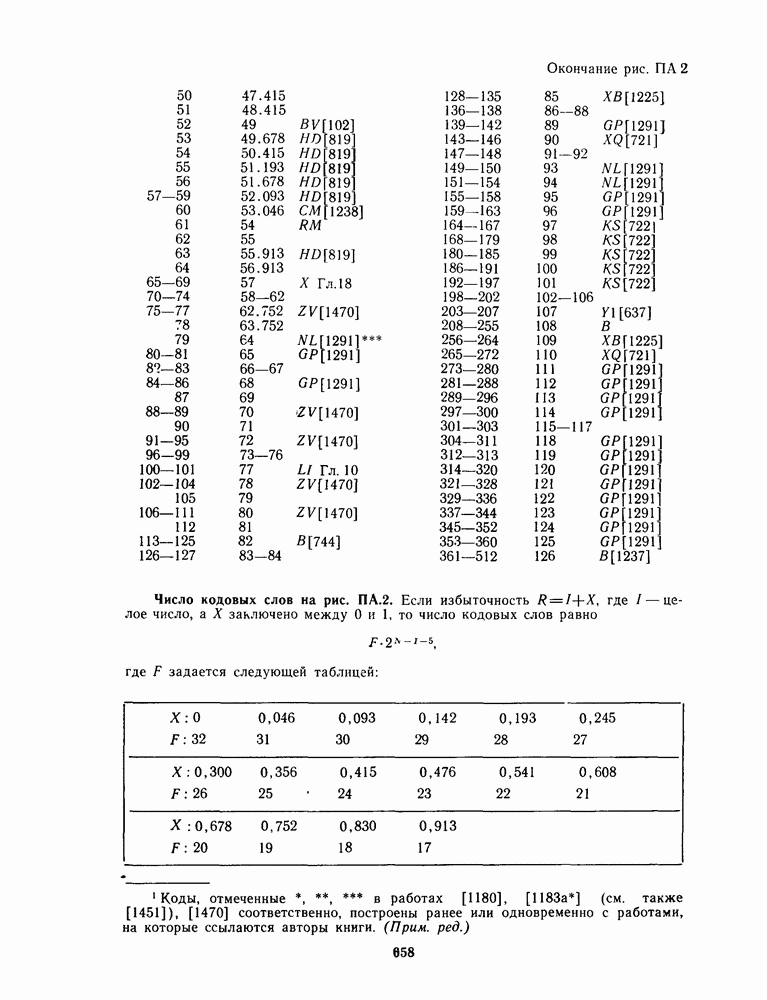
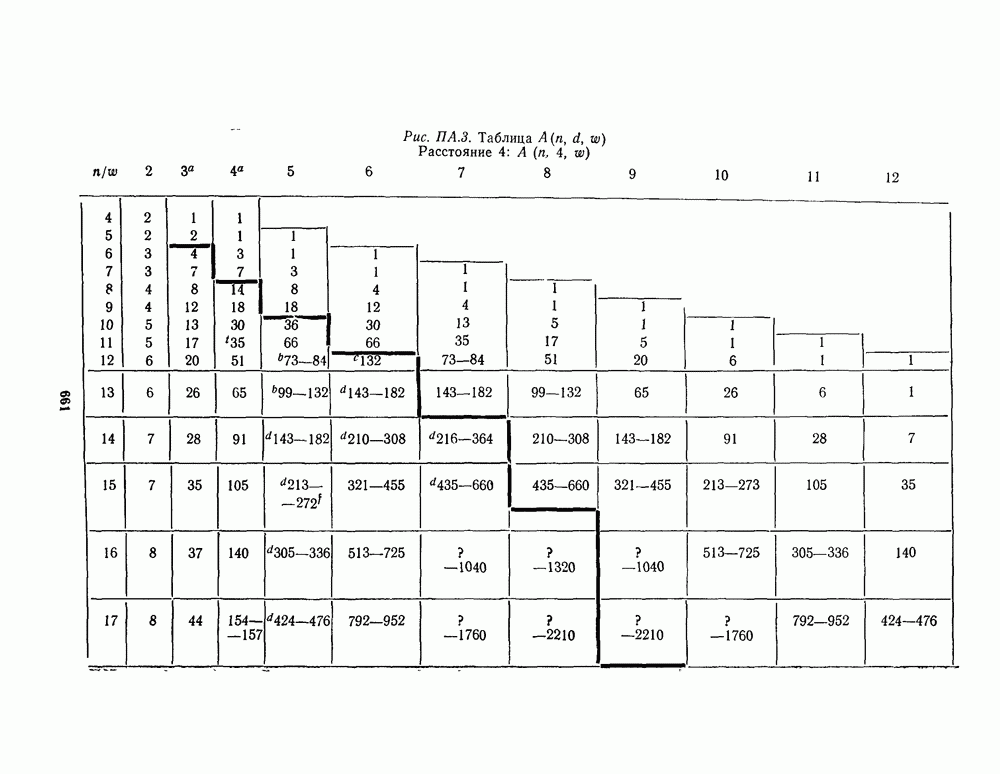
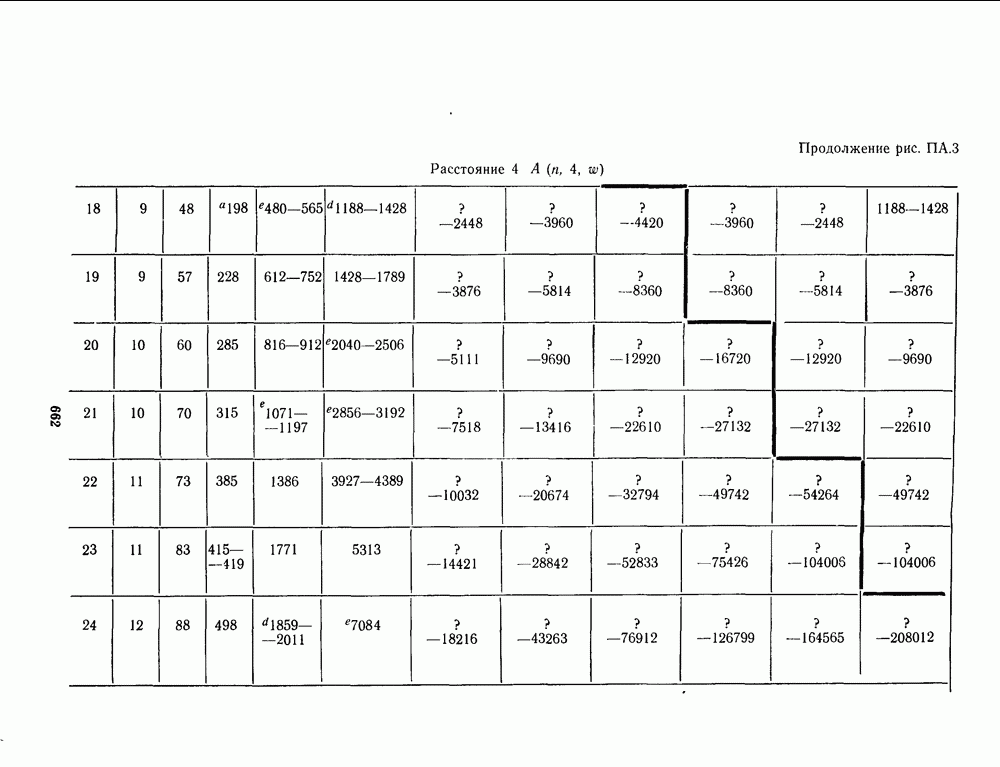
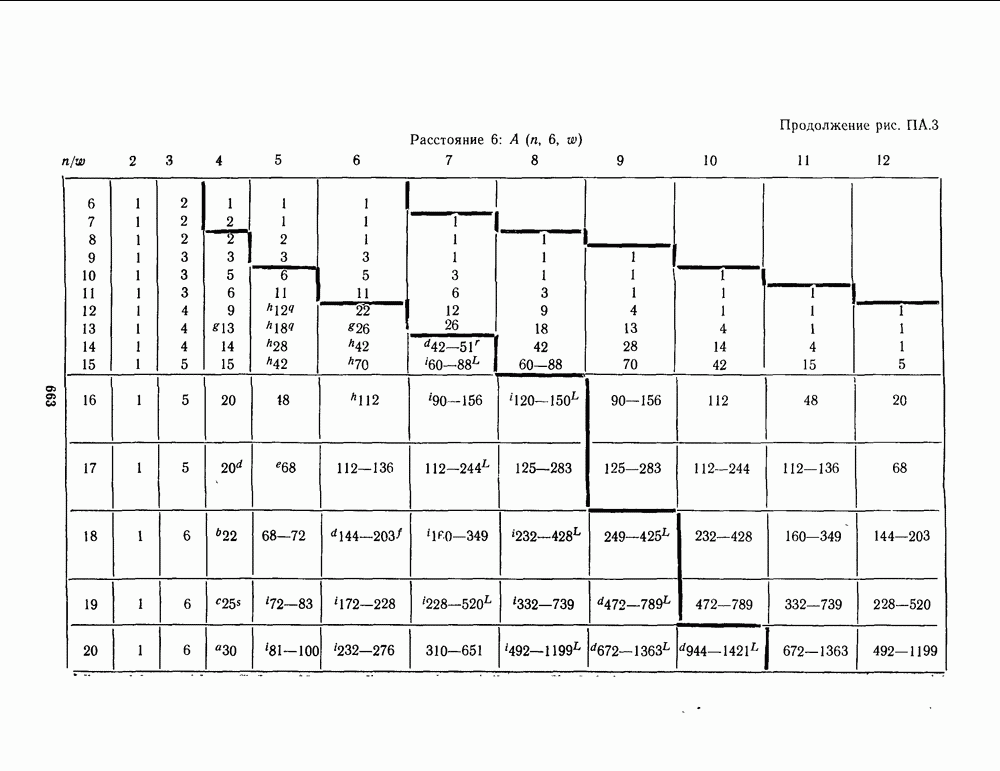
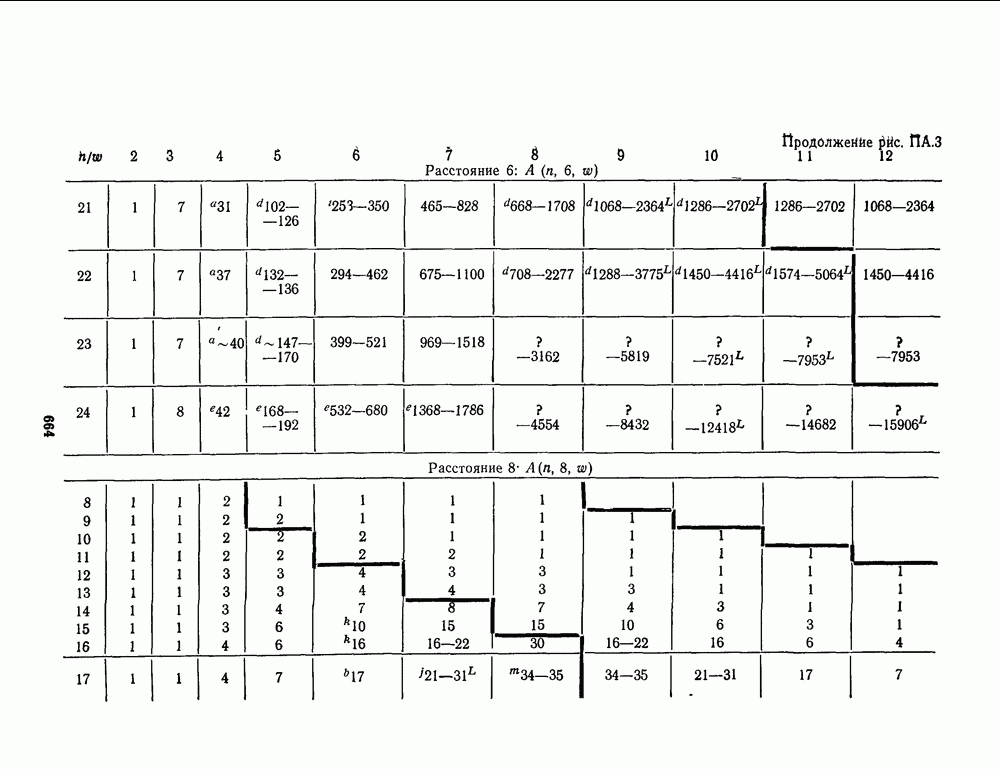
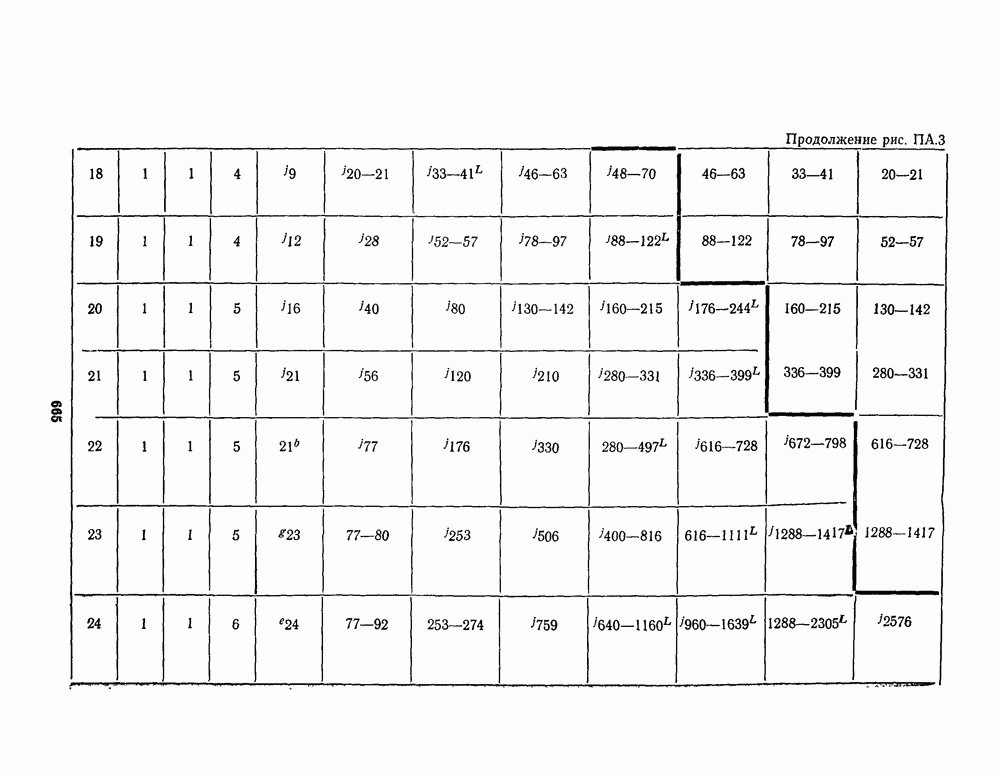
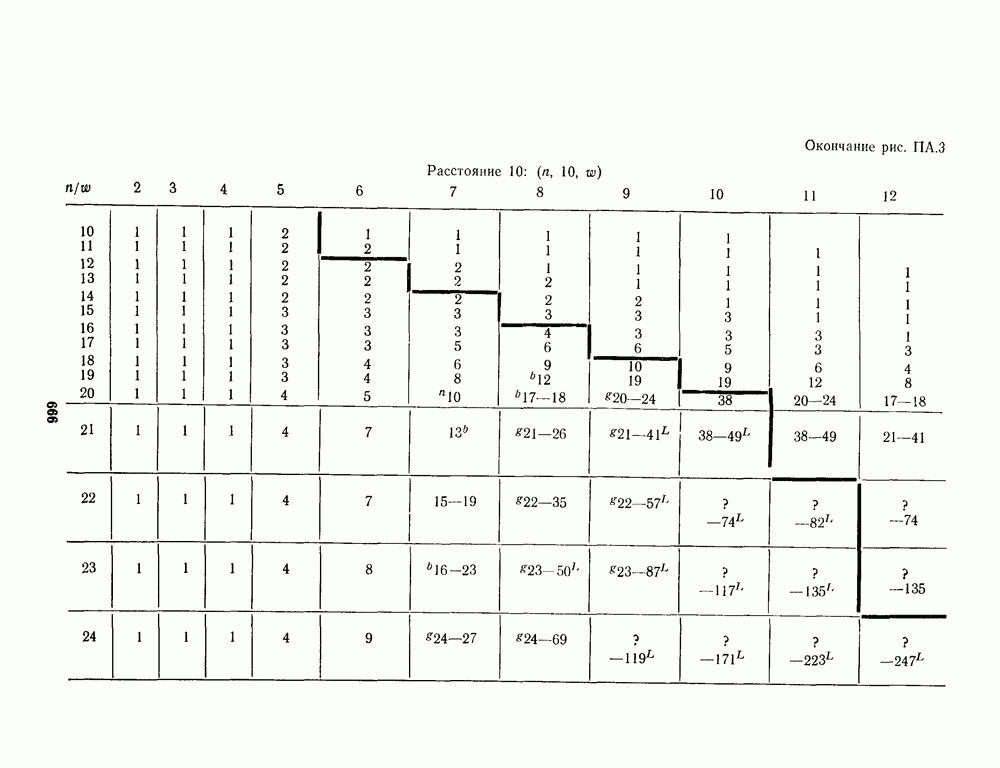
- ПРИЛОЖЕНИЕ А. ТАБЛИЦЫ НАИЛУЧШИХ ИЗВЕСТНЫХ КОДОВ
- ПРИЛОЖЕНИЕ В. КОНЕЧНЫЕ ГЕОМЕТРИИ