| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
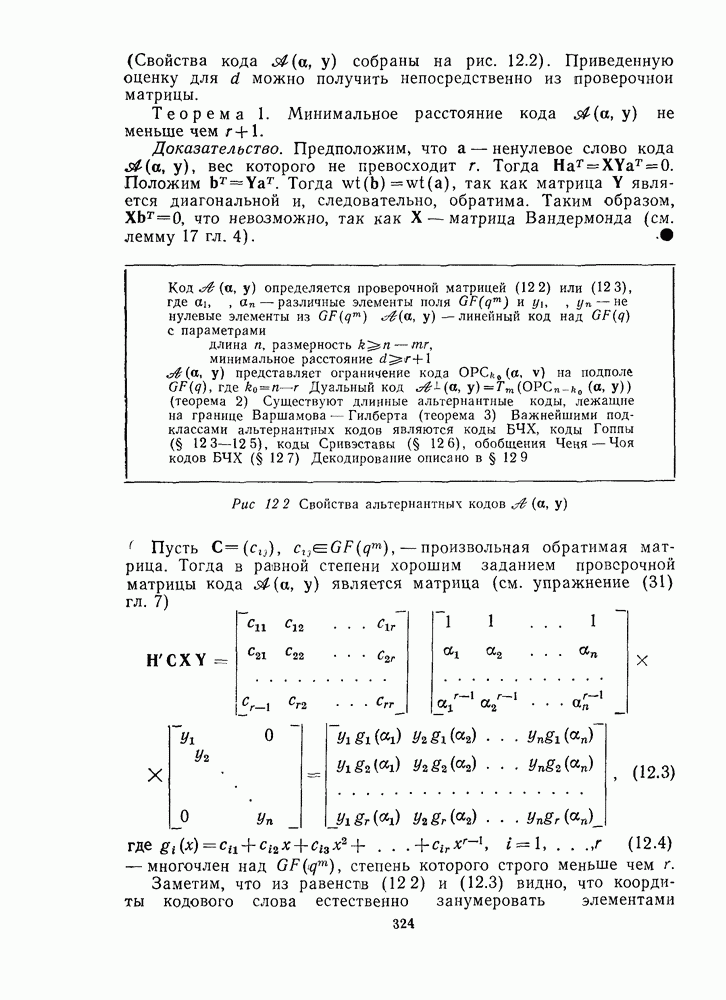
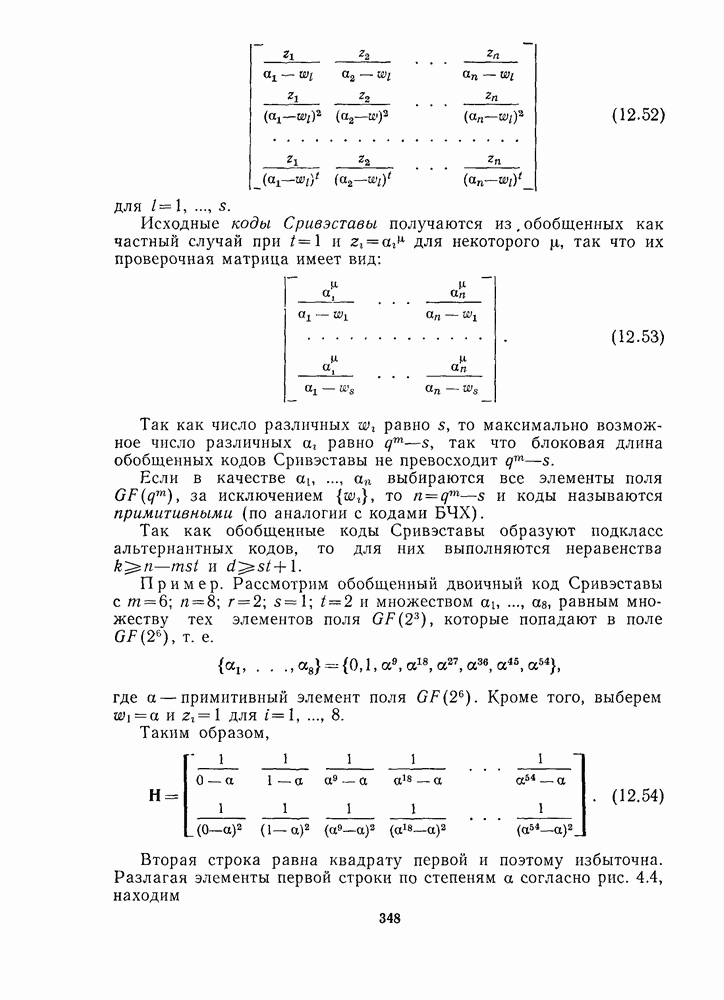
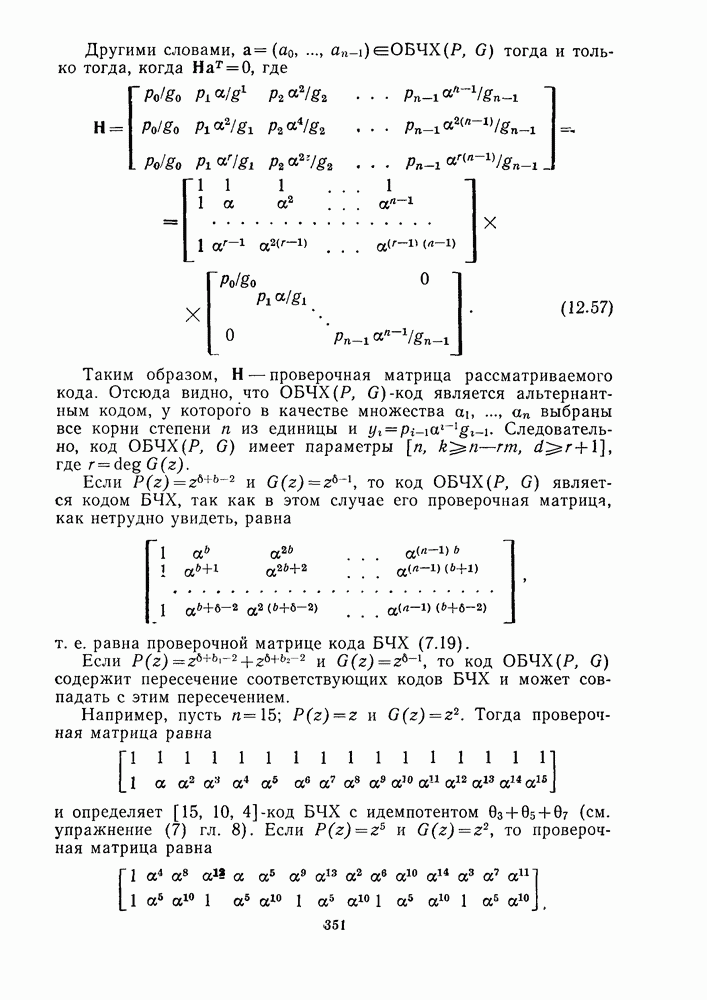
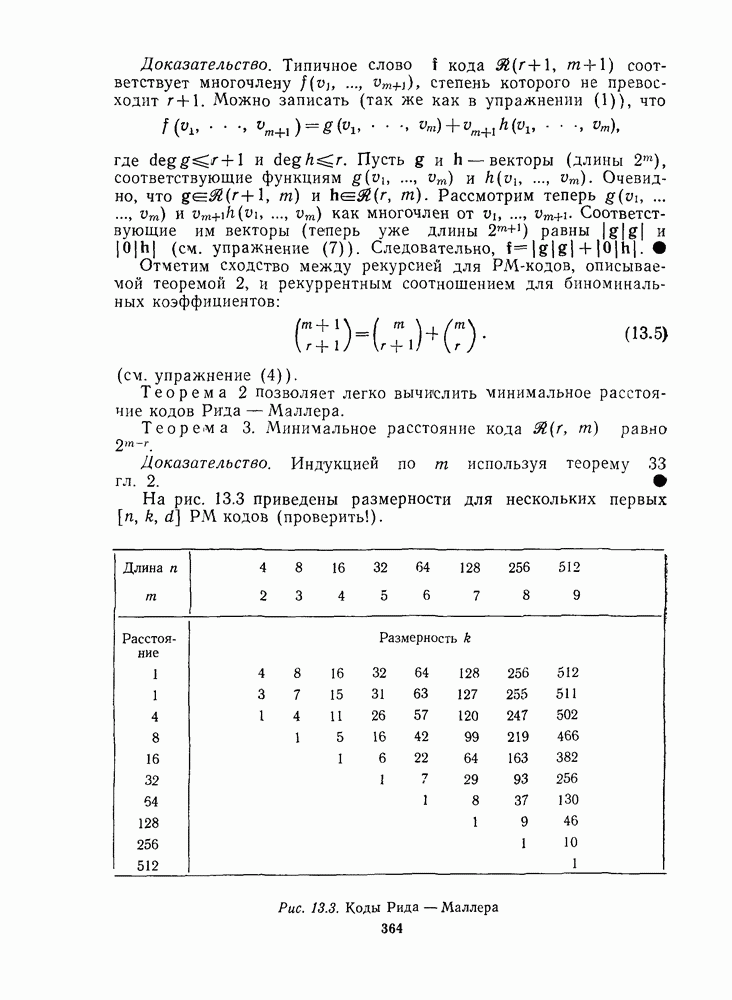
19.3. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ИНВАРИАНТОВ
Группы матриц. С помрщью заданной совокупности  невырожденных
невырожденных  -матриц можно образовать группу
-матриц можно образовать группу  умножая матрицы друг на друга всеми возможными способами. Таким образом, группа
умножая матрицы друг на друга всеми возможными способами. Таким образом, группа  содержит матрицы
содержит матрицы  Будем говорить, что группа
Будем говорить, что группа  порождается матрицами
порождается матрицами  Конечно, группа
Конечно, группа  может быть бесконечной, и в этом случае описанная здесь теория инвариантов прямо неприменима. (Однако см. Дьедонне и Керрол [375], Рэллис [1087] и Вейль [1410].)
может быть бесконечной, и в этом случае описанная здесь теория инвариантов прямо неприменима. (Однако см. Дьедонне и Керрол [375], Рэллис [1087] и Вейль [1410].)
Пример. Покажем, что группа порожденная матрицами

с которой мы встречались в § 19.2, действительно имеет порядок 192. Существенный момент заключается в обнаружении того (при случайном умножении матриц друг на друга), что содержит матрицы

Поэтому содержит матрицы

образующие подгруппу  порядка 16. Отсюда легко видеть, что группа является объединением 12 смежных классов по подгруппе
порядка 16. Отсюда легко видеть, что группа является объединением 12 смежных классов по подгруппе 

где матрицы  соответственно равны
соответственно равны

 Таким образом, группа 91 состоит из 192 матриц вида
Таким образом, группа 91 состоит из 192 матриц вида

где 
Для проверки достаточно убедиться в том, что каждая матрица из семейства (19.28) может быть представлена как произведение степеней матриц  что произведение двух матриц вида (19.28) имеет такой же вид и что матрица, обратная любой матрице из семейства (19.28), принадлежит этому же семейству. Следовательно, семейство матриц (19.28) является группой, которая порождается матрицами
что произведение двух матриц вида (19.28) имеет такой же вид и что матрица, обратная любой матрице из семейства (19.28), принадлежит этому же семейству. Следовательно, семейство матриц (19.28) является группой, которая порождается матрицами  Таким образом, группа действительно совпадает с семейством (19.28).
Таким образом, группа действительно совпадает с семейством (19.28).
Мы подробно разобрали этот пример, чтобы подчеркнуть, как важно начать с досконального изучения группы. (Другой возможный подход к изучению группы см. в [201; с. 160-161].)
Инварианты. Процитируем Германа Вейля [1409]: «Теория инвариантов возникла в середине XIX столетия отчасти подобно Минерве: взрослая дева, одетая в сияющие доспехи алгебры, она выпрыгнула из Юпитеровой головы Кэли». Теория инвариантов стала одним из ведущих направлений математики XIX столетия, но вышла из моды после работы Гилберта (см. Фишер [431] и Рейд [1108]). В последнее время, однако, интерес к ней возродился в связи с применениями в алгебраической геометрии (Дьедон-не и Керрол [375], Мамфорд [976]), физике (см., например, Агравала и Белпнфант [7] и ссылки, приведенные там), комбинаторике (Дубиле и др. [381], Рота [1125]) и в теории кодирования ([883, 894, 895]).
Имеется несколько различных типов инвариантов, но здесь инвариант определяется следующим образом.
Пусть  представляет собой группу, состоящую из
представляет собой группу, состоящую из  комплексных
комплексных  -матриц
-матриц  где
где  элемент матрицы
элемент матрицы  равен
равен  Другими словами,
Другими словами,  группа линейных преобразований переменных
группа линейных преобразований переменных  состоящая из преобразований
состоящая из преобразований

где
Имеет смысл точно описать, как многочлен  преобразуется матрицей
преобразуется матрицей  из группы Преобразованный многочлен имеет вид
из группы Преобразованный многочлен имеет вид

где каждое  заменяется выражением
заменяется выражением 
Другой способ описания этого преобразования состоит в представлении  в виде вектора-столбца. Тогда
в виде вектора-столбца. Тогда  преобразуется в многочлен
преобразуется в многочлен

где  обычное произведение матрицы и вектора. Можно проверить, что
обычное произведение матрицы и вектора. Можно проверить, что

Например, матрица  преобразует
преобразует 
Определение. Инвариантом группы  называется многочлен
называется многочлен  который остается неизменным при действии любого линейного преобразования из группы
который остается неизменным при действии любого линейного преобразования из группы  Другими словами,
Другими словами,  инвариант если
инвариант если  для всех
для всех 
Пример. Пусть  группа порядка
группа порядка  Тогда
Тогда  являются однородными инвариантами степени 2.
являются однородными инвариантами степени 2.
Даже если  не является инвариантом, то, как указывалось в § 19.2, его среднее по группе является таковым.
не является инвариантом, то, как указывалось в § 19.2, его среднее по группе является таковым.
Теорема 4. Пусть  произвольный многочлен. Тогда многочлен
произвольный многочлен. Тогда многочлен

является инвариантом группы
Доказательство. Любая матрица  преобразует правую часть выражения (19.32) в сумму
преобразует правую часть выражения (19.32) в сумму 

Так как матрица  пробегает всю группу то при фиксированной матрице
пробегает всю группу то при фиксированной матрице  произведение
произведение  также пробегает всю группу. Следовательно, выражение (19.33) равно
также пробегает всю группу. Следовательно, выражение (19.33) равно

что совпадает с  Таким образом,
Таким образом,  инвариант.
инвариант.
В более общем случае любая симметрическая функция от  многочленов
многочленов  является инвариантом
является инвариантом
Ясно, что если  инварианты то
инварианты то  (с — комплексное число) также являются инвариантами. Это эквивалентно утверждению о том, что множество
(с — комплексное число) также являются инвариантами. Это эквивалентно утверждению о том, что множество
инвариантов группы  которое мы обозначим через образует кольцо (см. с. 189).
которое мы обозначим через образует кольцо (см. с. 189).
Одна из основных задач теории инвариантов заключается в описании кольца Так как преобразования группы  не изменяют степень многочлена, то достаточно описать однородные инварианты (ибо любой инвариант представляет собой сумму однородных инвариантов).
не изменяют степень многочлена, то достаточно описать однородные инварианты (ибо любой инвариант представляет собой сумму однородных инвариантов).
Базисные инварианты. Наша цель — найти «базис» для инвариантов 5, т. е. найти множество базисных инвариантов таких, что любой инвариант может быть выражен через элементы этого множества. Существуют два различных типа базисов, которые можно было бы искать.
Определение. Многочлены  называются алгебраически зависимыми, если существует многочлен
называются алгебраически зависимыми, если существует многочлен  от
от  переменных с комплексными коэффициентами, не равными одновременно нулю, такой, что
переменных с комплексными коэффициентами, не равными одновременно нулю, такой, что  . В противном случае
. В противном случае  называются алгебраически независимыми. Следующая теорема представляет собой фундаментальный алгебраический результат.
называются алгебраически независимыми. Следующая теорема представляет собой фундаментальный алгебраический результат.
Теорема 7. (Джекобсон [687], т. 3, с. 154.) Любые  многочленов от
многочленов от  переменных алгебраически зависимы.
переменных алгебраически зависимы.
Первый тип базиса, который мы могли бы искать, представляет собой множество  алгебраически независимых инвариантов
алгебраически независимых инвариантов  Такое множество в самом деле является «базисом», так как по теореме 7 любой инвариант алгебраически зависит от
Такое множество в самом деле является «базисом», так как по теореме 7 любой инвариант алгебраически зависит от  и поэтому является корнем некоторого многочлена от
и поэтому является корнем некоторого многочлена от  Существование такого базиса обеспечивает следующая теорема.
Существование такого базиса обеспечивает следующая теорема.
Теорема 8. (Бернсайд [211, с. 357].) Всегда существует  алгебраически независимых инвариантов группы
алгебраически независимых инвариантов группы 
Доказательство. Рассмотрим многочлен

от переменных  Так как одна из матриц
Так как одна из матриц  единичная, то значение
единичная, то значение  является нулем этого многочлена. Если этот многочлен разложить по степеням
является нулем этого многочлена. Если этот многочлен разложить по степеням  то его коэффициенты являются инвариантами в силу замечания, следующего непосредственно после доказательства теоремы 4. Следовательно,
то его коэффициенты являются инвариантами в силу замечания, следующего непосредственно после доказательства теоремы 4. Следовательно,  алгебраическая функция от инвариантов. Аналогично каждая из переменных
алгебраическая функция от инвариантов. Аналогично каждая из переменных  является алгебраической функцией от инвариантов. Далее, если число алгебраически независимых инвариантов равнялось бы
является алгебраической функцией от инвариантов. Далее, если число алгебраически независимых инвариантов равнялось бы  то
то  независимых переменных
независимых переменных  были бы алгебраическими функциями от
были бы алгебраическими функциями от  переменных, что приводит к противоречию. Следовательно, число алгебраически независимых инвариантов по крайней мере равно
переменных, что приводит к противоречию. Следовательно, число алгебраически независимых инвариантов по крайней мере равно  Согласно теореме 7 это число не может быть больше чем
Согласно теореме 7 это число не может быть больше чем 
Пример. Для рассмотренной выше группы  в качестве алгебраически независимых инвариантов мы можем выбрать
в качестве алгебраически независимых инвариантов мы можем выбрать  Тогда любой инвариант является корнем многочлена от
Тогда любой инвариант является корнем многочлена от  Например,
Например,

Однако намного удобнее описание инвариантов как множества инвариантов  обладающих тем свойством, что любой инвариант является многочленом от
обладающих тем свойством, что любой инвариант является многочленом от  . В этом случае множество
. В этом случае множество  называется полиномиальным базисом (или целостностным базисом) для инвариантов группы
называется полиномиальным базисом (или целостностным базисом) для инвариантов группы  Конечно, если
Конечно, если  то по теореме 7 будут иметь место полиномиальные уравнения, связывающие
то по теореме 7 будут иметь место полиномиальные уравнения, связывающие  и называемые сизигиями.
и называемые сизигиями.
Например, многочлены  образуют полиномиальный базис для инвариантов
образуют полиномиальный базис для инвариантов  Их связывает сизигия
Их связывает сизигия 
Существование полиномиального базиса и метод его нахождения определяются следующей теоремой.
Теорема 9. (Нетер [997]; см. также Вейль [1410 с. 369].) Кольцо инвариантов конечной группы  комплексных
комплексных  -матриц имеет полиномиальный базис, состоящий не более чем из
-матриц имеет полиномиальный базис, состоящий не более чем из  инвариантов степени, не превышающей
инвариантов степени, не превышающей  где
где  порядок группы
порядок группы  Более того, этот базис может быть получен усреднением по
Более того, этот базис может быть получен усреднением по  всех одночленов вида
всех одночленов вида  где полная степень
где полная степень  не превосходит
не превосходит 
Доказательство. Пусть группа  состоит из преобразований (19.29). Предположим, что многочлен
состоит из преобразований (19.29). Предположим, что многочлен

где  комплексное число, является произвольным инвариантом группы (Сумма берется по всем наборам
комплексное число, является произвольным инвариантом группы (Сумма берется по всем наборам  для которых в многочлене
для которых в многочлене  имеется ненулевой член
имеется ненулевой член  хтет). Так как
хтет). Так как  инвариант, то он не изменится, если мы усредним его по группе, и поэтому
инвариант, то он не изменится, если мы усредним его по группе, и поэтому

Таким образом, каждый инвариант представляет собой линейную комбинацию специальных инвариантов (число которых бесконечно велико)

Далее  является (с точностью до мультипликативной константы) коэффициентом при и... в выражении
является (с точностью до мультипликативной константы) коэффициентом при и... в выражении

где 
Другими словами, значения  представляют собой степенные суммы
представляют собой степенные суммы  величин
величин

Любая степенная сумма  может быть записана как многочлен с рациональными коэффициентами от первых
может быть записана как многочлен с рациональными коэффициентами от первых  степенных сумм
степенных сумм  (упражнение (3)). Следовательно, любой инвариант
(упражнение (3)). Следовательно, любой инвариант  с индексом
с индексом  (являющийся коэффициентом в
(являющийся коэффициентом в  может быть записан как многочлен от специальных инвариантов
может быть записан как многочлен от специальных инвариантов  таких, что
таких, что  (являющихся коэффициентами в
(являющихся коэффициентами в  Следовательно, любой инвариант может быть записан как многочлен от
Следовательно, любой инвариант может быть записан как многочлен от  таких, что Число таких
таких, что Число таких  равно числу наборов
равно числу наборов  где
где  , а это число равно
, а это число равно  Наконец,
Наконец,  получается усреднением
получается усреднением  по группе.
по группе.
Теорема Молина. Так как из теоремы 9 мы знаем, что полиномиальный базис всегда существует, то мы можем уверенно двигаться дальше и попытаться найти его, используя методы, описанные в § 19.2.
Для проверки того, что найден базис, мы используем теорему Молина (теорема 2). Она утверждает, что если а — число линейно независимых однородных инвариантов группы  степени
степени  и
и

то

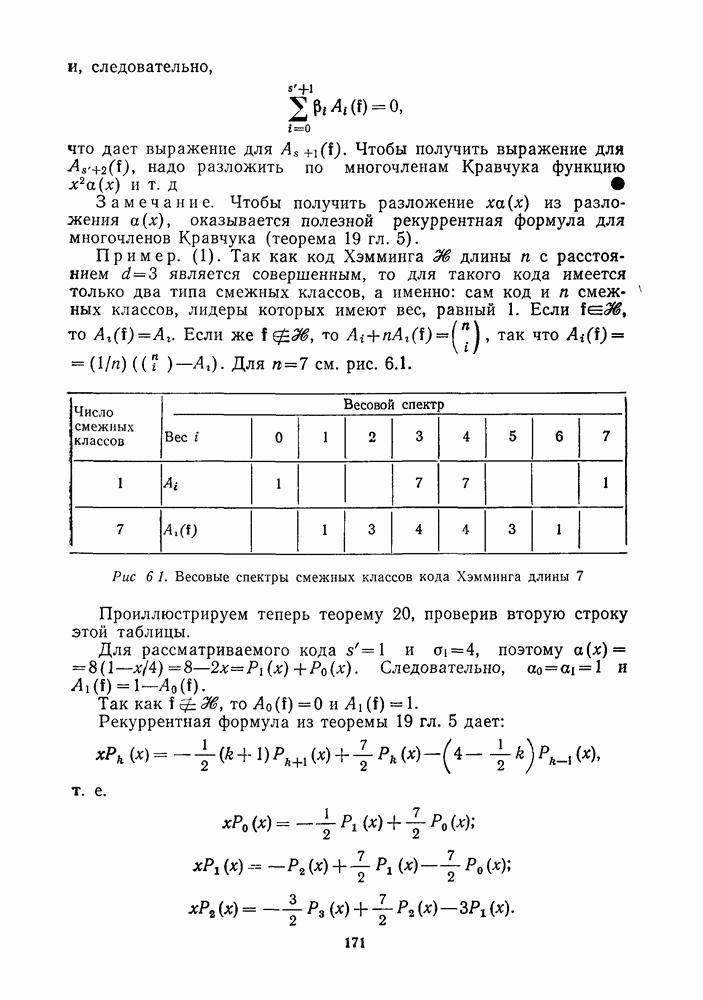
При доказательстве используется следующая теорема. Теорема 10. (Миллер и др. [955, с. 258], Серр [1185, с. 29].)
Число линейно независимых инвариантов  степени 1 равно
степени 1 равно

Доказательство. Пусть

Замена переменных  на которые действует группа на
на которые действует группа на  где
где  переводит матрицу
переводит матрицу  в матрицу
в матрицу  Мы можем выбрать
Мы можем выбрать  так, чтобы
так, чтобы  была диагональной матрицей (см. Бернсайд [211], с. 252). Далее
была диагональной матрицей (см. Бернсайд [211], с. 252). Далее  следовательно, диагональными элементами
следовательно, диагональными элементами  являются 0 или 1. Поэтому, изменив порядок переменных, мы можем считать, что
являются 0 или 1. Поэтому, изменив порядок переменных, мы можем считать, что

Обозначим через  число единиц на диагонали. Таким образом,
число единиц на диагонали. Таким образом,  если
если  и
и  если
если 
Любой линейный инвариант группы конечно, остается неподвижным при действии матрицы  и поэтому
и поэтому  . С другой стороны, согласно теореме 4
. С другой стороны, согласно теореме 4

является инвариантом  для любого
для любого  и поэтому
и поэтому 
Прежде чем доказывать теорему 2, введем некоторые обозначения. Соотношение (19.29) показывает, как преобразуются переменные  при действии матрицы
при действии матрицы  Индуцированная матрица кратности
Индуцированная матрица кратности  обозначаемая через
обозначаемая через  показывает, как
показывает, как  преобразует все
преобразует все  -кратные произведения переменных
-кратные произведения переменных  а именно
а именно  (Литлвуд [857, с. 122]). Например, матрица
(Литлвуд [857, с. 122]). Например, матрица

преобразует  в многочлены
в многочлены

соответственно. Таким образом, индуцированная матрица кратности 2 имеет вид

Доказательство теоремы 2. Чтобы доказать формулу (19.35), заметим, что равно числу линейно независимых инвариантов степени 1 группы  Согласно теореме 10
Согласно теореме 10

Следовательно, чтобы доказать теорему 2, достаточно показать, что след матрицы  равен коэффициенту при
равен коэффициенту при  в выражении
в выражении

где  (от — собственные значения матрицы
(от — собственные значения матрицы 
Соответствующей заменой переменных можно представить матрицы  и
и  в виде
в виде

и след  равен сумме
равен сумме  -кратных произведений элементов
-кратных произведений элементов  Но это в точности равно коэффициенту при
Но это в точности равно коэффициенту при  в разложении выражения (19.36) по
в разложении выражения (19.36) по  .
.
Стоит заметить, что ряд Молина не определяет однозначно группу. Например, существуют две группы  -матриц порядка 8, для которых
-матриц порядка 8, для которых

(а именно группа диэдра и абелева группа  . В действительности существуют абстрактные группы и
. В действительности существуют абстрактные группы и  чьи матричные представления могут быть сопоставлены попарно так, что каждое представление группы
чьи матричные представления могут быть сопоставлены попарно так, что каждое представление группы  имеет тот же ряд Молина, что и соответствующее представление группы
имеет тот же ряд Молина, что и соответствующее представление группы  (Дейд [324]).
(Дейд [324]).
Стандартный вид базисных инвариантов. Следующие обозначения очень полезны для описания кольца  инвариантов группы Обозначим множество комплексных чисел через С, и для заданных многочленов
инвариантов группы Обозначим множество комплексных чисел через С, и для заданных многочленов  обозначим через
обозначим через  множество всех многочленов от
множество всех многочленов от  с комплексными коэффициентами. Например, теорема За как раз утверждает, что
с комплексными коэффициентами. Например, теорема За как раз утверждает, что 
Обозначим также через  обычную прямую сумму. Например, утверждение вида
обычную прямую сумму. Например, утверждение вида  означает, что каждый инвариант группы
означает, что каждый инвариант группы  может быть единственным образом представлен в виде суммы
может быть единственным образом представлен в виде суммы  где
где  (Примером является приводимая ниже теорема 12.)
(Примером является приводимая ниже теорема 12.)
Используя эти обозначения, мы можем теперь задать наиболее удобный вид полиномиального базиса для
Определение. Хороший полиномиальный базис для  состоит из однородных инвариантов
состоит из однородных инвариантов  где
где  алгебраически независимы и
алгебраически независимы и

или если 

Другими словами, это означает, что любой инвариант 9 может быть записан как многочлен от  (если
(если  или как такой же многочлен плюс
или как такой же многочлен плюс  раз взятый другой такой многочлен, плюс ... (если
раз взятый другой такой многочлен, плюс ... (если  ). Грубо говоря, это означает, что при описании произвольного инварианта
). Грубо говоря, это означает, что при описании произвольного инварианта  играют роль «свободных» инвариантов, которые могут использоваться столько раз, сколько необходимо,
играют роль «свободных» инвариантов, которые могут использоваться столько раз, сколько необходимо,  играют роль «случайных» инвариантов, каждый из которых может использоваться не более одного раза.
играют роль «случайных» инвариантов, каждый из которых может использоваться не более одного раза.
Для хорошего полиномиального базиса  мы можем точно сказать, сколько существует сизигий. Если
мы можем точно сказать, сколько существует сизигий. Если  то сизигий нет. Если
то сизигий нет. Если  то имеется
то имеется  сизигий, выражающих произведения
сизигий, выражающих произведения  через
через 
Важно заметить, что ряд Молина может быть выписан только через степени хорошего полиномиального базиса. Пусть  Тогда
Тогда

или

(Это легко проверяется разложением выражений (19.38а) и (19.386) по степеням X и сравнением с выражениями (19.37а) и 
Приведем для пояснения несколько примеров.
(1). Для группы из § 19.2 многочлены  образуют хороший полиномиальный базис со степенями
образуют хороший полиномиальный базис со степенями  Действительно, согласно теореме За и формуле (19.11)
Действительно, согласно теореме За и формуле (19.11)

и

(2). Для группы 94, введенной выше, многочлены  образуют хороший полиномиальный базис, причем
образуют хороший полиномиальный базис, причем  Инварианты описываются следующим образом:
Инварианты описываются следующим образом:

Другими словами, любой инвариант группы может быть представлен единственным образом как многочлен от  плюс другой такой многочлен, взятый
плюс другой такой многочлен, взятый  раз. Например,
раз. Например,

Ряд Молина имеет вид

что согласуется с выражениями (19.386) и (19.39). Единственная сизигия имеет вид  Заметим, что выбор
Заметим, что выбор  уже не является хорошим полиномиальным базисом, так как инвариант
уже не является хорошим полиномиальным базисом, так как инвариант  не принадлежит множеству
не принадлежит множеству

К счастью, имеет место следующий результат.
Теорема 11. (Хочстер и Игон [657, утверждение 13]; независимо доказана также Дейдом [325].) Для инвариантов любой конечной группы комплексных  -матриц существует хороший полиномиальный базис.
-матриц существует хороший полиномиальный базис.
(Доказательство слишком сложно, чтобы приводить его здесь.)
Таким образом, мы знаем, что для любой группы ряд Молина может быть выписан в стандартной форме, задаваемой выражениями (19.38а) и (19.386) (со знаменателем, состоящим из произведения  сомножителей вида
сомножителей вида  и числителем, состоящим из суммы степеней X с положительными коэффициентами), и что может быть найден хороший полиномиальный базис, удовлетворяющий выражениям (19.37а) и (19.376), степени которого соответствуют степеням X, встречающимся в ряде Молина.
и числителем, состоящим из суммы степеней X с положительными коэффициентами), и что может быть найден хороший полиномиальный базис, удовлетворяющий выражениям (19.37а) и (19.376), степени которого соответствуют степеням X, встречающимся в ряде Молина.
С другой стороны, обратное утверждение несправедливо. Не всегда верно, что если ряд Молина выписан в виде (19.38а) или (19.386) (где сокращены общие сомножители и умножены
числитель и знаменатель на новые сомножители), то может быть найден хороший полиномиальный базис для степени которого соответствуют степеням X в  Это показывает следующий пример, приведенный Стенли [1262].
Это показывает следующий пример, приведенный Стенли [1262].
Пусть  обозначает группу порядка 8, порожденную матрицами
обозначает группу порядка 8, порожденную матрицами

Ряд Молина имеет вид

Существует хороший полиномиальный базис, соответствующий формуле (19.41), а именно

но не существует такого базиса, соответствующего формуле (19.40).
Задача (нерешенная). (19.1). Какому виду  соответствует хороший полиномиальный базис и какому нет?
соответствует хороший полиномиальный базис и какому нет?
Один важный частный случай был решен. Шефард и Тодд [1196] охарактеризовали те группы, для которых имеют место соотношения (19.37а) и (19.38а), т. е. для которых существует хороший полиномиальный базис, состоящий только из алгебраически независимых инвариантов. Эти группы известны как унитарные группы, порожденные отражениями. Полный список 37 неприводимых групп такого типа приведен в работе [1196].
Упражнение. (4). Пусть

где  переменные. Показать, что
переменные. Показать, что  представляет собой многочлен от
представляет собой многочлен от  с рациональными коэффициентами. [Указание. Воспользоваться упражнением (52) гл. 8; см. также [756].]
с рациональными коэффициентами. [Указание. Воспользоваться упражнением (52) гл. 8; см. также [756].]
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРОВ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Часть I: Глава 1. Линейные коды
- 1.1. ЛИНЕЙНЫЕ КОДЫ
- 1.2. СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.3. НА ПРИЕМНОМ КОНЦЕ
- 1.4. НЕМНОГО ПОДРОБНЕЕ О ДЕКОДИРОВАНИИ ЛИНЕЙНОГО КОДА
- 1.5. ВЕРОЯТНОСТЬ ОШИБКИ
- 1.6. ТЕОРЕМА ШЕННОНА О СУЩЕСТВОВАНИИ ХОРОШИХ КОДОВ
- 1.7. КОДЫ ХЭММИНГА
- 1.8. ДУАЛЬНЫЙ КОД
- 1.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (II)
- 1.10. НЕКОТОРЫЕ ОБЩИЕ СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.11. КРАТКОЕ СОДЕРЖАНИЕ ГЛ. 1
- Глава 2. Нелинейные коды, матрицы Адамара, t-схемы и код Голея
- 2.1. НЕЛИНЕЙНЫЕ КОДЫ
- 2.2. ГРАНИЦА ПЛОТКИНА
- 2.3. МАТРИЦЫ АДАМАРА И КОДЫ АДАМАРА
- 2.4. КОНФЕРЕНС-МАТРИЦЫ
- 2.5. t-СХЕМЫ
- 2.6. ВВЕДЕНИЕ В ДВОИЧНЫЙ КОД ГОЛЕЯ
- 2.7. СИСТЕМА ШТЕЙНЕРА S(5,6,12) И НЕЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОДНУ ОШИБКУ
- 2.8. ВВЕДЕНИЕ В КОД НОРДСТРОМА—РОБИНСОНА
- 2.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (III)
- Глава 3. Введение в коды БЧХ и конечные поля
- 3.1. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (I)
- 3.2. ПОСТРОЕНИЕ ПОЛЯ GF(16)
- 3.3. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (II)
- 3.4. ВЫЧИСЛЕНИЯ В КОНЕЧНОМ ПОЛЕ
- Глава 4. Конечные поля
- 4.2. КОНЕЧНЫЕ ПОЛЯ ОСНОВЫ ТЕОРИИ
- 4.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ
- 4.4. КАК НАХОДИТЬ НЕПРИВОДИМЫЕ МНОГОЧЛЕНЫ
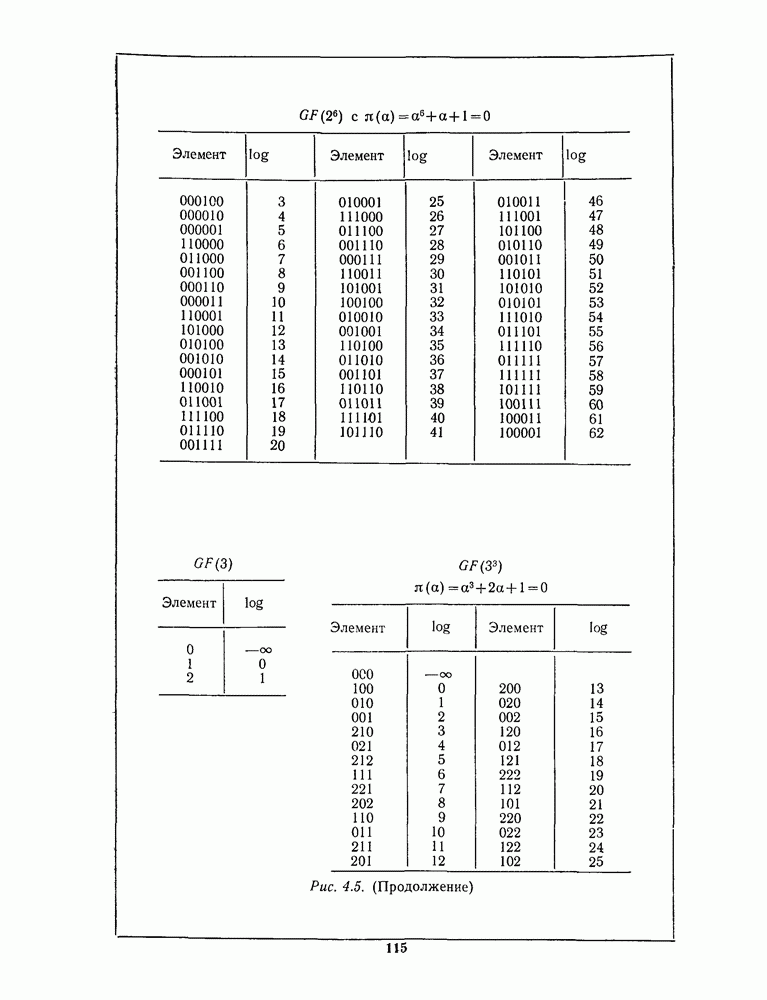
- 4.5. ТАБЛИЦЫ МАЛЫХ ПОЛЕЙ
- 4.6. ГРУППА АВТОМОРФИЗМОВ ПОЛЯ GF(p^m)
- 4.7. ЧИСЛО НЕПРИВОДИМЫХ МНОГОЧЛЕНОВ
- 4.8. БАЗИСЫ GF(p^m) НАД GF(p)
- 4.9. ЛИНЕАРИЗОВАННЫЕ МНОГОЧЛЕНЫ И НОРМАЛЬНЫЕ БАЗИСЫ
- Глава 5. Дуальные коды и их весовые спектры
- 5.2. ВЕСОВОЙ СПЕКТР КОДА, ДУАЛЬНОГО К ДВОИЧНОМУ ЛИНЕЙНОМУ КОДУ
- 5.3. ГРУППОВАЯ АЛГЕБРА
- 5.4. ХАРАКТЕРЫ
- 5.5. ТЕОРЕМА МАК-ВИЛЬЯМС ДЛЯ НЕЛИНЕЙНЫХ КОДОВ
- 5.6. ОБОБЩЕННЫЕ ТЕОРЕМЫ МАК-ВИЛЬЯМС ДЛЯ ЛИНЕЙНЫХ КОДОВ
- 5.7. СВОЙСТВА МНОГОЧЛЕНОВ КРАВЧУКА
- Глава 6. Коды, схемы и совершенные коды
- 6.2. ЧЕТЫРЕ ФУНДАМЕНТАЛЬНЫХ ПАРАМЕТРА КОДА
- 6.3. ЯВНАЯ ФОРМУЛА ДЛЯ СПЕКТРА ВЕСОВ И РАССТОЯНИЙ
- 6.4. ПОСТРОЕНИЕ СХЕМ ИЗ КОДОВ ПРИ …
- 6.5. ДУАЛЬНЫЙ КОД ТАКЖЕ ПОРОЖДАЕТ СХЕМЫ
- 6.6. ВЕСОВОЙ СПЕКТР КОДА, ПОЛУЧЕННОГО В РЕЗУЛЬТАТЕ СДВИГА
- 6.7. ПОСТРОЕНИЕ СХЕМ ИЗ НЕЛИНЕЙНЫХ КОДОВ ПРИ …
- 6.8. СОВЕРШЕННЫЕ КОДЫ
- 6.9. КОДЫ НАД GF(q)
- 6.10. НЕ СУЩЕСТВУЕТ НЕИЗВЕСТНЫХ СОВЕРШЕННЫХ КОДОВ
- Глава 7. Циклические коды
- 7.2. ОПРЕДЕЛЕНИЕ ЦИКЛИЧЕСКОГО КОДА
- 7.3. ПОРОЖДАЮЩИЙ МНОГОЧЛЕН
- 7.4. ПРОВЕРОЧНЫЙ МНОГОЧЛЕН
- 7.5. ДЕЛИТЕЛИ МНОГОЧЛЕНА x^n-1
- 7.6. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ t ОШИБОК
- 7.7. ИСПОЛЬЗОВАНИЕ МАТРИЦЫ НАД GF(q^m) ДЛЯ ЗАДАНИЯ КОДА НАД GF(q)
- 7.8. КОДИРОВАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- Глава 8. Циклические коды (продолжение): идемпотенты и многочлены Мэттсона-Соломона
- 8.2. ИДЕМПОТЕНТЫ
- 8.3. МИНИМАЛЬНЫЕ ИДЕАЛЫ, НЕПРИВОДИМЫЕ КОДЫ И ПРИМИТИВНЫЕ ИДЕМПОТЕНТЫ
- 8.4. ВЕСОВОЙ СПЕКТР МИНИМАЛЬНЫХ КОДОВ
- 8.5. ГРУППЫ АВТОМОРФИЗМОВ КОДА
- 8.6. МНОГОЧЛЕН МЭТТСОНА—СОЛОМОНА
- 8.7. НЕКОТОРЫЕ ВЕСОВЫЕ СПЕКТРЫ
- Глава 9. Коды БЧХ
- 9.2. ИСТИННОЕ МИНИМАЛЬНОЕ РАССТОЯНИЕ КОДА БЧХ
- 9.3. ЧИСЛО ИНФОРМАЦИОННЫХ СИМВОЛОВ КОДОВ БЧХ
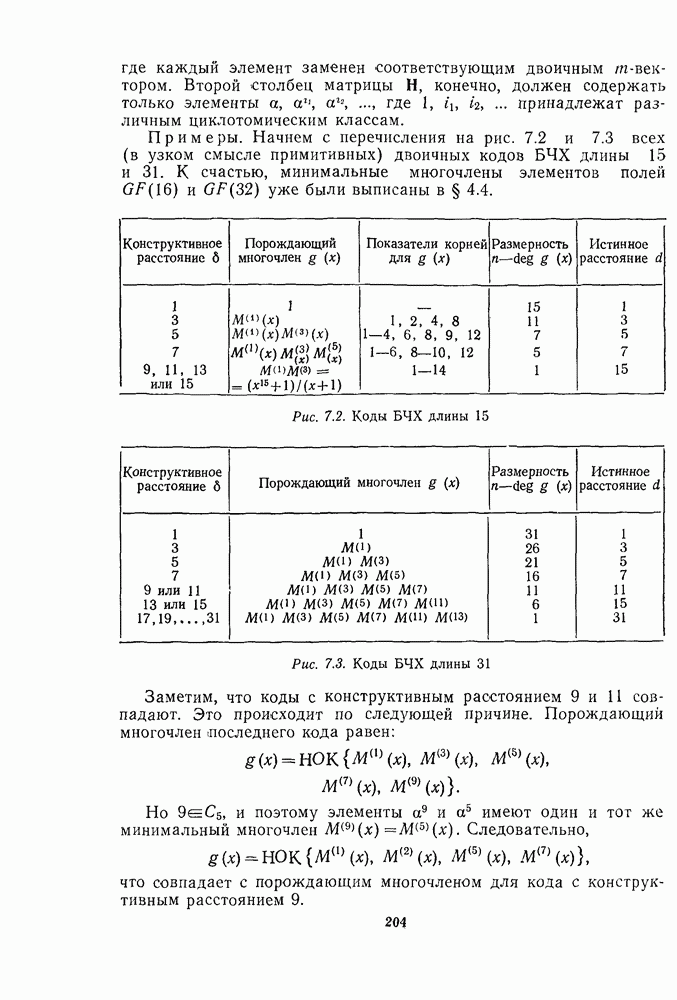
- 9.4. ТАБЛИЦА КОДОВ БЧХ
- 9.5. ДЛИННЫЕ КОДЫ БЧХ
- 9.6. ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 9.7. КВАДРАТНЫЕ УРАВНЕНИЯ НАД GF(2^m)
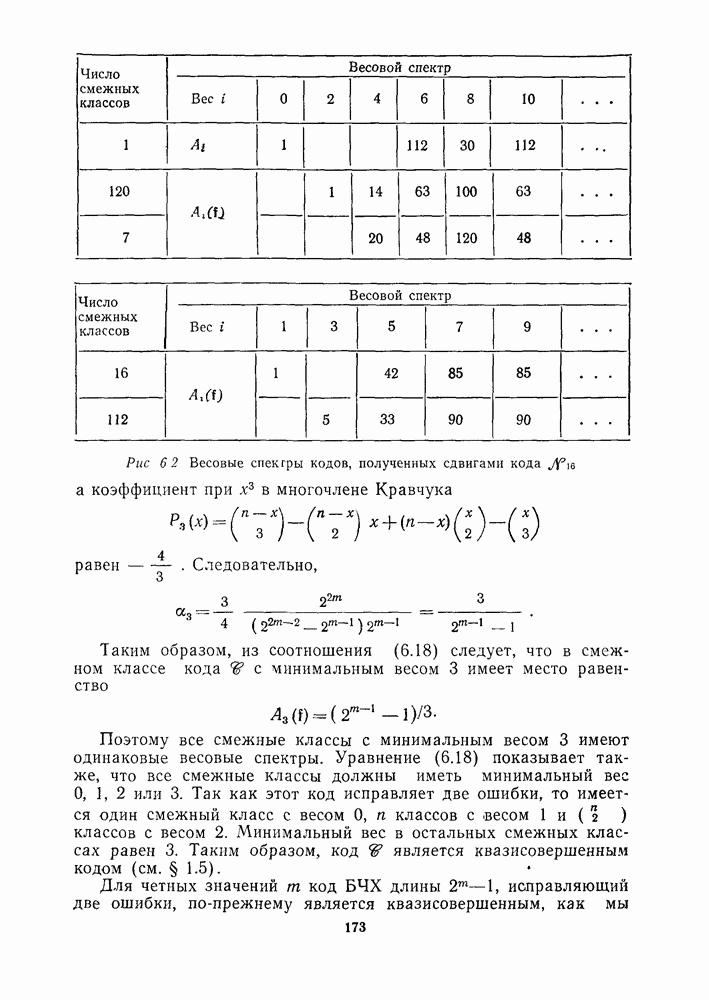
- 9.8. КВАЗИСОВЕРШЕННОСТЬ КОДОВ БЧХ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
- 9.9. ГРАНИЦА КАРЛИЦА—УШИЯМЫ
- 9.10. АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ НЕКОТОРЫХ ВЕСОВЫХ СПЕКТРОВ
- 9.11. КОДЫ НЕ-БЧХ, ИСПРАВЛЯЮЩИЕ ТРИ ОШИБКИ
- Глава 10. Коды Рида-Соломона и коды Юстесена
- 10.2. КОДЫ РИДА-СОЛОМОНА
- 10.3. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
- 10.4. ИДЕМПОТЕНТЫ КОДОВ РИДА-СОЛОМОНА
- 10.5. ОТОБРАЖЕНИЕ КОДОВ НАД GF(2^m) В ДВОИЧНЫЕ КОДЫ
- 10.6. ИСПРАВЛЕНИЕ ПАКЕТОВ ОШИБОК
- 10.7. КОДИРОВАНИЕ КОДОВ РИДА—СОЛОМОНА
- 10.9. ИЗБЫТОЧНЫЕ ВЫЧЕТНЫЕ КОДЫ
- 10.10. ДЕКОДИРОВАНИЕ КОДОВ РИДА-СОЛОМОНА
- 10.11. КОДЫ ЮСТЕСЕНА И КАСКАДНЫЕ КОДЫ
- Глава 11. Коды МДР
- 11.2. ПОРОЖДАЮЩАЯ И ПРОВЕРОЧНАЯ МАТРИЦЫ
- 11.3. ВЕСОВОЙ СПЕКТР КОДА МДР
- 11.4. МАТРИЦЫ, У КОТОРЫХ ВСЕ КВАДРАТНЫЕ ПОДМАТРИЦЫ НЕВЫРОЖДЕНЫ
- 11.5. КОДЫ МДР, ПОЛУЧЕННЫЕ ИЗ КОДОВ РИДА-СОЛОМОНА
- 11.6. n-МНОЖЕСТВА
- 11.7. ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ
- 11.8. ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
- Глава 12. Альтернантные коды, коды Гоппы и другие обобщения кодов БЧХ
- 12.2. АЛЬТЕРНАНТНЫЕ КОДЫ
- 12.3. КОДЫ ГОППЫ
- 12.4. ДАЛЬНЕЙШИЕ СВОЙСТВА КОДОВ ГОППЫ
- 12.5. ЦИКЛИЧНОСТЬ УДЛИНЕННЫХ КОДОВ ГОППЫ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
- 12.6. ОБОБЩЕННЫЕ КОДЫ СРИВЭСТАВЫ
- 12.7. ОБОБЩЕНИЕ ЧЕНЯ—ЧОЯ КОДОВ БЧХ
- 12.8. АЛГОРИТМ ЕВКЛИДА
- 12.9. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- Часть II: Глава 13. Коды Рида-Маллера
- 13.2. БУЛЕВЫ ФУНКЦИИ
- 13.3. КОДЫ РИДА-МАЛЛЕРА
- 13.4. РИДА-МАЛЕРА КОДЫ И ГЕОМЕТРИИ
- 13.5. ВЕКТОРЫ МИНИМАЛЬНОГО ВЕСА ПОРОЖДАЮТ КОД
- 13.6. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (I)
- 13.7. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (II)
- 13.8. ДРУГИЕ ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.9. ГРУППЫ АВТОМОРФИЗМОВ РИДА-МАЛЕРА КОДОВ
- 13.10. МНОГОЧЛЕНЫ МЭТТСОНА—СОЛОМОНА ДЛЯ РИДА-МАЛЕРА КОДОВ
- 13.11. ДЕЙСТВИЕ ПОЛНОЙ АФФИННОЙ ГРУППЫ НА МНОГОЧЛЕНАХ МЭТТСОНА—СОЛОМОНА
- Глава 14. Коды Рида-Маллера первого порядка
- 14.2. ПСЕВДОШУМОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 14.3. СМЕЖНЫЕ КЛАССЫ ПО КОДУ РИДА—МАЛЛЕРА ПЕРВОГО ПОРЯДКА
- 14.4. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ КОДА R(1, m)
- 14.5. МАКСИМАЛЬНО-НЕЛИНЕЙНЫЕ ФУНКЦИИ
- Глава 15. Коды Рида-Маллера первого порядка Кердока и Препараты
- 15.2. ВЕСОВОЙ СПЕКТР КОДА РИДА—МАЛЛЕРА ВТОРОГО ПОРЯДКА
- 15.3. СПЕКТР ВЕСОВ ПРОИЗВОЛЬНЫХ КОДОВ РИДА—МАЛЛЕРА
- 15.4. ПОДКОДЫ РАЗМЕРНОСТИ 2m В КОДАХ R(2, m)* И R(2, m)
- 15.5. КОД КЕРДОКА И ЕГО ОБОБЩЕНИЯ
- 15.6. КОД ПРЕПАРАТЫ
- 15.7. ОБОБЩЕНИЕ ГЕТАЛСА КОДОВ ПРЕПАРАТЫ
- Глава 16. Квадратично-вычетные коды
- 16.2. ОПРЕДЕЛЕНИЕ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.3. ИДЕМПОТЕНТЫ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.4. РАСШИРЕННЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.5. ГРУППА АВТОМОРФИЗМОВ КВ-КОДОВ
- 16.6. ДВОИЧНЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.7. ДВАЖДЫ ЦИРКУЛЯНТНЫЕ И КВАЗИЦИКЛИЧЕСКИЕ КОДЫ
- 16.8. КВАДРАТИЧНО-ВЫЧЕТНЫЕ И СИММЕТРИЧНЫЕ КОДЫ НАД GF{3)
- 16.9. ДЕКОДИРОВАНИЕ ЦИКЛИЧЕСКИХ И НЕКОТОРЫХ ДРУГИХ КОДОВ
- Глава 17. Границы для объема кода
- 17.2. ГРАНИЦЫ ДЛЯ A(n, d, w)
- 17.3. ГРАНИЦЫ ДЛЯ A(n, d)
- 17.4. ГРАНИЦЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 17.5. ГРАНИЦА ГРАЙСМЕРА
- 17.6. ПОСТРОЕНИЕ ЛИНЕЙНЫХ КОДОВ; АНТИКОДЫ
- 17.7. АСИМПТОТИЧЕСКИЕ ГРАНИЦЫ
- Глава 18. Методы комбинирования кодов
- I. ПРОИЗВЕДЕНИЕ КОДОВ И ИХ ОБОБЩЕНИЕ
- 18.2. ПРЯМОЕ ПРОИЗВЕДЕНИЕ КОДОВ
- 18.3. НЕ ВСЕ ЦИКЛИЧЕСКИЕ КОДЫ ЯВЛЯЮТСЯ ПРЯМЫМИ ПРОИЗВЕДЕНИЯМИ ЦИКЛИЧЕСКИХ КОДОВ
- 18.4. ДРУГОЙ СПОСОБ ПРЕДСТАВЛЕНИЯ НЕПРИВОДИМЫХ ЦИКЛИЧЕСКИХ кодов В ВИДЕ ПРОИЗВЕДЕНИЯ КОДОВ
- 18.5. КАСКАДНЫЕ КОДЫ: (*)-КОНСТРУКЦИЯ
- 18.6. ОБЩИЙ ПОДХОД К РАЗЛОЖЕНИЮ ЦИКЛИЧЕСКИХ КОДОВ
- II. ДРУГИЕ МЕТОДЫ КОМБИНИРОВАНИЯ КОДОВ
- 18.7. МЕТОДЫ ПОСТРОЕНИЯ, КОТОРЫЕ УВЕЛИЧИВАЮТ ДЛИНУ
- 18.7.1. КОНСТРУКЦИЯ X: ДОБАВЛЕНИЕ СУФФИКСОВ К КОДОВЫМ СЛОВАМ
- 18.7.2. КОНСТРУКЦИЯ Х4: КОМБИНИРОВАНИЕ ЧЕТЫРЕХ КОДОВ
- 18.7.3. КОДЫ, ИСПРАВЛЯЮЩИЕ ОДИНОЧНЫЕ И ДВОЙНЫЕ ОШИБКИ
- 18.7.4. КОНСТРУКЦИЯ …
- 18.7.5. КОНСТРУКЦИЯ ПИРЕТА
- 18.8. КОНСТРУКЦИИ, СВЯЗАННЫЕ С КАСКАДНЫМИ КОДАМИ
- 18.8.2. ОБОБЩЕННЫЕ КАСКАДНЫЕ КОДЫ ЗИНОВЬЕВА
- 18.9. МЕТОДЫ УКОРОЧЕНИЯ КОДОВ
- 18.9.2. КОНСТРУКЦИИ ХЕЛГЕРТА И СТИНАФФА
- Глава 19. Самодуальные коды и теория инвариантов
- 19.2. ВВЕДЕНИЕ В ТЕОРИЮ ИНВАРИАНТОВ
- 19.3. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ИНВАРИАНТОВ
- 19.4. ОБОБЩЕНИЯ ТЕОРЕМЫ ГЛИСОНА
- 19.5. НЕСУЩЕСТВОВАНИЕ НЕКОТОРЫХ ОЧЕНЬ ХОРОШИХ КОДОВ
- 19.6. ХОРОШИЕ САМОДУАЛЬНЫЕ КОДЫ СУЩЕСТВУЮТ
- Глава 20. Коды Голея
- 20.2. ГРУППА МАТЬЕ M24
- 20.3. ГРУППА М24 5-ТРАНЗИТИВНА
- 20.4. ПОРЯДОК ГРУППЫ М24 РАВЕН 24•23•22•21•20•48
- 20.5. СИСТЕМА ШТЕЙНЕРА S(5, 8, 24) ЕДИНСТВЕННА
- 20.6. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
- 20.7. ГРУППЫ АВТОМОРФИЗМОВ ТРОИЧНЫХ КОДОВ ГОЛЕЯ
- 20.8. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
- Глава 21. Схемы отношений
- 21.2. СХЕМЫ ОТНОШЕНИЙ
- 21.3. СХЕМА ОТНОШЕНИЙ ХЭММИНГА
- 21.4. МЕТРИЧЕСКИЕ СХЕМЫ
- 21.5. СИМПЛЕКТИЧЕСКИЕ ФОРМЫ
- 21.6. СХЕМА ДЖОНСОНА
- 21.7. ПОДМНОЖЕСТВА СХЕМ ОТНОШЕНИЙ
- 21.8. ПОДМНОЖЕСТВА СИМПЛЕКТИЧЕСКИХ ФОРМ
- 21.9. t-СХЕМЫ И ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
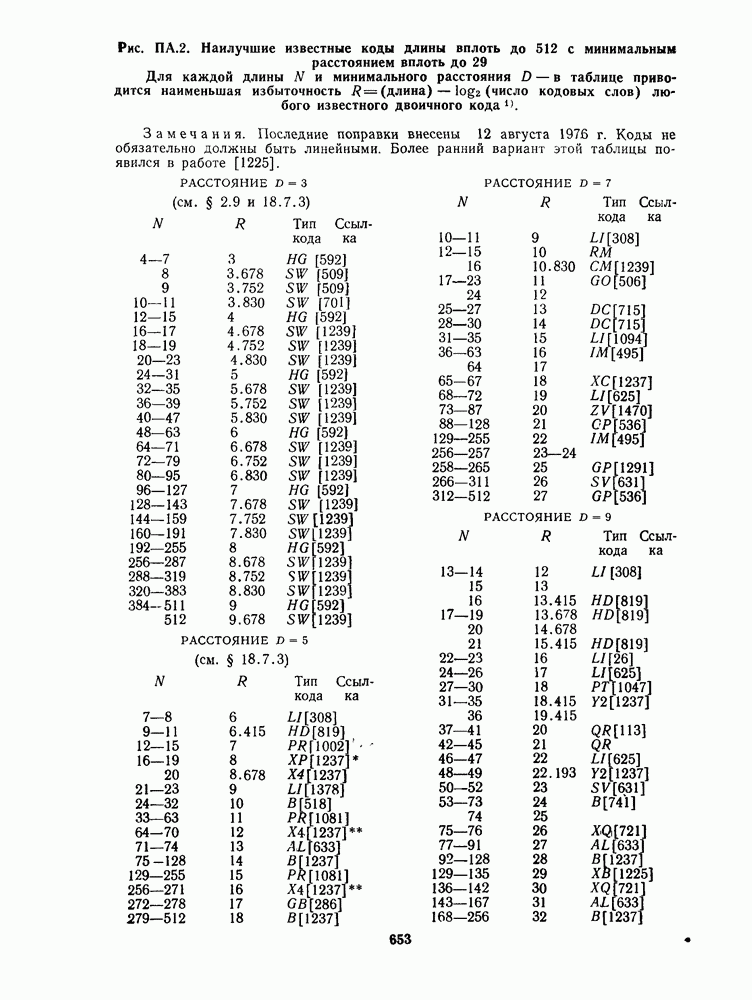
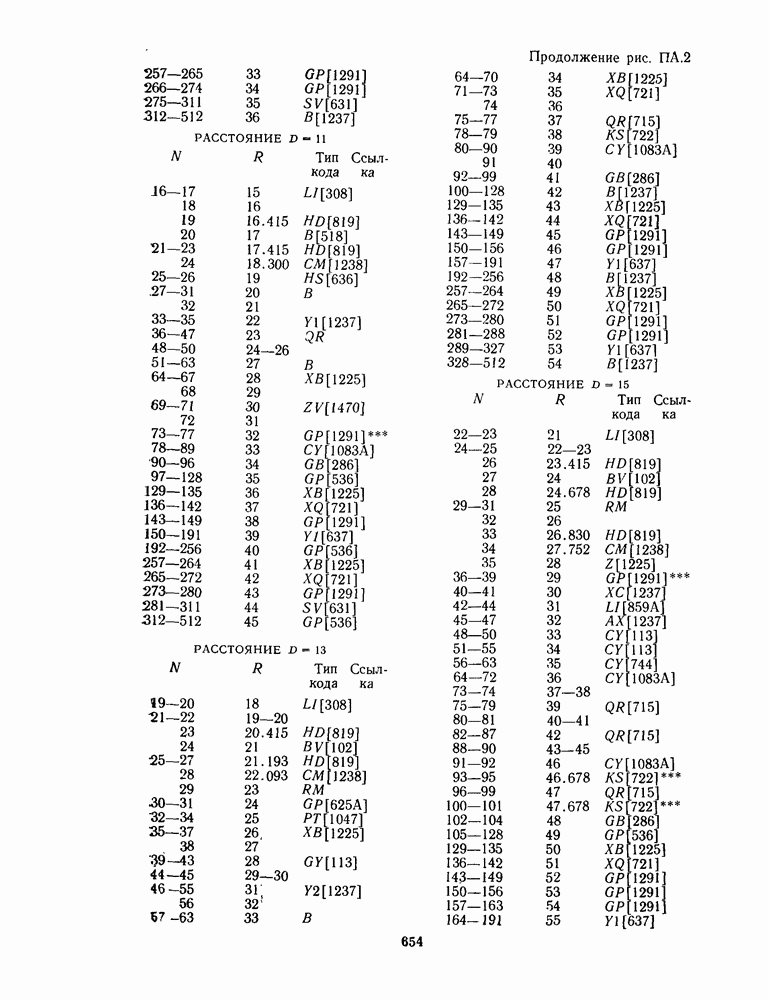
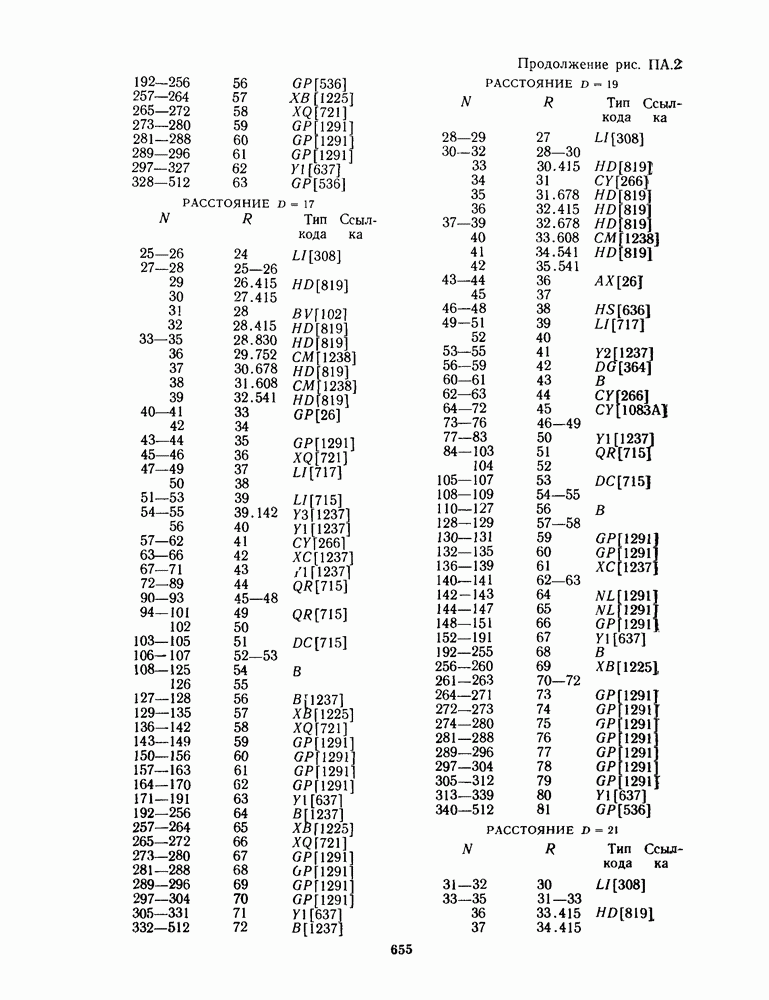
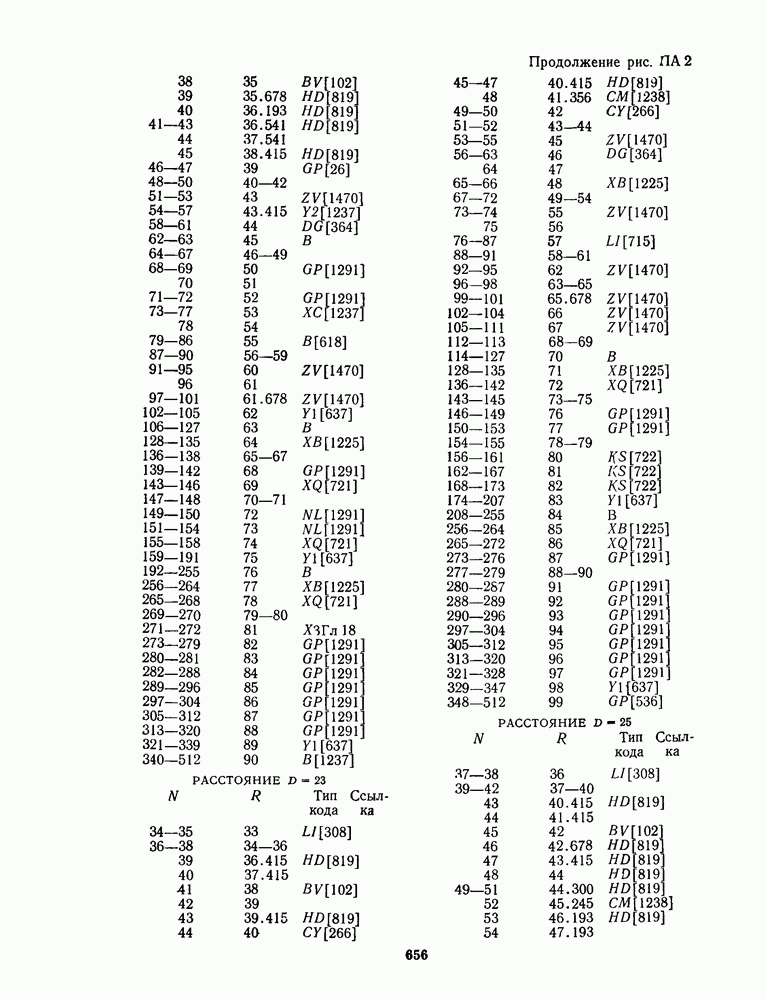
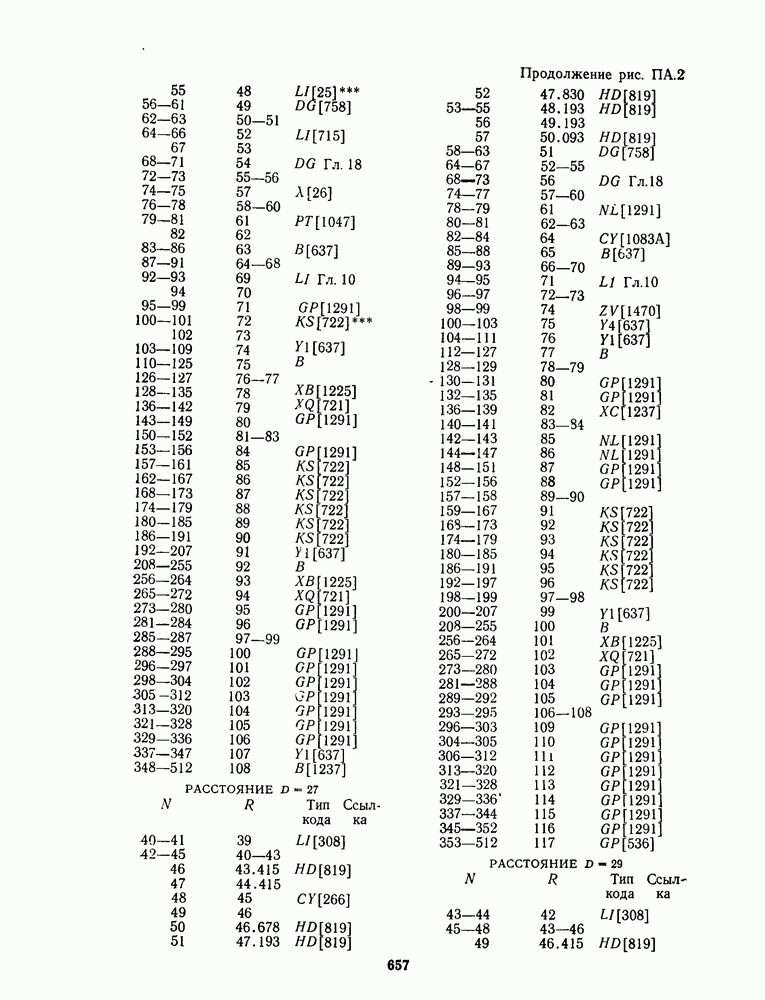
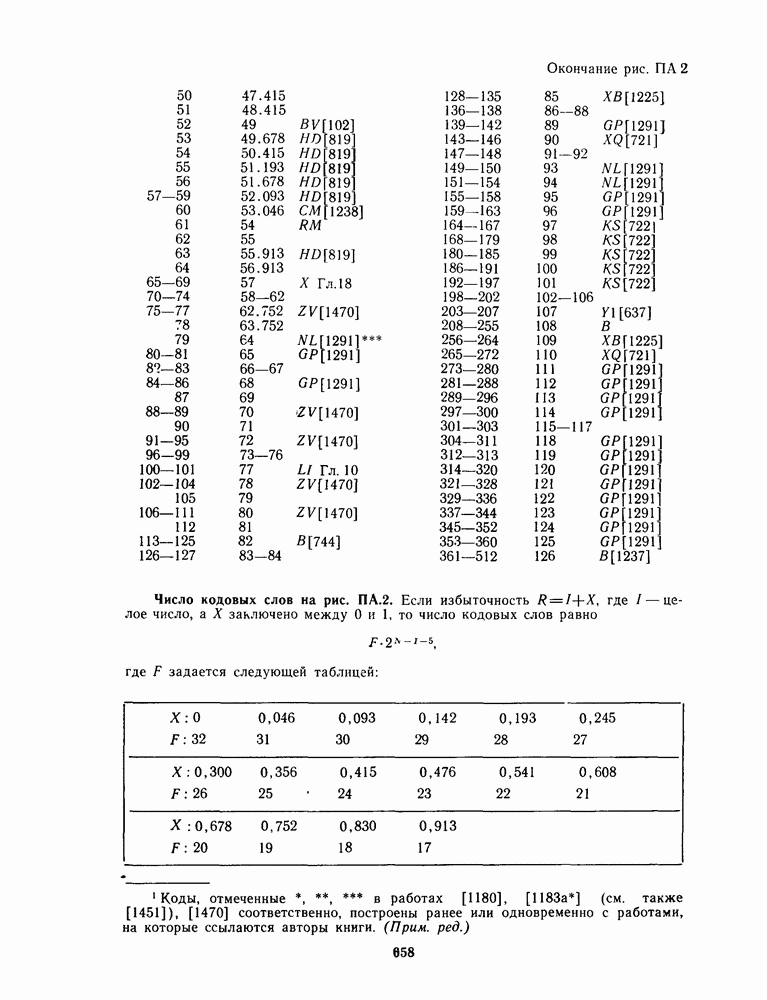
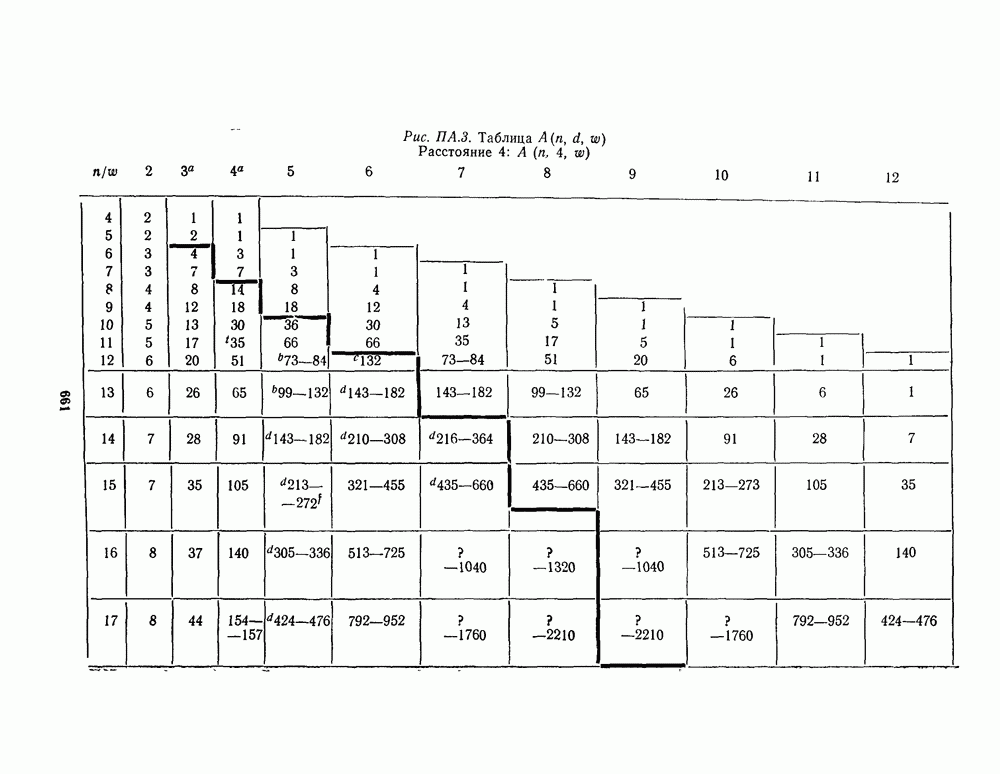
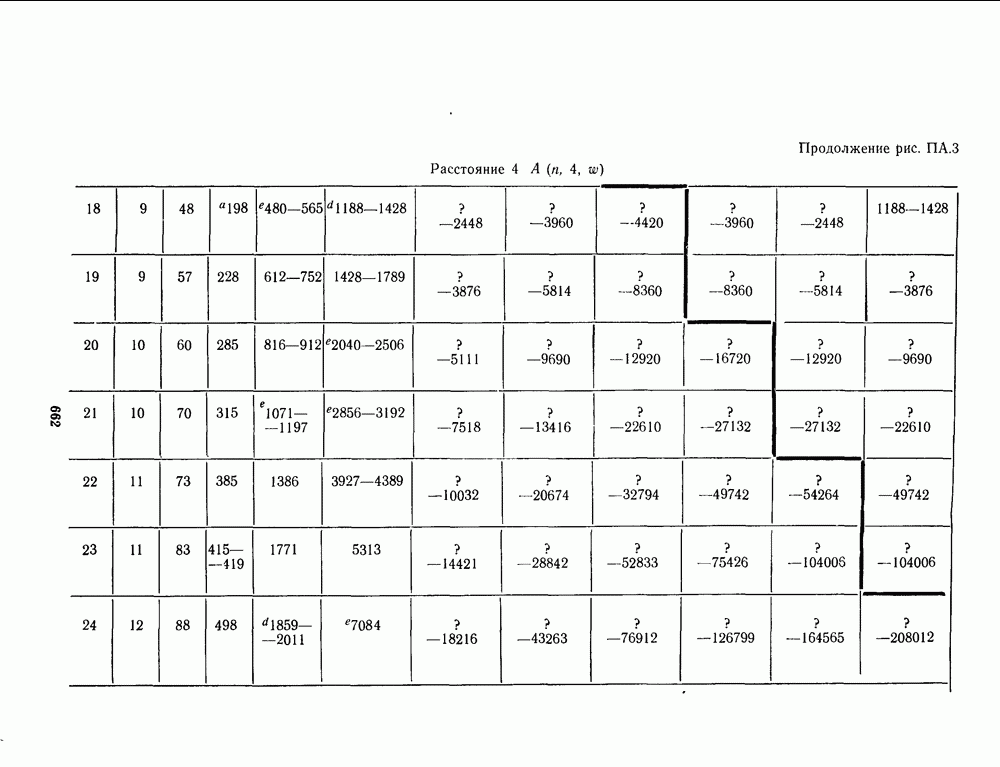
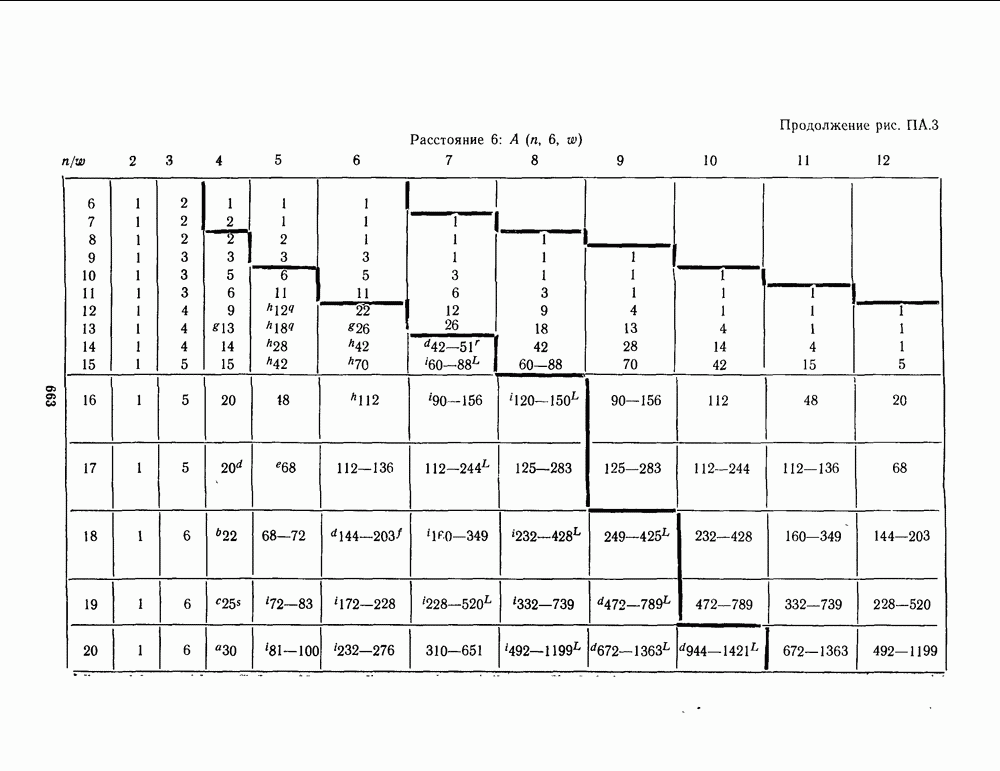
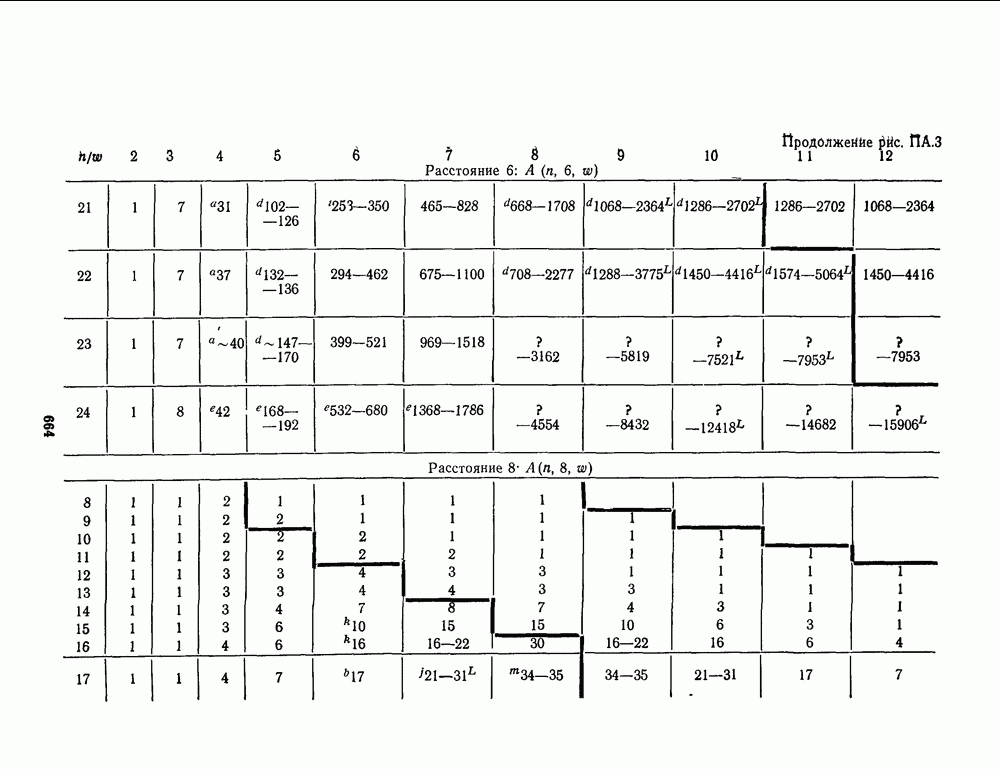
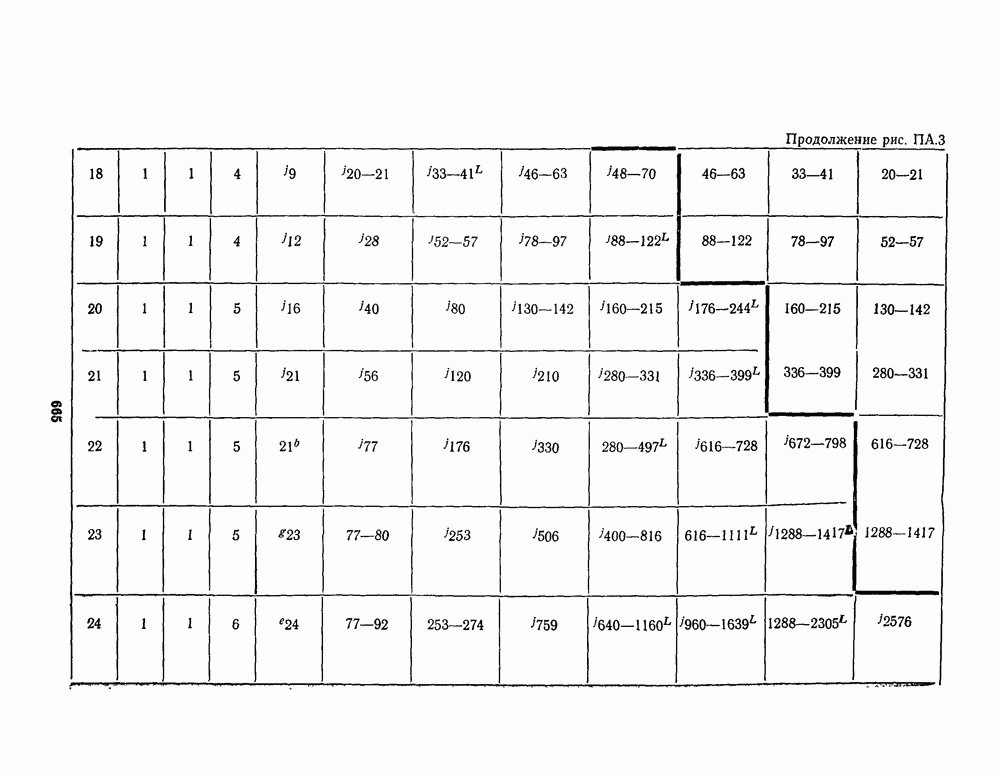
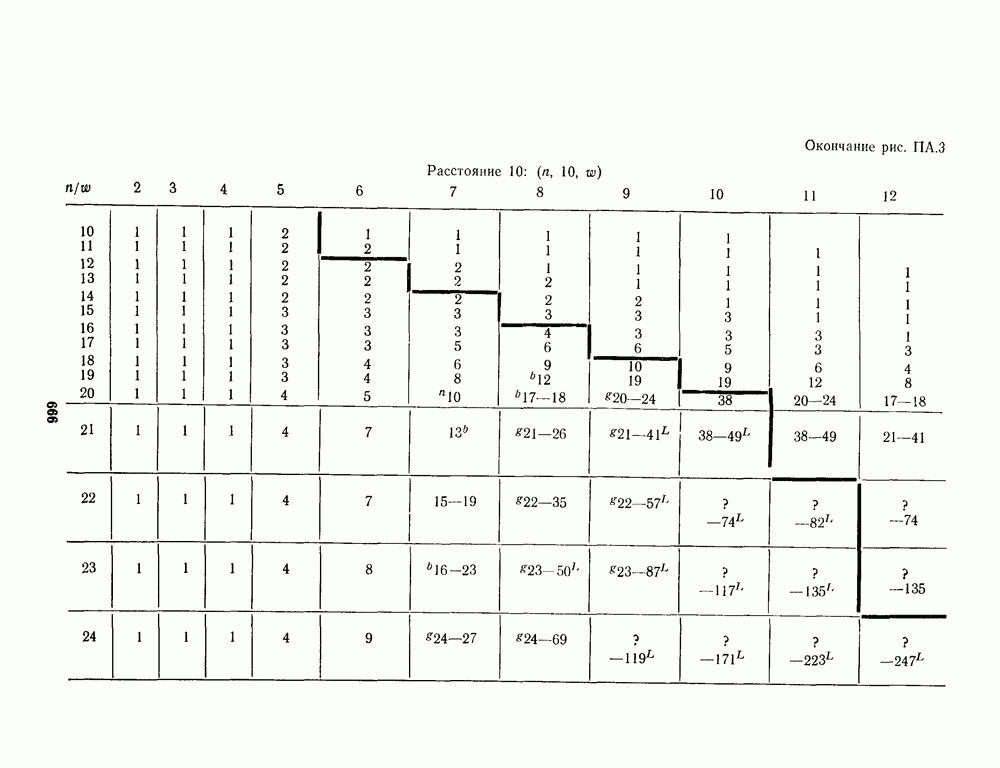
- ПРИЛОЖЕНИЕ А. ТАБЛИЦЫ НАИЛУЧШИХ ИЗВЕСТНЫХ КОДОВ
- ПРИЛОЖЕНИЕ В. КОНЕЧНЫЕ ГЕОМЕТРИИ