| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
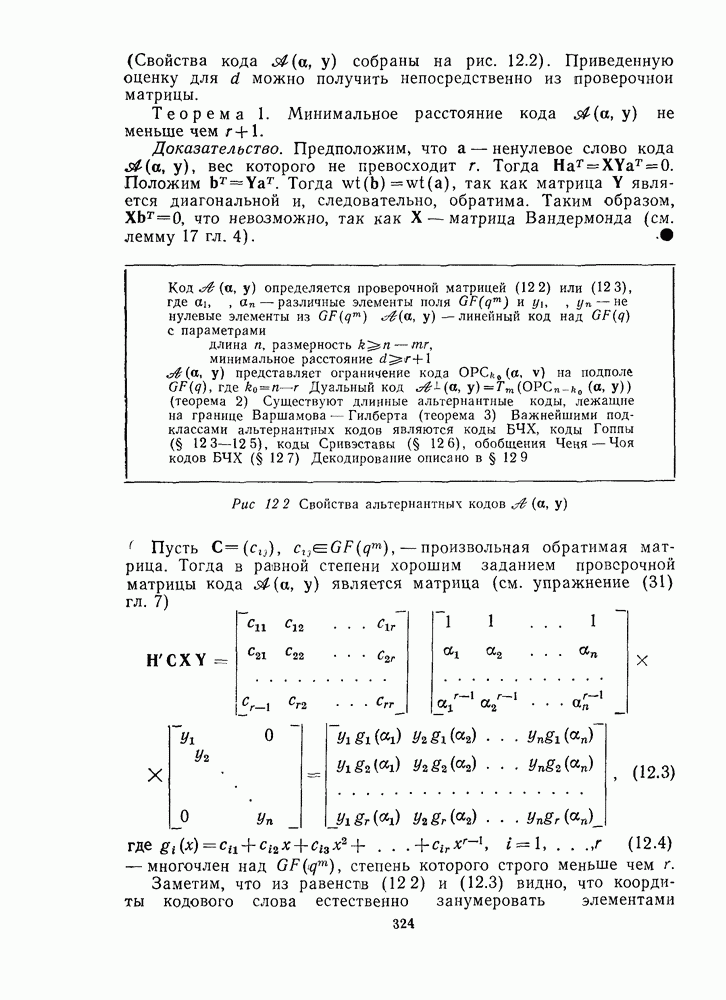
12.5. ЦИКЛИЧНОСТЬ УДЛИНЕННЫХ КОДОВ ГОППЫ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
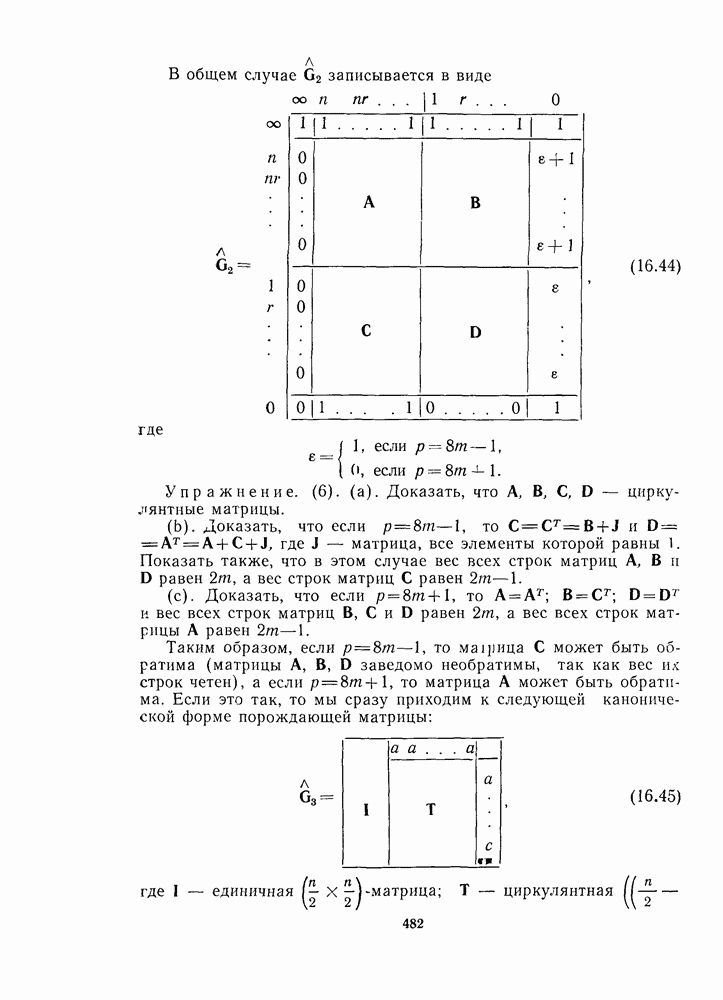
В данном параграфе доказывается, что некоторые расширенные двоичные коды Гоппы, исправляющие две ошибки, являются циклическими (обобщение примера 1 из § 12.3). Для этого находится группа подстановок, относительно которой код инвариантен, а затем показывается, что одна из этих подстановок состоит из единственного цикла.
Для рассматриваемых кодов многочлен Гоппы  является квадратным многочленом с различными корнями, а множество
является квадратным многочленом с различными корнями, а множество  состоит из всех элементов поля
состоит из всех элементов поля  не являющихся корнями
не являющихся корнями  Следовательно,
Следовательно,  -код, исправляющий две ошибки. Возможны два случая, зависящих от того, приводим или неприводим многочлен
-код, исправляющий две ошибки. Возможны два случая, зависящих от того, приводим или неприводим многочлен  . В соответствии с теоремой 16 и упражнением 6 гл. 9 многочлен
. В соответствии с теоремой 16 и упражнением 6 гл. 9 многочлен  может быть записан в виде
может быть записан в виде  где
где  — элемент поля
— элемент поля  со следом, равным
со следом, равным  неприводим, и со следом, равным 0, если
неприводим, и со следом, равным 0, если  приводим. Пусть
приводим. Пусть  расширенный код, получаемый из
расширенный код, получаемый из  добавлением общей проверки на четность, а его координаты перенумерованы элементами множества
добавлением общей проверки на четность, а его координаты перенумерованы элементами множества  Таким образом, блоковая длина кода
Таким образом, блоковая длина кода  равна
равна  если
если  неприводим, и
неприводим, и  если
если  приводим.
приводим.
Сначала рассмотрим неприводимый случай.
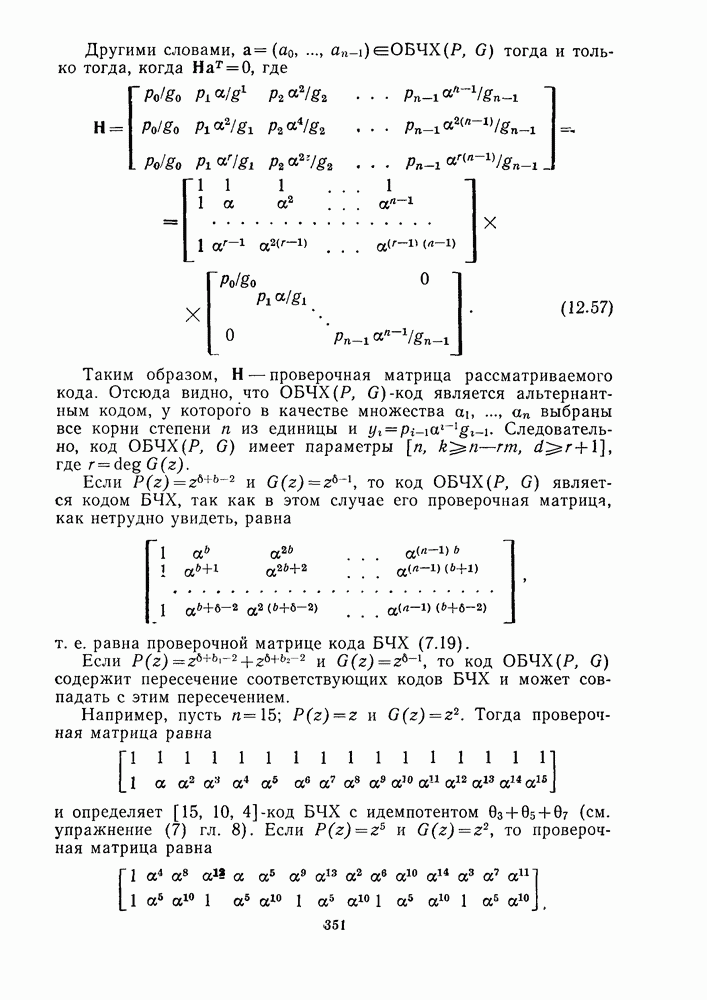
Теорема 10. Пусть  определенный выше расширенный
определенный выше расширенный  -код Гоппы, исправляющий две ошибки, где
-код Гоппы, исправляющий две ошибки, где  -неприводимый многочлен над
-неприводимый многочлен над  Тогда код
Тогда код  инвариантен относительно следующей группы
инвариантен относительно следующей группы  состоящей из
состоящей из  подстановок:
подстановок:

где

для всех  (Дополнительно о группе
(Дополнительно о группе  см. следующую теорему.)
см. следующую теорему.)
Доказательство, (i). Докажем прежде всего, что Код  инвариантен относительно подстановок
инвариантен относительно подстановок  (Заметим,
(Заметим,

Кодовыми словами являются

Этот [8, 2, 5]-код на самом деле эквивалентен коду Гоппы, рассмотренному в примере 1 из § 12.3.
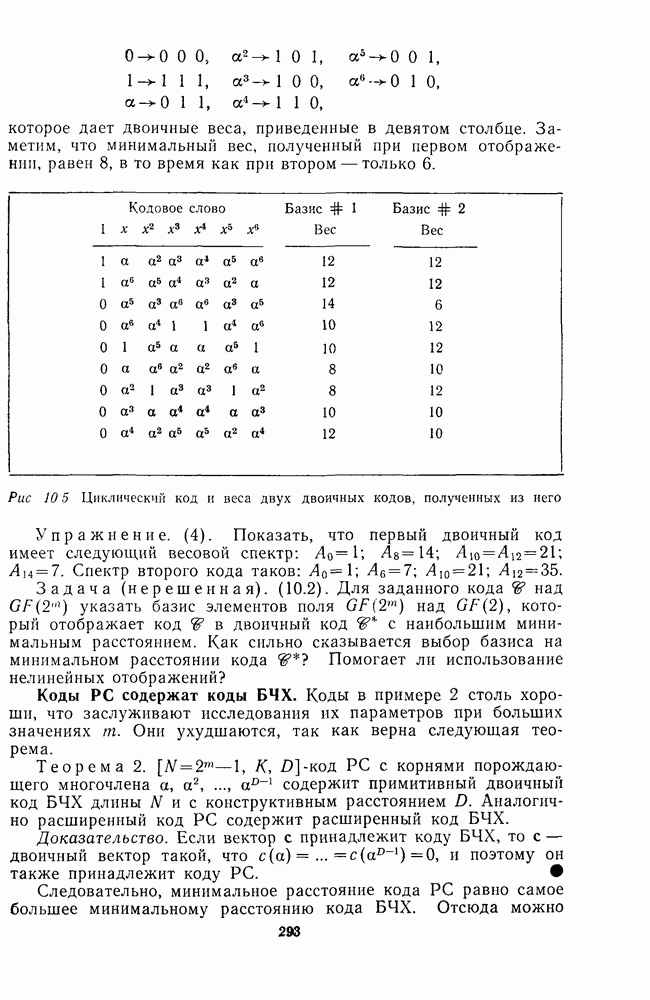
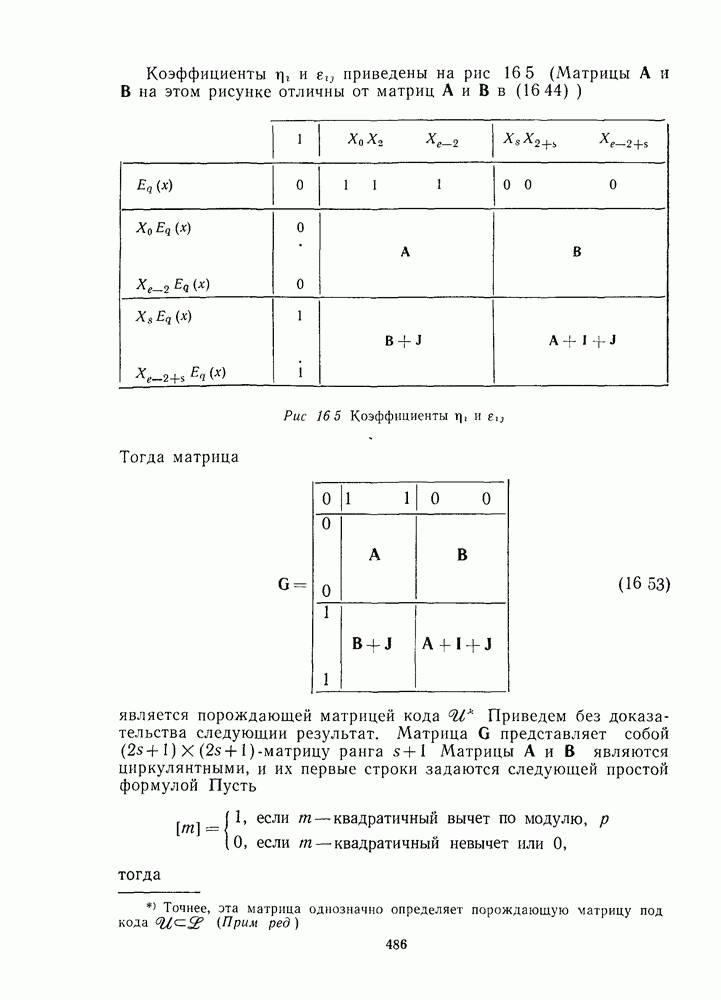
Упражнения. (14). Показать, что код Сривэставы (при  является кодом Гоппы, и, следовательно, для двоичных кодов Сривэставы
является кодом Гоппы, и, следовательно, для двоичных кодов Сривэставы 
(15). Показать, что двоичный код Сривэставы (12.53) при  является
является  -кодом и что минимальное расстояние дуального ему кода равно 4.
-кодом и что минимальное расстояние дуального ему кода равно 4.
(16). Показать, что двоичный код Сривэставы с  является
является  -кодом и что минимальное расстояние дуального ему кода равно 5.
-кодом и что минимальное расстояние дуального ему кода равно 5.
(17). Доказать, что при  обобщенные коды Сривэставы являются кодами МДР. Эти коды иногда называются кодами Габидулина.
обобщенные коды Сривэставы являются кодами МДР. Эти коды иногда называются кодами Габидулина.
(18). Пусть  двоичный примитивный обобщенный код Сривэставы с
двоичный примитивный обобщенный код Сривэставы с  для всех
для всех 
Доказать, что при  код определяется однозначно и равен примитивному коду БЧХ в узком смысле.
код определяется однозначно и равен примитивному коду БЧХ в узком смысле.
(ii). Доказать, что при  код
код  также определяется однозначно и что его расширение
также определяется однозначно и что его расширение  инвариантно относительно транзитивной группы подстановок.
инвариантно относительно транзитивной группы подстановок.
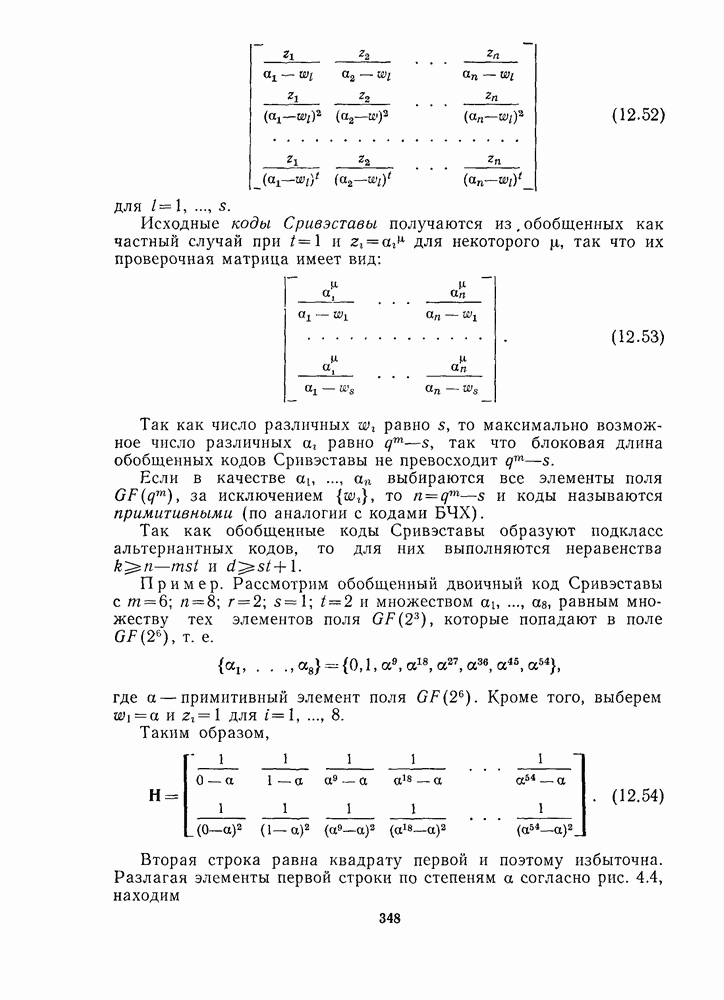
(19). Доказать следующие свойства для двоичных непримитивных обобщенных кодов Сривэставы с параметрами:  примитивный элемент поля
примитивный элемент поля  различные элементы поля
различные элементы поля  ненулевые элементы поля
ненулевые элементы поля  .
.
(i). Строки подматриц  в (12.51) являются избыточными. Следовательно, матрица
в (12.51) являются избыточными. Следовательно, матрица  может быть выбрана в виде правой части равенства (12.52) с заменой на а.
может быть выбрана в виде правой части равенства (12.52) с заменой на а.
(ii). Код с проверочной матрицей (12.54) является кодом этого типа.

затем  представляется матрицей
представляется матрицей  Например,
Например,  представляется матрицей
представляется матрицей

Заметим, что

так что 
Пусть  — группа, порождаемая подстановками
— группа, порождаемая подстановками  для всех
для всех  Из равенств (12.38) и
Из равенств (12.38) и

следует, что

и что порядок группы  равен
равен  Остается доказать, что группа, порожденная группой
Остается доказать, что группа, порожденная группой  и подстановкой С, задается (12.33). Это следует из равенства
и подстановкой С, задается (12.33). Это следует из равенства

Упражнение. (10). Доказать, что 
Докажем теперь, что код  эквивалентен циклическому коду.
эквивалентен циклическому коду.
Теорема 11. (Берлекэмп и Морено). Пусть, как и в теореме  — расширенный неприводимый двоичный код Гоппы, исправляющий две ошибки. Группа
— расширенный неприводимый двоичный код Гоппы, исправляющий две ошибки. Группа  задаваемая (12.33), содержит подстановку
задаваемая (12.33), содержит подстановку  которая представляет собой один цикл, содержащий все элементы множества
которая представляет собой один цикл, содержащий все элементы множества  Следовательно, координаты можно переупорядочить так, чтобы код
Следовательно, координаты можно переупорядочить так, чтобы код  стал циклическим.
стал циклическим.
Доказательство. Элементы множества  можно представить ненулевыми векторами
можно представить ненулевыми векторами  где
где  и вектор соответствует элементу
и вектор соответствует элементу  если
если  и вектор
и вектор  соответствует элементу
соответствует элементу  Кроме того, векторы
Кроме того, векторы  представляют один и тот же элемент для всех
представляют один и тот же элемент для всех  Действие подстановки
Действие подстановки  задаваемой (12.37), записывается в виде
задаваемой (12.37), записывается в виде

или, что эквивалентно, в векторной записи

Мы хотим найти такой элемент  чтобы подстановка
чтобы подстановка  состояла из одного цикла, т. е. хотим найти такое наименьшее число
состояла из одного цикла, т. е. хотим найти такое наименьшее число  для которого при некотором
для которого при некотором  число
число

равнялось бы  Собственные значения матрицы
Собственные значения матрицы  равны А, и
равны А, и  где
где

Собственные векторы задаются равенствами:

Запишем разложение вектора по собственным векторами

Тогда 
Пусть теперь  такое наименьшее целое число, что
такое наименьшее целое число, что

для некоторого  Тогда
Тогда

Подставляя (12.41) в (12.40), получаем:

Пусть  Тогда
Тогда  так что по теореме 8 гл. 4
так что по теореме 8 гл. 4  .
.
Предположим теперь, что  примитивный корень степени
примитивный корень степени  из единицы. Тогда
из единицы. Тогда  так что
так что  или
или 
Выберем  так, чтобы выполнялось условие
так, чтобы выполнялось условие  таким образом,
таким образом,

Теперь  является корнем многочлена
является корнем многочлена  следовательно,
следовательно,  по теореме 15 гл. 9. Тогда
по теореме 15 гл. 9. Тогда  и в силу (12.43) и теоремы 15 гл.
и в силу (12.43) и теоремы 15 гл.  лежит в поле
лежит в поле 
Согласно (12.42) должно выполняться условие  т. е.
т. е.

Но числа  взаимно просты, так что
взаимно просты, так что  является также примитивным корнем степени
является также примитивным корнем степени  из единицы. Следовательно,
из единицы. Следовательно,  является наименьшим целым числом, для которого выполняется равенство (12.44), и, таким образом, подстановка
является наименьшим целым числом, для которого выполняется равенство (12.44), и, таким образом, подстановка  состоит из единственного цикла. (Заметим, что равенство (12.41) справедливо при
состоит из единственного цикла. (Заметим, что равенство (12.41) справедливо при 
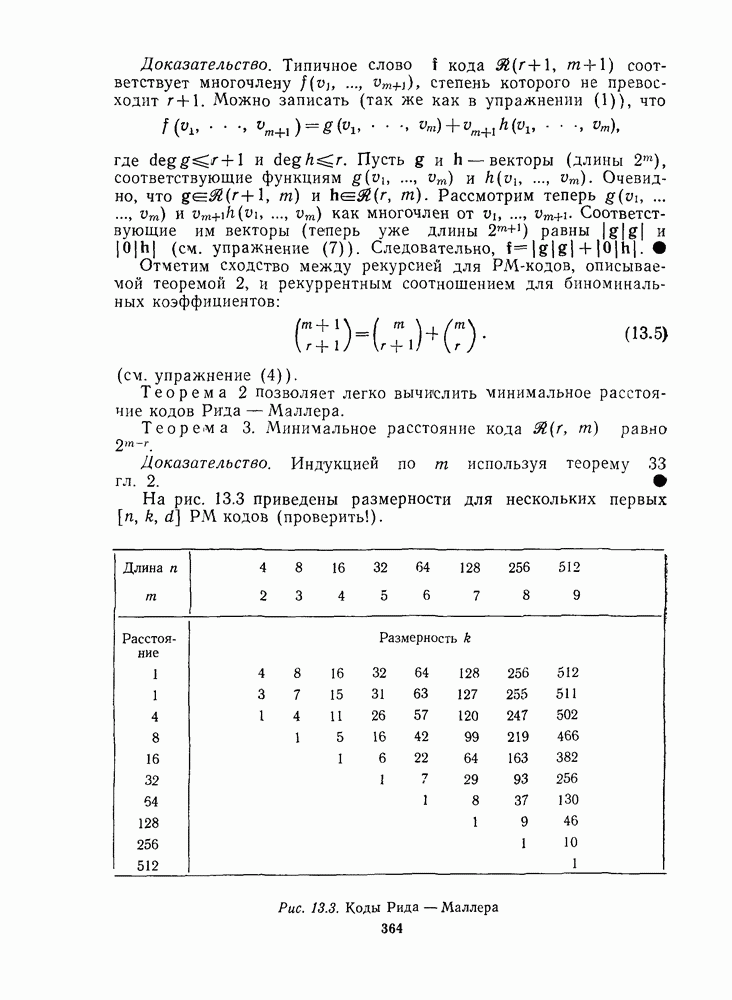
Согласно § 9.4 любой циклический код длины  является реверсивным. [Код (12.19) именно
является реверсивным. [Код (12.19) именно  Поэтому, так как мы знаем из теоремы 11, что
Поэтому, так как мы знаем из теоремы 11, что  циклический код, отсюда вытекает, что группа автоморфизмов кода
циклический код, отсюда вытекает, что группа автоморфизмов кода  содержит подстановку реверсию R (переводящую
содержит подстановку реверсию R (переводящую  в
в  при соответствующей нумерации координат и подстановку
при соответствующей нумерации координат и подстановку  (см. § 9.4). Порядок группы автоморфизмов кода
(см. § 9.4). Порядок группы автоморфизмов кода  согласно упражнению
согласно упражнению  равен по меньшей мере
равен по меньшей мере  На самом деле (см. упражнение
На самом деле (см. упражнение  подстановки
подстановки  принадлежат группе
принадлежат группе  и поэтому
и поэтому  в точности совпадает с группой, порожденной подстановками
в точности совпадает с группой, порожденной подстановками 
Конечно, группа автоморфизмов кода  может быть и больше группы
может быть и больше группы  что мы и увидим из приводимых ниже примеров.
что мы и увидим из приводимых ниже примеров.
Упражнение. (11). (i). Показать, что подстановка

принадлежит группе  фиксирует точку
фиксирует точку  и переводит
и переводит  Таким образом, эта подстановка является подстановкой
Таким образом, эта подстановка является подстановкой 
[Указание. Использовать разложение 
(ii). Доказать, что подстановка  является реверсией.
является реверсией.
Пример. Для иллюстрации теорем 10 и 11 рассмотрим  -код
-код  задаваемый (12.19) из § 12.3. Этот код, в частности, инвариантен относительно подстановок:
задаваемый (12.19) из § 12.3. Этот код, в частности, инвариантен относительно подстановок:

и

Как было показано в § 12.3, следующее переупорядочивание координат:  превращает этот код в циклический. Согласно (12.45) подстановка
превращает этот код в циклический. Согласно (12.45) подстановка  для этого кода равна
для этого кода равна  и через циклы записывается в виде
и через циклы записывается в виде 
Согласно теореме 11 этот код инвариантен относительно группы подстановок  порядок которой равен 54. На самом деле этот код инвариантен относительно гораздо большего множества подстановок.
порядок которой равен 54. На самом деле этот код инвариантен относительно гораздо большего множества подстановок.
Упражнение. (12). Доказать, что порядок группы автоморфизмов  -кода (12.19) равен 1296.
-кода (12.19) равен 1296.
Применяя теорему 11 к примеру 3 из § 12.3, получаем [17, 8, 6] циклический код, который на самом деле является квадратично-вычетным кодом (см. гл. 16) с группой автоморфизмов порядка 2448.
В качестве третьего примера выберем 
Тогда  циклический код с порождающим многочленом
циклический код с порождающим многочленом 
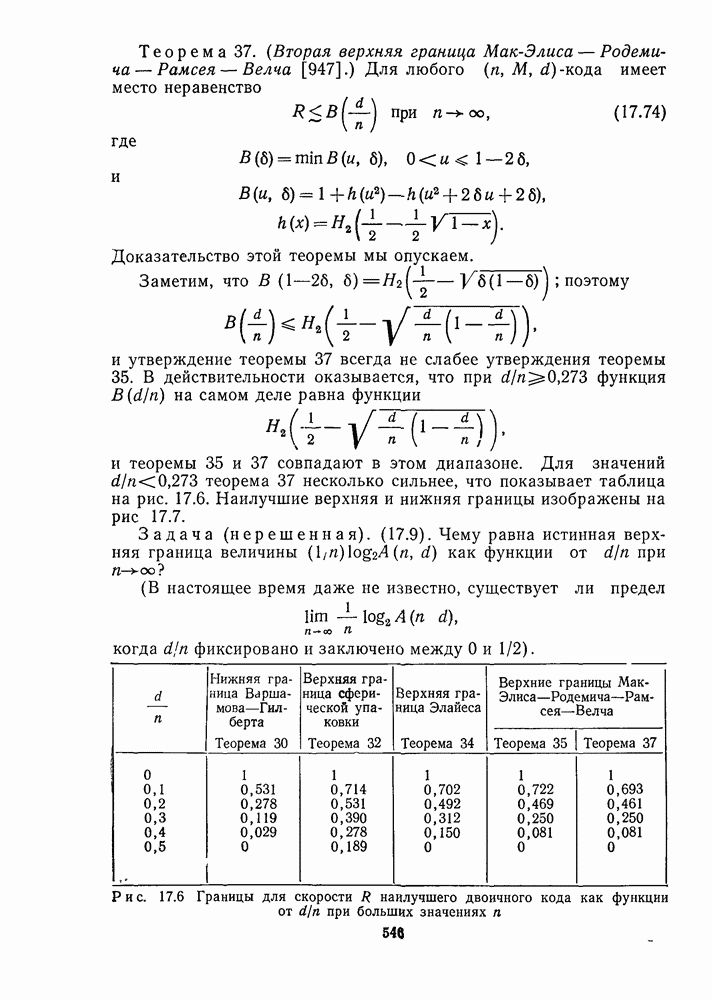
Случай, когда G(z) приводим. Аналогичный результат имеет место для приводимого многочлена над  скажем, для
скажем, для  где
где  Выберем теперь
Выберем теперь  координат кода
координат кода  занумеруем элементами множества
занумеруем элементами множества  Предполагая и
Предполагая и  снова определим подстановки
снова определим подстановки  равенствами (12.34). Это действительно подстановки на множестве
равенствами (12.34). Это действительно подстановки на множестве  так как
так как  меняют местами
меняют местами  а С просто фиксирует оба этих элемента.
а С просто фиксирует оба этих элемента.
Теорема 12. Если многочлен  приводим, то
приводим, то  расширенный код Гоппы
расширенный код Гоппы  инвариантен относительно группы
инвариантен относительно группы  состоящей из
состоящей из  подстановок вида
подстановок вида

действующих на множестве  Эта группа содержит подстановку
Эта группа содержит подстановку  представляющую собой один цикл, содержащий все элементы множества
представляющую собой один цикл, содержащий все элементы множества  Следовательно, код
Следовательно, код  эквивалентен циклическому коду.
эквивалентен циклическому коду.
Доказательство. Первое утверждение доказывается точно так же, как и в теореме 10. Заметим, что теперь  Для доказательства второго утверждения надо показать, что в поле
Для доказательства второго утверждения надо показать, что в поле  найдется элемент, скажем,
найдется элемент, скажем,  для которого ни при каком
для которого ни при каком  не выполняется равенство
не выполняется равенство 
Затем выберем  так, чтобы имело место равенство
так, чтобы имело место равенство

Это всегда можно сделать, так как  Тогда
Тогда  будет наименьшим целым числом, для которого будут выполняться равенства (12.41) и (12.42), что и завершит доказательство.
будет наименьшим целым числом, для которого будут выполняться равенства (12.41) и (12.42), что и завершит доказательство.
Итак, остается показать, что существует  для которого равенство (12.47) не выполняется ни при каком
для которого равенство (12.47) не выполняется ни при каком  Минимальное
Минимальное  для которого имеет место (12.47), должно быть делителем
для которого имеет место (12.47), должно быть делителем  Действительно, так как
Действительно, так как  то
то  следовательно, в силу (12.47) должно выполняться равенство
следовательно, в силу (12.47) должно выполняться равенство  где
где  Но так как
Но так как  минимально, то
минимально, то 
Обозначим через  число корней многочлена
число корней многочлена  лежащих в поле
лежащих в поле  при
при  Так как многочлен
Так как многочлен  делит многочлен
делит многочлен  а последний многочлен имеет в поле
а последний многочлен имеет в поле  точно
точно  корней (а именно все элементы
корней (а именно все элементы  за исключением 0 и 1), то и все корни многочлена
за исключением 0 и 1), то и все корни многочлена  также лежат в поле
также лежат в поле  так что
так что 
Число корней многочлена  которые не являются корнями (12.47) ни при каком
которые не являются корнями (12.47) ни при каком  равно
равно

где  функция Мебиуса, определенная в гл. 4.
функция Мебиуса, определенная в гл. 4.
Действительно, если  такой корень, то он будет учтен только в члене, соответствующем
такой корень, то он будет учтен только в члене, соответствующем  т. е. только один раз. С другой стороны, если
т. е. только один раз. С другой стороны, если  корень многочлена
корень многочлена  при
при  он также является корнем многочлена
он также является корнем многочлена  для произвольного
для произвольного  такого, что
такого, что  т. е. число раз его учета в сумме равно:
т. е. число раз его учета в сумме равно:

по теореме 14 гл. 4.
Наконец, опять по теореме 14 гл. 4 величина (12.48) равна:

что и требовалось доказать.
Упражнение. (13). Доказать, что этот код также реверсивен и что в качестве подстановки, осуществляющей реверсию, можно взять 
Следовательно, в рассматриваемом случае код  инвариантен относительно группы порядка
инвариантен относительно группы порядка  порожденной циклической подстановкой
порожденной циклической подстановкой  подстановкой
подстановкой  и подстановкой-реверсией
и подстановкой-реверсией  (см. упражнение (4) гл. 9).
(см. упражнение (4) гл. 9).
Задача (нерешенная). (12.3). Какие другие расширенные коды Гоппы являются циклическими?
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АВТОРОВ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- Часть I: Глава 1. Линейные коды
- 1.1. ЛИНЕЙНЫЕ КОДЫ
- 1.2. СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.3. НА ПРИЕМНОМ КОНЦЕ
- 1.4. НЕМНОГО ПОДРОБНЕЕ О ДЕКОДИРОВАНИИ ЛИНЕЙНОГО КОДА
- 1.5. ВЕРОЯТНОСТЬ ОШИБКИ
- 1.6. ТЕОРЕМА ШЕННОНА О СУЩЕСТВОВАНИИ ХОРОШИХ КОДОВ
- 1.7. КОДЫ ХЭММИНГА
- 1.8. ДУАЛЬНЫЙ КОД
- 1.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (II)
- 1.10. НЕКОТОРЫЕ ОБЩИЕ СВОЙСТВА ЛИНЕЙНОГО КОДА
- 1.11. КРАТКОЕ СОДЕРЖАНИЕ ГЛ. 1
- Глава 2. Нелинейные коды, матрицы Адамара, t-схемы и код Голея
- 2.1. НЕЛИНЕЙНЫЕ КОДЫ
- 2.2. ГРАНИЦА ПЛОТКИНА
- 2.3. МАТРИЦЫ АДАМАРА И КОДЫ АДАМАРА
- 2.4. КОНФЕРЕНС-МАТРИЦЫ
- 2.5. t-СХЕМЫ
- 2.6. ВВЕДЕНИЕ В ДВОИЧНЫЙ КОД ГОЛЕЯ
- 2.7. СИСТЕМА ШТЕЙНЕРА S(5,6,12) И НЕЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОДНУ ОШИБКУ
- 2.8. ВВЕДЕНИЕ В КОД НОРДСТРОМА—РОБИНСОНА
- 2.9. ПОСТРОЕНИЕ НОВЫХ КОДОВ ИЗ ЗАДАННЫХ КОДОВ (III)
- Глава 3. Введение в коды БЧХ и конечные поля
- 3.1. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (I)
- 3.2. ПОСТРОЕНИЕ ПОЛЯ GF(16)
- 3.3. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ (II)
- 3.4. ВЫЧИСЛЕНИЯ В КОНЕЧНОМ ПОЛЕ
- Глава 4. Конечные поля
- 4.2. КОНЕЧНЫЕ ПОЛЯ ОСНОВЫ ТЕОРИИ
- 4.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ
- 4.4. КАК НАХОДИТЬ НЕПРИВОДИМЫЕ МНОГОЧЛЕНЫ
- 4.5. ТАБЛИЦЫ МАЛЫХ ПОЛЕЙ
- 4.6. ГРУППА АВТОМОРФИЗМОВ ПОЛЯ GF(p^m)
- 4.7. ЧИСЛО НЕПРИВОДИМЫХ МНОГОЧЛЕНОВ
- 4.8. БАЗИСЫ GF(p^m) НАД GF(p)
- 4.9. ЛИНЕАРИЗОВАННЫЕ МНОГОЧЛЕНЫ И НОРМАЛЬНЫЕ БАЗИСЫ
- Глава 5. Дуальные коды и их весовые спектры
- 5.2. ВЕСОВОЙ СПЕКТР КОДА, ДУАЛЬНОГО К ДВОИЧНОМУ ЛИНЕЙНОМУ КОДУ
- 5.3. ГРУППОВАЯ АЛГЕБРА
- 5.4. ХАРАКТЕРЫ
- 5.5. ТЕОРЕМА МАК-ВИЛЬЯМС ДЛЯ НЕЛИНЕЙНЫХ КОДОВ
- 5.6. ОБОБЩЕННЫЕ ТЕОРЕМЫ МАК-ВИЛЬЯМС ДЛЯ ЛИНЕЙНЫХ КОДОВ
- 5.7. СВОЙСТВА МНОГОЧЛЕНОВ КРАВЧУКА
- Глава 6. Коды, схемы и совершенные коды
- 6.2. ЧЕТЫРЕ ФУНДАМЕНТАЛЬНЫХ ПАРАМЕТРА КОДА
- 6.3. ЯВНАЯ ФОРМУЛА ДЛЯ СПЕКТРА ВЕСОВ И РАССТОЯНИЙ
- 6.4. ПОСТРОЕНИЕ СХЕМ ИЗ КОДОВ ПРИ …
- 6.5. ДУАЛЬНЫЙ КОД ТАКЖЕ ПОРОЖДАЕТ СХЕМЫ
- 6.6. ВЕСОВОЙ СПЕКТР КОДА, ПОЛУЧЕННОГО В РЕЗУЛЬТАТЕ СДВИГА
- 6.7. ПОСТРОЕНИЕ СХЕМ ИЗ НЕЛИНЕЙНЫХ КОДОВ ПРИ …
- 6.8. СОВЕРШЕННЫЕ КОДЫ
- 6.9. КОДЫ НАД GF(q)
- 6.10. НЕ СУЩЕСТВУЕТ НЕИЗВЕСТНЫХ СОВЕРШЕННЫХ КОДОВ
- Глава 7. Циклические коды
- 7.2. ОПРЕДЕЛЕНИЕ ЦИКЛИЧЕСКОГО КОДА
- 7.3. ПОРОЖДАЮЩИЙ МНОГОЧЛЕН
- 7.4. ПРОВЕРОЧНЫЙ МНОГОЧЛЕН
- 7.5. ДЕЛИТЕЛИ МНОГОЧЛЕНА x^n-1
- 7.6. КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ t ОШИБОК
- 7.7. ИСПОЛЬЗОВАНИЕ МАТРИЦЫ НАД GF(q^m) ДЛЯ ЗАДАНИЯ КОДА НАД GF(q)
- 7.8. КОДИРОВАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- Глава 8. Циклические коды (продолжение): идемпотенты и многочлены Мэттсона-Соломона
- 8.2. ИДЕМПОТЕНТЫ
- 8.3. МИНИМАЛЬНЫЕ ИДЕАЛЫ, НЕПРИВОДИМЫЕ КОДЫ И ПРИМИТИВНЫЕ ИДЕМПОТЕНТЫ
- 8.4. ВЕСОВОЙ СПЕКТР МИНИМАЛЬНЫХ КОДОВ
- 8.5. ГРУППЫ АВТОМОРФИЗМОВ КОДА
- 8.6. МНОГОЧЛЕН МЭТТСОНА—СОЛОМОНА
- 8.7. НЕКОТОРЫЕ ВЕСОВЫЕ СПЕКТРЫ
- Глава 9. Коды БЧХ
- 9.2. ИСТИННОЕ МИНИМАЛЬНОЕ РАССТОЯНИЕ КОДА БЧХ
- 9.3. ЧИСЛО ИНФОРМАЦИОННЫХ СИМВОЛОВ КОДОВ БЧХ
- 9.4. ТАБЛИЦА КОДОВ БЧХ
- 9.5. ДЛИННЫЕ КОДЫ БЧХ
- 9.6. ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 9.7. КВАДРАТНЫЕ УРАВНЕНИЯ НАД GF(2^m)
- 9.8. КВАЗИСОВЕРШЕННОСТЬ КОДОВ БЧХ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
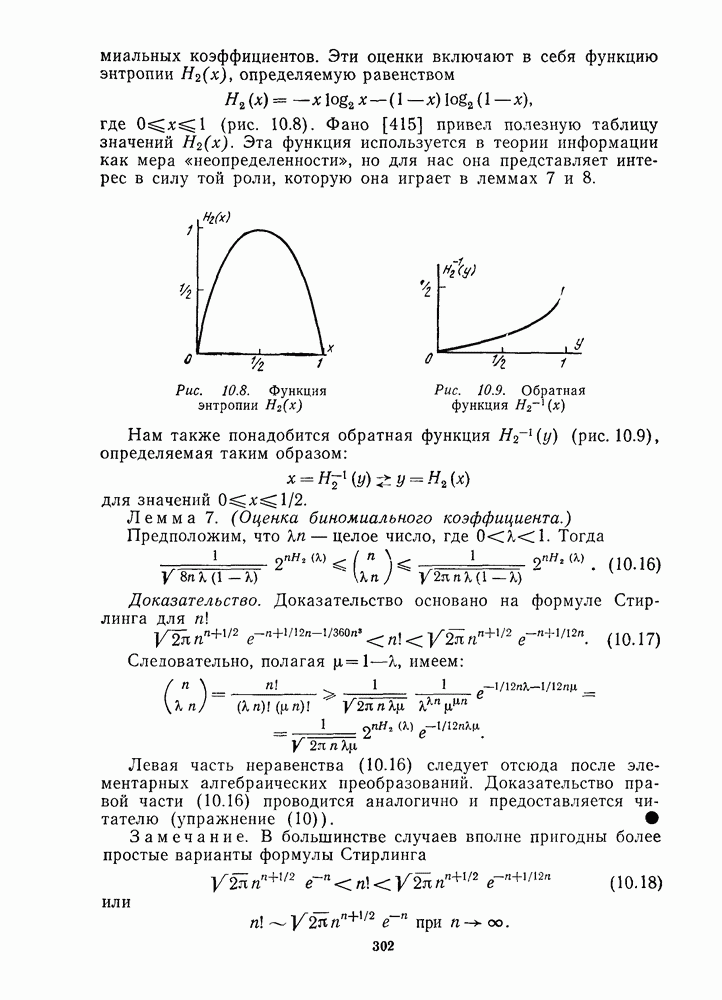
- 9.9. ГРАНИЦА КАРЛИЦА—УШИЯМЫ
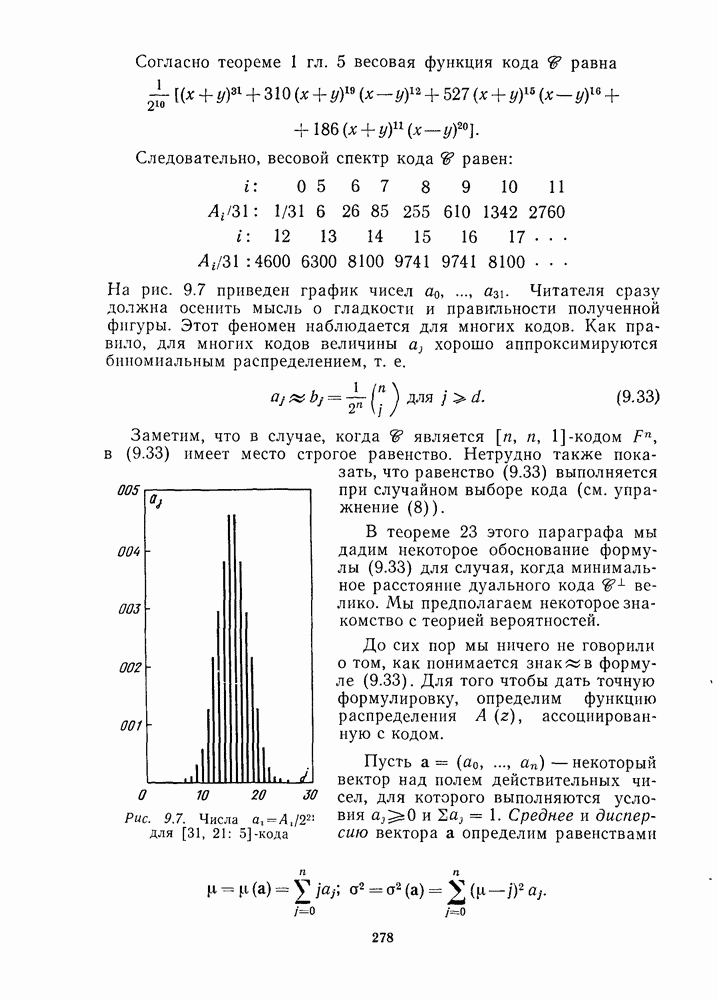
- 9.10. АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ НЕКОТОРЫХ ВЕСОВЫХ СПЕКТРОВ
- 9.11. КОДЫ НЕ-БЧХ, ИСПРАВЛЯЮЩИЕ ТРИ ОШИБКИ
- Глава 10. Коды Рида-Соломона и коды Юстесена
- 10.2. КОДЫ РИДА-СОЛОМОНА
- 10.3. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
- 10.4. ИДЕМПОТЕНТЫ КОДОВ РИДА-СОЛОМОНА
- 10.5. ОТОБРАЖЕНИЕ КОДОВ НАД GF(2^m) В ДВОИЧНЫЕ КОДЫ
- 10.6. ИСПРАВЛЕНИЕ ПАКЕТОВ ОШИБОК
- 10.7. КОДИРОВАНИЕ КОДОВ РИДА—СОЛОМОНА
- 10.9. ИЗБЫТОЧНЫЕ ВЫЧЕТНЫЕ КОДЫ
- 10.10. ДЕКОДИРОВАНИЕ КОДОВ РИДА-СОЛОМОНА
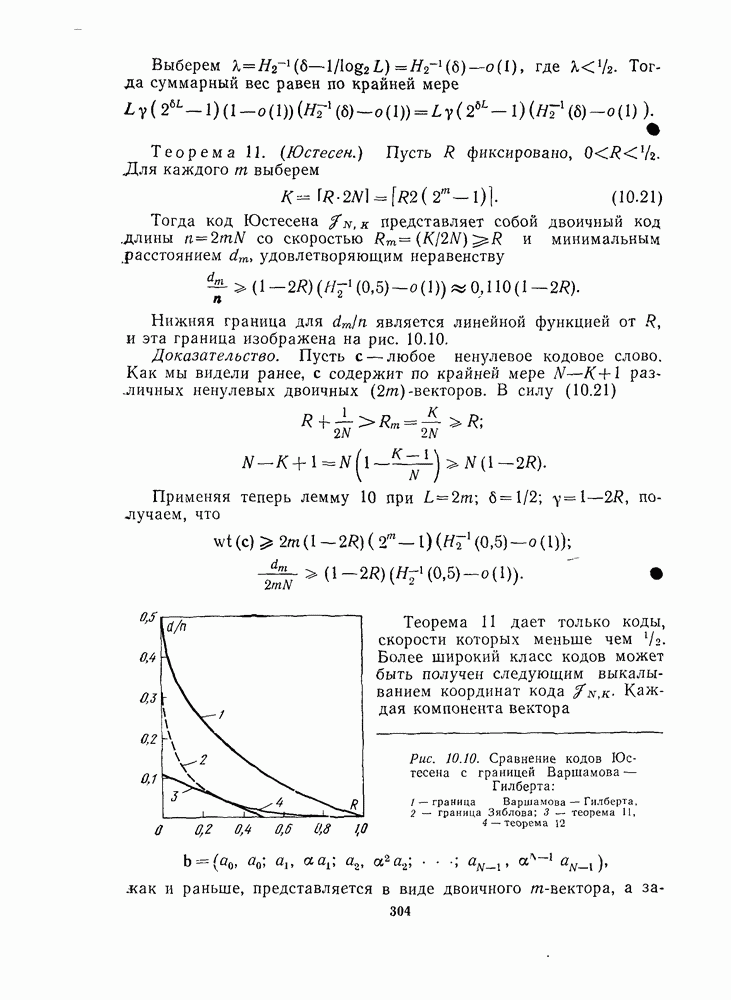
- 10.11. КОДЫ ЮСТЕСЕНА И КАСКАДНЫЕ КОДЫ
- Глава 11. Коды МДР
- 11.2. ПОРОЖДАЮЩАЯ И ПРОВЕРОЧНАЯ МАТРИЦЫ
- 11.3. ВЕСОВОЙ СПЕКТР КОДА МДР
- 11.4. МАТРИЦЫ, У КОТОРЫХ ВСЕ КВАДРАТНЫЕ ПОДМАТРИЦЫ НЕВЫРОЖДЕНЫ
- 11.5. КОДЫ МДР, ПОЛУЧЕННЫЕ ИЗ КОДОВ РИДА-СОЛОМОНА
- 11.6. n-МНОЖЕСТВА
- 11.7. ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ
- 11.8. ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
- Глава 12. Альтернантные коды, коды Гоппы и другие обобщения кодов БЧХ
- 12.2. АЛЬТЕРНАНТНЫЕ КОДЫ
- 12.3. КОДЫ ГОППЫ
- 12.4. ДАЛЬНЕЙШИЕ СВОЙСТВА КОДОВ ГОППЫ
- 12.5. ЦИКЛИЧНОСТЬ УДЛИНЕННЫХ КОДОВ ГОППЫ, ИСПРАВЛЯЮЩИХ ДВЕ ОШИБКИ
- 12.6. ОБОБЩЕННЫЕ КОДЫ СРИВЭСТАВЫ
- 12.7. ОБОБЩЕНИЕ ЧЕНЯ—ЧОЯ КОДОВ БЧХ
- 12.8. АЛГОРИТМ ЕВКЛИДА
- 12.9. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- Часть II: Глава 13. Коды Рида-Маллера
- 13.2. БУЛЕВЫ ФУНКЦИИ
- 13.3. КОДЫ РИДА-МАЛЛЕРА
- 13.4. РИДА-МАЛЕРА КОДЫ И ГЕОМЕТРИИ
- 13.5. ВЕКТОРЫ МИНИМАЛЬНОГО ВЕСА ПОРОЖДАЮТ КОД
- 13.6. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (I)
- 13.7. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ (II)
- 13.8. ДРУГИЕ ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.9. ГРУППЫ АВТОМОРФИЗМОВ РИДА-МАЛЕРА КОДОВ
- 13.10. МНОГОЧЛЕНЫ МЭТТСОНА—СОЛОМОНА ДЛЯ РИДА-МАЛЕРА КОДОВ
- 13.11. ДЕЙСТВИЕ ПОЛНОЙ АФФИННОЙ ГРУППЫ НА МНОГОЧЛЕНАХ МЭТТСОНА—СОЛОМОНА
- Глава 14. Коды Рида-Маллера первого порядка
- 14.2. ПСЕВДОШУМОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 14.3. СМЕЖНЫЕ КЛАССЫ ПО КОДУ РИДА—МАЛЛЕРА ПЕРВОГО ПОРЯДКА
- 14.4. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ КОДА R(1, m)
- 14.5. МАКСИМАЛЬНО-НЕЛИНЕЙНЫЕ ФУНКЦИИ
- Глава 15. Коды Рида-Маллера первого порядка Кердока и Препараты
- 15.2. ВЕСОВОЙ СПЕКТР КОДА РИДА—МАЛЛЕРА ВТОРОГО ПОРЯДКА
- 15.3. СПЕКТР ВЕСОВ ПРОИЗВОЛЬНЫХ КОДОВ РИДА—МАЛЛЕРА
- 15.4. ПОДКОДЫ РАЗМЕРНОСТИ 2m В КОДАХ R(2, m)* И R(2, m)
- 15.5. КОД КЕРДОКА И ЕГО ОБОБЩЕНИЯ
- 15.6. КОД ПРЕПАРАТЫ
- 15.7. ОБОБЩЕНИЕ ГЕТАЛСА КОДОВ ПРЕПАРАТЫ
- Глава 16. Квадратично-вычетные коды
- 16.2. ОПРЕДЕЛЕНИЕ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.3. ИДЕМПОТЕНТЫ КВАДРАТИЧНО-ВЫЧЕТНЫХ КОДОВ
- 16.4. РАСШИРЕННЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.5. ГРУППА АВТОМОРФИЗМОВ КВ-КОДОВ
- 16.6. ДВОИЧНЫЕ КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- 16.7. ДВАЖДЫ ЦИРКУЛЯНТНЫЕ И КВАЗИЦИКЛИЧЕСКИЕ КОДЫ
- 16.8. КВАДРАТИЧНО-ВЫЧЕТНЫЕ И СИММЕТРИЧНЫЕ КОДЫ НАД GF{3)
- 16.9. ДЕКОДИРОВАНИЕ ЦИКЛИЧЕСКИХ И НЕКОТОРЫХ ДРУГИХ КОДОВ
- Глава 17. Границы для объема кода
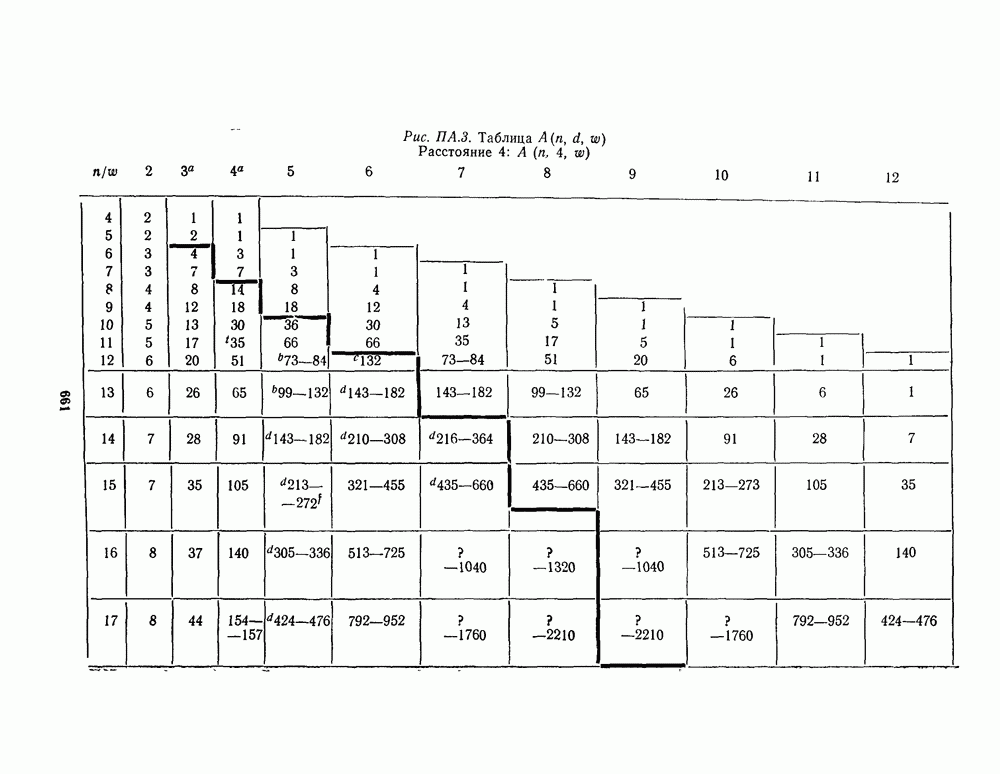
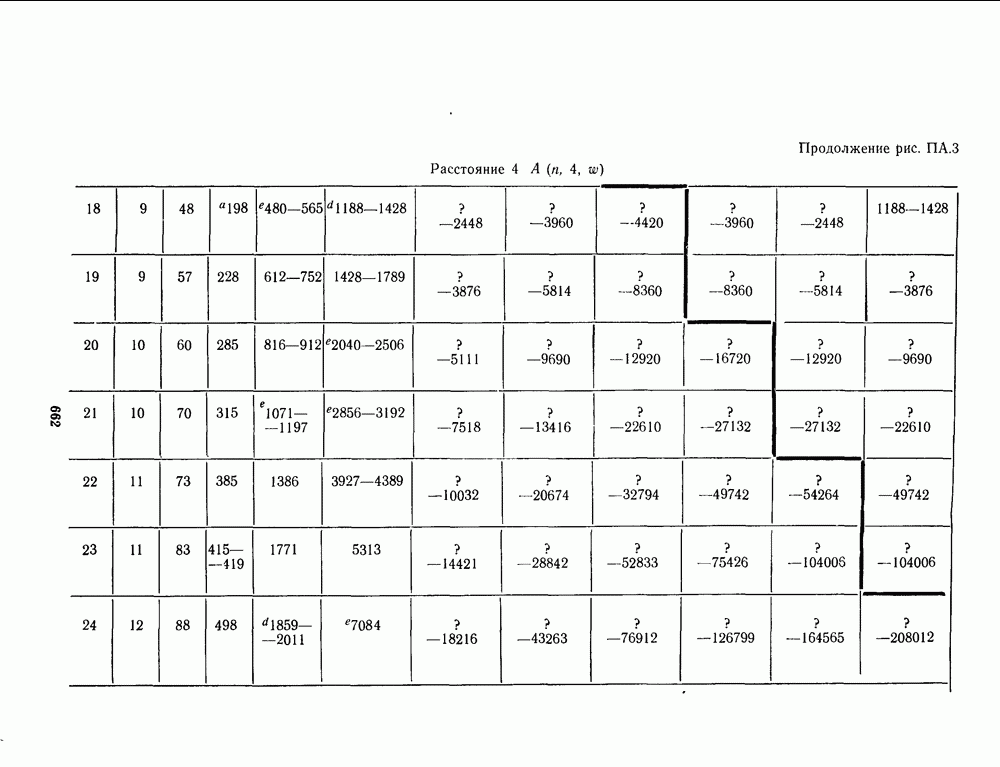
- 17.2. ГРАНИЦЫ ДЛЯ A(n, d, w)
- 17.3. ГРАНИЦЫ ДЛЯ A(n, d)
- 17.4. ГРАНИЦЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- 17.5. ГРАНИЦА ГРАЙСМЕРА
- 17.6. ПОСТРОЕНИЕ ЛИНЕЙНЫХ КОДОВ; АНТИКОДЫ
- 17.7. АСИМПТОТИЧЕСКИЕ ГРАНИЦЫ
- Глава 18. Методы комбинирования кодов
- I. ПРОИЗВЕДЕНИЕ КОДОВ И ИХ ОБОБЩЕНИЕ
- 18.2. ПРЯМОЕ ПРОИЗВЕДЕНИЕ КОДОВ
- 18.3. НЕ ВСЕ ЦИКЛИЧЕСКИЕ КОДЫ ЯВЛЯЮТСЯ ПРЯМЫМИ ПРОИЗВЕДЕНИЯМИ ЦИКЛИЧЕСКИХ КОДОВ
- 18.4. ДРУГОЙ СПОСОБ ПРЕДСТАВЛЕНИЯ НЕПРИВОДИМЫХ ЦИКЛИЧЕСКИХ кодов В ВИДЕ ПРОИЗВЕДЕНИЯ КОДОВ
- 18.5. КАСКАДНЫЕ КОДЫ: (*)-КОНСТРУКЦИЯ
- 18.6. ОБЩИЙ ПОДХОД К РАЗЛОЖЕНИЮ ЦИКЛИЧЕСКИХ КОДОВ
- II. ДРУГИЕ МЕТОДЫ КОМБИНИРОВАНИЯ КОДОВ
- 18.7. МЕТОДЫ ПОСТРОЕНИЯ, КОТОРЫЕ УВЕЛИЧИВАЮТ ДЛИНУ
- 18.7.1. КОНСТРУКЦИЯ X: ДОБАВЛЕНИЕ СУФФИКСОВ К КОДОВЫМ СЛОВАМ
- 18.7.2. КОНСТРУКЦИЯ Х4: КОМБИНИРОВАНИЕ ЧЕТЫРЕХ КОДОВ
- 18.7.3. КОДЫ, ИСПРАВЛЯЮЩИЕ ОДИНОЧНЫЕ И ДВОЙНЫЕ ОШИБКИ
- 18.7.4. КОНСТРУКЦИЯ …
- 18.7.5. КОНСТРУКЦИЯ ПИРЕТА
- 18.8. КОНСТРУКЦИИ, СВЯЗАННЫЕ С КАСКАДНЫМИ КОДАМИ
- 18.8.2. ОБОБЩЕННЫЕ КАСКАДНЫЕ КОДЫ ЗИНОВЬЕВА
- 18.9. МЕТОДЫ УКОРОЧЕНИЯ КОДОВ
- 18.9.2. КОНСТРУКЦИИ ХЕЛГЕРТА И СТИНАФФА
- Глава 19. Самодуальные коды и теория инвариантов
- 19.2. ВВЕДЕНИЕ В ТЕОРИЮ ИНВАРИАНТОВ
- 19.3. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ИНВАРИАНТОВ
- 19.4. ОБОБЩЕНИЯ ТЕОРЕМЫ ГЛИСОНА
- 19.5. НЕСУЩЕСТВОВАНИЕ НЕКОТОРЫХ ОЧЕНЬ ХОРОШИХ КОДОВ
- 19.6. ХОРОШИЕ САМОДУАЛЬНЫЕ КОДЫ СУЩЕСТВУЮТ
- Глава 20. Коды Голея
- 20.2. ГРУППА МАТЬЕ M24
- 20.3. ГРУППА М24 5-ТРАНЗИТИВНА
- 20.4. ПОРЯДОК ГРУППЫ М24 РАВЕН 24•23•22•21•20•48
- 20.5. СИСТЕМА ШТЕЙНЕРА S(5, 8, 24) ЕДИНСТВЕННА
- 20.6. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
- 20.7. ГРУППЫ АВТОМОРФИЗМОВ ТРОИЧНЫХ КОДОВ ГОЛЕЯ
- 20.8. КОДЫ ГОЛЕЯ … ЕДИНСТВЕННЫ
- Глава 21. Схемы отношений
- 21.2. СХЕМЫ ОТНОШЕНИЙ
- 21.3. СХЕМА ОТНОШЕНИЙ ХЭММИНГА
- 21.4. МЕТРИЧЕСКИЕ СХЕМЫ
- 21.5. СИМПЛЕКТИЧЕСКИЕ ФОРМЫ
- 21.6. СХЕМА ДЖОНСОНА
- 21.7. ПОДМНОЖЕСТВА СХЕМ ОТНОШЕНИЙ
- 21.8. ПОДМНОЖЕСТВА СИМПЛЕКТИЧЕСКИХ ФОРМ
- 21.9. t-СХЕМЫ И ОРТОГОНАЛЬНЫЕ ТАБЛИЦЫ
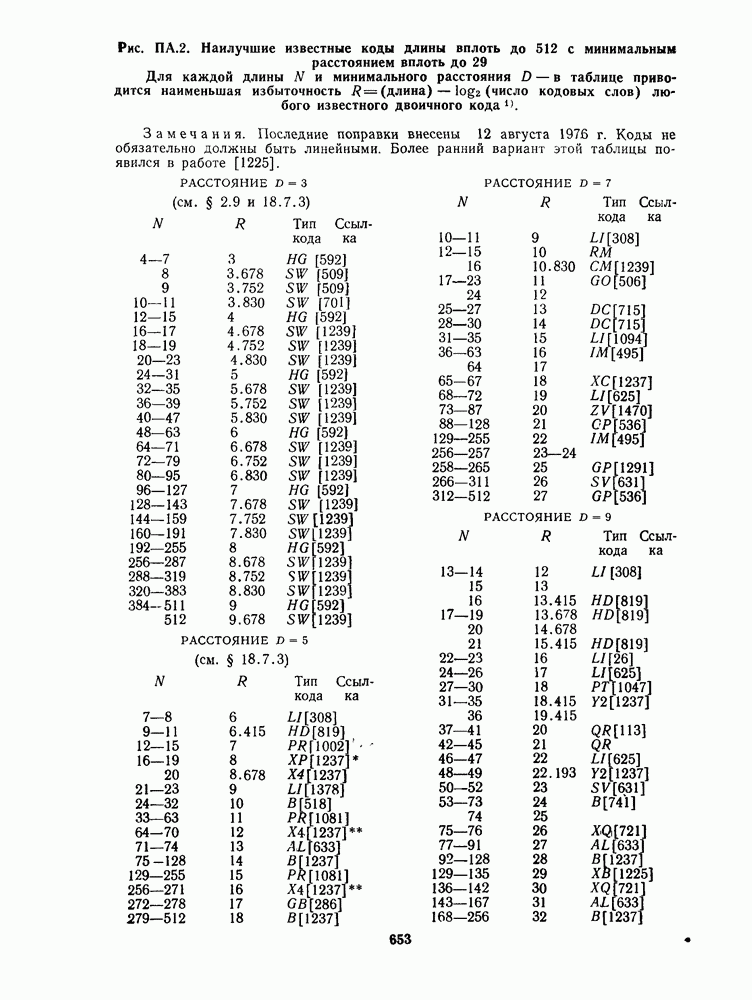
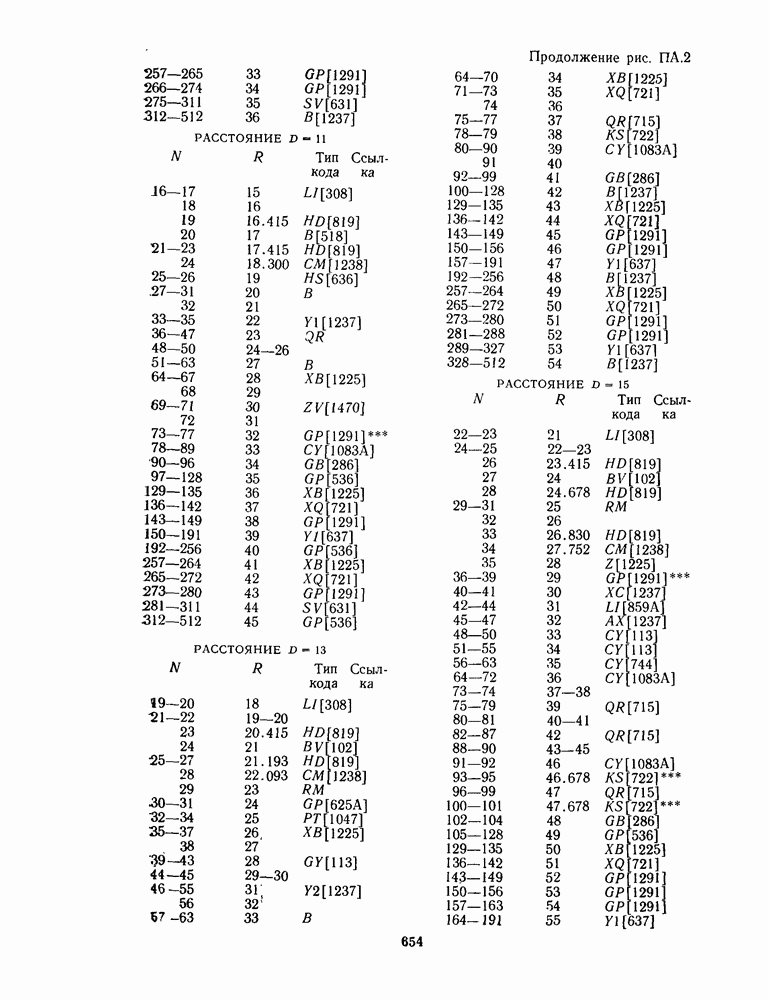
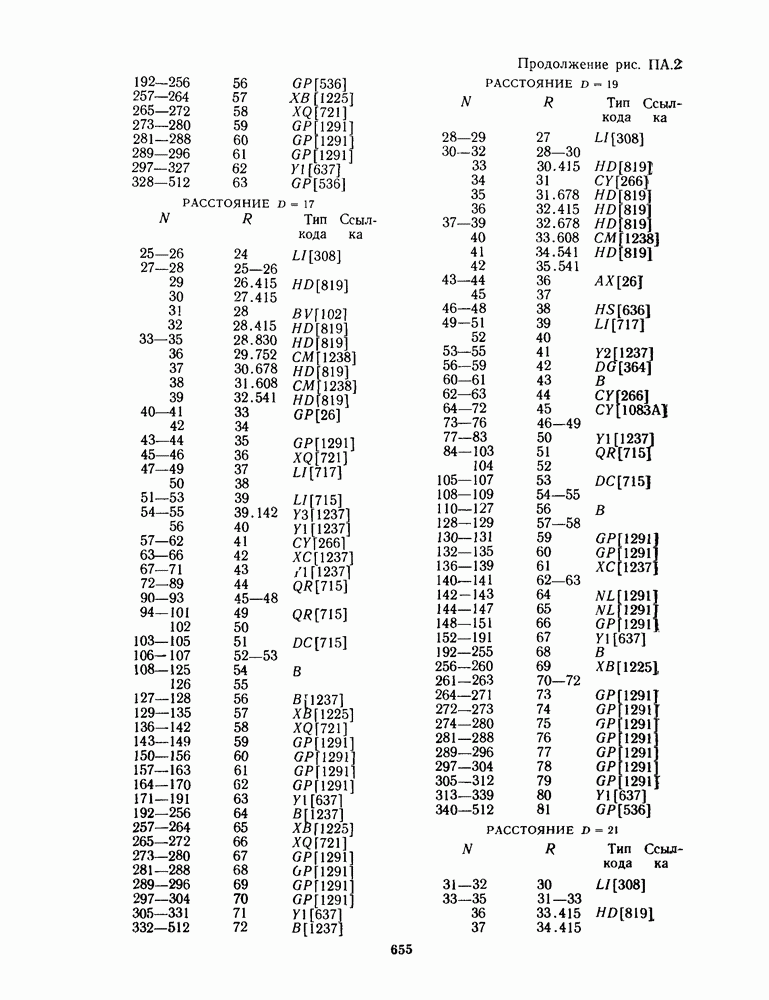
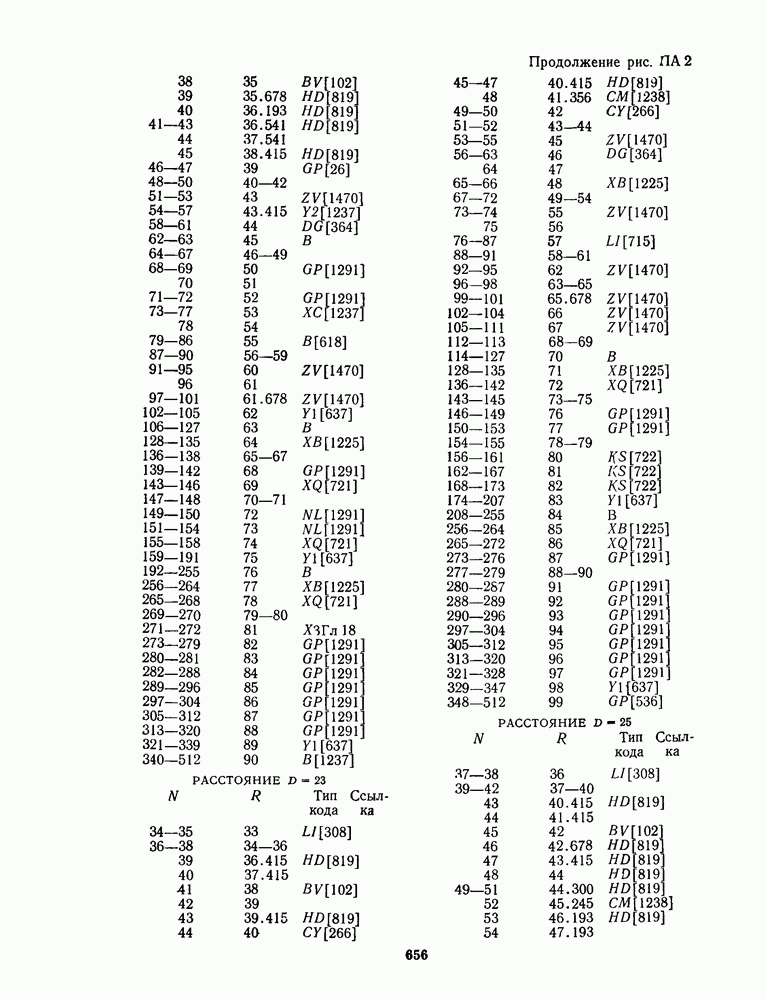
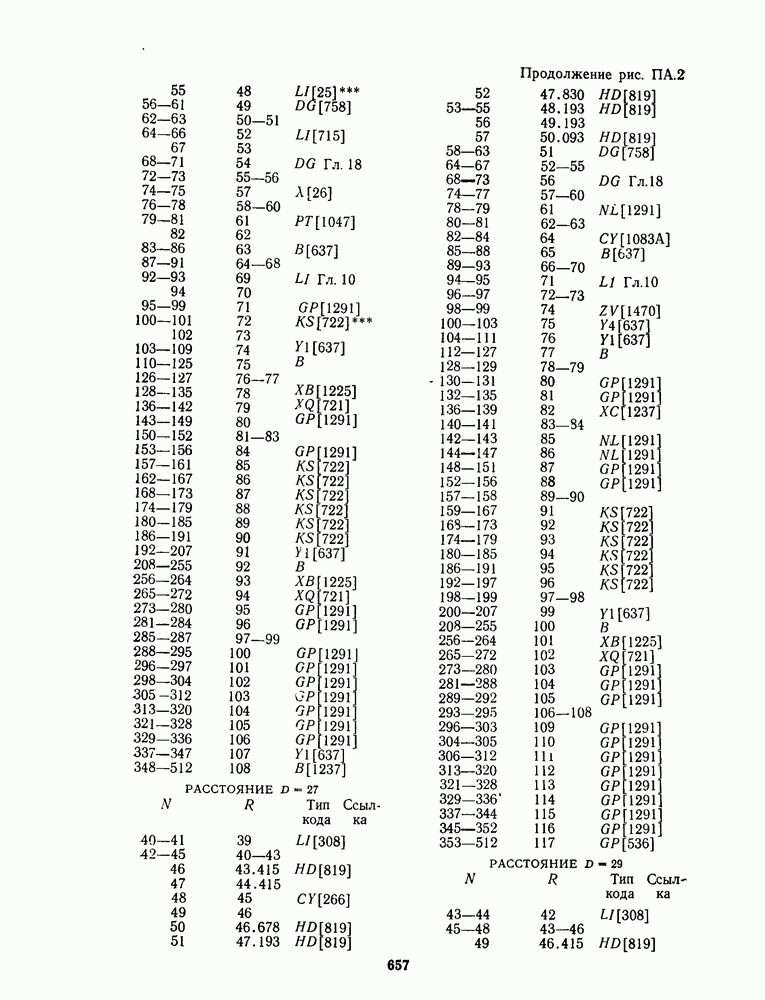
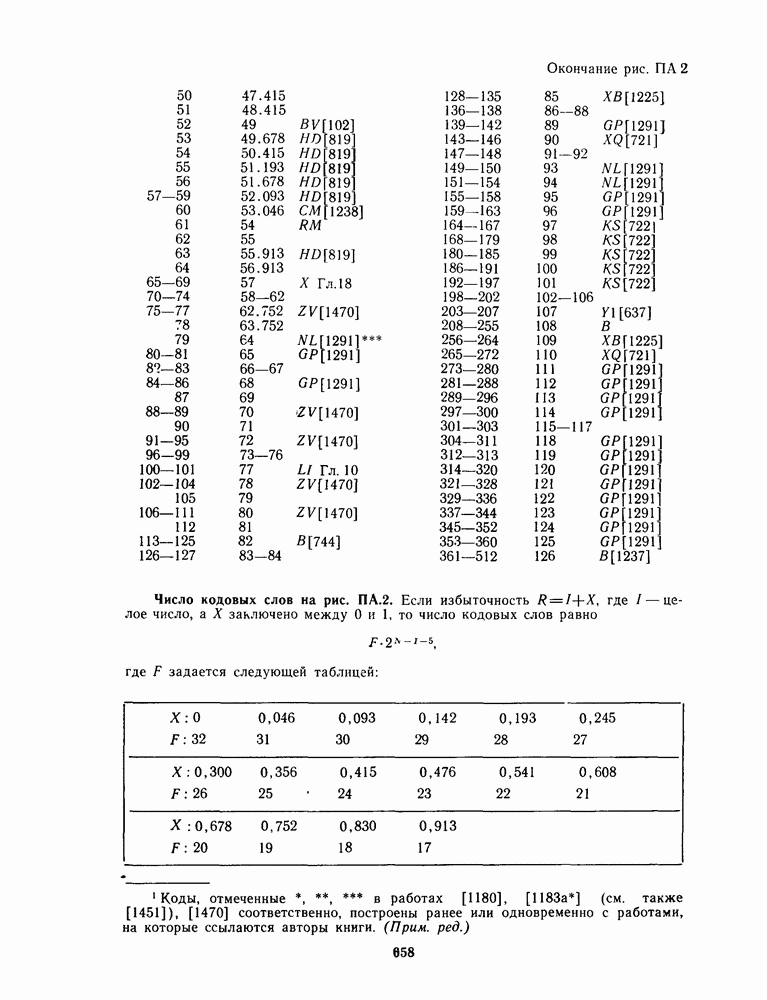
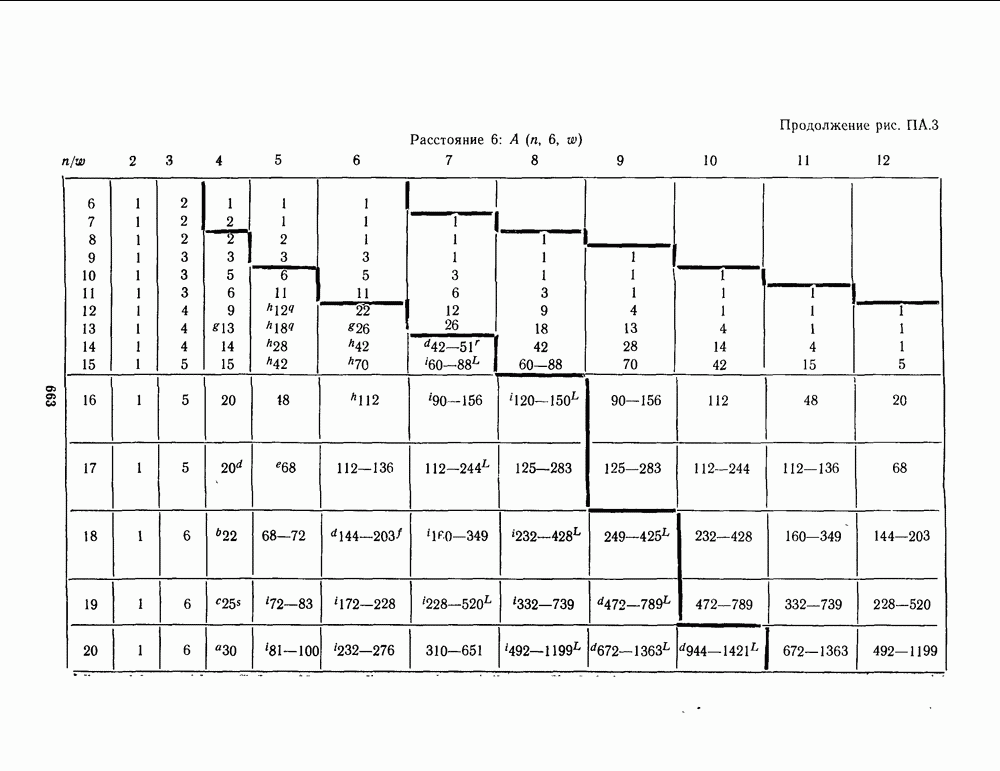
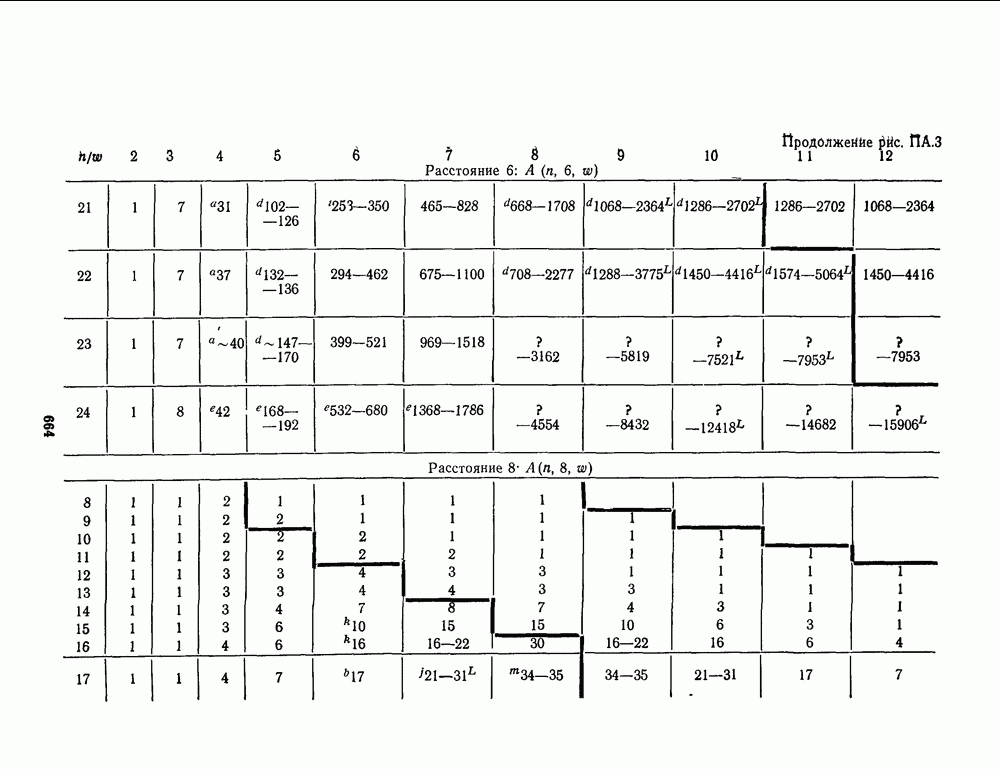
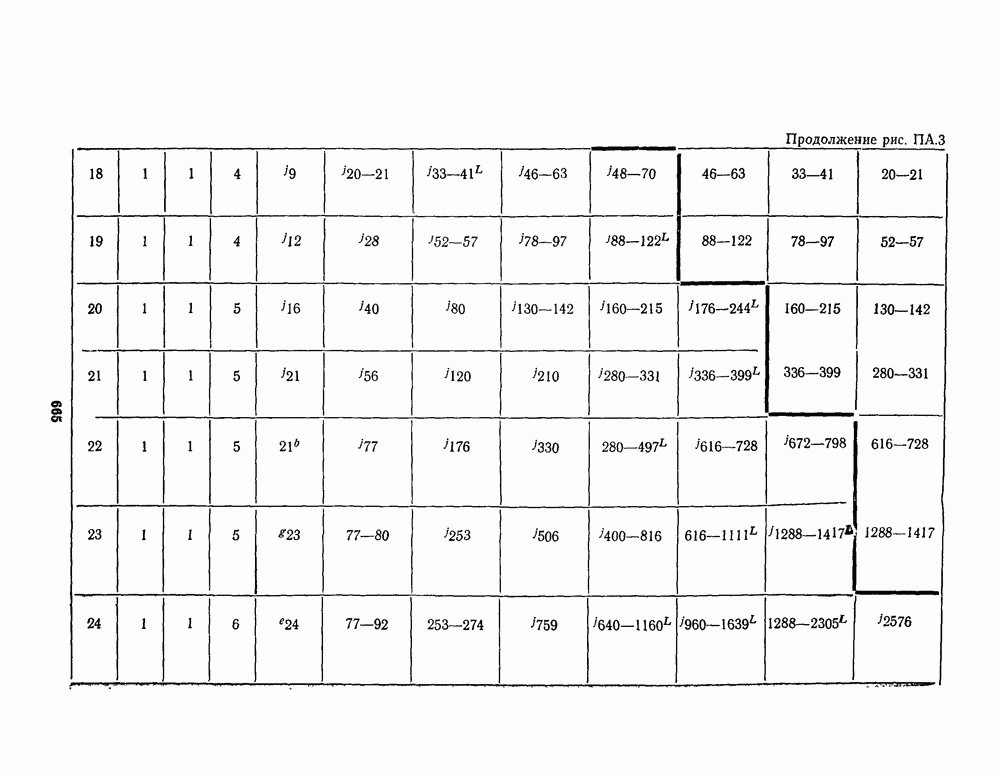
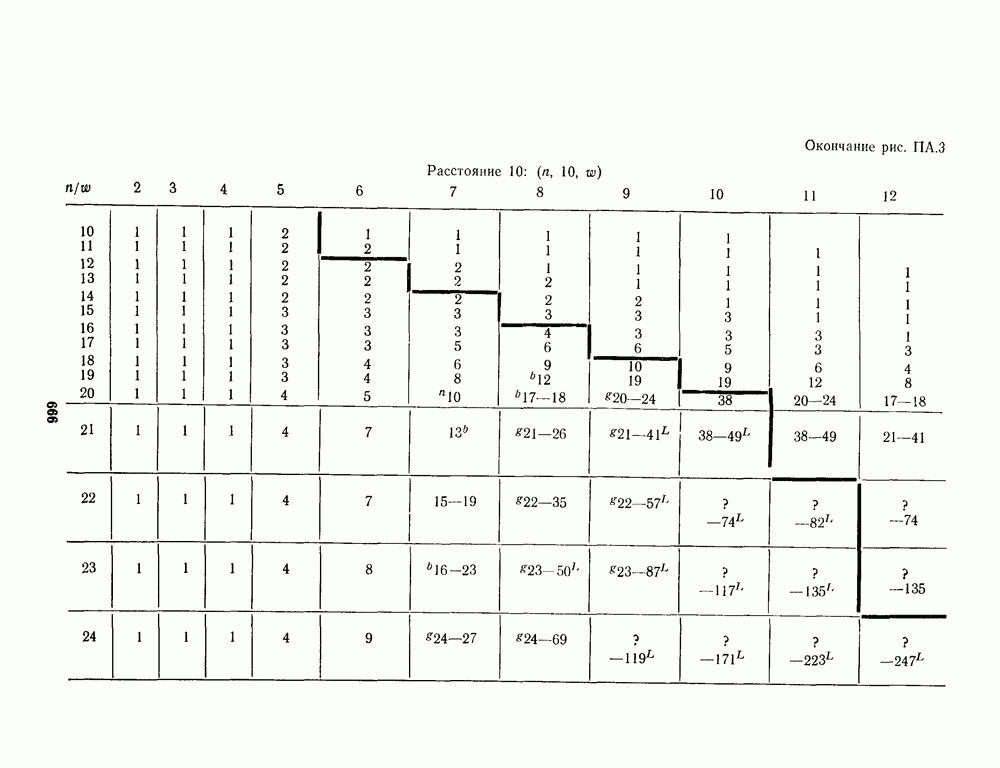
- ПРИЛОЖЕНИЕ А. ТАБЛИЦЫ НАИЛУЧШИХ ИЗВЕСТНЫХ КОДОВ
- ПРИЛОЖЕНИЕ В. КОНЕЧНЫЕ ГЕОМЕТРИИ